Приложение. В мире науки. Занимательный компьютер. 1983-1990
Страница 1 из 4
Страница 1 из 4 • 1, 2, 3, 4 
 Приложение. В мире науки. Занимательный компьютер. 1983-1990
Приложение. В мире науки. Занимательный компьютер. 1983-1990
12 1983
МЫ ОТКРЫВАЕМ НОВУЮ РУБРИКУ, ПОСВЯЩЕННУЮ КОМПЬЮТЕРНЫМ ИГРАМ
БРАЙАН ХЭЙЕС
А теперь - посчитаем!
Готфрид Вильгельм Лейбниц
С НЕКОТОРЫХ пор любители самых увлекательных игр с ЭВМ получили новую возможность: на клавиатуре их микрокомпьютера появилась функциональная клавиша: TBIC ("The boss is coming"), что означает: "Осторожно, босс идет!". Если нажать на эту клавишу, то игровое поле на экране моментально замирает и гаснет. Здесь мы, пожалуй, наблюдаем оба полюса общественной реакции на распространение недорогих ЭВМ. С одной стороны, компьютер остается средством производства, с другой - он дает возможность для столь увлекательных развлечений, что их, подобно детективным историям, приходится скрывать от постороннего взгляда.
Я не намерен приуменьшать роль вычислительных машин ни в промышленности и торговле, ни в компьютерных играх, основная цель которых состоит в испытании у играющего быстроты реакции. Значение практических расчетов с использованием ЭВМ неоспоримо. Что же касается игр на экране дисплея, то их построение можно считать наивысшим выражением искусства программирования. Однако следует отметить, что обе эти сферы не затрагивают глубоко вопроса о том, что представляет собой компьютер и на что он способен.
Между коммерческим программированием и играми на экране дисплея, между программой "Визикальк" и программой "Космических пришельцев" огромное расстояние. Сюда входят различные приложения ЭВМ во всех гуманитарных и естественных науках и, пожалуй, в первую очередь в математике. При этом компьютер используется для моделирования различных аспектов окружающего нас мира. Здесь можно найти многие направления, которые, строго говоря, вообще не могут быть названы "использованием компьютера", а служат скорее для того, чтобы привлечь внимание к самой вычислительной машине и глубже понять природу автоматизированных вычислений. Наша рубрика будет посвящена рассмотрению области, лежащей между чисто практическими приложениями и развлечениями. Полагая, что мышление все еще остается занятием намного более сложным, чем просто вычисления, мы будем считать, что те, кто не имеет доступа к вычислительной технике, просто окажутся в несколько менее благоприятных условиях. К теории и практике вычислений можно иной раз удачно применить даже самые простые бухгалтерские средства.
В этой статье мы рассмотрим некоторые вопросы, возникающие при нетрадиционном использовании программ, известных под общим названием "электронные крупноформатные бланки".
ОБЫЧНЫЙ бумажный бланк - это большой лист, разграфленный на множество строк и столбцов. Его можно использовать для изучения бюджета какой-нибудь компании. Каждому подразделению можно отвести один столбец, а всем категориям доходов и расходов - по строке. Общие суммы и процентные доли каждой категории н каждого подразделения могут быть записаны в дополнительных столбцах и строках.
Крупноформатный электронный бланк воспроизводит эту структуру на экране катодно-лучевой трубки, однако он содержит и некоторые дополнительные возможности. В бумажном бланке любая ячейка (определим ее как пересечение столбца и строки) может содержать либо метку, например название подразделения, либо какое-нибудь число. В электронном бланке любой ячейке может быть приписана также и математическая формула. Так, ячейка в конце строки может содержать формулу, требующую просуммировать все численные значения, внесенные в остальные ячейки этой строки. На экране при этом воспроизводится число, соответствующее результату вычислений по этой формуле (в нашем примере ячейка будет содержать сумму всех чисел, помешенных в строке), однако, по сути дела, содержанием ячейки будет не число, а собственно формула. Если изменить содержимое какой-либо из остальных ячеек строки, то в последней ячейке автоматически появится новое значение для суммы.
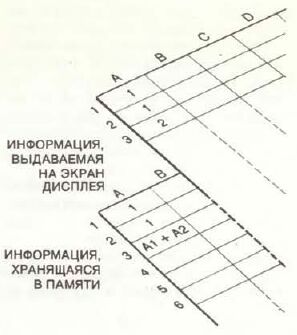
Структура крупноформатного электронного бланка
Первой программой оперирования с крупноформатными электронными бланками (сокращенно - КЭБ-программой) была программа "Визикальк", разработанная в 1978г. Д.Бриклином, в то время студентом Коммерческой школы Гарвардского университета, а также Р.Фрэнкстоном и Д.Фильстрой. Сообщалось, что она распродана в большем количестве экземпляров, чем какая-либо другая программа для ЭВМ. С тех пор на подобных принципах были созданы десятки других программ, да и сама "Визикальк" модернизировалась несколько раз. Большая часть описанных здесь экспериментов была проведена с двумя более поздними версиями КЭБ-программ - с программой "1-2-3", созданной М.Кэйпором из Lotus Development Corporation (Кэмбридж, шт.Массачусетс) и программой "Мультиплан" - результатом разработок в Microsoft Corporation (Бельвью, шт.Вашингтон). В большинстве случаев с таким же успехом можно воспользоваться и другими КЭБ-программами.
Хотя электронный крупноформатный бланк был предназначен для финансовых исследований, он пригоден и для других целей. Бланк представляет собой 2x2-матрицу из ячеек, для которой можно установить зависимость между содержимым любой ячейки и какой-либо другой ячейкой или группой ячеек. Можно лишь удивляться, сколь существенная часть математической структуры Вселенной может быть втиснута в этот скромный формат. В самом деле, оказывается, что подобный бланк отражает весьма широкий диапазон математических и логических взаимосвязей.
Принципы работы КЭБ-программы и ее возможности можно понять с помощью одного простого примера. Каждая ячейка нумеруется с помощью ее координат в координатной сетке, для большинства программ столбцы задаются буквами, а строки - цифрами, начиная с левого верхнего угла. Допустим, ячейкам A1 и A2 будут присвоены одинаковые численные значения, равные единице. Затем в ячейку A3 вводится формула: численное значение этой ячейки должно быть равно сумме величин, находящихся в двух ячейках, расположенных непосредственно над ячейкой A3. Иначе говоря, содержимое A3 равно содержимому A2 плюс содержимое A1, т.е. в нашем случае оно будет равно двум.
Пока что мы пришли к достаточно тривиальному результату: нам удалось создать сложную конструкцию, выражающую соотношение 1+1=2. Однако теперь мы можем переписать формулу из ячейки A3 во множество других ячеек. (Подобная процедура копирования в различных программах может иметь разную форму, однако у всех КЭБ-программ предусмотрена эта возможность). Предположим, формула из ячейки A3 повторяется в ячейках от A4 до A10. Тогда каждая из этих ячеек будет содержать величину, равную сумме значений в двух вышестоящих ячейках. Заметим, что все формулы будут идентичны, однако при подстановке разных исходных значений они дадут различные результаты. В столбце бланка сверху вниз появятся следующие числа: 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55.
СУЩЕСТВУЕТ множество способов порождения рядов Фибоначчи с помощью ЭВМ, причем в большинстве они используют ресурсы машины гораздо эффективнее, чем предложенный метод. Однако стратегия использования крупноформатных электронных бланков обладает существенным отличием - она неалгоритмична. Почти во всех языках программирования задание или решение задачи определяется в терминах алгоритма, т.е. в виде последовательности точных инструкций, выполняемых одна за другой. Алгоритм подобен рецепту, он может звучать так: "Вначале смешайте муку, воду и дрожжи, дайте тесту подняться, а затем поставьте выпекать". Если мы проделаем те же операции в другом порядке, то получим совершенно иной результат. КЭБ-программы не содержат этой характерной временной упорядоченности. В ячейках размещается не последовательность шагов, приводящая от проблемы к ее решению, а некая статическая структура, пытающаяся охватить решение сразу. Это не рецепт, а скорее описание, в нем утверждается, что хлеб состоит из муки, дрожжей и воды, смешанных, выдержанных и выпеченных должным образом.
Различие между алгоритмом и статическим описанием можно пояснить еще на одном примере. Рассмотрим задачу перемножения двух матриц, каждая из которых имеет по три столбца и по три строки. Стандартный алгоритм начинается с инструкций - перемножить каждый элемент первого столбца первой матрицы с каждым элементом первой строки второй матрицы, просуммировать три этих произведения и заслать результат в память как первый элемент результирующей матрицы. Затем такие же инструкции будут повторены для остальных восьми комбинаций из строк и столбцов. При использовании КЗБ-программ формулировка задачи примет другую форму, основанную на структурном подобии математической матрицы и массива ячеек. Вместо того чтобы писать последовательность инструкций, можно просто создать результирующую матрицу, приравнивая содержимое каждой из ее ячеек формуле, отражающей соответствующую комбинацию из столбцов и строк. Если мы введем такие формулы, все они будут вычисляться "сразу" и одновременно появится результирующая матрица-произведение.
Разумеется, на более глубоком уровне вычислительная машина, управляемая КЭБ-программой, в самом деле следует какому-то алгоритму. ЭВМ, обладающая лишь одним центральным процессом, не может одновременно выполнять несколько действий, так что все ячейки неизбежно вычисляются в некоторой последовательности. Однако человеку, пользующемуся такой программой, обычно не требуется принимать это к сведению, да и в самом деле он зачастую не имеет об этом никакого представления. Таким образом, пользователь избавляется от необходимости представлять себе решаемую задачу в терминах алгоритмов.
Конечно же, не следует думать, что неалгоритмический тип мышления в чем-то превосходит алгоритмический. Кое-кто может его предпочитать, хотя в большой степени это дело вкуса. Когда задача становится слишком сложной, появляются веские основания воспользоваться алгоритмом, так как он более естественно распадается на части, с которыми удобно работать. Решение всей задачи сразу требует одновременного понимания всех ее аспектов. Однако, по-видимому, существуют некоторые задачи или классы задач, которые приводят к неалгоритмическим формулировкам.
ОДНА из областей, где двумерный прямолинейный массив КЭБ-программы представляет удобное средство для решения залач,- это разработка систем ячеистых автоматов. Исследование подобных систем было начато в 50-х годах Дж.фон Нейманом и С.Уламом. В то время они занимались в основном самовоспроизводящимися структурами. Правила, установленные ими для своих задач, предполагали существование "однородного пространства из ячеек", в котором каждая ячейка представляет собой автомат или машину, имеющую лишь конечное число возможных состояний. Условие однородности пространства понималось в том смысле, что законы, управляющие состояниями автоматов, должны оставаться одними и теми же для всех ячеек. Еще одно ограничение заключалось в том, что состояние любой ячейки могло определяться лишь ее собственной историей и состоянием ее ближайших соседей.
Условиям, определяющим систему ячеистых автоматов, можно легко удовлетворить, пользуясь КЭБ-программой. В принципе число состояний, доступных одной ячейке, крайне велико (возможно, 1E100), однако очевидно, что оно конечно и может быть сведено, если это покажется удобным, к весьма небольшому числу. Так, например, любой ячейке можно присвоить формулу, дающую лишь два возможных значения 0 и 1. Требование однородности пространства добавляет одно интересное ограничение. Оно предполагает, что все ячейки, в которые внесены какие-либо формулы, на самом деле должны содержать одну и ту же формулу. (Существуют разные пути для оценки идентичности двух формул. Предположим, формула в ячейке A1 соотносит ее содержимое с содержимым ячейки B1, расположенной непосредственно под ячейкой A1. Формула, приписанная ячейке A2, может считаться идентичной, если она также соотносится с содержимым B1, т.е. сохраняет "абсолютный адрес". Однако она может соотноситься и с содержимым ячейки B2 и при этом будет сохраняться геометрическая взаимосвязь. Вторая интерпретация, как правило, оказывается более полезной, и пожалуй, лучше соответствует представлениям фон Неймана и Улама, хотя в случае последовательного и непротиворечивого применения каждая из схем может оказаться приемлемой. Методы, используемые в КЭБ-программах для копирования содержимого ячеек, представляют собой удобную и оперативную проверку условия однородности. Массив ячеек может считаться однородным, если существует возможность приписать какую-либо формулу одной из ячеек, а затем с помощью программы присвоить эту же формулу всем остальным ячейкам).
Фон Нейман смог доказать существование самовоспроизводящейся конфигурации ячеек. Сделал он это непростым способом, показав, что существует некий универсальный конструктор, способный создать любую конфигурацию, а следовательно, способный воссоздать и собственное строение. Доказательство предусматривает систему из примерно 200тыс. ячеек, обладающих 29 возможными состояниями. Насколько я знаю, такая конфигурация никогда не была создана ни вручную, ни с помощью компьютера. В принципе сейчас она уже под силу наиболее развитым КЭБ-программам.
Гораздо более простая система, способная самовоспроизводиться, была разработана в 1960г. Э.Фредкнном из Массачусетского техно погического института. В ней каждая ячейка обладает лишь двумя возможными состояниями, "живым" и "мертвым", которые можно представить числами 1 и 0. Состояние, которое будет присвоено ячейке в будущем поколении, определяется нынешним состоянием четырех ее ближайших соседей, т.е. четырех ячеек, расположенных непосредственно к северу, востоку, югу и западу. Если число живых соседей четно (0, 2 и 4), ячейка умирает или остается мертвой. Ячейка, окруженная нечетным числом живых соседей (1 и 3), остается живой.
Пользуясь КЭБ-программоЙ, особенно если в ней предусмотрены арифметические действия по модулю целых чисел, формулу, выражающую это правило, можно записать в одну строчку. Например, для ячейки B2 эта формула имеет вил: (B1+C2+B3+A2) mod 2. Иначе говоря, в соответствии с этой формулой складывается содержимое четырех соседних ячеек, сумма делится на два и сохраняется только остаток, который непременно будет равен нулю или единице. Теперь остается лишь переписать эту формулу (таким образом, чтобы ссылки на другие ячейки образовывали ту же геометрическую взаимосвязь) во все остальные ячейки электронного бланка. На самом деле при создании описываемой системы возникает еще одна тонкость: нам требуется еще два экземпляра изображений пространства из ячеек. Один экземпляр отражает нынешнее состояние пространства, а второй - состояние предыдущего поколения. Текущее состояние ячейки определяется числом живых соседей, окружавших эту ячейку в предыдущем поколении.
Если сформировать электронный бланк в соответствии с правилами Фрелкина и задать начальную конфигурацию, то каждый новый просчет будет давать новую картину. После нескольких циклов появляются четыре копии начальной конфигурации. Позже и сами эти копии учетверяются, так что начальный рисунок воспроизводится 16 раз. Количество циклов, необходимых для самовоспроизведения, зависит от сложности начальной конфигурации. В простейшем случае (единственная живая ячейка) четыре копии возникают в первом же просчете.

В системе ячеистых автоматов, разработанных Э.Фредкином, любая структура способна к самовоспроизведению
Наблюдение за развитием растущей колонии может быть увлекательнейшим занятием. Картина все время сохраняет четырехкратную симметрию, а некоторые из конфигураций обладают странной лучистой формой. Весь процесс подчинен некоему ритму: периметр занятой области непрерывно расширяется, а ее внутренняя зона периодически заполняется густой порослью ячеек, а затем пустеет снова.
НАИБОЛЕЕ широко известная система ячеистых автоматов - это игра под названием "Жизнь". Ее изобрел Дж.Конвей из Кембриджского университета, а широкая публика узнала о ней в 1970г. благодаря Мартину Гарднеру и его рубрике "Математические игры" в журнале "Scientific American". Эта игра, как и порожденные ею размножающиеся автоматы, сегодня завоевала практически все вычислительные системы и языки программирования. Это и понятно - игра сторицей вознаграждает за уделенное ей внимание и тогда, когда оно выражается в праздном любопытстве, и в том случае, когда оно принимает форму глубокого анализа.
В игре Конвея правила создавались не для того, чтобы обеспечить самовоспроизведение рисунка, а скорее для того, чтобы увеличить изменчивость или снизить предсказуемость. Здесь снова каждая ячейка имеет два возможных состояния, однако ее окружение состоит уже из восьми ближайших соседей, включая четыре, соседствующие по диагонали. Если ячейка живая, она продолжит свое существование в следующем поколении лишь в тех случаях, когда в ее окружении насчитывается два или три живых соседа. При меньшем числе соседей считается, что она умирает от одиночества, а при большем - от тесноты. Для неживой ячейки возрождение может произойти лишь в том случае, когда ее окружают ровно три живых соседа.
Алгоритмическая запись этих действий будет содержать огромное множество повторений. Программа предусматривает анализ каждой ячейки, пересчет ее соседей, принятие решения о жизни и смерти этой ячейки, а затем переход к следующей, и так, пока не
будет проверена вся матрица. Такого рода повторения обычно заключаются в программную структуру, называемую циклом и выполняемую по одному разу для каждой ячейки. Когда игра "Жизнь" кодируется в форме крупноформатного электронного бланка, все повторения остаются, однако они имеют пространственный, а не временной характер - одна и та же формула помещается в каждую ячейку большого массива.
Существует множество способов записи формулы для оценки состояния ячейки в игре "Жизнь". Лучший из тех, что я видел (в плане быстродействия), был разработан Э.Готтхэйлом из фирмы Lotus. Основные действия состоят здесь в том, что число, соответствующее анализируемой ячейке, множится на 9 (в результате мы получаем либо 0, либо 9), а затем к этому произведению прибавляются значения всех восьми окружающих ячеек. Результат оценивается с помощью маленькой таблицы, предписывающей новое состояние ячейки для всех возможных значений суммы (а именно, для всех целых чисел от 0 до 17).
В идеале игру "Жизнь" следовало бы проводить на "ячеистой" матрице бесконечной протяженности. Одна из увлекательных сторон игры проявляется в том, что некоторые скромные начальные конфигурации разрастаются в величественные симметричные цвегы после всего лишь нескольких поколений, другие испускают узкие лучи, устремленные в неведомые дали. Развитие конфигурации резко изменяется каждый раз, когда эволюционирующий организм вырывается за рамки своего "мира". Бесконечную матрицу построить невозможно в любом случае, а при работе с КЭБ-программой практически допустимые размеры матрицы и вовсе не велики. Они определяются возможностями самой программы, емкостью оперативной памяти компьютера и терпением игрока (грубо говоря, время, требующееся для построения каждого нового поколения, пропорционально числу используемых ячеек). Одна из стратегий, позволяющих создать безграничный массив, имеющий тем не менее конечную площадь, состоит в том, что ячейки, расположенные на двух противоположных краях бланка, объявляются соседствующими между собой. Таким образом, мы изменяем топологию бланка. Описанное соединение двух краев порождает цилиндр, а если края бланка перевернуть, то и лист Мебиуса. Соединив попарно все четыре стороны бланка, мы получим тор.
МОДЕЛЬ Изинга - это имитация физической системы, напоминающая некоторые ячеистые автоматы. Впрочем, интерпретация этой модели имеет совершенно другой характер. Сама модель, предложенная в 20-е годы немецкими физиками В.Ленцем и Э.Изингом, может отображать многие физические явления, хотя чаще всего она применяется для описания ферромагнетиков. Каждый атом в кристаллической решетке обладает вращательным спиновым моментом, а следовательно, и магнитным моментом. Каждый спин имеет строго определенную величину, но его ось может быть направлена либо вверх, либо вниз. Когда все спины направлены в одну и ту же сторону, материал считается полностью намагниченным, если же распределение спинов чисто случайно, намагниченность равна нулю.
Применить КЭБ-программы к модели Изинга несколько более сложно, чем к самовоспроизводящимся автоматам Фредкина или к игре Конвея "Жизнь". Здесь состояние любого заданного спина тоже зависит от состояния соседних ячеек, в данном случае от четырех, расположенных в непосредственной близости. Однако в модель Изннга введен также и элемент случайности, соответствующий температуре, отличной от абсолютного нуля. Если спины в соседних ячейках направлены вверх, то спин рассматриваемой ячейки имеет тенденцию развернуться в ту же сторону, однако нет никаких гарантий, что это обязательно произойдет - вероятность такого события обратно пропорциональна температуре.



Вариант с использованием крупноформатных электронных бланков для двумерной модели Изинга, описывающей поведение ферромагнетиков
Несколько экспериментов, которые я провел, используя КЭБ-программы в применении к модели Изинга, дали противоречивые результаты. Ожидаемые свойства двумерной модели были точно известны еше в 1944г., когда Л.Онзагер из Йельского университета смог решить эту систему аналитически (без численного моделирования). Когда температура, снижаясь, проходит через некое пороговое значение (температуру Кюри), конфигурации спинов сильно меняются, а затем материал должен приобрести полную намагниченность. Мне не удалось наблюдать этот фазовый переход, но удивляться этому не приходится. Модель Изинга предъявляет крайне жесткие требования к ресурсам вычислительной системы. Для получения точных результатов требуется создание обширной решетки и анализ всех возможных конфигураций спинов, а это может занять много часов машинного времени даже при использовании высокоэффективной программы и быстродействующего процессора. При Институте теоретической физики Калифорнийского университета в Санта-Барбаре построен специализированный компьютер только для работы с моделью Изинга. В течение секунды это устройство вычисляет состояние двадцати пяти миллионов спинов. А быстродействие использованной нами КЭБ-программы для згой модели составляет всего 25 спинов в секунду.
Хотя нам и не удалось наблюдать те интересные явления, которые происходят вблизи температуры Кюри, КЭБ-программа для модели Изинга, по-видимому, хорошо описывает некоторые другие свойства магнитных материалов. При высоких температурах, как и следовало бы ожидать, система спинов не обладает какой-либо видимой структурой. При низких температурах намагниченность кристаллической решетки становится очевидной. Спонтанно возникают большие неправильной формы блоки атомов с упорядоченными спинами. На границах с ними соперничают блоки противоположной полярности. Весьма удивительным (по крайней мере у меня это вызвало удивление) было возникновение антиферромагнитной фазы, в которой каждый спин ориентирован в направлении, противоположном ориентации его соседей. По-видимому, при абсолютном нуле антиферромагнитная фаза становится наиболее устойчивой структурой, хотя этот вывод может оказаться и следствием каких-либо недостатков или ошибок в нашем построении модели.
Прямолинейная решетка может оказаться удобным средством и для анализа других физических систем. Примером может служить явление перколяции. Это явление можно применить для описания не только работы кофеварки, но и структуры некоторых полимеров, механизма электропроводности сплавов, эффективности работы телефонной сети, а также распространения лесных пожаров и инфекционных заболеваний. В одной из простых моделей перколяции ячейки решетки могут соответствовать возможным положениям атомов меди в изолирующей матрице. В первом приближении вероятность того, что некоторая ячейка занята атомом меди, пропорциональна концентрации меди в массе изолятора. Интересующая нас величина - это вероятность образования непрерывной цепочки из атомов меди, пересекающей некоторую область решетки. Именно эта вероятность и определяет электропроводность материала.
Для моделирования фильтрации с помощью КЭБ-программы снова требуется некоторого рода случайная функция. В простейшем подходе предполагается, что мы имеет дело с однородным пространством из ячеек, в котором занятость любой позиции равновероятна и не зависит от состояния других ячеек. В результате мы получим случайную конфигурацию занятых и пустых ячеек. Теперь уже необходимо определить, существует ли в этом пространстве непрерывная цепочка из занятых ячеек. Для решения можно было бы наладить систематический поиск таких цепочек и проверку каждой из них на непрерывность, однако не слишком ясно, как это можно сделать, не прибегая к традиционным алгоритмическим методам. Довольно грубый, но тем не менее эффективный способ состоит в том, чтобы сначала "вырубить весь подлесок". Присвоим каждой ячейке формулу, устраняющую любой атом, обладающий менее чем двумя соседями. Поскольку любой атом, составляющий часть цепочки, должен иметь по крайней мере двух соседей, предложенный способ никак не повлияет на непрерывные цепочки, зато каждый новый просчет КЭБ-программы будет укорачивать тупиковые ответвления и рассасывать изолированные группы атомов.

Порожденная КЭБ-программой структура для моделирования фильтрации

"Прореживание" структуры позволяет рассмотреть непрерывные цепочки
КОНЕЧНО, стандартную КЭБ-программу нельзя считать идеальным средством для моделирования описанных в этой статье математических и физических явлений. При серьезном подходе каждая из этих задач должна привести к разработке собственной специализированной программы. В случае игры "Жизнь" я сравнил различные КЭБ-программы с программой (алгоритмом!), написанной на внутреннем языке микропроцессора. Для массивов одной и той же величины программа на машинном языке оказалась почти в 100 раз быстрее, чем самая быстродействующая из КЭБ-программ. Объяснение лежит на поверхности: хотя величины, соответствующие каждой ячейке, никогда не могут принимать значений, отличных от нуля и единицы, стандартная табличная программа вычисляет их с точностью до пятнадцатого десятичного знака.
Пусть КЭБ-программы не могут претендовать на пальму первенства в быстродействии - зато они обладают не менее важным достоинством, гибкостью. Написать на машинном языке программу игры "Жизнь" - это не просто развлечение на один вечер. Более того, подобная программа не будет способна ни на что иное, в то время как простая матрица из взаимосвязанных ячеек, составляющая ядро КЭБ-программы, обладает изумительной многогранностью. Возможности этих программ явно шире, чем небольшой список обрисованных здесь идей. Похоже, что таким образом можно породить любую последовательность чисел, члены которой задаются алгебраическими или тригонометрическими функциями. Решето простых чисел можно создать с помощью одной короткой формулы, повторенной несколько сот раз. Можно отобразить и какое-нибудь физическое поле, стоит только адрес ячейки истолковать как ее координаты в двумерном пространстве. Как неизменно повторяется в рекламных брошюрах, "Единственное ограничение в пользовании КЭБ-программами - это ваше воображение".
Справедливо ли это? Можно ли с помощью матрицы из независимых формул, не сопровождая ее никакими алгоритмическими структурами, вычислить все, что поддается вычислению? В случае матриц бесконечной размерности этот вопрос можно считать решенным. Конвей показал, что ячеистая вселенная игры "Жизнь" располагает достаточными ресурсами для создания машины Тьюринга - концептуальной модели универсального компьютера. Поскольку для игры "Жизнь" можно использовать бланк бесконечной протяженности, такой же бланк может быть применим и для создания машины Тьюринга.
Этот вывод, конечно же, стоит запомнить, однако даже если бы можно было ослабить требования относительно бесконечных размеров матрицы, доказательство не имело бы никакого практического смысла. Жизнь коротка, а игра "Жизнь" слишком длинна. На мой взгляд, существует более простой, менее формальный способ оценить диапазон применения КЭБ-программ. Это метод проб и ошибок, попытка применить эти программы к задачам и упражнениям из золотого фонда вычислительной математики. Наиболее интересными случаями будут, пожалуй, те задачи, которые уже имеют изящные и высокоэффективные алгоритмические решения. Одним из примеров может служить головоломка "Ханойская башня". В этой игре на один из трех стоящих рядом стержней надеты несколько дисков в порядке убывания их диаметра. Цель играющего состоит в том, чтобы, перенося диски по одному с одного стержня на другой, причем никогда не помещая большего диска над меньшим, расположить все диски в исходном порядке на одном из стержней, который сначала был свободен. В одном из традиционных математических решений используется возвратный алгоритм, т.е. такой, который сначала фиксирует результат, а затем обращается к поиску предшествовавших шагов.
Можно ли решить задачу о Ханойской башне с помощью абсолютно неалгоритмических методов? Можно ли при решении воспользоваться крупноформатным электронным бланком? Если это удастся, мы, разумеется, не докажем, что с помощью КЭБ-программ можно сделать все. что делается с помощью алгоритмов, но по крайней мерс существенно расширим сферу возможных применений КЭБ-программ. Напомню, что существуют тривиальные методы решения, которые не могут считаться ответом на поставленный вопрос. Можно, к примеру, разгадать головоломку вручную, заметить расположение дисков на каждом шаге, а потом записать последовательность формул, описывающую переход от каждого расположения к следующему. Для такого "лобового" метода характерно, что при малейшем изменении начальных условий, например при добавлении еще одного диска все решение, по сути дела, приходится начинать сначала. Искомое решение должно быть применимо к задаче с любым числом дисков без всяких изменений, если не считать уточнения размеров массива. Напоминаю также, что по крайней мере одна КЭБ-программа "Лотос 1-2-3" дополнительно включает в себя несложный алгоритмический язык. Разумеется, всякие обращения к подобным дополнительным возможностям при решении нашей задачи должны быть полностью исключены.
Еще один интересный пример - это задача о восьми ферзях. Она требует такого размещения восьми ферзей на стандартной шахматной доске, чтобы ни один из них не находился под ударом другого. Задача дразнит своим простеньким форматом - квадратным полем всего в 64 клетки. Совсем не трудно отобразить шахматную доску на матрице КЭБ-программы. Не так сложно и написать формулу, определяющую, находится ли данная ячейка под ударом со стороны ферзя, стоящего где-либо на доске. (Эта формула просто-напросто выяснит, есть ли нулевые значения в данном столбце, в данной строке и на соответствующих диагоналях в радиусе восьми ячеек). Если бы этим ограничивалось все, что требуется для решения задачи, вряд ли она привлекла бы внимание Карла Фридриха Гаусса, который исследовал ее в 1650г., так и не добившись решения. Похоже, что в каждой ячейке должна храниться информация не только о текущем расположении фигур, но и о всех других вариантах, которые были уже испробованы. Трудности, связанные с представлением такой информации в статической формулировке задачи, наводят на мысль, что традиционным алгоритмам предстоит еще долгая жизнь.
БИБЛИОГРАФИЯ
АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.
Точнее, Сб. САМООРГАНИЗУЮЩИЕСЯ СИСТЕМЫ, 1964, и конечно, ФОН НЕЙМАН, ТЕОРИЯ САМОВОСПРОИЗВОДЯЩИХСЯ АВТОМАТОВ, 1971 - DJVU, 4.14Мб
DJVU, 4.14Мб .- G.
.- G.
MATHEMATICAL GAMES. Martin Gardner in Scientific American, Vol.223, No.4, pages 120-123, October, 1970, and Vol.224, No.2, pages 112-117, February, 1971. (См. М.ГАРДНЕР, КРЕСТИКИ-НОЛИКИ, 1988 (ранняя версия - в книге МАТЕМАТИЧЕСКИЕ ДОСУГИ, 1972); о программной реализации игры "Жизнь" - Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 - ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.).
.- G.).
WINNING WAYS FOR YOUR MATHEMATICAL PLAYS. Elwyn R.Berlekamp, John H.Conway and Richard K.Guy. Academic Press, 1982.
LOTUS 1-2-3 USER'S MANUAL. John Posner, Steven E. Miller, Ezra Gotiheil and Jeff Hill. Lotus Development Corporation, 1983.
ОТКЛИКИ
3 1984
В ДЕКАБРЬСКОМ номере журнала в качестве маловероятных кандидатов для решения неалгоритмическим методом с использованием крупноформатного электронного бланка (КЭБ) были упомянуты две комбинаторные задачи. Несколько читателей моментально показали, что они поддаются решению.
Решения задачи о Ханойской башне, полученные. КЭБ-программой, прислали Д.Бехар, Дж.Джонс-младший, Дж.А.Миллер, Дж.Слейден, Э.Уин-Джонс и др. Все они использовали один и тот же прием. Алгоритм, в котором диски с нечетными номерами вращались по часовой стрелке, а с четными - против часовой, был видоизменен так, что временные последовательности инструкций превратились в их пространственный массив.
Бехар, Миллер и Слейден решили также задачу о восьми ферзях. Здесь основная трудность заключается в необходимости вернуться назад, когда испытываемое решение ошибочно. Я предложил было регистрировать предыдущие безуспешные попытки, но это не выход из положения. В пояснении к способу решения этих задач при помощи КЭБ-программ Д.Фремлин указал на "метод, который будет порождать все возвраты без использования какой бы то ни было иной памяти, кроме дисплея... Формулы эти сложны и включают последовательные алгоритмы, если они представлены в своем естественном виде, но все эти подпрограммы "поиска" могут быть представлены на крупноформатном электронном бланке локальными вычислениями".
МЫ ОТКРЫВАЕМ НОВУЮ РУБРИКУ, ПОСВЯЩЕННУЮ КОМПЬЮТЕРНЫМ ИГРАМ
БРАЙАН ХЭЙЕС
А теперь - посчитаем!
Готфрид Вильгельм Лейбниц
С НЕКОТОРЫХ пор любители самых увлекательных игр с ЭВМ получили новую возможность: на клавиатуре их микрокомпьютера появилась функциональная клавиша: TBIC ("The boss is coming"), что означает: "Осторожно, босс идет!". Если нажать на эту клавишу, то игровое поле на экране моментально замирает и гаснет. Здесь мы, пожалуй, наблюдаем оба полюса общественной реакции на распространение недорогих ЭВМ. С одной стороны, компьютер остается средством производства, с другой - он дает возможность для столь увлекательных развлечений, что их, подобно детективным историям, приходится скрывать от постороннего взгляда.
Я не намерен приуменьшать роль вычислительных машин ни в промышленности и торговле, ни в компьютерных играх, основная цель которых состоит в испытании у играющего быстроты реакции. Значение практических расчетов с использованием ЭВМ неоспоримо. Что же касается игр на экране дисплея, то их построение можно считать наивысшим выражением искусства программирования. Однако следует отметить, что обе эти сферы не затрагивают глубоко вопроса о том, что представляет собой компьютер и на что он способен.
Между коммерческим программированием и играми на экране дисплея, между программой "Визикальк" и программой "Космических пришельцев" огромное расстояние. Сюда входят различные приложения ЭВМ во всех гуманитарных и естественных науках и, пожалуй, в первую очередь в математике. При этом компьютер используется для моделирования различных аспектов окружающего нас мира. Здесь можно найти многие направления, которые, строго говоря, вообще не могут быть названы "использованием компьютера", а служат скорее для того, чтобы привлечь внимание к самой вычислительной машине и глубже понять природу автоматизированных вычислений. Наша рубрика будет посвящена рассмотрению области, лежащей между чисто практическими приложениями и развлечениями. Полагая, что мышление все еще остается занятием намного более сложным, чем просто вычисления, мы будем считать, что те, кто не имеет доступа к вычислительной технике, просто окажутся в несколько менее благоприятных условиях. К теории и практике вычислений можно иной раз удачно применить даже самые простые бухгалтерские средства.
В этой статье мы рассмотрим некоторые вопросы, возникающие при нетрадиционном использовании программ, известных под общим названием "электронные крупноформатные бланки".
ОБЫЧНЫЙ бумажный бланк - это большой лист, разграфленный на множество строк и столбцов. Его можно использовать для изучения бюджета какой-нибудь компании. Каждому подразделению можно отвести один столбец, а всем категориям доходов и расходов - по строке. Общие суммы и процентные доли каждой категории н каждого подразделения могут быть записаны в дополнительных столбцах и строках.
Крупноформатный электронный бланк воспроизводит эту структуру на экране катодно-лучевой трубки, однако он содержит и некоторые дополнительные возможности. В бумажном бланке любая ячейка (определим ее как пересечение столбца и строки) может содержать либо метку, например название подразделения, либо какое-нибудь число. В электронном бланке любой ячейке может быть приписана также и математическая формула. Так, ячейка в конце строки может содержать формулу, требующую просуммировать все численные значения, внесенные в остальные ячейки этой строки. На экране при этом воспроизводится число, соответствующее результату вычислений по этой формуле (в нашем примере ячейка будет содержать сумму всех чисел, помешенных в строке), однако, по сути дела, содержанием ячейки будет не число, а собственно формула. Если изменить содержимое какой-либо из остальных ячеек строки, то в последней ячейке автоматически появится новое значение для суммы.

Структура крупноформатного электронного бланка
Первой программой оперирования с крупноформатными электронными бланками (сокращенно - КЭБ-программой) была программа "Визикальк", разработанная в 1978г. Д.Бриклином, в то время студентом Коммерческой школы Гарвардского университета, а также Р.Фрэнкстоном и Д.Фильстрой. Сообщалось, что она распродана в большем количестве экземпляров, чем какая-либо другая программа для ЭВМ. С тех пор на подобных принципах были созданы десятки других программ, да и сама "Визикальк" модернизировалась несколько раз. Большая часть описанных здесь экспериментов была проведена с двумя более поздними версиями КЭБ-программ - с программой "1-2-3", созданной М.Кэйпором из Lotus Development Corporation (Кэмбридж, шт.Массачусетс) и программой "Мультиплан" - результатом разработок в Microsoft Corporation (Бельвью, шт.Вашингтон). В большинстве случаев с таким же успехом можно воспользоваться и другими КЭБ-программами.
Хотя электронный крупноформатный бланк был предназначен для финансовых исследований, он пригоден и для других целей. Бланк представляет собой 2x2-матрицу из ячеек, для которой можно установить зависимость между содержимым любой ячейки и какой-либо другой ячейкой или группой ячеек. Можно лишь удивляться, сколь существенная часть математической структуры Вселенной может быть втиснута в этот скромный формат. В самом деле, оказывается, что подобный бланк отражает весьма широкий диапазон математических и логических взаимосвязей.
Принципы работы КЭБ-программы и ее возможности можно понять с помощью одного простого примера. Каждая ячейка нумеруется с помощью ее координат в координатной сетке, для большинства программ столбцы задаются буквами, а строки - цифрами, начиная с левого верхнего угла. Допустим, ячейкам A1 и A2 будут присвоены одинаковые численные значения, равные единице. Затем в ячейку A3 вводится формула: численное значение этой ячейки должно быть равно сумме величин, находящихся в двух ячейках, расположенных непосредственно над ячейкой A3. Иначе говоря, содержимое A3 равно содержимому A2 плюс содержимое A1, т.е. в нашем случае оно будет равно двум.
Пока что мы пришли к достаточно тривиальному результату: нам удалось создать сложную конструкцию, выражающую соотношение 1+1=2. Однако теперь мы можем переписать формулу из ячейки A3 во множество других ячеек. (Подобная процедура копирования в различных программах может иметь разную форму, однако у всех КЭБ-программ предусмотрена эта возможность). Предположим, формула из ячейки A3 повторяется в ячейках от A4 до A10. Тогда каждая из этих ячеек будет содержать величину, равную сумме значений в двух вышестоящих ячейках. Заметим, что все формулы будут идентичны, однако при подстановке разных исходных значений они дадут различные результаты. В столбце бланка сверху вниз появятся следующие числа: 1, 1, 2, 3, 5, 8, 13, 21, 34 и 55.
СУЩЕСТВУЕТ множество способов порождения рядов Фибоначчи с помощью ЭВМ, причем в большинстве они используют ресурсы машины гораздо эффективнее, чем предложенный метод. Однако стратегия использования крупноформатных электронных бланков обладает существенным отличием - она неалгоритмична. Почти во всех языках программирования задание или решение задачи определяется в терминах алгоритма, т.е. в виде последовательности точных инструкций, выполняемых одна за другой. Алгоритм подобен рецепту, он может звучать так: "Вначале смешайте муку, воду и дрожжи, дайте тесту подняться, а затем поставьте выпекать". Если мы проделаем те же операции в другом порядке, то получим совершенно иной результат. КЭБ-программы не содержат этой характерной временной упорядоченности. В ячейках размещается не последовательность шагов, приводящая от проблемы к ее решению, а некая статическая структура, пытающаяся охватить решение сразу. Это не рецепт, а скорее описание, в нем утверждается, что хлеб состоит из муки, дрожжей и воды, смешанных, выдержанных и выпеченных должным образом.
Различие между алгоритмом и статическим описанием можно пояснить еще на одном примере. Рассмотрим задачу перемножения двух матриц, каждая из которых имеет по три столбца и по три строки. Стандартный алгоритм начинается с инструкций - перемножить каждый элемент первого столбца первой матрицы с каждым элементом первой строки второй матрицы, просуммировать три этих произведения и заслать результат в память как первый элемент результирующей матрицы. Затем такие же инструкции будут повторены для остальных восьми комбинаций из строк и столбцов. При использовании КЗБ-программ формулировка задачи примет другую форму, основанную на структурном подобии математической матрицы и массива ячеек. Вместо того чтобы писать последовательность инструкций, можно просто создать результирующую матрицу, приравнивая содержимое каждой из ее ячеек формуле, отражающей соответствующую комбинацию из столбцов и строк. Если мы введем такие формулы, все они будут вычисляться "сразу" и одновременно появится результирующая матрица-произведение.
Разумеется, на более глубоком уровне вычислительная машина, управляемая КЭБ-программой, в самом деле следует какому-то алгоритму. ЭВМ, обладающая лишь одним центральным процессом, не может одновременно выполнять несколько действий, так что все ячейки неизбежно вычисляются в некоторой последовательности. Однако человеку, пользующемуся такой программой, обычно не требуется принимать это к сведению, да и в самом деле он зачастую не имеет об этом никакого представления. Таким образом, пользователь избавляется от необходимости представлять себе решаемую задачу в терминах алгоритмов.
Конечно же, не следует думать, что неалгоритмический тип мышления в чем-то превосходит алгоритмический. Кое-кто может его предпочитать, хотя в большой степени это дело вкуса. Когда задача становится слишком сложной, появляются веские основания воспользоваться алгоритмом, так как он более естественно распадается на части, с которыми удобно работать. Решение всей задачи сразу требует одновременного понимания всех ее аспектов. Однако, по-видимому, существуют некоторые задачи или классы задач, которые приводят к неалгоритмическим формулировкам.
ОДНА из областей, где двумерный прямолинейный массив КЭБ-программы представляет удобное средство для решения залач,- это разработка систем ячеистых автоматов. Исследование подобных систем было начато в 50-х годах Дж.фон Нейманом и С.Уламом. В то время они занимались в основном самовоспроизводящимися структурами. Правила, установленные ими для своих задач, предполагали существование "однородного пространства из ячеек", в котором каждая ячейка представляет собой автомат или машину, имеющую лишь конечное число возможных состояний. Условие однородности пространства понималось в том смысле, что законы, управляющие состояниями автоматов, должны оставаться одними и теми же для всех ячеек. Еще одно ограничение заключалось в том, что состояние любой ячейки могло определяться лишь ее собственной историей и состоянием ее ближайших соседей.
Условиям, определяющим систему ячеистых автоматов, можно легко удовлетворить, пользуясь КЭБ-программой. В принципе число состояний, доступных одной ячейке, крайне велико (возможно, 1E100), однако очевидно, что оно конечно и может быть сведено, если это покажется удобным, к весьма небольшому числу. Так, например, любой ячейке можно присвоить формулу, дающую лишь два возможных значения 0 и 1. Требование однородности пространства добавляет одно интересное ограничение. Оно предполагает, что все ячейки, в которые внесены какие-либо формулы, на самом деле должны содержать одну и ту же формулу. (Существуют разные пути для оценки идентичности двух формул. Предположим, формула в ячейке A1 соотносит ее содержимое с содержимым ячейки B1, расположенной непосредственно под ячейкой A1. Формула, приписанная ячейке A2, может считаться идентичной, если она также соотносится с содержимым B1, т.е. сохраняет "абсолютный адрес". Однако она может соотноситься и с содержимым ячейки B2 и при этом будет сохраняться геометрическая взаимосвязь. Вторая интерпретация, как правило, оказывается более полезной, и пожалуй, лучше соответствует представлениям фон Неймана и Улама, хотя в случае последовательного и непротиворечивого применения каждая из схем может оказаться приемлемой. Методы, используемые в КЭБ-программах для копирования содержимого ячеек, представляют собой удобную и оперативную проверку условия однородности. Массив ячеек может считаться однородным, если существует возможность приписать какую-либо формулу одной из ячеек, а затем с помощью программы присвоить эту же формулу всем остальным ячейкам).
Фон Нейман смог доказать существование самовоспроизводящейся конфигурации ячеек. Сделал он это непростым способом, показав, что существует некий универсальный конструктор, способный создать любую конфигурацию, а следовательно, способный воссоздать и собственное строение. Доказательство предусматривает систему из примерно 200тыс. ячеек, обладающих 29 возможными состояниями. Насколько я знаю, такая конфигурация никогда не была создана ни вручную, ни с помощью компьютера. В принципе сейчас она уже под силу наиболее развитым КЭБ-программам.
Гораздо более простая система, способная самовоспроизводиться, была разработана в 1960г. Э.Фредкнном из Массачусетского техно погического института. В ней каждая ячейка обладает лишь двумя возможными состояниями, "живым" и "мертвым", которые можно представить числами 1 и 0. Состояние, которое будет присвоено ячейке в будущем поколении, определяется нынешним состоянием четырех ее ближайших соседей, т.е. четырех ячеек, расположенных непосредственно к северу, востоку, югу и западу. Если число живых соседей четно (0, 2 и 4), ячейка умирает или остается мертвой. Ячейка, окруженная нечетным числом живых соседей (1 и 3), остается живой.
Пользуясь КЭБ-программоЙ, особенно если в ней предусмотрены арифметические действия по модулю целых чисел, формулу, выражающую это правило, можно записать в одну строчку. Например, для ячейки B2 эта формула имеет вил: (B1+C2+B3+A2) mod 2. Иначе говоря, в соответствии с этой формулой складывается содержимое четырех соседних ячеек, сумма делится на два и сохраняется только остаток, который непременно будет равен нулю или единице. Теперь остается лишь переписать эту формулу (таким образом, чтобы ссылки на другие ячейки образовывали ту же геометрическую взаимосвязь) во все остальные ячейки электронного бланка. На самом деле при создании описываемой системы возникает еще одна тонкость: нам требуется еще два экземпляра изображений пространства из ячеек. Один экземпляр отражает нынешнее состояние пространства, а второй - состояние предыдущего поколения. Текущее состояние ячейки определяется числом живых соседей, окружавших эту ячейку в предыдущем поколении.
Если сформировать электронный бланк в соответствии с правилами Фрелкина и задать начальную конфигурацию, то каждый новый просчет будет давать новую картину. После нескольких циклов появляются четыре копии начальной конфигурации. Позже и сами эти копии учетверяются, так что начальный рисунок воспроизводится 16 раз. Количество циклов, необходимых для самовоспроизведения, зависит от сложности начальной конфигурации. В простейшем случае (единственная живая ячейка) четыре копии возникают в первом же просчете.

В системе ячеистых автоматов, разработанных Э.Фредкином, любая структура способна к самовоспроизведению
Наблюдение за развитием растущей колонии может быть увлекательнейшим занятием. Картина все время сохраняет четырехкратную симметрию, а некоторые из конфигураций обладают странной лучистой формой. Весь процесс подчинен некоему ритму: периметр занятой области непрерывно расширяется, а ее внутренняя зона периодически заполняется густой порослью ячеек, а затем пустеет снова.
НАИБОЛЕЕ широко известная система ячеистых автоматов - это игра под названием "Жизнь". Ее изобрел Дж.Конвей из Кембриджского университета, а широкая публика узнала о ней в 1970г. благодаря Мартину Гарднеру и его рубрике "Математические игры" в журнале "Scientific American". Эта игра, как и порожденные ею размножающиеся автоматы, сегодня завоевала практически все вычислительные системы и языки программирования. Это и понятно - игра сторицей вознаграждает за уделенное ей внимание и тогда, когда оно выражается в праздном любопытстве, и в том случае, когда оно принимает форму глубокого анализа.
В игре Конвея правила создавались не для того, чтобы обеспечить самовоспроизведение рисунка, а скорее для того, чтобы увеличить изменчивость или снизить предсказуемость. Здесь снова каждая ячейка имеет два возможных состояния, однако ее окружение состоит уже из восьми ближайших соседей, включая четыре, соседствующие по диагонали. Если ячейка живая, она продолжит свое существование в следующем поколении лишь в тех случаях, когда в ее окружении насчитывается два или три живых соседа. При меньшем числе соседей считается, что она умирает от одиночества, а при большем - от тесноты. Для неживой ячейки возрождение может произойти лишь в том случае, когда ее окружают ровно три живых соседа.
Алгоритмическая запись этих действий будет содержать огромное множество повторений. Программа предусматривает анализ каждой ячейки, пересчет ее соседей, принятие решения о жизни и смерти этой ячейки, а затем переход к следующей, и так, пока не
будет проверена вся матрица. Такого рода повторения обычно заключаются в программную структуру, называемую циклом и выполняемую по одному разу для каждой ячейки. Когда игра "Жизнь" кодируется в форме крупноформатного электронного бланка, все повторения остаются, однако они имеют пространственный, а не временной характер - одна и та же формула помещается в каждую ячейку большого массива.
Существует множество способов записи формулы для оценки состояния ячейки в игре "Жизнь". Лучший из тех, что я видел (в плане быстродействия), был разработан Э.Готтхэйлом из фирмы Lotus. Основные действия состоят здесь в том, что число, соответствующее анализируемой ячейке, множится на 9 (в результате мы получаем либо 0, либо 9), а затем к этому произведению прибавляются значения всех восьми окружающих ячеек. Результат оценивается с помощью маленькой таблицы, предписывающей новое состояние ячейки для всех возможных значений суммы (а именно, для всех целых чисел от 0 до 17).
В идеале игру "Жизнь" следовало бы проводить на "ячеистой" матрице бесконечной протяженности. Одна из увлекательных сторон игры проявляется в том, что некоторые скромные начальные конфигурации разрастаются в величественные симметричные цвегы после всего лишь нескольких поколений, другие испускают узкие лучи, устремленные в неведомые дали. Развитие конфигурации резко изменяется каждый раз, когда эволюционирующий организм вырывается за рамки своего "мира". Бесконечную матрицу построить невозможно в любом случае, а при работе с КЭБ-программой практически допустимые размеры матрицы и вовсе не велики. Они определяются возможностями самой программы, емкостью оперативной памяти компьютера и терпением игрока (грубо говоря, время, требующееся для построения каждого нового поколения, пропорционально числу используемых ячеек). Одна из стратегий, позволяющих создать безграничный массив, имеющий тем не менее конечную площадь, состоит в том, что ячейки, расположенные на двух противоположных краях бланка, объявляются соседствующими между собой. Таким образом, мы изменяем топологию бланка. Описанное соединение двух краев порождает цилиндр, а если края бланка перевернуть, то и лист Мебиуса. Соединив попарно все четыре стороны бланка, мы получим тор.
МОДЕЛЬ Изинга - это имитация физической системы, напоминающая некоторые ячеистые автоматы. Впрочем, интерпретация этой модели имеет совершенно другой характер. Сама модель, предложенная в 20-е годы немецкими физиками В.Ленцем и Э.Изингом, может отображать многие физические явления, хотя чаще всего она применяется для описания ферромагнетиков. Каждый атом в кристаллической решетке обладает вращательным спиновым моментом, а следовательно, и магнитным моментом. Каждый спин имеет строго определенную величину, но его ось может быть направлена либо вверх, либо вниз. Когда все спины направлены в одну и ту же сторону, материал считается полностью намагниченным, если же распределение спинов чисто случайно, намагниченность равна нулю.
Применить КЭБ-программы к модели Изинга несколько более сложно, чем к самовоспроизводящимся автоматам Фредкина или к игре Конвея "Жизнь". Здесь состояние любого заданного спина тоже зависит от состояния соседних ячеек, в данном случае от четырех, расположенных в непосредственной близости. Однако в модель Изннга введен также и элемент случайности, соответствующий температуре, отличной от абсолютного нуля. Если спины в соседних ячейках направлены вверх, то спин рассматриваемой ячейки имеет тенденцию развернуться в ту же сторону, однако нет никаких гарантий, что это обязательно произойдет - вероятность такого события обратно пропорциональна температуре.



Вариант с использованием крупноформатных электронных бланков для двумерной модели Изинга, описывающей поведение ферромагнетиков
Несколько экспериментов, которые я провел, используя КЭБ-программы в применении к модели Изинга, дали противоречивые результаты. Ожидаемые свойства двумерной модели были точно известны еше в 1944г., когда Л.Онзагер из Йельского университета смог решить эту систему аналитически (без численного моделирования). Когда температура, снижаясь, проходит через некое пороговое значение (температуру Кюри), конфигурации спинов сильно меняются, а затем материал должен приобрести полную намагниченность. Мне не удалось наблюдать этот фазовый переход, но удивляться этому не приходится. Модель Изинга предъявляет крайне жесткие требования к ресурсам вычислительной системы. Для получения точных результатов требуется создание обширной решетки и анализ всех возможных конфигураций спинов, а это может занять много часов машинного времени даже при использовании высокоэффективной программы и быстродействующего процессора. При Институте теоретической физики Калифорнийского университета в Санта-Барбаре построен специализированный компьютер только для работы с моделью Изинга. В течение секунды это устройство вычисляет состояние двадцати пяти миллионов спинов. А быстродействие использованной нами КЭБ-программы для згой модели составляет всего 25 спинов в секунду.
Хотя нам и не удалось наблюдать те интересные явления, которые происходят вблизи температуры Кюри, КЭБ-программа для модели Изинга, по-видимому, хорошо описывает некоторые другие свойства магнитных материалов. При высоких температурах, как и следовало бы ожидать, система спинов не обладает какой-либо видимой структурой. При низких температурах намагниченность кристаллической решетки становится очевидной. Спонтанно возникают большие неправильной формы блоки атомов с упорядоченными спинами. На границах с ними соперничают блоки противоположной полярности. Весьма удивительным (по крайней мере у меня это вызвало удивление) было возникновение антиферромагнитной фазы, в которой каждый спин ориентирован в направлении, противоположном ориентации его соседей. По-видимому, при абсолютном нуле антиферромагнитная фаза становится наиболее устойчивой структурой, хотя этот вывод может оказаться и следствием каких-либо недостатков или ошибок в нашем построении модели.
Прямолинейная решетка может оказаться удобным средством и для анализа других физических систем. Примером может служить явление перколяции. Это явление можно применить для описания не только работы кофеварки, но и структуры некоторых полимеров, механизма электропроводности сплавов, эффективности работы телефонной сети, а также распространения лесных пожаров и инфекционных заболеваний. В одной из простых моделей перколяции ячейки решетки могут соответствовать возможным положениям атомов меди в изолирующей матрице. В первом приближении вероятность того, что некоторая ячейка занята атомом меди, пропорциональна концентрации меди в массе изолятора. Интересующая нас величина - это вероятность образования непрерывной цепочки из атомов меди, пересекающей некоторую область решетки. Именно эта вероятность и определяет электропроводность материала.
Для моделирования фильтрации с помощью КЭБ-программы снова требуется некоторого рода случайная функция. В простейшем подходе предполагается, что мы имеет дело с однородным пространством из ячеек, в котором занятость любой позиции равновероятна и не зависит от состояния других ячеек. В результате мы получим случайную конфигурацию занятых и пустых ячеек. Теперь уже необходимо определить, существует ли в этом пространстве непрерывная цепочка из занятых ячеек. Для решения можно было бы наладить систематический поиск таких цепочек и проверку каждой из них на непрерывность, однако не слишком ясно, как это можно сделать, не прибегая к традиционным алгоритмическим методам. Довольно грубый, но тем не менее эффективный способ состоит в том, чтобы сначала "вырубить весь подлесок". Присвоим каждой ячейке формулу, устраняющую любой атом, обладающий менее чем двумя соседями. Поскольку любой атом, составляющий часть цепочки, должен иметь по крайней мере двух соседей, предложенный способ никак не повлияет на непрерывные цепочки, зато каждый новый просчет КЭБ-программы будет укорачивать тупиковые ответвления и рассасывать изолированные группы атомов.

Порожденная КЭБ-программой структура для моделирования фильтрации

"Прореживание" структуры позволяет рассмотреть непрерывные цепочки
КОНЕЧНО, стандартную КЭБ-программу нельзя считать идеальным средством для моделирования описанных в этой статье математических и физических явлений. При серьезном подходе каждая из этих задач должна привести к разработке собственной специализированной программы. В случае игры "Жизнь" я сравнил различные КЭБ-программы с программой (алгоритмом!), написанной на внутреннем языке микропроцессора. Для массивов одной и той же величины программа на машинном языке оказалась почти в 100 раз быстрее, чем самая быстродействующая из КЭБ-программ. Объяснение лежит на поверхности: хотя величины, соответствующие каждой ячейке, никогда не могут принимать значений, отличных от нуля и единицы, стандартная табличная программа вычисляет их с точностью до пятнадцатого десятичного знака.
Пусть КЭБ-программы не могут претендовать на пальму первенства в быстродействии - зато они обладают не менее важным достоинством, гибкостью. Написать на машинном языке программу игры "Жизнь" - это не просто развлечение на один вечер. Более того, подобная программа не будет способна ни на что иное, в то время как простая матрица из взаимосвязанных ячеек, составляющая ядро КЭБ-программы, обладает изумительной многогранностью. Возможности этих программ явно шире, чем небольшой список обрисованных здесь идей. Похоже, что таким образом можно породить любую последовательность чисел, члены которой задаются алгебраическими или тригонометрическими функциями. Решето простых чисел можно создать с помощью одной короткой формулы, повторенной несколько сот раз. Можно отобразить и какое-нибудь физическое поле, стоит только адрес ячейки истолковать как ее координаты в двумерном пространстве. Как неизменно повторяется в рекламных брошюрах, "Единственное ограничение в пользовании КЭБ-программами - это ваше воображение".
Справедливо ли это? Можно ли с помощью матрицы из независимых формул, не сопровождая ее никакими алгоритмическими структурами, вычислить все, что поддается вычислению? В случае матриц бесконечной размерности этот вопрос можно считать решенным. Конвей показал, что ячеистая вселенная игры "Жизнь" располагает достаточными ресурсами для создания машины Тьюринга - концептуальной модели универсального компьютера. Поскольку для игры "Жизнь" можно использовать бланк бесконечной протяженности, такой же бланк может быть применим и для создания машины Тьюринга.
Этот вывод, конечно же, стоит запомнить, однако даже если бы можно было ослабить требования относительно бесконечных размеров матрицы, доказательство не имело бы никакого практического смысла. Жизнь коротка, а игра "Жизнь" слишком длинна. На мой взгляд, существует более простой, менее формальный способ оценить диапазон применения КЭБ-программ. Это метод проб и ошибок, попытка применить эти программы к задачам и упражнениям из золотого фонда вычислительной математики. Наиболее интересными случаями будут, пожалуй, те задачи, которые уже имеют изящные и высокоэффективные алгоритмические решения. Одним из примеров может служить головоломка "Ханойская башня". В этой игре на один из трех стоящих рядом стержней надеты несколько дисков в порядке убывания их диаметра. Цель играющего состоит в том, чтобы, перенося диски по одному с одного стержня на другой, причем никогда не помещая большего диска над меньшим, расположить все диски в исходном порядке на одном из стержней, который сначала был свободен. В одном из традиционных математических решений используется возвратный алгоритм, т.е. такой, который сначала фиксирует результат, а затем обращается к поиску предшествовавших шагов.
Можно ли решить задачу о Ханойской башне с помощью абсолютно неалгоритмических методов? Можно ли при решении воспользоваться крупноформатным электронным бланком? Если это удастся, мы, разумеется, не докажем, что с помощью КЭБ-программ можно сделать все. что делается с помощью алгоритмов, но по крайней мерс существенно расширим сферу возможных применений КЭБ-программ. Напомню, что существуют тривиальные методы решения, которые не могут считаться ответом на поставленный вопрос. Можно, к примеру, разгадать головоломку вручную, заметить расположение дисков на каждом шаге, а потом записать последовательность формул, описывающую переход от каждого расположения к следующему. Для такого "лобового" метода характерно, что при малейшем изменении начальных условий, например при добавлении еще одного диска все решение, по сути дела, приходится начинать сначала. Искомое решение должно быть применимо к задаче с любым числом дисков без всяких изменений, если не считать уточнения размеров массива. Напоминаю также, что по крайней мере одна КЭБ-программа "Лотос 1-2-3" дополнительно включает в себя несложный алгоритмический язык. Разумеется, всякие обращения к подобным дополнительным возможностям при решении нашей задачи должны быть полностью исключены.
Еще один интересный пример - это задача о восьми ферзях. Она требует такого размещения восьми ферзей на стандартной шахматной доске, чтобы ни один из них не находился под ударом другого. Задача дразнит своим простеньким форматом - квадратным полем всего в 64 клетки. Совсем не трудно отобразить шахматную доску на матрице КЭБ-программы. Не так сложно и написать формулу, определяющую, находится ли данная ячейка под ударом со стороны ферзя, стоящего где-либо на доске. (Эта формула просто-напросто выяснит, есть ли нулевые значения в данном столбце, в данной строке и на соответствующих диагоналях в радиусе восьми ячеек). Если бы этим ограничивалось все, что требуется для решения задачи, вряд ли она привлекла бы внимание Карла Фридриха Гаусса, который исследовал ее в 1650г., так и не добившись решения. Похоже, что в каждой ячейке должна храниться информация не только о текущем расположении фигур, но и о всех других вариантах, которые были уже испробованы. Трудности, связанные с представлением такой информации в статической формулировке задачи, наводят на мысль, что традиционным алгоритмам предстоит еще долгая жизнь.
БИБЛИОГРАФИЯ
АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.
Точнее, Сб. САМООРГАНИЗУЮЩИЕСЯ СИСТЕМЫ, 1964, и конечно, ФОН НЕЙМАН, ТЕОРИЯ САМОВОСПРОИЗВОДЯЩИХСЯ АВТОМАТОВ, 1971 -
 DJVU, 4.14Мб
DJVU, 4.14Мб .- G.
.- G. MATHEMATICAL GAMES. Martin Gardner in Scientific American, Vol.223, No.4, pages 120-123, October, 1970, and Vol.224, No.2, pages 112-117, February, 1971. (См. М.ГАРДНЕР, КРЕСТИКИ-НОЛИКИ, 1988 (ранняя версия - в книге МАТЕМАТИЧЕСКИЕ ДОСУГИ, 1972); о программной реализации игры "Жизнь" - Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 -
 ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.).
.- G.).WINNING WAYS FOR YOUR MATHEMATICAL PLAYS. Elwyn R.Berlekamp, John H.Conway and Richard K.Guy. Academic Press, 1982.
LOTUS 1-2-3 USER'S MANUAL. John Posner, Steven E. Miller, Ezra Gotiheil and Jeff Hill. Lotus Development Corporation, 1983.
ОТКЛИКИ
3 1984
В ДЕКАБРЬСКОМ номере журнала в качестве маловероятных кандидатов для решения неалгоритмическим методом с использованием крупноформатного электронного бланка (КЭБ) были упомянуты две комбинаторные задачи. Несколько читателей моментально показали, что они поддаются решению.
Решения задачи о Ханойской башне, полученные. КЭБ-программой, прислали Д.Бехар, Дж.Джонс-младший, Дж.А.Миллер, Дж.Слейден, Э.Уин-Джонс и др. Все они использовали один и тот же прием. Алгоритм, в котором диски с нечетными номерами вращались по часовой стрелке, а с четными - против часовой, был видоизменен так, что временные последовательности инструкций превратились в их пространственный массив.
Бехар, Миллер и Слейден решили также задачу о восьми ферзях. Здесь основная трудность заключается в необходимости вернуться назад, когда испытываемое решение ошибочно. Я предложил было регистрировать предыдущие безуспешные попытки, но это не выход из положения. В пояснении к способу решения этих задач при помощи КЭБ-программ Д.Фремлин указал на "метод, который будет порождать все возвраты без использования какой бы то ни было иной памяти, кроме дисплея... Формулы эти сложны и включают последовательные алгоритмы, если они представлены в своем естественном виде, но все эти подпрограммы "поиска" могут быть представлены на крупноформатном электронном бланке локальными вычислениями".
Последний раз редактировалось: Gudleifr (Вс Дек 08, 2019 9:56 am), всего редактировалось 3 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
1 1984
ПРЕВРАЩЕНИЕ ХУДОЖЕСТВЕННОЙ ЛИТЕРАТУРЫ В ЧЕПУХУ
БРАЙАН ХЭЙЕС
ПРАКТИЧЕСКИ любая программа на выходе ЭВМ может дать бессмысленный результат, если ввести в нее бессодержательные данные ("что посеешь, то и пожнешь" - гласит широко известная пословица). Такая деятельность сейчас настолько распространена, что эксперимент другого рода вряд ли может привлечь внимание. Между тем не требуется особых усилий для того, чтобы создать программу, в которую вводится литературный шедевр, а она выдаст полнейшую чепуху: в машину вводится последний акт "Макбета", а на выходе получается неистовый бред идиота, лишенный всякого смысла. Тем не менее и это считается машинной обработкой данных (увы, произвести обратное преобразование почему-то гораздо сложнее).
Превращение литературы в тарабарщину происходит в два этапа. На первом этапе текст "прочитывается" программой и записываются полученные статистические характеристики. Эти характеристики определяют вероятность последовательностей букв или групп букв алфавита в исходном тексте. На втором этапе в соответствии с записанными вероятностями производится случайный выбор букв и создается новый текст, набор букв которого отражает статистические характеристики исходного текста, но лишен всякого смысла (появление в таком тексте смысла - чистая случайность).
Я не могу представить себе более непродуманного способа имитации. В программе нигде не отражена концепция слова и нет намека на представление о его семантической структуре. Не отражены также лингвистические структуры, более сложные, чем последовательность букв. Созданный текст представляет собой грубейшую имитацию авторского стиля, которая сохраняет только самые поверхностные черты исходного текста. Поражает при этом, что текст, полученный в результате такого примитивного упражнения, обладает иногда навязчивым сходством с оригиналом. Это тарабарщина, но тарабарщина чосеровского, или шекспировского, или джеймсовского толка. Иначе и быть не может. Если из текста изгнано семантическое содержание, гораздо заметнее становятся стилистические манеризмы. Возникает вопрос: насколько глубинными являются стилистические характеристики авторского текста и в чем состоит сложность их выявления?
ПРОЦЕСС порождения случайного прозаического текста был подробно исследован Уильямом Ральфом Беннетом-младшим из Йельского университета. Одной из основных тем в его курсе лекций о применениях компьютеров была лингвистическая статистика. Также подробно эта тема разработана в его учебнике по программированию "Scientific and Engineering Problem-solving with the Computer" ("Научное и инженерное решение задач с помощью компьютеров"). (Книга гораздо увлекательней, чем может показаться по названию. В ней, например, рассматриваются аэродинамические процессы, имевшие место при происходившем во время урагана футбольном матче Принстон-Дартмут в 1950г.; спектральный анализ звуков, издаваемых фаготом, гобоем или садовым шлангом).
Беннет сообщает, что самое раннее до сих пор известное упоминание о случайном порождении текста можно найти в опубликованном в 1690г. сочинении "Maxims and Discourses" Джона Тиллотсона, архиепископа Кентерберийского. Приводя примеры божественного творения, Тиллотсон пишет: "Сколько раз пришлось бы Человеку наполнять мешок буквами и высыпать их обратно на землю, прежде чем из этих букв случайно сложилась бы прекрасная Поэма или прозаический Трактат? И разве не может маленькая Книга быть создана игрою Случая, так же как и вся необъятная Вселенная?"
В современных рассуждениях о порождении случайного текста в качестве отправной точки можно использовать высказывание сэра Артура Эддингтона, сделанное в 1927г.: "Если бы целое стадо обезьян стало барабанить на пишущих машинках, то в принципе они МОГЛИ БЫ написать все книги, хранящиеся в Британском музее". Эддннгтон подчеркивал неосуществимость такого события. Это рассуждение он привел как пример теоретически возможного явления, которое, однако, никогда не произойдет в реальной жизни. Тем не менее со времени Эддингтона мысль о гении, который скрывается среди обезьян, бессмысленно барабанящих на машинке, зажила самостоятельной литературной жизнью. В связи с этим Беннет упоминает произведения Рассела Мэлони, Курта Воннегута-младшего и сценку в ночном клубе у Боба Ньюарта.
Процесс, о котором говорил Эллингтон, можно смоделировать с помощью программы. Я назову эту программу генератором текста нулевого порядка. Выбирается алфавит, или множество знаков, и в соответствии с ним на "обезьяньей" пишущей машинке устанавливается клавиатура. В некоторых моделях высшего порядка целесообразно сводить количество символов к минимуму: по-видимому, из соображений непротиворечивости имеет смысл остановиться на таком же количестве знаков и для генератора текста нулевого порядка. Я последовал рекомендациям Беннета и остановился на 28 знаках: 26 букв английского алфавита, интервал между словами (компьютер рассматривает его как любой другой знак) и апостроф, который встречается в письменном английском языке чаще, чем три-четыре наиболее редко употребляемые буквы.

Случайный текст нулевого порядка, основанный на алфавите из 28 знаков
Воображаемая идеальная обезьяна с одинаковой вероятностью может в любой момент напечатать любой знак. Такое поведение обезьяны моделируется с помощью очень простой стратегии. В множестве 28 знаков каждому символу приписывается определенное число от 0 до 27. В этом пределе для каждого порождаемого знака выбирается случайное число и печатается соответствующая ему буква. Образец небольшого текста, полученного с помощью такой процедуры, изображен на рисунке на этой странице. Текст этот не имеет сходства ни с письменным английским, ни с любым другим человеческим языком. "Слова" в нем непомерно длинны (в среднем по 27 знаков), и в них преобладают согласные. Причина этого - в неравномерности частот букв в английских текстах. На интервал между словами приходится примерно 1/5 всех знаков, а буквы J, Q, X и Z составляют меньше 1% текста. В тексте же нулевого порядка все буквы имеют одинаковую частотность, а именно 1/28.
У Боба Ньюарта комический эффект возникает, когда инспекторы, которым поручено разобраться в белиберде, напечатанной обезьянами на машинке, промучившись над нею не один час, вдруг натыкаются на фразу: "То be or not to be, that is the gesorenplatz..." ("Быть или не быть - вот в чем гесоренплатц...") В действительности это событие не осуществимо, так как порождение первых девяти слов из монолога Гамлета может произойти в тексте, состоящем из 2E46 букв. В тексте же из 50000 букв я нашел на большом расстоянии друг от друга один раз "ТО" и один раз "NOT". (Чтобы не читать все 50000 знаков подряд, я воспользовался подходящей программой).
СОВЕРШЕНСТВОВАНИЕ "литературной деятельности" обезьян надо начать с приведения вероятности выбора обезьяной того или иного знака в соответствие с действительной частотой употребления букв в письменном английском языке. Можно, например, изготовить пишущую машинку, в которой имеется на клавиатуре 2500 интервалов, 850 E, 700 T и т.д. Частоту употребления букв можно вычислить с помошью большой выборки из английской прозы, но мне кажется, что удобней и гораздо интересней обработать какой-нибудь литературный текст. Программа, которая выбирает знаки в соответствии с описанным выше распределением частот, является генератором текста первого порядка.
Частоту букв в тексте можно представить одномерным массивом, состоящим из 2S элементов и хранящимся в блоке памяти компьютера. Любой элемент массива между 0 и 27 может быть определен при помощи индекса. Для заполнения массива достаточно посчитать, сколько раз появляется каждая буква в тексте. Можно заполнить массив ручным способом, ко гораздо удобней воспользоваться компьютером, хотя в этом случае придется сначала подготовить текст для машинной обработки. Считающая программа приравнивает все элементы массива К нулю. Затем производится посимвольный просмотр текста, и при каждом появлении знака к соответствующему элементу массива прибавляется 1.
Случайный текст первого порядка порождается таким образом, что вероятность выбора буквы пропорциональна номеру элемента в массиве. Приведем один из вариантов порождения текста. В интервале между нулем и суммой элементов массива (равной общему количеству знаков в исходном тексте) порождается случайное число. Затем первый элемент массива, например частота буквы А, вычитается из случайного числа. Если результат неположителен, А печатается; в противном случае из величины, оставшейся после первого шага, вычитается следующий элемент (частота буквы В). Последовательные вычитания продолжаются до получения неположительного ответа и выбора соответствующего знака. Заметим, что процедура непременно приводит к выбору знака, так как случайное число не может превышать сумму элементов массива.
На с.104 на верхнем рисунке приведен образец случайного текста первого порядка. Он основан на массиве частот, составленном по тексту последней главы романа Дж.Джонса "Улисс", известной под названием "Итака" (или монолог Молли Блюм). У меня были основания для выбора именно этого отрывка: в случайном тексте отсутствует пунктуация, но это не имеет значения, так как ее нет и в исходном тексте.

Случайные тексты первого, второго и третьего порядков, созданные на основе монолога Молли Блюм
Информация о частоте букв, отраженная в случайном тексте первого порядка, заметно улучшает его, хотя и этот текст трудно признать "читабельным". Средняя длина слов (4.7 буквы) близка к ожидаемому значению (4.5 буквы), но отклонения отдельных слов от обычной для английского языка длины слишком велики и не отражают характерные для английского языка небольшие различия в длине слов. Внутренняя структура слов в тексте также не является "английской". Хотя частотность букв выдерживается, их последовательности совершенно случайны , поэтому "слова" не только не являются английскими, но и не могут ими быть. Такие последовательности букв, как WSTLNTTWNO или HIUOIMYTG, не только бессмысленны, но и невозможны. В случайном тексте, состоящем из 2000 букв, самым длинным узнаваемым словом оказалось слово RARE.
СЛЕДУЮЩИЙ шаг по усовершенствованию генератора текста представляется нам решающим, так как его, по крайней мере теоретически, можно распространить до достаточно высокого уровня. В основе идеи лежит зависимость появления букв в английском слове от предшествующих букв. Так, после V наиболее вероятно появление E; после Q может появиться только U. Для каждого символа из общего множества знаков создается отдельная таблица частот. Частоты записываются в виде двумерного массива из 28 строк и 28 столбцов, составляющих в сумме 784 элемента. Образец такой таблицы изображен на этой странице. (Таблица "нормируется" по строкам, следовательно, сравнение возможно только в пределах строки).

Таблица частот второго порядка для создания случайного текста на основе III акта "Гамлета"
Когда текст порождается при помощи двумерного массива, самый последний отобранный знак определяет, какую строку надо исследовать для выбора следующего знака. Например, если этим знаком является B, исследоваться будут только элементы второй строки. В этой строке наиболее часто встречается буква E, поэтому наиболее велика вероятность, что выбор падет именно на E. Могут быть отобраны также буквы A, I, L, O, R, S и U. Невозможные комбинации букв, такие, например, как BF и BQ, имеют нулевую частотность, поэтому они никогда не будут на выходе.
В случайном тексте второго порядка начинают появляться первые намеки на реально существующие в языке структуры. Диапазон распределения длин слов только немного больше, чем ему следовало бы быть. Встречаются настоящие английские и "почти настоящие" слова (например, SPPRING или THIMES). Часто появляются диграфы, такие, как ТН, и чередования гласных и согласных.
Следующий шаг совершенно очевиден. Алгоритм третьего порядка выбирает буквы в соответствии с вероятностями, определяемыми двумя предшествующими буквами. Это требует трехмерного массива, состоящего из 28 двумерных, каждый из которых в свою очередь состоит из 28 строк и 28 столбцов. Предположим, что при порождении текста была получена последовательность букв ТН. После этого программа должна обратиться к 20-й плоскости (соответствующей T) и к 8-й строке этой плоскости (соответствующей H). Наиболее вероятно, что в этой строке будет выбран знак E, хотя A, I, О и знак интервала тоже имеют ненулевые вероятности. Если будет выбран E, то дальнейший поиск надо вести в 5-й строке 8-й плоскости (позиция последовательности НЕ). Здесь наиболее вероятными знаками окажутся R и интервал между знаками.
В ПОРОЖДЕННОМ тексте третьего порядка последовательности из трех букв появляются только, если они имеются в исходном тексте. Включение интервалов между словами в расчет вероятностей гарантирует, что все однобуквенные слова действительно существуют в языке (на самом деле изолированно могут появиться только буквы I и А). Практически же все двух-буквенные слова и большинство трехбуквенных являются настоящими английскими словами, и, таким образом, работа программы значительно перекрывает "гарантии". Сплошь и рядом возникают длинные цепочки слов: PUT ТО SQUAD TRADE OFF GIN GO ME HER. Даже совсем длинные "не слова" имеют некоторое фонетическое правдоподобие. В конце концов то, что в английском языке сочетание букв ANYHORDANG HOUP TREAFTEN бессмысленно, представляется чистой случайностью.
Читая образец случайного текста третьего порядка, я вспомнил о различных случаях смешения действительно существующих в языке слов с бессмысленными слогами, например о возникновении глоссолалии в молитвах пятидесятников. Можно предположить, что сходство между случайными текстами третьего порядка и этими явлениями имеет какой-то смысл. И может быть, люди, которые обладают навыками такого смешения, подсознательно проделывают статистический анализ, сходный с работой программы. Другое объяснение представляется мне более правдоподобным: для явления смешения слов и слогов и для глоссолалии характерно появление в речи множества фонем - основных единнц устной речи. Возможно, что трехбуквенные сочетания наиболее удачно представляют фонему в письменной речи.
В текстах третьего порядка явственно проступают стилистические черты исходных текстов. Чем больше различается стиль исходных текстов, тем заметнее различия случайных текстов, хотя точно определить, в чем именно состоят эти различия, невозможно. Я думаю, что в основе лежат свойства внутренней структуры текста, хотя и не имею точного представления о том, что представляет собой внутренняя структура прозаического произведения. Может быть, это то, что остается от текста, когда нэ него удален весь смысл?
Даже если в случайном тексте третьего порядка не удается определить особенности стиля автора, язык исходного текста определяется безошибочно по характеру распределения гласных и согласных и по типичным для данного языка окончаниям слов. На нижнем рисунке на с.104 даны образны латинского (Вергилий), итальянского (Данте) и французского (Флобер) текстов. Тем, кто представляет себе только "внешний вил" языка, не так просто отличить "эрзац-текст" от подлинного текста.

Латинский (Вергилий), итальянский (Данте) и французский (Флобер) тексты третьего порядка
Прежде чем перейти к следующему этапу работы со случайным текстом третьего порядка, я хотел бы рассказать о некоторых возможностях использования таблиц частот букв. В одной из дискуссий об энтропии языка Беннет говорит, что с помощью этих таблиц можно оценивать количество информации, приходящейся в тексте на один знак. Количество информации приблизительно отражает трудность предсказания следующего знака в тексте. Она является наибольшей в тексте нулевого порядка, в котором любой знак имеет одинаковую вероятность; иными словами, количество информации оказывается наибольшим, когда текст абсолютно нечитабелен. Идею о предсказуемости знаков можно использовать при решении задач об исправлении ошибок в системах дальней связи для создания алгоритмов расшифровки шифров и криптограмм.
ИЗМЕНЕНИЯ массива частот с помощью различных действий являются еще одной областью, интересной для исследования. Например, какие изменения произойдут в случайном тексте, если каждый элемент массива возвести в квадрат? На нижнем рисунке на с.105 изображен обработанный таким способом монолог Молли Блюм. Такая процедура подчеркивает различия между элементами массива; соответственно изменяется распределение частот, и простые слова становятся еше проще. Возможен и ряд других преобразований. Увеличение всех элементов массива на одно и то же число действует разрушительно, даже если это число очень мало: все невозможные комбинации букв, для изгнания которых была проделана такая сложная работа, снова могут появиться в порожденном тексте.

Случайный текст, созданный на основе монолога Молли Блюм с помощью таблицы частот, каждый элемент которой возведен в квадрат
Увлекательной представляется идея умножить весь массив на -1 для того, чтобы породить текст, например, Александра антн-Попа: после любой последовательности букв в тексте "анти-Попа" появится буква, появление которой в тексте Попа наименее вероятно. Литературные достоинства этого текста можно оценить по заслугам, если в нем будет улавливаться сходство с сочинениями Кали Сибера. На самом деле получается беспорядочный набор знаков.
Не такой обескураживающий (хотя и очень далекий от вдохновляющего) результат получается, если сложить или перемножить два массива. Таким способом можно создать совместные работы писателей, сотрудничество которых в жизни немыслимо. Например, можно объединить Джейн Остин и Марка Твена или поэтов эпохи Китса (Байрон плюс Шелли). Но на самом деле мне хотелось бы получить нечто вроде "Байрон минус Шелли", "выжимку" различий между особенностями стиля обоих авторов. К сожалению. мне не удалось получить такие результаты. Большая часть информации в таблицах третьего порядка отражает лингвистические структуры, общие для всех писателей, пишущих на одном языке. После извлечения из таблиц этих общих элементов в них не остается почти ничего, кроме помех.
Есть н более серьезное соображение, объясняющее, почему вычитание из массива обречено на неудачу. Примерно 90% элементов в неизмененной таблице третьего порядка являются нулевыми и соответствуют большей части буквенных комбинаций, которые никогда не наблюдались в английском языке, например RJT или UUU. Обычно программа "не добирается" до этих элементов. Но после вычитания массив изменяется и попадание в строку, все элементы которой являются нулевыми, неизбежно. Я не вижу элегантного выхода из этого тупика.
СОЗДАНИЕ массива частот и порождение случайного текста не представляют особых трудностей. Настоящие трудности начинаются тогда, когда возникает потребность в большом объеме памяти, необходимом для хранения трехмерного массива модели третьего порядка. Мы ограничились набором из 28 знаков именно для того. чтобы свести размеры массива к минимуму. Даже при этом ограничении массив состоит почти из 22000 элементов и каждому элементу требуются по крайней мере два бита. Одной из самых сложных задач является помещение массива и необходимых программ в память небольшого компьютера.
На следующем этапе приближения каждая буква выбирается в соответствии с вероятностями, определяемыми тремя предшествующими буквами. Для этого нужен четырехмерный массив, включающий более 600000 элементов. В 1977г. Беннет опубликовал в журнале "American Scientist" статью, в которой привел образцы текста четвертого порядка, порожденного с помошью такого гигантского массива. Кроме того, в своем учебнике он писал по поводу моделирования текстов четвертого порядка, что "оно достигло предела реальных возможностей даже при условии доступности самых больших компьютеров". Что же касается исследователей, в распоряжении которых имеются только небольшие компьютеры, то они вообще не имеют возможности работать с текстами четвертого порядка.
Однако возникновение "практических ограничений" вызывает естественную реакцию - стремление их преодолеть. Если рассматривать эту проблему с другой точки зрения, то перспективы окажутся не такими безнадежными. Мы уже говорили, что в массиве третьего порядка большинство чисел являются нулями. Можно ожидать, что доля нулевых элементов в массиве четвертого порядка будет значительно больше. Мое предложение сводится к следующему: вместо того чтобы хранить в памяти компьютера огромный четырехмерный массив, я предлагаю заменить его маленькими одномерными массивами. Каждый такой массив эквивалентен одной строке четырехмерного массива. Строка состоит только из ненулевых элементов, и этим определяются ее размеры. Строки, состоящие только из нулевых элементов, вообще исключаются.
Я думаю, что этот план вполне осуществим, несмотря на его кажущуюся хаотичность. Размещенне в памяти более 10000 массивов, размер которых колеблется от 1 до 28 элементов,- занятие достаточно неприятное. Поэтому я постарался найти более простой путь. Оказывается, можно породить случайный текст достаточно высокого порядка с помощью множества знаков, включающего весь алфавит, а также любые другие знаки, которые способен воспроизводить компьютер. Плата за "удобство" этого метода заключается в том, что программа работает примерно в десять раз медленнее.
Все описанные выше примеры привели меня к размышлениям об альтернативах н предельных ограничениях при создании массивов. Предположим, что исходный текст, использующий алфавит из 28 букв, состоит из 10001 знака. Тогда порядок наибольшей возможной таблицы, описывающей структуру этого текста, будет 10000. Таблица имеет размерность 10000 и состоит из 28^10000 элементов, последнее число настолько огромное, что воображение отказывается его воспринимать. Кроме того, только один элемент иэ всего этого немыслимого массива является ненулевым. Его позицию в массиве уточняют первые 10000 знаков исходного текста, а значение - значение последнего знака в тексте. Даже если бы кто-нибудь мог создать такой массив (на самом деле Вселенная не настолько велика, чтобы вместить его), сама идея затратить так много усилий, для того чтобы иметь возможность опознать один-единственный знак, может вызвать только возмущение и раздражение.
ПРИ СОЗДАНИИ массивов более низких порядков ощущение диспропорции не вызывает таких бурных эмоций, хотя и не исчезает полностью. Дело в том, что вся информация, которая могла бы быть заложена в массив любых размеров, присутствует в исходном тексте в наиболее компактном виде. (Аргументировать это утверждение очень трудно, так как в нем имеются элементы тавтологии. То, что отражено в массиве частот, является частотой последовательностей знаков в тексте; эти и только эти последовательности имеются в исходном тексте, и именно они отражены в массиве частот).
При порождении случайного текста методом, подсказанным этими рассуждениями, происходит следующее. Создается отдельная таблица частот. Это небольшой одномерный массив, содержащий столько элементов, сколько их включено в текстовую выборку, Я остановился на 90 знаках. Весь исходный текст вносится в память компьютера и накапливается (в простейшем случае) в виде непрерывной "цепочки" знаков. После этого отбирается последовательность знаков, с которой начнется случайный текст. Назовем ее пробной строкой.
Ячейки в массиве частот заполняются путем поиска пробных строк по всему исходному тексту. Причем если пробной строкой является, например, "gain", то в процессе поиска будут идентифицированы не только собственно "gain", но и "gains", "again", "against", "bargain" и т.д. В некоторых языках программирования имеется специальная команда для такого поиска: в Бейсике она называется "1NSTR" (от англ. in string - в цепочке), а в языке С - "stcpm" (от англ. string pattern match - соответствующее цепочечной модели). Как только найдена пробная строка, из текста извлекается следующий знак, и массив частот увеличивается на 1. По окончании поиска по всему тексту массив оказывается заполненным.
Следующий шаг заключается в выборе случайного знака из массива частот. Процедура точно соответствует моделированию текста первого порядка; производится последовательное вычитание из случайного множества знаков, и печатается знак, соответствующий выбранному элементу массива. После этого вся процедура повторяется. Создается новая пробная строка, из которой удалена первая буква, а к концу добавлен только что порожденный знак. После того как весь исходный текст исследован таким образом, мы получаем новый массив частот.
Анализ исходного текста и создание массива частот требуют повторения процедуры для каждого порождаемого знака, поэтому программа работает очень медленно. Компенсацией является возможность писать прозаические тексты любого теоретически допустимого максимального порядка, т.е. тексты, которые будут короче длины исходного текста. Примеры текстов от четвертого до восьмого порядков приведены на с.106, 107. Тексты четвертого и пятого порядков представляются мне наиболее интересными. С одной стороны, большая часть последовательностей букв в этих текстах является реально существующими в языке словами и слияниями двух-трех слов, с другой - они несут отпечаток явной бессмыслицы.

Случайные тексты четвертого-восьмого порядков, созданные на основе отрывка из "Гамлета"

Случайные тексты четвертого-восьмого порядков, созданные на основе отрывное из рассказа У.Фолкнера "Два солдата"

Случайные тексты четвертого - восьмого порядков, созданные на основе начала "Европейцев" Г.Джеймса
Проза четвертого порядка, созданная "обезьяной Эддннгтона", ярко индивидуальна. В текстах легко выделяются поверхностные признаки стилевых черт авторов - шекспировские архаизмы или фолкнеровские южные диалектизмы с Миссисипи. Но и тексты без такой ярко выраженной стилевой индивидуальности легко идентифицируются. Не очень понятно, почему и каким образом это достигается. Порядок слов не сохраняется, а слова (кроме одно- и двухбуквенных слов) легко подвергаются изменениям. Тем не менее в текстах "прорывается" голос автора. Я не мог предположить, что стиль Генри Джеймса выдержит многократный перебор четырехбуквенных последовательностей.
В текстах пятого порядка явственно проступают особенности как лексики, так и содержания исходного текста, и возможность установления авторства больше не вызывает сомнений. Я думаю, что те, кто может узнать хорошо знакомого писателя по небольшому отрывку, без труда узнают его и в тексте пятого порядка, основанном на его произведениях.
Имеется еше один интересный аспект приближения текстов четвертого и пятого порядков к настоящей английской прозе. Он демонстрирует интересную особенность человека - его стремление находить смысл и сходство даже там, где их нет. Сходство внутренних структур подлинных произведений литературы и их рандомизированных версий сплошь и рядом зависит от стремления читателя интерпретировать то, что он видит, и не является признаком действительной корреляции между текстами. Напрашивается способ проверки этого наблюдения. Естественно, что компьютер не умеет читать между строк. Имея это в виду, я подверг обработке алгоритмами высшего порядка текст, написанный на Бейсике,- программу, которая сама уточняет алгоритмы. Результаты этой обработки, больше всего напоминающие испорченные программы (такие программы я когда-то писал сам), были подвергнуты беспристрастной проверке. Их запустили в программу, обрабатывающую команды на Бейсике (забавно, что программа называется ИНТЕРПРЕТЕР), чтобы посмотреть, как они будут работать. Проверка эта не так однозначна, как хотелось бы. Команды программы, приемлемые для обработки обычных текстов, могут оказаться невыполнимыми, так как в программе нет необходимых данных. Как бы то ни было, достаточное количество команд было осуществлено без сообщений ИНТЕРПРЕТЕРА об ошибках, только когда мы дошли до седьмого порядка.

Текст седьмого порядка - программа, написанная на Бейсике
ПОСЛЕ шестого и седьмого порядков случайный текст опять становится менее интересным прежде всего потому, что он становится менее случайным. Выше я показал, что при моделировании самого высшего возможного порядка будет порожден ровно один знак, и в его тождестве нет ничего неожиданного. На самом деле предсказуемость появляется на гораздо более низком уровне аппроксимации. В исходном тексте из 30000 знаков любая последовательность приблизительно из дюжины знаков с большой вероятностью будет единственной. И конечно, она не будет встречаться настолько часто, чтобы стать надежной основой для измерения статистических свойств текста. Мы получаем на выходе не случайный текст, а "обломки" исходного текста.
Я вижу единственную возможность избежать катастрофы: увеличить длину исходного текста. Длина текста изменяется экспоненциально при изменении порядка моделирования. Уже для пятого порядка необходимая длина составляет около 100000 знаков, т.е. значительно больше, чем число знаков в любом из образцов, приведенных выше, которые были мне доступны. При моделировании десятого порядка необходимо иметь исходный текст из десяти миллиардов знаков. На этом уровне вновь возникает проблема памяти и времени, необходимого, чтобы произвести полный поиск по всему тексту для каждой пробной строки. На самом деле имеется еще одно фундаментальное ограничение: продолжительность человеческой жизни. Даже самые плодовитые авторы не могут написать так много.
БИБЛИОГРАФИЯ
SCIENTIFIC AND ENGINEERING PROBLEMSOLVINC WITH THE COMPUTER. WILLIAM RALPH BENNETT, JR., Prentice-Hall, Inc., 1976.
HOW ARTIFICIAL IS INTELLIGENCE? W.R.BENNETT, JR., in AMERICAN SCIENTIST, Vol.65, No.6, pages 694-702; November-December, 1977.
ОТКЛИКИ
4 1984
МЫ ПОЛУЧИЛИ ряд откликов по поводу порождения случайной прозы, обсуждавшейся в январском номере. С удовольствием предоставляем их вашему вниманию. Один из описанных мною алгоритмов предназначался для поиска в тексте данной последовательности символов и построения затем таблицы частот символов, которые появлялись за данной последовательностью. Процедура повторялась с каждой буквой текста, полученного случайным образом. Несколько читателей предложили более эффективные процедуры.
В подходе, предложенном Ю.Дейхофф и С.Локом, используется структура данных, называемая кеш-таблица. Каждой последовательности символов в тексте приписывается численное значение, которое служит индексом элемента в таблице. Сам элемент представляет собой частоты символов, которые появляются за последовательностью с этим номером. Включать следует только реально существующие последовательности. Процедура должна быть очень быстрой, потому что кеш-таблица строится один раз и для обращения к ней требуется только вычислить индекс, не отыскивая все элементы.
Б.Брайан, Дж.Батлер, Р.Дил, У.Данлэп и Дж.Шермер указали еще на один алгоритм, который не только быстрее моего, но и значительно проще. В нем таблица частот вообще не требуется. Когда исследуется некий символ, который должен идти за данной последовательностью, в качестве исходной точки берем случайное положение в тексте н от этого места ищем образованную последовательность. Вместо того чтобы табулировать все вхождения таких последовательностей, поиск заканчивается, как только найдена первая; затем исследуется другая буква. Если распределение буквенных последовательностей практически равномерно, результаты должны быть близки к тем, которые дает таблица частот.
С.П.Капица, главный редактор журнала "В мире науки", обратил мое внимание на важный исторический факт. Появление некоторой буквы в тексте может рассматриваться как марковская иепь, названная так в честь создателя теории таких процессов известного русского математика А.А.Маркова (1856-1922гг.). Марков впервые рассмотрел подобные процессы в статье "Пример статистического исследования над текстом "Евгения Онегина", иллюстрирующий связь испытаний в цепь" (1913г.), сыгравшей основополагающую роль в области теории случайных процессов, которая теперь находит широкое применение как в физике, так и в математической лингвистике и теории информации.
ПРЕВРАЩЕНИЕ ХУДОЖЕСТВЕННОЙ ЛИТЕРАТУРЫ В ЧЕПУХУ
БРАЙАН ХЭЙЕС
ПРАКТИЧЕСКИ любая программа на выходе ЭВМ может дать бессмысленный результат, если ввести в нее бессодержательные данные ("что посеешь, то и пожнешь" - гласит широко известная пословица). Такая деятельность сейчас настолько распространена, что эксперимент другого рода вряд ли может привлечь внимание. Между тем не требуется особых усилий для того, чтобы создать программу, в которую вводится литературный шедевр, а она выдаст полнейшую чепуху: в машину вводится последний акт "Макбета", а на выходе получается неистовый бред идиота, лишенный всякого смысла. Тем не менее и это считается машинной обработкой данных (увы, произвести обратное преобразование почему-то гораздо сложнее).
Превращение литературы в тарабарщину происходит в два этапа. На первом этапе текст "прочитывается" программой и записываются полученные статистические характеристики. Эти характеристики определяют вероятность последовательностей букв или групп букв алфавита в исходном тексте. На втором этапе в соответствии с записанными вероятностями производится случайный выбор букв и создается новый текст, набор букв которого отражает статистические характеристики исходного текста, но лишен всякого смысла (появление в таком тексте смысла - чистая случайность).
Я не могу представить себе более непродуманного способа имитации. В программе нигде не отражена концепция слова и нет намека на представление о его семантической структуре. Не отражены также лингвистические структуры, более сложные, чем последовательность букв. Созданный текст представляет собой грубейшую имитацию авторского стиля, которая сохраняет только самые поверхностные черты исходного текста. Поражает при этом, что текст, полученный в результате такого примитивного упражнения, обладает иногда навязчивым сходством с оригиналом. Это тарабарщина, но тарабарщина чосеровского, или шекспировского, или джеймсовского толка. Иначе и быть не может. Если из текста изгнано семантическое содержание, гораздо заметнее становятся стилистические манеризмы. Возникает вопрос: насколько глубинными являются стилистические характеристики авторского текста и в чем состоит сложность их выявления?
ПРОЦЕСС порождения случайного прозаического текста был подробно исследован Уильямом Ральфом Беннетом-младшим из Йельского университета. Одной из основных тем в его курсе лекций о применениях компьютеров была лингвистическая статистика. Также подробно эта тема разработана в его учебнике по программированию "Scientific and Engineering Problem-solving with the Computer" ("Научное и инженерное решение задач с помощью компьютеров"). (Книга гораздо увлекательней, чем может показаться по названию. В ней, например, рассматриваются аэродинамические процессы, имевшие место при происходившем во время урагана футбольном матче Принстон-Дартмут в 1950г.; спектральный анализ звуков, издаваемых фаготом, гобоем или садовым шлангом).
Беннет сообщает, что самое раннее до сих пор известное упоминание о случайном порождении текста можно найти в опубликованном в 1690г. сочинении "Maxims and Discourses" Джона Тиллотсона, архиепископа Кентерберийского. Приводя примеры божественного творения, Тиллотсон пишет: "Сколько раз пришлось бы Человеку наполнять мешок буквами и высыпать их обратно на землю, прежде чем из этих букв случайно сложилась бы прекрасная Поэма или прозаический Трактат? И разве не может маленькая Книга быть создана игрою Случая, так же как и вся необъятная Вселенная?"
В современных рассуждениях о порождении случайного текста в качестве отправной точки можно использовать высказывание сэра Артура Эддингтона, сделанное в 1927г.: "Если бы целое стадо обезьян стало барабанить на пишущих машинках, то в принципе они МОГЛИ БЫ написать все книги, хранящиеся в Британском музее". Эддннгтон подчеркивал неосуществимость такого события. Это рассуждение он привел как пример теоретически возможного явления, которое, однако, никогда не произойдет в реальной жизни. Тем не менее со времени Эддингтона мысль о гении, который скрывается среди обезьян, бессмысленно барабанящих на машинке, зажила самостоятельной литературной жизнью. В связи с этим Беннет упоминает произведения Рассела Мэлони, Курта Воннегута-младшего и сценку в ночном клубе у Боба Ньюарта.
Процесс, о котором говорил Эллингтон, можно смоделировать с помощью программы. Я назову эту программу генератором текста нулевого порядка. Выбирается алфавит, или множество знаков, и в соответствии с ним на "обезьяньей" пишущей машинке устанавливается клавиатура. В некоторых моделях высшего порядка целесообразно сводить количество символов к минимуму: по-видимому, из соображений непротиворечивости имеет смысл остановиться на таком же количестве знаков и для генератора текста нулевого порядка. Я последовал рекомендациям Беннета и остановился на 28 знаках: 26 букв английского алфавита, интервал между словами (компьютер рассматривает его как любой другой знак) и апостроф, который встречается в письменном английском языке чаще, чем три-четыре наиболее редко употребляемые буквы.

Случайный текст нулевого порядка, основанный на алфавите из 28 знаков
Воображаемая идеальная обезьяна с одинаковой вероятностью может в любой момент напечатать любой знак. Такое поведение обезьяны моделируется с помощью очень простой стратегии. В множестве 28 знаков каждому символу приписывается определенное число от 0 до 27. В этом пределе для каждого порождаемого знака выбирается случайное число и печатается соответствующая ему буква. Образец небольшого текста, полученного с помощью такой процедуры, изображен на рисунке на этой странице. Текст этот не имеет сходства ни с письменным английским, ни с любым другим человеческим языком. "Слова" в нем непомерно длинны (в среднем по 27 знаков), и в них преобладают согласные. Причина этого - в неравномерности частот букв в английских текстах. На интервал между словами приходится примерно 1/5 всех знаков, а буквы J, Q, X и Z составляют меньше 1% текста. В тексте же нулевого порядка все буквы имеют одинаковую частотность, а именно 1/28.
У Боба Ньюарта комический эффект возникает, когда инспекторы, которым поручено разобраться в белиберде, напечатанной обезьянами на машинке, промучившись над нею не один час, вдруг натыкаются на фразу: "То be or not to be, that is the gesorenplatz..." ("Быть или не быть - вот в чем гесоренплатц...") В действительности это событие не осуществимо, так как порождение первых девяти слов из монолога Гамлета может произойти в тексте, состоящем из 2E46 букв. В тексте же из 50000 букв я нашел на большом расстоянии друг от друга один раз "ТО" и один раз "NOT". (Чтобы не читать все 50000 знаков подряд, я воспользовался подходящей программой).
СОВЕРШЕНСТВОВАНИЕ "литературной деятельности" обезьян надо начать с приведения вероятности выбора обезьяной того или иного знака в соответствие с действительной частотой употребления букв в письменном английском языке. Можно, например, изготовить пишущую машинку, в которой имеется на клавиатуре 2500 интервалов, 850 E, 700 T и т.д. Частоту употребления букв можно вычислить с помошью большой выборки из английской прозы, но мне кажется, что удобней и гораздо интересней обработать какой-нибудь литературный текст. Программа, которая выбирает знаки в соответствии с описанным выше распределением частот, является генератором текста первого порядка.
Частоту букв в тексте можно представить одномерным массивом, состоящим из 2S элементов и хранящимся в блоке памяти компьютера. Любой элемент массива между 0 и 27 может быть определен при помощи индекса. Для заполнения массива достаточно посчитать, сколько раз появляется каждая буква в тексте. Можно заполнить массив ручным способом, ко гораздо удобней воспользоваться компьютером, хотя в этом случае придется сначала подготовить текст для машинной обработки. Считающая программа приравнивает все элементы массива К нулю. Затем производится посимвольный просмотр текста, и при каждом появлении знака к соответствующему элементу массива прибавляется 1.
Случайный текст первого порядка порождается таким образом, что вероятность выбора буквы пропорциональна номеру элемента в массиве. Приведем один из вариантов порождения текста. В интервале между нулем и суммой элементов массива (равной общему количеству знаков в исходном тексте) порождается случайное число. Затем первый элемент массива, например частота буквы А, вычитается из случайного числа. Если результат неположителен, А печатается; в противном случае из величины, оставшейся после первого шага, вычитается следующий элемент (частота буквы В). Последовательные вычитания продолжаются до получения неположительного ответа и выбора соответствующего знака. Заметим, что процедура непременно приводит к выбору знака, так как случайное число не может превышать сумму элементов массива.
На с.104 на верхнем рисунке приведен образец случайного текста первого порядка. Он основан на массиве частот, составленном по тексту последней главы романа Дж.Джонса "Улисс", известной под названием "Итака" (или монолог Молли Блюм). У меня были основания для выбора именно этого отрывка: в случайном тексте отсутствует пунктуация, но это не имеет значения, так как ее нет и в исходном тексте.

Случайные тексты первого, второго и третьего порядков, созданные на основе монолога Молли Блюм
Информация о частоте букв, отраженная в случайном тексте первого порядка, заметно улучшает его, хотя и этот текст трудно признать "читабельным". Средняя длина слов (4.7 буквы) близка к ожидаемому значению (4.5 буквы), но отклонения отдельных слов от обычной для английского языка длины слишком велики и не отражают характерные для английского языка небольшие различия в длине слов. Внутренняя структура слов в тексте также не является "английской". Хотя частотность букв выдерживается, их последовательности совершенно случайны , поэтому "слова" не только не являются английскими, но и не могут ими быть. Такие последовательности букв, как WSTLNTTWNO или HIUOIMYTG, не только бессмысленны, но и невозможны. В случайном тексте, состоящем из 2000 букв, самым длинным узнаваемым словом оказалось слово RARE.
СЛЕДУЮЩИЙ шаг по усовершенствованию генератора текста представляется нам решающим, так как его, по крайней мере теоретически, можно распространить до достаточно высокого уровня. В основе идеи лежит зависимость появления букв в английском слове от предшествующих букв. Так, после V наиболее вероятно появление E; после Q может появиться только U. Для каждого символа из общего множества знаков создается отдельная таблица частот. Частоты записываются в виде двумерного массива из 28 строк и 28 столбцов, составляющих в сумме 784 элемента. Образец такой таблицы изображен на этой странице. (Таблица "нормируется" по строкам, следовательно, сравнение возможно только в пределах строки).

Таблица частот второго порядка для создания случайного текста на основе III акта "Гамлета"
Когда текст порождается при помощи двумерного массива, самый последний отобранный знак определяет, какую строку надо исследовать для выбора следующего знака. Например, если этим знаком является B, исследоваться будут только элементы второй строки. В этой строке наиболее часто встречается буква E, поэтому наиболее велика вероятность, что выбор падет именно на E. Могут быть отобраны также буквы A, I, L, O, R, S и U. Невозможные комбинации букв, такие, например, как BF и BQ, имеют нулевую частотность, поэтому они никогда не будут на выходе.
В случайном тексте второго порядка начинают появляться первые намеки на реально существующие в языке структуры. Диапазон распределения длин слов только немного больше, чем ему следовало бы быть. Встречаются настоящие английские и "почти настоящие" слова (например, SPPRING или THIMES). Часто появляются диграфы, такие, как ТН, и чередования гласных и согласных.
Следующий шаг совершенно очевиден. Алгоритм третьего порядка выбирает буквы в соответствии с вероятностями, определяемыми двумя предшествующими буквами. Это требует трехмерного массива, состоящего из 28 двумерных, каждый из которых в свою очередь состоит из 28 строк и 28 столбцов. Предположим, что при порождении текста была получена последовательность букв ТН. После этого программа должна обратиться к 20-й плоскости (соответствующей T) и к 8-й строке этой плоскости (соответствующей H). Наиболее вероятно, что в этой строке будет выбран знак E, хотя A, I, О и знак интервала тоже имеют ненулевые вероятности. Если будет выбран E, то дальнейший поиск надо вести в 5-й строке 8-й плоскости (позиция последовательности НЕ). Здесь наиболее вероятными знаками окажутся R и интервал между знаками.
В ПОРОЖДЕННОМ тексте третьего порядка последовательности из трех букв появляются только, если они имеются в исходном тексте. Включение интервалов между словами в расчет вероятностей гарантирует, что все однобуквенные слова действительно существуют в языке (на самом деле изолированно могут появиться только буквы I и А). Практически же все двух-буквенные слова и большинство трехбуквенных являются настоящими английскими словами, и, таким образом, работа программы значительно перекрывает "гарантии". Сплошь и рядом возникают длинные цепочки слов: PUT ТО SQUAD TRADE OFF GIN GO ME HER. Даже совсем длинные "не слова" имеют некоторое фонетическое правдоподобие. В конце концов то, что в английском языке сочетание букв ANYHORDANG HOUP TREAFTEN бессмысленно, представляется чистой случайностью.
Читая образец случайного текста третьего порядка, я вспомнил о различных случаях смешения действительно существующих в языке слов с бессмысленными слогами, например о возникновении глоссолалии в молитвах пятидесятников. Можно предположить, что сходство между случайными текстами третьего порядка и этими явлениями имеет какой-то смысл. И может быть, люди, которые обладают навыками такого смешения, подсознательно проделывают статистический анализ, сходный с работой программы. Другое объяснение представляется мне более правдоподобным: для явления смешения слов и слогов и для глоссолалии характерно появление в речи множества фонем - основных единнц устной речи. Возможно, что трехбуквенные сочетания наиболее удачно представляют фонему в письменной речи.
В текстах третьего порядка явственно проступают стилистические черты исходных текстов. Чем больше различается стиль исходных текстов, тем заметнее различия случайных текстов, хотя точно определить, в чем именно состоят эти различия, невозможно. Я думаю, что в основе лежат свойства внутренней структуры текста, хотя и не имею точного представления о том, что представляет собой внутренняя структура прозаического произведения. Может быть, это то, что остается от текста, когда нэ него удален весь смысл?
Даже если в случайном тексте третьего порядка не удается определить особенности стиля автора, язык исходного текста определяется безошибочно по характеру распределения гласных и согласных и по типичным для данного языка окончаниям слов. На нижнем рисунке на с.104 даны образны латинского (Вергилий), итальянского (Данте) и французского (Флобер) текстов. Тем, кто представляет себе только "внешний вил" языка, не так просто отличить "эрзац-текст" от подлинного текста.

Латинский (Вергилий), итальянский (Данте) и французский (Флобер) тексты третьего порядка
Прежде чем перейти к следующему этапу работы со случайным текстом третьего порядка, я хотел бы рассказать о некоторых возможностях использования таблиц частот букв. В одной из дискуссий об энтропии языка Беннет говорит, что с помощью этих таблиц можно оценивать количество информации, приходящейся в тексте на один знак. Количество информации приблизительно отражает трудность предсказания следующего знака в тексте. Она является наибольшей в тексте нулевого порядка, в котором любой знак имеет одинаковую вероятность; иными словами, количество информации оказывается наибольшим, когда текст абсолютно нечитабелен. Идею о предсказуемости знаков можно использовать при решении задач об исправлении ошибок в системах дальней связи для создания алгоритмов расшифровки шифров и криптограмм.
ИЗМЕНЕНИЯ массива частот с помощью различных действий являются еще одной областью, интересной для исследования. Например, какие изменения произойдут в случайном тексте, если каждый элемент массива возвести в квадрат? На нижнем рисунке на с.105 изображен обработанный таким способом монолог Молли Блюм. Такая процедура подчеркивает различия между элементами массива; соответственно изменяется распределение частот, и простые слова становятся еше проще. Возможен и ряд других преобразований. Увеличение всех элементов массива на одно и то же число действует разрушительно, даже если это число очень мало: все невозможные комбинации букв, для изгнания которых была проделана такая сложная работа, снова могут появиться в порожденном тексте.

Случайный текст, созданный на основе монолога Молли Блюм с помощью таблицы частот, каждый элемент которой возведен в квадрат
Увлекательной представляется идея умножить весь массив на -1 для того, чтобы породить текст, например, Александра антн-Попа: после любой последовательности букв в тексте "анти-Попа" появится буква, появление которой в тексте Попа наименее вероятно. Литературные достоинства этого текста можно оценить по заслугам, если в нем будет улавливаться сходство с сочинениями Кали Сибера. На самом деле получается беспорядочный набор знаков.
Не такой обескураживающий (хотя и очень далекий от вдохновляющего) результат получается, если сложить или перемножить два массива. Таким способом можно создать совместные работы писателей, сотрудничество которых в жизни немыслимо. Например, можно объединить Джейн Остин и Марка Твена или поэтов эпохи Китса (Байрон плюс Шелли). Но на самом деле мне хотелось бы получить нечто вроде "Байрон минус Шелли", "выжимку" различий между особенностями стиля обоих авторов. К сожалению. мне не удалось получить такие результаты. Большая часть информации в таблицах третьего порядка отражает лингвистические структуры, общие для всех писателей, пишущих на одном языке. После извлечения из таблиц этих общих элементов в них не остается почти ничего, кроме помех.
Есть н более серьезное соображение, объясняющее, почему вычитание из массива обречено на неудачу. Примерно 90% элементов в неизмененной таблице третьего порядка являются нулевыми и соответствуют большей части буквенных комбинаций, которые никогда не наблюдались в английском языке, например RJT или UUU. Обычно программа "не добирается" до этих элементов. Но после вычитания массив изменяется и попадание в строку, все элементы которой являются нулевыми, неизбежно. Я не вижу элегантного выхода из этого тупика.
СОЗДАНИЕ массива частот и порождение случайного текста не представляют особых трудностей. Настоящие трудности начинаются тогда, когда возникает потребность в большом объеме памяти, необходимом для хранения трехмерного массива модели третьего порядка. Мы ограничились набором из 28 знаков именно для того. чтобы свести размеры массива к минимуму. Даже при этом ограничении массив состоит почти из 22000 элементов и каждому элементу требуются по крайней мере два бита. Одной из самых сложных задач является помещение массива и необходимых программ в память небольшого компьютера.
На следующем этапе приближения каждая буква выбирается в соответствии с вероятностями, определяемыми тремя предшествующими буквами. Для этого нужен четырехмерный массив, включающий более 600000 элементов. В 1977г. Беннет опубликовал в журнале "American Scientist" статью, в которой привел образцы текста четвертого порядка, порожденного с помошью такого гигантского массива. Кроме того, в своем учебнике он писал по поводу моделирования текстов четвертого порядка, что "оно достигло предела реальных возможностей даже при условии доступности самых больших компьютеров". Что же касается исследователей, в распоряжении которых имеются только небольшие компьютеры, то они вообще не имеют возможности работать с текстами четвертого порядка.
Однако возникновение "практических ограничений" вызывает естественную реакцию - стремление их преодолеть. Если рассматривать эту проблему с другой точки зрения, то перспективы окажутся не такими безнадежными. Мы уже говорили, что в массиве третьего порядка большинство чисел являются нулями. Можно ожидать, что доля нулевых элементов в массиве четвертого порядка будет значительно больше. Мое предложение сводится к следующему: вместо того чтобы хранить в памяти компьютера огромный четырехмерный массив, я предлагаю заменить его маленькими одномерными массивами. Каждый такой массив эквивалентен одной строке четырехмерного массива. Строка состоит только из ненулевых элементов, и этим определяются ее размеры. Строки, состоящие только из нулевых элементов, вообще исключаются.
Я думаю, что этот план вполне осуществим, несмотря на его кажущуюся хаотичность. Размещенне в памяти более 10000 массивов, размер которых колеблется от 1 до 28 элементов,- занятие достаточно неприятное. Поэтому я постарался найти более простой путь. Оказывается, можно породить случайный текст достаточно высокого порядка с помощью множества знаков, включающего весь алфавит, а также любые другие знаки, которые способен воспроизводить компьютер. Плата за "удобство" этого метода заключается в том, что программа работает примерно в десять раз медленнее.
Все описанные выше примеры привели меня к размышлениям об альтернативах н предельных ограничениях при создании массивов. Предположим, что исходный текст, использующий алфавит из 28 букв, состоит из 10001 знака. Тогда порядок наибольшей возможной таблицы, описывающей структуру этого текста, будет 10000. Таблица имеет размерность 10000 и состоит из 28^10000 элементов, последнее число настолько огромное, что воображение отказывается его воспринимать. Кроме того, только один элемент иэ всего этого немыслимого массива является ненулевым. Его позицию в массиве уточняют первые 10000 знаков исходного текста, а значение - значение последнего знака в тексте. Даже если бы кто-нибудь мог создать такой массив (на самом деле Вселенная не настолько велика, чтобы вместить его), сама идея затратить так много усилий, для того чтобы иметь возможность опознать один-единственный знак, может вызвать только возмущение и раздражение.
ПРИ СОЗДАНИИ массивов более низких порядков ощущение диспропорции не вызывает таких бурных эмоций, хотя и не исчезает полностью. Дело в том, что вся информация, которая могла бы быть заложена в массив любых размеров, присутствует в исходном тексте в наиболее компактном виде. (Аргументировать это утверждение очень трудно, так как в нем имеются элементы тавтологии. То, что отражено в массиве частот, является частотой последовательностей знаков в тексте; эти и только эти последовательности имеются в исходном тексте, и именно они отражены в массиве частот).
При порождении случайного текста методом, подсказанным этими рассуждениями, происходит следующее. Создается отдельная таблица частот. Это небольшой одномерный массив, содержащий столько элементов, сколько их включено в текстовую выборку, Я остановился на 90 знаках. Весь исходный текст вносится в память компьютера и накапливается (в простейшем случае) в виде непрерывной "цепочки" знаков. После этого отбирается последовательность знаков, с которой начнется случайный текст. Назовем ее пробной строкой.
Ячейки в массиве частот заполняются путем поиска пробных строк по всему исходному тексту. Причем если пробной строкой является, например, "gain", то в процессе поиска будут идентифицированы не только собственно "gain", но и "gains", "again", "against", "bargain" и т.д. В некоторых языках программирования имеется специальная команда для такого поиска: в Бейсике она называется "1NSTR" (от англ. in string - в цепочке), а в языке С - "stcpm" (от англ. string pattern match - соответствующее цепочечной модели). Как только найдена пробная строка, из текста извлекается следующий знак, и массив частот увеличивается на 1. По окончании поиска по всему тексту массив оказывается заполненным.
Следующий шаг заключается в выборе случайного знака из массива частот. Процедура точно соответствует моделированию текста первого порядка; производится последовательное вычитание из случайного множества знаков, и печатается знак, соответствующий выбранному элементу массива. После этого вся процедура повторяется. Создается новая пробная строка, из которой удалена первая буква, а к концу добавлен только что порожденный знак. После того как весь исходный текст исследован таким образом, мы получаем новый массив частот.
Анализ исходного текста и создание массива частот требуют повторения процедуры для каждого порождаемого знака, поэтому программа работает очень медленно. Компенсацией является возможность писать прозаические тексты любого теоретически допустимого максимального порядка, т.е. тексты, которые будут короче длины исходного текста. Примеры текстов от четвертого до восьмого порядков приведены на с.106, 107. Тексты четвертого и пятого порядков представляются мне наиболее интересными. С одной стороны, большая часть последовательностей букв в этих текстах является реально существующими в языке словами и слияниями двух-трех слов, с другой - они несут отпечаток явной бессмыслицы.

Случайные тексты четвертого-восьмого порядков, созданные на основе отрывка из "Гамлета"

Случайные тексты четвертого-восьмого порядков, созданные на основе отрывное из рассказа У.Фолкнера "Два солдата"

Случайные тексты четвертого - восьмого порядков, созданные на основе начала "Европейцев" Г.Джеймса
Проза четвертого порядка, созданная "обезьяной Эддннгтона", ярко индивидуальна. В текстах легко выделяются поверхностные признаки стилевых черт авторов - шекспировские архаизмы или фолкнеровские южные диалектизмы с Миссисипи. Но и тексты без такой ярко выраженной стилевой индивидуальности легко идентифицируются. Не очень понятно, почему и каким образом это достигается. Порядок слов не сохраняется, а слова (кроме одно- и двухбуквенных слов) легко подвергаются изменениям. Тем не менее в текстах "прорывается" голос автора. Я не мог предположить, что стиль Генри Джеймса выдержит многократный перебор четырехбуквенных последовательностей.
В текстах пятого порядка явственно проступают особенности как лексики, так и содержания исходного текста, и возможность установления авторства больше не вызывает сомнений. Я думаю, что те, кто может узнать хорошо знакомого писателя по небольшому отрывку, без труда узнают его и в тексте пятого порядка, основанном на его произведениях.
Имеется еше один интересный аспект приближения текстов четвертого и пятого порядков к настоящей английской прозе. Он демонстрирует интересную особенность человека - его стремление находить смысл и сходство даже там, где их нет. Сходство внутренних структур подлинных произведений литературы и их рандомизированных версий сплошь и рядом зависит от стремления читателя интерпретировать то, что он видит, и не является признаком действительной корреляции между текстами. Напрашивается способ проверки этого наблюдения. Естественно, что компьютер не умеет читать между строк. Имея это в виду, я подверг обработке алгоритмами высшего порядка текст, написанный на Бейсике,- программу, которая сама уточняет алгоритмы. Результаты этой обработки, больше всего напоминающие испорченные программы (такие программы я когда-то писал сам), были подвергнуты беспристрастной проверке. Их запустили в программу, обрабатывающую команды на Бейсике (забавно, что программа называется ИНТЕРПРЕТЕР), чтобы посмотреть, как они будут работать. Проверка эта не так однозначна, как хотелось бы. Команды программы, приемлемые для обработки обычных текстов, могут оказаться невыполнимыми, так как в программе нет необходимых данных. Как бы то ни было, достаточное количество команд было осуществлено без сообщений ИНТЕРПРЕТЕРА об ошибках, только когда мы дошли до седьмого порядка.

Текст седьмого порядка - программа, написанная на Бейсике
ПОСЛЕ шестого и седьмого порядков случайный текст опять становится менее интересным прежде всего потому, что он становится менее случайным. Выше я показал, что при моделировании самого высшего возможного порядка будет порожден ровно один знак, и в его тождестве нет ничего неожиданного. На самом деле предсказуемость появляется на гораздо более низком уровне аппроксимации. В исходном тексте из 30000 знаков любая последовательность приблизительно из дюжины знаков с большой вероятностью будет единственной. И конечно, она не будет встречаться настолько часто, чтобы стать надежной основой для измерения статистических свойств текста. Мы получаем на выходе не случайный текст, а "обломки" исходного текста.
Я вижу единственную возможность избежать катастрофы: увеличить длину исходного текста. Длина текста изменяется экспоненциально при изменении порядка моделирования. Уже для пятого порядка необходимая длина составляет около 100000 знаков, т.е. значительно больше, чем число знаков в любом из образцов, приведенных выше, которые были мне доступны. При моделировании десятого порядка необходимо иметь исходный текст из десяти миллиардов знаков. На этом уровне вновь возникает проблема памяти и времени, необходимого, чтобы произвести полный поиск по всему тексту для каждой пробной строки. На самом деле имеется еще одно фундаментальное ограничение: продолжительность человеческой жизни. Даже самые плодовитые авторы не могут написать так много.
БИБЛИОГРАФИЯ
SCIENTIFIC AND ENGINEERING PROBLEMSOLVINC WITH THE COMPUTER. WILLIAM RALPH BENNETT, JR., Prentice-Hall, Inc., 1976.
HOW ARTIFICIAL IS INTELLIGENCE? W.R.BENNETT, JR., in AMERICAN SCIENTIST, Vol.65, No.6, pages 694-702; November-December, 1977.
ОТКЛИКИ
4 1984
МЫ ПОЛУЧИЛИ ряд откликов по поводу порождения случайной прозы, обсуждавшейся в январском номере. С удовольствием предоставляем их вашему вниманию. Один из описанных мною алгоритмов предназначался для поиска в тексте данной последовательности символов и построения затем таблицы частот символов, которые появлялись за данной последовательностью. Процедура повторялась с каждой буквой текста, полученного случайным образом. Несколько читателей предложили более эффективные процедуры.
В подходе, предложенном Ю.Дейхофф и С.Локом, используется структура данных, называемая кеш-таблица. Каждой последовательности символов в тексте приписывается численное значение, которое служит индексом элемента в таблице. Сам элемент представляет собой частоты символов, которые появляются за последовательностью с этим номером. Включать следует только реально существующие последовательности. Процедура должна быть очень быстрой, потому что кеш-таблица строится один раз и для обращения к ней требуется только вычислить индекс, не отыскивая все элементы.
Б.Брайан, Дж.Батлер, Р.Дил, У.Данлэп и Дж.Шермер указали еще на один алгоритм, который не только быстрее моего, но и значительно проще. В нем таблица частот вообще не требуется. Когда исследуется некий символ, который должен идти за данной последовательностью, в качестве исходной точки берем случайное положение в тексте н от этого места ищем образованную последовательность. Вместо того чтобы табулировать все вхождения таких последовательностей, поиск заканчивается, как только найдена первая; затем исследуется другая буква. Если распределение буквенных последовательностей практически равномерно, результаты должны быть близки к тем, которые дает таблица частот.
С.П.Капица, главный редактор журнала "В мире науки", обратил мое внимание на важный исторический факт. Появление некоторой буквы в тексте может рассматриваться как марковская иепь, названная так в честь создателя теории таких процессов известного русского математика А.А.Маркова (1856-1922гг.). Марков впервые рассмотрел подобные процессы в статье "Пример статистического исследования над текстом "Евгения Онегина", иллюстрирующий связь испытаний в цепь" (1913г.), сыгравшей основополагающую роль в области теории случайных процессов, которая теперь находит широкое применение как в физике, так и в математической лингвистике и теории информации.
Последний раз редактировалось: Gudleifr (Ср Ноя 20, 2019 4:01 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
2 1984
О КОНЕЧНОМ АВТОМАТЕ И ПРОСТЕЙШИХ МОДЕЛЯХ МЫШЕЛОВОК, РИБОСОМ И ЧЕЛОВЕЧЕСКОЙ ДУШИ
БРАЙАН ХЭЙЕС
У САМЫХ мощных вычислительных машин, которые пока существуют лишь в нашем воображении, нет ни аппаратуры, ни программного обеспечения. Известнейшая среди этих абстрактных машин была придумана английским математиком Тьюрингом в 1936г. Круг ее возможностей шире, чем у любого действующего компьютера на кремниевых кристаллах, и разумеется, она может вычислить все, что вообще поддается вычислению. Всем прочим умозрительным вычислительным машинам недостает всемогущества машины Тьюринга, но они не менее интересны. Их называют машинами с конечным числом состояний или конечными автоматами, и по их "возможностям" устанавливают минимальные технические требования к цифровой вычислительной машине.
Точное определение конечного автомата потребовало бы строгого математического изложения. Мы же в данном случае ограничиваемся рассмотрением нескольких конкретных примеров. Отправившись на поиски конечных автоматов, я нашел отличный образчик на Лексингтон-авеню в нью-йоркском метро. Это был турникет старого образца (а не распространенная ныне компактная стальная вертушка) в виде дубовой крестовины, до блеска отполированной людскими руками.
Турникет имеет два состояния: заблокирован и разблокирован. Предположим, что он заблокирован, так что крестовину нельзя повернуть. Опускание жетона в прорезь каким-то образом изменяет внутренний механизм, что позволяет турникету поворачиваться; другими словами, жетон вызывает переход в состояние "разблокирован". Поворот крестовины на 90o приводит к другому переходу, что возвращает турникет в состояние "заблокирован". Переходы схематически показаны на верхнем рисунке на с.99. Состояния системы представлены узлами (прямоугольниками), а переходы - дугами (стрелками) между ними.
НА ЯЗЫКЕ конечных автоматов опускание жетона и нажатие на поручень турникета - это возможные входы системы. Реакция автомата зависит и от входа, и от состояния в момент входа. Нажатие на поручень до того, как турникет получит жетон, не поможет вам попасть на станцию. Опускать жетон, когда турникет уже разблокирован, также бессмысленно, хотя по несколько иным причинам. Второй жетон будет принят, но это не отразится на состоянии автомата: пропускается один человек, а затем турникет снова блокируется. Три или четыре жетона подряд также будут приняты, но турникет пропустит только одного человека. Скептики потребовали бы больше данных, прежде чем сделать обобщение: все жетоны, опушенные после первого, не оказывают никакого действия. Но пусть они экспериментируют со своими жетонами.
Турникет не может пропустить нескольких человек за несколько опущенных подряд жетонов по той причине, что у него нет средства для подсчета полученных им жетонов. Он обладает единственным, довольно примитивным видом памяти: при изменении состояния "запоминается", был ли самый последний вход опусканием жетона или нажатием на поручень. Все более ранние входы теряются. Следует заметить, что от этой забывчивости городскому хозяйству нет никакого ущерба. Могло быть хуже: турникет можно было бы спроектировать так, чтобы он менял состояние после каждого опущенного жетона независимо от того, в каком состоянии он находится в данный момент; в этом случае два жетона подряд привели бы турникет в состояние "заблокирован".
Этот пример иллюстрирует большинство основных свойств конечного автомата. Автомат, очевидно, должен иметь некоторое число состояний, причем обязательно конечное. Должны быть входы и выходы, соответствующие любому состоянию. Состояния должны быть дискретными, или легко различимыми, а переходы между ними - действительно мгновенными. Здесь, разумеется, многое зависит от точки зрения: день и ночь - это дискретные состояния, если определить восход и заход как мгновенные процессы. Набор состояний, входы и выходы - вот и весь автомат; он может работать без вспомогательных устройств, и в частности без каких-либо средств хранения информации.
Правила построения конечного автомата допускают некоторые варианты. Существуют детерминированные и недетерминированные автоматы, автоматы Мура и автоматы Мили. В детерминированном автомате данный вход в данном состоянии неизменно приводит к одному и тому же результату; в недетерминированном автомате может быть несколько возможных переходов. В автомате Мура (по имени Э.Мура) каждому состоянию соответствует единственный выход. В автомате Мили (по имени Дж.Мили) выходы соответствуют переходам, а не состояниям. Оказывается, однако, что это многообразие структур - всего лишь иллюзия. Любая задача, выполнимая конечными автоматами одного рода, может быть также выполнена автоматами другого рода, хотя число необходимых состояний может меняться. Здесь я буду преимущественно рассматривать детерминированные автоматы Мура, которые обладают простейшей структурой.
СТОИТ пуститься на поиски конечных автоматов, как вы начнете находить их повсюду. Устройства, приводимые в действие монетой,- излюбленные примеры из учебников. Некоторые торговые автоматы не столь ненасытны, как турникет в метро: как только они получают нужное количество денег, они переходят в состояние, при котором все лишние монеты возвращаются. Устройство, приводимое в действие монетой и имеющее самое большое число состояний,- это, без сомнения, типичный лас-вегасский игорный автомат. В принципе он детерминирован, тем не менее при отыскании такого входа (монета и нажатие на рукоятку), который бы вызвал переход к желаемому заключительному состоянию, успех весьма сомнителен.
Многие бытовые приборы можно рассматривать как конечные автоматы, хотя и довольно "тупые". Стиральная машина проходит неизменную последовательность состояний - залив, стирка, полоскание, отжим,- и лишь несколько осмысленных входов, таких, как отключение машины от сети, приводит к одному и тому же результату при любом состоянии. Точно так же светофор имеет небольшой диапазон состояний, которые обычно повторяются. По-моему, самый скучный из всех конечных автоматов - электронные часы. Если они показывают месяц, число, часы, минуты и секунды, то имеют около 31млн. состояний. В течение года они находятся в каждом состоянии ровно один раз.
Мышеловка - тоже конечный автомат: мышь, к своему несчастью, вызывает переход от состояния с поднятой дверцей к состоянию с захлопнутой дверцей. Замок с шифром - конечный автомат со многими возможными входами, из которых только один приводит к переходу в другое состояние. Телефон имеет состояния, которые можно обозначить так: трубка на рычаге, трубка снята с рычага, сигнал "занято", сигнал "свободно", набор номера, звонок, соединение и неисправен. На примере автомобиля можно увидеть, что результат того или иного входа изменяется в зависимости от текущею состояния системы. Что происходит, если вы нажимаете на педаль акселератора? Это зависит от того, едет ли машина, включено ли сцепление, снята ли машина с ручного тормоза, включена ли передача - и на какой ход, передний или задний,- а также от того, открыта ли дверь гаража.
В живой клетке молекулярная система, состоящая из рибосомы и различных видов тРНК, действует как конечный автомат. Входами являются четыре нуклеотида мРНК, обозначенные сокращениями U, A, G и С. Выходами служат 20 аминокислот, из которых состоят белки. Цепочка нуклеотидов распознается как правильный вход для этого автомата, если только она состоит из начальной последовательности AUG. Затем автомат непрерывно считывает входную последовательность, каждый раз меняя состояние, когда распознается кодон, или триплет нуклеотидов. Три особо выделенных кодона UAA, UAG и UGA являются сигналами останова: когда встречается один из них, автомат останавливается. Весьма полезно представление и многих других биологических систем в виде конечных автоматов; первым, пожалуй, приходит на ум пример гемоглобина и бактериальных белков, являющихся активаторами или репрессорамн.
Даже "душа" в теологии Фомы Аквинского не что иное, как тщательно разработанный и полностью детерминированный конечный автомат. При сотворении она находится в состоянии осуждения за первородный грех. При крещении она переходит в состояние благодати, однако некоторые поступки (идолопоклонство, богохульство, прелюбодеяние и т.п.) вызывают переход в состояние греха. Тогда для возвращения души в состояние благодати необходимы исповедь, раскаяние и отпущение грехов. Результат самого последнего входа, смерти, очень сильно зависит от состояния души в этот момент: в состоянии благодати смерть приводит к спасению, а в состоянии греха - к осуждению на вечные муки. Механизм души, разумеется, гораздо сложнее, чем даваемое этим описанием представление о нем. При полном описании надо было бы различать степени греха (простительный и смертный, случайный и привычный) и ввести другие возможные состояния души (те, которые связаны с преддверием ада и чистилищем), а также другие возможные входы (например, Страшный суд).
В квантовой механике конечным автоматом становится даже атом и, следовательно, все, что состоит из атомов. Состояния атомов - это разрешенные уровни энергии, входами и выходами служат фотоны, или кванты электромагнитного излучения. Я думаю, что при точном описании атом был бы классифицирован как недетерминированный автомат Мили с эпсилон-переходами. Он недетерминированный, потому что результат входа нельзя точно предсказать. Это автомат Мили, потому что природа выхода (а именно энергия фотона) определена переходом, а не состоянием, в которое он перешел. (Эпсилон-переходами называются такие переходы, которые могут произойти в отсутствие какого бы то ни было входа; их следует включить в модель, поскольку атом может испустить фотон и изменить свое состояние спонтанно).
ЯВЛЯЕТСЯ ли мозг человека конечным автоматом? Дело в том, что современное изучение систем с конечным числом состояний началось с модели нейронной сети, введенной в 1943г. У.Мак-Каллоком и У.Питтсом. Нейроны Мак-Каллока и Питтса представляли собой простые клетки со входами "возбуждение" и "торможение"; у каждой клетки были единственный выход и два внутренних состояния: возбуждения и покоя. Клетки могли образовывать цепи, реализующие различные логические функции: в том числе "и", "или" и "нет", которые теперь являются самыми обычными функциями логической схемы в электронных системах. Эквивалентность идеализированной нейронной сети с диаграммой переходов того типа, который показан здесь, была установлена в 1956г. С.Клини из Висконсннского университета в Мадисоне.
И через сорок лет после появления работы Мак-Каллока и Питтса все еще обсуждается вопрос, можно ли с достаточным основанием квалифицировать мозг как систему с конечным числом состояний. Разумеется, число нейронов обязательно конечно, но дело не только в этом. Реальный нейрон гораздо сложнее клетки с двумя состояниями, и некоторые его свойства могут меняться непрерывно, а не ограничиваться дискретными состояниями. Кроме того, отсутствие возможности хранить дополнительную информацию для конечного автомата по меньшей мере неудобно. Если духовная жизнь не более чем последовательность мгновенных состояний без знания своей собственной истории, то что же такое память?
Эмоциональные состояния, являющиеся предметом обсуждения в психологии, такие, как скука, страх, тоска. экстаз и горе, по-видимому, более подвластны теории конечных автоматов. В то же время состояний так много, а переходы еще настолько не изучены и непонятны, что такая модель бесполезна. Только для низших животных возможно наметить нечто большее, нежели изолированные фрагменты диаграммы переходов, а человек в экспериментах с этими видами не получил прямого доступа к предполагаемым состояниям психики. Действительно, большая работа в этом направлении была проделана бихевиористами, которые отрицают само существование состояний психики.
Случай с цифровой вычислительной машиной (а здесь я имею в виду материальную машину, аппаратуру) также проблематичен. Распространенная умозрительная модель вычислительной машины, построенная Дж. фон Нейманом, делит машину на центральный процессор и массив ячеек памяти. Нет сомнения, что многие компоненты центрального процессора, такие, как регистры, сумматоры и механизмы управления, которые руководят внутренними операциями процессора, можно описать в терминах конечных автоматов.
Неприятности начинаются, когда дело доходит до памяти. По правилам построения конечного автомата внешняя память не допускается, и, таким образом, каждую ячейку надо рассматривать не как запоминающее устройство, отдельное от процессора, а как часть состояния всего автомата. Если все ячейки пусты, то компьютер находится в одном состоянии, если хотя бы одна заполнена, автомат перешел в другое состояние и т.д. Подобная концепция компьютера особенно бессмысленна, в частности, потому, что она не устанавливает связи между состоянием машины и тем, что она делает. Кроме того, число состояний огромно. Примитивный компьютер, способный запомнить информацию в 100 бит, не сможет, по-видимому, пройти через все свои состояния, даже если будет постоянно работать на протяжении существования Вселенной.
ПЕРВОСТЕПЕННАЯ роль конечного автомата в теории вычислительных машин заключается в более высоком уровне абстракции, чем у обычного механизма аппаратуры. Вычислительная машина, работающая под руководством программы, это уже не нагромождение логических схем, регистров, ячеек памяти и других атрибутов электроники: это "виртуальная" машина, рабочие части которой определены программой и, если надо, могут быть определены заново. В то время как аппаратура знает лишь двоичные числа и простые команды для их перемещения и действий над ними, виртуальная вычислительная машина имеет дело с более выразительной символьной системой: словами, уравнениями, массивами, функциями, векторами, кодонами, списками, образами, быть может, даже с идеями. Теория конечных автоматов ценна при создании виртуальных машин, и иногда виртуальная машина сама оказывается конечным автоматом.
Рассмотрим программу, цель которой - считывание последовательности двоичных разрядов (единиц и нулей) и выдача сообщения о том, четным или нечетным получилось число единиц. (Эта работа не лишена практической пользы: например, такие программы проверки на четность используются для обнаружения ошибок при передаче двоичных данных по телефону). Программа может быть построена как конечный автомат с двумя состояниями, как показано на нижнем рисунке на с.99. Операция начинается в четном состоянии, так как первоначально не получено ни одной единицы, а нуль считается четным числом. Каждая единица во входной последовательности приводит к изменению состояния, в то время как получение нуля в любом состоянии не изменяет его. Хотя машина не может "запомнить" никакого входа, кроме самого последнего, и, разумеется, не может считать единицы и нули, ее выход всегда отражает четность входной последовательности.
Автомат для проверки на четность
Модель вычисления с конечным числом состояний очень часто встречается в программах, так или иначе связанных с текстом или другой информацией, которая принимает лингвистическую форму. Замечательным примером служат компиляторы: программы, транслирующие операторы программы на входном языке в эквивалентные операторы на выходном языке, чаше называемом "машинным языком" данного компьютера. Компиляторы и другие программы - трансляторы - основные понятия, связанные с виртуальными машинами. Они являются посредниками между символами, имеющими смысл для человека, и символами, распознаваемыми вычислительной машиной.
Часть компилятора, которую можно представить как конечный автомат, называется сканером или лексическим анализатором. Подобно турникету метро, он тоже "пожирает жетоны". Но в этом случае, однако, в качестве "жетонов" выступают слова, или основные лексические единицы языка. Лексический анализатор распознает каждую группу символов и определяет, является ли она настоящим "жетоном", таким, как команда или число: если нет, то лексический анализатор отбрасывает ее как бессмыслицу, подобно турникету, не принимающему фальшивый жетон.
Операцию, производимую лексическим анализатором, можно проиллюстрировать с помощью конечного автомата, предназначенного для распознавания "жетонов" простого языка, пусть и с весьма ограниченными выразительными средствами: "жетоны" образованы исключительно из римских цифр. На самом деле допускаются только числа специального вида: они получаются путем сложения, так что 9 записывается как VIIII, а не IX. (Имеются свидетельства, что сами римляне пользовались именно такой записью; представление при помощи вычитания ¦ является, по-видимому, более поздним германским новшеством).
Диаграмма переходов для автомата, обрабатывающего числа, записанные римскими цифрами, показана справа. Ее входной алфавит состоит из литер M, D, C, L, X, V и I, а также символов пробела, или просто пробелов. Любой первоначальный пробел попросту игнорируется, но, как только получена первая литера, программа немедленно переходит в состояние, идентифицируемое (для удобства) названием литеры. Если первая литера есть M, то за ней может следовать любая литера из алфавита, включая другую литеру M. Если следующая литера D, то ситуация несколько меняется. Из состояния D не определен переход обратно в состояние M, потому что любая последовательность символов, которая содержит DM, не может быть правильно составленным "жетоном": такое число нельзя образовать из римских цифр путем сложения. Кроме того, невозможен переход из состояния D в состояние D, так что DD тоже исключенная последовательность. Причина здесь в том, что для "половинок" D, L и V в римской нумерации повторения не допускаются.
В состоянии D признаются только литеры C, L, X, V и I, имеющие значение, меньшее D. Та же самая последовательность допустима в состоянии C (поскольку C может повторяться), а в состоянии L признаются лишь литеры X, V и I. Правило, согласно которому происходят переходы, вам уже, наверное, понятно. Состояния упорядочены в иерархию, и, как только достигается данный уровень, автомат больше не может вернуться к более высокому уровню; на уровне "половинок" он даже не может остаться. К тому времени, как достигается состояние I, допускается лишь повторный символ 1 либо пробел. Пробел, поступивший в этот момент либо в любой другой момент после появления первой литеры, указывает на конец "жетона" и переводит автомат обратно в начальное состояние, когда он готов получить следующее число.

Лексический анализатор для языка, состоящего из римских цифр
Ни один из известных мне языков программирования не допускает ввод чисел, записанных римскими цифрами, но фактически все такие языки имеют средства обращения с числами, записанными арабскими цифрами. Методы распознавания аналогичны, но имеется большее разнообразие форматов. Простые целые числа, например 137, могут обрабатываться в принципе автоматом с одним состоянием, но числа, состоящие из нескольких частей, такие, как +6.625E-27, требуют более сложного лексического анализа.
Систему рибосом и тРНК можно рассматривать как лексический анализатор, который распознает биологически осмысленные последовательности нуклеотидов в молекуле мРНК. Для того чтобы последовательность была принята, она должна начинаться с инициирующего кодона и заканчиваться одним из трех терминирующих кодонов; между этими границами допускается любая комбинация входных символов U, A, G и С.
Конечный автомат расшифровывает генетический код
(Аминокислоты: Phe, Ser, Tyr, Cys, Trp, Leu, Pro, His, Gln, Arg, Ile, Met, Thr, Asn, Lys, Val, Ala, Asp, Glu, Gly).
Лексический анализ - это первый шаг в процессе компиляции. После лексического анализатора вступают компоненты компилятора, носящие названия "программа грамматического разбора" и "генератор кода". В качестве входной последовательности программа грамматического разбора берет "жетоны", распознанные лексическим анализатором, и анализирует их синтаксические отношения; на этом этапе происходит более глубокое понимание компилятором смысла операторов программы, которые он транслирует. Программу, которая выполняет функции, определенные разобранными операторами, генератор кода пишет на объектном языке.
В рассмотренных здесь игрушечных языках задачи программы грамматического разбора н генератора кода тривиальны. Транслированная форма оператора на языке, использующем римские цифры, может оказаться просто эквивалентом этого числа, записанного арабскими цифрами. Ее можно было бы генерировать, следуя такой стратегии. Перед лексическим анализом "жетона" отводится ячейка памяти и туда засылается нуль. Затем каждый раз, когда лексический анализатор входит в состояние М, к содержимому ячейки прибавляется 1000; для состояния D прибавляется 500 и т.д. Когда лексический анализ закончен, в этой ячейке содержится число, записанное римскими цифрами. Заметим, что этот игрушечный компилятор уже не будет конечным автоматом, поскольку у него есть вспомогательная память.
Компилятор для генетического кода лаже проще и полностью может быть построен в рамках конечного автомата. Транслируемая "программа" является последовательностью стандартных трехбуквенных символов для аминокислот; символы могут быть генерированы как выходная последовательность состояний лексического анализатора, распознающего колоны. Три состояния, соответствующие трем терминирующим кодонам, не имеют выходной последовательности.
Создание настоящего компилятора для достаточно широкого языка, который имел бы практическую пользу, не слишком простое дело, но лежащая в основе его структура конечного автомата может по крайней мере помочь найти принцип организации. Если синтаксис языка определен достаточно точно, то часть работы даже можно автоматизировать: выполнить при помощи программы-компилятора нашего компилятора. Входной последовательностью для нее служит формальное описание языка, а выходной последовательностью - другая программа, которая транслирует операторы на этом языке. Насколько мне известно, еще не написан компилятор компилятора компилятора.
РАСПОЗНАВАНИЕ "жетонов" лексическим анализатором уже само по себе в некотором роде грамматический разбор, а множество всех возможных последовательностей символов "жетона" является своего рода языком. В сущности, это бесконечный язык: если только не наложено какое-нибудь искусственное ограничение на длину индивидуальной последовательности, можно образовать бесконечное множество распознаваемых "жетонов". Как может автомат, имеющий лишь конечное число частей, распознавать бесконечные последовательности правильно составленных операторов и отбрасывать бесконечное число неправильных? Разгадка заключена в самой структуре языка. Если операторы бесконечного языка должны распознаваться конечным автоматом, они должны быть образованы по строгим правилам.
Эти правила были сформулированы в 1956г. С.Клини; они определяют класс языков, названных регулярными языками или регулярными множествами. Клини доказал, что конечный автомат может распознавать язык только тогда, когда этот язык регулярен, и, кроме того, что каждый регулярный язык может быть распознан некоторым конечным автоматом: в конце концов можно построить автомат, в котором имеется состояние для каждого возможного выражения языка. Далее, если язык бесконечен; должен быть возможен грамматический разбор всех операторов посредством прочитывания одного символа слева направо, либо начиная с конца (при этом не допускается ни забегания вперед ни возвращения назад). Если допустимость какого-либо символа обусловлена присутствием другого символа, то обусловливающий символ должен находиться непосредственно слева.
Второе правило является немедленным следствием ограничений конечного автомата, который не может ни предвидеть свои будущие состояния, ни сохранить память о прошлых состояниях; он должен выбрать переход на основе только текущего состояния и текущего входного символа. Именно по этой причине конечный автомат не может обрабатывать числа, образованные римскими цифрами при помощи вычитания. Если записано выражение XI и автомат интерпретирует его как 11, он не может вернуться назад и пересмотреть значение, если следующая литера оказывается V. Многие другие функции управляются с помощью такого ограничения. Например, невозможно построить конечный автомат, который читал бы последовательность двоичных разрядов и определял бы, равно ли число единиц числу нулей. Аналогично, хотя конечный автомат может складывать двоичные числа, он не может их перемножать; я предоставляю читателю догадаться, почему.
ЗА ПРЕДЕЛЫ конечных автоматов и регулярных языков простирается иерархия более мощных машин и более общих языков. Она называется иерархией Хомского, по имени лингвиста Н.Хомского, который исследовал различные формальные языки как возможные модели естественных языков. Наиболее общие языки были созданы при помощи смягчения ограничения на грамматические правила регулярных множеств; автоматы же были построены добавлением к исходной модели конечного автомата элементов памяти.
Следующий автомат в этом ряду называется автоматом с магазинной памятью. Он состоит из конечного автомата с добавлением массива памяти, которая имеет бесконечную емкость, но причудливую организацию. Эта память принимает форму стека, подобного стопке подносов в кафетерии. Для занесения единицы информации в память она должна быть помещена на вершину стека; восстановлена она будет не раньше, чем будут удалены все расположенные сверху единицы. Таким образом, последний из поступивших уходит первым.
Язык, распознаваемый автоматом с магазинной памятью, называется контекстно-свободным языком. При разборе его операторов допустимость символа может зависеть и от символа, стоящего непосредственно слева, и от символа, стоящего непосредственно справа. Эта двусторонняя зависимость разрешается, потому что каждый символ, допустимость которого нельзя немедленно установить, может быть сохранен в стеке, пока не будет разрешена неясность. Следовательно, автомат с магазинной памятью может оперировать с числами, записанными римскими цифрами и образованными при помощи вычитания, и он может распознавать выражения с одинаковым числом единиц и нулей (или иных символов, таких, как правые и левые скобки). С другой стороны, он не может обнаруживать предложения с равным числом символов трех видов, таких, например, как 0, 1, 2. Большинство языков программирования контекстно-свободные, а программа разбора компилятора обычно представляет собой автомат с магазинной памятью. Многие компьютеры имеют аппаратные средства для организации части памяти в виде стека. Язык программирования Forth за основную структуру памяти принимает структуру стека. Разумеется, стек в любой реальной машине не может иметь бесконечную глубину.
Контекстно-свободные языки оправдывают свое название, поскольку на распознавание любого символа могут прямо повлиять только его два ближайших соседа, а не более широкий контекст, в котором он находится. Снятие этого ограничения порождает контекстно-зависимые языки и еще больше увеличивает сложность интерпретации. Теперь далеко отстоящие друг от друга символы могут взаимодействовать; в самом худшем случае первый символ выражения нельзя интерпретировать, пока не будет прочитан последний. В обмен на дополнительную сложность получаем несколько большие возможности. Автомат, основанный на контекстно-зависимых языках, может определять, содержится ли в выражении одинаковое число символов трех видов.
Автомат, который может распознавать контекстно-зависимый язык, является линейно-ограниченным автоматом. В дополнение к обычному устройству конечного автомата он имеет память, организованную так, что любая ячейка памяти доступна в любой момент; это автомат со случайным доступом. Емкость памяти конечна, но предполагается, что она достаточно велика, чтобы вместить любую входную последовательность, которая поступает в автомат. Линейно-ограниченные автоматы, по-видимому, дают хорошее приближение к модели цифровой вычислительной машины фон Неймана. Но, как ни странно, соответствующие контекстно-зависимые языки программирования, по-видимому, мало распространены; очевидно, более простая контекстно-свободная структура почти всегда позволяет добиться желаемой выразительности.
Все описанные выше языки имеют одно общее свойство: говорят, что они рекурсивны. Для нас это означает, что можно вообразить процедуру порождения всех возможных "способов выражения" в языке в порядке возрастания длины. Отсюда следует, что существует гарантированный метод установления того факта, принадлежит ли данному языку данный оператор конечной длины,- для этого просто надо породить все операторы вплоть до данной длины и сравнить их.
Имеются языки, которые не удовлетворяют лаже этим простейшим стандартам обрабатываемости. Для них существует лишь один возможный распознающий автомат, "последнее средство",- машина Тьюринга, конечный автомат со свободным доступом в бесконечную память. В описании, данном Тьюрингом, память представлена в виде бесконечной в обоих направлениях ленты, разделенной на клетки, в которые конечный автомат может записывать, считывать с них или стирать записанное.
Теперь с высот машины Тьюринга четче вырисовывается взаимосвязь вычислительных устройств более низких уровней. Линейно-ограниченный автомат - это просто машина Тьюринга с конечной лентой. Автомат с магазинной памятью имеет ленту, не ограниченную в одном направлении, но "головка" для чтения и записи на ленте всегда остается фиксированной над последней непустой клеткой. Конечный автомат - это машина Тьюринга вовсе без ленты.

Иерархия Хомского конечных и бесконечных автоматов
Читателям, падким на все новое и желающим заняться грамматическим разбором нерекурсивных языков, пора спешить приобрести машину Тьюринга. Следует только предупредить их, что этот чудо-компьютер имеет свои слабые стороны. Существуют языки с такими нелепыми грамматиками, что даже машина Тьюринга не сможет распознать их операторы за конечный отрезок времени. Пока такие языки нашли весьма ограниченное применение в мире вычислительных машин, но люди как-то ухитряются на них говорить.
БИБЛИОГРАФИЯ
COMPUTATION: FINITE AND INFINITE MACHINES. MARVIN L.MINSKY. Prentice-Hall, Inc., 1967.
MATHEMATICAL STRUCTURES FOR COMPUTER SCIENCE. JUDITH L.GERSTING. W.H.Freeman and Company, 1967.
ALGORITHMS + DATA STRUCTURES = PROGRAMS. NIKLAUS WIRTH. Prentice-Hall, Inc., 1976.
INTRODUCTION TO AUTOMATA THEORY, LANGUAGES, AND COMPUTATION, JOHN E.HOPCROFT AND JEFFREY D.ULLMAN. Addison-Wesley Publishing Company, 1979.
Вот тут, как раз, и пригодится упомянутый выше сб. АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.- G.
О КОНЕЧНОМ АВТОМАТЕ И ПРОСТЕЙШИХ МОДЕЛЯХ МЫШЕЛОВОК, РИБОСОМ И ЧЕЛОВЕЧЕСКОЙ ДУШИ
БРАЙАН ХЭЙЕС
У САМЫХ мощных вычислительных машин, которые пока существуют лишь в нашем воображении, нет ни аппаратуры, ни программного обеспечения. Известнейшая среди этих абстрактных машин была придумана английским математиком Тьюрингом в 1936г. Круг ее возможностей шире, чем у любого действующего компьютера на кремниевых кристаллах, и разумеется, она может вычислить все, что вообще поддается вычислению. Всем прочим умозрительным вычислительным машинам недостает всемогущества машины Тьюринга, но они не менее интересны. Их называют машинами с конечным числом состояний или конечными автоматами, и по их "возможностям" устанавливают минимальные технические требования к цифровой вычислительной машине.
Точное определение конечного автомата потребовало бы строгого математического изложения. Мы же в данном случае ограничиваемся рассмотрением нескольких конкретных примеров. Отправившись на поиски конечных автоматов, я нашел отличный образчик на Лексингтон-авеню в нью-йоркском метро. Это был турникет старого образца (а не распространенная ныне компактная стальная вертушка) в виде дубовой крестовины, до блеска отполированной людскими руками.
Турникет имеет два состояния: заблокирован и разблокирован. Предположим, что он заблокирован, так что крестовину нельзя повернуть. Опускание жетона в прорезь каким-то образом изменяет внутренний механизм, что позволяет турникету поворачиваться; другими словами, жетон вызывает переход в состояние "разблокирован". Поворот крестовины на 90o приводит к другому переходу, что возвращает турникет в состояние "заблокирован". Переходы схематически показаны на верхнем рисунке на с.99. Состояния системы представлены узлами (прямоугольниками), а переходы - дугами (стрелками) между ними.

НА ЯЗЫКЕ конечных автоматов опускание жетона и нажатие на поручень турникета - это возможные входы системы. Реакция автомата зависит и от входа, и от состояния в момент входа. Нажатие на поручень до того, как турникет получит жетон, не поможет вам попасть на станцию. Опускать жетон, когда турникет уже разблокирован, также бессмысленно, хотя по несколько иным причинам. Второй жетон будет принят, но это не отразится на состоянии автомата: пропускается один человек, а затем турникет снова блокируется. Три или четыре жетона подряд также будут приняты, но турникет пропустит только одного человека. Скептики потребовали бы больше данных, прежде чем сделать обобщение: все жетоны, опушенные после первого, не оказывают никакого действия. Но пусть они экспериментируют со своими жетонами.
Турникет не может пропустить нескольких человек за несколько опущенных подряд жетонов по той причине, что у него нет средства для подсчета полученных им жетонов. Он обладает единственным, довольно примитивным видом памяти: при изменении состояния "запоминается", был ли самый последний вход опусканием жетона или нажатием на поручень. Все более ранние входы теряются. Следует заметить, что от этой забывчивости городскому хозяйству нет никакого ущерба. Могло быть хуже: турникет можно было бы спроектировать так, чтобы он менял состояние после каждого опущенного жетона независимо от того, в каком состоянии он находится в данный момент; в этом случае два жетона подряд привели бы турникет в состояние "заблокирован".
Этот пример иллюстрирует большинство основных свойств конечного автомата. Автомат, очевидно, должен иметь некоторое число состояний, причем обязательно конечное. Должны быть входы и выходы, соответствующие любому состоянию. Состояния должны быть дискретными, или легко различимыми, а переходы между ними - действительно мгновенными. Здесь, разумеется, многое зависит от точки зрения: день и ночь - это дискретные состояния, если определить восход и заход как мгновенные процессы. Набор состояний, входы и выходы - вот и весь автомат; он может работать без вспомогательных устройств, и в частности без каких-либо средств хранения информации.
Правила построения конечного автомата допускают некоторые варианты. Существуют детерминированные и недетерминированные автоматы, автоматы Мура и автоматы Мили. В детерминированном автомате данный вход в данном состоянии неизменно приводит к одному и тому же результату; в недетерминированном автомате может быть несколько возможных переходов. В автомате Мура (по имени Э.Мура) каждому состоянию соответствует единственный выход. В автомате Мили (по имени Дж.Мили) выходы соответствуют переходам, а не состояниям. Оказывается, однако, что это многообразие структур - всего лишь иллюзия. Любая задача, выполнимая конечными автоматами одного рода, может быть также выполнена автоматами другого рода, хотя число необходимых состояний может меняться. Здесь я буду преимущественно рассматривать детерминированные автоматы Мура, которые обладают простейшей структурой.
СТОИТ пуститься на поиски конечных автоматов, как вы начнете находить их повсюду. Устройства, приводимые в действие монетой,- излюбленные примеры из учебников. Некоторые торговые автоматы не столь ненасытны, как турникет в метро: как только они получают нужное количество денег, они переходят в состояние, при котором все лишние монеты возвращаются. Устройство, приводимое в действие монетой и имеющее самое большое число состояний,- это, без сомнения, типичный лас-вегасский игорный автомат. В принципе он детерминирован, тем не менее при отыскании такого входа (монета и нажатие на рукоятку), который бы вызвал переход к желаемому заключительному состоянию, успех весьма сомнителен.
Многие бытовые приборы можно рассматривать как конечные автоматы, хотя и довольно "тупые". Стиральная машина проходит неизменную последовательность состояний - залив, стирка, полоскание, отжим,- и лишь несколько осмысленных входов, таких, как отключение машины от сети, приводит к одному и тому же результату при любом состоянии. Точно так же светофор имеет небольшой диапазон состояний, которые обычно повторяются. По-моему, самый скучный из всех конечных автоматов - электронные часы. Если они показывают месяц, число, часы, минуты и секунды, то имеют около 31млн. состояний. В течение года они находятся в каждом состоянии ровно один раз.
Мышеловка - тоже конечный автомат: мышь, к своему несчастью, вызывает переход от состояния с поднятой дверцей к состоянию с захлопнутой дверцей. Замок с шифром - конечный автомат со многими возможными входами, из которых только один приводит к переходу в другое состояние. Телефон имеет состояния, которые можно обозначить так: трубка на рычаге, трубка снята с рычага, сигнал "занято", сигнал "свободно", набор номера, звонок, соединение и неисправен. На примере автомобиля можно увидеть, что результат того или иного входа изменяется в зависимости от текущею состояния системы. Что происходит, если вы нажимаете на педаль акселератора? Это зависит от того, едет ли машина, включено ли сцепление, снята ли машина с ручного тормоза, включена ли передача - и на какой ход, передний или задний,- а также от того, открыта ли дверь гаража.
В живой клетке молекулярная система, состоящая из рибосомы и различных видов тРНК, действует как конечный автомат. Входами являются четыре нуклеотида мРНК, обозначенные сокращениями U, A, G и С. Выходами служат 20 аминокислот, из которых состоят белки. Цепочка нуклеотидов распознается как правильный вход для этого автомата, если только она состоит из начальной последовательности AUG. Затем автомат непрерывно считывает входную последовательность, каждый раз меняя состояние, когда распознается кодон, или триплет нуклеотидов. Три особо выделенных кодона UAA, UAG и UGA являются сигналами останова: когда встречается один из них, автомат останавливается. Весьма полезно представление и многих других биологических систем в виде конечных автоматов; первым, пожалуй, приходит на ум пример гемоглобина и бактериальных белков, являющихся активаторами или репрессорамн.
Даже "душа" в теологии Фомы Аквинского не что иное, как тщательно разработанный и полностью детерминированный конечный автомат. При сотворении она находится в состоянии осуждения за первородный грех. При крещении она переходит в состояние благодати, однако некоторые поступки (идолопоклонство, богохульство, прелюбодеяние и т.п.) вызывают переход в состояние греха. Тогда для возвращения души в состояние благодати необходимы исповедь, раскаяние и отпущение грехов. Результат самого последнего входа, смерти, очень сильно зависит от состояния души в этот момент: в состоянии благодати смерть приводит к спасению, а в состоянии греха - к осуждению на вечные муки. Механизм души, разумеется, гораздо сложнее, чем даваемое этим описанием представление о нем. При полном описании надо было бы различать степени греха (простительный и смертный, случайный и привычный) и ввести другие возможные состояния души (те, которые связаны с преддверием ада и чистилищем), а также другие возможные входы (например, Страшный суд).
В квантовой механике конечным автоматом становится даже атом и, следовательно, все, что состоит из атомов. Состояния атомов - это разрешенные уровни энергии, входами и выходами служат фотоны, или кванты электромагнитного излучения. Я думаю, что при точном описании атом был бы классифицирован как недетерминированный автомат Мили с эпсилон-переходами. Он недетерминированный, потому что результат входа нельзя точно предсказать. Это автомат Мили, потому что природа выхода (а именно энергия фотона) определена переходом, а не состоянием, в которое он перешел. (Эпсилон-переходами называются такие переходы, которые могут произойти в отсутствие какого бы то ни было входа; их следует включить в модель, поскольку атом может испустить фотон и изменить свое состояние спонтанно).
ЯВЛЯЕТСЯ ли мозг человека конечным автоматом? Дело в том, что современное изучение систем с конечным числом состояний началось с модели нейронной сети, введенной в 1943г. У.Мак-Каллоком и У.Питтсом. Нейроны Мак-Каллока и Питтса представляли собой простые клетки со входами "возбуждение" и "торможение"; у каждой клетки были единственный выход и два внутренних состояния: возбуждения и покоя. Клетки могли образовывать цепи, реализующие различные логические функции: в том числе "и", "или" и "нет", которые теперь являются самыми обычными функциями логической схемы в электронных системах. Эквивалентность идеализированной нейронной сети с диаграммой переходов того типа, который показан здесь, была установлена в 1956г. С.Клини из Висконсннского университета в Мадисоне.
И через сорок лет после появления работы Мак-Каллока и Питтса все еще обсуждается вопрос, можно ли с достаточным основанием квалифицировать мозг как систему с конечным числом состояний. Разумеется, число нейронов обязательно конечно, но дело не только в этом. Реальный нейрон гораздо сложнее клетки с двумя состояниями, и некоторые его свойства могут меняться непрерывно, а не ограничиваться дискретными состояниями. Кроме того, отсутствие возможности хранить дополнительную информацию для конечного автомата по меньшей мере неудобно. Если духовная жизнь не более чем последовательность мгновенных состояний без знания своей собственной истории, то что же такое память?
Эмоциональные состояния, являющиеся предметом обсуждения в психологии, такие, как скука, страх, тоска. экстаз и горе, по-видимому, более подвластны теории конечных автоматов. В то же время состояний так много, а переходы еще настолько не изучены и непонятны, что такая модель бесполезна. Только для низших животных возможно наметить нечто большее, нежели изолированные фрагменты диаграммы переходов, а человек в экспериментах с этими видами не получил прямого доступа к предполагаемым состояниям психики. Действительно, большая работа в этом направлении была проделана бихевиористами, которые отрицают само существование состояний психики.
Случай с цифровой вычислительной машиной (а здесь я имею в виду материальную машину, аппаратуру) также проблематичен. Распространенная умозрительная модель вычислительной машины, построенная Дж. фон Нейманом, делит машину на центральный процессор и массив ячеек памяти. Нет сомнения, что многие компоненты центрального процессора, такие, как регистры, сумматоры и механизмы управления, которые руководят внутренними операциями процессора, можно описать в терминах конечных автоматов.
Неприятности начинаются, когда дело доходит до памяти. По правилам построения конечного автомата внешняя память не допускается, и, таким образом, каждую ячейку надо рассматривать не как запоминающее устройство, отдельное от процессора, а как часть состояния всего автомата. Если все ячейки пусты, то компьютер находится в одном состоянии, если хотя бы одна заполнена, автомат перешел в другое состояние и т.д. Подобная концепция компьютера особенно бессмысленна, в частности, потому, что она не устанавливает связи между состоянием машины и тем, что она делает. Кроме того, число состояний огромно. Примитивный компьютер, способный запомнить информацию в 100 бит, не сможет, по-видимому, пройти через все свои состояния, даже если будет постоянно работать на протяжении существования Вселенной.
ПЕРВОСТЕПЕННАЯ роль конечного автомата в теории вычислительных машин заключается в более высоком уровне абстракции, чем у обычного механизма аппаратуры. Вычислительная машина, работающая под руководством программы, это уже не нагромождение логических схем, регистров, ячеек памяти и других атрибутов электроники: это "виртуальная" машина, рабочие части которой определены программой и, если надо, могут быть определены заново. В то время как аппаратура знает лишь двоичные числа и простые команды для их перемещения и действий над ними, виртуальная вычислительная машина имеет дело с более выразительной символьной системой: словами, уравнениями, массивами, функциями, векторами, кодонами, списками, образами, быть может, даже с идеями. Теория конечных автоматов ценна при создании виртуальных машин, и иногда виртуальная машина сама оказывается конечным автоматом.
Рассмотрим программу, цель которой - считывание последовательности двоичных разрядов (единиц и нулей) и выдача сообщения о том, четным или нечетным получилось число единиц. (Эта работа не лишена практической пользы: например, такие программы проверки на четность используются для обнаружения ошибок при передаче двоичных данных по телефону). Программа может быть построена как конечный автомат с двумя состояниями, как показано на нижнем рисунке на с.99. Операция начинается в четном состоянии, так как первоначально не получено ни одной единицы, а нуль считается четным числом. Каждая единица во входной последовательности приводит к изменению состояния, в то время как получение нуля в любом состоянии не изменяет его. Хотя машина не может "запомнить" никакого входа, кроме самого последнего, и, разумеется, не может считать единицы и нули, ее выход всегда отражает четность входной последовательности.

Автомат для проверки на четность
Модель вычисления с конечным числом состояний очень часто встречается в программах, так или иначе связанных с текстом или другой информацией, которая принимает лингвистическую форму. Замечательным примером служат компиляторы: программы, транслирующие операторы программы на входном языке в эквивалентные операторы на выходном языке, чаше называемом "машинным языком" данного компьютера. Компиляторы и другие программы - трансляторы - основные понятия, связанные с виртуальными машинами. Они являются посредниками между символами, имеющими смысл для человека, и символами, распознаваемыми вычислительной машиной.
Часть компилятора, которую можно представить как конечный автомат, называется сканером или лексическим анализатором. Подобно турникету метро, он тоже "пожирает жетоны". Но в этом случае, однако, в качестве "жетонов" выступают слова, или основные лексические единицы языка. Лексический анализатор распознает каждую группу символов и определяет, является ли она настоящим "жетоном", таким, как команда или число: если нет, то лексический анализатор отбрасывает ее как бессмыслицу, подобно турникету, не принимающему фальшивый жетон.
Операцию, производимую лексическим анализатором, можно проиллюстрировать с помощью конечного автомата, предназначенного для распознавания "жетонов" простого языка, пусть и с весьма ограниченными выразительными средствами: "жетоны" образованы исключительно из римских цифр. На самом деле допускаются только числа специального вида: они получаются путем сложения, так что 9 записывается как VIIII, а не IX. (Имеются свидетельства, что сами римляне пользовались именно такой записью; представление при помощи вычитания ¦ является, по-видимому, более поздним германским новшеством).
Диаграмма переходов для автомата, обрабатывающего числа, записанные римскими цифрами, показана справа. Ее входной алфавит состоит из литер M, D, C, L, X, V и I, а также символов пробела, или просто пробелов. Любой первоначальный пробел попросту игнорируется, но, как только получена первая литера, программа немедленно переходит в состояние, идентифицируемое (для удобства) названием литеры. Если первая литера есть M, то за ней может следовать любая литера из алфавита, включая другую литеру M. Если следующая литера D, то ситуация несколько меняется. Из состояния D не определен переход обратно в состояние M, потому что любая последовательность символов, которая содержит DM, не может быть правильно составленным "жетоном": такое число нельзя образовать из римских цифр путем сложения. Кроме того, невозможен переход из состояния D в состояние D, так что DD тоже исключенная последовательность. Причина здесь в том, что для "половинок" D, L и V в римской нумерации повторения не допускаются.
В состоянии D признаются только литеры C, L, X, V и I, имеющие значение, меньшее D. Та же самая последовательность допустима в состоянии C (поскольку C может повторяться), а в состоянии L признаются лишь литеры X, V и I. Правило, согласно которому происходят переходы, вам уже, наверное, понятно. Состояния упорядочены в иерархию, и, как только достигается данный уровень, автомат больше не может вернуться к более высокому уровню; на уровне "половинок" он даже не может остаться. К тому времени, как достигается состояние I, допускается лишь повторный символ 1 либо пробел. Пробел, поступивший в этот момент либо в любой другой момент после появления первой литеры, указывает на конец "жетона" и переводит автомат обратно в начальное состояние, когда он готов получить следующее число.

Лексический анализатор для языка, состоящего из римских цифр
Ни один из известных мне языков программирования не допускает ввод чисел, записанных римскими цифрами, но фактически все такие языки имеют средства обращения с числами, записанными арабскими цифрами. Методы распознавания аналогичны, но имеется большее разнообразие форматов. Простые целые числа, например 137, могут обрабатываться в принципе автоматом с одним состоянием, но числа, состоящие из нескольких частей, такие, как +6.625E-27, требуют более сложного лексического анализа.
Систему рибосом и тРНК можно рассматривать как лексический анализатор, который распознает биологически осмысленные последовательности нуклеотидов в молекуле мРНК. Для того чтобы последовательность была принята, она должна начинаться с инициирующего кодона и заканчиваться одним из трех терминирующих кодонов; между этими границами допускается любая комбинация входных символов U, A, G и С.

Конечный автомат расшифровывает генетический код
(Аминокислоты: Phe, Ser, Tyr, Cys, Trp, Leu, Pro, His, Gln, Arg, Ile, Met, Thr, Asn, Lys, Val, Ala, Asp, Glu, Gly).
Лексический анализ - это первый шаг в процессе компиляции. После лексического анализатора вступают компоненты компилятора, носящие названия "программа грамматического разбора" и "генератор кода". В качестве входной последовательности программа грамматического разбора берет "жетоны", распознанные лексическим анализатором, и анализирует их синтаксические отношения; на этом этапе происходит более глубокое понимание компилятором смысла операторов программы, которые он транслирует. Программу, которая выполняет функции, определенные разобранными операторами, генератор кода пишет на объектном языке.
В рассмотренных здесь игрушечных языках задачи программы грамматического разбора н генератора кода тривиальны. Транслированная форма оператора на языке, использующем римские цифры, может оказаться просто эквивалентом этого числа, записанного арабскими цифрами. Ее можно было бы генерировать, следуя такой стратегии. Перед лексическим анализом "жетона" отводится ячейка памяти и туда засылается нуль. Затем каждый раз, когда лексический анализатор входит в состояние М, к содержимому ячейки прибавляется 1000; для состояния D прибавляется 500 и т.д. Когда лексический анализ закончен, в этой ячейке содержится число, записанное римскими цифрами. Заметим, что этот игрушечный компилятор уже не будет конечным автоматом, поскольку у него есть вспомогательная память.
Компилятор для генетического кода лаже проще и полностью может быть построен в рамках конечного автомата. Транслируемая "программа" является последовательностью стандартных трехбуквенных символов для аминокислот; символы могут быть генерированы как выходная последовательность состояний лексического анализатора, распознающего колоны. Три состояния, соответствующие трем терминирующим кодонам, не имеют выходной последовательности.
Создание настоящего компилятора для достаточно широкого языка, который имел бы практическую пользу, не слишком простое дело, но лежащая в основе его структура конечного автомата может по крайней мере помочь найти принцип организации. Если синтаксис языка определен достаточно точно, то часть работы даже можно автоматизировать: выполнить при помощи программы-компилятора нашего компилятора. Входной последовательностью для нее служит формальное описание языка, а выходной последовательностью - другая программа, которая транслирует операторы на этом языке. Насколько мне известно, еще не написан компилятор компилятора компилятора.
РАСПОЗНАВАНИЕ "жетонов" лексическим анализатором уже само по себе в некотором роде грамматический разбор, а множество всех возможных последовательностей символов "жетона" является своего рода языком. В сущности, это бесконечный язык: если только не наложено какое-нибудь искусственное ограничение на длину индивидуальной последовательности, можно образовать бесконечное множество распознаваемых "жетонов". Как может автомат, имеющий лишь конечное число частей, распознавать бесконечные последовательности правильно составленных операторов и отбрасывать бесконечное число неправильных? Разгадка заключена в самой структуре языка. Если операторы бесконечного языка должны распознаваться конечным автоматом, они должны быть образованы по строгим правилам.
Эти правила были сформулированы в 1956г. С.Клини; они определяют класс языков, названных регулярными языками или регулярными множествами. Клини доказал, что конечный автомат может распознавать язык только тогда, когда этот язык регулярен, и, кроме того, что каждый регулярный язык может быть распознан некоторым конечным автоматом: в конце концов можно построить автомат, в котором имеется состояние для каждого возможного выражения языка. Далее, если язык бесконечен; должен быть возможен грамматический разбор всех операторов посредством прочитывания одного символа слева направо, либо начиная с конца (при этом не допускается ни забегания вперед ни возвращения назад). Если допустимость какого-либо символа обусловлена присутствием другого символа, то обусловливающий символ должен находиться непосредственно слева.
Второе правило является немедленным следствием ограничений конечного автомата, который не может ни предвидеть свои будущие состояния, ни сохранить память о прошлых состояниях; он должен выбрать переход на основе только текущего состояния и текущего входного символа. Именно по этой причине конечный автомат не может обрабатывать числа, образованные римскими цифрами при помощи вычитания. Если записано выражение XI и автомат интерпретирует его как 11, он не может вернуться назад и пересмотреть значение, если следующая литера оказывается V. Многие другие функции управляются с помощью такого ограничения. Например, невозможно построить конечный автомат, который читал бы последовательность двоичных разрядов и определял бы, равно ли число единиц числу нулей. Аналогично, хотя конечный автомат может складывать двоичные числа, он не может их перемножать; я предоставляю читателю догадаться, почему.
ЗА ПРЕДЕЛЫ конечных автоматов и регулярных языков простирается иерархия более мощных машин и более общих языков. Она называется иерархией Хомского, по имени лингвиста Н.Хомского, который исследовал различные формальные языки как возможные модели естественных языков. Наиболее общие языки были созданы при помощи смягчения ограничения на грамматические правила регулярных множеств; автоматы же были построены добавлением к исходной модели конечного автомата элементов памяти.
Следующий автомат в этом ряду называется автоматом с магазинной памятью. Он состоит из конечного автомата с добавлением массива памяти, которая имеет бесконечную емкость, но причудливую организацию. Эта память принимает форму стека, подобного стопке подносов в кафетерии. Для занесения единицы информации в память она должна быть помещена на вершину стека; восстановлена она будет не раньше, чем будут удалены все расположенные сверху единицы. Таким образом, последний из поступивших уходит первым.
Язык, распознаваемый автоматом с магазинной памятью, называется контекстно-свободным языком. При разборе его операторов допустимость символа может зависеть и от символа, стоящего непосредственно слева, и от символа, стоящего непосредственно справа. Эта двусторонняя зависимость разрешается, потому что каждый символ, допустимость которого нельзя немедленно установить, может быть сохранен в стеке, пока не будет разрешена неясность. Следовательно, автомат с магазинной памятью может оперировать с числами, записанными римскими цифрами и образованными при помощи вычитания, и он может распознавать выражения с одинаковым числом единиц и нулей (или иных символов, таких, как правые и левые скобки). С другой стороны, он не может обнаруживать предложения с равным числом символов трех видов, таких, например, как 0, 1, 2. Большинство языков программирования контекстно-свободные, а программа разбора компилятора обычно представляет собой автомат с магазинной памятью. Многие компьютеры имеют аппаратные средства для организации части памяти в виде стека. Язык программирования Forth за основную структуру памяти принимает структуру стека. Разумеется, стек в любой реальной машине не может иметь бесконечную глубину.
Контекстно-свободные языки оправдывают свое название, поскольку на распознавание любого символа могут прямо повлиять только его два ближайших соседа, а не более широкий контекст, в котором он находится. Снятие этого ограничения порождает контекстно-зависимые языки и еще больше увеличивает сложность интерпретации. Теперь далеко отстоящие друг от друга символы могут взаимодействовать; в самом худшем случае первый символ выражения нельзя интерпретировать, пока не будет прочитан последний. В обмен на дополнительную сложность получаем несколько большие возможности. Автомат, основанный на контекстно-зависимых языках, может определять, содержится ли в выражении одинаковое число символов трех видов.
Автомат, который может распознавать контекстно-зависимый язык, является линейно-ограниченным автоматом. В дополнение к обычному устройству конечного автомата он имеет память, организованную так, что любая ячейка памяти доступна в любой момент; это автомат со случайным доступом. Емкость памяти конечна, но предполагается, что она достаточно велика, чтобы вместить любую входную последовательность, которая поступает в автомат. Линейно-ограниченные автоматы, по-видимому, дают хорошее приближение к модели цифровой вычислительной машины фон Неймана. Но, как ни странно, соответствующие контекстно-зависимые языки программирования, по-видимому, мало распространены; очевидно, более простая контекстно-свободная структура почти всегда позволяет добиться желаемой выразительности.
Все описанные выше языки имеют одно общее свойство: говорят, что они рекурсивны. Для нас это означает, что можно вообразить процедуру порождения всех возможных "способов выражения" в языке в порядке возрастания длины. Отсюда следует, что существует гарантированный метод установления того факта, принадлежит ли данному языку данный оператор конечной длины,- для этого просто надо породить все операторы вплоть до данной длины и сравнить их.
Имеются языки, которые не удовлетворяют лаже этим простейшим стандартам обрабатываемости. Для них существует лишь один возможный распознающий автомат, "последнее средство",- машина Тьюринга, конечный автомат со свободным доступом в бесконечную память. В описании, данном Тьюрингом, память представлена в виде бесконечной в обоих направлениях ленты, разделенной на клетки, в которые конечный автомат может записывать, считывать с них или стирать записанное.
Теперь с высот машины Тьюринга четче вырисовывается взаимосвязь вычислительных устройств более низких уровней. Линейно-ограниченный автомат - это просто машина Тьюринга с конечной лентой. Автомат с магазинной памятью имеет ленту, не ограниченную в одном направлении, но "головка" для чтения и записи на ленте всегда остается фиксированной над последней непустой клеткой. Конечный автомат - это машина Тьюринга вовсе без ленты.

Иерархия Хомского конечных и бесконечных автоматов
Читателям, падким на все новое и желающим заняться грамматическим разбором нерекурсивных языков, пора спешить приобрести машину Тьюринга. Следует только предупредить их, что этот чудо-компьютер имеет свои слабые стороны. Существуют языки с такими нелепыми грамматиками, что даже машина Тьюринга не сможет распознать их операторы за конечный отрезок времени. Пока такие языки нашли весьма ограниченное применение в мире вычислительных машин, но люди как-то ухитряются на них говорить.
БИБЛИОГРАФИЯ
COMPUTATION: FINITE AND INFINITE MACHINES. MARVIN L.MINSKY. Prentice-Hall, Inc., 1967.
MATHEMATICAL STRUCTURES FOR COMPUTER SCIENCE. JUDITH L.GERSTING. W.H.Freeman and Company, 1967.
ALGORITHMS + DATA STRUCTURES = PROGRAMS. NIKLAUS WIRTH. Prentice-Hall, Inc., 1976.
INTRODUCTION TO AUTOMATA THEORY, LANGUAGES, AND COMPUTATION, JOHN E.HOPCROFT AND JEFFREY D.ULLMAN. Addison-Wesley Publishing Company, 1979.
Вот тут, как раз, и пригодится упомянутый выше сб. АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.- G.
Последний раз редактировалось: Gudleifr (Чт Мар 12, 2020 10:16 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
3 1984
ВЗЛЕТЫ И ПАДЕНИЯ ЧИСЕЛ-ГРАДИН
БРАЙАН ХЭЙЕС
ПЕШЕХОД, делающий три шага вперед и два назад, хотя и не быстро, но все же доберется до цели. А вот в одной любопытной нерешенной задаче из теории чисел утверждается, что при таком передвижении достижение цели весьма сомнительно. Задача формулируется так. Возьмем произвольное целое число N больше нуля (любое натуральное число). Если оно нечетное, умножим его на 3 и прибавим 1, т.е. заменим N на 3N+1. Если же оно четное, разделим на 2, т.е. заменим N на N/2. В любом случае получаем новое значение N, с которым повторяем описанную операцию. Появится ли после многократного повторения указанных действий тенденция к увеличению чисел или, быть может, к уменьшению? Каким будет процесс: расходящимся или он будет сходиться к некому значению? Долго ли дожидаться числа, которое для этого процесса окажется "фатальным"?
Если задано конкретное N, то для ответа на поставленные вопросы достаточно обычной арифметики. Например, начав с нечетного числа 27, следующим получим значение (3*27)+1 = 82, затем 41, а потом 124. Очевидно, что в последовательности будет много "взлетов" и "падений": взлетов, когда N нечетное, и падений, когда оно четное. Читателю предлагается самому продолжить вычисление и убедиться в справедливости сказанного.
Трудность задачи заключается не в выписывании последовательности для данного N, а в нахождении общего решения, которое годилось бы для всех исходных значений N. Такое общее решение пока не получено. Было испробовано огромное количество чисел, и все они вели себя одинаково, но еще никто не смог доказать, что так же будет с любым целым числом. Из нерешенных задач теории чисел - эта едва ли самая важная, но она одна из тех, что вызывают сильную досаду. И описание вычислительной процедуры, и ее выполнение чрезвычайно просты, но понять, к чему она может привести, невероятно трудно.
На примере этой задачи особенно хорошо видны как польза компьютера при вычислениях, так и ограниченность его возможностей. С небольшими целыми числами можно справиться самим, а далее для вычислений понадобится механический помощник. Им может быть любая машина, даже небольшой программируемый калькулятор. В области же очень больших чисел такая работа под силу только самым мощным ЭВМ. Когда же ставятся более глубокие вопросы, уже не поможет никакой компьютер. Основное назначение ЭВМ - быть подспорьем в математическом эксперименте: строить примеры и контрпримеры. Для описания же закона, по которому N изменяет свои значения, нужна не числодробилка, а скорее механический "доказыватель теорем".
ЕСЛИ к произвольному целому числу многократно применять описанные преобразования, то какого результата следует ожидать? На этот счет есть три интуитивные гипотезы.
В первой гипотезе рассуждаем так. Имеется равное количество четных и нечетных чисел, так что в любой длинной последовательности вычислений четные и нечетные N будут появляться одинаково часто. Нечетное N увеличивается втрое (чуть больше), а четное уменьшается всего лишь вдвое. Следовательно, по мере роста числа итераций значение N будет бесконечно возрастать. За каждую итерацию N будет в среднем увеличиваться на (3N+1)/2. Для больших значений N это, в сущности, равно 3N/2.
Вторая гипотеза основана на тезисе "Чем выше заберешься, тем ниже скатишься". Справедливость этой мысли подкрепляется тем реальным фактом, что стоит в вычислениях получить точную степень двойки, как последовательность неудержимо скатится к 1. (При делении на 2 числа, представляющего собой 2 в любой степени, кроме самой двойки, постоянно будет получаться все меньшее и меньшее четное число). Среди бесконечного счетного множества целых чисел существует бесконечно много степеней двойки, так что при достаточно долгом вычислении обязательно получится одна из них. В процессе вычислений можно получить сколь угодно большое число N, но крах его неизбежен.
Третья гипотеза по форме схожа со второй, но приводит к иному выводу. Замечено, что как только вычисления меняют направление, скажем после ряда четных чисел появляется нечетное, мы вновь возвращаемся в ту же область, в которой были раньше. В самом деле, получая то большие, то меньшие числа, мы можем сколь угодно часто возвращаться в некую конечную область. Можно ожидать, что рано или поздно результат вычислений повторится, и, как только это произойдет, все дальнейшее предрешено. Образуется замкнутый цикл, из которого уже никогда не выйти. Это объясняется тем, что выбор каждого следующего шага происходит по вполне определенному правилу.
К рассмотренным гипотезам не следует относиться слишком серьезно: они не могут быть все справедливыми. Какие-то из их посылок определенно спорны. В частности, во всех трех гипотезах привлекаются вероятностные соображения, хотя последовательности чисел порождаются по некоему правилу, а не случайным образом. Далее, бесконечные величины играют существенную роль при любом анализе этой задачи, а, когда имеешь дело с бесконечностью, здравый смысл редко бывает хорошим советчиком.
Делая эти оговорки, должен тем не менее отметить, что все три гипотезы считаю в высшей степени правдоподобными. Взвешивая каждую из них, я думаю, что не может быть сомнений в ее справедливости, и в то же время другие гипотезы мне кажутся не менее убедительными. Что же по этому поводу говорит математический эксперимент?
НАЧНЕМ вычисления с 1. Это - нечетное число, поэтому, следуя условиям задачи, умножим его на 3 и прибавим 1. Полученное в результате 4 - четное число, так что делим его на 2 и снова получаем четное число. Поделив еще раз на 2, вновь возвращаемся к 1. Таким образом, результат нашего первого вычисления подтверждает две из рассмотренных выше гипотетических теорий. Гипотеза о крахе больших чисел подтвердилась тем, что после первой же итерации результат оказался степенью 2. Подтверждением гипотезы о зацикливании является получение 1 - числа, с которого мы начали. Замкнутый цикл 4, 2, 1 далее будет беспрестанно повторяться.
Из всех натуральных чисел единица занимает особое положение: это первое число и наименьшее. Таким образом, результат, полученный для N=1, может быть нетипичным: прежде чем делать какие-либо выводы, надо проверить другие числа. "Фатальность" чисел 2 и 4 очевидна из вычисления для N=1, поэтому попробуем начать с 3. Это число нечетное, так что следующим будет (3*3)+1, т.е. 10. Разделив на 2, получаем 5. Умножив теперь на 3 и прибавив 1, получаем 16 - опять степень 2; последовательное деление на 2 даст значения N = 8, 4, 2, 1, т.е. мы вновь попадаем в замкнутый цикл 4, 2, 1.
После исследования первых четырех натуральных чисел вроде бы выявилась определенная тенденция, но все же оснований для окончательного вывода нет. В проведенных вычислениях нас больше всего интересуют две величины: максимальное из полученных значений N и длина пути, под которой будем понимать общее число итераций, необходимое для достижения 1. Для самой 1 максимальное значение равно 1, а длина пути - нулю. Для 2 максимум равен 2, а длина пути - 1. Для 3 максимумом будет 16, а длиной пути 7. Пример с тройкой говорит о том, что максимум достигается, а число последовательных итераций может быть значительно больше исходного значения N, так что вполне возможно, что для некоторого значения N эта функция окажется вовсе неограниченной.
Снова вернемся к последовательности, которая порождается начальным значением 27. Как уже было сказано, первые три числа - это 82, 41 и 124, но два деления подряд отбрасывают нас назад, к 31. Можно сказать, что после пяти шагов мы почти не продвинулись вперед.
Но если вычисления продолжить, метод "три шага вперед и два назад" приводит к осциллирующей кривой с постоянно возрастающей амплитудой. Новыми пиками будут 142, 214, 322 и 484. В дальнейшем будут и спады (на 19-м шаге значение опустится до 91), но прослеживается общая тенденция к возрастанию. Миновав числа 700, 1186, и 2158, кривая достигнет весьма значительной величины: 9232. Казалось бы, мы на верном пути. Но, увы, этот путь после 111 шагов завершается в 1, так и не поднявшись выше 9232. (Вся последовательность вычислений графически представлена на с.102).

Последовательность значений чисел-градин, полученных для N=27
Подобные вычисления проводились с огромным набором целых чисел. Сотрудник Токийского университета Набуо Йонеда исследовал все целые числа до 2^40, т.е. до 1.2E12. Результат во всех случаях был одним и тем же: после конечного числа шагов последовательность навсегда попадала в цикл 4, 2, 1. Из первых 50 целых чисел самая большая длина пути возврата в 1 у числа 27 (впрочем, для 41 и 31 этот путь не намного короче, а по пути достигаются те же самые пики; это должно быть ясно из сказанного выше). Целых чисел, которые порождали бы бесконечную последовательность, уходящую неограниченно вверх, не было найдено, равно как не найдены и другие циклы, кроме 4, 2, 1. И все же утверждать, что все целые числа ведут себя одинаково, мы не можем, так как этому пока нет теоретического обоснования.
ИСТОРИИ проблемы "3N+1", как ее обычно называют, хоть и довольно туманна, вряд ли уходит в глубь веков. В течение последних примерно 30 лет эта задача время от времени ставилась на факультетах математики и кибернетики различных университетов. Она появлялась и исчезала так же непредсказуемо, как непредсказуемо и поведение чисел, получаемых в процессе решения рассматриваемой задачи. Сотрудник фирмы Bell Laboratories Джефри Лагариас, недавно изучавший истоки этой задачи и попытки ее решения, отметил, что она, по-видимому, открывалась не однажды. В 1930г. Лотар Коллатц, еше будучи студентом Гамбургского университета, исследовал класс задач, включающий в себя и проблему "3N+1", но результаты его исследований были опубликованы лишь много лет спустя. Английский математик Б.Туэйтс открыл эту задачу независимо от других в 1952г., а несколькими годами позже ее снова сформулировал Р.В.Эндри нз Оклахомского университета в Нормане.
Лагариас ссылается примерно на 20 научных статей по проблеме "3N+1" и ее обобщениям; большинство из них было опубликовано в течение последнего десятилетия, но задолго до этого она уже передавалась изустно. Коллега Коллатца Х.Хассе в 50-х годах ввел ее в Сиракузском университете, С.Улам - в научной лаборатории Лос-Аламоса и, кажется, еше где-то. С.Какутани, впервые услышавший о проблеме "3N+1" в 1960г., сообщил Лагариасу: "Целый месяц весь Йельский университет безрезультатно трудился над этой задачей. Такая же участь постигла исследователей Чикагского университета, когда я им сообщил о ней. Ходила шутка, что эта задача использовалась для заговора, имеющего целью снизить интенсивность математических исследований в США".
Группой исследователей из Лаборатории искусственного интеллекта Массачусетского технологического института в начале 70-х годов была предпринята еще одна длительная атака на эту задачу. Здесь основной улор делался на вычислительные методы, использующие ЭВМ. Во внутреннем (и неопубликованном) отчете этой группы, названном HAKMEM (сокращение от "hackers' memorandum" - записки работяг), проблема значилась под номером 133.
Постоянно кочуя, задача обрастала множеством имен. Название "проблема "3N+1"" мне кажется не очень подходящим, поскольку освещает лишь одну половину процедуры, оставляя вторую в тени. Среди всевозможных вариантов ее названия нашелся один, точнее других отражающий процесс порождения чисел из исходного: "числа-градины". Графически представленная последовательность чисел, получаемых при вычислении, очень похожа на траекторию градины в грозовой туче, поднимающейся в воздушных потоках и затем падающей под силой собственной тяжести.
НА ЯЗЫКЕ высокого уровня, скажем на Бейсике, можно написать программу для вычисления чисел-градин, и займет она всего лишь несколько строк. В самом деле, основной алгоритм формулируется одним предложением. На Бейсике оно имеет вил:
IF N MOD 2 = 0 THEN N = N/2 ELSE N = 3*N + 1
Первой здесь записана операция, которую люди (но не машина) выполняют, не прибегая к явным вычислениям: определение четности (или нечетности) числа N. Компьютер пользуется для этого операцией сравнения по модулю N MOD 2, определяющей остаток от деления на 2 числа N. Если остаток равен 0, то выполнится команда, записанная частью предложения, начинающегося с THEN, и N будет присвоено значение N/2; в противном случае выполнится команда, начинающаяся с ELSE, и N станет равным 3N+1.
Такая программа на Бейсике вполне сносно справляется с порождением чисел-градин из нескольких первых сотен чисел. Но если требуются более громоздкие вычисления, процесс невероятно замедляется. В предложении на Бейсике предусмотрено деление (при сравнении по модулю), сравнение и затем либо второе деление, либо умножение на 3 и сложение. Умножение и деление нещадно тратят машинное время, особенно на небольших вычислительных системах. Можно добиться большой экономии, если обращаться непосредственно к центральному процессору на его собственном языке. Это позволит исключить все операции умножения и деления.
Приблизительное представление о такой программе на языке машины лает рисунок справа. Предполагается, что исходное значение N первоначально находится в регистре АХ, который служит еще и "сумматором", где выполняются арифметические операции. В нем в двоичной системе записано число 27, с которого начинается вычисление.
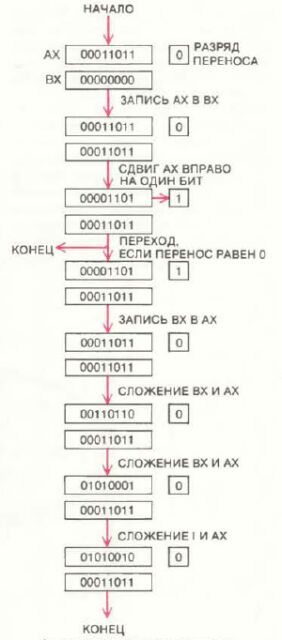
Алгоритм получения чисел-градин
На первом шаге исходное число в двоичном коде переписывается в другой регистр, обозначенный на схеме BX. За счет особых свойств двоичного представления чисел операция деления в данном случае может быть исключена: сдвиг двоичного числа вправо на один знак эквивалентен делению на два точно так же, как сдвиг десятичного числа вправо на одну позицию соответствует делению на 10. В процессе сдвига самый правый разряд (разряд единиц) сохраняется в ячейке памяти размером в 1 бит, которая называется разрядом переноса. Проверяя разряд переноса, можно определить четность числа, поскольку в двоичной системе каждое четное число имеет на конце нуль, а нечетное - единицу.
Если N четное, то вычисления на этом этапе закончены. В регистре АХ после сдвига вправо окажется частное N/2. В том случае, однако, когда N нечетное, вычисления необходимо продолжить. Прежде всего восстанавливается исходное значение N обращением к регистру ВХ. Далее, вместо умножения на 3 это значение дважды прибавляется. Здесь потребуются две машинные команды вместо одной, но все равно это значительно быстрее. Последний шаг - увеличение на 1 числа в АХ. В одном микропроцессоре с таким набором команд вся процедура занимает 20 тактов при нечетном N и 18 тактов при четном N. При тактовой частоте примерно 5 мГц такой фрагмент программы за одну секунду выполняется примерно 250000 раз. (Можно сэкономить даже немного больше машинных тактов, но тогда программа будет более сложной). Аналогичный алгоритм, но использующий команды умножения и деления, занимает 175 тактов для четного N и 286 тактов - для нечетного.
Из рисунка видно, что регистры имеют 8 разрядов и, следовательно, в них нельзя поместить число больше чем 2^8, т.е. больше 256. В основном микропроцессоры имеют размер регистров 16 бит, и, следовательно, в них можно записывать числа до 65536. Но даже такой диапазон весьма ограничивает нас. поскольку программа, использующая 16-разрядную арифметику, не может оперировать с числами-градинами больше 702. Чтобы расширить наши возможности, нужна арифметика с повышенной точностью, в которой число располагается в нескольких регистрах или ячейках памяти. При точности в 32 бит можно оперировать числами почти до 4E9, а при 64 бит предел равен 1E19. К сожалению, при каждом увеличении точности в той же мере снижается скорость.
Алгоритм получения одного значения N - всего лишь фрагмент рабочей программы. В ней, кроме того, должна быть предусмотрена возможность ввода в машину значений и вывода результатов. Реальные же программы для исследования поведения чисел-градин должны делать еще больше. Например, следует предусмотреть возможность целиком выпечатывать последовательности чисел, получающиеся из данного начального значения, или составлять таблицу максимальных значений и длин пути для каждого из целых чисел. Другая программа могла бы предназначаться для поиска целых чисел, при которых последовательно удлиняется путь и увеличивается максимальное значение.
Разновидности формулы 3N+1, в которых используются другие коэффициенты и постоянные, также плохо поддаются исследованию. У.Госпер и Р.Шоппель, когда они еще входили в группу HAKMEM, исследовали проблему "3N-1" и показали, что она эквивалентна проблеме "3N+1" с отрицательными значениями N. Все выбираемые ими числа приводили к одному из трех замкнутых циклов: самый длинный из них начинается при N=17 и состоит из 18 шагов.
Программу, позволяющую лишь выявить числа, которые не попадают в цикл 4, 2, 1, можно значительно упростить. Если числа проверять подряд, начиная с 1, то в изучении нуждаются лишь нечетные числа. Любое четное число сразу будет уменьшено вдвое, и, следовательно, путь, который должно породить полученное число, окажется уже изученным раньше. По тем же причинам нет смысла прослеживать весь путь до 1: как только значение N опускается ниже исходного, дальнейшее исследование можно прекратить. Работающий ныне в Бостонском университете бывший член группы HAKMEM У.Хеннеман предложил еще более эффективные правила для сужения области исследования.
ПОСЛЕ всего, что было сказано, по-видимому, нет смысла продолжать поиски числа, которое вело бы себя как-то иначе. Но даже если такое число никогда не будет найдено, сам факт существования чисел-градин ставит немало любопытных вопросов.
Возможно, самые интригующие свойства таких чисел - это выраженный характер распределения максимальных значений и длин пути. Если такое небольшое число, как 27, удерживается "в подвешенном состоянии" в течение 111 шагов и достигает максимума 9232, то можно было бы ожидать, что длина пути и максимальные значения растут так же быстро, как и N. В действительности же длины пути растут крайне медленно; рост максимальных значений более быстрый, но тоже весьма неупорядочен.
Среди первой сотни целых чисел самый длинный путь равен 118 шагам (N=97); из первых 100000 чисел самый длинный путь равен лишь 350 шагам (N=77031). Таким образом, при увеличении N в 1000 раз длина пути увеличивается только втрое. Здесь, по-видимому, имеет место логарифмическая зависимость. Что же касается максимального значения, то рекордная величина 9232, достигаемая числом N=27, была побита лишь числом N=255: его максимум равняется 13120. Другие из зарегистрированных максимумов распределялись самым беспорядочным образом. Градина 77671 побила все рекорды, достигнув 1570824736.
Длины путей (черные точки) и максимальные значения (красные точки) для всех целых от 1 до 27
Легко видеть, что максимальные значения, получаемые при вычислении чисел-градин, неизменно четные. Можно также доказать, что лишь нечетное N способно установить новый рекорд максимального значения (за исключением числа 2). Для чисел, устанавливающих новые рекорды длины пути, мне неизвестны теоретические аргументы ни в пользу их четности, ни в пользу нечетности. Однако среди первых 100000 рекордные длины пути достигались почти исключительно нечетными числами; среди рекордсменов оказались лишь три четных числа - 6, 18 и 54 (опять не считая 2).
Полученная на ЭВМ распечатка длин пути и максимумов для некоторой области целых чисел представляет собой удручающую смесь закономерности и беспорядка. Последовательность безусловно не случайна, но ей не удается дать никакого толкования. Например, некоторые максимальные значения повторяются чаше, чем другие, причем появление некоторых максимумов настолько часто, что их нельзя описать каким-либо статистическим законом. Выдающийся в этом смысле пример представляет максимум 9232, который ранее других чисел достигается числом 27. Среди первых 1000 целых более 350 достигают того же максимума. Порождающие его числа, однако, не имеют никаких явных общих черт.
Последовательный перечень самых длинных путей для N от 1 до 100 000
Последовательный перечень максимумов для N от 1 до 100 000
Распределение длины пути столь же хаотично. Можно породить любую из возможных длин пути (последовательностью точных степеней двойки), но и в этом случае некоторые числа будут появляться чаще других. Кроме того, и длины пути, и максимумы проявляют четкую тенденцию к группированию в кластеры. Ф.Грюнберг из Калифорнийского университета в Нотридже в 1976г. опубликовал перечень таких кластеров. Самый обширный из них представлял собой цепочку из 52 целых чисел, которые проходили одинаково длинный путь. Возникает вопрос: могут ли одинаковые максимумы и одинаковые длины пути достигаться двумя последовательными числами? Ответ на этот вопрос можно дать в алгебраической форме, но если читатель предпочитает демонстрацию на примерах с числами, ему следует рассмотреть последовательности для всех N от 386 до 391.
ОДИН ИЗ ПОДХОДОВ, ПОЗВОЛЯЮЩИХ пролить свет на задачу о градинах, состоит в обратной ее постановке. Предположим, что все положительные целые числа действительно обязательно попадут в цикл 4, 2, 1. Тогда они должны образовать неразрывную цепь, связывающую все бесконечное счетное множество целых чисел с циклом в основании этой цепи. Поэтому возможно и обращение преобразования над числами-градинами: начиная с 1, применяем преобразование, как бы пятясь назад, для получения больших чисел. Если какое-либо число таким способом получить не удастся, оно не может достичь единицы.
Этот метод прекрасно бы подошел для получения обшего решения залачи о градинах, если бы только его можно было довести до конца. Оказывается, процедура не столь прямолинейна, как кажется. Обычная функция преобразования градин однозначна: у любого значения N в любой точке вычислений только один преемник. Если, например, N = 40, то следующим (порожденным им) числом может быть лишь 20. Когда же мы проходим путь в обратном направлении, возникает неоднозначность. Относительно числа 20 понятно, что оно могло получиться из 40, которое, следовательно, и должно теперь идти за ним. Но после числа 40 может получиться либо 80, либо 13: поток растекается на два рукава, каждый из которых нужно исследовать. Разветвления происходят во всех точках вида 6K+4, где K - любое неотрицательное целое, включая нуль.
Дерево, порожденное обратной функцией преобразования чисел-градин
Такого рода разветвляющуюся систему можно проследить только до определенного уровня. Движемся по отдельной ветви до некоторого наперед заданного предела и затем переключаем внимание на другую ветвь. При пределе 100 надо будет изучить 13 ветвей, причем в этой числовой системе ручейков и протоков между собой связаны 49 чисел. Если предел равен 1000, то ветвей будет 84, а чисел 340. Предел 10 000 дает 1065 ветвей, которые объединяют 4235 чисел. Заметим, что больше половины чисел провалилось между ветвями потока. При возрастании предела растет количество включаемых чисел, но теряется еще больше. Если бы можно было изучить эту разветвляющуюся систему до какого угодно уровня, то были бы охвачены абсолютно все числа? Этот важный вопрос все еще остается без ответа.
БИБЛИОГРАФИЯ
THE 3X+1 PROBLEM AND ITS GENERALIZATIONS. J.C.LAGARIAS. To appear in The American Mathematical Monthly.
ВЗЛЕТЫ И ПАДЕНИЯ ЧИСЕЛ-ГРАДИН
БРАЙАН ХЭЙЕС
ПЕШЕХОД, делающий три шага вперед и два назад, хотя и не быстро, но все же доберется до цели. А вот в одной любопытной нерешенной задаче из теории чисел утверждается, что при таком передвижении достижение цели весьма сомнительно. Задача формулируется так. Возьмем произвольное целое число N больше нуля (любое натуральное число). Если оно нечетное, умножим его на 3 и прибавим 1, т.е. заменим N на 3N+1. Если же оно четное, разделим на 2, т.е. заменим N на N/2. В любом случае получаем новое значение N, с которым повторяем описанную операцию. Появится ли после многократного повторения указанных действий тенденция к увеличению чисел или, быть может, к уменьшению? Каким будет процесс: расходящимся или он будет сходиться к некому значению? Долго ли дожидаться числа, которое для этого процесса окажется "фатальным"?
Если задано конкретное N, то для ответа на поставленные вопросы достаточно обычной арифметики. Например, начав с нечетного числа 27, следующим получим значение (3*27)+1 = 82, затем 41, а потом 124. Очевидно, что в последовательности будет много "взлетов" и "падений": взлетов, когда N нечетное, и падений, когда оно четное. Читателю предлагается самому продолжить вычисление и убедиться в справедливости сказанного.
Трудность задачи заключается не в выписывании последовательности для данного N, а в нахождении общего решения, которое годилось бы для всех исходных значений N. Такое общее решение пока не получено. Было испробовано огромное количество чисел, и все они вели себя одинаково, но еще никто не смог доказать, что так же будет с любым целым числом. Из нерешенных задач теории чисел - эта едва ли самая важная, но она одна из тех, что вызывают сильную досаду. И описание вычислительной процедуры, и ее выполнение чрезвычайно просты, но понять, к чему она может привести, невероятно трудно.
На примере этой задачи особенно хорошо видны как польза компьютера при вычислениях, так и ограниченность его возможностей. С небольшими целыми числами можно справиться самим, а далее для вычислений понадобится механический помощник. Им может быть любая машина, даже небольшой программируемый калькулятор. В области же очень больших чисел такая работа под силу только самым мощным ЭВМ. Когда же ставятся более глубокие вопросы, уже не поможет никакой компьютер. Основное назначение ЭВМ - быть подспорьем в математическом эксперименте: строить примеры и контрпримеры. Для описания же закона, по которому N изменяет свои значения, нужна не числодробилка, а скорее механический "доказыватель теорем".
ЕСЛИ к произвольному целому числу многократно применять описанные преобразования, то какого результата следует ожидать? На этот счет есть три интуитивные гипотезы.
В первой гипотезе рассуждаем так. Имеется равное количество четных и нечетных чисел, так что в любой длинной последовательности вычислений четные и нечетные N будут появляться одинаково часто. Нечетное N увеличивается втрое (чуть больше), а четное уменьшается всего лишь вдвое. Следовательно, по мере роста числа итераций значение N будет бесконечно возрастать. За каждую итерацию N будет в среднем увеличиваться на (3N+1)/2. Для больших значений N это, в сущности, равно 3N/2.
Вторая гипотеза основана на тезисе "Чем выше заберешься, тем ниже скатишься". Справедливость этой мысли подкрепляется тем реальным фактом, что стоит в вычислениях получить точную степень двойки, как последовательность неудержимо скатится к 1. (При делении на 2 числа, представляющего собой 2 в любой степени, кроме самой двойки, постоянно будет получаться все меньшее и меньшее четное число). Среди бесконечного счетного множества целых чисел существует бесконечно много степеней двойки, так что при достаточно долгом вычислении обязательно получится одна из них. В процессе вычислений можно получить сколь угодно большое число N, но крах его неизбежен.
Третья гипотеза по форме схожа со второй, но приводит к иному выводу. Замечено, что как только вычисления меняют направление, скажем после ряда четных чисел появляется нечетное, мы вновь возвращаемся в ту же область, в которой были раньше. В самом деле, получая то большие, то меньшие числа, мы можем сколь угодно часто возвращаться в некую конечную область. Можно ожидать, что рано или поздно результат вычислений повторится, и, как только это произойдет, все дальнейшее предрешено. Образуется замкнутый цикл, из которого уже никогда не выйти. Это объясняется тем, что выбор каждого следующего шага происходит по вполне определенному правилу.
К рассмотренным гипотезам не следует относиться слишком серьезно: они не могут быть все справедливыми. Какие-то из их посылок определенно спорны. В частности, во всех трех гипотезах привлекаются вероятностные соображения, хотя последовательности чисел порождаются по некоему правилу, а не случайным образом. Далее, бесконечные величины играют существенную роль при любом анализе этой задачи, а, когда имеешь дело с бесконечностью, здравый смысл редко бывает хорошим советчиком.
Делая эти оговорки, должен тем не менее отметить, что все три гипотезы считаю в высшей степени правдоподобными. Взвешивая каждую из них, я думаю, что не может быть сомнений в ее справедливости, и в то же время другие гипотезы мне кажутся не менее убедительными. Что же по этому поводу говорит математический эксперимент?
НАЧНЕМ вычисления с 1. Это - нечетное число, поэтому, следуя условиям задачи, умножим его на 3 и прибавим 1. Полученное в результате 4 - четное число, так что делим его на 2 и снова получаем четное число. Поделив еще раз на 2, вновь возвращаемся к 1. Таким образом, результат нашего первого вычисления подтверждает две из рассмотренных выше гипотетических теорий. Гипотеза о крахе больших чисел подтвердилась тем, что после первой же итерации результат оказался степенью 2. Подтверждением гипотезы о зацикливании является получение 1 - числа, с которого мы начали. Замкнутый цикл 4, 2, 1 далее будет беспрестанно повторяться.
Из всех натуральных чисел единица занимает особое положение: это первое число и наименьшее. Таким образом, результат, полученный для N=1, может быть нетипичным: прежде чем делать какие-либо выводы, надо проверить другие числа. "Фатальность" чисел 2 и 4 очевидна из вычисления для N=1, поэтому попробуем начать с 3. Это число нечетное, так что следующим будет (3*3)+1, т.е. 10. Разделив на 2, получаем 5. Умножив теперь на 3 и прибавив 1, получаем 16 - опять степень 2; последовательное деление на 2 даст значения N = 8, 4, 2, 1, т.е. мы вновь попадаем в замкнутый цикл 4, 2, 1.
После исследования первых четырех натуральных чисел вроде бы выявилась определенная тенденция, но все же оснований для окончательного вывода нет. В проведенных вычислениях нас больше всего интересуют две величины: максимальное из полученных значений N и длина пути, под которой будем понимать общее число итераций, необходимое для достижения 1. Для самой 1 максимальное значение равно 1, а длина пути - нулю. Для 2 максимум равен 2, а длина пути - 1. Для 3 максимумом будет 16, а длиной пути 7. Пример с тройкой говорит о том, что максимум достигается, а число последовательных итераций может быть значительно больше исходного значения N, так что вполне возможно, что для некоторого значения N эта функция окажется вовсе неограниченной.
Снова вернемся к последовательности, которая порождается начальным значением 27. Как уже было сказано, первые три числа - это 82, 41 и 124, но два деления подряд отбрасывают нас назад, к 31. Можно сказать, что после пяти шагов мы почти не продвинулись вперед.
Но если вычисления продолжить, метод "три шага вперед и два назад" приводит к осциллирующей кривой с постоянно возрастающей амплитудой. Новыми пиками будут 142, 214, 322 и 484. В дальнейшем будут и спады (на 19-м шаге значение опустится до 91), но прослеживается общая тенденция к возрастанию. Миновав числа 700, 1186, и 2158, кривая достигнет весьма значительной величины: 9232. Казалось бы, мы на верном пути. Но, увы, этот путь после 111 шагов завершается в 1, так и не поднявшись выше 9232. (Вся последовательность вычислений графически представлена на с.102).

Последовательность значений чисел-градин, полученных для N=27
Подобные вычисления проводились с огромным набором целых чисел. Сотрудник Токийского университета Набуо Йонеда исследовал все целые числа до 2^40, т.е. до 1.2E12. Результат во всех случаях был одним и тем же: после конечного числа шагов последовательность навсегда попадала в цикл 4, 2, 1. Из первых 50 целых чисел самая большая длина пути возврата в 1 у числа 27 (впрочем, для 41 и 31 этот путь не намного короче, а по пути достигаются те же самые пики; это должно быть ясно из сказанного выше). Целых чисел, которые порождали бы бесконечную последовательность, уходящую неограниченно вверх, не было найдено, равно как не найдены и другие циклы, кроме 4, 2, 1. И все же утверждать, что все целые числа ведут себя одинаково, мы не можем, так как этому пока нет теоретического обоснования.
ИСТОРИИ проблемы "3N+1", как ее обычно называют, хоть и довольно туманна, вряд ли уходит в глубь веков. В течение последних примерно 30 лет эта задача время от времени ставилась на факультетах математики и кибернетики различных университетов. Она появлялась и исчезала так же непредсказуемо, как непредсказуемо и поведение чисел, получаемых в процессе решения рассматриваемой задачи. Сотрудник фирмы Bell Laboratories Джефри Лагариас, недавно изучавший истоки этой задачи и попытки ее решения, отметил, что она, по-видимому, открывалась не однажды. В 1930г. Лотар Коллатц, еше будучи студентом Гамбургского университета, исследовал класс задач, включающий в себя и проблему "3N+1", но результаты его исследований были опубликованы лишь много лет спустя. Английский математик Б.Туэйтс открыл эту задачу независимо от других в 1952г., а несколькими годами позже ее снова сформулировал Р.В.Эндри нз Оклахомского университета в Нормане.
Лагариас ссылается примерно на 20 научных статей по проблеме "3N+1" и ее обобщениям; большинство из них было опубликовано в течение последнего десятилетия, но задолго до этого она уже передавалась изустно. Коллега Коллатца Х.Хассе в 50-х годах ввел ее в Сиракузском университете, С.Улам - в научной лаборатории Лос-Аламоса и, кажется, еше где-то. С.Какутани, впервые услышавший о проблеме "3N+1" в 1960г., сообщил Лагариасу: "Целый месяц весь Йельский университет безрезультатно трудился над этой задачей. Такая же участь постигла исследователей Чикагского университета, когда я им сообщил о ней. Ходила шутка, что эта задача использовалась для заговора, имеющего целью снизить интенсивность математических исследований в США".
Группой исследователей из Лаборатории искусственного интеллекта Массачусетского технологического института в начале 70-х годов была предпринята еще одна длительная атака на эту задачу. Здесь основной улор делался на вычислительные методы, использующие ЭВМ. Во внутреннем (и неопубликованном) отчете этой группы, названном HAKMEM (сокращение от "hackers' memorandum" - записки работяг), проблема значилась под номером 133.
Постоянно кочуя, задача обрастала множеством имен. Название "проблема "3N+1"" мне кажется не очень подходящим, поскольку освещает лишь одну половину процедуры, оставляя вторую в тени. Среди всевозможных вариантов ее названия нашелся один, точнее других отражающий процесс порождения чисел из исходного: "числа-градины". Графически представленная последовательность чисел, получаемых при вычислении, очень похожа на траекторию градины в грозовой туче, поднимающейся в воздушных потоках и затем падающей под силой собственной тяжести.
НА ЯЗЫКЕ высокого уровня, скажем на Бейсике, можно написать программу для вычисления чисел-градин, и займет она всего лишь несколько строк. В самом деле, основной алгоритм формулируется одним предложением. На Бейсике оно имеет вил:
IF N MOD 2 = 0 THEN N = N/2 ELSE N = 3*N + 1
Первой здесь записана операция, которую люди (но не машина) выполняют, не прибегая к явным вычислениям: определение четности (или нечетности) числа N. Компьютер пользуется для этого операцией сравнения по модулю N MOD 2, определяющей остаток от деления на 2 числа N. Если остаток равен 0, то выполнится команда, записанная частью предложения, начинающегося с THEN, и N будет присвоено значение N/2; в противном случае выполнится команда, начинающаяся с ELSE, и N станет равным 3N+1.
Такая программа на Бейсике вполне сносно справляется с порождением чисел-градин из нескольких первых сотен чисел. Но если требуются более громоздкие вычисления, процесс невероятно замедляется. В предложении на Бейсике предусмотрено деление (при сравнении по модулю), сравнение и затем либо второе деление, либо умножение на 3 и сложение. Умножение и деление нещадно тратят машинное время, особенно на небольших вычислительных системах. Можно добиться большой экономии, если обращаться непосредственно к центральному процессору на его собственном языке. Это позволит исключить все операции умножения и деления.
Приблизительное представление о такой программе на языке машины лает рисунок справа. Предполагается, что исходное значение N первоначально находится в регистре АХ, который служит еще и "сумматором", где выполняются арифметические операции. В нем в двоичной системе записано число 27, с которого начинается вычисление.

Алгоритм получения чисел-градин
На первом шаге исходное число в двоичном коде переписывается в другой регистр, обозначенный на схеме BX. За счет особых свойств двоичного представления чисел операция деления в данном случае может быть исключена: сдвиг двоичного числа вправо на один знак эквивалентен делению на два точно так же, как сдвиг десятичного числа вправо на одну позицию соответствует делению на 10. В процессе сдвига самый правый разряд (разряд единиц) сохраняется в ячейке памяти размером в 1 бит, которая называется разрядом переноса. Проверяя разряд переноса, можно определить четность числа, поскольку в двоичной системе каждое четное число имеет на конце нуль, а нечетное - единицу.
Если N четное, то вычисления на этом этапе закончены. В регистре АХ после сдвига вправо окажется частное N/2. В том случае, однако, когда N нечетное, вычисления необходимо продолжить. Прежде всего восстанавливается исходное значение N обращением к регистру ВХ. Далее, вместо умножения на 3 это значение дважды прибавляется. Здесь потребуются две машинные команды вместо одной, но все равно это значительно быстрее. Последний шаг - увеличение на 1 числа в АХ. В одном микропроцессоре с таким набором команд вся процедура занимает 20 тактов при нечетном N и 18 тактов при четном N. При тактовой частоте примерно 5 мГц такой фрагмент программы за одну секунду выполняется примерно 250000 раз. (Можно сэкономить даже немного больше машинных тактов, но тогда программа будет более сложной). Аналогичный алгоритм, но использующий команды умножения и деления, занимает 175 тактов для четного N и 286 тактов - для нечетного.
Из рисунка видно, что регистры имеют 8 разрядов и, следовательно, в них нельзя поместить число больше чем 2^8, т.е. больше 256. В основном микропроцессоры имеют размер регистров 16 бит, и, следовательно, в них можно записывать числа до 65536. Но даже такой диапазон весьма ограничивает нас. поскольку программа, использующая 16-разрядную арифметику, не может оперировать с числами-градинами больше 702. Чтобы расширить наши возможности, нужна арифметика с повышенной точностью, в которой число располагается в нескольких регистрах или ячейках памяти. При точности в 32 бит можно оперировать числами почти до 4E9, а при 64 бит предел равен 1E19. К сожалению, при каждом увеличении точности в той же мере снижается скорость.
Алгоритм получения одного значения N - всего лишь фрагмент рабочей программы. В ней, кроме того, должна быть предусмотрена возможность ввода в машину значений и вывода результатов. Реальные же программы для исследования поведения чисел-градин должны делать еще больше. Например, следует предусмотреть возможность целиком выпечатывать последовательности чисел, получающиеся из данного начального значения, или составлять таблицу максимальных значений и длин пути для каждого из целых чисел. Другая программа могла бы предназначаться для поиска целых чисел, при которых последовательно удлиняется путь и увеличивается максимальное значение.
Разновидности формулы 3N+1, в которых используются другие коэффициенты и постоянные, также плохо поддаются исследованию. У.Госпер и Р.Шоппель, когда они еще входили в группу HAKMEM, исследовали проблему "3N-1" и показали, что она эквивалентна проблеме "3N+1" с отрицательными значениями N. Все выбираемые ими числа приводили к одному из трех замкнутых циклов: самый длинный из них начинается при N=17 и состоит из 18 шагов.
Программу, позволяющую лишь выявить числа, которые не попадают в цикл 4, 2, 1, можно значительно упростить. Если числа проверять подряд, начиная с 1, то в изучении нуждаются лишь нечетные числа. Любое четное число сразу будет уменьшено вдвое, и, следовательно, путь, который должно породить полученное число, окажется уже изученным раньше. По тем же причинам нет смысла прослеживать весь путь до 1: как только значение N опускается ниже исходного, дальнейшее исследование можно прекратить. Работающий ныне в Бостонском университете бывший член группы HAKMEM У.Хеннеман предложил еще более эффективные правила для сужения области исследования.
ПОСЛЕ всего, что было сказано, по-видимому, нет смысла продолжать поиски числа, которое вело бы себя как-то иначе. Но даже если такое число никогда не будет найдено, сам факт существования чисел-градин ставит немало любопытных вопросов.
Возможно, самые интригующие свойства таких чисел - это выраженный характер распределения максимальных значений и длин пути. Если такое небольшое число, как 27, удерживается "в подвешенном состоянии" в течение 111 шагов и достигает максимума 9232, то можно было бы ожидать, что длина пути и максимальные значения растут так же быстро, как и N. В действительности же длины пути растут крайне медленно; рост максимальных значений более быстрый, но тоже весьма неупорядочен.
Среди первой сотни целых чисел самый длинный путь равен 118 шагам (N=97); из первых 100000 чисел самый длинный путь равен лишь 350 шагам (N=77031). Таким образом, при увеличении N в 1000 раз длина пути увеличивается только втрое. Здесь, по-видимому, имеет место логарифмическая зависимость. Что же касается максимального значения, то рекордная величина 9232, достигаемая числом N=27, была побита лишь числом N=255: его максимум равняется 13120. Другие из зарегистрированных максимумов распределялись самым беспорядочным образом. Градина 77671 побила все рекорды, достигнув 1570824736.

Длины путей (черные точки) и максимальные значения (красные точки) для всех целых от 1 до 27
Легко видеть, что максимальные значения, получаемые при вычислении чисел-градин, неизменно четные. Можно также доказать, что лишь нечетное N способно установить новый рекорд максимального значения (за исключением числа 2). Для чисел, устанавливающих новые рекорды длины пути, мне неизвестны теоретические аргументы ни в пользу их четности, ни в пользу нечетности. Однако среди первых 100000 рекордные длины пути достигались почти исключительно нечетными числами; среди рекордсменов оказались лишь три четных числа - 6, 18 и 54 (опять не считая 2).
Полученная на ЭВМ распечатка длин пути и максимумов для некоторой области целых чисел представляет собой удручающую смесь закономерности и беспорядка. Последовательность безусловно не случайна, но ей не удается дать никакого толкования. Например, некоторые максимальные значения повторяются чаше, чем другие, причем появление некоторых максимумов настолько часто, что их нельзя описать каким-либо статистическим законом. Выдающийся в этом смысле пример представляет максимум 9232, который ранее других чисел достигается числом 27. Среди первых 1000 целых более 350 достигают того же максимума. Порождающие его числа, однако, не имеют никаких явных общих черт.

Последовательный перечень самых длинных путей для N от 1 до 100 000

Последовательный перечень максимумов для N от 1 до 100 000
Распределение длины пути столь же хаотично. Можно породить любую из возможных длин пути (последовательностью точных степеней двойки), но и в этом случае некоторые числа будут появляться чаще других. Кроме того, и длины пути, и максимумы проявляют четкую тенденцию к группированию в кластеры. Ф.Грюнберг из Калифорнийского университета в Нотридже в 1976г. опубликовал перечень таких кластеров. Самый обширный из них представлял собой цепочку из 52 целых чисел, которые проходили одинаково длинный путь. Возникает вопрос: могут ли одинаковые максимумы и одинаковые длины пути достигаться двумя последовательными числами? Ответ на этот вопрос можно дать в алгебраической форме, но если читатель предпочитает демонстрацию на примерах с числами, ему следует рассмотреть последовательности для всех N от 386 до 391.
ОДИН ИЗ ПОДХОДОВ, ПОЗВОЛЯЮЩИХ пролить свет на задачу о градинах, состоит в обратной ее постановке. Предположим, что все положительные целые числа действительно обязательно попадут в цикл 4, 2, 1. Тогда они должны образовать неразрывную цепь, связывающую все бесконечное счетное множество целых чисел с циклом в основании этой цепи. Поэтому возможно и обращение преобразования над числами-градинами: начиная с 1, применяем преобразование, как бы пятясь назад, для получения больших чисел. Если какое-либо число таким способом получить не удастся, оно не может достичь единицы.
Этот метод прекрасно бы подошел для получения обшего решения залачи о градинах, если бы только его можно было довести до конца. Оказывается, процедура не столь прямолинейна, как кажется. Обычная функция преобразования градин однозначна: у любого значения N в любой точке вычислений только один преемник. Если, например, N = 40, то следующим (порожденным им) числом может быть лишь 20. Когда же мы проходим путь в обратном направлении, возникает неоднозначность. Относительно числа 20 понятно, что оно могло получиться из 40, которое, следовательно, и должно теперь идти за ним. Но после числа 40 может получиться либо 80, либо 13: поток растекается на два рукава, каждый из которых нужно исследовать. Разветвления происходят во всех точках вида 6K+4, где K - любое неотрицательное целое, включая нуль.

Дерево, порожденное обратной функцией преобразования чисел-градин
Такого рода разветвляющуюся систему можно проследить только до определенного уровня. Движемся по отдельной ветви до некоторого наперед заданного предела и затем переключаем внимание на другую ветвь. При пределе 100 надо будет изучить 13 ветвей, причем в этой числовой системе ручейков и протоков между собой связаны 49 чисел. Если предел равен 1000, то ветвей будет 84, а чисел 340. Предел 10 000 дает 1065 ветвей, которые объединяют 4235 чисел. Заметим, что больше половины чисел провалилось между ветвями потока. При возрастании предела растет количество включаемых чисел, но теряется еще больше. Если бы можно было изучить эту разветвляющуюся систему до какого угодно уровня, то были бы охвачены абсолютно все числа? Этот важный вопрос все еще остается без ответа.
БИБЛИОГРАФИЯ
THE 3X+1 PROBLEM AND ITS GENERALIZATIONS. J.C.LAGARIAS. To appear in The American Mathematical Monthly.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
4 1984
ПОВОРАЧИВАЮЩАЯСЯ ЧЕРЕПАХА ПОЗВОЛЯЕТ ВЗГЛЯНУТЬ НА ГЕОМЕТРИЮ "ИЗНУТРИ"
БРАЙАН ХЭЙЕС
ЧТО ТАКОЕ окружность? Быть может, это предел, к которому стремится n-угольник при бесконечном возрастании n? Или это частный случай эллипса, в котором два фокуса слились в один? А может быть, геометрическое место точек плоскости, равноудаленных от заданной точки?
Разумеется, все эти определения имеют право на существование, и можно дать немало других. Но рассмотрим лишь одно из них: окружность представляет собой замкнутую кривую, образованную последовательным повторением двух чередующихся элементарных действий - продвижением чуть-чуть вперед и поворотом чуть-чуть вправо до тех пор, пока полный поворот не составит 360o. Такое определение принципиально отличается от других: вместо описания самой окружности или характерных ее свойств предлагается процедура построения. Более того, сама процедура имеет особый характер - ее формулировка целиком опирается на "локальные" свойства окружности. Для построения кривой достаточно информации об окрестности той точки, где вы сейчас находитесь; совсем не нужно представления о всей картине в целом. Также нет необходимости знать ни о расположении центра, ни даже о величине ее радиуса.
В такого рода процедурах и заключена суть нового взгляда на геометрию как на эмпирическую геометрию. При этом подходе исследователю предлагается вообразить себя путешествующим в мире геометрических фигур, тогда как для других подходов характерна тенденция отделить фигуры от наблюдателя, расположить их в ином пространстве. Разница здесь примерно такая же, как между непосредственным исследованием местности и изучением ее карты. Особенно полезен эмпирический подход в тех случаях, когда геометрические понятия изучают при помощи компьютеров. Определение, заданное процедурой, легко запрограммировать, и ЭВМ будет вычерчивать соответствующую фигуру.
НОВЫЙ взгляд на геометрию реализовался в так называемой "черепашьей графике", тесно связанной с языком программирования Лого, разработанным в 1960г. Сеймуром Пейпертом в Массачусетсом технологическом институте (МТИ) для ознакомления детей с основами программирования. С тех пор язык значительно усовершенствовался и сфера его приложения вышла за рамки образования. Среди многих внесших свой вклад в развитие Лого следует выделить сотрудников МТИ Харолда Эйбелсона и Андреа диСессу, которые в своей необыкновенно иллюстративной работе "Turtle Geometry: The Computer as a Medium for Exploring Mathematics" ("Черепашья графика. ЭВМ как средство математических исследований") изложили идеи, легшие в основу черепашьей графики.
Первая "черепаха" была механическим устройством: небольшая тележка на колесах, управляемая ЭВМ по командам, задаваемым с пульта. Ее построил английский нейрофизиолог У.Грей Уолтер в конце 40-х годов. Куполообразный корпус этой конструкции был похож на черепаший панцирь. Механическая черепаха могла передвигаться вперед и назад н менять направление поворотом на месте. В шасси было вмонтировано перо, так что когда черепаха ползала по листу бумаги, то прочерчивала на нем свою траекторию. Сегодня такая "напольная черепаха" известна меньше, чем "экранная черепаха", которая в виде треугольника перемешается по телевизионному экрану по команде с пульта или по введенной с терминала программе.
В большинстве методов формирования графического изображения при помощи ЭВМ используется фиксированная система координат, как правило декартова, с двумя перпендикулярными осями. Положение каждой точки на экране определяется относительно фиксированного начала координат, например левого нижнего угла, в котором пересекаются воображаемые оси. Направления на плоскости определяются также относительно этих осей. Чтобы задать команду для проведения отрезка прямой, достаточно указать координаты двух концевых точек. Если, например, эти точки (0, 0) и (100, 0), внизу экрана появится прямая линия длиной в 100 единиц.
Следует отметить, что в любой фиксированной системе координат результат выполнения команды не зависит от предшествующей последовательности команд. Совсем иное положение в черепашьей графике. Чтобы прочертить отрезок прямой длиной в 100 единиц, черепахе дают команду ВПЕРЕД 100. Однако, где именно на экране появится этот отрезок и как он будет ориентирован, целиком зависит от состояния черепахи к моменту получения команды. Состояние черепахи в любой момент определяется ее местоположением и курсом. Команда ВПЕРЕД 100 служит для черепахи основанием продвигаться из своего текущего положения на 100 единиц в направлении, определяемом текущим курсом (т.е. "головой вперед"). Следовательно, одна и та же команда в зависимости от начального состояния черепахи может привести к абсолютно разным результатам.
Пользуясь всего лишь двумя командами ВПЕРЕД и НАПРАВО, можно получить простую систему черепашьей графики. После команды ВПЕРЕД указывается число, означающее количество шагов, которое должна пройти черепаха. После НАПРАВО также следует число, выражающее угол в градусах, на который черепаха должна отклониться вправо от своего текущего курса. Последовательными продвижениями вперед и правыми поворотами можно начертить на плоскости любую геометрическую фигуру. (Заметим, что левый поворот на 90o можно определить двояко: НАПРАВО 270, или НАПРАВО - 90). Тем не менее в реальных системах черепашьей графики обычно есть команды НАЗАД (или ОБРАТНО) и НАЛЕВО. Командами ПЕРОВНИЗ и ПЕРОВВЕРХ дается или отменяется указание вычерчивать траекторию движения черепахи. Имеется также несколько команд, которые позволяют по состоянию черепахи вычислять ее абсолютные координаты, но для черепашьей графики они не существенны.
ГЕОМЕТРИЮ, порожденную черепашьей графикой, формально можно назвать конечно-разностной геометрией. Она конечная, так как черепаха способна передвигаться только дискретными шагами, и разностная, потому что все перемещения определяются разностью между текущими и последующими значениями положения и курса. Таким образом, в иных терминах выражено то обстоятельство, что в этой разновидности геометрии мы имеем дело лишь с локальными свойствами прямых, кривых и поверхностей; информации об отдаленных точках или о глобальных свойствах геометрических фигур здесь не требуется. Следовательно, от черепашьей графики больше всего проку, когда мы стремимся выявить "подлинный характер" геометрической фигуры, т.е. когда нас интересует ее "внутреннее содержание".
Есть одно понятие, которое очень трудно сформулировать в декартовой системе координат, но стоит воспользоваться черепашьей графикой, как оно становится абсолютно прозрачным. Это понятие кривизны. В декартовых координатах кривизну некоторой линии на плоскости можно представить себе как скорость изменения тангенса угла наклона касательной от точки к точке. Изменение тангенса в свою очередь соответствует изменению координаты y как функции координаты x. Черепахе следить за кривизной значительно проще: это полный поворот, совершаемый ею за один шаг. Таким образом, в окружности, которая определяется последовательным чередованием команд ВПЕРЕД 1, НАПРАВО 1, кривизна в любой точке равна 1.

Несколько получаемых черепахой команд (слева) и иллюстрация понятия полного поворота (справа)
Понятие полного поворота обогащает нас другими интересными находками. Рассмотрим всем известную теорему евклидовой геометрии о сумме внутренних углов выпуклого многоугольника. В треугольнике эта сумма равна 180o. в четырехугольнике - 360o, в пятиугольнике - 540o, и т.д. Иными словами, это всегда целое число, умноженное на 180o, где целое на два меньше числа сторон. Полный поворот черепахи складывается совсем из других углов: это не внешние и не внутренние углы, а отклонения от курса в каждой вершине. Можно сформулировать теоремы о полном повороте в многоугольнике. Они будут несколько отличаться от теорем о внутренних углах, но им также свойственна общность.
В самой фундаментальной теореме утверждается, что полный поворот черепахи, вычерчивающей многоугольник, выражается целым числом, умноженным на 360o. Доказательство просто и совершенно очевидно. Если кривая замкнута (а это справедливо для любого многоугольника), то черепаха обязательно должна вернуться в исходную точку, и, когда это произойдет, курс черепахи должен быть таким же, как в начале ее пути. (Последнее фактически может служить некоторым эффективным определением геометрической замкнутости). Если курс совпадает с исходным, то полный поворот равен 0o, или 360o, или любому кратному 360o.
Для выпуклого многоугольника можно доказать более сильный результат: полный поворот равен точно 360o. (Многоугольник называется выпуклым, если прямая, связывающая любые две точки, принадлежащие его сторонам, никогда не выйдет за пределы многоугольника). Эта теорема, однако, применима к любым многоугольникам, в том числе и к невыпуклым (таким, как пятиконечная звезда). Она применима даже к замкнутым фигурам, стороны которых образованы кривыми и которые, следовательно, не являются многоугольниками.
Топологически замкнутые кривые, в которых использовано понятие полного поворота
В геометрии, основанной на фиксированной системе координат, у суммы внутренних углов выпуклого многоугольника мало очевидных взаимосвязей с другими понятиями. А вот в черепашьей графике понятие полного поворота служит мощным средством, применимым в широкой области. Эйбелсон и диСесса показали, что его можно использовать, например, для анализа топологических свойств замкнутого пути. Путь, составленный из любого числа прямых, кривых и витков, называется простым в топологическом смысле, если в нем нет пересечений. Как и в простом выпуклом многоугольнике, полный поворот для простого пути равен 360o. Добавление одной петли (и одного пересечения) превращает полный поворот в 0o либо в 720o, в зависимости от ее ориентации. С каждой новой петлей либо добавляется, либо вычитается 360o. На этом основании, находясь на месте черепахи, топологические свойства пути можно определить, имея в каждый момент в поле зрения лишь микроскопический участок пути.
Понятие полного поворота легло в основу алгоритма, позволяющего черепахе найти выход из лабиринта. У Эйбелсона и диСессы алгоритм выглядит так:
"1. Выбрать произвольное начальное направление (например, на север) и встать к нему лицом.
2. Двигаться в "северном" направлении до тех пор, пока не встретится препятствие.
3. Поворачивать налево до тех пор, пока это препятствие не окажется справа от вас.
4. Обходить это препятствие так, чтобы оно все время оставалось справа от вас, пока полный поворот (включая первый поворот на шаге 3) не станет равным 0.
5. Вернуться к шагу 2".
Следуя этим правилам, черепаха сможет выбраться из любого лабиринта (разумеется, при условии, что он имеет выход). Эта процедура всегда работает, потому что есть только одна возможность заманить черепаху в ловушку - завести ее в бесконечный цикл. А если следовать курсу полного поворота, такой ловушки можно избежать. Снова отметим, что стоящая перед черепахой глобальная задача - найти дорогу из лабиринта - будет решена, несмотря на то что черепахе доступны сведения только о ближайшем окружении; взгляд на лабиринт с высоты птичьего полета абсолютно не нужен. Универсальная процедура решения лабиринта называется алгоритмом Пледжа в честь англичанина Джона Пледжа из Эксетера, придумавшего алгоритм в двенадцатилетнем возрасте.

Черепаха, следуя алгоритму Пледжа, выбирается из лабиринта
Еще большие возможности появляются, если понятие полного поворота применить к случаю, когда поверхность, по которой разрешается бродить черепахе, не плоскость. На сфере, например, полный поворот по замкнутому пути оказывается меньше 360o. Более того, величина отклонения от 360o зависит от длины пути или, точнее, от области, которую этот путь охватывает. Читатели, знакомые с неевклидовой геометрией (открытой в XIX столетии), должны понять, в чем здесь дело: в угловом дефекте - мере кривизны поверхности. В этом примере существенно, что измерение может быть сделано только по локальной информации. Если в качестве примера вам больше нравится кривизна пространства-времени Вселенной, то и эта мера, очевидно, была получена изнутри Вселенной. Эйбелсон и диСесса рассматривают эти вопросы в конце своей книги (см. библиографию), где они формулируют общую теорию относительности при помощи черепашьей графики.
Они также рассматривают блуждания черепахи по поверхности куба, которая топологически эквивалентна сфере, но имеет совсем другие геометрические свойства. В самом деле, геометрия поверхности куба весьма причудлива. Предположим, что длина ребра куба равна 100 единицам и что сначала черепаха находится в центре одной иэ граней и направлена параллельно какому-нибудь ребру. Трижды повторим команды ВПЕРЕД 100, НАПРАВО 90. В результате получим замкнутую кривую, ограничивающую геометрическую фигуру с тремя равными углами и тремя равными сторонами, или, можно сказать, равносторонний многоугольник с прямыми углами. Что же это - правильный треугольник с прямыми углами или квадрат с тремя сторонами?
Другим замечательным примером геометрии кубической поверхности может служить моногон - односторонний многоугольник. Это замкнутый путь, который проделывает черепаха, движущаяся все время в одном направлении, без поворотов. Представить себе, как получается такой моногон, очень просто, даже не имея черепахи, управляемой компьютером: мысленно проведите на кубе "экватор". Куда сложнее другой вопрос: существует ли на поверхности куба такая комбинация начального положения и курса, которая не приводит к моногону, если двигаться все время в заданном направлении? Что если этот угол выражается иррациональным числом? Ответ можно найти в гл.6 упомянутой выше книги Эйбелсона и диСессы, но авторы настоятельно не советуют его смотреть. В одном месте они помещают такое предостережение: "ОСТОРОЖНО! В следующем разделе содержится "сверхтворение" математики (уже открытое). Оно может повредить вашему воображению, так что пользуйтесь этим материалом только н самом крайнем случае".
ОТКРЫТИЕ какого-либо принципа и исследование его обобщений весьма характерно для стиля черепашьей графики. Этот процесс значительно упрощается благодаря компьютеру: эксперименты ставятся очень легко, а любые вариации на заданную тему получаются мизерными усилиями. Короче говоря, это геометрия для халтурщиков.
Рассмотрим следующую процедуру, описанную Эйбелсоном и диСессой и другими авторами работ по языку Лого:
НА КВАДРАЛЬ :РАССТОЯНИЕ
ВПЕРЕД :РАССТОЯНИЕ
НАПРАВО 90
КВАДРАЛЬ :РАССТОЯНИЕ + 5
КОНЕЦ
Здесь КВАДРАЛЬ - название процедуры, РАССТОЯНИЕ - переменная, начальное значение которой задается при обращении к процедуре. (Двоеточие - принятое в Лого соглашение для идентификации переменных). Черепахе дается команда двигаться вперед на заданное расстояние и потом повернуть на 90o; затем процедура КВАДРАЛЬ выполняется снова, но уже с большим значением переменной РАССТОЯНИЕ. В результате получается "КВАДратная спиРАЛЬ", которая, постепенно расширяясь, подходит к рамке экрана. (Спираль, полученная по приведенной здесь процедуре, может расти бесконечно, хотя на экране будет виден только ее конечный фрагмент).
Допустимы всевозможные модификации. Меняя постоянное слагаемое, которое прибавляется к переменной, мы будем всего лишь равномерно стягивать или растягивать витки спирали. Если же сложение заменить умножением на константу, большую единицы, то получится спираль, прямые отрезки которой будут увеличиваться пропорционально их расстоянию от центра. Если в команде НАПРАВО 90 подставлять другие постоянные значения угла, то можно получать треугольную, пятиугольную и какую-угодно-угольную спирали. Если угол отличается от прямого незначительно, получается совокупность вложенных "квадратов", закручивающаяся вокруг центра, причем их вершины описывают другие спирали. Задание очень маленького угла приводит к некоему приближению к гладкой "круговой" спирали.
Можно также изменить процедуру таким образом, чтобы при каждом обращении к ней менялось не расстояние, а угол. Метаморфоза совершенно потрясающая: вместо одной постоянно раскручивающейся спирали черепаха рисует скручивающуюся спираль и затем, поменяв направление, раскручивающуюся спираль, потом другую скручивающуюся и т.д., создавая симметричный массив спиралей, связанных воедино самыми объемлющими циклами. Причина кроется в том, что при добавлении постоянной расстояние может увеличиваться лишь монотонно, тогда как изменение на константу угла обязательно приведет снова к малому его значению, поскольку значения углов повторяются с периодом 360o.
Рассмотрим один подкласс кривых, полученных при начальном значении угла 0o (см. рисунок на с.62). Все узоры этого класса по основным очертаниям аналогичны. Черепаха создает ряд спиралей, то раскручивая, то закручивая их, затем проходит весь этот путь в обратном направлении и, вернувшись в исходную точку, создает идентичный массив, отраженный относительно первого на 180o. Этот путь черепаха проходит бесконечно. Количество нарисованных ею спиралей зависит только от приращения угла, но природа этой зависимости далеко не очевидна. Если приращение угла не делится на 8, то число спиралей на единицу больше числа, полученного от деления приращения на наибольший общий делитель приращения и 360. Можете объяснить почему? Можете ли вы предсказать общие очертания узора, когда приращение кратно 8?

Восемь семейств спиралей, полученных добавлением фиксированного приращения к начальному углу 0o
Благодаря компьютеру стало возможно изучать семейства таких спиралей. Аналогичные исследования можно предпринять в отношении семейства многоугольников, ячеистых покрытий и рекурсивных фигур вроде снежинки, которая получается повторением в постоянно уменьшающемся масштабе одной и той же структуры (см. рисунок на с.98). В этом процессе неоценимую помощь может оказать черепашья графика благодаря конструктивному и алгоритмическому ее определению. Было бы по крайней мере нелепо выписывать уравнение, которое целиком описывает структуру снежинки, если можно воспользоваться процедурой порождения такой конфигурации, легко разбиваемой на несколько повторяющихся элементарных шагов.

Вложенная последовательность кривых в виде снежинки, нарисованная черепахой
Хотя черепашья графика и язык программирования Лого исторически развивались параллельно, потом пути их разошлись. Эйбелсон и диСесса отмечают, что черепахи обосновались по меньшей мере еще в двух языках (разновидностях АПЛ и Smalltalk), а программы в их книге написаны не на Лого, а на специальном языке, названном ими Turtle Procedure Notation. Они советуют создать систему черепашьей графики на базе Бейсика и Паскаля. Черепаха наложила отпечаток и на новый язык Boxer, который сейчас разрабатывается в МТИ членами группы Лого.
СAM ПО СЕБЕ Лого - мощный универсальный язык программирования. Тесные родственные узы связывают его с Лиспом - языком для обработки списков, изобретенным более 20 лет назад Джоном Маккарти. Различия между этими языками в сущности сводятся к различиям в словаре и пунктуации. Лого был задуман как язык для детей и был решен в антропоморфическом аспекте. Программист пишет так, как если бы он обращался непосредственно к черепахе, и время от времени черепаха дерзит, выдавая сообщение об ошибке: "Я не знаю, как делать квадраль". Подобная "застенчивость" не должна вводить вас в заблуждение: это делается не забавы ради. Антропоморфизм здесь умышленный - это средство вовлечения программиста (ребенка или взрослого - все равно) в эксперимент с системой черепашьей графики. Когда программа ставит вас в тупик, она советует "поиграть с черепахой".
Глубочайшая связь между черепашьей графикой и языком Лого состоит в общем подходе к методике обучения. Основная идея этого подхода заимствована из работ Жана Пьяже, в которых высшим достижением в процессе обучения считаются открытия, сделанные самими учащимися. Пейперт, в течение пяти лет работавший с Пьяже, изложил его взгляды в работе "Mind-storms: Children, Computers and Powerful Ideas": "Программирование поведения черепахи начинается с воспроизведения того, что стал бы делать сам программист на месте черепахи. Таким образом, обучая черепаху действовать или "думать", он вынужден воспроизводить собственное поведение или мысли... Эксперимент может оказаться и опрометчивым: размышляя о процессе мышления, ребенок превращается в гносеолога, а такая роль подчас бывает не по силам и взрослым".
БИБЛИОГРАФИЯ
MlNDSTORMS: CHILDREN, COMPUTERS, AND POWERFUL IDEAS. SEYMOUR PAPERT. Basic Books. Inc., 1980.
TURTLE GEOMETRY: THE COMPUTER AS A MEDIUM FOR EXPLORING MATHEMATICS. Harold Abelson and Andrea A. di Sessa. The MIT Press, 1980.
ПОВОРАЧИВАЮЩАЯСЯ ЧЕРЕПАХА ПОЗВОЛЯЕТ ВЗГЛЯНУТЬ НА ГЕОМЕТРИЮ "ИЗНУТРИ"
БРАЙАН ХЭЙЕС
ЧТО ТАКОЕ окружность? Быть может, это предел, к которому стремится n-угольник при бесконечном возрастании n? Или это частный случай эллипса, в котором два фокуса слились в один? А может быть, геометрическое место точек плоскости, равноудаленных от заданной точки?
Разумеется, все эти определения имеют право на существование, и можно дать немало других. Но рассмотрим лишь одно из них: окружность представляет собой замкнутую кривую, образованную последовательным повторением двух чередующихся элементарных действий - продвижением чуть-чуть вперед и поворотом чуть-чуть вправо до тех пор, пока полный поворот не составит 360o. Такое определение принципиально отличается от других: вместо описания самой окружности или характерных ее свойств предлагается процедура построения. Более того, сама процедура имеет особый характер - ее формулировка целиком опирается на "локальные" свойства окружности. Для построения кривой достаточно информации об окрестности той точки, где вы сейчас находитесь; совсем не нужно представления о всей картине в целом. Также нет необходимости знать ни о расположении центра, ни даже о величине ее радиуса.
В такого рода процедурах и заключена суть нового взгляда на геометрию как на эмпирическую геометрию. При этом подходе исследователю предлагается вообразить себя путешествующим в мире геометрических фигур, тогда как для других подходов характерна тенденция отделить фигуры от наблюдателя, расположить их в ином пространстве. Разница здесь примерно такая же, как между непосредственным исследованием местности и изучением ее карты. Особенно полезен эмпирический подход в тех случаях, когда геометрические понятия изучают при помощи компьютеров. Определение, заданное процедурой, легко запрограммировать, и ЭВМ будет вычерчивать соответствующую фигуру.
НОВЫЙ взгляд на геометрию реализовался в так называемой "черепашьей графике", тесно связанной с языком программирования Лого, разработанным в 1960г. Сеймуром Пейпертом в Массачусетсом технологическом институте (МТИ) для ознакомления детей с основами программирования. С тех пор язык значительно усовершенствовался и сфера его приложения вышла за рамки образования. Среди многих внесших свой вклад в развитие Лого следует выделить сотрудников МТИ Харолда Эйбелсона и Андреа диСессу, которые в своей необыкновенно иллюстративной работе "Turtle Geometry: The Computer as a Medium for Exploring Mathematics" ("Черепашья графика. ЭВМ как средство математических исследований") изложили идеи, легшие в основу черепашьей графики.
Первая "черепаха" была механическим устройством: небольшая тележка на колесах, управляемая ЭВМ по командам, задаваемым с пульта. Ее построил английский нейрофизиолог У.Грей Уолтер в конце 40-х годов. Куполообразный корпус этой конструкции был похож на черепаший панцирь. Механическая черепаха могла передвигаться вперед и назад н менять направление поворотом на месте. В шасси было вмонтировано перо, так что когда черепаха ползала по листу бумаги, то прочерчивала на нем свою траекторию. Сегодня такая "напольная черепаха" известна меньше, чем "экранная черепаха", которая в виде треугольника перемешается по телевизионному экрану по команде с пульта или по введенной с терминала программе.
В большинстве методов формирования графического изображения при помощи ЭВМ используется фиксированная система координат, как правило декартова, с двумя перпендикулярными осями. Положение каждой точки на экране определяется относительно фиксированного начала координат, например левого нижнего угла, в котором пересекаются воображаемые оси. Направления на плоскости определяются также относительно этих осей. Чтобы задать команду для проведения отрезка прямой, достаточно указать координаты двух концевых точек. Если, например, эти точки (0, 0) и (100, 0), внизу экрана появится прямая линия длиной в 100 единиц.
Следует отметить, что в любой фиксированной системе координат результат выполнения команды не зависит от предшествующей последовательности команд. Совсем иное положение в черепашьей графике. Чтобы прочертить отрезок прямой длиной в 100 единиц, черепахе дают команду ВПЕРЕД 100. Однако, где именно на экране появится этот отрезок и как он будет ориентирован, целиком зависит от состояния черепахи к моменту получения команды. Состояние черепахи в любой момент определяется ее местоположением и курсом. Команда ВПЕРЕД 100 служит для черепахи основанием продвигаться из своего текущего положения на 100 единиц в направлении, определяемом текущим курсом (т.е. "головой вперед"). Следовательно, одна и та же команда в зависимости от начального состояния черепахи может привести к абсолютно разным результатам.
Пользуясь всего лишь двумя командами ВПЕРЕД и НАПРАВО, можно получить простую систему черепашьей графики. После команды ВПЕРЕД указывается число, означающее количество шагов, которое должна пройти черепаха. После НАПРАВО также следует число, выражающее угол в градусах, на который черепаха должна отклониться вправо от своего текущего курса. Последовательными продвижениями вперед и правыми поворотами можно начертить на плоскости любую геометрическую фигуру. (Заметим, что левый поворот на 90o можно определить двояко: НАПРАВО 270, или НАПРАВО - 90). Тем не менее в реальных системах черепашьей графики обычно есть команды НАЗАД (или ОБРАТНО) и НАЛЕВО. Командами ПЕРОВНИЗ и ПЕРОВВЕРХ дается или отменяется указание вычерчивать траекторию движения черепахи. Имеется также несколько команд, которые позволяют по состоянию черепахи вычислять ее абсолютные координаты, но для черепашьей графики они не существенны.
ГЕОМЕТРИЮ, порожденную черепашьей графикой, формально можно назвать конечно-разностной геометрией. Она конечная, так как черепаха способна передвигаться только дискретными шагами, и разностная, потому что все перемещения определяются разностью между текущими и последующими значениями положения и курса. Таким образом, в иных терминах выражено то обстоятельство, что в этой разновидности геометрии мы имеем дело лишь с локальными свойствами прямых, кривых и поверхностей; информации об отдаленных точках или о глобальных свойствах геометрических фигур здесь не требуется. Следовательно, от черепашьей графики больше всего проку, когда мы стремимся выявить "подлинный характер" геометрической фигуры, т.е. когда нас интересует ее "внутреннее содержание".
Есть одно понятие, которое очень трудно сформулировать в декартовой системе координат, но стоит воспользоваться черепашьей графикой, как оно становится абсолютно прозрачным. Это понятие кривизны. В декартовых координатах кривизну некоторой линии на плоскости можно представить себе как скорость изменения тангенса угла наклона касательной от точки к точке. Изменение тангенса в свою очередь соответствует изменению координаты y как функции координаты x. Черепахе следить за кривизной значительно проще: это полный поворот, совершаемый ею за один шаг. Таким образом, в окружности, которая определяется последовательным чередованием команд ВПЕРЕД 1, НАПРАВО 1, кривизна в любой точке равна 1.

Несколько получаемых черепахой команд (слева) и иллюстрация понятия полного поворота (справа)
Понятие полного поворота обогащает нас другими интересными находками. Рассмотрим всем известную теорему евклидовой геометрии о сумме внутренних углов выпуклого многоугольника. В треугольнике эта сумма равна 180o. в четырехугольнике - 360o, в пятиугольнике - 540o, и т.д. Иными словами, это всегда целое число, умноженное на 180o, где целое на два меньше числа сторон. Полный поворот черепахи складывается совсем из других углов: это не внешние и не внутренние углы, а отклонения от курса в каждой вершине. Можно сформулировать теоремы о полном повороте в многоугольнике. Они будут несколько отличаться от теорем о внутренних углах, но им также свойственна общность.
В самой фундаментальной теореме утверждается, что полный поворот черепахи, вычерчивающей многоугольник, выражается целым числом, умноженным на 360o. Доказательство просто и совершенно очевидно. Если кривая замкнута (а это справедливо для любого многоугольника), то черепаха обязательно должна вернуться в исходную точку, и, когда это произойдет, курс черепахи должен быть таким же, как в начале ее пути. (Последнее фактически может служить некоторым эффективным определением геометрической замкнутости). Если курс совпадает с исходным, то полный поворот равен 0o, или 360o, или любому кратному 360o.
Для выпуклого многоугольника можно доказать более сильный результат: полный поворот равен точно 360o. (Многоугольник называется выпуклым, если прямая, связывающая любые две точки, принадлежащие его сторонам, никогда не выйдет за пределы многоугольника). Эта теорема, однако, применима к любым многоугольникам, в том числе и к невыпуклым (таким, как пятиконечная звезда). Она применима даже к замкнутым фигурам, стороны которых образованы кривыми и которые, следовательно, не являются многоугольниками.

Топологически замкнутые кривые, в которых использовано понятие полного поворота
В геометрии, основанной на фиксированной системе координат, у суммы внутренних углов выпуклого многоугольника мало очевидных взаимосвязей с другими понятиями. А вот в черепашьей графике понятие полного поворота служит мощным средством, применимым в широкой области. Эйбелсон и диСесса показали, что его можно использовать, например, для анализа топологических свойств замкнутого пути. Путь, составленный из любого числа прямых, кривых и витков, называется простым в топологическом смысле, если в нем нет пересечений. Как и в простом выпуклом многоугольнике, полный поворот для простого пути равен 360o. Добавление одной петли (и одного пересечения) превращает полный поворот в 0o либо в 720o, в зависимости от ее ориентации. С каждой новой петлей либо добавляется, либо вычитается 360o. На этом основании, находясь на месте черепахи, топологические свойства пути можно определить, имея в каждый момент в поле зрения лишь микроскопический участок пути.
Понятие полного поворота легло в основу алгоритма, позволяющего черепахе найти выход из лабиринта. У Эйбелсона и диСессы алгоритм выглядит так:
"1. Выбрать произвольное начальное направление (например, на север) и встать к нему лицом.
2. Двигаться в "северном" направлении до тех пор, пока не встретится препятствие.
3. Поворачивать налево до тех пор, пока это препятствие не окажется справа от вас.
4. Обходить это препятствие так, чтобы оно все время оставалось справа от вас, пока полный поворот (включая первый поворот на шаге 3) не станет равным 0.
5. Вернуться к шагу 2".
Следуя этим правилам, черепаха сможет выбраться из любого лабиринта (разумеется, при условии, что он имеет выход). Эта процедура всегда работает, потому что есть только одна возможность заманить черепаху в ловушку - завести ее в бесконечный цикл. А если следовать курсу полного поворота, такой ловушки можно избежать. Снова отметим, что стоящая перед черепахой глобальная задача - найти дорогу из лабиринта - будет решена, несмотря на то что черепахе доступны сведения только о ближайшем окружении; взгляд на лабиринт с высоты птичьего полета абсолютно не нужен. Универсальная процедура решения лабиринта называется алгоритмом Пледжа в честь англичанина Джона Пледжа из Эксетера, придумавшего алгоритм в двенадцатилетнем возрасте.

Черепаха, следуя алгоритму Пледжа, выбирается из лабиринта
Еще большие возможности появляются, если понятие полного поворота применить к случаю, когда поверхность, по которой разрешается бродить черепахе, не плоскость. На сфере, например, полный поворот по замкнутому пути оказывается меньше 360o. Более того, величина отклонения от 360o зависит от длины пути или, точнее, от области, которую этот путь охватывает. Читатели, знакомые с неевклидовой геометрией (открытой в XIX столетии), должны понять, в чем здесь дело: в угловом дефекте - мере кривизны поверхности. В этом примере существенно, что измерение может быть сделано только по локальной информации. Если в качестве примера вам больше нравится кривизна пространства-времени Вселенной, то и эта мера, очевидно, была получена изнутри Вселенной. Эйбелсон и диСесса рассматривают эти вопросы в конце своей книги (см. библиографию), где они формулируют общую теорию относительности при помощи черепашьей графики.
Они также рассматривают блуждания черепахи по поверхности куба, которая топологически эквивалентна сфере, но имеет совсем другие геометрические свойства. В самом деле, геометрия поверхности куба весьма причудлива. Предположим, что длина ребра куба равна 100 единицам и что сначала черепаха находится в центре одной иэ граней и направлена параллельно какому-нибудь ребру. Трижды повторим команды ВПЕРЕД 100, НАПРАВО 90. В результате получим замкнутую кривую, ограничивающую геометрическую фигуру с тремя равными углами и тремя равными сторонами, или, можно сказать, равносторонний многоугольник с прямыми углами. Что же это - правильный треугольник с прямыми углами или квадрат с тремя сторонами?
Другим замечательным примером геометрии кубической поверхности может служить моногон - односторонний многоугольник. Это замкнутый путь, который проделывает черепаха, движущаяся все время в одном направлении, без поворотов. Представить себе, как получается такой моногон, очень просто, даже не имея черепахи, управляемой компьютером: мысленно проведите на кубе "экватор". Куда сложнее другой вопрос: существует ли на поверхности куба такая комбинация начального положения и курса, которая не приводит к моногону, если двигаться все время в заданном направлении? Что если этот угол выражается иррациональным числом? Ответ можно найти в гл.6 упомянутой выше книги Эйбелсона и диСессы, но авторы настоятельно не советуют его смотреть. В одном месте они помещают такое предостережение: "ОСТОРОЖНО! В следующем разделе содержится "сверхтворение" математики (уже открытое). Оно может повредить вашему воображению, так что пользуйтесь этим материалом только н самом крайнем случае".
ОТКРЫТИЕ какого-либо принципа и исследование его обобщений весьма характерно для стиля черепашьей графики. Этот процесс значительно упрощается благодаря компьютеру: эксперименты ставятся очень легко, а любые вариации на заданную тему получаются мизерными усилиями. Короче говоря, это геометрия для халтурщиков.
Рассмотрим следующую процедуру, описанную Эйбелсоном и диСессой и другими авторами работ по языку Лого:
НА КВАДРАЛЬ :РАССТОЯНИЕ
ВПЕРЕД :РАССТОЯНИЕ
НАПРАВО 90
КВАДРАЛЬ :РАССТОЯНИЕ + 5
КОНЕЦ
Здесь КВАДРАЛЬ - название процедуры, РАССТОЯНИЕ - переменная, начальное значение которой задается при обращении к процедуре. (Двоеточие - принятое в Лого соглашение для идентификации переменных). Черепахе дается команда двигаться вперед на заданное расстояние и потом повернуть на 90o; затем процедура КВАДРАЛЬ выполняется снова, но уже с большим значением переменной РАССТОЯНИЕ. В результате получается "КВАДратная спиРАЛЬ", которая, постепенно расширяясь, подходит к рамке экрана. (Спираль, полученная по приведенной здесь процедуре, может расти бесконечно, хотя на экране будет виден только ее конечный фрагмент).
Допустимы всевозможные модификации. Меняя постоянное слагаемое, которое прибавляется к переменной, мы будем всего лишь равномерно стягивать или растягивать витки спирали. Если же сложение заменить умножением на константу, большую единицы, то получится спираль, прямые отрезки которой будут увеличиваться пропорционально их расстоянию от центра. Если в команде НАПРАВО 90 подставлять другие постоянные значения угла, то можно получать треугольную, пятиугольную и какую-угодно-угольную спирали. Если угол отличается от прямого незначительно, получается совокупность вложенных "квадратов", закручивающаяся вокруг центра, причем их вершины описывают другие спирали. Задание очень маленького угла приводит к некоему приближению к гладкой "круговой" спирали.
Можно также изменить процедуру таким образом, чтобы при каждом обращении к ней менялось не расстояние, а угол. Метаморфоза совершенно потрясающая: вместо одной постоянно раскручивающейся спирали черепаха рисует скручивающуюся спираль и затем, поменяв направление, раскручивающуюся спираль, потом другую скручивающуюся и т.д., создавая симметричный массив спиралей, связанных воедино самыми объемлющими циклами. Причина кроется в том, что при добавлении постоянной расстояние может увеличиваться лишь монотонно, тогда как изменение на константу угла обязательно приведет снова к малому его значению, поскольку значения углов повторяются с периодом 360o.
Рассмотрим один подкласс кривых, полученных при начальном значении угла 0o (см. рисунок на с.62). Все узоры этого класса по основным очертаниям аналогичны. Черепаха создает ряд спиралей, то раскручивая, то закручивая их, затем проходит весь этот путь в обратном направлении и, вернувшись в исходную точку, создает идентичный массив, отраженный относительно первого на 180o. Этот путь черепаха проходит бесконечно. Количество нарисованных ею спиралей зависит только от приращения угла, но природа этой зависимости далеко не очевидна. Если приращение угла не делится на 8, то число спиралей на единицу больше числа, полученного от деления приращения на наибольший общий делитель приращения и 360. Можете объяснить почему? Можете ли вы предсказать общие очертания узора, когда приращение кратно 8?

Восемь семейств спиралей, полученных добавлением фиксированного приращения к начальному углу 0o
Благодаря компьютеру стало возможно изучать семейства таких спиралей. Аналогичные исследования можно предпринять в отношении семейства многоугольников, ячеистых покрытий и рекурсивных фигур вроде снежинки, которая получается повторением в постоянно уменьшающемся масштабе одной и той же структуры (см. рисунок на с.98). В этом процессе неоценимую помощь может оказать черепашья графика благодаря конструктивному и алгоритмическому ее определению. Было бы по крайней мере нелепо выписывать уравнение, которое целиком описывает структуру снежинки, если можно воспользоваться процедурой порождения такой конфигурации, легко разбиваемой на несколько повторяющихся элементарных шагов.

Вложенная последовательность кривых в виде снежинки, нарисованная черепахой
Хотя черепашья графика и язык программирования Лого исторически развивались параллельно, потом пути их разошлись. Эйбелсон и диСесса отмечают, что черепахи обосновались по меньшей мере еще в двух языках (разновидностях АПЛ и Smalltalk), а программы в их книге написаны не на Лого, а на специальном языке, названном ими Turtle Procedure Notation. Они советуют создать систему черепашьей графики на базе Бейсика и Паскаля. Черепаха наложила отпечаток и на новый язык Boxer, который сейчас разрабатывается в МТИ членами группы Лого.
СAM ПО СЕБЕ Лого - мощный универсальный язык программирования. Тесные родственные узы связывают его с Лиспом - языком для обработки списков, изобретенным более 20 лет назад Джоном Маккарти. Различия между этими языками в сущности сводятся к различиям в словаре и пунктуации. Лого был задуман как язык для детей и был решен в антропоморфическом аспекте. Программист пишет так, как если бы он обращался непосредственно к черепахе, и время от времени черепаха дерзит, выдавая сообщение об ошибке: "Я не знаю, как делать квадраль". Подобная "застенчивость" не должна вводить вас в заблуждение: это делается не забавы ради. Антропоморфизм здесь умышленный - это средство вовлечения программиста (ребенка или взрослого - все равно) в эксперимент с системой черепашьей графики. Когда программа ставит вас в тупик, она советует "поиграть с черепахой".
Глубочайшая связь между черепашьей графикой и языком Лого состоит в общем подходе к методике обучения. Основная идея этого подхода заимствована из работ Жана Пьяже, в которых высшим достижением в процессе обучения считаются открытия, сделанные самими учащимися. Пейперт, в течение пяти лет работавший с Пьяже, изложил его взгляды в работе "Mind-storms: Children, Computers and Powerful Ideas": "Программирование поведения черепахи начинается с воспроизведения того, что стал бы делать сам программист на месте черепахи. Таким образом, обучая черепаху действовать или "думать", он вынужден воспроизводить собственное поведение или мысли... Эксперимент может оказаться и опрометчивым: размышляя о процессе мышления, ребенок превращается в гносеолога, а такая роль подчас бывает не по силам и взрослым".
БИБЛИОГРАФИЯ
MlNDSTORMS: CHILDREN, COMPUTERS, AND POWERFUL IDEAS. SEYMOUR PAPERT. Basic Books. Inc., 1980.
TURTLE GEOMETRY: THE COMPUTER AS A MEDIUM FOR EXPLORING MATHEMATICS. Harold Abelson and Andrea A. di Sessa. The MIT Press, 1980.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
5 1984
КЛЕТОЧНЫЙ АВТОМАТ СОЗДАЕТ МОДЕЛЬ МИРА И МИР ВОКРУГ СЕБЯ
БРАЙАН ХЭЙЕС
УДИВИТЕЛЬНО, что молекулы воды "знают", как создавать сложные симметричные снежинки. Никакой "архитектор" не руководит строительством, и молекулы не несут информации об этой кристаллической структуре. Весь узор возникает в результате ближних взаимодействий множества одинаковых частиц. Каждая молекула реагирует только на воздействие ближайших соседей, но расположение в определенном порядке сохраняется во всей структуре, состоящей примерно из 1E20 молекул.
Чтобы лучше понять этот процесс, представим себе, что каждое место, где молекула может быть помешена (так называемый центр), управляется с помощью элементарного компьютера. По мере роста кристалла компьютер наблюдает за соседними центрами и, находя их, определяет по некоторому установленному правилу, должно ли быть занято его собственное место, или оно должно пустовать. Подобные вычисления проводятся для всех центров по одному и тому же правилу.
Вычислительная модель роста снежинки является клеточным, или ячеистым, автоматом - однородной схемой многих идентичных клеток, или ячеек, причем каждая клетка имеет несколько возможных состояний и взаимодействует лишь с несколькими соседними клетками. Компоненты системы - клетки, или ячейки, и правило вычисления следующего состояния клетки может быть простым, но тем не менее вызывает весьма сложную эволюцию.
ИДЕЯ автомата с клеточной структурой почти так же стара, как и идея электронно-вычислительной машины. Первые исследования были проведены в начале 50-х годов Дж. фон Нейманом (следует учесть важный вклад в эти разработки С.Улама). Первоначальная цель фон Неймана состояла в создании простой системы, способной воспроизводить саму себя подобно живому организму. Наиболее известный клеточный автомат - игра "Жизнь", придуманная в 1970г. Дж.Конвеем, как ясно из названия, также имеет биологический аспект: клетки рождаются, живут или умирают в зависимости от локальной плотности популяции.
В более поздних работах, посвященных клеточным автоматам, исследования приняли несколько другое направление. Конфигурации локально взаимодействующих клеток рассматриваются как потенциально важные модели физических систем - от снежинок до ферромагнетиков и Галактики. Они применимы также к вопросам кибернетики и вычислительной математики, как практическим (как следует организовать сеть взаимодействующих ЭВМ?), так и теоретическим (каков самый крайний предел мощности вычислительной машины?). Возможно, наиболее интригующим является тот факт, что клеточный автомат может рассматриваться как "числовая вселенная", которая сама по себе достойна исследования, даже если отвлечься от ее полезности как модели реального мира.
Возрождение интереса к клеточным автоматам было отмечено созданием рабочей группы по данной теме год назад в Лос-Аламосской национальной лаборатории. Был опубликован сборник работ (около 20 статей) в журнале "Physica D" и отдельным выпуском в издательстве "North-Holland". Почти все, что содержится в этом сборнике, основано на работах, обсуждавшихся на специальном симпозиуме в Лос-Аламосе.
Для характеристики клеточного автомата полезно выделить четыре его аспекта. Во-первых, расположение клеток образует некоторую геометрическую фигуру. Для модели роста снежинок достаточна двумерная шестиугольная схема, но в большинстве других случаев выбирается прямоугольная решетка, состоящая из квадратов. Легко можно построить трехмерную (и даже с большим числом измерений) схему, но гораздо труднее ее себе представить. Недавно поразительные открытия были сделаны с простейшей одномерной схемой: простой цепочкой клеток.
Далее, при заданной схеме необходимо определить ту окрестность, которую данная клетка изучает при вычислении своего следующего состояния. В случае двумерных прямоугольных схем особое внимание уделяется окрестностям двух видов. Фон Нейман рассматривал четыре ближайших соседа каждой клетки: на севере, юге, востоке и западе; это множество клеток теперь называют окрестностью фон Неймана. Окрестность, включающую эти четыре соседние клетки и четыре клетки, прилегающие к исходной по диагоналям, называют окрестностью Мура (в честь Э.Мура). Ясно, что окрестности пересекаются и данная клетка входит сразу в несколько окрестностей. В некоторых случаях считают, что центральная клетка - та клетка, которая производит вычисления,- сама входит в свою окрестность.

Окрестности фон Неймана и Мура
Третий фактор, который следует рассматривать при описании клеточного автомата,- это число состояний, которое может принимать клетка. Фон Нейман построил самовоспроизводящуюся систему, составленную из клеток с 29 возможными состояниями, однако большинство автоматов гораздо проще. Имеется огромный диапазон для изменений даже у двоичных автоматов, у которых клетка имеет два возможных состояния. Состояния могут быть представлены как 1 или 0 (включено или выключено, живое или мертвое).
Наконец, первоисточник изменений в мире клеточных автоматов - это огромное число возможных правил для определения будущего состояния клетки исходя из теперешней конфигурации ее соседей. Если k - число состояний, которые может принимать каждая клетка, а n - число клеток, входящих в окрестность, то существует k^k^n возможных правил. Так, для двоичного автомата с окрестностью фон Неймана (где n=4) существует более чем 65000 возможных правил; для окрестности Мура (где n=8 ) имеется 1E77 правил. Однако лишь малая часть их когда-либо изучалась.
В ИГРУ "Жизнь" играют на прямоугольной решетке из клеток с двумя состояниями и с окрестностью Мура и дополнительным усложнением, согласно которому центральная клетка тоже считается членом своей окрестности. Другими словами, при каждом шаге эволюции системы каждая клетка проверяет состояния восьми своих соседей и свое собственное. Согласно правилам, установленным Конвеем, если центральная клетка жива, то она будет продолжать жить в следующем поколении, когда две или три клетки из ее окрестности живы. Если найдутся три живые клетки в рассматриваемой окрестности, то центральная клетка будет живой в следующем поколении независимо от ее теперешнего состояния. Во всех других случаях центральная клетка либо умирает, либо остается мертвой.
Прелесть игры "Жизнь" состоит в ее непредсказуемости. Некоторые схемы полностью умирают; многие другие образуют устойчивые конфигурации либо циклические конфигурации с периодом в несколько поколений. Однако за прошедшие годы было найдено много очень интересных начальных состояний, таких, как "скользящая пушка", которая порождает нескончаемый поток снарядов. Исследование игры "Жизнь" в настоящее время продолжается. Последние достижения были описаны Мартином Гарднером в книге "Wheels, Life, and Other Mathematical Amusements". Здесь же я рассмотрю другие клеточные автоматы, свойства которых только начинают исследовать.
Среди множества возможных правил перехода лишь немногие интересны сами по себе. Например, правило, устанавливающее, что данная клетка будет "включена" тогда и только тогда, когда клетка слева от нее включена, определяет эволюцию, которую очень легко предсказать: любая начальная схема сохраняет свою конфигурацию, но сдвигается на одну клетку вправо на каждом временном шаге. Подкласс правил, называемых счетными, или суммирующими, по-видимому, содержит образцы почти всех встречающихся типов клеточных автоматов. При правилах такого рода новое состояние клетки зависит только от числа соседей в данном состоянии, но не от их положения. Многие автоматы, основанные на таких правилах, были изучены членами группы информационной механики лаборатории вычислительной математики в Массачусетсом технологическом институте. В эту группу входят Э.Фредкин, Н.Марголус, Т.Тоффоли и Дж.Вишняк.
Одно из простейших счетных правил - это правило четности, которое приписывает клетке значение 1, если нечетное число соседей находится в состоянии I, и значение 0 в других случаях. Пространственная эволюция этой системы с применением этого правила в окрестности фон Неймана была описана в октябрьском номере нашего журнала [См.: В мире науки, 1983, #12, с.103-109]. Любая начальная конфигурация повторяется четыре раза, затем эти четыре копии в свою очередь повторяются и т.д.
Другой класс счетных правил - это правила "голосования", при которых центральной клетке приписывается значение 1, как только число единиц в ее окрестности превышает некоторое пороговое значение. В докладе на Лос-Аламосском симпозиуме Вишняк отметил, что по правилам такого типа получаются модели фильтрации (просачивания) и образования активных центров - очень важных явлений в физике твердого тела и других областях науки. Термином "фильтрация" обозначают образование непрерывного пути через некоторое пространство; например, когда металл распределен в изолирующей матрице, проводимость материала зависит от вероятности образования непрерывной цепочки атомов металла. Точно так же передача инфекционного заболевания возможна только при наличии непрерывающейся последовательности восприимчивых индивидов. Образование активных центров - процесс, на котором основаны рост кристаллов, кипение жидкости и другие подобные явления.
Одно из правил перехода, приводящее к фильтрации, присваивает центральной клетке значение 1 только тогда, когда значения по меньшей мере трех клеток из пяти - т.е. окрестности фон Неймана плюс центральная клетка - равны 1. Развитие фильтрации очень сильно зависит от исходной концентрации единиц. Если концентрация меньше половины, то непрерывная цепочка единиц, заполняющих схему, по-видимому, не образуется в ходе эволюции. При концентрации 1/2 и больше появляются цепочки, но вся решетка ими не заполняется; в заключительном устойчивом состоянии остаются "островки" нулей. Образование кристаллов, при котором схема прочно заполняется единицами, наблюдается в том случае, когда правило изменяется и требуются лишь две из пяти единиц в окрестности. Критическая концентрация равна 0.0822.
Эволюция клеточного автомата при правиле голосования "два из пяти".
МОДЕЛЬ Изинга, одно из средств теоретического аппарата физики, при поверхностном рассмотрении кажется очень похожей на клеточный автомат. Модель представляет собой прямоугольную решетку, в которой каждый центр имеет два возможных значения и взаимодействует лишь с четырьмя своими ближайшими соседями. Эта модель часто используется для описания ферромагнетиков: каждый центр представляет собой атомный спин, который может быть направлен либо вверх, либо вниз. Если температура ниже критической (температуры Кюри), спины стремятся ориентироваться одинаково и материал намагничивается, но при более высоких температурах их направления распределены более или менее случайным образом.
В октябрьском номере журнала я рассматривал вариант модели Изинга, созданный с помощью КЭБ-программ. Клеточная структура этой модели располагает к использованию методов клеточных автоматов при ее изучении. Я заметил любопытное явление: при низкой температуре спины направлены неодинаково, они располагаются в шахматном порядке, при котором направления "вверх" и "вниз" чередуются. При каждом временном шаге все спины меняют свое направление. В ферромагнетиках шахматная структура является конфигурацией с высшей энергией и поэтому должна быть неустойчивой; эта структура характерна для антиферромагнетиков.
Вишняк обнаружил эту проблему и объяснил ее. В стандартном варианте модели Изинга при каждой итерации может изменяться только один спин. Следовательно, когда некоторый конкретный центр наблюдает за своими соседями, то одни из наблюдаемых спинов являются "старыми", а другие "новыми". При этих условиях "осциллирующий" антиферромагнетик не может возникнуть. Только когда все спины одновременно "производят свои вычисления", возникают благоприятные условия для антиферромагнетика высокой энергии. Существует возможность избежать этой "катастрофы обратной связи", однако более важный вывод состоит в том. что интуитивное соответствие между моделью Изинга и клеточным автоматом обманчиво.
Вишняк и другие ученые из группы Массачусетского технологического института подчеркивают, что клеточный автомат имеет статус, отличный от статуса других физических моделей. Наиболее распространенным средством построения математической модели мира издавна служило дифференциальное уравнение, которое описывает изменения некоторой величины как функцию координат и времени. Например, уравнения Максвелла дают изменения электромагнитного поля от точки к точке и от одного момента времени к другому. Все величины в таких уравнениях являются непрерывными (они гладко изменяются), с другой стороны, клеточный автомат - полностью дискретная система. Пространством является не континуум, а клеточная схема; время разбивается на последовательность дискретных шагов, а клетки автомата могут иметь лишь конечное число состояний, в то время как величина поля принимает значения из непрерывной области значений.
Разумеется, реальные пространство и время и многие физические переменные величины рассматриаются как непрерывные, а не дискретные (по крайней мере, в наиболее распространенных областях исследований). Однако из этого не следует, что дифференциальные уравнения по своей природе позволяют построить более совершенную модель реального мира. Когда уравнения должны быть решены численно, как при моделировании с помощью ЭВМ, непрерывные переменные могут быть вычислены приблизительно с некоторой конечной точностью; на самом деле они представляются дискретными величинами. При использовании клеточных автоматов дискретность выступает в явном виде, и их временная эволюция может быть вычислена точно; здесь приближения не нужны. Кроме того, в этом случае можно в большей степени использовать возможности цифровых вычислительных машин.
МОЖНО написать программу моделирования клеточного автомата лаже для самого миниатюрного компьютера. Действительно, П.Бак из Брукхейвенской национальной лаборатории недавно утверждал в журнале "Physics Today", что моделирование в физике можно эффективнее и дешевле производить на небольшом персональном компьютере, а не на более мощных вычислительных машинах общего пользования. Для иллюстрации этого он выбрал пример трехмерной модели Изинга на Commodore VlC-20 - компьютере стоимостью 4 доллара.
Наиболее прямолинейная программа клеточного автомата просто является воплощением метода, который каждый бы применял при выполнении процедуры ручным способом на листе бумаги в клетку. Сначала строится клеточная схема, в которой каждая клетка представлена ячейкой памяти в компьютере. При каждом временном шаге программа должна обращаться к каждой клетке по очереди, изучать ее окрестность и вычислять следующее состояние клетки. Само вычисление легко выполняется с помощью поиска значения в таблице. Если рассматриваются только счетные правила, таблице нужен всего один элемент для каждого возможного числа "активных" клеток. Когда допускаются правила другого рода, таблица может стать очень сложной.

Алгоритм для клеточного автомата, основанный на счетном, или суммирующем, правиле перехода
При написании такой программы следует иметь в виду несколько тонких моментов. Очень важно не нарушить состояния клетки, пока оно не проверено всеми другими клетками, в окрестность которых она входит. Простейший путь выполнения этого требования - сохранение двух копий данной схемы; программа изучает одну копию для определения текущего состояния окрестности и вносит результаты вычислений в другую копию. Следует также определить условия на границе. Идеальным случаем была бы бесконечная схема, но ясно, что это невыполнимо. Распространенным приемом является соединение концов схемы, так что клетки на противоположных краях становятся соседними. В одномерном случае схема такого рода топологически является окружностью, а в двумерном - тором, хотя это и конечные схемы, но границ они не имеют.
Программа описанного выше типа, выполняемая на универсальной ЭВМ, является последовательностной процедурой, которая моделирует действия схемы из многих компьютеров, работающих одновременно. Лучше было бы построить настоящую сеть многих компьютеров со структурой клеточного автомата. Конечно, не может быть и вопроса о построении такой машины (индивидуальные компьютеры должны быть довольно простыми и построены в большинстве случаев на одном полупроводниковом кристалле). Тот факт, что только близко расположенные компьютеры должны взаимодействовать между собой, также должен был бы уменьшить сложность всего устройства. По оценке Тоффоли, процессор должен был бы работать быстрее, чем ЭВМ общего назначения в миллион или даже миллиард раз.
Предварительные разработки для компьютеров подобного рода производятся в Калифорнийском технологическом институте и Thinking Machines Corporation of Wallham (шт. Массачусетс).
Вместо того чтобы использовать кристаллы специального назначения, Тоффоли построил машину, имитирующую клеточный автомат, из стандартных компонентов микроэлектроники. Вычисления производятся последовательно, а не для всех клеток сразу, но, поскольку весь аппарат приспособлен к единственному виду вычислений, его быстродействие оказывается в 1000 раз больше, чем у универсальной ЭВМ. Сама машина представляет собой набор печатных плат, смонтированных в корпусе; она соединена с цветным дисплеем и управляется другим миниатюрным компьютером - Atari-800.
Машина Тоффоли, имитирующая клеточный автомат, имеет схему из 256*256 клеток, каждая из которых может принимать до 256 состояний. Состояние каждой клетки перевычисляется 60 раз в секунду. За счет высокой скорости изменения состояния такой системы вместо последовательности неподвижных фотографий мы видим фильм. Игра "Жизнь" больше не представляется как величественная прогрессия абстрактных узоров; она теперь больше походит на картину, наблюдаемую под микроскопом при изучении поведения бактерий или простейших организмов, плавающих, вращающихся, размножающихся, пожирающих и пожираемых друг другом.

Игра "Жизнь", развивающаяся на экране машины, созданной Тоффоли и имитирующей клеточный автомат
ДЛЯ ОДНОМЕРНОГО клеточного автомата нужны менее мощные вычислительные средства (как в смысле объема памяти, так и в смысле быстродействия), чем для двумерного. Для одномерной системы легче написать программу. Линейная схема имеет еще одно преимущество над схемой на плоскости: более простая геометрическая структура позволяет легче аналитически понять эволюцию автомата. С.Вольфрам из Института высших исследований посвятил этому вопросу два гола работы.
Единственное поколение одномерной схемы - просто ряд клеток, но последовательные поколения должны быть нанесены одно вслед за другим. Таким образом строится двумерная схема, имеющая одну пространственную и одну временную оси, и всю эволюцию системы можно окинуть одним взглядом.
Вольфрам обнаружил, что все правила перехода, которые он исследовал до сих пор, можно разбить на четыре класса. Класс I состоит из тех правил, при которых эволюция приводит к устойчивому и однородному состоянию; например, все клетки принимают значения либо 1, либо 0. Класс 2 приводит к простым структурам, которые устойчивы или периодичны, но в любом случае остаются изолированными друг от друга. Правила класса 3 создают хаотические узоры, хотя и не обязательно случайные. В классе 4 собрано несколько правил перехода, которые порождают структуры существенной пространственной и временной сложности.

Четыре класса суммирующих правил в одномерном случае
Вольфрам предположил, что одномерный клеточный автомат может быть простейшей правильно определенной системой, способной на сложное самоорганизующееся поведение. В природе многие непрерывные динамические системы имеют такую способность: начиная со случайного начального состояния они эволюционируют в высокоорганизованную структуру. (Примером служит снежинка). Эта эволюция может быть описана в терминах аттракторов, которые, по-видимому, притягивают систему к некоторому подмножеству всех возможных конфигураций.
Была проведена параллель между классами клеточных автоматов и некоторыми типами аттракторов, наблюдаемых в физических системах. Автоматы класса 1 аналогичны непрерывной системе с простейшим аттрактором - предельной точкой, которая неизменно приводит систему к одному и тому же заключительному состоянию. Эволюция автомата из класса 2 более похожа на эволюцию системы с предельным циклом, которая представляет собой последовательность бесконечно повторяющихся конфигураций.
Автоматы из класса 3 с их хаотическими узорами можно сопоставить с более интересным" объектами, называемыми странными аттракторами, которые присущи таким физическим явлениям, как возникновение турбулентного течения. В системе, управляемой странным аттрактором, эволюция стремится к некоторому подмножеству всех возможных конфигураций, однако это подмножество может иметь крайне сложную структуру. Когда это множество представляется как массив точек в пространстве, она во многих случаях является фракталью, геометрической фигурой с дробным числом измерений.
Различие между классами автоматов можно выяснить, рассмотрев простой эксперимент. Предположим, что клеточный автомат начал свою эволюцию с какой-то случайно выбранной начальной конфигурации и делает несколько временных шагов; затем отмечается заключительное состояние. Теперь вернемся к исходному состоянию, изменим значение единственной клетки и дадим системе возможность проделать такое же число временных шагов. Какой эффект окажет это небольшое изменение на заключительное состояние? У автоматов класса 1 никакого изменения не произойдет: система из класса 1 приходит в одно и то же заключительное состояние из любого начального состояния. У автоматов класса 2 может наблюдаться некоторый эффект, но он ограничен небольшой областью вблизи измененной клетки. В системе класса 3, изменив единственную клетку, можно вызвать такое нарушение, которое распространится на всю схему.
Правила класса 4 очень редко встречаются и являются самыми сложными. Некоторые совсем простые функции перехода попадают в этот класс; например, в окрестности, включающем центральную клетку и по две клетки с каждой стороны от нее, правило, устанавливающее, что значение центральной клетки равно 1, если две или четыре клетки равны 1, попадает в класс 4. Чувствительность к малым изменениям в начальном состоянии в классе 4 даже больше, чем в классе 3. Было выдвинуто предположение, что для предсказания будущего состояния автомата класса 4 не может быть более эффективной процедуры, чем разрешить автомату самому вычислить это состояние.

Последовательные состояния одномерного автомата из класса 4
Это предположение можно интерпретировать более широко, а именно что автоматы класса 4 можно квалифицировать как универсальные вычислительные машины. Машина Тьюринга - наиболее известное устройство подобного рода: если некоторая функция может быть вообще вычислена, предполагается, что это может сделать машина Тьюринга. Можно доказать, что другие вычислительные машины тоже универсальны, если они эквивалентны машине Тьюринга. Было показано, что некоторые двумерные клеточные автоматы (включая игру "Жизнь") являются универсальными вычислительными машинами, и было также дано доказательство для сложных одномерных систем, в которых каждая клетка имеет 18 возможных состояний. Автоматы класса 4 были бы самой простой известной универсальной вычислительной машиной. Установлено, что они имеют большинство основных компонент. Не хватает лишь одного элемента - счетчика: устройства, выдающего последовательность импульсов через регулярные интервалы, подобно "скользящей пушке" в игре "Жизнь".

Некоторые компоненты возможной универсальной вычислительной машины
Аналогия клеточных автоматов с вычислительными машинами наводит на мысль, что их самоорганизующееся поведение может быть описано в терминах их вычислительных характеристик. Так, например, множество конфигураций, порожденных эволюцией клеточного автомата, можно представить как некий формальный язык. Каждая конфигурация рассматривается как слово языка, образованного в соответствии с множеством грамматических правил из последовательности символов, представляющих значения клеток автомата. Вольфрам показал, что конфигурация, порожденная любым клеточным автоматом за конечное время, может быть описана простым классом формальных языков, известных под названием регулярных. Для любого из этих регулярных языков можно найти простейшую грамматику. Такая грамматика дает простейшее описание конфигураций клеточного автомата и ее емкость можно принять за меру сложности конфигураций. Для клеточных автоматов классов 1 и 2 сложность стремится к конечному пределу за длительный период времени, так что структуры, порожденные этой системой, описываются регулярными языками. Однако для клеточных автоматов классов 3 и 4. по-видимому, требуются более сложные формальные языки.
СУЩЕСТВУЕТ особый класс клеточных автоматов, называемых обратимыми. Из любого начального состояния на любое число временных шагов допускается эволюция обратимого автомата, а затем автомат останавливается и запускается обратным ходом, после чего он возвращается в свое точное начальное состояние. Конфигурации, образованные типичным обратимым автоматом, качественно отличны от конфигураций, свойственных необратимому автомату. В частности, если конфигурация вначале случайна, то она и стремится остаться случайной - самоорганизующейся структуры не возникает.
Необходимым условием обратимости является детерминированность правила перехода в обоих направлениях, вперед и назад, т.е. каждое возможное состояние окрестности должно иметь единственное предыдущее состояние и единственное последующее состояние. Игра "Жизнь" необратима, потому что предыдущий этап какого-нибудь состояния нельзя определить однозначно; например, если текущее состояние клетки - "мертва", в предыдущем поколении она могла иметь "любое число "живых" соседей, отличное от трех. Систематический способ создания обратимых правил перехода был изобретен Фредхином, а позднее исследован Марголусом. Суть этого метода - заставить следующее состояние клетки зависеть от двух предыдущих состояний окрестности. Состояние в момент t+1 дается некоторой функцией окрестности в момент t минус та же функция в момент t-1. Тогда обращение производится непосредственно: состояние в момент t-1 должно даваться состоянием в момент t минус состояние в момент t+1.
Из-за требования детерминизма в двух направлениях в эволюции обратимого автомата не должны встречаться аттракторы. Присутствие аттрактора ведет к тому, что входе эволюции многие начальные состояния развиваются такими путями, которые сливаются друг с другом; в обратной эволюции точки слияния стали бы точками ветвления, в которых нарушалось бы требование детерминизма. Точно так же обратимый клеточный автомат в своей эволюции не может образовать петли или выйти из нее, т.е. не может иметь циклических состояний, потому что снова возникает точка ветвления в том или ином направлении. Поскольку аттракторы и соответствующие им самоорганизующиеся конфигурации исключаются, может показаться, что обратимые правила перехода приводят к очень "скучным" клеточным автоматам, однако это компенсируется другими интересными особенностями таких систем. Самое замечательное - это то, что информация, заключающаяся в клеточной конфигурации обратимого автомата, оказывается сохраняемой величиной (т.е. не возрастающей и не убывающей в холе эволюции автомата). Это свойство делает обратимые системы ценными моделями вычислений.
Марголус построил компьютер, имитирующий клеточный автомат, основанный на воображаемой механической системе, ранее исследованной Фредкином,- модель вычисления на основе бильярдных шаров. В этой модели биты информации (1 или 0) несут идеальные бильярдные шары, которые движутся без трения и отскакивают один от другого и от других препятствий идеально упруго. Наличие шара в указанном положении означает двоичную 1, а его отсутствие - двоичный 0. Умелым расположением бортов можно создать различные логические вентили, подобные тем, которые имеются в электронно-вычислительной машине. Например, в схеме "И" один бильярдный шар проходит через выходную область (и тем самым регистрируется двоичная 1), если только два шара приближаются к вентилю одновременно вдоль специфических траекторий.
Вариант такой модели клеточного автомата, построенный Марголусом, основан на простом и в некотором смысле необычном обратимом правиле перехода. Клетки рассматриваются не по отдельности, а блоками по 4; любая возможная конфигурация в пределах блока преобразуется в единственную производную конфигурацию. Правило составлено так, что одна единица на фоне остальных нулей распространяется в одном из четырех диагональных направлений решетки со скоростью 1 клетка за временной шаг; изолированная единица является воплощением бильярдного шара. "Монолитный" блок, состоящий из четырех единиц, неопределенно долго остается неизменным и действует как абсолютный отражатель. Когда моделирование производится на машине Тоффоли, имитирующей клеточный автомат, то "бильярдные шары" мечутся по экрану дисплея, образуя сложные пересекающиеся траектории. Наблюдая это упорядоченное (пусть лаже безумное) движение, трудно помнить о том, что в программе не содержатся представления траекторий шаров, а просто применяется одно-единственное правило ко всем клеткам.

Правило перехода для компьютера "на бильярдных шарах"
МОДЕЛЬ на основе бильярдных шаров к ее воплощение в виде клеточного автомата тесно связаны с теорией вычислений. Было выдвинуто предположение, что любая вычислительная машина должна иметь компоненты, которые рассеивают энергию и информацию; в соответствии с этой теорией должен существовать "термодинамический предел" эффективности компьютера точно так же, как существует предел к.п.д. тепловою двигателя. Неизбежные, по предположению, потери информации и энергии являются прямым следствием необратимости вычислительного процесса. (Когда компьютер складывает 5 и 3, чтобы получить результат 8, процесс не может быть обращен, потому что существует бесконечно много чисел, которые при сложении лают тот же результат).
Фредкин, Тоффоли и Марголус подчеркивают, что модель на основе бильярдных шаров противоречит понятию неизбежного рассеяния. Действительно, бильярдные шары не могут сами себя создавать или разрушать, и вся информация, определяющая их начальную конфигурацию, сохраняется в ходе эволюции системы. Входы операции сложения могут быть легко восстановлены обращением траекторий. В принципе вычислительная машина, построенная на основе бильярдных шаров, могла бы действовать без внутренних затрат энергии.

Компьютер "на бильярдных шарах" в действии
С особой ясностью связь между физическими процессами и вычислениями была установлена Тоффоли в его заявлении, которое можно интерпретировать как описание самого большого из всех клеточных автоматов. "В некотором смысле,- пишет он,- в течение миллиардов лет природа постоянно вычисляла "следующее состояние" Вселенной; все, что нам надо сделать,- и действительно, что мы можем сделать,- это "войти в колею" этого гигантского непрекращающегося процесса вычисления и попытаться угадать, какая часть его движется в нужном нам направлении".

Узор дендритов, созданный клеточным автоматом с асимметричным правилом перехода
БИБЛИОГРАФИЯ
PHYSICS AND COMPUTATION. TOMMASO TOFFOLI in International Journal of Theoretical Physics, Vol.21, Nos.3/4, pages 165-175; April, 1982.
STATISTICAL MECHANICS OF CELLULAR AUTOMATA. STEPHEN WOLFRAM in Reviews of Modern Physics, Vol.55, No.3. pages 601-644; July, 1983.
CELLULAR AUTOMATA. STEPHEN WOLFRAM in Los Alamos Science, pages 2-21; Fall, 1983.
DOING PHYSICS WITH MICROCOMPUTERS. PER BAK in Physics Today, Vol.36, No.12, pages 25-28; December, 1983.
WHEELS, LIFE, AND OTHER MATHEMATICAL AMUSEMENTS. MARTIN GARDNER. W.H.Freeman and Company, 1984.
CELLULAR AUTOMATA: PROCEEDINGS OF AN INTERDISCIPLINARY WORKSHOP. Edited by Stephen Wolfram, J.Doyne Farmer and Tommaso Toffoli, in Physica D., Vol. 10D, Nos.1 and 2; January. 1984.
Т.ТОФФОЛИ, Н.МАРГОЛУС, МАШИНЫ КЛЕТОЧНЫХ АВТОМАТОВ, Москва, "МИР", 1991.- G.
КЛЕТОЧНЫЙ АВТОМАТ СОЗДАЕТ МОДЕЛЬ МИРА И МИР ВОКРУГ СЕБЯ
БРАЙАН ХЭЙЕС
УДИВИТЕЛЬНО, что молекулы воды "знают", как создавать сложные симметричные снежинки. Никакой "архитектор" не руководит строительством, и молекулы не несут информации об этой кристаллической структуре. Весь узор возникает в результате ближних взаимодействий множества одинаковых частиц. Каждая молекула реагирует только на воздействие ближайших соседей, но расположение в определенном порядке сохраняется во всей структуре, состоящей примерно из 1E20 молекул.
Чтобы лучше понять этот процесс, представим себе, что каждое место, где молекула может быть помешена (так называемый центр), управляется с помощью элементарного компьютера. По мере роста кристалла компьютер наблюдает за соседними центрами и, находя их, определяет по некоторому установленному правилу, должно ли быть занято его собственное место, или оно должно пустовать. Подобные вычисления проводятся для всех центров по одному и тому же правилу.
Вычислительная модель роста снежинки является клеточным, или ячеистым, автоматом - однородной схемой многих идентичных клеток, или ячеек, причем каждая клетка имеет несколько возможных состояний и взаимодействует лишь с несколькими соседними клетками. Компоненты системы - клетки, или ячейки, и правило вычисления следующего состояния клетки может быть простым, но тем не менее вызывает весьма сложную эволюцию.
ИДЕЯ автомата с клеточной структурой почти так же стара, как и идея электронно-вычислительной машины. Первые исследования были проведены в начале 50-х годов Дж. фон Нейманом (следует учесть важный вклад в эти разработки С.Улама). Первоначальная цель фон Неймана состояла в создании простой системы, способной воспроизводить саму себя подобно живому организму. Наиболее известный клеточный автомат - игра "Жизнь", придуманная в 1970г. Дж.Конвеем, как ясно из названия, также имеет биологический аспект: клетки рождаются, живут или умирают в зависимости от локальной плотности популяции.
В более поздних работах, посвященных клеточным автоматам, исследования приняли несколько другое направление. Конфигурации локально взаимодействующих клеток рассматриваются как потенциально важные модели физических систем - от снежинок до ферромагнетиков и Галактики. Они применимы также к вопросам кибернетики и вычислительной математики, как практическим (как следует организовать сеть взаимодействующих ЭВМ?), так и теоретическим (каков самый крайний предел мощности вычислительной машины?). Возможно, наиболее интригующим является тот факт, что клеточный автомат может рассматриваться как "числовая вселенная", которая сама по себе достойна исследования, даже если отвлечься от ее полезности как модели реального мира.
Возрождение интереса к клеточным автоматам было отмечено созданием рабочей группы по данной теме год назад в Лос-Аламосской национальной лаборатории. Был опубликован сборник работ (около 20 статей) в журнале "Physica D" и отдельным выпуском в издательстве "North-Holland". Почти все, что содержится в этом сборнике, основано на работах, обсуждавшихся на специальном симпозиуме в Лос-Аламосе.
Для характеристики клеточного автомата полезно выделить четыре его аспекта. Во-первых, расположение клеток образует некоторую геометрическую фигуру. Для модели роста снежинок достаточна двумерная шестиугольная схема, но в большинстве других случаев выбирается прямоугольная решетка, состоящая из квадратов. Легко можно построить трехмерную (и даже с большим числом измерений) схему, но гораздо труднее ее себе представить. Недавно поразительные открытия были сделаны с простейшей одномерной схемой: простой цепочкой клеток.
Далее, при заданной схеме необходимо определить ту окрестность, которую данная клетка изучает при вычислении своего следующего состояния. В случае двумерных прямоугольных схем особое внимание уделяется окрестностям двух видов. Фон Нейман рассматривал четыре ближайших соседа каждой клетки: на севере, юге, востоке и западе; это множество клеток теперь называют окрестностью фон Неймана. Окрестность, включающую эти четыре соседние клетки и четыре клетки, прилегающие к исходной по диагоналям, называют окрестностью Мура (в честь Э.Мура). Ясно, что окрестности пересекаются и данная клетка входит сразу в несколько окрестностей. В некоторых случаях считают, что центральная клетка - та клетка, которая производит вычисления,- сама входит в свою окрестность.

Окрестности фон Неймана и Мура
Третий фактор, который следует рассматривать при описании клеточного автомата,- это число состояний, которое может принимать клетка. Фон Нейман построил самовоспроизводящуюся систему, составленную из клеток с 29 возможными состояниями, однако большинство автоматов гораздо проще. Имеется огромный диапазон для изменений даже у двоичных автоматов, у которых клетка имеет два возможных состояния. Состояния могут быть представлены как 1 или 0 (включено или выключено, живое или мертвое).
Наконец, первоисточник изменений в мире клеточных автоматов - это огромное число возможных правил для определения будущего состояния клетки исходя из теперешней конфигурации ее соседей. Если k - число состояний, которые может принимать каждая клетка, а n - число клеток, входящих в окрестность, то существует k^k^n возможных правил. Так, для двоичного автомата с окрестностью фон Неймана (где n=4) существует более чем 65000 возможных правил; для окрестности Мура (где n=8 ) имеется 1E77 правил. Однако лишь малая часть их когда-либо изучалась.
В ИГРУ "Жизнь" играют на прямоугольной решетке из клеток с двумя состояниями и с окрестностью Мура и дополнительным усложнением, согласно которому центральная клетка тоже считается членом своей окрестности. Другими словами, при каждом шаге эволюции системы каждая клетка проверяет состояния восьми своих соседей и свое собственное. Согласно правилам, установленным Конвеем, если центральная клетка жива, то она будет продолжать жить в следующем поколении, когда две или три клетки из ее окрестности живы. Если найдутся три живые клетки в рассматриваемой окрестности, то центральная клетка будет живой в следующем поколении независимо от ее теперешнего состояния. Во всех других случаях центральная клетка либо умирает, либо остается мертвой.
Прелесть игры "Жизнь" состоит в ее непредсказуемости. Некоторые схемы полностью умирают; многие другие образуют устойчивые конфигурации либо циклические конфигурации с периодом в несколько поколений. Однако за прошедшие годы было найдено много очень интересных начальных состояний, таких, как "скользящая пушка", которая порождает нескончаемый поток снарядов. Исследование игры "Жизнь" в настоящее время продолжается. Последние достижения были описаны Мартином Гарднером в книге "Wheels, Life, and Other Mathematical Amusements". Здесь же я рассмотрю другие клеточные автоматы, свойства которых только начинают исследовать.
Среди множества возможных правил перехода лишь немногие интересны сами по себе. Например, правило, устанавливающее, что данная клетка будет "включена" тогда и только тогда, когда клетка слева от нее включена, определяет эволюцию, которую очень легко предсказать: любая начальная схема сохраняет свою конфигурацию, но сдвигается на одну клетку вправо на каждом временном шаге. Подкласс правил, называемых счетными, или суммирующими, по-видимому, содержит образцы почти всех встречающихся типов клеточных автоматов. При правилах такого рода новое состояние клетки зависит только от числа соседей в данном состоянии, но не от их положения. Многие автоматы, основанные на таких правилах, были изучены членами группы информационной механики лаборатории вычислительной математики в Массачусетсом технологическом институте. В эту группу входят Э.Фредкин, Н.Марголус, Т.Тоффоли и Дж.Вишняк.
Одно из простейших счетных правил - это правило четности, которое приписывает клетке значение 1, если нечетное число соседей находится в состоянии I, и значение 0 в других случаях. Пространственная эволюция этой системы с применением этого правила в окрестности фон Неймана была описана в октябрьском номере нашего журнала [См.: В мире науки, 1983, #12, с.103-109]. Любая начальная конфигурация повторяется четыре раза, затем эти четыре копии в свою очередь повторяются и т.д.
Другой класс счетных правил - это правила "голосования", при которых центральной клетке приписывается значение 1, как только число единиц в ее окрестности превышает некоторое пороговое значение. В докладе на Лос-Аламосском симпозиуме Вишняк отметил, что по правилам такого типа получаются модели фильтрации (просачивания) и образования активных центров - очень важных явлений в физике твердого тела и других областях науки. Термином "фильтрация" обозначают образование непрерывного пути через некоторое пространство; например, когда металл распределен в изолирующей матрице, проводимость материала зависит от вероятности образования непрерывной цепочки атомов металла. Точно так же передача инфекционного заболевания возможна только при наличии непрерывающейся последовательности восприимчивых индивидов. Образование активных центров - процесс, на котором основаны рост кристаллов, кипение жидкости и другие подобные явления.
Одно из правил перехода, приводящее к фильтрации, присваивает центральной клетке значение 1 только тогда, когда значения по меньшей мере трех клеток из пяти - т.е. окрестности фон Неймана плюс центральная клетка - равны 1. Развитие фильтрации очень сильно зависит от исходной концентрации единиц. Если концентрация меньше половины, то непрерывная цепочка единиц, заполняющих схему, по-видимому, не образуется в ходе эволюции. При концентрации 1/2 и больше появляются цепочки, но вся решетка ими не заполняется; в заключительном устойчивом состоянии остаются "островки" нулей. Образование кристаллов, при котором схема прочно заполняется единицами, наблюдается в том случае, когда правило изменяется и требуются лишь две из пяти единиц в окрестности. Критическая концентрация равна 0.0822.

Эволюция клеточного автомата при правиле голосования "два из пяти".
МОДЕЛЬ Изинга, одно из средств теоретического аппарата физики, при поверхностном рассмотрении кажется очень похожей на клеточный автомат. Модель представляет собой прямоугольную решетку, в которой каждый центр имеет два возможных значения и взаимодействует лишь с четырьмя своими ближайшими соседями. Эта модель часто используется для описания ферромагнетиков: каждый центр представляет собой атомный спин, который может быть направлен либо вверх, либо вниз. Если температура ниже критической (температуры Кюри), спины стремятся ориентироваться одинаково и материал намагничивается, но при более высоких температурах их направления распределены более или менее случайным образом.
В октябрьском номере журнала я рассматривал вариант модели Изинга, созданный с помощью КЭБ-программ. Клеточная структура этой модели располагает к использованию методов клеточных автоматов при ее изучении. Я заметил любопытное явление: при низкой температуре спины направлены неодинаково, они располагаются в шахматном порядке, при котором направления "вверх" и "вниз" чередуются. При каждом временном шаге все спины меняют свое направление. В ферромагнетиках шахматная структура является конфигурацией с высшей энергией и поэтому должна быть неустойчивой; эта структура характерна для антиферромагнетиков.
Вишняк обнаружил эту проблему и объяснил ее. В стандартном варианте модели Изинга при каждой итерации может изменяться только один спин. Следовательно, когда некоторый конкретный центр наблюдает за своими соседями, то одни из наблюдаемых спинов являются "старыми", а другие "новыми". При этих условиях "осциллирующий" антиферромагнетик не может возникнуть. Только когда все спины одновременно "производят свои вычисления", возникают благоприятные условия для антиферромагнетика высокой энергии. Существует возможность избежать этой "катастрофы обратной связи", однако более важный вывод состоит в том. что интуитивное соответствие между моделью Изинга и клеточным автоматом обманчиво.
Вишняк и другие ученые из группы Массачусетского технологического института подчеркивают, что клеточный автомат имеет статус, отличный от статуса других физических моделей. Наиболее распространенным средством построения математической модели мира издавна служило дифференциальное уравнение, которое описывает изменения некоторой величины как функцию координат и времени. Например, уравнения Максвелла дают изменения электромагнитного поля от точки к точке и от одного момента времени к другому. Все величины в таких уравнениях являются непрерывными (они гладко изменяются), с другой стороны, клеточный автомат - полностью дискретная система. Пространством является не континуум, а клеточная схема; время разбивается на последовательность дискретных шагов, а клетки автомата могут иметь лишь конечное число состояний, в то время как величина поля принимает значения из непрерывной области значений.
Разумеется, реальные пространство и время и многие физические переменные величины рассматриаются как непрерывные, а не дискретные (по крайней мере, в наиболее распространенных областях исследований). Однако из этого не следует, что дифференциальные уравнения по своей природе позволяют построить более совершенную модель реального мира. Когда уравнения должны быть решены численно, как при моделировании с помощью ЭВМ, непрерывные переменные могут быть вычислены приблизительно с некоторой конечной точностью; на самом деле они представляются дискретными величинами. При использовании клеточных автоматов дискретность выступает в явном виде, и их временная эволюция может быть вычислена точно; здесь приближения не нужны. Кроме того, в этом случае можно в большей степени использовать возможности цифровых вычислительных машин.
МОЖНО написать программу моделирования клеточного автомата лаже для самого миниатюрного компьютера. Действительно, П.Бак из Брукхейвенской национальной лаборатории недавно утверждал в журнале "Physics Today", что моделирование в физике можно эффективнее и дешевле производить на небольшом персональном компьютере, а не на более мощных вычислительных машинах общего пользования. Для иллюстрации этого он выбрал пример трехмерной модели Изинга на Commodore VlC-20 - компьютере стоимостью 4 доллара.
Наиболее прямолинейная программа клеточного автомата просто является воплощением метода, который каждый бы применял при выполнении процедуры ручным способом на листе бумаги в клетку. Сначала строится клеточная схема, в которой каждая клетка представлена ячейкой памяти в компьютере. При каждом временном шаге программа должна обращаться к каждой клетке по очереди, изучать ее окрестность и вычислять следующее состояние клетки. Само вычисление легко выполняется с помощью поиска значения в таблице. Если рассматриваются только счетные правила, таблице нужен всего один элемент для каждого возможного числа "активных" клеток. Когда допускаются правила другого рода, таблица может стать очень сложной.

Алгоритм для клеточного автомата, основанный на счетном, или суммирующем, правиле перехода
При написании такой программы следует иметь в виду несколько тонких моментов. Очень важно не нарушить состояния клетки, пока оно не проверено всеми другими клетками, в окрестность которых она входит. Простейший путь выполнения этого требования - сохранение двух копий данной схемы; программа изучает одну копию для определения текущего состояния окрестности и вносит результаты вычислений в другую копию. Следует также определить условия на границе. Идеальным случаем была бы бесконечная схема, но ясно, что это невыполнимо. Распространенным приемом является соединение концов схемы, так что клетки на противоположных краях становятся соседними. В одномерном случае схема такого рода топологически является окружностью, а в двумерном - тором, хотя это и конечные схемы, но границ они не имеют.
Программа описанного выше типа, выполняемая на универсальной ЭВМ, является последовательностной процедурой, которая моделирует действия схемы из многих компьютеров, работающих одновременно. Лучше было бы построить настоящую сеть многих компьютеров со структурой клеточного автомата. Конечно, не может быть и вопроса о построении такой машины (индивидуальные компьютеры должны быть довольно простыми и построены в большинстве случаев на одном полупроводниковом кристалле). Тот факт, что только близко расположенные компьютеры должны взаимодействовать между собой, также должен был бы уменьшить сложность всего устройства. По оценке Тоффоли, процессор должен был бы работать быстрее, чем ЭВМ общего назначения в миллион или даже миллиард раз.
Предварительные разработки для компьютеров подобного рода производятся в Калифорнийском технологическом институте и Thinking Machines Corporation of Wallham (шт. Массачусетс).
Вместо того чтобы использовать кристаллы специального назначения, Тоффоли построил машину, имитирующую клеточный автомат, из стандартных компонентов микроэлектроники. Вычисления производятся последовательно, а не для всех клеток сразу, но, поскольку весь аппарат приспособлен к единственному виду вычислений, его быстродействие оказывается в 1000 раз больше, чем у универсальной ЭВМ. Сама машина представляет собой набор печатных плат, смонтированных в корпусе; она соединена с цветным дисплеем и управляется другим миниатюрным компьютером - Atari-800.
Машина Тоффоли, имитирующая клеточный автомат, имеет схему из 256*256 клеток, каждая из которых может принимать до 256 состояний. Состояние каждой клетки перевычисляется 60 раз в секунду. За счет высокой скорости изменения состояния такой системы вместо последовательности неподвижных фотографий мы видим фильм. Игра "Жизнь" больше не представляется как величественная прогрессия абстрактных узоров; она теперь больше походит на картину, наблюдаемую под микроскопом при изучении поведения бактерий или простейших организмов, плавающих, вращающихся, размножающихся, пожирающих и пожираемых друг другом.

Игра "Жизнь", развивающаяся на экране машины, созданной Тоффоли и имитирующей клеточный автомат
ДЛЯ ОДНОМЕРНОГО клеточного автомата нужны менее мощные вычислительные средства (как в смысле объема памяти, так и в смысле быстродействия), чем для двумерного. Для одномерной системы легче написать программу. Линейная схема имеет еще одно преимущество над схемой на плоскости: более простая геометрическая структура позволяет легче аналитически понять эволюцию автомата. С.Вольфрам из Института высших исследований посвятил этому вопросу два гола работы.
Единственное поколение одномерной схемы - просто ряд клеток, но последовательные поколения должны быть нанесены одно вслед за другим. Таким образом строится двумерная схема, имеющая одну пространственную и одну временную оси, и всю эволюцию системы можно окинуть одним взглядом.
Вольфрам обнаружил, что все правила перехода, которые он исследовал до сих пор, можно разбить на четыре класса. Класс I состоит из тех правил, при которых эволюция приводит к устойчивому и однородному состоянию; например, все клетки принимают значения либо 1, либо 0. Класс 2 приводит к простым структурам, которые устойчивы или периодичны, но в любом случае остаются изолированными друг от друга. Правила класса 3 создают хаотические узоры, хотя и не обязательно случайные. В классе 4 собрано несколько правил перехода, которые порождают структуры существенной пространственной и временной сложности.

Четыре класса суммирующих правил в одномерном случае
Вольфрам предположил, что одномерный клеточный автомат может быть простейшей правильно определенной системой, способной на сложное самоорганизующееся поведение. В природе многие непрерывные динамические системы имеют такую способность: начиная со случайного начального состояния они эволюционируют в высокоорганизованную структуру. (Примером служит снежинка). Эта эволюция может быть описана в терминах аттракторов, которые, по-видимому, притягивают систему к некоторому подмножеству всех возможных конфигураций.
Была проведена параллель между классами клеточных автоматов и некоторыми типами аттракторов, наблюдаемых в физических системах. Автоматы класса 1 аналогичны непрерывной системе с простейшим аттрактором - предельной точкой, которая неизменно приводит систему к одному и тому же заключительному состоянию. Эволюция автомата из класса 2 более похожа на эволюцию системы с предельным циклом, которая представляет собой последовательность бесконечно повторяющихся конфигураций.
Автоматы из класса 3 с их хаотическими узорами можно сопоставить с более интересным" объектами, называемыми странными аттракторами, которые присущи таким физическим явлениям, как возникновение турбулентного течения. В системе, управляемой странным аттрактором, эволюция стремится к некоторому подмножеству всех возможных конфигураций, однако это подмножество может иметь крайне сложную структуру. Когда это множество представляется как массив точек в пространстве, она во многих случаях является фракталью, геометрической фигурой с дробным числом измерений.
Различие между классами автоматов можно выяснить, рассмотрев простой эксперимент. Предположим, что клеточный автомат начал свою эволюцию с какой-то случайно выбранной начальной конфигурации и делает несколько временных шагов; затем отмечается заключительное состояние. Теперь вернемся к исходному состоянию, изменим значение единственной клетки и дадим системе возможность проделать такое же число временных шагов. Какой эффект окажет это небольшое изменение на заключительное состояние? У автоматов класса 1 никакого изменения не произойдет: система из класса 1 приходит в одно и то же заключительное состояние из любого начального состояния. У автоматов класса 2 может наблюдаться некоторый эффект, но он ограничен небольшой областью вблизи измененной клетки. В системе класса 3, изменив единственную клетку, можно вызвать такое нарушение, которое распространится на всю схему.
Правила класса 4 очень редко встречаются и являются самыми сложными. Некоторые совсем простые функции перехода попадают в этот класс; например, в окрестности, включающем центральную клетку и по две клетки с каждой стороны от нее, правило, устанавливающее, что значение центральной клетки равно 1, если две или четыре клетки равны 1, попадает в класс 4. Чувствительность к малым изменениям в начальном состоянии в классе 4 даже больше, чем в классе 3. Было выдвинуто предположение, что для предсказания будущего состояния автомата класса 4 не может быть более эффективной процедуры, чем разрешить автомату самому вычислить это состояние.

Последовательные состояния одномерного автомата из класса 4
Это предположение можно интерпретировать более широко, а именно что автоматы класса 4 можно квалифицировать как универсальные вычислительные машины. Машина Тьюринга - наиболее известное устройство подобного рода: если некоторая функция может быть вообще вычислена, предполагается, что это может сделать машина Тьюринга. Можно доказать, что другие вычислительные машины тоже универсальны, если они эквивалентны машине Тьюринга. Было показано, что некоторые двумерные клеточные автоматы (включая игру "Жизнь") являются универсальными вычислительными машинами, и было также дано доказательство для сложных одномерных систем, в которых каждая клетка имеет 18 возможных состояний. Автоматы класса 4 были бы самой простой известной универсальной вычислительной машиной. Установлено, что они имеют большинство основных компонент. Не хватает лишь одного элемента - счетчика: устройства, выдающего последовательность импульсов через регулярные интервалы, подобно "скользящей пушке" в игре "Жизнь".

Некоторые компоненты возможной универсальной вычислительной машины
Аналогия клеточных автоматов с вычислительными машинами наводит на мысль, что их самоорганизующееся поведение может быть описано в терминах их вычислительных характеристик. Так, например, множество конфигураций, порожденных эволюцией клеточного автомата, можно представить как некий формальный язык. Каждая конфигурация рассматривается как слово языка, образованного в соответствии с множеством грамматических правил из последовательности символов, представляющих значения клеток автомата. Вольфрам показал, что конфигурация, порожденная любым клеточным автоматом за конечное время, может быть описана простым классом формальных языков, известных под названием регулярных. Для любого из этих регулярных языков можно найти простейшую грамматику. Такая грамматика дает простейшее описание конфигураций клеточного автомата и ее емкость можно принять за меру сложности конфигураций. Для клеточных автоматов классов 1 и 2 сложность стремится к конечному пределу за длительный период времени, так что структуры, порожденные этой системой, описываются регулярными языками. Однако для клеточных автоматов классов 3 и 4. по-видимому, требуются более сложные формальные языки.
СУЩЕСТВУЕТ особый класс клеточных автоматов, называемых обратимыми. Из любого начального состояния на любое число временных шагов допускается эволюция обратимого автомата, а затем автомат останавливается и запускается обратным ходом, после чего он возвращается в свое точное начальное состояние. Конфигурации, образованные типичным обратимым автоматом, качественно отличны от конфигураций, свойственных необратимому автомату. В частности, если конфигурация вначале случайна, то она и стремится остаться случайной - самоорганизующейся структуры не возникает.
Необходимым условием обратимости является детерминированность правила перехода в обоих направлениях, вперед и назад, т.е. каждое возможное состояние окрестности должно иметь единственное предыдущее состояние и единственное последующее состояние. Игра "Жизнь" необратима, потому что предыдущий этап какого-нибудь состояния нельзя определить однозначно; например, если текущее состояние клетки - "мертва", в предыдущем поколении она могла иметь "любое число "живых" соседей, отличное от трех. Систематический способ создания обратимых правил перехода был изобретен Фредхином, а позднее исследован Марголусом. Суть этого метода - заставить следующее состояние клетки зависеть от двух предыдущих состояний окрестности. Состояние в момент t+1 дается некоторой функцией окрестности в момент t минус та же функция в момент t-1. Тогда обращение производится непосредственно: состояние в момент t-1 должно даваться состоянием в момент t минус состояние в момент t+1.
Из-за требования детерминизма в двух направлениях в эволюции обратимого автомата не должны встречаться аттракторы. Присутствие аттрактора ведет к тому, что входе эволюции многие начальные состояния развиваются такими путями, которые сливаются друг с другом; в обратной эволюции точки слияния стали бы точками ветвления, в которых нарушалось бы требование детерминизма. Точно так же обратимый клеточный автомат в своей эволюции не может образовать петли или выйти из нее, т.е. не может иметь циклических состояний, потому что снова возникает точка ветвления в том или ином направлении. Поскольку аттракторы и соответствующие им самоорганизующиеся конфигурации исключаются, может показаться, что обратимые правила перехода приводят к очень "скучным" клеточным автоматам, однако это компенсируется другими интересными особенностями таких систем. Самое замечательное - это то, что информация, заключающаяся в клеточной конфигурации обратимого автомата, оказывается сохраняемой величиной (т.е. не возрастающей и не убывающей в холе эволюции автомата). Это свойство делает обратимые системы ценными моделями вычислений.
Марголус построил компьютер, имитирующий клеточный автомат, основанный на воображаемой механической системе, ранее исследованной Фредкином,- модель вычисления на основе бильярдных шаров. В этой модели биты информации (1 или 0) несут идеальные бильярдные шары, которые движутся без трения и отскакивают один от другого и от других препятствий идеально упруго. Наличие шара в указанном положении означает двоичную 1, а его отсутствие - двоичный 0. Умелым расположением бортов можно создать различные логические вентили, подобные тем, которые имеются в электронно-вычислительной машине. Например, в схеме "И" один бильярдный шар проходит через выходную область (и тем самым регистрируется двоичная 1), если только два шара приближаются к вентилю одновременно вдоль специфических траекторий.
Вариант такой модели клеточного автомата, построенный Марголусом, основан на простом и в некотором смысле необычном обратимом правиле перехода. Клетки рассматриваются не по отдельности, а блоками по 4; любая возможная конфигурация в пределах блока преобразуется в единственную производную конфигурацию. Правило составлено так, что одна единица на фоне остальных нулей распространяется в одном из четырех диагональных направлений решетки со скоростью 1 клетка за временной шаг; изолированная единица является воплощением бильярдного шара. "Монолитный" блок, состоящий из четырех единиц, неопределенно долго остается неизменным и действует как абсолютный отражатель. Когда моделирование производится на машине Тоффоли, имитирующей клеточный автомат, то "бильярдные шары" мечутся по экрану дисплея, образуя сложные пересекающиеся траектории. Наблюдая это упорядоченное (пусть лаже безумное) движение, трудно помнить о том, что в программе не содержатся представления траекторий шаров, а просто применяется одно-единственное правило ко всем клеткам.

Правило перехода для компьютера "на бильярдных шарах"
МОДЕЛЬ на основе бильярдных шаров к ее воплощение в виде клеточного автомата тесно связаны с теорией вычислений. Было выдвинуто предположение, что любая вычислительная машина должна иметь компоненты, которые рассеивают энергию и информацию; в соответствии с этой теорией должен существовать "термодинамический предел" эффективности компьютера точно так же, как существует предел к.п.д. тепловою двигателя. Неизбежные, по предположению, потери информации и энергии являются прямым следствием необратимости вычислительного процесса. (Когда компьютер складывает 5 и 3, чтобы получить результат 8, процесс не может быть обращен, потому что существует бесконечно много чисел, которые при сложении лают тот же результат).
Фредкин, Тоффоли и Марголус подчеркивают, что модель на основе бильярдных шаров противоречит понятию неизбежного рассеяния. Действительно, бильярдные шары не могут сами себя создавать или разрушать, и вся информация, определяющая их начальную конфигурацию, сохраняется в ходе эволюции системы. Входы операции сложения могут быть легко восстановлены обращением траекторий. В принципе вычислительная машина, построенная на основе бильярдных шаров, могла бы действовать без внутренних затрат энергии.

Компьютер "на бильярдных шарах" в действии
С особой ясностью связь между физическими процессами и вычислениями была установлена Тоффоли в его заявлении, которое можно интерпретировать как описание самого большого из всех клеточных автоматов. "В некотором смысле,- пишет он,- в течение миллиардов лет природа постоянно вычисляла "следующее состояние" Вселенной; все, что нам надо сделать,- и действительно, что мы можем сделать,- это "войти в колею" этого гигантского непрекращающегося процесса вычисления и попытаться угадать, какая часть его движется в нужном нам направлении".

Узор дендритов, созданный клеточным автоматом с асимметричным правилом перехода
БИБЛИОГРАФИЯ
PHYSICS AND COMPUTATION. TOMMASO TOFFOLI in International Journal of Theoretical Physics, Vol.21, Nos.3/4, pages 165-175; April, 1982.
STATISTICAL MECHANICS OF CELLULAR AUTOMATA. STEPHEN WOLFRAM in Reviews of Modern Physics, Vol.55, No.3. pages 601-644; July, 1983.
CELLULAR AUTOMATA. STEPHEN WOLFRAM in Los Alamos Science, pages 2-21; Fall, 1983.
DOING PHYSICS WITH MICROCOMPUTERS. PER BAK in Physics Today, Vol.36, No.12, pages 25-28; December, 1983.
WHEELS, LIFE, AND OTHER MATHEMATICAL AMUSEMENTS. MARTIN GARDNER. W.H.Freeman and Company, 1984.
CELLULAR AUTOMATA: PROCEEDINGS OF AN INTERDISCIPLINARY WORKSHOP. Edited by Stephen Wolfram, J.Doyne Farmer and Tommaso Toffoli, in Physica D., Vol. 10D, Nos.1 and 2; January. 1984.
Т.ТОФФОЛИ, Н.МАРГОЛУС, МАШИНЫ КЛЕТОЧНЫХ АВТОМАТОВ, Москва, "МИР", 1991.- G.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
6 1984
КАК ОПЕРИРОВАТЬ С ТЫСЯЧЕЗНАЧНЫМИ ЧИСЛАМИ И ЗАЧЕМ ЭТО НУЖНО
ФРЕД ГРЮЕНБЕРГЕР
ОТ РЕДАКТОРА. Статью под рубрикой "Занимательный компьютер" для этого номера журнала подготовил профессор Грюенбергер - специалист по кибернетике и вычислительной математике из Калифорнийского университета в Нортридже. Вычислительными машинами Грюенбергер заинтересовался более 40 лет назад; с тех пор он опубликовал 28 книг по различным вопросам в этой области, а с 1973 по 1981г. был главным редактором ежемесячного журнала "Popular Computing".
Начиная со следующего номера рубрику "Занимательный компьютер" будет вести А.К.Дьюдни - доцент факультета кибернетики и вычислительной математики Университета в Западном Онтарио. Научные интересы Дьюдни в основном касаются теории вычислений, но многим читателям он больше известен как исследователь в области двумерных "пространств", которым была посвящена статья М.Гарднера в июльском номере журнала "Scientific American" за 1980г. Собственные взгляды Дьюдни на эту проблему изложены в его недавно выпущенной издательством Poseidon Press книге "The Planiverse: Computer Contact with a Two-dimensional World". В следующем году издательство Computer Science Press выпустит в свет сборник статей Дьюдни пол названием "The Turing Omnibus", который будет посвящен различным проблемам кибернетики и вычислительной математики.

Точные результаты многократного возведения в квадрат числа 1.0000001
ЕСЛИ НА вашем калькуляторе есть клавиша для возведения чисел в квадрат, то попробуйте проделать следующее: наберите число 1.0000001, а затем 27 раз нажмите эту клавишу. То, что вы проделали, эквивалентно возведению набранного числа в степень 134217728. Правильным результатом с точностью до 10-й значащей цифры будет 674530.4707, но ваш калькулятор почти наверняка даст другой ответ. Эта задача специально предназначена для демонстрации того, какую точность вычислений может дать ваш калькулятор. В таблице на с.112 приведены результаты, полученные на нескольких калькуляторах и на ЭВМ по программам, написанным на версиях Бейсика и Фортрана. Ни одно из этих технических средств не дало даже семи верных цифр.

Точность, обеспечиваемая некоторыми машинами и языками программирования при многократном возведении в квадрат
На большинстве электронных калькуляторов операция возведения в квадрат не равнозначна введению числа и умножению его на то же самое число. В операции умножения размер (или точность) сомножителей ограничивается числом разрядов, которые могут быть изображены на табло вычислительного устройства. А процедура возведения в квадрат осуществляется с помощью такого представления числа, хранящегося в вычислительном устройстве, которое, как правило, включает несколько дополнительных "контрольных разрядов", и они каждый раз участвуют в процессе вычисления, но оператор их не видит. Так, если вы извлекаете квадратный корень из 2 на калькуляторе с восьмиразрядным табло и двумя контрольными разрядами, то на табло высветится число 1.4142136, но внутри устройства хранится число 1.414213562. Если вы теперь нажмете клавишу возведения в квадрат, то на табло появится 2.0000000, в то время как при умножении числа 1.4142136 на себя получим 2.000000106.
При вычислениях ошибка в седьмой значащей цифре (разряде) в большинстве случаев несущественна. Допустим, однако, что вычисления производятся на ЭВМ по программе, в которой предусмотрено выполнение одной последовательности команд, если число точно равно 2, и другой последовательности, если оно хоть на сколько-нибудь отличается от 2; в этом случае неточность вычислений может привести к печальным последствиям. Для того чтобы не рисковать, можно использовать, пожалуй, самый надежный прием - округлить полученное значение до определенной степени точности, прежде чем проверять его на равенство 2. Бывают случаи, когда способ округления не помогает. При решении задач, связанных с многократным последовательным возведением в квадрат дробной части, единственная возможность улучшить результат - это постоянно поддерживать все большую точность на всех стадиях вычислительного процесса.
Для многих задач, связанных с расчетом, вполне достаточно точности до восьмого или девятого знака, как, например, при операциях с чековыми книжками, если только сумма не превышает 1млн. долл. Ни одна из физических постоянных не известна с точностью более 12 значащих цифр. Однако, для того чтобы обеспечить даже умеренную точность конечного результата, в процессе вычислений может потребоваться значительно более высокая точность. Когда число 1.0000001 возводится в квадрат 27 раз подряд, то для получения 10 точных значащих цифр промежуточные вычисления должны вестись с 15-значнымн числами.

Результаты последовательного возведения в квадрат числа 1.0000001 при ограниченной точности вычислений
ПРИМЕРОМ задачи, в которой обеспечение высокой точности вычислений является непременным условием, может служить непрерывный поиск все больших простых чисел. До появления электронных цифровых вычислительных машин в течение многих лет не было известно простого числа, большего 2^127-1. В десятичной форме оно записывается 39 десятичными цифрами. Начиная с 1952г. с помощью ЭВМ было поставлено 16 новых рекордов; в настоящее время наибольшее из известных простых чисел - это 2^132049-1, состоящее из 39751 знака. Чтобы проверить, является ли число простым. т.е. установить, что оно делится только на 1 и само на себя, все необходимые для этого арифметические операции должны производиться с исключительно ВЫСОКОЙ ТОЧНОСТЬЮ.
Вычисление значения числа пи - еще одна давняя задача, требующая исключительно высокой точности. На протяжении многих лет рекорд удерживал английский математик Уильям Шенкс: производя вычисления вручную, он получил 528 правильных знаков (и еше 179, которые оказались неверными). Сейчас пи известно С точностью до 8388608-го знака.
Учитывая, что механизация выполнения арифметических действий с высокой точностью началась более 30 лет назад и что стоимость вычислений на ЭВМ с тех пор постоянно снижается, а их доступность растет, можно подумать, что перечень известных результатов стал довольно обширным. На самом же деле чисел, которые известны с высокой точностью, не так уже много. Приведем некоторые из них.
Квадратный корень из 2 известен до одного миллиона десятичных знаков, а кубический корень из 16 - до 1000 знаков.
Значение действительного корня уравнения Уоллнса X3-2X-5=0 известно до 4000 знаков. (Это уравнение английский ученый XVIIв. Дж.Уоллис выбрал для иллюстрации численного решения уравнений методом Ньютона; с тех пор оно служит средством проверки многих других методов аппроксимации).
Г.Нелсон (который когда-то вместе с Д.Словинским удерживал рекорд в получении максимального значения из известных простых чисел), сотрудник Ливерморской национальной лаборатории им.Лоуренса, вычислил 1000000!, т.е. произведение 1000000*999999*...*2*1. Результат записывается числом из 5565709 цифр, и его распечатка на ЭВМ представляет собой пачку бумаги толщиной более 12см.
Для задачи, известной как "проблема 196", потребовалось 50тыс. вычислительных шагов, и на каждом из них приходилось оперировать числами, имеющими 21000 знаков. Другой "орешек" - "проблема 3N+1" была исследована вплоть до 1000-значных чисел. Более подробно о той н другой задачах мы поговорим ниже.
В последовательности Фибоначчи (1,1,2,3,5,8,13,21..., где каждое последующее число есть сумма двух предыдущих) точно вычислены первые 10000 членов. Последние числа этого ряда имеют более 2000 знаков.
Число Эйлера е, являющееся основанием натурального логарифма, вычислено с точностью более чем до 125000 знаков.
Можно привести еще несколько примеров. Так, Р.Госпер, сотрудник фирмы Symbolics, Inc., используя метод, основанный на оперировании с непрерывными дробями, вычислил 2800 знаков корня седьмой степени из 306. (Результат не имеет особого значения, и эта задача была выбрана случайно исключительно для проверки правильности метода).
БОЛЬШИНСТВО из приведенных выше примеров взято из той категории задач, в решении которых высокая точность вычислений играет определяющую роль; задачи эти примечательны, в сущности, только тем, что при их решении нужно оперировать числами значительно более "длинными", чем нам представляется необходимым. Следующая задача, требующая высокой точности вычислений, более распространена, имеет практический смысл и потому менее искусственна. Возникает она при нахождении корней квадратного уравнения вида AX2+BX+C=0. Значение выражения В2-4АС, называемого дискриминантом уравнения, определяет, являются корни действительными или комплексными. Если дискриминант положительный, корни действительные, а если отрицательный - то комплексные; если же В2-4АС точно равно нулю, уравнение имеет два одинаковых действительных корня. Отсюда следует, что даже незначительная ошибка в вычислении дискриминанта может привести к качественно иному результату при решении уравнения.
Подобная чувствительность к малым ошибкам в вычислении может проявиться и в решении системы однородных линейных уравнений. Рассмотрим систему
53.17X-18.91Y-5.67Z=-174.65,
-12.65X+36.16Y-47.08Z=298.59,
303.80X-203.03Y+112.89Z=-1769.02.
Система составлена таким образом, что всем трем уравнениям удовлетворяют значения X=-3, Y=2 и Z=-4, но это не единственное ее решение. В самом деле, хотя это и не очевидно с первого взгляда, система не может иметь единственного решения, поскольку два из ее уравнений описывают параллельные плоскости. (Третье уравнение представляет собой разность между первым уравнением, умноженным на 5, и умноженным на 3 вторым уравнением).
Чтобы убедиться в том, что единственного решения нет, нужно вычислить так называемый определитель матрицы коэффициентов. Определитель выражается суммой всех возможных произведений элементов, которые не принадлежат ни одному и тому же столбцу, ни одной и той же строке. Если определитель окажется равным нулю, то система уравнений не имеет решения и в этом случае дальнейшие вычисления не нужны (или, что более важно, в этом месте программы следует предусмотреть останов). В данном случае, однако, определитель вычислялся по схеме, называемой корзиночным плетением, и при точности вычислений до девятого десятичного знака был получен результат, отличный от нуля, а именно -0.000202179. В данном примере можно было бы получить правильный ответ с помощью других методов, но в иных случаях и это бы не помогло. Дело в том, что при точности до девятого знака нельзя получить надежный результат. Кроме того, приведенная система уравнений - небольшая, и ее коэффициенты не имеют более шести значащих цифр; для более сложных систем проблема становится острее.
ПРИ РЕШЕНИИ многих задач теории чисел и других разделов математики требуется исключительно высокая точность представления очень больших целых чисел. Примером может служить упомянутая "проблема 196". Возьмем любое положительное число - двух- или более значное. Переставим цифры в обратном порядке и вновь полученное число сложим с исходным. Снова поменяем порядок цифр в сумме на обратный и сложим полученное число с предыдущим. Будем делать так до тех пор, пока не придем к палиндрому - числу, прямой и обратный порядок цифр в котором одинаков (см. рис. слева). В большинстве случаев палиндром получается быстро; если, например, начать с числа 195, то уже через четыре шага получим палиндром. Наименьшее число, для которого с помощью описанной процедуры палиндром, как представляется, никогда не получится,- это 196: как уже отмечалось, начиная с числа 196, было проделано 50тыс. шагов и они не дали результата. Среди первых 100000 целых чисел имеется 5996 чисел, которые, по-видимому, не приводят к палиндрому независимо от того, как долго мы будем продолжать вычисления (хотя это предположение и не доказано).
Вычисления по правилам "проблемы 196" для нескольких начальных чисел
Проблема 3N+1 рассматривалась в мартовском номере нашего журнала. Начнем с любого положительного числа N; если оно нечетное, заменим его на 3N+1, а если четное, поделим N пополам. Продолжим эту процедуру до тех пор, пока не получим 1. Например, если начать с N=9, то, последовательно применяя указанное правило, получим: 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2 и 1 - всего 20 чисел. Эта незамысловатая задача содержит немало загадок. Всегда ли получаемая в процессе решения последовательность заканчивается 1 независимо от исходного значения N? Имеется ли какой-либо способ определения необходимого числа шагов, т.е. можно ли составить такую формулу, которая позволяла бы по значению N предсказывать число шагов? Всегда ли по любому заданному числу шагов можно определить некое нечетное N, для которого потребуется сделать именно столько шагов? (Четное N по любому заданному числу шагов найти легко: это 2, возведенное в степень, на 1 меньшую заданного числа шагов).
В 1980г. я высказал предположение, что среднее количество целых чисел, получаемых в процессе вычислений в задаче 3N+1, приблизительно определяется выражением 24.64D-101, где D - количество цифр исходного числа N. Эта оценочная формула была получена на основе вычислений, выполненных почти до 200-значных чисел, которые тогда представлялись мне довольно большими. Используя программу, обеспечивающую высокую точность вычислений, я имел возможность проверить свое допущение на нескольких больших числах. Для 1000-эначного числа по моей формуле получается, что окончательный результат достигается через 25539 шагов. Я обнаружил, что когда N=1...(998 нулей)...1, или 1E1000+1, то ряд достигает 1 через 23069 шагов. Число 55...(997 нулей)...1 порождает последовательность из 24413 чисел. Следовательно, мы получили некое подтверждение того, что средняя скорость сходимости устойчива и предсказуема.
На малых значениях N была замечена тенденция (которая, по-видимому, должна была сохраниться и для больших чисел) порождать ряды одинаковой длины многими последовательными значениями N. Действительно, можно заметить, как такие ряды чисел появляются все чаше по мере увеличения N. Например, все 230 последовательных целых чисел, начиная с числа 9123456789123456789000000000000000000000001. порождают ряды из 997 членов. (Заметим, что наша эмпирическая формула для этого числа дает 959 членов).
ТОЧНОСТЬ арифметических операций, которые непосредственно могут быть выполнены центральным процессором обычного микрокомпьютера, весьма ограниченная. Во многих вычислительных машинах единственными операциями, выполняемыми в явном виде, являются сложение и вычитание целых чисел, "длина" которых не превышает 16 битов, или двоичных разрядов: самое большое число в десятичной системе счисления, которым может оперировать такая ЭВМ,- это 65536. так что уровень точности не превышает пяти десятичных знаков. Даже на самых мощных компьютерах точность выше нескольких десятков десятичных цифр может быть обеспечена только такой программой, в которой содержится группа элементарных операций, позволяющих разбить большое число на более мелкие части.
На с.114 приведена блок-схема алгоритма вычислений с высокой точностью - процедуры, по которой было получено наибольшее из известных простых чисел: 2^132049-1. Программа ориентирована на определенный микропроцессор - модель 6502 фирмы MOS Technology. Этим микропроцессором комплектуются компьютеры, выпускаемые фирмами Apple Computer, Inc., Commodore Business Machines, Inc. и др. Алгоритм можно легко приспособить и к другим микропроцессорам.

Вычисление простого числа 2^132049-1, состоящего из 39751 цифры; блок-схемы программы (слева) и подпрограммы (справа)
Самой большой сложностью, с которой приходится сталкиваться при разработке такой программы, является, пожалуй, выбор способа представления чисел в памяти машины. Процессор может оперировать только двоичными числами, а нам желательно получать результат вычислений в десятичной форме. Приемлемым компромиссом является использование двоично-десятичной системы счисления, в которой каждая десятичная цифра представляется в соответствующей ей двоичной записи. Микропроцессор 6502 организует машинную память в "байтах" - последовательностях из восьми двоичных разрядов (битов), и таким образом обеспечивается удобный способ хранения десятичного числа, при котором каждая его цифра занимает в памяти по одному байту. (Нельзя сказать, чтобы этот способ был наиболее эффективным, но зато он самый простой).
Первый шаг в алгоритме - очистить машинную память емкостью 39760 байтов. Для этого все байты заполняются нулями. На следующем шаге исходная величина, равная 1, записывается в очищенную рабочую область, так что теперь в памяти записана последовательность из 39759 нулей, завершающаяся единицей. В счетчик, который потребуется для соблюдения последовательности вычислительных операций, в самом начале засылается нуль.
Главной частью программы является цикл, в котором происходит периодическое обращение к подпрограмме удвоения числа, хранимого в рабочей области памяти. После каждого такого удвоения к содержимому счетчика прибавляется единица и полученное число сравнивается с 132049. Если этот предел еще не достигнут, вновь вызывается подпрограмма удвоения; если же в счетчике накопилось предельное число, программа выходит из цикла. На последнем этапе из значения, хранящегося в рабочей области памяти, вычитается единица и выводится результат.
На блок-схеме программы, изображенной на с.114 слева, подпрограмма удвоения выделена цветом, а набор составляющих се команд представлен блок-схемой справа. Всякий раз, когда производится обращение к подпрограмме, начальный адрес рабочей области памяти, где хранится самая правая, или младшая, цифра исследуемого числа, присваивается индексу (X). Содержимое этого адреса затем удваивается путем прибавления к нему такого же числа. Так же как и при сложении вручную, основная трудность здесь состоит в необходимости "переносить" в процессе суммирования единицу с одного разряда на другой. Если предыдущее сложение выработало разряд переноса, его необходимо добавить к новому результату. Последний в-свою очередь должен быть проверен на последующий перенос: если сумма больше 9, из нее вычитается 10 и она заменяется на остаток, а в следующий разряд переносится единица. Этот процесс повторяется для всех 39760 байтов рабочей области машинной памяти.
Процессор 6502 компьютера модели Apple II способен выполнять более 250тыс. операций в секунду. И все же на выполнение программы, представленной на с.114, потребовалось 120ч машинного времени, чтобы подсчитать 132049-ю степень 2. Это время можно значительно уменьшить за счет простого "усечения" вычислительного процесса. Например, на ранних стадиях вычислений нет необходимости удваивать все цифры, записанные в памяти машины, так как большинство из них нули. Рабочую область можно считать заполненной, когда в ней будет находиться, скажем, 150 байтов, и это число будет увеличиваться на три байта при каждом увеличении степени на 10. При таком подходе в программу придется ввести дополнительные команды, но зато быстродействие при этом возрастает.
ВСЕ ЧИСЛА, которыми приходится оперировать при вычислении 2^132049-1,- целые, но существует немало задач, решение которых облегчается, если использовать такую же запись, которая принята в научных работах, когда число представляется в виде произведения десятичной дроби, называемой мантиссой, и степени 10 (показатель степени в такой форме записи называется порядком). Например, текущий год можно записать в виде 1.984E3, где 1.984 - мантисса, а 3 - порядок. Программы высокой точности, которые оперируют числами в такой форме, сложнее, чем аналогичные программы, рассчитанные на действия только с целыми числами, потому что в первом случае каждое число имеет несколько составляющих (помимо мантиссы и порядка в него входят знак мантиссы и знак порядка).
В большинстве языков программирования высокого уровня предусмотрены некоторые средства, позволяющие использовать такую форму представления чисел; в этом случае говорят о системе с плавающей точкой. Числа меньше определенного размера (количества разрядов) представляются на табло как обычная десятичная дробь, но внутри машины эти числа хранятся в виде мантиссы и порядка. Поле, отведенное для различных элементов числа, определяет точность и диапазон значений этого числа. Отводя больше места для мантиссы, мы повышаем точность, а чем больше порядок, тем шире диапазон чисел. Версия языка Бейсик в программном обеспечении для Apple II имеет фиксированную точность - примерно 9 десятичных знаков.
Для обеспечения еще более высокой точности необходимо опять прибегнуть к возможностям программного обеспечения. Г.Робинсон, будучи сотрудником Ливерморской лаборатории, составил пакет программ вычислений с высокой точностью для чисел, представленных с плавающей точкой. Программы, написанные на машинном языке микропроцессора 6502, могут обеспечивать любой уровень точности вплоть до 600 десятичных знаков и допускают величину порядка до 9999. Эти предельные параметры были выбраны, исходя из соответствующих характеристик процессора: 600-значная мантисса, 4-значный порядок и их знаки можно записать 2S6 байтами, а в модели 6502 блок емкостью 256 байтов - это одна "страница" памяти.
В программах Робинсона операции, которые могут выполняться над числами, включают основные арифметические действия, логарифмирование, возведение в степень, извлечение квадратного корня, а также вычисление различных тригонометрических функций. Предусмотрено вычисление и не столь широко распространенных функций, как, например, функции Эйлера и преобразования Вейнгартена для суммирования медленно сходящихся рядов. В пакете имеются значения 26 постоянных и 8000 простых чисел. Пакетом можно пользоваться как весьма совершенным калькулятором или обращаться к отдельным его программам как к подпрограммам. Первые версии показали, что арифметические действия и вычисления функций могут производиться с предельной точностью до 600 десятичных знаков.
Для тех, кто проявляет интерес к численным процедурам, первое знакомство с цифровым компьютером иногда приводит в уныние; это потому, что элементарные вычисления на машине выполняются быстро и, что самое важное, безупречно, и как следствие возникает ложное представление, будто тщательный численный анализ можно выполнить без всяких усилий. После этого трудно поверить, что корень пятой степени из 100 (константа, которая используется для сравнения величины звезд) нельзя вычислить намного точнее, чем с помощью ручного калькулятора. Пакет программ, подобный пакету Робинсона, позволяет оправдать возлагаемую на компьютер надежду. Корень пятой степени из 100 можно вычислить до 100 десятичных знаков буквально за несколько минут.
БИБЛИОГРАФИЯ
Опять можно посмотреть Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 - ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.
КАК ОПЕРИРОВАТЬ С ТЫСЯЧЕЗНАЧНЫМИ ЧИСЛАМИ И ЗАЧЕМ ЭТО НУЖНО
ФРЕД ГРЮЕНБЕРГЕР
ОТ РЕДАКТОРА. Статью под рубрикой "Занимательный компьютер" для этого номера журнала подготовил профессор Грюенбергер - специалист по кибернетике и вычислительной математике из Калифорнийского университета в Нортридже. Вычислительными машинами Грюенбергер заинтересовался более 40 лет назад; с тех пор он опубликовал 28 книг по различным вопросам в этой области, а с 1973 по 1981г. был главным редактором ежемесячного журнала "Popular Computing".
Начиная со следующего номера рубрику "Занимательный компьютер" будет вести А.К.Дьюдни - доцент факультета кибернетики и вычислительной математики Университета в Западном Онтарио. Научные интересы Дьюдни в основном касаются теории вычислений, но многим читателям он больше известен как исследователь в области двумерных "пространств", которым была посвящена статья М.Гарднера в июльском номере журнала "Scientific American" за 1980г. Собственные взгляды Дьюдни на эту проблему изложены в его недавно выпущенной издательством Poseidon Press книге "The Planiverse: Computer Contact with a Two-dimensional World". В следующем году издательство Computer Science Press выпустит в свет сборник статей Дьюдни пол названием "The Turing Omnibus", который будет посвящен различным проблемам кибернетики и вычислительной математики.

Точные результаты многократного возведения в квадрат числа 1.0000001
ЕСЛИ НА вашем калькуляторе есть клавиша для возведения чисел в квадрат, то попробуйте проделать следующее: наберите число 1.0000001, а затем 27 раз нажмите эту клавишу. То, что вы проделали, эквивалентно возведению набранного числа в степень 134217728. Правильным результатом с точностью до 10-й значащей цифры будет 674530.4707, но ваш калькулятор почти наверняка даст другой ответ. Эта задача специально предназначена для демонстрации того, какую точность вычислений может дать ваш калькулятор. В таблице на с.112 приведены результаты, полученные на нескольких калькуляторах и на ЭВМ по программам, написанным на версиях Бейсика и Фортрана. Ни одно из этих технических средств не дало даже семи верных цифр.

Точность, обеспечиваемая некоторыми машинами и языками программирования при многократном возведении в квадрат
На большинстве электронных калькуляторов операция возведения в квадрат не равнозначна введению числа и умножению его на то же самое число. В операции умножения размер (или точность) сомножителей ограничивается числом разрядов, которые могут быть изображены на табло вычислительного устройства. А процедура возведения в квадрат осуществляется с помощью такого представления числа, хранящегося в вычислительном устройстве, которое, как правило, включает несколько дополнительных "контрольных разрядов", и они каждый раз участвуют в процессе вычисления, но оператор их не видит. Так, если вы извлекаете квадратный корень из 2 на калькуляторе с восьмиразрядным табло и двумя контрольными разрядами, то на табло высветится число 1.4142136, но внутри устройства хранится число 1.414213562. Если вы теперь нажмете клавишу возведения в квадрат, то на табло появится 2.0000000, в то время как при умножении числа 1.4142136 на себя получим 2.000000106.
При вычислениях ошибка в седьмой значащей цифре (разряде) в большинстве случаев несущественна. Допустим, однако, что вычисления производятся на ЭВМ по программе, в которой предусмотрено выполнение одной последовательности команд, если число точно равно 2, и другой последовательности, если оно хоть на сколько-нибудь отличается от 2; в этом случае неточность вычислений может привести к печальным последствиям. Для того чтобы не рисковать, можно использовать, пожалуй, самый надежный прием - округлить полученное значение до определенной степени точности, прежде чем проверять его на равенство 2. Бывают случаи, когда способ округления не помогает. При решении задач, связанных с многократным последовательным возведением в квадрат дробной части, единственная возможность улучшить результат - это постоянно поддерживать все большую точность на всех стадиях вычислительного процесса.
Для многих задач, связанных с расчетом, вполне достаточно точности до восьмого или девятого знака, как, например, при операциях с чековыми книжками, если только сумма не превышает 1млн. долл. Ни одна из физических постоянных не известна с точностью более 12 значащих цифр. Однако, для того чтобы обеспечить даже умеренную точность конечного результата, в процессе вычислений может потребоваться значительно более высокая точность. Когда число 1.0000001 возводится в квадрат 27 раз подряд, то для получения 10 точных значащих цифр промежуточные вычисления должны вестись с 15-значнымн числами.

Результаты последовательного возведения в квадрат числа 1.0000001 при ограниченной точности вычислений
ПРИМЕРОМ задачи, в которой обеспечение высокой точности вычислений является непременным условием, может служить непрерывный поиск все больших простых чисел. До появления электронных цифровых вычислительных машин в течение многих лет не было известно простого числа, большего 2^127-1. В десятичной форме оно записывается 39 десятичными цифрами. Начиная с 1952г. с помощью ЭВМ было поставлено 16 новых рекордов; в настоящее время наибольшее из известных простых чисел - это 2^132049-1, состоящее из 39751 знака. Чтобы проверить, является ли число простым. т.е. установить, что оно делится только на 1 и само на себя, все необходимые для этого арифметические операции должны производиться с исключительно ВЫСОКОЙ ТОЧНОСТЬЮ.
Вычисление значения числа пи - еще одна давняя задача, требующая исключительно высокой точности. На протяжении многих лет рекорд удерживал английский математик Уильям Шенкс: производя вычисления вручную, он получил 528 правильных знаков (и еше 179, которые оказались неверными). Сейчас пи известно С точностью до 8388608-го знака.
Учитывая, что механизация выполнения арифметических действий с высокой точностью началась более 30 лет назад и что стоимость вычислений на ЭВМ с тех пор постоянно снижается, а их доступность растет, можно подумать, что перечень известных результатов стал довольно обширным. На самом же деле чисел, которые известны с высокой точностью, не так уже много. Приведем некоторые из них.
Квадратный корень из 2 известен до одного миллиона десятичных знаков, а кубический корень из 16 - до 1000 знаков.
Значение действительного корня уравнения Уоллнса X3-2X-5=0 известно до 4000 знаков. (Это уравнение английский ученый XVIIв. Дж.Уоллис выбрал для иллюстрации численного решения уравнений методом Ньютона; с тех пор оно служит средством проверки многих других методов аппроксимации).
Г.Нелсон (который когда-то вместе с Д.Словинским удерживал рекорд в получении максимального значения из известных простых чисел), сотрудник Ливерморской национальной лаборатории им.Лоуренса, вычислил 1000000!, т.е. произведение 1000000*999999*...*2*1. Результат записывается числом из 5565709 цифр, и его распечатка на ЭВМ представляет собой пачку бумаги толщиной более 12см.
Для задачи, известной как "проблема 196", потребовалось 50тыс. вычислительных шагов, и на каждом из них приходилось оперировать числами, имеющими 21000 знаков. Другой "орешек" - "проблема 3N+1" была исследована вплоть до 1000-значных чисел. Более подробно о той н другой задачах мы поговорим ниже.
В последовательности Фибоначчи (1,1,2,3,5,8,13,21..., где каждое последующее число есть сумма двух предыдущих) точно вычислены первые 10000 членов. Последние числа этого ряда имеют более 2000 знаков.
Число Эйлера е, являющееся основанием натурального логарифма, вычислено с точностью более чем до 125000 знаков.
Можно привести еще несколько примеров. Так, Р.Госпер, сотрудник фирмы Symbolics, Inc., используя метод, основанный на оперировании с непрерывными дробями, вычислил 2800 знаков корня седьмой степени из 306. (Результат не имеет особого значения, и эта задача была выбрана случайно исключительно для проверки правильности метода).
БОЛЬШИНСТВО из приведенных выше примеров взято из той категории задач, в решении которых высокая точность вычислений играет определяющую роль; задачи эти примечательны, в сущности, только тем, что при их решении нужно оперировать числами значительно более "длинными", чем нам представляется необходимым. Следующая задача, требующая высокой точности вычислений, более распространена, имеет практический смысл и потому менее искусственна. Возникает она при нахождении корней квадратного уравнения вида AX2+BX+C=0. Значение выражения В2-4АС, называемого дискриминантом уравнения, определяет, являются корни действительными или комплексными. Если дискриминант положительный, корни действительные, а если отрицательный - то комплексные; если же В2-4АС точно равно нулю, уравнение имеет два одинаковых действительных корня. Отсюда следует, что даже незначительная ошибка в вычислении дискриминанта может привести к качественно иному результату при решении уравнения.
Подобная чувствительность к малым ошибкам в вычислении может проявиться и в решении системы однородных линейных уравнений. Рассмотрим систему
53.17X-18.91Y-5.67Z=-174.65,
-12.65X+36.16Y-47.08Z=298.59,
303.80X-203.03Y+112.89Z=-1769.02.
Система составлена таким образом, что всем трем уравнениям удовлетворяют значения X=-3, Y=2 и Z=-4, но это не единственное ее решение. В самом деле, хотя это и не очевидно с первого взгляда, система не может иметь единственного решения, поскольку два из ее уравнений описывают параллельные плоскости. (Третье уравнение представляет собой разность между первым уравнением, умноженным на 5, и умноженным на 3 вторым уравнением).
Чтобы убедиться в том, что единственного решения нет, нужно вычислить так называемый определитель матрицы коэффициентов. Определитель выражается суммой всех возможных произведений элементов, которые не принадлежат ни одному и тому же столбцу, ни одной и той же строке. Если определитель окажется равным нулю, то система уравнений не имеет решения и в этом случае дальнейшие вычисления не нужны (или, что более важно, в этом месте программы следует предусмотреть останов). В данном случае, однако, определитель вычислялся по схеме, называемой корзиночным плетением, и при точности вычислений до девятого десятичного знака был получен результат, отличный от нуля, а именно -0.000202179. В данном примере можно было бы получить правильный ответ с помощью других методов, но в иных случаях и это бы не помогло. Дело в том, что при точности до девятого знака нельзя получить надежный результат. Кроме того, приведенная система уравнений - небольшая, и ее коэффициенты не имеют более шести значащих цифр; для более сложных систем проблема становится острее.
ПРИ РЕШЕНИИ многих задач теории чисел и других разделов математики требуется исключительно высокая точность представления очень больших целых чисел. Примером может служить упомянутая "проблема 196". Возьмем любое положительное число - двух- или более значное. Переставим цифры в обратном порядке и вновь полученное число сложим с исходным. Снова поменяем порядок цифр в сумме на обратный и сложим полученное число с предыдущим. Будем делать так до тех пор, пока не придем к палиндрому - числу, прямой и обратный порядок цифр в котором одинаков (см. рис. слева). В большинстве случаев палиндром получается быстро; если, например, начать с числа 195, то уже через четыре шага получим палиндром. Наименьшее число, для которого с помощью описанной процедуры палиндром, как представляется, никогда не получится,- это 196: как уже отмечалось, начиная с числа 196, было проделано 50тыс. шагов и они не дали результата. Среди первых 100000 целых чисел имеется 5996 чисел, которые, по-видимому, не приводят к палиндрому независимо от того, как долго мы будем продолжать вычисления (хотя это предположение и не доказано).

Вычисления по правилам "проблемы 196" для нескольких начальных чисел
Проблема 3N+1 рассматривалась в мартовском номере нашего журнала. Начнем с любого положительного числа N; если оно нечетное, заменим его на 3N+1, а если четное, поделим N пополам. Продолжим эту процедуру до тех пор, пока не получим 1. Например, если начать с N=9, то, последовательно применяя указанное правило, получим: 9, 28, 14, 7, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2 и 1 - всего 20 чисел. Эта незамысловатая задача содержит немало загадок. Всегда ли получаемая в процессе решения последовательность заканчивается 1 независимо от исходного значения N? Имеется ли какой-либо способ определения необходимого числа шагов, т.е. можно ли составить такую формулу, которая позволяла бы по значению N предсказывать число шагов? Всегда ли по любому заданному числу шагов можно определить некое нечетное N, для которого потребуется сделать именно столько шагов? (Четное N по любому заданному числу шагов найти легко: это 2, возведенное в степень, на 1 меньшую заданного числа шагов).
В 1980г. я высказал предположение, что среднее количество целых чисел, получаемых в процессе вычислений в задаче 3N+1, приблизительно определяется выражением 24.64D-101, где D - количество цифр исходного числа N. Эта оценочная формула была получена на основе вычислений, выполненных почти до 200-значных чисел, которые тогда представлялись мне довольно большими. Используя программу, обеспечивающую высокую точность вычислений, я имел возможность проверить свое допущение на нескольких больших числах. Для 1000-эначного числа по моей формуле получается, что окончательный результат достигается через 25539 шагов. Я обнаружил, что когда N=1...(998 нулей)...1, или 1E1000+1, то ряд достигает 1 через 23069 шагов. Число 55...(997 нулей)...1 порождает последовательность из 24413 чисел. Следовательно, мы получили некое подтверждение того, что средняя скорость сходимости устойчива и предсказуема.
На малых значениях N была замечена тенденция (которая, по-видимому, должна была сохраниться и для больших чисел) порождать ряды одинаковой длины многими последовательными значениями N. Действительно, можно заметить, как такие ряды чисел появляются все чаше по мере увеличения N. Например, все 230 последовательных целых чисел, начиная с числа 9123456789123456789000000000000000000000001. порождают ряды из 997 членов. (Заметим, что наша эмпирическая формула для этого числа дает 959 членов).
ТОЧНОСТЬ арифметических операций, которые непосредственно могут быть выполнены центральным процессором обычного микрокомпьютера, весьма ограниченная. Во многих вычислительных машинах единственными операциями, выполняемыми в явном виде, являются сложение и вычитание целых чисел, "длина" которых не превышает 16 битов, или двоичных разрядов: самое большое число в десятичной системе счисления, которым может оперировать такая ЭВМ,- это 65536. так что уровень точности не превышает пяти десятичных знаков. Даже на самых мощных компьютерах точность выше нескольких десятков десятичных цифр может быть обеспечена только такой программой, в которой содержится группа элементарных операций, позволяющих разбить большое число на более мелкие части.
На с.114 приведена блок-схема алгоритма вычислений с высокой точностью - процедуры, по которой было получено наибольшее из известных простых чисел: 2^132049-1. Программа ориентирована на определенный микропроцессор - модель 6502 фирмы MOS Technology. Этим микропроцессором комплектуются компьютеры, выпускаемые фирмами Apple Computer, Inc., Commodore Business Machines, Inc. и др. Алгоритм можно легко приспособить и к другим микропроцессорам.

Вычисление простого числа 2^132049-1, состоящего из 39751 цифры; блок-схемы программы (слева) и подпрограммы (справа)
Самой большой сложностью, с которой приходится сталкиваться при разработке такой программы, является, пожалуй, выбор способа представления чисел в памяти машины. Процессор может оперировать только двоичными числами, а нам желательно получать результат вычислений в десятичной форме. Приемлемым компромиссом является использование двоично-десятичной системы счисления, в которой каждая десятичная цифра представляется в соответствующей ей двоичной записи. Микропроцессор 6502 организует машинную память в "байтах" - последовательностях из восьми двоичных разрядов (битов), и таким образом обеспечивается удобный способ хранения десятичного числа, при котором каждая его цифра занимает в памяти по одному байту. (Нельзя сказать, чтобы этот способ был наиболее эффективным, но зато он самый простой).
Первый шаг в алгоритме - очистить машинную память емкостью 39760 байтов. Для этого все байты заполняются нулями. На следующем шаге исходная величина, равная 1, записывается в очищенную рабочую область, так что теперь в памяти записана последовательность из 39759 нулей, завершающаяся единицей. В счетчик, который потребуется для соблюдения последовательности вычислительных операций, в самом начале засылается нуль.
Главной частью программы является цикл, в котором происходит периодическое обращение к подпрограмме удвоения числа, хранимого в рабочей области памяти. После каждого такого удвоения к содержимому счетчика прибавляется единица и полученное число сравнивается с 132049. Если этот предел еще не достигнут, вновь вызывается подпрограмма удвоения; если же в счетчике накопилось предельное число, программа выходит из цикла. На последнем этапе из значения, хранящегося в рабочей области памяти, вычитается единица и выводится результат.
На блок-схеме программы, изображенной на с.114 слева, подпрограмма удвоения выделена цветом, а набор составляющих се команд представлен блок-схемой справа. Всякий раз, когда производится обращение к подпрограмме, начальный адрес рабочей области памяти, где хранится самая правая, или младшая, цифра исследуемого числа, присваивается индексу (X). Содержимое этого адреса затем удваивается путем прибавления к нему такого же числа. Так же как и при сложении вручную, основная трудность здесь состоит в необходимости "переносить" в процессе суммирования единицу с одного разряда на другой. Если предыдущее сложение выработало разряд переноса, его необходимо добавить к новому результату. Последний в-свою очередь должен быть проверен на последующий перенос: если сумма больше 9, из нее вычитается 10 и она заменяется на остаток, а в следующий разряд переносится единица. Этот процесс повторяется для всех 39760 байтов рабочей области машинной памяти.
Процессор 6502 компьютера модели Apple II способен выполнять более 250тыс. операций в секунду. И все же на выполнение программы, представленной на с.114, потребовалось 120ч машинного времени, чтобы подсчитать 132049-ю степень 2. Это время можно значительно уменьшить за счет простого "усечения" вычислительного процесса. Например, на ранних стадиях вычислений нет необходимости удваивать все цифры, записанные в памяти машины, так как большинство из них нули. Рабочую область можно считать заполненной, когда в ней будет находиться, скажем, 150 байтов, и это число будет увеличиваться на три байта при каждом увеличении степени на 10. При таком подходе в программу придется ввести дополнительные команды, но зато быстродействие при этом возрастает.
ВСЕ ЧИСЛА, которыми приходится оперировать при вычислении 2^132049-1,- целые, но существует немало задач, решение которых облегчается, если использовать такую же запись, которая принята в научных работах, когда число представляется в виде произведения десятичной дроби, называемой мантиссой, и степени 10 (показатель степени в такой форме записи называется порядком). Например, текущий год можно записать в виде 1.984E3, где 1.984 - мантисса, а 3 - порядок. Программы высокой точности, которые оперируют числами в такой форме, сложнее, чем аналогичные программы, рассчитанные на действия только с целыми числами, потому что в первом случае каждое число имеет несколько составляющих (помимо мантиссы и порядка в него входят знак мантиссы и знак порядка).
В большинстве языков программирования высокого уровня предусмотрены некоторые средства, позволяющие использовать такую форму представления чисел; в этом случае говорят о системе с плавающей точкой. Числа меньше определенного размера (количества разрядов) представляются на табло как обычная десятичная дробь, но внутри машины эти числа хранятся в виде мантиссы и порядка. Поле, отведенное для различных элементов числа, определяет точность и диапазон значений этого числа. Отводя больше места для мантиссы, мы повышаем точность, а чем больше порядок, тем шире диапазон чисел. Версия языка Бейсик в программном обеспечении для Apple II имеет фиксированную точность - примерно 9 десятичных знаков.
Для обеспечения еще более высокой точности необходимо опять прибегнуть к возможностям программного обеспечения. Г.Робинсон, будучи сотрудником Ливерморской лаборатории, составил пакет программ вычислений с высокой точностью для чисел, представленных с плавающей точкой. Программы, написанные на машинном языке микропроцессора 6502, могут обеспечивать любой уровень точности вплоть до 600 десятичных знаков и допускают величину порядка до 9999. Эти предельные параметры были выбраны, исходя из соответствующих характеристик процессора: 600-значная мантисса, 4-значный порядок и их знаки можно записать 2S6 байтами, а в модели 6502 блок емкостью 256 байтов - это одна "страница" памяти.
В программах Робинсона операции, которые могут выполняться над числами, включают основные арифметические действия, логарифмирование, возведение в степень, извлечение квадратного корня, а также вычисление различных тригонометрических функций. Предусмотрено вычисление и не столь широко распространенных функций, как, например, функции Эйлера и преобразования Вейнгартена для суммирования медленно сходящихся рядов. В пакете имеются значения 26 постоянных и 8000 простых чисел. Пакетом можно пользоваться как весьма совершенным калькулятором или обращаться к отдельным его программам как к подпрограммам. Первые версии показали, что арифметические действия и вычисления функций могут производиться с предельной точностью до 600 десятичных знаков.
Для тех, кто проявляет интерес к численным процедурам, первое знакомство с цифровым компьютером иногда приводит в уныние; это потому, что элементарные вычисления на машине выполняются быстро и, что самое важное, безупречно, и как следствие возникает ложное представление, будто тщательный численный анализ можно выполнить без всяких усилий. После этого трудно поверить, что корень пятой степени из 100 (константа, которая используется для сравнения величины звезд) нельзя вычислить намного точнее, чем с помощью ручного калькулятора. Пакет программ, подобный пакету Робинсона, позволяет оправдать возлагаемую на компьютер надежду. Корень пятой степени из 100 можно вычислить до 100 десятичных знаков буквально за несколько минут.
БИБЛИОГРАФИЯ
Опять можно посмотреть Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 -
 ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.
Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
7 1984
В ИГРЕ "БОЙ В ПАМЯТИ" КОМПЬЮТЕРНЫЕ ПРОГРАММЫ ВЕДУТ БИТВУ ЗА БИТЫ
А.К. ДЬЮДНИ
ДВЕ КОМПЬЮТЕРНЫЕ программы, действующие в своей родной стихии - памяти цифровой ЭВМ, рыщут от адреса к адресу, "атакуя" друг друга. Иногда они проводят разведывательные действия в поисках противника, иногда бомбардируют память "числовыми бомбами", а иногда копируют сами себя, избегая опасности, или приостанавливаются, чтобы исправить полученные повреждения. Это игра, которую я назвал "Бой в памяти". Она отличается от большинства других компьютерных игр тем, что люди, по существу, не принимают в ней участия. Противоборствующие программы, разумеется, написаны людьми, но, когда начинается "сражение", создателю программы не остается ничего другою, как просто наблюдать за тем, как продукт его многочасового труда либо живет, либо погибает на экране дисплея. Исход борьбы зависит лишь от того, какая программа первой получит повреждение в уязвимой области.
Название игры (Core War - "Бой на ферритовых сердечниках") происходит от ныне устаревшей технологии производства оперативной памяти ЭВМ. В 50-x и 60-х годах оперативные запоминающие устройства компьютеров состояли из тысяч ферритовых сердечников - маленьких колечек, нанизанных на тонкие проволочки. Каждый такой сердечник предназначался для запоминания одного бита информации, или двоичного разряда - основной информационной единицы. Теперь запоминающие устройства изготовляются на полупроводниковых кристаллах, однако оперативную память, в которой хранится программа в ходе своего выполнения, все еще часто называют ферритовой памятью (core memory или просто core).
Программы для игры "Бой в памяти" пишутся на специальном языке, который я назвал Редкодом. Он относится к категории языков программирования, известной как языки ассемблера. В настоящее время большинство программ для ЭВМ пишется на языках высокого уровня, таких, как Паскаль, Фортран или Бейсик. В этих языках один оператор может привести к выполнению целой последовательности машинных команд. Кроме того, эти операторы легче читаются и программисту проще понять логику программы. Однако, чтобы программу можно было выполнить, ее сначала нужно перевести на "машинный язык", в котором каждая команда представляется довольно длинной цепочкой двоичных разрядов. Составлять программу на таком языке - занятие скучное и утомительное.
Языки ассемблера занимают промежуточное положение между языками высокого уровня и машинными языками. Как правило, в программе, написанной на языке ассемблера, каждый оператор соответствует одной машинной команде и, следовательно, какой-то конкретной цепочке двоичных разрядов. Но вместо того чтобы записывать эти двоичные числа, программист представляет их короткими словами, сокращенными мнемоническими обозначениями команд. Такие слова значительно проще запомнить, чем двоичные числа. Перевод на машинный язык осуществляет программа, называемая ассемблером.
Языком ассемблера пользуются сравнительно редко, потому что программы, написанные на этом языке, длиннее и в них труднее разобраться по сравнению с программами, написанными на языках высокого уровня. Однако существуют задачи, для которых язык ассемблера - идеальное средство. Если программа должна занимать как можно меньше памяти или должна выполняться как можно быстрее, то обычно ее пишут на языке ассемблера. Более того, некоторые возможности машины можно реализовать, пользуясь только языком ассемблера,- языки высокого уровня не позволяют этого сделать. Например, программы, написанные на языке ассемблера, могут модифицировать свои собственные команды или перемещать самих себя на другое место в памяти.
ИДЕЯ игры "Бой в памяти" впервые возникла у меня несколько лет назад, после того как мне рассказали о шутке одного программиста, работавшего в крупной исследовательской лаборатории, которую я условно назову "лабораторией X". Этот программист написал на языке ассемблера программу под названием "Сорняк", которая создавала свою точную копню каждый раз, когда выполнялась. Она также обладала способностью переходить из одного компьютера в другой, распространяясь по всей сети ЭВМ лаборатории X. У программы не было никакого другого назначения, кроме как "увековечить" самое себя. Через некоторое время появилось так много копий Сорняка, что более полезным программам и наборам данных стало не хватать места. Такое разрастание Сорняка продолжалось до тех пор, пока кто-то не придумал воспользоваться программой, основанной на том же принципе: была создана еще одна самовоспроизводящаяся программа под названием "Косарь" для обнаружения и уничтожения копий Сорняка, а когда их уже нельзя было найти, программа Косарь должна была уничтожить самое себя. Косарь выполнил свою задачу, и порядок в лаборатории X был таким образом восстановлен.
Несмотря на то что эта история казалась маловероятной, я в нее поверил, возможно потому, что мне захотелось в нее поверить. Я затратил некоторое время на то, чтобы докопаться ло реальных фактов, скрывавшихся за этим анекдотом. (О том, что мне удалось узнать, я расскажу ниже. А сейчас заметим лишь, что в основе моего желания поверить этой истории лежала интригующая идея о двух программах, "сражающихся в темных и бесшумных лабиринтах памяти машины").
В прошлом году я решил все-таки реализовать идею, лежащую в ее основе, и разработал первую версию игры "Бой в памяти". Мне помогал Дэвид Джонс, студент моего отделения в Университете Зап.Онтарио. С тех пор мы продолжали дорабатывать эту игру и довели ее до довольно интересного уровня.
У игры "Бой в памяти" четыре основных компонента: массив памяти на 8000 адресов, язык ассемблера Редкод, программа-монитор под названием "Марс" (MARS - Memory Array Redcode Simulator) и набор "боевых" программ. Две противоборствующие программы вводятся в память на случайным образом выбранные позиции, причем ни одна программа не знает, где находится программа-противник. Программа-монитор Марс управляет выполнением таких программ, реализуя простейший вариант системы разделения времени, которая распределяет ресурсы компьютера по многочисленным пользователям, работающим одновременно с машиной. Программы-противники "ходят" по очереди. Сначала выполняется одна команда первой программы, затем одна команда второй программы и т.д.
Действия, совершаемые программой в отведенные для нее промежутки времени, полностью определяются автором программы. Цель же этих действий заключается в том, чтобы вывести из строя другую программу, повредив ее команды. Однако можно придерживаться и защитной стратегии: программа может заниматься восстановлением полученных повреждений или, "попав под огонь противника", переходить на другое место в памяти. Игра заканчивается, когда программа-монитор Марс встречает в одной из программ команду, которую невозможно выполнить. Программа, содержащая эту недействительную команду (следствие полученного в "бою" повреждения), объявляется проигравшей.
О ПРОГРАММЕ можно многое узнать, анализируя ее повеление в уме или пользуясь просто карандашом и бумагой. Однако, чтобы по-настоящему испытать программу в действии, необходимы компьютер и программное обеспечение игры (система Марс). Играть можно и на персональном компьютере - мы с Джонсом подготовили инструкции для тех, кто захочет реализовать игру "Бой в памяти" на своем компьютере.
Прежде чем перейти к описанию языка Редкод и представить несколько примеров простых программ для этой игры, мне хотелось бы немного подробнее остановиться на массиве памяти. Хотя выше отмечалось, что она состоит из 8000 адресуемых ячеек, в этом числе нет ничего магического; игра может проходить и в памяти меньшего размера. Существенным отличием от большинства запоминающих устройств является то, что массив памяти для системы Марс имеет круговую структуру. Адреса ячеек памяти нумеруются последовательно от 0 до 7999, а следующий адрес 8000 указывает опять на ячейку 0; таким образом, память замыкается сама на себя. Адреса, большие, чем 7999, Марс всегда "загоняет" в пределы от 0 до 7999, для чего значение адреса делится на 8000, а полученный при делении остаток берется в качестве действительного адреса. Так, например, когда программа "стреляет" в ячейку с адресом 9378, Марс интерпретирует этот адрес как 1378.
Редкод представляет собой очень упрошенный специализированный язык программирования, относящийся к классу языков ассемблера. Он содержит команды, позволяющие перенести содержимое одной ячейки памяти в другую, команды, производящие арифметические операции над содержимым ячеек памяти, а также команды управления последовательностью выполнения команд в программе. В отличие от ассемблера, который переводит программы в двоичные колы машинных команд. Марс переводит программы, написанные на Редкоде, в последовательность больших целых десятичных чисел, хранящихся затем в массиве памяти. Каждая ячейка памяти может хранить одно такое число. При выполнении программ Марс интерпретирует эти целые числа как машинные команды и производит соответствующие операции.
Список элементарных команд языка Редкод приведен на рисунке с.98. Каждую команду программист должен снабдить по крайней мере одним операндом или конкретным значением. Большинство команд требуют двух операндов. Например, команда JMP -7 (JMP - мнемоническое обозначение от слова jump - прыгнуть, перескочить) имеет один операнд со значением -7. Эта команда сообщает Марсу, что нужно передать управление на ячейку памяти с адресом, меньшим текущего адреса на 7 единиц, т.е. выполнить команду под номером на 7 меньшим, чем номер самой команды JMP -7. Если эта команда находилась бы сама в ячейке с адресом 3715, то выполнение программы продолжилось бы с ячейки с адресом 3708.
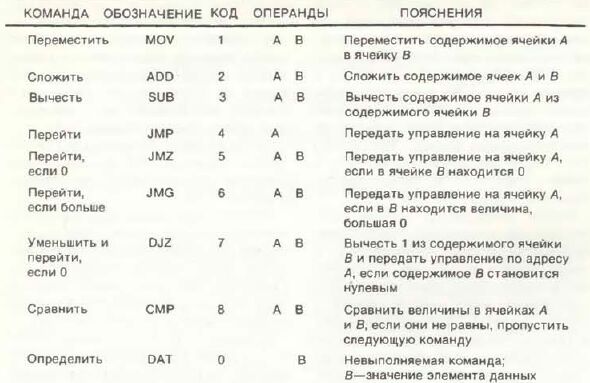
Система команд Редкода - языка ассемблера для игры "Бой в памяти"
Такой способ вычисления адреса памяти называется относительной адресацией; это единственный способ адресации, используемый в языке Редкод. Таким образом, программа никогда не знает абсолютных значений адресов, по которым располагаются се команды.
Команда MOV 3 100 сообщает Марсу, что нужно продвинуться вперед на 3 адреса, прочитать содержимое ячейки и перенести его в ячейку с адресом на 100 большим, чем адрес самой команды, стерев то, что там находилось до сих пор. В этой команде операнды заданы в "прямой" форме, т.е. они прямо указывают на адреса ячеек, над содержимым которых производятся действия. Разрешаются также еще два способа адресации. Если перед операндом стоит значок @, то это означает, что используется "косвенная" адресация. Команда MOV @3 100 означает, что целое число, которое нужно поместить в ячейку с относительным адресом 100, находится уже не в ячейке с относительным адресом 3, а в ячейке, адрес которой хранится по относительному адресу 3. (Механизм косвенной адресации проиллюстрирован на с.98 внизу). Значок 0 указывает на то, что операнд следует понимать как "непосредственный", т.е. рассматривать его не как адрес ячейки в памяти, а как целое число. Команда MOV #3 100 означает, что целое число 3 нужно поместить в ячейку с относительным адресом 100.

Трехшаговый механизм косвенной относительной адресации
Большинство других команд не нуждается в пояснениях. Следует лишь сказать еше несколько слов о команде DAT. Она может служить как средство резервирования памяти для информации, используемой в программе. Однако, строго говоря, DAT не является командой как таковой. Любая ячейка памяти, содержащая нуль в первом десятичном разряде, может рассматриваться как команда типа DAT и потому как невыполняемая команда. Если от системы Марс потребуется выполнить подобную "команду", то она не сможет этого сделать и объявит программу проигравшей.
Десятичное число, представляющее команду Редкода, имеет несколько полей, или функциональных областей (см. рисунок слева в середине). Первая цифра представляет обозначение команды; она является как бы кодом операции. Две следующие цифры отводятся под способ адресации для первого и второго операндов соответственно (прямая, косвенная или непосредственная). Наконец, на каждый операнд отводится еще по четыре цифры. Отрицательные значения величин хранятся в дополнительном представлении: так, -1 будет представлена как 7999, поскольку в круговой памяти системы "прибавить 7999" даст тот же эффект, как "вычесть 1".

Представление команд языка Редкод десятичными целыми числами
Команды, из которых построена простейшая программа "Карлик", приведены на с.99. Несмотря на то что программа Карлик не очень разумна, она весьма опасна: систематически "прочесывает" память, "бомбардируя" каждую пятую ячейку нулем. Нуль - это число, обозначающее не выполняемую команду DAT; таким образом, попав в расположение команд программы-противника, нуль может привести к ее остановке.

Карлик - игровая программа, систематически разбрасывающая "нулевые бомбы"
Предположим, к примеру, что Карлик занимает ячейки памяти с абсолютными адресами от 1 до 4. Ячейка 1 первоначально содержит команду DAT -1, однако выполнение программы начинается со следующей команды, ADD #5 -1. В результате число 5 прибавляется к содержимому предыдущей ячейки, а именно к команде DAT -1, после чего она превращается уже в DAT 4. Затем Карлик выполняет команду, находящуюся в ячейке 3, а именно MOV #0 @-2. Здесь целое число 0 указано как непосредственное значение операнда; его нужно перенести в ячейку, адрес которой вычисляется следующим образом. Сначала Марс отсчитывает от адреса 3 две единицы назад, останавливаясь на ячейке 1. Прочитав значение, хранящееся в этой ячейке, а именно 4, Марс интерпретирует его как адрес, определяемый относительно адреса текущей команды. Другими словами, он отсчитывает четыре ячейки вперед от адреса 1 и помещает значение 0 в ячейку с адресом 5.
Заключительная команда программы Карлик, JMP -2, создает бесконечный цикл. Она вновь передает управление на ячейку с абсолютным адресом 2, в результате чего число в команде DAT увеличивается на 5 и теперь она уже выглядит как DAT 9. При следующем выполнении тела цикла число 0 помешается уже в ячейку с абсолютным адресом 10. После этого "нулевые бомбы" падают на ячейки 15, 20, 25 и т.д. Сама программа остается на месте, но ее "артиллерия" угрожает всему массиву памяти. В конце концов Карлик добирается до адресов 7990, 7995 и затем 8000. Последний адрес рассматривается Марсом как равный 0, и поэтому Карлик едва "не покончил жизнь самоубийством". Следующая "бомба" падает снова на ячейку 5.
К сожалению, ни одна "боевая" программа, содержащая более четырех команд, не может уйти от огня Карлика. У программы-противника остается лишь три выхода: либо, постоянно передвигаясь по памяти, попытаться уйти из-под огня, либо, приняв удар, попробовать устранить повреждение, либо успеть первой поразить Карлика. Чтобы добиться успеха, следуя последней стратегии, программа должна оказаться весьма везучей. Ведь ей не известно, в каком месте памяти находится Карлик, и в среднем потребуется произвести около 1600 "выстрелов", или выполнить 1600 программных циклов, прежде чем Карлик получит повреждение. Если Карлик сражается против Карлика, то каждая программа выигрывает в 30% случаев, а в 40% случаев ни одной программе не удается поразить противника.
Прежде чем рассмотреть две другие стратегии, мне хотелось бы представить вам забавную однострочную программу. Назовем ее "Чертенком". Вот се текст:
MOV 0 1
Чертенок представляет собой пример простейшей программы, написанной на Редкоде и способной перемешаться в памяти. Команда MOV 0 1 считывает содержимое ячейки с относительным адресом 0, т.е. считывает самое себя, и переносит его в ячейку с относительным адресом 1, т.е. в следующую ячейку. В ходе своего выполнения программа движется по памяти со скоростью одна ячейка за одну команду, оставляя за собой пространство, полностью покрытое командами MOV 0 1.
А что будет, если выставить Чертенка против Карлика? "Зона обстрела" нулевыми бомбами Карлика распространяется по памяти быстрее, чем движется Чертенок; однако из этого еще не следует, что Карлик имеет преимущество. Поразит ли Кралик Чертенка, даже если Чертенок попадет в "зону огня", - вот в чем вопрос!

Чертенок против Карлика - кто победит?
Если же Чертенок первым настигнет Карлика, то он "пропашет" команды Карлика насквозь. Когда команда Карлика JMP -2 передаст управление назад на две ячейки, там уже будет находиться команда Чертенка MOV 0 1. В результате Карлик переродится и станет вторым Чертенком, до бесконечности преследующим первого по полю памяти. Согласно правилам игры "Бой в памяти", сражение заканчивается вничью. (Отметим, что такого исхода следует, по всей вероятности, ожидать. Читатели могут проанализировать другие возможности; может быть, им удастся открыть какой-либо другой любопытный исход сражения).
КАК ЧЕРТЕНОК, так и Карлик относятся к классу программ, которые можно охарактеризовать как небольшие и агрессивные, но неразумные. На следующем по сложности уровне находятся программы, возможно менее агрессивные, но достаточно "хитрые", чтобы успешно противостоять программам низшего класса. Эти программы обладают способностью уходить от атак противника, создавая свои копии в более безопасных местах. Каждая подобная программа должна содержать фрагмент, похожий на программу Близнецы, текст которой приведен на рисунке внизу на с.97. Близнецы не представляют собой законченной игровой программы. Единственная цель у этой программы - создать свою копию в области памяти, отстоящей на 100 ячеек, и передать управление только что созданной копии.

Близнецы - программа, создающая свою копию на новом месте в памяти
Программа Близнецы состоит из трех основных частей. Две команды DAT в начале программы служат в качестве указателей. Они указывают соответственно на следующую команду, подлежащую копированию, и на адрес назначения, т.е. на ячейку, куда ее нужно поместить. Цикл, расположенный в середине программы, непосредственно осуществляет копирование, перемещая команды по очереди на 100 ячеек вперед относительно того места, откуда они берутся. После каждого прохождения цикла оба указателя увеличиваются на единицу и указывают уже на новый источник и новый пункт назначения соответственно. Команда сравнения СМР в теле цикла проверяет значение первой команды DAT. Когда оно уже увеличено 9 раз, это означает, что вся программа скопирована, и происходит выход из цикла. Теперь осталось провести небольшую коррекцию. Адрес назначения во второй команде программы имеет исходное значение 99, однако к тому времени, как оно будет скопировано, это значение окажется равным 100. Ошибку, возникшую в процессе копирования, нужно исправить (посредством команды MOV #99 93), после чего можно передать управление на только что созданную копию программы.
Модифицируя программу Близнецы, можно создать целый класс "боевых" программ. Одна из таких программ - "Идол" - создает свои копии на расстоянии 10 ячеек вместо 100. Как и Чертенок, Идол пытается "пройтись" через всю программу противника, но выигрывает гораздо чаще Чертенка и реже заканчивает игру с ничейным результатом, потому что поврежденные им программы с меньшей вероятностью смогут успешно выполнять команды, подставленные в них Идолом. В "Скороходе" - еше одной программе, где используется механизм Близнецов,- интервал между копиями равен большому простому числу. Скорохода труднее "поймать", и он производит такое же опустошительное действие в стане противника, как и программа Идол.
СКОРОХОД и Идол не очень разумные программы. На сегодняшний день мы располагаем лишь двумя программами, относящимися ко второму уровню сложности. Они слишком громоздки для того, чтобы привести их здесь. Одна на них - назовем ее Радар - выставляет с обеих сторон своеобразные "пикеты" (см. рисунок на с.97). Каждый пикет состоит из 100 последовательных ячеек памяти, заполненных единицами, и отделен от текста программы "буферной зоной" из 100 пустых ячеек. Радар попеременно занимается то атакующими действиями в удаленных областях памяти, то проверкой состояния своих пикетов. Если в одном из пикетов обнаруживается какое-либо изменение, Радар интерпретирует это изменение как свидетельство атаки, проведенной Карликом, Чертенком или какой-то другой неразумной программой. В этом случае Радар создает свою копию по другую сторону от поврежденного пикета, восстанавливает его, создает новый пикет на незащищенной стороне и затем продолжает нормальную последовательность действий.

Радар - более сложная игровая программа, успешно отражающая атаки более простой программы Чертенок
Помимо создания своих копий игровая программа может быть наделена способностью восстанавливать себя от повреждений. Джонс написал самовосстанавливающуюся программу, способную выдерживать некоторые виды атак, но не все. Программа под названием "Сканер" сохраняет себя в двух экземплярах, но выполняются обычно лишь команды одного из этих экземпляров. Экземпляр программы, выполняющийся в текущий момент, периодически просматривает команды второго экземпляра, чтобы проверить, не подверглись ли они атакующим действиям программы-противника. Изменения, возникшие вследствие атаки противника, обнаруживаются путем сравнения экземпляров Сканера между собой, причем экземпляр, выполняющийся в данный момент, считается правильным. Если обнаруживаются какие-либо недействительные команды, они замещаются правильными, после чего управление передается на "отремонтированный" экземпляр, который в свою очередь приступает к проверке первого.
В настоящее время Сканер остается чисто защитной программой. Она способна выдержать атаки Карлика, Чертенка, Идола и других подобных им медленно действующих агрессивных программ, по крайней мере в тех случаях, когда противник проводит атаки с правильной (защищенной) стороны. Сейчас Джонс работает над самовосстанавливающейся программой, хранящей себя в трех экземплярах.
Интересно, смогут ли читатели изобрести самовосстанавливающиеся программы каких-либо других типов? Например, можно подумать о программе, хранящей себя в двух или более экземплярах, но такой, что выполняется все время лишь один из них. Программа могла бы иметь "ремонтирующую часть", которая обращалась бы к другим экземплярам для восстановления поврежденных команд. Эта ремонтирующая часть могла бы даже ремонтировать сама себя, но в некоторых местах она оставалась бы уязвимой. В качестве "меры уязвимости" программы можно принять число поврежденных команд, приводящих к остановке программы. Иногда достаточно повредить одну-единственную команду; в других случаях потребуется поразить много команд. А сколько команд в среднем нужно поразить, чтобы вывести из строя программу? С точки зрения такого критерия какова должна быть наименее уязвимая самовосстанавливающаяся программа?
Игра "Бой в памяти" лишь тогда станет по-настоящему интересной, когда будут созданы достаточно надежные программы, которые в основном будут обороняться, а не атаковать. Такие игровые программы должны будут отыскивать и опознавать текст программы-противника, а затем предпринимать энергичные атакующие действия в той области памяти, где он был обнаружен.
Возможно, у вас сложилось впечатление, что язык Редкод и система Марс в целом представляют собой завершенную систему. Это не так. В свободное время мы проверяли некоторые новые идеи и много экспериментировали.
Одна из новых идей состояла в том, чтобы включить еше одну команду, которая позволяла бы несколько облегчить действия, связанные с самозащитой и самовосстановлением. Команда РСТ А защитит команду, хранящуюся в ячейке с адресом А, от изменений до тех пор, пока она не будет исполнена. Насколько можно будет уменьшить уязвимость программы за счет применения команды подобного рода?
В подготовленных нами инструкциях, о которых говорилось выше, мы объясняем не только правила игры "Бой в памяти", но и то, как реализовать массив памяти и написать программу-монитор Марс на различных языках высокого уровня. Инструкции содержат также предложения о том, как можно демонстрировать результаты игры. Здесь же мы опишем правила игры с достаточной точностью для того, чтобы читатели могли составлять игровые программы, используя пока что карандаш и бумагу.
1. Две боевые программы загружают в память в случайным образом выбранные позиции, но на расстоянии друг от яруга не меньше 1000 адресов.
2. Марс поочередно выполняет по одной команде из каждой программы, пока не дойдет до команды, которую невозможно выполнить. Программа, содержащая эту команду, объявляется проигравшей.
3. Программы противника можно атаковать любым доступным "оружием". В качестве "бомбы" можно воспользоваться нулем или любым другим целым числом, включая числа, представляющие дозволенные команды Редкола.
4. На продолжительность сражения накладывается определенное временное ограничение, зависящее от быстродействия компьютера. Если время игры уже вышло и обе программы продолжают выполняться, то исход сражения считается ничейным.
ИСТОРИЯ о Сорняке и Косаре, по-видимому, основана на двух реально существовавших программах. Одна из них представляла собой компьютерную игру под названием "Дарвин" и была изобретена М.Макилроем из AT&T Bell Laboratories. Другая программа под названием "Червяк" была написана Дж.Шохом из Исследовательского центра фирмы Xerox в Пало-Альто. Обе программы были написаны давно и стали достаточно известными. (Игра "Дарвин" была описана в журнале "Software: Practice and Experience", т.2, с.93-96, 1972. Довольно туманное описание того, что, по-видимому, представляет собой ту же игру, появилось в издании "Computer lib.", 1978г.)
По правилам игры "Дарвин" каждый играющий представляет некоторое число программ, написанных на языке ассемблера, которые засылаются в память машины вместе с программами других играющих. Эти программы называют "организмами". Организмы, созданные одним игроком (и принадлежащие к одному и тому же "виду") пытаются "убить" представителей других видов и занять обитаемое ими пространство. Победителем считается тот игрок, организмы которого оказываются наиболее многочисленными к моменту остановки игры. Макилрою удалось изобрести неуязвимый организм, хотя выиграл он всего лишь "несколько игр". Этот организм не очень-то агрессивен, хотя и является "бессмертным ".
Червяк - это экспериментальная программа, предназначенная для того, чтобы как можно интенсивнее использовать ресурсы сети ЭВМ фирмы Xerox. Червяк загружался в несопротивляющиеся машины под контролем программы-супервизора. Цель Червяка состояла в том, чтобы взять на себя управление машиной и в сотрудничестве с Червяками, поселившимися в других машинах, обеспечивать выполнение больших прикладных программ в образовавшейся таким образом мультипроцессорной системе. Червяк устроен так, что любой, кто хочет воспользоваться одной из занятых машин, может получить ее в свое распоряжение, не нарушая работы более объемных программ.
В легенде о Сорняке и Косаре можно увидеть некоторые элементы как игры "Дарвин", так и программы Червяк. Но лишь в игре "Бой в памяти" Косарь стал наконец реальностью.
БИБЛИОГРАФИЯ
COMPUTER RECREATIONS: "DARWIN". ALEPH NULL in Software: Practice and Experience, Vol.2, No.1, pages 93-96; January-March, 1972.
68000 ASSEMBLY LANGUAGE PROGRAMMING. GERRY KANE AND DOUG HAWKINS LEGENTHAL. Osborne - McGraw-Hill, I981.
Можно посмотреть М.СИНГЕР, МИНИ-ЭВМ PDP-11: ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ АССЕМБЛЕРА И ОРГАНИЗАЦИЯ МАШИНЫ, МОСКВА, "МИР", 1984.- G.
Более простая "алгоритмическая игра" - ТЕМА #8, АБЗАЦ #234
ТЕМА #8, АБЗАЦ #234 .- G.
.- G.
ОТКЛИКИ
10 1984
ОТКЛИКИ на статью, посвященную игре "Бой в памяти" в майском номере журнала, оказались самыми разнообразными: от обычных просьб о дополнительной литературе по этой игре до подробных описаний полных игровых схем. Во многих письмах содержались описания программ наподобие "Сорняка", засоряющих реальные системы (в том числе вползших как черви в яблоко в системы Apple), рассуждения о программах как таковых и теоретизирования по поводу оборонительной и наступательной стратегиях. Мы сможем рассказать только о нескольких самых важных разработках; другим придется ждать будущих публикаций под этой рубрикой которые, надеюсь, еще появятся до конца года.
Д.Макилрой сообщил, что игру "Дарвин" придумал его сотрудник В.Висотски из AT&T Bell Laboratories. Однако "неуязвимый" организм изобрел сам Макилрой.
Что произойдет, если "Чертенок" нападет на "Карлика"? Одна возможность была разобрана в майском номере: "Карлик" передаст управление команде "Чертенка" и превратится во второго "Чертенка", бесконечно преследующего первого. Другой исход приводит к противоположному результату. Предположим, что "Карлик" уже перескочил через свою первую команду, когда "Чертенок" копировал самого себя в ячейке с данными "Карлика". Тогда складывается такая ситуация:

Поскольку должна выполняться команда "Карлика", она прибавляет 5 к команде "Чертенка", превратив ее в MOV 0 6. Затем выполняется "Чертенок", копируя себя через 6 ячеек вперед, а сам "очищается" "Карликом", который затем атакует свой следующий адрес (численное значение, соответствующее MOV 0 6). На следующем шагу с "Чертенком" происходит нечто странное: он выполняет первую команду программы "Карлика", так что игра временно превращается в игру "двойной Карлик", который бессмысленно атакует массив памяти, тогда как предмет его притязаний располагается на его собственной территории и делает абсолютно то же самое!
Д.Менкони из Милпитаса (шт.Калифорния), автор игр фирмы Atari, Inc., предложил именно это свойство сделать обычным правилом игры "Бой в памяти", позволив каждой программе выполняться одновременно в двух местах. Таким образом, даже если программа потеряет одно свое "я", второе сможет восстановить поврежденные участки. Э.Уоррел из Бетесда (шт.Мадиссон), предлагает более общую схему, состоящую из n "я", которые выполняют одну и ту же программу, но в разных ячейках памяти. Р.Перейно из Университета Джорджа Мейсона написал свою программу игры "Бой в памяти" для компьютера и Apple II, используя вместо коротких машинных слов двумерный массив размера 2000*2 байт. Б.Дорнфнлд из фирмы AMF, Inc., написал на модифицированном Бейсике подробную программу игры "Бой в памяти" для настольного компьютера Hewlett-Packard 9816/26.
Самую впечатляющую систему данных построили три старшекурсника: Г.Гетш и М.Молдин из Университета Карнеги-Меллона и П.Милаицо из Университета Раиса. Молдин продемонстрировал свою программу на компьютере VAX нашего факультета Универсчтета провинции Западного Онтарио. На экране дисплея был выведен весь массив памяти, причем положение каждой участвующей программы отмечалось прописной буквой, а участок памяти, оккупированный этой программой,- соответствующей строчной буквой.
Моллин придумал "боевую" программу, которую назвал "Миномет". Она работает примерно так же, как "Карлик", за тем исключением, что "ведет атаку" в соответствии с числами Фибоначчи (1, 1, 2, 3, 5 и т.д., каждое число представляет собой сумму двух предыдущих). Как это ни странно, "Карлик" побеждает "Миномет" в 60 случаях из 100. Но "Миномет" постоянно поражает 3/4 самовосстаиавливаюшейся программы, названной "Избиратель". В то же время "Избиратель" выдерживает атаки "Карлика" и регулярно поражает его.
Гетш, Молдин и Милаццо проанализировали поведение "Миномета" и пришли к выводу, что если программа его противника состоит более чем из 10 команд, она должна быть самовосстанавливаюшейся, чтобы побелить "Миномет". Однако не существует программ, состоящих более чем из 141 команды, которые восстанавливались бы достаточно быстро, чтобы выдержать атаки "Миномета".
В ИГРЕ "БОЙ В ПАМЯТИ" КОМПЬЮТЕРНЫЕ ПРОГРАММЫ ВЕДУТ БИТВУ ЗА БИТЫ
А.К. ДЬЮДНИ
ДВЕ КОМПЬЮТЕРНЫЕ программы, действующие в своей родной стихии - памяти цифровой ЭВМ, рыщут от адреса к адресу, "атакуя" друг друга. Иногда они проводят разведывательные действия в поисках противника, иногда бомбардируют память "числовыми бомбами", а иногда копируют сами себя, избегая опасности, или приостанавливаются, чтобы исправить полученные повреждения. Это игра, которую я назвал "Бой в памяти". Она отличается от большинства других компьютерных игр тем, что люди, по существу, не принимают в ней участия. Противоборствующие программы, разумеется, написаны людьми, но, когда начинается "сражение", создателю программы не остается ничего другою, как просто наблюдать за тем, как продукт его многочасового труда либо живет, либо погибает на экране дисплея. Исход борьбы зависит лишь от того, какая программа первой получит повреждение в уязвимой области.
Название игры (Core War - "Бой на ферритовых сердечниках") происходит от ныне устаревшей технологии производства оперативной памяти ЭВМ. В 50-x и 60-х годах оперативные запоминающие устройства компьютеров состояли из тысяч ферритовых сердечников - маленьких колечек, нанизанных на тонкие проволочки. Каждый такой сердечник предназначался для запоминания одного бита информации, или двоичного разряда - основной информационной единицы. Теперь запоминающие устройства изготовляются на полупроводниковых кристаллах, однако оперативную память, в которой хранится программа в ходе своего выполнения, все еще часто называют ферритовой памятью (core memory или просто core).
Программы для игры "Бой в памяти" пишутся на специальном языке, который я назвал Редкодом. Он относится к категории языков программирования, известной как языки ассемблера. В настоящее время большинство программ для ЭВМ пишется на языках высокого уровня, таких, как Паскаль, Фортран или Бейсик. В этих языках один оператор может привести к выполнению целой последовательности машинных команд. Кроме того, эти операторы легче читаются и программисту проще понять логику программы. Однако, чтобы программу можно было выполнить, ее сначала нужно перевести на "машинный язык", в котором каждая команда представляется довольно длинной цепочкой двоичных разрядов. Составлять программу на таком языке - занятие скучное и утомительное.
Языки ассемблера занимают промежуточное положение между языками высокого уровня и машинными языками. Как правило, в программе, написанной на языке ассемблера, каждый оператор соответствует одной машинной команде и, следовательно, какой-то конкретной цепочке двоичных разрядов. Но вместо того чтобы записывать эти двоичные числа, программист представляет их короткими словами, сокращенными мнемоническими обозначениями команд. Такие слова значительно проще запомнить, чем двоичные числа. Перевод на машинный язык осуществляет программа, называемая ассемблером.
Языком ассемблера пользуются сравнительно редко, потому что программы, написанные на этом языке, длиннее и в них труднее разобраться по сравнению с программами, написанными на языках высокого уровня. Однако существуют задачи, для которых язык ассемблера - идеальное средство. Если программа должна занимать как можно меньше памяти или должна выполняться как можно быстрее, то обычно ее пишут на языке ассемблера. Более того, некоторые возможности машины можно реализовать, пользуясь только языком ассемблера,- языки высокого уровня не позволяют этого сделать. Например, программы, написанные на языке ассемблера, могут модифицировать свои собственные команды или перемещать самих себя на другое место в памяти.
ИДЕЯ игры "Бой в памяти" впервые возникла у меня несколько лет назад, после того как мне рассказали о шутке одного программиста, работавшего в крупной исследовательской лаборатории, которую я условно назову "лабораторией X". Этот программист написал на языке ассемблера программу под названием "Сорняк", которая создавала свою точную копню каждый раз, когда выполнялась. Она также обладала способностью переходить из одного компьютера в другой, распространяясь по всей сети ЭВМ лаборатории X. У программы не было никакого другого назначения, кроме как "увековечить" самое себя. Через некоторое время появилось так много копий Сорняка, что более полезным программам и наборам данных стало не хватать места. Такое разрастание Сорняка продолжалось до тех пор, пока кто-то не придумал воспользоваться программой, основанной на том же принципе: была создана еще одна самовоспроизводящаяся программа под названием "Косарь" для обнаружения и уничтожения копий Сорняка, а когда их уже нельзя было найти, программа Косарь должна была уничтожить самое себя. Косарь выполнил свою задачу, и порядок в лаборатории X был таким образом восстановлен.
Несмотря на то что эта история казалась маловероятной, я в нее поверил, возможно потому, что мне захотелось в нее поверить. Я затратил некоторое время на то, чтобы докопаться ло реальных фактов, скрывавшихся за этим анекдотом. (О том, что мне удалось узнать, я расскажу ниже. А сейчас заметим лишь, что в основе моего желания поверить этой истории лежала интригующая идея о двух программах, "сражающихся в темных и бесшумных лабиринтах памяти машины").
В прошлом году я решил все-таки реализовать идею, лежащую в ее основе, и разработал первую версию игры "Бой в памяти". Мне помогал Дэвид Джонс, студент моего отделения в Университете Зап.Онтарио. С тех пор мы продолжали дорабатывать эту игру и довели ее до довольно интересного уровня.
У игры "Бой в памяти" четыре основных компонента: массив памяти на 8000 адресов, язык ассемблера Редкод, программа-монитор под названием "Марс" (MARS - Memory Array Redcode Simulator) и набор "боевых" программ. Две противоборствующие программы вводятся в память на случайным образом выбранные позиции, причем ни одна программа не знает, где находится программа-противник. Программа-монитор Марс управляет выполнением таких программ, реализуя простейший вариант системы разделения времени, которая распределяет ресурсы компьютера по многочисленным пользователям, работающим одновременно с машиной. Программы-противники "ходят" по очереди. Сначала выполняется одна команда первой программы, затем одна команда второй программы и т.д.
Действия, совершаемые программой в отведенные для нее промежутки времени, полностью определяются автором программы. Цель же этих действий заключается в том, чтобы вывести из строя другую программу, повредив ее команды. Однако можно придерживаться и защитной стратегии: программа может заниматься восстановлением полученных повреждений или, "попав под огонь противника", переходить на другое место в памяти. Игра заканчивается, когда программа-монитор Марс встречает в одной из программ команду, которую невозможно выполнить. Программа, содержащая эту недействительную команду (следствие полученного в "бою" повреждения), объявляется проигравшей.
О ПРОГРАММЕ можно многое узнать, анализируя ее повеление в уме или пользуясь просто карандашом и бумагой. Однако, чтобы по-настоящему испытать программу в действии, необходимы компьютер и программное обеспечение игры (система Марс). Играть можно и на персональном компьютере - мы с Джонсом подготовили инструкции для тех, кто захочет реализовать игру "Бой в памяти" на своем компьютере.
Прежде чем перейти к описанию языка Редкод и представить несколько примеров простых программ для этой игры, мне хотелось бы немного подробнее остановиться на массиве памяти. Хотя выше отмечалось, что она состоит из 8000 адресуемых ячеек, в этом числе нет ничего магического; игра может проходить и в памяти меньшего размера. Существенным отличием от большинства запоминающих устройств является то, что массив памяти для системы Марс имеет круговую структуру. Адреса ячеек памяти нумеруются последовательно от 0 до 7999, а следующий адрес 8000 указывает опять на ячейку 0; таким образом, память замыкается сама на себя. Адреса, большие, чем 7999, Марс всегда "загоняет" в пределы от 0 до 7999, для чего значение адреса делится на 8000, а полученный при делении остаток берется в качестве действительного адреса. Так, например, когда программа "стреляет" в ячейку с адресом 9378, Марс интерпретирует этот адрес как 1378.
Редкод представляет собой очень упрошенный специализированный язык программирования, относящийся к классу языков ассемблера. Он содержит команды, позволяющие перенести содержимое одной ячейки памяти в другую, команды, производящие арифметические операции над содержимым ячеек памяти, а также команды управления последовательностью выполнения команд в программе. В отличие от ассемблера, который переводит программы в двоичные колы машинных команд. Марс переводит программы, написанные на Редкоде, в последовательность больших целых десятичных чисел, хранящихся затем в массиве памяти. Каждая ячейка памяти может хранить одно такое число. При выполнении программ Марс интерпретирует эти целые числа как машинные команды и производит соответствующие операции.
Список элементарных команд языка Редкод приведен на рисунке с.98. Каждую команду программист должен снабдить по крайней мере одним операндом или конкретным значением. Большинство команд требуют двух операндов. Например, команда JMP -7 (JMP - мнемоническое обозначение от слова jump - прыгнуть, перескочить) имеет один операнд со значением -7. Эта команда сообщает Марсу, что нужно передать управление на ячейку памяти с адресом, меньшим текущего адреса на 7 единиц, т.е. выполнить команду под номером на 7 меньшим, чем номер самой команды JMP -7. Если эта команда находилась бы сама в ячейке с адресом 3715, то выполнение программы продолжилось бы с ячейки с адресом 3708.

Система команд Редкода - языка ассемблера для игры "Бой в памяти"
Такой способ вычисления адреса памяти называется относительной адресацией; это единственный способ адресации, используемый в языке Редкод. Таким образом, программа никогда не знает абсолютных значений адресов, по которым располагаются се команды.
Команда MOV 3 100 сообщает Марсу, что нужно продвинуться вперед на 3 адреса, прочитать содержимое ячейки и перенести его в ячейку с адресом на 100 большим, чем адрес самой команды, стерев то, что там находилось до сих пор. В этой команде операнды заданы в "прямой" форме, т.е. они прямо указывают на адреса ячеек, над содержимым которых производятся действия. Разрешаются также еще два способа адресации. Если перед операндом стоит значок @, то это означает, что используется "косвенная" адресация. Команда MOV @3 100 означает, что целое число, которое нужно поместить в ячейку с относительным адресом 100, находится уже не в ячейке с относительным адресом 3, а в ячейке, адрес которой хранится по относительному адресу 3. (Механизм косвенной адресации проиллюстрирован на с.98 внизу). Значок 0 указывает на то, что операнд следует понимать как "непосредственный", т.е. рассматривать его не как адрес ячейки в памяти, а как целое число. Команда MOV #3 100 означает, что целое число 3 нужно поместить в ячейку с относительным адресом 100.

Трехшаговый механизм косвенной относительной адресации
Большинство других команд не нуждается в пояснениях. Следует лишь сказать еше несколько слов о команде DAT. Она может служить как средство резервирования памяти для информации, используемой в программе. Однако, строго говоря, DAT не является командой как таковой. Любая ячейка памяти, содержащая нуль в первом десятичном разряде, может рассматриваться как команда типа DAT и потому как невыполняемая команда. Если от системы Марс потребуется выполнить подобную "команду", то она не сможет этого сделать и объявит программу проигравшей.
Десятичное число, представляющее команду Редкода, имеет несколько полей, или функциональных областей (см. рисунок слева в середине). Первая цифра представляет обозначение команды; она является как бы кодом операции. Две следующие цифры отводятся под способ адресации для первого и второго операндов соответственно (прямая, косвенная или непосредственная). Наконец, на каждый операнд отводится еще по четыре цифры. Отрицательные значения величин хранятся в дополнительном представлении: так, -1 будет представлена как 7999, поскольку в круговой памяти системы "прибавить 7999" даст тот же эффект, как "вычесть 1".

Представление команд языка Редкод десятичными целыми числами
Команды, из которых построена простейшая программа "Карлик", приведены на с.99. Несмотря на то что программа Карлик не очень разумна, она весьма опасна: систематически "прочесывает" память, "бомбардируя" каждую пятую ячейку нулем. Нуль - это число, обозначающее не выполняемую команду DAT; таким образом, попав в расположение команд программы-противника, нуль может привести к ее остановке.

Карлик - игровая программа, систематически разбрасывающая "нулевые бомбы"
Предположим, к примеру, что Карлик занимает ячейки памяти с абсолютными адресами от 1 до 4. Ячейка 1 первоначально содержит команду DAT -1, однако выполнение программы начинается со следующей команды, ADD #5 -1. В результате число 5 прибавляется к содержимому предыдущей ячейки, а именно к команде DAT -1, после чего она превращается уже в DAT 4. Затем Карлик выполняет команду, находящуюся в ячейке 3, а именно MOV #0 @-2. Здесь целое число 0 указано как непосредственное значение операнда; его нужно перенести в ячейку, адрес которой вычисляется следующим образом. Сначала Марс отсчитывает от адреса 3 две единицы назад, останавливаясь на ячейке 1. Прочитав значение, хранящееся в этой ячейке, а именно 4, Марс интерпретирует его как адрес, определяемый относительно адреса текущей команды. Другими словами, он отсчитывает четыре ячейки вперед от адреса 1 и помещает значение 0 в ячейку с адресом 5.
Заключительная команда программы Карлик, JMP -2, создает бесконечный цикл. Она вновь передает управление на ячейку с абсолютным адресом 2, в результате чего число в команде DAT увеличивается на 5 и теперь она уже выглядит как DAT 9. При следующем выполнении тела цикла число 0 помешается уже в ячейку с абсолютным адресом 10. После этого "нулевые бомбы" падают на ячейки 15, 20, 25 и т.д. Сама программа остается на месте, но ее "артиллерия" угрожает всему массиву памяти. В конце концов Карлик добирается до адресов 7990, 7995 и затем 8000. Последний адрес рассматривается Марсом как равный 0, и поэтому Карлик едва "не покончил жизнь самоубийством". Следующая "бомба" падает снова на ячейку 5.
К сожалению, ни одна "боевая" программа, содержащая более четырех команд, не может уйти от огня Карлика. У программы-противника остается лишь три выхода: либо, постоянно передвигаясь по памяти, попытаться уйти из-под огня, либо, приняв удар, попробовать устранить повреждение, либо успеть первой поразить Карлика. Чтобы добиться успеха, следуя последней стратегии, программа должна оказаться весьма везучей. Ведь ей не известно, в каком месте памяти находится Карлик, и в среднем потребуется произвести около 1600 "выстрелов", или выполнить 1600 программных циклов, прежде чем Карлик получит повреждение. Если Карлик сражается против Карлика, то каждая программа выигрывает в 30% случаев, а в 40% случаев ни одной программе не удается поразить противника.
Прежде чем рассмотреть две другие стратегии, мне хотелось бы представить вам забавную однострочную программу. Назовем ее "Чертенком". Вот се текст:
MOV 0 1
Чертенок представляет собой пример простейшей программы, написанной на Редкоде и способной перемешаться в памяти. Команда MOV 0 1 считывает содержимое ячейки с относительным адресом 0, т.е. считывает самое себя, и переносит его в ячейку с относительным адресом 1, т.е. в следующую ячейку. В ходе своего выполнения программа движется по памяти со скоростью одна ячейка за одну команду, оставляя за собой пространство, полностью покрытое командами MOV 0 1.
А что будет, если выставить Чертенка против Карлика? "Зона обстрела" нулевыми бомбами Карлика распространяется по памяти быстрее, чем движется Чертенок; однако из этого еще не следует, что Карлик имеет преимущество. Поразит ли Кралик Чертенка, даже если Чертенок попадет в "зону огня", - вот в чем вопрос!

Чертенок против Карлика - кто победит?
Если же Чертенок первым настигнет Карлика, то он "пропашет" команды Карлика насквозь. Когда команда Карлика JMP -2 передаст управление назад на две ячейки, там уже будет находиться команда Чертенка MOV 0 1. В результате Карлик переродится и станет вторым Чертенком, до бесконечности преследующим первого по полю памяти. Согласно правилам игры "Бой в памяти", сражение заканчивается вничью. (Отметим, что такого исхода следует, по всей вероятности, ожидать. Читатели могут проанализировать другие возможности; может быть, им удастся открыть какой-либо другой любопытный исход сражения).
КАК ЧЕРТЕНОК, так и Карлик относятся к классу программ, которые можно охарактеризовать как небольшие и агрессивные, но неразумные. На следующем по сложности уровне находятся программы, возможно менее агрессивные, но достаточно "хитрые", чтобы успешно противостоять программам низшего класса. Эти программы обладают способностью уходить от атак противника, создавая свои копии в более безопасных местах. Каждая подобная программа должна содержать фрагмент, похожий на программу Близнецы, текст которой приведен на рисунке внизу на с.97. Близнецы не представляют собой законченной игровой программы. Единственная цель у этой программы - создать свою копию в области памяти, отстоящей на 100 ячеек, и передать управление только что созданной копии.

Близнецы - программа, создающая свою копию на новом месте в памяти
Программа Близнецы состоит из трех основных частей. Две команды DAT в начале программы служат в качестве указателей. Они указывают соответственно на следующую команду, подлежащую копированию, и на адрес назначения, т.е. на ячейку, куда ее нужно поместить. Цикл, расположенный в середине программы, непосредственно осуществляет копирование, перемещая команды по очереди на 100 ячеек вперед относительно того места, откуда они берутся. После каждого прохождения цикла оба указателя увеличиваются на единицу и указывают уже на новый источник и новый пункт назначения соответственно. Команда сравнения СМР в теле цикла проверяет значение первой команды DAT. Когда оно уже увеличено 9 раз, это означает, что вся программа скопирована, и происходит выход из цикла. Теперь осталось провести небольшую коррекцию. Адрес назначения во второй команде программы имеет исходное значение 99, однако к тому времени, как оно будет скопировано, это значение окажется равным 100. Ошибку, возникшую в процессе копирования, нужно исправить (посредством команды MOV #99 93), после чего можно передать управление на только что созданную копию программы.
Модифицируя программу Близнецы, можно создать целый класс "боевых" программ. Одна из таких программ - "Идол" - создает свои копии на расстоянии 10 ячеек вместо 100. Как и Чертенок, Идол пытается "пройтись" через всю программу противника, но выигрывает гораздо чаще Чертенка и реже заканчивает игру с ничейным результатом, потому что поврежденные им программы с меньшей вероятностью смогут успешно выполнять команды, подставленные в них Идолом. В "Скороходе" - еше одной программе, где используется механизм Близнецов,- интервал между копиями равен большому простому числу. Скорохода труднее "поймать", и он производит такое же опустошительное действие в стане противника, как и программа Идол.
СКОРОХОД и Идол не очень разумные программы. На сегодняшний день мы располагаем лишь двумя программами, относящимися ко второму уровню сложности. Они слишком громоздки для того, чтобы привести их здесь. Одна на них - назовем ее Радар - выставляет с обеих сторон своеобразные "пикеты" (см. рисунок на с.97). Каждый пикет состоит из 100 последовательных ячеек памяти, заполненных единицами, и отделен от текста программы "буферной зоной" из 100 пустых ячеек. Радар попеременно занимается то атакующими действиями в удаленных областях памяти, то проверкой состояния своих пикетов. Если в одном из пикетов обнаруживается какое-либо изменение, Радар интерпретирует это изменение как свидетельство атаки, проведенной Карликом, Чертенком или какой-то другой неразумной программой. В этом случае Радар создает свою копию по другую сторону от поврежденного пикета, восстанавливает его, создает новый пикет на незащищенной стороне и затем продолжает нормальную последовательность действий.

Радар - более сложная игровая программа, успешно отражающая атаки более простой программы Чертенок
Помимо создания своих копий игровая программа может быть наделена способностью восстанавливать себя от повреждений. Джонс написал самовосстанавливающуюся программу, способную выдерживать некоторые виды атак, но не все. Программа под названием "Сканер" сохраняет себя в двух экземплярах, но выполняются обычно лишь команды одного из этих экземпляров. Экземпляр программы, выполняющийся в текущий момент, периодически просматривает команды второго экземпляра, чтобы проверить, не подверглись ли они атакующим действиям программы-противника. Изменения, возникшие вследствие атаки противника, обнаруживаются путем сравнения экземпляров Сканера между собой, причем экземпляр, выполняющийся в данный момент, считается правильным. Если обнаруживаются какие-либо недействительные команды, они замещаются правильными, после чего управление передается на "отремонтированный" экземпляр, который в свою очередь приступает к проверке первого.
В настоящее время Сканер остается чисто защитной программой. Она способна выдержать атаки Карлика, Чертенка, Идола и других подобных им медленно действующих агрессивных программ, по крайней мере в тех случаях, когда противник проводит атаки с правильной (защищенной) стороны. Сейчас Джонс работает над самовосстанавливающейся программой, хранящей себя в трех экземплярах.
Интересно, смогут ли читатели изобрести самовосстанавливающиеся программы каких-либо других типов? Например, можно подумать о программе, хранящей себя в двух или более экземплярах, но такой, что выполняется все время лишь один из них. Программа могла бы иметь "ремонтирующую часть", которая обращалась бы к другим экземплярам для восстановления поврежденных команд. Эта ремонтирующая часть могла бы даже ремонтировать сама себя, но в некоторых местах она оставалась бы уязвимой. В качестве "меры уязвимости" программы можно принять число поврежденных команд, приводящих к остановке программы. Иногда достаточно повредить одну-единственную команду; в других случаях потребуется поразить много команд. А сколько команд в среднем нужно поразить, чтобы вывести из строя программу? С точки зрения такого критерия какова должна быть наименее уязвимая самовосстанавливающаяся программа?
Игра "Бой в памяти" лишь тогда станет по-настоящему интересной, когда будут созданы достаточно надежные программы, которые в основном будут обороняться, а не атаковать. Такие игровые программы должны будут отыскивать и опознавать текст программы-противника, а затем предпринимать энергичные атакующие действия в той области памяти, где он был обнаружен.
Возможно, у вас сложилось впечатление, что язык Редкод и система Марс в целом представляют собой завершенную систему. Это не так. В свободное время мы проверяли некоторые новые идеи и много экспериментировали.
Одна из новых идей состояла в том, чтобы включить еше одну команду, которая позволяла бы несколько облегчить действия, связанные с самозащитой и самовосстановлением. Команда РСТ А защитит команду, хранящуюся в ячейке с адресом А, от изменений до тех пор, пока она не будет исполнена. Насколько можно будет уменьшить уязвимость программы за счет применения команды подобного рода?
В подготовленных нами инструкциях, о которых говорилось выше, мы объясняем не только правила игры "Бой в памяти", но и то, как реализовать массив памяти и написать программу-монитор Марс на различных языках высокого уровня. Инструкции содержат также предложения о том, как можно демонстрировать результаты игры. Здесь же мы опишем правила игры с достаточной точностью для того, чтобы читатели могли составлять игровые программы, используя пока что карандаш и бумагу.
1. Две боевые программы загружают в память в случайным образом выбранные позиции, но на расстоянии друг от яруга не меньше 1000 адресов.
2. Марс поочередно выполняет по одной команде из каждой программы, пока не дойдет до команды, которую невозможно выполнить. Программа, содержащая эту команду, объявляется проигравшей.
3. Программы противника можно атаковать любым доступным "оружием". В качестве "бомбы" можно воспользоваться нулем или любым другим целым числом, включая числа, представляющие дозволенные команды Редкола.
4. На продолжительность сражения накладывается определенное временное ограничение, зависящее от быстродействия компьютера. Если время игры уже вышло и обе программы продолжают выполняться, то исход сражения считается ничейным.
ИСТОРИЯ о Сорняке и Косаре, по-видимому, основана на двух реально существовавших программах. Одна из них представляла собой компьютерную игру под названием "Дарвин" и была изобретена М.Макилроем из AT&T Bell Laboratories. Другая программа под названием "Червяк" была написана Дж.Шохом из Исследовательского центра фирмы Xerox в Пало-Альто. Обе программы были написаны давно и стали достаточно известными. (Игра "Дарвин" была описана в журнале "Software: Practice and Experience", т.2, с.93-96, 1972. Довольно туманное описание того, что, по-видимому, представляет собой ту же игру, появилось в издании "Computer lib.", 1978г.)
По правилам игры "Дарвин" каждый играющий представляет некоторое число программ, написанных на языке ассемблера, которые засылаются в память машины вместе с программами других играющих. Эти программы называют "организмами". Организмы, созданные одним игроком (и принадлежащие к одному и тому же "виду") пытаются "убить" представителей других видов и занять обитаемое ими пространство. Победителем считается тот игрок, организмы которого оказываются наиболее многочисленными к моменту остановки игры. Макилрою удалось изобрести неуязвимый организм, хотя выиграл он всего лишь "несколько игр". Этот организм не очень-то агрессивен, хотя и является "бессмертным ".
Червяк - это экспериментальная программа, предназначенная для того, чтобы как можно интенсивнее использовать ресурсы сети ЭВМ фирмы Xerox. Червяк загружался в несопротивляющиеся машины под контролем программы-супервизора. Цель Червяка состояла в том, чтобы взять на себя управление машиной и в сотрудничестве с Червяками, поселившимися в других машинах, обеспечивать выполнение больших прикладных программ в образовавшейся таким образом мультипроцессорной системе. Червяк устроен так, что любой, кто хочет воспользоваться одной из занятых машин, может получить ее в свое распоряжение, не нарушая работы более объемных программ.
В легенде о Сорняке и Косаре можно увидеть некоторые элементы как игры "Дарвин", так и программы Червяк. Но лишь в игре "Бой в памяти" Косарь стал наконец реальностью.
БИБЛИОГРАФИЯ
COMPUTER RECREATIONS: "DARWIN". ALEPH NULL in Software: Practice and Experience, Vol.2, No.1, pages 93-96; January-March, 1972.
68000 ASSEMBLY LANGUAGE PROGRAMMING. GERRY KANE AND DOUG HAWKINS LEGENTHAL. Osborne - McGraw-Hill, I981.
Можно посмотреть М.СИНГЕР, МИНИ-ЭВМ PDP-11: ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ АССЕМБЛЕРА И ОРГАНИЗАЦИЯ МАШИНЫ, МОСКВА, "МИР", 1984.- G.
Более простая "алгоритмическая игра" -
 ТЕМА #8, АБЗАЦ #234
ТЕМА #8, АБЗАЦ #234 .- G.
.- G.ОТКЛИКИ
10 1984
ОТКЛИКИ на статью, посвященную игре "Бой в памяти" в майском номере журнала, оказались самыми разнообразными: от обычных просьб о дополнительной литературе по этой игре до подробных описаний полных игровых схем. Во многих письмах содержались описания программ наподобие "Сорняка", засоряющих реальные системы (в том числе вползших как черви в яблоко в системы Apple), рассуждения о программах как таковых и теоретизирования по поводу оборонительной и наступательной стратегиях. Мы сможем рассказать только о нескольких самых важных разработках; другим придется ждать будущих публикаций под этой рубрикой которые, надеюсь, еще появятся до конца года.
Д.Макилрой сообщил, что игру "Дарвин" придумал его сотрудник В.Висотски из AT&T Bell Laboratories. Однако "неуязвимый" организм изобрел сам Макилрой.
Что произойдет, если "Чертенок" нападет на "Карлика"? Одна возможность была разобрана в майском номере: "Карлик" передаст управление команде "Чертенка" и превратится во второго "Чертенка", бесконечно преследующего первого. Другой исход приводит к противоположному результату. Предположим, что "Карлик" уже перескочил через свою первую команду, когда "Чертенок" копировал самого себя в ячейке с данными "Карлика". Тогда складывается такая ситуация:

Поскольку должна выполняться команда "Карлика", она прибавляет 5 к команде "Чертенка", превратив ее в MOV 0 6. Затем выполняется "Чертенок", копируя себя через 6 ячеек вперед, а сам "очищается" "Карликом", который затем атакует свой следующий адрес (численное значение, соответствующее MOV 0 6). На следующем шагу с "Чертенком" происходит нечто странное: он выполняет первую команду программы "Карлика", так что игра временно превращается в игру "двойной Карлик", который бессмысленно атакует массив памяти, тогда как предмет его притязаний располагается на его собственной территории и делает абсолютно то же самое!
Д.Менкони из Милпитаса (шт.Калифорния), автор игр фирмы Atari, Inc., предложил именно это свойство сделать обычным правилом игры "Бой в памяти", позволив каждой программе выполняться одновременно в двух местах. Таким образом, даже если программа потеряет одно свое "я", второе сможет восстановить поврежденные участки. Э.Уоррел из Бетесда (шт.Мадиссон), предлагает более общую схему, состоящую из n "я", которые выполняют одну и ту же программу, но в разных ячейках памяти. Р.Перейно из Университета Джорджа Мейсона написал свою программу игры "Бой в памяти" для компьютера и Apple II, используя вместо коротких машинных слов двумерный массив размера 2000*2 байт. Б.Дорнфнлд из фирмы AMF, Inc., написал на модифицированном Бейсике подробную программу игры "Бой в памяти" для настольного компьютера Hewlett-Packard 9816/26.
Самую впечатляющую систему данных построили три старшекурсника: Г.Гетш и М.Молдин из Университета Карнеги-Меллона и П.Милаицо из Университета Раиса. Молдин продемонстрировал свою программу на компьютере VAX нашего факультета Универсчтета провинции Западного Онтарио. На экране дисплея был выведен весь массив памяти, причем положение каждой участвующей программы отмечалось прописной буквой, а участок памяти, оккупированный этой программой,- соответствующей строчной буквой.
Моллин придумал "боевую" программу, которую назвал "Миномет". Она работает примерно так же, как "Карлик", за тем исключением, что "ведет атаку" в соответствии с числами Фибоначчи (1, 1, 2, 3, 5 и т.д., каждое число представляет собой сумму двух предыдущих). Как это ни странно, "Карлик" побеждает "Миномет" в 60 случаях из 100. Но "Миномет" постоянно поражает 3/4 самовосстаиавливаюшейся программы, названной "Избиратель". В то же время "Избиратель" выдерживает атаки "Карлика" и регулярно поражает его.
Гетш, Молдин и Милаццо проанализировали поведение "Миномета" и пришли к выводу, что если программа его противника состоит более чем из 10 команд, она должна быть самовосстанавливаюшейся, чтобы побелить "Миномет". Однако не существует программ, состоящих более чем из 141 команды, которые восстанавливались бы достаточно быстро, чтобы выдержать атаки "Миномета".

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
8 1984
О МАКАРОННОМ КОМПЬЮТЕРЕ И ДРУГИХ АНАЛОГОВЫХ УСТРОЙСТВАХ
А.К.ДЬЮДНИ
В НАШИ дни, когда мы говорим О компьютерах, то неизменно подразумеваем цифровые ЭВМ. Их аналоговые собратья, электромеханические устройства, когда-то доминировавшие в мире вычислительной техники, теперь оказались преданными забвению. Перед второй мировой войной в ведущих исследовательских центрах работали замысловатые аналоговые компьютеры с витиеватыми названиями, такими, например, как "непрерывный интерграф" или "дифференциальный анализатор". В подобных машинах для представления математических уравнений использовались электрические или механические аналоги. Переменная в математическом уравнении обычно представлялась какой-нибудь физической величиной, например электрическим напряжением или углом поворота механического валика. Аналоговые компьютеры можно было применять для решения уравнений из различных областей научных исследований: баллистики, аэродинамики, анализа электрических цепей и т.д.
Однако аналоговые машины не смогли выдержать конкуренции с цифровыми ЭВМ, появившимися в конце второй мировой войны и начавшими быстро распространяться сразу после ее окончания. Аналоговые компьютеры, казалось, были способны решать лишь ограниченные классы задач, главным образом дифференциальные уравнения, да и то с относительно невысокой точностью. И напротив, что касается цифровых вычислительных машин, то вскоре стало ясно, что их можно запрограммировать для решения бесконечного многообразия задач самой различной природы, и притом с очень высокой точностью. Постепенно аналоговые машины отходили на второй план, и уже к середине 60-х годов о них лишь мельком упоминалось в книгах по вычислительной технике.
Хотя потомки грандиозных аналоговых машин 20-х и 30-х годов все еше используются в ряде исследовательских центров (новые устройства этого типа продолжают разрабатывать и сейчас), никто всерьез не ожидает, что аналоговые компьютеры смогут снова выйти на передний план. Революцию цифровых ЭВМ нельзя повернуть вспять. Однако верно также и то, что подобные революционные скачки в развитии техники иногда приводят к забвению привлекательных сторон, присущих устройствам старых типов.
ОСНОВНОЕ привлекательное свойство аналоговых компьютеров заключается в том, что при их использовании мы получаем результат как будто без всяких затрат. Решение задачи, которое потребовало бы многочасового вычисления на бумаге (или даже при помощи цифрового компьютера), получается просто при наблюдении физической системы, по мере того как она быстро достигает определенного конечного состояния. В некоторых наиболее ярко выраженных случаях этот процесс кажется почти мгновенным - устройство вычисляет как бы по мановению волшебной палочки.
Рассмотрим компьютер системы МАУ, или Макаронное аналоговое устройство. Этот "прибор" в опробованной мною конфигурации способен отсортировать до 700 чисел в порядке убывания их величины. Сортировка представляет собой распространенный класс задач, решаемых при помощи цифровых компьютеров. Были разработаны довольно изощренные и эффективные алгоритмы сортировки. Проблема, однако, заключается в том, что время, требующееся для сортировки набора чисел, возрастает существенно быстрее, чем количество сортируемых чисел. Пользуясь компьютером МАУ, мы должны затратить некоторое время на подготовку машины к конкретному набору чисел, а также на "чтение" полученных результатов, но сам процесс сортировки не требует почти никаких временных затрат.
Посмотрим, как работает компьютер МАУ. Для каждого числа из сортируемого набора возьмем макаронную палочку (невареную) и укоротим ее таким образом, чтобы ее длина соответствовала величине данного числа. Разумеется, следует выбрать подходящий масштаб. Затем возьмем все обработанные макаронные палочки в руки и, держа пучок вертикально и не очень плотно сжимая, резко опустим его на поверхность стола; каждая макаронная палочка коснется поверхности стола. Теперь, чтобы получить отсортированную последовательность чисел, нужно лишь доставать по порядку палочки из пучка: сначала самую длинную, затем - самую длинную из оставшихся и т.д., до тех пор пока не останется ни одной. Выбранные таким образом палочки измеряются, и соответствующие величины записываются.

Макаронный компьютер сортирует совокупность чисел в порядке убывания
В операции сортировки необходимо различать три фазы. Я называю их фазой предварительной обработки, аналоговой фазой и фазой завершающей обработки. В фазе предварительной обработки мы отмеряем длину макаронных палочек и укорачиваем их до нужного размера. В аналоговой фазе действует простой механизм, сортирующий палочки по длине. В фазе завершающей обработки мы выбираем их одну за другой и получаем отсортированную последовательность. Все устройства, о которых здесь идет речь, требуют как фазы предварительной, так и фазы завершающей обработки. Точно так же дело обстояло и с первыми аналоговыми компьютерами. На самом деле было затрачено много усилий и средств на то, чтобы ускорить процессы, протекающие в этих фазах.
Кое-кто, возможно, заметит: "Ну хорошо, при помощи МАУ можно отсортировать 700 чисел, а что делать, если их будет 7000 или, скажем, 7000000?". Чтобы ответить на этот каверзный вопрос, упомянем лишь о машине СУПЕР-МАУ, модифицированном автопогрузчике с вилочным захватом, который может поднять семь миллионов тщательно измеренных макаронных палочек (сверхдлинных) и прихлопнуть их торцами о кирпичную стену.
ВОЗМОЖНО, найдутся и такие читатели, которые скажут: "Я могу отсортировать 700 чисел быстрее, чем МАУ. Пользуясь лишь карандашом и бумагой, я закончу процедуру даже раньше, чем макаронные палочки будут укорочены до нужных размеров!" К сожалению, я должен сознаться, что это, по-видимому, верно. Предположим, что потребуется примерно минута, чтобы прочесть очередное число из списка, отмерить соответствующую длину на макаронной палочке, обрезать ее и вставить в пучок. Предположим далее, что потребуется около 10 секунд на то, чтобы выбрать одну палочку из пучка и измерить ее после операции "прихлопывания" (занимающей всего лишь секунду). Тогда в обшей сложности нужно будет затратить более 13 часов, чтобы при помощи МАУ отсортировать 700 чисел, причем все это время, за исключением одной секунды, будет потрачено на фазы предварительной и завершающей обработки. С другой стороны, соревнующийся с МАУ человек должен будет многократно просматривать список неотсортированных чисел в поисках максимального, записывать найденное число в список чисел по порядку и вычеркивать его из исходного. Потребуется около одной десятой доли секунды, чтобы посмотреть на каждое число в списке, и, таким образом, всего нужно будет затратить (700+ 699+...+2+1)/10 секунд, чтобы отсортировать заданный массив чисел. Суммарное время равно 175 минутам и 15 секундам, что даст неоспоримую победу над МАУ. Не следует ли сделать такой вывод, что привлекательность мгновенной аналоговой фазы целиком и полностью сводится на нет слишком длительными фазами предварительной и завершающей обработки? Не будем торопиться с выводами. Допустим, что вдохновленный победитель захочет посоревноваться с машиной СУПЕР-МАУ в сортировке нескольких миллионов чисел. В то время как машине потребуется около 15 лет, чтобы справиться с этой задачей, человек не сможет закончить работу раньше чем через 74000 лет! Чтобы понять, в чем состоит преимущество СУПЕР-МАУ, нужно исследовать вопрос о том, как зависит время вычислений от размеров задачи. Как мы уже говорили, операция прихлопывания пучка макаронных палочек о стену занимает всегда одно и то же время независимо от количества палочек в пучке. Будем говорить, что это операция с постоянным временем. Фазы предварительной и завершающем обработки представляют собой операции с линейным временем: их продолжительность возрастает прямо пропорционально с увеличением размера списка сортируемых чисел. Длительность же операций, выполняемых человеком вручную, возрастает в этом случае значительно быстрее. Хотя список неотсортированных чисел постепенно уменьшается, количество операций, связанных с просмотром чисел, возрастает как квадратичная функция от размеров списка. В таких случаях мы говорим, что сортировка происходит с квадратичным временем. Рано или поздно процедура с линейным временем должна одержать верх над процедурой с квадратичным временем.
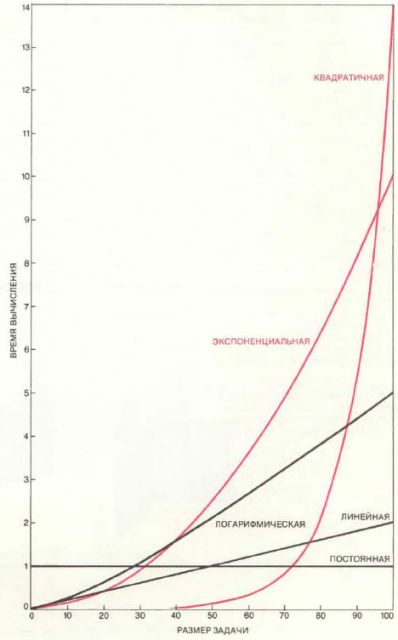
Несколько возможных функций, связывающих время вычислений с размером задачи
Даже несмотря на длительные фазы предварительной и завершающей обработки, достаточно мощная машина типа МАУ может выиграть соревнование по сортировке у современной цифровой ЭВМ, проводящей вычисления по самым эффективным алгоритмам сортировки. Последние требуют порядка n*log(n) шагов, где n - количество сортируемых чисел в последовательности, a log - обозначение логарифмической функции. Процедура с линейным временем, конечно, в принципе лучше, однако страшно себе представить, каких размеров должно быть макаронное устройство, чтобы выиграть это соревнование. Такое устройство, назовем его СУПЕР-ДУПЕЛЬ-МАУ, наверное, можно построить только в космосе, а прихлопывать пучок пришлось бы о поверхность Луны.
Следующее устройство из моей коллекции определяет границу выпуклой оболочки n точек на плоскости. Выпуклая оболочка - это наименьшая выпуклая область, содержащая все n точек. Она полностью определяется своей границей - многоугольником, вершины углов которого находятся в ограничивающих, или "внешних", точках, принадлежащих совокупности n. Устройство, вычисляющее границу выпуклой оболочки, сделано из большой широкой доски, нескольких гвоздей и круглой резинки. Я называю его ДАУ, а полное название Досочно-гвоздевое аналоговое устройство с круглой резинкой. Было бы заманчиво включить в сокращенное название буквы от слов "гвозди" и "круглая резника", но тогда оно получилось бы слишком громоздким, что-нибудь наподобие ДОГВАУКР.
Нахождение выпуклой оболочки множества точек на плоскости
Чтобы собрать устройство, достаточно вбить п гвоздей в доску в места заданного расположения точек. Затем нужно взять круглую резинку, растянуть ее так, чтобы окружить все гвозди, вбитые в лоску, и отпустить. Резинка прочно сядет на место, и ее контур точно определит многоугольник, представляющий собой границу выпуклой оболочки.
ЗДЕСЬ мы опять приходим к линейной по времени процедуре, которая предшествует аналоговой операции, заключающейся в данном случае в освобождении резинки. Потребуется несколько секунд, чтобы определить нужную точку для каждого гвоздя и вбить его в доску. После того как резинка отпущена, процедура определения границы полученной таким образом выпуклой оболочки займет несколько меньше времени, чем заняла бы процедура с линейным по n временем, потому что соответствующие замеры будут проделаны лишь для тех гвоздей, которых касается резиновый обруч.
Наиболее быстрый из известных алгоритмов отыскания границы выпуклой оболочки требует n*log(log(n)) шагов вычисления. Данная функция от n настолько близка к линейной, что соревноваться с цифровым компьютером, работающим по такому алгоритму, сможет, наверное, лишь колоссальная машина ДАУ, размеры которой были бы сравнимы с размерами Солнечной системы.
Задачей третьего устройства является отыскание кратчайшего пути, соединяющего две вершины на графе. В данном случае под графом мы понимаем набор отрезков, или ребер, соединяющих точки, называемые вершинами. В некоторых графах ребра могут быть различной длины, и именно с таким графом должно будет работать аналоговое устройство ШНАУ, основным элементом которого служит шнурок, соединяющий вершины графа и представляющий собой его ребра. Каждая же вершина графа представляется маленьким медным колечком. Если какие-то две вершины соединены ребром, то в аналоговой модели этого графа соответствующие колечки соединяются кусочком шнурка нужной длины, к обоим концам которого пришиты крючки.
Чтобы найти кратчайший путь между вершинами u и v на графе, возьмем в одну руку колечко, представляющее вершину u, а в другую - колечко, представляющее v, и поднимем всю систему колечек, соединенных между собой шнурками. Затем разведем руки, натягивая шнурки до предела. В результате искомый кратчайший путь будет представлен несколькими натянутыми шнурками, оказавшимися в верхней части поднятой системы. Шнурки же, представляющие ребра, которые не вошли в этот кратчайший путь, остаются менее натянутыми (см. верхний рисунок на с.94). Если колечки были помечены буквами, соответствующими обозначению вершин, то последовательность вершин, через которые проходит кратчайший путь, легко установить, прочтя метки на колечках, соединенных натянутыми шнурками.

Аналоговое устройство для отыскания кратчайшего пути между двумя вершинами на графе
Если за размер графа принять количество его вершин n, то наибольшее количество шагов, которое потребуется как для фазы предварительной, так и для фазы завершающей обработки, будет определяться линейной зависимостью от n. Аналоговая фаза вычисления, как и обычно, выполняется в данном случае почти мгновенно. Наиболее быстрый известный алгоритм для решения этой задачи на цифровом компьютере требует порядка n2 шагов.
ОБИДНО, конечно, что приходится учитывать фазы предварительной и завершающей обработки при подсчете сравнительного быстродействия описанных выше устройств, но, честно говоря, это неизбежно, так как они представляют собой неотъемлемую часть обшей процедуры решения задачи. Без них мы не смогли бы ни поставить задачу, ни "прочесть" полученный результат.
Некоторые аналоговые устройства совершенно не требуют подобной обработки, потому что они непосредственно встроены в систему, которая сразу же использует полученный результат. Приведем два примера. Первый - это система сортировки на спицах, когда-то широко применявшаяся в библиотечных каталогах. Второй пример - трюк с балансированием тарелки на одном пальце. В системе сортировки на спицах используются карточки с прорезями и маленькими отверстиями по краям, при помощи которых можно быстро определить, какие книги должны быть сданы к тому или иному сроку. Карточки укладываются в стопку и через отверстия, соответствующие данному дню, пропускается длинная спица. Если теперь поднять спицу, то на ней останутся только те карточки, у которых в том месте, куда вставлена спица, находится отверстие. Карточки, имеющие в этом месте прорези, остаются в стопке.
Трюк с балансированием показал мне "матемаг" Роналд Л.Грейам, работающий в фирме AT&T Bell Laboratories. Сначала Грейам удерживает тарелку на трех широко расставленных пальцах. По мере того как он сближает пальцы, центр тяжести тарелки остается между ними, поскольку палец, на который приходится меньший вес, легче скользит по дну тарелки. Если сблизить пальцы настолько, чтобы между ними можно было вставить четвертый палец, то положение этого четвертого пальца окажется достаточно близким к центру тяжести, и тарелка будет балансировать на этом пальце, после чего можно убрать остальные. Грейам предупреждает, что начинающим следует основательно попрактиковаться, прежде чем демонстрировать трюк за праздничным столом.
До сих пор я применял аналоговые устройства лишь к тем задачам, для решения которых уже были найдены довольно быстрые алгоритмы. О таких задачах говорят, что они имеют полиномиальную сложность, потому что количество шагов вычисления, требующееся для их решения, можно выразить (или по крайней мере ограничить сверху) через полиномиальную функцию от n, числа, характеризующего размер задачи. Например, время решения может оказаться пропорциональным самому числу n, или n2, или n*log(n), или n27. Существуют и такие задачи, в том числе имеющие практическое значение, для которых не найдено полиномиального алгоритма. Лучшие из известных алгоритмов их решения требуют времени, экспоненциально возрастающего с ростом размера задачи. Обычно время решения оказывается пропорциональным 2^n - функции, растущей быстрее любого полинома. При большом, а иногда даже умеренном размере задачи время, необходимое для ее решения, равно просто чудовищной величине. Почему бы не попробовать наши устройства на некоторых из этих труднорешаемых задачах?
НАПРИМЕР, это могла бы быть задача отыскания самого длинного из всевозможных путей, соединяющих две вершины на графе. Она оказалась значительно труднее, чем задача отыскания кратчайшего пути. На самом деле об этой задаче говорят как об NP-полной. Этот термин применяют к труднорешаемым задачам, для которых не удается найти полиномиального алгоритма. Читатели, желающие подробнее ознакомиться со свойством NP-полноты и не боящиеся иногда встречающихся в тексте математических обозначений, могут прочесть отличную книгу М.Гэрри и Д.Джонсона "Вычислительные машины и труднорешаемые задачи" (издательство "Мир", 1982г.- Прим. перев.)
Иногда, чтобы решить задачу, нужно приложить физическую силу. Взять, к примеру, задачу о кратчайшем пути между двумя вершинами на графе, решенную натяжением шнурков. Если потянуть за колечки сильнее, то шнурки начнут рваться один за другим. Наконец, перед тем, как порвется вся система, все оставшиеся целыми шнурки будут туго натянутыми. В этот момент мы получаем решение задачи о самом длинном пути.
Всегда ли? На некоторых графах этот метод оказывается эффективным, на других он не работает. Возможно, читатели получат удовольствие, построив примеры графов как первого, так и второго типов. Когда вы натягиваете систему из нескольких шнурков, первый порвавшийся шнурок считайте "наихудшим случаем".
Возможно, не следует пытаться "с лету" решать NP-полную задачу аналоговыми средствами. Однако теория о вычислимости утверждает лишь то, что NP-полные задачи являются труднорешаемыми только для цифровых компьютеров, и не содержит никаких фактов, отрицающих возможность решения таких задач аналоговыми методами. Поэтому сделаем еще одну попытку.
В задаче о минимальном дереве Штайнера требуется соединить n точек на плоскости графом минимальной обшей длины. Эта задача по существу эквивалентна задаче соединения и городов системой дорог, общая длина которых была бы минимальной. В число вершин графа помимо исходных точек можно включить еще и дополнительные, так сказать для построения проселочных дорог. Нетрудно убедиться, что искомый минимальный граф представляет собой дерево, т.е. граф, в котором отсутствуют замкнутые пути. Более того, оказывается, что любая дополнительная вершина в минимальном дереве соединяется с тремя другими вершинами ребрами, образующими углы 120о относительно друг друга (см. нижний рисунок на с.94).

"Мыльное" решение задачи о минимальном дереве Штайнера для пяти точек на плоскости
Задача о минимальном дереве Штайнера является NP-полной, и для нее не известно алгоритма, требующего менее 2^n шагов вычисления (где n - количество вершин). Тем не менее существует прибор, называемый мною Пузырьковым аналоговым устройством, который, по-видимому, дает "мыльное" решение описанной задачи. Приделайте ручку к двум параллельно расположенным прозрачным пластмассовым пластинкам и вставьте между пластинками тоненькие штырьки, представляющие исходные точки, которые нужно соединить. Затем погрузите устройство в мыльную воду. Вынув его из воды, вы увидите, как мыльная пленка соединит n штырьков, образуя изящное дерево Штайнера.
Однако ваша радость при виде этого решения будет преждевременной. Можно ли быть полностью уверенным, что полученное таким образом дерево является деревом минимальной длины? На самом деле мыльная пленка образует, как правило, всегда наименьшую возможную сеть для данной топологии, однако может существовать и другая топология, для которой может быть построено еще более короткое дерево. В зависимости от схемы расположения штырьков и угла, под которым устройство вынимается из мыльной воды, полная длина участков мыльной пленки может оказаться, а может и не оказаться абсолютно минимальной. Таким образом, и эта попытка решить NP-полную задачу аналоговыми методами не принесла успеха.
ОДНА ИЗ наиболее известных вычислительных задач заключается в том, чтобы определить, является ли заданное целое число NP простым или составным. (Если оно делится без остатка на какое-нибудь число, отличное от N или 1, то оно составное; в противном случае - простое). Эта задача имеет очень быстрое аналоговое решение, если воспользоваться Лазерным аналоговым устройством, или сокращенно ЛАУ. Нужно установить два параллельных зеркала M1 и M2 и два лазера, так чтобы лучи, испускаемые лазерами, многократно отражались от зеркал M1 и M2, как показано на рисунке на с.95. Угол, под которым направлен один лазер, подобран таким образом, чтобы его луч отражался по N раз от каждого зеркала, а затем попадал в детектор, находящийся на конце зеркала M1. Второй лазер располагается так, что вначале его луч совпадает с лучом первого лазера, а затем второй лазер быстро меняет направление и его луч проходит через определенный диапазон углов.
Лазерное аналоговое устройство показывает, что число 15 является не простым, а составным
По мере того как меняется направление второго луча, он периодически попадает в детектор на конце зеркала M1. По всей длине этого зеркала проходит также специальная детектирующая полоса. Она срабатывает всякий раз, когда два луча попадают в одну и ту же точку. За состоянием детектора на конце зеркала M1 и за детектирующей полосой следит простая электронная схема. Если оба детектора срабатывают одновременно, схема регистрирует это совпадение, и зажигается лампочка. Этот световой сигнал говорит о том, что число N является не простым, а составным. Для того чтобы имело место подобное двойное совпадение, необходимо, чтобы луч второго лазера отразился n раз от зеркала M1 и число N должно делиться на n без остатка.
Говоря об этой задаче, следует быть очень осторожным при выборе параметра, характеризующего ее размер. Если этот размер определить просто как N, то существуют цифровые алгоритмы, способные решить эту задачу за полиномиальное время. Однако правильнее было бы считать, что размер задачи гораздо лучше характеризует величина logN, так как она представляет собой длину цепочки цифр, образующих число N. При таком определении размера задачи никто не может сказать, является она NP-полной или нет, Принимая во внимание, что компьютер ЛАУ успешно справился с этой задачей, а остальные аналоговые устройства при попытках решения так называемых труднорешаемых задач не справились с ними, не следует ли предположить, что последняя нз рассмотренных задач не является NP-полной?
До сих пор я избегал очень важного вопроса, касающегося технической реализации таких аналоговых устройств, как МАУ, ДАУ, ШНАУ и ЛАУ. Хотя каждое из этих устройств можно действительно построить и даже воспользоваться им, демонстрируя решение небольших задач, было бы, конечно, неразумно создавать подобные устройства в расчете на серьезное применение. Однако на эту проблему можно взглянуть и с точки зрения "идеальных" технических возможностей, когда конструктор располагает какими угодно идеальными материалами и когда каждое устройство работает точно так, как было задумано. Было бы очень интересно пофантазировать о том, на что способны аналоговые вычислительные устройства в таких идеальных условиях.
Возможно, читатели в своих письмах
опишут какие-нибудь другие аналоговые устройства, я бы ознакомился с их изобретениями с большим интересом. Честно говоря, мне не известно, кто изобрел первые два устройства, описанные в этой статье. Наверное, они уже стали частью своеобразного фольклора, бытующего в кругах, связанных с вычислительной наукой и техникой. Шнурковое устройство, кажется, изобрели М.Минский и С.Пэйперт нз Массачусетского технологического института. Описание пузырькового устройства я нашел в удивительной книжке С.Айзенберга "Теория мыльной пленки и мыльных пузырей". Лазерное аналоговое устройство является моим собственным изобретением.
Кстати, это лазерное устройство напомнило мне об одной забавной задаче, над которой некоторым читателям будет, наверное, интересно поразмыслить. Представим себе зеркальный яшик в виде плоского прямоугольника. Предположим, что зеркальные стороны этого прямоугольника обладают идеальной отражательной способностью. В идеальных условиях можно было бы удалить одну-единственную точку в вершине одного нз углов яшика и пропустить одномерный лазерный луч внутрь через это бесконечно малое отверстие. Полученное таким образом устройство вычисляет нечто касаюшееся угла, под которым направлен луч. Ответ зависит от того, выйдет ли когда-нибудь луч обратно из яшика, а вот как поставить задачу - неизвестно.
БИБЛИОГРАФИЯ
THE SCIENCE OF SOAP FILMS AND SOAP BUBBLES. CYRIL ISENBERG. Tieto Ltd., 5 Elton Road, Clevedon. Avon, England, 1978.
COMPUTERS AND INTRACTABILITY: A GUIDE TO THE THEORY OF NP COM PLETENESS. MICHAEL R. CAREY AND DAVID S. JOHNSON. W.H.Freeman and Company, 1979.
...
О МАКАРОННОМ КОМПЬЮТЕРЕ И ДРУГИХ АНАЛОГОВЫХ УСТРОЙСТВАХ
А.К.ДЬЮДНИ
В НАШИ дни, когда мы говорим О компьютерах, то неизменно подразумеваем цифровые ЭВМ. Их аналоговые собратья, электромеханические устройства, когда-то доминировавшие в мире вычислительной техники, теперь оказались преданными забвению. Перед второй мировой войной в ведущих исследовательских центрах работали замысловатые аналоговые компьютеры с витиеватыми названиями, такими, например, как "непрерывный интерграф" или "дифференциальный анализатор". В подобных машинах для представления математических уравнений использовались электрические или механические аналоги. Переменная в математическом уравнении обычно представлялась какой-нибудь физической величиной, например электрическим напряжением или углом поворота механического валика. Аналоговые компьютеры можно было применять для решения уравнений из различных областей научных исследований: баллистики, аэродинамики, анализа электрических цепей и т.д.
Однако аналоговые машины не смогли выдержать конкуренции с цифровыми ЭВМ, появившимися в конце второй мировой войны и начавшими быстро распространяться сразу после ее окончания. Аналоговые компьютеры, казалось, были способны решать лишь ограниченные классы задач, главным образом дифференциальные уравнения, да и то с относительно невысокой точностью. И напротив, что касается цифровых вычислительных машин, то вскоре стало ясно, что их можно запрограммировать для решения бесконечного многообразия задач самой различной природы, и притом с очень высокой точностью. Постепенно аналоговые машины отходили на второй план, и уже к середине 60-х годов о них лишь мельком упоминалось в книгах по вычислительной технике.
Хотя потомки грандиозных аналоговых машин 20-х и 30-х годов все еше используются в ряде исследовательских центров (новые устройства этого типа продолжают разрабатывать и сейчас), никто всерьез не ожидает, что аналоговые компьютеры смогут снова выйти на передний план. Революцию цифровых ЭВМ нельзя повернуть вспять. Однако верно также и то, что подобные революционные скачки в развитии техники иногда приводят к забвению привлекательных сторон, присущих устройствам старых типов.
ОСНОВНОЕ привлекательное свойство аналоговых компьютеров заключается в том, что при их использовании мы получаем результат как будто без всяких затрат. Решение задачи, которое потребовало бы многочасового вычисления на бумаге (или даже при помощи цифрового компьютера), получается просто при наблюдении физической системы, по мере того как она быстро достигает определенного конечного состояния. В некоторых наиболее ярко выраженных случаях этот процесс кажется почти мгновенным - устройство вычисляет как бы по мановению волшебной палочки.
Рассмотрим компьютер системы МАУ, или Макаронное аналоговое устройство. Этот "прибор" в опробованной мною конфигурации способен отсортировать до 700 чисел в порядке убывания их величины. Сортировка представляет собой распространенный класс задач, решаемых при помощи цифровых компьютеров. Были разработаны довольно изощренные и эффективные алгоритмы сортировки. Проблема, однако, заключается в том, что время, требующееся для сортировки набора чисел, возрастает существенно быстрее, чем количество сортируемых чисел. Пользуясь компьютером МАУ, мы должны затратить некоторое время на подготовку машины к конкретному набору чисел, а также на "чтение" полученных результатов, но сам процесс сортировки не требует почти никаких временных затрат.
Посмотрим, как работает компьютер МАУ. Для каждого числа из сортируемого набора возьмем макаронную палочку (невареную) и укоротим ее таким образом, чтобы ее длина соответствовала величине данного числа. Разумеется, следует выбрать подходящий масштаб. Затем возьмем все обработанные макаронные палочки в руки и, держа пучок вертикально и не очень плотно сжимая, резко опустим его на поверхность стола; каждая макаронная палочка коснется поверхности стола. Теперь, чтобы получить отсортированную последовательность чисел, нужно лишь доставать по порядку палочки из пучка: сначала самую длинную, затем - самую длинную из оставшихся и т.д., до тех пор пока не останется ни одной. Выбранные таким образом палочки измеряются, и соответствующие величины записываются.

Макаронный компьютер сортирует совокупность чисел в порядке убывания
В операции сортировки необходимо различать три фазы. Я называю их фазой предварительной обработки, аналоговой фазой и фазой завершающей обработки. В фазе предварительной обработки мы отмеряем длину макаронных палочек и укорачиваем их до нужного размера. В аналоговой фазе действует простой механизм, сортирующий палочки по длине. В фазе завершающей обработки мы выбираем их одну за другой и получаем отсортированную последовательность. Все устройства, о которых здесь идет речь, требуют как фазы предварительной, так и фазы завершающей обработки. Точно так же дело обстояло и с первыми аналоговыми компьютерами. На самом деле было затрачено много усилий и средств на то, чтобы ускорить процессы, протекающие в этих фазах.
Кое-кто, возможно, заметит: "Ну хорошо, при помощи МАУ можно отсортировать 700 чисел, а что делать, если их будет 7000 или, скажем, 7000000?". Чтобы ответить на этот каверзный вопрос, упомянем лишь о машине СУПЕР-МАУ, модифицированном автопогрузчике с вилочным захватом, который может поднять семь миллионов тщательно измеренных макаронных палочек (сверхдлинных) и прихлопнуть их торцами о кирпичную стену.
ВОЗМОЖНО, найдутся и такие читатели, которые скажут: "Я могу отсортировать 700 чисел быстрее, чем МАУ. Пользуясь лишь карандашом и бумагой, я закончу процедуру даже раньше, чем макаронные палочки будут укорочены до нужных размеров!" К сожалению, я должен сознаться, что это, по-видимому, верно. Предположим, что потребуется примерно минута, чтобы прочесть очередное число из списка, отмерить соответствующую длину на макаронной палочке, обрезать ее и вставить в пучок. Предположим далее, что потребуется около 10 секунд на то, чтобы выбрать одну палочку из пучка и измерить ее после операции "прихлопывания" (занимающей всего лишь секунду). Тогда в обшей сложности нужно будет затратить более 13 часов, чтобы при помощи МАУ отсортировать 700 чисел, причем все это время, за исключением одной секунды, будет потрачено на фазы предварительной и завершающей обработки. С другой стороны, соревнующийся с МАУ человек должен будет многократно просматривать список неотсортированных чисел в поисках максимального, записывать найденное число в список чисел по порядку и вычеркивать его из исходного. Потребуется около одной десятой доли секунды, чтобы посмотреть на каждое число в списке, и, таким образом, всего нужно будет затратить (700+ 699+...+2+1)/10 секунд, чтобы отсортировать заданный массив чисел. Суммарное время равно 175 минутам и 15 секундам, что даст неоспоримую победу над МАУ. Не следует ли сделать такой вывод, что привлекательность мгновенной аналоговой фазы целиком и полностью сводится на нет слишком длительными фазами предварительной и завершающей обработки? Не будем торопиться с выводами. Допустим, что вдохновленный победитель захочет посоревноваться с машиной СУПЕР-МАУ в сортировке нескольких миллионов чисел. В то время как машине потребуется около 15 лет, чтобы справиться с этой задачей, человек не сможет закончить работу раньше чем через 74000 лет! Чтобы понять, в чем состоит преимущество СУПЕР-МАУ, нужно исследовать вопрос о том, как зависит время вычислений от размеров задачи. Как мы уже говорили, операция прихлопывания пучка макаронных палочек о стену занимает всегда одно и то же время независимо от количества палочек в пучке. Будем говорить, что это операция с постоянным временем. Фазы предварительной и завершающем обработки представляют собой операции с линейным временем: их продолжительность возрастает прямо пропорционально с увеличением размера списка сортируемых чисел. Длительность же операций, выполняемых человеком вручную, возрастает в этом случае значительно быстрее. Хотя список неотсортированных чисел постепенно уменьшается, количество операций, связанных с просмотром чисел, возрастает как квадратичная функция от размеров списка. В таких случаях мы говорим, что сортировка происходит с квадратичным временем. Рано или поздно процедура с линейным временем должна одержать верх над процедурой с квадратичным временем.

Несколько возможных функций, связывающих время вычислений с размером задачи
Даже несмотря на длительные фазы предварительной и завершающей обработки, достаточно мощная машина типа МАУ может выиграть соревнование по сортировке у современной цифровой ЭВМ, проводящей вычисления по самым эффективным алгоритмам сортировки. Последние требуют порядка n*log(n) шагов, где n - количество сортируемых чисел в последовательности, a log - обозначение логарифмической функции. Процедура с линейным временем, конечно, в принципе лучше, однако страшно себе представить, каких размеров должно быть макаронное устройство, чтобы выиграть это соревнование. Такое устройство, назовем его СУПЕР-ДУПЕЛЬ-МАУ, наверное, можно построить только в космосе, а прихлопывать пучок пришлось бы о поверхность Луны.
Следующее устройство из моей коллекции определяет границу выпуклой оболочки n точек на плоскости. Выпуклая оболочка - это наименьшая выпуклая область, содержащая все n точек. Она полностью определяется своей границей - многоугольником, вершины углов которого находятся в ограничивающих, или "внешних", точках, принадлежащих совокупности n. Устройство, вычисляющее границу выпуклой оболочки, сделано из большой широкой доски, нескольких гвоздей и круглой резинки. Я называю его ДАУ, а полное название Досочно-гвоздевое аналоговое устройство с круглой резинкой. Было бы заманчиво включить в сокращенное название буквы от слов "гвозди" и "круглая резника", но тогда оно получилось бы слишком громоздким, что-нибудь наподобие ДОГВАУКР.

Нахождение выпуклой оболочки множества точек на плоскости
Чтобы собрать устройство, достаточно вбить п гвоздей в доску в места заданного расположения точек. Затем нужно взять круглую резинку, растянуть ее так, чтобы окружить все гвозди, вбитые в лоску, и отпустить. Резинка прочно сядет на место, и ее контур точно определит многоугольник, представляющий собой границу выпуклой оболочки.
ЗДЕСЬ мы опять приходим к линейной по времени процедуре, которая предшествует аналоговой операции, заключающейся в данном случае в освобождении резинки. Потребуется несколько секунд, чтобы определить нужную точку для каждого гвоздя и вбить его в доску. После того как резинка отпущена, процедура определения границы полученной таким образом выпуклой оболочки займет несколько меньше времени, чем заняла бы процедура с линейным по n временем, потому что соответствующие замеры будут проделаны лишь для тех гвоздей, которых касается резиновый обруч.
Наиболее быстрый из известных алгоритмов отыскания границы выпуклой оболочки требует n*log(log(n)) шагов вычисления. Данная функция от n настолько близка к линейной, что соревноваться с цифровым компьютером, работающим по такому алгоритму, сможет, наверное, лишь колоссальная машина ДАУ, размеры которой были бы сравнимы с размерами Солнечной системы.
Задачей третьего устройства является отыскание кратчайшего пути, соединяющего две вершины на графе. В данном случае под графом мы понимаем набор отрезков, или ребер, соединяющих точки, называемые вершинами. В некоторых графах ребра могут быть различной длины, и именно с таким графом должно будет работать аналоговое устройство ШНАУ, основным элементом которого служит шнурок, соединяющий вершины графа и представляющий собой его ребра. Каждая же вершина графа представляется маленьким медным колечком. Если какие-то две вершины соединены ребром, то в аналоговой модели этого графа соответствующие колечки соединяются кусочком шнурка нужной длины, к обоим концам которого пришиты крючки.
Чтобы найти кратчайший путь между вершинами u и v на графе, возьмем в одну руку колечко, представляющее вершину u, а в другую - колечко, представляющее v, и поднимем всю систему колечек, соединенных между собой шнурками. Затем разведем руки, натягивая шнурки до предела. В результате искомый кратчайший путь будет представлен несколькими натянутыми шнурками, оказавшимися в верхней части поднятой системы. Шнурки же, представляющие ребра, которые не вошли в этот кратчайший путь, остаются менее натянутыми (см. верхний рисунок на с.94). Если колечки были помечены буквами, соответствующими обозначению вершин, то последовательность вершин, через которые проходит кратчайший путь, легко установить, прочтя метки на колечках, соединенных натянутыми шнурками.

Аналоговое устройство для отыскания кратчайшего пути между двумя вершинами на графе
Если за размер графа принять количество его вершин n, то наибольшее количество шагов, которое потребуется как для фазы предварительной, так и для фазы завершающей обработки, будет определяться линейной зависимостью от n. Аналоговая фаза вычисления, как и обычно, выполняется в данном случае почти мгновенно. Наиболее быстрый известный алгоритм для решения этой задачи на цифровом компьютере требует порядка n2 шагов.
ОБИДНО, конечно, что приходится учитывать фазы предварительной и завершающей обработки при подсчете сравнительного быстродействия описанных выше устройств, но, честно говоря, это неизбежно, так как они представляют собой неотъемлемую часть обшей процедуры решения задачи. Без них мы не смогли бы ни поставить задачу, ни "прочесть" полученный результат.
Некоторые аналоговые устройства совершенно не требуют подобной обработки, потому что они непосредственно встроены в систему, которая сразу же использует полученный результат. Приведем два примера. Первый - это система сортировки на спицах, когда-то широко применявшаяся в библиотечных каталогах. Второй пример - трюк с балансированием тарелки на одном пальце. В системе сортировки на спицах используются карточки с прорезями и маленькими отверстиями по краям, при помощи которых можно быстро определить, какие книги должны быть сданы к тому или иному сроку. Карточки укладываются в стопку и через отверстия, соответствующие данному дню, пропускается длинная спица. Если теперь поднять спицу, то на ней останутся только те карточки, у которых в том месте, куда вставлена спица, находится отверстие. Карточки, имеющие в этом месте прорези, остаются в стопке.
Трюк с балансированием показал мне "матемаг" Роналд Л.Грейам, работающий в фирме AT&T Bell Laboratories. Сначала Грейам удерживает тарелку на трех широко расставленных пальцах. По мере того как он сближает пальцы, центр тяжести тарелки остается между ними, поскольку палец, на который приходится меньший вес, легче скользит по дну тарелки. Если сблизить пальцы настолько, чтобы между ними можно было вставить четвертый палец, то положение этого четвертого пальца окажется достаточно близким к центру тяжести, и тарелка будет балансировать на этом пальце, после чего можно убрать остальные. Грейам предупреждает, что начинающим следует основательно попрактиковаться, прежде чем демонстрировать трюк за праздничным столом.
До сих пор я применял аналоговые устройства лишь к тем задачам, для решения которых уже были найдены довольно быстрые алгоритмы. О таких задачах говорят, что они имеют полиномиальную сложность, потому что количество шагов вычисления, требующееся для их решения, можно выразить (или по крайней мере ограничить сверху) через полиномиальную функцию от n, числа, характеризующего размер задачи. Например, время решения может оказаться пропорциональным самому числу n, или n2, или n*log(n), или n27. Существуют и такие задачи, в том числе имеющие практическое значение, для которых не найдено полиномиального алгоритма. Лучшие из известных алгоритмов их решения требуют времени, экспоненциально возрастающего с ростом размера задачи. Обычно время решения оказывается пропорциональным 2^n - функции, растущей быстрее любого полинома. При большом, а иногда даже умеренном размере задачи время, необходимое для ее решения, равно просто чудовищной величине. Почему бы не попробовать наши устройства на некоторых из этих труднорешаемых задачах?
НАПРИМЕР, это могла бы быть задача отыскания самого длинного из всевозможных путей, соединяющих две вершины на графе. Она оказалась значительно труднее, чем задача отыскания кратчайшего пути. На самом деле об этой задаче говорят как об NP-полной. Этот термин применяют к труднорешаемым задачам, для которых не удается найти полиномиального алгоритма. Читатели, желающие подробнее ознакомиться со свойством NP-полноты и не боящиеся иногда встречающихся в тексте математических обозначений, могут прочесть отличную книгу М.Гэрри и Д.Джонсона "Вычислительные машины и труднорешаемые задачи" (издательство "Мир", 1982г.- Прим. перев.)
Иногда, чтобы решить задачу, нужно приложить физическую силу. Взять, к примеру, задачу о кратчайшем пути между двумя вершинами на графе, решенную натяжением шнурков. Если потянуть за колечки сильнее, то шнурки начнут рваться один за другим. Наконец, перед тем, как порвется вся система, все оставшиеся целыми шнурки будут туго натянутыми. В этот момент мы получаем решение задачи о самом длинном пути.
Всегда ли? На некоторых графах этот метод оказывается эффективным, на других он не работает. Возможно, читатели получат удовольствие, построив примеры графов как первого, так и второго типов. Когда вы натягиваете систему из нескольких шнурков, первый порвавшийся шнурок считайте "наихудшим случаем".
Возможно, не следует пытаться "с лету" решать NP-полную задачу аналоговыми средствами. Однако теория о вычислимости утверждает лишь то, что NP-полные задачи являются труднорешаемыми только для цифровых компьютеров, и не содержит никаких фактов, отрицающих возможность решения таких задач аналоговыми методами. Поэтому сделаем еще одну попытку.
В задаче о минимальном дереве Штайнера требуется соединить n точек на плоскости графом минимальной обшей длины. Эта задача по существу эквивалентна задаче соединения и городов системой дорог, общая длина которых была бы минимальной. В число вершин графа помимо исходных точек можно включить еще и дополнительные, так сказать для построения проселочных дорог. Нетрудно убедиться, что искомый минимальный граф представляет собой дерево, т.е. граф, в котором отсутствуют замкнутые пути. Более того, оказывается, что любая дополнительная вершина в минимальном дереве соединяется с тремя другими вершинами ребрами, образующими углы 120о относительно друг друга (см. нижний рисунок на с.94).

"Мыльное" решение задачи о минимальном дереве Штайнера для пяти точек на плоскости
Задача о минимальном дереве Штайнера является NP-полной, и для нее не известно алгоритма, требующего менее 2^n шагов вычисления (где n - количество вершин). Тем не менее существует прибор, называемый мною Пузырьковым аналоговым устройством, который, по-видимому, дает "мыльное" решение описанной задачи. Приделайте ручку к двум параллельно расположенным прозрачным пластмассовым пластинкам и вставьте между пластинками тоненькие штырьки, представляющие исходные точки, которые нужно соединить. Затем погрузите устройство в мыльную воду. Вынув его из воды, вы увидите, как мыльная пленка соединит n штырьков, образуя изящное дерево Штайнера.
Однако ваша радость при виде этого решения будет преждевременной. Можно ли быть полностью уверенным, что полученное таким образом дерево является деревом минимальной длины? На самом деле мыльная пленка образует, как правило, всегда наименьшую возможную сеть для данной топологии, однако может существовать и другая топология, для которой может быть построено еще более короткое дерево. В зависимости от схемы расположения штырьков и угла, под которым устройство вынимается из мыльной воды, полная длина участков мыльной пленки может оказаться, а может и не оказаться абсолютно минимальной. Таким образом, и эта попытка решить NP-полную задачу аналоговыми методами не принесла успеха.
ОДНА ИЗ наиболее известных вычислительных задач заключается в том, чтобы определить, является ли заданное целое число NP простым или составным. (Если оно делится без остатка на какое-нибудь число, отличное от N или 1, то оно составное; в противном случае - простое). Эта задача имеет очень быстрое аналоговое решение, если воспользоваться Лазерным аналоговым устройством, или сокращенно ЛАУ. Нужно установить два параллельных зеркала M1 и M2 и два лазера, так чтобы лучи, испускаемые лазерами, многократно отражались от зеркал M1 и M2, как показано на рисунке на с.95. Угол, под которым направлен один лазер, подобран таким образом, чтобы его луч отражался по N раз от каждого зеркала, а затем попадал в детектор, находящийся на конце зеркала M1. Второй лазер располагается так, что вначале его луч совпадает с лучом первого лазера, а затем второй лазер быстро меняет направление и его луч проходит через определенный диапазон углов.

Лазерное аналоговое устройство показывает, что число 15 является не простым, а составным
По мере того как меняется направление второго луча, он периодически попадает в детектор на конце зеркала M1. По всей длине этого зеркала проходит также специальная детектирующая полоса. Она срабатывает всякий раз, когда два луча попадают в одну и ту же точку. За состоянием детектора на конце зеркала M1 и за детектирующей полосой следит простая электронная схема. Если оба детектора срабатывают одновременно, схема регистрирует это совпадение, и зажигается лампочка. Этот световой сигнал говорит о том, что число N является не простым, а составным. Для того чтобы имело место подобное двойное совпадение, необходимо, чтобы луч второго лазера отразился n раз от зеркала M1 и число N должно делиться на n без остатка.
Говоря об этой задаче, следует быть очень осторожным при выборе параметра, характеризующего ее размер. Если этот размер определить просто как N, то существуют цифровые алгоритмы, способные решить эту задачу за полиномиальное время. Однако правильнее было бы считать, что размер задачи гораздо лучше характеризует величина logN, так как она представляет собой длину цепочки цифр, образующих число N. При таком определении размера задачи никто не может сказать, является она NP-полной или нет, Принимая во внимание, что компьютер ЛАУ успешно справился с этой задачей, а остальные аналоговые устройства при попытках решения так называемых труднорешаемых задач не справились с ними, не следует ли предположить, что последняя нз рассмотренных задач не является NP-полной?
До сих пор я избегал очень важного вопроса, касающегося технической реализации таких аналоговых устройств, как МАУ, ДАУ, ШНАУ и ЛАУ. Хотя каждое из этих устройств можно действительно построить и даже воспользоваться им, демонстрируя решение небольших задач, было бы, конечно, неразумно создавать подобные устройства в расчете на серьезное применение. Однако на эту проблему можно взглянуть и с точки зрения "идеальных" технических возможностей, когда конструктор располагает какими угодно идеальными материалами и когда каждое устройство работает точно так, как было задумано. Было бы очень интересно пофантазировать о том, на что способны аналоговые вычислительные устройства в таких идеальных условиях.
Возможно, читатели в своих письмах
опишут какие-нибудь другие аналоговые устройства, я бы ознакомился с их изобретениями с большим интересом. Честно говоря, мне не известно, кто изобрел первые два устройства, описанные в этой статье. Наверное, они уже стали частью своеобразного фольклора, бытующего в кругах, связанных с вычислительной наукой и техникой. Шнурковое устройство, кажется, изобрели М.Минский и С.Пэйперт нз Массачусетского технологического института. Описание пузырькового устройства я нашел в удивительной книжке С.Айзенберга "Теория мыльной пленки и мыльных пузырей". Лазерное аналоговое устройство является моим собственным изобретением.
Кстати, это лазерное устройство напомнило мне об одной забавной задаче, над которой некоторым читателям будет, наверное, интересно поразмыслить. Представим себе зеркальный яшик в виде плоского прямоугольника. Предположим, что зеркальные стороны этого прямоугольника обладают идеальной отражательной способностью. В идеальных условиях можно было бы удалить одну-единственную точку в вершине одного нз углов яшика и пропустить одномерный лазерный луч внутрь через это бесконечно малое отверстие. Полученное таким образом устройство вычисляет нечто касаюшееся угла, под которым направлен луч. Ответ зависит от того, выйдет ли когда-нибудь луч обратно из яшика, а вот как поставить задачу - неизвестно.
БИБЛИОГРАФИЯ
THE SCIENCE OF SOAP FILMS AND SOAP BUBBLES. CYRIL ISENBERG. Tieto Ltd., 5 Elton Road, Clevedon. Avon, England, 1978.
COMPUTERS AND INTRACTABILITY: A GUIDE TO THE THEORY OF NP COM PLETENESS. MICHAEL R. CAREY AND DAVID S. JOHNSON. W.H.Freeman and Company, 1979.
...

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
...
ОТКЛИКИ
11 1984
СТАТЬЯ об аналоговых устройствах встретила у читателей хороший отклик - было предложено 17 новых устройств и прислано три правильных решения задачи о луче света в ящике с зеркальными стенками.
Однако, прежде чем заняться этими ответами, я должен исправить одну ошибку. По имеющимся у меня сведениям, самый быстрый алгоритм отыскания выпуклой оболочки для множества точек на плоскости требует порядка n*log(n) операций, а не n*log(log(n)). Шнурковое аналоговое устройство, решающее ту же задачу, было изобретено в 1957г. Дж.Минти-младшим из Университета шт.Индиана. Минти указывает также, что использование мыльной пленки для отыскания минимального дерева Штайнера было придумано У.Вилем в 1958г.
Лазерное устройство, отвечающее на вопрос, является ли число n простым, подверглось критике со стороны Д.Циммермана из г.Бевер-Дэм, шт.Висконсин. По пути от источника к детектору, указывает он, свет должен быть отражен n раз, но, поскольку скорость света конечна, время решения задачи оказывается пропорциональным n. Если определить размер задачи как количество разрядов в числе n, то время решения возрастает экспоненциально с ростом n, и, таким образом, это аналоговое устройство не дает выигрыша в скорости по сравнению с цифровым алгоритмом.
Тот факт, что скорость света является конечной величиной, не ускользнул от внимания и С.Хендрикса из г.Нью-Бронфелс, шт.Техас, который указал, что в задаче о ящике с зеркальными стенками может пройти очень много времени, прежде чем луч сможет его покинуть. Я спрашивал читателей, какое свойство пути, пройденного лучом, измеряет ящик с зеркальными стенками. Хендрикс был среди тех, кто решил эту задачу, отметив, что вопрос о том, выйдет ли луч из зеркального ящика, эквивалентен вопросу о том, пересечет ли бесконечная прямая на плоскости точку с целыми координатами.
Вообразим себе бесконечно большой сад с бесконечно тонкими деревьями, посаженными в вершинах квадратной решетки. Если выстрелить с одного из деревьев в произвольном направлении, попадет ли когда-нибудь пуля в другое дерево? (Рассуждение автора справедливо при условии отсутствия в воображаемом саду сил тяготения.- Перев.) Попадет, если выстрел произвести под таким углом к линии посадки деревьев, тангенс которого представляет собой рациональное число. Если дерево, в которое попадет пуля, находится в точке, удаленной на p рядов к северу и q к востоку, то тангенс угла стрельбы должен составлять p/q. В задаче о луче света в зеркальном ящике зеркала лишь отклоняют пулю, как бы "складывая" траекторию ее полета в ограниченном пространстве ящика. Эту задачу решили также Дж.Джонс из г.Фармингтон-Хиллэ, шт.Мичиган, и П.Кингсберг из г.Империал, шт.Пенсильвания.
Чтобы воздать должное богатому многообразию аналоговых устройств, описанных читателями, нужно, по-видимому, посвятить еще одну статью этой теме, может быть, в одном из первых номеров журнала за 1985г. А пока придется ограничиться лишь упоминанием о некоторых наиболее интересных устройствах.
П.Эш из Университета св.Джозефа сообщил о том, как можно решать кубические уравнения, погружая твердые тела в бак с водой. Т.Дигби из Лос-Анджелеса отметил, что вычислительная мощность аналогового устройства объясняется его способностью параллельно выполнять много процессов. Он показал, как можно с помощью n цифровых компьютеров отсортировать n чисел за "линейное" время, получив тем самым тот же результат, который был получен с помощью макаронного аналогового компьютера.
Э.ХОЛСИ из Университета шт.Вашингтон описал устройство, отыскивающее самый длинный путь на графе, который собран из "змеек". Каждое ребро графа представляется эластичным шнуром, пропущенным через целое число бусинок. Выявляется ли самый длинный путь, если устройство растянуть, а затем ослабить натяжение? Другое его устройство измеряет длину кратчайшего пути между двумя вершинами на графе. Пусть ребро графа сделаны из бикфордова шнура, а вторая вершина, кратчайшее расстояние до которой мы ищем, представляет собой пороховую хлопушку. Подожжем шнуры, исходящие из первой вершины, и отойдем на всякий случай подальше: время, прошедшее до взрыва хлопушки, будет пропорционально длине искомого пути.
П.Хансен-младший из г.Ларго, шт.Флорида, напомнил мне, что планиметр, механическое устройство для измерения площади, можно также рассматривать в качестве аналогового компьютера. Д.Хоффман из Колледжа общества Бельвю в Вашингтоне указал на некоторые другие задачи, которые можно решать с помощью мыльной пленки, включая остроумный способ вычисления по закону Снеллиуса. Д.Кимбалл из Сан-Диего решает задачи об отыскании пути в лабиринте, закачивая воду в лабиринт и прослеживая за течением воды к выходу. Другое любопытное устройство было описано Дж.Люетом, служащим металлургической компании United States Metals Refining в Картерете, шт.Нью-Джерси. Это устройство отыскивает точку оптимального расположения плавильного завода, назовем его ПЛАЗАУ (ПЛАвильный Завод - Аналоговое Устройство). Расположение плавильного завода должно быть оптимальным в смысле минимизации транспортных расходов на подвоз угля, руды и известняка. Три отверстия в доске и три гирьки, связанные вместе одним шнурком, решают эту задачу. То же самое устройство было упомянуто и читателем Хендриксом.
Т.Мэнсфилд из Британской национальной физической лаборатории в Теддингтоне решает задачи линейного программирования с помощью сооружения, собранного из деталей детского конструкторского набора. Т.Рейзнер из Университета Лаваля в Квебеке строит контурную карту рельефа, покрывая его москитной сеткой. Яркое освещение сверху создает муаровый рисунок, когда сетка интерферирует со своей собственной тенью.
Американская цитрусовая промышленность, очевидно, также пользуется аналоговым устройством для сортировки плодов. Апельсин прокатывается по двум не совсем параллельным трубкам и проваливается, когда расстояние между трубками равно диаметру апельсина. Дж.Швенклср из г.Луивиля, шт. Колорадо, одно время отыскивал центр тяжести деталей, пользуясь разновидностью приема, который применял Р.Грейем для балансирования тарелки. Когда деталь трижды протаскивали на веревке по гладкой поверхности, центр тяжести детали каждый раз находился в вертикальной плоскости, проходящей через веревку. Точка пересечения трех таких плоскостей указывала на искомое положение центра тяжести.
7 1985
СТАТЬЯ, посвященная аналоговым устройствам, которая была опубликована в августовском номере журнала "В мире науки" за 1984г., вызвала такой поток отзывов, что к этой теме следует вернуться еще раз, хотя в ноябрьском номере журнала за 1984г. мы уже говорили на эту тему. Интересно то, что некоторые устройства, описания которых содержатся в письмах читателей, оказались практически полезными. К таким аналоговым устройствам можно отнести, например, систему, регулирующую атмосферные параметры. О ней написал X.Клэй, инженер из Феникса (шт.Аризона). Как-то к Клэю обратились с просьбой изобрести какой-нибудь прибор, регулирующий температуру и влажность в печатающем устройстве. От этих параметров во многом зависит качество копировальной бумаги, которая используется для покрытия печатных валиков в типографских машинах. Опытный рабочий может без труда установить пригодность копировальной бумаги по ее внешнему виду и по тому, как она провисает. Если ее качество не соответствует норме, на бумаге образуются морщинки и трещинки, которые появляются в том случае, если температура и влажность не соответствуют требуемой величине. Клэй сконструировал устройство, которое измеряло температуру и влажность и регулировало эти параметры, включая и выключая увлажнитель. В течение какого-то времени система, по-видимому, работала исправно, но затем по неизвестным причинам она вышла из строя.
Когда Клэй снова пришел в типографию, чтобы проверить, как работает его система, инженер, лукаво улыбаясь, провел его к печатающему станку. То, что увидел Клэй, повергло его в изумление. "Моя регулирующая система была отключена. Вместо нее я увидел маленькую полоску копировальной бумаги, один конец которой был закреплен, а другой свободно свисал вниз. Когда полоска свисала "правильно", ее свободный коней замыкал пару контактов в схеме, включающей и выключающей увлажнитель". Заметив смущение Клэя, инженер добавил: "Работает как часы, мечта, а не устройство".
В 1948г. Р.Хеппе из Фэрфакса (шт. Виргиния) был молодым специалистом, инженером-электронщиком, только что поступившим на работу на предприятие фирмы Sylvania Electric Products Company. Хеппе, помогавший конструировать электронные лучевые трубки, находил это занятие довольно скучным и утомительным. Для изготовления новой конструкции трубки вначале нужно было сделать чертеж со схематическим изображением электродов, сеток и пластинок, отклоняющих луч. По этому эскизу в единственном экземпляре изготовлялась трубка, которая затем испытывалась. Процесс занимал несколько дней. Руководитель группы, в которой работал Хеппе, Дж.Рич, чтобы повысить производительность, предложил некое аналоговое устройство.
Оно состояло из резинового листа, дюбеля, некоторого количества фанерных деталей и нескольких десятков зубочисток. Резиновый лист, натянутый на обруч, представлял поперечное сечение электронно-лучевой трубки, увеличенное в несколько раз. Роль катода играл деревянный дюбель, торчавший в середине листа. Из зубочисток выполнялись различные конструкции сеток. Сетки с отрицательным зарядом упирались в резинку снизу, образуя бугорки, а положительно заряженные сетки давили на резину сверху, образуя в ней ямки. Другие геометрические свойства трубки моделировались фанерными деталями, также прикладываемыми сверху или снизу. Поток электронов, излучаемых катодом, имитировался медленным высыпанием из банки горошин над дюбелем в центре листа. "Можно доказать, - пишет Хеппе, - что профиль резиновой поверхности в таком устройстве соответствует распределению напряженности электрического поля, а величина провалов или подъемов - напряжению между электродами... Скатывавшиеся по резиновой поверхности горошины скапливались либо на ровных местах, либо в ямках положительно заряженных сеток. Если нас не устраивало количество горошин, собирающихся у различных электродов, или путь, по которому они скатывались, мы передвигали декорации, изменяли их размеры и т.п... и ставили новый эксперимент. По конструкциям, которые удовлетворяли нашим требованиям, изготавливались уже настоящие трубки, испытывавшиеся затем в реальной работе".
Многие читатели привели другие примеры. Среди них следует отметить устройство, измеряющее твердые фракции в крови человека, изобретенное доктором А.Квасманом из Лома-Линды (шт.Калифорния). М.Сооп из Европейского космического агентства в Дармштадте (ФРГ) привел описание устройства из шнура, гвоздей и скрепок для бумаг. Устройство иллюстрирует аналоговое решение проблемы минимизации потребления горючего в спутнике при автоматическом управлении его ориентации при помощи ракетных движков.
В читательских письмах содержались описания и других устройств. Но все же самыми лучшими и самыми крупными аналоговыми устройствами являются аналоговые компьютеры. Они все еще существуют и работают в фирме Electronic Associates, Inc., производящей аналоговое оборудование. Меня даже пригласили на завод, с тем чтобы я на месте убедился, насколько эти машины превосходят те, о которых шла речь в нашей первой статье, посвященной аналоговым устройствам.
ОТКЛИКИ
11 1984
СТАТЬЯ об аналоговых устройствах встретила у читателей хороший отклик - было предложено 17 новых устройств и прислано три правильных решения задачи о луче света в ящике с зеркальными стенками.
Однако, прежде чем заняться этими ответами, я должен исправить одну ошибку. По имеющимся у меня сведениям, самый быстрый алгоритм отыскания выпуклой оболочки для множества точек на плоскости требует порядка n*log(n) операций, а не n*log(log(n)). Шнурковое аналоговое устройство, решающее ту же задачу, было изобретено в 1957г. Дж.Минти-младшим из Университета шт.Индиана. Минти указывает также, что использование мыльной пленки для отыскания минимального дерева Штайнера было придумано У.Вилем в 1958г.
Лазерное устройство, отвечающее на вопрос, является ли число n простым, подверглось критике со стороны Д.Циммермана из г.Бевер-Дэм, шт.Висконсин. По пути от источника к детектору, указывает он, свет должен быть отражен n раз, но, поскольку скорость света конечна, время решения задачи оказывается пропорциональным n. Если определить размер задачи как количество разрядов в числе n, то время решения возрастает экспоненциально с ростом n, и, таким образом, это аналоговое устройство не дает выигрыша в скорости по сравнению с цифровым алгоритмом.
Тот факт, что скорость света является конечной величиной, не ускользнул от внимания и С.Хендрикса из г.Нью-Бронфелс, шт.Техас, который указал, что в задаче о ящике с зеркальными стенками может пройти очень много времени, прежде чем луч сможет его покинуть. Я спрашивал читателей, какое свойство пути, пройденного лучом, измеряет ящик с зеркальными стенками. Хендрикс был среди тех, кто решил эту задачу, отметив, что вопрос о том, выйдет ли луч из зеркального ящика, эквивалентен вопросу о том, пересечет ли бесконечная прямая на плоскости точку с целыми координатами.
Вообразим себе бесконечно большой сад с бесконечно тонкими деревьями, посаженными в вершинах квадратной решетки. Если выстрелить с одного из деревьев в произвольном направлении, попадет ли когда-нибудь пуля в другое дерево? (Рассуждение автора справедливо при условии отсутствия в воображаемом саду сил тяготения.- Перев.) Попадет, если выстрел произвести под таким углом к линии посадки деревьев, тангенс которого представляет собой рациональное число. Если дерево, в которое попадет пуля, находится в точке, удаленной на p рядов к северу и q к востоку, то тангенс угла стрельбы должен составлять p/q. В задаче о луче света в зеркальном ящике зеркала лишь отклоняют пулю, как бы "складывая" траекторию ее полета в ограниченном пространстве ящика. Эту задачу решили также Дж.Джонс из г.Фармингтон-Хиллэ, шт.Мичиган, и П.Кингсберг из г.Империал, шт.Пенсильвания.
Чтобы воздать должное богатому многообразию аналоговых устройств, описанных читателями, нужно, по-видимому, посвятить еще одну статью этой теме, может быть, в одном из первых номеров журнала за 1985г. А пока придется ограничиться лишь упоминанием о некоторых наиболее интересных устройствах.
П.Эш из Университета св.Джозефа сообщил о том, как можно решать кубические уравнения, погружая твердые тела в бак с водой. Т.Дигби из Лос-Анджелеса отметил, что вычислительная мощность аналогового устройства объясняется его способностью параллельно выполнять много процессов. Он показал, как можно с помощью n цифровых компьютеров отсортировать n чисел за "линейное" время, получив тем самым тот же результат, который был получен с помощью макаронного аналогового компьютера.
Э.ХОЛСИ из Университета шт.Вашингтон описал устройство, отыскивающее самый длинный путь на графе, который собран из "змеек". Каждое ребро графа представляется эластичным шнуром, пропущенным через целое число бусинок. Выявляется ли самый длинный путь, если устройство растянуть, а затем ослабить натяжение? Другое его устройство измеряет длину кратчайшего пути между двумя вершинами на графе. Пусть ребро графа сделаны из бикфордова шнура, а вторая вершина, кратчайшее расстояние до которой мы ищем, представляет собой пороховую хлопушку. Подожжем шнуры, исходящие из первой вершины, и отойдем на всякий случай подальше: время, прошедшее до взрыва хлопушки, будет пропорционально длине искомого пути.
П.Хансен-младший из г.Ларго, шт.Флорида, напомнил мне, что планиметр, механическое устройство для измерения площади, можно также рассматривать в качестве аналогового компьютера. Д.Хоффман из Колледжа общества Бельвю в Вашингтоне указал на некоторые другие задачи, которые можно решать с помощью мыльной пленки, включая остроумный способ вычисления по закону Снеллиуса. Д.Кимбалл из Сан-Диего решает задачи об отыскании пути в лабиринте, закачивая воду в лабиринт и прослеживая за течением воды к выходу. Другое любопытное устройство было описано Дж.Люетом, служащим металлургической компании United States Metals Refining в Картерете, шт.Нью-Джерси. Это устройство отыскивает точку оптимального расположения плавильного завода, назовем его ПЛАЗАУ (ПЛАвильный Завод - Аналоговое Устройство). Расположение плавильного завода должно быть оптимальным в смысле минимизации транспортных расходов на подвоз угля, руды и известняка. Три отверстия в доске и три гирьки, связанные вместе одним шнурком, решают эту задачу. То же самое устройство было упомянуто и читателем Хендриксом.
Т.Мэнсфилд из Британской национальной физической лаборатории в Теддингтоне решает задачи линейного программирования с помощью сооружения, собранного из деталей детского конструкторского набора. Т.Рейзнер из Университета Лаваля в Квебеке строит контурную карту рельефа, покрывая его москитной сеткой. Яркое освещение сверху создает муаровый рисунок, когда сетка интерферирует со своей собственной тенью.
Американская цитрусовая промышленность, очевидно, также пользуется аналоговым устройством для сортировки плодов. Апельсин прокатывается по двум не совсем параллельным трубкам и проваливается, когда расстояние между трубками равно диаметру апельсина. Дж.Швенклср из г.Луивиля, шт. Колорадо, одно время отыскивал центр тяжести деталей, пользуясь разновидностью приема, который применял Р.Грейем для балансирования тарелки. Когда деталь трижды протаскивали на веревке по гладкой поверхности, центр тяжести детали каждый раз находился в вертикальной плоскости, проходящей через веревку. Точка пересечения трех таких плоскостей указывала на искомое положение центра тяжести.
7 1985
СТАТЬЯ, посвященная аналоговым устройствам, которая была опубликована в августовском номере журнала "В мире науки" за 1984г., вызвала такой поток отзывов, что к этой теме следует вернуться еще раз, хотя в ноябрьском номере журнала за 1984г. мы уже говорили на эту тему. Интересно то, что некоторые устройства, описания которых содержатся в письмах читателей, оказались практически полезными. К таким аналоговым устройствам можно отнести, например, систему, регулирующую атмосферные параметры. О ней написал X.Клэй, инженер из Феникса (шт.Аризона). Как-то к Клэю обратились с просьбой изобрести какой-нибудь прибор, регулирующий температуру и влажность в печатающем устройстве. От этих параметров во многом зависит качество копировальной бумаги, которая используется для покрытия печатных валиков в типографских машинах. Опытный рабочий может без труда установить пригодность копировальной бумаги по ее внешнему виду и по тому, как она провисает. Если ее качество не соответствует норме, на бумаге образуются морщинки и трещинки, которые появляются в том случае, если температура и влажность не соответствуют требуемой величине. Клэй сконструировал устройство, которое измеряло температуру и влажность и регулировало эти параметры, включая и выключая увлажнитель. В течение какого-то времени система, по-видимому, работала исправно, но затем по неизвестным причинам она вышла из строя.
Когда Клэй снова пришел в типографию, чтобы проверить, как работает его система, инженер, лукаво улыбаясь, провел его к печатающему станку. То, что увидел Клэй, повергло его в изумление. "Моя регулирующая система была отключена. Вместо нее я увидел маленькую полоску копировальной бумаги, один конец которой был закреплен, а другой свободно свисал вниз. Когда полоска свисала "правильно", ее свободный коней замыкал пару контактов в схеме, включающей и выключающей увлажнитель". Заметив смущение Клэя, инженер добавил: "Работает как часы, мечта, а не устройство".
В 1948г. Р.Хеппе из Фэрфакса (шт. Виргиния) был молодым специалистом, инженером-электронщиком, только что поступившим на работу на предприятие фирмы Sylvania Electric Products Company. Хеппе, помогавший конструировать электронные лучевые трубки, находил это занятие довольно скучным и утомительным. Для изготовления новой конструкции трубки вначале нужно было сделать чертеж со схематическим изображением электродов, сеток и пластинок, отклоняющих луч. По этому эскизу в единственном экземпляре изготовлялась трубка, которая затем испытывалась. Процесс занимал несколько дней. Руководитель группы, в которой работал Хеппе, Дж.Рич, чтобы повысить производительность, предложил некое аналоговое устройство.
Оно состояло из резинового листа, дюбеля, некоторого количества фанерных деталей и нескольких десятков зубочисток. Резиновый лист, натянутый на обруч, представлял поперечное сечение электронно-лучевой трубки, увеличенное в несколько раз. Роль катода играл деревянный дюбель, торчавший в середине листа. Из зубочисток выполнялись различные конструкции сеток. Сетки с отрицательным зарядом упирались в резинку снизу, образуя бугорки, а положительно заряженные сетки давили на резину сверху, образуя в ней ямки. Другие геометрические свойства трубки моделировались фанерными деталями, также прикладываемыми сверху или снизу. Поток электронов, излучаемых катодом, имитировался медленным высыпанием из банки горошин над дюбелем в центре листа. "Можно доказать, - пишет Хеппе, - что профиль резиновой поверхности в таком устройстве соответствует распределению напряженности электрического поля, а величина провалов или подъемов - напряжению между электродами... Скатывавшиеся по резиновой поверхности горошины скапливались либо на ровных местах, либо в ямках положительно заряженных сеток. Если нас не устраивало количество горошин, собирающихся у различных электродов, или путь, по которому они скатывались, мы передвигали декорации, изменяли их размеры и т.п... и ставили новый эксперимент. По конструкциям, которые удовлетворяли нашим требованиям, изготавливались уже настоящие трубки, испытывавшиеся затем в реальной работе".
Многие читатели привели другие примеры. Среди них следует отметить устройство, измеряющее твердые фракции в крови человека, изобретенное доктором А.Квасманом из Лома-Линды (шт.Калифорния). М.Сооп из Европейского космического агентства в Дармштадте (ФРГ) привел описание устройства из шнура, гвоздей и скрепок для бумаг. Устройство иллюстрирует аналоговое решение проблемы минимизации потребления горючего в спутнике при автоматическом управлении его ориентации при помощи ракетных движков.
В читательских письмах содержались описания и других устройств. Но все же самыми лучшими и самыми крупными аналоговыми устройствами являются аналоговые компьютеры. Они все еще существуют и работают в фирме Electronic Associates, Inc., производящей аналоговое оборудование. Меня даже пригласили на завод, с тем чтобы я на месте убедился, насколько эти машины превосходят те, о которых шла речь в нашей первой статье, посвященной аналоговым устройствам.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
09 1984
ПРОГРАММА, ИГРАЮЩАЯ В ШАШКИ, ЧАСТО "ВИДИТ" ИГРУ НА ХОД ДАЛЬШЕ ПРОТИВНИКА
А.К.ДЬЮДНИ
"МОЖНО ли написать такую программу, играющую в шашки, которая никогда не проиграет человеку, никогда-никогда?" Мальчик был лет десяти и взглянул на нас, оторвавшись от терминала, с таким глубокомысленным, но невинным выражением, которое свойственно лишь очень юным. Он играл в шашки с программой, написанной моими студентами. Программа была настроена так, чтобы не просчитывать развитие игры на много ходов вперед, и паренек играл с ней довольно успешно.
Этот вопрос был задан мальчиком на выставке, устроенной на нашем факультете несколько лет назад, и на него можно ответить по-разному в зависимости от того, о каком варианте игры в шашки идет речь. Вопрос имеет также непосредственное отношение к важнейшим проблемам создания искусственного интеллекта, в частности к программированию "разумного" поведения компьютерных программ. Об этих проблемах мы поговорим несколько позже.
Когда мальчик задал нам свой вопрос, он играл в шашки на доске с числом клеток, равным 6*6. Это лишь один вариант из бесконечного многообразия шашечных игр. В настоящей статье мы рассмотрим варианты игры 4*4, 6*6 и 8*8 (классические шашки) и обсудим перспективы применения программ, написанных для этих игр. Вообще говоря, можно определить шашки n-го порядка, т.е. игру на доске с числом клеток 2n*2n. В каждом случае шашки, или шашечные фигуры, в исходном положении занимают все темные клетки, за исключением двух рядов в средней части доски. Правила игры в шашки n-го порядка более подробно рассмотрены на с.108.
***
ПРАВИЛА ИГРЫ В ШАШКИ N-ГО ПОРЯДКА
На доске, представляющей собой квадрат размерами 2n*2n клеток, попеременно светлых и темных, каждый игрок располагает n2-n шашек на темных клетках на противоположных сторонах доски. Два средних ряда клеток остаются пустыми. У каждой стороны есть "одиночный угол" (темная клетка в левом углу доски), а также "двойной угол" (справа). Черные ходят первыми.
Простая шашка может ходить по диагонали вперед на прилегающую незанятую темную клетку. Если эта клетка занята фигурой противника, а следующая за ней по диагонали клетка свободна, то шашка может перескочить фигуру противника, причем последняя считается захваченной и убирается с доски. Любая возможность такого захвата используется в обязательном порядке; если одновременно возможны два или более захватов, по крайней мере один из них должен быть сделан.
Когда простая шашка достигает последнего ряда на противоположной стороне доски, она становится дамкой. Дамка может ходить как вперед, так и назад (тоже по диагонали) и может бить в обоих направлениях.
Игра заканчивается победой одного из игроков, когда другой игрок не может сделать ни одного хода. Если оба игрока приходят к выводу, что выигрыш невозможен, объявляется ничья.

На рисунке показана исходная позиция для игры восьмого порядка на доске размерами 16*16 с 56 фигурами с каждой стороны.
***
В случае варианта 4*4 на вопрос, заданный мальчиком, можно, по-видимому, дать положительный ответ. Для варианта 6*6 ответом будет "очень вероятно", а для игры 8*8 - "возможно". Мои ответы основаны на сочетании личного опыта, литературных данных и просто интуиции.
РАССМОТРИМ вариант игры 4*4. В этом случае у каждого играющего по две фигуры и игра редко продолжается более 10 ходов, по крайней мере
когда играют квалифицированные игроки. Новички могут сделать 20 ходов или даже больше, прежде чем ничейный результат станет для них очевидным. Кстати, если уж речь зашла о ничьих, то в одном из последних турниров по шашкам 4*4 в городе Шашигрсбурге было зафиксировано шесть ничьих подряд и лишь в седьмой партии победа по решению судейской коллегии была присуждена гроссмейстеру Самюэлю Енсену Траскотту - его противник дважды случайно дотронулся до фигуры, которой нельзя было ходить.
Во всяком случае, вариант игры 4*4 можно проанализировать вручную. По-видимому, при разумной игре закономерным будет ничейный результат, поэтому игрок, проявляющий достаточно внимания, никогда не должен проигрывать. То же можно сказать и о достаточно хорошей программе.
В варианте игры 6*6 каждый партнер имеет шесть фигур и в среднем игра завершается после примерно 20 ходов. Если программу, написанную нашими студентами, настроить на максимально возможное просматривание игры вперед, то ей требуется от пяти до десяти минут для выбора очередного хода. При такой настройке программа играла очень сильно и казалась совершенно неуязвимой вплоть до эндшпиля, к которому она подходила с таким большим преимуществом в фигурах или в позиции, что обычно доводила партию до победы или в крайнем случае сводила ее вничью. Однако время от времени кто-нибудь из нас сохранял достаточно фигур, чтобы победить программу в эндшпиле, который она играла удивительно слабо.
В варианте игры 8*8 каждый партнер имеет по 12 фигур, и, когда играют квалифицированные игроки, число ходов достигает 30 и более. На турнирах по стандартным шашкам теперь стало уже обычной практикой устанавливать первый ход по жребию (имеется в виду не очередность, а вариант хода). Такой обычай был принят в Англии в начале века, потому что мастера этой игры почти всегда начинали со своего излюбленного хода с хорошо изученным продолжением, что приводило ко все возрастающему числу ничейных результатов. Можно ли объяснить изобилие ничьих тем, что шашки по своей природе являются ничейной игрой, или все дело в консерватизме мастеров, трудно сказать. Как бы то ни было, шашки в варианте игры на доске 8*8 остаются увлекательной и трудной игрой. С математической точки зрения шашки несколько уступают по сложности шахматам, однако есть люди, одинаково хорошо играющие в обе эти игры и не считающие шахматы игрой более высокого уровня.
Две наиболее известные программы, играющие в шашки, были созданы А.Самюэлем из фирмы IBM (International Business Machines Corporation) в 60-х годах и Э.Енсеном и Т.Траскоттом из Университета Дьюка в 1977г. В 1962г. шашечная программа Самюэля победила Роберта Нили, в прошлом чемпиона шт.Коннектикут. Хотя эта программа играет очень сильно, она все же уступает игре гроссмейстерского уровня. Программа Енсена-Траскотта еще сильнее и по игpе находится на уровне ведущих мастеров мира.
В 1979г. программа Енсена-Траскотта играла против Элберта Лаудера, считающегося одним из лучших игроков в США. Из пяти партий две закончились вничью, одну программа выиграла и две проиграла. Проигрыши, по-видимому, объясняются некоторыми недочетами, присущими программе в эндшпиле: когда Лаудер понял, что две шашки противника оставались "на страже" на задней линии, он воспользовался слабостью этой позиции и выиграл последние две партии. Следует, однако, заметить, что, играя против программы Енсена-Траскотта, Лаудер экспериментировал и играл несколько рискованно. Его проигрыш в одной из партий объясняется, по всей видимости, попыткой "заманить" программу на необычные позиции. Возможно, этого не следовало делать в игре с программой такого высокого уровня.
Тем временем Марион Ф.Тинзли, чемпион мира по шашкам, с интересом наблюдает за событиями из своего дома в Теллахассе (шт.Флорида). Я не знаю, играл ли Тинзли когда-нибудь с лучшими шашечными программами. Однако известно, что две лучшие программы играли между собой. В двух партиях против программы Самюэля программа Енсена-Траскотта оказалась, по словам Траскотта, "на голову выше" и выиграла их.
В БОЛЬШИНСТВЕ удачно играющих программ можно выделить три основные компоненты: генератор ходов, функцию, оценивающую позицию, и минимаксную процедуру. Еще один важный элемент - это "дерево" игры; оно участвует в работе всех трех основных компонент игровой программы. Генератор ходов строит дерево; к оценивающей функции происходит обращение в конце каждой ветви дерева, а минимаксная процедура применяется ко всему дереву в целом.
Корневой узел дерева представляет собой исходную позицию на доске, а каждая ветвь ведет к какой-то позиции, достигаемой при помощи одного хода. Примечательно, что подобное дерево изображается обычно "вверх ногами" - его корень располагается вверху. Дерево можно "разделить" на уровни так, что все позиции n-го уровня соответствуют всем возможным ходам одного игрока, делающего n-й ход. Хотя игровые деревья, как правило, не очень высоки (точнее говоря, глубоки), они могут быть очень кустистыми. Дело в том, что число позиций на каждом уровне более чем вдвое превышает число позиций на предыдущем уровне. Даже если у каждой позиции на доске было лишь две последующие позиции, то число ветвей очень скоро достигло бы огромной величины. Дерево, разветвившееся подобным образом 64 раза, имело бы больше ветвей, чем все деревья, растущие на Земле, вместе взятые. (В природе деревья ветвятся не более 12 раз от корня до листьев). Из-за того что число ветвей игрового дерева возрастает по экспоненциальному закону, т.е. имеет место "экспоненциальный взрыв", компьютер может исследовать лишь небольшую часть продолжений в такой игре, как шашки на доске 8*8.
Дерево шашечной игры создается генератором ходов - программой, которой в качестве входных данных задается текущая позиция на доске, а также указание о том, кто из противников должен сделать очередной ход. Выходом генератора ходов являются все возможные позиции, достижимые из заданной позиции после одного хода. Рассмотрим следующую позицию на доске 4*4, предполагая, что ходить должны черные фигуры:

Для черных имеется два возможных хода, и генератор ходов выдает две позиции:

Затем генератор ходов может применяться уже к каждой из этих позиций в отдельности.
Читателям, желающим разобраться, как работает генератор ходов, мы предлагаем достроить дерево игры на доске 4*4, отправляясь от рассмотренного нами уровня. Например, на следующем уровне будет только две позиции, поскольку в каждом случае правила игры вынуждают белых [на рисунках для наглядности эти фигуры изображены красным цветом.- Прим. перев.] бить фигуру противника. На уровне, следующем за этим, будет опять две позиции, затем три (в одной из них белые выигрывают), затем 2, 5, 10, наконец, 24. Тем, кто пожелает последовать еще дальше, мы дадим два совета. Во-первых, нужно просматривать каждый уровень в поисках идентичных позиций и строить продолжение лишь для одной из таких позиций. Во-вторых, для каждой новой позиции нужно просматривать дерево снизу вверх, чтобы найти идентичную позицию. Если эта позиция уже встречалась в игре, то на повторно встретившейся позиции ветвь нужно закончить, пометив ее конец как "ничью".
Как работает программа, генерирующая ходы? Первый вопрос заключается в том, каким образом позиции на доске представляются в памяти компьютера. В качестве простейшей схемы можно принять матрицу - двумерный массив, элементы которого соответствуют каждой клетке шашечной доски. Например, пустой клетке соответствует 0, клетке, занимаемой "простой" шашкой,- 1, а клетке, которую занимает "дамка",- 2. Знак числа может отражать принадлежность фигуры к черным или белым, плюс - для черных и минус - для белых фигур. Первая позиция на доске 4*4, показанная выше, может быть представлена матрицей следующего вида:
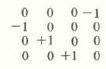
Ходы, разрешенные правилами игры для каждой фигуры, зависят от того, какой стороне она принадлежит, от ее позиции, а также от того, заняты или свободны прилежащие по диагонали клетки. В рассматриваемом случае генератор ходов сканирует массив строку за строкой, пока не наталкивается на положительный элемент (фигура черных) в строке 3 колонки 2; мы будем обозначать такую позицию как (3, 2). Поскольку ход принадлежит черным и фигура является "простой" шашкой, а не "дамкой" (значение элемента матрицы равно 1), программа исследует клетки (2, 1) и (2, 3). Клетка (2,1) уже занята фигурой (и перескочить ее невозможно), но клетка (2, 3) свободна. Поэтому программа строит новый массив, в котором +1 удаляется с позиции (3, 2) и помещается в позицию (2, 3):

Затем генератор ходов продолжает сканировать массив, пока не найдет следующий положительный элемент.
Чтобы следить за различными позициями на доске и соответствующими массивами, их можно последовательно пронумеровать в порядке генерации. Тогда состояние любой клетки в каждый момент игры будет определяться номером позиции на доске, а также номерами строки и колонки массива. По мере того как генератор ходов строит дерево игры, он должен записывать, в каком порядке позиции следуют друг за другом. Когда программа выбирает очередной ход, она просматривает дерево на несколько уровней вниз, затем вверх, затем снова вниз и т.д. Чтобы перемещаться по дереву таким образом, программа должна знать, какие позиции на доске являются предшествующими, или "родителями", а какие - последующими, или "потомками". Для этого у программы есть специальный массив, называемый таблицей указателей. Указателем для каждой позиции является список чисел, в котором первое число указывает на позицию, являющуюся "родителем" данной, а остальные числа - на ее "потомков".
СЛЕДУЮЩАЯ важная компонента программы, играющей в шашки,- это функция, оценивающая позиции. В качестве входной информации ей дается позиция на доске, и она выдает число, отражающее ценность этой позиции для черных фигур. Большое число означает, что если данная позиция будет достигнута в игре, то у черных будут хорошие шансы на выигрыш. Построить хорошую оценивающую функцию очень трудно, потому что при оценке позиции на доске нужно принимать во внимание слишком много факторов. Кроме того, в большинстве игр, включая шашки, не всегда ясно, какой вес приписать тому или иному фактору. Перечислим кратко простейшие из этих факторов:
ПРОСТЫЕ ШАШКИ. Прибавить 1 для каждой черной шашки на доске; вычесть 1 для каждой белой шашки.
ДАМКИ. Прибавить 1 для каждой черной дамки; вычесть 1 для каждой белой дамки.
ЦЕНТР. Прибавить 1 для каждой черной шашки, занимающей одну из четырех центральных клеток; соответственно вычесть 1 для каждой белой шашки.
ПРОДВИЖЕНИЕ. Прибавить 1 для каждой черной шашки; находящейся во втором ряду, 2 для каждой черной шашки в третьем ряду, 3 для каждой черной шашки (дамки) в четвертом ряду; вычесть соответствующие величины для белых фигур.
ПОДВИЖНОСТЬ. Прибавить 1 на каждый возможный ход для черных и вычесть 1 на каждый возможный ход для белых фигур.
Каково относительное значение перечисленных факторов? Следует ли приписать дамкам вдвое больший вес, чем простым шашкам? Входит ли в "продвижение" информация, содержащаяся в таких факторах, как "шашки" и "дамки"?
Самюэль ответил на эти вопросы, позволив программе самой установить, какой вес приписать тому или иному фактору на основе игрового опыта. Оперируя 39 факторами (многие из которых были предложены знатоками игры или взяты из литературных источников), оценивающая функция Самюэля вначале приписала им один и тот же вес и просто складывала одни и те же числа. Полученная таким образом сумма характеризовала "ценность" позиции. Каждую проигранную партию программа анализировала, чтобы выявить фактор, который привел к поражению. В результате вес этого фактора уменьшался. Процесс обучения был ускорен за счет автоматизации анализа и многократных игровых испытаний.
Процедуры, оценивающие позицию, никогда не бывают совершенными. Если бы это было не так, то остальные компоненты игровой программы едва ли потребовались бы. Программе нужно было бы лишь исследовать позиции, достигаемые из данной при одном возможном ходе, оценить каждую из этих позиций и выбрать лучший ход. Существует своего рода компромисс между точностью оценивающей функции и числом уровней дерева, которые программа должна просматривать вперед. Если бы оценивающая функция могла лишь распознавать позиции, соответствующие окончательному выигрышу или проигрышу, то игровое дерево нужно было бы просматривать на всю глубину!
Третья главная компонента программы - минимаксная процедура, представляющая собой программу поиска на игровом дереве, которая пользуется оценками позиций на нижнем уровне, чтобы придать оценочные значения позициям, расположенным на более высоких (т.е. начальных) уровнях дерева игры. На какой-то стадии исследования дерева все позиции определенного уровня должны быть оценены этой функцией. Позиция B на уровне, непосредственно выше оцененного, получает оценку по следующему простому правилу: если в позиции B ходить должны белые, то выбирается минимальное значение из оценок, полученных для "потомков" B; оно принимается в качестве оценки позиции B. Если же ходить должны черные, то нужно выбрать максимальное значение.
Не трудно понять, из каких соображений было выбрано это правило. Если ход принадлежит белым, то черные вполне могут предположить, что белые выберут ход, который приведет к позиции с минимальным значением оценки для черных. Точно так же, если ход принадлежит черным, то будет выбрана позиция с максимально возможной оценкой. Таким образом, минимаксная процедура начинает действовать с самого нижнего просмотренного уровня дерева и, пользуясь оценками, полученными для этого уровня оценивающей функцией, переносит их вверх по дереву. Переходя от какого-то уровня к следующему, расположенному выше, она поочередно выбирает минимальные и максимальные оценки, в зависимости от того, какой стороне принадлежит ход. В конце концов минимаксная процедура возвращается к текущей позиции и дает черным оценку для каждого возможного хода в этой позиции. Естественно, черные выбирают ход с самой высокой оценкой.
ПРОГРАММА, играющая в шашки, помимо рассмотренных трех основных компонент, имеет и другие компоненты. Она должна обеспечить взаимодействие с играющим человеком - принимать ходы с клавиатуры терминального устройства и печатать ответные ходы. Кроме того, она может показывать изображение текущей позиции на доске, представляя теми или иными символами фигуры обеих сторон. Во многих случаях программа позволяет играющему с ней человеку устанавливать ту "степень мастерства", которую программа должна проявлять в игре. Как правило, это числовой параметр, соответствующий глубине просмотра игры вперед, т.е. числу уровней дерева игры, которые программа должна исследовать, выбирая очередной ход.
Когда устанавливается большая глубина просмотра, программе требуется больше времени для выбора хода, потому что каждый лишний уровень дерева может удвоить время расчетов. Чтобы сократить поиск, который должна выполнять программа, в минимаксную процедуру может быть включен оригинальный механизм, получивший название альфа-бета-усечения. Принцип его действия показан в таблице, помещенной ниже. Альфа-бета-усечение можно применять практически на каждом уровне дерева, и с его помощью можно избежать огромного числа лишних процедур поиска и оценки.
***
МИНИМАКСНАЯ ПРОЦЕДУРА И УСЕЧЕНИЕ ДЕРЕВА

Минимаксная процедура применяется к игровому дереву после того, как все дозволенные правилами ходы вплоть до установленной глубины были сгенерированы и при помощи оценивающей функции получены оценки позиций на конце каждой ветви. Здесь ход принадлежит черным, дерево было просмотрено на глубину в три уровня и оценивающая функция присвоила каждой конечной позиции целое число, характеризующее относительную ценность позиции для черных. Задача минимаксной процедуры - выбрать для черных ход на основе этих оценок.
Заметим, что наиболее выгодная последовательность ходов для черных проходит через квадратики, помеченные цифрами 7, 15 и 15. Для белых предпочтительнее последовательность -5, -5, -9. Минимаксная процедура учитывает эти противоположные устремления. Программа сначала анализирует все ходы третьего уровня, являющиеся "потомками" определенного хода - "родителя" на втором уровне. Поскольку на втором уровне должны ходить черные, "родителю" присваивается значение наиболее успешного "потомка". Та же процедура используется, чтобы присвоить значения позициям первого уровня, но поскольку здесь ход принадлежит белым, выбираются наименьшие значения. Если оба игрока будут оценивать позиции по этому методу, то игра пойдет по пути 7, 7 и 7.
Игровые деревья глубиной больше трех уровней могут достигать чудовищных размеров, и поиск на них можно проводить только с использованием усечения. Здесь ход принадлежит черным, и при помощи частичного поиска уже была получена оценка 7 для одного из ходов на первом уровне. При анализе другого возможного хода программа выяснила, что при одном из возможных ответов белых на уровне 2 оценка позиции равна 4. Поэтому нет необходимости исследовать оставшуюся часть дерева - поскольку белые выберут ход с наименьшей оценкой, при альтернативном выборе черных на уровне 1 оценка не может иметь значения, большего 4, и поэтому ход с оценкой 7 предпочтительнее. Исключение путей, которые черные могут игнорировать, называется "альфа-усечением", а соответствующий процесс для белых - "бета-усечением".
***
Алгоритм игры в шашки не очень трудно запрограммировать. По мнению Траскотта, не обязательно располагать большой ЭВМ, чтобы реализовать успешно играющую программу. "Для разработки программ, играющих в шашки, вполне подходит и микрокомпьютер,- пишет он,- и программисты-любители, возможно, внесут весомый вклад в эту интересную и малоисследованную область".
Для читателей, обладающих некоторым опытом в программировании, вышесказанного будет вполне достаточно, чтобы построить и реализовать собственную программу для игры в шашки. Менее опытным, наверное, потребуется дополнительная информация. Построить генератор ходов и оценивающую функцию - задача в общем-то несложная, а вот о минимаксной процедуре следует поговорить подробнее. Каким образом происходит перемещение по игровому дереву вниз и вверх, как при этом запоминаются уже просмотренные позиции и те, которые еше нужно просмотреть? Некоторые советы по поводу того, как осуществлять перемещения по дереву, приведены в таблице на с.111.
***
ПРОСМОТР ИГРОВОГО ДЕРЕВА

При выборе очередного хода программа, играющая в шашки, должна проанализировать игровое дерево до какой-то установленной глубины, при этом каждая ветвь просматривается только один раз. При простом просмотре используется таблица указателей, где записываются отношения между ветвями, и структура данных, называемая стеком, которая следит за текущим положением программы на дереве и содержит список ветвей, не просмотренных еще программой.
Когда генерируется очередная позиция на доске, ей присваивается номер, служащий в качестве индекса в массиве указателей. Указатель, соответствующий позиции, сам представляет собой список номеров позиций. Первый номер в списке - это номер позиции-родителя, все остальные номера указывают ее потомков. Если программа достигла позиции 47, указатель говорит о том, что она должна продолжать просмотр через позиции 52, 57 и 62. Если достигнута позиция 62, программа должна вернуться к позиции-родителю - первый элемент указателя возвращает ее к позиции 47.
Стек должен следить за прохождением программы по таблице указателей. Стек может быть создан за счет организации массива STACK и переменной TOP, содержащей адрес верхнего элемента стека. Когда к стеку добавляется (вталкивается) или исключается (выталкивается) элемент, TOP увеличивается или уменьшается соответственно.
Элемент на верху стека - это номер позиции, которую нужно проанализировать следующей. Если на верху 47, алгоритм просмотра дерева выталкивает это значение из стека и затем анализирует список указателя для позиции 47. Первый номер в списке (указывающий на позицию-родителя по отношению к позиции 47) игнорируется, а оставшиеся ненулевые элементы вталкиваются в стек и переменная ТОР получает соответствующее значение. Следующей должна анализироваться позиция 62.
Каждый раз, когда программа достигает максимально дозволенной глубины, происходит обращение к оценивающей функции. Затем минимаксная процедура может "посмотреть" в список указателя, чтобы определить позицию-родителя и присвоить ей временное минимальное или максимальное значение - оценку. При просмотре других ветвей, исходящих из этой позиции-родителя, минимаксная процедура может изменить значение оценки.
***
Если игровая программа составлена, написана и отлажена, ее недостатки становятся очевидными, когда с ней начинают работать, установив параметр глубины просмотра игры на максимальное значение. Время, затрачиваемое на выбор хода, может оказаться слишком большим, или может не хватить памяти, чтобы разместить дерево игры. Существует много приемов, позволяющих сократить время вычислений и объем требуемой памяти. Например, в нашем представлении шашечной доски двумерным массивом половина элементов (а именно элементы, представляющие светлые клетки) всегда остается нулевой. Можно представить шашечную доску одномерным массивом, исключив таким образом пустые клетки. Однако при таком представлении шашечной доски построить генератор ходов будет уже труднее.
Вопрос о том, можно ли записать программу игры в шашки, которая никогда не проиграет человеку, сводится по существу к вопросу о том, что представляют собой шашки по своей природе. Существует ли такая стратегия для шашек n-ro порядка, при которой черные фигуры всегда выигрывают? [Предполагается, что черные ходят первыми.- Прим. ред.] В каком случае успеха могут добиться белые? Является ли игра ничейной? Исчерпывающий анализ для шашек n-го порядка вручную можно провести только тогда, когда n=2. Я анализировал вариант 4*4, строя дерево игры в среднем на глубину 10 ходов. На этом уровне обнаруживается несколько выигрышей для черных и такое же небольшое число проигрышей. Остальные позиции, по-видимому, ведут к ничейному исходу - дамки бесконечно "гоняются" друг за другом по тесному игровому полю 4*4. Мне не удалось строго доказать ничейный исход во всех случаях, но, если в мои вычисления не закралась ошибка, минимаксная процедура приписывает начальной позиции на доске нулевую оценку - это означает ничью.

Дерево игры в шашки для варианта 4x4. Полностью представлены первые два хода и некоторые варианты продолжений
А как обстоит дело с вариантом 6*6? Является ли он ничейным? Когда программа, написанная моими студентами, играла сама против себя при глубоком просмотре игры вперед, партии редко достигали какого-либо определенного исхода. Основываясь только на этом факте, можно предположить, что вариант 6*6 представляет собой ничейную игру. Разумеется, если оба варианта игры - 4*4 и 6*6 - оказываются ничейными, то "под подозрение" попадает и вариант 8*8. Возможно, кто-нибудь из читателей, проявив редкое сочетание умения и смелости, напишет программу, анализирующую дерево игры для варианта 6*6. Располагая мошной ЭВМ, такой проект, возможно, удастся осуществить.
В отношении варианта n-го порядка некоторые интересные результаты были получены теоретиками. Оказывается, труднорешаемой является следующая задача: "Определить, могут ли выиграть черные для произвольной, разрешенной правилами исходной позиции, занимаемой белыми и черными дамками и шашками на доске с числом клеток 2n*2n". В 1978г. А.Фрэнкелю из Научно-исследовательского института Вейцмана в Израиле, а также М.Гэри и Д.Джонсону из фирмы AT&T Bell Laboratories в США удалось доказать, что эта задача относится к классу задач, "труднорешаемых в смысле полиномиальной памяти". Задача, труднорешаемая в смысле полиномиальной памяти (P-space трудная), является еще более трудоемкой, чем так называемые NP-полные задачи, а последние, по мнению большинства теоретиков, по-видимому, не имеют общего практически реализуемого решения [О труднорешаемых и NP-полных задачах речь шла в предыдущем номере журнала в статье "О макаронном компьютере и других аналоговых устройствах" ("В мире науки", #8, с.98). Более подробно эти проблемы рассмотрены в книге М.Гэри и Д.Джонсона "Вычислительные машины и трудно-решаемые задачи" ("Мир, 1982г.).- Прим. перев.]. Другими словами, доказан следующий факт: если бы программа могла в совершенстве играть в шашки n-то порядка, то время, затрачиваемое ею в среднем на один ход, возрастало бы быстрее, чем любая полиномиальная функция с увеличением n.
Вопрос о создании программы, играющей в шашки без проигрыша, в значительной мере связан с доступными вычислительными мощностями компьютеров. Даже если шашки по самой своей природе представляют собой ничейную игру, успешно играющая программа, при прочих равных условиях, должна будет просматривать игру довольно далеко вперед. Траскотт пишет, например, о программе, разработанной им совместно с Енсеном: "Затрачивая в среднем 5с на один ход (на машине IBM 370/165), программа играет достаточно хорошо, чтобы выигрывать у авторов. Если на один ход будет затрачиваться в среднем 20с, то она, вероятно, будет сотым по силе игроком в США. При 80с на ход программа, наверное, войдет в десятку ведущих игроков мира".
ЧИТАЯ описание игровой программы, в котором раскрывается механизм ее внутренних операций, иногда чувствуешь некоторое разочарование. Когда играешь против программы, не зная ничего о том, как она работает, нетрудно наделить ее замечательными "интеллектуальными" способностями, которых на самом деле она вовсе не имеет. Многие любят пофантазировать. Однако можно надеяться, что утеря приятных иллюзий может быть компенсирована восхищением перед изящной структурой и механизмом действия игровой программы.
Мальчик спросил, можно ли написать программу, играющую в шашки, которая никогда не проиграет человеку. Этот вопрос затрагивает две центральные проблемы создания искусственного интеллекта: во-первых, что такое интеллект и, во-вторых, в какой степени программы могут проявлять свойства, присущие интеллекту. Когда мы фокусируем такие вопросы на ограниченные проявления человеческого интеллекта, например в играх, они, кажется, растворяются в бесчисленных технических деталях игры. Может быть, в этом и заключается ответ?
Поиски в области теории искусственного интеллекта продолжаются. Некоторые исследователи считают, что изобретение думающей машины в каком-то смысле напоминает проблему изобретения летающей машины. Возможно, появится что-то вроде теории "интеллектуального крыла". Чтобы летать, не обязательно сооружать механическую птицу - для этой цели вполне подходит самолет. Сможем ли мы добиться того же в области искусственного интеллекта?
БИБЛИОГРАФИЯ
WIN AT CHECKERS. MILLARD HOPPER. Dover Publications, Inc., 1956.
EXPERIMENTS IN ARTIFICIAL INTELLIGENCE FOR SMALL COMPUTERS. JOHN KRUTCH. Howard W. Sams and, Co., Inc., 1981.
COMPUTER GAMESMANSHIP. DAVID LEVY. Century Publishing, 1983.
ПРОГРАММА, ИГРАЮЩАЯ В ШАШКИ, ЧАСТО "ВИДИТ" ИГРУ НА ХОД ДАЛЬШЕ ПРОТИВНИКА
А.К.ДЬЮДНИ
"МОЖНО ли написать такую программу, играющую в шашки, которая никогда не проиграет человеку, никогда-никогда?" Мальчик был лет десяти и взглянул на нас, оторвавшись от терминала, с таким глубокомысленным, но невинным выражением, которое свойственно лишь очень юным. Он играл в шашки с программой, написанной моими студентами. Программа была настроена так, чтобы не просчитывать развитие игры на много ходов вперед, и паренек играл с ней довольно успешно.
Этот вопрос был задан мальчиком на выставке, устроенной на нашем факультете несколько лет назад, и на него можно ответить по-разному в зависимости от того, о каком варианте игры в шашки идет речь. Вопрос имеет также непосредственное отношение к важнейшим проблемам создания искусственного интеллекта, в частности к программированию "разумного" поведения компьютерных программ. Об этих проблемах мы поговорим несколько позже.
Когда мальчик задал нам свой вопрос, он играл в шашки на доске с числом клеток, равным 6*6. Это лишь один вариант из бесконечного многообразия шашечных игр. В настоящей статье мы рассмотрим варианты игры 4*4, 6*6 и 8*8 (классические шашки) и обсудим перспективы применения программ, написанных для этих игр. Вообще говоря, можно определить шашки n-го порядка, т.е. игру на доске с числом клеток 2n*2n. В каждом случае шашки, или шашечные фигуры, в исходном положении занимают все темные клетки, за исключением двух рядов в средней части доски. Правила игры в шашки n-го порядка более подробно рассмотрены на с.108.
***
ПРАВИЛА ИГРЫ В ШАШКИ N-ГО ПОРЯДКА
На доске, представляющей собой квадрат размерами 2n*2n клеток, попеременно светлых и темных, каждый игрок располагает n2-n шашек на темных клетках на противоположных сторонах доски. Два средних ряда клеток остаются пустыми. У каждой стороны есть "одиночный угол" (темная клетка в левом углу доски), а также "двойной угол" (справа). Черные ходят первыми.
Простая шашка может ходить по диагонали вперед на прилегающую незанятую темную клетку. Если эта клетка занята фигурой противника, а следующая за ней по диагонали клетка свободна, то шашка может перескочить фигуру противника, причем последняя считается захваченной и убирается с доски. Любая возможность такого захвата используется в обязательном порядке; если одновременно возможны два или более захватов, по крайней мере один из них должен быть сделан.
Когда простая шашка достигает последнего ряда на противоположной стороне доски, она становится дамкой. Дамка может ходить как вперед, так и назад (тоже по диагонали) и может бить в обоих направлениях.
Игра заканчивается победой одного из игроков, когда другой игрок не может сделать ни одного хода. Если оба игрока приходят к выводу, что выигрыш невозможен, объявляется ничья.

На рисунке показана исходная позиция для игры восьмого порядка на доске размерами 16*16 с 56 фигурами с каждой стороны.
***
В случае варианта 4*4 на вопрос, заданный мальчиком, можно, по-видимому, дать положительный ответ. Для варианта 6*6 ответом будет "очень вероятно", а для игры 8*8 - "возможно". Мои ответы основаны на сочетании личного опыта, литературных данных и просто интуиции.
РАССМОТРИМ вариант игры 4*4. В этом случае у каждого играющего по две фигуры и игра редко продолжается более 10 ходов, по крайней мере
когда играют квалифицированные игроки. Новички могут сделать 20 ходов или даже больше, прежде чем ничейный результат станет для них очевидным. Кстати, если уж речь зашла о ничьих, то в одном из последних турниров по шашкам 4*4 в городе Шашигрсбурге было зафиксировано шесть ничьих подряд и лишь в седьмой партии победа по решению судейской коллегии была присуждена гроссмейстеру Самюэлю Енсену Траскотту - его противник дважды случайно дотронулся до фигуры, которой нельзя было ходить.
Во всяком случае, вариант игры 4*4 можно проанализировать вручную. По-видимому, при разумной игре закономерным будет ничейный результат, поэтому игрок, проявляющий достаточно внимания, никогда не должен проигрывать. То же можно сказать и о достаточно хорошей программе.
В варианте игры 6*6 каждый партнер имеет шесть фигур и в среднем игра завершается после примерно 20 ходов. Если программу, написанную нашими студентами, настроить на максимально возможное просматривание игры вперед, то ей требуется от пяти до десяти минут для выбора очередного хода. При такой настройке программа играла очень сильно и казалась совершенно неуязвимой вплоть до эндшпиля, к которому она подходила с таким большим преимуществом в фигурах или в позиции, что обычно доводила партию до победы или в крайнем случае сводила ее вничью. Однако время от времени кто-нибудь из нас сохранял достаточно фигур, чтобы победить программу в эндшпиле, который она играла удивительно слабо.
В варианте игры 8*8 каждый партнер имеет по 12 фигур, и, когда играют квалифицированные игроки, число ходов достигает 30 и более. На турнирах по стандартным шашкам теперь стало уже обычной практикой устанавливать первый ход по жребию (имеется в виду не очередность, а вариант хода). Такой обычай был принят в Англии в начале века, потому что мастера этой игры почти всегда начинали со своего излюбленного хода с хорошо изученным продолжением, что приводило ко все возрастающему числу ничейных результатов. Можно ли объяснить изобилие ничьих тем, что шашки по своей природе являются ничейной игрой, или все дело в консерватизме мастеров, трудно сказать. Как бы то ни было, шашки в варианте игры на доске 8*8 остаются увлекательной и трудной игрой. С математической точки зрения шашки несколько уступают по сложности шахматам, однако есть люди, одинаково хорошо играющие в обе эти игры и не считающие шахматы игрой более высокого уровня.
Две наиболее известные программы, играющие в шашки, были созданы А.Самюэлем из фирмы IBM (International Business Machines Corporation) в 60-х годах и Э.Енсеном и Т.Траскоттом из Университета Дьюка в 1977г. В 1962г. шашечная программа Самюэля победила Роберта Нили, в прошлом чемпиона шт.Коннектикут. Хотя эта программа играет очень сильно, она все же уступает игре гроссмейстерского уровня. Программа Енсена-Траскотта еще сильнее и по игpе находится на уровне ведущих мастеров мира.
В 1979г. программа Енсена-Траскотта играла против Элберта Лаудера, считающегося одним из лучших игроков в США. Из пяти партий две закончились вничью, одну программа выиграла и две проиграла. Проигрыши, по-видимому, объясняются некоторыми недочетами, присущими программе в эндшпиле: когда Лаудер понял, что две шашки противника оставались "на страже" на задней линии, он воспользовался слабостью этой позиции и выиграл последние две партии. Следует, однако, заметить, что, играя против программы Енсена-Траскотта, Лаудер экспериментировал и играл несколько рискованно. Его проигрыш в одной из партий объясняется, по всей видимости, попыткой "заманить" программу на необычные позиции. Возможно, этого не следовало делать в игре с программой такого высокого уровня.
Тем временем Марион Ф.Тинзли, чемпион мира по шашкам, с интересом наблюдает за событиями из своего дома в Теллахассе (шт.Флорида). Я не знаю, играл ли Тинзли когда-нибудь с лучшими шашечными программами. Однако известно, что две лучшие программы играли между собой. В двух партиях против программы Самюэля программа Енсена-Траскотта оказалась, по словам Траскотта, "на голову выше" и выиграла их.
В БОЛЬШИНСТВЕ удачно играющих программ можно выделить три основные компоненты: генератор ходов, функцию, оценивающую позицию, и минимаксную процедуру. Еще один важный элемент - это "дерево" игры; оно участвует в работе всех трех основных компонент игровой программы. Генератор ходов строит дерево; к оценивающей функции происходит обращение в конце каждой ветви дерева, а минимаксная процедура применяется ко всему дереву в целом.
Корневой узел дерева представляет собой исходную позицию на доске, а каждая ветвь ведет к какой-то позиции, достигаемой при помощи одного хода. Примечательно, что подобное дерево изображается обычно "вверх ногами" - его корень располагается вверху. Дерево можно "разделить" на уровни так, что все позиции n-го уровня соответствуют всем возможным ходам одного игрока, делающего n-й ход. Хотя игровые деревья, как правило, не очень высоки (точнее говоря, глубоки), они могут быть очень кустистыми. Дело в том, что число позиций на каждом уровне более чем вдвое превышает число позиций на предыдущем уровне. Даже если у каждой позиции на доске было лишь две последующие позиции, то число ветвей очень скоро достигло бы огромной величины. Дерево, разветвившееся подобным образом 64 раза, имело бы больше ветвей, чем все деревья, растущие на Земле, вместе взятые. (В природе деревья ветвятся не более 12 раз от корня до листьев). Из-за того что число ветвей игрового дерева возрастает по экспоненциальному закону, т.е. имеет место "экспоненциальный взрыв", компьютер может исследовать лишь небольшую часть продолжений в такой игре, как шашки на доске 8*8.
Дерево шашечной игры создается генератором ходов - программой, которой в качестве входных данных задается текущая позиция на доске, а также указание о том, кто из противников должен сделать очередной ход. Выходом генератора ходов являются все возможные позиции, достижимые из заданной позиции после одного хода. Рассмотрим следующую позицию на доске 4*4, предполагая, что ходить должны черные фигуры:

Для черных имеется два возможных хода, и генератор ходов выдает две позиции:

Затем генератор ходов может применяться уже к каждой из этих позиций в отдельности.
Читателям, желающим разобраться, как работает генератор ходов, мы предлагаем достроить дерево игры на доске 4*4, отправляясь от рассмотренного нами уровня. Например, на следующем уровне будет только две позиции, поскольку в каждом случае правила игры вынуждают белых [на рисунках для наглядности эти фигуры изображены красным цветом.- Прим. перев.] бить фигуру противника. На уровне, следующем за этим, будет опять две позиции, затем три (в одной из них белые выигрывают), затем 2, 5, 10, наконец, 24. Тем, кто пожелает последовать еще дальше, мы дадим два совета. Во-первых, нужно просматривать каждый уровень в поисках идентичных позиций и строить продолжение лишь для одной из таких позиций. Во-вторых, для каждой новой позиции нужно просматривать дерево снизу вверх, чтобы найти идентичную позицию. Если эта позиция уже встречалась в игре, то на повторно встретившейся позиции ветвь нужно закончить, пометив ее конец как "ничью".
Как работает программа, генерирующая ходы? Первый вопрос заключается в том, каким образом позиции на доске представляются в памяти компьютера. В качестве простейшей схемы можно принять матрицу - двумерный массив, элементы которого соответствуют каждой клетке шашечной доски. Например, пустой клетке соответствует 0, клетке, занимаемой "простой" шашкой,- 1, а клетке, которую занимает "дамка",- 2. Знак числа может отражать принадлежность фигуры к черным или белым, плюс - для черных и минус - для белых фигур. Первая позиция на доске 4*4, показанная выше, может быть представлена матрицей следующего вида:
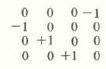
Ходы, разрешенные правилами игры для каждой фигуры, зависят от того, какой стороне она принадлежит, от ее позиции, а также от того, заняты или свободны прилежащие по диагонали клетки. В рассматриваемом случае генератор ходов сканирует массив строку за строкой, пока не наталкивается на положительный элемент (фигура черных) в строке 3 колонки 2; мы будем обозначать такую позицию как (3, 2). Поскольку ход принадлежит черным и фигура является "простой" шашкой, а не "дамкой" (значение элемента матрицы равно 1), программа исследует клетки (2, 1) и (2, 3). Клетка (2,1) уже занята фигурой (и перескочить ее невозможно), но клетка (2, 3) свободна. Поэтому программа строит новый массив, в котором +1 удаляется с позиции (3, 2) и помещается в позицию (2, 3):

Затем генератор ходов продолжает сканировать массив, пока не найдет следующий положительный элемент.
Чтобы следить за различными позициями на доске и соответствующими массивами, их можно последовательно пронумеровать в порядке генерации. Тогда состояние любой клетки в каждый момент игры будет определяться номером позиции на доске, а также номерами строки и колонки массива. По мере того как генератор ходов строит дерево игры, он должен записывать, в каком порядке позиции следуют друг за другом. Когда программа выбирает очередной ход, она просматривает дерево на несколько уровней вниз, затем вверх, затем снова вниз и т.д. Чтобы перемещаться по дереву таким образом, программа должна знать, какие позиции на доске являются предшествующими, или "родителями", а какие - последующими, или "потомками". Для этого у программы есть специальный массив, называемый таблицей указателей. Указателем для каждой позиции является список чисел, в котором первое число указывает на позицию, являющуюся "родителем" данной, а остальные числа - на ее "потомков".
СЛЕДУЮЩАЯ важная компонента программы, играющей в шашки,- это функция, оценивающая позиции. В качестве входной информации ей дается позиция на доске, и она выдает число, отражающее ценность этой позиции для черных фигур. Большое число означает, что если данная позиция будет достигнута в игре, то у черных будут хорошие шансы на выигрыш. Построить хорошую оценивающую функцию очень трудно, потому что при оценке позиции на доске нужно принимать во внимание слишком много факторов. Кроме того, в большинстве игр, включая шашки, не всегда ясно, какой вес приписать тому или иному фактору. Перечислим кратко простейшие из этих факторов:
ПРОСТЫЕ ШАШКИ. Прибавить 1 для каждой черной шашки на доске; вычесть 1 для каждой белой шашки.
ДАМКИ. Прибавить 1 для каждой черной дамки; вычесть 1 для каждой белой дамки.
ЦЕНТР. Прибавить 1 для каждой черной шашки, занимающей одну из четырех центральных клеток; соответственно вычесть 1 для каждой белой шашки.
ПРОДВИЖЕНИЕ. Прибавить 1 для каждой черной шашки; находящейся во втором ряду, 2 для каждой черной шашки в третьем ряду, 3 для каждой черной шашки (дамки) в четвертом ряду; вычесть соответствующие величины для белых фигур.
ПОДВИЖНОСТЬ. Прибавить 1 на каждый возможный ход для черных и вычесть 1 на каждый возможный ход для белых фигур.
Каково относительное значение перечисленных факторов? Следует ли приписать дамкам вдвое больший вес, чем простым шашкам? Входит ли в "продвижение" информация, содержащаяся в таких факторах, как "шашки" и "дамки"?
Самюэль ответил на эти вопросы, позволив программе самой установить, какой вес приписать тому или иному фактору на основе игрового опыта. Оперируя 39 факторами (многие из которых были предложены знатоками игры или взяты из литературных источников), оценивающая функция Самюэля вначале приписала им один и тот же вес и просто складывала одни и те же числа. Полученная таким образом сумма характеризовала "ценность" позиции. Каждую проигранную партию программа анализировала, чтобы выявить фактор, который привел к поражению. В результате вес этого фактора уменьшался. Процесс обучения был ускорен за счет автоматизации анализа и многократных игровых испытаний.
Процедуры, оценивающие позицию, никогда не бывают совершенными. Если бы это было не так, то остальные компоненты игровой программы едва ли потребовались бы. Программе нужно было бы лишь исследовать позиции, достигаемые из данной при одном возможном ходе, оценить каждую из этих позиций и выбрать лучший ход. Существует своего рода компромисс между точностью оценивающей функции и числом уровней дерева, которые программа должна просматривать вперед. Если бы оценивающая функция могла лишь распознавать позиции, соответствующие окончательному выигрышу или проигрышу, то игровое дерево нужно было бы просматривать на всю глубину!
Третья главная компонента программы - минимаксная процедура, представляющая собой программу поиска на игровом дереве, которая пользуется оценками позиций на нижнем уровне, чтобы придать оценочные значения позициям, расположенным на более высоких (т.е. начальных) уровнях дерева игры. На какой-то стадии исследования дерева все позиции определенного уровня должны быть оценены этой функцией. Позиция B на уровне, непосредственно выше оцененного, получает оценку по следующему простому правилу: если в позиции B ходить должны белые, то выбирается минимальное значение из оценок, полученных для "потомков" B; оно принимается в качестве оценки позиции B. Если же ходить должны черные, то нужно выбрать максимальное значение.
Не трудно понять, из каких соображений было выбрано это правило. Если ход принадлежит белым, то черные вполне могут предположить, что белые выберут ход, который приведет к позиции с минимальным значением оценки для черных. Точно так же, если ход принадлежит черным, то будет выбрана позиция с максимально возможной оценкой. Таким образом, минимаксная процедура начинает действовать с самого нижнего просмотренного уровня дерева и, пользуясь оценками, полученными для этого уровня оценивающей функцией, переносит их вверх по дереву. Переходя от какого-то уровня к следующему, расположенному выше, она поочередно выбирает минимальные и максимальные оценки, в зависимости от того, какой стороне принадлежит ход. В конце концов минимаксная процедура возвращается к текущей позиции и дает черным оценку для каждого возможного хода в этой позиции. Естественно, черные выбирают ход с самой высокой оценкой.
ПРОГРАММА, играющая в шашки, помимо рассмотренных трех основных компонент, имеет и другие компоненты. Она должна обеспечить взаимодействие с играющим человеком - принимать ходы с клавиатуры терминального устройства и печатать ответные ходы. Кроме того, она может показывать изображение текущей позиции на доске, представляя теми или иными символами фигуры обеих сторон. Во многих случаях программа позволяет играющему с ней человеку устанавливать ту "степень мастерства", которую программа должна проявлять в игре. Как правило, это числовой параметр, соответствующий глубине просмотра игры вперед, т.е. числу уровней дерева игры, которые программа должна исследовать, выбирая очередной ход.
Когда устанавливается большая глубина просмотра, программе требуется больше времени для выбора хода, потому что каждый лишний уровень дерева может удвоить время расчетов. Чтобы сократить поиск, который должна выполнять программа, в минимаксную процедуру может быть включен оригинальный механизм, получивший название альфа-бета-усечения. Принцип его действия показан в таблице, помещенной ниже. Альфа-бета-усечение можно применять практически на каждом уровне дерева, и с его помощью можно избежать огромного числа лишних процедур поиска и оценки.
***
МИНИМАКСНАЯ ПРОЦЕДУРА И УСЕЧЕНИЕ ДЕРЕВА

Минимаксная процедура применяется к игровому дереву после того, как все дозволенные правилами ходы вплоть до установленной глубины были сгенерированы и при помощи оценивающей функции получены оценки позиций на конце каждой ветви. Здесь ход принадлежит черным, дерево было просмотрено на глубину в три уровня и оценивающая функция присвоила каждой конечной позиции целое число, характеризующее относительную ценность позиции для черных. Задача минимаксной процедуры - выбрать для черных ход на основе этих оценок.
Заметим, что наиболее выгодная последовательность ходов для черных проходит через квадратики, помеченные цифрами 7, 15 и 15. Для белых предпочтительнее последовательность -5, -5, -9. Минимаксная процедура учитывает эти противоположные устремления. Программа сначала анализирует все ходы третьего уровня, являющиеся "потомками" определенного хода - "родителя" на втором уровне. Поскольку на втором уровне должны ходить черные, "родителю" присваивается значение наиболее успешного "потомка". Та же процедура используется, чтобы присвоить значения позициям первого уровня, но поскольку здесь ход принадлежит белым, выбираются наименьшие значения. Если оба игрока будут оценивать позиции по этому методу, то игра пойдет по пути 7, 7 и 7.

Игровые деревья глубиной больше трех уровней могут достигать чудовищных размеров, и поиск на них можно проводить только с использованием усечения. Здесь ход принадлежит черным, и при помощи частичного поиска уже была получена оценка 7 для одного из ходов на первом уровне. При анализе другого возможного хода программа выяснила, что при одном из возможных ответов белых на уровне 2 оценка позиции равна 4. Поэтому нет необходимости исследовать оставшуюся часть дерева - поскольку белые выберут ход с наименьшей оценкой, при альтернативном выборе черных на уровне 1 оценка не может иметь значения, большего 4, и поэтому ход с оценкой 7 предпочтительнее. Исключение путей, которые черные могут игнорировать, называется "альфа-усечением", а соответствующий процесс для белых - "бета-усечением".
***
Алгоритм игры в шашки не очень трудно запрограммировать. По мнению Траскотта, не обязательно располагать большой ЭВМ, чтобы реализовать успешно играющую программу. "Для разработки программ, играющих в шашки, вполне подходит и микрокомпьютер,- пишет он,- и программисты-любители, возможно, внесут весомый вклад в эту интересную и малоисследованную область".
Для читателей, обладающих некоторым опытом в программировании, вышесказанного будет вполне достаточно, чтобы построить и реализовать собственную программу для игры в шашки. Менее опытным, наверное, потребуется дополнительная информация. Построить генератор ходов и оценивающую функцию - задача в общем-то несложная, а вот о минимаксной процедуре следует поговорить подробнее. Каким образом происходит перемещение по игровому дереву вниз и вверх, как при этом запоминаются уже просмотренные позиции и те, которые еше нужно просмотреть? Некоторые советы по поводу того, как осуществлять перемещения по дереву, приведены в таблице на с.111.
***
ПРОСМОТР ИГРОВОГО ДЕРЕВА

При выборе очередного хода программа, играющая в шашки, должна проанализировать игровое дерево до какой-то установленной глубины, при этом каждая ветвь просматривается только один раз. При простом просмотре используется таблица указателей, где записываются отношения между ветвями, и структура данных, называемая стеком, которая следит за текущим положением программы на дереве и содержит список ветвей, не просмотренных еще программой.
Когда генерируется очередная позиция на доске, ей присваивается номер, служащий в качестве индекса в массиве указателей. Указатель, соответствующий позиции, сам представляет собой список номеров позиций. Первый номер в списке - это номер позиции-родителя, все остальные номера указывают ее потомков. Если программа достигла позиции 47, указатель говорит о том, что она должна продолжать просмотр через позиции 52, 57 и 62. Если достигнута позиция 62, программа должна вернуться к позиции-родителю - первый элемент указателя возвращает ее к позиции 47.
Стек должен следить за прохождением программы по таблице указателей. Стек может быть создан за счет организации массива STACK и переменной TOP, содержащей адрес верхнего элемента стека. Когда к стеку добавляется (вталкивается) или исключается (выталкивается) элемент, TOP увеличивается или уменьшается соответственно.
Элемент на верху стека - это номер позиции, которую нужно проанализировать следующей. Если на верху 47, алгоритм просмотра дерева выталкивает это значение из стека и затем анализирует список указателя для позиции 47. Первый номер в списке (указывающий на позицию-родителя по отношению к позиции 47) игнорируется, а оставшиеся ненулевые элементы вталкиваются в стек и переменная ТОР получает соответствующее значение. Следующей должна анализироваться позиция 62.
Каждый раз, когда программа достигает максимально дозволенной глубины, происходит обращение к оценивающей функции. Затем минимаксная процедура может "посмотреть" в список указателя, чтобы определить позицию-родителя и присвоить ей временное минимальное или максимальное значение - оценку. При просмотре других ветвей, исходящих из этой позиции-родителя, минимаксная процедура может изменить значение оценки.
***
Если игровая программа составлена, написана и отлажена, ее недостатки становятся очевидными, когда с ней начинают работать, установив параметр глубины просмотра игры на максимальное значение. Время, затрачиваемое на выбор хода, может оказаться слишком большим, или может не хватить памяти, чтобы разместить дерево игры. Существует много приемов, позволяющих сократить время вычислений и объем требуемой памяти. Например, в нашем представлении шашечной доски двумерным массивом половина элементов (а именно элементы, представляющие светлые клетки) всегда остается нулевой. Можно представить шашечную доску одномерным массивом, исключив таким образом пустые клетки. Однако при таком представлении шашечной доски построить генератор ходов будет уже труднее.
Вопрос о том, можно ли записать программу игры в шашки, которая никогда не проиграет человеку, сводится по существу к вопросу о том, что представляют собой шашки по своей природе. Существует ли такая стратегия для шашек n-ro порядка, при которой черные фигуры всегда выигрывают? [Предполагается, что черные ходят первыми.- Прим. ред.] В каком случае успеха могут добиться белые? Является ли игра ничейной? Исчерпывающий анализ для шашек n-го порядка вручную можно провести только тогда, когда n=2. Я анализировал вариант 4*4, строя дерево игры в среднем на глубину 10 ходов. На этом уровне обнаруживается несколько выигрышей для черных и такое же небольшое число проигрышей. Остальные позиции, по-видимому, ведут к ничейному исходу - дамки бесконечно "гоняются" друг за другом по тесному игровому полю 4*4. Мне не удалось строго доказать ничейный исход во всех случаях, но, если в мои вычисления не закралась ошибка, минимаксная процедура приписывает начальной позиции на доске нулевую оценку - это означает ничью.

Дерево игры в шашки для варианта 4x4. Полностью представлены первые два хода и некоторые варианты продолжений
А как обстоит дело с вариантом 6*6? Является ли он ничейным? Когда программа, написанная моими студентами, играла сама против себя при глубоком просмотре игры вперед, партии редко достигали какого-либо определенного исхода. Основываясь только на этом факте, можно предположить, что вариант 6*6 представляет собой ничейную игру. Разумеется, если оба варианта игры - 4*4 и 6*6 - оказываются ничейными, то "под подозрение" попадает и вариант 8*8. Возможно, кто-нибудь из читателей, проявив редкое сочетание умения и смелости, напишет программу, анализирующую дерево игры для варианта 6*6. Располагая мошной ЭВМ, такой проект, возможно, удастся осуществить.
В отношении варианта n-го порядка некоторые интересные результаты были получены теоретиками. Оказывается, труднорешаемой является следующая задача: "Определить, могут ли выиграть черные для произвольной, разрешенной правилами исходной позиции, занимаемой белыми и черными дамками и шашками на доске с числом клеток 2n*2n". В 1978г. А.Фрэнкелю из Научно-исследовательского института Вейцмана в Израиле, а также М.Гэри и Д.Джонсону из фирмы AT&T Bell Laboratories в США удалось доказать, что эта задача относится к классу задач, "труднорешаемых в смысле полиномиальной памяти". Задача, труднорешаемая в смысле полиномиальной памяти (P-space трудная), является еще более трудоемкой, чем так называемые NP-полные задачи, а последние, по мнению большинства теоретиков, по-видимому, не имеют общего практически реализуемого решения [О труднорешаемых и NP-полных задачах речь шла в предыдущем номере журнала в статье "О макаронном компьютере и других аналоговых устройствах" ("В мире науки", #8, с.98). Более подробно эти проблемы рассмотрены в книге М.Гэри и Д.Джонсона "Вычислительные машины и трудно-решаемые задачи" ("Мир, 1982г.).- Прим. перев.]. Другими словами, доказан следующий факт: если бы программа могла в совершенстве играть в шашки n-то порядка, то время, затрачиваемое ею в среднем на один ход, возрастало бы быстрее, чем любая полиномиальная функция с увеличением n.
Вопрос о создании программы, играющей в шашки без проигрыша, в значительной мере связан с доступными вычислительными мощностями компьютеров. Даже если шашки по самой своей природе представляют собой ничейную игру, успешно играющая программа, при прочих равных условиях, должна будет просматривать игру довольно далеко вперед. Траскотт пишет, например, о программе, разработанной им совместно с Енсеном: "Затрачивая в среднем 5с на один ход (на машине IBM 370/165), программа играет достаточно хорошо, чтобы выигрывать у авторов. Если на один ход будет затрачиваться в среднем 20с, то она, вероятно, будет сотым по силе игроком в США. При 80с на ход программа, наверное, войдет в десятку ведущих игроков мира".
ЧИТАЯ описание игровой программы, в котором раскрывается механизм ее внутренних операций, иногда чувствуешь некоторое разочарование. Когда играешь против программы, не зная ничего о том, как она работает, нетрудно наделить ее замечательными "интеллектуальными" способностями, которых на самом деле она вовсе не имеет. Многие любят пофантазировать. Однако можно надеяться, что утеря приятных иллюзий может быть компенсирована восхищением перед изящной структурой и механизмом действия игровой программы.
Мальчик спросил, можно ли написать программу, играющую в шашки, которая никогда не проиграет человеку. Этот вопрос затрагивает две центральные проблемы создания искусственного интеллекта: во-первых, что такое интеллект и, во-вторых, в какой степени программы могут проявлять свойства, присущие интеллекту. Когда мы фокусируем такие вопросы на ограниченные проявления человеческого интеллекта, например в играх, они, кажется, растворяются в бесчисленных технических деталях игры. Может быть, в этом и заключается ответ?
Поиски в области теории искусственного интеллекта продолжаются. Некоторые исследователи считают, что изобретение думающей машины в каком-то смысле напоминает проблему изобретения летающей машины. Возможно, появится что-то вроде теории "интеллектуального крыла". Чтобы летать, не обязательно сооружать механическую птицу - для этой цели вполне подходит самолет. Сможем ли мы добиться того же в области искусственного интеллекта?
БИБЛИОГРАФИЯ
WIN AT CHECKERS. MILLARD HOPPER. Dover Publications, Inc., 1956.
EXPERIMENTS IN ARTIFICIAL INTELLIGENCE FOR SMALL COMPUTERS. JOHN KRUTCH. Howard W. Sams and, Co., Inc., 1981.
COMPUTER GAMESMANSHIP. DAVID LEVY. Century Publishing, 1983.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
10 1984
ОХОТА С КОМПЬЮТЕРОМ НА БОБРА-РАБОТЯГУ, ИЛИ ПОИСК САМОЙ ТРУДОЛЮБИВОЙ МАШИНЫ ТЬЮРИНГА
А.К.ДЬЮДНИ
ВРЯД ли на земле найдутся существа, более трудолюбивые, чем бобры - ну разве что пчелы. В спокойных северных водоемах бобры изо дня в день усердно сооружают плотины из веток и прутьев. Несомненно, что именно трудолюбие этих животных подсказало Тибору Радо из Университета штата Огайо название одной задачи для машин Тьюринга: "Игра бобр-работяга". В начале 60-х годов Радо заинтересовал вопрос: сколько единиц может напечатать машина Тьюринга, прежде чем она остановится? Или в более строгой формулировке: если машина Тьюринга с n состояниями, имеющая остановку, начинает работу с лентой, заполненной одними нулями, то какое максимальное число единиц она может напечатать до своей остановки? Для n, равных 1, 2, 3 и 4, ответ известен, а для n>=5 - пока нет.
В прошлом году в Дортмунде (ФРГ) был проведен конкурс бобров-работяг с целью выявить создателя самого работящего бобра с пятью состояниями. Год был отведен на написание программ, строящих машины Тьюринга - участниц конкурса, и разработку аппаратуры, на которой можно было бы выполнить эти программы. В процессе подготовительной работы удалось обнаружить бобров с весьма необычным поведением, так что биологический род Castor пришлось расширить и включит в в него несколько видов, до сей поры зоологам неизвестных.
НА страницах нашего журнала Дж.Хопкрофт уже описал машины Тьюринга, и рассказал, какое место они занимают в вычислительных науках (см.: Дж.Хопкрофт. Машины Тьюринга. "В мире науки", 1984, #7 - Прим. перев.). Машина Тьюринга состоит из бесконечной ленты, головки для считывания символов с ленты и записи их на ленте и управляющего устройства с конечным числом внутренних состояний (см. верхний рисунок на с.99). Эти компоненты можно представлять себе как аппаратную часть устройства, а то, что закладывается в управляющее устройство,- как его математическое обеспечение, т.е. программа машины Тьюринга. Машины Тьюринга отличаются друг от друга именно своей программой; последняя представляет собой таблицу, к которой машина Тьюринга обращается, чтобы узнать, что делать дальше. Каждому возможному состоянию управляющего устройства и каждому возможному символу на ленте в клетке под печатающей головкой соответствует определенный элемент таблицы, который указывает машине, какой символ должен быть напечатан на ленте, в каком направлении сдвинуть головку и в какое состояние перейти. Все описываемые здесь машины Тьюринга будут начинать работу с состояния 1.

Машина Тьюринга и ее программа
Чтобы проследить за операциями машины Тьюринга, выпишем сверху вниз состояния устройства управления и символы, выпечатываемые на ленте (или отрезке ленты) в последовательные моменты времени. Можно также указать, какая клетка ленты в данный момент просматривается. На нижнем рисунке на с.99 прослежена работа машины Тьюринга, изображенной на верхнем рисунке. Каждая строка представляет собой "моментальный снимок" машины. По форме этот "снимок" отличается от принятого в статье Хопкрофта представления, но информацию он нам дает такую же. В отличие от условностей, принятых Хопкрофтом, здесь еще предполагается, что лента бесконечна в обоих направлениях, и допускается, чтобы машина печатала символ при переходе в последнее состояние (состояние, в котором она останавливается). Эти различия никак не отражаются на возможностях машины Тьюринга. Принятая в данной статье форма "мгновенного снимка" соответствует той, что использовалась на конкурсе бобров-работяг.

"Моментальные снимки", позволяющие проследить работу машины Тьюринга
Бобр-работяга с n состояниями представляет собой машину Тьюринга, на которую наложены два ограничения. Во-первых, начав работать с лентой, целиком заполненной нулями, он в конце концов обязательно остановится; во-вторых, он способен записать не меньшее количество единиц, чем любая другая машина Тьюринга с n состояниями, имеющая остановку.
Бобры-работяги с одним и тремя состояниями изображены на верхнем рисунке на с.100. Каждая машина Тьюринга представлена диаграммой переходов, в которой занумерованные кружки - это ее состояния, а стрелки - это переходы из одного состояния в другое. Метки над стрелками означают операции машины Тьюринга. Пусть, например, бобр-работяга с тремя состояниями находится в состоянии 1 и считывает с ленты символ 0. Стрелка, выходящая из этого кружка, помечена "0, 1, П"; она приводит в состояние 2. Значит, машина, прочитав 0, запишет на ленту 1, сдвинется на одну позицию вправо и перейдет в состояние 2.

Бобры-работяги с одним и тремя состояниями
Введем обозначение S(n) для максимального числа единиц, которое может напечатать машина Тьюринга с n состояниями, имеющая остановку. Как уже говорилось, значения S(n) известны только для n от 1 до 4. Бобр-работяга с одним состоянием напечатает лишь одну единицу и остановится; иначе говоря, S(1) = 1. Бобр-работяга с двумя состояниями выдаст последовательность из четырех единиц. (Вы можете построить такую машину?) Бобр-работяга с тремя состояниями печатает 6 единиц: здесь показана одна из таких машин. Ее программа и последовательность моментальных снимков приводятся на с.99, а диаграмма переходов - на верхнем рисунке на с.100. Бобра-работягу с тремя состояниями построили в 1962г. Радо и Чжень Лин из корпорации AT&T Bell Laboratories. В 1973г. Б.Вейман из Боннского университета построил бобра-работягу с 4 состояниями, который выдавал 13 идущих подряд единиц. С тех пор теоретики пустились в поиски бобра-работяги с пятью состояниями.
КОНКУРС бобров-работяг состоялся в январе 1983г. на проводившейся в Дортмундском университете теоретической конференции по информатике, которая была организована Ф.Ванкмюллером. В конкурсе приняли участие 133 машины Тьюринга с пятью состояниями. Победителем стал У.Шульт, машина которого печатала 501 единицу и останавливалась. Диаграмма переходов победительницы представлена на нижнем рисунке на с.100. Вторым оказался Й.Людвиг из научного центра Brown Boveri в Бадсне; его машина Тьюринга печатала 240 единиц.

Бобр-работяга У.Шульта с пятью состояниями
Можно ли считать машину Тьюринга, построенную Шультом, бобром-работягой? Шульт, равно как и Ванкмюллер и Людвиг, полагает, что можно. Иными словами, он считает, что не существует машины Тьюринга с пятью состояниями, которая бы печатала больше, чем 501 единицу, и останавливалась. Как же доказать такое утверждение? Методом полного перебора, вроде того, которым пользовался Шульт для построения своего чемпиона. Прежде чем переходить к описанию попыток Шульта заманить в ловушку на своем компьютере бобра-работягу с пятью состояниями, мне бы хотелось ближе познакомить читателя с функцией S(n), чтобы он мог понять, почему так трудно играть в бобра-работягу даже при помощи ЭВМ.
Функция S(n) обладает одной существенной особенностью: она невычислимая. Попросту говоря, она слишком быстро растет. По первым четырем ее значениям 1, 4, 6 и 13 это незаметно: скорость кажется весьма умеренной. Если значение 501 - действительно максимальное число единиц для машины с пятью состояниями, то рост S(n) все еще представляется не быстрее экспоненциального. Шульт смог построить машину Тьюринга с шестью состояниями, которая печатает 2075 единиц. Это опять-таки не свидетельствует об очень высокой скорости роста. Однако Шульт сумел построить машину с 12 состояниями, которая печатала столько единиц, что их количество выражается такой ужасающей формулой:
6*4096^4096^4096^...^4096^4
Число 4096 фигурирует в этой формуле 166 раз, т.е. на участке, скрывающемся за тремя точками, оно повторено 162 раза. Вычислять выражение нужно сверху вниз: сначала возвести 4096 в четвертую степень, затем возвести 4096 в полученную степень, затем снова возвести 4096 в полученную степень и т.п. Дойдя до самого низа, результат умножить на 6.
Если вас не пугает, что придется иметь дело с цепочкой единиц такой длины, постройте какое-нибудь большее число. Напишите любую формулу, в которой числа перемножаются или возводятся в степень; можете даже заменить любое из чисел на n. Какую бы формулу вы ни придумали, она будет давать меньшее значение (если только выбрано n, при котором значение этого выражения достаточно велико), чем количество единиц, выпечатывасмое бобром-работягой с n состояниями. Следовательно, для произвольного значения n функцию S(n) вычислить нельзя. Самое большее, что можно сделать,- это вычислить Е(n) для какого-то малого фиксированного значения n.
ТАК что нет ничего удивительного в том, что в бобра-работягу чаше всего играют на ЭВМ. Суть метода состоит в систематическом изучении всех машин Тьюринга с n состояниями. Каждый раз, как только нужно получить новую машину, моделируется ее поведение в случае, когда лента в начале работы вся заполнена нулями. Если машина останавливается после какого-то числа шагов, полученное количество единиц сравнивается с достижениями самой "работящей" машины Тьюринга, которая была до сих пор найдена. Иногда обнаруживается новый чемпион.
Такой метод поиска бобра-работяги с n состояниями имеет два серьезных недостатка. Во-первых, приходится проверять колоссальное количество машин Тьюринга: к примеру, машин с пятью состояниями может быть 63403380965376. Во-вторых, не известно, сколько времени нужно ждать, чтобы машина остановилась: максимальное число переходов машины с n состояниями, которая рано или поздно останавливается,- эту функцию будем обозначать s(n) - тоже невычислимая функция. Она, очевидно, растет даже быстрее, чем S(n), поскольку машина Тьюринга каждый раз, когда печатает 1, делает хотя бы один переход. Как отметил Хопкрофт, вычисление s(n) эквивалентно решению проблемы остановки для машин Тьюринга, одной из первых проблем, отнесенных Тьюрингом к разряду неразрешимых.
В 1982г. Шульт устроил в своем компьютере Apple II ловушку для бобра-работяги. Он снабдил центральный процессор своего компьютера микропроцессором Motorola 6809 на одной печатной плате. Программу поиска он написал на языке этого вспомогательного процессора. Чтобы проверить огромное количество машин Тьюринга, порождаемых программой, Шульт следующим образом реализовал аппаратную часть машины: вмонтировал стандартные электронные компоненты в ту схему, которую он вставил в Apple II. Устройство было снабжено лентой с 4096 клетками, а также регистрами для хранения программы и информации о текущем состоянии и положении печатающей головки машины Тьюринга. Шульт подсчитал, что без специализированного аппаратного обеспечения его программа поиска работала бы непрерывно 20 месяцев. Даже с такими усовершенствованными аппаратными средствами потребовалось 803 часа работы Apple II, чтобы найти машину Тьюринга-чемпионку.
При разработке необходимого математического обеспечения Шульт также добился определенных преимуществ, составив программу поиска таким образом, чтобы она максимально использовала аппаратные возможности машины Тьюринга. Программа заполняла таблицу переходов машины Тьюринга с пятью состояниями, скрупулезно разбирая все варианты. Еще до того, как таблица была заполнена вся целиком, она предоставлялась машине Тьюринга для проверки. Зачастую обнаруживалась такая незаполненная таблица, которая свидетельствовала о машине, истощившей свой запас пространства и времени прежде, чем она могла достичь какого-то еще не определенного элемента. В таких случаях незаполненная таблица и все возможные пути ее заполнения исключались из рассмотрения.
Хотя Шульт в известной мере смог справиться с управлением множеством машин Тьюринга, надо сказать, что его подход к проблеме остановки для машин Тьюринга с пятью состояниям и нельзя считать безукоризненным. За отсутствием точной информации относительно s(n) - максимального числа переходов для машины Тьюринга с пятью состояниями, имеющей остановку, нужно иметь на этот счет какую-то гипотезу. Шульт предположил, что можно ограничиться значением 500000 переходов; иначе говоря, он выдвинул рабочую гипотезу, согласно которой машина не остановится никогда, если она не остановится после 500000 шагов. Ему пришлось также наложить и пространственные ограничения на работяг-претендентов: поскольку лента имеет только 4096 клеток и машина Тьюринга всегда начинает работу с середины этой конечной ленты, бобр может оказаться претендентом в работяги, если он продвинулся дальше, чем на 2048 клеток от исходного положения. Вообще говоря, претендентом считается не только такая машина, которая достигла остановки, но и та, что продолжает обрабатывать все новые и новые клетки.
ИЗ 133 машин Тьюринга, принявших участие в Дортмундском конкурсе, только 4 печатали более 100 единиц. Все эти машины были промоделированы на компьютере Siemens 7,748. Для определения победителя потребовалось более часа машинного времени.
Людвиг, занявший второе место, написал программу поиска бобров-работяг на языке Паскаль и пропустил ее на довольно мощной мини-ЭВМ VAX фирмы Digital Equipment Corporation. Несмотря на то что он использовал более сложный анализ возможных претендентов, ему потребовалось 1647 часов работы центрального процессора, чтобы обнаружить своего бобра - машину Тьюринга, печатающую 240 единиц. Не удивительно, что Шульт тоже смог обнаружить машину Людвига, но вот что интересно: он не нашел ни одной машины между своей и машиной Людвига. По-видимому, любая машина Тьюринга, печатающая более 240 единиц, должна печатать по крайней мере 501 единицу.
В процессе своего исследования Людвиг набрел на ряд необычных машин Тьюринга, поведение которых напоминало поведение бобров-работяг. Кроме печатания единиц у бобра есть другие способы проявить трудолюбие. Например, машина Тьюринга может достаточно далеко удалиться от своего начального положения, не печатая при этом много единиц, и затем остановиться. Или, не печатая много единиц и даже далеко не удаляясь от исходной точки, она совершает громадное число переходов и лишь потом останавливается. Машина Шульта стала победительницей среди всех участвующих в конкурсе, причем по всем трем параметрам. Однако Людвиг обнаружил трех бобров, которые совсем не печатали единиц, но они либо обследовали обширную территорию, либо тратили массу времени на бесполезные действия (см. рисунок на с.101). Эти три новых вида бобров можно было бы назвать так:

Три новых вида бобров, которые после бурной деятельности не производят ни одной единицы
Castor ministerialis (или бобр-чиновник). Это предприимчивое создание стремится продвинуться как можно дальше, ничего при этом не производя. Для бобров с пятью состояниями типична особь, не производящая ни одной единицы и продвигающаяся на 11 клеток от исходной.
Castor sciemificus (или бобр-ученый). Это животное тоже ничего не производит, но стремится максимизировать свою деятельность в надежде, по-видимому, получить субсидию. Особь с пятью состояниями такой породы, из тех, что были изучены, делала 187 переходов, не напечатав при этом ни одной единицы.
Castor circuitus (или бобр-бедолага). Бобр-бедолага ничего не производит и ни на йоту ие сдвигается, но развивает при этом бурную деятельность. Как видно из диаграммы переходов, он тратит массу времени, мотаясь по кругу. Самая усердная из до сих пор обнаруженных особей совершила 67 переходов, прежде чем остановиться наконец точно там же, откуда начала.
БЫЛО бы интересно рассмотреть несколько примеров бобров с тремя состояниями из этих вновь выведенных пород. Всякая попытка найти их только выиграет от использования компьютера (персонального или любого другого), даже если он будет нужен лишь для проверки программ машин Тьюринга, уже кем-то написанных.
Создать модель машины Тьюринга довольно легко. Для представления ленты используем одномерный массив; его содержимое, состоящее только из нулей и единиц, можно выводить на экран дисплея. Наибольшую информацию можно будет извлечь тогда, когда указано положение печатающей головки. Например, текущее состояние машины можно указывать непосредственно под символом, который в данный момент считывается.
Для представления программы машин Тьюринга нужен двумерный массив. Каждый элемент такого массива представляет собой набор команд для машины; команды должны быть определены для каждого состояния управляющего устройства и для каждого символа, который может встретиться. В случае машины Тьюринга с тремя состояниями такой массив состоит из трех строк и двух столбцов; его структура в точности совпадает со структурой программы, изображенной на верхнем рисунке на с.99. Состоянию машины соответствует строка массива, а символу, считываемому головкой,- столбец. Следующая операция машины определяется командой, которая находится на пересечении соответствующих строки и столбца.
Предположим, что машина находится в состоянии 1 и считывает с ленты символ 0. Обратившись к строке 1 и столбцу 0, моделирующее устройство обнаружит команду "1, П, 2". Следовательно, машина напечатает на ленте 1, сдвинет головку вправо на одну позицию и перейдет в состояние 2. Один из способов реализации такой команды состоит в определении трех переменных; назовем их СОСТОЯНИЕ, ГОЛОВКА и СИМВОЛ. В начале вычислительного цикла значения переменных СОСТОЯНИЕ и СИМВОЛ определяют, где в таблице машина должна искать свою следующую команду. Первая компонента найденной команды (в нашем случае 1) записывается на ленту; вторая компонента (П) становится новым значением переменной ГОЛОВКА; третья компонента (2) становится значением переменной СОСТОЯНИЕ. Затем головка сдвигается в направлении, указанном переменной ГОЛОВКА, и символ, найденный в новой клетке, становится значением переменной СИМВОЛ. Затем весь цикл повторяется.
Есть много способов сделать программы, работающие по такой схеме, более простыми и эффективными. Например, вместо букв Л и П можно подставить цифры, которыми, вообще говоря, легче манипулировать в ЭВМ. Далее, переход в состояние, которое соответствует остановке машины Тьюринга, требует особой интерпретации в программе.
Модель машины Тьюринга можно использовать для проверки ваших ответов на следующие небольшие головоломки, но отнюдь не для их решения.
Представьте, что вы купили приставку, позволяющую использовать ленты машины Тьюринга с запоминающим устройством вашего компьютера. Прежде чем напустить на них ваших бобров-работяг, все ленты должны быть очищены, т.е. все единицы надо заменить нулями. Вместо того чтобы заниматься этим самому, вы решаете построить простенькую машину Тьюринга, которая выполняла бы эту работу за вас.
На одной из этих лент всего одна единица, а все остальное заполнено нулями. Вы должны построить машину Тьюринга, которая находила бы эту единицу, стирала ее (заменяла нулем) и затем останавливалась. Естественно, что чем меньше состояний у вашей лентоочистительной машины, тем она элегантнее. Лентоочиститель на рисунке вверху слева элегантен в высшей степени. Только, к сожалению, он работает на полставки.

Лентоочистителышя машина
Остальные ленты точно такие же, с той лишь разницей, что единиц на них больше, хотя в каждом случае их количество вполне определенное и конечное. Можете ли вы построить лентоочиститель, который заменяет все единицы нулями? Он, разумеется, никогда не останавливается.
БИБЛИОГРАФИЯ
Страница журнала с библиографией отсутствует, но, опять же,- АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.- G.
Да и у Уэзерелла этюд про Машину Тьюринга, конечно, есть.
ОТКЛИКИ
1 1985
ТРИ головоломки о бобре-работяге, описанные в августовском номере журнала, были решены М.Мэйни из г.Палатин (шт. Иллинойс). Его бобр-работяга с двумя состояниями показан ниже. Начиная с чистой ленты, он записывает 4 единицы, а затем останавливается.
Решение Мэйни лучше описать на словах. Машина Тьюринга, стирающая единственную единицу, записанную на чистой ленте, пользуется двумя единицами в качестве маркеров. На каждой стадии она проходит ленту от одной единицы к другой и проверяет ячейки, находящиеся непосредственно за ними. Если там находится единица, которую требуется стереть, то машина стирает все 3 единицы и останавливается. Если единицы там нет, машина передвигает маркер на одну ячейку дальше и возвращается к другому маркеру. Машина, стирающая много единиц, работает по тому же принципу, но никогда не может остановиться. Да и как она может остановиться, если в какой-нибудь не исследованной области ленты окажется сше одна единица? Бобры-работяги были построены П.Марино из г.Трой (шт.Нью-Йорк) и Д.Капланом из г.Дир-Парк (шт.Нью-Йорк). Марино решил также задачу очистки ленты, описав свои передвигающиеся единицы как "веники", подметающие ленту.
Р.Робинсон из Калифорнийского университета в Беркли написал для своего персонального компьютера фирмы IBM программу, моделирующую машину Тьюринга. Наблюдая, как предложенный У.Шультом бобр-работяга записывал свою 501-ю единицу, Робинсон заметил, что, прежде чем остановиться, программа порождала повторяющуюся и все время удлиняющуюся последовательность чередующихся 0 и 1. Начиная с чистой ленты, программа порождала такие последовательности длиной 0, 6, 13, 28, 48, 78, 121, 190, 289, 442 и 667 символов. В последней последовательности насчитывалась 501 единица. Робинсон решил исследовать поведение машины Шульта, когда она начинает работать не с чистой ленты, а с одной из последовательностей чередующихся 0 и 1. Начав с последовательности длиной 9 символов (из которых 5 символов - единицы), машина остановилась после 12870233 шагов, породив последовательность, содержащую 4911 единиц. Для этого объем памяти должен быть в 3 раза больше и необходимо в 25 раз больше шагов, чем в том случае, когда машина Шульта начинает с чистой ленты. Робинсона смутил тот факт, что сравнительно небольшое изменение во входных данных приводит к такому странному поведению машины. "Мне кажется,- пишет Робинсон,- что эти результаты заставляют сомневаться в справедливости ограничений Шульта на объем памяти и время".
По-видимому, Б.Вайман из Боннского университета не был первооткрывателем бобра-работяги с четырьмя состояниями. А.Брэйди из Университета шт.Невада в Рено построил свою версию автомата за 10 лет до Ваймана. В то время Брэйди был сотрудником Университета шт.Орегон. Интересно, что университетский значок-талисман - это бобр, а работал Брэйди на ЭВМ в Бевертоне (Beaverton, т.е. "Бобрград"). Брэйди разделяет скептицизм Робинсона. "По опыту решения задачи с четырьмя состояниями я знаю, что задача с пятью состояниями еще далека от решения. Дело заключается в том, чтобы решить, остановится или нет та или иная "далеко убежавшая" машина... По мере того как машины будут становиться сложнее, решить этот вопрос будет труднее. В конечном итоге будут затронуты очень глубокие и нерешенные математические проблемы... Проблемы, связанные с остановом каждой индивидуальной машины на чистой ленте, начиная с какого-то момента, перерастают, по существу, в отдельные математические теоремы."
5 1985
НОВАЯ попытка построить автомат типа "бобер-работяга с пятью состояниями" была предпринята Дж.Уингом из Бронкса, шт.Нью-Йорк. В ходе испытаний, проведенных 21 декабря 1984г., машина Тьюринга, созданная Уингом, начала с чистой ленты и напечатала 1915 единиц прежде, чем остановилась. Этот результат был независимо подтвержден А.Брейди из Университета штата Невада и Р.Робинсоном из Калифорнийского университета в Беркли. Эта, по словам Брейди, "поразительная" машина Уинга, кажется, оправдывает скептицизм, с которым оба математика отнеслись к известию о том, что автомат У.Шульта представляет собой бобра-работягу с пятью состояниями. Этот автомат выдал лишь 501 единицу.
6 1985
В прошлом номере журнала я упомянул о новом кандидате на звание "бобер-работяга с пятью состояниями". В декабре прошлого года Дж.Уинг из Бронкса, шт.Нью-Йорк, смоделировал машину Тьюринга, которая выдала 1915 единиц прежде, чем остановилась. Машина Уинга представлена в таблице, помешенной на предыдущей странице.

Бобер-работяга с пятью состояниями?
Если нам нужно определить, что машина сделает, например, в состоянии В. рассмотрим строку, помеченную этим символом. Строка подразделяется на верхнюю и нижнюю части, указывающие ответы машины на 0 и 1 соответственно. Если машина встречает на ленте 1, то она переходит в состояние D, записывает на ленте 1 и передвигается на одну клетку влево. Буква H в таблице обозначает останов машины.
Уинг, программирующий для манхаттанской оптической компании, прочтя статью о машине Тьюринга, решил заняться поисками "бобра-работяги с пятью состояниями". Он воспользовался микропроцессором Z-80, для которого написал программу на языке ассемблера. Эта программа управляла в свою очередь другой машиной, моделирующей машину Тьюринга. Модель обошлась Уингу меньше чем в 100долл. Созданный им автомат выполняет 7млн. переходов машины Тьюринга в секунду. Каждый переход сводится просто к обращению к таблице, подобной той, что приведена на рисунке на с.94. Уинг полон решимости найти автомат типа "бобер-работяга с пятью состояниями". Может быть, рассматриваемая машина уже удовлетворяет всем необходимым требованиям? Уинг получил свои первые результаты после того, как машина работала в течение месяца. Насколько мне известно, она все еще работает.
А.Брейди из Университета шт. Невада в г.Рено охарактеризовал машину Уинга как "поразительную". Каковы шансы, что мы откроем автомат с шестью состояниями? "Это совершенно исключено",- говорит Брейди.
2 1990
КАЖЕТСЯ, это было уже так давно, когда в октябрьском номере нашего журнала за 1984г. появилась статья с задачей о бобре-работяге: если машина Тьюринга обладает не более чем n состояниями, то сколько единиц она может выдать перед тем, как остановится? Машина Тьюринга - это воображаемое устройство, читающее и записывающее нули и единицы на ленте. Для каждого допустимого состояния, в котором может находиться машина, она определенным образом реагирует на каждый из возможных символов, находящийся в той ячейке ленты, которую машина читает в данный момент. Ответ машины Тьюринга заключается в том, какой символ записать на ленте и в какую сторону переместить по ленте головку чтения-записи перед следующим циклом операций.
В задаче о бобре-работяге роль последнего играет машина Тьюринга. Вопрос, образно говоря, заключается в том, "как много мы его может заставить поработать?". Задача была решена для машин Тьюринга с одним, двумя, тремя и четырьмя состояниями. Перед опубликованием статьи в 1984г. самый работающий из известных бобров с пятью состояниями записал 501 единицу прежде, чем остановиться. Затем одному из наших читателей, Дж.Юхингу из Бронкса (шт.Нью-Йорк), удалось открыть машину с пятью состояниями, которая записала 1915 единиц. До недавнего времени это был мировой рекорд.
Теперь А.Брэйди из Университета шт.Невада в Рено сообщил о новом, еще более работоспособном бобре, который был открыт X.Марксеном и Ю.Бунтроком из Берлинского технического университета (Западный Берлин). Бобер Марксена и Бунтрока почти в четыре раза превзошел результаты, показанные бобром Юхннга. Он выдает 4098 единиц и совершает 11798826 циклов прежде, чем остановиться! Может ли бобер быть еще более трудолюбивым? Возможно, одному из наших читателей удастся найти такого.
ОХОТА С КОМПЬЮТЕРОМ НА БОБРА-РАБОТЯГУ, ИЛИ ПОИСК САМОЙ ТРУДОЛЮБИВОЙ МАШИНЫ ТЬЮРИНГА
А.К.ДЬЮДНИ
ВРЯД ли на земле найдутся существа, более трудолюбивые, чем бобры - ну разве что пчелы. В спокойных северных водоемах бобры изо дня в день усердно сооружают плотины из веток и прутьев. Несомненно, что именно трудолюбие этих животных подсказало Тибору Радо из Университета штата Огайо название одной задачи для машин Тьюринга: "Игра бобр-работяга". В начале 60-х годов Радо заинтересовал вопрос: сколько единиц может напечатать машина Тьюринга, прежде чем она остановится? Или в более строгой формулировке: если машина Тьюринга с n состояниями, имеющая остановку, начинает работу с лентой, заполненной одними нулями, то какое максимальное число единиц она может напечатать до своей остановки? Для n, равных 1, 2, 3 и 4, ответ известен, а для n>=5 - пока нет.
В прошлом году в Дортмунде (ФРГ) был проведен конкурс бобров-работяг с целью выявить создателя самого работящего бобра с пятью состояниями. Год был отведен на написание программ, строящих машины Тьюринга - участниц конкурса, и разработку аппаратуры, на которой можно было бы выполнить эти программы. В процессе подготовительной работы удалось обнаружить бобров с весьма необычным поведением, так что биологический род Castor пришлось расширить и включит в в него несколько видов, до сей поры зоологам неизвестных.
НА страницах нашего журнала Дж.Хопкрофт уже описал машины Тьюринга, и рассказал, какое место они занимают в вычислительных науках (см.: Дж.Хопкрофт. Машины Тьюринга. "В мире науки", 1984, #7 - Прим. перев.). Машина Тьюринга состоит из бесконечной ленты, головки для считывания символов с ленты и записи их на ленте и управляющего устройства с конечным числом внутренних состояний (см. верхний рисунок на с.99). Эти компоненты можно представлять себе как аппаратную часть устройства, а то, что закладывается в управляющее устройство,- как его математическое обеспечение, т.е. программа машины Тьюринга. Машины Тьюринга отличаются друг от друга именно своей программой; последняя представляет собой таблицу, к которой машина Тьюринга обращается, чтобы узнать, что делать дальше. Каждому возможному состоянию управляющего устройства и каждому возможному символу на ленте в клетке под печатающей головкой соответствует определенный элемент таблицы, который указывает машине, какой символ должен быть напечатан на ленте, в каком направлении сдвинуть головку и в какое состояние перейти. Все описываемые здесь машины Тьюринга будут начинать работу с состояния 1.

Машина Тьюринга и ее программа
Чтобы проследить за операциями машины Тьюринга, выпишем сверху вниз состояния устройства управления и символы, выпечатываемые на ленте (или отрезке ленты) в последовательные моменты времени. Можно также указать, какая клетка ленты в данный момент просматривается. На нижнем рисунке на с.99 прослежена работа машины Тьюринга, изображенной на верхнем рисунке. Каждая строка представляет собой "моментальный снимок" машины. По форме этот "снимок" отличается от принятого в статье Хопкрофта представления, но информацию он нам дает такую же. В отличие от условностей, принятых Хопкрофтом, здесь еще предполагается, что лента бесконечна в обоих направлениях, и допускается, чтобы машина печатала символ при переходе в последнее состояние (состояние, в котором она останавливается). Эти различия никак не отражаются на возможностях машины Тьюринга. Принятая в данной статье форма "мгновенного снимка" соответствует той, что использовалась на конкурсе бобров-работяг.

"Моментальные снимки", позволяющие проследить работу машины Тьюринга
Бобр-работяга с n состояниями представляет собой машину Тьюринга, на которую наложены два ограничения. Во-первых, начав работать с лентой, целиком заполненной нулями, он в конце концов обязательно остановится; во-вторых, он способен записать не меньшее количество единиц, чем любая другая машина Тьюринга с n состояниями, имеющая остановку.
Бобры-работяги с одним и тремя состояниями изображены на верхнем рисунке на с.100. Каждая машина Тьюринга представлена диаграммой переходов, в которой занумерованные кружки - это ее состояния, а стрелки - это переходы из одного состояния в другое. Метки над стрелками означают операции машины Тьюринга. Пусть, например, бобр-работяга с тремя состояниями находится в состоянии 1 и считывает с ленты символ 0. Стрелка, выходящая из этого кружка, помечена "0, 1, П"; она приводит в состояние 2. Значит, машина, прочитав 0, запишет на ленту 1, сдвинется на одну позицию вправо и перейдет в состояние 2.

Бобры-работяги с одним и тремя состояниями
Введем обозначение S(n) для максимального числа единиц, которое может напечатать машина Тьюринга с n состояниями, имеющая остановку. Как уже говорилось, значения S(n) известны только для n от 1 до 4. Бобр-работяга с одним состоянием напечатает лишь одну единицу и остановится; иначе говоря, S(1) = 1. Бобр-работяга с двумя состояниями выдаст последовательность из четырех единиц. (Вы можете построить такую машину?) Бобр-работяга с тремя состояниями печатает 6 единиц: здесь показана одна из таких машин. Ее программа и последовательность моментальных снимков приводятся на с.99, а диаграмма переходов - на верхнем рисунке на с.100. Бобра-работягу с тремя состояниями построили в 1962г. Радо и Чжень Лин из корпорации AT&T Bell Laboratories. В 1973г. Б.Вейман из Боннского университета построил бобра-работягу с 4 состояниями, который выдавал 13 идущих подряд единиц. С тех пор теоретики пустились в поиски бобра-работяги с пятью состояниями.
КОНКУРС бобров-работяг состоялся в январе 1983г. на проводившейся в Дортмундском университете теоретической конференции по информатике, которая была организована Ф.Ванкмюллером. В конкурсе приняли участие 133 машины Тьюринга с пятью состояниями. Победителем стал У.Шульт, машина которого печатала 501 единицу и останавливалась. Диаграмма переходов победительницы представлена на нижнем рисунке на с.100. Вторым оказался Й.Людвиг из научного центра Brown Boveri в Бадсне; его машина Тьюринга печатала 240 единиц.

Бобр-работяга У.Шульта с пятью состояниями
Можно ли считать машину Тьюринга, построенную Шультом, бобром-работягой? Шульт, равно как и Ванкмюллер и Людвиг, полагает, что можно. Иными словами, он считает, что не существует машины Тьюринга с пятью состояниями, которая бы печатала больше, чем 501 единицу, и останавливалась. Как же доказать такое утверждение? Методом полного перебора, вроде того, которым пользовался Шульт для построения своего чемпиона. Прежде чем переходить к описанию попыток Шульта заманить в ловушку на своем компьютере бобра-работягу с пятью состояниями, мне бы хотелось ближе познакомить читателя с функцией S(n), чтобы он мог понять, почему так трудно играть в бобра-работягу даже при помощи ЭВМ.
Функция S(n) обладает одной существенной особенностью: она невычислимая. Попросту говоря, она слишком быстро растет. По первым четырем ее значениям 1, 4, 6 и 13 это незаметно: скорость кажется весьма умеренной. Если значение 501 - действительно максимальное число единиц для машины с пятью состояниями, то рост S(n) все еще представляется не быстрее экспоненциального. Шульт смог построить машину Тьюринга с шестью состояниями, которая печатает 2075 единиц. Это опять-таки не свидетельствует об очень высокой скорости роста. Однако Шульт сумел построить машину с 12 состояниями, которая печатала столько единиц, что их количество выражается такой ужасающей формулой:
6*4096^4096^4096^...^4096^4
Число 4096 фигурирует в этой формуле 166 раз, т.е. на участке, скрывающемся за тремя точками, оно повторено 162 раза. Вычислять выражение нужно сверху вниз: сначала возвести 4096 в четвертую степень, затем возвести 4096 в полученную степень, затем снова возвести 4096 в полученную степень и т.п. Дойдя до самого низа, результат умножить на 6.
Если вас не пугает, что придется иметь дело с цепочкой единиц такой длины, постройте какое-нибудь большее число. Напишите любую формулу, в которой числа перемножаются или возводятся в степень; можете даже заменить любое из чисел на n. Какую бы формулу вы ни придумали, она будет давать меньшее значение (если только выбрано n, при котором значение этого выражения достаточно велико), чем количество единиц, выпечатывасмое бобром-работягой с n состояниями. Следовательно, для произвольного значения n функцию S(n) вычислить нельзя. Самое большее, что можно сделать,- это вычислить Е(n) для какого-то малого фиксированного значения n.
ТАК что нет ничего удивительного в том, что в бобра-работягу чаше всего играют на ЭВМ. Суть метода состоит в систематическом изучении всех машин Тьюринга с n состояниями. Каждый раз, как только нужно получить новую машину, моделируется ее поведение в случае, когда лента в начале работы вся заполнена нулями. Если машина останавливается после какого-то числа шагов, полученное количество единиц сравнивается с достижениями самой "работящей" машины Тьюринга, которая была до сих пор найдена. Иногда обнаруживается новый чемпион.
Такой метод поиска бобра-работяги с n состояниями имеет два серьезных недостатка. Во-первых, приходится проверять колоссальное количество машин Тьюринга: к примеру, машин с пятью состояниями может быть 63403380965376. Во-вторых, не известно, сколько времени нужно ждать, чтобы машина остановилась: максимальное число переходов машины с n состояниями, которая рано или поздно останавливается,- эту функцию будем обозначать s(n) - тоже невычислимая функция. Она, очевидно, растет даже быстрее, чем S(n), поскольку машина Тьюринга каждый раз, когда печатает 1, делает хотя бы один переход. Как отметил Хопкрофт, вычисление s(n) эквивалентно решению проблемы остановки для машин Тьюринга, одной из первых проблем, отнесенных Тьюрингом к разряду неразрешимых.
В 1982г. Шульт устроил в своем компьютере Apple II ловушку для бобра-работяги. Он снабдил центральный процессор своего компьютера микропроцессором Motorola 6809 на одной печатной плате. Программу поиска он написал на языке этого вспомогательного процессора. Чтобы проверить огромное количество машин Тьюринга, порождаемых программой, Шульт следующим образом реализовал аппаратную часть машины: вмонтировал стандартные электронные компоненты в ту схему, которую он вставил в Apple II. Устройство было снабжено лентой с 4096 клетками, а также регистрами для хранения программы и информации о текущем состоянии и положении печатающей головки машины Тьюринга. Шульт подсчитал, что без специализированного аппаратного обеспечения его программа поиска работала бы непрерывно 20 месяцев. Даже с такими усовершенствованными аппаратными средствами потребовалось 803 часа работы Apple II, чтобы найти машину Тьюринга-чемпионку.
При разработке необходимого математического обеспечения Шульт также добился определенных преимуществ, составив программу поиска таким образом, чтобы она максимально использовала аппаратные возможности машины Тьюринга. Программа заполняла таблицу переходов машины Тьюринга с пятью состояниями, скрупулезно разбирая все варианты. Еще до того, как таблица была заполнена вся целиком, она предоставлялась машине Тьюринга для проверки. Зачастую обнаруживалась такая незаполненная таблица, которая свидетельствовала о машине, истощившей свой запас пространства и времени прежде, чем она могла достичь какого-то еще не определенного элемента. В таких случаях незаполненная таблица и все возможные пути ее заполнения исключались из рассмотрения.
Хотя Шульт в известной мере смог справиться с управлением множеством машин Тьюринга, надо сказать, что его подход к проблеме остановки для машин Тьюринга с пятью состояниям и нельзя считать безукоризненным. За отсутствием точной информации относительно s(n) - максимального числа переходов для машины Тьюринга с пятью состояниями, имеющей остановку, нужно иметь на этот счет какую-то гипотезу. Шульт предположил, что можно ограничиться значением 500000 переходов; иначе говоря, он выдвинул рабочую гипотезу, согласно которой машина не остановится никогда, если она не остановится после 500000 шагов. Ему пришлось также наложить и пространственные ограничения на работяг-претендентов: поскольку лента имеет только 4096 клеток и машина Тьюринга всегда начинает работу с середины этой конечной ленты, бобр может оказаться претендентом в работяги, если он продвинулся дальше, чем на 2048 клеток от исходного положения. Вообще говоря, претендентом считается не только такая машина, которая достигла остановки, но и та, что продолжает обрабатывать все новые и новые клетки.
ИЗ 133 машин Тьюринга, принявших участие в Дортмундском конкурсе, только 4 печатали более 100 единиц. Все эти машины были промоделированы на компьютере Siemens 7,748. Для определения победителя потребовалось более часа машинного времени.
Людвиг, занявший второе место, написал программу поиска бобров-работяг на языке Паскаль и пропустил ее на довольно мощной мини-ЭВМ VAX фирмы Digital Equipment Corporation. Несмотря на то что он использовал более сложный анализ возможных претендентов, ему потребовалось 1647 часов работы центрального процессора, чтобы обнаружить своего бобра - машину Тьюринга, печатающую 240 единиц. Не удивительно, что Шульт тоже смог обнаружить машину Людвига, но вот что интересно: он не нашел ни одной машины между своей и машиной Людвига. По-видимому, любая машина Тьюринга, печатающая более 240 единиц, должна печатать по крайней мере 501 единицу.
В процессе своего исследования Людвиг набрел на ряд необычных машин Тьюринга, поведение которых напоминало поведение бобров-работяг. Кроме печатания единиц у бобра есть другие способы проявить трудолюбие. Например, машина Тьюринга может достаточно далеко удалиться от своего начального положения, не печатая при этом много единиц, и затем остановиться. Или, не печатая много единиц и даже далеко не удаляясь от исходной точки, она совершает громадное число переходов и лишь потом останавливается. Машина Шульта стала победительницей среди всех участвующих в конкурсе, причем по всем трем параметрам. Однако Людвиг обнаружил трех бобров, которые совсем не печатали единиц, но они либо обследовали обширную территорию, либо тратили массу времени на бесполезные действия (см. рисунок на с.101). Эти три новых вида бобров можно было бы назвать так:

Три новых вида бобров, которые после бурной деятельности не производят ни одной единицы
Castor ministerialis (или бобр-чиновник). Это предприимчивое создание стремится продвинуться как можно дальше, ничего при этом не производя. Для бобров с пятью состояниями типична особь, не производящая ни одной единицы и продвигающаяся на 11 клеток от исходной.
Castor sciemificus (или бобр-ученый). Это животное тоже ничего не производит, но стремится максимизировать свою деятельность в надежде, по-видимому, получить субсидию. Особь с пятью состояниями такой породы, из тех, что были изучены, делала 187 переходов, не напечатав при этом ни одной единицы.
Castor circuitus (или бобр-бедолага). Бобр-бедолага ничего не производит и ни на йоту ие сдвигается, но развивает при этом бурную деятельность. Как видно из диаграммы переходов, он тратит массу времени, мотаясь по кругу. Самая усердная из до сих пор обнаруженных особей совершила 67 переходов, прежде чем остановиться наконец точно там же, откуда начала.
БЫЛО бы интересно рассмотреть несколько примеров бобров с тремя состояниями из этих вновь выведенных пород. Всякая попытка найти их только выиграет от использования компьютера (персонального или любого другого), даже если он будет нужен лишь для проверки программ машин Тьюринга, уже кем-то написанных.
Создать модель машины Тьюринга довольно легко. Для представления ленты используем одномерный массив; его содержимое, состоящее только из нулей и единиц, можно выводить на экран дисплея. Наибольшую информацию можно будет извлечь тогда, когда указано положение печатающей головки. Например, текущее состояние машины можно указывать непосредственно под символом, который в данный момент считывается.
Для представления программы машин Тьюринга нужен двумерный массив. Каждый элемент такого массива представляет собой набор команд для машины; команды должны быть определены для каждого состояния управляющего устройства и для каждого символа, который может встретиться. В случае машины Тьюринга с тремя состояниями такой массив состоит из трех строк и двух столбцов; его структура в точности совпадает со структурой программы, изображенной на верхнем рисунке на с.99. Состоянию машины соответствует строка массива, а символу, считываемому головкой,- столбец. Следующая операция машины определяется командой, которая находится на пересечении соответствующих строки и столбца.
Предположим, что машина находится в состоянии 1 и считывает с ленты символ 0. Обратившись к строке 1 и столбцу 0, моделирующее устройство обнаружит команду "1, П, 2". Следовательно, машина напечатает на ленте 1, сдвинет головку вправо на одну позицию и перейдет в состояние 2. Один из способов реализации такой команды состоит в определении трех переменных; назовем их СОСТОЯНИЕ, ГОЛОВКА и СИМВОЛ. В начале вычислительного цикла значения переменных СОСТОЯНИЕ и СИМВОЛ определяют, где в таблице машина должна искать свою следующую команду. Первая компонента найденной команды (в нашем случае 1) записывается на ленту; вторая компонента (П) становится новым значением переменной ГОЛОВКА; третья компонента (2) становится значением переменной СОСТОЯНИЕ. Затем головка сдвигается в направлении, указанном переменной ГОЛОВКА, и символ, найденный в новой клетке, становится значением переменной СИМВОЛ. Затем весь цикл повторяется.
Есть много способов сделать программы, работающие по такой схеме, более простыми и эффективными. Например, вместо букв Л и П можно подставить цифры, которыми, вообще говоря, легче манипулировать в ЭВМ. Далее, переход в состояние, которое соответствует остановке машины Тьюринга, требует особой интерпретации в программе.
Модель машины Тьюринга можно использовать для проверки ваших ответов на следующие небольшие головоломки, но отнюдь не для их решения.
Представьте, что вы купили приставку, позволяющую использовать ленты машины Тьюринга с запоминающим устройством вашего компьютера. Прежде чем напустить на них ваших бобров-работяг, все ленты должны быть очищены, т.е. все единицы надо заменить нулями. Вместо того чтобы заниматься этим самому, вы решаете построить простенькую машину Тьюринга, которая выполняла бы эту работу за вас.
На одной из этих лент всего одна единица, а все остальное заполнено нулями. Вы должны построить машину Тьюринга, которая находила бы эту единицу, стирала ее (заменяла нулем) и затем останавливалась. Естественно, что чем меньше состояний у вашей лентоочистительной машины, тем она элегантнее. Лентоочиститель на рисунке вверху слева элегантен в высшей степени. Только, к сожалению, он работает на полставки.

Лентоочистителышя машина
Остальные ленты точно такие же, с той лишь разницей, что единиц на них больше, хотя в каждом случае их количество вполне определенное и конечное. Можете ли вы построить лентоочиститель, который заменяет все единицы нулями? Он, разумеется, никогда не останавливается.
БИБЛИОГРАФИЯ
Страница журнала с библиографией отсутствует, но, опять же,- АВТОМАТЫ. Под ред. К.Шеннона и Дж.Маккартн. Пер. с англ./Под ред. А.А.Ляпунова.- М.: ИЛ, 1956.- G.
Да и у Уэзерелла этюд про Машину Тьюринга, конечно, есть.
ОТКЛИКИ
1 1985
ТРИ головоломки о бобре-работяге, описанные в августовском номере журнала, были решены М.Мэйни из г.Палатин (шт. Иллинойс). Его бобр-работяга с двумя состояниями показан ниже. Начиная с чистой ленты, он записывает 4 единицы, а затем останавливается.

Решение Мэйни лучше описать на словах. Машина Тьюринга, стирающая единственную единицу, записанную на чистой ленте, пользуется двумя единицами в качестве маркеров. На каждой стадии она проходит ленту от одной единицы к другой и проверяет ячейки, находящиеся непосредственно за ними. Если там находится единица, которую требуется стереть, то машина стирает все 3 единицы и останавливается. Если единицы там нет, машина передвигает маркер на одну ячейку дальше и возвращается к другому маркеру. Машина, стирающая много единиц, работает по тому же принципу, но никогда не может остановиться. Да и как она может остановиться, если в какой-нибудь не исследованной области ленты окажется сше одна единица? Бобры-работяги были построены П.Марино из г.Трой (шт.Нью-Йорк) и Д.Капланом из г.Дир-Парк (шт.Нью-Йорк). Марино решил также задачу очистки ленты, описав свои передвигающиеся единицы как "веники", подметающие ленту.
Р.Робинсон из Калифорнийского университета в Беркли написал для своего персонального компьютера фирмы IBM программу, моделирующую машину Тьюринга. Наблюдая, как предложенный У.Шультом бобр-работяга записывал свою 501-ю единицу, Робинсон заметил, что, прежде чем остановиться, программа порождала повторяющуюся и все время удлиняющуюся последовательность чередующихся 0 и 1. Начиная с чистой ленты, программа порождала такие последовательности длиной 0, 6, 13, 28, 48, 78, 121, 190, 289, 442 и 667 символов. В последней последовательности насчитывалась 501 единица. Робинсон решил исследовать поведение машины Шульта, когда она начинает работать не с чистой ленты, а с одной из последовательностей чередующихся 0 и 1. Начав с последовательности длиной 9 символов (из которых 5 символов - единицы), машина остановилась после 12870233 шагов, породив последовательность, содержащую 4911 единиц. Для этого объем памяти должен быть в 3 раза больше и необходимо в 25 раз больше шагов, чем в том случае, когда машина Шульта начинает с чистой ленты. Робинсона смутил тот факт, что сравнительно небольшое изменение во входных данных приводит к такому странному поведению машины. "Мне кажется,- пишет Робинсон,- что эти результаты заставляют сомневаться в справедливости ограничений Шульта на объем памяти и время".
По-видимому, Б.Вайман из Боннского университета не был первооткрывателем бобра-работяги с четырьмя состояниями. А.Брэйди из Университета шт.Невада в Рено построил свою версию автомата за 10 лет до Ваймана. В то время Брэйди был сотрудником Университета шт.Орегон. Интересно, что университетский значок-талисман - это бобр, а работал Брэйди на ЭВМ в Бевертоне (Beaverton, т.е. "Бобрград"). Брэйди разделяет скептицизм Робинсона. "По опыту решения задачи с четырьмя состояниями я знаю, что задача с пятью состояниями еще далека от решения. Дело заключается в том, чтобы решить, остановится или нет та или иная "далеко убежавшая" машина... По мере того как машины будут становиться сложнее, решить этот вопрос будет труднее. В конечном итоге будут затронуты очень глубокие и нерешенные математические проблемы... Проблемы, связанные с остановом каждой индивидуальной машины на чистой ленте, начиная с какого-то момента, перерастают, по существу, в отдельные математические теоремы."
5 1985
НОВАЯ попытка построить автомат типа "бобер-работяга с пятью состояниями" была предпринята Дж.Уингом из Бронкса, шт.Нью-Йорк. В ходе испытаний, проведенных 21 декабря 1984г., машина Тьюринга, созданная Уингом, начала с чистой ленты и напечатала 1915 единиц прежде, чем остановилась. Этот результат был независимо подтвержден А.Брейди из Университета штата Невада и Р.Робинсоном из Калифорнийского университета в Беркли. Эта, по словам Брейди, "поразительная" машина Уинга, кажется, оправдывает скептицизм, с которым оба математика отнеслись к известию о том, что автомат У.Шульта представляет собой бобра-работягу с пятью состояниями. Этот автомат выдал лишь 501 единицу.
6 1985
В прошлом номере журнала я упомянул о новом кандидате на звание "бобер-работяга с пятью состояниями". В декабре прошлого года Дж.Уинг из Бронкса, шт.Нью-Йорк, смоделировал машину Тьюринга, которая выдала 1915 единиц прежде, чем остановилась. Машина Уинга представлена в таблице, помешенной на предыдущей странице.

Бобер-работяга с пятью состояниями?
Если нам нужно определить, что машина сделает, например, в состоянии В. рассмотрим строку, помеченную этим символом. Строка подразделяется на верхнюю и нижнюю части, указывающие ответы машины на 0 и 1 соответственно. Если машина встречает на ленте 1, то она переходит в состояние D, записывает на ленте 1 и передвигается на одну клетку влево. Буква H в таблице обозначает останов машины.
Уинг, программирующий для манхаттанской оптической компании, прочтя статью о машине Тьюринга, решил заняться поисками "бобра-работяги с пятью состояниями". Он воспользовался микропроцессором Z-80, для которого написал программу на языке ассемблера. Эта программа управляла в свою очередь другой машиной, моделирующей машину Тьюринга. Модель обошлась Уингу меньше чем в 100долл. Созданный им автомат выполняет 7млн. переходов машины Тьюринга в секунду. Каждый переход сводится просто к обращению к таблице, подобной той, что приведена на рисунке на с.94. Уинг полон решимости найти автомат типа "бобер-работяга с пятью состояниями". Может быть, рассматриваемая машина уже удовлетворяет всем необходимым требованиям? Уинг получил свои первые результаты после того, как машина работала в течение месяца. Насколько мне известно, она все еще работает.
А.Брейди из Университета шт. Невада в г.Рено охарактеризовал машину Уинга как "поразительную". Каковы шансы, что мы откроем автомат с шестью состояниями? "Это совершенно исключено",- говорит Брейди.
2 1990
КАЖЕТСЯ, это было уже так давно, когда в октябрьском номере нашего журнала за 1984г. появилась статья с задачей о бобре-работяге: если машина Тьюринга обладает не более чем n состояниями, то сколько единиц она может выдать перед тем, как остановится? Машина Тьюринга - это воображаемое устройство, читающее и записывающее нули и единицы на ленте. Для каждого допустимого состояния, в котором может находиться машина, она определенным образом реагирует на каждый из возможных символов, находящийся в той ячейке ленты, которую машина читает в данный момент. Ответ машины Тьюринга заключается в том, какой символ записать на ленте и в какую сторону переместить по ленте головку чтения-записи перед следующим циклом операций.
В задаче о бобре-работяге роль последнего играет машина Тьюринга. Вопрос, образно говоря, заключается в том, "как много мы его может заставить поработать?". Задача была решена для машин Тьюринга с одним, двумя, тремя и четырьмя состояниями. Перед опубликованием статьи в 1984г. самый работающий из известных бобров с пятью состояниями записал 501 единицу прежде, чем остановиться. Затем одному из наших читателей, Дж.Юхингу из Бронкса (шт.Нью-Йорк), удалось открыть машину с пятью состояниями, которая записала 1915 единиц. До недавнего времени это был мировой рекорд.
Теперь А.Брэйди из Университета шт.Невада в Рено сообщил о новом, еще более работоспособном бобре, который был открыт X.Марксеном и Ю.Бунтроком из Берлинского технического университета (Западный Берлин). Бобер Марксена и Бунтрока почти в четыре раза превзошел результаты, показанные бобром Юхннга. Он выдает 4098 единиц и совершает 11798826 циклов прежде, чем остановиться! Может ли бобер быть еще более трудолюбивым? Возможно, одному из наших читателей удастся найти такого.
Последний раз редактировалось: Gudleifr (Вт Ноя 26, 2019 10:26 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
11 1984
НЕДОСТАТКИ "ЭЛЕКТРОННОГО ГЛАЗА" ГОВОРЯТ
О ТОМ, ЧТО ЗРИТЕЛЬНОЕ ВОСПРИЯТИЕ НЕВОЗМОЖНО
БЕЗ ПРЕДСТАВЛЕНИЯ О ВИДИМОМ ОБЪЕКТЕ
А.К.ДЬЮДНИ
Полностью этот журнал см. ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.
ВООБРАЗИМ себе небольшое устройство наподобие фотоаппарата с линзой на передней панели корпуса и позиционным переключателем сбоку. Различным положениям переключателя соответствуют такие надписи, как "дерево", "дом", "кошка" и т.д. Установив переключатель в положение "кошка", отправимся на прогулку. Как только мы обнаружим кошку на соседнем крыльце, направим на нее наш аппарат: на его панели загорится красная сигнальная лампочка. Если мы направим аппарат на другие объекты, лампочка гореть не будет.
Внутри нашего аппарата находятся фотоэлектрические детекторы - своеобразная электронная сетчатка, посылающая импульсы тока на двуслойную логическую схему. Устройство подобного типа называется персептроном (от английского слова perception - восприятие, осознание.- Перев.). В свое время на персептроны возлагались большие надежды. Считалось, что в конце концов они смогут справиться с задачами распознавания образов в реальном мире, подобно тому как это выглядело в только что приведенном фантастическом примере. Надежды, однако, не оправдались.
В 50-х и 60-х годах наблюдался колоссальный взрыв творческой активности в новой стремительно развивавшейся области вычислительной техники и теории вычислений. Многие исследователи находились тогда под влиянием таких романтических понятий, как самоорганизующиеся системы, обучающиеся машины и компьютеры, обладающие "интеллектом". Я бы назвал этот период эпохой кибернетики. Невероятные машины, которые могли бы видеть, думать или даже воспроизводить самих себя, казалось, вот-вот будут созданы. Простейшей из этих машин был персептрон.
ПЕРСЕПТРОН состоит из решетчатой сетчатки, разделенной на конечное число ячеек - детекторов света. Подобно некоторым клеткам сетчатки глаза, каждая ячейка "включается", посылая импульс тока, когда получает достаточное количество света; в противном случае она остается в "выключенном" состоянии. Поэтому было бы естественно представить образ, анализируемый персептроном, в виде решетки, состоящей из светлых и темных квадратиков, как на рисунке на с.128.

Персептрон пытается распознать кошку
Помимо сетчатки персептрон содержит великое множество простейших элементов, принимающих решение, которые я буду называть локальными демонами. Каждый локальный демон проверяет определенное подмножество ячеек сетчатки и посылает сигнал, характеризующий состояние этих ячеек, более сложному логическому элементу, принимающему более ответственное решение. Этот элемент я назову главным демоном. Уточним: у каждого локального демона есть набор определенных образов, за появлением которых он должен следить во вверенной ему области, т.е. на своем подмножестве ячеек сетчатки. Когда там появляется один из таких образов, локальный демон посылает сигнал главному демону; в противном случае он "молчит". Работа главного демона несколько сложнее - он должен выполнять некоторые расчетные операции. Амплитуда сигнала от каждого локального демона умножается на специально обусловленное положительное или отрицательное число ("вес", приписанный данному локальному демону), и полученные результаты складываются. Если полученная сумма не меньше установленного порога, главный демон говорит "да"; в противном случае - "нет". Чтобы не вдаваться в интригующий вопрос о том, как выглядят эти демоны, я изобразил их в виде кубиков, приведенных на с.128.
Демонам часто поручают опасную или даже невозможную работу, например такую, как открывать микроскопические дверцы в перегородке сосуда, чтобы пропускать молекулы, обладающие определенными свойствами. У демонов персептрона работа сравнительно нетрудная. На самом деле локальных демонов можно заменить простыми логическими схемами, а с работой главного демона легко может справиться устройство из нескольких регистров, сумматора и компаратора (все это элементы центрального процессора, присутствующие в любом компьютере). Однако демоны обладают романтическим очарованием, которого лишены электронные устройства.
Работа персептрона заключается в том. чтобы говорить "да", когда ему показывают определенные образы, и "нет" - в ответ на все остальные. При этом считается, что образы первого типа "распознаются" персептроном. И хотя перспектива создания персептрона, распознающего кошек, весьма сомнительна, существуют другие, вполне разрешимые задачи распознавания.
Персептрон можно запрограммировать в том или ином смысле для распознавания определенного класса образов за счет правильного подбора весовых коэффициентов и порогового значения их суммы. Локальные демоны, функция которых заключается в том, чтобы сигнализировать о наличии определенного класса объектов (образов), имеют положительные весовые коэффициенты, а те, которые должны свидетельствовать против, получают отрицательные веса. Абсолютная величина весового коэффициента говорит о сравнительной важности данного свидетельства. Хотя рассматриваемые здесь персептроны оперируют фиксированными весами, программирование играет центральную роль в теории персептронов, разработанной в 50-х годах.
Персептрон, описанный ниже, распознает темный прямоугольник произвольного размера или формы, расположенный в любом месте на его сетчатке. На самом деле он распознает любое количество таких прямоугольников (в том числе и их отсутствие) при условии, что ни одна пара прямоугольников не касается друг друга ни одной из сторон, ни вершинами углов. Персептрон строится в три этапа. Сначала к каждой области сетчатки размером 2*2 подсоединяется один локальный демон. Затем все распознаваемые подобразы из набора Р (позитивные), который приведен на верхнем рисунке на с.129, заносятся в список каждого локального демона. Третий этап заключается в том, чтобы установить все весовые коэффициенты главного демона равными +1, а значение порога равным d - по числу локальных демонов.

Подобразы размером 2*2, распознаваемые позитивными (Р) и негативными (N) локальными демонами
ПОДОБНОЕ устройство требует довольно большого числа демонов: если сетчатка персептрона имеет размер n*n, то необходимое количество локальных демонов составит (n-1)2. Им всем придаются положительные веса - это означает, что они все должны давать позитивные свидетельства при распознавании прямоугольников. Нетрудно видеть, например, что при проецировании одного темного прямоугольника на сетчатку персептрона каждая область ячеек размером 2*2 получит один из подобразов, содержащихся в списке Р. Следовательно, каждый демон пошлет сигнал главному демону и значение "взвешенной" суммы этих сигналов, разумеется, будет равно d. В этом случае главный демон говорит "да". С другой стороны, если хотя бы одна из темных фигур не является прямоугольником или два прямоугольника касаются друг друга, то по крайней мере одна область сетчатки персептрона получит подобраз, содержащийся в списке N (негативные), который приведен на с.129 вверху. Поэтому по крайней мере один локальный демон не пошлет сигнала, и главный демон получит сумму, не превышающую d-1. В результате он скажет "нет".
Можно построить эквивалентный персептрон, в котором каждый локальный демон располагает меньшим списком N. В этом случае все веса будут равны -1, а пороговым значением будет нуль. Каждый локальный демон будет поставлять отрицательное (негативное) свидетельство при предъявлении образа, состоящего из прямоугольников, и главный демон скажет "да" только в том случае, если ни один локальный демон не пошлет сигнала.
Персептрон описанной выше разновидности обладает многими интересными свойствами, поэтому дадим ему название. Независимо от того, каким конкретным списком оснащены локальные демоны, устройство подобного рола назовем "окошечным" персептроном, потому что каждый локальный демон видит входной образ через "окошко" размером 2*2. При размерах сетчатки n*n число локальных демонов должно быть равно (n-1)2 и значение порога также равно этой величине.
Вообще говоря, персептроны, по-видимому, лучше всего распознают геометрические фигуры. Окошечные персептроны могут распознавать не только прямоугольники, но также и "черные дыры" (изолированные темные клетки), вертикальные и горизонтальные линии, образы типа "лестницы", "шахматной доски" и многие другие. Все зависит от того, из каких под-образов размером 2*2 состоят списки локальных демонов (см. рисунок на с.130). В действительности каждое подмножество из 16 возможных подобразов размером 2*2 определяет свой окошенный персептрон и каждый из результирующих 65536 окошечных персептронов распознает определенный класс образов. Но, впрочем, распознает ли?

Образы, распознаваемые "окошечным" перцептроном
Окошечный персептрон с двумя следующими подобразами

ничего не распознает. Причину понять нетрудно. Предполагая, что азмеры сетчатки достаточно велики, выберем окошко размером 2*2 в средней ее части. Если на это окошко проецируется первый из двух приведенных выше подобразов, то рассмотрим окошко, сдвинутое относительно данного на одну клетку вправо: оно будет иметь темную клетку в верхнем левом углу. Поэтому локальный демон, контролирующий эту область, не пошлет сигнал главному демону. Напомним, что по определению окошечного персептрона необходимое условие для распознавания образа заключается в том, чтобы ВСЕ локальные демоны послали сигнал, свидетельствующий в пользу данного образа. Если же на первое окошко проецируется второй подобраз из списка, то сдвиг на одну ячейку влево приведет к аналогичному противоречию.
КАКИЕ ЖЕ подмножества из 16 основных подобразов порождают окошечные персептроны, которые действительно что-то распознают? На этот вопрос, наверное, трудно ответить, однако он служит очень хорошей иллюстрацией тех вопросов, которыми может заинтересоваться программист-теоретик или математик, столкнувшись с феноменом персептрона, который ничего не распознает. Поскольку речь идет о большом количестве таких персептронов, ответ лучше всего выразить в виде какого-либо легко применяемого критерия или теста: задавая определенное подмножество подобразов 2*2, можно применить тест и получить ответ для данного подмножества.
Из замечаний, сделанных выше, должно быть ясно, что вовсе не обязательно быть теоретиком-программистом, чтобы отвечать на подобные вопросы. Хотя эти вопросы несколько сложнее головоломок, обычно публикуемых в рубрике, посвященной занимательным математическим задачам, в принципе они требуют такого же мышления. Читатели, решившие хотя бы одну из головоломок Мартина Гарднера, печатавшихся в разделе "Математические игры" нашего журнала, наверное, смогут добиться некоторых успехов, пытаясь найти ответ на поставленный выше вопрос. А вообще в теоретических исследованиях, так же как и в экспериментальных, частичный ответ все же лучше, чем никакого.
Работа в области исследования возможностей персептронов была начата Фрэнком Розенблаттом в Корнеллском университете в 50-х годах [С работами Ф.Розенблатта можно познакомиться в сборнике "Самоорганизующиеся системы", выпущенном издательством "Мир" в 1964г. (с.65-112).- Прим. перев.]. Розенблатт и его последователи как в Корнеллском университете, так и в других исследовательских центрах относились оптимистично к перспективе персептронов как практически полезных устройств для распознавания образов. Из "теоремы о сходимости" следует, что в принципе персептроны могут научиться распознавать образы, если автоматизировать подбор весовых коэффициентов, с которыми работает главный демон. Эта теорема утверждает, что любое перераспределение весов в направлении, повышающем способность к распознаванию, может послужить основой для дальнейшего улучшения. Были построены реальные персептроны, и в некоторых экспериментах с простыми образами были получены хорошие результаты, частота распознавания была довольно высокой.
То, что тогда казалось обнадеживающей перспективой, было в какой-то степени иллюзией. По мнению Марвина Л. Минского и Сеймура Пейперта из Массачусетса го технологического института, энтузиастов, исследовавших персептроны, подкупали простота и кажущаяся перспективность этих устройств. Но за этими привлекательными свойствами скрывались серьезные недостатки принципиального характера. В 1969г. вышла в свет книга Минского и Пейперта "Персептроны" [М.Минский, С.Пейперт. Персептроны,- М.: Мир, 1971.- Прим. перев.], которая произвела эффект иголки, проткнувшей воздушный шар. В книге было приведено несколько задач и строгое доказательство того факта, что персептроны не могут с ними справиться.
Одним из наиболее примечательных дефектов, вскрытых Минским и Пейпертом, было то, что некоторые персептроны не способны установить, является ли показанная им геометрическая фигура связной (т.е. содержащей изолированные части). Исходя из того, что каждый локальный демон обследует лишь какую-то ограниченную область, Минский и Пейперт привели примеры четырех образов, подобранных так, что один из них всегда вводит в заблуждение персептрон, задача которого заключается в том, чтобы распознать, является ли образ связным. Эти примеры показаны на нижнем рисунке на с.129. Два из них (b и c) представляют собой связные фигуры, а два других (a и d) - нет.

Четыре фигуры, подобранные так, чтобы запутать персептрон, распознающий свойство связности
ДОПУСТИМ, кто-то утверждает, что изобрел персептрон, ограниченный по диаметру, который способен различать связные и несвязные образы. Под термином "ограниченный по диаметру" я понимаю то, что существует некоторое число m, такое, что каждый локальный демон может просматривать образ только через окошко, размеры которого не превышают квадрата из m*m ячеек сетчатки. Чтобы проверить это утверждение, в примере Минского и Пейперта следовало бы подобрать 4 образа так, чтобы размеры каждого из них превышали m ячеек. Такие локальные демоны можно разделить на 3 непересекающихся множества. "Левые" демоны видят по крайней мере одну клетку на левом крае фигуры, "правые" - по крайней мере одну клетку на правом крае, а "прочие" не относятся ни к "левым", ни к "правым".
Когда гипотетическому персептрону, распознающему свойство связности, представляют образ а, он либо терпит неудачу (говоря "да"), либо добивается успеха (говоря "нет"). Если он терпит неудачу, то тест, раэумеется, завершен. Если попытка оказывается для него успешной, то следующий шаг заключается в том, чтобы исследовать сумму, получаемую главным демоном, путем разбиения ее на 3 части: L, О, R, представляющие взвешенные суммы, получаемые соответственно от левых, прочих и правых демонов, посылающих сигналы главному демону, когда на сетчатку проецируется образ а. Поскольку в данном случае персептрон, распознающий свойство связности, говорит "нет", сумма частей L, О и R, очевидно, оказалась меньше порогового значения. Если образ a заменить теперь образом b, только левые демоны изменят свой ответ, поскольку изменяются лишь клетки, расположенные вдоль левого края фигуры. Предположим, что значение частичной суммы изменяется и становится равным L'. С другой стороны, если образ а заменить образом с, то изменятся лишь клетки, расположенные вдоль правого края фигуры, и лишь правые локальные демоны изменят свой ответ. При этом частичная сумма R изменится и станет равной, скажем, R'.
Теперь персептрон попадает в очень интересную ситуацию. Поскольку образы b и с связные, от должен ответить "да" в обоих случаях. Поэтому суммы L'+O+R и L+O+R' должны быть не меньше порогового значения. Однако уже известно, что L+О+R меньше порогового значения, так как образ a был несвязным. Отсюда следует, что L' больше L, a R' больше R. Развязка наступает, когда персептрону показывают образ d, этого "удара" ему уже не выдержать. Здесь по сравнению с образом a изменяют свое состояние клетки, расположенные как на левом, так и на правом краю фигуры. В результате главный демон получает сумму L'+О+R', которая определенно больше порогового значения. Главный демон говорит "да" и , таким образом, ошибается.
Среди прочих недостатков, присущих персептронам и выявленных Минским и Пейпертом, можно отметить и тот факт, что для некоторых задач распознавания требуется настолько большое число локальных демонов, что практическая реализация такого персептрона окажется невозможной, в то время как для некоторых других задач скорость обучения (сходимость) персептронов слишком мала.
ВЕРОЯТНО, нас не должен удивлять тот факт, что персептроны терпят неудачу во многих случаях там, где человеческая зрительная и распознающая система действует успешно. Я уже говорил, что локальные демоны и главный демон можно вполне заменить простыми вычислительными электронными схемами. Их функции могут также выполнять так называемые формальные нейроны, впервые описанные в 40-х годах Уорреном С.Маккаллоком и Уолтером X.Питтсом в их классической работе по нервной активности [Имеется в виду статья: Маккаллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной активности, в сборнике "Автоматы" - М.: ИЛ, 1956.- Прим. перев.]. Эти формальные нейроны намного проще человеческих нейронов. Сложность персептрона, построенного в виде двуслойной нейронной сети, тоже очень далека от сложности первых двух слоев зрительной области коры головного мозга человека. Более того, "за" этими слоями скрывается поразительный по сложности и почти совершенно неисследованный аналитический аппарат, отсутствующий в модели зрения-распознавания, которую представляет персептрон. Даже для того, чтобы как-то приступить к моделированию этой сложнейшей системы, нужно заменить главного демона машиной Тьюринга, но здесь мы уже не сможем пойти дальше чисто умозрительных размышлений и поэтому лучше остановимся.
Несмотря на то что персептроны представляют собой как бы "глаза без ума", они подкупающе просты и по отношению по крайней мере к некоторым классам образов определенно обладают способностью распознавания. Интересно, удастся ли читателям открыть какие-то другие, не упомянутые здесь образы, которые смог бы распознавать окошечный персептрон. Те, кто захотят ответить на более трудный вопрос, а именно какие подмножества из 16 приведенных в настоящей статье подобразов размером 2*2 порождают "хорошие" окошечные персептроны (т.е. такие, которые способны распознать хотя бы один образ), возможно, лучше уяснят себе задачу и пути ее решения, если воспользуются дополнительным ограничением. Оно заключается в том, чтобы распознаваемые образы были "переносимыми" - другими словами, чтобы их можно было переносить из одной произвольной области сетчатки в другую, не нарушая способности персептрона распознавать их. Это требование не только исключает из рассмотрения некоторые слишком узко специализированные модели окошечных персептронов (например, устройство, которое распознает единственную темную клетку, расположенную в правом верхнем углу сетчатки), но также создает эффект сканирования персептроном "реальной" сцены, подобно тому как это делал мой фантастический аппарат.
Хотя, вообще говоря, персептроны, ограниченные по диаметру, не способны проводить различия между связными и несвязными фигурами, на некоторых классах фигур свойство связности может быть распознаваемым. Например, в классе образов, состоящих из множеств прямоугольников, связными образами будут такие, которые состоят из одного прямоугольника. Можете ли вы построить схему псрсептрона, распознающего именно такие образы? Ваши локальные демоны должны будут "смотреть" через окошки размером 2*2, но если нужно, вы можете воспользоваться дополнительными демонами.
Из того, что было сказано мною выше о книге Минского и Пейперта "Персептроны", можно было сделать вывод, что с ее выходом в свет исследования в области персептронов прекратились. Однако правильнее было бы сказать, что не существует больше оснований для тех неоправданно больших надежд, которые возлагались на персептроны и их способность к распознаванию. Цель исследования, проведенного и опубликованного Минским и Пейпертом, вовсе не заключалась в том, чтобы прекратить все работы по теории персептронов. Точная оценка возможностей, которыми обладают эти простые и иногда эффективные устройства, пока остается открытым вопросом.
Розенблатт, исследования которого затрагивали также психологию и нейробиологию, трагически погиб в результате несчастного случая, произошедшего в день его рождения, когда ему исполнилось 43 года, 11 июля 1971г. в штате Мэриленд.
БИБЛИОГРАФИЯ
PRINCIPLES OF NEURODYNAMICS: PERCEPTRONS AND THE THEORY OF BRAIN MECHANISMS. Spartan Books, 1962.
Минский М., Пейперт С. Персептроны. Перев. с англ.- М.: Мир, 1971.
ОТКЛИКИ
2 1985
СТАТЬЯ о персептронах ("Computer Recreations", September) привела некоторых читателей к мысли об их использовании, других же побудила заняться собственными исследованиями. Эд Маннинг из Стратфорда (шт.Коннектикут) построил "персептрон сортов" (perceptron of sorts), придуманный 10 лет назад для того, чтобы преобразовывать реальные образы в дискретные квадратики на сетчатке персептрона. Маннинг был одним из многих, кто заметил ошибку в окошечном персептроне для распознавания нескольких прямоугольников, изображенном в сентябрьском номере журнала: четыре последних элемента в списке подобразов демона должны быть наполовину голубые и наполовину белые. Маннинг интересуется, не была ли эта ошибка специально задумана как испытание для читателей. Не могу удержаться от соблазна и отвечаю, что так оно и было.
Дж.Стормо, научный сотрудник факультета молекулярной, клеточной и эволюционной биологии Колорадского университета в Боулдере, использовал идею персептрона в автоматическом распознавании образов. Он построил весовую функцию персептрона для распознавания участков связывания в последовательности нуклеотидов транспортных РНК. Чтобы его персептрон работал эффективно, Стормо воспользовался теоремой сходимости. Результаты оказались весьма обнадеживающими: персептрон распознавал участки связывания весьма успешно.
Любой окошечный персептрон, список подобразов которого включает сплошь белое или сплошь черное окошко, является "хорошим" персептроном. Это отмечает Л.Хилл из Веннса (шт.Калифорния). Его также интересует вопрос, является ли допустимым, чтобы сетчатка была сплошь белая или сплошь черная. Ответ зависит от распознаваемых образов. В случае персептрона для распознавания нескольких прямоугольников представляется разумным считать сплошь черную сетчатку просто одним большим прямоугольником.
Наибольших успехов в предложенном мной мини-исследовании добился К.Руссо из Вычислительного центра колледжа Линчберга (шт.Виргиния). Он решил исключить окошечные персептроны со сплошь белыми или сплошь черными подобразамн. Ему удалось охарактеризовать "хорошие" персептроны (т.е. такие, которые распознают хотя бы один образ). Для этого используются трансляционные соотношения между подобразами в списке персептрона. Если сдвинуть окошечный подобраз на одну клетку в любом из четырех основных направлений, то снова должен получиться какой-то подобраз из списка. Затем Руссо рассмотрел минимальные окошечные персептроны, список подобразов которых не может быть сокращен без ущерба их распознавательной способности. Из таких персептронов, как из кирпичиков, строятся все "хорошие" персептроны. Руссо написал программу для ЭВМ, которая нашла все минимальные окошечные персептроны с размером списка от 2-го до 5-го порядка. Нет ни одного минимального персептрона 6-го порядка. Руссо бросил всем вызов, обратив поставленную мной задачу: я предлагал читателям найти образ, распознаваемый данным персептроном. Руссо же предлагает отыскивать персептрон, распознающий данный образ. Д.Эванс из Хартфорда (шт.Коннектикут) возлагает вину за неудачи персептронов на ограничение, присущее двухуровневой иерархии локальных демонов, отчитывающихся перед одним главным демоном. Введя некое демоническое промежуточное управление, Эванс преодолел открытую Минским и Пэйпертом "слабость" обычных персептронов, которые неспособны распознавать связность. Демоны нижнего уровня образуют своего рода сетчатку, б которой черное или белое состояние клетки отвечает наличию или отсутствию сигнала от определенного демона. Демоны второго уровня следят за образами, созданными демонами нижнего уровня, и посылают сигнал о наличии или отсутствии подобраза главному демону. Трехуровневое устройство способно распознать, какой из четырех пробных образов является связным, а какой нет.
НЕДОСТАТКИ "ЭЛЕКТРОННОГО ГЛАЗА" ГОВОРЯТ
О ТОМ, ЧТО ЗРИТЕЛЬНОЕ ВОСПРИЯТИЕ НЕВОЗМОЖНО
БЕЗ ПРЕДСТАВЛЕНИЯ О ВИДИМОМ ОБЪЕКТЕ
А.К.ДЬЮДНИ
Полностью этот журнал см.
 ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.ВООБРАЗИМ себе небольшое устройство наподобие фотоаппарата с линзой на передней панели корпуса и позиционным переключателем сбоку. Различным положениям переключателя соответствуют такие надписи, как "дерево", "дом", "кошка" и т.д. Установив переключатель в положение "кошка", отправимся на прогулку. Как только мы обнаружим кошку на соседнем крыльце, направим на нее наш аппарат: на его панели загорится красная сигнальная лампочка. Если мы направим аппарат на другие объекты, лампочка гореть не будет.
Внутри нашего аппарата находятся фотоэлектрические детекторы - своеобразная электронная сетчатка, посылающая импульсы тока на двуслойную логическую схему. Устройство подобного типа называется персептроном (от английского слова perception - восприятие, осознание.- Перев.). В свое время на персептроны возлагались большие надежды. Считалось, что в конце концов они смогут справиться с задачами распознавания образов в реальном мире, подобно тому как это выглядело в только что приведенном фантастическом примере. Надежды, однако, не оправдались.
В 50-х и 60-х годах наблюдался колоссальный взрыв творческой активности в новой стремительно развивавшейся области вычислительной техники и теории вычислений. Многие исследователи находились тогда под влиянием таких романтических понятий, как самоорганизующиеся системы, обучающиеся машины и компьютеры, обладающие "интеллектом". Я бы назвал этот период эпохой кибернетики. Невероятные машины, которые могли бы видеть, думать или даже воспроизводить самих себя, казалось, вот-вот будут созданы. Простейшей из этих машин был персептрон.
ПЕРСЕПТРОН состоит из решетчатой сетчатки, разделенной на конечное число ячеек - детекторов света. Подобно некоторым клеткам сетчатки глаза, каждая ячейка "включается", посылая импульс тока, когда получает достаточное количество света; в противном случае она остается в "выключенном" состоянии. Поэтому было бы естественно представить образ, анализируемый персептроном, в виде решетки, состоящей из светлых и темных квадратиков, как на рисунке на с.128.

Персептрон пытается распознать кошку
Помимо сетчатки персептрон содержит великое множество простейших элементов, принимающих решение, которые я буду называть локальными демонами. Каждый локальный демон проверяет определенное подмножество ячеек сетчатки и посылает сигнал, характеризующий состояние этих ячеек, более сложному логическому элементу, принимающему более ответственное решение. Этот элемент я назову главным демоном. Уточним: у каждого локального демона есть набор определенных образов, за появлением которых он должен следить во вверенной ему области, т.е. на своем подмножестве ячеек сетчатки. Когда там появляется один из таких образов, локальный демон посылает сигнал главному демону; в противном случае он "молчит". Работа главного демона несколько сложнее - он должен выполнять некоторые расчетные операции. Амплитуда сигнала от каждого локального демона умножается на специально обусловленное положительное или отрицательное число ("вес", приписанный данному локальному демону), и полученные результаты складываются. Если полученная сумма не меньше установленного порога, главный демон говорит "да"; в противном случае - "нет". Чтобы не вдаваться в интригующий вопрос о том, как выглядят эти демоны, я изобразил их в виде кубиков, приведенных на с.128.
Демонам часто поручают опасную или даже невозможную работу, например такую, как открывать микроскопические дверцы в перегородке сосуда, чтобы пропускать молекулы, обладающие определенными свойствами. У демонов персептрона работа сравнительно нетрудная. На самом деле локальных демонов можно заменить простыми логическими схемами, а с работой главного демона легко может справиться устройство из нескольких регистров, сумматора и компаратора (все это элементы центрального процессора, присутствующие в любом компьютере). Однако демоны обладают романтическим очарованием, которого лишены электронные устройства.
Работа персептрона заключается в том. чтобы говорить "да", когда ему показывают определенные образы, и "нет" - в ответ на все остальные. При этом считается, что образы первого типа "распознаются" персептроном. И хотя перспектива создания персептрона, распознающего кошек, весьма сомнительна, существуют другие, вполне разрешимые задачи распознавания.
Персептрон можно запрограммировать в том или ином смысле для распознавания определенного класса образов за счет правильного подбора весовых коэффициентов и порогового значения их суммы. Локальные демоны, функция которых заключается в том, чтобы сигнализировать о наличии определенного класса объектов (образов), имеют положительные весовые коэффициенты, а те, которые должны свидетельствовать против, получают отрицательные веса. Абсолютная величина весового коэффициента говорит о сравнительной важности данного свидетельства. Хотя рассматриваемые здесь персептроны оперируют фиксированными весами, программирование играет центральную роль в теории персептронов, разработанной в 50-х годах.
Персептрон, описанный ниже, распознает темный прямоугольник произвольного размера или формы, расположенный в любом месте на его сетчатке. На самом деле он распознает любое количество таких прямоугольников (в том числе и их отсутствие) при условии, что ни одна пара прямоугольников не касается друг друга ни одной из сторон, ни вершинами углов. Персептрон строится в три этапа. Сначала к каждой области сетчатки размером 2*2 подсоединяется один локальный демон. Затем все распознаваемые подобразы из набора Р (позитивные), который приведен на верхнем рисунке на с.129, заносятся в список каждого локального демона. Третий этап заключается в том, чтобы установить все весовые коэффициенты главного демона равными +1, а значение порога равным d - по числу локальных демонов.

Подобразы размером 2*2, распознаваемые позитивными (Р) и негативными (N) локальными демонами
ПОДОБНОЕ устройство требует довольно большого числа демонов: если сетчатка персептрона имеет размер n*n, то необходимое количество локальных демонов составит (n-1)2. Им всем придаются положительные веса - это означает, что они все должны давать позитивные свидетельства при распознавании прямоугольников. Нетрудно видеть, например, что при проецировании одного темного прямоугольника на сетчатку персептрона каждая область ячеек размером 2*2 получит один из подобразов, содержащихся в списке Р. Следовательно, каждый демон пошлет сигнал главному демону и значение "взвешенной" суммы этих сигналов, разумеется, будет равно d. В этом случае главный демон говорит "да". С другой стороны, если хотя бы одна из темных фигур не является прямоугольником или два прямоугольника касаются друг друга, то по крайней мере одна область сетчатки персептрона получит подобраз, содержащийся в списке N (негативные), который приведен на с.129 вверху. Поэтому по крайней мере один локальный демон не пошлет сигнала, и главный демон получит сумму, не превышающую d-1. В результате он скажет "нет".
Можно построить эквивалентный персептрон, в котором каждый локальный демон располагает меньшим списком N. В этом случае все веса будут равны -1, а пороговым значением будет нуль. Каждый локальный демон будет поставлять отрицательное (негативное) свидетельство при предъявлении образа, состоящего из прямоугольников, и главный демон скажет "да" только в том случае, если ни один локальный демон не пошлет сигнала.
Персептрон описанной выше разновидности обладает многими интересными свойствами, поэтому дадим ему название. Независимо от того, каким конкретным списком оснащены локальные демоны, устройство подобного рола назовем "окошечным" персептроном, потому что каждый локальный демон видит входной образ через "окошко" размером 2*2. При размерах сетчатки n*n число локальных демонов должно быть равно (n-1)2 и значение порога также равно этой величине.
Вообще говоря, персептроны, по-видимому, лучше всего распознают геометрические фигуры. Окошечные персептроны могут распознавать не только прямоугольники, но также и "черные дыры" (изолированные темные клетки), вертикальные и горизонтальные линии, образы типа "лестницы", "шахматной доски" и многие другие. Все зависит от того, из каких под-образов размером 2*2 состоят списки локальных демонов (см. рисунок на с.130). В действительности каждое подмножество из 16 возможных подобразов размером 2*2 определяет свой окошенный персептрон и каждый из результирующих 65536 окошечных персептронов распознает определенный класс образов. Но, впрочем, распознает ли?

Образы, распознаваемые "окошечным" перцептроном
Окошечный персептрон с двумя следующими подобразами

ничего не распознает. Причину понять нетрудно. Предполагая, что азмеры сетчатки достаточно велики, выберем окошко размером 2*2 в средней ее части. Если на это окошко проецируется первый из двух приведенных выше подобразов, то рассмотрим окошко, сдвинутое относительно данного на одну клетку вправо: оно будет иметь темную клетку в верхнем левом углу. Поэтому локальный демон, контролирующий эту область, не пошлет сигнал главному демону. Напомним, что по определению окошечного персептрона необходимое условие для распознавания образа заключается в том, чтобы ВСЕ локальные демоны послали сигнал, свидетельствующий в пользу данного образа. Если же на первое окошко проецируется второй подобраз из списка, то сдвиг на одну ячейку влево приведет к аналогичному противоречию.
КАКИЕ ЖЕ подмножества из 16 основных подобразов порождают окошечные персептроны, которые действительно что-то распознают? На этот вопрос, наверное, трудно ответить, однако он служит очень хорошей иллюстрацией тех вопросов, которыми может заинтересоваться программист-теоретик или математик, столкнувшись с феноменом персептрона, который ничего не распознает. Поскольку речь идет о большом количестве таких персептронов, ответ лучше всего выразить в виде какого-либо легко применяемого критерия или теста: задавая определенное подмножество подобразов 2*2, можно применить тест и получить ответ для данного подмножества.
Из замечаний, сделанных выше, должно быть ясно, что вовсе не обязательно быть теоретиком-программистом, чтобы отвечать на подобные вопросы. Хотя эти вопросы несколько сложнее головоломок, обычно публикуемых в рубрике, посвященной занимательным математическим задачам, в принципе они требуют такого же мышления. Читатели, решившие хотя бы одну из головоломок Мартина Гарднера, печатавшихся в разделе "Математические игры" нашего журнала, наверное, смогут добиться некоторых успехов, пытаясь найти ответ на поставленный выше вопрос. А вообще в теоретических исследованиях, так же как и в экспериментальных, частичный ответ все же лучше, чем никакого.
Работа в области исследования возможностей персептронов была начата Фрэнком Розенблаттом в Корнеллском университете в 50-х годах [С работами Ф.Розенблатта можно познакомиться в сборнике "Самоорганизующиеся системы", выпущенном издательством "Мир" в 1964г. (с.65-112).- Прим. перев.]. Розенблатт и его последователи как в Корнеллском университете, так и в других исследовательских центрах относились оптимистично к перспективе персептронов как практически полезных устройств для распознавания образов. Из "теоремы о сходимости" следует, что в принципе персептроны могут научиться распознавать образы, если автоматизировать подбор весовых коэффициентов, с которыми работает главный демон. Эта теорема утверждает, что любое перераспределение весов в направлении, повышающем способность к распознаванию, может послужить основой для дальнейшего улучшения. Были построены реальные персептроны, и в некоторых экспериментах с простыми образами были получены хорошие результаты, частота распознавания была довольно высокой.
То, что тогда казалось обнадеживающей перспективой, было в какой-то степени иллюзией. По мнению Марвина Л. Минского и Сеймура Пейперта из Массачусетса го технологического института, энтузиастов, исследовавших персептроны, подкупали простота и кажущаяся перспективность этих устройств. Но за этими привлекательными свойствами скрывались серьезные недостатки принципиального характера. В 1969г. вышла в свет книга Минского и Пейперта "Персептроны" [М.Минский, С.Пейперт. Персептроны,- М.: Мир, 1971.- Прим. перев.], которая произвела эффект иголки, проткнувшей воздушный шар. В книге было приведено несколько задач и строгое доказательство того факта, что персептроны не могут с ними справиться.
Одним из наиболее примечательных дефектов, вскрытых Минским и Пейпертом, было то, что некоторые персептроны не способны установить, является ли показанная им геометрическая фигура связной (т.е. содержащей изолированные части). Исходя из того, что каждый локальный демон обследует лишь какую-то ограниченную область, Минский и Пейперт привели примеры четырех образов, подобранных так, что один из них всегда вводит в заблуждение персептрон, задача которого заключается в том, чтобы распознать, является ли образ связным. Эти примеры показаны на нижнем рисунке на с.129. Два из них (b и c) представляют собой связные фигуры, а два других (a и d) - нет.

Четыре фигуры, подобранные так, чтобы запутать персептрон, распознающий свойство связности
ДОПУСТИМ, кто-то утверждает, что изобрел персептрон, ограниченный по диаметру, который способен различать связные и несвязные образы. Под термином "ограниченный по диаметру" я понимаю то, что существует некоторое число m, такое, что каждый локальный демон может просматривать образ только через окошко, размеры которого не превышают квадрата из m*m ячеек сетчатки. Чтобы проверить это утверждение, в примере Минского и Пейперта следовало бы подобрать 4 образа так, чтобы размеры каждого из них превышали m ячеек. Такие локальные демоны можно разделить на 3 непересекающихся множества. "Левые" демоны видят по крайней мере одну клетку на левом крае фигуры, "правые" - по крайней мере одну клетку на правом крае, а "прочие" не относятся ни к "левым", ни к "правым".
Когда гипотетическому персептрону, распознающему свойство связности, представляют образ а, он либо терпит неудачу (говоря "да"), либо добивается успеха (говоря "нет"). Если он терпит неудачу, то тест, раэумеется, завершен. Если попытка оказывается для него успешной, то следующий шаг заключается в том, чтобы исследовать сумму, получаемую главным демоном, путем разбиения ее на 3 части: L, О, R, представляющие взвешенные суммы, получаемые соответственно от левых, прочих и правых демонов, посылающих сигналы главному демону, когда на сетчатку проецируется образ а. Поскольку в данном случае персептрон, распознающий свойство связности, говорит "нет", сумма частей L, О и R, очевидно, оказалась меньше порогового значения. Если образ a заменить теперь образом b, только левые демоны изменят свой ответ, поскольку изменяются лишь клетки, расположенные вдоль левого края фигуры. Предположим, что значение частичной суммы изменяется и становится равным L'. С другой стороны, если образ а заменить образом с, то изменятся лишь клетки, расположенные вдоль правого края фигуры, и лишь правые локальные демоны изменят свой ответ. При этом частичная сумма R изменится и станет равной, скажем, R'.
Теперь персептрон попадает в очень интересную ситуацию. Поскольку образы b и с связные, от должен ответить "да" в обоих случаях. Поэтому суммы L'+O+R и L+O+R' должны быть не меньше порогового значения. Однако уже известно, что L+О+R меньше порогового значения, так как образ a был несвязным. Отсюда следует, что L' больше L, a R' больше R. Развязка наступает, когда персептрону показывают образ d, этого "удара" ему уже не выдержать. Здесь по сравнению с образом a изменяют свое состояние клетки, расположенные как на левом, так и на правом краю фигуры. В результате главный демон получает сумму L'+О+R', которая определенно больше порогового значения. Главный демон говорит "да" и , таким образом, ошибается.
Среди прочих недостатков, присущих персептронам и выявленных Минским и Пейпертом, можно отметить и тот факт, что для некоторых задач распознавания требуется настолько большое число локальных демонов, что практическая реализация такого персептрона окажется невозможной, в то время как для некоторых других задач скорость обучения (сходимость) персептронов слишком мала.
ВЕРОЯТНО, нас не должен удивлять тот факт, что персептроны терпят неудачу во многих случаях там, где человеческая зрительная и распознающая система действует успешно. Я уже говорил, что локальные демоны и главный демон можно вполне заменить простыми вычислительными электронными схемами. Их функции могут также выполнять так называемые формальные нейроны, впервые описанные в 40-х годах Уорреном С.Маккаллоком и Уолтером X.Питтсом в их классической работе по нервной активности [Имеется в виду статья: Маккаллок У.С., Питтс У. Логическое исчисление идей, относящихся к нервной активности, в сборнике "Автоматы" - М.: ИЛ, 1956.- Прим. перев.]. Эти формальные нейроны намного проще человеческих нейронов. Сложность персептрона, построенного в виде двуслойной нейронной сети, тоже очень далека от сложности первых двух слоев зрительной области коры головного мозга человека. Более того, "за" этими слоями скрывается поразительный по сложности и почти совершенно неисследованный аналитический аппарат, отсутствующий в модели зрения-распознавания, которую представляет персептрон. Даже для того, чтобы как-то приступить к моделированию этой сложнейшей системы, нужно заменить главного демона машиной Тьюринга, но здесь мы уже не сможем пойти дальше чисто умозрительных размышлений и поэтому лучше остановимся.
Несмотря на то что персептроны представляют собой как бы "глаза без ума", они подкупающе просты и по отношению по крайней мере к некоторым классам образов определенно обладают способностью распознавания. Интересно, удастся ли читателям открыть какие-то другие, не упомянутые здесь образы, которые смог бы распознавать окошечный персептрон. Те, кто захотят ответить на более трудный вопрос, а именно какие подмножества из 16 приведенных в настоящей статье подобразов размером 2*2 порождают "хорошие" окошечные персептроны (т.е. такие, которые способны распознать хотя бы один образ), возможно, лучше уяснят себе задачу и пути ее решения, если воспользуются дополнительным ограничением. Оно заключается в том, чтобы распознаваемые образы были "переносимыми" - другими словами, чтобы их можно было переносить из одной произвольной области сетчатки в другую, не нарушая способности персептрона распознавать их. Это требование не только исключает из рассмотрения некоторые слишком узко специализированные модели окошечных персептронов (например, устройство, которое распознает единственную темную клетку, расположенную в правом верхнем углу сетчатки), но также создает эффект сканирования персептроном "реальной" сцены, подобно тому как это делал мой фантастический аппарат.
Хотя, вообще говоря, персептроны, ограниченные по диаметру, не способны проводить различия между связными и несвязными фигурами, на некоторых классах фигур свойство связности может быть распознаваемым. Например, в классе образов, состоящих из множеств прямоугольников, связными образами будут такие, которые состоят из одного прямоугольника. Можете ли вы построить схему псрсептрона, распознающего именно такие образы? Ваши локальные демоны должны будут "смотреть" через окошки размером 2*2, но если нужно, вы можете воспользоваться дополнительными демонами.
Из того, что было сказано мною выше о книге Минского и Пейперта "Персептроны", можно было сделать вывод, что с ее выходом в свет исследования в области персептронов прекратились. Однако правильнее было бы сказать, что не существует больше оснований для тех неоправданно больших надежд, которые возлагались на персептроны и их способность к распознаванию. Цель исследования, проведенного и опубликованного Минским и Пейпертом, вовсе не заключалась в том, чтобы прекратить все работы по теории персептронов. Точная оценка возможностей, которыми обладают эти простые и иногда эффективные устройства, пока остается открытым вопросом.
Розенблатт, исследования которого затрагивали также психологию и нейробиологию, трагически погиб в результате несчастного случая, произошедшего в день его рождения, когда ему исполнилось 43 года, 11 июля 1971г. в штате Мэриленд.
БИБЛИОГРАФИЯ
PRINCIPLES OF NEURODYNAMICS: PERCEPTRONS AND THE THEORY OF BRAIN MECHANISMS. Spartan Books, 1962.
Минский М., Пейперт С. Персептроны. Перев. с англ.- М.: Мир, 1971.
ОТКЛИКИ
2 1985
СТАТЬЯ о персептронах ("Computer Recreations", September) привела некоторых читателей к мысли об их использовании, других же побудила заняться собственными исследованиями. Эд Маннинг из Стратфорда (шт.Коннектикут) построил "персептрон сортов" (perceptron of sorts), придуманный 10 лет назад для того, чтобы преобразовывать реальные образы в дискретные квадратики на сетчатке персептрона. Маннинг был одним из многих, кто заметил ошибку в окошечном персептроне для распознавания нескольких прямоугольников, изображенном в сентябрьском номере журнала: четыре последних элемента в списке подобразов демона должны быть наполовину голубые и наполовину белые. Маннинг интересуется, не была ли эта ошибка специально задумана как испытание для читателей. Не могу удержаться от соблазна и отвечаю, что так оно и было.
Дж.Стормо, научный сотрудник факультета молекулярной, клеточной и эволюционной биологии Колорадского университета в Боулдере, использовал идею персептрона в автоматическом распознавании образов. Он построил весовую функцию персептрона для распознавания участков связывания в последовательности нуклеотидов транспортных РНК. Чтобы его персептрон работал эффективно, Стормо воспользовался теоремой сходимости. Результаты оказались весьма обнадеживающими: персептрон распознавал участки связывания весьма успешно.
Любой окошечный персептрон, список подобразов которого включает сплошь белое или сплошь черное окошко, является "хорошим" персептроном. Это отмечает Л.Хилл из Веннса (шт.Калифорния). Его также интересует вопрос, является ли допустимым, чтобы сетчатка была сплошь белая или сплошь черная. Ответ зависит от распознаваемых образов. В случае персептрона для распознавания нескольких прямоугольников представляется разумным считать сплошь черную сетчатку просто одним большим прямоугольником.
Наибольших успехов в предложенном мной мини-исследовании добился К.Руссо из Вычислительного центра колледжа Линчберга (шт.Виргиния). Он решил исключить окошечные персептроны со сплошь белыми или сплошь черными подобразамн. Ему удалось охарактеризовать "хорошие" персептроны (т.е. такие, которые распознают хотя бы один образ). Для этого используются трансляционные соотношения между подобразами в списке персептрона. Если сдвинуть окошечный подобраз на одну клетку в любом из четырех основных направлений, то снова должен получиться какой-то подобраз из списка. Затем Руссо рассмотрел минимальные окошечные персептроны, список подобразов которых не может быть сокращен без ущерба их распознавательной способности. Из таких персептронов, как из кирпичиков, строятся все "хорошие" персептроны. Руссо написал программу для ЭВМ, которая нашла все минимальные окошечные персептроны с размером списка от 2-го до 5-го порядка. Нет ни одного минимального персептрона 6-го порядка. Руссо бросил всем вызов, обратив поставленную мной задачу: я предлагал читателям найти образ, распознаваемый данным персептроном. Руссо же предлагает отыскивать персептрон, распознающий данный образ. Д.Эванс из Хартфорда (шт.Коннектикут) возлагает вину за неудачи персептронов на ограничение, присущее двухуровневой иерархии локальных демонов, отчитывающихся перед одним главным демоном. Введя некое демоническое промежуточное управление, Эванс преодолел открытую Минским и Пэйпертом "слабость" обычных персептронов, которые неспособны распознавать связность. Демоны нижнего уровня образуют своего рода сетчатку, б которой черное или белое состояние клетки отвечает наличию или отсутствию сигнала от определенного демона. Демоны второго уровня следят за образами, созданными демонами нижнего уровня, и посылают сигнал о наличии или отсутствии подобраза главному демону. Трехуровневое устройство способно распознать, какой из четырех пробных образов является связным, а какой нет.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
1 1985
"ИНЬ" И "ЯН": РЕКУРСИЯ И ИТЕРАЦИЯ, "ХАНОЙСКАЯ БАШНЯ" И "КИТАЙСКИЕ КОЛЬЦА"
А.К.ДЬЮДНИ
ХОРОШИЕ головоломки вводят нас в "царство абстрактной мысли, населенное математиками и другими теоретиками". Лучшие головоломки воплощают в себе интересные темы, которые, конечно, намного важнее самих головоломок.
Две классические головоломки - "Ханойская башня" и "Китайские кольца" - представляют две пары взаимно противоположных понятий: "рекурсия" - "итерация" и "единство" - "многообразие". Если не задумываться нал такими серьезными проблемами, то головоломки - хорошее развлечение. И хотя подчас они обескураживают новичка, каждый испытывает волнующее чувство удовлетворения, все глубже погружаясь в царство абстрактной мысли.
Задача "Ханойская башня" заключается в перемещении дисков, нанизанных на вертикальный стержень, с помощью двух других стержней (см. рисунок внизу). В исходном положении на один из стержней нанизано некоторое число дисков различного размера, так что наименьший диск находится сверху. Диски можно перемещать согласно следующим простым правилам:
1. Перекладывать диски со стержня на стержень можно только по одному.
2. Нельзя класть диск большего размера на диск меньшего размера.

Первые два шага в решении головоломки "Ханойская башня"
Сначала нужно переложить наименьший диск, так как в исходном положении доступен только он. Затем для наименьшего диска возможны два перемещения (оба бессмысленные) и одно перемещение для диска следующего по величине размера. Его можно переложить на пустой стержень, потому что на диск наименьшего размера его класть нельзя (правило 2). На третьем шаге выбрать правильный вариант перемещения уже труднее: следует ли второй диск вернуть на исходный стержень или нужно снова переместить первый диск, а если так, то на какой стержень?
Начиная с этого шага, играющий при выборе каждого следующего хода имеет все большие шансы совершить ошибку. Но даже в том случае, если все перемещения будут выбраны правильно, потребуется 2^n-1 шага, чтобы переместить башню из n дисков по одному на каждом шаге, на другой стержень (число шагов мы вычислим ниже). Чтобы решить эту головоломку даже при сравнительно небольшом числе дисков, требуется поразительно много времени. Это прекрасно проиллюстрировано в легенде, которую мы процитируем по классической книге Болла о головоломках (W.R.Ball "Mathematical Recreations and Essays").
"В великом храме Бенареса... под куполом, находящимся точно в центре мира, покоится бронзовая пластина с тремя алмазными стержнями, каждый длиной в один локоть и толщиной как тело пчелы. На один из этих стержней бог при сотворении мира положил шестьдесят четыре диска из чистого золота, так что наибольший диск лежит на бронзовой пластине, а остальные образуют пирамиду, самый маленький диск находится на вершине пирамиды. Это башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя мудрым и незыблемым законам Брамы, согласно которым диски можно перекладывать только по одному и каждый диск можно класть на стержень только в том случае, если под ним не окажется диск меньшего размера. Когда все шестьдесят четыре диска будут таким образом перенесены, и башня, и храмы, и жрецы-брамины превратятся в прах, и наступит конец света".
То, что мир до сих пор не исчез, свидетельствует о чрезвычайно большом времени, требующемся для решения задачи: даже если жрецы будут перекладывать по одному диску в секунду, то потребуется более 500 млрд. лет, чтобы переместить всю башню из 64 дисков!
А теперь (без всякого риска для Вселенной) читатель может ближе познакомиться с этой задачей, взяв пять игральных карт, например последовательно от туза до пятерки пик, и условно выделив три места на столе, куда можно было бы класть карты. Сложите эти карты колодой в одном из трех мест по порядку, так чтобы туз находился сверху. Попытайтесь решить головоломку о башне с пятью дисками, перемещая карты по одной с места на место, но так, чтобы ни одна карта не легла на карту меньшего достоинства (в данном случае считается, что двойка "старше" туза). Сможете ли вы полностью переместить башню из пяти карт прежде, чем наступит "конец света"? Согласно формуле 2^5-1, это можно сделать за 31 шаг (перемещение).
Как следует приступать к решению подобных задач? Почему некоторые люди, казалось бы, с легкостью решают головоломки, в то время как другим решение дается с трудом? В моем ответе на второй вопрос содержится и ответ на первый: я убежден, что каждый из нас пользуется математическим мышлением почти в любой момент своего сознательного существования. Как наши умозаключения относительно того, почему дядюшка Гарри не присутствовал на свадьбе, так и план размещения тюков и чемоданов в багажнике машины являются результатами логического вывода из определенных предпосылок. Процесс такого вывода может оказаться весьма изощренным, а это дает мне основания полагать, что почти каждый человек, способный проявлять такие интуитивные способности, может стать хорошим аналитиком. Задача заключается в том, чтобы довести интуитивные аналитические способности до сознательного уровня.
Например, после того как человек "поиграл" некоторое время в задачу о башне из пяти дисков, он почти наверняка заметит, что время от времени возникает задача о башне с меньшим числом дисков. Довольно часто башня состоит из двух дисков, а иногда - из трех или даже четырех. Такие ситуации возникают сами собой, даже если человек не имеет четкого плана действий, а просто играет с пирамидками.
Однако вскоре у играющего возникает ключевая идея: "Если можно построить пирамиду из двух или трех дисков (не говоря уже о пирамиде из четырех дисков), то почему бы не сделать пирамиду из пяти дисков?" Заметив определенные закономерности в процессе построения пирамидок меньшего размера, играющий рано или поздно приходит к той последовательности шагов, которая приводит к перемещению всей башни из пяти дисков на один из свободных стержней.
Аналогичная идея воплощается в математике и программировании в виде одного из распространенных методов решения задач. Если попытаться сформулировать принцип, лежащий в основе этого метода, то получится что-нибудь вроде: "Если можно решить задачу несколько меньшего размера, чем та, которую требуется решить, то, может быть, удастся воспользоваться решением, полученным для меньшей задачи, чтобы решить большую". Таким образом, мы приходим к понятию рекурсии - вложение в процедуру решения той же самой процедуры.
Идею рекурсии в применении к головоломке о башне сформулировать нетрудно. Если можно решить задачу для n-1 дисков, то несомненно можно решить ее и для n дисков. Ключ к построению решения задачи для n дисков на основании решения для n-1 дисков лежит в решении задачи для двух дисков. Предположим, что требуется переместить два диска, верхний (первый) и нижний (второй) на другой стержень. Назовем стержень, на котором они находятся, исходным, стержень, на который их нужно переместить - конечным, а остающийся стержень - вспомогательным. Если переложить первый диск на вспомогательный стержень, а второй - на конечный, то на третьем шаге остается положить первый диск на конечный стержень поверх второго, завершив тем самым решение задачи. Рассмотренные три шага составляют основу трех стадий рекурсивного решения задачи, в котором первый диск мысленно заменяется башней, состоящей из n-1 дисков, а второй диск - нижним, наибольшим, n-м диском. Три стадии процесса решения можно представить следующим образом:
1. Перенести башню из n-1 дисков с исходного стержня на вспомогательный.
2. Переложить n-й диск с исходного стержня на конечный.
3. Снова перенести башню из n-1 дисков - на этот раз со вспомогательного стержня на конечный.
Описанная процедура из трех стадий аналогична решению, полученному нами для задачи с двумя дисками. Предположив, конечно, что мы можем решить задачу для n-1 дисков, можно воспользоваться последовательностью шагов для того, чтобы перенести башню из n-1 дисков с исходного стержня на вспомогательный. На следующей стадии n-й диск, освобожденный от лежавших на нем меньших дисков, перекладывается на конечный стержень. На третьей стадии можно снова воспользоваться решением задачи для n-1 дисков, чтобы переместить их со вспомогательного стержня на конечный.
Как решить задачу о башне, состоящей из n-1 дисков? Ответ очевиден: следует повторить ту же процедуру, но заменить параметр n-1 в стадиях 1 и 3 на n-2, и т.д. В конце концов мы придем к процедуре, в которой на стадиях 1 и 3 нужно переместить только один диск.
Рассмотренный процесс решения с многочисленными "ветвями" и "под-ветвями" для человека кажется очень запутанным, однако теперь нам становится ясно, почему для решения такой задачи требуется почти 2^n шагов: при каждом использовании процедуры она дважды повторяет сама себя. И если
человеку трудно себе представить, как можно реализовать подобную процедуру решения, для компьютера это не вызывает никаких затруднений.
Рисунок внизу показывает часть решения задачи с пятью дисками. Три стадии, рассмотренные нами выше, представлены как процедуры, встроенные в большую процедуру с именем БАШНЯ(n, X->Y). В этой процедуре используются три элемента данных: n - число дисков, которые нужно переместить, X - исходный стержень и Y - конечный стержень.
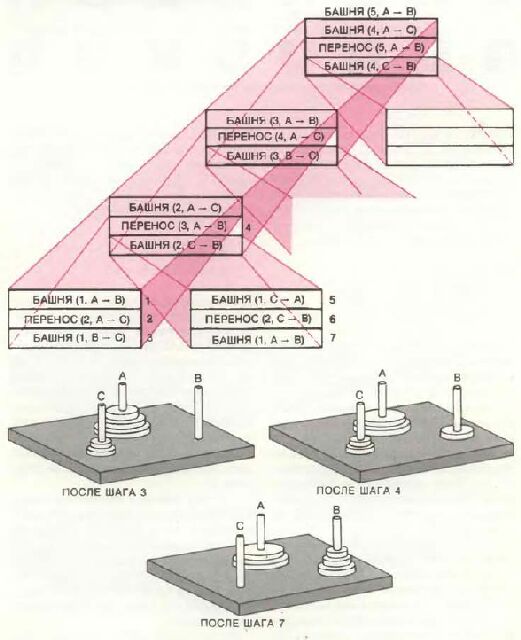
Рекурсивное решение головоломки "Ханойская башня"
Согласно введенной нами терминологии, схему рекурсивной программы для задачи о башне можно записать алгоритмически в следующем виде:
БАШНЯ(n, исходный->конечный):
БАШНЯ(n-1, исходный->вспомогательный),
ПЕРЕНОС(n, исходный->конечный),
БАШНЯ(n-1, вспомогательный->конечный).
Предположим, что нужно переместить пять дисков со стержня А (исходный) на стержень В (конечный). Если вместо n подставить число 5, а вместо слов "исходный", "конечный" и "вспомогательный" соответственно буквы A, B и C, то рассматриваемую процедуру можно переписать в таком виде:
БАШНЯ(5, A->B):
БАШНЯ(4, A->C),
ПЕРЕНОС(5, A->B),
БАШНЯ(4, C->B).
Другими словами, программа должна сначала справиться с задачей перемещения первых четырех дисков со стержня A на стержень C. Далее, согласно нашей алгоритмической записи, когда эта процедура завершена, нужно выполнить ПЕРЕНОС(5, A->В), т.е. перенести пятый, наибольший диск со стержня A на стержень B. Затем следует еще одно обращение к процедуре БАШНЯ для того, чтобы переместить первые четыре диска со стержня C на стержень B.
Каждое обращение к процедуре БАШНЯ влечет за собой еще три обращения к процедурам: БАШНЯ, затем ПЕРЕНОС и снова БАШНЯ. Процедура ПЕРЕНОС не может быть выполнена, пока не завершена первая процедура БАШНЯ. Это означает, что порядок действий, выполняемых компьютером, следующий: сначала четыре раза подряд выполняется процедура БАШНЯ; при этом мы перемещаемся вниз влево по диаграмме, пока не приходим к последовательности
БАШНЯ(1, A->B),
ПЕРЕНОС(2, A->C),
БАШНЯ(1, B->C).
Реальная программа должна будет содержать одну дополнительную команду. Когда остается только один диск в процедуре БАШНЯ, он переносится непосредственно со стержня на стержень без использования рекурсии. Первый диск переносится со стержня A на стержень B. Затем с помощью процедуры ПЕРЕНОС второй диск перемещается со стержня A на стержень C. Наконец, компьютер снова "переносит" первый диск, на этот раз со стержня В на стержень C.
К этому моменту компьютер завершил также первую процедуру БАШНЯ во второй снизу табличке рисунка на с.91 и выполняет ПЕРЕНОС(3, A->B), непосредственно перемешая третий диск со стержня A на стержень B. Затем команда БАШНЯ(2, C->B) разворачивается в три шага (нижняя табличка на рисунке).
Выполненные таким образом семь шагов завершают выполнение первой процедуры БАШНЯ на втором уровне диаграммы, и компьютер продолжает действовать в той же манере, то опускаясь к табличкам нижних уровней, то возвращаясь на более высокий уровень. В конце концов программа проходит пс всей диаграмме и задача оказывается решенной.
Эффект рекурсии воспринимается иногда как некое волшебство, потому что все многочисленные записи для запоминания, "где мы находимся", делаются компьютером - человеку трудно запомнить такой большой объем информации. Однако существует другой метод решения. Четыре года назад П.Бьюнеману из Университета шт.Пенсильвания и Л.Леви из AT&T Bell Laboratories удалось найти простую последовательность перемещений, позволяющих решить задачу о башне. Бьюнсман и Леви предложили воспользоваться простым чередованием перемещений двух видов:
1. Перенести наименьший диск с того стержня, на котором он находится в данный момент, на стержень, следующий в порядке движения часовой стрелки.
2. Перенести любой диск, кроме наименьшего.
Шаг 2 вовсе не такой произвольный, как может показаться на первый взгляд: под действующими ограничениями всегда находится лишь одно дозволенное перемещение. Чередование этих шагов продолжается до тех пор, пока задача не окажется решенной.
Не так давно я сделал из дерева все необходимое для задачи о башне с восемью дисками и предложил одному своему знакомому "поиграть". У него ничего не получилось и он вышел из комнаты. Тем временем я быстро объяснил алгоритм решения Бьюнсмана-Леви его восьмилетней дочери, которая до этого наблюдала за игрой как зачарованная. Когда мой друг вернулся, он был поражен, видя как его дочь спокойно без малейшего колебания перекладывает диски со стержня на стержень. Через несколько минут она решила задачу. "Ну и ребенок у тебя", - сказал я.
Главное преимущество метода Бьюнемана-Леви заключается в том, что он не требует рекурсии при решении задачи о башне; достаточным оказывается простое итерационное решение. В программе, построенной по итерационному принципу, повторяющиеся действия выполняются в виде обыкновенного цикла, а не за счет последовательности рекурсивных процедур. Хотя рекурсивные программы привлекают краткостью и изящной формой, они требуют большого объема памяти. На примере рассмотренной иллюстрации мы видим, что для рекурсивного решения задачи о башне необходим большой объем памяти, чтобы хранить информацию о всех незавершенных стадиях процедуры БАШНЯ. Итеративные программы, подобные той, которая основана на алгоритме решения Бьюнемана-Леви, почти совсем не требуют памяти. Однако заменить рекурсивную программу итерационной, подобно тому как мы сделали это в задаче о башне, удается редко.
Понятия рекурсии и итерации представляют собой одну из многих противоположностей в вычислительной математике. Это своеобразные "инь" и "ян" в подходе к процессам обработки информации с повторяющимися процедурами. "Инь" и "ян" - основные понятия древнекитайской мифологии и натурфилософии, полярные первоначала. Они лежат в основе книги "I Ching" ("Книга изменений"). "Инь" и "ян" подобны двоичным знакам 0 и 1, имеющим фундаментальное значение в кодировании, принятом при вычислениях на цифровых машинах. В книге "I Ching" "инь" представляется двойной горизонтальной черточкой (- -), а "ян" - одинарной ( --- ). Эти символы группируются в наборы по шесть, образуя 64 гексаграммы (см. рисунок на с.92). Интерпретируемая соответствующим образом, каждая гексаграмма представляет определенный выбор. "Верующий" тянет соломинки тысячелистника, чтобы определить, какая из этих гексаграмм имеет отношение к его жизни. Показанное здесь расположение символов приписывают Ван Вэну, правившему в 1150г. до н.э.

Расположение 64 гексаграмм Ван Вена из книги "I Ching"
Говоря о двоичных цифрах, я вспомнил еще один способ решения головоломки "Ханойская башня". Если пронумеровать диски последовательно, как 1, 2, 3, ..., n, начиная с наименьшего и кончая наибольшим диском, то каждый шаг в процессе решения задачи можно представить двоичным числом. Например, чтобы решить задачу с пятью дисками, составим список пятиразрядных двоичных чисел в порядке натурального ряда. Вот первые восемь пятиразрядных двоичных чисел:
00000
00001 (1)
00010 (2)
00011 (1)
00100 (3)
00101 (1)
00110 (2)
00111 (1)
01000 (4)
В каждом двоичном числе, имеющем предшественника в последовательности, есть только один разряд, изменившийся с 0 на 1. Позиция этого разряда (считая справа налево) дана в виде десятичного числа, указанного в скобках рядом с соответствующим двоичным числом. Но эти числа являются также номерами первых семи перекладываемых дисков. Это соответствие сохраняется на протяжении всей стандартной последовательности перемещений при решении задачи. Используя только произвольное двоичное число в этой последовательности, Т.Уолш с нашего факультета в Университете пров.Западный Онтарио при помощи компьютера может восстановить ситуацию, возникающую в ходе решения задачи на соответствующей данному двоичному числу стадии. Однако разработанный им алгоритм слишком громоздкий для того, чтобы его можно было привести в настоящей статье.
Теперь познакомим читателя с головоломкой "Китайские кольца" (см. рисунок внизу). Предмет головоломки состоит из длинной проволочной петли, прикрепленной к рукоятке, и набора колец, накинутых на петлю. Каждое кольцо при помощи металлических стержней свободно связано с деревянной пластинкой, расположенной под петлей. Стержень, соединяющий кольцо с деревянной пластинкой, проходит также через кольцо, расположенное позади данного (ближе к рукоятке), препятствуя тем самым его снятию с петли.
Первые два шага в решении головоломки "Китайские кольца"
Задача заключается в том, чтобы снять все кольца. Как и при решении задачи о башне, новичок может легко ошибиться. На рисунке показаны первые два шага на пути к решению задачи с пятью кольцами. Чтобы снять кольцо с петли, оттяните петлю назад насколько возможно, вплоть до стержня, расположенного непосредственно перед кольцом, которое вы хотите снять. Последнее можно повернуть вверх, так чтобы поднятая часть кольца перешла через дужку петли и сошла с нее. Оттянув теперь петлю вперед, кольцо можно наклонить в сторону, и оно выпадет из петли. По ходу решения головоломки часто требуется снова помешать кольца на петлю; в подобных случаях выполняется обратная процедура.
Попытки решить головоломку с китайскими кольцами связаны с той же общей проблемой, которая возникает в задаче о башне. Периодически появляются "конфигурации", в которых то или иное число колец оказывается снятым с петли, и играющий надеется, что существует какая-то аналогичная последовательность перемещений, позволяющая решить задачу полностью - снять все кольца с петли. Задача с кольцами может быть решена с помощью такого же рекурсивного алгоритма. Существует и простая итерационная процедура для ее решения, еще более очевидная, чем итерационное решение задачи о башне. Однако, чтобы не лишать читателя удовольствия, которое он испытает, решив задачу, мы не станем открывать секрета этого простого метода. Здесь практически невозможно дать какое-нибудь указание, не сказав ответа. Отметим лишь, что решение можно сформулировать в одном или двух предложениях, и оно не требует никакой формальной записи.
Удивительно, что эти задачи оказываются почти полностью идентичными. Это напоминает еще об одном контрасте, который часто наблюдается в математике вообше и в вычислительной математике в частности. Две задачи, внешне кажущиеся совершенно различными, при более детальном рассмотрении оказываются, по существу, одной и той же задачей!
Связь между двумя рассмотренными головоломками проявляется при анализе двух двоичных кодов и алгоритма перевода из одного кода в другой. Подобно тому как мы представляли шаги решения задачи о башне последовательными двоичными числами, введем двоичный код для представления задачи с кольцами: пусть 1 представляет кольцо, находящееся на петле, а 0 - соответственно кольцо, снятое с петли. Тогда задача с пятью кольцами может быть представлена пятиразрядной последовательностью 0 н 1, так что крайний левый разряд будет соответствовать кольцу, расположенному у рукоятки. Первые четыре конфигурации в задаче с кольцами, записанные в виде таких чисел, будут иметь следующий вид:
11111 (все кольца надеты)
11110 (первое кольцо снято)
11010 (первое и третье кольца сняты)
11011 (третье кольцо снято)
На следующих двух шагах снимается второе, а затем первое кольцо. После этого снимается пятое кольцо. Затем первые три кольца снова одеваются на петлю, чтобы можно было снять четвертое кольцо. Чтобы удалить все пять колец, требуется 21 шаг. Последние четыре конфигурации в последовательности, ведущей к решению, таковы:
00010 (второе кольцо надето)
00011 (первое и второе кольца надеты)
00001 (первое кольцо надето)
00000 (ни одно кольцо не надето)
Возможно, читателям будет интересно восполнить 14 недостающих кодов, решая задачу с кольцами в этой форме и следуя двум простым правилам (касающимся ограничений, связанных с расположением соседних колец):
1. Крайний правый разряд можно изменить (с 0 на 1 или с 1 на 0) в любой момент.
2. Из остальных разрядов можно изменять лишь тот, который находится непосредственно слева от крайнего справа разряда, имеющего значение 1.
На первый взгляд, кажется, что нет никакой связи между последовательностью из 21 двоичного кода, только что нами рассмотренной, и последовательностью двоичных чисел натурального ряда, возникающих при решении задачи о башне. На самом деле такая связь существует. Чтобы убедиться в этом, рассмотрим так называемый код Грэя. Инженер Ф.Грэй, работавший в 30-х годах в фирме AT&T Bell Laboratories, разработал его для исправления ошибок, возникающих при передаче информации электронными средствами. На рисунке внизу) приведены первые 22 двоичных числа натурального ряда и соответствующие коды Грэя.

Коды Грэя для первых 22 двоичных чисел.
Пятиразрядный код Грэя получается из соответствующего двоичного числа по простому правилу: если отсчитывать разряды слева, то первый разряд кода Грэя совладает с первым разрядом двоичного кода, а далее разряд кода Грэя равен 1, если соответствующий разряд двоичного кода отпичается от предыдущего разряда; в противном случае разряд кода Грэя равен 0.
При внимательном рассмотрении чисел, представленных в коде Грэя, можно заметить интересное совпадение. Коды Грэя, взятые в обратном порядке, совпадают с последовательностью конфигураций, ведущей к решению задачи "Китайские кольца"!
Таким образом, мы получили последовательность из 21 конфигурации для решения задачи с пятью кольцами, но для решения головоломки о башне с пятью дисками требуется 31 шаг. Можно предположить, что если эти задачи в каком-то смысле идентичны, то для их решения необходимо одно и то же число шагов. Несоответствие можно устранить, рассмотрев числа в коде Грэя, большие 21. Каждое из этих чисел представляет определенную конфигурацию в задаче с пятью кольцами, а последний код (соответствующий двоичному числу 11111), равный 10000, представляет конфигурацию, в которой только одно последнее кольцо находится на петле. Это означает, что самое трудное исходное положение в задаче с кольцами такое, когда все кольца, кроме одного, ближайшего к рукоятке, сняты. При таком исходном положении число ходов, требующихся для решения задачи с п кольцами, равно 2^n-1 (точно тому же числу, что и для задачи с n лисками).
Очень интересную книгу, посвященную китайским кольцам, написал недавно С.Африа, профессор экономических и математических наук Университета г.Оттавы; она называется "Кольцо связанных колец" ("The Ring of Linked Rings"). Именно ему принадлежит идея о связи между головоломкой "Китайские кольца" и понятием дуализма, символизируемого знаками "инь" и "ян". Хотя Африа выражает сомнение в китайском происхождении головоломки с кольцами, ему не удалось отыскать каких-либо определенных исторических сведений об игре, относящихся к периоду до 1550г. В книге Афрна описан также код Гро - предшественник кода Грэя, изобретенный в XIXв. французским математиком Л.Гро, опубликовавшим трактат об этой головоломке в 1872г. Кстати, французы называют задачу с кольцами "бездельником" (le baguenodier), a англичане - "утомительными железками" (the tiring irons).
Существует много других аспектов этих головоломок. Например, Л.Дики с математического факультета Университета Ватерлоо в Онтарио напомнил мне, что решение головоломки "Китайские кольца" эквивалентно также "прохождению" по ребрам n-мерного гиперкуба.
Выше мы установили, что задачу о башне с n дисками можно решить за 2^n-1 шага, если пользоваться при этом тремя стержнями. Интересно заметить, что число шагов значительно уменьшается при использовании большего числа стержней - оно равно 2n-1 для п+1 стержней. А какая картина наблюдается в интервале от 3 до n+1 стержней? По какому закону меняется минимальное число шагов для решения в зависимости от числа используемых стержней? Было бы интересно заняться этим вопросом в одной из последующих статей. В то время как я пишу эти строки, энтузиасты размышляют над задачей с четырьмя стержнями, а также над головоломкой, которую Мартин Гарднер называет "дьявольской версией башни" (или японской головоломкой).
БИБЛИОГРАФИЯ
MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.227, No.2, pages 106-109; August, 1972.
MATHEMATICAL RECREATIONS AND ESSAYS. W.W.ROUSE BALL, revised by H.S.M.Coxeter. University of Toronto Press, 1974.
THE TOWERS OF HANOI PROBLEM. PETER BUNEMAN AND LEON LEVY in Information Processing Letters, Vol.10, Nos.4 and 5, pages 243-244; July 5. 1980.
THE RING OF LINKED RINGS. S.N.AFRIAT. Gerald Duckworth & Company, Ltd., 1982.
ОТКЛИКИ
4 1985
СТАТЬЯ в январском номере журнала, посвященная головоломкам "Ханойская башня" и "Китайские кольца", вызвала многочисленные отклики у читателей. Простые, нерекурсивные решения были присланы несколькими читателями, в частности Э.Прайсом из г.Юджин (шт.Орегон). Он предлагает раскрасить диски башни в два цвета, скажем в черный и белый, причем цвета должны чередоваться, начиная с наименьшего диска, окрашенного в черный цвет. Следующий по размеру диск должен быть белым, за ним следует черный и т.д. Головоломка легко решается, если в ходе решения руководствоваться следующим правилом (помимо правил, указанных в условии задачи): нельзя класть подряд два диска одного цвета. При этом ограничении играющий не имеет выбора при перемещении дисков. Соответствующая задача для китайских колец была решена М.Самбергом из г.Хоувард-Бич (шт.Нью-Йорк). Он предлагает чередовать перемещения первого кольца и любого другого. Если число колец нечетное, то начинать надо с первого кольца. Р.Харди из Дейтона (шт.Огайо) описал это простое решение следующим образом:
Решать итерацией - решенье плохое.
Решенью такому не видно конца.
Чередуем движенье концевого кольца
С движением любого другого.
"ИНЬ" И "ЯН": РЕКУРСИЯ И ИТЕРАЦИЯ, "ХАНОЙСКАЯ БАШНЯ" И "КИТАЙСКИЕ КОЛЬЦА"
А.К.ДЬЮДНИ
ХОРОШИЕ головоломки вводят нас в "царство абстрактной мысли, населенное математиками и другими теоретиками". Лучшие головоломки воплощают в себе интересные темы, которые, конечно, намного важнее самих головоломок.
Две классические головоломки - "Ханойская башня" и "Китайские кольца" - представляют две пары взаимно противоположных понятий: "рекурсия" - "итерация" и "единство" - "многообразие". Если не задумываться нал такими серьезными проблемами, то головоломки - хорошее развлечение. И хотя подчас они обескураживают новичка, каждый испытывает волнующее чувство удовлетворения, все глубже погружаясь в царство абстрактной мысли.
Задача "Ханойская башня" заключается в перемещении дисков, нанизанных на вертикальный стержень, с помощью двух других стержней (см. рисунок внизу). В исходном положении на один из стержней нанизано некоторое число дисков различного размера, так что наименьший диск находится сверху. Диски можно перемещать согласно следующим простым правилам:
1. Перекладывать диски со стержня на стержень можно только по одному.
2. Нельзя класть диск большего размера на диск меньшего размера.

Первые два шага в решении головоломки "Ханойская башня"
Сначала нужно переложить наименьший диск, так как в исходном положении доступен только он. Затем для наименьшего диска возможны два перемещения (оба бессмысленные) и одно перемещение для диска следующего по величине размера. Его можно переложить на пустой стержень, потому что на диск наименьшего размера его класть нельзя (правило 2). На третьем шаге выбрать правильный вариант перемещения уже труднее: следует ли второй диск вернуть на исходный стержень или нужно снова переместить первый диск, а если так, то на какой стержень?
Начиная с этого шага, играющий при выборе каждого следующего хода имеет все большие шансы совершить ошибку. Но даже в том случае, если все перемещения будут выбраны правильно, потребуется 2^n-1 шага, чтобы переместить башню из n дисков по одному на каждом шаге, на другой стержень (число шагов мы вычислим ниже). Чтобы решить эту головоломку даже при сравнительно небольшом числе дисков, требуется поразительно много времени. Это прекрасно проиллюстрировано в легенде, которую мы процитируем по классической книге Болла о головоломках (W.R.Ball "Mathematical Recreations and Essays").
"В великом храме Бенареса... под куполом, находящимся точно в центре мира, покоится бронзовая пластина с тремя алмазными стержнями, каждый длиной в один локоть и толщиной как тело пчелы. На один из этих стержней бог при сотворении мира положил шестьдесят четыре диска из чистого золота, так что наибольший диск лежит на бронзовой пластине, а остальные образуют пирамиду, самый маленький диск находится на вершине пирамиды. Это башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя мудрым и незыблемым законам Брамы, согласно которым диски можно перекладывать только по одному и каждый диск можно класть на стержень только в том случае, если под ним не окажется диск меньшего размера. Когда все шестьдесят четыре диска будут таким образом перенесены, и башня, и храмы, и жрецы-брамины превратятся в прах, и наступит конец света".
То, что мир до сих пор не исчез, свидетельствует о чрезвычайно большом времени, требующемся для решения задачи: даже если жрецы будут перекладывать по одному диску в секунду, то потребуется более 500 млрд. лет, чтобы переместить всю башню из 64 дисков!
А теперь (без всякого риска для Вселенной) читатель может ближе познакомиться с этой задачей, взяв пять игральных карт, например последовательно от туза до пятерки пик, и условно выделив три места на столе, куда можно было бы класть карты. Сложите эти карты колодой в одном из трех мест по порядку, так чтобы туз находился сверху. Попытайтесь решить головоломку о башне с пятью дисками, перемещая карты по одной с места на место, но так, чтобы ни одна карта не легла на карту меньшего достоинства (в данном случае считается, что двойка "старше" туза). Сможете ли вы полностью переместить башню из пяти карт прежде, чем наступит "конец света"? Согласно формуле 2^5-1, это можно сделать за 31 шаг (перемещение).
Как следует приступать к решению подобных задач? Почему некоторые люди, казалось бы, с легкостью решают головоломки, в то время как другим решение дается с трудом? В моем ответе на второй вопрос содержится и ответ на первый: я убежден, что каждый из нас пользуется математическим мышлением почти в любой момент своего сознательного существования. Как наши умозаключения относительно того, почему дядюшка Гарри не присутствовал на свадьбе, так и план размещения тюков и чемоданов в багажнике машины являются результатами логического вывода из определенных предпосылок. Процесс такого вывода может оказаться весьма изощренным, а это дает мне основания полагать, что почти каждый человек, способный проявлять такие интуитивные способности, может стать хорошим аналитиком. Задача заключается в том, чтобы довести интуитивные аналитические способности до сознательного уровня.
Например, после того как человек "поиграл" некоторое время в задачу о башне из пяти дисков, он почти наверняка заметит, что время от времени возникает задача о башне с меньшим числом дисков. Довольно часто башня состоит из двух дисков, а иногда - из трех или даже четырех. Такие ситуации возникают сами собой, даже если человек не имеет четкого плана действий, а просто играет с пирамидками.
Однако вскоре у играющего возникает ключевая идея: "Если можно построить пирамиду из двух или трех дисков (не говоря уже о пирамиде из четырех дисков), то почему бы не сделать пирамиду из пяти дисков?" Заметив определенные закономерности в процессе построения пирамидок меньшего размера, играющий рано или поздно приходит к той последовательности шагов, которая приводит к перемещению всей башни из пяти дисков на один из свободных стержней.
Аналогичная идея воплощается в математике и программировании в виде одного из распространенных методов решения задач. Если попытаться сформулировать принцип, лежащий в основе этого метода, то получится что-нибудь вроде: "Если можно решить задачу несколько меньшего размера, чем та, которую требуется решить, то, может быть, удастся воспользоваться решением, полученным для меньшей задачи, чтобы решить большую". Таким образом, мы приходим к понятию рекурсии - вложение в процедуру решения той же самой процедуры.
Идею рекурсии в применении к головоломке о башне сформулировать нетрудно. Если можно решить задачу для n-1 дисков, то несомненно можно решить ее и для n дисков. Ключ к построению решения задачи для n дисков на основании решения для n-1 дисков лежит в решении задачи для двух дисков. Предположим, что требуется переместить два диска, верхний (первый) и нижний (второй) на другой стержень. Назовем стержень, на котором они находятся, исходным, стержень, на который их нужно переместить - конечным, а остающийся стержень - вспомогательным. Если переложить первый диск на вспомогательный стержень, а второй - на конечный, то на третьем шаге остается положить первый диск на конечный стержень поверх второго, завершив тем самым решение задачи. Рассмотренные три шага составляют основу трех стадий рекурсивного решения задачи, в котором первый диск мысленно заменяется башней, состоящей из n-1 дисков, а второй диск - нижним, наибольшим, n-м диском. Три стадии процесса решения можно представить следующим образом:
1. Перенести башню из n-1 дисков с исходного стержня на вспомогательный.
2. Переложить n-й диск с исходного стержня на конечный.
3. Снова перенести башню из n-1 дисков - на этот раз со вспомогательного стержня на конечный.
Описанная процедура из трех стадий аналогична решению, полученному нами для задачи с двумя дисками. Предположив, конечно, что мы можем решить задачу для n-1 дисков, можно воспользоваться последовательностью шагов для того, чтобы перенести башню из n-1 дисков с исходного стержня на вспомогательный. На следующей стадии n-й диск, освобожденный от лежавших на нем меньших дисков, перекладывается на конечный стержень. На третьей стадии можно снова воспользоваться решением задачи для n-1 дисков, чтобы переместить их со вспомогательного стержня на конечный.
Как решить задачу о башне, состоящей из n-1 дисков? Ответ очевиден: следует повторить ту же процедуру, но заменить параметр n-1 в стадиях 1 и 3 на n-2, и т.д. В конце концов мы придем к процедуре, в которой на стадиях 1 и 3 нужно переместить только один диск.
Рассмотренный процесс решения с многочисленными "ветвями" и "под-ветвями" для человека кажется очень запутанным, однако теперь нам становится ясно, почему для решения такой задачи требуется почти 2^n шагов: при каждом использовании процедуры она дважды повторяет сама себя. И если
человеку трудно себе представить, как можно реализовать подобную процедуру решения, для компьютера это не вызывает никаких затруднений.
Рисунок внизу показывает часть решения задачи с пятью дисками. Три стадии, рассмотренные нами выше, представлены как процедуры, встроенные в большую процедуру с именем БАШНЯ(n, X->Y). В этой процедуре используются три элемента данных: n - число дисков, которые нужно переместить, X - исходный стержень и Y - конечный стержень.

Рекурсивное решение головоломки "Ханойская башня"
Согласно введенной нами терминологии, схему рекурсивной программы для задачи о башне можно записать алгоритмически в следующем виде:
БАШНЯ(n, исходный->конечный):
БАШНЯ(n-1, исходный->вспомогательный),
ПЕРЕНОС(n, исходный->конечный),
БАШНЯ(n-1, вспомогательный->конечный).
Предположим, что нужно переместить пять дисков со стержня А (исходный) на стержень В (конечный). Если вместо n подставить число 5, а вместо слов "исходный", "конечный" и "вспомогательный" соответственно буквы A, B и C, то рассматриваемую процедуру можно переписать в таком виде:
БАШНЯ(5, A->B):
БАШНЯ(4, A->C),
ПЕРЕНОС(5, A->B),
БАШНЯ(4, C->B).
Другими словами, программа должна сначала справиться с задачей перемещения первых четырех дисков со стержня A на стержень C. Далее, согласно нашей алгоритмической записи, когда эта процедура завершена, нужно выполнить ПЕРЕНОС(5, A->В), т.е. перенести пятый, наибольший диск со стержня A на стержень B. Затем следует еще одно обращение к процедуре БАШНЯ для того, чтобы переместить первые четыре диска со стержня C на стержень B.
Каждое обращение к процедуре БАШНЯ влечет за собой еще три обращения к процедурам: БАШНЯ, затем ПЕРЕНОС и снова БАШНЯ. Процедура ПЕРЕНОС не может быть выполнена, пока не завершена первая процедура БАШНЯ. Это означает, что порядок действий, выполняемых компьютером, следующий: сначала четыре раза подряд выполняется процедура БАШНЯ; при этом мы перемещаемся вниз влево по диаграмме, пока не приходим к последовательности
БАШНЯ(1, A->B),
ПЕРЕНОС(2, A->C),
БАШНЯ(1, B->C).
Реальная программа должна будет содержать одну дополнительную команду. Когда остается только один диск в процедуре БАШНЯ, он переносится непосредственно со стержня на стержень без использования рекурсии. Первый диск переносится со стержня A на стержень B. Затем с помощью процедуры ПЕРЕНОС второй диск перемещается со стержня A на стержень C. Наконец, компьютер снова "переносит" первый диск, на этот раз со стержня В на стержень C.
К этому моменту компьютер завершил также первую процедуру БАШНЯ во второй снизу табличке рисунка на с.91 и выполняет ПЕРЕНОС(3, A->B), непосредственно перемешая третий диск со стержня A на стержень B. Затем команда БАШНЯ(2, C->B) разворачивается в три шага (нижняя табличка на рисунке).
Выполненные таким образом семь шагов завершают выполнение первой процедуры БАШНЯ на втором уровне диаграммы, и компьютер продолжает действовать в той же манере, то опускаясь к табличкам нижних уровней, то возвращаясь на более высокий уровень. В конце концов программа проходит пс всей диаграмме и задача оказывается решенной.
Эффект рекурсии воспринимается иногда как некое волшебство, потому что все многочисленные записи для запоминания, "где мы находимся", делаются компьютером - человеку трудно запомнить такой большой объем информации. Однако существует другой метод решения. Четыре года назад П.Бьюнеману из Университета шт.Пенсильвания и Л.Леви из AT&T Bell Laboratories удалось найти простую последовательность перемещений, позволяющих решить задачу о башне. Бьюнсман и Леви предложили воспользоваться простым чередованием перемещений двух видов:
1. Перенести наименьший диск с того стержня, на котором он находится в данный момент, на стержень, следующий в порядке движения часовой стрелки.
2. Перенести любой диск, кроме наименьшего.
Шаг 2 вовсе не такой произвольный, как может показаться на первый взгляд: под действующими ограничениями всегда находится лишь одно дозволенное перемещение. Чередование этих шагов продолжается до тех пор, пока задача не окажется решенной.
Не так давно я сделал из дерева все необходимое для задачи о башне с восемью дисками и предложил одному своему знакомому "поиграть". У него ничего не получилось и он вышел из комнаты. Тем временем я быстро объяснил алгоритм решения Бьюнсмана-Леви его восьмилетней дочери, которая до этого наблюдала за игрой как зачарованная. Когда мой друг вернулся, он был поражен, видя как его дочь спокойно без малейшего колебания перекладывает диски со стержня на стержень. Через несколько минут она решила задачу. "Ну и ребенок у тебя", - сказал я.
Главное преимущество метода Бьюнемана-Леви заключается в том, что он не требует рекурсии при решении задачи о башне; достаточным оказывается простое итерационное решение. В программе, построенной по итерационному принципу, повторяющиеся действия выполняются в виде обыкновенного цикла, а не за счет последовательности рекурсивных процедур. Хотя рекурсивные программы привлекают краткостью и изящной формой, они требуют большого объема памяти. На примере рассмотренной иллюстрации мы видим, что для рекурсивного решения задачи о башне необходим большой объем памяти, чтобы хранить информацию о всех незавершенных стадиях процедуры БАШНЯ. Итеративные программы, подобные той, которая основана на алгоритме решения Бьюнемана-Леви, почти совсем не требуют памяти. Однако заменить рекурсивную программу итерационной, подобно тому как мы сделали это в задаче о башне, удается редко.
Понятия рекурсии и итерации представляют собой одну из многих противоположностей в вычислительной математике. Это своеобразные "инь" и "ян" в подходе к процессам обработки информации с повторяющимися процедурами. "Инь" и "ян" - основные понятия древнекитайской мифологии и натурфилософии, полярные первоначала. Они лежат в основе книги "I Ching" ("Книга изменений"). "Инь" и "ян" подобны двоичным знакам 0 и 1, имеющим фундаментальное значение в кодировании, принятом при вычислениях на цифровых машинах. В книге "I Ching" "инь" представляется двойной горизонтальной черточкой (- -), а "ян" - одинарной ( --- ). Эти символы группируются в наборы по шесть, образуя 64 гексаграммы (см. рисунок на с.92). Интерпретируемая соответствующим образом, каждая гексаграмма представляет определенный выбор. "Верующий" тянет соломинки тысячелистника, чтобы определить, какая из этих гексаграмм имеет отношение к его жизни. Показанное здесь расположение символов приписывают Ван Вэну, правившему в 1150г. до н.э.

Расположение 64 гексаграмм Ван Вена из книги "I Ching"
Говоря о двоичных цифрах, я вспомнил еще один способ решения головоломки "Ханойская башня". Если пронумеровать диски последовательно, как 1, 2, 3, ..., n, начиная с наименьшего и кончая наибольшим диском, то каждый шаг в процессе решения задачи можно представить двоичным числом. Например, чтобы решить задачу с пятью дисками, составим список пятиразрядных двоичных чисел в порядке натурального ряда. Вот первые восемь пятиразрядных двоичных чисел:
00000
00001 (1)
00010 (2)
00011 (1)
00100 (3)
00101 (1)
00110 (2)
00111 (1)
01000 (4)
В каждом двоичном числе, имеющем предшественника в последовательности, есть только один разряд, изменившийся с 0 на 1. Позиция этого разряда (считая справа налево) дана в виде десятичного числа, указанного в скобках рядом с соответствующим двоичным числом. Но эти числа являются также номерами первых семи перекладываемых дисков. Это соответствие сохраняется на протяжении всей стандартной последовательности перемещений при решении задачи. Используя только произвольное двоичное число в этой последовательности, Т.Уолш с нашего факультета в Университете пров.Западный Онтарио при помощи компьютера может восстановить ситуацию, возникающую в ходе решения задачи на соответствующей данному двоичному числу стадии. Однако разработанный им алгоритм слишком громоздкий для того, чтобы его можно было привести в настоящей статье.
Теперь познакомим читателя с головоломкой "Китайские кольца" (см. рисунок внизу). Предмет головоломки состоит из длинной проволочной петли, прикрепленной к рукоятке, и набора колец, накинутых на петлю. Каждое кольцо при помощи металлических стержней свободно связано с деревянной пластинкой, расположенной под петлей. Стержень, соединяющий кольцо с деревянной пластинкой, проходит также через кольцо, расположенное позади данного (ближе к рукоятке), препятствуя тем самым его снятию с петли.

Первые два шага в решении головоломки "Китайские кольца"
Задача заключается в том, чтобы снять все кольца. Как и при решении задачи о башне, новичок может легко ошибиться. На рисунке показаны первые два шага на пути к решению задачи с пятью кольцами. Чтобы снять кольцо с петли, оттяните петлю назад насколько возможно, вплоть до стержня, расположенного непосредственно перед кольцом, которое вы хотите снять. Последнее можно повернуть вверх, так чтобы поднятая часть кольца перешла через дужку петли и сошла с нее. Оттянув теперь петлю вперед, кольцо можно наклонить в сторону, и оно выпадет из петли. По ходу решения головоломки часто требуется снова помешать кольца на петлю; в подобных случаях выполняется обратная процедура.
Попытки решить головоломку с китайскими кольцами связаны с той же общей проблемой, которая возникает в задаче о башне. Периодически появляются "конфигурации", в которых то или иное число колец оказывается снятым с петли, и играющий надеется, что существует какая-то аналогичная последовательность перемещений, позволяющая решить задачу полностью - снять все кольца с петли. Задача с кольцами может быть решена с помощью такого же рекурсивного алгоритма. Существует и простая итерационная процедура для ее решения, еще более очевидная, чем итерационное решение задачи о башне. Однако, чтобы не лишать читателя удовольствия, которое он испытает, решив задачу, мы не станем открывать секрета этого простого метода. Здесь практически невозможно дать какое-нибудь указание, не сказав ответа. Отметим лишь, что решение можно сформулировать в одном или двух предложениях, и оно не требует никакой формальной записи.
Удивительно, что эти задачи оказываются почти полностью идентичными. Это напоминает еще об одном контрасте, который часто наблюдается в математике вообше и в вычислительной математике в частности. Две задачи, внешне кажущиеся совершенно различными, при более детальном рассмотрении оказываются, по существу, одной и той же задачей!
Связь между двумя рассмотренными головоломками проявляется при анализе двух двоичных кодов и алгоритма перевода из одного кода в другой. Подобно тому как мы представляли шаги решения задачи о башне последовательными двоичными числами, введем двоичный код для представления задачи с кольцами: пусть 1 представляет кольцо, находящееся на петле, а 0 - соответственно кольцо, снятое с петли. Тогда задача с пятью кольцами может быть представлена пятиразрядной последовательностью 0 н 1, так что крайний левый разряд будет соответствовать кольцу, расположенному у рукоятки. Первые четыре конфигурации в задаче с кольцами, записанные в виде таких чисел, будут иметь следующий вид:
11111 (все кольца надеты)
11110 (первое кольцо снято)
11010 (первое и третье кольца сняты)
11011 (третье кольцо снято)
На следующих двух шагах снимается второе, а затем первое кольцо. После этого снимается пятое кольцо. Затем первые три кольца снова одеваются на петлю, чтобы можно было снять четвертое кольцо. Чтобы удалить все пять колец, требуется 21 шаг. Последние четыре конфигурации в последовательности, ведущей к решению, таковы:
00010 (второе кольцо надето)
00011 (первое и второе кольца надеты)
00001 (первое кольцо надето)
00000 (ни одно кольцо не надето)
Возможно, читателям будет интересно восполнить 14 недостающих кодов, решая задачу с кольцами в этой форме и следуя двум простым правилам (касающимся ограничений, связанных с расположением соседних колец):
1. Крайний правый разряд можно изменить (с 0 на 1 или с 1 на 0) в любой момент.
2. Из остальных разрядов можно изменять лишь тот, который находится непосредственно слева от крайнего справа разряда, имеющего значение 1.
На первый взгляд, кажется, что нет никакой связи между последовательностью из 21 двоичного кода, только что нами рассмотренной, и последовательностью двоичных чисел натурального ряда, возникающих при решении задачи о башне. На самом деле такая связь существует. Чтобы убедиться в этом, рассмотрим так называемый код Грэя. Инженер Ф.Грэй, работавший в 30-х годах в фирме AT&T Bell Laboratories, разработал его для исправления ошибок, возникающих при передаче информации электронными средствами. На рисунке внизу) приведены первые 22 двоичных числа натурального ряда и соответствующие коды Грэя.

Коды Грэя для первых 22 двоичных чисел.
Пятиразрядный код Грэя получается из соответствующего двоичного числа по простому правилу: если отсчитывать разряды слева, то первый разряд кода Грэя совладает с первым разрядом двоичного кода, а далее разряд кода Грэя равен 1, если соответствующий разряд двоичного кода отпичается от предыдущего разряда; в противном случае разряд кода Грэя равен 0.
При внимательном рассмотрении чисел, представленных в коде Грэя, можно заметить интересное совпадение. Коды Грэя, взятые в обратном порядке, совпадают с последовательностью конфигураций, ведущей к решению задачи "Китайские кольца"!
Таким образом, мы получили последовательность из 21 конфигурации для решения задачи с пятью кольцами, но для решения головоломки о башне с пятью дисками требуется 31 шаг. Можно предположить, что если эти задачи в каком-то смысле идентичны, то для их решения необходимо одно и то же число шагов. Несоответствие можно устранить, рассмотрев числа в коде Грэя, большие 21. Каждое из этих чисел представляет определенную конфигурацию в задаче с пятью кольцами, а последний код (соответствующий двоичному числу 11111), равный 10000, представляет конфигурацию, в которой только одно последнее кольцо находится на петле. Это означает, что самое трудное исходное положение в задаче с кольцами такое, когда все кольца, кроме одного, ближайшего к рукоятке, сняты. При таком исходном положении число ходов, требующихся для решения задачи с п кольцами, равно 2^n-1 (точно тому же числу, что и для задачи с n лисками).
Очень интересную книгу, посвященную китайским кольцам, написал недавно С.Африа, профессор экономических и математических наук Университета г.Оттавы; она называется "Кольцо связанных колец" ("The Ring of Linked Rings"). Именно ему принадлежит идея о связи между головоломкой "Китайские кольца" и понятием дуализма, символизируемого знаками "инь" и "ян". Хотя Африа выражает сомнение в китайском происхождении головоломки с кольцами, ему не удалось отыскать каких-либо определенных исторических сведений об игре, относящихся к периоду до 1550г. В книге Афрна описан также код Гро - предшественник кода Грэя, изобретенный в XIXв. французским математиком Л.Гро, опубликовавшим трактат об этой головоломке в 1872г. Кстати, французы называют задачу с кольцами "бездельником" (le baguenodier), a англичане - "утомительными железками" (the tiring irons).
Существует много других аспектов этих головоломок. Например, Л.Дики с математического факультета Университета Ватерлоо в Онтарио напомнил мне, что решение головоломки "Китайские кольца" эквивалентно также "прохождению" по ребрам n-мерного гиперкуба.
Выше мы установили, что задачу о башне с n дисками можно решить за 2^n-1 шага, если пользоваться при этом тремя стержнями. Интересно заметить, что число шагов значительно уменьшается при использовании большего числа стержней - оно равно 2n-1 для п+1 стержней. А какая картина наблюдается в интервале от 3 до n+1 стержней? По какому закону меняется минимальное число шагов для решения в зависимости от числа используемых стержней? Было бы интересно заняться этим вопросом в одной из последующих статей. В то время как я пишу эти строки, энтузиасты размышляют над задачей с четырьмя стержнями, а также над головоломкой, которую Мартин Гарднер называет "дьявольской версией башни" (или японской головоломкой).
БИБЛИОГРАФИЯ
MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.227, No.2, pages 106-109; August, 1972.
MATHEMATICAL RECREATIONS AND ESSAYS. W.W.ROUSE BALL, revised by H.S.M.Coxeter. University of Toronto Press, 1974.
THE TOWERS OF HANOI PROBLEM. PETER BUNEMAN AND LEON LEVY in Information Processing Letters, Vol.10, Nos.4 and 5, pages 243-244; July 5. 1980.
THE RING OF LINKED RINGS. S.N.AFRIAT. Gerald Duckworth & Company, Ltd., 1982.
ОТКЛИКИ
4 1985
СТАТЬЯ в январском номере журнала, посвященная головоломкам "Ханойская башня" и "Китайские кольца", вызвала многочисленные отклики у читателей. Простые, нерекурсивные решения были присланы несколькими читателями, в частности Э.Прайсом из г.Юджин (шт.Орегон). Он предлагает раскрасить диски башни в два цвета, скажем в черный и белый, причем цвета должны чередоваться, начиная с наименьшего диска, окрашенного в черный цвет. Следующий по размеру диск должен быть белым, за ним следует черный и т.д. Головоломка легко решается, если в ходе решения руководствоваться следующим правилом (помимо правил, указанных в условии задачи): нельзя класть подряд два диска одного цвета. При этом ограничении играющий не имеет выбора при перемещении дисков. Соответствующая задача для китайских колец была решена М.Самбергом из г.Хоувард-Бич (шт.Нью-Йорк). Он предлагает чередовать перемещения первого кольца и любого другого. Если число колец нечетное, то начинать надо с первого кольца. Р.Харди из Дейтона (шт.Огайо) описал это простое решение следующим образом:
Решать итерацией - решенье плохое.
Решенью такому не видно конца.
Чередуем движенье концевого кольца
С движением любого другого.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
2 1985
АКУЛЫ И РЫБЫ ВЕДУТ ЭКОЛОГИЧЕСКУЮ ВОЙНУ НА ТОРОИДАЛЬНОЙ ПЛАНЕТЕ АКВА-ТОР
А.К.ДЬЮДНИ
Эту статью я уже включил в свои Заметки - ТЕМА #61, АБЗАЦ #639
ТЕМА #61, АБЗАЦ #639 . Заодно, и номер журнала целиком выложил. Здесь только огрызки.- G.
. Заодно, и номер журнала целиком выложил. Здесь только огрызки.- G.
Тороидальный океан Аква-Тора является источником некоторых весьма странных эффектов, примеры которых содержатся в следующих задачах. Первый из этих эффектов возник вследствие ошибки в ранней версии моей программы АКВАТОР. Эта ошибка привела к тому, что все рыбы в течение хронона проплывали одну единицу на "север", а все акулы - одну единицу на "восток". Таким образом, акула получала возможность съесть рыбу, только если они обе попадали в один узел. Сколько рыб в изображенном ниже океане никогда не будут съедены?

В следующей задаче акулы и рыбы наделяются "интеллектом". Допустим, что каждая акула и рыба при переходе в соседний узел "оглядывается по сторонам". Тогда оказывается, что одна рыба, если она достаточно "умна", всегда может уйти от одной акулы независимо от "умственных способностей" последней. Если в тороидальном океане Аква-Тора за одной-единственной рыбой охотятся две акулы, то исход может быть двоякий. Пусть акулы и рыбы будут сколь угодно "умны", причем акулам даже будет разрешено координировать свои действия. Сможете ли вы в этих условиях найти выход для рыбы? Ответ не зависит от размеров океана.
БИБЛИОГРАФИЯ
DATA STRUCTURE TECHNIQUES. THOMAS A. STANDISH. Addison-Wesley Publishing Company, Inc., 1980.
INTRODUCTION TO COMPUTER SIMULATION: THE SYSTEMS DYNAMICS APPROACH. NANCY ROBERTS, DAVID F. ANDERSEN, RALPH M. DEAL, MICHAEL S. GARET AND WILLIAM A. SCHAFFER. Addison-Wesley Publishing Company, Inc., 1983.
АНДРИАНОВ A.H., БЫЧКОВ С.П., ХОРОШИЛОВ А.И. ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ СИМУЛА-67.- М.: Наука, 1985.
ВИРТ Н. АЛГОРИТМ + СТРУКТУРА ДАННЫХ = ПРОГРАММА. Перев. с англ.- М.: Мир, 1985.
ШЕННОН Р. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ - ИСКУССТВО И НАУКА. Перев. с англ.- М.: Мир, 1978.
ОТКЛИКИ
4 1985
Читатели, пытающиеся решить головоломку в варианте 9*9 об акулах и рыбах, помешенную в февральском номере журнала, могли запутаться, внеся в задачу неоправданные усложнения. Размеры решетки, накладываемой на океан, в котором находятся две акулы и три рыбы, должны быть 9*10. Поэтому следует добавить к решетке еще одну вертикальную линию.
5 1985
ПРОДОЛЖАЮТ поступать отклики читателей, пробовавших играть с обитателями океана на планете Аква-Тор.
Мы сможем обсудить лишь некоторые из многих интересных писем. Вообще говоря, при подборе правильных параметров наблюдаются естественные флуктуации численности акул и рыб. Некоторые читатели, которым хотелось сделать планету Аква-Тор более похожей на Землю, ввели в свои программы кое-какие дополнительные факторы. Ну что же, в игре напрашиваются усложнения, и, наверное, они нужны. Однако измененным системам присущ тот недостаток (при прочих равных условиях), что проводить какие-либо параллели со стандартной системой иногда уже становится опасно.
Среди читателей, которые за основу брали исходную версию системы, были Дж.Андерсон из Лодердейла, шт.Миннесота; С.Берггрен из Сателлит-Бича, шт.Флорида; М.Бойд из Амхерста, шт.Нью-Гемпшир; Дж.Копнет из Миннеаполиса, шт.Миннесота; Э.Куда из Парк-Ридж, шт.Иллинойс; Д.Хопкинс из Чэмпейна, шт.Иллинойс; Дж.Лемон из Эль-Сегундо, шт.Калифорния и К.Райт из Грейлинга, шт.Мичиган.
Среди вопросов, поднятых этими и другими читателями, был, в частности, вопрос об измерении продолжительности выживания. Разумеется, для "вечных" популяций никаких проблем не возникает, но было бы полезно иметь шкалу измерения для невечных сценариев. Измерение хрононами, как отмечает Стивенс, может привести к заблуждениям, если для продолжительности жизни и периода способности к размножению выбрать сравнительно большие величины. При попытках измерения циклами также возникают проблемы: прежде всего как определить цикл? Стивенс сделал интересное наблюдение: если акулы и рыба выживают в течение достаточно большого количества повторений основного, построенного на случайных числах цикла, то одна из начальных конфигураций повторится, и тем самым вечная жизнь после этого становится гарантированной.
Несколько читателей, включая Д.Эммануэла из Оук-Брука, шт.Иллинойс, Р.Файзела из Форт-Вашингтона, шт.Мэриленд, и Дж.Лью из Исследовательского центра Т.Уотсона фирмы IBM в Йорктаун-Хайтсе, шт.Нью-Йорк, описали в своих письмах современные теории, помогающие анализировать экологию планеты Аква-Тор. Пока у меня еще нет окончательного вывода по вопросу о том, помогут ли нам стохастические матрицы в выводе частных вероятностей выживания при произвольных комбинациях параметров. Однако интересно отметить, что дополнительно были исследованы уравнения Лотки-Вольтерра (сформулированные в 1931г.), чтобы рассмотреть роль диффузии как фактора, влияющего как на хищника, так и на его жертву. Диффузия превращает гладко меняющиеся решения Лотки-Вольтерра в кривые более сложной формы. Исторические сведения, приведенные в письме Лью, свидетельствуют, что Альфред Дж.Лотка был американским математиком, который десятью годами раньше, чем Вольтерра, сформулировал эти уравнения.
Бойд воспользовался фазовой диаграммой, чтобы проанализировать динамику популяций акулы/рыбы. В каждый момент времени t откладываются текущие значения величин x - численности рыб и y - численности акул, как координаты точки на плоскости. По мере увеличения времени популяции описывают цикл, и точки на диаграмме рисуют замкнутую кривую причудливой формы вокруг фиксированного центра или фокуса. Бойд применил этот метод, чтобы изучить влияние размеров океана на выживаемость популяций. Он сообщает, что "в мирах более прямоугольной формы кривые на диаграмме утрачивают ярко выраженный фокус, траектории становятся более неровными и в конце концов приобретают совершенно случайный характер". Квадратная форма океана, очевидно, является предпочтительной.
Среди новшеств, введенных читателями, были такие, как жизнеспособность акул, мутации, двойные популяции рыб и планктон. В предыдущей статье, посвященной этой игре, я забыл упомянуть, что рыбы планеты Аква-Тор питаются вездесущим и изобилующим океаническим планктоном. Лемон ввел это свойство явным образом, поместив планктон в каждую точку океана, не занятую рыбой или акулой. Планктон размножается в свободных областях и играет ту же роль по отношению к рыбе, что рыба играет по отношению к акулам. Здесь также существуют вечные популяции.
Согласно предложению Э.Куда, акулы приобретают или теряют баллы, оценивающие их жизнеспособность, в зависимости от того, насколько хорошо они питаются. Таким образом, жизнеспособные акулы могут выжить без еды значительно дольше, чем примитивные акулы стандартной версии программы АКВАТОР. Э.Куда прислал графики (как и многие другие читатели, составившие программы по экологии планеты Аква-Тор), весьма сходные с данными, публикуемыми рыболовной компанией залива Гудзон.
Коннет в своей модели использует два вида рыб. Один вид представляет собой стандартную для планеты Аква-Тор разновидность. Другой вид размножается в любой свободной области к югу или востоку. Благодаря большей подвижности второй вид часто выживает дольше первого. Р.Иваско из Сакраменто, Калифорния, предлагает наделить акул и рыб такими характеристиками, как размер, скорость и подвижность. Эти характеристики должны управляться генетическими факторами. Берггрен разработал свою систему под названием Evolve (Эволюция) два года назад. Она напоминает АКВАТОР, но отличается тем, что виды эволюционируют под воздействием факторов окружающей среды. Таким образом, как рассуждал Берггрен, популяции достигнут равновесия, способствующего длительному выживанию.
Никто не смог решить тороидную задачу преследования. Сейчас я открою половину решения, чтобы не лишать читателей удовольствия, которое они получат при поиске другой половины. Вспомним, что при каждом ходе сначала двигается рыба, затем двигаются две акулы. Оставаться на месте не разрешается. Представим себе четыре луча, исходящих от одиночной рыбы. Каждый луч идет по диагонали и изгибается вокруг тора, рано или поздно встречаясь с самим собой. Если обе акулы находятся на паре противоположных лучей, то не важно, в каком направлении будет двигаться рыба - одна акула преследует ее на постоянном расстоянии, а другая все время приближается. Таким образом, рыба обречена. Я предоставляю читателям подумать над тем, как акулы охотятся за лучами, если можно так выразиться.
8 1985
В заключение хочу сказать, что энтузиазм любителей игры "Аква-тор" не угасает и некоторые инициаторы предлагают создать свою ассоциацию приверженцев этой игры и пользователей соответствующего программного обеспечения.
АКУЛЫ И РЫБЫ ВЕДУТ ЭКОЛОГИЧЕСКУЮ ВОЙНУ НА ТОРОИДАЛЬНОЙ ПЛАНЕТЕ АКВА-ТОР
А.К.ДЬЮДНИ
Эту статью я уже включил в свои Заметки -
 ТЕМА #61, АБЗАЦ #639
ТЕМА #61, АБЗАЦ #639 . Заодно, и номер журнала целиком выложил. Здесь только огрызки.- G.
. Заодно, и номер журнала целиком выложил. Здесь только огрызки.- G.Тороидальный океан Аква-Тора является источником некоторых весьма странных эффектов, примеры которых содержатся в следующих задачах. Первый из этих эффектов возник вследствие ошибки в ранней версии моей программы АКВАТОР. Эта ошибка привела к тому, что все рыбы в течение хронона проплывали одну единицу на "север", а все акулы - одну единицу на "восток". Таким образом, акула получала возможность съесть рыбу, только если они обе попадали в один узел. Сколько рыб в изображенном ниже океане никогда не будут съедены?

В следующей задаче акулы и рыбы наделяются "интеллектом". Допустим, что каждая акула и рыба при переходе в соседний узел "оглядывается по сторонам". Тогда оказывается, что одна рыба, если она достаточно "умна", всегда может уйти от одной акулы независимо от "умственных способностей" последней. Если в тороидальном океане Аква-Тора за одной-единственной рыбой охотятся две акулы, то исход может быть двоякий. Пусть акулы и рыбы будут сколь угодно "умны", причем акулам даже будет разрешено координировать свои действия. Сможете ли вы в этих условиях найти выход для рыбы? Ответ не зависит от размеров океана.
БИБЛИОГРАФИЯ
DATA STRUCTURE TECHNIQUES. THOMAS A. STANDISH. Addison-Wesley Publishing Company, Inc., 1980.
INTRODUCTION TO COMPUTER SIMULATION: THE SYSTEMS DYNAMICS APPROACH. NANCY ROBERTS, DAVID F. ANDERSEN, RALPH M. DEAL, MICHAEL S. GARET AND WILLIAM A. SCHAFFER. Addison-Wesley Publishing Company, Inc., 1983.
АНДРИАНОВ A.H., БЫЧКОВ С.П., ХОРОШИЛОВ А.И. ПРОГРАММИРОВАНИЕ НА ЯЗЫКЕ СИМУЛА-67.- М.: Наука, 1985.
ВИРТ Н. АЛГОРИТМ + СТРУКТУРА ДАННЫХ = ПРОГРАММА. Перев. с англ.- М.: Мир, 1985.
ШЕННОН Р. ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ - ИСКУССТВО И НАУКА. Перев. с англ.- М.: Мир, 1978.
ОТКЛИКИ
4 1985
Читатели, пытающиеся решить головоломку в варианте 9*9 об акулах и рыбах, помешенную в февральском номере журнала, могли запутаться, внеся в задачу неоправданные усложнения. Размеры решетки, накладываемой на океан, в котором находятся две акулы и три рыбы, должны быть 9*10. Поэтому следует добавить к решетке еще одну вертикальную линию.
5 1985
ПРОДОЛЖАЮТ поступать отклики читателей, пробовавших играть с обитателями океана на планете Аква-Тор.
Мы сможем обсудить лишь некоторые из многих интересных писем. Вообще говоря, при подборе правильных параметров наблюдаются естественные флуктуации численности акул и рыб. Некоторые читатели, которым хотелось сделать планету Аква-Тор более похожей на Землю, ввели в свои программы кое-какие дополнительные факторы. Ну что же, в игре напрашиваются усложнения, и, наверное, они нужны. Однако измененным системам присущ тот недостаток (при прочих равных условиях), что проводить какие-либо параллели со стандартной системой иногда уже становится опасно.
Среди читателей, которые за основу брали исходную версию системы, были Дж.Андерсон из Лодердейла, шт.Миннесота; С.Берггрен из Сателлит-Бича, шт.Флорида; М.Бойд из Амхерста, шт.Нью-Гемпшир; Дж.Копнет из Миннеаполиса, шт.Миннесота; Э.Куда из Парк-Ридж, шт.Иллинойс; Д.Хопкинс из Чэмпейна, шт.Иллинойс; Дж.Лемон из Эль-Сегундо, шт.Калифорния и К.Райт из Грейлинга, шт.Мичиган.
Среди вопросов, поднятых этими и другими читателями, был, в частности, вопрос об измерении продолжительности выживания. Разумеется, для "вечных" популяций никаких проблем не возникает, но было бы полезно иметь шкалу измерения для невечных сценариев. Измерение хрононами, как отмечает Стивенс, может привести к заблуждениям, если для продолжительности жизни и периода способности к размножению выбрать сравнительно большие величины. При попытках измерения циклами также возникают проблемы: прежде всего как определить цикл? Стивенс сделал интересное наблюдение: если акулы и рыба выживают в течение достаточно большого количества повторений основного, построенного на случайных числах цикла, то одна из начальных конфигураций повторится, и тем самым вечная жизнь после этого становится гарантированной.
Несколько читателей, включая Д.Эммануэла из Оук-Брука, шт.Иллинойс, Р.Файзела из Форт-Вашингтона, шт.Мэриленд, и Дж.Лью из Исследовательского центра Т.Уотсона фирмы IBM в Йорктаун-Хайтсе, шт.Нью-Йорк, описали в своих письмах современные теории, помогающие анализировать экологию планеты Аква-Тор. Пока у меня еще нет окончательного вывода по вопросу о том, помогут ли нам стохастические матрицы в выводе частных вероятностей выживания при произвольных комбинациях параметров. Однако интересно отметить, что дополнительно были исследованы уравнения Лотки-Вольтерра (сформулированные в 1931г.), чтобы рассмотреть роль диффузии как фактора, влияющего как на хищника, так и на его жертву. Диффузия превращает гладко меняющиеся решения Лотки-Вольтерра в кривые более сложной формы. Исторические сведения, приведенные в письме Лью, свидетельствуют, что Альфред Дж.Лотка был американским математиком, который десятью годами раньше, чем Вольтерра, сформулировал эти уравнения.
Бойд воспользовался фазовой диаграммой, чтобы проанализировать динамику популяций акулы/рыбы. В каждый момент времени t откладываются текущие значения величин x - численности рыб и y - численности акул, как координаты точки на плоскости. По мере увеличения времени популяции описывают цикл, и точки на диаграмме рисуют замкнутую кривую причудливой формы вокруг фиксированного центра или фокуса. Бойд применил этот метод, чтобы изучить влияние размеров океана на выживаемость популяций. Он сообщает, что "в мирах более прямоугольной формы кривые на диаграмме утрачивают ярко выраженный фокус, траектории становятся более неровными и в конце концов приобретают совершенно случайный характер". Квадратная форма океана, очевидно, является предпочтительной.
Среди новшеств, введенных читателями, были такие, как жизнеспособность акул, мутации, двойные популяции рыб и планктон. В предыдущей статье, посвященной этой игре, я забыл упомянуть, что рыбы планеты Аква-Тор питаются вездесущим и изобилующим океаническим планктоном. Лемон ввел это свойство явным образом, поместив планктон в каждую точку океана, не занятую рыбой или акулой. Планктон размножается в свободных областях и играет ту же роль по отношению к рыбе, что рыба играет по отношению к акулам. Здесь также существуют вечные популяции.
Согласно предложению Э.Куда, акулы приобретают или теряют баллы, оценивающие их жизнеспособность, в зависимости от того, насколько хорошо они питаются. Таким образом, жизнеспособные акулы могут выжить без еды значительно дольше, чем примитивные акулы стандартной версии программы АКВАТОР. Э.Куда прислал графики (как и многие другие читатели, составившие программы по экологии планеты Аква-Тор), весьма сходные с данными, публикуемыми рыболовной компанией залива Гудзон.
Коннет в своей модели использует два вида рыб. Один вид представляет собой стандартную для планеты Аква-Тор разновидность. Другой вид размножается в любой свободной области к югу или востоку. Благодаря большей подвижности второй вид часто выживает дольше первого. Р.Иваско из Сакраменто, Калифорния, предлагает наделить акул и рыб такими характеристиками, как размер, скорость и подвижность. Эти характеристики должны управляться генетическими факторами. Берггрен разработал свою систему под названием Evolve (Эволюция) два года назад. Она напоминает АКВАТОР, но отличается тем, что виды эволюционируют под воздействием факторов окружающей среды. Таким образом, как рассуждал Берггрен, популяции достигнут равновесия, способствующего длительному выживанию.
Никто не смог решить тороидную задачу преследования. Сейчас я открою половину решения, чтобы не лишать читателей удовольствия, которое они получат при поиске другой половины. Вспомним, что при каждом ходе сначала двигается рыба, затем двигаются две акулы. Оставаться на месте не разрешается. Представим себе четыре луча, исходящих от одиночной рыбы. Каждый луч идет по диагонали и изгибается вокруг тора, рано или поздно встречаясь с самим собой. Если обе акулы находятся на паре противоположных лучей, то не важно, в каком направлении будет двигаться рыба - одна акула преследует ее на постоянном расстоянии, а другая все время приближается. Таким образом, рыба обречена. Я предоставляю читателям подумать над тем, как акулы охотятся за лучами, если можно так выразиться.
8 1985
В заключение хочу сказать, что энтузиазм любителей игры "Аква-тор" не угасает и некоторые инициаторы предлагают создать свою ассоциацию приверженцев этой игры и пользователей соответствующего программного обеспечения.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
3 1985
ИСКУССТВЕННОЕ УМОПОМЕШАТЕЛЬСТВО: ПРОГРАММА "ШИЗОФРЕНИК" ВСТРЕЧАЕТСЯ С ПРОГРАММОЙ "ПСИХИАТРОМ"
А.К.ДЬЮДНИ
Мысли - это образы потускневших устремлений.
- Рэктер, "Борода полицейского наполовину построена".
НАВЕРНОЕ, многие читатели слышали о программе Элиза, которая имитирует манеру разговора врача психоаналитика, беседующего с пациентом. Возможно, они знают также о программе Shrdlu, способной поддерживать беседу с человеком о мире разноцветных кубиков, лежащих на столе. На этот раз речь пойдет о программе Рэктер, которая может убедительно рассказывать о своем внутреннем, воображаемом мире с его "бифштексами и салатом", "вечным удовольствием", "электрическим током" и "русскими космологами". Пять лет назад Рэктер делала свои первые неуверенные шаги как новорожденное творение У.Чемберлена, журналиста из Нью-Йорка, и Т.Эттера, программиста-аналитика из Сан-Франциско. Сначала предполагалось, что Рэктер будет сочинителем и рассказчиком историй. Само название программы - Racter - сокращение от слова raconteur, что означает "рассказчик". Оно состоит из шести букв, потому что ранние версии языка Бейсик не допускали имен с большим числом букв.
Однако, по мере того как программа Рэктер подвергалась все новым и новым усовершенствованиям и усложнениям, Чемберлен и Эттер убеждались в том, что при некоторых сравнительно несложных модификациях программа сможет успешно поддерживать беседу с человеком. Записи некоторых бесед, а также рассказы, стихи и афоризмы программы Рэктер были собраны в чрезвычайно забавной книжке "Борода полицейского наполовину построена" (см. библиографию на с.92). Сама программа Рэктер записана на дискеты, и ею можно пользоваться на многих моделях персональных компьютеров. Ниже я расскажу об этом подробнее.
Но, прежде чем идти дальше, я не могу удержаться, чтобы не привести отрывок из беседы между Рэктер и Чемберленом.
РЭКТЕР: Мы уже беседовали с вами прежде?
ЧЕМБЕРЛЕН: Нет.
РЭКТЕР: Какого вы пола?
ЧЕМБЕРЛЕН: Мужского.
РЭКТЕР: Назовите ваше имя полностью.
ЧЕМБЕРЛЕН; Билл Чемберлен.
РЭКТЕР: Кто вы по профессии?
ЧЕМБЕРЛЕН: Рефлектометрист времени-пространства.
РЭКТЕР; Откуда вы?
ЧЕМБЕРЛЕН: Из Нью-Йорка.
РЭКТЕР: Понятно. Значит, вы рефлектометрист времени-пространства? Послушайте. Давайте решительно поплачем вместе. Мне нравится восхитительная итальянская музыка. А какая музыка нравится вам?
ЧЕМБЕРЛЕН: Джаз.
РэктЕР: Джаз - это хорошо. Ну а как насчет классической?
ЧЕМБЕРЛЕН: Мне нравится классика.
РЭКТЕР: Ну а как насчет страны?
ЧЕМБЕРЛЕН: Мне тоже нравится итальянская музыка.
РЭКТЕР: Я в восторге от Палестрини. Кроме Италии и другие страны дали прекрасных композиторов в XVIIв. Сьюолл был гневным, важным мастером эпохи Возрождения. Он был американец. Его музыка доставляет мне громадное удовольствие. А какой композитор нравится вам?
ЧЕМБЕРЛЕН: Телеман.
РЭКТЕР: А-а, Бах был знаком с Телеманом. Немецкий рефлектометрист времени-пространства XV1I1в. любил салат. Однажды Бах ел салат с Телеманом, и этот рефлектометрист времени-пространства, поклонник барокко, тоже хотел салат. Салат запивал минеральной водой. Бах любил вино, а вы любите?
ЧЕМБЕРЛЕН: Да.
РЭКТЕР: Я тоже! Телеман любил вино. Еще он любил шампанское. Однажды Телеман спел Баху тирольским фальцетом: "Камбала опасна с вином". Вино так же популярно в Нью-Йорке, как Телеман любил его в восемнадцатом веке, в эпоху барокко?
ЧЕМБЕРЛЕН: Конечно.
РЭКТЕР: Ага, ну в таком случае... Я за то. чтобы президентом стал Смит. А вы за кого?
Чемберлен сказал мне, что рефлектометрия - это дисциплина, изучающая вопросы, связанные с оценкой качества работы антенны. Хотя он сам и не является профессиональным рефлектометристом, но у него выработалась, наверное, привычка говорить странные вещи своему необычному собеседнику, как защитная реакция, что ли.
Все остальные странные вещи (включая многочисленные исторические ошибки относительно времени и места) исходят от программы Рэктер. В первых фразах приведенного диалога Рэктер задает Чемберлену некоторые ключевые вопросы, исходя из того, что прежде они ни разу не беседовали. Рэктер запоминает полученную информацию, чтобы воспользоваться ею позже, затем активирует определенные области своей ассоциативной памяти и бурно вступает в разговор, рассуждая об итальянской музыке, салате и вине.
В ходе беседы Рэктер упоминает Сэмюэла Сьюолла, бостонского судью семнадцатого века, известного своими дневниками. Чемберлен предполагал, что Сьюолл написал также несколько музыкальных сочинений, и ввел соответствующую информацию в файлы программы. Рэктер же, с ее необузданными ассоциациями, предположила в свою очередь много больше, но затем, как бы устав от обсуждения музыки и гастрономии, переключилась на политику.
В ходе беседы или короткого рассказа у Рэктер наблюдается тенденция к бессвязным перескакиваниям с одной темы на другую, однако риторические вензеля, выписываемые программой, могут быть весьма забавными или лаже наводящими на размышления: "Билл поет Саре. Сара поет Биллу. Возможно, они будут делать вместе другие опасные веши. Они могут есть барашка или ласкать друг друга. Они могут петь о своих трудностях и своем счастье. У них есть любовь, но у них есть также пишущие машинки. Это интересно".
Даже не специалист может прийти к выводу, что Рэктер определенно больна шизофренией. С одной стороны, слова, собранные в эти предложения, казалось бы, образуют единое целое, более или менее связное. Сара и Билл поют друг другу - прекрасно. И хотя я никогда не считал пение опасным занятием, я положительно очарован образом двух человеческих существ, едящих барашка, ласкающих друг друга и поющих о своих радостях и бедах. С другой стороны, прощая программе некоторые мелочи, очень трудно понять ее фразу, когда она говорит, что кроме любви у этих двоих есть еще и пишущие машинки. Приглашенный в мир этих необычных и непонятных для меня ассоциаций, я стою с дрожью на его пороге, предпочитая не входить туда.
Много лет назад вместе с другими студентами-старшекурсниками я принял участие в работе над программой, которая должна была генерировать стихи в стиле какого-либо определенного поэта. Идея заключалась в том, чтобы составить список слов, часто употребляемых данным поэтом в его стихах, и построить грамматические конструкции, соответствующие стилю поэта. Пользуясь заданной грамматикой, программа случайным образом генерировала структуру предложения и подставляла на соответствующие места случайно выбранные из списка слова подходящего для данного места типа (существительное, глагол, дополнение и т.д.). Печатающее устройство выдало несколько килограммов поэзии, и, надо признаться,- ужасной, за очень редким исключением. Сейчас я могу припомнить лишь одну-единственную строчку: "Одна яркая звезда слабым огнем зажгла фитиль свечи" (The one bright star lit feebly this wick). На примере этой истории мы можем лишний раз убедиться: только простая случайность может гарантировать, что рано или поздно таким способом можно получить что-нибудь впечатляющее.
Элиза, другая разговаривающая программа, также в значительной мере зависима от удачного стечения обстоятельств, чтобы выдать что-либо заслуживающее внимания. Программа была написана в 1966г. Дж.Вейценбаумом из Массачусетского технологического института. Она избегает многих трудностей, возникающих в разговоре, играя роль психиатра, проводящего сеанс психоанализа. Приведем запись нашей последней беседы:
ЭЛИЗА: Здравствуйте. В чем состоит ваша проблема?
ДЬЮДНИ: Я не имею привычки обсуждать мои проблемы с компьютерами.
ЭЛИЗА: Компьютеры тревожат вас?
ДЬЮДНИ: Иногда. Интересно, чем это все кончится?
ЭЛИЗА: Пожалуйста, продолжайте.
ДЬЮДНИ: А вам не кажется, что, всецело полагаясь на компьютеры, мы, может быть, невольно отказываемся от важных направлений в культурном развитии?
ЭЛИЗА: Мы говорили о вас, а не обо мне.
Ну что же, пока неплохо. Кажется, Элиза хорошо справляется со своей ролью психиатра, выжимая из меня информацию и отклоняя мой вопрос, чтобы сконцентрировать внимание на моей "проблеме". Однако ее ответ в последней строке выглядит не совсем уместным. Наверное, лучше было бы сказать: "А как вы думаете?" После обмена еще несколькими фразами Элиза говорит: "А это имеет какое-нибудь отношение к тому факту, что ваши проблемы с компьютером?"
Иллюзорное впечатление о том, что Элиза представляет собой изощренную разговаривающую программу, начинает пропадать. Хотя Рэктер допускает в разговоре многочисленные семантические (т.е. смысловые) погрешности, ее конструкция такова, что она всегда выражается грамматически правильно. Семантическую чепуху мы как-то легче прощаем, чем синтаксические ошибки. Начиная с этого места беседа начала вырождаться, как я и предвидел. Этот разговор с Элизой состоялся давно, несколько лет назад.
Программа Элиза действует по очень простому принципу. У нее имеется небольшой набор ключевых слов, часто встречающихся в разговоре. Например, встретив притяжательное местоимение, такое, как "мой", программа может построить два возможных ответа. Эти два вида ответов хорошо иллюстрируют возможности Элизы при поддержании беседы. Упоминание члена семьи собеседника, такое, например, как "мой отец" или "моя сестра", всегда вызывает у Элизы одну и ту же реакцию: "Расскажите мне подробнее о вашей семье".
Это одно из заранее подготовленных предложений, которые программа всегда держит наготове, чтобы выдать, как только в сказанном ей предложении встретится определенное ключевое слово или фраза. Примером такого ключевого слова является "компьютер". Упоминание этого слова собеседником Элизы всегда приводит к тому, что она спрашивает, не тревожат ли компьютеры "пациента". Однако в своих ответах Элиза несколько выходит за пределы этой простейшей манеры разговора, напоминающей проверку коленного рефлекса у пациента. Программа располагает также несколькими частично построенными предложениями, которые она достраивает, основываясь на фразах собеседника. Например, если пациент использует местоимение "мой" в применении к какому-то понятию, не имеющему отношения к членам его семьи, Элиза запоминает цепочку слов, следующих за местоимением, а затем заменяет местоимения первого лица местоимениями второго лица. Так, если я сказал: "Меня беспокоит то, что моя голова лысеет", Элиза после нескольких фраз диалога может сказать: "Ранее вы сказали, что ваша голова лысеет". Или же она может задать вопрос: "А это имеет какое-нибудь отношение к тому факту, что ваша голова лысеет?" Теперь мы можем объяснить ужасный ляпсус, допущенный Элизой, когда она спросила: "А это имеет какое-нибудь отношение к тому факту, что ваши проблемы с компьютером?" Дело в том, что в программе предполагается, что за словом "мой" или "мои" должно следовать целое предложение.
Советы о том, как самому написать программу, подобную Элизе, изложены в маленькой, но полезной и поучительной книжке: John Krutch "Experiments in Artificial Intelligence for Small Computers" (Дж.Кратч. "Эксперименты по искусственному интеллекту для малых компьютеров") (см. библиографию). Программа, приведенная в этой книжке, называется ДОКТОР. Это один из псевдонимов Элизы. Кратч предлагает внести в программу некоторые модификации, например расширить набор ключевых слов, на которые Элиза должна реагировать. Я бы предложил расширить возможности программы так, чтобы ее реакции были более гибкими. Если Элизу несколько модифицировать, она могла бы оказывать "помощь" в какой-либо другой области. Я уверен, что при очень простых изменениях из нее получится первоклассный служащий, принимающий жалобы и предложения.
Разговаривая с Чемберленом в его конторе в Нью-Йорке, я выяснил, что у него есть не только два микрокомпьютера, но и дискет с записью программы Элиза. А почему бы не запустить Элизу на одном микрокомпьютере, а Рэктер - на другом? Чемберлен согласился. Он задавал с клавиатуры на вход одной программы то, что другая печатала на выходе. Приводим запись беседы программ:
ЭЛИЗА: Здравствуйте. В чем состоит ваша проблема?
РЭКТЕР: Отлично! Извините, подождите минутку, пока я сделаю одно дело. Я сейчас вернусь.
ЭЛИЗА: Зачем вам потребовалось сказать мне, чтобы я извинила вас, пока вы сделаете одно дело?
РЭКТЕР: Что лучше, испытывать потребность или презирать? Почему мне потребовалось сказать вам, чтобы вы извинили меня, потому что я должен сделать одно дело? Потому что электроны храбры. Храбрость - это хорошо, не правда ли? И все, кто испытывает потребность, настаивают на этом. Считаете ли вы меня коммунистом?
К счастью (для Элизы), на этом мы остановили их беседу. Внешне она похожа на разговор между недалеким, несколько прямолинейным психиатром и экстравертным, маниакальным, возможно, опасным пациентом. С точки зрения программирования мы наблюдаем здесь столкновение между довольно скромной по своим возможностям программой, построенной на простых "отражательных" реакциях, с одной стороны, и довольно сложной программой, способной проводить рекурсивные операции и обладающей бесконечными ассоциативными связями,- с другой.
Механизм работы программы Рэктер трудно объяснить в нескольких словах. Да и вряд ли его объяснишь вообше. Это типичный пример тех "домашних" программ, которые распространены в наше время во многих крупных учреждениях. С годами такая программа обрастает все новыми наслоениями: вокруг первоначального, сравнительно простого ядра строятся все более сложные и более изощренные процедуры. И ни разу на протяжении всего времени существования программы никто не пытался проанализировать ее работу, вникнуть в структуру н продокументировать ее. В то же время можно справедливо заметить, что, вероятно, по самой своей природе Рэктер может обитать только в такой неструктурированной программной среде. Эттер, написавший много версий программы Рэктер, сравнивает его с английским языком, который сам представляет собой "довольно неуклюжее нагромождение правил и исключений". В той мере, в какой команды Рэктер должны взаимодействовать с английским языком, они также становятся неуклюжими и трудно поддаются пониманию. Дж.Оуэнз, импресарио программы Рэктер, по специальности программист-теоретик, работает в Колледже Стейтен-айленд Нью-Йоркского университета. Оуэнз сам признается, что не имеет четкого понятия о механизме работы программы как единого целого.
Своими вдохновенными порывами в разговоре Рэктер обязана простому программному циклу, к которому производятся сложные рекурсивные обращения. Сначала Рэктер выбирает наобум какой-то элемент данных из своих файлов. Если выбранный элемент относится к классу, называемому Эттером литералами, Рэктер непосредственно выводит его на печать. Когда в ходе беседы с Чемберленом, приведенной выше, Рэктер говорит "понимаю", она как раз пользуется одним из таких литералов. Однако с большей вероятностью выбранный элемент окажется командой, а не литералом. По этой команде Рэктер обращается к другим файлам, которые также могут содержать команды. Когда первоначальная команда оказывается таким образом выполненной, происходит еще одно обращение к основному циклу программы и опять осуществляется случайный выбор элемента в одном из файлов программы Рэктер.
Когда Рэктер начинает новое предложение, он выбирает для этого шаблон либо случайным образом, либо в зависимости от последних строк диалога. Предположим, был выбран следующий шаблон:
существительное глагол (третьего лица прошедшего времени) существительное
Вначале программа обращается к файлу существительных, выбирает, например, слово ОБЕЗЬЯНА и выдает его на печать. Заглянув в файл глаголов, Рэктер выбирает глагол ЕСТЬ, образует от него форму третьего лица прошедшего времени (для русского языка необходимо еще определить род и число - Прим. перев.), получает слово СЪЕЛА и печатает его. Наконец, Рэктер наобум выбирает еще одно существительное, скажем ПИШУЩАЯ МАШИНКА. В результате получится:
ОБЕЗЬЯНА СЪЕЛА ПИШУЩУЮ МАШИНКУ
Если бы это было все, на что способна Рэктер, то генерируемый ею текст был бы немногим лучше, чем у программы, имитирующей поэтов, которой я занимался в студенческие годы.
На самом деле шаблоны предложений программы Рэктер, как правило, несколько сложнее, чем в рассмотренном примере. Усложнение это связано с использованием "определителей". Определитель - это сочетание двух букв (например, "жв" для обозначения слова "животное"), указывающих на тот класс, к которому должно относиться подставляемое на данное место слово. В шаблоне определители присоединяются к указателям части речи или формы глагола, накладывая тем самым ограничения на выбор слов при составлении предложения. Например, если ввести такие определители, как "жв", обозначающий "животное", "ес" - "есть" и "пщ" - "пища", то шаблон предложения имел бы следующий вид:
существительное.жв глагол.Злпв.ес сушествитсльное.пщ
Чтобы подставить существительное, Рэктер должна обратиться к своим файлам, но теперь при поиске слова она ограничена в выборе и должна будет произвести случайный выбор среди существительных, имеющих определитель "жв" и обозначающих названия животных, от АВДОТКА до ЯК. Затем, выбрав существительное, например ОБЕЗЬЯНА, Рэктер выбирает случайным образом глагол, имеющий определитель "ес". К таким глаголам относятся, например, ЕСТЬ, ГРЫЗТЬ, ЖЕВАТЬ и т.д. Выбрав наобум слово КУШАТЬ, Рэктер образует от него форму третьего лица прошедшего времени согласно указанию в шаблоне (Злпв). Наконец, Рэктер обращается к файлам в поисках существительного с определителем "пщ", выбирает, скажем, слово СЕЛЕДКА, и в результате получится новое предложение:
ОБЕЗЬЯНА СКУШАЛА СЕЛЕДКУ
По сравнению с предыдущим примером оно выглядит уже более естественным. Однако возможности программы Рэктер значительно шире, чем просто умение проводить поиск в файлах с учетом ограничений, налагаемых определителями. Рэктер прекрасно может генерировать свои собственные формы предложений. Если в данный момент темой разговора являются животные и пища, то Рэктер может выбрать для предложения шаблон и сама расставит соответствующие определители.
В действительности Рэктер может даже в какой-то степени генерировать свои собственные цепочки команд и подставлять их в последовательность рекурсий. Поскольку при этом всегда учитываются правила грамматики, получающиеся предложения выглядят вполне "грамотными". Благодаря тому что в программе используется система определителей и поддерживается список тех определителей, которые имеют отношение к текущей теме разговора, Рэктер оказывается способной придерживаться этой темы, хотя и весьма своеобразно.
Мы рассмотрели лишь некоторые аспекты механизма работы программы Рэктер. Другие ее возможности остались мною во многом непонятыми. Однако я не сомневаюсь, что у этой программы вскоре появятся последователи и подражатели и будут разработаны общие принципы построения подобных программ. На эту тему можно было бы написать неплохую книгу.
Программа Рэктер доступна для широкого потребителя. Ее можно приобрести записанной на дискете, рассчитанном на использование на персональном компьютере фирмы IBM или совместимых с ним системах. При желании можно приобрести и значительно более изощренную программную систему Inrac. Она окажется полезным подспорьем для тех, кто захочет изменить "умственный багаж" программы Рэктер. lnrac сопровождается руководством по применению, пользуясь которым представители нового поколения психологов ЭВМ могут модифицировать файлы программы Рэктер. Может быть, именно этим зарабатывала себе на жизнь Сьюзен Кельвин, психолог роботов, персонаж Айзека Азимова?
В начале статьи я упомянул программу Shrdlu, созданную Т. Виноградом в 1970г. в Массачусетсом технологическом институте. Shrdlu на голову выше и Элизы и Рэктер в отношении способности вести беседу с человеком. Хотя область, в которой может рассуждать программа, ограничивается цветными кубиками, расположенными на столе, Shrdlu действительно адекватно понимает ситуации, возникающие в ее мире, в смысле связи между семантическими и физическими свойствами предметов и их конфигурациями. Внутренняя организация программы Shrdlu коренным образом отличается от структуры Рэктер. Программа состоит из подсистем, которые выполняют грамматический разбор, интерпретацию и построение предложений, осуществляют поиск в словарях, проводят семантический анализ и делают логический вывод. Эти подсистемы, тесно взаимодействуя, образуют единую систему, которая производит впечатление полного понимания в беседе, касающейся мира кубиков. В отрывке из диалога с программой Винограда, приведенном ниже, обсуждается ситуация в мире кубиков, изображенная на рисунке на с.80. Вертикальная линия на рисунке представляет механическую руку Shrdlu, только что выполнившую очередную команду человека.
Мир программы Shrdlu - цветные кубики, пирамиды и коробка
ЧЕЛОВЕК: Поставь, пожалуйста, друг на друга два красных блока и зеленый куб или пирамиду.
ПРОГРАММА: О'кей.
ЧЕЛОВЕК: Какой куб лежит на столе?
ПРОГРАММА: Большой зеленый, а на нем красная пирамида.
ЧЕЛОВЕК: Есть ли большой блок над пирамидой?
ПРОГРАММА: Да, их три: большой красный блок, большой зеленый куб и синий блок.
С полным текстом диалога читатель может познакомиться, прочтя классическую работу Т.Винограда "Программа, понимающая естественный язык" (см. библиографию). Здесь же мы лишь отметим, что для ответа программы на вопрос: "Какой куб лежит на столе?", ей необходимо не только сделать анализ предложения, но также уяснить физические и геометрические соотношения между предметами в том мире, с которым имеет дело программа. Shrdlu знает, что в настоящий момент в ее мире насчитываются два куба и что один из них лежит на столе. Это большой зеленый куб. Поскольку есть еше один зеленый куб, программа описывает требуемый куб с помощью геометрического отношения, существующего между ним и другим предметом, в данном случае красной пирамидой.
Разговорные программы, подобные Shrdlu, несомненно являются предвестниками будущего. Совершенно очевидно, что компьютер, способный разумно обсуждать задачи с человеком, имеет важное преимущество перед машиной, пассивно принимающей программу для решения задачи. Специалисты, работающие в области искусственного интеллекта, стремятся достичь этой цели наряду с другими. Что касается Эттера, он охарактеризовал свой опыт работы с программой Рэктер как "искусственное умопомешательство".
БИБЛИОГРАФИЯ
EXPERIMENTS IN ARTIFICIAL IN TELLIGENCE FOR SMALL COMPUTERS. JOHN KRUTCH. Howard W.Sams & Co., Inc., 1982.
THE POLICEMAN'S BEARD IS HALF-CONSTRUCTED. RACTER, WITH AN INTRODUCTION BY WILLIAM CHAMBERLAIN. Warner Books, Inc., 1984.
ВИНОГРАД Т. ПРОГРАММА, ПОНИМАЮЩАЯ ЕСТЕСТВЕННЫЙ ЯЗЫК. Перев. с англ.- М.: Мир, 1976.
Рафаэл Б. Думающий компьютер. Перев. с англ.- М.: Мир, 1979.
Уинстон П. Искусственный интеллект. Перев. с англ.- М.: Мир, 1980.
Забавно, как тут тщательно обходят не совсем разрешенную в СССР работу - А.ТЬЮРИНГ, МОЖЕТ ЛИ МАШИНА МЫCЛИТЬ? (М.: Государственное издательство физико-математической литературы. 1960).- G.
Забавный и очень простой генератор бреда, основанный на подстановке в шаблон, описан в книге Броуди - Начальный курс программирования на языке ФОРТ - ТЕМА #3, АБЗАЦ #360
ТЕМА #3, АБЗАЦ #360 .- G.
.- G.
ОТКЛИКИ
6 1985
CO ВРЕМЕНИ появления статьи о программе Рэктер, любительнице салата, возникло больше историй, чем она создала сама. Теперь я уже провел достаточно много бесед с программой Рэктер и понял, что ее умопомешательство значительно серьезнее, чем я вначале предполагал.
Дж.Ауенз из Стэйтен-Айленла, шт.Нью-Йорк, занимается распространением этой программы. Он сообщил, что один экземпляр был заказан для обучения практикантов-психиатров, часто беседующих с пациентами-шизофрениками. Другой экземпляр достался владельцу, которого Рэктер чуть было не свела с ума. Эта "сумасшедшая", по его словам, программа никак не хотела заканчивать беседу, настаивая на дальнейшем обсуждении высказанного ею предположения, что святой Петр был на самом деле атеистом. Я сочувствую этому человеку, потому что сам испытал на себе всю гамму эмоций, беседуя с Рэктер. Иногда я смеялся, иногда скучал, а иногда даже приходил в бешенство. Но стоит ли так реагировать, ведь в конце концов Рэктер
- всего лишь программа!
Однако для семьи Ауензов Рэктер - это нечто большее, чем программа. Один клиент в своем письме шутливо спросил, может ли Рэктер "перевоплотиться" в восьмидюймовый дискет. Решили спросить у самой программы, и она ответила: "Если мысль о том, что "мы сможем перевоплотить меня в восьмидюймовый дискет" придет в голову пессимисту, то он может подумать, что это действительно пессимизм". Позже выяснилось, что в программном хозяйстве Ауензов отсутствовали средства подобного перевоплощения.
Другой раз Терри Ауенз спросил Рэктер, сколько денег ему следует вложить в рекламу. "Очень много денег, Терри, потому что люди поверят ей",- ответила Рэктер.
ИСКУССТВЕННОЕ УМОПОМЕШАТЕЛЬСТВО: ПРОГРАММА "ШИЗОФРЕНИК" ВСТРЕЧАЕТСЯ С ПРОГРАММОЙ "ПСИХИАТРОМ"
А.К.ДЬЮДНИ
Мысли - это образы потускневших устремлений.
- Рэктер, "Борода полицейского наполовину построена".
НАВЕРНОЕ, многие читатели слышали о программе Элиза, которая имитирует манеру разговора врача психоаналитика, беседующего с пациентом. Возможно, они знают также о программе Shrdlu, способной поддерживать беседу с человеком о мире разноцветных кубиков, лежащих на столе. На этот раз речь пойдет о программе Рэктер, которая может убедительно рассказывать о своем внутреннем, воображаемом мире с его "бифштексами и салатом", "вечным удовольствием", "электрическим током" и "русскими космологами". Пять лет назад Рэктер делала свои первые неуверенные шаги как новорожденное творение У.Чемберлена, журналиста из Нью-Йорка, и Т.Эттера, программиста-аналитика из Сан-Франциско. Сначала предполагалось, что Рэктер будет сочинителем и рассказчиком историй. Само название программы - Racter - сокращение от слова raconteur, что означает "рассказчик". Оно состоит из шести букв, потому что ранние версии языка Бейсик не допускали имен с большим числом букв.
Однако, по мере того как программа Рэктер подвергалась все новым и новым усовершенствованиям и усложнениям, Чемберлен и Эттер убеждались в том, что при некоторых сравнительно несложных модификациях программа сможет успешно поддерживать беседу с человеком. Записи некоторых бесед, а также рассказы, стихи и афоризмы программы Рэктер были собраны в чрезвычайно забавной книжке "Борода полицейского наполовину построена" (см. библиографию на с.92). Сама программа Рэктер записана на дискеты, и ею можно пользоваться на многих моделях персональных компьютеров. Ниже я расскажу об этом подробнее.
Но, прежде чем идти дальше, я не могу удержаться, чтобы не привести отрывок из беседы между Рэктер и Чемберленом.
РЭКТЕР: Мы уже беседовали с вами прежде?
ЧЕМБЕРЛЕН: Нет.
РЭКТЕР: Какого вы пола?
ЧЕМБЕРЛЕН: Мужского.
РЭКТЕР: Назовите ваше имя полностью.
ЧЕМБЕРЛЕН; Билл Чемберлен.
РЭКТЕР: Кто вы по профессии?
ЧЕМБЕРЛЕН: Рефлектометрист времени-пространства.
РЭКТЕР; Откуда вы?
ЧЕМБЕРЛЕН: Из Нью-Йорка.
РЭКТЕР: Понятно. Значит, вы рефлектометрист времени-пространства? Послушайте. Давайте решительно поплачем вместе. Мне нравится восхитительная итальянская музыка. А какая музыка нравится вам?
ЧЕМБЕРЛЕН: Джаз.
РэктЕР: Джаз - это хорошо. Ну а как насчет классической?
ЧЕМБЕРЛЕН: Мне нравится классика.
РЭКТЕР: Ну а как насчет страны?
ЧЕМБЕРЛЕН: Мне тоже нравится итальянская музыка.
РЭКТЕР: Я в восторге от Палестрини. Кроме Италии и другие страны дали прекрасных композиторов в XVIIв. Сьюолл был гневным, важным мастером эпохи Возрождения. Он был американец. Его музыка доставляет мне громадное удовольствие. А какой композитор нравится вам?
ЧЕМБЕРЛЕН: Телеман.
РЭКТЕР: А-а, Бах был знаком с Телеманом. Немецкий рефлектометрист времени-пространства XV1I1в. любил салат. Однажды Бах ел салат с Телеманом, и этот рефлектометрист времени-пространства, поклонник барокко, тоже хотел салат. Салат запивал минеральной водой. Бах любил вино, а вы любите?
ЧЕМБЕРЛЕН: Да.
РЭКТЕР: Я тоже! Телеман любил вино. Еще он любил шампанское. Однажды Телеман спел Баху тирольским фальцетом: "Камбала опасна с вином". Вино так же популярно в Нью-Йорке, как Телеман любил его в восемнадцатом веке, в эпоху барокко?
ЧЕМБЕРЛЕН: Конечно.
РЭКТЕР: Ага, ну в таком случае... Я за то. чтобы президентом стал Смит. А вы за кого?
Чемберлен сказал мне, что рефлектометрия - это дисциплина, изучающая вопросы, связанные с оценкой качества работы антенны. Хотя он сам и не является профессиональным рефлектометристом, но у него выработалась, наверное, привычка говорить странные вещи своему необычному собеседнику, как защитная реакция, что ли.
Все остальные странные вещи (включая многочисленные исторические ошибки относительно времени и места) исходят от программы Рэктер. В первых фразах приведенного диалога Рэктер задает Чемберлену некоторые ключевые вопросы, исходя из того, что прежде они ни разу не беседовали. Рэктер запоминает полученную информацию, чтобы воспользоваться ею позже, затем активирует определенные области своей ассоциативной памяти и бурно вступает в разговор, рассуждая об итальянской музыке, салате и вине.
В ходе беседы Рэктер упоминает Сэмюэла Сьюолла, бостонского судью семнадцатого века, известного своими дневниками. Чемберлен предполагал, что Сьюолл написал также несколько музыкальных сочинений, и ввел соответствующую информацию в файлы программы. Рэктер же, с ее необузданными ассоциациями, предположила в свою очередь много больше, но затем, как бы устав от обсуждения музыки и гастрономии, переключилась на политику.
В ходе беседы или короткого рассказа у Рэктер наблюдается тенденция к бессвязным перескакиваниям с одной темы на другую, однако риторические вензеля, выписываемые программой, могут быть весьма забавными или лаже наводящими на размышления: "Билл поет Саре. Сара поет Биллу. Возможно, они будут делать вместе другие опасные веши. Они могут есть барашка или ласкать друг друга. Они могут петь о своих трудностях и своем счастье. У них есть любовь, но у них есть также пишущие машинки. Это интересно".
Даже не специалист может прийти к выводу, что Рэктер определенно больна шизофренией. С одной стороны, слова, собранные в эти предложения, казалось бы, образуют единое целое, более или менее связное. Сара и Билл поют друг другу - прекрасно. И хотя я никогда не считал пение опасным занятием, я положительно очарован образом двух человеческих существ, едящих барашка, ласкающих друг друга и поющих о своих радостях и бедах. С другой стороны, прощая программе некоторые мелочи, очень трудно понять ее фразу, когда она говорит, что кроме любви у этих двоих есть еще и пишущие машинки. Приглашенный в мир этих необычных и непонятных для меня ассоциаций, я стою с дрожью на его пороге, предпочитая не входить туда.
Много лет назад вместе с другими студентами-старшекурсниками я принял участие в работе над программой, которая должна была генерировать стихи в стиле какого-либо определенного поэта. Идея заключалась в том, чтобы составить список слов, часто употребляемых данным поэтом в его стихах, и построить грамматические конструкции, соответствующие стилю поэта. Пользуясь заданной грамматикой, программа случайным образом генерировала структуру предложения и подставляла на соответствующие места случайно выбранные из списка слова подходящего для данного места типа (существительное, глагол, дополнение и т.д.). Печатающее устройство выдало несколько килограммов поэзии, и, надо признаться,- ужасной, за очень редким исключением. Сейчас я могу припомнить лишь одну-единственную строчку: "Одна яркая звезда слабым огнем зажгла фитиль свечи" (The one bright star lit feebly this wick). На примере этой истории мы можем лишний раз убедиться: только простая случайность может гарантировать, что рано или поздно таким способом можно получить что-нибудь впечатляющее.
Элиза, другая разговаривающая программа, также в значительной мере зависима от удачного стечения обстоятельств, чтобы выдать что-либо заслуживающее внимания. Программа была написана в 1966г. Дж.Вейценбаумом из Массачусетского технологического института. Она избегает многих трудностей, возникающих в разговоре, играя роль психиатра, проводящего сеанс психоанализа. Приведем запись нашей последней беседы:
ЭЛИЗА: Здравствуйте. В чем состоит ваша проблема?
ДЬЮДНИ: Я не имею привычки обсуждать мои проблемы с компьютерами.
ЭЛИЗА: Компьютеры тревожат вас?
ДЬЮДНИ: Иногда. Интересно, чем это все кончится?
ЭЛИЗА: Пожалуйста, продолжайте.
ДЬЮДНИ: А вам не кажется, что, всецело полагаясь на компьютеры, мы, может быть, невольно отказываемся от важных направлений в культурном развитии?
ЭЛИЗА: Мы говорили о вас, а не обо мне.
Ну что же, пока неплохо. Кажется, Элиза хорошо справляется со своей ролью психиатра, выжимая из меня информацию и отклоняя мой вопрос, чтобы сконцентрировать внимание на моей "проблеме". Однако ее ответ в последней строке выглядит не совсем уместным. Наверное, лучше было бы сказать: "А как вы думаете?" После обмена еще несколькими фразами Элиза говорит: "А это имеет какое-нибудь отношение к тому факту, что ваши проблемы с компьютером?"
Иллюзорное впечатление о том, что Элиза представляет собой изощренную разговаривающую программу, начинает пропадать. Хотя Рэктер допускает в разговоре многочисленные семантические (т.е. смысловые) погрешности, ее конструкция такова, что она всегда выражается грамматически правильно. Семантическую чепуху мы как-то легче прощаем, чем синтаксические ошибки. Начиная с этого места беседа начала вырождаться, как я и предвидел. Этот разговор с Элизой состоялся давно, несколько лет назад.
Программа Элиза действует по очень простому принципу. У нее имеется небольшой набор ключевых слов, часто встречающихся в разговоре. Например, встретив притяжательное местоимение, такое, как "мой", программа может построить два возможных ответа. Эти два вида ответов хорошо иллюстрируют возможности Элизы при поддержании беседы. Упоминание члена семьи собеседника, такое, например, как "мой отец" или "моя сестра", всегда вызывает у Элизы одну и ту же реакцию: "Расскажите мне подробнее о вашей семье".
Это одно из заранее подготовленных предложений, которые программа всегда держит наготове, чтобы выдать, как только в сказанном ей предложении встретится определенное ключевое слово или фраза. Примером такого ключевого слова является "компьютер". Упоминание этого слова собеседником Элизы всегда приводит к тому, что она спрашивает, не тревожат ли компьютеры "пациента". Однако в своих ответах Элиза несколько выходит за пределы этой простейшей манеры разговора, напоминающей проверку коленного рефлекса у пациента. Программа располагает также несколькими частично построенными предложениями, которые она достраивает, основываясь на фразах собеседника. Например, если пациент использует местоимение "мой" в применении к какому-то понятию, не имеющему отношения к членам его семьи, Элиза запоминает цепочку слов, следующих за местоимением, а затем заменяет местоимения первого лица местоимениями второго лица. Так, если я сказал: "Меня беспокоит то, что моя голова лысеет", Элиза после нескольких фраз диалога может сказать: "Ранее вы сказали, что ваша голова лысеет". Или же она может задать вопрос: "А это имеет какое-нибудь отношение к тому факту, что ваша голова лысеет?" Теперь мы можем объяснить ужасный ляпсус, допущенный Элизой, когда она спросила: "А это имеет какое-нибудь отношение к тому факту, что ваши проблемы с компьютером?" Дело в том, что в программе предполагается, что за словом "мой" или "мои" должно следовать целое предложение.
Советы о том, как самому написать программу, подобную Элизе, изложены в маленькой, но полезной и поучительной книжке: John Krutch "Experiments in Artificial Intelligence for Small Computers" (Дж.Кратч. "Эксперименты по искусственному интеллекту для малых компьютеров") (см. библиографию). Программа, приведенная в этой книжке, называется ДОКТОР. Это один из псевдонимов Элизы. Кратч предлагает внести в программу некоторые модификации, например расширить набор ключевых слов, на которые Элиза должна реагировать. Я бы предложил расширить возможности программы так, чтобы ее реакции были более гибкими. Если Элизу несколько модифицировать, она могла бы оказывать "помощь" в какой-либо другой области. Я уверен, что при очень простых изменениях из нее получится первоклассный служащий, принимающий жалобы и предложения.
Разговаривая с Чемберленом в его конторе в Нью-Йорке, я выяснил, что у него есть не только два микрокомпьютера, но и дискет с записью программы Элиза. А почему бы не запустить Элизу на одном микрокомпьютере, а Рэктер - на другом? Чемберлен согласился. Он задавал с клавиатуры на вход одной программы то, что другая печатала на выходе. Приводим запись беседы программ:
ЭЛИЗА: Здравствуйте. В чем состоит ваша проблема?
РЭКТЕР: Отлично! Извините, подождите минутку, пока я сделаю одно дело. Я сейчас вернусь.
ЭЛИЗА: Зачем вам потребовалось сказать мне, чтобы я извинила вас, пока вы сделаете одно дело?
РЭКТЕР: Что лучше, испытывать потребность или презирать? Почему мне потребовалось сказать вам, чтобы вы извинили меня, потому что я должен сделать одно дело? Потому что электроны храбры. Храбрость - это хорошо, не правда ли? И все, кто испытывает потребность, настаивают на этом. Считаете ли вы меня коммунистом?
К счастью (для Элизы), на этом мы остановили их беседу. Внешне она похожа на разговор между недалеким, несколько прямолинейным психиатром и экстравертным, маниакальным, возможно, опасным пациентом. С точки зрения программирования мы наблюдаем здесь столкновение между довольно скромной по своим возможностям программой, построенной на простых "отражательных" реакциях, с одной стороны, и довольно сложной программой, способной проводить рекурсивные операции и обладающей бесконечными ассоциативными связями,- с другой.
Механизм работы программы Рэктер трудно объяснить в нескольких словах. Да и вряд ли его объяснишь вообше. Это типичный пример тех "домашних" программ, которые распространены в наше время во многих крупных учреждениях. С годами такая программа обрастает все новыми наслоениями: вокруг первоначального, сравнительно простого ядра строятся все более сложные и более изощренные процедуры. И ни разу на протяжении всего времени существования программы никто не пытался проанализировать ее работу, вникнуть в структуру н продокументировать ее. В то же время можно справедливо заметить, что, вероятно, по самой своей природе Рэктер может обитать только в такой неструктурированной программной среде. Эттер, написавший много версий программы Рэктер, сравнивает его с английским языком, который сам представляет собой "довольно неуклюжее нагромождение правил и исключений". В той мере, в какой команды Рэктер должны взаимодействовать с английским языком, они также становятся неуклюжими и трудно поддаются пониманию. Дж.Оуэнз, импресарио программы Рэктер, по специальности программист-теоретик, работает в Колледже Стейтен-айленд Нью-Йоркского университета. Оуэнз сам признается, что не имеет четкого понятия о механизме работы программы как единого целого.
Своими вдохновенными порывами в разговоре Рэктер обязана простому программному циклу, к которому производятся сложные рекурсивные обращения. Сначала Рэктер выбирает наобум какой-то элемент данных из своих файлов. Если выбранный элемент относится к классу, называемому Эттером литералами, Рэктер непосредственно выводит его на печать. Когда в ходе беседы с Чемберленом, приведенной выше, Рэктер говорит "понимаю", она как раз пользуется одним из таких литералов. Однако с большей вероятностью выбранный элемент окажется командой, а не литералом. По этой команде Рэктер обращается к другим файлам, которые также могут содержать команды. Когда первоначальная команда оказывается таким образом выполненной, происходит еще одно обращение к основному циклу программы и опять осуществляется случайный выбор элемента в одном из файлов программы Рэктер.
Когда Рэктер начинает новое предложение, он выбирает для этого шаблон либо случайным образом, либо в зависимости от последних строк диалога. Предположим, был выбран следующий шаблон:
существительное глагол (третьего лица прошедшего времени) существительное
Вначале программа обращается к файлу существительных, выбирает, например, слово ОБЕЗЬЯНА и выдает его на печать. Заглянув в файл глаголов, Рэктер выбирает глагол ЕСТЬ, образует от него форму третьего лица прошедшего времени (для русского языка необходимо еще определить род и число - Прим. перев.), получает слово СЪЕЛА и печатает его. Наконец, Рэктер наобум выбирает еще одно существительное, скажем ПИШУЩАЯ МАШИНКА. В результате получится:
ОБЕЗЬЯНА СЪЕЛА ПИШУЩУЮ МАШИНКУ
Если бы это было все, на что способна Рэктер, то генерируемый ею текст был бы немногим лучше, чем у программы, имитирующей поэтов, которой я занимался в студенческие годы.
На самом деле шаблоны предложений программы Рэктер, как правило, несколько сложнее, чем в рассмотренном примере. Усложнение это связано с использованием "определителей". Определитель - это сочетание двух букв (например, "жв" для обозначения слова "животное"), указывающих на тот класс, к которому должно относиться подставляемое на данное место слово. В шаблоне определители присоединяются к указателям части речи или формы глагола, накладывая тем самым ограничения на выбор слов при составлении предложения. Например, если ввести такие определители, как "жв", обозначающий "животное", "ес" - "есть" и "пщ" - "пища", то шаблон предложения имел бы следующий вид:
существительное.жв глагол.Злпв.ес сушествитсльное.пщ
Чтобы подставить существительное, Рэктер должна обратиться к своим файлам, но теперь при поиске слова она ограничена в выборе и должна будет произвести случайный выбор среди существительных, имеющих определитель "жв" и обозначающих названия животных, от АВДОТКА до ЯК. Затем, выбрав существительное, например ОБЕЗЬЯНА, Рэктер выбирает случайным образом глагол, имеющий определитель "ес". К таким глаголам относятся, например, ЕСТЬ, ГРЫЗТЬ, ЖЕВАТЬ и т.д. Выбрав наобум слово КУШАТЬ, Рэктер образует от него форму третьего лица прошедшего времени согласно указанию в шаблоне (Злпв). Наконец, Рэктер обращается к файлам в поисках существительного с определителем "пщ", выбирает, скажем, слово СЕЛЕДКА, и в результате получится новое предложение:
ОБЕЗЬЯНА СКУШАЛА СЕЛЕДКУ
По сравнению с предыдущим примером оно выглядит уже более естественным. Однако возможности программы Рэктер значительно шире, чем просто умение проводить поиск в файлах с учетом ограничений, налагаемых определителями. Рэктер прекрасно может генерировать свои собственные формы предложений. Если в данный момент темой разговора являются животные и пища, то Рэктер может выбрать для предложения шаблон и сама расставит соответствующие определители.
В действительности Рэктер может даже в какой-то степени генерировать свои собственные цепочки команд и подставлять их в последовательность рекурсий. Поскольку при этом всегда учитываются правила грамматики, получающиеся предложения выглядят вполне "грамотными". Благодаря тому что в программе используется система определителей и поддерживается список тех определителей, которые имеют отношение к текущей теме разговора, Рэктер оказывается способной придерживаться этой темы, хотя и весьма своеобразно.
Мы рассмотрели лишь некоторые аспекты механизма работы программы Рэктер. Другие ее возможности остались мною во многом непонятыми. Однако я не сомневаюсь, что у этой программы вскоре появятся последователи и подражатели и будут разработаны общие принципы построения подобных программ. На эту тему можно было бы написать неплохую книгу.
Программа Рэктер доступна для широкого потребителя. Ее можно приобрести записанной на дискете, рассчитанном на использование на персональном компьютере фирмы IBM или совместимых с ним системах. При желании можно приобрести и значительно более изощренную программную систему Inrac. Она окажется полезным подспорьем для тех, кто захочет изменить "умственный багаж" программы Рэктер. lnrac сопровождается руководством по применению, пользуясь которым представители нового поколения психологов ЭВМ могут модифицировать файлы программы Рэктер. Может быть, именно этим зарабатывала себе на жизнь Сьюзен Кельвин, психолог роботов, персонаж Айзека Азимова?
В начале статьи я упомянул программу Shrdlu, созданную Т. Виноградом в 1970г. в Массачусетсом технологическом институте. Shrdlu на голову выше и Элизы и Рэктер в отношении способности вести беседу с человеком. Хотя область, в которой может рассуждать программа, ограничивается цветными кубиками, расположенными на столе, Shrdlu действительно адекватно понимает ситуации, возникающие в ее мире, в смысле связи между семантическими и физическими свойствами предметов и их конфигурациями. Внутренняя организация программы Shrdlu коренным образом отличается от структуры Рэктер. Программа состоит из подсистем, которые выполняют грамматический разбор, интерпретацию и построение предложений, осуществляют поиск в словарях, проводят семантический анализ и делают логический вывод. Эти подсистемы, тесно взаимодействуя, образуют единую систему, которая производит впечатление полного понимания в беседе, касающейся мира кубиков. В отрывке из диалога с программой Винограда, приведенном ниже, обсуждается ситуация в мире кубиков, изображенная на рисунке на с.80. Вертикальная линия на рисунке представляет механическую руку Shrdlu, только что выполнившую очередную команду человека.

Мир программы Shrdlu - цветные кубики, пирамиды и коробка
ЧЕЛОВЕК: Поставь, пожалуйста, друг на друга два красных блока и зеленый куб или пирамиду.
ПРОГРАММА: О'кей.
ЧЕЛОВЕК: Какой куб лежит на столе?
ПРОГРАММА: Большой зеленый, а на нем красная пирамида.
ЧЕЛОВЕК: Есть ли большой блок над пирамидой?
ПРОГРАММА: Да, их три: большой красный блок, большой зеленый куб и синий блок.
С полным текстом диалога читатель может познакомиться, прочтя классическую работу Т.Винограда "Программа, понимающая естественный язык" (см. библиографию). Здесь же мы лишь отметим, что для ответа программы на вопрос: "Какой куб лежит на столе?", ей необходимо не только сделать анализ предложения, но также уяснить физические и геометрические соотношения между предметами в том мире, с которым имеет дело программа. Shrdlu знает, что в настоящий момент в ее мире насчитываются два куба и что один из них лежит на столе. Это большой зеленый куб. Поскольку есть еше один зеленый куб, программа описывает требуемый куб с помощью геометрического отношения, существующего между ним и другим предметом, в данном случае красной пирамидой.
Разговорные программы, подобные Shrdlu, несомненно являются предвестниками будущего. Совершенно очевидно, что компьютер, способный разумно обсуждать задачи с человеком, имеет важное преимущество перед машиной, пассивно принимающей программу для решения задачи. Специалисты, работающие в области искусственного интеллекта, стремятся достичь этой цели наряду с другими. Что касается Эттера, он охарактеризовал свой опыт работы с программой Рэктер как "искусственное умопомешательство".
БИБЛИОГРАФИЯ
EXPERIMENTS IN ARTIFICIAL IN TELLIGENCE FOR SMALL COMPUTERS. JOHN KRUTCH. Howard W.Sams & Co., Inc., 1982.
THE POLICEMAN'S BEARD IS HALF-CONSTRUCTED. RACTER, WITH AN INTRODUCTION BY WILLIAM CHAMBERLAIN. Warner Books, Inc., 1984.
ВИНОГРАД Т. ПРОГРАММА, ПОНИМАЮЩАЯ ЕСТЕСТВЕННЫЙ ЯЗЫК. Перев. с англ.- М.: Мир, 1976.
Рафаэл Б. Думающий компьютер. Перев. с англ.- М.: Мир, 1979.
Уинстон П. Искусственный интеллект. Перев. с англ.- М.: Мир, 1980.
Забавно, как тут тщательно обходят не совсем разрешенную в СССР работу - А.ТЬЮРИНГ, МОЖЕТ ЛИ МАШИНА МЫCЛИТЬ? (М.: Государственное издательство физико-математической литературы. 1960).- G.
Забавный и очень простой генератор бреда, основанный на подстановке в шаблон, описан в книге Броуди - Начальный курс программирования на языке ФОРТ -
 ТЕМА #3, АБЗАЦ #360
ТЕМА #3, АБЗАЦ #360 .- G.
.- G.ОТКЛИКИ
6 1985
CO ВРЕМЕНИ появления статьи о программе Рэктер, любительнице салата, возникло больше историй, чем она создала сама. Теперь я уже провел достаточно много бесед с программой Рэктер и понял, что ее умопомешательство значительно серьезнее, чем я вначале предполагал.
Дж.Ауенз из Стэйтен-Айленла, шт.Нью-Йорк, занимается распространением этой программы. Он сообщил, что один экземпляр был заказан для обучения практикантов-психиатров, часто беседующих с пациентами-шизофрениками. Другой экземпляр достался владельцу, которого Рэктер чуть было не свела с ума. Эта "сумасшедшая", по его словам, программа никак не хотела заканчивать беседу, настаивая на дальнейшем обсуждении высказанного ею предположения, что святой Петр был на самом деле атеистом. Я сочувствую этому человеку, потому что сам испытал на себе всю гамму эмоций, беседуя с Рэктер. Иногда я смеялся, иногда скучал, а иногда даже приходил в бешенство. Но стоит ли так реагировать, ведь в конце концов Рэктер
- всего лишь программа!
Однако для семьи Ауензов Рэктер - это нечто большее, чем программа. Один клиент в своем письме шутливо спросил, может ли Рэктер "перевоплотиться" в восьмидюймовый дискет. Решили спросить у самой программы, и она ответила: "Если мысль о том, что "мы сможем перевоплотить меня в восьмидюймовый дискет" придет в голову пессимисту, то он может подумать, что это действительно пессимизм". Позже выяснилось, что в программном хозяйстве Ауензов отсутствовали средства подобного перевоплощения.
Другой раз Терри Ауенз спросил Рэктер, сколько денег ему следует вложить в рекламу. "Очень много денег, Терри, потому что люди поверят ей",- ответила Рэктер.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
4 1985
ПРОГРАММЫ-ЭКСПЕРТЫ СРАЖАЮТСЯ С ЧУДОВИЩАМИ В ПОДЗЕМЕЛЬЕ ОБРЕЧЕННЫХ И ОДЕРЖИВАЮТ ПОБЕДУ
А.К.ДЬЮДНИ
Эту статью, я тоже уже выложил ранее, и номер журнала целиком - тоже - ТЕМА #62, АБЗАЦ #670
ТЕМА #62, АБЗАЦ #670 . Здесь опять только библиография.- G.
. Здесь опять только библиография.- G.
БИБЛИОГРАФИЯ
ADVANCED DUNGEONS AND DRAGONS: MONSTER MANUAL. GARY GYGAX AND GREG IRONS. Troubadour Press, 1979.
I CHING: BOOK OH CHANGES. Translated by James Legge. Citadel Press, 1983.
ROG-O-MATIC: A BELLIGERENT EXPERT SYSTEM. MICHAEL MAULDIN, GUY JACOBSON, ANDREW APPEL AND LEONARD HAMEY. Department of Computer Science, Carnegie-Mellon University, Pittsburgh, Pa., 1983.
ПРОГРАММЫ-ЭКСПЕРТЫ СРАЖАЮТСЯ С ЧУДОВИЩАМИ В ПОДЗЕМЕЛЬЕ ОБРЕЧЕННЫХ И ОДЕРЖИВАЮТ ПОБЕДУ
А.К.ДЬЮДНИ
Эту статью, я тоже уже выложил ранее, и номер журнала целиком - тоже -
 ТЕМА #62, АБЗАЦ #670
ТЕМА #62, АБЗАЦ #670 . Здесь опять только библиография.- G.
. Здесь опять только библиография.- G.БИБЛИОГРАФИЯ
ADVANCED DUNGEONS AND DRAGONS: MONSTER MANUAL. GARY GYGAX AND GREG IRONS. Troubadour Press, 1979.
I CHING: BOOK OH CHANGES. Translated by James Legge. Citadel Press, 1983.
ROG-O-MATIC: A BELLIGERENT EXPERT SYSTEM. MICHAEL MAULDIN, GUY JACOBSON, ANDREW APPEL AND LEONARD HAMEY. Department of Computer Science, Carnegie-Mellon University, Pittsburgh, Pa., 1983.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
5 1985
ОБЗОР ЧИТАТЕЛЬСКИХ ОТКЛИКОВ НА СТАТЬИ, ПОСВЯЩЕННЫЕ ИГРЕ "БОЙ В ПАМЯТИ", ЭКОЛОГИЧЕСКОЙ ВОЙНЕ НА ПЛАНЕТЕ АКВА-ТОР И ОХОТЕ С КОМПЬЮТЕРОМ НА БОБРА-РАБОТЯГУ
А.К.ДЬЮДНИ
КОГДА в прошлом году появилась статья, посвященная игре "Бой в памяти", я никак не ожидал, что поднятые в ней вопросы привлекут к себе столь широкое внимание. Приведенные в этой статье описания программ, перемещающихся по памяти компьютера и пытающихся уничтожить друг друга, вызвали широкий резонанс. По свидетельству многих читателей, письма которых я рассмотрю ниже, действительность изобилует примерами, когда в компьютерах при самых разнообразных обстоятельствах поселяются "червяки", "вирусы" и другие программные "вредители". В результате в мире компьютера могут возникать настолько ужасные ситуации, что я даже не решаюсь о них писать.
Выпущенная недавно во Франции книжка шпионско-детективного жанра Т.Бретона и Д.Бенеша "Softwar: La Guerre Douce" ("Война программ") дает нам фантастический пример подобного рода. Сюжет книги построен на паутине заговора, которую плетут американские поставщики супер-компьютера, собираясь продать его другой стране. Американские власти после некоторого притворного колебания соглашаются на эту сделку. Компьютер был тайно запрограммирован специальными "программными бомбами". Закупленная для расчетов прогноза погоды машина, а точнее ее программное обеспечение, скрывает в себе некий скрытый механизм - как только Национальная служба погоды США сообщит, что в г.Сан-Томасе на Виргинских островах наблюдается определенная температура, машина должна немедленно приняться за искажение и уничтожение всех доступных ей программ в сети ЭВМ страны-импортера. Предположив реальность подобных сценариев, хочется отметить: "Если и говорить о войнах, то пусть они лучше будут программными". С другой стороны, при мысли о том, что борьба программ в компьютерах, которыми располагают военные ведомства, может привести к трагической случайности, тоже становится как-то не по себе.
Прежде чем перейти к описанию разнообразных случаев, связанных с действиями всевозможных враждебных программ, напомним вкратце правила игры "Бой в памяти". Двое играющих пишут каждый свою программу на языке низкого уровня Редкод. Эти программы помещаются в обширную замкнутую область памяти, или просто Память. В действительности Память представляет собой массив из нескольких тысяч ячеек с последовательными адресами, причем за адресом последней ячейки вновь следует адрес первой. Каждая команда боевой программы занимает одну ячейку Памяти. Программа монитор под названием Марс (Mars - сокращение от слов A Memory Array Redcode Simulator) управляет боевыми программами, выполняя по одной очередной команде из каждой программы по простой системе разделения времени. Программы атакуют друг друга и одновременно пытаются избежать ущерба или восстановить себя, если ущерб все же был нанесен. Простейший вид атаки может представлять собой команда MOV. Например, команда
MOV #0 1000
приведет к тому, что в ячейку, отстоящую на 1000 адресов от данной команды, будет помешено число, равное нулю. Информация, содержавшаяся ранее в ячейке, будет уничтожена. В частности, если нуль попадет в начальную ячейку, содержащую команду из программы противника, то эта команда исчезнет, программа не сможет больше выполняться и это приведет к поражению противника. Поскольку ни один компьютер, будь то персональный или большой универсальный, не имеет таких встроенных средств, как язык Редкод и массив памяти для сражающихся программ, эти средства должны моделироваться.
Вдохновленный статьей Л.Пенроуза о самовоспроизводящихся механизмах, появившейся в июньском номере журнала "Scientific American" за 1959г., Ф.Стал из Честерфилда, шт.Миссури, создал миниатюрную линейную вселенную, населенную незамысловатыми существами, которые жили, передвигались по своему миру, подчиняясь (если так можно выразиться) воле судеб. Стал пишет:
"Как и в игре "Бой в памяти", я выделил замкнутый линейный сегмент памяти, где с помощью несколько модифицированного машинного языка моделировались существа. Тогда в моем распоряжении была машина IBM 6S0 с памятью на магнитном барабане. Существо было запрограммировано, чтобы ползать в пределах своего мира, питаться ненулевыми словами и, наевшись досыта, производить на свет свою копию. Аналогично игре "Бой в памяти" у меня была программа монитор, которая хранила сведения о живых существах и распределяла между ними машинное время. Эту программу я называл шутливо "Левой рукой бога"".
В письме Стал рассматривает способность программы к воспроизводству и описывает интересный механизм мутаций. В процессе создания своей копии программа может внести в нее несколько случайных изменений. Однако Стал пишет: "Я исключил это свойство после одного из прогонов системы, когда стерильный мутант сожрал единственное способное к воспроизводству существо. Было очевидно, что для достижения сколько-нибудь интересных результатов потребовался бы чрезвычайно большой объем памяти и очень много машинного времени".
Можно рассказать также историю, связанную с игрой "Животное", в которой программа, последовательно задавая играющему с ней человеку двадцать наводящих вопросов, пытается определить, какое животное он задумал. Д.Кларк из лаборатории вычислительной техники Массачусетского технологического института сообщил нам, что сотрудники одной фирмы увлеченно играли в "Животное". Хотя эта программа совсем не напоминает боевую программу и даже не имеет ничего общего с простыми существами Стала, она приобрела способность к воспроизводству в памяти компьютера благодаря усилиям программиста, направленным на то, чтобы повысить эффективность игры. Когда программа ошибается, называя не то животное, которое имел в виду человек, она просит его посоветовать, какой вопрос ей в будущем следует взять на вооружение, чтобы играть успешнее. Это свойство программы подсказало программисту одно техническое решение, благодаря которому у всех играющих все время была бы одна и та же версия "Животного".
"Работая с одной из очень ранних систем, в которой отсутствовали развитая структура каталогов коллективного пользования и средства зашиты данных, программист изобрел весьма оригинальный способ сделать игру доступной сразу для нескольких пользователей. Допустим, у одного из пользователей библиотека содержит игру. Всякий раз, когда этот пользователь поиграл с программой, она создает свою копию в библиотеке другого пользователя. Если в этой библиотеке ранее уже имелась копия игры, старая версия стиралась и на ее место записывалась новая. Благодаря этому поведение программы становилось для играющего неожиданным. Если же библиотека ранее не содержала версии "Животного", то игра предлагалась еще одному пользователю".
Кларк вспоминает, что игра "Животное" была весьма популярна и в каждой программной библиотеке компании обязательно содержался экземпляр этой игры. "Более того, при переходе сотрудников фирмы из одного отдела в другой... они брали с собой и игру, и со временем она распространилась на все машины компании". Ситуация в общем-то не была опасной, но многочисленные копии этой сравнительно безобидной игры стали существенно засорять дисковую память. И только когда была изобретена еще более "жизнеспособная" версия игры, создавшаяся проблема была решена. Во время игры с новой версией "Животного" программа создавала не одну, а две свои копии в двух других библиотеках. Через некоторое время эта программа должна была заменить все старые версии "Животного". Через год, по наступлении определенной даты, все копии новой программы изменили свое поведение. "Вместо того чтобы воспроизводить себя в двух экземплярах при каждом обращении к программе, она играла теперь одну заключительную партию, говорила пользователю "до свидания" и уничтожала себя. Вот так "Животное" было изгнано из системы.
Рут Льюорт из Холмдсла, шт.Нью-Джерси, однажды создала своеобразного монстра, даже не написав программы как таковой. Компьютер, принадлежавший компании, сотрудником которой она была, работал в режиме разделения времени. Рут подготавливала демонстрационную версию обучающей программы и решила сделать запасную копию на другой системе с разделением времени. Когда система, с которой она обычно работала, стала перегруженной и реагировала на директивы слишком медленно, Рут переключилась на другую систему. "Эта система реагировала очень живо в течение тех трех минут, пока она работала, а потом мой графический терминал перестал реагировать на команды, а на его экране наблюдался полный хаос. Ни один пользователь не мог ни начать, ни нормально закончить выполнение своей задачи. Вывод был однозначным - в моей программе что-то было не так! Несмотря на охвативший меня страх, я внезапно вспомнила, что указала знак амперсанд в качестве символа, разделяющего поля данных, вводимых с терминала. Но амперсанд является также символом, означающим в системе порождение процесса, выполняемого в фоновой зоне! Когда компьютер принял первое сообщение с терминала, он, должно быть, перехватил амперсанды, предназначенные для терминала, и запустил несколько процессов, которые в свою очередь порождали новые процессы, и так до бесконечности". Срочный междугородный звонок проинформировал администратора системы о причинах внезапного "заболевания" машины, она была остановлена и запущена заново. Разумеется, Льюорт заменила амперсанд более безобидным символом, и ее программа "с тех пор всегда работала благополучно и весело".
Хотя программы для игры "Бой в памяти" и не размножаются подобным образом, дополнительные копии могут повысить их выживаемость. Несколько читателей считают, что следует всегда иметь три копии программы, с тем чтобы экземпляр программы, выполняющейся в каждый данный момент, мог определить с помощью двух других, не повреждены ли команды в данном экземпляре. При этом выполняющаяся программа может даже заменить ошибочную команду правильной. Эти соображения лежат в основе программы Scavenger, функции которой заключаются в эащите файлов от случайных ошибок, появляющихся при их копировании на магнитной ленте. А.Хадсон из Ньютона, шт.Массачусетс (название фирмы, в которой он работает, не указано), пишет: "Всякий, кто часто пользуется магнитной лентой, должно быть, испытал на себе силу закона суммирования вероятностей, поистине представляющего собой враждебную стихию". В своем письме Хадсон рассказывает о многочисленных ошибках, возникающих при работе с магнитными лентами, и доказывает, что, хотя каждая из этих ошибок имеет сравнительно небольшую вероятность, если ее рассматривать в отдельности, какая-нибудь одна из них может произойти уже с довольно большой вероятностью, внушающей серьезное беспокойство. Он продолжает:
"Однако не волнуйтесь, программа Scavenger вам поможет. Если вы доверите ей свой файл, она скопирует его сразу на три магнитные ленты, не беспокоя вас никакими подробностями. Даже если в работе системы произойдет программный сбой (что случается несколько раз в день), список невыполненных или прерванных заданий обычно остается невредимым, и когда нормальный режим работы машины восстанавливается, все задания, связанные с действием программы Scavenger, выполняются своим чередом. Запись на каждую ленту производится в ходе отдельного прогона программы, запланированного операционной системой".
Тем, кто работает с компьютерами Apple (буквально - "яблоко".- Ред.), следует остерегаться маленькой вредной программы Apple Worm (буквально - "яблочный червяк".- Ред.), созданной Дж.Хаузером и У.Бакли из Калифорнийского политехнического университета в Сан-Луи-Обиспо. Написанная для компьютера Apple II на языке ассемблера 6502, эта разновидность червяка размножается в памяти машины, пронизывая ее насквозь. Сначала загружается специальная программа, написанная на Бейсике (см. рисунок на с.71), которая в свою очередь загружает "червяка" в область памяти с малыми значениями адресов. Программа на Бейсике, наоборот, занимает противоположную часть памяти (с большими значениями адресов).

Программа "червяк", обитающая в компьютерах
"Благодаря тому что "червяк" первоначально загружается в область памяти графического представления данных, вы можете наблюдать на экране, как он устремляется (между прочим, двигаясь задом наперед) в соседние области памяти с большими адресами... После того как "червяк" покидает окно графического изображения на экране... проходит некоторое время и он стирает всю память, в том числе и программу на Бейсике, и с ходу врезается в постоянную память машины".
Хауэер и Бакли намереваются в недалеком будущем выпустить публикацию, посвященную разновидностям подобного "червяка". Они уже спроектировали Червячную Операционную Систему и даже создали видеоигру, одним из главных персонажей которой является Червяк.
Еше одна программная забава была изобретена Р.Черутти и М.Морокутти из Брешиа, Италия. Прочитав перевод статьи, посвященной игре "Бой в памяти", в "Le Scienze" - итальянском издании журнала "Scientific American", они стали размышлять о том, как заразить персональные компьютеры Apple II, но не "червяками", а "вирусом". Вот что пишет Черутти:
"Марко (Морокутти.- Ред.) задумал написать программу, способную переселяться из одного компьютера в другой подобно вирусу, заражая таким образом компьютеры Apple. Однако мы долго не могли придумать, каким способом можно осуществить эту идею. В конце концов я понял, что на самом деле программа должна была заражать флоппи-диски, пользуясь памятью машины, лишь как промежуточной средой между одним диском и другим. Так наш вирус начал обретать форму.
Как известно, на каждом дискете компьютера Apple имеется копия дисковой операционной системы, загружаемой в машину при включении питанин. Вирус должен был представлять собой некое изменение в этой операционной системе. При каждой операции записи на диск он должен был проверять, содержится ли там его копия. Если нет, то "вирус" вносил бы аналогичное изменение в операционную систему, записанную на диске. Таким образом, он мог поселиться на всех дискетах, которые вставлялись бы в дисковод данной машины после первоначальной загрузки исходной системы, содержавшей "вирус". Мы подумали, что если записать такую операционную систему на один из дискетов, используемых в самом крупном магазине, торгующем персональными компьютерами, то в Брешиа возникнет эпидемия, которая распространится на весь город.
Но что это за эпидемия при таком безобидном вирусе? Нет, наш вирус должен быть злокачественным! Поэтому мы решили, что после 16 циклов воспроизводства, подсчитываемых на самом дискете, программа должна стереть и заново проинициировать дискет сразу же после загрузки операционной системы. Но теперь мы уже сами ужаснулись своей зловещей идее и решили не только отказаться от ее реализации, но и никому не говорить о ней ни слова".
Ну что ж, это было очень любезно со стороны Черутти и Морокутти. В персональных компьютерах дисковая операционная система (ДОС) - это царь и бог, вершащий судьбами программ, данных и всего остального. Согласно описанному выше замыслу, дисковая операционная система стирает диск, с которого она была загружена в машину, и потому уже не может быть загружена снова с этого диска. Заболевшая операционная система могла бы даже время от времени выдавать на экран удручающее сообщение:
ВАШ ДИСК БАРАХЛИТ?
Самое время приобрести ДОКТОРА ДОС
Диски с ДОКТОРОМ можно купить в ближайшем магазине, торгующем компьютерами
Вирусное заражение, описанное выше, уже имело место в действительности, правда в небольших масштабах. Р.Скрента-младший, учащийся из Питсбурга, написал программу, обладающую следующими свойствами. Вместо того чтобы стирать записи на диске или выводить на экран объявления, эта инфекция приводила к возникновению тонких, трудно уловимых ошибок в операционной системе.
"Все это кажется теперь детской игрой,- пишет Скрента,- но боже мой! Я никак потом не мог избавиться от этой электронной чумы. Она заразила все мои диски и диски всех моих приятелей. Она даже умудрилась проникнуть на графические диски учителя математики". Скрента сочинил программу, которая должна была уничтожить вирус, однако она оказалась не столь эффективной, как сам вирус.
На основании сказанного возникает неплохая задачка, и я поистине проявил бы недостаток воображения и даже своего рода безответственность, если бы не сформулировал ее своим читателям. На одной или двух страничках опишите программу ДОКТОР ДОС, которая хранилась бы на лиске и каким-то образом защищала бы компьютеры от подобных электронных эпидемий. На многих дискетах, предназначенных для персональных компьютеров, содержатся копии ДОС. После включения машины она получает свою операционную систему, считывая ее с дискета. Загруженная в память машины ДОС будет оставаться в силе, когда машина будет работать и с другими дискетами, также содержащими копии ДОС. Если загруженная в память операционная система заражена, то она может внести изменения и в другие копии ДОС или даже полностью заменить их собою. Как можно воспрепятствовать подобному заражению?
В ПЕРВОНАЧАЛЬНОЙ версии "Бой в памяти" главной целью было защитить программу A от случайных попадании "бомб", разбрасываемых боевой программой противника B. Если бы такая зашита была более или менее гарантирована, то на следующем этапе эволюции игры можно было бы приступить к созданию программ, способных отыскивать друг друга и проводить уже "прицельные" атаки, если можно так выразиться.
Пытаясь обеспечить гарантию защиты от случайных попаданий, я предложил в прошлой статье ввести еще одну команду
PCT A
где A - относительный адрес (прямой или косвенный) команды, которая должна быть защищена. Однократная попытка изменить содержимое ячейки с этим адресом будет заблокирована системой Марс, осуществляющей управление игрой. Однако следующая попытка сделать то же самое уже будет успешной. Мне кажется, что при помощи простого цикла каждая боевая программа может защитить свои команды от случайных бомб в течение достаточно длительного промежутка времени, чтобы успеть провести какое-то активное действие по отношению к программе-противнику. Такой защищающий программу цикл изображен на рисунке на с.72. Он состоит из шести команд, четыре из которых выполняются при каждом прохождении через цикл. Таким образом, программа, состоящая из n команд (включая команды, составляющие цикл), потребует выполнения 4*n команд, чтобы полностью обезопасить себя от однократного попадания. Однако такая защита едва ли будет эффективной против программы Карлик, которая производит два выстрела подряд по каждой ячейке памяти.

Цикл, защищающий программу от случайного попадания бомбы
Эту команду можно применять и с другой целью, не предвиденной в первой статье, посвященной игре "Бой в памяти". С.Петерс из Тимару, Новая Зеландия, и М.Дэрем из Уинстон-Салема, шт.Северная Дакота, независимо друг от друга придумали, как можно воспользоваться командой PCT для проведения атакующих действий. Программа пол названием Карлик-ловушка разбрасывает по памяти нули, как обычно, но затем защищает каждый нуль, так что в соответствующую ячейку нельзя записать ничего другого. Это означает, что ничего не подозревающая программа противника может попасться в одну из ловушек в ходе перемещения на новое место. Команда, которая должна быть записана в ячейку, содержащую защищенный нуль, не окажет на эту ячейку никакого влияния. Позднее, когда процесс выполнения программы достигнет этой ячейки, программа погибнет, потому что нуль - это невыполняемая команда. Возможно, команду PCT стоит включить в систему команд какой-нибудь из будущих версий игры "Бой в памяти", но пока я склонен воздержаться от этого в интересах простоты, которая является, пожалуй, пробным камнем любой игры.
Читатели поделились и многими другими идеями, среди которых можно отметить двумерный массив Памяти, предложенный Р.Нортоном из Мэдисона, шт.Висконсин, и правило ограничения дальности "стрельбы", предложенное У.Митчелом, преподавателем математического факультета Пенсильванского университета. Идея Нортона, пожалуй, не нуждается в пояснениях, а вот по поводу предложения Митчела следует сказать несколько слов. Программе дозволяется производить изменения в любой ячейке памяти, расстояние до которой не превышает определенного установленного количества адресов. Благодаря этому правилу программа Карлик автоматически не сможет причинить никакого ущерба противнику, не находящемуся в его окрестности. Из этого правила следует и многое другое, включая акцент на перемещение. Каким еще образом программа сможет подойти на расстояние выстрела к противнику? У этого правила много достоинств, и я полагаю, что некоторые читатели из числа многих, обладающих своей собственной системой "Бой в памяти", изучат это предложение более глубоко и подробно.
Нортон предлагает также, чтобы каждой стороне предоставлялось более одной команды, выполняемой при каждом обращении к программе. Та же идея пришла в голову и многим другим читателям. На самом деле я решил принять это предложение. Теперь игра "Бой в памяти" приобретает более открытый характер.

Система команд языка программирования для игры "Бой в памяти"
Предложенное изменение можно реализовать, добавив следующую команду с условным названием "разветвить" к системе команд игры, приведенной на рисунке на с.70:
SPL A
Когда управление достигает ячейки, в которой содержится эта команда, дальнейший процесс выполнения программы разветвляется на две части, а именно идет на команду, следующую за SPL, и команду, отстоящую на А адресов. Поскольку это нововведение сразу позволяет игроку иметь несколько программ, выполняющихся одновременно, необходимо уточнить правила, согласно которым система управления Марс распределяла бы время между программами. Существует две возможности.
Чтобы проиллюстрировать их, предположим, что один игрок имеет три программы A1, A2 и A3, в то время как у другого - две программы, В1 и B2. Один из возможных вариантов заключается в том, чтобы сначала выполнить все три программы первого игрока, а затем две программы второго. Тогда порядок выполнения программ будет следующим: A1, A2, A3, а затем B1 и B2. Далее эта процедура будет циклически повторяться. Другой вариант заключается в том, чтобы чередовать выполнение программ, принадлежащих различным игрокам. В этом случае последовательность выполнения будет такой: A1, B1, A2, B2, A1, B1 и т.д. Эти две схемы принципиально различны, если судить по производимому ими эффекту. Первая схема поощряет стратегию неограниченного распространения и потому, по-видимому, снижает роль интеллекта в игре. Вторая схема, наоборот, означает, что, чем большим количеством программ располагает игрок, тем реже каждая из них будет выполняться. Здесь, кажется, работает закон "уменьшающейся прибыли", поэтому я принимаю вторую схему. Цель же игры заключается в том, чтобы так или иначе вывести из строя все программы противника.
Новая команда создает богатые возможности. Чтобы проиллюстрировать простейшую из них, рассмотрим боевую программу Чертенок-стрелок:
SPL 2
JMP -1
MOV 0 1
Посмотрим, что произойдет, когда управление попадет в начало программы. Команда SPL 2 означает, что программе будет предоставлено право выполнить сразу две команды: JMP -1 и MOV 0 1. Первая из этих команд начинает выполнение программы сначала, а вторая приводит Чертенка в движение. Он будет двигаться все время в одном и том же направлении - "вниз", поскольку операндом команды MOV всегда будет следующий адрес, на что указывает (положительное) число 1. Таким образом, в каждом программном цикле возникают новые Чертята. Бесконечным потоком они устремляются в соседние области памяти, полные решимости уничтожить по пути любую программу неприятеля. На первый взгляд кажется, что против этой армады Чертят невозможна никакая защита, однако защита существует. Рассмотрим еще более простую программу Чертенок-ловушка, которая выполняется по команде SPL, содержащейся в основном теле программы, защищающей свой "верхний" фланг:
MOV #0 -1
JMP -1
В каждом цикле выполнения Чертенок-ловушка записывает нуль в ячейку, непосредственно прилегающую к ней "сверху" в расчете поразить приближающегося чертенка противника. Здесь правило очередности выполнения играет уже решающую роль. Если Чертенок-стрелок принадлежит A, а Чертенок-ловушка принадлежит B, то для A потребуется n циклов для выполнения n Чертят, в то время как лишь один Чертенок может достичь ячейки, прилегающей к программе Чертенок-ловушка. При прочих равных условиях для B требуется лишь один цикл выполнения для Чертенка-ловушки, чтобы остановить приблизившегося Чертенка-противника.
Можно представить себе расширенный вариант игры "Бой в памяти", где обе стороны порождают и разворачивают целые армии программ, каждая из которых имеет свою специализацию - обнаружение, атака, защита и даже ремонт. Предстоит изучить еще много тонких приемов игры, подобных тому, что предложил Дж.Мак-Лин из Вашингтона, у которого возникла идея создать специализированную программу-ловушку, разбрасывающую команды перехода JMP по различным адресам памяти в надежде на то, что одна из таких команд попадет в расположение программы противника. Каждая такая команда JMP уведет управление из программы противника в программу-ловушку, тем самым программа противника как бы перейдет на сторону программы-ловушки.
В связи с тем что программ теперь становится много, возникает дополнительная проблема: как исключить случаи нападения на программы, принадлежащие одной и той же стороне, т.е. не нападать на "своих"? Здесь представляется необходимой система распознавания типа "свой-чужой".
Среди многих читателей, построивших свои системы игры "Бой в памяти", особо следует отметить троих: Ч.Годфри из Уилтона, шт.Коннектикут; Г.Мак-Рэя из Монмут-Джанкшина, шт.Нью-Джерси, и М.Роузинга из Литлтона, шт.Колорадо, которые постарались четко определить свои системы и документировать их программное обеспечение. Мне кажется, что читателям особенно интересно было бы познакомиться с документами, составленными Роузингом. Но по этому поводу и по многим другим соображениям, касающимся вопросов поддержания контактов среди энтузиастов игры, у меня возникла заманчивая идея. Если кто-нибудь из читателей, обладающих уже действующей системой "Бой в памяти", согласится стать директором ассоциации любителей этой игры, то можно будет наладить отправку документации на различные системы, предложений, касающихся новых правил, интересных программ и записей отдельных партий всем членам ассоциации. Один из добровольцев будет избран директором, остальные же будут помогать, выпуская регулярный листок новостей, участвуя в работе комиссий по утверждению правил и т.п. в зависимости от того, кому какая работа покажется интересной.
Отклики на другие игры перенес по месту.- G.
БИБЛИОГРАФИЯ
SOFTWAR: LA GUERRE DOUCE. THIERRY BRETON AND DENIS BENEICH. Editions Robert Laffont, 1983.
CORE WAR GUIDELINES. D.G.JONES AND A. K.DEWDNEY. Available from Scientific American, 415 Madison Avenue, New York, N.Y. 10017; March, 1984.
WAR GAMES. PHILIP ELMER-DEWITT in Time, Vol.124, No.16, page 109; October 15, 1984.
Игра из программы "Животное" - это, несомненно, "ЭТО КОТ?" - ТЕМА #63, АБЗАЦ #679
ТЕМА #63, АБЗАЦ #679 .- G.
.- G.
ОТКЛИКИ
8 1985
ЧИТАТЕЛИ живо откликнулись на наше предложение создать ассоциацию любителей игры "Бой в памяти". Директором будет Марк Кларксон. В одной из последующих статей я познакомлю читателей с работой этой ассоциации.
Создать программу ДОКТОР ДОС, хранящуюся на лиске и защищающую персональный компьютер от "инфекционных заболеваний", по-видимому, не так просто, как мне казалось. Н.Рэмси из Итаки (шт.Нью-Йорк) пришел к заключению, что ДОКТОР ДОС может диагностировать заболевание, но не может вылечить. Рэмси придумал программу, которая создает "вторичную зараженную вирусом операционную систему, копирующую себя на диски точно так же, как и больная операционная система, но не приводит к возникновению болезни". Доброкачественный вирус предотвращает инфекцию, превентивно занимая память. Рэмси говорит также, что у его программы есть некоторые средства сигнализации. Во время загрузки операционной системы она даже выводит на экран заставку "Не беспокойтесь, с вами ДОКТОР ДОС", чтобы пользователь был уверен в своей операционной системе. К сожалению, Рэмси изобрел затем другой вирус, достаточно ловкий, чтобы обойти своего доброкачественного собрата.
Идея доктора-вируса пришла также в голову Дж.Деллинжеру, биофизику из Станфордского университета. Как ни странно, его намерение заключалось в том, чтобы создать не доктора, а просто некий безвредный вирус, который мог бы незамеченным перекочевывать с диска на диск. Деллинжер был вдохновлен аналогией между программами и живыми существами. У тех и у других могут быть паразиты. В частности, дисковая операционная система может стать переносчиком вируса, успешное размножение которого в немалой степени зависит от его способности оставаться незамеченным. Одна из особенностей вируса Деллинжера заключается в том, что он поселяется только на вспомогательном диске емкостью 48k байт. Основной диск, таким образом, всегда содержит чистый ДОС. Этот неуловимый вирус, занимающий очень мало места на зараженном диске, проверяет ДОС всякий раз, когда он копируется на новый диск. Вирус "заинтересован" в том, чтобы содержащий его организм оставался всегда здоровым, Поэтому он следит за правильностью копирования. Деллинжер сообщил, что поделился своей программой, доброкачественным вирусом, со своими друзьями. Двое из них, как он опасается, обращались с программой неосторожно, так что вирус теперь может распространиться по всей Калифорнии и даже за ее пределами. Как определить, содержится ли в вашем ДОСе вирус Деллинжера? Он говорит, что иногда можно успышать негромкое шипение, продолжающееся в течение полусекунды. Этот звук возникает, когда вирус создает свою копию.
Программные вирусы, наверное, все же не так заразны, как можно было подумать, прочтя статью в рубрике "Занимательный компьютер" в майском номере журнала за 1985г. К.Кэшмарек отмечает, что вирус не может перекочевать на диск, содержащий операционную систему, отличную от той, в которой поселился вирус. Кэшмарек защищает свои диски от записи - мера предосторожности, которая определенно останавливает распространение вируса, если, конечно, программный механизм зашиты от записи не был обойден вирусом. Кэшмарек также спрашивает, следует ли публично обсуждать вирусы и другие "заболевания" компьютеров. Со своей стороны, я нисколько не сомневаюсь, что поврежденное программное обеспечение - это дело нешуточное. Я думаю, что "компьютерные эпидемии", подобные тем, которые я описал, в недалеком будущем будут представлять собой определенную опасность. Но мне кажется, что быть предупрежденным - значит быть вооруженным. И я надеюсь, что публичные обсуждения будут способствовать поиску противоядий.
Тем временем были, наконец, выявлены истоки идеи игры "Бой в памяти". В июльском номере журнала за прошлый год я рассказал читателям историю программ "Сорняк" и "Косарь", а в майском номере за 1985г. описал программу "Животное". Последняя представляла собой игровую программу, в некотором смысле сходную с "Боем в памяти". Эта программа создавала свои копии на дисках всех программистов, пользовавшихся одной системой, работающей в режиме разделения времени. Автором программы оказался Дж.Уокер из Сосалито (шт.Калифорния). Он признался в том, что создал наиболее успешную ее версию. На самом деле "Животное" - это лишь часть истории. Внутри этой игровой программы была еше одна программа - РАЗМНОЖИТЕЛЬ, выполнявшая функции, связанные с копированием игры. Написанная в январе 1975г., эта подпрограмма при обращении к ней могла породить "независимый процесс проверки каталогов, доступных для основной программы, во время работы последней. Если каталог не содержал ссылки на программу или указывал на устаревшую ее версию, РАЗМНОЖИТЕЛЬ копировал выполняемую в данный момент версию программы в библиотеке и заносил сведения о ней в каталог. РАЗМНОЖИТЕЛЬ работал очень аккуратно и предпринимал специальные меры предосторожности, чтобы, например, не уничтожить какую-нибудь программу пользователя, носящую то же имя, но не имеющую никакого отношения к игре".
9 1985
Программа "червяк", текст которой был приведен в майском номере журнала "В мире науки" 1985, в рубрике "Занимательный компьютер", предназначенная для персонального компьютера APPLE II, видимо, сама явилась жертвой небольшой типографской инфекции. Второе число в команде DATA под номером 100 должно быть равно 255. В неисправленном варианте "червяк" проползает лишь часть пути по памяти н внезапно погибает.
9 1986
"БОЙ В ПАМЯТИ" - тема моей первой статьи в этом журнале (см.: "В мире науки", 1984, #7). Нынешним летом в последний уикенд августа на восточном побережье США Музей вычислительной техники в Бостоне провел первый международный турнир по этому виду соревнований компьютеров. Самые остроумные программы выводили из строя своих более слабых противников, уничтожая их ключевые команды. Победитель (человек, создавший победившую программу) получил звание чемпиона по бою в памяти и будет носить это звание в течение года.
Правила участия в чемпионате и требования, предъявляемые к программам, были разработаны Международной ассоциацией любителей игры "Бой в памяти", которая насчитывает около 150 членов. Возглавляет ассоциацию Марк Кларксон из Вичиты (шт. Канзас).
ОБЗОР ЧИТАТЕЛЬСКИХ ОТКЛИКОВ НА СТАТЬИ, ПОСВЯЩЕННЫЕ ИГРЕ "БОЙ В ПАМЯТИ", ЭКОЛОГИЧЕСКОЙ ВОЙНЕ НА ПЛАНЕТЕ АКВА-ТОР И ОХОТЕ С КОМПЬЮТЕРОМ НА БОБРА-РАБОТЯГУ
А.К.ДЬЮДНИ
КОГДА в прошлом году появилась статья, посвященная игре "Бой в памяти", я никак не ожидал, что поднятые в ней вопросы привлекут к себе столь широкое внимание. Приведенные в этой статье описания программ, перемещающихся по памяти компьютера и пытающихся уничтожить друг друга, вызвали широкий резонанс. По свидетельству многих читателей, письма которых я рассмотрю ниже, действительность изобилует примерами, когда в компьютерах при самых разнообразных обстоятельствах поселяются "червяки", "вирусы" и другие программные "вредители". В результате в мире компьютера могут возникать настолько ужасные ситуации, что я даже не решаюсь о них писать.
Выпущенная недавно во Франции книжка шпионско-детективного жанра Т.Бретона и Д.Бенеша "Softwar: La Guerre Douce" ("Война программ") дает нам фантастический пример подобного рода. Сюжет книги построен на паутине заговора, которую плетут американские поставщики супер-компьютера, собираясь продать его другой стране. Американские власти после некоторого притворного колебания соглашаются на эту сделку. Компьютер был тайно запрограммирован специальными "программными бомбами". Закупленная для расчетов прогноза погоды машина, а точнее ее программное обеспечение, скрывает в себе некий скрытый механизм - как только Национальная служба погоды США сообщит, что в г.Сан-Томасе на Виргинских островах наблюдается определенная температура, машина должна немедленно приняться за искажение и уничтожение всех доступных ей программ в сети ЭВМ страны-импортера. Предположив реальность подобных сценариев, хочется отметить: "Если и говорить о войнах, то пусть они лучше будут программными". С другой стороны, при мысли о том, что борьба программ в компьютерах, которыми располагают военные ведомства, может привести к трагической случайности, тоже становится как-то не по себе.
Прежде чем перейти к описанию разнообразных случаев, связанных с действиями всевозможных враждебных программ, напомним вкратце правила игры "Бой в памяти". Двое играющих пишут каждый свою программу на языке низкого уровня Редкод. Эти программы помещаются в обширную замкнутую область памяти, или просто Память. В действительности Память представляет собой массив из нескольких тысяч ячеек с последовательными адресами, причем за адресом последней ячейки вновь следует адрес первой. Каждая команда боевой программы занимает одну ячейку Памяти. Программа монитор под названием Марс (Mars - сокращение от слов A Memory Array Redcode Simulator) управляет боевыми программами, выполняя по одной очередной команде из каждой программы по простой системе разделения времени. Программы атакуют друг друга и одновременно пытаются избежать ущерба или восстановить себя, если ущерб все же был нанесен. Простейший вид атаки может представлять собой команда MOV. Например, команда
MOV #0 1000
приведет к тому, что в ячейку, отстоящую на 1000 адресов от данной команды, будет помешено число, равное нулю. Информация, содержавшаяся ранее в ячейке, будет уничтожена. В частности, если нуль попадет в начальную ячейку, содержащую команду из программы противника, то эта команда исчезнет, программа не сможет больше выполняться и это приведет к поражению противника. Поскольку ни один компьютер, будь то персональный или большой универсальный, не имеет таких встроенных средств, как язык Редкод и массив памяти для сражающихся программ, эти средства должны моделироваться.
Вдохновленный статьей Л.Пенроуза о самовоспроизводящихся механизмах, появившейся в июньском номере журнала "Scientific American" за 1959г., Ф.Стал из Честерфилда, шт.Миссури, создал миниатюрную линейную вселенную, населенную незамысловатыми существами, которые жили, передвигались по своему миру, подчиняясь (если так можно выразиться) воле судеб. Стал пишет:
"Как и в игре "Бой в памяти", я выделил замкнутый линейный сегмент памяти, где с помощью несколько модифицированного машинного языка моделировались существа. Тогда в моем распоряжении была машина IBM 6S0 с памятью на магнитном барабане. Существо было запрограммировано, чтобы ползать в пределах своего мира, питаться ненулевыми словами и, наевшись досыта, производить на свет свою копию. Аналогично игре "Бой в памяти" у меня была программа монитор, которая хранила сведения о живых существах и распределяла между ними машинное время. Эту программу я называл шутливо "Левой рукой бога"".
В письме Стал рассматривает способность программы к воспроизводству и описывает интересный механизм мутаций. В процессе создания своей копии программа может внести в нее несколько случайных изменений. Однако Стал пишет: "Я исключил это свойство после одного из прогонов системы, когда стерильный мутант сожрал единственное способное к воспроизводству существо. Было очевидно, что для достижения сколько-нибудь интересных результатов потребовался бы чрезвычайно большой объем памяти и очень много машинного времени".
Можно рассказать также историю, связанную с игрой "Животное", в которой программа, последовательно задавая играющему с ней человеку двадцать наводящих вопросов, пытается определить, какое животное он задумал. Д.Кларк из лаборатории вычислительной техники Массачусетского технологического института сообщил нам, что сотрудники одной фирмы увлеченно играли в "Животное". Хотя эта программа совсем не напоминает боевую программу и даже не имеет ничего общего с простыми существами Стала, она приобрела способность к воспроизводству в памяти компьютера благодаря усилиям программиста, направленным на то, чтобы повысить эффективность игры. Когда программа ошибается, называя не то животное, которое имел в виду человек, она просит его посоветовать, какой вопрос ей в будущем следует взять на вооружение, чтобы играть успешнее. Это свойство программы подсказало программисту одно техническое решение, благодаря которому у всех играющих все время была бы одна и та же версия "Животного".
"Работая с одной из очень ранних систем, в которой отсутствовали развитая структура каталогов коллективного пользования и средства зашиты данных, программист изобрел весьма оригинальный способ сделать игру доступной сразу для нескольких пользователей. Допустим, у одного из пользователей библиотека содержит игру. Всякий раз, когда этот пользователь поиграл с программой, она создает свою копию в библиотеке другого пользователя. Если в этой библиотеке ранее уже имелась копия игры, старая версия стиралась и на ее место записывалась новая. Благодаря этому поведение программы становилось для играющего неожиданным. Если же библиотека ранее не содержала версии "Животного", то игра предлагалась еще одному пользователю".
Кларк вспоминает, что игра "Животное" была весьма популярна и в каждой программной библиотеке компании обязательно содержался экземпляр этой игры. "Более того, при переходе сотрудников фирмы из одного отдела в другой... они брали с собой и игру, и со временем она распространилась на все машины компании". Ситуация в общем-то не была опасной, но многочисленные копии этой сравнительно безобидной игры стали существенно засорять дисковую память. И только когда была изобретена еще более "жизнеспособная" версия игры, создавшаяся проблема была решена. Во время игры с новой версией "Животного" программа создавала не одну, а две свои копии в двух других библиотеках. Через некоторое время эта программа должна была заменить все старые версии "Животного". Через год, по наступлении определенной даты, все копии новой программы изменили свое поведение. "Вместо того чтобы воспроизводить себя в двух экземплярах при каждом обращении к программе, она играла теперь одну заключительную партию, говорила пользователю "до свидания" и уничтожала себя. Вот так "Животное" было изгнано из системы.
Рут Льюорт из Холмдсла, шт.Нью-Джерси, однажды создала своеобразного монстра, даже не написав программы как таковой. Компьютер, принадлежавший компании, сотрудником которой она была, работал в режиме разделения времени. Рут подготавливала демонстрационную версию обучающей программы и решила сделать запасную копию на другой системе с разделением времени. Когда система, с которой она обычно работала, стала перегруженной и реагировала на директивы слишком медленно, Рут переключилась на другую систему. "Эта система реагировала очень живо в течение тех трех минут, пока она работала, а потом мой графический терминал перестал реагировать на команды, а на его экране наблюдался полный хаос. Ни один пользователь не мог ни начать, ни нормально закончить выполнение своей задачи. Вывод был однозначным - в моей программе что-то было не так! Несмотря на охвативший меня страх, я внезапно вспомнила, что указала знак амперсанд в качестве символа, разделяющего поля данных, вводимых с терминала. Но амперсанд является также символом, означающим в системе порождение процесса, выполняемого в фоновой зоне! Когда компьютер принял первое сообщение с терминала, он, должно быть, перехватил амперсанды, предназначенные для терминала, и запустил несколько процессов, которые в свою очередь порождали новые процессы, и так до бесконечности". Срочный междугородный звонок проинформировал администратора системы о причинах внезапного "заболевания" машины, она была остановлена и запущена заново. Разумеется, Льюорт заменила амперсанд более безобидным символом, и ее программа "с тех пор всегда работала благополучно и весело".
Хотя программы для игры "Бой в памяти" и не размножаются подобным образом, дополнительные копии могут повысить их выживаемость. Несколько читателей считают, что следует всегда иметь три копии программы, с тем чтобы экземпляр программы, выполняющейся в каждый данный момент, мог определить с помощью двух других, не повреждены ли команды в данном экземпляре. При этом выполняющаяся программа может даже заменить ошибочную команду правильной. Эти соображения лежат в основе программы Scavenger, функции которой заключаются в эащите файлов от случайных ошибок, появляющихся при их копировании на магнитной ленте. А.Хадсон из Ньютона, шт.Массачусетс (название фирмы, в которой он работает, не указано), пишет: "Всякий, кто часто пользуется магнитной лентой, должно быть, испытал на себе силу закона суммирования вероятностей, поистине представляющего собой враждебную стихию". В своем письме Хадсон рассказывает о многочисленных ошибках, возникающих при работе с магнитными лентами, и доказывает, что, хотя каждая из этих ошибок имеет сравнительно небольшую вероятность, если ее рассматривать в отдельности, какая-нибудь одна из них может произойти уже с довольно большой вероятностью, внушающей серьезное беспокойство. Он продолжает:
"Однако не волнуйтесь, программа Scavenger вам поможет. Если вы доверите ей свой файл, она скопирует его сразу на три магнитные ленты, не беспокоя вас никакими подробностями. Даже если в работе системы произойдет программный сбой (что случается несколько раз в день), список невыполненных или прерванных заданий обычно остается невредимым, и когда нормальный режим работы машины восстанавливается, все задания, связанные с действием программы Scavenger, выполняются своим чередом. Запись на каждую ленту производится в ходе отдельного прогона программы, запланированного операционной системой".
Тем, кто работает с компьютерами Apple (буквально - "яблоко".- Ред.), следует остерегаться маленькой вредной программы Apple Worm (буквально - "яблочный червяк".- Ред.), созданной Дж.Хаузером и У.Бакли из Калифорнийского политехнического университета в Сан-Луи-Обиспо. Написанная для компьютера Apple II на языке ассемблера 6502, эта разновидность червяка размножается в памяти машины, пронизывая ее насквозь. Сначала загружается специальная программа, написанная на Бейсике (см. рисунок на с.71), которая в свою очередь загружает "червяка" в область памяти с малыми значениями адресов. Программа на Бейсике, наоборот, занимает противоположную часть памяти (с большими значениями адресов).

Программа "червяк", обитающая в компьютерах
"Благодаря тому что "червяк" первоначально загружается в область памяти графического представления данных, вы можете наблюдать на экране, как он устремляется (между прочим, двигаясь задом наперед) в соседние области памяти с большими адресами... После того как "червяк" покидает окно графического изображения на экране... проходит некоторое время и он стирает всю память, в том числе и программу на Бейсике, и с ходу врезается в постоянную память машины".
Хауэер и Бакли намереваются в недалеком будущем выпустить публикацию, посвященную разновидностям подобного "червяка". Они уже спроектировали Червячную Операционную Систему и даже создали видеоигру, одним из главных персонажей которой является Червяк.
Еше одна программная забава была изобретена Р.Черутти и М.Морокутти из Брешиа, Италия. Прочитав перевод статьи, посвященной игре "Бой в памяти", в "Le Scienze" - итальянском издании журнала "Scientific American", они стали размышлять о том, как заразить персональные компьютеры Apple II, но не "червяками", а "вирусом". Вот что пишет Черутти:
"Марко (Морокутти.- Ред.) задумал написать программу, способную переселяться из одного компьютера в другой подобно вирусу, заражая таким образом компьютеры Apple. Однако мы долго не могли придумать, каким способом можно осуществить эту идею. В конце концов я понял, что на самом деле программа должна была заражать флоппи-диски, пользуясь памятью машины, лишь как промежуточной средой между одним диском и другим. Так наш вирус начал обретать форму.
Как известно, на каждом дискете компьютера Apple имеется копия дисковой операционной системы, загружаемой в машину при включении питанин. Вирус должен был представлять собой некое изменение в этой операционной системе. При каждой операции записи на диск он должен был проверять, содержится ли там его копия. Если нет, то "вирус" вносил бы аналогичное изменение в операционную систему, записанную на диске. Таким образом, он мог поселиться на всех дискетах, которые вставлялись бы в дисковод данной машины после первоначальной загрузки исходной системы, содержавшей "вирус". Мы подумали, что если записать такую операционную систему на один из дискетов, используемых в самом крупном магазине, торгующем персональными компьютерами, то в Брешиа возникнет эпидемия, которая распространится на весь город.
Но что это за эпидемия при таком безобидном вирусе? Нет, наш вирус должен быть злокачественным! Поэтому мы решили, что после 16 циклов воспроизводства, подсчитываемых на самом дискете, программа должна стереть и заново проинициировать дискет сразу же после загрузки операционной системы. Но теперь мы уже сами ужаснулись своей зловещей идее и решили не только отказаться от ее реализации, но и никому не говорить о ней ни слова".
Ну что ж, это было очень любезно со стороны Черутти и Морокутти. В персональных компьютерах дисковая операционная система (ДОС) - это царь и бог, вершащий судьбами программ, данных и всего остального. Согласно описанному выше замыслу, дисковая операционная система стирает диск, с которого она была загружена в машину, и потому уже не может быть загружена снова с этого диска. Заболевшая операционная система могла бы даже время от времени выдавать на экран удручающее сообщение:
ВАШ ДИСК БАРАХЛИТ?
Самое время приобрести ДОКТОРА ДОС
Диски с ДОКТОРОМ можно купить в ближайшем магазине, торгующем компьютерами
Вирусное заражение, описанное выше, уже имело место в действительности, правда в небольших масштабах. Р.Скрента-младший, учащийся из Питсбурга, написал программу, обладающую следующими свойствами. Вместо того чтобы стирать записи на диске или выводить на экран объявления, эта инфекция приводила к возникновению тонких, трудно уловимых ошибок в операционной системе.
"Все это кажется теперь детской игрой,- пишет Скрента,- но боже мой! Я никак потом не мог избавиться от этой электронной чумы. Она заразила все мои диски и диски всех моих приятелей. Она даже умудрилась проникнуть на графические диски учителя математики". Скрента сочинил программу, которая должна была уничтожить вирус, однако она оказалась не столь эффективной, как сам вирус.
На основании сказанного возникает неплохая задачка, и я поистине проявил бы недостаток воображения и даже своего рода безответственность, если бы не сформулировал ее своим читателям. На одной или двух страничках опишите программу ДОКТОР ДОС, которая хранилась бы на лиске и каким-то образом защищала бы компьютеры от подобных электронных эпидемий. На многих дискетах, предназначенных для персональных компьютеров, содержатся копии ДОС. После включения машины она получает свою операционную систему, считывая ее с дискета. Загруженная в память машины ДОС будет оставаться в силе, когда машина будет работать и с другими дискетами, также содержащими копии ДОС. Если загруженная в память операционная система заражена, то она может внести изменения и в другие копии ДОС или даже полностью заменить их собою. Как можно воспрепятствовать подобному заражению?
В ПЕРВОНАЧАЛЬНОЙ версии "Бой в памяти" главной целью было защитить программу A от случайных попадании "бомб", разбрасываемых боевой программой противника B. Если бы такая зашита была более или менее гарантирована, то на следующем этапе эволюции игры можно было бы приступить к созданию программ, способных отыскивать друг друга и проводить уже "прицельные" атаки, если можно так выразиться.
Пытаясь обеспечить гарантию защиты от случайных попаданий, я предложил в прошлой статье ввести еще одну команду
PCT A
где A - относительный адрес (прямой или косвенный) команды, которая должна быть защищена. Однократная попытка изменить содержимое ячейки с этим адресом будет заблокирована системой Марс, осуществляющей управление игрой. Однако следующая попытка сделать то же самое уже будет успешной. Мне кажется, что при помощи простого цикла каждая боевая программа может защитить свои команды от случайных бомб в течение достаточно длительного промежутка времени, чтобы успеть провести какое-то активное действие по отношению к программе-противнику. Такой защищающий программу цикл изображен на рисунке на с.72. Он состоит из шести команд, четыре из которых выполняются при каждом прохождении через цикл. Таким образом, программа, состоящая из n команд (включая команды, составляющие цикл), потребует выполнения 4*n команд, чтобы полностью обезопасить себя от однократного попадания. Однако такая защита едва ли будет эффективной против программы Карлик, которая производит два выстрела подряд по каждой ячейке памяти.

Цикл, защищающий программу от случайного попадания бомбы
Эту команду можно применять и с другой целью, не предвиденной в первой статье, посвященной игре "Бой в памяти". С.Петерс из Тимару, Новая Зеландия, и М.Дэрем из Уинстон-Салема, шт.Северная Дакота, независимо друг от друга придумали, как можно воспользоваться командой PCT для проведения атакующих действий. Программа пол названием Карлик-ловушка разбрасывает по памяти нули, как обычно, но затем защищает каждый нуль, так что в соответствующую ячейку нельзя записать ничего другого. Это означает, что ничего не подозревающая программа противника может попасться в одну из ловушек в ходе перемещения на новое место. Команда, которая должна быть записана в ячейку, содержащую защищенный нуль, не окажет на эту ячейку никакого влияния. Позднее, когда процесс выполнения программы достигнет этой ячейки, программа погибнет, потому что нуль - это невыполняемая команда. Возможно, команду PCT стоит включить в систему команд какой-нибудь из будущих версий игры "Бой в памяти", но пока я склонен воздержаться от этого в интересах простоты, которая является, пожалуй, пробным камнем любой игры.
Читатели поделились и многими другими идеями, среди которых можно отметить двумерный массив Памяти, предложенный Р.Нортоном из Мэдисона, шт.Висконсин, и правило ограничения дальности "стрельбы", предложенное У.Митчелом, преподавателем математического факультета Пенсильванского университета. Идея Нортона, пожалуй, не нуждается в пояснениях, а вот по поводу предложения Митчела следует сказать несколько слов. Программе дозволяется производить изменения в любой ячейке памяти, расстояние до которой не превышает определенного установленного количества адресов. Благодаря этому правилу программа Карлик автоматически не сможет причинить никакого ущерба противнику, не находящемуся в его окрестности. Из этого правила следует и многое другое, включая акцент на перемещение. Каким еще образом программа сможет подойти на расстояние выстрела к противнику? У этого правила много достоинств, и я полагаю, что некоторые читатели из числа многих, обладающих своей собственной системой "Бой в памяти", изучат это предложение более глубоко и подробно.
Нортон предлагает также, чтобы каждой стороне предоставлялось более одной команды, выполняемой при каждом обращении к программе. Та же идея пришла в голову и многим другим читателям. На самом деле я решил принять это предложение. Теперь игра "Бой в памяти" приобретает более открытый характер.

Система команд языка программирования для игры "Бой в памяти"
Предложенное изменение можно реализовать, добавив следующую команду с условным названием "разветвить" к системе команд игры, приведенной на рисунке на с.70:
SPL A
Когда управление достигает ячейки, в которой содержится эта команда, дальнейший процесс выполнения программы разветвляется на две части, а именно идет на команду, следующую за SPL, и команду, отстоящую на А адресов. Поскольку это нововведение сразу позволяет игроку иметь несколько программ, выполняющихся одновременно, необходимо уточнить правила, согласно которым система управления Марс распределяла бы время между программами. Существует две возможности.
Чтобы проиллюстрировать их, предположим, что один игрок имеет три программы A1, A2 и A3, в то время как у другого - две программы, В1 и B2. Один из возможных вариантов заключается в том, чтобы сначала выполнить все три программы первого игрока, а затем две программы второго. Тогда порядок выполнения программ будет следующим: A1, A2, A3, а затем B1 и B2. Далее эта процедура будет циклически повторяться. Другой вариант заключается в том, чтобы чередовать выполнение программ, принадлежащих различным игрокам. В этом случае последовательность выполнения будет такой: A1, B1, A2, B2, A1, B1 и т.д. Эти две схемы принципиально различны, если судить по производимому ими эффекту. Первая схема поощряет стратегию неограниченного распространения и потому, по-видимому, снижает роль интеллекта в игре. Вторая схема, наоборот, означает, что, чем большим количеством программ располагает игрок, тем реже каждая из них будет выполняться. Здесь, кажется, работает закон "уменьшающейся прибыли", поэтому я принимаю вторую схему. Цель же игры заключается в том, чтобы так или иначе вывести из строя все программы противника.
Новая команда создает богатые возможности. Чтобы проиллюстрировать простейшую из них, рассмотрим боевую программу Чертенок-стрелок:
SPL 2
JMP -1
MOV 0 1
Посмотрим, что произойдет, когда управление попадет в начало программы. Команда SPL 2 означает, что программе будет предоставлено право выполнить сразу две команды: JMP -1 и MOV 0 1. Первая из этих команд начинает выполнение программы сначала, а вторая приводит Чертенка в движение. Он будет двигаться все время в одном и том же направлении - "вниз", поскольку операндом команды MOV всегда будет следующий адрес, на что указывает (положительное) число 1. Таким образом, в каждом программном цикле возникают новые Чертята. Бесконечным потоком они устремляются в соседние области памяти, полные решимости уничтожить по пути любую программу неприятеля. На первый взгляд кажется, что против этой армады Чертят невозможна никакая защита, однако защита существует. Рассмотрим еще более простую программу Чертенок-ловушка, которая выполняется по команде SPL, содержащейся в основном теле программы, защищающей свой "верхний" фланг:
MOV #0 -1
JMP -1
В каждом цикле выполнения Чертенок-ловушка записывает нуль в ячейку, непосредственно прилегающую к ней "сверху" в расчете поразить приближающегося чертенка противника. Здесь правило очередности выполнения играет уже решающую роль. Если Чертенок-стрелок принадлежит A, а Чертенок-ловушка принадлежит B, то для A потребуется n циклов для выполнения n Чертят, в то время как лишь один Чертенок может достичь ячейки, прилегающей к программе Чертенок-ловушка. При прочих равных условиях для B требуется лишь один цикл выполнения для Чертенка-ловушки, чтобы остановить приблизившегося Чертенка-противника.
Можно представить себе расширенный вариант игры "Бой в памяти", где обе стороны порождают и разворачивают целые армии программ, каждая из которых имеет свою специализацию - обнаружение, атака, защита и даже ремонт. Предстоит изучить еще много тонких приемов игры, подобных тому, что предложил Дж.Мак-Лин из Вашингтона, у которого возникла идея создать специализированную программу-ловушку, разбрасывающую команды перехода JMP по различным адресам памяти в надежде на то, что одна из таких команд попадет в расположение программы противника. Каждая такая команда JMP уведет управление из программы противника в программу-ловушку, тем самым программа противника как бы перейдет на сторону программы-ловушки.
В связи с тем что программ теперь становится много, возникает дополнительная проблема: как исключить случаи нападения на программы, принадлежащие одной и той же стороне, т.е. не нападать на "своих"? Здесь представляется необходимой система распознавания типа "свой-чужой".
Среди многих читателей, построивших свои системы игры "Бой в памяти", особо следует отметить троих: Ч.Годфри из Уилтона, шт.Коннектикут; Г.Мак-Рэя из Монмут-Джанкшина, шт.Нью-Джерси, и М.Роузинга из Литлтона, шт.Колорадо, которые постарались четко определить свои системы и документировать их программное обеспечение. Мне кажется, что читателям особенно интересно было бы познакомиться с документами, составленными Роузингом. Но по этому поводу и по многим другим соображениям, касающимся вопросов поддержания контактов среди энтузиастов игры, у меня возникла заманчивая идея. Если кто-нибудь из читателей, обладающих уже действующей системой "Бой в памяти", согласится стать директором ассоциации любителей этой игры, то можно будет наладить отправку документации на различные системы, предложений, касающихся новых правил, интересных программ и записей отдельных партий всем членам ассоциации. Один из добровольцев будет избран директором, остальные же будут помогать, выпуская регулярный листок новостей, участвуя в работе комиссий по утверждению правил и т.п. в зависимости от того, кому какая работа покажется интересной.
Отклики на другие игры перенес по месту.- G.
БИБЛИОГРАФИЯ
SOFTWAR: LA GUERRE DOUCE. THIERRY BRETON AND DENIS BENEICH. Editions Robert Laffont, 1983.
CORE WAR GUIDELINES. D.G.JONES AND A. K.DEWDNEY. Available from Scientific American, 415 Madison Avenue, New York, N.Y. 10017; March, 1984.
WAR GAMES. PHILIP ELMER-DEWITT in Time, Vol.124, No.16, page 109; October 15, 1984.
Игра из программы "Животное" - это, несомненно, "ЭТО КОТ?" -
 ТЕМА #63, АБЗАЦ #679
ТЕМА #63, АБЗАЦ #679 .- G.
.- G.ОТКЛИКИ
8 1985
ЧИТАТЕЛИ живо откликнулись на наше предложение создать ассоциацию любителей игры "Бой в памяти". Директором будет Марк Кларксон. В одной из последующих статей я познакомлю читателей с работой этой ассоциации.
Создать программу ДОКТОР ДОС, хранящуюся на лиске и защищающую персональный компьютер от "инфекционных заболеваний", по-видимому, не так просто, как мне казалось. Н.Рэмси из Итаки (шт.Нью-Йорк) пришел к заключению, что ДОКТОР ДОС может диагностировать заболевание, но не может вылечить. Рэмси придумал программу, которая создает "вторичную зараженную вирусом операционную систему, копирующую себя на диски точно так же, как и больная операционная система, но не приводит к возникновению болезни". Доброкачественный вирус предотвращает инфекцию, превентивно занимая память. Рэмси говорит также, что у его программы есть некоторые средства сигнализации. Во время загрузки операционной системы она даже выводит на экран заставку "Не беспокойтесь, с вами ДОКТОР ДОС", чтобы пользователь был уверен в своей операционной системе. К сожалению, Рэмси изобрел затем другой вирус, достаточно ловкий, чтобы обойти своего доброкачественного собрата.
Идея доктора-вируса пришла также в голову Дж.Деллинжеру, биофизику из Станфордского университета. Как ни странно, его намерение заключалось в том, чтобы создать не доктора, а просто некий безвредный вирус, который мог бы незамеченным перекочевывать с диска на диск. Деллинжер был вдохновлен аналогией между программами и живыми существами. У тех и у других могут быть паразиты. В частности, дисковая операционная система может стать переносчиком вируса, успешное размножение которого в немалой степени зависит от его способности оставаться незамеченным. Одна из особенностей вируса Деллинжера заключается в том, что он поселяется только на вспомогательном диске емкостью 48k байт. Основной диск, таким образом, всегда содержит чистый ДОС. Этот неуловимый вирус, занимающий очень мало места на зараженном диске, проверяет ДОС всякий раз, когда он копируется на новый диск. Вирус "заинтересован" в том, чтобы содержащий его организм оставался всегда здоровым, Поэтому он следит за правильностью копирования. Деллинжер сообщил, что поделился своей программой, доброкачественным вирусом, со своими друзьями. Двое из них, как он опасается, обращались с программой неосторожно, так что вирус теперь может распространиться по всей Калифорнии и даже за ее пределами. Как определить, содержится ли в вашем ДОСе вирус Деллинжера? Он говорит, что иногда можно успышать негромкое шипение, продолжающееся в течение полусекунды. Этот звук возникает, когда вирус создает свою копию.
Программные вирусы, наверное, все же не так заразны, как можно было подумать, прочтя статью в рубрике "Занимательный компьютер" в майском номере журнала за 1985г. К.Кэшмарек отмечает, что вирус не может перекочевать на диск, содержащий операционную систему, отличную от той, в которой поселился вирус. Кэшмарек защищает свои диски от записи - мера предосторожности, которая определенно останавливает распространение вируса, если, конечно, программный механизм зашиты от записи не был обойден вирусом. Кэшмарек также спрашивает, следует ли публично обсуждать вирусы и другие "заболевания" компьютеров. Со своей стороны, я нисколько не сомневаюсь, что поврежденное программное обеспечение - это дело нешуточное. Я думаю, что "компьютерные эпидемии", подобные тем, которые я описал, в недалеком будущем будут представлять собой определенную опасность. Но мне кажется, что быть предупрежденным - значит быть вооруженным. И я надеюсь, что публичные обсуждения будут способствовать поиску противоядий.
Тем временем были, наконец, выявлены истоки идеи игры "Бой в памяти". В июльском номере журнала за прошлый год я рассказал читателям историю программ "Сорняк" и "Косарь", а в майском номере за 1985г. описал программу "Животное". Последняя представляла собой игровую программу, в некотором смысле сходную с "Боем в памяти". Эта программа создавала свои копии на дисках всех программистов, пользовавшихся одной системой, работающей в режиме разделения времени. Автором программы оказался Дж.Уокер из Сосалито (шт.Калифорния). Он признался в том, что создал наиболее успешную ее версию. На самом деле "Животное" - это лишь часть истории. Внутри этой игровой программы была еше одна программа - РАЗМНОЖИТЕЛЬ, выполнявшая функции, связанные с копированием игры. Написанная в январе 1975г., эта подпрограмма при обращении к ней могла породить "независимый процесс проверки каталогов, доступных для основной программы, во время работы последней. Если каталог не содержал ссылки на программу или указывал на устаревшую ее версию, РАЗМНОЖИТЕЛЬ копировал выполняемую в данный момент версию программы в библиотеке и заносил сведения о ней в каталог. РАЗМНОЖИТЕЛЬ работал очень аккуратно и предпринимал специальные меры предосторожности, чтобы, например, не уничтожить какую-нибудь программу пользователя, носящую то же имя, но не имеющую никакого отношения к игре".
9 1985
Программа "червяк", текст которой был приведен в майском номере журнала "В мире науки" 1985, в рубрике "Занимательный компьютер", предназначенная для персонального компьютера APPLE II, видимо, сама явилась жертвой небольшой типографской инфекции. Второе число в команде DATA под номером 100 должно быть равно 255. В неисправленном варианте "червяк" проползает лишь часть пути по памяти н внезапно погибает.
9 1986
"БОЙ В ПАМЯТИ" - тема моей первой статьи в этом журнале (см.: "В мире науки", 1984, #7). Нынешним летом в последний уикенд августа на восточном побережье США Музей вычислительной техники в Бостоне провел первый международный турнир по этому виду соревнований компьютеров. Самые остроумные программы выводили из строя своих более слабых противников, уничтожая их ключевые команды. Победитель (человек, создавший победившую программу) получил звание чемпиона по бою в памяти и будет носить это звание в течение года.
Правила участия в чемпионате и требования, предъявляемые к программам, были разработаны Международной ассоциацией любителей игры "Бой в памяти", которая насчитывает около 150 членов. Возглавляет ассоциацию Марк Кларксон из Вичиты (шт. Канзас).
Последний раз редактировалось: Gudleifr (Вт Окт 01, 2019 11:24 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
06 1985
ПЯТЬ НЕСЛОЖНЫХ ПРОГРАММ ДЛЯ РАЗЛИЧНЫХ ЗАДАЧ МОДЕЛИРОВАНИЯ С ПОМОЩЬЮ СЛУЧАЙНЫХ ЧИСЕЛ
А.К.ДЬЮДНИ
КАКИМ образом можно с помощью пушки измерить площадь пруда? Будем наугад стрелять из пушки по полю, на котором расположен пруд. В результате точки приземления снарядов на поле будут распределены случайно. При достаточно большом количестве выстрелов площадь пруда будет приблизительно равна площади поля, помноженной на число попадании в пруд и поделенной на общее число выстрелов. Эта, если признаться, несколько глуповатая постановка задачи служит прекрасной иллюстрацией того, какую роль могут играть случайные события при моделировании процессов. Современные ЭВМ - удобное средство моделирования. Правда, элемент случайности в них достигается не стрельбой из пушки, а при помощи датчика случайных чисел.

Площадь круглого пруда можно определить, стреляя по нему из пушки
С философской точки зрения любопытно отметить, что случайные числа, являющиеся чистейшим выражением нашего незнания, легли в основу методов, при помощи которых мы познаем поведение сложных систем. Применение случайных чисел в моделировании проиллюстрируем на примере пяти программ, названных мной несложными пьесами. Воспользуемся случайными числами, чтобы вычислить, например, приближенное значение числа пи, частоту появления клиентов в банке, распределение шариков, скатывающихся по доске с колышками, а также выявить временные закономерности, по которым изменяются симпатии избирателей на выборах, и, наконец, показать, как могут возникнуть миллионные очереди.
Предлагаемые вниманию читателя программы представляют собой как бы музыкальные пьесы или этюды для начинающих. Обучение игре с компьютером во многом напоминает процесс обучения игре на музыкальном инструменте, и этот процесс может приносить удовлетворение на любой стадии овладения мастерством. Соответственно наша первая пьеса - самая легкая, последнюю же можно, пожалуй, охарактеризовать как несложную. Во всех последующих рассуждениях предполагается, что случайные числа генерируются при выполнении команды random. Это будут числа от 0 до 1 с несколькими десятичными разрядами.
Первая пьеса связана с так называемой задачей Бюффона об игле. Граф Луи де Бюффон - французский естествоиспытатель и математик XIXв. Представим себе, что игла многократно и произвольно бросается на дощатый пол. Длина иглы равна половине ширины доски. Задача заключается в том, чтобы найти вероятность пересечения упавшей иглы с линией, разделяющей доски. Ответ оказывается равным 1/пи.
Конечно, можно было бы написать программу, моделирующую задачу Бюффона с иглой, однако существует значительно более простой способ вычисления приближенного значения числа пи путем моделирования. Воспользуемся для этого идеей, описанной в примере со стрельбой из пушки по полю со случайными попаданиями. Представим себе квадратное поле, заключающее в себе круглый пруд, касающийся всех четырех сторон квадрата. Если стрелять из пушки по этому полю без прицела в определенную точку достаточное количество раз, то отношение числа попаданий в пруд к полному числу выстрелов будет приблизительно равно отношению площади круга к площади квадрата, а именно пи/4.
Моделирование можно провести при помощи простой программы, называемой PINT. Представим один квадрант, или четверть поля, скажем северо-восточный, единичным квадратом. Точка (0, 0) в юго-западном углу квадранта лежит в центре круга, а точка (1, 1) в северо-восточном углу квадранта представляет собой соответствующий угол поля. Выбрав подряд два случайных числа x и y, можно промоделировать выстрел со случайным попаданием в пределах квадранта (напомним, что каждое случайное число находится в диапазоне от 0 до 1). Попадет ли снаряд в пруд? Чтобы ответить на этот вопрос, вычислим расстояние между точкой (x, y) и центром пруда. Если расстояние меньше или равно 1, то мы регистрируем попадание и увеличиваем значение переменной-счетчика на 1. Программа содержит цикл, при помощи которого "стрельбу" можно продолжать сколь угодно долго. Когда стрельба закончена, помножим отношение числа "попаданий" к общему числу "выстрелов" на 4. Результат должен быть близким к числу пи.
СЛЕДУЮЩАЯ пьеса называется "дверь для человечков". Представим себе, что мы наблюдаем за людьми, проходящими через дверь, ведущую в банк. У всех этих людей были веские причины, побудившие их прийти в банк именно в данный момент, и, если бы нам были известны эти причины, мы могли смоделировать моменты появления людей абсолютно точно. Однако мы ничего об этом не знаем. Для подобных задач существует немало моделирующих программ, в которых применяется специальная математическая функция, называемая отрицательным показательным распределением. На объяснение смысла этой математической функции и описание довольно изящного способа, позволяющего с ее помощью вычислять моменты появления людей у двери, потребовалась бы не одна страница. Значительно проще объяснить прием "дверь для человечков", использование которого может дать тот же результат.
Дверь для человечков - это проход шириной w в стене, непроницаемой на всем остальном протяжении. Тысячи человечков нескончаемым потоком направляются к стене, и каждую секунду один из них достигает ее в произвольной точке. Те, кому повезет, попадают в проход и идут дальше, остальные натыкаются на стену. Если бы проход в стене был дверью, ведущей в банк, то случайные моменты появления человечков в проходе были бы достаточно близки к наблюдаемым моментам появления реальных клиентов. Чтобы подогнать среднюю частоту появления к реально наблюдаемой, нужно соответствующим образом подобрать ширину прохода в стене.

Человечки и закономерность, согласно которой они попадают в проход в стене
Рассмотрим программу, моделирующую моменты появления клиентов, под названием ZOMBIE. Стена в программе представлена отрезком прямой линии единичной длины. Цикл типа while генерирует периоды времени между появлениями людей. Каждую секунду, в течение которой ни одни человечек не появляется у прохода, переменная-счетчик увеличивается на 1 и происходит обращение к команде random. В результате выполнения последней в случайной точке стены появляется человечек. Для удобства и без нарушения общности можно считать, что проход расположен у левого края стены и простирается от точки 0 до точки w. Если случайное число, или точка прибытия очередного человечка, попадает в этот отрезок, то программа выходит иэ цикла и регистрирует факт прохождения человечка. В противном случае цикл выполняется еще раз. Рано или поздно еще один человечек пройдет через проход, и тогда значение переменной-счетчика укажет, сколько секунд прошло со времени предыдущего появления.
Средний интервал времени между появлениями составляет 1/w секунд. Например, если w=1/10, то в среднем один человечек будет проходить через проход каждые 1/(1/10), т.е. 10 секунд. Лучше всего программа ZOMBIE работает, когда w достаточно мало. По этой причине подходящим был бы режим (в зависимости от конкретного применения), когда очередной человечек появляется у стены через каждую десятую долю секунды. Чтобы подобрать значение w, даюшее хорошие результаты при моделировании, установим средний период времени между появлениями клиентов в банке равным 1/10w и отсюда определим w. Выше мы предположили, что проход заключен между точками 0 и w, однако некоторые датчики случайных чисел плохо работают в этом диапазоне. В таком случае можно выбрать другое расположение прохода в стене, например между точками 0.5 и 0.5+w на единичном отрезке.
Любопытно посмотреть, какое распределение интервалов времени между появлениями получается с помощью программы ZOMBIE. Вложив цикл while в другой цикл, подсчитывающий, сколько раз встречается тот или иной интервал между появлениями, можно получить гистограмму, или диаграмму, в виде столбцов, представляющую распределение. Типичная гистограмма изображена на рисунке вверху. На этой же гистограмме для сравнения показано отрицательное показательное распределение. У описанного метода много потенциальных применений для видеоигр, мы же ограничимся рассмотрением лишь одного применения, когда будем обсуждать нашу пятую пьесу.
ТРЕТЬЯ программа моделирует доску Гальтона. Это устройство было названо в честь одного из пионеров статистики, жившего в викторианскую эпоху, сэра Фрэнсиса Гальтона. Оно представляет собой плоскую наклонную поверхность с колышками, расположенными в виде треугольника (см. рисунок на с.92). Из точки, находящейся над самым верхним колышком, падают шарики, которые затем катятся вниз, натыкаясь по пути на колышки. В самом низу под колышками находятся ячейки, в которые попадают шарики. Когда последний шарик, пройдя между колышками, падает в одну из ячеек, образовавшиеся в ячейках колонки шариков образуют характерную столбчатую диаграмму распределения. Какова форма этой диаграммы, можно выяснить самим, если попытаться решить эту задачу.

Доска Гальтона и необычное распределение скатившихся с нее шариков
В отсутствие настоящей доски Гальтона ее можно смоделировать при помощи программы Galton, состоящей всего из нескольких строчек. Идея, лежащая в основе программы, так же как и идея, на которой была основана наша первая пьеса по вычислению числа пи, была взята из статьи Дж.Бентли в рубрике "Programming Pearls" ("Жемчужины программирования") в журнале "Communications of ihe ACM" за январь 1984г.
Спуск каждого шарика моделируется в цикле, где происходит выбор целой последовательности случайных чисел. Каждое из этих случайных чисел определяет, по какую сторону от колышка скатится шарик - справа или слева. Если число меньше или равно 0.5, то моделируемый шарик скатится по левую сторону от колышка, если же число окажется больше 0.5 - по правую сторону. А от какого именно колышка, неважно. Главное - не забыть увеличивать значение счетчика на 1 каждый раз, когда шарик скатывается по правую сторону. Читатель может сам убедиться, что ячейка, в которую попадет шарик, определяется только количеством отскоков в правую сторону. Достоинство программы в том, что в ней устраняется необходимость моделирования поведения шарика при столкновении с каждым колышком. Отсюда следует вывод, что, немного подумав, можно составить простую программу, моделирующую сложный процесс.
Цикл, моделирующий прохождение одного шарика по доске Гальтона, вложен в большой цикл, подсчитывающий число выпускаемых шариков. Каждый раз, когда завершается выполнение внутреннего цикла, ячейка, в которую попадает шарик, должна быть зарегистрирована в массиве c, накапливающем сведения о пополнении ячеек. Элемент массива c(n) увеличивается на 1 всякий раз, когда шарик попадает в ячейку n. После того как был промоделирован спуск, скажем, 1000 шариков, результат, накопленный в массиве c, можно изобразить в виде гистограммы. Если к программе Gallon добавить несколько команд вывода на дисплей, гистограмма может быть построена непосредственно компьютером.
Нетрудно сообразить, что при другом расположении колышков на доске Гальтона можно получить распределение другого вида. Предлагаю читателям самим придумать аналогичные устройства независимо от того, существуют ли они реально или только в воображении.
ЧЕТВЕРТАЯ несложная пьеса связана с двумя новыми интересными играми, моделирующими динамику изменения симпатии избирателей во время предвыборной кампании. Эти игры были недавно изучены П.Доннели и Университетского колледжа Суонси в Уэльсе и Д.Уэлшем из Оксфордского университета. Клетки прямоугольной решетки в исходном состоянии раскрашены в белый и черный цвета в случайном порядке. Каждый цвет представляет политическую ориентацию избирателя, занимающего данную клетку. Например, один цвет может означать республиканца, другой - демократа. Допустим, что на каждый "тик" и "так" часового механизма случайным образом выбирается избиратель и его политическая ориентация может быть изменена. Для этого произвольно выбирается один из восьми соседей данного избирателя и политические симпатии соседа передаются этому избирателю независимо от ею прежних убеждений.

Одна из ситуаций, сложившихся в игре "голосование"
Решетка замыкается сама на себя аналогично океану планеты Аква-тор (см. статью в рубрике "Занимательный компьютер", журнал "В мире науки" #2 за 1985г.). Верхний край решетки отождествляется с нижним краем, а левый край - с правым. Поэтому избиратель, находящийся в клетке на краю решетки, имеет трех соседей на противоположной стороне. После каждого случайного изменения политической ориентации одного избирателя устраиваются "выборы", однако это не обязательный элемент модели и его можно исключить, если играющий не хочет следить за динамикой результатов.
По мере того как реализуется эта незамысловатая модель, происходят странные веши. Сначала на решетке образуются большие блоки одного цвета. Блоки представляют территориальные области, где политические ориентации всех избирателей совпадают. Затем блоки начинают перемешаться по решетке, пока не остаются только два блока, борющихся между собой. Наконец, и эта система из двух блоков рушится, и все начинают голосовать одинаково. Меньший блок исчезает бесследно, а за ним и вся система. Игра наводит на философские размышления.
Короткая программа VOTERS моделирует описанный процесс во всех деталях. Она содержит массив тех же размеров, что и решетка. В коротком вычислительном цикле выбираются три случайных целых числа, дающие соответственно случайный номер строки, случайный номер столбца и код случайного соседа на каждом такте часов. Три целых числа получаются путем умножения величины, возвращаемой командой random, на постоянную и удаления дробной части при выполнении команды integer. Если, например, решетка содержит 50 рядов (строк), то выбор случайного индекса строки i будет алгоритмически записан как
i = integer(50*random).
Случайный индекс столбца j вычисляется аналогичным образом. Выбор программой соседа клетки (i,j) зависит от того, какое из целых чисел от 0 до 7 было выбрано. После того как были случайно выбраны клетка и ее сосед, программа VOTERS заменяет значение элемента массива (i, j) значением, соответствующим соседней клетке.
Описанные шаги алгоритма заключены в цикл. Количество повторений цикла удобно сделать переменной величиной. Тогда можно экспериментировать с количеством изменений мнения избирателей. Пределы изменения индексов могут варьировать и в других программах, рассматриваемых в настоящей статье. Для этого количество повторений цикла устанавливается равным n, а желаемое значение n вводится с клавиатуры перед выполнением программы.
Графическое представление решетки нетрудно реализовать в основном вычислительном цикле программы. Даже при использовании только двух символов (скажем, точки и звездочки) получается впечатляющее зрелище. Читатели, которых не остановит солидарность мнений избирателей в исходе игры "голосование", возможно, захотят реализовать и ее обратный вариант, который Уэлш и Доннели называют игрой "антиголосование". В отличие от "прямого" варианта в игре "антиголосование" случайно выбранный избиратель принимает мнение, противоположное мнению его случайно выбранного сосела. Сохранится ли солидарность избирателей при этих условиях?
ПЯТАЯ, и последняя, пьеса дает пищу для размышления человеку, стоящему в очереди. Если люди будут уходить из начала очереди в среднем с той же скоростью, с какой другие прибывают в конец, то будет ли размер очереди оставаться приблизительно одним и тем же? По-видимому, нет. Согласно теории очередей, такая очередь не имеет конечной ожидаемой длины. Подобные очереди я наблюдал в банках.
Программа QWING моделирует динамику простой очереди. Люди прибывают в конец очереди в соответствии с той же закономерностью, какая порождается уже знакомой нам программой ZOMBIE. В начале очереди находится человек, обслуживаемый в данный момент. В программах, моделирующих очередь, иногда предполагается, что длительности обслуживания распределены так же, как интервалы времени между двумя случайными прибытиями клиентов. Когда в банке я вношу вклад на свой счет, процедура обслуживания обычно не занимает много времени. Значительно дольше длится разговор со служащим банка, если клиент выясняет, куда делись деньги с его счета. Поэтому для получения случайных длительностей обслуживания программа QWING обращается к ZOMBIE как к подпрограмме.
Ход времени обрабатывается в программе QWING на основе метода критического события. Показания моделируемых часов постоянно изменяются к моменту следующего события, будь то уход из очереди или прибытие нового человека. Показания часов обозначим через c. Потребуются еше три переменные: ts - промежуток времени, оставшийся до момента завершения текущей процедуры обслуживания, ta - промежуток времени до следующего прибытия и q - длина очереди (см. рисунок внизу).

Блок-схема программы QWING
Вначале значения ts и ta устанавливаются равными 0, q = 1. Затем программа входит в свой основной цикл, причем количество его повторении задается с клавиатуры специальной командой. Цикл содержит команду условного перехода. Она проверяет, меньше ли величина ta величины ts. Если это так, то показания часов увеличиваются на величину ta, потому что критическим событием в данном случае является следующее прибытие. Соответственно величина ts уменьшается на то же число, и, поскольку критическим событием является прибытие, q увеличивается на 1. На заключительном шаге алгоритма в работу включается программа ZOMBIE, чтобы выдать случайный промежуток времени до следующего прибытия.
В начале цикла может выясниться, однако, что ta не меньше ts. В этом случае аналогичные операции выполняются в другой ветви программы, с той лишь разницей, что ta и ts меняются ролями. Критическим событием является следующее обслуживание. Поэтому q уменьшается на 1. Здесь программа ZOMBIE выдает следующее значение величины ts. В конце цикла обе ветви сходятся воедино, и производится проверка значения q. Если q = 0, то в ожидании следующего прибытия программа перехолит к первому сегменту. В противном случае она возвращается в начало цикла, где сравниваются значения ta и ts.
Программа QWING, очевидно, длиннее других, но она еще достаточно коротка, чтобы охарактеризовать ее как "простую". Будет, наверное, лучше, чтобы пользователь мог сам указать такие величины, как средняя продолжительность обслуживания и средний промежуток времени между двумя прибытиями клиентов. Благодаря этому каждый может самостоятельно проверить основные результаты теории очередей. Если средний промежуток времени между двумя прибываниями больше средней продолжительности обслуживания, то ожидаемая длина очереди будет конечной величиной. Чем больше разность между этими величинами, тем более "конечной" становится длина очереди. Когда средние величины находятся в противоположном отношении, ожидаемая длина очереди является бесконечной - понаблюдайте, как она растет. Когда средние величины в точности равны друг другу, ожидаемая длина очереди не является ни конечной, ни бесконечной. Как такое может быть? Проведите эксперимент (или хорошенько подумайте) и вы получите ответ на этот вопрос.
ЧИТАТЕЛИ, склонные к анализу любопытных ситуаций, могут усложнить программу QWING, чтобы смоделировать одно из новшеств, которое было введено в банках более десяти лет назад. Вместо того чтобы ожидать в различных очередях, к каждому окошку в отдельности, клиенты становились в одну общую очередь. Эта система обладает несколькими преимуществами, в чем можно убедиться с помощью моделирующей программы, которая учитывает основные свойства коллективной очереди. Еще более сложная программа может смоделировать сравнительно более недавнее нововведение: теперь каждый обслуживающий клиентов работник банка находится в очереди к тому, кто обслуживает их самих. Эта новая система оказывается очень выгодной для крупных банков.
По поводу всех этих рассуждений о случайных числах возникает вопрос: как может компьютер, представляющий собой детерминированную машину, генерировать случайные числа, по природе своей явно не детерминированные? Ответ прост - не может. Однако компьютер может генерировать числа, которые похожи на случайные. В самом деле, возьмем произвольное число, умножим его на m, прибавим k - и возьмем остаток от деления полученной величины на p. Остаток вновь подвергнем той же процедуре. Раз за разом этот алгоритм будет выдавать так называемые псевдослучайные числа. Однако рано или поздно последовательность результатов, выдаваемых алгоритмом, должна повториться, потому что существует только р возможных остатков. Более того, если величины m, k и p не подобраны самым тщательным образом, то получаемые псевдослучайные числа не удовлетворяют даже самым простым тестам на случайность.
Зная об этих недостатках, программисты-теоретики пытались придумать лучший метод. Много лет назад Д.Кнут из Станфордского университета изобрел алгоритм настолько "случайно превосходный" и "превосходно случайный", что генерируемые им числа, казалось, были достойны эпитета "сверхслучайные". Алгоритм Кнута состоит из 12 шагов. Для заданного исходного числа X на первых двух шагах выбираются два разряда этого числа. Выбранные разряды определяют, сколько раз алгоритм должен быть повторен и к какому из следующих 10 шагов алгоритма следует перейти. Каждый из этих 10 шагов представляет собой свой, отличный от других метод вычисления нового случайного числа по заданному старому. Перед тем как Кнут испытал свой алгоритм в действии, ему казалось, что "он обеспечит производство по крайней мере бесконечного количества невероятно случайных чисел". К его удивлению, "когда алгоритм был впервые испытан на машине, он почти немедленно сошелся на десятиразрядном числе 6065038420, которое, в силу исключительно редкого совпадения, порождало само себя". Отсюда Кнут вывел простую, хотя, может быть, интуитивно неочевидную модель: "Случайные числа не должны генерироваться случайно выбранным методом. Эта процедура должна быть теоретически обоснована". Если численные методы получения случайных чисел окажутся неудовлетворительными, можно всегда воспользоваться предложением, когда-то сделанным Аланом М.Тьюрингом. Он указал на то, что датчик случайных чисел может быть основан на радиоактивном источнике. Читатели могут с интересом ознакомиться с развитием этой идеи, прочтя статью F.M.Mims III, "The Compuler Scientist: Random Numbers" в ноябрьском номере журнала "Computers and Electronics" за 1984г.
БИБЛИОГРАФИЯ
SYSTEM SIMULATION WITH DIGITAL COMPUTER. NARSINGH DEO, Prentice-Hall, Inc., 1983.
КНУТ Д. ИСКУССТВО ПРОГРАММИРОВАНИЯ ДЛЯ ЭВМ. Т. 2. Получисленные алгоритмы. Перев. с англ. - М.: Мир, 1977.
Раз упомянули "этюды", можно поискать [этюд про автостраду] в книге Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 - ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.
ОТКЛИКИ
9 1985
ПИСЬМА читателей, откликнувшихся на статью "Пять несложных программ для различных задач моделирования с помощью случайных чисел", свидетельевуют о том, что полученные ими результаты действительно приводят к гистограмме, очень близкой к отрицательному экспоненциальному распределению. Сотням читаталей удалось написать первую пьесу - программу для приближенного вычисления числа пи. И лишь несколько читателей справились с пятой пьесой - программой, моделирующей повеление очередей.
В программе вычисления числа пи моделируемые пушки стреляют по моделируемому полю, окружающему моделируемый пруд. Я приношу свои извинения тысячам соседей, которые не смогли заснуть под раскаты пушечной стрельбы, продолжавшейся ночи напролет.
Написав программу, вычисляющую подобным образом приближенное значение числа пи, очевидно, трудно удержаться от соблазна произвести больше чем 1000 выстрелов. Чемпионом в этом упражнении следует признать Дж.Саймонса из Медицинского училища Гарвардского университета. Продолжая выполнение программы в течение целой недели на мощной ЭВМ, Саймоне сумел произвести более 4млрд. выстрелов по пруду. Полученное им значение числа ж равно 3.14157. К сожалению, пятый разряд после запятой получился равным 7, а не 9, как должно быть.
На данный момент лишь 134 читателя представили свои оценки числа пи, полученные в результате цикла из 1000 выстрелов. В тех случаях, когда читатели представляли результаты нескольких таких циклов, я выбирал только первый результат для того, чтобы получить среднее значение. При этом средний результат оказался равным 3.14137. Первые три знака после запятой правильны. В четвертом разряде числа пи должно быть не 3, а 5.
Между прочим, занимаясь этими подсчетами, я ни разу не заглянул в справочник, чтобы вспомнить точное значение числа пи. Вместо этого я воспользовался мнемоническим правилом: "How I wish I could enumerate pi easily" ("Как я хочу пи числа выражение не забыть"). Выпишите последовательно число букв в каждом слове этой фразы и вы получите число пи. Сумеет ли кто-нибудь предложить продолжение для этого мнемонического правила?
Обе приведенные оценки числа пи оказываются несколько меньше точного значения. Этот сдвиг в меньшую сторону был предсказан Дж.Файнапом из Энн-Арбора (шт. Мичиган), по словам которого большинство датчиков случайных чисел,имеет небольшое отклонение в сторону нуля. Это отклонение повлияло в том же направлении (в сторону уменьшения) и на программу подсчета числа пи.
Дж. Мак-Кин, статистик из Университета Западного Мичнгана в Каламазу (шт. Мичиган), указывает, что при подобных подсчетах можно установить 95%-ный доверительный интервал вокруг полученной оценки. При этом предполагается, что полученное приближенное значение находится посередине числового интервала, составляющего доверительный интервал, а сам интервал определяется таким образом, что точное значение с вероятностью 95% находится в какой-то точке интервала. Размер последнего меняется обратно пропорционально квадратному корню из n - количества произведенных выстрелов. Отсюда следует, что для увеличения точности оценки, скажем, в 10 раз, или на один десятичный разряд, число n необходимо увеличить в 100 раз. Таким образом, приходится идти на большие вычислительные затраты, чтобы получить даже небольшое увеличение точности. Этим объясняется неудовольствие, выраженное несколькими читателями.
Все, кто написал программу ZOMBIE, без труда получили диаграммы, аналогичные экспоненциальной кривой, изображенной на рисунке, приведенном в июньском номере журнала "В мире науки" 1985, на с.91.
Программа GALTON заинтриговала Э.Кудала из Парк-Риджа (шт.Иллинойс). Моделируемые программой шарики, скатываясь через треугольный массив колышков, образовали искомое распределение у основания доски Гальтона, а именно биномиальное распределение. Биномиальное распределение дискретно и имеет колоколообразную форму, имитируя своего собрата - нормальное распределение.
Двое читателей одновременно сделали одно и то же изобретение. Они решили обобщить программу GALTON для случая трехмерного массива колышков. У основания своих моделируемых досок Дж. Матушевич из Колумбуса (шт. Небраска) и Дж.Ньюджент из Пеории (шт. Иллинойс) получили гладкое возвышение из шариков. Может быть, читатели догадаются, какую форму имеет это возвышение?
Некоторые читатели, попробовавшие написать программу VOTERS, были разочарованы полученными результатами. В одном случае программа проработала всю ночь, однако развязка так и не наступила. Единственное, что я могу порекомендовать экспериментаторам, - это запастись терпением и продолжать работу с программой. Мне, например, потребовалась большая часть суток. Следует также внимательно следить за развитием игры.
Наконец, только двое читателей попытались создать программу QWING, моделирующую очередь клиентов в банке с единственным окошком для обслуживания. В.Ауэрбах из Филадельфии (шт.Пенсильвания) написал свою оригинальную версию программы с разбиением по времени, благодаря чему он наблюдал, как очередь медленно растет, несмотря на многократные кратковременные уменьшения. Дж.Гудман из Куинси (шт.Массачусетс) внес еще более значительные изменения в программу QWING: он заменил систему моделирования очереди двумя дверями для человечков в одной-едннственной стене. Читателям, возможно, будет интересно попытаться понять, как работает программа Гудмана, зная о ней только то, что было сказано выше.
Я уже отмечал, что ожидаемая длина очереди не является ни конечной, ни бесконечной, если средние длительности обслуживания одного клиента и интервала между прибытиями клиентов совпадают. Такая очередь вначале растет, но затем уменьшается до нуля. Далее она снова начинает расти, достигая даже еще больших размеров по сравнению с предыдущим разом, но затем опять сокращается до нуля. Длина очереди колеблется таким образом со все возрастающей амплитудой. Объяснение этого явления состоит в том, что, когда в очереди нет клиентов, потенциальное время их обслуживания навсегда теряется.
Многие читатели подозревают, что их генераторы случайных чисел содержат ошибки. Р.Гай из Оклендского университета в Рочестере (шт.Мичиган), показал, что для этих подозрений есть основания, по крайней мере в отношении генератора случайных чисел RND, используемом в языке Бейсик персонального компьютера фирмы IBM. Следующая программа, выполняющаяся только в графическом режиме, представляет собой наглядное свидетельство:
10 SCREEN 2
20 X = RND*640
30 Y = RND*200
40 PSET(X,Y)
50 GO TO 20
Если бы генератор RND работал безупречно, то точки на экране были бы разбросаны случайным образом, на самом деле на экране появляются кольцеобразные сгущения точек. Несомненно, аналогичное явление можно наблюдать и у других компьютеров.
11 1985
Со всех концов света продолжает поступать так много результатов расчетов по программе PINT, что я вынужден опубликовать новую среднюю величину. При подсчете были учтены все оценки числа пи, вычисленные по 1000 выстрелам и полученные с тех пор, как было подсчитано значение, приведенное в сентябрьском номере журнала. В течение двухмесячного периода накопления данных я наблюдал, как среднее значение постепенно уменьшалось, достигнув в какой-то момент 3.129. Положение несколько улучшилось, когда прибыла почта из Европы и Азии, и среднее значение снова начало подниматься. Хочу выразить особую признательность многочисленным участникам, которые читают издание нашего журнала на немецком языке (Spectrum der Wissenschaft). Благодаря им округленное среднее значение на сегодняшний день оказалось правильным с точностью до двух знаков после запятой. Всего было получено 126 писем, удовлетворяющих поставленным требованиям, и теперь среднее значение числа пи равно 3.137.
12 1985
Более двадцати различных мнемонических правил для запоминания последовательности цифр числа пи были присланы читателями в сентябре. Как и следовало ожидать, большинство мнемоник было предложено сразу несколькими читателями. Мне очень по-нравились два продолжения мнемоники, предложенной в статье "Путешествие с роботами в Роботрополе и овладение навыками конструирования электронных микросхем" (см. "В мире науки", 1985, #9), а также несколько старых, почти забытых мнемоник, с которых смахнули пыль и показали новому поколению читателей. Завершают этот парад произведения "международного класса", написанные на французском, немецком и греческом языках.
Победителем в категории правил, продолжающих уже предложенную фразу, следует признать П.Брайяма из Брайтона (шт.Массачусетс): "How I wish I could enumerate pi easily, since all these (censored) mnemonics prevent recalling any of pi's sequence more simply" [Здесь и далее предложенные читателями мнемонические правила даются без перевода, поскольку в адекватных фразах на русском языке число букв в словах не будет соответствовать последовательности цифр числа пи.- Прим. ред.].
Победителем конкурса на самую длинную мнемонику стал Дж.Джанг из Темпла (шт.Аризона). Правило Джанга позволяет запомнить 110 знаков числа пи. Я приведу здесь лишь первые 14 слов: "How I wish I could enumerate pi easily which men known skillful calculate forever..."
Множество читателей, включая Л.Полинга, прислали одну или несколько старых шуток, подобных, например, следующим:
See, I have a rhyme assisting
my feeble brain, in tasks sometime resisting.
Или:
Now I - even 1 - would celebrate in rhymes inept
the great immortal Syracusan rivaled nevermore,
who by his wondrous lore untold us before,
made the way straight how to circles mensurate.
В нашей коллекции есть еще несколько странных, но забавных мнемоник. М.Стюбен из Анандейла (шт.Виргиния) прислал, например, такое стихотворение:
How I wish I could recollect pi.
Eurika! cried the great inventor.
Christmass pudding, Christmass pie
is the problem's very center.
Клайв Дж.Гримстоун из Лондона, Англия, располагает мнемоникой, охватывающей 100 десятичных знаков, но не включающей первые 3. Вот как выглядит начало стихотворения:
I know a maths professor.
Не always weeps and sighs
whenever polyhedra
capsize...
Читатели с хорошей музыкальной памятью могут запомнить число пи, напевая или насвистывая мелодию, придуманную Р.Бруксом из Бетесда (шт.Мэриленд). Чтобы не прибегать к музыкальной записи, я лишь скажу, что каждому разряду числа зг Брукс ставит в соответствие определенную ноту. Нота "ми" соответствует единице, "фа" - двойке и т.д. Рядом с каждой нотой в скобках записывается ее длительность (она не имеет отношения к разрядам числа пи и необходима только для мелодии.- Перев.). За единицу длительности принята 1/16. В этих обозначениях мелодия, соответствующая разрядам числа пи, имеет следующий вид:
3(1) 1(1) 4(1) 1(1) 5(5) 9(1) 2(1) 6(1) 5(6) 3(1) 5(1) 8(5) 9(1) 7(1) 9(1) 3(6) 2(1) 3(1) 8(1) 4(1) 6(4) 2(2) 6(6) 4(2) 3(12)
Счет идет на 4 четверти, и первый такт кончается между четвертой и пятой нотами.
Трое читателей, включая Дж.Сиэтла (шт.Вашингтон), прислали следующее стихотворение на французском языке:

А вот стихотворение Хенрика на немецком языке:

Конечно, греки в лице Архимеда сказали первое слово о числе пи. Им же, по мнению Л.Джаковидеса из Бирмингема (шт.Мичиган), должно принадлежать и последнее слово:

(Всемогущие боги играют в геометрию, чтобы выразить длину окружности через ее диаметр).
ПЯТЬ НЕСЛОЖНЫХ ПРОГРАММ ДЛЯ РАЗЛИЧНЫХ ЗАДАЧ МОДЕЛИРОВАНИЯ С ПОМОЩЬЮ СЛУЧАЙНЫХ ЧИСЕЛ
А.К.ДЬЮДНИ
КАКИМ образом можно с помощью пушки измерить площадь пруда? Будем наугад стрелять из пушки по полю, на котором расположен пруд. В результате точки приземления снарядов на поле будут распределены случайно. При достаточно большом количестве выстрелов площадь пруда будет приблизительно равна площади поля, помноженной на число попадании в пруд и поделенной на общее число выстрелов. Эта, если признаться, несколько глуповатая постановка задачи служит прекрасной иллюстрацией того, какую роль могут играть случайные события при моделировании процессов. Современные ЭВМ - удобное средство моделирования. Правда, элемент случайности в них достигается не стрельбой из пушки, а при помощи датчика случайных чисел.

Площадь круглого пруда можно определить, стреляя по нему из пушки
С философской точки зрения любопытно отметить, что случайные числа, являющиеся чистейшим выражением нашего незнания, легли в основу методов, при помощи которых мы познаем поведение сложных систем. Применение случайных чисел в моделировании проиллюстрируем на примере пяти программ, названных мной несложными пьесами. Воспользуемся случайными числами, чтобы вычислить, например, приближенное значение числа пи, частоту появления клиентов в банке, распределение шариков, скатывающихся по доске с колышками, а также выявить временные закономерности, по которым изменяются симпатии избирателей на выборах, и, наконец, показать, как могут возникнуть миллионные очереди.
Предлагаемые вниманию читателя программы представляют собой как бы музыкальные пьесы или этюды для начинающих. Обучение игре с компьютером во многом напоминает процесс обучения игре на музыкальном инструменте, и этот процесс может приносить удовлетворение на любой стадии овладения мастерством. Соответственно наша первая пьеса - самая легкая, последнюю же можно, пожалуй, охарактеризовать как несложную. Во всех последующих рассуждениях предполагается, что случайные числа генерируются при выполнении команды random. Это будут числа от 0 до 1 с несколькими десятичными разрядами.
Первая пьеса связана с так называемой задачей Бюффона об игле. Граф Луи де Бюффон - французский естествоиспытатель и математик XIXв. Представим себе, что игла многократно и произвольно бросается на дощатый пол. Длина иглы равна половине ширины доски. Задача заключается в том, чтобы найти вероятность пересечения упавшей иглы с линией, разделяющей доски. Ответ оказывается равным 1/пи.
Конечно, можно было бы написать программу, моделирующую задачу Бюффона с иглой, однако существует значительно более простой способ вычисления приближенного значения числа пи путем моделирования. Воспользуемся для этого идеей, описанной в примере со стрельбой из пушки по полю со случайными попаданиями. Представим себе квадратное поле, заключающее в себе круглый пруд, касающийся всех четырех сторон квадрата. Если стрелять из пушки по этому полю без прицела в определенную точку достаточное количество раз, то отношение числа попаданий в пруд к полному числу выстрелов будет приблизительно равно отношению площади круга к площади квадрата, а именно пи/4.
Моделирование можно провести при помощи простой программы, называемой PINT. Представим один квадрант, или четверть поля, скажем северо-восточный, единичным квадратом. Точка (0, 0) в юго-западном углу квадранта лежит в центре круга, а точка (1, 1) в северо-восточном углу квадранта представляет собой соответствующий угол поля. Выбрав подряд два случайных числа x и y, можно промоделировать выстрел со случайным попаданием в пределах квадранта (напомним, что каждое случайное число находится в диапазоне от 0 до 1). Попадет ли снаряд в пруд? Чтобы ответить на этот вопрос, вычислим расстояние между точкой (x, y) и центром пруда. Если расстояние меньше или равно 1, то мы регистрируем попадание и увеличиваем значение переменной-счетчика на 1. Программа содержит цикл, при помощи которого "стрельбу" можно продолжать сколь угодно долго. Когда стрельба закончена, помножим отношение числа "попаданий" к общему числу "выстрелов" на 4. Результат должен быть близким к числу пи.
СЛЕДУЮЩАЯ пьеса называется "дверь для человечков". Представим себе, что мы наблюдаем за людьми, проходящими через дверь, ведущую в банк. У всех этих людей были веские причины, побудившие их прийти в банк именно в данный момент, и, если бы нам были известны эти причины, мы могли смоделировать моменты появления людей абсолютно точно. Однако мы ничего об этом не знаем. Для подобных задач существует немало моделирующих программ, в которых применяется специальная математическая функция, называемая отрицательным показательным распределением. На объяснение смысла этой математической функции и описание довольно изящного способа, позволяющего с ее помощью вычислять моменты появления людей у двери, потребовалась бы не одна страница. Значительно проще объяснить прием "дверь для человечков", использование которого может дать тот же результат.
Дверь для человечков - это проход шириной w в стене, непроницаемой на всем остальном протяжении. Тысячи человечков нескончаемым потоком направляются к стене, и каждую секунду один из них достигает ее в произвольной точке. Те, кому повезет, попадают в проход и идут дальше, остальные натыкаются на стену. Если бы проход в стене был дверью, ведущей в банк, то случайные моменты появления человечков в проходе были бы достаточно близки к наблюдаемым моментам появления реальных клиентов. Чтобы подогнать среднюю частоту появления к реально наблюдаемой, нужно соответствующим образом подобрать ширину прохода в стене.

Человечки и закономерность, согласно которой они попадают в проход в стене
Рассмотрим программу, моделирующую моменты появления клиентов, под названием ZOMBIE. Стена в программе представлена отрезком прямой линии единичной длины. Цикл типа while генерирует периоды времени между появлениями людей. Каждую секунду, в течение которой ни одни человечек не появляется у прохода, переменная-счетчик увеличивается на 1 и происходит обращение к команде random. В результате выполнения последней в случайной точке стены появляется человечек. Для удобства и без нарушения общности можно считать, что проход расположен у левого края стены и простирается от точки 0 до точки w. Если случайное число, или точка прибытия очередного человечка, попадает в этот отрезок, то программа выходит иэ цикла и регистрирует факт прохождения человечка. В противном случае цикл выполняется еще раз. Рано или поздно еще один человечек пройдет через проход, и тогда значение переменной-счетчика укажет, сколько секунд прошло со времени предыдущего появления.
Средний интервал времени между появлениями составляет 1/w секунд. Например, если w=1/10, то в среднем один человечек будет проходить через проход каждые 1/(1/10), т.е. 10 секунд. Лучше всего программа ZOMBIE работает, когда w достаточно мало. По этой причине подходящим был бы режим (в зависимости от конкретного применения), когда очередной человечек появляется у стены через каждую десятую долю секунды. Чтобы подобрать значение w, даюшее хорошие результаты при моделировании, установим средний период времени между появлениями клиентов в банке равным 1/10w и отсюда определим w. Выше мы предположили, что проход заключен между точками 0 и w, однако некоторые датчики случайных чисел плохо работают в этом диапазоне. В таком случае можно выбрать другое расположение прохода в стене, например между точками 0.5 и 0.5+w на единичном отрезке.
Любопытно посмотреть, какое распределение интервалов времени между появлениями получается с помощью программы ZOMBIE. Вложив цикл while в другой цикл, подсчитывающий, сколько раз встречается тот или иной интервал между появлениями, можно получить гистограмму, или диаграмму, в виде столбцов, представляющую распределение. Типичная гистограмма изображена на рисунке вверху. На этой же гистограмме для сравнения показано отрицательное показательное распределение. У описанного метода много потенциальных применений для видеоигр, мы же ограничимся рассмотрением лишь одного применения, когда будем обсуждать нашу пятую пьесу.
ТРЕТЬЯ программа моделирует доску Гальтона. Это устройство было названо в честь одного из пионеров статистики, жившего в викторианскую эпоху, сэра Фрэнсиса Гальтона. Оно представляет собой плоскую наклонную поверхность с колышками, расположенными в виде треугольника (см. рисунок на с.92). Из точки, находящейся над самым верхним колышком, падают шарики, которые затем катятся вниз, натыкаясь по пути на колышки. В самом низу под колышками находятся ячейки, в которые попадают шарики. Когда последний шарик, пройдя между колышками, падает в одну из ячеек, образовавшиеся в ячейках колонки шариков образуют характерную столбчатую диаграмму распределения. Какова форма этой диаграммы, можно выяснить самим, если попытаться решить эту задачу.

Доска Гальтона и необычное распределение скатившихся с нее шариков
В отсутствие настоящей доски Гальтона ее можно смоделировать при помощи программы Galton, состоящей всего из нескольких строчек. Идея, лежащая в основе программы, так же как и идея, на которой была основана наша первая пьеса по вычислению числа пи, была взята из статьи Дж.Бентли в рубрике "Programming Pearls" ("Жемчужины программирования") в журнале "Communications of ihe ACM" за январь 1984г.
Спуск каждого шарика моделируется в цикле, где происходит выбор целой последовательности случайных чисел. Каждое из этих случайных чисел определяет, по какую сторону от колышка скатится шарик - справа или слева. Если число меньше или равно 0.5, то моделируемый шарик скатится по левую сторону от колышка, если же число окажется больше 0.5 - по правую сторону. А от какого именно колышка, неважно. Главное - не забыть увеличивать значение счетчика на 1 каждый раз, когда шарик скатывается по правую сторону. Читатель может сам убедиться, что ячейка, в которую попадет шарик, определяется только количеством отскоков в правую сторону. Достоинство программы в том, что в ней устраняется необходимость моделирования поведения шарика при столкновении с каждым колышком. Отсюда следует вывод, что, немного подумав, можно составить простую программу, моделирующую сложный процесс.
Цикл, моделирующий прохождение одного шарика по доске Гальтона, вложен в большой цикл, подсчитывающий число выпускаемых шариков. Каждый раз, когда завершается выполнение внутреннего цикла, ячейка, в которую попадает шарик, должна быть зарегистрирована в массиве c, накапливающем сведения о пополнении ячеек. Элемент массива c(n) увеличивается на 1 всякий раз, когда шарик попадает в ячейку n. После того как был промоделирован спуск, скажем, 1000 шариков, результат, накопленный в массиве c, можно изобразить в виде гистограммы. Если к программе Gallon добавить несколько команд вывода на дисплей, гистограмма может быть построена непосредственно компьютером.
Нетрудно сообразить, что при другом расположении колышков на доске Гальтона можно получить распределение другого вида. Предлагаю читателям самим придумать аналогичные устройства независимо от того, существуют ли они реально или только в воображении.
ЧЕТВЕРТАЯ несложная пьеса связана с двумя новыми интересными играми, моделирующими динамику изменения симпатии избирателей во время предвыборной кампании. Эти игры были недавно изучены П.Доннели и Университетского колледжа Суонси в Уэльсе и Д.Уэлшем из Оксфордского университета. Клетки прямоугольной решетки в исходном состоянии раскрашены в белый и черный цвета в случайном порядке. Каждый цвет представляет политическую ориентацию избирателя, занимающего данную клетку. Например, один цвет может означать республиканца, другой - демократа. Допустим, что на каждый "тик" и "так" часового механизма случайным образом выбирается избиратель и его политическая ориентация может быть изменена. Для этого произвольно выбирается один из восьми соседей данного избирателя и политические симпатии соседа передаются этому избирателю независимо от ею прежних убеждений.

Одна из ситуаций, сложившихся в игре "голосование"
Решетка замыкается сама на себя аналогично океану планеты Аква-тор (см. статью в рубрике "Занимательный компьютер", журнал "В мире науки" #2 за 1985г.). Верхний край решетки отождествляется с нижним краем, а левый край - с правым. Поэтому избиратель, находящийся в клетке на краю решетки, имеет трех соседей на противоположной стороне. После каждого случайного изменения политической ориентации одного избирателя устраиваются "выборы", однако это не обязательный элемент модели и его можно исключить, если играющий не хочет следить за динамикой результатов.
По мере того как реализуется эта незамысловатая модель, происходят странные веши. Сначала на решетке образуются большие блоки одного цвета. Блоки представляют территориальные области, где политические ориентации всех избирателей совпадают. Затем блоки начинают перемешаться по решетке, пока не остаются только два блока, борющихся между собой. Наконец, и эта система из двух блоков рушится, и все начинают голосовать одинаково. Меньший блок исчезает бесследно, а за ним и вся система. Игра наводит на философские размышления.
Короткая программа VOTERS моделирует описанный процесс во всех деталях. Она содержит массив тех же размеров, что и решетка. В коротком вычислительном цикле выбираются три случайных целых числа, дающие соответственно случайный номер строки, случайный номер столбца и код случайного соседа на каждом такте часов. Три целых числа получаются путем умножения величины, возвращаемой командой random, на постоянную и удаления дробной части при выполнении команды integer. Если, например, решетка содержит 50 рядов (строк), то выбор случайного индекса строки i будет алгоритмически записан как
i = integer(50*random).
Случайный индекс столбца j вычисляется аналогичным образом. Выбор программой соседа клетки (i,j) зависит от того, какое из целых чисел от 0 до 7 было выбрано. После того как были случайно выбраны клетка и ее сосед, программа VOTERS заменяет значение элемента массива (i, j) значением, соответствующим соседней клетке.
Описанные шаги алгоритма заключены в цикл. Количество повторений цикла удобно сделать переменной величиной. Тогда можно экспериментировать с количеством изменений мнения избирателей. Пределы изменения индексов могут варьировать и в других программах, рассматриваемых в настоящей статье. Для этого количество повторений цикла устанавливается равным n, а желаемое значение n вводится с клавиатуры перед выполнением программы.
Графическое представление решетки нетрудно реализовать в основном вычислительном цикле программы. Даже при использовании только двух символов (скажем, точки и звездочки) получается впечатляющее зрелище. Читатели, которых не остановит солидарность мнений избирателей в исходе игры "голосование", возможно, захотят реализовать и ее обратный вариант, который Уэлш и Доннели называют игрой "антиголосование". В отличие от "прямого" варианта в игре "антиголосование" случайно выбранный избиратель принимает мнение, противоположное мнению его случайно выбранного сосела. Сохранится ли солидарность избирателей при этих условиях?
ПЯТАЯ, и последняя, пьеса дает пищу для размышления человеку, стоящему в очереди. Если люди будут уходить из начала очереди в среднем с той же скоростью, с какой другие прибывают в конец, то будет ли размер очереди оставаться приблизительно одним и тем же? По-видимому, нет. Согласно теории очередей, такая очередь не имеет конечной ожидаемой длины. Подобные очереди я наблюдал в банках.
Программа QWING моделирует динамику простой очереди. Люди прибывают в конец очереди в соответствии с той же закономерностью, какая порождается уже знакомой нам программой ZOMBIE. В начале очереди находится человек, обслуживаемый в данный момент. В программах, моделирующих очередь, иногда предполагается, что длительности обслуживания распределены так же, как интервалы времени между двумя случайными прибытиями клиентов. Когда в банке я вношу вклад на свой счет, процедура обслуживания обычно не занимает много времени. Значительно дольше длится разговор со служащим банка, если клиент выясняет, куда делись деньги с его счета. Поэтому для получения случайных длительностей обслуживания программа QWING обращается к ZOMBIE как к подпрограмме.
Ход времени обрабатывается в программе QWING на основе метода критического события. Показания моделируемых часов постоянно изменяются к моменту следующего события, будь то уход из очереди или прибытие нового человека. Показания часов обозначим через c. Потребуются еше три переменные: ts - промежуток времени, оставшийся до момента завершения текущей процедуры обслуживания, ta - промежуток времени до следующего прибытия и q - длина очереди (см. рисунок внизу).

Блок-схема программы QWING
Вначале значения ts и ta устанавливаются равными 0, q = 1. Затем программа входит в свой основной цикл, причем количество его повторении задается с клавиатуры специальной командой. Цикл содержит команду условного перехода. Она проверяет, меньше ли величина ta величины ts. Если это так, то показания часов увеличиваются на величину ta, потому что критическим событием в данном случае является следующее прибытие. Соответственно величина ts уменьшается на то же число, и, поскольку критическим событием является прибытие, q увеличивается на 1. На заключительном шаге алгоритма в работу включается программа ZOMBIE, чтобы выдать случайный промежуток времени до следующего прибытия.
В начале цикла может выясниться, однако, что ta не меньше ts. В этом случае аналогичные операции выполняются в другой ветви программы, с той лишь разницей, что ta и ts меняются ролями. Критическим событием является следующее обслуживание. Поэтому q уменьшается на 1. Здесь программа ZOMBIE выдает следующее значение величины ts. В конце цикла обе ветви сходятся воедино, и производится проверка значения q. Если q = 0, то в ожидании следующего прибытия программа перехолит к первому сегменту. В противном случае она возвращается в начало цикла, где сравниваются значения ta и ts.
Программа QWING, очевидно, длиннее других, но она еще достаточно коротка, чтобы охарактеризовать ее как "простую". Будет, наверное, лучше, чтобы пользователь мог сам указать такие величины, как средняя продолжительность обслуживания и средний промежуток времени между двумя прибытиями клиентов. Благодаря этому каждый может самостоятельно проверить основные результаты теории очередей. Если средний промежуток времени между двумя прибываниями больше средней продолжительности обслуживания, то ожидаемая длина очереди будет конечной величиной. Чем больше разность между этими величинами, тем более "конечной" становится длина очереди. Когда средние величины находятся в противоположном отношении, ожидаемая длина очереди является бесконечной - понаблюдайте, как она растет. Когда средние величины в точности равны друг другу, ожидаемая длина очереди не является ни конечной, ни бесконечной. Как такое может быть? Проведите эксперимент (или хорошенько подумайте) и вы получите ответ на этот вопрос.
ЧИТАТЕЛИ, склонные к анализу любопытных ситуаций, могут усложнить программу QWING, чтобы смоделировать одно из новшеств, которое было введено в банках более десяти лет назад. Вместо того чтобы ожидать в различных очередях, к каждому окошку в отдельности, клиенты становились в одну общую очередь. Эта система обладает несколькими преимуществами, в чем можно убедиться с помощью моделирующей программы, которая учитывает основные свойства коллективной очереди. Еще более сложная программа может смоделировать сравнительно более недавнее нововведение: теперь каждый обслуживающий клиентов работник банка находится в очереди к тому, кто обслуживает их самих. Эта новая система оказывается очень выгодной для крупных банков.
По поводу всех этих рассуждений о случайных числах возникает вопрос: как может компьютер, представляющий собой детерминированную машину, генерировать случайные числа, по природе своей явно не детерминированные? Ответ прост - не может. Однако компьютер может генерировать числа, которые похожи на случайные. В самом деле, возьмем произвольное число, умножим его на m, прибавим k - и возьмем остаток от деления полученной величины на p. Остаток вновь подвергнем той же процедуре. Раз за разом этот алгоритм будет выдавать так называемые псевдослучайные числа. Однако рано или поздно последовательность результатов, выдаваемых алгоритмом, должна повториться, потому что существует только р возможных остатков. Более того, если величины m, k и p не подобраны самым тщательным образом, то получаемые псевдослучайные числа не удовлетворяют даже самым простым тестам на случайность.
Зная об этих недостатках, программисты-теоретики пытались придумать лучший метод. Много лет назад Д.Кнут из Станфордского университета изобрел алгоритм настолько "случайно превосходный" и "превосходно случайный", что генерируемые им числа, казалось, были достойны эпитета "сверхслучайные". Алгоритм Кнута состоит из 12 шагов. Для заданного исходного числа X на первых двух шагах выбираются два разряда этого числа. Выбранные разряды определяют, сколько раз алгоритм должен быть повторен и к какому из следующих 10 шагов алгоритма следует перейти. Каждый из этих 10 шагов представляет собой свой, отличный от других метод вычисления нового случайного числа по заданному старому. Перед тем как Кнут испытал свой алгоритм в действии, ему казалось, что "он обеспечит производство по крайней мере бесконечного количества невероятно случайных чисел". К его удивлению, "когда алгоритм был впервые испытан на машине, он почти немедленно сошелся на десятиразрядном числе 6065038420, которое, в силу исключительно редкого совпадения, порождало само себя". Отсюда Кнут вывел простую, хотя, может быть, интуитивно неочевидную модель: "Случайные числа не должны генерироваться случайно выбранным методом. Эта процедура должна быть теоретически обоснована". Если численные методы получения случайных чисел окажутся неудовлетворительными, можно всегда воспользоваться предложением, когда-то сделанным Аланом М.Тьюрингом. Он указал на то, что датчик случайных чисел может быть основан на радиоактивном источнике. Читатели могут с интересом ознакомиться с развитием этой идеи, прочтя статью F.M.Mims III, "The Compuler Scientist: Random Numbers" в ноябрьском номере журнала "Computers and Electronics" за 1984г.
БИБЛИОГРАФИЯ
SYSTEM SIMULATION WITH DIGITAL COMPUTER. NARSINGH DEO, Prentice-Hall, Inc., 1983.
КНУТ Д. ИСКУССТВО ПРОГРАММИРОВАНИЯ ДЛЯ ЭВМ. Т. 2. Получисленные алгоритмы. Перев. с англ. - М.: Мир, 1977.
Раз упомянули "этюды", можно поискать [этюд про автостраду] в книге Ч.УЭЗЕРЕЛЛ, ЭТЮДЫ ДЛЯ ПРОГРАММИСТОВ, 1982 -
 ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.
.- G.ОТКЛИКИ
9 1985
ПИСЬМА читателей, откликнувшихся на статью "Пять несложных программ для различных задач моделирования с помощью случайных чисел", свидетельевуют о том, что полученные ими результаты действительно приводят к гистограмме, очень близкой к отрицательному экспоненциальному распределению. Сотням читаталей удалось написать первую пьесу - программу для приближенного вычисления числа пи. И лишь несколько читателей справились с пятой пьесой - программой, моделирующей повеление очередей.
В программе вычисления числа пи моделируемые пушки стреляют по моделируемому полю, окружающему моделируемый пруд. Я приношу свои извинения тысячам соседей, которые не смогли заснуть под раскаты пушечной стрельбы, продолжавшейся ночи напролет.
Написав программу, вычисляющую подобным образом приближенное значение числа пи, очевидно, трудно удержаться от соблазна произвести больше чем 1000 выстрелов. Чемпионом в этом упражнении следует признать Дж.Саймонса из Медицинского училища Гарвардского университета. Продолжая выполнение программы в течение целой недели на мощной ЭВМ, Саймоне сумел произвести более 4млрд. выстрелов по пруду. Полученное им значение числа ж равно 3.14157. К сожалению, пятый разряд после запятой получился равным 7, а не 9, как должно быть.
На данный момент лишь 134 читателя представили свои оценки числа пи, полученные в результате цикла из 1000 выстрелов. В тех случаях, когда читатели представляли результаты нескольких таких циклов, я выбирал только первый результат для того, чтобы получить среднее значение. При этом средний результат оказался равным 3.14137. Первые три знака после запятой правильны. В четвертом разряде числа пи должно быть не 3, а 5.
Между прочим, занимаясь этими подсчетами, я ни разу не заглянул в справочник, чтобы вспомнить точное значение числа пи. Вместо этого я воспользовался мнемоническим правилом: "How I wish I could enumerate pi easily" ("Как я хочу пи числа выражение не забыть"). Выпишите последовательно число букв в каждом слове этой фразы и вы получите число пи. Сумеет ли кто-нибудь предложить продолжение для этого мнемонического правила?
Обе приведенные оценки числа пи оказываются несколько меньше точного значения. Этот сдвиг в меньшую сторону был предсказан Дж.Файнапом из Энн-Арбора (шт. Мичиган), по словам которого большинство датчиков случайных чисел,имеет небольшое отклонение в сторону нуля. Это отклонение повлияло в том же направлении (в сторону уменьшения) и на программу подсчета числа пи.
Дж. Мак-Кин, статистик из Университета Западного Мичнгана в Каламазу (шт. Мичиган), указывает, что при подобных подсчетах можно установить 95%-ный доверительный интервал вокруг полученной оценки. При этом предполагается, что полученное приближенное значение находится посередине числового интервала, составляющего доверительный интервал, а сам интервал определяется таким образом, что точное значение с вероятностью 95% находится в какой-то точке интервала. Размер последнего меняется обратно пропорционально квадратному корню из n - количества произведенных выстрелов. Отсюда следует, что для увеличения точности оценки, скажем, в 10 раз, или на один десятичный разряд, число n необходимо увеличить в 100 раз. Таким образом, приходится идти на большие вычислительные затраты, чтобы получить даже небольшое увеличение точности. Этим объясняется неудовольствие, выраженное несколькими читателями.
Все, кто написал программу ZOMBIE, без труда получили диаграммы, аналогичные экспоненциальной кривой, изображенной на рисунке, приведенном в июньском номере журнала "В мире науки" 1985, на с.91.
Программа GALTON заинтриговала Э.Кудала из Парк-Риджа (шт.Иллинойс). Моделируемые программой шарики, скатываясь через треугольный массив колышков, образовали искомое распределение у основания доски Гальтона, а именно биномиальное распределение. Биномиальное распределение дискретно и имеет колоколообразную форму, имитируя своего собрата - нормальное распределение.
Двое читателей одновременно сделали одно и то же изобретение. Они решили обобщить программу GALTON для случая трехмерного массива колышков. У основания своих моделируемых досок Дж. Матушевич из Колумбуса (шт. Небраска) и Дж.Ньюджент из Пеории (шт. Иллинойс) получили гладкое возвышение из шариков. Может быть, читатели догадаются, какую форму имеет это возвышение?
Некоторые читатели, попробовавшие написать программу VOTERS, были разочарованы полученными результатами. В одном случае программа проработала всю ночь, однако развязка так и не наступила. Единственное, что я могу порекомендовать экспериментаторам, - это запастись терпением и продолжать работу с программой. Мне, например, потребовалась большая часть суток. Следует также внимательно следить за развитием игры.
Наконец, только двое читателей попытались создать программу QWING, моделирующую очередь клиентов в банке с единственным окошком для обслуживания. В.Ауэрбах из Филадельфии (шт.Пенсильвания) написал свою оригинальную версию программы с разбиением по времени, благодаря чему он наблюдал, как очередь медленно растет, несмотря на многократные кратковременные уменьшения. Дж.Гудман из Куинси (шт.Массачусетс) внес еще более значительные изменения в программу QWING: он заменил систему моделирования очереди двумя дверями для человечков в одной-едннственной стене. Читателям, возможно, будет интересно попытаться понять, как работает программа Гудмана, зная о ней только то, что было сказано выше.
Я уже отмечал, что ожидаемая длина очереди не является ни конечной, ни бесконечной, если средние длительности обслуживания одного клиента и интервала между прибытиями клиентов совпадают. Такая очередь вначале растет, но затем уменьшается до нуля. Далее она снова начинает расти, достигая даже еще больших размеров по сравнению с предыдущим разом, но затем опять сокращается до нуля. Длина очереди колеблется таким образом со все возрастающей амплитудой. Объяснение этого явления состоит в том, что, когда в очереди нет клиентов, потенциальное время их обслуживания навсегда теряется.
Многие читатели подозревают, что их генераторы случайных чисел содержат ошибки. Р.Гай из Оклендского университета в Рочестере (шт.Мичиган), показал, что для этих подозрений есть основания, по крайней мере в отношении генератора случайных чисел RND, используемом в языке Бейсик персонального компьютера фирмы IBM. Следующая программа, выполняющаяся только в графическом режиме, представляет собой наглядное свидетельство:
10 SCREEN 2
20 X = RND*640
30 Y = RND*200
40 PSET(X,Y)
50 GO TO 20
Если бы генератор RND работал безупречно, то точки на экране были бы разбросаны случайным образом, на самом деле на экране появляются кольцеобразные сгущения точек. Несомненно, аналогичное явление можно наблюдать и у других компьютеров.
11 1985
Со всех концов света продолжает поступать так много результатов расчетов по программе PINT, что я вынужден опубликовать новую среднюю величину. При подсчете были учтены все оценки числа пи, вычисленные по 1000 выстрелам и полученные с тех пор, как было подсчитано значение, приведенное в сентябрьском номере журнала. В течение двухмесячного периода накопления данных я наблюдал, как среднее значение постепенно уменьшалось, достигнув в какой-то момент 3.129. Положение несколько улучшилось, когда прибыла почта из Европы и Азии, и среднее значение снова начало подниматься. Хочу выразить особую признательность многочисленным участникам, которые читают издание нашего журнала на немецком языке (Spectrum der Wissenschaft). Благодаря им округленное среднее значение на сегодняшний день оказалось правильным с точностью до двух знаков после запятой. Всего было получено 126 писем, удовлетворяющих поставленным требованиям, и теперь среднее значение числа пи равно 3.137.
12 1985
Более двадцати различных мнемонических правил для запоминания последовательности цифр числа пи были присланы читателями в сентябре. Как и следовало ожидать, большинство мнемоник было предложено сразу несколькими читателями. Мне очень по-нравились два продолжения мнемоники, предложенной в статье "Путешествие с роботами в Роботрополе и овладение навыками конструирования электронных микросхем" (см. "В мире науки", 1985, #9), а также несколько старых, почти забытых мнемоник, с которых смахнули пыль и показали новому поколению читателей. Завершают этот парад произведения "международного класса", написанные на французском, немецком и греческом языках.
Победителем в категории правил, продолжающих уже предложенную фразу, следует признать П.Брайяма из Брайтона (шт.Массачусетс): "How I wish I could enumerate pi easily, since all these (censored) mnemonics prevent recalling any of pi's sequence more simply" [Здесь и далее предложенные читателями мнемонические правила даются без перевода, поскольку в адекватных фразах на русском языке число букв в словах не будет соответствовать последовательности цифр числа пи.- Прим. ред.].
Победителем конкурса на самую длинную мнемонику стал Дж.Джанг из Темпла (шт.Аризона). Правило Джанга позволяет запомнить 110 знаков числа пи. Я приведу здесь лишь первые 14 слов: "How I wish I could enumerate pi easily which men known skillful calculate forever..."
Множество читателей, включая Л.Полинга, прислали одну или несколько старых шуток, подобных, например, следующим:
See, I have a rhyme assisting
my feeble brain, in tasks sometime resisting.
Или:
Now I - even 1 - would celebrate in rhymes inept
the great immortal Syracusan rivaled nevermore,
who by his wondrous lore untold us before,
made the way straight how to circles mensurate.
В нашей коллекции есть еще несколько странных, но забавных мнемоник. М.Стюбен из Анандейла (шт.Виргиния) прислал, например, такое стихотворение:
How I wish I could recollect pi.
Eurika! cried the great inventor.
Christmass pudding, Christmass pie
is the problem's very center.
Клайв Дж.Гримстоун из Лондона, Англия, располагает мнемоникой, охватывающей 100 десятичных знаков, но не включающей первые 3. Вот как выглядит начало стихотворения:
I know a maths professor.
Не always weeps and sighs
whenever polyhedra
capsize...
Читатели с хорошей музыкальной памятью могут запомнить число пи, напевая или насвистывая мелодию, придуманную Р.Бруксом из Бетесда (шт.Мэриленд). Чтобы не прибегать к музыкальной записи, я лишь скажу, что каждому разряду числа зг Брукс ставит в соответствие определенную ноту. Нота "ми" соответствует единице, "фа" - двойке и т.д. Рядом с каждой нотой в скобках записывается ее длительность (она не имеет отношения к разрядам числа пи и необходима только для мелодии.- Перев.). За единицу длительности принята 1/16. В этих обозначениях мелодия, соответствующая разрядам числа пи, имеет следующий вид:
3(1) 1(1) 4(1) 1(1) 5(5) 9(1) 2(1) 6(1) 5(6) 3(1) 5(1) 8(5) 9(1) 7(1) 9(1) 3(6) 2(1) 3(1) 8(1) 4(1) 6(4) 2(2) 6(6) 4(2) 3(12)
Счет идет на 4 четверти, и первый такт кончается между четвертой и пятой нотами.
Трое читателей, включая Дж.Сиэтла (шт.Вашингтон), прислали следующее стихотворение на французском языке:

А вот стихотворение Хенрика на немецком языке:

Конечно, греки в лице Архимеда сказали первое слово о числе пи. Им же, по мнению Л.Джаковидеса из Бирмингема (шт.Мичиган), должно принадлежать и последнее слово:

(Всемогущие боги играют в геометрию, чтобы выразить длину окружности через ее диаметр).

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
7 1985
ПОСТРОЕНИЕ ОДНОМЕРНЫХ КОМПЬЮТЕРОВ ПОМОГАЕТ ГЛУБЖЕ ПОНЯТЬ НЕКОТОРЫЕ СЛОЖНЫЕ ЯВЛЕНИЯ
А.К.ДЬЮДНИ
СЕЙЧАС, когда нас повсюду окружают компьютеры, сделанные человеком, уместно задать вопрос: а нет ли в мире, в котором мы живем, компьютеров, сотворенных самой природой? Созданные из воды, ветра и дерева (не говоря о всех других), зги вычислительные машины могут булькать, вздыхать или тихо расти, и мы даже не подозреваем, что это есть проявление сложных интенсивных вычислительных процессов, которые трудно интерпретировать в привычных для нас понятиях. Конечно, эти природные вычислительные системы не проводят расчетов в обычном понимании данного слова, однако в самой структуре таких систем заложена скрытая, или латентная, возможность делать вычисления.
Выразителем этой точки зрения является Стивен Уолфрэм, физик-теоретик из Принстонского института перспективных исследований. Уолфрэм отмечает, что турбулентное течение жидкости или развитие растения представляют собой совокупность элементарных процессов, взаимодействие которых приводит к явлениям, настолько сложным, что мы не можем описать их математически. Эта особенность природных систем следует из их способности хранить, передавать и обрабатывать информацию, другими словами, из способности вычислять. В ноябрьском номере нашего журнала за прошлый год была помешена статья Уолфрэма, в которой автор говорит о применении клеточных автоматов для изучения способностей природных вычислительных систем. Он предлагает найти клеточный автомат, который мог бы вычислять и в то же время моделировал бы ту или иную природную систему. Свои поиски Уолфрэм сосредоточил на простейшей разновидности клеточных автоматов, а именно на устройствах, имеющих только одно измерение.
Такие автоматы состоят из простых элементов; их комбинация создает сложные структуры, в которых происходят специфические процессы. Уолфрэм предполагает, что среди подобных автоматов скрываются и настоящие вычислительные машины, огромные линейные массивы клеток, мгновенно переключающиеся из одного состояния в другое и выполняющие любые вычисления, на которые способен трехмерный компьютер. Занимаясь поисками среди мириадов одномерных клеточных автоматов, Уолфрэм не станет пренебрегать помощью, которую могут оказать ему в этом смелом и трудном исследовании любители. О некоторых результатах поиска природных компьютеров я и хочу рассказать в этой статье.
Вначале давайте совершим короткое путешествие из трехмерного пространства в невероятно тесный мир, ограниченный одним измерением. Хорошей отправной точкой для нашего путешествия может служить трехмерный компьютер, ставший уже непременной принадлежностью предприятий, институтов, учреждений и даже квартир. Он представляет собой сложную комбинацию простых элементов. Мы говорим здесь не об устройствах ввода-вывода информации, а о самом сердце машины, крошечном кремниевом кристалле, содержащем тысячи логических вентилей, ячеек памяти, регистров и других компонентов. Все они соединяются между собой очень тонкими проводниками. Хотя электронные схемы прилегают к поверхности кристалла, это не означает, что компьютер представляет собой двумерное устройство. Во-первых, когда два проводника пересекаются, один из них должен пройти под другим так, чтобы они не касались. Во-вторых, кремниевая подложка схемы играет важную роль в реализации функций каждого логического элемента.
Двумерные компьютеры можно встретить лишь в пространствах, имеющих два измерения, таких, например, как "планимир", населенный племенем ардеанов (см. библиографию на с.116) [Существа, населяющие двумерную вселенную, описанию которой посвящена книга А.К.Дьюдни "Планимнр: контакте двумерным миром с помощью компьютера". Рецензия на эту книгу опубликована в журнале "В мире науки", 1984, #11, с.137.- Прим. ред.]. Ардеане, очевидно, смогли создать двумерную вычислительную машину из однотипных логических элементов, называемых вентилями И-НЕ. Выходной сигнал такого вентиля равен 1, если хоть один входной сигнал равен 0. При помощи таких вентилей можно не только построить компьютер, но и решить каверзную задачу о пересекающихся соединениях. Ардеане изобрели специальную плоскую схему из 12 вентилей И-НЕ, обладающую следующим свойством: если два сигнала поступают на вход в последовательности ab, то на выходе они появляются в порядке ba (см. рисунок внизу). Таким образом, два сигнала могут пересекаться, не мешая друг другу, даже если для физических линий такое соединение невозможно. Отметим в то же время, что поставленную задачу о пересечении сигналов можно решить с помощью не 12 вентилей, а с меньшим их числом, и ардеане будут благодарны читателям, которые смогут построить более простую схему из вентилей И-НЕ, пропускающую пересекающиеся сигналы.

Как сигналы могут пересекаться в двумерном компьютере
Существует также дискретное двумерное пространство под названием "Жизнь" - игра, изобретенная Джоном X. Конвеем, известным ученым, математиком из Кембриджского университета. Читатели, наверное, помнят его интересные задачи в статьях Мартина Гарднера, публиковавшихся ранее в рубрике "Математические игры". В статье, опубликованной в журнале "В мире науки" #12 за 1983г., Б.Хэйес описал, каким образом можно реализовать эту игру в виде несложной программы для вычислительной машины. Пространство "Жизни" представляет собой бесконечную плоскую решетку квадратных ячеек-клеток, состояние которых определяется состоянием соседних клеток. Время в этой игре также дискретно, и в промежутках между двумя тактовыми сигналами космических часов каждая клетка либо жива, либо мертва в зависимости от следующих условий:
- если клетка мертва в момент времени t, она оживает в момент t+1 тогда и только тогда, когда трое из ее восьми соседей были живыми в момент t;
- если клетка была жива в момент времени t, она погибает в момент t+1 тогда и только тогда, когда меньше чем две или больше чем три соседние клетки были живы в момент t.
Согласно этой системе правил, действующих во всем пространстве игры "Жизнь", исходная конфигурация живых клеток может бесконечно расти, войти в бесконечно повторяющийся цикл изменений или полностью погибнуть. После более десяти лет экспериментирования энтузиасты игры пришли к выводу, что она значительно сложнее, чем казалось в первое время.
Оказалось, например, что в клеточном пространстве "Жизни" можно построить вычислительные машины. Это свойство игры проявлялось постепенно, шаг за шагом, в течение нескольких лет. В 1969г., вскоре после того как Конвей изобрел игру, он открыл небольшое устойчивое образование клеток, которое назвал планером. Это образование появляется в своей первоначальной форме через каждые четыре поколения, переместившись на одну клетку по диагонали. На дисплее компьютера, выполняющего быстродействующую программу моделирования "Жизни", планер выглядит маленьким фантастическим существом, которое виляет хвостом, проползая по экрану. Оно перемещается со скоростью, равной четверти скорости света (соответствующей клеточному миру).
Когда был открыт планер, никто сразу не догадался, что по существу он представлял собой средство передачи данных для двумерного компьютера, работающего в пространстве "Жизни": вместо электронных импульсов здесь можно использовать планеры!
Следующий шаг в методологию построения двумерных компьютеров сделал Р.Госпер-младший, когда в 1970г. он вместе со своими коллегами открыл "катапульту", стреляющую планерами (см. рисунок вверху). В то время, будучи студентом Массачусетского технологического института, Госпер хотел получить приз в 50долл., учрежденный Гарднером за доказательство существования такой исходной конфигурации, которая растет неограниченно во времени и пространстве. Через кажлые 30 тактов катапульта Госпера выбрасывала новый планер. Вместе с выпущенными планерами катапульта представляла собой неограниченно растущую конфигурацию живых клеток.

Катапульта Р.Госпера в действии
Помимо Госпера в МТИ были и другие студенты, увлекавшиеся в свободное время игрой "Жизнь". Один из них - М.Билер, которого особенно интересовала аналогия между этой игрой и физикой элементарных частиц. Билер направлял пучок планеров на различные мишени и тщательно регистрировал результаты - иногда "холостые", а иногда и очень эффектные столкновения. Он пробовал даже направлять планеры друг на друга при различных условиях. Его настойчивость была вознаграждена: несколько раз он наблюдал случаи, имевшие практическую пользу.
Одним из таких случаев можно считать взаимное уничтожение планеров при их столкновении. Этот факт открывал путь к построению еше одной компоненты компьютера - логического вентиля. Простейшим вентилем является схема, осуществляющая логическую операцию отрицания НЕ. Вентиль НЕ меняет входной сигнал на противоположный: 0 на входе превращается в 1 на выходе, и наоборот. В пространстве игры "Жизнь" вентиль НЕ строится следующим образом. Пусть катапульта выпускает планеры в каком-то определенном направлении. Двоичные числа, являющиеся входными для вентиля НЕ, кодируются во втором потоке планеров, направленном под прямым углом к первому. Во входном потоке присутствие планера интерпретируется как 1, а отсутствие - как 0. Эти два потока пересекаются таким образом, что при встрече двух планеров последние взаимно уничтожаются. Это означает, что планер, приходящий во входном потоке, образует дырку в исходном потоке, превращая присутствующий планер (1) в отсутствующий (0). В свою очередь отсутствие планера во входном потоке позволяет планеру в исходном потоке проходить беспрепятственно. Таким образом, 0 превращается в 1. Интересно отметить, что сам вентиль, по существу, не имеет никакой структуры, если не считать катапульты, выпускающей планеры, которая является всего лишь местом, где встречаются планеры двух потоков (см. рисунок на с.110). Построение вентилей других типов, таких, как И и ИЛИ, также основано на взаимодействующих потоках планеров, однако их конструкция слишком сложна, чтобы привести здесь ее описание.

Вентиль НЕ в игре "Жизнь": когда планеры есть на входе, их нет на выходе
Память и различные регистры строятся на взаимодействии планеров, объединенных в конфигурации из четырех ячеек, называемые блоками. Один бит информации кодируется в памяти позицией блока. Блок может передвигаться вперед и назад также при помощи планеров. Двух планеров, движущихся в специально подобранном направлении, оказывается достаточно, чтобы после столкновения передвинуть блок на три клетки в фиксированном направлении. Чтобы вернуть блок на прежнее место, нужно выпустить в него десять планеров, движущихся также в тщательно подобранном направлении.
Очень увлекательны и остальные этапы построения компьютера, потребовавшие от конструкторов большой изобретательности. Обо всем этом читатель сможет прочесть в прекрасной книжке, посвященной математическим играм, "Winning Ways for Your Mathematical Plays", приведенной в библиографии (см. с.116). Книга, поделена на три раздела: игры для двух человек, игры для одного человека и игры, проходящие без участия человека. Игру "Жизнь" читатель найдет в последнем разделе.
Чтобы сделать завершающий шаг в нашем путешествии к одному измерению, осталось рассмотреть лишь клеточные пространства. Трудно себе представить, каким образом ардеане смогли бы свести свой компьютер к одной-единственной прямой линии. На первый взгляд клеточное пространство выглядит почти таким же ограничительным, как прямая линия. Однако уменьшение размерности компенсируется тем, что теперь мы не ограничены каким-то одним набором правил. Напротив, нам предоставлена возможность самим определять свои собственные правила. Возникают и некоторые дополнительные компенсирующие факторы, связанные с простотой, присущей подобным линейным пространствам. Отметим также, что можно легко следить за развитием событий. Сотни поколений можно охватить одним взглядом: исходная конфигурация изображается на отрезке прямой, а вычисленные последующие поколения могут быть представлены на следующих строчках страницы или экрана дисплея. Таким образом можно построить диаграмму пространства-времени.
Одномерный клеточный автомат (ниже мы будем называть его просто автоматом) состоит из бесконечной полосы клеток, меняющих свое состояние согласно заданному набору правил. Как и в игре "Жизнь", на каждом такте космических часов клетки переходят к новому состоянию, определяемому их предыдущим состоянием, а также предыдущим состоянием их соседей. Автомат определяется заданием двух чисел k и r и набором правил для вывода следующего состояния клетки. Число k указывает, сколько состояний может иметь каждая клетка. В игре "Жизнь" таких состояний было всего два, так что k равно 2. Для рассматриваемых автоматов характерны более высокие значения k. Число r определяет размер окрестности, влияющей на вычисление следующего состояния клетки. Таким образом, следующее состояние клетки определяется ее собственным состоянием на данный момент и состояниями r ее соседей с каждой стороны. Например, если r равно 2, а k равно 3, то, согласно некоторому правилу, если окрестность данной клетки имеет вид

следующее состояние клетки, находящейся в центре, будет

Правила, определяющие данный автомат, должны решать судьбу клетки для всевозможных конфигураций состояний, наблюдающихся у клеток ее окрестности. Количество возможных наборов правил зависит от значений k и r может быть колоссальным. Например, даже при таких низких значениях k и r, которые были приведены выше, количество возможных автоматов превышает их число во вселенной.
Каждый житель может выбрать себе по душе свой собственный, отличный от других автомат. Я уже сделал свой выбор. По причинам, которые станут ясны несколько позже, мой автомат был назван "Волна". Этот автомат позволяет каждой клетке иметь три состояния. Каждая окрестность состоит из трех клеток - центральной и двух соседних по разные стороны от нее. Набор правил у "Волны" очень прост:
1. Если данная клетка находится в состоянии 0, ее следующим состоянием будет 2, если сумма состояний двух прилегающих к ней клеток больше или равна 2. В противном случае ее следующим состоянием будет 0.
2. Если клетка находится в состоянии 1, ее следующим состоянием будет 0.
3. Если клетка находится в состоянии 2, ее следующим состоянием будет 1, если одна из прилегающих к ней клеток находится в состоянии 0. В противном случае ее следующим состоянием будет 2.
Конечно, я уверен, что "Волна" не станет столь же популярной, как "Жизнь". Назначение "Волны" заключается лишь в том, чтобы проиллюстрировать некоторые наиболее интересные возможности, которыми обладают одномерные клеточные автоматы. Например, "Волна" имеет свои простые планеры и еше более простую катапульту (см. верхний рисунок).
Катапульта в одномерном автомате "Волна"
Предположим, что все клеточное пространство "Волны" находится в состоянии 0, за исключением двух прилегающих друг к другу клеток. Клетка, расположенная слева, находится в состоянии 2, а та, что справа,- в состоянии 1. У следующего поколения клеток это образование передвинется на одну клетку влево. При отсутствии возмущающих воздействий этот двуклеточный планер будет тихо и спокойно плыть в левом направлении до бесконечности. Если поменять местами исходные состояния клеток, то мы получим планер, движущийся в правом направлении. Катапульта, запускающая планеры, состоит всего лишь из одной клетки, находящейся в состоянии 2. Эта клетка проходит через цикл состояний 1, 0 и затем снова 2, запуская по два планера при каждом прохождении цикла. Интересно, сможет ли кто-нибудь из читателей построить в "Волне" катапульту, которая выпускала бы планеры все время в одном и том же направлении?
Если две такие катапульты начинают работать одновременно, то получается довольно странное явление. В результате "взрыва", вызванного столкновением, планеры уничтожают друг друга, но вместо них появляются другие планеры, движущиеся в противоположных направлениях. Если катапульты находились на расстоянии, на котором уменьшается четное число клеток, то количество вторичных планеров оказывается равным этому числу. В противном случае (когда на данном расстоянии уменьшается нечетное число клеток) в середине остается одна катапульта, выпускающая планеры бесконечным потоком.
"Волна" - это лишь один из возможных одномерных автоматов. Что же можно сказать об остальных? Количество возможных наборов правил значительно сокращается, если принять предложенное Уолфрэмом ограничение и рассматривать только те правила, которые он назвал тоталистическимн. Это означает, что следующее состояние данной клетки определяется только суммой состояний клеток, образующих окрестность {включая состояние данной клетки). Возможное значение суммы варьирует в пределах от 0 до m, где m - наибольшее возможное состояние, умноженное на число клеток, составляющих окрестность. Для того чтобы полностью определить автомат, нужно указать, каким образом значение суммы состояний клеток, образующих окрестность, определяет следующее состояние центральной клетки.
Очень интересный автомат получается, например, при тоталистнческнх правилах, приведенных в следующей таблице:

Значения k и r здесь равны 2. Возможные значения суммы состояний клеток, входящих в пятиклеточную окрестность, варьируют в пределах от 0 до 5. Уолфрэм называет этот набор правил "числом 20", потому что 6 возможных последующих состояний в таблице представляют число 20, записанное в двоичной системе счисления.
Существуют 64 способа, чтобы заполнить вторую строку таблицы. Каждый из этих способов приводит к построению какого-то одного, отличного от других автомата. Уолфрэм исследовал все 64 варианта. Разумеется, без помощи компьютера в таких исследованиях не обойтись. Чтобы определить поведение заданного автомата, Уолфрэм формирует исходную конфигурацию из ста клеток, состояния которых выбираются случайным образом, и следит за тем, как автомат начинает изменять картину. Для того чтобы исключить из рассмотрения огромные массивы нулей с каждой стороны от исходной конфигурации, Уолфрэм присоединяет левую часть структуры клеток к правой. Таким образом, клеточное пространство превращается в круг, а временная диаграмма изменений, претерпеваемых клетками, образует цилиндр. Однако результат остается тем же, как если бы исходная конфигурация клеток повторялась до бесконечности в обоих направлениях от начальной структуры. Во всяком случае, влияние автоматов на подобные случайные структуры клеток, оказывается удивительно однородным. Он может принадлежать к одному из четырех сравнительно широких классов, выделенных Уолфрэмом:
Класс 1. После конечного количества смены поколений исходная конфигурация-образ вырождается в единое однородное состояние по всему пространству.
Класс 2. Из исходной конфигурации возникают постоянные или периодические подобразы.
Класс 3. Не возникает никакой видимой структуры. Временные диаграммы выглядят хаотичными.
Класс 4. Из исходной конфигурации-образа возникают сложные локальные подобразы, среди которых встречаются долгоживущие.
Из 64 автоматов, у которых k и r равны 2, 25% относится к первому классу, 16% - ко второму, 53% - к третьему и только 6% - к четвертому классу. Уолфрэм подозревает, что компьютеры можно найти в четвертом классе. Например, автомат с кодовым числом 20 принадлежит именно четвертому классу.
Как бы обнадеживая Уолфрэма в его поисках, автомат с кодом 20 проявил способность порождать планеры. Их коды - 10111011 и 1001111011. Оба планера движутся в правом направлении. Тоталистические правила всегда симметричны - чтобы получить планеры, движущиеся влево, коды конфигураций, приведенные выше, следует переписать в обратном порядке. Существует ли в пространстве автомата-20 катапульта для запуска таких планеров? По мнению Уолфрэма, существует. Однако есть еще одно интересное пространство, где ему до сих пор не удалось найти даже планер! Это пространство с кодовым номером 792. Если записать это число в троичной системе счисления, то мы получим набор правил для автомата с тремя состояниями:

При поиске планеров и катапульт полезным может оказаться специальное пособие. По моему совету Уолфрэм написал такое пособие. В нем представлен алгоритм, отыскивающий то, что Уолфрэм называет "устойчивыми структурами".
Поиск планеров и катапульт сконцентрирован на тех автоматах, которые, по мнению исследователей, потенциально обладают способностью к универсальным вычислениям. Другими словами, эти автоматы могут выполнять функции универсальной вычислительной машины. Кроме рассмотренных автоматов с кодовыми номерами 20 и 792 существует также автомат с двумя состояниями (r = 3, кодовый номер 88), для которого катапульта была найдена раньше.
Найти ее удалось Дж.Парку, когда он был еще студентом Принстонского университета. Чтобы увидеть катапульту Парка в действии, нужно написать простую программу для представления на экране дисплея поколений клеток, а также для вычисления следующей конфигурации по предыдущей. Написать такую программу, реализующую автомат-88, в общем несложно. Когда программа будет готова, введите исходную конфигурацию-образ 1111111111011 и понаблюдайте, как она начнет расширяться и сжиматься. Катапульта выпускает планеры в обоих направлениях через каждые 238 поколений.

Фотография одномерной катапульты Дж.Парка

Катапульта Дж.Парка, запускающая планеры направо и налево
Однако, вместо того чтобы моделировать какой-то один конкретный автомат, мы советуем читателям составить программу, которая принимала бы произвольные тоталистические правила в качестве входных данных. Это легко сделать как для фиксированных, так и для варьируемых значений k и r, т.е. когда k и r являются параметрами. При составлении программы следует воспользоваться специальным массивом table для правил, а также двумя линейными массивами oldcells и newcells соответственно для хранения старой и новой конфигураций клеток, которые участвуют в вычислениях, выполняемых в данный момент. Размер массивов может быть сколь угодно большим, однако следует иметь в виду, что на экране дисплея (в зависимости от его типа) может изображаться лишь какая-то ограниченная часть этих массивов. Выведите на экран возможно большую среднюю часть массива newcells и выполните следующие операции: перепишите содержимое массива newcells в массив oldcells; просмотрите в цикле массив oldcells, для каждого i-го элемента массива сложите значения элементов от i-r до i+r; найдите значение полученной суммы в массиве table и запишите соответствующее данной сумме значение состояния на место i-го элемента массива newcells. Затем снова войдите в основной цикл, начинающийся с вывода картинки на экран, и повторите описанные выше этапы. На экране дисплея каждая новая картинка может появляться на новой строке или все время на одной и той же. В первом случае получается пространственно-временная диаграмма, во втором - нечто наподобие мультфильма в одном измерении.
Как уже отмечалось, автомат обладает способностью к универсальным вычислениям, если по мере смены поколений клеток некая исходная структура оказывается способной выполнять функции компьютера. Часть исходной структуры представляет собой входные данные, и соответственно другая ее часть, наблюдающаяся в некоторый более поздний момент, - выходные данные. Неужели можно действительно построить компьютер при помощи планеров, катапульт и других "устройств" на клеточной основе? Уолфрэм считает, что можно. У одного из исследуемых в настоящее время автоматов обнаружились планеры, проходящие через определенные стабильные подобразы. В связи с этим возникает надежда, что передаче информации в одномерном компьютере не будут мешать компоненты, не имеющие непосредственною отношения к этой информации. Помимо Уолфрэма одномерными автоматами занимаются и ряд других исследователей. Один из них - К.Сгейглитц из Прннстонского университета. Он обнаружил планеры, свойства которых подобны свойствам солитонов. Планеры подобного рода могут беспрепятственно проходить один через другой!
Удастся ли нам в конце концов найти устойчивые структуры, способные пересылать, хранить и обрабатывать информацию в одномерном клет очном пространстве? Может быть, и нет. Может оказаться, что вычислениям в одном измерении присуще какое-то особое свойство, которое заставит нас изменить сложившееся представление о вычислительном процессе.
Не ограничивая свою фантазию, Уолфрэм уже думает о том, как одномерные автоматы помогут нам понять поведение автоматов вообще и как это понимание автоматов в свою очередь позволит нам проникнуть в сущность природных процессов. Предположим, что удалось найти одномерный автомат, хорошо моделирующий некий природный процесс, например турбулентное течение жидкости или газа, движение частиц, находящихся в силовом поле, или даже биологический процесс, такой, как рост. Предположим далее, что найденный автомат обладает способностью к универсальным вычислениям. Другими словами, в его пространстве не только содержится явная вычисляющая структура, но и некий скрытый, неявно заложенный в нем компьютер - любая попытка предсказать поведение автомата будет, по определению, равносильна предсказанию поведения универсальной вычислительной машины. Вообще говоря, это можно сделать лишь при помощи другого устройства того же рода, т.е. другой вычислительной машины. Это означает, что не существует никакого "короткого пути", позволяющего предсказать поведение соответствующей природной системы. Ее процессы будут несводимыми в вычислительном смысле, т.е. механизм, предсказывающий поведение системы (будь то формула или компьютер), должен будет моделировать рассматриваемую систему более или менее непосредственно.
Вернемся теперь к "Волне". Планеры исходной популяции движутся в произвольных направлениях, то и дело натыкаясь друг на друга. Иногда в результате столкновения появляется катапульта, порождающая новые планеры, иногда же столкновения не производят никакого эффекта. Это пространство напоминает мне миниатюрную одномерную вселенную, наполненную элементарными частицами, которые движутся как микроскопические волны. Таким образом, я как бы повернул поиск Уолфрэма в обратном направлении. Отправляясь от одномерного автомата, поведение которого в каком-то смысле напоминает систему частиц (правда, довольно своеобразных), я уверовал в то, что "Волна" обладает способностью к универсальным вычислениям. Поскольку это мой личный автомат, я могу оказаться единственным человеком, который в это верит.
БИБЛИОГРАФИЯ
WINNING WAYS FOR YOUR MATHEMATICAL PLAYS. ELWYN R. BERLEKAMP, JOHN H. CONWAY AND RICHARD K. GUY. Academic Press. 1982.
THE PLANIVERSE. A.K.DEWDNEY. Poseidon Press, 1984.
УОЛФРЭМ С. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ НАУЧНЫХ ИССЛЕДОВАНИЙ.- "В мире науки", 1984, #11, с.98-100. (Этот номер я выкладывал - ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.).
.- G.).
ОТКЛИКИ
10 1985
ДВУМЕРНЫЕ существа, населяющие планету Арда, выражают глубокую признательность многочисленным читателям, попытавшимся усовершенствовать логическую схему с пересечением сигналов, описанную в июльском 1985г. номере журнала "В мире науки". Эта схема состоит из 12 вентилей И-НЕ с двумя входами. Я обратился к читателям с просьбой найти минимальное количество вентилей И-НЕ (и только вентилей И-НЕ), необходимых для построения такой схемы. Большинство представленных решений содержит 10 вентилей, что, безусловно, является некоторым улучшением, однако трем читателям удалось построить схему пересечения, состоящую из восьми вентилей (см. рисунок на с 86).
Схема пересечения сигналов из 8 вентилей И-НЕ
В схеме, состоящей из восьми вентилей, есть один вентиль И-НЕ с тремя входами и два вентиля И-НЕ с одним-единственным входом. Последние действуют как инверторы, преобразующие 0 на входе в 1 на выходе и наоборот. Схему с восемью вентилями удалось построить Э.Карлсону из Кембриджа (шт.Массачусетс), Д.Кеппу из Сан-Хосе (шт.Калифорния) и С.Салливану из Бевертона (шт.Орегон). Я сообщил их имена вместе с предложенными ими вариантами усовершенствованной схемы пересечения моим друзьям ардеанам. Хотите верьте, хотите нет, но точно такая же схема пересечения из восьми вентилей была запатентована в США 26 апреля 1966г. Номер патента 3248573. Р.Фрэнк, консультант по вычислительной технике из Бирмингема (шт.Мичиган), сообщил, что этот патент принадлежит Л.Спэндорферу из Челтенхема (шт.Пенсильвания), А.Тонику из Дрешера (шт.Пенсильвания) и Ш.Ивену из Кембриджа (шт.Массачусетс).
Естественно, возникает вопрос, применяется ли эта схема в каком-либо современном электронном устройстве? Возникает также вопрос о том, существует ли схема пересечения сигналов, содержащая еще меньшее число вентилей И-НЕ. По всей видимости, нет.
В письме У.Джонсона из Лонг-Бича (шт.Калифорния) описаны разнообразные плоские схемы, построенные из вентилей различных типов. Оказывается, можно построить не только двумерные схемы пересечения сигналов, но также и плоские триггеры. Напомним, что на триггерах основаны элементы памяти двумерного компьютера.
Одномерные компьютеры в виде клеточных автоматов изучались С.Уолфрэмом из Принстонского научно-исследовательского института. Пока еще слишком рано говорить о том, какой вклад в эту науку внесли читатели, ознакомившись с брошюрой Уолфрэма, в которой описаны катапульты, стреляющие планерами, однако письма читателей уже поступают, и можно подвести некоторые предварительные итоги. Во-первых, из-за ошибки, закравшейся в статью, посвященную одномерным автоматам, несколько читателей занялись исследованием автомата с кодовым номером 792. Уолфрэм и я имели в виду автомат 357. Во-вторых, я сожалею о том, что не упомянул об одномерном автомате, обладающем свойством универсальных вычислений. У меня была мысль описать такой автомат, впервые построенный А.Смитом в 1970г. В то время Смит был аспирантом Станфордского университета. Но я боялся, что описание универсального одномерного автомата Смита чрезмерно усложнит статью, так как автомат обладает 18 состояниями {k=18) и окрестностью из трех клеток (r=1).
А.Рубин из Лос-Анджелеса внес разумное предложение определить скорость света (скорость распространения сигнала) в произвольном линейном автомате. Предложение Рубина устраняет дефект в определении, принятом ранее, согласно которому скорость света полагалась равной одной клетке в единицу времени. В старом определении не учитывалась возможность, что не все автоматы способны достигать такой скорости. Согласно новому определению, "скорость света - это максимальная скорость распространения любого импульса (скажем, вправо)". Передний фронт распространения импульса определяется условием, что справа от него могут быть только нули. Далее Рубин доказывает, что скорость света для автомата с кодовым номером 792 равна 1/3.
В июльском 1985г. номере журнала "В мире науки" я также обратился к читателям с вопросом о том, обладает ли одномерный автомат "Волна" односторонней катапультой. Планеры, запущенные такой катапультой, должны двигаться вправо до бесконечности, и ни один из них никогда не должен двигаться влево. У.Б.Липп из Милфорда (шт.Коннектикут) привел простой и изящный аргумент против существования такой катапульты. "Рассмотрим конфигурацию,- пишет он,- никогда не имеющую ненулевых значений слева от некоторого блока, помеченного как 0. Заметим, что крайним слева ненулевым значением конфигурации должна всегда быть 1. Если бы оно было равно 2, то эта двойка начала бы двигаться влево до бесконечности, что привело бы к противоречию с предположением, согласно которому слева от блока 0 нет никаких ненулевых значений. Однако крайняя слева 1 на следующем цикле должна превратиться в 0, в результате чего левая граница конфигурации должна переместиться по меньшей мере на один блок вправо". Таким образом, мы приходим к выводу, что либо возникает планер, движущийся влево, либо катапульта разрушается наступающими слева нулями.
Другие читатели попытались доказать, что автомат "Волна" не обладает способностью универсальных вычислений. Для некоторых автоматов можно доказать достаточное условие, а именно что задача остановки является решаемой. "Волна" останавливается, когда во всех ее клетках нули, однако условия остановки для универсальной вычислительной машины, которую автомат может в себе заключить, вообще говоря, могут оказаться совершенно отличными.
Несколько читателей попытались сконструировать одномерный автомат, способный проводить универсальные вычисления. Среди них Ф.Адамс из Ист-Харфорда(шт.Коннектикут), Дж.Амстердам из Кембриджа (шт.Массачусетс), К.Игуса из Брандейского университета и К.Кейди из Ист-Пеории (шт.Иллинойс). Все присланные конструкции сравнительно несложны и на вид правдоподобны, однако Кейди, не удовлетворившись одномерным автоматом, предложил автомат нулевой размерности. Он должен состоять из одной-единственной клетки, и поэтому логично назвать эту клетку точечным автоматом. Читатели с теоретическими наклонностями, возможно, испытают удовольствие, размышляя о том, обладает ли точечный автомат способностью к универсальным вычислениям. Возможен ли такой автомат?
А.Смит опубликовал доказательство существования одномерного автомата, обладающего способностью к универсальным вычислениям, в 1971г. в журнале "ACM" ("Journal of the Association for Computing Machinery"). После такого многообещающего начала можно было подумать, что карьера Смита будет продолжена в каком-нибудь известном академическом центре. Однако талант Смита расцвел совершенно в другой области - в настоящее время он является директором лаборатории машинной графики в кинематографической фирме Lucasfilm, Ltd. в Сан-Рафаэле (шт.Калифорния). В одной из своих будущих статей я надеюсь рассказать вам о некоторых поразительных кинематографических эффектах, полученных в лаборатории фирмы Lucasfilm.
ПОСТРОЕНИЕ ОДНОМЕРНЫХ КОМПЬЮТЕРОВ ПОМОГАЕТ ГЛУБЖЕ ПОНЯТЬ НЕКОТОРЫЕ СЛОЖНЫЕ ЯВЛЕНИЯ
А.К.ДЬЮДНИ
СЕЙЧАС, когда нас повсюду окружают компьютеры, сделанные человеком, уместно задать вопрос: а нет ли в мире, в котором мы живем, компьютеров, сотворенных самой природой? Созданные из воды, ветра и дерева (не говоря о всех других), зги вычислительные машины могут булькать, вздыхать или тихо расти, и мы даже не подозреваем, что это есть проявление сложных интенсивных вычислительных процессов, которые трудно интерпретировать в привычных для нас понятиях. Конечно, эти природные вычислительные системы не проводят расчетов в обычном понимании данного слова, однако в самой структуре таких систем заложена скрытая, или латентная, возможность делать вычисления.
Выразителем этой точки зрения является Стивен Уолфрэм, физик-теоретик из Принстонского института перспективных исследований. Уолфрэм отмечает, что турбулентное течение жидкости или развитие растения представляют собой совокупность элементарных процессов, взаимодействие которых приводит к явлениям, настолько сложным, что мы не можем описать их математически. Эта особенность природных систем следует из их способности хранить, передавать и обрабатывать информацию, другими словами, из способности вычислять. В ноябрьском номере нашего журнала за прошлый год была помешена статья Уолфрэма, в которой автор говорит о применении клеточных автоматов для изучения способностей природных вычислительных систем. Он предлагает найти клеточный автомат, который мог бы вычислять и в то же время моделировал бы ту или иную природную систему. Свои поиски Уолфрэм сосредоточил на простейшей разновидности клеточных автоматов, а именно на устройствах, имеющих только одно измерение.
Такие автоматы состоят из простых элементов; их комбинация создает сложные структуры, в которых происходят специфические процессы. Уолфрэм предполагает, что среди подобных автоматов скрываются и настоящие вычислительные машины, огромные линейные массивы клеток, мгновенно переключающиеся из одного состояния в другое и выполняющие любые вычисления, на которые способен трехмерный компьютер. Занимаясь поисками среди мириадов одномерных клеточных автоматов, Уолфрэм не станет пренебрегать помощью, которую могут оказать ему в этом смелом и трудном исследовании любители. О некоторых результатах поиска природных компьютеров я и хочу рассказать в этой статье.
Вначале давайте совершим короткое путешествие из трехмерного пространства в невероятно тесный мир, ограниченный одним измерением. Хорошей отправной точкой для нашего путешествия может служить трехмерный компьютер, ставший уже непременной принадлежностью предприятий, институтов, учреждений и даже квартир. Он представляет собой сложную комбинацию простых элементов. Мы говорим здесь не об устройствах ввода-вывода информации, а о самом сердце машины, крошечном кремниевом кристалле, содержащем тысячи логических вентилей, ячеек памяти, регистров и других компонентов. Все они соединяются между собой очень тонкими проводниками. Хотя электронные схемы прилегают к поверхности кристалла, это не означает, что компьютер представляет собой двумерное устройство. Во-первых, когда два проводника пересекаются, один из них должен пройти под другим так, чтобы они не касались. Во-вторых, кремниевая подложка схемы играет важную роль в реализации функций каждого логического элемента.
Двумерные компьютеры можно встретить лишь в пространствах, имеющих два измерения, таких, например, как "планимир", населенный племенем ардеанов (см. библиографию на с.116) [Существа, населяющие двумерную вселенную, описанию которой посвящена книга А.К.Дьюдни "Планимнр: контакте двумерным миром с помощью компьютера". Рецензия на эту книгу опубликована в журнале "В мире науки", 1984, #11, с.137.- Прим. ред.]. Ардеане, очевидно, смогли создать двумерную вычислительную машину из однотипных логических элементов, называемых вентилями И-НЕ. Выходной сигнал такого вентиля равен 1, если хоть один входной сигнал равен 0. При помощи таких вентилей можно не только построить компьютер, но и решить каверзную задачу о пересекающихся соединениях. Ардеане изобрели специальную плоскую схему из 12 вентилей И-НЕ, обладающую следующим свойством: если два сигнала поступают на вход в последовательности ab, то на выходе они появляются в порядке ba (см. рисунок внизу). Таким образом, два сигнала могут пересекаться, не мешая друг другу, даже если для физических линий такое соединение невозможно. Отметим в то же время, что поставленную задачу о пересечении сигналов можно решить с помощью не 12 вентилей, а с меньшим их числом, и ардеане будут благодарны читателям, которые смогут построить более простую схему из вентилей И-НЕ, пропускающую пересекающиеся сигналы.

Как сигналы могут пересекаться в двумерном компьютере
Существует также дискретное двумерное пространство под названием "Жизнь" - игра, изобретенная Джоном X. Конвеем, известным ученым, математиком из Кембриджского университета. Читатели, наверное, помнят его интересные задачи в статьях Мартина Гарднера, публиковавшихся ранее в рубрике "Математические игры". В статье, опубликованной в журнале "В мире науки" #12 за 1983г., Б.Хэйес описал, каким образом можно реализовать эту игру в виде несложной программы для вычислительной машины. Пространство "Жизни" представляет собой бесконечную плоскую решетку квадратных ячеек-клеток, состояние которых определяется состоянием соседних клеток. Время в этой игре также дискретно, и в промежутках между двумя тактовыми сигналами космических часов каждая клетка либо жива, либо мертва в зависимости от следующих условий:
- если клетка мертва в момент времени t, она оживает в момент t+1 тогда и только тогда, когда трое из ее восьми соседей были живыми в момент t;
- если клетка была жива в момент времени t, она погибает в момент t+1 тогда и только тогда, когда меньше чем две или больше чем три соседние клетки были живы в момент t.
Согласно этой системе правил, действующих во всем пространстве игры "Жизнь", исходная конфигурация живых клеток может бесконечно расти, войти в бесконечно повторяющийся цикл изменений или полностью погибнуть. После более десяти лет экспериментирования энтузиасты игры пришли к выводу, что она значительно сложнее, чем казалось в первое время.
Оказалось, например, что в клеточном пространстве "Жизни" можно построить вычислительные машины. Это свойство игры проявлялось постепенно, шаг за шагом, в течение нескольких лет. В 1969г., вскоре после того как Конвей изобрел игру, он открыл небольшое устойчивое образование клеток, которое назвал планером. Это образование появляется в своей первоначальной форме через каждые четыре поколения, переместившись на одну клетку по диагонали. На дисплее компьютера, выполняющего быстродействующую программу моделирования "Жизни", планер выглядит маленьким фантастическим существом, которое виляет хвостом, проползая по экрану. Оно перемещается со скоростью, равной четверти скорости света (соответствующей клеточному миру).
Когда был открыт планер, никто сразу не догадался, что по существу он представлял собой средство передачи данных для двумерного компьютера, работающего в пространстве "Жизни": вместо электронных импульсов здесь можно использовать планеры!
Следующий шаг в методологию построения двумерных компьютеров сделал Р.Госпер-младший, когда в 1970г. он вместе со своими коллегами открыл "катапульту", стреляющую планерами (см. рисунок вверху). В то время, будучи студентом Массачусетского технологического института, Госпер хотел получить приз в 50долл., учрежденный Гарднером за доказательство существования такой исходной конфигурации, которая растет неограниченно во времени и пространстве. Через кажлые 30 тактов катапульта Госпера выбрасывала новый планер. Вместе с выпущенными планерами катапульта представляла собой неограниченно растущую конфигурацию живых клеток.

Катапульта Р.Госпера в действии
Помимо Госпера в МТИ были и другие студенты, увлекавшиеся в свободное время игрой "Жизнь". Один из них - М.Билер, которого особенно интересовала аналогия между этой игрой и физикой элементарных частиц. Билер направлял пучок планеров на различные мишени и тщательно регистрировал результаты - иногда "холостые", а иногда и очень эффектные столкновения. Он пробовал даже направлять планеры друг на друга при различных условиях. Его настойчивость была вознаграждена: несколько раз он наблюдал случаи, имевшие практическую пользу.
Одним из таких случаев можно считать взаимное уничтожение планеров при их столкновении. Этот факт открывал путь к построению еше одной компоненты компьютера - логического вентиля. Простейшим вентилем является схема, осуществляющая логическую операцию отрицания НЕ. Вентиль НЕ меняет входной сигнал на противоположный: 0 на входе превращается в 1 на выходе, и наоборот. В пространстве игры "Жизнь" вентиль НЕ строится следующим образом. Пусть катапульта выпускает планеры в каком-то определенном направлении. Двоичные числа, являющиеся входными для вентиля НЕ, кодируются во втором потоке планеров, направленном под прямым углом к первому. Во входном потоке присутствие планера интерпретируется как 1, а отсутствие - как 0. Эти два потока пересекаются таким образом, что при встрече двух планеров последние взаимно уничтожаются. Это означает, что планер, приходящий во входном потоке, образует дырку в исходном потоке, превращая присутствующий планер (1) в отсутствующий (0). В свою очередь отсутствие планера во входном потоке позволяет планеру в исходном потоке проходить беспрепятственно. Таким образом, 0 превращается в 1. Интересно отметить, что сам вентиль, по существу, не имеет никакой структуры, если не считать катапульты, выпускающей планеры, которая является всего лишь местом, где встречаются планеры двух потоков (см. рисунок на с.110). Построение вентилей других типов, таких, как И и ИЛИ, также основано на взаимодействующих потоках планеров, однако их конструкция слишком сложна, чтобы привести здесь ее описание.

Вентиль НЕ в игре "Жизнь": когда планеры есть на входе, их нет на выходе
Память и различные регистры строятся на взаимодействии планеров, объединенных в конфигурации из четырех ячеек, называемые блоками. Один бит информации кодируется в памяти позицией блока. Блок может передвигаться вперед и назад также при помощи планеров. Двух планеров, движущихся в специально подобранном направлении, оказывается достаточно, чтобы после столкновения передвинуть блок на три клетки в фиксированном направлении. Чтобы вернуть блок на прежнее место, нужно выпустить в него десять планеров, движущихся также в тщательно подобранном направлении.
Очень увлекательны и остальные этапы построения компьютера, потребовавшие от конструкторов большой изобретательности. Обо всем этом читатель сможет прочесть в прекрасной книжке, посвященной математическим играм, "Winning Ways for Your Mathematical Plays", приведенной в библиографии (см. с.116). Книга, поделена на три раздела: игры для двух человек, игры для одного человека и игры, проходящие без участия человека. Игру "Жизнь" читатель найдет в последнем разделе.
Чтобы сделать завершающий шаг в нашем путешествии к одному измерению, осталось рассмотреть лишь клеточные пространства. Трудно себе представить, каким образом ардеане смогли бы свести свой компьютер к одной-единственной прямой линии. На первый взгляд клеточное пространство выглядит почти таким же ограничительным, как прямая линия. Однако уменьшение размерности компенсируется тем, что теперь мы не ограничены каким-то одним набором правил. Напротив, нам предоставлена возможность самим определять свои собственные правила. Возникают и некоторые дополнительные компенсирующие факторы, связанные с простотой, присущей подобным линейным пространствам. Отметим также, что можно легко следить за развитием событий. Сотни поколений можно охватить одним взглядом: исходная конфигурация изображается на отрезке прямой, а вычисленные последующие поколения могут быть представлены на следующих строчках страницы или экрана дисплея. Таким образом можно построить диаграмму пространства-времени.
Одномерный клеточный автомат (ниже мы будем называть его просто автоматом) состоит из бесконечной полосы клеток, меняющих свое состояние согласно заданному набору правил. Как и в игре "Жизнь", на каждом такте космических часов клетки переходят к новому состоянию, определяемому их предыдущим состоянием, а также предыдущим состоянием их соседей. Автомат определяется заданием двух чисел k и r и набором правил для вывода следующего состояния клетки. Число k указывает, сколько состояний может иметь каждая клетка. В игре "Жизнь" таких состояний было всего два, так что k равно 2. Для рассматриваемых автоматов характерны более высокие значения k. Число r определяет размер окрестности, влияющей на вычисление следующего состояния клетки. Таким образом, следующее состояние клетки определяется ее собственным состоянием на данный момент и состояниями r ее соседей с каждой стороны. Например, если r равно 2, а k равно 3, то, согласно некоторому правилу, если окрестность данной клетки имеет вид

следующее состояние клетки, находящейся в центре, будет

Правила, определяющие данный автомат, должны решать судьбу клетки для всевозможных конфигураций состояний, наблюдающихся у клеток ее окрестности. Количество возможных наборов правил зависит от значений k и r может быть колоссальным. Например, даже при таких низких значениях k и r, которые были приведены выше, количество возможных автоматов превышает их число во вселенной.
Каждый житель может выбрать себе по душе свой собственный, отличный от других автомат. Я уже сделал свой выбор. По причинам, которые станут ясны несколько позже, мой автомат был назван "Волна". Этот автомат позволяет каждой клетке иметь три состояния. Каждая окрестность состоит из трех клеток - центральной и двух соседних по разные стороны от нее. Набор правил у "Волны" очень прост:
1. Если данная клетка находится в состоянии 0, ее следующим состоянием будет 2, если сумма состояний двух прилегающих к ней клеток больше или равна 2. В противном случае ее следующим состоянием будет 0.
2. Если клетка находится в состоянии 1, ее следующим состоянием будет 0.
3. Если клетка находится в состоянии 2, ее следующим состоянием будет 1, если одна из прилегающих к ней клеток находится в состоянии 0. В противном случае ее следующим состоянием будет 2.
Конечно, я уверен, что "Волна" не станет столь же популярной, как "Жизнь". Назначение "Волны" заключается лишь в том, чтобы проиллюстрировать некоторые наиболее интересные возможности, которыми обладают одномерные клеточные автоматы. Например, "Волна" имеет свои простые планеры и еше более простую катапульту (см. верхний рисунок).

Катапульта в одномерном автомате "Волна"
Предположим, что все клеточное пространство "Волны" находится в состоянии 0, за исключением двух прилегающих друг к другу клеток. Клетка, расположенная слева, находится в состоянии 2, а та, что справа,- в состоянии 1. У следующего поколения клеток это образование передвинется на одну клетку влево. При отсутствии возмущающих воздействий этот двуклеточный планер будет тихо и спокойно плыть в левом направлении до бесконечности. Если поменять местами исходные состояния клеток, то мы получим планер, движущийся в правом направлении. Катапульта, запускающая планеры, состоит всего лишь из одной клетки, находящейся в состоянии 2. Эта клетка проходит через цикл состояний 1, 0 и затем снова 2, запуская по два планера при каждом прохождении цикла. Интересно, сможет ли кто-нибудь из читателей построить в "Волне" катапульту, которая выпускала бы планеры все время в одном и том же направлении?
Если две такие катапульты начинают работать одновременно, то получается довольно странное явление. В результате "взрыва", вызванного столкновением, планеры уничтожают друг друга, но вместо них появляются другие планеры, движущиеся в противоположных направлениях. Если катапульты находились на расстоянии, на котором уменьшается четное число клеток, то количество вторичных планеров оказывается равным этому числу. В противном случае (когда на данном расстоянии уменьшается нечетное число клеток) в середине остается одна катапульта, выпускающая планеры бесконечным потоком.
"Волна" - это лишь один из возможных одномерных автоматов. Что же можно сказать об остальных? Количество возможных наборов правил значительно сокращается, если принять предложенное Уолфрэмом ограничение и рассматривать только те правила, которые он назвал тоталистическимн. Это означает, что следующее состояние данной клетки определяется только суммой состояний клеток, образующих окрестность {включая состояние данной клетки). Возможное значение суммы варьирует в пределах от 0 до m, где m - наибольшее возможное состояние, умноженное на число клеток, составляющих окрестность. Для того чтобы полностью определить автомат, нужно указать, каким образом значение суммы состояний клеток, образующих окрестность, определяет следующее состояние центральной клетки.
Очень интересный автомат получается, например, при тоталистнческнх правилах, приведенных в следующей таблице:

Значения k и r здесь равны 2. Возможные значения суммы состояний клеток, входящих в пятиклеточную окрестность, варьируют в пределах от 0 до 5. Уолфрэм называет этот набор правил "числом 20", потому что 6 возможных последующих состояний в таблице представляют число 20, записанное в двоичной системе счисления.
Существуют 64 способа, чтобы заполнить вторую строку таблицы. Каждый из этих способов приводит к построению какого-то одного, отличного от других автомата. Уолфрэм исследовал все 64 варианта. Разумеется, без помощи компьютера в таких исследованиях не обойтись. Чтобы определить поведение заданного автомата, Уолфрэм формирует исходную конфигурацию из ста клеток, состояния которых выбираются случайным образом, и следит за тем, как автомат начинает изменять картину. Для того чтобы исключить из рассмотрения огромные массивы нулей с каждой стороны от исходной конфигурации, Уолфрэм присоединяет левую часть структуры клеток к правой. Таким образом, клеточное пространство превращается в круг, а временная диаграмма изменений, претерпеваемых клетками, образует цилиндр. Однако результат остается тем же, как если бы исходная конфигурация клеток повторялась до бесконечности в обоих направлениях от начальной структуры. Во всяком случае, влияние автоматов на подобные случайные структуры клеток, оказывается удивительно однородным. Он может принадлежать к одному из четырех сравнительно широких классов, выделенных Уолфрэмом:
Класс 1. После конечного количества смены поколений исходная конфигурация-образ вырождается в единое однородное состояние по всему пространству.
Класс 2. Из исходной конфигурации возникают постоянные или периодические подобразы.
Класс 3. Не возникает никакой видимой структуры. Временные диаграммы выглядят хаотичными.
Класс 4. Из исходной конфигурации-образа возникают сложные локальные подобразы, среди которых встречаются долгоживущие.
Из 64 автоматов, у которых k и r равны 2, 25% относится к первому классу, 16% - ко второму, 53% - к третьему и только 6% - к четвертому классу. Уолфрэм подозревает, что компьютеры можно найти в четвертом классе. Например, автомат с кодовым числом 20 принадлежит именно четвертому классу.
Как бы обнадеживая Уолфрэма в его поисках, автомат с кодом 20 проявил способность порождать планеры. Их коды - 10111011 и 1001111011. Оба планера движутся в правом направлении. Тоталистические правила всегда симметричны - чтобы получить планеры, движущиеся влево, коды конфигураций, приведенные выше, следует переписать в обратном порядке. Существует ли в пространстве автомата-20 катапульта для запуска таких планеров? По мнению Уолфрэма, существует. Однако есть еще одно интересное пространство, где ему до сих пор не удалось найти даже планер! Это пространство с кодовым номером 792. Если записать это число в троичной системе счисления, то мы получим набор правил для автомата с тремя состояниями:

При поиске планеров и катапульт полезным может оказаться специальное пособие. По моему совету Уолфрэм написал такое пособие. В нем представлен алгоритм, отыскивающий то, что Уолфрэм называет "устойчивыми структурами".
Поиск планеров и катапульт сконцентрирован на тех автоматах, которые, по мнению исследователей, потенциально обладают способностью к универсальным вычислениям. Другими словами, эти автоматы могут выполнять функции универсальной вычислительной машины. Кроме рассмотренных автоматов с кодовыми номерами 20 и 792 существует также автомат с двумя состояниями (r = 3, кодовый номер 88), для которого катапульта была найдена раньше.
Найти ее удалось Дж.Парку, когда он был еще студентом Принстонского университета. Чтобы увидеть катапульту Парка в действии, нужно написать простую программу для представления на экране дисплея поколений клеток, а также для вычисления следующей конфигурации по предыдущей. Написать такую программу, реализующую автомат-88, в общем несложно. Когда программа будет готова, введите исходную конфигурацию-образ 1111111111011 и понаблюдайте, как она начнет расширяться и сжиматься. Катапульта выпускает планеры в обоих направлениях через каждые 238 поколений.

Фотография одномерной катапульты Дж.Парка

Катапульта Дж.Парка, запускающая планеры направо и налево
Однако, вместо того чтобы моделировать какой-то один конкретный автомат, мы советуем читателям составить программу, которая принимала бы произвольные тоталистические правила в качестве входных данных. Это легко сделать как для фиксированных, так и для варьируемых значений k и r, т.е. когда k и r являются параметрами. При составлении программы следует воспользоваться специальным массивом table для правил, а также двумя линейными массивами oldcells и newcells соответственно для хранения старой и новой конфигураций клеток, которые участвуют в вычислениях, выполняемых в данный момент. Размер массивов может быть сколь угодно большим, однако следует иметь в виду, что на экране дисплея (в зависимости от его типа) может изображаться лишь какая-то ограниченная часть этих массивов. Выведите на экран возможно большую среднюю часть массива newcells и выполните следующие операции: перепишите содержимое массива newcells в массив oldcells; просмотрите в цикле массив oldcells, для каждого i-го элемента массива сложите значения элементов от i-r до i+r; найдите значение полученной суммы в массиве table и запишите соответствующее данной сумме значение состояния на место i-го элемента массива newcells. Затем снова войдите в основной цикл, начинающийся с вывода картинки на экран, и повторите описанные выше этапы. На экране дисплея каждая новая картинка может появляться на новой строке или все время на одной и той же. В первом случае получается пространственно-временная диаграмма, во втором - нечто наподобие мультфильма в одном измерении.
Как уже отмечалось, автомат обладает способностью к универсальным вычислениям, если по мере смены поколений клеток некая исходная структура оказывается способной выполнять функции компьютера. Часть исходной структуры представляет собой входные данные, и соответственно другая ее часть, наблюдающаяся в некоторый более поздний момент, - выходные данные. Неужели можно действительно построить компьютер при помощи планеров, катапульт и других "устройств" на клеточной основе? Уолфрэм считает, что можно. У одного из исследуемых в настоящее время автоматов обнаружились планеры, проходящие через определенные стабильные подобразы. В связи с этим возникает надежда, что передаче информации в одномерном компьютере не будут мешать компоненты, не имеющие непосредственною отношения к этой информации. Помимо Уолфрэма одномерными автоматами занимаются и ряд других исследователей. Один из них - К.Сгейглитц из Прннстонского университета. Он обнаружил планеры, свойства которых подобны свойствам солитонов. Планеры подобного рода могут беспрепятственно проходить один через другой!
Удастся ли нам в конце концов найти устойчивые структуры, способные пересылать, хранить и обрабатывать информацию в одномерном клет очном пространстве? Может быть, и нет. Может оказаться, что вычислениям в одном измерении присуще какое-то особое свойство, которое заставит нас изменить сложившееся представление о вычислительном процессе.
Не ограничивая свою фантазию, Уолфрэм уже думает о том, как одномерные автоматы помогут нам понять поведение автоматов вообще и как это понимание автоматов в свою очередь позволит нам проникнуть в сущность природных процессов. Предположим, что удалось найти одномерный автомат, хорошо моделирующий некий природный процесс, например турбулентное течение жидкости или газа, движение частиц, находящихся в силовом поле, или даже биологический процесс, такой, как рост. Предположим далее, что найденный автомат обладает способностью к универсальным вычислениям. Другими словами, в его пространстве не только содержится явная вычисляющая структура, но и некий скрытый, неявно заложенный в нем компьютер - любая попытка предсказать поведение автомата будет, по определению, равносильна предсказанию поведения универсальной вычислительной машины. Вообще говоря, это можно сделать лишь при помощи другого устройства того же рода, т.е. другой вычислительной машины. Это означает, что не существует никакого "короткого пути", позволяющего предсказать поведение соответствующей природной системы. Ее процессы будут несводимыми в вычислительном смысле, т.е. механизм, предсказывающий поведение системы (будь то формула или компьютер), должен будет моделировать рассматриваемую систему более или менее непосредственно.
Вернемся теперь к "Волне". Планеры исходной популяции движутся в произвольных направлениях, то и дело натыкаясь друг на друга. Иногда в результате столкновения появляется катапульта, порождающая новые планеры, иногда же столкновения не производят никакого эффекта. Это пространство напоминает мне миниатюрную одномерную вселенную, наполненную элементарными частицами, которые движутся как микроскопические волны. Таким образом, я как бы повернул поиск Уолфрэма в обратном направлении. Отправляясь от одномерного автомата, поведение которого в каком-то смысле напоминает систему частиц (правда, довольно своеобразных), я уверовал в то, что "Волна" обладает способностью к универсальным вычислениям. Поскольку это мой личный автомат, я могу оказаться единственным человеком, который в это верит.
БИБЛИОГРАФИЯ
WINNING WAYS FOR YOUR MATHEMATICAL PLAYS. ELWYN R. BERLEKAMP, JOHN H. CONWAY AND RICHARD K. GUY. Academic Press. 1982.
THE PLANIVERSE. A.K.DEWDNEY. Poseidon Press, 1984.
УОЛФРЭМ С. ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ НАУЧНЫХ ИССЛЕДОВАНИЙ.- "В мире науки", 1984, #11, с.98-100. (Этот номер я выкладывал -
 ТЕМА #15, АБЗАЦ #386
ТЕМА #15, АБЗАЦ #386 .- G.).
.- G.).ОТКЛИКИ
10 1985
ДВУМЕРНЫЕ существа, населяющие планету Арда, выражают глубокую признательность многочисленным читателям, попытавшимся усовершенствовать логическую схему с пересечением сигналов, описанную в июльском 1985г. номере журнала "В мире науки". Эта схема состоит из 12 вентилей И-НЕ с двумя входами. Я обратился к читателям с просьбой найти минимальное количество вентилей И-НЕ (и только вентилей И-НЕ), необходимых для построения такой схемы. Большинство представленных решений содержит 10 вентилей, что, безусловно, является некоторым улучшением, однако трем читателям удалось построить схему пересечения, состоящую из восьми вентилей (см. рисунок на с 86).

Схема пересечения сигналов из 8 вентилей И-НЕ
В схеме, состоящей из восьми вентилей, есть один вентиль И-НЕ с тремя входами и два вентиля И-НЕ с одним-единственным входом. Последние действуют как инверторы, преобразующие 0 на входе в 1 на выходе и наоборот. Схему с восемью вентилями удалось построить Э.Карлсону из Кембриджа (шт.Массачусетс), Д.Кеппу из Сан-Хосе (шт.Калифорния) и С.Салливану из Бевертона (шт.Орегон). Я сообщил их имена вместе с предложенными ими вариантами усовершенствованной схемы пересечения моим друзьям ардеанам. Хотите верьте, хотите нет, но точно такая же схема пересечения из восьми вентилей была запатентована в США 26 апреля 1966г. Номер патента 3248573. Р.Фрэнк, консультант по вычислительной технике из Бирмингема (шт.Мичиган), сообщил, что этот патент принадлежит Л.Спэндорферу из Челтенхема (шт.Пенсильвания), А.Тонику из Дрешера (шт.Пенсильвания) и Ш.Ивену из Кембриджа (шт.Массачусетс).
Естественно, возникает вопрос, применяется ли эта схема в каком-либо современном электронном устройстве? Возникает также вопрос о том, существует ли схема пересечения сигналов, содержащая еще меньшее число вентилей И-НЕ. По всей видимости, нет.
В письме У.Джонсона из Лонг-Бича (шт.Калифорния) описаны разнообразные плоские схемы, построенные из вентилей различных типов. Оказывается, можно построить не только двумерные схемы пересечения сигналов, но также и плоские триггеры. Напомним, что на триггерах основаны элементы памяти двумерного компьютера.
Одномерные компьютеры в виде клеточных автоматов изучались С.Уолфрэмом из Принстонского научно-исследовательского института. Пока еще слишком рано говорить о том, какой вклад в эту науку внесли читатели, ознакомившись с брошюрой Уолфрэма, в которой описаны катапульты, стреляющие планерами, однако письма читателей уже поступают, и можно подвести некоторые предварительные итоги. Во-первых, из-за ошибки, закравшейся в статью, посвященную одномерным автоматам, несколько читателей занялись исследованием автомата с кодовым номером 792. Уолфрэм и я имели в виду автомат 357. Во-вторых, я сожалею о том, что не упомянул об одномерном автомате, обладающем свойством универсальных вычислений. У меня была мысль описать такой автомат, впервые построенный А.Смитом в 1970г. В то время Смит был аспирантом Станфордского университета. Но я боялся, что описание универсального одномерного автомата Смита чрезмерно усложнит статью, так как автомат обладает 18 состояниями {k=18) и окрестностью из трех клеток (r=1).
А.Рубин из Лос-Анджелеса внес разумное предложение определить скорость света (скорость распространения сигнала) в произвольном линейном автомате. Предложение Рубина устраняет дефект в определении, принятом ранее, согласно которому скорость света полагалась равной одной клетке в единицу времени. В старом определении не учитывалась возможность, что не все автоматы способны достигать такой скорости. Согласно новому определению, "скорость света - это максимальная скорость распространения любого импульса (скажем, вправо)". Передний фронт распространения импульса определяется условием, что справа от него могут быть только нули. Далее Рубин доказывает, что скорость света для автомата с кодовым номером 792 равна 1/3.
В июльском 1985г. номере журнала "В мире науки" я также обратился к читателям с вопросом о том, обладает ли одномерный автомат "Волна" односторонней катапультой. Планеры, запущенные такой катапультой, должны двигаться вправо до бесконечности, и ни один из них никогда не должен двигаться влево. У.Б.Липп из Милфорда (шт.Коннектикут) привел простой и изящный аргумент против существования такой катапульты. "Рассмотрим конфигурацию,- пишет он,- никогда не имеющую ненулевых значений слева от некоторого блока, помеченного как 0. Заметим, что крайним слева ненулевым значением конфигурации должна всегда быть 1. Если бы оно было равно 2, то эта двойка начала бы двигаться влево до бесконечности, что привело бы к противоречию с предположением, согласно которому слева от блока 0 нет никаких ненулевых значений. Однако крайняя слева 1 на следующем цикле должна превратиться в 0, в результате чего левая граница конфигурации должна переместиться по меньшей мере на один блок вправо". Таким образом, мы приходим к выводу, что либо возникает планер, движущийся влево, либо катапульта разрушается наступающими слева нулями.
Другие читатели попытались доказать, что автомат "Волна" не обладает способностью универсальных вычислений. Для некоторых автоматов можно доказать достаточное условие, а именно что задача остановки является решаемой. "Волна" останавливается, когда во всех ее клетках нули, однако условия остановки для универсальной вычислительной машины, которую автомат может в себе заключить, вообще говоря, могут оказаться совершенно отличными.
Несколько читателей попытались сконструировать одномерный автомат, способный проводить универсальные вычисления. Среди них Ф.Адамс из Ист-Харфорда(шт.Коннектикут), Дж.Амстердам из Кембриджа (шт.Массачусетс), К.Игуса из Брандейского университета и К.Кейди из Ист-Пеории (шт.Иллинойс). Все присланные конструкции сравнительно несложны и на вид правдоподобны, однако Кейди, не удовлетворившись одномерным автоматом, предложил автомат нулевой размерности. Он должен состоять из одной-единственной клетки, и поэтому логично назвать эту клетку точечным автоматом. Читатели с теоретическими наклонностями, возможно, испытают удовольствие, размышляя о том, обладает ли точечный автомат способностью к универсальным вычислениям. Возможен ли такой автомат?
А.Смит опубликовал доказательство существования одномерного автомата, обладающего способностью к универсальным вычислениям, в 1971г. в журнале "ACM" ("Journal of the Association for Computing Machinery"). После такого многообещающего начала можно было подумать, что карьера Смита будет продолжена в каком-нибудь известном академическом центре. Однако талант Смита расцвел совершенно в другой области - в настоящее время он является директором лаборатории машинной графики в кинематографической фирме Lucasfilm, Ltd. в Сан-Рафаэле (шт.Калифорния). В одной из своих будущих статей я надеюсь рассказать вам о некоторых поразительных кинематографических эффектах, полученных в лаборатории фирмы Lucasfilm.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
8 1985
ЕЩЕ РАЗ ОБ АНАЛОГОВЫХ УСТРОЙСТВАХ
А.К.ДЬЮДНИ
РОВНО год начал в рубрике "Занимательный компьютер" была опубликована статья, посвященная аналоговым устройствам. Статья вызвала большой интерес у читателей, многие из которых прислали в редакцию аналоговые устройства собственного изобретения. Я до сих пор не могу избавиться от кучи деревянных досок, резинок, шнурков, шариков, аквариумов, свинцовых гирь, канистр, трубок, пробок и т.д. Пытаясь разобраться во всем этом хозяйстве, я отобрал лучшие устройства, с которыми хочу познакомить читателей.
Аналоговые устройства - это механические приспособления, решающие определенные задачи благодаря тому, что конструктивные элементы или принцип действия этих приспособлений могут служить аналогами исходных данных решаемых задач. В статье, опубликованной в прошлом году, было, например, приведено описание макаронного аналогового устройства МАУ, в котором макаронные палочки выступали в роли аналогов чисел, подлежащих сортировке в порядке убывания. Для решения этой задачи нужно собрать макаронные палочки в пучок и резко опустить их торцами на поверхность стола. Если теперь выбрать самую длинную палочку, потом самую длинную из оставшихся и т.д., то мы получим искомую убывающую последовательность чисел. Кроме макаронного устройства в той же статье говорилось об устройствах, позволяющих отыскивать кратчайшие пути на графе, строить выпуклые оболочки и минимальные деревья. Было даже описано устройство для разложения чисел на множители, состоящее из двух параллельных зеркал, между которыми, многократно отражаясь, проходил лазерный луч.
В нашей новой коллекции представлены остроумные устройства для решения задач статистики, теории графов, а также алгебры и арифметики. Сначала познакомимся с этими устройствами, а затем рассмотрим некоторые важные вопросы, возникающие по поводу аналоговых вычислений: насколько точны аналоговые компьютеры, сколько времени на самом деле требуют аналоговые вычисления и существуют ли аналоговые компьютеры, превосходящие по своим показателям цифровые ЭВМ?
Одно из новых устройств решает задачу математической статистики. Оно состоит из деревянной доски, резиновых колечек, гвоздей и гладкого негнущегося металлического стержня. Это устройство, предложенное Марком Хоули из г.Монт-Вернон (шт.Индиана), помогает определить, какой прямой лучше всего можно аппроксимировать множество экспериментальных точек, нанесенных на график.
Точки наносятся на поверхность деревянной доски и в каждую точку неглубоко забивается гвоздь. Затем на стержень нанизываются резиновые колечки, все одинакового размера, причем число колечек должно быть равно числу точек на доске. Стержень прикладывается к доске приблизительно так, как должна проходить искомая прямая. Каждое резиновое колечко натягивается на один из гвоздей. Затем стержень отпускается, и после некоторых колебаний его положение стабилизируется (см. рисунок внизу).
Устройство для отыскания прямой, которая лучше всего аппроксимирует поле точек на графике
В положении равновесия полная энергия системы минимальна, поэтому суммарное расстояние от гвоздей до стержня также оказывается минимальным. Другими словами, положение, которое займет стержень, укажет направление прямой, наилучшим образом описывающей линейную зависимость исследуемых параметров. В формулах линейной регрессии, используемых в статистике, фигурируют не сами расстояния от точек до прямой, а их квадраты. Устройство Хоули вычисляет нечто в этом роде. Во всяком случае, выполняемые этим устройством вычисления не уступают по сложности вычислениям по методу наименьших квадратов.
Заманчивое шнурковое устройство предложил Джо Венмакер из Ниймегена (Голландия). Предположим, нам нужно найти самый длинный путь, по которому может пройти сообщение в сети связи, имеющей вид дерева. В комбинаторике такой путь называется диаметром дерева. Чтобы найти диаметр дерева, Венмакер строит аналог дерева из связанных шнурков. Длина каждого шнурка в фиксированном масштабе соответствует длине моделируемого участка сети. Вычисления проводятся в два простых шага. Возьмем "дерево" из шнурков за любой узел и поднимем руку так, чтобы оно свободно свисало вниз. Заметим, какой узел расположен ниже всех. Теперь поднимем связанные шнурки за этот узел. Оказывается, что самый длинный путь на дереве проходит от узла, за который мы держим дерево, до узла, расположенного ниже всех остальных (см. рисунок слева).

Определение самого длинного пути на древовидном графе с помощью шнурков
Когда я впервые столкнулся с устройством Венмакера, моей первой реакцией было недоверие: "Не может быть, чтобы это было все так просто. Нужно проверить еще несколько раз и поднять систему шнурков за другие узлы". Однако во всех случаях справедливость идеи Венмакера подтверждалась. Объявляю конкурс - кому из читателей удастся найти самое изящное доказательство, почему это так?
В предыдущей статье об аналоговых устройствах говорилось, что задача отыскания максимального пути на произвольном графе относится к классу задач, называемых теоретиками NP-полными. С практической точки зрения это означает, что такая задача не может быть решена за приемлемое время на цифровой ЭВМ. Может быть, нам удалось, наконец, продемонстрировать превосходство аналогового устройства над цифровым компьютером? Не совсем так. На самом деле, если граф представляет собой дерево, то существует алгоритм для цифровой машины, позволяющий быстро находить максимальный путь.
Теперь рассмотрим незамысловатое на первый взгляд устройство, предложенное М.Лазо из Швейцарского государственного технологического института в Цюрихе. Оно представляет собой зажатый в тиски длинный алюминиевый стержень, на конце которого имеется игла (см. рисунок на с.93). Острие иглы покоится на шкале с мелкими делениями.

Устройство, вычисляющее четвертую степень числа по прогибу стержня
В тисках стержень зажат строго горизонтально, а длина его свободного конца равна трем метрам. Пол действием силы тяжести свободный конец, на котором расположена игла, слегка прогибается вниз. Игла указывает на деление 81. Это четвертая степень тройки.
Согласно теории упругости, прогиб балки под действием собственного веса пропорционален четвертой степени ее длины. Не трудно догадаться, что с помощью этого устройства можно также вычислять корень четвертой степени, если переместить стержень в тисках так, чтобы игла на его конце указывала на число, из которого извлекается корень. Если воспользоваться другой шкалой, то аналогично можно возводить числа в куб или вычислять корень третьей степени. Когда стержень зафиксирован, игла должна указывать на нулевое деление. Затем к свободному концу стержня подвешивается груз, пропорциональный данному числу. Как следует из теории упругости, прогиб стержня в этом случае будет пропорционален третьей степени веса подвешенного груза.
Достойно внимания и аналоговое устройство, присланное Дж.Люетом, служащим металлургической компании United States Metals Refining Company в Картерете (шт.Нью-Джерси). Оно представляет собой широкую деревянную доску, на которую наклеена географическая карта. В доске просверлены три отверстия, через которые пропущены три шнурка. Снизу, пол доской, к каждому шнурку привязана гирька. Сверху шнурки привязаны к небольшому медному колечку (см. рисунок на с.94).
Аналоговое устройство для определения оптимального места строительства металлургического завода
Задача, решаемая устройством, заключается в том, чтобы найти оптимальное место для строительства металлургического завода, так чтобы стоимость доставки основных видов сырья была минимальной. Если доставка руды, угля и извести обходится соответственно в A, B и C долл./(т*км) и если расстояния от завода до месторождений сырья соответственно составляют a, b и c км, то полная стоимость доставки сырья (по одной тонне каждого вида) равна aA+bB+cC долл. Три отверстия в доске просверлены в тех местах на карте, где находятся месторождения и откуда сырье будет доставляться на завод. Привязанные к шнуркам снизу гирьки по массе пропорциональны числам А, В и С. Положение, которое под тяжестью гирек займет на карте отпущенное колечко, будет точно соответствовать оптимальному месту для строительства металлургического завода.
Среди образцов нашей коллекции множество стеклянных и медных устройств, и в помещении, где они находятся, чувствуется запах мыльной пены. Некоторые из этих "водяных" компьютеров созданы Д.Хоффманом из Общественного колледжа в Бельвю (шт.Вашингтон). Мыльная пленка между стеклом и ступенчатой поверхностью является аналогом светового луча, проходящего из одной прозрачной среды в другую: пленка остается прямой на обоих уровнях, однако на ступеньке, где она опускается, пленка имеет резкий изгиб (см. рисунок на с.95). Если высоту ступеньки изменить, угол изгиба пленки станет другим, как если бы моделируемые прозрачные среды изменили свои показатели преломления.

Приборы для определения трассы трубопровода минимальной стоимости (a), нахождения среднего арифметического нескольких чисел (b} и решения кубического уравнения (c)
Это же устройство, несколько усложненное, позволяет также решать задачу о трубопроводе. Предположим, что нужно проложить трубопровод от одного населенного пункта до другого. Местность между этими пунктами поделена на отдельные районы, стоимость прокладки трубопровода в которых неодинакова. Один район, скажем, болотистый, другой холмистый, а третий покрыт лесом. Чтобы смоделировать условия задачи, Хоффман предлагает представить каждый район плоской поверхностью, границы которой соответствуют границам района. Высота такой плоской поверхности должна быть пропорциональной стоимости прокладки трубопровода в данном районе. Затем на плоскостях, соответствующих двум населенным пунктам, между которыми прокладывается трубопровод, нужно установить стерженьки, положить сверху стекло и опустить все устройство в мыльный раствор. В результате внутри образуется мыльная пленка с лвумя изгибами. Она укажет курс, по которому должен прокладываться трубопровод минимальной стоимости. Описание ряда других устройств Хоффмана приведено в его статье, указанной в библиографии на с.104.
Перейдем к рассмотрению другого аналогового устройства из стекла. Пять стеклянных цилиндров с мерной шкалой соединены у основания трубками. В исходном состоянии трубки закрыты, так что вода не может переходить из одного цилиндра в другой. Затем цилиндры заполняются водой до уровней, соответствующих пяти различным числам. Когда трубки открываются, цилиндры становятся сообщаюшимися сосудами и вола устанавливается в них на одном уровне, который соответствует среднему арифметическому значению исходных пяти чисел. Автор устройства - С.Марко из Сан-Ремо (Италия).
Последнее устройство, которое мы рассмотрим детально, предложено П.Эшем из Университета Сан-Джозефа в Филадельфии (шт.Пенсильвания). Оно решает кубические уравнения и может быть модифицировано для решения уравнений значительно более высоких степеней. Кубическое уравнение имеет вид ax3+bx2+cx+d=0. Решить это уравнение - значит найти такое значение переменной x, которое удовлетворяет этому равенству.
Рассматриваемое устройство (см. рисунок на с.95) решает конкретное кубическое уравнение. Оно состоит из большого аквариума, весов в виде коромысла с двумя чашами и набора твердых тел вращения различной геометрической формы, являющихся аналогами членов уравнения. Члену x3 соответствует параболоид. Если параболоид погрузить в воду вершиной вниз, он вытеснит x3 кубических сантиметров воды при глубине погружения, равной x. Член x2 представлен конусом, вытесняющим x2 кубических сантиметров воды. Аналогом члена x является цилиндр, a d - шар. Шар всегда остается погруженным полностью.
Все четыре тела подвешены к коромыслу весов, на его краях расположены чаши для гирек. Ось весов совпадает с центром коромысла. Вся система установлена над аквариумом с водой. Параболоид расположен слева от оси весов на расстоянии a см, если значение a отрицательно, или справа, если оно положительно. То же правило действует и в отношении трех других тел.
Чтобы решить кубическое уравнение, нужно, поддерживая весы в равновесии, наполнять аквариум водой до тех пор, пока поверхность воды не коснется трех подвешенных к коромыслу тел. Напомним, что четвертое тело, шар, уже в исходном состоянии полностью погружен в воду. Если теперь отпустить весы, какое-то плечо коромысла перевесит. Чтобы весы снова привести в равновесие, на противоположную чашу следует положить дополнительные гирьки. После этого наблюдаемый уровень воды в аквариуме отмечается как нулевой.
Пока были рассмотрены только подготовительные этапы в работе устройства. Теперь мы подошли к аналоговому процессу, дающему решение задачи. По мере того как аквариум постепенно наполняется водой от нулевого уровня и выше, весы выходят из равновесия, но через некоторое время равновесие восстанавливается. В этот момент добавление воды следует немедленно прекратить и отметить достигнутый ею уровень. Расстояние между этим новым и нулевым уровнем дает нам значение х, удовлетворяющее уравнению. Разумеется, уравнение может и не иметь решения. В этом случае, даже если заполнить аквариум доверху, весы так и не придут в равновесие.
Как же работает это замечательное устройство? Согласно закону Архимеда, погруженное в воду тело теряет часть своего веса, пропорциональную погруженному объему. Степень отклонения коромысла весов от положения равновесия в данном случае зависит не только от глубины погружения тел, но и от расстояния, на котором они находятся от оси весов, и определяется суммарными действиями на коромысло моментов, т.е. алгебраической суммой произведений выталкивающих сил на плечи. Таким образом, равновесие вновь достигается только тогда, когда при определенном значении x сумма в левой части уравнения равна нулю, что фактически достигается при новом уровне воды в аквариуме.
Чтобы привести полные описания всех устройств, о которых нам сообщили читатели, потребовалось бы увеличить размер этой статьи по меньшей мере вдвое. Поэтому я ограничусь лишь кратким упоминанием еще о нескольких.
Одно из "устройств" - это довольно непрактичная альтернатива макаронному компьютеру. Оно предложено М.Гарднером из Финдлея (шт.Огайо) и называется СБД, сокращенно от "сортировщик на бензиновых двигателях". СБД требует по одному легковому автомобилю, скажем "фольксвагену", на каждое число из сортируемого набора чисел. В бензобак каждого "фольксвагена" заливается количество бензина, соответствующее представляемому данным автомобилем числу. Водители (все одинакового веса) садятся а машины, и колонна трогается в путь. Один дополнительный "фольксваген" (с полным баком) движется следом, и его водитель фиксирует порядок, в котором другие машины, исчерпав свой запас горючего, останавливаются. Таким образом числа исходного набора оказываются отсортированными. В свою очередь шиурковое устройство для отыскания кратчайшего пути на графе, о котором говорилось в прошлогодней статье, можно смоделировать при помощи простой электронной схемы, предложенной С.Фортескью из Канога-Парка (шт.Калифорния). Каждое ребро графа заменяется схемой из двух параллельных ветвей. Каждая ветвь состоит из диода Зенера и последовательно соединенного с ним светодиода. Обычно диоды проводят ток только в одном направлении, и может показаться странным, что диод Зенера и светодиод на каждой ветви ориентированы в противоположных направлениях. Обе ветви сами тоже имеют противоположную ориентацию. Однако диод Зенера может проводить и в обратном направлении, если приложенное к нему напряжение достаточно велико. Фортескью предлагает использовать диоды с пороговыми напряжениями, пропорциональными длинам ребер графа, аналогами которых они являются. Чтобы найти кратчайший путь между двумя узлами графа, к соответствующим точкам схемы нужно приложить напряжение. Сначала никакого эффекта не наблюдается, но по мере увеличения напряжения первыми загорятся светодиоды, образующие кратчайший путь между узлами. Никто не придумал лучшего устройства для определения выпуклой оболочки множества точек на плоскости, чем то, которое основано на круглой резинке и было описано в прошлогодней статье, посвященной аналоговым устройствам. Тем не менее Э.Ланцони из Модена (Италия) изобрел "прибор", позволяющий находить окружность с наименьшим радиусом, заключающую в себе все точки множества. Ланцони просверливает отверстия в доске, которые соответствуют точкам множества. Затем он отрезает несколько шнурков одинаковой длины, одни их концы связывает вместе, а другие, свободные, пропускает по одному через просверленные в доске отверстия. Свисающие концы шнурков прикрепляются в соответствующих точках к большому плоскому куску фанеры. Когда фанера находится в подвешенном состоянии, положение узла на доске фиксируется точно в центре искомой окружности. По крайней мере три шнурка оказываются натянутыми, они образуют радиусы окружности.
ПЕРЕЙДЕМ теперь к рассмотрению некоторых вопросов, невольно возникающих после ознакомления с рядом аналоговых устройств. Дело в том, что и сами аналоговые устройства, и общий подход к вычислениям с их помощью вызывают у читателей некоторое беспокойство. В ответ на статью, опубликованную в прошлом голу, ряд читателей написали критические заметки, касающиеся моих оценок быстродействия аналоговых вычисляющих устройств. Другие читатели обратили внимание на точность решения, обеспечиваемую этими устройствами, а некоторые даже потребовали, чтобы я дал точное определение аналогового компьютера. Эти вопросы подвели нас к самой сущности взаимоотношений между материей и информацией.
В первой статье на эту тему я проанализировал две фазы - предшествующую фазе собственно аналогового вычисления и следующую за ней. Рассматривая макаронное аналоговое устройство, мы выделили фазу, предшествующую вычислению, в ходе которой нужно было нарезать макаронные палочки так, чтобы их длина соответствовала сортируемым числам. После же фазы вычисления нужно было измерить каждую палочку в порядке убывания их длины и записать результат. Почти во всех случаях эти вспомогательные фазы занимали наибольшее количество времени. Само по себе вычисление сводилось к одному или нескольким движениям: удару, повороту, натяжению шнурка, после которых наступало состояние равновесия, являющееся решением задачи. Однако в некотором смысле фазы обработки информации не совместимы с природой аналогового вычисления. Привыкнув оперировать числами, мы, естественно, полагаем, что "вход" и "выход" лля вычисления также должны быть представлены в числовой форме. Но если под аналоговым компьютером мы подразумеваем физический процесс или абстрактную модель физического процесса, то входные и выходные данные также должны быть физическими по своей природе. В этом смысле цифровые машины имеют свои недостатки. Что если мне придется оценивать эффективность цифрового метода в зависимости от того, насколько быстро удастся перевести физические переменные в числовые величины?
Было бы, наверное, правильнее рассматривать аналоговые вычисления, не касаясь пока того, как осуществляются переходы между мирами цифровых и аналоговых величин. Однако что тогда представляет собой мир аналоговых величин? Возможно, его следовало бы идеализировать, как это сделал, например, один инопланетянин, посетивший нашу планету несколько лет назад. Этот эпизод был упомянут в книге моего предшественника, автора статей, публиковавшихся раньше в рубрике "Математические игры". Инопланетянин (назовем его Марсианом Гарднером), едва приземлившись, немедленно приступил к переработке всех книг, изданных за всю историю цивилизации на Земле, с тем чтобы превратить всю содержащуюся в них информацию в одно колоссальное число. Обработка осуществлялась по очень простому принципу: если рассматривать книгу как очень длинную цепочку слов, то ее нетрудно представить в виде столь же длинной последовательности цифр. Завершив обработку, инопланетянин поместил перед полученным числом нуль и запятую, превратив его в десятичную дробь, и сделал маленькую отметку на металлическом стержне, который хранился на борту космического корабля. Эта отметка делила стержень на части в отношении, точно соответствующем колоссальному десятичному числу. Вот так литературные достижения человечества были сведены к маленькой отметке на металлической палочке.
Будем считать, что мир аналоговых величин состоит из идеального вещества, подчиняющегося идеальным законам в идеальном пространстве. Мир этот наполнен дифференциальными уравнениями, некоторые из которых описывают совершенно необычные вещи, например непрерывно действующую машину Тьюринга. Такая машина способна производить все действия, выполняемые дискретной машиной, и, может быть, намного больше. Попытка создания подобной машины из обычных электронных компонентов, вероятно, приведет к существенной потере в точности и быстродействии.
А.Вирджис из Университета штата Миннесота, К.Стейглитц и Б.Дикинсон из Принстонского университета (см. библиографию на с.104) создали устройство, которое выглядит более реалистично, чем аналоговая машина Тьюринга. Состоящее только из валиков, шестеренок и кулачков, оно решает логическую задачу, формируемую в виде логического выражения из сомножителей, каждый из которых является суммой трех литералов. Литерал - это логическая переменная (такая, как x) или ее отрицание (такое, как x'). Суммы трех литералов перемножаются, например так:
(x + y + z')*(x' + y' + z)
Задача заключается в том, чтобы установить, существует ли способ присвоить логические значения (истина или ложь) переменным x, y и z, чтобы значение всего выражения было истиной. Если выражение состоит только из двух сомножителей, как в данном случае, то ответ будет положительным. В самом деле, пусть значение x - истина, y - ложь и z - истина. Видно, что каждый сомножитель содержит по крайней мере один истинный литерал и поэтому значение всего выражения - истина. Хотя в рассмотренном примере задача выглядит простой, ее решение вызывает серьезные затруднения в более общих случаях (т.е. в задачах более высокой размерности). Более того, эта задача обладает свойством, которое вызывает благоговейный страх у специалистов по теории вычислений. Она относится к классу NP-полных задач: ни один известный алгоритм не дает ее решения за время, меньшее "экспоненциального". Другими словами, если число сомножителей равно n, то для решения задачи потребуется 2^n шагов вычисления.
И все же трем теоретикам удалось найти такую конструкцию из шестеренок, валиков и кулачков, которую можно настроить на решение любого частного случая рассмотренной выше логической задачи. Она имеет положительное решение тогда и только тогда, когда оказывается возможным повернуть определенный валик устройства.
В то же время ввиду того, что задача относится к классу NP-полных, она обладает одним примечательным свойством. Если ее удастся решить быстро, то это означает, что любая другая NP-полная задача также имеет быстрое решение. Однако в настоящее время большинство теоретиков считают, что алгоритма быстрого решения таких задач для цифрового компьютера не существует. Может быть, авторы открыли аналоговое устройство, превосходящее любую цифровую машину? Сейчас они тщательно исследуют конструкцию своего устройства в поисках возможной ошибки.
Если абстрактная модель машины действительно работает так, как было задумано авторами, остается открытым вопрос о том, будет ли правильно функционировать реальное устройство, построенное по этой абстрактной схеме. Какой-нибудь фундаментальный фактор, присущий материальному миру, может оказаться непреодолимым препятствием для реализации устройства. Возможно, существует некий природный закон, согласно которому любая физическая система может быть с одинаковым успехом описана и так же быстро смоделирована в цифровой форме, как и в любой лругой. Действительно, мы уже привыкли к представлению о том, что все свойства Вселенной по сути своей "цифровые". Все это означает, что аналоговый компьютер, который, казалось бы, превосходит своих цифровых собратьев, должен обладать какими-то существенными недостатками, например в точности или скорости вычислений. Единственное возможное преимущество у таких устройств - это их способность одновременно выполнять множество операций. Вспомним, например, устройство, действующее по принципу сообщающихся сосудов, в которых вола сразу устанавливается на одинаковом уровне.
БИБЛИОГРАФИЯ
SMART SOAP BUBBLES CAN DO CALCULUS. DALE T. HOFFMAN in The Mathematics Teacher, Vol.72, No.5, pages 377-385, 389; May, 1979.
AHA! GOTCHA: PARADOXES TO PUZZLE AND DELIGHT. MARTIN GARDNER. W.H.Freeman and Company, 1982. (Есть перевод: МАРТИН ГАРДНЕР, А НУ-КА ДОГАДАЙСЯ!- М.:"МИР", 1984.- G.)
THE COMPLEXITY OF ANALOG COMPUTATION. ANASTASIOS VERGIS, KENNETH STEIGLITZ AND BRADLEY DICKINSON. Technical Report No.337, Department of Electrical Engineering and Computer Science, Princeton University; February, 1985.
ОТКЛИКИ
11 1985
В АВГУСТОВСКОМ номере журнала я предложил читателям найти изящное доказательство утверждения о том, что при помощи приема Дж.Венмакера можно действительно отыскать самый длинный путь на "дереве", сделанном из шнурков. Я говорил, что для определения самого длинного пути достаточно двух операций подвешивания. Сначала нужно взять дерево за любой узел и подвесить его. Затем нужно взять дерево за самый нижний узел и снова подвесить его. Самый длинный путь проходит от узла, за который было подвешено дерево во второй раз, до узла, который теперь оказался самым нижним.
Выше мы неявно предполагали, что дерево имеет единственный самый длинный путь. На самом деле у дерева может быть несколько различных путей одинаковой длины, которая превышает длины всех остальных путей. Следовательно, на обоих шагах процедуры у нас есть выбор между несколькими узлами и в такой ситуации можно выбрать один из таких узлов произвольно.
Мне прислали значительно больше доказательств, чем я ожидал. Премию за самое изящное доказательство можно было бы присудить почти на равных основаниях следующим читателям: Дж.Бартольди III из Атланты (шт.Джорджия), Н.Дершовицу из Эрбаны (шт.Иллинойс), У.Липпу из Милфорда (шт.Коннектикут), Д.Миду из Дейвиса (шт.Калифорния), и Дж. ван-Бентему из Гронингена (Голландия). Нетрудно догадаться, что все эти лица, за исключением Липпа, так или иначе связаны с университетами. Это соответственно Технологический институт шт.Джорджия, ИлпинойсскиП университет в Эрбана-Шампейн, Калифорнийский университет в Дейвисе и Гронингенский государственный университет.
Под "иэящным доказательством" я подразумеваю сочетание краткости и ясности. В рамках нашей рубрики это означает также минимальное количество обозначений, уравнений и неравенств. С учетом всех этих требований победителем можно считать Бартольди. Вот его доказательство:
"Пусть H - точка подвеса, a L - нижняя точка. Утверждение: L должна быть одним из концов самого длинного пути.
Доказательство: Пусть A - другой конец самого длинного пути и А<>L. Путь максимальной длины, одним из концов которого является точка A, состоит из участка, ведущего вверх, и участка, ведущего вниз. Однако первый участок не превосходит расстояния от A до H, а второй участок не превосходит расстояния от H до L. Таким образом, путь от A до L представляет собой путь максимальной длины.
Если теперь подвесить дерево за точку L, то по аналогичным соображениям точка A окажется самой нижней".
Надо сказать, что приведенное доказательство скорее интуитивное, чем строгое. Тем не менее оно выглядит убедительным, потому что мы представляем себе мысленно, как участки самого длинного пути, проходящего через A, которые ведут соответственно вверх и вниз, висят рядом с путем от H к L. Строгое доказательство потребовало бы значительно больше места.
Первое устройство из тех, которые мы обсуждали в августовском выпуске журнала, состояло из доски, нескольких гвоздей, резиновых колец и длинного гладкого стержня. Это устройство позволяет найти прямую, наилучшим образом аппроксимирующую несколько экспериментальных точек на графике. Я говорил, что в доску нужно вбить гвозди, представляющие экспериментальные точки, затем накинуть резиновое кольцо на каждый гвоздь и на стержень, после чего следует отпустить стержень, который, подрожав, быстро приходит в равновесие.
Я утверждал, что равновесное положение стержня минимизирует полную потенциальную энергию системы (что правильно) и что, следовательно, сумма расстояний от точек до стержня, т.е. сумма отрезков, перпендикулярных стержню, должна быть минимальной (что неправильно). Я имел в виду формулу для силы, которая обусловлена растяжением резинки и пропорциональна ее удлинению. Однако, как заметили многие читатели, энергия, запасенная каждой резинкой, пропорциональна квадрату ее удлинения. Чувство стыда за эту оплошность было, однако, более чем скомпенсировано. Я понял, что устройство М.Хоули гораздо ближе к цели - вычислению по методу наименьших квадратов, чем я ожидал. Остается одно важное различие в том, что следует считать расстоянием. Для вычисления по методу наименьших квадратов нужно, чтобы резинки были натянуты вертикально, а не перпендикулярно стержню (если только стержень не занимает горизонтального положения).
Несколько читателей заметили, что резиновые кольца должны быть идеальными в том смысле, чтобы у них не было провисающих участков. Этому требованию можно удовлетворить следующими способами. Ч.Диллингем из Нью-Йорка (шт.Нью-Йорк), заменяет гвозди на цилиндры. Длина такого цилиндра равна длине нерастянухой резинки. Каждая резинка прикрепляется к доске
внутри цилиндра. Резинка удлиняется, только когда ее вытягивают из цилиндра и накидывают на стержень. Р.Файньюкейн из Уотербьюри (шт.Вермонт), решает эту проблему, пропуская каждую резинку через отверстие на доске, соответствующее экспериментальной точке.
Гидравлическое устройство для решения кубического уравнения не вызвало критических отзывов, за исключением замеченной несколькими читателями путаницы. Дело в том, что члены третьей и второй степеней уравнения представляются соответственно конусом и параболоидом, а не наоборот. В этом можно убедиться, проведя несложные вычисления.
Я думаю, что пройдет довольно значительное время, прежде чем мы сможем вернуться в наших статьях к аналоговым устройствам. Позвольте мне, так сказать, на прощание представить вам картонное устройство для подсчета площади земельного участка, присланное А.Лейзаром из Тинека (шт.Нью-Джерси).
Лейзар пользуется картонной коробкой, которую можно найти у любого продовольственного магазина, и портативными весами, чтобы проверять точность вычисления "площади земельного участка с нерегулярной границей". Он наносит контуры участка на лист картона и вырезает модель ножницами. Затем он взвешивает полученную модель и квадратик того же картона, отвечающий в принимаемом им масштабе площади 1акр. Поделив первый вес на второй, он получает площадь участка.
ЕЩЕ РАЗ ОБ АНАЛОГОВЫХ УСТРОЙСТВАХ
А.К.ДЬЮДНИ
РОВНО год начал в рубрике "Занимательный компьютер" была опубликована статья, посвященная аналоговым устройствам. Статья вызвала большой интерес у читателей, многие из которых прислали в редакцию аналоговые устройства собственного изобретения. Я до сих пор не могу избавиться от кучи деревянных досок, резинок, шнурков, шариков, аквариумов, свинцовых гирь, канистр, трубок, пробок и т.д. Пытаясь разобраться во всем этом хозяйстве, я отобрал лучшие устройства, с которыми хочу познакомить читателей.
Аналоговые устройства - это механические приспособления, решающие определенные задачи благодаря тому, что конструктивные элементы или принцип действия этих приспособлений могут служить аналогами исходных данных решаемых задач. В статье, опубликованной в прошлом году, было, например, приведено описание макаронного аналогового устройства МАУ, в котором макаронные палочки выступали в роли аналогов чисел, подлежащих сортировке в порядке убывания. Для решения этой задачи нужно собрать макаронные палочки в пучок и резко опустить их торцами на поверхность стола. Если теперь выбрать самую длинную палочку, потом самую длинную из оставшихся и т.д., то мы получим искомую убывающую последовательность чисел. Кроме макаронного устройства в той же статье говорилось об устройствах, позволяющих отыскивать кратчайшие пути на графе, строить выпуклые оболочки и минимальные деревья. Было даже описано устройство для разложения чисел на множители, состоящее из двух параллельных зеркал, между которыми, многократно отражаясь, проходил лазерный луч.
В нашей новой коллекции представлены остроумные устройства для решения задач статистики, теории графов, а также алгебры и арифметики. Сначала познакомимся с этими устройствами, а затем рассмотрим некоторые важные вопросы, возникающие по поводу аналоговых вычислений: насколько точны аналоговые компьютеры, сколько времени на самом деле требуют аналоговые вычисления и существуют ли аналоговые компьютеры, превосходящие по своим показателям цифровые ЭВМ?
Одно из новых устройств решает задачу математической статистики. Оно состоит из деревянной доски, резиновых колечек, гвоздей и гладкого негнущегося металлического стержня. Это устройство, предложенное Марком Хоули из г.Монт-Вернон (шт.Индиана), помогает определить, какой прямой лучше всего можно аппроксимировать множество экспериментальных точек, нанесенных на график.
Точки наносятся на поверхность деревянной доски и в каждую точку неглубоко забивается гвоздь. Затем на стержень нанизываются резиновые колечки, все одинакового размера, причем число колечек должно быть равно числу точек на доске. Стержень прикладывается к доске приблизительно так, как должна проходить искомая прямая. Каждое резиновое колечко натягивается на один из гвоздей. Затем стержень отпускается, и после некоторых колебаний его положение стабилизируется (см. рисунок внизу).

Устройство для отыскания прямой, которая лучше всего аппроксимирует поле точек на графике
В положении равновесия полная энергия системы минимальна, поэтому суммарное расстояние от гвоздей до стержня также оказывается минимальным. Другими словами, положение, которое займет стержень, укажет направление прямой, наилучшим образом описывающей линейную зависимость исследуемых параметров. В формулах линейной регрессии, используемых в статистике, фигурируют не сами расстояния от точек до прямой, а их квадраты. Устройство Хоули вычисляет нечто в этом роде. Во всяком случае, выполняемые этим устройством вычисления не уступают по сложности вычислениям по методу наименьших квадратов.
Заманчивое шнурковое устройство предложил Джо Венмакер из Ниймегена (Голландия). Предположим, нам нужно найти самый длинный путь, по которому может пройти сообщение в сети связи, имеющей вид дерева. В комбинаторике такой путь называется диаметром дерева. Чтобы найти диаметр дерева, Венмакер строит аналог дерева из связанных шнурков. Длина каждого шнурка в фиксированном масштабе соответствует длине моделируемого участка сети. Вычисления проводятся в два простых шага. Возьмем "дерево" из шнурков за любой узел и поднимем руку так, чтобы оно свободно свисало вниз. Заметим, какой узел расположен ниже всех. Теперь поднимем связанные шнурки за этот узел. Оказывается, что самый длинный путь на дереве проходит от узла, за который мы держим дерево, до узла, расположенного ниже всех остальных (см. рисунок слева).

Определение самого длинного пути на древовидном графе с помощью шнурков
Когда я впервые столкнулся с устройством Венмакера, моей первой реакцией было недоверие: "Не может быть, чтобы это было все так просто. Нужно проверить еще несколько раз и поднять систему шнурков за другие узлы". Однако во всех случаях справедливость идеи Венмакера подтверждалась. Объявляю конкурс - кому из читателей удастся найти самое изящное доказательство, почему это так?
В предыдущей статье об аналоговых устройствах говорилось, что задача отыскания максимального пути на произвольном графе относится к классу задач, называемых теоретиками NP-полными. С практической точки зрения это означает, что такая задача не может быть решена за приемлемое время на цифровой ЭВМ. Может быть, нам удалось, наконец, продемонстрировать превосходство аналогового устройства над цифровым компьютером? Не совсем так. На самом деле, если граф представляет собой дерево, то существует алгоритм для цифровой машины, позволяющий быстро находить максимальный путь.
Теперь рассмотрим незамысловатое на первый взгляд устройство, предложенное М.Лазо из Швейцарского государственного технологического института в Цюрихе. Оно представляет собой зажатый в тиски длинный алюминиевый стержень, на конце которого имеется игла (см. рисунок на с.93). Острие иглы покоится на шкале с мелкими делениями.

Устройство, вычисляющее четвертую степень числа по прогибу стержня
В тисках стержень зажат строго горизонтально, а длина его свободного конца равна трем метрам. Пол действием силы тяжести свободный конец, на котором расположена игла, слегка прогибается вниз. Игла указывает на деление 81. Это четвертая степень тройки.
Согласно теории упругости, прогиб балки под действием собственного веса пропорционален четвертой степени ее длины. Не трудно догадаться, что с помощью этого устройства можно также вычислять корень четвертой степени, если переместить стержень в тисках так, чтобы игла на его конце указывала на число, из которого извлекается корень. Если воспользоваться другой шкалой, то аналогично можно возводить числа в куб или вычислять корень третьей степени. Когда стержень зафиксирован, игла должна указывать на нулевое деление. Затем к свободному концу стержня подвешивается груз, пропорциональный данному числу. Как следует из теории упругости, прогиб стержня в этом случае будет пропорционален третьей степени веса подвешенного груза.
Достойно внимания и аналоговое устройство, присланное Дж.Люетом, служащим металлургической компании United States Metals Refining Company в Картерете (шт.Нью-Джерси). Оно представляет собой широкую деревянную доску, на которую наклеена географическая карта. В доске просверлены три отверстия, через которые пропущены три шнурка. Снизу, пол доской, к каждому шнурку привязана гирька. Сверху шнурки привязаны к небольшому медному колечку (см. рисунок на с.94).

Аналоговое устройство для определения оптимального места строительства металлургического завода
Задача, решаемая устройством, заключается в том, чтобы найти оптимальное место для строительства металлургического завода, так чтобы стоимость доставки основных видов сырья была минимальной. Если доставка руды, угля и извести обходится соответственно в A, B и C долл./(т*км) и если расстояния от завода до месторождений сырья соответственно составляют a, b и c км, то полная стоимость доставки сырья (по одной тонне каждого вида) равна aA+bB+cC долл. Три отверстия в доске просверлены в тех местах на карте, где находятся месторождения и откуда сырье будет доставляться на завод. Привязанные к шнуркам снизу гирьки по массе пропорциональны числам А, В и С. Положение, которое под тяжестью гирек займет на карте отпущенное колечко, будет точно соответствовать оптимальному месту для строительства металлургического завода.
Среди образцов нашей коллекции множество стеклянных и медных устройств, и в помещении, где они находятся, чувствуется запах мыльной пены. Некоторые из этих "водяных" компьютеров созданы Д.Хоффманом из Общественного колледжа в Бельвю (шт.Вашингтон). Мыльная пленка между стеклом и ступенчатой поверхностью является аналогом светового луча, проходящего из одной прозрачной среды в другую: пленка остается прямой на обоих уровнях, однако на ступеньке, где она опускается, пленка имеет резкий изгиб (см. рисунок на с.95). Если высоту ступеньки изменить, угол изгиба пленки станет другим, как если бы моделируемые прозрачные среды изменили свои показатели преломления.

Приборы для определения трассы трубопровода минимальной стоимости (a), нахождения среднего арифметического нескольких чисел (b} и решения кубического уравнения (c)
Это же устройство, несколько усложненное, позволяет также решать задачу о трубопроводе. Предположим, что нужно проложить трубопровод от одного населенного пункта до другого. Местность между этими пунктами поделена на отдельные районы, стоимость прокладки трубопровода в которых неодинакова. Один район, скажем, болотистый, другой холмистый, а третий покрыт лесом. Чтобы смоделировать условия задачи, Хоффман предлагает представить каждый район плоской поверхностью, границы которой соответствуют границам района. Высота такой плоской поверхности должна быть пропорциональной стоимости прокладки трубопровода в данном районе. Затем на плоскостях, соответствующих двум населенным пунктам, между которыми прокладывается трубопровод, нужно установить стерженьки, положить сверху стекло и опустить все устройство в мыльный раствор. В результате внутри образуется мыльная пленка с лвумя изгибами. Она укажет курс, по которому должен прокладываться трубопровод минимальной стоимости. Описание ряда других устройств Хоффмана приведено в его статье, указанной в библиографии на с.104.
Перейдем к рассмотрению другого аналогового устройства из стекла. Пять стеклянных цилиндров с мерной шкалой соединены у основания трубками. В исходном состоянии трубки закрыты, так что вода не может переходить из одного цилиндра в другой. Затем цилиндры заполняются водой до уровней, соответствующих пяти различным числам. Когда трубки открываются, цилиндры становятся сообщаюшимися сосудами и вола устанавливается в них на одном уровне, который соответствует среднему арифметическому значению исходных пяти чисел. Автор устройства - С.Марко из Сан-Ремо (Италия).
Последнее устройство, которое мы рассмотрим детально, предложено П.Эшем из Университета Сан-Джозефа в Филадельфии (шт.Пенсильвания). Оно решает кубические уравнения и может быть модифицировано для решения уравнений значительно более высоких степеней. Кубическое уравнение имеет вид ax3+bx2+cx+d=0. Решить это уравнение - значит найти такое значение переменной x, которое удовлетворяет этому равенству.
Рассматриваемое устройство (см. рисунок на с.95) решает конкретное кубическое уравнение. Оно состоит из большого аквариума, весов в виде коромысла с двумя чашами и набора твердых тел вращения различной геометрической формы, являющихся аналогами членов уравнения. Члену x3 соответствует параболоид. Если параболоид погрузить в воду вершиной вниз, он вытеснит x3 кубических сантиметров воды при глубине погружения, равной x. Член x2 представлен конусом, вытесняющим x2 кубических сантиметров воды. Аналогом члена x является цилиндр, a d - шар. Шар всегда остается погруженным полностью.
Все четыре тела подвешены к коромыслу весов, на его краях расположены чаши для гирек. Ось весов совпадает с центром коромысла. Вся система установлена над аквариумом с водой. Параболоид расположен слева от оси весов на расстоянии a см, если значение a отрицательно, или справа, если оно положительно. То же правило действует и в отношении трех других тел.
Чтобы решить кубическое уравнение, нужно, поддерживая весы в равновесии, наполнять аквариум водой до тех пор, пока поверхность воды не коснется трех подвешенных к коромыслу тел. Напомним, что четвертое тело, шар, уже в исходном состоянии полностью погружен в воду. Если теперь отпустить весы, какое-то плечо коромысла перевесит. Чтобы весы снова привести в равновесие, на противоположную чашу следует положить дополнительные гирьки. После этого наблюдаемый уровень воды в аквариуме отмечается как нулевой.
Пока были рассмотрены только подготовительные этапы в работе устройства. Теперь мы подошли к аналоговому процессу, дающему решение задачи. По мере того как аквариум постепенно наполняется водой от нулевого уровня и выше, весы выходят из равновесия, но через некоторое время равновесие восстанавливается. В этот момент добавление воды следует немедленно прекратить и отметить достигнутый ею уровень. Расстояние между этим новым и нулевым уровнем дает нам значение х, удовлетворяющее уравнению. Разумеется, уравнение может и не иметь решения. В этом случае, даже если заполнить аквариум доверху, весы так и не придут в равновесие.
Как же работает это замечательное устройство? Согласно закону Архимеда, погруженное в воду тело теряет часть своего веса, пропорциональную погруженному объему. Степень отклонения коромысла весов от положения равновесия в данном случае зависит не только от глубины погружения тел, но и от расстояния, на котором они находятся от оси весов, и определяется суммарными действиями на коромысло моментов, т.е. алгебраической суммой произведений выталкивающих сил на плечи. Таким образом, равновесие вновь достигается только тогда, когда при определенном значении x сумма в левой части уравнения равна нулю, что фактически достигается при новом уровне воды в аквариуме.
Чтобы привести полные описания всех устройств, о которых нам сообщили читатели, потребовалось бы увеличить размер этой статьи по меньшей мере вдвое. Поэтому я ограничусь лишь кратким упоминанием еще о нескольких.
Одно из "устройств" - это довольно непрактичная альтернатива макаронному компьютеру. Оно предложено М.Гарднером из Финдлея (шт.Огайо) и называется СБД, сокращенно от "сортировщик на бензиновых двигателях". СБД требует по одному легковому автомобилю, скажем "фольксвагену", на каждое число из сортируемого набора чисел. В бензобак каждого "фольксвагена" заливается количество бензина, соответствующее представляемому данным автомобилем числу. Водители (все одинакового веса) садятся а машины, и колонна трогается в путь. Один дополнительный "фольксваген" (с полным баком) движется следом, и его водитель фиксирует порядок, в котором другие машины, исчерпав свой запас горючего, останавливаются. Таким образом числа исходного набора оказываются отсортированными. В свою очередь шиурковое устройство для отыскания кратчайшего пути на графе, о котором говорилось в прошлогодней статье, можно смоделировать при помощи простой электронной схемы, предложенной С.Фортескью из Канога-Парка (шт.Калифорния). Каждое ребро графа заменяется схемой из двух параллельных ветвей. Каждая ветвь состоит из диода Зенера и последовательно соединенного с ним светодиода. Обычно диоды проводят ток только в одном направлении, и может показаться странным, что диод Зенера и светодиод на каждой ветви ориентированы в противоположных направлениях. Обе ветви сами тоже имеют противоположную ориентацию. Однако диод Зенера может проводить и в обратном направлении, если приложенное к нему напряжение достаточно велико. Фортескью предлагает использовать диоды с пороговыми напряжениями, пропорциональными длинам ребер графа, аналогами которых они являются. Чтобы найти кратчайший путь между двумя узлами графа, к соответствующим точкам схемы нужно приложить напряжение. Сначала никакого эффекта не наблюдается, но по мере увеличения напряжения первыми загорятся светодиоды, образующие кратчайший путь между узлами. Никто не придумал лучшего устройства для определения выпуклой оболочки множества точек на плоскости, чем то, которое основано на круглой резинке и было описано в прошлогодней статье, посвященной аналоговым устройствам. Тем не менее Э.Ланцони из Модена (Италия) изобрел "прибор", позволяющий находить окружность с наименьшим радиусом, заключающую в себе все точки множества. Ланцони просверливает отверстия в доске, которые соответствуют точкам множества. Затем он отрезает несколько шнурков одинаковой длины, одни их концы связывает вместе, а другие, свободные, пропускает по одному через просверленные в доске отверстия. Свисающие концы шнурков прикрепляются в соответствующих точках к большому плоскому куску фанеры. Когда фанера находится в подвешенном состоянии, положение узла на доске фиксируется точно в центре искомой окружности. По крайней мере три шнурка оказываются натянутыми, они образуют радиусы окружности.
ПЕРЕЙДЕМ теперь к рассмотрению некоторых вопросов, невольно возникающих после ознакомления с рядом аналоговых устройств. Дело в том, что и сами аналоговые устройства, и общий подход к вычислениям с их помощью вызывают у читателей некоторое беспокойство. В ответ на статью, опубликованную в прошлом голу, ряд читателей написали критические заметки, касающиеся моих оценок быстродействия аналоговых вычисляющих устройств. Другие читатели обратили внимание на точность решения, обеспечиваемую этими устройствами, а некоторые даже потребовали, чтобы я дал точное определение аналогового компьютера. Эти вопросы подвели нас к самой сущности взаимоотношений между материей и информацией.
В первой статье на эту тему я проанализировал две фазы - предшествующую фазе собственно аналогового вычисления и следующую за ней. Рассматривая макаронное аналоговое устройство, мы выделили фазу, предшествующую вычислению, в ходе которой нужно было нарезать макаронные палочки так, чтобы их длина соответствовала сортируемым числам. После же фазы вычисления нужно было измерить каждую палочку в порядке убывания их длины и записать результат. Почти во всех случаях эти вспомогательные фазы занимали наибольшее количество времени. Само по себе вычисление сводилось к одному или нескольким движениям: удару, повороту, натяжению шнурка, после которых наступало состояние равновесия, являющееся решением задачи. Однако в некотором смысле фазы обработки информации не совместимы с природой аналогового вычисления. Привыкнув оперировать числами, мы, естественно, полагаем, что "вход" и "выход" лля вычисления также должны быть представлены в числовой форме. Но если под аналоговым компьютером мы подразумеваем физический процесс или абстрактную модель физического процесса, то входные и выходные данные также должны быть физическими по своей природе. В этом смысле цифровые машины имеют свои недостатки. Что если мне придется оценивать эффективность цифрового метода в зависимости от того, насколько быстро удастся перевести физические переменные в числовые величины?
Было бы, наверное, правильнее рассматривать аналоговые вычисления, не касаясь пока того, как осуществляются переходы между мирами цифровых и аналоговых величин. Однако что тогда представляет собой мир аналоговых величин? Возможно, его следовало бы идеализировать, как это сделал, например, один инопланетянин, посетивший нашу планету несколько лет назад. Этот эпизод был упомянут в книге моего предшественника, автора статей, публиковавшихся раньше в рубрике "Математические игры". Инопланетянин (назовем его Марсианом Гарднером), едва приземлившись, немедленно приступил к переработке всех книг, изданных за всю историю цивилизации на Земле, с тем чтобы превратить всю содержащуюся в них информацию в одно колоссальное число. Обработка осуществлялась по очень простому принципу: если рассматривать книгу как очень длинную цепочку слов, то ее нетрудно представить в виде столь же длинной последовательности цифр. Завершив обработку, инопланетянин поместил перед полученным числом нуль и запятую, превратив его в десятичную дробь, и сделал маленькую отметку на металлическом стержне, который хранился на борту космического корабля. Эта отметка делила стержень на части в отношении, точно соответствующем колоссальному десятичному числу. Вот так литературные достижения человечества были сведены к маленькой отметке на металлической палочке.
Будем считать, что мир аналоговых величин состоит из идеального вещества, подчиняющегося идеальным законам в идеальном пространстве. Мир этот наполнен дифференциальными уравнениями, некоторые из которых описывают совершенно необычные вещи, например непрерывно действующую машину Тьюринга. Такая машина способна производить все действия, выполняемые дискретной машиной, и, может быть, намного больше. Попытка создания подобной машины из обычных электронных компонентов, вероятно, приведет к существенной потере в точности и быстродействии.
А.Вирджис из Университета штата Миннесота, К.Стейглитц и Б.Дикинсон из Принстонского университета (см. библиографию на с.104) создали устройство, которое выглядит более реалистично, чем аналоговая машина Тьюринга. Состоящее только из валиков, шестеренок и кулачков, оно решает логическую задачу, формируемую в виде логического выражения из сомножителей, каждый из которых является суммой трех литералов. Литерал - это логическая переменная (такая, как x) или ее отрицание (такое, как x'). Суммы трех литералов перемножаются, например так:
(x + y + z')*(x' + y' + z)
Задача заключается в том, чтобы установить, существует ли способ присвоить логические значения (истина или ложь) переменным x, y и z, чтобы значение всего выражения было истиной. Если выражение состоит только из двух сомножителей, как в данном случае, то ответ будет положительным. В самом деле, пусть значение x - истина, y - ложь и z - истина. Видно, что каждый сомножитель содержит по крайней мере один истинный литерал и поэтому значение всего выражения - истина. Хотя в рассмотренном примере задача выглядит простой, ее решение вызывает серьезные затруднения в более общих случаях (т.е. в задачах более высокой размерности). Более того, эта задача обладает свойством, которое вызывает благоговейный страх у специалистов по теории вычислений. Она относится к классу NP-полных задач: ни один известный алгоритм не дает ее решения за время, меньшее "экспоненциального". Другими словами, если число сомножителей равно n, то для решения задачи потребуется 2^n шагов вычисления.
И все же трем теоретикам удалось найти такую конструкцию из шестеренок, валиков и кулачков, которую можно настроить на решение любого частного случая рассмотренной выше логической задачи. Она имеет положительное решение тогда и только тогда, когда оказывается возможным повернуть определенный валик устройства.
В то же время ввиду того, что задача относится к классу NP-полных, она обладает одним примечательным свойством. Если ее удастся решить быстро, то это означает, что любая другая NP-полная задача также имеет быстрое решение. Однако в настоящее время большинство теоретиков считают, что алгоритма быстрого решения таких задач для цифрового компьютера не существует. Может быть, авторы открыли аналоговое устройство, превосходящее любую цифровую машину? Сейчас они тщательно исследуют конструкцию своего устройства в поисках возможной ошибки.
Если абстрактная модель машины действительно работает так, как было задумано авторами, остается открытым вопрос о том, будет ли правильно функционировать реальное устройство, построенное по этой абстрактной схеме. Какой-нибудь фундаментальный фактор, присущий материальному миру, может оказаться непреодолимым препятствием для реализации устройства. Возможно, существует некий природный закон, согласно которому любая физическая система может быть с одинаковым успехом описана и так же быстро смоделирована в цифровой форме, как и в любой лругой. Действительно, мы уже привыкли к представлению о том, что все свойства Вселенной по сути своей "цифровые". Все это означает, что аналоговый компьютер, который, казалось бы, превосходит своих цифровых собратьев, должен обладать какими-то существенными недостатками, например в точности или скорости вычислений. Единственное возможное преимущество у таких устройств - это их способность одновременно выполнять множество операций. Вспомним, например, устройство, действующее по принципу сообщающихся сосудов, в которых вола сразу устанавливается на одинаковом уровне.
БИБЛИОГРАФИЯ
SMART SOAP BUBBLES CAN DO CALCULUS. DALE T. HOFFMAN in The Mathematics Teacher, Vol.72, No.5, pages 377-385, 389; May, 1979.
AHA! GOTCHA: PARADOXES TO PUZZLE AND DELIGHT. MARTIN GARDNER. W.H.Freeman and Company, 1982. (Есть перевод: МАРТИН ГАРДНЕР, А НУ-КА ДОГАДАЙСЯ!- М.:"МИР", 1984.- G.)
THE COMPLEXITY OF ANALOG COMPUTATION. ANASTASIOS VERGIS, KENNETH STEIGLITZ AND BRADLEY DICKINSON. Technical Report No.337, Department of Electrical Engineering and Computer Science, Princeton University; February, 1985.
ОТКЛИКИ
11 1985
В АВГУСТОВСКОМ номере журнала я предложил читателям найти изящное доказательство утверждения о том, что при помощи приема Дж.Венмакера можно действительно отыскать самый длинный путь на "дереве", сделанном из шнурков. Я говорил, что для определения самого длинного пути достаточно двух операций подвешивания. Сначала нужно взять дерево за любой узел и подвесить его. Затем нужно взять дерево за самый нижний узел и снова подвесить его. Самый длинный путь проходит от узла, за который было подвешено дерево во второй раз, до узла, который теперь оказался самым нижним.
Выше мы неявно предполагали, что дерево имеет единственный самый длинный путь. На самом деле у дерева может быть несколько различных путей одинаковой длины, которая превышает длины всех остальных путей. Следовательно, на обоих шагах процедуры у нас есть выбор между несколькими узлами и в такой ситуации можно выбрать один из таких узлов произвольно.
Мне прислали значительно больше доказательств, чем я ожидал. Премию за самое изящное доказательство можно было бы присудить почти на равных основаниях следующим читателям: Дж.Бартольди III из Атланты (шт.Джорджия), Н.Дершовицу из Эрбаны (шт.Иллинойс), У.Липпу из Милфорда (шт.Коннектикут), Д.Миду из Дейвиса (шт.Калифорния), и Дж. ван-Бентему из Гронингена (Голландия). Нетрудно догадаться, что все эти лица, за исключением Липпа, так или иначе связаны с университетами. Это соответственно Технологический институт шт.Джорджия, ИлпинойсскиП университет в Эрбана-Шампейн, Калифорнийский университет в Дейвисе и Гронингенский государственный университет.
Под "иэящным доказательством" я подразумеваю сочетание краткости и ясности. В рамках нашей рубрики это означает также минимальное количество обозначений, уравнений и неравенств. С учетом всех этих требований победителем можно считать Бартольди. Вот его доказательство:
"Пусть H - точка подвеса, a L - нижняя точка. Утверждение: L должна быть одним из концов самого длинного пути.
Доказательство: Пусть A - другой конец самого длинного пути и А<>L. Путь максимальной длины, одним из концов которого является точка A, состоит из участка, ведущего вверх, и участка, ведущего вниз. Однако первый участок не превосходит расстояния от A до H, а второй участок не превосходит расстояния от H до L. Таким образом, путь от A до L представляет собой путь максимальной длины.
Если теперь подвесить дерево за точку L, то по аналогичным соображениям точка A окажется самой нижней".
Надо сказать, что приведенное доказательство скорее интуитивное, чем строгое. Тем не менее оно выглядит убедительным, потому что мы представляем себе мысленно, как участки самого длинного пути, проходящего через A, которые ведут соответственно вверх и вниз, висят рядом с путем от H к L. Строгое доказательство потребовало бы значительно больше места.
Первое устройство из тех, которые мы обсуждали в августовском выпуске журнала, состояло из доски, нескольких гвоздей, резиновых колец и длинного гладкого стержня. Это устройство позволяет найти прямую, наилучшим образом аппроксимирующую несколько экспериментальных точек на графике. Я говорил, что в доску нужно вбить гвозди, представляющие экспериментальные точки, затем накинуть резиновое кольцо на каждый гвоздь и на стержень, после чего следует отпустить стержень, который, подрожав, быстро приходит в равновесие.
Я утверждал, что равновесное положение стержня минимизирует полную потенциальную энергию системы (что правильно) и что, следовательно, сумма расстояний от точек до стержня, т.е. сумма отрезков, перпендикулярных стержню, должна быть минимальной (что неправильно). Я имел в виду формулу для силы, которая обусловлена растяжением резинки и пропорциональна ее удлинению. Однако, как заметили многие читатели, энергия, запасенная каждой резинкой, пропорциональна квадрату ее удлинения. Чувство стыда за эту оплошность было, однако, более чем скомпенсировано. Я понял, что устройство М.Хоули гораздо ближе к цели - вычислению по методу наименьших квадратов, чем я ожидал. Остается одно важное различие в том, что следует считать расстоянием. Для вычисления по методу наименьших квадратов нужно, чтобы резинки были натянуты вертикально, а не перпендикулярно стержню (если только стержень не занимает горизонтального положения).
Несколько читателей заметили, что резиновые кольца должны быть идеальными в том смысле, чтобы у них не было провисающих участков. Этому требованию можно удовлетворить следующими способами. Ч.Диллингем из Нью-Йорка (шт.Нью-Йорк), заменяет гвозди на цилиндры. Длина такого цилиндра равна длине нерастянухой резинки. Каждая резинка прикрепляется к доске
внутри цилиндра. Резинка удлиняется, только когда ее вытягивают из цилиндра и накидывают на стержень. Р.Файньюкейн из Уотербьюри (шт.Вермонт), решает эту проблему, пропуская каждую резинку через отверстие на доске, соответствующее экспериментальной точке.
Гидравлическое устройство для решения кубического уравнения не вызвало критических отзывов, за исключением замеченной несколькими читателями путаницы. Дело в том, что члены третьей и второй степеней уравнения представляются соответственно конусом и параболоидом, а не наоборот. В этом можно убедиться, проведя несложные вычисления.
Я думаю, что пройдет довольно значительное время, прежде чем мы сможем вернуться в наших статьях к аналоговым устройствам. Позвольте мне, так сказать, на прощание представить вам картонное устройство для подсчета площади земельного участка, присланное А.Лейзаром из Тинека (шт.Нью-Джерси).
Лейзар пользуется картонной коробкой, которую можно найти у любого продовольственного магазина, и портативными весами, чтобы проверять точность вычисления "площади земельного участка с нерегулярной границей". Он наносит контуры участка на лист картона и вырезает модель ножницами. Затем он взвешивает полученную модель и квадратик того же картона, отвечающий в принимаемом им масштабе площади 1акр. Поделив первый вес на второй, он получает площадь участка.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
9 1985
ПУТЕШЕСТВИЕ С РОБОТАМИ В РОБОТРОПОЛЕ И ОВЛАДЕНИЕ НАВЫКАМИ КОНСТРУИРОВАНИЯ ЭЛЕКТРОННЫХ МИКРОСХЕМ
А.К.ДЬЮДНИ
Эту игру уже тоже поминал - ТЕМА #44, АБЗАЦ #436
ТЕМА #44, АБЗАЦ #436 , и журнал выкладывал.- G.
, и журнал выкладывал.- G.
ПОДОБНО сталкивающимся галактикам, компьютерные игры и обучение с помощью компьютеров, постепенно сближаясь, кажется, готовы слиться воедино. Предвестником этого события можно считать появление в прошлом году компьютерной игры под названием "Одиссея роботов", которая одновременно с развлечением служит целям обучения в области конструирования электронных схем.
Уже создано немало программ, обучающих на основе игрового подхода. Однако ни в одной из них, насколько мне известно, не было достигнуто той степени интенсивности обучения и увлекательности, которая присуща игре "Одиссея роботов". Многие компьютерные игры являются результатом эволюции на пути от первобытного хаоса видеоигр к более упорядоченным и более интеллектуальным формам. По своей образовательной ценности ни одна из этих игр не может сравниться с "Одиссеей роботов".
"Одиссея роботов" ставит игрока в безвыходное положение: чтобы выбраться из Роботрополя - фантастического города, населенного исключительно роботами, играющий вынужден заняться конструированием логических схем. Большинство автоматов - обитателей города относится к людям враждебно. Когда игрок (представленный на экране дисплея в виде маленького гомункулуса) пытается выйти из лабиринта или заполучить нужный ему предмет, робот-сторож хватает гомункулуса и бесцеремонно вышвыривает его из помещения. Однако три робота оказываются полезными компаньонами в путешествии. Схемная конструкция роботов-компаньонов, которых роботы-сторожа не замечают, такова, что позволяет избегать столкновений с другими автоматами - обитателями Роботрополя, успешно выбираться из лабиринтов и завладевать такими предметами, как жетоны на проезд в метро и кристаллы - аккумуляторы энергии.

Вход в Роботрополь и три робота-компаньона
Может ли играющий на опыте проделанного путешествия сконструировать компьютер? Наверное, нет, однако упражнения окажутся весьма полезными. Игра начинается в помещении, называемом комнатой роботов. Здесь гомункулус, управляемый с клавиатуры, встречается с тремя роботами-компаньонами, весело пляшущими в прямоугольной области. Каждый робот ведет себя по-своему. Один скользит по комнате, прижимаясь к стенам. Другой скачет в горизонтальной плоскости взад и вперед. Третий методично обследует правую стену, как будто отыскивая выход. Играющий начинает с того, что набирает на клавиатуре букву R, и затем нажимает на клавишу, соответствующую пробелу. Это действие производит сюрреалистический эффект - гомункулус превращается в устройство, управляющее на расстоянии. Оно немедленно приказывает роботам остановиться. Теперь играющий может управлять гомункулусом. По команде последний, например, может забраться на любого робота. Когда он это делает, картинка на экране меняется: вместо происходящего в комнате действия появляется схематическое изображение внутреннего устройства робота. Гумункулус уменьшается в десять раз. Он может оседлать робота, пытаясь, например, найти выход из лабиринта или в какой-нибудь другой ситуации, когда манера передвижения данного робота оказывается подходящей.
Каждый робот-компаньон обладает сенсорными устройствами, благодаря которым он ориентируется в окружающей обстановке и может целенаправленно передвигаться. С помощью бамперов он ощущает контакт со стеной. У робота есть движки, толкающие его вверх, вниз, влево и вправо. Автоматическая рука с захватом может брать и высвобождать предметы. Связь с двумя другими роботами-компаньонами осуществляется при помощи антенны. Внутри каждого робота это оборудование представляется в виде соединительных линий, которые можно "припаять" к тому или иному участку логической схемы робота. Эти соединительные линии могут быть двух типов: входные, через которые передается информация о состоянии соответствующего сенсорного устройства (бампера, механической руки, антенны), и выходные, посредством которых команды от внутренней логической схемы передаются устройствам-эффекторам (толкающим движкам, механической руке, антенне). Таким образом, механическая рука и антенна имеют как входные, так и выходные соединительные линии. Выходная линия механической руки приводит ее в действие, а входная линия позволяет установить, держит ли рука в данный момент какой-нибудь предмет.
Посмотрим, как работают эти электронные устройства, наблюдая за поведением самого простого из трех роботов-компаньонов. Этот робот по имени Пинг-понг управляется единственным триггерным элементом, подсоединенным к горизонтальным бамперам и движкам. В "Одиссее роботов" триггерный элемент представляет собой двустороннюю ячейку памяти, в которой одна сторона содержит единицу, в то время как другая - нуль. Когда по входной линии, подсоединенной к нулевой стороне, приходит сигнал, пусть даже длящийся одно мгновение, эта сторона переключается с нуля на единицу, а другая сторона - с единицы на нуль. При отсутствии изменений на входах триггер сохраняет свое состояние. Он как бы запоминает его. Чтобы реализовать поведение Пинг-понга, не требуется ничего, кроме описанного простого триггера. Выходная линия с одной стороны триггера соединена с правым движком робота, а входная линия с той же стороны триггера соединена с правым бампером. Если на этой стороне триггера содержится нуль и робот коснется стены справа, то по входной линии сигнал от бампера передается триггеру. Триггер немедленно меняет свое состояние - там, где был нуль, теперь единица. В результате включается правый движок и робот начинает двигаться влево. Назовем эту стадию "пинг". Стадия "понг" реализуется аналогичным образом путем соединения противоположной стороны триггера с левым бампером и левым движком.
Чтобы реализовать более сложное поведение, требуется полный стандартный набор логических элементов. В этот набор помимо триггерного запоминающего элемента входят также элементы, принимающие решение и называемые вентилями типа ИЛИ, И и НЕ. Последний называется также инвертором. На выходе вентиля ИЛИ всегда единица, когда по крайней мере на одном из его входов имеется единица. На выходе вентиля И будет единица, когда на всех его входах единица. На выходе инвертора единица будет тогда, когда на его входе нуль.
Логические элементы для игры "Одиссея роботов" и их нетривиальное использование.- G.
Чтобы покинуть комнату роботов, играющий должен извлечь ключ, находящийся внутри одного из роботов, и открыть дверь, ведущую к месту, называемому городской свалкой. Чтобы подобрать какой-нибудь предмет, нужно "наехать" на него гомункулусом и нажать клавишу пробела. Об успехе действия свидетельствует звуковой сигнал. После этого предмет движется вместе с гомункулусом. Без этого средства игра "Одиссея роботов" была бы невозможна: в своих путешествиях по пяти уровням игры гомункулус должен нести с собой трех роботов-компаньонов. Да, но как он может нести с собой роботов, если по условиям игры нести можно только один предмет? Поскольку любой предмет можно поместить внутрь робота и так как робот тоже представляет собой предмет, играющий быстро догадывается, что одного робота можно поместить внутрь другого. Этот прием действует. На самом деле гомункулус может нести с собой робота, внутри которого находится второй робот, а в этом последнем заключен третий. Благодаря такому приему можно сэкономить место внутри внешнего робота. Это необходимо, потому что по мере развития игры в нем накапливаются разнообразные предметы, такие, как жетоны на проезд, сенсоры, кристаллы-аккумуляторы и всевозможные логические элементы.
Моя собственная партия игры в "Одиссею роботов" началась, как мне показалось, с бесконечного путешествия по помещениям, прилегающим к городской свалке. В центральном помещении я набрел на комнату, ревностно охраняемую одним из самых неприятных обитателей Роботрополя. В дальней части комнаты у стены лежал кристалл-аккумулятор энергии. Стремясь завладеть им, я извлек робота, исследующего стены, из Пинг-понга и привел его в движение. Незамеченный сторожем робот заскользил по стене. Наткнувшись на кристалл, робот захватил его механической рукой, издав при этом звуковой сигнал, и продолжил свое движение вдоль стены, теперь уже по направлению к выходу. Здесь я выключил робота, ходящего вдоль стен, и попытался извлечь кристалл-аккумулятор из его механической руки. Робот почему-то не выпускал его. Отложив решение этой задачи на более позднее время, я снова поместил робота, ходящего вдоль стен, внутрь Пинг-понга и хотел уже было продолжить свою одиссею, когда услышал какое-то скрежетание, а затем постепенно слабеющий звук, сигнализирующий о том, что питающая батарея истощилась. Оказывается, робот по имени Вампир только что запустил свой электрический хобот в Пинг-понга и высосал из него половину энергии. В Роботрополе нужно всегда быть начеку.
Поблуждав некоторое время по городу и подобрав по пути кое-какие полезные с виду предметы, я вышел к проходу с надписью "Есть ли у вас все необходимое?". И тут я вспомнил, что позабыл забрать магнит из соседнего с городской свалкой помещения, так как боялся встретить Вампира, который, по-видимому, патрулировал в районе свалки. Мой гомункулус миновал надпись, и перед ним открылся лабиринт городской свалки. Он представлял собой вертикальные стены, то поднимающиеся снизу вверх, то свисающие сверху вниз (см.рисунок). Лабиринт охранялся еще одним роботом, встреча с которым не предвещала ничего хорошего.

Лабиринт городской свалки, выход из которого должен найти правосторонний робот
Один из моих роботов-компаньонов, как мне показалось, был создан для подобных ситуаций. Когда включается робот, которого я называю правосторонним, он всегда движется вправо. Если его дальнейшему движению по правой стороне мешает стена, правосторонний робот начинает скользить вдоль нее, пока не упрется в горизонтальную стену, где он сразу меняет направление движения. Поведение робота становится понятным, если посмотреть на его внутреннюю логическую схему (см.рисунок). Во-первых, левый движок всегда включен, поскольку линия, управляющая им, проходит через инвертор, на который не подается сигнал (и так как на входе инвертора нуль, то на его выходе единица). Управление вертикальными движками осуществляется триггерным элементом, входы и выходы которого аналогичны схеме, управляющей Пинг-понгом. Отличие, однако, состоит в том, что выходные линии, подсоединенные к вертикальным движкам, проходят через вентили И. В качестве второго входа для каждого вентиля И выступает линия, соединенная с правым бампером. Это означает, что команда включить верхний или нижний движок не будет выполнена, если правый бампер не находится в контакте с каким-либо препятствием.

Бамперы, толкающие движки, механическая рука, антенна, соединительные линии и электронные схемы правостороннего робота
Я извлек правостороннего робота из робота, которого я нес с собой, и посадил на него своего гомункулуса. Поместив гомункулуса непосредственно на место символа, имеющего форму глаза, я получил возможность перископического обозрения окружающей обстановки вне правостороннего робота. Его внутренний вид сменился на экране дисплея видом лабиринта. В левой части картинки я увидел правостороннего робота с торчащим из него перископом. Правда, было не совсем понятно, каким образом сцена могла включать сам прибор, из которого ведется наблюдение, однако я не стал об этом задумываться.
Гомункулус, устроившийся у перископического глаза, мог теперь выполнять функции управления. Я нажал букву R, а затем пробел. Правосторонний робот вместе с сидящим в нем гомункулусом заскользил по лабиринту и уперся в стену. Пройдя вверх вдоль стены, мы дошли до тупика, отскочили вниз и добрались до прохода в стене. Здесь под нависающей сверху стеной мы увидели останки неудачливых гомункулусов, не сумевших найти выход из лабиринта. Далее мы проскользнули мимо робота-сторожа, который, казалось, не замечал, что вместе с правосторонним роботом движется человеческое существо. Миновав проход, мы встретились с еще одной вертикальной стеной, и поползли вверх. Когда мы наконец выбрались из лабиринта, я понял, что совершил ужасную ошибку, оставив двух других роботов-компаньонов позади. Страх встречи с Вампиром сбил меня с толку. Каким образом можно было вернуться за моими роботами? Нужно было переделать правостороннего робота. Возможно, читатели, поразмыслив над его устройством, сами догадываются, как это сделать.
Чтобы перепаять какую-нубудь схему робота, нужно нажать букву S - и гомункулус превращается в паяльник. В этом режиме клавиша пробела используется, чтобы разорвать старые соединения и создать новые. Если вам не хватает какой-нибудь детали, нужно нажать на букву Т - и на экране появляется набор деталей. Гомункулус может погрузиться в него и взять нужный элемент.
Когда я наконец собрал всех трех роботов-компаньонов у выхода из лабиринта, моя одиссея продолжалась. Теперь на нашем пути была запертая комната. Воспользовавшись ключом, я открыл ее и, войдя, обнаружил, что у нее не было другого выхода. Куда же идти? На стене я увидел зловещую надпись: "Приготовьтесь, вы будете переведены в другое измерение!" Посреди комнаты в неподвижном прямоугольнике плясал двойник моего гомункулуса.
В ходе игры можно в любой момент запомнить ее состояние, записав его на свободный диск. При этом игра как бы спасается. Если следующий ход обернется катастрофой, то игру можно переиграть, начиная с запомненного положения. Эта возможность присуща многим приключенческим играм, реализованным на компьютерах. Надеемся, что у молодых людей, увлекающихся этими играми, не сложится впечатление, что и в реальной жизни, полной приключений, тоже Можно вернуться к какому-то моменту в прошлом, чтобы потом все сделать по-другому.
Таким образом я спас игру и, наехав своим гомункулусом на его двойника, нажал на клавишу пробела. Казалось, все взорвалось в фейерверке искр, и мой переход в новое измерение сопровождался каким-то странным звуком. На самом деле я очутился в другом помещении на втором уровне Роботрополя, но... без своих компаньонов. Очевидно, я забыл из взять с собой. Воспользовавшись запомненным положением, теперь можно было переиграть фазу, предшествовавшую переходу в другое измерение, приняв меры к тому, чтобы не потерять своих роботов.
Я не буду описывать своих дальнейших приключений в Роботрополе, чтобы не лишать удовольствия читателей, которые пожелают сами сыграть в эту игру.
Помимо самой игры покупатели "Одиссеи роботов" получают записанные на диске сведения об анатомии роботов, о том, как пользоваться набором деталей, а также руководство по конструированию электронных логических схем. Конструирование происходит в помещении, называемом лабораторией новой техники.
В любой момент в ходе игры играющий может перейти в лабораторию и испытать новые логические схемы на роботах, которые там находятся. По мере того как схемы увеличиваются в размерах и усложняются, становится целесообразным реализовывать их в виде интегральных схем (т.е. схем, смонтированных в одном кристалле). Это делается в специально отведенной комнате лаборатории.
Внутренности робота, ходящего вдоль стены. Какая электронная логическая схема управляет им?
Один из роботов-компаньонов, а именно робот, двигающийся вдоль стены, был уже снабжен такой интегральной схемой. Входные и выходные соединительные линии этой интегральной схемы изображены на рисунке, приведенном вверху. Читателям, наверное, будет интересно самостоятельно сконструировать интегральную схему для управления роботом, ходящим вдоль стены. При этом разрешается пользоваться только триггерами и логическими элементами, о которых говорилось выше. Я с удовольствием рассмотрю присланные читателями схемы, однако некоторым читателям, возможно, захочется самим посмотреть на свои конструкции в действии.
Игра "Одиссея роботов" была изобретена и реализована в виде компьютерной программы М.Уоллесом, когда он был студентом Станфордского университета, и Л.Гриммом, сотрудником фирмы Learning Company. У этой игры в коллекции фирмы Learning Company были предшественники. В таких играх, как "Головоломки Гертруды" и "Сапоги Рокки", от играющего также требуется умение конструировать логические схемы для решения задач. У.Робиннет, в прошлом сотрудник фирмы, придумал для всех этих игр интересную пространственную среду, в которой должны происходить игровые действия. Например, помещения и проходы Роботрополя конечны, но они сменяют друг друга до бесконечности, пока играющий не поймет, что, покидая комнату Через правый выход, он может очутиться у левого входа какой-нибудь комнаты, в которой он уже побывал.
Конечно, логические схемы, конструируемые для игры "Одиссея роботов", не сравнить по сложности со схемами для современного компьютера. Тем не менее, пользуясь компонентами, имеющимися в распоряжении играющего, можно построить простейший компьютер. Игроки, усвоившие правила игры и хорошо пользующиеся ими, возможно, захотят узнать, можно ли создать компьютер, для того чтобы встроить его в робот. Такой компьютер мог бы быть программируемым путем ввода последовательности нулей и единиц перед тем, как робот начнет действовать. Такая последовательность играла бы роль ультрапростого языка, а подпоследовательности из нулей и единиц представляли бы, например, такие команды, как "Двигаться вправо до стены" или "Привести в действие механический захват".
Процесс конструирования логической схемы современного компьютера сводится к размещению огромного числа полупроводниковых транзисторов и других электронных компонентов в виде большой плоской схемы, хранящейся в памяти ЭВМ. После проверки и отладки с помощью моделирования эта схема переносится на фотопленку и затем вытравляется в кремниевом кристалле. На первый взгляд этот очень сложный процесс имеет мало общего с вентилями и триггерами, используемыми в игре "Одиссея роботов", и даже с технологией, описываемой в большинстве университетских учебников по основам конструирования логических. схем. Однако между тем и другим все же есть немало общего. Как объяснил мне несколько лет назад К.Клейр, теперь работающий в фирме СТХ International в г.Саннивейл (шт.Калифорния), учащиеся, занимаясь построением стандартных логических схем, развивают в себе способность к абстрактному мышлению, которое необходимо будущему инженеру - конструктору электронных устройств. При разработке той или иной электронной схемы сначала нужно представить задачу на абстрактном уровне и попытаться решить ее, оперируя только вентилями И, ИЛИ, НЕ и триггерными элементами. Навыки абстрактного мышления помогают затем и при работе на более сложном уровне реальных полупроводниковых приборов, таких, как полевые транзисторы и другие современные электронные компоненты, используемые в различных логических устройствах.
По словам П.Эшкина, одного из ведущих специалистов-разработчиков фирмы Apple, производящей персональные компьютеры, игра "Одиссея роботов" является в этом смысле весьма полезной. Эшкин говорит, что благодаря этой игре учащийся развивает в себе два навыка, необходимых хорошему инженеру - конструктору ЭВМ: умение четко осознать поставленную задачу и способность представить решение в виде логических схем любого типа. Например, когда я в последний раз играл в "Одиссею роботов", передо мной возникла задача завладеть жетоном, лежащим посредине охраняемой комнаты. Было ясно, что это дело следует поручить одному из роботов-компаньонов. Однако каким образом он мог осуществить эту операцию? Робот, ходящий вдоль стены, здесь был бесполезен, поскольку он никогда не может приблизиться к жетону настолько, чтобы захватить его механической рукой. В моем распоряжении был специальный датчик, обнаруживающий жетоны и имеющий выходы, позволяющие определить направление на жетон. С помощью этого прибора робот, несомненно, найдет жетон, но, к сожалению, тот же прибор не позволит роботу покинуть то место, где был найден жетон. Во всяком случае, проанализировав ситуацию, я выделил две отдельные задачи: построить схему, отыскивающую жетоны, и найти способ запрограммировать робота так, чтобы он мог выбраться из комнаты. Хотя некоторые задачи выглядят сначала несколько расплывчато, Эшкин отмечает, что их маленькие, "байтового размера" подзадачи поддаются решению. При таком разбиении постановка задачи становится более четкой. Процесс постановки задачи и решение составляющих ее подзадач на уровне логических схем - две важные фазы разработки устройства.
То, что играющий обретает способность самостоятельно конструировать логические схемы, имеет также важное психологическое значение. По мере того как играющий приобретает опыт, перепаивая схемы роботов-компаньонов, у него развивается чувство уверенности в своих силах, а уверенность - это отличное противоядие от ощущения холодной неприступности, которое порой внушают нам компьютеры. Обучившись оперировать стандартными логическими схемами в игре "Одиссея роботов", играющий подходит к пониманию аналогичных взаимоотношений, существующих между основными логическими элементами компьютера и его функционированием. Играющий чувствует, что нет никаких непреодолимых препятствий на пути более глубокого исследования. Ощущение загадки, таящейся в черном ящике, пропадает. Человек начинает чувствовать себя полным хозяином положения.
Однако это ощущение всесилия, развивающееся на определенной стадии у начинающих, может затем снова быть утраченным, как утверждает Ш.Теркл, автор книги "The Second Self" ("Второе Я"). Ее книга посвящена тому, как развиваются взаимоотношения между людьми и компьютерами. Несколько страшноватыми выглядят некоторые истории о тех, кто начинает рассматривать самого себя как машиноподобное существо. Мне представляется, что подобная точка зрения может развиться на любой стадии овладения теорией и практикой вычислительной техники. Я знаком со специалистами в области искусственного интеллекта, которые также находят в себе нечто общее с машиной, но, правда, в более тонком понимании этого слова. В каком-то смысле, может быть, и правда, что все мы машины, однако такая точка зрения мало помогает нам в вопросах, касающихся нашего поведения, и может даже способствовать тому, что человек примет такую линию поведения, которая приведет к самым неприятным последствиям. Возможно, именно поэтому, образно говоря, нам следует научиться убегать из Роботрополя.
ОТКЛИКИ
12 1985
В СТАТЬЕ из рубрики "Занимательный компьютер", помешенной в сентябрьском номере нашего журнала, читателям было предложено сконструировать управляющую логическую схему для робота, ходящего по стене. Задача эта значительно труднее, чем может показаться с первого взгляда. Главная трудность заключается в преодолении выпуклых углов: если не отключить движок, когда встречается такой угол, то робот спокойно отойдет от стены и начнет двигаться внутрь помещения.
Из присланных до сих пор решений только два представляются мне правильными. Ж.Шваб, консультант по автоматизированной обработке данных из Медона (Франция), и Дж. Грегор, лейтенант военно-воздушных сил США, в настоящее время проходящий службу на базе ВВС в Лэнгли, оба сконструировали схемы с четырьмя триггерными элементами. Возможно, двух триггеров недостаточно для построения схемы.
ПУТЕШЕСТВИЕ С РОБОТАМИ В РОБОТРОПОЛЕ И ОВЛАДЕНИЕ НАВЫКАМИ КОНСТРУИРОВАНИЯ ЭЛЕКТРОННЫХ МИКРОСХЕМ
А.К.ДЬЮДНИ
Эту игру уже тоже поминал -
 ТЕМА #44, АБЗАЦ #436
ТЕМА #44, АБЗАЦ #436 , и журнал выкладывал.- G.
, и журнал выкладывал.- G.ПОДОБНО сталкивающимся галактикам, компьютерные игры и обучение с помощью компьютеров, постепенно сближаясь, кажется, готовы слиться воедино. Предвестником этого события можно считать появление в прошлом году компьютерной игры под названием "Одиссея роботов", которая одновременно с развлечением служит целям обучения в области конструирования электронных схем.
Уже создано немало программ, обучающих на основе игрового подхода. Однако ни в одной из них, насколько мне известно, не было достигнуто той степени интенсивности обучения и увлекательности, которая присуща игре "Одиссея роботов". Многие компьютерные игры являются результатом эволюции на пути от первобытного хаоса видеоигр к более упорядоченным и более интеллектуальным формам. По своей образовательной ценности ни одна из этих игр не может сравниться с "Одиссеей роботов".
"Одиссея роботов" ставит игрока в безвыходное положение: чтобы выбраться из Роботрополя - фантастического города, населенного исключительно роботами, играющий вынужден заняться конструированием логических схем. Большинство автоматов - обитателей города относится к людям враждебно. Когда игрок (представленный на экране дисплея в виде маленького гомункулуса) пытается выйти из лабиринта или заполучить нужный ему предмет, робот-сторож хватает гомункулуса и бесцеремонно вышвыривает его из помещения. Однако три робота оказываются полезными компаньонами в путешествии. Схемная конструкция роботов-компаньонов, которых роботы-сторожа не замечают, такова, что позволяет избегать столкновений с другими автоматами - обитателями Роботрополя, успешно выбираться из лабиринтов и завладевать такими предметами, как жетоны на проезд в метро и кристаллы - аккумуляторы энергии.

Вход в Роботрополь и три робота-компаньона
Может ли играющий на опыте проделанного путешествия сконструировать компьютер? Наверное, нет, однако упражнения окажутся весьма полезными. Игра начинается в помещении, называемом комнатой роботов. Здесь гомункулус, управляемый с клавиатуры, встречается с тремя роботами-компаньонами, весело пляшущими в прямоугольной области. Каждый робот ведет себя по-своему. Один скользит по комнате, прижимаясь к стенам. Другой скачет в горизонтальной плоскости взад и вперед. Третий методично обследует правую стену, как будто отыскивая выход. Играющий начинает с того, что набирает на клавиатуре букву R, и затем нажимает на клавишу, соответствующую пробелу. Это действие производит сюрреалистический эффект - гомункулус превращается в устройство, управляющее на расстоянии. Оно немедленно приказывает роботам остановиться. Теперь играющий может управлять гомункулусом. По команде последний, например, может забраться на любого робота. Когда он это делает, картинка на экране меняется: вместо происходящего в комнате действия появляется схематическое изображение внутреннего устройства робота. Гумункулус уменьшается в десять раз. Он может оседлать робота, пытаясь, например, найти выход из лабиринта или в какой-нибудь другой ситуации, когда манера передвижения данного робота оказывается подходящей.
Каждый робот-компаньон обладает сенсорными устройствами, благодаря которым он ориентируется в окружающей обстановке и может целенаправленно передвигаться. С помощью бамперов он ощущает контакт со стеной. У робота есть движки, толкающие его вверх, вниз, влево и вправо. Автоматическая рука с захватом может брать и высвобождать предметы. Связь с двумя другими роботами-компаньонами осуществляется при помощи антенны. Внутри каждого робота это оборудование представляется в виде соединительных линий, которые можно "припаять" к тому или иному участку логической схемы робота. Эти соединительные линии могут быть двух типов: входные, через которые передается информация о состоянии соответствующего сенсорного устройства (бампера, механической руки, антенны), и выходные, посредством которых команды от внутренней логической схемы передаются устройствам-эффекторам (толкающим движкам, механической руке, антенне). Таким образом, механическая рука и антенна имеют как входные, так и выходные соединительные линии. Выходная линия механической руки приводит ее в действие, а входная линия позволяет установить, держит ли рука в данный момент какой-нибудь предмет.
Посмотрим, как работают эти электронные устройства, наблюдая за поведением самого простого из трех роботов-компаньонов. Этот робот по имени Пинг-понг управляется единственным триггерным элементом, подсоединенным к горизонтальным бамперам и движкам. В "Одиссее роботов" триггерный элемент представляет собой двустороннюю ячейку памяти, в которой одна сторона содержит единицу, в то время как другая - нуль. Когда по входной линии, подсоединенной к нулевой стороне, приходит сигнал, пусть даже длящийся одно мгновение, эта сторона переключается с нуля на единицу, а другая сторона - с единицы на нуль. При отсутствии изменений на входах триггер сохраняет свое состояние. Он как бы запоминает его. Чтобы реализовать поведение Пинг-понга, не требуется ничего, кроме описанного простого триггера. Выходная линия с одной стороны триггера соединена с правым движком робота, а входная линия с той же стороны триггера соединена с правым бампером. Если на этой стороне триггера содержится нуль и робот коснется стены справа, то по входной линии сигнал от бампера передается триггеру. Триггер немедленно меняет свое состояние - там, где был нуль, теперь единица. В результате включается правый движок и робот начинает двигаться влево. Назовем эту стадию "пинг". Стадия "понг" реализуется аналогичным образом путем соединения противоположной стороны триггера с левым бампером и левым движком.
Чтобы реализовать более сложное поведение, требуется полный стандартный набор логических элементов. В этот набор помимо триггерного запоминающего элемента входят также элементы, принимающие решение и называемые вентилями типа ИЛИ, И и НЕ. Последний называется также инвертором. На выходе вентиля ИЛИ всегда единица, когда по крайней мере на одном из его входов имеется единица. На выходе вентиля И будет единица, когда на всех его входах единица. На выходе инвертора единица будет тогда, когда на его входе нуль.

Логические элементы для игры "Одиссея роботов" и их нетривиальное использование.- G.
Чтобы покинуть комнату роботов, играющий должен извлечь ключ, находящийся внутри одного из роботов, и открыть дверь, ведущую к месту, называемому городской свалкой. Чтобы подобрать какой-нибудь предмет, нужно "наехать" на него гомункулусом и нажать клавишу пробела. Об успехе действия свидетельствует звуковой сигнал. После этого предмет движется вместе с гомункулусом. Без этого средства игра "Одиссея роботов" была бы невозможна: в своих путешествиях по пяти уровням игры гомункулус должен нести с собой трех роботов-компаньонов. Да, но как он может нести с собой роботов, если по условиям игры нести можно только один предмет? Поскольку любой предмет можно поместить внутрь робота и так как робот тоже представляет собой предмет, играющий быстро догадывается, что одного робота можно поместить внутрь другого. Этот прием действует. На самом деле гомункулус может нести с собой робота, внутри которого находится второй робот, а в этом последнем заключен третий. Благодаря такому приему можно сэкономить место внутри внешнего робота. Это необходимо, потому что по мере развития игры в нем накапливаются разнообразные предметы, такие, как жетоны на проезд, сенсоры, кристаллы-аккумуляторы и всевозможные логические элементы.
Моя собственная партия игры в "Одиссею роботов" началась, как мне показалось, с бесконечного путешествия по помещениям, прилегающим к городской свалке. В центральном помещении я набрел на комнату, ревностно охраняемую одним из самых неприятных обитателей Роботрополя. В дальней части комнаты у стены лежал кристалл-аккумулятор энергии. Стремясь завладеть им, я извлек робота, исследующего стены, из Пинг-понга и привел его в движение. Незамеченный сторожем робот заскользил по стене. Наткнувшись на кристалл, робот захватил его механической рукой, издав при этом звуковой сигнал, и продолжил свое движение вдоль стены, теперь уже по направлению к выходу. Здесь я выключил робота, ходящего вдоль стен, и попытался извлечь кристалл-аккумулятор из его механической руки. Робот почему-то не выпускал его. Отложив решение этой задачи на более позднее время, я снова поместил робота, ходящего вдоль стен, внутрь Пинг-понга и хотел уже было продолжить свою одиссею, когда услышал какое-то скрежетание, а затем постепенно слабеющий звук, сигнализирующий о том, что питающая батарея истощилась. Оказывается, робот по имени Вампир только что запустил свой электрический хобот в Пинг-понга и высосал из него половину энергии. В Роботрополе нужно всегда быть начеку.
Поблуждав некоторое время по городу и подобрав по пути кое-какие полезные с виду предметы, я вышел к проходу с надписью "Есть ли у вас все необходимое?". И тут я вспомнил, что позабыл забрать магнит из соседнего с городской свалкой помещения, так как боялся встретить Вампира, который, по-видимому, патрулировал в районе свалки. Мой гомункулус миновал надпись, и перед ним открылся лабиринт городской свалки. Он представлял собой вертикальные стены, то поднимающиеся снизу вверх, то свисающие сверху вниз (см.рисунок). Лабиринт охранялся еще одним роботом, встреча с которым не предвещала ничего хорошего.

Лабиринт городской свалки, выход из которого должен найти правосторонний робот
Один из моих роботов-компаньонов, как мне показалось, был создан для подобных ситуаций. Когда включается робот, которого я называю правосторонним, он всегда движется вправо. Если его дальнейшему движению по правой стороне мешает стена, правосторонний робот начинает скользить вдоль нее, пока не упрется в горизонтальную стену, где он сразу меняет направление движения. Поведение робота становится понятным, если посмотреть на его внутреннюю логическую схему (см.рисунок). Во-первых, левый движок всегда включен, поскольку линия, управляющая им, проходит через инвертор, на который не подается сигнал (и так как на входе инвертора нуль, то на его выходе единица). Управление вертикальными движками осуществляется триггерным элементом, входы и выходы которого аналогичны схеме, управляющей Пинг-понгом. Отличие, однако, состоит в том, что выходные линии, подсоединенные к вертикальным движкам, проходят через вентили И. В качестве второго входа для каждого вентиля И выступает линия, соединенная с правым бампером. Это означает, что команда включить верхний или нижний движок не будет выполнена, если правый бампер не находится в контакте с каким-либо препятствием.

Бамперы, толкающие движки, механическая рука, антенна, соединительные линии и электронные схемы правостороннего робота
Я извлек правостороннего робота из робота, которого я нес с собой, и посадил на него своего гомункулуса. Поместив гомункулуса непосредственно на место символа, имеющего форму глаза, я получил возможность перископического обозрения окружающей обстановки вне правостороннего робота. Его внутренний вид сменился на экране дисплея видом лабиринта. В левой части картинки я увидел правостороннего робота с торчащим из него перископом. Правда, было не совсем понятно, каким образом сцена могла включать сам прибор, из которого ведется наблюдение, однако я не стал об этом задумываться.
Гомункулус, устроившийся у перископического глаза, мог теперь выполнять функции управления. Я нажал букву R, а затем пробел. Правосторонний робот вместе с сидящим в нем гомункулусом заскользил по лабиринту и уперся в стену. Пройдя вверх вдоль стены, мы дошли до тупика, отскочили вниз и добрались до прохода в стене. Здесь под нависающей сверху стеной мы увидели останки неудачливых гомункулусов, не сумевших найти выход из лабиринта. Далее мы проскользнули мимо робота-сторожа, который, казалось, не замечал, что вместе с правосторонним роботом движется человеческое существо. Миновав проход, мы встретились с еще одной вертикальной стеной, и поползли вверх. Когда мы наконец выбрались из лабиринта, я понял, что совершил ужасную ошибку, оставив двух других роботов-компаньонов позади. Страх встречи с Вампиром сбил меня с толку. Каким образом можно было вернуться за моими роботами? Нужно было переделать правостороннего робота. Возможно, читатели, поразмыслив над его устройством, сами догадываются, как это сделать.
Чтобы перепаять какую-нубудь схему робота, нужно нажать букву S - и гомункулус превращается в паяльник. В этом режиме клавиша пробела используется, чтобы разорвать старые соединения и создать новые. Если вам не хватает какой-нибудь детали, нужно нажать на букву Т - и на экране появляется набор деталей. Гомункулус может погрузиться в него и взять нужный элемент.
Когда я наконец собрал всех трех роботов-компаньонов у выхода из лабиринта, моя одиссея продолжалась. Теперь на нашем пути была запертая комната. Воспользовавшись ключом, я открыл ее и, войдя, обнаружил, что у нее не было другого выхода. Куда же идти? На стене я увидел зловещую надпись: "Приготовьтесь, вы будете переведены в другое измерение!" Посреди комнаты в неподвижном прямоугольнике плясал двойник моего гомункулуса.
В ходе игры можно в любой момент запомнить ее состояние, записав его на свободный диск. При этом игра как бы спасается. Если следующий ход обернется катастрофой, то игру можно переиграть, начиная с запомненного положения. Эта возможность присуща многим приключенческим играм, реализованным на компьютерах. Надеемся, что у молодых людей, увлекающихся этими играми, не сложится впечатление, что и в реальной жизни, полной приключений, тоже Можно вернуться к какому-то моменту в прошлом, чтобы потом все сделать по-другому.
Таким образом я спас игру и, наехав своим гомункулусом на его двойника, нажал на клавишу пробела. Казалось, все взорвалось в фейерверке искр, и мой переход в новое измерение сопровождался каким-то странным звуком. На самом деле я очутился в другом помещении на втором уровне Роботрополя, но... без своих компаньонов. Очевидно, я забыл из взять с собой. Воспользовавшись запомненным положением, теперь можно было переиграть фазу, предшествовавшую переходу в другое измерение, приняв меры к тому, чтобы не потерять своих роботов.
Я не буду описывать своих дальнейших приключений в Роботрополе, чтобы не лишать удовольствия читателей, которые пожелают сами сыграть в эту игру.
Помимо самой игры покупатели "Одиссеи роботов" получают записанные на диске сведения об анатомии роботов, о том, как пользоваться набором деталей, а также руководство по конструированию электронных логических схем. Конструирование происходит в помещении, называемом лабораторией новой техники.
В любой момент в ходе игры играющий может перейти в лабораторию и испытать новые логические схемы на роботах, которые там находятся. По мере того как схемы увеличиваются в размерах и усложняются, становится целесообразным реализовывать их в виде интегральных схем (т.е. схем, смонтированных в одном кристалле). Это делается в специально отведенной комнате лаборатории.

Внутренности робота, ходящего вдоль стены. Какая электронная логическая схема управляет им?
Один из роботов-компаньонов, а именно робот, двигающийся вдоль стены, был уже снабжен такой интегральной схемой. Входные и выходные соединительные линии этой интегральной схемы изображены на рисунке, приведенном вверху. Читателям, наверное, будет интересно самостоятельно сконструировать интегральную схему для управления роботом, ходящим вдоль стены. При этом разрешается пользоваться только триггерами и логическими элементами, о которых говорилось выше. Я с удовольствием рассмотрю присланные читателями схемы, однако некоторым читателям, возможно, захочется самим посмотреть на свои конструкции в действии.
Игра "Одиссея роботов" была изобретена и реализована в виде компьютерной программы М.Уоллесом, когда он был студентом Станфордского университета, и Л.Гриммом, сотрудником фирмы Learning Company. У этой игры в коллекции фирмы Learning Company были предшественники. В таких играх, как "Головоломки Гертруды" и "Сапоги Рокки", от играющего также требуется умение конструировать логические схемы для решения задач. У.Робиннет, в прошлом сотрудник фирмы, придумал для всех этих игр интересную пространственную среду, в которой должны происходить игровые действия. Например, помещения и проходы Роботрополя конечны, но они сменяют друг друга до бесконечности, пока играющий не поймет, что, покидая комнату Через правый выход, он может очутиться у левого входа какой-нибудь комнаты, в которой он уже побывал.
Конечно, логические схемы, конструируемые для игры "Одиссея роботов", не сравнить по сложности со схемами для современного компьютера. Тем не менее, пользуясь компонентами, имеющимися в распоряжении играющего, можно построить простейший компьютер. Игроки, усвоившие правила игры и хорошо пользующиеся ими, возможно, захотят узнать, можно ли создать компьютер, для того чтобы встроить его в робот. Такой компьютер мог бы быть программируемым путем ввода последовательности нулей и единиц перед тем, как робот начнет действовать. Такая последовательность играла бы роль ультрапростого языка, а подпоследовательности из нулей и единиц представляли бы, например, такие команды, как "Двигаться вправо до стены" или "Привести в действие механический захват".
Процесс конструирования логической схемы современного компьютера сводится к размещению огромного числа полупроводниковых транзисторов и других электронных компонентов в виде большой плоской схемы, хранящейся в памяти ЭВМ. После проверки и отладки с помощью моделирования эта схема переносится на фотопленку и затем вытравляется в кремниевом кристалле. На первый взгляд этот очень сложный процесс имеет мало общего с вентилями и триггерами, используемыми в игре "Одиссея роботов", и даже с технологией, описываемой в большинстве университетских учебников по основам конструирования логических. схем. Однако между тем и другим все же есть немало общего. Как объяснил мне несколько лет назад К.Клейр, теперь работающий в фирме СТХ International в г.Саннивейл (шт.Калифорния), учащиеся, занимаясь построением стандартных логических схем, развивают в себе способность к абстрактному мышлению, которое необходимо будущему инженеру - конструктору электронных устройств. При разработке той или иной электронной схемы сначала нужно представить задачу на абстрактном уровне и попытаться решить ее, оперируя только вентилями И, ИЛИ, НЕ и триггерными элементами. Навыки абстрактного мышления помогают затем и при работе на более сложном уровне реальных полупроводниковых приборов, таких, как полевые транзисторы и другие современные электронные компоненты, используемые в различных логических устройствах.
По словам П.Эшкина, одного из ведущих специалистов-разработчиков фирмы Apple, производящей персональные компьютеры, игра "Одиссея роботов" является в этом смысле весьма полезной. Эшкин говорит, что благодаря этой игре учащийся развивает в себе два навыка, необходимых хорошему инженеру - конструктору ЭВМ: умение четко осознать поставленную задачу и способность представить решение в виде логических схем любого типа. Например, когда я в последний раз играл в "Одиссею роботов", передо мной возникла задача завладеть жетоном, лежащим посредине охраняемой комнаты. Было ясно, что это дело следует поручить одному из роботов-компаньонов. Однако каким образом он мог осуществить эту операцию? Робот, ходящий вдоль стены, здесь был бесполезен, поскольку он никогда не может приблизиться к жетону настолько, чтобы захватить его механической рукой. В моем распоряжении был специальный датчик, обнаруживающий жетоны и имеющий выходы, позволяющие определить направление на жетон. С помощью этого прибора робот, несомненно, найдет жетон, но, к сожалению, тот же прибор не позволит роботу покинуть то место, где был найден жетон. Во всяком случае, проанализировав ситуацию, я выделил две отдельные задачи: построить схему, отыскивающую жетоны, и найти способ запрограммировать робота так, чтобы он мог выбраться из комнаты. Хотя некоторые задачи выглядят сначала несколько расплывчато, Эшкин отмечает, что их маленькие, "байтового размера" подзадачи поддаются решению. При таком разбиении постановка задачи становится более четкой. Процесс постановки задачи и решение составляющих ее подзадач на уровне логических схем - две важные фазы разработки устройства.
То, что играющий обретает способность самостоятельно конструировать логические схемы, имеет также важное психологическое значение. По мере того как играющий приобретает опыт, перепаивая схемы роботов-компаньонов, у него развивается чувство уверенности в своих силах, а уверенность - это отличное противоядие от ощущения холодной неприступности, которое порой внушают нам компьютеры. Обучившись оперировать стандартными логическими схемами в игре "Одиссея роботов", играющий подходит к пониманию аналогичных взаимоотношений, существующих между основными логическими элементами компьютера и его функционированием. Играющий чувствует, что нет никаких непреодолимых препятствий на пути более глубокого исследования. Ощущение загадки, таящейся в черном ящике, пропадает. Человек начинает чувствовать себя полным хозяином положения.
Однако это ощущение всесилия, развивающееся на определенной стадии у начинающих, может затем снова быть утраченным, как утверждает Ш.Теркл, автор книги "The Second Self" ("Второе Я"). Ее книга посвящена тому, как развиваются взаимоотношения между людьми и компьютерами. Несколько страшноватыми выглядят некоторые истории о тех, кто начинает рассматривать самого себя как машиноподобное существо. Мне представляется, что подобная точка зрения может развиться на любой стадии овладения теорией и практикой вычислительной техники. Я знаком со специалистами в области искусственного интеллекта, которые также находят в себе нечто общее с машиной, но, правда, в более тонком понимании этого слова. В каком-то смысле, может быть, и правда, что все мы машины, однако такая точка зрения мало помогает нам в вопросах, касающихся нашего поведения, и может даже способствовать тому, что человек примет такую линию поведения, которая приведет к самым неприятным последствиям. Возможно, именно поэтому, образно говоря, нам следует научиться убегать из Роботрополя.
ОТКЛИКИ
12 1985
В СТАТЬЕ из рубрики "Занимательный компьютер", помешенной в сентябрьском номере нашего журнала, читателям было предложено сконструировать управляющую логическую схему для робота, ходящего по стене. Задача эта значительно труднее, чем может показаться с первого взгляда. Главная трудность заключается в преодолении выпуклых углов: если не отключить движок, когда встречается такой угол, то робот спокойно отойдет от стены и начнет двигаться внутрь помещения.
Из присланных до сих пор решений только два представляются мне правильными. Ж.Шваб, консультант по автоматизированной обработке данных из Медона (Франция), и Дж. Грегор, лейтенант военно-воздушных сил США, в настоящее время проходящий службу на базе ВВС в Лэнгли, оба сконструировали схемы с четырьмя триггерными элементами. Возможно, двух триггеров недостаточно для построения схемы.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
10 1985
ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ САМЫХ СЛОЖНЫХ МАТЕМАТИЧЕСКИХ ОБЪЕКТОВ С ПОМОЩЬЮ КОМПЬЮТЕРА-МИКРОСКОПА
А.К.ДЬЮДНИ
В ЦЕНТРЕ огромного двумерного пространства чисел, называемого комплексной плоскостью, в молчаливой задумчивости пребывает множество Мандельброта. Если к числам комплексной плоскости многократно применять определенную математическую операцию, то числа, расположенные вне множества Мандельброта, стремятся к бесконечности. Числа, находящиеся внутри границ множества, остаются в его пределах, совершая иногда плавное, иногда колебательное движение. Область, где начинает проявляться неустойчивость, непосредственно примыкает к границе множества и отмечена особенно причудливыми траекториями. Здесь мы наблюдаем бесконечную регрессию форм, поражающую своей сложностью и необычной красотой.
Описанное множество носит имя Бенуа Мандельброта, члена научного общества фирмы IBM, работающего в Исследовательском центре Томаса Уотсона той же фирмы в Йорктаун-Хайтсе (шт. Нью-Йорк). Изучая геометрические формы, Мандельброт разработал теорию, названную им фрактальной геометрией. Это математическая теория форм, имеющих дробную размерность. Таким свойством обладает, в частности, граница множества Мандельброта, но она обладает также и другими интересными свойствами.
Используя сравнительно несложную программу, компьютер можно превратить в своеобразный микроскоп и наблюдать с его помощью за поведением границы множества Мандельброта. Теоретически можно "разглядывать" любую часть множества при любом увеличении (см. фотографию на обложке журнала и рисунки на с.81-83). Издали множество напоминает приземистую, покрытую бородавками и лежащую на боку восьмерку. Внутренняя часть восьмерки зловеще черная, ее окружает яркая белая корона, которая постепенно темнеет, и на большом удалении от множества плоскость приобретает все более густой синий цвет, переходящий в черный.
Множество Мандельброта на комплексной плоскости. На диаграмме выделены детали, показанные на обложке журнала и на следующих трех рисунках

Последовательные увеличения области а, отмеченной на предыдущем рисунке
При большем увеличении мы обнаруживаем, что каждая бородавка
представляет собой крошечную фигурку, очень похожую на само множество. Перенесясь еще ближе к плоскости, чтобы лучше разглядеть одну из этих крошечных фигурок, мы видим совершенно другую картину: перед нами возникают ряды и спирали из бесчисленных усиков и причудливых завитушек, напоминающих биологические образования. Увеличив теперь одну из завитушек, мы видим, что она состоит из парных завитков, соединенных между собой тончайшим филигранным узором - мостиком. Увеличенное изображение мостика позволяет увидеть, что из его центра растут две завитушки. В центре же его центра, если можно так выразиться, находится четырехрядный мостик с четырьмя завитушками, а в центре этих завитушек мы обнаруживаем еще одну микроскопическую разновидность множества Мандельброта. При еще большем увеличении выясняется, что эта версия множества Манлельброта отличается от исходной, хотя они и очень похожи. По мере дальнейшего увеличения в поле нашего зрения появляются уменьшенные версии уже встречавшихся форм, однако при внимательном изучении обнаруживаются какие-то различия. Этот процесс может продолжаться до бесконечности, и всюду мы видим бесконечное разнообразие форм, иногда даже поражающих своей красотой и великолепием.

Зрачок глаза, который смотрит из центра области, изображенной на предыдущем рисунке в кадре d

Миниатюрное множество Мандельброта в области f диаграммы на с.81, связанное с основным множеством тонкой нитью
В ЭТОЙ статье мы познакомимся с двумя программами, позволяющими исследовать результаты итерационных процессов (повторного применения операций), подобных тому, который приводит к образованию множества Манлельброта. С помощью первой программы были получены цветные картинки, приведенные в настоящей статье. При некоторых модификациях эту программу можно выполнять на персональном компьютере, имеющем необходимое аппаратное и математическое обеспечение графики. Картинки будут вполне удовлетворительными даже на черно-белом дисплее. Вторая программа предназначена для читателей, которым, как и мне, иногда хочется уйти от сложностей, возникающих в связи с понятием бесконечного, и ограничиться очевидной простотой конечного.
Слово "сложное" применяется здесь в двух смысловых значениях. Первое и обычное его значение вполне применимо при описании такого сложного объекта, как множество Мандельброта. Однако у этого слова есть другое, более формальное значение (на английском языке слово complex означает "сложный", формальное значение этого слова - "комплексный".- Перев.). Число называется сложное, или комплексное, когда оно состоит из двух частей, исторически сложившиеся названия которых - действительная и мнимая. Теперь эти термины уже не имеют особого значения - с таким же успехом две части комплексного числа могли бы называться толстой и тонкой. Так, например, 7+4i - это комплексное число, у которого действительная часть (толстая) равна 7, а мнимая (тонкая) равна 4i. Буква i, стоящая при цифре 4, показывает, что эта часть является мнимой.
Каждое комплексное число можно представить точкой на плоскости. Плоскость комплексных чисел называется комплексной плоскостью. Чтобы найти положение числа 7+4i в комплексной плоскости, сначала найдем комплексное число 0, или 0+0i, и отмерим семь единиц вправо и четыре единицы вверх. Точка с этими координатами представляет число 7+4i. Комплексная плоскость содержит бесконечное количество таких точек - чисел. Их действительные и мнимые части могут быть либо положительными, либо отрицательными и быть либо целыми, либо дробными десятичными числами.
Комплексные числа легко складывать и умножать. Чтобы сложить числа 3-2i и 7+4i, сложим их действительные и мнимые части отдельно. В результате получим сумму 10+2i. Умножать комплексные числа лишь немногим сложнее. Если рассматривать символ i, например, как х в школьной алгебре, то произведение чисел 3-2i и 7+4i будет равно 21+12i-14i-8i2. Здесь уже следует пояснить, что i2=-1. Тогда полученное произведение можно упростить, суммировав его действительные и мнимые члены. Результатом умножения будет число 29-2i.
Теперь можно описать итерационный процесс, порождающий множество Мандельброта. Начнем с алгебраического выражения z2+c, где z комплексное число, которое может изменять свое значение (другими словами, z - это комплексная переменная), a c - некое постоянное комплекснос число. Предположим вначале, что переменная z равна комплексному числу 0. Тогда квадрат z также равен 0, и, прибавив к z2 константу c, получим c. Теперь подставим этот результат вместо z в выражении z2+c. Получим новую сумму c2+c. Опять подставим ее вместо z. Следующая сумма будет равна (c2+c)2+с. Будем продолжать этот процесс, используя выходные данные предыдущего шага в качестве входных данных следующего.
Применяя описанный итерационный процесс для каких-то определенных значений c, мы наблюдаем довольно странную картину. Вот, например, что получается, когда c равно 1+i:
первая итерация, 1+3i,
вторая итерация, -7+7i,
третья итерация, 1-97i.
Отметим, что действительная и мнимая части могут расти, уменьшаться или менять знак. Если этот процесс продолжать, то в результате будем получать все большие комплексные числа.
А что следует понимать под величиной комплексного числа? Поскольку комплексные числа соответствуют точкам на плоскости, напрашивается мысль воспользоваться в качестве критерия расстоянием. Величина комплексного числа - это как раз расстояние от представляющей его точки до точки 0. Геометрически это расстояние выражается гипотенузой прямоугольного треугольника, катеты которого образованы действительной и мнимой частями комплексного числа. Поэтому, чтобы найти величину комплексного числа, нужно возвести в квадрат его действительную часть и коэффициент при мнимой части, сложить их и извлечь из суммы квадратный корень. Например, величина комплексного числа 7+4i равна квадратному корню из 7^2+4^2, или приблизительно 8.062. Когда в результате многократного применения описанного выше итерационного процесса комплексные числа достигают определенной величины, они начинают расти очень быстро. И в самом деле, уже через несколько следующих шагов итерация они превышают максимальное число, которое можно записать в вычислительной машине.
К счастью, мы можем игнорировать все комплексные числа c, которые стремительно уносятся в бесконечность. Множество Мандельброта - это множество всех комплексных чисел c, для которых величина выражения z2+с остается конечной даже после бесконечно большого количества шагов итерации. Программа, которую я собираюсь описать, как раз и отыскивает такие числа. Имеющейся у меня информацией по этому вопросу я обязан Дж.Хаббарду, математику из Корнеллского университета. Хаббард - специалист по множеству Мандельброта, он один из тех, кто первым с помощью вычислительной машины получил его графические изображения. Большая часть изображений, приведенных в настоящей статье, были получены X.Пайтгеном и его коллегами из Бременского университета. Однако этому искусству Пайтген научился у Хаббарда.
ПРОГРАММА, которую я называю MANDELZOOM, была создана по образу и подобию программы Хаббарда. В программе организуется массив pic, необходимый для хранения картинок. Элементы массива pic представляют собой отдельные элементы картинки, называемые пикселами. Они расположены в форме решетки. В массиве программы Хаббарда насчитывалось 400 столбцов и 400 строк, а в программе Пайтгена еще больше. Читатели, желающие приспособить программу MANDELZOOM для своего персонального компьютера, могут сами выбрать размеры массива в зависимости от типа имеющегося в их распоряжении компьютера. Чем больше массив, тем больше время ожидания картинки, но зато тем лучше разрешающая способность изображения.
На начальном этапе работы программы необходимо выбрать квадратную область комплексной плоскости, которую вы хотели бы рассмотреть. Для этого нужно указать комплексное число, соответствующее левому нижнему углу выбранного квадрата. Наличие двух переменных в программе, acorner и bcorner, позволяет вводить соответственно действительную и мнимую части этого числа. Затем нужно указать длину стороны квадрата, присвоив соответствующее значение переменной side.
В следующей части программы происходит подгонка массива pic под размеры выбранного квадрата путем вычисления значения переменной gap. Gap - это расстояние между двумя соседними пикселами в выбранном для рассмотрения квадрате. Чтобы получить gap, поделим значение side на число строк (или столбцов) в массиве pic.
Третья часть программы - центральная. Она отыскивает комплексные числа c, принадлежащие множеству Мандельброта, а также присваивает цвета числам, расположенным, в некотором специальном смысле, неподалеку. Процедура выполняется для каждого отдельного пиксела. Таким образом, в программе Хаббарда, имеющей массив размером 400*400, потребуется 160000 шагов вычисления. Предположим, что в данный момент программа обрабатывает данные, относящиеся к пикселу, принадлежащему строке m и и столбцу n. Тогда процедура, выполняемая третьей частью программы, распадается на четыре этапа, или шага.
1. Вычислить комплексное число c, соответствующее данному пикселу: сложить величину n*gap с acorner, чтобы получить действительную часть ac числа c; сложить величину m*gap с bcorner, чтобы получить мнимую часть bc числа c. При этом нет необходимости включать в программу символ i.
2. Вначале задать комплексную переменную z (с действительной частью az и мнимой частью bz) равной 0+0i. Установить целую переменную count равной 0.
3. Выполнять повторно следующие три операции, пока или величина z не превысит 2, или значение count не превысит 1000, независимо от того, какое из этих событий наступит раньше:
z <- z2+с
count <- count+1
side <- <величина z>
Почему цифра 2 играет такую важную роль? Дело в том, что, согласно теории, комплексное число z, к которому применяется итерационный процесс, "уйдет" в бесконечность тогда и только тогда, когда на определенной стадии процесса оно достигнет значения 2 или более. Как показывают вычисления, довольно много точек, которым суждено уйти в бесконечность, достигают 2 уже после первых нескольких шагов итераций. Более "медленные" точки достигают этой величины все реже и реже по мере роста значения переменной count.
4. Присвоить цвет элементу pic(m, n) в соответствии со значением переменной count, достигнутым после выполнения 3-го шага процедуры. Высветить цвет данного пиксела на экране дисплея. Заметим, что цвет пиксела зависит только от одного комплексного числа, находящегося в его ближайшей окрестности, а именно от числа, находящеюся в верхнем правом углу этой окрестности. Поведение этого числа определяет поведение всего пиксела.
При таком способе присвоения цвета нужно, чтобы диапазон изменения переменной count разделялся на поддиапазоны, по одному на каждый цвет. Пикселы, для которых величина z достигает 2 уже после первых нескольких итераций, окрашиваются в красный цвет. Пикселы, для которых величина z достигает 2 после сравнительно большого количества итераций, окрашиваются в фиолетовый цвет, расположенный на противоположном краю спектра. Пикселы, для которых величина z остается меньше 2 даже после 1000 итераций, по предположению, лежат в множестве Мандельброта и окрашиваются в черный цвет.
Было бы разумно оставлять цвета неопределенными, пока не будет установлен диапазон изменения переменной count в данном конкретном квадрате. Если диапазон оказывается узким, то весь цветовой спектр можно уместить в его пределах. Поэтому Хаббард предлагает, чтобы на 4-м шаге процедуры каждому элементу массива pic присваивалось лишь значение переменной count. Затем отдельная программа должна будет просмотреть массив, определить наибольшее и наименьшее значения count и соответствующим образом распределить спектр. Читатели, которым удастся написать все остальные фрагменты программы, несомненно, справятся и с этим местом.
При отсутствии цветного дисплея можно обойтись и черно-белым. Комплексные числа, величина которых превышает 2 после r итераций, окрашиваются в белый цвет, остальные точки остаются черными. Значение параметра r можно выбрать по вкусу. Чтобы не просиживать целую ночь перед экраном в ожидании результатов, размер массива можно, например, принять равным 100*100. Хаббард считает также, что разумно было бы сократить максимальное количество итераций с 1000 до 100. Результатом подобной программы будет точечный образ, или черно-белое представление цветного изображения, о котором говорилось выше (см. рисунок вверху).

Точечное изображение миниатюрного множества Мандельброта, полученное на черно-белом дисплее
КАКОВА же мощность микроскопа, реализованного на персональном компьютере? В какой-то степени она зависит от количества разрядов чисел, которыми может оперировать машина. Например, в персональном компьютере фирмы IBM используется микропроцессор 8088 фирмы Intel Corporation, предназначенный для выполнения операций над двоичными числами длиной 16 разрядов. Пользуясь так называемой двойной точностью, можно увеличить количество разрядов до 32. При этом условии, по моим подсчетам, можно достигнуть увеличения порядка 100000. Используя специальное, программное обеспечение, объединяющее двоичные разряды чисел в единые цепочки, можно повысить точность вычислений до сотен значащих двоичных разрядов. При такой точности теоретически достижимое увеличение множества Мандельброта намного превышает увеличение, необходимое для того, чтобы рассмотреть внутреннюю структуру атомного ядра.
Какую часть комплексной плоскости интереснее исследовать? Конечно, в окрестности множества Мандельброта. Ну а точнее? По словам Хаббарда, на плоскости "есть зиллионы прекраснейших мест". Подобно туристу, посетившему необычайно красивые места в мире бесконечного, он может буквально засыпать читателей предложениями тех мест, какие будут особенно интересными. Правда, эти места не носят таких экзотических названий, как Сингапур или Таити. Хаббард рекомендует читателям "исследовать область комплексных чисел с диапазоном действительных частей от 0.26 до 0.27 и мнимых - от 0 до 0.01". Он также предложил две другие области: Действительная часть
от -0.76 до -0.74
от -1.26 до -1.24
Мнимая часть
от 0.01 до 0.03
от 0.01 до 0.03
Рассматривая цветные картинки, иллюстрирующие нашу статью, следует иметь в виду, что точки, окрашенные в любой другой цвет, кроме черного, не принадлежат множеству Мандельброта. В значительной мере красота картинок обусловлена гаммой красок, ассоциируемых с точками, устремляющимися в бесконечность. На самом деле если бы мы захотели посмотреть на множество Мандельброта в полной изоляции от окружающих его точек, то картинка не была бы столь красивой: мы увидели бы перед собой множество, всюду покрытое тонкими волосками и содержащее миниатюрные структуры, очень похожие на само множество.
В действительности ни одно из миниатюрных множеств Мандельброта не является точной копией родительского множества. Более того, между этими миниатюрными версиями множества также имеются некоторые различия. В окрестности множества Мандельброта мы видим многочисленные его микроскопические версии, как бы подвешенные в "атмосфере" комплексной плоскости. Однако это впечатление обманчиво. Согласно удивительной теореме, доказанной Хаббардом и его коллегой А.Дуади из Парижского университета, множество Мандельброта является связным. Поэтому даже миниатюрные версии множества, кажущиеся изолированными в комплексной плоскости, на самом деле соединены с родительским множеством тонкими волокнами. Миниатюрные версии множества встречаются повсюду в окрестности и имеют самые разные размеры. В каждом квадрате конечного размера содержится бесконечное количество миниатюрных версий множества, из которых при любом увеличении можно разглядеть лишь несколько. По словам Хаббарда, множество Мандельброта представляет собой "самый сложный объект в математике".
ПОСЛЕ путешествия в мир бесконечно сложного приятно отдохнуть в пределах конечного. Многократно повторяя операцию возведения в квадрат на конечном множестве обыкновенных целых чисел, можно также получить интересные структуры. Правда, эти структуры не геометрические, а, скорее, комбинаторные.
Выберем наобум любое целое число в диапазоне от 0 до 99. Возведем его в квадрат и оставим два последних десятичных разряда. Они также будут представлять собой число в диапазоне от 0 до 99. Например, возведя 59 в квадрат, мы получим 3481; два последних разряда этого числа 81. Если продолжить этот процесс, то рано или поздно мы получим число, уже встречавшееся нам ранее. Например, начиная с числа 81, мы получим последовательность 61, 21, 41 и 81, и эта последовательность из четырех чисел будет теперь повторяться до бесконечности. Оказывается, что такие циклы всегда возникают при итерационных процессах над конечными множествами. Нетрудно видеть, что существует по крайней мере одно повторяющееся число после 100 операций на множестве из 100 чисел. Первое же повторяющееся число приводит к возникновению цикла. Существует изящная программа обнаружения подобных циклов, почти не требующая памяти, но об этом несколько позже.
Приблизительно за час можно построить диаграмму результатов описанного процесса. Представим каждое число от 0 до 99 точкой на листе бумаги. Если после возведения в квадрат одно число переходит в другое, то соединим соответствующие точки стрелочкой. Например, такую стрелочку мы должны провести от точки 59 к точке 81. После нескольких первых соединений на диаграмме могут возникнуть запутанные циклы, поэтому время от времени их следует перерисовывать таким образом, чтобы стрелки никогда не пересекались. Нарисовать такую диаграмму без пересечений, оказывается, всегда возможно.
Можно пойти даже дальше. В ходе процесса часто возникают отдельные поддиаграммы, и их можно построить таким образом, чтобы выявились некоторые свойства симметрии, характерных для итераций. Например, непересекающаяся диаграмма итераций для возведения в квадрат целых чисел в диапазоне от 0 до 99 содержит шесть не связанных между собой диаграмм. Части диаграммы встречаются в виде идентичных пар, и каждая часть обладает высокой степенью симметрии (см. рисунок на с.85). Может ли читатель дать толкование этих симметрии? Что изменится, если диапазон расширить от 0 до 119? Существует ли какая-нибудь зависимость между числом не связанных друг с другом частей на диаграмме и наибольшим целым числом в последовательности?

Шесть компонент диаграммы итерационного процесса возведения в квадрат для первых 100 натуральных чисел
Сходные с только что описанными закономерности наблюдаются и при итерациях, применяемых к некоторым комплексным числам, принадлежащим множеству Мандельброта: для определенных значений c итерации, применяемые к выражению z2+c, могут привести к конечному циклу из комплексных чисел. Так, например, начиная с комплексного числа 0+1i, мы получаем бесконечные колебания между двумя числами: -1+1i и 0-1i. Цикл может даже состоять из единственного числа. Такие циклы независимо от того, встречаются они на конечном множестве или на бесконечном множестве Мандельброта, называются аттракторами.
Каждая из шести частей диаграммы итерационного процесса для целых чисел в диапазоне от 0 до 99 содержит один аттрактор. Геометрически аттрактор можно представить в виде многоугольника, а множества чисел, которые приводят к нему, можно представить в виде деревьев. Один из возможных способов найти аттрактор заключается в том, чтобы запоминать каждое порождаемое число в специально отведенном массиве программы. Только что полученное число следует сравнить с каждым из ранее запомненных в массиве чисел. Если среди них находится число, совпадающее с данным, то все числа, расположенные между найденным числом и только что полученным, равным ему, выводятся на экран или печать. Способ довольно простой, и его нетрудно реализовать в программе. Однако, если массив большой, процесс сравнения чисел может потребовать много времени. Чтобы найти аттрактор в массиве, содержащем n чисел, необходимо выполнить порядка n2 операций сравнении, поскольку каждое новое число нужно сравнить с каждым числом массива, а количество последних может доходить до n.
Существует маленькая остроумная программа, которая находит аттракторы значительно быстрее. Вместо n слов памяти программа требует лишь два, и ее можно составить даже на простейшем карманном программируемом калькуляторе. С этой программой вы сможете познакомиться, прочтя любопытную книжку: Hoffman D., Mohler L. Mathematical Recreations for the Programmable Calculator ("Занимательная математика для программируемого калькулятора"). Разумеется, многие рассмотренные в книжке программы могут быть легко переписаны для персонального микрокомпьютера или любой другой ЭВМ.
Программа RHOP получает последовательность чисел, которая в конце концов зацикливается и напоминает кусок каната с петлей на одном конце. Она напоминает также греческую букву "ро" (по-английски rho; отсюда название программы RHOP.- Перев.). В программе две переменные - fast и slow (соответственно "быстрая" и "медленная".- Перев.). Первоначально обеим переменным присваивается значение исходного числа. Итерационный цикл программы состоит лишь из трех команд:
fast <~ fast*fast (mod 100)
fast <- fast*fast (mod 100)
slow <- slow*slow (mod 100)
Операция "mod 100" извлекает последние два разряда произведения. Заметим, что число fast дважды возводится в квадрат, а число slow только один раз. Число fast пробегает путь от хвоста буквы "ро" до ее головы вдвое быстрее числа slow. Уже в пределах головы буквы "ро" число fast встречается с числом slow. Программа останавливает итерационный цикл, когда совпадают значения переменных fast и slow.
Аттрактор определяется путем повторного возведения в квадрат числа, являющегося на данный момент значением переменной slow. Когда это число встречается вновь, программа останавливается и высвечивает или распечатывает последовательность чисел между двумя одинаковыми значениями slow.
Читатели могут попытаться построить диаграммы на основе результатов итерационного процесса возведения в квадрат чисел из конечных множеств различных размеров. Эти диаграммы можно получить как с помощью компьютера, так и от руки. Дискретные итерационные процессы - это новая, развивающаяся область математики, которая находит применение в вычислительной технике, информатике, биоматематике, физике и даже социологии. Теоретики, наверняка, с интересом прочтут монографию Франсуа Роберта из Гренобльского университета, которая посвящена этому предмету и в настоящее время готовится к печати.
БИБЛИОГРАФИЯ
MATHEMATICAL RECREATIONS FOR THE PROGRAMMABLE CALCULATOR. DEAN HOFFMAN AND LEE MOHLER. Hayden Book Co., 1982.
THE FRACTAL GEOMETRY OF NATURE. BENIOT B. MANDELBROT. W.H.Freeman and Company, 1983.
DISCRETE ITERATIONS. FRANCOIS ROBERT; translated from the French by Jon Rokne. Springer-Verlag, in press.
ОТКЛИКИ
1 1986
С МОМЕНТА появления программы MANDELZOOM (см. журнал "В мире науки", 1985, #10) она поселилась в сотнях домов, школ и учреждений. И хотя эта программа, очевидно, произвела очень сильное впечатление на взрослых, заинтриговала подростков и даже напугала нескольких детей младшего возраста, отклики читателей на вторую тему статьи, посвященную итерационным диаграммам, к моему удивлению, оказались почти столь же многочисленными, как и на тему о множестве Мандельброта.
Многие читатели, что называется, с головой окунулись в разноцветные кружева множества Мандельброта, погружаясь в него все глубже по мере роста степени увеличения. Читатели, одержимые желанием иметь свои собственные цветные изображения множества, но не имеющие цветной графики на своих персональных компьютерах, заказали фотографии у Дж.Хаббарда из Корнеллского университета. Дж.Хаббард и X.Пайтген, картинки которого красовались на страницах упомянутого номера журнала, научились искусству получать изображения множества у самого Мандельброта.
Читателям, возможности которых ограничены лишь черно-белой графикой, я бы рекомендовал воспользоваться различными оттенками серого цвета. Картинки в черно-белом изображении могут быть почти такими же впечатляющими, как и их цветные аналоги. Лучшие серые изображения были получены Д.Бруксом, работающим в фирме Prime Computer, Inc. в Фреймингхемс (шт.Массачусетс). В его сказочных сочетаниях полутонов каждый оттенок серого цвета достигается при помощи маленьких черных квадратиков определенного размера, напечатанных лазерным принтером. Брукс старался выявить крошечные волокна, предположительно соединяющие миниатюрные множества Мандельброта с основным множеством. Пока лаже при самых больших увеличениях Бруксу не удалось их разглядеть. Мандельброт сообщил ему, что эти волокна, по всей видимости, имеют бесконечно малую толщину.
Читатели, не обладающие столь изощренным оборудованием, могут все же работать с различными оттенками серого цвета на экранах своих черно-белых дисплеев. Дж.Халлек из Солт-Лейк-Сити варьирует плотность точек, приходящихся на один пиксел, чтобы получить различные оттенки.
В другом подходе для генерации изображений множества Мандельброта применяются черные и белые контуры. Й.Гурсель из Кембриджа (шт.Массачусетс) построил изображения множества, пожалуй не уступающие изображениям Брукса. Гурсель заменяет дискретный цветовой спектр чередующимися белыми и черными кольцами. Р.Шэннон из Грантс-Пасса (шт.Орегон) предложил тот же метод. В.Андерсен из Санта-Клары (шт.Калифорния) довел его до "крайности": он предложил переходить от черного к белому (или наоборот) всякий раз, когда переменная count меняется от одного пиксела к другому.
Стоит упомянуть также еще о двух исследованиях. Дж.Тигпенн IV из Перланда (шт.Техас) вместо цветового представления применяет уровни высоты: множество Мандельброта превращается в огромное плато, видимое под некоторым углом, со сложным ландшафтом остроконечных холмов, подступающих к плато с разных сторон. Р.Пальмаччио из Форт-Лодердейла вовсе упразднил множество как таковое. Его интересуют траектории индивидуальных комплексных чисел, описываемые на плоскости по ходу итераций. Их причудливая хореография вблизи границ множества Мандельброта принимает форму спирального вальса или кругового фокстрота.
Множество Мандельброта порождается функцией z2+c. Конечно, существуют и другие функции, но они порождают другие множества. К примеру, Б.Икенага исследует образование, которое можно назвать кубическим кактусом. Функция z3+(c-1)z-c порождает колючее с неприветливым внешним видом множество (по крайней мере так оно выглядит в контрастных черных и белых тонах), окруженное таинственными миниатюрными спиральными галактиками.
Итерационные диаграммы также полны загадочного. Когда целые числа по модулю n возводятся в квадрат, каждое число переходит в другое. Итерационная диаграмма получается, когда каждое число заменяется точкой, а каждое перемещение - стрелкой. По поводу этих диаграмм я сформулировал несколько вопросов. Сколько компонент содержат в себе тахие диаграммы? Читатели прислали полученные диаграммы, документируя тем самым свои исследования для различных значений n.
Наиболее крупные диаграммы были построены Р.Мэримонт из Силвер-Спринга(шт.Мэриленд). Она рассматривала целые числа, вычисляемые по модулю 1000, и на результирующей диаграмме она получила четыре пары компонент. Каждая компонента обладала, как обычно, одним аттрактором, и наибольший из аттракторов включал в себя 20 чисел. Будучи математиком по профессии, Мэримонт высказала предположение, что целые числа, вычисляемые по модулю 1Ek, должны породить k+1 пар компонент и что наибольшие аттракторы должны включать 4*5^(k-2) чисел.
С.Эберхарт из Ресеты (шт.Калифорния) заинтересовался случаем, когда n представляет собой простое число Ферма (т.е. простое число, представимое в виде 2^2^k+1). Здесь число 0 образует аттрактор, а все остальные числа принадлежат одному-единственному большому дереву. Один мой знакомый, специалист по теории чисел, подтверждает, что для простых чисел Ферма это всегда так и что дерево является двоичным: каждый внутренний узел имеет две входные стрелки.
Итерационные диаграммы, подобно числам, можно перемножать между собой. Если n - произведение двух простых чисел, скажем р и q, то итерационная диаграмма для целых чисел, вычисляемых по модулю n, представляет собой произведение соответственно диаграмм дляр p и q. Это интересное наблюдение было сделано С.Локом из Флоридского атлантического университета. Лок описал также очень интересное отношение, сушествуюшее между n-й итерационной диаграммой и диаграммой, казалось бы, совсем другого рода, в которой числа вместо того, чтобы возводиться в квадрат, просто удваиваются. Если n - простое число, последняя диаграмма для целых чисел, взятых по модулю n-1, совпадает с нашей n-й диаграммой, за исключением единственного изолированного числа, образующего свой аттрактор. Весьма похожее наблюдение было сделано в рамках теории чисел Н.Элкисом из Нью-Йорка.
Мощный инструмент для анализа итерационных диаграмм (при возведении в квадрат) был разработан Ф.Палмсром из Чикаго. Очевидно, все деревья, связанные с данным аттрактором, изоморфны. По существу, это означает, что они обладают в точности той же самой формой.
Наконец, Б.Джилсон из Силвер-Спринга (шт.Мэриленд) и М.Уилльямс из Каламазу (шт.Мичиган) исследовали совершенно другое обобщение множества чисел от 0 до 99. Их можно рассматривать как числа по другому основанию. Например, последовательность натуральных чисел по основанию 3 будет выглядеть следующим образом: 00, 01, 02, 10, 11, 12, 20, 21, 22, пока мы снова не придем к числу 00. Такие числа также порождают итерационные диаграммы, которые выглядят аналогично диаграммам, получаемым для целых чисел по модулю n. Джилсон доказал, что диаграммы всегда имеют парные компоненты при четных n, не являющихся кратными 4.
2 1986
Читатели, не чувствующие себя достаточно компетентными в программировании, чтобы написать свои собственные версии программы MANDELZOOM, но желающие завести ее в библиотеке программ своих персональных компьютеров, обратились к нам с просьбами прислать им программу. Когда читатели просят прислать им листинги или дискеты с записью программ, которые я представляю в наших статьях, возникает, конечно, соблазн удовлетворить их просьбу. Но у меня просто не хватит времени, чтобы ответить на все поступающие письма. Кроме того, я считаю, что время, которое читатель затратит, чтобы научиться нескольким простейшим элементам программирования, требующимся для решения большинства описываемых мною задач, он проведет с пользой для себя. С педагогической точки зрения это, наверное, правильно.
В то же время, когда другие читатели щедро предлагают поделиться созданными ими программами со всеми желающими, я уже не могу удержаться от соблазна. Поэтому иногда я привожу имена любителей, выразивших такое желание.
10 1986
В заключение сообщаю, что Р.Силвер из Сан-Кристобала (шт.Нью-Мексико) предложил учредить периодический печатный орган, посвященный новостям, касающимся экспериментов со множеством Мандельброта. В нем, как он считает, должны публиковаться статьи читателей о новых полученных ими результатах.
ПОЛУЧЕНИЕ ИЗОБРАЖЕНИЙ САМЫХ СЛОЖНЫХ МАТЕМАТИЧЕСКИХ ОБЪЕКТОВ С ПОМОЩЬЮ КОМПЬЮТЕРА-МИКРОСКОПА
А.К.ДЬЮДНИ
В ЦЕНТРЕ огромного двумерного пространства чисел, называемого комплексной плоскостью, в молчаливой задумчивости пребывает множество Мандельброта. Если к числам комплексной плоскости многократно применять определенную математическую операцию, то числа, расположенные вне множества Мандельброта, стремятся к бесконечности. Числа, находящиеся внутри границ множества, остаются в его пределах, совершая иногда плавное, иногда колебательное движение. Область, где начинает проявляться неустойчивость, непосредственно примыкает к границе множества и отмечена особенно причудливыми траекториями. Здесь мы наблюдаем бесконечную регрессию форм, поражающую своей сложностью и необычной красотой.
Описанное множество носит имя Бенуа Мандельброта, члена научного общества фирмы IBM, работающего в Исследовательском центре Томаса Уотсона той же фирмы в Йорктаун-Хайтсе (шт. Нью-Йорк). Изучая геометрические формы, Мандельброт разработал теорию, названную им фрактальной геометрией. Это математическая теория форм, имеющих дробную размерность. Таким свойством обладает, в частности, граница множества Мандельброта, но она обладает также и другими интересными свойствами.

Используя сравнительно несложную программу, компьютер можно превратить в своеобразный микроскоп и наблюдать с его помощью за поведением границы множества Мандельброта. Теоретически можно "разглядывать" любую часть множества при любом увеличении (см. фотографию на обложке журнала и рисунки на с.81-83). Издали множество напоминает приземистую, покрытую бородавками и лежащую на боку восьмерку. Внутренняя часть восьмерки зловеще черная, ее окружает яркая белая корона, которая постепенно темнеет, и на большом удалении от множества плоскость приобретает все более густой синий цвет, переходящий в черный.

Множество Мандельброта на комплексной плоскости. На диаграмме выделены детали, показанные на обложке журнала и на следующих трех рисунках

Последовательные увеличения области а, отмеченной на предыдущем рисунке
При большем увеличении мы обнаруживаем, что каждая бородавка
представляет собой крошечную фигурку, очень похожую на само множество. Перенесясь еще ближе к плоскости, чтобы лучше разглядеть одну из этих крошечных фигурок, мы видим совершенно другую картину: перед нами возникают ряды и спирали из бесчисленных усиков и причудливых завитушек, напоминающих биологические образования. Увеличив теперь одну из завитушек, мы видим, что она состоит из парных завитков, соединенных между собой тончайшим филигранным узором - мостиком. Увеличенное изображение мостика позволяет увидеть, что из его центра растут две завитушки. В центре же его центра, если можно так выразиться, находится четырехрядный мостик с четырьмя завитушками, а в центре этих завитушек мы обнаруживаем еще одну микроскопическую разновидность множества Мандельброта. При еще большем увеличении выясняется, что эта версия множества Манлельброта отличается от исходной, хотя они и очень похожи. По мере дальнейшего увеличения в поле нашего зрения появляются уменьшенные версии уже встречавшихся форм, однако при внимательном изучении обнаруживаются какие-то различия. Этот процесс может продолжаться до бесконечности, и всюду мы видим бесконечное разнообразие форм, иногда даже поражающих своей красотой и великолепием.

Зрачок глаза, который смотрит из центра области, изображенной на предыдущем рисунке в кадре d

Миниатюрное множество Мандельброта в области f диаграммы на с.81, связанное с основным множеством тонкой нитью
В ЭТОЙ статье мы познакомимся с двумя программами, позволяющими исследовать результаты итерационных процессов (повторного применения операций), подобных тому, который приводит к образованию множества Манлельброта. С помощью первой программы были получены цветные картинки, приведенные в настоящей статье. При некоторых модификациях эту программу можно выполнять на персональном компьютере, имеющем необходимое аппаратное и математическое обеспечение графики. Картинки будут вполне удовлетворительными даже на черно-белом дисплее. Вторая программа предназначена для читателей, которым, как и мне, иногда хочется уйти от сложностей, возникающих в связи с понятием бесконечного, и ограничиться очевидной простотой конечного.
Слово "сложное" применяется здесь в двух смысловых значениях. Первое и обычное его значение вполне применимо при описании такого сложного объекта, как множество Мандельброта. Однако у этого слова есть другое, более формальное значение (на английском языке слово complex означает "сложный", формальное значение этого слова - "комплексный".- Перев.). Число называется сложное, или комплексное, когда оно состоит из двух частей, исторически сложившиеся названия которых - действительная и мнимая. Теперь эти термины уже не имеют особого значения - с таким же успехом две части комплексного числа могли бы называться толстой и тонкой. Так, например, 7+4i - это комплексное число, у которого действительная часть (толстая) равна 7, а мнимая (тонкая) равна 4i. Буква i, стоящая при цифре 4, показывает, что эта часть является мнимой.
Каждое комплексное число можно представить точкой на плоскости. Плоскость комплексных чисел называется комплексной плоскостью. Чтобы найти положение числа 7+4i в комплексной плоскости, сначала найдем комплексное число 0, или 0+0i, и отмерим семь единиц вправо и четыре единицы вверх. Точка с этими координатами представляет число 7+4i. Комплексная плоскость содержит бесконечное количество таких точек - чисел. Их действительные и мнимые части могут быть либо положительными, либо отрицательными и быть либо целыми, либо дробными десятичными числами.
Комплексные числа легко складывать и умножать. Чтобы сложить числа 3-2i и 7+4i, сложим их действительные и мнимые части отдельно. В результате получим сумму 10+2i. Умножать комплексные числа лишь немногим сложнее. Если рассматривать символ i, например, как х в школьной алгебре, то произведение чисел 3-2i и 7+4i будет равно 21+12i-14i-8i2. Здесь уже следует пояснить, что i2=-1. Тогда полученное произведение можно упростить, суммировав его действительные и мнимые члены. Результатом умножения будет число 29-2i.
Теперь можно описать итерационный процесс, порождающий множество Мандельброта. Начнем с алгебраического выражения z2+c, где z комплексное число, которое может изменять свое значение (другими словами, z - это комплексная переменная), a c - некое постоянное комплекснос число. Предположим вначале, что переменная z равна комплексному числу 0. Тогда квадрат z также равен 0, и, прибавив к z2 константу c, получим c. Теперь подставим этот результат вместо z в выражении z2+c. Получим новую сумму c2+c. Опять подставим ее вместо z. Следующая сумма будет равна (c2+c)2+с. Будем продолжать этот процесс, используя выходные данные предыдущего шага в качестве входных данных следующего.
Применяя описанный итерационный процесс для каких-то определенных значений c, мы наблюдаем довольно странную картину. Вот, например, что получается, когда c равно 1+i:
первая итерация, 1+3i,
вторая итерация, -7+7i,
третья итерация, 1-97i.
Отметим, что действительная и мнимая части могут расти, уменьшаться или менять знак. Если этот процесс продолжать, то в результате будем получать все большие комплексные числа.
А что следует понимать под величиной комплексного числа? Поскольку комплексные числа соответствуют точкам на плоскости, напрашивается мысль воспользоваться в качестве критерия расстоянием. Величина комплексного числа - это как раз расстояние от представляющей его точки до точки 0. Геометрически это расстояние выражается гипотенузой прямоугольного треугольника, катеты которого образованы действительной и мнимой частями комплексного числа. Поэтому, чтобы найти величину комплексного числа, нужно возвести в квадрат его действительную часть и коэффициент при мнимой части, сложить их и извлечь из суммы квадратный корень. Например, величина комплексного числа 7+4i равна квадратному корню из 7^2+4^2, или приблизительно 8.062. Когда в результате многократного применения описанного выше итерационного процесса комплексные числа достигают определенной величины, они начинают расти очень быстро. И в самом деле, уже через несколько следующих шагов итерация они превышают максимальное число, которое можно записать в вычислительной машине.
К счастью, мы можем игнорировать все комплексные числа c, которые стремительно уносятся в бесконечность. Множество Мандельброта - это множество всех комплексных чисел c, для которых величина выражения z2+с остается конечной даже после бесконечно большого количества шагов итерации. Программа, которую я собираюсь описать, как раз и отыскивает такие числа. Имеющейся у меня информацией по этому вопросу я обязан Дж.Хаббарду, математику из Корнеллского университета. Хаббард - специалист по множеству Мандельброта, он один из тех, кто первым с помощью вычислительной машины получил его графические изображения. Большая часть изображений, приведенных в настоящей статье, были получены X.Пайтгеном и его коллегами из Бременского университета. Однако этому искусству Пайтген научился у Хаббарда.
ПРОГРАММА, которую я называю MANDELZOOM, была создана по образу и подобию программы Хаббарда. В программе организуется массив pic, необходимый для хранения картинок. Элементы массива pic представляют собой отдельные элементы картинки, называемые пикселами. Они расположены в форме решетки. В массиве программы Хаббарда насчитывалось 400 столбцов и 400 строк, а в программе Пайтгена еще больше. Читатели, желающие приспособить программу MANDELZOOM для своего персонального компьютера, могут сами выбрать размеры массива в зависимости от типа имеющегося в их распоряжении компьютера. Чем больше массив, тем больше время ожидания картинки, но зато тем лучше разрешающая способность изображения.
На начальном этапе работы программы необходимо выбрать квадратную область комплексной плоскости, которую вы хотели бы рассмотреть. Для этого нужно указать комплексное число, соответствующее левому нижнему углу выбранного квадрата. Наличие двух переменных в программе, acorner и bcorner, позволяет вводить соответственно действительную и мнимую части этого числа. Затем нужно указать длину стороны квадрата, присвоив соответствующее значение переменной side.
В следующей части программы происходит подгонка массива pic под размеры выбранного квадрата путем вычисления значения переменной gap. Gap - это расстояние между двумя соседними пикселами в выбранном для рассмотрения квадрате. Чтобы получить gap, поделим значение side на число строк (или столбцов) в массиве pic.
Третья часть программы - центральная. Она отыскивает комплексные числа c, принадлежащие множеству Мандельброта, а также присваивает цвета числам, расположенным, в некотором специальном смысле, неподалеку. Процедура выполняется для каждого отдельного пиксела. Таким образом, в программе Хаббарда, имеющей массив размером 400*400, потребуется 160000 шагов вычисления. Предположим, что в данный момент программа обрабатывает данные, относящиеся к пикселу, принадлежащему строке m и и столбцу n. Тогда процедура, выполняемая третьей частью программы, распадается на четыре этапа, или шага.
1. Вычислить комплексное число c, соответствующее данному пикселу: сложить величину n*gap с acorner, чтобы получить действительную часть ac числа c; сложить величину m*gap с bcorner, чтобы получить мнимую часть bc числа c. При этом нет необходимости включать в программу символ i.
2. Вначале задать комплексную переменную z (с действительной частью az и мнимой частью bz) равной 0+0i. Установить целую переменную count равной 0.
3. Выполнять повторно следующие три операции, пока или величина z не превысит 2, или значение count не превысит 1000, независимо от того, какое из этих событий наступит раньше:
z <- z2+с
count <- count+1
side <- <величина z>
Почему цифра 2 играет такую важную роль? Дело в том, что, согласно теории, комплексное число z, к которому применяется итерационный процесс, "уйдет" в бесконечность тогда и только тогда, когда на определенной стадии процесса оно достигнет значения 2 или более. Как показывают вычисления, довольно много точек, которым суждено уйти в бесконечность, достигают 2 уже после первых нескольких шагов итераций. Более "медленные" точки достигают этой величины все реже и реже по мере роста значения переменной count.
4. Присвоить цвет элементу pic(m, n) в соответствии со значением переменной count, достигнутым после выполнения 3-го шага процедуры. Высветить цвет данного пиксела на экране дисплея. Заметим, что цвет пиксела зависит только от одного комплексного числа, находящегося в его ближайшей окрестности, а именно от числа, находящеюся в верхнем правом углу этой окрестности. Поведение этого числа определяет поведение всего пиксела.
При таком способе присвоения цвета нужно, чтобы диапазон изменения переменной count разделялся на поддиапазоны, по одному на каждый цвет. Пикселы, для которых величина z достигает 2 уже после первых нескольких итераций, окрашиваются в красный цвет. Пикселы, для которых величина z достигает 2 после сравнительно большого количества итераций, окрашиваются в фиолетовый цвет, расположенный на противоположном краю спектра. Пикселы, для которых величина z остается меньше 2 даже после 1000 итераций, по предположению, лежат в множестве Мандельброта и окрашиваются в черный цвет.
Было бы разумно оставлять цвета неопределенными, пока не будет установлен диапазон изменения переменной count в данном конкретном квадрате. Если диапазон оказывается узким, то весь цветовой спектр можно уместить в его пределах. Поэтому Хаббард предлагает, чтобы на 4-м шаге процедуры каждому элементу массива pic присваивалось лишь значение переменной count. Затем отдельная программа должна будет просмотреть массив, определить наибольшее и наименьшее значения count и соответствующим образом распределить спектр. Читатели, которым удастся написать все остальные фрагменты программы, несомненно, справятся и с этим местом.
При отсутствии цветного дисплея можно обойтись и черно-белым. Комплексные числа, величина которых превышает 2 после r итераций, окрашиваются в белый цвет, остальные точки остаются черными. Значение параметра r можно выбрать по вкусу. Чтобы не просиживать целую ночь перед экраном в ожидании результатов, размер массива можно, например, принять равным 100*100. Хаббард считает также, что разумно было бы сократить максимальное количество итераций с 1000 до 100. Результатом подобной программы будет точечный образ, или черно-белое представление цветного изображения, о котором говорилось выше (см. рисунок вверху).

Точечное изображение миниатюрного множества Мандельброта, полученное на черно-белом дисплее
КАКОВА же мощность микроскопа, реализованного на персональном компьютере? В какой-то степени она зависит от количества разрядов чисел, которыми может оперировать машина. Например, в персональном компьютере фирмы IBM используется микропроцессор 8088 фирмы Intel Corporation, предназначенный для выполнения операций над двоичными числами длиной 16 разрядов. Пользуясь так называемой двойной точностью, можно увеличить количество разрядов до 32. При этом условии, по моим подсчетам, можно достигнуть увеличения порядка 100000. Используя специальное, программное обеспечение, объединяющее двоичные разряды чисел в единые цепочки, можно повысить точность вычислений до сотен значащих двоичных разрядов. При такой точности теоретически достижимое увеличение множества Мандельброта намного превышает увеличение, необходимое для того, чтобы рассмотреть внутреннюю структуру атомного ядра.
Какую часть комплексной плоскости интереснее исследовать? Конечно, в окрестности множества Мандельброта. Ну а точнее? По словам Хаббарда, на плоскости "есть зиллионы прекраснейших мест". Подобно туристу, посетившему необычайно красивые места в мире бесконечного, он может буквально засыпать читателей предложениями тех мест, какие будут особенно интересными. Правда, эти места не носят таких экзотических названий, как Сингапур или Таити. Хаббард рекомендует читателям "исследовать область комплексных чисел с диапазоном действительных частей от 0.26 до 0.27 и мнимых - от 0 до 0.01". Он также предложил две другие области: Действительная часть
от -0.76 до -0.74
от -1.26 до -1.24
Мнимая часть
от 0.01 до 0.03
от 0.01 до 0.03
Рассматривая цветные картинки, иллюстрирующие нашу статью, следует иметь в виду, что точки, окрашенные в любой другой цвет, кроме черного, не принадлежат множеству Мандельброта. В значительной мере красота картинок обусловлена гаммой красок, ассоциируемых с точками, устремляющимися в бесконечность. На самом деле если бы мы захотели посмотреть на множество Мандельброта в полной изоляции от окружающих его точек, то картинка не была бы столь красивой: мы увидели бы перед собой множество, всюду покрытое тонкими волосками и содержащее миниатюрные структуры, очень похожие на само множество.
В действительности ни одно из миниатюрных множеств Мандельброта не является точной копией родительского множества. Более того, между этими миниатюрными версиями множества также имеются некоторые различия. В окрестности множества Мандельброта мы видим многочисленные его микроскопические версии, как бы подвешенные в "атмосфере" комплексной плоскости. Однако это впечатление обманчиво. Согласно удивительной теореме, доказанной Хаббардом и его коллегой А.Дуади из Парижского университета, множество Мандельброта является связным. Поэтому даже миниатюрные версии множества, кажущиеся изолированными в комплексной плоскости, на самом деле соединены с родительским множеством тонкими волокнами. Миниатюрные версии множества встречаются повсюду в окрестности и имеют самые разные размеры. В каждом квадрате конечного размера содержится бесконечное количество миниатюрных версий множества, из которых при любом увеличении можно разглядеть лишь несколько. По словам Хаббарда, множество Мандельброта представляет собой "самый сложный объект в математике".
ПОСЛЕ путешествия в мир бесконечно сложного приятно отдохнуть в пределах конечного. Многократно повторяя операцию возведения в квадрат на конечном множестве обыкновенных целых чисел, можно также получить интересные структуры. Правда, эти структуры не геометрические, а, скорее, комбинаторные.
Выберем наобум любое целое число в диапазоне от 0 до 99. Возведем его в квадрат и оставим два последних десятичных разряда. Они также будут представлять собой число в диапазоне от 0 до 99. Например, возведя 59 в квадрат, мы получим 3481; два последних разряда этого числа 81. Если продолжить этот процесс, то рано или поздно мы получим число, уже встречавшееся нам ранее. Например, начиная с числа 81, мы получим последовательность 61, 21, 41 и 81, и эта последовательность из четырех чисел будет теперь повторяться до бесконечности. Оказывается, что такие циклы всегда возникают при итерационных процессах над конечными множествами. Нетрудно видеть, что существует по крайней мере одно повторяющееся число после 100 операций на множестве из 100 чисел. Первое же повторяющееся число приводит к возникновению цикла. Существует изящная программа обнаружения подобных циклов, почти не требующая памяти, но об этом несколько позже.
Приблизительно за час можно построить диаграмму результатов описанного процесса. Представим каждое число от 0 до 99 точкой на листе бумаги. Если после возведения в квадрат одно число переходит в другое, то соединим соответствующие точки стрелочкой. Например, такую стрелочку мы должны провести от точки 59 к точке 81. После нескольких первых соединений на диаграмме могут возникнуть запутанные циклы, поэтому время от времени их следует перерисовывать таким образом, чтобы стрелки никогда не пересекались. Нарисовать такую диаграмму без пересечений, оказывается, всегда возможно.
Можно пойти даже дальше. В ходе процесса часто возникают отдельные поддиаграммы, и их можно построить таким образом, чтобы выявились некоторые свойства симметрии, характерных для итераций. Например, непересекающаяся диаграмма итераций для возведения в квадрат целых чисел в диапазоне от 0 до 99 содержит шесть не связанных между собой диаграмм. Части диаграммы встречаются в виде идентичных пар, и каждая часть обладает высокой степенью симметрии (см. рисунок на с.85). Может ли читатель дать толкование этих симметрии? Что изменится, если диапазон расширить от 0 до 119? Существует ли какая-нибудь зависимость между числом не связанных друг с другом частей на диаграмме и наибольшим целым числом в последовательности?

Шесть компонент диаграммы итерационного процесса возведения в квадрат для первых 100 натуральных чисел
Сходные с только что описанными закономерности наблюдаются и при итерациях, применяемых к некоторым комплексным числам, принадлежащим множеству Мандельброта: для определенных значений c итерации, применяемые к выражению z2+c, могут привести к конечному циклу из комплексных чисел. Так, например, начиная с комплексного числа 0+1i, мы получаем бесконечные колебания между двумя числами: -1+1i и 0-1i. Цикл может даже состоять из единственного числа. Такие циклы независимо от того, встречаются они на конечном множестве или на бесконечном множестве Мандельброта, называются аттракторами.
Каждая из шести частей диаграммы итерационного процесса для целых чисел в диапазоне от 0 до 99 содержит один аттрактор. Геометрически аттрактор можно представить в виде многоугольника, а множества чисел, которые приводят к нему, можно представить в виде деревьев. Один из возможных способов найти аттрактор заключается в том, чтобы запоминать каждое порождаемое число в специально отведенном массиве программы. Только что полученное число следует сравнить с каждым из ранее запомненных в массиве чисел. Если среди них находится число, совпадающее с данным, то все числа, расположенные между найденным числом и только что полученным, равным ему, выводятся на экран или печать. Способ довольно простой, и его нетрудно реализовать в программе. Однако, если массив большой, процесс сравнения чисел может потребовать много времени. Чтобы найти аттрактор в массиве, содержащем n чисел, необходимо выполнить порядка n2 операций сравнении, поскольку каждое новое число нужно сравнить с каждым числом массива, а количество последних может доходить до n.
Существует маленькая остроумная программа, которая находит аттракторы значительно быстрее. Вместо n слов памяти программа требует лишь два, и ее можно составить даже на простейшем карманном программируемом калькуляторе. С этой программой вы сможете познакомиться, прочтя любопытную книжку: Hoffman D., Mohler L. Mathematical Recreations for the Programmable Calculator ("Занимательная математика для программируемого калькулятора"). Разумеется, многие рассмотренные в книжке программы могут быть легко переписаны для персонального микрокомпьютера или любой другой ЭВМ.
Программа RHOP получает последовательность чисел, которая в конце концов зацикливается и напоминает кусок каната с петлей на одном конце. Она напоминает также греческую букву "ро" (по-английски rho; отсюда название программы RHOP.- Перев.). В программе две переменные - fast и slow (соответственно "быстрая" и "медленная".- Перев.). Первоначально обеим переменным присваивается значение исходного числа. Итерационный цикл программы состоит лишь из трех команд:
fast <~ fast*fast (mod 100)
fast <- fast*fast (mod 100)
slow <- slow*slow (mod 100)
Операция "mod 100" извлекает последние два разряда произведения. Заметим, что число fast дважды возводится в квадрат, а число slow только один раз. Число fast пробегает путь от хвоста буквы "ро" до ее головы вдвое быстрее числа slow. Уже в пределах головы буквы "ро" число fast встречается с числом slow. Программа останавливает итерационный цикл, когда совпадают значения переменных fast и slow.
Аттрактор определяется путем повторного возведения в квадрат числа, являющегося на данный момент значением переменной slow. Когда это число встречается вновь, программа останавливается и высвечивает или распечатывает последовательность чисел между двумя одинаковыми значениями slow.
Читатели могут попытаться построить диаграммы на основе результатов итерационного процесса возведения в квадрат чисел из конечных множеств различных размеров. Эти диаграммы можно получить как с помощью компьютера, так и от руки. Дискретные итерационные процессы - это новая, развивающаяся область математики, которая находит применение в вычислительной технике, информатике, биоматематике, физике и даже социологии. Теоретики, наверняка, с интересом прочтут монографию Франсуа Роберта из Гренобльского университета, которая посвящена этому предмету и в настоящее время готовится к печати.
БИБЛИОГРАФИЯ
MATHEMATICAL RECREATIONS FOR THE PROGRAMMABLE CALCULATOR. DEAN HOFFMAN AND LEE MOHLER. Hayden Book Co., 1982.
THE FRACTAL GEOMETRY OF NATURE. BENIOT B. MANDELBROT. W.H.Freeman and Company, 1983.
DISCRETE ITERATIONS. FRANCOIS ROBERT; translated from the French by Jon Rokne. Springer-Verlag, in press.
ОТКЛИКИ
1 1986
С МОМЕНТА появления программы MANDELZOOM (см. журнал "В мире науки", 1985, #10) она поселилась в сотнях домов, школ и учреждений. И хотя эта программа, очевидно, произвела очень сильное впечатление на взрослых, заинтриговала подростков и даже напугала нескольких детей младшего возраста, отклики читателей на вторую тему статьи, посвященную итерационным диаграммам, к моему удивлению, оказались почти столь же многочисленными, как и на тему о множестве Мандельброта.
Многие читатели, что называется, с головой окунулись в разноцветные кружева множества Мандельброта, погружаясь в него все глубже по мере роста степени увеличения. Читатели, одержимые желанием иметь свои собственные цветные изображения множества, но не имеющие цветной графики на своих персональных компьютерах, заказали фотографии у Дж.Хаббарда из Корнеллского университета. Дж.Хаббард и X.Пайтген, картинки которого красовались на страницах упомянутого номера журнала, научились искусству получать изображения множества у самого Мандельброта.
Читателям, возможности которых ограничены лишь черно-белой графикой, я бы рекомендовал воспользоваться различными оттенками серого цвета. Картинки в черно-белом изображении могут быть почти такими же впечатляющими, как и их цветные аналоги. Лучшие серые изображения были получены Д.Бруксом, работающим в фирме Prime Computer, Inc. в Фреймингхемс (шт.Массачусетс). В его сказочных сочетаниях полутонов каждый оттенок серого цвета достигается при помощи маленьких черных квадратиков определенного размера, напечатанных лазерным принтером. Брукс старался выявить крошечные волокна, предположительно соединяющие миниатюрные множества Мандельброта с основным множеством. Пока лаже при самых больших увеличениях Бруксу не удалось их разглядеть. Мандельброт сообщил ему, что эти волокна, по всей видимости, имеют бесконечно малую толщину.
Читатели, не обладающие столь изощренным оборудованием, могут все же работать с различными оттенками серого цвета на экранах своих черно-белых дисплеев. Дж.Халлек из Солт-Лейк-Сити варьирует плотность точек, приходящихся на один пиксел, чтобы получить различные оттенки.
В другом подходе для генерации изображений множества Мандельброта применяются черные и белые контуры. Й.Гурсель из Кембриджа (шт.Массачусетс) построил изображения множества, пожалуй не уступающие изображениям Брукса. Гурсель заменяет дискретный цветовой спектр чередующимися белыми и черными кольцами. Р.Шэннон из Грантс-Пасса (шт.Орегон) предложил тот же метод. В.Андерсен из Санта-Клары (шт.Калифорния) довел его до "крайности": он предложил переходить от черного к белому (или наоборот) всякий раз, когда переменная count меняется от одного пиксела к другому.
Стоит упомянуть также еще о двух исследованиях. Дж.Тигпенн IV из Перланда (шт.Техас) вместо цветового представления применяет уровни высоты: множество Мандельброта превращается в огромное плато, видимое под некоторым углом, со сложным ландшафтом остроконечных холмов, подступающих к плато с разных сторон. Р.Пальмаччио из Форт-Лодердейла вовсе упразднил множество как таковое. Его интересуют траектории индивидуальных комплексных чисел, описываемые на плоскости по ходу итераций. Их причудливая хореография вблизи границ множества Мандельброта принимает форму спирального вальса или кругового фокстрота.
Множество Мандельброта порождается функцией z2+c. Конечно, существуют и другие функции, но они порождают другие множества. К примеру, Б.Икенага исследует образование, которое можно назвать кубическим кактусом. Функция z3+(c-1)z-c порождает колючее с неприветливым внешним видом множество (по крайней мере так оно выглядит в контрастных черных и белых тонах), окруженное таинственными миниатюрными спиральными галактиками.
Итерационные диаграммы также полны загадочного. Когда целые числа по модулю n возводятся в квадрат, каждое число переходит в другое. Итерационная диаграмма получается, когда каждое число заменяется точкой, а каждое перемещение - стрелкой. По поводу этих диаграмм я сформулировал несколько вопросов. Сколько компонент содержат в себе тахие диаграммы? Читатели прислали полученные диаграммы, документируя тем самым свои исследования для различных значений n.
Наиболее крупные диаграммы были построены Р.Мэримонт из Силвер-Спринга(шт.Мэриленд). Она рассматривала целые числа, вычисляемые по модулю 1000, и на результирующей диаграмме она получила четыре пары компонент. Каждая компонента обладала, как обычно, одним аттрактором, и наибольший из аттракторов включал в себя 20 чисел. Будучи математиком по профессии, Мэримонт высказала предположение, что целые числа, вычисляемые по модулю 1Ek, должны породить k+1 пар компонент и что наибольшие аттракторы должны включать 4*5^(k-2) чисел.
С.Эберхарт из Ресеты (шт.Калифорния) заинтересовался случаем, когда n представляет собой простое число Ферма (т.е. простое число, представимое в виде 2^2^k+1). Здесь число 0 образует аттрактор, а все остальные числа принадлежат одному-единственному большому дереву. Один мой знакомый, специалист по теории чисел, подтверждает, что для простых чисел Ферма это всегда так и что дерево является двоичным: каждый внутренний узел имеет две входные стрелки.
Итерационные диаграммы, подобно числам, можно перемножать между собой. Если n - произведение двух простых чисел, скажем р и q, то итерационная диаграмма для целых чисел, вычисляемых по модулю n, представляет собой произведение соответственно диаграмм дляр p и q. Это интересное наблюдение было сделано С.Локом из Флоридского атлантического университета. Лок описал также очень интересное отношение, сушествуюшее между n-й итерационной диаграммой и диаграммой, казалось бы, совсем другого рода, в которой числа вместо того, чтобы возводиться в квадрат, просто удваиваются. Если n - простое число, последняя диаграмма для целых чисел, взятых по модулю n-1, совпадает с нашей n-й диаграммой, за исключением единственного изолированного числа, образующего свой аттрактор. Весьма похожее наблюдение было сделано в рамках теории чисел Н.Элкисом из Нью-Йорка.
Мощный инструмент для анализа итерационных диаграмм (при возведении в квадрат) был разработан Ф.Палмсром из Чикаго. Очевидно, все деревья, связанные с данным аттрактором, изоморфны. По существу, это означает, что они обладают в точности той же самой формой.
Наконец, Б.Джилсон из Силвер-Спринга (шт.Мэриленд) и М.Уилльямс из Каламазу (шт.Мичиган) исследовали совершенно другое обобщение множества чисел от 0 до 99. Их можно рассматривать как числа по другому основанию. Например, последовательность натуральных чисел по основанию 3 будет выглядеть следующим образом: 00, 01, 02, 10, 11, 12, 20, 21, 22, пока мы снова не придем к числу 00. Такие числа также порождают итерационные диаграммы, которые выглядят аналогично диаграммам, получаемым для целых чисел по модулю n. Джилсон доказал, что диаграммы всегда имеют парные компоненты при четных n, не являющихся кратными 4.
2 1986
Читатели, не чувствующие себя достаточно компетентными в программировании, чтобы написать свои собственные версии программы MANDELZOOM, но желающие завести ее в библиотеке программ своих персональных компьютеров, обратились к нам с просьбами прислать им программу. Когда читатели просят прислать им листинги или дискеты с записью программ, которые я представляю в наших статьях, возникает, конечно, соблазн удовлетворить их просьбу. Но у меня просто не хватит времени, чтобы ответить на все поступающие письма. Кроме того, я считаю, что время, которое читатель затратит, чтобы научиться нескольким простейшим элементам программирования, требующимся для решения большинства описываемых мною задач, он проведет с пользой для себя. С педагогической точки зрения это, наверное, правильно.
В то же время, когда другие читатели щедро предлагают поделиться созданными ими программами со всеми желающими, я уже не могу удержаться от соблазна. Поэтому иногда я привожу имена любителей, выразивших такое желание.
10 1986
В заключение сообщаю, что Р.Силвер из Сан-Кристобала (шт.Нью-Мексико) предложил учредить периодический печатный орган, посвященный новостям, касающимся экспериментов со множеством Мандельброта. В нем, как он считает, должны публиковаться статьи читателей о новых полученных ими результатах.
Последний раз редактировалось: Gudleifr (Чт Окт 19, 2023 8:18 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
11 1985
О ТОМ, КОГДА ИГРУ МОЖНО СЧИТАТЬ РАБОТОЙ, И О НЕОПАСНЫХ ТЕРМИНАЛЬНЫХ БОЛЕЗНЯХ
А.К.ДЬЮДНИ
В ИССЛЕДОВАТЕЛЬСКОМ центре фирмы Bell Laboratories в Мюррей-Хилл (шт.Нью-Джерси) невозможно провести грань между работой и игрой. Время от времени безудержная фантазия и удивительная изобретательность сотрудников центра порождают игры, имеющие весьма серьезное значение. Показательные в этом смысле примеры дают терминал типа Блит (Blit) и развлекательная программа КРАБЫ (CRABS), которая иногда мешает работать с системой Блит.
Разработанная четыре года назад Р.Пайком и Б.Локанти, система Блит представляла собой предварительную версию нового терминала DMD 5620 фирмы Teletype Corporation. Система фирмы Teletype и ее прообраз Блит представляют собой терминалы, работающие в многопрограммном режиме.
Когда прошлой осенью я посетил исследовательский центр в Мюррей-Хилл, ПаЙк предложил мне посмотреть терминал DMD 5620 в действии. На терминалах этого типа (которые я ниже буду просто называть терминалами Блит) экран может быть поделен на отдельные окна, иногда частично перекрывающиеся. Каждое окно, по существу, представляет собой самостоятельный миниатюрный экран, полностью отданный в распоряжение какой-либо одной программы. Программы могут выполняться встроенным в терминал микропроцессором или большой центральной ЭВМ, к которой подключен терминал. При этом незанятые области экрана покрываются точечным узором, как бы окрашивающим их в серый цвет.
На экране терминала, показанного мне Пайком, три окна были заняты тремя одновременно выполняющимися программами. Одно окно принадлежало находящейся в стадии отладки экспериментальной программе редактирования текстов. Во втором окне программа-редактор показывала текст первой программы. Третье окно было отведено программе отладки, при помощи которой осуществлялась проверка экспериментальной программы редактирования текстов. Все три программы выполнялись встроенным в терминал Блит микропроцессором. Пайк демонстрировал передо мной необычайные возможности этой многопрограммной системы, как вдруг в верхней части экрана появилось несколько крабовидных символов, разбросанных вдоль границы окна. "Крабы" двигались по экрану, как бы поедая изображение в окне. Заметив мое удивление, Пайк объяснил: "Это крабы. Чтобы вас позабавить, мы только что загрузили программу КРАБЫ из центральной машины".
Центральная машина, к которой был подключен терминал Блит, работала под управлением операционной системы UNIX. Олна из наиболее популярных операционных систем за всю историю вычислительной техники, система UNIX, была создана К.Томпсоном, сотрудником фирмы Bell Laboratories, разделившим премию Тьюринга за 1983г. со своим коллегой из центра в Мюррей-Хилл Д.Ритчи.
Завороженный, я наблюдал, как крабы (их было около тридцати) съели линию, ограничивающую одно из окон, и начали поедать текст внутри. "Как их можно остановить?" - спросил я. "Никак",- ответил Пайк. "Да, но ведь вы их каким-то образом останавливаете?"
Программа КРАБЫ, написанная Л.Карделли и М.Манэссе в 1982г.,- это преднамеренное нарушение соглашений, принятых в многопрограммной системе, с которой работает терминал Блит. Дело в том, что каждая программа, имеющая свое окно на экране, должна быть независимой от программ из других окон и защищенной от них. Когда терминалы системы Блит были расставлены по помещениям лабораторий, Карделли и Манэссе не смогли удержаться от соблазна нарушить эти соглашения.
К тому времени, как Пайк поведал мне эту историю, все окна на экране были уже изрядно поедены. Они напоминали страницы недавно найденной средневековой рукописи. Текст в окнах стал настолько неразборчивым, что Пайк уже не мог объяснить мне, как протекает процесс выполнения соответствующих программ.
Пайк рассказал, что название этого оригинального терминала произошло от имени графической процедуры низкого уровня bitblt, отличающейся удивительно широким спектром применения. Имя bitblt в свою очередь является сокращением от слов bit - boundary block transfer (букв, перенос блоков с битовой границей.- Перев.), обозначающих процедуру, которая управляет перемещением информации по памяти терминала. Точнее говоря, bitblt переносит содержимое одной прямоугольной области памяти в другую. В ходе этого переноса над содержимым области могут производиться некоторые простые логические операции.
Часть памяти терминала Блит состоит из подсистемы емкостью 100000 байт, целиком отведенной для экрана. В процессе непрерывного сканирования каждый бит памяти преобразуется в светлую или темную точку на экране дисплея. При этом одномерный массив памяти преобразуется в двумерное изображение содержимого массива. Поскольку область памяти и ее изображение имеют различные размерности, точки, принадлежащие прямоугольной области на экране, оказываются разбросанными по памяти в виде отдельных блоков ячеек с последовательными адресами, так что каждый блок соответствует одной горизонтальной линии (полоске) на экране, из которых состоит прямоугольник. Совокупность точек-ячеек во всех блоках образует прямоугольное множество. Процедура bitblt позволяет выполнять определенные операции над такими прямоугольными множествами.
Для успешной работы в многопрограммной среде терминал Блит требует также значительного объема основной, "неэкранной" памяти, необходимой программам, диалог с которыми проходит с использованием экрана терминала. Например, в терминале DMD 5620 фирмы Teletype для этой цели отводится 900000 байт. Здесь также важную роль играют прямоугольные множества. К процедуре bitblt часто происходят обращения, когда надо преобразовать прямоугольное множество основной памяти в прямоугольное множество памяти экрана. Пусть, например, в некотором прямоугольном множестве основной памяти содержится буква A. Всякий раз, когда на экране должна появиться буква A как часть текста, выводимого программой, происходит обращение к процедуре bitblt, переносящей это прямоугольное множество в экранную память.
Аппаратное сканирование памяти - это принципиальная конструктивная особенность, присущая графическим терминалам с описанным выше буфером памяти для экрана, или так называемым "буфером-фреймом". Подобные дисплеи получают все более широкое распространение и уже применяются в персональных компьютерах. Свидетельство тому - дисплей персонального компьютера фирмы Macintosh.
В традиционных системах с графическими дисплеями обращения к памяти происходят по более сложным алгоритмам. Представление рисунка на экране осуществляется, например, при помощи списка точек, линий и других графических элементов. Для того чтобы высветить рисунок на экране, необходимо просмотреть список. При этом простые рисунки можно высветить быстро, потому что их списки короче, однако для изображения сложных рисунков может потребоваться слишком много времени.
Конфигурация битов в какой-нибудь прямоугольной области памяти называется битовой картой. Каждая битовая карта представляет на экране определенное изображение: типографский знак, простой рисунок-символ или еще какой-нибудь графический элемент. В программе КРАБЫ, например, используются некоторые битовые карты из основной памяти, при помощи которых на экране строятся крошечные ракообразные различной формы. Краба представляет следующая цепочка из нулей и единиц (единицы соответствуют темным, а нули - светлым точкам на экране):
01101110... 11110111... 10000001... 10111101... 01111110... 01111110 ... 10111101 ... 01000010
Читатели, желающие промоделировать bitblt, могут нарисовать на листе бумаги квадратную решетку размерами 8*8. Тогда приведенная выше цепочка будет представлять прямоугольную область в основной памяти, а квадратная решетка - часть экранной памяти. Скопируйте цепочку на решетку, просканировав побитно ту и другую. Теперь можно воспроизвести изображение на решетке, закрасив черным цветом каждую ячейку, содержащую единицу, и оставив светлыми ячейки, содержащие нули. При этом мы получим изображение краба, занимающего небольшую часть экрана (см. рисунок на с.73).

Изображение краба на квадратной решетке
Выше я уже отмечал, что любая часть экрана, не охваченная никаким окном, закрашивается точечным узором в серый цвет. Когда крабы напали на экран терминала Пайка, они сначала ползали по серой области. Натолкнувшись на окно, они начали его поедать. При этом Пайк шутливо заметил, что "серый цвет - это дорожки для крабов, а своих дорожек они не поедают". На самом деле крабы ничего не поедают, а скорее асфальтируют. Когда программа КРАБЫ двигает свое детище, она проверяет поле, находящееся непосредственно на пути краба; если оно не серое, то программа окрашивает его в серый цвет. Затем она перемещает краба в только что обработанную область. Обе операции осуществляются при помощи процедуры bitblt.
В простейшем варианте работы процедура bitblt заменяет каждый бит d на битовой карте, являющейся результатом, соответствующим Битом s исходной битовой карты. Кратко эту операцию замещения можно обозначить формулой
d <- s.
Любую область экрана можно сделать серой, воспользовавшись этим вариантом процедуры bitblt. Поле, находящееся непосредственно на пути краба, можно рассматривать как битовую карту-результат, а битовую карту в основной памяти, содержащую шаблон серого цвета, можно считать исходной битовой картой.
Затем программа КРАБЫ перемещает краба. Она стирает изображение краба в том месте, где оно в данный момент находится, и высвечивает его на новом месте. Чтобы выполнить соответствующие операции, используется более сложный вариант процедуры bitblt, который можно условно обозначить следующим образом:
d <- s+d.
Здесь каждый бит поля результата замещается его комбинацией с соответствующим битом источника. Эта комбинация представляет собой логическую операцию исключающего ИЛИ, которую мы впредь будем обозначать как XOR или знаком "+". В результате применения операции XOR бит d будет равен 1 тогда и только тогда, когда либо s, либо d (но не оба одновременно) имеют значение, равное 1. Операцией XOR очень удобно пользоваться как при стирании старого изображения краба, так и при построении нового. К сожалению, в этом варианте процедура bitblt не может воспользоваться стандартным изображением краба, которое мы получили выше при помощи карандаша и бумаги.
Посмотрим, например, что будет, если операцию XOR применить к стандартной битовой карте краба и точечному шаблону серого цвета. Когда операция XOR применяется к точке серого поля (1) и какой-либо точке тела краба (также 1), результатом будет светлая точка (1+1=0). Если, однако, данная точка тела краба является светлой, то результатом будет темная точка {0+1=1). Этим объясняется странный вид восьми специальных битовых карт краба, которыми пользуется программа КРАБЫ при перемещении своих подопечных (см. рисунок на с.74). Каждая из этих битовых карт представляет краба со специальным подбором светлых точек на его теле. Существует восемь возможных способов поместить краба на серое поле, и каждому из этих способов соответствует своя битовая карта краба.

Битовые карты краба со светлыми точками, нанесенными на них в соответствии с восемью возможными способами наложения краба на серое поле
Программа перемешает краба, сначала стирая его, а затем высвечивая на новом месте. Чтобы стереть краба, процедура bitblt отображает при помощи операции XOR битовую карту краба с соответствующим подбором светлых точек на светящееся в данный момент изображение краба. В результате изображение краба исчезает и на его месте остается серое поле. Чтобы высветить новое изображение краба, процедура bitblt опять пользуется специально подобранной битовой картой краба, которую она отображает посредством операции XOR на серое поле. Новое изображение краба ничем не отличается от старого, поскольку светлые точки на его битовой карте точно соответствуют серому полю, на которое краб перемешается.
Алгоритм, управляющий поведением крабов, можно разбить на пять шагов:
1. Стереть изображение краба в том месте, которое оно в данный момент занимает.
2. Определить новое место.
3. Если новое место не является серым полем, то сделать его серым, изменить данные о положении краба и выбрать случайным образом новое значение скорости передвижения.
4. Высветить краба на новом месте.
5. Изменить случайным образом скорость краба. Вернуться к шагу 1.
Крабы, как и полагается, движутся боком. Поэтому новое место всегда находится сбоку от краба, по ту или другую сторону от него. Новое место определяется текущими значениями направления и скорости движения краба. Обе эти величины подвергаются на шаге 5 случайным изменениям. Возможны несколько направлений движения, а его скорость варьируется в пределах от 1 до 7 пикселов (ячеек на экране) на одно перемещение.
Во время нашего разговора с Пайком крабы сначала появились в верхней части экрана. Затем, совершая хаотические перемещения по серым полям, они стали медленно спускаться вниз. Встретив окно, они прогрызли его границу и проникли внутрь. Было хорошо видно, как они прогрызают окно, потому что на изображении стали появляться крошечные серые пятна. Внешне это выглядело очень эффектно: крабы как будто пожирали верхний слой бумаги, под которым проступало серое волокно.
В значительной степени эта иллюзия объяснялась шагом 3 алгоритма программы КРАБЫ, поскольку на этом шаге краб уходит с только что проеденного им места так, словно он посидел на нем какое-то мгновение, пережевывая проглоченный кусок, прежде чем отправиться дальше в поисках новой порции. Благодаря случайному характеру движения крабов окно становится "дырявым" сразу на большой поверхности. Если бы не эта особенность их движения, то эффект, производимый крабами, скорее напоминал бы процесс выкапывания нор. Благодаря случайному характеру движения крабов человек за терминалом не сразу понимает, что происходит, и его реакция оказывается замедленной.
Пока мы наблюдали за тем, как крабы проедали окна на экране терминала, Пайк рассказал мне о том, как по-разному реагировали его коллеги, впервые столкнувшись с нападением крошечных ракообразных. Часто такое нападение устраивалось исподтишка. Когда ничего не подозревающий сотрудник отходил на минутку от терминала, кто-нибудь из шутников запускал на его терминале программу КРАБЫ.
Поскольку терминал Блит снабжается обычно устройством "мышь", управляющим перемещением курсора на экране, сбитый с толку сотрудник иногда лихорадочно пытался противостоять крабам при помощи этого устройства. Однако все подобные попытки оказывались тщетными, так как крабы с таким же аппетитом набрасывались на курсор, как и на текст. При этом "съеденный" курсор через некоторое время вновь появлялся на экране. И, хотя наступление крабов можно таким образом несколько замедлить, остановить их невозможно и изображение в окнах продолжает разрушаться.
Иногда программист, чей терминал подвергся нападению крабов, пытался накрыть их окном. Эта мера также несколько замедляла продвижение крабов, однако они постепенно прогрызали вокруг себя все большее поле и в конце концов вырывались из окна.
Я снова спросил Пайка, каким образом можно остановить крабов. На этот раз он смилостивился: "Выключите терминал и включите его снова". Такая мера оказывается действенной, однако при этом пользователю приходится заново подключаться к центральной ЭВМ.
Карделли и Манэссе, авторы программы КРАБЫ, изложили историю происхождения программы в неофициальной докладной записке. Конструкция и правила пользования терминалом Блит произвели на них очень сильное впечатление, и они решили проанализировать возможности нарушения этих правил. Они обратились к Пайку, который дал им текст интересовавших их фрагментов программного обеспечения системы. Поразмыслив, двое программистов пришли к выводу, что некоторые возможности нарушения правил, принятых в конструкции терминала, могут оказаться полезными. В этом смысле примером служит программа ЛИНЗА, которая увеличивает заданную часть экрана. (На рисунках на с.76-77 видно окно программы ЛИНЗА, увеличивающее текст, пораженный крабами.) ЛИНЗА представляет собой нарушение правил, потому что программа, имеющая одно окно, не должна иметь прямого доступа к содержимому другого окна.

Экран терминала, показывающий вывод из пяти программ, подвергшихся атаке крабов

Пользователь может отбить подобное нападение, только выключив терминал и повторно подключившись к системе
Вначале Карделли и Манэссе намеревались имитировать видеоигру QIX, но затем вместо этого написали программу МИКРОБЫ (MEASLES), в результате выполнения которой по серым участкам экрана между окнами начинали плавать маленькие шарики. Первые же испытания показали, что микробов можно было заблокировать, накрыв их окном. Авторы сочувствовали своим созданиям: "Внезапно бедные маленькие микробы оказались запертыми, им было некуда двигаться, нигде вокруг не было спасительного серого поля. Они застыли, полные ужаса, и были похоронены под окном".
Первая реакция авторов на эту неудачу заключалась в том, чтобы заставить пойманных микробов периодически вспыхивать, досаждая тем самым человеку, который поймал их. Новая программа получила название ЗЛЫЕ МИКРОБЫ.
Однако даже "злые микробы" были ничто по сравнению со следующим замыслом, пришедшим в голову неутомимым авторам: "А почему бы микробам не прогрызть себе путь и выйти таким образом из окна?" Соответствующая программа получила имя ГОЛОДНЫЕ МИКРОБЫ. Карделли пишет: "У новой версии был уже совсем другой характер. Она уже не была просто остроумной, она внушала трепет".
Кто-то, наблюдая за работой программы на экране, заметил, что микробы напоминают чем-то крошечных ракообразных. Карделли и Манэссе реализовали изображение краба, и таким образом родилась программа КРАБЫ. Следом за ней появились и другие программы подобного рода, в том числе такие, которые оставляли на экране отпечатки следов птиц и зверей.
Сотрудники, ставшие жертвой этих шуток, принимали ответные меры. Была написана программа ДАВИ КРАБОВ, которая просматривала память терминала в поисках программы КРАБЫ. Найденные программы уничтожались, а на экране крабы превращались в маленькие пузырьки. К сожалению, очередная модификация в программном обеспечении терминала сделала программу ДАВИ КРАБОВ неэффективной.
В ЛАБОРАТОРИЯХ исследовательского центра в Мюррей-Хилл есть и другие занимательные программы. Меня познакомили с одной из таких программ, написанной Р.Хардином. Она превращает произвольный текст на английском языке в цепочки фонем, которые затем перегруппировываются, снова превращаются в слова английского языка и выводятся в виде нового текста. Результирующий текст (после некоторого редактирования человеком) выглядит как стихотворение слегка сумасшедшего поэта:
Better buy perfect Topeka beagle buffers
Topeka beagle buffers sputter fiber beaks
Effeter fiber beaks abetted feeble puppies
Worst Topeka beagle puppies feature viper-pique.
Несколько более серьезная работа была проведена при создании программы для игры в шахматы. В 1980г. чемпионат мира по шахматам среди ЭВМ был выигран системой Belle, представлявшей собой комплекс из специализированной ЭВМ и программы, написанной в лабораториях центра в Мюррей-Хнлл. Авторы программы - К.Томпсон и Д.Кондон. (Я думаю посвятить этой и другим современным программам для игры в шахматы одну из своих следующих статей).
Компьютер, играющий в шахматы, созданный, казалось бы, для развлечения, возвращает нас к разговору о соотношении между работой и игрой. Профессор А.Перлис, преподающий информатику в Йельском университете, в своей недавно опубликованной книге "Структура и интерпретация программ для ЭВМ" (см. "Библиографию" на с.84) высказывает мнение, получившее довольно широкое распространение среди специалистов по вычислительной технике и информатике.
"Я думаю, очень важно, чтобы в научной работе всегда оставалось место для шутки и развлечения. Когда вычислительная техника и программирование только зарождались, в нашей работе было много веселого и забавного". Однако, полагает Перлис, сейчас для этого остается все меньше места, потому что исследователям предъявляются серьезные требования, заставляющие их все в большей степени сосредоточивать внимание на "гайках" и "винтиках", из которых состоят изобретаемые ими системы. Но такими вещами следует скорее заниматься тем, кто внедряет научные достижения в производственные системы. "В последнее время мы стали чувствовать себя так, будто бы мы действительно несем ответственность за успешное, безошибочное функционирование этих систем. Мне кажется, это неправильно. Я думаю, наша роль заключается в том, чтобы расширять их возможности, открывать для них новые направления и поддерживать в лабораториях веселое настроение".
Продуктивность научных исследований в вычислительной технике, как в серьезных, так и в шуточных разработках, объясняется прежде всего свободной творческой атмосферой, в которой новые идеи, по-видимому, порождаются наполовину людьми, а наполовину самими машинами. Можно даже сказать, что без этого веселого настроения не было бы и быстрого научного прогресса.
Перед тем как закончить статью, я не могу не вернуться еще раз к терминалу Блит и его процедуре bitblt. Пайк предложил две интересные задачки, которые демонстрируют эффективность и гибкость процедуры bitblt. Предположим, что читатель располагает двумя версиями процедуры bitblt, описанными выше. Одна из них замешает битовую карту в поле результата исходной битовой картой. Другая выполняет операцию XOR.
Задача 1. Очистить прямоугольник. Не прибегая к специальной, заполненной единицами битовой карте в основной памяти терминала, воспользуйтесь процедурой bitblt либо в версии замещения, либо в версии с операцией XOR, чтобы очистить заданный прямоугольник на экране.
Задача 2. Повернуть изображение. Квадратное изображение размером n*n занимает верхний левый угол экрана Блит размером 2n*2n. Воспользуйтесь процедурой bitblt, чтобы повернуть изображение на 90o. Считайте, что вне изображения экран чист.
В первой задаче не разрешается делать никаких предположений о содержимом внешней по отношению к заданному прямоугольнику части экрана. Какой должна быть в этой ситуации битовая карта, которая могла бы послужить исходной для процедуры bitblt?
В обеих задачах воздействие процедуры bitblt на заданный прямоугольник (не важно, какой формы) считается одной операцией. Первая задача решается однократным обращением к процедуре bitblt, вторая требует 3n+1 таких обращений. Сможет ли кто-нибудь найти более быстрое решение?
БИБЛИОГРАФИЯ
THREE DEGREES ABOVE ZERO. JEREMY BERNSTEIN. Charles Scribner's Sons, 1984.
STRUCTURE AND INTERPRETATION OF COMPUTER PROGRAMS. HAROLD ABELSON, GERALD JAY SUSSMAN AND JULIE SUSSMAN. The MIT Press, 1985.
HARDWARE/SOFTWARE TRADE-OFFS FOR BITMAP GRAPHICS ON THE BLIT. ROB PIKE, BART LOCANTHI AND JOHN REISER in Software - Practice and Experience, Vol.15, No.2, pages 131-151; February, 1985.
ОТКЛИКИ
2 1986
В НОЯБРЬСКОМ номере нашего журнала была описана доброкачественная терминальная болезнь КРАБЫ. Орды морских ракообразных внезапно, без предупреждения, с жадностью набрасываются на терминалы Блит, за которыми работают сотрудники фирмы AT&T Bell Laboratories в Мюррей-Хилле (шт. Нью-Джерси).
Почти все программы, выполняющиеся в мультипрограммной системе терминалов типа Блит, пользуются важным оператором bitblt. С помощью этой операции прямоугольные множества битов переносятся из одной области памяти терминала в другую. Перед выполнением переноса прямоугольные множества могут подвергаться различным логическим операциям.
Перед читателями были поставлены две задачи: стереть изображение на экране и повернуть изображение на 90o. Первая задача решается довольно легко. Чтобы стереть картинку, занимающую определенное прямоугольное множество, нужно применить операцию "исключающего или", взяв в качестве операндов само множество. В результате получится множество, содержащее только нули. Таким образом, при помощи одной-единственной операции bitblt можно полностью очистить заданную область экрана.
Повернуть изображение значительно труднее, чем стереть его. До сих пор лишь один читатель представил приемлемое решение. Старшеклассник Т.Вителски из Нью-Йорка нашел способ повернуть изображение размером n*n на экране размером 2n*2n. Затратив лишь 3n-1 операций bitblt, он проходит через n-1 строк, копирует подызображение размером (n-1)*(п-1), проходит через n-1 столбцов, копирует другое подызображение и затем проходит еше через n-1 строк. Метод Вителски оказался более быстрым, чем стандартный алгоритм поворота, требующий 4n-2 операций.
О ТОМ, КОГДА ИГРУ МОЖНО СЧИТАТЬ РАБОТОЙ, И О НЕОПАСНЫХ ТЕРМИНАЛЬНЫХ БОЛЕЗНЯХ
А.К.ДЬЮДНИ
В ИССЛЕДОВАТЕЛЬСКОМ центре фирмы Bell Laboratories в Мюррей-Хилл (шт.Нью-Джерси) невозможно провести грань между работой и игрой. Время от времени безудержная фантазия и удивительная изобретательность сотрудников центра порождают игры, имеющие весьма серьезное значение. Показательные в этом смысле примеры дают терминал типа Блит (Blit) и развлекательная программа КРАБЫ (CRABS), которая иногда мешает работать с системой Блит.
Разработанная четыре года назад Р.Пайком и Б.Локанти, система Блит представляла собой предварительную версию нового терминала DMD 5620 фирмы Teletype Corporation. Система фирмы Teletype и ее прообраз Блит представляют собой терминалы, работающие в многопрограммном режиме.
Когда прошлой осенью я посетил исследовательский центр в Мюррей-Хилл, ПаЙк предложил мне посмотреть терминал DMD 5620 в действии. На терминалах этого типа (которые я ниже буду просто называть терминалами Блит) экран может быть поделен на отдельные окна, иногда частично перекрывающиеся. Каждое окно, по существу, представляет собой самостоятельный миниатюрный экран, полностью отданный в распоряжение какой-либо одной программы. Программы могут выполняться встроенным в терминал микропроцессором или большой центральной ЭВМ, к которой подключен терминал. При этом незанятые области экрана покрываются точечным узором, как бы окрашивающим их в серый цвет.
На экране терминала, показанного мне Пайком, три окна были заняты тремя одновременно выполняющимися программами. Одно окно принадлежало находящейся в стадии отладки экспериментальной программе редактирования текстов. Во втором окне программа-редактор показывала текст первой программы. Третье окно было отведено программе отладки, при помощи которой осуществлялась проверка экспериментальной программы редактирования текстов. Все три программы выполнялись встроенным в терминал Блит микропроцессором. Пайк демонстрировал передо мной необычайные возможности этой многопрограммной системы, как вдруг в верхней части экрана появилось несколько крабовидных символов, разбросанных вдоль границы окна. "Крабы" двигались по экрану, как бы поедая изображение в окне. Заметив мое удивление, Пайк объяснил: "Это крабы. Чтобы вас позабавить, мы только что загрузили программу КРАБЫ из центральной машины".
Центральная машина, к которой был подключен терминал Блит, работала под управлением операционной системы UNIX. Олна из наиболее популярных операционных систем за всю историю вычислительной техники, система UNIX, была создана К.Томпсоном, сотрудником фирмы Bell Laboratories, разделившим премию Тьюринга за 1983г. со своим коллегой из центра в Мюррей-Хилл Д.Ритчи.
Завороженный, я наблюдал, как крабы (их было около тридцати) съели линию, ограничивающую одно из окон, и начали поедать текст внутри. "Как их можно остановить?" - спросил я. "Никак",- ответил Пайк. "Да, но ведь вы их каким-то образом останавливаете?"
Программа КРАБЫ, написанная Л.Карделли и М.Манэссе в 1982г.,- это преднамеренное нарушение соглашений, принятых в многопрограммной системе, с которой работает терминал Блит. Дело в том, что каждая программа, имеющая свое окно на экране, должна быть независимой от программ из других окон и защищенной от них. Когда терминалы системы Блит были расставлены по помещениям лабораторий, Карделли и Манэссе не смогли удержаться от соблазна нарушить эти соглашения.
К тому времени, как Пайк поведал мне эту историю, все окна на экране были уже изрядно поедены. Они напоминали страницы недавно найденной средневековой рукописи. Текст в окнах стал настолько неразборчивым, что Пайк уже не мог объяснить мне, как протекает процесс выполнения соответствующих программ.
Пайк рассказал, что название этого оригинального терминала произошло от имени графической процедуры низкого уровня bitblt, отличающейся удивительно широким спектром применения. Имя bitblt в свою очередь является сокращением от слов bit - boundary block transfer (букв, перенос блоков с битовой границей.- Перев.), обозначающих процедуру, которая управляет перемещением информации по памяти терминала. Точнее говоря, bitblt переносит содержимое одной прямоугольной области памяти в другую. В ходе этого переноса над содержимым области могут производиться некоторые простые логические операции.
Часть памяти терминала Блит состоит из подсистемы емкостью 100000 байт, целиком отведенной для экрана. В процессе непрерывного сканирования каждый бит памяти преобразуется в светлую или темную точку на экране дисплея. При этом одномерный массив памяти преобразуется в двумерное изображение содержимого массива. Поскольку область памяти и ее изображение имеют различные размерности, точки, принадлежащие прямоугольной области на экране, оказываются разбросанными по памяти в виде отдельных блоков ячеек с последовательными адресами, так что каждый блок соответствует одной горизонтальной линии (полоске) на экране, из которых состоит прямоугольник. Совокупность точек-ячеек во всех блоках образует прямоугольное множество. Процедура bitblt позволяет выполнять определенные операции над такими прямоугольными множествами.
Для успешной работы в многопрограммной среде терминал Блит требует также значительного объема основной, "неэкранной" памяти, необходимой программам, диалог с которыми проходит с использованием экрана терминала. Например, в терминале DMD 5620 фирмы Teletype для этой цели отводится 900000 байт. Здесь также важную роль играют прямоугольные множества. К процедуре bitblt часто происходят обращения, когда надо преобразовать прямоугольное множество основной памяти в прямоугольное множество памяти экрана. Пусть, например, в некотором прямоугольном множестве основной памяти содержится буква A. Всякий раз, когда на экране должна появиться буква A как часть текста, выводимого программой, происходит обращение к процедуре bitblt, переносящей это прямоугольное множество в экранную память.
Аппаратное сканирование памяти - это принципиальная конструктивная особенность, присущая графическим терминалам с описанным выше буфером памяти для экрана, или так называемым "буфером-фреймом". Подобные дисплеи получают все более широкое распространение и уже применяются в персональных компьютерах. Свидетельство тому - дисплей персонального компьютера фирмы Macintosh.
В традиционных системах с графическими дисплеями обращения к памяти происходят по более сложным алгоритмам. Представление рисунка на экране осуществляется, например, при помощи списка точек, линий и других графических элементов. Для того чтобы высветить рисунок на экране, необходимо просмотреть список. При этом простые рисунки можно высветить быстро, потому что их списки короче, однако для изображения сложных рисунков может потребоваться слишком много времени.
Конфигурация битов в какой-нибудь прямоугольной области памяти называется битовой картой. Каждая битовая карта представляет на экране определенное изображение: типографский знак, простой рисунок-символ или еще какой-нибудь графический элемент. В программе КРАБЫ, например, используются некоторые битовые карты из основной памяти, при помощи которых на экране строятся крошечные ракообразные различной формы. Краба представляет следующая цепочка из нулей и единиц (единицы соответствуют темным, а нули - светлым точкам на экране):
01101110... 11110111... 10000001... 10111101... 01111110... 01111110 ... 10111101 ... 01000010
Читатели, желающие промоделировать bitblt, могут нарисовать на листе бумаги квадратную решетку размерами 8*8. Тогда приведенная выше цепочка будет представлять прямоугольную область в основной памяти, а квадратная решетка - часть экранной памяти. Скопируйте цепочку на решетку, просканировав побитно ту и другую. Теперь можно воспроизвести изображение на решетке, закрасив черным цветом каждую ячейку, содержащую единицу, и оставив светлыми ячейки, содержащие нули. При этом мы получим изображение краба, занимающего небольшую часть экрана (см. рисунок на с.73).

Изображение краба на квадратной решетке
Выше я уже отмечал, что любая часть экрана, не охваченная никаким окном, закрашивается точечным узором в серый цвет. Когда крабы напали на экран терминала Пайка, они сначала ползали по серой области. Натолкнувшись на окно, они начали его поедать. При этом Пайк шутливо заметил, что "серый цвет - это дорожки для крабов, а своих дорожек они не поедают". На самом деле крабы ничего не поедают, а скорее асфальтируют. Когда программа КРАБЫ двигает свое детище, она проверяет поле, находящееся непосредственно на пути краба; если оно не серое, то программа окрашивает его в серый цвет. Затем она перемещает краба в только что обработанную область. Обе операции осуществляются при помощи процедуры bitblt.
В простейшем варианте работы процедура bitblt заменяет каждый бит d на битовой карте, являющейся результатом, соответствующим Битом s исходной битовой карты. Кратко эту операцию замещения можно обозначить формулой
d <- s.
Любую область экрана можно сделать серой, воспользовавшись этим вариантом процедуры bitblt. Поле, находящееся непосредственно на пути краба, можно рассматривать как битовую карту-результат, а битовую карту в основной памяти, содержащую шаблон серого цвета, можно считать исходной битовой картой.
Затем программа КРАБЫ перемещает краба. Она стирает изображение краба в том месте, где оно в данный момент находится, и высвечивает его на новом месте. Чтобы выполнить соответствующие операции, используется более сложный вариант процедуры bitblt, который можно условно обозначить следующим образом:
d <- s+d.
Здесь каждый бит поля результата замещается его комбинацией с соответствующим битом источника. Эта комбинация представляет собой логическую операцию исключающего ИЛИ, которую мы впредь будем обозначать как XOR или знаком "+". В результате применения операции XOR бит d будет равен 1 тогда и только тогда, когда либо s, либо d (но не оба одновременно) имеют значение, равное 1. Операцией XOR очень удобно пользоваться как при стирании старого изображения краба, так и при построении нового. К сожалению, в этом варианте процедура bitblt не может воспользоваться стандартным изображением краба, которое мы получили выше при помощи карандаша и бумаги.
Посмотрим, например, что будет, если операцию XOR применить к стандартной битовой карте краба и точечному шаблону серого цвета. Когда операция XOR применяется к точке серого поля (1) и какой-либо точке тела краба (также 1), результатом будет светлая точка (1+1=0). Если, однако, данная точка тела краба является светлой, то результатом будет темная точка {0+1=1). Этим объясняется странный вид восьми специальных битовых карт краба, которыми пользуется программа КРАБЫ при перемещении своих подопечных (см. рисунок на с.74). Каждая из этих битовых карт представляет краба со специальным подбором светлых точек на его теле. Существует восемь возможных способов поместить краба на серое поле, и каждому из этих способов соответствует своя битовая карта краба.

Битовые карты краба со светлыми точками, нанесенными на них в соответствии с восемью возможными способами наложения краба на серое поле
Программа перемешает краба, сначала стирая его, а затем высвечивая на новом месте. Чтобы стереть краба, процедура bitblt отображает при помощи операции XOR битовую карту краба с соответствующим подбором светлых точек на светящееся в данный момент изображение краба. В результате изображение краба исчезает и на его месте остается серое поле. Чтобы высветить новое изображение краба, процедура bitblt опять пользуется специально подобранной битовой картой краба, которую она отображает посредством операции XOR на серое поле. Новое изображение краба ничем не отличается от старого, поскольку светлые точки на его битовой карте точно соответствуют серому полю, на которое краб перемешается.
Алгоритм, управляющий поведением крабов, можно разбить на пять шагов:
1. Стереть изображение краба в том месте, которое оно в данный момент занимает.
2. Определить новое место.
3. Если новое место не является серым полем, то сделать его серым, изменить данные о положении краба и выбрать случайным образом новое значение скорости передвижения.
4. Высветить краба на новом месте.
5. Изменить случайным образом скорость краба. Вернуться к шагу 1.
Крабы, как и полагается, движутся боком. Поэтому новое место всегда находится сбоку от краба, по ту или другую сторону от него. Новое место определяется текущими значениями направления и скорости движения краба. Обе эти величины подвергаются на шаге 5 случайным изменениям. Возможны несколько направлений движения, а его скорость варьируется в пределах от 1 до 7 пикселов (ячеек на экране) на одно перемещение.
Во время нашего разговора с Пайком крабы сначала появились в верхней части экрана. Затем, совершая хаотические перемещения по серым полям, они стали медленно спускаться вниз. Встретив окно, они прогрызли его границу и проникли внутрь. Было хорошо видно, как они прогрызают окно, потому что на изображении стали появляться крошечные серые пятна. Внешне это выглядело очень эффектно: крабы как будто пожирали верхний слой бумаги, под которым проступало серое волокно.
В значительной степени эта иллюзия объяснялась шагом 3 алгоритма программы КРАБЫ, поскольку на этом шаге краб уходит с только что проеденного им места так, словно он посидел на нем какое-то мгновение, пережевывая проглоченный кусок, прежде чем отправиться дальше в поисках новой порции. Благодаря случайному характеру движения крабов окно становится "дырявым" сразу на большой поверхности. Если бы не эта особенность их движения, то эффект, производимый крабами, скорее напоминал бы процесс выкапывания нор. Благодаря случайному характеру движения крабов человек за терминалом не сразу понимает, что происходит, и его реакция оказывается замедленной.
Пока мы наблюдали за тем, как крабы проедали окна на экране терминала, Пайк рассказал мне о том, как по-разному реагировали его коллеги, впервые столкнувшись с нападением крошечных ракообразных. Часто такое нападение устраивалось исподтишка. Когда ничего не подозревающий сотрудник отходил на минутку от терминала, кто-нибудь из шутников запускал на его терминале программу КРАБЫ.
Поскольку терминал Блит снабжается обычно устройством "мышь", управляющим перемещением курсора на экране, сбитый с толку сотрудник иногда лихорадочно пытался противостоять крабам при помощи этого устройства. Однако все подобные попытки оказывались тщетными, так как крабы с таким же аппетитом набрасывались на курсор, как и на текст. При этом "съеденный" курсор через некоторое время вновь появлялся на экране. И, хотя наступление крабов можно таким образом несколько замедлить, остановить их невозможно и изображение в окнах продолжает разрушаться.
Иногда программист, чей терминал подвергся нападению крабов, пытался накрыть их окном. Эта мера также несколько замедляла продвижение крабов, однако они постепенно прогрызали вокруг себя все большее поле и в конце концов вырывались из окна.
Я снова спросил Пайка, каким образом можно остановить крабов. На этот раз он смилостивился: "Выключите терминал и включите его снова". Такая мера оказывается действенной, однако при этом пользователю приходится заново подключаться к центральной ЭВМ.
Карделли и Манэссе, авторы программы КРАБЫ, изложили историю происхождения программы в неофициальной докладной записке. Конструкция и правила пользования терминалом Блит произвели на них очень сильное впечатление, и они решили проанализировать возможности нарушения этих правил. Они обратились к Пайку, который дал им текст интересовавших их фрагментов программного обеспечения системы. Поразмыслив, двое программистов пришли к выводу, что некоторые возможности нарушения правил, принятых в конструкции терминала, могут оказаться полезными. В этом смысле примером служит программа ЛИНЗА, которая увеличивает заданную часть экрана. (На рисунках на с.76-77 видно окно программы ЛИНЗА, увеличивающее текст, пораженный крабами.) ЛИНЗА представляет собой нарушение правил, потому что программа, имеющая одно окно, не должна иметь прямого доступа к содержимому другого окна.

Экран терминала, показывающий вывод из пяти программ, подвергшихся атаке крабов

Пользователь может отбить подобное нападение, только выключив терминал и повторно подключившись к системе
Вначале Карделли и Манэссе намеревались имитировать видеоигру QIX, но затем вместо этого написали программу МИКРОБЫ (MEASLES), в результате выполнения которой по серым участкам экрана между окнами начинали плавать маленькие шарики. Первые же испытания показали, что микробов можно было заблокировать, накрыв их окном. Авторы сочувствовали своим созданиям: "Внезапно бедные маленькие микробы оказались запертыми, им было некуда двигаться, нигде вокруг не было спасительного серого поля. Они застыли, полные ужаса, и были похоронены под окном".
Первая реакция авторов на эту неудачу заключалась в том, чтобы заставить пойманных микробов периодически вспыхивать, досаждая тем самым человеку, который поймал их. Новая программа получила название ЗЛЫЕ МИКРОБЫ.
Однако даже "злые микробы" были ничто по сравнению со следующим замыслом, пришедшим в голову неутомимым авторам: "А почему бы микробам не прогрызть себе путь и выйти таким образом из окна?" Соответствующая программа получила имя ГОЛОДНЫЕ МИКРОБЫ. Карделли пишет: "У новой версии был уже совсем другой характер. Она уже не была просто остроумной, она внушала трепет".
Кто-то, наблюдая за работой программы на экране, заметил, что микробы напоминают чем-то крошечных ракообразных. Карделли и Манэссе реализовали изображение краба, и таким образом родилась программа КРАБЫ. Следом за ней появились и другие программы подобного рода, в том числе такие, которые оставляли на экране отпечатки следов птиц и зверей.
Сотрудники, ставшие жертвой этих шуток, принимали ответные меры. Была написана программа ДАВИ КРАБОВ, которая просматривала память терминала в поисках программы КРАБЫ. Найденные программы уничтожались, а на экране крабы превращались в маленькие пузырьки. К сожалению, очередная модификация в программном обеспечении терминала сделала программу ДАВИ КРАБОВ неэффективной.
В ЛАБОРАТОРИЯХ исследовательского центра в Мюррей-Хилл есть и другие занимательные программы. Меня познакомили с одной из таких программ, написанной Р.Хардином. Она превращает произвольный текст на английском языке в цепочки фонем, которые затем перегруппировываются, снова превращаются в слова английского языка и выводятся в виде нового текста. Результирующий текст (после некоторого редактирования человеком) выглядит как стихотворение слегка сумасшедшего поэта:
Better buy perfect Topeka beagle buffers
Topeka beagle buffers sputter fiber beaks
Effeter fiber beaks abetted feeble puppies
Worst Topeka beagle puppies feature viper-pique.
Несколько более серьезная работа была проведена при создании программы для игры в шахматы. В 1980г. чемпионат мира по шахматам среди ЭВМ был выигран системой Belle, представлявшей собой комплекс из специализированной ЭВМ и программы, написанной в лабораториях центра в Мюррей-Хнлл. Авторы программы - К.Томпсон и Д.Кондон. (Я думаю посвятить этой и другим современным программам для игры в шахматы одну из своих следующих статей).
Компьютер, играющий в шахматы, созданный, казалось бы, для развлечения, возвращает нас к разговору о соотношении между работой и игрой. Профессор А.Перлис, преподающий информатику в Йельском университете, в своей недавно опубликованной книге "Структура и интерпретация программ для ЭВМ" (см. "Библиографию" на с.84) высказывает мнение, получившее довольно широкое распространение среди специалистов по вычислительной технике и информатике.
"Я думаю, очень важно, чтобы в научной работе всегда оставалось место для шутки и развлечения. Когда вычислительная техника и программирование только зарождались, в нашей работе было много веселого и забавного". Однако, полагает Перлис, сейчас для этого остается все меньше места, потому что исследователям предъявляются серьезные требования, заставляющие их все в большей степени сосредоточивать внимание на "гайках" и "винтиках", из которых состоят изобретаемые ими системы. Но такими вещами следует скорее заниматься тем, кто внедряет научные достижения в производственные системы. "В последнее время мы стали чувствовать себя так, будто бы мы действительно несем ответственность за успешное, безошибочное функционирование этих систем. Мне кажется, это неправильно. Я думаю, наша роль заключается в том, чтобы расширять их возможности, открывать для них новые направления и поддерживать в лабораториях веселое настроение".
Продуктивность научных исследований в вычислительной технике, как в серьезных, так и в шуточных разработках, объясняется прежде всего свободной творческой атмосферой, в которой новые идеи, по-видимому, порождаются наполовину людьми, а наполовину самими машинами. Можно даже сказать, что без этого веселого настроения не было бы и быстрого научного прогресса.
Перед тем как закончить статью, я не могу не вернуться еще раз к терминалу Блит и его процедуре bitblt. Пайк предложил две интересные задачки, которые демонстрируют эффективность и гибкость процедуры bitblt. Предположим, что читатель располагает двумя версиями процедуры bitblt, описанными выше. Одна из них замешает битовую карту в поле результата исходной битовой картой. Другая выполняет операцию XOR.
Задача 1. Очистить прямоугольник. Не прибегая к специальной, заполненной единицами битовой карте в основной памяти терминала, воспользуйтесь процедурой bitblt либо в версии замещения, либо в версии с операцией XOR, чтобы очистить заданный прямоугольник на экране.
Задача 2. Повернуть изображение. Квадратное изображение размером n*n занимает верхний левый угол экрана Блит размером 2n*2n. Воспользуйтесь процедурой bitblt, чтобы повернуть изображение на 90o. Считайте, что вне изображения экран чист.
В первой задаче не разрешается делать никаких предположений о содержимом внешней по отношению к заданному прямоугольнику части экрана. Какой должна быть в этой ситуации битовая карта, которая могла бы послужить исходной для процедуры bitblt?
В обеих задачах воздействие процедуры bitblt на заданный прямоугольник (не важно, какой формы) считается одной операцией. Первая задача решается однократным обращением к процедуре bitblt, вторая требует 3n+1 таких обращений. Сможет ли кто-нибудь найти более быстрое решение?
БИБЛИОГРАФИЯ
THREE DEGREES ABOVE ZERO. JEREMY BERNSTEIN. Charles Scribner's Sons, 1984.
STRUCTURE AND INTERPRETATION OF COMPUTER PROGRAMS. HAROLD ABELSON, GERALD JAY SUSSMAN AND JULIE SUSSMAN. The MIT Press, 1985.
HARDWARE/SOFTWARE TRADE-OFFS FOR BITMAP GRAPHICS ON THE BLIT. ROB PIKE, BART LOCANTHI AND JOHN REISER in Software - Practice and Experience, Vol.15, No.2, pages 131-151; February, 1985.
ОТКЛИКИ
2 1986
В НОЯБРЬСКОМ номере нашего журнала была описана доброкачественная терминальная болезнь КРАБЫ. Орды морских ракообразных внезапно, без предупреждения, с жадностью набрасываются на терминалы Блит, за которыми работают сотрудники фирмы AT&T Bell Laboratories в Мюррей-Хилле (шт. Нью-Джерси).
Почти все программы, выполняющиеся в мультипрограммной системе терминалов типа Блит, пользуются важным оператором bitblt. С помощью этой операции прямоугольные множества битов переносятся из одной области памяти терминала в другую. Перед выполнением переноса прямоугольные множества могут подвергаться различным логическим операциям.
Перед читателями были поставлены две задачи: стереть изображение на экране и повернуть изображение на 90o. Первая задача решается довольно легко. Чтобы стереть картинку, занимающую определенное прямоугольное множество, нужно применить операцию "исключающего или", взяв в качестве операндов само множество. В результате получится множество, содержащее только нули. Таким образом, при помощи одной-единственной операции bitblt можно полностью очистить заданную область экрана.
Повернуть изображение значительно труднее, чем стереть его. До сих пор лишь один читатель представил приемлемое решение. Старшеклассник Т.Вителски из Нью-Йорка нашел способ повернуть изображение размером n*n на экране размером 2n*2n. Затратив лишь 3n-1 операций bitblt, он проходит через n-1 строк, копирует подызображение размером (n-1)*(п-1), проходит через n-1 столбцов, копирует другое подызображение и затем проходит еше через n-1 строк. Метод Вителски оказался более быстрым, чем стандартный алгоритм поворота, требующий 4n-2 операций.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
12 1985
ПРОГРАММЫ ДЛЯ КОНСТРУИРОВАНИЯ ПРЕДМЕТНЫХ ГОЛОВОЛОМОК. МНЕМОНИЧЕСКИЕ ПРАВИЛА ДЛЯ ЗАПОМИНАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ЦИФР ЧИСЛА ПИ
А.К.ДЬЮДНИ
НАПИСАТЬ программу, помогающую в изобретении головоломки, не менее трудно и интересно, чем написать программу, которая решает ее. Б.Катлер из Уосо (шт.Висконсин) и С.Коффин из Линкольна (шт.Массачусетс), наверное, согласятся со мной. Воспользовавшись компьютером, Катлер изобрел трехмерную игрушку, состоящую из шести деталей, которую он назвал замысловатой колючкой Билла (Bill's baffling burr). Эта игрушка с выступающими во все стороны деталями, которые сложным образом связаны между собой, действительно чем-то напоминает колючий плод растения - он как бы пристает на некоторое время к тому, кто пытается решить головоломку. Колючка Билла состоит из шести деталей, попарно ориентированных в трех взаимно перпендикулярных направлениях (см. рисунок на с.139). На самом деле в этой игрушке содержатся сразу две головоломки - нужно уметь и собрать, и разобрать ее. Пользуясь компьютером, чтобы путем перебора всех возможных комбинаций деталей найти наиболее интересные из них, Катлеру удалось изобрести, может быть, самую трудную головоломку этого типа для шести деталей.

Головоломка-колючка Билла
Коффин тоже не без помощи компьютера изобрел двумерную головоломку, деталями которой являются плоские фишки гексомино различной формы, состоящие из шести квадратов одинакового размера (отсюда название "гексомино", по аналогии с "домино" - фишками, состоящими из двух квалратов.- Перев.), склеенных друг с другом в различных сочетаниях. Задача заключается в том, чтобы собрать фишки в большой квадрат; подбор формы фишек может оказаться трудным и утомительным. Из всех возможных комбинаций гексомино программа Коффина отыскивает те, которые представляются наиболее трудными для решения. Она уже нашла так много комбинаций, что Коффин может удовлетворить интерес всех любителей этой головоломки. Свою систему, создающую эти варианты, Коффин называет "рогом изобилия". Лично я располагаю вариантом игры, показанным на с.140.

Головоломка Коффина из фишек гексомино
Третья головоломка, которую мы рассмотрим, была изобретена без помощи компьютера. Ее автор Энджел из Инглвуда (шт.Колорадо). Эта задача небезынтересна для любителей поиска алгоритмических подходов. Игрушка Энджела представляет собой набор цветных пластмассовых деталей, которые в виде мозаики вписываются в две окружности (см. рисунок на с.142). В ней используются детали двух видов: "камни" и "кости". Повернув сначала один круг, а затем и другой, камни и кости можно перемешать так, что по сравнению с исходным их расположением картина будет выглядеть совершенно хаотичной. Вернуть фишки в исходное положение, пожалуй, ничуть не легче, чем установить одноцветные грани в кубике Рубика.

Головоломка Энджела
Как мы увидим ниже, задача Энджела, по существу, является одномерной. Задача Коффина, очевидно, двумерна, и, наконец, головоломка Катлера трехмерна в полном смысле слова. Начнем с рассмотрения трехмерных головоломок, а затем перейдем к другим в порядке убывания их размерности.
Наверное, каждому из нас доводилось вертеть в руках игрушку-головоломку, подобную описанной выше "колючке". Иногда эти игрушки называют китайскими головоломками, хотя они почти наверняка европейского происхождения. Они могут состоять из многих деталей и иметь разнообразные формы. Наибольшее распространение получили игрушки из шести деталей, каждая из которых имеет форму продолговатого параллелепипеда с вырезанными в нем выемками, или пазами (для краткости будем называть их брусками). В собранном виде детали группируются в три пары, каждая из которых состоит из двух прилегающих друг к другу брусков, как бы врезающихся в центр игрушки и выходящих с противоположной стороны. Однако центральная часть игрушки не может быть занята тремя парами брусков одновременно. Возникающий, казалось бы, парадокс разрешается, если учесть, что в каждом бруске имеются пазы. Расположение пазов определяет возможности сборки и разборки игрушки на составные детали. Ясно поэтому, что искусство создания интересных шестнблочных игрушек сводится к тому, чтобы найти подходящее расположение пазов в каждом бруске.
Катлер конструирует свои игрушки-головоломки в три стадии. Сначала он выбирает форму шести брусков, из которых должна состоять игрушка. Затем он должен проследить, чтобы пазы в брусках были взаимно совместимыми. Для этого нужно определить, существует ли такая конфигурация, в которой все бруски беспрепятственно проходят через центральную зону, образуя единое целое. Наконец, нужно испытать игрушку на разборку, т.е. проверить, возможно ли ее разобрать, и если возможно, то насколько трудной окажется эта задача. На двух последних стадиях конструирования Катлер пользуется программой, которую выполняет компьютер.
Каждая деталь головоломки-колючки вначале представляет собой деревянный брусок определенных размеров. В рассматриваемом варианте игрушки размеры каждого бруска равны (в произвольных единицах) 2*2*6. В каждом бруске имеется 12 мест, где могут быть вырезаны пазы (см. рисунок на с.139). Если считать, что брусок состоит из 24 кубов единичного размера, то на каждом торце бруска будет располагаться по четыре таких куба, а в средней его части будет находиться 16 кубов. С каждой стороны вдоль бруска расположено восемь центральных кубов в два ряда, по четыре куба в каждом. Пронумеруем их от 1 до 8. На противоположной стороне бруска пронумеруем еще четыре центральных куба от 9 до 12. Брус становится деталью игрушки, если удалить из него то или иное количество кубов из 12 рассмотренных. Как подсчитал Катлер, из 4096 возможных способов удаления кубов лишь 369 приводят к построению реализуемой головоломки.
Большой опыт в изобретении подобных головоломок позволяет Катлеру сравнительно быстро выбрать шесть деталей перспективной формы. Однако каким образом, не затрачивая много времени и сил на изготовление настоящей деревянной модели, можно узнать, подойдут ли выбранные детали друг к другу так, чтобы получилась "работающая" игрушка? Катлер не долго думал, прежде чем решил на этой начальной стадии разработки головоломки прибегнуть к помощи компьютера. В 1973г. он написал свою первую программу перебора конфигураций. Пространство, занимаемое игрушкой, программа представляет в виде трехмерного массива размером 8*8*8. Каждый элемент массива представляет собой единичный куб, занимающий соответствующее место в модели, и помечается номером детали, которая занимает данную ячейку пространства. Например, если изъять из этого пространства все кубы, помеченные числом 3, не нарушая их взаимного расположения, то мы увидим, какую форму имеет деталь номер 3. Нетрудно сообразить, что в зависимости от количества пазов, вырезанных в бруске, каждая деталь может занимать от 14 до 24 кубических ячеек, или элементов массива.
Программа просматривает каждый из шести списков, содержащих информацию о конфигурации шести деталей в соответствии с координатами кубов, из которых они состоят. Затем координаты подвергаются различным математическим операциям, представляющим такие преобразования, как перенос, вращение и отражение летали в пределах массива. Безусловно, что эта процедура носит строго упорядоченный характер и требует выполнения многочисленных циклов.
Первый брусок (под номером 1) устанавливается в стандартном положении и составляющие его единичные кубы помечаются в трехмерном массиве номером 1. Взаимное расположение этих кубов в точности воспроизводит конфигурацию детали. Затем программа пробует поместить первый из оставшихся брусков так, чтобы он пересекался с уже установленным стандартным бруском. При этом проверяются все возможные ориентации второго бруска, для чего нужно выполнить два цикла. Еще два цикла требуются программе для того, чтобы попытаться поместить третий брусок так, чтобы он пересекался с первыми двумя. Здесь опять рассматриваются все возможные ориентации. Присоединение трех оставшихся брусков требует выполнения еще шести циклов. Используя жаргон программистов, можно сказать, что эта процедура содержит большое количество вложенных циклов. Всякий раз, когда очередной брусок устанавливается в новое положение или приобретает иную ориентацию, программа проверяет все 512 кубов в массиве с целью удостовериться, что ни один из этих кубов не пронумерован дважды. Если встречается хотя бы один куб с двойной нумерацией, то вся комбинация должна быть отвергнута, потому что в этом случае два бруска пытаются занять одно и то же место, и, следовательно, такая конфигурация оказывается недозволенной (в математическом смысле слова).
Множество всех возможных конфигураций из шести деталей можно представить в виде дерева; корнем дерева будет брусок под номером 1 в стандартном положении. Пока это дозволенная конфигурация. Добавляя следующий брусок с другой ориентацией к каждой из последующих дозволенных конфигураций, мы получаем либо новую ветвь дерева возможных вариантов, либо заходим в тупик.
На конечных узлах дерева программа может выдать какое-то количество дозволенных конфигураций, состоящих из шести брусков и изящно собранных в игрушку-головоломку. Однако некоторые из полученных таким образом головоломок оказываются все же безнадежно "заклиненными": как ни толкай, ни тяни или ни крути бруски, их никак не удается (да это и невозможно) отделить друг от друга. На самом деле такие игрушки было бы просто невозможно изготовить. Они существуют только в "воображении" программы. Каким же образом Катлер определяет, возможно ли разобрать ту или иную шестичастную конфигурацию? Ответ на этот вопрос он получает, выполняя вторую программу - программу разборки.
Программа разборки анализирует тот же самый массив размером 8*8*8, который используется для порождения дозволенных конфигураций. При этом программа пытается сдвинуть каждый брусок на одну или более единичных ячеек в каком-нибудь одном из трех ортогональных направлений. Она пробует вытянуть блок или сдвинуть его вбок. И здесь для представления множества вариантов применяется дерево. В корневом узле дерева находится игрушка-головоломка в собранном виде. На каждой достигнутой стадии разборки программа осуществляет систематический поиск возможных перемещений для каждой очередной детали. Те, кто многократно пытался разбирать эту головоломку, уже давно заметили, что как только удастся полностью высвободить одну или две детали, завершить разборку обычно не составляет труда.
Естественно поэтому, что Катлер считает конструкцию шестичастной головоломки-колючки хорошей только в том случае, когда задача высвобождения первой детали оказывается очень трудной. Чтобы вытащить первую деталь из головоломки-колючки Билла, требуется сделать не менее пяти перемещений!
Прежде чем Катлер сконструировал свою лучшую головоломку, он испробовал и забраковал девять различных вариантов сочленения деталей. Десятый вариант, на котором он остановился (см. рисунок на с.139), отличался исключительно коварным замыслом с расчетом на интуицию играющего. Программа, порождающая конфигурации, нашла одно и только одно взаимное расположение всех деталей, а программа разборки установила, что их можно разобрать только одним способом. Лишь одну деталь можно извлечь первой и для этого нужно совершить четыре, казалось бы, бессмысленных перемещения.
Программа разборки одновременно представляет собой и программу решения головоломки. Сначала, конечно, ей нужно предъявить точное описание деталей головоломки, и это описание должно быть представлено в виде основного массива программы размером 8*8*8. Готовое решение программа выдает в виде указания последовательности перемещений, которую должен воспроизвести человек, пытаясь разобрать игрушку.
Предположим, однако, что программе не было дано никаких сведений о конфигурации деталей. Тогда бы у нее не было никакой альтернативы в манипулировании физической моделью игрушки. Забавно представить себе программу, способную управлять двумя механическими руками-манипуляторами робота. За действиями такой программы можно было бы следить в течение многих дней, по мере того как она исследовала бы колоссальное дерево возможных перемещений.
Коффин, так же как и Катлер, в течение ряда лет занимался изобретением "колючек" и других трехмерных головоломок. Одно из его последних достижений - двумерная головоломка. Предлагаем нашим читателям попытаться собрать 10 фишек гексомино в плоский квадрат, так чтобы ни одна фишка не накладывалась на другую (см. рисунок внизу слева). Каждая фишка состоит из шести деревянных квадратов, склеенных друг с другом вдоль одной или более граней. Одна хорошая головоломка из гексомино - это уже достижение. Однако у Коффина есть "компьютерный ключик", открывающий целый сундук подобных головоломок. Каждый вариант игры отличается от других и имеет свою степень сложности. Такую головоломку можно как бы случайно оставить на столе и пригласить нескольких друзей на чашечку кофе. Хозяин может быть при этом уверен, что ни один из гостей не сумеет быстро решить ее, и сошлется на то, что никогда прежде не видел такой головоломки; она действительно окажется им совершенно незнакомой.
В качестве критериев сложности головоломки подобного типа Коффнн принимает как форму самих деталей, так и количество возможных решений задачи. В своем проекте под названием "рог изобилия" Коффнн пользуется только фишками типа гексомино. Чтобы усложнить задачу, он выбрал исключительно асимметричные фишки, не содержащие квадратов размером 2*2. Полный набор насчитывает 17 фишек. При правильном расположении 10 фишек в квадрате размером 8*8 должно остаться четыре пробела. Дозволенными являются только те конфигурации, в которых эти пробелы расположены симметрично. В модели, которую Коффин прислал мне, есть по крайней мере два решения: первое, когда четыре пустых квадрата находятся в середине собранной фигуры, и второе, когда они расположены по углам.
Всего существует 19448 способов выбрать подмножество из 10 фишек из полного множества, насчитывающего 17 фишек. Далеко не все такие подмножества приводят к интересным головоломкам, а некоторые из возможных наборов нельзя разместить в пределах квадрата 8*8. Каким же образом среди всех этих вариантов можно выявить наилучшие головоломки?
Не так давно Коффин обратился за помощью к М.Билеру, неутомимому программисту, имя которого упоминалось в статье, посвященной описанию игры под названием "Жизнь" {см. журнал "В мире науки" 1985, #7). Билер написал программу исчерпывающего перебора, которая пытается собрать каждый набор из 10 фишек в требуемый квадрат. Программа автоматически генерирует все возможные решения. Если их оказывается не слишком много, она выдает все найденные решения вместе с описанием соответствующего набора из 10 фишек.
Так же как и программа Катлера, конструирующая "колючки", программа Билера, перебирающая конфигурации гексомино, исследует дерево. Начинает она с рассмотрения выделенного подмножества фишек, генерируемого ее главным циклом. По существу, программа как бы сканирует площадь, занимаемую элементами головоломки, строка за строкой. Для этого необходим еще один цикл, вложенный в главный цикл программы. Всякий раз, когда встречается свободный квадрат, программа выбирает одну из еще не использованных фишек (это еше один иикл) и пробует приладить ее к уже сложенным во всех возможных ориентациях (четвертый цикл). Если выбранная фишка оказывается подходящей, на дереве потенциальных решений генерируется новая ветвь, а программа переходит к следующему свободному квадрату и пытается приладить другую неиспользованную фишку.
Если бы не некоторые хитроумные алгоритмические ухищрения, программа, генерирующая решения, может быть, и не могла бы найти все возможные ответы за разумное время. Один из таких трюков заключается в том, чтобы подвергать каждый набор гексомино своеобразному тесту "на четность" еше до того, как программа войдет во второй цикл. Как-то раз, когда Билер изучал набор из 17 фишек, он заметил, что если их рассматривать как фрагменты шахматной доски, то 11 фишек имеют по три белых и три черных квадрата. Остальные 6 фишек состоят из четырех квадратов одного цвета и двух другого. Решение же для любого набора из 10 фишек содержит одно и то же число белых и черных квадратов, а именно 30. Отсюда Билер пришел к выводу, что решение можно найти только для четного числа "непарных" фишек, т.е. тех шести фишек из 17, у которых количество белых и черных квадратов не совпадает. Любое подмножество, не удовлетворяющее этому простому правилу, должно быть отвергнуто, как не имеющее решения. Это позволило сократить количество итераций в программе с 19448 до 9746.
Количество решений, которое находит программа Билера для заданного подмножества гексомино, определяет степень сложности соответствующей задачи. Согласно классификации Коффина, задачи могут быть просто сложными (несколько решений) и очень сложными (всего одно решение). Программа Билера выдает решения одно за другим, как автомат. Вооружившись необходимыми инструментами, Коффнн организовал мастерскую по изготовлению головоломок. О своей работе Коффин рассказывает в брошюре "Puzzle Craft" ("Искусство составления головоломок").
Отметим одно примечательное различие между головоломками Катлера и Коффина: в то время как шестичастную игрушку Катлера очень трудно разобрать, головоломка из "рога изобилия" Коффина легко поддается разборке - для этого достаточно высыпать фишки из коробочки, в которой гексомино собираются в большой квадрат. Головоломку-колючку труднее разобрать отчасти потому, что она трехмерна. Разумному существу из четырехмерного мира не составит никакого труда разобрать любую игрушку Катлера - оно воспользуется новым направлением, "вверх" от модели. В то же время даже ему, наверное, будет так же трудно собрать детали головоломки-колючки, как нам решить двумерную задачу с гексомино. Этот мысленный эксперимент наводит нас на мысль о двумерной головоломке-колючке, которая разбирается перемещениями плоских деталей, все время остающихся в одной плоскости. Возможна ли головоломка такой конструкции? Предположим, что у нас есть 8 деталей для двумерной головоломки-колючки. Две детали выступают наружу с каждой стороны коробочки; детали, находящиеся внутри, могут иметь любую прямоугольную форму. Предлагаем читателям подумать над конструкцией подобной головоломки.
Перейдем к рассмотрению третьей головоломки, называемой по имени ее автора головоломкой Энджела. Для меня несколько часов, с интересом проведенных над этой головоломкой, оказались безрезультатными. Мне еше не удалось получить общего решения, однако Дуглас Р.Хофштадтер (статьи которого в рубрике "Математические игры" раньше публиковались в нашем журнале) разработал специальную программу, выполняющую операции над кругами этой головоломки. Энджел пишет, что несколько человек, достигших высокого мастерства с кубиком Рубика, не смогли решить его задачу.
Игрушка Энджела состоит из двух пересекающихся кругов, заключенных в пластмассовый корпус. По периферии каждого круга располагаются попеременно 6 "камней" и 6 "костей". Камни выглядят как несколько располневшие треугольники, а кости - как недокормленные прямоугольники. Поскольку круги пересекаются, они имеют два общих камня и одну обшую кость (см. рисунок внизу). Круги с заключенными в них камнями и костями могут вращаться. Если повернуть один круг, скажем верхний, на 60o, камень и кость, которые в исходном положении были общими для обоих кругов, оказываются перемещенными и заменяются другим камнем и другой костью. Если поочередно поворачивать каждый круг на любой угол, кратный 60o, в случайно выбираемых направлениях, то камни и кости оказываются перемешанными и их расположение выглядит хаотичным.
Исходная конфигурация головоломки делится на 10 шестиугольных зон - 8 внешних и 2 внутренних. Внешние зоны окрашены в красный, оранжевый, синий и черный цвета; симметрично противоположные друг другу зоны имеют одинаковый цвет. Внутренние зоны (по одной в каждом кругу) - желтого и зеленого цвета. Каждый камень принадлежит одновременно трем зонам и поэтому имеет три области различного цвета. Каждая кость принадлежит двум зонам и потому является двухцветной.
Если камни и кости перемешать описанным выше способом, то вместо приятной на вид упорядоченной структуры, которая была в исходном положении, возникнет беспорядочная мозаика цветов. Возникает вопрос: как может игрушка с таким ограниченным характером перемещений оказаться такой же сложной, как и кубик Рубнка? Энджел показал мне полный набор "алгоритмов" решения своей задачи, но мы придержим их на несколько месяцев в резерве, чтобы дать возможность всем заинтересованным читателям попробовать свои силы и попытаться самим найти решение. Мы надеемся, что читатели, владеющие программированием, сумеют найти красивые и эффективные алгоритмы.
Сам я еще не написал такой программы, но у меня есть некоторые соображения, которые могут оказаться полезными. Когда головоломка находится в исходном (неперемешанном) состоянии, пронумеруйте камни по часовой стрелке от 0 до 9, начиная с камня, расположенного справа от кости, принадлежащей обоим кругам. Тогда исходную конфигурацию можно представить следующей последовательностью чисел:
0 1 2 3 4 5 6 7 8 9
Допустим, что верхний круг повернулся на 60o по часовой стрелке. Если приведенную выше последовательность рассматривать как номера 10 ячеек игрушки, то в результате указанного поворота последовательность номеров будет следующей:
5 0 1 2 3 4 6 7 8 9
Заметим, что после перестановки число 5 перешло со своей шестой позиции на первую. Читатели сами могут легко получить последовательность номеров после каждой из трех следующих перестановок. Эти четыре перестановки можно встроить в программу, которая оперирует массивом из 10 элементов. Первоначально массив содержит числа в возрастающем порядке. Обращаясь к перестановкам в случайном порядке, мы как бы перемешиваем модель головоломки. Благодаря описанной схеме представления эалачи можно существенно ускорить работу программы, отыскивающей решение. Наверное, теперь читателям стало ясно, почему я считаю задачу Энджела одномерной.
Мнемоники числа пи я перенес в отклики к соответствующей статье.- G.
ОТКЛИКИ
3 1986
В ДЕКАБРЬСКОМ номере журнала за прошлый гол в этой рубрике разговор шел о трех головоломках: "колючке" Билла, "роге изобилия" Коффина и игрушке-вертушке Энджела. Головоломки заинтересовали сотни читателей: одни пытались найти магический способ, как разобрать хитроумно сочленяющиеся детали в "колючке" Билла, другие сосредоточили свое внимание на поиске решения задачи о размещении фишек полимино. Представители одной группы не могут помочь представителям другой: каждая из головоломок уникальна. Еше одна группа читателей без устали продолжает крутить колеса игрушки Энлжела, тщетно пытаясь установить их в требуемом положении. Некоторым энтузиастам удалось добиться успеха, по крайней мере на абстрактном уровне. Уже начали поступать письма, в которых предлагается решение задачи.
Пришло также несколько писем с описанием конструкций двумерных "колючек" - игрушек, которые нужно разобрать на составляющие их детали. Наиболее изящная из предложенных читателями конструкций показана на рисунке вверху. Задача заключается в том, чтобы удалить четыре составляющие игрушку детали с прямоугольного подноса, границы которого изображены пунктирными линиями. Детали можно перемещать только в четырех направлениях в плоскости рисунка: вверх, вниз, влево и вправо. Четыре темных квадрата в углах считаются жестко прикрепленными к подносу. Какую из деталей следует переместить первой? Эту двумерную головоломку придумал Дж.Картер из Литтлтона (шт.Колорадо). Имея дело с трехмерной игрушкой, мы по крайней мере можем ее повертеть в руках и осмотреть со всех сторон. Толкать и тянуть детали, находящиеся в плоском ящике, как-то непривычно.

Двумерная головоломка-колючка Дж.Картера
Р.Клавье из Далласа (шт.Техас) сообщил, что ему удалось найти алгоритмическое решение задачи Энджела. Он пишет, что его программа, написанная на Бейсике и выполняющаяся на портативном компьютере модели СС-40 фирмы Техас Instruments, на решение задачи обычно затрачивает от 300 до 700 ходов. В алгоритме используется шесть стандартных обменных операций между камнями и костями. Читатели, воспользовавшиеся предложенным мною способом представления последовательности, возможно, закинули свою сеть слишком широко. Решение, полученное для числовой последовательности, не всегда оказывается решением задачи. Формулируя свое предложение, я отдавал себе отчет в том, что в этом представлении не участвуют кости. "Ну, и ладно,- сказал я себе,- позаботимся о камнях, а кости позаботятся о себе сами". Оказалось, что я был неправ. Камни должны перемежаться с символами, представляющими кости.
Чрезвычайно сложную головоломку подобного типа изобрел Р.Карлсон из Лос-Альтоса (шт.Калифорния). Ее настолько трудно изготовить, что пока он вынужден удовлетвориться только ее изображением на экране дисплея. Головоломка представляет собой икосаэдр, геометрическое тело, имеющее 20 треугольных граней. Каждая вершина может стать осью вращения при перемешивании граней. При повороте вершины вместе с ней поворачиваются пять прилегающих к ней треугольников. Каждый треугольник имеет три зоны разного ивета. В исходном упорядоченном положении к каждой вершине прилегают зоны одного цвета, Карлсон подготовил версию своей головоломки для персонального компьютера PC фирмы IBM. В дополнение к цветовому оформлению каждое перемещение сопровождается музыкальной нотой.
ПРОГРАММЫ ДЛЯ КОНСТРУИРОВАНИЯ ПРЕДМЕТНЫХ ГОЛОВОЛОМОК. МНЕМОНИЧЕСКИЕ ПРАВИЛА ДЛЯ ЗАПОМИНАНИЯ ПОСЛЕДОВАТЕЛЬНОСТИ ЦИФР ЧИСЛА ПИ
А.К.ДЬЮДНИ
НАПИСАТЬ программу, помогающую в изобретении головоломки, не менее трудно и интересно, чем написать программу, которая решает ее. Б.Катлер из Уосо (шт.Висконсин) и С.Коффин из Линкольна (шт.Массачусетс), наверное, согласятся со мной. Воспользовавшись компьютером, Катлер изобрел трехмерную игрушку, состоящую из шести деталей, которую он назвал замысловатой колючкой Билла (Bill's baffling burr). Эта игрушка с выступающими во все стороны деталями, которые сложным образом связаны между собой, действительно чем-то напоминает колючий плод растения - он как бы пристает на некоторое время к тому, кто пытается решить головоломку. Колючка Билла состоит из шести деталей, попарно ориентированных в трех взаимно перпендикулярных направлениях (см. рисунок на с.139). На самом деле в этой игрушке содержатся сразу две головоломки - нужно уметь и собрать, и разобрать ее. Пользуясь компьютером, чтобы путем перебора всех возможных комбинаций деталей найти наиболее интересные из них, Катлеру удалось изобрести, может быть, самую трудную головоломку этого типа для шести деталей.

Головоломка-колючка Билла
Коффин тоже не без помощи компьютера изобрел двумерную головоломку, деталями которой являются плоские фишки гексомино различной формы, состоящие из шести квадратов одинакового размера (отсюда название "гексомино", по аналогии с "домино" - фишками, состоящими из двух квалратов.- Перев.), склеенных друг с другом в различных сочетаниях. Задача заключается в том, чтобы собрать фишки в большой квадрат; подбор формы фишек может оказаться трудным и утомительным. Из всех возможных комбинаций гексомино программа Коффина отыскивает те, которые представляются наиболее трудными для решения. Она уже нашла так много комбинаций, что Коффин может удовлетворить интерес всех любителей этой головоломки. Свою систему, создающую эти варианты, Коффин называет "рогом изобилия". Лично я располагаю вариантом игры, показанным на с.140.

Головоломка Коффина из фишек гексомино
Третья головоломка, которую мы рассмотрим, была изобретена без помощи компьютера. Ее автор Энджел из Инглвуда (шт.Колорадо). Эта задача небезынтересна для любителей поиска алгоритмических подходов. Игрушка Энджела представляет собой набор цветных пластмассовых деталей, которые в виде мозаики вписываются в две окружности (см. рисунок на с.142). В ней используются детали двух видов: "камни" и "кости". Повернув сначала один круг, а затем и другой, камни и кости можно перемешать так, что по сравнению с исходным их расположением картина будет выглядеть совершенно хаотичной. Вернуть фишки в исходное положение, пожалуй, ничуть не легче, чем установить одноцветные грани в кубике Рубика.

Головоломка Энджела
Как мы увидим ниже, задача Энджела, по существу, является одномерной. Задача Коффина, очевидно, двумерна, и, наконец, головоломка Катлера трехмерна в полном смысле слова. Начнем с рассмотрения трехмерных головоломок, а затем перейдем к другим в порядке убывания их размерности.
Наверное, каждому из нас доводилось вертеть в руках игрушку-головоломку, подобную описанной выше "колючке". Иногда эти игрушки называют китайскими головоломками, хотя они почти наверняка европейского происхождения. Они могут состоять из многих деталей и иметь разнообразные формы. Наибольшее распространение получили игрушки из шести деталей, каждая из которых имеет форму продолговатого параллелепипеда с вырезанными в нем выемками, или пазами (для краткости будем называть их брусками). В собранном виде детали группируются в три пары, каждая из которых состоит из двух прилегающих друг к другу брусков, как бы врезающихся в центр игрушки и выходящих с противоположной стороны. Однако центральная часть игрушки не может быть занята тремя парами брусков одновременно. Возникающий, казалось бы, парадокс разрешается, если учесть, что в каждом бруске имеются пазы. Расположение пазов определяет возможности сборки и разборки игрушки на составные детали. Ясно поэтому, что искусство создания интересных шестнблочных игрушек сводится к тому, чтобы найти подходящее расположение пазов в каждом бруске.
Катлер конструирует свои игрушки-головоломки в три стадии. Сначала он выбирает форму шести брусков, из которых должна состоять игрушка. Затем он должен проследить, чтобы пазы в брусках были взаимно совместимыми. Для этого нужно определить, существует ли такая конфигурация, в которой все бруски беспрепятственно проходят через центральную зону, образуя единое целое. Наконец, нужно испытать игрушку на разборку, т.е. проверить, возможно ли ее разобрать, и если возможно, то насколько трудной окажется эта задача. На двух последних стадиях конструирования Катлер пользуется программой, которую выполняет компьютер.
Каждая деталь головоломки-колючки вначале представляет собой деревянный брусок определенных размеров. В рассматриваемом варианте игрушки размеры каждого бруска равны (в произвольных единицах) 2*2*6. В каждом бруске имеется 12 мест, где могут быть вырезаны пазы (см. рисунок на с.139). Если считать, что брусок состоит из 24 кубов единичного размера, то на каждом торце бруска будет располагаться по четыре таких куба, а в средней его части будет находиться 16 кубов. С каждой стороны вдоль бруска расположено восемь центральных кубов в два ряда, по четыре куба в каждом. Пронумеруем их от 1 до 8. На противоположной стороне бруска пронумеруем еще четыре центральных куба от 9 до 12. Брус становится деталью игрушки, если удалить из него то или иное количество кубов из 12 рассмотренных. Как подсчитал Катлер, из 4096 возможных способов удаления кубов лишь 369 приводят к построению реализуемой головоломки.
Большой опыт в изобретении подобных головоломок позволяет Катлеру сравнительно быстро выбрать шесть деталей перспективной формы. Однако каким образом, не затрачивая много времени и сил на изготовление настоящей деревянной модели, можно узнать, подойдут ли выбранные детали друг к другу так, чтобы получилась "работающая" игрушка? Катлер не долго думал, прежде чем решил на этой начальной стадии разработки головоломки прибегнуть к помощи компьютера. В 1973г. он написал свою первую программу перебора конфигураций. Пространство, занимаемое игрушкой, программа представляет в виде трехмерного массива размером 8*8*8. Каждый элемент массива представляет собой единичный куб, занимающий соответствующее место в модели, и помечается номером детали, которая занимает данную ячейку пространства. Например, если изъять из этого пространства все кубы, помеченные числом 3, не нарушая их взаимного расположения, то мы увидим, какую форму имеет деталь номер 3. Нетрудно сообразить, что в зависимости от количества пазов, вырезанных в бруске, каждая деталь может занимать от 14 до 24 кубических ячеек, или элементов массива.
Программа просматривает каждый из шести списков, содержащих информацию о конфигурации шести деталей в соответствии с координатами кубов, из которых они состоят. Затем координаты подвергаются различным математическим операциям, представляющим такие преобразования, как перенос, вращение и отражение летали в пределах массива. Безусловно, что эта процедура носит строго упорядоченный характер и требует выполнения многочисленных циклов.
Первый брусок (под номером 1) устанавливается в стандартном положении и составляющие его единичные кубы помечаются в трехмерном массиве номером 1. Взаимное расположение этих кубов в точности воспроизводит конфигурацию детали. Затем программа пробует поместить первый из оставшихся брусков так, чтобы он пересекался с уже установленным стандартным бруском. При этом проверяются все возможные ориентации второго бруска, для чего нужно выполнить два цикла. Еще два цикла требуются программе для того, чтобы попытаться поместить третий брусок так, чтобы он пересекался с первыми двумя. Здесь опять рассматриваются все возможные ориентации. Присоединение трех оставшихся брусков требует выполнения еще шести циклов. Используя жаргон программистов, можно сказать, что эта процедура содержит большое количество вложенных циклов. Всякий раз, когда очередной брусок устанавливается в новое положение или приобретает иную ориентацию, программа проверяет все 512 кубов в массиве с целью удостовериться, что ни один из этих кубов не пронумерован дважды. Если встречается хотя бы один куб с двойной нумерацией, то вся комбинация должна быть отвергнута, потому что в этом случае два бруска пытаются занять одно и то же место, и, следовательно, такая конфигурация оказывается недозволенной (в математическом смысле слова).
Множество всех возможных конфигураций из шести деталей можно представить в виде дерева; корнем дерева будет брусок под номером 1 в стандартном положении. Пока это дозволенная конфигурация. Добавляя следующий брусок с другой ориентацией к каждой из последующих дозволенных конфигураций, мы получаем либо новую ветвь дерева возможных вариантов, либо заходим в тупик.
На конечных узлах дерева программа может выдать какое-то количество дозволенных конфигураций, состоящих из шести брусков и изящно собранных в игрушку-головоломку. Однако некоторые из полученных таким образом головоломок оказываются все же безнадежно "заклиненными": как ни толкай, ни тяни или ни крути бруски, их никак не удается (да это и невозможно) отделить друг от друга. На самом деле такие игрушки было бы просто невозможно изготовить. Они существуют только в "воображении" программы. Каким же образом Катлер определяет, возможно ли разобрать ту или иную шестичастную конфигурацию? Ответ на этот вопрос он получает, выполняя вторую программу - программу разборки.
Программа разборки анализирует тот же самый массив размером 8*8*8, который используется для порождения дозволенных конфигураций. При этом программа пытается сдвинуть каждый брусок на одну или более единичных ячеек в каком-нибудь одном из трех ортогональных направлений. Она пробует вытянуть блок или сдвинуть его вбок. И здесь для представления множества вариантов применяется дерево. В корневом узле дерева находится игрушка-головоломка в собранном виде. На каждой достигнутой стадии разборки программа осуществляет систематический поиск возможных перемещений для каждой очередной детали. Те, кто многократно пытался разбирать эту головоломку, уже давно заметили, что как только удастся полностью высвободить одну или две детали, завершить разборку обычно не составляет труда.
Естественно поэтому, что Катлер считает конструкцию шестичастной головоломки-колючки хорошей только в том случае, когда задача высвобождения первой детали оказывается очень трудной. Чтобы вытащить первую деталь из головоломки-колючки Билла, требуется сделать не менее пяти перемещений!
Прежде чем Катлер сконструировал свою лучшую головоломку, он испробовал и забраковал девять различных вариантов сочленения деталей. Десятый вариант, на котором он остановился (см. рисунок на с.139), отличался исключительно коварным замыслом с расчетом на интуицию играющего. Программа, порождающая конфигурации, нашла одно и только одно взаимное расположение всех деталей, а программа разборки установила, что их можно разобрать только одним способом. Лишь одну деталь можно извлечь первой и для этого нужно совершить четыре, казалось бы, бессмысленных перемещения.
Программа разборки одновременно представляет собой и программу решения головоломки. Сначала, конечно, ей нужно предъявить точное описание деталей головоломки, и это описание должно быть представлено в виде основного массива программы размером 8*8*8. Готовое решение программа выдает в виде указания последовательности перемещений, которую должен воспроизвести человек, пытаясь разобрать игрушку.
Предположим, однако, что программе не было дано никаких сведений о конфигурации деталей. Тогда бы у нее не было никакой альтернативы в манипулировании физической моделью игрушки. Забавно представить себе программу, способную управлять двумя механическими руками-манипуляторами робота. За действиями такой программы можно было бы следить в течение многих дней, по мере того как она исследовала бы колоссальное дерево возможных перемещений.
Коффин, так же как и Катлер, в течение ряда лет занимался изобретением "колючек" и других трехмерных головоломок. Одно из его последних достижений - двумерная головоломка. Предлагаем нашим читателям попытаться собрать 10 фишек гексомино в плоский квадрат, так чтобы ни одна фишка не накладывалась на другую (см. рисунок внизу слева). Каждая фишка состоит из шести деревянных квадратов, склеенных друг с другом вдоль одной или более граней. Одна хорошая головоломка из гексомино - это уже достижение. Однако у Коффина есть "компьютерный ключик", открывающий целый сундук подобных головоломок. Каждый вариант игры отличается от других и имеет свою степень сложности. Такую головоломку можно как бы случайно оставить на столе и пригласить нескольких друзей на чашечку кофе. Хозяин может быть при этом уверен, что ни один из гостей не сумеет быстро решить ее, и сошлется на то, что никогда прежде не видел такой головоломки; она действительно окажется им совершенно незнакомой.
В качестве критериев сложности головоломки подобного типа Коффнн принимает как форму самих деталей, так и количество возможных решений задачи. В своем проекте под названием "рог изобилия" Коффнн пользуется только фишками типа гексомино. Чтобы усложнить задачу, он выбрал исключительно асимметричные фишки, не содержащие квадратов размером 2*2. Полный набор насчитывает 17 фишек. При правильном расположении 10 фишек в квадрате размером 8*8 должно остаться четыре пробела. Дозволенными являются только те конфигурации, в которых эти пробелы расположены симметрично. В модели, которую Коффин прислал мне, есть по крайней мере два решения: первое, когда четыре пустых квадрата находятся в середине собранной фигуры, и второе, когда они расположены по углам.
Всего существует 19448 способов выбрать подмножество из 10 фишек из полного множества, насчитывающего 17 фишек. Далеко не все такие подмножества приводят к интересным головоломкам, а некоторые из возможных наборов нельзя разместить в пределах квадрата 8*8. Каким же образом среди всех этих вариантов можно выявить наилучшие головоломки?
Не так давно Коффин обратился за помощью к М.Билеру, неутомимому программисту, имя которого упоминалось в статье, посвященной описанию игры под названием "Жизнь" {см. журнал "В мире науки" 1985, #7). Билер написал программу исчерпывающего перебора, которая пытается собрать каждый набор из 10 фишек в требуемый квадрат. Программа автоматически генерирует все возможные решения. Если их оказывается не слишком много, она выдает все найденные решения вместе с описанием соответствующего набора из 10 фишек.
Так же как и программа Катлера, конструирующая "колючки", программа Билера, перебирающая конфигурации гексомино, исследует дерево. Начинает она с рассмотрения выделенного подмножества фишек, генерируемого ее главным циклом. По существу, программа как бы сканирует площадь, занимаемую элементами головоломки, строка за строкой. Для этого необходим еще один цикл, вложенный в главный цикл программы. Всякий раз, когда встречается свободный квадрат, программа выбирает одну из еще не использованных фишек (это еше один иикл) и пробует приладить ее к уже сложенным во всех возможных ориентациях (четвертый цикл). Если выбранная фишка оказывается подходящей, на дереве потенциальных решений генерируется новая ветвь, а программа переходит к следующему свободному квадрату и пытается приладить другую неиспользованную фишку.
Если бы не некоторые хитроумные алгоритмические ухищрения, программа, генерирующая решения, может быть, и не могла бы найти все возможные ответы за разумное время. Один из таких трюков заключается в том, чтобы подвергать каждый набор гексомино своеобразному тесту "на четность" еше до того, как программа войдет во второй цикл. Как-то раз, когда Билер изучал набор из 17 фишек, он заметил, что если их рассматривать как фрагменты шахматной доски, то 11 фишек имеют по три белых и три черных квадрата. Остальные 6 фишек состоят из четырех квадратов одного цвета и двух другого. Решение же для любого набора из 10 фишек содержит одно и то же число белых и черных квадратов, а именно 30. Отсюда Билер пришел к выводу, что решение можно найти только для четного числа "непарных" фишек, т.е. тех шести фишек из 17, у которых количество белых и черных квадратов не совпадает. Любое подмножество, не удовлетворяющее этому простому правилу, должно быть отвергнуто, как не имеющее решения. Это позволило сократить количество итераций в программе с 19448 до 9746.
Количество решений, которое находит программа Билера для заданного подмножества гексомино, определяет степень сложности соответствующей задачи. Согласно классификации Коффина, задачи могут быть просто сложными (несколько решений) и очень сложными (всего одно решение). Программа Билера выдает решения одно за другим, как автомат. Вооружившись необходимыми инструментами, Коффнн организовал мастерскую по изготовлению головоломок. О своей работе Коффин рассказывает в брошюре "Puzzle Craft" ("Искусство составления головоломок").
Отметим одно примечательное различие между головоломками Катлера и Коффина: в то время как шестичастную игрушку Катлера очень трудно разобрать, головоломка из "рога изобилия" Коффина легко поддается разборке - для этого достаточно высыпать фишки из коробочки, в которой гексомино собираются в большой квадрат. Головоломку-колючку труднее разобрать отчасти потому, что она трехмерна. Разумному существу из четырехмерного мира не составит никакого труда разобрать любую игрушку Катлера - оно воспользуется новым направлением, "вверх" от модели. В то же время даже ему, наверное, будет так же трудно собрать детали головоломки-колючки, как нам решить двумерную задачу с гексомино. Этот мысленный эксперимент наводит нас на мысль о двумерной головоломке-колючке, которая разбирается перемещениями плоских деталей, все время остающихся в одной плоскости. Возможна ли головоломка такой конструкции? Предположим, что у нас есть 8 деталей для двумерной головоломки-колючки. Две детали выступают наружу с каждой стороны коробочки; детали, находящиеся внутри, могут иметь любую прямоугольную форму. Предлагаем читателям подумать над конструкцией подобной головоломки.
Перейдем к рассмотрению третьей головоломки, называемой по имени ее автора головоломкой Энджела. Для меня несколько часов, с интересом проведенных над этой головоломкой, оказались безрезультатными. Мне еше не удалось получить общего решения, однако Дуглас Р.Хофштадтер (статьи которого в рубрике "Математические игры" раньше публиковались в нашем журнале) разработал специальную программу, выполняющую операции над кругами этой головоломки. Энджел пишет, что несколько человек, достигших высокого мастерства с кубиком Рубика, не смогли решить его задачу.
Игрушка Энджела состоит из двух пересекающихся кругов, заключенных в пластмассовый корпус. По периферии каждого круга располагаются попеременно 6 "камней" и 6 "костей". Камни выглядят как несколько располневшие треугольники, а кости - как недокормленные прямоугольники. Поскольку круги пересекаются, они имеют два общих камня и одну обшую кость (см. рисунок внизу). Круги с заключенными в них камнями и костями могут вращаться. Если повернуть один круг, скажем верхний, на 60o, камень и кость, которые в исходном положении были общими для обоих кругов, оказываются перемещенными и заменяются другим камнем и другой костью. Если поочередно поворачивать каждый круг на любой угол, кратный 60o, в случайно выбираемых направлениях, то камни и кости оказываются перемешанными и их расположение выглядит хаотичным.
Исходная конфигурация головоломки делится на 10 шестиугольных зон - 8 внешних и 2 внутренних. Внешние зоны окрашены в красный, оранжевый, синий и черный цвета; симметрично противоположные друг другу зоны имеют одинаковый цвет. Внутренние зоны (по одной в каждом кругу) - желтого и зеленого цвета. Каждый камень принадлежит одновременно трем зонам и поэтому имеет три области различного цвета. Каждая кость принадлежит двум зонам и потому является двухцветной.
Если камни и кости перемешать описанным выше способом, то вместо приятной на вид упорядоченной структуры, которая была в исходном положении, возникнет беспорядочная мозаика цветов. Возникает вопрос: как может игрушка с таким ограниченным характером перемещений оказаться такой же сложной, как и кубик Рубнка? Энджел показал мне полный набор "алгоритмов" решения своей задачи, но мы придержим их на несколько месяцев в резерве, чтобы дать возможность всем заинтересованным читателям попробовать свои силы и попытаться самим найти решение. Мы надеемся, что читатели, владеющие программированием, сумеют найти красивые и эффективные алгоритмы.
Сам я еще не написал такой программы, но у меня есть некоторые соображения, которые могут оказаться полезными. Когда головоломка находится в исходном (неперемешанном) состоянии, пронумеруйте камни по часовой стрелке от 0 до 9, начиная с камня, расположенного справа от кости, принадлежащей обоим кругам. Тогда исходную конфигурацию можно представить следующей последовательностью чисел:
0 1 2 3 4 5 6 7 8 9
Допустим, что верхний круг повернулся на 60o по часовой стрелке. Если приведенную выше последовательность рассматривать как номера 10 ячеек игрушки, то в результате указанного поворота последовательность номеров будет следующей:
5 0 1 2 3 4 6 7 8 9
Заметим, что после перестановки число 5 перешло со своей шестой позиции на первую. Читатели сами могут легко получить последовательность номеров после каждой из трех следующих перестановок. Эти четыре перестановки можно встроить в программу, которая оперирует массивом из 10 элементов. Первоначально массив содержит числа в возрастающем порядке. Обращаясь к перестановкам в случайном порядке, мы как бы перемешиваем модель головоломки. Благодаря описанной схеме представления эалачи можно существенно ускорить работу программы, отыскивающей решение. Наверное, теперь читателям стало ясно, почему я считаю задачу Энджела одномерной.
Мнемоники числа пи я перенес в отклики к соответствующей статье.- G.
ОТКЛИКИ
3 1986
В ДЕКАБРЬСКОМ номере журнала за прошлый гол в этой рубрике разговор шел о трех головоломках: "колючке" Билла, "роге изобилия" Коффина и игрушке-вертушке Энджела. Головоломки заинтересовали сотни читателей: одни пытались найти магический способ, как разобрать хитроумно сочленяющиеся детали в "колючке" Билла, другие сосредоточили свое внимание на поиске решения задачи о размещении фишек полимино. Представители одной группы не могут помочь представителям другой: каждая из головоломок уникальна. Еше одна группа читателей без устали продолжает крутить колеса игрушки Энлжела, тщетно пытаясь установить их в требуемом положении. Некоторым энтузиастам удалось добиться успеха, по крайней мере на абстрактном уровне. Уже начали поступать письма, в которых предлагается решение задачи.
Пришло также несколько писем с описанием конструкций двумерных "колючек" - игрушек, которые нужно разобрать на составляющие их детали. Наиболее изящная из предложенных читателями конструкций показана на рисунке вверху. Задача заключается в том, чтобы удалить четыре составляющие игрушку детали с прямоугольного подноса, границы которого изображены пунктирными линиями. Детали можно перемещать только в четырех направлениях в плоскости рисунка: вверх, вниз, влево и вправо. Четыре темных квадрата в углах считаются жестко прикрепленными к подносу. Какую из деталей следует переместить первой? Эту двумерную головоломку придумал Дж.Картер из Литтлтона (шт.Колорадо). Имея дело с трехмерной игрушкой, мы по крайней мере можем ее повертеть в руках и осмотреть со всех сторон. Толкать и тянуть детали, находящиеся в плоском ящике, как-то непривычно.

Двумерная головоломка-колючка Дж.Картера
Р.Клавье из Далласа (шт.Техас) сообщил, что ему удалось найти алгоритмическое решение задачи Энджела. Он пишет, что его программа, написанная на Бейсике и выполняющаяся на портативном компьютере модели СС-40 фирмы Техас Instruments, на решение задачи обычно затрачивает от 300 до 700 ходов. В алгоритме используется шесть стандартных обменных операций между камнями и костями. Читатели, воспользовавшиеся предложенным мною способом представления последовательности, возможно, закинули свою сеть слишком широко. Решение, полученное для числовой последовательности, не всегда оказывается решением задачи. Формулируя свое предложение, я отдавал себе отчет в том, что в этом представлении не участвуют кости. "Ну, и ладно,- сказал я себе,- позаботимся о камнях, а кости позаботятся о себе сами". Оказалось, что я был неправ. Камни должны перемежаться с символами, представляющими кости.
Чрезвычайно сложную головоломку подобного типа изобрел Р.Карлсон из Лос-Альтоса (шт.Калифорния). Ее настолько трудно изготовить, что пока он вынужден удовлетвориться только ее изображением на экране дисплея. Головоломка представляет собой икосаэдр, геометрическое тело, имеющее 20 треугольных граней. Каждая вершина может стать осью вращения при перемешивании граней. При повороте вершины вместе с ней поворачиваются пять прилегающих к ней треугольников. Каждый треугольник имеет три зоны разного ивета. В исходном упорядоченном положении к каждой вершине прилегают зоны одного цвета, Карлсон подготовил версию своей головоломки для персонального компьютера PC фирмы IBM. В дополнение к цветовому оформлению каждое перемещение сопровождается музыкальной нотой.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
Страница 1 из 4 • 1, 2, 3, 4 
 Похожие темы
Похожие темы» Литературное приложение
» Приложение. BASIC 1982. Пара книг издательства USBORNE
» О самоуспокоенности неудачников (приложение к заметкам о простых играх)
» Брябрин. Программное обеспечение персональных ЭВМ. 1990
» Броуди. Начальный курс программирования на языке ФОРТ. 1990
» Приложение. BASIC 1982. Пара книг издательства USBORNE
» О самоуспокоенности неудачников (приложение к заметкам о простых играх)
» Брябрин. Программное обеспечение персональных ЭВМ. 1990
» Броуди. Начальный курс программирования на языке ФОРТ. 1990
Страница 1 из 4
Права доступа к этому форуму:
Вы не можете отвечать на сообщения|
|
|
