Приложение. В мире науки. Занимательный компьютер. 1983-1990
Страница 2 из 4
Страница 2 из 4 •  1, 2, 3, 4
1, 2, 3, 4 
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
1 1986
ИССЛЕДОВАНИЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В ПЕРВОБЫТНОМ КОМПЬЮТЕРНОМ ОКЕАНЕ, НАСЕЛЕННОМ ФЛИБАМИ
А.К.ДЬЮДНИ
ПРЕДСТАВИМ себе абстрактное море, населенное абстрактными организмами, которые условно назовем конечными живыми капельками (от английского названия finite living blobs) или для краткости флибами (flibs). Каждый флиб снабжен наипростейшим аппаратом принятия решений. По существу, это биологический эквивалент того, что математики называют конечным автоматом. Флиб содержит в себе также одну хромосому, состоящую из цепочки символов, которая является колом, определяющим автомат. Флибы обитают в первобытном цифровом "бульоне", постоянно подвергающемся изменениям. Чтобы выжить, флиб должен уметь точно предугадывать эти изменения.
В первобытном бульоне, сваренном мною недавно в моем компьютере, флибы, которые плохо предсказывали изменения в окружающей среде, все вымерли. Те же, которые обладали способностью к предсказанию, произвели на свет потомство, причем отдельным его представителям удалось даже превзойти своих предков. В конечном итоге как результат эволюционного процесса возникла линия безошибочных предсказателей.
Флибы и их эволюционные тенденции хорошо иллюстрируют вид программирования, известный под названием "метод генетического алгоритма". Основанный Дж.Холландом в Мичиганском университете в 60-х голах, этот метод позволяет иногда решать трудные задачи путем создания "эволюционной последовательности" приближенных решений. Новые решения получаются путем "скрещивания и размножения" лучших решений, полученных к данному моменту. Через некоторое время появляется новое решение, превосходящее своих "родителей", и это решение в свою очередь заносится в список будущих "производителей". Генетические алгоритмы применялись с переменным успехом в задачах, связанных с системами классификации, распознавания образов и некоторых, пока немногочисленных задачах из других областей. В моем компьютерном первобытном бульоне лри помощи этого метода удалось получить флибы, стоящие на более высокой ступени развития. Объясняется ли мой успех обшей эффективностью метола генетического алгоритма или же простотой задачи, перед которой были поставлены флибы? На этот вопрос ответить трудно. Во всяком случае над ним стоит поразмыслить, а само явление может быть воспроизведено любым читателем, в распоряжении которого имеется компьютер.
Конечный автомат обладает конечным числом состояний. Под действием входного сигнала он автоматически переходит из одного состояния в другое. Автоматы, на основе которых построены флибы, сами тоже порождают сигналы. Входные и выходные сигналы представляются в автомате символами. Приняв сигнал, автомат меняет свое состояние и вырабатывает другой сигнал.
Процесс удобно представлять в виде таблицы переходов из одного состояния в другое. Например, конечный автомат, который может принимать три состояния А, В и С, реагировать на входные сигналы в виде нулей и единиц, а также генерировать аналогичные сигналы, можно полностью описать таблицей размером 3*4. Для каждого состояния, в котором может находиться автомат, и для каждого символа, который он может получить, в таблице есть два элемента. Первый элемент соответствует выходному символу, а второй указывает, каким должно быть следующее состояние автомата:

Автомат, который описывается приведенной таблицей, в некоторый момент времени может оказаться в состоянии С. Если он принимает 1, то, согласно таблице, должен выдать 0 и перейти к состоянию А.
Другое, более наглядное представление лает диаграмма переходов между состояниями. На этой диаграмме в кружках записываются состояния, а соединяющие кружки стрелки указывают переходы. Если автомат, получив определенный символ, переходит из одного состояния в другое, то на диаграмме следует изобразить стрелку, ведущую от кружка, соответствующего первому состоянию, к другому кружку, соответствующему новому состоянию автомата. У одного конца стрелку помечают символом входного сигнала, обусловившего данный переход, а у другого конца - символом, выходного сигнала (см. рисунок на с.102).
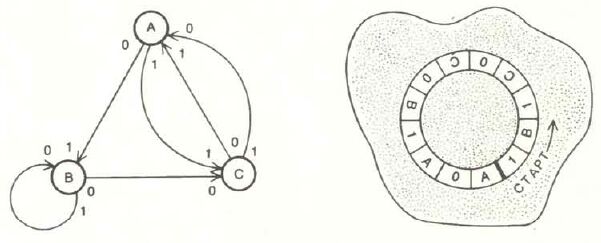
Диаграмма переходов между состояниями (слева) и соответствующий флиб со своей хромосомой (справа)
Конечный автомат всегда начинает работу с какого-то первоначального состояния, называемого исходным. С каждым тактом воображаемого часового механизма на вход автомата прибывает новый символ, генерируется выходной символ и автомат переходит в следующее состояние. Автоматы, на основе которых построены флибы, могут получать и посылать только два вида символов - 0 и 1.
Ну а как интерпретировать поведение флиба, если нам почти ничего не известно о биологии этого существа? В этом и заключается одно из удовольствий, доставляемых нам абстракцией. Символы, принимаемые автоматом, можно рассматривать как сенсорное восприятие окружающей среды. Соответственно выходные символы можно считать реакцией организма на изменение в окружающей среде.
На самом деле понятие флиба настолько гибкое, что входные и выходные символы можно трактовать как самые разнообразные явления. Например, входной сигнал может представлять химический или температурный градиент. Соответственно выходной символ может быть командой, управляющей "ресничками", при помощи которых передвигается организм, или командой, вызывающей образование спор. Одной из наиболее важных задач для любого существа, желающего в процессе эволюции развиться до сколько-нибудь приемлемого уровня (скажем, университетского профессора), является способность предсказывать изменения в окружающей среде. Для флиба окружающая среда представляется нескончаемой последовательностью нулей и единиц. Поскольку принимаемые флибом символы означают существенные события в окружающей его среде, его способность предсказывать следующий символ, очевидно, даст ему некоторое преимущество, в особенности если в рамках более конкретной интерпретации модели шансы на выживание у флиба при этом условии возрастают.
Большинство флибов в этом смысле довольно плохо предсказывает изменения в окружающей среде. Например, флиб, определенный приведенной выше таблицей переходов, отвечает на принимаемую из среды последовательность
0111000010110...
такой последовательностью символов:
100001100I000...
В каждый момент времени выходной символ флиба представляет собой предсказываемый им символ, который должен поступить из среды в следующий момент. Чтобы определить количество правильных предсказаний, нужно сдвинуть выходную последовательность на один символ вправо и сравнить ее побитно с входной последовательностью. Подсчитаем количество совпадающих символов. В рассматриваемом случае флиб сумел правильно предсказать лишь 6 из 12 входных символов - результат не лучший, чем при чисто случайном угадывании.
Вообще не следует требовать слишком много от конечного автомата. Например, нельзя требовать от флиба правильного предсказания в условиях непериодической среды. Здесь читателю следует немного поразмыслить. Почему правильно предсказанная последовательность входных символов должна обязательно состоять из одной и той же основной цепочки, которая бесконечно повторяется? Например, флиб с тремя состояниями, не справившийся с только что рассмотренным тестом, достиг блестящего успеха, столкнувшись с такой последовательностью символов:
010011010011010011...
Здесь окружающая среда все время "выбивает" один и тот же ритм - 010011.
Существует несколько десятков различных флибов с тремя состояниями, но лишь очень немногие из них могут предсказать эту последовательность безошибочно. Среди флибов с числом состояний больше трех безошибочные предсказатели для данной последовательности входных символов встречаются редко и по мере роста количества состояний встречаются все реже и реже. Способность к предсказанию очень сильно зависит от периода последовательности: ни один флиб с n состояниями не сможет предсказать последовательность, состоящую из бесконечно повторяющейся основной цепочки символов, если эта цепочка слишком длинная. Очевидно, существует зависимость между количеством возможных состояний флиба и наибольшим периодом в последовательности, которую он может точно предсказать. Читателям, наверное, будет интересно попробовать найти эту зависимость. Каков наибольший период последовательности, которую может предсказать флиб с n состояниями?
Функционально флиб представляет собой несколько более сложное "устройство", чем просто конечный автомат, пытающийся предсказать повеление окружающей его среды. Напомним, что он сше обладает и хромосомой. Флибы периодически размножаются (механизм этого размножения нам не известен). Исследование хромосомы и ее отношения к конечному автомату флиба показывает нам, каким образом унаследованные гены определяют повеление организмов. Начнем с таблицы переходов и будем выбирать из нее строки по одной сверху вниз. Соединим концы выбранных таким образом строк в олну полосу, а затем присоединим начало полосы к ее концу. В результате получается круглая хромосома.
Перед заключительной операцией соединения хромосома нашего экземпляра флиба с тремя состояниями примет вид цепочки, состоящей из 12 генов:
1B1C0C0B1A0A
Строго говоря, символы этой цепочки являются аллелями. Аллель - это ген определенного типа, который появляется в заданном локусе. Ген как таковой может быть указан либо по имени, либо по его локусу. Так, например, седьмой символ слева управляет выходным символом флиба, когда тот находится в состоянии B и получает 1 на входе. Соответствующий локус имеет номер 7.
Не так давно я создал в своем персональном компьютере первобытный бульон, населенный десятью флибами с четырьмя состояниями. Прежде чем прошло 1000 единиц времени, которые я называю хрононами, ни одного из исходных флибов уже не было в живых. Их место заняли флибы, обладающие лучшей способностью к предсказанию. На экране дисплея демонстрируются лучший и худший результаты, достигнутые живущими на данный момент представителями популяции. Наихудший показатель изменяется довольно часто и в сравнительно широких пределах, в то время как наилучший показатель медленно возрастает (см. рисунок на с. 103). Как раз, когда я уже почти оставил надежду получить в результате эволюции безошибочного предсказателя, он внезапно появился, и наилучший показатель сразу подпрыгнул до 100.

Бульон, населенный десятью фпибоми (вверху), и безошибочный предсказатель (внизу)
Пора уже, наверное, объяснить читателю, каким образом флибы эволюционируют в моем первобытном компьютерном бульоне. Время от времени периодически в среду попадает космический луч, который поражает случайно выбранную хромосому и случайный локус, в результате чего тот или иной ген перехолит из одной аллели в другую. Рассмотрим, например, хромосому флиба с четырьмя состояниями. Ген третьего локуса управляет выходным символом при переходе из состояния A, когда существо принимает на входе 1:
0D1C0D0B1A0C1B1A
Попавший в этот ген космический луч слегка изменяет хромосому:
0D0C0D0B1A0C1B1A
Другим источником вариаций в множестве генов популяции является "спаривание" существ. Когда настает сезон размножения, гены флиба, достигшего наилучших результатов в предсказывании, перемешиваются с генами другого производителя, выбранного случайным образом. Получающаяся в результате особь несет в себе свойства обоих родителей. Часть хромосомы происходит от родителя, успешно предсказывающего состояние среды, а другая часть - от родителя, выигравшего право на размножение по лотерее. Механизм перемешивания хромосом напоминает явление перекреста (или кроссинговера), наблюдаемое в настоящих хромосомах. Можно проиллюстрировать перекрещивание хромосомы флиба, комбинируя первую (неизменную) хромосому, приведенную выше, с другой хромосомой:
1A1^B0D1A^0C1D1B0C
Стрелки указывают на точки перекреста, выбираемые случайным образом. Хромосома полученного флиба идентична хромосоме второго родителя вплоть до первой точки, на которую указывает стрелка. В интервале между двумя точками она идентична хромосоме первого родителя, а после второй точки мы опять видим фрагмент хромосомы второго родителя (см. рисунок на с.104):

Перекрещивание двух хромосом родителей и получающаяся в результате хромосома потомка (справа)
1A1C0D0B0C1D1B0C
До того как начать работать нал программой, я был настроен несколько скептически по поводу эффективности механизма перекрещивания хромосом. Однако к моему удивлению выяснилось, что, когда один из родителей является хорошим предсказателем, потомство, как правило, также хорошо справляется с задачей предсказывания.
Читатели сами могут убедиться в этом, написав программу под названием АВТОСУП. Листинг программы не занял бы больше одной страницы. Она состоит из четырех модулей, вложенных в цикл. В программе можно установить верхний предел показателей предсказания, или счета. Пока наилучший достигнутый счет не превышает предельного значения, выполнение программы (всех ее четырех модулей) должно продолжаться.
В первом модуле производится подсчет результатов, показанных десятью флибами для 100 сигналов, поступающих из окружающей среды. Во втором модуле выявляются флибы, показавшие самый лучший и самый худший результаты. В третьем модуле флиб, достигший наилучшего показателя, спаривается со случайно выбранной особью популяции. Их потомок замещает флиб с наихудшим результатом. В четвертом и последнем модуле космический луч ударяет в случайно выбранную особь и вызывает мутацию. Непосредственно перед входом в третий модуль (модуль размножения) производится выбор случайного числа. Если число оказывается ниже определенного порогового значения, то программа минует модуль размножения и сразу переходит к модулю мутаций. Пороговое значение можно устанавливать произвольно. Однако некоторые значения оказываются предпочтительными: если модуль размножения выполняется слишком часто, то гены флиба, добившегося наилучшего результата на данный момент, быстро становятся доминирующими в небольшой популяции. Генофонд таким образом обедняется, и эволюция становится очень медленной, если вообще не прекращается. Впрочем, эволюция замедляется так или иначе, по мере того как возрастают показатели флнбов. Флиб, добившийся наилучших результатов, остается на сцене все дольше, потому что вероятность появления "более высоко организованного" флиба становится все меньше.
В программе АВТОСУП следует организовать четыре массива. Назовем их ХРОМ, СОСТ, СЧЕТ и СРЕД. ХРОМ - это двумерный массив, расчитанный на 10 флнбов и 16 генов. ХРОМ(i, j) относится к j-му гену i-го флиба. СОСТ и СЧЕТ описывают соответственно текущее состояние и счет (т.е. показатель предсказания) для всех 10 флибов. Четвертый массив СРЕД используется для генерирования сигналов, поступающих из внешней среды. Этот массив вводится с клавиатуры перед выполнением программы.
Показатели флнбов рассчитываются в двойном цикле. Во внешнем цикле генерируются 100 символов среды, а во внутреннем - счет каждого флиба увеличивается на 1, если он правильно предсказал следующий символ. Флибы с четырьмя состояниями могут с успехом использоваться в средах с периодом, равным 6; предсказание в этих условиях будет для них задачей средней трудности. Чтобы появились безошибочные предсказатели в среде с периодом 8, программа может проработать целый день, в то время как со средой с периодом 4 программа справится очень легко. В этом модуле программы полезными оказываются следующие два приема. При помошн первого из них каждый следующий символ среды формируется на основе индекса внешнего цикла i. Для этого индекс i вычисляется по модулю 6. Результатом этой операции является остаток от деления i на 6. Полученное число может быть использовано для индексирования массива СРЕД. По мере того как индекс i пробегает значения от 1 до 100, вычисляемый вторичный индекс повторно пробегает через массив СРЕД, порождая нужную последовательность символов среды. По известному индексу текущего символа следующий символ легко вычисляется. Этот символ поочередно сравнивается с предсказанием, сделанным каждым флибом.
Второй прием позволяет программе быстро находить следующее состояние флиба и соответствующий выходной символ просто путем просмотра хромосомы флиба. В массиве сост вместо букв A, B, C, D для представления состояний используются цифры 0, 1, 2, 3. Если переменную, содержащую символ среды, назвать СИМВ, то выходной символ i-го флиба можно определить, воспользовавшись сначала простой формулой
l = 4*СОСТ(i)+2*СИМВ.
Затем нужно найти значение элемента ХРОМ(i, l). Когда существо находится в состоянии i и получен входной символ СИМВ, значение выходного символа находится в локусе l хромосомы i-ro флиба. Следующее состояние содержится в локусе l+1.
В модуле, который выявляет наилучшую и наихудшую особи, используется стандартный прием, задаваемый в качестве упражнения в элементарных курсах программирования: при заданном массиве из n чисел нужно написать программу, определяющую наибольшее из этих чисел. Для решения задачи нужно установить значение переменной МАКС в нуль и затем просматривать массив в простом цикле. Каждый элемент массива сравнивается с переменной МАКС. Если его значение оказывается больше МАКС, то оно присваивается как новое значение переменной МАКС. При этом запоминается также индекс элемента. Ту же процедуру можно обратить для отыскания наименьшего числа. Для этого нужно установить исходное значение переменной МИН равным 100 и заменять его элементами, которые оказываются меньше текущего значения МИН.
В третьем модуле флнб, достигший наилучших результатов, спаривается со случайно выбранным членом популяции. Единственное затруднение, возникающее при написании этого сегмента, связано с выбором двух точек перекреста. Мне кажется, что легче всего эту задачу можно решить, выбирая две целые случайные величины в диапазоне от 1 до 16; назовем эти величины C1 и C2. Если C1 больше С2, то их значения нужно поменять местами. После некоторого размышления читатели смогут организовать три цикла с индексом, пробегающим значение от 1 до C1, от C1 до C2 и от C2 до 16, построив тем самым механизм перемещения строк множества хромосом для спариваемых особей в строку, которую ранее занимала хромосома флиба с наихудшим результатом.
В четвертом модуле должны быть выбраны случайные значения индекса флиба и номера локуса. Четность номера локуса говорит о том, чтб подлежит мутации - ген состояния или ген выходного символа. Если номер данного локуса четный, то к хранящемуся в локусе значению прибавляется 1 по модулю 2. Тем самым значение бита меняется на противоположное. Если же номер локуса нечетный, то к соответствующему элементу массива следует прибавить 1 по модулю 4. Таким образом, состояние, хранящееся в данном локусе, изменяется.
Не совершил ли я какого-нибудь жульничества? Конечно, систематическое изменение состояний от 0 к 1, затем к 2, к 3 и опять к 0 едва ли назовешь случайным процессом. На это я могу ответить, что он случайный в достаточной мере: поскольку количество состояний очень мало, результаты работы программы не должны сильно отличаться от случая, когда состояния выбираются с большей степенью случайности. Можно усмотреть также небольшое жульничество в моем небрежном выборе C1 и C2. Дело в том, что этот метод гарантирует преимущество отдельных подцепочек перед другими. Однако и в этом случае, я думаю, различия между программой АВТОСУП и какой-нибудь статистически более корректной программой генетической селекции будут не очень существенными. Так или иначе, процессы жонглирования генами и поражения хромосом космическими лучами настолько интенсивны, что флибу-чемпиону иногда очень трудно узнать своих внуков.
В программе АВТОСУП нам осталось рассмотреть лишь ее начало и конец. Исходная популяция флибов, населяющая среду, должна быть выбрана случайным образом. Для каждого гена каждого флиба должно быть выбрано целое число из подходящего диапазона и присвоено этому гену. Наконец, когда какому-либо флибу удается превзойти пороговое значение результата, указанное во внешнем цикле, программа должна выдать достигнутый результат на экран.
Читателей, желающих пуститься в это генетическое приключение, следует предупредить, что им придется провести значительную исследовательскую работу. Возможно, некоторые исследователи даже пристрастятся к этой работе. В числе интересных вопросов, на которые нужно найти ответ, находится вопрос о присутствии эволюционного процесса и о его скорости. Когда период поступления сигналов о состоянии окружающей среды слишком большой для того, чтобы в результате эволюции мог появиться безошибочный предсказатель с четырьмя состояниями, то как тогда флибам удается приспособиться и выжить? Как изменение длины периода влияет на время, требующееся для выведения безошибочного предсказателя? Ничто в описании программы АВТОСУП не препятствует ее расширению для флибов с пятью или шестью состояниями. Можно даже изменить программу так, чтобы исследовать непериодические среды или среды, которые время от времени меняют свою основную цепочку символов.
Описанная эволюция автоматов была задумана под влиянием книги: L.J.Fogel, A.J.Owens, M.J.Walsh, "Artificial Intelligence through Simulated Evolution" ("Искусственный интеллект как результат моделируемой эволюции"), появившейся в начале 60-х годов. В этой книге была описана серия экспериментов по эволюции автоматов. Автоматы должны были предсказывать периодические последовательности и могли эволюционировать аналогично нашим флибам. Однако в этом строгом научном исследовании размножение и генетический перекрест не фигурировали.
Ввести в модель свойство генетического перекреста мне посоветовал Холланд. Как уже отмечалось, Холланд является признанным отцом генетического алгоритма. Его последователи, число которых постоянно растет, недавно собрались на свою первую крупную конференцию, состоявшуюся в Университете Карнеги-Меллона. Они обсудили широкий круг вопросов теории и ее практических приложений. В нескольких докладах рассматривалась задача, которая может послужить интересным введением в область генетического программирования.
Речь идет о задаче коммивояжера, которая заключается в следующем: по заданной географической карте с n городами, соединенными сетью дорог, требуется найти кратчайший маршрут, включающий все n городов. Этот маршрут позволяет коммивояжеру минимизировать дорожные затраты.
Вполне возможно, что маршрут минимальной длины может возникнуть в результате эволюции, подобно тому как возникают безошибочные предсказатели из "низших" флибов. Каждый маршрут может быть закодирован в хромосоме. Кратчайшие из существующих на данный момент маршрутов можно размножать в надежде получить потомство из еще более коротких путей. Хромосомы потомства можно получить в результате механизма перекреста родительских хромосом.
Интересная проблема связана с выбором хорошего представления для маршрута. Если, например, пользоваться просто списком городов в порядке их посещения, то полученное потомство может даже не соответствовать никакому маршруту. Чтобы обойти затруднение, авторы одного из докладов - Дж.Греффенштетт, Р.Гопал, Б.Росмайта и Д. ван Гухт из Вандербильтского университета - предлагают хромосому остроумной конструкции. Например, маршрут из пяти городов, скажем a, c, e, d, b, можно представить в виде последовательности 12321. Чтобы получить такую цепочку чисел, используется некий стандартный порядок, в котором перечислены города, например a, b, c, d, e. Если нам задан маршруту c, e, d, b, то будем систематически удалять города из стандартного списка, чтобы получить указанный маршрут. Сначала удалим a, затем c, e и т.д. Перед тем как удалить город из стандартного списка, заметим его порядковый номер в этом уменьшающемся списке: a - первый, c - второй, e - третий, d - второй и, наконец, b - первый. Примечательно, что при перекрещивании двух таких хромосом результат всегда является каким-нибудь маршрутом (см. рисунок на с.106). Пользуясь таким представлением маршрутов, их можно размножать и проводить среди них селекцию.

Два родигтльских маршрута коммивояжера (вверху) и маршрут-потомок (внизу), полученный в результате перекрещивания хромосом
Большинство поклонников генетических алгоритмов признают, что задача коммивояжера представляет для них самый серьезный вызов. Хотя эксперименты, в которых применялось только что описанное представление, не принесли впечатляющих результатов, были разработаны некоторые другие алгоритмы, более успешно работающие при решении этой задачи.
И все же ни один из генетических алгоритмов не смог справиться с задачей коммивояжера в требуемом смысле. Несомненно, прежде всего это объясняется сложностью самой задачи. Поскольку она принадлежит к классу задач, называемых теоретиками NP-полными, она, возможно, обречена навсегда остаться неразрешимой в практическом смысле.
ARTIFICIAL INTELLIGENCE THROUGH SIMULATED EVOLUTION. LAWRENCE J.FOGEL, ALVIN J.OWENS AND MICHAEL J. WALSH, John Wiley & Sons, Inc., 1966 (Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. Пер. с англ. М.: "МИР", 1969.- G.).
ADAPTATION IN NATURAL AND AR TIFICIAL SYSTEMS. JOHN H. HOLLAND University of Michigan Press, 1975.
GENETIC ALGORITHMS FOR THE TRAVELING SALESMAN PROBLEM. JOHN GREFENSTETTE, RAJEEV GOPAL, BRIAN ROSMAITA AND DIRK VAN GUCHI in Proceedings of an International Conference on Genetic Algorithms and Their Applications, edited by John J. Grefenstette. The Robotics Institute, Carnegie-Mellon University, 1985.
ОТКЛИКИ
4 1986
В ЯНВАРСКОМ номере журнала в рубрике "Занимательный компьютер" речь шла о флнбах - конечных "живых организмах", пытающихся предсказывать изменения в окружающей их среде. В первобытном компьютерном бульоне лучший представитель каждого поколения скрещивает свои хромосомы со случайно выбранным флибом. В результате эволюционного процесса возникают все более удачливые предсказатели, пока на свет не появляется организм, безошибочно предсказывающий изменения в среде.
По существу, флиб представляет собой конечный автомат. Другими словами, он обладает конечным числом состояний и для каждого принимаемого им сигнала (0 или 1) он вырабатывает ответный сигнал и переходит в новое состояние. Сигнал, генерируемый флибом на каждом цикле процесса, является предсказанием следующего сигнала, который должен быть им получен из внешней среды.
Некоторые читатели поставили перед своими флибами непосильные для них задачи. Никакая эволюция не породит флиба, способного предсказывать последовательности случайно генерируемых битов. Точно так же никогда не возникнут флибы, предсказывающие простые числа. От них можно требовать предсказания периодически повторяющихся двоичных последовательностей. Например, существует флиб с четырьмя состояниями, предсказывающий повторяющуюся восьмисимвольную последовательность 01100010. Однако даже повторяющаяся последовательность может выйти за пределы предсказательной способности флиба, если основная цепочка окажется слишком длинной по отношению к числу его состояний. На самом деле ни один флиб с четырьмя состояниями не сможет предсказать повторяющуюся последовательность 010010111. Почему?
Простейший ответ на этот вопрос можно получить с помощью процедуры, которую я называю "ползучей индукцией". Представим себе флиб с одним состоянием. Он может предсказать бесконечно повторяющуюся основную последовательность 01. Для каждого из двух возможных сигналов, получаемых флибом, он вырабатывает один ответ: получив на входе 0, флиб отвечает 1 и переходит в то же самое состояние. Если он получает 1, то в ответ вырабатывает 0. Цепочка из трех символов, скажем 011, выходит за пределы возможностей флиба с одним состоянием просто потому, что автомат не имеет в своем наборе достаточного количества ответов. В то же время флиб с двумя состояниями располагает четырьмя возможными ответами, по два на каждое состояние. Таким образом, он может предсказать цепочку из четырех символов, но не справляется с цепочкой из пяти символов: когда дело доходит до пятого символа, флиб должен повторить один из своих предыдущих ответов. Принцип доказательства ясен. Флиб с n состояниями может предсказать последовательность, состоящую из 2n символов, но не 2n+1. Можно найти приятное развлечение в том, чтобы составить последовательность из 8 бит, а затем сконструировать флиба, который ее предскажет. Совершенный предсказатель, полученный таким образом, будет единственным в своем роде. Об успехе программы AUTOSOUP можно судить, сравнивая совершенного предсказателя, порожденного программой в ходе эволюции, с флибом, который уже был построен "вручную".
Несколько читателей придумали, как можно ускорить работу программы AUTOSOUP. Например, практически не имеет смысла проверять существующую на данный момент популяцию флибов на последовательности из 100 символов, если основная цепочка содержит лишь 6 символов. В результате однократного повторения цепочки будет задана последовательность из 12 символов, которой оказывается вполне достаточно.
Ф.Каарет из Принстонского университета указал также на то, что количество команд в программе можно уменьшить, если оценивать показатели только двух флибов при каждом выполнении основного цикла, а не всей популяции. В конце концов, измениться могли лишь (самое большее) два флиба: флиб с наихудшим результатом был заменен новым гибридом и еще один флиб, который, возможно, был поражен космическим лучом.
Ускорение, полученное путем сокращения тестовой последовательности символов окружающей среды и за счет устранения теста для старых флибов, приблизительно одно и то же. Теперь у нас должно хватить времени для того, чтобы получить в результате эволюции флибы с n состояниями, способные предсказать повторяющиеся цепочки символов длиной до 2n.
Из письма Э.Кудала из Парк-Риджа (шт.Иллинойс) мы узнали, что ему неприятно было посылать последнего флнба прямо на тот свет. Вместо этого он стал скрещивать на каждом цикле худшего флиба с лучшим. Следуя этой схеме, Кудал смог менее чем за 40 поколений вывести флибов, способных предсказывать цепочки из шести символов.
ИССЛЕДОВАНИЕ ГЕНЕТИЧЕСКИХ АЛГОРИТМОВ В ПЕРВОБЫТНОМ КОМПЬЮТЕРНОМ ОКЕАНЕ, НАСЕЛЕННОМ ФЛИБАМИ
А.К.ДЬЮДНИ
ПРЕДСТАВИМ себе абстрактное море, населенное абстрактными организмами, которые условно назовем конечными живыми капельками (от английского названия finite living blobs) или для краткости флибами (flibs). Каждый флиб снабжен наипростейшим аппаратом принятия решений. По существу, это биологический эквивалент того, что математики называют конечным автоматом. Флиб содержит в себе также одну хромосому, состоящую из цепочки символов, которая является колом, определяющим автомат. Флибы обитают в первобытном цифровом "бульоне", постоянно подвергающемся изменениям. Чтобы выжить, флиб должен уметь точно предугадывать эти изменения.
В первобытном бульоне, сваренном мною недавно в моем компьютере, флибы, которые плохо предсказывали изменения в окружающей среде, все вымерли. Те же, которые обладали способностью к предсказанию, произвели на свет потомство, причем отдельным его представителям удалось даже превзойти своих предков. В конечном итоге как результат эволюционного процесса возникла линия безошибочных предсказателей.
Флибы и их эволюционные тенденции хорошо иллюстрируют вид программирования, известный под названием "метод генетического алгоритма". Основанный Дж.Холландом в Мичиганском университете в 60-х голах, этот метод позволяет иногда решать трудные задачи путем создания "эволюционной последовательности" приближенных решений. Новые решения получаются путем "скрещивания и размножения" лучших решений, полученных к данному моменту. Через некоторое время появляется новое решение, превосходящее своих "родителей", и это решение в свою очередь заносится в список будущих "производителей". Генетические алгоритмы применялись с переменным успехом в задачах, связанных с системами классификации, распознавания образов и некоторых, пока немногочисленных задачах из других областей. В моем компьютерном первобытном бульоне лри помощи этого метода удалось получить флибы, стоящие на более высокой ступени развития. Объясняется ли мой успех обшей эффективностью метола генетического алгоритма или же простотой задачи, перед которой были поставлены флибы? На этот вопрос ответить трудно. Во всяком случае над ним стоит поразмыслить, а само явление может быть воспроизведено любым читателем, в распоряжении которого имеется компьютер.
Конечный автомат обладает конечным числом состояний. Под действием входного сигнала он автоматически переходит из одного состояния в другое. Автоматы, на основе которых построены флибы, сами тоже порождают сигналы. Входные и выходные сигналы представляются в автомате символами. Приняв сигнал, автомат меняет свое состояние и вырабатывает другой сигнал.
Процесс удобно представлять в виде таблицы переходов из одного состояния в другое. Например, конечный автомат, который может принимать три состояния А, В и С, реагировать на входные сигналы в виде нулей и единиц, а также генерировать аналогичные сигналы, можно полностью описать таблицей размером 3*4. Для каждого состояния, в котором может находиться автомат, и для каждого символа, который он может получить, в таблице есть два элемента. Первый элемент соответствует выходному символу, а второй указывает, каким должно быть следующее состояние автомата:

Автомат, который описывается приведенной таблицей, в некоторый момент времени может оказаться в состоянии С. Если он принимает 1, то, согласно таблице, должен выдать 0 и перейти к состоянию А.
Другое, более наглядное представление лает диаграмма переходов между состояниями. На этой диаграмме в кружках записываются состояния, а соединяющие кружки стрелки указывают переходы. Если автомат, получив определенный символ, переходит из одного состояния в другое, то на диаграмме следует изобразить стрелку, ведущую от кружка, соответствующего первому состоянию, к другому кружку, соответствующему новому состоянию автомата. У одного конца стрелку помечают символом входного сигнала, обусловившего данный переход, а у другого конца - символом, выходного сигнала (см. рисунок на с.102).

Диаграмма переходов между состояниями (слева) и соответствующий флиб со своей хромосомой (справа)
Конечный автомат всегда начинает работу с какого-то первоначального состояния, называемого исходным. С каждым тактом воображаемого часового механизма на вход автомата прибывает новый символ, генерируется выходной символ и автомат переходит в следующее состояние. Автоматы, на основе которых построены флибы, могут получать и посылать только два вида символов - 0 и 1.
Ну а как интерпретировать поведение флиба, если нам почти ничего не известно о биологии этого существа? В этом и заключается одно из удовольствий, доставляемых нам абстракцией. Символы, принимаемые автоматом, можно рассматривать как сенсорное восприятие окружающей среды. Соответственно выходные символы можно считать реакцией организма на изменение в окружающей среде.
На самом деле понятие флиба настолько гибкое, что входные и выходные символы можно трактовать как самые разнообразные явления. Например, входной сигнал может представлять химический или температурный градиент. Соответственно выходной символ может быть командой, управляющей "ресничками", при помощи которых передвигается организм, или командой, вызывающей образование спор. Одной из наиболее важных задач для любого существа, желающего в процессе эволюции развиться до сколько-нибудь приемлемого уровня (скажем, университетского профессора), является способность предсказывать изменения в окружающей среде. Для флиба окружающая среда представляется нескончаемой последовательностью нулей и единиц. Поскольку принимаемые флибом символы означают существенные события в окружающей его среде, его способность предсказывать следующий символ, очевидно, даст ему некоторое преимущество, в особенности если в рамках более конкретной интерпретации модели шансы на выживание у флиба при этом условии возрастают.
Большинство флибов в этом смысле довольно плохо предсказывает изменения в окружающей среде. Например, флиб, определенный приведенной выше таблицей переходов, отвечает на принимаемую из среды последовательность
0111000010110...
такой последовательностью символов:
100001100I000...
В каждый момент времени выходной символ флиба представляет собой предсказываемый им символ, который должен поступить из среды в следующий момент. Чтобы определить количество правильных предсказаний, нужно сдвинуть выходную последовательность на один символ вправо и сравнить ее побитно с входной последовательностью. Подсчитаем количество совпадающих символов. В рассматриваемом случае флиб сумел правильно предсказать лишь 6 из 12 входных символов - результат не лучший, чем при чисто случайном угадывании.
Вообще не следует требовать слишком много от конечного автомата. Например, нельзя требовать от флиба правильного предсказания в условиях непериодической среды. Здесь читателю следует немного поразмыслить. Почему правильно предсказанная последовательность входных символов должна обязательно состоять из одной и той же основной цепочки, которая бесконечно повторяется? Например, флиб с тремя состояниями, не справившийся с только что рассмотренным тестом, достиг блестящего успеха, столкнувшись с такой последовательностью символов:
010011010011010011...
Здесь окружающая среда все время "выбивает" один и тот же ритм - 010011.
Существует несколько десятков различных флибов с тремя состояниями, но лишь очень немногие из них могут предсказать эту последовательность безошибочно. Среди флибов с числом состояний больше трех безошибочные предсказатели для данной последовательности входных символов встречаются редко и по мере роста количества состояний встречаются все реже и реже. Способность к предсказанию очень сильно зависит от периода последовательности: ни один флиб с n состояниями не сможет предсказать последовательность, состоящую из бесконечно повторяющейся основной цепочки символов, если эта цепочка слишком длинная. Очевидно, существует зависимость между количеством возможных состояний флиба и наибольшим периодом в последовательности, которую он может точно предсказать. Читателям, наверное, будет интересно попробовать найти эту зависимость. Каков наибольший период последовательности, которую может предсказать флиб с n состояниями?
Функционально флиб представляет собой несколько более сложное "устройство", чем просто конечный автомат, пытающийся предсказать повеление окружающей его среды. Напомним, что он сше обладает и хромосомой. Флибы периодически размножаются (механизм этого размножения нам не известен). Исследование хромосомы и ее отношения к конечному автомату флиба показывает нам, каким образом унаследованные гены определяют повеление организмов. Начнем с таблицы переходов и будем выбирать из нее строки по одной сверху вниз. Соединим концы выбранных таким образом строк в олну полосу, а затем присоединим начало полосы к ее концу. В результате получается круглая хромосома.
Перед заключительной операцией соединения хромосома нашего экземпляра флиба с тремя состояниями примет вид цепочки, состоящей из 12 генов:
1B1C0C0B1A0A
Строго говоря, символы этой цепочки являются аллелями. Аллель - это ген определенного типа, который появляется в заданном локусе. Ген как таковой может быть указан либо по имени, либо по его локусу. Так, например, седьмой символ слева управляет выходным символом флиба, когда тот находится в состоянии B и получает 1 на входе. Соответствующий локус имеет номер 7.
Не так давно я создал в своем персональном компьютере первобытный бульон, населенный десятью флибами с четырьмя состояниями. Прежде чем прошло 1000 единиц времени, которые я называю хрононами, ни одного из исходных флибов уже не было в живых. Их место заняли флибы, обладающие лучшей способностью к предсказанию. На экране дисплея демонстрируются лучший и худший результаты, достигнутые живущими на данный момент представителями популяции. Наихудший показатель изменяется довольно часто и в сравнительно широких пределах, в то время как наилучший показатель медленно возрастает (см. рисунок на с. 103). Как раз, когда я уже почти оставил надежду получить в результате эволюции безошибочного предсказателя, он внезапно появился, и наилучший показатель сразу подпрыгнул до 100.

Бульон, населенный десятью фпибоми (вверху), и безошибочный предсказатель (внизу)
Пора уже, наверное, объяснить читателю, каким образом флибы эволюционируют в моем первобытном компьютерном бульоне. Время от времени периодически в среду попадает космический луч, который поражает случайно выбранную хромосому и случайный локус, в результате чего тот или иной ген перехолит из одной аллели в другую. Рассмотрим, например, хромосому флиба с четырьмя состояниями. Ген третьего локуса управляет выходным символом при переходе из состояния A, когда существо принимает на входе 1:
0D1C0D0B1A0C1B1A
Попавший в этот ген космический луч слегка изменяет хромосому:
0D0C0D0B1A0C1B1A
Другим источником вариаций в множестве генов популяции является "спаривание" существ. Когда настает сезон размножения, гены флиба, достигшего наилучших результатов в предсказывании, перемешиваются с генами другого производителя, выбранного случайным образом. Получающаяся в результате особь несет в себе свойства обоих родителей. Часть хромосомы происходит от родителя, успешно предсказывающего состояние среды, а другая часть - от родителя, выигравшего право на размножение по лотерее. Механизм перемешивания хромосом напоминает явление перекреста (или кроссинговера), наблюдаемое в настоящих хромосомах. Можно проиллюстрировать перекрещивание хромосомы флиба, комбинируя первую (неизменную) хромосому, приведенную выше, с другой хромосомой:
1A1^B0D1A^0C1D1B0C
Стрелки указывают на точки перекреста, выбираемые случайным образом. Хромосома полученного флиба идентична хромосоме второго родителя вплоть до первой точки, на которую указывает стрелка. В интервале между двумя точками она идентична хромосоме первого родителя, а после второй точки мы опять видим фрагмент хромосомы второго родителя (см. рисунок на с.104):

Перекрещивание двух хромосом родителей и получающаяся в результате хромосома потомка (справа)
1A1C0D0B0C1D1B0C
До того как начать работать нал программой, я был настроен несколько скептически по поводу эффективности механизма перекрещивания хромосом. Однако к моему удивлению выяснилось, что, когда один из родителей является хорошим предсказателем, потомство, как правило, также хорошо справляется с задачей предсказывания.
Читатели сами могут убедиться в этом, написав программу под названием АВТОСУП. Листинг программы не занял бы больше одной страницы. Она состоит из четырех модулей, вложенных в цикл. В программе можно установить верхний предел показателей предсказания, или счета. Пока наилучший достигнутый счет не превышает предельного значения, выполнение программы (всех ее четырех модулей) должно продолжаться.
В первом модуле производится подсчет результатов, показанных десятью флибами для 100 сигналов, поступающих из окружающей среды. Во втором модуле выявляются флибы, показавшие самый лучший и самый худший результаты. В третьем модуле флиб, достигший наилучшего показателя, спаривается со случайно выбранной особью популяции. Их потомок замещает флиб с наихудшим результатом. В четвертом и последнем модуле космический луч ударяет в случайно выбранную особь и вызывает мутацию. Непосредственно перед входом в третий модуль (модуль размножения) производится выбор случайного числа. Если число оказывается ниже определенного порогового значения, то программа минует модуль размножения и сразу переходит к модулю мутаций. Пороговое значение можно устанавливать произвольно. Однако некоторые значения оказываются предпочтительными: если модуль размножения выполняется слишком часто, то гены флиба, добившегося наилучшего результата на данный момент, быстро становятся доминирующими в небольшой популяции. Генофонд таким образом обедняется, и эволюция становится очень медленной, если вообще не прекращается. Впрочем, эволюция замедляется так или иначе, по мере того как возрастают показатели флнбов. Флиб, добившийся наилучших результатов, остается на сцене все дольше, потому что вероятность появления "более высоко организованного" флиба становится все меньше.
В программе АВТОСУП следует организовать четыре массива. Назовем их ХРОМ, СОСТ, СЧЕТ и СРЕД. ХРОМ - это двумерный массив, расчитанный на 10 флнбов и 16 генов. ХРОМ(i, j) относится к j-му гену i-го флиба. СОСТ и СЧЕТ описывают соответственно текущее состояние и счет (т.е. показатель предсказания) для всех 10 флибов. Четвертый массив СРЕД используется для генерирования сигналов, поступающих из внешней среды. Этот массив вводится с клавиатуры перед выполнением программы.
Показатели флнбов рассчитываются в двойном цикле. Во внешнем цикле генерируются 100 символов среды, а во внутреннем - счет каждого флиба увеличивается на 1, если он правильно предсказал следующий символ. Флибы с четырьмя состояниями могут с успехом использоваться в средах с периодом, равным 6; предсказание в этих условиях будет для них задачей средней трудности. Чтобы появились безошибочные предсказатели в среде с периодом 8, программа может проработать целый день, в то время как со средой с периодом 4 программа справится очень легко. В этом модуле программы полезными оказываются следующие два приема. При помошн первого из них каждый следующий символ среды формируется на основе индекса внешнего цикла i. Для этого индекс i вычисляется по модулю 6. Результатом этой операции является остаток от деления i на 6. Полученное число может быть использовано для индексирования массива СРЕД. По мере того как индекс i пробегает значения от 1 до 100, вычисляемый вторичный индекс повторно пробегает через массив СРЕД, порождая нужную последовательность символов среды. По известному индексу текущего символа следующий символ легко вычисляется. Этот символ поочередно сравнивается с предсказанием, сделанным каждым флибом.
Второй прием позволяет программе быстро находить следующее состояние флиба и соответствующий выходной символ просто путем просмотра хромосомы флиба. В массиве сост вместо букв A, B, C, D для представления состояний используются цифры 0, 1, 2, 3. Если переменную, содержащую символ среды, назвать СИМВ, то выходной символ i-го флиба можно определить, воспользовавшись сначала простой формулой
l = 4*СОСТ(i)+2*СИМВ.
Затем нужно найти значение элемента ХРОМ(i, l). Когда существо находится в состоянии i и получен входной символ СИМВ, значение выходного символа находится в локусе l хромосомы i-ro флиба. Следующее состояние содержится в локусе l+1.
В модуле, который выявляет наилучшую и наихудшую особи, используется стандартный прием, задаваемый в качестве упражнения в элементарных курсах программирования: при заданном массиве из n чисел нужно написать программу, определяющую наибольшее из этих чисел. Для решения задачи нужно установить значение переменной МАКС в нуль и затем просматривать массив в простом цикле. Каждый элемент массива сравнивается с переменной МАКС. Если его значение оказывается больше МАКС, то оно присваивается как новое значение переменной МАКС. При этом запоминается также индекс элемента. Ту же процедуру можно обратить для отыскания наименьшего числа. Для этого нужно установить исходное значение переменной МИН равным 100 и заменять его элементами, которые оказываются меньше текущего значения МИН.
В третьем модуле флнб, достигший наилучших результатов, спаривается со случайно выбранным членом популяции. Единственное затруднение, возникающее при написании этого сегмента, связано с выбором двух точек перекреста. Мне кажется, что легче всего эту задачу можно решить, выбирая две целые случайные величины в диапазоне от 1 до 16; назовем эти величины C1 и C2. Если C1 больше С2, то их значения нужно поменять местами. После некоторого размышления читатели смогут организовать три цикла с индексом, пробегающим значение от 1 до C1, от C1 до C2 и от C2 до 16, построив тем самым механизм перемещения строк множества хромосом для спариваемых особей в строку, которую ранее занимала хромосома флиба с наихудшим результатом.
В четвертом модуле должны быть выбраны случайные значения индекса флиба и номера локуса. Четность номера локуса говорит о том, чтб подлежит мутации - ген состояния или ген выходного символа. Если номер данного локуса четный, то к хранящемуся в локусе значению прибавляется 1 по модулю 2. Тем самым значение бита меняется на противоположное. Если же номер локуса нечетный, то к соответствующему элементу массива следует прибавить 1 по модулю 4. Таким образом, состояние, хранящееся в данном локусе, изменяется.
Не совершил ли я какого-нибудь жульничества? Конечно, систематическое изменение состояний от 0 к 1, затем к 2, к 3 и опять к 0 едва ли назовешь случайным процессом. На это я могу ответить, что он случайный в достаточной мере: поскольку количество состояний очень мало, результаты работы программы не должны сильно отличаться от случая, когда состояния выбираются с большей степенью случайности. Можно усмотреть также небольшое жульничество в моем небрежном выборе C1 и C2. Дело в том, что этот метод гарантирует преимущество отдельных подцепочек перед другими. Однако и в этом случае, я думаю, различия между программой АВТОСУП и какой-нибудь статистически более корректной программой генетической селекции будут не очень существенными. Так или иначе, процессы жонглирования генами и поражения хромосом космическими лучами настолько интенсивны, что флибу-чемпиону иногда очень трудно узнать своих внуков.
В программе АВТОСУП нам осталось рассмотреть лишь ее начало и конец. Исходная популяция флибов, населяющая среду, должна быть выбрана случайным образом. Для каждого гена каждого флиба должно быть выбрано целое число из подходящего диапазона и присвоено этому гену. Наконец, когда какому-либо флибу удается превзойти пороговое значение результата, указанное во внешнем цикле, программа должна выдать достигнутый результат на экран.
Читателей, желающих пуститься в это генетическое приключение, следует предупредить, что им придется провести значительную исследовательскую работу. Возможно, некоторые исследователи даже пристрастятся к этой работе. В числе интересных вопросов, на которые нужно найти ответ, находится вопрос о присутствии эволюционного процесса и о его скорости. Когда период поступления сигналов о состоянии окружающей среды слишком большой для того, чтобы в результате эволюции мог появиться безошибочный предсказатель с четырьмя состояниями, то как тогда флибам удается приспособиться и выжить? Как изменение длины периода влияет на время, требующееся для выведения безошибочного предсказателя? Ничто в описании программы АВТОСУП не препятствует ее расширению для флибов с пятью или шестью состояниями. Можно даже изменить программу так, чтобы исследовать непериодические среды или среды, которые время от времени меняют свою основную цепочку символов.
Описанная эволюция автоматов была задумана под влиянием книги: L.J.Fogel, A.J.Owens, M.J.Walsh, "Artificial Intelligence through Simulated Evolution" ("Искусственный интеллект как результат моделируемой эволюции"), появившейся в начале 60-х годов. В этой книге была описана серия экспериментов по эволюции автоматов. Автоматы должны были предсказывать периодические последовательности и могли эволюционировать аналогично нашим флибам. Однако в этом строгом научном исследовании размножение и генетический перекрест не фигурировали.
Ввести в модель свойство генетического перекреста мне посоветовал Холланд. Как уже отмечалось, Холланд является признанным отцом генетического алгоритма. Его последователи, число которых постоянно растет, недавно собрались на свою первую крупную конференцию, состоявшуюся в Университете Карнеги-Меллона. Они обсудили широкий круг вопросов теории и ее практических приложений. В нескольких докладах рассматривалась задача, которая может послужить интересным введением в область генетического программирования.
Речь идет о задаче коммивояжера, которая заключается в следующем: по заданной географической карте с n городами, соединенными сетью дорог, требуется найти кратчайший маршрут, включающий все n городов. Этот маршрут позволяет коммивояжеру минимизировать дорожные затраты.
Вполне возможно, что маршрут минимальной длины может возникнуть в результате эволюции, подобно тому как возникают безошибочные предсказатели из "низших" флибов. Каждый маршрут может быть закодирован в хромосоме. Кратчайшие из существующих на данный момент маршрутов можно размножать в надежде получить потомство из еще более коротких путей. Хромосомы потомства можно получить в результате механизма перекреста родительских хромосом.
Интересная проблема связана с выбором хорошего представления для маршрута. Если, например, пользоваться просто списком городов в порядке их посещения, то полученное потомство может даже не соответствовать никакому маршруту. Чтобы обойти затруднение, авторы одного из докладов - Дж.Греффенштетт, Р.Гопал, Б.Росмайта и Д. ван Гухт из Вандербильтского университета - предлагают хромосому остроумной конструкции. Например, маршрут из пяти городов, скажем a, c, e, d, b, можно представить в виде последовательности 12321. Чтобы получить такую цепочку чисел, используется некий стандартный порядок, в котором перечислены города, например a, b, c, d, e. Если нам задан маршруту c, e, d, b, то будем систематически удалять города из стандартного списка, чтобы получить указанный маршрут. Сначала удалим a, затем c, e и т.д. Перед тем как удалить город из стандартного списка, заметим его порядковый номер в этом уменьшающемся списке: a - первый, c - второй, e - третий, d - второй и, наконец, b - первый. Примечательно, что при перекрещивании двух таких хромосом результат всегда является каким-нибудь маршрутом (см. рисунок на с.106). Пользуясь таким представлением маршрутов, их можно размножать и проводить среди них селекцию.

Два родигтльских маршрута коммивояжера (вверху) и маршрут-потомок (внизу), полученный в результате перекрещивания хромосом
Большинство поклонников генетических алгоритмов признают, что задача коммивояжера представляет для них самый серьезный вызов. Хотя эксперименты, в которых применялось только что описанное представление, не принесли впечатляющих результатов, были разработаны некоторые другие алгоритмы, более успешно работающие при решении этой задачи.
И все же ни один из генетических алгоритмов не смог справиться с задачей коммивояжера в требуемом смысле. Несомненно, прежде всего это объясняется сложностью самой задачи. Поскольку она принадлежит к классу задач, называемых теоретиками NP-полными, она, возможно, обречена навсегда остаться неразрешимой в практическом смысле.
ARTIFICIAL INTELLIGENCE THROUGH SIMULATED EVOLUTION. LAWRENCE J.FOGEL, ALVIN J.OWENS AND MICHAEL J. WALSH, John Wiley & Sons, Inc., 1966 (Фогель Л., Оуэнс А., Уолш М. Искусственный интеллект и эволюционное моделирование. Пер. с англ. М.: "МИР", 1969.- G.).
ADAPTATION IN NATURAL AND AR TIFICIAL SYSTEMS. JOHN H. HOLLAND University of Michigan Press, 1975.
GENETIC ALGORITHMS FOR THE TRAVELING SALESMAN PROBLEM. JOHN GREFENSTETTE, RAJEEV GOPAL, BRIAN ROSMAITA AND DIRK VAN GUCHI in Proceedings of an International Conference on Genetic Algorithms and Their Applications, edited by John J. Grefenstette. The Robotics Institute, Carnegie-Mellon University, 1985.
ОТКЛИКИ
4 1986
В ЯНВАРСКОМ номере журнала в рубрике "Занимательный компьютер" речь шла о флнбах - конечных "живых организмах", пытающихся предсказывать изменения в окружающей их среде. В первобытном компьютерном бульоне лучший представитель каждого поколения скрещивает свои хромосомы со случайно выбранным флибом. В результате эволюционного процесса возникают все более удачливые предсказатели, пока на свет не появляется организм, безошибочно предсказывающий изменения в среде.
По существу, флиб представляет собой конечный автомат. Другими словами, он обладает конечным числом состояний и для каждого принимаемого им сигнала (0 или 1) он вырабатывает ответный сигнал и переходит в новое состояние. Сигнал, генерируемый флибом на каждом цикле процесса, является предсказанием следующего сигнала, который должен быть им получен из внешней среды.
Некоторые читатели поставили перед своими флибами непосильные для них задачи. Никакая эволюция не породит флиба, способного предсказывать последовательности случайно генерируемых битов. Точно так же никогда не возникнут флибы, предсказывающие простые числа. От них можно требовать предсказания периодически повторяющихся двоичных последовательностей. Например, существует флиб с четырьмя состояниями, предсказывающий повторяющуюся восьмисимвольную последовательность 01100010. Однако даже повторяющаяся последовательность может выйти за пределы предсказательной способности флиба, если основная цепочка окажется слишком длинной по отношению к числу его состояний. На самом деле ни один флиб с четырьмя состояниями не сможет предсказать повторяющуюся последовательность 010010111. Почему?
Простейший ответ на этот вопрос можно получить с помощью процедуры, которую я называю "ползучей индукцией". Представим себе флиб с одним состоянием. Он может предсказать бесконечно повторяющуюся основную последовательность 01. Для каждого из двух возможных сигналов, получаемых флибом, он вырабатывает один ответ: получив на входе 0, флиб отвечает 1 и переходит в то же самое состояние. Если он получает 1, то в ответ вырабатывает 0. Цепочка из трех символов, скажем 011, выходит за пределы возможностей флиба с одним состоянием просто потому, что автомат не имеет в своем наборе достаточного количества ответов. В то же время флиб с двумя состояниями располагает четырьмя возможными ответами, по два на каждое состояние. Таким образом, он может предсказать цепочку из четырех символов, но не справляется с цепочкой из пяти символов: когда дело доходит до пятого символа, флиб должен повторить один из своих предыдущих ответов. Принцип доказательства ясен. Флиб с n состояниями может предсказать последовательность, состоящую из 2n символов, но не 2n+1. Можно найти приятное развлечение в том, чтобы составить последовательность из 8 бит, а затем сконструировать флиба, который ее предскажет. Совершенный предсказатель, полученный таким образом, будет единственным в своем роде. Об успехе программы AUTOSOUP можно судить, сравнивая совершенного предсказателя, порожденного программой в ходе эволюции, с флибом, который уже был построен "вручную".
Несколько читателей придумали, как можно ускорить работу программы AUTOSOUP. Например, практически не имеет смысла проверять существующую на данный момент популяцию флибов на последовательности из 100 символов, если основная цепочка содержит лишь 6 символов. В результате однократного повторения цепочки будет задана последовательность из 12 символов, которой оказывается вполне достаточно.
Ф.Каарет из Принстонского университета указал также на то, что количество команд в программе можно уменьшить, если оценивать показатели только двух флибов при каждом выполнении основного цикла, а не всей популяции. В конце концов, измениться могли лишь (самое большее) два флиба: флиб с наихудшим результатом был заменен новым гибридом и еще один флиб, который, возможно, был поражен космическим лучом.
Ускорение, полученное путем сокращения тестовой последовательности символов окружающей среды и за счет устранения теста для старых флибов, приблизительно одно и то же. Теперь у нас должно хватить времени для того, чтобы получить в результате эволюции флибы с n состояниями, способные предсказать повторяющиеся цепочки символов длиной до 2n.
Из письма Э.Кудала из Парк-Риджа (шт.Иллинойс) мы узнали, что ему неприятно было посылать последнего флнба прямо на тот свет. Вместо этого он стал скрещивать на каждом цикле худшего флиба с лучшим. Следуя этой схеме, Кудал смог менее чем за 40 поколений вывести флибов, способных предсказывать цепочки из шести символов.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
2 1986
О ЛИНЕЙКАХ КОЛОМБА И ИХ ПРИМЕНЕНИИ В РАДИОАСТРОНОМИИ
А.К.ДЬЮДНИ
ПРИ ПОМОЩИ простой линейки длиной в один фут с 13 делениями, каждое из которых соответствует одному дюйму, можно измерить 12 различных расстояний. Возможно ли так усовершенствовать это знакомое всем устройство, чтобы число измеряемых с его помощью расстояний было больше числа нанесенных на нем делений? Оказывается, да: например, на стандартной линейке можно оставить лишь пять делений и при этом измерить 10 различных расстояний. Каждое такое расстояние заключено между некоторой парой делений и вычисляется как разность между целыми числами, которыми помечены эти деления. Того же результата можно достичь, даже воспользовавшись 11-дюймовой линейкой. Читатели, которые после некоторых размышлений придумают, как это можно сделать, создадут тем самым так называемую линейку Коломба.
Поиск таких линеек - весьма интересное занятие, в котором большую помощь может оказать компьютер. Решая эту задачу, вы не просто удовлетворяете свое любопытство, а участвуете в серьезном исследовании. Дело в том, что необходимость в линейках Коломба возникает в целом ряде областей науки и техники.
Эти устройства являются изобретением Соломона У. Коломба, профессора математики и электроники Южнокалифорнийского университета. В течение двух десятилетий он и его коллеги занимались поиском и изучением свойств этих линеек. Устройства подобного рода могут применяться в теории кодирования, рентгеновской кристаллографии, конструировании электронных схем, радиоастрономии.
Одним из исследователей, в работе которых линейки Коломба играют важную роль, является Д.Робертсон, геофизик, работающий в Роквилле (шт.Мэриленд) в Национальном геодезическом центре Национальной службы США по океану и атмосфере. Он применяет радиоастрономический метод - интерферометрию с очень длинной базой - не для того, чтобы фиксировать местоположение радиоисточников, а чтобы выполнить точные измерения параметров Земли. Занимаясь уже в течение нескольких лет поиском линеек, он обращается за помощью к читателям. В результате, возможно, удастся точнее определить размеры, форму и параметры движения нашей планеты.
Прежде чем откликнуться на просьбу Робертсона, нам, наверное, следует вникнуть в принципы, лежащие в основе линеек Коломба. Хотя линейки могут быть произвольной длины, пока изучены лишь линейки малых размеров. Первые три линейки можно описать несколько абстрактно тремя последовательностями чисел:
0, 1
0, 1, 3
0, 1, 4, 6
Чтобы представить себе линейку как физический объект, можно мысленно пометить левый конец "пустой" линейки длиной n единиц наименьшим числом последовательности, т.е. 0. Правый конец пометим наибольшим числом n; им может быть 1, 3 или 6. Промежуточными числами пометим деления, нанесенные на соответствующих расстояниях от левого конца линейки, т.е. от 0 (см. рисунок на с.103).

Три идеальные линейки Коломба и диаграммы их расстояний
Простой способ проверить, какие расстояния из диапазона от 0 до n можно измерить одной из этих маленьких линеек, заключается в том, чтобы нарисовать диаграмму расстояний на линейке. Для этого каждому целому числу на линейке поставим в соответствие точку на листе бумаги и пометим точку данным числом. Затем каждую пару точек соединим линией, помеченной разностью между целыми числами, расположенными на концах линии. Если каждое расстояние в диапазоне от 0 до n появляется на одной и только на одной линии диаграммы расстояний, то линейка Коломба называется идеальной. Все три линейки на иллюстрации идеальные - факт, в котором можно убедиться, взглянув на соответствующие диаграммы расстояний. На каждой диаграмме ни одно расстояние не появляется более одного раза, и все возможные расстояния в диапазоне от 0 до n присутствуют.
Среди линеек Коломба идеальные встречаются очень редко. На самом деле все существующие идеальные линейки были только что рассмотрены. Для значений n больших 6 "неидеальность" может проявляться двояким образом: либо какое-то расстояние встречается более одного раза, либо не встречается вовсе.
Вот так, в самом начале поиска больших (и лучших) линеек мы столкнулись с суровой действительностью. Однако откуда известно, что идеальных линеек больших размеров не существует? Коломб представил короткое и изящное доказательство этого факта.
Он предлагает рассмотреть не сами деления на линейке, а интервалы между ними. Если линейка идеальна, то множество всех интервалов между последовательными делениями образует ряд 1, 2, 3... до m-1 в некотором порядке (m - количество делений). Коломб спрашивает: "Где расположен единичный интервал?". Если он прилегает к любому интервалу, длина которого меньше m-1, то оба эти интервала вместе дают расстояние, меньшее m. Но это расстояние уже должно было встретиться в виде одного из интервалов где-то еще, потому что все расстояния от 1 до m-1 расположены соответственно между последовательными делениями. Указанные соображения приводят нас к несколько неожиданному выводу, что единичный интервал должен прилегать к интервалу длиной m-1. Более того, по другую сторону от единичного интервала никаких интервалов больше нет, ибо он располагается на одном из концов линейки.
Полученный нами результат представляет собой как бы один поворот ручки того, что математики называют "колбасной машиной". Далее, Коломб спрашивает: "Где располагается интервал длиной 2 единицы?" Повернем ручку еще раз. Если интервал длиной 2 единицы прилегает к любому интервалу длиной меньше m-2, то взятые вместе эти два интервала образуют расстояние, уже встречавшееся где-то еще. На этот раз мы уже не можем считать, что интервал длиной 2 единицы прилегает к интервалу длиной m-2. Их суммарная длина m уже измеряется комбинацией интервалов длиной 1 и m-1 с одного конца линейки.
Таким образом, колбасная машина останавливается, и мы приходим к выводу, что есть только один интервал, к которому может прилегать интервал длиной 2 единицы, а именно интервал длиной m-1. Поскольку у любой линейки есть только два конца, идеальная линейка не может содержать больше трех интервалов: 1, m-1 и 2. Доказательство завершается, когда мы вспоминаем, что три интервала требуют четырех делений. Таким образом, при m=4 интервалы равны 1, 3, 2, а соответствующие деления образуют последовательность 0, 1, 4, 6.
Столкнувшись с полным отсутствием идеальных линеек, имеющих более 4 делений, математик попытается "отыграться", построив новое определение. Продемонстрируем пример определения, возникшего в результате подобных попыток. Наилучшим приближением к невозможной идеальной линейке с пятью делениями является такая линейка, которая содержит каждое расстояние не более одного раза, но может и не содержать всех расстояний, которые должна была бы иметь идеальная линейка того же размера. Этому условию легко удовлетворить, подобрав достаточно длинную линейку. Среди всевозможных линеек с пятью делениями, содержащих каждое расстояние максимум по одному разу, выявим самую короткую. Такая линейка будет называться линейкой Коломба пятого порядка. Линейка Коломба порядка m определяется аналогичным образом. Поскольку это определение включает также первые три линейки как частный случай, оно как бы сглаживает разрыв в свойстве "идеальности", наблюдающийся при переходе через значение m, равное 4.
Г.Тэйлор, коллега Коломба, представил имеющуюся на данный момент информацию о линейках Коломба в виде приведенной вверху таблицы. В диапазоне от двух до 24 делений мы располагаем как точными знаниями, так и некоторыми гипотезами относительно размеров линеек Коломба. Зона, которую я называю идеальной, заключается между двумя и четырьмя делениями. Далее простирается зона знания, охватывающая линейки Коломба, имеющие до 13 делений. В этой области известны все линейки минимального размера. Другими словами, в каждом конкретном случае не существует линейки Коломба меньшей длины с тем же количеством делений. Линейка Коломба с 5 делениями имеет длину 11 единиц. Линейка Коломба с 13 делениями имеет длину 106 единиц.

Длина линеек Коломбо и линеек, близких к этому классу
За 13 делениями начинается зона, которую я называю зоной полумрака. Эта зона (назовем ее более уважительно зоной исследований) содержит только те линейки, относительно которых еще нельзя с уверенностью сказать, что они являются линейками Коломба. Для каждого количества делений в таблице указана длина линейки. Однако могут существовать и линейки меньшего размера. На самом деле имеется формула, которая дает нижний предел для этих размеров. Постоянно увеличивающийся разрыв между значениями, получаемыми по формуле, и длинами найденных к настоящему моменту линеек свидетельствует либо о слабости оценки по формуле, либо о том, что линейки, найденные для каждого значения числа делений, имеют тенденцию "ухудшаться" с ростом последнего.
Зона знания была расширена до границы в 13 делений благодаря усилиям Робертсона. В ходе непрерывной работы ЭВМ в течение месяца его программа произвела исчерпывающий перебор всех потенциальных линеек Коломба с 13 делениями и нашла самую короткую. Если для поиска линеек Коломба с 14 и более делениями потребуется еще больше машинного времени, то, наверное, немногие читатели заинтересуются этим поиском.
Вместо этого можно предложить им тактику "компьютерных налетов" на зону исследований, в результате которых можно получить линейки, обладающие меньшими размерами, чем найденные до сих пор. Очень полезной для всех поисков подобного рода является программа под названием CHECKER. Однако прежде чем применить эту программу, необходимо задать способ проверки наличия одинаковых разностей между всеми возможными парами целых чисел в данном массиве. При самом простом подходе можно организовать массив таких разностей, а затем просмотреть его в поисках дублирующихся значений, опираясь на довольно неуклюжий и требующий много времени алгоритм.
Редко бывает так, чтобы алгоритм, обеспечивающий наиболее быстрое решение задачи, можно было реализовать с помощью самой короткой программы. Однако здесь мы сталкиваемся как раз с таким случаем. Поскольку предполагается, что все разности отличаются друг от друга (т.е. одинаковых разностей не существует), то ими можно воспользоваться как адресами в специальном массиве check. Вначале в массиве check хранятся только нули. Каждый раз, когда вычисляется новая разность, значение, хранящееся по соответствующему адресу, меняется с 0 на 1. Таким образом, по мере того, как программа CHECKER проводит дальнейшие вычисления, она может наткнуться на единицу, уже записанную по данному адресу, а это означает, что "новая" разность уже встречалась где-то раньше. В этом случае рассматриваемая линейка не может принадлежать к классу Коломба, поскольку она не обладает основным свойством, присущим линейкам Коломба: каждое расстояние должно встречаться не более одного раза.
Описанный метод, использующий значения разностей в качестве адресов, представляет собой простую разновидность того, что специалисты по вычислительной математике и программированию называют хешированием. Во многих задачах, связанных с информационным поиском, хеширование обеспечивает самый быстрый доступ к данным.
Для тех, кто хотел бы подробнее ознакомиться с программой CHECKER, опишем в общих чертах ее структуру. С помощью двух вложенных циклов генерируются все возможные пары целых чисел из входного массива. В первом цикле генерируются индексы i, а во втором - индексы j. Программа вычисляет абсолютное значение разности и присваивает его в качестве значения переменной diff. На следующем шаге алгоритма программа CHECKER использует значение diff в качестве хеш-кода. В алгоритмических обозначениях можно записать:
если check(diff) = 1
то вывести "не коломбова" и выход
в противном случае check (diff) <- 1
Если программа ни разу не выведет сообщение "не коломбова", то можно считать, что рассматриваемая линейка успешно прошла главный тест. Однако каков ее размер? Существует несколько способов получить ответ на этот вопрос.
Прежде всего можно воспользоваться программой CHECKER в ее основном варианте без каких-либо дополнительных программ. Я представляю себе читателя, склонившегося над клавиатурой и увлеченно работающего с программой CHECKER. Он проводит разведку в зоне исследований на высоте 14 делений в поисках линейки короче 127 единиц - именно такую длину имеет лучшая из известных на сегодня линеек. Читатель, совершающий полет в сложных метеорологических условиях, не знает, в какую сторону повернуть. Только что он ввел последовательность из 14 делений. Наибольшим числом этой последовательности было 124. С неописуемым волнением он видит, как на экране начинает высвечиваться сообщение: "Поздравляю! Последовательность подходит". Введя это поздравительное сообщение в программу, читатель дает себе слово всегда пробовать ее исключительно для потенциально рекордных последовательностей.
Возможно, читатель нашел свой рекордный набор делений, последовав совету Коломба и исследуя только те линейки, у которых наиболее длинные интервалы встречаются в средней части. У таких линеек интервалы уменьшаются при приближении к концам, однако точные закономерности читателям предстоит найти самим. Коломб заверяет нас, что многие хорошие линейки, хотя и не обязательно наилучшие, обладают этим свойством.
Программу CHECKER можно несколько модифицировать, чтобы придать изысканиям характер коротких пробных попыток. В программе STEP CHECKER целые числа вводятся по одному. После того как введено очередное число, программа вычисляет все разности между только что введенным числом и теми, которые уже хранились в памяти. На самом деле STEP CHECKER - это просто версия программы CHECKER, в которой инструкция ввода заменяет внешний цикл. Последовательность считается подходящей, если при обработке последнего введенного числа программа не выдала сообщения "не коломбова".
Наконец, программу STEP CHECKER можно встроить в автоматическую систему, подобную разработанной Робертсоном. Его программа, которую я могу назвать EXHAUST (от англ. exhaustive - исчерпывающий), поскольку она производит исчерпывающий перебор, систематически порождая новые линейки путем добавления новых интервалов. После добавления каждого нового интервала программа STEP CHECKER проверяет полученную таким образом последовательность, или линейку.
Робертсон построил свою программу исходя из того, что новые интервалы (и соответственно новые деления) должны добавляться к линейке слева направо. Читатели, которые следили за ходом доказательства Коломба (о несуществовании идеальных линеек для числа делений больше 4), вспомнят, что интервалы должны иметь длину 1,2,... ,m-1 в некотором порядке. Хотя это было справедливо только в отношении идеальных линеек, нечто подобное, вообще говоря, справедливо также в отношении линеек Коломба. Большинство, хотя и не все, интервалов длиной от 1 до m-1 между последовательными делениями на линейках, приближающихся к идеальным, встречается в некотором порядке. Отметим, однако, что у таких линеек встречаются интервалы даже больше m-1.
Алгоритм Робертсона порождает новые интервалы в пошаговом режиме. Эти интервалы хранятся в массиве, который мы назовем spaces. Программа EXHAUST просматривает массив и добавляет к нему каждый раз по одному новому интервалу. Конечно, в алгоритме используются некоторые простые тесты, облегчающие работу программы. С помощью одного из них можно проследить, чтобы новый интервал не совпадал с одним из уже имеющихся в массиве spaces, а с помощью второго - чтобы суммарная длина всех интервалов, образующих линейку, не превосходила минимальную известную длину для линейки с данным числом делений.
Программа EXHAUST, кажется, с большим энтузиазмом отыскивает новые линейки. Сначала она полагает первый элемент массива spaces равным 1 и добавляет по единице к следующему интервалу, так чтобы он отличался от первого. Затем она начинает добавлять по единице к третьему интервалу, следя за тем, чтобы это расстояние не только отличалось от первых двух, но также удовлетворяло условию, заложенному в программе STEP CHECKER, согласно которому все расстояния, содержащиеся в линейке, должны отличаться друг от друга. Всякий раз, когда появляется новый элемент (интервал), программа суммирует все элементы массива и сравнивает полученную сумму с длиной самой короткой известной к данному моменту линейки. Если сумма оказывается меньше, программа переходит к следующему интервалу. Если нет, то она возвращается к предыдущему элементу и продолжает перебор.
Программа Робертсона работает значительно быстрее, если первый элемент массива spaces положить равным 2, а не 1. На самом деле прогон программы, занимающий целые сутки, сократится на несколько часов. Читатели могут поразмыслить над тем, почему и в этом случае поиск остается исчерпывающим.
Конечно, эффективность алгоритма поиска можно повысить за счет включения других тестов и эвристических приемов. Эти тесты и эвристики могут особенно сильно повлиять на эффективность, если они налагают дополнительные ограничения на возможные значения элементов массива spaces. Возможно, существует процедура, работающая со значительно более узкими диапазонами этих значений. Обработка массива во многом подобна счету. А счет будет выполнен намного быстрее, если уменьшить количество возможных вариантов в каждом элементе массива spaces. В любом случае читатели, сумевшие найти рекордного бобра-работягу, построить новые катапульты, стреляющие планерами, и добившиеся многих других результатов в своих исследованиях, смогут найти свой собственный подход к решению задач из зоны исследований Коломба. О лучших находках будет рассказано в одной из наших следующих статей. Интересно, кто первым найдет две различные линейки, имеющие больше 6 делений, но измеряющие один и тот же набор отличных друг от друга расстояний. Линейки, представляющие собой взаимные зеркальные отображения, не считаются различными.
Успешное решение задачи будет означать несостоятельность "теоремы", предложенной швейцарским математиком Софи Пиккард в 1939г. Согласно этой теореме, две линейки, измеряющие один и тот же набор отличных друг от друга расстояний, должны быть идентичными. Теорема очень понравилась специалистам по рентгеновской кристаллографии, поскольку она помогала им разрешать неопределенности в дифракционных картинках. К сожалению, эта теорема оказалась не справедливой для многих пар линеек, имеющих 6 делений. Может быть она остается справедливой для всех линеек более высокого порядка. Этот вопрос можно рассмотреть, выбрав в качестве объекта исследований линейки, имеющие всего 7 делений.
Однако какое это все имеет отношение к задаче, которой занимается Робертсон? Дело в том, что линейка Коломба иногда используется в радиоастрономии для разрешения удаленных радиоисточников и для измерения параметров нашей планеты. В первом случае несколько антенн располагаются на прямой линии протяженностью несколько километров. Позиции антенн соответствуют делениям на линейке Коломба (см. рисунок на с.105). Для того чтобы определить положение удаленного радиоисточника, необходимо найти угол между линией базы антенн и направлением волнового фронта, поступающего от источника. Все антенны настроены на одну и ту же длину волны. Точное время прибытия сигнала к каждой антенне может быть установлено путем анализа записи принимаемых сигналов. Полное число длин волны, укладывающееся в интервале между данной парой антенн, называется полной разностью фаз. Обычно она состоит из целого числа и дробной части, которая называется сдвигом по фазе. Если удается восстановить полную разность фаз, то искомый угол между направлением на источник и линией базы нетрудно вычислить по известной длине волны и скорости света c. Однако по сигналам, принятым каждой парой антенн, можно определить лишь сдвиг по фазе, но не полную разность фаз.

Пары радиотелескопических антенн, расположенных по линейке Коломба, позволяют определить разность фаз приходящих сигналов
В действительности полная разность фаз вычисляется с применением анализа Фурье по данным, зафиксированным многими парами антенн. Однако если расстояние между одной парой антенн оказывается равным расстоянию между какой-нибудь другой парой, то обе они дают одну и ту же информацию о сдвиге по фазе. Избыточность информации означает ее потерю. Точность вычисления искомого угла наиболее высока в том случае, когда каждая пара антенн фиксирует отличный от других сдвиг по фазе. Это условие выполняется за счет размещения антенн по тому же принципу, по которому располагаются деления на линейке Коломба.
Еще один способ определения положения удаленного радиоисточника заключается в том, чтобы воспользоваться лишь двумя приемниками, сканирующими одновременно весь набор длин волн, на которых ведутся наблюдения. Прием на две антенны на нескольких различных волнах позволяет получить ту же информацию о полной разности фаз между принимаемыми сигналами, какую дало бы использование нескольких антенн, настроенных на одну и ту же длину волны. Здесь опять возникает опасность появления избыточной информации. Ни одна пара длин волн, на которых ведется наблюдение, не должна иметь разность, совпадающую с разностью между какой-либо другой парой. И хотя линейка Коломба здесь остается как бы невидимой, она все же присутствует в неявной форме.
Робертсон применяет второй метод не для фиксации радиоисточников, а для того, чтобы определить местоположение самих антенн. Для целей, которые он преследует, недостаточно знать, что вторая антенна находится в Уэстфорде (шт.Массачусетс). Ему нужно знать ее положение с точностью до нескольких сантиметров. Такой точности можно достичь, если воспользоваться очень далеким, практически точечным источником, таким, как квазар. Установить точное положение точки на земной поверхности по отношению к далекому радиоисточнику равносильно тому, чтобы точно установить значения таких фундаментальных земных параметров, как диаметр планеты, ориентация оси ее вращения и продолжительность суток. На уровне сантиметров и микросекунд эти параметры являются переменными величинами из-за воздействия годовых, сезонных и даже метеорологических вариаций, которые иногда подчиняются известным закономерностям, а иногда остаются совершенно необъяснимыми.
БИБЛИОГРАФИЯ
MINIMUM-REDUNDANCY LINEAR ARRAYS. ALAN T. MOFFET in IEEE Transactions on Antennas and Propagation, Vol.AP-16, No.2, pages 172-175; February, 1963.
APPLICATIONS OF NUMBERED UNDIRECTED GRAPHS. GARY S. BLOOM AND SOLOMON W. GOLOMB in Proceedings of the IEEE, Vol.65. No.4, pages 562-570; April, 1977.
GOLOMB'S GRACEFUL CURVE. MARTIN GARDNER in Wheels, Life and Other Mathematical Amusements. W.H.Freeman and Company, 1983. (М.ГАРДНЕР, КРЕСТИКИ-НОЛИКИ, 1988.- G.)
VARIATIONS IN THE ROTATION OF THE EARTH. W.E.CARTER, D.S.ROBERTSON, J.E.PETTEY, B.D.TAPLEY. В.Е.SCHUTZ, R.J.EANES AND MIAO LUFENG in Science, Vol.224, No.4652, pages 957-961; June 1, 1984.
ОТКЛИКИ
5 1986
ЛИНЕЙКИ Коломба, предмет статьи в февральском номере нашего журнала, оказались самой трудной задачей из тех, с которыми читатели сталкивались до сих пор. Многие были званы, да немногие избраны, так сказать. Несколько читателей попытались заработать приз в 100долл., учрежденный изобретателем линеек Соломоном У. Коломбом из Южнокалифорнийского университета.
Линейка Коломба с n делениями - это кратчайшая возможная линейка, обладающая следующими свойствами: у нее n делений (включая концы), отстоящих друг от друга на расстояния, равные целым числам, и она измеряет все возможные интервалы, которые представляются суммой целых чисел, от единицы до интервала, равного длине линейки, причем каждый интервал измеряется единственным способом. Интервал может быть измерен линейкой только в том случае, если он оказался равным расстоянию между какими-нибудь двумя делениями линейки. Если одно и то же расстояние можно измерить более чем одной парой делений, то линейка уже не принадлежит классу линеек Коломба.
Ко времени публикации статьи не было известно ни одной линейки Коломба, обладающей более чем 13 делениями, а кратчайшая известная линейка с 15 делениями имела длину 155 единиц. Однако вскоре после этого Д.Робертсон из Национальной службы США по исследованию атмосферы и океана открыл более короткую линейку с 15 делениями. Ее длина 153 единицы. Затем во время рождественских каникул Дж.Шерер из Исследовательского центра Томаса Уотсона фирмы IBM запрограммировал простаивающий компьютер для исчерпывающего поиска линеек, и теперь появились линейки Коломба с 14 и 15 делениями. Линейка с 14 делениями имеет длину 127 единиц, и ее деления расположены в точках 0, 5, 28, 38, 41, 49, 50, 68, 75, 92, 107, 121, 123 и 127. Линейка Коломба с 15 делениями имеет длину 151 единицу, и ее деления расположены соответственно в точках 0, 6, 7, 15, 28, 40, 51, 75, 89, 92, 94, 121, 131, 147 и 151. Шерер пишет, что он сэкономил много машинного времени, предположив, что среднее деление линейки находится слева от ее геометрического центра.
По другой задаче, поставленной Коломбом, мы получили письма читателей с заявками на премию в 100долл. Однако все присланные до сих пор решения недействительны, поскольку они основаны на неправильном понимании задачи. Коломб попросил прояснить ситуацию, переформулировав условие задачи. Найти две различные линейки (не обязательно минимальной длины) с одинаковым количеством делений, превышающим число 6, которые измеряют один и тот же набор расстояний, причем опять-таки ни одно из этих расстояний не может быть измерено никакой линейкой более чем одной парой делений. Линейки, являющиеся зеркальным отражением друг друга, например такие, как 0, 2, 5, 6 и 0, 1, 4, 6, не считаются различными. Существует бесконечно много пар линеек (почти все они не минимальные), которые решают аналог задачи Коломба для шести делений. Например, такую пару образуют следующие линейки: 0, 1, 4, 10, 12, 17 и 0, 1, 8, 11, 13, 17. Они не являются зеркальным отражением друг друга. Это существенно разные линейки, но обе они измеряют все расстояния в диапазоне от 1 до 17, кроме 14 и 15. Награда достанется тому, кто первым найдет такую пару линеек с числом делений, большим шести.
О ЛИНЕЙКАХ КОЛОМБА И ИХ ПРИМЕНЕНИИ В РАДИОАСТРОНОМИИ
А.К.ДЬЮДНИ
ПРИ ПОМОЩИ простой линейки длиной в один фут с 13 делениями, каждое из которых соответствует одному дюйму, можно измерить 12 различных расстояний. Возможно ли так усовершенствовать это знакомое всем устройство, чтобы число измеряемых с его помощью расстояний было больше числа нанесенных на нем делений? Оказывается, да: например, на стандартной линейке можно оставить лишь пять делений и при этом измерить 10 различных расстояний. Каждое такое расстояние заключено между некоторой парой делений и вычисляется как разность между целыми числами, которыми помечены эти деления. Того же результата можно достичь, даже воспользовавшись 11-дюймовой линейкой. Читатели, которые после некоторых размышлений придумают, как это можно сделать, создадут тем самым так называемую линейку Коломба.
Поиск таких линеек - весьма интересное занятие, в котором большую помощь может оказать компьютер. Решая эту задачу, вы не просто удовлетворяете свое любопытство, а участвуете в серьезном исследовании. Дело в том, что необходимость в линейках Коломба возникает в целом ряде областей науки и техники.
Эти устройства являются изобретением Соломона У. Коломба, профессора математики и электроники Южнокалифорнийского университета. В течение двух десятилетий он и его коллеги занимались поиском и изучением свойств этих линеек. Устройства подобного рода могут применяться в теории кодирования, рентгеновской кристаллографии, конструировании электронных схем, радиоастрономии.
Одним из исследователей, в работе которых линейки Коломба играют важную роль, является Д.Робертсон, геофизик, работающий в Роквилле (шт.Мэриленд) в Национальном геодезическом центре Национальной службы США по океану и атмосфере. Он применяет радиоастрономический метод - интерферометрию с очень длинной базой - не для того, чтобы фиксировать местоположение радиоисточников, а чтобы выполнить точные измерения параметров Земли. Занимаясь уже в течение нескольких лет поиском линеек, он обращается за помощью к читателям. В результате, возможно, удастся точнее определить размеры, форму и параметры движения нашей планеты.
Прежде чем откликнуться на просьбу Робертсона, нам, наверное, следует вникнуть в принципы, лежащие в основе линеек Коломба. Хотя линейки могут быть произвольной длины, пока изучены лишь линейки малых размеров. Первые три линейки можно описать несколько абстрактно тремя последовательностями чисел:
0, 1
0, 1, 3
0, 1, 4, 6
Чтобы представить себе линейку как физический объект, можно мысленно пометить левый конец "пустой" линейки длиной n единиц наименьшим числом последовательности, т.е. 0. Правый конец пометим наибольшим числом n; им может быть 1, 3 или 6. Промежуточными числами пометим деления, нанесенные на соответствующих расстояниях от левого конца линейки, т.е. от 0 (см. рисунок на с.103).

Три идеальные линейки Коломба и диаграммы их расстояний
Простой способ проверить, какие расстояния из диапазона от 0 до n можно измерить одной из этих маленьких линеек, заключается в том, чтобы нарисовать диаграмму расстояний на линейке. Для этого каждому целому числу на линейке поставим в соответствие точку на листе бумаги и пометим точку данным числом. Затем каждую пару точек соединим линией, помеченной разностью между целыми числами, расположенными на концах линии. Если каждое расстояние в диапазоне от 0 до n появляется на одной и только на одной линии диаграммы расстояний, то линейка Коломба называется идеальной. Все три линейки на иллюстрации идеальные - факт, в котором можно убедиться, взглянув на соответствующие диаграммы расстояний. На каждой диаграмме ни одно расстояние не появляется более одного раза, и все возможные расстояния в диапазоне от 0 до n присутствуют.
Среди линеек Коломба идеальные встречаются очень редко. На самом деле все существующие идеальные линейки были только что рассмотрены. Для значений n больших 6 "неидеальность" может проявляться двояким образом: либо какое-то расстояние встречается более одного раза, либо не встречается вовсе.
Вот так, в самом начале поиска больших (и лучших) линеек мы столкнулись с суровой действительностью. Однако откуда известно, что идеальных линеек больших размеров не существует? Коломб представил короткое и изящное доказательство этого факта.
Он предлагает рассмотреть не сами деления на линейке, а интервалы между ними. Если линейка идеальна, то множество всех интервалов между последовательными делениями образует ряд 1, 2, 3... до m-1 в некотором порядке (m - количество делений). Коломб спрашивает: "Где расположен единичный интервал?". Если он прилегает к любому интервалу, длина которого меньше m-1, то оба эти интервала вместе дают расстояние, меньшее m. Но это расстояние уже должно было встретиться в виде одного из интервалов где-то еще, потому что все расстояния от 1 до m-1 расположены соответственно между последовательными делениями. Указанные соображения приводят нас к несколько неожиданному выводу, что единичный интервал должен прилегать к интервалу длиной m-1. Более того, по другую сторону от единичного интервала никаких интервалов больше нет, ибо он располагается на одном из концов линейки.
Полученный нами результат представляет собой как бы один поворот ручки того, что математики называют "колбасной машиной". Далее, Коломб спрашивает: "Где располагается интервал длиной 2 единицы?" Повернем ручку еще раз. Если интервал длиной 2 единицы прилегает к любому интервалу длиной меньше m-2, то взятые вместе эти два интервала образуют расстояние, уже встречавшееся где-то еще. На этот раз мы уже не можем считать, что интервал длиной 2 единицы прилегает к интервалу длиной m-2. Их суммарная длина m уже измеряется комбинацией интервалов длиной 1 и m-1 с одного конца линейки.
Таким образом, колбасная машина останавливается, и мы приходим к выводу, что есть только один интервал, к которому может прилегать интервал длиной 2 единицы, а именно интервал длиной m-1. Поскольку у любой линейки есть только два конца, идеальная линейка не может содержать больше трех интервалов: 1, m-1 и 2. Доказательство завершается, когда мы вспоминаем, что три интервала требуют четырех делений. Таким образом, при m=4 интервалы равны 1, 3, 2, а соответствующие деления образуют последовательность 0, 1, 4, 6.
Столкнувшись с полным отсутствием идеальных линеек, имеющих более 4 делений, математик попытается "отыграться", построив новое определение. Продемонстрируем пример определения, возникшего в результате подобных попыток. Наилучшим приближением к невозможной идеальной линейке с пятью делениями является такая линейка, которая содержит каждое расстояние не более одного раза, но может и не содержать всех расстояний, которые должна была бы иметь идеальная линейка того же размера. Этому условию легко удовлетворить, подобрав достаточно длинную линейку. Среди всевозможных линеек с пятью делениями, содержащих каждое расстояние максимум по одному разу, выявим самую короткую. Такая линейка будет называться линейкой Коломба пятого порядка. Линейка Коломба порядка m определяется аналогичным образом. Поскольку это определение включает также первые три линейки как частный случай, оно как бы сглаживает разрыв в свойстве "идеальности", наблюдающийся при переходе через значение m, равное 4.
Г.Тэйлор, коллега Коломба, представил имеющуюся на данный момент информацию о линейках Коломба в виде приведенной вверху таблицы. В диапазоне от двух до 24 делений мы располагаем как точными знаниями, так и некоторыми гипотезами относительно размеров линеек Коломба. Зона, которую я называю идеальной, заключается между двумя и четырьмя делениями. Далее простирается зона знания, охватывающая линейки Коломба, имеющие до 13 делений. В этой области известны все линейки минимального размера. Другими словами, в каждом конкретном случае не существует линейки Коломба меньшей длины с тем же количеством делений. Линейка Коломба с 5 делениями имеет длину 11 единиц. Линейка Коломба с 13 делениями имеет длину 106 единиц.

Длина линеек Коломбо и линеек, близких к этому классу
За 13 делениями начинается зона, которую я называю зоной полумрака. Эта зона (назовем ее более уважительно зоной исследований) содержит только те линейки, относительно которых еще нельзя с уверенностью сказать, что они являются линейками Коломба. Для каждого количества делений в таблице указана длина линейки. Однако могут существовать и линейки меньшего размера. На самом деле имеется формула, которая дает нижний предел для этих размеров. Постоянно увеличивающийся разрыв между значениями, получаемыми по формуле, и длинами найденных к настоящему моменту линеек свидетельствует либо о слабости оценки по формуле, либо о том, что линейки, найденные для каждого значения числа делений, имеют тенденцию "ухудшаться" с ростом последнего.
Зона знания была расширена до границы в 13 делений благодаря усилиям Робертсона. В ходе непрерывной работы ЭВМ в течение месяца его программа произвела исчерпывающий перебор всех потенциальных линеек Коломба с 13 делениями и нашла самую короткую. Если для поиска линеек Коломба с 14 и более делениями потребуется еще больше машинного времени, то, наверное, немногие читатели заинтересуются этим поиском.
Вместо этого можно предложить им тактику "компьютерных налетов" на зону исследований, в результате которых можно получить линейки, обладающие меньшими размерами, чем найденные до сих пор. Очень полезной для всех поисков подобного рода является программа под названием CHECKER. Однако прежде чем применить эту программу, необходимо задать способ проверки наличия одинаковых разностей между всеми возможными парами целых чисел в данном массиве. При самом простом подходе можно организовать массив таких разностей, а затем просмотреть его в поисках дублирующихся значений, опираясь на довольно неуклюжий и требующий много времени алгоритм.
Редко бывает так, чтобы алгоритм, обеспечивающий наиболее быстрое решение задачи, можно было реализовать с помощью самой короткой программы. Однако здесь мы сталкиваемся как раз с таким случаем. Поскольку предполагается, что все разности отличаются друг от друга (т.е. одинаковых разностей не существует), то ими можно воспользоваться как адресами в специальном массиве check. Вначале в массиве check хранятся только нули. Каждый раз, когда вычисляется новая разность, значение, хранящееся по соответствующему адресу, меняется с 0 на 1. Таким образом, по мере того, как программа CHECKER проводит дальнейшие вычисления, она может наткнуться на единицу, уже записанную по данному адресу, а это означает, что "новая" разность уже встречалась где-то раньше. В этом случае рассматриваемая линейка не может принадлежать к классу Коломба, поскольку она не обладает основным свойством, присущим линейкам Коломба: каждое расстояние должно встречаться не более одного раза.
Описанный метод, использующий значения разностей в качестве адресов, представляет собой простую разновидность того, что специалисты по вычислительной математике и программированию называют хешированием. Во многих задачах, связанных с информационным поиском, хеширование обеспечивает самый быстрый доступ к данным.
Для тех, кто хотел бы подробнее ознакомиться с программой CHECKER, опишем в общих чертах ее структуру. С помощью двух вложенных циклов генерируются все возможные пары целых чисел из входного массива. В первом цикле генерируются индексы i, а во втором - индексы j. Программа вычисляет абсолютное значение разности и присваивает его в качестве значения переменной diff. На следующем шаге алгоритма программа CHECKER использует значение diff в качестве хеш-кода. В алгоритмических обозначениях можно записать:
если check(diff) = 1
то вывести "не коломбова" и выход
в противном случае check (diff) <- 1
Если программа ни разу не выведет сообщение "не коломбова", то можно считать, что рассматриваемая линейка успешно прошла главный тест. Однако каков ее размер? Существует несколько способов получить ответ на этот вопрос.
Прежде всего можно воспользоваться программой CHECKER в ее основном варианте без каких-либо дополнительных программ. Я представляю себе читателя, склонившегося над клавиатурой и увлеченно работающего с программой CHECKER. Он проводит разведку в зоне исследований на высоте 14 делений в поисках линейки короче 127 единиц - именно такую длину имеет лучшая из известных на сегодня линеек. Читатель, совершающий полет в сложных метеорологических условиях, не знает, в какую сторону повернуть. Только что он ввел последовательность из 14 делений. Наибольшим числом этой последовательности было 124. С неописуемым волнением он видит, как на экране начинает высвечиваться сообщение: "Поздравляю! Последовательность подходит". Введя это поздравительное сообщение в программу, читатель дает себе слово всегда пробовать ее исключительно для потенциально рекордных последовательностей.
Возможно, читатель нашел свой рекордный набор делений, последовав совету Коломба и исследуя только те линейки, у которых наиболее длинные интервалы встречаются в средней части. У таких линеек интервалы уменьшаются при приближении к концам, однако точные закономерности читателям предстоит найти самим. Коломб заверяет нас, что многие хорошие линейки, хотя и не обязательно наилучшие, обладают этим свойством.
Программу CHECKER можно несколько модифицировать, чтобы придать изысканиям характер коротких пробных попыток. В программе STEP CHECKER целые числа вводятся по одному. После того как введено очередное число, программа вычисляет все разности между только что введенным числом и теми, которые уже хранились в памяти. На самом деле STEP CHECKER - это просто версия программы CHECKER, в которой инструкция ввода заменяет внешний цикл. Последовательность считается подходящей, если при обработке последнего введенного числа программа не выдала сообщения "не коломбова".
Наконец, программу STEP CHECKER можно встроить в автоматическую систему, подобную разработанной Робертсоном. Его программа, которую я могу назвать EXHAUST (от англ. exhaustive - исчерпывающий), поскольку она производит исчерпывающий перебор, систематически порождая новые линейки путем добавления новых интервалов. После добавления каждого нового интервала программа STEP CHECKER проверяет полученную таким образом последовательность, или линейку.
Робертсон построил свою программу исходя из того, что новые интервалы (и соответственно новые деления) должны добавляться к линейке слева направо. Читатели, которые следили за ходом доказательства Коломба (о несуществовании идеальных линеек для числа делений больше 4), вспомнят, что интервалы должны иметь длину 1,2,... ,m-1 в некотором порядке. Хотя это было справедливо только в отношении идеальных линеек, нечто подобное, вообще говоря, справедливо также в отношении линеек Коломба. Большинство, хотя и не все, интервалов длиной от 1 до m-1 между последовательными делениями на линейках, приближающихся к идеальным, встречается в некотором порядке. Отметим, однако, что у таких линеек встречаются интервалы даже больше m-1.
Алгоритм Робертсона порождает новые интервалы в пошаговом режиме. Эти интервалы хранятся в массиве, который мы назовем spaces. Программа EXHAUST просматривает массив и добавляет к нему каждый раз по одному новому интервалу. Конечно, в алгоритме используются некоторые простые тесты, облегчающие работу программы. С помощью одного из них можно проследить, чтобы новый интервал не совпадал с одним из уже имеющихся в массиве spaces, а с помощью второго - чтобы суммарная длина всех интервалов, образующих линейку, не превосходила минимальную известную длину для линейки с данным числом делений.
Программа EXHAUST, кажется, с большим энтузиазмом отыскивает новые линейки. Сначала она полагает первый элемент массива spaces равным 1 и добавляет по единице к следующему интервалу, так чтобы он отличался от первого. Затем она начинает добавлять по единице к третьему интервалу, следя за тем, чтобы это расстояние не только отличалось от первых двух, но также удовлетворяло условию, заложенному в программе STEP CHECKER, согласно которому все расстояния, содержащиеся в линейке, должны отличаться друг от друга. Всякий раз, когда появляется новый элемент (интервал), программа суммирует все элементы массива и сравнивает полученную сумму с длиной самой короткой известной к данному моменту линейки. Если сумма оказывается меньше, программа переходит к следующему интервалу. Если нет, то она возвращается к предыдущему элементу и продолжает перебор.
Программа Робертсона работает значительно быстрее, если первый элемент массива spaces положить равным 2, а не 1. На самом деле прогон программы, занимающий целые сутки, сократится на несколько часов. Читатели могут поразмыслить над тем, почему и в этом случае поиск остается исчерпывающим.
Конечно, эффективность алгоритма поиска можно повысить за счет включения других тестов и эвристических приемов. Эти тесты и эвристики могут особенно сильно повлиять на эффективность, если они налагают дополнительные ограничения на возможные значения элементов массива spaces. Возможно, существует процедура, работающая со значительно более узкими диапазонами этих значений. Обработка массива во многом подобна счету. А счет будет выполнен намного быстрее, если уменьшить количество возможных вариантов в каждом элементе массива spaces. В любом случае читатели, сумевшие найти рекордного бобра-работягу, построить новые катапульты, стреляющие планерами, и добившиеся многих других результатов в своих исследованиях, смогут найти свой собственный подход к решению задач из зоны исследований Коломба. О лучших находках будет рассказано в одной из наших следующих статей. Интересно, кто первым найдет две различные линейки, имеющие больше 6 делений, но измеряющие один и тот же набор отличных друг от друга расстояний. Линейки, представляющие собой взаимные зеркальные отображения, не считаются различными.
Успешное решение задачи будет означать несостоятельность "теоремы", предложенной швейцарским математиком Софи Пиккард в 1939г. Согласно этой теореме, две линейки, измеряющие один и тот же набор отличных друг от друга расстояний, должны быть идентичными. Теорема очень понравилась специалистам по рентгеновской кристаллографии, поскольку она помогала им разрешать неопределенности в дифракционных картинках. К сожалению, эта теорема оказалась не справедливой для многих пар линеек, имеющих 6 делений. Может быть она остается справедливой для всех линеек более высокого порядка. Этот вопрос можно рассмотреть, выбрав в качестве объекта исследований линейки, имеющие всего 7 делений.
Однако какое это все имеет отношение к задаче, которой занимается Робертсон? Дело в том, что линейка Коломба иногда используется в радиоастрономии для разрешения удаленных радиоисточников и для измерения параметров нашей планеты. В первом случае несколько антенн располагаются на прямой линии протяженностью несколько километров. Позиции антенн соответствуют делениям на линейке Коломба (см. рисунок на с.105). Для того чтобы определить положение удаленного радиоисточника, необходимо найти угол между линией базы антенн и направлением волнового фронта, поступающего от источника. Все антенны настроены на одну и ту же длину волны. Точное время прибытия сигнала к каждой антенне может быть установлено путем анализа записи принимаемых сигналов. Полное число длин волны, укладывающееся в интервале между данной парой антенн, называется полной разностью фаз. Обычно она состоит из целого числа и дробной части, которая называется сдвигом по фазе. Если удается восстановить полную разность фаз, то искомый угол между направлением на источник и линией базы нетрудно вычислить по известной длине волны и скорости света c. Однако по сигналам, принятым каждой парой антенн, можно определить лишь сдвиг по фазе, но не полную разность фаз.

Пары радиотелескопических антенн, расположенных по линейке Коломба, позволяют определить разность фаз приходящих сигналов
В действительности полная разность фаз вычисляется с применением анализа Фурье по данным, зафиксированным многими парами антенн. Однако если расстояние между одной парой антенн оказывается равным расстоянию между какой-нибудь другой парой, то обе они дают одну и ту же информацию о сдвиге по фазе. Избыточность информации означает ее потерю. Точность вычисления искомого угла наиболее высока в том случае, когда каждая пара антенн фиксирует отличный от других сдвиг по фазе. Это условие выполняется за счет размещения антенн по тому же принципу, по которому располагаются деления на линейке Коломба.
Еще один способ определения положения удаленного радиоисточника заключается в том, чтобы воспользоваться лишь двумя приемниками, сканирующими одновременно весь набор длин волн, на которых ведутся наблюдения. Прием на две антенны на нескольких различных волнах позволяет получить ту же информацию о полной разности фаз между принимаемыми сигналами, какую дало бы использование нескольких антенн, настроенных на одну и ту же длину волны. Здесь опять возникает опасность появления избыточной информации. Ни одна пара длин волн, на которых ведется наблюдение, не должна иметь разность, совпадающую с разностью между какой-либо другой парой. И хотя линейка Коломба здесь остается как бы невидимой, она все же присутствует в неявной форме.
Робертсон применяет второй метод не для фиксации радиоисточников, а для того, чтобы определить местоположение самих антенн. Для целей, которые он преследует, недостаточно знать, что вторая антенна находится в Уэстфорде (шт.Массачусетс). Ему нужно знать ее положение с точностью до нескольких сантиметров. Такой точности можно достичь, если воспользоваться очень далеким, практически точечным источником, таким, как квазар. Установить точное положение точки на земной поверхности по отношению к далекому радиоисточнику равносильно тому, чтобы точно установить значения таких фундаментальных земных параметров, как диаметр планеты, ориентация оси ее вращения и продолжительность суток. На уровне сантиметров и микросекунд эти параметры являются переменными величинами из-за воздействия годовых, сезонных и даже метеорологических вариаций, которые иногда подчиняются известным закономерностям, а иногда остаются совершенно необъяснимыми.
БИБЛИОГРАФИЯ
MINIMUM-REDUNDANCY LINEAR ARRAYS. ALAN T. MOFFET in IEEE Transactions on Antennas and Propagation, Vol.AP-16, No.2, pages 172-175; February, 1963.
APPLICATIONS OF NUMBERED UNDIRECTED GRAPHS. GARY S. BLOOM AND SOLOMON W. GOLOMB in Proceedings of the IEEE, Vol.65. No.4, pages 562-570; April, 1977.
GOLOMB'S GRACEFUL CURVE. MARTIN GARDNER in Wheels, Life and Other Mathematical Amusements. W.H.Freeman and Company, 1983. (М.ГАРДНЕР, КРЕСТИКИ-НОЛИКИ, 1988.- G.)
VARIATIONS IN THE ROTATION OF THE EARTH. W.E.CARTER, D.S.ROBERTSON, J.E.PETTEY, B.D.TAPLEY. В.Е.SCHUTZ, R.J.EANES AND MIAO LUFENG in Science, Vol.224, No.4652, pages 957-961; June 1, 1984.
ОТКЛИКИ
5 1986
ЛИНЕЙКИ Коломба, предмет статьи в февральском номере нашего журнала, оказались самой трудной задачей из тех, с которыми читатели сталкивались до сих пор. Многие были званы, да немногие избраны, так сказать. Несколько читателей попытались заработать приз в 100долл., учрежденный изобретателем линеек Соломоном У. Коломбом из Южнокалифорнийского университета.
Линейка Коломба с n делениями - это кратчайшая возможная линейка, обладающая следующими свойствами: у нее n делений (включая концы), отстоящих друг от друга на расстояния, равные целым числам, и она измеряет все возможные интервалы, которые представляются суммой целых чисел, от единицы до интервала, равного длине линейки, причем каждый интервал измеряется единственным способом. Интервал может быть измерен линейкой только в том случае, если он оказался равным расстоянию между какими-нибудь двумя делениями линейки. Если одно и то же расстояние можно измерить более чем одной парой делений, то линейка уже не принадлежит классу линеек Коломба.
Ко времени публикации статьи не было известно ни одной линейки Коломба, обладающей более чем 13 делениями, а кратчайшая известная линейка с 15 делениями имела длину 155 единиц. Однако вскоре после этого Д.Робертсон из Национальной службы США по исследованию атмосферы и океана открыл более короткую линейку с 15 делениями. Ее длина 153 единицы. Затем во время рождественских каникул Дж.Шерер из Исследовательского центра Томаса Уотсона фирмы IBM запрограммировал простаивающий компьютер для исчерпывающего поиска линеек, и теперь появились линейки Коломба с 14 и 15 делениями. Линейка с 14 делениями имеет длину 127 единиц, и ее деления расположены в точках 0, 5, 28, 38, 41, 49, 50, 68, 75, 92, 107, 121, 123 и 127. Линейка Коломба с 15 делениями имеет длину 151 единицу, и ее деления расположены соответственно в точках 0, 6, 7, 15, 28, 40, 51, 75, 89, 92, 94, 121, 131, 147 и 151. Шерер пишет, что он сэкономил много машинного времени, предположив, что среднее деление линейки находится слева от ее геометрического центра.
По другой задаче, поставленной Коломбом, мы получили письма читателей с заявками на премию в 100долл. Однако все присланные до сих пор решения недействительны, поскольку они основаны на неправильном понимании задачи. Коломб попросил прояснить ситуацию, переформулировав условие задачи. Найти две различные линейки (не обязательно минимальной длины) с одинаковым количеством делений, превышающим число 6, которые измеряют один и тот же набор расстояний, причем опять-таки ни одно из этих расстояний не может быть измерено никакой линейкой более чем одной парой делений. Линейки, являющиеся зеркальным отражением друг друга, например такие, как 0, 2, 5, 6 и 0, 1, 4, 6, не считаются различными. Существует бесконечно много пар линеек (почти все они не минимальные), которые решают аналог задачи Коломба для шести делений. Например, такую пару образуют следующие линейки: 0, 1, 4, 10, 12, 17 и 0, 1, 8, 11, 13, 17. Они не являются зеркальным отражением друг друга. Это существенно разные линейки, но обе они измеряют все расстояния в диапазоне от 1 до 17, кроме 14 и 15. Награда достанется тому, кто первым найдет такую пару линеек с числом делений, большим шести.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
3 1986
ИССЛЕДОВАНИЕ ЗВЕЗДНЫХ СКОПЛЕНИЙ С ПОМОЩЬЮ КОМПЬЮТЕРНОГО ТЕЛЕСКОПА
А.К.ДЬЮДНИ
ДАЛЕКО в космическом пространстве под музыку гравитационных сил в хороводе кружится скопление звезд. На протяжении человеческой жизни их движение мы почти не замечаем, но если рассматривать его в другом временном масштабе, когда годы эквивалентны секундам, то можно увидеть причудливые переплетения звездных траекторий. Иногда две звезды, приблизившись друг к другу, исполняют парный танец, а затем одна из них стремительно уносится в окружающее пространство.
С помощью мощного телескопа можно рассмотреть структуру некоторых звездных скоплений нашей Галактики, но он не позволяет сжать годы в секунды - это может сделать только компьютер. Кроме того, компьютер можно запрограммировать так, что он будет играть роль своеобразного телескопа, позволяющего разглядывать гипотетические звездные скопления. При этом можно наблюдать движение отдельных объектов скопления в космическом временном масштабе, получая последовательность фотоснимков, на которых фиксируются пунктирные траектории каждой звезды, вьющиеся и переплетающиеся с траекториями других звезд скопления (см. рисунок на с.91).

Четыре звезды кружатся в космическом хороводе в течение нескольких лет и затем покидают сцену
Объясняется ли эволюция звездных скоплений, наблюдаемая астрономами, только гравитационными силами? Компьютеры помогают дать ответ как на этот вопрос, так и на другие, связанные с ним. В мае 1984г. в Принстонском университете на очередном 113-м симпозиуме Международного астрономического общества, на этот раз целиком посвященном динамике звездных скоплений, теоретики и специалисты по моделированию обсуждали проблему соответствия между гипотетическими и реальными звездными скоплениями.
Поставить космический балет при помощи компьютера сравнительно несложно. В принципе взаимодействия между звездами, входящими в скопление, описываются простым классическим законом: каждая звезда в паре с каждой другой звездой испытывает действие гравитационной силы, пропорциональной произведению масс звезд рассматриваемой пары и обратно пропорциональной квадрату расстояния между ними. Вычисления по этой формуле выполнить нетрудно: нужно перемножить массы звезд, полученное произведение умножить на коэффициент пропорциональности (гравитационную постоянную) и результат разделить на квадрат расстояния между звездами. Суммарный эффект всех парных взаимодействий, по-видимому, полностью определяет характер изменений, претерпеваемых со временем звездным скоплением. Программа CLUSTER вычисляет результирующую силу, действующую на каждую звезду, и перемещает эту звезду в следующее по времени положение. Процедура циклически повторяется на заданном отрезке времени, соответствующем нескольким столетиям, по принятому в модели масштабу.
Правда, вводить с клавиатуры координаты и скорости большого числа звезд - занятие довольно скучное, но зато вы видите, как перед вами на экране разворачивается эволюция миниатюрной вселенной. Звезды в центральной части скопления движутся по неустойчивым хаотическим орбитам, а те, которые находятся в периферийных областях, медленно уплывают, останавливаются и плавно возвращаются назад. Наиболее интересно наблюдать, как звезды сталкиваются и как некоторые из них покидают скопление.
Когда две звезды сближаются, они сообщают друг другу колоссальные гравитационные ускорения и после столкновения стремительно расходятся в разные стороны. Стремительный выход отдельных звезд за пределы скопления обычно является результатом одного или более таких сближений. Звезда, покинувшая скопление, может вернуться в него, а может и не вернуться. Астрономическое тело обладает определенной скоростью отрыва, зависящей от его массы и массы того тела или объекта, от которого оно отрывается. Если звезда, удаляющаяся от скопления, достигла этой скорости, она никогда к нему не вернется. Те, кто еще не имеют опыта в моделировании звездных скоплений, наверное, часто будут наблюдать "побеги" звезд из составленных ими конфигураций скоплений. На самом деле в звездных скоплениях, построенных новичками, звездный хоровод быстро распадается. Лучше всего начинать с несложных двойных или тройных звездных систем.
Программа CLUSTER имеет простую структуру. Она состоит из цикла инициализации, за которым следует двойной цикл, в котором вычисляются изменения скорости, ускорения и положения каждой звезды как результат суммарного воздействия со стороны остальных звезд. Здесь мы рассмотрим простейшую версию программы, в которой такие величины, как интервал между двумя соседними моментами времени, коэффициент пропорциональности в формуле притяжения и массы звезд, являются как бы "встроенными", т.е. фиксированными. Несмотря на свою простоту, даже эта версия программы CLUSTER способна моделировать почти все явления, присущие звездным скоплениям. В программе используются три множества массивов. В массивах первого множества хранятся значения ускорений, которыми обладают звезды на данный момент в каждом направлении по трем осям координат. Имена этих массивов соответственно ax, ay и az. Таким образом, ax(i), ay{i) и az(i) указывают компоненты ускорения i-й звезды по осям x, y и z. Элементы этих трех массивов не обязательно инициализировать (т.е. присваивать им начальные значения) перед выполнением программы. Массивы второй группы vx, vy и vz хранят значения скоростей: vx(i), vy(i) и vz(i) указывают соответственно компоненты скорости i-й звезды вдоль осей x, y и z. Массивы третьей группы предназначены для координат положения звезд: x(i), y(i) и z(i) соответственно указывают координаты положения i-й звезды в данный момент по осям x, y и z. Элементы массивов x, y, z и vx, vy и vz следует инициализировать в начале программы.
Вслед за блоком инициализации идет главная часть программы CLUSTER. Двойной цикл может повторяться автоматически до бесконечности, или же программист должен указать, при каких условиях производится повторное выполнение цикла. Во внешнем цикле каждая звезда рассматривается по очереди и компоненты ее ускорения устанавливаются равными нулю. После этого во внутреннем цикле вычисляются силы, действуюшне на каждую звезду со стороны остальных звезд, входящих в скопление.
Предположим, к примеру, что индекс внешнего цикла равен i, а индекс внутреннего цикла - j. Во внутреннем цикле вначале производится проверка, не равен ли индекс i индексу j. Если индексы оказываются равными, программа не вычисляет силу, поскольку звезда сама себя не притягивает. Во всяком случае, это вычисление привело бы к попытке деления на нуль. (Это, пожалуй, единственная ситуация, в которой я мог бы искренне посочувствовать компьютеру). Когда i и j не равны друг другу, программа CLUSTER пользуется формулой евклидова расстояния между звездами: разности координат по осям x, y и z возводятся в квадрат и складываются друг с другом. В результате мы получаем, конечно, квадрат расстояния. Затем производится проверка, не равно ли полученное расстояние нулю. Если да, то нужно дать сигнал тревоги в той или иной форме, потому что компьютеру вскоре придется выполнить операцию деления на нуль. Моя версия программы в таких случаях выдаст сообщение "Столкновение!"
Если все в порядке, команды внутреннего цикла завершают вычисление расстояния между звездами, беря квадратный корень из квадрата расстояния, вычисленного ранее. Затем производится деление числа I000 на квадрат полученного расстояния и в результате этого деления получается значение силы. Наконец, последняя задача, которую нужно решить во внутреннем цикле,- это определить компоненты ускорения i-й звезды. Для этого необходимо суммировать все силы, действующие со стороны других звезд. Например, компонента ускорения i-й звезды по оси x может быть выражена в общем виде следующим образом:
ax(i) <- ax(i) + f*(x(j) - x(i))/d.
Здесь f и d представляют соответственно силу и расстояние. Отношение проекции расстояния между звездами i и j на ось x к полному расстоянию в точности соответствует составляющей силы, действующей на звезду i вдоль оси x. Компоненты ускорения звезды вдоль осей у и z вычисляются аналогичным образом.
Завершают программу два цикла, следующие один за другим. В первом осуществляется изменение значения скорости, а во втором - положения. Здесь возникает одна тонкость, на которую обратил мое внимание Дж.Хаббард, математик из Корнеллского университета, чей совет по поводу вычислений, выполняемых над множеством Мандельброта, оказался в высшей степени полезным (см. статью в рубрике "Занимательный компьютер" в журнале "В мире науки", 1985, #10). Дело в том, что можно вычислять координаты положения звезды до вычисления ее скорости, и получающиеся при этом результаты выглядят достаточно правдоподобными. Однако со временем движение звезд станет неестественным, поскольку при таком вычислении координат положения и скоростей звезд будет нарушаться закон сохранения энергии.
В цикле изменения скорости к текущему значению этой переменной просто прибавляется ускорение согласно следующей формуле:
vx(i) <- vx(i) + ax(i).
Здесь предполагается, что временной интервал между двумя последовательными моментами равен единице времени, через которую выражается скорость. Аналогичные формулы применяются для вычисления составляющих vy и vz. Вычисления координат, выполняемые в последнем цикле, также очень просты:
x(i) <- x(i) + vx(i).
Аналогичным образом изменяются элементы массивов y и z. На основе данных, получаемых в последнем цикле, программа CLUSTER определяет положение каждой звезды на двумерной поверхности экрана дисплея. При этом первые две координаты "наносятся" на экран, а третья координата по оси z игнорируется. Таким образом, можно представить себе, что мы наблюдаем скопление через иллюминатор, роль которого играет экран. Значения величин, вычисляемых в программе моделирования скопления, иногда оказываются очень малыми, а иногда и очень большими. По этой причине мы советуем вользоваться арифметическими операциями с двойной точностью так, чтобы округления не нарушали картины.
Время, затрачиваемое программой CLUSTER на один вычислительный цикл, зависит от количества звезд в системе. Системы, насчитывающие около 10 звезд, отличаются интересным (с эстетической точки зрения) повелением, но для того, чтобы достичь реалистичной сложности, количество звезд должно быть порядка 100 или лаже 1000. К сожалению, число шагов алгоритма в основном вычислительном цикле возрастает как квадрат числа звезд в скоплении. И хотя специалисты по моделированию звездных систем нашли интересный способ обойти это ограничение, возникает рял других проблем, осложняющих моделирование.
Наиболее серьезная проблема связана с тем обстоятельством, что мы пытаемся с помощью дискретной модели описать поведение по существу непрерывной системы. Непрерывные гладкие орбиты аппроксимируются последовательностью скачков, траектория которых все дальше удаляется от истинной орбиты, по которой звезда движется в скоплении. Неточности подобного рода можно в какой-то степени скорректировать при наличии статистической регулярности, но когда звезды подходят друг к другу на очень малое расстояние, дискретная модель неестественно и непоправимо усиливает эффекты, связанные с большими гравитационными ускорениями.
Если, например, в ходе выполнения вычислительного цикла одна звезда (Стелла) оказывается в непосредственной близости от другой звезды (Астер), мощное гравитационное поле резко увеличивает компоненты ускорения обеих звезд. Это увеличение на последующих шагах вычисления распространяется на компоненты скорости, а затем и на координаты положения звезд. На следующей итерации процесса моделирования Стелла оказывается уже очень далеко от Астера и не может "выплатить гравитационного долга". Таким образом возник излишек кинетической энергии. За счет этого эффекта искусственные звездные скопления распадаются быстрее реальных. Есть два пути преодоления указанного затруднения. Первый путь трудный, второй проще. В первом случае необходимо вычислять кеплеровские орбиты для пары близко сошедшихся звезд. Теоретики предпочитают этот метол прежде всего потому, что формулы, по которым вычисляются орбиты, являются абсолютно точными. Более простой, но иногда неточный метод обработки данных, описывающих ситуации, когда звезды приближаются друг к другу, заключается в том, чтобы уменьшить масштаб шагов по времени в основном вычислительном цикле. Возможно, читатели пожелают взять на вооружение этот прием и воспользоваться им при составлении усовершенствованной версии программы - SUPERCLUSTER.
Программу SUPERCLUSTER можно получить путем несложной модификации программы CLUSTER. Во-первых, в программе SUPERCLUSTER массы звезд, входящих в скопление, могут быть различными. Это изменение можно легко реализовать, введя перед началом выполнения программы значения масс в массив m. Расчет гравитационной силы несколько усложняется: сила уже не является функцией только 1/d2, она теперь пропорциональна произведению масс, деленному на d2. Кроме того, новая версия программы отличается тем, что звезды подразделяются на спектральные типы. Как и для масс, в программе организуется массив spec, элементы которого должны быть заданы перед началом выполнения программы. Однако этот массив используется только в фазе высвечивания звезд на экране после очередной итерации вычислений. Цвет звезд изменяется в пределах от голубого до красного. Зеленый цвет отсутствует. Третье усовершенствование программы CLUSTER состоит в том, что шаг по времени берется произвольным.
В программе SUPERCLUSTER используется переменная delta. значение которой равно интервалу между двумя последовательными моментами времени. Эта величина устанавливается перед началом выполнения основных вычислительных циклов. Конечно, эта переменная должна повлиять на формулы, по которым вычисляются изменения как скорости, так и положения звезд: в формуле для скорости на нее множится ускорение, а в формуле для координат на нее множится скорость.
Рассмотрим теперь простой способ, позволяющий обрабатывать данные, описывающие ситуации, возникающие при сближении звезд. Прежде всего нужно четко установить критерий "близости". Затем в программу нужно ввести проверку, соответствующую выбранному критерию. Проверка должна производиться сразу после вычисления расстояния между двумя звездами. Если зафиксировано "сближение", программа SUPERCLUSTER заменяет значение delta, уменьшая ее до одной десятой от ее текущей величины,- по крайней мере до тех пор, пока ни одна пара звезд уже не будет удовлетворять критерию близости. Этот прием, конечно, помогает смягчить внезапные скачки гравитации в дискретной модели. Однако он создает еше более серьезные проблемы, когда звезды по-настоящему близко подходят лруг к другу. Если расстояние между звездами уменьшается, скажем, в 10 раз, то гравитационная сила увеличивается в 100 раз! К счастью, опасные сближения случаются довольно редко. Метод уменьшения временного интервала был стандартным средством, которым обычно пользовались специалисты, профессионально занимающиеся моделированием звездных скоплений.
Чтобы программа SUPERCLUSTER давала небессмысленные с астрономической точки зрения результаты, нужно ввести единицы измерения расстояния, массы, а также некоторые другие характеристики физической реальности. В астрономии принята удобная мера расстояния, называемая астрономической единицей (АЕ) и соответствующая среднему расстоянию от Земли ло Солнца. Массу можно измерять, приняв за единицу массу Солнца, а время лучше всего измерять в годах. При этих условиях универсальная постоянная гравитационною притяжения булет приблизительно равна 39. В программе SUPERCLUSTER используется именно это значение в отличие от 1000, принятого в программе CLUSTER.
Теперь все готово к тому, чтобы запустить любую из рассмотренных нами программ. В качестве предварительного упражнения для программы CLUSTER можно взять четыре звезды. Расположим их по вершинам квадрата, размер которого на экране был бы 3-5см. Помимо координат x и y, соответствующих плоскости экрана, для каждой звезды следует задать также, вообще говоря, ненулевое значение координаты z. В противном случае пространство, в котором движутся звезды, будет ограничено плоскостью и сближения между ними будут наблюдаться намного чаще. Компоненты скоростей должны быть небольшими (скажем, в пределах от -5
до +5), а направление скоростей должно быть выбрано так, чтобы звезды двигались по часовой стрелке по замкнутым траекториям.
Программу SUPERCLUSTER можно попробовать в действии на звездной системе, изображенной на рисунке на с.92. Эта система образована звездами, являющимися ближайшими соседями Солнечной системы в нашей Галактике. Что случилось бы, если бы Солнце и несколько соседних с ним звезд были отрезаны (в гравитационном смысле) от остальной части Галактики и предоставлены сами себе на неограниченное время? Каким было бы движение звезд? Образовали бы они звездное скопление или рассеялись? Этот вопрос может иметь, а может и не иметь научного значения, однако сам по себе он интересен. Кроме того, точные координаты и скорости известны нам лишь лля нескольких ближайших звезд (см. таблицу на с.93).

Могли бы звезды соседней с нашей галактики образовать звездное скопление?
Параметры всех (за исключением трех) звезд, ближайших соседей Солнечной системы
Звездные скопления бывают либо открытыми (рассеянными), либо шаровыми. Открытые скопления насчитывают несколько тысяч звезд, в то время как число звезд в шаровых скоплениях может достигать нескольких миллионов. Пока исследователи, среди которых можно назвать н Дж.Джернигена, работающего в Калифорнийском университете в Беркли, ограничивались моделированием лишь открытых звездных скоплений и не очень многочисленных. Шаровые скопления пока остаются неприступными. Тем не менее Джерниген и некоторые другие пионеры моделирования, например такие, как Аарсет также из Калифорнийского университета в Беркли, уже на протяжении десятилетий наблюдают коллапсы звездных скоплений, моделируемых на ЭВМ. В качестве количественной характеристики коллапса рассматривается сферический объем, занимающий центральную часть скопления и содержащий в себе 10% его полной массы. Радиус этой сферы называют десятипроцентным радиусом. Явление коллапса начинается, когда десятипроцентный радиус уменьшается со временем. При этом центральная часть скопления неизбежно становится все плотнее н плотнее. Но, поскольку моделируемые звезды являются математическими точками, в таких звездных скоплениях никогда не происходит ничего страшного. В них не возникает никаких черных дыр. Это подтверждают и теоретики, занимающиеся моделированием звездных скоплений. У нас также пока мало свидетельств тому, что подобные ярко выраженные коллапсы случаются и в реальных скоплениях звезд. Какие-то факторы, по-видимому, мешают возникновению коллапса.

Шаровое звездное скопление Мессье 13 в созвездии Геркулеса
Как традиционные, так и современные эксперименты по моделированию звездных скоплений могут дать ключ к этой загадке. Во многих случаях начинающийся коллапс центральной части скопления фактически останавливался несколькими двойными звездными системами, расположенными в центре моделируемого скопления. В одном из экспериментов Джернигена достаточным для этого, по-видимому, оказалось присутствие лишь одной такой системы. Как это можно объяснить? По мнению аспиранта Д.Портера, работающего под руководством Джернигена, объяснение может заключаться в том, что "очень плотные двойные звездные системы вращаются с такой колоссальной скоростью, что отталкивают приближающиеся к ним звезды по касательной, и последние либо вращаются по круговым орбитам вокруг центра скопления, либо лаже возвращаются в область меньшей плотности, окружающую ядро скопления и называемую короной. Это, наверное, и есть тот механизм, который предотвраoает чрезмерное уплотнение ядра скопления".
В свое время Джeрниген занимался наблюдением звезд - источников рентгеновского излучения. Когда его исследования сконцентрировались на поисках источников рентгеновского излучения в звездных скоплениях, он стал все больше интересоваться природой звездных скоплений как таковых. Моделирование показалось ему эффективным средством исследования.
Джерннген внес важный вклад в технику моделирования, повышающий его эффективность. В программе CLUSTER и других подобных программах один вычислительный никл для п звезд требует n2 шагов вычисления. Цикл Джерннгена требует лишь п*log(n) шагов. Он разбивает моделируемое скопление на пары соседних звезд. Затем каждая такая пара заменяется некоторой фиктивной массой и скоростью, описывающими результирующее поведение пары. Затем тот же процесс применяется уже к парам звезд так, как если бы они были отдельными звездами. По мере того как развивается этот процесс разбиения на пары, возникают все новые узлы масс в структуре данных, называемой деревом. При этом корневой узел дерева представляет уже все скопление звезд. Теперь можно вычислить характеристики движения как для центрального узла, так и для всех ветвей дерева, вплоть до индивидуальных звезд.
Принадлежит ли будущее этому методу? По мнению самого Джернигена, он определенно помогает ускорить вычисления. Однако будущие поколения программ, моделирующих звездные скопления, скорее всего будут основаны на гибридном методе, применяемом А.Лайтмемом из Астрофизического центра обсерватории Гарвардского колледжа и Астрофизической обсерватории Смитсона, а также С.Макмнлланом из Иллинойсского университета в Урбана-Шампейне. Согласно их методу, к звездам ядра скопления применяется непосредственно моделирование, описанное выше, а к звездам, находящимся вне ядра, применяются статистические методы моделирования так как если бы они представляли собой газ.
Читателям, владеющим языком программирования АПЛ, будет интересно познакомиться с новой публикацией Г.Чентнна из Исследовательского центра Т.Уотсона фирмы IBM в Йорктаун-Хайтсс (шт.Нью-Йорк). Она называется "An APL2 Gallery of Mathematical Physics" ("Галерея математической физики на АПЛ-2") и представляет собой брошюру на 56 страницах, в которой приведены объяснения пяти важнейших физических теорий, включая как ньютоновское, так и релятивистское движение тел в космическом пространстве. Каждая рассмотренная теория иллюстрируется распечатками компьютерных программ, написанных на языке АПЛ.
AN APL2 GALLERY OF MATHEMATICAL PHYSICS - A COURSE OUTLINE. GREGORY J. CHAITIN, IBM Research, P.O.Box 218, Yorktown Heights, N.Y. 10598; 1985.
DIRECT N-BODY CALCULATIONS. SVERRE J. AARSETH in Dynamics of Star Clusters, edited by Jeremy Goodman and Piet Hut. D.Reidel Publishing Company, 1985.
A UNIFIED N-BODY AND STATISTICAL TREATMENT OF STELLAR DYNAMICS. ALAN P. LIGHTMAN AND STEPHEN L.W. MCMILLAN in Dynamics of Star Clusters, edited by Jeremy Goodman and Piet Hut. D.Reidel Publishing Company, 1985.
ОТКЛИКИ
6 1986
В РУБРИКЕ "Занимательный компьютер" в январском номере нашего журнала речь шла о двух программах, CLUSTER и SUPERCLUSTER, которые моделируют эволюцию звездного скопления. Приятно сознавать, что по крайней мере в не скольких тысячах домов они породили новый вид развлечения, вытеснивший на время увлечение телевидением. Некоторые читатели написали о тех проблемах, с которыми они столкнулись при попытке самостоятельно моделировать поведение звезд в скоплении. Но причины этих проблем заключаются не в звездах, а в наших собственных ошибках.
Б.Дэвис из Энн-Арбора (шт.Мичиган) и П.Фортескью из Ла-Холла (шт.Калифорния), реализуя программу SUPERCLUSTER, испытали трудности при составлении уравнений ускорения. Мне кажется, эти трудности можно устранить, заменив силу f в уравнении, приведенном на с.92, ускорением a, возникающим под действием этой силы. Чтобы получить a, нужно разделить f на массу притягиваемой звезды. Э.Одлицко из фирмы AT&T Bell Laboratories указал на то, что координаты звезд, приведенные в таблице на с.93, выражены в тысячах астрономических единиц, а не просто в астрономических единицах. Ну что же, теперь наша Вселенная будет эволюционировать правильно.
Когда наблюдаешь работу программ CLUSTER и SUPERCLUSTER на экране дисплея, то порой очень трудно различить, какие звезды ближе к наблюдателю, а какие дальше. А.Инглиш из Делрей-Бича (шт.Флорида) и П.Стирнз из Лоди (шт.Калифорния) написали специальные отображающие программы, которые генерируют два изображения скопления, расположенные вплотную друг к другу, одно как видимое правым глазом и одно - как левым. Читатели, которые сумеют освоить приемы видения стереоскопического изображения, увидят звездные скопления так же, как и гиперкубы, в захватывающей дыхание глубокой перспективе. (О стереоскопии киперкубов - в том самом 6-м номере, где напечатаны Отклики.- G.).
Некоторые читатели уже составляли программы, подобные программе SUPERCLUSTER, но применяли их не к звездным скоплениям, а к нашей Солнечной системе. Программу SUPERCLUSTER также можно применить для этой цели. Читатели могут сами посмотреть в справочниках величины масс, скоростей и координаты 10 основных небесных тел Солнечной системы на какой-то момент времени и, запустив программу, наблюдать "свысока" за эволюцией системы. Уже через несколько минут наступит 2000 год. Дж.Филипс из Сан-Луи (шт.Миссури) написал программу, моделирующую поведение системы Земля-Луна, включив в нее маленький невесомый космический корабль. Запустить его с Земли так. чтобы он вышел на орбиту вокруг Луны,- задача не такая уж простая. Читатели, добившиеся определенных успехов в этой области, могут попробовать запустить космический корабль так, чтобы он прошел вблизи от всех планет-гигантов Солнечной системы и вышел за се пределы.
У.Хофф из ШампеЙна (шт.Иллинойс) вычислял прирашение времени в модели звездных скоплений динамически, введя переменную dvmax в начале программы. По ходу расчетов движения звезд программа всегда вычисляет максимальное ускорение amax. На следующем этапе моделирования величина прирашения времени равна частному от деления dvmax на amax. Благодаря этой модификации изменения скорости звезд не могут превысить величины dvmax.
ИССЛЕДОВАНИЕ ЗВЕЗДНЫХ СКОПЛЕНИЙ С ПОМОЩЬЮ КОМПЬЮТЕРНОГО ТЕЛЕСКОПА
А.К.ДЬЮДНИ
ДАЛЕКО в космическом пространстве под музыку гравитационных сил в хороводе кружится скопление звезд. На протяжении человеческой жизни их движение мы почти не замечаем, но если рассматривать его в другом временном масштабе, когда годы эквивалентны секундам, то можно увидеть причудливые переплетения звездных траекторий. Иногда две звезды, приблизившись друг к другу, исполняют парный танец, а затем одна из них стремительно уносится в окружающее пространство.
С помощью мощного телескопа можно рассмотреть структуру некоторых звездных скоплений нашей Галактики, но он не позволяет сжать годы в секунды - это может сделать только компьютер. Кроме того, компьютер можно запрограммировать так, что он будет играть роль своеобразного телескопа, позволяющего разглядывать гипотетические звездные скопления. При этом можно наблюдать движение отдельных объектов скопления в космическом временном масштабе, получая последовательность фотоснимков, на которых фиксируются пунктирные траектории каждой звезды, вьющиеся и переплетающиеся с траекториями других звезд скопления (см. рисунок на с.91).

Четыре звезды кружатся в космическом хороводе в течение нескольких лет и затем покидают сцену
Объясняется ли эволюция звездных скоплений, наблюдаемая астрономами, только гравитационными силами? Компьютеры помогают дать ответ как на этот вопрос, так и на другие, связанные с ним. В мае 1984г. в Принстонском университете на очередном 113-м симпозиуме Международного астрономического общества, на этот раз целиком посвященном динамике звездных скоплений, теоретики и специалисты по моделированию обсуждали проблему соответствия между гипотетическими и реальными звездными скоплениями.
Поставить космический балет при помощи компьютера сравнительно несложно. В принципе взаимодействия между звездами, входящими в скопление, описываются простым классическим законом: каждая звезда в паре с каждой другой звездой испытывает действие гравитационной силы, пропорциональной произведению масс звезд рассматриваемой пары и обратно пропорциональной квадрату расстояния между ними. Вычисления по этой формуле выполнить нетрудно: нужно перемножить массы звезд, полученное произведение умножить на коэффициент пропорциональности (гравитационную постоянную) и результат разделить на квадрат расстояния между звездами. Суммарный эффект всех парных взаимодействий, по-видимому, полностью определяет характер изменений, претерпеваемых со временем звездным скоплением. Программа CLUSTER вычисляет результирующую силу, действующую на каждую звезду, и перемещает эту звезду в следующее по времени положение. Процедура циклически повторяется на заданном отрезке времени, соответствующем нескольким столетиям, по принятому в модели масштабу.
Правда, вводить с клавиатуры координаты и скорости большого числа звезд - занятие довольно скучное, но зато вы видите, как перед вами на экране разворачивается эволюция миниатюрной вселенной. Звезды в центральной части скопления движутся по неустойчивым хаотическим орбитам, а те, которые находятся в периферийных областях, медленно уплывают, останавливаются и плавно возвращаются назад. Наиболее интересно наблюдать, как звезды сталкиваются и как некоторые из них покидают скопление.
Когда две звезды сближаются, они сообщают друг другу колоссальные гравитационные ускорения и после столкновения стремительно расходятся в разные стороны. Стремительный выход отдельных звезд за пределы скопления обычно является результатом одного или более таких сближений. Звезда, покинувшая скопление, может вернуться в него, а может и не вернуться. Астрономическое тело обладает определенной скоростью отрыва, зависящей от его массы и массы того тела или объекта, от которого оно отрывается. Если звезда, удаляющаяся от скопления, достигла этой скорости, она никогда к нему не вернется. Те, кто еще не имеют опыта в моделировании звездных скоплений, наверное, часто будут наблюдать "побеги" звезд из составленных ими конфигураций скоплений. На самом деле в звездных скоплениях, построенных новичками, звездный хоровод быстро распадается. Лучше всего начинать с несложных двойных или тройных звездных систем.
Программа CLUSTER имеет простую структуру. Она состоит из цикла инициализации, за которым следует двойной цикл, в котором вычисляются изменения скорости, ускорения и положения каждой звезды как результат суммарного воздействия со стороны остальных звезд. Здесь мы рассмотрим простейшую версию программы, в которой такие величины, как интервал между двумя соседними моментами времени, коэффициент пропорциональности в формуле притяжения и массы звезд, являются как бы "встроенными", т.е. фиксированными. Несмотря на свою простоту, даже эта версия программы CLUSTER способна моделировать почти все явления, присущие звездным скоплениям. В программе используются три множества массивов. В массивах первого множества хранятся значения ускорений, которыми обладают звезды на данный момент в каждом направлении по трем осям координат. Имена этих массивов соответственно ax, ay и az. Таким образом, ax(i), ay{i) и az(i) указывают компоненты ускорения i-й звезды по осям x, y и z. Элементы этих трех массивов не обязательно инициализировать (т.е. присваивать им начальные значения) перед выполнением программы. Массивы второй группы vx, vy и vz хранят значения скоростей: vx(i), vy(i) и vz(i) указывают соответственно компоненты скорости i-й звезды вдоль осей x, y и z. Массивы третьей группы предназначены для координат положения звезд: x(i), y(i) и z(i) соответственно указывают координаты положения i-й звезды в данный момент по осям x, y и z. Элементы массивов x, y, z и vx, vy и vz следует инициализировать в начале программы.
Вслед за блоком инициализации идет главная часть программы CLUSTER. Двойной цикл может повторяться автоматически до бесконечности, или же программист должен указать, при каких условиях производится повторное выполнение цикла. Во внешнем цикле каждая звезда рассматривается по очереди и компоненты ее ускорения устанавливаются равными нулю. После этого во внутреннем цикле вычисляются силы, действуюшне на каждую звезду со стороны остальных звезд, входящих в скопление.
Предположим, к примеру, что индекс внешнего цикла равен i, а индекс внутреннего цикла - j. Во внутреннем цикле вначале производится проверка, не равен ли индекс i индексу j. Если индексы оказываются равными, программа не вычисляет силу, поскольку звезда сама себя не притягивает. Во всяком случае, это вычисление привело бы к попытке деления на нуль. (Это, пожалуй, единственная ситуация, в которой я мог бы искренне посочувствовать компьютеру). Когда i и j не равны друг другу, программа CLUSTER пользуется формулой евклидова расстояния между звездами: разности координат по осям x, y и z возводятся в квадрат и складываются друг с другом. В результате мы получаем, конечно, квадрат расстояния. Затем производится проверка, не равно ли полученное расстояние нулю. Если да, то нужно дать сигнал тревоги в той или иной форме, потому что компьютеру вскоре придется выполнить операцию деления на нуль. Моя версия программы в таких случаях выдаст сообщение "Столкновение!"
Если все в порядке, команды внутреннего цикла завершают вычисление расстояния между звездами, беря квадратный корень из квадрата расстояния, вычисленного ранее. Затем производится деление числа I000 на квадрат полученного расстояния и в результате этого деления получается значение силы. Наконец, последняя задача, которую нужно решить во внутреннем цикле,- это определить компоненты ускорения i-й звезды. Для этого необходимо суммировать все силы, действующие со стороны других звезд. Например, компонента ускорения i-й звезды по оси x может быть выражена в общем виде следующим образом:
ax(i) <- ax(i) + f*(x(j) - x(i))/d.
Здесь f и d представляют соответственно силу и расстояние. Отношение проекции расстояния между звездами i и j на ось x к полному расстоянию в точности соответствует составляющей силы, действующей на звезду i вдоль оси x. Компоненты ускорения звезды вдоль осей у и z вычисляются аналогичным образом.
Завершают программу два цикла, следующие один за другим. В первом осуществляется изменение значения скорости, а во втором - положения. Здесь возникает одна тонкость, на которую обратил мое внимание Дж.Хаббард, математик из Корнеллского университета, чей совет по поводу вычислений, выполняемых над множеством Мандельброта, оказался в высшей степени полезным (см. статью в рубрике "Занимательный компьютер" в журнале "В мире науки", 1985, #10). Дело в том, что можно вычислять координаты положения звезды до вычисления ее скорости, и получающиеся при этом результаты выглядят достаточно правдоподобными. Однако со временем движение звезд станет неестественным, поскольку при таком вычислении координат положения и скоростей звезд будет нарушаться закон сохранения энергии.
В цикле изменения скорости к текущему значению этой переменной просто прибавляется ускорение согласно следующей формуле:
vx(i) <- vx(i) + ax(i).
Здесь предполагается, что временной интервал между двумя последовательными моментами равен единице времени, через которую выражается скорость. Аналогичные формулы применяются для вычисления составляющих vy и vz. Вычисления координат, выполняемые в последнем цикле, также очень просты:
x(i) <- x(i) + vx(i).
Аналогичным образом изменяются элементы массивов y и z. На основе данных, получаемых в последнем цикле, программа CLUSTER определяет положение каждой звезды на двумерной поверхности экрана дисплея. При этом первые две координаты "наносятся" на экран, а третья координата по оси z игнорируется. Таким образом, можно представить себе, что мы наблюдаем скопление через иллюминатор, роль которого играет экран. Значения величин, вычисляемых в программе моделирования скопления, иногда оказываются очень малыми, а иногда и очень большими. По этой причине мы советуем вользоваться арифметическими операциями с двойной точностью так, чтобы округления не нарушали картины.
Время, затрачиваемое программой CLUSTER на один вычислительный цикл, зависит от количества звезд в системе. Системы, насчитывающие около 10 звезд, отличаются интересным (с эстетической точки зрения) повелением, но для того, чтобы достичь реалистичной сложности, количество звезд должно быть порядка 100 или лаже 1000. К сожалению, число шагов алгоритма в основном вычислительном цикле возрастает как квадрат числа звезд в скоплении. И хотя специалисты по моделированию звездных систем нашли интересный способ обойти это ограничение, возникает рял других проблем, осложняющих моделирование.
Наиболее серьезная проблема связана с тем обстоятельством, что мы пытаемся с помощью дискретной модели описать поведение по существу непрерывной системы. Непрерывные гладкие орбиты аппроксимируются последовательностью скачков, траектория которых все дальше удаляется от истинной орбиты, по которой звезда движется в скоплении. Неточности подобного рода можно в какой-то степени скорректировать при наличии статистической регулярности, но когда звезды подходят друг к другу на очень малое расстояние, дискретная модель неестественно и непоправимо усиливает эффекты, связанные с большими гравитационными ускорениями.
Если, например, в ходе выполнения вычислительного цикла одна звезда (Стелла) оказывается в непосредственной близости от другой звезды (Астер), мощное гравитационное поле резко увеличивает компоненты ускорения обеих звезд. Это увеличение на последующих шагах вычисления распространяется на компоненты скорости, а затем и на координаты положения звезд. На следующей итерации процесса моделирования Стелла оказывается уже очень далеко от Астера и не может "выплатить гравитационного долга". Таким образом возник излишек кинетической энергии. За счет этого эффекта искусственные звездные скопления распадаются быстрее реальных. Есть два пути преодоления указанного затруднения. Первый путь трудный, второй проще. В первом случае необходимо вычислять кеплеровские орбиты для пары близко сошедшихся звезд. Теоретики предпочитают этот метол прежде всего потому, что формулы, по которым вычисляются орбиты, являются абсолютно точными. Более простой, но иногда неточный метод обработки данных, описывающих ситуации, когда звезды приближаются друг к другу, заключается в том, чтобы уменьшить масштаб шагов по времени в основном вычислительном цикле. Возможно, читатели пожелают взять на вооружение этот прием и воспользоваться им при составлении усовершенствованной версии программы - SUPERCLUSTER.
Программу SUPERCLUSTER можно получить путем несложной модификации программы CLUSTER. Во-первых, в программе SUPERCLUSTER массы звезд, входящих в скопление, могут быть различными. Это изменение можно легко реализовать, введя перед началом выполнения программы значения масс в массив m. Расчет гравитационной силы несколько усложняется: сила уже не является функцией только 1/d2, она теперь пропорциональна произведению масс, деленному на d2. Кроме того, новая версия программы отличается тем, что звезды подразделяются на спектральные типы. Как и для масс, в программе организуется массив spec, элементы которого должны быть заданы перед началом выполнения программы. Однако этот массив используется только в фазе высвечивания звезд на экране после очередной итерации вычислений. Цвет звезд изменяется в пределах от голубого до красного. Зеленый цвет отсутствует. Третье усовершенствование программы CLUSTER состоит в том, что шаг по времени берется произвольным.
В программе SUPERCLUSTER используется переменная delta. значение которой равно интервалу между двумя последовательными моментами времени. Эта величина устанавливается перед началом выполнения основных вычислительных циклов. Конечно, эта переменная должна повлиять на формулы, по которым вычисляются изменения как скорости, так и положения звезд: в формуле для скорости на нее множится ускорение, а в формуле для координат на нее множится скорость.
Рассмотрим теперь простой способ, позволяющий обрабатывать данные, описывающие ситуации, возникающие при сближении звезд. Прежде всего нужно четко установить критерий "близости". Затем в программу нужно ввести проверку, соответствующую выбранному критерию. Проверка должна производиться сразу после вычисления расстояния между двумя звездами. Если зафиксировано "сближение", программа SUPERCLUSTER заменяет значение delta, уменьшая ее до одной десятой от ее текущей величины,- по крайней мере до тех пор, пока ни одна пара звезд уже не будет удовлетворять критерию близости. Этот прием, конечно, помогает смягчить внезапные скачки гравитации в дискретной модели. Однако он создает еше более серьезные проблемы, когда звезды по-настоящему близко подходят лруг к другу. Если расстояние между звездами уменьшается, скажем, в 10 раз, то гравитационная сила увеличивается в 100 раз! К счастью, опасные сближения случаются довольно редко. Метод уменьшения временного интервала был стандартным средством, которым обычно пользовались специалисты, профессионально занимающиеся моделированием звездных скоплений.
Чтобы программа SUPERCLUSTER давала небессмысленные с астрономической точки зрения результаты, нужно ввести единицы измерения расстояния, массы, а также некоторые другие характеристики физической реальности. В астрономии принята удобная мера расстояния, называемая астрономической единицей (АЕ) и соответствующая среднему расстоянию от Земли ло Солнца. Массу можно измерять, приняв за единицу массу Солнца, а время лучше всего измерять в годах. При этих условиях универсальная постоянная гравитационною притяжения булет приблизительно равна 39. В программе SUPERCLUSTER используется именно это значение в отличие от 1000, принятого в программе CLUSTER.
Теперь все готово к тому, чтобы запустить любую из рассмотренных нами программ. В качестве предварительного упражнения для программы CLUSTER можно взять четыре звезды. Расположим их по вершинам квадрата, размер которого на экране был бы 3-5см. Помимо координат x и y, соответствующих плоскости экрана, для каждой звезды следует задать также, вообще говоря, ненулевое значение координаты z. В противном случае пространство, в котором движутся звезды, будет ограничено плоскостью и сближения между ними будут наблюдаться намного чаще. Компоненты скоростей должны быть небольшими (скажем, в пределах от -5
до +5), а направление скоростей должно быть выбрано так, чтобы звезды двигались по часовой стрелке по замкнутым траекториям.
Программу SUPERCLUSTER можно попробовать в действии на звездной системе, изображенной на рисунке на с.92. Эта система образована звездами, являющимися ближайшими соседями Солнечной системы в нашей Галактике. Что случилось бы, если бы Солнце и несколько соседних с ним звезд были отрезаны (в гравитационном смысле) от остальной части Галактики и предоставлены сами себе на неограниченное время? Каким было бы движение звезд? Образовали бы они звездное скопление или рассеялись? Этот вопрос может иметь, а может и не иметь научного значения, однако сам по себе он интересен. Кроме того, точные координаты и скорости известны нам лишь лля нескольких ближайших звезд (см. таблицу на с.93).

Могли бы звезды соседней с нашей галактики образовать звездное скопление?

Параметры всех (за исключением трех) звезд, ближайших соседей Солнечной системы
Звездные скопления бывают либо открытыми (рассеянными), либо шаровыми. Открытые скопления насчитывают несколько тысяч звезд, в то время как число звезд в шаровых скоплениях может достигать нескольких миллионов. Пока исследователи, среди которых можно назвать н Дж.Джернигена, работающего в Калифорнийском университете в Беркли, ограничивались моделированием лишь открытых звездных скоплений и не очень многочисленных. Шаровые скопления пока остаются неприступными. Тем не менее Джерниген и некоторые другие пионеры моделирования, например такие, как Аарсет также из Калифорнийского университета в Беркли, уже на протяжении десятилетий наблюдают коллапсы звездных скоплений, моделируемых на ЭВМ. В качестве количественной характеристики коллапса рассматривается сферический объем, занимающий центральную часть скопления и содержащий в себе 10% его полной массы. Радиус этой сферы называют десятипроцентным радиусом. Явление коллапса начинается, когда десятипроцентный радиус уменьшается со временем. При этом центральная часть скопления неизбежно становится все плотнее н плотнее. Но, поскольку моделируемые звезды являются математическими точками, в таких звездных скоплениях никогда не происходит ничего страшного. В них не возникает никаких черных дыр. Это подтверждают и теоретики, занимающиеся моделированием звездных скоплений. У нас также пока мало свидетельств тому, что подобные ярко выраженные коллапсы случаются и в реальных скоплениях звезд. Какие-то факторы, по-видимому, мешают возникновению коллапса.

Шаровое звездное скопление Мессье 13 в созвездии Геркулеса
Как традиционные, так и современные эксперименты по моделированию звездных скоплений могут дать ключ к этой загадке. Во многих случаях начинающийся коллапс центральной части скопления фактически останавливался несколькими двойными звездными системами, расположенными в центре моделируемого скопления. В одном из экспериментов Джернигена достаточным для этого, по-видимому, оказалось присутствие лишь одной такой системы. Как это можно объяснить? По мнению аспиранта Д.Портера, работающего под руководством Джернигена, объяснение может заключаться в том, что "очень плотные двойные звездные системы вращаются с такой колоссальной скоростью, что отталкивают приближающиеся к ним звезды по касательной, и последние либо вращаются по круговым орбитам вокруг центра скопления, либо лаже возвращаются в область меньшей плотности, окружающую ядро скопления и называемую короной. Это, наверное, и есть тот механизм, который предотвраoает чрезмерное уплотнение ядра скопления".
В свое время Джeрниген занимался наблюдением звезд - источников рентгеновского излучения. Когда его исследования сконцентрировались на поисках источников рентгеновского излучения в звездных скоплениях, он стал все больше интересоваться природой звездных скоплений как таковых. Моделирование показалось ему эффективным средством исследования.
Джерннген внес важный вклад в технику моделирования, повышающий его эффективность. В программе CLUSTER и других подобных программах один вычислительный никл для п звезд требует n2 шагов вычисления. Цикл Джерннгена требует лишь п*log(n) шагов. Он разбивает моделируемое скопление на пары соседних звезд. Затем каждая такая пара заменяется некоторой фиктивной массой и скоростью, описывающими результирующее поведение пары. Затем тот же процесс применяется уже к парам звезд так, как если бы они были отдельными звездами. По мере того как развивается этот процесс разбиения на пары, возникают все новые узлы масс в структуре данных, называемой деревом. При этом корневой узел дерева представляет уже все скопление звезд. Теперь можно вычислить характеристики движения как для центрального узла, так и для всех ветвей дерева, вплоть до индивидуальных звезд.
Принадлежит ли будущее этому методу? По мнению самого Джернигена, он определенно помогает ускорить вычисления. Однако будущие поколения программ, моделирующих звездные скопления, скорее всего будут основаны на гибридном методе, применяемом А.Лайтмемом из Астрофизического центра обсерватории Гарвардского колледжа и Астрофизической обсерватории Смитсона, а также С.Макмнлланом из Иллинойсского университета в Урбана-Шампейне. Согласно их методу, к звездам ядра скопления применяется непосредственно моделирование, описанное выше, а к звездам, находящимся вне ядра, применяются статистические методы моделирования так как если бы они представляли собой газ.
Читателям, владеющим языком программирования АПЛ, будет интересно познакомиться с новой публикацией Г.Чентнна из Исследовательского центра Т.Уотсона фирмы IBM в Йорктаун-Хайтсс (шт.Нью-Йорк). Она называется "An APL2 Gallery of Mathematical Physics" ("Галерея математической физики на АПЛ-2") и представляет собой брошюру на 56 страницах, в которой приведены объяснения пяти важнейших физических теорий, включая как ньютоновское, так и релятивистское движение тел в космическом пространстве. Каждая рассмотренная теория иллюстрируется распечатками компьютерных программ, написанных на языке АПЛ.
AN APL2 GALLERY OF MATHEMATICAL PHYSICS - A COURSE OUTLINE. GREGORY J. CHAITIN, IBM Research, P.O.Box 218, Yorktown Heights, N.Y. 10598; 1985.
DIRECT N-BODY CALCULATIONS. SVERRE J. AARSETH in Dynamics of Star Clusters, edited by Jeremy Goodman and Piet Hut. D.Reidel Publishing Company, 1985.
A UNIFIED N-BODY AND STATISTICAL TREATMENT OF STELLAR DYNAMICS. ALAN P. LIGHTMAN AND STEPHEN L.W. MCMILLAN in Dynamics of Star Clusters, edited by Jeremy Goodman and Piet Hut. D.Reidel Publishing Company, 1985.
ОТКЛИКИ
6 1986
В РУБРИКЕ "Занимательный компьютер" в январском номере нашего журнала речь шла о двух программах, CLUSTER и SUPERCLUSTER, которые моделируют эволюцию звездного скопления. Приятно сознавать, что по крайней мере в не скольких тысячах домов они породили новый вид развлечения, вытеснивший на время увлечение телевидением. Некоторые читатели написали о тех проблемах, с которыми они столкнулись при попытке самостоятельно моделировать поведение звезд в скоплении. Но причины этих проблем заключаются не в звездах, а в наших собственных ошибках.
Б.Дэвис из Энн-Арбора (шт.Мичиган) и П.Фортескью из Ла-Холла (шт.Калифорния), реализуя программу SUPERCLUSTER, испытали трудности при составлении уравнений ускорения. Мне кажется, эти трудности можно устранить, заменив силу f в уравнении, приведенном на с.92, ускорением a, возникающим под действием этой силы. Чтобы получить a, нужно разделить f на массу притягиваемой звезды. Э.Одлицко из фирмы AT&T Bell Laboratories указал на то, что координаты звезд, приведенные в таблице на с.93, выражены в тысячах астрономических единиц, а не просто в астрономических единицах. Ну что же, теперь наша Вселенная будет эволюционировать правильно.
Когда наблюдаешь работу программ CLUSTER и SUPERCLUSTER на экране дисплея, то порой очень трудно различить, какие звезды ближе к наблюдателю, а какие дальше. А.Инглиш из Делрей-Бича (шт.Флорида) и П.Стирнз из Лоди (шт.Калифорния) написали специальные отображающие программы, которые генерируют два изображения скопления, расположенные вплотную друг к другу, одно как видимое правым глазом и одно - как левым. Читатели, которые сумеют освоить приемы видения стереоскопического изображения, увидят звездные скопления так же, как и гиперкубы, в захватывающей дыхание глубокой перспективе. (О стереоскопии киперкубов - в том самом 6-м номере, где напечатаны Отклики.- G.).
Некоторые читатели уже составляли программы, подобные программе SUPERCLUSTER, но применяли их не к звездным скоплениям, а к нашей Солнечной системе. Программу SUPERCLUSTER также можно применить для этой цели. Читатели могут сами посмотреть в справочниках величины масс, скоростей и координаты 10 основных небесных тел Солнечной системы на какой-то момент времени и, запустив программу, наблюдать "свысока" за эволюцией системы. Уже через несколько минут наступит 2000 год. Дж.Филипс из Сан-Луи (шт.Миссури) написал программу, моделирующую поведение системы Земля-Луна, включив в нее маленький невесомый космический корабль. Запустить его с Земли так. чтобы он вышел на орбиту вокруг Луны,- задача не такая уж простая. Читатели, добившиеся определенных успехов в этой области, могут попробовать запустить космический корабль так, чтобы он прошел вблизи от всех планет-гигантов Солнечной системы и вышел за се пределы.
У.Хофф из ШампеЙна (шт.Иллинойс) вычислял прирашение времени в модели звездных скоплений динамически, введя переменную dvmax в начале программы. По ходу расчетов движения звезд программа всегда вычисляет максимальное ускорение amax. На следующем этапе моделирования величина прирашения времени равна частному от деления dvmax на amax. Благодаря этой модификации изменения скорости звезд не могут превысить величины dvmax.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
4 1986
ОТ ШАХМАТНЫХ ПРОГРАММ К СПЕЦИАЛИЗИРОВАННЫМ ШАХМАТНЫМ КОМПЬЮТЕРАМ
А.К.ДЬЮДНИ
ЕСЛИ бы программа CRAY BLITZ могла запоминать не только шахматные ходы, она навечно сохранила бы в своей памяти события 15 октября 1985г., когда состоялся последний тур шахматного чемпионата Северной Америки среди компьютеров, приуроченного к очередной конференции Ассоциации специалистов по вычислительной технике. Перед участниками на сцене зала заседаний отеля "Радиссон" в Денвере было установлено пять столов, отделенных от зрителей барьером. За каждым столом напротив друг друга сидели представители двух команд - программисты и консультанты. Иногда они шутили, а иногда их лица выражали ожидание и глубокие раздумья. Над каждым столом висели экраны, на которые проектировались позиции на шахматной доске.
В турнире принимали участие 10 программ - претендентов на звание чемпиона Северной Америки. Их названия звучат странно и непривычно, что свидетельствует о различном происхождении программ и о честолюбивых замыслах их создателей: AWIT, ВЕВЕ, CHAOS, CRAY BLITZ, HITECH, INTELLIGENT SOFTWARE, LACHEX, OSTRICH, PHOENIX и SPOC (см. таблицу на с.95). В этом списке отсутствуют названия трех программ из числа тех, что имели наибольший успех на компьютерной шахматной арене в течение нескольких последних лет: BELLE, CHESS 4.7 и NUCHESS.

Участники чемпионата Северной Америки 1985г. по шахматам среди компьютеров
Самый большой интерес вызвала встреча между CRAY BLITZ и HITECH. Первую программу за столом соревнований представляют Р.Хьят из Южно-Миссисипского университета, А.Гауер, шахматный эксперт из того же университета и X.Нельсон из Лоуренсовской национальной лаборатории в Ливерморе. Напротив: X.Берлинер из Университета Карнеги - Меллона и М.Кемпбелл, один из аспирантов того же университета, шахматист высокого класса. Берлинер выступает сразу в двух лицах - и как шахматный консультант, и как программист в команде HITECH. По мере того как развиваются события на доске, напряжение возрастает. Берлинер часто встает из-за стола с усталой улыбкой. Как-то проходя мимо меня, он пробормотал: "Уж слишком это напоминает мне то время, когда я сам играл на чемпионатах США!" (В течение нескольких лет в конце 50-х - начале 60-х годов Берлинер входил в десятку лучших игроков США).
В отличие от чемпионата страны, когда в игровом зале царит мертвая тишина, этот турнир протекает в оживленной атмосфере. Кругом слышатся разговоры, иногда даже смех, постукивают клавиши терминалов, игру постоянно комментирует в микрофон темпераментный по натуре судья М.Валво, консультант по вычислительной технике, мастер международного класса по шахматам из Седона (шт.Аризона): "Слабый ход черных. Король все еще находится в слишком уязвимом положении, а сдвоенные пешки на c5 и c6 затрудняют защиту". Рядом член команды CRAY BLITZ воскликнул, ни к кому конкретно не обращаясь: "Забавно! Я думал, она сыграет королем на f3". Шахматисты-профессионалы пока еше замечают погрешности в игре компьютера, а программисты в свою очередь все еще удивляются способностям своих творений.
На протяжении всего заключительного этапа игры было видно, что HITECH имеет преимущество над своим соперником. В начале игры CRAY BLITZ попала в трудное положение, выйти из которого можно было либо с материальными потерями, либо уступив инициативу. В сложившейся ситуации CRAY BLITZ была вынуждена неудачно расположить свои пешки. HITECH продолжала развивать преимущество.
К полуночи почти все было кончено. Большинство игр завершилось, и специалисты настаивали, чтобы победа была присуждена программе HITECH. Команда CRAY BLITZ просила судью Валво разрешить им сдаться. Он предложил сделать еше два хода: если положение белых не улучшится, то они могут признать себя побежденными. Положение не улучшилось, и они сдались. HITECH стала чемпионом Северной Америки, по существу королем компьютерных шахмат. И хотя CRAY BLITZ пока остается официальным чемпионом мира (этот титул был завоеван ею в 1983г. и защищать его предстоит лишь в июне этого года), победа HITECH наряду с ее победами в трех других турнирах производит внушительное впечатление. На сегодняшний день HITECH почти наверняка является самой сильной в мире компьютерной программой, играющей в шахматы.
Представители соперничавших команд улыбаются, обмениваются мнениями о только что закончившемся турнире. Повлияло ли на его исход отсутствие программ BELLE, CHESS 4.7 и NUCHESS? "Конечно, было бы интересно посмотреть на игру BELLE и некоторых других программ,- сказал один из организаторов турнира,- но я не думаю, что исход соревнований был бы иным". Он отметил, что по составу программ и машин, принимавших участие в турнире, между чемпионатом Северной Америки и чемпионатом мира почти нет разницы. Разговор перешел к обсуждению поединка между Каспаровым и Карповым, затем шахматной теории. "Я не шучу,- говорит, очевидно, сведущий участник разговора,- программа, способная анализировать ситуации на 20 ходов вперед и оценивающая позиции лишь с точки зрения материального преимущества, может обыграть любого гроссмейстера". Возник спор, но ненадолго. Уже через несколько минут зал опустел. Чемпионат Северной Америки завершился.
Высказывание, касающееся способности программы, предвидящей развитие игры вперед на 20 ходов, заслуживает внимания. Графически шахматную игру можно представить в виде разветвленного дерева, состоящего из узлов и соединяющих их линий. При этом дерево как бы перевернуто - его корневой узел находится вверху. Каждый узел соответствует одной из возможных позиций, т.е. тому или иному расположению фигур на шахматной доске, которое может быть достигнуто после определенного числа ходов, дозволенных правилами. Узел соединяется со своим "потомком" линией в том случае, если позиция, представляемая последними, получается из той, которая ей предшествовала до того, как был сделан один ход фигурой или пешкой. На шахматном дереве всякую партию можно отождествить с каким-нибудь одним конкретным путем, ведущим из корневого узла (соответствующего исходной позиции, когда еше не было сделано ни одного хода) к какому-то конечному узлу, представляющему, как правило, такую позицию, в которой на шахматной доске остается лишь несколько фигур и одна из сторон либо получает мат, либо вынуждена сдаться.
Программа, играющая в шахматы, должна исследовать по возможности лишь ту часть игрового дерева, которая оказывается необходимой. Исходя из узла, представляющего позицию, сложившуюся в игре на данный момент, она исследует все узлы - потомки данного (слой 1), затем все узлы - потомки этих потомков (слой 2) и т.д. Средняя глубина исследования дерева игры является мерой "интеллекта" программы, под которым понимается ее способность наперед видеть возможные позиции и производить их оценку на каждом уровне дерева. Программа анализирует позиции и каждой из них ставит в соответствие определенное числовое значение, которое отражает степень "выгодности" достижения этой позиции. Пользуясь так называемой минимаксной процедурой, программа возвращает некоторые из полученных значений вверх по дереву на слой 1. Узел, получивший наибольшее значение, и определяет следующий ход.
Существует довольно интересная связь между двумя упомянутыми составляющими, которые определяют интеллект программы: чем лучше механизм оценивания позиций, тем меньше необходимая глубина исследования дерева игры. На самом деле если бы программа обладала идеальной схемой оценивания, то ей никогда не потребовалось бы просматривать дерево глубже, чем на один слой. В то же время программа с очень простой схемой оценивания, чтобы демонстрировать достаточно хорошую игру, должна просматривать дерево глубже. Возникает вопрос: насколько глубоким должен быть поиск при оценивании позиций только с точки зрения обеспечения материального преимущества, чтобы программа могла успешно соперничать с игроком гроссмейстерского класса? Достаточно ли будет 20 слоев?
Звание гроссмейстера присваивается международной шахматной федерацией игрокам, отличившимся в международных соревнованиях (федерация не рассматривает результаты, достигнутые компьютерами). Гроссмейстеры обычно имеют "рэйтинг" выше 2400 баллов. К началу чемпионата Северной Америки по шахматам среди компьютеров HITECH сыграла 21 партию в турнирах с шахматистами высокого класса и набрала 2233 балла. Это самый высокий в мире результат, достигнутый компьютером. По словам Берлинера, имевшего в свое время рэйтинг 2443 балла, рэйтинг HITECH возрастал в среднем на 8 баллов за игру на турнирах, проводившихся в США. Означает ли это, что через двадцать с лишним игр машина превзойдет своего создателя?
В связи с этим невольно задаешься вопросом, насколько хорошими игроками станут в конце концов компьютеры. Станет ли компьютер когда-либо лучшим в мире шахматистом? Д.Леви, в прошлом шахматист, а теперь бизнесмен и литератор, не раз заключал пари в спорах по данному вопросу. В 1968г. он поспорил на 500долл. с Дж.Маккарти из Станфордского университета, утверждая, что на протяжении следующих 10 лет ни одному компьютеру не удастся его обыграть. В августе 1978г. на канадской выставке в Торонто Леви получил свои 500 долл. Там он выиграл соревнование с программой CHESS 4.5, созданной в Северо-Западном
университете. На следующие 6 лет Леви заключил пари уже на 6000 долл. В апреле 1984г. Леви, находясь в Лондоне, сыграл по телефону матч с CRAY BLITZ и опять выиграл.
Удача воодушевила Леви до такой степени, что он предложил в Денвере новое пари на сумму 100тыс. долл.: в течение следующих 10 лет любой компьютер будет побежден игроком - человеком, которого выберет Леви. Если кто-нибудь примет пари Леви, то, наверное, выставит против него не просто программу, а специализированный компьютер. Пока желающих заключить это пари не нашлось.
Два лучших участника Североамериканского турнира, HITECH и ВЕВЕ, по существу представляют собой такие шахматные машины. Интересно отметить, что программа, выставленная самим Леви, INTELLIGENT SOFTWARE, заняла на турнире третье место. Она написана для компьютера Apple IIe, в котором нет никаких изощренных аппаратных средств, за исключением платы акселератора, представляющей собой электронную схему, удваивающую быстродействие машины. Вероятно, Леви удалось разработать лучшую схему оценивания позиций.
Шахматные знатоки, присутствовавшие на чемпионате, сходятся на том, что лучшая партия на чемпионате была сыграна во втором туре между CRAY BLITZ и ВЕВЕ, продуктом коммерческого предпринимательства. Т.Шерцер из компании SYS-10, Inc., разработавший ВЕВЕ, возил свое изобретение на несколько турниров, состоявшихся в последние годы. ВЕВЕ - это не просто программа, а специализированная шахматная машина. Упомянутая партия имела важное значение не только потому, что была наиболее интересной на чемпионате, но и потому, что в ней CRAY BLITZ потерпела первое поражение за три года.
Читатели, располагающие шахматной доской, могут проследить за игрой между CRAY BLITZ и ВЕВЕ, рассмотрев 50 ходов, приведенных ниже. Фигуры обозначены заглавными буквами: Кр - король, Ф - ферзь, С - слон, К - конь, Л - ладья. Клетки, или поля, шахматной доски обозначаются буквенными и цифровыми координатами. Если доска установлена перед вами так, что нижнее левое поле черное, то по горизонтали поля нумеруются слева направо латинскими буквами a, Ь, c, d. e, f, g, h, а по вертикали - цифрами от 1 до 8 снизу вверх. Обозначения, применяемые для записи ходов игры, как это приведено ниже, иногда совершенно однозначны, например Крb1 (король ходит на поле b1), а иногда не совсем понятны, например Kf3 (конь ходит на f3). Какой из двух коней? В данном случае лишь один конь может ходить на поле f3. Ход пешки обозначается просто указанием поля, на которое она ходит, скажем e4. Партию записал Валво:
CRAY BLITZ (белые) - ВЕВЕ (черные)
1. e4 c5
2. Кf3 d6
3. d4 cd
(Обозначение cd означает, что пешка с поля c бьет пешку на поле d).
4. К:d4 Кf6
(Знак ":" означает, что фигура бьет фигуру или пешку противника).
5. КcЗ g6
6. Сg5 Сg7
7. Фd2 Кcб
8. 0-0-0 0-0
(Рокировка: у белых на ферзевом фланге, у черных на королевском).
9. Кb3 Лe8
10. Сc4 Kg4
Черные сыграли Кg4, готовясь к тому, чтобы затем сыграть 11... С:c3. Черные, наверное, считали, что после этого белые вынуждены будут сыграть 12. bc. Однако черные, должно быть, передумали, проанализировав другой возможный ход белых. Если С:c5, то Ф:c3! Ход К:f2 станет бессмысленным, если одна из ладей белых сыграет на f1, в то время как ход белых С:f7+ (шах) был бы для черных роковым.
11. h3 Кge5
12. Сb5 a6
13. Сe2 a5
14. СЬ5 Сe6
15. Кd5 a4
16. Кd4 Сd7
Положение белых становится отчаянным. Пешка черных (a4) создает угрозу на королевском фланге белых.
17. К:c6 bc
18. К:e7+ Л:e7
19. С:e7 Ф:e7
20. Сe2 Фe6
21. Крb1 Лb8
(Положение фигур на доске после 21 -го хода показано на рисунке слева). Черные угрожают ходом 22... Лb2+ , затем последует 23. Крb2 Кc4, "вилка", в результате которой белые проигрывают ферзя.

Положение после 21-го хода
22. b3 ab
23. cb Сe8
24. Крc2 Кd7
25. f3 Лa8
26. Крc1 Кc5
27. Фc2 Фf6
28. Сc4 Фа1
29. Крd2 Ф:a2
Более сильный ход был бы 29...Сc3+ , шах, за которым последовал бы 30. Крe2 Л:a2!
30. Ф:a2 Л:a2+
31. Крc1 d5
32. ed cd
33. С:d5 Сb5
34. Лhe1 Кd3+
Материальный перевес черных на одну фигуру может стать ощутимее в результате очередного размена. В игре шахматистов в этой позиции белые, наверное, признали бы себя побежденными.
35. Л:d3 С:d3
36. Лe8+ Сf8
37. g4 Крg7
38. Ле3 Сa3+
39. Крd1 Лa1+
40. Крd2 Сf1
41. Крc3 Лc1+
42. Крd2 Лc5
43. Крe1 С:h3
44. Сc4 h5
45. gh gh
46. Крf2 h4
47. Лd3 Сf5
48. Лd4 h3
49. Лh4 Лс7
Сделав ход 50. Лh5, белые сдались
Программа CRAY BLITZ выполняется на компьютере CRAY XM-P 48. Славящийся своим быстродействием и большим числом процессоров CRAY тем не менее представляет собой универсальную ЭВМ, а не специализированную шахматную машину. Очевидно, система ВЕВЕ, аппаратные средства которой специально предназначены для игры в шахматы, превзошла комбинацию машины CRAY и программы CRAY BLITZ.
Система HITECH в определенном смысле еще более специализирована. Когда Университет Карнеги-Меллона был еще Технологическим институтом Карнеги, там была разработана программа TECH, играющая в шахматы. Имя HITECH отражает тот факт, что Берлинер, Кемпбелл и другие ее разработчики: К.Эбелинг, Г.Гетш, Э.Пэлей и Л.Сломер, приспособили заложенные в программе ТЕСН принципы к новой технике на сверхбольших интегральных схемах (СБИС) и с параллельным режимом работы. Машина HITECH представляет собой компьютер Sun с процессором специальной конструкции, который Берлинер называет поисковым. Компьютер Sun выполняет три программы: интерфейс с пользователем, управляющую программу и программу "оракул". Последняя представляет собой то, что специалисты в области шахматных программ называют "книгой". Это обширный каталог известных в шахматной литературе дебютов и их вариаций. База данных оракула содержит также значительный объем других сведений из теории шахмат, которые нетрудно пополнять. Когда поисковый процессор исследует возможные варианты развития игры из заданной позиции, он прибегает к этой информации и с помощью оракула выбирает ту, которая имеет отношение к данной позиции.
Сам же поисковый процессор состоит из микропроцессора и нескольких аппаратных модулей, которые генерируют ходы, оценивают их, проверяют, не повторяются ли ходы, и т.д. Микропроцессор координирует действия, выполняемые этими модулями. Генератор ходов состоит из 64 СБИС, по одной микросхеме на каждое поле шахматной доски. Каждая микросхема "просматривает" всю доску, чтобы определить, может ли какая-нибудь фигура или пешка пойти на контролируемое ею поле. Она определяет наилучший ход, пользуясь такими стандартными критериями, как возможность взятия фигуры или пешки противника или обеспечение господства в центре доски. Одновременно другие 63 микросхемы заняты той же работой (параллельный режим). Если на доске 10 фигур, то подобная архитектура аппаратных средств означает, что ходы генерируются в 10 раз быстрее при прочих равных условиях.
Процедура оценивания должна вовремя поспевать за генерацией ходов. На первой стадии оценивание производится самим генератором ходов, В нем содержится своего рода "эксперт", который оценивает все ходы, генерируемые каждой из 64 микросхем. Каждая такая микросхема вычисляет значение, характеризующее силу наилучшего из рассмотренных ею ходов и передает это значение выбирающему ход "эксперту". Числа, генерируемые микросхемами, дублируются привлекающими внимание звуковыми сигналами. "Эксперт" располагает их в порядке громкости (т.е. эффективности ходов).
Затем HITECH приступает к поиску на игровом дереве, следуя вариантам, выбранным "экспертом" из всех возможных в данной позиции. Затем производится еще одно оценивание, теперь уже для каждой новой позиции, генерируемой на дереве игры. Пользуясь познаниями шахматной теории (поставляемыми оракулом), применимыми к данной позиции, модуль оценивания рассматривает каждую из них независимо от того, находится ли эта позиция на горизонте средней глубины просмотра или нет. В этом заключаются преимущества и сама сущность параллелизма - дополнительная работа не требует дополнительного времени. Управляющая программа компьютера Sun сообщает поисковому процессору, на какую глубину следует исследовать дерево игры и нужно ли продолжить поиск на большую глубину, когда это исследование закончено. Таким образом системе HITECH удается достичь средней глубины просмотра, равной 8 слоям, а в отдельных случаях проводить исследование вплоть до 14 слоев. Все же эти цифры могут показаться еще далекими от 20 слоев, потребность в которых не исключена для победы над гроссмейстером. В то же время параллельный режим работы HITECH и довольно умелое использование теоретических положений о решении шахматных комбинаций в процессе исследования дерева игры могут компенсировать относительно небольшую глубину поиска. Во всяком случае, на следующем чемпионате мира по шахматам среди компьютеров, который состоится в Колоне (ФРГ) в июне этого года, HITECH, по-видимому, будет одной из сильнейших претенденток на звание чемпиона.
HITECH - новейшая в мире шахматная машина. А первая машина для игры в шахматы была изобретена в 1890г. испанским инженером Л.Торресом-и-Кеведо. Используя механические рычаги, блоки и электромеханические переключатели, она играла ладьей и королем против короля. Сопернику отводилась роль манипулирования "голым" королем, чтобы избежать мата. Машина Торреса-и-Кеведо всегда выигрывала.
Предлагаем читателям самим построить алгоритм стратегии машины, играющей двумя указанными фигурами против короля противника. Естественно, следует предполагать, что король, которым играет человек, в исходной позиции не находится в положении "пат" (т.е. у него есть по крайней мере один ход, при котором он не попадает под шах). Задача, таким образом, заключается в том, чтобы указать, пользуясь как можно меньшим числом различных правил, что должна делать машина, чтобы поставить мат из произвольного исходного положения. Позицию на доске, показанную на с.97, можно принять за исходную.

Как поставить мат, имея ладью и короля?
Машина играет белыми и должна ходить первой. Как можно поставить мат черному королю, пользуясь ладьей и королем? Белые могли бы, например, начать с хода ладьей на поле d. После этого черный король не сможет уйти левее поля e. Маневр можно повторить, если король черных послушно уйдет вправо. Но что, если он останется на поле e, курсируя по нему то вверх, то вниз? Лучшее решение будет опубликовано независимо от того, будет ли оно алгоритмическим или описательным, т.е. выраженным на естественном языке.
CLASSIC CHESS PROBLEMS. KENNETH S.HOWARD. Dover Publications, Inc., 1970.
COMPUTER GAMESMANSHIP. DAVID LEVY. Simon and Schuster, 1984.
БОТВИННИК М.М. АЛГОРИТМ ИГРЫ В ШАХМАТЫ.- М.: Наука, 1968.
БОТВИННИК М.М. О КИБЕРНЕТИЧЕСКОЙ ЦЕЛИ ИГРЫ.- М.: "Советское радио", 1975.
БОТВИННИК М.М. О РЕШЕНИИ НЕТОЧНЫХ ПЕРЕБОРНЫХ ЗАДАЧ.- М.: "Советское радио", 1979.
ОТКЛИКИ
7 1986
В апрельском номере журнала я рассказывал читателям о машине, играющей в шахматы, которую в 1890г. изобрел испанский инженер Л.Торрес-и-Кеведо. Машина всегда ставила мат черному королю, играя королем и ладьей против любого игрока-человека. Какова была конструкция этой машины? Сравнительно старое, но тем не менее отличное описание приведено в книге Д.Леви "Шахматы и компьютеры" (David Levy "Chess and Computers"). Каким образом нужно запрограммировать ходы этой машины? Я предложил читателям попытаться придумать алгоритмы, отличающиеся такой же стопроцентной эффективностью.
Подходы к решению этой задачи, не говоря уже об алгоритмических стилях, отличались таким разнообразием, что было трудно выбрать какое-то одно, наиболее изящное решение. Трое читателей, С.Лидделл из Снлвер-Спрннга (шт.Мэриленд), П.Кэннифф из Марлтона (шт.Нью-Джерси) и С.Перрис из Бейтон-Ружа (шт.Луизиана), не только воспользовались надежными алгоритмами, обеспечивающими мат черным, но составили также и программы, чтобы экспериментально подтвердить эффективность выбранных алгоритмов.
В алгоритме Лидделла, пожалуй лучшем из трех, используется стратегия "поворачивая разделяй". Алгоритм поворачивает доску в поисках таких позиций, в которых черный король находится не меньше чем на две линии выше белого короля. По крайней мере одна такая позиция всегда существует, но в большинстве случаев их две. Если алгоритм находит лишь одну такую позицию, он выбирает ее в качестве цели. Если таких позиций оказывается две, то программа выбирает ту, в которой черный король находится ближе к дальнему концу доски. После того как позиция выбрана, программа "отрезает" часть доски при помоши ладьи так, чтобы черный король не мог выйти из отрезанной зоны. Если же белая ладья находится в таком положении, что не может сразу отрезать путь черному королю, то она перемешается на дальний конец доски. Тогда независимо от хода черных программа может отрезать нужную часть доски на следующем ходе. Вся эта процедура требует, самое большее, двух ходов белых.
Таким образом, Лидделл реализует стратегию белых, заключающуюся в том, чтобы последовательно оттеснить короля черных в угол доски. Важное преимущество описанного алгоритма заключается в его вращательной симметрии. Если черный король "не выше" по отношению к белому, программа просто поворачивает доску, пока это условие не будет выполнено.
В нескольких стратегиях, представленных различными читателями, применена ключевая шахматная концепция оппозиции. Если королей разделяет только одно поле и один из королей должен делать ход, то этот король не может придвигаться к другому на любое соседнее с ним поле: он должен либо соблюдать ту же дистанцию, либо двигаться в противоположную сторону. Пожалуй, наилучшая стратегия, использующая оппозицию, была предложена А.Гиллилендом из Арлингтона (шт.Виргиния). Приведем (в слегка перефразированной форме) применяемые им правила:
1. Ладья всегда занимает первую или восьмую горизонталь. Если она подвергается атаке на одной горизонтали, она переходит на другую.
2. Белый король движется к центру доски и пытается оттеснить короля черных к зоне, контролируемой ладьей.
3. Белые стремятся достичь оппозиции, в которой короли находятся на одной горизонтали; их разделяет одно поле, и ход принадлежит белым. Чтобы достичь оппозиции, белые иногда вынуждены сделать лишний ход ладьей, временно нарушая правило 1.
4. Когда белые достигают оппозиции, они делают шах черному королю, совершая ход ладьей на вертикаль, занимаемую черным королем, тем самым оттесняя его на одну вертикаль ближе к краю доски.
5. Правила 3 и 4 применяются повторно, пока черный король не достигнет края доски. Затем применение правила 4 дает мат.
Гиллиленд утверждает, что его стратегия всегда приносит успех. Он отмечает также, что алгоритм, обеспечивающий мат за минимальное количество ходов, вероятно, не будет самым коротким по числу машинных команд.
ОТ ШАХМАТНЫХ ПРОГРАММ К СПЕЦИАЛИЗИРОВАННЫМ ШАХМАТНЫМ КОМПЬЮТЕРАМ
А.К.ДЬЮДНИ
ЕСЛИ бы программа CRAY BLITZ могла запоминать не только шахматные ходы, она навечно сохранила бы в своей памяти события 15 октября 1985г., когда состоялся последний тур шахматного чемпионата Северной Америки среди компьютеров, приуроченного к очередной конференции Ассоциации специалистов по вычислительной технике. Перед участниками на сцене зала заседаний отеля "Радиссон" в Денвере было установлено пять столов, отделенных от зрителей барьером. За каждым столом напротив друг друга сидели представители двух команд - программисты и консультанты. Иногда они шутили, а иногда их лица выражали ожидание и глубокие раздумья. Над каждым столом висели экраны, на которые проектировались позиции на шахматной доске.
В турнире принимали участие 10 программ - претендентов на звание чемпиона Северной Америки. Их названия звучат странно и непривычно, что свидетельствует о различном происхождении программ и о честолюбивых замыслах их создателей: AWIT, ВЕВЕ, CHAOS, CRAY BLITZ, HITECH, INTELLIGENT SOFTWARE, LACHEX, OSTRICH, PHOENIX и SPOC (см. таблицу на с.95). В этом списке отсутствуют названия трех программ из числа тех, что имели наибольший успех на компьютерной шахматной арене в течение нескольких последних лет: BELLE, CHESS 4.7 и NUCHESS.

Участники чемпионата Северной Америки 1985г. по шахматам среди компьютеров
Самый большой интерес вызвала встреча между CRAY BLITZ и HITECH. Первую программу за столом соревнований представляют Р.Хьят из Южно-Миссисипского университета, А.Гауер, шахматный эксперт из того же университета и X.Нельсон из Лоуренсовской национальной лаборатории в Ливерморе. Напротив: X.Берлинер из Университета Карнеги - Меллона и М.Кемпбелл, один из аспирантов того же университета, шахматист высокого класса. Берлинер выступает сразу в двух лицах - и как шахматный консультант, и как программист в команде HITECH. По мере того как развиваются события на доске, напряжение возрастает. Берлинер часто встает из-за стола с усталой улыбкой. Как-то проходя мимо меня, он пробормотал: "Уж слишком это напоминает мне то время, когда я сам играл на чемпионатах США!" (В течение нескольких лет в конце 50-х - начале 60-х годов Берлинер входил в десятку лучших игроков США).
В отличие от чемпионата страны, когда в игровом зале царит мертвая тишина, этот турнир протекает в оживленной атмосфере. Кругом слышатся разговоры, иногда даже смех, постукивают клавиши терминалов, игру постоянно комментирует в микрофон темпераментный по натуре судья М.Валво, консультант по вычислительной технике, мастер международного класса по шахматам из Седона (шт.Аризона): "Слабый ход черных. Король все еще находится в слишком уязвимом положении, а сдвоенные пешки на c5 и c6 затрудняют защиту". Рядом член команды CRAY BLITZ воскликнул, ни к кому конкретно не обращаясь: "Забавно! Я думал, она сыграет королем на f3". Шахматисты-профессионалы пока еше замечают погрешности в игре компьютера, а программисты в свою очередь все еще удивляются способностям своих творений.
На протяжении всего заключительного этапа игры было видно, что HITECH имеет преимущество над своим соперником. В начале игры CRAY BLITZ попала в трудное положение, выйти из которого можно было либо с материальными потерями, либо уступив инициативу. В сложившейся ситуации CRAY BLITZ была вынуждена неудачно расположить свои пешки. HITECH продолжала развивать преимущество.
К полуночи почти все было кончено. Большинство игр завершилось, и специалисты настаивали, чтобы победа была присуждена программе HITECH. Команда CRAY BLITZ просила судью Валво разрешить им сдаться. Он предложил сделать еше два хода: если положение белых не улучшится, то они могут признать себя побежденными. Положение не улучшилось, и они сдались. HITECH стала чемпионом Северной Америки, по существу королем компьютерных шахмат. И хотя CRAY BLITZ пока остается официальным чемпионом мира (этот титул был завоеван ею в 1983г. и защищать его предстоит лишь в июне этого года), победа HITECH наряду с ее победами в трех других турнирах производит внушительное впечатление. На сегодняшний день HITECH почти наверняка является самой сильной в мире компьютерной программой, играющей в шахматы.
Представители соперничавших команд улыбаются, обмениваются мнениями о только что закончившемся турнире. Повлияло ли на его исход отсутствие программ BELLE, CHESS 4.7 и NUCHESS? "Конечно, было бы интересно посмотреть на игру BELLE и некоторых других программ,- сказал один из организаторов турнира,- но я не думаю, что исход соревнований был бы иным". Он отметил, что по составу программ и машин, принимавших участие в турнире, между чемпионатом Северной Америки и чемпионатом мира почти нет разницы. Разговор перешел к обсуждению поединка между Каспаровым и Карповым, затем шахматной теории. "Я не шучу,- говорит, очевидно, сведущий участник разговора,- программа, способная анализировать ситуации на 20 ходов вперед и оценивающая позиции лишь с точки зрения материального преимущества, может обыграть любого гроссмейстера". Возник спор, но ненадолго. Уже через несколько минут зал опустел. Чемпионат Северной Америки завершился.
Высказывание, касающееся способности программы, предвидящей развитие игры вперед на 20 ходов, заслуживает внимания. Графически шахматную игру можно представить в виде разветвленного дерева, состоящего из узлов и соединяющих их линий. При этом дерево как бы перевернуто - его корневой узел находится вверху. Каждый узел соответствует одной из возможных позиций, т.е. тому или иному расположению фигур на шахматной доске, которое может быть достигнуто после определенного числа ходов, дозволенных правилами. Узел соединяется со своим "потомком" линией в том случае, если позиция, представляемая последними, получается из той, которая ей предшествовала до того, как был сделан один ход фигурой или пешкой. На шахматном дереве всякую партию можно отождествить с каким-нибудь одним конкретным путем, ведущим из корневого узла (соответствующего исходной позиции, когда еше не было сделано ни одного хода) к какому-то конечному узлу, представляющему, как правило, такую позицию, в которой на шахматной доске остается лишь несколько фигур и одна из сторон либо получает мат, либо вынуждена сдаться.
Программа, играющая в шахматы, должна исследовать по возможности лишь ту часть игрового дерева, которая оказывается необходимой. Исходя из узла, представляющего позицию, сложившуюся в игре на данный момент, она исследует все узлы - потомки данного (слой 1), затем все узлы - потомки этих потомков (слой 2) и т.д. Средняя глубина исследования дерева игры является мерой "интеллекта" программы, под которым понимается ее способность наперед видеть возможные позиции и производить их оценку на каждом уровне дерева. Программа анализирует позиции и каждой из них ставит в соответствие определенное числовое значение, которое отражает степень "выгодности" достижения этой позиции. Пользуясь так называемой минимаксной процедурой, программа возвращает некоторые из полученных значений вверх по дереву на слой 1. Узел, получивший наибольшее значение, и определяет следующий ход.
Существует довольно интересная связь между двумя упомянутыми составляющими, которые определяют интеллект программы: чем лучше механизм оценивания позиций, тем меньше необходимая глубина исследования дерева игры. На самом деле если бы программа обладала идеальной схемой оценивания, то ей никогда не потребовалось бы просматривать дерево глубже, чем на один слой. В то же время программа с очень простой схемой оценивания, чтобы демонстрировать достаточно хорошую игру, должна просматривать дерево глубже. Возникает вопрос: насколько глубоким должен быть поиск при оценивании позиций только с точки зрения обеспечения материального преимущества, чтобы программа могла успешно соперничать с игроком гроссмейстерского класса? Достаточно ли будет 20 слоев?
Звание гроссмейстера присваивается международной шахматной федерацией игрокам, отличившимся в международных соревнованиях (федерация не рассматривает результаты, достигнутые компьютерами). Гроссмейстеры обычно имеют "рэйтинг" выше 2400 баллов. К началу чемпионата Северной Америки по шахматам среди компьютеров HITECH сыграла 21 партию в турнирах с шахматистами высокого класса и набрала 2233 балла. Это самый высокий в мире результат, достигнутый компьютером. По словам Берлинера, имевшего в свое время рэйтинг 2443 балла, рэйтинг HITECH возрастал в среднем на 8 баллов за игру на турнирах, проводившихся в США. Означает ли это, что через двадцать с лишним игр машина превзойдет своего создателя?
В связи с этим невольно задаешься вопросом, насколько хорошими игроками станут в конце концов компьютеры. Станет ли компьютер когда-либо лучшим в мире шахматистом? Д.Леви, в прошлом шахматист, а теперь бизнесмен и литератор, не раз заключал пари в спорах по данному вопросу. В 1968г. он поспорил на 500долл. с Дж.Маккарти из Станфордского университета, утверждая, что на протяжении следующих 10 лет ни одному компьютеру не удастся его обыграть. В августе 1978г. на канадской выставке в Торонто Леви получил свои 500 долл. Там он выиграл соревнование с программой CHESS 4.5, созданной в Северо-Западном
университете. На следующие 6 лет Леви заключил пари уже на 6000 долл. В апреле 1984г. Леви, находясь в Лондоне, сыграл по телефону матч с CRAY BLITZ и опять выиграл.
Удача воодушевила Леви до такой степени, что он предложил в Денвере новое пари на сумму 100тыс. долл.: в течение следующих 10 лет любой компьютер будет побежден игроком - человеком, которого выберет Леви. Если кто-нибудь примет пари Леви, то, наверное, выставит против него не просто программу, а специализированный компьютер. Пока желающих заключить это пари не нашлось.
Два лучших участника Североамериканского турнира, HITECH и ВЕВЕ, по существу представляют собой такие шахматные машины. Интересно отметить, что программа, выставленная самим Леви, INTELLIGENT SOFTWARE, заняла на турнире третье место. Она написана для компьютера Apple IIe, в котором нет никаких изощренных аппаратных средств, за исключением платы акселератора, представляющей собой электронную схему, удваивающую быстродействие машины. Вероятно, Леви удалось разработать лучшую схему оценивания позиций.
Шахматные знатоки, присутствовавшие на чемпионате, сходятся на том, что лучшая партия на чемпионате была сыграна во втором туре между CRAY BLITZ и ВЕВЕ, продуктом коммерческого предпринимательства. Т.Шерцер из компании SYS-10, Inc., разработавший ВЕВЕ, возил свое изобретение на несколько турниров, состоявшихся в последние годы. ВЕВЕ - это не просто программа, а специализированная шахматная машина. Упомянутая партия имела важное значение не только потому, что была наиболее интересной на чемпионате, но и потому, что в ней CRAY BLITZ потерпела первое поражение за три года.
Читатели, располагающие шахматной доской, могут проследить за игрой между CRAY BLITZ и ВЕВЕ, рассмотрев 50 ходов, приведенных ниже. Фигуры обозначены заглавными буквами: Кр - король, Ф - ферзь, С - слон, К - конь, Л - ладья. Клетки, или поля, шахматной доски обозначаются буквенными и цифровыми координатами. Если доска установлена перед вами так, что нижнее левое поле черное, то по горизонтали поля нумеруются слева направо латинскими буквами a, Ь, c, d. e, f, g, h, а по вертикали - цифрами от 1 до 8 снизу вверх. Обозначения, применяемые для записи ходов игры, как это приведено ниже, иногда совершенно однозначны, например Крb1 (король ходит на поле b1), а иногда не совсем понятны, например Kf3 (конь ходит на f3). Какой из двух коней? В данном случае лишь один конь может ходить на поле f3. Ход пешки обозначается просто указанием поля, на которое она ходит, скажем e4. Партию записал Валво:
CRAY BLITZ (белые) - ВЕВЕ (черные)
1. e4 c5
2. Кf3 d6
3. d4 cd
(Обозначение cd означает, что пешка с поля c бьет пешку на поле d).
4. К:d4 Кf6
(Знак ":" означает, что фигура бьет фигуру или пешку противника).
5. КcЗ g6
6. Сg5 Сg7
7. Фd2 Кcб
8. 0-0-0 0-0
(Рокировка: у белых на ферзевом фланге, у черных на королевском).
9. Кb3 Лe8
10. Сc4 Kg4
Черные сыграли Кg4, готовясь к тому, чтобы затем сыграть 11... С:c3. Черные, наверное, считали, что после этого белые вынуждены будут сыграть 12. bc. Однако черные, должно быть, передумали, проанализировав другой возможный ход белых. Если С:c5, то Ф:c3! Ход К:f2 станет бессмысленным, если одна из ладей белых сыграет на f1, в то время как ход белых С:f7+ (шах) был бы для черных роковым.
11. h3 Кge5
12. Сb5 a6
13. Сe2 a5
14. СЬ5 Сe6
15. Кd5 a4
16. Кd4 Сd7
Положение белых становится отчаянным. Пешка черных (a4) создает угрозу на королевском фланге белых.
17. К:c6 bc
18. К:e7+ Л:e7
19. С:e7 Ф:e7
20. Сe2 Фe6
21. Крb1 Лb8
(Положение фигур на доске после 21 -го хода показано на рисунке слева). Черные угрожают ходом 22... Лb2+ , затем последует 23. Крb2 Кc4, "вилка", в результате которой белые проигрывают ферзя.

Положение после 21-го хода
22. b3 ab
23. cb Сe8
24. Крc2 Кd7
25. f3 Лa8
26. Крc1 Кc5
27. Фc2 Фf6
28. Сc4 Фа1
29. Крd2 Ф:a2
Более сильный ход был бы 29...Сc3+ , шах, за которым последовал бы 30. Крe2 Л:a2!
30. Ф:a2 Л:a2+
31. Крc1 d5
32. ed cd
33. С:d5 Сb5
34. Лhe1 Кd3+
Материальный перевес черных на одну фигуру может стать ощутимее в результате очередного размена. В игре шахматистов в этой позиции белые, наверное, признали бы себя побежденными.
35. Л:d3 С:d3
36. Лe8+ Сf8
37. g4 Крg7
38. Ле3 Сa3+
39. Крd1 Лa1+
40. Крd2 Сf1
41. Крc3 Лc1+
42. Крd2 Лc5
43. Крe1 С:h3
44. Сc4 h5
45. gh gh
46. Крf2 h4
47. Лd3 Сf5
48. Лd4 h3
49. Лh4 Лс7
Сделав ход 50. Лh5, белые сдались
Программа CRAY BLITZ выполняется на компьютере CRAY XM-P 48. Славящийся своим быстродействием и большим числом процессоров CRAY тем не менее представляет собой универсальную ЭВМ, а не специализированную шахматную машину. Очевидно, система ВЕВЕ, аппаратные средства которой специально предназначены для игры в шахматы, превзошла комбинацию машины CRAY и программы CRAY BLITZ.
Система HITECH в определенном смысле еще более специализирована. Когда Университет Карнеги-Меллона был еще Технологическим институтом Карнеги, там была разработана программа TECH, играющая в шахматы. Имя HITECH отражает тот факт, что Берлинер, Кемпбелл и другие ее разработчики: К.Эбелинг, Г.Гетш, Э.Пэлей и Л.Сломер, приспособили заложенные в программе ТЕСН принципы к новой технике на сверхбольших интегральных схемах (СБИС) и с параллельным режимом работы. Машина HITECH представляет собой компьютер Sun с процессором специальной конструкции, который Берлинер называет поисковым. Компьютер Sun выполняет три программы: интерфейс с пользователем, управляющую программу и программу "оракул". Последняя представляет собой то, что специалисты в области шахматных программ называют "книгой". Это обширный каталог известных в шахматной литературе дебютов и их вариаций. База данных оракула содержит также значительный объем других сведений из теории шахмат, которые нетрудно пополнять. Когда поисковый процессор исследует возможные варианты развития игры из заданной позиции, он прибегает к этой информации и с помощью оракула выбирает ту, которая имеет отношение к данной позиции.
Сам же поисковый процессор состоит из микропроцессора и нескольких аппаратных модулей, которые генерируют ходы, оценивают их, проверяют, не повторяются ли ходы, и т.д. Микропроцессор координирует действия, выполняемые этими модулями. Генератор ходов состоит из 64 СБИС, по одной микросхеме на каждое поле шахматной доски. Каждая микросхема "просматривает" всю доску, чтобы определить, может ли какая-нибудь фигура или пешка пойти на контролируемое ею поле. Она определяет наилучший ход, пользуясь такими стандартными критериями, как возможность взятия фигуры или пешки противника или обеспечение господства в центре доски. Одновременно другие 63 микросхемы заняты той же работой (параллельный режим). Если на доске 10 фигур, то подобная архитектура аппаратных средств означает, что ходы генерируются в 10 раз быстрее при прочих равных условиях.
Процедура оценивания должна вовремя поспевать за генерацией ходов. На первой стадии оценивание производится самим генератором ходов, В нем содержится своего рода "эксперт", который оценивает все ходы, генерируемые каждой из 64 микросхем. Каждая такая микросхема вычисляет значение, характеризующее силу наилучшего из рассмотренных ею ходов и передает это значение выбирающему ход "эксперту". Числа, генерируемые микросхемами, дублируются привлекающими внимание звуковыми сигналами. "Эксперт" располагает их в порядке громкости (т.е. эффективности ходов).
Затем HITECH приступает к поиску на игровом дереве, следуя вариантам, выбранным "экспертом" из всех возможных в данной позиции. Затем производится еще одно оценивание, теперь уже для каждой новой позиции, генерируемой на дереве игры. Пользуясь познаниями шахматной теории (поставляемыми оракулом), применимыми к данной позиции, модуль оценивания рассматривает каждую из них независимо от того, находится ли эта позиция на горизонте средней глубины просмотра или нет. В этом заключаются преимущества и сама сущность параллелизма - дополнительная работа не требует дополнительного времени. Управляющая программа компьютера Sun сообщает поисковому процессору, на какую глубину следует исследовать дерево игры и нужно ли продолжить поиск на большую глубину, когда это исследование закончено. Таким образом системе HITECH удается достичь средней глубины просмотра, равной 8 слоям, а в отдельных случаях проводить исследование вплоть до 14 слоев. Все же эти цифры могут показаться еще далекими от 20 слоев, потребность в которых не исключена для победы над гроссмейстером. В то же время параллельный режим работы HITECH и довольно умелое использование теоретических положений о решении шахматных комбинаций в процессе исследования дерева игры могут компенсировать относительно небольшую глубину поиска. Во всяком случае, на следующем чемпионате мира по шахматам среди компьютеров, который состоится в Колоне (ФРГ) в июне этого года, HITECH, по-видимому, будет одной из сильнейших претенденток на звание чемпиона.
HITECH - новейшая в мире шахматная машина. А первая машина для игры в шахматы была изобретена в 1890г. испанским инженером Л.Торресом-и-Кеведо. Используя механические рычаги, блоки и электромеханические переключатели, она играла ладьей и королем против короля. Сопернику отводилась роль манипулирования "голым" королем, чтобы избежать мата. Машина Торреса-и-Кеведо всегда выигрывала.
Предлагаем читателям самим построить алгоритм стратегии машины, играющей двумя указанными фигурами против короля противника. Естественно, следует предполагать, что король, которым играет человек, в исходной позиции не находится в положении "пат" (т.е. у него есть по крайней мере один ход, при котором он не попадает под шах). Задача, таким образом, заключается в том, чтобы указать, пользуясь как можно меньшим числом различных правил, что должна делать машина, чтобы поставить мат из произвольного исходного положения. Позицию на доске, показанную на с.97, можно принять за исходную.

Как поставить мат, имея ладью и короля?
Машина играет белыми и должна ходить первой. Как можно поставить мат черному королю, пользуясь ладьей и королем? Белые могли бы, например, начать с хода ладьей на поле d. После этого черный король не сможет уйти левее поля e. Маневр можно повторить, если король черных послушно уйдет вправо. Но что, если он останется на поле e, курсируя по нему то вверх, то вниз? Лучшее решение будет опубликовано независимо от того, будет ли оно алгоритмическим или описательным, т.е. выраженным на естественном языке.
CLASSIC CHESS PROBLEMS. KENNETH S.HOWARD. Dover Publications, Inc., 1970.
COMPUTER GAMESMANSHIP. DAVID LEVY. Simon and Schuster, 1984.
БОТВИННИК М.М. АЛГОРИТМ ИГРЫ В ШАХМАТЫ.- М.: Наука, 1968.
БОТВИННИК М.М. О КИБЕРНЕТИЧЕСКОЙ ЦЕЛИ ИГРЫ.- М.: "Советское радио", 1975.
БОТВИННИК М.М. О РЕШЕНИИ НЕТОЧНЫХ ПЕРЕБОРНЫХ ЗАДАЧ.- М.: "Советское радио", 1979.
ОТКЛИКИ
7 1986
В апрельском номере журнала я рассказывал читателям о машине, играющей в шахматы, которую в 1890г. изобрел испанский инженер Л.Торрес-и-Кеведо. Машина всегда ставила мат черному королю, играя королем и ладьей против любого игрока-человека. Какова была конструкция этой машины? Сравнительно старое, но тем не менее отличное описание приведено в книге Д.Леви "Шахматы и компьютеры" (David Levy "Chess and Computers"). Каким образом нужно запрограммировать ходы этой машины? Я предложил читателям попытаться придумать алгоритмы, отличающиеся такой же стопроцентной эффективностью.
Подходы к решению этой задачи, не говоря уже об алгоритмических стилях, отличались таким разнообразием, что было трудно выбрать какое-то одно, наиболее изящное решение. Трое читателей, С.Лидделл из Снлвер-Спрннга (шт.Мэриленд), П.Кэннифф из Марлтона (шт.Нью-Джерси) и С.Перрис из Бейтон-Ружа (шт.Луизиана), не только воспользовались надежными алгоритмами, обеспечивающими мат черным, но составили также и программы, чтобы экспериментально подтвердить эффективность выбранных алгоритмов.
В алгоритме Лидделла, пожалуй лучшем из трех, используется стратегия "поворачивая разделяй". Алгоритм поворачивает доску в поисках таких позиций, в которых черный король находится не меньше чем на две линии выше белого короля. По крайней мере одна такая позиция всегда существует, но в большинстве случаев их две. Если алгоритм находит лишь одну такую позицию, он выбирает ее в качестве цели. Если таких позиций оказывается две, то программа выбирает ту, в которой черный король находится ближе к дальнему концу доски. После того как позиция выбрана, программа "отрезает" часть доски при помоши ладьи так, чтобы черный король не мог выйти из отрезанной зоны. Если же белая ладья находится в таком положении, что не может сразу отрезать путь черному королю, то она перемешается на дальний конец доски. Тогда независимо от хода черных программа может отрезать нужную часть доски на следующем ходе. Вся эта процедура требует, самое большее, двух ходов белых.
Таким образом, Лидделл реализует стратегию белых, заключающуюся в том, чтобы последовательно оттеснить короля черных в угол доски. Важное преимущество описанного алгоритма заключается в его вращательной симметрии. Если черный король "не выше" по отношению к белому, программа просто поворачивает доску, пока это условие не будет выполнено.
В нескольких стратегиях, представленных различными читателями, применена ключевая шахматная концепция оппозиции. Если королей разделяет только одно поле и один из королей должен делать ход, то этот король не может придвигаться к другому на любое соседнее с ним поле: он должен либо соблюдать ту же дистанцию, либо двигаться в противоположную сторону. Пожалуй, наилучшая стратегия, использующая оппозицию, была предложена А.Гиллилендом из Арлингтона (шт.Виргиния). Приведем (в слегка перефразированной форме) применяемые им правила:
1. Ладья всегда занимает первую или восьмую горизонталь. Если она подвергается атаке на одной горизонтали, она переходит на другую.
2. Белый король движется к центру доски и пытается оттеснить короля черных к зоне, контролируемой ладьей.
3. Белые стремятся достичь оппозиции, в которой короли находятся на одной горизонтали; их разделяет одно поле, и ход принадлежит белым. Чтобы достичь оппозиции, белые иногда вынуждены сделать лишний ход ладьей, временно нарушая правило 1.
4. Когда белые достигают оппозиции, они делают шах черному королю, совершая ход ладьей на вертикаль, занимаемую черным королем, тем самым оттесняя его на одну вертикаль ближе к краю доски.
5. Правила 3 и 4 применяются повторно, пока черный король не достигнет края доски. Затем применение правила 4 дает мат.
Гиллиленд утверждает, что его стратегия всегда приносит успех. Он отмечает также, что алгоритм, обеспечивающий мат за минимальное количество ходов, вероятно, не будет самым коротким по числу машинных команд.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
5 1986
ДВЕ НЕЗАМЫСЛОВАТЫЕ ПРОГРАММЫ ДЕМОНСТРИРУЮТ ГЕНИАЛЬНЫЕ СПОСОБНОСТИ В ТЕСТАХ НА УМСТВЕННОЕ РАЗВИТИЕ
А.К.ДЬЮДНИ
НАВЕРНОЕ, всем знаком старый шуточный номер, который часто показывают в цирке и на ярмарочных клоунадах. На сцену выходит мужчина с могучей мускулатурой в сопровождении сравнительно хрупкой ассистентки. Мужчина берется за штангу невероятных размеров, и С нечеловеческим напряжением сил ему удается поднять ее над головой. Зрители аплодируют, однако аплодисменты тут же сменяются смехом, когда ассистентка небрежно подхватывает штангу одной рукой и уносит ее за кулисы.
Существуют две компьютерные программы, которые как бы воспроизводят этот комический номер, показывая нам, чего в действительности стоят умственные "мускулы", демонстрируемые теми, кто набирает высокий балл по результатам обычного теста на умственное развитие. Обе программы работают, если не на уровне гения, то близком к нему, решая две задачи, широко используемые в тестах: дополнение числовой последовательности и поиск геометрических аналогий. Однако, разобравшись в механизме работы этих программ (что можно сделать без особого труда), невольно удивляешься тому, насколько они, если можно так выразиться, глупы.
Мне вовсе не хочется обижать читателей, считающих себя щедро одаренными умственными способностями, и если я с иронией говорю о тесте умственного развития, то делаю это умышленно. Цель этого теста, как нам говорят, заключается в том, чтобы определить, каков уровень умственного развития индивидуума. Интеллект относится к тем немногим качествам, которыми человек гордится, если они у него есть, и испытывает неудовлетворение, если их у него нет. Однако говорить об интеллекте, когда речь пойдет об обычном тесте на умственное развитие, по-видимому, в корне ошибочно. Эта точка зрения убедительно аргументирована С.Гоулдом из Гарвардского университета в его книге, посвященной тестам на умственные способности (см. библиографию на с.104). В основном его рассуждения сводятся к следующему. Традиционные тесты такого рода основаны на неявно допускаемом ошибочном предположении, что человеческий интеллект, подобно физической силе,- это некий обобщенный физиологический показатель, поддающийся количественному измерению при помощи последовательности задач, упорядоченных по уровню сложности.
Хороший пример задач подобного рода - продолжение числовой последовательности. Каким должно быть следующее число в последовательности 2, 4, 6, 8,...? Или, например, в последовательности 2,4,8,14,...? Или 1,2,6,24,...? Количество правильных ответов на такие вопросы, выраженное в процентах, измеряет ваше "общее умственное развитие", подобно тому, как динамометр измеряет вес, который вы можете поднять, и, стало быть, силу ваших рук. Заметим, что если результаты теста трактуются как мера "общего умственного развития", то должно существовать некое "ядро" - центральная способность или несколько таких способностей, которые могли бы служить критерием общего умственного развития. Поскольку в самом понятии общего умственного развития предполагается наличие сильной взаимозависимости, или корреляции, между наиболее важными центральными способностями, то не так уж существенно, какие конкретно задачи были включены в тест. Одна задача не хуже и не лучше других.
Одна из рассматриваемых здесь программ, решающих задачи из тестов на умственное развитие, представляет собой упрощенную версию программы, написанной М.Феенстра, студентом из Роттердама. Программа под названием HI Q решает два вида задач, часто встречающихся в стандартных тестах, а именно дополнение числовой последовательности и обнаружение цифровых аналогий. Недавно Феенстра опробовал свою программу на ряде тестов, приведенных в книге Г.Айзенка "Know Your Own I.Q." ("Ваш коэффициент умственного развития"). Суммарное количество очков, набранных программой, оказалось равным примерно 160. И хотя условия и результаты эксперимента не были тщательно зафиксированы, едва ли следует сомневаться в том, что программа покажет хорошие результаты в реальных условиях, в которых проводятся подобные тесты.
Программа, которую мы здесь рассмотрим, называется SE Q. Она копирует поведение программы HI Q при решении задач на продолжение числовой последовательности. У читателей, которые напишут и испытают программу SE Q, возможно, сложится впечатление, что их умственные способности в решении числовых задач значительно повысятся. В основу программы положена довольно простая идея. Когда задана последовательность чисел и требуется найти следующее число, никто не пытается сразу угадать его. Стремятся найти правило, которому подчиняются заданные члены последовательности. Заметим, что с математической точки зрения для любой конечной последовательности чисел существует бесконечное количество правил, которым она подчиняется. Таким образом, задача сводится к отысканию простого правила, задающего последовательность.
В программе SE Q рассматриваются лишь два вида правил: аддитивные и мультипликативные. Например, чтобы найти следующее число в последовательности 2, 4, 8, 14,..., можно попытаться найти аддитивное правило, а лучший способ поиска такого правила заключается в построении так называемой пирамиды разностей (см. рисунок на с.90). В основании пирамиды лежит заданная последовательность чисел, и пирамида строится снизу вверх вычислением разностей между каждым последующим и предыдущим числами, находящимися на предыдущем уровне пирамиды. Так, первое число на втором уровне пирамиды есть разница первых двух чисел первого уровня, а именно 2 и 4. Их разность равна 2, и, таким образом, 2 - это первое число на втором уровне. Аналогично два других числа на втором уровне находятся вычитанием: 8-4=4 и 14-8 = 6; полученная в результате последовательность на втором уровне: 2, 4, 6. С помощью аналогичной процедуры находим числа третьего уровня пирамиды - их два, причем оба равны 2.

Продолжение числовой последовательности методом пирамиды. Предлагается решить две задачи, приведенные внизу
Равенство всех чисел на определенном уровне пирамиды является своеобразным сигналом, говорящим о том, что процесс наращивания пирамиды вверх следует прекратить и достраивать ее сбоку. Предположим, что третье число в третьем ряду пирамиды также должно быть равно 2. Но в таком случае логично считать, что следующее число во втором ряду пирамиды должно получаться путем прибавления к последнему числу 2, т.е. 6+2=8. В свою очередь это число можно прибавить к последнему члену последовательности на первом уровне пирамиды: 14+8=22; и действительно, 22 - это правильный ответ, за получение которого, согласно условиям теста, начисляют полное число баллов. Стоит таким образом прийти к последовательности одинаковых чисел на верхнем уровне пирамиды, как все остальные уровни будут достраиваться путем применения соответствующего правила к каждому нижележащему уровню вплоть до основания.
Очень многие задачи из тестов, касающиеся числовых последовательностей, сводятся к этой простой процедуре. Читатели, хорошо помнящие алгебру из курса средней школы, сразу же видят, что приведенные в качестве примера последовательности обладают свойствами полиномов. Любой полином, вычисленный для последовательного набора целых значений аргумента, дает последовательность, из которой можно построить пирамиду разностей. При достаточно большом количестве вычисленных значений на верхнем уровне пирамиды в конце концов получится последовательность одинаковых чисел. Количество требующихся для этого уровней минус единица - это степень полинома. Последовательность 2, 4, 8, 14, дающая постоянную последовательность, состоящую из двоек, на третьем уровне пирамиды разностей, образуется, например, в процессе последовательного вычисления значений квадратичного полинома, или полинома второй степени: x2-х+2.
К сожалению, не все задачи на числовые последовательности можно решить путем построения пирамиды разностей. Например, последовательность 1, 2, 6, 24,... дает пирамиду разностей, на верхнем уровне которой находятся числа 3 и 14. Однако быстрый рост членов последовательности говорит в пользу ее геометрического характера: соседние члены геометрической прогрессии отличаются друг от друга на постоянный множитель, а не на постоянную прибавляемую или вычитаемую величину. Разумно поэтому было бы построить множество величин, являющихся частным от деления соседних членов последовательности друг на друга, а не их разности (см. рисунок на с.90). Вычисляя частные от деления каждой пары чисел в последовательности 1, 2, 6, 24,..., мы получаем на втором уровне пирамиды числа 2, 3, 4,... Вторая последовательность говорит о резком изменении правила, задающего последовательность: третий ряд пирамиды нужно строить уже по разностям, а не по частным от деления. Наверное, ни у кого не возникнет сомнения в том, что в конце второго ряда должно стоять число 5? Таким образом, ответ будет равен 120, т.е. произведению 24, последнего заданного числа в первом ряду, и 5.
Программа SE Q, решающая задачи на продолжение числовых последовательностей, строит пирамиды, рассматривая как последовательности из разностей между соседними членами нижнего уровня, так и последовательности частных от их деления друг на друга. Более того, она исследует соседние пары чисел последовательности в поисках более общих аддитивных и мультипликативных правил. В аддитивном правиле первый член каждой пары может предварительно быть умножен на константу k, перед тем как произвести обычное сложение, а в мультипликативном правиле после обычного умножения к результату может быть прибавлена константа k. Написать такую программу - это довольно несложное упражнение для начинающих программистов (см. рисунок справа).

Алгоритм программы SE Q
Несколько простых формул, на которых основаны общие правила построения пирамиды, представляют собой главную часть программы SE Q. Предположим, что числа заданной последовательности уже были присвоены в качестве значений четырем переменным a(1), a{2), a(3), a(4). Чтобы получить второй ряд, b(1), b(2), b(3), программа пытается применить либо обобщенную формулу разности вида b(1) <- a(2) - k*a(1), либо обобщенную формулу частного вида b(1) <- [a(2) - k]/a(1). В обоих случаях k означает произвольное целое число из определенного диапазона. Программа пытается также сделать аналогичные подстановки для b(2) и b(3) при одном и том же значении константы k: для b(2) она пробует формулу a(3)-k*a(2) или [a(3)-k]/a(2), а для b(3) она пробует a(4)-k*a(3) или [а(4)-k]/a(3).
Третий ряд, c(1), c(2), получается еше проще: программа пробует подставлять лишь формулу простой разности c(1) <- b(2)-b(1) и c(2) <- b(3)-b(2) или простого частного: c(1) <- b(2)/b(1) и c(2) <- b(3)/b(2). Очевидно, в тестах на умственное развитие очень редко встречаются задачи с числовыми последовательностями более сложными, чем те, которые охватываются рассмотренными формулами.
При построении пирамиды программа SE Q каждый раз пробует применить обобщенную формулу для вычисления значений b и простую формулу для значений c. Таким образом, программа создается как бы из четырех сегментов. Каждый сегмент представляет собой цикл с какой-то одной комбинацией подстановочных формул. Например, в одном из таких сегментов сначала применяются три обобщенные формулы частного вида b{1) <- [a(2)-k]/а(1) для вычисления значений b(l), b(2) и b(3), образующих второй уровень пирамиды. Затем в этом сегменте применяются две простые формулы разности вида c(1) <- b(2)-b(l), чтобы получить значения c(1) и c(2) третьего уровня пирамиды. Весь набор из пяти формул вложен в так называемый цикл полного перебора возможностей, в котором пробуется каждое значение константы k, Феенстра рекомендует ограничивать значения к диапазоном от -5 до 5.
Внутри цикла, после того как вычисляются новые значения c(1) и c(2), они проверяются на равенство. Если они оказываются равными, то их общее значение присваивается переменной c, а текущее значение константы к присваивается переменной kk. Сразу за циклом расположены операторы, строящие искомое число, продолжающее заданную последовательность (если решение было найдено) по значениям c и kk. В рассматриваемом примере получаем b(4), новый член второго уровня, путем прибавления c к значению b(3). Ответ, т.е. значение a(5), получается затем умножением a(4) на b(4) и прибавлением значения kk к произведению.
Таким образом, двух операторов в конце каждого цикла оказывается достаточно, чтобы получить решение задачи, если поиск, осуществляемый в цикле, оказался успешным. Конкретный вид этих операторов зависит от формул, применяемых в соответствующем цикле, и я предоставляю читателям, желающим самостоятельно написать программу SE Q, установить, какими должны быть операторы, завершающие каждый цикл. Чтобы выделить переменную, представляющую наибольший интерес в каждом конкретном случае, воспользуйтесь приемами алгебры. И конечно, если один из описанных циклов программы приводит к решению задачи, то оно должно быть выведено на печать специальным оператором печати. При этом программа может уже не выполнять оставшиеся циклы и остановиться, или же она может выполнить все циклы, чтобы найти другие решения. Выполняя все циклы своей программы, Феенстра выявил несколько "некорректных" задач в тестах, имевших более одного правильного ответа. Если ни в одном из четырех циклов не удается найти никакого решения, то разумно на этот случай предусмотреть вывод на печать сообщения о неудаче поиска. Каким именно должно быть это сообщение - дело вкуса. Те, кто хочет придать своей программе оттенок одушевленности, могут, например, заложить в нее сообщение "Помогите!".

Мини-тест на умственное развитие, составленный из вопросов, заимствованных из книги Г.Айзенка "Ваш коэффициент умственного развития"
Программу SE Q можно испытать на вопросах, взятых из нескольких широко известных книжек, посвященных тестированию. В книге Айзенка приведено восемь полных тестов, при помощи которых читатель якобы может определить коэффициент своего умственного развития. Тесты включают вопросы нескольких различных видов, обычно присутствующих в стандартных тестах, например вопросы о недостающем числе, недостающей букве, недостающем слове, неподходящем слове, о перетасованных словах и геометрических аналогиях (см. рисунок слева). В каждой категории вопросов обычно имеются несколько подтипов. Например, в книге Айзенка есть три типа вопросов о недостающем числе, а именно обычные задачи на дополнение числовой последовательности, уже рассмотренные выше, и два других типа задач, которые можно проиллюстрировать следующими двумя примерами:

В каждом случае экзаменующийся потенциальный гений должен указать недостающее число в соответствии с "уловленным" им правилом. Программа Феенстры HI Q справляется с такими вопросами при помощи процедур, в которых применяются формулы того же типа, что и в рассмотренной выше программе продолжения числовой последовательности. Предлагаю читателям попробовать свои силы. В следующем номере журнала будут даны ответы к двум приведенным выше задачам, а также к задачам, представленным на рисунках на с.90 и 92.
Хотя программа HI Q отвечает лишь на вопросы одного важного класса из числа предлагаемых в тестах на проверку умственного развития, решение задач, относящихся к другим классам, также можно автоматизировать. В самом деле, программа, решающая задачи на геометрические аналогии, была написана более 20 лет назад Т.Эвансом как часть его диссертации на звание доктора философии, которую он защитил в Массачусетском технологическом институте. Несмотря на то что все это звучит весьма серьезно, основные идеи, заложенные в программе Эванса, можно легко понять.
Все геометрические задачи, которые она призвана решать, сводятся к следующему: фигура A относится к фигуре B, как фигура C относится к одной из, скажем, четырех фигур, приведенных в качестве потенциального ответа. Программа выбирает подходящую фигуру, сначала пытаясь определить набор простых правил, трансформирующих фигуру A в фигуру B (см. рисунок справа). Затем она повторяет эту процедуру с фигурой C и каждой из четырех фигур - потенциальных решений задачи. В каждом случае генерируется набор правил, при помощи которых фигуру С можно трансформировать в искомую фигуру. Фигура, получающаяся в результате применения тех правил трансформации, которые ближе всего к правилам, трансформирующим фигуру A в фигуру B, выбирается в качестве ответа.
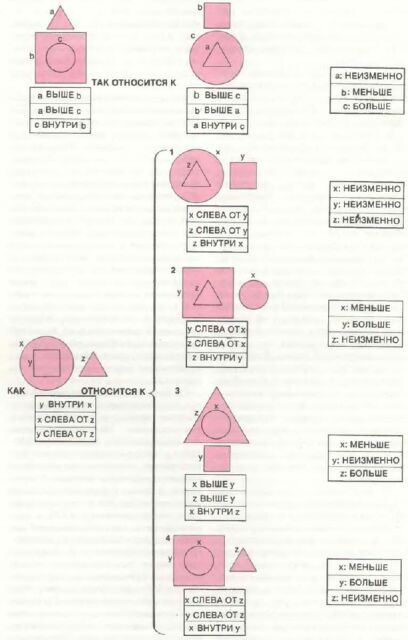
Алгоритм решения задач на геометрические аналогии, приведенный в диссертации Т.Эванса
В программе Эванса пять раз повторяется, по существу, одна и та же операция. Каждый раз две фигуры, исходная и производная, служат в качестве входных данных. Для каждой такой пары фигур программа вырабатывает трехкомпонентное табличное описание процесса трансформации, в результате которого исходная фигура превращается в производную. Сначала программа перечисляет пространственные взаимоотношения между составными частями исходной фигуры, затем она перечисляет пространственные отношения между составляющими производной фигуры. В обоих описаниях рассматриваются лишь три пространственных отношения; ВЫШЕ, СЛЕВА ОТ и ВНУТРИ. Наконец, программа описывает, каким образом изменяются составляющие детали второй фигуры по сравнению с составляющими первой. Изменения эти могут быть четырех видов; каждая деталь может: изменить свой размер, оказаться повернутой, быть отражением или же вовсе исчезнуть.
Предположим, фигуры A, B и C состоят из трех частей каждая: круга, квадрата и треугольника. На фигурах A и B программа может обозначить треугольники буквой a, квадраты - буквой b и круги - буквой c, однако она не пытается обозначить детали фигуры С аналогичным образом. Вместо этого она присваивает трем составляющим фигуры C произвольные обозначения x, y и z. Затем она создает трехкомпонентное табличное описание для пары фигур A и B и еще четыре описания, по одному для каждой пары фигур C и фигуры из числа кандидатов на ответ. В последних четырех таблицах повсюду используются обозначения x, y и z. Завершающая операция программы Эванса состоит в том, чтобы произвести все возможные подстановки a, b и c вместо x, y и z. Поскольку x, y и z можно переставить лишь шестью различными способами, количество производимых подстановок в программе также равно шести. Одна из подстановок может превратить табличное описание пары фигур A и B в соответствующее табличное описание фигуры C и одной из фигур - кандидатов на ответ. Эта последняя фигура и представляет собой решение задачи. Если точного соответствия найти не удалось, то программа может подсчитать степень относительного успеха при подстановках и выбрать подстановку, дающую наилучший результат.
Патрик Уинстон описывает программу поиска геометрических аналогий в своей книге "Artificial Intelligence" (в переводе "Искусственный интеллект", см. библиографию). Уинстон утверждает, что программа "работает хорошо" и объясняет ее успех применением эффективной системы представления знаний, касающихся геометрических фигур, которыми оперирует программа. Например, вместо того чтобы указывать, каким образом такие отношения, как ВЫШЕ, СЛЕВА ОТ или ВНУТРИ, изменяются от картинки к картинке, программа могла бы описывать, как одна фигура на первой картинке трансформируется в другую фигуру на второй картинке. Такая программа могла бы оказаться чрезвычайно громоздкой и к тому же неэффективной, поскольку ей нужно было бы проверить намного большее количество подстановок по сравнению с программой Эванса. В действительности поиск хорошего представления является центральной проблемой в задаче создания искусственного интеллекта. Очень часто удачно выбранное представление оказывается ключевым фактором, позволяющим компьютеру имитировать некоторые аспекты человеческого мышления, проявляемого при решении различных задач.
По аналогичным причинам представление объектов в сознании человека также является в настоящее время предметом оживленных дискуссий среди исследователей, занимающихся изучением природы человеческого интеллекта. В этом смысле необходимость изучения искусственного интеллекта часто объясняется, помимо всего прочего, и тем, что оно представляет собой попытку продемонстрировать "доказательство существования" механистического описания человеческих способностей. При этом рассуждают примерно так: если компьютерная программа оказывается в состоянии моделировать какой-то элемент человеческого поведения, то представление поведения, заложенное в программе, может по крайней мере служить моделью внутреннего представления того же элемента поведения в человеческом мозгу. Однако на самом деле успешное моделирование человеческого поведения зачастую проливает очень мало света на внутренние процессы, характерные для человеческой психики. Мы не можем с уверенностью утверждать, что существует какая-либо связь между механизмом работы программ Феенстры и Эванса и тем, как аналогичные задачи решаются людьми. Вероятно, человеческий разум при решении той или иной конкретной задачи пользуется более универсальными стратегиями.
Это последнее предположение как бы замыкает круг наших рассуждений и возвращает нас к вопросу о природе человеческого интеллекта и о том, как его можно измерить. Уже отмечалось, что С.Гоулд охарактеризовал тесты на умственное развитие как принципиальное заблуждение. В своей критике он делает акцент на двух главных недостатках, присущих самой концепции тестов: неправомерной материализации сугубо абстрактного понятия и ранжировании этой материализованной абстракции в одном-единственном измерении. В значительной степени эта наша склонность "делать вещи" из того, что в лучшем случае является лишь туманными абстракциями, объясняется самой природой языка. Более того, когда мы убеждаем себя в том, что имеем дело с реальной вещью, у нас срабатывает рефлекс попытаться измерить ее.
Требуя единой количественной меры, мы совершаем вторую принципиальную ошибку, а именно ошибку ранжирования. Мы хотим свести сложные явления к одной шкале. Подобные методы привели нас к хорошей физике, но они также привели к плохим социальным теориям. В частности, я имею в виду тестирование интеллекта. Для XXв. это примерно то же самое, чем была для XIXв. краниометрия - система измерений черепа человека с помощью антропологических инструментов. В обоих случаях целые расовые группы людей оказались "измерены" принципиально ошибочно не только потому, что само по себе это измерение было почти бессмысленным, но и потому, что процесс измерения в значительной мере был подвержен предубеждениям, как сознательным, так и неосознанным.
Гоулд энергично атакует биологический детерминизм, мнение о том, что поведение человека определяется его генами, и предостерегает нас от той точки зрения, что способности нашего мозга являются прямым следствием естественного отбора. "Наш мозг - это компьютер колоссальной сложности,- пишет он.- Если установить гораздо более простой компьютер для бухгалтерских расчетов на фабрике, то он может также выполнять и многие другие более сложные функции, не связанные с его непосредственной ролью. Эти дополнительные способности являются неизбежным следствием структурной конструкции машины, а не его приспособления. Наши значительно более сложные биологические компьютеры также были созданы с некоторой целью, однако они обладают почти ужасающим многообразием дополнительных способностей, включая большую часть того, что, как мне кажется, делает нас людьми".
И именно здесь Гоулд затронул то, что, на мой взгляд, должно тревожить нас в оценке относительно простой компьютерной программы, которая, подвергшись тесту на умственное развитие, получает балл на уровне гения. Измеряет ли этот балл умственное развитие компьютера? Если нет, то каким образом можно измерить интеллект машины независимо от того, сделана она из кремния или пластмассы или еще какого-нибудь материала? Ответ: наверное, не прогоном программы через набор тестов на умственное развитие.
БИБЛИОГРАФИЯ
THE MISMEASURE OF MAN. STEPHEN JAY GOULD. W.W.Norton & Company, Inc., 1981.
KNOW YOUR OWN I.Q. H.J.EYSENCK. Penguin Books, 1984.
АЙЗЕНК Г. ПРОВЕРЬТЕ СВОИ СПОСОБНОСТИ. Перев. с англ.- М.: Мир, 1972.
УИНСТОН П. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ. Перев. с англ.- М.: Мир, 1980.
ОТКЛИКИ
6 1986
В майском номере журнала речь шла о тестах на умственное развитие, и там перед читателями было поставлено несколько вопросов относительно числовых последовательностей. Первая задача мини-теста может послужить хорошим примером неоднозначности, обычно присутствующей в подобных задачах. Нужно было продолжить последовательность 3, 7, 16, 35,... Если из каждого члена последовательности вычесть удвоенный предыдущий член, то получится последовательность 1, 2, 3, ... - второй ряд пирамиды. Согласно этому правилу, следующий член должен быть равен: 35*2+4, т.е. 74. В то же время если построить простую пирамиду разностей в три ряда, то в третьем ряду мы получим 5 и 10. Разумно поэтому достроить этот ряд числом 15. Но тогда соответственно исходную последовательность нужно дополнить числом 69. Следует сказать, что программы, описанные в нашей предыдущей статье, упустили бы этот ответ. Теперь приведем ответы на вопросы мини-теста: отсутствующая буква - это 3 (если считать, что в алфавите нет буквы е); отсутствующее слово - БАР; неподходящее слово - ЛЮБОВЬ; неитальянский город - Тонопа; правильная геометрическая аналогия та, что под номером 2.
Две числовые последовательности на с.92 дополняются соответственно числами 350 и 22: Задача с первой числовой последовательностью, приведенной на с.90, решается путем применения обобщенного правила разностей при k=3, а затем обобщенного правила частного; отсутствующий член равен 324. Задача со второй последовательностью должна остаться неприступной для всех, кроме, может быть, самых терпеливых любителей головоломок, если решающие не написали программу SE Q. Задача может быть решена путем применения двух правил частного. Значение к в первом правиле равно 5. Отсутствующий член равен - 65551.
9 1986
Статья о программах, проходящих тесты на умственное развитие (см. "В мире науки", 1986, #5), вдохновила многих читателей попробовать свои силы в мини-тесте. А некоторые написали даже свои собственные версии программы HI Q. П.Кук из Садбери (шт.Массачусетс), как и многие другие читатели, удивляется, как это удалось Марселю Феенстра, изобретателю программы HI Q, добиться результата в 160 очков. По словам самого Феенстра, эту идею подсказал ему его товарищ из Австралии К.Хардинг, набравший рекордную сумму баллов по тестам на умственное развитие. Харлинг предложил создать программу, которая могла бы подвергаться тестам, основанным на задачках по дополнению последовательностей, подобных тем, что содержатся в книге Г.Айзенка "Know Your Own I.Q." (Айзенк Г. Проверьте свои способности.- М.: Мир, 1972). В своей программе Феенстра принял систему оценки результатов, предложенную в книге Айзенка.
ДВЕ НЕЗАМЫСЛОВАТЫЕ ПРОГРАММЫ ДЕМОНСТРИРУЮТ ГЕНИАЛЬНЫЕ СПОСОБНОСТИ В ТЕСТАХ НА УМСТВЕННОЕ РАЗВИТИЕ
А.К.ДЬЮДНИ
НАВЕРНОЕ, всем знаком старый шуточный номер, который часто показывают в цирке и на ярмарочных клоунадах. На сцену выходит мужчина с могучей мускулатурой в сопровождении сравнительно хрупкой ассистентки. Мужчина берется за штангу невероятных размеров, и С нечеловеческим напряжением сил ему удается поднять ее над головой. Зрители аплодируют, однако аплодисменты тут же сменяются смехом, когда ассистентка небрежно подхватывает штангу одной рукой и уносит ее за кулисы.
Существуют две компьютерные программы, которые как бы воспроизводят этот комический номер, показывая нам, чего в действительности стоят умственные "мускулы", демонстрируемые теми, кто набирает высокий балл по результатам обычного теста на умственное развитие. Обе программы работают, если не на уровне гения, то близком к нему, решая две задачи, широко используемые в тестах: дополнение числовой последовательности и поиск геометрических аналогий. Однако, разобравшись в механизме работы этих программ (что можно сделать без особого труда), невольно удивляешься тому, насколько они, если можно так выразиться, глупы.
Мне вовсе не хочется обижать читателей, считающих себя щедро одаренными умственными способностями, и если я с иронией говорю о тесте умственного развития, то делаю это умышленно. Цель этого теста, как нам говорят, заключается в том, чтобы определить, каков уровень умственного развития индивидуума. Интеллект относится к тем немногим качествам, которыми человек гордится, если они у него есть, и испытывает неудовлетворение, если их у него нет. Однако говорить об интеллекте, когда речь пойдет об обычном тесте на умственное развитие, по-видимому, в корне ошибочно. Эта точка зрения убедительно аргументирована С.Гоулдом из Гарвардского университета в его книге, посвященной тестам на умственные способности (см. библиографию на с.104). В основном его рассуждения сводятся к следующему. Традиционные тесты такого рода основаны на неявно допускаемом ошибочном предположении, что человеческий интеллект, подобно физической силе,- это некий обобщенный физиологический показатель, поддающийся количественному измерению при помощи последовательности задач, упорядоченных по уровню сложности.
Хороший пример задач подобного рода - продолжение числовой последовательности. Каким должно быть следующее число в последовательности 2, 4, 6, 8,...? Или, например, в последовательности 2,4,8,14,...? Или 1,2,6,24,...? Количество правильных ответов на такие вопросы, выраженное в процентах, измеряет ваше "общее умственное развитие", подобно тому, как динамометр измеряет вес, который вы можете поднять, и, стало быть, силу ваших рук. Заметим, что если результаты теста трактуются как мера "общего умственного развития", то должно существовать некое "ядро" - центральная способность или несколько таких способностей, которые могли бы служить критерием общего умственного развития. Поскольку в самом понятии общего умственного развития предполагается наличие сильной взаимозависимости, или корреляции, между наиболее важными центральными способностями, то не так уж существенно, какие конкретно задачи были включены в тест. Одна задача не хуже и не лучше других.
Одна из рассматриваемых здесь программ, решающих задачи из тестов на умственное развитие, представляет собой упрощенную версию программы, написанной М.Феенстра, студентом из Роттердама. Программа под названием HI Q решает два вида задач, часто встречающихся в стандартных тестах, а именно дополнение числовой последовательности и обнаружение цифровых аналогий. Недавно Феенстра опробовал свою программу на ряде тестов, приведенных в книге Г.Айзенка "Know Your Own I.Q." ("Ваш коэффициент умственного развития"). Суммарное количество очков, набранных программой, оказалось равным примерно 160. И хотя условия и результаты эксперимента не были тщательно зафиксированы, едва ли следует сомневаться в том, что программа покажет хорошие результаты в реальных условиях, в которых проводятся подобные тесты.
Программа, которую мы здесь рассмотрим, называется SE Q. Она копирует поведение программы HI Q при решении задач на продолжение числовой последовательности. У читателей, которые напишут и испытают программу SE Q, возможно, сложится впечатление, что их умственные способности в решении числовых задач значительно повысятся. В основу программы положена довольно простая идея. Когда задана последовательность чисел и требуется найти следующее число, никто не пытается сразу угадать его. Стремятся найти правило, которому подчиняются заданные члены последовательности. Заметим, что с математической точки зрения для любой конечной последовательности чисел существует бесконечное количество правил, которым она подчиняется. Таким образом, задача сводится к отысканию простого правила, задающего последовательность.
В программе SE Q рассматриваются лишь два вида правил: аддитивные и мультипликативные. Например, чтобы найти следующее число в последовательности 2, 4, 8, 14,..., можно попытаться найти аддитивное правило, а лучший способ поиска такого правила заключается в построении так называемой пирамиды разностей (см. рисунок на с.90). В основании пирамиды лежит заданная последовательность чисел, и пирамида строится снизу вверх вычислением разностей между каждым последующим и предыдущим числами, находящимися на предыдущем уровне пирамиды. Так, первое число на втором уровне пирамиды есть разница первых двух чисел первого уровня, а именно 2 и 4. Их разность равна 2, и, таким образом, 2 - это первое число на втором уровне. Аналогично два других числа на втором уровне находятся вычитанием: 8-4=4 и 14-8 = 6; полученная в результате последовательность на втором уровне: 2, 4, 6. С помощью аналогичной процедуры находим числа третьего уровня пирамиды - их два, причем оба равны 2.

Продолжение числовой последовательности методом пирамиды. Предлагается решить две задачи, приведенные внизу
Равенство всех чисел на определенном уровне пирамиды является своеобразным сигналом, говорящим о том, что процесс наращивания пирамиды вверх следует прекратить и достраивать ее сбоку. Предположим, что третье число в третьем ряду пирамиды также должно быть равно 2. Но в таком случае логично считать, что следующее число во втором ряду пирамиды должно получаться путем прибавления к последнему числу 2, т.е. 6+2=8. В свою очередь это число можно прибавить к последнему члену последовательности на первом уровне пирамиды: 14+8=22; и действительно, 22 - это правильный ответ, за получение которого, согласно условиям теста, начисляют полное число баллов. Стоит таким образом прийти к последовательности одинаковых чисел на верхнем уровне пирамиды, как все остальные уровни будут достраиваться путем применения соответствующего правила к каждому нижележащему уровню вплоть до основания.
Очень многие задачи из тестов, касающиеся числовых последовательностей, сводятся к этой простой процедуре. Читатели, хорошо помнящие алгебру из курса средней школы, сразу же видят, что приведенные в качестве примера последовательности обладают свойствами полиномов. Любой полином, вычисленный для последовательного набора целых значений аргумента, дает последовательность, из которой можно построить пирамиду разностей. При достаточно большом количестве вычисленных значений на верхнем уровне пирамиды в конце концов получится последовательность одинаковых чисел. Количество требующихся для этого уровней минус единица - это степень полинома. Последовательность 2, 4, 8, 14, дающая постоянную последовательность, состоящую из двоек, на третьем уровне пирамиды разностей, образуется, например, в процессе последовательного вычисления значений квадратичного полинома, или полинома второй степени: x2-х+2.
К сожалению, не все задачи на числовые последовательности можно решить путем построения пирамиды разностей. Например, последовательность 1, 2, 6, 24,... дает пирамиду разностей, на верхнем уровне которой находятся числа 3 и 14. Однако быстрый рост членов последовательности говорит в пользу ее геометрического характера: соседние члены геометрической прогрессии отличаются друг от друга на постоянный множитель, а не на постоянную прибавляемую или вычитаемую величину. Разумно поэтому было бы построить множество величин, являющихся частным от деления соседних членов последовательности друг на друга, а не их разности (см. рисунок на с.90). Вычисляя частные от деления каждой пары чисел в последовательности 1, 2, 6, 24,..., мы получаем на втором уровне пирамиды числа 2, 3, 4,... Вторая последовательность говорит о резком изменении правила, задающего последовательность: третий ряд пирамиды нужно строить уже по разностям, а не по частным от деления. Наверное, ни у кого не возникнет сомнения в том, что в конце второго ряда должно стоять число 5? Таким образом, ответ будет равен 120, т.е. произведению 24, последнего заданного числа в первом ряду, и 5.
Программа SE Q, решающая задачи на продолжение числовых последовательностей, строит пирамиды, рассматривая как последовательности из разностей между соседними членами нижнего уровня, так и последовательности частных от их деления друг на друга. Более того, она исследует соседние пары чисел последовательности в поисках более общих аддитивных и мультипликативных правил. В аддитивном правиле первый член каждой пары может предварительно быть умножен на константу k, перед тем как произвести обычное сложение, а в мультипликативном правиле после обычного умножения к результату может быть прибавлена константа k. Написать такую программу - это довольно несложное упражнение для начинающих программистов (см. рисунок справа).

Алгоритм программы SE Q
Несколько простых формул, на которых основаны общие правила построения пирамиды, представляют собой главную часть программы SE Q. Предположим, что числа заданной последовательности уже были присвоены в качестве значений четырем переменным a(1), a{2), a(3), a(4). Чтобы получить второй ряд, b(1), b(2), b(3), программа пытается применить либо обобщенную формулу разности вида b(1) <- a(2) - k*a(1), либо обобщенную формулу частного вида b(1) <- [a(2) - k]/a(1). В обоих случаях k означает произвольное целое число из определенного диапазона. Программа пытается также сделать аналогичные подстановки для b(2) и b(3) при одном и том же значении константы k: для b(2) она пробует формулу a(3)-k*a(2) или [a(3)-k]/a(2), а для b(3) она пробует a(4)-k*a(3) или [а(4)-k]/a(3).
Третий ряд, c(1), c(2), получается еше проще: программа пробует подставлять лишь формулу простой разности c(1) <- b(2)-b(1) и c(2) <- b(3)-b(2) или простого частного: c(1) <- b(2)/b(1) и c(2) <- b(3)/b(2). Очевидно, в тестах на умственное развитие очень редко встречаются задачи с числовыми последовательностями более сложными, чем те, которые охватываются рассмотренными формулами.
При построении пирамиды программа SE Q каждый раз пробует применить обобщенную формулу для вычисления значений b и простую формулу для значений c. Таким образом, программа создается как бы из четырех сегментов. Каждый сегмент представляет собой цикл с какой-то одной комбинацией подстановочных формул. Например, в одном из таких сегментов сначала применяются три обобщенные формулы частного вида b{1) <- [a(2)-k]/а(1) для вычисления значений b(l), b(2) и b(3), образующих второй уровень пирамиды. Затем в этом сегменте применяются две простые формулы разности вида c(1) <- b(2)-b(l), чтобы получить значения c(1) и c(2) третьего уровня пирамиды. Весь набор из пяти формул вложен в так называемый цикл полного перебора возможностей, в котором пробуется каждое значение константы k, Феенстра рекомендует ограничивать значения к диапазоном от -5 до 5.
Внутри цикла, после того как вычисляются новые значения c(1) и c(2), они проверяются на равенство. Если они оказываются равными, то их общее значение присваивается переменной c, а текущее значение константы к присваивается переменной kk. Сразу за циклом расположены операторы, строящие искомое число, продолжающее заданную последовательность (если решение было найдено) по значениям c и kk. В рассматриваемом примере получаем b(4), новый член второго уровня, путем прибавления c к значению b(3). Ответ, т.е. значение a(5), получается затем умножением a(4) на b(4) и прибавлением значения kk к произведению.
Таким образом, двух операторов в конце каждого цикла оказывается достаточно, чтобы получить решение задачи, если поиск, осуществляемый в цикле, оказался успешным. Конкретный вид этих операторов зависит от формул, применяемых в соответствующем цикле, и я предоставляю читателям, желающим самостоятельно написать программу SE Q, установить, какими должны быть операторы, завершающие каждый цикл. Чтобы выделить переменную, представляющую наибольший интерес в каждом конкретном случае, воспользуйтесь приемами алгебры. И конечно, если один из описанных циклов программы приводит к решению задачи, то оно должно быть выведено на печать специальным оператором печати. При этом программа может уже не выполнять оставшиеся циклы и остановиться, или же она может выполнить все циклы, чтобы найти другие решения. Выполняя все циклы своей программы, Феенстра выявил несколько "некорректных" задач в тестах, имевших более одного правильного ответа. Если ни в одном из четырех циклов не удается найти никакого решения, то разумно на этот случай предусмотреть вывод на печать сообщения о неудаче поиска. Каким именно должно быть это сообщение - дело вкуса. Те, кто хочет придать своей программе оттенок одушевленности, могут, например, заложить в нее сообщение "Помогите!".

Мини-тест на умственное развитие, составленный из вопросов, заимствованных из книги Г.Айзенка "Ваш коэффициент умственного развития"
Программу SE Q можно испытать на вопросах, взятых из нескольких широко известных книжек, посвященных тестированию. В книге Айзенка приведено восемь полных тестов, при помощи которых читатель якобы может определить коэффициент своего умственного развития. Тесты включают вопросы нескольких различных видов, обычно присутствующих в стандартных тестах, например вопросы о недостающем числе, недостающей букве, недостающем слове, неподходящем слове, о перетасованных словах и геометрических аналогиях (см. рисунок слева). В каждой категории вопросов обычно имеются несколько подтипов. Например, в книге Айзенка есть три типа вопросов о недостающем числе, а именно обычные задачи на дополнение числовой последовательности, уже рассмотренные выше, и два других типа задач, которые можно проиллюстрировать следующими двумя примерами:

В каждом случае экзаменующийся потенциальный гений должен указать недостающее число в соответствии с "уловленным" им правилом. Программа Феенстры HI Q справляется с такими вопросами при помощи процедур, в которых применяются формулы того же типа, что и в рассмотренной выше программе продолжения числовой последовательности. Предлагаю читателям попробовать свои силы. В следующем номере журнала будут даны ответы к двум приведенным выше задачам, а также к задачам, представленным на рисунках на с.90 и 92.
Хотя программа HI Q отвечает лишь на вопросы одного важного класса из числа предлагаемых в тестах на проверку умственного развития, решение задач, относящихся к другим классам, также можно автоматизировать. В самом деле, программа, решающая задачи на геометрические аналогии, была написана более 20 лет назад Т.Эвансом как часть его диссертации на звание доктора философии, которую он защитил в Массачусетском технологическом институте. Несмотря на то что все это звучит весьма серьезно, основные идеи, заложенные в программе Эванса, можно легко понять.
Все геометрические задачи, которые она призвана решать, сводятся к следующему: фигура A относится к фигуре B, как фигура C относится к одной из, скажем, четырех фигур, приведенных в качестве потенциального ответа. Программа выбирает подходящую фигуру, сначала пытаясь определить набор простых правил, трансформирующих фигуру A в фигуру B (см. рисунок справа). Затем она повторяет эту процедуру с фигурой C и каждой из четырех фигур - потенциальных решений задачи. В каждом случае генерируется набор правил, при помощи которых фигуру С можно трансформировать в искомую фигуру. Фигура, получающаяся в результате применения тех правил трансформации, которые ближе всего к правилам, трансформирующим фигуру A в фигуру B, выбирается в качестве ответа.

Алгоритм решения задач на геометрические аналогии, приведенный в диссертации Т.Эванса
В программе Эванса пять раз повторяется, по существу, одна и та же операция. Каждый раз две фигуры, исходная и производная, служат в качестве входных данных. Для каждой такой пары фигур программа вырабатывает трехкомпонентное табличное описание процесса трансформации, в результате которого исходная фигура превращается в производную. Сначала программа перечисляет пространственные взаимоотношения между составными частями исходной фигуры, затем она перечисляет пространственные отношения между составляющими производной фигуры. В обоих описаниях рассматриваются лишь три пространственных отношения; ВЫШЕ, СЛЕВА ОТ и ВНУТРИ. Наконец, программа описывает, каким образом изменяются составляющие детали второй фигуры по сравнению с составляющими первой. Изменения эти могут быть четырех видов; каждая деталь может: изменить свой размер, оказаться повернутой, быть отражением или же вовсе исчезнуть.
Предположим, фигуры A, B и C состоят из трех частей каждая: круга, квадрата и треугольника. На фигурах A и B программа может обозначить треугольники буквой a, квадраты - буквой b и круги - буквой c, однако она не пытается обозначить детали фигуры С аналогичным образом. Вместо этого она присваивает трем составляющим фигуры C произвольные обозначения x, y и z. Затем она создает трехкомпонентное табличное описание для пары фигур A и B и еще четыре описания, по одному для каждой пары фигур C и фигуры из числа кандидатов на ответ. В последних четырех таблицах повсюду используются обозначения x, y и z. Завершающая операция программы Эванса состоит в том, чтобы произвести все возможные подстановки a, b и c вместо x, y и z. Поскольку x, y и z можно переставить лишь шестью различными способами, количество производимых подстановок в программе также равно шести. Одна из подстановок может превратить табличное описание пары фигур A и B в соответствующее табличное описание фигуры C и одной из фигур - кандидатов на ответ. Эта последняя фигура и представляет собой решение задачи. Если точного соответствия найти не удалось, то программа может подсчитать степень относительного успеха при подстановках и выбрать подстановку, дающую наилучший результат.
Патрик Уинстон описывает программу поиска геометрических аналогий в своей книге "Artificial Intelligence" (в переводе "Искусственный интеллект", см. библиографию). Уинстон утверждает, что программа "работает хорошо" и объясняет ее успех применением эффективной системы представления знаний, касающихся геометрических фигур, которыми оперирует программа. Например, вместо того чтобы указывать, каким образом такие отношения, как ВЫШЕ, СЛЕВА ОТ или ВНУТРИ, изменяются от картинки к картинке, программа могла бы описывать, как одна фигура на первой картинке трансформируется в другую фигуру на второй картинке. Такая программа могла бы оказаться чрезвычайно громоздкой и к тому же неэффективной, поскольку ей нужно было бы проверить намного большее количество подстановок по сравнению с программой Эванса. В действительности поиск хорошего представления является центральной проблемой в задаче создания искусственного интеллекта. Очень часто удачно выбранное представление оказывается ключевым фактором, позволяющим компьютеру имитировать некоторые аспекты человеческого мышления, проявляемого при решении различных задач.
По аналогичным причинам представление объектов в сознании человека также является в настоящее время предметом оживленных дискуссий среди исследователей, занимающихся изучением природы человеческого интеллекта. В этом смысле необходимость изучения искусственного интеллекта часто объясняется, помимо всего прочего, и тем, что оно представляет собой попытку продемонстрировать "доказательство существования" механистического описания человеческих способностей. При этом рассуждают примерно так: если компьютерная программа оказывается в состоянии моделировать какой-то элемент человеческого поведения, то представление поведения, заложенное в программе, может по крайней мере служить моделью внутреннего представления того же элемента поведения в человеческом мозгу. Однако на самом деле успешное моделирование человеческого поведения зачастую проливает очень мало света на внутренние процессы, характерные для человеческой психики. Мы не можем с уверенностью утверждать, что существует какая-либо связь между механизмом работы программ Феенстры и Эванса и тем, как аналогичные задачи решаются людьми. Вероятно, человеческий разум при решении той или иной конкретной задачи пользуется более универсальными стратегиями.
Это последнее предположение как бы замыкает круг наших рассуждений и возвращает нас к вопросу о природе человеческого интеллекта и о том, как его можно измерить. Уже отмечалось, что С.Гоулд охарактеризовал тесты на умственное развитие как принципиальное заблуждение. В своей критике он делает акцент на двух главных недостатках, присущих самой концепции тестов: неправомерной материализации сугубо абстрактного понятия и ранжировании этой материализованной абстракции в одном-единственном измерении. В значительной степени эта наша склонность "делать вещи" из того, что в лучшем случае является лишь туманными абстракциями, объясняется самой природой языка. Более того, когда мы убеждаем себя в том, что имеем дело с реальной вещью, у нас срабатывает рефлекс попытаться измерить ее.
Требуя единой количественной меры, мы совершаем вторую принципиальную ошибку, а именно ошибку ранжирования. Мы хотим свести сложные явления к одной шкале. Подобные методы привели нас к хорошей физике, но они также привели к плохим социальным теориям. В частности, я имею в виду тестирование интеллекта. Для XXв. это примерно то же самое, чем была для XIXв. краниометрия - система измерений черепа человека с помощью антропологических инструментов. В обоих случаях целые расовые группы людей оказались "измерены" принципиально ошибочно не только потому, что само по себе это измерение было почти бессмысленным, но и потому, что процесс измерения в значительной мере был подвержен предубеждениям, как сознательным, так и неосознанным.
Гоулд энергично атакует биологический детерминизм, мнение о том, что поведение человека определяется его генами, и предостерегает нас от той точки зрения, что способности нашего мозга являются прямым следствием естественного отбора. "Наш мозг - это компьютер колоссальной сложности,- пишет он.- Если установить гораздо более простой компьютер для бухгалтерских расчетов на фабрике, то он может также выполнять и многие другие более сложные функции, не связанные с его непосредственной ролью. Эти дополнительные способности являются неизбежным следствием структурной конструкции машины, а не его приспособления. Наши значительно более сложные биологические компьютеры также были созданы с некоторой целью, однако они обладают почти ужасающим многообразием дополнительных способностей, включая большую часть того, что, как мне кажется, делает нас людьми".
И именно здесь Гоулд затронул то, что, на мой взгляд, должно тревожить нас в оценке относительно простой компьютерной программы, которая, подвергшись тесту на умственное развитие, получает балл на уровне гения. Измеряет ли этот балл умственное развитие компьютера? Если нет, то каким образом можно измерить интеллект машины независимо от того, сделана она из кремния или пластмассы или еще какого-нибудь материала? Ответ: наверное, не прогоном программы через набор тестов на умственное развитие.
БИБЛИОГРАФИЯ
THE MISMEASURE OF MAN. STEPHEN JAY GOULD. W.W.Norton & Company, Inc., 1981.
KNOW YOUR OWN I.Q. H.J.EYSENCK. Penguin Books, 1984.
АЙЗЕНК Г. ПРОВЕРЬТЕ СВОИ СПОСОБНОСТИ. Перев. с англ.- М.: Мир, 1972.
УИНСТОН П. ИСКУССТВЕННЫЙ ИНТЕЛЛЕКТ. Перев. с англ.- М.: Мир, 1980.
ОТКЛИКИ
6 1986
В майском номере журнала речь шла о тестах на умственное развитие, и там перед читателями было поставлено несколько вопросов относительно числовых последовательностей. Первая задача мини-теста может послужить хорошим примером неоднозначности, обычно присутствующей в подобных задачах. Нужно было продолжить последовательность 3, 7, 16, 35,... Если из каждого члена последовательности вычесть удвоенный предыдущий член, то получится последовательность 1, 2, 3, ... - второй ряд пирамиды. Согласно этому правилу, следующий член должен быть равен: 35*2+4, т.е. 74. В то же время если построить простую пирамиду разностей в три ряда, то в третьем ряду мы получим 5 и 10. Разумно поэтому достроить этот ряд числом 15. Но тогда соответственно исходную последовательность нужно дополнить числом 69. Следует сказать, что программы, описанные в нашей предыдущей статье, упустили бы этот ответ. Теперь приведем ответы на вопросы мини-теста: отсутствующая буква - это 3 (если считать, что в алфавите нет буквы е); отсутствующее слово - БАР; неподходящее слово - ЛЮБОВЬ; неитальянский город - Тонопа; правильная геометрическая аналогия та, что под номером 2.
Две числовые последовательности на с.92 дополняются соответственно числами 350 и 22: Задача с первой числовой последовательностью, приведенной на с.90, решается путем применения обобщенного правила разностей при k=3, а затем обобщенного правила частного; отсутствующий член равен 324. Задача со второй последовательностью должна остаться неприступной для всех, кроме, может быть, самых терпеливых любителей головоломок, если решающие не написали программу SE Q. Задача может быть решена путем применения двух правил частного. Значение к в первом правиле равно 5. Отсутствующий член равен - 65551.
9 1986
Статья о программах, проходящих тесты на умственное развитие (см. "В мире науки", 1986, #5), вдохновила многих читателей попробовать свои силы в мини-тесте. А некоторые написали даже свои собственные версии программы HI Q. П.Кук из Садбери (шт.Массачусетс), как и многие другие читатели, удивляется, как это удалось Марселю Феенстра, изобретателю программы HI Q, добиться результата в 160 очков. По словам самого Феенстра, эту идею подсказал ему его товарищ из Австралии К.Хардинг, набравший рекордную сумму баллов по тестам на умственное развитие. Харлинг предложил создать программу, которая могла бы подвергаться тестам, основанным на задачках по дополнению последовательностей, подобных тем, что содержатся в книге Г.Айзенка "Know Your Own I.Q." (Айзенк Г. Проверьте свои способности.- М.: Мир, 1972). В своей программе Феенстра принял систему оценки результатов, предложенную в книге Айзенка.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
6 1986
ПРОГРАММА, ВРАЩАЮЩАЯ НА ЭКРАНЕ ДИСПЛЕЯ ЧЕТЫРЕХМЕРНЫЕ ГИПЕРКУБЫ
А.К.ДЬЮДНИ
"Мой муж буквально растворился в воздухе, и я думаю, что вы в какой-то степени причастны к этому!" - Я узнал женщину, говорившую со мной по телефону. Это была Черил, и она была явно не в себе. Ее муж Мэги, мой специальный помощник по микрокомпьютерам в Университете шт.Западный Онтарио, по всей видимости, исчез, наблюдая за поведением компьютерной программы, которую я предложил ему написать. Программа вращает четырехмерный аналог куба, называемый гиперкубом, и проектирует его на экран дисплея. Черил взволнованно продолжала: "По экрану движется какой-то странный узор, а вещи моего мужа свалены в кучу у кресла. Он, наверное, был в этих странных цветных очках с картонной оправой. А это что? Боже мой, его носки остались в туфлях!"
Мне стало ясно, что здесь имело место классическое проявление четырехмерного помешательства. Его жертвы убеждены, что они вышли за пределы обычного пространства и очутились в четырехмерном мире, невидимом для остальных людей. Это иллюзорное впечатление, что человек стал невидимым, может быть настолько сильным, что затрагивает восприятие и других людей: жертва помешательства может войти в комнату полную людей и остаться незамеченной. К счастью, случай с Мэги закончился благополучно, но об этом потом. А пока расскажу о программе, вращающей гиперкубы, сделав предварительно одно предупреждение, к которому, надеюсь, читатели отнесутся достаточно серьезно. Те, кто склонен к помешательству, как Мэги, не должны писать эту программу и тем более наблюдать за ее работой на экране дисплея. К потенциальным жертвам можно отнести всех, у кого наблюдался навязчивый интерес к пространствам высших размерностей, а также тех, кто, пусть даже не часто, но задумывался о заманчивых перспективах неизведанных пространств и миров.
Четвертое измерение стало предметом физических и метафизических размышлений по крайней мере с конца прошлого столетия. Идея четвертого измерения имела наибольший успех в специальной и обшей теориях относительности Эйнштейна. В этих теориях пространство и время в совокупности образуют четырехмерный континуум, в котором все события во Вселенной оказываются как бы навсегда замороженными. Такая концепция Вселенной может подвергаться модификациям в количестве измерений. Например, в так называемых теориях Клейна-Калузы вводится семь или более дополнительных измерений в форме миниатюрных гиперпузырьков, прикрепленных к каждой точке пространства-времени (см. статью Дэниела 3. Фридмана и Питера ван Ньювенхойзена "Скрытые измерения пространства-времени", опубликованную в майском номере нашего журнала за 1985г.).
Четвертое измерение, с которым я познакомился, а познакомившись, полюбил его,- это дитя математики. Читатели, находящиеся в обыкновенных комнатах, имеют трехмерную систему координат, так сказать, у себя над головой. Три плоскости встречаются в каждом углу комнаты, и из этого угла исходят три линии, каждая из которых является пересечением двух плоскостей. Каждая линия перпендикулярна двум другим. Может ли читатель представить себе еще одну, четвертую линию, перпендикулярную этим трем? Наверное нет, но именно этого требуют математики, сооружая чисто абстрактную конструкцию, называемую четырехмерным пространством. Теперь вам предоставляется возможность самим исследовать это пространство, не подвергая себя непосредственной опасности. Для этого нужно лишь написать программу, которую я называю HYPERCUBE (гиперкуб).
Если говорить о происхождении этой программы, то вспомним, что еще в середине 60-х годов А.Нолл, в то время работавший в фирме Bell Laboratories, отснял фильм, в котором представлены двумерные тени, отбрасываемые четырехмерными объектами, движущимися в четырехмерном гиперпространстве. Однако в ее теперешнем виде программа была разработана Т.Бэнкоффом и его коллегами по лаборатории компьютерной графики в Университете Брауна, и настоящая статья была написана под влиянием впечатления, которое произвели на меня замечательные изображения, порожденные программой (см. рисунки на с.99, 101 и 102). Бэнкофф, профессор математики, возглавляет визуальные исследования поверхностей и пространств высших размерностей в дополнение к своим геометрическим исследованиям. В 1978г. совместно с Ч.Строессом он продемонстрировал генерируемый компьютером десятиминутный цветной фильм "Гиперкуб: проекции и разрезы". Этот фильм уже успел стать классическим в математическом подполье. Бэнкофф, вероятно, также является ведущим исследователем жизни и творчества Эдвина Аббота, английского священника и учителя, который в 1884г. написал сказку о воображаемой жизни в двумерном мире ("Flatiand", см. библиографию на с.116).

Поворот четырехмерного гиперкуба через измерения 2 и 4, проецируемый на обычное трехмерное пространство
Бэнкоффу и его коллегам удалось создать потрясающие изображения, иллюстрирующие свойства четырехмерных объектов. Например, рисунки на с.99 изображают вращение четырехмерного гиперкуба в четырехмерном пространстве. Чтобы лучше понять эти картинки, рассмотрим тень, отбрасываемую обычным кубом на плоскость: эта тень может напоминать квадрат, заключенный в другом квадрате. Если затенить соответствующие грани куба, то тень представляет собой квадрат с квадратным отверстием внутри (см.нижний рисунок на с.100).
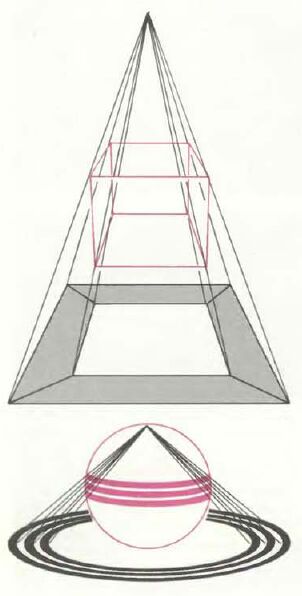
Проекции куба и сферы
Аналогично, когда гиперкуб освещен из точки, расположенной "над" обычным пространством в четвертом измерении, трехмерная тень, отбрасываемая гиперкубом, может напоминать куб, заключенный в другом кубе. Внутренний куб окружен шестью шестигранниками, которые можно рассматривать как искаженные кубы. Четыре искаженных куба, прилегающих к граням внутреннего куба, образуют в совокупности сплошное тело, торообразная поверхность которого показана на изображениях Бэнкоффа. Два других искаженных куба - внутренний и внешний - также образуют тор, который здесь не показан. Когда гиперкуб вращается, возникает ощущение, что квадратное отверстие в видимом торе надвигается на зрителя. Те, кто напишет свою версию программы HYPERCUBE, станут свидетелями других подобных эффектов, хотя уже и не таких реалистичных или "непрерывных".
Изображения, приведенные на с.101 и 102, взяты из фильма "Гиперсфера: расслоение и проекции", который готовят к выпуску Бэнкофф и его коллеги Г.Кошак, Д.Лэйдлоу и Д.Марголис. Гиперсфера представляет собой гораздо более сложный объект по сравнению с гиперкубом, и я не стану детально описывать ее. Тем не менее эти изображения можно в какой-то степени лучше понять, воспользовавшись аналогией с обычной сферой. Если в исходном положении сфера покоится на плоскости, касающейся южного полюса сферы, а источник света в исходном положении находится на ее северном полюсе, то тень, отбрасываемая на плоскость линиями параллелей сферы, будет представлять собой ряд концентрических окружностей (см. нижний рисунок на с.100). Если сфера начинает поворачиваться, а источник света остается в фиксированном положении, то тени-окружности будут становиться неконцентрическимн, а теневое изображение любой окружности, целиком лежащей в плоскости источника света, будет представлять собой прямую линию.

Последовательность вложенных торов, которые по аналогии с параллелями на сфере являются проекциями гиперсферы на три измерения

Проецируемое движение торов по мере вращения гиперсферы аналогично проекции движения параллелей во время вращения сферы
Аналогичным образом трехмерная "тень", отбрасываемая гиперсферой, может рассматриваться как ряд концентрических торов (см. рисунок на с.101). Когда гиперсфера вращается, торы как бы раздуваются и проносятся один за другим. При этом любой тор, проходящий через источник света, становится бесконечно большим (см. рисунок на с.102).
Рассмотрение аналогий в различных размерностях - ценное подспорье для построения и понимания четырехмерных объектов. Например, гиперкуб получается из куба точно так же, как куб получается из квадрата. Чтобы получить куб из квадрата, будем поднимать квадрат в направлении, перпендикулярном его плоскости, до высоты, равной его стороне (см. верхний рисунок на с.100). Полученный в результате куб имеет 8 вершин (вдвое больше, чем у исходного квадрата) и 12 ребер - 4 стороны исходного квадрата и 4 стороны вновь полученного верхнего квадрата, а еще 4 получаются соединением вершин исходного квадрата с вершинами верхнего квадрата. Кроме того, у куба 6 квадратных граней - одна, совпадающая с исходным квадратом, одна - с поднятым и по одной грани-стене, воздвигнутой между каждой из 4 пар сторон, принадлежащих исходному и поднятому квадратам.

Квадрат порождает куб, а куб порождает гиперкуб
Если представить на мгновение, что у нас есть еще одно дополнительное измерение, то ту же операцию можно повторить уже для куба. В самом деле, "поднимем" куб из обычного пространства в направлении дополнительного измерения на "высоту", равную грани куба (смотри рисунок вверху). В результате получится гиперкуб. Но каково же все-таки направление дополнительного измерения? Я не могу этого объяснить. Даже фотография с изображением моей руки, указывающей в направлении четвертого измерения, не помогла бы. На ней рука была бы просто невидимой.
Тем не менее количество вершин, ребер, граней и гиперграней (обыкновенных кубов), из которых состоит гиперкуб, можно легко подсчитать. Количество вершин равно количеству вершин в исходном кубе плюс их количество в перенесенном кубе - всего 16. Каждая из 8 вершин исходного куба соединяется ребром с одной из 8 вершин перенесенного куба, и, кроме того, есть еще 12 ребер в каждом из этих двух кубов. Таким образом, всего гиперкуб насчитывает 8+12+12=32 ребра. Аналогично можно показать, что число обычных граней гиперкуба равно 24, а число гиперграней равно 8.
Должен выразить признательность Д.Лэйдлоу, объяснившему мне механизм программы HYPERCUBE. Версия программы, которую я здесь опишу, генерирует изображение гиперкуба, показывая лишь его вершины и ребра. Более того, изображения, генерируемые программой, не обязательно представляют один куб внутри другого; на самом деле изображение зависит от того, каким образом реализована программа и как она выполняется. Всякий раз при повороте гиперкуба его вершины переходят в новое положение и возникает новое, сбивающее с толку изображение объекта. Однако, когда у вас накопится некоторый опыт в экспериментировании, изображения станут в каком-то смысле понятными и вы почувствуете себя на пороге чего-то волнующе грандиозного и манящего.
В программе 16 вершин гиперкуба пронумерованы от 0 до 15 по простой схеме. Если каждый из этих номеров представить в двоичном виде и составить массив из элементов по четыре бита, то мы получим миниатюрную систему координат. Например, двоичное представление числа 13 состоит из 1 (одной восьмерки), 1 (одной четверки), 0 (ни одной двойки) и 1 (одной единицы). Таким образом, это число можно записать в виде (1, 1, 0, 1). Такая запись уже дает нам практически систему координат для представления положения вершин гиперкуба. (Это не есть положение, которое напоминает куб внутри другого куба). Чтобы перейти к более удобной системе координат, заменим нули на -1 и помножим каждый элемент массива на достаточно большое число, чтобы построить на экране дисплея изображение приемлемых размеров. Например, если в качестве такого множителя выбрать число 10, то координаты 13-й вершины будут представлены как (10, 10, -10, 10).
Конструируя программу HYPERCUBE, мы повсеместно сталкиваемся с размерностями. Двумерная матрица, или массив, vert хранит исходные координаты вершин. Поскольку всего насчитывается 16 вершин, каждая из которых задается четырьмя координатами, vert представляет собой матрицу размером 16*4 - всего 64 числа. Vert{i, j) - это j-я координата i-й вершины. Программа HYPERCUBE сохраняет матрицу vert неизменной, она определяется в начале программы, и ее содержимое переносится затем в другую матрицу размерами 16*4, назовем ее cube. Эту матрицу можно считать рабочей, ее содержимое постоянно меняется при поворотах гиперкуба, выполняемых программой.
После инициализации матрицы vert программу можно условно разбить на три главных раздела: выбор желаемого поворота гиперкуба, вычисление координат повернутого гиперкуба и представление (высвечивание) результатов поворота на экране дисплея. Если бы вращаемый объект был трехмерным, то поворот можно было бы выбрать, указав ось вращения и угол поворота вокруг этой оси. Однако при повороте четырехмерного объекта выбор оси вращения не определяет плоскости, в которой происходит поворот. Напомним, что существуют два неэквивалентных направления, перпендикулярные заданной плоскости. В то же время даже для четырехмерного гиперпространства остается справедливым, как и в обычном пространстве, то, что поворот может повлиять только на два измерения. Когда поворачивается трехмерный объект, во вращательном движении принимают участие два измерения, в то время как третье остается неподвижным. Аналогично, при повороте четырехмерного объекта два его измерения меняют ориентацию в пространстве, а два других остаются неподвижными.
Существует много способов поворота четырехмерного объекта в новое положение. Однако оказывается, что любое положение может быть достигнуто последовательностью таких поворотов, которые ограничиваются плоскими движениями, определяемыми координатными осями окружающего четырехмерного пространства. В четырехмерном пространстве мы имеем 4 координатные оси, пронумерованные, скажем, от 1 до 4, и существует 6 способов разбиения их на пары. Следовательно, мы имеем 6 плоскостей в четырехмерном пространстве, определяемых координатными осями: плоскость 1-2, т.е. плоскость, заданная осями 1 и 2, плоскость 1-3, плоскость 1-4, плоскость 2-3, плоскость 2-4 и плоскость 3-4.
Для каждой из этих шести плоскостей есть свой вид поворота, который определяется квадратной матрицей размером 4*4. т.е. состоящей из 16 чисел. Назовем эти 6 матриц поворота соответственно rot12, rot13, rot14, rot23, rot24 и rot34. Работая с программой, вы должны указать имя матрицы для выбранного поворота и величину угла поворота. Например, напечатав на клавиатуре терминала "rot23", а затем "60", вы тем самым задаете программе команду выполнить поворот на 60o в плоскости, заданной второй и третьей осями координат.
Предположим, вы хотите повернуть гиперкуб в плоскости третьего и четвертого измерений. Пожалуй, это самый загадочный из возможных поворотов. Для этого используется матрица rot34. В качестве ее элементов могут встретиться нули, единицы и три других числа, расположенные следующим образом:

Выбранный вами угол поворота в градусах запоминается в переменной ang, причем величины а и b зависят от значения ang: a равно cos(ang), a b равно sin(ang), где sin и cos - обычные тригонометрические функции угла синус и косинус.
Правило получения остальных пяти матриц поворота довольно простое. Величина a появляется на главной диагонали каждой матрицы в положениях, соответствующих измерениям, которые затрагиваются при повороте. Величина b появляется на всех других пересечениях строк и колонок, соответствующих измерениям, которые участвуют в повороте. Все остальные элементы на главной диагонали равны 1, а прочие элементы матрицы равны 0. Например, матрица rot13 имеет следующий вид:

Когда нужная матрица поворота выбрана, значения ее элементов присваиваются программой HYPERCUBE специальной матрице rote. Это присвоение удобно выполнять в виде двойного цикла: внутренний цикл - для последовательности величин, расположенных по строке матрицы, а внешний - для последовательности строк.
Координаты вершин повернутого гиперкуба вычисляются путем "умножения" матрицы cube на выбранную матрицу поворота rote. Произведение этих двух матриц временно запоминается в третьей матрице, назовем ее temp, и оно дает координаты повернутого гиперкуба. Это произведение вычисляется по правилам умножения матриц, и для вычисления используется стандартная операция перемножения числовых матриц. Последняя заключается в большом количестве всевозможных перемножений, выполняемых в тройном цикле.
Так же как vert и cude, матрица temp имеет размер 16*4 и состоит из 64 чисел. Она дает четыре координаты для каждой из 16 вершин гиперкуба в новом положении. Каждый элемент матрицы temp(i ,j) определяется двумя индексами i и j. Например, элемент temp(13, 3) задает третью координату 13-й вершины повернутого гиперкуба. Его значение является суммой четырех произведений чисел, выбранных в точном определенном порядке из матрицы cube и матрицы rote (см. рисунок на с.103). В качестве индекса внутреннего цикла программы можно взять букву k, пробегающую значения от 1 до 4, и этот цикл будет возвращать значение одного элемента матрицы temp. Цикл по k заключается затем в промежуточный цикл по индексу j. В цикле по j вычисляются все четыре координаты i-й вершины повернутого гиперкуба в соответствии с только что описанной процедурой. Другими словами, этот цикл заполняет все 4 элемента i-й строки матрицы temp. Наконец, цикл по j заключается во внешний цикл с индексом i. В цикле по i вычисляются все 16 строк матрицы temp, и когда этот цикл завершается, матрица temp дает координаты всех вершин повернутого гиперкуба, представшего перед нами в своем новом положении и, так сказать, во всей своей красе. Чтобы показать его на экране дисплея, потребуется еще один двойной цикл, заменяющий координаты старого положения гиперкуба в матрице cube его новыми, только что вычисленными координатами из матрицы temp.

Вершина гиперкуба, поворачиваясь, уходит из трехмерного в четырехмерное пространство
У гиперкуба четыре измерения, а у экрана дисплея только два. Поэтому разумно было бы условиться, что, скажем, первые два измерения (или координаты) гиперкуба соответствуют координатам экрана. Простейший способ представления третьего и четвертого измерений гиперкуба заключается просто в том, чтобы игнорировать их. Именно так и работает метод отображения, который я здесь опишу, но его можно усовершенствовать (в результате чего проекция объекта может выглядеть демонически сложной), если попытаться сделать третье и четвертое измерения несколько более наглядными.
Чтобы отобразить "скелет" гиперкуба, программе нужно лишь показать его ребра. Поскольку у гиперкуба 32 ребра, то та часть программы, которая ответственна за отображение на экран, должна лишь провести соответствующие линии между 32 парами вершин. Но в каком порядке? Практически существует неограниченное количество вариантов, и поэтому ответ на этот вопрос, по-видимому, зависит от личного вкуса. Тем не менее трудно удержаться от соблазна изобразить ребра как след Эйлера. Он назван так в честь знаменитого математика Леонарда Эйлера. След Эйлера можно нарисовать карандашом, не отрывая его от бумаги и не проводя ни одной линии более одного раза. Последовательно нарисованные ребра гиперкуба в виде следа Эйлера имеют общую вершину.
В обход, пересекая, вверх и вниз скачет след Эйлера по мере того, как он проходит через вершины. Очень изящным представляется следующий порядок соединения вершин гиперкуба: 0, 1, 3, 2, 6, 14, 10, 8, 9, 11, 3, 7, 15, 14, 12, 13, 9, 1, 5, 7, 6, 4, 12, 8, 0, 4, 5, 13, 15, 11, 10, 2, 0. Эти вершины хранятся в массиве trail с индексом i. Таким образом, i-я вершина в последовательности из 33 вершин обозначается как trail(i). Для каждого значения i выполняются команды выборки первой и второй координаты как элемента trail(i), так и trail (i+1). Затем нужно выполнить команду, которая рисует на экране линию, соединяющую две заданные точки. Команды выборки и графическая команда вложены в единый цикл с индексом i, который от каждой точки-вершины последовательности проводит линию к следующей точке.
Теперь несколько слов о некоторых визуальных (и психологических) осложнениях. Существуют два стандартных метода представления третьего измерения гиперкуба. Ортографический метод просто игнорирует третье измерение, и все вершины проецируются на плоскую поверхность экрана вне зависимости от расстояния между ними и экраном. В перспективе из одной точки вершины проецируются на экран так, как будто они являются тенями от света точечного источника, расположенного в центре экрана и на некотором расстоянии позади гиперкуба. Наблюдение этих теней на экране эквивалентно наблюдению гиперкуба с обратной стороны, однако визуально вид сзади неотличим от вида спереди.
Чтобы добиться эффекта перспективы из одной точки, в программе HYPERCUBE принимается, что третья координата вершины равна расстоянию между вершиной и экраном по линии, ведущей к воображаемому источнику света. Пользуясь признаками подобия треугольников, программа определяет множитель, необходимый для того, чтобы преобразовать первые две координаты вершины в координаты на экране дисплея. Например, если воображаемый источник света находится на расстоянии 20 единиц от экрана, вершина с координатами (5, -7, 11, 18 ) может быть спроецирована на экран путем умножения каждой из первых двух координат на 20 и деления результата на разность 20-11, т.е. число 9.
К сожалению, здесь мне не удастся уместить полное описание процесса, при помощи которого создаются стереоскопические изображения, показывающие четвертое измерение гиперкуба. Существует общий метод построения стереоскопических изображений, и в будущем я надеюсь посвятить этой теме одну из своих статей. Однако для программы HYPERCUBE Бэнкофф и его коллеги применили значительно более простой метод. Для каждого положения гиперкуба создаем два новых изображения путем применения матрицы rot14 с углом поворота на 3o в одном направлении и на 3o в другом. Направление первого измерения параллельно горизонтальной линии зрения, а четвертое измерение - это цель, достигаемая процедурой. Два небольших поворота хорошо аппроксимируют вид гиперкуба для наблюдателя. Нужно лишь представить себе, как две линии зрения сходятся около центра гиперкуба под углом 6o.
Читатели, желающие получить удовольствие, наблюдая пространственное (трехмерное) изображение, могут сделать себе стереоскопические очки из красного и синего целлофана. В данном случае программа HYPERCUBE должна выполняться дважды, по одному разу для каждого маленького поворота. Изображение, получающееся в результате первого поворота, окрашивается в синий цвет, а в результате второго - в красный.
Лично я предпочитаю не возиться с целлофаном и научился сливать два изображения в единое стереоскопическое просто усилием воли. Мой метод требует, чтобы два повернутых изображения были уменьшены в размерах и перенесены на прилегающие друг к другу и не перекрывающиеся позиции на экране. Они должны быть одного и того же цвета, поэтому можно вполне обойтись черно-белым монитором, и расстояние между ними не должно превышать расстояния между зрачками наблюдателя. Не таращите глаза на сами изображения, а вместо этого смотрите на какую-нибудь точку между ними, представив, что она находится бесконечно далеко. Тогда два гиперкуба придут в движение, с легкими колебаниями начнут сближаться и, наконец, сольются в единое целое.
Даже если третье и четвертое измерения не подвергать специальной обработке, программа HYPERCUBE может генерировать изображения, очень напоминающие картинки Бэнкоффа. При последовательных поворотах на небольшие углы в третьем и четвертом измерениях читатели могут наблюдать, как два довольно грубой формы тора раздуваются, сжимаются и восстанавливают свою прежнюю форму, подобно их более "гладким" аналогам на иллюстрации, изображающей вращение гиперсферы.
Программа HYPERCUBE, очевидно, явилась причиной исчезновения моего друга Мэги. История этого четырехмерного помешательства закончилась благополучно. Как и следовало ожидать, он позвонил и говорил об удивительных вещах: "Вы, наверное, подумаете, что я сошел с ума,- сказал он. (Эта фраза всегда является верным признаком...) - Я только что плавал в четвертом измерении. Я видел, как мимо меня проносилось поперечное сечение моего дома. Тогда я подплыл ближе и пощекотал почки моей кошке..."
Я избавлю читателя от дальнейших подробностей нашего разговора. Достаточно сказать, что я уговорил Мэги не запускать больше программу HYPERCUBE и проводить исследования исключительно в интеллектуальной плоскости. Он сказал, что последовал моему совету и теперь заявляет, что сделал множество замечательных открытий, пользуясь своим усилившимся внутренним зрением. Отметим, кстати, две придуманные им задачи, которые, кажется, достойны того, чтобы читатели над ними поразмыслили.
Давайте подумаем над такой последовательностью объектов: единичный отрезок прямой линии, единичный квадрат, единичный куб и т.д. Тогда n-м членом последовательности будет n-мерный аналог куба. Теперь попробуем провести два мысленных эксперимента над этими объектами. Проведем диагональ в n -мерном кубе и впишем n-мерную сферу n-мерный куб; диагональ проходит от одной вершины к противоположной. Как будет изменяться ее длина по мере того, как n будет постепенно увеличиваться, и как будет меняться объем n-мерной сферы с ростом n? Ответы Мэги выглядят, мягко говоря, странноватыми. Я приведу их в следующей статье.
БИБЛИОГРАФИЯ
THE FOURTH DIMENSION SIMPLY EXPLAINED: A Collection of essays Selected from those Submitted in the Scientific American's Prize Competition. Edited by Henry P. Manning. Dover Publications, Inc., 1960.
FLATLAND: A ROMANCE OF MANY DIMENSIONS. EDWIN A.ABBOTT. New American Library, 1984. (Есть перевод: Э.ЭББОТ, ФЛАТЛАНДИЯ, Д.БЮРГЕР, СФЕРЛАНДИЯ, М.: "МИР", 1976.- G.).
THE FOURTH DIMENSION: TOWARD A GEOMETRY OF HIGHER REALITY. RUDY RUCKER. Houghton Mifflin Company, 1984.
THE SHAPE OF SPACE; HOW TO VISUALIZE SURFACES AND THREE-DIMENSIONAL MANIFOLDS. JEFFREY R. WEEKS. Marcel Dekker, Inc., 1985.
ОТКЛИКИ
7 1986
В ЖУРНАЛЕ за прошлый месяц было рассказано о четырехмерном помешательстве моего ассистента Мэги. Он утверждал, что попал в четвертое измерение и открыл у гиперкубов кое-какие интересные свойства. Его интересовало, какова длина диагонали n-мерного гиперкуба и каким будет объем n-мерной гиперсферы, вписанной в n-мерный гиперкуб. Признаться, мне показалось, что его ответы на эти вопросы были сумасбродны, потому что они противоречили обычной интуиции. Длина диагонали безгранично растет, по мере того как увеличивается размерность гиперкуба. В то же время объем вписанной гиперсферы становится все меньше и меньше!
Впрочем, первый ответ нетрудно объяснить, если формулу евклидова расстояния перенести на высшие размерности: длина диагонали п-мерного гиперкуба просто пропорциональна квадратному корню из n и безгранично возрастает по мере того, как увеличивается значение n. Я не знаю, каким образом можно элементарно объяснить уменьшение объема вписанной гиперсферы, однако Т.Бэнкофф из Университета Брауна, которому с помощью компьютера удалось получить изображения вращающейся гиперсферы, рассмотренные в предыдущей статье, выдвинул довольно убедительный аргумент.
Объем гиперсферы можно грубо аппроксимировать объемом вписанного гипервосьмигранника. Каким образом мы можем представить себе вписанный гипервосьмигранник? Каждая вершина обычного восьмигранника, вписанного в куб, касается одной из граней куба. По аналогии каждая вершина гипервосьмигранника лежит в центре одной из гиперграней гиперкуба. После этой подсказки нетрудно вычислить объем гипервосьмигранника, и он действительно уменьшается по мере роста размерности.
Отбросив апрельские шутки, должен сознаться, что этими интригующими задачками я обязан не Мэги, а Р.Грехему, признанному "матемагу", работающему в фирме AT&T Bell Laboratories.
9 1986
Статья о геометрических телах высших размерностей (см. "В мире науки" 1986, #6) не вызвала у читателей никаких отклонений в психике. Все написавшие свою собственную версию программы HYPERCUBE сохранили душевное здоровье и физическую материальность. Правда, был выявлен поразительный случай ясновидения и предсказания будущего. Д.Эклейн из Рамни (шт.Нью-Гэмпшир) создал подобную программу за несколько месяцев до того, как я описал свою. Программа Эклейна дает все эффекты, производимые программой HYPERCUBE, но использует лишь четыре плоскости вращения вместо шести. Э.Холси из Сиэтла (шт. Вашингтон) не удовлетворился "мышиной возней" с программой HYPERCUBE. Он пошел дальше, к более сложным телам высоких размерностей, включая четырехмерный усеченный многогранник, четырехмерный симплекс и другие сложные объекты.
Наконец, следует отметить работу Э.Бекера из Риверхеда (шт.Нью-Йорк), который вплотную повстречался с гипердодекаэдром (см. рисунок вверху на с.96). Обычный додекаэдр - это классическое геометрическое тело с 12 гранями. Гипердодекаэдр Бекера состоит из 120 обычных додекаэдров, построенных из 1200 линий. Фигура, изображенная на рисунке, была получена путем проектирования этого чудовищного объекта на трехмерное пространство с последующим смешением каждого из составляющих додекаэдров на небольшое расстояние в заданном направлении. Получается так, что каждая линия одновременно принадлежит трем додекаэдрам. Бекер пишет: "Плоские поверхности ограничены ребрами в их смещенном и несмещенном положениях. Соответственно я заменил каждую линию... чем-то вроде Y-образной рейки, в результате чего более понятной становится общая структура объекта, по крайней мере для моего трехмерного пространственного воображения".

Проекция четырехмерного гипердодекаэдра Э.Бекера
ПРОГРАММА, ВРАЩАЮЩАЯ НА ЭКРАНЕ ДИСПЛЕЯ ЧЕТЫРЕХМЕРНЫЕ ГИПЕРКУБЫ
А.К.ДЬЮДНИ
"Мой муж буквально растворился в воздухе, и я думаю, что вы в какой-то степени причастны к этому!" - Я узнал женщину, говорившую со мной по телефону. Это была Черил, и она была явно не в себе. Ее муж Мэги, мой специальный помощник по микрокомпьютерам в Университете шт.Западный Онтарио, по всей видимости, исчез, наблюдая за поведением компьютерной программы, которую я предложил ему написать. Программа вращает четырехмерный аналог куба, называемый гиперкубом, и проектирует его на экран дисплея. Черил взволнованно продолжала: "По экрану движется какой-то странный узор, а вещи моего мужа свалены в кучу у кресла. Он, наверное, был в этих странных цветных очках с картонной оправой. А это что? Боже мой, его носки остались в туфлях!"
Мне стало ясно, что здесь имело место классическое проявление четырехмерного помешательства. Его жертвы убеждены, что они вышли за пределы обычного пространства и очутились в четырехмерном мире, невидимом для остальных людей. Это иллюзорное впечатление, что человек стал невидимым, может быть настолько сильным, что затрагивает восприятие и других людей: жертва помешательства может войти в комнату полную людей и остаться незамеченной. К счастью, случай с Мэги закончился благополучно, но об этом потом. А пока расскажу о программе, вращающей гиперкубы, сделав предварительно одно предупреждение, к которому, надеюсь, читатели отнесутся достаточно серьезно. Те, кто склонен к помешательству, как Мэги, не должны писать эту программу и тем более наблюдать за ее работой на экране дисплея. К потенциальным жертвам можно отнести всех, у кого наблюдался навязчивый интерес к пространствам высших размерностей, а также тех, кто, пусть даже не часто, но задумывался о заманчивых перспективах неизведанных пространств и миров.
Четвертое измерение стало предметом физических и метафизических размышлений по крайней мере с конца прошлого столетия. Идея четвертого измерения имела наибольший успех в специальной и обшей теориях относительности Эйнштейна. В этих теориях пространство и время в совокупности образуют четырехмерный континуум, в котором все события во Вселенной оказываются как бы навсегда замороженными. Такая концепция Вселенной может подвергаться модификациям в количестве измерений. Например, в так называемых теориях Клейна-Калузы вводится семь или более дополнительных измерений в форме миниатюрных гиперпузырьков, прикрепленных к каждой точке пространства-времени (см. статью Дэниела 3. Фридмана и Питера ван Ньювенхойзена "Скрытые измерения пространства-времени", опубликованную в майском номере нашего журнала за 1985г.).
Четвертое измерение, с которым я познакомился, а познакомившись, полюбил его,- это дитя математики. Читатели, находящиеся в обыкновенных комнатах, имеют трехмерную систему координат, так сказать, у себя над головой. Три плоскости встречаются в каждом углу комнаты, и из этого угла исходят три линии, каждая из которых является пересечением двух плоскостей. Каждая линия перпендикулярна двум другим. Может ли читатель представить себе еще одну, четвертую линию, перпендикулярную этим трем? Наверное нет, но именно этого требуют математики, сооружая чисто абстрактную конструкцию, называемую четырехмерным пространством. Теперь вам предоставляется возможность самим исследовать это пространство, не подвергая себя непосредственной опасности. Для этого нужно лишь написать программу, которую я называю HYPERCUBE (гиперкуб).
Если говорить о происхождении этой программы, то вспомним, что еще в середине 60-х годов А.Нолл, в то время работавший в фирме Bell Laboratories, отснял фильм, в котором представлены двумерные тени, отбрасываемые четырехмерными объектами, движущимися в четырехмерном гиперпространстве. Однако в ее теперешнем виде программа была разработана Т.Бэнкоффом и его коллегами по лаборатории компьютерной графики в Университете Брауна, и настоящая статья была написана под влиянием впечатления, которое произвели на меня замечательные изображения, порожденные программой (см. рисунки на с.99, 101 и 102). Бэнкофф, профессор математики, возглавляет визуальные исследования поверхностей и пространств высших размерностей в дополнение к своим геометрическим исследованиям. В 1978г. совместно с Ч.Строессом он продемонстрировал генерируемый компьютером десятиминутный цветной фильм "Гиперкуб: проекции и разрезы". Этот фильм уже успел стать классическим в математическом подполье. Бэнкофф, вероятно, также является ведущим исследователем жизни и творчества Эдвина Аббота, английского священника и учителя, который в 1884г. написал сказку о воображаемой жизни в двумерном мире ("Flatiand", см. библиографию на с.116).

Поворот четырехмерного гиперкуба через измерения 2 и 4, проецируемый на обычное трехмерное пространство
Бэнкоффу и его коллегам удалось создать потрясающие изображения, иллюстрирующие свойства четырехмерных объектов. Например, рисунки на с.99 изображают вращение четырехмерного гиперкуба в четырехмерном пространстве. Чтобы лучше понять эти картинки, рассмотрим тень, отбрасываемую обычным кубом на плоскость: эта тень может напоминать квадрат, заключенный в другом квадрате. Если затенить соответствующие грани куба, то тень представляет собой квадрат с квадратным отверстием внутри (см.нижний рисунок на с.100).

Проекции куба и сферы
Аналогично, когда гиперкуб освещен из точки, расположенной "над" обычным пространством в четвертом измерении, трехмерная тень, отбрасываемая гиперкубом, может напоминать куб, заключенный в другом кубе. Внутренний куб окружен шестью шестигранниками, которые можно рассматривать как искаженные кубы. Четыре искаженных куба, прилегающих к граням внутреннего куба, образуют в совокупности сплошное тело, торообразная поверхность которого показана на изображениях Бэнкоффа. Два других искаженных куба - внутренний и внешний - также образуют тор, который здесь не показан. Когда гиперкуб вращается, возникает ощущение, что квадратное отверстие в видимом торе надвигается на зрителя. Те, кто напишет свою версию программы HYPERCUBE, станут свидетелями других подобных эффектов, хотя уже и не таких реалистичных или "непрерывных".
Изображения, приведенные на с.101 и 102, взяты из фильма "Гиперсфера: расслоение и проекции", который готовят к выпуску Бэнкофф и его коллеги Г.Кошак, Д.Лэйдлоу и Д.Марголис. Гиперсфера представляет собой гораздо более сложный объект по сравнению с гиперкубом, и я не стану детально описывать ее. Тем не менее эти изображения можно в какой-то степени лучше понять, воспользовавшись аналогией с обычной сферой. Если в исходном положении сфера покоится на плоскости, касающейся южного полюса сферы, а источник света в исходном положении находится на ее северном полюсе, то тень, отбрасываемая на плоскость линиями параллелей сферы, будет представлять собой ряд концентрических окружностей (см. нижний рисунок на с.100). Если сфера начинает поворачиваться, а источник света остается в фиксированном положении, то тени-окружности будут становиться неконцентрическимн, а теневое изображение любой окружности, целиком лежащей в плоскости источника света, будет представлять собой прямую линию.

Последовательность вложенных торов, которые по аналогии с параллелями на сфере являются проекциями гиперсферы на три измерения

Проецируемое движение торов по мере вращения гиперсферы аналогично проекции движения параллелей во время вращения сферы
Аналогичным образом трехмерная "тень", отбрасываемая гиперсферой, может рассматриваться как ряд концентрических торов (см. рисунок на с.101). Когда гиперсфера вращается, торы как бы раздуваются и проносятся один за другим. При этом любой тор, проходящий через источник света, становится бесконечно большим (см. рисунок на с.102).
Рассмотрение аналогий в различных размерностях - ценное подспорье для построения и понимания четырехмерных объектов. Например, гиперкуб получается из куба точно так же, как куб получается из квадрата. Чтобы получить куб из квадрата, будем поднимать квадрат в направлении, перпендикулярном его плоскости, до высоты, равной его стороне (см. верхний рисунок на с.100). Полученный в результате куб имеет 8 вершин (вдвое больше, чем у исходного квадрата) и 12 ребер - 4 стороны исходного квадрата и 4 стороны вновь полученного верхнего квадрата, а еще 4 получаются соединением вершин исходного квадрата с вершинами верхнего квадрата. Кроме того, у куба 6 квадратных граней - одна, совпадающая с исходным квадратом, одна - с поднятым и по одной грани-стене, воздвигнутой между каждой из 4 пар сторон, принадлежащих исходному и поднятому квадратам.

Квадрат порождает куб, а куб порождает гиперкуб
Если представить на мгновение, что у нас есть еще одно дополнительное измерение, то ту же операцию можно повторить уже для куба. В самом деле, "поднимем" куб из обычного пространства в направлении дополнительного измерения на "высоту", равную грани куба (смотри рисунок вверху). В результате получится гиперкуб. Но каково же все-таки направление дополнительного измерения? Я не могу этого объяснить. Даже фотография с изображением моей руки, указывающей в направлении четвертого измерения, не помогла бы. На ней рука была бы просто невидимой.
Тем не менее количество вершин, ребер, граней и гиперграней (обыкновенных кубов), из которых состоит гиперкуб, можно легко подсчитать. Количество вершин равно количеству вершин в исходном кубе плюс их количество в перенесенном кубе - всего 16. Каждая из 8 вершин исходного куба соединяется ребром с одной из 8 вершин перенесенного куба, и, кроме того, есть еще 12 ребер в каждом из этих двух кубов. Таким образом, всего гиперкуб насчитывает 8+12+12=32 ребра. Аналогично можно показать, что число обычных граней гиперкуба равно 24, а число гиперграней равно 8.
Должен выразить признательность Д.Лэйдлоу, объяснившему мне механизм программы HYPERCUBE. Версия программы, которую я здесь опишу, генерирует изображение гиперкуба, показывая лишь его вершины и ребра. Более того, изображения, генерируемые программой, не обязательно представляют один куб внутри другого; на самом деле изображение зависит от того, каким образом реализована программа и как она выполняется. Всякий раз при повороте гиперкуба его вершины переходят в новое положение и возникает новое, сбивающее с толку изображение объекта. Однако, когда у вас накопится некоторый опыт в экспериментировании, изображения станут в каком-то смысле понятными и вы почувствуете себя на пороге чего-то волнующе грандиозного и манящего.
В программе 16 вершин гиперкуба пронумерованы от 0 до 15 по простой схеме. Если каждый из этих номеров представить в двоичном виде и составить массив из элементов по четыре бита, то мы получим миниатюрную систему координат. Например, двоичное представление числа 13 состоит из 1 (одной восьмерки), 1 (одной четверки), 0 (ни одной двойки) и 1 (одной единицы). Таким образом, это число можно записать в виде (1, 1, 0, 1). Такая запись уже дает нам практически систему координат для представления положения вершин гиперкуба. (Это не есть положение, которое напоминает куб внутри другого куба). Чтобы перейти к более удобной системе координат, заменим нули на -1 и помножим каждый элемент массива на достаточно большое число, чтобы построить на экране дисплея изображение приемлемых размеров. Например, если в качестве такого множителя выбрать число 10, то координаты 13-й вершины будут представлены как (10, 10, -10, 10).
Конструируя программу HYPERCUBE, мы повсеместно сталкиваемся с размерностями. Двумерная матрица, или массив, vert хранит исходные координаты вершин. Поскольку всего насчитывается 16 вершин, каждая из которых задается четырьмя координатами, vert представляет собой матрицу размером 16*4 - всего 64 числа. Vert{i, j) - это j-я координата i-й вершины. Программа HYPERCUBE сохраняет матрицу vert неизменной, она определяется в начале программы, и ее содержимое переносится затем в другую матрицу размерами 16*4, назовем ее cube. Эту матрицу можно считать рабочей, ее содержимое постоянно меняется при поворотах гиперкуба, выполняемых программой.
После инициализации матрицы vert программу можно условно разбить на три главных раздела: выбор желаемого поворота гиперкуба, вычисление координат повернутого гиперкуба и представление (высвечивание) результатов поворота на экране дисплея. Если бы вращаемый объект был трехмерным, то поворот можно было бы выбрать, указав ось вращения и угол поворота вокруг этой оси. Однако при повороте четырехмерного объекта выбор оси вращения не определяет плоскости, в которой происходит поворот. Напомним, что существуют два неэквивалентных направления, перпендикулярные заданной плоскости. В то же время даже для четырехмерного гиперпространства остается справедливым, как и в обычном пространстве, то, что поворот может повлиять только на два измерения. Когда поворачивается трехмерный объект, во вращательном движении принимают участие два измерения, в то время как третье остается неподвижным. Аналогично, при повороте четырехмерного объекта два его измерения меняют ориентацию в пространстве, а два других остаются неподвижными.
Существует много способов поворота четырехмерного объекта в новое положение. Однако оказывается, что любое положение может быть достигнуто последовательностью таких поворотов, которые ограничиваются плоскими движениями, определяемыми координатными осями окружающего четырехмерного пространства. В четырехмерном пространстве мы имеем 4 координатные оси, пронумерованные, скажем, от 1 до 4, и существует 6 способов разбиения их на пары. Следовательно, мы имеем 6 плоскостей в четырехмерном пространстве, определяемых координатными осями: плоскость 1-2, т.е. плоскость, заданная осями 1 и 2, плоскость 1-3, плоскость 1-4, плоскость 2-3, плоскость 2-4 и плоскость 3-4.
Для каждой из этих шести плоскостей есть свой вид поворота, который определяется квадратной матрицей размером 4*4. т.е. состоящей из 16 чисел. Назовем эти 6 матриц поворота соответственно rot12, rot13, rot14, rot23, rot24 и rot34. Работая с программой, вы должны указать имя матрицы для выбранного поворота и величину угла поворота. Например, напечатав на клавиатуре терминала "rot23", а затем "60", вы тем самым задаете программе команду выполнить поворот на 60o в плоскости, заданной второй и третьей осями координат.
Предположим, вы хотите повернуть гиперкуб в плоскости третьего и четвертого измерений. Пожалуй, это самый загадочный из возможных поворотов. Для этого используется матрица rot34. В качестве ее элементов могут встретиться нули, единицы и три других числа, расположенные следующим образом:

Выбранный вами угол поворота в градусах запоминается в переменной ang, причем величины а и b зависят от значения ang: a равно cos(ang), a b равно sin(ang), где sin и cos - обычные тригонометрические функции угла синус и косинус.
Правило получения остальных пяти матриц поворота довольно простое. Величина a появляется на главной диагонали каждой матрицы в положениях, соответствующих измерениям, которые затрагиваются при повороте. Величина b появляется на всех других пересечениях строк и колонок, соответствующих измерениям, которые участвуют в повороте. Все остальные элементы на главной диагонали равны 1, а прочие элементы матрицы равны 0. Например, матрица rot13 имеет следующий вид:

Когда нужная матрица поворота выбрана, значения ее элементов присваиваются программой HYPERCUBE специальной матрице rote. Это присвоение удобно выполнять в виде двойного цикла: внутренний цикл - для последовательности величин, расположенных по строке матрицы, а внешний - для последовательности строк.
Координаты вершин повернутого гиперкуба вычисляются путем "умножения" матрицы cube на выбранную матрицу поворота rote. Произведение этих двух матриц временно запоминается в третьей матрице, назовем ее temp, и оно дает координаты повернутого гиперкуба. Это произведение вычисляется по правилам умножения матриц, и для вычисления используется стандартная операция перемножения числовых матриц. Последняя заключается в большом количестве всевозможных перемножений, выполняемых в тройном цикле.
Так же как vert и cude, матрица temp имеет размер 16*4 и состоит из 64 чисел. Она дает четыре координаты для каждой из 16 вершин гиперкуба в новом положении. Каждый элемент матрицы temp(i ,j) определяется двумя индексами i и j. Например, элемент temp(13, 3) задает третью координату 13-й вершины повернутого гиперкуба. Его значение является суммой четырех произведений чисел, выбранных в точном определенном порядке из матрицы cube и матрицы rote (см. рисунок на с.103). В качестве индекса внутреннего цикла программы можно взять букву k, пробегающую значения от 1 до 4, и этот цикл будет возвращать значение одного элемента матрицы temp. Цикл по k заключается затем в промежуточный цикл по индексу j. В цикле по j вычисляются все четыре координаты i-й вершины повернутого гиперкуба в соответствии с только что описанной процедурой. Другими словами, этот цикл заполняет все 4 элемента i-й строки матрицы temp. Наконец, цикл по j заключается во внешний цикл с индексом i. В цикле по i вычисляются все 16 строк матрицы temp, и когда этот цикл завершается, матрица temp дает координаты всех вершин повернутого гиперкуба, представшего перед нами в своем новом положении и, так сказать, во всей своей красе. Чтобы показать его на экране дисплея, потребуется еще один двойной цикл, заменяющий координаты старого положения гиперкуба в матрице cube его новыми, только что вычисленными координатами из матрицы temp.

Вершина гиперкуба, поворачиваясь, уходит из трехмерного в четырехмерное пространство
У гиперкуба четыре измерения, а у экрана дисплея только два. Поэтому разумно было бы условиться, что, скажем, первые два измерения (или координаты) гиперкуба соответствуют координатам экрана. Простейший способ представления третьего и четвертого измерений гиперкуба заключается просто в том, чтобы игнорировать их. Именно так и работает метод отображения, который я здесь опишу, но его можно усовершенствовать (в результате чего проекция объекта может выглядеть демонически сложной), если попытаться сделать третье и четвертое измерения несколько более наглядными.
Чтобы отобразить "скелет" гиперкуба, программе нужно лишь показать его ребра. Поскольку у гиперкуба 32 ребра, то та часть программы, которая ответственна за отображение на экран, должна лишь провести соответствующие линии между 32 парами вершин. Но в каком порядке? Практически существует неограниченное количество вариантов, и поэтому ответ на этот вопрос, по-видимому, зависит от личного вкуса. Тем не менее трудно удержаться от соблазна изобразить ребра как след Эйлера. Он назван так в честь знаменитого математика Леонарда Эйлера. След Эйлера можно нарисовать карандашом, не отрывая его от бумаги и не проводя ни одной линии более одного раза. Последовательно нарисованные ребра гиперкуба в виде следа Эйлера имеют общую вершину.
В обход, пересекая, вверх и вниз скачет след Эйлера по мере того, как он проходит через вершины. Очень изящным представляется следующий порядок соединения вершин гиперкуба: 0, 1, 3, 2, 6, 14, 10, 8, 9, 11, 3, 7, 15, 14, 12, 13, 9, 1, 5, 7, 6, 4, 12, 8, 0, 4, 5, 13, 15, 11, 10, 2, 0. Эти вершины хранятся в массиве trail с индексом i. Таким образом, i-я вершина в последовательности из 33 вершин обозначается как trail(i). Для каждого значения i выполняются команды выборки первой и второй координаты как элемента trail(i), так и trail (i+1). Затем нужно выполнить команду, которая рисует на экране линию, соединяющую две заданные точки. Команды выборки и графическая команда вложены в единый цикл с индексом i, который от каждой точки-вершины последовательности проводит линию к следующей точке.
Теперь несколько слов о некоторых визуальных (и психологических) осложнениях. Существуют два стандартных метода представления третьего измерения гиперкуба. Ортографический метод просто игнорирует третье измерение, и все вершины проецируются на плоскую поверхность экрана вне зависимости от расстояния между ними и экраном. В перспективе из одной точки вершины проецируются на экран так, как будто они являются тенями от света точечного источника, расположенного в центре экрана и на некотором расстоянии позади гиперкуба. Наблюдение этих теней на экране эквивалентно наблюдению гиперкуба с обратной стороны, однако визуально вид сзади неотличим от вида спереди.
Чтобы добиться эффекта перспективы из одной точки, в программе HYPERCUBE принимается, что третья координата вершины равна расстоянию между вершиной и экраном по линии, ведущей к воображаемому источнику света. Пользуясь признаками подобия треугольников, программа определяет множитель, необходимый для того, чтобы преобразовать первые две координаты вершины в координаты на экране дисплея. Например, если воображаемый источник света находится на расстоянии 20 единиц от экрана, вершина с координатами (5, -7, 11, 18 ) может быть спроецирована на экран путем умножения каждой из первых двух координат на 20 и деления результата на разность 20-11, т.е. число 9.
К сожалению, здесь мне не удастся уместить полное описание процесса, при помощи которого создаются стереоскопические изображения, показывающие четвертое измерение гиперкуба. Существует общий метод построения стереоскопических изображений, и в будущем я надеюсь посвятить этой теме одну из своих статей. Однако для программы HYPERCUBE Бэнкофф и его коллеги применили значительно более простой метод. Для каждого положения гиперкуба создаем два новых изображения путем применения матрицы rot14 с углом поворота на 3o в одном направлении и на 3o в другом. Направление первого измерения параллельно горизонтальной линии зрения, а четвертое измерение - это цель, достигаемая процедурой. Два небольших поворота хорошо аппроксимируют вид гиперкуба для наблюдателя. Нужно лишь представить себе, как две линии зрения сходятся около центра гиперкуба под углом 6o.
Читатели, желающие получить удовольствие, наблюдая пространственное (трехмерное) изображение, могут сделать себе стереоскопические очки из красного и синего целлофана. В данном случае программа HYPERCUBE должна выполняться дважды, по одному разу для каждого маленького поворота. Изображение, получающееся в результате первого поворота, окрашивается в синий цвет, а в результате второго - в красный.
Лично я предпочитаю не возиться с целлофаном и научился сливать два изображения в единое стереоскопическое просто усилием воли. Мой метод требует, чтобы два повернутых изображения были уменьшены в размерах и перенесены на прилегающие друг к другу и не перекрывающиеся позиции на экране. Они должны быть одного и того же цвета, поэтому можно вполне обойтись черно-белым монитором, и расстояние между ними не должно превышать расстояния между зрачками наблюдателя. Не таращите глаза на сами изображения, а вместо этого смотрите на какую-нибудь точку между ними, представив, что она находится бесконечно далеко. Тогда два гиперкуба придут в движение, с легкими колебаниями начнут сближаться и, наконец, сольются в единое целое.
Даже если третье и четвертое измерения не подвергать специальной обработке, программа HYPERCUBE может генерировать изображения, очень напоминающие картинки Бэнкоффа. При последовательных поворотах на небольшие углы в третьем и четвертом измерениях читатели могут наблюдать, как два довольно грубой формы тора раздуваются, сжимаются и восстанавливают свою прежнюю форму, подобно их более "гладким" аналогам на иллюстрации, изображающей вращение гиперсферы.
Программа HYPERCUBE, очевидно, явилась причиной исчезновения моего друга Мэги. История этого четырехмерного помешательства закончилась благополучно. Как и следовало ожидать, он позвонил и говорил об удивительных вещах: "Вы, наверное, подумаете, что я сошел с ума,- сказал он. (Эта фраза всегда является верным признаком...) - Я только что плавал в четвертом измерении. Я видел, как мимо меня проносилось поперечное сечение моего дома. Тогда я подплыл ближе и пощекотал почки моей кошке..."
Я избавлю читателя от дальнейших подробностей нашего разговора. Достаточно сказать, что я уговорил Мэги не запускать больше программу HYPERCUBE и проводить исследования исключительно в интеллектуальной плоскости. Он сказал, что последовал моему совету и теперь заявляет, что сделал множество замечательных открытий, пользуясь своим усилившимся внутренним зрением. Отметим, кстати, две придуманные им задачи, которые, кажется, достойны того, чтобы читатели над ними поразмыслили.
Давайте подумаем над такой последовательностью объектов: единичный отрезок прямой линии, единичный квадрат, единичный куб и т.д. Тогда n-м членом последовательности будет n-мерный аналог куба. Теперь попробуем провести два мысленных эксперимента над этими объектами. Проведем диагональ в n -мерном кубе и впишем n-мерную сферу n-мерный куб; диагональ проходит от одной вершины к противоположной. Как будет изменяться ее длина по мере того, как n будет постепенно увеличиваться, и как будет меняться объем n-мерной сферы с ростом n? Ответы Мэги выглядят, мягко говоря, странноватыми. Я приведу их в следующей статье.
БИБЛИОГРАФИЯ
THE FOURTH DIMENSION SIMPLY EXPLAINED: A Collection of essays Selected from those Submitted in the Scientific American's Prize Competition. Edited by Henry P. Manning. Dover Publications, Inc., 1960.
FLATLAND: A ROMANCE OF MANY DIMENSIONS. EDWIN A.ABBOTT. New American Library, 1984. (Есть перевод: Э.ЭББОТ, ФЛАТЛАНДИЯ, Д.БЮРГЕР, СФЕРЛАНДИЯ, М.: "МИР", 1976.- G.).
THE FOURTH DIMENSION: TOWARD A GEOMETRY OF HIGHER REALITY. RUDY RUCKER. Houghton Mifflin Company, 1984.
THE SHAPE OF SPACE; HOW TO VISUALIZE SURFACES AND THREE-DIMENSIONAL MANIFOLDS. JEFFREY R. WEEKS. Marcel Dekker, Inc., 1985.
ОТКЛИКИ
7 1986
В ЖУРНАЛЕ за прошлый месяц было рассказано о четырехмерном помешательстве моего ассистента Мэги. Он утверждал, что попал в четвертое измерение и открыл у гиперкубов кое-какие интересные свойства. Его интересовало, какова длина диагонали n-мерного гиперкуба и каким будет объем n-мерной гиперсферы, вписанной в n-мерный гиперкуб. Признаться, мне показалось, что его ответы на эти вопросы были сумасбродны, потому что они противоречили обычной интуиции. Длина диагонали безгранично растет, по мере того как увеличивается размерность гиперкуба. В то же время объем вписанной гиперсферы становится все меньше и меньше!
Впрочем, первый ответ нетрудно объяснить, если формулу евклидова расстояния перенести на высшие размерности: длина диагонали п-мерного гиперкуба просто пропорциональна квадратному корню из n и безгранично возрастает по мере того, как увеличивается значение n. Я не знаю, каким образом можно элементарно объяснить уменьшение объема вписанной гиперсферы, однако Т.Бэнкофф из Университета Брауна, которому с помощью компьютера удалось получить изображения вращающейся гиперсферы, рассмотренные в предыдущей статье, выдвинул довольно убедительный аргумент.
Объем гиперсферы можно грубо аппроксимировать объемом вписанного гипервосьмигранника. Каким образом мы можем представить себе вписанный гипервосьмигранник? Каждая вершина обычного восьмигранника, вписанного в куб, касается одной из граней куба. По аналогии каждая вершина гипервосьмигранника лежит в центре одной из гиперграней гиперкуба. После этой подсказки нетрудно вычислить объем гипервосьмигранника, и он действительно уменьшается по мере роста размерности.
Отбросив апрельские шутки, должен сознаться, что этими интригующими задачками я обязан не Мэги, а Р.Грехему, признанному "матемагу", работающему в фирме AT&T Bell Laboratories.
9 1986
Статья о геометрических телах высших размерностей (см. "В мире науки" 1986, #6) не вызвала у читателей никаких отклонений в психике. Все написавшие свою собственную версию программы HYPERCUBE сохранили душевное здоровье и физическую материальность. Правда, был выявлен поразительный случай ясновидения и предсказания будущего. Д.Эклейн из Рамни (шт.Нью-Гэмпшир) создал подобную программу за несколько месяцев до того, как я описал свою. Программа Эклейна дает все эффекты, производимые программой HYPERCUBE, но использует лишь четыре плоскости вращения вместо шести. Э.Холси из Сиэтла (шт. Вашингтон) не удовлетворился "мышиной возней" с программой HYPERCUBE. Он пошел дальше, к более сложным телам высоких размерностей, включая четырехмерный усеченный многогранник, четырехмерный симплекс и другие сложные объекты.
Наконец, следует отметить работу Э.Бекера из Риверхеда (шт.Нью-Йорк), который вплотную повстречался с гипердодекаэдром (см. рисунок вверху на с.96). Обычный додекаэдр - это классическое геометрическое тело с 12 гранями. Гипердодекаэдр Бекера состоит из 120 обычных додекаэдров, построенных из 1200 линий. Фигура, изображенная на рисунке, была получена путем проектирования этого чудовищного объекта на трехмерное пространство с последующим смешением каждого из составляющих додекаэдров на небольшое расстояние в заданном направлении. Получается так, что каждая линия одновременно принадлежит трем додекаэдрам. Бекер пишет: "Плоские поверхности ограничены ребрами в их смещенном и несмещенном положениях. Соответственно я заменил каждую линию... чем-то вроде Y-образной рейки, в результате чего более понятной становится общая структура объекта, по крайней мере для моего трехмерного пространственного воображения".

Проекция четырехмерного гипердодекаэдра Э.Бекера

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
7 1986
ПРОГРАММЫ, МОДЕЛИРУЮЩИЕ ЭВОЛЮЦИЮ БИОЛОГИЧЕСКИХ ВИДОВ ПАЛЕОЗОЯ И ЭВОЛЮЦИЮ АНГЛИЙСКИХ ФАМИЛИЙ
А.К.ДЬЮДНИ
В ЮЖНОЙ части Онтарио и в западной части штата Нью-Йорк находятся богатые ископаемыми остатками выходы девонской горной породы. Одно такое "месторождение" расположено неподалеку от моего дома. Там, в карьере, сохраняющем следы доисторической жизни, я однажды увидел череп трилобита, уставившегося на меня из слоя глинистого сланца. Поглощенный процессом осторожного извлечения остатков, я вдруг услышал шарканье чьих-то ног и, резко повернувшись, увидел за своей спиной солидного бородатого мужчину. "Роскошный экземпляр Phacops raw,- сказал он.- Жаль, что они все вымерли". Незнакомец оказался профессором палеонтологии, его фамилия была Смит. "Интересно, - полюбопытствовал я вслух,- почему они вымерли?" Профессор Смит посмотрел задумчиво вдаль и затем в ответ на мой вопрос спросил: "Интересно, почему фамилия Смит такая распространенная?"
Чтобы точно ответить на эти вопросы, нужно было бы, наверное, проследить за сложным и необратимым взаимодействием генетических факторов и условий окружающей среды. Однако приближенные ответы дают нам две компьютерные программы, которые моделируют эволюцию биологических видов и фамилий при помощи одного и того же механизма. Первая программа по замыслу должна была моделировать "великие вымирания" в палеозойскую эру. Ее первоначальная версия была создана Д.Раупом, известным палеонтологом из Чикагского университета. Программа строит филогенетическое дерево, причем его структурные элементы выбираются произвольно: на каждом такте геологических часов кончик каждой ветви дерева с определенной вероятностью либо растет, либо разветвляется, либо отмирает. Картина этого случайного эволюционного процесса, порождаемого программой, удивительно напоминает хронику, зафиксированную ископаемыми находками, и в ней, в частности, также присутствует явление массового вымирания видов.
Вторая программа моделирует процесс распространения и исчезновения английских фамилий за период с 1350г. до настоящего времени. Программа эта - результат творческой деятельности К.Стерджеса и Б.Хэггета, сотрудников британского министерства обороны. Стерджес и Хэггет в свободное время увлекаются генеалогией. Они заинтересовались, почему в исторических документах многие древние фамилии постепенно исчезают. Может ли подобное исчезновение быть случайным событием? Чтобы выяснить, в чем тут дело, они написали моделирующую программу. Согласно полученным результатам, три четверти фамилий, распространенных в 1350г., по чисто случайным причинам исчезли на протяжении последующих 636 лет.
Каждый читатель, желающий совершить путешествие в вероятностной машине времени, может сам написать упрощенную версию любой из этих двух программ, сохранив наиболее существенные свойства, присущие оригиналам. При помощи первой программы вы проделаете путешествне длительностью в несколько сот миллионов лет, наблюдая за тем, как биологические виды и роды, состоящие из неизвестных и безымянных существ, становятся более разнообразными или вымирают. Вторая программа охватывает всего несколько сот лет, но исследуемая ею проблема по-человечески нам более интересна. Какие фамилии выйдут победителями: Смиты или Смедли?
Программа, которую я назвал PALEOTREE, начинает свою работу с единственного первородного существа. Чтобы наша модель носила палеонтологический смысл, присвоим этому существу какое-нибудь научное имя, например Paleoplasmus radiculus. Впрочем, читатели могут сами поупражняться в латыни и выбрать любое другое имя. В произвольно заданный момент времени программа представляет полную популяцию P.radiculus в виде одного узла, или точки, в структуре данных, называемой деревом. Любая популяция существ, принадлежащих той же биологической категории, что и P.radiculus, и происходящих из нее, также представляется в виде узла - в программе не производится подсчета количества живущих особей, их популяция представляется целиком.
За одно мгновение реального времени в модели проходят миллионы лет, и на каждом шаге программа рассматривает результаты эволюционного процесса. Старая популяция существ может сохраниться в неизменном виде на протяжении следующих нескольких миллионов лет. Если это так, то исходный узел на дереве порождает новый узел, связанный прямой линией с первым. Может случиться и так, что исходная популяция не только выживает, но н порождает новую биологическую категорию. Подобный исход можно представить в виде Y-образного разветвления. Одна из этих ветвей ведет к новому узлу, являющемуся продолжением исходной биологической категории, а вторая ведет к другому новому узлу, представляющему начало новой категории. Наконец, возможен и такой вариант, когда исходная популяция вымирает. В этом случае исходный узел становится тупиковым и у него нет никаких отростков.
Судьба каждого узла, порожденного на дереве, решается программой PALEOTREE случайным образом: продолжит ли популяция свое существование в неизменном виде, породит ли она новую биологическую категорию или целиком окажется вымершей? Конечно, строго говоря, эти три возможности далеко не полностью отражают все богаство структуры биологической эволюции. Из всего сказанного о программе следует, что все существа, произошедшие от одного и того же общего предка, являются монофилогенетическими, т.е. они достаточно близки друг к другу, чтобы их можно было отнести к одной и той же биологической категории, и поэтому они принадлежат одному и тому же дереву. Однако иногда эволюционный процесс приводит к возникновению новой широкой категории или к массовому вымиранию, когда исчезают старые категории. Таксономисты различают много подобных категорий - от подвидов до типов и царств. Для простоты в программе PALEOTREE представлены только две категории: вид и род, однако годятся и любые другие названия этих двух категорий.
В нашей программе из одного рода может произойти другой. Механизм такого происхождения довольно прост: из старого рода выделяется новый вид, на основе которого впоследствии развивается целый род. И то, что было просто ветвью на эволюционном дереве, уже само становится деревом. Разумеется, дерево (или род) может и полностью отмереть, когда исчезнут все составляющие его виды. Количество видов, из которых состоит род на данный момент, можно назвать разнообразием рода. Оно отражает не только генетическое богатство, но и вероятность выживания рода. Для изображения результатов работы программы PALEOTREE есть изящный графический способ. Каждый род представляется симметричной фигурой из горизонтальных прямоугольников, напоминающей веретено. Каждый прямоугольник представляет соответствующую эпоху, а горизонтальный размер прямоугольника - разнообразие рода в данную эпоху. Получающиеся в результате фигуры изображены на рисунке внизу.


Процесс эволюционного развития, ветвление и образование новых видов в биологических родах, моделируемые программой Д.Раупа, аналогичной программе PALEOTREE
Нетрудно, и даже полезно, поупражняться в построении дерева и соответствующего веретена вручную. Нарисуйте точку на листе бумаги и бросьте пару игральных костей. Если сумма выпавших чисел будет равна 2, 3 или 4, то вид немедленно вымирает. P.radiculus оказывается мертворожденным, и из точки на бумаге не появляется никаких ответвлений. Если сумма равна 9 или 10, то появляются ответвления - вид развивается. От исходной точки вверх отходят два коротких отрезка, и на конце каждого из них изображается еще по одной точке. Если выпадает любая другая сумма, вид сохраняется неизменным. В этом случае от исходной точки вверх отходит один отрезок, заканчивающийся точкой. В каждую эпоху этот эксперимент повторяется для каждого еще не вымершего вида. В результате описанной процедуры возникает дерево, а на веретенообразной диаграмме длина каждого прямоугольника соответствует количеству точек на данном уровне дерева (см. рисунок на с.84).

Судьба видов, образующих род, определяется бросанием игральных костей
При однократном бросании костей вероятность того, что вид исчезнет в следующей эпохе, равна 1/6, или 0,167, вероятность ветвления равна 7/36, или 0,194, а вероятность того, что вид останется без изменений, равна 23/36, или 0,639. Эти вероятности приблизительно соответствуют значениям, принятым в программе PALEOTREE, и поэтому приводят к аналогичным деревьям. Поскольку вероятность вымирания вида несколько меньше, чем вероятность ветвления, можно полагать, что некоторые деревья будут расти до бесконечности. Так ли это на самом деле? Интересно, к какому выводу придут читатели, пожелающие провести бессонную ночь в поисках ответа?
Чтобы построить веретенообразную диаграмму, вовсе не обязательно прослеживать за деревом каждого рода. Программа PALEOTREE просто подсчитывает количество видов, из которых состоит род в каждую данную эпоху, и следит за ветвлениями родов. Обе функции можно реализовать при помощи двумерного массива history. Каждый столбец представляет род, а строка - эпоху. Таким образом, history(i, j) - это количество видов, из которых состоит роду на момент времени, соответствующий эпохе i. После того как программа смоделирует эволюционный процесс для заданного числа шагов по времени, или эпох, массив history можно распечатать и воспользоваться значениями его элементов для построения веретенообразных диаграмм от руки. Читатели, располагающие некоторым опытом в графическом программировании, могут попытаться составить дополнительную программу, автоматически строящую диаграммы, однако детальное описание этой процедуры потребовало бы самостоятельной статьи.
Чтобы работать с программой PALEOTREE в ее простейшем варианте, вначале нужно указать с клавиатуры число эпох, или "поколений". Это число запоминается программой в переменной numgen; оно является
максимальным значением, которые может принимать индекс i в массиве history. По мере того как программа выполняет свой внешний цикл, значение i последовательно увеличивается на 1, начиная от 1 и кончая numgen. В этот цикл вложен второй цикл с индексом, пробегающим значения j в массиве history, при этом каждое значение j соответствует определенному роду. Чтобы определить максимальное значение индекса j, введена переменная max. Поскольку в исходном состоянии существует лишь один род, значение переменной max вначале устанавливается равным 1. По мере того как повторяется выполнение внешнего цикла, количество родов то возрастает, то убывает. Для каждой новой эпохи значение max устанавливается равным числу родов, существовавших в предыдущую эпоху. Перед выполнением цикла с индексом j переменной lmax присваивается значение max, и j пробегает значения от 1 до lmax.
Во втором цикле программа PALEOTREE подсчитывает количество видов, из которых состоит на данный момент род j, и запоминает это число во временной переменной temp. Затем программа входит в свой третий, самый внутренний цикл, где определяется судьба каждого вида, принадлежащего j-му роду. Индекс k этого внутреннего цикла можно рассматривать как счетчик видов. Он пробегает значения от 1 по temp, и значение temp заносится также в элемент history(i+1, j) массива, и таким образом указывается количество видов j-го рода в следующей эпохе i+1.
Для каждого вида, или, другими словами, для каждого значения k, выбирается случайное число в диапазоне от 0 до 1. Это делается посредством оператора, генерирующего случайные числа. Конкретный вид этого оператора зависит от языка программирования, которым вы пользуетесь. Если случайное число оказывается меньше 0,15, то k-й вид вымирает и элемент массива history(i+1, j) уменьшается на 1. Если значение случайного числа больше 0,8, то от k-го вида отделяется новый вид и элемент history(i+1, j) увеличивается на 1. Таким образом, виды вымирают с вероятностью 0.15 и порождают новые виды с вероятностью 0.2.
В написанной Раупом программе, на основе которой была создана программа PALEOTREE, новый род определялся посредством ретроспективного анализа, слишком сложного для того, чтобы описывать его в настоящей статье. Однако Рауп заметил, что в достаточной мере сходные результаты можно получить и более простым путем. Предположим, что из каждого вида может произойти новый род с довольно маленькой вероятностью, скажем 0.02. Это предположение нужно встроить во внутренний цикл. Если случайное число, определяющее судьбу k-го вида, окажется больше 0.98, то программа PALEOTREE прерывает на мгновение обычный порядок работы, чтобы создать новый род вместо нового вида.
Относительно этой части программы следует сделать несколько важных технических замечаний. Сначала значение max увеличивается на 1 и i-и элемент нового столбца в массиве history, а именно history(i, max), устанавливается равным индексу рода j, от которого произошел новый род. Таким образом в массиве можно запомнить информацию, касающуюся происхождения нового рода. Это позволяет читателю (или программе графического отображения) установить происхождение каждого рода. В эпоху i+1, на первой стадии своей эволюции, вновь созданный род состоит лишь из одного-единственного вида. Поэтому элемент массива history (i+1, max) полагается равным 1, после чего эволюция идет своим обычным ходом.
При тех значениях вероятностей, которые мы установили в программе, какие-то роды практически неизбежно обречены на вымирание. В таком случае столбец массива history, соответствующий исчезнувшему роду, становится нулевым и значение max должно быть уменьшено на 1. В некоторых языках программирования это может привести к осложнениям. Вместо того чтобы игнорировать такой столбец массива, самый внутренний цикл может выполниться один или два раза, несмотря на то что переменная temp равна 0. Дело в том, что в некоторых языках программирования предполагается, что подобные циклы должны выполняться по уменьшению от 1 до 0, и таким образом уже обреченный было род получает шанс чудо-подобного воскресения. Чтобы избежать этой ситуации, в начало внутреннего цикла следует вставить процедуру проверки значения переменной temp, и если она оказывается равной 0, то весь внутренний цикл должен быть пропущен.
Как всегда, некоторым читателям, наверное, захочется немного поэкспериментировать с предложенной программой. Например, как изменится разнообразие рода, если вероятность вымирания вида увеличить с 0.15 до 0.2? Приведет ли равновероятность вымирания и ветвления к тому, что все живое прекратит свое существование? Было бы интересно познакомиться с результатами, полученными читателями, в которых наблюдаются массовые вымирания или очень незначительный процент выживания.
Наверное, никого не удивит то, что вторая из рассматриваемых в этой статье программ весьма сходна с программой PALEOTREE как по своей структуре, так и по выполняемым функциям. Напомним, что она моделирует выживание и вымирание фамилий. На самом деле эта программа может быть получена из PALEOTREE, если убрать из нее процедуру, генерирующую новый род. Назовем нашу вторую программу NEOTREE.
Как и в первой программе, здесь имеется массив history, в котором регистрируются все события по мере того, как идет время. Однако первоначально массив history содержит уже не один элемент, а 1000. Эти элементы представляют 1000 английских фамилий из числа наиболее распространенных в 1350г. Было бы, наверное, смешно (хотя и не лишено определенного антикварного шарма), если бы мы действительно ввели в программу 1000 реальных фамилий. Но ограничимся тем, что каждый столбец массива history будет представлять какую-то одну фамилию, которая, к сожалению, просто соответствует порядковому номеру столбца. Исходное значение элемента в каждом из 1000 столбцов равно 1. Оно представляет одну английскую семью: мать, отца и нескольких детей. В действительности программа прослеживает лишь за представителями мужского пола, т.е. за теми членами семьи, которые могут передать свою фамилию следующему поколению.
В данном случае было нереалистично по аналогии с программой PALEOTREE ограничить возможность ветвления семьи двумя новыми в каждом поколении. В программе NEOTREE каждая семья может "породить" от 0 до 6 новых семей в каждом поколении. Самый внутренний цикл программы обрабатывает фамилии аналогично тому, как внутренний цикл программы PALEOTREE оперировал с родами. Например, когда программа рассматривает j-ю фамилию, переменная temp устанавливается равной количеству семей, носящих на данный момент j-ю фамилию. В свою очередь каждая семья рассматривается в самом внутреннем цикле. Здесь при помощи датчика случайных чисел определяется количество представителей мужского пола, которые происходят из данной семьи и заводят свои собственные семьи.
Стерджес и Хэггет в своей работе пользовались таблицей, составленной по данным статистического анализа генеалогических записей и устанавливающей вероятности семи возможных событий для каждой семьи (см. рисунок вверху). Например, по статистике с вероятностью 0,317 в семье не окажется ни одного представителя мужского пола следующего поколения, у которого впоследствии будет собственная семья. С вероятностью 0,364 в семье окажется один такой представитель и т.д.

Статистические данные о числе потомков мужского пола и вероятности продолжения рода за период с 1350 г. по настоящее время
Между случайными числами, порождаемыми программой и значениями вероятностей, указанными в таблице, о которой мы только что говорили, нетрудно установить соответствие. Например, если случайное число оказывается меньше или равно 0.317, то у данной семьи не будет потомков мужского пола, которые создадут свои семьи в следующем поколении; в этом случае семья (а может быть, и фамилия, которую она носит) прекратит свое существование. Если случайное число находится в промежутке от 0.317 до 0.681 (сумма 0.317 и 0.364), то в семье окажется один потомок, потенциальный глава новой семьи. Другими словами, случайное число будет попадать во второй диапазон приблизительно 364 раза из 1000, что соответствует вероятности, полученной по данным статистического анализа. Оставшаяся часть таблицы строится аналогичным образом.
После того как программа NEOTREE определила судьбу данной семьи на следующее поколение, она действует точно так же, как и PALEOTREE. По достижении i-го поколения число семей, носящих фамилию j, запоминается в переменной temp. Индекс к самого внутреннего цикла пробегает значения от 1 до temp, и значение temp присваивается элементу массива history(i+1, j), как и раньше. Для каждой семьи с фамилией j, которая не дает ни одного потомка мужского пола, потенциального основателя новой семьи, элемент history(i+1, j) уменьшается на 1. Это отражает тот факт, что в следующем поколении число семей, носящих фамилию j, будет на одну меньше. Для каждой семьи с фамилией j, дающей одного потомка мужского пола, элемент массива history(i+1, j) остается без изменений. Для каждой семьи, дающей двух потомков мужского пола, значение history (i+i, j) увеличивается на 1 и т.д.
В некотором смысле программы PALEOTREE и NEOTREE приводят к противоположным результатам. Например, в программе NEOTREE принимается, что каждое новое поколение наступает через 28 лет и, таким образом, за период с 1350 по 1986г. сменяются 22 или 23 поколения; другими словами, требуется провести 22 или 23 цикла вычислений. Какая часть фамилий исчезнет за это время? Стерджес и Хэггет установили, что количество фамилий неуклонно уменьшается и что за 636-летний период исчезает почти три четверти фамилий. Может быть, некоторые читатели наберутся терпения и продолжат выполнение программы NEOTREE до тех пор, пока не установят, в каком году из 1000 исходных фамилий сохранится только одна.
Как и следовало ожидать, результаты моделирования с помощью программы PALEOTREE были совершенно иными. Несмотря на исчезновение отдельных родов, жизнь постепенно становится все более разнообразной. По мере того как одна эпоха сменяет другую, суммарное количество родов имеет тенденцию к возрастанию. Поэтому естественно предполагать, что некоторые роды станут настолько многочисленными и разнообразными, что практически окажутся полностью застрахованными от случайного вымирания в течение всего времени существования Вселенной. Тем не менее первоначальная версия программы Раупа давала необычайно много случаев вымирания, и этот результат был озадачивающим.
Программа PALEOTREE была создана в 70-е годы, когда внимание многих исследователей было приковано к свидетельствам массовых вымираний, зафиксированным в хронологии ископаемых остатков. Если верить этим свидетельствам, то подобные массовые исчезновения видов могли объясняться какими-то геологическими или космическими катаклизмами. Работая совместно с С.Гоулдом из Гарвардского университета и другими коллегами, Рауп высказал предположение, что быстро выполняющаяся программа моделирования, подобная программе PALEOTREE, может служить в качестве "нулевой гипотезы": если при такой работе программы будут наблюдаться явления массового вымирания, аналогичные тем, что наблюдаются в хронологии ископаемых остатков, то, возможно, для их объяснения совсем не обязательно было бы делать предположение о каких-либо катастрофических событиях.
Честно говоря, перед тем как писать свою программу, Рауп не имел оснований сомневаться в существовании таких явлений, как массовое вымирание видов. Он ожидал, что между результатами моделирования с помощью программы и широкими флуктуациями, наблюдаемыми в палеонтологии, не будет сколько-нибудь существенной корреляции. Однако в действительности такая корреляция была установлена и носила ярко выраженный характер. Некоторые филогенетические линии, порождаемые программой, ветвились и распространялись широко, в то время как другие заходили в тупик, так же как и по хронологии ископаемых находок. Наблюдались даже такие явления, когда сразу несколько линий одновременно обрывались, свидетельствуя о вымирании видов. Для чего тогда нужно было связывать эти явления с периодами оледенения или столкновениями Земли с астероидами, если массовые исчезновения биологических видов можно объяснить чисто случайными причинами?
С.Стэнли из Университета Джонса Гопкинса подверг критике результаты и их интерпретацию Раупом вскоре после их опубликования. Стэнли отметил, что число видов, которое программа допускала в одном роду, было нереалистично малым. А чем меньше видов насчитывается в роду, тем более вероятно, что случайные флуктуации их численности приведут к полному исчезновению рода. В реальных условиях количество видов в роду обычно достаточно велико, чтобы успешно противостоять таким флуктуациям. Поэтому в отличие от массовых исчезновений, полученных при моделировании по программе Раупа, реальные вымирания видов, зафиксированные в палеонтологии, могут и не быть результатом обычных статистических закономерностей. Рауп признал справедливость критических замечаний Стэнли и теперь придерживается той точки зрения, что реальные массовые вымирания, вероятно, не были результатом чисто случайных событий.
Одна из причин относительно малого разнообразия родов, наблюдавшегося в результатах Раупа, заключалась в том, что первоначально в программе организовывались слишком маленькие массивы. Такие массивы искусственно ограничивали каждый род, самое большее, 40 видами. Как отметил Рауп: "Мы не понимали тогда, насколько важную роль играет этот фактор". Его программа не помешала более одного вида в один элемент массива в отличие от программы PALEOTREE, потому что Рауп хотел проследить за развитием эволюционного дерева для каждого вида в отдельности, чтобы потом можно было внимательно изучить процесс случайного образования видов.
Еще одна причина сравнительно небольшого разнообразия видов заключается в том, что и программа Раупа, и программа PALEOTREE начинают с одного-единственного вида. Такая модель была бы, наверное, более подходящей для аппроксимации ранних этапов биологической эволюции, когда разнообразие видов было еще невелико. Читатели, которые желают убедиться в справедливости критических замечаний Стэнли, могут, например, в качестве исходных данных принять массив history, содержащий 100 родов, каждый из которых состоит из 100 видов. Будут ли при этих условиях наблюдаться массовые вымирания? В одной из наших следующих статей я рассмотрю наиболее интересные результаты, полученные читателями как в отношении трилобитов, так и в отношении Смитов.
БИБЛИОГРАФИЯ
STOCHASTIC MODELS OF PHYLOGENY AND THE EVOLUTION OF DIVERSITY, DAVID M. RAUP, STEPHEN J. GOULD, THOMAS J.M. SCHOPF AND DANIEL S. SIMBERLOFF in The Journal of Geology, Vol.81, No.5, pages 525-542; September, 1973.
PROBABILISTIC MODELS IN EVOLUTIONARY PALEOBIOLOGY. DAVID M. RAUP in Paleontology and Paleoenvironments: Readings from American Scientist, edited by Brian J. Skinner. William Kaufmann, Inc., 1981.
ОТКЛИКИ
10 1986
ПРОГРАММА NEOTREE, моделирующая процесс исчезновения фамилий, захватила воображение большего числа читателей, чем программа PALEOTREE, которая моделирует эволюцию биологических родов и видов. Обе программы рассматривались в июльском номере нашего журнала.
Для того чтобы проследить за эволюцией одного биологического рода, многие читатели обошлись без компьютера, ограничившись бросанием пары игральных костей. Напомним, что при выпадении суммы, равной 2, 3 или 4, данный биологический вид "вымирает", а 9 или 10 означает возникновение нового вида, все остальные значения суммы не приводят ни к каким изменениям. Вероятности, соответствующие этим событиям, равны 6/36, 7/36 и 23/36. В ходе своих собственных экспериментов я заметил, что ветвящиеся деревья, фиксирующие историю эволюции, часто отмирают. А какой процент выживающих деревьев будет жить вечно? Этот вопрос показался мне очень интересным. И. Джек Гуд из Блэксбурга показал, что вероятность того, что дерево окажется конечным, равна 6/7. Следовательно, в среднем седьмая часть моих деревьев обречена на бессмертие. Р.Соловэй из Калифорнийского университета в Беркли пришел к тому же выводу путем элементарных рассуждений. А тем временем Э.Каудал в Парк-Ридже (шт.Иллинойс) по многу раз прогонял программу, чтобы проследить за полной эволюцией дерева. Считая, что все деревья должны быть конечными, Каудал потратил целый вечер, генерируя самые различные деревья, чтобы определить их средние размеры. Он пишет, что время от времени возникали деревья, заполнявшие весь экран, и специально встроенное в программу условие, фиксирующее "переполнение", прекращало дальнейшее выполнение программы. Не подозревая, что истинным виновником этого явления была бесконечность дерева, он задал себе вопрос: какие последствия для теоретической палеонтологии означает ограниченный размер экрана? Он пишет: "Не будет ли Д.Раупу (из Чикагского университета) интересно узнать, что... вечные циклы лишь совпадают с ошибками переполнения в вечном центральном процессоре?"
Все читатели, экспериментировавшие с программой NEOTREE, получили идентичные результаты в опытах с 1000 исходных фамилий. При обычной статистике рождаемости особей мужского и женского пола количество фамилий сокращалось на три четверти уже через 20 поколений. Например, Дж.Кокс из Оттавы (Канада) получил результаты, согласно которым половина фамилий исчезает уже через три поколения, а две трети - через 10 поколений. После этого наблюдалась некая стабильность. М.Кэммен из Пэннтэд-Поуста (шт.Нью-Йорк) так объясняет это явление: "После, скажем, 50 поколений большинство фамилий имеют более 100 из живущих носителей мужского пола, способных завести свою собственную семью". Интересно, а может ли получиться так, что число фамилий сократится до одной-единственной? К.Элберт из Нью-Йорка считает, что такая возможность исключена. Опыт работы с программой NEOTREE показывает, что следует запастись "исключительным терпением" в ожидании этого события. Результат, как всегда, зависит от исходной модели. Например, в рамках абстрактной модели с непрерывным ростом населения 200 фамилий, возможно, станут вечными. Однако ни один компьютер не сможет вместить информацию о бесконечном населении. Какое-то значение окажется предельным. При ограничении на численность населения количество фамилий начнет сокращаться. И наконец, через 10^10^100 лет либо фамилия Смит, либо Хэн окажется навсегда утерянной.
ПРОГРАММЫ, МОДЕЛИРУЮЩИЕ ЭВОЛЮЦИЮ БИОЛОГИЧЕСКИХ ВИДОВ ПАЛЕОЗОЯ И ЭВОЛЮЦИЮ АНГЛИЙСКИХ ФАМИЛИЙ
А.К.ДЬЮДНИ
В ЮЖНОЙ части Онтарио и в западной части штата Нью-Йорк находятся богатые ископаемыми остатками выходы девонской горной породы. Одно такое "месторождение" расположено неподалеку от моего дома. Там, в карьере, сохраняющем следы доисторической жизни, я однажды увидел череп трилобита, уставившегося на меня из слоя глинистого сланца. Поглощенный процессом осторожного извлечения остатков, я вдруг услышал шарканье чьих-то ног и, резко повернувшись, увидел за своей спиной солидного бородатого мужчину. "Роскошный экземпляр Phacops raw,- сказал он.- Жаль, что они все вымерли". Незнакомец оказался профессором палеонтологии, его фамилия была Смит. "Интересно, - полюбопытствовал я вслух,- почему они вымерли?" Профессор Смит посмотрел задумчиво вдаль и затем в ответ на мой вопрос спросил: "Интересно, почему фамилия Смит такая распространенная?"
Чтобы точно ответить на эти вопросы, нужно было бы, наверное, проследить за сложным и необратимым взаимодействием генетических факторов и условий окружающей среды. Однако приближенные ответы дают нам две компьютерные программы, которые моделируют эволюцию биологических видов и фамилий при помощи одного и того же механизма. Первая программа по замыслу должна была моделировать "великие вымирания" в палеозойскую эру. Ее первоначальная версия была создана Д.Раупом, известным палеонтологом из Чикагского университета. Программа строит филогенетическое дерево, причем его структурные элементы выбираются произвольно: на каждом такте геологических часов кончик каждой ветви дерева с определенной вероятностью либо растет, либо разветвляется, либо отмирает. Картина этого случайного эволюционного процесса, порождаемого программой, удивительно напоминает хронику, зафиксированную ископаемыми находками, и в ней, в частности, также присутствует явление массового вымирания видов.
Вторая программа моделирует процесс распространения и исчезновения английских фамилий за период с 1350г. до настоящего времени. Программа эта - результат творческой деятельности К.Стерджеса и Б.Хэггета, сотрудников британского министерства обороны. Стерджес и Хэггет в свободное время увлекаются генеалогией. Они заинтересовались, почему в исторических документах многие древние фамилии постепенно исчезают. Может ли подобное исчезновение быть случайным событием? Чтобы выяснить, в чем тут дело, они написали моделирующую программу. Согласно полученным результатам, три четверти фамилий, распространенных в 1350г., по чисто случайным причинам исчезли на протяжении последующих 636 лет.
Каждый читатель, желающий совершить путешествие в вероятностной машине времени, может сам написать упрощенную версию любой из этих двух программ, сохранив наиболее существенные свойства, присущие оригиналам. При помощи первой программы вы проделаете путешествне длительностью в несколько сот миллионов лет, наблюдая за тем, как биологические виды и роды, состоящие из неизвестных и безымянных существ, становятся более разнообразными или вымирают. Вторая программа охватывает всего несколько сот лет, но исследуемая ею проблема по-человечески нам более интересна. Какие фамилии выйдут победителями: Смиты или Смедли?
Программа, которую я назвал PALEOTREE, начинает свою работу с единственного первородного существа. Чтобы наша модель носила палеонтологический смысл, присвоим этому существу какое-нибудь научное имя, например Paleoplasmus radiculus. Впрочем, читатели могут сами поупражняться в латыни и выбрать любое другое имя. В произвольно заданный момент времени программа представляет полную популяцию P.radiculus в виде одного узла, или точки, в структуре данных, называемой деревом. Любая популяция существ, принадлежащих той же биологической категории, что и P.radiculus, и происходящих из нее, также представляется в виде узла - в программе не производится подсчета количества живущих особей, их популяция представляется целиком.
За одно мгновение реального времени в модели проходят миллионы лет, и на каждом шаге программа рассматривает результаты эволюционного процесса. Старая популяция существ может сохраниться в неизменном виде на протяжении следующих нескольких миллионов лет. Если это так, то исходный узел на дереве порождает новый узел, связанный прямой линией с первым. Может случиться и так, что исходная популяция не только выживает, но н порождает новую биологическую категорию. Подобный исход можно представить в виде Y-образного разветвления. Одна из этих ветвей ведет к новому узлу, являющемуся продолжением исходной биологической категории, а вторая ведет к другому новому узлу, представляющему начало новой категории. Наконец, возможен и такой вариант, когда исходная популяция вымирает. В этом случае исходный узел становится тупиковым и у него нет никаких отростков.
Судьба каждого узла, порожденного на дереве, решается программой PALEOTREE случайным образом: продолжит ли популяция свое существование в неизменном виде, породит ли она новую биологическую категорию или целиком окажется вымершей? Конечно, строго говоря, эти три возможности далеко не полностью отражают все богаство структуры биологической эволюции. Из всего сказанного о программе следует, что все существа, произошедшие от одного и того же общего предка, являются монофилогенетическими, т.е. они достаточно близки друг к другу, чтобы их можно было отнести к одной и той же биологической категории, и поэтому они принадлежат одному и тому же дереву. Однако иногда эволюционный процесс приводит к возникновению новой широкой категории или к массовому вымиранию, когда исчезают старые категории. Таксономисты различают много подобных категорий - от подвидов до типов и царств. Для простоты в программе PALEOTREE представлены только две категории: вид и род, однако годятся и любые другие названия этих двух категорий.
В нашей программе из одного рода может произойти другой. Механизм такого происхождения довольно прост: из старого рода выделяется новый вид, на основе которого впоследствии развивается целый род. И то, что было просто ветвью на эволюционном дереве, уже само становится деревом. Разумеется, дерево (или род) может и полностью отмереть, когда исчезнут все составляющие его виды. Количество видов, из которых состоит род на данный момент, можно назвать разнообразием рода. Оно отражает не только генетическое богатство, но и вероятность выживания рода. Для изображения результатов работы программы PALEOTREE есть изящный графический способ. Каждый род представляется симметричной фигурой из горизонтальных прямоугольников, напоминающей веретено. Каждый прямоугольник представляет соответствующую эпоху, а горизонтальный размер прямоугольника - разнообразие рода в данную эпоху. Получающиеся в результате фигуры изображены на рисунке внизу.


Процесс эволюционного развития, ветвление и образование новых видов в биологических родах, моделируемые программой Д.Раупа, аналогичной программе PALEOTREE
Нетрудно, и даже полезно, поупражняться в построении дерева и соответствующего веретена вручную. Нарисуйте точку на листе бумаги и бросьте пару игральных костей. Если сумма выпавших чисел будет равна 2, 3 или 4, то вид немедленно вымирает. P.radiculus оказывается мертворожденным, и из точки на бумаге не появляется никаких ответвлений. Если сумма равна 9 или 10, то появляются ответвления - вид развивается. От исходной точки вверх отходят два коротких отрезка, и на конце каждого из них изображается еще по одной точке. Если выпадает любая другая сумма, вид сохраняется неизменным. В этом случае от исходной точки вверх отходит один отрезок, заканчивающийся точкой. В каждую эпоху этот эксперимент повторяется для каждого еще не вымершего вида. В результате описанной процедуры возникает дерево, а на веретенообразной диаграмме длина каждого прямоугольника соответствует количеству точек на данном уровне дерева (см. рисунок на с.84).

Судьба видов, образующих род, определяется бросанием игральных костей
При однократном бросании костей вероятность того, что вид исчезнет в следующей эпохе, равна 1/6, или 0,167, вероятность ветвления равна 7/36, или 0,194, а вероятность того, что вид останется без изменений, равна 23/36, или 0,639. Эти вероятности приблизительно соответствуют значениям, принятым в программе PALEOTREE, и поэтому приводят к аналогичным деревьям. Поскольку вероятность вымирания вида несколько меньше, чем вероятность ветвления, можно полагать, что некоторые деревья будут расти до бесконечности. Так ли это на самом деле? Интересно, к какому выводу придут читатели, пожелающие провести бессонную ночь в поисках ответа?
Чтобы построить веретенообразную диаграмму, вовсе не обязательно прослеживать за деревом каждого рода. Программа PALEOTREE просто подсчитывает количество видов, из которых состоит род в каждую данную эпоху, и следит за ветвлениями родов. Обе функции можно реализовать при помощи двумерного массива history. Каждый столбец представляет род, а строка - эпоху. Таким образом, history(i, j) - это количество видов, из которых состоит роду на момент времени, соответствующий эпохе i. После того как программа смоделирует эволюционный процесс для заданного числа шагов по времени, или эпох, массив history можно распечатать и воспользоваться значениями его элементов для построения веретенообразных диаграмм от руки. Читатели, располагающие некоторым опытом в графическом программировании, могут попытаться составить дополнительную программу, автоматически строящую диаграммы, однако детальное описание этой процедуры потребовало бы самостоятельной статьи.
Чтобы работать с программой PALEOTREE в ее простейшем варианте, вначале нужно указать с клавиатуры число эпох, или "поколений". Это число запоминается программой в переменной numgen; оно является
максимальным значением, которые может принимать индекс i в массиве history. По мере того как программа выполняет свой внешний цикл, значение i последовательно увеличивается на 1, начиная от 1 и кончая numgen. В этот цикл вложен второй цикл с индексом, пробегающим значения j в массиве history, при этом каждое значение j соответствует определенному роду. Чтобы определить максимальное значение индекса j, введена переменная max. Поскольку в исходном состоянии существует лишь один род, значение переменной max вначале устанавливается равным 1. По мере того как повторяется выполнение внешнего цикла, количество родов то возрастает, то убывает. Для каждой новой эпохи значение max устанавливается равным числу родов, существовавших в предыдущую эпоху. Перед выполнением цикла с индексом j переменной lmax присваивается значение max, и j пробегает значения от 1 до lmax.
Во втором цикле программа PALEOTREE подсчитывает количество видов, из которых состоит на данный момент род j, и запоминает это число во временной переменной temp. Затем программа входит в свой третий, самый внутренний цикл, где определяется судьба каждого вида, принадлежащего j-му роду. Индекс k этого внутреннего цикла можно рассматривать как счетчик видов. Он пробегает значения от 1 по temp, и значение temp заносится также в элемент history(i+1, j) массива, и таким образом указывается количество видов j-го рода в следующей эпохе i+1.
Для каждого вида, или, другими словами, для каждого значения k, выбирается случайное число в диапазоне от 0 до 1. Это делается посредством оператора, генерирующего случайные числа. Конкретный вид этого оператора зависит от языка программирования, которым вы пользуетесь. Если случайное число оказывается меньше 0,15, то k-й вид вымирает и элемент массива history(i+1, j) уменьшается на 1. Если значение случайного числа больше 0,8, то от k-го вида отделяется новый вид и элемент history(i+1, j) увеличивается на 1. Таким образом, виды вымирают с вероятностью 0.15 и порождают новые виды с вероятностью 0.2.
В написанной Раупом программе, на основе которой была создана программа PALEOTREE, новый род определялся посредством ретроспективного анализа, слишком сложного для того, чтобы описывать его в настоящей статье. Однако Рауп заметил, что в достаточной мере сходные результаты можно получить и более простым путем. Предположим, что из каждого вида может произойти новый род с довольно маленькой вероятностью, скажем 0.02. Это предположение нужно встроить во внутренний цикл. Если случайное число, определяющее судьбу k-го вида, окажется больше 0.98, то программа PALEOTREE прерывает на мгновение обычный порядок работы, чтобы создать новый род вместо нового вида.
Относительно этой части программы следует сделать несколько важных технических замечаний. Сначала значение max увеличивается на 1 и i-и элемент нового столбца в массиве history, а именно history(i, max), устанавливается равным индексу рода j, от которого произошел новый род. Таким образом в массиве можно запомнить информацию, касающуюся происхождения нового рода. Это позволяет читателю (или программе графического отображения) установить происхождение каждого рода. В эпоху i+1, на первой стадии своей эволюции, вновь созданный род состоит лишь из одного-единственного вида. Поэтому элемент массива history (i+1, max) полагается равным 1, после чего эволюция идет своим обычным ходом.
При тех значениях вероятностей, которые мы установили в программе, какие-то роды практически неизбежно обречены на вымирание. В таком случае столбец массива history, соответствующий исчезнувшему роду, становится нулевым и значение max должно быть уменьшено на 1. В некоторых языках программирования это может привести к осложнениям. Вместо того чтобы игнорировать такой столбец массива, самый внутренний цикл может выполниться один или два раза, несмотря на то что переменная temp равна 0. Дело в том, что в некоторых языках программирования предполагается, что подобные циклы должны выполняться по уменьшению от 1 до 0, и таким образом уже обреченный было род получает шанс чудо-подобного воскресения. Чтобы избежать этой ситуации, в начало внутреннего цикла следует вставить процедуру проверки значения переменной temp, и если она оказывается равной 0, то весь внутренний цикл должен быть пропущен.
Как всегда, некоторым читателям, наверное, захочется немного поэкспериментировать с предложенной программой. Например, как изменится разнообразие рода, если вероятность вымирания вида увеличить с 0.15 до 0.2? Приведет ли равновероятность вымирания и ветвления к тому, что все живое прекратит свое существование? Было бы интересно познакомиться с результатами, полученными читателями, в которых наблюдаются массовые вымирания или очень незначительный процент выживания.
Наверное, никого не удивит то, что вторая из рассматриваемых в этой статье программ весьма сходна с программой PALEOTREE как по своей структуре, так и по выполняемым функциям. Напомним, что она моделирует выживание и вымирание фамилий. На самом деле эта программа может быть получена из PALEOTREE, если убрать из нее процедуру, генерирующую новый род. Назовем нашу вторую программу NEOTREE.
Как и в первой программе, здесь имеется массив history, в котором регистрируются все события по мере того, как идет время. Однако первоначально массив history содержит уже не один элемент, а 1000. Эти элементы представляют 1000 английских фамилий из числа наиболее распространенных в 1350г. Было бы, наверное, смешно (хотя и не лишено определенного антикварного шарма), если бы мы действительно ввели в программу 1000 реальных фамилий. Но ограничимся тем, что каждый столбец массива history будет представлять какую-то одну фамилию, которая, к сожалению, просто соответствует порядковому номеру столбца. Исходное значение элемента в каждом из 1000 столбцов равно 1. Оно представляет одну английскую семью: мать, отца и нескольких детей. В действительности программа прослеживает лишь за представителями мужского пола, т.е. за теми членами семьи, которые могут передать свою фамилию следующему поколению.
В данном случае было нереалистично по аналогии с программой PALEOTREE ограничить возможность ветвления семьи двумя новыми в каждом поколении. В программе NEOTREE каждая семья может "породить" от 0 до 6 новых семей в каждом поколении. Самый внутренний цикл программы обрабатывает фамилии аналогично тому, как внутренний цикл программы PALEOTREE оперировал с родами. Например, когда программа рассматривает j-ю фамилию, переменная temp устанавливается равной количеству семей, носящих на данный момент j-ю фамилию. В свою очередь каждая семья рассматривается в самом внутреннем цикле. Здесь при помощи датчика случайных чисел определяется количество представителей мужского пола, которые происходят из данной семьи и заводят свои собственные семьи.
Стерджес и Хэггет в своей работе пользовались таблицей, составленной по данным статистического анализа генеалогических записей и устанавливающей вероятности семи возможных событий для каждой семьи (см. рисунок вверху). Например, по статистике с вероятностью 0,317 в семье не окажется ни одного представителя мужского пола следующего поколения, у которого впоследствии будет собственная семья. С вероятностью 0,364 в семье окажется один такой представитель и т.д.

Статистические данные о числе потомков мужского пола и вероятности продолжения рода за период с 1350 г. по настоящее время
Между случайными числами, порождаемыми программой и значениями вероятностей, указанными в таблице, о которой мы только что говорили, нетрудно установить соответствие. Например, если случайное число оказывается меньше или равно 0.317, то у данной семьи не будет потомков мужского пола, которые создадут свои семьи в следующем поколении; в этом случае семья (а может быть, и фамилия, которую она носит) прекратит свое существование. Если случайное число находится в промежутке от 0.317 до 0.681 (сумма 0.317 и 0.364), то в семье окажется один потомок, потенциальный глава новой семьи. Другими словами, случайное число будет попадать во второй диапазон приблизительно 364 раза из 1000, что соответствует вероятности, полученной по данным статистического анализа. Оставшаяся часть таблицы строится аналогичным образом.
После того как программа NEOTREE определила судьбу данной семьи на следующее поколение, она действует точно так же, как и PALEOTREE. По достижении i-го поколения число семей, носящих фамилию j, запоминается в переменной temp. Индекс к самого внутреннего цикла пробегает значения от 1 до temp, и значение temp присваивается элементу массива history(i+1, j), как и раньше. Для каждой семьи с фамилией j, которая не дает ни одного потомка мужского пола, потенциального основателя новой семьи, элемент history(i+1, j) уменьшается на 1. Это отражает тот факт, что в следующем поколении число семей, носящих фамилию j, будет на одну меньше. Для каждой семьи с фамилией j, дающей одного потомка мужского пола, элемент массива history(i+1, j) остается без изменений. Для каждой семьи, дающей двух потомков мужского пола, значение history (i+i, j) увеличивается на 1 и т.д.
В некотором смысле программы PALEOTREE и NEOTREE приводят к противоположным результатам. Например, в программе NEOTREE принимается, что каждое новое поколение наступает через 28 лет и, таким образом, за период с 1350 по 1986г. сменяются 22 или 23 поколения; другими словами, требуется провести 22 или 23 цикла вычислений. Какая часть фамилий исчезнет за это время? Стерджес и Хэггет установили, что количество фамилий неуклонно уменьшается и что за 636-летний период исчезает почти три четверти фамилий. Может быть, некоторые читатели наберутся терпения и продолжат выполнение программы NEOTREE до тех пор, пока не установят, в каком году из 1000 исходных фамилий сохранится только одна.
Как и следовало ожидать, результаты моделирования с помощью программы PALEOTREE были совершенно иными. Несмотря на исчезновение отдельных родов, жизнь постепенно становится все более разнообразной. По мере того как одна эпоха сменяет другую, суммарное количество родов имеет тенденцию к возрастанию. Поэтому естественно предполагать, что некоторые роды станут настолько многочисленными и разнообразными, что практически окажутся полностью застрахованными от случайного вымирания в течение всего времени существования Вселенной. Тем не менее первоначальная версия программы Раупа давала необычайно много случаев вымирания, и этот результат был озадачивающим.
Программа PALEOTREE была создана в 70-е годы, когда внимание многих исследователей было приковано к свидетельствам массовых вымираний, зафиксированным в хронологии ископаемых остатков. Если верить этим свидетельствам, то подобные массовые исчезновения видов могли объясняться какими-то геологическими или космическими катаклизмами. Работая совместно с С.Гоулдом из Гарвардского университета и другими коллегами, Рауп высказал предположение, что быстро выполняющаяся программа моделирования, подобная программе PALEOTREE, может служить в качестве "нулевой гипотезы": если при такой работе программы будут наблюдаться явления массового вымирания, аналогичные тем, что наблюдаются в хронологии ископаемых остатков, то, возможно, для их объяснения совсем не обязательно было бы делать предположение о каких-либо катастрофических событиях.
Честно говоря, перед тем как писать свою программу, Рауп не имел оснований сомневаться в существовании таких явлений, как массовое вымирание видов. Он ожидал, что между результатами моделирования с помощью программы и широкими флуктуациями, наблюдаемыми в палеонтологии, не будет сколько-нибудь существенной корреляции. Однако в действительности такая корреляция была установлена и носила ярко выраженный характер. Некоторые филогенетические линии, порождаемые программой, ветвились и распространялись широко, в то время как другие заходили в тупик, так же как и по хронологии ископаемых находок. Наблюдались даже такие явления, когда сразу несколько линий одновременно обрывались, свидетельствуя о вымирании видов. Для чего тогда нужно было связывать эти явления с периодами оледенения или столкновениями Земли с астероидами, если массовые исчезновения биологических видов можно объяснить чисто случайными причинами?
С.Стэнли из Университета Джонса Гопкинса подверг критике результаты и их интерпретацию Раупом вскоре после их опубликования. Стэнли отметил, что число видов, которое программа допускала в одном роду, было нереалистично малым. А чем меньше видов насчитывается в роду, тем более вероятно, что случайные флуктуации их численности приведут к полному исчезновению рода. В реальных условиях количество видов в роду обычно достаточно велико, чтобы успешно противостоять таким флуктуациям. Поэтому в отличие от массовых исчезновений, полученных при моделировании по программе Раупа, реальные вымирания видов, зафиксированные в палеонтологии, могут и не быть результатом обычных статистических закономерностей. Рауп признал справедливость критических замечаний Стэнли и теперь придерживается той точки зрения, что реальные массовые вымирания, вероятно, не были результатом чисто случайных событий.
Одна из причин относительно малого разнообразия родов, наблюдавшегося в результатах Раупа, заключалась в том, что первоначально в программе организовывались слишком маленькие массивы. Такие массивы искусственно ограничивали каждый род, самое большее, 40 видами. Как отметил Рауп: "Мы не понимали тогда, насколько важную роль играет этот фактор". Его программа не помешала более одного вида в один элемент массива в отличие от программы PALEOTREE, потому что Рауп хотел проследить за развитием эволюционного дерева для каждого вида в отдельности, чтобы потом можно было внимательно изучить процесс случайного образования видов.
Еще одна причина сравнительно небольшого разнообразия видов заключается в том, что и программа Раупа, и программа PALEOTREE начинают с одного-единственного вида. Такая модель была бы, наверное, более подходящей для аппроксимации ранних этапов биологической эволюции, когда разнообразие видов было еще невелико. Читатели, которые желают убедиться в справедливости критических замечаний Стэнли, могут, например, в качестве исходных данных принять массив history, содержащий 100 родов, каждый из которых состоит из 100 видов. Будут ли при этих условиях наблюдаться массовые вымирания? В одной из наших следующих статей я рассмотрю наиболее интересные результаты, полученные читателями как в отношении трилобитов, так и в отношении Смитов.
БИБЛИОГРАФИЯ
STOCHASTIC MODELS OF PHYLOGENY AND THE EVOLUTION OF DIVERSITY, DAVID M. RAUP, STEPHEN J. GOULD, THOMAS J.M. SCHOPF AND DANIEL S. SIMBERLOFF in The Journal of Geology, Vol.81, No.5, pages 525-542; September, 1973.
PROBABILISTIC MODELS IN EVOLUTIONARY PALEOBIOLOGY. DAVID M. RAUP in Paleontology and Paleoenvironments: Readings from American Scientist, edited by Brian J. Skinner. William Kaufmann, Inc., 1981.
ОТКЛИКИ
10 1986
ПРОГРАММА NEOTREE, моделирующая процесс исчезновения фамилий, захватила воображение большего числа читателей, чем программа PALEOTREE, которая моделирует эволюцию биологических родов и видов. Обе программы рассматривались в июльском номере нашего журнала.
Для того чтобы проследить за эволюцией одного биологического рода, многие читатели обошлись без компьютера, ограничившись бросанием пары игральных костей. Напомним, что при выпадении суммы, равной 2, 3 или 4, данный биологический вид "вымирает", а 9 или 10 означает возникновение нового вида, все остальные значения суммы не приводят ни к каким изменениям. Вероятности, соответствующие этим событиям, равны 6/36, 7/36 и 23/36. В ходе своих собственных экспериментов я заметил, что ветвящиеся деревья, фиксирующие историю эволюции, часто отмирают. А какой процент выживающих деревьев будет жить вечно? Этот вопрос показался мне очень интересным. И. Джек Гуд из Блэксбурга показал, что вероятность того, что дерево окажется конечным, равна 6/7. Следовательно, в среднем седьмая часть моих деревьев обречена на бессмертие. Р.Соловэй из Калифорнийского университета в Беркли пришел к тому же выводу путем элементарных рассуждений. А тем временем Э.Каудал в Парк-Ридже (шт.Иллинойс) по многу раз прогонял программу, чтобы проследить за полной эволюцией дерева. Считая, что все деревья должны быть конечными, Каудал потратил целый вечер, генерируя самые различные деревья, чтобы определить их средние размеры. Он пишет, что время от времени возникали деревья, заполнявшие весь экран, и специально встроенное в программу условие, фиксирующее "переполнение", прекращало дальнейшее выполнение программы. Не подозревая, что истинным виновником этого явления была бесконечность дерева, он задал себе вопрос: какие последствия для теоретической палеонтологии означает ограниченный размер экрана? Он пишет: "Не будет ли Д.Раупу (из Чикагского университета) интересно узнать, что... вечные циклы лишь совпадают с ошибками переполнения в вечном центральном процессоре?"
Все читатели, экспериментировавшие с программой NEOTREE, получили идентичные результаты в опытах с 1000 исходных фамилий. При обычной статистике рождаемости особей мужского и женского пола количество фамилий сокращалось на три четверти уже через 20 поколений. Например, Дж.Кокс из Оттавы (Канада) получил результаты, согласно которым половина фамилий исчезает уже через три поколения, а две трети - через 10 поколений. После этого наблюдалась некая стабильность. М.Кэммен из Пэннтэд-Поуста (шт.Нью-Йорк) так объясняет это явление: "После, скажем, 50 поколений большинство фамилий имеют более 100 из живущих носителей мужского пола, способных завести свою собственную семью". Интересно, а может ли получиться так, что число фамилий сократится до одной-единственной? К.Элберт из Нью-Йорка считает, что такая возможность исключена. Опыт работы с программой NEOTREE показывает, что следует запастись "исключительным терпением" в ожидании этого события. Результат, как всегда, зависит от исходной модели. Например, в рамках абстрактной модели с непрерывным ростом населения 200 фамилий, возможно, станут вечными. Однако ни один компьютер не сможет вместить информацию о бесконечном населении. Какое-то значение окажется предельным. При ограничении на численность населения количество фамилий начнет сокращаться. И наконец, через 10^10^100 лет либо фамилия Смит, либо Хэн окажется навсегда утерянной.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
9 1986
ФАНТАСТИЧЕСКИЙ ПОЛЕТ НАД НЕОБИТАЕМОЙ БАЗОЙ ДАННЫХ
А.К.ДЬЮДНИ
Эту статью я уже упоминал - ТЕМА #67, АБЗАЦ #732
ТЕМА #67, АБЗАЦ #732 . И журнал выкладывал. Особенно обратите в нем внимание на "предваряющую" статью - про реальные тренажеры.- G.
. И журнал выкладывал. Особенно обратите в нем внимание на "предваряющую" статью - про реальные тренажеры.- G.
Я лихорадочно изучал приборную панель самолета "Чессна 182". Наверное, с моей стороны было неразумно пытаться совершить полет в одиночку без надлежащей подготовки. Может быть, следовало взять с собой опытного пилота? На чикагском аэродроме Мейгс-Филд не было видно ни души, даже ни один механик не вышел покурить на солнышке. Единственно на что я мог положиться в этой сумасбродкой затее - это на руководство для пилота, на изучение которого я потратил не больше 10 минут.
Думаю, что я чувствовал бы себя увереннее, если бы у меня в руках была ручка управления или штурвал. Еще ребенком я по многу раз смотрел фильмы о приключениях летчиков-асов и хорошо запомнил основные приемы управления самолетом. Однако в этом самолете все было по-другому. Он управлялся с клавиатуры стоящего передо мной терминала.
Со вздохом я раскрыл страницу 46 руководства. Клавиша F2 слегка приоткрывает дроссель, клавиша F4 широко раскрывает его. Будучи человеком не совсем безрассудным, я с опаской нажал на клавишу F2. Мягкий шум двигателя несколько усилился. Взлетная дорожка побежала мне навстречу, и на какое-то мгновение мною овладела паника. Самолет почти сразу же начал уходить в сторону от бетонной полосы. По невежеству я не прочел ничего о руле горизонтального управления или о переднем шасси. Спасти меня могли только элероны - клавиша 4 (левый крен) и клавиша 6 (правый крен). К моему полному изумлению, одна из них стала медленно, но верно возвращать самолет на взлетную полосу.
Всего в ста метрах впереди показались голубые воды озера Мичиган. Прибавляю газ - F2, F2, F2, F2. Прибавляю еще. Мотор звучит все мощнее, но самолет упорно отказывается взлетать. Взлетная полоса побежала подо мной еше быстрее, и меня опять охватила паника. Какая же волшебная клавиша поднимет меня в воздух? Вся моя жизнь пронеслась предо мной. Сцены из далекого детства: вот я управляю моделью самолета, это можно было делать лишь с помощью двух закрылков на хвосте. Руль высоты! Я стал лихорадочно искать "руль высоты" в своем руководстве. Этот руль управляет углом атаки самолета, при его помощи можно приподнять нос самолета. Нажимаю на клавишу 2, и как раз вовремя, еше немного и передо мной разверзлась бы водяная могила. Страшная граница между сушей и водой стала отступать. Самолет был в воздухе! Он набирал высоту как будто по своей воле. Внизу все четче проступала перспектива западной береговой линии озера Мичиган, и в течение какого-то времени я продолжал полет в северном направлении, загипнотизированный своим достижением.
Как уже, наверное, догадались многие читатели, моя кабина находилась в комнате, а роль ручек управления играли клавиши на терминале моего персонального компьютера, который выполнял программу имитации полета. Однако знакомая обстановка ничуть не снижала остроту ощущений. Тот факт, что и самолет, и ландшафт лишь имитировались компьютером, даже усиливал воображение. В этих условиях можно было совершать такие действия, на которые никто бы не отважился, сидя в кабине настоящего самолета. Ведь счет, предъявленный за аварию, будет тоже воображаемым. Я сделал вираж в юго-западном направлении и стал приближаться к Чикаго. Мне захотелось пронестись нал Мичиган-авеню и произвести впечатление на многочисленных водителей и пассажиров движущегося по этой оживленной улице транспорта. Часы, вмонтированные в приборную панель самолета, показывали 4ч 30мин., как раз начало вечернего часа пик.
Приближаясь к Чикаго, я стал замечать что-то неладное. Были видны лишь несколько зданий, расположенных вдоль берега озера, а на улицах никакого транспорта. Людей тоже не было видно. Может быть, началась атомная война? Я заметил, что принял за часы высотомер с двумя стрелками, но даже несмотря на то, что сейчас было значительно раньше 4ч 30мин., полное отсутствие людей на улицах такого большого города казалось странным. Хотя и неохотно, но я пришел к выводу: в программе имитации полета просто не нашлось места для людей. Ее база данных и без того была перегружена описанием североамериканского ландшафта, не говоря уже о всевозможных географических подробностях, необходимых для моделирования четырех больших городов и более 20 аэродромов.
В последующих полетах я уже все меньше и меньше думал о недостатке в людском обществе. Слишком интересен был сам полет. В этом со мной, наверное, согласятся многие из тех, кто совершал подобные воздушные путешествия. Программа называется FLIGHT SIMULATOR (Имитатор полета), и в течение уже многих месяцев она была одной из наиболее популярных, если не самой популярной из всех занимательных программ для персональных компьютеров. Существует немало других программ имитации полета, которые можно купить или приобрести бесплатно в различных ассоциациях. Однако как FLIGHT SIMULATOR, так и ряд других аналогичных программ своей популярностью обязаны Б.Артвику, инженеру-программисту из Шампейна (шт.Иллинойс). Более чем кто-либо другой Артвик способствовал "взлету" программ имитации полета, и благодаря его усилиям они теперь могут выполняться на персональных компьютерах. В течение долгого времени компьютерная имитация полета применялась исключительно с целью обучения летчиков (см. статью Р.Хабера "Моделирование условий полета"). Теперь же эти средства доступны практически каждому.
Рассмотрим, в чем должны заключаться особенности таких программ, чтобы поддерживать у пользователя иллюзию реального полета. Во-первых, они должны создавать и несколько раз в секунду воссоздавать ландшафт, видимый из какой-то фиксированной точки. По мере того как моделируемый аэроплан бороздит моделируемые небеса, точка наблюдения перемешается, и поэтому черты проплывающего на экране ландшафта должны вычисляться заново. Более того, для каждой точки наблюдения возможны различные углы зрения. Угол зрения определяется результатами имитации физических особенностей аэроплана, находящегося в полете. Например, если самолет делает крен в сторону, чтобы совершить поворот, угол зрения, так же как н точка наблюдения, должен соответственно меняться. В основном цикле вычислений применяется ряд трюков и осуществляется поиск компромиссных решений, что само по себе не менее увлекательно, чем имитация полета в целом.
Географическая база данных является одним из главных компонентов программы FLIGHT SIMULATOR. Она включает обширный список объектов, необходимых для воссоздания ландшафта территории, над которой желает полетать пользователь (или в которую он не хочет врезаться). Вы можете получить доступ к "сцене" вашего полета, обратившись к иерархической информационной системе и прослеживая за данными "сверху вниз". В массиве памяти под названием USA (США) хранятся названия районов, таких, как Чикаго, Нью-Йорк и Сиэтл. Положение самолета задается тремя координатами: x - широта, у - высота над уровнем моря (в метрах) и z - долгота. Программа FLIGHT SIMULATOR сравнивает эти координаты с предельными значениями, ограничивающими каждый район в массиве США. Если, например, х и z задают точку, принадлежащую району Чикаго, то программа выполняет операцию, называемую загрузкой базы данных. В результате этой операции список, в котором хранится информация о районе Чикаго, загружается с магнитного лиска в оперативную память компьютера.
Когда в ходе своего первого полета я сделал вираж, повернув по направлению к Чикаго, сначала я не увндел никаких зданий. Однако некоторое время спустя показалась башня Сирз-Тауэр. Затем стали проступать и ее детали. В этом как раз и заключается стратегия программы, позволяющая ей уложиться в пределы имеющегося объема памяти и быстродействия: особенности ландшафта не отображаются на экране до тех пор, пока в них нет реальной необходимости. В программу встроены две специальные тестирующие процедуры, управляющие появлением и исчезновением на экране тех или иных деталей ландшафта. Первая из них ifin2d следит лишь за двумя координатами - широтой и долготой самолета. Выше уже говорилось, каким образом географические районы ассоциируются с этими двумя координатами.
Вторая тестирующая процедура ifin3d определяет расстояние до заданной детали ландшафта, и если она находится достаточно близко, программа отображает ее на экране. По мере того как я приближался к Чикаго, процедура ifin3d постоянно вычисляла расстояние от самолета до тех или иных зданий или других ориентиров города, видимых с воздуха. Когда мой самолет приблизился к башне Сирз-Тауэр на расстояние 12800м, на экране внезапно появилась миниатюрная копия этого сооружения в виде нескольких мерцающих точек. Когда же расстояние до башни уменьшилось до 7680м, появились уже некоторые неразличимые ранее детали. Для каждых трех новых значений координат FLIGHT SIMULATOR быстро просматривает список, хранящий все видимые особенности ландшафта, и проверяет их согласно критериям отображения объектов, на которых основана процедура ifin3d. Если объект удовлетворяет критериям, программа отображает его на экране таким, каким он должен быть виден из данной точки. Если же объект не проходит теста, он не отображается, и программа переходит к проверке следующего объекта в списке.

Вид статуи Свободы из кабины самолета, построенной программой FLIGHT SIMULATOR
Вообще говоря, каждый объект или каждая особенность моделируемого ландшафта определяется в программе списком точек, линий и поверхностей. Поскольку изображение вычисляется пять раз в секунду, достаточно часто для того, чтобы воспользоваться инерционностью человеческого зрения, линии и поверхности должны отображаться за минимально возможное время. Поэтому даже элементарные графические операции были реализованы в программе самым тщательным образом. Артвик описал эти операции в своей замечательной книге "Microcomputer Displays, Graphics, and Animation" ("Микрокомпьютерные изображения, графика и мультипликация").
Например, в основном методе, применяемом для изображения линии, операции умножения и деления не применяются, поскольку для их выполнения требуется в 10 и даже в 100 раз больше времени по сравнению с операциями сложения и вычитания. В данном случае метод изображения линии основан на тщательном анализе временных затрат на каждую выполняемую команду. Получившийся в результате остроумный алгоритм изображения линии по существу состоит лишь из четырех команд: сложения, сравнения, перехода к команды отображения. Пусть, например, точка с координатами {a, b) была только что высвечена на линии с (положительным) наклоном 1/4. Программа входит в цикл, в котором она повторно прибавляет 1 к значению координаты a и 1/4 к специальной сумме, называемой ошибкой прослеживания, и затем тестирует текущее значение этой суммы. Если ошибка прослеживания оказывается большей или равной какому-нибудь целому числу, то программа выходит из цикла и высвечивает следующую точку, в данном случае с координатами (a+4, b+1).
Поверхности программа изображает посредством метода, который едва ли поддается описанию, но зато чрезвычайно быстро реализуется в компьютере. В нескольких словах этот процесс можно представить следующим образом. Программа изображает многоугольник, ограничивающий данную поверхность, и затем "заштриховывает" его внутреннюю область. После того как вычислена форма многоугольника, специальная графическая процедура вначале определяет сканирующие линии, пересекающие на экране полученный многоугольник. Для каждой такой линии сканирования определяются пересекаемые ею стороны многоугольника, а затем эти стороны сортируются (упорядочиваются) в соответствии с порядком, в котором линия сканирования пересекает их слева направо. Затем процедура рассматривает каждый пиксел, или элемент изображения, на линии сканирования по порядку слева направо. Когда линия встречается с первой стороной многоугольника, она начинает высвечивать точки определенного цвета, выбранного для представления данной поверхности. Как только линия сканирования доходит до следующей стороны, отображение точек прекращается. При встрече со следующей стороной отображение возобновляется и т.д.

По смертельно опасному курсу на Манхаттенский мост
Описанный метод включения-выключения отображения вдоль линии сканирования экрана основан на фундаментальном положении топологии на плоскости: любой многоугольник делит плоскость на две части - внутреннюю и внешнюю. Поэтому любая линия, пересекаюшая сторону многоугольника, переходит из внутренней части (принадлежащей отображаемой области) во внешнюю (не принадлежащую ей) или наоборот. Большинство поверхностей, отображаемых программой FLIGHT SIMULATOR, ограничены сравнительно простыми многоугольниками. Например, после того как я покинул зону аэродрома Мейгс-Филд, передо мной до самого горизонта протянулась береговая линия озера Мичиган. Эта линия представляла собой несколько сторон многоугольника, очерчивающих залив, ограниченный отмелью, тянущейся в северном направлении. Голубые линии воды в заливе прерывались в зоне отмели и затем снова возникали, заполняя главную часть озера.
Специалисты, работающие с графическими программами, часто размышляли над так называемой проблемой скрытой линии. Каким образом программа должна изображать трехмерное непрозрачное тело, чтобы видна была только та грань, которая находится ближе к наблюдателю? Некоторые методы, применимые к этой задаче, требуют решения трудоемких уравнений, на что уходит слишком много времени. FLIGHT SIMULATOR едва ли может себе это позволить. Решение Артвика, применимое лишь к простым ландшафтам, заключается в том, чтобы при изображении объекта ближайшая к наблюдателю грань заштриховывалась последней. Части объекта, которые должны оставаться невидимыми для наблюдателя, просто затираются теми, которые должны быть видны. Представление двух башен Международного торгового центра в Нью-Йорке дает нам хороший пример применения этого грубого, но эффективного метода. При любом угле зрения ближайшие части здания закрывают более далекие и ближняя башня "затмевает" дальнюю.
После того как я узнал, что Чикаго необитаем, я решил вернуться на Мейгс-Филд. Владелец самолета, наверное, уже беспокоится. И все же я хотел еше многому научиться. Во-первых, мне было как-то не по себе оттого, что я не знал назначения нескольких рычагов управления. Во-вторых, я так и не попытался выяснить какую-нибудь фигуру высшего пилотажа. Для этой цели я вылетел в зону озера Мичиган.
Моим излюбленным средством управления были элероны. При нажатии на клавишу левого элерона самолет делает крен влево: горизонт передо мной наклонился вправо, и весь ландшафт, казалось начал сползать по склону. Не противореча законам аэродинамики, нос "Чессны" все это время поворачивал влево. Вернув крыло в горизонтальное положение и продолжая полет по прямой, я нажал несколько раз на клавишу 8 и почти физически почувствовал, как нос самолета нырнул вниз. За окном моей кабины горизонт резко поднялся вверх. Самолет пикировал. Спидометр показывал скорость, превышающую 150 миль/ч. Я попытался воспользоваться горизонтальным рулем. Клавиша со знаком "плюс" слегка повернула руль вправо, и самолет начал вращаться, вызывая неприятные ощущения. Вернув руль в нейтральное положение, я стал наблюдать, как простирающийся подо мной ландшафт обманчиво медленно надвигается на меня. Настало время приступить к выполнению фигуры.
Пилоты входят в петли значительно реже, чем программисты в циклы. Интуиция подсказывала, что для маневра понадобится довольно большая скорость. Сначала вниз, затем вверх и потом вниз головой. Нажимать клавиши мне нравилось меньше, чем твердо поворачивать на себя ручку управления, но я тем не менее старательно нажимал на клавишу 2. Самолет с ревом вышел из пике в горизонтальный полет, а затем устремился вверх в голубую твердь небес. Я увидел, как линия горизонта ушла подо мной вниз, и стал ждать. У меня не было никакой уверенности в том, что фигура удастся. Все замерло в тишине. Может быть, самолет зависнет и рухнет на землю? Приборы не могли мне ничего подсказать, лишь о половине из них я имел какое-то представление, да и то смутное.
Внезапно на экране появился перевернутый ландшафт - сверху зеленая земля, а снизу голубое небо. Неужели маневр удался? Я был слишком разгорячен, чтобы ответить на свой вопрос. Полный мрачной решимости, я продолжал эксперимент. Теперь передо мной во все стороны раскинулась земля. Затем горизонт занял свое нормальное положение. Я попытался опустить нос самолета, чтобы предотвратить еще одну петлю. Горизонт покачнулся и замер на месте. Да, фигура удалась! Видимо, я принадлежу к числу тех одаренных людей, которые могут обучиться летному делу экспериментально, почти безо всякой предварительной подготовки. Впереди показался аэродром Мейгс-Филл. Как только совершу посадку, пойду приму душ.
Главная посадочная полоса аэродрома протянулась с севера на юг. Я находился к юго-востоку от аэродрома и решил лететь на запад, а поравнявшись с посадочной полосой, повернуть на север. Реализовать этот план мне почему-то не удалось. Никак не удавалось зайти на посадочную полосу, и, кроме того, я приближался к аэродрому на слишком большой высоте. Все это было подобно кошмару, когда за одним несчастьем приходит другое. Я резко опустил нос самолета, чтобы побыстрее снизиться, стараясь в то же время дотянуть еще несколько метров в направлении на восток. Однако посадочная полоса ушла с экрана, и к тому же я потерял горизонт. Земля стала быстро приближаться, зазвучал сигнал тревоги. Черт побери! Я врезался в землю. Это стало очевидно, когда ветровое стекло кабины покрылось трещинами и на их фоне появилась крупная надпись "Авария". Погиб я или нет? Очень жаль, если база данных Чикаго лишится своего последнего обитателя.

Три оси, вокруг которых может поворачивать самолет
Чтобы моделировать все эти приключения, FLIGHT SIMULATOR должна постоянно делать новые вычисления вида на ландшафт из кабины самолета. Рычаги управления самолетом можно сгруппировать по направлениям вращения вокруг трех осей (см. рисунок). Так, элероны поворачивают самолет вокруг продольной оси, проходящей через носовую и хвостовую части самолета и называемой осью крена. Руль высоты вызывает поворот вокруг линии, параллельной крыльям, или оси тангажа (наклона). Руль направления поворачивает самолет вокруг вертикальной линии по отношению к пилоту, или оси рыскания. Если в какой-то момент положение самолета задано координатами x, y и z, то как программа определяет, где будет самолет мгновением позже?
Направление самолета и его скорость в данный момент образуют вектор, и по нему вычисляется новое положение машины. Программа определяет новое направление самолета (и, следовательно, новый угол зрения) из физических уравнений полета. На каждом цикле отображения программа задает новые начальные данные для этих уравнений, соответствующие текущему состоянию управляющих механизмов и условиям окружающей среды, таким, как давление и плотность воздуха, скорость ветра и температура. В уравнениях полета учтены физические параметры самолета, и к начальным данным уравнении применяются физические законы. Здесь работают такие силы, как вес, тяговое усилие двигателя, подъемная сила крыла и лобовое сопротивление воздуха. Учитываются также инерционные факторы, зависящие от массы и геометрической формы самолета. Решение уравнений дает новое направление полета.
Уравнения эти слишком сложны для того, чтобы микрокомпьютер мог решить их за приемлемое время, поэтому Артвик заменил их таблицами уже вычисленных значений. Одна из таблиц, например, содержит величины подъема самолета, соответствующие каждому дискретному значению угла атаки. Причем разность между двумя соседними значениями угла атаки составляет десятую долю градуса. Использование таблиц дает еше одно дополнительное преимущество: характер полета можно изменить, просто заменив таблицы, и новых формул выводить не надо.
Читатели, которых захватывают фигуры высшего пилотажа, могут воспользоваться готовой программой, имитирующей полет для любой распространенной марки домашнего компьютера. Артвик руководил созданием наиболее известной программы, распространяемой компанией Microsoft Corporation (Бельвю, шт.Вашингтон). Он сыграл также важную роль в разработке программы FLIGHT SIMULATOR II (Имитатор полета II). Обе программы могут выполняться компьютерами Apple II, IBM PC, Commodore 64 и Atari. Третья программа Артвика была создана недавно для персонального компьютера Macintosh.
После первых учебных полетов у читателей может возникнуть желание повторить захватывающие приключения, о которых поветствуется в новой книге Ч.Гулика "Сорок грандиозных приключений в имитируемом полете". Каждое из описываемых в ней приключений начинается, когда читатель запускает любую из упомянутых выше программ имитации полета и вводит необходимые данные из книги Гулика. Эти данные включают в себя такие параметры, как широта, долгота, высота, положение управляющих механизмов, время дня и т.д.
Между прочим, вы можете оказаться в нескольких стах метрах от Манхаттенского моста и лететь по курсу, который приведет вас прямо под мост. Другая острая ситуация, "Мертвый номер у Сан-Клементе", заключается в том, что мотор самолета выходит из строя на высоте 5000 футов над островом Сан-Клементе у калифорнийского побережья Тихого океана. Сможете ли вы посадить самолет на планирующем полете? Третье приключение называется "Зона сумрака". Вы находитесь на травянистой взлетной полосе. Часы на приборной доске показывают три минуты первого ночи, но еще не совсем темно. Часть самолета, видимая из заднего бокового окна кабины, совершенно черная. Самолет медленно отрывается от земли, и после этого в окно уже ничего не видно. Никакой информации о ландшафте не дает и радар. Что бы вы стали делать в такой ситуации? Впрочем, лично я предпочитаю необитаемую базу данных.
БИБЛИОГРАФИЯ
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARTWICK. Prentice-Hall, Inc., 1984.
40 GREAT FLIGHT SIMULATOR ADVENTURES. CHARLES GULICK. COMPUTE! Publications, 1985.
ОТКЛИКИ
12 1986
О ПРОГРАММАХ, имитирующих на домашних компьютерах полет в воздушном пространстве, речь шла в сентябрьском номере журнала. Обладателям такой программы, созданной фирмой Microsoft X.Нью-холл из Спрингфилда (шт.Массачусетс) предлагает головокружительный трюк - попытаться сделать мертвую петлю над Манхаттенским мостом. В нижней части петли самолет должен пролететь под мостом.
Появились и более быстрые игры. Дж.Казиановичу из Порт-Джеферсона (шт.Нью-Йорк) очень нравится программа JET, выпущенная фирмой Sublogic Corporation и написанная Ч.Гаем и Б.Артвиком. События в программе JET развиваются намного быстрее, чем в других программах подобного рода. Здесь можно попробовать планирующий полет, бомбежку на бреющем полете и даже воздушный бой. Казианович, считающий себя воздушным дьяволом, проносится, едва не касаясь земли, над своим аэродромом н испытывает предельные возможности программы. Иногда возникают забавные проблемы, связанные с ландшафтом: оказывается, можно пролететь гору насквозь, не разбившись. Казианович устремляет свой самолет прямо в склон горы, а затем, оттянув на себя ручку управления, взмывает вверх над вершиной.
ФАНТАСТИЧЕСКИЙ ПОЛЕТ НАД НЕОБИТАЕМОЙ БАЗОЙ ДАННЫХ
А.К.ДЬЮДНИ
Эту статью я уже упоминал -
 ТЕМА #67, АБЗАЦ #732
ТЕМА #67, АБЗАЦ #732 . И журнал выкладывал. Особенно обратите в нем внимание на "предваряющую" статью - про реальные тренажеры.- G.
. И журнал выкладывал. Особенно обратите в нем внимание на "предваряющую" статью - про реальные тренажеры.- G.Я лихорадочно изучал приборную панель самолета "Чессна 182". Наверное, с моей стороны было неразумно пытаться совершить полет в одиночку без надлежащей подготовки. Может быть, следовало взять с собой опытного пилота? На чикагском аэродроме Мейгс-Филд не было видно ни души, даже ни один механик не вышел покурить на солнышке. Единственно на что я мог положиться в этой сумасбродкой затее - это на руководство для пилота, на изучение которого я потратил не больше 10 минут.
Думаю, что я чувствовал бы себя увереннее, если бы у меня в руках была ручка управления или штурвал. Еще ребенком я по многу раз смотрел фильмы о приключениях летчиков-асов и хорошо запомнил основные приемы управления самолетом. Однако в этом самолете все было по-другому. Он управлялся с клавиатуры стоящего передо мной терминала.
Со вздохом я раскрыл страницу 46 руководства. Клавиша F2 слегка приоткрывает дроссель, клавиша F4 широко раскрывает его. Будучи человеком не совсем безрассудным, я с опаской нажал на клавишу F2. Мягкий шум двигателя несколько усилился. Взлетная дорожка побежала мне навстречу, и на какое-то мгновение мною овладела паника. Самолет почти сразу же начал уходить в сторону от бетонной полосы. По невежеству я не прочел ничего о руле горизонтального управления или о переднем шасси. Спасти меня могли только элероны - клавиша 4 (левый крен) и клавиша 6 (правый крен). К моему полному изумлению, одна из них стала медленно, но верно возвращать самолет на взлетную полосу.
Всего в ста метрах впереди показались голубые воды озера Мичиган. Прибавляю газ - F2, F2, F2, F2. Прибавляю еще. Мотор звучит все мощнее, но самолет упорно отказывается взлетать. Взлетная полоса побежала подо мной еше быстрее, и меня опять охватила паника. Какая же волшебная клавиша поднимет меня в воздух? Вся моя жизнь пронеслась предо мной. Сцены из далекого детства: вот я управляю моделью самолета, это можно было делать лишь с помощью двух закрылков на хвосте. Руль высоты! Я стал лихорадочно искать "руль высоты" в своем руководстве. Этот руль управляет углом атаки самолета, при его помощи можно приподнять нос самолета. Нажимаю на клавишу 2, и как раз вовремя, еше немного и передо мной разверзлась бы водяная могила. Страшная граница между сушей и водой стала отступать. Самолет был в воздухе! Он набирал высоту как будто по своей воле. Внизу все четче проступала перспектива западной береговой линии озера Мичиган, и в течение какого-то времени я продолжал полет в северном направлении, загипнотизированный своим достижением.
Как уже, наверное, догадались многие читатели, моя кабина находилась в комнате, а роль ручек управления играли клавиши на терминале моего персонального компьютера, который выполнял программу имитации полета. Однако знакомая обстановка ничуть не снижала остроту ощущений. Тот факт, что и самолет, и ландшафт лишь имитировались компьютером, даже усиливал воображение. В этих условиях можно было совершать такие действия, на которые никто бы не отважился, сидя в кабине настоящего самолета. Ведь счет, предъявленный за аварию, будет тоже воображаемым. Я сделал вираж в юго-западном направлении и стал приближаться к Чикаго. Мне захотелось пронестись нал Мичиган-авеню и произвести впечатление на многочисленных водителей и пассажиров движущегося по этой оживленной улице транспорта. Часы, вмонтированные в приборную панель самолета, показывали 4ч 30мин., как раз начало вечернего часа пик.
Приближаясь к Чикаго, я стал замечать что-то неладное. Были видны лишь несколько зданий, расположенных вдоль берега озера, а на улицах никакого транспорта. Людей тоже не было видно. Может быть, началась атомная война? Я заметил, что принял за часы высотомер с двумя стрелками, но даже несмотря на то, что сейчас было значительно раньше 4ч 30мин., полное отсутствие людей на улицах такого большого города казалось странным. Хотя и неохотно, но я пришел к выводу: в программе имитации полета просто не нашлось места для людей. Ее база данных и без того была перегружена описанием североамериканского ландшафта, не говоря уже о всевозможных географических подробностях, необходимых для моделирования четырех больших городов и более 20 аэродромов.
В последующих полетах я уже все меньше и меньше думал о недостатке в людском обществе. Слишком интересен был сам полет. В этом со мной, наверное, согласятся многие из тех, кто совершал подобные воздушные путешествия. Программа называется FLIGHT SIMULATOR (Имитатор полета), и в течение уже многих месяцев она была одной из наиболее популярных, если не самой популярной из всех занимательных программ для персональных компьютеров. Существует немало других программ имитации полета, которые можно купить или приобрести бесплатно в различных ассоциациях. Однако как FLIGHT SIMULATOR, так и ряд других аналогичных программ своей популярностью обязаны Б.Артвику, инженеру-программисту из Шампейна (шт.Иллинойс). Более чем кто-либо другой Артвик способствовал "взлету" программ имитации полета, и благодаря его усилиям они теперь могут выполняться на персональных компьютерах. В течение долгого времени компьютерная имитация полета применялась исключительно с целью обучения летчиков (см. статью Р.Хабера "Моделирование условий полета"). Теперь же эти средства доступны практически каждому.
Рассмотрим, в чем должны заключаться особенности таких программ, чтобы поддерживать у пользователя иллюзию реального полета. Во-первых, они должны создавать и несколько раз в секунду воссоздавать ландшафт, видимый из какой-то фиксированной точки. По мере того как моделируемый аэроплан бороздит моделируемые небеса, точка наблюдения перемешается, и поэтому черты проплывающего на экране ландшафта должны вычисляться заново. Более того, для каждой точки наблюдения возможны различные углы зрения. Угол зрения определяется результатами имитации физических особенностей аэроплана, находящегося в полете. Например, если самолет делает крен в сторону, чтобы совершить поворот, угол зрения, так же как н точка наблюдения, должен соответственно меняться. В основном цикле вычислений применяется ряд трюков и осуществляется поиск компромиссных решений, что само по себе не менее увлекательно, чем имитация полета в целом.
Географическая база данных является одним из главных компонентов программы FLIGHT SIMULATOR. Она включает обширный список объектов, необходимых для воссоздания ландшафта территории, над которой желает полетать пользователь (или в которую он не хочет врезаться). Вы можете получить доступ к "сцене" вашего полета, обратившись к иерархической информационной системе и прослеживая за данными "сверху вниз". В массиве памяти под названием USA (США) хранятся названия районов, таких, как Чикаго, Нью-Йорк и Сиэтл. Положение самолета задается тремя координатами: x - широта, у - высота над уровнем моря (в метрах) и z - долгота. Программа FLIGHT SIMULATOR сравнивает эти координаты с предельными значениями, ограничивающими каждый район в массиве США. Если, например, х и z задают точку, принадлежащую району Чикаго, то программа выполняет операцию, называемую загрузкой базы данных. В результате этой операции список, в котором хранится информация о районе Чикаго, загружается с магнитного лиска в оперативную память компьютера.
Когда в ходе своего первого полета я сделал вираж, повернув по направлению к Чикаго, сначала я не увндел никаких зданий. Однако некоторое время спустя показалась башня Сирз-Тауэр. Затем стали проступать и ее детали. В этом как раз и заключается стратегия программы, позволяющая ей уложиться в пределы имеющегося объема памяти и быстродействия: особенности ландшафта не отображаются на экране до тех пор, пока в них нет реальной необходимости. В программу встроены две специальные тестирующие процедуры, управляющие появлением и исчезновением на экране тех или иных деталей ландшафта. Первая из них ifin2d следит лишь за двумя координатами - широтой и долготой самолета. Выше уже говорилось, каким образом географические районы ассоциируются с этими двумя координатами.
Вторая тестирующая процедура ifin3d определяет расстояние до заданной детали ландшафта, и если она находится достаточно близко, программа отображает ее на экране. По мере того как я приближался к Чикаго, процедура ifin3d постоянно вычисляла расстояние от самолета до тех или иных зданий или других ориентиров города, видимых с воздуха. Когда мой самолет приблизился к башне Сирз-Тауэр на расстояние 12800м, на экране внезапно появилась миниатюрная копия этого сооружения в виде нескольких мерцающих точек. Когда же расстояние до башни уменьшилось до 7680м, появились уже некоторые неразличимые ранее детали. Для каждых трех новых значений координат FLIGHT SIMULATOR быстро просматривает список, хранящий все видимые особенности ландшафта, и проверяет их согласно критериям отображения объектов, на которых основана процедура ifin3d. Если объект удовлетворяет критериям, программа отображает его на экране таким, каким он должен быть виден из данной точки. Если же объект не проходит теста, он не отображается, и программа переходит к проверке следующего объекта в списке.

Вид статуи Свободы из кабины самолета, построенной программой FLIGHT SIMULATOR
Вообще говоря, каждый объект или каждая особенность моделируемого ландшафта определяется в программе списком точек, линий и поверхностей. Поскольку изображение вычисляется пять раз в секунду, достаточно часто для того, чтобы воспользоваться инерционностью человеческого зрения, линии и поверхности должны отображаться за минимально возможное время. Поэтому даже элементарные графические операции были реализованы в программе самым тщательным образом. Артвик описал эти операции в своей замечательной книге "Microcomputer Displays, Graphics, and Animation" ("Микрокомпьютерные изображения, графика и мультипликация").
Например, в основном методе, применяемом для изображения линии, операции умножения и деления не применяются, поскольку для их выполнения требуется в 10 и даже в 100 раз больше времени по сравнению с операциями сложения и вычитания. В данном случае метод изображения линии основан на тщательном анализе временных затрат на каждую выполняемую команду. Получившийся в результате остроумный алгоритм изображения линии по существу состоит лишь из четырех команд: сложения, сравнения, перехода к команды отображения. Пусть, например, точка с координатами {a, b) была только что высвечена на линии с (положительным) наклоном 1/4. Программа входит в цикл, в котором она повторно прибавляет 1 к значению координаты a и 1/4 к специальной сумме, называемой ошибкой прослеживания, и затем тестирует текущее значение этой суммы. Если ошибка прослеживания оказывается большей или равной какому-нибудь целому числу, то программа выходит из цикла и высвечивает следующую точку, в данном случае с координатами (a+4, b+1).
Поверхности программа изображает посредством метода, который едва ли поддается описанию, но зато чрезвычайно быстро реализуется в компьютере. В нескольких словах этот процесс можно представить следующим образом. Программа изображает многоугольник, ограничивающий данную поверхность, и затем "заштриховывает" его внутреннюю область. После того как вычислена форма многоугольника, специальная графическая процедура вначале определяет сканирующие линии, пересекающие на экране полученный многоугольник. Для каждой такой линии сканирования определяются пересекаемые ею стороны многоугольника, а затем эти стороны сортируются (упорядочиваются) в соответствии с порядком, в котором линия сканирования пересекает их слева направо. Затем процедура рассматривает каждый пиксел, или элемент изображения, на линии сканирования по порядку слева направо. Когда линия встречается с первой стороной многоугольника, она начинает высвечивать точки определенного цвета, выбранного для представления данной поверхности. Как только линия сканирования доходит до следующей стороны, отображение точек прекращается. При встрече со следующей стороной отображение возобновляется и т.д.

По смертельно опасному курсу на Манхаттенский мост
Описанный метод включения-выключения отображения вдоль линии сканирования экрана основан на фундаментальном положении топологии на плоскости: любой многоугольник делит плоскость на две части - внутреннюю и внешнюю. Поэтому любая линия, пересекаюшая сторону многоугольника, переходит из внутренней части (принадлежащей отображаемой области) во внешнюю (не принадлежащую ей) или наоборот. Большинство поверхностей, отображаемых программой FLIGHT SIMULATOR, ограничены сравнительно простыми многоугольниками. Например, после того как я покинул зону аэродрома Мейгс-Филд, передо мной до самого горизонта протянулась береговая линия озера Мичиган. Эта линия представляла собой несколько сторон многоугольника, очерчивающих залив, ограниченный отмелью, тянущейся в северном направлении. Голубые линии воды в заливе прерывались в зоне отмели и затем снова возникали, заполняя главную часть озера.
Специалисты, работающие с графическими программами, часто размышляли над так называемой проблемой скрытой линии. Каким образом программа должна изображать трехмерное непрозрачное тело, чтобы видна была только та грань, которая находится ближе к наблюдателю? Некоторые методы, применимые к этой задаче, требуют решения трудоемких уравнений, на что уходит слишком много времени. FLIGHT SIMULATOR едва ли может себе это позволить. Решение Артвика, применимое лишь к простым ландшафтам, заключается в том, чтобы при изображении объекта ближайшая к наблюдателю грань заштриховывалась последней. Части объекта, которые должны оставаться невидимыми для наблюдателя, просто затираются теми, которые должны быть видны. Представление двух башен Международного торгового центра в Нью-Йорке дает нам хороший пример применения этого грубого, но эффективного метода. При любом угле зрения ближайшие части здания закрывают более далекие и ближняя башня "затмевает" дальнюю.
После того как я узнал, что Чикаго необитаем, я решил вернуться на Мейгс-Филд. Владелец самолета, наверное, уже беспокоится. И все же я хотел еше многому научиться. Во-первых, мне было как-то не по себе оттого, что я не знал назначения нескольких рычагов управления. Во-вторых, я так и не попытался выяснить какую-нибудь фигуру высшего пилотажа. Для этой цели я вылетел в зону озера Мичиган.
Моим излюбленным средством управления были элероны. При нажатии на клавишу левого элерона самолет делает крен влево: горизонт передо мной наклонился вправо, и весь ландшафт, казалось начал сползать по склону. Не противореча законам аэродинамики, нос "Чессны" все это время поворачивал влево. Вернув крыло в горизонтальное положение и продолжая полет по прямой, я нажал несколько раз на клавишу 8 и почти физически почувствовал, как нос самолета нырнул вниз. За окном моей кабины горизонт резко поднялся вверх. Самолет пикировал. Спидометр показывал скорость, превышающую 150 миль/ч. Я попытался воспользоваться горизонтальным рулем. Клавиша со знаком "плюс" слегка повернула руль вправо, и самолет начал вращаться, вызывая неприятные ощущения. Вернув руль в нейтральное положение, я стал наблюдать, как простирающийся подо мной ландшафт обманчиво медленно надвигается на меня. Настало время приступить к выполнению фигуры.
Пилоты входят в петли значительно реже, чем программисты в циклы. Интуиция подсказывала, что для маневра понадобится довольно большая скорость. Сначала вниз, затем вверх и потом вниз головой. Нажимать клавиши мне нравилось меньше, чем твердо поворачивать на себя ручку управления, но я тем не менее старательно нажимал на клавишу 2. Самолет с ревом вышел из пике в горизонтальный полет, а затем устремился вверх в голубую твердь небес. Я увидел, как линия горизонта ушла подо мной вниз, и стал ждать. У меня не было никакой уверенности в том, что фигура удастся. Все замерло в тишине. Может быть, самолет зависнет и рухнет на землю? Приборы не могли мне ничего подсказать, лишь о половине из них я имел какое-то представление, да и то смутное.
Внезапно на экране появился перевернутый ландшафт - сверху зеленая земля, а снизу голубое небо. Неужели маневр удался? Я был слишком разгорячен, чтобы ответить на свой вопрос. Полный мрачной решимости, я продолжал эксперимент. Теперь передо мной во все стороны раскинулась земля. Затем горизонт занял свое нормальное положение. Я попытался опустить нос самолета, чтобы предотвратить еще одну петлю. Горизонт покачнулся и замер на месте. Да, фигура удалась! Видимо, я принадлежу к числу тех одаренных людей, которые могут обучиться летному делу экспериментально, почти безо всякой предварительной подготовки. Впереди показался аэродром Мейгс-Филл. Как только совершу посадку, пойду приму душ.
Главная посадочная полоса аэродрома протянулась с севера на юг. Я находился к юго-востоку от аэродрома и решил лететь на запад, а поравнявшись с посадочной полосой, повернуть на север. Реализовать этот план мне почему-то не удалось. Никак не удавалось зайти на посадочную полосу, и, кроме того, я приближался к аэродрому на слишком большой высоте. Все это было подобно кошмару, когда за одним несчастьем приходит другое. Я резко опустил нос самолета, чтобы побыстрее снизиться, стараясь в то же время дотянуть еще несколько метров в направлении на восток. Однако посадочная полоса ушла с экрана, и к тому же я потерял горизонт. Земля стала быстро приближаться, зазвучал сигнал тревоги. Черт побери! Я врезался в землю. Это стало очевидно, когда ветровое стекло кабины покрылось трещинами и на их фоне появилась крупная надпись "Авария". Погиб я или нет? Очень жаль, если база данных Чикаго лишится своего последнего обитателя.

Три оси, вокруг которых может поворачивать самолет
Чтобы моделировать все эти приключения, FLIGHT SIMULATOR должна постоянно делать новые вычисления вида на ландшафт из кабины самолета. Рычаги управления самолетом можно сгруппировать по направлениям вращения вокруг трех осей (см. рисунок). Так, элероны поворачивают самолет вокруг продольной оси, проходящей через носовую и хвостовую части самолета и называемой осью крена. Руль высоты вызывает поворот вокруг линии, параллельной крыльям, или оси тангажа (наклона). Руль направления поворачивает самолет вокруг вертикальной линии по отношению к пилоту, или оси рыскания. Если в какой-то момент положение самолета задано координатами x, y и z, то как программа определяет, где будет самолет мгновением позже?
Направление самолета и его скорость в данный момент образуют вектор, и по нему вычисляется новое положение машины. Программа определяет новое направление самолета (и, следовательно, новый угол зрения) из физических уравнений полета. На каждом цикле отображения программа задает новые начальные данные для этих уравнений, соответствующие текущему состоянию управляющих механизмов и условиям окружающей среды, таким, как давление и плотность воздуха, скорость ветра и температура. В уравнениях полета учтены физические параметры самолета, и к начальным данным уравнении применяются физические законы. Здесь работают такие силы, как вес, тяговое усилие двигателя, подъемная сила крыла и лобовое сопротивление воздуха. Учитываются также инерционные факторы, зависящие от массы и геометрической формы самолета. Решение уравнений дает новое направление полета.
Уравнения эти слишком сложны для того, чтобы микрокомпьютер мог решить их за приемлемое время, поэтому Артвик заменил их таблицами уже вычисленных значений. Одна из таблиц, например, содержит величины подъема самолета, соответствующие каждому дискретному значению угла атаки. Причем разность между двумя соседними значениями угла атаки составляет десятую долю градуса. Использование таблиц дает еше одно дополнительное преимущество: характер полета можно изменить, просто заменив таблицы, и новых формул выводить не надо.
Читатели, которых захватывают фигуры высшего пилотажа, могут воспользоваться готовой программой, имитирующей полет для любой распространенной марки домашнего компьютера. Артвик руководил созданием наиболее известной программы, распространяемой компанией Microsoft Corporation (Бельвю, шт.Вашингтон). Он сыграл также важную роль в разработке программы FLIGHT SIMULATOR II (Имитатор полета II). Обе программы могут выполняться компьютерами Apple II, IBM PC, Commodore 64 и Atari. Третья программа Артвика была создана недавно для персонального компьютера Macintosh.
После первых учебных полетов у читателей может возникнуть желание повторить захватывающие приключения, о которых поветствуется в новой книге Ч.Гулика "Сорок грандиозных приключений в имитируемом полете". Каждое из описываемых в ней приключений начинается, когда читатель запускает любую из упомянутых выше программ имитации полета и вводит необходимые данные из книги Гулика. Эти данные включают в себя такие параметры, как широта, долгота, высота, положение управляющих механизмов, время дня и т.д.
Между прочим, вы можете оказаться в нескольких стах метрах от Манхаттенского моста и лететь по курсу, который приведет вас прямо под мост. Другая острая ситуация, "Мертвый номер у Сан-Клементе", заключается в том, что мотор самолета выходит из строя на высоте 5000 футов над островом Сан-Клементе у калифорнийского побережья Тихого океана. Сможете ли вы посадить самолет на планирующем полете? Третье приключение называется "Зона сумрака". Вы находитесь на травянистой взлетной полосе. Часы на приборной доске показывают три минуты первого ночи, но еще не совсем темно. Часть самолета, видимая из заднего бокового окна кабины, совершенно черная. Самолет медленно отрывается от земли, и после этого в окно уже ничего не видно. Никакой информации о ландшафте не дает и радар. Что бы вы стали делать в такой ситуации? Впрочем, лично я предпочитаю необитаемую базу данных.
БИБЛИОГРАФИЯ
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARTWICK. Prentice-Hall, Inc., 1984.
40 GREAT FLIGHT SIMULATOR ADVENTURES. CHARLES GULICK. COMPUTE! Publications, 1985.
ОТКЛИКИ
12 1986
О ПРОГРАММАХ, имитирующих на домашних компьютерах полет в воздушном пространстве, речь шла в сентябрьском номере журнала. Обладателям такой программы, созданной фирмой Microsoft X.Нью-холл из Спрингфилда (шт.Массачусетс) предлагает головокружительный трюк - попытаться сделать мертвую петлю над Манхаттенским мостом. В нижней части петли самолет должен пролететь под мостом.
Появились и более быстрые игры. Дж.Казиановичу из Порт-Джеферсона (шт.Нью-Йорк) очень нравится программа JET, выпущенная фирмой Sublogic Corporation и написанная Ч.Гаем и Б.Артвиком. События в программе JET развиваются намного быстрее, чем в других программах подобного рода. Здесь можно попробовать планирующий полет, бомбежку на бреющем полете и даже воздушный бой. Казианович, считающий себя воздушным дьяволом, проносится, едва не касаясь земли, над своим аэродромом н испытывает предельные возможности программы. Иногда возникают забавные проблемы, связанные с ландшафтом: оказывается, можно пролететь гору насквозь, не разбившись. Казианович устремляет свой самолет прямо в склон горы, а затем, оттянув на себя ручку управления, взмывает вверх над вершиной.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
10 1986
КОМПЬЮТЕР В РОЛИ ИСКУСНОГО МАГА-ИЛЛЮЗИОНИСТА
А.К.ДЬЮДНИ
ВСТРЕТИВ в одном предложении слова "маг" и "компьютер", человек рационалистического склада ума придет, наверное, в некоторое недоумение, считая такое сочетание слов противоречивым. Каким образом магия, атрибут призрачного мира, от которого мы оградились стеной логики, может проникнуть в компьютер, являющийся, пожалуй, самым ярким воплощением нашей рациональности? Конечно, смысловой диссонанс вносит слово "маг" как символ чего-то сверхъестественного. На самом деле магия иллюзионистов - это часть нашего естественного мира, а занимающиеся ею - последовательно и логически мыслящие люди.
Чтобы провести сеанс магии, достаточно, хотя и не всегда необходимо, выполнение трех условий: присутствие публики, наличие реквизита и умение демонстрировать фокусы. Мне приходилось наблюдать действия иллюзионистов без реквизита, но никогда без публики. Публика, вообще говоря, может быть какой угодно, но речь сейчас не о ней. Что же касается реквизита, то в качестве его можно с успехом использовать и компьютер, и ниже я буду всюду предполагать, что наш маг всегда прибегает к помощи материализованного по крайней мере микрокомпьютера. Простенькие программы позволяют машине "угадывать" вынутую наобум из колоды карту или задуманное число к полному изумлению незадачливого добровольца из публики. Для этого достаточно располагать хотя бы портативным электронным калькулятором.
Вот и все, что касается публики и реквизита, остальное - искусство демонстрации фокуса. Оно заключается в умении формализовать внутреннюю логику трюка и трансформировать ее в наглядное действие. Дух настоящей магии может поддерживаться лишь до тех пор, пока маг в состоянии внушать доверие зрителю и манипулировать его представлениями, в которые он уже уверовал. Каждое такое представление, кажется, неизбежно ведет к следующему, пока не наступит поразительная развязка. Иногда, для того чтобы трюк имел успех, еще до его демонстрации необходимо "заговорить" зрителя, используя массу псевдонаучных концепций из области вычислительной техники и прикладной математики. Советуем вам пользоваться ими совершенно свободно с неискушенными зрителями и соблюдать осторожность, когда вы имеете дело со знающей публикой. Вот, например, как можно представить первый магический номер из нашей программы.
"Леди и джентльмены, рано или поздно это должно было свершиться. Крупные открытия в области искусственного интеллекта позволили компьютерам читать мысли человека. Теория рекурсивного нондетерминизма гарантирует, что определенный неполиномиальный алгоритм, который впервые описал известный тибетский ученый, профессор Ян Ки, всегда выйдет из бесконечных циклов. Шаг за шагом программа циклически просматривает полубесконечную стохастическую структуру данных, отыскивая логические примитивы и составляя из них запросы к базе данных... (Можно продолжать в том же духе еще некоторое время). Попрошу кого-нибудь из зрителей подойти ко мне. Пожалуйста".
Затем маг поднимает вытащенную зрителем из колоды игральную карту так, чтобы все ее видели. Допустим, это шестерка треф. Тут возникает дополнительная возможность подшутить над вызвавшимся зрителем. Факир говорит: "Пожалуйста, прижмите карту ко лбу и постарайтесь сосредоточиться. Ваш мозг и мозг компьютера должны достигнуть состояния имитируемой одновременности".
После этого он подходит к клавиатуре компьютера и запускает программу. На экране немедленно появляется сообщение. Факир зачитывает вслух следующий диалог с машиной:
"СУБЪЕКТ СОСРЕДОТОЧИЛСЯ?" (Сообщения и вопросы компьютера напечатаны прописными буквами).
"Да". (Это наш маг набрал ответ на клавиатуре).
"КАРТА ТЕМНОЙ МАСТИ?" "Да".
"МАСТИ ТРЕФ?" "Да".
"ВОСЬМЕРКА ИЛИ МЛАДШЕ?" "Да".
"ПЯТЕРКА ИЛИ СТАРШЕ?" "Да".
"ПЯТЕРКА ИЛИ ШЕСТЕРКА?" "Да".
"ШЕСТЕРКА?" "Да".
Задавая вопросы, программа раз за разом сужает круг поиска. Как ни странно, отвечаем мы ей всегда утвердительно, как булто программа заранее знает ответ и требует лишь подтверждения. Читатели уже, наверное, заинтригованы: в чем тут фокус? Обычно я очень неохотно удовлетворяю подобное любопытство: у фокусников существует неписаное правило, запрещающее раскрывать секреты ремесла. В конце концов факир может зарабатывать свой хлеб, только сохраняя вокруг себя ореол таинственности, поэтому я не могу открыть секреты всех трюков, описанных в настоящей статье. Хотя для этого остроумного карточного трюка у меня имеется разрешение объяснить его читателям. Оно получено от Кристофера Моргана, в прошлом факира. В настоящее время Морган работает администратором в фирме Lotus Development Corporation в Кембридже и, очевидно, его хлеб насущный уже не зависит целиком и полностью от магии.
Когда доброволец из публики вытаскивает карту из колоды, факир запоминает ее, затем грациозно подходит к клавиатуре и набирает слово "да" на каждый вопрос. Однако каждое такое "да" может сопровождаться незаметным нажатием на клавишу пробела. Эта последняя операция на самом деле не влияет на ответ на предыдущий вопрос, но зато определяет содержание следующего. Так, когда знаменитая программа профессора Яна Ки спрашивает: "СУБЪЕКТ СОСРЕДОТОЧИЛСЯ?", факир набирает "да" с пробелом только в том случае, если карта темной масти. Если она оказывается красной масти, факир набирает "да" без пробела. Таким образом программа получает достаточно информации, чтобы задать правильный вопрос на следующем этапе. Если факир набрал "да" с пробелом, программа спрашивает: "КАРТА ТЕМНОЙ МАСТИ?", в противном случае вопрос меняется: "КАРТА КРАСНОЙ МАСТИ?"
При помощи этого приема факир управляет программой по мере ее продвижения по неявному двоичному дереву выбора; скрытая в нем логика охватывает все возможные альтернативы, позволяющие идентифицировать любую карту в колоде (см. рисунок на с.97). Например, после того как определен цвет масти выбранной карты, следует выбор в новой альтернативе. Когда компьютер уже знает, что карта темной масти, факир может незаметно сообщить ей, какой именно из двух темных мастей принадлежит карта - пик или треф. Если карта красной масти, то на следующем этапе нужно выбрать черви или бубны. Все остальные альтернативы предназначены для определения достоинства карты: от туза, двойки и тройки до валета, дамы и короля. Поскольку всего существует 13 градаций достоинства карты, для ее идентификации требуется четыре вопроса.

Скрытое дерево решений для компьютерного карточного фокуса Кристофера Моргана
Важно, чтобы факир отвлекал внимание зрителей каждый раз, когда он касается клавиши пробела. Проще всего воспользоваться для этого клавишей возврата каретки (впрочем, она называется по-разному, но на нее нужно нажимать при каждом вводе информации в машину). Поскольку на нее нужно нажимать всякий раз, когда факир отвечает на очередной вопрос, можно делать это красивым размашистым жестом правой руки, в то время как палец левой руки незаметно касается расположенной внизу и протягивающейся вдоль почти всей клавиатуры клавиши пробела, Попрактиковавшись, можно добиться в этом деле совершенства.
Программа, которую я называю ЯН КИ, несколько длинновата, но писать ее очень легко. Она подразделяется на 31 маленькую секцию, что соответствует полному набору возможных вопросов, задаваемых машиной в процессе работы. Все секции имеют одну и ту же основную алгоритмическую структуру:
XX вывести "КАРТА ТЕМНОЙ МАСТИ?"
ввести строку символов
подсчитать количество символов
если их число равно 4
то переход на YY иначе переход на ZZ
Здесь XX - это номер программной строки, или метка, на которую в программе передается управление после первого ввода слова "да" с пробелом, как в моем примере. Выведя на экран вопрос, соответствующий данной секции, программа принимает строку символов, являющихся ответом мага, и просто подсчитывает их. Если было набрано три символа, значит маг должен был нажать на клавишу пробела. В этом случае управление передается программной секции с меткой YY, которая начинается с вопроса "МАСТИ ТРЕФ?" Если же маг не нажимал на пробел, то программа передает управление на секцию с меткой ZZ, которая начинается с вопроса "МАСТИ ПИК?" Будущий маг должен тщательно запомнить процесс принятия решений, заложенный в программе и использующий в качестве входных данных наличие или отсутствие пробела в ответе на каждый вопрос.
Следующий номер запрограммированной магии был предложен М.Рореггером, читателем из Линца (Австрия). Компьютерный маг, упомянув о тех же самых сомнительных теориях, описанных выше, теперь уже заявляет, что вторая программа может отгадывать мысли человека еще до того, как они приходят ему в голову! К сожалению, продолжает маг, исследования в этой области еще не завершены и поэтому программа добивается успеха не во всех случаях, но в большинстве. Из публики приглашается желающий, его усаживают в кресло и просят выбрать одно из двух чисел (или бит): 0 или 1. Чтобы доброволец не отвлекался, глядя на экран компьютера, лучше всего расположить машину и кресло таким образом, чтобы и экран и человек, сидящий в кресле, были обращены к зрителям.
Человек называет вслух цифру, а маг и публика сравнивают ее с цифрой, уже появившейся на экране. Если они совпадают, маг мудро кивает головой. Если же цифры оказываются разными, он объясняет, что должно пройти некоторое время, прежде чем программа сможет настроиться на психические процессы, проходящие в мозгу данного субъекта. (В самом деле, добровольца из публики всегда можно упрекнуть в том, что он порождает "статический фон"). Маг нажимает на клавишу, и программа предсказывает следующий бит, выбираемый человеком. Его опять просят назвать какую-нибудь из этих двух цифр и т.д. Эксперимент продолжается до тех пор, пока программа не "синхронизируется или почти не синхронизируется со структурой пространства-времени в мозгу данного субъекта". Всякий раз, когда участник эксперимента называет число, маг кивает головой и улыбается, если машина угадывает его, и терпеливо хмурит брови, если попытка оказывается неудачной.
Сначала результаты, достигаемые программой, кажутся не лучшими, чем при чисто случайном угадывании; ее предсказывания оказываются правильными лишь приблизительно в 50% случаев. Однако, по мере того как эксперимент продолжается, результаты заметно улучшаются, программа угадывает числа уже по крайней мере в 60% случаев, а иногда и гораздо чаще. Вот как она работает.
В программе под названием PREDICTABIT (предсказатель бит) имеется массив subject размером 16 на 2. Каждая из 16 строк массива нумеруется одной из 16 возможных последовательностей из четырех следующих друг за другом бит. Столбцы массива соответствуют двум возможным вариантам выбора значения бит: 0 и 1. Правым элементом строки является число случаев, в которых субъект выбрал 0 сразу после того, как им была выбрана последовательность бит, соответствующая номеру строки. Вторым элементом той же строки является число случаев, когда вслед за данной последовательностью из четырех бит он выбрал 1.
Предположим, в четырех предшествующих попытках человек выбрал биты 0, 1, 1, 1. Программа рассматривает эти биты как единое двоичное число и преобразует их к десятичному эквиваленту, в данном случае 7. Если элемент массива subject
(7, 0) равен 4, a subject (7, 1) равен 2, то это означает, что вслед за последовательностью 0, 1, 1, 1 человек выбрал в четырех случаях 0 и только в двух случаях 1. Таким образом, анализируя результаты предыдущих испытаний, зафиксированные в массиве, программа предсказывает, что следующее число, выбранное человеком, будет 0. Алгоритм программы, скрывающийся за этим описанием, уже, наверное, понятен. В своей простейшей форме программа состоит из шести простых циклических секций:
Ввести очередной бит
Модифицировать массив по старому индексу
Сдвинуть переменные
Сформировать новый индекс последовательности
Сравнить элементы массива subject
Сделать предсказание
Как только человек из публики называет очередное число, маг вводит его в машину. В четырех переменных first, second, third к fourth (соответственно первый, второй, третий и четвертый) хранятся четыре числа, выбранных человеком в непосредственно предшествующих попытках. Переменная под названием index хранит номер строки массива, вычисленный по текущим значениям переменных от "первого" до "четвертого". Если только что введенный бит был 0, программа прибавляет 1 к элементу массива subject (index, 0). В противном случае 1 прибавляется к элементу subject (index, 1).
В третьей секции программы сдвигаются значения четырех переменных следующим образом:
fourth <- введенный бит
third <- fourth
second <- third
first <- second
Программа формирует новый индекс последовательности, вычисляя следующую сумму произведений: 1*first + 2*second + 4*third +8*fourth. Затем программа сравнивает элементы subject{index, 0) и subject (index, 1) для только что вычисленного значения переменной index. Если subject (index, 0) больше, чем subject (index, 1), то программа выводит на экран в качестве предсказываемого ею числа 0, в противном случае выводится 1. Для успешной демонстрации фокусов программа должна также предсказать первые четыре числа, называемые испытуемым, чтобы заполнить первые четыре переменные конкретными значениями. Эти исходные значения можно, конечно, ввести и заранее, выбрав, например, все нули.
Если факир пожелает время от времени объявлять, каков процент удач в работе программы PREDICTABIT, в ней можно предусмотреть еще одну операцию. Для этого нужно ввести дополнительную переменную, скажем score (счет), и непосредственно перед секцией сдвига переменных вставить несколько дополнительных команд, сравнивающих значение переменной fourth с последним числом, названным человеком. Если они оказываются равными, к значению переменной score прибавляется 1. По завершении очередного этапа демонстрации программа делит значение score на полное число совершенных попыток, умножает частное на 100 и высвечивает результат на экране.
Трюк с предсказанием оказывается более или менее успешным, потому что люди, совершая случайный выбор между двумя альтернативами, подсознательно следуют каким-то правилам. Например, если вы выберете подряд два раза 0, естественно у вас возникает желание в качестве следующем цифры назвать 1. Как бы борясь с этим желанием, многие люди могут, правда, и в третий раз назвать 0, но тогда соблазн выбрать в следующий раз 1 становится еще больше. Вероятность того, что следующей цифрой будет 1, тем больше, чем больше было пулей в предшествующей последовательности. Конечно, при чисто случайном выборе предыдущие цифры совершенно не оказывают никакого влияния на выбор в данной попытке. Вероятность выбора 1 на следующем шаге всегда остается одной и той же, а именно 0.5.
Возможно, при случайном выборе числа человек руководствуется даже более тонкими факторами. Однако если эти факторы в какой-то мере зависят от предшествующих попыток, то программа PREDICTABIT должна работать успешно. Между прочим, я пришел к выводу, что в подобных экспериментах очень важно избегать людей, которые, если можно так выразиться, слишком изобретательны. Они склонны придерживаться каких-то вполне осознанных правил, а затем внезапно менять их в ходе сеанса, что, конечно, приводит к катастрофическим результатам. Чтобы помешать субъекту стать слишком непредсказуемым, можно отвлекать его внимание какой-нибудь чепухой, например: "Когда я нажму на эту клавишу, программа предскажет следующее число, о котором вы подумаете. Очень важно, чтобы в данный момент вы еще не думали о вашем числе. В противном случае программа несправедливо получит преимущество, ибо сможет прочесть ваши мысли непосредственно". В продолжении всего сеанса факир должен сдерживать желание человека назвать цифру до того, как сам факир нажмет на клавишу. Напомним, что в этот момент в машину вводится цифра, выбранная человеком в предыдущей попытке.
В следующем номере магической программы компьютер выступает одновременно и в роли мага и в роли реквизита. Человек, ассистирующий магу, протягивает вызвавшемуся из публики колоду обычных игральных карт и произносит что-нибудь вроде: "Пожалуйста, займите место перед электронным воплощением великого мага, уже ушедшего из нашего мира". Чтобы произвести еще большее впечатление на публику, можно привести также утонченные аналоги между духом и программным обеспечением. Если потребуется, можно поговорить о теориях профессора Яна Ки. Наконец, ассистент мага просит человека из публики нажать на клавишу пробела. Вслед за этим на экране последовательно появляются команды из "потустороннего мира" (после выполнения каждого очередного указания следует нажать на клавишу пробела, и на экране высвечивается следующее):
ТЩАТЕЛЬНО ПЕРЕМЕШАЙТЕ КАРТЫ, ВЫРОВНЯЙТЕ КОЛОДУ И ПОЛОЖИТЕ ЕЕ НА СТОЛ ЛИЦОМ ВНИЗ (пробел).
ПОДСНИМИТЕ КОЛОДУ ПРИМЕРНО В СЕРЕДИНЕ, ЗАПОМНИТЕ НИЖНЮЮ КАРТУ ИЗ СНЯТЫХ И ВЕРНИТЕ ИХ В КОЛОДУ (пробел).
СДАЙТЕ КАРТЫ ЛИЦОМ ВНИЗ НА ШЕСТЬ МАЛЕНЬКИХ СТОПОК (пробел).
ПРОСМОТРИТЕ КАЖДУЮ СТОПКУ, ПОКА НЕ ОПРЕДЕЛИТЕ ТУ, В КОТОРОЙ НАХОДИТСЯ ПОДСНЯТАЯ РАНЕЕ КАРТА (пробел).
ТЕПЕРЬ СДАВАЙТЕ ПО ОДНОЙ КАРТЕ ИЗ ЭТОЙ СТОПКИ, КЛАДИТЕ КАРТЫ ЛИЦОМ ВВЕРХ, СОСРЕДОТОЧЬТЕСЬ НА ИСКОМОЙ КАРТЕ И НАЖМИТЕ НА КЛАВИШУ ПРОБЕЛА, КОГДЫ ВЫ СОЧТЕТЕ, ЧТО Я ГОТОВ РЕШИТЬ, ЭТА ЛИ КАРТА БЫЛА ВАМИ ПОДСНЯТА {пробел).
По мере того как человек из публики сдает карты одну за другой, программа передает нам решение ушедшего из жизни мага. В первый раз он отвечает "нет". Нажатие клавиши пробела говорит магу о том, что сдана следующая карта. Его дух опять отвечает "нет". После еще нескольких карт дух внезапно восклицает (образно говоря): "СТОП, ВОТ ОНА!"
Третья программа из нашей серии, пожалуй, самая простая. Я назвал ее HOUDINI. Эта программа просто высвечивает приведенные выше указания одно за другим, пока человек из публики не начинает сдавать карты из той стопки, которая содержит запомненную им карту. На экране появляется "стоп", когда сдается четвертая карта. Эта или следующая карта всегда будет искомой.
Программа HOUDINI настолько проста, что едва ли нуждается в описании. Однако в процессе ее выполнения ассистент электронного мага должен все время быть около человека из публики, разделяя его растущее изумление и следя при этом, чтобы все шло, как надо. Например, подснимать колоду необходимо как можно ближе к ее середине, чтобы разница в количестве карт в каждой половине не превышала нескольких карт. Порядок карт в шести стопках также должен строго сохраняться во время их просмотра в поисках первоначально подснятой карты. Наконец, маг-ассистент должен вовремя интерпретировать команду "стоп". Если искомой является четвертая карта, то он должен сказать, что кремниевый дух машины прочел мысли субъекта. Если же это не четвертая, а пятая карта, то маг-ассистент советует после четвертой карты сразу открыть пятую. "Прыгающий ЛИСП,- говорит маг-ассистент,- я должен был догадаться, великий Хаудини прочел карты путем прямого ясновидения!"
Сдерживая свое обещание не раскрывать секрета всех представленных здесь магических номеров, объяснение этого последнего трюка я оставляю читателю. Правильный ответ будет опубликован в следующем номере журнала, так что не посылайте мне писем с вашими мыслями но этому поводу. Они придут слишком поздно. Добавлю, что HOUDINI - это переложенный на компьютерный язык известный трюк нью-йоркского иллюзиониста X.Лорейни под названием "Стоп!"
Последний номер, связанный с чтением чужих мыслей, принадлежит Мартину Гарднеру; для исполнения номера достаточно иметь небольшой карманный калькулятор. Как обычно, факир приглашает желающего из публики. Передав ему калькулятор, факир отворачивается, демонстративно прикладывает руку ко лбу и бормочет некоторое время всякую чепуху об электронном единстве с калькуляторами. Наконец, обращаясь к человеку из публики, факир говорит: "Выберите любую строку или столбец или главную диагональ числовой клавиатуры калькулятора, которая представляет собой квадрат из чисел от 1 до 9. Введите цифры из выбранной вами линии в любом порядке. Готово? У вас на дисплее должно быть трехзначное число. Теперь нажмите на клавишу со энаком умножения и выберите другую линию, т.е. любую другую строку или столбец, или большую диагональ маленького квадрата. Выбрали? Отлично. Опять введите три цифры из этой линии в любом порядке. На дисплее должно быть другое трехзначное число. Когда вы нажмете на клавишу со знаком равенства, на экране появится произведение двух трехзначных чисел. Видите его? Это волшебное число. Выберите любой ненулевой разряд этого числа и, не называя мне его, сообщите оставшиеся цифры. В каком порядке - неважно, я лишь хочу, чтобы вы освободили от них свое сознание и сосредоточились на цифре, которую вы мне не назвали. Очень хорошо. Теперь сосредоточьтесь на этой очень важной цифре, и, если мне немного повезет, я смогу ее угадать".
У читателей есть месяц, чтобы объяснить, каким образом факир определяет недостающую цифру. Посмотрите внимательно на рисунок на с.98. В одной из будущих статей я сообшу об удачах и неудачах читателей, попытавших счастья с магическими программами, представленными в этом номере.
Магическое произведение двух чисел
БИБЛИОГРАФИЯ
MATHEMATICS, MAGIC AND MYSTERY. MARTIN GARDNER. Dover Publications, Inc., 1956. (Есть перевод: МАТЕМАТИЧЕСКИЕ ЧУДЕСА И ТАЙНЫ, МАРТИН ГАРДНЕР, М.: "НАУКА", 1978.- G.).
THE CONJURER'S CALCULATOR (MAGIC WITH A POCKET COMPUTER). JOHN C. SHERWOOD. Micky Hades International, Box 476, Calgary, Alberta, 1976.
THE MAGIC BOOK: THE COMPLETE BEGINNER'S GUIDE TO ANYTIME, ANYWHERE, SLEIGHT-OF HAND MAGIC. Putnam Publishing, 1977.
ОТКЛИКИ
11 1986
В СТАТЬЕ, посвященной компьютерной магии, опубликованной в предыдущем номере журнала, внутренняя логика двух трюков осталась необъясненной. Первый из них был основан на известном фокусе X. Лорейни, нью-йоркского мага. Доброволец из публики вытаскивает карту из хорошо перемешанной колоды и возвращает ее на место. Затем он сдает карты в шесть стопок и находит ту стопку, которая содержит вытянутую им ранее карту. Компьютер повелевает добровольцу сдавать по одной карте из этой стопки. После того как сдана очередная карта, компьютер указывает, следует ли продолжать сдавать или остановиться, угадывая тем самым выбранную карту в сдаваемой стопке.
Каким же образом компьютер останавливается на нужной карте? Ответ заключается в том, что, когда человек сдает колоду на шесть стопок, из центральной части исходной колоды в каждую стопку попадает по одной карте из каждых шести. Каждая из шести карт, находившихся в середине исходной колоды, занимает одно и то же относительное положение в маленьких стопках, а именно она всегда будет четвертой. Поскольку человек сдает карты только из стопки, содержащей выбранную карту, компьютер всегда оказывается в состоянии угадать ее, остановившись после того, как сдана четвертая карта.
Второй нераскрытый в прошлый раз трюк основан на выборе цифр на клавиатуре обыкновенного карманного калькулятора. Доброволец из публики вводит два трехразрядных числа, выполняет над ними операцию умножения и называет все разряды результата, кроме одного. Каким образом факиру удается отгадать этот разряд?
Согласно инструкциям факира, каждое трехразрядное число, выбранное добровольцем, должно представлять собой три десятичных цифры, взятых либо со строки, либо со столбца, либо с главной диагонали цифровой клавиатуры калькулятора. Но любое такое число обладает мистическим свойством "троечности" после выбрасывания девяток. Когда все разряды числа складываются между собой, их сумма может представлять одно- или двухразрядное число. Если сумма является двухразрядной, то сумма самих разрядов дает одноразрядное число. В любом случае окончательный одноразрядный результат кратен трем. Например, число 471, набранное на клавишах первой колонки клавиатуры, сводится к 12, а затем и к 3, которое, разумеется, кратно 3. В то же время, когда человек перемножает два трехразрядных числа, обладающих описанными свойствами, и произведение подвергается той же самой процедуре, результат получается равным 9. Эта процедура равносильна перемножению по модулю 9 - отсюда мой термин "выбрасывание девяток". Если отсутствует какой-нибудь разряд произведения, скажем x, то в результате отбрасывания 9 для остающихся разрядов имеем 9-x. Это число вычисляется магом по мере того, как человек зачитывает все, кроме одного, разряды произведения. Таким образом, по известной величине 9-x можно немедленно указать значение х.
1 1987
АБСОЛЮТНОЕ большинство писем, присланных читателями в ответ на статью о компьютерной магии, содержали ответы на вопрос, поставленный в этой статье, но объяснение было опубликовано уже в следующем номере. Вопрос был о том, каким образом факир, располагая лишь карманным калькулятором, мог "прочесть" мысли человека? Объяснение заключалось в том, что любое число, составленное из цифр, расположенных на одной из линий клавиатуры калькулятора, делится на 3. Я не буду еще раз подробно останавливаться на этом трюке, но хотел бы обратить внимание читателей на то, что обычно в статьях нашей рубрики ставятся вопросы двух типов и между ними существует одно принципиальное различие.
Вопросы первого типа требуют небольшого размышления. Ответы на такие вопросы публикуются в следующем номере журнала. При постановке вопроса автор предупреждает читателей, что ответ будет опубликован задолго до того, как придут первые отклики.
Вопросы второго типа требуют более солидной проработки. Как правило, чтобы ответить на них, необходимо воспользоваться компьютером, и при постановке таких вопросов автор просит читателя присылать ответы. На размышления предоставляется достаточно много времени. Если письмо выслано через две-три недели после публикации статьи, то у него имеются хорошие шансы попасть на мой стол, прежде чем обзор читательских писем отправится в печать. Обычно такой обзор появляется через три месяца после выхода статьи.
К.Фалвес из Тинека (шт.Нью-Джерси) предложил еще один вариант трюка с калькулятором. Как и прежде, факир просит добровольца из публики выбрать два числа из цифр, лежащих на одной линии клавиатуры калькулятора, и перемножить их, воспользовавшись калькулятором. В предложенном мною варианте доброволец не должен был называть одну из цифр произведения, а факиру нужно было "угадать" ее путем выбрасывания девяток. Несколько более занятным выглядит этот фокус, если доброволец из публики называет все цифры, но при этом добавляет возраст своей собачки или кошечки. Если возраст животного не превышает 9 лет, то факир может легко его подсчитать: "Мадам, духи поведали мне, что вашему Рексику пять лет".
Р.Малленикс, инженер, работающий в фирме Georgia Power Company в Валдосте (шт. Джорджия), рассказал мне о своем коротком, но поучительном приключении с программой PREDICTABIT, которая должна предсказывать следующий бит, называемый человеком. После сравнительно длинной цепочки нулей и единиц частота правильных предсказаний должна повышаться. Это объясняется тем, что в подсознании человека, пытающегося выбирать цифры совершенно случайно, все же существуют некоторые уловимые закономерности. Малленикс добился сравнительно скромного успеха, играя с приятелем. Программа показывала результаты, точность которых была близка к 60%. Однако, когда приятель понял, как работает программа, он начал называть цифры, пользуясь разложением числа пи. Число случаев правильного предсказания снизилось до 43%. Ну что же, я предупреждал читателей. Клиентов следует выбирать в среде доверчивых людей, кроме того, их нужно постоянно отвлекать какой-нибудь болтовней так, чтобы они не успевали задуматься.
КОМПЬЮТЕР В РОЛИ ИСКУСНОГО МАГА-ИЛЛЮЗИОНИСТА
А.К.ДЬЮДНИ
ВСТРЕТИВ в одном предложении слова "маг" и "компьютер", человек рационалистического склада ума придет, наверное, в некоторое недоумение, считая такое сочетание слов противоречивым. Каким образом магия, атрибут призрачного мира, от которого мы оградились стеной логики, может проникнуть в компьютер, являющийся, пожалуй, самым ярким воплощением нашей рациональности? Конечно, смысловой диссонанс вносит слово "маг" как символ чего-то сверхъестественного. На самом деле магия иллюзионистов - это часть нашего естественного мира, а занимающиеся ею - последовательно и логически мыслящие люди.
Чтобы провести сеанс магии, достаточно, хотя и не всегда необходимо, выполнение трех условий: присутствие публики, наличие реквизита и умение демонстрировать фокусы. Мне приходилось наблюдать действия иллюзионистов без реквизита, но никогда без публики. Публика, вообще говоря, может быть какой угодно, но речь сейчас не о ней. Что же касается реквизита, то в качестве его можно с успехом использовать и компьютер, и ниже я буду всюду предполагать, что наш маг всегда прибегает к помощи материализованного по крайней мере микрокомпьютера. Простенькие программы позволяют машине "угадывать" вынутую наобум из колоды карту или задуманное число к полному изумлению незадачливого добровольца из публики. Для этого достаточно располагать хотя бы портативным электронным калькулятором.
Вот и все, что касается публики и реквизита, остальное - искусство демонстрации фокуса. Оно заключается в умении формализовать внутреннюю логику трюка и трансформировать ее в наглядное действие. Дух настоящей магии может поддерживаться лишь до тех пор, пока маг в состоянии внушать доверие зрителю и манипулировать его представлениями, в которые он уже уверовал. Каждое такое представление, кажется, неизбежно ведет к следующему, пока не наступит поразительная развязка. Иногда, для того чтобы трюк имел успех, еще до его демонстрации необходимо "заговорить" зрителя, используя массу псевдонаучных концепций из области вычислительной техники и прикладной математики. Советуем вам пользоваться ими совершенно свободно с неискушенными зрителями и соблюдать осторожность, когда вы имеете дело со знающей публикой. Вот, например, как можно представить первый магический номер из нашей программы.
"Леди и джентльмены, рано или поздно это должно было свершиться. Крупные открытия в области искусственного интеллекта позволили компьютерам читать мысли человека. Теория рекурсивного нондетерминизма гарантирует, что определенный неполиномиальный алгоритм, который впервые описал известный тибетский ученый, профессор Ян Ки, всегда выйдет из бесконечных циклов. Шаг за шагом программа циклически просматривает полубесконечную стохастическую структуру данных, отыскивая логические примитивы и составляя из них запросы к базе данных... (Можно продолжать в том же духе еще некоторое время). Попрошу кого-нибудь из зрителей подойти ко мне. Пожалуйста".
Затем маг поднимает вытащенную зрителем из колоды игральную карту так, чтобы все ее видели. Допустим, это шестерка треф. Тут возникает дополнительная возможность подшутить над вызвавшимся зрителем. Факир говорит: "Пожалуйста, прижмите карту ко лбу и постарайтесь сосредоточиться. Ваш мозг и мозг компьютера должны достигнуть состояния имитируемой одновременности".
После этого он подходит к клавиатуре компьютера и запускает программу. На экране немедленно появляется сообщение. Факир зачитывает вслух следующий диалог с машиной:
"СУБЪЕКТ СОСРЕДОТОЧИЛСЯ?" (Сообщения и вопросы компьютера напечатаны прописными буквами).
"Да". (Это наш маг набрал ответ на клавиатуре).
"КАРТА ТЕМНОЙ МАСТИ?" "Да".
"МАСТИ ТРЕФ?" "Да".
"ВОСЬМЕРКА ИЛИ МЛАДШЕ?" "Да".
"ПЯТЕРКА ИЛИ СТАРШЕ?" "Да".
"ПЯТЕРКА ИЛИ ШЕСТЕРКА?" "Да".
"ШЕСТЕРКА?" "Да".
Задавая вопросы, программа раз за разом сужает круг поиска. Как ни странно, отвечаем мы ей всегда утвердительно, как булто программа заранее знает ответ и требует лишь подтверждения. Читатели уже, наверное, заинтригованы: в чем тут фокус? Обычно я очень неохотно удовлетворяю подобное любопытство: у фокусников существует неписаное правило, запрещающее раскрывать секреты ремесла. В конце концов факир может зарабатывать свой хлеб, только сохраняя вокруг себя ореол таинственности, поэтому я не могу открыть секреты всех трюков, описанных в настоящей статье. Хотя для этого остроумного карточного трюка у меня имеется разрешение объяснить его читателям. Оно получено от Кристофера Моргана, в прошлом факира. В настоящее время Морган работает администратором в фирме Lotus Development Corporation в Кембридже и, очевидно, его хлеб насущный уже не зависит целиком и полностью от магии.
Когда доброволец из публики вытаскивает карту из колоды, факир запоминает ее, затем грациозно подходит к клавиатуре и набирает слово "да" на каждый вопрос. Однако каждое такое "да" может сопровождаться незаметным нажатием на клавишу пробела. Эта последняя операция на самом деле не влияет на ответ на предыдущий вопрос, но зато определяет содержание следующего. Так, когда знаменитая программа профессора Яна Ки спрашивает: "СУБЪЕКТ СОСРЕДОТОЧИЛСЯ?", факир набирает "да" с пробелом только в том случае, если карта темной масти. Если она оказывается красной масти, факир набирает "да" без пробела. Таким образом программа получает достаточно информации, чтобы задать правильный вопрос на следующем этапе. Если факир набрал "да" с пробелом, программа спрашивает: "КАРТА ТЕМНОЙ МАСТИ?", в противном случае вопрос меняется: "КАРТА КРАСНОЙ МАСТИ?"
При помощи этого приема факир управляет программой по мере ее продвижения по неявному двоичному дереву выбора; скрытая в нем логика охватывает все возможные альтернативы, позволяющие идентифицировать любую карту в колоде (см. рисунок на с.97). Например, после того как определен цвет масти выбранной карты, следует выбор в новой альтернативе. Когда компьютер уже знает, что карта темной масти, факир может незаметно сообщить ей, какой именно из двух темных мастей принадлежит карта - пик или треф. Если карта красной масти, то на следующем этапе нужно выбрать черви или бубны. Все остальные альтернативы предназначены для определения достоинства карты: от туза, двойки и тройки до валета, дамы и короля. Поскольку всего существует 13 градаций достоинства карты, для ее идентификации требуется четыре вопроса.

Скрытое дерево решений для компьютерного карточного фокуса Кристофера Моргана
Важно, чтобы факир отвлекал внимание зрителей каждый раз, когда он касается клавиши пробела. Проще всего воспользоваться для этого клавишей возврата каретки (впрочем, она называется по-разному, но на нее нужно нажимать при каждом вводе информации в машину). Поскольку на нее нужно нажимать всякий раз, когда факир отвечает на очередной вопрос, можно делать это красивым размашистым жестом правой руки, в то время как палец левой руки незаметно касается расположенной внизу и протягивающейся вдоль почти всей клавиатуры клавиши пробела, Попрактиковавшись, можно добиться в этом деле совершенства.
Программа, которую я называю ЯН КИ, несколько длинновата, но писать ее очень легко. Она подразделяется на 31 маленькую секцию, что соответствует полному набору возможных вопросов, задаваемых машиной в процессе работы. Все секции имеют одну и ту же основную алгоритмическую структуру:
XX вывести "КАРТА ТЕМНОЙ МАСТИ?"
ввести строку символов
подсчитать количество символов
если их число равно 4
то переход на YY иначе переход на ZZ
Здесь XX - это номер программной строки, или метка, на которую в программе передается управление после первого ввода слова "да" с пробелом, как в моем примере. Выведя на экран вопрос, соответствующий данной секции, программа принимает строку символов, являющихся ответом мага, и просто подсчитывает их. Если было набрано три символа, значит маг должен был нажать на клавишу пробела. В этом случае управление передается программной секции с меткой YY, которая начинается с вопроса "МАСТИ ТРЕФ?" Если же маг не нажимал на пробел, то программа передает управление на секцию с меткой ZZ, которая начинается с вопроса "МАСТИ ПИК?" Будущий маг должен тщательно запомнить процесс принятия решений, заложенный в программе и использующий в качестве входных данных наличие или отсутствие пробела в ответе на каждый вопрос.
Следующий номер запрограммированной магии был предложен М.Рореггером, читателем из Линца (Австрия). Компьютерный маг, упомянув о тех же самых сомнительных теориях, описанных выше, теперь уже заявляет, что вторая программа может отгадывать мысли человека еще до того, как они приходят ему в голову! К сожалению, продолжает маг, исследования в этой области еще не завершены и поэтому программа добивается успеха не во всех случаях, но в большинстве. Из публики приглашается желающий, его усаживают в кресло и просят выбрать одно из двух чисел (или бит): 0 или 1. Чтобы доброволец не отвлекался, глядя на экран компьютера, лучше всего расположить машину и кресло таким образом, чтобы и экран и человек, сидящий в кресле, были обращены к зрителям.
Человек называет вслух цифру, а маг и публика сравнивают ее с цифрой, уже появившейся на экране. Если они совпадают, маг мудро кивает головой. Если же цифры оказываются разными, он объясняет, что должно пройти некоторое время, прежде чем программа сможет настроиться на психические процессы, проходящие в мозгу данного субъекта. (В самом деле, добровольца из публики всегда можно упрекнуть в том, что он порождает "статический фон"). Маг нажимает на клавишу, и программа предсказывает следующий бит, выбираемый человеком. Его опять просят назвать какую-нибудь из этих двух цифр и т.д. Эксперимент продолжается до тех пор, пока программа не "синхронизируется или почти не синхронизируется со структурой пространства-времени в мозгу данного субъекта". Всякий раз, когда участник эксперимента называет число, маг кивает головой и улыбается, если машина угадывает его, и терпеливо хмурит брови, если попытка оказывается неудачной.
Сначала результаты, достигаемые программой, кажутся не лучшими, чем при чисто случайном угадывании; ее предсказывания оказываются правильными лишь приблизительно в 50% случаев. Однако, по мере того как эксперимент продолжается, результаты заметно улучшаются, программа угадывает числа уже по крайней мере в 60% случаев, а иногда и гораздо чаще. Вот как она работает.
В программе под названием PREDICTABIT (предсказатель бит) имеется массив subject размером 16 на 2. Каждая из 16 строк массива нумеруется одной из 16 возможных последовательностей из четырех следующих друг за другом бит. Столбцы массива соответствуют двум возможным вариантам выбора значения бит: 0 и 1. Правым элементом строки является число случаев, в которых субъект выбрал 0 сразу после того, как им была выбрана последовательность бит, соответствующая номеру строки. Вторым элементом той же строки является число случаев, когда вслед за данной последовательностью из четырех бит он выбрал 1.
Предположим, в четырех предшествующих попытках человек выбрал биты 0, 1, 1, 1. Программа рассматривает эти биты как единое двоичное число и преобразует их к десятичному эквиваленту, в данном случае 7. Если элемент массива subject
(7, 0) равен 4, a subject (7, 1) равен 2, то это означает, что вслед за последовательностью 0, 1, 1, 1 человек выбрал в четырех случаях 0 и только в двух случаях 1. Таким образом, анализируя результаты предыдущих испытаний, зафиксированные в массиве, программа предсказывает, что следующее число, выбранное человеком, будет 0. Алгоритм программы, скрывающийся за этим описанием, уже, наверное, понятен. В своей простейшей форме программа состоит из шести простых циклических секций:
Ввести очередной бит
Модифицировать массив по старому индексу
Сдвинуть переменные
Сформировать новый индекс последовательности
Сравнить элементы массива subject
Сделать предсказание
Как только человек из публики называет очередное число, маг вводит его в машину. В четырех переменных first, second, third к fourth (соответственно первый, второй, третий и четвертый) хранятся четыре числа, выбранных человеком в непосредственно предшествующих попытках. Переменная под названием index хранит номер строки массива, вычисленный по текущим значениям переменных от "первого" до "четвертого". Если только что введенный бит был 0, программа прибавляет 1 к элементу массива subject (index, 0). В противном случае 1 прибавляется к элементу subject (index, 1).
В третьей секции программы сдвигаются значения четырех переменных следующим образом:
fourth <- введенный бит
third <- fourth
second <- third
first <- second
Программа формирует новый индекс последовательности, вычисляя следующую сумму произведений: 1*first + 2*second + 4*third +8*fourth. Затем программа сравнивает элементы subject{index, 0) и subject (index, 1) для только что вычисленного значения переменной index. Если subject (index, 0) больше, чем subject (index, 1), то программа выводит на экран в качестве предсказываемого ею числа 0, в противном случае выводится 1. Для успешной демонстрации фокусов программа должна также предсказать первые четыре числа, называемые испытуемым, чтобы заполнить первые четыре переменные конкретными значениями. Эти исходные значения можно, конечно, ввести и заранее, выбрав, например, все нули.
Если факир пожелает время от времени объявлять, каков процент удач в работе программы PREDICTABIT, в ней можно предусмотреть еще одну операцию. Для этого нужно ввести дополнительную переменную, скажем score (счет), и непосредственно перед секцией сдвига переменных вставить несколько дополнительных команд, сравнивающих значение переменной fourth с последним числом, названным человеком. Если они оказываются равными, к значению переменной score прибавляется 1. По завершении очередного этапа демонстрации программа делит значение score на полное число совершенных попыток, умножает частное на 100 и высвечивает результат на экране.
Трюк с предсказанием оказывается более или менее успешным, потому что люди, совершая случайный выбор между двумя альтернативами, подсознательно следуют каким-то правилам. Например, если вы выберете подряд два раза 0, естественно у вас возникает желание в качестве следующем цифры назвать 1. Как бы борясь с этим желанием, многие люди могут, правда, и в третий раз назвать 0, но тогда соблазн выбрать в следующий раз 1 становится еще больше. Вероятность того, что следующей цифрой будет 1, тем больше, чем больше было пулей в предшествующей последовательности. Конечно, при чисто случайном выборе предыдущие цифры совершенно не оказывают никакого влияния на выбор в данной попытке. Вероятность выбора 1 на следующем шаге всегда остается одной и той же, а именно 0.5.
Возможно, при случайном выборе числа человек руководствуется даже более тонкими факторами. Однако если эти факторы в какой-то мере зависят от предшествующих попыток, то программа PREDICTABIT должна работать успешно. Между прочим, я пришел к выводу, что в подобных экспериментах очень важно избегать людей, которые, если можно так выразиться, слишком изобретательны. Они склонны придерживаться каких-то вполне осознанных правил, а затем внезапно менять их в ходе сеанса, что, конечно, приводит к катастрофическим результатам. Чтобы помешать субъекту стать слишком непредсказуемым, можно отвлекать его внимание какой-нибудь чепухой, например: "Когда я нажму на эту клавишу, программа предскажет следующее число, о котором вы подумаете. Очень важно, чтобы в данный момент вы еще не думали о вашем числе. В противном случае программа несправедливо получит преимущество, ибо сможет прочесть ваши мысли непосредственно". В продолжении всего сеанса факир должен сдерживать желание человека назвать цифру до того, как сам факир нажмет на клавишу. Напомним, что в этот момент в машину вводится цифра, выбранная человеком в предыдущей попытке.
В следующем номере магической программы компьютер выступает одновременно и в роли мага и в роли реквизита. Человек, ассистирующий магу, протягивает вызвавшемуся из публики колоду обычных игральных карт и произносит что-нибудь вроде: "Пожалуйста, займите место перед электронным воплощением великого мага, уже ушедшего из нашего мира". Чтобы произвести еще большее впечатление на публику, можно привести также утонченные аналоги между духом и программным обеспечением. Если потребуется, можно поговорить о теориях профессора Яна Ки. Наконец, ассистент мага просит человека из публики нажать на клавишу пробела. Вслед за этим на экране последовательно появляются команды из "потустороннего мира" (после выполнения каждого очередного указания следует нажать на клавишу пробела, и на экране высвечивается следующее):
ТЩАТЕЛЬНО ПЕРЕМЕШАЙТЕ КАРТЫ, ВЫРОВНЯЙТЕ КОЛОДУ И ПОЛОЖИТЕ ЕЕ НА СТОЛ ЛИЦОМ ВНИЗ (пробел).
ПОДСНИМИТЕ КОЛОДУ ПРИМЕРНО В СЕРЕДИНЕ, ЗАПОМНИТЕ НИЖНЮЮ КАРТУ ИЗ СНЯТЫХ И ВЕРНИТЕ ИХ В КОЛОДУ (пробел).
СДАЙТЕ КАРТЫ ЛИЦОМ ВНИЗ НА ШЕСТЬ МАЛЕНЬКИХ СТОПОК (пробел).
ПРОСМОТРИТЕ КАЖДУЮ СТОПКУ, ПОКА НЕ ОПРЕДЕЛИТЕ ТУ, В КОТОРОЙ НАХОДИТСЯ ПОДСНЯТАЯ РАНЕЕ КАРТА (пробел).
ТЕПЕРЬ СДАВАЙТЕ ПО ОДНОЙ КАРТЕ ИЗ ЭТОЙ СТОПКИ, КЛАДИТЕ КАРТЫ ЛИЦОМ ВВЕРХ, СОСРЕДОТОЧЬТЕСЬ НА ИСКОМОЙ КАРТЕ И НАЖМИТЕ НА КЛАВИШУ ПРОБЕЛА, КОГДЫ ВЫ СОЧТЕТЕ, ЧТО Я ГОТОВ РЕШИТЬ, ЭТА ЛИ КАРТА БЫЛА ВАМИ ПОДСНЯТА {пробел).
По мере того как человек из публики сдает карты одну за другой, программа передает нам решение ушедшего из жизни мага. В первый раз он отвечает "нет". Нажатие клавиши пробела говорит магу о том, что сдана следующая карта. Его дух опять отвечает "нет". После еще нескольких карт дух внезапно восклицает (образно говоря): "СТОП, ВОТ ОНА!"
Третья программа из нашей серии, пожалуй, самая простая. Я назвал ее HOUDINI. Эта программа просто высвечивает приведенные выше указания одно за другим, пока человек из публики не начинает сдавать карты из той стопки, которая содержит запомненную им карту. На экране появляется "стоп", когда сдается четвертая карта. Эта или следующая карта всегда будет искомой.
Программа HOUDINI настолько проста, что едва ли нуждается в описании. Однако в процессе ее выполнения ассистент электронного мага должен все время быть около человека из публики, разделяя его растущее изумление и следя при этом, чтобы все шло, как надо. Например, подснимать колоду необходимо как можно ближе к ее середине, чтобы разница в количестве карт в каждой половине не превышала нескольких карт. Порядок карт в шести стопках также должен строго сохраняться во время их просмотра в поисках первоначально подснятой карты. Наконец, маг-ассистент должен вовремя интерпретировать команду "стоп". Если искомой является четвертая карта, то он должен сказать, что кремниевый дух машины прочел мысли субъекта. Если же это не четвертая, а пятая карта, то маг-ассистент советует после четвертой карты сразу открыть пятую. "Прыгающий ЛИСП,- говорит маг-ассистент,- я должен был догадаться, великий Хаудини прочел карты путем прямого ясновидения!"
Сдерживая свое обещание не раскрывать секрета всех представленных здесь магических номеров, объяснение этого последнего трюка я оставляю читателю. Правильный ответ будет опубликован в следующем номере журнала, так что не посылайте мне писем с вашими мыслями но этому поводу. Они придут слишком поздно. Добавлю, что HOUDINI - это переложенный на компьютерный язык известный трюк нью-йоркского иллюзиониста X.Лорейни под названием "Стоп!"
Последний номер, связанный с чтением чужих мыслей, принадлежит Мартину Гарднеру; для исполнения номера достаточно иметь небольшой карманный калькулятор. Как обычно, факир приглашает желающего из публики. Передав ему калькулятор, факир отворачивается, демонстративно прикладывает руку ко лбу и бормочет некоторое время всякую чепуху об электронном единстве с калькуляторами. Наконец, обращаясь к человеку из публики, факир говорит: "Выберите любую строку или столбец или главную диагональ числовой клавиатуры калькулятора, которая представляет собой квадрат из чисел от 1 до 9. Введите цифры из выбранной вами линии в любом порядке. Готово? У вас на дисплее должно быть трехзначное число. Теперь нажмите на клавишу со энаком умножения и выберите другую линию, т.е. любую другую строку или столбец, или большую диагональ маленького квадрата. Выбрали? Отлично. Опять введите три цифры из этой линии в любом порядке. На дисплее должно быть другое трехзначное число. Когда вы нажмете на клавишу со знаком равенства, на экране появится произведение двух трехзначных чисел. Видите его? Это волшебное число. Выберите любой ненулевой разряд этого числа и, не называя мне его, сообщите оставшиеся цифры. В каком порядке - неважно, я лишь хочу, чтобы вы освободили от них свое сознание и сосредоточились на цифре, которую вы мне не назвали. Очень хорошо. Теперь сосредоточьтесь на этой очень важной цифре, и, если мне немного повезет, я смогу ее угадать".
У читателей есть месяц, чтобы объяснить, каким образом факир определяет недостающую цифру. Посмотрите внимательно на рисунок на с.98. В одной из будущих статей я сообшу об удачах и неудачах читателей, попытавших счастья с магическими программами, представленными в этом номере.

Магическое произведение двух чисел
БИБЛИОГРАФИЯ
MATHEMATICS, MAGIC AND MYSTERY. MARTIN GARDNER. Dover Publications, Inc., 1956. (Есть перевод: МАТЕМАТИЧЕСКИЕ ЧУДЕСА И ТАЙНЫ, МАРТИН ГАРДНЕР, М.: "НАУКА", 1978.- G.).
THE CONJURER'S CALCULATOR (MAGIC WITH A POCKET COMPUTER). JOHN C. SHERWOOD. Micky Hades International, Box 476, Calgary, Alberta, 1976.
THE MAGIC BOOK: THE COMPLETE BEGINNER'S GUIDE TO ANYTIME, ANYWHERE, SLEIGHT-OF HAND MAGIC. Putnam Publishing, 1977.
ОТКЛИКИ
11 1986
В СТАТЬЕ, посвященной компьютерной магии, опубликованной в предыдущем номере журнала, внутренняя логика двух трюков осталась необъясненной. Первый из них был основан на известном фокусе X. Лорейни, нью-йоркского мага. Доброволец из публики вытаскивает карту из хорошо перемешанной колоды и возвращает ее на место. Затем он сдает карты в шесть стопок и находит ту стопку, которая содержит вытянутую им ранее карту. Компьютер повелевает добровольцу сдавать по одной карте из этой стопки. После того как сдана очередная карта, компьютер указывает, следует ли продолжать сдавать или остановиться, угадывая тем самым выбранную карту в сдаваемой стопке.
Каким же образом компьютер останавливается на нужной карте? Ответ заключается в том, что, когда человек сдает колоду на шесть стопок, из центральной части исходной колоды в каждую стопку попадает по одной карте из каждых шести. Каждая из шести карт, находившихся в середине исходной колоды, занимает одно и то же относительное положение в маленьких стопках, а именно она всегда будет четвертой. Поскольку человек сдает карты только из стопки, содержащей выбранную карту, компьютер всегда оказывается в состоянии угадать ее, остановившись после того, как сдана четвертая карта.
Второй нераскрытый в прошлый раз трюк основан на выборе цифр на клавиатуре обыкновенного карманного калькулятора. Доброволец из публики вводит два трехразрядных числа, выполняет над ними операцию умножения и называет все разряды результата, кроме одного. Каким образом факиру удается отгадать этот разряд?
Согласно инструкциям факира, каждое трехразрядное число, выбранное добровольцем, должно представлять собой три десятичных цифры, взятых либо со строки, либо со столбца, либо с главной диагонали цифровой клавиатуры калькулятора. Но любое такое число обладает мистическим свойством "троечности" после выбрасывания девяток. Когда все разряды числа складываются между собой, их сумма может представлять одно- или двухразрядное число. Если сумма является двухразрядной, то сумма самих разрядов дает одноразрядное число. В любом случае окончательный одноразрядный результат кратен трем. Например, число 471, набранное на клавишах первой колонки клавиатуры, сводится к 12, а затем и к 3, которое, разумеется, кратно 3. В то же время, когда человек перемножает два трехразрядных числа, обладающих описанными свойствами, и произведение подвергается той же самой процедуре, результат получается равным 9. Эта процедура равносильна перемножению по модулю 9 - отсюда мой термин "выбрасывание девяток". Если отсутствует какой-нибудь разряд произведения, скажем x, то в результате отбрасывания 9 для остающихся разрядов имеем 9-x. Это число вычисляется магом по мере того, как человек зачитывает все, кроме одного, разряды произведения. Таким образом, по известной величине 9-x можно немедленно указать значение х.
1 1987
АБСОЛЮТНОЕ большинство писем, присланных читателями в ответ на статью о компьютерной магии, содержали ответы на вопрос, поставленный в этой статье, но объяснение было опубликовано уже в следующем номере. Вопрос был о том, каким образом факир, располагая лишь карманным калькулятором, мог "прочесть" мысли человека? Объяснение заключалось в том, что любое число, составленное из цифр, расположенных на одной из линий клавиатуры калькулятора, делится на 3. Я не буду еще раз подробно останавливаться на этом трюке, но хотел бы обратить внимание читателей на то, что обычно в статьях нашей рубрики ставятся вопросы двух типов и между ними существует одно принципиальное различие.
Вопросы первого типа требуют небольшого размышления. Ответы на такие вопросы публикуются в следующем номере журнала. При постановке вопроса автор предупреждает читателей, что ответ будет опубликован задолго до того, как придут первые отклики.
Вопросы второго типа требуют более солидной проработки. Как правило, чтобы ответить на них, необходимо воспользоваться компьютером, и при постановке таких вопросов автор просит читателя присылать ответы. На размышления предоставляется достаточно много времени. Если письмо выслано через две-три недели после публикации статьи, то у него имеются хорошие шансы попасть на мой стол, прежде чем обзор читательских писем отправится в печать. Обычно такой обзор появляется через три месяца после выхода статьи.
К.Фалвес из Тинека (шт.Нью-Джерси) предложил еще один вариант трюка с калькулятором. Как и прежде, факир просит добровольца из публики выбрать два числа из цифр, лежащих на одной линии клавиатуры калькулятора, и перемножить их, воспользовавшись калькулятором. В предложенном мною варианте доброволец не должен был называть одну из цифр произведения, а факиру нужно было "угадать" ее путем выбрасывания девяток. Несколько более занятным выглядит этот фокус, если доброволец из публики называет все цифры, но при этом добавляет возраст своей собачки или кошечки. Если возраст животного не превышает 9 лет, то факир может легко его подсчитать: "Мадам, духи поведали мне, что вашему Рексику пять лет".
Р.Малленикс, инженер, работающий в фирме Georgia Power Company в Валдосте (шт. Джорджия), рассказал мне о своем коротком, но поучительном приключении с программой PREDICTABIT, которая должна предсказывать следующий бит, называемый человеком. После сравнительно длинной цепочки нулей и единиц частота правильных предсказаний должна повышаться. Это объясняется тем, что в подсознании человека, пытающегося выбирать цифры совершенно случайно, все же существуют некоторые уловимые закономерности. Малленикс добился сравнительно скромного успеха, играя с приятелем. Программа показывала результаты, точность которых была близка к 60%. Однако, когда приятель понял, как работает программа, он начал называть цифры, пользуясь разложением числа пи. Число случаев правильного предсказания снизилось до 43%. Ну что же, я предупреждал читателей. Клиентов следует выбирать в среде доверчивых людей, кроме того, их нужно постоянно отвлекать какой-нибудь болтовней так, чтобы они не успевали задуматься.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
11 1986
ПРОГРАММЫ, ГЕНЕРИРУЮЩИЕ УЗОРЫ ДЛЯ ОБОЕВ
А.К.ДЬЮДНИ
ОБЫЧНЫЕ обои печатаются вращающимся цилиндром, на котором выгравирован узор. При каждом обороте цилиндра отпечатывается одно и то же изображение. А вот компьютер может воспроизводить затейливые узоры, которые я называю "обоями для ума" и которые, вообще говоря, не повторяются или во всяком случае повторяются не полностью. Изображение все время проявляется в новых конфигурациях, слева и справа, внизу и вверху. Интересно понаблюдать за тем, что изменяется и что сохраняется от одной картинки к другой.
Цветные образчики в моей коллекции демонстрируют результаты, полученные с использованием трех существенно различающихся методов. Компьютерные программы, при помощи которых были получены изображения, не одинаковы по сложности - среди них есть и простые, и не очень сложные. Они принадлежат трем нашим читателям: Дж.Коннету из Миннесотского университета, Б.Мартину из Бирмингема (Англия) и Т.Смиту из Эсседона (Австралия). Программа Коннета основана на окружности, но в ее причудливых узорах проступают и квадраты. Ввиду ее двойственной природы мне пришлось назвать ее CIRCLE2 (КРУГ2). В нескольких словах, в ней применяется формула окружности x2+y2, для того чтобы придать тот или иной цвет точке с координатами x и y. Подробности я опишу ниже. А пока замечу, возможно, к вашему удивлению (а поначалу и к моему), что в обоях подобного рода таится нечто большее, чем множество концентрических окружностей: по мере того как вы отходите назад от стены, все более отчетливо могут проступать на ней изящные структуры квадратной формы (см. рисунки на с.93).

Окружности и квадраты по модулям 2, 3 и 4, полученные по программе Дж.Коннета CIRCLE2
Наверное, не стоит удивляться тому, что программа CIRCLE2 родилась под влиянием множества Мандельброта, о чем речь шла в октябрьском номере нашего журнала за 1985г. Открытие этого множества принадлежит Б.Мандельброту из исследовательского центра Томаса Уотсона фирмы IBM. Богатство формы и красок в графическом изображении множеств Мандельброта основано на единственной математической функции, применяющейся повторно к собственному результату для каждого комплексного числа из заданной области на плоскости. Всякий раз, когда итерируемое значение функции достигает абсолютного значения 2, количество итераций, необходимых для достижения этого значения, определяет цвет соответствующей точки.
Коннет не располагает цветным монитором, поэтому он решил поставить черный цвет в соответствие точкам, для которых абсолютная величина достигает 2 после четного числа итераций, и белый - точкам, для которых количество итераций нечетно. Таким образом, Коннету удалось получить достаточно хорошие изображения множества Мандельброта, но он этим не удовлетворился и занялся исследованием других формул. В конце концов он остановился на формуле x2+y2 и отказался от итераций. Его программа систематически сканирует решетчатую область на плоскости. Для каждой точки (x, y) она вычисляет значение формулы и выделяет целую часть из полученного результата. Если это целое число оказывается четным, точка (x, y) окрашивается в черный цвет, если нечетным, то в белый (остается неокрашенной).
Боюсь, что я уже потерял половину своей аудитории. Читатели, наверное, поняли, как устроена программа, и бросились к своим компьютерам, чтобы ввести ее в память машины. Конечно же, программа очень проста. В алгоритмической записи программа CIRCLE2 состоит из секции ввода, за которой следует двойной цикл:
input corna, cornb
input side
for i <- 1 to 100
- for j <- 1 to 100
- - x <- corna+(side*i/100)
- - y <- cornb +{side*j/100)
- - z <- x2 + y2
- - c <- int(z)
- - if c is even, then plot(i, j)
Сначала программа ждет ввода координат (corna, cornb) левого нижнего угла исследуемого квадрата. Переменная side представляет длину стороны этого квадрата. Например, если ввести значения - 15 и - 20 в качестве координат левого нижнего угла квадрата и 87 как длину его стороны, то программа изобразит массив точек 100*100, заключенный в квадратной области со стороной 87 единиц, левый нижний угол которой будет находиться в точке с координатами (-15, -20). В моей версии программы индексы циклов пробегают значения от 1 до 100, однако эти пределы следует выбирать таким образом, чтобы квадрат лежал в пределах экрана того монитора, которым вы располагаете. На моем мониторе при выбранных предельных значениях квадрат получается довольно маленьким.
Двойной цикл проходит через квадратную решетку и для каждой пары индексов (i, j) вычисляет координаты точки (x, y), которой соответствует эта пара. Затем в теле цикла x и y возводятся в квадрат, сумма полученных квадратов присваивается переменной z и из этого значения извлекается целая часть. Наибольшее целое число, большее или равное сумме квадратов x и y, хранится как значение переменной c. Если c делится на 2, то точка (х, у) высвечивается на экране в виде цветного элемента изображения или как темная точка при выводе картинки на печатающее устройство. Если значение переменной с оказывается нечетным, то соответствующая точка не высвечивается или не печатается.
Читателям, которые пожелают воспроизвести обои Коннета, не следует думать о том, правильно ли они поняли, каким цветом нужно изображать "четные" и "нечетные" точки. Большинство рисунков не утрачивают свою красоту при выборе любых цветов. На самом деле количество цветов может быть больше двух. Вместо того чтобы определять, четно или нечетно значение переменной c, его можно делить на число, соответствующее количеству цветов, которым вы располагаете. Тогда величина остатка от деления будет определять тот или иной цвет. Например, чтобы получить изображения, приведенные на с.93, были выбраны соответственно два цвета для верхнего узора, три для среднего и четыре для нижнего.
Чем меньше исследуемый квадрат, тем плоскость кажется наблюдателю ближе и тем сильнее "увеличение", под которым рассматривает изображение программа CIRCLE2. Однако в отличие от процедуры раскрашивания окрестности множества Мандельброта программа Коннета не содержит в себе бесконечной регрессии все уменьшающихся узоров. При большом увеличении в окрестности начала координат (0, 0) появляется семейство концентрических окружностей. При еще большем увеличении в середине экрана возникает черный диск; целая часть суммы квадратов координат для каждой точки диска равна нулю. Затем уже весь экран становится темным.
Обои Коннета выглядят значительно интереснее при уменьшении увеличения, когда вы как бы отходите от стены. Концентрические круги будто растворяются в замысловатом узоре первичных и вторичных окружностей, напоминающих муаровые кружева. По мере снижения степени увеличения, как по мановению волшебной палочки, появляются все новые и новые отличающиеся от предыдущих узоры. Может быть, здесь все же скрывается бесконечная регрессия? Я уверен, что читатели сумеют понять, в чем тут дело, а через три месяца я опубликую наиболее интересные ответы.
Б.Мартин из Астонского университета в Бирмингеме был также вдохновлен свойствами множества Мандельброта. Он принял на вооружение идею Мандельброта итерировать формулу от начального числового значения - зародыша, но на этом сходство их методов заканчивается. В то время как узоры Мандельброта возникают из комплексных чисел, обои Мартина основаны на итерациях, применяемых к обычным действительным числам. Более того, числовые зародыши для множества Мандельброта представляют собой бесчисленные точки, принадлежащие заданной области на плоскости, а программа Мартина выращивает свои узоры из одного-единственного зародыша.
Мартин предлагает, например, следующие две формулы, которые могут породить потрясающие, отличающиеся довольно сложным узором изображения (см. фото на обложке журнала, а также рисунки на с.94, 95 и 96):
x <- y-sign(x)*[abs(b*x-c)]^(1/2)
у <- a - x
Здесь функция sign(x) принимает значения 1 или -1 в зависимости от того, положителен или отрицателен аргумент x. Функция abs(b*x-c) дает абсолютную величину выражения b*x-c. Изображения могут варьировать довольно значительно в зависимости от выбираемых значений a, b и c - числовых параметров в формуле.


"Фрактальные" обои, порожденные программой Б.Мартина HOPALONG
Сами формулы записаны в сокращенной математической форме. Здесь предполагается, что каждый раз новые значения x и y вычисляются в правой части формул и присваиваются x и y в левой части, после чего эти значения снова подставляются в правую часть для вычисления следующих x и y. Таким образом, программа, которую я назвал HOPALONG (попрыгунья), скачет от одной точки к другой. Процесс начинается в точке, где и x, и y равны 0, т.е. в начале координат. Следующая точка может уже располагаться справа вверху, а точка за ней - слева внизу. Компьютер высвечивает точки настолько быстро, что у наблюдателя возникает ощущение миниатюрного электронного дождя, падающего на экран; на нем появляются сотни, а затем и тысячи точек. Вскоре начинает вырисовываться узор. Если, например, параметр a принять равным -200, b равным 0.1 и c равным -80, то возникает восьмиугольный узор (см. нижний рисунок слева). Если рассматривать изображение под увеличением и раскрашивать точку в зависимости от количества скачков, требующихся, чтобы достичь ее, то изображение превращается в удивительные вензеля (см. верхний рисунок слева). Для других значений a, b и c можно получить новые узоры. Можно принять, например, a = 0.4, b = 1 и c = 0 (см. верхний рисунок на с.95) или принять а = -3.14, b = 0.3 и с = 0.3 (см. нижний рисунок на с.95).

Магические символы, полученные по итерационной формуле Мартина
Алгоритм программы HOPALONG почти так же прост, как и программы CIRCLE2:
input num
input a, b, c
x <- 0
y <- 0
for i <- 1 to num
- plot(x, y)
- xx <- y-sign(x)*[abs(b*x-c)]^(1/2)
- yy <- a-x
- x <- xx
- y <- yy
И опять множество читателей бросились, наверное, к своим компьютерам, чтобы тотчас ввести и запустить программу. Те же, кто останутся с нами, будут вознаграждены более подробным описанием программы Мартина и познакомятся также с третьей программой, производящей рисунки для обоев.
Перед выполнением программы HOPALONG нужно ввести количество итераций, которое присваивается в качестве значения переменной num. Затем нужно ввести также значения параметров a, b и c. Чем больше величина num, тем более тонким и замысловатым становится узор. Если, например, num принять равной 10000, программа высветит на экране 10000 точек, но для некоторых значений a, b и c это лишь только начало. При a = -1000, b = 0.1 и c = -10 и небольших увеличениях изображение напоминает корку четырехдольного лимона (см. нижний рисунок на с.96). По мере того как число итерадий возрастает от 10000 точек до 100000 н затем до 600000, кружева становятся все более н более тонкими и красивыми (см. верх рисунка на с.96).
Модель стебля растения и его сосудистая система, порожденные программой НОРАLONG
Этот алгоритм можно несколько усовершенствовать. Например, в него можно ввести средство, обеспечивающее перемещение точек, не попадающих на экран, или сжатие внеэкранных областей, чтобы сделать их видимыми. Если в алгоритм введены такие средства, то перед началом выполнения программы следует задать еще три дополнительных параметра, определяющих положенне и масштаб картинки. В этом случае тело главного цикла нужно модифицировать: сразу после вычисления x и y в усовершенствованной версии программы HOPALONG осуществляются сдвиг полученных значений x и y и умножение результатов на масштабный множитель.
Аналогия с обоями не укрылась и от Мартина: "Мне кажется, что мы находимся на пороге взрыва в области создания узоров, имеющей важное коммерческое значение. Возможно, мы станем свидетелями создания автоматизированного дизайнера, художника по узорам на обоях и тканях,- это может произойти уже в ближайшие несколько лет. Клиент будет сам подбирать себе рисунок по вкусу, задавая компьютеру несколько числовых параметров". Мартин оптимистически смотрит и на возможность применения подобных программ в математической биологии. Посмотрим-ка снова на четырехдольный лимон. При сильном увеличении мы можем видеть детали, весьма напоминающие сосудистую систему; а может быть, это поперечное сечение внешнего слоя односемядольного растения? Об этих и о других узорах Мартин пишет следующее: "Очевидно, эти любопытные конфигурации показывают нам, что правила, по которым строятся сложнейшие ткани живых организмов, могут быть до абсурда простыми".
Возможно, читатели заинтересуются исследованием образов, порождаемых двумя другими итерационными формулами, также предложенными Мартином:
x <- y-sin(x) и
у <- a-x
В этих формулах требуется указать значение лишь одного параметра a. Мартину удалось обнаружить ряд в высшей степени интересных узоров, когда а лежит в окрестности 0.07 от числа пи.
Обои третьей разновидности следует приберечь для комнат, отведенных для глубоких и серьезных размышлений. Узоры здесь самые разные, от персидских хитросплетений до неистовых образов южноамериканских индейских культур (см. нижний рисунок на с.97 и на с.98 ). Методы, при помощи которых были получены эти образы, абсолютно непохожи на рассмотренные выше. Т.Смит из австралийской фирмы PICA Pty. Ltd. разработал тонкие вариации самовоспроизводящегося клеточного автомата, изобретенного в 1960г. Э.Фредкиным из Массачусетского технологического института (см. статью Б.Хейеса в рубрике "Занимательный компьютер" в декабрьском номере журнала за 1983г.). В идее этого автомата кроется удивительная возможность для порождения разнообразных узоров, и Смит начал исследования этих огромных возможностей.
Что собой представляет клеточный автомат Фредкина? Представьте себе бесконечную двумерную решетку из квадратных клеток. В каждый данный момент времени каждая клетка может находиться в одном из двух возможных состояний: она может быть либо живой, либо мертвой. Система управляется воображаемыми часами, при тактовых сигналах которых могут меняться состояния клеток. Судьба каждой клетки определяется окружающими ее четырьмя соседними клетками: если число живых соседей на одном такте часов четно, то на следующем такте данная клетка будет мертвой независимо от ее предыдущего состояния. Если же число живых соседей оказывается нечетным, то на следующем такте клетка будет живой. Это правило применяется одновременно ко всем клеткам решетки.
Автомат Фредкина очень напоминает игру "Жизнь", изобретенную Дж.Конвеем из Кембриджского университета. Эту игру мы не раз обсуждали в статьях нашей рубрики. Однако автомат Фредкина появился на свет раньше игры Конвея и он намного проще. Более того, он обладает одним удивительным свойством, отсутствующим у игры "Жизнь",- любая исходная конфигурация живых клеток, проходя через ряд поколений (тактов часового механизма), производит четыре своих копии. Еще через несколько поколений таких копий насчитывается уже 16, затем 64 и т.д. Обои самых интересных образцов появляются в течение жизни промежуточных поколений клеток на стадии создания новых копий исходных популяций живых клеток.
Программа Смита, печатающая обобщенные обои Фредкина, обладает весьма универсальными свойствами и называется PATTERN BREEDER (генератор узоров). Правила, определяющие судьбу клетки, не обязательно зависят от состояния четырех соседних клеток. Перед выполнением программы можно задать конфигурацию окружающих клеток, или "активную окрестность" для каждой клетки. Затем уже программа применяет то же самое правило "четный-нечетный", которое было выбрано в исходной версии автомата Фредкина. Каждый раз, когда на очередном такте часов число живых клеток в активной окрестности данной клетки четное, зга клетка должна умереть в следующем поколении. В противном случае она будет живой.
PATTERN BREEDER работает с любой исходной конфигурацией клеток, заданной пользователем. Например, исходная конфигурация, обозначенная буквой a на верхнем рисунке справа, создает красную часть узора, показанного на рисунке внизу. Для каждой данной клетки и на каждой стадии эволюционного процесса активная окрестность остается той же. Сама по себе она является довольно сложным узором, в который входят все цветные клетки в матрице 5*5, также обозначенной буквой а на верхнем рисунке на с.97. Заметим, что активная окрестность в данном случае включает н саму клетку, судьба которой определяется окрестностью.

Правила, порождающие клеточные автоматы в программе Т.Смита PATTERN

Два наложенных друг на друга изображения, порожденные программой PATTERN BREEDER
Чтобы применить решающее правило, нужно подсчитать число живых клеток в активной окрестности; если рассматриваемая клетка в данный момент жива, ее тоже надо учесть при подсчете. Исходные конфигурации и соответствующие каждой из них активные окрестности показаны также для двух других изображений. Пара, обозначенная буквой b, соответствует синей части изображения, приведенного на нижнем рисунке на с.97, а пара, обозначенная буквой c, соответствует рисунку на с.98. Активная окрестность c обладает дополнительным усложняющим свойством: клетка, судьба которой определяется окрестностью, сама осциллирует в последующих поколениях слева направо и обратно в центр окрестности. Программа Смита содержит в себе библиотеку исходных конфигураций и активных окрестностей, из которых пользователь может выбирать интересующие его варианты. В настоящее время программа может выполняться только на персональных компьютерах Apple фирмы Macintosh.

Абстракция в стиле майя, полученная программой Смита
Я не буду описывать программу PATTERN BREEDER во всей ее сложности, но приведу здесь более простую программу под названием FREDKIN. Читатели, обладающие некоторой подготовкой в программировании, смогут затем превратить эту программу в более общий алгоритм, обладающий кое-какими свойствами PATTERN BREEDER Смита:
Ввести исходную конфигурацию
S:
Для каждой клетки массива на экране
- count <- 0
- Для каждого соседа этой клетки
- - Если сосед живой
- - то count <- count+1
- Если значение count четно
- - то cell <- 0
- - иначе cell <- 1
- Вывести cell
Ввести go
Переход на S
Одна из привлекательных особенностей алгоритмической записи заключается в том, что в вашем распоряжении имеется много различных уровней описания. Конечно, грань, отделяющая общность описания от безответственной туманности, очень тонка. Читатели, наверное, заметят, что описание программы FREDKIN в том виде, в каком оно было приведено выше, отличается большей общностью по сравнению с алгоритмами, рассмотренными ранее. Например, для выполнения инструкции "Ввести исходную конфигурацию" потребуется указание нескольких инструкций на любом из распространенных языков программирования. Эти инструкции будут объединены в двойной цикл с двумя индексами i и j. Еще один двойной цикл скрывается за инструкцией "Для каждой клетки массива на экране". Здесь два индекса соответствуют координатам точек на экране дисплея или на принтере.
В своем главном цикле программа FREDKIN просто реализует применение правила, управляющего эволюцией заданной конфигурации. Она подсчитывает количество живых членов активной окрестности для каждой клетки (x, y) и затем, если это количество оказывается нечетным, высвечивает или выводит на печать клетку в виде точки. Последняя инструкция главного цикла требует ввода значения для переменной go. Здесь пользователь может ввести любое число, после чего программа FREDKIN построит свой следующий узор. Таким образом, процесс выполнения программы может быть прерван, чтобы можно было внимательно рассмотреть особенно понравившийся узор. Данный алгоритм, может быть, и не отвечает полностью требованиям структурного программирования, но работает прекрасно. Иногда, как мы видим, инструкции GOTO и связанные с ними уловки оказываются все же полезными.
Через три месяца я опубликую наиболее интересные образцы обоев для ума, присланные к тому времени нашими читателями. Остальные же войдут в мою коллекцию, которую в виде книги я представлю вам, если когда-нибудь вернусь к этой теме.
БИБЛИОГРАФИЯ
MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.224, No.2, pages 112-117; February, 1971.
COMPUTER RECREATIONS. BRIAN HAYES in Scientific American, Vol.249, No.4, pages 22-36; October 1983. (Это просто ссылка на пост в начале темы.- G.).
ОТКЛИКИ
2 1987
В СТАТЬЕ, посвященной программам, генерирующим узоры для обоев, которая была опубликована в ноябрьском за 1986г. номере нашего журнала, речь шла о почти повторяющейся структуре рисунков, создаваемых компьютером и весьма подходящих для обоев. Однако на самом деле изображения подобного рода были известны еще предыдущему поколению читателей. М.Россману, журналисту и политическому комментатору из Беркли (шт.Калифорния) принадлежит фраза "обои для ума". Он первым применил ее в 1971г., описывая деликатные узоры - галлюцинации, которые при закрытых глазах наблюдали люди, принявшие дозу препарата ЛСД. Россман писал: "Это было похоже на обои, узор которых никогда не выглядел полосатым, но был преимущественно повторяющимся: здесь были упорядоченные "созвездия" попугаев, морских звезд, электрических лампочек и снежных хлопьев, сложнейшие неописуемые образы, подобные пятнам, используемым в тесте Роршаха [Герман Роршах - швейцарский врач-психиатр, скончавшийся в 1922г. Его именем назван один из тестов на умственное развитие и характер человека. Тест основан на том, как человек интерпретирует чернильные пятна в категориях, позволяющих понять его эмоциональные и интеллектуальные особенности.- Прим. перев.], причудливо сменяющие друг друга, эволюционирующие один из другого, как в бесконечной цепи метаморфоз, оживленных как в мультипликационном фильме".
Читатели, наверное, помнят, что самая простая программа, создающая изображения такого рода обоев, принадлежала Дж.Коннету из Миннесотского университета. Согласно его "рецепту", координаты каждого пиксела должны возводиться в квадрат и складываться между собой. Результат усекается до ближайшего целого числа. Если полученное целое число четно, пиксел будет окрашен в черный цвет, если же оно нечетно, пиксел будет белым. Сходство создаваемого узора с узорами на обоях заключается в наличии горизонтальных и вертикальных повторений и муаровой фактуры рисунка, достигаемой наложением друг на друга двух неявно выраженных узоров. Первый из этих узоров представляет собой прямоугольную решетку пикселов, соответствующую геометрии экрана. Второй узор - это семейство концентрических колец из тех точек на плоскости, для которых процедура Коннета дает нечетные числа. Подобный рисунку на обоях этот узор возникает в результате повторяющейся интерференции его элементов в горизонтальном и вертикальном направлениях. Несколько последовательно расположенных точек решетки может попасть во внутреннюю область кольца, следующие несколько точек - во внешнюю и т.д. По мере того как растет расстояние от центра, кольца становятся все тоньше, попадания н промахи наблюдаются вдоль любой линии, состоящей из точек решетки.
П.Брауну из Симн-Вэлли (шт.Калифорния) этот процесс показался невыносимо медленным. Экран его компьютера заполнялся так долго, что он решил ограничиться лишь частичной выборкой из полной картинки и высвечивать лишь каждый девятый пиксел как по горизонтали, так и по вертикали. В этой сжатой форме изображение выглядело совершенно непохожим на исходное. На самом деле Браун изменил размер решетки, в результате чего изменился характер интерференции узоров.
О.Смит из Порт-Таунсенда (шт.Вашингтон) пришел к выводу, что можно значительно изменить рисунок муарового узора, просто изменив закон, по которому определяется цвет точки. Как и многие другие читатели, Смит экспериментировал с формулами, отличными от формулы Коннета. Например, некоторые суммы или произведения простых тригонометрических функций порождают буйные вихревые узоры, напоминающие роскошно разукрашенные внутренние стороны обложки дорогих книг в твердом высококачественном переплете. Смит отмечает также, что подобные муаровые узоры и другие изображения, порождаемые интерференционными эффектами, часто возникают в компьютерной графике. Причем в большинстве случаев эти изображения возникают как побочные, нежелательные эффекты при отладке графических программ со сложными регулярными вариациями изображения.
Я был очень тронут миниатюрным воспроизводимым вручную мультфильмом, присланным Д.Рэймондом из Оринды (шт.Калифорния). Фильм состоит из подобранной последовательности крошечных отпечатков обоев Коннета с постепенно увеличивающимся размером решетки. Отпечатки плотно сшиты между собой в виде маленькой книжечки, и если быстро перелистывать страницы, держа их большим пальцем, то можно наблюдать короткий мультипликационный фильм.
ПРОГРАММЫ, ГЕНЕРИРУЮЩИЕ УЗОРЫ ДЛЯ ОБОЕВ
А.К.ДЬЮДНИ
ОБЫЧНЫЕ обои печатаются вращающимся цилиндром, на котором выгравирован узор. При каждом обороте цилиндра отпечатывается одно и то же изображение. А вот компьютер может воспроизводить затейливые узоры, которые я называю "обоями для ума" и которые, вообще говоря, не повторяются или во всяком случае повторяются не полностью. Изображение все время проявляется в новых конфигурациях, слева и справа, внизу и вверху. Интересно понаблюдать за тем, что изменяется и что сохраняется от одной картинки к другой.
Цветные образчики в моей коллекции демонстрируют результаты, полученные с использованием трех существенно различающихся методов. Компьютерные программы, при помощи которых были получены изображения, не одинаковы по сложности - среди них есть и простые, и не очень сложные. Они принадлежат трем нашим читателям: Дж.Коннету из Миннесотского университета, Б.Мартину из Бирмингема (Англия) и Т.Смиту из Эсседона (Австралия). Программа Коннета основана на окружности, но в ее причудливых узорах проступают и квадраты. Ввиду ее двойственной природы мне пришлось назвать ее CIRCLE2 (КРУГ2). В нескольких словах, в ней применяется формула окружности x2+y2, для того чтобы придать тот или иной цвет точке с координатами x и y. Подробности я опишу ниже. А пока замечу, возможно, к вашему удивлению (а поначалу и к моему), что в обоях подобного рода таится нечто большее, чем множество концентрических окружностей: по мере того как вы отходите назад от стены, все более отчетливо могут проступать на ней изящные структуры квадратной формы (см. рисунки на с.93).

Окружности и квадраты по модулям 2, 3 и 4, полученные по программе Дж.Коннета CIRCLE2
Наверное, не стоит удивляться тому, что программа CIRCLE2 родилась под влиянием множества Мандельброта, о чем речь шла в октябрьском номере нашего журнала за 1985г. Открытие этого множества принадлежит Б.Мандельброту из исследовательского центра Томаса Уотсона фирмы IBM. Богатство формы и красок в графическом изображении множеств Мандельброта основано на единственной математической функции, применяющейся повторно к собственному результату для каждого комплексного числа из заданной области на плоскости. Всякий раз, когда итерируемое значение функции достигает абсолютного значения 2, количество итераций, необходимых для достижения этого значения, определяет цвет соответствующей точки.
Коннет не располагает цветным монитором, поэтому он решил поставить черный цвет в соответствие точкам, для которых абсолютная величина достигает 2 после четного числа итераций, и белый - точкам, для которых количество итераций нечетно. Таким образом, Коннету удалось получить достаточно хорошие изображения множества Мандельброта, но он этим не удовлетворился и занялся исследованием других формул. В конце концов он остановился на формуле x2+y2 и отказался от итераций. Его программа систематически сканирует решетчатую область на плоскости. Для каждой точки (x, y) она вычисляет значение формулы и выделяет целую часть из полученного результата. Если это целое число оказывается четным, точка (x, y) окрашивается в черный цвет, если нечетным, то в белый (остается неокрашенной).
Боюсь, что я уже потерял половину своей аудитории. Читатели, наверное, поняли, как устроена программа, и бросились к своим компьютерам, чтобы ввести ее в память машины. Конечно же, программа очень проста. В алгоритмической записи программа CIRCLE2 состоит из секции ввода, за которой следует двойной цикл:
input corna, cornb
input side
for i <- 1 to 100
- for j <- 1 to 100
- - x <- corna+(side*i/100)
- - y <- cornb +{side*j/100)
- - z <- x2 + y2
- - c <- int(z)
- - if c is even, then plot(i, j)
Сначала программа ждет ввода координат (corna, cornb) левого нижнего угла исследуемого квадрата. Переменная side представляет длину стороны этого квадрата. Например, если ввести значения - 15 и - 20 в качестве координат левого нижнего угла квадрата и 87 как длину его стороны, то программа изобразит массив точек 100*100, заключенный в квадратной области со стороной 87 единиц, левый нижний угол которой будет находиться в точке с координатами (-15, -20). В моей версии программы индексы циклов пробегают значения от 1 до 100, однако эти пределы следует выбирать таким образом, чтобы квадрат лежал в пределах экрана того монитора, которым вы располагаете. На моем мониторе при выбранных предельных значениях квадрат получается довольно маленьким.
Двойной цикл проходит через квадратную решетку и для каждой пары индексов (i, j) вычисляет координаты точки (x, y), которой соответствует эта пара. Затем в теле цикла x и y возводятся в квадрат, сумма полученных квадратов присваивается переменной z и из этого значения извлекается целая часть. Наибольшее целое число, большее или равное сумме квадратов x и y, хранится как значение переменной c. Если c делится на 2, то точка (х, у) высвечивается на экране в виде цветного элемента изображения или как темная точка при выводе картинки на печатающее устройство. Если значение переменной с оказывается нечетным, то соответствующая точка не высвечивается или не печатается.
Читателям, которые пожелают воспроизвести обои Коннета, не следует думать о том, правильно ли они поняли, каким цветом нужно изображать "четные" и "нечетные" точки. Большинство рисунков не утрачивают свою красоту при выборе любых цветов. На самом деле количество цветов может быть больше двух. Вместо того чтобы определять, четно или нечетно значение переменной c, его можно делить на число, соответствующее количеству цветов, которым вы располагаете. Тогда величина остатка от деления будет определять тот или иной цвет. Например, чтобы получить изображения, приведенные на с.93, были выбраны соответственно два цвета для верхнего узора, три для среднего и четыре для нижнего.
Чем меньше исследуемый квадрат, тем плоскость кажется наблюдателю ближе и тем сильнее "увеличение", под которым рассматривает изображение программа CIRCLE2. Однако в отличие от процедуры раскрашивания окрестности множества Мандельброта программа Коннета не содержит в себе бесконечной регрессии все уменьшающихся узоров. При большом увеличении в окрестности начала координат (0, 0) появляется семейство концентрических окружностей. При еще большем увеличении в середине экрана возникает черный диск; целая часть суммы квадратов координат для каждой точки диска равна нулю. Затем уже весь экран становится темным.
Обои Коннета выглядят значительно интереснее при уменьшении увеличения, когда вы как бы отходите от стены. Концентрические круги будто растворяются в замысловатом узоре первичных и вторичных окружностей, напоминающих муаровые кружева. По мере снижения степени увеличения, как по мановению волшебной палочки, появляются все новые и новые отличающиеся от предыдущих узоры. Может быть, здесь все же скрывается бесконечная регрессия? Я уверен, что читатели сумеют понять, в чем тут дело, а через три месяца я опубликую наиболее интересные ответы.
Б.Мартин из Астонского университета в Бирмингеме был также вдохновлен свойствами множества Мандельброта. Он принял на вооружение идею Мандельброта итерировать формулу от начального числового значения - зародыша, но на этом сходство их методов заканчивается. В то время как узоры Мандельброта возникают из комплексных чисел, обои Мартина основаны на итерациях, применяемых к обычным действительным числам. Более того, числовые зародыши для множества Мандельброта представляют собой бесчисленные точки, принадлежащие заданной области на плоскости, а программа Мартина выращивает свои узоры из одного-единственного зародыша.
Мартин предлагает, например, следующие две формулы, которые могут породить потрясающие, отличающиеся довольно сложным узором изображения (см. фото на обложке журнала, а также рисунки на с.94, 95 и 96):
x <- y-sign(x)*[abs(b*x-c)]^(1/2)
у <- a - x
Здесь функция sign(x) принимает значения 1 или -1 в зависимости от того, положителен или отрицателен аргумент x. Функция abs(b*x-c) дает абсолютную величину выражения b*x-c. Изображения могут варьировать довольно значительно в зависимости от выбираемых значений a, b и c - числовых параметров в формуле.


"Фрактальные" обои, порожденные программой Б.Мартина HOPALONG
Сами формулы записаны в сокращенной математической форме. Здесь предполагается, что каждый раз новые значения x и y вычисляются в правой части формул и присваиваются x и y в левой части, после чего эти значения снова подставляются в правую часть для вычисления следующих x и y. Таким образом, программа, которую я назвал HOPALONG (попрыгунья), скачет от одной точки к другой. Процесс начинается в точке, где и x, и y равны 0, т.е. в начале координат. Следующая точка может уже располагаться справа вверху, а точка за ней - слева внизу. Компьютер высвечивает точки настолько быстро, что у наблюдателя возникает ощущение миниатюрного электронного дождя, падающего на экран; на нем появляются сотни, а затем и тысячи точек. Вскоре начинает вырисовываться узор. Если, например, параметр a принять равным -200, b равным 0.1 и c равным -80, то возникает восьмиугольный узор (см. нижний рисунок слева). Если рассматривать изображение под увеличением и раскрашивать точку в зависимости от количества скачков, требующихся, чтобы достичь ее, то изображение превращается в удивительные вензеля (см. верхний рисунок слева). Для других значений a, b и c можно получить новые узоры. Можно принять, например, a = 0.4, b = 1 и c = 0 (см. верхний рисунок на с.95) или принять а = -3.14, b = 0.3 и с = 0.3 (см. нижний рисунок на с.95).

Магические символы, полученные по итерационной формуле Мартина
Алгоритм программы HOPALONG почти так же прост, как и программы CIRCLE2:
input num
input a, b, c
x <- 0
y <- 0
for i <- 1 to num
- plot(x, y)
- xx <- y-sign(x)*[abs(b*x-c)]^(1/2)
- yy <- a-x
- x <- xx
- y <- yy
И опять множество читателей бросились, наверное, к своим компьютерам, чтобы тотчас ввести и запустить программу. Те же, кто останутся с нами, будут вознаграждены более подробным описанием программы Мартина и познакомятся также с третьей программой, производящей рисунки для обоев.
Перед выполнением программы HOPALONG нужно ввести количество итераций, которое присваивается в качестве значения переменной num. Затем нужно ввести также значения параметров a, b и c. Чем больше величина num, тем более тонким и замысловатым становится узор. Если, например, num принять равной 10000, программа высветит на экране 10000 точек, но для некоторых значений a, b и c это лишь только начало. При a = -1000, b = 0.1 и c = -10 и небольших увеличениях изображение напоминает корку четырехдольного лимона (см. нижний рисунок на с.96). По мере того как число итерадий возрастает от 10000 точек до 100000 н затем до 600000, кружева становятся все более н более тонкими и красивыми (см. верх рисунка на с.96).

Модель стебля растения и его сосудистая система, порожденные программой НОРАLONG
Этот алгоритм можно несколько усовершенствовать. Например, в него можно ввести средство, обеспечивающее перемещение точек, не попадающих на экран, или сжатие внеэкранных областей, чтобы сделать их видимыми. Если в алгоритм введены такие средства, то перед началом выполнения программы следует задать еще три дополнительных параметра, определяющих положенне и масштаб картинки. В этом случае тело главного цикла нужно модифицировать: сразу после вычисления x и y в усовершенствованной версии программы HOPALONG осуществляются сдвиг полученных значений x и y и умножение результатов на масштабный множитель.
Аналогия с обоями не укрылась и от Мартина: "Мне кажется, что мы находимся на пороге взрыва в области создания узоров, имеющей важное коммерческое значение. Возможно, мы станем свидетелями создания автоматизированного дизайнера, художника по узорам на обоях и тканях,- это может произойти уже в ближайшие несколько лет. Клиент будет сам подбирать себе рисунок по вкусу, задавая компьютеру несколько числовых параметров". Мартин оптимистически смотрит и на возможность применения подобных программ в математической биологии. Посмотрим-ка снова на четырехдольный лимон. При сильном увеличении мы можем видеть детали, весьма напоминающие сосудистую систему; а может быть, это поперечное сечение внешнего слоя односемядольного растения? Об этих и о других узорах Мартин пишет следующее: "Очевидно, эти любопытные конфигурации показывают нам, что правила, по которым строятся сложнейшие ткани живых организмов, могут быть до абсурда простыми".
Возможно, читатели заинтересуются исследованием образов, порождаемых двумя другими итерационными формулами, также предложенными Мартином:
x <- y-sin(x) и
у <- a-x
В этих формулах требуется указать значение лишь одного параметра a. Мартину удалось обнаружить ряд в высшей степени интересных узоров, когда а лежит в окрестности 0.07 от числа пи.
Обои третьей разновидности следует приберечь для комнат, отведенных для глубоких и серьезных размышлений. Узоры здесь самые разные, от персидских хитросплетений до неистовых образов южноамериканских индейских культур (см. нижний рисунок на с.97 и на с.98 ). Методы, при помощи которых были получены эти образы, абсолютно непохожи на рассмотренные выше. Т.Смит из австралийской фирмы PICA Pty. Ltd. разработал тонкие вариации самовоспроизводящегося клеточного автомата, изобретенного в 1960г. Э.Фредкиным из Массачусетского технологического института (см. статью Б.Хейеса в рубрике "Занимательный компьютер" в декабрьском номере журнала за 1983г.). В идее этого автомата кроется удивительная возможность для порождения разнообразных узоров, и Смит начал исследования этих огромных возможностей.
Что собой представляет клеточный автомат Фредкина? Представьте себе бесконечную двумерную решетку из квадратных клеток. В каждый данный момент времени каждая клетка может находиться в одном из двух возможных состояний: она может быть либо живой, либо мертвой. Система управляется воображаемыми часами, при тактовых сигналах которых могут меняться состояния клеток. Судьба каждой клетки определяется окружающими ее четырьмя соседними клетками: если число живых соседей на одном такте часов четно, то на следующем такте данная клетка будет мертвой независимо от ее предыдущего состояния. Если же число живых соседей оказывается нечетным, то на следующем такте клетка будет живой. Это правило применяется одновременно ко всем клеткам решетки.
Автомат Фредкина очень напоминает игру "Жизнь", изобретенную Дж.Конвеем из Кембриджского университета. Эту игру мы не раз обсуждали в статьях нашей рубрики. Однако автомат Фредкина появился на свет раньше игры Конвея и он намного проще. Более того, он обладает одним удивительным свойством, отсутствующим у игры "Жизнь",- любая исходная конфигурация живых клеток, проходя через ряд поколений (тактов часового механизма), производит четыре своих копии. Еще через несколько поколений таких копий насчитывается уже 16, затем 64 и т.д. Обои самых интересных образцов появляются в течение жизни промежуточных поколений клеток на стадии создания новых копий исходных популяций живых клеток.
Программа Смита, печатающая обобщенные обои Фредкина, обладает весьма универсальными свойствами и называется PATTERN BREEDER (генератор узоров). Правила, определяющие судьбу клетки, не обязательно зависят от состояния четырех соседних клеток. Перед выполнением программы можно задать конфигурацию окружающих клеток, или "активную окрестность" для каждой клетки. Затем уже программа применяет то же самое правило "четный-нечетный", которое было выбрано в исходной версии автомата Фредкина. Каждый раз, когда на очередном такте часов число живых клеток в активной окрестности данной клетки четное, зга клетка должна умереть в следующем поколении. В противном случае она будет живой.
PATTERN BREEDER работает с любой исходной конфигурацией клеток, заданной пользователем. Например, исходная конфигурация, обозначенная буквой a на верхнем рисунке справа, создает красную часть узора, показанного на рисунке внизу. Для каждой данной клетки и на каждой стадии эволюционного процесса активная окрестность остается той же. Сама по себе она является довольно сложным узором, в который входят все цветные клетки в матрице 5*5, также обозначенной буквой а на верхнем рисунке на с.97. Заметим, что активная окрестность в данном случае включает н саму клетку, судьба которой определяется окрестностью.

Правила, порождающие клеточные автоматы в программе Т.Смита PATTERN

Два наложенных друг на друга изображения, порожденные программой PATTERN BREEDER
Чтобы применить решающее правило, нужно подсчитать число живых клеток в активной окрестности; если рассматриваемая клетка в данный момент жива, ее тоже надо учесть при подсчете. Исходные конфигурации и соответствующие каждой из них активные окрестности показаны также для двух других изображений. Пара, обозначенная буквой b, соответствует синей части изображения, приведенного на нижнем рисунке на с.97, а пара, обозначенная буквой c, соответствует рисунку на с.98. Активная окрестность c обладает дополнительным усложняющим свойством: клетка, судьба которой определяется окрестностью, сама осциллирует в последующих поколениях слева направо и обратно в центр окрестности. Программа Смита содержит в себе библиотеку исходных конфигураций и активных окрестностей, из которых пользователь может выбирать интересующие его варианты. В настоящее время программа может выполняться только на персональных компьютерах Apple фирмы Macintosh.

Абстракция в стиле майя, полученная программой Смита
Я не буду описывать программу PATTERN BREEDER во всей ее сложности, но приведу здесь более простую программу под названием FREDKIN. Читатели, обладающие некоторой подготовкой в программировании, смогут затем превратить эту программу в более общий алгоритм, обладающий кое-какими свойствами PATTERN BREEDER Смита:
Ввести исходную конфигурацию
S:
Для каждой клетки массива на экране
- count <- 0
- Для каждого соседа этой клетки
- - Если сосед живой
- - то count <- count+1
- Если значение count четно
- - то cell <- 0
- - иначе cell <- 1
- Вывести cell
Ввести go
Переход на S
Одна из привлекательных особенностей алгоритмической записи заключается в том, что в вашем распоряжении имеется много различных уровней описания. Конечно, грань, отделяющая общность описания от безответственной туманности, очень тонка. Читатели, наверное, заметят, что описание программы FREDKIN в том виде, в каком оно было приведено выше, отличается большей общностью по сравнению с алгоритмами, рассмотренными ранее. Например, для выполнения инструкции "Ввести исходную конфигурацию" потребуется указание нескольких инструкций на любом из распространенных языков программирования. Эти инструкции будут объединены в двойной цикл с двумя индексами i и j. Еще один двойной цикл скрывается за инструкцией "Для каждой клетки массива на экране". Здесь два индекса соответствуют координатам точек на экране дисплея или на принтере.
В своем главном цикле программа FREDKIN просто реализует применение правила, управляющего эволюцией заданной конфигурации. Она подсчитывает количество живых членов активной окрестности для каждой клетки (x, y) и затем, если это количество оказывается нечетным, высвечивает или выводит на печать клетку в виде точки. Последняя инструкция главного цикла требует ввода значения для переменной go. Здесь пользователь может ввести любое число, после чего программа FREDKIN построит свой следующий узор. Таким образом, процесс выполнения программы может быть прерван, чтобы можно было внимательно рассмотреть особенно понравившийся узор. Данный алгоритм, может быть, и не отвечает полностью требованиям структурного программирования, но работает прекрасно. Иногда, как мы видим, инструкции GOTO и связанные с ними уловки оказываются все же полезными.
Через три месяца я опубликую наиболее интересные образцы обоев для ума, присланные к тому времени нашими читателями. Остальные же войдут в мою коллекцию, которую в виде книги я представлю вам, если когда-нибудь вернусь к этой теме.
БИБЛИОГРАФИЯ
MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.224, No.2, pages 112-117; February, 1971.
COMPUTER RECREATIONS. BRIAN HAYES in Scientific American, Vol.249, No.4, pages 22-36; October 1983. (Это просто ссылка на пост в начале темы.- G.).
ОТКЛИКИ
2 1987
В СТАТЬЕ, посвященной программам, генерирующим узоры для обоев, которая была опубликована в ноябрьском за 1986г. номере нашего журнала, речь шла о почти повторяющейся структуре рисунков, создаваемых компьютером и весьма подходящих для обоев. Однако на самом деле изображения подобного рода были известны еще предыдущему поколению читателей. М.Россману, журналисту и политическому комментатору из Беркли (шт.Калифорния) принадлежит фраза "обои для ума". Он первым применил ее в 1971г., описывая деликатные узоры - галлюцинации, которые при закрытых глазах наблюдали люди, принявшие дозу препарата ЛСД. Россман писал: "Это было похоже на обои, узор которых никогда не выглядел полосатым, но был преимущественно повторяющимся: здесь были упорядоченные "созвездия" попугаев, морских звезд, электрических лампочек и снежных хлопьев, сложнейшие неописуемые образы, подобные пятнам, используемым в тесте Роршаха [Герман Роршах - швейцарский врач-психиатр, скончавшийся в 1922г. Его именем назван один из тестов на умственное развитие и характер человека. Тест основан на том, как человек интерпретирует чернильные пятна в категориях, позволяющих понять его эмоциональные и интеллектуальные особенности.- Прим. перев.], причудливо сменяющие друг друга, эволюционирующие один из другого, как в бесконечной цепи метаморфоз, оживленных как в мультипликационном фильме".
Читатели, наверное, помнят, что самая простая программа, создающая изображения такого рода обоев, принадлежала Дж.Коннету из Миннесотского университета. Согласно его "рецепту", координаты каждого пиксела должны возводиться в квадрат и складываться между собой. Результат усекается до ближайшего целого числа. Если полученное целое число четно, пиксел будет окрашен в черный цвет, если же оно нечетно, пиксел будет белым. Сходство создаваемого узора с узорами на обоях заключается в наличии горизонтальных и вертикальных повторений и муаровой фактуры рисунка, достигаемой наложением друг на друга двух неявно выраженных узоров. Первый из этих узоров представляет собой прямоугольную решетку пикселов, соответствующую геометрии экрана. Второй узор - это семейство концентрических колец из тех точек на плоскости, для которых процедура Коннета дает нечетные числа. Подобный рисунку на обоях этот узор возникает в результате повторяющейся интерференции его элементов в горизонтальном и вертикальном направлениях. Несколько последовательно расположенных точек решетки может попасть во внутреннюю область кольца, следующие несколько точек - во внешнюю и т.д. По мере того как растет расстояние от центра, кольца становятся все тоньше, попадания н промахи наблюдаются вдоль любой линии, состоящей из точек решетки.
П.Брауну из Симн-Вэлли (шт.Калифорния) этот процесс показался невыносимо медленным. Экран его компьютера заполнялся так долго, что он решил ограничиться лишь частичной выборкой из полной картинки и высвечивать лишь каждый девятый пиксел как по горизонтали, так и по вертикали. В этой сжатой форме изображение выглядело совершенно непохожим на исходное. На самом деле Браун изменил размер решетки, в результате чего изменился характер интерференции узоров.
О.Смит из Порт-Таунсенда (шт.Вашингтон) пришел к выводу, что можно значительно изменить рисунок муарового узора, просто изменив закон, по которому определяется цвет точки. Как и многие другие читатели, Смит экспериментировал с формулами, отличными от формулы Коннета. Например, некоторые суммы или произведения простых тригонометрических функций порождают буйные вихревые узоры, напоминающие роскошно разукрашенные внутренние стороны обложки дорогих книг в твердом высококачественном переплете. Смит отмечает также, что подобные муаровые узоры и другие изображения, порождаемые интерференционными эффектами, часто возникают в компьютерной графике. Причем в большинстве случаев эти изображения возникают как побочные, нежелательные эффекты при отладке графических программ со сложными регулярными вариациями изображения.
Я был очень тронут миниатюрным воспроизводимым вручную мультфильмом, присланным Д.Рэймондом из Оринды (шт.Калифорния). Фильм состоит из подобранной последовательности крошечных отпечатков обоев Коннета с постепенно увеличивающимся размером решетки. Отпечатки плотно сшиты между собой в виде маленькой книжечки, и если быстро перелистывать страницы, держа их большим пальцем, то можно наблюдать короткий мультипликационный фильм.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
12 1986
КОМПЬЮТЕР-КАРИКАТУРИСТ И УДИВИТЕЛЬНОЕ ПУТЕШЕСТВИЕ В ФИЗИОНОМИЧЕСКОМ ПРОСТРАНСТВЕ
НЕ УЗНАТЬ это лицо, пожалуй, невозможно. Эти ннэкорасположенные крупные уши, выразительные скулы, высокая прическа в стиле "помпадур". Лицо Роналда Рейгана знакомо всем, однако его быстрее узнаешь на карикатуре, чем на фотографии. Конечно, искусство карикатуры требует глубокого проникновения в человеческую природу. Если тут н найдется место для компьютера, то лишь в роли тривиального вспомогательного средства, что-то наподобие эскизного блокнота для сохранения промежуточных результатов творческих поисков карикатуриста и представления их в визуальной форме.
Но только ли в этой роли? Все карикатуры, изображенные на рисунке внизу, построены программой, которую составила Сьюзен Брениан, научный сотрудник исследовательской лаборатории фирмы Hewlett-Packard в Пало-Альто (шт.Калифорния). При работе с программой удобно пользоваться манипулятором типа "мышь", световым пером или каким-нибудь другим аналогом карандаша, однако это вовсе не обязательно. Результаты едва ли зависят от таких качеств, как твердость руки и тренированный глаз. Как только черты с фотографии лица введены в машину, всю остальную работу выполняет уже программа, которая совершенно самостоятельно рисует карикатуру. Как она это делает? На этот вопрос можно дать короткий и обманчиво простой ответ: программа сравнивает "фотографию" представленного ей лица с неким "среднестатистическим" лицом, хранящимся в памяти компьютера. Те черты, которые наиболее сильно отличаются от соответствующих черт среднестатистического лица, подвергаются изменениям в масштабе, подчеркивающим эти отличия.

Трансформация изображения лица Роналда Рейгана при построении карикатуры с помощью программы FACEBENDER, авторам которой является С.Бреннан
Программа Бреннан явилась как бы естественным результатом, с одной стороны, ее собственного таланта как художника-карикатуриста, а с другой - ее научного интереса к процессам, протекающим в человеческом мозгу при распознавании изображений, и в частности при узнавании лиц. Эти процессы уже давно стали загадкой для психологов и других специалистов, интересующихся работой мозга и высшей нервной деятельностью, а карикатуры, по-видимому, играют особую роль в этих процессах, потому что, когда их узнают, то узнают практически мгновенно. Может быть, вместо того чтобы хранить в памяти все черты лица своего знакомого, мы храним лишь его карикатуру? Чтобы разобраться в этом вопросе, Бреннан изобрела простой метод создания карикатуры и представила его описание в диссертации, которую она защищала в Массачусетском технологическом институте. Она и теперь продолжает интересоваться этими вопросами, но уже в свободное время. Свои рабочие часы она посвящает экспериментам в области новых форм общения между человеком и машиной, основанных, в частности, на понимании машиной естественного языка.
Метод построения карикатуры, изобретенный Бреннан, напоминает трюк, которым часто пользуются художники-мультипликаторы, работающие с компьютером. Они называют его "усреднением". Представим себе два рисунка, изображающих такие знакомые нам предметы, как яблоко и банан. Оба рисунка - контурные очертания плодов и получены путем соединения точек отрезками прямых линий (см. рисунок на с.154). Каждой точке на изображении яблока поставим в соответствие точку на изображении банана. Если теперь соединить соответствующие точки отрезками прямых линий и отметить точками середины этих линий, то, соединив эти средние точки, мы получим контур совершенно нового фрукта, представляющего собой нечто среднее между яблоком и бананом - "банаблоко".
Превращение яблока в банан и карикатура на банан
При помощи тех же линий, которые соединяют банан и яблоко, можно также получить изображение гротескного, карикатурного банана, если так можно выразиться, с точки зрения яблока. Для этого продолжим каждую линию за пределы банана на половину ее длины и на конце отрезка поставим точку. Если теперь соединить между собой все полученные таким образом точки, то мы построим контурный рисунок карикатурного банана. Аналогично, продолжив соединительные линии между бананом и яблоком за пределы яблока, мы получим карикатурное изображение яблока, с точки зрения банана. Подобную процедуру можно применить и к портретам. Каждая пара физиономий в каком-то смысле представляет собой две взаимные карикатуры. Однако самые удачные карикатуры получаются на основе сравнения данной физиономии с нормальным, так сказать "среднестатистическим" лицом.
Изображения таких нормальных лиц программа Бреннан строит по нескольким десяткам портретов реальных людей. В закодированном виде эти портреты хранятся в базе данных компьютера, насчитывающей их несколько сот. Для работы с этими портретами были выбраны наиболее характерные точки, лучше всего отражающие особенности любого лица. Точки упорядочены и помечены в соответствии с их положением на плоскости относительно координатных осей. В качестве начала координат выбран левый верхний угол плоскости изображения. Значения координат увеличиваются слева направо и сверху вниз. Масштаб при этом выбирается таким образом, чтобы центр левого зрачка находился в точке с координатами (135, 145), а центр правого - в точке (190, 145). Координаты соответственных точек каждого лица усредняются и, таким образом, для каждой представительной точки человеческого лица мы имеем нормальное ее положение. Например, усредненное значение координат внешнего конца левой брови дает положение на координатной плоскости этой характерной точки для нормального, или среднестатистического, лица. При помощи такого усреднения программа строит три нормальных портрета: среднестатистическое мужское лицо, среднестатистическое женское лицо и полностью усредненный, лишенный каких-либо половых признаков абстрактный портрет. Этот последний портрет и служит основой для большинства карикатур.

Бесполое среднестатистическое лицо
Для того чтобы программа могла нарисовать карикатуру, основанную на нормальном портрете, ей нужно представить цифровое описание реального лица. Как правило, при этом пользуются фотографией, и программа поочередно запрашивает координаты (или положение) 186 ключевых точек на фотографии. Например, когда программа ожидает ввода данных о шести точках, описывающих форму левой брови, пользователь последовательно передвигает курсор и отмечает положение соответствующих точек на левой брови на приложенной к экрану фотографии.
Образно говоря, программа Бреннан, как космический корабль, совершает путешествие в физиономическом пространстве и исследует его. Введенные в машину значения координат точек, определяющих портрет на фотографии, можно представить в виде единого упорядоченного массива данных. В результате получается список чисел, которые можно рассматривать как координатные значения одной-единственной точки в многомерном пространстве. В самом деле, как абстрактное нормальное лицо, так и лицо на фотографии представляются 186 точками, каждая из которых имеет два координатных значения. Получающийся в результате список из 372 чисел для каждого лица является представлением точки в 372-мерном пространстве. В принципе каждому конкретному лицу можно поставить в соответствие точку в пространстве физиономий, и любые две физиономии в этом пространстве можно соединить прямой линией.
В данном случае не следует особо глубоко задумываться о таинственных свойствах пространства высокой размерности. Многомерное физиономическое пространство - это просто удобная абстракция, позволяющая количественно описывать сходство и различие между лицами. У знакомых нам понятий, таких, как прямая линия и расстояние между двумя точками, есть непосредственные аналоги и в пространстве любой высокой размерности. Все точки, лежащие в физиономическом пространстве на одной прямой линии, представляют собой пропорциональные изменения координатных значений. Расстояние между двумя точками в этом пространстве служит мерой сходства между соответствующими им лицами: схожие лица - близкие соседи в физиономическом пространстве, несхожие расположены далеко друг от друга.
Абстрактный, или среднестатистический, человеческий портрет в физиономическом пространстве можно представить себе лежащим в центре скопления точек, соответствующих изображениям реальных человеческих лиц. Каждое реальное лицо соединено с абстрактным портретом ("нормой") прямой линией. Точки же, лежащие на этой линии, есть последовательность промежуточных физиономий, все более похожих на реальное лицо, представленное конечной точкой отрезка. Если же продолжить эту линию, то принадлежащие продолжению точки уже будут соответствовать карикатурным изображениям данного лица. Однако для карикатурных преувеличений существует предел, за которым в изображении уже трудно узнать не только конкретного человека, но и человека вообще. Такие изображения вырождаются в хаотические сплетения линий и принадлежат области физиономического пространства, которую Бреннан называет "безликой".
Идея о представлении каждого лица точкой в многомерном пространстве, наводит на мысль еще об одном интересном преобразовании. Поскольку любые два лица в этом пространстве можно соединить прямой линией, то программе можно задать построение последовательности промежуточных физиономий. По мнению Бреннан, такие последовательности выглядят особенно интригующими, когда две конечные точки прямо соответствуют мужскому и женскому лицам. Так, без особого труда программа преобразует, например, лицо Элизабет Тейлор в портрет покойного президента Джона Кеннеди.

Элизабет Тейлор (в роли Клеопатры) встречается с бывшим президентом Кеннеди в физиономическом пространстве
Читатель может повторить некоторые из карикатурных подвигов Бреннан, написав свою, упрощенную версию ее программы. Назовем ее FACEBENDER (карикатура). В качестве входных данных ей нужна информация по крайней мере о двух лицах: абстрактной "норме" и лице, карикатурное изображение которого требуется построить. Координаты точек элементов абстрактного лица - нормы были любезно предоставлены нам Сьюзен Бреннан (см. рисунок на с.156). В такой же форме читателям нужно самим представить лицо для карикатуры. При отсутствии средств графико-цифрового преобразования без особого труда можно преобразовать фотографию любимого человека (возможно, самого себя) в аналогичный перечень точек с указанием их координат. Однако Бренная предупреждает, что лицо на фотографии должно иметь спокойное нейтральное выражение, даже небольшая улыбка может превратиться в чудовищную гримасу. Лицо на фотографии должно быть снято строго "анфас"; если оно слегка повернуто в сторону, FACEBENDER повернет его еще больше.

Координаты ключевых точек для абстрактного лица
Чтобы выбрать подходящий масштаб для координатных осей, считайте, что координаты левого и правого зрачка те же, что и у абстрактной нормы: центр левого зрачка должен находиться в точке (135, 145), а правого - в точке (190, 145). (Напомним, что на горизонтальной оси координат значения возрастают слева направо, а на вертикальной - сверху вниз). После того как масштаб установлен, необходимо найти координаты остальных ключевых точек лица путем тщательных измерений. В схеме, используемой Бреннан, представительные точки человеческого портрета распределены по 39 характерным элементам. Каждый элемент - это последовательность соединенных между собой точек. Их порядок зависит от ориентации данного элемента (черты лица): для черт, имеющих в основном горизонтальную ориентацию, точки перечислены слева направо, а для черт, ориентированных вертикально, они перечислены сверху вниз.
Бреннан признается, что ключевые точки на человеческом портрете в основном выбираются методом проб и ошибок; в этом смысле приведенный здесь портрет президента весьма показателен и может служить образцом. Важно, чтобы преобразования фотографий человеческих лиц в списки координат, вводимые в базу данных программы, выполнялись одним человеком.
Программа FACEBENDER хранит два цифровых массива - face и norm (соответственно лицо и норма). Третий массив disp нужен для воспроизведения лица на экране дисплея. Все три массива имеют по 186 строк и по 2 столбца: по одной точке на строку и по одному координатному значению на столбец. Точки расположены в специально подобранном порядке, который задан в списке данных для абстрактного портрета. Преимущество такого упорядочения в том, что в результирующем рисунке линии проводятся между точками, расположенными в массиве по соседству друг к другу. Однако не все соседние в массиве точки соединяются линиями. Линии прерываются, когда завершено изображение одной черты лица и начинается изображение другой.
Первый элемент, который рисует программа,- это зрачок левого глаза, затем изображается зрачок правого глаза. На рисунке зрачок может быть представлен либо как точка, либо как небольшой кружок. (Во втором варианте лицо выглядит более приветливым). При изображении всех остальных элементов используется одна и та же техника - соседние точки в массиве соединяются линиями. Для этого нужен специальный массив features (черты, характерные элементы), указывающий, когда следует сделать разрыв между последней точкой одного элемента и первой точкой следующего. Массив задает количество точек в каждом элементе, а соответствующими пропусками управляет двойной цикл (см. рисунок на с.156).

Ключевой фрагмент программы FACEBENDER
Поскольку два элемента лица уже были нарисованы, процедура отображения начинается с третьего элемента, а именно с радужной оболочки левого глаза. Первая точка этого элемента является третьей точкой в массиве disp, проиндексированном переменной i. Поэтому исходное значение i равно 3. Массив features проиндексирован другой переменной, j, которая пробегает значения от 1 до 37, поскольку остается еще 37 черт. Внутри цикла по j введена еще одна переменная count (счетчик), которая следит за количеством линий, уже нарисованных в данном элементе. При каждом новом прохождении цикла по j значение переменной count устанавливается равным 1, а значение j увеличивается на 1. Значение индекса i также каждый раз увеличивается на 1, оно указывает на переход к очередной точке массива disp, который в данный момент участвует в процессе быстро протекающего соединения точек на экране.
Цикл по индексу j содержит в себе второй цикл, while (ожидание). Он сравнивает количество точек элемента j, уже соединенных между собой, с полным количеством точек данного элемента. Когда эти два числа оказываются равными, программа выходит из цикла while, так как изображение данного элемента завершено. Если в этом элементе остаются еще не соединенные точки, программа проводит на экране линию между точками, индексы которых в массиве disp равны соответственно i и i+1. Конечно, я описываю этот процесс, пользуясь сокращенными обозначениями. На самом деле в команде отображения линии на экране координаты точек будут указаны в виде disp(i, 1) и disp(i, 2) для первой точки и disp(i+1, 1), disp(i+1, 2) - для второй.
Главным компонентом программы FACEBENDER является процедура "преувеличения". Ее внутренняя структура, пожалуй, даже проще, чем у только что рассмотренной процедуры отображения (см. нижний рисунок на с.156). Для каждой из 186 точек в массивах face и norm подсчитывается значение элемента нового массива bend (искажение). В этом новом массиве закодирована будущая карикатура. Значения координат каждой точки в массиве bend вычисляются путем прибавления к соответствующей координате массива norm определенной величины, которая увеличивает разрыв между положениями точек, взятых из массивов face и norm. Фактор преувеличения/вводится в программу пользователем перед началом выполнения программы. На этот фактор умножается разность между соответствующими горизонтальными и соответствующими вертикальными координатами массивов face и norm.
Осталось лишь рассмотреть вопросы, связанные с компоновкой программы, а также с настройкой процедуры отображения, впрочем, последнее уже не обязательно. Проще всего, наверное, организовать программу таким образом, чтобы обе основные процедуры отображения и преувеличения были вложены в интерактивный иикл диалога с пользователем, в котором программа могла бы, например, спрашивать: "Нарисовать еще одну линию?" Программа должна также запрашивать пользователя о величине фактора преувеличения. Команду ввода этой величины следует расположить в программе таким образом, чтобы можно было попробовать различные факторы, не вводя заново массива face, так будет удобнее наблюдать, как влияет на карикатуру величина фактора f
.
Качество рисунков можно несколько улучшить, если точки соединять не прямолинейными отрезками, а участками кривых, так называемыми сплайнами; контуры рисунка при этом сглаживаются. Программа Бреннан, как правило, соединяет соседние точки сплайнами. При подготовке этой статьи я понимал, что объяснить технику рисования сплайнами довольно трудно, к тому же статьи в рубрике "Занимательный компьютер" в основном посвящаются описанию несложных программ. Я спросил Бреннан, нельзя ли воспользоваться каким-нибудь другим, упрощенным методом. Можно ли, например, пользоваться отрезками прямых? К нашему обоюдному удивлению, карикатуры, нарисованные прямыми линиями, оказались почти такими же выразительными, как и те, которые выполнены сплайнами. На самом деле все рисунки, помешенные в этой статье, были сделаны с применением прямых линий. Таким образом, можно избежать сложных, трудоемких методов с относительно небольшими потерями в эстетическом отношении. Теперь читатели могут приступить к преобразованию в цифровую форму фотографий своих любимых.
Генератор карикатур Бреннан был применен в нескольких экспериментальных исследованиях по узнаванию лиц. Изображения, построенные ее программой, передавались по телефонным линиям как часть эксперимента по проведению телеконференций, осуществляемого в лаборатории средств массовой информации Массачусетского технологического института. В прошлом году Бреннан провела эксперименты совместно с Джиллиан Роудс из Университета в Отаго (Новая Зеландия), в то время аспиранткой, которая работала с Роджером Шепардом из Станфордского университета. Были сгенерированы карикатуры на преподавателей и студентов психологического факультета Станфордского университета. Затем карикатуры наряду с обычными рисованы ми портретами были подвергнуты тестам на узнавание.
Результаты эксперимента Бреннан подытожила следующим образом: "Генератор карикатур оказался в этих исследованиях очень полезным, потому что благодаря ему мы могли непрерывно варьировать стимулирование и управлять им. В предыдущих экспериментах подобного рода карикатуры приходилось сравнивать непосредственно с фотографиями или какими-то другими изображениями, стиль выполнения которых был относительно далеким от изображения карикатуры, и поэтому эксперименты не были свободны от эффектов, связанных с характером представления. Нельзя сказать, что карикатуры существенно ПРЕВЗОШЛИ обычные рисунки в плане узнавания ("наилучшими" в этом смысле оказались рисунки с небольшими преувеличениями), но зато, когда гротескные карикатуры узнавались, они узнавались значительно быстрее - почти вдвое БЫСТРЕЕ, чем реалистические изображения тех же самых людей".
Бреннан предложила также ряд других экспериментов с генератором карикатур. Например, было бы очень интересно воссоздать абстрактный портрет-норму, интуитивно принимаемую карикатуристами. Имея в руках карикатуру на известного человека, выполненную известным мастером, с помощью программы Бреннан можно попытаться обратить процесс построения карикатуры и восстановить нормальное человеческое лицо, отпечатавшееся где-то в подсознании художника, т.е. лицо, из которого было "выведено" преувеличение в карикатуре. Будут ли полученные таким образом из карикатур нормы отличаться при использовании различных оригиналов? Будут ли нормы, отпечатавшиеся в подсознании различных художников, отличаться друг от друга?
БИБЛИОГРАФИЯ
CARICATURE GENERATOR: THE DYNAMICS EXAGGERATION OF FACES BY COMPUTER. SUSAN E. BRENNAN in Leonardo, Vol.18, No.3, pages 170-178; 1985.
FACE TO FACE: IT'S THE EXPRESSION THAT BEARS THE MESSAGE. JEANNE MCDERMOTT in Smithsonian, Vol.16, No.12, pages 112-123; March. 1986.
ОТКЛИКИ
3 1987
В ДЕКАБРЬСКОМ номере журнала за прошлый год в рубрике "Занимательный компьютер" была помешена статья с описанием программы, строящей карикатуры и созданной под влиянием работы С.Бреннан, сотрудницы фирмы Hewlett-Packard Laboratories в Пало-Альто (шт.Калифорния). В качестве входных данных в программу вводится цифровая версия портрета, карикатурное изображение которого должна построить программа. Введенный цифровой портрет программа сравнивает со среднестатистическим лицом, также хранящимся в памяти компьютера в цифровой форме. Затем программа увеличивает каждую черту представленного ей портрета с коэффициентом, пропорциональным тому расстоянию, на которое отстоят друг от друга соответствующие точки двух портретов. Если, например, ухо окажется несколько большим, чем у среднестатистического лица, то программа сделает его еще большим, помножив расстояния мгжду соответствующими точками на множитель искажения k.
Читателей, которые хотели бы сами реализовать программу FACE-BENDER, возможно, несколько отпугивает перспектива перевода в цифровую форму своего собственного лица с фотографии. П.Макалузо из Уайт-Плейнза (шт.Нью-Йорк) в качестве исходного портрета для карикатуры использует среднестатистическое лицо. "Главное,- пишет Макалузо,- подобрать диапазон вариаций таким образом, чтобы он соответствовал размеру данной черты лица. Так, например, величина уха может варьировать в более широких пределах, чем ямочка на подбородке. Лля каждой черты лниы мы просто строим "описываюший" ее прямоугольник, вычислив максимально возможные и минимально возможные координаты x и y для этой черты". В этих зафиксированных диапазонах фактор искажения выбирается с использованием датчика случайных чисел в ходе выполнения программы. Таким образом, пользуясь версией программы FACEBENDER, созданной Макалузо, можно без труда получить целую галерею портретов. Одна из построенных этой программой карикатур напоминает портрет Леонардо да Винчи. Она показана слева.

Карикатура на среднестатистическое лицо
Читатель из Пасалина (шт.Калифорния), известный нам только по своим инициалам Д.М.И., сделал предложение, позволяющее избежать "безликости" - ужасного состояния программы, когда коэффициент искажения становится слишком большим. Все черты лица превращаются при этом в какое-то невообразимое и неузнаваемое птичье гнездо из многоугольников. Представим себе, что лицо, предназначенное для карикатуры, наложено на среднестатистическое лицо и что соответственные точки обоих портретов связаны между собой пружинками. Теперь, когда искажающая процедура пытается переместить представительные точки введенного лица, она встречает со стороны пружинок определенное сопротивление. На относительно небольшие искажения оно оказывает пренебрежимо малое воздействие, но при увеличении размеров искажения сопротивление пружинок растет и в конечном итоге не позволяет изображению стать "безликим".
КОМПЬЮТЕР-КАРИКАТУРИСТ И УДИВИТЕЛЬНОЕ ПУТЕШЕСТВИЕ В ФИЗИОНОМИЧЕСКОМ ПРОСТРАНСТВЕ
НЕ УЗНАТЬ это лицо, пожалуй, невозможно. Эти ннэкорасположенные крупные уши, выразительные скулы, высокая прическа в стиле "помпадур". Лицо Роналда Рейгана знакомо всем, однако его быстрее узнаешь на карикатуре, чем на фотографии. Конечно, искусство карикатуры требует глубокого проникновения в человеческую природу. Если тут н найдется место для компьютера, то лишь в роли тривиального вспомогательного средства, что-то наподобие эскизного блокнота для сохранения промежуточных результатов творческих поисков карикатуриста и представления их в визуальной форме.
Но только ли в этой роли? Все карикатуры, изображенные на рисунке внизу, построены программой, которую составила Сьюзен Брениан, научный сотрудник исследовательской лаборатории фирмы Hewlett-Packard в Пало-Альто (шт.Калифорния). При работе с программой удобно пользоваться манипулятором типа "мышь", световым пером или каким-нибудь другим аналогом карандаша, однако это вовсе не обязательно. Результаты едва ли зависят от таких качеств, как твердость руки и тренированный глаз. Как только черты с фотографии лица введены в машину, всю остальную работу выполняет уже программа, которая совершенно самостоятельно рисует карикатуру. Как она это делает? На этот вопрос можно дать короткий и обманчиво простой ответ: программа сравнивает "фотографию" представленного ей лица с неким "среднестатистическим" лицом, хранящимся в памяти компьютера. Те черты, которые наиболее сильно отличаются от соответствующих черт среднестатистического лица, подвергаются изменениям в масштабе, подчеркивающим эти отличия.


Трансформация изображения лица Роналда Рейгана при построении карикатуры с помощью программы FACEBENDER, авторам которой является С.Бреннан
Программа Бреннан явилась как бы естественным результатом, с одной стороны, ее собственного таланта как художника-карикатуриста, а с другой - ее научного интереса к процессам, протекающим в человеческом мозгу при распознавании изображений, и в частности при узнавании лиц. Эти процессы уже давно стали загадкой для психологов и других специалистов, интересующихся работой мозга и высшей нервной деятельностью, а карикатуры, по-видимому, играют особую роль в этих процессах, потому что, когда их узнают, то узнают практически мгновенно. Может быть, вместо того чтобы хранить в памяти все черты лица своего знакомого, мы храним лишь его карикатуру? Чтобы разобраться в этом вопросе, Бреннан изобрела простой метод создания карикатуры и представила его описание в диссертации, которую она защищала в Массачусетском технологическом институте. Она и теперь продолжает интересоваться этими вопросами, но уже в свободное время. Свои рабочие часы она посвящает экспериментам в области новых форм общения между человеком и машиной, основанных, в частности, на понимании машиной естественного языка.
Метод построения карикатуры, изобретенный Бреннан, напоминает трюк, которым часто пользуются художники-мультипликаторы, работающие с компьютером. Они называют его "усреднением". Представим себе два рисунка, изображающих такие знакомые нам предметы, как яблоко и банан. Оба рисунка - контурные очертания плодов и получены путем соединения точек отрезками прямых линий (см. рисунок на с.154). Каждой точке на изображении яблока поставим в соответствие точку на изображении банана. Если теперь соединить соответствующие точки отрезками прямых линий и отметить точками середины этих линий, то, соединив эти средние точки, мы получим контур совершенно нового фрукта, представляющего собой нечто среднее между яблоком и бананом - "банаблоко".

Превращение яблока в банан и карикатура на банан
При помощи тех же линий, которые соединяют банан и яблоко, можно также получить изображение гротескного, карикатурного банана, если так можно выразиться, с точки зрения яблока. Для этого продолжим каждую линию за пределы банана на половину ее длины и на конце отрезка поставим точку. Если теперь соединить между собой все полученные таким образом точки, то мы построим контурный рисунок карикатурного банана. Аналогично, продолжив соединительные линии между бананом и яблоком за пределы яблока, мы получим карикатурное изображение яблока, с точки зрения банана. Подобную процедуру можно применить и к портретам. Каждая пара физиономий в каком-то смысле представляет собой две взаимные карикатуры. Однако самые удачные карикатуры получаются на основе сравнения данной физиономии с нормальным, так сказать "среднестатистическим" лицом.
Изображения таких нормальных лиц программа Бреннан строит по нескольким десяткам портретов реальных людей. В закодированном виде эти портреты хранятся в базе данных компьютера, насчитывающей их несколько сот. Для работы с этими портретами были выбраны наиболее характерные точки, лучше всего отражающие особенности любого лица. Точки упорядочены и помечены в соответствии с их положением на плоскости относительно координатных осей. В качестве начала координат выбран левый верхний угол плоскости изображения. Значения координат увеличиваются слева направо и сверху вниз. Масштаб при этом выбирается таким образом, чтобы центр левого зрачка находился в точке с координатами (135, 145), а центр правого - в точке (190, 145). Координаты соответственных точек каждого лица усредняются и, таким образом, для каждой представительной точки человеческого лица мы имеем нормальное ее положение. Например, усредненное значение координат внешнего конца левой брови дает положение на координатной плоскости этой характерной точки для нормального, или среднестатистического, лица. При помощи такого усреднения программа строит три нормальных портрета: среднестатистическое мужское лицо, среднестатистическое женское лицо и полностью усредненный, лишенный каких-либо половых признаков абстрактный портрет. Этот последний портрет и служит основой для большинства карикатур.

Бесполое среднестатистическое лицо
Для того чтобы программа могла нарисовать карикатуру, основанную на нормальном портрете, ей нужно представить цифровое описание реального лица. Как правило, при этом пользуются фотографией, и программа поочередно запрашивает координаты (или положение) 186 ключевых точек на фотографии. Например, когда программа ожидает ввода данных о шести точках, описывающих форму левой брови, пользователь последовательно передвигает курсор и отмечает положение соответствующих точек на левой брови на приложенной к экрану фотографии.
Образно говоря, программа Бреннан, как космический корабль, совершает путешествие в физиономическом пространстве и исследует его. Введенные в машину значения координат точек, определяющих портрет на фотографии, можно представить в виде единого упорядоченного массива данных. В результате получается список чисел, которые можно рассматривать как координатные значения одной-единственной точки в многомерном пространстве. В самом деле, как абстрактное нормальное лицо, так и лицо на фотографии представляются 186 точками, каждая из которых имеет два координатных значения. Получающийся в результате список из 372 чисел для каждого лица является представлением точки в 372-мерном пространстве. В принципе каждому конкретному лицу можно поставить в соответствие точку в пространстве физиономий, и любые две физиономии в этом пространстве можно соединить прямой линией.
В данном случае не следует особо глубоко задумываться о таинственных свойствах пространства высокой размерности. Многомерное физиономическое пространство - это просто удобная абстракция, позволяющая количественно описывать сходство и различие между лицами. У знакомых нам понятий, таких, как прямая линия и расстояние между двумя точками, есть непосредственные аналоги и в пространстве любой высокой размерности. Все точки, лежащие в физиономическом пространстве на одной прямой линии, представляют собой пропорциональные изменения координатных значений. Расстояние между двумя точками в этом пространстве служит мерой сходства между соответствующими им лицами: схожие лица - близкие соседи в физиономическом пространстве, несхожие расположены далеко друг от друга.
Абстрактный, или среднестатистический, человеческий портрет в физиономическом пространстве можно представить себе лежащим в центре скопления точек, соответствующих изображениям реальных человеческих лиц. Каждое реальное лицо соединено с абстрактным портретом ("нормой") прямой линией. Точки же, лежащие на этой линии, есть последовательность промежуточных физиономий, все более похожих на реальное лицо, представленное конечной точкой отрезка. Если же продолжить эту линию, то принадлежащие продолжению точки уже будут соответствовать карикатурным изображениям данного лица. Однако для карикатурных преувеличений существует предел, за которым в изображении уже трудно узнать не только конкретного человека, но и человека вообще. Такие изображения вырождаются в хаотические сплетения линий и принадлежат области физиономического пространства, которую Бреннан называет "безликой".
Идея о представлении каждого лица точкой в многомерном пространстве, наводит на мысль еще об одном интересном преобразовании. Поскольку любые два лица в этом пространстве можно соединить прямой линией, то программе можно задать построение последовательности промежуточных физиономий. По мнению Бреннан, такие последовательности выглядят особенно интригующими, когда две конечные точки прямо соответствуют мужскому и женскому лицам. Так, без особого труда программа преобразует, например, лицо Элизабет Тейлор в портрет покойного президента Джона Кеннеди.

Элизабет Тейлор (в роли Клеопатры) встречается с бывшим президентом Кеннеди в физиономическом пространстве
Читатель может повторить некоторые из карикатурных подвигов Бреннан, написав свою, упрощенную версию ее программы. Назовем ее FACEBENDER (карикатура). В качестве входных данных ей нужна информация по крайней мере о двух лицах: абстрактной "норме" и лице, карикатурное изображение которого требуется построить. Координаты точек элементов абстрактного лица - нормы были любезно предоставлены нам Сьюзен Бреннан (см. рисунок на с.156). В такой же форме читателям нужно самим представить лицо для карикатуры. При отсутствии средств графико-цифрового преобразования без особого труда можно преобразовать фотографию любимого человека (возможно, самого себя) в аналогичный перечень точек с указанием их координат. Однако Бренная предупреждает, что лицо на фотографии должно иметь спокойное нейтральное выражение, даже небольшая улыбка может превратиться в чудовищную гримасу. Лицо на фотографии должно быть снято строго "анфас"; если оно слегка повернуто в сторону, FACEBENDER повернет его еще больше.

Координаты ключевых точек для абстрактного лица
Чтобы выбрать подходящий масштаб для координатных осей, считайте, что координаты левого и правого зрачка те же, что и у абстрактной нормы: центр левого зрачка должен находиться в точке (135, 145), а правого - в точке (190, 145). (Напомним, что на горизонтальной оси координат значения возрастают слева направо, а на вертикальной - сверху вниз). После того как масштаб установлен, необходимо найти координаты остальных ключевых точек лица путем тщательных измерений. В схеме, используемой Бреннан, представительные точки человеческого портрета распределены по 39 характерным элементам. Каждый элемент - это последовательность соединенных между собой точек. Их порядок зависит от ориентации данного элемента (черты лица): для черт, имеющих в основном горизонтальную ориентацию, точки перечислены слева направо, а для черт, ориентированных вертикально, они перечислены сверху вниз.
Бреннан признается, что ключевые точки на человеческом портрете в основном выбираются методом проб и ошибок; в этом смысле приведенный здесь портрет президента весьма показателен и может служить образцом. Важно, чтобы преобразования фотографий человеческих лиц в списки координат, вводимые в базу данных программы, выполнялись одним человеком.
Программа FACEBENDER хранит два цифровых массива - face и norm (соответственно лицо и норма). Третий массив disp нужен для воспроизведения лица на экране дисплея. Все три массива имеют по 186 строк и по 2 столбца: по одной точке на строку и по одному координатному значению на столбец. Точки расположены в специально подобранном порядке, который задан в списке данных для абстрактного портрета. Преимущество такого упорядочения в том, что в результирующем рисунке линии проводятся между точками, расположенными в массиве по соседству друг к другу. Однако не все соседние в массиве точки соединяются линиями. Линии прерываются, когда завершено изображение одной черты лица и начинается изображение другой.
Первый элемент, который рисует программа,- это зрачок левого глаза, затем изображается зрачок правого глаза. На рисунке зрачок может быть представлен либо как точка, либо как небольшой кружок. (Во втором варианте лицо выглядит более приветливым). При изображении всех остальных элементов используется одна и та же техника - соседние точки в массиве соединяются линиями. Для этого нужен специальный массив features (черты, характерные элементы), указывающий, когда следует сделать разрыв между последней точкой одного элемента и первой точкой следующего. Массив задает количество точек в каждом элементе, а соответствующими пропусками управляет двойной цикл (см. рисунок на с.156).

Ключевой фрагмент программы FACEBENDER
Поскольку два элемента лица уже были нарисованы, процедура отображения начинается с третьего элемента, а именно с радужной оболочки левого глаза. Первая точка этого элемента является третьей точкой в массиве disp, проиндексированном переменной i. Поэтому исходное значение i равно 3. Массив features проиндексирован другой переменной, j, которая пробегает значения от 1 до 37, поскольку остается еще 37 черт. Внутри цикла по j введена еще одна переменная count (счетчик), которая следит за количеством линий, уже нарисованных в данном элементе. При каждом новом прохождении цикла по j значение переменной count устанавливается равным 1, а значение j увеличивается на 1. Значение индекса i также каждый раз увеличивается на 1, оно указывает на переход к очередной точке массива disp, который в данный момент участвует в процессе быстро протекающего соединения точек на экране.
Цикл по индексу j содержит в себе второй цикл, while (ожидание). Он сравнивает количество точек элемента j, уже соединенных между собой, с полным количеством точек данного элемента. Когда эти два числа оказываются равными, программа выходит из цикла while, так как изображение данного элемента завершено. Если в этом элементе остаются еще не соединенные точки, программа проводит на экране линию между точками, индексы которых в массиве disp равны соответственно i и i+1. Конечно, я описываю этот процесс, пользуясь сокращенными обозначениями. На самом деле в команде отображения линии на экране координаты точек будут указаны в виде disp(i, 1) и disp(i, 2) для первой точки и disp(i+1, 1), disp(i+1, 2) - для второй.
Главным компонентом программы FACEBENDER является процедура "преувеличения". Ее внутренняя структура, пожалуй, даже проще, чем у только что рассмотренной процедуры отображения (см. нижний рисунок на с.156). Для каждой из 186 точек в массивах face и norm подсчитывается значение элемента нового массива bend (искажение). В этом новом массиве закодирована будущая карикатура. Значения координат каждой точки в массиве bend вычисляются путем прибавления к соответствующей координате массива norm определенной величины, которая увеличивает разрыв между положениями точек, взятых из массивов face и norm. Фактор преувеличения/вводится в программу пользователем перед началом выполнения программы. На этот фактор умножается разность между соответствующими горизонтальными и соответствующими вертикальными координатами массивов face и norm.
Осталось лишь рассмотреть вопросы, связанные с компоновкой программы, а также с настройкой процедуры отображения, впрочем, последнее уже не обязательно. Проще всего, наверное, организовать программу таким образом, чтобы обе основные процедуры отображения и преувеличения были вложены в интерактивный иикл диалога с пользователем, в котором программа могла бы, например, спрашивать: "Нарисовать еще одну линию?" Программа должна также запрашивать пользователя о величине фактора преувеличения. Команду ввода этой величины следует расположить в программе таким образом, чтобы можно было попробовать различные факторы, не вводя заново массива face, так будет удобнее наблюдать, как влияет на карикатуру величина фактора f
.
Качество рисунков можно несколько улучшить, если точки соединять не прямолинейными отрезками, а участками кривых, так называемыми сплайнами; контуры рисунка при этом сглаживаются. Программа Бреннан, как правило, соединяет соседние точки сплайнами. При подготовке этой статьи я понимал, что объяснить технику рисования сплайнами довольно трудно, к тому же статьи в рубрике "Занимательный компьютер" в основном посвящаются описанию несложных программ. Я спросил Бреннан, нельзя ли воспользоваться каким-нибудь другим, упрощенным методом. Можно ли, например, пользоваться отрезками прямых? К нашему обоюдному удивлению, карикатуры, нарисованные прямыми линиями, оказались почти такими же выразительными, как и те, которые выполнены сплайнами. На самом деле все рисунки, помешенные в этой статье, были сделаны с применением прямых линий. Таким образом, можно избежать сложных, трудоемких методов с относительно небольшими потерями в эстетическом отношении. Теперь читатели могут приступить к преобразованию в цифровую форму фотографий своих любимых.
Генератор карикатур Бреннан был применен в нескольких экспериментальных исследованиях по узнаванию лиц. Изображения, построенные ее программой, передавались по телефонным линиям как часть эксперимента по проведению телеконференций, осуществляемого в лаборатории средств массовой информации Массачусетского технологического института. В прошлом году Бреннан провела эксперименты совместно с Джиллиан Роудс из Университета в Отаго (Новая Зеландия), в то время аспиранткой, которая работала с Роджером Шепардом из Станфордского университета. Были сгенерированы карикатуры на преподавателей и студентов психологического факультета Станфордского университета. Затем карикатуры наряду с обычными рисованы ми портретами были подвергнуты тестам на узнавание.
Результаты эксперимента Бреннан подытожила следующим образом: "Генератор карикатур оказался в этих исследованиях очень полезным, потому что благодаря ему мы могли непрерывно варьировать стимулирование и управлять им. В предыдущих экспериментах подобного рода карикатуры приходилось сравнивать непосредственно с фотографиями или какими-то другими изображениями, стиль выполнения которых был относительно далеким от изображения карикатуры, и поэтому эксперименты не были свободны от эффектов, связанных с характером представления. Нельзя сказать, что карикатуры существенно ПРЕВЗОШЛИ обычные рисунки в плане узнавания ("наилучшими" в этом смысле оказались рисунки с небольшими преувеличениями), но зато, когда гротескные карикатуры узнавались, они узнавались значительно быстрее - почти вдвое БЫСТРЕЕ, чем реалистические изображения тех же самых людей".
Бреннан предложила также ряд других экспериментов с генератором карикатур. Например, было бы очень интересно воссоздать абстрактный портрет-норму, интуитивно принимаемую карикатуристами. Имея в руках карикатуру на известного человека, выполненную известным мастером, с помощью программы Бреннан можно попытаться обратить процесс построения карикатуры и восстановить нормальное человеческое лицо, отпечатавшееся где-то в подсознании художника, т.е. лицо, из которого было "выведено" преувеличение в карикатуре. Будут ли полученные таким образом из карикатур нормы отличаться при использовании различных оригиналов? Будут ли нормы, отпечатавшиеся в подсознании различных художников, отличаться друг от друга?
БИБЛИОГРАФИЯ
CARICATURE GENERATOR: THE DYNAMICS EXAGGERATION OF FACES BY COMPUTER. SUSAN E. BRENNAN in Leonardo, Vol.18, No.3, pages 170-178; 1985.
FACE TO FACE: IT'S THE EXPRESSION THAT BEARS THE MESSAGE. JEANNE MCDERMOTT in Smithsonian, Vol.16, No.12, pages 112-123; March. 1986.
ОТКЛИКИ
3 1987
В ДЕКАБРЬСКОМ номере журнала за прошлый год в рубрике "Занимательный компьютер" была помешена статья с описанием программы, строящей карикатуры и созданной под влиянием работы С.Бреннан, сотрудницы фирмы Hewlett-Packard Laboratories в Пало-Альто (шт.Калифорния). В качестве входных данных в программу вводится цифровая версия портрета, карикатурное изображение которого должна построить программа. Введенный цифровой портрет программа сравнивает со среднестатистическим лицом, также хранящимся в памяти компьютера в цифровой форме. Затем программа увеличивает каждую черту представленного ей портрета с коэффициентом, пропорциональным тому расстоянию, на которое отстоят друг от друга соответствующие точки двух портретов. Если, например, ухо окажется несколько большим, чем у среднестатистического лица, то программа сделает его еще большим, помножив расстояния мгжду соответствующими точками на множитель искажения k.
Читателей, которые хотели бы сами реализовать программу FACE-BENDER, возможно, несколько отпугивает перспектива перевода в цифровую форму своего собственного лица с фотографии. П.Макалузо из Уайт-Плейнза (шт.Нью-Йорк) в качестве исходного портрета для карикатуры использует среднестатистическое лицо. "Главное,- пишет Макалузо,- подобрать диапазон вариаций таким образом, чтобы он соответствовал размеру данной черты лица. Так, например, величина уха может варьировать в более широких пределах, чем ямочка на подбородке. Лля каждой черты лниы мы просто строим "описываюший" ее прямоугольник, вычислив максимально возможные и минимально возможные координаты x и y для этой черты". В этих зафиксированных диапазонах фактор искажения выбирается с использованием датчика случайных чисел в ходе выполнения программы. Таким образом, пользуясь версией программы FACEBENDER, созданной Макалузо, можно без труда получить целую галерею портретов. Одна из построенных этой программой карикатур напоминает портрет Леонардо да Винчи. Она показана слева.

Карикатура на среднестатистическое лицо
Читатель из Пасалина (шт.Калифорния), известный нам только по своим инициалам Д.М.И., сделал предложение, позволяющее избежать "безликости" - ужасного состояния программы, когда коэффициент искажения становится слишком большим. Все черты лица превращаются при этом в какое-то невообразимое и неузнаваемое птичье гнездо из многоугольников. Представим себе, что лицо, предназначенное для карикатуры, наложено на среднестатистическое лицо и что соответственные точки обоих портретов связаны между собой пружинками. Теперь, когда искажающая процедура пытается переместить представительные точки введенного лица, она встречает со стороны пружинок определенное сопротивление. На относительно небольшие искажения оно оказывает пренебрежимо малое воздействие, но при увеличении размеров искажения сопротивление пружинок растет и в конечном итоге не позволяет изображению стать "безликим".

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
1 1987
ИГРА "ЗВЕЗДНЫЙ БОЙ" ДЛЯ ДОМАШНИХ КОМПЬЮТЕРОВ
А.К.ДЬЮДНИ
Упоминал, журнал выкладывал - ТЕМА #67, АБЗАЦ #735
ТЕМА #67, АБЗАЦ #735 .- G.
.- G.
В НАЧАЛЕ 70-х годов я часто засиживался до позднего вечера в своем университетском кабинете в надежде на то, что студенты уже не будут отвлекать меня от работы. К моему несчастью, в расположенной рядом по коридору исследовательской лаборатории по машинной графике почти постоянно задерживались студенты, проводившие вечера за своей излюбленной игрой, называвшейся тогда по-разному: то "Звездный бой", то "Космическая война". [Вроде бы, "SpaceWar!". Почему у Дьюдни всплыл "STAR TREK", не знаю.- G.] "Стреляй! Скорее! Попал, попал!- то и дело доносились возгласы увлеченных игроков через плотно закрытую дверь моего кабинета.- Берегись, ракеты!" Этот шум не давал мне сосредоточиться. И, оказавшись не в состоянии работать, я обычно присоединялся к играющим. Полный твердой решимости вернуться к более серьезным занятиям после небольшого развлечения, я отправлялся в соседнюю лабораторию понаблюдать за игрой.
Игра "Звездный бой" в какой-то мере была основана на сюжете популярного многосерийного телевизионного фильма под таким же названием. Игра повторяет эпизоды боя между космическим кораблем "Энтерпрайз" и крейсером вооруженных сил клингов. Поклонники этой телевизионной программы, наверное, помнят, что "Энтерпрайз" совершил путешествие в ту область Вселенной, где люди еще никогда не бывали. Это путешествие совершалось под флагом союза сотрудничавших цивилизаций, называемого Федерацией. Главенствующую роль в союзе играла Человеческая раса. Клинги были представителями звероподобной волосатой расы, соперничавшей с Федерацией в борьбе за господство над Млечным Путем, а может быть, и над всей Вселенной.
Хотя первоначально игра "Звездный бой" могла выполняться лишь на мощном компьютере, оснащенном специальными графическими средствами, сейчас аналогичную программу вполне можно написать и для персонального компьютера. Два космических корабля описывают орбитальные траектории вокруг звезды, находящейся в центре, стреляя друг по другу ракетами и пытаясь в свою очередь уклониться от ракет противника. Как сами корабли, так и ракеты, которыми они обстреливают друг друга, подвержены гравитационному притяжению, и, таким образом, законы орбитального движения в значительной мере определяют характер игры. Пилоты, не обладающие достаточным интуитивным чутьем к законам небесной механики, либо сжигают свои корабли, неосторожно приблизившись к Солнцу, либо, не сумев сманеврировать, пересекают обманчивые траектории смертоносных ракет. Сторона, космический корабль которой взрывается первым, считается проигравшей.
Было время, когда различные версии игры "Звездный бой" распространились на сотни университетов и других учреждений. Официально это не одобрялось, но втайне все получали от игры много удовольствия. Хотя эта игра так часто мешала мне работать, теперь, через много лет я вспоминаю о ней с очень теплым чувством. "Звездный бой" - это лишь одна из многих увлекательных игр, созданных студентами. Большинство таких игр быстро превращались в законченные пакеты программ, представлявшие собой уже коммерческий продукт. По-видимому, игры внесли значительный вклад в ту революцию, которая произошла в области домашних компьютеров. Версии игры "Звездный бой" поступили в широкую продажу лишь сравнительно недавно, хотя в "подпольном" виде они кочевали уже давно.
Версия "Звездного боя", описанная в настоящей статье, вернет читателя к тем временам, когда появились первые компьютерные игры, окруженные атмосферой таинства и романтики. На ее примере я смогу посвятить читателя в секреты, без которых не обойтись при программировании игр. Прежде всего нужно стараться поддерживать непрерывное движение на экране. Поэтому вычисления в программе, реализующей игру "Звездный бой", должны быть как можно проще и выполняться как можно быстрее. С этой проблемой мы уже сталкивались в статье, посвященной программам, имитирующим полет (см.: "В мире науки", 1986, #9, с.92). К счастью, мир "Звездного боя" намного проще той детальной цифровой географии, которая должна раскрываться перед пилотом, сидящим за клавиатурой.
Вторая цель, стоящая перед программистом, заключается в том, чтобы создать реалистическую гравитационную среду. С этой проблемой читатели также уже сталкивались, правда, в несколько другой форме. В мартовском номере журнала рассказывалось об искусственной вселенной, за эволюцией которой можно наблюдать, сидя в кресле перед своим домашним компьютером. Звезды, населяющие этот мир, кружат причудливый хоровод, движимые силами их взаимного притяжения. Траектории кораблей и ракет в игре "Звездный бой" управляются более простым гравитационным влиянием. Лишь Солнце, находящееся в центре, оказывает ощутимое гравитационное воздействие.
Чтобы вступить в орбитальную дуэль, двое играющих усаживаются перед клавиатурой компьютера и нажимают на клавиши, специально отведенные в программе для управления кораблями. Один из играющих (по-видимому, более волосатый) принимает командование кораблем клингов, другому вверяется судьба корабля Федерации. Вначале на экране видны лишь Солнце, расположенное в центре, и два космических корабля. Солнце изображено в виде маленького диска, а корабли - крошечными символами, размеры которых достаточны лишь для того, чтобы отличить "своего" от "чужого".
В начале игры оба корабля находятся в состоянии свободного падения по направлению к Солнцу. Игроки немедленно меняют курс, стремясь уйти с траектории, ведущей к светилу, и включают ракетные двигатели кораблей, чтобы вывести их на безопасные орбиты. Корабль, коснувшийся Солнца, немедленно испаряется, и игра, конечно, оказывается проигранной.
Как только корабли выходят на заданные орбиты, каждый игрок начинает попытки уничтожить своего противника. Один из крайних тактических замыслов заключается в том, чтобы выждать, пока корабль противника не окажется поблизости. Тогда быстрым залпом его можно уничтожить. Другой крайний замысел, пожалуй, похитрее: можно попытаться произвести прицельные выстрелы с противоположной от Солнца стороны. На экране от ведущего огонь корабля отделяются яркие световые точки (в телевизионной программе называвшиеся фотонными торпедами) и прожигают траектории вокруг Солнца в виде плавно закругляющихся смертоносных линий. Если кораблем противника управляет пилот, не обладающий высочайшим мастерством, корабль наверняка попадет под удар одной из выпущенных по нему ракет и, взорвавшись, разлетится на осколки, подобные звездной пыли. На экране это событие мгновенно знаменуется облаком светящихся точек и крупной надписью: ПОБЕДУ ОДЕРЖАЛА ФЕДЕРАЦИЯ или ПОБЕДИЛИ ВООРУЖЕННЫЕ СИЛЫ КЛИНГОВ.
Поскольку боевые действия вблизи Солнца обычно очень интенсивны, осторожные игроки предпочитают держаться на более далеких орбитах. Основной недостаток подобной стратегии состоит в том, что возникает потребность в перезарядке солнечных элементов питания (системы управления кораблем питаются от солнечных батарей). Когда запасы электроэнергии исчерпываются, корабль должен немедленно приблизиться к Солнцу и пополнить энергетические запасы. На удаленных орбитах фотонный поток слаб и корабль подвергается риску потерять управление.
В игре есть еще одна тонкость, о которой следует помнить, находясь на удаленных от Солнца орбитах. Дело в том, что боевое пространство "Звездного боя" как бы "тороидально". Другими словами, если корабль подходит слишком близко к краю экрана, он исчезает и появляется на противоположной его стороне.
Каждый корабль обладает неограниченным запасом ракет, но в каждый данный момент в полете может находиться не более 10 из них. Ракета подчиняется тем же физическим законам, что и корабли. Она остается активной до тех пор, пока не поразит корабль (возможно, даже и свой), либо пока у нее не кончится горючее. Таковы правила игры.
Программа, которую я назову TREK, будет, наверное, самой крупной из тех, что когда-либо рассматривались в статьях рубрики "Занимательный компьютер", и, возможно, не столько из-за своей сложности, сколько из-за масштабов. Поэтому некоторые более или менее стандартные процедуры мы рассмотрим лишь кратко, в общих чертах. Тем не менее программисты-новички, в особенности те, у кого есть возможность проконсультироваться у опытных специалистов, могут попытаться написать собственную программу с надеждой на успех.




"Энтерпрайз" и крейсер клингов обстреливают друг друга ракетами
Программа TREK циклически проходит через шесть основных секций до тех пор, пока оба корабля существуют:
- Опрос клавиш
- Корректировка положения кораблей и ракет
- Проверка на столкновения
- Изменение энергетических ресурсов кораблей
- Управление ракетами
- Вывод изображения на экран
Многие читатели найдут программу TREK сравнительно несложной, может быть, за исключением первой секции. Для некоторых такая процедура, как опрос клавиш, будет в новинку, однако при программировании игр без нее, пожалуй, не обойтись. В большинстве языков высокого уровня имеются специальные операторы, позволяющие проверить, была ли нажата та или иная клавиша.
Например, в языке Бейсик версии Microsoft соответствующий оператор выглядит следующим образом:
ON KEY(K) GOSUB N
После того как выполняется команда On key, программа, перед тем как выполнять каждый следующий оператор, проверяет, не была ли нажата клавиша k. Если была, то управление в программе переходит на первый оператор в строке под номером n. В этой строке начинается подпрограмма, назначение которой заключается в том, чтобы зафиксировать каким-то образом тот факт, что клавиша k была нажата. Обычно это делается путем присвоения определенного значения переменной, играющей роль "флажка". На клавиатуре персонального компьютера IBM имеется 14 клавиш, которые можно опросить указанным способом: 10 функциональных клавиш и четыре клавиши управления курсором. Каждому играющему нужно отвести по четыре клавиши, скажем функциональные клавиши F1, F2, F3 и F4 для корабля Федерации и четыре клавиши управления курсором для корабля клингов. Числа, соответствующие первым четырем клавишам,- от 1 до 4, а другим четырем - от 11 до 14. Здесь нужно посмотреть коды клавиш в руководстве по программированию на том или ином компьютере.
Для каждой стороны первая из выделенных ей клавиш управляет мощностью двигателя, две следующие служат для изменения направления и последняя - для стрельбы ракетами. Клавиша двигателя сообщает кораблю фиксированный импульс мощности, действующий в течение одного программного цикла. Каждое нажатие на клавишу направления поворачивает соответствующий корабль на угол, равный 10град. При нажатии на клавишу стрельбы корабль выпускает один снаряд. Прежде чем начать игру, советуем налепить на клавиши маленькие квадратики с обозначениями их функций. Они будут напоминать играющим назначение каждой клавиши.
В программе должно быть по одному оператору On key для каждой из восьми клавиш управления. Оператор On key не выполняется, если ему не предшествует оператор Кеу(k) оn. Все процедуры, к которым обращается программа по каждой команде On key, очень просты и в сущности одинаковы. Каждая такая процедура состоит из двух операторов. Первый оператор присваивает переменной-флажку значение 1 для последующего анализа в ходе выполнения программы, а второй оператор возвращает управление на то место в программе, откуда произошло обращение к данной процедуре по команде On key. Переменные-флажки для управления "Энтерпрайзом", можно, например, назвать fdgo, fdrt, fdlt и fdfr. Эти названия означают соответственно "Федерация вперед" (Federation go) - включение двигателя, "Федерация вправо" (Federation right), "Федерация влево" (Federation left) - эти повороты делаются соответственно по и против часовой стрелки - и "Федерация огонь" (Fedaration fire) - старт боевой ракеты. Аналогично для крейсера клингов переменные kngo, knrt, knlt и knfr соответственно регистрируют нажатие клавиш импульса, направления и стрельбы.
После того как процедура присваивает переменной-флажку значение 1, в состоянии одного из кораблей происходит изменение. Например, в случае если fdgo становится равной 1, секция программы, управляющая положением кораблей, создает небольшое дополнительное ускорение (в пределах между 2 и 5, кому как нравится) в движении корабля "Энтерпрайз". Затем программа должна сбросить флажок в 0.

Корабль клингов не смог уйти от огня
Управлять положением двух космических кораблей и несколькими ракетами значительно проще, чем смоделировать движение такого же числа массивных звезд. Суммарная масса боевой техники пренебрежимо мала по сравнению с массой расположенного в центре системы Солнца, поэтому взаимным гравитационным притяжением, действующим между кораблями и ракетами, мы пренебрегаем. По заданному расстоянию от каждого объекта до Солнца программа TREK вычисляет ускорение этого объекта, обусловленное радиально направленной силой притяжения, по этому ускорению вычисляется изменение скорости объекта и, наконец, его перемещение.
Даже при таком в принципе простом характере вычислений они отнимают значительное количество машинного времени. Для выполнения этих вычислений требуются операции сложения, умножения и извлечения квадратного корня. Чтобы избежать замедления темпа, в котором проводится игра, в программе TREK используется таблица: для каждого возможного расстояния от объекта до Солнца массив под названием force (сила) указывает заранее вычисленное ускорение, которое должен испытывать объект (см. таблицу). Поскольку мир этой игры "тороидален", новое положение объекта, вычисляемое по величине ускорения в массиве force, должно определяться по модулю, равному максимальному горизонтальному или вертикальному расстоянию, представленному на прямоугольном экране дисплея.

Часть таблицы ускорения и его формула
В двух других массивах содержатся даннные о скорости и положении обоих космических кораблей, а также до 20 выпушенных ими ракет. Эти массивы называются соответственно vel (от velocity - скорость) и pos (от position - положение). Каждый массив содержит два стобца и 22 строки. В первых двух строках находятся данные о космических кораблях, а в остальных 20 - о ракетах. Так, например, в первой строке массива vel два элемента vel(1,1) и vel(1,2) указывают соответственно составляющие скорости по горизонтальной оси x и по вертикальной оси y для корабля "Энтерпрайз". Аналогично, элементы vel(2,1) и vel(2,2) задают две взаимно перпендикулярные компоненты скорости для крейсера клингов. Специальная переменная misnum (от missile - ракета и number - число) позволяет программе следить за количеством ракет, активных в каждый данный момент. Значение misnum изменяется в пределах от 2 (т.е. ни одной ракеты, только сами корабли) до 22 (т.е. 2 корабля и 20 боевых ракет).
Разместив все данные о кораблях и снарядах в единых массивах, мы создаем более короткую и более быструю программу. Для вычисления новых скоростей и положений требуется лишь один цикл. Однако для определения изменений скорости и положения кораблей требуются еще две переменные fdor и knor. Их значения выражены в градусах, причем если угол равен 0, то корабль смотрит строго на восток, если угол равен 90, то корабль смотрит на север, и т.д. Всякий раз, когда игрок нажимает клавишу направления, значение одной из этих переменных изменяется на 10град. в ту или другую сторону.
Цикл для определения нового положения объекта проиндексирован переменной i, принимающей значения от 1 до 22. Для каждого значения i программа вычисляет ускорение: текущие значения x и y, указанные в i-й строке массива pos, возводятся в квадрат и складываются. Затем из полученной суммы программа извлекает квадратный корень и результат усекается до ближайшего целого числа, меньшего или равного этому результату. Усеченная таким образом величина представляет собой приблизительно расстояние от Солнца до точки, в которой находится объект с индексом i. Это целое число используется затем в качестве индекса в таблице ускорений, по которой программа определяет силу притяжения к Солнцу. [Обратите внимание. Что проще: извечь из числа корень, усечь до целого и посмотреть в таблице или тупо разделить 800 на число?- G.]
Для каждого из двух космических кораблей к компонентам ускорения, обусловленного притяжением к Солнцу, нужно прибавить компоненты ускорения, получаемого в результате импульсов двигателя. Если значение какого-либо флажка, либо fdgo, либо kngo, установлено в 1 (другими словами, если была нажата клавиша двигателя) и соответствующий корабль еще не исчерпал запасы топлива, программа должна умножить постоянную импульса (его абсолютную величину) на горизонтальную и вертикальную компоненты. На своем компьютере я выбрал константу импульса равной 3, что обеспечивает космическим кораблям достаточно хорошую маневренность. Для "Энтерпрайза" горизонтальная компонента равна утроенному значению косинуса fdor, а вертикальная - утроенному значению синуса fdor. Для корабля клингов компоненты импульса вычисляются аналогично по углу knor. После того как эти вычисления завершены, программа снова устанавливает значения флажков fdgo и kngo равными 0, ускорители заглушаются до тех пор, пока вновь не будет нажата одна из клавиш, включающих двигатель.
Когда индекс i становится больше 2, процедура расчета импульса пропускается, поскольку однажды выпущенные по цели боевые ракеты уже находятся в пассивном полете. В оставшейся части цикла корректировки вычисляются новые скорости и положения движущихся на экране объектов. Для каждого объекта численное значение ускорения прибавляется к текущему значению скорости, а величина скорости - к соответствующей координате положения. Такое упрощение в вычислениях достигнуто за счет соответствующего выбора величины одиночного импульса и солнечного притяжения, при котором минимальный промежуток времени в основном программном цикле оказывается равным единице.
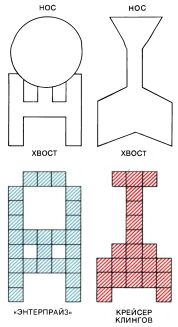
Символы кораблей и их изображения на экране
Чтобы провести проверку на контакт между различными движущимися объектами, программа прежде всего должна установить, находятся ли корабли вне границ солнечного диска. Поскольку расстояние между каждым кораблем и Солнцем уже было вычислено, то остается лишь проверить, превышает ли это расстояние радиус Солнца, скажем, 10 единиц. Если один из кораблей коснулся светила, программа выводит на экран соответствующее сообщение, например: КЛИНГИ ИСПАРИЛИСЬ. Затем управление передается секции изображения на экране очередной картинки.
В ходе второй проверки на контакт нужно определить, не находится ли какой-нибудь снаряд в пределах порогового маленького расстояния до одного из космических кораблей. Здесь используется простой, но эффективный прием: сначала вычисляется разность между значениями координат снаряда и корабля по оси x, затем по оси y после чего эти две разности складываются, и таким образом мы избегаем операций возведения в квадрат и извлечения квадратного корня; результат почти не отличается от вычисленного обычным способом. Если сумма двух разностей оказывается меньше,скажем, 4, то программа фиксирует попадание. На экране появляется сообщение, например такое: ЭНТЕРПРАЙЗ ПОРАЖЕН РАКЕТОЙ. КЛИНГИ ОДЕРЖАЛИ ПОБЕДУ. Проверка для всех выпущенных на данный момент ракет производится в одном цикле. Его индекс пробегает значения от 3 до misnum, т.е. до числа ракет плюс 2.
Чтобы изменить запасы энергии, которыми располагают корабли, программа делит значение ускорения, обусловленного притяжением к Солнцу и получаемого из таблицы, на 60. Поскольку величина ускорения растет при приближении к Солнцу, корабль получает больше энергии благодаря более интенсивному потоку солнечных фотонов. Получаемая энергия прибавляется затем к энергетической переменной fdfl или knfl в зависимости от того, для какого корабля проводятся вычисления. Каждая из этих переменных уменьшается на 0,1 при нажатии на клавишу двигателя. Это уменьшение производится в секции корректировки положения. Считается, что корабль исчерпал свои запасы энергии, когда в его баке остается меньше одной единицы солнечного топлива. Вначале в баке каждого корабля имеется по 10 единиц топлива. Управление боевыми ракетами осуществляется с помощью специального массива time (время), хранящего число программных циклов, в которых выражается "возраст" каждой ракеты. Когда число циклов достигает 25, соответствующая ракета выводится из массива pos, счетчик сбрасывается на 0 и значение переменной misnum уменьшается на 1. Удалить ракету из pos можно двумя способами. Первый способ легче реализовать в программе, но он замедляет темп игры. В этом случае программа пробегает массив, начиная со значения индекса, соответствующего удаляемой ракете, и уменьшает номер строки каждого элемента на 1. Таким образом, последний передвигаемый элемент имеет индекс misnum. Он перемещается на строку с номером misnum - 1. Та же самая операция выполняется над массивами vel и time. Более быстрый способ основан на учете индекса ракеты, который тем меньше, чем старше ракета, поскольку она была раньше добавлена к списку. Поэтому можно следить за ракетами, не передвигая их индексов. Ракеты, возраст которых достиг 25 программных циклов, должны находиться в начале последовательно расположенных ракет в каждом массиве, и только они подлежат удалению. Аналогичным образом, новые ракеты всегда добавляются в конец последовательности.
Введем две новые переменные old (старый) и new (новый), которые будут служить в качестве указателей на самую старую и самую новую ракету в каждом массиве. По мере того как одни снаряды удаляются, а другие добавляются к спискам, изменению подвергаются лишь значения old и new. В таком случае можно воспользоваться арифметическими действиями, выполняемыми по модулю, и тем самым поддерживать циклическое перемещение ракет по массивам. Когда нужно добавить новую ракету при значении индекса, равном 23, программа берет индекс по модулю 23, получает 0 и прибавляет к нему число 3, чтобы не подменить координаты космического корабля координатами одной из ракет. Значения old и new подвергаются той же самой операции. Такая структура данных называется круговой очередью. Если мы решили воспользоваться этим приемом, то секция программы, вычисляющая коррекции положения, должна быть модифицирована: каждый цикл нужно разбить на два меньших цикла, один для кораблей и другой для ракет.
Когда играющий нажимает клавишу стрельбы, программа сначала проверяет, сколько снарядов активны на данный момент у данной стороны. Если их насчитывается меньше 10, то анализируются значения переменных-флажков fdfr и knfr. Если, например, fdfr равна 1, то программа прибавляет 1 к количеству ракет на стороне Федерации, увеличивает на 1 значение misnum и затем помещает координаты положения и скорости корабля "Энтерпрайз" в соответствующие элементы массивов pos и vel. При этом к координатам положения прибавляется по 4 единицы и по 2 к координатам скорости. Эти увеличения происходят в том направлении, в котором корабль движется в данный момент. Например, горизонтальная координата ракеты, выпускаемой "Энтерпрайзом", равна учетверенному косинусу угла fdor плюс текущая горизонтальная координата положения корабля в данный момент; для вертикальной координаты мы берем соответственно учетверенное значение синуса fdor. Таким образом, сразу после запуска ракета уже достаточно удалена от своего корабля, иначе он был бы мгновенно уничтожен своей собственной фотонной торпедой. Аналогичная процедура применяется к координатам скорости снаряда. Это означает, что в момент запуска скорость ракеты относительно корабля составляет две единицы на один временной цикл. Другими словами, скорость снаряда на две единицы больше, чем у запустившего его корабля.
Последняя из числа основных секций программы TREK изображает на экране Солнце, два корабля и все активные к данному моменту ракеты. Программа рисует круг радиусом 10 единиц в центральной части экрана и затем просматривает массив pos. Корабли Федерации и клингов представлены маленькими символическими изображениями. Одно из этих изображений по существу представляет собой кружок (в фильме "Энтерпрайз" имел форму диска с двумя слегка выступающими двигателями). Корабль клингов имеет угловатую форму. Читатели могут сами выбрать символы для представления на экране кораблей, учитывая, чтобы принадлежность корабля и направление его движения можно было определить с первого взгляда. При изображении на экране символов обоих кораблей программа TREK пользуется специальными списками точек, по которым строится изображение и которые можно переносить и подвергать поворотам, моделируя тем самым изменения в положении и ориентации кораблей. Для выполнения этих операций программа обращается к массиву pos и переменным fdor и knor.
С ракетами дело обстоит проще: каждая изображается на экране в виде точки. Это происходит в ходе выполнения одного цикла при последовательном просмотре массива pos.
Использование программы TREK сопряжено с некоторым неудобством, возникающим в связи с конструктивными особенностями большинства переменных дисплеев. Дело в том, что экраны этих дисплеев работают в режиме запоминания изображения: объект, однажды "нарисованный" на экране, остается на нем продолжительное время. Чтобы избежать загромождения экрана "остатками" изображений кораблей и ракет из предшествующих стадий игры, программа должна рисовать каждый объект дважды. Сначала она рисует его на старой позиции черным, а затем изображает его на новой позиции светлым.
Остальные подробности реализации игры я оставляю ее будущим энтузиастам, "треккерам". Несмотря на некоторые хитрости, при помощи которых удается ускорить программу, вы все же можете остаться неудовлетворенными темпом игры. Возможно, по этой причине вы назовете свою программу не TREK, а TRAKTOR. Чтобы попытаться ускорить работу программы, попробуйте ее откомпилировать или наложите более жесткие ограничения на число активных боевых ракет, разрешенных для каждой стороны.
Я описал здесь лишь основную, так сказать, скелетную версию игры "Звездный бой". Существуют и более замысловатые версии, их число растет и они также получают распространение. Появились варианты игры с тремя и более кораблями, лазерными пушками, цветным изображением и высветкой текущих показателей игры. Я должен выразить признательность Дж.Гроффу из Клирватера (шт.Флорида), напомнившему мне об этой классической игре, родившейся в подполье, и познакомившему меня с версией игры, в которой поведение клингов автоматизировано. Люди, пытающиеся отстаивать честь Федерации, все время терпят поражение в борьбе с программой Гроффа.
занимательный компьютер
Ну что же, я предлагаю читателям, которым удастся создать собственные работающие версии "Звездного боя", рассказать в своих письмах о стратегиях и остроумных решениях, благодаря которым они добивались ускорения действия. О лучших результатах я расскажу в одной из следующих статей.
БИБЛИОГРАФИЯ
STAR FLEET TECHNICAL MANUAL. Designed by FRANZ JOSEPH. Ballantine Books, 1975.
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARTWICK. Prentice-Hall, 1985.
ОТКЛИКИ
4 1987
ИГРА ПОД названием "Звездный бой" (Star trek), о которой речь шла в первом номере журнала за этот год, оказывается, существовала, если не по названию, то по сути, еще задолго до появления на телевизионных экранах популярного многосерийного фильма с этим названием. Р.Нельсон-младший из Остина (шт.Техас) вспоминает, как в начале 60-х годов появилась игра под названием "Космическая война" - прабабушка всех игр, в которых космические корабли охотятся друг за другом. Программа была написана для ЭВМ PDP-1 в Массачусетском технологическом институте. Авторы игры, аспиранты МТИ, очень гордились своим изобретением. Об этом можно прочитать в августовском номере журнала "Creative Computing" за 1981г. (см. библиографию). Машина PDP-1 была плохо приспособлена для программирования подобных игр, и входные параметры вводились в нее с операторского пульта. Дж.Грэтц, один из авторов игры, вспоминает, в какой атмосфере проходили состязания: "Если мы загорались какой-нибудь идеей, для нас не было ничего невозможного... "Космическая война" прекрасно работала с ключей регистра операторского пульта, правда, монитор терминала был расположен несколько в стороне, так что один из игроков получал преимущество, потому что ему было удобнее наблюдать за событиями на экране. Важнее было, наверное, то, что двое возбужденных бойцов теснились в ограниченном пространстве, рассчитанном на одного спокойно работающего оператора, поэтому постоянно возникала опасность поломки оборудования".
Программа варианта "Космической войны", описанная в январском номере журнала, не удовлетворила К.Ван-Еселтайна из Скулкрафта (шт.Мичиган). Она показалась ему настолько медленной, что он назвал ее "Звездным трактором" (Star truck). Она стала достойной названия "Звездный бой" (Star trek) лишь после того, как он нашел способ удалить большую часть арифметических операций с плавающей запятой из главного цикла программы. Чтобы не вычислять квадратных корней по ходу выполнения программы, он заранее рассчитал двумерный массив расстояний от всех возможных точек (x, y) до начала координат (0, 0). Теперь расстояние между любыми двумя точками (x1, y1) и (x2, y2) можно получить очень просто, посмотрев в таблице расстояние для координат (x2-x1, y2-y2). Ван-Еселтайн затабулировал также значения синуса и косинуса в двух массивах по 36 элементов в каждом, по одному элементу на каждые 10 градусов. Кроме того, он пришел к выводу, что с ракетами легче управляться, если их всегда ровно 20. Разумеется, на любой конкретный момент многие из них могут оказаться виртуальными, в этом случае они просто не отображаются. Далее, массивы, задающие скорость, должны быть не двумерными, а спаренными одномерными. На многих персональных компьютерах такое простое новое определение может дать значительную экономию времени. Целеустремленные читатели, несомненно, сами дойдут до многих других усовершенствований, позволяющих ускорить программу Ван-Еселтайна.
THE ORIGIN OF SPACEBAR. J.M.GRAETZ in Creative Computing, Vol.7, No.8, pages 56-67; August, 1981.
ИГРА "ЗВЕЗДНЫЙ БОЙ" ДЛЯ ДОМАШНИХ КОМПЬЮТЕРОВ
А.К.ДЬЮДНИ
Упоминал, журнал выкладывал -
 ТЕМА #67, АБЗАЦ #735
ТЕМА #67, АБЗАЦ #735 .- G.
.- G. В НАЧАЛЕ 70-х годов я часто засиживался до позднего вечера в своем университетском кабинете в надежде на то, что студенты уже не будут отвлекать меня от работы. К моему несчастью, в расположенной рядом по коридору исследовательской лаборатории по машинной графике почти постоянно задерживались студенты, проводившие вечера за своей излюбленной игрой, называвшейся тогда по-разному: то "Звездный бой", то "Космическая война". [Вроде бы, "SpaceWar!". Почему у Дьюдни всплыл "STAR TREK", не знаю.- G.] "Стреляй! Скорее! Попал, попал!- то и дело доносились возгласы увлеченных игроков через плотно закрытую дверь моего кабинета.- Берегись, ракеты!" Этот шум не давал мне сосредоточиться. И, оказавшись не в состоянии работать, я обычно присоединялся к играющим. Полный твердой решимости вернуться к более серьезным занятиям после небольшого развлечения, я отправлялся в соседнюю лабораторию понаблюдать за игрой.
Игра "Звездный бой" в какой-то мере была основана на сюжете популярного многосерийного телевизионного фильма под таким же названием. Игра повторяет эпизоды боя между космическим кораблем "Энтерпрайз" и крейсером вооруженных сил клингов. Поклонники этой телевизионной программы, наверное, помнят, что "Энтерпрайз" совершил путешествие в ту область Вселенной, где люди еще никогда не бывали. Это путешествие совершалось под флагом союза сотрудничавших цивилизаций, называемого Федерацией. Главенствующую роль в союзе играла Человеческая раса. Клинги были представителями звероподобной волосатой расы, соперничавшей с Федерацией в борьбе за господство над Млечным Путем, а может быть, и над всей Вселенной.
Хотя первоначально игра "Звездный бой" могла выполняться лишь на мощном компьютере, оснащенном специальными графическими средствами, сейчас аналогичную программу вполне можно написать и для персонального компьютера. Два космических корабля описывают орбитальные траектории вокруг звезды, находящейся в центре, стреляя друг по другу ракетами и пытаясь в свою очередь уклониться от ракет противника. Как сами корабли, так и ракеты, которыми они обстреливают друг друга, подвержены гравитационному притяжению, и, таким образом, законы орбитального движения в значительной мере определяют характер игры. Пилоты, не обладающие достаточным интуитивным чутьем к законам небесной механики, либо сжигают свои корабли, неосторожно приблизившись к Солнцу, либо, не сумев сманеврировать, пересекают обманчивые траектории смертоносных ракет. Сторона, космический корабль которой взрывается первым, считается проигравшей.
Было время, когда различные версии игры "Звездный бой" распространились на сотни университетов и других учреждений. Официально это не одобрялось, но втайне все получали от игры много удовольствия. Хотя эта игра так часто мешала мне работать, теперь, через много лет я вспоминаю о ней с очень теплым чувством. "Звездный бой" - это лишь одна из многих увлекательных игр, созданных студентами. Большинство таких игр быстро превращались в законченные пакеты программ, представлявшие собой уже коммерческий продукт. По-видимому, игры внесли значительный вклад в ту революцию, которая произошла в области домашних компьютеров. Версии игры "Звездный бой" поступили в широкую продажу лишь сравнительно недавно, хотя в "подпольном" виде они кочевали уже давно.
Версия "Звездного боя", описанная в настоящей статье, вернет читателя к тем временам, когда появились первые компьютерные игры, окруженные атмосферой таинства и романтики. На ее примере я смогу посвятить читателя в секреты, без которых не обойтись при программировании игр. Прежде всего нужно стараться поддерживать непрерывное движение на экране. Поэтому вычисления в программе, реализующей игру "Звездный бой", должны быть как можно проще и выполняться как можно быстрее. С этой проблемой мы уже сталкивались в статье, посвященной программам, имитирующим полет (см.: "В мире науки", 1986, #9, с.92). К счастью, мир "Звездного боя" намного проще той детальной цифровой географии, которая должна раскрываться перед пилотом, сидящим за клавиатурой.
Вторая цель, стоящая перед программистом, заключается в том, чтобы создать реалистическую гравитационную среду. С этой проблемой читатели также уже сталкивались, правда, в несколько другой форме. В мартовском номере журнала рассказывалось об искусственной вселенной, за эволюцией которой можно наблюдать, сидя в кресле перед своим домашним компьютером. Звезды, населяющие этот мир, кружат причудливый хоровод, движимые силами их взаимного притяжения. Траектории кораблей и ракет в игре "Звездный бой" управляются более простым гравитационным влиянием. Лишь Солнце, находящееся в центре, оказывает ощутимое гравитационное воздействие.
Чтобы вступить в орбитальную дуэль, двое играющих усаживаются перед клавиатурой компьютера и нажимают на клавиши, специально отведенные в программе для управления кораблями. Один из играющих (по-видимому, более волосатый) принимает командование кораблем клингов, другому вверяется судьба корабля Федерации. Вначале на экране видны лишь Солнце, расположенное в центре, и два космических корабля. Солнце изображено в виде маленького диска, а корабли - крошечными символами, размеры которых достаточны лишь для того, чтобы отличить "своего" от "чужого".
В начале игры оба корабля находятся в состоянии свободного падения по направлению к Солнцу. Игроки немедленно меняют курс, стремясь уйти с траектории, ведущей к светилу, и включают ракетные двигатели кораблей, чтобы вывести их на безопасные орбиты. Корабль, коснувшийся Солнца, немедленно испаряется, и игра, конечно, оказывается проигранной.
Как только корабли выходят на заданные орбиты, каждый игрок начинает попытки уничтожить своего противника. Один из крайних тактических замыслов заключается в том, чтобы выждать, пока корабль противника не окажется поблизости. Тогда быстрым залпом его можно уничтожить. Другой крайний замысел, пожалуй, похитрее: можно попытаться произвести прицельные выстрелы с противоположной от Солнца стороны. На экране от ведущего огонь корабля отделяются яркие световые точки (в телевизионной программе называвшиеся фотонными торпедами) и прожигают траектории вокруг Солнца в виде плавно закругляющихся смертоносных линий. Если кораблем противника управляет пилот, не обладающий высочайшим мастерством, корабль наверняка попадет под удар одной из выпущенных по нему ракет и, взорвавшись, разлетится на осколки, подобные звездной пыли. На экране это событие мгновенно знаменуется облаком светящихся точек и крупной надписью: ПОБЕДУ ОДЕРЖАЛА ФЕДЕРАЦИЯ или ПОБЕДИЛИ ВООРУЖЕННЫЕ СИЛЫ КЛИНГОВ.
Поскольку боевые действия вблизи Солнца обычно очень интенсивны, осторожные игроки предпочитают держаться на более далеких орбитах. Основной недостаток подобной стратегии состоит в том, что возникает потребность в перезарядке солнечных элементов питания (системы управления кораблем питаются от солнечных батарей). Когда запасы электроэнергии исчерпываются, корабль должен немедленно приблизиться к Солнцу и пополнить энергетические запасы. На удаленных орбитах фотонный поток слаб и корабль подвергается риску потерять управление.
В игре есть еще одна тонкость, о которой следует помнить, находясь на удаленных от Солнца орбитах. Дело в том, что боевое пространство "Звездного боя" как бы "тороидально". Другими словами, если корабль подходит слишком близко к краю экрана, он исчезает и появляется на противоположной его стороне.
Каждый корабль обладает неограниченным запасом ракет, но в каждый данный момент в полете может находиться не более 10 из них. Ракета подчиняется тем же физическим законам, что и корабли. Она остается активной до тех пор, пока не поразит корабль (возможно, даже и свой), либо пока у нее не кончится горючее. Таковы правила игры.
Программа, которую я назову TREK, будет, наверное, самой крупной из тех, что когда-либо рассматривались в статьях рубрики "Занимательный компьютер", и, возможно, не столько из-за своей сложности, сколько из-за масштабов. Поэтому некоторые более или менее стандартные процедуры мы рассмотрим лишь кратко, в общих чертах. Тем не менее программисты-новички, в особенности те, у кого есть возможность проконсультироваться у опытных специалистов, могут попытаться написать собственную программу с надеждой на успех.




"Энтерпрайз" и крейсер клингов обстреливают друг друга ракетами
Программа TREK циклически проходит через шесть основных секций до тех пор, пока оба корабля существуют:
- Опрос клавиш
- Корректировка положения кораблей и ракет
- Проверка на столкновения
- Изменение энергетических ресурсов кораблей
- Управление ракетами
- Вывод изображения на экран
Многие читатели найдут программу TREK сравнительно несложной, может быть, за исключением первой секции. Для некоторых такая процедура, как опрос клавиш, будет в новинку, однако при программировании игр без нее, пожалуй, не обойтись. В большинстве языков высокого уровня имеются специальные операторы, позволяющие проверить, была ли нажата та или иная клавиша.
Например, в языке Бейсик версии Microsoft соответствующий оператор выглядит следующим образом:
ON KEY(K) GOSUB N
После того как выполняется команда On key, программа, перед тем как выполнять каждый следующий оператор, проверяет, не была ли нажата клавиша k. Если была, то управление в программе переходит на первый оператор в строке под номером n. В этой строке начинается подпрограмма, назначение которой заключается в том, чтобы зафиксировать каким-то образом тот факт, что клавиша k была нажата. Обычно это делается путем присвоения определенного значения переменной, играющей роль "флажка". На клавиатуре персонального компьютера IBM имеется 14 клавиш, которые можно опросить указанным способом: 10 функциональных клавиш и четыре клавиши управления курсором. Каждому играющему нужно отвести по четыре клавиши, скажем функциональные клавиши F1, F2, F3 и F4 для корабля Федерации и четыре клавиши управления курсором для корабля клингов. Числа, соответствующие первым четырем клавишам,- от 1 до 4, а другим четырем - от 11 до 14. Здесь нужно посмотреть коды клавиш в руководстве по программированию на том или ином компьютере.
Для каждой стороны первая из выделенных ей клавиш управляет мощностью двигателя, две следующие служат для изменения направления и последняя - для стрельбы ракетами. Клавиша двигателя сообщает кораблю фиксированный импульс мощности, действующий в течение одного программного цикла. Каждое нажатие на клавишу направления поворачивает соответствующий корабль на угол, равный 10град. При нажатии на клавишу стрельбы корабль выпускает один снаряд. Прежде чем начать игру, советуем налепить на клавиши маленькие квадратики с обозначениями их функций. Они будут напоминать играющим назначение каждой клавиши.
В программе должно быть по одному оператору On key для каждой из восьми клавиш управления. Оператор On key не выполняется, если ему не предшествует оператор Кеу(k) оn. Все процедуры, к которым обращается программа по каждой команде On key, очень просты и в сущности одинаковы. Каждая такая процедура состоит из двух операторов. Первый оператор присваивает переменной-флажку значение 1 для последующего анализа в ходе выполнения программы, а второй оператор возвращает управление на то место в программе, откуда произошло обращение к данной процедуре по команде On key. Переменные-флажки для управления "Энтерпрайзом", можно, например, назвать fdgo, fdrt, fdlt и fdfr. Эти названия означают соответственно "Федерация вперед" (Federation go) - включение двигателя, "Федерация вправо" (Federation right), "Федерация влево" (Federation left) - эти повороты делаются соответственно по и против часовой стрелки - и "Федерация огонь" (Fedaration fire) - старт боевой ракеты. Аналогично для крейсера клингов переменные kngo, knrt, knlt и knfr соответственно регистрируют нажатие клавиш импульса, направления и стрельбы.
После того как процедура присваивает переменной-флажку значение 1, в состоянии одного из кораблей происходит изменение. Например, в случае если fdgo становится равной 1, секция программы, управляющая положением кораблей, создает небольшое дополнительное ускорение (в пределах между 2 и 5, кому как нравится) в движении корабля "Энтерпрайз". Затем программа должна сбросить флажок в 0.

Корабль клингов не смог уйти от огня
Управлять положением двух космических кораблей и несколькими ракетами значительно проще, чем смоделировать движение такого же числа массивных звезд. Суммарная масса боевой техники пренебрежимо мала по сравнению с массой расположенного в центре системы Солнца, поэтому взаимным гравитационным притяжением, действующим между кораблями и ракетами, мы пренебрегаем. По заданному расстоянию от каждого объекта до Солнца программа TREK вычисляет ускорение этого объекта, обусловленное радиально направленной силой притяжения, по этому ускорению вычисляется изменение скорости объекта и, наконец, его перемещение.
Даже при таком в принципе простом характере вычислений они отнимают значительное количество машинного времени. Для выполнения этих вычислений требуются операции сложения, умножения и извлечения квадратного корня. Чтобы избежать замедления темпа, в котором проводится игра, в программе TREK используется таблица: для каждого возможного расстояния от объекта до Солнца массив под названием force (сила) указывает заранее вычисленное ускорение, которое должен испытывать объект (см. таблицу). Поскольку мир этой игры "тороидален", новое положение объекта, вычисляемое по величине ускорения в массиве force, должно определяться по модулю, равному максимальному горизонтальному или вертикальному расстоянию, представленному на прямоугольном экране дисплея.

Часть таблицы ускорения и его формула
В двух других массивах содержатся даннные о скорости и положении обоих космических кораблей, а также до 20 выпушенных ими ракет. Эти массивы называются соответственно vel (от velocity - скорость) и pos (от position - положение). Каждый массив содержит два стобца и 22 строки. В первых двух строках находятся данные о космических кораблях, а в остальных 20 - о ракетах. Так, например, в первой строке массива vel два элемента vel(1,1) и vel(1,2) указывают соответственно составляющие скорости по горизонтальной оси x и по вертикальной оси y для корабля "Энтерпрайз". Аналогично, элементы vel(2,1) и vel(2,2) задают две взаимно перпендикулярные компоненты скорости для крейсера клингов. Специальная переменная misnum (от missile - ракета и number - число) позволяет программе следить за количеством ракет, активных в каждый данный момент. Значение misnum изменяется в пределах от 2 (т.е. ни одной ракеты, только сами корабли) до 22 (т.е. 2 корабля и 20 боевых ракет).
Разместив все данные о кораблях и снарядах в единых массивах, мы создаем более короткую и более быструю программу. Для вычисления новых скоростей и положений требуется лишь один цикл. Однако для определения изменений скорости и положения кораблей требуются еще две переменные fdor и knor. Их значения выражены в градусах, причем если угол равен 0, то корабль смотрит строго на восток, если угол равен 90, то корабль смотрит на север, и т.д. Всякий раз, когда игрок нажимает клавишу направления, значение одной из этих переменных изменяется на 10град. в ту или другую сторону.
Цикл для определения нового положения объекта проиндексирован переменной i, принимающей значения от 1 до 22. Для каждого значения i программа вычисляет ускорение: текущие значения x и y, указанные в i-й строке массива pos, возводятся в квадрат и складываются. Затем из полученной суммы программа извлекает квадратный корень и результат усекается до ближайшего целого числа, меньшего или равного этому результату. Усеченная таким образом величина представляет собой приблизительно расстояние от Солнца до точки, в которой находится объект с индексом i. Это целое число используется затем в качестве индекса в таблице ускорений, по которой программа определяет силу притяжения к Солнцу. [Обратите внимание. Что проще: извечь из числа корень, усечь до целого и посмотреть в таблице или тупо разделить 800 на число?- G.]
Для каждого из двух космических кораблей к компонентам ускорения, обусловленного притяжением к Солнцу, нужно прибавить компоненты ускорения, получаемого в результате импульсов двигателя. Если значение какого-либо флажка, либо fdgo, либо kngo, установлено в 1 (другими словами, если была нажата клавиша двигателя) и соответствующий корабль еще не исчерпал запасы топлива, программа должна умножить постоянную импульса (его абсолютную величину) на горизонтальную и вертикальную компоненты. На своем компьютере я выбрал константу импульса равной 3, что обеспечивает космическим кораблям достаточно хорошую маневренность. Для "Энтерпрайза" горизонтальная компонента равна утроенному значению косинуса fdor, а вертикальная - утроенному значению синуса fdor. Для корабля клингов компоненты импульса вычисляются аналогично по углу knor. После того как эти вычисления завершены, программа снова устанавливает значения флажков fdgo и kngo равными 0, ускорители заглушаются до тех пор, пока вновь не будет нажата одна из клавиш, включающих двигатель.
Когда индекс i становится больше 2, процедура расчета импульса пропускается, поскольку однажды выпущенные по цели боевые ракеты уже находятся в пассивном полете. В оставшейся части цикла корректировки вычисляются новые скорости и положения движущихся на экране объектов. Для каждого объекта численное значение ускорения прибавляется к текущему значению скорости, а величина скорости - к соответствующей координате положения. Такое упрощение в вычислениях достигнуто за счет соответствующего выбора величины одиночного импульса и солнечного притяжения, при котором минимальный промежуток времени в основном программном цикле оказывается равным единице.

Символы кораблей и их изображения на экране
Чтобы провести проверку на контакт между различными движущимися объектами, программа прежде всего должна установить, находятся ли корабли вне границ солнечного диска. Поскольку расстояние между каждым кораблем и Солнцем уже было вычислено, то остается лишь проверить, превышает ли это расстояние радиус Солнца, скажем, 10 единиц. Если один из кораблей коснулся светила, программа выводит на экран соответствующее сообщение, например: КЛИНГИ ИСПАРИЛИСЬ. Затем управление передается секции изображения на экране очередной картинки.
В ходе второй проверки на контакт нужно определить, не находится ли какой-нибудь снаряд в пределах порогового маленького расстояния до одного из космических кораблей. Здесь используется простой, но эффективный прием: сначала вычисляется разность между значениями координат снаряда и корабля по оси x, затем по оси y после чего эти две разности складываются, и таким образом мы избегаем операций возведения в квадрат и извлечения квадратного корня; результат почти не отличается от вычисленного обычным способом. Если сумма двух разностей оказывается меньше,скажем, 4, то программа фиксирует попадание. На экране появляется сообщение, например такое: ЭНТЕРПРАЙЗ ПОРАЖЕН РАКЕТОЙ. КЛИНГИ ОДЕРЖАЛИ ПОБЕДУ. Проверка для всех выпущенных на данный момент ракет производится в одном цикле. Его индекс пробегает значения от 3 до misnum, т.е. до числа ракет плюс 2.
Чтобы изменить запасы энергии, которыми располагают корабли, программа делит значение ускорения, обусловленного притяжением к Солнцу и получаемого из таблицы, на 60. Поскольку величина ускорения растет при приближении к Солнцу, корабль получает больше энергии благодаря более интенсивному потоку солнечных фотонов. Получаемая энергия прибавляется затем к энергетической переменной fdfl или knfl в зависимости от того, для какого корабля проводятся вычисления. Каждая из этих переменных уменьшается на 0,1 при нажатии на клавишу двигателя. Это уменьшение производится в секции корректировки положения. Считается, что корабль исчерпал свои запасы энергии, когда в его баке остается меньше одной единицы солнечного топлива. Вначале в баке каждого корабля имеется по 10 единиц топлива. Управление боевыми ракетами осуществляется с помощью специального массива time (время), хранящего число программных циклов, в которых выражается "возраст" каждой ракеты. Когда число циклов достигает 25, соответствующая ракета выводится из массива pos, счетчик сбрасывается на 0 и значение переменной misnum уменьшается на 1. Удалить ракету из pos можно двумя способами. Первый способ легче реализовать в программе, но он замедляет темп игры. В этом случае программа пробегает массив, начиная со значения индекса, соответствующего удаляемой ракете, и уменьшает номер строки каждого элемента на 1. Таким образом, последний передвигаемый элемент имеет индекс misnum. Он перемещается на строку с номером misnum - 1. Та же самая операция выполняется над массивами vel и time. Более быстрый способ основан на учете индекса ракеты, который тем меньше, чем старше ракета, поскольку она была раньше добавлена к списку. Поэтому можно следить за ракетами, не передвигая их индексов. Ракеты, возраст которых достиг 25 программных циклов, должны находиться в начале последовательно расположенных ракет в каждом массиве, и только они подлежат удалению. Аналогичным образом, новые ракеты всегда добавляются в конец последовательности.
Введем две новые переменные old (старый) и new (новый), которые будут служить в качестве указателей на самую старую и самую новую ракету в каждом массиве. По мере того как одни снаряды удаляются, а другие добавляются к спискам, изменению подвергаются лишь значения old и new. В таком случае можно воспользоваться арифметическими действиями, выполняемыми по модулю, и тем самым поддерживать циклическое перемещение ракет по массивам. Когда нужно добавить новую ракету при значении индекса, равном 23, программа берет индекс по модулю 23, получает 0 и прибавляет к нему число 3, чтобы не подменить координаты космического корабля координатами одной из ракет. Значения old и new подвергаются той же самой операции. Такая структура данных называется круговой очередью. Если мы решили воспользоваться этим приемом, то секция программы, вычисляющая коррекции положения, должна быть модифицирована: каждый цикл нужно разбить на два меньших цикла, один для кораблей и другой для ракет.
Когда играющий нажимает клавишу стрельбы, программа сначала проверяет, сколько снарядов активны на данный момент у данной стороны. Если их насчитывается меньше 10, то анализируются значения переменных-флажков fdfr и knfr. Если, например, fdfr равна 1, то программа прибавляет 1 к количеству ракет на стороне Федерации, увеличивает на 1 значение misnum и затем помещает координаты положения и скорости корабля "Энтерпрайз" в соответствующие элементы массивов pos и vel. При этом к координатам положения прибавляется по 4 единицы и по 2 к координатам скорости. Эти увеличения происходят в том направлении, в котором корабль движется в данный момент. Например, горизонтальная координата ракеты, выпускаемой "Энтерпрайзом", равна учетверенному косинусу угла fdor плюс текущая горизонтальная координата положения корабля в данный момент; для вертикальной координаты мы берем соответственно учетверенное значение синуса fdor. Таким образом, сразу после запуска ракета уже достаточно удалена от своего корабля, иначе он был бы мгновенно уничтожен своей собственной фотонной торпедой. Аналогичная процедура применяется к координатам скорости снаряда. Это означает, что в момент запуска скорость ракеты относительно корабля составляет две единицы на один временной цикл. Другими словами, скорость снаряда на две единицы больше, чем у запустившего его корабля.
Последняя из числа основных секций программы TREK изображает на экране Солнце, два корабля и все активные к данному моменту ракеты. Программа рисует круг радиусом 10 единиц в центральной части экрана и затем просматривает массив pos. Корабли Федерации и клингов представлены маленькими символическими изображениями. Одно из этих изображений по существу представляет собой кружок (в фильме "Энтерпрайз" имел форму диска с двумя слегка выступающими двигателями). Корабль клингов имеет угловатую форму. Читатели могут сами выбрать символы для представления на экране кораблей, учитывая, чтобы принадлежность корабля и направление его движения можно было определить с первого взгляда. При изображении на экране символов обоих кораблей программа TREK пользуется специальными списками точек, по которым строится изображение и которые можно переносить и подвергать поворотам, моделируя тем самым изменения в положении и ориентации кораблей. Для выполнения этих операций программа обращается к массиву pos и переменным fdor и knor.
С ракетами дело обстоит проще: каждая изображается на экране в виде точки. Это происходит в ходе выполнения одного цикла при последовательном просмотре массива pos.
Использование программы TREK сопряжено с некоторым неудобством, возникающим в связи с конструктивными особенностями большинства переменных дисплеев. Дело в том, что экраны этих дисплеев работают в режиме запоминания изображения: объект, однажды "нарисованный" на экране, остается на нем продолжительное время. Чтобы избежать загромождения экрана "остатками" изображений кораблей и ракет из предшествующих стадий игры, программа должна рисовать каждый объект дважды. Сначала она рисует его на старой позиции черным, а затем изображает его на новой позиции светлым.
Остальные подробности реализации игры я оставляю ее будущим энтузиастам, "треккерам". Несмотря на некоторые хитрости, при помощи которых удается ускорить программу, вы все же можете остаться неудовлетворенными темпом игры. Возможно, по этой причине вы назовете свою программу не TREK, а TRAKTOR. Чтобы попытаться ускорить работу программы, попробуйте ее откомпилировать или наложите более жесткие ограничения на число активных боевых ракет, разрешенных для каждой стороны.
Я описал здесь лишь основную, так сказать, скелетную версию игры "Звездный бой". Существуют и более замысловатые версии, их число растет и они также получают распространение. Появились варианты игры с тремя и более кораблями, лазерными пушками, цветным изображением и высветкой текущих показателей игры. Я должен выразить признательность Дж.Гроффу из Клирватера (шт.Флорида), напомнившему мне об этой классической игре, родившейся в подполье, и познакомившему меня с версией игры, в которой поведение клингов автоматизировано. Люди, пытающиеся отстаивать честь Федерации, все время терпят поражение в борьбе с программой Гроффа.
занимательный компьютер
Ну что же, я предлагаю читателям, которым удастся создать собственные работающие версии "Звездного боя", рассказать в своих письмах о стратегиях и остроумных решениях, благодаря которым они добивались ускорения действия. О лучших результатах я расскажу в одной из следующих статей.
БИБЛИОГРАФИЯ
STAR FLEET TECHNICAL MANUAL. Designed by FRANZ JOSEPH. Ballantine Books, 1975.
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARTWICK. Prentice-Hall, 1985.
ОТКЛИКИ
4 1987
ИГРА ПОД названием "Звездный бой" (Star trek), о которой речь шла в первом номере журнала за этот год, оказывается, существовала, если не по названию, то по сути, еще задолго до появления на телевизионных экранах популярного многосерийного фильма с этим названием. Р.Нельсон-младший из Остина (шт.Техас) вспоминает, как в начале 60-х годов появилась игра под названием "Космическая война" - прабабушка всех игр, в которых космические корабли охотятся друг за другом. Программа была написана для ЭВМ PDP-1 в Массачусетском технологическом институте. Авторы игры, аспиранты МТИ, очень гордились своим изобретением. Об этом можно прочитать в августовском номере журнала "Creative Computing" за 1981г. (см. библиографию). Машина PDP-1 была плохо приспособлена для программирования подобных игр, и входные параметры вводились в нее с операторского пульта. Дж.Грэтц, один из авторов игры, вспоминает, в какой атмосфере проходили состязания: "Если мы загорались какой-нибудь идеей, для нас не было ничего невозможного... "Космическая война" прекрасно работала с ключей регистра операторского пульта, правда, монитор терминала был расположен несколько в стороне, так что один из игроков получал преимущество, потому что ему было удобнее наблюдать за событиями на экране. Важнее было, наверное, то, что двое возбужденных бойцов теснились в ограниченном пространстве, рассчитанном на одного спокойно работающего оператора, поэтому постоянно возникала опасность поломки оборудования".
Программа варианта "Космической войны", описанная в январском номере журнала, не удовлетворила К.Ван-Еселтайна из Скулкрафта (шт.Мичиган). Она показалась ему настолько медленной, что он назвал ее "Звездным трактором" (Star truck). Она стала достойной названия "Звездный бой" (Star trek) лишь после того, как он нашел способ удалить большую часть арифметических операций с плавающей запятой из главного цикла программы. Чтобы не вычислять квадратных корней по ходу выполнения программы, он заранее рассчитал двумерный массив расстояний от всех возможных точек (x, y) до начала координат (0, 0). Теперь расстояние между любыми двумя точками (x1, y1) и (x2, y2) можно получить очень просто, посмотрев в таблице расстояние для координат (x2-x1, y2-y2). Ван-Еселтайн затабулировал также значения синуса и косинуса в двух массивах по 36 элементов в каждом, по одному элементу на каждые 10 градусов. Кроме того, он пришел к выводу, что с ракетами легче управляться, если их всегда ровно 20. Разумеется, на любой конкретный момент многие из них могут оказаться виртуальными, в этом случае они просто не отображаются. Далее, массивы, задающие скорость, должны быть не двумерными, а спаренными одномерными. На многих персональных компьютерах такое простое новое определение может дать значительную экономию времени. Целеустремленные читатели, несомненно, сами дойдут до многих других усовершенствований, позволяющих ускорить программу Ван-Еселтайна.
THE ORIGIN OF SPACEBAR. J.M.GRAETZ in Creative Computing, Vol.7, No.8, pages 56-67; August, 1981.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
2 1987
О ФРАКТАЛЬНЫХ ГОРАХ, ГРАФТАЛЬНЫХ РАСТЕНИЯХ И ДРУГИХ ГРАФИЧЕСКИХ ЧУДЕСАХ ФИРМЫ PIXAR
А.К.ДЬЮДНИ
Я ПРЕДСТАВЛЯЮ себе появление первого полнометражного фильма, созданного компьютером. Год 1991. По лестнице спускаюсь в партер зрительного зала с большой сумкой, набитой пакетиками с синтетическими кукурузными хлопьями и бутылками с прохладительными напитками, уже не содержащими обычных натуральных ингредиентов. Медленно гаснет свет в зале, занавес раздвигается и серебряный экран оживает сценой из фильма, созданного по мотивам трилогии Дж.Толкейна "Властелин колец". Фродо Хоббит прогуливается по узкой горной долине. Вдали острые заснеженные горные вершины упираются в самое небо. На переднем плане в ярких солнечных лучах поблескивают экзотические деревья и диковинные травы. Эту сцену сменяет другая - волшебник смотрит в хрустальный шар. В центре шара появляется крепость, ее стены объяты пламенем.
Сейчас трудно сказать, насколько убедительными будут казаться движения и голос Фродо в таком фильме, но я уверен, что горы, растения, хрустальный шар и пламя получатся превосходно. Этим успехом фильм будет в значительной мере обязан новому программному обеспечению и аппаратуре, созданным фирмой Pixar (в прошлом лаборатория компьютерной графики Lucasfilm). Посетив эту удивительную мекку компьютерной графики в Сан-Рафаэле (шт.Калифорния), я готов поделиться с читателями всеми секретами построения изображений гор и растений. Любой, кто располагает домашним компьютером, сможет теперь самостоятельно создавать убедительные изображения подобных объектов. Правда, объем этой статьи не позволит подробно рассмотреть процедуру формирования изображения хрустального шара и пламени, но тем не менее я постараюсь осветить в обших чертах принципы, на основе которых создаются их изображения.
В нашем гипотетическом фильме камера может как бы приближать к нам заснеженные вершины гор, возвышающиеся за спиной Фродо. Более
устрашающие горные хребты, наверное, трудно себе представить. Каждая крупная вершина состоит из отдельных более мелких пиков, а те в свою очередь состоят из еше более мелких и т.д. Здесь перед нами раскрывается бесконечная регрессия пиков. Даже Орк (из упомянутого фильма) - зигзагообразный зверь с толстокожими жесткими ступнями чувствовал бы себя неуютно на подобных склонах с острыми выступами.

Фрактальные горы, построенные компьютером, имитируют природные
Создать изображение такого горного хребта в принципе не сложно. Предположим для простоты, что наша территория имеет треугольную форму. Исходный большой треугольник можно поделить на четыре треугольника меньших размеров, нанеся точки на середине каждой стороны треугольника и соединив эти точки между собой. Каждый из вновь образованных треугольников поделим аналогичным образом. Этот процесс можно продолжать до тех пор, пока не будут достигнуты пределы оптического разрешения или машинного времени компьютера. Полученную в итоге довольно скучноватую решетку треугольников можно несколько оживить, прибегнув к вертикальным вариациям. Каждый раз, найдя среднюю точку на стороне треугольника, ее можно поднять или опустить на некоторое случайным образом выбранное расстояние. Вертикальные перемещения, которые, вообще говоря, должны уменьшаться по мере того, как треугольники становятся все меньше, преобразуют треугольники в горный ландшафт с пиками и расщелинами (см. верхний рисунок на с.106).

Гора получается делением треугольника
Почему благодаря этому методу удается построить достаточно естественно выглядящие горы? Отчасти, наверное, потому, что описанный процесс позволяет построить объект, обладающий фрактальными свойствами: при нарастающем увеличении объекта видны все более и более мелкие его детали. Бенуа Мандельброт, неутомимый "фракталист", работающий в исследовательском центре Томаса Уотсона фирмы IBM в Йорктаун-Хайтсе (шт.Нью-Йорк), в качестве примера, объясняющего свойства таких объектов, использует береговую линию. Допустим, что вы должны измерить длину береговой линии Франции при помощи мерного шеста длиной в один километр. Перебрасывая мерный шест с одного конца на другой, пройдем вдоль всей береговой линии и подсчитаем число отмеренных километров. Конечно, при этом мы не учтем множество мелких заливчиков и мысов, поэтому наш окончательный результат будет не очень точным. Повторив эксперимент с метровой палочкой, получим более точный и больший по величине результат. Но и в этом случае бесчисленное множество мельчайших выступов и впадин окажется неучтенным. Несомненно, сантиметровая палочка еще больше уточнит результат измерения.
Общая закономерность, таким образом, заключается в том, что измеренная длина береговой линии увеличивается с уменьшением длины измерительного прибора. Отношение измеренной длины контура к длине мерной палочки [Очевидно, автор имеет в виду отношение истинной длины контура к измеренной при помощи мерной палочки.- Прим. перев.] - это особое число. Оно называется фрактальной размерностью. Фрактальная размерность отличается от обычного понятия размерности тем, что она обычно выражается дробным числом. Береговая линия, например, может иметь фрактальную размерность, равную 3/2. Такой объект можно представлять себе как нечто промежуточное между одномерным объектом (прямой линией) и двумерным объектом (плоскостью). Если береговая линия относительно прямолинейная, ее фрактальная размерность будет близка к 1, если же береговая линия сильно изрезана, ее фрактальная размерность будет приближаться к 2. Такая линия как бы стремится заполнить двумерное плоское пространство.
Фрактальная модель природного объекта влечет за собой явление бесконечной регрессии формы. С точки зрения компьютерной графики бесконечная регрессия - это в общем-то высокие материи. Достаточно того, чтобы ландшафт имел детали при всех возможных уровнях увеличения. В пределах разрешения экрана горную поверхность можно изобразить с достаточно мелкими деталями, которые можно построить, пользуясь описанным выше процессом последовательного деления треугольников. Хотя полное описание алгоритма, используемого для изображения горного ландшафта, из-за его сложности привести в данной статье не представляется возможным, существует простая программа MOUNTAIN (гора), которая изображает пик Мандельброта в поперечном сечении. Программа MOUNTAIN хорошо иллюстрирует основную идею перемещения точек деления вдоль вертикальной оси. Художник-фракталист начинает рисунок с одного горизонтального отрезка прямой. Определив среднюю точку отрезка, он отклоняет ее вверх или вниз на случайно выбираемое расстояние. Каждый из двух новых отрезков снова делится пополам, и средняя точка подвергается перемещению. Этот процесс можно продолжать неопределенно долго, так же как и деление треугольников.
В программе MOUNTAIN имеются два массива: points (точки) и lines (линии). В них хранится информация о горном профиле. Каждый массив содержит две колонки и некоторое количество строк (скажем, 2048 ), достаточное, чтобы достичь разрешения экрана. В двух столбцах массива points хранятся координаты, а в двух столбцах массива lines - индексы. Каждая линия задается двумя точками в массиве points - значениями координат начальной и конечной точек линии. Чтобы пользователь мог визуально следить за интересным процессом последовательных делений отрезков и образования контуров горного хребта из исходного ничем не приметного многоугольника, программа останавливается на каждом новом поколении точек и ожидает, какое решение он примет. При завершении главного и единственного цикла программа запрашивает пользователя, нужна ли еще одна итерация. Если он отвечает "да", управление опять передается на начало программы.
В теле главного цикла текущие множества точек и линий преобразуются в новые множества, вдвое более многочисленные. С этой целью программа просматривает массив lines строку за строкой, находит индексы соответствующих точек и извлекает их координаты из массива points. По известным координатам конечных точек отрезка прямой вычисляются координаты средней точки отрезка, и координата по оси у изменяется случайным образом. Приведенная ниже формальная запись алгоритма может послужить основой для создания программы. В этой записи переменные j и k указывают на строки массивов points и lines, которые в данный момент заполняются значениями, полученными в результате последнего деления. В переменных pts и lns хранится количество точек и линий, составляющих профиль горы перед последним входом в тело главного цикла. Первоначально j равно pts, а k равно lns. Индекс i пробегает значения от 1 до lns.
j <- j+1
k <- k+1
а <- lines(i, 1)
b <- lines(i, 2)
xl <- points(a, 1)
y1 <- points(a, 2)
x2 <- points(b, 1)
y2 <- points(b, 2)
points(j, l) <- (x1+x2)/2
points(j, 2) <- {y1+y2)/2+random(range)
lines(i, 2) <- j
lines(k, 1) <- j
lines(k, 2) <- b
Эта часть программы MOUNTAIN почти не нуждается в дополнительных пояснениях. После того как вычислены координаты j-й точки значение индекса j запоминается как указатель на вторую точку i-й линии и на первую точку k-й линии. Первая точка i-й линии остается той же, что и прежде, а вторая точка k-й линии идентична исходной второй точке i-й линии; эта точка имеет индекс b. Когда тело цикла полностью выполнено, значения переменных pts и Ins должны быть установлены равными последним значениям j и k соответственно. Значение переменной range первоначально устанавливается пользователем как максимально возможная величина случайного вертикального смещения для точек деления. После каждого выполнения тела цикла значение этой переменной должно быть уменьшено вдвое, чтобы сохранить пропорцию между масштабом случайных вариаций и размером форм, подвергающихся этим вариациям. Функция random(range) выражает выбор случайного числа в диапазоне от 0 до текущего значения переменной range.
Если горы за спиной у Фродо выглядят впечатляющими, то окружающие его со всех сторон растения и деревья никак им не уступают. Они выглядят и реалистично, и в то же время как-то сказочно-причудливо. Реалистичными они выглядят вследствие того, что ветвятся аналогично настоящим растениям, а необычными они кажутся потому, что не принадлежат знакомым видам. В распоряжении графического дизайнера так много различных параметров, что он не может устоять перед искушением создать нечто новое.
Эти новые "вилы" растений можно, пожалуй, назвать "графтальными", потому что они основаны на графах и имеют неявно выраженную фрактальную природу. Говоря о неявной фрактальной природе, я имею в виду, что правила построения топологии растений могли бы применяться (но не применяются) вплоть до предела, накладываемого разрешением экрана. Короче говоря, ветви не разветвляются до бесконечности. После того как граф, лежащий в основе растений, построен, из него можно вывести мириады убедительно выглядящих видов, интерпретируя этот граф по-разному в отношении размеров, цвета, густоты, фактуры и т.д.
Графы, определяющие топологию того или иного растения, генерируются при помощи L-систем, образующих класс грамматик, которые были введены датским биологом и математиком Аристидом Линденмеером в 1968г. L-система по существу представляет собой набор правил, позволяющих выводить новые цепочки символов из старых. Эти правила задают способ подстановки последовательностей символов на место одного исходного символа. Пользуясь, например, алфавитом из символов 0, 1, а также скобками [ и ], можно построить множество сложных ботанических форм, если воспользоваться следующими правилами:
0 -> 1[0]1[0]0
1 -> 11
[ -> [
] -> ]
Чтобы посмотреть, как работают эти правила, допустим, что у нас есть одна исходная цепочка символов, состоящая из единственного символа 0. Последовательно заменяя его и каждый встречающийся далее символ соответствующей ему цепочкой по приведенным правилам, получим такую последовательность символьных цепочек:
0
1[0]1[0]0
11[1[0]1[0]0]11[1[0]1[0]0]1[0]1[0]0
Подобные цепочки можно преобразовать в древовидные графы, если каждое число (0 или 1) представить в виде отрезка прямой, а каждую скобку - точкой ветвления. Отрезки, соответствующие 0 и 1, имеют одинаковую длину, но обычно отличаются тем, что ветки типа 1 остаются голыми, а на конце каждой ветки типа 0 находится лист.
Например, стебель (или ствол) цепочки 1[0]1[0]0 состоит из трех символов, не заключенных в скобки. Отрезок типа 1 продолжается другим таким же отрезком и завершается отрезком типа 0. Две ветки, каждая из которых состоит из единственного отрезка 0, отделяются от стебля, описанного этой формулой. Первая ветвь отходит от конца первого отрезка, а вторая - от конца второго отрезка. Прежде чем мы перейдем к рассмотрению нижнего рисунка на с.106, читатели могут попрактиковаться в построении первых нескольких поколений структуры. Для достижения большей реалистичности в описанную модель можно ввести некоторые дополнительные свойства, например наложить условие, согласно которому для каждого данного стебля (независимо от того, является ли он стволом или веткой) вторичные ветви должны отходить поочередно влево и вправо. Читатели, желающие составить собственные графтальные программы, могут ограничиться этой упрощенной моделью растений. При помощи рассмотренной грамматики профессионалы, работающие в фирме Pixar, получают довольно красивые растения, подобные тем, что показаны на верхнем рисунке справа.
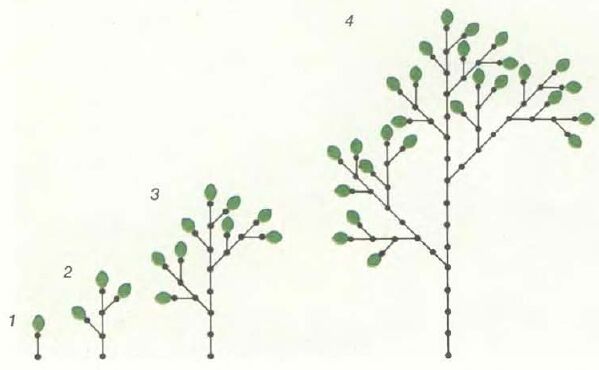
Четыре поколения графтального растения

Графтальные растения фирмы Pixar
Состоящая из двух частей программа под названием PLANT (растение) строит n-ю цепочку в рассмотренной выше последовательности и затем трансформирует ее в изображение в виде контурного рисунка. В первой части программы генерируемые ею цепочки запоминаются в двух символьных массивах stringA и stringB. Каждое поколение растений занимает один из этих массивов поочередно: данное поколение в одном массиве выводится из предыдущего поколения, которое содержится в другом массиве. Хранить в этих массивах символы не обязательно. С тем же успехом можно воспользоваться цифрами 0, 1, 2 и 3 при условии, что программа будет правильно выполнять подстановки.
Правила L-системы встроены в программе в условные операторы. Например, приведенная ниже процедура, записанная в алгоритмическом виде, может служить для преобразования 0 на i-позиции цепочки символов stringA в девять новых символов, которые будут записаны в цепочку stringB:
если stringA(i) = 0, тогда
stringB(j) <- 1
stringB(j+1) <- 2
stringB(j+2) <- 0
stringB(j+3) <- 3
stringB(j+4) <- 1
stringB(j+5) <- 2
stringB(j+6) <- 0
stringB(j+7) <- 3
stringB(j+8 ) <- 0
j <- j+9
Здесь 0 и 1 обозначают сами себя, а 2 и 3 обозначают соответственно [ и ]. Если i-й символ цепочки stringA оказывается равным 0, то программа подставляет последовательность символов 1, 2, 0, 3, 1, 2, 0, 3, 0 в девять прилегающих друг к другу позиций массива stringB, начиная от индекса j (первая еще не заполненная позиция в массиве stringB). Единственный цикл в первой части программы PLANT содержит четыре таких условных оператора, по одному на каждый из возможных символов. Индекс j в цикле играет роль указателя на тот символ в текущем поколении, который обрабатывается в данный момент. Тело этого цикла выполняется для стольких поколений, сколько потребуется худож-ннку-графталисту для воплощения его творческих замыслов. На каждой стадии программа PLANT может запрашивать пользователя, нужна ли еше одна (еще более длинная) цепочка символов.
Во второй, графической части программы PLANT цепочка символов, полученная в результате выполнения первой части программы, превращается в рисунок. Процедура отображения рекурсивна. Пока не встретится левая скобка, или 2, программа рисует последовательность линейных отрезков в заданном направлении. Когда встречается левая скобка, следующий отрезок прямой проводится в новом направлении, под углом 45o (против часовой стрелки) к прежнему. Эта подпроцедура завершается при появлении соответствующей правой скобки. Здесь можно нарисовать листик (его форма и цвет выбираются произвольно). Появление еще одной левой скобки означает повторное выполнение подпроцедуры, с той лишь разницей, что теперь направление меняется на угол 45o по часовой стрелке.
В программе PLANT используется множитель масштаба, величина которого зависит от сложности изображаемого растения. Например, растение в n-м поколении имеет высоту порядка 2^n отрезков. Если на высоте экрана укладываются 200 пикселов, то элементарные отрезки должны быть короче 200/2^n. Изобретательные читатели, несомненно, поэкспериментируют с различными вариантами генерирующих грамматик, углов ветвления и формы листиков. В результате этих вариаций на экране появятся пейзажи из различных трав, кустарников и деревьев (хотя, наверное, и не очень реалистичных).
Хрустальный шар в гипотетическом фильме Толкейна выполняется по методу трассирования лучей, пламя на стенах крепости имитируется путем прослеживания за движением большой совокупности мелких частиц.
Метод трассирования лучей требует задания трехмерной геометрии изображаемой сцены и положения источника света. Покидая источник, каждый луч света следует по сложной траектории, многократно отражаясь и преломляясь. Глаз наблюдателя, который смотрит на сцену, перехватит лишь некоторые лучи и упустит многие другие. Чтобы сэкономить машинное время и память, трассировка лучей осуществляется в обратном направлении. Допустим, что лучи исходят га глаза наблюдателя. Широкий пучок лучей распространяется по сцене. Если луч встречает на своем пути отражающую поверхность, его направление меняется в соответствии с законами оптики. В конце концов луч попадет на поглощающую поверхность и примет тот цвет, который по условию соответствует данной поверхности. Этот цвет присваивается пикселу, который соответствует направлению исходного луча.
Пример изображения, получаемого с использованием метода трассирования лучей, показан на нижнем рисунке на с. 107. В сцене с бильярдными шарами лучи описывают сравнительно простые траектории. Тем не менее на поверхности шаров мы можем видеть отражение бильярдного зала и человека с кием в руках, наблюдающего за движением шаров после очередного удара.

Метод трассирования лучей: построенное компьютером изображение бильярдных шаров
Большая система частиц, которой можно воспользоваться для воспроизведения пламени на стенках крепости, является как бы логическим продолжением тех маленьких облачков из светящихся точек, которые символизировали миниатюрные взрывы в видео- и компьютерных играх. Однако система частиц, разработанная фирмой Pixar, намного сложнее. В определенной области экрана в непрерывном движении живет стая крошечных частиц. Под управлением программы каждая точечная частичка движется в соответствии со строгими динамическими законами. Она рождается, некоторое время живет и двигается, может даже произвести на свет несколько новых частиц и наконец умирает.
Возможности подобной системы частиц были с блеском продемонстрированы в сцене из фильма "Звездный марш II - Гнев хана". На мертвую планету, поверхность которой усеяна кратерами, падает бомба "генезиса". От ее взрыва распространяется причудливо искрящееся кольцо пламени, в конце концов охватывающего всю планету. Когда пламя утихает, мы вил им, что поверхность планеты чудесным образом преобразовалась - теперь она покрыта цветущей роскошной биосферой. Этот эффект был продемонстрирован специалистами фирмы Pixar в те времена, когда она была еще лабораторией компьютерной графики под названием Lucasfilm. Распространяющееся огненное кольцо состояло из ансамблей частиц, в которых отдельные частицы иногда порождали новые ансамбли. Частицы этих новых ансамблей устремлялись высоко вверх над поверхностью планеты, изменяли свой цвет и затем падали вниз под действием гравитационных сил.

Кадр из фильма "Звездный марш II"
Э.Смит, возглавляющий отдел исследований и разработок фирмы Pixar, провел меня по ее лабораториям во время моего визита в Сан-Рафаэль. Смит уже знаком читателям нашего журнала по своим работам в области клеточных автоматов (см. рубрику "Занимательный компьютер": "В мире науки", 1985, #10). Кроме Смита, первым применившим графтальный подход к "компьютерной растительности", я познакомился с Л.Карпентером, специализирующимся на построении изображений гор с помощью фракталий, Р.Куком, экспертом по методу трассирования лучей, и У.Ривсом, изобретателем ансамблей частиц. В разгаре дискуссии о путях развития графического программного обеспечения Смит немало удивил меня, сказав, что главная цель его фирмы состоит не столько в создании специальных эффектов для голливудских фильмов, сколько в разработке специализированного графического компьютера Pixar Image Computer.
Основу графического компьютера фирмы Pixar составляет оперативная память объемом 24 мегабайт для хранения массива 2000*2000 элементов изображения. Этим обеспечивается более чем достаточное разрешение для большинства приложений. Каждый элемент изображения (пиксел) представлен 48 битами памяти, что позволяет хранить обширную информацию, скажем, о цвете и прозрачности изображения. Огромная память компьютера Pixar будет управляться четырьмя работающими параллельно высокопроизводительными полностью программируемыми процессами. Они в состоянии выполнять около 40млн. операций в секунду, обеспечивая быстродействие на несколько порядков выше по сравнению с быстродействием обычных компьютеров. Блок отображения графической информации взаимодействует с памятью компьютера со скоростью 480 мегабайт в секунду.
Первые образцы нового компьютера фирмы Pixar были выпущены в мае прошлого года. Они предназначены для работы в комплексе с медицинскими приборами, с дистанционными датчиками, со средствами инженерного проектирования, а также для создания мультипликационных фильмов. Может быть, именно с помощью таких компьютеров и будет создан мой гипотетический фильм.
БИБЛИОГРАФИЯ
DISTRIBUTED RAY TRACING. ROBERT L.COOK, THOMAS PORTER AND LOREN CARPENTER in Computer Graphics, Vol.18, No.3, pages 137-145; July, 1984.
3-D FRACTALS. MICHIEL VAN DE PANNE in Creative Computing, Vol.11, No.7, pages 78-82; July, 1985.
ОТКЛИКИ
5 1987
ОДИН из наших читателей, У.Слэттери из Джеймстауна
(шт.Род-Айленд), обвинил меня в некомпетентности. В статье, помещенной в февральском номере журнала, в
которой речь шла о программах, рисующих горы и растения, на с.106 было приведено изображение фрактальной горы, построенной методом деления треугольников. Упрек Слэттери заключался в том, что я не смог узнать в этом рисунке... шляпу Шерлока Холмса. Возможно, меня следовало бы даже арестовать за то, что я ввел в заблуждение читателей. И сделать это, наверное, должен великий детектив.
Дж.Маккарти, известный ученый, специалист по информатике из Стан-Фордского университета, высказал более серьезные замечания по поводу фрактальных гор. Он отметил, что у подножия реальных гор, подвергающихся эрозии, образуется немало речных долин. Фрактальные же горы лишены этой особенности, и, по мнению Маккарти, пейзаж должен был бы включать множество озер. Не является ли сходство фрактальных и реальных гор просто оптической иллюзией? Маккарти предостерегает против поспешного принятия фрактальных объектов в качестве моделей реальных и считает, что этот вопрос требует более глубокого изучения.
Поперечное сечение объекта, названного в статье горой Мандельброта, может, по-видимому, представлять не одну гору, а целый горный хребет. Об этом свидетельствуют компьютерные изображения, присланные К.Райтом из Грейлинга (шт.Мичиган). Чтобы вернуться к механизму одиночного горообразования, можно, например, несколько скорректировать случайные отклонения линейных отрезков, образующих профиль горы Мандельброта. Если отклонение вверх сделать более вероятным, чем вниз, то пик горы, по-видимому, становится выразительнее.
Программа, рисующая гору Мандельброта, требует неоправданно большого объема памяти, поскольку она формирует два массива для хранения чередующихся поколений точек, образующихся при последовательном разбиении профиля. Р.Ланг из Линкольн-Сентера (шт.Массачусетс) считает, что достаточно одного массива. По существу, тот же алгоритм, который был предложен в статье, можно легко модифицировать так, чтобы использовался один-единственный массив, хранящий точки профиля, подвергающегося разбиению.
О ФРАКТАЛЬНЫХ ГОРАХ, ГРАФТАЛЬНЫХ РАСТЕНИЯХ И ДРУГИХ ГРАФИЧЕСКИХ ЧУДЕСАХ ФИРМЫ PIXAR
А.К.ДЬЮДНИ
Я ПРЕДСТАВЛЯЮ себе появление первого полнометражного фильма, созданного компьютером. Год 1991. По лестнице спускаюсь в партер зрительного зала с большой сумкой, набитой пакетиками с синтетическими кукурузными хлопьями и бутылками с прохладительными напитками, уже не содержащими обычных натуральных ингредиентов. Медленно гаснет свет в зале, занавес раздвигается и серебряный экран оживает сценой из фильма, созданного по мотивам трилогии Дж.Толкейна "Властелин колец". Фродо Хоббит прогуливается по узкой горной долине. Вдали острые заснеженные горные вершины упираются в самое небо. На переднем плане в ярких солнечных лучах поблескивают экзотические деревья и диковинные травы. Эту сцену сменяет другая - волшебник смотрит в хрустальный шар. В центре шара появляется крепость, ее стены объяты пламенем.
Сейчас трудно сказать, насколько убедительными будут казаться движения и голос Фродо в таком фильме, но я уверен, что горы, растения, хрустальный шар и пламя получатся превосходно. Этим успехом фильм будет в значительной мере обязан новому программному обеспечению и аппаратуре, созданным фирмой Pixar (в прошлом лаборатория компьютерной графики Lucasfilm). Посетив эту удивительную мекку компьютерной графики в Сан-Рафаэле (шт.Калифорния), я готов поделиться с читателями всеми секретами построения изображений гор и растений. Любой, кто располагает домашним компьютером, сможет теперь самостоятельно создавать убедительные изображения подобных объектов. Правда, объем этой статьи не позволит подробно рассмотреть процедуру формирования изображения хрустального шара и пламени, но тем не менее я постараюсь осветить в обших чертах принципы, на основе которых создаются их изображения.
В нашем гипотетическом фильме камера может как бы приближать к нам заснеженные вершины гор, возвышающиеся за спиной Фродо. Более
устрашающие горные хребты, наверное, трудно себе представить. Каждая крупная вершина состоит из отдельных более мелких пиков, а те в свою очередь состоят из еше более мелких и т.д. Здесь перед нами раскрывается бесконечная регрессия пиков. Даже Орк (из упомянутого фильма) - зигзагообразный зверь с толстокожими жесткими ступнями чувствовал бы себя неуютно на подобных склонах с острыми выступами.

Фрактальные горы, построенные компьютером, имитируют природные
Создать изображение такого горного хребта в принципе не сложно. Предположим для простоты, что наша территория имеет треугольную форму. Исходный большой треугольник можно поделить на четыре треугольника меньших размеров, нанеся точки на середине каждой стороны треугольника и соединив эти точки между собой. Каждый из вновь образованных треугольников поделим аналогичным образом. Этот процесс можно продолжать до тех пор, пока не будут достигнуты пределы оптического разрешения или машинного времени компьютера. Полученную в итоге довольно скучноватую решетку треугольников можно несколько оживить, прибегнув к вертикальным вариациям. Каждый раз, найдя среднюю точку на стороне треугольника, ее можно поднять или опустить на некоторое случайным образом выбранное расстояние. Вертикальные перемещения, которые, вообще говоря, должны уменьшаться по мере того, как треугольники становятся все меньше, преобразуют треугольники в горный ландшафт с пиками и расщелинами (см. верхний рисунок на с.106).

Гора получается делением треугольника
Почему благодаря этому методу удается построить достаточно естественно выглядящие горы? Отчасти, наверное, потому, что описанный процесс позволяет построить объект, обладающий фрактальными свойствами: при нарастающем увеличении объекта видны все более и более мелкие его детали. Бенуа Мандельброт, неутомимый "фракталист", работающий в исследовательском центре Томаса Уотсона фирмы IBM в Йорктаун-Хайтсе (шт.Нью-Йорк), в качестве примера, объясняющего свойства таких объектов, использует береговую линию. Допустим, что вы должны измерить длину береговой линии Франции при помощи мерного шеста длиной в один километр. Перебрасывая мерный шест с одного конца на другой, пройдем вдоль всей береговой линии и подсчитаем число отмеренных километров. Конечно, при этом мы не учтем множество мелких заливчиков и мысов, поэтому наш окончательный результат будет не очень точным. Повторив эксперимент с метровой палочкой, получим более точный и больший по величине результат. Но и в этом случае бесчисленное множество мельчайших выступов и впадин окажется неучтенным. Несомненно, сантиметровая палочка еще больше уточнит результат измерения.
Общая закономерность, таким образом, заключается в том, что измеренная длина береговой линии увеличивается с уменьшением длины измерительного прибора. Отношение измеренной длины контура к длине мерной палочки [Очевидно, автор имеет в виду отношение истинной длины контура к измеренной при помощи мерной палочки.- Прим. перев.] - это особое число. Оно называется фрактальной размерностью. Фрактальная размерность отличается от обычного понятия размерности тем, что она обычно выражается дробным числом. Береговая линия, например, может иметь фрактальную размерность, равную 3/2. Такой объект можно представлять себе как нечто промежуточное между одномерным объектом (прямой линией) и двумерным объектом (плоскостью). Если береговая линия относительно прямолинейная, ее фрактальная размерность будет близка к 1, если же береговая линия сильно изрезана, ее фрактальная размерность будет приближаться к 2. Такая линия как бы стремится заполнить двумерное плоское пространство.
Фрактальная модель природного объекта влечет за собой явление бесконечной регрессии формы. С точки зрения компьютерной графики бесконечная регрессия - это в общем-то высокие материи. Достаточно того, чтобы ландшафт имел детали при всех возможных уровнях увеличения. В пределах разрешения экрана горную поверхность можно изобразить с достаточно мелкими деталями, которые можно построить, пользуясь описанным выше процессом последовательного деления треугольников. Хотя полное описание алгоритма, используемого для изображения горного ландшафта, из-за его сложности привести в данной статье не представляется возможным, существует простая программа MOUNTAIN (гора), которая изображает пик Мандельброта в поперечном сечении. Программа MOUNTAIN хорошо иллюстрирует основную идею перемещения точек деления вдоль вертикальной оси. Художник-фракталист начинает рисунок с одного горизонтального отрезка прямой. Определив среднюю точку отрезка, он отклоняет ее вверх или вниз на случайно выбираемое расстояние. Каждый из двух новых отрезков снова делится пополам, и средняя точка подвергается перемещению. Этот процесс можно продолжать неопределенно долго, так же как и деление треугольников.
В программе MOUNTAIN имеются два массива: points (точки) и lines (линии). В них хранится информация о горном профиле. Каждый массив содержит две колонки и некоторое количество строк (скажем, 2048 ), достаточное, чтобы достичь разрешения экрана. В двух столбцах массива points хранятся координаты, а в двух столбцах массива lines - индексы. Каждая линия задается двумя точками в массиве points - значениями координат начальной и конечной точек линии. Чтобы пользователь мог визуально следить за интересным процессом последовательных делений отрезков и образования контуров горного хребта из исходного ничем не приметного многоугольника, программа останавливается на каждом новом поколении точек и ожидает, какое решение он примет. При завершении главного и единственного цикла программа запрашивает пользователя, нужна ли еще одна итерация. Если он отвечает "да", управление опять передается на начало программы.
В теле главного цикла текущие множества точек и линий преобразуются в новые множества, вдвое более многочисленные. С этой целью программа просматривает массив lines строку за строкой, находит индексы соответствующих точек и извлекает их координаты из массива points. По известным координатам конечных точек отрезка прямой вычисляются координаты средней точки отрезка, и координата по оси у изменяется случайным образом. Приведенная ниже формальная запись алгоритма может послужить основой для создания программы. В этой записи переменные j и k указывают на строки массивов points и lines, которые в данный момент заполняются значениями, полученными в результате последнего деления. В переменных pts и lns хранится количество точек и линий, составляющих профиль горы перед последним входом в тело главного цикла. Первоначально j равно pts, а k равно lns. Индекс i пробегает значения от 1 до lns.
j <- j+1
k <- k+1
а <- lines(i, 1)
b <- lines(i, 2)
xl <- points(a, 1)
y1 <- points(a, 2)
x2 <- points(b, 1)
y2 <- points(b, 2)
points(j, l) <- (x1+x2)/2
points(j, 2) <- {y1+y2)/2+random(range)
lines(i, 2) <- j
lines(k, 1) <- j
lines(k, 2) <- b
Эта часть программы MOUNTAIN почти не нуждается в дополнительных пояснениях. После того как вычислены координаты j-й точки значение индекса j запоминается как указатель на вторую точку i-й линии и на первую точку k-й линии. Первая точка i-й линии остается той же, что и прежде, а вторая точка k-й линии идентична исходной второй точке i-й линии; эта точка имеет индекс b. Когда тело цикла полностью выполнено, значения переменных pts и Ins должны быть установлены равными последним значениям j и k соответственно. Значение переменной range первоначально устанавливается пользователем как максимально возможная величина случайного вертикального смещения для точек деления. После каждого выполнения тела цикла значение этой переменной должно быть уменьшено вдвое, чтобы сохранить пропорцию между масштабом случайных вариаций и размером форм, подвергающихся этим вариациям. Функция random(range) выражает выбор случайного числа в диапазоне от 0 до текущего значения переменной range.
Если горы за спиной у Фродо выглядят впечатляющими, то окружающие его со всех сторон растения и деревья никак им не уступают. Они выглядят и реалистично, и в то же время как-то сказочно-причудливо. Реалистичными они выглядят вследствие того, что ветвятся аналогично настоящим растениям, а необычными они кажутся потому, что не принадлежат знакомым видам. В распоряжении графического дизайнера так много различных параметров, что он не может устоять перед искушением создать нечто новое.
Эти новые "вилы" растений можно, пожалуй, назвать "графтальными", потому что они основаны на графах и имеют неявно выраженную фрактальную природу. Говоря о неявной фрактальной природе, я имею в виду, что правила построения топологии растений могли бы применяться (но не применяются) вплоть до предела, накладываемого разрешением экрана. Короче говоря, ветви не разветвляются до бесконечности. После того как граф, лежащий в основе растений, построен, из него можно вывести мириады убедительно выглядящих видов, интерпретируя этот граф по-разному в отношении размеров, цвета, густоты, фактуры и т.д.
Графы, определяющие топологию того или иного растения, генерируются при помощи L-систем, образующих класс грамматик, которые были введены датским биологом и математиком Аристидом Линденмеером в 1968г. L-система по существу представляет собой набор правил, позволяющих выводить новые цепочки символов из старых. Эти правила задают способ подстановки последовательностей символов на место одного исходного символа. Пользуясь, например, алфавитом из символов 0, 1, а также скобками [ и ], можно построить множество сложных ботанических форм, если воспользоваться следующими правилами:
0 -> 1[0]1[0]0
1 -> 11
[ -> [
] -> ]
Чтобы посмотреть, как работают эти правила, допустим, что у нас есть одна исходная цепочка символов, состоящая из единственного символа 0. Последовательно заменяя его и каждый встречающийся далее символ соответствующей ему цепочкой по приведенным правилам, получим такую последовательность символьных цепочек:
0
1[0]1[0]0
11[1[0]1[0]0]11[1[0]1[0]0]1[0]1[0]0
Подобные цепочки можно преобразовать в древовидные графы, если каждое число (0 или 1) представить в виде отрезка прямой, а каждую скобку - точкой ветвления. Отрезки, соответствующие 0 и 1, имеют одинаковую длину, но обычно отличаются тем, что ветки типа 1 остаются голыми, а на конце каждой ветки типа 0 находится лист.
Например, стебель (или ствол) цепочки 1[0]1[0]0 состоит из трех символов, не заключенных в скобки. Отрезок типа 1 продолжается другим таким же отрезком и завершается отрезком типа 0. Две ветки, каждая из которых состоит из единственного отрезка 0, отделяются от стебля, описанного этой формулой. Первая ветвь отходит от конца первого отрезка, а вторая - от конца второго отрезка. Прежде чем мы перейдем к рассмотрению нижнего рисунка на с.106, читатели могут попрактиковаться в построении первых нескольких поколений структуры. Для достижения большей реалистичности в описанную модель можно ввести некоторые дополнительные свойства, например наложить условие, согласно которому для каждого данного стебля (независимо от того, является ли он стволом или веткой) вторичные ветви должны отходить поочередно влево и вправо. Читатели, желающие составить собственные графтальные программы, могут ограничиться этой упрощенной моделью растений. При помощи рассмотренной грамматики профессионалы, работающие в фирме Pixar, получают довольно красивые растения, подобные тем, что показаны на верхнем рисунке справа.

Четыре поколения графтального растения

Графтальные растения фирмы Pixar
Состоящая из двух частей программа под названием PLANT (растение) строит n-ю цепочку в рассмотренной выше последовательности и затем трансформирует ее в изображение в виде контурного рисунка. В первой части программы генерируемые ею цепочки запоминаются в двух символьных массивах stringA и stringB. Каждое поколение растений занимает один из этих массивов поочередно: данное поколение в одном массиве выводится из предыдущего поколения, которое содержится в другом массиве. Хранить в этих массивах символы не обязательно. С тем же успехом можно воспользоваться цифрами 0, 1, 2 и 3 при условии, что программа будет правильно выполнять подстановки.
Правила L-системы встроены в программе в условные операторы. Например, приведенная ниже процедура, записанная в алгоритмическом виде, может служить для преобразования 0 на i-позиции цепочки символов stringA в девять новых символов, которые будут записаны в цепочку stringB:
если stringA(i) = 0, тогда
stringB(j) <- 1
stringB(j+1) <- 2
stringB(j+2) <- 0
stringB(j+3) <- 3
stringB(j+4) <- 1
stringB(j+5) <- 2
stringB(j+6) <- 0
stringB(j+7) <- 3
stringB(j+8 ) <- 0
j <- j+9
Здесь 0 и 1 обозначают сами себя, а 2 и 3 обозначают соответственно [ и ]. Если i-й символ цепочки stringA оказывается равным 0, то программа подставляет последовательность символов 1, 2, 0, 3, 1, 2, 0, 3, 0 в девять прилегающих друг к другу позиций массива stringB, начиная от индекса j (первая еще не заполненная позиция в массиве stringB). Единственный цикл в первой части программы PLANT содержит четыре таких условных оператора, по одному на каждый из возможных символов. Индекс j в цикле играет роль указателя на тот символ в текущем поколении, который обрабатывается в данный момент. Тело этого цикла выполняется для стольких поколений, сколько потребуется худож-ннку-графталисту для воплощения его творческих замыслов. На каждой стадии программа PLANT может запрашивать пользователя, нужна ли еше одна (еще более длинная) цепочка символов.
Во второй, графической части программы PLANT цепочка символов, полученная в результате выполнения первой части программы, превращается в рисунок. Процедура отображения рекурсивна. Пока не встретится левая скобка, или 2, программа рисует последовательность линейных отрезков в заданном направлении. Когда встречается левая скобка, следующий отрезок прямой проводится в новом направлении, под углом 45o (против часовой стрелки) к прежнему. Эта подпроцедура завершается при появлении соответствующей правой скобки. Здесь можно нарисовать листик (его форма и цвет выбираются произвольно). Появление еще одной левой скобки означает повторное выполнение подпроцедуры, с той лишь разницей, что теперь направление меняется на угол 45o по часовой стрелке.
В программе PLANT используется множитель масштаба, величина которого зависит от сложности изображаемого растения. Например, растение в n-м поколении имеет высоту порядка 2^n отрезков. Если на высоте экрана укладываются 200 пикселов, то элементарные отрезки должны быть короче 200/2^n. Изобретательные читатели, несомненно, поэкспериментируют с различными вариантами генерирующих грамматик, углов ветвления и формы листиков. В результате этих вариаций на экране появятся пейзажи из различных трав, кустарников и деревьев (хотя, наверное, и не очень реалистичных).
Хрустальный шар в гипотетическом фильме Толкейна выполняется по методу трассирования лучей, пламя на стенах крепости имитируется путем прослеживания за движением большой совокупности мелких частиц.
Метод трассирования лучей требует задания трехмерной геометрии изображаемой сцены и положения источника света. Покидая источник, каждый луч света следует по сложной траектории, многократно отражаясь и преломляясь. Глаз наблюдателя, который смотрит на сцену, перехватит лишь некоторые лучи и упустит многие другие. Чтобы сэкономить машинное время и память, трассировка лучей осуществляется в обратном направлении. Допустим, что лучи исходят га глаза наблюдателя. Широкий пучок лучей распространяется по сцене. Если луч встречает на своем пути отражающую поверхность, его направление меняется в соответствии с законами оптики. В конце концов луч попадет на поглощающую поверхность и примет тот цвет, который по условию соответствует данной поверхности. Этот цвет присваивается пикселу, который соответствует направлению исходного луча.
Пример изображения, получаемого с использованием метода трассирования лучей, показан на нижнем рисунке на с. 107. В сцене с бильярдными шарами лучи описывают сравнительно простые траектории. Тем не менее на поверхности шаров мы можем видеть отражение бильярдного зала и человека с кием в руках, наблюдающего за движением шаров после очередного удара.

Метод трассирования лучей: построенное компьютером изображение бильярдных шаров
Большая система частиц, которой можно воспользоваться для воспроизведения пламени на стенках крепости, является как бы логическим продолжением тех маленьких облачков из светящихся точек, которые символизировали миниатюрные взрывы в видео- и компьютерных играх. Однако система частиц, разработанная фирмой Pixar, намного сложнее. В определенной области экрана в непрерывном движении живет стая крошечных частиц. Под управлением программы каждая точечная частичка движется в соответствии со строгими динамическими законами. Она рождается, некоторое время живет и двигается, может даже произвести на свет несколько новых частиц и наконец умирает.
Возможности подобной системы частиц были с блеском продемонстрированы в сцене из фильма "Звездный марш II - Гнев хана". На мертвую планету, поверхность которой усеяна кратерами, падает бомба "генезиса". От ее взрыва распространяется причудливо искрящееся кольцо пламени, в конце концов охватывающего всю планету. Когда пламя утихает, мы вил им, что поверхность планеты чудесным образом преобразовалась - теперь она покрыта цветущей роскошной биосферой. Этот эффект был продемонстрирован специалистами фирмы Pixar в те времена, когда она была еще лабораторией компьютерной графики под названием Lucasfilm. Распространяющееся огненное кольцо состояло из ансамблей частиц, в которых отдельные частицы иногда порождали новые ансамбли. Частицы этих новых ансамблей устремлялись высоко вверх над поверхностью планеты, изменяли свой цвет и затем падали вниз под действием гравитационных сил.

Кадр из фильма "Звездный марш II"
Э.Смит, возглавляющий отдел исследований и разработок фирмы Pixar, провел меня по ее лабораториям во время моего визита в Сан-Рафаэль. Смит уже знаком читателям нашего журнала по своим работам в области клеточных автоматов (см. рубрику "Занимательный компьютер": "В мире науки", 1985, #10). Кроме Смита, первым применившим графтальный подход к "компьютерной растительности", я познакомился с Л.Карпентером, специализирующимся на построении изображений гор с помощью фракталий, Р.Куком, экспертом по методу трассирования лучей, и У.Ривсом, изобретателем ансамблей частиц. В разгаре дискуссии о путях развития графического программного обеспечения Смит немало удивил меня, сказав, что главная цель его фирмы состоит не столько в создании специальных эффектов для голливудских фильмов, сколько в разработке специализированного графического компьютера Pixar Image Computer.
Основу графического компьютера фирмы Pixar составляет оперативная память объемом 24 мегабайт для хранения массива 2000*2000 элементов изображения. Этим обеспечивается более чем достаточное разрешение для большинства приложений. Каждый элемент изображения (пиксел) представлен 48 битами памяти, что позволяет хранить обширную информацию, скажем, о цвете и прозрачности изображения. Огромная память компьютера Pixar будет управляться четырьмя работающими параллельно высокопроизводительными полностью программируемыми процессами. Они в состоянии выполнять около 40млн. операций в секунду, обеспечивая быстродействие на несколько порядков выше по сравнению с быстродействием обычных компьютеров. Блок отображения графической информации взаимодействует с памятью компьютера со скоростью 480 мегабайт в секунду.
Первые образцы нового компьютера фирмы Pixar были выпущены в мае прошлого года. Они предназначены для работы в комплексе с медицинскими приборами, с дистанционными датчиками, со средствами инженерного проектирования, а также для создания мультипликационных фильмов. Может быть, именно с помощью таких компьютеров и будет создан мой гипотетический фильм.
БИБЛИОГРАФИЯ
DISTRIBUTED RAY TRACING. ROBERT L.COOK, THOMAS PORTER AND LOREN CARPENTER in Computer Graphics, Vol.18, No.3, pages 137-145; July, 1984.
3-D FRACTALS. MICHIEL VAN DE PANNE in Creative Computing, Vol.11, No.7, pages 78-82; July, 1985.
ОТКЛИКИ
5 1987
ОДИН из наших читателей, У.Слэттери из Джеймстауна
(шт.Род-Айленд), обвинил меня в некомпетентности. В статье, помещенной в февральском номере журнала, в
которой речь шла о программах, рисующих горы и растения, на с.106 было приведено изображение фрактальной горы, построенной методом деления треугольников. Упрек Слэттери заключался в том, что я не смог узнать в этом рисунке... шляпу Шерлока Холмса. Возможно, меня следовало бы даже арестовать за то, что я ввел в заблуждение читателей. И сделать это, наверное, должен великий детектив.
Дж.Маккарти, известный ученый, специалист по информатике из Стан-Фордского университета, высказал более серьезные замечания по поводу фрактальных гор. Он отметил, что у подножия реальных гор, подвергающихся эрозии, образуется немало речных долин. Фрактальные же горы лишены этой особенности, и, по мнению Маккарти, пейзаж должен был бы включать множество озер. Не является ли сходство фрактальных и реальных гор просто оптической иллюзией? Маккарти предостерегает против поспешного принятия фрактальных объектов в качестве моделей реальных и считает, что этот вопрос требует более глубокого изучения.
Поперечное сечение объекта, названного в статье горой Мандельброта, может, по-видимому, представлять не одну гору, а целый горный хребет. Об этом свидетельствуют компьютерные изображения, присланные К.Райтом из Грейлинга (шт.Мичиган). Чтобы вернуться к механизму одиночного горообразования, можно, например, несколько скорректировать случайные отклонения линейных отрезков, образующих профиль горы Мандельброта. Если отклонение вверх сделать более вероятным, чем вниз, то пик горы, по-видимому, становится выразительнее.
Программа, рисующая гору Мандельброта, требует неоправданно большого объема памяти, поскольку она формирует два массива для хранения чередующихся поколений точек, образующихся при последовательном разбиении профиля. Р.Ланг из Линкольн-Сентера (шт.Массачусетс) считает, что достаточно одного массива. По существу, тот же алгоритм, который был предложен в статье, можно легко модифицировать так, чтобы использовался один-единственный массив, хранящий точки профиля, подвергающегося разбиению.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
3 1987
АНАЛИЗ РЕЗУЛЬТАТОВ ПЕРВОГО ТУРНИРА ПО КОМПЬЮТЕРНОЙ ИГРЕ "БОЙ В ПАМЯТИ"
А.К.ДЬЮДНИ
"БОЙ В ПАМЯТИ" - игра, участники которой, компьютерные программы, пытаются уничтожить друг друга, привлекла к себе внимание в конце прошлого года, когда в музее вычислительной техники в Бостоне (шт.Массачусетс) состоялся первый международный турнир, организованный ее энтузиастами. В турнире принимала участие 31 программа, три из них, оказавшиеся самыми боеспособными, стали призерами соревнований. Абсолютным чемпионом была объявлена программа MICE (мышка). Ее автору Ч.Уэнделлу из Рочестера был вручен приз - специально изготовленная декоративная панель с элементами памяти для игры "Бой в памяти" в ее первоначальной версии, относящейся к тому времени, когда появились первые игровые программы, способные вести бой и выполнявшиеся на компьютере CDC 6600.
Игра "Бой в памяти" уже дважды была темой статей в рубрике "Занимательный компьютер" (см. "В мире науки". 1984, #7 и 1985, #5). Созданные людьми боевые программы начинают самостоятельную жизнь, вступая в сражение с противником на поле компьютерной памяти. Область памяти, отведенная под поле боя, называется CORE (сердечник) - так называлась оперативная память компьютера в те времена, когда ее ячейки представляли собой миниатюрные колечки из ферромагнитных сплавов. Эта игра стала настолько популярной, что ее любители организовали свое международное общество. Недавно это общество несколько изменило правила игры и теперь игроки будут придерживаться ее новой версии.
Основу игры составляют боевые программы, написанные на специальном языке низкого уровня пол названием Редкод (Redcode). Именно такие программы и выступали на недавнем турнире. При помощи 10 простых команд программа может перемешать информацию из одной ячейки памяти в другую, складывать и вычитать числа, изменять порядок выполнения команд и даже выполнять несколько команд одновременно (см. рисунок на с.98 ). Рассмотрим, например, одну из основных команд на перемещение информации MOV. Она состоит из трех частей - кода команды и двух адресов - и занимает одну ячейку памяти. В общем виде команда записывается как MOV A B. Если A, скажем, равно 102, а В равно - 5, то программа обратится к ячейке, отстоящей от данной ячейки на 102 адреса, и, прочтя информацию, которая там хранится, поместит ее в ячейку, расположенную на 5 адресов до ячейки, хранящей команду MOV.

Сведения о Редкоде, языке ассемблера для игры "Бой в памяти"
Простейшая программа на языке Редкод состоит всего из одной команды MOV 0 1. Эта программа IMP (будем называть ее чертенком) перемещает содержимое ячейки с относительным адресом 0 (т.е. саму команду MOV) в ячейку с относительным адресом 1, т.е. в ячейку, расположенную на один адрес впереди. Команды языка Редкод обычно выполняются последовательно. Это означает, что после выполнения команды MOV 0 1 компьютер попытается выполнить команду, записанную в следующей ячейке. Но там теперь находится команда MOV 0 1, только что скопированная туда из ячейки с предшествующим адресом. В результате чертенок прыгает от адреса к адресу по памяти компьютера, сокрушая все на своем пути. Позади он оставляет след из команд MOV 0 1.
Чертенок может похитить самое главное в программе противника, а именно право на выполнение. Чтобы понять, как это происходит, предположим, что у нас есть боевая программа, выполняющаяся, как обычно, в том порядке, в каком расположены ее команды. Чертенок вторгается в пределы этой программы, заменяя ее команды бесконечной последовательностью MOV 0 1. Рано или поздно наша программа, наверное, передаст управление на поврежденный участок. Но в этом случае она сразу превратится в нового чертенка. Выступая под старым флагом, она вынуждена теперь следовать на поводу у противника, чертенка, до тех пор, пока сражение не кончится.
Чтобы обезопасить себя от нападения чертенка, программа для "Боя в памяти" должна по крайней мере содержать в себе специальный барьер. Этот предохранительный барьер состоит из двух команд, выполняющихся циклически:
MOV #0 -1
JMP -1
Первая команда перемещает целое число 0, записанное как #0, в ячейку с относительным адресом -1. Другими словами, при каждом выполнении команды MOV ячейка, расположенная непосредственно "над" ней (только оттуда следует ожидать вторжения чертенка), заполняется числом 0. Вторая команда JMP является командой перехода, или передачи управления. После того как она выполнена, управление переходит на ячейку с относительным адресом -1, т.е. на ячейку, расположенную непосредственно над командой MOV. При каждом цикле выполнения программа сбрасывает нулевую бомбу на то место, куда перед этим мог добраться чертенок,- на ячейку, прилегающую к барьеру сверху, В результате чертенок уничтожается.
Игра "Бой в памяти" основана на двух правилах. Первое заключается в том, что программы-соперники выполняют свои команды по очереди. За чередованием ходов следит управляющая система Марс (MARS - от слов Memory Array Redcode Simulator). Из этого несколько неуклюжего военного названия следует, что Марс имитирует действия компьютера. Марс постоянно изменяет содержимое ячеек оперативной памяти в соответствии с выполняемыми командами языка Редкод. Каждой стороне предоставляется право выполнения лишь одной команды, после чего выполняется команда программы противника. Второе правило состоит в том, что когда одна из программ не может выполнить свою очередную команду, то эта программа считается проигравшей.
Выполнение программы может разделиться на несколько линий. Если в программе, написанной на языке Редкод, встречается команда SPL A, то дальнейшее выполнение программы как бы идет по двум линиям. Одна линия начинается с команды, непосредственно следующей за SPL A, a другая перескакивает на команду с относительным адресом A. К сожалению, Марс не может выполнить обе эти команды одновременно, одну команду система выполняет на одном ходе, предоставленном данной программе, а вторую - на следующем ходе. Таким образом сводится на нет, казалось бы, важное преимущество: чем больше у программы различных линий выполнения, тем медленнее выполняется каждая из этих линий. Но в итоге подобное замедление оказывается оправданным. Если у программы есть несколько линий выполнения, то она считается проигравшей лишь в том случае, когда ни одна из этих линий не может быть продолжена. Эта ситуация возникает, когда система Марс, ожидая найти выполнимую команду языка Редкод, находит лишь то, что можно, образно выражаясь, назвать воронками от взорванных снарядов и бомб.
Чтобы проиллюстрировать возможности команды SPL, рассмотрим, к примеру, пять первых команд моей собственной программы, принявшей участие в турнире "Вой в памяти". Я назвал ее COMMANDO (десантник-диверсант) по причинам, о
которых скажу несколько позже.
MOV #0 -1
JMP -1
SPL -2
MOV 10 113
SPL 112
...
В первых двух командах читатели, наверное, узнали барьер, предохраняющий программу от вторжения чертенка. Выполнение самой программы начинается с третьей команды: SPL -2. На следующих двух ходах, предоставленных программе COMMANDO, будут выполнены первая и четвертая команды, а затем при следующих двух очередных ходах - вторая и пятая команды. Каждая линия программы развивается независимо от другой и с вдвое меньшей скоростью, если можно так выразиться. В рассматриваемом нами примере COMMANDO сначала запускает свой оборонительный фрагмент, который в дальнейшем работает самостоятельно. Затем она запускает своего собственного чертенка (начиная с ячейки, отстоящей на 10 адресов от второй команды MOV) в далекую ячейку (отстоящую на 113 адресов). Второй чертенок запускается следующей командой SPL.
Остальные команды программы COMMANDO предназначены для того, чтобы скопировать всю программу в другую область, которая удалена на 100 адресов от ее теперешнего положения. Новая копия программы, как десантник, только что приземлившийся на территории противника, запускается командой JMP в исходной программе. Старый экземпляр COMMANDO, за исключением барьерного фрагмента, прекращает свое существование и больше не выполняется. Затем описанный процесс повторяется для нового экземпляра программы, который в свою очередь копируется на новое место в памяти.
Ну а насколько успешно выступила программа COMMANDO против своих соперников? Турнир был организован так, чтобы между программами-участниками (а их, как уже отмечалось, было 31) состоялось как можно больше поединков. Розыгрыш по полной круговой системе, когда каждый участник встречается со всеми другими участниками, потребовал бы проведения 465 поединков и занял бы слишком много времени. Поэтому участники были поделены произвольно на две приблизительно равные группы: группа I и группа II. Затем внутри каждой группы был проведен турнир по полной круговой системе.
Известие о том, что COMMANDO стала победителем турнира в группе II, я встретил со смешанным чувством. С одной стороны, я был очень горд тем, что мое кибернетическое творение так хорошо проявило себя в действии. В то же время я испытывал некоторое беспокойство при мысли о том, что моя программа может оказаться победителем соревнований. Дело в том, что я согласился выступить в роли комментатора финальных состязаний и чувствовал, что мне трудно будет сохранить объективность.
Четыре лучшие программы из каждой группы выступили затем в новом круговом турнире. Победителями в этом турнире оказались три программы: CHANG1 - автор М.Чанг из Флорал-Парка (шт.Нью-Йорк) и две программы Ч.Уэнделла MIDGET и MICE. Моя программа COMMANDO, получив смертельное ранение, пала смертью храбрых. Интересно сложился финал, выигранный программой MICE. MIDGET и MICE свели свои поединки с CHANG1 вничью, но MICE получила решающее выигрышное очко, добившись победы в поединке с MIDGET.
Матч между каждой парой финалистов состоял из четырех боев, проводившихся один за другим. Поединки были ограничены по времени: каждая сторона могла сделать не более 15тыс. ходов (команд), что приблизительно соответствует двум минутам машинного времени. Две встречающиеся в поединке боевые программы помещались в выбранные случайным образом непересекающиеся области памяти, после чего они запускались. Получилось так, что бои, проведенные между всеми парами программ, закончились с одним и тем же результатом. В частности, все бои между программами MICE и CHANG1 завершились вничью.
Очень интересно наблюдать за развитием боя. На турнире использовался дисплей, на котором отображалось поле боя в виде последовательности полос с клеточной структурой (см. рисунок на с.97). Каждая клетка представляла одну ячейку (и один адрес) в памяти, причем последняя клетка в нижнем ряду была соседней по отношению к первой клетке в верхнем ряду. Таким образом, поле боя было замкнутым. Программа, которой предоставлялся первый ход, в исходном положении занимала область памяти, начинавшуюся с адреса 0, и ее команды последовательно заполняли прилегающие ячейки. Клетки, занятые этой программой, окрашивались в голубой цвет. Программа-соперник занимала произвольно выбранную область ячеек, не пересекавшуюся с областью, занятой первой программой. На экране эта область окрашивалась в ярко-красный цвет. А вообще цвет любой клетки на дисплее определялся тем, какая из соперничавших программ изменила ее содержимое последней. Таким образом, перед глазами наблюдателя разворачивалась картина сражения.

Одна из начальных и одна из завершающих стадий в сражении между программами MICE (красный) и CHANG1 (синий)
На темно-синем фоне экрана МICE и CHANG1 переползали с места на место, запускали чертиков, разбрасывали бомбы и воспроизводили сами себя (самопроизвольным делением). Проследим за тем, как развивались события в одном типичном бою между этими программами. CHANG1 возникла в виде голубой полоски в левом верхнем углу экрана, а появление на свет программы MICE было ознаменовано красной полоской, возникшей несколько ближе чем на полпути к нижнему краю экрана. Почти сразу же и очень быстро "мышки" начали разбегаться по экрану.
Одна из самых коротких известных мне самовоспроизводящихся программ MICE состоит всего из восьми команд, две из которых создают новую копию программы в области памяти, отстоящей на 833 адреса от положения, занимаемого ею на момент копирования (см. рисунок справа). Эти две команды демонстрируют некоторые дополнительные возможности языка Редкод:
loop MOV @ptr <5
DJN loop ptr
Здесь слово loop (цикл) представляет собой просто метку, обозначающую адрес (в данном случае ячейки, в которой содержится команда MOV). Благодаря использованию меток написание программы на Редкоде значительно упрощается. По команде DJN (уменьшение и переход к ненулевому значению операнда) происходит передача управления на команду, помеченную меткой loop, если значение величины, хранящейся в ячейке с другим адресом (помеченным меткой ptr), не равно нулю. Значок @ означает способ адресации, называемый косвенным: при выполнении команды MOV перемешается не содержимое ячейки, помеченной как ptr, а содержимое содержимого, если можно так выразиться. Число, хранящееся по адресу ptr, является адресом той ячейки, содержимое которой следует переместить. В данном случае это содержимое представляет собой одну из команд программы MICE.

Участники чемпионата игр "Бой в памяти"
Число, хранящееся в ячейке с адресом ptr, все время изменяется благодаря функции уменьшения, содержащейся в команде DJN. Исходное значение этого числа равно последнему адресу программы, затем оно постепенно уменьшается до 0 и здесь цикл копирования завершается. Аналогичным образом адреса, по которым должны разместиться команды программы на новом месте, также заданы косвенно. Ячейка с относительным адресом 5 первоначально хранит число 833, и первая команда, перемещаемая программой, приземлится в ячейке, отстоящей на 832 адреса от команды MOV. Как показывает значок <, адрес назначения уменьшается при каждом выполнении команды MOV. Мышки копируют себя как бы от хвоста к голове.
Команда SPL (от англ. split - разветвление), следующая сразу же за циклом копирования, передает управление только что созданному экземпляру программы MICE. Но вслед за рождением отпрыска старый экземпляр программы выполняется сначала. В принципе количество отпрысков, порождаемых подобной программой, не ограничено. И каждая новая программа работает, следуя все той же процедуре. Действительно, получаются такие же мышки!
Так было и в типичном сражении с программой CHANG1. Мышки размножались с невероятной быстротой. Вскоре весь экран был усеян маленькими красными полосками. Тем временем CHANG1 запустила своеобразную фабрику, производящую на свет чертиков и спускающую их "вниз по течению". Эта фабрика была построена всего лишь из трех команд:
SPL 2
JMP -1
MOV 0 1
Когда управление достигает команды SPL, процесс выполнения команд разветвляется на две ветви. Одна из них начинается с команды MOV 0 1. Другая ветвь выполняет команду JMP -1, которая начинает весь описанный процесс заново. Тем временем один чертенок уже покинул конвейер и отправился на охоту за мышками. Основная проблема, возникающая при массовом производстве чертиков, заключается в том, что большое число независимых линий выполнения замедляет каждый из выполняемых процессов. 1000 чертиков движутся в 1000 раз медленнее, чем один чертенок. Во всяком случае, роковая орда чертиков стала медленно спускаться из верхней части экрана в виде все удлинявшейся сплошной голубой полосы. Смогут ли они перехитрить мышек?
Пока размножались чертики, несколько экземпляров программы MICE, или несколько мышек, были убиты бомбами, брошенными программой CHANG1. Такая бомба представляет собой обычно число 0, "сбрасываемое" командой MOV предположительно на территорию противника. Ключевая команда в программе Чанга - это MOV #0 @-4. Нулевая бомба падает в ячейку, адрес которой содержится в ячейке четырьмя адресами "выше" команды MOV. Адрес назначения постоянно увеличивается на 16 единиц, тем самым обеспечивается равномерный обстрел "по площади".
В то время как некоторые мышки погибали от бомб, чертики тоже начали причинять вред противнику. Однако в каждом экземпляре программы MICE заложена возможность самоубийства. Программа постоянно проверяет свою первую команду, которая представляет собой команду описания данных и должна содержать в себе число 0. Если там уже не 0, то программа совершает переход на (невыполнимую) команду описания данных и таким образом предпочитает погибнуть, чем стать жертвой крошечного неприятеля.
Но если одни мышки погибали под бомбами, а другие, так сказать, кончали жизнь самоубийством, чтобы избежать плена, то как же им удалось все-таки выжить? Объяснение, конечно, заключается в их чрезвычайной плодовитости. Ведь в конце концов многие новые экземпляры приземлились на голову противника. На самом деле незадолго до истечения времени поединка один из экземпляров программы MICE приземлился прямо на территории основной программы CHANG1 и уничтожил ее. Однако к этому моменту CHANG1 создала достаточно много чертиков, чтобы протянуть время до финального звонка. Поединок завершился с ничейным исходом. Искусство создания программ для игры "Бой в памяти" находится еше в своей начальной стадии. Конечно, здесь будут сделаны свои открытия и будет наблюдаться постепенный неуклонный прогресс. Какому-нибудь изобретательному программисту, возможно, удастся открыть абсолютно надежное средство против угрозы чертиков, другой сумеет найти простой способ самовосстановления поврежденной программы.
Боевые программы следующих поколений, наверное, будут длиннее теперешних призеров, но зато их "живучесть" будет на несколько порядков величины выше. Они будут способны заниматься разведкой, оставлять ложный след и наносить внезапные сокрушительные удары по противнику. Эти тенденции, возможно, проявятся уже на втором международном турнире по игре "Бой в памяти", который должен состояться осенью этого года в музее вычислительной техники. А пока читатели имеют возможность солидно подготовиться, вложив в программы всю свою изобретательность и коварство.
Своим успехом прошлогодний турнир был в значительной степени обязан М. и Б.Кларксонам, а также Г.Беллу, возглавляющему музей вычислительной техники, и Оливеру Стримпелу, куратору музея. В заключение нужно, наверное, сказать несколько слов о самом музее.
Музей вычислительной техники в Бостоне, пожалуй, единственный в мире музей, экспозиция которого целиком посвящена компьютерам. Размешенный в перестроенном (и теперь роскошном) здании бывшего складского помещения на набережной, он демонстрирует компьютеры - от чудовищ, собранных на вакуумных электронных лампах, до персональных компьютеров, полностью предназначенных для игр. Стены помещения украшены удивительной графикой; здесь представлена полная компьютерная система NORAD SAGE и многие другие экспонаты как развлекательного, так и образовательного плана. Читатели, которые будут в Бостоне и посетят старинный корабль в бостонской бухте, могут заглянуть и в музей вычислительной техники, это буквально в двух шагах от бухты.
ОТКЛИКИ
6 1987
За время, прошедшее с момента выхода в свет нашей статьи, посвященной первому международному турниру по компьютерной игре "Бой в памяти", число членов международной ассоциации любителей игры возросло, по словам ее председателя М.Кларксона, в четыре раза. Тем не менее Кларксон по-прежнему приглашает желающих присоединиться к ассоциации. В то же время У.Р.Бакли, редактор бюллетеня "Новости войны в памяти", отметил соответствующее увеличение числа подписчиков на это издание. Бакли сообщает, что бюллетень будет официальным органом ассоциации, в котором ее члены будут публиковать свои сообщения, рассказывающие о новых тактических приемах, будут высказывать свои мысли, касающиеся дальнейшего совершенствования игры и повышения класса игроков.
7 1987
ПО МЕРЕ ТОГО как под влиянием статей из рубрики "Занимательный компьютер" продолжают возникать различные любительские ассоциации, эти статьи все в большей степени играют роль "доски объявлений" этих ассоциаций. В этом месяце два объявления для любителей игры "Бой в памяти". Читатели, обращающиеся к М.Кларксону, президенту международного общества любителей этой игры, с просьбой выслать им "Правила игры "Бой в памяти"", должны запастись терпением. Пожар, случившийся в доме Кларксона в январе, является причиной длительной задержки в выполнении запросов. Продолжают поступать заявки от желающих принять участие во втором международном турнире по игре "Бой в памяти", который планируется провести в Бостоне этой осенью. О подробностях будет сообщено в последующих статьях.
12 1988
Наконец, для увлекающихся игрой "Бой в памяти", сообщим, что III международный турнир по этой игре состоится 3-4 декабря в штаб-квартире Международного общества по игре "Бой в памяти"в Хантингтон-Биче (шт.Калифорния).
АНАЛИЗ РЕЗУЛЬТАТОВ ПЕРВОГО ТУРНИРА ПО КОМПЬЮТЕРНОЙ ИГРЕ "БОЙ В ПАМЯТИ"
А.К.ДЬЮДНИ
"БОЙ В ПАМЯТИ" - игра, участники которой, компьютерные программы, пытаются уничтожить друг друга, привлекла к себе внимание в конце прошлого года, когда в музее вычислительной техники в Бостоне (шт.Массачусетс) состоялся первый международный турнир, организованный ее энтузиастами. В турнире принимала участие 31 программа, три из них, оказавшиеся самыми боеспособными, стали призерами соревнований. Абсолютным чемпионом была объявлена программа MICE (мышка). Ее автору Ч.Уэнделлу из Рочестера был вручен приз - специально изготовленная декоративная панель с элементами памяти для игры "Бой в памяти" в ее первоначальной версии, относящейся к тому времени, когда появились первые игровые программы, способные вести бой и выполнявшиеся на компьютере CDC 6600.
Игра "Бой в памяти" уже дважды была темой статей в рубрике "Занимательный компьютер" (см. "В мире науки". 1984, #7 и 1985, #5). Созданные людьми боевые программы начинают самостоятельную жизнь, вступая в сражение с противником на поле компьютерной памяти. Область памяти, отведенная под поле боя, называется CORE (сердечник) - так называлась оперативная память компьютера в те времена, когда ее ячейки представляли собой миниатюрные колечки из ферромагнитных сплавов. Эта игра стала настолько популярной, что ее любители организовали свое международное общество. Недавно это общество несколько изменило правила игры и теперь игроки будут придерживаться ее новой версии.
Основу игры составляют боевые программы, написанные на специальном языке низкого уровня пол названием Редкод (Redcode). Именно такие программы и выступали на недавнем турнире. При помощи 10 простых команд программа может перемешать информацию из одной ячейки памяти в другую, складывать и вычитать числа, изменять порядок выполнения команд и даже выполнять несколько команд одновременно (см. рисунок на с.98 ). Рассмотрим, например, одну из основных команд на перемещение информации MOV. Она состоит из трех частей - кода команды и двух адресов - и занимает одну ячейку памяти. В общем виде команда записывается как MOV A B. Если A, скажем, равно 102, а В равно - 5, то программа обратится к ячейке, отстоящей от данной ячейки на 102 адреса, и, прочтя информацию, которая там хранится, поместит ее в ячейку, расположенную на 5 адресов до ячейки, хранящей команду MOV.

Сведения о Редкоде, языке ассемблера для игры "Бой в памяти"
Простейшая программа на языке Редкод состоит всего из одной команды MOV 0 1. Эта программа IMP (будем называть ее чертенком) перемещает содержимое ячейки с относительным адресом 0 (т.е. саму команду MOV) в ячейку с относительным адресом 1, т.е. в ячейку, расположенную на один адрес впереди. Команды языка Редкод обычно выполняются последовательно. Это означает, что после выполнения команды MOV 0 1 компьютер попытается выполнить команду, записанную в следующей ячейке. Но там теперь находится команда MOV 0 1, только что скопированная туда из ячейки с предшествующим адресом. В результате чертенок прыгает от адреса к адресу по памяти компьютера, сокрушая все на своем пути. Позади он оставляет след из команд MOV 0 1.
Чертенок может похитить самое главное в программе противника, а именно право на выполнение. Чтобы понять, как это происходит, предположим, что у нас есть боевая программа, выполняющаяся, как обычно, в том порядке, в каком расположены ее команды. Чертенок вторгается в пределы этой программы, заменяя ее команды бесконечной последовательностью MOV 0 1. Рано или поздно наша программа, наверное, передаст управление на поврежденный участок. Но в этом случае она сразу превратится в нового чертенка. Выступая под старым флагом, она вынуждена теперь следовать на поводу у противника, чертенка, до тех пор, пока сражение не кончится.
Чтобы обезопасить себя от нападения чертенка, программа для "Боя в памяти" должна по крайней мере содержать в себе специальный барьер. Этот предохранительный барьер состоит из двух команд, выполняющихся циклически:
MOV #0 -1
JMP -1
Первая команда перемещает целое число 0, записанное как #0, в ячейку с относительным адресом -1. Другими словами, при каждом выполнении команды MOV ячейка, расположенная непосредственно "над" ней (только оттуда следует ожидать вторжения чертенка), заполняется числом 0. Вторая команда JMP является командой перехода, или передачи управления. После того как она выполнена, управление переходит на ячейку с относительным адресом -1, т.е. на ячейку, расположенную непосредственно над командой MOV. При каждом цикле выполнения программа сбрасывает нулевую бомбу на то место, куда перед этим мог добраться чертенок,- на ячейку, прилегающую к барьеру сверху, В результате чертенок уничтожается.
Игра "Бой в памяти" основана на двух правилах. Первое заключается в том, что программы-соперники выполняют свои команды по очереди. За чередованием ходов следит управляющая система Марс (MARS - от слов Memory Array Redcode Simulator). Из этого несколько неуклюжего военного названия следует, что Марс имитирует действия компьютера. Марс постоянно изменяет содержимое ячеек оперативной памяти в соответствии с выполняемыми командами языка Редкод. Каждой стороне предоставляется право выполнения лишь одной команды, после чего выполняется команда программы противника. Второе правило состоит в том, что когда одна из программ не может выполнить свою очередную команду, то эта программа считается проигравшей.
Выполнение программы может разделиться на несколько линий. Если в программе, написанной на языке Редкод, встречается команда SPL A, то дальнейшее выполнение программы как бы идет по двум линиям. Одна линия начинается с команды, непосредственно следующей за SPL A, a другая перескакивает на команду с относительным адресом A. К сожалению, Марс не может выполнить обе эти команды одновременно, одну команду система выполняет на одном ходе, предоставленном данной программе, а вторую - на следующем ходе. Таким образом сводится на нет, казалось бы, важное преимущество: чем больше у программы различных линий выполнения, тем медленнее выполняется каждая из этих линий. Но в итоге подобное замедление оказывается оправданным. Если у программы есть несколько линий выполнения, то она считается проигравшей лишь в том случае, когда ни одна из этих линий не может быть продолжена. Эта ситуация возникает, когда система Марс, ожидая найти выполнимую команду языка Редкод, находит лишь то, что можно, образно выражаясь, назвать воронками от взорванных снарядов и бомб.
Чтобы проиллюстрировать возможности команды SPL, рассмотрим, к примеру, пять первых команд моей собственной программы, принявшей участие в турнире "Вой в памяти". Я назвал ее COMMANDO (десантник-диверсант) по причинам, о
которых скажу несколько позже.
MOV #0 -1
JMP -1
SPL -2
MOV 10 113
SPL 112
...
В первых двух командах читатели, наверное, узнали барьер, предохраняющий программу от вторжения чертенка. Выполнение самой программы начинается с третьей команды: SPL -2. На следующих двух ходах, предоставленных программе COMMANDO, будут выполнены первая и четвертая команды, а затем при следующих двух очередных ходах - вторая и пятая команды. Каждая линия программы развивается независимо от другой и с вдвое меньшей скоростью, если можно так выразиться. В рассматриваемом нами примере COMMANDO сначала запускает свой оборонительный фрагмент, который в дальнейшем работает самостоятельно. Затем она запускает своего собственного чертенка (начиная с ячейки, отстоящей на 10 адресов от второй команды MOV) в далекую ячейку (отстоящую на 113 адресов). Второй чертенок запускается следующей командой SPL.
Остальные команды программы COMMANDO предназначены для того, чтобы скопировать всю программу в другую область, которая удалена на 100 адресов от ее теперешнего положения. Новая копия программы, как десантник, только что приземлившийся на территории противника, запускается командой JMP в исходной программе. Старый экземпляр COMMANDO, за исключением барьерного фрагмента, прекращает свое существование и больше не выполняется. Затем описанный процесс повторяется для нового экземпляра программы, который в свою очередь копируется на новое место в памяти.
Ну а насколько успешно выступила программа COMMANDO против своих соперников? Турнир был организован так, чтобы между программами-участниками (а их, как уже отмечалось, было 31) состоялось как можно больше поединков. Розыгрыш по полной круговой системе, когда каждый участник встречается со всеми другими участниками, потребовал бы проведения 465 поединков и занял бы слишком много времени. Поэтому участники были поделены произвольно на две приблизительно равные группы: группа I и группа II. Затем внутри каждой группы был проведен турнир по полной круговой системе.
Известие о том, что COMMANDO стала победителем турнира в группе II, я встретил со смешанным чувством. С одной стороны, я был очень горд тем, что мое кибернетическое творение так хорошо проявило себя в действии. В то же время я испытывал некоторое беспокойство при мысли о том, что моя программа может оказаться победителем соревнований. Дело в том, что я согласился выступить в роли комментатора финальных состязаний и чувствовал, что мне трудно будет сохранить объективность.
Четыре лучшие программы из каждой группы выступили затем в новом круговом турнире. Победителями в этом турнире оказались три программы: CHANG1 - автор М.Чанг из Флорал-Парка (шт.Нью-Йорк) и две программы Ч.Уэнделла MIDGET и MICE. Моя программа COMMANDO, получив смертельное ранение, пала смертью храбрых. Интересно сложился финал, выигранный программой MICE. MIDGET и MICE свели свои поединки с CHANG1 вничью, но MICE получила решающее выигрышное очко, добившись победы в поединке с MIDGET.
Матч между каждой парой финалистов состоял из четырех боев, проводившихся один за другим. Поединки были ограничены по времени: каждая сторона могла сделать не более 15тыс. ходов (команд), что приблизительно соответствует двум минутам машинного времени. Две встречающиеся в поединке боевые программы помещались в выбранные случайным образом непересекающиеся области памяти, после чего они запускались. Получилось так, что бои, проведенные между всеми парами программ, закончились с одним и тем же результатом. В частности, все бои между программами MICE и CHANG1 завершились вничью.
Очень интересно наблюдать за развитием боя. На турнире использовался дисплей, на котором отображалось поле боя в виде последовательности полос с клеточной структурой (см. рисунок на с.97). Каждая клетка представляла одну ячейку (и один адрес) в памяти, причем последняя клетка в нижнем ряду была соседней по отношению к первой клетке в верхнем ряду. Таким образом, поле боя было замкнутым. Программа, которой предоставлялся первый ход, в исходном положении занимала область памяти, начинавшуюся с адреса 0, и ее команды последовательно заполняли прилегающие ячейки. Клетки, занятые этой программой, окрашивались в голубой цвет. Программа-соперник занимала произвольно выбранную область ячеек, не пересекавшуюся с областью, занятой первой программой. На экране эта область окрашивалась в ярко-красный цвет. А вообще цвет любой клетки на дисплее определялся тем, какая из соперничавших программ изменила ее содержимое последней. Таким образом, перед глазами наблюдателя разворачивалась картина сражения.

Одна из начальных и одна из завершающих стадий в сражении между программами MICE (красный) и CHANG1 (синий)
На темно-синем фоне экрана МICE и CHANG1 переползали с места на место, запускали чертиков, разбрасывали бомбы и воспроизводили сами себя (самопроизвольным делением). Проследим за тем, как развивались события в одном типичном бою между этими программами. CHANG1 возникла в виде голубой полоски в левом верхнем углу экрана, а появление на свет программы MICE было ознаменовано красной полоской, возникшей несколько ближе чем на полпути к нижнему краю экрана. Почти сразу же и очень быстро "мышки" начали разбегаться по экрану.
Одна из самых коротких известных мне самовоспроизводящихся программ MICE состоит всего из восьми команд, две из которых создают новую копию программы в области памяти, отстоящей на 833 адреса от положения, занимаемого ею на момент копирования (см. рисунок справа). Эти две команды демонстрируют некоторые дополнительные возможности языка Редкод:
loop MOV @ptr <5
DJN loop ptr
Здесь слово loop (цикл) представляет собой просто метку, обозначающую адрес (в данном случае ячейки, в которой содержится команда MOV). Благодаря использованию меток написание программы на Редкоде значительно упрощается. По команде DJN (уменьшение и переход к ненулевому значению операнда) происходит передача управления на команду, помеченную меткой loop, если значение величины, хранящейся в ячейке с другим адресом (помеченным меткой ptr), не равно нулю. Значок @ означает способ адресации, называемый косвенным: при выполнении команды MOV перемешается не содержимое ячейки, помеченной как ptr, а содержимое содержимого, если можно так выразиться. Число, хранящееся по адресу ptr, является адресом той ячейки, содержимое которой следует переместить. В данном случае это содержимое представляет собой одну из команд программы MICE.

Участники чемпионата игр "Бой в памяти"
Число, хранящееся в ячейке с адресом ptr, все время изменяется благодаря функции уменьшения, содержащейся в команде DJN. Исходное значение этого числа равно последнему адресу программы, затем оно постепенно уменьшается до 0 и здесь цикл копирования завершается. Аналогичным образом адреса, по которым должны разместиться команды программы на новом месте, также заданы косвенно. Ячейка с относительным адресом 5 первоначально хранит число 833, и первая команда, перемещаемая программой, приземлится в ячейке, отстоящей на 832 адреса от команды MOV. Как показывает значок <, адрес назначения уменьшается при каждом выполнении команды MOV. Мышки копируют себя как бы от хвоста к голове.
Команда SPL (от англ. split - разветвление), следующая сразу же за циклом копирования, передает управление только что созданному экземпляру программы MICE. Но вслед за рождением отпрыска старый экземпляр программы выполняется сначала. В принципе количество отпрысков, порождаемых подобной программой, не ограничено. И каждая новая программа работает, следуя все той же процедуре. Действительно, получаются такие же мышки!
Так было и в типичном сражении с программой CHANG1. Мышки размножались с невероятной быстротой. Вскоре весь экран был усеян маленькими красными полосками. Тем временем CHANG1 запустила своеобразную фабрику, производящую на свет чертиков и спускающую их "вниз по течению". Эта фабрика была построена всего лишь из трех команд:
SPL 2
JMP -1
MOV 0 1
Когда управление достигает команды SPL, процесс выполнения команд разветвляется на две ветви. Одна из них начинается с команды MOV 0 1. Другая ветвь выполняет команду JMP -1, которая начинает весь описанный процесс заново. Тем временем один чертенок уже покинул конвейер и отправился на охоту за мышками. Основная проблема, возникающая при массовом производстве чертиков, заключается в том, что большое число независимых линий выполнения замедляет каждый из выполняемых процессов. 1000 чертиков движутся в 1000 раз медленнее, чем один чертенок. Во всяком случае, роковая орда чертиков стала медленно спускаться из верхней части экрана в виде все удлинявшейся сплошной голубой полосы. Смогут ли они перехитрить мышек?
Пока размножались чертики, несколько экземпляров программы MICE, или несколько мышек, были убиты бомбами, брошенными программой CHANG1. Такая бомба представляет собой обычно число 0, "сбрасываемое" командой MOV предположительно на территорию противника. Ключевая команда в программе Чанга - это MOV #0 @-4. Нулевая бомба падает в ячейку, адрес которой содержится в ячейке четырьмя адресами "выше" команды MOV. Адрес назначения постоянно увеличивается на 16 единиц, тем самым обеспечивается равномерный обстрел "по площади".
В то время как некоторые мышки погибали от бомб, чертики тоже начали причинять вред противнику. Однако в каждом экземпляре программы MICE заложена возможность самоубийства. Программа постоянно проверяет свою первую команду, которая представляет собой команду описания данных и должна содержать в себе число 0. Если там уже не 0, то программа совершает переход на (невыполнимую) команду описания данных и таким образом предпочитает погибнуть, чем стать жертвой крошечного неприятеля.
Но если одни мышки погибали под бомбами, а другие, так сказать, кончали жизнь самоубийством, чтобы избежать плена, то как же им удалось все-таки выжить? Объяснение, конечно, заключается в их чрезвычайной плодовитости. Ведь в конце концов многие новые экземпляры приземлились на голову противника. На самом деле незадолго до истечения времени поединка один из экземпляров программы MICE приземлился прямо на территории основной программы CHANG1 и уничтожил ее. Однако к этому моменту CHANG1 создала достаточно много чертиков, чтобы протянуть время до финального звонка. Поединок завершился с ничейным исходом. Искусство создания программ для игры "Бой в памяти" находится еше в своей начальной стадии. Конечно, здесь будут сделаны свои открытия и будет наблюдаться постепенный неуклонный прогресс. Какому-нибудь изобретательному программисту, возможно, удастся открыть абсолютно надежное средство против угрозы чертиков, другой сумеет найти простой способ самовосстановления поврежденной программы.
Боевые программы следующих поколений, наверное, будут длиннее теперешних призеров, но зато их "живучесть" будет на несколько порядков величины выше. Они будут способны заниматься разведкой, оставлять ложный след и наносить внезапные сокрушительные удары по противнику. Эти тенденции, возможно, проявятся уже на втором международном турнире по игре "Бой в памяти", который должен состояться осенью этого года в музее вычислительной техники. А пока читатели имеют возможность солидно подготовиться, вложив в программы всю свою изобретательность и коварство.
Своим успехом прошлогодний турнир был в значительной степени обязан М. и Б.Кларксонам, а также Г.Беллу, возглавляющему музей вычислительной техники, и Оливеру Стримпелу, куратору музея. В заключение нужно, наверное, сказать несколько слов о самом музее.
Музей вычислительной техники в Бостоне, пожалуй, единственный в мире музей, экспозиция которого целиком посвящена компьютерам. Размешенный в перестроенном (и теперь роскошном) здании бывшего складского помещения на набережной, он демонстрирует компьютеры - от чудовищ, собранных на вакуумных электронных лампах, до персональных компьютеров, полностью предназначенных для игр. Стены помещения украшены удивительной графикой; здесь представлена полная компьютерная система NORAD SAGE и многие другие экспонаты как развлекательного, так и образовательного плана. Читатели, которые будут в Бостоне и посетят старинный корабль в бостонской бухте, могут заглянуть и в музей вычислительной техники, это буквально в двух шагах от бухты.
ОТКЛИКИ
6 1987
За время, прошедшее с момента выхода в свет нашей статьи, посвященной первому международному турниру по компьютерной игре "Бой в памяти", число членов международной ассоциации любителей игры возросло, по словам ее председателя М.Кларксона, в четыре раза. Тем не менее Кларксон по-прежнему приглашает желающих присоединиться к ассоциации. В то же время У.Р.Бакли, редактор бюллетеня "Новости войны в памяти", отметил соответствующее увеличение числа подписчиков на это издание. Бакли сообщает, что бюллетень будет официальным органом ассоциации, в котором ее члены будут публиковать свои сообщения, рассказывающие о новых тактических приемах, будут высказывать свои мысли, касающиеся дальнейшего совершенствования игры и повышения класса игроков.
7 1987
ПО МЕРЕ ТОГО как под влиянием статей из рубрики "Занимательный компьютер" продолжают возникать различные любительские ассоциации, эти статьи все в большей степени играют роль "доски объявлений" этих ассоциаций. В этом месяце два объявления для любителей игры "Бой в памяти". Читатели, обращающиеся к М.Кларксону, президенту международного общества любителей этой игры, с просьбой выслать им "Правила игры "Бой в памяти"", должны запастись терпением. Пожар, случившийся в доме Кларксона в январе, является причиной длительной задержки в выполнении запросов. Продолжают поступать заявки от желающих принять участие во втором международном турнире по игре "Бой в памяти", который планируется провести в Бостоне этой осенью. О подробностях будет сообщено в последующих статьях.
12 1988
Наконец, для увлекающихся игрой "Бой в памяти", сообщим, что III международный турнир по этой игре состоится 3-4 декабря в штаб-квартире Международного общества по игре "Бой в памяти"в Хантингтон-Биче (шт.Калифорния).
Последний раз редактировалось: Gudleifr (Вт Окт 29, 2019 9:01 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
4 1987
ТРЕХМЕРНЫЕ ВЕРСИИ ИГРЫ "ЖИЗНЬ"
А.К.ДЬЮДНИ
У ПОПУЛЯРНОЙ ИГРЫ "Жизнь" с клеточными автоматами, игровые ситуации в которой разворачиваются на двумерном поле, теперь стали появляться трехмерные аналоги. К.Бейс, специалист по программированию в Южно-Каролинском университете, исследовал множество трехмерных версий, две из которых он считает заслуживающими наибольшего внимания. Бейс назвал их "Жизнь 4555" и "Жизнь 5766". В обеих этих версиях присутствуют многие свойства исходного варианта {такие образования, как "мигалки" и "планеры"), и одна из них, несомненно, станет достойным последователем игры, изобретенной в 1968г. Дж.Конвеем из Кембриджского университета.
Игра Коивея, как, наверное, помнят многие читатели по нескольким статьям М.Гарднера в рубрике "Математические игры", разворачивается на бесконечной двумерной решетке квадратных клеток. Каждая клетка имеет восемь соседей (четыре по углам и четыре по сторонам) и может находиться в одном из двух состояний, живом или мертвом. Игра управляется часами, задающими такт. При каждом тактовом сигнале часов одни клетки могут оживать, другие умирать. Судьба каждой клетки определяется числом ее соседей, живых на данный момент. Например, если на каком-то такте у живой клетки окажется менее двух или более трех живых соседей, то на следующем такте она должна умереть. Здесь как бы моделируются неблагоприятные для клетки условия - недостаток питания или перенаселенность в среде обитания. В то же время мертвая клетка может снова ожить на следующем такте, если у нее в данный момент насчитывается ровно три живых соседа. Для рождения клетки, таким образом, необходимо наличие трех "родителей".
Конвей назвал свою игру "Жизнь" просто потому, что клетки могут быть либо живыми, либо мертвыми. Однако вскоре стало очевидно, что это название оказалось более подходящим, чем могло показаться с первого взгляда. Дело в том, что всевозможные образования из живых клеток демонстрируют сложное поведение, в чем-то подобное поведению живых организмов (см. верхний рисунок на с.90). Оно носит циклический характер, на каждом такте часов конфигурации изменяются, но после некоторого конечного числа тактов исходные конфигурации возникают вновь. Некоторые образования остаются на месте, другие же путешествуют по всей решетке, перемещаясь за один такт на одну клетку в горизонтальном, вертикальном или диагональном направлении. Клеточные конфигурации обоих типов имеют образные названия. Среди стационарных конфигураций различают "маяки", "ульи", "мигалки" и "блоки". Примерами конфигураций-путешественников являются "планеры" и "космические корабли". Однако возможности игры Конвея не ограничиваются лишь имитацией природных явлений. Как я уже указывал в статье в рубрике "Занимательный компьютер" в июльском номере журнала за 1985г., в плоском клеточном "пространстве" игры "Жизнь" можно построить даже компьютер.

Некоторые формы двумерной игры "Жизнь" Дж.X.Конвея
Поэтому было бы, наверное, не удивительно, если бы в трехмерном клеточном пространстве аналоги игры Конвея оказались способными порождать еще более фантастичные конфигурации. Такими аналогами и являются уже упомянутые версии Бейса "Жизнь 4555" и "Жизнь 5766". Здесь клетка представляет собой уже не квадрат, а куб, а число кубов-соседей равно не 8, а 26.
Названия "Жизнь 4555" и "Жизнь 5766" были взяты из лаконичного лексикона, придуманного Бейсом. Первые две цифры служат критерием при определении судьбы живой клетки. Первая цифра указывает наименьшее число соседей, при котором клетка еше не погибает голодной смертью, а вторая цифра - максимальное число соседей, при котором клетка еще не погибает от перенаселенности среды обитания. Третья н четвертая цифры определяют судьбу мертвой клетки. Третья цифра указывает минимальное, а четвертая - максимальное число живых соседей, при котором мертвая клетка становится живой. (В каждой из рассматриваемых версий "Жизни" третья и четвертая цифры в названии версии будут совпадать, однако, вообще говоря, это не всегда так). Таким образом, согласно системе обозначений Бейса, первоначальная версия игры Конвея будет иметь название "Жизнь 2333".
Правила игры "Жизнь 4555" так же просты, как и для варианта 2333. Живая на данный момент клетка умирает, если у нее менее четырех или более пяти живых соседей. В то же время мертвая клетка оживает, если у нее ровно пять живых соседей. Исследуя многочисленные варианты игры в этой области определяющих числовых параметров, Бейс впервые заинтересовался вариантом 4555, когда заметил, как на экране компьютера "Макинтош" начала вырисовываться любопытная конфигурация кубических "клеток", показанная на нижнем рисунке на с.90. Это был трехмерный планер, который циклически проходит через четыре различных превращения, прежде чем вернуться к исходному состоянию. Каждая из этих конфигураций состояла из 10 кубических "клеток", образующих продолговатый странным образом притупленный объект, движущийся в пространстве подобно дивану, совершающему свободное падение.

Планер в "Жизни 4555"
Бейс решил провести более полное исследование варианта 4555, поставив ряд экспериментов с "первобытным бульоном". Задав в исходном состоянии случайным образом выбранные конфигурации живых клеток, он следил за эволюцией своего клеточного мира. В каждом поколении одни клетки-кубики умирали, другие оживали. Число клеток с каждым новым поколением уменьшалось, однако Бейс обнаружил некоторые любопытные стабильные образования, остававшиеся неизменными из поколения в поколение. Эти образования напоминали пьедесталы, кресты, ступеньки, шары и спортивные штанги (см. рисунок на с.91). Другие исходные конфигурации порождали все новые стабильные образования, а также циклические, которым Бейс присваивал такие имена, как "ротор" или даже "лягающий мустанг".

Стабильные и циклические формы "Жизни 4555"
Подобно физику, исследующему элементарные частицы, Бейс устраивал столкновения между планерами и другими мелкими конфигурациями, причем объекты сталкивались под всевозможными углами. "Среди наиболее удивительных столкновений,- пишет он,- можно выделить столкновение планера с шариком, при котором суммарная масса осколков увеличивается до 29, что само по себе не так уж примечательно. Но затем после нескольких поколений внезапно снова появляется планер, несколько переместившийся от места столкновения".
Все то, что развивается из первобытного бульона, и даже результаты столкновений планеров между собой и с другим объектами Бейс называет природой. Некоторые конфигурации получить нетрудно. Другие же, более экзотические образования требуют для своего воссоздания значительно больших усилий. Можно, например, сцепить друг с другом несколько конфигураций, имеющих форму арки, и получить таким образом новое стабильное образование, которое Бейс называет галереей. Возникает полный архитектурный ансамбль из заборов, лестниц, стен и цепей. Стены можно закручивать в спирали и множество других экзотических стабильных форм, ограниченных лишь воображением энтузиаста, исследующего возможности "Жизни 4555" (см. рисунок внизу).

Планер проходит через стабильную улитку в трехмерном пространстве игры К.Бейса "Жизнь 4555"
Следует обратить внимание и на некоторые другие интересные явления. Среди прочих образовании часто встречается объект из 7 кубиков под названием "привет". В отсутствие другого такого же привета это образование погибает. Планер, встретившись с приветом, оказывается захваченным и не может продолжить свое путешествие. Второй планер может случайно освободить своего собрата, столкнувшись с приветом и взорвав его.
Из двух наиболее плодотворных трехмерных версий, открытых Бейсом, "Жизнь 4555", по-видимому, нравится ему больше. Здесь можно отметить одно любопытное обстоятельство: цифры в названии "Жизнь 4555" получаются прибавлением 2 к соответствующим цифрам названия версии Конвея 2333. Возможно, это совпадение послужит предзнаменованием того, что именно "Жизнь 4555" станет достойным преемником игры Конвея.
Однако, строго говоря, "Жизнь 5766" имеет больше сходства с игрой Конвея по сравнению с вариантом 4555. В частности, при некоторых условиях "Жизнь 5766" моделирует версию Конвея на плоскости. Эти условия сформулированы в теореме, на которую наткнулся в своих исследованиях Бейс.
Представим себе, что мы смотрим сверху на плоскую решетку игры Конвея и видим какую-то конфигурацию живых (квадратных) клеток. Теперь поместим непосредственно над каждой клеткой конфигурации и под ней по одному живому кубу. Следуя правилам игры "Жизнь 5766", эти кубические "клетки" будут неограниченно долго точно копировать поведение "бутерброда" из клеток Конвея тогда (и только тогда), когда будут выполнены два условия:
1. Ни одна живая клетка на плоскости никогда не имеет 5 живых соседей.
2. Ни одна мертвая клетка на плоскости никогда не имеет 6 живых соседей.
Многие конфигурации "Жизни", в том числе и планер Конвея, удовлетворяют указанным условиям. Планер в пространстве "Жизни 5766" можно создать, преобразовав клетки двумерного планера в кубы. Такой планер занимает два прилегающих друг к другу слоя клеток в трехмерном пространстве и будет двигаться всегда в пределах этих слоев (см. рисунок на с.92).

Планер в трехмерной игре Бейса "Жизнь 5766"
Многие другие простые объекты "Жизни" Конвея, такие, как маяк, улей, мигалка и блок, а также более экзотические образования, такие, как лодка и часы, также удовлетворяют условиям теоремы Бейса. Эти объекты существуют в двухслойном виде как конфигурации "Жизни 5766", которые ведут себя точно так же, как и их двумерные аналоги. К сожалению, не все конфигурации игры Конвея удовлетворяют критериям теоремы. Среди этих "неподдающихся" объектов - знаменитая катапульта, запускающая планеры, которая была открыта Р.Госпером в 1970г., когда он был еще студентом Массачусетского технологического института. Проследив за катапультой, мы видим, что на любой стадии се жизненного цикла у нее имеются живые клетки с пятью живыми соседями. Любые нарушения какого-либо условия теоремы Бейса приводят к отклонению от модели. "Когда это происходит,- рассказывает Бейс,- объект, до тех пор ограниченный двумя плоскостями, почти во всех случаях превращается в округлую трехмерную массу, которая обычно довольно быстро погибает".
Можно добиться более полного моделирования версии Конвея на основе "Жизни 5766", если воздвигнуть то, что Бейс называет барьером времени-пространства. Он состоит из единой поверхности живых клеток, в которой как бы просверлены дырки (см. рисунок на с.93). Дырки расположены таким образом, чтобы каждый куб в барьере имел ровно 7 соседей. Клетки-кубы, принадлежащие барьеру, едва-едва избегают гибели от перенаселения среды, в то время как любой куб, непосредственно прилегающий к барьеру, всегда будет иметь более 6 живых соседей и потому никогда не оживет. Образующейся в результате мертвой зоной с каждой стороны от барьера можно воспользоваться для точного воспроизведения "Жизни" Конвея. Для этого нужно соорудить два параллельных барьера времени-пространства на расстоянии четырех кубов друг от друга. Из четырех заключенных между ними плоскостей две центральные могут поддерживать все формы жизни, потому что теперь условия теоремы Бейса удовлетворяются для любой популяции живых клеток, находящихся посередине этого "бутерброда".

Два барьера времени-пространства в "Жизни 5766"
Несмотря на то что "Жизнь 5766" способна в той или иной мере имитировать версию Конвея, ее клеточный мир все же не так красив и привлекателен. Как свидетельствует Бейс, случайно выбранные первобытные бульоны "Жизни 5766", кажется, всегда достигают "установившегося состояния" быстрее по сравнению с "Жизнью 4555". Неустановившийся характер "Жизни 4555" говорит о ее более богатых вычислительных возможностях. В самом деле, "Жизнь 4555" изобилует стабильными и осциллирующими формами, которые обладают свойством симметрии. Возможно, окончательное решение вопроса о том, какая версия станет наиболее достойным преемником "Жизни" Конвея, будет зависеть от того, удастся ли смоделировать двумерную игру при помощи "Жизни 4555". В случае успеха эта версия окажется во всех отношениях лучше, чем "Жизнь 5766".
Бейс написал брошюру на 40 страницах под названием "Трехмерная игра "Жизнь"". Она содержит в себе все, о чем мы здесь говорили, и много больше, включая советы по эффективному программированию игр. Бейс располагает также программой для компьютера "Макинтош", которая моделирует обе версии трехмерной жизни.
Программу, вычисляющую и показывающую последовательные поколения любой формы трехмерной версии игры, написать нетрудно, по крайней мере в принципе. Программу можно даже модифицировать так, чтобы она пробовала различные правила, и, может быть, читателям удастся открыть третью удачную трехмерную версию "Жизни", которую Бейс мог упустить в своих исследованиях.
Два больших трехмерных массива cells (клетки) и newcells (новые клетки) имеют три индекса i, j и k, соответствующие трем координатам клеточного пространства. Содержимое каждого элемента массива показывает, жива или мертва соответствующая клетка. Пусть 1 означает живое состояние а 0 - мертвое.
Не удивительно, что для вычисления статуса каждой клетки в каждом поколении требуются три вложенных цикла. Самый внешний цикл с индексом i служит для вычисления последовательности плоскостей, проходящих через все пространство игры. В этот цикл вложены два других с индексами j и k. В цикле по j происходит вычисление последовательных строк в пределах каждой плоскости, а в цикле по k вычисляется состояние последовательных клеток в строке. В качестве руководства можно воспользоваться следующей схемой:
for i = 1 to 30
- for j = 1 to 30
- - for к = I to 30
- - - вычислить соседей
- - - определить состояние
- - - высветить живые клетки
Число 30, конечно, выбрано произвольно. Однако лишь читателям, обладающим неограниченным терпением, можно поэкспериментировать с числами, большими 30, потому что время вычислений становится очень большим.
Во внутреннем цикле перед программой стоят три основные задачи. Чтобы решить задачу вычисления соседей, программе нужно исследовать состояние 26 соседей каждой клетки и подсчитать число живых на данный момент. Это можно сделать при помощи трех миниатюрных циклов или путем перечисления всех возможных координат 26 клеток. Если воспользоваться конструкцией с циклами, то их можно расписать по следующему алгоритму:
tot <- 0
for l = i-1 to i+1
- for m = j-1 to j+1
- - for n = k-1 to k+1
- - - if cells(l, m, n) = 1
- - - - then tot <- tot+1
tot <- tot-cells(i, j, k)
Здесь переменная tot (от слова total - полный) хранит суммарное число живых соседей. Последняя строчка в алгоритме нужна для того, чтобы состояние самой клетки cells(i, j, k) не влияло на подсчитываемую сумму.
Определив величину tot - полное число живых соседей, программа должна затем определить новое состояние рассматриваемой в данный момент клетки cells (i, j, k). Задача определения состояния сводится к простой проверке значения tot в отношении к состоянию клетки cells {i, j, k):
if cells{i, j, k) = 0
- then if tot = 5
- - then newcells(i, j, k) <- 1
- - else newcells(i, j, k) <- 0
if cells(i, j, k) = 1
- then if tot < 4 or tot > 5
- - then newcells(i, j, к) <- 0
- - else newcells{i, j, k) <- 1
Здесь я предполагал, что читатель программирует игру "Жизнь 4555". Можно несколько изменить алгоритм, чтобы приспособить его к версии 5766 или сделать его достаточно общим, чтобы охватить любые трехмерные правила. Рассмотрим последнюю возможность.
В универсальном виде описанный выше алгоритм вычисления состояния можно записать, воспользовавшись четырьмя переменными, которые Бейс назвал как el, eu, fl, fu. Буквы е и/означают соответственно среду (environment) и плодовитость (fertility), а буквы l и u соответственно нижний (lower) и верхний (upper). Таким образом, el н eu - это нижняя и верхняя границы, в которые должна попасть клетка, чтобы продолжить жизнь в следующем поколении. Клетка останется живой, если число окружающих ее живых соседей больше или равно el, но меньше или равно величине eu. Аналогично, величины fl и fu - это границы, в которые должна попасть мертвая клетка, чтобы ожить в следующем поколении. Это произойдет, если число живых кубов в окрестности клетки больше или равно fl, но меньше или равно fu. В этих обозначениях общий алгоритм приобретает следующий вид:
if cells{i, j, k) = 0
- then if tot < fl or tot > fu
- - then newcells(i, j, k) <- 1
- - else newcells(i, j, k) <- 0
if cells(i, j, k) = 1
- then if tot < el or tot > eu
- - then newcells(i, j, к) <- 0
- - else newcells{i, j, k) <- 1
Здесь в любой версии трехмерной жизни программа должна перевести содержимое массива newcells в массив cells при помощи тройного цикла. Таким образом, массив newcells освобождается для следующего поколения живых кубов.
В заключительной стадии рассматриваемого нами алгоритма, обозначенной как "высветить живые клеткн", программа должна изобразить соответствующий куб при условии, что он находится в живом состоянии. При изображении кубов на экране мы советуем закрашивать видимые поверхности. Если оставлять рисунок в скелетном виде, то изображение получается очень сложным и непонятным. Простейший способ сделать невидимыми кубы, расположенные за видимыми поверхностями, заключается в том, чтобы i - индекс внешнего цикла - пробегал значения, соответствующие оси, ведущей из глубины экрана к зрителю. Тот печальный факт, что некоторые кубики становятся, таким образом, невидимыми,- единственный недостаток, присущий всем трехмерным версиям "Жизни". Мы не имеет возможности охватить взглядом все, что происходит в пространстве, как мы могли это сделать в двумерной версии Конвея. В то же время этот недостаток любой трехмерной игры присущ и всему нашему трехмерному миру. Мы не можем видеть всего того, что в нем происходит. И можно сказать, что это к нашему счастью.
После того как в программе реализована последняя стадия, процесс ее выполнения становится довольно медленным. Можно добиться некоторого ускорения, заменив кубы сферами (на самом деле заштрихованными дисками, размеры которых изменяются в зависимости от их "глубины" на экране). Нужно сказать, что в брошюре Бейса, о которой мы говорили, есть рецепты, позволяющие добиться увеличения скорости на несколько порядков.
Как всегда, я с радостью расскажу обо всех необычных, интересных явлениях, которые будут открыты читателями. Во-первых, удастся ли неутомимым исследователям, всегда стремящимся к обобщению, найти какие-нибудь формы трехмерной жизни (стоящие такого названия), которые, возможно, упустил Бейс? Во-вторых, читателям, наверное, будет интересно поэкспериментировать со своими собственными рецептами первобытного бульона. Ну а в остальном, кто знает, сколько еще существует неоткрытых планеров, космических кораблей, катапульт и других интересных образований! Но чтобы не дублировать результатов, достигнутых Бейсом, следует обязательно изучить брошюру "Трехмерная игра "Жизнь"".
БИБЛИОГРАФИЯ
WINNING WAYS FOR YOUR MATHEMATICAL PLAYS, Vol.2; Games in Particular. Elwyn R. Berlekamp, John H. Conway and Richard K. Guy. Academic Press, 1982.
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. Bruce A. Art-wick. Prentice-Hall, Inc., 1984.
ОТКЛИКИ
7 1987
Вот еще одно объявление: К.Бейс, импрессарио игры "Трехмерная жизнь", сообщает, что он намеревается учредить регулярный бюллетень и что через несколько месяцев появится его первый номер. В апрельском номере журнала мы говорили о двух трехмерных версиях клеточных автоматов, недавно открытых и исследуемых Бейсом. Вместо клеток-квадратов, рождающихся, живущих и умирающих в исходной версии двумерной игры, придуманной математиком Дж.Конвеем, в трехмерном пространстве Бейса рождаются, живут и умирают клетки кубической формы. Поскольку Бейс получил уже около 500 писем, он считает, что учреждение специального бюллетеня будет оправданно. Он надеется выпускать журнал раз в квартал. Туда войдут все интересные наблюдения, сделанные им самим или подписчиками журнала.
Бейс продолжает поиски удачных трехмерных аналогов игры Конвея. Недавно он нашел два критерия, которые, по-видимому, уверенно позволяют различать удачные и неудачные варианты игры. Первый критерий заключается в том, что биологическая среда, или "первобытный бульон", не должна расти беспредельно. Другими словами, если начать со случайного набора живых клеток, они не должны иметь тенденцию к безграничному распространению. Согласно второму критерию, время от времени среда должна порождать планеры - циклические конфигурации живых кубических клеток, перемещающихся по экрану как единое целое.
Об одном из трехмерных вариантов игры сообщил К.Пирсон из Нанаймо (Британская Колумбия), написавший Бейсу о книге П.Антони "Окс" (P.Anthony, "Ox"), в которой автор упоминает об одном из возможных вариантов трехмерной "Жизни". Этот вариант, следуя лаконичному лексикону самого Бейса, нужно назвать "Жизнь 6777". По правилам "Жизни 6777" живая кубическая клетка умрет в следующем поколении, если у нес меньше шести или больше семи живых соседей в текущем поколении. Мертвая клетка оживает в следующем поколении в том случае, если в данном поколении у нее ровно семь живых соседей. Бейс сообщает, что он уже исследовал предложенную версию трехмерной "Жизни" и нашел, что она не удовлетворяет первому критерию.
В настоящее время Бейс сосредоточил свое внимание на двух вариантах, потенциально достойных преемниках игры Конвея. (Как, наверное, помнят многие читатели, это варианты "Жизнь 4555" и "Жизнь 5766".) Исследуя эти варианты, Бейс занимается главным образом поиском "катапульты", стреляющей "планерами". Катапульта - это конфигурация клеток, постоянно выпускающая планеры в одном или более фиксированных направлениях.
ТРЕХМЕРНЫЕ ВЕРСИИ ИГРЫ "ЖИЗНЬ"
А.К.ДЬЮДНИ
У ПОПУЛЯРНОЙ ИГРЫ "Жизнь" с клеточными автоматами, игровые ситуации в которой разворачиваются на двумерном поле, теперь стали появляться трехмерные аналоги. К.Бейс, специалист по программированию в Южно-Каролинском университете, исследовал множество трехмерных версий, две из которых он считает заслуживающими наибольшего внимания. Бейс назвал их "Жизнь 4555" и "Жизнь 5766". В обеих этих версиях присутствуют многие свойства исходного варианта {такие образования, как "мигалки" и "планеры"), и одна из них, несомненно, станет достойным последователем игры, изобретенной в 1968г. Дж.Конвеем из Кембриджского университета.
Игра Коивея, как, наверное, помнят многие читатели по нескольким статьям М.Гарднера в рубрике "Математические игры", разворачивается на бесконечной двумерной решетке квадратных клеток. Каждая клетка имеет восемь соседей (четыре по углам и четыре по сторонам) и может находиться в одном из двух состояний, живом или мертвом. Игра управляется часами, задающими такт. При каждом тактовом сигнале часов одни клетки могут оживать, другие умирать. Судьба каждой клетки определяется числом ее соседей, живых на данный момент. Например, если на каком-то такте у живой клетки окажется менее двух или более трех живых соседей, то на следующем такте она должна умереть. Здесь как бы моделируются неблагоприятные для клетки условия - недостаток питания или перенаселенность в среде обитания. В то же время мертвая клетка может снова ожить на следующем такте, если у нее в данный момент насчитывается ровно три живых соседа. Для рождения клетки, таким образом, необходимо наличие трех "родителей".
Конвей назвал свою игру "Жизнь" просто потому, что клетки могут быть либо живыми, либо мертвыми. Однако вскоре стало очевидно, что это название оказалось более подходящим, чем могло показаться с первого взгляда. Дело в том, что всевозможные образования из живых клеток демонстрируют сложное поведение, в чем-то подобное поведению живых организмов (см. верхний рисунок на с.90). Оно носит циклический характер, на каждом такте часов конфигурации изменяются, но после некоторого конечного числа тактов исходные конфигурации возникают вновь. Некоторые образования остаются на месте, другие же путешествуют по всей решетке, перемещаясь за один такт на одну клетку в горизонтальном, вертикальном или диагональном направлении. Клеточные конфигурации обоих типов имеют образные названия. Среди стационарных конфигураций различают "маяки", "ульи", "мигалки" и "блоки". Примерами конфигураций-путешественников являются "планеры" и "космические корабли". Однако возможности игры Конвея не ограничиваются лишь имитацией природных явлений. Как я уже указывал в статье в рубрике "Занимательный компьютер" в июльском номере журнала за 1985г., в плоском клеточном "пространстве" игры "Жизнь" можно построить даже компьютер.

Некоторые формы двумерной игры "Жизнь" Дж.X.Конвея
Поэтому было бы, наверное, не удивительно, если бы в трехмерном клеточном пространстве аналоги игры Конвея оказались способными порождать еще более фантастичные конфигурации. Такими аналогами и являются уже упомянутые версии Бейса "Жизнь 4555" и "Жизнь 5766". Здесь клетка представляет собой уже не квадрат, а куб, а число кубов-соседей равно не 8, а 26.
Названия "Жизнь 4555" и "Жизнь 5766" были взяты из лаконичного лексикона, придуманного Бейсом. Первые две цифры служат критерием при определении судьбы живой клетки. Первая цифра указывает наименьшее число соседей, при котором клетка еше не погибает голодной смертью, а вторая цифра - максимальное число соседей, при котором клетка еще не погибает от перенаселенности среды обитания. Третья н четвертая цифры определяют судьбу мертвой клетки. Третья цифра указывает минимальное, а четвертая - максимальное число живых соседей, при котором мертвая клетка становится живой. (В каждой из рассматриваемых версий "Жизни" третья и четвертая цифры в названии версии будут совпадать, однако, вообще говоря, это не всегда так). Таким образом, согласно системе обозначений Бейса, первоначальная версия игры Конвея будет иметь название "Жизнь 2333".
Правила игры "Жизнь 4555" так же просты, как и для варианта 2333. Живая на данный момент клетка умирает, если у нее менее четырех или более пяти живых соседей. В то же время мертвая клетка оживает, если у нее ровно пять живых соседей. Исследуя многочисленные варианты игры в этой области определяющих числовых параметров, Бейс впервые заинтересовался вариантом 4555, когда заметил, как на экране компьютера "Макинтош" начала вырисовываться любопытная конфигурация кубических "клеток", показанная на нижнем рисунке на с.90. Это был трехмерный планер, который циклически проходит через четыре различных превращения, прежде чем вернуться к исходному состоянию. Каждая из этих конфигураций состояла из 10 кубических "клеток", образующих продолговатый странным образом притупленный объект, движущийся в пространстве подобно дивану, совершающему свободное падение.

Планер в "Жизни 4555"
Бейс решил провести более полное исследование варианта 4555, поставив ряд экспериментов с "первобытным бульоном". Задав в исходном состоянии случайным образом выбранные конфигурации живых клеток, он следил за эволюцией своего клеточного мира. В каждом поколении одни клетки-кубики умирали, другие оживали. Число клеток с каждым новым поколением уменьшалось, однако Бейс обнаружил некоторые любопытные стабильные образования, остававшиеся неизменными из поколения в поколение. Эти образования напоминали пьедесталы, кресты, ступеньки, шары и спортивные штанги (см. рисунок на с.91). Другие исходные конфигурации порождали все новые стабильные образования, а также циклические, которым Бейс присваивал такие имена, как "ротор" или даже "лягающий мустанг".

Стабильные и циклические формы "Жизни 4555"
Подобно физику, исследующему элементарные частицы, Бейс устраивал столкновения между планерами и другими мелкими конфигурациями, причем объекты сталкивались под всевозможными углами. "Среди наиболее удивительных столкновений,- пишет он,- можно выделить столкновение планера с шариком, при котором суммарная масса осколков увеличивается до 29, что само по себе не так уж примечательно. Но затем после нескольких поколений внезапно снова появляется планер, несколько переместившийся от места столкновения".
Все то, что развивается из первобытного бульона, и даже результаты столкновений планеров между собой и с другим объектами Бейс называет природой. Некоторые конфигурации получить нетрудно. Другие же, более экзотические образования требуют для своего воссоздания значительно больших усилий. Можно, например, сцепить друг с другом несколько конфигураций, имеющих форму арки, и получить таким образом новое стабильное образование, которое Бейс называет галереей. Возникает полный архитектурный ансамбль из заборов, лестниц, стен и цепей. Стены можно закручивать в спирали и множество других экзотических стабильных форм, ограниченных лишь воображением энтузиаста, исследующего возможности "Жизни 4555" (см. рисунок внизу).

Планер проходит через стабильную улитку в трехмерном пространстве игры К.Бейса "Жизнь 4555"
Следует обратить внимание и на некоторые другие интересные явления. Среди прочих образовании часто встречается объект из 7 кубиков под названием "привет". В отсутствие другого такого же привета это образование погибает. Планер, встретившись с приветом, оказывается захваченным и не может продолжить свое путешествие. Второй планер может случайно освободить своего собрата, столкнувшись с приветом и взорвав его.
Из двух наиболее плодотворных трехмерных версий, открытых Бейсом, "Жизнь 4555", по-видимому, нравится ему больше. Здесь можно отметить одно любопытное обстоятельство: цифры в названии "Жизнь 4555" получаются прибавлением 2 к соответствующим цифрам названия версии Конвея 2333. Возможно, это совпадение послужит предзнаменованием того, что именно "Жизнь 4555" станет достойным преемником игры Конвея.
Однако, строго говоря, "Жизнь 5766" имеет больше сходства с игрой Конвея по сравнению с вариантом 4555. В частности, при некоторых условиях "Жизнь 5766" моделирует версию Конвея на плоскости. Эти условия сформулированы в теореме, на которую наткнулся в своих исследованиях Бейс.
Представим себе, что мы смотрим сверху на плоскую решетку игры Конвея и видим какую-то конфигурацию живых (квадратных) клеток. Теперь поместим непосредственно над каждой клеткой конфигурации и под ней по одному живому кубу. Следуя правилам игры "Жизнь 5766", эти кубические "клетки" будут неограниченно долго точно копировать поведение "бутерброда" из клеток Конвея тогда (и только тогда), когда будут выполнены два условия:
1. Ни одна живая клетка на плоскости никогда не имеет 5 живых соседей.
2. Ни одна мертвая клетка на плоскости никогда не имеет 6 живых соседей.
Многие конфигурации "Жизни", в том числе и планер Конвея, удовлетворяют указанным условиям. Планер в пространстве "Жизни 5766" можно создать, преобразовав клетки двумерного планера в кубы. Такой планер занимает два прилегающих друг к другу слоя клеток в трехмерном пространстве и будет двигаться всегда в пределах этих слоев (см. рисунок на с.92).

Планер в трехмерной игре Бейса "Жизнь 5766"
Многие другие простые объекты "Жизни" Конвея, такие, как маяк, улей, мигалка и блок, а также более экзотические образования, такие, как лодка и часы, также удовлетворяют условиям теоремы Бейса. Эти объекты существуют в двухслойном виде как конфигурации "Жизни 5766", которые ведут себя точно так же, как и их двумерные аналоги. К сожалению, не все конфигурации игры Конвея удовлетворяют критериям теоремы. Среди этих "неподдающихся" объектов - знаменитая катапульта, запускающая планеры, которая была открыта Р.Госпером в 1970г., когда он был еще студентом Массачусетского технологического института. Проследив за катапультой, мы видим, что на любой стадии се жизненного цикла у нее имеются живые клетки с пятью живыми соседями. Любые нарушения какого-либо условия теоремы Бейса приводят к отклонению от модели. "Когда это происходит,- рассказывает Бейс,- объект, до тех пор ограниченный двумя плоскостями, почти во всех случаях превращается в округлую трехмерную массу, которая обычно довольно быстро погибает".
Можно добиться более полного моделирования версии Конвея на основе "Жизни 5766", если воздвигнуть то, что Бейс называет барьером времени-пространства. Он состоит из единой поверхности живых клеток, в которой как бы просверлены дырки (см. рисунок на с.93). Дырки расположены таким образом, чтобы каждый куб в барьере имел ровно 7 соседей. Клетки-кубы, принадлежащие барьеру, едва-едва избегают гибели от перенаселения среды, в то время как любой куб, непосредственно прилегающий к барьеру, всегда будет иметь более 6 живых соседей и потому никогда не оживет. Образующейся в результате мертвой зоной с каждой стороны от барьера можно воспользоваться для точного воспроизведения "Жизни" Конвея. Для этого нужно соорудить два параллельных барьера времени-пространства на расстоянии четырех кубов друг от друга. Из четырех заключенных между ними плоскостей две центральные могут поддерживать все формы жизни, потому что теперь условия теоремы Бейса удовлетворяются для любой популяции живых клеток, находящихся посередине этого "бутерброда".

Два барьера времени-пространства в "Жизни 5766"
Несмотря на то что "Жизнь 5766" способна в той или иной мере имитировать версию Конвея, ее клеточный мир все же не так красив и привлекателен. Как свидетельствует Бейс, случайно выбранные первобытные бульоны "Жизни 5766", кажется, всегда достигают "установившегося состояния" быстрее по сравнению с "Жизнью 4555". Неустановившийся характер "Жизни 4555" говорит о ее более богатых вычислительных возможностях. В самом деле, "Жизнь 4555" изобилует стабильными и осциллирующими формами, которые обладают свойством симметрии. Возможно, окончательное решение вопроса о том, какая версия станет наиболее достойным преемником "Жизни" Конвея, будет зависеть от того, удастся ли смоделировать двумерную игру при помощи "Жизни 4555". В случае успеха эта версия окажется во всех отношениях лучше, чем "Жизнь 5766".
Бейс написал брошюру на 40 страницах под названием "Трехмерная игра "Жизнь"". Она содержит в себе все, о чем мы здесь говорили, и много больше, включая советы по эффективному программированию игр. Бейс располагает также программой для компьютера "Макинтош", которая моделирует обе версии трехмерной жизни.
Программу, вычисляющую и показывающую последовательные поколения любой формы трехмерной версии игры, написать нетрудно, по крайней мере в принципе. Программу можно даже модифицировать так, чтобы она пробовала различные правила, и, может быть, читателям удастся открыть третью удачную трехмерную версию "Жизни", которую Бейс мог упустить в своих исследованиях.
Два больших трехмерных массива cells (клетки) и newcells (новые клетки) имеют три индекса i, j и k, соответствующие трем координатам клеточного пространства. Содержимое каждого элемента массива показывает, жива или мертва соответствующая клетка. Пусть 1 означает живое состояние а 0 - мертвое.
Не удивительно, что для вычисления статуса каждой клетки в каждом поколении требуются три вложенных цикла. Самый внешний цикл с индексом i служит для вычисления последовательности плоскостей, проходящих через все пространство игры. В этот цикл вложены два других с индексами j и k. В цикле по j происходит вычисление последовательных строк в пределах каждой плоскости, а в цикле по k вычисляется состояние последовательных клеток в строке. В качестве руководства можно воспользоваться следующей схемой:
for i = 1 to 30
- for j = 1 to 30
- - for к = I to 30
- - - вычислить соседей
- - - определить состояние
- - - высветить живые клетки
Число 30, конечно, выбрано произвольно. Однако лишь читателям, обладающим неограниченным терпением, можно поэкспериментировать с числами, большими 30, потому что время вычислений становится очень большим.
Во внутреннем цикле перед программой стоят три основные задачи. Чтобы решить задачу вычисления соседей, программе нужно исследовать состояние 26 соседей каждой клетки и подсчитать число живых на данный момент. Это можно сделать при помощи трех миниатюрных циклов или путем перечисления всех возможных координат 26 клеток. Если воспользоваться конструкцией с циклами, то их можно расписать по следующему алгоритму:
tot <- 0
for l = i-1 to i+1
- for m = j-1 to j+1
- - for n = k-1 to k+1
- - - if cells(l, m, n) = 1
- - - - then tot <- tot+1
tot <- tot-cells(i, j, k)
Здесь переменная tot (от слова total - полный) хранит суммарное число живых соседей. Последняя строчка в алгоритме нужна для того, чтобы состояние самой клетки cells(i, j, k) не влияло на подсчитываемую сумму.
Определив величину tot - полное число живых соседей, программа должна затем определить новое состояние рассматриваемой в данный момент клетки cells (i, j, k). Задача определения состояния сводится к простой проверке значения tot в отношении к состоянию клетки cells {i, j, k):
if cells{i, j, k) = 0
- then if tot = 5
- - then newcells(i, j, k) <- 1
- - else newcells(i, j, k) <- 0
if cells(i, j, k) = 1
- then if tot < 4 or tot > 5
- - then newcells(i, j, к) <- 0
- - else newcells{i, j, k) <- 1
Здесь я предполагал, что читатель программирует игру "Жизнь 4555". Можно несколько изменить алгоритм, чтобы приспособить его к версии 5766 или сделать его достаточно общим, чтобы охватить любые трехмерные правила. Рассмотрим последнюю возможность.
В универсальном виде описанный выше алгоритм вычисления состояния можно записать, воспользовавшись четырьмя переменными, которые Бейс назвал как el, eu, fl, fu. Буквы е и/означают соответственно среду (environment) и плодовитость (fertility), а буквы l и u соответственно нижний (lower) и верхний (upper). Таким образом, el н eu - это нижняя и верхняя границы, в которые должна попасть клетка, чтобы продолжить жизнь в следующем поколении. Клетка останется живой, если число окружающих ее живых соседей больше или равно el, но меньше или равно величине eu. Аналогично, величины fl и fu - это границы, в которые должна попасть мертвая клетка, чтобы ожить в следующем поколении. Это произойдет, если число живых кубов в окрестности клетки больше или равно fl, но меньше или равно fu. В этих обозначениях общий алгоритм приобретает следующий вид:
if cells{i, j, k) = 0
- then if tot < fl or tot > fu
- - then newcells(i, j, k) <- 1
- - else newcells(i, j, k) <- 0
if cells(i, j, k) = 1
- then if tot < el or tot > eu
- - then newcells(i, j, к) <- 0
- - else newcells{i, j, k) <- 1
Здесь в любой версии трехмерной жизни программа должна перевести содержимое массива newcells в массив cells при помощи тройного цикла. Таким образом, массив newcells освобождается для следующего поколения живых кубов.
В заключительной стадии рассматриваемого нами алгоритма, обозначенной как "высветить живые клеткн", программа должна изобразить соответствующий куб при условии, что он находится в живом состоянии. При изображении кубов на экране мы советуем закрашивать видимые поверхности. Если оставлять рисунок в скелетном виде, то изображение получается очень сложным и непонятным. Простейший способ сделать невидимыми кубы, расположенные за видимыми поверхностями, заключается в том, чтобы i - индекс внешнего цикла - пробегал значения, соответствующие оси, ведущей из глубины экрана к зрителю. Тот печальный факт, что некоторые кубики становятся, таким образом, невидимыми,- единственный недостаток, присущий всем трехмерным версиям "Жизни". Мы не имеет возможности охватить взглядом все, что происходит в пространстве, как мы могли это сделать в двумерной версии Конвея. В то же время этот недостаток любой трехмерной игры присущ и всему нашему трехмерному миру. Мы не можем видеть всего того, что в нем происходит. И можно сказать, что это к нашему счастью.
После того как в программе реализована последняя стадия, процесс ее выполнения становится довольно медленным. Можно добиться некоторого ускорения, заменив кубы сферами (на самом деле заштрихованными дисками, размеры которых изменяются в зависимости от их "глубины" на экране). Нужно сказать, что в брошюре Бейса, о которой мы говорили, есть рецепты, позволяющие добиться увеличения скорости на несколько порядков.
Как всегда, я с радостью расскажу обо всех необычных, интересных явлениях, которые будут открыты читателями. Во-первых, удастся ли неутомимым исследователям, всегда стремящимся к обобщению, найти какие-нибудь формы трехмерной жизни (стоящие такого названия), которые, возможно, упустил Бейс? Во-вторых, читателям, наверное, будет интересно поэкспериментировать со своими собственными рецептами первобытного бульона. Ну а в остальном, кто знает, сколько еще существует неоткрытых планеров, космических кораблей, катапульт и других интересных образований! Но чтобы не дублировать результатов, достигнутых Бейсом, следует обязательно изучить брошюру "Трехмерная игра "Жизнь"".
БИБЛИОГРАФИЯ
WINNING WAYS FOR YOUR MATHEMATICAL PLAYS, Vol.2; Games in Particular. Elwyn R. Berlekamp, John H. Conway and Richard K. Guy. Academic Press, 1982.
MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. Bruce A. Art-wick. Prentice-Hall, Inc., 1984.
ОТКЛИКИ
7 1987
Вот еще одно объявление: К.Бейс, импрессарио игры "Трехмерная жизнь", сообщает, что он намеревается учредить регулярный бюллетень и что через несколько месяцев появится его первый номер. В апрельском номере журнала мы говорили о двух трехмерных версиях клеточных автоматов, недавно открытых и исследуемых Бейсом. Вместо клеток-квадратов, рождающихся, живущих и умирающих в исходной версии двумерной игры, придуманной математиком Дж.Конвеем, в трехмерном пространстве Бейса рождаются, живут и умирают клетки кубической формы. Поскольку Бейс получил уже около 500 писем, он считает, что учреждение специального бюллетеня будет оправданно. Он надеется выпускать журнал раз в квартал. Туда войдут все интересные наблюдения, сделанные им самим или подписчиками журнала.
Бейс продолжает поиски удачных трехмерных аналогов игры Конвея. Недавно он нашел два критерия, которые, по-видимому, уверенно позволяют различать удачные и неудачные варианты игры. Первый критерий заключается в том, что биологическая среда, или "первобытный бульон", не должна расти беспредельно. Другими словами, если начать со случайного набора живых клеток, они не должны иметь тенденцию к безграничному распространению. Согласно второму критерию, время от времени среда должна порождать планеры - циклические конфигурации живых кубических клеток, перемещающихся по экрану как единое целое.
Об одном из трехмерных вариантов игры сообщил К.Пирсон из Нанаймо (Британская Колумбия), написавший Бейсу о книге П.Антони "Окс" (P.Anthony, "Ox"), в которой автор упоминает об одном из возможных вариантов трехмерной "Жизни". Этот вариант, следуя лаконичному лексикону самого Бейса, нужно назвать "Жизнь 6777". По правилам "Жизни 6777" живая кубическая клетка умрет в следующем поколении, если у нес меньше шести или больше семи живых соседей в текущем поколении. Мертвая клетка оживает в следующем поколении в том случае, если в данном поколении у нее ровно семь живых соседей. Бейс сообщает, что он уже исследовал предложенную версию трехмерной "Жизни" и нашел, что она не удовлетворяет первому критерию.
В настоящее время Бейс сосредоточил свое внимание на двух вариантах, потенциально достойных преемниках игры Конвея. (Как, наверное, помнят многие читатели, это варианты "Жизнь 4555" и "Жизнь 5766".) Исследуя эти варианты, Бейс занимается главным образом поиском "катапульты", стреляющей "планерами". Катапульта - это конфигурация клеток, постоянно выпускающая планеры в одном или более фиксированных направлениях.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
5 1987
МАШИНКИ БРАЙТЕНБЕРГА - АВТОМАТЫ С СИНТЕТИЧЕСКОЙ ПСИХОЛОГИЕЙ
А.К.ДЬЮДНИ
На эту статью уже ссылался и журнал выкладывал - ТЕМА #44, АБЗАЦ #436
ТЕМА #44, АБЗАЦ #436 .- G.
.- G.
Широкая равнина жужжит сотнями игрушечных машинок. Одни скапливаются у основания гигантских лампочек, другие ищут себе места потемнее или же нерешительно слоняются между светом и тенью. Что это за страна, какой безумный мир? Этот мир можно назвать миром синтетической психологии. Изобрел его Валентино Брайтенберг, сотрудник Института биологической кибернетики им.Макса Планка в Тюбингене. Тезис Брайтенберга о том, что биологическое повеление легче синтезировать, чем анализировать, наглядно иллюстрируется машинками, населяющими широкую равнину. Пользуясь лишь элементарными механизмами и электрическими устройствами, управляемыми простейшими схемами, можно имитировать поведение, в котором, по мнению Брайтенберга, проявляется любовь, агрессия, страх и предвидение. Полное описание эксперимента Брайтенберга можно найти в его небольшой занятной книжке под названием "Машинки: эксперименты по синтетической психологии" (V.Braiienberg "Vehicles: Experiments in Synthetic Psychology").
Но перед тем как отправиться в мир машинок Брайтенберга, я хотел бы рассказать свою собственную историю, которая также иллюстрирует его тезис. Один профессор принес как-то раз на занятия по искусственному интеллекту любопытный предмет. Это был золотистый шар, который, как он заявил (конечно, в шутку), выпал прямо на его глазах из НЛО утром, как раз когда он направлялся в университетский городок. Повернувшись спиной к аудитории, он что-то покрутил, и шар начал жужжать. Когда профессор положил его на гладкий пол, шар внезапно пришел в движение и покатился, как бы по своей воле. Натолкнувшись на какое-нибудь препятствие, например ножку стула, он на мгновение останавливался, затем, объехав препятствие, продолжал свой путь. Один раз шар даже выкатился за открытую дверь. Пожужжав и потолкавшись с минуту в углу, он внезапно снова выкатился из тупика, как будто удовлетворенный результатами проведенного исследования. Читателям, возможно, будет интересно поразмыслить о том, какая таинственная сила управляла шаром, каким образом ему удавалось объезжать препятствия. Ответ будет дан через месяц, в следующем номере нашего журнала.
У машинок Брайтенберга есть одно общее свойство с описанным золотым шаром; лишь посвященным известно, как они работают, остальные могут только в недоумении пожимать плечами. Я взял на себя смелость несколько упростить и формализовать игру Брайтенберга, так чтобы читатели смогли присоединиться к посвященным и принять участие в приключениях.
Машинку Брайтенберга можно себе представить как игрушечный автомобиль с двумя независимыми задними ведущими колесами и двумя ведомыми передними наподобие обычных роликов (см. рисунок). Разница в скорости вращения задних колес определяет направление, в котором движется машинка.
Колеса прикреплены к платформе в виде сплошного параллелепипеда. К боковым ее граням можно прикрепить различные датчики. Электрические цепи, соединяющие датчики с задними колесами, завершают конструкцию машинки. Соединительные проводники располагаются на верхней грани платформы подобно печатной схеме. В конструкцию машинки можно включить еще одну деталь - прямоугольную крышку, закрывающую электронную схему на верхней грани. Крышка служит не для того, чтобы защитить мозг машинки от дождя (у природы синтетической психологии нет плохой погоды), а чтобы скрыть ее от любопытных глаз посторонних. Нам не хочется, чтобы все видели, как просты на самом деле наши миниатюрные схемы. Пусть непосвященные наблюдатели дадут свободу своему воображению и переберут самые фантастические версии относительно того, что "на уме" у машинок и как они работают. Не будем портить им удовольствия.
У машинки стандартной модели имеются два "глаза", или фоторецептора, с широким углом зрения, которые установлены на передней грани платформы. Каждый рецептор направлен немного в сторону от продольной оси; при таком расположении рецепторов световой источник, расположенный впереди и слева от машинки, подействует на левый рецептор сильнее, чем на правый.
Рецепторы электрически соединены с моторчиками, приводящими в движение задние колеса. Сигналы, передаваемые по соединительным линиям, представляют собой последовательности дискретных электрических импульсов. Чем больше света падает на данный рецептор, тем больше импульсов он посылает по своей выходной линии. При низких уровнях освещенности передается всего несколько импульсов в секунду. При высокой освещенности количество импульсов велико. Будем считать, что в обоих случаях импульсы посылаются равной длительности. На другом конце линий последовательности импульсов преобразуются в команды, управляющие работой моторчиков. Чем больше импульсов в секунду прибывает на данное колесо, тем быстрее крутит его моторчик.
В простейшей модели глаза машинки непосредственно соединяются двумя линиями с задними колесами. Возможны два варианта: либо проводники перекрещены, либо - нет. В последнем случае каждый проводник соединяет глаз с колесом, находящимся по ту же сторону от продольной оси. Что произойдет, если поставить такую машинку посреди бесконечной темной равнины, местами освещенной ярко горящими лампочками? Если машинка окажется поблизости от одной из лампочек и будет ориентирована передом к ней, она сразу придет в движение и немедленно начнет поворачивать в сторону от света, как бы напуганная его яркостью. Такая "боязливая" машинка, постепенно замедляясь, убежит в темноту; далее она будет медленно ползать по равнине, избегая ярко освещенных мест. Когда машинка окажется между двумя близко расположенными лампочками, она стремительно разгонится и, подобно испуганному кролику, поспешит выйти из зтого неприятного и опасного места.
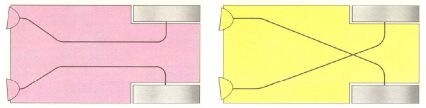
Прямые (слева) и перекрещивающиеся (справа) соединения приводят к разному поведению
Такое поведение машинки, возможно, озадачит постороннего наблюдателя, однако оно имеет очень простое объяснение. Если впереди по ходу машинки, например слева, появляется источник света, ее левый глаз получит больше света, чем правый, Следовательно, левый моторчик будет вращаться быстрее, чем правый: машинка начнет разворачиваться вправо, удаляясь от источника света. Если источник света появится справа, машинка повернет влево, в сторону от источника. Как только источник света пропадает из поля зрения машинки, она тут же замедляет движение и ее скорость уже регулируется средней освещенностью, создаваемой удаленными источниками.
Ну а как будет вести себя машинка с перекрещенными проводниками? Ее поведение будет противоположным. Если поставить такую машинку на большом удалении от всех лампочек, она начнет медленно двигаться по направлению к той лампочке, свет которой доминирует в ее поле зрения. По мере приближения к лампочке машинка будет двигаться все быстрее и быстрее. Наконец, на самой высокой скорости она врежется в лампочку и разобьет ее. Не покажется ли постороннему наблюдателю, что машинка с перекрещенными проводниками ведет себя агрессивно?
В отсутствие каких-либо электронных устройств между рецепторами и моторами эти две описанные машинки фактически исчерпывают весь доступный репертуар поведения. Чтобы добиться более сложного поведения, нужно ввести устройство, подобное так называемому абстрактному нейрону. Назовем его нейродом, чтобы не путать с настоящим нейроном.
Нейрод, по существу, представляет собой формальный вычислительный элемент, получающий импульсы от других нейродов или рецепторов. Импульсы передаются по проводникам. При определенных условиях нейрод и сам порождает импульсы. Вся система синхронизируется часовым механизмом, выдающим тактовые импульсы с частотой, скажем, 100 тактов в секунду. Нейрод выдает импульс в конце очередного такта - причем только в конце такта,- если число импульсов, полученных им от других нейродов в продолжение завершающегося такта, больше или равно установленному заранее значению. (Время прохождения любого импульса между любыми двумя непосредственно соединенными нейродами всегда несколько меньше длительности одного такта.) Установленное число, управляющее поведением нейрода, называется его порогом.
В самом общем случае можно сказать, что импульсы передаются от нейродов к нейродам по проводникам двух видов - возбуждения и торможения. Нейрод срабатывает, если получает достаточное количество импульсов по линиям возбуждения, так что пороговое значение оказывается превзойденным. В то же время нейрод не сможет сработать в конце данного такта, если в его продолжение он получил импульс по линии торможения.
Часовой механизм управляет также рецепторами и моторами. Рецептор может послать сигнал только в конце такта. Срабатывая на каждом такте, он будет посылать 100 импульсов в секунду, достигая тем самым максимального уровня активности, на котором может работать рецептор. Моторы тоже могут получать максимум 100 импульсов в секунду от управляющих ими нейродов. Будем также предполагать, что каждый импульс, достигший мотора, поворачивает его колесо на некий небольшой угол. Такие устройства действительно существуют и называются шаговыми двигателями.
Если теперь в управляющую схему, которая до сих пор была ультрапростейшей, ввести два нейрода, поведение двух рассмотренных выше машинок коренным образом изменится: боязливые машинки станут светолюбивыми, а агрессивные превратятся в робких. Однако их поведение не станет просто противоположным, изменение будет более тонким. В обоих случаях мы вставляем один нейрод с порогом 10 посередине каждого проводника, соединяющего рецептор с мотором, а участок проводника между рецептором и нейродом заменяется проводником тормозящего типа. Следовательно, когда нейрод получает импульс от рецептора, он ничего не посылает мотору, работой которого управляет. И наоборот, когда нейрод не получает импульсов от рецептора, он срабатывает и посылает импульс мотору. Другими словами, чем выше частота импульсов, посылаемых глазом, тем медленнее крутится мотор, и, наоборот, чем ниже частота импульсов от глаза, тем быстрее крутится мотор.
Теперь представим себе, каким будет поведение первой машинки, той, у которой проводники не перекрещены. При приближении к источнику света она двигается прямо на него, постепенно замедляясь. Наконец, она останавливается, глядя на лампочку в молчаливом восторге. Что же касается второй машинки, то перекрещенные проводники теперь заставляют ее медленно удаляться от ближайшего источника света, а затем, набирая скорость, стремительно убегать в самое темное место.
Причины такого поведения обеих машинок должны быть ясны любому, кто знает их управляющие схемы. В обоих случаях чем больше света попадает в рецепторы, тем медленнее вращаются моторы. Однако в первом случае более ярко освещенный глаз управляет более медленным мотором по ту же сторону от продольной оси. Благодаря этому отклонение от осевого направления корректируется. Во втором случае более ярко освещенный глаз управляет более медленным мотором по другую сторону от продольной оси, что лишь усиливает наметившееся отклонение.
До сих пор реакция моторов на сигналы, подаваемые рецепторами, была либо прямо, либо обратно пропорциональна частоте этих сигналов. При помощи простой схемы из четырех нейродов реакцию моторов можно сделать нелинейной. Повеление четырехнейродной схемы остается совершенно непримечательным до тех пор, пока рецептор посылает импульсы с частотой меньше 50 импульсов в секунду: чем больше импульсов в секунду поступает от рецептора, тем быстрее вращается мотор. Однако при частоте, превышающей 50 импульсов в секунду, поведение машинки становится интереснее. Вращение мотора начинает замедляться: чем больше импульсов в секунду поступает от рецептора, тем медленнее вращается мотор.
Чтобы объяснить, как работает схема управления из четырех нейродов, необходимо ввести понятие частоты импульсов. Частота импульсов - это среднее количество импульсов, приходящееся на один такт. Например, рецептор, посылающий 50 импульсов в секунду, работает с частотой 1/2, поскольку 50 импульсов в секунду, деленные на 100 тактов в секунду, дают нам 1/2 импульса на один такт (напомним, что часы отсчитывают 100 тактов в секунду). Так как нейрод или рецептор могут вырабатывать сигнал только в конце такта, частота импульсов никогда не превышает 1. Схема из четырех нейродов построена таким образом, что если глаз посылает импульсы с частотой меньшей 1/2, то все импульсы достигают мотора. Если же частота импульсов выше 1/2, то схема начинает действовать как сеть: чем больше посылается импульсов, тем меньшее их число достигает мотора.
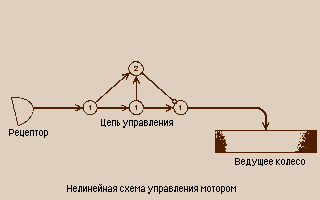
Четырехнейродная управляющая схема состоит из трехнейродной цепочки с порогом 1 и дополнительного нейрода с порогом 2 (см. рисунок). Первые два нейрода с порогом 1 посылают импульсы нейроду с порогом 2, который в свою очередь посылает импульс торможения третьему нейроду с порогом 1 в цепочке. Суммарный эффект этой схемы, если можно так выразиться, сводится к тому, чтобы в любой последовательности плотно прилегающие друг к другу импульсов, проходящих через это миниатюрное нервное сплетение, "убить" все импульсы, кроме первого. Предлагаю читателям самим убедиться в том, что схема работает именно так. При этом предполагается, что при частоте импульсов, меньшей 1/2, никакие два импульса не прилегают вплотную друг к другу. Однако при частотах выше 1/2 появляются скопления импульсов.
Предлагаю также поразмыслить над тем, каким будет поведение машинок, если каждый тормозящий проводник, ведущий от рецептора, заменить возбуждающим проводником, а каждый нейрод с порогом 0 заменить четырехнейродной нелинейной схемой. Вблизи источника света, там, где частота импульсов, посылаемых рецептором, выше 1/2, машинка с неперекрещенными соединениями между рецепторами и моторами будет вести себя как светолюбивое существо. Вдали же от источников света она становится пугливой и избегает освещенных мест. В то же время машинка с перекрещенными соединениями становится то нерешительной и боязливой, то агрессивной. При частоте импульсов, превышающей границу 1/2, она ведет себя агрессивно, устремляясь к ближайшей лампочке со все возрастающей скоростью. При частотах, меньших граничного значения, она становится нерешительной и боязливо отворачивается от света.

Теперь представим себе великую равнину, населенную машинками всех шести разновидностей (см. рисунок). Около каждой лампочки мы увидим, наверное, небольшую группу тихих ее обожателей. Несколько поодаль по извилистым орбитам будут нерешительно кружить машинки с неустойчивым характером. Еще дальше в темноте мы увидим боязливых и робких, либо тихо ползающих, либо испуганно проносящихся по сложным траекториям. Время от времени сцены тихого обожания в окрестности той или иной лампочки будут нарушаться прибытием агрессивной машинки. Если лампочка будет при этом уничтожена, машинки начнут разбегаться кто куда в поисках другого источника света. Машинка же, виновная в гибели лампочки (если только она сама благополучно пережила столкновение), покинет сцену последней, двигаясь медленнее машинок - обожателей лампочки.
Поведенческие возможности машинок, оснащенных нейродами, практически неограниченны. На самом деле систему нейродов можно соединить таким образом, чтобы получился настоящий компьютер. Однако для чего нужен мощный мозг при таких ограниченных сенсорных возможностях? Можно, конечно, оборудовать машинки более совершенным зрительным аппаратом, снабдить их слуховыми и осязательными рецепторами. При наличии таких органов чувств можно сделать окружающую среду более сложной, интересной и разнообразной. Усовершенствованная зрительная система будет состоять уже не только из рецепторов с широким углом зрения, но и из узко фокусируемых, которые будут взаимно дополнять друг друга. Визуальные рецепторы можно снабдить фильтрами, так чтобы машинки могли различать цвета и чувствовать тепло (в форме инфракрасного излучения). Слуховые рецепторы могут представлять собой некое примитивное подобие ушей, настроенных на различные частотные диапазоны. В качестве осязательных рецепторов я бы выбрал длинные усики-антенны, вытягивающиеся далеко вперед. Природу равнины можно затем разнообразить звуковыми и тепловыми источниками. Машинки и сами могли бы выделять тепло. Некоторые лампочки могли бы издавать звук.
Когда я читал книжку Брайтенберга, мое внимание привлек следующий фрагмент. Описывая богатые возможности машинок, управляемых системами нейродов, Брайтенберг пишет: "Вы уже, наверное, в какой-то степени представляете себе, что может делать машинка, снабженная подобным мозгом, однако, увидев все это в действии, вы все же будете удивлены. Например, какая-то машинка может быть совершенно неподвижной в течение нескольких часов и затем внезапно прийти в движение, заметив светло-зеленую машинку, издающую звук определенной частоты и передвигающуюся со скоростью, не превышающей 5см/с".

Это описание натолкнуло меня на мысль о машинках-хищниках, бросающихся на любую другую машинку, попадающую в их поле зрения (см. рисунок). Я сконструировал ту часть мозга хищника, которая управляет преследованием жертвы, и предлагаю читателям в качестве упражнения самим разработать конструкцию такой машинки. Возможно, читателям будет интересно изобрести другие модели мозга, вызывающие то или иное поведение.
Мозг сконструированной мною машинки-хищника построен из трех уровней взаимосвязанных нейродов. Первый уровень представляет собой модель сетчатки, выделяющей значимую информацию из тех сигналов, которые поступают от трех визуальных рецепторов с малым углом зрения. Нейроды второго уровня решают, появилась ли в поле зрения жертва. Третий уровень системы состоит из двух моторных нейродов, которые управляют ведущими колесами.
Рассмотрим данную модель подробнее. Сетчатка состоит из четырех нейродов, каждый из которых реагирует на определенные сочетания светлых и темных пятен в поле зрения трех фоторецептороа. Два нейрода в левой части схемы срабатывают, если какой-нибудь темный объект (в данном случае машинка) попадает в поле зрения самого левого или двух левых рецепторов. Эти два нейрода соединены линиями возбуждения с нейродом порога 1 на втором уровне мозга.
Нейрод второго уровня срабатывает а конце данного такта, если один из двух нейродов сетчатки сработал на предыдущем такте. Следовательно, он посылает сигнал, когда в левой части поля зрения появляется машинка. Нейрод второго уровня одновременно посылает импульсы возбуждения моторному нейроду, управляющему правым ведущим колесом, и импульсы торможения моторному нейроду, управляющему левым ведущим колесом. Таким образом, машинка начинает поворачивать влево, так что мишень сместится в центральную часть сетчатки. Нейроды правой стороны мозга хищника работают как зеркальное отражение левых. Центральный нейрод порога 0 на втором уровне соединен одной линией торможения с центральным фоторецептором и двумя линиями возбуждения с моторными нейродами. Нейрод с нулевым порогом будете продвигать машинку прямо вперед при условии, что ни один из двух других нейродов второго уровня не работает, поскольку каждый из них может затормозить соответствующий моторный нейрод.
Очевидно синтезировать машинку Брайтенберга намного проще, чем анализировать внутренний механизм биологической нервной системы, даже такой примитивной, как у крупной морской улитки Aplysia (см.статью: Eric R.Kandel. Small Systems of Neurons, "Scientific American", September, 1979 - P.К.Кендел "Малые нейронные системы"). Несомненно, наблюдатели, знакомые с правилами игры в синтетическую психологию, смогут понять конструкцию многих машинок Брайтенберга, просто синтезировав свои собственные аналоги. В то же время машинки Брайтенберга говорят о том, что даже самые примитивные нервные системы могут демонстрировать поведение, кажущееся сложным и удивительным. Во всяком случае, нейрофизиологи имеют дело с существами, сложность которых на несколько порядков величины выше, чем у описанных здесь машинок.
М.А.Арбиб - специалист по информатике и мозгу, недавно перешедший в Южно-КаролинскиЙ университет,- занимается координацией исследований в области, расположенной на стыке нейрофизиологии, информатики и науки, изучающей поведение. У Арбиба есть тоже своя "машинка" для изучения деятельности мозга - моделируемая компьютером лягушка, ее научное (латинское) название Rana compulciiri.v (лягушка компьютерная). В настоящее время мозг лягушки реализован лишь частично: построена грубая модель сетчатки, довольно развитый тектум и почти ничего больше. Однако уже сейчас лягушка прыгает, огибая препятствия, и отличает "добычу" от неживых предметов. Кроме того, она демонстрирует способность к простому обучению. По мнению Арбиба, сейчас наблюдается возрождение интереса к нейронным моделям как в плане имитации живых существ, так и в плане изучения их возможностей как вычислительных систем. Несколько исследователей, работающих в первой области, создали компьютерные модели изолированных нейронных систем простых сушеств, таких, как кузнечики, лягушки и морские слизни. Эти модели уже привели к проверяемым предсказаниям. Небольшая группа инженеров, работающих во второй области, занимается изучением формальных нейронов как элементов параллельного компьютера.
Пропасть, лежащая между синтезом и анализом, не означает, конечно, что машинки Брайтенберга должны рассматриваться просто как игрушки. В моделях подобного рода настораживает (наверное, больше, чем пропасть между синтезом и анализом) тенденция некоторых наблюдателей характеризовать действия машинок в терминах человеческого поведения - говорить, что машинки "любят" или "ненавидят", основываясь на поведении, которое лишь кажется сложным и вовсе не является таковым на самом деле. В высказываниях Брайтенберга, по-видимому, подразумевается, что в принципе явления любви и ненависти, проявляющиеся в поведении человека, настолько же определенны, как и в "нервных системах" машинок. Совершая переход от простого к сложному и в то же время от абстрактных существ к реальным, мы вынуждены заключить, что любовь и ненависть существовали почти с самого начала.
В своей книге Брайтенберг тщательно подбирает последовательность машинок от простых к сложным. В конце книги он объясняет, каким образом каждое предположение как в плане поведения, так и в плане конструкции основано на реальных наблюдениях. В заключение заметим, что способность зрительной системы, состоящей из многих визуальных рецепторов с узким полем зрения, различать предметы, наверное, может послужить в конце концов объяснением тому, как в людном помещении муха выбирает, на чей нос сесть.
БИБЛИОГРАФИЯ
INТRОDUСТЮN ТО NERVOUS SYSTEMS. THEODORE HOLMES BULLOCK, RICHARD ORKAND AND АLАП GRINNELL. W.Н.Freeman and Соmраnу, 1977.
SMALL SYSTEMS OF NEURONS. ERIC R. KANDEL in Scieпtific Americaп, Vol.241, No.3, pages 66-76; September, 1979.
VEHICLES: EXPERIMENTS lN SYNTHEТIC PSYCHOLOGY. Valentino
Braitenberg. The MIT Press, 1984.
ОТКЛИКИ
6 1987
В РУБРИКЕ "Занимательный компьютер" в статье, посвященной машинкам Брайтенберга и другим электронным устройствам из мира синтетической психологии, я поставил перед читателями задачу попытаться объяснить поведение золотистого шара, выпавшего из неопознанного летательного объекта. Приведенный в действие шар начинает с тихим жужжанием кататься по гладкому полу. Каким образом он двигается, если у него нет никаких выступающих наружу деталей - ни колесиков, ни ножек? Шар избегает также препятствий: при встрече с препятствием он объезжает его. Каким образом он это делает?
Несколько лет назад в США и Канале продавалась игрушка под названием "луноход". Она состояла из двух полых прозрачных пластмассовых полусфер, которые, защелкиваясь, образовывали шар. Внутрь сферы помешалась маленькая игрушечная машинка с электромоторчиком, работающим от батарейки. Чтобы привести игрушку в действие, электромотор машинки включался перед тем, как ее опускали в одну из полусфер. Шар диаметром 10см катался по полу, потому что находящаяся внутри машинка постоянно пыталась заехать на внутреннюю стенку сферы, и последняя, выходя из статического равновесия, двигалась в том направлении, в котором в данный момент была ориентирована машинка.
Когда же сфера натыкалась на препятствие, например на ножку стула, машинка забиралась по стенке сферы еше выше. В некоторой точке начинал срабатывать эффект встроенного в правое колесо машинки проскальзывания. Машинка начинала смещаться вправо ло тех пор, пока не находила свободного от препятствия направления. Таким образом сфера объезжала препятствия. Стоит лишь закрасить поверхность сферы, чтобы скрыть автомашинку, как зрители приходят в полное недоумение. Какие только фантастические предположения не высказывают люди, пытаясь угадать, что находится внутри этого таинственного шара, прибывшего к нам из космического пространства.
8 1987
ОТКЛИКИ на статью в майском номере о машинках Брайтенберга были полны энтузиазма. В них было все - от практических предложений до философских обобщений. Напомним, что машинки Брайтенберга - это чисто символические творения. Они представляют собой платформу с печатной платой, двумя передними и двумя задними колесами, набор сенсоров (обычно два глаза) впереди и два моторчика, вращающие задние колеса. Построенные даже на простейших электронных схемах, машинки демонстрируют удивительно разнообразное поведение. Есть и светолюбивые машинки, замирающие в молчаливом восторге перед светящимися шарами, есть и агрессивные, которые набрасываются на источники света, стремительно выезжая из окружающей тьмы.
Дж.Коппола из Шеррилла (шт.Нью-Йорк) утверждает, что приблизительно за 30долл. можно построить настоящую машинку с фанерным корпусом, стандартными моторчиками и электронными компонентами. Машинку конструкции Копполы удобно модифицировать для исследования различных типов поведения. Любители конструировать могут сами сделать такие машинки с различным характером поведения и устроить соревнование своих детищ в каком-нибудь городском парке при свете ярких уличных фонарей.
Т.Напье из Дрешера (шт.Пенсильвания) напомнил мне о замысловатой машинке, сконструированной в 50-х годах У.Уолтером из Бристольского университета. Устройство это называлось черепахой. По словам Напье, "у него было одно ведущее колесо и два свободно вращающихся на неподвижной оси поддерживающих колесика. Управляющий моторчик поворачивал ведущее колесо и его движущий мотор вокруг вертикальной оси. И управляющий, и движущий моторы работали постоянно, но их можно было переключать на вдвое меньшее число оборотов при помощи двух реле. Эти реле управлялись схемой на двух электронных лампах, на входе которой был фотоэлемент, поворачивающийся вместе с ведущим колесом рулевым механизмом. Поскольку движущий и рулевой моторы имели лишь два состояния и никогда не выключались, черепаха двигалась к источнику света по циклоидной траектории".
Чтобы получить изменяющееся поведение у машинки Брайтенберга, я предложил схему, состоящую и четырех нейродов, простейших вычислительных элементов, являющихся абстрактными эквивалентами нейронов мозга. Ф.Палмер из Чикаго указал на то, что достаточно будет и двух нейродов. В его схеме проводник, несущий входной сигнал, разветвляется на две линии, каждая из которых подсоединяется к нейроду с порогом 1. При этом один из нейродов действует тормозящим образом на другой. Последний передает то, что остается от сигнала, в качестве выхода системы.
Р.Барух из Бэй-Сайда (шт.Нью-Йорк) сделал одно любопытное наблюдение. Он согласен с Брайтенбергом, что посторонние наблюдатели могут подумать, что даже такие простые машинки обладают способностью проявлять эмоции. Барух замечает, что, возможно, отношение к нашим собственным эмоциям можно объяснить аналогичным образом. Он пишет: "Может быть, человеческий мозг с его мириадами сложных обратных связей лишь иллюзорно рассматривает себя как нечто обладающее эмоциями и разумом в обычном понимании этого слова, хотя на самом деле за этими понятиями не скрывается ничего, кроме переключательных схем".
МАШИНКИ БРАЙТЕНБЕРГА - АВТОМАТЫ С СИНТЕТИЧЕСКОЙ ПСИХОЛОГИЕЙ
А.К.ДЬЮДНИ
На эту статью уже ссылался и журнал выкладывал -
 ТЕМА #44, АБЗАЦ #436
ТЕМА #44, АБЗАЦ #436 .- G.
.- G.Широкая равнина жужжит сотнями игрушечных машинок. Одни скапливаются у основания гигантских лампочек, другие ищут себе места потемнее или же нерешительно слоняются между светом и тенью. Что это за страна, какой безумный мир? Этот мир можно назвать миром синтетической психологии. Изобрел его Валентино Брайтенберг, сотрудник Института биологической кибернетики им.Макса Планка в Тюбингене. Тезис Брайтенберга о том, что биологическое повеление легче синтезировать, чем анализировать, наглядно иллюстрируется машинками, населяющими широкую равнину. Пользуясь лишь элементарными механизмами и электрическими устройствами, управляемыми простейшими схемами, можно имитировать поведение, в котором, по мнению Брайтенберга, проявляется любовь, агрессия, страх и предвидение. Полное описание эксперимента Брайтенберга можно найти в его небольшой занятной книжке под названием "Машинки: эксперименты по синтетической психологии" (V.Braiienberg "Vehicles: Experiments in Synthetic Psychology").
Но перед тем как отправиться в мир машинок Брайтенберга, я хотел бы рассказать свою собственную историю, которая также иллюстрирует его тезис. Один профессор принес как-то раз на занятия по искусственному интеллекту любопытный предмет. Это был золотистый шар, который, как он заявил (конечно, в шутку), выпал прямо на его глазах из НЛО утром, как раз когда он направлялся в университетский городок. Повернувшись спиной к аудитории, он что-то покрутил, и шар начал жужжать. Когда профессор положил его на гладкий пол, шар внезапно пришел в движение и покатился, как бы по своей воле. Натолкнувшись на какое-нибудь препятствие, например ножку стула, он на мгновение останавливался, затем, объехав препятствие, продолжал свой путь. Один раз шар даже выкатился за открытую дверь. Пожужжав и потолкавшись с минуту в углу, он внезапно снова выкатился из тупика, как будто удовлетворенный результатами проведенного исследования. Читателям, возможно, будет интересно поразмыслить о том, какая таинственная сила управляла шаром, каким образом ему удавалось объезжать препятствия. Ответ будет дан через месяц, в следующем номере нашего журнала.
У машинок Брайтенберга есть одно общее свойство с описанным золотым шаром; лишь посвященным известно, как они работают, остальные могут только в недоумении пожимать плечами. Я взял на себя смелость несколько упростить и формализовать игру Брайтенберга, так чтобы читатели смогли присоединиться к посвященным и принять участие в приключениях.

Машинку Брайтенберга можно себе представить как игрушечный автомобиль с двумя независимыми задними ведущими колесами и двумя ведомыми передними наподобие обычных роликов (см. рисунок). Разница в скорости вращения задних колес определяет направление, в котором движется машинка.
Колеса прикреплены к платформе в виде сплошного параллелепипеда. К боковым ее граням можно прикрепить различные датчики. Электрические цепи, соединяющие датчики с задними колесами, завершают конструкцию машинки. Соединительные проводники располагаются на верхней грани платформы подобно печатной схеме. В конструкцию машинки можно включить еще одну деталь - прямоугольную крышку, закрывающую электронную схему на верхней грани. Крышка служит не для того, чтобы защитить мозг машинки от дождя (у природы синтетической психологии нет плохой погоды), а чтобы скрыть ее от любопытных глаз посторонних. Нам не хочется, чтобы все видели, как просты на самом деле наши миниатюрные схемы. Пусть непосвященные наблюдатели дадут свободу своему воображению и переберут самые фантастические версии относительно того, что "на уме" у машинок и как они работают. Не будем портить им удовольствия.
У машинки стандартной модели имеются два "глаза", или фоторецептора, с широким углом зрения, которые установлены на передней грани платформы. Каждый рецептор направлен немного в сторону от продольной оси; при таком расположении рецепторов световой источник, расположенный впереди и слева от машинки, подействует на левый рецептор сильнее, чем на правый.
Рецепторы электрически соединены с моторчиками, приводящими в движение задние колеса. Сигналы, передаваемые по соединительным линиям, представляют собой последовательности дискретных электрических импульсов. Чем больше света падает на данный рецептор, тем больше импульсов он посылает по своей выходной линии. При низких уровнях освещенности передается всего несколько импульсов в секунду. При высокой освещенности количество импульсов велико. Будем считать, что в обоих случаях импульсы посылаются равной длительности. На другом конце линий последовательности импульсов преобразуются в команды, управляющие работой моторчиков. Чем больше импульсов в секунду прибывает на данное колесо, тем быстрее крутит его моторчик.
В простейшей модели глаза машинки непосредственно соединяются двумя линиями с задними колесами. Возможны два варианта: либо проводники перекрещены, либо - нет. В последнем случае каждый проводник соединяет глаз с колесом, находящимся по ту же сторону от продольной оси. Что произойдет, если поставить такую машинку посреди бесконечной темной равнины, местами освещенной ярко горящими лампочками? Если машинка окажется поблизости от одной из лампочек и будет ориентирована передом к ней, она сразу придет в движение и немедленно начнет поворачивать в сторону от света, как бы напуганная его яркостью. Такая "боязливая" машинка, постепенно замедляясь, убежит в темноту; далее она будет медленно ползать по равнине, избегая ярко освещенных мест. Когда машинка окажется между двумя близко расположенными лампочками, она стремительно разгонится и, подобно испуганному кролику, поспешит выйти из зтого неприятного и опасного места.

Прямые (слева) и перекрещивающиеся (справа) соединения приводят к разному поведению
Такое поведение машинки, возможно, озадачит постороннего наблюдателя, однако оно имеет очень простое объяснение. Если впереди по ходу машинки, например слева, появляется источник света, ее левый глаз получит больше света, чем правый, Следовательно, левый моторчик будет вращаться быстрее, чем правый: машинка начнет разворачиваться вправо, удаляясь от источника света. Если источник света появится справа, машинка повернет влево, в сторону от источника. Как только источник света пропадает из поля зрения машинки, она тут же замедляет движение и ее скорость уже регулируется средней освещенностью, создаваемой удаленными источниками.
Ну а как будет вести себя машинка с перекрещенными проводниками? Ее поведение будет противоположным. Если поставить такую машинку на большом удалении от всех лампочек, она начнет медленно двигаться по направлению к той лампочке, свет которой доминирует в ее поле зрения. По мере приближения к лампочке машинка будет двигаться все быстрее и быстрее. Наконец, на самой высокой скорости она врежется в лампочку и разобьет ее. Не покажется ли постороннему наблюдателю, что машинка с перекрещенными проводниками ведет себя агрессивно?
В отсутствие каких-либо электронных устройств между рецепторами и моторами эти две описанные машинки фактически исчерпывают весь доступный репертуар поведения. Чтобы добиться более сложного поведения, нужно ввести устройство, подобное так называемому абстрактному нейрону. Назовем его нейродом, чтобы не путать с настоящим нейроном.
Нейрод, по существу, представляет собой формальный вычислительный элемент, получающий импульсы от других нейродов или рецепторов. Импульсы передаются по проводникам. При определенных условиях нейрод и сам порождает импульсы. Вся система синхронизируется часовым механизмом, выдающим тактовые импульсы с частотой, скажем, 100 тактов в секунду. Нейрод выдает импульс в конце очередного такта - причем только в конце такта,- если число импульсов, полученных им от других нейродов в продолжение завершающегося такта, больше или равно установленному заранее значению. (Время прохождения любого импульса между любыми двумя непосредственно соединенными нейродами всегда несколько меньше длительности одного такта.) Установленное число, управляющее поведением нейрода, называется его порогом.
В самом общем случае можно сказать, что импульсы передаются от нейродов к нейродам по проводникам двух видов - возбуждения и торможения. Нейрод срабатывает, если получает достаточное количество импульсов по линиям возбуждения, так что пороговое значение оказывается превзойденным. В то же время нейрод не сможет сработать в конце данного такта, если в его продолжение он получил импульс по линии торможения.
Часовой механизм управляет также рецепторами и моторами. Рецептор может послать сигнал только в конце такта. Срабатывая на каждом такте, он будет посылать 100 импульсов в секунду, достигая тем самым максимального уровня активности, на котором может работать рецептор. Моторы тоже могут получать максимум 100 импульсов в секунду от управляющих ими нейродов. Будем также предполагать, что каждый импульс, достигший мотора, поворачивает его колесо на некий небольшой угол. Такие устройства действительно существуют и называются шаговыми двигателями.
Если теперь в управляющую схему, которая до сих пор была ультрапростейшей, ввести два нейрода, поведение двух рассмотренных выше машинок коренным образом изменится: боязливые машинки станут светолюбивыми, а агрессивные превратятся в робких. Однако их поведение не станет просто противоположным, изменение будет более тонким. В обоих случаях мы вставляем один нейрод с порогом 10 посередине каждого проводника, соединяющего рецептор с мотором, а участок проводника между рецептором и нейродом заменяется проводником тормозящего типа. Следовательно, когда нейрод получает импульс от рецептора, он ничего не посылает мотору, работой которого управляет. И наоборот, когда нейрод не получает импульсов от рецептора, он срабатывает и посылает импульс мотору. Другими словами, чем выше частота импульсов, посылаемых глазом, тем медленнее крутится мотор, и, наоборот, чем ниже частота импульсов от глаза, тем быстрее крутится мотор.
Теперь представим себе, каким будет поведение первой машинки, той, у которой проводники не перекрещены. При приближении к источнику света она двигается прямо на него, постепенно замедляясь. Наконец, она останавливается, глядя на лампочку в молчаливом восторге. Что же касается второй машинки, то перекрещенные проводники теперь заставляют ее медленно удаляться от ближайшего источника света, а затем, набирая скорость, стремительно убегать в самое темное место.
Причины такого поведения обеих машинок должны быть ясны любому, кто знает их управляющие схемы. В обоих случаях чем больше света попадает в рецепторы, тем медленнее вращаются моторы. Однако в первом случае более ярко освещенный глаз управляет более медленным мотором по ту же сторону от продольной оси. Благодаря этому отклонение от осевого направления корректируется. Во втором случае более ярко освещенный глаз управляет более медленным мотором по другую сторону от продольной оси, что лишь усиливает наметившееся отклонение.
До сих пор реакция моторов на сигналы, подаваемые рецепторами, была либо прямо, либо обратно пропорциональна частоте этих сигналов. При помощи простой схемы из четырех нейродов реакцию моторов можно сделать нелинейной. Повеление четырехнейродной схемы остается совершенно непримечательным до тех пор, пока рецептор посылает импульсы с частотой меньше 50 импульсов в секунду: чем больше импульсов в секунду поступает от рецептора, тем быстрее вращается мотор. Однако при частоте, превышающей 50 импульсов в секунду, поведение машинки становится интереснее. Вращение мотора начинает замедляться: чем больше импульсов в секунду поступает от рецептора, тем медленнее вращается мотор.
Чтобы объяснить, как работает схема управления из четырех нейродов, необходимо ввести понятие частоты импульсов. Частота импульсов - это среднее количество импульсов, приходящееся на один такт. Например, рецептор, посылающий 50 импульсов в секунду, работает с частотой 1/2, поскольку 50 импульсов в секунду, деленные на 100 тактов в секунду, дают нам 1/2 импульса на один такт (напомним, что часы отсчитывают 100 тактов в секунду). Так как нейрод или рецептор могут вырабатывать сигнал только в конце такта, частота импульсов никогда не превышает 1. Схема из четырех нейродов построена таким образом, что если глаз посылает импульсы с частотой меньшей 1/2, то все импульсы достигают мотора. Если же частота импульсов выше 1/2, то схема начинает действовать как сеть: чем больше посылается импульсов, тем меньшее их число достигает мотора.

Четырехнейродная управляющая схема состоит из трехнейродной цепочки с порогом 1 и дополнительного нейрода с порогом 2 (см. рисунок). Первые два нейрода с порогом 1 посылают импульсы нейроду с порогом 2, который в свою очередь посылает импульс торможения третьему нейроду с порогом 1 в цепочке. Суммарный эффект этой схемы, если можно так выразиться, сводится к тому, чтобы в любой последовательности плотно прилегающие друг к другу импульсов, проходящих через это миниатюрное нервное сплетение, "убить" все импульсы, кроме первого. Предлагаю читателям самим убедиться в том, что схема работает именно так. При этом предполагается, что при частоте импульсов, меньшей 1/2, никакие два импульса не прилегают вплотную друг к другу. Однако при частотах выше 1/2 появляются скопления импульсов.
Предлагаю также поразмыслить над тем, каким будет поведение машинок, если каждый тормозящий проводник, ведущий от рецептора, заменить возбуждающим проводником, а каждый нейрод с порогом 0 заменить четырехнейродной нелинейной схемой. Вблизи источника света, там, где частота импульсов, посылаемых рецептором, выше 1/2, машинка с неперекрещенными соединениями между рецепторами и моторами будет вести себя как светолюбивое существо. Вдали же от источников света она становится пугливой и избегает освещенных мест. В то же время машинка с перекрещенными соединениями становится то нерешительной и боязливой, то агрессивной. При частоте импульсов, превышающей границу 1/2, она ведет себя агрессивно, устремляясь к ближайшей лампочке со все возрастающей скоростью. При частотах, меньших граничного значения, она становится нерешительной и боязливо отворачивается от света.

Теперь представим себе великую равнину, населенную машинками всех шести разновидностей (см. рисунок). Около каждой лампочки мы увидим, наверное, небольшую группу тихих ее обожателей. Несколько поодаль по извилистым орбитам будут нерешительно кружить машинки с неустойчивым характером. Еще дальше в темноте мы увидим боязливых и робких, либо тихо ползающих, либо испуганно проносящихся по сложным траекториям. Время от времени сцены тихого обожания в окрестности той или иной лампочки будут нарушаться прибытием агрессивной машинки. Если лампочка будет при этом уничтожена, машинки начнут разбегаться кто куда в поисках другого источника света. Машинка же, виновная в гибели лампочки (если только она сама благополучно пережила столкновение), покинет сцену последней, двигаясь медленнее машинок - обожателей лампочки.
Поведенческие возможности машинок, оснащенных нейродами, практически неограниченны. На самом деле систему нейродов можно соединить таким образом, чтобы получился настоящий компьютер. Однако для чего нужен мощный мозг при таких ограниченных сенсорных возможностях? Можно, конечно, оборудовать машинки более совершенным зрительным аппаратом, снабдить их слуховыми и осязательными рецепторами. При наличии таких органов чувств можно сделать окружающую среду более сложной, интересной и разнообразной. Усовершенствованная зрительная система будет состоять уже не только из рецепторов с широким углом зрения, но и из узко фокусируемых, которые будут взаимно дополнять друг друга. Визуальные рецепторы можно снабдить фильтрами, так чтобы машинки могли различать цвета и чувствовать тепло (в форме инфракрасного излучения). Слуховые рецепторы могут представлять собой некое примитивное подобие ушей, настроенных на различные частотные диапазоны. В качестве осязательных рецепторов я бы выбрал длинные усики-антенны, вытягивающиеся далеко вперед. Природу равнины можно затем разнообразить звуковыми и тепловыми источниками. Машинки и сами могли бы выделять тепло. Некоторые лампочки могли бы издавать звук.
Когда я читал книжку Брайтенберга, мое внимание привлек следующий фрагмент. Описывая богатые возможности машинок, управляемых системами нейродов, Брайтенберг пишет: "Вы уже, наверное, в какой-то степени представляете себе, что может делать машинка, снабженная подобным мозгом, однако, увидев все это в действии, вы все же будете удивлены. Например, какая-то машинка может быть совершенно неподвижной в течение нескольких часов и затем внезапно прийти в движение, заметив светло-зеленую машинку, издающую звук определенной частоты и передвигающуюся со скоростью, не превышающей 5см/с".

Это описание натолкнуло меня на мысль о машинках-хищниках, бросающихся на любую другую машинку, попадающую в их поле зрения (см. рисунок). Я сконструировал ту часть мозга хищника, которая управляет преследованием жертвы, и предлагаю читателям в качестве упражнения самим разработать конструкцию такой машинки. Возможно, читателям будет интересно изобрести другие модели мозга, вызывающие то или иное поведение.
Мозг сконструированной мною машинки-хищника построен из трех уровней взаимосвязанных нейродов. Первый уровень представляет собой модель сетчатки, выделяющей значимую информацию из тех сигналов, которые поступают от трех визуальных рецепторов с малым углом зрения. Нейроды второго уровня решают, появилась ли в поле зрения жертва. Третий уровень системы состоит из двух моторных нейродов, которые управляют ведущими колесами.
Рассмотрим данную модель подробнее. Сетчатка состоит из четырех нейродов, каждый из которых реагирует на определенные сочетания светлых и темных пятен в поле зрения трех фоторецептороа. Два нейрода в левой части схемы срабатывают, если какой-нибудь темный объект (в данном случае машинка) попадает в поле зрения самого левого или двух левых рецепторов. Эти два нейрода соединены линиями возбуждения с нейродом порога 1 на втором уровне мозга.
Нейрод второго уровня срабатывает а конце данного такта, если один из двух нейродов сетчатки сработал на предыдущем такте. Следовательно, он посылает сигнал, когда в левой части поля зрения появляется машинка. Нейрод второго уровня одновременно посылает импульсы возбуждения моторному нейроду, управляющему правым ведущим колесом, и импульсы торможения моторному нейроду, управляющему левым ведущим колесом. Таким образом, машинка начинает поворачивать влево, так что мишень сместится в центральную часть сетчатки. Нейроды правой стороны мозга хищника работают как зеркальное отражение левых. Центральный нейрод порога 0 на втором уровне соединен одной линией торможения с центральным фоторецептором и двумя линиями возбуждения с моторными нейродами. Нейрод с нулевым порогом будете продвигать машинку прямо вперед при условии, что ни один из двух других нейродов второго уровня не работает, поскольку каждый из них может затормозить соответствующий моторный нейрод.
Очевидно синтезировать машинку Брайтенберга намного проще, чем анализировать внутренний механизм биологической нервной системы, даже такой примитивной, как у крупной морской улитки Aplysia (см.статью: Eric R.Kandel. Small Systems of Neurons, "Scientific American", September, 1979 - P.К.Кендел "Малые нейронные системы"). Несомненно, наблюдатели, знакомые с правилами игры в синтетическую психологию, смогут понять конструкцию многих машинок Брайтенберга, просто синтезировав свои собственные аналоги. В то же время машинки Брайтенберга говорят о том, что даже самые примитивные нервные системы могут демонстрировать поведение, кажущееся сложным и удивительным. Во всяком случае, нейрофизиологи имеют дело с существами, сложность которых на несколько порядков величины выше, чем у описанных здесь машинок.
М.А.Арбиб - специалист по информатике и мозгу, недавно перешедший в Южно-КаролинскиЙ университет,- занимается координацией исследований в области, расположенной на стыке нейрофизиологии, информатики и науки, изучающей поведение. У Арбиба есть тоже своя "машинка" для изучения деятельности мозга - моделируемая компьютером лягушка, ее научное (латинское) название Rana compulciiri.v (лягушка компьютерная). В настоящее время мозг лягушки реализован лишь частично: построена грубая модель сетчатки, довольно развитый тектум и почти ничего больше. Однако уже сейчас лягушка прыгает, огибая препятствия, и отличает "добычу" от неживых предметов. Кроме того, она демонстрирует способность к простому обучению. По мнению Арбиба, сейчас наблюдается возрождение интереса к нейронным моделям как в плане имитации живых существ, так и в плане изучения их возможностей как вычислительных систем. Несколько исследователей, работающих в первой области, создали компьютерные модели изолированных нейронных систем простых сушеств, таких, как кузнечики, лягушки и морские слизни. Эти модели уже привели к проверяемым предсказаниям. Небольшая группа инженеров, работающих во второй области, занимается изучением формальных нейронов как элементов параллельного компьютера.
Пропасть, лежащая между синтезом и анализом, не означает, конечно, что машинки Брайтенберга должны рассматриваться просто как игрушки. В моделях подобного рода настораживает (наверное, больше, чем пропасть между синтезом и анализом) тенденция некоторых наблюдателей характеризовать действия машинок в терминах человеческого поведения - говорить, что машинки "любят" или "ненавидят", основываясь на поведении, которое лишь кажется сложным и вовсе не является таковым на самом деле. В высказываниях Брайтенберга, по-видимому, подразумевается, что в принципе явления любви и ненависти, проявляющиеся в поведении человека, настолько же определенны, как и в "нервных системах" машинок. Совершая переход от простого к сложному и в то же время от абстрактных существ к реальным, мы вынуждены заключить, что любовь и ненависть существовали почти с самого начала.
В своей книге Брайтенберг тщательно подбирает последовательность машинок от простых к сложным. В конце книги он объясняет, каким образом каждое предположение как в плане поведения, так и в плане конструкции основано на реальных наблюдениях. В заключение заметим, что способность зрительной системы, состоящей из многих визуальных рецепторов с узким полем зрения, различать предметы, наверное, может послужить в конце концов объяснением тому, как в людном помещении муха выбирает, на чей нос сесть.
БИБЛИОГРАФИЯ
INТRОDUСТЮN ТО NERVOUS SYSTEMS. THEODORE HOLMES BULLOCK, RICHARD ORKAND AND АLАП GRINNELL. W.Н.Freeman and Соmраnу, 1977.
SMALL SYSTEMS OF NEURONS. ERIC R. KANDEL in Scieпtific Americaп, Vol.241, No.3, pages 66-76; September, 1979.
VEHICLES: EXPERIMENTS lN SYNTHEТIC PSYCHOLOGY. Valentino
Braitenberg. The MIT Press, 1984.
ОТКЛИКИ
6 1987
В РУБРИКЕ "Занимательный компьютер" в статье, посвященной машинкам Брайтенберга и другим электронным устройствам из мира синтетической психологии, я поставил перед читателями задачу попытаться объяснить поведение золотистого шара, выпавшего из неопознанного летательного объекта. Приведенный в действие шар начинает с тихим жужжанием кататься по гладкому полу. Каким образом он двигается, если у него нет никаких выступающих наружу деталей - ни колесиков, ни ножек? Шар избегает также препятствий: при встрече с препятствием он объезжает его. Каким образом он это делает?
Несколько лет назад в США и Канале продавалась игрушка под названием "луноход". Она состояла из двух полых прозрачных пластмассовых полусфер, которые, защелкиваясь, образовывали шар. Внутрь сферы помешалась маленькая игрушечная машинка с электромоторчиком, работающим от батарейки. Чтобы привести игрушку в действие, электромотор машинки включался перед тем, как ее опускали в одну из полусфер. Шар диаметром 10см катался по полу, потому что находящаяся внутри машинка постоянно пыталась заехать на внутреннюю стенку сферы, и последняя, выходя из статического равновесия, двигалась в том направлении, в котором в данный момент была ориентирована машинка.
Когда же сфера натыкалась на препятствие, например на ножку стула, машинка забиралась по стенке сферы еше выше. В некоторой точке начинал срабатывать эффект встроенного в правое колесо машинки проскальзывания. Машинка начинала смещаться вправо ло тех пор, пока не находила свободного от препятствия направления. Таким образом сфера объезжала препятствия. Стоит лишь закрасить поверхность сферы, чтобы скрыть автомашинку, как зрители приходят в полное недоумение. Какие только фантастические предположения не высказывают люди, пытаясь угадать, что находится внутри этого таинственного шара, прибывшего к нам из космического пространства.
8 1987
ОТКЛИКИ на статью в майском номере о машинках Брайтенберга были полны энтузиазма. В них было все - от практических предложений до философских обобщений. Напомним, что машинки Брайтенберга - это чисто символические творения. Они представляют собой платформу с печатной платой, двумя передними и двумя задними колесами, набор сенсоров (обычно два глаза) впереди и два моторчика, вращающие задние колеса. Построенные даже на простейших электронных схемах, машинки демонстрируют удивительно разнообразное поведение. Есть и светолюбивые машинки, замирающие в молчаливом восторге перед светящимися шарами, есть и агрессивные, которые набрасываются на источники света, стремительно выезжая из окружающей тьмы.
Дж.Коппола из Шеррилла (шт.Нью-Йорк) утверждает, что приблизительно за 30долл. можно построить настоящую машинку с фанерным корпусом, стандартными моторчиками и электронными компонентами. Машинку конструкции Копполы удобно модифицировать для исследования различных типов поведения. Любители конструировать могут сами сделать такие машинки с различным характером поведения и устроить соревнование своих детищ в каком-нибудь городском парке при свете ярких уличных фонарей.
Т.Напье из Дрешера (шт.Пенсильвания) напомнил мне о замысловатой машинке, сконструированной в 50-х годах У.Уолтером из Бристольского университета. Устройство это называлось черепахой. По словам Напье, "у него было одно ведущее колесо и два свободно вращающихся на неподвижной оси поддерживающих колесика. Управляющий моторчик поворачивал ведущее колесо и его движущий мотор вокруг вертикальной оси. И управляющий, и движущий моторы работали постоянно, но их можно было переключать на вдвое меньшее число оборотов при помощи двух реле. Эти реле управлялись схемой на двух электронных лампах, на входе которой был фотоэлемент, поворачивающийся вместе с ведущим колесом рулевым механизмом. Поскольку движущий и рулевой моторы имели лишь два состояния и никогда не выключались, черепаха двигалась к источнику света по циклоидной траектории".
Чтобы получить изменяющееся поведение у машинки Брайтенберга, я предложил схему, состоящую и четырех нейродов, простейших вычислительных элементов, являющихся абстрактными эквивалентами нейронов мозга. Ф.Палмер из Чикаго указал на то, что достаточно будет и двух нейродов. В его схеме проводник, несущий входной сигнал, разветвляется на две линии, каждая из которых подсоединяется к нейроду с порогом 1. При этом один из нейродов действует тормозящим образом на другой. Последний передает то, что остается от сигнала, в качестве выхода системы.
Р.Барух из Бэй-Сайда (шт.Нью-Йорк) сделал одно любопытное наблюдение. Он согласен с Брайтенбергом, что посторонние наблюдатели могут подумать, что даже такие простые машинки обладают способностью проявлять эмоции. Барух замечает, что, возможно, отношение к нашим собственным эмоциям можно объяснить аналогичным образом. Он пишет: "Может быть, человеческий мозг с его мириадами сложных обратных связей лишь иллюзорно рассматривает себя как нечто обладающее эмоциями и разумом в обычном понимании этого слова, хотя на самом деле за этими понятиями не скрывается ничего, кроме переключательных схем".
Последний раз редактировалось: Gudleifr (Сб Май 27, 2023 12:19 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
6 1987
ПРОГРАММИРОВАНИЕ МЕЛОДИЧНОГО ЗВУЧАНИЯ РАБОТАЮЩЕГО КОМПЬЮТЕРА
А.К.ДЬЮДНИ
ЗВУКИ, издаваемые работающим компьютером, я впервые услышал в 1965г. В вычислительном центре Мичиганского университета к компьютеру IBM 7090 был подключен простой электромагнитный датчик - приемник, соединенный с динамиком. По ходу выполнения компьютерной программы тот или иной регистр машины меняет свое содержимое тысячи раз в секунду. Воспринимаемое на слух щелканье регистров представляло собой удивительный поток ни на что не похожих звуков. Жужжание сменялось визгом, затем слышался треск, потом завывание. Временами звук резко переходил от басов к высоким нотам. Эти изменения звука, по-видимому, объяснялись двойным циклом в программе - внутренний цикл выполнялся все быстрее и быстрее, порождая звук все более высокого тока. В целом эта симфония напоминала дыхание кита.
С тех пор было написано много программ, позволяющих исследовать различные аспекты мелодии, гармонии и ритма. Хотя домашние компьютеры обычно не снабжаются электромагнитными датчиками, приставленными к регистру-сумматору, в большинстве случаев у них имеются небольшие динамики, подсоединенные к простейшим генераторам звуков. В наиболее распространенных языках программирования есть инструкции, выполнение которых сопровождается различными звуковыми сигналами. При помощи этого простого средства можно, с одной стороны, делать программы звучащими, а с другой - делать звучащие программы. В первом случае инструкция, генерирующая звуки, просто вставляется в программу, предназначенную для вычислений. Я остановлюсь коротко на этом случае несколько ниже. Во втором случае программа специально предназначается для создания мелодических, гармонических или ритмических эффектов. Описанные здесь две программы, пожалуй, похожи на программы первой разновидности. Лишь несколько генерирующих звук инструкций вставлены в, казалось бы, совершенно обычную последовательность инструкций.
Мелодию, рассматриваемую просто как произвольную последовательность нот, нетрудно генерировать при помощи программы. На самом деле такая программа может состоять из одного-единственного цикла. Процедура принятия решений, встроенная в цикл, определяет, какой будет следующая нота и какова будет ее продолжительность. Этот процесс можно произвольно усложнять, накладывая на него всевозможные ограничения. Мне кажется, что уже существуют программы этого типа, способные генерировать довольно складные мелодии в том или ином традиционном стиле. Я с удовольствием прочту письма читателей, которым что-либо известно о таких программах. А пока пусть известные мне алгоритмы исполнят нам свои мелодии.
Самыми скромными кандидатами на должность композитора являются простейшие арифметические алгоритмы. Выходные численные данные этих алгоритмов легко преобразуются в ноты при помощи самых разнообразных формул. Простой пример дает нам формула итерационного линейного присвоения:
x <- (a*x+b) mod m.
Эта формула порождает целый процесс. При заданных заранее параметpах a, b и m исходное значение x преобразуется в числовую последовательность путем итерирования (повторного выполнения) формулы присвоения. Выражение "mod m" является сокращением от выражения "по модулю m", означающего, что результат вычисленного в скобках выражения должен интерпретироваться подобно показаниям стрелки часов с циферблатом из m часовых делений. Так, например, 10 по модулю 8 - это 2. Следовательно, если m равно 8 и если параметры a, b и исходное значение x - целые, то в результате итераций получаем последовательность чисел, лежащих в диапазоне от 0 до 7.
Эта числовая последовательность легко преобразуется в последовательность нот при помощи простой таблицы:


Частоты гаммы со ступенью в полтона от среднего "до" до "до" следующей октавы
В программе, которую я назвал SOLFEGGIO (пение по нотам), вместо названия нот элементы таблицы содержат числовые значения, соответствующие частотам (число периодов в секунду) музыкальной гаммы "до-мажор", начинающейся со среднего "до".

Всю эту программу можно представить в обычной алгоритмической записи следующим коротким алгоритмом:
ввести a, b, x
for i = 1 to 100
- x <- (х*a+b) mod 8
- note <- notes(x)
- сыграть note
В моей версии SOLFEGGIO числа в таблице notes (ноты) непосредственно используются инструкцией, генерирующей тон определенной высоты. В большинстве языков программирования для персональных компьютеров имеются также средства, позволяющие управлять продолжительностью звука. Пока для простоты будем считать, что эта продолжительность фиксирована н равна, скажем, половине секунды.
Теперь перед теми, кто обладает арифметическим (в отличие от музыкального) "слухом", открывается целый мир, наполненный невероятными мелодиями. В зависимости от выбора значений трех параметров формулы мы услышим либо однообразные сочинения, играющиеся как стакатто, либо странные повторяющиеся мелодии на нескольких нотах, либо причудливую музыку с внезапными скачками и быстрыми фразами. К последней категории относилась и маленькая, удивительно запоминающаяся пьеса, к сожалению навсегда утерянная, потому что я не записал принятых для нее параметров. Предложенный мною выше алгоритм порождает мелодии длиной 100 нот. Возможно, будущие исследователи в этой новой музыкальной области захотят сократить эту длину, для того чтобы успеть опробовать большее число вариантов.
Конечно, программу SOLFEGGIO можно и нужно усовершенствовать. Выберем большее значение для модуля m, оно должно быть достаточно большим, чтобы охватывать две или более диатонические октавы. Это ограничение на самом деле не является жестким: вместо диатонической гаммы можно, например, воспользоваться гаммами из 12 нот, отстоящих друг от друга на полтона. Можно даже выбрать ультрасовременное музыкальное построение - "линейное присвоение", в котором числа x, полученные алгоритмом, указывают на частоты, вычисляемые путем прибавления определенной константы, скажем 100. Если в какой-то момент значение x оказывается равным 183, то программа сыграет ноту с частотой 283. Интересно, какие еше возможности придут на ум читателю? А пока вот вам занимательный вопрос. Для заданных значений a, b и m, сколько нот будет сыграно, прежде чем мелодия начнет повторяться?
Гармония также входит теперь в сферу вокальных возможностей многих домашних компьютеров. Компьютеры, имеющие два или более динамиков, смогут исполнить весь репертуар программы, которую я назвал CANON. На самом деле энтузиасты, наверное, значительно разовьют эту идею. Существует система MIDI - цифровой интерфейс для музыкальных инструментов. Это электронный "черный ящик", преобразующий сигналы, генерируемые компьютером, в команды, управляющие электронными музыкальными инструментами, такими, как электроорган и многоканальные синтезаторы. (Статья, посвященная взаимодействию между компьютером и электронными музыкальными инструментами, опубликована в апрельском номере журнала; см. статью: М.Мэттьюз, Дж.Пирс. Компьютер в роли музыкального инструмента, "В мире науки", 1987, #4, с.72.).
Программа CANON в соответствии с определением музыкального термина "канон" генерирует композицию на два голоса, каждый из которых исполняет практически одну и ту же мелодию, но, как правило, на разной высоте и со сдвигом по времени. Получается очень интересная разновидность хорового пения. Канон представляет собой простейшую форму полифонии, или контрапункта (соединение в одновременное звучание двух или более мелодически самостоятельных голосов, укладывающихся в один и тот же ритм).
Такая каноническая композиция составляется из двух голосов, удовлетворяющих четырем критериям. Во-первых, все ноты имеют одну и туже продолжительность. Во-вторых, один голос вступает вслед за другим. В-третьих, мелодии, исполняемые обоими голосами, идентичны, за исключением того, что один из голосов транспонирован вверх на некоторый стандартный музыкальный интервал (унисон, чистая кварта, чистая квинта или октава). В-четвертых, оба голоса вместе, как пары одновременно звучащих нот, должны удовлетворять определенным гармоническим правилам, изложенным в любом музыкальном учебнике. Эти правила в основном касаются дозволенных гармонических интервалов (см. рисунок на с.100) и устанавливают форму участвующих в композиции мелодических линий. В интересах простоты последнее мы здесь опускаем.

Таблица консонантных гармонических интервалов
Пример подобной композиции показан на верхнем рисунке на с.101. Композиция была написана не машиной, а человеком. Посмотрев на нее, мы быстро замечаем, что, начиная с какого-то места, композитор уже устает от строгих ограничений, накладываемых всеми четырьмя критериями. Третье правило обычно нарушается в первую очередь - достаточным оказывается и то, что второй голос имитирует первый лишь по духу.

Пример канона на два голоса, взятый из учебника
С другой стороны, компьютерную программу эти ограничения нисколько не угнетают. Программа CANON работает без устали, пока не завершит свою пьесу. Однако, как правило, порождаемая программой мелодия, звучит скучновато. Поэтому я сгенерировал множество коротких канонов и записал самые интересные образцы. Эти избранные фрагменты можно затем соединять в более длинные пьесы (см. нижний рисунок на с.101). Описанный эксперимент был проведен десять лет назад с участием Г.Утаса - одного из моих студентов в Университете Западного Онтарио.

Два канона, сочиненные компьютером, сливаются в один
CANON сочиняет пьесу, как бы считая цифры по порядку. Пусть, например, программе было предписано сочинить крошечную композицию в стиле "канон" длиной в 6 нот. По причинам, которые вскоре станут очевидными, диапазон тонов, ограничивающих каждую мелодическую линию, невелик, скажем, 6 ступеней гаммы вверх и вниз от тоники - главного опорного звука. Множество из 13 возможных нот можно представить как цифры в системе счисления по основанию 13, или в "тринадцатиричном" счислении. Цифра 0 представляет тон, расположенный шестью ступенями ниже тоники, а "цифра" 13 - тон шестью ступенями выше тоники. Программа CANON работает очень просто, считая по порядку через все шестиразрядные числа в тринадцатеричной системе счисления. В конце концов каждое из этих чисел представляет какую-никакую, но мелодию.
Всякий раз, когда программа CANON генерирует новую мелодическую линию, она транспонирует ее вверх на квинту и переносит (по времени) на определенное количество нот, например на две. Затем она сравнивает полученные пары тонов, которые в результате предыдущей операции должны звучать одновременно. Если ни одна из полученных пар не нарушает правил гармонии, то пьеса принимается как удовлетворяющая канону и либо сразу распечатывается для сидящего у компьютера композитора, либо записывается в файл для последующей выдачи.
Программа CANON, в частности, требует, чтобы композитор перед началом выполнения программы указал следующие три параметра: int - интервал, на который должны отстоять друг от друга голоса, del - задержка, после которой вступает второй голос, и num - количество нот в каждой мелодической линии. Ноты генерируемой мелодии хранятся в массиве mel. В алгоритмической записи программу CANON можно представить в следующем виде:
ввести int, del, num
mel(l) <- 7
for i <= 2 to num
- mel{i) <- 1
found <- "ложь"
while found = "ложь"
- увеличить mel
- for j = 1 to num-del
- - сравнить melU) и mel(j+del)+int
- - if они гармоничны then found <- "истина"
вывести mel
продолжить или нет
Алгоритм начинается с присвоения элементу mel(1), первой ноте канона, значения 7. Эта нота является тоникой, и она не будет меняться. Оставшиеся элементы массива mel все начинаются с нулевых значений. Цикл типа while проверяет значение булевской, или логической, переменной found (найдено), которая в исходном состоянии имеет значение "ложь". Переменной found присваивается значение "истина", если при выполнении остальных инструкций тела цикла найдена мелодическая линия, удовлетворяющая требованиям канона. Сначала увеличивается содержимое массива mel. Это делается путем просмотра массива справа налево. В процессе просмотра считающая процедура отыскивает элемент массива, значение которого меньше 13. Найдя такой элемент, она увеличивает его на 1 и устанавливает все остальные элементы справа (если они есть) в ноль. Это происходит точно так же, как и при обычном счете, только роль цифры 9 в данном случае играет "цифра" 13. Например, 3572+1 = 3573, 3579 + 1 = 3580 и 3599 + 1 = 3600.
Следующая операция, выполняемая в цикле, заключается в сравнении каждой ноты mel(j) с нотой mel(j+del)+int. Другими словами, программа прибавляет значение int к ноте, расположенной на del элементов после mel(j), и по вычисленной разности между двумя тонами обращается к таблице гармонических правил, соответствующих канону. Если эта разность оказывается гармоничной во всех парах от 1 до num-del, то логической переменной found присваивается значение "истина". (Ноты, следующие за num-del, играются без аккомпанемента второго голоса, поэтому уже не нужно смотреть никаких разностей в таблице правил). После того как мелодическая линия найдена и распечатана, программа спрашивает композитора: "Хотите продолжить?" Если он отвечает "да", управление в программе снова переходит на инструкцию, в которой переменной found присваивается значение "ложь", и программа продолжает процесс счета с того места, где она остановилась.
Можно, конечно, проигрывать мелодические сочетания, найденные программой CANON, через миниатюрный динамик собственного домашнего компьютера. Однако музыкально одаренные читатели, наверное, быстро научатся напевать сгенерированные последовательности нот или же записывать их вместе с нотами второго голоса на нотной бумаге. Тогда найденный канон можно будет опробовать на клавиатуре пианино или другого музыкального инструмента, так сказать, во всем его гармоническом великолепии.
Ритм - значительно более тонкая музыкальная форма, чем думают, наверное, многие читатели. Традиционная европейская музыка, впрочем, никогда не была ритмически изощренной. С другой стороны, современная популярная музыка вобрала в себя чрезвычайно богатое многообразие ритмических форм. Большинство этих ритмов прямо или косвенно происходят из традиционной музыки Африки или Азии. Это относится к рок-музыке, джазу, карибской и латино-американской музыке. Все более заметный вклад в современную западную музыку вносят ритмы, выбиваемые пальцами на паре барабанов. Эти ритмы происходят из индийских музыкальных форм, таких, как рага.
Программа, которую я назвал BEAT, позволяет задавать простые ритмы как последовательности нулей и единиц. Последние преобразуются в звуки по мере того, как программа повторно пробегает через последовательность. Всякий раз, встретив 1, программа посылает короткий звуковой сигнал, а 0 не сопровождается никаким сигналом.
Программа BEAT настолько проста, что ее алгоритм можно представить без всяких предисловий. Ее структура похожа на структуру программы SOLFEGGIO (программу, которая исполняет музыку в стиле "линейного присвоения"). Единственный масснв pulse хранит ритм, заданный программистом перед началом выполнения программы.
ввести pulse, num, dur
for i = 1 to 25
- for j = I to num
- - k <- 1
- - while k <= dur
- - - k <- k+1
- - if pulse(j) = 1
- - - then звук
Переменные num (от слова number - число) и dur (от слова duration - продолжительность) относятся соответственно к размеру вводимого массива и продолжительности интервала между звуковыми сигналами. Во внешнем цикле указано, что основной ритмический интервал, задаваемый массивом pulse, должен проигрываться 25 раз. Этот параметр можно легко изменить, если читатели встретят ритмы, которые им хотелось бы послушать подольше. Следующий внутренний иикл управляет индексом массива; алгоритм по очереди просматривает каждый элемент массива, решая посылать или не посылать звуковой сигнал. Сколько времени нужно ждать между двумя "звуковыми событиями"? Этот вопрос решается посредством специального цикла ожидания, в котором просто идет счет от 1 до значения переменной dur. Затем, если элемент массива pulse(j) оказывается равным I, программа BEAT посылает звуковой сигнал; каким именно будет звук, зависит от конструктивных особенностей компьютера. Если величина dur мала, ритм будет быстрым. Если dur велико, ритм будет медленным.
Как и рассмотренные выше ее предшественницы, программа BEAT может быть усовершенствована. Можно, например, сочинять ритмы для целых ударных установок, если есть возможность ввести звуковые сигналы различного тона (низкие тона могли бы представлять большие барабаны, высокие - колокольчики и тарелки). И хотя звуки будут, по-видимому, далеки от реальных, сами по себе ритмы могут быть безупречными. Можно усложнить массив pulse, пользуясь в качестве его значений целыми числами 0, 1, 2 и 3, представляющими соответственно паузу, звук солирующего барабана высокого тона, звук барабана низкого тона и, наконец, одновременный улар по обоим барабанам. При этом каждое значение массива pulse, исследуемое во внутреннем цикле, должно быть декодировано набором инструкций "if ... then" (если ... то), которые решают, следует ли в данный момент сделать паузу, сыграть на каком-то одном "барабане" или на обоих сразу. Правда, в последнем случае два тона звучат вслед друг за другом как ближайшее возможное приближение к одновременности. Если при этом два последовательных звука будут разделены слишком большим временным интервалом, то цикл ожидания можно будет встроить внутрь конструкций "if ... then", так чтобы для каждого из четырех возможных вариантов была своя продолжительность. В случае паузы и двух последовательных звуков значение продолжительности dur должно быть заменено на два новых значения, одно из которых больше, а другое меньше dur. В обоих случаях новое значение будет отличаться от старого на величину, равную продолжительности одного звукового сигнала.
Более совершенная версия программы BEAT наверняка сможет сыграть кое-какие интересные ритмы, подобные приведенным на с.99. Приведенные партитуры интерпретируются как последовательности дискретных событий, привязанных к одному и тому же общему отсчету времени. Вдохновленный композитор сможет легко преобразовать их в содержимое массива pulse.

Образцы ритмов для программы BEAT
После этих экскурсов в царство мелодии, гармонии и ритма я все же хочу вернуться к заинтриговавшей меня идее о двух ролях, которые могут играть компьютерные программы. В первой роли программа вычисляет то, что она вычисляет, и ничего более. Во второй роли программа снабжается одной-двумя звуковыми инструкциями по соседству с каждым внутренним циклом, внешним циклом и условной конструкцией (оператор if). Во втором случае программа как бы поет песню о задаче, которую решает. Тот, кто часто слушает свою излюбленную программу (будь она развлекательной или производственной), через некоторое время научится чувствовать по звуку, как она работает. У меня нет сомнения в том, что некоторые ошибки в новых версиях программы можно будет выявить на слух.
БИБЛИОГРАФИЯ
POLYPHONIC COMPOSITION. OWEN SWINDALE. Oxford University Press, 1962.
STUDIES FOR THE CONTEMPORARY DRUMMER. JOHN XEPOLEAS AND WARREN NUNES. Hansen House, 1981.
COMPUTERS AND MUSIC. Special issue of Byte, Vol.11, No.5; June, 1986.
ОТКЛИКИ
9 1987
В июньском номере журнала в статье, посвященной компьютерной музыке, я предложил читателям поразмыслить, каким образом можно получить неповторяющиеся последовательности нот, выбирая числа по модулю m. Выборку следует начинать с исходного числа и далее все время умножать имеющееся число на a, прибавлять b и брать остаток от деления полученного результата на m. Если числа a и m не имеют общего множителя большего единицы, то последовательность будет максимально длинной. Она также порождает самую необычную музыку.
П. де Йонг отмечает, что при помощи хаоса ему удавалось создавать очень странную музыку. Читатели и сами могут синтезировать аналогичные звуки, превращая числа, которые генерирует программа CHAOS2 в музыкальные ноты. Вне хаотических зон будут получаться простые, повторяющиеся музыкальные фразы, внутри же этих зон музыка будет воплощением хаоса.
ПРОГРАММИРОВАНИЕ МЕЛОДИЧНОГО ЗВУЧАНИЯ РАБОТАЮЩЕГО КОМПЬЮТЕРА
А.К.ДЬЮДНИ
ЗВУКИ, издаваемые работающим компьютером, я впервые услышал в 1965г. В вычислительном центре Мичиганского университета к компьютеру IBM 7090 был подключен простой электромагнитный датчик - приемник, соединенный с динамиком. По ходу выполнения компьютерной программы тот или иной регистр машины меняет свое содержимое тысячи раз в секунду. Воспринимаемое на слух щелканье регистров представляло собой удивительный поток ни на что не похожих звуков. Жужжание сменялось визгом, затем слышался треск, потом завывание. Временами звук резко переходил от басов к высоким нотам. Эти изменения звука, по-видимому, объяснялись двойным циклом в программе - внутренний цикл выполнялся все быстрее и быстрее, порождая звук все более высокого тока. В целом эта симфония напоминала дыхание кита.
С тех пор было написано много программ, позволяющих исследовать различные аспекты мелодии, гармонии и ритма. Хотя домашние компьютеры обычно не снабжаются электромагнитными датчиками, приставленными к регистру-сумматору, в большинстве случаев у них имеются небольшие динамики, подсоединенные к простейшим генераторам звуков. В наиболее распространенных языках программирования есть инструкции, выполнение которых сопровождается различными звуковыми сигналами. При помощи этого простого средства можно, с одной стороны, делать программы звучащими, а с другой - делать звучащие программы. В первом случае инструкция, генерирующая звуки, просто вставляется в программу, предназначенную для вычислений. Я остановлюсь коротко на этом случае несколько ниже. Во втором случае программа специально предназначается для создания мелодических, гармонических или ритмических эффектов. Описанные здесь две программы, пожалуй, похожи на программы первой разновидности. Лишь несколько генерирующих звук инструкций вставлены в, казалось бы, совершенно обычную последовательность инструкций.
Мелодию, рассматриваемую просто как произвольную последовательность нот, нетрудно генерировать при помощи программы. На самом деле такая программа может состоять из одного-единственного цикла. Процедура принятия решений, встроенная в цикл, определяет, какой будет следующая нота и какова будет ее продолжительность. Этот процесс можно произвольно усложнять, накладывая на него всевозможные ограничения. Мне кажется, что уже существуют программы этого типа, способные генерировать довольно складные мелодии в том или ином традиционном стиле. Я с удовольствием прочту письма читателей, которым что-либо известно о таких программах. А пока пусть известные мне алгоритмы исполнят нам свои мелодии.
Самыми скромными кандидатами на должность композитора являются простейшие арифметические алгоритмы. Выходные численные данные этих алгоритмов легко преобразуются в ноты при помощи самых разнообразных формул. Простой пример дает нам формула итерационного линейного присвоения:
x <- (a*x+b) mod m.
Эта формула порождает целый процесс. При заданных заранее параметpах a, b и m исходное значение x преобразуется в числовую последовательность путем итерирования (повторного выполнения) формулы присвоения. Выражение "mod m" является сокращением от выражения "по модулю m", означающего, что результат вычисленного в скобках выражения должен интерпретироваться подобно показаниям стрелки часов с циферблатом из m часовых делений. Так, например, 10 по модулю 8 - это 2. Следовательно, если m равно 8 и если параметры a, b и исходное значение x - целые, то в результате итераций получаем последовательность чисел, лежащих в диапазоне от 0 до 7.
Эта числовая последовательность легко преобразуется в последовательность нот при помощи простой таблицы:


Частоты гаммы со ступенью в полтона от среднего "до" до "до" следующей октавы
В программе, которую я назвал SOLFEGGIO (пение по нотам), вместо названия нот элементы таблицы содержат числовые значения, соответствующие частотам (число периодов в секунду) музыкальной гаммы "до-мажор", начинающейся со среднего "до".

Всю эту программу можно представить в обычной алгоритмической записи следующим коротким алгоритмом:
ввести a, b, x
for i = 1 to 100
- x <- (х*a+b) mod 8
- note <- notes(x)
- сыграть note
В моей версии SOLFEGGIO числа в таблице notes (ноты) непосредственно используются инструкцией, генерирующей тон определенной высоты. В большинстве языков программирования для персональных компьютеров имеются также средства, позволяющие управлять продолжительностью звука. Пока для простоты будем считать, что эта продолжительность фиксирована н равна, скажем, половине секунды.
Теперь перед теми, кто обладает арифметическим (в отличие от музыкального) "слухом", открывается целый мир, наполненный невероятными мелодиями. В зависимости от выбора значений трех параметров формулы мы услышим либо однообразные сочинения, играющиеся как стакатто, либо странные повторяющиеся мелодии на нескольких нотах, либо причудливую музыку с внезапными скачками и быстрыми фразами. К последней категории относилась и маленькая, удивительно запоминающаяся пьеса, к сожалению навсегда утерянная, потому что я не записал принятых для нее параметров. Предложенный мною выше алгоритм порождает мелодии длиной 100 нот. Возможно, будущие исследователи в этой новой музыкальной области захотят сократить эту длину, для того чтобы успеть опробовать большее число вариантов.
Конечно, программу SOLFEGGIO можно и нужно усовершенствовать. Выберем большее значение для модуля m, оно должно быть достаточно большим, чтобы охватывать две или более диатонические октавы. Это ограничение на самом деле не является жестким: вместо диатонической гаммы можно, например, воспользоваться гаммами из 12 нот, отстоящих друг от друга на полтона. Можно даже выбрать ультрасовременное музыкальное построение - "линейное присвоение", в котором числа x, полученные алгоритмом, указывают на частоты, вычисляемые путем прибавления определенной константы, скажем 100. Если в какой-то момент значение x оказывается равным 183, то программа сыграет ноту с частотой 283. Интересно, какие еше возможности придут на ум читателю? А пока вот вам занимательный вопрос. Для заданных значений a, b и m, сколько нот будет сыграно, прежде чем мелодия начнет повторяться?
Гармония также входит теперь в сферу вокальных возможностей многих домашних компьютеров. Компьютеры, имеющие два или более динамиков, смогут исполнить весь репертуар программы, которую я назвал CANON. На самом деле энтузиасты, наверное, значительно разовьют эту идею. Существует система MIDI - цифровой интерфейс для музыкальных инструментов. Это электронный "черный ящик", преобразующий сигналы, генерируемые компьютером, в команды, управляющие электронными музыкальными инструментами, такими, как электроорган и многоканальные синтезаторы. (Статья, посвященная взаимодействию между компьютером и электронными музыкальными инструментами, опубликована в апрельском номере журнала; см. статью: М.Мэттьюз, Дж.Пирс. Компьютер в роли музыкального инструмента, "В мире науки", 1987, #4, с.72.).
Программа CANON в соответствии с определением музыкального термина "канон" генерирует композицию на два голоса, каждый из которых исполняет практически одну и ту же мелодию, но, как правило, на разной высоте и со сдвигом по времени. Получается очень интересная разновидность хорового пения. Канон представляет собой простейшую форму полифонии, или контрапункта (соединение в одновременное звучание двух или более мелодически самостоятельных голосов, укладывающихся в один и тот же ритм).
Такая каноническая композиция составляется из двух голосов, удовлетворяющих четырем критериям. Во-первых, все ноты имеют одну и туже продолжительность. Во-вторых, один голос вступает вслед за другим. В-третьих, мелодии, исполняемые обоими голосами, идентичны, за исключением того, что один из голосов транспонирован вверх на некоторый стандартный музыкальный интервал (унисон, чистая кварта, чистая квинта или октава). В-четвертых, оба голоса вместе, как пары одновременно звучащих нот, должны удовлетворять определенным гармоническим правилам, изложенным в любом музыкальном учебнике. Эти правила в основном касаются дозволенных гармонических интервалов (см. рисунок на с.100) и устанавливают форму участвующих в композиции мелодических линий. В интересах простоты последнее мы здесь опускаем.

Таблица консонантных гармонических интервалов
Пример подобной композиции показан на верхнем рисунке на с.101. Композиция была написана не машиной, а человеком. Посмотрев на нее, мы быстро замечаем, что, начиная с какого-то места, композитор уже устает от строгих ограничений, накладываемых всеми четырьмя критериями. Третье правило обычно нарушается в первую очередь - достаточным оказывается и то, что второй голос имитирует первый лишь по духу.

Пример канона на два голоса, взятый из учебника
С другой стороны, компьютерную программу эти ограничения нисколько не угнетают. Программа CANON работает без устали, пока не завершит свою пьесу. Однако, как правило, порождаемая программой мелодия, звучит скучновато. Поэтому я сгенерировал множество коротких канонов и записал самые интересные образцы. Эти избранные фрагменты можно затем соединять в более длинные пьесы (см. нижний рисунок на с.101). Описанный эксперимент был проведен десять лет назад с участием Г.Утаса - одного из моих студентов в Университете Западного Онтарио.

Два канона, сочиненные компьютером, сливаются в один
CANON сочиняет пьесу, как бы считая цифры по порядку. Пусть, например, программе было предписано сочинить крошечную композицию в стиле "канон" длиной в 6 нот. По причинам, которые вскоре станут очевидными, диапазон тонов, ограничивающих каждую мелодическую линию, невелик, скажем, 6 ступеней гаммы вверх и вниз от тоники - главного опорного звука. Множество из 13 возможных нот можно представить как цифры в системе счисления по основанию 13, или в "тринадцатиричном" счислении. Цифра 0 представляет тон, расположенный шестью ступенями ниже тоники, а "цифра" 13 - тон шестью ступенями выше тоники. Программа CANON работает очень просто, считая по порядку через все шестиразрядные числа в тринадцатеричной системе счисления. В конце концов каждое из этих чисел представляет какую-никакую, но мелодию.
Всякий раз, когда программа CANON генерирует новую мелодическую линию, она транспонирует ее вверх на квинту и переносит (по времени) на определенное количество нот, например на две. Затем она сравнивает полученные пары тонов, которые в результате предыдущей операции должны звучать одновременно. Если ни одна из полученных пар не нарушает правил гармонии, то пьеса принимается как удовлетворяющая канону и либо сразу распечатывается для сидящего у компьютера композитора, либо записывается в файл для последующей выдачи.
Программа CANON, в частности, требует, чтобы композитор перед началом выполнения программы указал следующие три параметра: int - интервал, на который должны отстоять друг от друга голоса, del - задержка, после которой вступает второй голос, и num - количество нот в каждой мелодической линии. Ноты генерируемой мелодии хранятся в массиве mel. В алгоритмической записи программу CANON можно представить в следующем виде:
ввести int, del, num
mel(l) <- 7
for i <= 2 to num
- mel{i) <- 1
found <- "ложь"
while found = "ложь"
- увеличить mel
- for j = 1 to num-del
- - сравнить melU) и mel(j+del)+int
- - if они гармоничны then found <- "истина"
вывести mel
продолжить или нет
Алгоритм начинается с присвоения элементу mel(1), первой ноте канона, значения 7. Эта нота является тоникой, и она не будет меняться. Оставшиеся элементы массива mel все начинаются с нулевых значений. Цикл типа while проверяет значение булевской, или логической, переменной found (найдено), которая в исходном состоянии имеет значение "ложь". Переменной found присваивается значение "истина", если при выполнении остальных инструкций тела цикла найдена мелодическая линия, удовлетворяющая требованиям канона. Сначала увеличивается содержимое массива mel. Это делается путем просмотра массива справа налево. В процессе просмотра считающая процедура отыскивает элемент массива, значение которого меньше 13. Найдя такой элемент, она увеличивает его на 1 и устанавливает все остальные элементы справа (если они есть) в ноль. Это происходит точно так же, как и при обычном счете, только роль цифры 9 в данном случае играет "цифра" 13. Например, 3572+1 = 3573, 3579 + 1 = 3580 и 3599 + 1 = 3600.
Следующая операция, выполняемая в цикле, заключается в сравнении каждой ноты mel(j) с нотой mel(j+del)+int. Другими словами, программа прибавляет значение int к ноте, расположенной на del элементов после mel(j), и по вычисленной разности между двумя тонами обращается к таблице гармонических правил, соответствующих канону. Если эта разность оказывается гармоничной во всех парах от 1 до num-del, то логической переменной found присваивается значение "истина". (Ноты, следующие за num-del, играются без аккомпанемента второго голоса, поэтому уже не нужно смотреть никаких разностей в таблице правил). После того как мелодическая линия найдена и распечатана, программа спрашивает композитора: "Хотите продолжить?" Если он отвечает "да", управление в программе снова переходит на инструкцию, в которой переменной found присваивается значение "ложь", и программа продолжает процесс счета с того места, где она остановилась.
Можно, конечно, проигрывать мелодические сочетания, найденные программой CANON, через миниатюрный динамик собственного домашнего компьютера. Однако музыкально одаренные читатели, наверное, быстро научатся напевать сгенерированные последовательности нот или же записывать их вместе с нотами второго голоса на нотной бумаге. Тогда найденный канон можно будет опробовать на клавиатуре пианино или другого музыкального инструмента, так сказать, во всем его гармоническом великолепии.
Ритм - значительно более тонкая музыкальная форма, чем думают, наверное, многие читатели. Традиционная европейская музыка, впрочем, никогда не была ритмически изощренной. С другой стороны, современная популярная музыка вобрала в себя чрезвычайно богатое многообразие ритмических форм. Большинство этих ритмов прямо или косвенно происходят из традиционной музыки Африки или Азии. Это относится к рок-музыке, джазу, карибской и латино-американской музыке. Все более заметный вклад в современную западную музыку вносят ритмы, выбиваемые пальцами на паре барабанов. Эти ритмы происходят из индийских музыкальных форм, таких, как рага.
Программа, которую я назвал BEAT, позволяет задавать простые ритмы как последовательности нулей и единиц. Последние преобразуются в звуки по мере того, как программа повторно пробегает через последовательность. Всякий раз, встретив 1, программа посылает короткий звуковой сигнал, а 0 не сопровождается никаким сигналом.
Программа BEAT настолько проста, что ее алгоритм можно представить без всяких предисловий. Ее структура похожа на структуру программы SOLFEGGIO (программу, которая исполняет музыку в стиле "линейного присвоения"). Единственный масснв pulse хранит ритм, заданный программистом перед началом выполнения программы.
ввести pulse, num, dur
for i = 1 to 25
- for j = I to num
- - k <- 1
- - while k <= dur
- - - k <- k+1
- - if pulse(j) = 1
- - - then звук
Переменные num (от слова number - число) и dur (от слова duration - продолжительность) относятся соответственно к размеру вводимого массива и продолжительности интервала между звуковыми сигналами. Во внешнем цикле указано, что основной ритмический интервал, задаваемый массивом pulse, должен проигрываться 25 раз. Этот параметр можно легко изменить, если читатели встретят ритмы, которые им хотелось бы послушать подольше. Следующий внутренний иикл управляет индексом массива; алгоритм по очереди просматривает каждый элемент массива, решая посылать или не посылать звуковой сигнал. Сколько времени нужно ждать между двумя "звуковыми событиями"? Этот вопрос решается посредством специального цикла ожидания, в котором просто идет счет от 1 до значения переменной dur. Затем, если элемент массива pulse(j) оказывается равным I, программа BEAT посылает звуковой сигнал; каким именно будет звук, зависит от конструктивных особенностей компьютера. Если величина dur мала, ритм будет быстрым. Если dur велико, ритм будет медленным.
Как и рассмотренные выше ее предшественницы, программа BEAT может быть усовершенствована. Можно, например, сочинять ритмы для целых ударных установок, если есть возможность ввести звуковые сигналы различного тона (низкие тона могли бы представлять большие барабаны, высокие - колокольчики и тарелки). И хотя звуки будут, по-видимому, далеки от реальных, сами по себе ритмы могут быть безупречными. Можно усложнить массив pulse, пользуясь в качестве его значений целыми числами 0, 1, 2 и 3, представляющими соответственно паузу, звук солирующего барабана высокого тона, звук барабана низкого тона и, наконец, одновременный улар по обоим барабанам. При этом каждое значение массива pulse, исследуемое во внутреннем цикле, должно быть декодировано набором инструкций "if ... then" (если ... то), которые решают, следует ли в данный момент сделать паузу, сыграть на каком-то одном "барабане" или на обоих сразу. Правда, в последнем случае два тона звучат вслед друг за другом как ближайшее возможное приближение к одновременности. Если при этом два последовательных звука будут разделены слишком большим временным интервалом, то цикл ожидания можно будет встроить внутрь конструкций "if ... then", так чтобы для каждого из четырех возможных вариантов была своя продолжительность. В случае паузы и двух последовательных звуков значение продолжительности dur должно быть заменено на два новых значения, одно из которых больше, а другое меньше dur. В обоих случаях новое значение будет отличаться от старого на величину, равную продолжительности одного звукового сигнала.
Более совершенная версия программы BEAT наверняка сможет сыграть кое-какие интересные ритмы, подобные приведенным на с.99. Приведенные партитуры интерпретируются как последовательности дискретных событий, привязанных к одному и тому же общему отсчету времени. Вдохновленный композитор сможет легко преобразовать их в содержимое массива pulse.

Образцы ритмов для программы BEAT
После этих экскурсов в царство мелодии, гармонии и ритма я все же хочу вернуться к заинтриговавшей меня идее о двух ролях, которые могут играть компьютерные программы. В первой роли программа вычисляет то, что она вычисляет, и ничего более. Во второй роли программа снабжается одной-двумя звуковыми инструкциями по соседству с каждым внутренним циклом, внешним циклом и условной конструкцией (оператор if). Во втором случае программа как бы поет песню о задаче, которую решает. Тот, кто часто слушает свою излюбленную программу (будь она развлекательной или производственной), через некоторое время научится чувствовать по звуку, как она работает. У меня нет сомнения в том, что некоторые ошибки в новых версиях программы можно будет выявить на слух.
БИБЛИОГРАФИЯ
POLYPHONIC COMPOSITION. OWEN SWINDALE. Oxford University Press, 1962.
STUDIES FOR THE CONTEMPORARY DRUMMER. JOHN XEPOLEAS AND WARREN NUNES. Hansen House, 1981.
COMPUTERS AND MUSIC. Special issue of Byte, Vol.11, No.5; June, 1986.
ОТКЛИКИ
9 1987
В июньском номере журнала в статье, посвященной компьютерной музыке, я предложил читателям поразмыслить, каким образом можно получить неповторяющиеся последовательности нот, выбирая числа по модулю m. Выборку следует начинать с исходного числа и далее все время умножать имеющееся число на a, прибавлять b и брать остаток от деления полученного результата на m. Если числа a и m не имеют общего множителя большего единицы, то последовательность будет максимально длинной. Она также порождает самую необычную музыку.
П. де Йонг отмечает, что при помощи хаоса ему удавалось создавать очень странную музыку. Читатели и сами могут синтезировать аналогичные звуки, превращая числа, которые генерирует программа CHAOS2 в музыкальные ноты. Вне хаотических зон будут получаться простые, повторяющиеся музыкальные фразы, внутри же этих зон музыка будет воплощением хаоса.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
7 1987
ПРОГРАММЫ ДЛЯ "БЫКОВ" И "МЕДВЕДЕЙ", ИГРАЮЩИХ НА БИРЖЕ
А.К.ДЬЮДНИ
ЗАЛ БИРЖИ, в котором совершается купля-продажа акций, иногда называют ямой. Здесь можно увидеть мужчин и женщин, громко кричащих, отчаянно жестикулирующих и лихорадочно вычисляющих что-то на клочках бумаги или на конвертах. В этом бедламе крики и жесты естественны для тех, кто продает и покупает акции. Будет ли этот процесс когда-нибудь автоматизирован? Наступит ли такой день, когда компьютеры раз и навсегда наведут тишину в яме?
Частично процесс купли-продажи акций автоматизируется уже сейчас, в том числе дома или в рабочем кабинете человека, играющего на бирже. Наши читатели могут сами написать программы, которые проводят общий или технический анализ, позволяющий предсказывать курс акций. Более непосредственное отношение к бирже имеют программы, написанные специалистами с Уолл-стрита [Уолл-стрит - улица в Нью-Йорке, на которой находится знаменитая американская фондовая биржа.- Прим. ред.]. Среди этих программ есть такие, которые рассчитывают конечный итог сложных сделок с большим количеством продаваемых и покупаемых акций с учетом не только текущего их курса, но и тенденций на будущее. Сделки, совершаемые при помощи подобных программ, известные как "программные сделки", по мнению некоторых специалистов, оказались виновницами резкого падения курса акций, наблюдавшегося в течение одного дня на нью-йоркской бирже в сентябре прошлого года. Еще ближе к яме программы, применяемые как вспомогательное средство непосредственно в процессе купли-продажи, о чем будет упомянуто в конце статьи. Может быть даже, что эти программы будут усовершенствованы до такой степени, чтобы непосредственно осуществлять сделки, но эта идея, конечно, натолкнется на трудности и даже возражения.
Сначала давайте совершим экскурсию на биржу. Очередная сделка начинается с того, что некто решил сделать капиталовложение, купив, скажем, 100 акций фирмы United Suspenders ("Объединенные подтяжки"). Человек, желающий приобрести акции, дает соответствующее поручение биржевому маклеру, который (за определенное вознаграждение) передает этот заказ непосредственно на биржу, где продаются акции фирмы United Suspenders. На бирже агент, занимающийся акциями этой фирмы, оформляет документ о продаже акций. Через некоторое время соответствующая сумма денег переводится со счета человека, покупающего акции, на счет их владельца. С этого момента акции официально становятся собственностью покупающего.
Если затем курс акций фирмы United Suspenders повышается, нынешний их владелец (или владелица) может продать их снова, но уже по более высокой цене и получить таким образом прибыль. Если же курс акций этой фирмы падает, их владелец может либо оставить акции у себя (в надежде на последующее повышение курса), либо продать их, оставшись в убытке. В первом случае владелец акций настроен оптимистически, он играет на повышение, а благоприятная для этого ситуация на биржевом жаргоне называется bull market, в буквальном переводе "рынок быка". В такой ситуации курс акций большинства акционерных обществ растет, казалось бы, беспредельно, и среди людей, вложивших свой капитал в акции, царит атмосфера оптимизма. Владелец акций считает, что их надо придержать, в надежде на то, что их курс, так же как и курс акций большинства других фирм, в конце концов тоже начнет расти. В противоположной ситуации владелец акций настроен пессимистически, он играет на понижение, а ситуация называется bear market, или "рынок медведя". Цена акций падает, атмосфера среди их владельцев становится тревожной, иногда даже панической. Крайнее проявление подобных тенденций, подобное тому, которое поразило Уолл-стрит в 1929г., приводит к краху биржи. Влияние биржевого краха на всю финансовую систему может оказаться катастрофическим. Рушится банковская система, фирмы объявляются банкротами, заводы и фабрики закрываются, что влечет за собой массовую безработицу,- короче говоря, возникает кризис.
Руководствуется ли владелец акций исключительно царящей в деловых кругах атмосферой, решая вопрос о том, покупать или продавать акции? Можно твердо ответить: руководствуется лишь иногда. Когда эта атмосфера не столь определенна, решение о купле или продаже акций может основываться на более тонком анализе. Существует два традиционных подхода - общий анализ и технический анализ. Общий анализ основан на сведениях о финансовом состоянии и перспективах компании, учредившей акции. Об этом подходе мы поговорим позже.
Технический подход очень привлекает любителей всевозможных графиков, таблиц и вообще цифровых показателей. Основываясь на предположении о том, что поведение курса акций в прошлом позволяет предсказывать их будущую стоимость, сторонник технического анализа пользуется различными приемами предсказания. Простейший из этих приемов заключается в продолжении наблюдаемой тенденции в изменении цены акций соответственно вверх или вниз. Предположим, например, что акции фирмы United Suspenders продавались в течение некоторого времени по цене около 10долл. и недавно цена начала расти. Если изменение было плавным и линейным, то специалист класса "B", т.е. новичок, изучив график изменения курса акций за последний период (см. верхний рисунок на с.87), возможно, приложит к графику линейку и продолжит линию. Если на данный момент цена одной акции составляет 15долл. и график изменения цены показывает повышение на 1 долл. в день, то специалист, наверное, приобретет 100 акций в надежде получать прибыль по 100долл. в день. Увы! В тот же день, когда он купил акции, их цена начала падать.

Неожиданные ситуации в изменении цен на акции
Понаблюдаем теперь за специалистом класса "Б" (практикант), который, изучив динамику изменения цены на акции на протяжении последующих дней и недель, заметил, что график изменения курса акций фирмы United Suspenders имеет пилообразную форму. Он заметил также, что каждое последующее максимальное значение выше предыдущего. Опять в ход идет линейка; на этот раз с ее помощью проводятся две линии (см. средний и нижний графики на с.87). Одна линия ограничивает кривую изменения цены снизу, другая - сверху. Между ними пролегает "канал", в пределах которого колеблется курс акций фирмы. Свойствами открытого им канала специалист класса "Б" может воспользоваться несколькими способами. Он может приобрести акции по любой текущей цене с намерением продержать их достаточно долго для того, чтобы в полной мере извлечь выгоду из долговременной тенденции повышения курса. Возможно, однако, что специалист выждет момент, когда цена на акции United Suspenders в очередной раз достигнет нижней границы канала. Это подходящий момент для того, чтобы купить акции с целью быстрого получения прибыли.
Момент, когда цена достигает верхней границы канала, также представляет интерес для игрока на бирже: он может продать акции, совершив очень быстрый оборот капитала. Например, он может взять в долг, скажем, 100 акций, когда их цена равна 20долл. за акцию, немедленно продать их по этой же цене, а заплатить за них уже позже, когда их цена достигнет 15 долл. Взятые в долг акции будут оплачены по новой цене, и в результате вкладчик получает разницу - по 5долл. за каждую акцию.
Однако в любом из описанных случаев человека, играющего на бирже, подстерегают очевидные опасности. Например, специалист класса "Б" может приобрести 100 акций фирмы United Suspenders в момент, когда цена на эти акции достигнет нижней границы канала. Убежденный, что цена вновь поднимется вверх, подобно теннисному мячу, отскочившему от земли, он с ужасом видит, что она продолжает падать! Пораженный, специалист класса "Б" обращается к своему приятелю, специалисту класса "А", т.е. эксперту.
"Вероятно, это новый канал",- говорит приятель, лишь на мгновение оторвавшись от своих собственных графиков. Ход событий на протяжении последующих недель подтверждает справедливость его предположения: курс акций фирмы United Suspenders начинает теперь постепенно падать с такими же колебаниями, которые наблюдались при росте. Каким образом специалист класса "А" понял, что начался нисходящий канал? "История повторяется, мой друг,- прошлой весной было то же самое".
Рассмотренные примеры - хотя они, наверное, очень далеки от реальности - я привел для того, чтобы ввести понятия тенденции и канала. Конечно, на самом деле анализ может быть значительно сложнее. Исследование изменения курса акций за длительный промежуток времени показывает наличие локальных изменений почти при любом увеличении времени. Мелкие изменения охватываются более крупными, и т.д. до бесконечности. График изменения цены демонстрирует почти фрактальные свойства: при любом увеличении мы наблюдаем аналогичные структуры.
Еще один важный инструмент в наборе специалиста-аналитика - это скользящее среднее. Если на диаграмму вместо цены на данный лень наносить значения цены, усредненные за неделю или даже месяц, то кратковременные флуктуации сглаживаются (см. рисунок вверху). Многие читатели, наверное, могут догадаться, что значение скользящего среднего для данного дня вычисляется путем усреднения цены на акции за предшествующие n дней. Усредненная величина обладает как бы "встроенным терпением". Если даже цена колеблется около одного и того же стабильного уровня, среднее остается постоянным. Если курс акций взлетает или стремительно падает, средняя величина смещается медленно, как бы нехотя, в том же направлении. Возвращаясь к своему стабильному уровню, график цены может подойти к скользящему среднему, подобно блудному сыну, вернувшемуся домой.

Скользящее среднее за 10 дней определяет полосу курса акций
При помощи скользящего среднего можно ввести еще одно понятие, которое специалисты-аналитики называют полосой. Если вычислить скользящее среднее и сместить его вверх и вниз так, чтобы получились две новые кривые, цена на акции будет большую часть времени колебаться в области, ограниченной этими двумя кривыми. Плавные кривые, образующие границы полосы, анализировать значительно проще, чем кривую цены, резко колеблющуюся в пределах полосы. Если полоса обнаруживает определенную тенденцию или закономерность, у специалиста-аналитика, играющего на бирже, возникает искушение воспользоваться этим. Полоса может также сигнализировать о том, что акции переоценены или недооценены. Например, когда время от времени цена выходит за пределы верхней границы полосы, некоторые специалисты считают это признаком переоценки, и в таких случаях курс акций может вскоре резко упасть.
Рассмотренные приемы и многие другие описаны в книге R.Schwabach "The Dow Jones-Irwin Guide lo Investment Software" (Роберт Швейбах, "Руководство по программному обеспечению операций по капиталовложению").
Как указывает Швейбах, в настоящее время существует около 200 программ, которые владельцы микрокомпьютеров, интересующиеся вопросами капиталовложений, могут приобрести. В книге описаны лучшие программы, осуществляющие как технический, так и общий анализ. Кроме того, в ней приведены сведения о вспомогательных программах обработки финансовых данных и даже о тех программах, которые позволяют при помощи модемов подсоединять микрокомпьютер к большим машинам информационных центров. В этом случае, по словам Швейбаха, специалист-аналитик получает доступ к "золотой жиле". Он может анализировать всевозможную информацию, касающуюся прошлого, и даже данные о цене акций, поступающие в реальном масштабе времени с самой биржи.
Читатель, проявляющий особый интерес к проблеме, может написать свои собственные программы и, не слишком приближаясь к опасной границе между неслыханным обогащением и банкротством, попробовать свои силы в техническом анализе и вкусить от его скромных плодов. Однако для этого нужно прежде всего располагать данными о цене акций. Существует два возможных источника таких данных: один из них реальный, другой воображаемый. Самый простой и самый дешевый способ получить реальные данные о ценах на акции - это заглянуть в финансовый раздел газеты, где приведены интересующие вас цены. Данные об акциях выбранных фирм могут быть занесены в 10 массивов, являющихся частью программы, которую я назвал TECHNIX. Имена массивов можно взять по названиям акций, а их размер выбрать в соответствии с периодом времени, за который вы хотите проанализировать их цены. Например, можно организовать массивы с названиями imb, itt, gm и т.д., а размер принять достаточным для того, чтобы вместить данные наблюдений за 365 дней. Более дорогой, но зато и более быстрый способ заполнения этих массивов - это стать абонентом информационной службы, которая поставляет нужные данные по запросу через модем.
Нетрудно (причем без всяких затрат) сгенерировать и искусственные цены. Можно, например, заполнить 365 элементов массива usp (акции фирмы United Suspenders) за несколько секунд, обратившись к специальной процедуре, порождающей фрактальные цены. Возможно, читатели помнят статью из рубрики "Занимательный компьютер" в декабрьском номере журнала, в которой речь шла о фрактальных горах. Программа, названная мной MOUNTAIN, рисовала поперечное сечение воображаемой горы путем повторяющейся операции деления и вертикального смешения, выполняемой на исходном отрезке прямой. Как быстро подметили читатели, испытавшие программу в работе, она может построить целый горный хребет так же легко, как и одну гору. На самом деле, если полученную в результате линию сжать по горизонтали, представляемый ею ландшафт, определенно, приобретает финансовый характер - он станет похож на график изменения стоимости акций, которые активно покупались и продавались на протяжении гола. Здесь наблюдаются отдельные взлеты и падения, а также намечаются тенденции и каналы.
Если заполнить хотя бы один массив реальными или вымышленными ценами, программа TECHNIX пустит в ход целую батарею несложных орудий технического анализа. Простейшее из этих орудий - скользящее среднее. Его действие описывает следующий короткий алгоритм:
ввести period
ввести day
for i = period to day
- sum <- 0
- for j = i-period to i
- - sum <- sum+usp(j)
- average <- sum/period
- высветить average
Здесь period - это число последовательных дней, участвующих в процедуре усреднения, а day - переменная, обозначающая текущий день биржевых операций и равная значению индекса в массиве usp.
Этот алгоритм можно модифицировать так, чтобы программа рисовала полосы курса акций, для чего нужно ввести еще одну переменную band. Значение переменной hand должно отражать типичный диапазон колебания цены акций интересующей фирмы. Если, например, цены на акции фирмы United Suspenders отклонялись не более чем на 4% от своей номинальной стоимости на протяжении последних нескольких месяцев, то пользователь программы TECHNIX перед ее выполнением введет для переменной band значение 4. Приведенный выше алгоритм можно легко дополнить, так, чтобы программа рисовала кривые, ограничивающие полосу изменения цены. Верхняя кривая получается построением графика функции average+(band*average)/100. Нижняя кривая строится по аналогичной формуле с той лишь разницей, что вместо знака плюс нужно поставить минус.
Канал изменения цены нарисовать не сложнее, чем полосу. Если специалист-аналитик замечает, что в последнее время в изменении цены наметилась линейная тенденция, он указывает интересующий период времени, вводя значения переменных day1 и day2 с клавиатуры; day1 - это первый день выбранного периода, а day2 - последний. Программа TECHNIX сначала находит линию, отражающую тенденцию, наблюдавшуюся в указанный период, а затем переносит эту линию вверх и вниз, чтобы установить пределы канала.
Линию, характеризующую тенденцию изменения цены, можно найти несколькими способами. Возможно, самый быстрый и простой способ заключается в разбиении данных об изменении цены на две половины. Назовем день, лежащий посередине между day1 и day2, middle (середина).
Программа TECHNIX вычисляет две средние величины: среднюю цену акций за период от dayl до middle и среднюю цену за период от middle до dayl. Назовем эти две средние величины как avp1 и avp2. Остается лишь найти индексы, соответствующие двум дням, лежащим посередине каждого из этих двух периодов. Они вычисляются очевидным образом. Назовем их m1 и m2. Теперь линия, характеризующая тенденцию, определяется как прямая, проходящая через точки с координатами (m1, avpl) и (m2, avp2). Далее программа TECHNIX переносит построенную линию вверх, пока она не окажется выше или на уровне максимальной цены, наблюдавшейся в рассматриваемый период времени. Затем аналогичным образом производится перенос линии вниз, чтобы установить нижнюю границу канала, или его основание.
Значение координаты линии тенденции по оси ординат на n-й день рассматриваемого периода выражается с виду сложной, но, по существу, очень простой формулой:
y = (avp2-avp1)*(n-m1)/(m2-m1)+avp1
Эта формула представляет собой обычное уравнение прямой линии: y+m*х+b, где m (коэффициент наклона) = (avp2-avp1)/(m2-m1), x = n-m1, a b (величина, равная отрезку, отсекаемому прямой на оси ординат) = avp1.
Можно провести интересный эксперимент, который позволит нам судить об эффективности технического анализа применительно к программе TECHNIX. Процесс определения канала можно автоматизировать, если принять, например, что ширина канала не должна превышать какой-то определенной части его длины, скажем четверти. Цены на акции, либо взятые из реального источника, либо полученные процедурой, генерирующей фрактальные данные, должны вводиться в экспериментальную программу "день за днем". Как только будет обнаружен канал изменения цены, программа дождется, пока график цены не коснется или почти коснется одной из линий, ограничивающих зону канала. Если это будет верхняя линия, программа совершит быстрый оборот капитала и тотчас продаст взятые в долг акции по высокой цене, дожидаясь для оплаты первого же понижения. Если же это будет нижняя линия, программа приобретет акции и получит прибыль, продав их при следующем максимуме. Разумеется, существует опасность, что, коснувшись границы, цена акций будет продолжать изменяться по прямой линии. В этом случае программа окажется в убытке.
Можно пользоваться и другими стратегиями, но они очень трудно поддаются количественному анализу. Если простейшая стратегия, основанная на самой сущности технического анализа, не приносит прибыли, то какие у нас будут основания полагать, что, следуя более замысловатым стратегиям, мы добьемся существенно лучших результатов?
Здесь мы подошли к фундаментальному вопросу о том, насколько эффективны технические методы предсказания вообще. Согласно Б.Г.Молкилу (В.G.Malkiel), автору популярной книги "A Random Walk Down Wall-Slreet" ("Случайный путь по Уолл-стриту"), вообще говоря, не существует надежного способа предсказания курса акций,чтобы постоянно и успешно выигрывать на бирже. Другими словами, с таким же успехом средний специалист-аналитик может приобрести набор случайно выбранных акций, принадлежащих самым различным компаниям. Если это действительно так, то описанный выше эксперимент должен дать в принципе одни и те же результаты как для фрактальных цен, так и для цен, взятых из реальных источников. Я буду благодарен читателям, которые проведут эксперимент и сообщат о его результатах.
Профессор Молкил относится несколько более снисходительно к вкладчикам, руководствующимся в своем выборе акций соображениями общего, или фундаментального, характера. Например, какой долг имеет фирма United Suspenders? Какова прибыль в расчете на одну акцию? Находится ли цена акций в разумном соответствии с размером выплачиваемой по ним прибыли? Является ли компания United Suspenders относительно небольшой и с хорошей перспективой роста? Руководство Швейбаха, о котором говорилось выше, содержит также раздел, посвященный программам, которые исследуют общие показатели и помогают вкладчику разобраться в работе сложного финансового механизма.
Наибольшее впечатление производят на меня программы, работающие в самом тесном контакте с человеком, находящемся в гуще событий на самой бирже, специалистом, который устанавливает цену на акции фирмы, поручившей ему свои дела на бирже. Ему разрешается извлекать для себя выгоду из биржевых операций взамен на обязательство поддерживать должный порядок во всем, что касается акций, вверенных ему фирмой. Этот специалист имеет возможность подработать, продавая акции по более высокой цене (по цене спроса), чем он их приобрел (по цене предложения). Он может также иногда совершить выгодную покупку акций, если видит, что цена пойдет вверх, или продать акции перед тем, как цена на них упадет. Таким образом специалист может заработать довольно много денег, но справедливости ради надо заметить, что и проиграть он может так же много.
В связи с участившимися в последнее время скандалами по поводу махинаций с "внутренней" торговлей акциями, а также периодически возникающими сомнениями относительно той роли, которую играют специалисты подобного рода, возникает вопрос, не следует ли заменить такого агента специализированной биржевой программой? Но тут сразу же возникает еше один вопрос: до какой степени биржевого агента можно заменить программой?
Правильным ответом конечно будет - "до некоторой степени". Например, на бирже акций в Торонто в настоящее время действует самая совершенная в мире автоматизированная система. Известная под названием CATS (от Computer Assisted Trading System), она снимает часть нагрузки с агента, руководящего торговлей акциями на бирже. Она автоматически оформляет небольшие сделки по купле и продаже акций в соответствии с текущими ценами спроса и предложения. В то же время запросы о сделках, совершаемых по цене выше и ниже этих уровней, также высвечиваются на экранах терминалов. Эти запросы делаются продающими и покупающими агентами, надеющимися на то, что цена изменится в скором времени в желаемом ими направлении. Пользуясь этой информацией, любой из зарегистрированных агентов, обладающих доступом к одному из 300 видеотерминалов системы CATS, разбросанных по всей Канаде, может более или менее успешно предугадать, в каком направлении будут изменяться цены. То, что запросы и предложения теперь высвечиваются всем на обозрение, раздражает некоторых специалистов в Торонто. Сведения о предлагаемых сделках, которые раньше были известны только им одним, теперь стали, можно сказать, наполовину всеобщим достоянием.
Насколько полно и точно можно описать роль агента фирмы на бирже, чтобы запрограммировать его функции? По мнению одного из бывших таких агентов, с которыми я недавно беседовал, не все здесь можно запрограммировать. "Иногда, решая вопрос о том, как будет меняться курс акций, мы руководствуемся интуитивным чутьем". Интересно, до какой степени успешными могут оказаться разработанные недавно приемы опроса специалистов с целью извлечь максимальное количество их знаний, на основе которых строится база знаний автоматизированной системы. Какой объем знаний будет необходимым для создания экспертной системы, принимающей достаточно быстро надежные и обоснованные решения? В октябрьском номере журнала мы, наверное, вернемся к этой теме, обсудив мнение некоторых экспертов.
БИБЛИОГРАФИЯ
THE WALL STREET JUNGLE. RICHARD NEY. Grove Press, Inc., 1970.
A RANDOM WALK DOWN WAII STREET. BURTON G. MALKIEL. W.W.Norton&Company, 1985.
ОТКЛИКИ
10 1987
В ИЮЛЬСКОМ номере журнала мы обсуждали возможности применения компьютера на бирже акций. Это обсуждение можно условно разбить на три этапа. Мы как бы продвигались от периферии к центру биржи. Сначала мы говорили о том, что индивидуальные вкладчики капитала, обладающие доступом к компьютеру, могут приобрести одну из сотен программ, предназначенных для технического или фундаментального анализа цен на акции. Ближе к самой бирже крупные финансовые организации пользуются помощью компьютеров для вычислений, результаты которых позволяют им предсказывать цены на куплю или продажу акций в будущем. Наконец, в самом центре биржи работают специалисты, непосредственно осуществляющие торговлю акциями определенной фирмы на определенной бирже. Мы обсуждали вопрос о том, можно ли заменить таких специалистов, полностью или частично, компьютерной программой. Сможет ли программа управлять всеми сделками по купле и продаже акций, вовремя изменять их цену? С этим вопросом я обратился к читателям-"экспертам", и надо сказать они меня не разочаровали.
А.С.Браун, финансист-консультант из Нью-Йорка, несколько лет назад написал докторскую диссертацию по техническому анализу, которую он защищал на финансовом факультете Чикагского университета. Браун считает, что нельзя доверяться техническому анализу. Высказанное мной предостережение по этому поводу показалось Брауну слабым. "Существуют убедительные свидетельства того, что методы технического анализа не работают как средство получения прибыли. Более того, они опасны". Особенно опасна, по мнению Брауна, стратегия покупки акций, когда их цена падает, в ожидании ее подъема в ближайшем будущем. Такая стратегия сродни порочной системе картежника, удваивающего ставку после каждого проигрыша. Следуя этой стратегии, можно все покупать и покупать акции по мере снижения их курса, каждый раз рассчитывая на поворот тенденции, пока они совсем не обесценятся.
Ч.Дж.Хиггинс, работающий на факультете финансов и автоматизированных информационных систем в Университете Лойола Мэримаунт в Лос-Анджелесе, тщательно проанализировал один из технических методов, сходных с методом исследования канала цен, который мы обсуждали в статье. По мнению Хиггинса, решающую роль здесь играет стоимость самой сделки. Изученные Хиггинсом данные показывают, что большинство ценных бумаг не принесли каких-либо значительных прибылей сверх обшей усредненной тенденции в изменении курса акций. "Однако многие ценные бумаги действительно приносили высокие прибыли... когда стоимость сделок была низкой или нулевой". Это указывает на то, что специалисты по акциям, биржевые маклеры и другие дельцы, работающие непосредственно на бирже (платя очень мало или вовсе ничего за совершение сделки), могут получать значительную прибыль, говорит Хиггинс.
В шестидесятых и семидесятых годах физик М.Осборн занимался изучением методов торговли акциями. Он прочел несколько курсов по биржевым финансовым операциям в аспирантуре для будущих бизнесменов и администраторов в Калифорнийском университете в Беркли. По мнению Осборна, проживающего теперь в Хиллкрест-Хайтсе, (шт.Мэриленд), алгоритмы торговли акциями в течение какого-то времени использовались на практике, по крайней мере в качестве системы правил, которые применялись человеком, ведущим торговлю. Осборн, изучавший в свое время все более и более изощренные алгоритмы торговли, написал на эту тему в общей сложности два тома статей. Он пришел к выводу, что все это становится слишком сложным для специалиста, пытающегося извлечь крупную прибыль, совершая операции в самой гуще биржи.
ПРОГРАММЫ ДЛЯ "БЫКОВ" И "МЕДВЕДЕЙ", ИГРАЮЩИХ НА БИРЖЕ
А.К.ДЬЮДНИ
ЗАЛ БИРЖИ, в котором совершается купля-продажа акций, иногда называют ямой. Здесь можно увидеть мужчин и женщин, громко кричащих, отчаянно жестикулирующих и лихорадочно вычисляющих что-то на клочках бумаги или на конвертах. В этом бедламе крики и жесты естественны для тех, кто продает и покупает акции. Будет ли этот процесс когда-нибудь автоматизирован? Наступит ли такой день, когда компьютеры раз и навсегда наведут тишину в яме?
Частично процесс купли-продажи акций автоматизируется уже сейчас, в том числе дома или в рабочем кабинете человека, играющего на бирже. Наши читатели могут сами написать программы, которые проводят общий или технический анализ, позволяющий предсказывать курс акций. Более непосредственное отношение к бирже имеют программы, написанные специалистами с Уолл-стрита [Уолл-стрит - улица в Нью-Йорке, на которой находится знаменитая американская фондовая биржа.- Прим. ред.]. Среди этих программ есть такие, которые рассчитывают конечный итог сложных сделок с большим количеством продаваемых и покупаемых акций с учетом не только текущего их курса, но и тенденций на будущее. Сделки, совершаемые при помощи подобных программ, известные как "программные сделки", по мнению некоторых специалистов, оказались виновницами резкого падения курса акций, наблюдавшегося в течение одного дня на нью-йоркской бирже в сентябре прошлого года. Еще ближе к яме программы, применяемые как вспомогательное средство непосредственно в процессе купли-продажи, о чем будет упомянуто в конце статьи. Может быть даже, что эти программы будут усовершенствованы до такой степени, чтобы непосредственно осуществлять сделки, но эта идея, конечно, натолкнется на трудности и даже возражения.
Сначала давайте совершим экскурсию на биржу. Очередная сделка начинается с того, что некто решил сделать капиталовложение, купив, скажем, 100 акций фирмы United Suspenders ("Объединенные подтяжки"). Человек, желающий приобрести акции, дает соответствующее поручение биржевому маклеру, который (за определенное вознаграждение) передает этот заказ непосредственно на биржу, где продаются акции фирмы United Suspenders. На бирже агент, занимающийся акциями этой фирмы, оформляет документ о продаже акций. Через некоторое время соответствующая сумма денег переводится со счета человека, покупающего акции, на счет их владельца. С этого момента акции официально становятся собственностью покупающего.
Если затем курс акций фирмы United Suspenders повышается, нынешний их владелец (или владелица) может продать их снова, но уже по более высокой цене и получить таким образом прибыль. Если же курс акций этой фирмы падает, их владелец может либо оставить акции у себя (в надежде на последующее повышение курса), либо продать их, оставшись в убытке. В первом случае владелец акций настроен оптимистически, он играет на повышение, а благоприятная для этого ситуация на биржевом жаргоне называется bull market, в буквальном переводе "рынок быка". В такой ситуации курс акций большинства акционерных обществ растет, казалось бы, беспредельно, и среди людей, вложивших свой капитал в акции, царит атмосфера оптимизма. Владелец акций считает, что их надо придержать, в надежде на то, что их курс, так же как и курс акций большинства других фирм, в конце концов тоже начнет расти. В противоположной ситуации владелец акций настроен пессимистически, он играет на понижение, а ситуация называется bear market, или "рынок медведя". Цена акций падает, атмосфера среди их владельцев становится тревожной, иногда даже панической. Крайнее проявление подобных тенденций, подобное тому, которое поразило Уолл-стрит в 1929г., приводит к краху биржи. Влияние биржевого краха на всю финансовую систему может оказаться катастрофическим. Рушится банковская система, фирмы объявляются банкротами, заводы и фабрики закрываются, что влечет за собой массовую безработицу,- короче говоря, возникает кризис.
Руководствуется ли владелец акций исключительно царящей в деловых кругах атмосферой, решая вопрос о том, покупать или продавать акции? Можно твердо ответить: руководствуется лишь иногда. Когда эта атмосфера не столь определенна, решение о купле или продаже акций может основываться на более тонком анализе. Существует два традиционных подхода - общий анализ и технический анализ. Общий анализ основан на сведениях о финансовом состоянии и перспективах компании, учредившей акции. Об этом подходе мы поговорим позже.
Технический подход очень привлекает любителей всевозможных графиков, таблиц и вообще цифровых показателей. Основываясь на предположении о том, что поведение курса акций в прошлом позволяет предсказывать их будущую стоимость, сторонник технического анализа пользуется различными приемами предсказания. Простейший из этих приемов заключается в продолжении наблюдаемой тенденции в изменении цены акций соответственно вверх или вниз. Предположим, например, что акции фирмы United Suspenders продавались в течение некоторого времени по цене около 10долл. и недавно цена начала расти. Если изменение было плавным и линейным, то специалист класса "B", т.е. новичок, изучив график изменения курса акций за последний период (см. верхний рисунок на с.87), возможно, приложит к графику линейку и продолжит линию. Если на данный момент цена одной акции составляет 15долл. и график изменения цены показывает повышение на 1 долл. в день, то специалист, наверное, приобретет 100 акций в надежде получать прибыль по 100долл. в день. Увы! В тот же день, когда он купил акции, их цена начала падать.

Неожиданные ситуации в изменении цен на акции
Понаблюдаем теперь за специалистом класса "Б" (практикант), который, изучив динамику изменения цены на акции на протяжении последующих дней и недель, заметил, что график изменения курса акций фирмы United Suspenders имеет пилообразную форму. Он заметил также, что каждое последующее максимальное значение выше предыдущего. Опять в ход идет линейка; на этот раз с ее помощью проводятся две линии (см. средний и нижний графики на с.87). Одна линия ограничивает кривую изменения цены снизу, другая - сверху. Между ними пролегает "канал", в пределах которого колеблется курс акций фирмы. Свойствами открытого им канала специалист класса "Б" может воспользоваться несколькими способами. Он может приобрести акции по любой текущей цене с намерением продержать их достаточно долго для того, чтобы в полной мере извлечь выгоду из долговременной тенденции повышения курса. Возможно, однако, что специалист выждет момент, когда цена на акции United Suspenders в очередной раз достигнет нижней границы канала. Это подходящий момент для того, чтобы купить акции с целью быстрого получения прибыли.
Момент, когда цена достигает верхней границы канала, также представляет интерес для игрока на бирже: он может продать акции, совершив очень быстрый оборот капитала. Например, он может взять в долг, скажем, 100 акций, когда их цена равна 20долл. за акцию, немедленно продать их по этой же цене, а заплатить за них уже позже, когда их цена достигнет 15 долл. Взятые в долг акции будут оплачены по новой цене, и в результате вкладчик получает разницу - по 5долл. за каждую акцию.
Однако в любом из описанных случаев человека, играющего на бирже, подстерегают очевидные опасности. Например, специалист класса "Б" может приобрести 100 акций фирмы United Suspenders в момент, когда цена на эти акции достигнет нижней границы канала. Убежденный, что цена вновь поднимется вверх, подобно теннисному мячу, отскочившему от земли, он с ужасом видит, что она продолжает падать! Пораженный, специалист класса "Б" обращается к своему приятелю, специалисту класса "А", т.е. эксперту.
"Вероятно, это новый канал",- говорит приятель, лишь на мгновение оторвавшись от своих собственных графиков. Ход событий на протяжении последующих недель подтверждает справедливость его предположения: курс акций фирмы United Suspenders начинает теперь постепенно падать с такими же колебаниями, которые наблюдались при росте. Каким образом специалист класса "А" понял, что начался нисходящий канал? "История повторяется, мой друг,- прошлой весной было то же самое".
Рассмотренные примеры - хотя они, наверное, очень далеки от реальности - я привел для того, чтобы ввести понятия тенденции и канала. Конечно, на самом деле анализ может быть значительно сложнее. Исследование изменения курса акций за длительный промежуток времени показывает наличие локальных изменений почти при любом увеличении времени. Мелкие изменения охватываются более крупными, и т.д. до бесконечности. График изменения цены демонстрирует почти фрактальные свойства: при любом увеличении мы наблюдаем аналогичные структуры.
Еще один важный инструмент в наборе специалиста-аналитика - это скользящее среднее. Если на диаграмму вместо цены на данный лень наносить значения цены, усредненные за неделю или даже месяц, то кратковременные флуктуации сглаживаются (см. рисунок вверху). Многие читатели, наверное, могут догадаться, что значение скользящего среднего для данного дня вычисляется путем усреднения цены на акции за предшествующие n дней. Усредненная величина обладает как бы "встроенным терпением". Если даже цена колеблется около одного и того же стабильного уровня, среднее остается постоянным. Если курс акций взлетает или стремительно падает, средняя величина смещается медленно, как бы нехотя, в том же направлении. Возвращаясь к своему стабильному уровню, график цены может подойти к скользящему среднему, подобно блудному сыну, вернувшемуся домой.

Скользящее среднее за 10 дней определяет полосу курса акций
При помощи скользящего среднего можно ввести еще одно понятие, которое специалисты-аналитики называют полосой. Если вычислить скользящее среднее и сместить его вверх и вниз так, чтобы получились две новые кривые, цена на акции будет большую часть времени колебаться в области, ограниченной этими двумя кривыми. Плавные кривые, образующие границы полосы, анализировать значительно проще, чем кривую цены, резко колеблющуюся в пределах полосы. Если полоса обнаруживает определенную тенденцию или закономерность, у специалиста-аналитика, играющего на бирже, возникает искушение воспользоваться этим. Полоса может также сигнализировать о том, что акции переоценены или недооценены. Например, когда время от времени цена выходит за пределы верхней границы полосы, некоторые специалисты считают это признаком переоценки, и в таких случаях курс акций может вскоре резко упасть.
Рассмотренные приемы и многие другие описаны в книге R.Schwabach "The Dow Jones-Irwin Guide lo Investment Software" (Роберт Швейбах, "Руководство по программному обеспечению операций по капиталовложению").
Как указывает Швейбах, в настоящее время существует около 200 программ, которые владельцы микрокомпьютеров, интересующиеся вопросами капиталовложений, могут приобрести. В книге описаны лучшие программы, осуществляющие как технический, так и общий анализ. Кроме того, в ней приведены сведения о вспомогательных программах обработки финансовых данных и даже о тех программах, которые позволяют при помощи модемов подсоединять микрокомпьютер к большим машинам информационных центров. В этом случае, по словам Швейбаха, специалист-аналитик получает доступ к "золотой жиле". Он может анализировать всевозможную информацию, касающуюся прошлого, и даже данные о цене акций, поступающие в реальном масштабе времени с самой биржи.
Читатель, проявляющий особый интерес к проблеме, может написать свои собственные программы и, не слишком приближаясь к опасной границе между неслыханным обогащением и банкротством, попробовать свои силы в техническом анализе и вкусить от его скромных плодов. Однако для этого нужно прежде всего располагать данными о цене акций. Существует два возможных источника таких данных: один из них реальный, другой воображаемый. Самый простой и самый дешевый способ получить реальные данные о ценах на акции - это заглянуть в финансовый раздел газеты, где приведены интересующие вас цены. Данные об акциях выбранных фирм могут быть занесены в 10 массивов, являющихся частью программы, которую я назвал TECHNIX. Имена массивов можно взять по названиям акций, а их размер выбрать в соответствии с периодом времени, за который вы хотите проанализировать их цены. Например, можно организовать массивы с названиями imb, itt, gm и т.д., а размер принять достаточным для того, чтобы вместить данные наблюдений за 365 дней. Более дорогой, но зато и более быстрый способ заполнения этих массивов - это стать абонентом информационной службы, которая поставляет нужные данные по запросу через модем.
Нетрудно (причем без всяких затрат) сгенерировать и искусственные цены. Можно, например, заполнить 365 элементов массива usp (акции фирмы United Suspenders) за несколько секунд, обратившись к специальной процедуре, порождающей фрактальные цены. Возможно, читатели помнят статью из рубрики "Занимательный компьютер" в декабрьском номере журнала, в которой речь шла о фрактальных горах. Программа, названная мной MOUNTAIN, рисовала поперечное сечение воображаемой горы путем повторяющейся операции деления и вертикального смешения, выполняемой на исходном отрезке прямой. Как быстро подметили читатели, испытавшие программу в работе, она может построить целый горный хребет так же легко, как и одну гору. На самом деле, если полученную в результате линию сжать по горизонтали, представляемый ею ландшафт, определенно, приобретает финансовый характер - он станет похож на график изменения стоимости акций, которые активно покупались и продавались на протяжении гола. Здесь наблюдаются отдельные взлеты и падения, а также намечаются тенденции и каналы.
Если заполнить хотя бы один массив реальными или вымышленными ценами, программа TECHNIX пустит в ход целую батарею несложных орудий технического анализа. Простейшее из этих орудий - скользящее среднее. Его действие описывает следующий короткий алгоритм:
ввести period
ввести day
for i = period to day
- sum <- 0
- for j = i-period to i
- - sum <- sum+usp(j)
- average <- sum/period
- высветить average
Здесь period - это число последовательных дней, участвующих в процедуре усреднения, а day - переменная, обозначающая текущий день биржевых операций и равная значению индекса в массиве usp.
Этот алгоритм можно модифицировать так, чтобы программа рисовала полосы курса акций, для чего нужно ввести еще одну переменную band. Значение переменной hand должно отражать типичный диапазон колебания цены акций интересующей фирмы. Если, например, цены на акции фирмы United Suspenders отклонялись не более чем на 4% от своей номинальной стоимости на протяжении последних нескольких месяцев, то пользователь программы TECHNIX перед ее выполнением введет для переменной band значение 4. Приведенный выше алгоритм можно легко дополнить, так, чтобы программа рисовала кривые, ограничивающие полосу изменения цены. Верхняя кривая получается построением графика функции average+(band*average)/100. Нижняя кривая строится по аналогичной формуле с той лишь разницей, что вместо знака плюс нужно поставить минус.
Канал изменения цены нарисовать не сложнее, чем полосу. Если специалист-аналитик замечает, что в последнее время в изменении цены наметилась линейная тенденция, он указывает интересующий период времени, вводя значения переменных day1 и day2 с клавиатуры; day1 - это первый день выбранного периода, а day2 - последний. Программа TECHNIX сначала находит линию, отражающую тенденцию, наблюдавшуюся в указанный период, а затем переносит эту линию вверх и вниз, чтобы установить пределы канала.
Линию, характеризующую тенденцию изменения цены, можно найти несколькими способами. Возможно, самый быстрый и простой способ заключается в разбиении данных об изменении цены на две половины. Назовем день, лежащий посередине между day1 и day2, middle (середина).
Программа TECHNIX вычисляет две средние величины: среднюю цену акций за период от dayl до middle и среднюю цену за период от middle до dayl. Назовем эти две средние величины как avp1 и avp2. Остается лишь найти индексы, соответствующие двум дням, лежащим посередине каждого из этих двух периодов. Они вычисляются очевидным образом. Назовем их m1 и m2. Теперь линия, характеризующая тенденцию, определяется как прямая, проходящая через точки с координатами (m1, avpl) и (m2, avp2). Далее программа TECHNIX переносит построенную линию вверх, пока она не окажется выше или на уровне максимальной цены, наблюдавшейся в рассматриваемый период времени. Затем аналогичным образом производится перенос линии вниз, чтобы установить нижнюю границу канала, или его основание.
Значение координаты линии тенденции по оси ординат на n-й день рассматриваемого периода выражается с виду сложной, но, по существу, очень простой формулой:
y = (avp2-avp1)*(n-m1)/(m2-m1)+avp1
Эта формула представляет собой обычное уравнение прямой линии: y+m*х+b, где m (коэффициент наклона) = (avp2-avp1)/(m2-m1), x = n-m1, a b (величина, равная отрезку, отсекаемому прямой на оси ординат) = avp1.
Можно провести интересный эксперимент, который позволит нам судить об эффективности технического анализа применительно к программе TECHNIX. Процесс определения канала можно автоматизировать, если принять, например, что ширина канала не должна превышать какой-то определенной части его длины, скажем четверти. Цены на акции, либо взятые из реального источника, либо полученные процедурой, генерирующей фрактальные данные, должны вводиться в экспериментальную программу "день за днем". Как только будет обнаружен канал изменения цены, программа дождется, пока график цены не коснется или почти коснется одной из линий, ограничивающих зону канала. Если это будет верхняя линия, программа совершит быстрый оборот капитала и тотчас продаст взятые в долг акции по высокой цене, дожидаясь для оплаты первого же понижения. Если же это будет нижняя линия, программа приобретет акции и получит прибыль, продав их при следующем максимуме. Разумеется, существует опасность, что, коснувшись границы, цена акций будет продолжать изменяться по прямой линии. В этом случае программа окажется в убытке.
Можно пользоваться и другими стратегиями, но они очень трудно поддаются количественному анализу. Если простейшая стратегия, основанная на самой сущности технического анализа, не приносит прибыли, то какие у нас будут основания полагать, что, следуя более замысловатым стратегиям, мы добьемся существенно лучших результатов?
Здесь мы подошли к фундаментальному вопросу о том, насколько эффективны технические методы предсказания вообще. Согласно Б.Г.Молкилу (В.G.Malkiel), автору популярной книги "A Random Walk Down Wall-Slreet" ("Случайный путь по Уолл-стриту"), вообще говоря, не существует надежного способа предсказания курса акций,чтобы постоянно и успешно выигрывать на бирже. Другими словами, с таким же успехом средний специалист-аналитик может приобрести набор случайно выбранных акций, принадлежащих самым различным компаниям. Если это действительно так, то описанный выше эксперимент должен дать в принципе одни и те же результаты как для фрактальных цен, так и для цен, взятых из реальных источников. Я буду благодарен читателям, которые проведут эксперимент и сообщат о его результатах.
Профессор Молкил относится несколько более снисходительно к вкладчикам, руководствующимся в своем выборе акций соображениями общего, или фундаментального, характера. Например, какой долг имеет фирма United Suspenders? Какова прибыль в расчете на одну акцию? Находится ли цена акций в разумном соответствии с размером выплачиваемой по ним прибыли? Является ли компания United Suspenders относительно небольшой и с хорошей перспективой роста? Руководство Швейбаха, о котором говорилось выше, содержит также раздел, посвященный программам, которые исследуют общие показатели и помогают вкладчику разобраться в работе сложного финансового механизма.
Наибольшее впечатление производят на меня программы, работающие в самом тесном контакте с человеком, находящемся в гуще событий на самой бирже, специалистом, который устанавливает цену на акции фирмы, поручившей ему свои дела на бирже. Ему разрешается извлекать для себя выгоду из биржевых операций взамен на обязательство поддерживать должный порядок во всем, что касается акций, вверенных ему фирмой. Этот специалист имеет возможность подработать, продавая акции по более высокой цене (по цене спроса), чем он их приобрел (по цене предложения). Он может также иногда совершить выгодную покупку акций, если видит, что цена пойдет вверх, или продать акции перед тем, как цена на них упадет. Таким образом специалист может заработать довольно много денег, но справедливости ради надо заметить, что и проиграть он может так же много.
В связи с участившимися в последнее время скандалами по поводу махинаций с "внутренней" торговлей акциями, а также периодически возникающими сомнениями относительно той роли, которую играют специалисты подобного рода, возникает вопрос, не следует ли заменить такого агента специализированной биржевой программой? Но тут сразу же возникает еше один вопрос: до какой степени биржевого агента можно заменить программой?
Правильным ответом конечно будет - "до некоторой степени". Например, на бирже акций в Торонто в настоящее время действует самая совершенная в мире автоматизированная система. Известная под названием CATS (от Computer Assisted Trading System), она снимает часть нагрузки с агента, руководящего торговлей акциями на бирже. Она автоматически оформляет небольшие сделки по купле и продаже акций в соответствии с текущими ценами спроса и предложения. В то же время запросы о сделках, совершаемых по цене выше и ниже этих уровней, также высвечиваются на экранах терминалов. Эти запросы делаются продающими и покупающими агентами, надеющимися на то, что цена изменится в скором времени в желаемом ими направлении. Пользуясь этой информацией, любой из зарегистрированных агентов, обладающих доступом к одному из 300 видеотерминалов системы CATS, разбросанных по всей Канаде, может более или менее успешно предугадать, в каком направлении будут изменяться цены. То, что запросы и предложения теперь высвечиваются всем на обозрение, раздражает некоторых специалистов в Торонто. Сведения о предлагаемых сделках, которые раньше были известны только им одним, теперь стали, можно сказать, наполовину всеобщим достоянием.
Насколько полно и точно можно описать роль агента фирмы на бирже, чтобы запрограммировать его функции? По мнению одного из бывших таких агентов, с которыми я недавно беседовал, не все здесь можно запрограммировать. "Иногда, решая вопрос о том, как будет меняться курс акций, мы руководствуемся интуитивным чутьем". Интересно, до какой степени успешными могут оказаться разработанные недавно приемы опроса специалистов с целью извлечь максимальное количество их знаний, на основе которых строится база знаний автоматизированной системы. Какой объем знаний будет необходимым для создания экспертной системы, принимающей достаточно быстро надежные и обоснованные решения? В октябрьском номере журнала мы, наверное, вернемся к этой теме, обсудив мнение некоторых экспертов.
БИБЛИОГРАФИЯ
THE WALL STREET JUNGLE. RICHARD NEY. Grove Press, Inc., 1970.
A RANDOM WALK DOWN WAII STREET. BURTON G. MALKIEL. W.W.Norton&Company, 1985.
ОТКЛИКИ
10 1987
В ИЮЛЬСКОМ номере журнала мы обсуждали возможности применения компьютера на бирже акций. Это обсуждение можно условно разбить на три этапа. Мы как бы продвигались от периферии к центру биржи. Сначала мы говорили о том, что индивидуальные вкладчики капитала, обладающие доступом к компьютеру, могут приобрести одну из сотен программ, предназначенных для технического или фундаментального анализа цен на акции. Ближе к самой бирже крупные финансовые организации пользуются помощью компьютеров для вычислений, результаты которых позволяют им предсказывать цены на куплю или продажу акций в будущем. Наконец, в самом центре биржи работают специалисты, непосредственно осуществляющие торговлю акциями определенной фирмы на определенной бирже. Мы обсуждали вопрос о том, можно ли заменить таких специалистов, полностью или частично, компьютерной программой. Сможет ли программа управлять всеми сделками по купле и продаже акций, вовремя изменять их цену? С этим вопросом я обратился к читателям-"экспертам", и надо сказать они меня не разочаровали.
А.С.Браун, финансист-консультант из Нью-Йорка, несколько лет назад написал докторскую диссертацию по техническому анализу, которую он защищал на финансовом факультете Чикагского университета. Браун считает, что нельзя доверяться техническому анализу. Высказанное мной предостережение по этому поводу показалось Брауну слабым. "Существуют убедительные свидетельства того, что методы технического анализа не работают как средство получения прибыли. Более того, они опасны". Особенно опасна, по мнению Брауна, стратегия покупки акций, когда их цена падает, в ожидании ее подъема в ближайшем будущем. Такая стратегия сродни порочной системе картежника, удваивающего ставку после каждого проигрыша. Следуя этой стратегии, можно все покупать и покупать акции по мере снижения их курса, каждый раз рассчитывая на поворот тенденции, пока они совсем не обесценятся.
Ч.Дж.Хиггинс, работающий на факультете финансов и автоматизированных информационных систем в Университете Лойола Мэримаунт в Лос-Анджелесе, тщательно проанализировал один из технических методов, сходных с методом исследования канала цен, который мы обсуждали в статье. По мнению Хиггинса, решающую роль здесь играет стоимость самой сделки. Изученные Хиггинсом данные показывают, что большинство ценных бумаг не принесли каких-либо значительных прибылей сверх обшей усредненной тенденции в изменении курса акций. "Однако многие ценные бумаги действительно приносили высокие прибыли... когда стоимость сделок была низкой или нулевой". Это указывает на то, что специалисты по акциям, биржевые маклеры и другие дельцы, работающие непосредственно на бирже (платя очень мало или вовсе ничего за совершение сделки), могут получать значительную прибыль, говорит Хиггинс.
В шестидесятых и семидесятых годах физик М.Осборн занимался изучением методов торговли акциями. Он прочел несколько курсов по биржевым финансовым операциям в аспирантуре для будущих бизнесменов и администраторов в Калифорнийском университете в Беркли. По мнению Осборна, проживающего теперь в Хиллкрест-Хайтсе, (шт.Мэриленд), алгоритмы торговли акциями в течение какого-то времени использовались на практике, по крайней мере в качестве системы правил, которые применялись человеком, ведущим торговлю. Осборн, изучавший в свое время все более и более изощренные алгоритмы торговли, написал на эту тему в общей сложности два тома статей. Он пришел к выводу, что все это становится слишком сложным для специалиста, пытающегося извлечь крупную прибыль, совершая операции в самой гуще биржи.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
8 1987
АЛГОРИТМИЧЕСКИЕ ГОЛОВОЛОМКИ
А.К.ДЬЮДНИ
ГОРОДА Задаченск и Решенск отстоят друг от друга на 100км. Как-то погожим июньским днем в полдень из этих городов выходят навстречу друг другу два поезда, причем каждый движется со скоростью 50км в час. В тот же момент пчела, уютно пристроившаяся на головной фаре поезда в Задаченске, вылетает в направлении Решенска и летит вдоль железнодорожного пути со скоростью 90км в час.
Встретившись с поездом, идущим из Решенска, пчела резко разворачивается и летит обратно все с той же скоростью 90км в час. Встретившись с поездом, идущим из Задаченска, она опять разворачивается и летит в противоположном направлении. Таким образом пчела снует между поездами до тех пор, пока они не встретятся. Какова будет полная длина пути, проделанного пчелой? Ответ к этой известной задачке, который будет дан в конце статьи, короткий. Это просто число.
Однако существуют задачи и другого рода, которые можно назвать алгоритмическими головоломками, и ответы к ним выглядят намного сложнее. Решить такую задачу - значит указать последовательность процедур, позволяющих прийти к желаемому результату. Другими словами, ответ представляет собой алгоритм. В литературе, посвященной головоломкам, приводится немало подобных задач. К числу известных относится, например, задача о том, как разделить жидкость в сосуде на три равные части посредством последовательности переливаний с использованием других сосудов определенной емкости или как можно без потерь с помощью одной лодки переправить на другой берег реки волка, козла и капусту. К этому же классу относится и задача о том, каким образом можно определить фальшивую монету (отличающуюся по массе) в кучке монет посредством последовательности взвешиваний на рычажных весах.
Различие в ответах на обычную задачу и алгоритмическую головоломку проще всего пояснить на конкретном примере. Начав с железнодорожных путей, пойдем по ним и дальше, продолжая тему первого примера. Допустим теперь, что поезда, движущиеся навстречу друг другу, при встрече не сталкиваются, а вовремя притормаживают. С шипением и грохотом они останавливаются друг перед другом. (При этом мне почему-то представляются два огромных старинных паровоза). Между поездами лежит короткий отрезок железнодорожного полотна и маленькое боковое ответвление, длина которого позволяет разместить лишь один вагон или локомотив (см. верхний рисунок на с.85). Очевидно, кто-то сделал серьезную ошибку при составлении расписания. Единственный способ выйти из затруднения и разминуться заключается в том, чтобы машинисты каким-то образом воспользовались боковым путем. В этой задаче так же, как и в последующих, мы будем предполагать, что каждый вагон и каждый локомотив с обеих сторон имеют устройство сцепления. Кроме того, на каждом поезде есть сцепщик, который, бегая по путям, может сцеплять и отцеплять вагоны.

Каким образом могут разминуться поезда?
Вытирая пот с лица красным в горошек носовым платком, машинист поезда, следующего из Задаченска, восклицает: "Я не знаю, как мы сможем пропустить друг друга. У нас есть только вон то небольшое ответвление". Машинист из Решенска настроен более оптимистично. Он излагает план, следуя которому поезда могут разминуться. Возможно ли это? Прежде чем читать дальше, давайте взглянем на рисунок. Для конкретности на нем изображены два поезда, каждый из пяти вагонов. В общей формулировке этой алгоритмической головоломки поезда имеют по n вагонов.
Подходя к решению этой сравнительно простой задачи, читатель, наверно, будет говорить себе под нос: "Так, посмотрим... А почему бы не провести состав из Задаченска по боковому пути по одному вагону? Поезд из Решенска мог бы сновать как челнок взад и вперед, затаскивая каждый раз новый вагон задаченского поезда на боковой путь, затем, проезжая мимо него по основному пути на всю свою длину и прицепляя его с другой стороны, чтобы вывести с бокового пути перед тем, как вернуться за следующим вагоном".
Такое описание может послужить отправной точкой для построения ответа к алгоритмической головоломке, но его нужно сделать более ясным и четким. Воспользуемся для этого алгоритмической системой записи, введя некоторые вспомогательные обозначения. При решении задачи можно выделить четыре участка железнодорожного полотна: участок от Задаченска до бокового пути (обозначим его A); отрезок основного пути между стрелками, соединяющими его с боковым путем (B); сам боковой путь {B') и участок от бокового пути до Решенска (C). Такая команда, как "Вперед к A", означает, что поезд из Решенска, состоящий из локомотива и вагонов, прицепленных к нему на данный момент, продвигается вперед до тех пор, пока полностью не окажется на участке пути A.
Напомним, что у каждого поезда по n вагонов. Локомотив задаченского поезда обозначим через P1, а его вагоны пронумеруем как Р2, РЗ и т.д. Команда "Прицепить Pk" означает, что к данному моменту решенский поезд находится вплотную к k-му элементу задаченского поезда; состав из Решенска мягко подкатывается к вагону Pk и сцепляется с ним. Те из вас, кто когда-нибудь жил вблизи железнодорожной станции,наверное, хорошо помнят очень характерный, ни на что другое не похожий звук, которым сопровождается сцепка вагонов.
Теперь можно записать алгоритм решения:
расцепить поезд Р
for k = 1 to n+1
- вперед к A
- прицепить Pk
- назад к C
- вперед к B'
- отцепить Pk
- назад к C
- вперед к A
- назад к B'
- прицепить Pk
- назад к C
- отцепить Pk
сцепить поезд P
Сначала поезд из Задаченска расцепляется на отдельные вагоны и мы имеем n вагонов и локомотив. Затем в алгоритме начинается цикл из 11 шагов. Всю работу выполняет поезд из Решенска. Ни разу не отцепив ни одного из своих вагонов, он сначала проходит вперед на участок А, где сцепляется с первым элементом (k = 1) задаченского состава, т.е. с локомотивом. Он буксирует локомотив назад к участку С и после перевода стрелок загоняет его на боковой путь В', здесь локомотив отцепляется. Затем состав из Решенска снова возвращается на участок C, стрелки переводятся, и он идет вперед к участку A. После этого он возвращается, проходит на боковой путь, снова прицепляется к оставленному там локомотиву задаченского состава и буксирует его на участок C, где отцепляет и оставляет его. Ту же последовательность шагов поезд выполняет для каждого из оставшихся вагонов задаченского состава. Когда главный цикл завершен, все вагоны задаченского поезда оказываются на участке дороги между решенским составом и Решенском. Теперь, как только поезд придет в себя от утомительных алгоритмических процедур, он запыхтит и тронется в направлении к Решенску.
Еще одна алгоритмическая головоломка возникает, когда поезд из Задаченска, завершая свое путешествие, подъезжает к Решенску. Машинист, глядя на пробегающие мимо него пригороды, вдруг с ужасом вспоминает, что забыл взять с собой пакетик с бутербродами. Делать нечего, придется возвращаться обратно. Он нажимает на тормоза, и постепенно тяжелый состав из n вагонов останавливается. Пятиться всю дорогу до Задаченска не
очень-то удобно. К счастью, машинист замечает справа небольшое боковое ответвление - тупик. Его длина достаточна лишь для одного вагона, у разветвления есть управляющие стрелки. Вдохновленный алгоритмическим достижением машиниста из Решенска, наш скромный герой тоже хочет попробовать свои силы.
Прежде всего машинист задаченского состава рисует на клочке бумаги схему пути (см. нижний рисунок). Затем он расписывает алгоритм и тщательно проверяет его, водя пальцем по бумаге то туда, то сюда и бормоча что-то себе под нос. После проверки алгоритма он начинает длительную серию отцеплений, буксировок и сцеплений, пока это все не заканчивается тем, что поезд оказывается полностью развернутым в обратном направлении. Причем не только порядок, в котором следовали локомотив и вагоны, сохранился, но и сами вагоны и локомотив оказались повернутыми в обратном направлении. Каким образом машинист проделал этот маневр? Лучшие решения читателей будут опубликованы в одном из следующих номеров журнала. Под словом "лучшее" подразумевается наиболее ясное и наиболее остроумное решение. Эта задача не так бесхитростна, как может показаться на первый взгляд.

Как поезд может развернуться, чтобы машинист вернулся в город, откуда прибыл?
Уже на пути в Задаченск машинист понял, что решение задачи потребовало очень больших энергетических затрат. Угольный тендер паровоза оказался почти пустым. Количество работы, затраченной во время маневров поезда, было пропорционально n2. В самом деле, если измерять массу в количестве вагонов, а расстояние в их длине, то работа будет пропорциональна числу вагонов n и расстоянию n. Только теперь, по пути домой, машинист задаченского поезда подумал о том, что, возможно, существует более эффективное решение. Давайте подумаем тоже, возможно ли развернуть состав за меньшее число шагов, скажем, порядка n(3/2) или даже n*log(n)?
Чтобы еще лучше потренировать однорельсовые умы в искусстве алгоритмических головоломок, вот еще одна маленькая задачка. Локомотив без вагонов приближается к поворотному кругу, на котором стоят два пустых вагона. Между вагонами расположен небольшой железнодорожный мост, прочность которого позволяет выдержать один вагон, но локомотива он уже не выдержит (см. верхний рисунок). Машинист локомотива должен развернуть вагоны так, чтобы они поменялись местами. Как и в предыдущих задачах, все сцепления и расцепления должны производиться только в неподвижном состоянии. Длина моста не превышает длины одного вагона. Завершив свою работу, локомотив должен покинуть поворотный круг. Решение задачи представляет собой простой алгоритм без циклов. С этим алгоритмом читатели ознакомятся в очередном номере журнала.

Локомотив должен поменять вагоны местами, не пересекая опасного моста
Со следующими двумя алгоритмическими головоломками я не был знаком раньше. Они продолжают транспортную тему, начатую в задачах о поездах, однако переводят наши исследования на более высокую ступень - теперь мы будем заниматься грузовиками. Задачи этой серии я буду называть задачами разведчика пустыни. В первой задаче патрульный автомобиль разведчика пустыни имеет бак, вмещающий 10 галлонов бензина. Бак автомобиля заполняется из цистерн емкостью 50 галлонов. Несколько таких цистерн хранятся на складе. Если автомобиль может везти в качестве груза одну цистерну с бензином и если он затрачивает 1 галлон горючего на 10 миль пути независимо от того, везет он с собой цистерну или нет, то каково максимальное расстояние, на которое он может удалиться от базы, прежде чем у него иссякнет горючее? Ответ, конечно, зависит от количества цистерн с бензином, хранящихся на базе. Как и во всех алгоритмических головоломках, предположим, что число цистерн на базе равно n.

На какое максимальное расстояние сможет уехать грузовик, располагая n цистернами с горючим?
Если n= 1, то ответ получить несложно. Автомобиль заправляет свой бак из единственной цистерны, грузит ее в кузов и отправляется в путь под жарким солнцем пустыни. Заправляясь при необходимости из цистерны, автомобиль, очевидно, пройдет 500 миль, прежде чем горючее будет полностью исчерпано. А как далеко он сможет уехать на двух цистернах? Поскольку автомобиль может везти с собой лишь одну цистерну, то, очевидно, он отвезет первую цистерну на какое-то расстояние в пустыню, заправится из нее, если это необходимо, а затем вернется на базу за второй. Вторую цистерну разведчик повезет по той же дороге. Он может остановиться для заправки, а может и не останавливаться у первой, оставленной им в пустыне цистерны, прежде чем продолжить свое путешествие. Как далеко он сможет уехать, совершая такие челночные перемещения между пунктами, в которых он оставляет запасы горючего? Внезапно задача перестает казаться тривиальной.
Приведем короткий алгоритм, позволяющий патрульному автомобилю проехать путь длиной 600 миль:
заправить бак и погрузить первую цистерну
вперед 100 миль
снять цистерну и заправиться
назад на базу за второй цистерной
заправиться и погрузить цистерну
вперед 100 миль
заправиться из первой цистерны
вперед 100 миль
снять цистерну и заправиться
назад к первой цистерне
заправиться и погрузить цистерну
вперед 100 миль
На этой стадии алгоритма автомобиль удалился от базы на 200 миль. У него две цистерны: в одной осталось 10 галлонов, а в другой - 30 галлонов бензина. Поездка продолжается после того, как водитель заправляет машину из первой цистерны (оставляя ее пустой), погружает в кузов вторую цистерну и уезжает, скрываясь за барханами. Таким образом, он сможет проехать еще 400 миль, прежде чем у него кончится горючее. Полное расстояние от базы составит 600 миль. Поскольку увеличение расстояния по сравнению с первым случаем, когда на базе была лишь одна цистерна, составляет всего 100 миль, у читателя, наверное, возникнет справедливое подозрение, что существует лучший алгоритм решения этой задачи. Действительно, можно добиться лучшего результата.
Ну а как далеко сможет уехать разведчик пустыни, если на базе имеется n цистерн с бензином? Как и во всех алгоритмических головоломках, простой численный ответ или даже формула не годятся. Требуется составить алгоритм, дающий тот или иной ответ.
В другой части громадной песчаной территории проходит патрульный маршрут противника, объезжаемый им другим способом. В произвольных пунктах замкнутого маршрута самолет сбрасывает n цистерн с горючим. В каждой цистерне содержится определенное количество бензина, однако это количество может варьировать в значительных пределах от одной цистерны к другой (см. рисунок вверху). Поскольку этот маршрут пролегает через неприятельскую территорию, машина и водитель сбрасываются на парашютах. Они приземляются у одной из цистерн, заправляются и начинают объезд. Бензобак машины растягивающийся: он может вместить любое количество горючего независимо от того, какой емкости цистерна ему встретится на пути.

Откуда должна начать путешествие машина, чтобы успешно объехать весь маршрут?
Как ни странно, по мере того как машина продвигается по маршруту, горючее никогда не оказывается исчерпанным, прежде чем она достигнет следующего пункта заправки. Другими словами, полное количество горючего в цистернах таково, что его как раз достаточно, чтобы машина могла полностью объехать маршрут, не больше и не меньше. Это странно, потому что, как я уже говорил, выбор пунктов для расположения цистерн с горючим и его количество в каждой цистерне совершенно произвольны. Например, вполне может случиться так, что машина начнет путешествие от цистерны, не содержащей достаточного количества горючего для того, чтобы можно было добраться до другой ближайшей цистерны, и разведчик застрянет посреди пустыни. В чем тут секрет?
Наш разведчик пустыни знает об этих патрульных поездках противника и откровенно озадачен ими. О противнике известно, что он сумасшедший и необыкновенно удачливый. Младший по чину помощник нашего разведчика, который проводит бессонные ночи в своей палатке, решая различные головоломки, находит ответ. "По-видимому, сэр, дело в том, что независимо от того, куда сбрасываются цистерны и сколько горючего они содержат, всегда можно найти такой пункт, начав с которого противник сумеет пройти весь маршрут".
Предлагаю читателям самим поразмыслить и открыть секрет. Разумеется, речь идет об алгоритме. Требуется шаг за шагом описать процедуру, в результате выполнения которой можно найти по крайней мере один заправочный пункт, где машина может начать (и завершить) свою патрульную поездку. Алгоритм должен также указывать направление, в котором следует двигаться машине. Ошибка в направлении может привести к катастрофе. Лучшие ответы к этой задаче так же, как и к железнодорожным задачам, будут опубликованы в одном из ближайших номеров журнала.
В начале статьи я обещал дать ответ на задачу о двух поездах и пчеле. Интересные головоломки часто отличаются тем, что вводят в заблуждение решающего, в особенности когда задача имеет простое решение. Описывая бесконечный процесс, в котором пчела мечется между двумя поездами, я намеренно пытался запутать читателей. Чтобы решить задачу, необходимо лишь понять, что пчела находится в полете ровно столько времени, сколько требуется поездам для того, чтобы встретиться. Половину расстояния между Задаченском и Решенском они преодолевают ровно за час. Следовательно, пчела, скорость полета которой всегда равна 90км/ч, пролетит 90км.
С этой задачей связана одна легенда, за правдивость которой я, впрочем, не могу поручиться. Говорят, что в свое время кто-то задал эту задачку Джону фон Нейману, одному из величайших математиков нынешнего столетия. Он тотчас ответил: "Конечно, 90 километров".
"Я так и знал,- сказал спрашивающий его,- что вы найдете легкий способ".
"Какой легкий способ?" - сказал фон Нейман. Оказывается, он просуммировал в уме бесконечный ряд.
БИБЛИОГРАФИЯ
AMUSEMENTS IN MATHEMATICS. HENRY ERNEST DUDENEY. Dover Publications, Inc., 1958.
ОТКЛИКИ
9 1987
ЧИТАТЕЛИ с "одноколейными умами" теперь уже наверняка решили задачу, предложенную в прошлом номере журнала, где требовалось поменять местами два железнодорожных вагона, между которыми находился мост. Вагоны стояли на круговом пути, а локомотив был на другом пути, соединяющемся с круговым стрелкой. Мост достаточно прочен, чтобы выдержать только один вагон; локомотива он не выдержит. Каким образом локомотив сможет поменять вагоны местами?
Локомотив заходит на круговой путь, подходит к вагону A и заталкивает его на мост. Затем он пятится назад, подходит к вагону B, прицепляет его, подводит к краю моста и сцепляет вагоны A и B. Далее локомотив и прицепленные к нему вагоны, пройдя через стрелку, выезжают на прямой путь, где вагон А отцепляется. Теперь локомотив опять подводит вагон В к мосту и, отцепив, оставляет его там. Наконец, локомотив проходит по кругу, стягивает вагон B с моста, оставляет его на новом месте и возвращается за вагоном A.
12 1987
Я БЫЛ ПОРАЖЕН обилием читательских откликов на статью, опубликованную в августовском номере журнала и посвященную алгоритмическим головоломкам. На этот раз не нужно было писать никаких программ, требовалось лишь построить несколько алгоритмов подзаправки автомашины в пустыне и железнодорожных маневров. Несколько сот "одноколейных умов" прислали мне результаты своих исследований, и мне приятно сознавать, что я дал людям столько пищи для размышлений. Алгоритмическая головоломка - это задача, имеющая алгоритмическое решение, т.е. рецепт или процедура, следуя которой, можно прийти к заданной цели. Головоломки с поездами были проще отчасти потому, что я привел решение одной из них. Конечно, очень трудно было отобрать лучшее решение из множества ответов, присланных ко второй головоломке, в которой требовалось развернуть весь состав, пользуясь лишь одним тупиком, вмещавшим только один вагон. Отобрав более или менее произвольно одно из лучших решений, присланных раньше других, я представляю здесь алгоритм, предложенный Д.Ауенбаем из Уэст-Ковина (шт.Калифорния). Буквой A обозначен участок железнодорожного полотна от Задаченска до тупика, B обозначает сам тупик и C - основной участок пути от тупика B до Решенска. Через Pk обозначен k-й вагон поезда.
Расцепить поезд P
вперед к B
назад к C
for k = 1 to n
- вперед к A
- прицепить Pk
- назад к C
- вперед к B
- отцепить Рk
- назад к C
- вперед к A
- назад к B
- прицепить Pk
В другом варианте решения процедура начинается не с первого вагона, а с последнего. Как подметили некоторые читатели, приведенное выше решение требует затрат, пропорциональных n3, поскольку n вагонов поезда нужно протащить назад и вперед n раз на пути, длина которого приблизительно равна длине состава из n вагонов.
В первой задаче о разведчике пустыни требовалось определить, какое расстояние сможет преодолеть патрульная автомашина при наличии n цистерн с горючим. В исходном состоянии горючее хранится в цистернах на базе, емкость каждой цистерны равна 50 галлонам. Автомашина может везти в кузове только одну цистерну. Каким образом следует расположить в пустыне склады, доставив туда предварительно горючее все той же автомашиной, чтобы максимально увеличить расстояние, на которое автомашина сможет удалиться от базы? В статье я привел алгоритм, гарантирующий возможность проехать расстояние 600 миль при наличии двух цистерн с горючим. Однако оптимальное расстояние, как показали У.Липп и многие другие читатели из Милфорда (шт.Коннектикут), равно 733.33 мили. В своем живо написанном письме под заглавием "Побьем рекорд! Даешь 733 мили всего на двух цистернах!" Липп показал, как можно превзойти результат 666 миль, о возможности достижения которого я говорил в статье. Вот его алгоритм (в слегка отредактированной форме):
Заправить автомашину из первой цистерны
Погрузить вторую цистерну
Вперед на 50 миль
Разгрузить вторую цистерну
Назад на базу
Заправить бак из первой цистерны
Погрузить первую цистерну
Вперед на 100 миль
Разгрузить первую цистерну
Заправить бак из первой цистерны
Назад на 50 миль ко второй цистерне
Погрузить вторую цистерну
Вперед на 50 миль к первой цистерне
Заправить бак из первой цистерны
Вперед на 33.33 мили
Разгрузить вторую цистерну
Назад на 33.33 мили к первой цистерне
Погрузить первую цистерну
Вперед на 33.33 мили ко второй цистерне
На этом этапе патрульная автомашина находится уже на расстоянии 133.33 мили от базы. Теперь нужно просто погрузить вторую цистерну (еще полную) и проехать вперед на расстояние 600 миль.
Обобщая этот алгоритм, мы не сможем прийти к оптимальному алгоритму при числе цистерн n > 2. Например, при его помощи мы не сможем достичь оптимального расстояния 860 миль при наличии 3 цистерн с горючим. Я приведу общий алгоритм (для числа цистерн n >= 6) через месяц, а также дам решение ко второй задаче о разведчике пустыни.
1 1988
ПОТОК писем со всех концов света по поводу статьи в августовском номере журнала, посвященной алгоритмическим головоломкам, не иссякает. Мы продолжаем разговор на эту тему, как и было обещано в предыдущей статье, в которой мы вернулись к алгоритмическим головоломкам. Прежде чем отправиться в пустыню и лать ответы к двум последним задачкам, сформулированным в первой статье об алгоритмических головоломках, я должен исправить ошибку, допущенную мною в рассуждениях о задачах с поездами. М.Блам, специалист по вычислительной математике из Калифорнийского университета в Беркли, заметил, что объем работы, требующейся, чтобы пропустить один поезд мимо другого по приведенному в статье алгоритму, на самом деле пропорционален n3 а не n2, как утверждалось в статье (напомним, что n - число вагонов поезда). Грубо говоря, каждый из n вагонов поезда перемещается на n единиц длины n раз. Бламу удалось придумать такой алгоритм, который решает ту же задачу при затратах работы, пропорциональных п2*log(n). К сожалению, недостаток места не позволяет мне привести здесь алгоритм Блама.
По условиям первой задачи о "разведчике пустыни" автомашина могла везти в своем кузове цистерну бензина емкостью 50 галлонов и имела бензобак, вмещавший 10 галлонов. В прошлой статье было показано, что, имея на базе лве цистерны горючего, автомашина может удалиться от базы на максимальное расстояние, равное 733,3 мили, прежде чем запас горючего будет полностью исчерпан.
Алгоритмы, представленные Ч.Новогорски из Нэплза (шт.Флорида) и Н.Рокком из Уинтерсвиля (шт.Огайо), свидетельствуют о том, что, имея три цистерны горючего, автомашина может удалиться от базы на расстояние 860 миль. Результаты большинства других читателей, попробовавших свои силы в этой задаче, были меньше этой величины. На самом деле даже общие формулы, представленные большинством читателей, дали более низкий результат, когда вместо n, количества цистерн в обшем случае, было подставлено число 3. Я не могу поэтому поручиться за правильность формул, подобных той, которую прислал Л.Лейнвебер из Кливленда (шт.Огайо). Однако она является типичным представителем тех формул из числа представленных читателями, которые дают наилучшие результаты:

Здесь греческая буква сигма означает суммирование последовательности величин 100/(2i-1), получающихся при различных i, принимающего значения от 1 до n. Формула означает, таким образом, что нужно сложить все n величин и полученную сумму помножить на 5.
Во второй задаче о разведчике пустыни автомашину можно было заправлять на n складах с горючим, расположенных в произвольных пунктах кругового маршрута, объезжаемого автомашиной. Количество горючего на каждом складе также произвольно, но горючего на всех складах должно быть ровно столько, сколько необходимо, чтобы машина могла полностью объехать свой маршрут (конечно, при условии, что она не начнет поездку от неподходящего склада). Ее собственный бензобак может вместить любое количество горючего, а в исходном состоянии он пуст. Нужно определить, откуда машина должна начать поездку.
Ряд читателей, включая А.Лавриджа из Лонг-Бнча (шт.Калифорния), придумали очень интересный прием, при помоши которого можно решить эту задачу. Представим себе, что автомашина совершает "пробную" поездку, стартуя у произвольно выбранного склада и двигаясь в произвольном направлении. Попутно будем рисовать график количества бензина в
баке, как функцию пройденного расстояния, и не будем останавливаться, даже если горючее полностью исчерпалось. В этом случае график просто перейдет в отрицательную область. После каждой заправки на складе горючего кривая резко поднимается вверх и затем начинает постепенно снижаться. В конце концов машина вернется к исходной точке. Теперь водитель должен проанализировать график и выбрать тот склад, при приближении к которому машина имела минимальное количество бензина (перед заправкой). От этого склада и следует начинать поездку.
АЛГОРИТМИЧЕСКИЕ ГОЛОВОЛОМКИ
А.К.ДЬЮДНИ
ГОРОДА Задаченск и Решенск отстоят друг от друга на 100км. Как-то погожим июньским днем в полдень из этих городов выходят навстречу друг другу два поезда, причем каждый движется со скоростью 50км в час. В тот же момент пчела, уютно пристроившаяся на головной фаре поезда в Задаченске, вылетает в направлении Решенска и летит вдоль железнодорожного пути со скоростью 90км в час.
Встретившись с поездом, идущим из Решенска, пчела резко разворачивается и летит обратно все с той же скоростью 90км в час. Встретившись с поездом, идущим из Задаченска, она опять разворачивается и летит в противоположном направлении. Таким образом пчела снует между поездами до тех пор, пока они не встретятся. Какова будет полная длина пути, проделанного пчелой? Ответ к этой известной задачке, который будет дан в конце статьи, короткий. Это просто число.
Однако существуют задачи и другого рода, которые можно назвать алгоритмическими головоломками, и ответы к ним выглядят намного сложнее. Решить такую задачу - значит указать последовательность процедур, позволяющих прийти к желаемому результату. Другими словами, ответ представляет собой алгоритм. В литературе, посвященной головоломкам, приводится немало подобных задач. К числу известных относится, например, задача о том, как разделить жидкость в сосуде на три равные части посредством последовательности переливаний с использованием других сосудов определенной емкости или как можно без потерь с помощью одной лодки переправить на другой берег реки волка, козла и капусту. К этому же классу относится и задача о том, каким образом можно определить фальшивую монету (отличающуюся по массе) в кучке монет посредством последовательности взвешиваний на рычажных весах.
Различие в ответах на обычную задачу и алгоритмическую головоломку проще всего пояснить на конкретном примере. Начав с железнодорожных путей, пойдем по ним и дальше, продолжая тему первого примера. Допустим теперь, что поезда, движущиеся навстречу друг другу, при встрече не сталкиваются, а вовремя притормаживают. С шипением и грохотом они останавливаются друг перед другом. (При этом мне почему-то представляются два огромных старинных паровоза). Между поездами лежит короткий отрезок железнодорожного полотна и маленькое боковое ответвление, длина которого позволяет разместить лишь один вагон или локомотив (см. верхний рисунок на с.85). Очевидно, кто-то сделал серьезную ошибку при составлении расписания. Единственный способ выйти из затруднения и разминуться заключается в том, чтобы машинисты каким-то образом воспользовались боковым путем. В этой задаче так же, как и в последующих, мы будем предполагать, что каждый вагон и каждый локомотив с обеих сторон имеют устройство сцепления. Кроме того, на каждом поезде есть сцепщик, который, бегая по путям, может сцеплять и отцеплять вагоны.

Каким образом могут разминуться поезда?
Вытирая пот с лица красным в горошек носовым платком, машинист поезда, следующего из Задаченска, восклицает: "Я не знаю, как мы сможем пропустить друг друга. У нас есть только вон то небольшое ответвление". Машинист из Решенска настроен более оптимистично. Он излагает план, следуя которому поезда могут разминуться. Возможно ли это? Прежде чем читать дальше, давайте взглянем на рисунок. Для конкретности на нем изображены два поезда, каждый из пяти вагонов. В общей формулировке этой алгоритмической головоломки поезда имеют по n вагонов.
Подходя к решению этой сравнительно простой задачи, читатель, наверно, будет говорить себе под нос: "Так, посмотрим... А почему бы не провести состав из Задаченска по боковому пути по одному вагону? Поезд из Решенска мог бы сновать как челнок взад и вперед, затаскивая каждый раз новый вагон задаченского поезда на боковой путь, затем, проезжая мимо него по основному пути на всю свою длину и прицепляя его с другой стороны, чтобы вывести с бокового пути перед тем, как вернуться за следующим вагоном".
Такое описание может послужить отправной точкой для построения ответа к алгоритмической головоломке, но его нужно сделать более ясным и четким. Воспользуемся для этого алгоритмической системой записи, введя некоторые вспомогательные обозначения. При решении задачи можно выделить четыре участка железнодорожного полотна: участок от Задаченска до бокового пути (обозначим его A); отрезок основного пути между стрелками, соединяющими его с боковым путем (B); сам боковой путь {B') и участок от бокового пути до Решенска (C). Такая команда, как "Вперед к A", означает, что поезд из Решенска, состоящий из локомотива и вагонов, прицепленных к нему на данный момент, продвигается вперед до тех пор, пока полностью не окажется на участке пути A.
Напомним, что у каждого поезда по n вагонов. Локомотив задаченского поезда обозначим через P1, а его вагоны пронумеруем как Р2, РЗ и т.д. Команда "Прицепить Pk" означает, что к данному моменту решенский поезд находится вплотную к k-му элементу задаченского поезда; состав из Решенска мягко подкатывается к вагону Pk и сцепляется с ним. Те из вас, кто когда-нибудь жил вблизи железнодорожной станции,наверное, хорошо помнят очень характерный, ни на что другое не похожий звук, которым сопровождается сцепка вагонов.
Теперь можно записать алгоритм решения:
расцепить поезд Р
for k = 1 to n+1
- вперед к A
- прицепить Pk
- назад к C
- вперед к B'
- отцепить Pk
- назад к C
- вперед к A
- назад к B'
- прицепить Pk
- назад к C
- отцепить Pk
сцепить поезд P
Сначала поезд из Задаченска расцепляется на отдельные вагоны и мы имеем n вагонов и локомотив. Затем в алгоритме начинается цикл из 11 шагов. Всю работу выполняет поезд из Решенска. Ни разу не отцепив ни одного из своих вагонов, он сначала проходит вперед на участок А, где сцепляется с первым элементом (k = 1) задаченского состава, т.е. с локомотивом. Он буксирует локомотив назад к участку С и после перевода стрелок загоняет его на боковой путь В', здесь локомотив отцепляется. Затем состав из Решенска снова возвращается на участок C, стрелки переводятся, и он идет вперед к участку A. После этого он возвращается, проходит на боковой путь, снова прицепляется к оставленному там локомотиву задаченского состава и буксирует его на участок C, где отцепляет и оставляет его. Ту же последовательность шагов поезд выполняет для каждого из оставшихся вагонов задаченского состава. Когда главный цикл завершен, все вагоны задаченского поезда оказываются на участке дороги между решенским составом и Решенском. Теперь, как только поезд придет в себя от утомительных алгоритмических процедур, он запыхтит и тронется в направлении к Решенску.
Еще одна алгоритмическая головоломка возникает, когда поезд из Задаченска, завершая свое путешествие, подъезжает к Решенску. Машинист, глядя на пробегающие мимо него пригороды, вдруг с ужасом вспоминает, что забыл взять с собой пакетик с бутербродами. Делать нечего, придется возвращаться обратно. Он нажимает на тормоза, и постепенно тяжелый состав из n вагонов останавливается. Пятиться всю дорогу до Задаченска не
очень-то удобно. К счастью, машинист замечает справа небольшое боковое ответвление - тупик. Его длина достаточна лишь для одного вагона, у разветвления есть управляющие стрелки. Вдохновленный алгоритмическим достижением машиниста из Решенска, наш скромный герой тоже хочет попробовать свои силы.
Прежде всего машинист задаченского состава рисует на клочке бумаги схему пути (см. нижний рисунок). Затем он расписывает алгоритм и тщательно проверяет его, водя пальцем по бумаге то туда, то сюда и бормоча что-то себе под нос. После проверки алгоритма он начинает длительную серию отцеплений, буксировок и сцеплений, пока это все не заканчивается тем, что поезд оказывается полностью развернутым в обратном направлении. Причем не только порядок, в котором следовали локомотив и вагоны, сохранился, но и сами вагоны и локомотив оказались повернутыми в обратном направлении. Каким образом машинист проделал этот маневр? Лучшие решения читателей будут опубликованы в одном из следующих номеров журнала. Под словом "лучшее" подразумевается наиболее ясное и наиболее остроумное решение. Эта задача не так бесхитростна, как может показаться на первый взгляд.

Как поезд может развернуться, чтобы машинист вернулся в город, откуда прибыл?
Уже на пути в Задаченск машинист понял, что решение задачи потребовало очень больших энергетических затрат. Угольный тендер паровоза оказался почти пустым. Количество работы, затраченной во время маневров поезда, было пропорционально n2. В самом деле, если измерять массу в количестве вагонов, а расстояние в их длине, то работа будет пропорциональна числу вагонов n и расстоянию n. Только теперь, по пути домой, машинист задаченского поезда подумал о том, что, возможно, существует более эффективное решение. Давайте подумаем тоже, возможно ли развернуть состав за меньшее число шагов, скажем, порядка n(3/2) или даже n*log(n)?
Чтобы еще лучше потренировать однорельсовые умы в искусстве алгоритмических головоломок, вот еще одна маленькая задачка. Локомотив без вагонов приближается к поворотному кругу, на котором стоят два пустых вагона. Между вагонами расположен небольшой железнодорожный мост, прочность которого позволяет выдержать один вагон, но локомотива он уже не выдержит (см. верхний рисунок). Машинист локомотива должен развернуть вагоны так, чтобы они поменялись местами. Как и в предыдущих задачах, все сцепления и расцепления должны производиться только в неподвижном состоянии. Длина моста не превышает длины одного вагона. Завершив свою работу, локомотив должен покинуть поворотный круг. Решение задачи представляет собой простой алгоритм без циклов. С этим алгоритмом читатели ознакомятся в очередном номере журнала.

Локомотив должен поменять вагоны местами, не пересекая опасного моста
Со следующими двумя алгоритмическими головоломками я не был знаком раньше. Они продолжают транспортную тему, начатую в задачах о поездах, однако переводят наши исследования на более высокую ступень - теперь мы будем заниматься грузовиками. Задачи этой серии я буду называть задачами разведчика пустыни. В первой задаче патрульный автомобиль разведчика пустыни имеет бак, вмещающий 10 галлонов бензина. Бак автомобиля заполняется из цистерн емкостью 50 галлонов. Несколько таких цистерн хранятся на складе. Если автомобиль может везти в качестве груза одну цистерну с бензином и если он затрачивает 1 галлон горючего на 10 миль пути независимо от того, везет он с собой цистерну или нет, то каково максимальное расстояние, на которое он может удалиться от базы, прежде чем у него иссякнет горючее? Ответ, конечно, зависит от количества цистерн с бензином, хранящихся на базе. Как и во всех алгоритмических головоломках, предположим, что число цистерн на базе равно n.

На какое максимальное расстояние сможет уехать грузовик, располагая n цистернами с горючим?
Если n= 1, то ответ получить несложно. Автомобиль заправляет свой бак из единственной цистерны, грузит ее в кузов и отправляется в путь под жарким солнцем пустыни. Заправляясь при необходимости из цистерны, автомобиль, очевидно, пройдет 500 миль, прежде чем горючее будет полностью исчерпано. А как далеко он сможет уехать на двух цистернах? Поскольку автомобиль может везти с собой лишь одну цистерну, то, очевидно, он отвезет первую цистерну на какое-то расстояние в пустыню, заправится из нее, если это необходимо, а затем вернется на базу за второй. Вторую цистерну разведчик повезет по той же дороге. Он может остановиться для заправки, а может и не останавливаться у первой, оставленной им в пустыне цистерны, прежде чем продолжить свое путешествие. Как далеко он сможет уехать, совершая такие челночные перемещения между пунктами, в которых он оставляет запасы горючего? Внезапно задача перестает казаться тривиальной.
Приведем короткий алгоритм, позволяющий патрульному автомобилю проехать путь длиной 600 миль:
заправить бак и погрузить первую цистерну
вперед 100 миль
снять цистерну и заправиться
назад на базу за второй цистерной
заправиться и погрузить цистерну
вперед 100 миль
заправиться из первой цистерны
вперед 100 миль
снять цистерну и заправиться
назад к первой цистерне
заправиться и погрузить цистерну
вперед 100 миль
На этой стадии алгоритма автомобиль удалился от базы на 200 миль. У него две цистерны: в одной осталось 10 галлонов, а в другой - 30 галлонов бензина. Поездка продолжается после того, как водитель заправляет машину из первой цистерны (оставляя ее пустой), погружает в кузов вторую цистерну и уезжает, скрываясь за барханами. Таким образом, он сможет проехать еще 400 миль, прежде чем у него кончится горючее. Полное расстояние от базы составит 600 миль. Поскольку увеличение расстояния по сравнению с первым случаем, когда на базе была лишь одна цистерна, составляет всего 100 миль, у читателя, наверное, возникнет справедливое подозрение, что существует лучший алгоритм решения этой задачи. Действительно, можно добиться лучшего результата.
Ну а как далеко сможет уехать разведчик пустыни, если на базе имеется n цистерн с бензином? Как и во всех алгоритмических головоломках, простой численный ответ или даже формула не годятся. Требуется составить алгоритм, дающий тот или иной ответ.
В другой части громадной песчаной территории проходит патрульный маршрут противника, объезжаемый им другим способом. В произвольных пунктах замкнутого маршрута самолет сбрасывает n цистерн с горючим. В каждой цистерне содержится определенное количество бензина, однако это количество может варьировать в значительных пределах от одной цистерны к другой (см. рисунок вверху). Поскольку этот маршрут пролегает через неприятельскую территорию, машина и водитель сбрасываются на парашютах. Они приземляются у одной из цистерн, заправляются и начинают объезд. Бензобак машины растягивающийся: он может вместить любое количество горючего независимо от того, какой емкости цистерна ему встретится на пути.

Откуда должна начать путешествие машина, чтобы успешно объехать весь маршрут?
Как ни странно, по мере того как машина продвигается по маршруту, горючее никогда не оказывается исчерпанным, прежде чем она достигнет следующего пункта заправки. Другими словами, полное количество горючего в цистернах таково, что его как раз достаточно, чтобы машина могла полностью объехать маршрут, не больше и не меньше. Это странно, потому что, как я уже говорил, выбор пунктов для расположения цистерн с горючим и его количество в каждой цистерне совершенно произвольны. Например, вполне может случиться так, что машина начнет путешествие от цистерны, не содержащей достаточного количества горючего для того, чтобы можно было добраться до другой ближайшей цистерны, и разведчик застрянет посреди пустыни. В чем тут секрет?
Наш разведчик пустыни знает об этих патрульных поездках противника и откровенно озадачен ими. О противнике известно, что он сумасшедший и необыкновенно удачливый. Младший по чину помощник нашего разведчика, который проводит бессонные ночи в своей палатке, решая различные головоломки, находит ответ. "По-видимому, сэр, дело в том, что независимо от того, куда сбрасываются цистерны и сколько горючего они содержат, всегда можно найти такой пункт, начав с которого противник сумеет пройти весь маршрут".
Предлагаю читателям самим поразмыслить и открыть секрет. Разумеется, речь идет об алгоритме. Требуется шаг за шагом описать процедуру, в результате выполнения которой можно найти по крайней мере один заправочный пункт, где машина может начать (и завершить) свою патрульную поездку. Алгоритм должен также указывать направление, в котором следует двигаться машине. Ошибка в направлении может привести к катастрофе. Лучшие ответы к этой задаче так же, как и к железнодорожным задачам, будут опубликованы в одном из ближайших номеров журнала.
В начале статьи я обещал дать ответ на задачу о двух поездах и пчеле. Интересные головоломки часто отличаются тем, что вводят в заблуждение решающего, в особенности когда задача имеет простое решение. Описывая бесконечный процесс, в котором пчела мечется между двумя поездами, я намеренно пытался запутать читателей. Чтобы решить задачу, необходимо лишь понять, что пчела находится в полете ровно столько времени, сколько требуется поездам для того, чтобы встретиться. Половину расстояния между Задаченском и Решенском они преодолевают ровно за час. Следовательно, пчела, скорость полета которой всегда равна 90км/ч, пролетит 90км.
С этой задачей связана одна легенда, за правдивость которой я, впрочем, не могу поручиться. Говорят, что в свое время кто-то задал эту задачку Джону фон Нейману, одному из величайших математиков нынешнего столетия. Он тотчас ответил: "Конечно, 90 километров".
"Я так и знал,- сказал спрашивающий его,- что вы найдете легкий способ".
"Какой легкий способ?" - сказал фон Нейман. Оказывается, он просуммировал в уме бесконечный ряд.
БИБЛИОГРАФИЯ
AMUSEMENTS IN MATHEMATICS. HENRY ERNEST DUDENEY. Dover Publications, Inc., 1958.
ОТКЛИКИ
9 1987
ЧИТАТЕЛИ с "одноколейными умами" теперь уже наверняка решили задачу, предложенную в прошлом номере журнала, где требовалось поменять местами два железнодорожных вагона, между которыми находился мост. Вагоны стояли на круговом пути, а локомотив был на другом пути, соединяющемся с круговым стрелкой. Мост достаточно прочен, чтобы выдержать только один вагон; локомотива он не выдержит. Каким образом локомотив сможет поменять вагоны местами?
Локомотив заходит на круговой путь, подходит к вагону A и заталкивает его на мост. Затем он пятится назад, подходит к вагону B, прицепляет его, подводит к краю моста и сцепляет вагоны A и B. Далее локомотив и прицепленные к нему вагоны, пройдя через стрелку, выезжают на прямой путь, где вагон А отцепляется. Теперь локомотив опять подводит вагон В к мосту и, отцепив, оставляет его там. Наконец, локомотив проходит по кругу, стягивает вагон B с моста, оставляет его на новом месте и возвращается за вагоном A.
12 1987
Я БЫЛ ПОРАЖЕН обилием читательских откликов на статью, опубликованную в августовском номере журнала и посвященную алгоритмическим головоломкам. На этот раз не нужно было писать никаких программ, требовалось лишь построить несколько алгоритмов подзаправки автомашины в пустыне и железнодорожных маневров. Несколько сот "одноколейных умов" прислали мне результаты своих исследований, и мне приятно сознавать, что я дал людям столько пищи для размышлений. Алгоритмическая головоломка - это задача, имеющая алгоритмическое решение, т.е. рецепт или процедура, следуя которой, можно прийти к заданной цели. Головоломки с поездами были проще отчасти потому, что я привел решение одной из них. Конечно, очень трудно было отобрать лучшее решение из множества ответов, присланных ко второй головоломке, в которой требовалось развернуть весь состав, пользуясь лишь одним тупиком, вмещавшим только один вагон. Отобрав более или менее произвольно одно из лучших решений, присланных раньше других, я представляю здесь алгоритм, предложенный Д.Ауенбаем из Уэст-Ковина (шт.Калифорния). Буквой A обозначен участок железнодорожного полотна от Задаченска до тупика, B обозначает сам тупик и C - основной участок пути от тупика B до Решенска. Через Pk обозначен k-й вагон поезда.
Расцепить поезд P
вперед к B
назад к C
for k = 1 to n
- вперед к A
- прицепить Pk
- назад к C
- вперед к B
- отцепить Рk
- назад к C
- вперед к A
- назад к B
- прицепить Pk
В другом варианте решения процедура начинается не с первого вагона, а с последнего. Как подметили некоторые читатели, приведенное выше решение требует затрат, пропорциональных n3, поскольку n вагонов поезда нужно протащить назад и вперед n раз на пути, длина которого приблизительно равна длине состава из n вагонов.
В первой задаче о разведчике пустыни требовалось определить, какое расстояние сможет преодолеть патрульная автомашина при наличии n цистерн с горючим. В исходном состоянии горючее хранится в цистернах на базе, емкость каждой цистерны равна 50 галлонам. Автомашина может везти в кузове только одну цистерну. Каким образом следует расположить в пустыне склады, доставив туда предварительно горючее все той же автомашиной, чтобы максимально увеличить расстояние, на которое автомашина сможет удалиться от базы? В статье я привел алгоритм, гарантирующий возможность проехать расстояние 600 миль при наличии двух цистерн с горючим. Однако оптимальное расстояние, как показали У.Липп и многие другие читатели из Милфорда (шт.Коннектикут), равно 733.33 мили. В своем живо написанном письме под заглавием "Побьем рекорд! Даешь 733 мили всего на двух цистернах!" Липп показал, как можно превзойти результат 666 миль, о возможности достижения которого я говорил в статье. Вот его алгоритм (в слегка отредактированной форме):
Заправить автомашину из первой цистерны
Погрузить вторую цистерну
Вперед на 50 миль
Разгрузить вторую цистерну
Назад на базу
Заправить бак из первой цистерны
Погрузить первую цистерну
Вперед на 100 миль
Разгрузить первую цистерну
Заправить бак из первой цистерны
Назад на 50 миль ко второй цистерне
Погрузить вторую цистерну
Вперед на 50 миль к первой цистерне
Заправить бак из первой цистерны
Вперед на 33.33 мили
Разгрузить вторую цистерну
Назад на 33.33 мили к первой цистерне
Погрузить первую цистерну
Вперед на 33.33 мили ко второй цистерне
На этом этапе патрульная автомашина находится уже на расстоянии 133.33 мили от базы. Теперь нужно просто погрузить вторую цистерну (еще полную) и проехать вперед на расстояние 600 миль.
Обобщая этот алгоритм, мы не сможем прийти к оптимальному алгоритму при числе цистерн n > 2. Например, при его помощи мы не сможем достичь оптимального расстояния 860 миль при наличии 3 цистерн с горючим. Я приведу общий алгоритм (для числа цистерн n >= 6) через месяц, а также дам решение ко второй задаче о разведчике пустыни.
1 1988
ПОТОК писем со всех концов света по поводу статьи в августовском номере журнала, посвященной алгоритмическим головоломкам, не иссякает. Мы продолжаем разговор на эту тему, как и было обещано в предыдущей статье, в которой мы вернулись к алгоритмическим головоломкам. Прежде чем отправиться в пустыню и лать ответы к двум последним задачкам, сформулированным в первой статье об алгоритмических головоломках, я должен исправить ошибку, допущенную мною в рассуждениях о задачах с поездами. М.Блам, специалист по вычислительной математике из Калифорнийского университета в Беркли, заметил, что объем работы, требующейся, чтобы пропустить один поезд мимо другого по приведенному в статье алгоритму, на самом деле пропорционален n3 а не n2, как утверждалось в статье (напомним, что n - число вагонов поезда). Грубо говоря, каждый из n вагонов поезда перемещается на n единиц длины n раз. Бламу удалось придумать такой алгоритм, который решает ту же задачу при затратах работы, пропорциональных п2*log(n). К сожалению, недостаток места не позволяет мне привести здесь алгоритм Блама.
По условиям первой задачи о "разведчике пустыни" автомашина могла везти в своем кузове цистерну бензина емкостью 50 галлонов и имела бензобак, вмещавший 10 галлонов. В прошлой статье было показано, что, имея на базе лве цистерны горючего, автомашина может удалиться от базы на максимальное расстояние, равное 733,3 мили, прежде чем запас горючего будет полностью исчерпан.
Алгоритмы, представленные Ч.Новогорски из Нэплза (шт.Флорида) и Н.Рокком из Уинтерсвиля (шт.Огайо), свидетельствуют о том, что, имея три цистерны горючего, автомашина может удалиться от базы на расстояние 860 миль. Результаты большинства других читателей, попробовавших свои силы в этой задаче, были меньше этой величины. На самом деле даже общие формулы, представленные большинством читателей, дали более низкий результат, когда вместо n, количества цистерн в обшем случае, было подставлено число 3. Я не могу поэтому поручиться за правильность формул, подобных той, которую прислал Л.Лейнвебер из Кливленда (шт.Огайо). Однако она является типичным представителем тех формул из числа представленных читателями, которые дают наилучшие результаты:

Здесь греческая буква сигма означает суммирование последовательности величин 100/(2i-1), получающихся при различных i, принимающего значения от 1 до n. Формула означает, таким образом, что нужно сложить все n величин и полученную сумму помножить на 5.
Во второй задаче о разведчике пустыни автомашину можно было заправлять на n складах с горючим, расположенных в произвольных пунктах кругового маршрута, объезжаемого автомашиной. Количество горючего на каждом складе также произвольно, но горючего на всех складах должно быть ровно столько, сколько необходимо, чтобы машина могла полностью объехать свой маршрут (конечно, при условии, что она не начнет поездку от неподходящего склада). Ее собственный бензобак может вместить любое количество горючего, а в исходном состоянии он пуст. Нужно определить, откуда машина должна начать поездку.
Ряд читателей, включая А.Лавриджа из Лонг-Бнча (шт.Калифорния), придумали очень интересный прием, при помоши которого можно решить эту задачу. Представим себе, что автомашина совершает "пробную" поездку, стартуя у произвольно выбранного склада и двигаясь в произвольном направлении. Попутно будем рисовать график количества бензина в
баке, как функцию пройденного расстояния, и не будем останавливаться, даже если горючее полностью исчерпалось. В этом случае график просто перейдет в отрицательную область. После каждой заправки на складе горючего кривая резко поднимается вверх и затем начинает постепенно снижаться. В конце концов машина вернется к исходной точке. Теперь водитель должен проанализировать график и выбрать тот склад, при приближении к которому машина имела минимальное количество бензина (перед заправкой). От этого склада и следует начинать поездку.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
9 1987
СТРАННАЯ ПРИВЛЕКАТЕЛЬНОСТЬ ХАОСА
А.К.ДЬЮДНИ
ХАОС ОБЛАДАЕТ странной привлекательностью для ума, способного увидеть в нем закономерности. Некоторые физические системы в своем хаотическом поведении в каком-то смысле стремятся к упорядоченности, в которой мы наблюдаем такие закономерности. К тому же внешние проявления этих закономерностей сами по себе кажутся нам какими-то странно привлекательными. Кое-кто из читателей уже, наверное, знает, что геометрические формы, лежащие в основе хаоса, называются странными, или хаотическими, аттракторами (см.: Дж.П.Кратчфилд, Дж.Д.Фармер, Н.X.Пэкард, Р.Шоу. Хаос, "В мире науки", 1987, #2). Странные аттракторы (от англ. attractive - привлекательный, притягательный) можно генерировать и с помощью персонального компьютера.
Но прежде чем отправиться в страну хаоса, читателям нужно вооружиться необходимыми доспехами - интуитивным пониманием основных физических понятий, которые нам встретятся. В частности, что такое аттрактор? Грубо говоря, аттрактор - это обобщение понятия равновесия, это то состояние, к которому приходит в конце концов система, то, к чему она притягивается. Простым примером физической системы, иллюстрирующей понятие аттрактора, служит маятник. Представим обычный движущийся маятник, который под воздействием сил трения замедляется и в конце концов останавливается. Движение маятника можно описать посредством так называемой фазовой диаграммы, или диаграммы состояний, по одной оси которой откладывается угол, составляемый маятником с вертикалью, а по другой - скорость изменения этого угла. Движение качающегося маятника на фазовой диаграмме представляется точкой, движущейся вокруг начала отсчета. По мере того как маятник теряет энергию, эта точка приближается по спирали к точке начала отсчета, где в конце концов и останавливается. В данном случае начало отсчета выступает в роли аттрактора, поскольку оно как бы притягивает к себе точку, представляющую движение маятника на фазовой диаграмме. Конечно, в аттракторе, состоящем из одной-единственной точки, нет ничего странного.
Несколько более замысловатый аттрактор характеризует движение старинных настенных часов с грузом на цепочке. Груз играет роль механизма, подкачивающего энергию к маятнику, благодаря чему он не замедляет своего движения. Если запустить часы энергичным толчком маятника, он замедляется до темпа, обусловленного механизмом груза, и затем характер его движения остается неизменным. Однако если запустить часы слабым толчком, то маятник ведет себя подобно обычному, энергетически независимому маятнику - он постепенно замедляется и останавливается. В случае слишком сильного начального толчка движение маятника на фазовой диаграмме представляется спиралью, обвивающейся все более плотно вокруг круговой орбиты. Здесь аттрактор является кругом. И в данном случае окружность не кажется нам более странным объектом, чем точка.
Обыкновенному маятнику можно придать хаотическое поведение, подвергнув его вертикальной вибрации: если точка подвеса начнет двигаться вверх и вниз, совершая гармонические колебания под действием электромотора, то маятник может качаться совершенно непредсказуемым образом, без всяких признаков периодичности.
Однако, чтобы синтезировать хаос, я выбрал другую физическую систему, а именно три усилителя, первый из которых выдает на выходе сигнал x, поступающий на два других усилителя. Второй усилитель выдает сигнал 1-x, имея на входе x. На вход третьего усилителя поступают два сигнала: x и 1-х. На выходе он выдает произведение входных сигналов x(1-х), которое подается на вход первого усилителя. Сюда же подается управляющее напряжение r. Эту систему завершает еще один компонент - устройство, на короткие промежутки времени выдающее на выходе тот сигнал, который в данный момент поступает ему на вход. Это устройство находится на выходе первого усилителя. Описанная электронная схема из трех усилителей порождает танец напряжения, который становится все более неистовым по мере того, как управляющее напряжение r постепенно увеличивается.
При r меньше 3 и первоначальном ненулевом значении x схема в течение короткого времени выдает осциллирующий сигнал, но затем приходит к некоторому фиксированному значению x, которое остается уже неизменным. Это значение представляет собой аттрактор в виде одной точки. Если управляющее напряжение r повысить до уровня, несколько превышающего 3, сигнал начинает колебаться между двумя значениями x. На этом уровне r о системе можно сказать, что она бистабильна и что аттрактор состоит из двух точек. При дальнейшем увеличении r сигнал колеблется уже около четырех точек. Если увеличить r еще больше, мы придем к аттрактору из восьми точек и т.д. При каждом небольшом повороте ручки, управляющей напряжением r, число точек удваивается, а когда напряжение достигает определенного значения, лежащего приблизительно посередине между 3 и 4, сигнал, вырабатываемый схемой, внезапно "сходит с ума". С огромной электронной скоростью он начинает бесконечно гоняться за простыми, повторяющимися закономерностями, которые были присущи ему ранее. Теперь его поведение управляется странным аттрактором, обладающим потенциально бесконечным количеством значений. В результате получается хаос.
Читатели, знакомые с электроникой, возможно, захотят сами собрать подобную схему. Другие же смогут смоделировать ее на компьютере (неважно, большом или маленьком) и увидеть этот танец во всей его красе на экране дисплея. Для этого нужно написать простую программу, решающую итерационным методом уравнение x <- x(1-x). Программа, которую я назову CHAOS1, имеет ядро, состоящее из шести инструкций:
x <- 0.3
for i <- 1 to 200
- x <- rx(1-x)
for i <- 1 to 300
- x <- rх(1-х)
- plot(200x, 100)
Исходное значение переменной х равно 0.3. Сначала программа CHAOS1 входит в цикл, итерирующий основное уравнение 200 раз, чтобы выйти из промежуточного, неустановившегося режима. Этот неустановившийся режим присущ свойствам самого уравнения и не является результатом приближенных вычислений. Причина этого явления будет пояснена ниже в геометрической интерпретации. Затем программа входит в новый цикл, итерирующий уравнение еще 300 раз и высвечивающий каждое значение x на экране.
Параметр 100 в графической инструкции plot приведенного выше алгоритма принят произвольно; в данном случае экран имеет размеры 200 на 200. Горизонтальная координата 200x распределяет вычисленные значения x (всегда находящиеся в интервале от 0 до 1) вдоль одной строки на экране, установленной на высоте 100 - как раз посередине гипотетического экрана.
В зависимости от устанавливаемого значения управляющего параметра f программа высветит либо одну и ту же точку на экране 300 раз, либо несколько точек, меньше чем 300 раз каждую. Она может даже попытаться уловить хаос, высвечивая 300 различных точек странного аттрактора. Если увеличить число шагов итерационного процесса, картина странного аттрактора будет уже полнее. В любом случае, после того как итерационный процесс установился, значения x начинают прыгать систематическим образом от одной точки аттрактора к другой. Аттракторы называют также орбитами независимо от того, конечно или бесконечно количество их точек.
Полная картина поведения рассмотренной простой схемы с усилителями возникает по мере того, как программа строит ряд изображений, расположенных одно под другим (см. рисунок справа). Эти изображения соответствуют ряду значений управляющего параметра r, изменяющихся от 2,9 до 4,0, скажем, за 200 шагов от верхнего до нижнего края экрана. Более изящную картинку можно получить, если увеличить число шагов, скажем, до 4000, однако в этом случае диаграмма не поместится ни на каком экране, и чтобы увидеть ее целиком, нужно распечатать ее на бумаге.

На бифуркационной диаграмме показан переход к хаосу
При значениях r, меньших 3,56 (более точное значение этого порога равно 3,56994571869), аттракторы нашей простой динамической системы, запечатленной в итерационном уравнении x <- x(1-х), состоят из нескольких точек. Эти точки, представляющие нехаотическое поведение, образуют три большие полосы и бесконечное количество полос меньшего размера. Аттракторы становятся странными, когда значение г приближается к 3,56. Здесь начинается хаос; до этого плавно разветвлявшиеся линии внезапно превращаются в сумасшедшие зигзаги и россыпи. Странно и то, что хаотическое поведение время от времени прерывается, по мере того как значение r продолжает приближаться к 4.
Получаемое таким образом изображение называется бифуркационной диаграммой. Если посмотреть на нее немного сбоку, то можно, наверное, подумать, что это хаотический спектр звезды x. Изображение украшено кривыми линиями и привлекательными теневыми складками. Почему диаграмма обладает такими декоративными свойствами - загадка, которую можно объяснить только при помощи теории хаоса. Мы еще коснемся этой темы ниже. А пока читателей, наверное, волнует другая загадка: почему это, казалось бы, невинное уравнение ведет себя так странно?
Поведение уравнения при нехаотических значениях параметра r может быть промоделировано геометрически, если мы нарисуем параболу, описываемую уравнением y = rx(1-x), где x - значение по оси абсцисс, а y - значение по оси ординат. Наложим на эту параболу прямую линию y = x. Описываемая процедура прослеживается на верхнем рисунке на с.98, где значение r установлено равным 3.3 и аттрактор системы состоит из двух точек. Чтобы показать, как ведет себя система, было выбрано начальное значение x. Я принял его равным 0.3, хотя можно было с таким же успехом выбрать любое другое значение.

Геометрическое моделирование простой системы приводит к возникновению двухточечного аттрактора
Первая итерация для уравнения моделируется проведением вертикальной линии, начинающейся в точке x = 0.3 в основании графика. Мы продолжаем эту линию до тех пор, пока она не дойдет до графика параболы. Точку, в которой линия касается параболы, обозначим A. Высота этой точки равна соответствующему значению координаты y. На втором шаге итерационного процесса это значение y вводится обратно в уравнение в качестве значения переменной x. Графически эта процедура соответствует измерению высоты пересечения вертикальной прямой и параболы, откладыванию измеренного расстояния по горизонтальной оси и проведению новой вертикальной линии от полученной отметки на горизонтальной оси до пересечения с параболой. Здесь эта процедура проводится в сокращенной версии, путем проведения горизонтальной линии от точки A до диагональной прямой y = x. Новую точку пересечения обозначим B. Заметим, что точка B и точка начала отсчета находятся в диагонально противоположных углах квадрата, сторона которого равна значению y, полученному на первом шаге итераций. Поэтому значение y снова можно ввести в систему, проведя вертикальную линию из точки B до пересечения с параболой (в точке C). Постоянно повторяя процедуру проведения вертикальных прямых до пересечения с параболой и горизонтальных линий до пересечения с диагональной прямой, мы получаем прямоугольные траектории, стремящиеся как бы по спирали к квадрату.
Наша геометрическая процедура шаг за шагом имитирует алгоритм программы CHAOS1. Те две точки, в которых результирующий квадрат пересекает параболу, соответствуют двухточечному аттрактору. Предприимчивые программисты, возможно, заинтересуются задачей генерирования подобных рисунков на компьютере. Если они это сделают, то, наверное, смогут глубже понять природу рассматриваемого нами "простого" итерационного уравнения. Интересно, как будут выглядеть рисунки, когда наступит хаос? Значения параметра r, приводящие к хаотическому поведению, выглядят случайными, но являются ли они на самом деле случайными?
Идеей совершить путешествие в страну хаоса я обязан группе читателей, среди которых был и Дж.П.Кратчфилд, один из авторов статьи "Хаос", о которой мы уже упоминали. Как объясняют Кратчфилд и его коллеги, соавторы статьи, "ключ к пониманию хаотического поведения лежит в понимании простых операций растяжения и свертывания, происходящих в пространстве состояний". В рассмотренном примере простой системы усилителей пространство состояний соответствует отрезку линии, содержащему точки аттрактора и точку, представляющую текущее значение х. Где тут возникает растяжение и свертывание?
Итерирование уравнения x <- rx(1-x) сводится к отображению точек на отрезке между 0 и 1 в участок параболической кривой. Точки, расположенные поблизости друг от друга на единичном отрезке, в особенности те, что лежат в окрестности 0, оказываются разнесенными дальше друг от друга, когда они отображаются на параболическую кривую. Это происходит, конечно, тогда, когда число rx(1-x) заменяет x. Свертывание возникает благодаря симметричности параболы; кроме вершины параболы для любого значения rx(1-x) всегда можно найти две точки единичного отрезка, отображающиеся в это значение. Это, конечно, точки x и 1-x.
Структура бифуркационной диаграммы была довольно подробно исследована теоретиками. Границы областей хаотического поведения устанавливаются максимальным и минимальным значениями, итерируемыми от x = 0.5. Кривые, за которыми следуют минимумы и максимумы, а также кривые, за которыми следуют "вуали", так причудливо свешивающиеся в хаотических областях, являются графиками простых полиномов по r. В местах наибольшего сгущения тени наблюдается самая высокая концентрация точек странных аттракторов. В пустых полосах, упомянутых выше, хаос уступает место порядку. Теория говорит, что для каждого целого числа существует полоса (она может быть сколь угодно узкой) с орбитами точно такого размера. Наконец, читателей, знакомых со свойствами хаоса, наверное, не удивит тот факт, что странные аттракторы, лаже в такой простенькой системе, которую мы исследовали, обладают фрактальной природой: рисунок из бесконечного числа точек имеет интересные узоры, повторяющиеся при любой степени увеличения рисунка, подобно множеству Мандельброта, описанному в журнале "В мире науки", 1985, #10. Более сложные динамические системы описываются уравнениями Энона, названными так в честь французского математика Мишеля Энона. Так называемые отображения Энона не только описывают физические системы, подобные движущимся астероидам или капающим водопроводным кранам, но генерируют также чудесные изображения. Отображение Энона состоит из пары уравнения. Рассмотрим следующий пример:
x <- x*cos(a)-(y-x2)sin(a)
y <- x*sin(a)+(y-x2)cos(a)
По текущим значениям двух переменных x и y в правых частях уравнений вычисляются новые значения (также обозначаемые через x и y) в левых частях.
В программе CHAOS2 эти два уравнения используются для создания изображений порядка и хаоса, присущих широкому классу динамических систем. Основной фрагмент программы CHAOS2 очень похож на аналогичный фрагмент программы CHAOS1:
input x, y
for i <- 1 to 1000
- хх <- x*cos(a)-(y-x2)sin(a)
- у <- x*sin(a)+(y-x2)cos(a)
- x <- xx
- plot (100x, 100y)
Различия между этими программами объясняются двумя причинами: в программе CHAOS2 мы имеем две итерируемые переменные вместо одной, и система, описываемая отображением Энона, является консервативной, а не диссипативной. Поскольку у нас два уравнения, необходимо ввести временную переменную xx для нового значения x, в то время пока текущее значение x используется еще во втором уравнении. Тот факт, что описываемая динамическая система консервативна, означает, что предварительный итерационный цикл для исключения промежуточных значений в неустановившемся режиме может быть опущен. Потери энергии, объясняющиеся трением или какими-либо другими факторами, здесь отсутствуют. Следовательно, здесь нет и аттракторов как таковых. Однако можно сказать, что каждая вычисленная системой орбита является своим собственным аттрактором. Как бы то ни было, странность (или хаос) определенно присутствует в отображении Энона. Наконец, отметим, что при любом значении параметра а результирующая система имеет множество орбит и благодаря свойству консервативности любая исходная пара значений x и y будет представлять точку, уже находящуюся на одной из орбит, таким образом, притяжение здесь является, если можно так выразиться, мгновенным. По этой причине в программе CHAOS2 не используются стандартные исходные значения для итерируемых переменных. Они должны быть введены перед выполнением основного цикла.
Построение программы CHAOS2 завершается, если перед ее основной частью поставить инструкцию ввода, позволяющую программисту выбрать значение a. Как и в программе CHAOS1, каждое новое значение a приводит к новой системе. Но поскольку система двумерна, выборка орбит занимает все свободное место и мы не можем теперь систематически варьировать параметр a, не вызывая на экране такого хаоса, который уже нежелателен.
Поэтому пользователь программы CHAOS2 задает исходную орбиту, вводя координаты одной из ее точек. Затем, откинувшись в кресле, он может с интересом наблюдать, как на экране возникает орбита. Она может оказаться кривой линией (нарисованной как бы пунктиром), либо чем-то более необычным. Например, на нижнем рисунке на с.98 показана последовательность из 38 орбит, построенных с использованием отображения Энона, со значением а, равным 1.111. При постепенном удалении от центра изображения видим, как орбиты образуют гнездо из замкнутых траекторий, затем внезапно появляются маленькие "островки": отдельные орбиты, вклинившиеся между более крупными, вложенными друг в друга орбитами. Двигаясь дальше, мы видим, как продолжается рисунок из вложенных орбит, сменяющийся хаосом. Во внешних частях изображения опять появляются островки вперемешку с кластерами случайно разбросанных точек, предвещающих наступление хаоса. Одна из хаотических областей (заключенная на рисунке в прямоугольную рамку) показана в увеличенном виде. Читателям, которые захотят рассматривать диаграммы Энона в увеличенном масштабе, мы советуем пользоваться самыми точными арифметическими операциями, имеющимися на их компьютерах.

Последовательные орбиты отображения Энона (слева) вырождаются в хаос (справа)
Как я уже говорил выше, отображения Энона представляют широкое многообразие консервативных физических систем, например таких, как астероиды, движущиеся по орбитам вокруг Солнца. К сожалению, орбиты на наших диаграммах - это не те орбиты, по которым движутся астероиды, а лишь фазовые их представления. На только что рассмотренных диаграммах по горизонтальной оси можно откладывать параметр, характеризующий положение астероида в пространстве, например расстояние до Солнца; по вертикальной оси можно откладывать скорость в радиальном направлении, или скорость изменения расстояния до Солнца. Каждая точка орбиты, вычисленной при помощи отображения Энона, представляет пару величин: расстояние до Солнца и скорость астероида, движущегося под определенным углом по отношению к направлению на Солнце, т.е. когда астероид проходит через вертикальную плоскость, составляющую этот угол с направлением на Солнце. Последовательные точки, вычисленные при помощи отображения, представляют последовательные появления астероида на этой плоскости. Островки, упомянутые выше,- это резонансные полосы, возникающие из-за возмущений орбиты астероида более крупными телами Солнечной системы, такими, как Юпитер. В хаотических областях положение и скорость астероида будут изменяться, по существу, случайным образом каждый раз, когда астероид будет вновь появляться на плоскости. Его движение непредсказуемо.
С эстетической точки зрения заслуживают внимания некоторые другие изображения, полученные при помощи отображений Энона. Независимо от их физической интерпретации, они выглядят весьма своеобразно, напоминая какие-то причудливые водные организмы (см. рисунок на с.99).

Отображение Энона генерирует различные фигуры при a = 0.264 (слева) и a = 1.5732 (справа)
Читатель из голландского города Лейден П. де Йонг предложил недавно некоторые интересные итерационные формулы, генерирующие весьма своеобразные формы и изображения. Он рекомендует обратить внимание на следующие формулы с четырьмя параметрами:
x <- sin(ax)-cos(bx)
y <- sin(cx)-cos(dy)
Начинаем с нулевых значений x и y. Затем, чтобы получить изображение того, что де Йонг называет "цыплячьими ножками", подставим a = 2.01; b = -2.53; c = 1,61 и d = -0.33. При значениях этих параметров соответственно -2.7; -0.9; -0.86; -2.2 получим "катапульту", стреляющую точками", а если их значения равны -2.24; 0.43; -0.65 и -2.43, то можно увидеть "пасхальное яичко, украшающее само себя".
Подобно де Йонгу, читатели могут изобретать свои собственные итерационные формулы и экспериментировать с ними.
БИБЛИОГРАФИЯ
HENON MAPPING WITH PASCAL. GORDON HUGHES in Byte, Vol.11, No.13, pages 161-192; December, 1986.
ОТКЛИКИ
1 1988
Свойства хаоса были исследованы многочисленными читателями, пожелавшими и сумевшими запрограммировать итерационную формулу, приведенную в статье нашей рубрики в октябрьском номере журнала. На самом деле несколько энтузиастов, среди них X.Марк из Сафферна (шт.Нью-Йорк), последовали моему предложению и проследили за самим итерационным процессом, наблюдая за паутиной, сплетающейся вокруг параболы. Сходимость процесса можно наблюдать по мере того, как эта паутина принимает стабильную форму. В отличие от этого в хаотическом режиме она заполняет целую область экрана запутанной структурой белых квадратов, не устанавливающихся ни в какую стабильную картину. Ч.Плантц из Уэст-Браунсвиля (шт.Пенсильвания) воспользовался своим персональным компьютером как микроскопом, нацелив его на дугу бифуркационной диаграммы, имеющую форму стремени, как раз над одной из хаотических областей. Но он обнаружил там не "соль и перец", как я, возможно, предсказал бы ему, а скорее слои и складчатые структуры, вторгающиеся в зоны хаоса.
СТРАННАЯ ПРИВЛЕКАТЕЛЬНОСТЬ ХАОСА
А.К.ДЬЮДНИ
ХАОС ОБЛАДАЕТ странной привлекательностью для ума, способного увидеть в нем закономерности. Некоторые физические системы в своем хаотическом поведении в каком-то смысле стремятся к упорядоченности, в которой мы наблюдаем такие закономерности. К тому же внешние проявления этих закономерностей сами по себе кажутся нам какими-то странно привлекательными. Кое-кто из читателей уже, наверное, знает, что геометрические формы, лежащие в основе хаоса, называются странными, или хаотическими, аттракторами (см.: Дж.П.Кратчфилд, Дж.Д.Фармер, Н.X.Пэкард, Р.Шоу. Хаос, "В мире науки", 1987, #2). Странные аттракторы (от англ. attractive - привлекательный, притягательный) можно генерировать и с помощью персонального компьютера.
Но прежде чем отправиться в страну хаоса, читателям нужно вооружиться необходимыми доспехами - интуитивным пониманием основных физических понятий, которые нам встретятся. В частности, что такое аттрактор? Грубо говоря, аттрактор - это обобщение понятия равновесия, это то состояние, к которому приходит в конце концов система, то, к чему она притягивается. Простым примером физической системы, иллюстрирующей понятие аттрактора, служит маятник. Представим обычный движущийся маятник, который под воздействием сил трения замедляется и в конце концов останавливается. Движение маятника можно описать посредством так называемой фазовой диаграммы, или диаграммы состояний, по одной оси которой откладывается угол, составляемый маятником с вертикалью, а по другой - скорость изменения этого угла. Движение качающегося маятника на фазовой диаграмме представляется точкой, движущейся вокруг начала отсчета. По мере того как маятник теряет энергию, эта точка приближается по спирали к точке начала отсчета, где в конце концов и останавливается. В данном случае начало отсчета выступает в роли аттрактора, поскольку оно как бы притягивает к себе точку, представляющую движение маятника на фазовой диаграмме. Конечно, в аттракторе, состоящем из одной-единственной точки, нет ничего странного.
Несколько более замысловатый аттрактор характеризует движение старинных настенных часов с грузом на цепочке. Груз играет роль механизма, подкачивающего энергию к маятнику, благодаря чему он не замедляет своего движения. Если запустить часы энергичным толчком маятника, он замедляется до темпа, обусловленного механизмом груза, и затем характер его движения остается неизменным. Однако если запустить часы слабым толчком, то маятник ведет себя подобно обычному, энергетически независимому маятнику - он постепенно замедляется и останавливается. В случае слишком сильного начального толчка движение маятника на фазовой диаграмме представляется спиралью, обвивающейся все более плотно вокруг круговой орбиты. Здесь аттрактор является кругом. И в данном случае окружность не кажется нам более странным объектом, чем точка.
Обыкновенному маятнику можно придать хаотическое поведение, подвергнув его вертикальной вибрации: если точка подвеса начнет двигаться вверх и вниз, совершая гармонические колебания под действием электромотора, то маятник может качаться совершенно непредсказуемым образом, без всяких признаков периодичности.
Однако, чтобы синтезировать хаос, я выбрал другую физическую систему, а именно три усилителя, первый из которых выдает на выходе сигнал x, поступающий на два других усилителя. Второй усилитель выдает сигнал 1-x, имея на входе x. На вход третьего усилителя поступают два сигнала: x и 1-х. На выходе он выдает произведение входных сигналов x(1-х), которое подается на вход первого усилителя. Сюда же подается управляющее напряжение r. Эту систему завершает еще один компонент - устройство, на короткие промежутки времени выдающее на выходе тот сигнал, который в данный момент поступает ему на вход. Это устройство находится на выходе первого усилителя. Описанная электронная схема из трех усилителей порождает танец напряжения, который становится все более неистовым по мере того, как управляющее напряжение r постепенно увеличивается.
При r меньше 3 и первоначальном ненулевом значении x схема в течение короткого времени выдает осциллирующий сигнал, но затем приходит к некоторому фиксированному значению x, которое остается уже неизменным. Это значение представляет собой аттрактор в виде одной точки. Если управляющее напряжение r повысить до уровня, несколько превышающего 3, сигнал начинает колебаться между двумя значениями x. На этом уровне r о системе можно сказать, что она бистабильна и что аттрактор состоит из двух точек. При дальнейшем увеличении r сигнал колеблется уже около четырех точек. Если увеличить r еще больше, мы придем к аттрактору из восьми точек и т.д. При каждом небольшом повороте ручки, управляющей напряжением r, число точек удваивается, а когда напряжение достигает определенного значения, лежащего приблизительно посередине между 3 и 4, сигнал, вырабатываемый схемой, внезапно "сходит с ума". С огромной электронной скоростью он начинает бесконечно гоняться за простыми, повторяющимися закономерностями, которые были присущи ему ранее. Теперь его поведение управляется странным аттрактором, обладающим потенциально бесконечным количеством значений. В результате получается хаос.
Читатели, знакомые с электроникой, возможно, захотят сами собрать подобную схему. Другие же смогут смоделировать ее на компьютере (неважно, большом или маленьком) и увидеть этот танец во всей его красе на экране дисплея. Для этого нужно написать простую программу, решающую итерационным методом уравнение x <- x(1-x). Программа, которую я назову CHAOS1, имеет ядро, состоящее из шести инструкций:
x <- 0.3
for i <- 1 to 200
- x <- rx(1-x)
for i <- 1 to 300
- x <- rх(1-х)
- plot(200x, 100)
Исходное значение переменной х равно 0.3. Сначала программа CHAOS1 входит в цикл, итерирующий основное уравнение 200 раз, чтобы выйти из промежуточного, неустановившегося режима. Этот неустановившийся режим присущ свойствам самого уравнения и не является результатом приближенных вычислений. Причина этого явления будет пояснена ниже в геометрической интерпретации. Затем программа входит в новый цикл, итерирующий уравнение еще 300 раз и высвечивающий каждое значение x на экране.
Параметр 100 в графической инструкции plot приведенного выше алгоритма принят произвольно; в данном случае экран имеет размеры 200 на 200. Горизонтальная координата 200x распределяет вычисленные значения x (всегда находящиеся в интервале от 0 до 1) вдоль одной строки на экране, установленной на высоте 100 - как раз посередине гипотетического экрана.
В зависимости от устанавливаемого значения управляющего параметра f программа высветит либо одну и ту же точку на экране 300 раз, либо несколько точек, меньше чем 300 раз каждую. Она может даже попытаться уловить хаос, высвечивая 300 различных точек странного аттрактора. Если увеличить число шагов итерационного процесса, картина странного аттрактора будет уже полнее. В любом случае, после того как итерационный процесс установился, значения x начинают прыгать систематическим образом от одной точки аттрактора к другой. Аттракторы называют также орбитами независимо от того, конечно или бесконечно количество их точек.
Полная картина поведения рассмотренной простой схемы с усилителями возникает по мере того, как программа строит ряд изображений, расположенных одно под другим (см. рисунок справа). Эти изображения соответствуют ряду значений управляющего параметра r, изменяющихся от 2,9 до 4,0, скажем, за 200 шагов от верхнего до нижнего края экрана. Более изящную картинку можно получить, если увеличить число шагов, скажем, до 4000, однако в этом случае диаграмма не поместится ни на каком экране, и чтобы увидеть ее целиком, нужно распечатать ее на бумаге.

На бифуркационной диаграмме показан переход к хаосу
При значениях r, меньших 3,56 (более точное значение этого порога равно 3,56994571869), аттракторы нашей простой динамической системы, запечатленной в итерационном уравнении x <- x(1-х), состоят из нескольких точек. Эти точки, представляющие нехаотическое поведение, образуют три большие полосы и бесконечное количество полос меньшего размера. Аттракторы становятся странными, когда значение г приближается к 3,56. Здесь начинается хаос; до этого плавно разветвлявшиеся линии внезапно превращаются в сумасшедшие зигзаги и россыпи. Странно и то, что хаотическое поведение время от времени прерывается, по мере того как значение r продолжает приближаться к 4.
Получаемое таким образом изображение называется бифуркационной диаграммой. Если посмотреть на нее немного сбоку, то можно, наверное, подумать, что это хаотический спектр звезды x. Изображение украшено кривыми линиями и привлекательными теневыми складками. Почему диаграмма обладает такими декоративными свойствами - загадка, которую можно объяснить только при помощи теории хаоса. Мы еще коснемся этой темы ниже. А пока читателей, наверное, волнует другая загадка: почему это, казалось бы, невинное уравнение ведет себя так странно?
Поведение уравнения при нехаотических значениях параметра r может быть промоделировано геометрически, если мы нарисуем параболу, описываемую уравнением y = rx(1-x), где x - значение по оси абсцисс, а y - значение по оси ординат. Наложим на эту параболу прямую линию y = x. Описываемая процедура прослеживается на верхнем рисунке на с.98, где значение r установлено равным 3.3 и аттрактор системы состоит из двух точек. Чтобы показать, как ведет себя система, было выбрано начальное значение x. Я принял его равным 0.3, хотя можно было с таким же успехом выбрать любое другое значение.

Геометрическое моделирование простой системы приводит к возникновению двухточечного аттрактора
Первая итерация для уравнения моделируется проведением вертикальной линии, начинающейся в точке x = 0.3 в основании графика. Мы продолжаем эту линию до тех пор, пока она не дойдет до графика параболы. Точку, в которой линия касается параболы, обозначим A. Высота этой точки равна соответствующему значению координаты y. На втором шаге итерационного процесса это значение y вводится обратно в уравнение в качестве значения переменной x. Графически эта процедура соответствует измерению высоты пересечения вертикальной прямой и параболы, откладыванию измеренного расстояния по горизонтальной оси и проведению новой вертикальной линии от полученной отметки на горизонтальной оси до пересечения с параболой. Здесь эта процедура проводится в сокращенной версии, путем проведения горизонтальной линии от точки A до диагональной прямой y = x. Новую точку пересечения обозначим B. Заметим, что точка B и точка начала отсчета находятся в диагонально противоположных углах квадрата, сторона которого равна значению y, полученному на первом шаге итераций. Поэтому значение y снова можно ввести в систему, проведя вертикальную линию из точки B до пересечения с параболой (в точке C). Постоянно повторяя процедуру проведения вертикальных прямых до пересечения с параболой и горизонтальных линий до пересечения с диагональной прямой, мы получаем прямоугольные траектории, стремящиеся как бы по спирали к квадрату.
Наша геометрическая процедура шаг за шагом имитирует алгоритм программы CHAOS1. Те две точки, в которых результирующий квадрат пересекает параболу, соответствуют двухточечному аттрактору. Предприимчивые программисты, возможно, заинтересуются задачей генерирования подобных рисунков на компьютере. Если они это сделают, то, наверное, смогут глубже понять природу рассматриваемого нами "простого" итерационного уравнения. Интересно, как будут выглядеть рисунки, когда наступит хаос? Значения параметра r, приводящие к хаотическому поведению, выглядят случайными, но являются ли они на самом деле случайными?
Идеей совершить путешествие в страну хаоса я обязан группе читателей, среди которых был и Дж.П.Кратчфилд, один из авторов статьи "Хаос", о которой мы уже упоминали. Как объясняют Кратчфилд и его коллеги, соавторы статьи, "ключ к пониманию хаотического поведения лежит в понимании простых операций растяжения и свертывания, происходящих в пространстве состояний". В рассмотренном примере простой системы усилителей пространство состояний соответствует отрезку линии, содержащему точки аттрактора и точку, представляющую текущее значение х. Где тут возникает растяжение и свертывание?
Итерирование уравнения x <- rx(1-x) сводится к отображению точек на отрезке между 0 и 1 в участок параболической кривой. Точки, расположенные поблизости друг от друга на единичном отрезке, в особенности те, что лежат в окрестности 0, оказываются разнесенными дальше друг от друга, когда они отображаются на параболическую кривую. Это происходит, конечно, тогда, когда число rx(1-x) заменяет x. Свертывание возникает благодаря симметричности параболы; кроме вершины параболы для любого значения rx(1-x) всегда можно найти две точки единичного отрезка, отображающиеся в это значение. Это, конечно, точки x и 1-x.
Структура бифуркационной диаграммы была довольно подробно исследована теоретиками. Границы областей хаотического поведения устанавливаются максимальным и минимальным значениями, итерируемыми от x = 0.5. Кривые, за которыми следуют минимумы и максимумы, а также кривые, за которыми следуют "вуали", так причудливо свешивающиеся в хаотических областях, являются графиками простых полиномов по r. В местах наибольшего сгущения тени наблюдается самая высокая концентрация точек странных аттракторов. В пустых полосах, упомянутых выше, хаос уступает место порядку. Теория говорит, что для каждого целого числа существует полоса (она может быть сколь угодно узкой) с орбитами точно такого размера. Наконец, читателей, знакомых со свойствами хаоса, наверное, не удивит тот факт, что странные аттракторы, лаже в такой простенькой системе, которую мы исследовали, обладают фрактальной природой: рисунок из бесконечного числа точек имеет интересные узоры, повторяющиеся при любой степени увеличения рисунка, подобно множеству Мандельброта, описанному в журнале "В мире науки", 1985, #10. Более сложные динамические системы описываются уравнениями Энона, названными так в честь французского математика Мишеля Энона. Так называемые отображения Энона не только описывают физические системы, подобные движущимся астероидам или капающим водопроводным кранам, но генерируют также чудесные изображения. Отображение Энона состоит из пары уравнения. Рассмотрим следующий пример:
x <- x*cos(a)-(y-x2)sin(a)
y <- x*sin(a)+(y-x2)cos(a)
По текущим значениям двух переменных x и y в правых частях уравнений вычисляются новые значения (также обозначаемые через x и y) в левых частях.
В программе CHAOS2 эти два уравнения используются для создания изображений порядка и хаоса, присущих широкому классу динамических систем. Основной фрагмент программы CHAOS2 очень похож на аналогичный фрагмент программы CHAOS1:
input x, y
for i <- 1 to 1000
- хх <- x*cos(a)-(y-x2)sin(a)
- у <- x*sin(a)+(y-x2)cos(a)
- x <- xx
- plot (100x, 100y)
Различия между этими программами объясняются двумя причинами: в программе CHAOS2 мы имеем две итерируемые переменные вместо одной, и система, описываемая отображением Энона, является консервативной, а не диссипативной. Поскольку у нас два уравнения, необходимо ввести временную переменную xx для нового значения x, в то время пока текущее значение x используется еще во втором уравнении. Тот факт, что описываемая динамическая система консервативна, означает, что предварительный итерационный цикл для исключения промежуточных значений в неустановившемся режиме может быть опущен. Потери энергии, объясняющиеся трением или какими-либо другими факторами, здесь отсутствуют. Следовательно, здесь нет и аттракторов как таковых. Однако можно сказать, что каждая вычисленная системой орбита является своим собственным аттрактором. Как бы то ни было, странность (или хаос) определенно присутствует в отображении Энона. Наконец, отметим, что при любом значении параметра а результирующая система имеет множество орбит и благодаря свойству консервативности любая исходная пара значений x и y будет представлять точку, уже находящуюся на одной из орбит, таким образом, притяжение здесь является, если можно так выразиться, мгновенным. По этой причине в программе CHAOS2 не используются стандартные исходные значения для итерируемых переменных. Они должны быть введены перед выполнением основного цикла.
Построение программы CHAOS2 завершается, если перед ее основной частью поставить инструкцию ввода, позволяющую программисту выбрать значение a. Как и в программе CHAOS1, каждое новое значение a приводит к новой системе. Но поскольку система двумерна, выборка орбит занимает все свободное место и мы не можем теперь систематически варьировать параметр a, не вызывая на экране такого хаоса, который уже нежелателен.
Поэтому пользователь программы CHAOS2 задает исходную орбиту, вводя координаты одной из ее точек. Затем, откинувшись в кресле, он может с интересом наблюдать, как на экране возникает орбита. Она может оказаться кривой линией (нарисованной как бы пунктиром), либо чем-то более необычным. Например, на нижнем рисунке на с.98 показана последовательность из 38 орбит, построенных с использованием отображения Энона, со значением а, равным 1.111. При постепенном удалении от центра изображения видим, как орбиты образуют гнездо из замкнутых траекторий, затем внезапно появляются маленькие "островки": отдельные орбиты, вклинившиеся между более крупными, вложенными друг в друга орбитами. Двигаясь дальше, мы видим, как продолжается рисунок из вложенных орбит, сменяющийся хаосом. Во внешних частях изображения опять появляются островки вперемешку с кластерами случайно разбросанных точек, предвещающих наступление хаоса. Одна из хаотических областей (заключенная на рисунке в прямоугольную рамку) показана в увеличенном виде. Читателям, которые захотят рассматривать диаграммы Энона в увеличенном масштабе, мы советуем пользоваться самыми точными арифметическими операциями, имеющимися на их компьютерах.

Последовательные орбиты отображения Энона (слева) вырождаются в хаос (справа)
Как я уже говорил выше, отображения Энона представляют широкое многообразие консервативных физических систем, например таких, как астероиды, движущиеся по орбитам вокруг Солнца. К сожалению, орбиты на наших диаграммах - это не те орбиты, по которым движутся астероиды, а лишь фазовые их представления. На только что рассмотренных диаграммах по горизонтальной оси можно откладывать параметр, характеризующий положение астероида в пространстве, например расстояние до Солнца; по вертикальной оси можно откладывать скорость в радиальном направлении, или скорость изменения расстояния до Солнца. Каждая точка орбиты, вычисленной при помощи отображения Энона, представляет пару величин: расстояние до Солнца и скорость астероида, движущегося под определенным углом по отношению к направлению на Солнце, т.е. когда астероид проходит через вертикальную плоскость, составляющую этот угол с направлением на Солнце. Последовательные точки, вычисленные при помощи отображения, представляют последовательные появления астероида на этой плоскости. Островки, упомянутые выше,- это резонансные полосы, возникающие из-за возмущений орбиты астероида более крупными телами Солнечной системы, такими, как Юпитер. В хаотических областях положение и скорость астероида будут изменяться, по существу, случайным образом каждый раз, когда астероид будет вновь появляться на плоскости. Его движение непредсказуемо.
С эстетической точки зрения заслуживают внимания некоторые другие изображения, полученные при помощи отображений Энона. Независимо от их физической интерпретации, они выглядят весьма своеобразно, напоминая какие-то причудливые водные организмы (см. рисунок на с.99).

Отображение Энона генерирует различные фигуры при a = 0.264 (слева) и a = 1.5732 (справа)
Читатель из голландского города Лейден П. де Йонг предложил недавно некоторые интересные итерационные формулы, генерирующие весьма своеобразные формы и изображения. Он рекомендует обратить внимание на следующие формулы с четырьмя параметрами:
x <- sin(ax)-cos(bx)
y <- sin(cx)-cos(dy)
Начинаем с нулевых значений x и y. Затем, чтобы получить изображение того, что де Йонг называет "цыплячьими ножками", подставим a = 2.01; b = -2.53; c = 1,61 и d = -0.33. При значениях этих параметров соответственно -2.7; -0.9; -0.86; -2.2 получим "катапульту", стреляющую точками", а если их значения равны -2.24; 0.43; -0.65 и -2.43, то можно увидеть "пасхальное яичко, украшающее само себя".
Подобно де Йонгу, читатели могут изобретать свои собственные итерационные формулы и экспериментировать с ними.
БИБЛИОГРАФИЯ
HENON MAPPING WITH PASCAL. GORDON HUGHES in Byte, Vol.11, No.13, pages 161-192; December, 1986.
ОТКЛИКИ
1 1988
Свойства хаоса были исследованы многочисленными читателями, пожелавшими и сумевшими запрограммировать итерационную формулу, приведенную в статье нашей рубрики в октябрьском номере журнала. На самом деле несколько энтузиастов, среди них X.Марк из Сафферна (шт.Нью-Йорк), последовали моему предложению и проследили за самим итерационным процессом, наблюдая за паутиной, сплетающейся вокруг параболы. Сходимость процесса можно наблюдать по мере того, как эта паутина принимает стабильную форму. В отличие от этого в хаотическом режиме она заполняет целую область экрана запутанной структурой белых квадратов, не устанавливающихся ни в какую стабильную картину. Ч.Плантц из Уэст-Браунсвиля (шт.Пенсильвания) воспользовался своим персональным компьютером как микроскопом, нацелив его на дугу бифуркационной диаграммы, имеющую форму стремени, как раз над одной из хаотических областей. Но он обнаружил там не "соль и перец", как я, возможно, предсказал бы ему, а скорее слои и складчатые структуры, вторгающиеся в зоны хаоса.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
10 1987
"ЛЕСТНИЦА СЛОВ": ЛИНГВИСТИЧЕСКИЕ ГОЛОВОЛОМКИ И ВОЗМОЖНОСТИ КОМПЬЮТЕРА
А.К.ДЬЮДНИ
НИКТО не знает, когда и при каких обстоятельствах исчезла марсианская цивилизация, лишь пещера у подножия горы Олимп хранит печальную память об этой древней и удивительной культуре. В самом дальнем углу пещеры стоит камень с высеченными на нем словами. Камень закрыт занавесом из пыльной ткани неизвестного нам состава. Раздвинув занавес, мы видим надписи, напоминающие словарь: одни слова расположены слева, другие - справа. У основания каменной дощечки высечены два предложения. Они соотносятся между собой любопытным образом. Дело в том, что первое предложение можно преобразовать во второе, последовательно заменяя составляющие его слова их эквивалентами из словаря. Каждое слово предложения, содержащееся в левой части словаря, можно заменить соответствующим ему словом из правой части.
Марсианскиепредложениянесодержатпробелов. Действительно, благодаря исключительной плавности и выразительности старомарсианского языка, пробелы в нем вовсе не нужны. Зачастую существует сразу много способов разбить марсианское предложение на составляющие его слова. Однако, как правило, лишь несколько таких разбиений имеют разумный смысл в данном контексте. Процесс подстановки слов по словарю можно проиллюстрировать на примере предложения, с которого начинается этот абзац. Если бы слово "одержатпробелов" входило в левую колонку словаря, а в правой колонке ему бы соответствовало слово "утвсебетайныйсмысл", то это последнее можно было бы подставить вместо первого, в результате чего получилось бы другое предложение: марсианскиепредложениянесутвсебетайныйсмысл.
Мудрецы марсианской древности считали, что всю необходимую информацию можно получить, начав с одного основного предложения и подставляя слова согласно словарю мудрости, единственный уцелевший фрагмент которого спрятан в пещере. Это основное предложение высечено первым в основании каменной дощечки у горы Олимп (см. рисунок внизу слева). Вообще говоря, компьютер будет не в состоянии установить, было ли выведено то или иное заданное предложение из другого заданного предложения. Другими словами, невозможно написать такую программу (неважно, насколько длинна программа и насколько высоко быстродействие компьютера), которая могла бы для любого заданного словаря и любых двух слов (или предложений) на входе установить, возможен ли переход от первого слова ко второму. Ниже я объясню, почему. А пока пусть читатели попробуют преобразовать первое предложение, высеченное на камне, во второе. (В данном случае такое преобразование возможно).

Марсианский словарь мудрости
Эта задачка о преобразовании предложений является представителем целого семейства головоломок, в которых производятся замены слов, предложений и даже целых абзацев другими словами, предложениями и абзацами. Одним из родоначальников этого направления в головоломках был и преподобный Чарлз Доджсон, известный также как Льюис Кэрролл. Среди множества других математических затей и головоломок, придуманных Кэрроллом во время его оксфордских прогулок, есть и игра под названием "Лестница слов". В этой игре нужно выбрать какие-нибудь два слова, принадлежащие одному языку и называемые источником и целью, а затем попытаться преобразовать первое слово во второе, заменяя каждый раз по одной букве.
Если оба слова состоят из одного и того же числа букв, то задача выглядит тривиально. Однако сумеете ли вы выдержать условие, чтобы все промежуточные цепочки букв были также словами выбранного языка? Это уже совсем другое дело, но и с этой задачей люди, поднаторевшие в словесных играх, справляются довольно легко. Начнем, например, со слова horse (лошадь). За один шаг его можно превратить в слово house (дом). Сделав еще один шаг, мы получим слово mouse (мышь). С помощью подобной алхимии лошадь, кажется, можно превратить практически во все что угодно, лишь бы название состояло из пяти букв. Действительно ли это возможно?
Чтобы ответить на этот вопрос в общей форме, необходимо построить грамматику переходов. Поскольку я противник заумной терминологии, я назвал это сетью слов. Полная сеть для английского языка была бы совершенно чудовищным образованием. Каждое слово языка было бы представлено в этой сети одним и только одним узлом. Чтобы удовлетворить требования игры "Лестница слов", две точки, или узла, соединяются в сети линией, если соответствующие им слова отличаются ровно на одну букву. Для того чтобы найти все слова, в которые можно превратить, например, слово horse (лошадь), нужно просто просмотреть всю сеть, начиная со слова horse и прибавляя к списку все повстречавшиеся в пути слова. Полное исследование такого пути было бы равносильно тому, чтобы потянуть сеть за узел horse и вытащить все узлы, соединяющиеся с ним. То, что мы вытащим, будет, наверное, напоминать порванную во многих местах рыболовную сеть. Конечно, абсолютное большинство слов не будет вытащено вслед за словом horse; например, любое слово, состоящее более чем из пяти букв, останется внизу.
Вытащим ли мы все пятибуквенные слова? Другими словами, возможно ли построить лестницу от слова horse к любому другому пятибуквенному слову английского языка? Я должен сознаться, что не знаю ответа на этот вопрос, но судя по откликам читателей на предыдущие задачи, я готов поспорить, что кто-нибудь сумеет решить и эту задачу. Необходимые для этого пособия - словарь в форме, читаемой компьютером, и программа, просматривающая словарь в поисках связанных друг с другом слов, т.е. слов, отличающихся одной буквой. Каждый раз, когда какое-то слово добавляется к списку слов, связанных со словом horse, программа вычеркивает его из словаря в памяти и снова пробегает через весь список, сравнивая каждое встреченное в нем слово со всеми словами все уменьшающегося словаря. Если слово из словаря отличается на одну букву от слова в списке, то первое добавляется к списку и процесс повторяется сначала. Различные словари, наверное, дадут различные результаты, не так ли? Возможно. С другой стороны, два в достаточной мере полных словаря могут дать один и тот же результат. Иначе говоря, сети могут оказаться настолько плотными, что их топология будет практически одинаковой.
Ответ на вопрос о том, связаны ли между собой все n-буквенные слова, для малых n можно получить практически вручную. Конечно же, все однобуквенные слова связаны между собой в сети слов. Вопрос о двухбуквенных словах можно решить здесь и сейчас. Согласно моему словарику, вот все двухбуквенные слова английского языка:
aa, ad, ae, ah, ai, am, an, ar, as, at, aw, ax, ay, ba, be, bi, bo, by, da, de, do, ef, eh, el, em, en, er, es, et, ex, fa, go, ha, he, hi, ho, id, if, in, is, it, jo, ka, la, li, lo, ma, me, mi, mu, my, na, no, nu, od, oe, of, oh, om, on, op, or, os, ow, ox, oy, pa, pe, pi, re, si, so, ta, ti, to, um, up, us, ut, we, wo, xi, xu, ya, ye.
Проведя небольшую работу, мы убеждаемся, что все эти слова связаны между собой. В самом деле, во-первых, все двухбуквенные слова, начинающиеся с одной и той же буквы, взаимно связаны. Это позволяет нам объединить такие слова в группы. Остается только заметить, что группа "a" связана с четырьмя другими группами слов, начинающихся с гласной буквы, далее, что группа "b" связана с другими 16 группами слов, начинающихся с согласных, и, наконец, что группы "a" и "b" также связаны между собой.
Возможно, на основании проверки, проведенной для двух наименьших значений n, кое-кто наберется смелости утверждать, что все n-буквенные слова английского языка тоже связаны между собой. Утверждение выглядит очень интригующим, что пожалуй характерно и для других абстрактных игр со словами. Читатели, располагающие компьютером, возможно, попытаются проверить справедливость этого утверждения для других малых значений л, например для л, равного 3 (см. рисунок вверху). А те, у кого нет компьютера, должны будут довольствоваться задачей по превращению слова hate (ненависть) в слово love (любовь). Или, еще лучше, попробуйте преобразовать слово evil (зло) Bgood (добро), углубив в процессе свое понимание вопросов морали и логики.

Сеть трехбуквенных слов
Игра "Лестница слов" представляет собой простой частный случай так называемой системы текстовых преобразований. Два главных компонента такой системы - это множество текстов, над которыми выполняются преобразования, и правила преобразований. Тексты могут представлять собой слова, предложения или абзацы, которые на самом деле являются лишь цепочками букв, независимо от того, каким образом было выбрано множество текстов. Правило преобразования представляет собой процедуру подстановки вместо части заданной цепочки букв другой цепочки. Обычно при применении процедуры подстановки используется словарь.
В "Лестнице слов", например, множество дозволенных цепочек букв состоит из всех английских слов по заданному словарю. Процедура преобразования заключается в том, чтобы по слову, заданному "на входе", сгенерировать другое слово, отличающееся от первого на одну букву и также принадлежащее словарю. В данном случае роль словаря играет просто список слов.
Большинство издаваемых словарей имеют элементы, состоящие из слов, которые "определены" посредством других слов. Здесь мы сталкиваемся с цепочкой переходов другого вида - более сложного по сравнению с "Лестницей слов". Представим, например, что мы начинаем с одного английского слова, смотрим на его значение в словаре и составляем список всех слов, встретившихся в его определении. Затем мы смотрим на значения слов из составленного списка, добавляем встреченные слова к списку и продолжаем этот процесс. Поскольку в английском языке содержится конечное число слов (не могу поручиться за другие языки), процесс приобретает вскоре циклический характер, если можяо так выразиться, т.е. определенные слова начинают встречаться повторно. Они определены частично через самих себя. Можно было бы назвать их "первичными" словами. К подобным словам следует отнестись с особым вниманием: возможно, они составляют неопределяемую понятийную основу английского языка.
Такое исследование, или, во всяком случае, нечто весьма сходное, было проведено Робертом Эмслером, сотрудником фирмы Bell Communications Research. Эмслер воспользовался словарем-тезаурусом, который был модифицирован таким образом, что определение каждого слова было сведено к некоторому набору "родовых" слов, служащих для обозначения широких классов понятий, к которым данное слово имеет отношение. Родовые слова были дополнены вспомогательными словами, позволяющими выделить данное слово среди других членов рола. Применив программу, подобную описанной выше, Эмслер провел исследование своего специального словаря и в общем нашел то, что предсказывали лингвисты-теоретики: первичные слова, которые использовались в определениях других первичных слов. Среди них такие слова, как "пища", "человек", "вещь", "инструмент" и "группа". Первичные слова занимали внешние участки ветвей структуры, представляющей "переплетенную иерархию" - нечто подобное лесу, в котором ветви различных деревьев срослись между собой. Первичные слова расположены "вверху" структуры. Направление вверх соответствует большей общности понятия.
Главная идея Эмслера заключалась в том, что словари обладают более глубокой структурой и говорят нам больше о языке, чем люди привыкли считать. Было бы удивительно, если бы относительно простая схема с родовыми словами не привела к нескольким аномалиям. Определение слова barbecue (целиком зажаренная туша), например, свелось к тому, что это "животное, зажаренное на костре". Таким образом, появилось новое животное, занявшее свое место в животном царстве где-то между антилопой и ящерицей.
Исследование Эмслера имеет приложения к схемам поиска информации в тех случаях, когда пользователь хочет найти частные понятия, принадлежащие широкому классу. В настоящее время Эмслер перестраивает свою переплетенную иерархию для словаря научно-технических терминов, подготавливаемого для печати издательством McGrow-Hill.
Еще одна цепочка преобразований была исследована Роном Хардином, научным сотрудником фирмы AT&T Bell Laboratories в Мюррей-Хилле (шт.Нью-Джерси). В течение многих лет Хардин увлекался изобретением курьезных текстовых преобразований. Предметом его последнего увлечения стал словарь "The New Collins Thesaurus". Обычно пользователь такого словаря ищет в нем синонимы к определенному слову или классу слов. Можно представить себе, что каждое слово в этом словаре принадлежит небольшому гнезду слов, имеющих практически одно и то же значение. Однако не все гнезда далеко отстоят друг от друга. Иногда они частично перекрываются. Как следствие, некоторые пары слов, сами по себе и не являющиеся синонимами, могут иметь общие синонимы. Здесь таится источник многих забавных противоречий. Рассмотрим, например, следующие цепочки, обнаруженные Хардином. Каждое из слов этих цепочек было найдено в гнезде синонимов слова-предшественника:
- приемлемый -> так себе -> заурядный -> непервосортный -> гнилой -> неприемлемый
- надежный -> твердый -> упрямый -> капризный -> непредсказуемый -> ненадежный
С помощью компьютера Хардин сгенерировал несколько тысяч подобных цепочек. В каждой из этих цепочек исходное слово постепенно превращается в свой антоним. Абсолютное большинство цепочек, построенных Хардином, не превосходят по длине приведенные два примера. Все это лишний раз напоминает нам о том, что естественный язык обладает свойством "текучести", что смысловое значение слов существенно зависит от контекста и что каждое слово обладает некоторой неопределенностью, которую можно рассматривать и как благословение, и как проклятие. Представим себе сцену перекрестного допроса свидетеля в зале суда. Адвокат пытается прояснить некоторые стороны характера подзащитного.
"В своих свидетельских показаниях вы утверждали, что Уотсон надежный человек. Не хотите ли вы тем самым сказать, что у него "твердый" характер?"
"Да".
"Действительно. Наверное, можно также сказать, что время от времени обвиняемый был даже упрям в своей твердости?"
"Ну ... я думаю да".
"А иногда, конечно, его упрямство казалось уже капризом, не так ли?"
"Я не уверен".
"Не уверены? Ну, ну, доктор Финч, быть упрямым и капризным - это практически одно и то же".
"Наверное".
"Однако капризный человек непредсказуем и, другими словами, попросту ненадежен. Таким образом вы противоречите своим предшествующим показаниям".
На рисунке вверху приведено еще несколько цепочек Хардина, в которых обращается исходный смысл слова. Его работа со словарем "The New Collins Thesaurus" на самом деле не была такой простой, как это может показаться. Словарь организован по словам-заголовкам. Когда пользователь словаря хочет подыскать нужное ему слово в данном контексте, он находит сначала слово-заголовок, наиболее близкое по смыслу. Под заголовком перечислены другие слова, организованные по смысловому значению слова заголовка. Например, под заголовком express можно найти его смысловые значения, относящиеся к речи и к скорости (express можно перевести как "срочный", "скорый" и как "определенный", "точно выраженный"). Главная задача, стоявшая перед Хардином, заключалась в том, чтобы связать логично и последовательно значения различных слов-заголовков. Как выразился Хардин: "Если предположить, что различия, проводимые между понятиями, когда отличаются их смысловые значения, не должны пропадать при распространении этих понятий... то невозможно будет связать словарь непротиворечивым образом".

Несколько из найденных Харбином примеров постепенного превращения исходного слова в антоним
Поэтому Хардин придумал алгоритм, систематически просматривающий все пары взаимосвязанных слов-заголовков и вычисляющий силу связи между различными смысловыми значениями, которые могут принимать эти слова. Наиболее сильно связанные смысловые значения включались затем в своеобразную сеть слов - паутину, которую плетет алгоритм. При этом различия между смысловыми значениями слов, как правило, остаются достаточно четкими, хотя в некоторых случаях они несколько размываются. Когда построение сети слов завершается, в дело вступает второй алгоритм, отыскивающий кратчайший путь между любыми двумя смысловыми значениями. Хардину нужно было только задавать различные пары слов и наблюдать, как строится его вавилонская башня, названная им по аналогии с библейской башней, сооружение которой, согласно преданиям, окончилось неудачей из-за "смешения языков" различных народов, принимавших участие в строительстве. Башня Хардина представляет собой мини-том, который будет, наверное, интересен как лингвистам, так и адвокатам.
Одно из более ранних текстовых преобразований Хардина уже упоминалось в статье нашей рубрики в журнале #11 за 1985г. Тогда я процитировал стихотворение "Topeka Beagle Buffers", которое было получено путем преобразования текста известного детского стихотворения "Peter Piper". В принципе это преобразование было не сложнее того, что лежит в основании вавилонской башни Хардина.
Вот, например, как Хардин преобразовал стихотворение, начинающееся со слов "Twas the night before Christmas" (то была ночь перед рождеством), в другое стихотворение, начинающееся строкой "Tweeze denied beef worker isthmuth" (бессмысленное сочетание слов, в котором от первой строки осталась лишь ритмическая основа - Ред.). Сначала он разложил все слова исходного текста на цепочку слогов, или фонем, классифицируемых по группам согласно приблизительному сходству в звучании. Сделав то же самое со стандартным словарем, Хардин воспользовался затем компьютерной программой, которая перегруппировала фонемы в новые слова, игнорируя границы между словами исходного текста, там, где это было необходимо. Прежде чем это сумасшедшее стихотворение было завершено, Хардину и его коллегам из фирмы Bell Laboratories пришлось отшлифовать вручную некоторые шероховатости в версии, построенной компьютером. Полученное в результате стихотворение, наверное, оставит любого человека, празднующего рождество, в недоумении относительно того, о чем говорилось в исходной версии (см. рисунок справа).

Первые несколько строк стихотворения "Tweeze denied beef worker isthmuth"
Теперь нам остается вернуться к задаче о преобразовании марсианских предложений. Почему компьютер не может, вообще говоря, при заданном словаре допустимых подстановок и двух словах (произвольной длины) установить, можно ли прийти от первого слова ко второму при помощи последовательности подстановок по словарю? Эта задача называется задачей Туе, в честь норвежского математика Акселя Туе.
Многие люди, не знакомые с теорией вычислений (и даже некоторые знакомые с ней), по-видимому, не отдают себе отчета в том, что возможности компьютера небеспредельны: есть такие вещи, которые ему не по силам. Одним из первых, кто указал на то, что всем компьютерам ло самой их природе присуши некоторые ограничения, был английский математик Алан М. Тьюринг, которого можно, наверное, назвать основателем теории вычислений. Тьюринг придумал абстрактную вычислительную машину, названную (правда, не им) машиной Тьюринга. В принципе это простое устройство способно выполнить любое вычисление, которое под силу любому существующему или гипотетическому компьютеру. Тьюринг доказал, что одна машина Тьюринга не способна установить по состояниям другой машины Тьюринга, заданным на ее входе, остановится ли когда-нибудь вторая машина или нет. Выражаясь более конкретно, невозможно написать такую программу, которая по заданной ей в качестве входных данных второй программе и ее входных данных всегда сможет установить, закончит ли когда-нибудь вторая программа процесс обработки своих данных.
Теорема Тьюринга имеет по крайней мере одно практическое приложение. В одном учебном заведении работал некий эксперт по системному программированию, который пришел к выводу, что мощный компьютер вычислительного центра тратит слишком много времени на выполнение учебных программ студентов-новичков в программировании. Главная причина задержек, по-видимому, заключалась в том, что многие из этих программ содержали в себе незапланированные бесконечные циклы. Если бы учебные программы можно было просматривать перед их выполнением при помощи другой программы, обнаруживающей бесконечные циклы, то удалось бы сэкономить много времени. К сожалению, написать такую программу было невозможно, о чем поведал эксперту один из студентов, знакомых с работами Тьюринга.
Исходя из неразрешимости задачи определения останова, нетрудно доказать даже непосвященному человеку, что сформулированная выше задача о преобразовании марсианских предложений также неразрешима. Доказательство сводится к тому, чтобы показать, что задача о преобразовании марсианских предложений является частным случаем задачи об определении останова.
Идея доказательства относительно проста. Состояние компьютера на любой заданный момент кодируется длинной цепочкой символов. В этой цепочке описывается содержимое памяти и рабочих регистров машины. Существует и такая цепочка символов, которая соответствует останову компьютера,- когда все вычисления, проводимые по программе, завершены. Допустим, нас интересует, остановится или нет некая программа. Мы переводим ее в набор правил, согласно которым может изменяться состояние машины и тем самым кодирующая его цепочка символов, на пути от исходного состояния к заданному состоянию останова. Эти правила являются правилами подстановки одной подцепочки символов вместо другой. Каждое применение такого правила приводит к появлению новой промежуточной цепочки символов, соответствующей выполнению очередного шага по мере того, как компьютер обрабатывает данные по программе в процессе, который, как мы надеемся, рано или поздно будет завершен. Другими словами, правила подстановки позволяют этому виртуальному компьютеру переходить от одного состояния к другому в ходе выполнения программы.
Если, например, в каком-то месте программы текущее содержимое регистра нужно записать в определенную ячейку памяти, то соответствующее этой операции правило заменяет участок цепочки символов, кодирующей состояние машины, подставляя туда новое содержимое данной ячейки памяти, под которую отведен этот участок. Процедура преобразования исходной цепочки символов в конечную цепочку завершается успешно в том и только в том случае, если компьютер, выполняющий программу, в конце концов остановит обработку данных. Поскольку, согласно теореме Тьюринга, мы не можем всегда предсказать, остановится ли когда-нибудь компьютер или нет, то рассматриваемое преобразование цепочек символов, вообще говоря, неосуществимо.
Однако, даже не прибегая к подобным высоко научным аргументам, неразрешимость задачи о преобразовании марсианских предложений можно понять на интуитивном уровне. Если слово-источник возможно преобразовать в слово-цель, то программа, систематически пробующая все допустимые подстановки, рано или поздно должна открыть правильную последовательность подстановок. Ну, а если преобразование невозможно, каким образом мы можем это выяснить? Как долго нам придется ждать? Во всяком случае, читателям, которые не сумеют успешно справиться с нашим частным случаем задачи о преобразовании марсианских предложений, придется ждать месяц.
БИБЛИОГРАФИЯ
THE THEORY OF COMPUTER SCIENCE: A PROGRAMMING APPROACH. J.M.BRADY. Chapman and Hall, Ltd., 1977.
THE OFFICIAL SCRABBLER PLAYERS DICTIONARY. Pocket Books, 1978.
THE OXFORD GUIDE TO WORD GAMES. TONY AUGARDE. Oxford University Press, 1984.
ОТКЛИКИ
2 1988
Я НЕ ПЕРЕСТАЮ удивляться изобретательности наших читателей. В статье, опубликованной в октябрьском номере журнала, я посоветовал читателям, не располагающим компьютерами, не утруждать себя решением некоторых проблем, возникающих в игре со словами, и с удивлением обнаружил, что именно эти читатели нашли интересные решения.
В частности, был сформулирован вопрос о возможности преобразования одного n-буквенного слова в другое при помощи цепочки промежуточных слов. При переходе от одного промежуточного слова к другому разрешалось заменять лишь одну букву. В результате получается лестница слов. Например, в случае n=2 все двухбуквенные слова английского языка (по словарю, которым я пользовался) оказались связанными друг с другом лестницами слов. Я оставил открытым вопрос о том, связаны ли все n-буквенные слова между собой для больших значений n. Оказалось, что для исследования связей между словами можно вполне обойтись и без компьютера.
В качестве решения трехбуквенной задачи многие читатели предложили слово gnu. А для n = 5 несколько человек назвали слово xylem. Решение задачи заключалось в том, чтобы найти слово, которое невозможно соединить ни с одним другим словом. Если такое слово нашлось, то общий вопрос задачи имеет отрицательный ответ. Согласно исследованиям Дж.Миллера из Сан-Франииско, в английском языке существует 1217 слов, с которыми невозможно связать слово horse (лошадь), приведенное в статье в качестве примера. У Миллера есть программа, которая отыскивает всевозможные лестницы между словами. Она написана для персонального компьютера фирмы IBM.
Очень интересная разновидность лестницы слов была предложена П.Блассом из Флорхем-Парка (шт.Нью-Джерси). Вдобавок к замене одной буквы еще разрешается словам ползать, подобно червякам, уменьшаясь или удлиняясь на одну букву в начале или в конце слова.
Воспользовавшись одним или двумя промежуточными словами (такими, как orad), Дж.Эрхард из Ричмонда (шт.Виргиния) нашел способ превратить зло (evif) в добро (good). Д.Фарр из Фрэмингхема (шт.Массачусетс) продемонстрировал лестнииу слов от solid (сплошной) к plane (плоский). По пути он проделал кувырки (flips) и скольжение (slide).
В задаче о марсианском тексте мы имеем дело с текстовыми операциями другого рода. При заданном словаре, в котором указаны все дозволенные подстановки одних цепочек вместо других, нужно преобразовать исходное слово в конечное. Задача была решена А.Перту III из Сиэтла (шт.Вашингтон) и Э.Гротом из Скотсдэйла (шт.Аризона). Она легко решается после того, как вы догадаетесь, что несколько элементов словаря означают простые правила, при помощи которых можно манипулировать символами текста.
Очень забавны вычислительные фокусы со словами, придуманные Р.Хардином. О них шла речь в октябрьском номере журнала. Читатели, наверное, помнят странное стихотворение, начинающееся словами "Tweeze Denied Beef Worker Istmuth" (бессмысленное сочетание слов. - Ред.), которое по звучанию удивительно напоминает знакомое всем рождественское стихотворение К.К.Мура. Искусством трансформации поэтических произведений уже давно овладели люди, не обладавшие компьютерами. Р.Рид, математик, увлекающийся играми, из Университета Ватерлоо в Онтарио рассказал мне о забавной французской книжонке, содержащей всевозможные искажения известных стихотворений.
В английской литературе также существуют образчики подобного рола. Двое наших читателей прислали очаровательное стихотворение пол названием "Ladle Rat Rotten Hat" (Очевидно, это искаженное название сказки о Красной Шапочке: Little Red Riding Hood - дословно: "маленький красный капюшончик". В искаженной форме что-то вроде: "Хлебай из гнилой крысиной норы".- Ред.). Действительно, для таких произведений компьютер едва ли необходим. Д.Вуд из Монреаля (пров.Квебек, Канада) написал импровизацию на тему песенки "It Came upon the Midnight Clear", звучащую следующим образом: "Eat cane a pond am I'd knight a glare" (бессмысленное сочетание слов, которое при беглом чтении очень созвучно исходной строке.- Ред.). Наконец, Р.Тилден из Соммервилла (шт.Массачусетс) напомнил мне, что известный американский карикатурист Уолт Келли дал нескольким своим произведениям шутливые названия такого же рода.
MOTS D'HEURES: GOUSSES, RAMES. THE D'ANTIN MANUSCRIPT. LUIS D'ANTIN VAN ROOTEN. Penguin Books, 1980.
"ЛЕСТНИЦА СЛОВ": ЛИНГВИСТИЧЕСКИЕ ГОЛОВОЛОМКИ И ВОЗМОЖНОСТИ КОМПЬЮТЕРА
А.К.ДЬЮДНИ
НИКТО не знает, когда и при каких обстоятельствах исчезла марсианская цивилизация, лишь пещера у подножия горы Олимп хранит печальную память об этой древней и удивительной культуре. В самом дальнем углу пещеры стоит камень с высеченными на нем словами. Камень закрыт занавесом из пыльной ткани неизвестного нам состава. Раздвинув занавес, мы видим надписи, напоминающие словарь: одни слова расположены слева, другие - справа. У основания каменной дощечки высечены два предложения. Они соотносятся между собой любопытным образом. Дело в том, что первое предложение можно преобразовать во второе, последовательно заменяя составляющие его слова их эквивалентами из словаря. Каждое слово предложения, содержащееся в левой части словаря, можно заменить соответствующим ему словом из правой части.
Марсианскиепредложениянесодержатпробелов. Действительно, благодаря исключительной плавности и выразительности старомарсианского языка, пробелы в нем вовсе не нужны. Зачастую существует сразу много способов разбить марсианское предложение на составляющие его слова. Однако, как правило, лишь несколько таких разбиений имеют разумный смысл в данном контексте. Процесс подстановки слов по словарю можно проиллюстрировать на примере предложения, с которого начинается этот абзац. Если бы слово "одержатпробелов" входило в левую колонку словаря, а в правой колонке ему бы соответствовало слово "утвсебетайныйсмысл", то это последнее можно было бы подставить вместо первого, в результате чего получилось бы другое предложение: марсианскиепредложениянесутвсебетайныйсмысл.
Мудрецы марсианской древности считали, что всю необходимую информацию можно получить, начав с одного основного предложения и подставляя слова согласно словарю мудрости, единственный уцелевший фрагмент которого спрятан в пещере. Это основное предложение высечено первым в основании каменной дощечки у горы Олимп (см. рисунок внизу слева). Вообще говоря, компьютер будет не в состоянии установить, было ли выведено то или иное заданное предложение из другого заданного предложения. Другими словами, невозможно написать такую программу (неважно, насколько длинна программа и насколько высоко быстродействие компьютера), которая могла бы для любого заданного словаря и любых двух слов (или предложений) на входе установить, возможен ли переход от первого слова ко второму. Ниже я объясню, почему. А пока пусть читатели попробуют преобразовать первое предложение, высеченное на камне, во второе. (В данном случае такое преобразование возможно).

Марсианский словарь мудрости
Эта задачка о преобразовании предложений является представителем целого семейства головоломок, в которых производятся замены слов, предложений и даже целых абзацев другими словами, предложениями и абзацами. Одним из родоначальников этого направления в головоломках был и преподобный Чарлз Доджсон, известный также как Льюис Кэрролл. Среди множества других математических затей и головоломок, придуманных Кэрроллом во время его оксфордских прогулок, есть и игра под названием "Лестница слов". В этой игре нужно выбрать какие-нибудь два слова, принадлежащие одному языку и называемые источником и целью, а затем попытаться преобразовать первое слово во второе, заменяя каждый раз по одной букве.
Если оба слова состоят из одного и того же числа букв, то задача выглядит тривиально. Однако сумеете ли вы выдержать условие, чтобы все промежуточные цепочки букв были также словами выбранного языка? Это уже совсем другое дело, но и с этой задачей люди, поднаторевшие в словесных играх, справляются довольно легко. Начнем, например, со слова horse (лошадь). За один шаг его можно превратить в слово house (дом). Сделав еще один шаг, мы получим слово mouse (мышь). С помощью подобной алхимии лошадь, кажется, можно превратить практически во все что угодно, лишь бы название состояло из пяти букв. Действительно ли это возможно?
Чтобы ответить на этот вопрос в общей форме, необходимо построить грамматику переходов. Поскольку я противник заумной терминологии, я назвал это сетью слов. Полная сеть для английского языка была бы совершенно чудовищным образованием. Каждое слово языка было бы представлено в этой сети одним и только одним узлом. Чтобы удовлетворить требования игры "Лестница слов", две точки, или узла, соединяются в сети линией, если соответствующие им слова отличаются ровно на одну букву. Для того чтобы найти все слова, в которые можно превратить, например, слово horse (лошадь), нужно просто просмотреть всю сеть, начиная со слова horse и прибавляя к списку все повстречавшиеся в пути слова. Полное исследование такого пути было бы равносильно тому, чтобы потянуть сеть за узел horse и вытащить все узлы, соединяющиеся с ним. То, что мы вытащим, будет, наверное, напоминать порванную во многих местах рыболовную сеть. Конечно, абсолютное большинство слов не будет вытащено вслед за словом horse; например, любое слово, состоящее более чем из пяти букв, останется внизу.
Вытащим ли мы все пятибуквенные слова? Другими словами, возможно ли построить лестницу от слова horse к любому другому пятибуквенному слову английского языка? Я должен сознаться, что не знаю ответа на этот вопрос, но судя по откликам читателей на предыдущие задачи, я готов поспорить, что кто-нибудь сумеет решить и эту задачу. Необходимые для этого пособия - словарь в форме, читаемой компьютером, и программа, просматривающая словарь в поисках связанных друг с другом слов, т.е. слов, отличающихся одной буквой. Каждый раз, когда какое-то слово добавляется к списку слов, связанных со словом horse, программа вычеркивает его из словаря в памяти и снова пробегает через весь список, сравнивая каждое встреченное в нем слово со всеми словами все уменьшающегося словаря. Если слово из словаря отличается на одну букву от слова в списке, то первое добавляется к списку и процесс повторяется сначала. Различные словари, наверное, дадут различные результаты, не так ли? Возможно. С другой стороны, два в достаточной мере полных словаря могут дать один и тот же результат. Иначе говоря, сети могут оказаться настолько плотными, что их топология будет практически одинаковой.
Ответ на вопрос о том, связаны ли между собой все n-буквенные слова, для малых n можно получить практически вручную. Конечно же, все однобуквенные слова связаны между собой в сети слов. Вопрос о двухбуквенных словах можно решить здесь и сейчас. Согласно моему словарику, вот все двухбуквенные слова английского языка:
aa, ad, ae, ah, ai, am, an, ar, as, at, aw, ax, ay, ba, be, bi, bo, by, da, de, do, ef, eh, el, em, en, er, es, et, ex, fa, go, ha, he, hi, ho, id, if, in, is, it, jo, ka, la, li, lo, ma, me, mi, mu, my, na, no, nu, od, oe, of, oh, om, on, op, or, os, ow, ox, oy, pa, pe, pi, re, si, so, ta, ti, to, um, up, us, ut, we, wo, xi, xu, ya, ye.
Проведя небольшую работу, мы убеждаемся, что все эти слова связаны между собой. В самом деле, во-первых, все двухбуквенные слова, начинающиеся с одной и той же буквы, взаимно связаны. Это позволяет нам объединить такие слова в группы. Остается только заметить, что группа "a" связана с четырьмя другими группами слов, начинающихся с гласной буквы, далее, что группа "b" связана с другими 16 группами слов, начинающихся с согласных, и, наконец, что группы "a" и "b" также связаны между собой.
Возможно, на основании проверки, проведенной для двух наименьших значений n, кое-кто наберется смелости утверждать, что все n-буквенные слова английского языка тоже связаны между собой. Утверждение выглядит очень интригующим, что пожалуй характерно и для других абстрактных игр со словами. Читатели, располагающие компьютером, возможно, попытаются проверить справедливость этого утверждения для других малых значений л, например для л, равного 3 (см. рисунок вверху). А те, у кого нет компьютера, должны будут довольствоваться задачей по превращению слова hate (ненависть) в слово love (любовь). Или, еще лучше, попробуйте преобразовать слово evil (зло) Bgood (добро), углубив в процессе свое понимание вопросов морали и логики.

Сеть трехбуквенных слов
Игра "Лестница слов" представляет собой простой частный случай так называемой системы текстовых преобразований. Два главных компонента такой системы - это множество текстов, над которыми выполняются преобразования, и правила преобразований. Тексты могут представлять собой слова, предложения или абзацы, которые на самом деле являются лишь цепочками букв, независимо от того, каким образом было выбрано множество текстов. Правило преобразования представляет собой процедуру подстановки вместо части заданной цепочки букв другой цепочки. Обычно при применении процедуры подстановки используется словарь.
В "Лестнице слов", например, множество дозволенных цепочек букв состоит из всех английских слов по заданному словарю. Процедура преобразования заключается в том, чтобы по слову, заданному "на входе", сгенерировать другое слово, отличающееся от первого на одну букву и также принадлежащее словарю. В данном случае роль словаря играет просто список слов.
Большинство издаваемых словарей имеют элементы, состоящие из слов, которые "определены" посредством других слов. Здесь мы сталкиваемся с цепочкой переходов другого вида - более сложного по сравнению с "Лестницей слов". Представим, например, что мы начинаем с одного английского слова, смотрим на его значение в словаре и составляем список всех слов, встретившихся в его определении. Затем мы смотрим на значения слов из составленного списка, добавляем встреченные слова к списку и продолжаем этот процесс. Поскольку в английском языке содержится конечное число слов (не могу поручиться за другие языки), процесс приобретает вскоре циклический характер, если можяо так выразиться, т.е. определенные слова начинают встречаться повторно. Они определены частично через самих себя. Можно было бы назвать их "первичными" словами. К подобным словам следует отнестись с особым вниманием: возможно, они составляют неопределяемую понятийную основу английского языка.
Такое исследование, или, во всяком случае, нечто весьма сходное, было проведено Робертом Эмслером, сотрудником фирмы Bell Communications Research. Эмслер воспользовался словарем-тезаурусом, который был модифицирован таким образом, что определение каждого слова было сведено к некоторому набору "родовых" слов, служащих для обозначения широких классов понятий, к которым данное слово имеет отношение. Родовые слова были дополнены вспомогательными словами, позволяющими выделить данное слово среди других членов рола. Применив программу, подобную описанной выше, Эмслер провел исследование своего специального словаря и в общем нашел то, что предсказывали лингвисты-теоретики: первичные слова, которые использовались в определениях других первичных слов. Среди них такие слова, как "пища", "человек", "вещь", "инструмент" и "группа". Первичные слова занимали внешние участки ветвей структуры, представляющей "переплетенную иерархию" - нечто подобное лесу, в котором ветви различных деревьев срослись между собой. Первичные слова расположены "вверху" структуры. Направление вверх соответствует большей общности понятия.
Главная идея Эмслера заключалась в том, что словари обладают более глубокой структурой и говорят нам больше о языке, чем люди привыкли считать. Было бы удивительно, если бы относительно простая схема с родовыми словами не привела к нескольким аномалиям. Определение слова barbecue (целиком зажаренная туша), например, свелось к тому, что это "животное, зажаренное на костре". Таким образом, появилось новое животное, занявшее свое место в животном царстве где-то между антилопой и ящерицей.
Исследование Эмслера имеет приложения к схемам поиска информации в тех случаях, когда пользователь хочет найти частные понятия, принадлежащие широкому классу. В настоящее время Эмслер перестраивает свою переплетенную иерархию для словаря научно-технических терминов, подготавливаемого для печати издательством McGrow-Hill.
Еще одна цепочка преобразований была исследована Роном Хардином, научным сотрудником фирмы AT&T Bell Laboratories в Мюррей-Хилле (шт.Нью-Джерси). В течение многих лет Хардин увлекался изобретением курьезных текстовых преобразований. Предметом его последнего увлечения стал словарь "The New Collins Thesaurus". Обычно пользователь такого словаря ищет в нем синонимы к определенному слову или классу слов. Можно представить себе, что каждое слово в этом словаре принадлежит небольшому гнезду слов, имеющих практически одно и то же значение. Однако не все гнезда далеко отстоят друг от друга. Иногда они частично перекрываются. Как следствие, некоторые пары слов, сами по себе и не являющиеся синонимами, могут иметь общие синонимы. Здесь таится источник многих забавных противоречий. Рассмотрим, например, следующие цепочки, обнаруженные Хардином. Каждое из слов этих цепочек было найдено в гнезде синонимов слова-предшественника:
- приемлемый -> так себе -> заурядный -> непервосортный -> гнилой -> неприемлемый
- надежный -> твердый -> упрямый -> капризный -> непредсказуемый -> ненадежный
С помощью компьютера Хардин сгенерировал несколько тысяч подобных цепочек. В каждой из этих цепочек исходное слово постепенно превращается в свой антоним. Абсолютное большинство цепочек, построенных Хардином, не превосходят по длине приведенные два примера. Все это лишний раз напоминает нам о том, что естественный язык обладает свойством "текучести", что смысловое значение слов существенно зависит от контекста и что каждое слово обладает некоторой неопределенностью, которую можно рассматривать и как благословение, и как проклятие. Представим себе сцену перекрестного допроса свидетеля в зале суда. Адвокат пытается прояснить некоторые стороны характера подзащитного.
"В своих свидетельских показаниях вы утверждали, что Уотсон надежный человек. Не хотите ли вы тем самым сказать, что у него "твердый" характер?"
"Да".
"Действительно. Наверное, можно также сказать, что время от времени обвиняемый был даже упрям в своей твердости?"
"Ну ... я думаю да".
"А иногда, конечно, его упрямство казалось уже капризом, не так ли?"
"Я не уверен".
"Не уверены? Ну, ну, доктор Финч, быть упрямым и капризным - это практически одно и то же".
"Наверное".
"Однако капризный человек непредсказуем и, другими словами, попросту ненадежен. Таким образом вы противоречите своим предшествующим показаниям".
На рисунке вверху приведено еще несколько цепочек Хардина, в которых обращается исходный смысл слова. Его работа со словарем "The New Collins Thesaurus" на самом деле не была такой простой, как это может показаться. Словарь организован по словам-заголовкам. Когда пользователь словаря хочет подыскать нужное ему слово в данном контексте, он находит сначала слово-заголовок, наиболее близкое по смыслу. Под заголовком перечислены другие слова, организованные по смысловому значению слова заголовка. Например, под заголовком express можно найти его смысловые значения, относящиеся к речи и к скорости (express можно перевести как "срочный", "скорый" и как "определенный", "точно выраженный"). Главная задача, стоявшая перед Хардином, заключалась в том, чтобы связать логично и последовательно значения различных слов-заголовков. Как выразился Хардин: "Если предположить, что различия, проводимые между понятиями, когда отличаются их смысловые значения, не должны пропадать при распространении этих понятий... то невозможно будет связать словарь непротиворечивым образом".

Несколько из найденных Харбином примеров постепенного превращения исходного слова в антоним
Поэтому Хардин придумал алгоритм, систематически просматривающий все пары взаимосвязанных слов-заголовков и вычисляющий силу связи между различными смысловыми значениями, которые могут принимать эти слова. Наиболее сильно связанные смысловые значения включались затем в своеобразную сеть слов - паутину, которую плетет алгоритм. При этом различия между смысловыми значениями слов, как правило, остаются достаточно четкими, хотя в некоторых случаях они несколько размываются. Когда построение сети слов завершается, в дело вступает второй алгоритм, отыскивающий кратчайший путь между любыми двумя смысловыми значениями. Хардину нужно было только задавать различные пары слов и наблюдать, как строится его вавилонская башня, названная им по аналогии с библейской башней, сооружение которой, согласно преданиям, окончилось неудачей из-за "смешения языков" различных народов, принимавших участие в строительстве. Башня Хардина представляет собой мини-том, который будет, наверное, интересен как лингвистам, так и адвокатам.
Одно из более ранних текстовых преобразований Хардина уже упоминалось в статье нашей рубрики в журнале #11 за 1985г. Тогда я процитировал стихотворение "Topeka Beagle Buffers", которое было получено путем преобразования текста известного детского стихотворения "Peter Piper". В принципе это преобразование было не сложнее того, что лежит в основании вавилонской башни Хардина.
Вот, например, как Хардин преобразовал стихотворение, начинающееся со слов "Twas the night before Christmas" (то была ночь перед рождеством), в другое стихотворение, начинающееся строкой "Tweeze denied beef worker isthmuth" (бессмысленное сочетание слов, в котором от первой строки осталась лишь ритмическая основа - Ред.). Сначала он разложил все слова исходного текста на цепочку слогов, или фонем, классифицируемых по группам согласно приблизительному сходству в звучании. Сделав то же самое со стандартным словарем, Хардин воспользовался затем компьютерной программой, которая перегруппировала фонемы в новые слова, игнорируя границы между словами исходного текста, там, где это было необходимо. Прежде чем это сумасшедшее стихотворение было завершено, Хардину и его коллегам из фирмы Bell Laboratories пришлось отшлифовать вручную некоторые шероховатости в версии, построенной компьютером. Полученное в результате стихотворение, наверное, оставит любого человека, празднующего рождество, в недоумении относительно того, о чем говорилось в исходной версии (см. рисунок справа).

Первые несколько строк стихотворения "Tweeze denied beef worker isthmuth"
Теперь нам остается вернуться к задаче о преобразовании марсианских предложений. Почему компьютер не может, вообще говоря, при заданном словаре допустимых подстановок и двух словах (произвольной длины) установить, можно ли прийти от первого слова ко второму при помощи последовательности подстановок по словарю? Эта задача называется задачей Туе, в честь норвежского математика Акселя Туе.
Многие люди, не знакомые с теорией вычислений (и даже некоторые знакомые с ней), по-видимому, не отдают себе отчета в том, что возможности компьютера небеспредельны: есть такие вещи, которые ему не по силам. Одним из первых, кто указал на то, что всем компьютерам ло самой их природе присуши некоторые ограничения, был английский математик Алан М. Тьюринг, которого можно, наверное, назвать основателем теории вычислений. Тьюринг придумал абстрактную вычислительную машину, названную (правда, не им) машиной Тьюринга. В принципе это простое устройство способно выполнить любое вычисление, которое под силу любому существующему или гипотетическому компьютеру. Тьюринг доказал, что одна машина Тьюринга не способна установить по состояниям другой машины Тьюринга, заданным на ее входе, остановится ли когда-нибудь вторая машина или нет. Выражаясь более конкретно, невозможно написать такую программу, которая по заданной ей в качестве входных данных второй программе и ее входных данных всегда сможет установить, закончит ли когда-нибудь вторая программа процесс обработки своих данных.
Теорема Тьюринга имеет по крайней мере одно практическое приложение. В одном учебном заведении работал некий эксперт по системному программированию, который пришел к выводу, что мощный компьютер вычислительного центра тратит слишком много времени на выполнение учебных программ студентов-новичков в программировании. Главная причина задержек, по-видимому, заключалась в том, что многие из этих программ содержали в себе незапланированные бесконечные циклы. Если бы учебные программы можно было просматривать перед их выполнением при помощи другой программы, обнаруживающей бесконечные циклы, то удалось бы сэкономить много времени. К сожалению, написать такую программу было невозможно, о чем поведал эксперту один из студентов, знакомых с работами Тьюринга.
Исходя из неразрешимости задачи определения останова, нетрудно доказать даже непосвященному человеку, что сформулированная выше задача о преобразовании марсианских предложений также неразрешима. Доказательство сводится к тому, чтобы показать, что задача о преобразовании марсианских предложений является частным случаем задачи об определении останова.
Идея доказательства относительно проста. Состояние компьютера на любой заданный момент кодируется длинной цепочкой символов. В этой цепочке описывается содержимое памяти и рабочих регистров машины. Существует и такая цепочка символов, которая соответствует останову компьютера,- когда все вычисления, проводимые по программе, завершены. Допустим, нас интересует, остановится или нет некая программа. Мы переводим ее в набор правил, согласно которым может изменяться состояние машины и тем самым кодирующая его цепочка символов, на пути от исходного состояния к заданному состоянию останова. Эти правила являются правилами подстановки одной подцепочки символов вместо другой. Каждое применение такого правила приводит к появлению новой промежуточной цепочки символов, соответствующей выполнению очередного шага по мере того, как компьютер обрабатывает данные по программе в процессе, который, как мы надеемся, рано или поздно будет завершен. Другими словами, правила подстановки позволяют этому виртуальному компьютеру переходить от одного состояния к другому в ходе выполнения программы.
Если, например, в каком-то месте программы текущее содержимое регистра нужно записать в определенную ячейку памяти, то соответствующее этой операции правило заменяет участок цепочки символов, кодирующей состояние машины, подставляя туда новое содержимое данной ячейки памяти, под которую отведен этот участок. Процедура преобразования исходной цепочки символов в конечную цепочку завершается успешно в том и только в том случае, если компьютер, выполняющий программу, в конце концов остановит обработку данных. Поскольку, согласно теореме Тьюринга, мы не можем всегда предсказать, остановится ли когда-нибудь компьютер или нет, то рассматриваемое преобразование цепочек символов, вообще говоря, неосуществимо.
Однако, даже не прибегая к подобным высоко научным аргументам, неразрешимость задачи о преобразовании марсианских предложений можно понять на интуитивном уровне. Если слово-источник возможно преобразовать в слово-цель, то программа, систематически пробующая все допустимые подстановки, рано или поздно должна открыть правильную последовательность подстановок. Ну, а если преобразование невозможно, каким образом мы можем это выяснить? Как долго нам придется ждать? Во всяком случае, читателям, которые не сумеют успешно справиться с нашим частным случаем задачи о преобразовании марсианских предложений, придется ждать месяц.
БИБЛИОГРАФИЯ
THE THEORY OF COMPUTER SCIENCE: A PROGRAMMING APPROACH. J.M.BRADY. Chapman and Hall, Ltd., 1977.
THE OFFICIAL SCRABBLER PLAYERS DICTIONARY. Pocket Books, 1978.
THE OXFORD GUIDE TO WORD GAMES. TONY AUGARDE. Oxford University Press, 1984.
ОТКЛИКИ
2 1988
Я НЕ ПЕРЕСТАЮ удивляться изобретательности наших читателей. В статье, опубликованной в октябрьском номере журнала, я посоветовал читателям, не располагающим компьютерами, не утруждать себя решением некоторых проблем, возникающих в игре со словами, и с удивлением обнаружил, что именно эти читатели нашли интересные решения.
В частности, был сформулирован вопрос о возможности преобразования одного n-буквенного слова в другое при помощи цепочки промежуточных слов. При переходе от одного промежуточного слова к другому разрешалось заменять лишь одну букву. В результате получается лестница слов. Например, в случае n=2 все двухбуквенные слова английского языка (по словарю, которым я пользовался) оказались связанными друг с другом лестницами слов. Я оставил открытым вопрос о том, связаны ли все n-буквенные слова между собой для больших значений n. Оказалось, что для исследования связей между словами можно вполне обойтись и без компьютера.
В качестве решения трехбуквенной задачи многие читатели предложили слово gnu. А для n = 5 несколько человек назвали слово xylem. Решение задачи заключалось в том, чтобы найти слово, которое невозможно соединить ни с одним другим словом. Если такое слово нашлось, то общий вопрос задачи имеет отрицательный ответ. Согласно исследованиям Дж.Миллера из Сан-Франииско, в английском языке существует 1217 слов, с которыми невозможно связать слово horse (лошадь), приведенное в статье в качестве примера. У Миллера есть программа, которая отыскивает всевозможные лестницы между словами. Она написана для персонального компьютера фирмы IBM.
Очень интересная разновидность лестницы слов была предложена П.Блассом из Флорхем-Парка (шт.Нью-Джерси). Вдобавок к замене одной буквы еще разрешается словам ползать, подобно червякам, уменьшаясь или удлиняясь на одну букву в начале или в конце слова.
Воспользовавшись одним или двумя промежуточными словами (такими, как orad), Дж.Эрхард из Ричмонда (шт.Виргиния) нашел способ превратить зло (evif) в добро (good). Д.Фарр из Фрэмингхема (шт.Массачусетс) продемонстрировал лестнииу слов от solid (сплошной) к plane (плоский). По пути он проделал кувырки (flips) и скольжение (slide).
В задаче о марсианском тексте мы имеем дело с текстовыми операциями другого рода. При заданном словаре, в котором указаны все дозволенные подстановки одних цепочек вместо других, нужно преобразовать исходное слово в конечное. Задача была решена А.Перту III из Сиэтла (шт.Вашингтон) и Э.Гротом из Скотсдэйла (шт.Аризона). Она легко решается после того, как вы догадаетесь, что несколько элементов словаря означают простые правила, при помощи которых можно манипулировать символами текста.
Очень забавны вычислительные фокусы со словами, придуманные Р.Хардином. О них шла речь в октябрьском номере журнала. Читатели, наверное, помнят странное стихотворение, начинающееся словами "Tweeze Denied Beef Worker Istmuth" (бессмысленное сочетание слов. - Ред.), которое по звучанию удивительно напоминает знакомое всем рождественское стихотворение К.К.Мура. Искусством трансформации поэтических произведений уже давно овладели люди, не обладавшие компьютерами. Р.Рид, математик, увлекающийся играми, из Университета Ватерлоо в Онтарио рассказал мне о забавной французской книжонке, содержащей всевозможные искажения известных стихотворений.
В английской литературе также существуют образчики подобного рола. Двое наших читателей прислали очаровательное стихотворение пол названием "Ladle Rat Rotten Hat" (Очевидно, это искаженное название сказки о Красной Шапочке: Little Red Riding Hood - дословно: "маленький красный капюшончик". В искаженной форме что-то вроде: "Хлебай из гнилой крысиной норы".- Ред.). Действительно, для таких произведений компьютер едва ли необходим. Д.Вуд из Монреаля (пров.Квебек, Канада) написал импровизацию на тему песенки "It Came upon the Midnight Clear", звучащую следующим образом: "Eat cane a pond am I'd knight a glare" (бессмысленное сочетание слов, которое при беглом чтении очень созвучно исходной строке.- Ред.). Наконец, Р.Тилден из Соммервилла (шт.Массачусетс) напомнил мне, что известный американский карикатурист Уолт Келли дал нескольким своим произведениям шутливые названия такого же рода.
MOTS D'HEURES: GOUSSES, RAMES. THE D'ANTIN MANUSCRIPT. LUIS D'ANTIN VAN ROOTEN. Penguin Books, 1980.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
11 1987
КОМПЬЮТЕР ПРИНИМАЕТ ГОСТЕЙ
А.К.ДЬЮДНИ
НЕДАВНО я устроил вечеринку, на которой сам присутствовать не мог. Восемь приглашенных мною персон были не похожи друг на друга ни по характеру, ни по роду занятий, ни по своим увлечениям. Среди них был, например, штангист Уолтер (или сокращенно Уолли). Уолтер был безнадежно влюблен в принцессу Пенелопу, утонченную, очень чувствительную женщину с аристократическими манерами, которая была также в числе приглашенных. В течение всего вечера Уолтер все время старался быть поближе к принцессе Пенелопе, в то время как она, наоборот, старалась держаться от него на расстоянии. Если оперировать количественными категориями, то Уолтеру, наверное, хотелось бы провести весь вечер на расстоянии одного метра от Пенелопы - быть еше ближе просто не позволяли приличия. Со своей стороны, Пенелопа чувствовала себя неловко, если ее поклонник находился к ней ближе, чем на пять метров. Однако, если Уолтер отдалялся еше больше, Пенелопа уже сама начинала маневрировать, чтобы несколько сократить расстояние между ними. По-видимому, ей все же нравилось находиться в поле зрения Уолтера.

Список гостей на компьютерной вечеринке
Наверное, немногие наши читатели будут удивлены, узнав, что вечеринка состоялась в моем компьютере. Гости были представлены на экране дисплея в виде алфавитно-цифровых символов: например, Уолтера представляла буква W, а Пенелопу - буква P. По ходу вечеринки восемь моих гостей блуждали по комнате, казалось бы, в бесконечных поисках социального равновесия. Образовывавшиеся время от времени небольшие группы тесно общающихся людей распадались после присоединения к ним какой-нибудь новой персоны, которая каким-то непостижимым образом нарушала тонкий баланс, сложившийся в группе. Каждый из приглашенных старался придерживаться некоторой идеальной дистанции по отношению к другим. Он или она всегда перемещались в направлении, минимизирующем их неприятные ощущения. В условиях моей чисто абстрактной (и в то же время довольно типичной) вечеринки ощущение дискомфорта того или иного гостя измерялось суммой расхождений между идеальными и реальными дистанциями по отношению ко всем другим гостям.
Все гости находились в одной прямоугольной комнате, значительную часть которой занимал широкий стол, уставленный всевозможными деликатесами. У каждой персоны была своя идеальная дистанция как по отношению к столу, так и по отношению к каждой другой персоне. Те, кто был на диете, предпочитали держаться на расстоянии полутора-двух метров от стола, в то время как другие гости чувствовали себя неуютно, если не были от него на расстоянии вытянутой руки. Однако это не означало, что любой гость, не находящийся на диете, сразу же направится к столу. Например, Артур, художник, был бы не прочь отведать чего-нибудь со стола, но Берни, бизнесмен (которого Артур не мог терпеть), загородил ему дорогу, говоря со своим собеседником о каких-то финансовых операциях.
Программа, которая провела описанную вечеринку, называется PARTY PLANNER (устроитель вечеринок). Так назвал ее автор Ричард Голдстейн, художник-программист, увлекающийся изобретением игр и живущий в Лос-Анджелесе (шт.Калифорния). Рич Голд (он предпочитает, чтобы его называли так), широко известен как автор игры "Маленькие компьютерные человечки", в которой воспроизводится изображение дома в поперечном сечении, где манекен (маленький компьютерный человечек) снует туда-сюда, занимаясь своими повседневными делами.
Название PARTY PLANNER Голд дал своей программе наполовину в шутку, наполовину всерьез. Он утверждает, что, закодировав вероятные взаимоотношения между гостями, приглашенными на прием, можно при помощи компьютерной модели предсказать, как будет развиваться общение между гостями, в терминах социальной динамики. Можно даже определить оптимальное расположение стола с закусками. Впрочем, проверить, насколько утверждения Голда соответствуют действительности, смогут, наверное, сами читатели, которые напишут свои собственные версии программы и попытаются применить ее на практике. Настоящие гости смогут по крайней мере посмеяться, наблюдая за поведением своих карикатурных представлений на экране дисплея.
Компьютерную вечеринку Голда можно провести в комнате, условно разделенной на 600 квадратов, которые организованы в массив размером 20*30. Каждый гость занимает один квадратный. элемент этого массива. Программа PARTY PLANNER работает, рассматривая каждого приглашенного по очереди: она "мысленно" перемешает гостя на каждый из прилегающих восьми квадратов. В каждом положении программа вычисляет суммарное ощущение дискомфорта, испытываемое данной персоной. Тот из соседних квадратов, в котором сумма неприятных ощущений минимальна, выбирается в качестве нового положения гостя.
Организация такой вечеринки требует минимального опыта в программировании. Массив размером 20*30 назовем room (комната). Поскольку элементами этого массива будут алфавитно-цифровые символы, room надо описать в программе как символьный массив. Стены и стол с закусками обозначаются фиксированными символами (см. рисунок на с.83, стол обозначен символами Т).

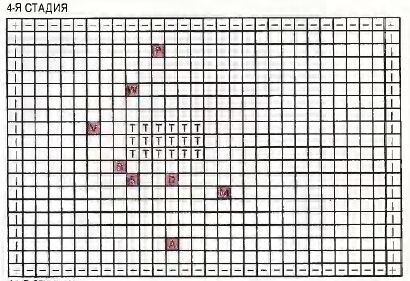
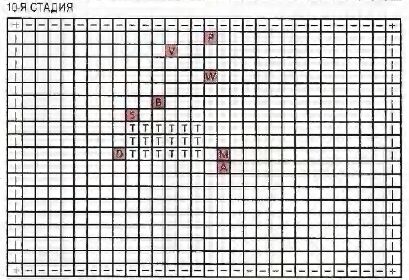





Восемь стадий вечеринки
Программа PARTY PLANNER имеет довольно простую структуру, и ее можно описать на двух уровнях - внешнем и внутреннем. Сначала рассмотрим цикл, в пределах которого все гости бесконечно движутся по комнате, пока пользователь не нажмет клавишу пробела на клавиатуре. В алгоритмических обозначениях внешний уровень программы можно представить следующим образом:
повторять
- for i <- 1 to 8
- - переместить i-го гостя
- вывести на экран room
до нажатия пробела
Внутри первого цикла "повторять" организован второй цикл, в котором восемь персон перемещаются на новые позиции. Ниже я раскрою все секреты процедуры перемещения i-го гостя. Процедура вывода на экран требует двойного цикла, в котором просматривается массив room после того, как вычислены новые позиции всех гостей. Используя, например, индексы j и k, процедура будет анализировать каждый элемент массива room(j, k) и выводить на экран символ, хранящийся в этом элементе, в соответствующей позиции.
Перемещение i-го гостя представляет собой уже более сложную операцию, поскольку его новая позиция будет зависеть от расположения всех других персон с учетом тех расстояний, на которых данный гость предпочитает находиться от остальных. Программа должна содержать таблицу, в каждом элементе которой дано расстояние, идеальное для гостя, указанного номером строки, по отношению к гостю, указанному номером столбца (см. рисунок вверху).

Матрица идеальных расстояний
Такой массив, назовем его ideal (идеальный), должен быть оформлен в программе либо как файл данных, либо как набор операторов типа data. Элемент массива ideal(i, j) указывает расстояние, на котором i-й гость предпочитает находиться от j-го. Эта величина совсем не обязательно совпадает с величиной ideal(j, i). Например, Уолтер предпочитает находиться на расстоянии одного метра от Пенелопы, однако сама Пенелопа предпочитает, чтобы их разделяло не менее пяти метров.
В двух массивах x и y хранятся текущие координаты восьми персон. Во время любого вычислительного цикла i-я персона занимает квадрат с координатами x(i) и y(i). Сумма неприятных ощущений i-й персоны вычисляется следующим образом:
presum <- sum
sum <- 0
for j <- 1 to 8
- dist2 <- [x(i)-x(j)]2+[y{i)-y(j)]2
- dist <- sqrt(dist2)
- sum <- sum+abs[dist-ideal(i,j)]
Тело цикла for пробегается не только для текущей позиции i-го гостя с координатами x(i), y(i), но и для восьми прилегающих позиций, что в сумме дает 9 вычислений. При каждом новом вычислении текущее значение переменной sum запоминается в переменной presum, а затем это значение используется для сравнения. Далее переменной sum присваивается нулевое значение и вычисляется расстояние dist от i-й персоны до j-й. После этого вычисляется абсолютное значение разности между реальным и идеальным расстоянием (с точки зрения i-го гостя) и полученный результат прибавляется к накопленному значению суммы.
Всякий раз, когда вычислено новое значение sum, программа сравнивает его с предыдущим значением, запомненным в переменной presum. Если новая сумма меньше предыдущей, то программа запоминает соответствующие координаты. Следующий алгоритмический фрагмент показывает, как это можно сделать:
if sum < presum
- then xx <- x(i)
- - yy <- y(i)
Таким образом, можно все время хранить те координаты, которые пока что минимизируют сумму неприятных ощущений для i-й персоны. После того как проведены расчеты для всех 9 позиций, i-я персона перемещается в ту позицию, которая дает минимальную сумму неприятных ощущений. Эти девять вычислений проще всего организовать в виде двойного цикла с использованием переменных x и y вместо элементов массива x(i) и y(i). Таким образом, значение переменной x будет варьировать в пределах от x(i)-1 до x(i)+1, а y будет меняться соответственно от y(i)-1 до y(i)+1. Построить цикл можно просто, прибавив значения приращений dx и dy к величинам x(i) и y(i) соответственно:
for dx <- -1 to 1
- for dy <- -1 to 1
- - x <- x(i)+dx
- - y <- y(i)+dy
Наконец, желающим написать программу для проведения вечера нужно напомнить еще об одной детали: гости не должны проходить сквозь стены или забираться на стол с угощениями. Поэтому всякий раз при выборе очередной пары координат для вычислений программа должна сравнивать их с определенными граничными значениями, которые соответствуют контурам стен и стола. В массиве room, используемом в описываемой версии программы, четырем стенам соответствуют значения x = 1, x = 30, y = 1 и y = 20. Если значение какой-либо координаты i-й персоны совпадает с соответствующим значением координаты стены, вычисление суммы неприятных ощущений для данного квадрата не должно проводиться. То же самое можно сказать и относительно стола, который в моей комнате занимает прямоугольную область, ограниченную по оси x значениями координат от 10 до 15, а по y - от 9 до 11. Если значение x принадлежит первому диапазону, а y - второму, то гость, занимающий данную позицию, неминуемо нанесет ущерб собственности хозяина. Поэтому для позиций с такими координатами вычисления также не проводятся. Кое-кто, возможно, будет настаивать и на соблюдении еще одного требования: чтобы гости не переходили друг через друга. Однако на хорошо спланированных приемах это случается не так уж часто, поэтому данное условие можно не предусматривать.
Перед началом выполнения программы PARTY PLANNER следует выбрать и указать исходные позиции всех приглашенных. Это можно сделать, либо введя соответствующие координатные значения, либо предоставив программе возможность самой выбрать эти значения произвольным образом. В последнем случае нужно наложить условие, чтобы выбор не пал на квадраты, занятые столом или стеной.
Мэги, мой помощник по вопросам кибернетики, поэкспериментировал с несколькими вариантами программы PARTY PLANNER. Почему, рассудил он, каждый из приглашенных должен обязательно иметь некоторую идеальную дистанцию по отношению ко всем остальным гостям? Возможно, кое-кому совершенно неважно, на каком расстоянии он находится от некоторых других гостей. Если это так, то Мэги заполняет соответствующую ячейку матрицы идеальных дистанций значением -1. Когда программа доходит до места, где она должна вычислить ощущения данной персоны по отношению к другим, она сначала просматривает значения идеальных дистанций в матрице. Если значение равно -1, то вычисление не производится, ибо рассматриваемая в данный момент другая персона никак не влияет на сумму приятных или неприятных ощущений того гостя, для которого эта сумма подсчитывается.
Я рекомендую читателям поэкспериментировать с различными конфигурациями комнаты, числом приглашенных и массивом идеальных дистанций. Голд предлагает даже проводить то, что он называет "иррациональными вечеринками", когда гости приглашаются как бы с улицы. Другими словами, массив идеальных дистанций заполняется случайными целыми числами, принадлежащими определенному диапазону, например от 1 до 25.
Интересно поэкспериментировать и с различными заранее составленными списками гостей. В этом случае результаты их встречи можно предсказать до того, как они соберутся в одной комнате. Например, если все значения идеальных дистанций превышают размеры комнаты, то приглашенные будут прижиматься к стенам, тщетно пытаясь избегать контактов с остальными гостями. (Мне приходилось бывать на таких приемах). Если же, с другой стороны, идеальные дистанции достаточно малы, то гости тесно сплачиваются в одну группу, увлеченно беседуя около стола с закусками. Весьма забавные результаты можно получить, установив "замыкающийся круг" односторонних симпатий: A любит B, но B терпеть не может A. В то же время B любит C, но C ненавидит B. Эта цепочка взаимоотношений продолжается до тех пор, пока не замкнется снова на A. В зависимости от расположения гостей в начальный момент мы будем наблюдать те или иные вариации всеобщего бесконечного преследования с возникающими время от времени романтическими завихрениями и тупиковыми ситуациями.
Понятие идеальной дистанции не является чисто математической фикцией. Психологи в своих исследованиях пользуются аналогичным понятием, называемым социальной дистанцией. В наших повседневных взаимоотношениях с другими людьми мы склонны придерживаться определенной дистанции в зависимости от нашего природного темперамента, общительности и отношения к тому или иному человеку. Вопросы, связанные с изучением социальных дистанций, образуют целое научное направление. К открытиям в этой области можно отнести то, что социальные дистанции определяются отчасти такими факторами, как культурный уровень, социальная роль и половая принадлежность. Например, жители Северной Америки иногда чувствуют себя немного неловко, общаясь с людьми из тех стран, где социальные дистанции меньше. Это явление можно изучить, подобрав соответствующим образом группу в программе PARTY PLANNER. Допустим, половина гостей предпочитает находиться на расстоянии одной трети метра от собеседников, а другая половина чувствует себя непринужденно, когда дистанция составляет один метр. Будут ли гости бесконечно переходить с места на место или же в конце концов возникнет какая-то стабильная конфигурация?
Этот вопрос волей-неволей приводит нас в область, изучающую поведение динамических систем. Если интерпретировать описанную выше вечеринку на языке абстрактных понятий, то она состоит из матрицы дистанций, двумерного клеточного пространства (оно может быть как конечным, так и бесконечным) и множества символов, перемещающихся по очереди в соответствии со значениями потенциальной функции. С точки зрения какого-то определенного символа (т.е. гостя), пространство представляет собой холмистую равнину. Высота любой точки этого динамического ландшафта является значением потенциальной функции для данного символа. Это значение представляет собой просто сумму разностей между дистанциями матрицы и реальными дистанциями, отделяющими данный символ от остальных.
Движение символа аналогично движению шарика, катящегося под действием силы тяжести - шарик всегда предпочитает катиться "под гору". Согласно этой аналогии, Голд иногда образно говорит, что гости, приглашенные на его компьютерные вечеринки, постоянно пребывают в поисках "долины удовольствия". В то же время каждый из символов располагается в своем собственном ландшафте, вообще говоря отличающемся от других. То, что для одного гостя "долина удовольствия", для другого - "холм несчастья" (см. рисунок на с.85).

Штангист Уолли спускается с "холма несчастья" по направлению к принцессе Пенелопе
При заданном клеточном пространстве, будь то гостиная или бесконечная плоскость, или замкнутое тороидальное пространство, разновидности которого так часто встречались в статьях нашей рубрики, абстрактного исследователя всегда интересуют простые вопросы: какие матрицы дистанций гарантируют, что символы рано или поздно придут в статическое состояние? При каких матрицах в поведении системы гарантированно возникают периодические закономерности? Отметим, что второй вопрос имеет смысл только в случае бесконечного пространства. В конечном же пространстве какая-то конфигурация должна неизбежно повториться. После этого поведение символов станет полностью периодическим. Поэтому перефразируем второй вопрос следующим образом: при каких матрицах дистанций в бесконечном пространстве никогда не возникнет периодического поведения?
Особенно интересную версию программы PARTY PLANNER Голд написал применительно к географии. Представьте себе, что вы пригласили в качестве гостей программы (в очень большую комнату) восемь крупнейших городов США. Другими словами, пусть идеальные дистанции между любыми двумя гостями соответствуют расстояниям между городами. Удивительно, что при произвольном исходном расположении таких гостей они, поблуждав какое-то время согласно правилам игры, останавливаются в конце концов в позициях, точно соответствующих географическому расположению городов относительно друг друга. Читатели, которые попробуют провести этот эксперимент, возможно, будут озадачены, когда перед ними возникнет географическая карта, перевернутая вверх ногами или наклоненная под каким-то углом к своей обычной ориентации, однако во всем остальном эта карта будет бесспорно правильной. Предположительно, это явление будет наблюдаться для любого набора расстояний между точками на плоскости.
Как художник Голд является представителем направления, которое он называет алгоритмическим символизмом. Программа PARTY PLANNER была создана вовсе не потому, что Голд испытывал затруднения, планируя свои вечеринки, она была следствием его занятий живописью. Вот что он пишет: "Эти композиции должны были состоять из самых разнообразных предметов, таких как апельсины, яблоки, скрипки, молотки и т.д. Я хотел построить композицию так, чтобы сходные между собой предметы располагались по соседству друг от друга, в то время как предметы, не похожие друг на друга, разделяло большое расстояние. Я построил матрицу, содержащую идеальные дистанции от каждого данного предмета до каждого другого, однако вскоре мне стало ясно, что найти в уме подходящее расположение очень трудно... И я подумал, а что если бы я смог оживить... эти предметы и позволил им свободно блуждать по полотну, отыскивая удобное для них положение? Я совсем не ожидал, что увижу такой красивый танец в исполнении предметов, пытающихся минимизировать свои неприятные ощущения. Так родилась идея устроителя вечеринок!"
Отметим, что любители компьютерных игр в США, вместо того чтобы потеть над созданием своей собственной программы, могут приобрести у Голда дискеты с готовой программой для персонального компьютера IBM и совместимых с ним машин, а также версию для компьютеров серии APPLE.
К теме настоящей статьи мы вернемся через четыре месяца, а не через три, как это было до сих пор. То же самое касается всех наших будущих публикаций - мы будем возвращаться к ним через четыре месяца со времени появления их в журнале. Я с удовольствием готов посвятить одну страничку "светской хронике", где будут описаны наиболее интересные вечеринки, устроенные нашими читателями.
БИБЛИОГРАФИЯ
THE EFFECTS OF PERSONAL SPACE AND TERRITORY ON HUMAN COMMUNICATION. E.T.HALL in Nonverbal Communication in Human Interaction, edited by Mark L. Knapp. Holt, Rinehart and Winston, 1978.
MODERN COMPUTER PEOPLE. Activision. Inc., Mountain View, Calif., 1985.
ОТКЛИКИ
В СТАТЬЕ нашей рубрики в ноябрьском номере мы обсуждали программу Рнча Голда, которая моделирует на персональном компьютере вечеринку с несколькими приглашенными людьми. Помещение, в котором собираются гости, представляет собой квадратную решетку на экране дисплея. Гости перемещаются с клетки на клетку в поисках наибольшего комфорта. У каждого приглашенного есть своя предпочтительная дистанция по отношению к каждому другому участнику вечеринки. Он (или она) перемешается в том направлении, которое уменьшает чувство дискомфорта в сложившейся на данный момент конфигурации. Чувство дискомфорта вычисляется путем суммирования разностей между предпочтительной и реальной дистанцией по отношению к каждому гостю.
Основной цикл программ был предельно простым. По мнению А.Чарльзворта из Университета шт.Виргиния, такая простота может несколько исказить картину. Чарльзворт занимался изучением параллельных программных систем, называемых системами "мультирандеву". Если бы каждый гость был представлен в виде отдельного процесса на языке параллельного программирования, то "после каждой итерации все такие процессы могли бы проводить "совещание", чтобы поделиться информацией о новом расположении гостей". Однако и в нашей обычной последовательной модели можно избежать искажений, если не перемешать гостей до тех пор, пока степень дискомфорта каждого из них не будет подсчитана.
А.Пенсер из Хантсвилля (шт.Алабама) остался неудовлетворенным по поводу функции, с помощью которой вычисляется степень дискомфортности гостей. Он предпочел бы разности между идеальными и реальными расстояниями возводить в квадрат. Насколько существенными будут отличия в поведении тех же гостей при тех же исходных положениях? Очевидно, силы взаимного притяжения и отталкивания будут значительно сильнее зависеть от расстояния между гостями.
Как я уже говорил в конце своей статьи в ноябрьском номере, существует даже своеобразная наука - проксемика. У.Икингер-младший из Мэрилендского университета построил как-то шестиугольную решетку, которую можно, подобно ковру, расстелить на полу, чтобы наблюдать за расстояниями, разделяющими различных участников сборища. Икингер очень увлечен программами, которые моделируют поведение гостей, и хотел бы связаться со всеми энтузиастами в США, разделяющими его увлечение.
КОМПЬЮТЕР ПРИНИМАЕТ ГОСТЕЙ
А.К.ДЬЮДНИ
НЕДАВНО я устроил вечеринку, на которой сам присутствовать не мог. Восемь приглашенных мною персон были не похожи друг на друга ни по характеру, ни по роду занятий, ни по своим увлечениям. Среди них был, например, штангист Уолтер (или сокращенно Уолли). Уолтер был безнадежно влюблен в принцессу Пенелопу, утонченную, очень чувствительную женщину с аристократическими манерами, которая была также в числе приглашенных. В течение всего вечера Уолтер все время старался быть поближе к принцессе Пенелопе, в то время как она, наоборот, старалась держаться от него на расстоянии. Если оперировать количественными категориями, то Уолтеру, наверное, хотелось бы провести весь вечер на расстоянии одного метра от Пенелопы - быть еше ближе просто не позволяли приличия. Со своей стороны, Пенелопа чувствовала себя неловко, если ее поклонник находился к ней ближе, чем на пять метров. Однако, если Уолтер отдалялся еше больше, Пенелопа уже сама начинала маневрировать, чтобы несколько сократить расстояние между ними. По-видимому, ей все же нравилось находиться в поле зрения Уолтера.

Список гостей на компьютерной вечеринке
Наверное, немногие наши читатели будут удивлены, узнав, что вечеринка состоялась в моем компьютере. Гости были представлены на экране дисплея в виде алфавитно-цифровых символов: например, Уолтера представляла буква W, а Пенелопу - буква P. По ходу вечеринки восемь моих гостей блуждали по комнате, казалось бы, в бесконечных поисках социального равновесия. Образовывавшиеся время от времени небольшие группы тесно общающихся людей распадались после присоединения к ним какой-нибудь новой персоны, которая каким-то непостижимым образом нарушала тонкий баланс, сложившийся в группе. Каждый из приглашенных старался придерживаться некоторой идеальной дистанции по отношению к другим. Он или она всегда перемещались в направлении, минимизирующем их неприятные ощущения. В условиях моей чисто абстрактной (и в то же время довольно типичной) вечеринки ощущение дискомфорта того или иного гостя измерялось суммой расхождений между идеальными и реальными дистанциями по отношению ко всем другим гостям.
Все гости находились в одной прямоугольной комнате, значительную часть которой занимал широкий стол, уставленный всевозможными деликатесами. У каждой персоны была своя идеальная дистанция как по отношению к столу, так и по отношению к каждой другой персоне. Те, кто был на диете, предпочитали держаться на расстоянии полутора-двух метров от стола, в то время как другие гости чувствовали себя неуютно, если не были от него на расстоянии вытянутой руки. Однако это не означало, что любой гость, не находящийся на диете, сразу же направится к столу. Например, Артур, художник, был бы не прочь отведать чего-нибудь со стола, но Берни, бизнесмен (которого Артур не мог терпеть), загородил ему дорогу, говоря со своим собеседником о каких-то финансовых операциях.
Программа, которая провела описанную вечеринку, называется PARTY PLANNER (устроитель вечеринок). Так назвал ее автор Ричард Голдстейн, художник-программист, увлекающийся изобретением игр и живущий в Лос-Анджелесе (шт.Калифорния). Рич Голд (он предпочитает, чтобы его называли так), широко известен как автор игры "Маленькие компьютерные человечки", в которой воспроизводится изображение дома в поперечном сечении, где манекен (маленький компьютерный человечек) снует туда-сюда, занимаясь своими повседневными делами.
Название PARTY PLANNER Голд дал своей программе наполовину в шутку, наполовину всерьез. Он утверждает, что, закодировав вероятные взаимоотношения между гостями, приглашенными на прием, можно при помощи компьютерной модели предсказать, как будет развиваться общение между гостями, в терминах социальной динамики. Можно даже определить оптимальное расположение стола с закусками. Впрочем, проверить, насколько утверждения Голда соответствуют действительности, смогут, наверное, сами читатели, которые напишут свои собственные версии программы и попытаются применить ее на практике. Настоящие гости смогут по крайней мере посмеяться, наблюдая за поведением своих карикатурных представлений на экране дисплея.
Компьютерную вечеринку Голда можно провести в комнате, условно разделенной на 600 квадратов, которые организованы в массив размером 20*30. Каждый гость занимает один квадратный. элемент этого массива. Программа PARTY PLANNER работает, рассматривая каждого приглашенного по очереди: она "мысленно" перемешает гостя на каждый из прилегающих восьми квадратов. В каждом положении программа вычисляет суммарное ощущение дискомфорта, испытываемое данной персоной. Тот из соседних квадратов, в котором сумма неприятных ощущений минимальна, выбирается в качестве нового положения гостя.
Организация такой вечеринки требует минимального опыта в программировании. Массив размером 20*30 назовем room (комната). Поскольку элементами этого массива будут алфавитно-цифровые символы, room надо описать в программе как символьный массив. Стены и стол с закусками обозначаются фиксированными символами (см. рисунок на с.83, стол обозначен символами Т).








Восемь стадий вечеринки
Программа PARTY PLANNER имеет довольно простую структуру, и ее можно описать на двух уровнях - внешнем и внутреннем. Сначала рассмотрим цикл, в пределах которого все гости бесконечно движутся по комнате, пока пользователь не нажмет клавишу пробела на клавиатуре. В алгоритмических обозначениях внешний уровень программы можно представить следующим образом:
повторять
- for i <- 1 to 8
- - переместить i-го гостя
- вывести на экран room
до нажатия пробела
Внутри первого цикла "повторять" организован второй цикл, в котором восемь персон перемещаются на новые позиции. Ниже я раскрою все секреты процедуры перемещения i-го гостя. Процедура вывода на экран требует двойного цикла, в котором просматривается массив room после того, как вычислены новые позиции всех гостей. Используя, например, индексы j и k, процедура будет анализировать каждый элемент массива room(j, k) и выводить на экран символ, хранящийся в этом элементе, в соответствующей позиции.
Перемещение i-го гостя представляет собой уже более сложную операцию, поскольку его новая позиция будет зависеть от расположения всех других персон с учетом тех расстояний, на которых данный гость предпочитает находиться от остальных. Программа должна содержать таблицу, в каждом элементе которой дано расстояние, идеальное для гостя, указанного номером строки, по отношению к гостю, указанному номером столбца (см. рисунок вверху).

Матрица идеальных расстояний
Такой массив, назовем его ideal (идеальный), должен быть оформлен в программе либо как файл данных, либо как набор операторов типа data. Элемент массива ideal(i, j) указывает расстояние, на котором i-й гость предпочитает находиться от j-го. Эта величина совсем не обязательно совпадает с величиной ideal(j, i). Например, Уолтер предпочитает находиться на расстоянии одного метра от Пенелопы, однако сама Пенелопа предпочитает, чтобы их разделяло не менее пяти метров.
В двух массивах x и y хранятся текущие координаты восьми персон. Во время любого вычислительного цикла i-я персона занимает квадрат с координатами x(i) и y(i). Сумма неприятных ощущений i-й персоны вычисляется следующим образом:
presum <- sum
sum <- 0
for j <- 1 to 8
- dist2 <- [x(i)-x(j)]2+[y{i)-y(j)]2
- dist <- sqrt(dist2)
- sum <- sum+abs[dist-ideal(i,j)]
Тело цикла for пробегается не только для текущей позиции i-го гостя с координатами x(i), y(i), но и для восьми прилегающих позиций, что в сумме дает 9 вычислений. При каждом новом вычислении текущее значение переменной sum запоминается в переменной presum, а затем это значение используется для сравнения. Далее переменной sum присваивается нулевое значение и вычисляется расстояние dist от i-й персоны до j-й. После этого вычисляется абсолютное значение разности между реальным и идеальным расстоянием (с точки зрения i-го гостя) и полученный результат прибавляется к накопленному значению суммы.
Всякий раз, когда вычислено новое значение sum, программа сравнивает его с предыдущим значением, запомненным в переменной presum. Если новая сумма меньше предыдущей, то программа запоминает соответствующие координаты. Следующий алгоритмический фрагмент показывает, как это можно сделать:
if sum < presum
- then xx <- x(i)
- - yy <- y(i)
Таким образом, можно все время хранить те координаты, которые пока что минимизируют сумму неприятных ощущений для i-й персоны. После того как проведены расчеты для всех 9 позиций, i-я персона перемещается в ту позицию, которая дает минимальную сумму неприятных ощущений. Эти девять вычислений проще всего организовать в виде двойного цикла с использованием переменных x и y вместо элементов массива x(i) и y(i). Таким образом, значение переменной x будет варьировать в пределах от x(i)-1 до x(i)+1, а y будет меняться соответственно от y(i)-1 до y(i)+1. Построить цикл можно просто, прибавив значения приращений dx и dy к величинам x(i) и y(i) соответственно:
for dx <- -1 to 1
- for dy <- -1 to 1
- - x <- x(i)+dx
- - y <- y(i)+dy
Наконец, желающим написать программу для проведения вечера нужно напомнить еще об одной детали: гости не должны проходить сквозь стены или забираться на стол с угощениями. Поэтому всякий раз при выборе очередной пары координат для вычислений программа должна сравнивать их с определенными граничными значениями, которые соответствуют контурам стен и стола. В массиве room, используемом в описываемой версии программы, четырем стенам соответствуют значения x = 1, x = 30, y = 1 и y = 20. Если значение какой-либо координаты i-й персоны совпадает с соответствующим значением координаты стены, вычисление суммы неприятных ощущений для данного квадрата не должно проводиться. То же самое можно сказать и относительно стола, который в моей комнате занимает прямоугольную область, ограниченную по оси x значениями координат от 10 до 15, а по y - от 9 до 11. Если значение x принадлежит первому диапазону, а y - второму, то гость, занимающий данную позицию, неминуемо нанесет ущерб собственности хозяина. Поэтому для позиций с такими координатами вычисления также не проводятся. Кое-кто, возможно, будет настаивать и на соблюдении еще одного требования: чтобы гости не переходили друг через друга. Однако на хорошо спланированных приемах это случается не так уж часто, поэтому данное условие можно не предусматривать.
Перед началом выполнения программы PARTY PLANNER следует выбрать и указать исходные позиции всех приглашенных. Это можно сделать, либо введя соответствующие координатные значения, либо предоставив программе возможность самой выбрать эти значения произвольным образом. В последнем случае нужно наложить условие, чтобы выбор не пал на квадраты, занятые столом или стеной.
Мэги, мой помощник по вопросам кибернетики, поэкспериментировал с несколькими вариантами программы PARTY PLANNER. Почему, рассудил он, каждый из приглашенных должен обязательно иметь некоторую идеальную дистанцию по отношению ко всем остальным гостям? Возможно, кое-кому совершенно неважно, на каком расстоянии он находится от некоторых других гостей. Если это так, то Мэги заполняет соответствующую ячейку матрицы идеальных дистанций значением -1. Когда программа доходит до места, где она должна вычислить ощущения данной персоны по отношению к другим, она сначала просматривает значения идеальных дистанций в матрице. Если значение равно -1, то вычисление не производится, ибо рассматриваемая в данный момент другая персона никак не влияет на сумму приятных или неприятных ощущений того гостя, для которого эта сумма подсчитывается.
Я рекомендую читателям поэкспериментировать с различными конфигурациями комнаты, числом приглашенных и массивом идеальных дистанций. Голд предлагает даже проводить то, что он называет "иррациональными вечеринками", когда гости приглашаются как бы с улицы. Другими словами, массив идеальных дистанций заполняется случайными целыми числами, принадлежащими определенному диапазону, например от 1 до 25.
Интересно поэкспериментировать и с различными заранее составленными списками гостей. В этом случае результаты их встречи можно предсказать до того, как они соберутся в одной комнате. Например, если все значения идеальных дистанций превышают размеры комнаты, то приглашенные будут прижиматься к стенам, тщетно пытаясь избегать контактов с остальными гостями. (Мне приходилось бывать на таких приемах). Если же, с другой стороны, идеальные дистанции достаточно малы, то гости тесно сплачиваются в одну группу, увлеченно беседуя около стола с закусками. Весьма забавные результаты можно получить, установив "замыкающийся круг" односторонних симпатий: A любит B, но B терпеть не может A. В то же время B любит C, но C ненавидит B. Эта цепочка взаимоотношений продолжается до тех пор, пока не замкнется снова на A. В зависимости от расположения гостей в начальный момент мы будем наблюдать те или иные вариации всеобщего бесконечного преследования с возникающими время от времени романтическими завихрениями и тупиковыми ситуациями.
Понятие идеальной дистанции не является чисто математической фикцией. Психологи в своих исследованиях пользуются аналогичным понятием, называемым социальной дистанцией. В наших повседневных взаимоотношениях с другими людьми мы склонны придерживаться определенной дистанции в зависимости от нашего природного темперамента, общительности и отношения к тому или иному человеку. Вопросы, связанные с изучением социальных дистанций, образуют целое научное направление. К открытиям в этой области можно отнести то, что социальные дистанции определяются отчасти такими факторами, как культурный уровень, социальная роль и половая принадлежность. Например, жители Северной Америки иногда чувствуют себя немного неловко, общаясь с людьми из тех стран, где социальные дистанции меньше. Это явление можно изучить, подобрав соответствующим образом группу в программе PARTY PLANNER. Допустим, половина гостей предпочитает находиться на расстоянии одной трети метра от собеседников, а другая половина чувствует себя непринужденно, когда дистанция составляет один метр. Будут ли гости бесконечно переходить с места на место или же в конце концов возникнет какая-то стабильная конфигурация?
Этот вопрос волей-неволей приводит нас в область, изучающую поведение динамических систем. Если интерпретировать описанную выше вечеринку на языке абстрактных понятий, то она состоит из матрицы дистанций, двумерного клеточного пространства (оно может быть как конечным, так и бесконечным) и множества символов, перемещающихся по очереди в соответствии со значениями потенциальной функции. С точки зрения какого-то определенного символа (т.е. гостя), пространство представляет собой холмистую равнину. Высота любой точки этого динамического ландшафта является значением потенциальной функции для данного символа. Это значение представляет собой просто сумму разностей между дистанциями матрицы и реальными дистанциями, отделяющими данный символ от остальных.
Движение символа аналогично движению шарика, катящегося под действием силы тяжести - шарик всегда предпочитает катиться "под гору". Согласно этой аналогии, Голд иногда образно говорит, что гости, приглашенные на его компьютерные вечеринки, постоянно пребывают в поисках "долины удовольствия". В то же время каждый из символов располагается в своем собственном ландшафте, вообще говоря отличающемся от других. То, что для одного гостя "долина удовольствия", для другого - "холм несчастья" (см. рисунок на с.85).

Штангист Уолли спускается с "холма несчастья" по направлению к принцессе Пенелопе
При заданном клеточном пространстве, будь то гостиная или бесконечная плоскость, или замкнутое тороидальное пространство, разновидности которого так часто встречались в статьях нашей рубрики, абстрактного исследователя всегда интересуют простые вопросы: какие матрицы дистанций гарантируют, что символы рано или поздно придут в статическое состояние? При каких матрицах в поведении системы гарантированно возникают периодические закономерности? Отметим, что второй вопрос имеет смысл только в случае бесконечного пространства. В конечном же пространстве какая-то конфигурация должна неизбежно повториться. После этого поведение символов станет полностью периодическим. Поэтому перефразируем второй вопрос следующим образом: при каких матрицах дистанций в бесконечном пространстве никогда не возникнет периодического поведения?
Особенно интересную версию программы PARTY PLANNER Голд написал применительно к географии. Представьте себе, что вы пригласили в качестве гостей программы (в очень большую комнату) восемь крупнейших городов США. Другими словами, пусть идеальные дистанции между любыми двумя гостями соответствуют расстояниям между городами. Удивительно, что при произвольном исходном расположении таких гостей они, поблуждав какое-то время согласно правилам игры, останавливаются в конце концов в позициях, точно соответствующих географическому расположению городов относительно друг друга. Читатели, которые попробуют провести этот эксперимент, возможно, будут озадачены, когда перед ними возникнет географическая карта, перевернутая вверх ногами или наклоненная под каким-то углом к своей обычной ориентации, однако во всем остальном эта карта будет бесспорно правильной. Предположительно, это явление будет наблюдаться для любого набора расстояний между точками на плоскости.
Как художник Голд является представителем направления, которое он называет алгоритмическим символизмом. Программа PARTY PLANNER была создана вовсе не потому, что Голд испытывал затруднения, планируя свои вечеринки, она была следствием его занятий живописью. Вот что он пишет: "Эти композиции должны были состоять из самых разнообразных предметов, таких как апельсины, яблоки, скрипки, молотки и т.д. Я хотел построить композицию так, чтобы сходные между собой предметы располагались по соседству друг от друга, в то время как предметы, не похожие друг на друга, разделяло большое расстояние. Я построил матрицу, содержащую идеальные дистанции от каждого данного предмета до каждого другого, однако вскоре мне стало ясно, что найти в уме подходящее расположение очень трудно... И я подумал, а что если бы я смог оживить... эти предметы и позволил им свободно блуждать по полотну, отыскивая удобное для них положение? Я совсем не ожидал, что увижу такой красивый танец в исполнении предметов, пытающихся минимизировать свои неприятные ощущения. Так родилась идея устроителя вечеринок!"
Отметим, что любители компьютерных игр в США, вместо того чтобы потеть над созданием своей собственной программы, могут приобрести у Голда дискеты с готовой программой для персонального компьютера IBM и совместимых с ним машин, а также версию для компьютеров серии APPLE.
К теме настоящей статьи мы вернемся через четыре месяца, а не через три, как это было до сих пор. То же самое касается всех наших будущих публикаций - мы будем возвращаться к ним через четыре месяца со времени появления их в журнале. Я с удовольствием готов посвятить одну страничку "светской хронике", где будут описаны наиболее интересные вечеринки, устроенные нашими читателями.
БИБЛИОГРАФИЯ
THE EFFECTS OF PERSONAL SPACE AND TERRITORY ON HUMAN COMMUNICATION. E.T.HALL in Nonverbal Communication in Human Interaction, edited by Mark L. Knapp. Holt, Rinehart and Winston, 1978.
MODERN COMPUTER PEOPLE. Activision. Inc., Mountain View, Calif., 1985.
ОТКЛИКИ
В СТАТЬЕ нашей рубрики в ноябрьском номере мы обсуждали программу Рнча Голда, которая моделирует на персональном компьютере вечеринку с несколькими приглашенными людьми. Помещение, в котором собираются гости, представляет собой квадратную решетку на экране дисплея. Гости перемещаются с клетки на клетку в поисках наибольшего комфорта. У каждого приглашенного есть своя предпочтительная дистанция по отношению к каждому другому участнику вечеринки. Он (или она) перемешается в том направлении, которое уменьшает чувство дискомфорта в сложившейся на данный момент конфигурации. Чувство дискомфорта вычисляется путем суммирования разностей между предпочтительной и реальной дистанцией по отношению к каждому гостю.
Основной цикл программ был предельно простым. По мнению А.Чарльзворта из Университета шт.Виргиния, такая простота может несколько исказить картину. Чарльзворт занимался изучением параллельных программных систем, называемых системами "мультирандеву". Если бы каждый гость был представлен в виде отдельного процесса на языке параллельного программирования, то "после каждой итерации все такие процессы могли бы проводить "совещание", чтобы поделиться информацией о новом расположении гостей". Однако и в нашей обычной последовательной модели можно избежать искажений, если не перемешать гостей до тех пор, пока степень дискомфорта каждого из них не будет подсчитана.
А.Пенсер из Хантсвилля (шт.Алабама) остался неудовлетворенным по поводу функции, с помощью которой вычисляется степень дискомфортности гостей. Он предпочел бы разности между идеальными и реальными расстояниями возводить в квадрат. Насколько существенными будут отличия в поведении тех же гостей при тех же исходных положениях? Очевидно, силы взаимного притяжения и отталкивания будут значительно сильнее зависеть от расстояния между гостями.
Как я уже говорил в конце своей статьи в ноябрьском номере, существует даже своеобразная наука - проксемика. У.Икингер-младший из Мэрилендского университета построил как-то шестиугольную решетку, которую можно, подобно ковру, расстелить на полу, чтобы наблюдать за расстояниями, разделяющими различных участников сборища. Икингер очень увлечен программами, которые моделируют поведение гостей, и хотел бы связаться со всеми энтузиастами в США, разделяющими его увлечение.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
12 1987
"ПОСЛЕ ГВУ": КОМПЬЮТЕРНАЯ ИГРА, В КОТОРОЙ МОДЕЛИРУЕТСЯ СТРАТЕГИЯ БОЯ С ПРИМЕНЕНИЕМ ЯДЕРНОГО ОРУЖИЯ
А.К.ДЬЮДНИ
Эту статью я уже выложил (и журнал - там много интересного про компьютеры) - ТЕМА #69, АБЗАЦ #750
ТЕМА #69, АБЗАЦ #750 .- G.
.- G.
БИБЛИОГРАФИЯ
FIGHTS, GAMES, AND DEBATES. ANATOL RAPOPORT. University of Michigan Press, 1960.
THE EVOLUTION OF COOPERATION. ROBERT AXELROD. Basic Books, 1984.
РИЧАРД ДОКИНЗ, ЭГОИСТИЧНЫЙ ГЕН.- G.
ОТКЛИКИ
4 1988
ИГРА под названием ГВУ (Гарантированное взаимное уничтожение) была темой нашей статьи в декабрьском номере журнала за прошлый год. Придуманная в 1985г. Т.Хомер-Диксоном и К.Оливо из Массачусетского технологического института, игра моделирует стратегию двух сверхдержав, балансирующих на грани между войной и миром. Были проведены эксперименты, в которых студенты МТИ, сидя за клавиатурами компьютеров, играли роль руководителей государств. Какой стратегии придерживаться? Воздерживаться от нападения и получать таким образом относительно скромную прибавку к очковому балансу или начать военные действия в надежде значительно изменить этот баланс в свою пользу? По мере того как развиваются события, потенциальный выигрыш стороны, принявшей решение атаковать первой, резко возрастает.
Несмотря на тот факт, что перед частью студентов была поставлена цель достичь наибольшего количества очков, чему лучше всего способствует мирная политика, многие из них не стали ее придерживаться. В их числе оказался и Д.Фармер из Миссисога (Канала, провинция Онтарио), попытавшийся проанализировать сходную игру, применив принципы теории игр. В теории рассматриваются лишь так называемые матрицы игры в отрыве от последующих ходов. Теория также требует максимально увеличивать счет, сводя к минимуму потери на каждом этапе игры. Чтобы воспользоваться теорией, Фармер нашел способ генерировать новые игровые матрицы, отражающие последующий ход игры. В своем письме Фармер рассмотрел пример с пятью центральными матрицами игры ГВУ. По мнению Фармера, наиболее благоприятный момент для нападения возникает на втором этапе. Однако он заключает: "Перед лицом все возрастающей угрозы опустошительного первого удара, чтобы следовать мирной стратегии, нужно руководствоваться соображениями, выходящими за пределы теории игр. С другой стороны, если негативные последствия будущих военных сценариев сделать менее негативными, то даже теория отдаст предпочтение мирной стратегии. Переговоры о разоружении способствуют уменьшению угрозы войны в будущем, модифицируя таким образом баланс очков в положительном направлении".
В последних стадиях игры ГВУ возникает ситуация, известная под названием "Дилеммы арестованного": вознаграждение за признание (соответствующее за нападение в ГВУ) становится настолько большим, что возникает соблазн "нажать кнопку". И все же турнир по игре "Дилемма арестованного", проведенный несколько лет назад в Мичиганском университете, показал, что наилучшей стратегией в игре была стратегия "око за око", т.е. пока ваш оппонент воздерживается, вам тоже лучше воздерживаться. Теперь студенты (и вообще все желающие) могут проводить свои собственные турниры по игре "Дилемма арестованного". Уже существует программное обеспечение игры для компьютера Макинтош, а вскоре будут готовы и программы для персонального компьютера фирмы IBM и совместимых с ним компьютеров. Авторы этих программ - Л.Беркхолдер и К.Уолтон из Университета Карнеги-Меллона.
"ПОСЛЕ ГВУ": КОМПЬЮТЕРНАЯ ИГРА, В КОТОРОЙ МОДЕЛИРУЕТСЯ СТРАТЕГИЯ БОЯ С ПРИМЕНЕНИЕМ ЯДЕРНОГО ОРУЖИЯ
А.К.ДЬЮДНИ
Эту статью я уже выложил (и журнал - там много интересного про компьютеры) -
 ТЕМА #69, АБЗАЦ #750
ТЕМА #69, АБЗАЦ #750 .- G.
.- G.БИБЛИОГРАФИЯ
FIGHTS, GAMES, AND DEBATES. ANATOL RAPOPORT. University of Michigan Press, 1960.
THE EVOLUTION OF COOPERATION. ROBERT AXELROD. Basic Books, 1984.
РИЧАРД ДОКИНЗ, ЭГОИСТИЧНЫЙ ГЕН.- G.
ОТКЛИКИ
4 1988
ИГРА под названием ГВУ (Гарантированное взаимное уничтожение) была темой нашей статьи в декабрьском номере журнала за прошлый год. Придуманная в 1985г. Т.Хомер-Диксоном и К.Оливо из Массачусетского технологического института, игра моделирует стратегию двух сверхдержав, балансирующих на грани между войной и миром. Были проведены эксперименты, в которых студенты МТИ, сидя за клавиатурами компьютеров, играли роль руководителей государств. Какой стратегии придерживаться? Воздерживаться от нападения и получать таким образом относительно скромную прибавку к очковому балансу или начать военные действия в надежде значительно изменить этот баланс в свою пользу? По мере того как развиваются события, потенциальный выигрыш стороны, принявшей решение атаковать первой, резко возрастает.
Несмотря на тот факт, что перед частью студентов была поставлена цель достичь наибольшего количества очков, чему лучше всего способствует мирная политика, многие из них не стали ее придерживаться. В их числе оказался и Д.Фармер из Миссисога (Канала, провинция Онтарио), попытавшийся проанализировать сходную игру, применив принципы теории игр. В теории рассматриваются лишь так называемые матрицы игры в отрыве от последующих ходов. Теория также требует максимально увеличивать счет, сводя к минимуму потери на каждом этапе игры. Чтобы воспользоваться теорией, Фармер нашел способ генерировать новые игровые матрицы, отражающие последующий ход игры. В своем письме Фармер рассмотрел пример с пятью центральными матрицами игры ГВУ. По мнению Фармера, наиболее благоприятный момент для нападения возникает на втором этапе. Однако он заключает: "Перед лицом все возрастающей угрозы опустошительного первого удара, чтобы следовать мирной стратегии, нужно руководствоваться соображениями, выходящими за пределы теории игр. С другой стороны, если негативные последствия будущих военных сценариев сделать менее негативными, то даже теория отдаст предпочтение мирной стратегии. Переговоры о разоружении способствуют уменьшению угрозы войны в будущем, модифицируя таким образом баланс очков в положительном направлении".
В последних стадиях игры ГВУ возникает ситуация, известная под названием "Дилеммы арестованного": вознаграждение за признание (соответствующее за нападение в ГВУ) становится настолько большим, что возникает соблазн "нажать кнопку". И все же турнир по игре "Дилемма арестованного", проведенный несколько лет назад в Мичиганском университете, показал, что наилучшей стратегией в игре была стратегия "око за око", т.е. пока ваш оппонент воздерживается, вам тоже лучше воздерживаться. Теперь студенты (и вообще все желающие) могут проводить свои собственные турниры по игре "Дилемма арестованного". Уже существует программное обеспечение игры для компьютера Макинтош, а вскоре будут готовы и программы для персонального компьютера фирмы IBM и совместимых с ним компьютеров. Авторы этих программ - Л.Беркхолдер и К.Уолтон из Университета Карнеги-Меллона.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
1 1988
МНОЖЕСТВО МАНДЕЛЬБРОТА И РОДСТВЕННЫЕ ЕМУ МНОЖЕСТВА ЖЮЛИА
А.К.ДЬЮДНИ
С МОМЕНТА публикации первой статьи о множестве Мандельброта в октябрьском номере нашего журнала за 1985г. оно приобрело самую большую популярность у любителей математических трюков. Их привлекает как внешняя красота множества, так и его глубокая сущность. На самом деле красота множества Мандельброта - это лишь вуаль, за которой скрывается его значимость: в замысловатом узоре из тонких линий и завитков вблизи границы множества закодированы различные формы хаоса и упорядоченности (см. верхний рисунок на с.90).

Множество Мандельброта (слева), часть которого (в квадрате) увеличена (справа)
В упомянутой статье наш рассказ о множестве Мандельброта был далеко не полным. Множество имеет некоторую важную связь со свойствами устойчивости и хаоса в динамических системах. Эта связь проходит через родственные множества, называемые множествами Жюлиа по имени французского математика Гастона Жюлиа. Каждой точке, принадлежащей множеству Мандельброта (и не принадлежащей ему), соответствует одно множество Жюлиа. Множества Жюлиа с их фрактальной природой тоже по-своему красивы (см. нижний рисунок на с.90). Но прежде чем рассказывать о них, мы вернемся еще раз к множеству, носящему имя Бенуа Мандельброта, ученого, работающего в Исследовательском центре Томаса Уотсона фирмы IBM в Йорктаун-Хайтсе (шт.Нью-Йорк).

Множество Жюлиа (слева), соответствующее центральной части верхнего правого рисунка; увеличенная часть (справа)
Множество Мандельброта - обитатель комплексной плоскости, т.е. обычной плоскости, каждая точка которой характеризуется двумя координатными значениями. Точнее говоря, каждая точка комплексной плоскости представляется числом вида a+bi. Числа a и b можно считать координатами точки: a - вещественная часть комплексного числа a+bi, а b - его мнимая часть. Число i отчасти служит для того, чтобы различать эти две координаты между собой. Комплексные числа можно складывать, суммируя их соответственные координаты по отдельности; результат представляет собой другое комплексное число. Их можно также умножать друг на друга, следуя при этом правилам умножения многочленов:
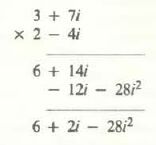
Чтобы представить результат в виде комплексного числа, член 28i2 нужно привести к стандартной форме, воспользовавшись самым важным свойством мнимых величин, а именно тем, что i2 = -1. Таким образом, выражение 6+2i-28i2 приводится к виду 34+2i. Теперь мы можем представить основную формулу, которая открывает нам множество Мандельброта, порождает также множества Жюлиа и в некотором смысле превращает порядок в хаос:
z <- z2+c.
Здесь z и c - это комплексные числа, каждое из них имеет мнимую и вещественную части. Число z возводится в квадрат и c прибавляется к результату согласно правилам умножения и сложения комплексных чисел. Формула как бы оживает, если начать последовательно вычислять значения сумм, подставляя в формулу каждый раз значение z, полученное на предыдущем шаге. Получающаяся в результате этого итерационного процесса последовательность комплексных чисел образует причудливый узор на комплексной плоскости. На каждом шаге новое комплексное число z лежит на некотором расстоянии от предшествующего. Это расстояние очень важно для вычисления множества Мандельброта.
Интересно представить полученную последовательность комплексных чисел (точек на комплексной плоскости) как блуждания исходной точки. Стремится ли она к бесконечности, все дальше удаляясь от начала координат комплексной плоскости? Некоторые комплексные числа действительно стремятся в бесконечность, другие навсегда ограничены в своем движении определенной областью, имеющей сложную форму. Их тюрьма, или область, где они содержатся, имеет фрактальные стены.
Как уже говорилось, итерационный процесс длится до бесконечности. Однако, каким образом выбираются константа c и исходное значение z? Можно, например, сделать число z равным нулю и выбирать различные значения c. Вырвется ли узник в данном случае на свободу? Будем повторять эксперимент снова и снова, систематически варьируя значение c в определенной области комплексной плоскости. Если узнику удается бежать, окрашиваем точку c в белый цвет, в противном случае делаем ее черной. Стены области, из которой не удается бежать, принимают форму множества Мандельброта. Если вместо того, чтобы окрашивать всех беглецов в белый цвет, придавать им окраску в зависимости от скорости побега, то изображение становится еще красивее.
Согласно только что описанному правилу, исходное значение числа z равно 0, или точнее, 0+0i. А что изменится, если процесс начать с какого-нибудь другого значения, скажем, z = 3.5+6i? Примет ли результирующее множество другую форму? Действительно, в результате мы всегда получаем деформированную версию множества Мандельброта. Обычно предпочтение отдается его канонической форме.
Если следовать противоположному правилу, когда значение c фиксировано, a z играет роль исходной точки, получающееся в результате итерационного процесса множество уже отличается по виду от множества Мандельброта. Оно, или вернее его граница, называется множеством Жюлиа. Множество Жюлиа не единственно, на самом деле имеется целое множество таких множеств: для каждого фиксированного значения c в формуле итераций мы получаем свое, отличное от других, множество Жюлиа, заполненное "узниками".
Я был вдохновлен на то, чтобы вернуться еше раз к множеству Мандельброта, прочтя книгу сотрудников Бременского университета Х.-О. Пайтгена и П.Рихтера "Красоты фракталов" (см. библиографию к статье на с.104). Эта крупноформатная книга, содержащая потрясающие черно-белые и цветные иллюстрации, с одинаковым успехом может служить и математическим учебным пособием, и украшением журнального столика. Вся теория, касающаяся множества Мандельброта и связанных с ним множеств Жюлиа, а также других аналогичных сложных систем, изложена в книге в виде математических теорем с доходчивым их описанием.
Рассмотрим смысл одной из теорем. Читатель, написавший программу для построения изображений множеств Жюлиа, возможно заметит, что для некоторых значений c множества получаются связными и графически выглядят как единое целое, в то время как для других значений с они оказываются несвязными. Что же обусловливает это различие? Ответ и прост и изящен: если выбранная точка c принадлежит множеству Мандельброта, то соответствующее множество Жюлиа будет связным. Если же c не принадлежит множеству Мандельброта, то множество Жюлиа будет несвязным.
Можно сделать нечто вроде мультипликационного фильма, иллюстрирующего смысл данной теоремы. Проведем прямую L от произвольной точки, принадлежащей множеству Мандельброта, к другой точке, не принадлежащей ему, и представим себе, что точка c медленно, но неуклонно продвигается вдоль линии L из внутренней области множества Мандельброта по направлению к его границе. Соответствующее множество Жюлиа будет становиться все более сжатым, постоянно уменьшаясь в размере, а когда точка с достигнет границы множества Мандельброта, множество Жюлиа сожмется до хрупкого дендритного скелета, практически не занимающего никакой площади. Когда с выйдет за границу множества Мандельброта, сопутствующее ему множество Жюлиа как бы взрывается, превращаясь во фрактальную пыль.
Читатели, которые пожелают и смогут написать программу, могут исследовать свойства множества Мандельброта и сопутствующих ему множеств Жюлиа, реализовав некоторые основные алгоритмы на том языке, которым они обычно пользуются. Во всех подобных алгоритмах присутствует итерационный процесс, зависящий существенным образом от следующей теоремы: если абсолютная величина итерируемой переменной z достигает 2, то ей суждено убежать в бесконечность, откуда она уже никогда не вернется. В основном именно этот критерий отличает беглецов от узников. Алгоритм содержит 100 шагов итераций, позволяющих переменной z достичь значения 2. Этот критерий, конечно, не срабатывает во всех 100% случаев, поскольку некоторое относительно небольшое количество беглецов не успевает достичь абсолютной величины 2 за 100 итераций. Можно было бы сделать число итераций равным, скажем, 1000, чтобы получить более точную картинку, но для этого потребовалось бы много машинного времени, даже на мощных компьютерах.
Абсолютная величина комплексного числа a+bi равна просто квадратному корню из a2+b2, другими словами, она представляет собой расстояние от начала координат, или нулевой точки. Основной алгоритм итераций имеет следующий вид:
n <- 0
while n<100 and abs(z)<2
- z <- z2 + c
- n <- n+1
раскрасить данную точку
Здесь n - индекс цикла с исходным значением 0. На каждом шаге цикла while, управляющего итерационным процессом, значение переменной n увеличивается на 1. Цикл while продолжается, "проворачивая мясорубку" итерационной формулы до тех пор, пока n не достигнет 100 или абсолютная величина z не достигнет 2. При выполнении любого из этих условий алгоритм выходит из цикла. Читателю предоставляется самому выбрать способ раскраски точек изображения. Этот способ, конечно, должен каким-то несложным образом зависеть от величины n, т.е. от той скорости, с которой точке удалось достичь расстояния 2, а также от того факта, удалось ли ей достичь этого расстояния. Читателям следует также не упускать из виду, что точка изображения на экране будет иметь, вообще говоря, другие координаты, отличающиеся от координат точки на комплексной плоскости.
Программа, написанная читателями, должна содержать отдельную процеруру вычислении абсолютной величины z, которая в приведенном выше алгоритме была представлена как abs(z). На самом деле, поскольку в большинстве языков программирования отсутствуют средства для работы с комплексными числами, переменную z нужно хранить в виде двух частей, скажем x (вещественная часть) и y (мнимая часть), то же касается и числа c, части которого можно обозначить соответственно как a и b. Следующий алгоритм будет уже несколько ближе к работающей программе:
n <- 0
while n <100 and x2+y2<4
- xx <- x2-y2+a
- y <- 2xy+b
- x <- xx
- n <- n+1
раскрасить данную точку
Наблюдательный читатель, наверное, заметит маленький трюк, введенный в эту версию итерационного процесса: вместо того чтобы сравнивать квадратный корень из выражения x2+y2 с 2, мы сравниваем само это выражение с 4. Результат тот же, но с помощью этого приема можно избежать многократного обращения к функции извлечения квадратного корня, выполнение которой требует относительно большого времени. Переменная xx временно содержит только что вычисленное значение x, пока вычисляется новое значение y. Таким образом, старое значение x сохраняется для дальнейших вычислений, пока его не заменит значение xx.
Программа, которую я назвал MANDELZOOM, плод моих первых попыток в данной области, предпринятых еще два года назад, будет представлена теперь в несколько более детальном виде. Она содержит основной итерационный алгоритм внутри цикла, в котором систематически варьируется комплексное число c и, как следствие, его части a и b. Если экран, на котором строится изображение, имеет размер 100*100 пикселов (точечных элементов изображения, образующих квадратную решетку), то программа будет основана на следующем двойном цикле:
gap <- side/100
a <- acorner
for j <- 1 to 100
- a <- a+gap
- b <- bcorner
- for k <- 1 to 100
- - b <- b+gap
- - x <- 0
- - y <- 0
- - [алгоритм итераций]
Однако, прежде чем программа MANDELZOOM доходит до этих операторов, она позволяет пользователю задать комплексное число, располагающееся в одном из углов квадрата, на котором строится изображение. Этот угол будет иметь координаты acorner, bcorner, наименьшие значения a и b, принимаемые комплексными числами в пределах данного квадрата. Квадрат, выбираемый пользователем программы, является как бы окном, через которое мы можем наблюдать изображение. Его можно сделать очень маленьким и тогда мы будем наблюдать в увеличенном виде ту часть множества, над которой располагается окно. Программа требует также указать значение переменной side, т.е. размер стороны квадрата на комплексной плоскости. Затем алгоритм вычисляет расстояние между последовательными комплексными числами c, задавая тем самым соответствующие приращения переменным a и b (это расстояние обозначено как gap).
Значения индексов j и k не участвуют ни в каких вычислениях внутри двойного цикла, поэтому эти индексы можно заменить какими-нибудь величинами, представляющими интерес. Например, вместо того чтобы пробегать значения от 1 до 100, индексы j и k могли бы пробегать через 100 последовательных точек на координатных осях экрана. После того как основная итерационная процедура присвоила определенное цветовое значение итерируемой точке z, точка с координатами (j, k) окрашивается в соответствующий цвет.
Рассмотрение программы MANDELZOOM будет неполным, если не упомянуть о модификации, предложенной Пайтгеном. Вместо того чтобы сравнивать абсолютную величину итерируемой переменной z с 2, можно в качестве порогового значения принять 100 или даже 1000. В конце концов, после того как абсолютная величина комплексной переменной достигла 2, она растет очень быстро и достигает значений порядка 100 или 1000 за несколько шагов итерационного процесса. И все же при различных исходных значениях итерируемые точки проходят пороговые величины с различными скоростями. Скорости тоже можно окрашивать, причем с плавными переходами между различными цветами. Красный цвет может, например, постепенно переходить в оранжевый, конечно, при условии, что цветовая палитра компьютера достаточно богата. Во всяком случае, цветные изображения, приведенные в данной статье, были получены именно этим способом. Пайтген считает, что распределение скоростей напоминает электрическое поле, как бы создаваемое вокруг множества Мандельброта. Градиенты напряженности "поля" представлены в воображаемом ландшафте Мандельброта (см. рисунок на с.89) в виде склонов горного хребта, окружающего то, что можно было бы назвать озером Мандельброта.

Множество Мандельброта в виде озера; горы представляют динамику окружающих точек
Хотя я не считаю, что слово ZOOM стало для меня навязчивым, я все же должен последовать примеру программы MANDELZOOM и назвать программу, генерирующую изображения множеств Жюлиа, JULIAZOOM. (Одно из значений слова ZOOM - это "рассматривать под большим увеличением"). Здесь мы также можем вплотную приблизиться к множеству и исследовать его как бы под очень сильной лупой. В программе JULIAZOOM применяется тот же основной алгоритм итераций, что и в программе MANDELZOOM, однако здесь у него уже несколько иная, так сказать, оправа.
Сначала программа запрашивает у пользователя значения величины xcorner, ycorner и side ("угол x", "угол y" и "сторона" соответственно). Она также запрашивает значение c в виде его составляющих a и b. Затем выполняется двойной цикл, кое в чем существенно отличающийся от цикла программы MANDELZOOM:
gap <- side/100
x <- xcorner
for j <- 1 to 100
- x <- x+gap
- у <- ycorner
- for k = 1 to 100
- - y <- y+gap
[алгоритм итераций]
Основной алгоритм итераций окрашивает точки экрана в зависимости от скорости, с которой итерационный процесс достигает (или вообще не достигает) порогового значения 2. Некоторые из наиболее эффектных графических результатов были получены при использовании самых простых правил окрашивания точек. На цветных мониторах даже трех цветов, присваиваемых по следующему правилу, оказывается достаточно, чтобы получить прекрасные изображения: окрасить в первый цвет точки со значениями n от 0 до 10, вторым цветом - точки со значениями n от 11 до 20, третьим цветом - точки со значениями n от 21 до 30, затем для следующих десяти значений n вернуться к первому цвету и т.д. На нецветных мониторах можно воспользоваться черно-белыми (или зелено-желтыми) контрастами, чередуя оба цвета для каждых десяти последовательных значений n.
Вооружившись работающей версией программы MANDELZOOM или JULIAZOOM (а может быть, обеими программами), читатели смогут заняться своими собственными исследованиями этих красивых и интересных фрактальных множеств. Можно побродить по комплексной плоскости в окрестностях множеств или же рассмотреть какие-то области под сильным увеличением, воспользовавшись компьютерным микроскопом, который был описан выше. Вплоть до предельной разрешающей способности, зависящей от точности арифметических операций у того или иного компьютера, эти множества предстают перед наблюдателем в виде удивительных узоров. Будущим исследователям микрокосма фрактальных объектов можно порекомендовать следующие интересные области, с координатными значениями, изменяющимися в пределах:
Множества Жюлна:
x и y от -1.8 до +1.8
Множество Мандельброта:
x от -2.25 до +0.75 и
y от -1.8 до +1.5
В сентябрьском номере журнала мы затронули тему хаоса в динамических системах, таких как механические маятники и электронные схемы. Свойства этих систем характеризуются простой итерационной формулой, в качестве переменных здесь выступают не комплексные, а обычные вещественные числа:
x <- rx(1-x).
Эта формула, очевидно, квадратична: если раскрыть скобки в правой части, то появится член, содержащий x в квадрате. В зависимости от выбранного значения параметра r, формула ведет себя либо просто, либо странно, если ее начать итерировать. При каждом значении r итерируемая переменная x образует орбиту, т.е. набор значений, которые x систематически посещает. В районе критического значения параметра 3.5699 переменная начинает быстро и более или менее непредсказуемо осциллировать между некоторыми значениями. Такое поведение формулы соответствует ситуации, когда описываемая ею физическая система, будь то двойной маятник или электронная схема, никак не может найти положение стабильности. Ее состояние постоянно меняется непредсказуемым образом, другими словами, наступает хаос.
Аналогичное явление наблюдается и в поведении комплексной итерационной формулы, рассматриваемой в данной статье, z <- z2+c. Однако в этом случае для каждого значения параметра c возникает уже не одна орбита - аттрактор. Их количество зависит от того, каким было выбрано исходное значение переменной z. Если абсолютная величина исходного значения z относительно мала, то переменная будет стремиться к определенной точке. Если же абсолютная величина исходного значения z будет достаточно большой, то в дальнейшем она будет неограниченно возрастать, и аттрактором будет уже бесконечность. И определенная точка, к которой стремится z, и бесконечность представляют собой две отдельные одноточечные орбиты - аттракторы для точек на комплексной плоскости. Граница между "зонами их притяжения" - это множество Жюлиа, невероятно тонкое и сморщенное. Оно тоже является орбитой, но не является аттрактором в строгом смысле слова. Точки, уже содержащиеся в этой пограничной области, совершают в ней беспорядочные скачки. Непосредственно вычислить множество Жюлиа непросто, потому что точность выполнения арифметических операций компьютером может не позволить точно указать точки, которые с самого начала должны находиться на границе, а когда начинается итерационный процесс, точность еще более снижается и итерируемые переменные уходят из поля зрения.
Как уже говорилось, каждому возможному значению параметра c соответствует свое, отличное от других множество Жюлиа. Множество Мандельброта в некотором смысле охватывает все возможные множества Жюлиа. Оно описывает судьбу переменной, выходящей из начала координат комплексной плоскости, для всех возможных значений параметра c. Для некоторых множеств Жюлиа область хаоса представляет собой лишь тонкую древовидную структуру или лаже некую симметричную россыпь точек, область, как бы посыпанную перцем. Читатели, наверное, помнят, что такие множества Жюлиа соответствуют значениям c, находящимся на границе множества Мандельброта или за его пределами.
Недавно мы встретились с Пайтгеном на конференции в Асиломаре (шт.Калифорния). Когда мы прогуливались вдоль пляжа, разговаривая о том, о сем, он охарактеризовал множество Мандельброта как своего рода огромную книгу, в которой каждое множество Жюлиа - не более чем страничка. По тому положению, которое занимает точка c в множестве Мандельброта, можно предсказать поведение итерируемой переменной, характеризуя обшую форму и размер сопутствующего множества Жюлиа. Здесь дело не только в том, будет ли оно связным или несвязным. Если, к примеру, выбрать c из перешейка между основной частью множества Мандельброта и одной из его "точек", то соответствующее множество Жюлиа окажется сжатым в структуру, также состоящую из перешейков и точек. Аналогия, согласно которой множество Мандельброта является как бы словарем для множеств Жюлиа, предполагает фундаментальное различие между этими множествами. Структура множества Жюлна подобна самой себе (в различном масштабе), в то время как для множества Мандельброта (даже для его границы) это не так. В противном случае, как говорит Пайтген. множество Мандельброта не обладало бы способностью кодировать в себе несчетные количества родственных множеств Жюлиа.

Шесть множеств Жюлиа; некоторые из них связные (a, b, c и e), а другие нет (d и f).
В упомянутой книге "Красоты фракталов" есть еще много интересного. Я весьма признателен Пайтгену за те изображения, которые он предоставил для иллюстрации в настоящей статье. Не все они получены описанными здесь способами, однако рецепты изготовления всех изображений даны в книге.
В качестве заключительного замечания об исследованиях, ведущихся в настоящее время специалистами в области динамических систем, я упомяну еще об одном объекте, таящемся в пространстве высшей размерности, чудовище, порождаемом кубическими итерациями, формула которых, в отличие от формулы Мандельброта. содержит z3 вместо z2. Этот объект четырехмерный, его завивающиеся щупальца тянутся от главного "тела" и образуют причудливую картину, которую мы не способны увидеть. Однако ее трехмерные поперечные сечения могут быть вычислены и представлены подобно тому, как это сделано на рисунке на с.92.

Трехмерное поперечное сечение четырехмерного множества Мандельброта
БИБЛИОГРАФИЯ
THE BEAUTY OH FRACTALS. HEIRV OTTO PEITGEN AND PETER H. RICHTER. Springer-Verlag, 1986.
ОТКЛИКИ
5 1988
В СТАТЬЕ январского номера мы вновь обратились к множеству Мандельброта и рассказали о мириадах родственных ему множеств, носящих имя Жюлиа, французского математика, одного из ведущих специалистов в области динамических систем. Программы, порождающие множества Жюлиа, настолько же просты, как и те, с помощью которых можно получать множества Мандельброта. Поэтому сотни наших читателей, а может быть уже и тысячи, написали свои собственные программы или собираются сделать это. В США издается специальный журнал о фракталах под названием "AMYGDALA". В нем приводятся различные полезные советы для тех, кто пишет программы, которые порождают множество Мандельброта или другие фрактальные множества. На его страницах программисты делятся своими секретами и рекламируют написанные ими программы.
В конце упомянутой статьи я продемонстрировал трехмерное чудовище, которое в действительности представляло собой поперечное сечение четырехмерного множества Мандельброта. Хайнц-Отто Пайтген, западногерманский математик и художник, раскрыл "рецепт" четырехмерного множества. Нужно итерировать уравнение z <- z3-3a2z+b, где a и b комплексные параметры. Какие точки играют в четырехмерном множестве ключевую роль подобно точке z = 0? На самом деле существуют сразу две такие точки, а именно z = +a и z = -a. Следовательно, мы имеем не одно, а два четырехмерных множества Мандельброта.
Г.Тичаут из Эверетта (шт. Вашингтон) пишет, что он рассматривает множества Мандельброта и Жюлиа как сечения четырехмерного множества, хотя его четырехмерное множество не совпадает с множеством Пайтгена. Основная итерационная формула z <- z2+c порождает множество Мандельброта, когда z остается постоянным, а c варьирует. Она же порождает множество Жюлиа, если c фиксировано, а z варьирует. Но z и c вместе определяют четыре измерения, по два на каждый параметр. Если собрать вместе все множества Жюлиа не в одномерную, а в двумерную совокупность, то возникает супермножество. М.Хармен из Кемберли (Англия) поделился размышлениями о таком же объекте.
Однако четырехмерный приз следует все же присудить У.Дженксу из Стамфорда (шт.Коннектикут). Не удовлетворенный обычными комплексными числами, Дженкс изобрел свои собственные числа, состоящие из четырех частей. Его числа аналогичны так называемым кватернионам, сложному множеству чисел, которое было изобретено математиками прошлого столетия и которым теперь пользуются физики. Дженкс прислал мне трехмерные представления своего объекта в виде последовательности из 29 его сечений.
Конечно, читатели, увлекающиеся построением изображений множества Мандельброта, хотели бы терять при этом поменьше времени - ведь кроме изображений итерационный процесс породил и множество обкусанных от нетерпения ногтей. Д.Холт из Силвер-Спринга (шт.Мэриленд) обнаружил, что скорость можно повысить на 8%, если вместо процедуры возведения числа в квадрат воспользоваться обычной операцией умножения числа само на себя. В его программном обеспечении эта операция выполняется быстрее, чем возведение в квадрат.
Наконец, рисунок внизу на с.89 представляет собой еще один экспонат в постоянно пополняющейся коллекции изображений множества Мандельброта. Он прислан Дж.Лойлессом из Лилберна (шт.Джорджия). При этом он воспользовался системой "XT турбо-клоун с арифметическим сопроцессором 8087 и 24-точечным принтером Тошиба 321".

Изображение множества Мандельброта, полученное Дж.Лойлессом
МНОЖЕСТВО МАНДЕЛЬБРОТА И РОДСТВЕННЫЕ ЕМУ МНОЖЕСТВА ЖЮЛИА
А.К.ДЬЮДНИ
С МОМЕНТА публикации первой статьи о множестве Мандельброта в октябрьском номере нашего журнала за 1985г. оно приобрело самую большую популярность у любителей математических трюков. Их привлекает как внешняя красота множества, так и его глубокая сущность. На самом деле красота множества Мандельброта - это лишь вуаль, за которой скрывается его значимость: в замысловатом узоре из тонких линий и завитков вблизи границы множества закодированы различные формы хаоса и упорядоченности (см. верхний рисунок на с.90).

Множество Мандельброта (слева), часть которого (в квадрате) увеличена (справа)
В упомянутой статье наш рассказ о множестве Мандельброта был далеко не полным. Множество имеет некоторую важную связь со свойствами устойчивости и хаоса в динамических системах. Эта связь проходит через родственные множества, называемые множествами Жюлиа по имени французского математика Гастона Жюлиа. Каждой точке, принадлежащей множеству Мандельброта (и не принадлежащей ему), соответствует одно множество Жюлиа. Множества Жюлиа с их фрактальной природой тоже по-своему красивы (см. нижний рисунок на с.90). Но прежде чем рассказывать о них, мы вернемся еще раз к множеству, носящему имя Бенуа Мандельброта, ученого, работающего в Исследовательском центре Томаса Уотсона фирмы IBM в Йорктаун-Хайтсе (шт.Нью-Йорк).

Множество Жюлиа (слева), соответствующее центральной части верхнего правого рисунка; увеличенная часть (справа)
Множество Мандельброта - обитатель комплексной плоскости, т.е. обычной плоскости, каждая точка которой характеризуется двумя координатными значениями. Точнее говоря, каждая точка комплексной плоскости представляется числом вида a+bi. Числа a и b можно считать координатами точки: a - вещественная часть комплексного числа a+bi, а b - его мнимая часть. Число i отчасти служит для того, чтобы различать эти две координаты между собой. Комплексные числа можно складывать, суммируя их соответственные координаты по отдельности; результат представляет собой другое комплексное число. Их можно также умножать друг на друга, следуя при этом правилам умножения многочленов:
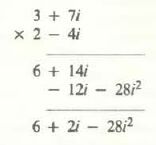
Чтобы представить результат в виде комплексного числа, член 28i2 нужно привести к стандартной форме, воспользовавшись самым важным свойством мнимых величин, а именно тем, что i2 = -1. Таким образом, выражение 6+2i-28i2 приводится к виду 34+2i. Теперь мы можем представить основную формулу, которая открывает нам множество Мандельброта, порождает также множества Жюлиа и в некотором смысле превращает порядок в хаос:
z <- z2+c.
Здесь z и c - это комплексные числа, каждое из них имеет мнимую и вещественную части. Число z возводится в квадрат и c прибавляется к результату согласно правилам умножения и сложения комплексных чисел. Формула как бы оживает, если начать последовательно вычислять значения сумм, подставляя в формулу каждый раз значение z, полученное на предыдущем шаге. Получающаяся в результате этого итерационного процесса последовательность комплексных чисел образует причудливый узор на комплексной плоскости. На каждом шаге новое комплексное число z лежит на некотором расстоянии от предшествующего. Это расстояние очень важно для вычисления множества Мандельброта.
Интересно представить полученную последовательность комплексных чисел (точек на комплексной плоскости) как блуждания исходной точки. Стремится ли она к бесконечности, все дальше удаляясь от начала координат комплексной плоскости? Некоторые комплексные числа действительно стремятся в бесконечность, другие навсегда ограничены в своем движении определенной областью, имеющей сложную форму. Их тюрьма, или область, где они содержатся, имеет фрактальные стены.
Как уже говорилось, итерационный процесс длится до бесконечности. Однако, каким образом выбираются константа c и исходное значение z? Можно, например, сделать число z равным нулю и выбирать различные значения c. Вырвется ли узник в данном случае на свободу? Будем повторять эксперимент снова и снова, систематически варьируя значение c в определенной области комплексной плоскости. Если узнику удается бежать, окрашиваем точку c в белый цвет, в противном случае делаем ее черной. Стены области, из которой не удается бежать, принимают форму множества Мандельброта. Если вместо того, чтобы окрашивать всех беглецов в белый цвет, придавать им окраску в зависимости от скорости побега, то изображение становится еще красивее.
Согласно только что описанному правилу, исходное значение числа z равно 0, или точнее, 0+0i. А что изменится, если процесс начать с какого-нибудь другого значения, скажем, z = 3.5+6i? Примет ли результирующее множество другую форму? Действительно, в результате мы всегда получаем деформированную версию множества Мандельброта. Обычно предпочтение отдается его канонической форме.
Если следовать противоположному правилу, когда значение c фиксировано, a z играет роль исходной точки, получающееся в результате итерационного процесса множество уже отличается по виду от множества Мандельброта. Оно, или вернее его граница, называется множеством Жюлиа. Множество Жюлиа не единственно, на самом деле имеется целое множество таких множеств: для каждого фиксированного значения c в формуле итераций мы получаем свое, отличное от других, множество Жюлиа, заполненное "узниками".
Я был вдохновлен на то, чтобы вернуться еше раз к множеству Мандельброта, прочтя книгу сотрудников Бременского университета Х.-О. Пайтгена и П.Рихтера "Красоты фракталов" (см. библиографию к статье на с.104). Эта крупноформатная книга, содержащая потрясающие черно-белые и цветные иллюстрации, с одинаковым успехом может служить и математическим учебным пособием, и украшением журнального столика. Вся теория, касающаяся множества Мандельброта и связанных с ним множеств Жюлиа, а также других аналогичных сложных систем, изложена в книге в виде математических теорем с доходчивым их описанием.
Рассмотрим смысл одной из теорем. Читатель, написавший программу для построения изображений множеств Жюлиа, возможно заметит, что для некоторых значений c множества получаются связными и графически выглядят как единое целое, в то время как для других значений с они оказываются несвязными. Что же обусловливает это различие? Ответ и прост и изящен: если выбранная точка c принадлежит множеству Мандельброта, то соответствующее множество Жюлиа будет связным. Если же c не принадлежит множеству Мандельброта, то множество Жюлиа будет несвязным.
Можно сделать нечто вроде мультипликационного фильма, иллюстрирующего смысл данной теоремы. Проведем прямую L от произвольной точки, принадлежащей множеству Мандельброта, к другой точке, не принадлежащей ему, и представим себе, что точка c медленно, но неуклонно продвигается вдоль линии L из внутренней области множества Мандельброта по направлению к его границе. Соответствующее множество Жюлиа будет становиться все более сжатым, постоянно уменьшаясь в размере, а когда точка с достигнет границы множества Мандельброта, множество Жюлиа сожмется до хрупкого дендритного скелета, практически не занимающего никакой площади. Когда с выйдет за границу множества Мандельброта, сопутствующее ему множество Жюлиа как бы взрывается, превращаясь во фрактальную пыль.
Читатели, которые пожелают и смогут написать программу, могут исследовать свойства множества Мандельброта и сопутствующих ему множеств Жюлиа, реализовав некоторые основные алгоритмы на том языке, которым они обычно пользуются. Во всех подобных алгоритмах присутствует итерационный процесс, зависящий существенным образом от следующей теоремы: если абсолютная величина итерируемой переменной z достигает 2, то ей суждено убежать в бесконечность, откуда она уже никогда не вернется. В основном именно этот критерий отличает беглецов от узников. Алгоритм содержит 100 шагов итераций, позволяющих переменной z достичь значения 2. Этот критерий, конечно, не срабатывает во всех 100% случаев, поскольку некоторое относительно небольшое количество беглецов не успевает достичь абсолютной величины 2 за 100 итераций. Можно было бы сделать число итераций равным, скажем, 1000, чтобы получить более точную картинку, но для этого потребовалось бы много машинного времени, даже на мощных компьютерах.
Абсолютная величина комплексного числа a+bi равна просто квадратному корню из a2+b2, другими словами, она представляет собой расстояние от начала координат, или нулевой точки. Основной алгоритм итераций имеет следующий вид:
n <- 0
while n<100 and abs(z)<2
- z <- z2 + c
- n <- n+1
раскрасить данную точку
Здесь n - индекс цикла с исходным значением 0. На каждом шаге цикла while, управляющего итерационным процессом, значение переменной n увеличивается на 1. Цикл while продолжается, "проворачивая мясорубку" итерационной формулы до тех пор, пока n не достигнет 100 или абсолютная величина z не достигнет 2. При выполнении любого из этих условий алгоритм выходит из цикла. Читателю предоставляется самому выбрать способ раскраски точек изображения. Этот способ, конечно, должен каким-то несложным образом зависеть от величины n, т.е. от той скорости, с которой точке удалось достичь расстояния 2, а также от того факта, удалось ли ей достичь этого расстояния. Читателям следует также не упускать из виду, что точка изображения на экране будет иметь, вообще говоря, другие координаты, отличающиеся от координат точки на комплексной плоскости.
Программа, написанная читателями, должна содержать отдельную процеруру вычислении абсолютной величины z, которая в приведенном выше алгоритме была представлена как abs(z). На самом деле, поскольку в большинстве языков программирования отсутствуют средства для работы с комплексными числами, переменную z нужно хранить в виде двух частей, скажем x (вещественная часть) и y (мнимая часть), то же касается и числа c, части которого можно обозначить соответственно как a и b. Следующий алгоритм будет уже несколько ближе к работающей программе:
n <- 0
while n <100 and x2+y2<4
- xx <- x2-y2+a
- y <- 2xy+b
- x <- xx
- n <- n+1
раскрасить данную точку
Наблюдательный читатель, наверное, заметит маленький трюк, введенный в эту версию итерационного процесса: вместо того чтобы сравнивать квадратный корень из выражения x2+y2 с 2, мы сравниваем само это выражение с 4. Результат тот же, но с помощью этого приема можно избежать многократного обращения к функции извлечения квадратного корня, выполнение которой требует относительно большого времени. Переменная xx временно содержит только что вычисленное значение x, пока вычисляется новое значение y. Таким образом, старое значение x сохраняется для дальнейших вычислений, пока его не заменит значение xx.
Программа, которую я назвал MANDELZOOM, плод моих первых попыток в данной области, предпринятых еще два года назад, будет представлена теперь в несколько более детальном виде. Она содержит основной итерационный алгоритм внутри цикла, в котором систематически варьируется комплексное число c и, как следствие, его части a и b. Если экран, на котором строится изображение, имеет размер 100*100 пикселов (точечных элементов изображения, образующих квадратную решетку), то программа будет основана на следующем двойном цикле:
gap <- side/100
a <- acorner
for j <- 1 to 100
- a <- a+gap
- b <- bcorner
- for k <- 1 to 100
- - b <- b+gap
- - x <- 0
- - y <- 0
- - [алгоритм итераций]
Однако, прежде чем программа MANDELZOOM доходит до этих операторов, она позволяет пользователю задать комплексное число, располагающееся в одном из углов квадрата, на котором строится изображение. Этот угол будет иметь координаты acorner, bcorner, наименьшие значения a и b, принимаемые комплексными числами в пределах данного квадрата. Квадрат, выбираемый пользователем программы, является как бы окном, через которое мы можем наблюдать изображение. Его можно сделать очень маленьким и тогда мы будем наблюдать в увеличенном виде ту часть множества, над которой располагается окно. Программа требует также указать значение переменной side, т.е. размер стороны квадрата на комплексной плоскости. Затем алгоритм вычисляет расстояние между последовательными комплексными числами c, задавая тем самым соответствующие приращения переменным a и b (это расстояние обозначено как gap).
Значения индексов j и k не участвуют ни в каких вычислениях внутри двойного цикла, поэтому эти индексы можно заменить какими-нибудь величинами, представляющими интерес. Например, вместо того чтобы пробегать значения от 1 до 100, индексы j и k могли бы пробегать через 100 последовательных точек на координатных осях экрана. После того как основная итерационная процедура присвоила определенное цветовое значение итерируемой точке z, точка с координатами (j, k) окрашивается в соответствующий цвет.
Рассмотрение программы MANDELZOOM будет неполным, если не упомянуть о модификации, предложенной Пайтгеном. Вместо того чтобы сравнивать абсолютную величину итерируемой переменной z с 2, можно в качестве порогового значения принять 100 или даже 1000. В конце концов, после того как абсолютная величина комплексной переменной достигла 2, она растет очень быстро и достигает значений порядка 100 или 1000 за несколько шагов итерационного процесса. И все же при различных исходных значениях итерируемые точки проходят пороговые величины с различными скоростями. Скорости тоже можно окрашивать, причем с плавными переходами между различными цветами. Красный цвет может, например, постепенно переходить в оранжевый, конечно, при условии, что цветовая палитра компьютера достаточно богата. Во всяком случае, цветные изображения, приведенные в данной статье, были получены именно этим способом. Пайтген считает, что распределение скоростей напоминает электрическое поле, как бы создаваемое вокруг множества Мандельброта. Градиенты напряженности "поля" представлены в воображаемом ландшафте Мандельброта (см. рисунок на с.89) в виде склонов горного хребта, окружающего то, что можно было бы назвать озером Мандельброта.

Множество Мандельброта в виде озера; горы представляют динамику окружающих точек
Хотя я не считаю, что слово ZOOM стало для меня навязчивым, я все же должен последовать примеру программы MANDELZOOM и назвать программу, генерирующую изображения множеств Жюлиа, JULIAZOOM. (Одно из значений слова ZOOM - это "рассматривать под большим увеличением"). Здесь мы также можем вплотную приблизиться к множеству и исследовать его как бы под очень сильной лупой. В программе JULIAZOOM применяется тот же основной алгоритм итераций, что и в программе MANDELZOOM, однако здесь у него уже несколько иная, так сказать, оправа.
Сначала программа запрашивает у пользователя значения величины xcorner, ycorner и side ("угол x", "угол y" и "сторона" соответственно). Она также запрашивает значение c в виде его составляющих a и b. Затем выполняется двойной цикл, кое в чем существенно отличающийся от цикла программы MANDELZOOM:
gap <- side/100
x <- xcorner
for j <- 1 to 100
- x <- x+gap
- у <- ycorner
- for k = 1 to 100
- - y <- y+gap
[алгоритм итераций]
Основной алгоритм итераций окрашивает точки экрана в зависимости от скорости, с которой итерационный процесс достигает (или вообще не достигает) порогового значения 2. Некоторые из наиболее эффектных графических результатов были получены при использовании самых простых правил окрашивания точек. На цветных мониторах даже трех цветов, присваиваемых по следующему правилу, оказывается достаточно, чтобы получить прекрасные изображения: окрасить в первый цвет точки со значениями n от 0 до 10, вторым цветом - точки со значениями n от 11 до 20, третьим цветом - точки со значениями n от 21 до 30, затем для следующих десяти значений n вернуться к первому цвету и т.д. На нецветных мониторах можно воспользоваться черно-белыми (или зелено-желтыми) контрастами, чередуя оба цвета для каждых десяти последовательных значений n.
Вооружившись работающей версией программы MANDELZOOM или JULIAZOOM (а может быть, обеими программами), читатели смогут заняться своими собственными исследованиями этих красивых и интересных фрактальных множеств. Можно побродить по комплексной плоскости в окрестностях множеств или же рассмотреть какие-то области под сильным увеличением, воспользовавшись компьютерным микроскопом, который был описан выше. Вплоть до предельной разрешающей способности, зависящей от точности арифметических операций у того или иного компьютера, эти множества предстают перед наблюдателем в виде удивительных узоров. Будущим исследователям микрокосма фрактальных объектов можно порекомендовать следующие интересные области, с координатными значениями, изменяющимися в пределах:
Множества Жюлна:
x и y от -1.8 до +1.8
Множество Мандельброта:
x от -2.25 до +0.75 и
y от -1.8 до +1.5
В сентябрьском номере журнала мы затронули тему хаоса в динамических системах, таких как механические маятники и электронные схемы. Свойства этих систем характеризуются простой итерационной формулой, в качестве переменных здесь выступают не комплексные, а обычные вещественные числа:
x <- rx(1-x).
Эта формула, очевидно, квадратична: если раскрыть скобки в правой части, то появится член, содержащий x в квадрате. В зависимости от выбранного значения параметра r, формула ведет себя либо просто, либо странно, если ее начать итерировать. При каждом значении r итерируемая переменная x образует орбиту, т.е. набор значений, которые x систематически посещает. В районе критического значения параметра 3.5699 переменная начинает быстро и более или менее непредсказуемо осциллировать между некоторыми значениями. Такое поведение формулы соответствует ситуации, когда описываемая ею физическая система, будь то двойной маятник или электронная схема, никак не может найти положение стабильности. Ее состояние постоянно меняется непредсказуемым образом, другими словами, наступает хаос.
Аналогичное явление наблюдается и в поведении комплексной итерационной формулы, рассматриваемой в данной статье, z <- z2+c. Однако в этом случае для каждого значения параметра c возникает уже не одна орбита - аттрактор. Их количество зависит от того, каким было выбрано исходное значение переменной z. Если абсолютная величина исходного значения z относительно мала, то переменная будет стремиться к определенной точке. Если же абсолютная величина исходного значения z будет достаточно большой, то в дальнейшем она будет неограниченно возрастать, и аттрактором будет уже бесконечность. И определенная точка, к которой стремится z, и бесконечность представляют собой две отдельные одноточечные орбиты - аттракторы для точек на комплексной плоскости. Граница между "зонами их притяжения" - это множество Жюлиа, невероятно тонкое и сморщенное. Оно тоже является орбитой, но не является аттрактором в строгом смысле слова. Точки, уже содержащиеся в этой пограничной области, совершают в ней беспорядочные скачки. Непосредственно вычислить множество Жюлиа непросто, потому что точность выполнения арифметических операций компьютером может не позволить точно указать точки, которые с самого начала должны находиться на границе, а когда начинается итерационный процесс, точность еще более снижается и итерируемые переменные уходят из поля зрения.
Как уже говорилось, каждому возможному значению параметра c соответствует свое, отличное от других множество Жюлиа. Множество Мандельброта в некотором смысле охватывает все возможные множества Жюлиа. Оно описывает судьбу переменной, выходящей из начала координат комплексной плоскости, для всех возможных значений параметра c. Для некоторых множеств Жюлиа область хаоса представляет собой лишь тонкую древовидную структуру или лаже некую симметричную россыпь точек, область, как бы посыпанную перцем. Читатели, наверное, помнят, что такие множества Жюлиа соответствуют значениям c, находящимся на границе множества Мандельброта или за его пределами.
Недавно мы встретились с Пайтгеном на конференции в Асиломаре (шт.Калифорния). Когда мы прогуливались вдоль пляжа, разговаривая о том, о сем, он охарактеризовал множество Мандельброта как своего рода огромную книгу, в которой каждое множество Жюлиа - не более чем страничка. По тому положению, которое занимает точка c в множестве Мандельброта, можно предсказать поведение итерируемой переменной, характеризуя обшую форму и размер сопутствующего множества Жюлиа. Здесь дело не только в том, будет ли оно связным или несвязным. Если, к примеру, выбрать c из перешейка между основной частью множества Мандельброта и одной из его "точек", то соответствующее множество Жюлиа окажется сжатым в структуру, также состоящую из перешейков и точек. Аналогия, согласно которой множество Мандельброта является как бы словарем для множеств Жюлиа, предполагает фундаментальное различие между этими множествами. Структура множества Жюлна подобна самой себе (в различном масштабе), в то время как для множества Мандельброта (даже для его границы) это не так. В противном случае, как говорит Пайтген. множество Мандельброта не обладало бы способностью кодировать в себе несчетные количества родственных множеств Жюлиа.

Шесть множеств Жюлиа; некоторые из них связные (a, b, c и e), а другие нет (d и f).
В упомянутой книге "Красоты фракталов" есть еще много интересного. Я весьма признателен Пайтгену за те изображения, которые он предоставил для иллюстрации в настоящей статье. Не все они получены описанными здесь способами, однако рецепты изготовления всех изображений даны в книге.
В качестве заключительного замечания об исследованиях, ведущихся в настоящее время специалистами в области динамических систем, я упомяну еще об одном объекте, таящемся в пространстве высшей размерности, чудовище, порождаемом кубическими итерациями, формула которых, в отличие от формулы Мандельброта. содержит z3 вместо z2. Этот объект четырехмерный, его завивающиеся щупальца тянутся от главного "тела" и образуют причудливую картину, которую мы не способны увидеть. Однако ее трехмерные поперечные сечения могут быть вычислены и представлены подобно тому, как это сделано на рисунке на с.92.

Трехмерное поперечное сечение четырехмерного множества Мандельброта
БИБЛИОГРАФИЯ
THE BEAUTY OH FRACTALS. HEIRV OTTO PEITGEN AND PETER H. RICHTER. Springer-Verlag, 1986.
ОТКЛИКИ
5 1988
В СТАТЬЕ январского номера мы вновь обратились к множеству Мандельброта и рассказали о мириадах родственных ему множеств, носящих имя Жюлиа, французского математика, одного из ведущих специалистов в области динамических систем. Программы, порождающие множества Жюлиа, настолько же просты, как и те, с помощью которых можно получать множества Мандельброта. Поэтому сотни наших читателей, а может быть уже и тысячи, написали свои собственные программы или собираются сделать это. В США издается специальный журнал о фракталах под названием "AMYGDALA". В нем приводятся различные полезные советы для тех, кто пишет программы, которые порождают множество Мандельброта или другие фрактальные множества. На его страницах программисты делятся своими секретами и рекламируют написанные ими программы.
В конце упомянутой статьи я продемонстрировал трехмерное чудовище, которое в действительности представляло собой поперечное сечение четырехмерного множества Мандельброта. Хайнц-Отто Пайтген, западногерманский математик и художник, раскрыл "рецепт" четырехмерного множества. Нужно итерировать уравнение z <- z3-3a2z+b, где a и b комплексные параметры. Какие точки играют в четырехмерном множестве ключевую роль подобно точке z = 0? На самом деле существуют сразу две такие точки, а именно z = +a и z = -a. Следовательно, мы имеем не одно, а два четырехмерных множества Мандельброта.
Г.Тичаут из Эверетта (шт. Вашингтон) пишет, что он рассматривает множества Мандельброта и Жюлиа как сечения четырехмерного множества, хотя его четырехмерное множество не совпадает с множеством Пайтгена. Основная итерационная формула z <- z2+c порождает множество Мандельброта, когда z остается постоянным, а c варьирует. Она же порождает множество Жюлиа, если c фиксировано, а z варьирует. Но z и c вместе определяют четыре измерения, по два на каждый параметр. Если собрать вместе все множества Жюлиа не в одномерную, а в двумерную совокупность, то возникает супермножество. М.Хармен из Кемберли (Англия) поделился размышлениями о таком же объекте.
Однако четырехмерный приз следует все же присудить У.Дженксу из Стамфорда (шт.Коннектикут). Не удовлетворенный обычными комплексными числами, Дженкс изобрел свои собственные числа, состоящие из четырех частей. Его числа аналогичны так называемым кватернионам, сложному множеству чисел, которое было изобретено математиками прошлого столетия и которым теперь пользуются физики. Дженкс прислал мне трехмерные представления своего объекта в виде последовательности из 29 его сечений.
Конечно, читатели, увлекающиеся построением изображений множества Мандельброта, хотели бы терять при этом поменьше времени - ведь кроме изображений итерационный процесс породил и множество обкусанных от нетерпения ногтей. Д.Холт из Силвер-Спринга (шт.Мэриленд) обнаружил, что скорость можно повысить на 8%, если вместо процедуры возведения числа в квадрат воспользоваться обычной операцией умножения числа само на себя. В его программном обеспечении эта операция выполняется быстрее, чем возведение в квадрат.
Наконец, рисунок внизу на с.89 представляет собой еще один экспонат в постоянно пополняющейся коллекции изображений множества Мандельброта. Он прислан Дж.Лойлессом из Лилберна (шт.Джорджия). При этом он воспользовался системой "XT турбо-клоун с арифметическим сопроцессором 8087 и 24-точечным принтером Тошиба 321".

Изображение множества Мандельброта, полученное Дж.Лойлессом

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
Re: Приложение. В мире науки. Занимательный компьютер. 1983-1990
2 1988
ВОСПРОИЗВЕДЕНИЕ "ЖИВЫХ" СЦЕН НА ЭКРАНЕ ДИСПЛЕЯ: ЗАДАЧИ ДЛЯ НАЧИНАЮЩИХ ПРОГРАММИСТОВ
А.К.ДЬЮДНИ
ЭФФЕКТИВНЫЕ кинофокусы не всегда требуют сложного технического оборудования или финансовой поддержки крупных киностудий. Любители фантастических сюжетов теперь сами могут воспроизводить удивительные явления, хотя и ограниченного репертуара, на экранах своих домашних компьютеров с помощью того, что можно было бы назвать программами видеоэффектов. Представим на минуту, что по экрану компьютера внезапно поползли червяки. Программа видеоэффектов способна создать такую "живую" сцену. Или, например, экран может превратиться в водяную поверхность с расходящимися кругами от падающих дождевых капель. Создать этот эффект тоже в общем-то довольно просто. И наконец, вообразим, что наш экран - это иллюминатор, через который видна Вселенная с взрывающимися или стремительно пробегающими мимо звездами, как будто мы находимся на борту космического корабля, с колоссальной скоростью пролетающего по звездному коридору. Подобная иллюзия достигается при помощи третьей, довольно экономной программы.
Экономия средств, на мой взгляд, одно из главных свойств программ подобного рода. Если достигается какой-то поразительный эффект, то лучше, если порождающая его программа оказывается чрезвычайно короткой. Как же лучше всего ввести читателей в таинственный мир удивительных явлений, видимых на экране дисплея и скрывающихся за ним. Судя по сравнительно небольшой, но всегда присутствующей части получаемых мною писем, многие начинающие любители компьютерных игр с грустью смотрят на страницы статей нашей рубрики, чувствуя свою неспособность превратить представленные в них алгоритмы в работающие программы. Они остаются лишь пассивными зрителями, когда мимо них в ярком парадном шествии проходят множества Мандельброта, лестницы слов, сотворенные компьютерами карикатуры, сосуды с первобытным бульоном и звездные скопления. Они могут лишь мечтать о тон радости, которую испытывают авторы программ, видя, как алгоритмы обретают плоть и кровь и оживают на экране дисплея.
Поэтому на этот раз я решил помочь таким читателям и не ограничиваться лишь общим описанием приемов, с помощью которых можно воспроизводить упомянутые выше видеоэффекты. Я расскажу обо всех "винтиках и гаечках", которые превращают алгоритм в программу. Я объясню, как населить экран ползающими червяками, не только на универсальном алгоритмическом языке, но и на конкретном языке программирования - Бейсик. Не ограничиваясь объяснением того, как нужно строить сам алгоритм, я приведу пример преобразования, который поможет читателям лучше понять как прошлые, так и будущие статьи нашей рубрики. Возможно, начинающие программисты почувствуют, что в них самих тоже произошло важное преобразование.
Кто бы смог удержаться от соблазна написать программу, порождающую на экране симпатичных копошащихся червячков? Энтузиазм читателей, наверное, не очень пострадает, когда они узнают, что каждый червяк на экране представляет собой не что иное, как цепочку окружностей. Впрочем, чтобы составить программу для какого-нибудь видеоэффекта (и вообще любую программу), нужно на время абстрагироваться от эмоций и сосредоточиться на анализе. Каким же образом заставить червяка двигаться? Добавляя новую окружность у головы и удаляя старую у хвоста: в результате появляется ощущение движения, как будто бы червяк ползет,- конечно, это иллюзия, но фокус тем не менее удается.
Идея программы WORMS (червяки) зародилась у меня, когда я впервые увидел подобный эффект на экране моего новенького компьютера SUN. Кто-то занес эффектную графическую программу в каталог системных и прикладных программ, обычно поставляемых в комплекте с машиной. Этот кто-то, по-видимому, подумал, что зрелище копошащихся на большом экране дисплея SUN червей убедит покупателей, что высокая цена на машину вполне оправдана.
Действительно, решение написать эту программу пришло, когда я задумался над тем, каким образом достигается впечатление, что червяк ползет. Пристально вглядываясь в экран, я вскоре понял, что эффект движения достигается каждый раз за счет добавления новой окружности к голове червяка и стирания старой в хвосте. "Ага,- сказал я себе,- это просто". Я сразу представил себе коротенькую программку, но затем подумал о том, что программа, стирающая старую окружность, должна помнить, где находится эта окружность. А поскольку каждое звено червяка рано или поздно нужно будет стереть, положение каждой окружности нужно запоминать.
Простейшая структура данных, позволяющая запоминать большое число однородных элементов данных, это массив. Следовательно, теперь нужно было подумать о том, как можно запоминать окружности в массиве. На каком бы языке мы ни писали программу, графическая команда "нарисовать окружность" (или стереть ее, проведя по ее контуру черной линией) обычно требует указания двух координатных значений, а именно центра окружности и радиуса. Радиус всех окружностей, из которых строятся звенья червяков, будет постоянной величиной, а вот координаты центра должны меняться от одной окружности к другой. Поэтому необходимо хранить лишь координаты центров. Так как, вообще говоря, абсцисса центра отличается от ординаты, то координатные значения центров удобнее хранить не в одном, а в двух массивах. Назовем их xcirc и ycirc. Таким образом, элемент xcirc(i) будет хранить координату i-й окружности по оси x, а ycirc(i) - по оси y.
Теперь мы подошли к главной трудности в программе WORMS: нужно, чтобы она каким-то образом добавляла к массиву новые окружности и удаляла из него старые. Подобно червяку, сами массивы будут состоять из цепочек окружностей. Однако массивы не движутся по экрану. Мы заведем специальную переменную, называемую указателем, в которой будет храниться та позиция массива, где в данный момент содержится координата последней, хвостовой окружности червяка. И в математике, и в программнрованин чудодейственной силой обладает простая процедура - присвоение имени. Назвав переменную-указатель tail (хвост), я сразу же догадался, какой должна быть главная, ключевая команда в программе WORMS:
tail <- tail+1.
Другими словами, на каждом шаге основного цикла программы указатель хвоста будет продвигаться в массиве на одну поэииию.
Если, например, последнее значение tail было равно 7, то координаты хвостовой окружности червяка хранились соответственно в элементах xcirc(7) и ycirc(7). Когда мы выполним команду приращения, приведенную выше, новое значение переменной tail будет равно 8. Тем временем мы должны будем нарисовать новую окружность и поместить ее координаты в массивы xcirc и ycirc. Логично поместить их на ту позицию, которую в данный момент занимают координаты старого хвоста, а именно позицию 7.
Пока что я не имею ни малейшего понятия, каким образом программа должна определять то место, где нужно рисовать новые головные окружности на экране,- это отдельный вопрос, к которому мы перейдем позже. Часто трудности при составлении программы объясняются той путаницей, которая возникает в голове, когда мы хотим учесть сразу много различных действий.
Еще не приступая к построению наброска алгоритма программы WORMS на бумаге, я уже принял решение, что нужно завести два массива, хранящие координаты всех окружностей, составляющих на данный момент тело червяка. Указатель tail должен продвигаться вдоль каждого массива, заменяя координаты старой хвостовой окружности координатами новой головной. Однако что произойдет, когда указатель tail достигнет конца массива? Конечно же, он должен снова перескочить на начало, для чего нужно воспользоваться вычислениями по некоторому модулю. Если, скажем, червяк состоит из 10 колец и старое значение указателя tail равно 9, то его новое значение должно быть равно 0. Пока наш алгоритм имеет следующий вид:
цикл
- tail <- tail+1 (по какому-то модулю)
- выбрать координаты новой головы
- подставить в xcirc {tail) и ycirc{tail)
- нарисовать новую голову
- стереть хвост
конец цикла
Главная польза алгоритмического подхода к построению компьютерной программы заключается как раз в неопределенности и гибкости алгоритмического языка. В любом месте алгоритма можно написать что угодно, лишь бы это имело какой-то потенциальный смысл, который можно уточнить позже. Например, сейчас я пока отложил вопрос о том, как программа должна определить координаты новой головы, просто записав "выбрать координаты новой головы". В подробном алгоритме это, возможно, превратится в несколько строк. Но даже при такой грубой детализации, подставив пока эту фразу, я сразу же яснее представил себе, какой должна быть структура программы. Я даже нашел ошибку: как программа сможет "стереть хвост", если она не знает, где он находится? Дело в том, что выше в теле цикла на место этих координат были записаны координаты новой головы. Стереть старый хвост следовало раньше, до того как на место старых были подставлены новые координаты. Я внес в алгоритм соответствующие коррективы. Возможно, читатели захотят сами внести исправления, прежде чем посмотреть, как это было сделано у меня.
Теперь настало время сделать второй проход по алгоритму. Какой именно цикл я подразумевал, заключив в него весь остальной алгоритм? Пытаясь ответить на этот вопрос, я сразу же натолкнулся на другую проблему: как должна завершаться программа? Сначала я подумал о простейшей схеме с фиксированным числом повторений, или итераций, реализуемой посредством оператора цикла FOR, в котором некоторый индекс автоматически отсчитывает несколько тысяч итераций, в то время как червяк будет ползать по экрану. Но лучше было бы закончить карьеру червяка, когда будет нажата какая-нибудь клавиша. Таким образом, программа будет снова и снова выполнять цикл, пока человек не нажмет определенную клавишу.
Следует также уточнить, что конкретно подразумевается под словами "по какому-то модулю" в первом операторе цикла. Этот модуль должен быть равен размеру массива. Однако тут возникает еще один вопрос, какой длины будет червяк? Я произвольно выбрал 25 звеньев, решив, что червяк такой длины будет выглядеть достаточно правдоподобно.
Теперь алгоритм программы WORMS принял уже следующий вид (здесь mod означает "по модулю"):
repeat
- tail <- tail+1 (mod 25)
- стереть хвост
- выбрать координаты новой головы
- подставить в xcirc(tail) и ycirc(tail)
- нарисовать новую голову
until нажатие клавиши
Продолжая уточнять алгоритм, я решил заменить фразу "стереть хвост" чем-то более близким к тому языку программирования, которым я намереваюсь в конце концов воспользоваться. Поскольку я хотел стереть старую окружность, нарисовав черный круг там, где раньше был белый (на моем нормально черном экране), я подставил выражение "черная окружность в circ(tail)", что означает черную окружность с центром в точке с координатами xcirc(tail) и ycirc(tail).
Теперь я приступаю к фразе "выбрать координаты новой головы". Посредством какого механизма программа может решить, где следует нарисовать новую головную окружность? Очевидно, она должна быть в непосредственной близости от предыдущей и где-то "впереди" от нее. Более того, чтобы извивания и повороты червяка выглядели естественно, новое направление не должно слишком резко отличаться от предшествующего. Здесь решение проблемы заключалось просто в том, чтобы ввести одну-единственную новую переменную dir (от слова direction - направление). Она должна содержать текущее направление движения червяка, выраженное в градусах. При каждом повторении главного цикла программа будет произвольно либо увеличивать, либо уменьшать значение dir на 10o.
Пришло время решить, насколько близко друг от друга должны быть окружности и какого они должны быть размера. В качестве пробного значения радиуса можно принять, например, 4. Чтобы червяк выглядел как единое целое, нужно, чтобы окружности частично перекрывали друг друга. Далее я заменил фразу "выбрать координаты новой головы" следующим фрагментом:
change <- случайное число
if change < 0.5
- then dir <- dir + 10
- else dir <- dir - 10
x <- xcirc(tail-1)
y <- ycirc{tail-1)
newx <- x+4*cos(dir)
newy <- y+4*sin(dir)
В этом алгоритмическом фрагменте случайным образом выбирается число, присваиваемое переменной change (изменение). Большинство языков программирования имеет оператор выбора случайного числа в диапазоне от 0 до 1. Поскольку случайное число этого диапазона будет меньше 0.5 в среднем в 50% случаев, переменная dir будет увеличиваться в среднем через раз. Конечно, эта статистика справедлива лишь при большом количестве испытаний. На коротких же промежутках времени переменная dir будет меняться непредсказуемым образом в ту или иную сторону на 10o. Переменные x и y - это просто координаты предыдущей головной окружности. Последние два оператора представляют собой элементарные тригонометрические вычисления, при помощи которых мы получаем изменения x и y, приведенные к радиусу, равному 4. Таким образом, координаты новой головы выбраны.
Осталось лишь сделать еще два шага, чтобы окончательно уточнить алгоритм. Запомнить координаты новой головы в элементах xcirc(tail) и ycirc(tail) можно очень просто, при помощи двух операторов присваивания. Чтобы нарисовать новую голову, можно воспользоваться графической псевдокомандой, при помощи которой мы ранее стирали хвост.
Наконец, нужно инициализировать (т.е. присвоить начальные значения) массивы и переменные перед выполнением алгоритма. В данном случае указателю tail присвоим значение 1, а элементам массивов xcirc(l) и ycirc(1) - по 100 каждому. Остальным элементам этих массивов автоматически присвоены нулевые значения. Переменная направления dir имела исходное значение 0. Таким образом, червяк "начинался" в точке с координатами (100, 100) и двигался под углом 0 к горизонту. Точка (100, 100) лишь условно обозначает координаты центра окружности; на экране в зависимости от типа компьютера эти координаты могут быть иными.
Одна проблема все же осталась: а что, если червяк уползет за пределы экрана? Чтобы решить ее, я наделил программу еще одним свойством. Если координатные значения x или y выходят за диапазон, соответствующий размерам экрана, то они автоматически преобразуются в координаты точки, расположенной на его противоположном крае. Предположив, что наш гипотетический экран имеет диапазон координатных значений от 0 до 199, мы можем воспользоваться следующими операторами, преобразующими координаты так, чтобы они всегда находились в пределах выбранного диапазона:
newx <- newx mod 200
newy <- newy mod 200
Возможность вычисления по задан ному модулю имеется практически во всех языках программирования. При этом преобразуемое число (newx) делится на заданный модуль (200) и в качестве результата берется остаток от деления. Теперь переменная, которой присваивается остаток (newx) имеет значение, вычисленное по модулю.
Ну вот и все, что касается программы WORMS. Или может быть правильнее было бы назвать ее WORM (червяк)? Ведь алгоритм порождает лишь одного червяка. Чтобы к названию программы по праву добавить окончание S, читатели могут завести по одному набору массивов и переменных для каждого червяка, который должен появиться на экране. Рассмотренный выше алгоритм полностью приведен на рисунке внизу. Рядом приведена эквивалентная программа на языке Бейсик. Как педагог я был бы весьма разочарован, узнав, что кто-нибудь из наших читателей просто-напросто скопировал мою программу на Бейсике в свою машину, не усвоив объяснений того, о чем так подробно говорилось выше.

Превращение алгоритма WORMS (червяки) в программу на языке Бейсик
Сравнив строка за строкой алгоритм и программу, мы обнаружим довольно близкое сходство между ними. Действительно, два основных блока операторов в алгоритме практически не претерпели никаких изменений при переводе на Бейсик (для машины IBM PC Бейсик, версия 3.0). Основные различия связаны со свойствами реализации ввода с клавиатуры в языке Бейсик IBM PC, а также отсутствием цикла типа repeat в данной версии Бейсика.
В первом случае KEY(1) (функциональная клавиша F1 на клавиатуре компьютера IBM PC) была выбрана в качестве выключателя, на который пользователь программы может нажать, когда ему надоест наблюдать за тем, как червяк ползает по экрану. В строке 70 программы эта клавиша активизируется, сообщая системе, реализующей команды Бейсика, что нужно постоянно проверять, не поступил ли сигнал от клавиши F1. В строке 90 команда KEYOFF удаляет пояснительный текст в нижней части экрана, чтобы освободить место для червяков. Однако главная команда, использующая клавишу F1, содержится в строке 60. Здесь программе надлежит совершить переход на строку 290, если пользователь нажал на клавишу F1. В строке 290 экран очищается и выполнение программы завершается командой END.
Во втором случае ввиду отсутствия в языке цикла типа repeat было необходимо построить эквивалентную последовательность выполнения операторов с помощью команды перехода GOTO на строку 280 программы. В результате программа будет снова и снова возвращаться на строку 110, пока кто-нибудь не нажмет на клавишу F1. Тело цикла выделено в программе двумя строками комментария под номерами 100 и 270. Эти комментарии были вставлены лля того, чтобы читатели лучше видели структуру цикла в программе.
Есть и другие отличия между алгоритмом и программой, связанные со свойствами языка Бейсик. В строке 10 устанавливается размер массивов, равный 25 элементам для каждого массива. В строке под номером 80 устанавливается высокая разрешающая способность экрана для компьютера марки IBM PC. Здесь точки изображения располагаются очень близко друг к другу. В строке 110 новая переменная wastail принимает значение переменной tail непосредственно перед тем, как последняя получает приращение. Следовательно, переменную wastail можно подставить в алгоритме вместо выражения tail-1 там, где вычисляются значения x и y. Однако главная причина введения переменной wastail заключается в том, что tail как индекс массива не может принимать нулевое значение в данной версии языка Бейсик. В связи с этим в строке 120 единица прибавляется после того, как взят модуль, но не прежде. Записывая алгоритм, я допустил неточность, небрежно предположив, что индекс tail должен пробегать значения от 0 до 24. Реальная команда, при помощи которой рисуется окружность на языке Бейсик IBM PC, содержится в строке 130. Центр окружности находится в точке с координатами XCIRC(TAIL), YCIRC(TAIL), радиус равен 4, а цвет обозначен цифрой 0 (черный).
В строке 150 значение переменной DIR получает приращение не в 10o, а на эквивалентную величину 0.1745рад. (В версии Бейсика для компьютера IBM PC углы не измеряются в градусах). В строках 200 и 210 переменные NEWX и NEWY ограничиваются значениями 600 и 200 соответственно. Это делается для того, чтобы координаты не выходили за пределы экрана для компьютера IBM PC. Средство Бейсика, позволяющее выделять модуль, хорошо работает для положительных чисел, но не работает с отрицательными. Поэтому, когда червяк пытается уползти с экрана в отрицательном направлении, модуль берется с прибавлением соответствующего размера экрана, так как это сделано в строках 220 и 230. Червяк, уползающий с одного края прямоугольника, появляется сразу же на другом краю. В строке 290 команда SCREEN 0 очищает экран для возможных в дальнейшем текстов.
Читатели, которые пожелают усовершенствовать свою версию программы, могут вставить перед началом цикла команду RANDOMIZE, не позволяя, таким образом, червяку повторять тот же путь. Можно также предусмотреть возможность повторного запуска программы после ее остановки. Можно, например, трассировать путь червяка пунктирной линией из точечек, подобно тому, как мы сделали это на верхнем рисунке, приведенном на с.83.

Червяк, оставляющий след (вверху), дождевые капли (слева внизу) и звездный взрыв (справа внизу)
Программы для других уже упомянутых видеоэффектов теперь, наверное, могут быть написаны даже новичками, если они к тому же воспользуются некоторыми подсказками. Программа, которую я назвал RAINDROPS (дождевые капли), случайным образом выбирает точку на экране дисплея и описывает вокруг нее последовательность концентрических окружностей возрастающего радиуса. Затем программа выбирает другую точку и повторяет процедуру построения окружностей. RAINDROPS продолжает работать до тех пор, пока "хозяин погоды" не нажмет клавишу. Таким образом, программа строится из двух циклов: внешнего цикла, в котором выбирается точка, и внутреннего цикла, в котором рисуются окружности вокруг выбранной точки. Программа преобразует два случайных числа в диапазоне между 0 и 1 в координаты точки на экране путем умножения этих чисел на соответствующие размеры экрана. Получаемая в результате точка (x, y) становится центром последовательности окружностей, рисуемых во внутреннем цикле. Пусть индекс k пробегает значения от 1 до 25 по мере того, как на экране строятся белые (или какого-нибудь другого цвета) окружности. Центры всех этих окружностей находятся в точке с координатами (x, y), а радиусы принимают значения, равные 4k. Проще, конечно, оставлять нарисованные таким образом окружности неподвижными. Однако эффект был бы более реалистичным, если бы несколько окружностей, или даже одна, распространялись, подобно волне. Для этого программа RAINDROPS должна стирать (перерисовывать черным цветом) окружность радиуса 4(k-1) всякий раз после того, как нарисована окружность радиуса 4k.
Программа STARBURST (звездный взрыв) демонстрирует эффект космического взрыва. По существу тот же эффект можно интерпретировать как полет вдоль огромного звездного коридора, наблюдаемого из иллюминатора космического корабля, который движется с околосветовой скоростью. Звезды каждый раз перемещаются на небольшое расстояние вдоль линий перспективы по направлению к наблюдателю. Величина сдвига возрастает по мере того, как звезды приближаются к наблюдателю. Создается впечатление, что объекты, находящиеся ближе, движутся с большей скоростью по сравнению с удаленными объектами. Программа STARBURST несколько сложнее, чем RAJNDROPS. Она должна постоянно следить за всеми звездами, находящимися в пределах экрана. Для этого читатели могут воспользоваться массивом, назвав его, скажем, stars (звезды) - а правильнее будет сказать двумя массивами, как в программе WORMS,- чтобы хранить координаты x и y каждой звезды. Координата z оказывается скрытой в кажущемся движении звезд.
Когда звезда впервые появляется в исходной точке (100, 100), ее перемещения вначале очень малы, но затем они растут по мере того, как звезда приближается к наблюдателю (или наоборот - наблюдатель приближается к звезде). Величина приращения обратно пропорциональна z - кажущемуся расстоянию от наблюдателя. При составлении программы можно запланировать, например, по 25 сдвигов на каждую звезду, прежде чем она выйдет за пределы экрана. Таким образом, расстояние z до любой данной звезды можно принять равным 25-k, где k: - количество итераций в расчете кажущихся расстояний до этой звезды.
В большом цикле программы на каждом шаге создается одна новая звезда, а для всех остальных звезд координаты, хранящиеся в массивах, получают приращения.
ОТКЛИКИ
6 1988
БОЛЬШИНСТВО программистов (как новичков, так и опытных), заинтересовавшихся видео-эффектами, описанными в нашей рубрике в февральском номере, выбрали для своих упражнений задачу с червяками. С.Африа из Оттавы, предыдущее письмо которого касалось головоломки о ханойской башне, рассмотренной нами еще в начале 1985г., отмечает, что ползающие червяки представляют собой особенно эффектное зрелище, когда программа выполняется в откомпилированной форме.
У.Клементсу из Беверли-Хилла (шт.Калифорния) не понравилось поведение червяков на краях экрана. Вместо того чтобы позволять им уползать за пределы одного края и появляться на противоположной стороне экрана, программа Клементса изменяет направление их движения на величину +2.5 или -2.5 в зависимости от того, превосходит ли переменная change (изменение) значение 0.5.
Случай с Р.Скоттом-младшим из Мэдисона (шт.Виргиния), наверное, типичен для тех читателей, чьи компьютеры работают с версией Бэйсика, отличающейся от версии, которой мы пользовались в наших примерах. Червяки программы WORMS отказываются ползать по экранам их компьютеров. Подобные отличия, кажущиеся фатальными, обычно не очень значительны, и их легко обойти после того, как они выявлены.
ВОСПРОИЗВЕДЕНИЕ "ЖИВЫХ" СЦЕН НА ЭКРАНЕ ДИСПЛЕЯ: ЗАДАЧИ ДЛЯ НАЧИНАЮЩИХ ПРОГРАММИСТОВ
А.К.ДЬЮДНИ
ЭФФЕКТИВНЫЕ кинофокусы не всегда требуют сложного технического оборудования или финансовой поддержки крупных киностудий. Любители фантастических сюжетов теперь сами могут воспроизводить удивительные явления, хотя и ограниченного репертуара, на экранах своих домашних компьютеров с помощью того, что можно было бы назвать программами видеоэффектов. Представим на минуту, что по экрану компьютера внезапно поползли червяки. Программа видеоэффектов способна создать такую "живую" сцену. Или, например, экран может превратиться в водяную поверхность с расходящимися кругами от падающих дождевых капель. Создать этот эффект тоже в общем-то довольно просто. И наконец, вообразим, что наш экран - это иллюминатор, через который видна Вселенная с взрывающимися или стремительно пробегающими мимо звездами, как будто мы находимся на борту космического корабля, с колоссальной скоростью пролетающего по звездному коридору. Подобная иллюзия достигается при помощи третьей, довольно экономной программы.
Экономия средств, на мой взгляд, одно из главных свойств программ подобного рода. Если достигается какой-то поразительный эффект, то лучше, если порождающая его программа оказывается чрезвычайно короткой. Как же лучше всего ввести читателей в таинственный мир удивительных явлений, видимых на экране дисплея и скрывающихся за ним. Судя по сравнительно небольшой, но всегда присутствующей части получаемых мною писем, многие начинающие любители компьютерных игр с грустью смотрят на страницы статей нашей рубрики, чувствуя свою неспособность превратить представленные в них алгоритмы в работающие программы. Они остаются лишь пассивными зрителями, когда мимо них в ярком парадном шествии проходят множества Мандельброта, лестницы слов, сотворенные компьютерами карикатуры, сосуды с первобытным бульоном и звездные скопления. Они могут лишь мечтать о тон радости, которую испытывают авторы программ, видя, как алгоритмы обретают плоть и кровь и оживают на экране дисплея.
Поэтому на этот раз я решил помочь таким читателям и не ограничиваться лишь общим описанием приемов, с помощью которых можно воспроизводить упомянутые выше видеоэффекты. Я расскажу обо всех "винтиках и гаечках", которые превращают алгоритм в программу. Я объясню, как населить экран ползающими червяками, не только на универсальном алгоритмическом языке, но и на конкретном языке программирования - Бейсик. Не ограничиваясь объяснением того, как нужно строить сам алгоритм, я приведу пример преобразования, который поможет читателям лучше понять как прошлые, так и будущие статьи нашей рубрики. Возможно, начинающие программисты почувствуют, что в них самих тоже произошло важное преобразование.
Кто бы смог удержаться от соблазна написать программу, порождающую на экране симпатичных копошащихся червячков? Энтузиазм читателей, наверное, не очень пострадает, когда они узнают, что каждый червяк на экране представляет собой не что иное, как цепочку окружностей. Впрочем, чтобы составить программу для какого-нибудь видеоэффекта (и вообще любую программу), нужно на время абстрагироваться от эмоций и сосредоточиться на анализе. Каким же образом заставить червяка двигаться? Добавляя новую окружность у головы и удаляя старую у хвоста: в результате появляется ощущение движения, как будто бы червяк ползет,- конечно, это иллюзия, но фокус тем не менее удается.
Идея программы WORMS (червяки) зародилась у меня, когда я впервые увидел подобный эффект на экране моего новенького компьютера SUN. Кто-то занес эффектную графическую программу в каталог системных и прикладных программ, обычно поставляемых в комплекте с машиной. Этот кто-то, по-видимому, подумал, что зрелище копошащихся на большом экране дисплея SUN червей убедит покупателей, что высокая цена на машину вполне оправдана.
Действительно, решение написать эту программу пришло, когда я задумался над тем, каким образом достигается впечатление, что червяк ползет. Пристально вглядываясь в экран, я вскоре понял, что эффект движения достигается каждый раз за счет добавления новой окружности к голове червяка и стирания старой в хвосте. "Ага,- сказал я себе,- это просто". Я сразу представил себе коротенькую программку, но затем подумал о том, что программа, стирающая старую окружность, должна помнить, где находится эта окружность. А поскольку каждое звено червяка рано или поздно нужно будет стереть, положение каждой окружности нужно запоминать.
Простейшая структура данных, позволяющая запоминать большое число однородных элементов данных, это массив. Следовательно, теперь нужно было подумать о том, как можно запоминать окружности в массиве. На каком бы языке мы ни писали программу, графическая команда "нарисовать окружность" (или стереть ее, проведя по ее контуру черной линией) обычно требует указания двух координатных значений, а именно центра окружности и радиуса. Радиус всех окружностей, из которых строятся звенья червяков, будет постоянной величиной, а вот координаты центра должны меняться от одной окружности к другой. Поэтому необходимо хранить лишь координаты центров. Так как, вообще говоря, абсцисса центра отличается от ординаты, то координатные значения центров удобнее хранить не в одном, а в двух массивах. Назовем их xcirc и ycirc. Таким образом, элемент xcirc(i) будет хранить координату i-й окружности по оси x, а ycirc(i) - по оси y.
Теперь мы подошли к главной трудности в программе WORMS: нужно, чтобы она каким-то образом добавляла к массиву новые окружности и удаляла из него старые. Подобно червяку, сами массивы будут состоять из цепочек окружностей. Однако массивы не движутся по экрану. Мы заведем специальную переменную, называемую указателем, в которой будет храниться та позиция массива, где в данный момент содержится координата последней, хвостовой окружности червяка. И в математике, и в программнрованин чудодейственной силой обладает простая процедура - присвоение имени. Назвав переменную-указатель tail (хвост), я сразу же догадался, какой должна быть главная, ключевая команда в программе WORMS:
tail <- tail+1.
Другими словами, на каждом шаге основного цикла программы указатель хвоста будет продвигаться в массиве на одну поэииию.
Если, например, последнее значение tail было равно 7, то координаты хвостовой окружности червяка хранились соответственно в элементах xcirc(7) и ycirc(7). Когда мы выполним команду приращения, приведенную выше, новое значение переменной tail будет равно 8. Тем временем мы должны будем нарисовать новую окружность и поместить ее координаты в массивы xcirc и ycirc. Логично поместить их на ту позицию, которую в данный момент занимают координаты старого хвоста, а именно позицию 7.
Пока что я не имею ни малейшего понятия, каким образом программа должна определять то место, где нужно рисовать новые головные окружности на экране,- это отдельный вопрос, к которому мы перейдем позже. Часто трудности при составлении программы объясняются той путаницей, которая возникает в голове, когда мы хотим учесть сразу много различных действий.
Еще не приступая к построению наброска алгоритма программы WORMS на бумаге, я уже принял решение, что нужно завести два массива, хранящие координаты всех окружностей, составляющих на данный момент тело червяка. Указатель tail должен продвигаться вдоль каждого массива, заменяя координаты старой хвостовой окружности координатами новой головной. Однако что произойдет, когда указатель tail достигнет конца массива? Конечно же, он должен снова перескочить на начало, для чего нужно воспользоваться вычислениями по некоторому модулю. Если, скажем, червяк состоит из 10 колец и старое значение указателя tail равно 9, то его новое значение должно быть равно 0. Пока наш алгоритм имеет следующий вид:
цикл
- tail <- tail+1 (по какому-то модулю)
- выбрать координаты новой головы
- подставить в xcirc {tail) и ycirc{tail)
- нарисовать новую голову
- стереть хвост
конец цикла
Главная польза алгоритмического подхода к построению компьютерной программы заключается как раз в неопределенности и гибкости алгоритмического языка. В любом месте алгоритма можно написать что угодно, лишь бы это имело какой-то потенциальный смысл, который можно уточнить позже. Например, сейчас я пока отложил вопрос о том, как программа должна определить координаты новой головы, просто записав "выбрать координаты новой головы". В подробном алгоритме это, возможно, превратится в несколько строк. Но даже при такой грубой детализации, подставив пока эту фразу, я сразу же яснее представил себе, какой должна быть структура программы. Я даже нашел ошибку: как программа сможет "стереть хвост", если она не знает, где он находится? Дело в том, что выше в теле цикла на место этих координат были записаны координаты новой головы. Стереть старый хвост следовало раньше, до того как на место старых были подставлены новые координаты. Я внес в алгоритм соответствующие коррективы. Возможно, читатели захотят сами внести исправления, прежде чем посмотреть, как это было сделано у меня.
Теперь настало время сделать второй проход по алгоритму. Какой именно цикл я подразумевал, заключив в него весь остальной алгоритм? Пытаясь ответить на этот вопрос, я сразу же натолкнулся на другую проблему: как должна завершаться программа? Сначала я подумал о простейшей схеме с фиксированным числом повторений, или итераций, реализуемой посредством оператора цикла FOR, в котором некоторый индекс автоматически отсчитывает несколько тысяч итераций, в то время как червяк будет ползать по экрану. Но лучше было бы закончить карьеру червяка, когда будет нажата какая-нибудь клавиша. Таким образом, программа будет снова и снова выполнять цикл, пока человек не нажмет определенную клавишу.
Следует также уточнить, что конкретно подразумевается под словами "по какому-то модулю" в первом операторе цикла. Этот модуль должен быть равен размеру массива. Однако тут возникает еще один вопрос, какой длины будет червяк? Я произвольно выбрал 25 звеньев, решив, что червяк такой длины будет выглядеть достаточно правдоподобно.
Теперь алгоритм программы WORMS принял уже следующий вид (здесь mod означает "по модулю"):
repeat
- tail <- tail+1 (mod 25)
- стереть хвост
- выбрать координаты новой головы
- подставить в xcirc(tail) и ycirc(tail)
- нарисовать новую голову
until нажатие клавиши
Продолжая уточнять алгоритм, я решил заменить фразу "стереть хвост" чем-то более близким к тому языку программирования, которым я намереваюсь в конце концов воспользоваться. Поскольку я хотел стереть старую окружность, нарисовав черный круг там, где раньше был белый (на моем нормально черном экране), я подставил выражение "черная окружность в circ(tail)", что означает черную окружность с центром в точке с координатами xcirc(tail) и ycirc(tail).
Теперь я приступаю к фразе "выбрать координаты новой головы". Посредством какого механизма программа может решить, где следует нарисовать новую головную окружность? Очевидно, она должна быть в непосредственной близости от предыдущей и где-то "впереди" от нее. Более того, чтобы извивания и повороты червяка выглядели естественно, новое направление не должно слишком резко отличаться от предшествующего. Здесь решение проблемы заключалось просто в том, чтобы ввести одну-единственную новую переменную dir (от слова direction - направление). Она должна содержать текущее направление движения червяка, выраженное в градусах. При каждом повторении главного цикла программа будет произвольно либо увеличивать, либо уменьшать значение dir на 10o.
Пришло время решить, насколько близко друг от друга должны быть окружности и какого они должны быть размера. В качестве пробного значения радиуса можно принять, например, 4. Чтобы червяк выглядел как единое целое, нужно, чтобы окружности частично перекрывали друг друга. Далее я заменил фразу "выбрать координаты новой головы" следующим фрагментом:
change <- случайное число
if change < 0.5
- then dir <- dir + 10
- else dir <- dir - 10
x <- xcirc(tail-1)
y <- ycirc{tail-1)
newx <- x+4*cos(dir)
newy <- y+4*sin(dir)
В этом алгоритмическом фрагменте случайным образом выбирается число, присваиваемое переменной change (изменение). Большинство языков программирования имеет оператор выбора случайного числа в диапазоне от 0 до 1. Поскольку случайное число этого диапазона будет меньше 0.5 в среднем в 50% случаев, переменная dir будет увеличиваться в среднем через раз. Конечно, эта статистика справедлива лишь при большом количестве испытаний. На коротких же промежутках времени переменная dir будет меняться непредсказуемым образом в ту или иную сторону на 10o. Переменные x и y - это просто координаты предыдущей головной окружности. Последние два оператора представляют собой элементарные тригонометрические вычисления, при помощи которых мы получаем изменения x и y, приведенные к радиусу, равному 4. Таким образом, координаты новой головы выбраны.
Осталось лишь сделать еще два шага, чтобы окончательно уточнить алгоритм. Запомнить координаты новой головы в элементах xcirc(tail) и ycirc(tail) можно очень просто, при помощи двух операторов присваивания. Чтобы нарисовать новую голову, можно воспользоваться графической псевдокомандой, при помощи которой мы ранее стирали хвост.
Наконец, нужно инициализировать (т.е. присвоить начальные значения) массивы и переменные перед выполнением алгоритма. В данном случае указателю tail присвоим значение 1, а элементам массивов xcirc(l) и ycirc(1) - по 100 каждому. Остальным элементам этих массивов автоматически присвоены нулевые значения. Переменная направления dir имела исходное значение 0. Таким образом, червяк "начинался" в точке с координатами (100, 100) и двигался под углом 0 к горизонту. Точка (100, 100) лишь условно обозначает координаты центра окружности; на экране в зависимости от типа компьютера эти координаты могут быть иными.
Одна проблема все же осталась: а что, если червяк уползет за пределы экрана? Чтобы решить ее, я наделил программу еще одним свойством. Если координатные значения x или y выходят за диапазон, соответствующий размерам экрана, то они автоматически преобразуются в координаты точки, расположенной на его противоположном крае. Предположив, что наш гипотетический экран имеет диапазон координатных значений от 0 до 199, мы можем воспользоваться следующими операторами, преобразующими координаты так, чтобы они всегда находились в пределах выбранного диапазона:
newx <- newx mod 200
newy <- newy mod 200
Возможность вычисления по задан ному модулю имеется практически во всех языках программирования. При этом преобразуемое число (newx) делится на заданный модуль (200) и в качестве результата берется остаток от деления. Теперь переменная, которой присваивается остаток (newx) имеет значение, вычисленное по модулю.
Ну вот и все, что касается программы WORMS. Или может быть правильнее было бы назвать ее WORM (червяк)? Ведь алгоритм порождает лишь одного червяка. Чтобы к названию программы по праву добавить окончание S, читатели могут завести по одному набору массивов и переменных для каждого червяка, который должен появиться на экране. Рассмотренный выше алгоритм полностью приведен на рисунке внизу. Рядом приведена эквивалентная программа на языке Бейсик. Как педагог я был бы весьма разочарован, узнав, что кто-нибудь из наших читателей просто-напросто скопировал мою программу на Бейсике в свою машину, не усвоив объяснений того, о чем так подробно говорилось выше.

Превращение алгоритма WORMS (червяки) в программу на языке Бейсик
Сравнив строка за строкой алгоритм и программу, мы обнаружим довольно близкое сходство между ними. Действительно, два основных блока операторов в алгоритме практически не претерпели никаких изменений при переводе на Бейсик (для машины IBM PC Бейсик, версия 3.0). Основные различия связаны со свойствами реализации ввода с клавиатуры в языке Бейсик IBM PC, а также отсутствием цикла типа repeat в данной версии Бейсика.
В первом случае KEY(1) (функциональная клавиша F1 на клавиатуре компьютера IBM PC) была выбрана в качестве выключателя, на который пользователь программы может нажать, когда ему надоест наблюдать за тем, как червяк ползает по экрану. В строке 70 программы эта клавиша активизируется, сообщая системе, реализующей команды Бейсика, что нужно постоянно проверять, не поступил ли сигнал от клавиши F1. В строке 90 команда KEYOFF удаляет пояснительный текст в нижней части экрана, чтобы освободить место для червяков. Однако главная команда, использующая клавишу F1, содержится в строке 60. Здесь программе надлежит совершить переход на строку 290, если пользователь нажал на клавишу F1. В строке 290 экран очищается и выполнение программы завершается командой END.
Во втором случае ввиду отсутствия в языке цикла типа repeat было необходимо построить эквивалентную последовательность выполнения операторов с помощью команды перехода GOTO на строку 280 программы. В результате программа будет снова и снова возвращаться на строку 110, пока кто-нибудь не нажмет на клавишу F1. Тело цикла выделено в программе двумя строками комментария под номерами 100 и 270. Эти комментарии были вставлены лля того, чтобы читатели лучше видели структуру цикла в программе.
Есть и другие отличия между алгоритмом и программой, связанные со свойствами языка Бейсик. В строке 10 устанавливается размер массивов, равный 25 элементам для каждого массива. В строке под номером 80 устанавливается высокая разрешающая способность экрана для компьютера марки IBM PC. Здесь точки изображения располагаются очень близко друг к другу. В строке 110 новая переменная wastail принимает значение переменной tail непосредственно перед тем, как последняя получает приращение. Следовательно, переменную wastail можно подставить в алгоритме вместо выражения tail-1 там, где вычисляются значения x и y. Однако главная причина введения переменной wastail заключается в том, что tail как индекс массива не может принимать нулевое значение в данной версии языка Бейсик. В связи с этим в строке 120 единица прибавляется после того, как взят модуль, но не прежде. Записывая алгоритм, я допустил неточность, небрежно предположив, что индекс tail должен пробегать значения от 0 до 24. Реальная команда, при помощи которой рисуется окружность на языке Бейсик IBM PC, содержится в строке 130. Центр окружности находится в точке с координатами XCIRC(TAIL), YCIRC(TAIL), радиус равен 4, а цвет обозначен цифрой 0 (черный).
В строке 150 значение переменной DIR получает приращение не в 10o, а на эквивалентную величину 0.1745рад. (В версии Бейсика для компьютера IBM PC углы не измеряются в градусах). В строках 200 и 210 переменные NEWX и NEWY ограничиваются значениями 600 и 200 соответственно. Это делается для того, чтобы координаты не выходили за пределы экрана для компьютера IBM PC. Средство Бейсика, позволяющее выделять модуль, хорошо работает для положительных чисел, но не работает с отрицательными. Поэтому, когда червяк пытается уползти с экрана в отрицательном направлении, модуль берется с прибавлением соответствующего размера экрана, так как это сделано в строках 220 и 230. Червяк, уползающий с одного края прямоугольника, появляется сразу же на другом краю. В строке 290 команда SCREEN 0 очищает экран для возможных в дальнейшем текстов.
Читатели, которые пожелают усовершенствовать свою версию программы, могут вставить перед началом цикла команду RANDOMIZE, не позволяя, таким образом, червяку повторять тот же путь. Можно также предусмотреть возможность повторного запуска программы после ее остановки. Можно, например, трассировать путь червяка пунктирной линией из точечек, подобно тому, как мы сделали это на верхнем рисунке, приведенном на с.83.

Червяк, оставляющий след (вверху), дождевые капли (слева внизу) и звездный взрыв (справа внизу)
Программы для других уже упомянутых видеоэффектов теперь, наверное, могут быть написаны даже новичками, если они к тому же воспользуются некоторыми подсказками. Программа, которую я назвал RAINDROPS (дождевые капли), случайным образом выбирает точку на экране дисплея и описывает вокруг нее последовательность концентрических окружностей возрастающего радиуса. Затем программа выбирает другую точку и повторяет процедуру построения окружностей. RAINDROPS продолжает работать до тех пор, пока "хозяин погоды" не нажмет клавишу. Таким образом, программа строится из двух циклов: внешнего цикла, в котором выбирается точка, и внутреннего цикла, в котором рисуются окружности вокруг выбранной точки. Программа преобразует два случайных числа в диапазоне между 0 и 1 в координаты точки на экране путем умножения этих чисел на соответствующие размеры экрана. Получаемая в результате точка (x, y) становится центром последовательности окружностей, рисуемых во внутреннем цикле. Пусть индекс k пробегает значения от 1 до 25 по мере того, как на экране строятся белые (или какого-нибудь другого цвета) окружности. Центры всех этих окружностей находятся в точке с координатами (x, y), а радиусы принимают значения, равные 4k. Проще, конечно, оставлять нарисованные таким образом окружности неподвижными. Однако эффект был бы более реалистичным, если бы несколько окружностей, или даже одна, распространялись, подобно волне. Для этого программа RAINDROPS должна стирать (перерисовывать черным цветом) окружность радиуса 4(k-1) всякий раз после того, как нарисована окружность радиуса 4k.
Программа STARBURST (звездный взрыв) демонстрирует эффект космического взрыва. По существу тот же эффект можно интерпретировать как полет вдоль огромного звездного коридора, наблюдаемого из иллюминатора космического корабля, который движется с околосветовой скоростью. Звезды каждый раз перемещаются на небольшое расстояние вдоль линий перспективы по направлению к наблюдателю. Величина сдвига возрастает по мере того, как звезды приближаются к наблюдателю. Создается впечатление, что объекты, находящиеся ближе, движутся с большей скоростью по сравнению с удаленными объектами. Программа STARBURST несколько сложнее, чем RAJNDROPS. Она должна постоянно следить за всеми звездами, находящимися в пределах экрана. Для этого читатели могут воспользоваться массивом, назвав его, скажем, stars (звезды) - а правильнее будет сказать двумя массивами, как в программе WORMS,- чтобы хранить координаты x и y каждой звезды. Координата z оказывается скрытой в кажущемся движении звезд.
Когда звезда впервые появляется в исходной точке (100, 100), ее перемещения вначале очень малы, но затем они растут по мере того, как звезда приближается к наблюдателю (или наоборот - наблюдатель приближается к звезде). Величина приращения обратно пропорциональна z - кажущемуся расстоянию от наблюдателя. При составлении программы можно запланировать, например, по 25 сдвигов на каждую звезду, прежде чем она выйдет за пределы экрана. Таким образом, расстояние z до любой данной звезды можно принять равным 25-k, где k: - количество итераций в расчете кажущихся расстояний до этой звезды.
В большом цикле программы на каждом шаге создается одна новая звезда, а для всех остальных звезд координаты, хранящиеся в массивах, получают приращения.
ОТКЛИКИ
6 1988
БОЛЬШИНСТВО программистов (как новичков, так и опытных), заинтересовавшихся видео-эффектами, описанными в нашей рубрике в февральском номере, выбрали для своих упражнений задачу с червяками. С.Африа из Оттавы, предыдущее письмо которого касалось головоломки о ханойской башне, рассмотренной нами еще в начале 1985г., отмечает, что ползающие червяки представляют собой особенно эффектное зрелище, когда программа выполняется в откомпилированной форме.
У.Клементсу из Беверли-Хилла (шт.Калифорния) не понравилось поведение червяков на краях экрана. Вместо того чтобы позволять им уползать за пределы одного края и появляться на противоположной стороне экрана, программа Клементса изменяет направление их движения на величину +2.5 или -2.5 в зависимости от того, превосходит ли переменная change (изменение) значение 0.5.
Случай с Р.Скоттом-младшим из Мэдисона (шт.Виргиния), наверное, типичен для тех читателей, чьи компьютеры работают с версией Бэйсика, отличающейся от версии, которой мы пользовались в наших примерах. Червяки программы WORMS отказываются ползать по экранам их компьютеров. Подобные отличия, кажущиеся фатальными, обычно не очень значительны, и их легко обойти после того, как они выявлены.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
Страница 2 из 4 •  1, 2, 3, 4
1, 2, 3, 4 
 Похожие темы
Похожие темы» Литературное приложение
» Приложение. BASIC 1982. Пара книг издательства USBORNE
» О самоуспокоенности неудачников (приложение к заметкам о простых играх)
» Брябрин. Программное обеспечение персональных ЭВМ. 1990
» Броуди. Начальный курс программирования на языке ФОРТ. 1990
» Приложение. BASIC 1982. Пара книг издательства USBORNE
» О самоуспокоенности неудачников (приложение к заметкам о простых играх)
» Брябрин. Программное обеспечение персональных ЭВМ. 1990
» Броуди. Начальный курс программирования на языке ФОРТ. 1990
Страница 2 из 4
Права доступа к этому форуму:
Вы не можете отвечать на сообщения