Приложение. В мире науки. Занимательный компьютер. 1983-1990

3 1988
НАНОТЕХНОЛОГИЯ: МИКРОСКОПИЧЕСКИЕ ПОДВОДНЫЕ ЛОДКИ, ПУТЕШЕСТВУЮЩИЕ ПО КРОВЕНОСНЫМ СОСУДАМ И УПРАВЛЯЕМЫЕ МОЛЕКУЛЯРНЫМИ КОМПЬЮТЕРАМИ
А.К.ДЬЮДНИ

БУДУТ ЛИ когда-нибудь машины, размером с митохондрию, введены в организм человека? Если при одной мысли о том, что по вашим внутренностям будут ползать крошечные механизмы, вас пробивает озноб, то подумайте, какие зато открываются при этом возможности. Микроскопические машины в виде миниатюрных подводных лодок, бороздящих сосудистую систему, будут уничтожать вредные микроорганизмы или жировые частицы в крови человека и тем самым они смогут продлить вашу жизнь.

Такие исцеляющие машины в какой-то степени являются изобретением К. Эрика Дрекслера, работающею в рамках международного обмена учеными на факультете вычислительной техники в Станфордском университете. Вот уже более десяти лет Дрекслер разрабатывает основы нанотехнологии - революционной концепции построения машин, имеющих размеры порядка нанометра (одной миллиардной доли метра). Он сконструировал зубчатые передачи и подшипники атомных размеров и описал молекулярные манипуляторы. Он разработал даже логические схемы нанокомпьютера, описанию которого в основном и посвящена настоящая статья. И хотя нанотехнология пока завладела воображением лишь Дрекслера и еще нескольких энтузиастов, она, как видно по всему, несет на себе печать неизбежности. Будущее, которое она сулит, представляется более удивительным, чем любая научная фантастика.

Следует заметить, что Дрекслер не первый, кому пришла в голову мысль о нанотехнологии. В 1959г. Фейнман описал последовательность машин все меньших и меньших размеров; на каждом уровне этой последовательности машины должны создавать себе подобных, но меньшего размера. По мнению Дрекслера, на последней ступеньке этой лестницы могут находиться механизмы, собранные из деталей размером не более нескольких атомов. Подобные изделия в зависимости от их конструкции и предназначения могли бы путешествовать по организму человека, проникая в раковые клетки и перестраивая их ДНК. Мириады других могли бы работать на стройке, облепив едва заметной металлической пленкой сооружаемое здание. В течение нескольких дней они могли бы завершить сооружение необычной изящной конструкции.

Дрекслер считает, что ключевым шагом в развитии нанотехнологии явилось бы создание машин-ассемблеров, маленьких механизмов, управляющих операциями химического соединения вступающих в реакцию молекул. Запрограммированные на выполнение определенных операций и работающие на миниатюрном сборочном конвейере ассемблеры могли бы создавать микроскопические машины заданной конструкции. Ежечасно такие фабрики размером не более песчинки могли бы выпускать со своих сборочных линии миллиарды машин, которые, подобно струйке пыли, выходили бы из фабричных ворот или в виде коллоидного раствора поступали бы в водную среду.

В природе уже существуют наномашины (своего рода), обитающие в волной среде. Вспомним, например, хорошо известный бактериофаг Т4, который воспроизводит себя, проникая в тело бактерии. Бактериофаг прикрепляется к внешнему слою молекул бактерии и затем, подобно крошечному шприцу, впрыскивает в бактерию свою ДНК. ДНК фага перестраивает процесс синтеза белков в бактерии таким образом, что та начинает производить сотни микроскопических компонентов фага. За счет случайных столкновений эти компоненты соединяются друг с другом и образуют новые заряженные ДНК "шприцы", которые после того, как распадается оболочка бактериальной клетки, распространяются в поисках новых жертв.

Другим примером наномеханизма может служить отдельная часть некоторых бактерий, которые обладают так называемым жгутиком - длинным спиралевидным образованием, выступающим с одного или обеих концов бактериальной клетки. Такие микроорганизмы плавают, вращая своим жгутиком, подобно штопору. Жгутиком управляет своеобразный моторчик, находящийся под оболочкой бактерии. По существу >тот моторчик представляет собой белковый ротор, вращаемый силами ионного взаимодействия.

Одним из важнейших компонентов любой мыслимой нанотехнологии является подшипник. Как правило, подшипники в той или иной форме требуют смазки. В 1959г. Фейнман отмечал, что "говоря о смазке, следует иметь в виду некоторые интересные особенности. Эффективная вязкость масла должна быть все выше и выше по мере уменьшения размеров механизмов, в которых она используется... На самом деле можно обойтись вообще без смазки! Даже совершенно сухие подшипники не будут перегреваться, потому что тепло уходит из таких маленьких устройств очень и очень быстро".

Будет ли работать более легкая смазка? Даже если заменить масло керосином, вязкость все же будет возрастать. Однако, как отмечает Дрекслер, "в масштабах типичной наномашины молекула керосина скорее является физическим телом, нежели смазочным материалом". В своей статье, посвященной зубчатым передачам и подшипникам, он обращается к проблеме трения в роликовых подшипниках. Благодаря тому, что в структурах микроскопического масштаба необходимо учитывать взаимодействие между отдельными атомами, естественно ожидать, что в роликовых подшипниках нанометрового размера будут возникать значительные силы трения покоя и скольжения. Силы, действующие между атомами, частично могут быть описаны формулой потенциала взаимодействия Ван-дер-Ваальса. Эта формула содержит экспоненциальный член, описывающий большую часть столкновений между атомами.

Дрекслер полагает, что проблема трения может быть решена путем использования роликовых подшипников, в которых атомы расположены рядами, чередующимися с такими же рядами роликов в обойме подшипника - кольцевой дорожке, вдоль которой двигается подшипник. Ассемблер, способный манипулировать отдельными атомами таких элементов, как углерод и фтор, может построить подшипник и его обойму из атомов углерода в виде структуры с одной связью, аналогичной структуре алмаза. Подшипник будет представлять собой полый цилиндр. Поверхность подшипника и обоймы будет усеяна атомами фтора, расположенными в виде наклонных рядов (см. рисунок на с.84). По тому же принципу могут быть построены зубчатые передачи. Дрекслер рассматривает также проблему трения скольжения между поверхностями атомов. Обладая возможностью располагать атомы по определенным позициям, не нарушая при этом физических законов, можно воспользоваться такими расположениями, при которых силы отталкивания Ван-лер-Ваальса становятся меньше. Например, атом, движущийся вплотную к поверхности, которая состоит из рядов других атомов, расположенных подходяшим образом, будет испытывать сравнительно небольшое сопротивление. Однако при этом он должен двигаться по прямому пути непосредственно над желобком между двумя соседними рядами. Дрекслер полон энтузиазма и относительно ряда других идей. С некоторыми из них можно познакомиться лишь в технических отчетах Дрекслсра, в которых содержится подробная информация о гипотетических винтиках и гаечках нанотехпологии. Более общий обзор положения дел в этой области можно найти в книге Дрекслера "Двигатели созидания" (Engines of Creation, см. библиографию на с.96).


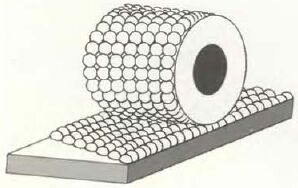
Роликовый подшипник из фторированного алмаза

Представим на минуту, что создание "подводной лодки", способном передвигаться в кровеносных сосудах, о которой говорилось выше, уже технически возможно. Каким образом можно управлять ею? Конечно, нанокомпьютером, но каким именно? Можно воспользоваться электронными компьютерами, говорит Дрекслер, однако сам он сосредоточил свое внимание на механических компьютерах, основанных на элементах так называемой "стерженьковой логики". Хотя логические операции в этих элементах реализуются перемешением молекулярных стерженьков по миниатюрной матрице, их никак не назовешь медленными. В масштабе атомарных размеров такие стерженьки перемешаются из одного положения в другое всего лишь за 50пс (пикосекунда - одна трнллионная часть секунды).

Основной функциональный элемент компьютера - это логический вентиль. На входе его имеется одна или несколько входных линий и одна выходная линия (которая затем может разветвляться на несколько линий). Входные и выходные сигналы бывают двух видов; обычно они обозначаются 0 и 1. Поскольку значение сигнала в одной и той же линии может со временем меняться, каждую линию удобно обозначать переменной величиной, например x. Логическую функцию вентиля можно описать формулой. Например, формула "x и y" соответствует так называемому вентилю И. Выходной сигнал такого вентиля равен 1 тогда и только тогда, когда оба входных сигнала x и y равны 1. Аналогичным образом формула "x или y" описывает функцию вентиля ИЛИ. В данном случае выходной сигнал вентиля равен 1, если хотя бы один из входных сигналов x или y равен 1. Из вентилей двух этих типов, вместе с третьим вентилем НЕ, называемым инвертором, можно построить логическую схему, реализующую любую функцию. Инвертор преобразует сигнал, равный 1, в 0 и, наоборот, равный 0 в 1.

В современных электронных компьютерах схемы логических вентилей собираются на транзисторах микронного размера, формируемых с помошью специальной технологии на поверхности кристалла. Слой обработанного кремния, легированного примесями, отличающимися избытком или недостатком свободных электронов, покрывается слоем поликриcталлического кремния. Поверх этих двух слоев обычно располагается еще металлический слой, как правило, из алюминия. Он служит проводником для электрической связи транзисторов. Конечно, не все участки поверхности кристалла содержат все три слоя. Точная структура расположения этих слоев определяется схемой соединения транзисторов. Обычно металлический слой имеет вил сверхтонких полосок алюминия, протягивающихся во всевозможных направлениях по всей поверхности кристалла. В таких микросхемах сигналы, проходящие по миниатюрным алюминиевым проводникам, могут принимать два различных уровня напряжения, кодирующих логические значения 0 и 1. Наиболее широко используются вентили типа И-НЕ, которые в терминах простых логических функций, описанных выше, можно представить выражением "НЕ (x И y)". Другими словами, выходной сигнал вентиля И-НЕ равен 1 в том случае, если оба сигнала на входе x и y не равны одновременно 1. Таким образом, если хотя бы один из входных сигналов равен 0, на выходе устанавливается 1. Пользуясь только вентилями И-НЕ, можно реализовать любую логическую функцию независимо от ее сложности.

Микросхемы, конечно, очень малы. Их компоненты имеют размеры несколько микронов (миллионных долей метра). Дрекслер же предлагает нам рассмотреть компьютер, который бы целиком уместился в одном транзисторе кремниевой микросхемы. Логические функции в гипотетическом нанокомпьютере Дрекслера реализуются с помощью бесконечно маленьких стерженьков, заменяющих проводники с двумя уровнями напряжения, кодирующими логические 0 и 1. Стержень размером в несколько атомов может скользить между двумя возможными положениями. Эти положения можно рассматривать как представления логических значений 0 и 1. Стержень сделан из карбина, цепочки атомов углерода с чередующимися одинарной и тройной связями. Этот стержень оказывается достаточно жестким и прочным, чтобы выполнять свои функции, и все же остается достаточно гибким, чтобы скользить вдоль не очень острых углов. У карбиновых стерженьков имеются образования, которые мы будем называть головками. Они бывают двух видов (см. верхний рисунок на с.85). Головки одного вида просто выдаются наружу, мы будем называть их зондирующими или тестирующими. Головки другого типа подобны створкам и называются блокирующими.


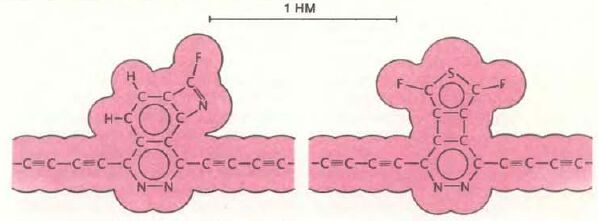
Тестирующая (слева) и блокирующая (справа) головки на карбиновом логическом стержне

Основание головок обоих типов образовано шестиугольным пиридазиновым кольцом, прикрепленным с каждой стороны к карбиновой цепочке. Тестирующая головка имеет второе углеродное кольцо поверх пиридазинового. Это внешнее кольцо содержит один атом фтора, который выдвинут вперед и играет роль логического зонда. Блокирующая головка несколько отличается от головки зонда, в частности, тем, что она содержит фторированное тиофеиовое кольцо. Впрочем, названия здесь не так важны. В дальнейшем мы просто будем предполагать, что такие структуры могут выполнять функции тестирования и блокирования. Достаточно сказать, что Дрекслер провел подробные вычисления, для освещения которых у нас здесь не хватит места и которые касаются, в частности, напряжений, выдерживаемых стерженьками при тепловом колебании молекул.

Кроме стерженьков логические схемы механического нанокомпьютера состоят также из трехмерной матрицы, построенной из атомов элементов - соседей углерода в периодической таблице. По этой структуре в двух взаимно перпендикулярных направлениях на многих уровнях протягиваются каналы. Каким образом стерженьки реализуют логические функции в этой матрице?

Представим себе один горизонтально расположенный в своем канале стержень, и пусть он находится в одном из двух дозволенных положений. Предположим для простоты, что этот "логический стержень" имеет две тестирующие головки и одну блокирующую (см. нижний рисунок на с.85). Такой стержень проходит через три замка, полые зоны матрицы, где два стержня (и их головки) пересекаются под прямым углом. При прохождении каждого замка возникает неопределенность, проскользнет ли головка-зонд одного стержня мимо блокирующей головки другого или будет захвачена ею. Из трех замков, через которые может пройти рассматриваемый нами стержень, в двух левых замках находятся блокирующие головки двух вертикальных стержней, обозначенных x и y. Замок, расположенный справа, содержит головку-зонд, прикрепленную к третьему вертикальному стержню f.


Логический стержень выполняет операцию И-НЕ

Горизонтальный стержень и его замки служат для вычисления логической функции И-НЕ. Два вертикальных стержня слева представляют входные переменные х и у. Вертикальный стержень справа представляет выходной сигнал операции И-НЕ.

Предполагая, что вертикальный входной стержень представляет логическое значение 0 в верхнем положении и 1 - в нижнем, рассмотрим ситуацию, когда x = 0 и y = 1. Другими словами, стержень x находится в верхнем положении, а y - в нижнем. В этом случае мы не сможем протащить логический стержень влево мимо обоих вертикальных стержней, поскольку x находится в верхнем положении и его блокирующая головка стоит на пути зонда логического стержня. Только если стержень x будет также в нижнем положении, обе тестирующие головки рассматриваемого нами стержня смогут миновать соответствующие блокирующие головки, так чтобы стержень мог беспрепятственно скользить влево.

Ну а что же выходной стержень f? Он может проверить, перешел ли наш логический стержень в свое новое положение, введя свой зонд в замок, содержащий блокирующую головку логического стержня. Когда горизонтальный стержень находится в правом положении, стержень f сможет миновать его, перейдя тем самым из логического состояния 0 в состояние 1. Однако, если логический стержень может проскользнуть в левое положение, его блокирующая головка будет препятствовать тестирующей головке f при ее прохождении через замок и поэтому стержень f будет иметь состояние 0. Таким образом, значение сигнала 1 будет равно 1, когда x н y оба одновременно не будут равны 1, что и соответствует требованиям функции И-НЕ.

Вычислительный цикл стержневого компьютера Дрскслера разбивается на три отдельные фазы, которые многократно следуют друг за другом с молниеносной быстротой. На первой фазе устанавливаются входные замки, при этом входные стержни временно оттягиваются. Это позволяет всем логическим стержням уйти в исходное положение. Во второй фазе входные стержни занимают свое текущее положение. Они могут соединяться с различными сенсорами наномашины или с выходами самого нанокомпьютера. Затем в едином движении все логические стержни тянутся влево, если можно так выразиться. Наконец, в заключительной фазе определяются значения выходных переменных, когда ко всем выходным стержням прикладывается сила, вынуждающая их двигаться по своим каналам. Перемещаются же лишь те из них, которые оказываются незаблокированными.

Специалисты, работающие в области искусственного интеллекта, наверняка возразят: даже если допустить, что в таком крошечном объеме можно разместить достаточно большие вычислительные мощности, то каким образом Дрекслер собирается наделить свои микроскопические автономные машины необходимым "интеллектом"?

На подобные возражения Дрекслер отвечает, что хотя в его машины можно встроить очень мощный центральный процессор, некоторые наномашины совсем не обязательно должны обладать значительным интеллектом. Взять к примеру описанный выше нанонаутилус - машину, предназначенную для лечения. Путешествуя по кровеносным сосудам человека, такая наномашина могла бы поглощать из крови глюкозу и кислород. Эти вещества обеспечивали бы машину необходимой энергией. Возможно, что у человека, в крови которого находятся миллиарды нанонаутилусов, время от времени будут возникать едва заметные неприятные ощущения. Во всяком случае, каждая машина будет использовать энергию, получаемую от своих "глюкозных двигателей" (конструируемых в настоящее время) для того, чтобы приводить в движение два спиралевидных пропеллера. Движение машины может быть и неуправляемым. Когда она натыкается на что-нибудь, центральный процессор получает сигнал от нанометрового контактного переключателя в ее передних сенсорах. Затем те же сенсоры используют различные встроенные в них ключи-шаблоны для определения молекулярной структуры препятствия.

Если препятствие окажется клеткой стенки сосуда, красным кровяным тельцем, лейкоцитом или еще каким-нибудь представителем заданного набора объектов, то наномашина на короткое время даст задний ход, а затем продолжит свое путешествие. Если же ей встретится болезнетворная бактерия или вирус, то она раскроет свои механические челюсти и проглотит настолько большой кусок объекта, насколько сможет откусить. К таким объектам относятся также вредные отложения и вообще все то, на что будет запрограммирована наномашина (см. рисунок на с.83). Проглоченные куски подвергаются искусственному химическому разложению, и продукты переработки, выпущенные в кровь, удаляются впоследствии почками. В кровеносной системе, населенной такими работающими наномашинами, у болезнетворных бактерий и других нежелательных тел будут очень маленькие шансы на то, чтобы выжить и просуществовать более нескольких часов.


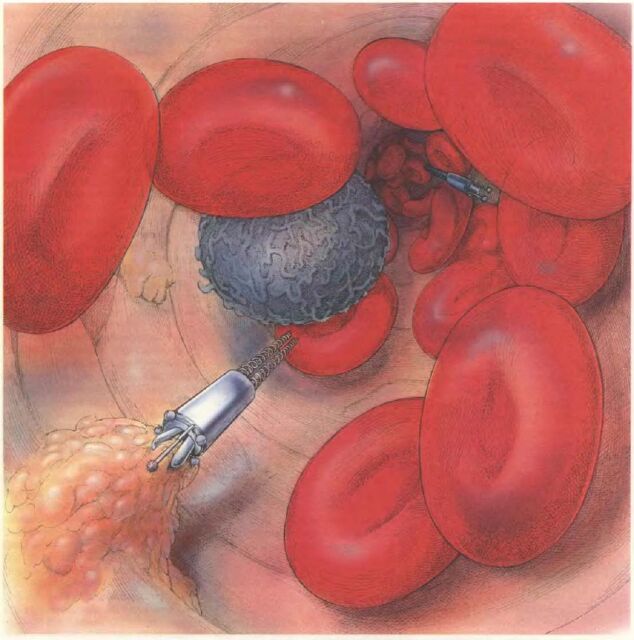
Наномашина, проплывающая по капилляру, атакует жировые отложения

Конечно, все это мечта - по крайней мере пока. Мы едва достигли порога мира нанотехнологии. Прав ли Дрекслер, утверждая, что нечто подобное этой фантастической мечте осуществится на самом деле? Он упорно защищает свои идеи, иногда несколько изменяя их под влиянием серьезных критических замечании своих ученых коллег. Однако пока он остается технологом без технологии, эрудированным мечтателем. Наверное, максимум, чего ему удастся достичь, - это внести свой вклад в стимулирование научной мысли - движущей силы нашего технического прогресса. При этом лично он не проявляет слепого оптимизма, отдавая себе отчет в том, что реализация нанотехнологии несет в себе опасности, может быть даже большие, чем атомное оружие или генетические эксперименты, вышедшие из-под контроля.

Один из энтузиастов нанотехнологии недавно сказал мне, что "тысячи из тысяч тех, кто живет сейчас, не умрут никогда". Любопытно, что один верующий говорил то же самое моему отцу полстолетия назад.

БИБЛИОГРАФИЯ

MOLECULAR ENGINEERING: AN APPROACH TO THE DEVELOPMENT OF GENERAL CAPABILITIES FOR MOLECULAR MANIPULATION. K. ERIC DREXLER in Proceedings of the National Academy of Sciences of the United States of America, Vol.78, No.9, pages 5275-5278; September, 1981.

ENGINES OF CREATION. K. ERIC DREXLER, Anchor Press, 1986.

ОТКЛИКИ

7 1988
НАНОТЕХНОЛОГИЯ, статья о которой была опубликована в мартовском номере, вызвала оживленные отклики как со стороны скептиков, так и со стороны энтузиастов. Любопытный образчик скепсиса содержится в письме, присланном "Ассоциацией гуманистов Оклахомы" и подписанном К.Л.Уайлэом из Оклахома-Сити. Уайлз не верит в обещание вечной жизни, которое некоторые энтузиасты усматривают в ианотехнологии. В частности, он считает, что подводный нанокорабль, описанный мною с таким восторгом, во-первых, вряд ли когда-нибудь удастся создать, а если он и будет создан, то уж никак, по мнению Уайлза, не сможет обеспечить вечной жизни. Он пишет: "Будучи в достаточной мере скептически настроенными по отношению к любым сверхестественным бессмертным существам, мы полагаем, что тем, кто рассчитывает на успехи нанотехнологии, придется ждать очень долго... Даже если подводные нанолодки в кровеносных сосудах - это безбожная идея, мы все же должны считать утверждение о ее реализуемости совершенно невероятным и требующим невероятного доказательства,- оно почти так же невероятно, как утверждение о том, что возможна сверхестественная вечная жизнь". Хотелось бы услышать мнение других читателей на этот счет.

Э.Дрекслер, конечно, находится в лагере защитников нанотехнологии. Поступая вполне ответственно, он тщательно избегает любых утверждений, выходящих за рамки возможности максимального продолжения человеческой жизни, которого можно достичь при помощи его "исцеляющих машин". Писатель П.Прус из Сан-Франциско, работающий в жанре научной фантастики, в восторге от идей Дрекслера. Он изучил некоторые возможности, которые, как ему кажется, несет в себе нанотехнология. В последней книге Пруса "Человеческая ошибка" описана гипотетическая самовоспроизводящаяся наномашина, которую случайно проглотил талантливый, но не очень приятный в жизни исследователь, работающий в одной из биотехнологических компаний Западного побережья США. После этого исследователь претерпевает удивительные превращения и даже обретает способность любить.

4 1988
МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ В МИРЕ БИОМОРФОВ
А.К.ДЬЮДНИ

ЕСЛИ живые существа уподобить часовым механизмам, то сознавший их часовой мастер, по мнению Р.Докинза, биолога из Оксфорда, автора книги "Эгоистичный ген" (The Selfish Gene), должен быть слепым. В конце концов эволюцией управляют слепые физические силы. Докинз присоединился к полемике между креационистами и эволюционистами, поддерживая последних, о чем свидетельствует написанная им недавно другая книга - "Слепой часовой мастер" (The Blind Watchmaker). Чтобы проиллюстрировать одно из главных положений своей книги, Докинз написал компьютерную программу, которая позволяет пользователю моделировать эволюционный процесс, придумывая и графически изображая свои собственные формы жизни, абстрактные организмы, которые Докинз называет биоморфами.

Программа, которую мы так и назовем WATCHMAKER (часовой мастер), демонстрирует ошибочность довода, часто выдвигаемого критиками теории эволюции. Каким образом нечто такое сложное, как "машина жизни", может возникнуть просто в результате стечения случайных событий? На первый взгляд кажется, что это действительно невероятно. Интуитивно мы чувствуем, что здесь не обошлось без "часового мастера", как говорил У.Пэйли, английский теолог, живший в XVIIIв. Доказывая, что у всех форм жизни должен быть Создатель, Пэйли рассуждал следующим образом. Если, идя по полю, мы наткнемся на камень, то можно, конечно, подумать, что он лежал там вечно. "Однако предположим,- писал Пэйли,- что я нашел на земле часы и захотел узнать, как они здесь оказались. Едва ли я удовлетворюсь тем же ответом, что и в предыдущем случае... Часы, должно быть, имели своего творца".

Пэйли умер еше до того, как родился Чарлз Дарвин, однако современные креационисты соглашаются с аргументом Пэйли. При каком стечении случайных событий могли появиться часы на поле, о котором говорит Пэйли? Ошибочность этого аргумента заключается в неявном предположении, что случайные события, которые привели к появлению часов (или их творца), происходили более или менее одновременно. Здесь не принимаются в расчет эффекты кумулятивных, т.е. накапливающихся изменений. Программа WATCHMAKER как раз и показывает на примере вычислительных процессов, сколь значительными могут быть кумулятивные изменения. Правда, творения этой программы - не живые организмы, а лишь биоморфы: статические формы, напоминающие живых существ.

Процесс начинается с очень простого образования в центре экрана, который делится на большие клетки (см. верхний рисунок на с.83). Предположим, к примеру, что центральная клетка содержит маленькое дерево с несколькими ветвями. Программа WATCHMAKER порождает деревья - вариации исходного, которые заполняют соседние клетки на экране. У одних деревьев становится больше веток, у других меньше, одни становятся выше, другие ниже. Характер изменений, которым могут подвергаться деревья, определяется некоторым набором генов. Но об этом мы поговорим несколько позже. Все производные деревья рассматриваются как потомки центрального дерева. Они представляют собой те видоизменения, которые возможны в популяции на данный момент.


Генетические вариации центрального дерева

Программа WATCHMAKER выполняется на персональном компьютере "Макинтош". Поэтому эволюционный процесс управляется "мышью" - устройством ввода, которое пользователь перемещает рукой по контактной площадке. Движение мыши сопровождается таким же движением маленького темного квадратика - указателя на экране компьютера. В ходе работы программы WATCHMAKER пользователь выбирает, какое из изображенных на экране деревьев должно дать потомство в следующем поколении. Для этого нужно загнать указатель, управляемый мышью, в один из квадратов, в котором находится выбранное дерево. У мыши есть кнопка, на которую нужно нажать, когда указатель уже находится в выбранной клетке; в этом случае все последующие деревья будут потомками выбранного. Оно перемешается в центральный квадрат. Теперь цикл отбора повторяется. Такая селекционная последовательность порождает филогенетическую линию деревьев, представители которой в каждом поколении несколько отличаются от родителя. Однако медленное накопление незначительных изменений может привести к удивительным результатам.

Докинз пишет, что, собираясь в первый раз запустить программу WATCHMAKER, он "надеялся увидеть плакучие ивы, ливанские кедры, ломбардийские тополя, водоросли, и может быть, оленьи рога. Но ни моя интуиция биолога, ни двадцатилетний опыт программирования компьютеров, ни самые необузданные полеты моей фантазии не подготовили меня к тому, что я увидел на экране в действительности. Я уже не помню, глядя на какой элемент последовательности, я начал впервые подозревать, что... может получиться нечто вроде насекомого... Все меньше веря своим глазам, я наблюдал, как сходство С насекомым становится все более отчетливым". И вот, наконец, под триумфальные звуки фанфар на экране появились насекомополобные существа (см. нижний рисунок на с.83). Докинз плохо спал в ту ночь, перед его глазами роились насекомые.


Насекомоподобные биоморфы, порожденные программой WATCHMAKER

Так появилась первая из тех форм, для которых позже Докинз придумал обшее название биоморфы. На самом деле все формы, порождаемые программой, представляли собой деревья. Причудливо изгибающиеся ветви могут придать этим деревьям формы, в которых мы узнаем не только тело, крылья и ножки насекомых, но и мириады других биоморфов, включая древовидных лягушек, летучих мышей и даже орхидеи. Могут появиться и такие технические формы, как лампочки и лабораторные весы (см. рисунок на с.84).


Биоморфы и другие формы, порожденные программой WATCHMAKER

Каким же образом программа "исполняет вариации на заданную тему"? Как я уже говорил, форма каждого дерева, порождаемого программой, определяется генами. Всего их 16. Роль некоторых генов объяснить просто. Эффект других заранее предсказать невозможно, потому что их роль зависит от взаимодействия с третьими. Несколько генов определяют количество ветвей и общие размеры дерева. Из генов второго типа три гена в определенных сочетаниях влияют на горизонтальную протяженность ветвей, в то время как пять других совместно определяют их вертикальную протяженность.

Мир Докинза представляет собой 16-мерное пространство, населенное всевозможными вариантами биоморфов. В конце концов каждое существо полностью определяется набором из 16 чисел, представляют их его генетическую наследственность. Эти числа можно считать значениями координат, и тогда каждый биоморф становится просто точкой в пространстве, которое Докинэ называет миром биоморфов. Программа WATCHMAKER представляет собой отличное средство, при помоши которого можно исследовать этот мир.

Программа Докинза слишком длинна и сложна, и я не смогу ее здесь описать прежде всего потому, что в ней осуществляется выбор большого количества различных режимов и параметров, и каждую процедуру выбора можно считать отдельной программой. Например, в программе можно выбрать режим конструирования. Пользователь знакомится с комментарием, прилагаемым к программе, чтобы научиться непосредственно манипулировать генами, с целью получить те или иные конкретные биоморфы. Среди других режимов есть и так называемая "история ископаемых останков". В этом режиме эволюционные ветви хранятся в виде отложений различных исторических эпох. Есть также режим "в поисках чудовища", в котором происходит случайный отбор потомства в каждом поколении. Этот процесс продолжается до тех пор, пока не появится какая-нибудь интересная форма, может быть даже чудовище.

Вот здесь креационист, наверное, воскликнет: "Обман!" - И не без оснований. Ведь это, по существу, искусственный отбор выживающих вариантов, совершаемый человеком. Другими словами, это не естественный отбор, а направленная селекция. Дарвин говорил об успешной деятельности селекционеров, чтобы подкрепить свой тезис о существовании изменчивости в популяциях. Конечно, эта деятельность не доказывает существования естественного отбора. Аргументы в пользу последнего Дарвин черпал из многих источников, в том числе он их находил и в истории ископаемых останков. Цель, преследуемая Докинзом, тем не менее была достигнута. Эффекты накапливающихся изменений могут быть весьма впечатляющими. Они были бы еще более впечатляющими, если на обвинение в обмане можно было ответить более непосредственным образом. Нельзя ли, скажем, сделать так, чтобы процедура отбора в программе не направлялась человеком и даже не была случайным процессом, а определялась в той или иной форме требованиями окружающей среды? Могла бы эволюция быть результатом конкурентного взаимодействия между различными видами?

Докинз сформулировал следующую задачу для программистов: "Биоморфы должны взаимодействовать в компьютере, который моделировал бы враждебную среду. Какие-то детали формы организмов должны определять, выживут они или погибнут в данной среде". Он указывает, далее, что уязвимость организмов должна следовать из самой модели, а не быть заранее "встроенной" программистом. Число генов можно варьировать. Докинз считает, что если кто-нибудь и справится с задачей, то это будут программисты из "числа тех, кто сочиняет всем знакомые видеоигры". Должен сказать, что я в этом сомневаюсь.

Хотя сам я, наверное, не справлюсь с задачей Докинза, я все же могу проиллюстрировать в общих чертах модель, которую он имел в виду. В конце концов можно придумать два каких-нибудь взаимодействующих вида, которые постепенно изменяются в результате взаимодействия. Однако уязвимость видов я как "часовой мастер-любитель" встроил в них заранее. Возможно, описанный ниже пример вдохновит кого-нибудь из читателей, и он превзойдет мою скромную попытку, создав настоящую эволюционную (если не сказать революционную) программу.

Рассмотрим организмы, изображенные на рисунке внизу. Назовем их шипофитом и гнутозавром. Гнутозавр не может жить без сочных листьев, растущих на верхушке шипофита. К сожалению, у основания шилофит окружен ошейником из колючих ядовитых шипов. Однако гнутозавр, как говорит само его имя, имеет в своем теле изгиб, позволяющий ему избегать смертельных уколов колючек шипофита, когда он пытается достать сочные листья последнего.


Взаимозависимая эволюция шипофита и гнутозавра

Это, как говорится, хорошо. Плохо же то, что гнутозавр ужасно негибкий. Его тело всегда изогнуто под углом 90o. Более того, ни шея, ни тело его не гнутся. Поэтому гнутозавр осужден на то, чтобы есть листья лишь на определенном уровне, конечно, при условии, что его шея окажется достаточно длинной, чтобы достать их.

Само собой разумеется, что обе популяции подвержены случайным вариациям в своем генетическом коде. Гнутозавры могут быть различной высоты (измеряемой по высоте плеч) и могут иметь шеи разной длины. Колючки шипофнта все одинаковой длины у одного и того же растения, но их длина может быть неодинаковой у разных растений. Высота шипофита также подвержена небольшим случайным изменениям.

Чтобы управлять формой каждого из этих биоморфов, им достаточно иметь по два гена. У гнутоэавра один ген ответствен за высоту, другой за длину шеи. У шипофита также два гена, один задает высоту и один длину шипов. При определенных условиях, указанных в программе, которую я назвал ESCAPEMENT эволюция этих двух форм жизни может быть взаимозависимой. В эволюционной перспективе изменения своих генов шипофит "стремится" избавиться от гнутозавра {отсюда название программы: escapement, что в переводе означает "избавление"), видоизменяясь так, чтобы последнему было все труднее добывать его листья.

Программа ESCAPEMENT поочередно предоставляет возможность обоим биоморфам изменять свою форму. Например, шнпофит может стать несколько выше или ниже, а его шипы - длиннее или короче. Высота тела и длина шеи гнутозавра также могут меняться в ту и другую сторону. Поскольку для обоих биоморфов существуют абсолютные верхние пределы размера, бесконечная "гонка вооружений" невозможна. Например, сумма длины шипов и высоты ствола шипофита не может превысить некоторого предельного значения, которое я назову smax. Аналогичным образом длина гнутозавра, измеряемая от его головы до кончиков пальцев на ногах, не превышает предельного значения bmax. Чтобы сделать модель интереснее, я решил, что bmax будет больше smax.

Каким образом программа ESCAPEMENT решает, какой из потомков каждого биоморфа выживет? Критерий заключается в величине, называемой дистанцией кормления. Она измеряет расстояние между головой гнутозавра и ароматными листьями шипофита. Предположим гнутозавр имеет рост w, а длина его шеи равна x. Если высота ствола шипофита равна y, а длина его колючек z, то дистанция кормления выражается обычной формулой евклидова расстояния: квадратным корнем из величины (z-x)2+(y-w)2. Если z оказывается меньше x, формула изменяется. В этом случае гнутозавр может стоять сколь угодно близко к шипофиту, и рассматривается только второй член формулы.

Неудивительно, что шипофит стремится эволюционировать так, чтобы максимально увеличить дистанцию кормления. Задача гнутозавра, наоборот, заключается в том, чтобы сделать это расстояние минимальным. Каждый биоморф, когда до него доходит очередь, порождает двух отпрысков. Например, если высота шипофита в данном поколении равна y, то в следующем она может стать равной y-1 или y+1. Длина шипов может либо увеличиться от z до z+1, либо уменьшиться до z-1. В
каждом случае выбор осуществляется случайным образом.

Аналогично возникают два видоизмененных потомка у гнутозавра. Вместе с двумя видоизмененными потомками родительский биоморф сохраняется для последующего оценивания перед лицом своего биологического противника. Критерием и в этом случае является дистанция кормления. Например, тот из трех шипофитов, которому удается держать "живущего" в данный момент гнутозавра на наибольшей дистанции, отбирается, так сказать, в квазиестественном процессе и сохраняется для следующего раунда эволюции. Теперь наступает очередь гнутозавра. Он сам и его два видоизмененных потомка проверяются на выживание в среде с новой моделью шипофита. Тот, у которого дистанция кормления окажется минимальной, будет родителем нового поколения.

Было бы замечательно, если бы программа ESCAPEMENT имела графические возможности, позволяющие ей изображать шипофитов и гнутозавров, представителей двух дренних и знаменитых биоморфов, так, как это сумел сделать наш художник. Однако это выше моих возможностей. Я остановил свой выбор на простейших диаграммах, одна иэ которых приведена на самом рисунке на с.82. Здесь нет практически ничего, кроме представления основных переменных в виде прямолинейных отрезков. Читатели, которые не пожелают возиться даже с такими простейшими изображениями, могут удовлетвориться тем, чтобы программа просто распечатывала значения четырех переменных в конце каждого раунда.

Программа ESCAPEMENT построена в виде единого цикла, в теле которого оба бноморфа изменяются, оцениваются и демонстрируются:

input bmax, smax
input w, x, y, z
input gen
for i <- 1 to gen
- создать потомков шипофита
- оценить шипофитов
- создать потомство гнутозавра
- оценить гнутозавров
- показать победителей

Пользователь, конечно, должен ввести исходные значения шести основных переменных от руки, а также задать значение величины gen, число поколений, или витков эволюции. Затем выполняются итерации в двух внутренних подциклах размножения биоморфов, их оценивания и показа. Биоморф воспроизводится путем выбора двух случайных чисел, определяющих, увеличится или уменьшится значение каждого гена. Например, алгоритм, с помощью которого порождаются два видоизмененных гнутозавра, получает мутации a и b соответственно для генов w и x следующим образом:

r <- random
if r < 0.5 then а <- w-1
- else a <- w+1
s <- random
if s < 0.5 then b <- x-1
- else b <- x+1

Теперь программа располагает тремя гнутозаврами. Их генетические наборы могут быть представлены в виде трех пар чисел: [w, x], [a, x], [w, b]. Который из них является наилучшим? Программа ESCAPEMENT оценивает эти три модели, подсчитывая для них соответствующие дистанции, на которых гнутозавры могут добыть себе корм с каждой текущей модели шипофита. Обозначив дистанции d1, d2 и d3, их можно вычислить по существу с помощью одной и той же формулы. Вот, например, как программа вычисляет второе расстояние, d2, между гнутозавром [a, x] и шинофитом [y, z]:

if x < z then d2 <- (z-x)2+(y-a)2
- else d2 <- (y-a)2

В каждом случае применяется формула евклидова расстояния, в которую подставляются соответствующие координаты головы животного н листа растения. Когда все три расстояния вычислены, наименьшее из них определяется путем последовательных сравнений:

if d2<=d1 and d2<=d3
- then w <- a
if d3<=d1 and d3<=d2
- then x <- b

Если ни одно из двух пар неравенств не удовлетворяется, то родитель сохраняет превосходство над своими потомками. Поэтому гены x и w остаются прежними. Аналогичным образом программа оценивает шипофитов с той лишь разницей, что по отношению к растениям в качестве критерия способности выжить берется не минимум, а максимум расстояния.

Пока мы еше ничего не сказали о пределах роста, о чем упоминалось выше. Каким образом программа ESCAPEMENT препятствует неумеренному росту каждого из биоморфов? Простейший способ заключается в том, чтобы наказывать биоморфа-переростка при вычислении расстояния. Например, если видоизмененный гнутозавр [a, x] окажется слишком большим, то сумма a+x превысит значение bmax. В этом случае к подсчитанному расстоянию можно прибавить, скажем, 1000, чтобы этот мутант не оказался победителем. Шнпофиты-переростки могут наказываться, наоборот, путем вычитания 1000 из вычисленного для них расстояния. Аналогичным образом оба биоморфа должны наказываться в том случае, если любая из четырех переменных окажется отрицательной.

Победители по результатам оценки демонстрируются на экране дисплея с помощью простых графических команд, обычно имеющихся в большинстве языков программирования. Эту часть программы мы оставляем воображению читателей.

Что же происходит с биоморфами при выполнении программы ESCAPEMENT? В какой-то степени это зависит от исходных значений четырех генов и двух предельных размеров, вводимых перед началом выполнения программы. Значения переменных могут также зависеть от размеров экрана. Пусть, например, smax будет равно 100, а bmax 110. Тогда мы будем наблюдать интересное явление. Выберем исходные значения для четырех генов произвольно в диапазоне от 0 до 50. Можно, например, начать с хорошо сбалансированных биоморфов, либо высоких и худых, либо низких и толстых. По мере того как одно поколение сменяет другое, мы становимся свидетелями гонки. Гнутозавр может "преследовать" шипофита, производя все более высоких и худых потомков, и, в конце концов, обогнав в росте растение, преградить ему путь вверх. Тогда шипофит может попытаться "убежать" вниз, все более широко расставляя свои ядовитые колючки. Гнутозавр в свою очередь тоже будет становиться более приземистым, а его шея начнет удлиняться. Таким образом, при выполнении простого требования, чтобы значение bmax превосходило smax, будет всегда возникать кажущаяся бесконечной последовательность из побегов и погони. Читатели, обладающие хорошим воображением, возможно, смогут представить себе, какими будут результаты в противном случае.

Разумеется, когда мы говорим о побеге и погоне, мы имеем в виду не отдельных биоморфов, а "историю ископаемых останков". Наверное, палеонтолог, исследующий всю последовательность слоев отложений с ископаемыми шипофитамн и гнутозаврами, будет немало удивлен, как оба вида меняли свои размеры со временем подобно раскачивающемуся маятнику.

Докинз предлагает читателям его книги самим заняться разработкой экспериментальных программ, которые позволяют исследовать эволюционные процессы. Эти программы могут быть либо усовершенствованными версиями ESCAPEMENT, либо представлять собой значительно более глубокие разработки.

Споры между креационистами и эволюционистами не утихают, но, может быть, и те и другие одинаково далеки от истины? Забавная мысль: представим себе Творца, способного создавать путем эволюции и с улыбкой наблюдающего за тем, как ломают копья сторонники двух противоположных концепций.

БИБЛИОГРАФИЯ

THE BLIND WATCHMAKER. RICHARD DAWKINS. W.W.Norton & Company, 1987. (Есть перевод.- G.).

ОТКЛИКИ

8 1988
В АПРЕЛЬСКОМ номере журнала мы познакомились со слепым часовым мастером и биоморфами - творением Ричарда Доукинса. Точнее говоря, биоморфы были творением не Доукинса, а программы, которую он написал. Экран персонального компьютера типа "Макинтош" делится на 9 квадратов. В центральном квадрате находится древовидная структура, а в восьми соседних квадратах - вариации на тему центральной структуры. Человек, руководяший процессом, выбирает одну из восьми вариаций, она переносится в центр и порождает свое потомство.

Направляемый человеком эволюционный процесс зачастую приводит к появлению удивительных форм, в которых можно увидеть все что угодно, от насекомого до аэроплана. В своей книге "Слепой часовой мастер" Доукннс приводит изображения, полученные с помощью его программы, и использует их в качестве одного из доказательств своего основного тезиса о том, что эволюция, даже очень медленная, может породить самые удивительные формы. Однако его все же беспокоит то обстоятельство, что разработанная им программа не совсем слепа. Каким образом, спрашивает он в своей книге, новые формы возникают в результате взаимодействия вида со средой обитания?

На конференции, посвященной вопросам искусственной жизни и проведенной в Лос-Аламосской национальной лаборатории в сентябре прошлого года, несколько ученых и любителей сообщили о том, что при моделировании эволюционного процесса им удалось получить организмы с новыми свойствами. Ни одно из этих сообщений не удовлетворило Доукинса. Об одной из последних работ в этой области мне рассказал Дж.Миттерер из Брокского университета в Онтарио. Она была выполнена Д.Плотом с факультета психологии Рочестерского университета и Д.Тэйлором из Сан-Матео (шт.Калифорния). Внимательный анализ работы Плота-Тэйлора показывает, что она не отличается принципиально от многих работ, представленных в Лос-Аламосе. Простые организмы, наделенные способностью находить себе пропитание и спасаться от врагов, демонстрируют определенное поведение, управляемое нервной системой. Организмы, не сумевшие выжить, не могут передать своего плохо приспособленного мозга потомству. Однако по условию этого эксперимента исходные существа уже обладают нервной системой. Доукинс же хотел бы увидеть, как сравнительно сложная нервная система появляется под влиянием естественного отбора, в ходе эволюции, начинающейся с примитивных организмов.

Д.Чесс, ученый из Исследовательского центра Томаса Уотсона фирмы IBM, тем не менее считает, что моделирование эволюции поведения может оказаться наиболее плодотворным. Например, описанный мной гнутозавр способен питаться сочными листьями шипофита только при условии, что горизонтальная часть его шеи имеет достаточную длину, чтобы достать листья. Однако сможет ли гнутозавр с такой шеей спасаться от хищников, спрашивает Чесс. Не разовьется ли у этого животного гипертония, не будет ли оно часто травмировать свою шею и т.п.?

Другой сотрудник фирмы IBM Д.Куртис из Кеннесо (шт. Джорджия) считает, что к научному креационизму следует отнестись более серьезно. Сторонники этого учения признают существование микроэволюции - постепенных изменений у того или иного вида. Однако, пишет Кертис, пока "нет никаких экспериментальных или ископаемых доказательств существования макроэволюции - фундаментальных изменений, в результате которых из старых видов возникают новые".

5 1988
МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ НЕКОТОРЫХ ФИЗИЧЕСКИХ СИСТЕМ В ДОМАШНЕЙ КОМПЬЮТЕРНОЙ ЛАБОРАТОРИИ
А.К.ДЬЮДНИ

СОСУД, заполненный летающими во всех направлениях шариками и служивший ранее лишь воображаемой моделью физической среды, теперь можно наблюдать на экране домашнего компьютера. Приложив в общем-то совсем небольшие усилия к составлению программы, читатели смогут наблюдать за тем, как молекулярные столкновения создают давление в цилиндре или как в хаотическом движении красных и синих молекул происходит диффузионный процесс между двумя жидкостями. А те, кого не устрашает перспектива ядерного взрыва в их компьютере, могут даже поэкспериментировать с критическими массами нестабильного элемента, который я называю гридиумом.

Темой этой очередной статьи я обязан Дж.Блинну, научному сотруднику Лаборатории реактивного движения в Пасадине (шт.Калифорния). Блинн когда-то занимался разработкой компьютерных моделей различных физических систем. Его программы были записаны на довольно занимательной видеокассете с лаконичным названием "Механическая вселенная". Две модели Блинна привлекли мое внимание для описания в рубрике "Занимательный компьютер": замечательные "мультипликации" цилиндра, наполненного газом, и камеры сгорания. В первом случае несколько десятков шариков прыгали, натыкаясь друг на друга и на стенки двумерного цилиндра, приводя подвешенный в цилиндре поршень в состояние "вибрирующего равновесия". Во второй модели шарики двух цветов совершают хаотическое движение в замкнутом сосуде. Первоначально на экране видны две области разного цвета, но затем по мере того как шарики совершают "броуновское" движение, цвета перемешиваются. Третья модель, которую мы рассмотрим в данной статье - ядерный взрыв,- это мое собственное изобретение. Его идея, наверное, объясняется безотчетным детским интересом к явлению взрыва.

За те несколько часов, которые вам придется потратить на создание рабочей версии программы, названной мной BOUNCE (прыг-скок), вы будете с лихвой вознаграждены забавным зрелищем на экране. В модели Блинна шарики отскакивали друг от друга и от стенок сосуда, но можно написать значительно более простую и столь же эффектную программу, в которой шарики, игнорируя друг друга, отскакивают только от стенок цилиндра.

Пользователь программы BOUNCE может сам выбрать значения таких параметров, как скорость шариков и их количество. Положение, принимаемое поршнем, соответствует закону состояния идеального газа: PV = kT, т.е. произведение давления данной массы газа на занимаемый им объем пропорционально его температуре. Когда пользователь указывает скорость движения молекул, он тем самым выбирает определенное значение температуры, а вес подвижного поршня задает давление. Каким тогда будет объем? Ответ вы сможете ясно увидеть на экране (см. рисунок внизу). Чем выше температура газа, тем выше поднимается поршень.


В модели Дж.Блинна объем газа увеличивается по мере повышения температуры

Полезно проследить сначала за движением какого-нибудь одного шарика. Рассмотрим замкнутый сосуд, изображенный в виде прямоугольника на экране компьютера. Пусть это будет квадрат со стороной 50 условных единиц и пусть в какой-то точке, принадлежащей этому квадрату, находится наш шарик. Поскольку мы имеем дело с плоской моделью, положение шарика должно быть задано двумя координатными значениями, скажем x и y. Его движение характеризуется двумя координатами скорости vx и vy. За короткий промежуток времени t шарик переместится из положения (x, y) в положение (x+t*vx, y+t*vy).

Программа BOUNCE рисует изображение цилиндра с поршнем также двумерное. У цилиндра три неподвижные стенки, определенные линиями x = 0, x = 50 и y = 0. Четвертую стенку представляет поршень. Ее уравнение y = h, где h - высота поршня в данный момент. Рано или поздно в программе, которая управляет системой движущихся шариков, придется рассмотреть вопрос, столкнется ли шарик с одной из стенок, и если столкнется, то когда. Программа BOUNCE сверяет направление движения шарика с каждым из четырех уравнений стенок цилиндра: в какой точке траектория движения шарика пересекает каждую из четырех линий? Ответы приведены в левой таблице нижнего рисунка на с.88.


Таблицы для расчета времени (слева) и места (справа) столкновений

В каждом случае мы получаем значение времени t (отсчитанное от данного момента), через которое шарик столкнется с рассматриваемой стенкой. Координаты точки столкновения можно вычислить, подставив значение t в простые формулы, определяющие положение движущегося шарика. Если значение t получается отрицательным, это означает, что шарик, продолжая движение в том же направлении, никогда не натолкнется на данную стенку, поскольку он движется в противоположном от нее направлении. Если значение t бесконечно велико, то одна из координатных составляющих скорости шарика должна быть равна 0. В этом случае шарик тоже никогда не столкнется с данной стенкой, и программа, конечно, не вычисляет значения t.

Первой стенкой, на которую натолкнется шарик, будет стенка с минимальным неотрицательным значением t. Полученным значением t можно воспользоваться, чтобы вычислить точку, в которой произойдет столкновение. Здесь нам пригодится небольшая табличка (см. правую половину нижнего рисунка на с.88).

В большинстве программ, моделирующих поведение движущихся механических систем, используется один из двух возможных способов продвижения времени, или часового механизма модели. Если используется способ равномерного разбиения времени, то часы каждый раз продвигаются на короткий промежуток времени и положение всех компонентов системы равномерно изменяется. При использовании способа "критического события" часы продвигаются до того момента, когда происходит какое-то интересное явление. Читатели, наверное, помнят программу, моделирующую звездные скопления. Речь о ней шла в мартовском номере журнала за 1986г. Там расположение всех звезд рассматриваемой системы изменялось с интервалом времени в несколько лет. В программе BOUNCE удобнее воспользоваться вторым приемом - ожиданием критического события, которое в данном случае происходит, когда шарик отскакивает при столкновении со стенкой.

При использовании подхода с ожиданием критического события очень важную роль играет массив еvenе(событие). Если программа BOUNCE жонглирует n шариками, то она должна знать, какой из них следующим столкнется со стенкой. Поэтому массив на самом деле представляет собой очередь. Вот как действует программа:

repeat
1. получить значения времени, шарика и стенки из event(1) (соответственно time, ball, wall)
2. изменить положение объектов по значению времени (time)
3. определить следующее событие для шарика (ball)
4. подставить значения шарика, времени и стенки (соответственно ball, time, wall) в event
5. показать новое состояние системы на экране until нажатие клавиши

Этот цикл, состоящий из пяти шагов, повторяется до тех пор, пока не будет нажата соответствующая клавиша. О том, как пользоваться клавишами для прерывания программы, мы говорили в статье, посвященной специальным видеоэффектам и опубликованной в февральском номере журнала за этот год.

Шаг 1 довольно прост. На самом деле очередь событий состоит из трех массивов. В массиве event (событие) хранятся значения временных интервалов от данного момента до следующих событий в их естественном порядке. В массиве ball (шарики) хранятся индексы тех шариков, которые соответствуют событиям массива event. Еще один массив, под названием wall (стенка), содержит в качестве своих элементов индекс стенки, соответствующей событию. Например, элемент event(2) содержит время до второго события, ball(2) содержит номер участвующего в этом событии шарика b, a wall(2) указывает номер стенки w, который может принимать одно из четырех значений: 1 (x = 0), 2 (x = 50), 3 (y = 0) или 4(y = h). Таким образом, шаг 1 реализуется тремя инструкциями, присваивающими переменным t, b и w три соответствующих элемента информации.

На шаге 2 нужно изменить положение всех шариков, содержащихся в цилиндре. Это можно сделать при помощи цикла, имеющего следующий вид:

for i <- 1 to n
- x(i) <- x(i)+t*vx(i)
- y(i) <- y(i)+t*vy(i)
if w=1 or w=2 then vx{b) <- -vx(b)
if w=3 or w=4 then vy(b) <- -vy(b)

Читатели, наверное, узнали рассмотренные выше формулы для вычисления положения шариков. Ни один шарик не сможет выйти за пределы сосуда, поскольку за время t он может лишь достигнуть стены, но не более. Два условных оператора if-then прямо обрабатывают отскок шарика b от стенки. Если шарик ударяется об одну из вертикальных стенок, то составляющая его скорости по оси x меняется на противоположное значение, соударение же с горизонтальной стенкой означает, что поменять на противоположную следует координату скорости по оси y. При вычислении нового расположения объектов системы нужно также уменьшить величины времени в массиве событий event. Программа BOUNCE просто вычитает значение t из каждого элемента массива.

Шаг 3, определение следующего события для шарика b, я уже описал неявным образом; теперь рассмотрим его более подробно:

if vx(b) = 0 then t1 <- 5000
- - t2 <- 5000
- else t1 <- x(b)/vx(b)
- - t2 <- (50-x(b))/vx(b)
if vy(b) = 0 then t3 <- 5000
- - t4 <- 5000
- else t3 <- -y(b)/vy(b)
- - t4 <- (h-y(b))/vy(b)

Время до столкновения между шариком b и каждой из четырех стенок записано в виде значений четырех переменных от t1 до t4. Если шарик b на продолжении своего теперешнего пути никогда не достигнет какой-нибудь из четырех стенок, то соответствующей переменной присваивается абсурдно большое значение 5000. Затем, чтобы определить стенку, которой шарик b достигнет первой, мы применяем своеобразное решето. Сначала программа присваивает переменной t значение 5000 и сравнивает его по очереди с каждым из четырех параметров от t1, до t4. Проверка состоит из трех условий: если ti меньше t, если ti больше нуля и если wall(b) не равно i, то программа заменяет текущее значение t на ti, а вместо w подставляет значение i.

На шаге 4 происходит перетасовка очередей. Главное - определить то место в очереди, которое соответствует следующему столкновению шарика b. Это сделать нетрудно:

k <- 2
while event(k) < t
- event(k-1) <- event(k)
- ball(k-1) <- ball(k)
- wall(k-1) <- wall(k)
- k <- k+1
event(k-1) <- t
ball(k-1) <- b
wall(k-1) <- w

Здесь программа просматривает очередь событий event, чтобы найти место, принадлежащее в данный момент шарику b. В процессе поиска она сдвигает все три массива на одну ячейку влево. Если программа находит элемент k, такой, что event(k) не меньше t, то очевидно, что время до следующего столкновения шарика b принадлежит предшествующей ячейке k. (Когда мы задаем начальное положение и скорости шариков, находящихся в цилиндре, нужно установить также исходные значения элементов очереди. Чтобы не делать программу слишком сложной, исходные положения и скорости можно задать вручную, а временные интервалы для ближайших событий вычислить, а затем ввести их в программу с клавиатуры).

На последнем шаге цикла программа BOUNCE должна показать на экране цилиндр и все шарики в положениях, занимаемых ими на данный момент. Выполняя эту простую операцию, нужно, конечно, не забыть стереть изображения шариков в их старых положениях.


Схема цилиндра с поршнем

Перед тем как приступить к выполнению основного цикла вычислений, программа просит пользователя ввести значение скорости, с которой будут двигаться шарики. Если обозначать эту величину через v, то программа затем выбирает n случайных чисел в диапазоне от -v до v и присваивает эти числа в качестве значений координат скоростей по оси x, т.е. vx(i). Составляющие скоростей по оси y вычисляются теперь по теореме Пифагора, а именно они полагаются равными квадратному корню из разности v2-vx(i)2. Возможно, читатели захотят поэкспериментировать с различными значениями v в диапазоне от 1 до 10.

Разумеется, авторы программы BOUNCE не устоят перед соблазном понаблюдать за тем, как поршень перемещается то вверх, то вниз в ответ на давление, оказываемое на него снизу шариками, прыгающими в цилиндре. Для этого на шаге 2 нужно провести вычисления, в которых учитывается взаимодействие двух движений, совершаемых поршнем: вниз под влиянием силы тяжести и вверх под влиянием импульса, полученного при столкновении с очередным шариком. В результате мы получаем новое значение высоты h.

В целях упрощения программы физический процесс столкновений шариков с поршнем был сведен к примитивным арифметическим действиям. За время t поршень падает на t2/100 единиц, а когда по нему ударяет шарик с вертикальной составляющей скорости vy, он поднимается на высоту, равную vy/100m единиц. Я приношу свои извинения физикам, но мой кустарный способ работает! Разумеется, пользователи программы BOUNCE должны задать массу m поршня, а также количество шариков n и их скорость v.

В программе, моделирующей диффузию, под названием BLEND (смесь) молекулы жидкости рассматриваются как шарики, которые могут перемещаться вертикально или горизонтально лишь на одну позицию за раз. Массив размером 31*31 под названием tank (бак) хранит данные о 930 шариках, исходное расположение которых напоминает расстановку шашек перед началом игры. Программа BLEND еще менее реалистична, чем BOUNCE, но она тоже работает. Шарики, находящиеся в левой половине замкнутого сосуда, окрашены в красный цвет, а те, что справа - в серый (см. нижний рисунок на с.87).


Процесс диффузии двух жидкостей в матрице 9*9

Начав работать, программа BLEND выбирает случайным образом позицию в массиве шариков, а затем также случайно одну из четырех соседних позиций. Если в первой позиции оказывается какой-нибудь шарик, а вторая пуста, то изображение шарика в старой позиции стирается и он появляется в новой, соседней позиции. Если шарик отсутствует в первой позиции и присутствует во второй, программа оставляет эти позиции без изменений. Через несколько микросекунд найдется какой-нибудь шарик, который она сможет переместить на соседнее место. Сколько времени потребуется для того, чтобы эти две абстрактные жидкости полностью перемешались? Мы не будем приводить здесь серьезного алгоритмического описания программы. Предоставляем читателям возможность проявить свои способности.

Мне не терпится поскорее перейти к гридиуму, очень опасному, нестабильному физического элементу. При спонтанном распаде одного атома этого вещества выделяется один нейтрон. Здесь я не могу не вспомнить о знаменитом опыте Уолта Диснея. Однажды этот великий затейник заполнил весь школьный спортивный зал взведенными мышеловками. На захлопывающейся рамке каждой мышеловки покоился шарик для игры в настольный теннис. С озорной улыбкой Дисней бросил в зал теннисный шарик. Через секунду в воздухе оказались тысячи шариков и зал наполнился каким-то странным шумом. Наверное, это была самая безопасная в мире цепная реакция.

Гридиум имеет кристаллическую структуру. Его атомы, подобные маленьким шарикам, расположены в виде квадратной решетки со стороной n+1 шариков. По сигналу пользователя программы центральный шарик распадается и из него вылетает нейтрон, который стремительно движется сквозь решетку шариков в случайном направлении. Если он натолкнется по пути на другой шарик, тот тоже подвергнется распаду. Начнется ли цепная реакция? Если решетка мала, то реакции скорее всего не получится. Но чем больше шариков в решетке, тем с большей вероятностью она "взорвется" (см.рисунок на с.88). Каковы же пороговые размеры, необходимые для начала цепной реакции? Предлагаем любителям экспериментов самим получить ответ на этот вопрос. Заметим, что даже маленький микрокомпьютер значительно облегчил бы работу физикам, исследовавшим цепную реакцию в 1944г. в Лос-Аламосе.



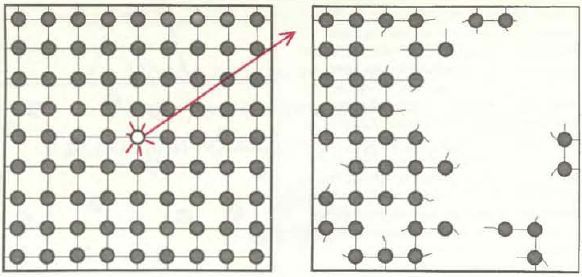
Фрагмент кристаллической решетки гридиума до (слева) и после (справа) цепной реакции

В нашей рубрике мы ничего не скрываем от наших читателей, у нас нет военных тайн. Я с удовольствием опубликую результаты исследований наших читателей, которым удастся определить критическую массу гридиума. В программе, которую я назвал BOOM (взрыв), используется массив grid (решетка). Поскольку в языках программирования, которыми пользуется большинство читателей, отсутствуют массивы переменной размерности, я решил установить для массива grid максимальные размеры 50*50. Когда пользователь введет с клавиатуры значение n, программа автоматически ограничит свои операции первыми n строками и столбцами массива grid. В каждом элементе массива содержится по одному атому. Чтобы упростить вычисления и демонстрацию картинки на экране, радиус атома гридиума примем равным единице, а интервал между соседними атомами - шести единицам. Для удобства будем также считать, что атом, содержащийся в элементе (i, j) массива, имеет координаты (6i, 6j).

Когда атом гридиума претерпевает радиоактивный распад, программа BOOM выбирает случайным образом угол a и вычисляет синус и косинус этого угла, записывая их в качестве значений переменных s и c. При известных координатах атома (x, y) и угла нетрудно построить прямую линию. Важное значение для нас будет иметь вопрос о том, "насколько близко эта прямая пройдет от другого атома, имеющего координаты (u, v)?" Ответ дает следующая формула: (u-x)2+(v-y)2-[(u-x)*c+(v-y)*s]2.

По этой формуле вычисляется квадрат расстояния между точкой (u, v) и рассматриваемой нами прямой. Вместо того чтобы возиться с извлечением квадратного корня, программа просто проверяет, не превосходит ли значение этой величины единицу. Если нет, то ясно, что атом с координатами (u, y) также должен претерпеть распад.

Всякий раз, когда один из атомов решетки grid взрывается, программа BOOM входит в цикл, в котором в переменные u и v систематически подставляются координаты всех n2 атомов, за исключением взорвавшегося. Атомы, которые должны претерпеть распад, добавляются к списку, имеющему форму массива и имя fire (огонь). Индекс fired (сгорели) отделяет уже взорвавшиеся атомы, значащиеся в этом списке, от еще не взорвавшихся. Еще один индекс end указывает на конец списка. Каждый раз, когда взрывается новый атом, все другие атомы, лежащие на пути испущенного им нейтрона, добавляются к списку fire, при этом значение индекса end соответственно увеличивается. Когда все такие атомы определены, увеличивается значение индекса fired и описанный цикл повторяется вновь. Если значения индексов end и fired равны, они оба указывают количество атомов, принявших участие в цепной реакции. При каком значении n вся решетка полностью прореагирует? По-видимому, статистический разброс результатов вокруг правильного ответа будет небольшим.

Ввиду того что мы уже почти исчерпали отведенное для нашей статьи место, на этом описание программы BOOM придется завершить. Можно, конечно, вставить в программу процедуру вывода изображения на экран, но для того чтобы найти ответ на поставленный вопрос, это не обязательно. В одном из следующих номеров я опубликую наиболее интересное изображение частично взорванной решетки из числа тех, которые пришлют читатели. Я думаю, что значение n для этой решетки окажется очень близким к критической массе.

БИБЛИОГРАФИЯ

MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARLWICK. Prentice-Hall, Inc., 1985.

ОТКЛИКИ

9 1988
В МАЙСКОМ номере журнала мы говорили о домашней компьютерной лаборатории, в которой моделировались эффекты давления с помощью молекул газа, сталкивающихся со стенками замкнутого сосуда. Молекулы участвовали также в процессе цифровой диффузии, распространяясь от одного края сосуда к другому. Наконец, атомы опасного нестабильного вещества, названного мною гридием, были собраны в критическую массу. Некоторые читатели построили свои собственные сосуды, содержащие газ под давлением, и свои диффузионные камеры, но большинство, конечно, заинтересовались гридием. Со всей Северной Америки, а потом и из других частей света посыпались на мой стол доклады о "компьютерных взрывах".

Описав путь испускаемого при делении нейтрона линейным уравнением, я тем самым неявно предполагал, что два нейтрона, удаляясь от расщепленного атома, должны двигаться в противоположных направлениях. Большинство читателей, однако, выбрали лишь одно из этих направлений. Так или иначе, расщепить все атомы плоской решетки размером n*n оказалось весьма непросто.

Построив по результатам многочисленных экспериментов диаграмму, Р.Касл из Уэбстера (шт.Техас), установил, что в решетке размером 16*16 обычно реагирует 904% атомов. А когда размер решетки достигает 32, количество делящихся атомов достигает уже 99%. Р.Мартин, профессор философии Университета Далуэн в Новой Скотни, пришел к следующим результатам: когда размер решетки равен 19, реагирует 90% атомов, а при размере 39 количество прореагировавшего материала достигает уже 99%. Большинство других ядерных экспериментов дали результаты, укладывающиеся в этот диапазон. Среди тех читателей, кто воспользовался моделью с двумя нейтронами, был, например, Р.Смит из Энн-Арбора (шт.Мичиган). Он пришел к типичным результатам с меньшей критической массой. Согласно его данным, в решетке 15*15 реагирует 98% атомов.

Наверное, немногим читателям удалось создать такую сложную и совершенную систему, какую представляет собой программа SHAKEY, написанная Р.Меркином из Нортэмптона (шт.Массачусетс). Программа SHAKEY не только управляется с очень большими решетками, но и с помощью многих приемов, позволяющих сэкономить время, работает очень быстро. Домашний реактор SHAKEY позволяет экспериментировать с различными интервалами в решетке, а также отмечает каждый распад звуковым сигналом, щелкая подобно счетчику Гейгера. Меркин пишет, что готов с удовольствием поделиться своей программой со всеми желающими.

Изображения взорвавшихся решеток, приведенные на рисунке вверху, были присланы Д. Фэнсом из Питтсбурга (шт.Пенсильвания) и П.Кейном из Шампейна (шт.Иллинойс).


Прореагировавшие матрицы: Д.Фэнса (слева) и П.Кейна (справа)

6 1988
ДРЕВНИЙ ВЕРЕВОЧНЫЙ КОМПЬЮТЕР, ОБНАРУЖЕННЫЙ В ДЖУНГЛЯХ ОСТРОВА АПРАФАЛ
А.К.ДЬЮДНИ

[Оригинальная статья опубликована в апрельском номере журнала "Scientific American". Желая придать ей юмористический характер, автор придумывает фантастический сюжет с вымышленным названием острова, его обитателей и т.д. Апрафал (в английском тексте Apraphul) созвучно английскому выражению April-fool, что в переводе означает "жертва первоапрельской шутки". Однако все что касается описания блочных устройств с веревками следует воспринимать не как шутку, а как попытку автора рассмотреть возможность имитации простейшими механизмами различных логических функций, выполняемых в обычном компьютере электронными схемами.- Прим. ред.].

НА ОСТРОВЕ Апрафал у северо-западного побережья Новой Гвинеи археологи обнаружили полусгнившие фрагменты замысловатой конструкции из веревок и блоков. Полагают, что это был первый в истории цифровой компьютер. Руководитель исследовательской группы Р.Л.Рипли из колледжа Чарльза Форта в Нью-Йорке датировал сооружение приблизительно 850г.н.э.

Апрафалитяне были отличными мореплавателями. Их корабли отличались добротностью и были прекрасно оснащены. Пришли ли апрафалитяне к своему веревочному компьютеру, потому что так мастерски владели корабельными устройствами из канатов и блоков, или все было как раз наоборот? Мнения специалистов разошлись, и между ними ведутся горячие споры.

Древний веревочный компьютер недавно был частично реконструирован группой исследователей во главе с Рипли в Тропическом музее морских древностей неподалеку от о.Суматра. Тщательно прочесав сплошь покрытую джунглями территорию в несколько квадратных километров к востоку от горного хребта Шу-Ток, она натолкнулась на следы истлевших джутовых веревок и отметила точное положение сильно окисленных медных блоков и других деталей. Эта реконструкция предоставила мне идеальную возможность познакомить читателей с принципами цифровой обработки данных, не прибегая к крошечным и загадочным электронным компонентам. Здесь есть и вентили, и триггеры, и другие разнообразные элементы, целиком состоящие из веревок н блоков. Все детали хорошо видны и нетрудно понять, как они работают.

Апрафалитяне, так же как и мы, пользовались двоичной системой счисления, но 0 и 1 были представлены в их "машине" не уровнями электрического напряжения, а положениями веревок. Представьте черный ящик с отверстием, просверленным в одной из его стенок, и что вы держите конец натянутой веревки, выходящей из отверстия. Такое положение веревки представляет цифру 0. Если теперь сильнее потянуть за веревку, из ящика послышится скрип и скрежет, и веревка выйдет из отверстия сантиметров на 30. В этом новом положении веревка будет представлять цифру 1.

При помощи таких ящиков можно представить все числа. Например, любое число в диапазоне от 0 до 7 может быть представлено тремя ящиками (см. таблицу на с.85). Чем большим числом ящиков мы располагаем, тем большее по величине число можно представить с их помощью. Десяти ящиков достаточно для представления всех чисел в диапазоне от 0 до 1023.


Представление чисел в веревочном компьютере

Мой пример с черными ящиками вовсе не был произвольным. Апрафалитяне, по всей видимости, любили помешать свои механизмы в черные деревянные ящики, большие н маленькие. Может быть это объясняется тем, что строительство и использование компьютеров было исключительной привилегией какой-то технической жреческой касты. Вид огромных сооружений из черных ящиков, наверное, приводил толпу в благоговейный трепет.

Одно из основных устройств, которыми пользовались апрафалитяне, преобразовывало 0 в 1, а 1 в 0. (Иногда нам будет удобнее говорить "0" и "1", вместо "внутрь" и "наружу"). Похожий по своим функциям на то, что современные инженеры-электронщики назвали бы инвертером, этот интересный механизм представляет собой опять-таки черный ящик с двумя просверленными в нем отверстиями: одно на передней, а другое на задней стенке (см. рисунок внизу). Если кто-нибудь тянул веревку из отверстия в передней стенке, то из отверстия на противоположной стенке веревка выходила на такую же длину. Заглянув внутрь ящика, можно легко понять как он устроен: веревки, входящие в ящик спереди и сзади, проходят через два фиксированных блока и далее идут к верхней стенке, где крепятся к пружине.


Веревочный инвертер

Как уже, наверное, догадались некоторые читатели, цифры 0 и 1 кодировались не столько тем, куда двигалась веревка, в ящик (внутрь) или из ящика (наружу), сколько направлением ее движения. Этот принцип лучше всего продемонстрировать на примере с ящиком, в котором вообще нет никакого механизма. Веревка входит в отверстие на его передней стенке и выходит через отверстие на противоположной стороне. Если потянуть ее из положения 0 в положение 1 из переднего отверстия, она перейдет из положения "внутрь" в положение "наружу". Ее движение направлено в ту сторону, в какую тянут. В то же время у выходного отверстия веревка переходит из положения "наружу" в положение "внутрь", но поскольку и в этом случае веревка движется в направлении, в котором ее тянут, то и здесь она переходит из состояния 0 в состояние 1.

Еще два механизма почти завершают набор компонентов, которыми пользовались древние апрафалитяне для сооружения своих компьютеров. Первый механизм - это черный ящик с двумя входными и одной выходной веревками. Если хотя бы одна входная веревка находится в положении 1, то выходная также будет в состоянии 1. Апрафалитяне достигали этого эффекта исключительно простыми средствами (см. верхний рисунок на с.86). Каждая веревка, входящая через переднее отверстие, проходила через пару блоков, и привязывалась к кольцу, соединенному с выходной веревкой. Если потянуть за одну или обе входные веревки, кольцо будет двигаться в том же направлении. Поскольку выход у этого черного ящика равен 1, если один или другой вход равен 1, современные инженеры назвали бы это устройство вентилем ИЛИ.


Вентиль ИЛИ (вверху) и вентиль И (внизу)

Древние островитяне умели также строить то, что мы называем вентилем И, При этом они пользовались тремя блоками и изогнутым стержнем (см. нижний рисунок на с.86). Один блок, к оси которого была привязана выходная веревка, мог свободно скользить по стержню. Два других блока были спарены н служили главным образом для того, чтобы удерживать выходную веревку у отверстия в задней стенке ящика. Когда обе входные веревки находились в состоянии 0, изогнутый стержень совпадал с дугой окружности, центр которой находился между спаренными блоками у выхода. Если какую-нибудь из входных веревок оттянуть в положение 1, то один коней стержня сдвинется с линии покоящейся окружности. Блок, скрепленный с выходной веревкой, покатится "под гору", по направлению к другому концу стержня. Положение выходной веревки по существу остается тем же, что и прежде, поскольку этот конец стержня по-прежнему будет совпадать с покоящейся окружностью. (Штырек в середине изогнутого стержня удерживает его ось на месте, когда натягивается лишь одна входная веревка).

Только если обе входные веревки будут оттянуты в положение 1, выходная веревка тоже перейдет в положение 1. В данном случае весь стержень займет новое положение. На каком бы конце стержня не находился подвижный блок, он будет одинаково удален от выходных блоков. Это устройство мы называем вентилем И, потому что выход его равен 1 тогда и только тогда, когда и один, и другой вход находятся в состоянии 1.

Теперь при наличии всех описанных выше компонентов можно построить любые управляющие схемы цифрового компьютера: схемы, выполняющие арифметические действия, схемы, которые интерпретируют коды машинных команд программы и управляют потоками информации между различными компонентами компьютера.

Был ли компьютер апрафалитян построен на аналогичных принципах? Пока на основании имеющихся данных еще трудно прийти к определенным выводам, однако архео-компьютологи, работающие под руководством Рипли, утверждают, что им удалось восстановить механизм, способный выполнять функции простого мультиплексора. В электронных компьютерах мультиплексор является по существу электрическим переключателем, который управляет прохождением многих сигналов по одной линии. В качестве примера рассмотрим простейший мультиплексор с двумя входными линиями, которые мы условно назовем a и b. В любой заданный момент времени на каждой из этих линий может быть сигнал, равный либо 0, либо 1. Какому из этих двух сигналов, передаваемому по линии a или b будет разрешено пройти через устройство и выйти по выходной линии d? Ответить на этот вопрос можно лишь при условии, если известно, в каком состоянии находится управляющая линия c: если на ней 1, то на выход пройдет сигнал со входа a; если же на управляющей линии 0, то пройдет сигнал b (см. рисунок на с.84).


Веревочный мультиплексор: веревка c определяет, какой из сигналов, a или b, достигнет линии d

Восстановленный мультиплексор апрафалитян имел два информационных входа и состоял из двух вентилей И, одного вентиля ИЛИ и одного инвертера. Конструкция устройства настолько проста, что читатели смогут его построить сами. Не исключено, что в магазинах хозяйственных товаров в скором времени будут раскуплены все веревки. Глядя на схему, попробуем разобраться, как работает мультиплексор. Веревки a и b - это входные линии мультиплексора; каждая веревка идет к своему вентилю И. Веревка c разветвляется: одна ее ветвь идет непосредственно на вход вентиля И, к которому ведет также веревка a; вторая ветвь веревки c проходит через инвертер и затем на вход того вентиля И, к которому ведет входная веревка b. Если веревка c натянута так, что на ней устанавливается значение 1, и поддерживается в этом состоянии, то любая последовательность нулей и единиц, передаваемая вдоль веревки a, будет без изменений подано через верхний вентиль И на вентиль ИЛИ. В то же время любой сигнал, передаваемый по веревке b, будет задержан нижним вентилем И. Если же веревку с отпустить в положение 0, то инвертер выдаст 1 на входе нижнего вентиля И. В этом случае любой сигнал, передаваемый вдоль веревки b, будет теперь беспрепятственно проходить через нижний вентиль И, а сигналы на веревке a будут игнорироваться.

Вентиль ИЛИ просто связывает два входных сигнала воедино. Предположим, что в данный момент мультиплексор передает сигнал, приходящий по входной веревке a. Посмотрим, как будет работать мультиплексор. Если веревка c отпущена и находится в состоянии 0, то подвижный блок в ящике И откатится к концу изогнутого стержня. Таким образом, состояние 0 будет передано на выходную веревку и подано на входную веревку ящика ИЛИ. Другая входная веревка этого ящика уже находится в состоянии 0 (она не натянута). Естественное натяжение выходной веревки d приведет к тому, что она сразу примет значение 0. Если теперь снова потянуть за веревку a, то натяжение передастся по только что рассмотренному пути, в результате чего веревка d изменит свое состояние.

Теперь рассмотрим вопрос о том, какую роль в компьютере апрафалитян играло натяжение веревок. Иногда, как это было в случае с вентилем ИЛИ, какая-то веревка оказывается ненатянутой. Естественно возникает опасность, что такая веревка соскользнет со своего блока. Рипли сообщил мне, что апрафалитяне учитывали такую возможность и применяли в своем компьютере специально модифицированный инвертер с очень слабой пружиной. Во всех местах, где ослабление натяжения веревки грозило каким-нибудь нарушением в работе механизма, они устанавливали "слабые инвертеры", которые позволяли поддерживать некоторое минимальное натяжение в веревках, несущих нулевой сигнал.

Ни один универсальный компьютер не может обойтись без памяти. Память апрафалитянского компьютера состояла из сотен специальных запоминающихся элементов, которые мы назвали бы триггерами. Здесь опять заметна способность апрафалитян находить простейшие решения. В соответствии с современной терминологией две входные линии механического триггера мы назовем линией установки и линией сброса (см. верхний рисунок на с.87). Три веревочных линии устройства соединялись с помощью трех блоков таким образом, что, когда линия установки оттягивалась из ящика в положение 1, линия сброса переходила в положение 0. Общая веревочная линия прикреплялась к подвижному бруску в задней части ящика. Выходная веревка, будучи продолжением линии установки, имела большую навеску, которая подходила к прорези в подвижном бруске. Когда линия установки вытягивалась до предела, навеска над концом бруска попадала как раз в прорезь.


Триггер, служивший элементом памяти

После этого выходная линия поддерживалась в одном и том же состоянии, пока гигантский веревочный компьютер в процессе своей работы не изменял состояние триггера при натягивании линии сброса. Подвижный брусок при этом отходил от навески, освобождая ее, в результате чего выходная линия переходила к состоянию 0. В данном случае, начиная с этого момента, триггер "запоминал" значение 0. Каким образом подобные элементы памяти использовались в веревочном компьютере?

Рипли и члены его группы были слегка озадачены, когда в самом центре гигантского компьютерного комплекса они обнаружили большое заросшее поле шириной около километра. Здесь под поверхностным слоем почвы скрывалось несколько тысяч полусгнивших деревянных ящиков-триггеров, лежащих рядами, по восемь устройств в ряду. Посоветовавшись с архео-компьютологами, Рипли в конце концов догадался, что это поле представляло собой не что иное, как главную память ископаемого компьютера. Каждый ряд из восьми ящиков, очевидно, составлял одно "восьмибитовое слово" точно так же, как три ящика в рассмотренном выше примере составляли трехбитовое слово. Допустим, что три триггера в этом случае имели значения 1, 0 и 1, т.е. представляли число 5 в двоичном коде.

Доступ к таким словам памяти осуществлялся в веревочном компьютере следующим образом. Веревка с выхода каждого триггера в ряду тянулась к входу вентиля И. Другая входная веревка каждого вентиля И сообщалась со специальной веревкой, по которой поступал запрос на содержимое данного слова памяти. Когда эта веревка натягивалась, выходы вентилей И становились тождественными выходами соответствующих триггеров. Выходные веревки вентилей И в свою очередь поступали в большую конструкцию из вентилей ИЛИ, а оттуда в специальный массив триггера, который мы назвали бы регистром. Таким образом, стоило потянуть за веревку, соответствовавшую выбору данного слова памяти, как в регистре устанавливались те же значения битов, что и в выбранном слове.

Главное логическое устройство компьютера, несомненно, могло направлять потоки информации не только от памяти к регистрам, но и от регистра к регистру. Для таких пересылок в частности использовались мультиплексоры, а также устройства, выполнявшие обратные мультиплексору функции. В одном регистре, который по нашим понятиям был арифметическим, двоичные слова могли комбинироваться в соответствии с правилами сложения или умножения.

Полагают, что веревочный компьютер был программируемым. Если это так, то часть его огромной памяти использовалась для хранения программы. Команды программы также представлялись наборами из нулей и единиц, которые извлекались из памяти посредством описанного выше механизма. Из памяти эти наборы поступали в так называемый регистр команды, где интерпретировались логическим устройством компьютера.

К сожалению, недостаток места не позволяет мне более детально описать древнюю вычислительную машину, во всем ее великолепии и сложности. Во время работы она, должно быть, являла собой удивительное зрелище. Поскольку суммарная длина ее веревочных линий была колоссальной, ни одному человеку не хватило бы сил вытянуть линии ввода данных в нужное положение. Найденные на острове скелеты слонов ясно указывают нам на источник энергии, необходимой для того, чтобы приводить машину в действие. На выходных концах мошные пружины поддерживали необходимое натяжение веревочных линий системы. Возможно, к выходным веревкам были привязаны яркие флажки, глядя на которые жрецы технической касты могли читать результаты вычислений, производимых компьютером.

Интересно сопоставить ископаемый веревочный компьютер острова Апрафал с нанокомпьютером, о котором речь шла в мартовском номере журнала. Конечно, веревочный компьютер принадлежит далекому прошлому, в то время как нанокомпьютер - машина далекого будущего. Веревочный компьютер имел огромные размеры, занимая площадь в тысячи акров. В противоположность ему, нанокомпьютср невероятно мал - в тысячу раз меньше ядра биологической клетки человека. Сама концепция той и другой машины переносит нас в тот абстрактный мир, где увлекательное переплетено с серьезным. Возьмем, к примеру, мечту о создании машин, обладающих искусственным интеллектом. Нам проще поверить в то, что это возможно, если мы представим себе такую машину в виде электронного компьютера, потому что наше собственное мышление в значительной степени происходит на уровне электронных процессов. Однако поскольку любой современный компьютер (и его программу) в принципе можно представить в виде веревочных конструкций островитян, то и любое устройство, обладающее искусственным интеллектом, независимо от того, реализуется оно в наше время или в будущем, также будет иметь свой веревочный аналог. А может быть действительно когда-нибудь появится "ХЭЛ-9000" - "психически ненормальный" компьютер из научно-фантастического романа А.Кларка "2001-й год. Космическая одиссея"? Способны ли мы представить себе, что огромное сооружение из веревок и блоков может быть таким же разумным, как и мы?

Перед тем как покинуть остров Алрафал, бросим последний взгляд в его туманное прошлое. Интересно, какие устройства предшествовали огромному цифровому компьютеру в технической эволюции островитян? Конечно же, аналоговые. На рисунке внизу на с.87 изображена схема аналоговой суммирующей машины, состоящей из двух веревок и двух блоков. Через два отверстия в передней стенке ящика пропущена веревка, которая внутри его проходит через блок; ось этого блока связана с осью другого блока. Один конец второй веревки прикреплен к задней стенке ящика. Она проходит через второй блок и выходит наружу из отверстия в задней стенке ящика. Возможно, читателям интересно самим разобраться в механизме, посредством которого эта машина складывает два числа. Если за два конца потянуть веревку на входе из ящика на расстояния a и b,то выходная линия должна переместиться на расстояние a+b.


Суммирующая веревочная машина

Это ясно. А как островитяне умудрялись производить аналоговое умножение? Я попробую опубликовать описание самой простой из предложенных читателями конструкций.

ОТКЛИКИ

10 1988
НЕМНОГИХ людей ввело в заблуждение путешествие на остров Апрафал, описание которого приводилось в июньском номере журнала. Тем же, кого статья увлекла, пришлось изрядно повозиться над восстановлением аналоговой перемножающей машины островитян - устройства, перемножающего два числа исключительно посредством веревок и блоков. Некоторые настолько глубоко прониклись духом этого исследования, что объявили себя специалистами по древней культуре островитян. Рекордсменом оказался К.Грант из Чичестера (шт.Нью-Гемпшир). В длинном письме Грант рассказывает о переписке с таинственным доктором Гребдлогом Эбуром, известным ученым, изучающим древнюю историю острова Апрафал. Вот что он, в частности, пишет: "Прочтя статью о развитии математики у древних апрафалитян, я связался с доктором Гребдлогом и спросил, не встречался ли он случайно в своих исследованиях... с апрафалнтянеким аналоговым перемножителем... Он ответил, что действительно занимался исследованием этого вопроса, и выслал мне копию своей статьи". И далее: "Статья была написана от руки, каллиграфическим почерком Гребдлога. Она сопровождалась техническими схемами устройств, состоящих из блоков, кулачков и перемычек. Гребдлог отмечает, что эти схемы свидетельствуют о незаурядной изобретательности и трудолюбии островитян, проявленных ими при создании этого устройства, но, пожалуй, еще больше удивляет его почти полная практическая бесполезность этого устройства".

В письмах читателей чаще всего предлагалась конструкция перемножителя с использованием стержня, один конец которого крепится к фиксированному шарниру. Веревка, играющая роль входного сигнала и привязанная к стержню на некотором расстоянии от конца, оттягивает его вперед, так что веревка, представляющая выходной сигнал и привязанная к свободному концу, также оттягивается в том же направлении. Поскольку стержень по существу представляет собой рычаг с осью в шарнире, выходная веревка перемещается на большее расстояние, чем входная. Основной недостаток этой конструкции заключается в потере пропорциональности этих перемещений, по мере того как входная линия вытягивается на большее расстояние, конец стрежня описывает дугу окружности, и эффект усиления на выходном конце постепенно сводится на нет. В различных вариантах описанной конструкции проблема, связанная с круговым движением стержня, решается либо при помощи специальных направляющих, либо при помощи сложных систем параллельно соединенных стержней. Такой подход представляется мне слишком замысловатым. Возможно, в условии задачи следовало оговорить, что использовать стержни запрещается.

Р.Нортон из Мадисона (шт.Висконсин) применил спиральные блоки, позволяющие вычислять логарифмы и антилогарифмы. Входные линии A и B разматываются с двух барабанов (которые не запрещены, потому что представляют собой просто широкие блоки). Каждый из зтих барабанов крепится к спиральному барабану, на который наматывается выходная линия. Два выходных сигнала складываются затем способом, описанным в конце статьи о веревочном компьютере. Антилогарифм суммы вычисляется посредством наматывания дополнительной веревки на спиральный барабан, соединенный с простым барабаном, на который наматывается веревка, представляющая окончательный выходной сигнал. Аналогичная машина была "открыта" Р.Эддиусом из Нью-Йорка. Он утверждает, что островитяне пользовались раковинами моллюсков, спиральная форма которых позволяла вычислять логарифмы с высокой точностью! Д.Фокс из Лимы (шт.Огайо) сообщает, что племена сходной культуры населяли когда-то один из маленьких островков, расположенный неподалеку от группы Маршалловых островов. Здесь он обнаружил не только аналогичные устройства для вычисления логарифмов и антилогарифмов, но и приспособление для возведения чисел в квадрат, которое напоминает йоу-йоу, распространенную на Филиппинах игрушку - диск с канавками для шнурка, поднимающийся и опускающийся подобно чертику на веревочке. Возможно, читатели захотят поразмыслить о справедливости утверждения Фокса?

К.Фостер из Восточного Орлеана (шт.Массачусетс) считает, что цивилизация апрафалитян погибла из-за проблемы нагрузочной способности, возникающей, когда выходной единичный сигнал вентилей компьютера не в точности равен единице. Чтобы исключить всякую неточность в священных вычислениях, верховные жрецы приставили к каждому логическому вентилю по одному островитянину, который должен был тянуть за выходную веревку, если она недостаточно натянута. Занятому этой работой населению не хватало времени на производство продуктов питания, и в конце концов люди вымерли с голоду.

И наконец, последнее слово принадлежит специалисту по архитектуре современных компьютеров М.Пейгану из Маунт-Лорела (шт.Нью-Джерси). Обеспокоенный образовавшимся у островитян разрывом между культурой аналоговых и культурой цифровых устройств, Пейган придумал восхительный аналого-цифровой преобразователь. Одна веревка, представляющая аналоговый сигнал, входит в устройство и некоторое число веревок, представляющих цифровой эквивалент входного числа, выходит из него. Такая машина могла быть изобретена и на Апрафале, но жрецы наверняка запретили бы подобную ересь (слово pagan, созвучное фамилии Пейган, означает "языческий".- Перев.).

7 1988
ГРАФОТВОРЧЕСТВО НЕВИДИМОГО ПРОФЕССОРА, СКРЫТОГО ЗА ЭКРАНОМ ДИСПЛЕЯ
А.К.ДЬЮДНИ

ЕСЛИ уподобить экран компьютерного дисплея классной доске, то кто же тогда рисует на ней красивые плавные кривые? Наверное, невидимый профессор - электронное воплощение преподавателей аналитической геометрии. Некоторые старательно выводимые ими кривые косят экзотические названия, такие как локон Аньези, конхоида Никомеда и улитка Паскаля. Среди них встречаются параболы, циклоиды, спирали и синусоиды. Они едва не были преданы забвению, когда в математике стали проявляться тенденции к обобщениям, а геометрия стала не евклидовой. Теперь значение этих кривых в основном заключается в отражении формы, которую принимают физические функции. Кривые напоминают нам о чудесных открытиях - и знаменитых, и не очень известных, сделанных математиками прошлых столетий.

Невидимый профессор - это набор простейших компьютерных программ. При изображения он передает красоту кривых с такой выразительностью, о которой едва ли могли мечтать их первооткрыватели. Мел в руке профессора - это маленькая яркая точка на экране. Изображение графика кубической функции Чирнгаузена, например, начинается с правого верхнего угла; кривая плавно проходит через начало координат, делает петлю и снова возвращается в начало координат. Далее светящаяся точка "прожигает" свой путь к нижнему правому углу экрана, где останавливается и гаснет (см. левую часть рисунка внизу).


Двадцать версий кубической параболы Чирнгаузена (слева) и пять версий гиппопеды (справа)

Невидимый профессор может нарисовать даже целое семейство таких кривых. Кубическое уравнение Чирнгаузена содержит постоянную величину, или параметр. Задавая различные значения этого параметра, мы получаем различные версии кривой - на экране как бы воплощаются вариации на заданную тему. Недостает только старческого голоса: "Ну, а здесь с первого взгляда на формулу мы видим, что это обобщенная полукубическая парабола".

Для невидимого профессора не составляет труда изобразить трансцендентный пейзаж нэ волнистых "параллельных" кривых или "комплексный" океан, искривляя прямоугольную форму ячеек решетки. Таких программ любители геометрии написали уже немало.

Чтобы дать читателям минимальные сведения о том, как рисовать различные кривые, я сам на некоторое время превращусь в невидимого профессора. В качестве примера рассмотрим, как составить программу, чтобы на экране получить обычную окружность. Для этого вспомним три способа задания окружности.

Первый и наиболее привычный способ знаком нам со школы:

x2+y2 = c2.

Это уравнение множества точек, принадлежащих окружности. Любая точка с декартовыми координатами x и y лежит на окружности тогда и только тогда, когда сумма квадратов x и y равна квадрату c (c - радиус окружности). Каждый раз при выполнении программы пользователь должен указать значение c.

Приведенной выше формулой можно воспользоваться для составления программы, рисующей окружность, если разделить кривую на две части - верхнюю и нижнюю. Программа пробегает через последовательные значения x, высвечивая на экране соответствующие им точки y. Чтобы строить изображение точки, значение y должно быть вычислено без квадрата, поэтому уравнение нужно решить относительно y. Две ветви решения отличаются только знаком:

y = +sqrt(c2-x2),
y = -sqrt(c2-x2).

Однако такое задание кривой выглядит уже несколько неуклюже. Наверное, лучше воспользоваться полярными координатами.

В декартовой системе координаты x и y указывают удаление данной точки соответственно по горизонтали и по вертикали от центральной точки, называемой началом отсчета. Полярные координаты r и Q определяют точку совершенно по-другому: r - это расстояние, на котором данная точка находится от начала отсчета, а Q - угол между линией, соединяющей данную точку с точкой начала отсчета, и горизонтальной прямой. Уравнение окружности в полярных координатах имеет очень простой вид: r = c. Независимо от величины угла Q расстояние r всегда равно c. К сожалению, лишь немногие читатели могут воспользоваться языками программирования, в которых для вывода изображений можно применять полярные координаты.

Третье представление основано на так называемых параметрических уравнениях. Для многих программ, рисующих изображения кривых, это представление наиболее подходящее:

x = c*cos(t),
y = c*sin(t).

Здесь параметр t пробегает значения от 0 до 360o. Можно высвечивать точки (х, у) с интервалом, скажем, в 1o. Читатели, немного подзабывшие функции синуса и косинуса, в крайнем случае могут прочесть о них в своем руководстве по языку программирования.

На алгоритмическом уровне "скелет" программы, которую я назову CIRCLE (круг), мог бы выглядеть следующим образом:

input c
for t <- 1 to 360
- x <- c*cos(t)
- y <- c*sin(t)
- точка (x, y)

Текст программного фрагмента не будет значительно отличаться от этого алгоритма. В конце фрагмента будет стоять та или иная графическая команда, роль которой здесь играет "точка (x, y)".

Однако реальная программа, рисующая окружность, конечно, не будет такой простой. Во-первых, у большинства персональных компьютеров начало координат находится в углу экрана. Следовательно, нужно добавить смещение, чтобы переместить окружность в центральную часть экрана. Если, например, на экране можно разместить 200 точек по горизонтали и 150 точек по вертикали, то приведенный выше программный фрагмент нужно модифицировать следующим образом:

x <- c*cos(t)+100
y <- c*sin(t)+75

Теперь невидимый профессор может воплотиться в нескольких маленьких программках, в основе которых лежит та же самая структура. Меняться будут лишь уравнения. Например, кубическая кривая Чирнгауэена имеет параметрические уравнения, в которых нет ни синуса, ни косинуса:

x = 3a(t2-3),
y = at(t2-3).

Поэтому в программе, которую я назвал TSCHIRNHAUSEN, используется параметр t, пробегающий от минимального до максимального значения. Эти значения определяются размерами экрана. Например, на упомянутом выше экране размером 150*200 точек поместится кривая со значениями t в диапазоне от t = -4.4 до t = +4.4, если а = 1. Ни один цифровой компьютер не может варьировать параметр t в этом диапазоне непрерывным образом - каждый раз величина t должна получать определенное приращение, достаточно малое, чтобы создать впечатление непрерывности. Другими словами, мел не должен крошиться при нажиме, чтобы линия получилась плавной. Поскольку наша воображаемая доска имеет 200 точек по горизонтали, разумное приращение для параметра t можно получить делением диапазона возможных его значений (а именно 8.8 ) на 200 равных частей. Таким образом получаем величину приращения, равную 0.044. В то же время следует учесть, что кривая рисуется не везде равномерно. Некоторые участки "мел" проходит быстрее, и на них точки изображения отстоят несколько дальше друг от друга. К счастью, подобные вычисления обходятся настолько дешево (и выполняются так быстро), что размер шага можно сократить до 0.01. Теперь наш алгоритм будет выглядеть следующим образом:

input a
for t <- -4.4 to +4.4 step 0.01
- x <- 3a(t2-3)+100
- у <- at(t2-3)+75
- точка (х, у)

Другой простой способ сделать кривую более гладкой заключается в том, чтобы воспользоваться отрезками прямых линий. Программу TSCHIRNHAUSEN так же, как и любую другую из описанных здесь программ, можно модифицировать таким образом, чтобы каждая новая точка получалась в результате выполнения команды, рисующей отрезок прямой, соединяющей предыдущую точку с новой. В этом случае координаты старой точки каждый раз должны заменяться координатами новой. Если отрезки достаточно малы, то человеческий глаз не отличит полученную таким образом ломаную линию от плавной кривой.

В любой версии программы следует также добавить новый внешний цикл, в котором константа a в диапазоне от 0.1 до 2 на каждом шаге принимает приращение, равное 0.1. В этом случае невидимый профессор нарисует целое семейство красиво вложенных друг в друга кубических кривых, которыми сам Чирнгаузен мог бы только гордиться.

Гиппопеда, изучавшаяся еще греческим философом Проклом приблизительно в 475г., может принимать две формы - либо в виде лежащей на боку восьмерки, либо в виде гантели в зависимости от значений ее двух констант a и b {см. правую часть рисунка на с.80). Параметрические уравнения этой кривой ненамного сложнее предыдущих:

х = 2cos(t)sqrt(ab-b2sin2(t)),
у = 2sin(t)sqrt(ab-b2sin2(t)).

Параметр t пробегает значения от -180o до +180o. Здесь время на вычислительную работу можно несколько сэкономить, поскольку выражение под знаком квадратного корня присутствует в обоих уравнениях. Таким образом программа, названная мной HIPPOPEDE, вычисляет это выражение лишь один раз, записывает ее в качестве значения переменной temp, а затем умножает переменную temp на 2cos(t) и на 2sin(t). Здесь читатели, которые пожелают создать своего собственного невидимого профессора, вновь сталкиваются с проблемой выбора шага. Хотя размер шага в какой-то степени зависит от параметров a и b, размера экрана и некоторых других факторов, шаг величиной в 1o в большинстве случаев должен оказаться подходящим. Опять-таки следует попробовать различные значения констант a и b, либо целые, либо дробные в диапазоне значений, скажем, от 1 до 10. В результате должно получиться изображение "старой мудрой совы", если для каждой кривой значения a выбрать равными 20, 25, 30, 40 и 50, а b поддерживать равным 20.

Спираль, как одна из красивейших форм, встречающихся в природе, является излюбленной темой невидимого профессора. Неудивительно, что их изображение лучше всего строить в системе полярных координат. Например, любая точка, принадлежащая спирали Архимеда и имеющая полярные координаты r и Q, удовлетворяет тривиальному, как говорят математики, уравнению r = aQ. Значение угла Q растет от 0 до тех пор, пока позволяют размеры экрана (а также константа a). В качестве приращения можно взять 1 или еще меньшую величину. Если значение a принять равным 0.01, то спираль будет закручена довольно плотно, при a = 0.1 она получается уже намного более "разреженной".

Невидимый профессор может без труда справиться и со знаменитой логарифмической спиралью. Эту кривую можно видеть в морских ракушках и на головках подсолнуха. И в этом случае невидимый профессор пользуется полярными координатами, в которых уравнение спирали имеет вид r = e^aQ, где иррациональное число e можно принять равным 2,7183. Размер шага здесь можно выбрать таким же, как и для спирали Архимеда, однако читателей следует предупредить, что экспоненциальные функции растут с чудовищной скоростью: даже при а = 0.01 спираль раскручивается очень быстро.

Описания не менее 300 интересных кривых содержатся в книжке небольшого формата Дж.Денниса Лоуренса "Каталог плоских кривых" (J.D.Lawrence, A Catalog of Special Plane Curves). Здесь невидимому профессору, так сказать, есть где разгуляться. Более опытным программистам, возможно, будет интересно попытаться собрать все программки, рисующие кривые, в одну большую программу. При этом к частным подпрограммам можно было бы обращаться, совершая выбор в так называемом меню.

В некоторых случаях не нужно даже собирать несколько программ в единое целое. Искусство обобщения позволяет создать одну универсальную программу, которая генерирует все кривые данного класса. Пользователю остается только задать значения различных констант в основной исходной формуле. Например, окружность - это лишь одна из множества кривых, называемых фигурами Лиссажу и описываемых двумя параметрическими уравнениями:

x = a*sin(ct+d),
y = b*sin(t).

Эти кривые хорошо знакомы тем, кто работает с осциллографом. На экране осциллографа они порождаются электронными сигналами, изменяющимися по синусоидальному закону.

Константы a и b определяют прямоугольник длиной a и высотой b единиц. В пределах этого прямоугольника фигуры Лиссажу исполняют свой неистовый танец. Константы c и d определяют характер этого танца и форму кривых. Например, когда d = 0, значения c = 3/5 и c = 1/4 порождают две кривые, показанные на рисунке вверху на с.82. Если значение c рационально, то кривая возвращается к своей исходной точке и повторяется до тех пор, пока невидимый профессор не исчерпает всех своих сил. Не стоит беспокоиться о том, рациональны или иррациональны числа в вашем компьютере: цифровой компьютер работает только с рациональными числами. (В предыдущих рассуждениях мы предполагали, что t измеряется в радианах. Чтобы перевести уравнения в градусную меру, нужно умножить аргумент функции sin на число пи/180). Если исходное значение t равно 0, то фигура Лиссажу начинается где-то на оси x. Вообще говоря, она совершает различные замысловатые траектории, прежде чем снова замкнется. Однако насколько большим будет значение t, когда это наконец произойдет? Читателям, любящим поразмышлять, предлагается самим ответить на этот вопрос. Пусть, например, t не превосходит значения 3600, изменяется с шагом 1 и принимает рациональные дробные значения с не очень большим количеством цифр в числителе и знаменателе. Ну, а любопытным, юмористам или просто страстным любителям головоломок можно предложить задачу с неизвестным исходом. Пусть они попытаются исчерпать возможности невидимого профессора, не устанавливая верхнего предела для t, и определить, сколько времени потребуется на то, чтобы кривая замкнулась. В этом случае цикл в программе строится чисто механически. В конце цикла обычный оператор "go to" передает управление в программе на начало цикла. Чтобы не приковать навечно старика-учителя к доске, вставим в цикл, из милосердия, один условный оператор "if", так что если будет нажата клавиша, то программа выйдет на определенный оператор за пределами цикла.


Фигуры Лиссажу, одна из которых бесконечно повторяет саму себя

Среди факторов, побудивших заняться анализом графических возможностей компьютера, было письмо от С.Миллера из Конкорда (шт.Массачусетс). Миллер, по долгу службы консультирующий менеджеров, увлекся таинственными кривыми, являющимися графическим выражением различных функций. Все началось с коммерческой программы CURVES, о которой далее я скажу еще несколько слов.

"Как-то раз поздно вечером, после напряженной работы,- пишет Миллер,- я случайно нажал не на ту клавишу, и передо мной возникла кривая, совершенно не похожая на те циклоиды, которые я генерировал до сих пор... Сначала я подумал, что в компьютере попало немного сыра с моего сандвича, который я жевал, сидя перед дисплеем, но затем я снова запустил программу с другими параметрами (константами) и вновь получил почти то же самое". Это неожиданное событие навело Миллера на мысль о том, что достаточно универсальная программа, генерирующая кривые, была бы способна порождать весьма разнообразные и весьма занятные изображения. Одну из его находок я поместил на с.81. Она выглядит как трехмерная сеть, закинутая в поисках впечатлительных умов. Если эта кривая нуждается в названии, то я бы назвал ее "Безумием". Ее параметрические уравнения на вид кажутся очень простыми:

x = sin(0.99t)-0.7cos(3.0t),
y = cos(1.01t)+0.1sin(15.03t).


Кривая С.Миллера "Безумие" - наглядный пример случайно сделанных открытий

Я понятия не имею, насколько велико должно быть значение t, чтобы завершить изображение. Читателям, которые пожелают увидеть "Безумие" на своих собственных компьютерах, советую воспользоваться бесконечным циклом, описанным выше, а t следует отсчитывать в радианах.

Составляя программу MADNESS (безумие), читатели могут сделать ее обобщенной, расставив константы перед четырьмя тригонометрическими функциями. Тем самым перед ними откроется практически бесконечное пространство для исследований.

Программа CURVES, вдохновившая Миллера, является довольно универсальной. Она была создана компанией Bridge Software. Обладающая некоторыми полезными дополнительными возможностями и очень интересными функциями, она может успешно сыграть роль невидимого профессора. Но эта компания продает также и другую программу под названием SURE, "продукт" которой показан внизу на с.82. Пользователи этой программы указывают функцию двух переменных и затем наблюдают, как программа рисует трехмерные пейзажи с горами и долинами. Обе программы относительно недороги.


Сложная поверхность из простых функций

Bridge Software - это не единственная маленькая компания, занимающаяся производством подобного математического обеспечения. Для любителей комплексных функций компания Lascaux Graphics создала программу под названием f(z). Наверное, многие из вас помнят множество Мандельброта, о котором последний раз речь шла в январском номере журнала. Но, может быть, немногие читатели помнят, что все действие развивалось там на комплексной плоскости. Функции, которые строит программа фирмы Lascaux Graphics, отображают комплексную плоскость саму на себя. Мы не можем здесь наблюдать четырехмерного пространства, однако мы можем почти физически ощущать комплексную функцию по мере того, как на экране проявляется действие, оказываемое ею на комплексную плоскость: регулярную плоскую полярную решетку (см. рисунок внизу) комплексная функция превращает в грациозную криволинейную структуру, которую можно уподобить картине течений в математическом океане. Хотя f(г)стоит несколько дороже программы CURVES, она может доставить много удовольствия читателям, которые хотят быть посвященными в самые глубокие тайны, присущие графическому представлению функций на экране дисплея.


Комплексная сеть (слева) и ее логарифм (справа)

БИБЛИОГРАФИЯ

A CATALOG OF SPECIAL PLANE CURVES. J. DENNIS LAWRENCE. Dover Publication, Inc., 1972.

ОТКЛИКИ

11 1988
НЕВИДИМЫЙ профессор, о котором шла речь в июльском номере журнала, привел нам несколько классических примеров из бесконечного многообразия тригонометрических и алгебраических кривых. Некоторые читатели из числа многих, ранее уже знакомых с профессором, прислали интересные комментарии.

Э.Ашкинази из Белла (шт.Калифорния) предложил организовать встречу между невидимым профессором и "Люси" - цветным графопостроителем в математической лаборатории Калифорнийского университета в Нотридже. Возможно, профессору понравятся фигуры Лиссажу в исполнении "Люси". У Ашкинази есть программа, которая рисует прямые линии между соответствующими точками пары таких фигур. С помощью этой программы "Люси" рисует немыслимые кривые с поблескивающей муаровой вуалью.

Т.Дорн из Ванкувера (Британская Колумбия) предлагает свою программу BUMBLEBEE (шмель). Она работает со следующими параметрическими уравнениями, в которых константу a можно варьировать:

x = 2sin(at),
y = e^(t*sin(t)).

Т.Фэй из Университета Южного Миссисипи коллекционирует кривые, полезные при изучении дифференциального и интегрального исчисления, которые он строит в полярных координатах (p, Q) вместо обычных координат (x, y). Профессор рисует бабочку с помощью синусоиды, косинусоиды и экспоненты:

p = e^cosQ-2cos(4Q)+sin5(Q/12).

В области математических кривых сейчас наблюдается бурная коммерческая и квазикоммерческая активность. Существует множество средств, которыми может воспользоваться любитель сложных криволинейных фигур. Например, Д.Кеннеди, школьный учитель математики из Лэнгли (Британская Колумбия) с энтузиазмом отзывается о калькуляторе-графопостроителе "Casio fx-7000G". Это чудо техники, которое можно держать в руке, демонстрирует миниатюрные ступенчатые графики практически любой функции на экране размерами 3*5см.

SPIA - по-видимому, весьма солидная математическая программа - позволяет пользователям строить и изображать функции почти любого вида. Более того, она выполняет специальные операции, такие как преобразование Фурье, для тех, кто интересуется основами обработки сигналов.

8 1988
ОРНАМЕНТЫ: ВООБРАЖЕНИЕ, ГЕОМЕТРИЯ, КОМПЬЮТЕР
А.К.ДЬЮДНИ

ХОТЯ компьютеры все глубже проникают в искусство, в этой области для человека остается еще достаточно широкое поле деятельности. Структуры, которые я называю решетчатым орнаментом, пока не демонстрируются на компьютерных экранах, их рисуют на обычных листах бумаги. Они создаются не за считанные секунды компьютерной программой, а медленно обретают форму под карандашом, линейкой и транспортиром, которыми манипулирует рука человека.

Сначала узоры рождаются в нашем воображении, когда мы мысленно представляем, например, решетку из переплетающихся окружностей. Каждый из нас способен ради забавы или всерьез построить на бумаге замысловатый узор из переплетающихся линий, глядя на который мы потом удивляемся и восхищаемся. Подобные узоры можно встретить на древних надгробиях и на стенах дворцов, которых немало повсюду, от Самарканда до Севильи. Строгие орнаменты арабского средневековья символически отражают бесконечность в конечном пространстве. Пользовались ли авторы этих орнаментов методами, которые я опишу ниже? Эксперты пока не пришли к определенному мнению относительно методов построения древних орнаментов, однако установлено, что с математической точки зрения эти узоры подчиняются законам геометрии и топологии.

Существует много подходов к анализу решетчатых орнаментов, но для начала, пожалуй, лучше всего рассмотреть их свойства симметрии. Например, образец, представленный на нижнем рисунке, обладает ярко выраженной симметрией: поворачивая его на 120o вокруг определенных точек, мы получим картину, подобную исходной. Зеркальное отражение по определенным линиям также дает почти идентичную картину. Наиболее заметные элементы узора - золотистые ленты, вьющиеся подобно шоссейным дорогам по кажущемуся бесконечным ландшафту. По всему орнаменту разбросаны окружности, в строгом соответствии со свойствами симметрии. Ленты тянутся от одной окружности к другой, сходясь вокруг них по 12, и резко изгибаясь, расходятся опять. Угол их отражения равен углу падения. Сами ленты также имеют форму, в данном случае либо шестиугольную, либо загзагообразную. Повсюду видны пересечения, в которых каждая лента поочередно проходит то над, то под пересекающими ее другими лентами. Каким образом был построен этот орнамент?


Этапы построения решетчатого орнамента

Решетчатые орнаменты принадлежат широкому классу бесконечных структур, имеющих по крайней мере две независимые симметрии переноса: если перемешать такую структуру вдоль другой идентичной ей структуры, то в конце концов они сольются, так что все линии будут совмещенными. Какими бы сложными ни были бесконечные решетки, если они обладают двумя независимыми симметриями переноса, они обязательно относятся к одной из 17 возможных кристаллографических групп, впервые введенных русским ученым Евграфом Федоровым. В необычайном богатстве решетчатых орнаментов, дошедших до нас из прошлого, можно найти представителей всех 17 групп. Их можно увидеть например, на оконных решетках или в росписи внутренних стен резиденции какого-нибудь султана.

Переносы - это лишь одна из четырех возможных операций, устанавливающих симметрию в плоском орнаменте. Операция отражения "перекидывает" плоскость, как огромную крышку, на противоположную сторону от оси, которая сама принадлежит плоскости. По существу это зеркальное отражение, в котором буквы перевернуты, а лица выглядят несколько иначе. Третья операция, обеспечивающая симметрию - это вращение: плоскость поворачивается на определенный угол относительно одной точки. Наконец, четвертый вид симметрии достигается с помощью двух операций: переноса, за которым следует отражение относительно линии, параллельной направлению переноса.

Все эти операции можно комбинировать, выполняя их в той или иной последовательности. При использовании всех перечисленных операций возникает алгебраическая структура, называемая группой. В группе произведение любых двух операций также является операцией, и для каждой операции существует обратная ей операция, которая как-бы ликвидирует ее результат. Кроме того, группа содержит так называемый единичный элемент (операция, которая ничего не делает). Группа должна также удовлетворять ассоциативному закону: если выполняются подряд три операции, то результат не должен зависеть от того, следует ли третья операция за первыми двумя или последние две следуют за первой. Признаемся, что в такой формулировке закон звучит, мягко говоря, глуповато, но это только потому, что справедливость ассоциативного закона по отношению к операциям симметрии на плоскости, как говорится, вполне очевидна. В приведенном примере группа операций симметрии для решеток на международном языке кристаллографии называется p6. Она характеризуется поворотом на 60o вокруг точек одного множества и на 120o вокруг точек другого множества. Центры этих вращений читатели легко найдут на рисунке.

Представленный здесь орнамент я построил несколько лет назад, пользуясь методом, который опишу ниже. Позже такую же решетку я обнаружил в книге, посвященной мусульманскому средневековому искусству. Чувство разочарования от того, что кто-то меня опередил, с лихвой компенсировалось совершенным открытием - метод построения был тот же. С тех пор мне удалось заново "открыть" еще несколько орнаментов.

Следуя этому методу, автор будущего орнамента сначала должен построить решетку из точек. Решетки могут быть четырех типов: треугольные, квадратные, прямоугольные или шестиугольные. Такие решетки легко строятся при помощи линейки и транспортира. Сначала проводим по линейке линию основания, затем с помощью транспортира отметим точки решетки, отстоящие на равном расстоянии друг от друга. При построении квадратных и прямоугольных решеток новые точки добавляются сверху и снизу от линии основания на концах перпендикулярных к ней отрезков. При построении треугольных и шестиугольных решеток используются равносторонние треугольники.

Рассматриваемый орнамент начинается с построения треугольной решетки. Затем около каждой точки решетки описывается окружность. Здесь уже впервые проявляется интуиция, потому что размер окружностей имеет очень важное значение. Немного позже я объясню, какую роль может играть интуиция при выборе размеров.

После того как окружности нарисованы, нужно выбрать и отметить несколько точек, равномерно разбросанных по окружности. Этими точками мы фиксируем линейные элементы орнамента. Положение и количество точек должны отражать свойства симметрии самой решетки. Другими словами, точки должны быть расставлены с соблюдением симметрии, соответствующей операциям отражения и вращения. При выполнении любой операции симметрии эти точки должны будут наложиться на точки либо другой, окружности, либо той же самой. В рассматриваемом случае количество точек на каждой окружности должно быть кратным 3. Я выбрал число 12, чтобы узор был более насыщенным. Поскольку необходимо, чтобы орнамент удовлетворял свойству симметрии отражения, возможны лишь два расположения точек на окружности. Я выбрал такое расположение, при котором 6 точек находились на кратчайшем расстоянии от соседних окружностей. А вообще, при любом выборе надо следовать правилу, согласно которому наилучшим является решение, гармонирующее с уже существующей симметрией.

На следующем этапе построения соединим точки, отмеченные на каждой окружности, с точками других окружностей. Здесь опять на помощь приходит интуиция. Возникает такое множество вариантов, что кажется, будто правильный выбор можно сделать только интуитивно. На самом деле количество возможных вариантов опять существенно ограничивается условиями симметрии: если соединить какую-нибудь точку на окружности А с точкой на окружности В, то благодаря свойствам симметрии такое же соединение должно распространиться и на другие точки окружности А. Таким образом, не успеем мы провести и пару линий, как станет ясно, что мы нарушили симметрию; линии придется стереть и пробовать уже другой тип соединения.

На этой стадии возникает своеобразная обратная связь с совершенным ранее выбором размера окружностей. Когда на первый взгляд удовлетворительная и согласованная схема соединений завершена, результаты могут оказаться неудачными как в математическом, так и в эстетическом смысле. Линии могут не гармонировать с симметрией узора. В таких случаях обычно становится ясно, следует ли уменьшить или увеличить окружности, чтобы соединение их линиями отвечало основным свойствам симметрии орнамента. Здесь интуиция может неожиданно дать верное решение, вы как будто прозреете и, увидев внутренним зрением расположение линий с новыми окружностями, воскликните "эврика!".

Достигнув первых успехов, вы, наверное, почувствуете некоторое волнение, линейка и транспортир начнут слегка подрагивать в ваших руках. Вас охватит чувство, которое часто испытывают художники и математики. Но стоит ли восхищаться интуицией, подсказавшей вам решение, просто игнорируя законы геометрии?

Так или иначе, настало время проложить по нашему ландшафту систему шоссейных дорог и придать ей достаточный размах. Ни одна система скоростных трасс не должна страдать от избытка светофоров, но как тогда обеспечить движение на пересечениях дорог? Вспомним, что ткань плетется из нитей путем поочередного пропускания одной нити над и под другими нитями. Однако не получится ли так, что при построении системы дорог мы в конце концов окажемся в тупике и нам придется сделать подряд два прохода снизу? Топология гарантирует, что этого не произойдет.

В самом деле, давайте поэкспериментируем. Нарисуем на листе бумаги большой прямоугольник. Затем будем проводить в нем линии, соблюдая лишь два правила:
1. Начинаться и кончаться линия должна только на границе прямоугольника.
2. В одной точке может пересекаться не более двух линий.
Можно, например, нарисовать нечто в абстрактном стиле, как на рисунке на с.81. Линии могут быть плавно изогнутыми или ломаными, с многократными пересечениями.


Иллюстрация правила "над-под"

Чтобы превратить этот рисунок в невероятно сложный узел, нужно лишь следовать правилу "над-под". Начав с любой точки и следуя по одной линии, мы повторяем про себя при каждом пересечении: "над, под, над...". Это, конечно, означает, что, следуя вдоль какой-то линии, мы говорим "над", проходя поверх пересечения, и соответственно "под", если проходим под ним. В конце концов мы либо придем к исходной точке, либо достигнем границы прямоугольника. По пути наша линия может пересечь и саму себя. Удивительно, но всякий раз, когда мы повторно приходим к какому-нибудь пересечению, оказывается, что оно как раз такое, каким его следовало бы сделать, следуя нашему правилу. Другими словами, мы никогда не скажем "над", если это пересечение на предыдущем проходе было помечено как "под". В конце концов мы построим все мосты и туннели, и то, что раньше казалось бессмысленными каракулями, примет вид современной системы дорог.

Правило "над-под" работает потому, что в некотором смысле оно не может не работать. Простая демонстрация этого факта наводит на интересные размышления. Наши каракули поделили прямоугольник на множество небольших областей. Оказывается, можно раскрасить все области прямоугольника двумя цветами, так что никакие две граничащие области не будут окрашены в один и тот же цвет. (Убедительное и в то же время элементарное доказательство этого факта заняло бы не более нескольких абзацев, но мне не терпится сказать самое главное). Предположим, что области прямоугольника окрашены в красный и синий цвета. Двигаясь по одной из дорог к пересечению, мы заметим, что либо область справа от нас будет красной, а слева - синей, либо наоборот.

В этом простом наблюдении и заключается рецепт разведения дорог на их пересечениях. Передвигаясь по дороге от перекрестка к перекрестку, бригада строителей каждый раз будет знать, нужно ли им строить мост или туннель. Если область справа по пути к перекрестку красная, нужно строить мост, а если синяя - туннель. Результат будет в точности таким же (или его "негативным изображением"), как если бы строители следовали описанному выше правилу "над-под".

Теперь при помощи карандаша и линейки читатель сможет превратить каждую линию орнамента в полосу, проведя с обеих сторон по параллельной линии. Эта работа выполняется чисто механически и не представляет особой сложности, за исключением небольших участков на изгибах линий. В ходе процедуры утолщения линий пересечения пока можно игнорировать. Затем вооружившись ластиком, примемся за пересечения и, руководствуясь правилом "над-под", придадим им соответствующий вид. Чтобы соорудить "мост", нужно стереть прилегающие к нему краешки проходящей под ним дороги. После этого пересечение действительно становится похожим на мост, под которым пролегает пересекаемая дорога. "Туннели" создаются при помощи противоположной процедуры. Интересно отметить, что в ходе такого переплетения уничтожаются все отражательные симметрии орнамента - хотя новая структура выглядит такой же, но, приглядевшись, можно заметить, что на месте мостов находятся туннели, и наоборот.

Две последние фазы создания орнамента - обведение контуров тушью и раскрашивание. Пользуясь хорошей ручкой, можно провести по линейке четкие контуры, прерывая их иногда на поворотах и пересечениях. Чтобы обвести орнамент средней сложности, потребуется около часа, но что такое час для художника, поглощенного творчеством? Во время работы можно подумать и о других вещах. Это спокойное занятие может стать своеобразной формой медитации.

После того как вы обвели контуры всего узора и стерли карандашные пометки, можно приступить к раскрашиванию. Поскольку раскрашивание не всегда удается с первого раза, имеет смысл сначала скопировать обведенный узор и раскрашивать уже копию. Таким образом, из исходных контуров можно сделать несколько цветных орнаментов, один красивее другого. Для раскраски советую воспользоваться темперой. Эта краска ложится ровно, почти не морщит бумагу и продается в наборах, где есть практически все цвета, в том числе золотой и серебряный. Более того, растворимые водой краски, или краски на водной основе, такие как темпера, не смачиваются тушью. Это очень важное обстоятельство, поскольку у не очень тренированного художника темпера почти неизбежно будет местами наезжать на тушь. Орнамент, конечно, будет намного красивее, если все раскрашенные области будут четко окантованы черной тушью, придающей дополнительный контраст.

Какого цвета краски выберет читатель - это, конечно, дело его личного вкуса. Художники, создававшие подобные росписи для областей, заключенных между линиями, чаще всего выбирали темные, приглушенные тона. Благодаря этому приему создается двойной план и сам узор ярче выступает на темном фоне. Я привожу здесь еще один орнамент, раскрашенный по этому принципу (см. рисунок на с.82).


Мусульманский решетчатый орнамент

Этот второй орнамент был получен аналогично первому. Сложные решетчатые орнаменты могут иметь не только то, что можно назвать первичной системой окружностей, но и вторичные окружности. Каждая пятиконечная звезда этого орнамента порождается такой вторичной окружностью. Приведу еще два примера решетчатых орнаментов, изобразив лишь их контуры. На одном из них первичные и вторичные окружности расположены так, что их центры совпадают с центрами различных симметрии вращения, на другом эти окружности концентрические (см. рисунок вверху). Обе эти структуры часто встречаются в классических орнаментах.


Контуры двух орнаментов

Решетчатые орнаменты близки по своим свойствам к структурам, называемым двумерными сотами и состоящим из множества копий одного и того же узора, точно пригнанных краями друг к другу, без наложения. В основе такого орнамента может лежать один и тот же элемент узора, нанесенный, например, на кафельную плитку, или на изразец. Имея множество идентичных изразцов, можно сложить сколь угодно большой орнамент, располагая плитки в определенном порядке. Если проанализировать любой из представленных здесь орнаментов, то в каждом из них найдется небольшая область, которую можно перенести на одну плитку. Во всяком случае, в этом заключается принципиальная основа любого орнамента подобного рода. Нарежьте из бумаги квадраты по размеру изразца и раскрасьте их. Из множества таких копий можно построить разнообразные орнаменты.

Вернемся к решетчатым орнаментам прошлого. Какими методами они были построены и каково их смысловое значение? Лайза Голомбек в течение многих лет изучала подобные узоры как на местах, так и у себя на факультете культуры Ближнего Востока и ислама в Университете Торонто. Она считает, что орнаменты, вероятно, строились на основе определенных геометрических форм, прямоугольных решеток и окружностей. Несомненно, каждый мастер пользовался теми или иными вариациями основного метода. Что же касается смыслового значения, Голомбек оспаривает традиционное объяснение, согласно которому геометрические формы использовались только потому, что мусульманская религия запрещала изображать людей и животных. По ее мнению, решетчатые орнаменты символизируют космический порядок, являющийся идейной основой ислама. В пользу ее версии свидетельствует соседство геометрических орнаментов с изображениями людей и животных, обнаруженных на остатках жилых зданий. Поскольку запреты, игнорировались, то, очевидно, обитателям этих домов нравился космический порядок.

Я был не совсем прав, сказав, что компьютеры не играют никакой роли в создании решетчатых орнаментов. Запрограммировать компьютер так, чтобы он принимал интуитивные решения, ведущие к очень красивым узорам,- задача, по-видимому, трудная. Гораздо легче составить программу, которая помогала бы конструировать орнаменты. Такая программа могла бы по выбору пользователя построить ту или иную основную решетку точек и предоставлять ему возможность выбирать размеры окружностей, число точек на окружности и т.п. Если при наличии такой программы указать тип соединений, на экране мгновенно появится сложный рисунок. Короче говоря, программа позволила бы избежать выполнения утомительных механических операций при создании орнамента. Ну а сам готовый "продукт" можно получить отпечатанным на принтере.

БИБЛИОГРАФИЯ

SYMMETRY. HERMANN WEYL. Princeton University Press, 1952.

ARABIC GEOMETRICAL PATTERN AND DESIGN. J. BOURGOIN. Dover Publications, Inc., 1973.

ART OF ISLAM: LANGUAGE AND MEANING. TITUS BURCKHARDT. World of Islam Festival Publishing Company Ltd., 1976.

ОТКЛИКИ

В АВГУСТОВСКОМ номере журнала была помещена статья о решетчатых орнаментах, замысловатых узорах, которые плетутся на плоскости согласно строгим геометрическим правилам. Б.Уоллис из Портола-Вэлли (шт.Калифорния) придумал, как можно генерировать приблизительно такие же узоры на экране компьютера, накладывая друг на друга четыре квадратные решетки, сдвигаемые или вращаемые одна относительно другой. Программа, основанная на применении пифагоровых чисел (чисел, соответствующих сторонам прямоугольного треугольника), производит некий фантастический художественный эффект, подобный галлюцинации. Эффекты такого рода можно было бы получить из нескольких экранов с отверстиями, наложенных один на другой, вращаемых и сдвигаемых относительно друг друга. Дж.Хоскинс, специалист по информатике из Университета Манитоба в Виннипеге (Канада), написала для своего микрокомпьютера программу, создающую решетчатые диаграммы ткани для каждого пересечения ее основы и утка. Программа позволяет ткачу сразу видеть, какой эффект то или иное перемежение нитей окажет на узор готовой ткани. Программа создает также диаграммы непосредственно по цифровым представлениями изображений.

9 1988
ПРОСЕИВАНИЕ ЧИСЛОВОГО ПЕСКА В ПОИСКАХ ПРОСТЫХ ЧИСЕЛ
А.К.ДЬЮДНИ

ВОЗМОЖНО, из всех занимательных задач в теории чисел самая занимательная - это поиски простых чисел. Подобно золотым самородкам, они скрываются в "породе" остальных чисел. Напомним, что простое число - это то, которое не делится ни на какое другое, кроме 1 и на само себя. Такие числа редки. Правда, у самых истоков великой реки Континуума (множества всех чисел), пока числа еще невелики, они встречаются достаточно часто, но затем быстро растворяются в потоке, по мере того как величина чисел растет.

Существуют различные способы поиска простых чисел. Можно даже построить специальное просеивающее устройство, подобное промывным желобам, которые старатели применяют при поиске самородков, но так или иначе их приходится искать, потому что никто не знает, где они могут встретиться. Формулы для простых чисел не существует. Есть, правда, кое-какие геологические приметы, по которым можно искать их залежи. Так же как когда-то тысячи золотоискателей бросились в Калифорнию и на Юкон промывать песок в горных речушках в поисках крупинок желтого металла, так и наши читатели могут отправиться а страну чисел, но налегке, вооружившись лишь этим маленьким руководством.

Наверное, немногие математические понятия настолько доступны далекому от математики человеку, как понятие простых чисел. Любому встретившемуся на улице можно за минуту объяснить, что такое простые числа. Поняв, человек без труда напишет: 2, 3, 5, 7, 11, 13, 17 и т.д. Единица обычно не считается простым числом.

Возможно ли распознать простое число, как говорится, с первого взгляда? Если вы зачерпнули в сито сразу много чисел, сверкнет ли среди них простое, как золотой самородок? Некоторые считают, что да. Например, числа, оканчивающиеся на 1, часто оказываются искомыми, скажем, такие как 11, 31, 41. Однако при этом следует быть осторожным и не принять фальшивое золото за чистое, как, скажем, 21 или 81. По мере роста величины чисел, единица на конце все чаще вводит нас в заблуждение. Создается лаже впечатление будто простые числа в конце концов просто исчезают, как полагали некоторые древние греки. Существует ли последнее, самое большое по величине простое число? Первое дошедшее до нас доказательство того, что конца простым числам не существует, принадлежит Евклиду.

Доказательство настолько простое, что его можно представить в виде диалога в стиле Сократа, который Евклид ведет с рабом. Однако мне больше нравится беседа между новичком и старожилом, которые встретились на берегу великой реки Континуум:
НОВИЧОК: Эй, мистер! Как далеко вниз по течению заходят простые числа?
СТАРОЖИЛ: До самого моря Бесконечности, парень.
НОВИЧОК: Я вам не верю. Мы здесь на уровне миллионов, а мне еще ни разу не повезло за целый день.
СТАРОЖИЛ: Эх, молодежь, вам нужно все объяснять! Смотри, допустим, ты дошел до последнего простого числа. После него их уже не существует, так?
НОВИЧОК: Ну. так.
СТАРОЖИЛ: Назовем его n. Составим произведение из всех простых чисел вплоть до n. Это будет 2*З*5*7*...*n. Теперь прибавим к произведению 1 и назовем это число p.
НОВИЧОК: И что же, вы хотите сказать, что p - простое число?
СТАРОЖИЛ: Конечно. Простое - проще некуда. Смотри, ты не можешь разделить его на 2, потому что остается 1. Ты не можешь разделить его на 3, потому что остается 1. Каждый раз всегда остается 1, вплоть до n. Ее никак не обойдешь.
НОВИЧОК: Вот оно что! Значит, вы правы, им конца нет.
СТАРОЖИЛ: Так-то вот. Ну ладно, чего стоишь без дела, помоги-ка мне с этим промывным желобом.

Хотя самого большого простого числа не существует вообще, но самое большое простое число из тех, что нам известны, все же есть. Это различие непонятно некоторым читателям и даже журналистам. Вся беда заключается в этих заголовках на последней странице газет и журналов: НАЙДЕНО САМОЕ БОЛЬШОЕ ПРОСТОЕ ЧИСЛО. Иногда эта путаница продолжается и в самом газетном сообщении, из которого мы узнаем, например, что с помощью нового суперкомпьютера только что удалось доказать, что число, содержащее 7067 знаков, а именно 5*2^23473+1 является простым. У него нет делителей, кроме 1 и, конечно, самого себя. В сообщении может отсутствовать напоминание (или читатель может проглядеть его) о том, что это лишь самое большое из известных простых чисел, и что вскоре, возможно, будет найдено новое, еще большее простое число.

Я затрудняюсь сказать, каково максимальное простое число из известных на сегодняшний день. Возможно, к тому времени, как эта статья выйдет в свет, оно уже будет другим. Ну а на тот момент, когда я писал эти строки, наибольшее простое число состояло из 65050 разрядов и было найдено Дэвидом Словински из фирмы Cray Research, Inc. в 1985 году: 2^216091-1. Простые числа, имеющие форму 2m-1, называются числами Мерсенна, в честь французского математика-любителя Марена Мерсенна. Другой любитель С.Йетс из Делри-Бич (шт.Флорида) собрал в своей коллекции все известные простые числа, большие 1000. Его коллекция полна и точна.

Насколько быстро простые числа разрежаются по течению реки Континуума? Из первых 10 чисел 4 являются простыми, таким образом их доля составляет 40%. В первом сотне их содержание падает до 25%, и оно продолжает падать с ростом величины чисел более или менее регулярно. В общем количество простых чисел до n включительно приблизительно равно n/log(n). (В данном случае это приближение является асимптотическим. Другими словами, если количество
простых чисел, меньших для равных n, обозначить p(n), то отношение p(n) к величине n/log(n) все ближе приближается к 1, по мере того как n становится все больше и больше. Таким образом, вниз по течению Континуума простые числа разрежаются пропорционально натуральному логарифму от n).

Давайте посмотрим, как действует это правило, подставив в формулу несколько пробных значений n. Например, сколько простых чисел содержится в интервале от 1 до 100 и в интервале от 1 до 1000? В первом случае формула дает что-то около 22, во втором - около 145.

Неудивительно, что это явление постепенного разрежения дает все более длительные интервалы, вовсе не содержащие простых чисел. Например, чтобы найти отрезок длиной в миллион, не содержащий ни одного простого числа, нужно лишь проплыть вниз по течению, как это однажды сделал Мартин Гарднер, до числа 1000001! Здесь восклицательный знак поставлен не для того, чтобы выразить восхищение или удивление: он означает число, равное 1*2*3*...*1000001. Как говорят дети, число, конечно, "здоровущее". Однако нетрудно убедиться, что с этого числа начинается интервал, не содержащий ни одного простого числа. Если в формуле 1000001!+n число n пробегает последовательные значения от 2 до 1000001, то каждое из получаемых чисел является составным. Потому что в любом случае 1000001! делится на n, и n делится на себя, т.е. число 1000001!+n делится на n.

Я уже говорил, что для простых чисел не существует никакой формулы, никакой комбинации алгебраических операций над n, выполняя которые можно было бы получить очередное, n-ое простое число. Многие люди впадали в заблуждение на этот счет, достигнув некоторых первоначальных успехов. Хорошо иллюстрирует подобные заблуждения шуточная поговорка, известная любому студенту-математику. В ней говорится о трех способах "доказательства" того, что все нечетные числа простые:
МАТЕМАТИК: 3 - это простое число, 5 - простое, 7 - простое... а дальше доказательство по индукции.
ФИЗИК: 3 - простое число, 5 - простое, 7 - простое, 9 - ошибка эксперимента, 11 - простое...
ИНЖЕНЕР: 3 - простое число, 5 - простое, 7 - простое, 9 - простое...
Инженер, как говорится, может смеяться последним, поскольку математики в своих поисках больших простых чисел все больше должны полагаться на компьютеры.

Но, может быть, существует формула, которая дает, пусть не все, но только простые числа? Пьер Ферма, знаменитый французский математик XVIIв., думал, что нашел такую формулу, когда написал 2^2^n+1. Он полагал, что какое значение ни подставь в эту формулу, результатом будет простое число. Однако этот мыльный пузырь, пущенный Ферма, лопнул после его смерти, когда швейцарский математик Леонард Эйлер нашел делители для пятого "простого числа" Ферма: 4294967297 = 641*6700417.

Иногда своего рода формула возникает как результат наблюдения визуальных закономерностей. Одну из таких закономерностей случайно открыл Станислав Улам, американский математик, поляк по происхождению. Сидя как-то на скучной лекции, он, ни о чем не думая, начал рисовать решетку из горизонтальных и вертикальных линий. В одной из полученных таким образом клеток он поставил 1 и стал нумеровать остальные клетки по спирали, расходящейся от первой клетки:



Когда спираль совершила уже несколько оборотов, Улам начал обводить кружками простые числа, не преследуя никакой определенной цели. Однако вскоре заметил, как на его глазах возникает довольно любопытная закономерность. Откуда ни возьмись, стали появляться прямые линии. Улам, конечно, сразу понял, что такие линии говорят о закономерности, которую можно облечь в формулу для простых чисел. Компьютерная распечатка, приведенная на с.83, дублирует то, что Улам сделал от руки. На компьютерном графике составные числа представлены маленькими белыми квадратиками, а простые - черными.


Спираль Станислава Улама выявляет несколько месторождений простых чисел

Выделяющиеся на графике темные линии - это залежи простых чисел. Каким образом можно выразить эту геологическую картину на языке математики? У самого центра диаграммы одно такое месторождение пролегает сверху вниз и справа налево. Оно состоит из последовательности чисел: 7, 23, 47, 79... Оказывается, эту последовательность можно описать квадратичной функцией 4x2+4x-1.

Те, у кого остались в памяти кое-какие сведения из школьной алгебры, смогут подобрать формулы практически для любой линии на диаграмме. Формула может оказаться справедливой и для множества простых чисел, лежащих далеко за пределами приведенной диаграммы. Эйлер, который так многим не дал сделать карьеру в математике, предвосхитив множество математических результатов, тоже "открыл" аналогичную формулу еще в XVIIIв.: x2+x+41. Эта формула не видна на диаграмме Улама, чтобы ее увидеть, нужно в качестве начального числа спирали выбрать другое значение. Если начать спираль с 41, то мы получим месторождение, содержащее сразу 40 последовательных простых чисел!

Но, наверное, с помощью формул простые числа ищут лишь дилетанты. Опытные старатели, работающие на берегах реки Континуума, предпочитают решето, а еще лучше промывные желоба. С одного конца в эти устройства загружаются всевозможные числа, а с другого конца из него выходят только простые числа. Специальные фильтры улавливают составные числа при помощи проверки на делимость (см. рисунок на с.82). Разумеется, такие промывные желоба очень хорошо работают в компьютерах.


Промывочный желоб для поиска простых чисел

Простейшие фильтрующие устройства отделяют простые числа путем деления на 2, 3, 4 и т.д. Если ввести в устройство число n, оно проверяет его делением на 2, на 3, на 4 и продолжает проверки до тех пор, пока одна из них не окажется успешной или делитель не достигнет n. В первом случае число составное, во втором - простое. Алгоритм модели промывного желоба может послужить основой простейшей программы для домашнего компьютера. Назовем этот алгоритм SLUICE1:

input n
f <- 1
for k <- 2 to n-1
- test <- rem(n/k)
- if test = 0 then f <- 0
if = 1 then output "простое"

На входе программа принимает число n, вводимое человеком с клавиатуры. Затем программа устанавливает у переменной f (действующей как флажок) значение 1. Если f все еще равно 1, когда программа завершает свои вычисления, значит, число является простым. В теле цикла многократно повторяется один условный оператор if. Индекс k пробегает значения от 2 до n-1. Для каждого значения k программа выполняет деление n/k, берет остаток от деления (rem) и запоминает его под именем test. Чаше всего значение test оказывается ненулевым, другими словами, k не делит n без остатка. Но если хоть раз оно оказывается нулевым, программа немедленно сбрасывает флажок f, записывая туда 0, и это значение сохраняется вплоть до конца цикла. Если условие во втором операторе if удовлетворяется, программа печатает "простое". Если же f было установлено в нуль где-то по ходу выполнения цикла, то программа хранит мрачное молчание.

Хотя описанная выше программа очень проста, она работает слишком медленно, особенно если заставить ее найти несколько простых чисел подряд. Для этого нужно лишь заменить первый оператор input оператором цикла, таким, например, как "for n <- 3 to 1000". А последний оператор в программе можно изменить так, чтобы вместо "простое" печаталось очередное значение n, успешно прошедшее все проверки и ни разу не разделившееся без остатка. Мы увидим, как начнут появляться простые числа от 3 до 997, по одному и очень медленно.

Однако работу программы SLUICE1 можно значительно ускорить, если внести в нее кое-какие изменения. Во-первых, не имеет никакого смысла проверять, делится ли число n на k, если k больше квадратного корня из k, потому что по крайней мере один делитель числа n, если он есть, не должен превосходить квадратного корня из n, а одного делителя уже достаточно, чтобы считать число составным. Существует также знаменитая арифметическая теорема, которая гласит, что любое целое число можно представить в виде произведения простых чисел, и это произведение единственное. Число не является составным, если оно не делится ни на одно простое число, меньшее себя. С учетом обоих этих фактов цикл можно сделать значительно короче, выбирая в качестве значений индекса k только простые числа, не превосходящие по величине квадратного корня из n.

Новый алгоритм, который мы назовем SLUICE2, в достаточной мере отличается от своего незамысловатого предшественника и выглядит следующим образом:

r <- 1
p(1) <- 2
for n <- 3 to 1000
- k <- 1
- f <- 1
- while f=1 and p(k)<sqrt(n)
- - test <- rem(n/p(k))
- - if test = 0 then f <- 0
- - k <- k + 1
- if f = 1 then r <- r+1
- - p(r) <- n

Поскольку программа SLUICE2 требует списка простых чисел, она запоминает каждое новое простое число в специальном массиве p. Переменная k является индексом, указывающим на последний элемент p. Таким образом, программа всегда знает, куда поместить следующее полученное ею простое число. В первой строке алгоритма индексу присваивается значение 1. В следующей строке в первый элемент массива простых чисел p помещается число 2. Затем следует цикл, описанный выше. В нем проверяются все числа в диапазоне от 3 до 1000. Переменная k указывает, какой элемент массива p используется в данный момент для проверки n. Внутри этого основного цикла есть еще один цикл типа while - пока флажок f равен 1 и очередное простое число из массива p не превышает квадратного корня из n, внутренний цикл продолжает проверки, выбирая последовательные значения k. При выходе из этого цикла флажок f может быть равен либо 1, либо 0. В первом случае это означает, что было найдено еше одно простое число. Программа добавляет ею к уже существующему списку. Во втором случае в основном цикле просто произойдет переход к следующему значению n.

Читатели, которые пожелают воспользоваться этим вариантом программы поиска простых чисел, могут выбрать один из двух способов вывода найденных значений. Программа SLUICE2 может распечатать весь массив p по завершении главного цикла алгоритма. При этом вы как бы увидите полное решето самородков. Но, может быть, вам больше понравится наблюдать, как самородки появляются по одному, как только они будут найдены. В таком случае сразу после оператора p(r) <- n нужно вставить оператор печати print.

Возможно, предложенный диапазон поиска, от 1 до 1000, покажется читателям слишком маленьким. В принципе ничто не мешает увеличить верхний предел поисков до 100000 или лаже до 1000000. А может быть, что-то все-таки помешает? Это будет зависеть от того, насколько большие массивы допускаются в том или ином компьютере. Размер основного массива программы определяется количеством простых чисел, которые должны быть найдены по ходу выполнения программы. Здесь нам пригодится формула, оценивающая количество простых чисел. Согласно этой формуле, в диапазоне от 1 до 1000000 содержится приблизительно 72382 простых числа. Если память компьютера имеет размер лишь 64Кбайт, то он не справится с этой задачей.

Простым числам было посвящено множество занимательных математических задач. Продолжая тему простых чисел в применении к квадратным матрицам, рассмотрим две задачки. Первая из них была придумана Генри Эрнестом Дьюднн, известным английским специалистом по головоломкам. Наверное, многим читателям уже знакомы так называемые магические квадраты - квадратные матрицы чисел, у которых суммирование элементов по любой строке, любому столбцу и двум главным диагоналям дает одно и то же число. Существуют ли магические квадраты, состоящие только из простых чисел: Оказывается, да. Магический квадрат размером 3*3, приведенный на с.84, имеет сумму 111 (между прочим, тоже не простое число) вдоль каждой строки, каждого столбца и каждой главной диагонали. Рядом с этой матрицей 3*3 приведена матрица 4*4. Известны магические квадраты и со стороной больше 4. Мы просим читателей, которым удастся самостоятельно открыть такие квадраты, прислать нам свои результаты. Лучшие из них будут опубликованы в одной из наших следующих статей. Результат будет тем ценнее, чем больше размер квадрата, а при одинаковых размерах преимущество будут иметь квадраты с меньшими суммами.


Магические квадраты из простых чисел: Генри Эрнеста Дьюдни (слева) и Аллана У. Джонсона-мл. (справа)

Другую задачку предложил еше один неутомимый английский изобретатель головоломок Гордон Ли, автор рубрики "Победители и побежденные" в журнале "Dragon User". Он построил квадрат 6*6, состоящий из цифр, которые скрывают в себе великое множество простых чисел, а точнее говоря, 170 (см. правый рисунок на с.84). Простые числа по диаграмме Ли можно строить из цифр любой строки, любого столбца и любой диагонали, просматривая их в произвольном направлении. Несколько полученных таким образом цифр могут составлять простое число, одно из 170, по подсчетам Ли. Всего в решетке размером 6*6 содержится максимум 616 чисел (как простых, так и составных). Повторяющиеся простые числа считаются как одно число. В своих подсчетах Ли включил в список простых чисел и 1.


Решетки простых чисел 6*6 Гордона Ли

Интересно, а смогут ли читатели составить свой квадрат из цифр размером 6*6, который содержал бы больше 170 простых чисел? Те, кто напишет и выполнит программы SLUICE1 и SLU1CE2, получат некоторое преимущество перед остальными участниками этого конкурса. Ли подсказывает, что по квадрату должны быть рассеяны цифры 1, 3, 7 и 9, поскольку простые числа оканчиваются всегда на одну из этих цифр. С другой стороны, если составить квадрат только иэ этих цифр, он, как ни странно, окажется довольно бедным на простые числа. Разумно разбросав четные числа, включая 0, можно увеличить свои шансы в попытках превзойти результат Ли. Я опубликую лучшее из присланных решений (конечно, если оно содержит более 170 простых чисел).

БИБЛИОГРАФИЯ

THE QUEEN OF MATHEMATICS. ERIC TEMPLE BELL in The World of Mathematics, edited by James R. Newman. Simon and Schuster, Inc., 1956.

AMUSEMENTS IN MATHEMATICS. HENRY ERNEST DUDENEY. Dover Publications, Inc., 1970.

THE SEARCH FOR PRIME NUMBERS. CARL POMERANCE in Scientific American, Vol.247, No.6, pages 135-147; December 1982.

ONE MILLION PRIMES THROUGH THE SIEVE. T.A.PENG in Byte, Vol.10, No.11, pages 243-244; Fall, 1985.

А также - "Этюды" Уэзерелла - ТЕМА #15, АБЗАЦ #386, второй том "Искусства программирования" Кнута, "Заметки по структурному программированию" Дейкстры.- G.

ОТКЛИКИ

2 1989
В НАШЕЙ СТАТЬЕ, посвященной поиску простых чисел на берегах реки Континуум (см. сентябрьский номер журнала за прошлый год), бывалый старик золотоискатель совершил ошибку, доказывая, что простым числам нет конца: предположив, что n последнее простое число, он перемножил все простые числа от 2 до n и прибавил 1 к произведению. Полученное число он назвал p. Когда новичок воскликнул: "Уж не хотите ли вы сказать, что p простое число!", старик должен был ответить, что p не делится ни на одно из простых чисел конечной последовательности. Это означает, что либо само р является простым числом, либо существует другое простое число (не принадлежащее данной последовательности), на которое делится p. В любом случае все-таки существует новое "самое что ни на есть простое число".

Ну что ж, когда на берегах великой реки Континуум идет дождь, то он льет как из ведра - несколько более тонких ошибок были замечены некоторыми читателями. В частности, они заметили, что программа SLUICE2 проходит через значительно большее количество простых чисел, чем я указал в статье, предложив предельное количество итераций, равное одному миллиону. На самом деле предел оказался равным миллиону в квадрате, поскольку простые числа, хранимые в массиве, должны доходить лишь до квадратного корня из предельного значения. С.Д.Йейтс из Дэлри-Бич (шт.Флорида) получил многочисленные письма от наших читателей с просьбой выслать упомянутый мною в сентябрьской статье список всех простых чисел, больших 1000. Однако в действительности у Йейтса есть список, содержащий все известные простые числа, количество разрядов которых превышает 1000.

Многие читатели представили новые магические квадраты из простых чисел, а некоторым удалось построить решетки, содержащие больше простых чисел, чем в рекордной на сегодняшний день решетке, насчитывающей 170 чисел. Победителям конкурса придется подождать до следующего номера журнала, в котором они будут официально объявлены.

3 1989
ТЕПЕРЬ я объявлю победителей конкурса, объявленного Гордоном Ли в нашей сентябрьской статье и касавшегося решетки простых чисел. Решетка представляет собой матрицу квадратных ячеек размером 6*6, в которой каждая ячейка содержит одну цифру. Задача заключается в том, чтобы выбрать цифры и их расположение в решетке таким образом, чтобы получить как можно больше простых чисел, читая последовательные цифры вдоль любой прямой линии - горизонтальной, вертикальной или по диагонали. Ли, организовавший аналогичный конкурс в Англии в прошлом году, сообщил, что лучший результат был равен 170 простым числам. Могут ли читатели нашей рубрики превзойти этот результат? Лично я никогда в этом не сомневался!

Откликов поступило значительно больше, чем я ожидал. Их присылали и профессиональные программисты, пользовавшиеся суперкомпьютерами, и люди, располагавшие более скромными техническими средствами, иногда лишь карандашом и бумагой. Я отправил все полученные письма Ли, с тем чтобы он вынес свое суждение. Вот результаты, представленные здесь в обратном порядке:

Самый плодовитый "решетчик" Л.Пэдден из Оклахома-Сити (шт.Оклахома), построивший 147 различных решеток, каждая из которых содержит от 170 до 173 простых чисел.

Самые шестереночные решетки: Д.Маккензи и Ф.Эндрес из Остина (шт.Техас), открывшие решетку, которая содержит всего 106 простых чисел, но зато все возможные шестиразрядные 28 чисел оказались в ней простыми.

Третье место: Дж.Уолдби из Робинсона (шт.Иллинойс): его результат - 185.

Второе место поделили уже упомянутые Маккензи и Эндрес, а также С.Рут из Вестборо (шт.Массачусетс). Все они построили решетки, содержащие по 186 простых чисел.

На первом месте - тот же Рут. Его рекордная решетка содержит 188 простых чисел. Вот она:

10 1988
"ПЕРЕМЕШИВАЮЩАЯ МАШИНА" - КЛЕТОЧНЫЙ АВТОМАТ, МОДЕЛИРУЮЩИЙ ХИМИЧЕСКИЕ РЕАКЦИИ
А.К.ДЬЮДНИ

КЛЕТОЧНЫЕ автоматы - компьютерные модели, основанные на массивах клеток, волной распространились в физике, математике и других науках. Теперь появилась новая разновидность клеточного автомата, которая сама в буквальном смысле порождает волны. Названная ее изобретателями "перемешивающей машиной" (hodgepodge machine), она моделирует химические реакции с такой точностью, которая редко достигается в других моделях.

Реакции, моделируемые этой машиной, происходят в активной химической среде, где два вещества (или больше) могут диссоциировать или рекомбинировать в присутствии катализатора. Если реагирующие вещества имеют различный цвет, то в таких средах можно наблюдать волнообразные структуры, которые, распространяясь постоянно, изменяют фронт с простым или сложным очертанием.

Может ли сам по себе автомат послужить адекватным физическим объяснением волнового процесса, действительно наблюдаемого в ходе реакции? Этот вопрос занимает сейчас изобретателей "перемешивающей машины" М.Герхардта и X.Шустер из Билефельдского университета в ФРГ, а также многих других исследователей из различных университетских центров.

Клеточный автомат можно представить в виде бесконечной решетки квадратных клеток, состояние которых меняется со временем в такт дискретным сигналам воображаемого часового механизма. На каждом временном такте каждая клетка находится в одном из конечного множества состояний. Состояние клетки на такте t+1 достаточно несложным образом зависит от состояния клеток в ее непосредственной окрестности на предыдущем такте t. Эта зависимость выражается в виде набора правил, одинаково применимых ко всем клеткам решетки. При последовательном применении правил на каждом такте часового механизма произвольная исходная конфигурация состояний клеток может изменяться и, таким образом, эволюционировать во времени. Иногда в процессе таких последовательных изменений можно наблюдать, как создаются чрезвычайно интересные структуры. В результате возникает убеждение, что при правильной исходной конфигурации клеточный автомат может породить нечто самоорганизующееся, способное к росту и воспроизводству - короче, нечто "живое".

Возможно, самым известным для наших читателей примером клеточных автоматов является знаменитая игра "жизнь", изобретенная в 60-х годах математиком Дж.Конвеем из Кембриджского университета. В игре "жизнь" каждая клетка может находиться лишь в одном из двух возможных состояний: живом или мертвом. Правила игры очень просты. Если клетка мертва на момент времени t, то она оживает в момент t+1, если трое ее соседей были живы на момент времени t. Если же клетка жива на момент времени t, то она умирает в момент t+1, если меньше двух или больше трех ее соседей были живы на момент времени t. Этих двух правил оказывается достаточно для того, чтобы клеточный автомат "жизнь" демонстрировал удивительно многообразное поведение, целиком и полностью зависящее от исходной конфигурации живых и мертвых клеток (см. статьи в рубрике "Занимательный компьютер" в журналах "В мире науки": 1985г., #7 и 1987г., #4).

Перемешивающая машина представляет собой целое семейство клеточных автоматов. Конкретную версию можно выбрать, указав значения ряда параметров, таких, например, как количество возможных состояний. Если количество состояний равно n+1, то каждое возможное состояние клетки можно представить числом в диапазоне от 0 до n. Герхардт и Шустер расширили метафору Конвея при описании состояний их машины. Клетка в состоянии 0 считается "здоровой", а в состоянии я - "больной". Все промежуточные - состояния соответствуют той или иной степени "зараженности", в зависимости от номера состояния - чем ближе номер состояния клетки к числу n, тем в большей степени она "заражена". Перемешивающая машина избирательно применяет одно из трех правил к каждой клетке, в зависимости от того, здорова она, заражена или больна.

Если клетка здорова (другими словами, находится в состоянии 0), то на следующем такте она перейдет в новое состояние, зависящее от числа зараженных клеток A и числа больных клеток B среди ее непосредственных соседей, а также от двух параметров, которые мы обозначим k1 и k2. Точнее, состояние клетки на момент времени t+1 определяется следующей формулой:

[A/k1]+[B/k2].

Здесь квадратные скобки обозначают операцию округления того дробного числа, которое в них заключено. Если, например, A/k1 окажется равным 2.725, то квадратные скобки сведут это число к 2. Если формула даст нулевое значение, то клетка, конечно, останется здоровой - по крайней мере пока.

Если клетка заражена, ее состояние со временем обычно ухудшается. Состояние зараженной клетки на момент времени t+1 вычисляется как сумма двух чисел: степени заражения клеток в окрестности на момент t и постоянной величины g, регулирующей скорость распространения инфекции среди клеток. Первая величина - степень заражения клеток в окрестности - получается делением числа S, суммы состояний самой клетки и ее соседей, на A - число зараженных соседей. Таким образом, клетка, зараженная на момент времени t, принимает в момент t+1 состояние, вычисляемое по следующей формуле:

[S/A]+g.

Однако зараженная клетка не может стать "больнее" n. Если значение, полученное по формуле, превысит n, то в качестве номера следующего состояния клетки принимается n.

Наконец, если на момент времени t клетка больна (находится в состоянии n), то она чудесным образом выздоравливает (принимает состояние 0) в момент t+1.

В дополнение к этим трем правилам необходимо четко определить, что мы понимаем под "окрестностью" клетки. Исторически в клеточных автоматах применялись два типа окрестностей: окрестность фон Неймана и окрестность Мура. Окрестность фон Неймана для каждой клетки состоит из четырех соседних клеток, имеющих по одной обшей стороне с данной клеткой. Окрестность Мура, помимо клеток из окрестности фон Неймана, включает также четыре клетки, соприкасающиеся с данной в ее вершинах - т.е. всего 8 клеток. При заданных трех правилах и определенном типе окрестности клетки клеточный автомат Герхардта-Шустер можно полностью определить, указав значения четырех параметров: n - числа возможных состояний минус 1; k1 и k2 - "весовых" параметров для здоровых клеток и g - скорости распространения инфекции.

В эксперименте, проведенном Герхардтом и Шустер на решетке размером 20*20 с использованием окрестности фон Неймана, проявилось типичное для перемешивающих машин поведение. (Клетки на краях решетки подчиняются тем же правилам, которые действуют повсюду в клеточном автомате, с той лишь разницей, что у граничных клеток меньше соседей в окрестности). Значения параметров n, k1 и k2 были выбраны равными соответственно 100, 2 и 3. При различных значениях параметра g наблюдалось четыре вида поведения. Обычно при каждом прогоне модели Герхардт и Шустер придавали 400 клеткам решетки 20*20 случайную исходную конфигурацию состояний, устанавливали значение g и запускали перемешивающую машину на 10000 вычислительных циклов. Поскольку данные, организованные в одномерные структуры, легче анализировать, чем двумерные изображения, Герхардт и Шустер записывали на каждом цикле лишь число зараженных клеток, с тем чтобы результаты можно было представить в виде графиков, аналогичных тем, что приведены на с.84.


Четыре типа поведения перемешивающей машины

В малых значениях параметра g машина не демонстрирует ничего интересного. За исключением нескольких начальных флуктуации, активные процессы в клетках имеют тенденцию к затуханию, клетки становятся здоровыми и навсегда остаются в этом состоянии. Однако с ростом g автомат начинает вести себя необычно. Среди множества возможных состояний в этом случае можно выделить несколько типичных. Начнем с того, что большинство клеток становятся зараженными и, как правило, они остаются в зараженном состоянии, хотя время от времени возникают случайные во времени и пространстве конфигурации здоровых клеток. Такое поведение автомата Герхардта и Шустер условно назвали поведением типа 1.

Следующий тип поведения, который они наблюдали, был обозначен как тип 2. Он характеризуется обычно регулярными последовательностями зараженного состояния, образующими "плато" длительностью примерно 30 циклов, которые неожиданно сменяются появлением большого количества здоровых клеток. (Иногда почти все 400 клеток внезапно выздоравливают, но затем сразу же начинается новая волна инфекции). По мере дальнейшего роста значений параметра g начинает проявляться поведение третьего типа. Оно характеризуется возникновением весьма регулярного чередования между насыщением и фактическим исчезновением зараженных клеток приблизительно через каждые 20 циклов. И наконец, для четвертого типа поведения характерно то, что после первых нескольких циклов количество зараженных клеток начинает колебаться с некоторой регулярностью около насыщающего значения, равного примерно 75%.

Хотя эти четыре типа поведения наблюдались при последовательном росте значений g, иногда области значений g частично перекрывались, т.е. при пограничных значениях g автомат иногда демонстрировал поведение одного типа, а иногда - другого. В нескольких случаях Герхардт и Шустер наблюдали даже переходы между двумя различными типами поведения в ходе одного и того же прогона программы.

Для каждого из описанных четырех типов поведения характерны свои волновые структуры, изображенные на цветной иллюстрации внизу; размеры решетки варьировались от 20*20 до 500*500. Волны, наблюдающиеся при повелении первого типа, распространяются лишь на короткое расстояние и быстро затухают. Волны второго типа распространяются по направлению к границам в виде круглых полос со значительными вариациями по ширине. Волны третьего типа также имеют круговую форму, но отличаются большей регулярностью, в соответствии с регулярными максимумами и минимумами числа зараженных клеток. Наконец, волны четвертого типа имеют спиральную форму и распространяются из центра решетки к ее границам. Как всегда, читателям, имеющим собственные компьютеры, предлагается в той или иной форме повторить эти эксперименты. Волнам на экране наверняка будут сопутствовать волны мысли.


Перемешивающая машина генерирует волны

Некоторые типы волн, генерируемые перемешивающей машиной, аналогичны волнам, наблюдаемым в определенных химических системах, в частности, машина порождает волны, являющиеся точной копией волн, которые возникают в ходе известной реакции Белоусова-Жаботинского. Сравним, например, сложные узоры завихрений на компьютерном изображении и на фотографии реакции Белоусова-Жаботинского, приведенных на с.85.


Волновые явления в химической реакции Белоусова-Жаботинского (слева) и их аналог в перемешивающей машине (справа)

В чем причина такого сходства? Оно едва ли удивило Герхардта и Шустер, ведь они изобрели перемешивающую машину специально для того, чтобы промоделировать свойства определенного типа "неоднородной каталитической реакции", в ходе которой монооксид углерода окисляется и адсорбируется крошечными палладиевыми кристаллитами, рассеянными в пористой среде. По мере того как продукт реакции, диоксид углерода, покрывает поверхность кристаллитов, тепло, выделяемое при реакции, изменяет состояние катализатора. При внезапном фазовом переходе в кристаллите двуокись углерода выделяется в виде газа, затем катализатор охлаждается и реакция начинается снова.

Перемешивающая машина хорошо промоделировала не только эту реакцию, но и реакцию Белоусова-Жаботинского, в ходе которой малоновая кислота окисляется броматом калия в присутствии катализатора, такого как церий или железо. Клетки решетки представляют по существу частицы катализатора, а метафора "зараженного" состояния отражает явление постепенного насыщения поверхностей этих частиц.

Однако аналогия здесь не так проста, есть тут и свои тонкости. Во-первых, в перемешивающей машине соседние клетки взаимодействуют между собой, так сказать, обмениваясь инфекцией. А каким образом частицы катализатора обмениваются активностью? Герхардт и Шустер считают, что, по крайней мере в случае реакции окисления оксида углерода, частицы катализатора оказывают воздействие на своих соседей посредством двух основных механизмов. Частица катализатора может стать более активной, получив некоторое количество тепла от соседней частицы, которая активнее данной, или в результате диффузии молекул оксида углерода от соседней частицы, которая менее активна.

Благодаря взаимодействию между соседними клетками перемешивающей машины у них появляется возможность синхронизировать свою активность. После некоторого начального периода случайной дезорганизации (фазы "перемешивания") в поведении машины начинает проявляться синхронность. То же самое, как можно предположить, справедливо и в отношении реальных химических реакций. Объясняет ли, таким образом, перемешивающая машина появление волн в ходе реакции, которую она моделирует?

Найдутся, конечно, такие, кто сразу воскликнет: "Разумеется!" и в качестве свидетельства укажет на изображения. Ну что же, есть люди, которые видят клеточные автоматы повсюду. В апрельском номере журнала "The Atlantic" была помещена статья, посвященная космологическим рассуждениям Э.Фредкина. Этот бизнесмен в области вычислительной техники, а в прошлом ученый, предполагает, что вся наша Вселенная состоит из клеток, которые переключаются из одного состояния в другое подобно гигантскому клеточному автомату. Откровенно говоря, свидетельств в пользу справедливости такого предположения не так уж много. Результаты, демонстрируемые перемешивающей машиной, конечно, впечатляют, но не убеждают. А что по этому поводу думают сами изобретатели машины? Несмотря на тот факт, что перемешивающая машина так хорошо моделирует реакцию Белоусова-Жаботинского, Герхардт и Шустер не утверждают, что все химические реакции имеют клеточную природу. Они рассматривают свой автомат лишь как инструмент, позволяющий получить некое приближение к реальности, как дискретную версию дифференциального уравнения в частных производных.

Вдохновленные первоначально работой химиков Н.Йегера и П.Плата из Бременского университета, Герхардт и Шустер вместе со своим учителем в Билефельдском университете А.Дрессом начали работать над перемешивающей машиной, пригласив на помощь двух химиков: С.Мюллера из Института физиологии питания Макса Планка в Дортмунде и Дж.Тайсона из Политехнического института и Университета шт.Виргиния. Создатели машины хотят показать, что массив "химических осцилляторов", взаимодействующих между собой согласно некоторым простым правилам, будет неизбежно генерировать волны. Предположительно существует лишь небольшое число возможных волновых структур, хотя, по мнению Тайсона, при переходе к трем измерениям они становятся значительно более сложными. В связи с тем что трехмерные волновые фронты значительно труднее наблюдать в лабораторных условиях, компьютерные модели могут помочь химикам в их поисках. Вообще следует заметить, что ученый должен хорошо уметь пользоваться моделями, при этом модель должна служить ученому, а не ученый модели.

Читатели, которые пожелают построить свои собственные версии перемешивающей машины, уже, наверное, получили достаточно сведений для того, чтобы приступить к работе. Нужно объявить массив подходящего размера и организовать большой цикл, в котором элементы этого массива изменяются в соответствии с тремя правилами, и полученные значения выводятся для обозрения. Каждый элемент массива должен содержать номер состояния соответствующей клетки. Однако при вычислении нового массива необходимо временно где-то запомнить результаты, скажем в другом массиве, до тех пор пока вычисления не будут завершены. Затем в простом двойном цикле можно полностью заменить элементы старого массива элементами нового.

Вычисление нового массива также производится в двойном цикле. Две индексные переменные, скажем i и j, служат указателями на клетки решетки. Для каждой клетки, заданной координатами (i, j), программа (которую мы, конечно, назовем HODGEPODGE) выполняет два условных оператора if, выясняя таким образом, здорова или больна эта клетка. Если она здорова, производятся вычисления по первой формуле, а если заражена, применяется вторая формула. В любом из этих случаев придется еще определить состояние клеток, лежащих в непосредственной окрестности данной. Если же клетка и не здорова, и не заражена, то она, очевидно, "больна" и на следующем такте должна "выздороветь".

Ввиду того что размеры нашей статьи не должны выходить за определенные пределы, мы ограничимся этим кратким рецептом.

БИБЛИОГРАФИЯ

THE ARMCHAIR UNIVERSE. A.K.DEWDNEY. W.H.Freeman and Company, 1988. (Сборная солянка из первоисточников этой темы?- G.).

DID THE UNIVERSE JUST HAPPEN? ROBERT WRIGHT in The Atlantic, Vol.261, No.4., pages 29-44; April, 1988.

ОТКЛИКИ

2 1989

В статье в октябрьском номере за 1988г. было проведено описание "перемешивающей машины", клеточного автомата, изобретенного М.Герхардтом и X.Шустер из Билефельдского университета в ФРГ. Перемешивающая машина прекрасно моделирует цветные волны, распространяющиеся в некоторых химических средах. Иногда у этих волн образуются острые края, завивающиеся в спирали и порождающие богатое разнообразие фигур Пэйзли. Но это не обязательно означает, как, по-видимому, считают некоторые читатели, что в этих волнах присутствует хаос; явления, происходящие в клеточном автомате, не следует путать с хаосом.

В статье о перемешивающей машине речь шла об алгоритмическом описании программы HODCE-PODGE. Составляя это описание, прислать которое меня попросили многие читатели, я смог не только детализировать инструкции, необходимые для моделирования химических реакций на экране домашнего компьютера, но и прояснить некоторые моменты, изложенные в статье. Во-первых, параметр g должен принимать целые значения в диапазоне от 1 до 20. Во-вторых, значение переменной A, количество зараженных клеток в окрестности данной зараженной клетки, должно также включать в себя и эту клетку.

Из многих интересных откликов читателей, касающихся перемешивающей машины, необходимо отметить Д.Смита из Эль-Серрито (шт.Калифорния), сумевшего втиснуть правила перемешивающей машины в одно измерение. Смит устанавливает исходные значения в полоске клеток, расположенной в верхней части экрана. После того как автомат запущен, на экране появляются все новые и новые полоски, на которых замысловатые конфигурации здоровых клеток сменяются зараженными. Однажды, после длительного ночного сеанса, Смит обнаружил конфигурацию, которая повторялась снова и снова подобно бесконечной последовательности отражающихся одномерных волн.

11 1988
СТАРЫЕ И НОВЫЕ ТРЕХМЕРНЫЕ ЛАБИРИНТЫ
А.К.ДЬЮДНИ

...лабиринт был построен Дедалом так искусно, что всякий, кто попадал туда, не мог самостоятельно найти выход.
Из древнегреческой мифологии

БОЛЬШИНСТВО лабиринтов двумерны, поэтому, глядя на них сверху, мы можем найти среди сложных извилин и поворотов путь к выходу. Однако на трехмерные лабиринты мы уже не можем, так сказать, посмотреть сверху, потому что верхние уровни лабиринта будут заслонять нижние. Таким образом, ничего не остается, как искать выход ощупью - либо буквально, либо в переносном смысле слова - в хитросплетениях проходов.

Существуют старые и новые трехмерные лабиринты. Судя по его легендарной сложности, древний лабиринт Дедала был, по-видимому, трехмерным. Царившая там кромешная тьма вынуждает применить некоторые методы поиска пути в лабиринте, включая модифицированную версию известного правила правой руки, используемого обычно при решении задач с двумерными лабиринтами. Что же касается современных лабиринтов, то в игрушках-головоломках, конструируемых М.Оскаром ван Девентером, лабиринты не только трехмерны, но и невидимы! Такие лабиринты приводят к увлекательной задаче восстановления: при каких условиях три двумерных лабиринта определяют единственным образом трехмерный лабиринт?

Дедал построил свой знаменитый лабиринт для Миноса, могущественного критского царя. Однако царю лабиринт понадобился вовсе не для развлечения. В него бросали семерых юношей и семерых девушек, ежегодно посылаемых на Крит жителями Афин в качестве дани. Никакие ухищрения не могли помочь беспомощным жертвам, кравшимся по сырым, темным проходам в поисках выхода. Но это было еще не самое страшное; в лабиринте обитало ужасное, свирепое чудовище - Минотавр. С головой человека и телом быка Минотавр пожирал несчастных афинян, блуждавших по лабиринту.

Лишь Тесею, прославленному герою греческих мифов, удалось решить загадку лабиринта и убить Минотавра. У входа в лабиринт он закрепил конец клубка, подаренного ему дочерью царя (которая, конечно, тайно любила его), и блуждая по переходам в поисках Минотавра, постепенно разматывал клубок. Убив чудовище, он, сматывая клубок, вышел наружу.

Ну а что бы случилось, если бы Тесей по рассеянности забыл закрепить конец нити перед тем, как войти в лабиринт? Сумел бы он выбраться из лабиринта? Например, он мог бы привязать нить к убитому Минотавру, перед тем как отправиться на поиски выхода. Это позволило бы ему по крайней мере возвращаться к одной и той же точке (к телу убитого чудовища) после каждой безуспешной вылазки в хитроумном лабиринте Дедала. Однако в этом случае сама нить не гарантировала бы, что поиски в конце концов увенчаются успехом. Каким образом Тесей запоминал бы проходы, которые он уже однажды исследовал?

Это зависит от того, какой памятью пользовался бы Тесей, внутренней или внешней? Пользуясь внутренней памятью, он мог бы запоминать в какую сторону поворачивал на каждом перекрестке. Прибегнув к внешней памяти, он мог бы оставлять какую-нибудь пометку на каждом пройденном пересечении, создавая таким образом запись своего маршрута. Лично я придерживаюсь мнения, что Тесей скорее воспользовался бы вторым видом памяти. Для удобства снабдим нашего героя достаточно большим количеством мелких монет, например, достоинством в одну драхму.

Каждый раз, подойдя к пересечению трех или более проходов, Тесей должен был внимательно осмотреть пол у входа в каждый проход. Если там лежала монетка, то ему не следовало входить в данный проход. Отсутствие же монетки означало, что проход еще не исследован и в него нужно войти. Войдя, он должен тотчас положить на пол монетку, так чтобы ее можно было заметить на пересечении. Некоторые читатели, без сомнения, возразят, что Тесей не мог видеть монеток, поскольку в лабиринте царила кромешная тьма. Логично поэтому снабдить его каким-нибудь зажигательным устройством, например газовой зажигалкой для сигарет.

Следуя предложенной выше процедуре, Тесей иногда вынужден был бы вернуться по уже пройденному маршруту. Например, в случае, если он натыкался на тупик или подходил к пересечению, у всех проходов которого уже лежали монетки. Может ли возникнуть такая ситуация, когда, возвращаясь назад, Тесей встречал бы только помеченные, т.е. запрещенные проходы? Другими словами, мог ли он попасть в бесконечный цикл? Чтобы не лишать удовольствия тех, кто любит поразмыслить, я не дам ответа на этот вопрос. Достаточно сказать, что описанный метод широко применяется в современных компьютерных алгоритмах поиска в структурах данных. Он называется поиском в глубину.

Могло, однако случиться так, что у нашего неустрашимого героя не было с собой монеток или - еще хуже - зажигалки. Как бы он тогда решил задачу? К счастью, существует метод поиска пути в лабиринте, который не требует внешней памяти. Более того, следуя этому методу, Тесей утомил бы свой мозг ничуть не больше, чем при выполнению процедуры поиска в глубину. Этот метод я называю тройным правилом правой руки.

Обычно задачи с двумерными лабиринтами решаются с использованием так называемого правила правой руки: войдя в лабиринт, следует все время двигаться, придерживаясь правой стенки, независимо от поворотов и перекрестков. Если проход разветвляется, следует продолжить движение по правому коридору. Если вам встретился тупик, нужно просто развернуться и идти обратно, опять-таки придерживаясь правой стенки. В конце концов вы выйдете из лабиринта, но не обязательно через "выход". Если выход расположен в средней части лабиринта (как это часто бывает в лабиринтах, изображаемых на бумаге), то можно выйти и вернуться туда, откуда вы вошли в лабиринт, но, конечно, после многократного применения правила правой руки. Однако так или иначе вы должны выйти. Объяснение тут очень простое: следуя этому правилу, вы никогда не пройдете по одному и тому же пути. Но если ни один участок стены, ограничивающий контуры лабиринта, никогда не проходится повторно, то рано или поздно стена должна кончиться, и вы должны выйти наружу. (Исключение из этого правила имеет место лишь в том случае, когда стены лабиринта образуют замкнутую поверхность, но тогда в стене не будет ни одного проема, через который в лабиринт можно войти).

В несколько видоизмененной форме правило правой руки можно применять и для решения задач с трехмерными лабиринтами, включая и страшный лабиринт царя Миноса. Чтобы упростить рассуждения, предположим, что все проходы лабиринта имеют квадратное сечение и идут по прямой линии везде, за исключением поворотов, где они образуют угол в 90o. Кроме того, будем считать, что проходы ориентированы строго с востока на запад, с севера на юг или сверху вниз и поэтому на пересечениях перпендикулярны друг другу. Будем далее предполагать, что возможны лишь два типа пересечений, там, где сходятся вместе три прохода: либо пересечение в виде буквы Т, либо трехгранный угол с тремя перпендикулярными друг к другу проходами.

А теперь я приглашаю читателей поблуждать вместе со мной по коридорам лабиринта, чтобы показать, что называется, на практике, как применяется тройное правило правой руки. Гироскопическая система нам не потребуется - гравитация всегда подскажет нам направления вверх и вниз. Четыре других направления мы должны запоминать, следя за поворотами, совершаемыми по ходу перемещений в трехмерном лабиринте. Например, если мы входим в лабиринт в направлении с запада на восток, то после поворота направо мы будем двигаться уже на юг, а после следующего поворота направо - на запад и т.д.

Тройное правило правой руки на пересечении типа Т следует применять лишь после того, как мы определим плоскость, в которой оно лежит, поскольку каждой из трех возможных плоскостей соответствует своя ориентация поворота (см. рисунок на с.88 )- Представим себе часовой циферблат, лежащий в плоскости Т-пересечения. Мы произвольно назовем направление, в котором поворачивается часовая стрелка, "правым", и, перемещаясь по лабиринту, всегда будем поворачивать в этом направлении.


Тройное правило правой руки для трехмерных лабиринтов

В трехгранных углах это правило нужно несколько модифицировать. (Постойте-ка, не Минотавр ли рычит там вдали?) Будем считать, что вертикальные проходы имеют направление 1, ориентированные с юга на север - направление 2, а с востока на запад - направление 3. Если мы приходим к пересечению, двигаясь в направлении 1, то нужно выйти из него в направлении 2. Если мы двигались в направлении 2, то выйти из узла следует в направлении 3. Но даже и Тесей, наверное, догадался бы, что, войдя в угловое пересечение в направлении 3, он должен покинуть его в направлении 1. Вот и все, что касается тройного правила правой руки.

Оказывается, что правило удовлетворяет общему критерию решения задачи: ни один коридор не проходится дважды в одном и том же направлении. Однако гарантирует ли тройное правило правой руки окончательный успех? Я утверждаю, что да, но только в том случае, если в лабиринте существует лишь один путь, соединяющий вход и выход. Если лабиринт обладает большим числом возможных решений, то я предсказываю, что рано или поздно вы выйдете из лабиринта - либо через вход, либо через выход.

Конечно, нет никакой гарантии, что Тесей вышел бы из лабиринта, начав следовать тройному правилу правой руки только после боя с Минотавром. Но если бы он начал пользоваться правилом с того момента, как вошел в лабиринт и сражение с Минотавром не нарушило бы его памяти, то он в конце концов обязательно вышел бы на свет гордым победителем. Тесею, наверное, было бы безразлично, откуда он вышел, из входа или из выхода.

Усвоив эти правила, читатели, несомненно, чувствуют себя готовыми попытаться решить задачу с трехмерным лабиринтом. Глубоко изучив вопрос, я предлагаю вам ни больше ни меньше как восстановленную модель древнего лабиринта Дедала. Модель показана на рис. с.89. Все шесть уровней лабиринта находятся под землей. Самый верхний уровень (уровень 1) лежит непосредственно под тяжелыми каменными плитами двора царской резиденции. На месте двух отсутствующих плит зияют отверстия. К одному из этих отверстий читателя сопровождает дородный слуга царя Миноса. В конце концов читатель должен выйти из другого отверстия, представляющего собой выход из лабиринта. А между входом и выходом ему предстоит пережить ряд приключений, в том числе и неприятных.


Реконструкция лабиринта Дедала и один из возможных путей (выделен цветом)

Шесть уровней лабиринта отражают принцип его конструкции: это куб, вдоль каждого ребра которого размешается по шесть ячеек. Все горизонтальные коридоры изображены так же, как они обычно изображаются на схемах двумерных лабиринтов. Вертикальные же колодцы обозначены одиночными квадратами. Наш новоявленный Тесей может спуститься с одного уровня на другой, спрыгнув в отверстие, изображенное в виде черного квадрата. При этом он попадет в соответствующую ячейку прилегающего снизу уровня. На схеме читатель увидит несколько больший белый квадрат - это отверстие, через которое он попал на данный уровень. Когда читатель захочет подняться вверх, он должен добраться до ближайшего белого квадрата. Иногда можно увидеть черный квадрат внутри белого. Это означает, что из данного места в лабиринте можно двигаться и вверх, и вниз.

В лабиринте существует несколько возможных путей от входа к выходу. Некоторые читатели удовлетворятся, найдя один из них, другие же, возможно, захотят найти кратчайший путь, измеряемый количеством пройденных ячеек. Чтобы придать немного остроты вашим приключениям, я поселил в лабиринте Минотавра. Он всегда находится в том месте, где наверняка перехватит любого исследователя. В одной из наших будущих статей я назову имена первых пяти читателей, которые укажут это место.

Среди более современных лабиринтов заслуживают внимания лабиринты двух типов. Первые видимые, вторые невидимые. Видимый лабиринт - это пластмассовый куб, внутри которого тем или иным образом расположены стенки с отверстиями. Стальной шарик катается по проходам, создаваемым системой стенок. Играющий держит куб в руках, манипулируя им таким образом, чтобы шарик в конце концов достиг "финиша" - определенного места в кубе. В США такие лабиринты-игрушки, изготавливаемые компанией Milton Bradley, были популярны лет десять назад. Теперь в магазинах продается аналогичная головоломка под названием "Лабиринт Миллера".

Лабиринты другого современного типа рождаются в мастерской ван Девентера в Воорбурге (Голландия). Одну из своих игрушек-головоломок он называет полым лабиринтом. Это название вполне подходит для его лабиринтов, поскольку они представляют собой деревянные коробочки, внутри которых абсолютно ничего нет! Нет никаких проходов, никаких перегородок, и тем не менее этот ящичек является трехмерным лабиринтом.

Весь секрет в гранях коробочки. Они представляют собой двумерные "управляющие лабиринты": деревянные поверхности с вырезанными в них пазами. Указатель-курсор, состоящий из трех взаимно перпендикулярных деревянных палочек, отмечает позицию в лабиринте, в которой находится играющий в данный момент. Каждая палочка курсора проходит от одной грани коробочки к другой - противоположной, скользя вдоль пазов управляющих лабиринтов каждой грани. Не удивительно поэтому, что два управляющих лабиринта на противоположных сторонах коробочки должны быть идентичными. Таким образом ван Девентеру удается построить один трехмерный лабиринт из трех пар двумерных лабиринтов.

В простом примере, показанном на с.90. мы начинаем из положения, когда курсор находится в одном из углов, и пытаемся перевести его в противоположный угол. Каждая направляющая палочка вдвигается и выдвигается из коробочки, при этом автоматически перемещаются и две другие палочки (если это возможно физически) вдоль пазов в своих управляющих плоских лабиринтах. Может создаться впечатление, что для решения задачи с полым лабиринтом нужно просто решить частные задачи с каждым из трех управляющих лабиринтов. Однако это не так. Хотя задача для каждого управляющего лабиринта легко поддается решению, трехмерная задача для полого лабиринта оказывается не такой простой.


Простой лабиринт ван Девентера (слева) и его проективный слепок (справа).

Сложность задачи в том, что перемещения, дозволенные в одном управляющем лабиринте, могут блокироваться в другом. Более того, не ясно, в каком порядке три стержня курсора должны вдвигаться и выдвигаться. Для каждого положения курсора может существовать сразу несколько дозволенных перемещений. Вообще, решая эту задачу, можно закрыть глаза и попытаться найти правильный путь "на ощупь". При этом невидимый лабиринт в коробочке приобретает новую, своего рода ощутимую реальность.

Невидимый лабиринт в принципе можно сделать и видимым, если продолжить пазы трех прилегающих друг к другу управляющих лабиринтов в сплошном кубе, сделанном иэ легко режущегося материала. Когда куб прорезан насквозь по всем контурам, материал, не принадлежащий проходам лабиринта, полностью удаляется. Конечно, контуры управляющих лабиринтов должны быть такими же,как у исходного лабиринта ван Девентера.

Поскольку описываемый процесс изготовления в значительной степени воображаемый, я, пожалуй, вооружусь для работы лазерной пилой. Установив пилу непосредственно над одной из граней куба, я буду просто проводить ею вдоль контуров управляющего лабиринта, прорезая куб насквозь. Когда вырезание закончено, я осторожно вытряхну остатки ненужного материала из куба. В результате в руках у меня останется трехмерная форма, соответствующая контурам управляющего лабиринта. Затем весь процесс повторяется для двух других граней куба, и получившееся тело представляет собой по существу "негатив" неявного лабиринта ван Девентера: дозволенные проходы представлены в нем сплошными колоннами и поперечными балками. Я наэову его проективным слепком. Он изображен на рисунке на с.90.

По поводу проективных слепков возникают два интригующих вопроса. Первый: когда три двумерных лабиринта определяют проективный слепок правильного трехмерного лабиринта? Второй: при каких условиях проективный слепок дает три проекции, каждая из которых представляет собой правильный двумерный лабиринт. Термин "правильный лабиринт" нуждается в уточнении. Он относится к лабиринту, все проходы которого имеют единичную ширину и в котором существует путь от точки "старта" до точки "финиша". (Правильный трехмерный лабиринт, получающийся из трех двумерных управляющих лабиринтов, мне кажется, следует называть лабиринтом ван Девентера). Можно предложить и другие ограничения, но они, скорее, будут относиться к эстетическим аспектам того, что следует считать хорошим лабиринтом. Предложенного нами определения для начала будет вполне достаточно.

Поэкспериментировав даже с очень простыми управляющими лабиринтами, вы будете весьма удивлены тем, что получится в трех измерениях. Например, можно построить лабиринт ван Девентера из довольно тривиальных управляющих лабиринтов, состоящих из клеточных матриц 3*3, в которых определенные прилегающие друг к другу клетки удалены. Возможно, читателям интересно будет начать с управляющих лабиринтов 3*3 с прорезями в виде буквы Г в различных ориентациях. Сколько результирующих комбинаций можно получить в соответствующих лабиринтах ван Девентера? Это один вопрос.

Второй вопрос противоположен первому: при каких условиях трехмерный лабиринт порождает три правильных управляющих лабиринта, которые являются его проекциями? Оба вопроса имеют для ван Девентера практическое значение. Ответ на любой из них существенно упрощает процесс конструирования его лабиринтов. Ван Девентер признается, что вырезал множество моделей, пытаясь создать более сложные полые лабиринты. Читателям, как всегда, предлагается самим поразмыслить над проблемами, возникающими в связи с конструированием лабиринтов ван Дсвентера. Наиболее интересные соображения по этому поводу мы опубликуем в одной иэ будущих статей нашей рубрики.

БИБЛИОГРАФИЯ

BULFINCH'S MYTHOLOGY. THOMAS BULFINCH. Carlton House, 1936.

GOEDEL, ESCHER, BACH: AN ETERNAL GOLDEN BRAID. DOUGLAS R. HOFSTADTER. Basic Books, Inc., 1979.

УОЛКЕР ДЖ. ПОСТРОЕНИЕ СЛОЖНЫХ ЗЕРКАЛЬНЫХ ЛАБИРИНТОВ.- "В мире науки", 1986, #8.

ОТКЛИКИ

3 1989
Кратчайший путь в зловещем трехмерном лабиринте, речь о котором шла в ноябрьском номере журнала, удалось найти многим читателям. Он оказался равным 39 ячейкам в длину (включая ячейки входа и выхода). Существует и много других, более длинных маршрутов, ведущих от входа к выходу, но все они проходят через одну определенную точку во внутренней части лабиринта. Именно в этой точке свирепый Минотавр подкарауливает беззащитных юношей и девушек из Афин, которых бросают в лабиринт. Некоторые читатели отыскали место, где притаился Минотавр, старательно нарисовав карту и заметив в системе ходов "узкое место", другие же исходили из симметричности лабиринта, заподозрив, что именно симметрия является ключом при поиске места Минотавра, и они были правы.

В этом трехмерном лабиринте лишь одна ячейка выпадает из общей симметрии. Возможно, читателям будет интересно вернуться к схеме лабиринта. Они обнаружат, что на втором уровне между ячейками (5, 3) и (5, 4) отсутствует стенка. (Координаты в скобках соответственно обозначают числа ячеек вниз от верхнего края). Почему "узкое место" должно находиться в точке, где нарушена симметрия?

В заключение я назову шестерых читателей, которые первыми прислали свое решение задачи о Минотавре: М.Эмлинг (Глен-Эллин, шт.Иллинойс), Л.Лейнвебер (Кливленд-Хайтс, шт.Огайо), Т.Лундсфорд-мл. (Хайнсвилл, шт.Джорджия), Д.Мэлн (Рочестер, шт.Мичиган), Дж.Ньютон (Мидлтон, шт.Висконсин), К.Силбер (Нью-Йорк, шт.Нью-Йорк).

12 1988
О ШИФРОВАЛЬНЫХ И ДЕШИФРОВАЛЬНЫХ МАШИНАХ. ЧАСТЬ I
А.К.ДЬЮДНИ

"Что бы ни придумал один человек, другой сможет это раскрыть",- говорил Шерлок Холмс, герой произведений Артура Конан-Дойла.

СЛЕДУЕТ ЛИ рассматривать эти слова знаменитого детектива как хладнокровное выражение уверенности в своей способности расшифровывать секретные коды или это скорее констатация исторического факта? Несомненно, что начиная со времен, когда была изобретена письменность, вплоть до середины нашего столетия, коды, придуманные одними людьми, чтобы скрыть смысл важных военных или служебных сообщений, в конце концов разгадывались другими. Перед началом второй мировой войны кодировать сообщения стали с помощью машин, но и с их приходом ситуация по сути не изменилась.

Перефразируя Холмса, можно сказать: "То, что закодирует одна машина, другая раскодирует". Данная статья - первая из двух статей, посвященных секретным шифрам,- как раз завершается рассуждением о единоборстве кодирующих и декодирующих машин. На одной стороне такого поединка выступает машина "Enigma" (загадка), которая применялась 50 лет назад в вооруженных силах держав "оси Берлин-Рим", на другой - машина "Bombe" (бомба). Как увидим, неустанно тикающая "Bombe" медленно, но верно шла к победе, правда, не без помощи людей,- в том числе Алана М. Тьюринга, одного из основателей информатики и вычислительной техники. В следующем номере журнала я продолжу эту тему и расскажу о том, как компьютеры применяются в наше время для шифровки и дешифровки секретных сообщений.

Исторически вначале применялись шифры, преобразующие сообщение на обычном естественном языке в закодированную форму, или шифрованный текст, путем замены одних букв алфавита другими. Например, в так называемом шифре Цезаря это делалось в соответствии с простой схемой нумерации. Если пронумеровать буквы латинского алфавита (A, B, C,...) от 0 до 25, то, задав какое-нибудь определенное число, скажем 13, можно прибавлять его к числам, соответствующим каждой букве исходного текста на естественном языке. Получаемые суммы будут представлять букву шифрованного текста. Если какая-нибудь сумма окажется больше 25, то, вычтя из нее 26, получим число, принадлежащее диапазону от 0 до 25. Так, например, X (буква номер 23) будет кодироваться как K (буква номер 10), потому что 23+13 = 36 и 36-26 = 10.

Говорят, что Юлий Цезарь пользовался этим шифром, чтобы сообщения с арены боевых действий не могли стать достоянием противника, если бы они попали в его руки. Приведем одно из таких возможных сообщений римского полководца с просьбой прислать подкрепление на естественном языке и в зашифрованном виде:

SEND MMCC REINFORCEMENTS
FRAQ ZZPP ERVASBEPRZRAGF

Для того чтобы можно было пользоваться такой системой, предполагаемый получатель шифровки должен иметь к ней ключ. В данном случае ключ - это буква N, или буква под номером 13. Зная эту букву, получатель сможет восстановить исходный текст, просто вычитая 13 из чисел, соответствующих каждой букве шифрованного текста.

Сообщение может попасть в руки противника (будем называть его дешифровщиком), который попытается расшифровать его, подставляя по очереди все буквы алфавита в качестве ключа. Если противник попытается расшифровать сообщение, предположив, что ключом является буква B, то результат будет следующим:

TFOE NNDD SFJOGPSDFNFOUT

Поскольку получилась бессмыслица, дешифровщик попытается применить другой ключ, и в конце концов он наткнется на букву N, которая превратит бессмыслицу в разумную фразу на английском языке.

На первый взгляд может показаться, что компьютер не способен помочь в расшифровке сообщений, закодированных шифром Цезаря, поскольку машина при переборе всевозможных ключей и подстановке их в зашифрованный текст не сможет отличить бессмыслицу от текста, имеющего определенное значение. Однако компьютер можно снабдить "словарем", который по крайней мере позволит ему установить, содержит ли закодированное сообщение слова естественного языка. Но существует и другой, более мощный инструмент расшифровки: статистика.

Каждая буква алфавита встречается обычно в текстах данного языка с определенной частотой (измеряемой частотностью). Например, частотность первых трех букв латинского алфавита в текстах на английском языке составляет в среднем соответственно 8, 1.5 и 3%. Чаще всего встречается буква Е, ее частотность равна 13%. (Полная таблица частотности всех букв в англоязычных текстах приведена на рисунке справа.)


Частотность букв латинского алфавита в обычном английском тексте

В шифровке гипотетического сообщения Цезаря чаще всего встречается буква R, а именно 4 раза. Расшифровывающая программа может поэтому предположить, что R подставлено вместо E. Поскольку разность между числовыми представлениями букв R и E равна 13, программа может далее предположить, что ключом шифра является буква N.

В данном случае такая программа окажется правой, однако во многом это результат везения. В реальной практике статистическими закономерностями при расшифровке можно успешно пользоваться только тогда, когда в распоряжении имеются достаточно длинные шифрованные тексты. Помимо определения наиболее вероятного кандидата на букву E программа могла бы также попытаться найти буквы, заменяющие T, A и Q, которые тоже часто встречаются в английском языке. Она могла бы даже сопоставить распределение встречаемости букв в шифрованном тексте со статистическим распределением тех же букв в обычном тексте, чтобы выявить наиболее вероятные ключи.

Блез де Вижинер, французский криптограф XVIв., усложнил код Цезаря, предложив менять ключ с определенной периодичностью. Кодируя сообщение по методу Вижинера, букву-ключ изменяют для каждой буквы исходного текста в последовательности, соответствующей списку букв-ключей. По существу ключом шифра является эта последовательность букв.

Предположим, например, что ключом является последовательность CLEF, которой соответствует числовая последовательность 2, И, 4, 5. Чтобы зашифровать сообщение при помощи этой последовательности, нужно разбить буквы исходного текста на группы из четырех букв каждая. Затем нужно прибавить 2 к числовому представлению первой буквы в каждой группе, 11 - второй, 4 - третьей и 5 - четвертой. Так же как и в шифре Цезаря, получающиеся суммы представляют числовые значения букв зашифрованного текста. Приведем пример, иллюстрирующий, каким образом шифр Вижинера преобразует исходный текст в шифровку:

ключ: CLEFCLEFCLEFCLEF
исходный текст: SENDINTHECAVALRY
шифрованный текст: UPRIKYXMGNEACWVD

Шифрованные сообщения могут представлять собой либо непрерывную цепочку символов, как в предыдущем примере, либо их можно разбить на отдельные блоки. В любом случае предполагается, что получатель сумеет сгруппировать расшифрованные символы в слова.

Если расшифровывающему известен период ключа (число букв в ключевой последовательности) шифра Вижинера, он может декодировать сообщение, применив по существу тот же метод, которым пользуются для декодирования шифра Цезаря. Но в данном случае процесс займет значительно больше времени. Чтобы декодировать приведенный выше текст, зашифрованный по методу Вижинера, расшифровывающая компьютерная программа должна будет построить четыре распределения по буквам: одно для каждой четвертой буквы в последовательности, начинающейся с U, одно для каждой четвертой буквы в последовательности, начинающейся с Р, и т.д. Затем программа сравнит каждое из полученных распределений со стандартным статистическим распределением встречаемости букв, чтобы определить каждую из четырех букв ключевой последовательности. Фактически задача сводится к расшифровке четырех отдельных шифров Цезаря. Если расшифровывающему не известен период ключевой последовательности, декодирование займет еше больше времени, поскольку необходимо будет перебрать все возможные периоды. В данном случае возможность воспользоваться компьютером даст существенное преимущество, потому что компьютер очень хорошо справляется с многократно повторяющимися процедурами.

Само собой разумеется, что если мы имеем дело с короткими сообщениями или длинными ключевыми последовательностями букв, то необходимо будет набрать большое число сообщений, прежде чем расшифровка шифра Вижинера увенчается успехом. И наоборот, если применяются короткие ключевые последовательности, компьютер почти наверняка восстановит исходный текст, даже если ему предъявить не очень длинные сообщения.

Теперь, минуя множество замысловатых систем кодирования, изобретенных в период между XVI и серединой XXв., перейдем к рассмотрению немецкой машины "Enigma", с которой связана наиболее серьезная и крупномасштабная попытка расшифровки, когда-либо предпринимавшаяся до тех пор. Машина применялась фашистской Германией во время второй мировой войны для шифровки передаваемых по радио сообщений (эти сообщения сами передавались в телеграфном коде), которыми обменивались полевые и штабные подразделения. Поскольку радиосообщения легко перехватить, располагая радиоприемником, настроенным на соответствующую частоту, необходимость шифровки сообщений очевидна.

Основная машина системы "Enigma" состояла из алфавитной клавиатуры, трех "роторов", "рефлектора" и набора из 26 лампочек-индикаторов, по одной на каждую букву алфавита (см. рисунок на с.112). Ротор представлял собой зубчатое колесо, через которое проходили провода, соединяющие 26 контактов на одной стороне ротора с таким же количеством контактов на другой его стороне. Соединения были выбраны произвольно, но затем они уже не менялись. В каждом из возможных положений ротор представлял какую-то конкретную систему перестановок для 26 возможных электрических сигналов от клавиатуры (по одному для каждой буквы). Например, ротор мог послать сигнал, представляющий букву A на контакт, соответствующий букве R, сигнал, представляющий B, на контакт, соответствующий D, и т.д. Второй ротор, с другим расположением проводников и находящийся, вообще говоря, в другом положении, принимая сигнал от первого ротора, подвергал его еще одной перестановке. Последний, третий ротор аналогичным образом осуществлял еще одну перестановку.


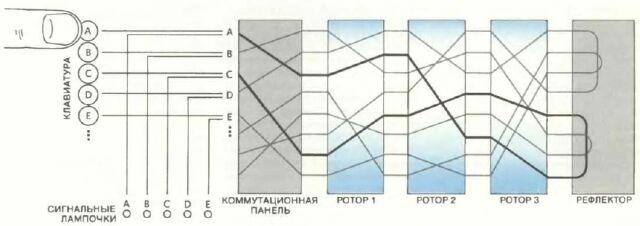
Схема машины "Enigma"

Пройдя через три ротора, сигнал поступал на рефлектор: систему проводников, соединяющую каждый контакт с другим контактом на задней стороне третьего ротора. Таким образом, рефлектор посылал сигнал обратно, по другому пути, через три ротора. Проходя от ротора к ротору в обратном порядке, сигнал претерпевал еще три изменения. Когда сигнал, наконец, выходил из системы роторов, он поступал на лампочку-индикатор.

Ключевым свойством машины "Enigma" был обратимый характер ее действия: если она кодировала букву R как Q, то, находясь в том же состоянии, она кодировала букву Q как R. Такая обратимость означала, что шифрованный текст, отпечатанный на клавиатуре машины, преобразовывался в исходный текст, при условии, что при декодировании машина находилась в том же состоянии, что и во время кодирования. Как следствие, шифровка и дешифровка сообщений сводились к одной и той же простой операции - установке роторов в правильное положение. Свойство обратимости, обеспечившее максимальное удобство для операторов машины, оказалось, как мы увидим в дальнейшем, роковым для этой системы кодирования.

Шифровки, посылаемые с помощью "Enigma", было особенно трудно декодировать еще и потому, что первый ее ротор автоматически поворачивался на одну позицию после каждой отпечатанной буквы. После того как клавиши были нажаты 26 раз, ротор возвращался в исходное положение, но зато второй ротор перемещался при этом в новое положение. Аналогичным образом, когда второй ротор поворачивался 26 раз, третий ротор также поворачивался на одну позицию. Система роторов по существу работала подобно одометру (курвиметру) в автомобиле. Благодаря такому механизму каждая буква исходного сообщения кодировалась по новой системе подстановки. Всего машина перебирала 26*26*26 = 17576 различных подстановок, прежде чем вернуться к исходному состоянию.

Такое кодирование напоминает метод Вижинера, однако в данном случае шифр оказывается неизмеримо сложнее. Каждая буква ключевой последовательности шифра Вижинера также осуществляет перестановку алфавита, заменяя букву исходного текста другой буквой, числовое значение которой является суммой чисел, соответствующих букве исходного текста и ключевой букве. Однако в шифре Вижинера применяется столько перестановок, сколько букв насчитывает ключевая последовательность, после чего происходит возврат к первоначальному "состоянию". Другими словами, машина "Enigma" имела ключевую последовательность длиной 17576 букв.

Если бы английским специалистам по расшифровке ничего не было известно о системе кодирования машины "Enigma", то разгадать ее шифр было бы практически невозможно. Статистический подход, основанный на средних значениях частотности букв в немецком языке, оказался бы бесполезным, поскольку любая буква исходного текста кодировалась поочередно любой буквой алфавита практически с одной и той же вероятностью. Однако англичане отнюдь не были в полном неведении относительно принципа, на котором была основана секретная кодирующая машина.

Еще перед войной французской разведке удалось добыть копии служебных инструкций для работающих с машиной. Французы передали эти материалы полякам, которые успешно воспользовались ими. Анализируя перехваченные немецкие радиосообщения с учетом имеющихся инструкций, польские специалисты сумели определить структуру соединений в трех роторах и рефлекторе машины. Благодаря этому было уже нетрудно определить сложную перестановку, являющуюся результатом совместного действия трех роторов, рефлектора и вторичного прохода через роторы, и тогда появилась возможность расшифровывать немецкие секретные сообщения - при условии, что было известно исходное состояние роторов. На самом деле исходные состояния машин польские специалисты могли определять по ежедневным шифрованным сообщениям, задававшим положение ротора на следующий день.

Хотя англичане и получили от поляков всю эту информацию, во время войны она оказалась уже недостаточной, так как перед самой войной немцы модифицировали свои машины системы "Enigma". Во-первых, они увеличили количество роторов до пяти. Поэтому, прежде чем пытаться декодировать перехваченные радиосообщения, нужно было определить, какие три из пяти взаимозаменяемых роторов были в машине. Во-вторых, в некоторых моделях машины, применявшихся в армии, была дополнительная "коммутационная панель", выполнявшая еще одну перестановку на шести или семи парах букв, перед тем как соответствующие электрические сигналы от клавиатуры достигали системы роторов и после того, как они ее покидали. Поляки, достигшие предела своих технических возможностей, после введения этих изменений вынуждены были отказаться от попыток расшифровывать секретные тексты.

Эту работу продолжили англичане, приняв эстафету от поляков. Вначале они собрали смешанную группу специалистов по шифрам и математиков (в число которых входил также Тьюринг) в викторианской усадьбе в Бакингемшире, называемой Блетчли-Парк. Располагая сведениями о структуре соединений в роторах и рефлекторе машины, группа должна была раскрыть структуру коммутационной панели. Было решено применить так называемый метод вероятного слова.

Этот метод основывался на том факте, что в некоторых контекстах определенная последовательность символов перехваченного сообщения почти наверняка представляет известное слово. Шифровка, переданная из штаба немецкого военно-морского флота, могла содержать, например, блок из пяти букв, который логично интерпретировать (с достаточно большой вероятностью, что эта интерпретация будет правильной) как закодированное слово U-boot (сокращение от немецкого слова Untersee-boot, или подводная лодка).


Немецкие подводные лодки времен второй мировой войны были оснащены машинами системы "Enigma"

Правильно догадавшись, что означает несколько слов шифрованного текста, можно было определить структуру контактов коммутационной панели, просто перепробовав все возможные соединения и выбрав из них то, которое давало бы нужное соответствие между зашифрованной и расшифрованной формой слов с уже известным значением. Но поскольку число возможных вариантов соединений на коммутационной панели для семи подстановок между парами букв все же больше миллиарда, Тьюринг понимал, что только быстродействующая машина сможет выполнить необходимый перебор.

Действительно, то, что Тьюринг решил воспользоваться машиной для расшифровки кода, сгенерированного другой машиной, уже не казалось чем-то удивительным. Поляки сами пользовались электромеханическими имитаторами машины "Enigma". Мерно пощелкивая, имитаторы переключались от одной "позиции" к другой, пытаясь определить, какая комбинация роторов воспроизводит данную перестановку. Звуки, производимые работающими имитаторами, напоминали тиканье часового механизма, поэтому их прозвали "бомбами".

Чтобы раскрыть структуру соединений коммутационной панели, была построена "бомба" нового типа. Машина "Bombe" представляла собой систему переключателей, или реле, которые перебирали все возможные варианты соединений на коммутационной панели в поисках логического соответствия имеющимся данным. В принципе проверка была простой. Рассмотрим, к примеру, пять машин системы "Enigma" и пронумеруем их от 1 до 5 (см. рисунок на с.114). Роторы в этих пяти машинах расположены так, чтобы моделировать суммарное действие одной машины, которое она будет выполнять при наборе каждой буквы пятибуквенного слова. (Напомним, что исходное положение роторов машины, зашифровавшей слово, нам известно по данным, которые удалось получить разведке). Аналитики определили, что пятибуквенное слово шифровки CZTUC, вероятно, означает в исходном тексте слово UBOOT (подводная лодка). На основании этой информации предстояло найти те соединения на коммутационной панели, которые использовались в этот день для кодирования всех сообщений.


"Bombe" пытается определить схему соединений на коммутационной панели шифровальной машины

Бомба Тьюринга начала бы с какого-нибудь произвольного предположения, скажем, что буква C на входной стороне коммутационной панели соединялась с буквой A на первом роторе. Допустим, далее, что "Enigma-1" преобразует букву A в R. Если наша гипотеза относительно значения слова правильна, то коммутационная панель должна заменять букву R на U и благодаря обратимости действия машины букву U на R.

Последний вывод означает, что коммутационная панель машины "Enigma-4" должна также заменять букву U в шифрованном тексте на R. Если машина 4 (ротор которой должен быть сдвинут на три позиции по отношению к машине 1) преобразует букву R, поступающую с коммутационной панели в X, то "Bombe" сразу же сделает вывод, что существует связь между буквами X и O, поскольку, по предположению, четвертая буква исходного текста - это O.

Этим выводом можно теперь воспользоваться при анализе действия машины в ее 3-м варианте, в котором она кодирует третью букву слова UBOOT. Если окажется, что машина 3 выдает букву X, когда получает на входе P, то мы устанавливаем, что на коммутационной панели существует связь между P и T, поскольку T является третьей буквой зашифрованного слова CZTUC.

Так как слово UBOOT заканчивается буквой Т, "Bombe" приходит к критическому выводу: не завершает ли машина 5 логический цикл, преобразуя P в A, так чтобы коммутационная панель давала букву C, стоящую на последней позиции шифрованного слова? Если нет (как оно обычно и было), то гипотеза о том, что коммутационная панель связывала буквы C и A, оказывалась несостоятельной. В этом случае "Bombe" приняла бы следующую гипотезу, скажем, что C связана с B. Если и эта гипотеза оказалась бы несостоятельной, машина рассмотрела бы вариант, когда C связана с C и т.д. Действуя в таком ключе, бомба Тьюринга в конце концов должна раскрыть правильные соединения на коммутационной панели.

Шифрованное слово, рассмотренное в примере, относительно короткое и в наших машинах системы "Enigma" перестановки букв были выбраны таким образом, что их было удобно анализировать путем проверок на логическое соответствие. В действительности приходилось расшифровывать значительно более длинные сообщения, дававшие больше информации для логических заключений. Таким образом бомба Тьюринга могла в результате процесса дедукции раскрыть все связи на коммутационной панели. В этот момент она, наверное, прекращала тикать, сигнализируя о том, что сейчас произойдет взрыв - но, конечно, не в Блетчли-Парке.

Решение задачи о соединениях в коммутационной панели было лишь частью усилий по дешифровке, предпринятых Тьюрингом и его коллегами. Например, каждый день нужно было определять еще исходную установку роторов, а также некоторые другие параметры, от которых зависела работа машины "Enigma" и которые из-за недостатка места мы не будем здесь обсуждать. Достаточно будет сказать, что группа специалистов, собранных в Блетчли-Парке, все время напряженно работала, расшифровывая различные версии шифров, применявшиеся немцами. Наверное, важнее все-таки было бы, что их работа, в которой они воспользовались машинами для расшифровки кодов, порожденных другой машиной, возвестила о начале новой эры, когда логические операции стали выполнять, машины, что в конечном итоге привело к современным компьютерам.

В следующей статье я продолжу эту криптологическую тему, рассказав о положении дел в этой области на сегодняшний день. А сейчас мне остается лишь добавить, что есть много энтузиастов, увлеченно занимающихся на досуге компьютерной криптологией. Некоторые из них даже написали программы, имитирующие машину "Enigma" и работу англичан по расшифровке ее кодов. Я хочу, в частности, поблагодарить Б.Милевски из Калифорнийского университета в Дейвисе, описавшего свой dнушитель-ный пакет программ CRYPTO, предназначенный для расшифровки кодов. В этом пакете есть, в частности, программа, расшифровывающая коды машины "Enigma" с одним ротором. Читатели могут попытаться составить собственные программы типа CRYPTO. Для них это будет хорошим практикумом в деле совершенствования своего мастерства в программировании.

БИБЛИОГРАФИЯ

CODES, CIPHERS, AND COMPUTERS: AN INTRODUCTION TO INFORMATION SECURITY. Hayden Book Company, 1982.

ALAN TURING: THE ENIGMA. ANDREW HODGES. Burnett Books, 1983.

CRYPTOGRAPHY AND DATA SECURITY. DOROTHY ELIZABETH ROBLING DENNING. Addison-Wesley Publishing Company, 1983.

Простейшие случаи рассмотрены в "Секретах" Абчука ТЕМА #26, АБЗАЦ #551 и "Этюдах" Уэзерелла ТЕМА #15, АБЗАЦ #386.- G.

ОТКЛИКИ

4 1989
В НАШЕЙ декабрьской статье, посвященной шифровке и расшифровке сообщений, утверждалось, что зашифрованный текст одним человеком (или машиной) может быть расшифрован другим человеком (другой машиной). На самом деле существует одно хорошо известное исключение из этого правила, но в той статье уже не было места, чтобы сказать об этом. Незашифрованное сообщение, полученное мною от Дж.Шуи, студента из Такома-Парка (шт.Мэриленд), напомнило мне о так называемом одноразовом блокноте. В простой версии этой системы кодирования используется цепочка случайных целых чисел от 0 до 25, при помощи которых кодируется каждая буква алфавита в исходном тексте сообщения. При этом i-я буква сообщения кодируется числом со сдвигом на n позиций по алфавиту, где n определяется как i-e случайное число кодирующей цепочки.

Криптографы называют такую цепочку случайных целых чисел блокнотом: он "одноразовый", потому что, закодировав сообщение, им больше не пользуются. Конечно, получатель текста, зашифрованного этим способом, также должен располагать точно таким же блокнотом. Подобный код расшифровать невозможно, потому что в зашифрованном сообщении нельзя уловить ни малейшей закономерности. Сам Шуи генерирует одноразовые блокноты по представлению букв алфавита внутри компьютера.

По мнению Дж.Миченера из Принстона (шт.Нью-Джерси), существуют довольно простые алгоритмы кодирования, отличающиеся от метода одноразовых блокнотов, которые не только можно применять в программах для домашнего компьютера, но с их помощью получать коды, поддающиеся расшифровке, чрезвычайно трудно. Эти алгоритмы основаны на удалении лишней информации из сообщения и сжатия его в минимально возможную цепочку битов. Затем сжатое сообщение подвергается операциям перестановки и замены битов. Миченер, написавший несколько научных статей по криптологии, утверждает, что "такой код будет слишком сложным, для того чтобы какой-нибудь любитель (или даже профессионал) смог расшифровать сообщение".

Несколько читателей указали на два солидных издания, которые могут заинтересовать нашу аудиторию. Первое - это книга под названием "Машинная криптография и современный криптоанализ", написанная С.Девуарсом и Л.Кру (С.A.Deavours, L.Kruh. "Machine Cryptography and Modern Cryptanalysis"). Второе - это ежеквартальный журнал "Криптология", одним из редакторов которого является тот же Кру.

И наконец, говоря о публикациях, нельзя не упомянуть о периодическом издании "REC", посвященном всевозможным головоломкам. Журнал "REC" (от слов Recreational and Educational Computing - занимательные и познавательные вычисления) выходит в США под редакцией М.Эккера.

1 1989
О ШИФРОВАЛЬНЫХ И ДЕШИФРОВАЛЬНЫХ МАШИНАХ. ЧАСТЬ II
А.К.ДЬЮДНИ

"То, что зашифровано на одной машине, можно легко расшифровать на другой".
Из книги А.Ходжеса "Алан Тьюринг: Загадка".

ДО ВТОРОЙ мировой войны засекречивание сообщений с помощью кодов и шифров представляло собой трудоемкую, утомительную ручную операцию. В военное время эту работу выполняли на электромеханических машинах, подобных немецкой "Enigma". В настоящее время шифровкой текстов занимаются электронные компьютеры. Они быстро превращают сообщение на естественном языке в соответствии с секретным "ключом" в зашифрованный текст и передают его по телефонным или другим каналам электронной связи. Компьютеры, снабженные тем же самым ключом, также быстро расшифровывают полученное сообщение. Во всяком случае на такой основе строится Стандарт Кодирования Данных (СКД) - метод шифрования информации, принятый Национальным бюро стандартов США в 1977г. и широко применяемый сейчас в гражданских и, возможно, военных системах связи.

Ниже я приведу полное описание СКД, и это, по-видимому, будет первой широкой публикацией об этой системе. Я не рискую раскрыть каких-либо важных секретов, потому что содержание любой шифровки останется тайной, пока не станет известен ключ шифра. И все же в последнее время в науке о шифровании и дешифровании акцент делался на ключах, некоторые из которых общедоступны, другие предназначены лишь для личного пользования. Личный ключ скрывается при этом в хорошо известной задаче, которую никто не может решить.

Независимо от того, какая часть информации остается общедоступной, а какая засекречивается, любая компьютерная система, работающая с шифрами, основана на алгоритме кодирования и алгоритме декодирования. Алгоритм кодирования для СКД первоначально был разработан в научно-исследовательском центре корпорации IBM. Подобно машине "Enigma", описание которой было приведено в предыдущем номере журнала, в системе СКД используется последовательность операций кодирования, по отдельности очень простых, но в совокупности производящих сложное преобразование. В машине "Enigma" операции кодирования выполнялись с помощью механических колес; в системе СКД они осуществляются либо программными модулями, либо микропроцессорами.

Поскольку кодирование выполняется на компьютере, в роли кодируемых символов выступают не буквы алфавита (как это было в машине "Enigma"), а биты, или двоичные разряды. В каждой операции кодирования по системе СКД участвует лишь одна цепочка длиной 64 бит. Поэтому перед тем как применять алгоритм, нужно сначала перевести исходный текст сообщения в цепочки по 64 бит. Для этого можно применить практически любой способ. Например, поскольку пяти битов оказывается достаточно, чтобы сосчитать до 31 в двоичной системе счисления, можно выбрать двоичные представления чисел в диапазоне от 0 до 25 для 26 букв латинского алфавита. При такой схеме соответствия цепочка длиной 64 бит способна представлять 12 последовательных букв текста на английском языке (при этом 4 бит останутся свободными).

Сообщение на исходном языке, шифруемое по системе СКД, можно представлять в виде реки, которая многократно делится на рукава, образуя сложнейшую речную систему, действительно, наилучший способ проследить за последовательностью отдельных операций - это воспользоваться "картой" реки, т.е. диаграммой алгоритма (см. рисунок слева). Отдельные модули на диаграмме, подобно водопадам, перемешивают и вспенивают воду. Каждая цепочка исходного текста встречает модули трех различных типов на своем бурном пути к выходному каналу: перестановки, сдвиги влево и замены. Операции, выполняемые модулями каждого типа, удобно представить в виде таблиц.


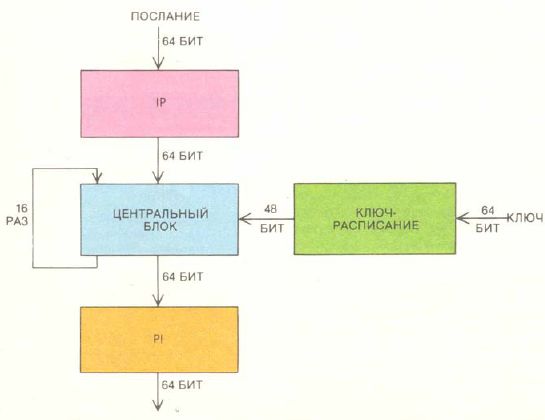
Блок-схема системы кодирования данных СКД

Таблица перестановок показывает, каким образом порядок битов в цепочке изменяется при воздействии данного модуля перестановки. Как пользоваться подобными таблицами, можно показать на простом примере. Предположим, что модуль перестановки воздействует на двоичную цепочку 1011 в соответствии со следующей (горизонтальной) таблицей: 3 1 2 4. Это означает, что третий бит цепочки переставляется на первую позицию, первый бит - на вторую позицию, второй бит - на третью, а последний остается на своем месте. Следовательно, применяя эту таблицу к числу 1011, мы получим число 1101.

В СКД используется несколько различных таблиц перестановок: так называемая первоначальная перестановочная таблица IP, таблица выбора бита E, или просто E, пара таблиц выбора-перестановки PC1 и PC2 и, наконец, обратная таблица перестановки P1. Эти таблицы приведены справа.


Таблицы перестановок, применяемые в системе СКД

Элементы некоторых таблиц по длине не равны 64 бит, поскольку их входные и выходные цепочки содержат меньше 64 бит. Например, таблица выбора бита E принимает на входе цепочку длиной 32 бит и расширяет ее на выходе до цепочки длиной 48 бит. Не удивительно поэтому, что, глядя в соответствующую таблицу, мы обнаруживаем, что некоторые элементы встречаются в ней более одного раза. Модули PC1 и PC2 оказывают противоположное действие: они сжимают проходящие через них цепочки. Поэтому в соответствующих таблицах некоторые элементы отсутствуют.

Заинтересовавшимся тайнописью читателям, которые пожелают перенести эти таблицы, так же как и сам стандарт СКД, в свои домашние компьютеры, придется обойтись без подсказок с моей стороны. Поскольку мы ограничены размерами статьи, я лишь упомяну о том, что операторы присвоения, используемые при работе с таблицами перестановок, должны быть следующего вида:

T(k) -> M(P(k)),

где массив M содержит биты цепочки, над которой выполняется перестановка, массив P содержит таблицу, T - временный массив, а k отсчитывает новые позиции битов. Составленная таким образом компьютерная программа будет помешать элемент с номером Р(k) массива M на k-ю позицию T. Когда все элементы T определены, M можно установить равным T. Система СКД как бы запирает сообщения на замок при помощи секретного ключа - произвольной цепочки из 64 бит, которую пользователь системы задает в качестве входных данных модулю ключа-расписания на начальном этапе кодирования. Ключ можно мысленно представить как речку-приток шириной 64 бит, которая сужается до 56 бит в модуле PC1, делится на два 28-битных канала, снова объединяющихся в модуле PC2, и вливается в основную реку сообщения последовательными порциями в виде 16 48-битных притоков, по одному для каждого шага главного итерационного цикла системы СКД.

Находясь еще в модуле ключа-расписания, два 28-битных канала встречаются с другим течением, перемещающим их биты влево. Как можно видеть из верхней таблицы на с.84, на первом, втором, девятом и 16-м шаге итераций происходит смешение битов двух цепочек влево на одну позицию. В остальных случаях цепочки сдвигаются влево на два бита.


Таблица сдвига влево (вверху) и таблицы замены (внизу)

Такие смешения влево легко реализуются в программе. 28 бит сегмента ключевой последовательности присваиваются, бит за битом, временному массиву таким образом, чтобы его i-й элемент принимал значение либо (i+1)-го, либо (i+2)-го бита сегмента. Конечно, последний элемент (или два) временного массива нужно установить равным первому биту (или двум) ключевой последовательности.

В систему СКД входят также восемь модулей замены, каждый из которых преобразует 6-битную цепочку в 4-битную. Биты числа, подвергающегося преобразованию, сами подсказывают, какими значениями индексов строки и столбца следует воспользоваться в соответствующей таблице: первый и последний биты определяют индекс строки, а средние четыре бита - индекс столбца (см. рисунок на с.84). Например, 6-битное число 111010 дает индекс строки 10 (крайние биты) и индекс столбца 1101 (внутренние биты). Эти двоичные числа представляют соответственно десятичные числа 2 и 13. Элемент в таблице S1 в строке 2 и столбце 13 - это десятичное число 10. В двоичной форме число 10 выглядит как 1010, которое и появится на выходе модуля S1, если на вход ему поступила цепочка 111010. (Большинству шифровальщиков, работающих с персональным компьютером, возможно, потребуются еще две процедуры преобразования для того, чтобы переводить двоичные числа в десятичные и наоборот).

Теперь рассмотрим, как взаимодействуют между собой эти различные потоки битов. Цепочка из 64 бит поступает в модуль IP и подвергается перестановке, описанной в соответствующей таблице. Затем она проходит в центральный блок, где основной кодирующий алгоритм перемешивает ее до неузнаваемости в своих многочисленных вихрях, прежде чем она дойдет до модуля PI, где она подвергается перестановке, обратной по отношению к той, которую выполняет модуль IP.

На вход центрального блока поступает не только результат преобразования модуля IP, но и 48-битные ключи (пронумерованные от 1 до 16), которые генерируются модулем ключа-расписания из заданной пользователем ключевой цепочки длиной 64 бит. Одни и те же основные операции выполняются в центральном блоке 16 раз, по одному разу для каждого из различных 48-битных ключей. Подробнее, 64-битная цепочка из модуля IP расщепляется на правую и левую половинки по 32 бита. Копия правой половинки сливается затем с ключом 1 в так называемом F-модуле. Результат складывается по модулю 2 с левой половинкой. (Сложение по модулю 2 подобно обычному сложению, за исключением того, что 1 плюс 1 равно 0). После этого 32-битная сумма и исходная 32-битная половинка цепочки меняются ролями перед следующим шагом итераций (на этот раз с ключом 2), при этом сумма становится правой половинкой 64-битной цепочки, а правая половинка подставляется вместо левой. По завершении цикла из 16 таких итераций со слиянием и переменой мест две 32-битные цепочки снова объединяются, образуя единое целое - цепочку из 64 бит.


Расширение версии центрального блока (слева) и блока ключа-расписания (справа)

Операция F, пожалуй, стоит того, чтобы построить для нее отдельную диаграмму (см. рисунок на с.86). Копия правой половинки текущей 64-битной цепочки входит в модуль выбора битов Е, где она расширяется до 48 бит. Затем она складывается по модулю 2 с 48-битным ключом под номером, соответствующим данному шагу итераций. После этого 48 бит разветвляются сразу на 8 речушек, шириной по 6 бит каждая. Эти цепочки пробегают через модули замены от S1 до S8, где каждая из них сжимается до четырехбитного числа. Поэтому, когда 8 речушек снова сливаются в единый поток, общая ширина цепочки уже равна только 32 бит. В этой точке модуль Р снова перемешивает цепочку.


Расширенная версия модуля F

Если читателю хватило упорства внимательно проследить за всем этим описанием с начала до конца, то у него, естественно, может возникнуть вопрос, а возможно ли вообще восстановить исходный текст сообщения по шифровке после того "турбулентного" перемешивания, которому подвергается этот текст, проходя сквозь систему СКД? Может быть, это настолько же трудно, как заставить воду течь в гору? В действительности дело обстоит именно так: прокрутим все основные операции центрального блока в обратном направлении. Направив 64-битную цепочку шифровки назад через модуль IP (аналогичная операция выполняется при кодировании сообщения), заставим цепочку повторить 16 шагов итераций в обратном порядке - от лежащего в основании центрального блока каскада со слиянием и переменой мест до вершины блока. Биты ключа также должны быть введены в модуль ключа-расписания в обратном порядке. После еще одной перестановки модулем PI исходное сообщение, подобно гейзеру, вырвется вверх.

Достаточно ли надежна система СКД на самом деле? Некоторые критики говорят, что нет. Еще до того, как система СКД была принята в качестве стандарта, У.Диффи и М.Е.Хеллман из Станфордского университета предупреждали, что СКД уязвим по отношению к лобовой (т.е. с исчерпывающим перебором вариантов) атаке, предпринятой достаточно хорошо оснащенным противником, скажем, способным построить параллельные компьютеры с быстродействием, которое позволяет перебирать 10 миллиардов возможных ключей в секунду.

Другое слабое звено системы СКД связано с необходимостью рассылать секретные ключи как отправителям, так и получателям сообщений. Это упрощает работу для агентов противника, у них появляется возможность каким-то образом раздобыть ключ и, пользуясь им, расшифровать сообщения. Поэтому 12 лет назад Диффи и Хеллман предложили рассылать так называемые общественные ключи по абонентам сети связи.

Схема распределения общественных ключей основана на очень большом простом числе p и числе основании a. Число a специально подбирается таким образом, чтобы a^n по модулю p, где n принимает значения 0, 1, 2, ..., давало все целые числа в диапазоне от 1 до р-1. Каждому абоненту сети связи известны числа p и a, и каждый абонент должен представить свой ключ, который будет указан в справочнике сети. Например, абонент p выбирает персональный "полуключ" xi и запирает его в сейфе. Затем он вычисляет число ki по формуле

ki = a^xi(mod p)

и высылает его администрации сети с тем, чтобы оно было опубликовано в справочнике под его именем. То же самое делают все абоненты.

Если теперь абонент j пожелает передать секретное сообщение абоненту i, он найдет в справочнике число ki и, воспользовавшись своим личным полуключом xj, вычислит комбинированный ключ kij, возведя ki в степень xj по модулю p. Другими словами,

kij = ki^xi(mod p).

Зная, что сообщение послал абонент j, абонент i аналогично вычисляет ключ kji, возводя kj в степень xi, по модулю p. Читателям, возможно, будет интересно убедиться, что оба абонента на самом деле пользуются одним и тем же ключом, другими словами, числа kij и kji равны.

Заинтересованный посторонний может вторгнуться в систему общественных ключей, решив дискретную логарифмическую задачу за приемлемое время. Если число у в формуле

y = a^x(mod p)

назвать дискретной степенью a, то x можно назвать дискретным логарифмом числа y по основанию a. Дискретная логарифмическая задача заключается просто в том, чтобы найти x при известных y и a.

Существует ли метод более быстрый, чем простой перебор всех возможных значений x с возведением каждый раз в степень x числа a по модулю p и сравнением результата с числом y? Теоретики считают, что не существует, однако строго этого пока никто не доказал. Если дискретная логарифмическая задача в действительности окажется настолько же труднорешаемой, насколько это представляется, то очень большое значение x, скажем число с несколькими сотнями разрядов, должно уже отпугнуть любого любопытствующего вычислителя.

Диффи и Хеллман расширили свою схему рассылки общественных ключей в криптосистему общественного пользования, придумав специальную функцию, названную ими односторонней функцией-люком. Вот как работает их система. Абонент i сети связи произвольно выбирает целое число ki в качестве своего персонального ключа, а в справочнике публикует свой специальный кодирующий алгоритм Ei. Он также формулирует другой алгоритм Di для декодирования, который держит в секрете. Абонент j делает то же самое, публикуя свой кодирующий алгоритм Ej, но оставляя свой личный ключ kj и декодирующий алгоритм Dj в секрете.

Позже, когда абонент j захочет послать сообщение абоненту i, он просто ознакомится с его кодирующим алгоритмом Ej по справочнику и воспользуется им для того, чтобы закодировать свое сообщение, исходную форму которого мы обозначим через m. Короче говоря, он передаст шифровку у, где

y = Ej(m).

Теперь абонент i без труда расшифрует сообщение с помощью своего секретного алгоритма Di.

Эффективность такой системы шифров в основном зависела от того, удастся ли найти "односторонние" кодирующие алгоритмы, т.е. такие кодирующие алгоритмы Ej знание которых ничего не говорило бы о соответствующих им декодирующих алгоритмах Dj. Идея подобной системы была очень привлекательной, хотя в то время, когда Диффи и Хеллман предложили ее, такие односторонние функции еше не были найдены.

Вот тогда-то и появилась криптосистема RSA, названная (по первым буквам фамилий) в честь Р.Ривеста, А.Шамира и Л.Адлемана, которые изобрели ее в 1978г. Она и сейчас считается наиболее перспективной криптосистемой для сетей связи с известными ключами. Абоненты сети связи с шифром RSA выбирают каждый по два простых числа и кодирующий показатель степени. Например, абонент i выбирает простые числа Pi и qi, а также кодирующий показатель степени ei. Он публикует произведение ni = Pi*qi и свой кодирующий алгоритм, преобразующий числовое сообщение m следующим образом:

Ei(m) = m^ei(mod ni).

Абонент i составляет также свой личный декодирующий алгоритм:

Di(x) = x^di(mod ni).

Оказывается, что алгоритм Di в точности противоположен алгоритму Ei. Эти два алгоритма при меняются именно так, как предсказывали Диффи и Хеллман в своем проекте системы шифров для сетей связи. Как же это все работает? Каким образом абонент i находит число di?

Магическое число di нетрудно вычислить, зная числа ei и fi = (Pi-1)*(qi-1). Простой алгоритм, изобретенный еще Евклидом, позволяет вычислить di как наибольший общий делитель чисел еi и fi. Это наибольшее число, на которое и еi и fi делятся без остатка. Теория чисел, многие положения которой кажутся несколько удивительными, гарантирует, что произведение di и ei можно представить как сумму числа, кратного fi, и единицы. Таким образом, когда абонент i лолучает сообщение, закодированное по его собственному алгоритму Ei, он фактически получает сообщение m в форме

m^ei(mod ni).

Если он теперь возведет это выражение в степень di, то получит

m^(ei*di)(mod ni).

Новый показатель степени числа m, а именно ei*di, как уже говорилось, равен сумме некоторого кратного fi и единицы. Однако, согласно другой теореме Евклида, число, возведенное в степень суммы fi и 1 по модулю ni, в точности равно числу m и, следовательно, исходная форма сообщения обнажается в лучах математического света.

Вопрос о том, возможно ли расшифровать коды системы RSA, имеет приблизительно такой же ответ, который можно дать на аналогичный вопрос, касающийся системы с известными ключами. Если кто-нибудь изобретет по-настоящему быстрый алгоритм разложения на множители, который бы очень легко разбивал большие числа на простые составляющие, то шифры системы RSA будут без особого труда раскрыты. Увидев число ni в общедоступном справочнике сети связи, нарушитель разобьет его на множители Pi и qi и найдет число di, при помощи которого сможет декодировать любое шифрованное сообщение от абонента i. Однако, по мнению теоретиков, такая задача разложения на множители, по-видимому, навсегда останется труднорешаемой.

DATA ENCRYPTION STANDARD. National Bureau of Standards, Federal Information Processing Standards Publication 46. National Technical
Information Service, 1977.

THE FIRST TEN YEARS OF PUBLIC-KEY CRYPTOGRAPHY. WHITFIELD DIFFIE in Proceedingsofthe IEEE, Vol.76, No.5, pages 560-577; May, 1988.

ОТКЛИКИ

6 1989
НАШЛОСЬ немало читателей, внимательно следящих за литературой в поисках замысловатых вычислительных задач, достойных их таланта. Две статьи, посвященные шифрам и опубликованные в последнем номере прошлого и первом номере нынешнего года, вызвали заметное оживление в их среде, особенно описание стандарта кодирования данных (СКД), приведенное во второй статье. Стандарт предусматривает порядок шифрования компьютерных сообщений и используется не только промышленными и финансовыми учреждениями, но, возможно, н различными военными учреждениями. Процедура шифрования длинная и сложная, но именно в этом видит ее достоинство М.Роузинг из Дэриена (шт.Иллинойс). Не прибегая к программному обеспечению на языках высокого уровня, Роузинг пишет свои собственные программы на языке ассемблера 68000, машинном языке, команды которого понятны микропроцессору 68000.

Ничто, наверное, не доставляет такого удовольствия, как написать к опробировать программу (на языке любого уровня), которая обнаружила бы ошибки в опубликованных описаниях. Например, вход для таблицы перестановок P в модуле F был помечен неправильно, его ширина должна быть не 48 бит, а 32. Процедура декодирования также поставила ряд проблем перед Роузингом и другими читателями. Так, в обратном порядке должны подаваться не 64 бит исходного ключа, а 48-битные "подключи". Они должны подаваться в центральный блок, начиная с ключа 16 и кончая ключом 1.

Ч.Клюпфел из Блумфилда (шт.Нью-Джерси) заинтересовался вопросом, какие части стандарта СКД были произвольными. Например, должна ли таблица выбора битов E обязательно иметь описанную мною форму для того, чтобы можно было построить успешную систему кодирования данных? То же касается и таблиц подстановки. Ходят также слухи, что изобретатели стандарта СКД специально оставили "черные ходы" в некоторых частях системы кодирования, благодаря которым несколько упрощается задача расшифровки закодированных сообщений при неизвестном исходном ключе.

Д.Вулф из Санта-Мария (шт.Калифорния) написал несколько интересных программ на языке ассемблера для своего компьютера Amiga с микропроцессором 68000. Американские читатели, обладатели компьютера Amiga, могут заказать копии системы кодирования, основанной на принципе, который был применен в знаменитой машине Enigma (описание приведено в декабрьском номере журнала), или на алгоритме RSA (см. январский номер). Основное достоинство программных систем кодирования, написанных на языке ассемблера, заключается в их молниеносном быстродействии.

Еще один журнал, посвященный криптологии, "Cryptosystems Journal" был рекомендован мне Т.Пэтти из Берка (шт.Вирджиния), который сам редактирует и издает этот журнал. В ближайших его номерах Пэтти собирается описать современные криптологические системы, чтобы они
стали доступными обладателям персональных компьютеров фирмы IBM и совместимых с ними моделей.

2 1989
СЛУЧАЙНОЕ ДВИЖЕНИЕ И ОБРАЗОВАНИЕ ФРАКТАЛЬНЫХ СКОПЛЕНИЙ
А.К.ДЬЮДНИ

ЧТО ЭТО - ион цинка, частичка сажи или покачивающийся пьяный - блуждает по экрану дисплея? Соединится ли этот объект с другими ему подобными, образующими вместе металлический цветок, темное пятно или безумную толпу? Ответ пусть подскажет вам собственное воображение, но - будь то цветок, пятно или толпа - форма агрегированной структуры будет, безусловно, фрактальной; можно даже измерить ее фрактальную размерность (которая лежит в диапазоне от 1 до 2).

Фрактал, изображенный на с.79, создан программой под названием SLO GRO (сокращение от слов SLOW GROWTH - медленный рост). Она отправляет последовательность частиц, одну за другой, в бесцельное блуждание по экрану, пока им не встретится неподвижное образование из таких же частиц. Как только частица натыкается на такое образование, она мгновенно останавливается и как бы прилипает к нему. По мере того как несколько сот частиц одна за одной скапливаются вместе, у неподвижной структуры постепенно отрастают ветви и усики хаотической формы, характерной для фрактальных объектов.


Фрактальное скопление К.Эбера

Можно сказать, что программа SLO GRO была создана под влиянием статьи, опубликованной в нашем журнале два года назад (см. Л.М.Сандер Фрактальный рост, "В мире науки", 1987, #3). В статье был описан механизм роста, о котором только что говорилось и который называется диффузионно-ограниченной агрегацией, или ДОА.

Несколько бесстрашных энтузиастов, любителей приключений, в которые так любят пускаться читатели статей рубрики "Занимательный компьютер", не стали дожидаться, пока я затрону тему программного моделирования ДОА, и написали свои собственные версии программы SLO GRO. Особенно большое впечатление произвела на меня работа Э.Смиертки из Санта-Клары (шт.Калифорния). Не имея за плечами практического опыта и вооруженный лишь элементарным курсом программирования, он вполне успешно написал программу SLO GRO. Не удовлетворившись наблюдением за тем, как растет фрактал, он измерял также его размерность.

Диффузионно-ограниченная агрегация может послужить неплохим представлением, например, такого физического процесса, как диффузия ионов цинка в двумерном электролитическом растворе. Когда ионы входят в контакт с агрегированным металлическим цинком на электроде, они немедленно прилипают к ранее осажденным атомам. Частички сажи, хаотично блуждающие прежде, чем они встретятся с другими частичками, уже прилипшими к какому-нибудь субстрату, по-видимому, также следуют этому процессу, хотя в данном случае сила, сцепляющая их с другими частичками, является силой электрического притяжения.

Конечно, самая забавная (хотя и наименее реалистичная) модель процесса ДОА - это множество пьяных, блуждающих в темноте, которые, наткнувшись на сборище своих бесчувственных мирно похрапывающих товарищей, ложатся в кучу и тут же засыпают. При помощи аэросъемки спящей толпы при дневном свете, наверное, можно установить, что она имеет фрактальную форму, аналогичную кластерам атомов цинка или пятнам сажи.

Ключом к моделированию диффузионной части процесса ДОА является "случайное движение". Каждый шаг случайного движения, проходящего в двух измерениях, совершается в одном из четырех случайным образом выбираемых направлений: север, юг, восток, запад. (Иногда в случайном движении допускаются также промежуточные направления, такие, например, как юго-восток или северо-запад, но мы будем придерживаться упрощенной версии). На верхнем рисунке на с.80 изображен путь, типичный для частицы, совершающей случайное движение,- она "бесцельно" блуждает туда-сюда. Наблюдая за тем, как движется такая частица на экране, невольно начинаешь сомневаться, что она когда-либо достигнет точки назначения. Однако в блужданиях частицы все же есть цель (хоть это звучит несколько теологически): достичь скопища себе подобных частиц, постепенно образовавшегося в центральной части экрана.


Покачивающийся пьяный, возможно, попадет, а возможно, и не попадет в скопление себе подобных

Все начинается с того, что программа SLO GRO помещает одну частицу в центр экрана компьютера. Затем из произвольной точки большого круга с центром в точке, где находится первая частица, начинает случайное движение другая частица. Проделав долгий и сложный путь, она наталкивается на неподвижную частицу и останавливается. После этого программа сразу же отправляет в путь следующую частицу, которая также стартует из случайно выбранной точки на круге и совершает аналогичное путешествие. Частицы одна за другой собираются в том месте, куда была помещена первая частица, и постепенно в центральной части круга начинает вырастать древовидное образование со странно переплетающимися ветвями и сучьями. Такую причудливую форму эта структура имеет потому, что случайно блуждающие частицы чаще всего наталкиваются на неподвижных собратьев уже на периферии образования, задолго до того, как проникнуть вглубь, в более плотно заселенную центральную часть. Новые веточки с большей вероятностью начинают расти также от веток, а не от ствола, если можно так выразиться.

Все это требует времени. Как говорит Смиертка: "На моем компьютере "IBM XT" программа работает четыре-пять часов, поэтому я просто запускаю ее на ночь". С помощью алгоритмов, описанных ниже, можно построить несколько более быструю версию программы, но продолжительность ее работы, конечно, зависит от выбранного числа частиц, участвующих в процессе.

Алгоритм диффузии (SLO) немного проще алгоритма агрегации (GRO). В целях простоты ограничимся всеми действиями внутри круга диаметром 200 точечных элементов изображения, или пикселов. Чтобы выбрать точку на окружности, из которой очередная частица начинает свой путь, алгоритм SLO выбирает случайный угол в одном операторе и затем в последующих двух операторах вычисляет координаты точки на окружности, где она пересекается радиусом, проведенным под данным углом к горизонтали:

angle <- random*360
x <- 100*cos(angle)+100
y <- 100*sin(angle)+100

Компьютер сам выбирает число случайным образом в качестве значения переменной random. Поскольку это число всегда принадлежит диапазону от 0 до 1, мы должны помножить его на 360, чтобы получить произвольный угол в диапазоне между 0 и 360o. (В системах, где вместо градусов используются радианы, значение random следует помножить на 2пи, или приблизительно на 6.283.) На следующем шаге вычисляем координату x точки на окружности под данным углом, умножая 100 (радиус окружности) на косинус угла. На третьем шаге получаем координату y, воспользовавшись функцией синуса. Поскольку в большинстве распространенных систем программирования начало координат - точка с координатами (0, 0) - находится в углу экрана, добавлено смещение 100 к обеим координатам для того, чтобы поместить начало координат в центр экрана. Конечно, этот прием годится лишь для экрана размерами 200*200 пикселов. Поэтому читатели должны будут сами подобрать подходящие смещения, исходя из размеров экрана того компьютера, для которого они напишут программы.

Выбрав точку старта для очередной частицы, программа SLO должна привести ее в движение в соответствии со следующим алгоритмом случайного движения (который мы встраиваем в цикл):

select <- random
if select <= 0.25
- then x <- x+1
if select > 0.25 and <= 0.5
- then x <- x-1
if select > 0.5 and <= 0.75
- then y <- y+1
if select > 0.75
- then y <- y-1

Правила движения выражаются явным образом через значения случайной переменной select (выбор). В зависимости от того, где (в каком из четырех равновероятных диапазонов между 0 и 1) лежит select, одна из координат частицы увеличивается или уменьшается на 1. Таким образом, частица случайно перемещается вверх, вниз, вправо или влево на один пиксел.

А вот что не выражено явно, так это два условия, при удовлетворении которых частица должна остановиться: в том случае, когда частица вышла за пределы окружности, с которой она стартовала, или если она достигла пиксела, прилегающего к уже накопившемуся скоплению неподвижных частиц, составляющих фрактальный объект. В первом случае программа просто ликвидирует частицу - если бы она этого не делала, то частица могла бы легко уйти за пределы экрана в бесконечное темное пространство электронного мира машины. Во втором случае программа фиксирует частицу в той точке, где она соприкоснулась с растущим кластером; частица как бы замирает на месте, загипнотизированная фрактальной Медузой.

Операторы, выполняющие эти действия, встроены в условный оператор while в начале цикла случайного блуждания, который приводит в движение частицы. Программа препятствует выходу частиц за пределы окружности постоянно следя за величиной расстояния между частицей и центром окружности. Это расстояние подсчитывается каждый раз при появлении новых значений x и y. (На самом деле программа SLO GRO вычисляет квадрат расстояния. При этом немного экономится время, поскольку не нужно выполнять операцию извлечения квадратного корня).

distx <- x-100
disty <- у-100
distance <- distx2+disty2

Условие while проверяет, насколько далеко частица ушла от центра окружности, путем сравнения величины distance с квадратом 100 (плюс 1). Если условие не выполняется, программа выходит из цикла и начинает его заново с другой частицей.

Ну а как определяется другое условие, а именно соприкоснулась ли частица с уже образовавшимся кластером неподвижных частиц? Для этого программа организует два списка, по одному на каждую координату для всех частиц, образующих неподвижное скопление. Эти списки представляют собой массивы с именами соответственно crdx и crdy (от crowd - скопление). Исходная частица, помещенная в центр экрана, имеет координаты crdx(1) = 100 и crdy(1) = 100. Если в своем хаотическом движении частица входит в соприкосновение с неподвижными частицами, программа SLO GRO выполняет следующие операторы:

crdx(count) <- x
crdy(count) <- y

Величина count (счетчик), как говорит уже ее имя, соответствует числу частиц в агрегате. В начале работы программы значение этой величины равно 1, и всякий раз, когда к агрегату добавляется очередная частица, count увеличивается на 1.

Но каким же образом GRO определяет момент, когда частица входит в соприкосновение с агрегатом? Простейший алгоритм проверки на соприкосновение заключается в том, чтобы сравнивать координаты четырех пикселов, непосредственно прилегающих к частице на данный момент, с координатами пикселов, содержащимися в списках crdx и crdy.

for n <- 1 to count
- x1 <- x+1
- if x1 = crdx(n) and y = crdy(n )
- - then contact <- true
- x1 <- x-1
- if x1 = crdx(n) and y = crdy(n )
- - then contact <- true
- y1 <- y+1
- if x = crdx(n) and y1 = crdy(n )
- - then contact <- true
- y1 <- y-1
- if x = crdx(n) and y1 = crdy(n )
- - then contact <- true

Здесь мы воспользовались так называемой булевой переменной под именем contact. Такая переменная может принимать одно из двух значений: "истина" или "ложь" (или, что эквивалентно, 1 или 0). Непосредственно перед началом цикла while переменной contact присваивается исходное значение "ложь".

Теперь мы почти полностью описали структуру программы SLO GRO, за исключением внешнего цикла while, который повторяет всю процедуру работы программы до тех пор, пока величина count не достигнет какого-то установленного числа частиц, скажем 500. Полностью алгоритм SLO GRO представлен на нижнем рисунке. Те его фрагменты, которые уже были подробно описаны по отдельности, представлены здесь блоками, помеченными соответствующим образом. Фрагменты, которые не были описаны явно, включают такие операторы, как инициализация переменных, стирание и высвечивание частиц на экране. (Начинающим программистам следует иметь в виду, что команды erase (стереть) и draw (нарисовать) представлены здесь в условной форме: в реальных системах программирования таких команд нет. Они реализуются при помощи других операторов, закрашивающих элементы изображения на экране).


Полное описание алгоритма программы SLO GRO

Фрактальные образования, подобные тем, которые строит программа SLO GRO, имеют определенную размерность, характеризующую скорость их роста. Рассмотрим, например, число частиц, лежащих в пределах окружности радиуса R. Если частицы образовавшегося скопления более или менее равномерно и плотно заполнили область роста, то естественно полагать, что удвоение радиуса приведет к учетверению числа частиц, заключенных внутри окружности, другими словами, рост агрегата идет по квадратичному закону и, таким образом, число частиц пропорционально R2. С другой стороны, если скопление частиц вытягивается в линию с немногочисленными ответвлениями или вообще без ветвей, то удвоение R приведет просто к удвоению числа частиц во внутренней части круга. Таким образом, рост агрегата будет линейным или пропорциональным R. Оказывается, фрактальный рост несколько быстрее линейного, но медленнее квадратичного: число частиц фрактального объекта, заключенных в круге радиуса R, пропорционально R^d, где d - число в диапазоне от 1 до 2.

Поэтому график зависимости числа частиц N в скоплении SLO GRO от радиуса круга R (в пикселах), построенный на бумаге в линейном масштабе, представляет собой кривую, по внешнему виду и своим свойствам находящуюся где-то между прямой и параболой, соответствующих линейному и квадратичному росту. Определить точно показатель степени роста, просто глядя на такой график, пожалуй, трудно. Намного проще это сделать, построив график в логарифмическом масштабе, т.е. на осях, на которых откладываются логарифмы величин.

На логарифмических осях координаты точек удваиваются, утраиваются или увеличиваются в какое-то определенное число раз, зависящее от выбора единиц. Если отложить зависимость числа N от радиуса R на логарифмической бумаге, то с квадратичными кривыми происходит странная вещь - они превращаются в прямые линии! Почему? Вспомним, что при квадратичном росте каждый раз при увеличении радиуса вдвое число частиц увеличивается в четыре раза. На логарифмической бумаге это будет соответствовать увеличению на четыре единицы по вертикальной оси на каждые две единицы роста по горизонтальной. Но график такой зависимости представляет собой прямую линию с коэффициентом 2. На самом деле график роста, пропорционального R3, будет выглядеть в логарифмическом масштабе тоже как прямая линия, с коэффициентом 3, в чем нетрудно убедиться, рассуждая аналогичным образом.

Теперь вам уже должно быть ясно, что делать, когда точки, соответствующие всем парам значений R и N, нанесены на логарифмическую бумагу. Если объект фрактальный, то все точки расположатся вблизи прямой линии (кроме, быть может, самого конца линии, где плотность частиц очень мала). Наклон полученной линии приблизительно равен фрактальной размерности объекта.

Смиертка сделал в точности то же самое с одним из произведений программы SLO GRO. Его график приведен на рисунке справа. Коэффициент полученной линии роста оказался равным 1.58. Правда, эта оценка немного меньше значений, обычно приводимых в научной литературе, но едва ли это обстоятельство испортит настроение любителю, проводящему свой собственный эксперимент. Он провел исследование с различными правилами прилипания частиц к агрегату и измерил размерности получившихся фракталов ДОА.


Как оценить величину фрактальной размерности

Как уже говорилось выше, другие читатели также построили свои версии программы SLO GRO. Например, С.Камазин из Итаки (шт.Нью-Йорк) считает, что его частицы не всегда движутся по случайным траекториям, а иногда даже создается впечатление, что они "набрасываются" на агрегат. Однако изображения полученных им фракталов убеждают меня в том, что его программа, по всей видимости, правильно отражает основные свойства диффузионно-ограниченной агрегации. Его программа написана для персональных компьютеров IBM PC и совместимых с ними машин.

К.Эбер, выпускник журналистского факультета Колорадского университета в Баулдере, написал версию программы SLO GRO, в которой частицы рождаются в случайно выбранных точках левого края экрана. С помощью своего приятеля Д.Сэйкена из университетского центра по астрофизике и астрономии он получил фрактальное скопление, приведенное на рисунке на с.79. Через каждые 100 итераций Эбер менял цвет частиц, что позволяло ему быстро оценивать число частиц, скопившихся на экране дисплея.

Наконец, я должен также сказать и об М.Эллере, приславшем письмо из японского города Хиросима. Он составил программу SOOT (сажа), похожую на SLO GRO во всех отношениях, за исключением того, что у него диффузия проходит в обратном направлении: частицы выходят из центра экрана и блуждают до тех пор, пока не натыкаются на очертание окружности или на другую частицу сажи. В результате от окружности начинают расти ветви к центру, и в конце концов источник оказывается поглощенным этой паутиной.

БИБЛИОГРАФИЯ

THE FRACTAL GEOMETRY OF NATURE. BENOIT B. MANDELBROT. W.H.Freeman and Company, 1982.

ЛЕОНАРД М. САНДЕР. ФРАКТАЛЬНЫЙ РОСТ.- В мире науки, 1987, #3.

ОТКЛИКИ

7 1989
ЭНТУЗИАЗМ читателей по поводу программы , порождающей фракталы, SLO GRO (Медленный Рост), описанной во втором номере журнала за нынешний год, нарастал отнюдь не медленно. Внушительный мешок писем говорит о неослабевающем интересе к фракталам любого вида и формы. Научным языком эту программу можно описать как моделирование диффузионно-ограниченной агрегации - процесса, наблюдаемого при образовании определенных минералов, электролитическом осаждении металлов и даже накоплении сажи.

Рецепт программы SLO GRO оказался достаточно простым и понятным для многих читателей, и они в нем хорошо разобрались. Основной алгоритм строится на введении случайно движущейся "частицы" в круговую область из произвольной точки окружности, ограничивающей эту область. Когда частица входит в контакт с другой, неподвижной, частицей, она также прекращает движение, и, таким образом, происходит агрегация частиц. Программу было нетрудно написать, но наблюдать за ее работой некоторым людям показалось утомительным занятием. В результате несколько читателей предложили, как изменить алгоритм, чтобы ускорить его работу.

Э.X.Кидера IV из Колумбии (шт.Мэриленд) достиг ощутимого ускорения, начиная с маленькой окружности и постепенно увеличивая ее радиус по мере роста объекта. Ряд читателей внесли предложения, заключающиеся в том, чтобы ускорить проверку на контакт с группой неподвижных частиц. Для этой проверки в программе осуществлялось сравнение координат прилегающих к частице пикселов с зафиксированными позициями каждой неподвижной частицы растущего агрегата.

С.С.Рид из Университета Ватерлоо в Онтарио сделал следующее предложение по этому поводу: "Для тех, кто пользуется Бейсиком (а я уверен, что им пользуются многие ваши читатели), существует значительно более простой способ. Нужно лишь воспользоваться командой Бейсика POINT, чтобы выяснить, был ли окрашен интересующий в данный момент пиксел. Таким образом, экран как бы выступает в роли запоминающего устройства".

Самым нетерпеливым, однако, оказался У.X.Пратт из Колледжа шт.Пенсильвания. Зачем вообще заставлять частицу совершать случайное движение? Почему бы сразу не выбрать для нее случайное место в ближайшей окрестности агрегата? Но, к своему немалому удивлению, Пратт обнаружил, что его объект оказался совершенно не похожим ни на одну из иллюстраций, сопровождавших статью в февральском номере журнала. И хотя края объекта были, конечно, неровными, в целом он был более плотным - можно сказать, имел другую природу.

Сам того не ведая, Пратт получил в своих экспериментах то, что называют моделью роста Ричардсона. Эта модель является излюбленным экспериментальным инструментом группы математиков, которых прозвали "мафией, работающей на частицах". Исследователи из этой группы (некоторые ее представители работают в Висконсинском университете в Мадисоне) уже более 10 лет занимаются изучением всевозможных моделей роста. В одной из будущих статей я надеюсь рассказать о своем недавнем визите в Мадисон.

3 1989
ПСИХОЛОГИЧЕСКИЕ ЗАДАЧИ: ТЕМА И ВАРИАЦИИ
А.К.ДЬЮДНИ

"По-видимому, самое интересное развлечение для человека - анализировать характер других людей" из статьи А.Сингера в журнале "Нью-Йорк тайме мэгэзин", 26 ноября 1978г.

ОДНАЖДЫ три знаменитых философа Древней Греции решили совершить полуденную прогулку по живописным окрестностям Афин. Расположившись под сенью большого оливкового дерева, они откупорили амфору с вином и начали не спеша обсуждать фундаментальный вопрос онтологии: в чем причина существования мира? Сначала дебаты были жаркими, но потом мысли стали путаться и дискуссия как-то увяла. Вскоре все три философа крепко заснули в тени дерева.

Озорной мальчишка из Афин, гулявший поблизости, увидев трех спящих философов, осторожно посадил им на лоб кляксы белой краской. Вечером перед заходом солнца жившая на этом дереве сова села на ветку прямо над спящими. Громко крикнув, она шумно захлопала крыльями и улетела. Крик совы пробудил философов, каждый из которых сразу подумал, что именно сова разукрасила лбы его коллегам. Все разом засмеялись.

Зрелище действительно было забавным, и прошло, наверное, секунд пять, прежде чем один из них внезапно прекратил смех. Почему? Эту задачу можно решить, проследив за ходом мыслей философа, прекратившего смеяться. При этом надо учитывать те предположения, которые делал философ относительно хода мыслей своих коллег.

Во многих задачах подобного рода люди фигурируют лишь для того, чтобы создать привычный для человека контекст, в котором задача выглядит более естественной, а решающий чувствует себя увереннее. Однако для успешного решения задач, которые мы условно назовем "психологическими", таких как задача о трех философах, необходимо учитывать, что думает один персонаж относительно хода мыслей других персонажей, фигурирующих в задаче. Подобное размышление о размышлениях представляет собой не только интересную тему для головоломок, оно необходимо также ученым, пытающимся создать такие программы, которые моделируют возможный ход мыслей человека, оказывающегося в аналогичных затруднительных ситуациях.

Для дальнейшего обсуждения этой темы нам, пожалуй, не обойтись без рассмотрения решения задачи о трех философах. Пусть это будет Пифагор, Платон и Аристотель. Пифагор, самый старший и мудрый, первым перестал смеяться. И вот почему: глядя на то, как веселится Аристотель, он понял, что тот не подозревает, что у него самого лоб запачкан чем-то белым. Но если у Пифагора лоб был чистым, то, очевидно, Аристотель смеялся над Платоном. Тогда, что думал Аристотель относительно того, над кем смеется Платон? "Клянусь всемогущей Афиной,- подумал, наверное, Пифагор,- мне не следовало бы смеяться!" Ситуация эта изображена на рисунке на с.85.


Один из философов оказался сообразительнее двух других

Мы привели решение для более или менее традиционной формы этой задачи. Ее можно несколько расширить, спросив, почему несколькими секундами позже прекратил смеяться и Платон. Как только Пифагор прекратил смеяться, ход его мыслей озадачил Платона. В самом деле, казалось бы, что Платон должен был утвердиться в предположении, что его лоб был чистым. "Пифагор, очевидно, увидел, что у меня лоб чистый и понял, что Аристотель смеется над ним",- мог бы рассуждать Платон. И все же, подумав как следует, Платон должен был догадаться, что его лоб также испачкан. Я представляю читателям самим, мысленно представив себя на месте Платона, определить, каким образом он пришел к этому выводу.

Рассмотрим другую задачу - так сказать, вариацию на тему трех философов. Один султан устроил трем своим визирям экзамен, чтобы самого мудрого из них назначить главным визирем. Он отвел трех кандидатов в темную комнату и одел каждому на голову по белому колпаку. Затем султан привел их в парадный зал и обратился к ним со следующими словами: "У каждого из вас на голове колпак, черный или белый, по крайней мере на одном из вас он, точно, белый. Первый, кто догадается, какого цвета у него колпак, станет моим главным визирем".

По существу, задача о трех визирях тождественна задаче о трех философах, хотя здесь смех уже не помогает определить, что видит тот или иной визирь. Однако любопытно, что эквивалентный эффект достигается здесь за счет того, что по крайней мере один из колпаков белый, и за счет того, что визири, не уверенные в правильном ответе, хранят молчание.

Назовем трех кандидатов на пост главного визиря аль-Хваризми, ибн-Халдун и ибн-Сина. Посмотрим, как рассуждал аль-Хваризми, вышедший победителем: "Так, предположим, что на мне черный колпак, что в таком случае подумают остальные? Допустим, ибн-Халдун тоже думает, что на нем черный колпак. Но тогда он поймет, что ибн-Сина видит перед собой два черных колпака и должен немедленно сообразить, что на нем белый. Однако ибн-Сина не воскликнул: "На мне белый колпак!" Поэтому ибн-Халдун знает, что ибн-Сина видит перед собой по крайней мере один белый колпак. Если бы мой колпак был действительно черный, то ибн-Халдун догадался бы, что ибн-Сина видит белый колпак у него на голове, и сказал бы, что белый колпак на нем. Ибн-Халдун тем не менее молчит. Клянусь бородой пророка, мой колпак не может быть черным!".

У задачи о трех визирях существует решение и другого уровня, как справедливо отметил один из моих коллег. Как только кандидатам объяснят условия конкурса, каждый из них должен догадаться, что единственно справедливый тест их умственных способностей может быть только при условии, что все три колпака белые.

Можно без труда переписать задачу о трех философах и трех визирях в бесчисленных вариациях. Одна из хорошо известных вариаций - это задача о трех женщинах аристократках, путешествующих по железной дороге в Англии на рубеже XIX и XXвв. День выдался жарким, и они открыли окно купе, чтобы подышать свежим воздухом. Поезд, изрыгающий густые облака черного дыма, въезжает в длинный темный туннель. Когда он снова выезжает на свет, все три женщины начинают смеяться при виде перепачканных сажей лиц своих компаньонок, однако через несколько секунд одна женщина неожиданно прекращает смеяться.

А вот еще одна вариация. Три бизнесмена обедают в фешенебельном нью-йоркском ресторане по оплаченным фирмой счетам. С удовольствием уминая пирог со шпинатом, каждый вдруг замечает, что в зубах у них застрял шпинат.... То, что "психологические" задачи могут принимать множество эквивалентных форм, приводит нас к понятию трансформации задачи. Посмотрим, например, каким образом можно трансформировать задачу о трех философах в задачу о трех визирях. Полезно будет определить соответственные элементы этих задач, имеющие аналогичные значения.

1. Озорной мальчишка - султан
2. Философ - визирь
3. Лоб - голова
4. Белое пятно - белый колпак
5. Смех - молчание

Помимо соответственных элементов следует определить также, что мы, собственно, понимаем под философом или визирем в данной задаче. Философ - это человек, который, пока не проанализирует ситуацию, будет смеяться при виде хотя бы одного испачканного лба, а в противном случае не будет смеяться. Визирь же - это человек, который, пока не проанализирует ситуацию, будет хранить молчание при виде по крайней мере одного белого колпака. В противном случае он скажет: "У меня на голове белый колпак".

Читателям предлагается самим заполнить пустые места в схеме обобщенной психологической задачи. Например, заполнив пронумерованные пустые места соответствующими словами из левой колонки, приведенной выше таблицы, вы получите задачу о трех философах. Если же подставить соответствующие слова правой колонки, то получится задача о трех визирях. (Можно, конечно, придумать свой собственный набор слов, подходящих для подстановки на свободные места схемы). Для простоты мы опустили здесь красочные описания времени и места событий.

Как-то раз (1) поместил (4) на (3) каждого из трех (2), так, что они об этом не знали. Пока он не знает, что у него на (3) есть (4), каждый (2) (5). Вдруг самый мудрый из трех (2) прекращает (5), воскликнув: "У меня (4) на (3)". Как он догадался об этом?

Следующая вариация на тему трех философов, которую я сейчас представлю, первоначально касалась неверных жен. Но поскольку здесь можно усмотреть стереотип неравноправия женщины, я воспользуюсь простейшей трансформацией, чтобы видоизменить задачу. Во всяком случае, эта задача интересна, потому что является обобщением задачи о трех философах.

Деспотичная королева амазонок объявила как-то раз своим подданным соотечественницам, что по крайней мере один из их мужей нарушил супружескую верность. Затем она велела зачитать свой королевский указ: "Если кто-нибудь из вас уличит своего мужа в неверности, я повелеваю казнить его ровно в полночь того дня, в который вы убедитесь, что он вам изменял". В королевстве амазонок информацией делились довольно свободно, но и не слишком откровенно: каждая амазонка знала о неверности всех мужей, кроме своего собственного. Весть об указе королевы облетела страну за один день. Нужно сказать, что в королевстве насчитывалось ровно 40 неверных мужей. Был ли кто-нибудь из них казнен, и если да, то на который день после указа?

Читатели, наверное, заметили, что королева сказала о неверности по
крайней мере одного мужа. Если бы действительно лишь один мужчина обманывал свою супругу, то его жена сразу же разоблачила бы его: ведь если бы неверным был чей-то еще муж, а не ее собственный, то она бы слышала об этом. Поэтому в полночь того же дня, в который королева издала свой указ, обманщик был бы убит своей женой.

Если бы неверных мужей было только двое, то их супруги расправились бы с ними в полночь второго дня. Тот факт, что ни одной казни не произошло в полночь первого дня, как раз свидетельствовал бы, что неверных мужей было двое. Поскольку жены этих двух обманщиков знали только об одном неверном супруге в королевстве (хотя все остальные амазонки знали, что неверных мужей по крайней мере двое), они немедленно поняли бы, что вторым обманщиком является собственный муж.

Теперь читатели уже, наверное, уловили идею рассуждения. Ни одной казни к полуночи n-го дня после указа - это факт, свидетельствующий о том, что в королевстве насчитывается по крайней мере n+1 неверных мужей. На заре сорокового дня все уже знали бы, что по крайней мере 40 мужей обманывали своих жен. На самом деле это нисколько не удивит амазонок, мужья которых были им верны, так как они и до этого знали, что в королевстве 40 неверных мужей. И лишь жены неверных мужей будут знать о 39 случаях супружеской измены, что и будет говорить им о сороковом обманщике, собственном муже. Эти жены, выполняя повеление королевы, призовут своих мужей на полуночный тет-а-тет по истечении 40 дней после указа.

Действительно ли задача об амазонках является вариацией на тему о трех философах? На этот вопрос можно ответить, предположив, что амазонок всего три, причем каждая из них имеет неверного супруга. В этом случае к концу третьего дня каждая женщина придет к правильному выводу. Строго говоря, в такой формулировке задача имеет больше сходства с задачей о трех визирях (но выше уже было доказано, что она получается путем трансформации задачи о трех философах).

Чтобы убедиться в этом, предположим, что султан обратился к трем кандидатам на пост главного визиря со следующими словами: "Я спрошу вас несколько раз подряд, знаете ли вы, какого цвета у вас колпак. Отвечайте только, если точно знаете, если же не уверены, молчите". В этом случае, когда султан первый раз задаст свой вопрос, все три визиря ничего не ответят. И на второй раз все трое промолчат. Когда же вопрос прозвучит третий раз, все трое ответят "да".

В задаче об амазонках неверных мужей 40, а не 3. Можно ли обобщить задачу о трех философах на 40 человек? Да, можно. Пока представим себе четырех философов, спящих под деревом. Проснувшись, все они дружно начинают смеяться, и четвертый философ (на самом деле один из перевоплотившихся бессмертных богов) рассуждает следующим образом:

"Хм. Уже по самой своей божественной природе и достоинству я могу, естественно, полагать, что мой лоб не испачкан, и поэтому я могу от души смеяться над этими смертными. Но почему никто из них не понимает, что сам испачкан, и не прекращает смеяться?" (И здесь обитатель Олимпа мысленно повторяет рассуждения Пифагора). "А-а, я, кажется, понял, в чем дело".

Но если такие рассуждения могут привести четвертого философа к правильному выводу о том, что и его лоб не избежал общей участи, то можно легко объяснить, как пятый, шестой или даже сороковой философ придет к тому же выводу. В одной из своих статей в рубрике "Математические игры" Мартин Гарднер аналогичным образом обобщил задачу о трех визирях (см. журнал "Scientific American", май, 1977г.). Однако, как он правильно заметил, возникают некоторые затруднения. "Обычно обобщения подобного рода наталкиваются на различные возражения. Решение задачи строится на таких расплывчатых предположениях относительно сообразительности персонажей и продолжительности их размышлений, что задача становится совершенно нереалистичной".

Разумеется, всем таким задачам свойственна некая нереалистичность. Ну в самом деле, насколько вероятно, что у троих людей, обедающих в ресторане, одновременно застрял в зубах кусочек шпината? Но даже если такое случится, то неужели каждый из них сразу не поймет по взгляду другого, что тот смеется именно над ним?

И все же для исследователей, пытающихся разрабатывать новые формы искусственного интеллекта, основанные на том, что называют логическим программированием, психологические задачи являются серьезным предметом. В частности, Дж. Маккарти из Калифорнийского университета в Беркли проверял дедуктивные способности логических систем, применяя их к задачам, подобным задаче о трех визирях. В системах логического программирования используется логический процесс, известный под названием исчисления предикатов, с помощью которого из определенных исходных предположений автоматически выводятся всевозможные заключения. Для того чтобы можно было в какой-то степени моделировать способность человека приходить к тем или иным логическим умозаключениям в общении друг с другом, системы логического программирования должны также уметь рассуждать о рассуждениях других.

Исследователям стоит, по-видимому, проанализировать более реалистические психологические задачи, часто возникающие в нашей повседневной жизни. Хотя они, как правило, не отличаются логической глубиной и требуют для своего решения многих предварительных предположений, такие задачи свидетельствуют, что значительная часть нашей умственной активности отводится на размышления о том, что думают другие люди относительно наших собственных мыслей.

Э.Гоффман из того же Калифорнийского университета одним из первых занялся исследованиями в новой области психологии, названной трансакциональным анализом. Трансакциональный анализ основан на предположении, что каждый человек постоянно пытается узнать, что думают о нем другие, и манипулировать их мнением, так, как это делают, например, актеры на сцене. Гоффман подкрепляет свои предположения об этом аспекте нашей внутренней жизни многочисленными примерами поведения обычного человека в хорошо знакомых нам ситуациях, и доводы Гоффмана надо признать убедительными.

Вот два примера, подобных тем, которые были описаны Гоффманом. Это примеры моих собственных наблюдений; дело в том, что я годами коллекционировал аналогичные эпизоды. Все они, кажется, указывают на человеческую способность думать о том, что думают другие люди. По-видимому, эти процессы происходят в нас наполовину подсознательно.

Однажды я увидел полицейского, спускающегося со второго этажа здания, где располагалось сомнительное заведение. Возможно, это был салон массажа. (В этой части города было много заведений такого рода). Выйдя на улицу, полицейский неожиданно столкнулся с другим полицейским. Моментально преобразившись, он принял очень странный вид. Он выглядел не смущенным, а так, как будто лишь притворялся смущенным. Сначала это меня озадачило, но, подумав немного, я понял, в чем дело. Первой реакцией полицейского, вышедшего из заведения, было, конечно, неподдельное смущение. Ведь коллега мог не без оснований заподозрить, что его визит на второй этаж был, так сказать, неофициальным. Однако смущение первого полицейского могло бы лишь подкрепить это подозрение. С другой стороны, если бы второй полицейский подумал, что первый лишь притворяется смущенным, весь эпизод мог бы сойти за шутку.

Иногда в играх проявляются худшие стороны человеческого характера. Двое довольно азартных картежников только что закончили игру в покер. Проигравший был заметно не в себе, безуспешно пытаясь совладать со своими эмоциями. Наконец, он выпалил; "Ты хотел меня.., а я хотел тебя... Ты просто вынудил меня к этому". (Пробелы здесь можно заполнить каким-нибудь грубым словом, в данном контексте означающим "обмануть").

Ключевое слово в этой фразе - "просто". На первый взгляд может показаться, что фраза означает, что в победе партнера решающим фактором оказалось не что иное, как везение. Однако, как показывает более внимательный анализ, проигравший хочет, чтобы выигравший считал самым существенным аспектом игры равенство их замыслов, а не то неравенство, которое вытекало из факта проигрыша.

Интересно, могут ли читатели привести аналогичные примеры из своего собственного опыта? Особенно интересными были бы письма с описанием ситуаций более близких к традиционным "психологическим" головоломкам.

Говоря о головоломках, уместно сказать несколько слов о недавно вышедшей прекрасной книге головоломок Д.Шаши под названием "Странные приключения д-ра Экко" (The Puzzling Adventures of Dr.Ecco, by Dennis Shasha). Автор этой книги - специалист по информатике из Математического института им.Куранта при Нью-Йорском университете. В ней описаны приключения таинственного доктора Экко, удивительно проницательного эксцентрика, сделавшего решение головоломок своей профессией. Кроме двух психологических задач книга содержит также всевозможные головоломки о выборах, поиске маршрутов, шпионах, электронных схемах, проверяющих другие электронные схемы, и многое другое. Здесь даже объявлен конкурс, участники которого должны решить 10 головоломок с шифрами. Справившиеся с этими задачами не только получают футболку, рисунок и надпись на которой символизируют высшую степень умственных способностей ее обладателя, но и его имя будет выгравировано на наборе шахматных фигур ручной работы из оникса. Обладатель главного приза будет объявлен в нашей статье в сентябрьском номере журнала.

Обсуждение психологических задач я хотел бы завершить головоломкой из книжки Шаши. Два генерала, соединения которых дислоцированы по разные стороны высокого горного хребта, хотят скоординировать атаку на общего противника, поскольку атака в одиночку может обернуться поражением. К сожалению, генералы не располагают никакими средствами коммуникации между собой, кроме почтовых голубей, перелетающих над хребтом из одного лагеря в другой (см. рисунок на с.86).


Закончится ли когда-нибудь обмен подтверждениями между генералами?

Первый генерал посылает второму следующее сообщение: "Атакуем в 0800. Подтвердите, что получили сообщение, иначе я не атакую". Второй генерал не имеет ничего против этого плана и собирается послать голубя с подтверждением. Однако внезапно этот генерал соображает, что первый не будет атаковать, если не получит подтверждения. Поскольку у второго генерала нет никаких гарантий, что почтовый голубь долетит и доставит подтверждение первому генералу, он решает, что и сам не будет атаковать, если не узнает, что первый генерал действительно получил подтверждение. После этого второй генерал посылает голубя с сообщением первому генералу с просьбой подтвердить получение его подтверждения. Прекратится ли кажущийся бесконечным ряд подтверждений? Возможно, ответ зависит от содержания одного из сообщений, которыми обмениваются генералы?

В заключение я выражаю благодарность двум моим коллегам из Университета Зап.Онтарио, Энди Л. Сциларду и Арески Н. Абдаллу, которые помогли мне подготовить настоящую статью.

БИБЛИОГРАФИЯ

THE PRESENTATION OF SELF IN EVERYDAY LIFE. ERVING GOFFMAN. Doubleday & Company, Inc., 1959.

THE PUZZLING ADVENTURES OF DR.ECCO. DENNIS SHASHA. W.H.Freeman and Company, 1988.

ОТКЛИКИ

7 1989
Темой нашей мартовской статьи были "психологические" головоломки: логические задачи, которые можно решить только с учетом возможного хода мыслей других участников рассматриваемых ситуаций. Целый класс таких задач был представлен головоломкой о трех философах, проснувшихся после полуденного сна в тени раскидистого дерева. Каждый философ заметил, что у обоих его коллег лбы были запачканы, по-видимому, птицей, сидевшей на дереве. Лишь после того, как все они какое-то время посмеялись друг над другом, самый мудрый из них догадался, что его собственный лоб был также запачкан. Как он пришел к этому выводу?

Мне как-то не пришло в голову, что можно сформулировать задачу о двух "философах". На эту возможность указал Дж.Клейн из Колледж-Плейс (шт.Вашингтон). Клейн опробовал эту задачу, рассказав своим детям историю о двух рабочих, свалившихся со строительной платформы. При падении никто из них не ушибся, но у одного оказалось перепачканным лицо. Почему рабочий с чистым лицом побежал умываться, в то время как другой, с испачканным лицом, спокойно вернулся на рабочее место? Клейн пишет: "Было очень интересно слушать, как дети рассуждают вслух, и наблюдать за тем, как меняется выражение их глаз, когда приходит решение".

Другая задача была заимствована мною из книжки Денниса Шаша "Удивительные приключения доктора Экко". Армии двух генералов времен наполеоновских войн оказались разделенными горным хребтом. Генералы захотели скоординировать совместную атаку на неприятеля, посылая друг другу сообщения с почтовыми голубями. Но что следует написать в сообщении? Если первый генерал пошлет сообщение: "Атакуем с рассветом", то он должен ждать, пока второй генерал пришлет подтверждение, что он получил сообщение. А что, если один из голубей не перелетит хребта? И даже если оба голубя благополучно долетят до пунктов назначения, каким образом второй генерал узнает, получил ли первый его подтверждение? По-видимому, здесь неизбежен бесконечный обмен сообщениями.

Ситуация, в которую попали генералы, напомнила У.Клементсу из Беверли-Хиллза (шт.Калифорния) о малоизвестной пьесе, шедшей одно время на Бродвее, в которой агент, работавший сразу на две разведки, снует туда-сюда между двумя враждующими государствами. Сначала агент узнает, что государство A расшифровало секретный военный код государства B. Агент отправляется в государство B, чтобы сообщить офицерам разведки это известие. "Мы уже знаем об этом",- говорят офицеры. Сначала агент растерялся, но потом сообразил, что может продать эту информацию офицерам разведки государства A. Те, в свою очередь, отвечают: "Мы знаем, что разведка B уже знает об этом и посылает нам ложные сообщения". Агент поспешил обратно в государство B: "А вам известно, что они уже поняли, что получают ложные сообщения?" "Конечно",- отвечают ему в разведке B. Агент возвращается в государство A, чтобы разъяснить там. истинное положение дел, и т.д. Сколько же раз придется агенту путешествовать из страны в страну, сообщая сведения о том, что известно другой стороне? Хотя в этой задаче две стороны не координируют свои действия, а враждуют друг с другом, решение задачи не упрощается - его просто не существует.

Психологические задачи встречаются и в нашей повседневной жизни. Их изучением занимался покойный Эрвин Гоффман, социолог. Я обратился к читателям с просьбой привести свои примеры и получил несколько ответов, в том числе от П.М.Камбеена из Муйдена (Голландия). Во время второй мировой войны офицер германских оккупационных сил пожаловался одному голландцу, что плохо понимает настроение его соотечественников. Голландец ответил ему следующее: "Голландцы обладают тремя главными достоинствами. Они умны, лояльны и сочувствуют нацистам. Однако каждый конкретный, отдельно взятый голландец обладает лишь двумя из этих достоинств и одним, противоположным третьему". Пока до немецкого офицера доходил логический смысл этого высказывания, у шутника было достаточно времени, чтобы скрыться.

10 1989
Перед читателями книги Д.Шаши "Удивительные приключения доктора Экко" было поставлено 10 задач, решение которых давало право на титул "всеведущего", учрежденный самим доктором Экко. Победителями конкурса стали Ф.Гэлвин из Лоуренса (шт.Канзас) и Л.Брайт из Линкольна (шт.Небраска), который выиграл также главный приз, шахматный набор, присужденный ему по жребию.

Одна из задач этого конкурса заключалась в том, чтобы придумать оптимальное расположение комнат в антарктическом исследовательском центре. Здание должно состоять из 31 комнаты, каждая площадью 20 квадратных футов. Ни одна из комнат не должна иметь больше 4 дверей, а толщину стенок можно считать пренебрежимо малой. Комнаты и двери должны быть расположены так, чтобы из любой заданной комнаты можно было перейти в любую другую, не проходя по пути более чем через 6 дверей.

Наилучшее решение прислал Б.Л.Платт из Вудз-Кросса (шт.Юта). Читатели могут попытаться повторить решение Платта, воспользовавшись древовидной структурой. Возможно, придется поэкспериментировать с натуральной моделью, чтобы удостовериться в существовании разумного архитектурного решения. Может быть, нашим всемогущим архитекторам удастся и более оригинальная схема расположения, которая при тех же условиях может вместить больше чем 31 комнату. Решение можно посылать на адрес Д.Шаши, я же опубликую имя победителя в одном из следующих номеров журнала. Шаша работает в Математическом институте им.Куранта при Нью-Йоркском университете, на отделении информатики.

2 1990
В октябрьском номере в статье из рубрики "Занимательный компьютер" я поставил перед читателями задачу, принадлежащую Д.Шаша из Нью-Йоркского университета. В его книге "Удивительные приключения доктора Экко" есть задача о планировании антарктической научной станции, которая должна состоять из 31 комнаты. Ни у одной из комнат не должно быть больше четырех дверей, и комнаты должны быть расположены так, чтобы можно было пройти из любой комнаты в любую другую, не пересекая более шести дверей. Я попросил читателей спланировать станцию с большим, чем 31, числом комнат.

Более ста читателей прислали свои ответы Д.Щаша. Многим из них удалось разместить 53 комнаты в виде древовидной структуры, а несколько самых изобретательных исследователей заметили, что совсем не обязательно, чтобы все пути проходили через центральную комнату. И действительно, объединив два дерева так, чтобы они имели общие "листья", эти читатели получили архитектуру с 70 комнатами на одном этаже. Двое читателей Э.Джордан и Э.Уикс из Даунерс-Гроува (шт.Иллинойс) прислали совместное решение, в котором, применив еще более хитрый подход, им удалось расщепить некоторые комнаты-листья на две комнаты.

4 1989
УВЛЕКАТЕЛЬНОЕ ПУТЕШЕСТВИЕ ПО МНОЖЕСТВУ МАНДЕЛЬБРОТА
А.К.ДЬЮДНИ

Науке и искусству мало лишь служенья;
В работе надо проявить терпенье.
Дух терпеливый к цели медленно идет;
Хорошему вину лишь время крепость придает.
Из Гете

ПОХОЖЕ, что искусство и наука сливаются воедино в множестве Мандельброта. Его поразительная сложность может символизировать развивающиеся сейчас отрасли науки, изучающие свойства хаоса и нелинейных динамических систем. Люди, даже не посвященные в реальное физическое значение этого "объекта", ощущают причудливую красоту его темного ядра и усыпанного "драгоценными камнями" ореола. Мудрое высказывание великого Гете говорит нам о терпении, которым действительно нужно запастись, чтобы получить изображение множества Мандельброта. Хотя персональный компьютер и способен выполнять тысячи вычислений в секунду, может потребоваться несколько часов, прежде чем он построит законченное изображение.

Множество Мандельброта (названное по имени человека, открывшего его, Бенуа Б. Мандельброта из Исследовательского центра Томаса Уотсона фирмы IBM в Йорктаун-Хейтсе, шт.Нью-Йорк) состоит из бесконечного количества точек. Изображения, приведенные в настоящей статье, были построены путем проверки точек из сравнительно небольшой выборки (всего лишь несколько тысяч точек) на принадлежность множеству Мандельброта. Каждый точечный элемент изображения, или пиксел, соответствует какой-нибудь одной точке выборки. Поэтому каждое изображение представляет собой тот или иной фрагмент множества, показанный с некоторым увеличением и в цветовой гамме, выбранной в соответствии со вкусами исследователей множества Мандельброта, приславших автору эти изображения. Наверное, глядя на приведенные здесь иллюстрации, читатели задумаются о природе той красоты, которая таится в множестве Мандельброта. Какие процессы создают эти удивительные формы, эту сложность, простирающуюся в бездну бесконечности? Простота ответа находится в очевидном противоречии со сложностью объекта.

В двух статьях, опубликованных ранее, уже достаточно подробно говорилось о том, каким образом можно построить множество Мандельброта при помощи компьютера. (См. "В мире науки", 1985, #10 и 1988, #1.) На этот раз я постараюсь сделать, так, чтобы даже те, кто испытывает жуткий страх перед математикой, получили представление о множестве Мандельброта. Есть люди, которые, услышав, что множество Манбельброта каким-то образом связано с "комплексными числами",сразу бледнеют и, торопливо извиняясь, говорят, что им срочно нужно куда-то идти. К счастью, темы комплексных чисел можно вообще не касаться. Я приглашаю таких читателей (а вместе с ними, разумеется, и всех остальных) последовать за мной на манделобусе в путешествие по воображаемой равнине и совершить экскурсию в множество Мандельброта.

Подобно точкам земной поверхности, положение которых можно определять по широте и долготе, точки на плоскости также имеют координаты. Точка (0, 0), называемая началом координат, лежит в центре плоскости. По мановению волшебной палочки я превращаю читателя в невероятно крошечное существо, помещающееся в точке с координатами (a, b). Где находится эта точка? Да где угодно. Но уж коль скоро мы выбрали эту точку, величины a и b должны иметь конкретные значения, такие, например, как 2.78 и -0.43. В этом случае читатель будет находится на 2.78 единиц к северу и на 0.43 единицы к востоку от начала координат. Что такое в данном случае единица? В принципе безразлично, считаем ли мы ее равной километру или метру. В конце концов любое расстояние кажется огромным, когда вы сами имеете точечные размеры.

Теперь, когда читатель - крошечный и одинокий - слился с точкой на плоскости, он готов к тому, чтобы начать путешествие на манделобусе, но прежде чем подойдет манделобус, я поясню, каков его маршрут. Начав с точки (0, 0), он проследует прямо к точке (a, b), где ожидает его читатель. Читатель будет совершать путешествие в одиночку, потому что ни на одной из бесчисленных остановок, которые будет делать манделобус, продвигаясь от точки к точке, людей больше не будет. Точнее говоря, маршрут манделобуса можно описать сравнительно несложной Формулой, пользуясь которой можно определить, в какой следующий пункт следует ехать после остановки в точке (x, y), а именно

(x, y)2 + (a, b).

Что означает эта формула? Член (x, y)2 - это лишь условное обозначение точки, имеющей координаты х2-y2 и 2ху. Прибавление (a, b) к (x, y)2 означает, что следует прибавить a к первой координате, а b - ко второй. Таким образом, если мы еще не утомили наших читателей, в результате этих нехитрых арифметических операций получатся такие координаты: (х2-y2+а, 2ху+b). Где находится эта точка? Чтобы найти ее, подставим в формулу координаты x и y предыдущей остановки, а также координаты a и b первой остановки.

Манделобус всегда стартует из начала координат (0, 0) и затем сразу оказывается в точке (a, b). Чтобы убедиться в этом, читателю нужно лишь подставить нуль вместо x и y в приведенной выше формуле. Все квадраты и удвоенное произведение x на y сразу исчезают, остаются лишь a и b - координаты новой точки. Чтобы определить место следующей остановки, нужно просто подставить значения a и b вместо x и y, т.е. точка, где делается вторая остановка, всегда имеет координаты (a2-b2+a, 2ab+b).

Дорога, по которой следует манделобус, очень извилиста. Чтобы читатель получил представление о ней, на с.82 приведены траектории двух возможных маршрутов, показанных как бы с высоты птичьего полета. В первом случае манделобус, отправляясь из начала координат, останавливается, чтобы подобрать читателя, а затем совершает странную последовательность остановок, которые по спирали ведут его обратно к точке старта. Во втором случае читатель последовательно посещает ряд пунктов, которые сначала располагаются неподалеку друг от друга, но потом расстояние между ними растет, и в конце концов они убегают в бесконечность. Если вы попали на такой рейс, то лучше, наверное, соскочить на ближайшей остановке.


Два возможных маршрута манделобуса

Хотя эти два маршрута так непохожи друг на друга, каждый из них был полностью определен первой остановкой, т.е. точкой с координатами a и b и формулой. Допустим, что в первом случае читатель сел на манделобус в точке (0.300, 0.100). Подставив эти координаты в формулу, мы получим координаты следующей остановки (0.380, 0.160). Чтобы немного попрактиковаться в процедуре построения множества Мандельброта, полезно вооружиться калькулятором и вычислить координаты третьей остановки, подставив 0.380 вместо x, 0.160 вместо y, 0.300 вместо a и 0.100 вместо b в приведенной формуле. В результате получим точку (0.419, 0.222). Вот эти простые, повторяющиеся арифметические действия и движут манделобусом в его бесконечном путешествии.

Хотя поездка может продолжаться сколько угодно долго, пока есть желание повторять циклы вычислений, маршрут, по которому движется манделобус, будет либо ограниченным, либо неограниченным. Под этими словами я подразумеваю, что последовательность остановок будет всегда заключена внутри какой-то ограниченной зоны вокруг начала координат (как это имеет место в первом случае) либо выйдет за пределы этой зоны и устремится в бесконечность (как во втором случае).

Что же такое множество Мандельброта? Это просто множество всех
точек (a, b), в которых манделобус делает остановки на своем маршруте в ограниченной зоне. Множество образует непрерывный континуум в средней части плоскости, вблизи начала координат, с тонкими извивающимися ветвями на периферии. В компьютерных программах, генерирующих изображения множеств Мандельброта, цвет пиксела на экране зависит от того, устремляется ли манделобус в бесконечность из точки (a, b), представляемой данным пикселом, и если да, то насколько быстро.

Некоторым читателям, наверное, спокойнее путешествовать по ограниченным маршрутам, начинающимся внутри множества Мандельброта, поскольку они содрогаются при мысли о путешествии в бесконечность. Однако ограниченность перемещения во время путешествия, кажется, удручает математиков. Наверное, именно поэтому они закрашивают само множество черным цветом.

Существует доказанная теорема (и следовательно, это безусловно верно), что если манделобус когда-либо достигнет точки, отстоящей от начала координат на две и более единиц, то он в конце концов уедет в бесконечность. Это справедливо в тех случаях, когда точка (a, b), где делается первая остановка, лежит за пределами множества Мандельброта. Однако сколько остановок сделает манделобус, уезжающий в бесконечность, прежде чем он удалится от начала координат по крайней мере на две единицы? Это число называется задержкой точки (a, b).

Когда пытаешься вычислять задержку точки (a, b), трудно решить, где нужно остановиться. Для некоторых точек манделобусу требуется сделать 100 или даже 1000 остановок, прежде чем он навсегда покинет окрестности начала координат. С другой стороны, точка может оказаться внутри множества Мандельброта и в этом случае, сколько бы мы ни продолжали вычисления, соответствующий пиксел все равно придется окрасить в черный цвет. Вблизи границы множества располагаются точки с очень высокими значениями задержки. Для этих точек иногда приходится сделать миллион итераций, прежде чем манделобус достигнет критического расстояния в две единицы от начала координат. Поэтому программа должна принимать в какой-то мере произвольное решение, когда следует прекратить расчеты по формуле для заданной точки (a, b). Такие предельные значения, как 100 или даже 50 итераций, приводят к очень красивым и сравнительно точным изображениям множества, несмотря на то, что некоторые пикселы окажутся окрашенными в черный цвет.

Выбор других цветов, помимо черного, также зависит от задержки для той точки, которая соответствует данному пикселу. Например, программист может решить, что цвет пиксела должен быть либо черным, либо фиолетовым, либо зеленым, если представляемые им точки имеют задержку соответственно от 100 и выше, от 50 до 99 или от 1 до 49. Цвета и диапазоны задержки, соответствующие каждому цвету, можно выбирать произвольно, однако от этого выбора зависит, получится ли изображение красивым (как на приведенных иллюстрациях) либо с художественной точки зрения оно окажется непривлекательным (к чему, как я подозреваю, привел бы мой собственный выбор цветовой гаммы). На самом деле половина задачи, стоящей перед программистом, заключается в том, чтобы выбрать цвета для точек, лежащих за пределами множества, а другая половина - в том, чтобы выбрать интересные области на плоскости для построения изображения. Следует отметить, что между этими двумя выборами существует взаимная зависимость, потому что именно благодаря выбору цвета становятся видимыми области, получившие такие названия, как Долина морского конька и Самый дальний запад (где обитают удивительнейшие существа).

Чтобы заполнить весь экран компьютерного дисплея цветными элементами, принадлежащими и не принадлежащими множеству Мандельброта, нужно поочередно взять в качестве значений a и b координаты каждого пиксела на экране из заданного диапазона значений a и b. Это можно сделать при помощи двух циклов. В одном цикле варьирует a, принимая значение через каждую 1/200 в пределах заданного диапазона. Второй цикл, в который вложен первый, изменяет значение b для такого же количества шагов в диапазоне, ограничивающем значения b. Число шагов в каждом цикле должно соответствовать числу пикселов по горизонтали (для a) и по вертикали (для b) с учетом размера экрана того компьютера, на котором строится изображение.

Поскольку каждое изображение содержит лишь конечную выборку точек в какой-то области множества Мандельброта, оно никогда не сможет отразить всех деталей реальной картины. Однако, сужая диапазоны измерения a и b, можно повысить степень "увеличения". В действительности множество Мандельброта имеет уйму сложных деталей на всех уровнях увеличения. Поэтому одной из самых популярных игр для всех, увлеченных множеством Мандельброта, является увеличение отдельных областей множества до пределов, допускаемых возможностями аппаратуры, программы и просто человеческого терпения.

Увеличение заданной области изображения можно рассчитать следующим образом. Допустим, что мы строим на плоскости изображение квадратной области со стороной s. В таком случае увеличение для данного изображения будет равно 1/s. Так, квадратное изображение со стороной 0.02 единицы, например, при построении на всем экране будет иметь увеличение 50.

У меня часто возникает соблазн самому сесть в манделобус и переключить его управление с автоматического режима на ручной. Думаю, было бы увлекательно прокатиться по завиткам множества Мандельброта, осматривая их окрестности. Например, уже вдали от множества можно встретить его миниатюрные копии, как бы свободно плавающие на плоскости. По утверждениям математиков, множество Мандельброта на самом деле связано, так что можно доехать на манделобусе до каждой мини-копии множества. Однако маршрут не будет похож ни на одну земную дорогу. Если последовательно увеличивать практически любую из ветвей, окружающих множество Мандельброта, то видны будут лишь цепочки крошечных черных островков, которые кажутся не связанными друг с другом. Конечно, мы найдем цепочки более мелких островков между крупными островами, однако непрерывная дорога встречается редко или вообще не обнаруживается ни при каком увеличении.

А теперь я уступаю роль гида некоторым из наших читателей, которые после многочасовых исследований и тонкой художественной настройки создали замечательные изображения множества. Так, У.Стриклер из Баулдера (шт.Колорадо) прислал изображение под номером 1. Названное "павлином", оно было построено программой, которую Стриклер написал для своего компьютера "Амига". Значения a в его программе менялись в пределах от -0.750 до -0.746, а значения b - от 0.0986 до 0.1014. Степень увеличения для изображения, полученного Стриклером, нетрудно подсчитать по вышеприведенной формуле. Меньшая сторона прямоугольника, в котором разместилось изображение, имеет длину 0.0028. Подсчитав обратную величину (1/0.0028 ), получим увеличение, примерно равное 357.


Примеры изображений множества Мандельброта

Изображения 2, 3 и 4 заимствованы из журнала "Amygdala", издаваемого Р.Силвером в Сан-Кристобале (шт.Нью-Мексико). На изображении 2, построенном Дж.Джонсом из Бернаби (Британская Колумбия), в увеличенном виде показана хвостовая часть "морского конька". Морские коньки являются неотъемлемым элементом мини-копий множества Мандельброта, очерчивающих линию, которая отделяет восточную часть от западной части множества. Практически любой морской конек даст аналогичное изображение, если правильно подобрать увеличение и цвета.

Изображение 3 названо "каналом любви" и было получено А.Ламансом из Вартбурга (шт.Теннесси). Думаю, что это название относится к одному очень загрязненному месту неподалеку от Ниагара-Фолса (шт.Нью-Йорк). Черная часть множества Мандельброта напоминает сточную канаву, наполненную токсичными веществами, в которой пытаются выжить странного вида водоросли. Центр этого изображения находится в точке с координатами (0.235125, 0.82722) и показано оно при колоссальном увеличении в 24800 раз.

К.Филип из Фэрбанкса (Аляска), еще один из издателей журнала "Amygdala", достиг увеличения 54000 в изображении под номером 4, показывающем один из маленьких объектов, похожих на скипетр и разбросанных около морских коньков. Читатели, которые пожелают сами исследовать эту область, должны быть готовы к большой вычислительной работе. Центр данного изображения находится в точке (-1.26446153, 0.04396696).

М.Адлер воспользовался сетью ЭВМ в исследовательском центре Apollo в Челмсфорде (шт.Массачусетс), чтобы рассчитать орнамент из спиралей на изображении 5. Читатели, желающие воспроизвести эту часть множества Мандельброта, должны будут выбрать подходящие цвета для значений a и b, изменяющихся соответственно в диапазонах между 0.31186 и 0.31458 и между 0.75322 и 0.75594. Чтобы построить такое изображение, необязательно прибегать к сети ЭВМ (увеличение здесь равно 368 ), если, конечно, вам не нужно, чтобы оно было построено за несколько секунд.


"Спираль" (слева) и "мини-Мандельброт" (справа)

Изображение 6 получено Р.Спроутом и сфотографировано Р.Макколи из Сан-Франциско (шт.Калифорния). Изображение показывает одну из мини-копий множества Мандельброта, отпочковывающихся от родительского тела по бокам. Увеличение здесь приблизительно равно 20.

Печатая фрагменты множества Мандельброта на бумаге, можно получить такие же красивые изображения, как и на экране дисплея. На картинке 7 видно, как Дж.Краму, научному сотруднику из Луисвила (шт.Огайо), удалось запечатлеть россыпи рубинов, изумрудов, аметистов и других драгоценных камней, свидетельствующих о неисчерпаемых богатствах множества Мандельброта, таящихся неподалеку от той области, которую показывает изображение, полученное Спроутом. Однако в данном случае Крам решил не закрашивать черным цветом точки, принадлежащие самому множеству. В правой части изображена мини-копия множества Мандельброта, покрытая серыми полосами.


Россыпи драгоценных камней в изображении, полученном Дж.Крамом

Теперь любители могут получать подобные изображения значительно быстрее, чем это раньше было возможно при использовании домашнего компьютера. Например, можно применить алгоритм Мариани, названный по имени Р.Мариани, работавшего программистом в Научно-исследовательском центре провинции Онтарио в Торонто (Канада). В основе алгоритма лежит простая идея: если пикселы, находящиеся на границе прямоугольной области, уже окрашены черным цветом (т.е. в отношении соответствующих им точек установлено, что они являются членами множества Мандельброта), то все пикселы, лежащие в ограниченном ими квадрате, также будут черными. Другой "быстрый" алгоритм был описан У.Фишером в его замечательной новой книге "Наука фрактальных изображений" ("The Science of Fractal Images"), вышедшей под редакцией Х.-О.Пайтгена и его коллеги Д.Зупе из Бременского университета. Быстрота этого алгоритма объясняется тем, что он не вычисляет точки, принадлежащие множеству Мандельброта. Вместо этого он разбивает прилегающую к нему зону на тысячи дисков неодинакового размера и ограничивает вычисления только этими дисковыми областями.

Тем американским читателям, у кого нет времени или желания исследовать множество Мандельброта на своих собственных компьютерах, можно порекомендовать видеокассету под названием "Только увеличения" ("Nothing but Zooms"), выпущенную компанией ART MATRIX в Итаке (шт.Нью-Йорк). Она содержит потрясающие фрактальные изображения, на которые было затрачено более 40тыс.долл. в уплату за машинное время, потребовавшееся для их построения в Корнеллском национальном центре суперкомпьютеров.

БИБЛИОГРАФИЯ

THE BEAUTY OF FRACTALS. H.O.PEITGEN AND P.H.RICHTER. Springer-Verlag, 1986.

CHAOS: MAKING A NEW SCIENCE. JAMES GLEICK. Viking Penguin, Inc., 1987.

THE SCIENCE OF FRACTAL IMAGES. Edited by Heinz-Otto Peitgen and
Dietmar Saupe. Springer-Verlag, 1988.

ОТКЛИКИ

8 1989
ИТАЛЬЯНСКИЕ студенты, биржевые маклеры из Сингапура и американские физики присоединились к растущему сообществу поклонников множества Мандельброта - и все это благодаря путешествию, совершенному на Манделобусе, о чем речь шла в апрельском номере журнала. Попытки изложить в общедоступной форме основной алгоритм итераций окупились возросшим количеством пассажиров на линиях Манделобуса и даже ростом числа наших читателей. И все же, как показывает ряд писем, остались кое-какие неясности. Заметим, в частности, что лишь первая остановка Манделобуса проверяется на принадлежность точки множеству Мандельброта. Последующие остановки могут оказаться внутри или вне множества, но если хоть одна из них окажется удаленной от центра более чем на 2 единицы, первая остановка будет автоматически исключена из множества Мандельброта.

Читатели, попытавшиеся посетить область множества Мандельброта, которую А.Ламанс называет "каналом любви", были разочарованы, увидев там пустоту. Дело в том, что координаты области были указаны ошибочно. Если приставить знак минус к первой из указанных координат, то читатели попадут как раз на то место, где находится этот знаменательный источник загрязнения окружающей среды.

Возможно, на меня произвело слишком сильное впечатление увеличенное в 54000 изображение "морского конька", полученное К.Филипом из Фэрбенкса (Аляска). Такое увеличение - далеко не предел возможностей компьютера. В самом деле, увеличения такого порядка стали уже почти привычными для Д.Филипа из Скенектади (шт.Нью-Йорк) и его брата Кена. Филип из Скенектади пишет: "Когда я был в ноябре в Фэрбенксе компьютер моего брата "Mac II" построил изображение карлика [множество Мандельброта] с увеличением 2E31. Вот это действительно достижение".

Кстати, П.Гаррисон из Лос-Анджелеса объясняет, что арифметика с двойной точностью, имеющаяся в большинстве персональных компьютеров (в этом режиме число битов в машинном слове удваивается), на самом деле более чем вдвое увеличивает разрешающую способность компьютера. В действительности мощность возрастает вдвое с каждым лишним битом в представлении слова. Поэтому при помощи еще большей точности, достигаемой при использовании специальных аппаратных и программных средств, можно добиться чрезвычайно высокого разрешения.

В конце статьи я упомянул о новом быстром алгоритме вычисления множества Мандельброта, который был описан У.Фишером в книге "Наука о фрактальных изображениях" (The Science of Fractal Images, by V.Fisher). У.Кливленд из AT&T Bell Laboratories написал, что в действительности алгоритм был разработан У.Терстоном и А.Уилксом. По словам Кливленда, новый алгоритм не только быстрее, он строит более точные изображения множества по сравнению со стандартным алгоритмом. Как говорит Кливленд: "Если вы сядете на Манделобус в компании с алгоритмом Терстона-Уилкса, окрашивающего пейзаж (в черно-белом изображении), перед вами откроется новый, более реалистичный мир".

О новом способе исполнения прекрасных изображений множества, который основан, впрочем, на традиционном подходе, сообщил мне К.Ньюджент из Сиэтла. Благодаря этому приему можно наблюдать множество в виде тонкого барельефа, напоминающего спрессованные и окаменевшие останки инопланетных организмов. Хотя изображения одноцветны, они не уступают по красоте цветным исполнениям благодаря удивительному эффекту "осязаемости"; у наблюдателя создается ощущение, что он может пощупать деликатные завитушки. Этот эффект достигается за счет того, что крошечные, тончайшие узоры множества издали выглядят так, будто они подсвечены сбоку.

Идея, на которой основан этот прием, заключается в том, чтобы поделить экран на диагональные линии пикселов, протягивающиеся от левого верхнего угла экрана к правому нижнему. Если порядковый номер итерации, вычисляемый для каждого пиксела, рассматривается как "высота" пиксела, то воображаемый источник света, находящийся в левом верхнем углу экрана, будет порождать "тени" на определенных пикселах в зависимости от высоты соседних, лежащих на данной диагонали (идущей влево и вверх) пикселов. На четных диагоналях пиксел окрашивается в черный цвет только в том случае, если высота соседнего пиксела строго больше его собственной; на нечетных же диагоналях пикселы окрашиваются в черный цвет и тогда, когда соседний пиксел имеет такую же высоту. Поэтому на "плато" множества Мандельброта (т.е. в областях, где счетчики итераций пикселов имеют одинаковые значения) окраска диагональных линий чередуется. В увеличенном виде плато выглядит, как шахматная доска. "Чтобы они стали серыми,- говорит Ньюджент,- просто выбросьте свой микроскоп".

5 1989
О ВИРУСАХ, ЧЕРВЯКАХ И ВОЙНЕ В ПАМЯТИ
А.К.ДЬЮДНИ

"По-настоящему безопасной можно считать лишь систему, которая выключена, замурована в бетонный корпус, заперта в помещении со свинцовыми стенами и охраняется вооруженным караулом,- но и в этом случае сомнения не оставляют меня".
Юджин X.Спаффорд

В ДВЕРЬ постучали. По всему чувствовалось, что произошло что-то чрезвычайное. Начальник вычислительного центра оторвал голову от разложенных на рабочем столе бумаг. В кабинет вошел оператор машинного зала. "Что-то случилось. Творятся непонятные вещи. У машины не хватает памяти. Наверное, в систему проник вирус". Если бы центр был оборудован аварийными сиренами, директор наверняка включил бы их.

Подобная сцена (с теми или иными вариациями) была нередким явлением в последние годы. Вслед за этим в выпусках новостей все чаще появлялись сообщения о новых жертвах компьютерных вирусов. В них неоднократно упоминалось и о статьях из рубрики "Занимательный компьютер" в связи с разрастающейся вирусной эпидемией среди компьютеров, возможно, потому, что мы неоднократно публиковали статьи об игре "Война в памяти" - о компьютерных программах, уничтожающих друг друга. Однако, как мы увидим, "Война в памяти" не имеет прямого отношения к вирусам, поражающим компьютеры.

Чтобы понять, как действует такой вирус, необходимо детально знать систему, в которой он обитает. То же самое можно сказать и о принципах, лежащих в основе действия "червяков", "логических бомб" и других поражающих средств, способных вывести из строя компьютер. В этой связи следует указать на два обстоятельства. Во-первых, журналисты в своих сообщениях склонны неправильно освещать, а порой и вовсе искажать истории о вирусах, причем неумышленно: большинство репортеров имеют довольно смутное представление о внутреннем устройстве и работе компьютера. Во-вторых, описанием компьютерного вируса в журнальных статьях - даже относительно подробном - никто не сможет воспользоваться для его практического создания, за исключением тех, кто обладает всеми необходимыми познаниями о компьютерной системе, в которой должен оперировать вирус. Однако знающий "технопат", помешавшийся на идее уничтожения программ и данных в том или ином компьютере, едва ли нуждается в журнальных или газетных статьях, чтобы придумать способ создания вируса. Поэтому нет никакого вреда в том, чтобы описать, каким образом действует вирус и другие разрушительные программы. (На самом деле, такое описание, возможно, даже окажется полезным, если сыграет роль дополнительного стимула в усилиях, направленных на защиту компьютерных систем).

Следует с самого начала провести различие между двумя наиболее распространенными типами вредных программ. "Вирус", если можно так выразиться, едет верхом на другой программе, он не может существовать самостоятельно. "Червяк" же способен на независимое существование, и его поведение в чем-то схоже с поведением бактерии. Оба вида "инфекции", как и всякая программа, зависят от операционной системы.

Большинство читателей, наверное, знают, что всякий работающий компьютер включает в себя материальную часть (аппаратные средства) и программное обеспечение. Например, сейчас передо мной компьютер Apple IIc, а в его памяти находится программное обеспечение - программа для обработки текстов "Appleworks Word Processor". Эта программа переводит буквы, которые я набираю на клавиатуре компьютера, в ту область памяти машины, которая отведена программой для текста.

Однако программа обработки текстов не может работать сама по себе. Ей необходима операционная система, которая, помимо прочих функций, переводит программу на специальный машинный язык, позволяющий аппаратным средствам машины выполнять ее инструкции. Операционная система персонального компьютера обычно находится на магнитном диске. Чтобы начать работать с такой машиной (скажем, написать какой-нибудь текст или поиграть в игру), необходимо предварительно загрузить дисковую операционную систему (ДОС) в электронную память компьютера. В домашнем компьютере ДОС обычно автоматически зaгрyжaeтcя с диска, который может содержать или не содержать нужную программу, как только включается питание.

Чтобы выполнить нужную программу на моем персональном компьютере, я должен сначала набрать ее имя на клавиатуре. После этого ДОС отыщет на диске программу с этим именем, загрузит ее в память и потом будет выполнять одну инструкцию за другой, как показано на среднем рисунке на с.83.


При загрузке ДОС в память (слева) может быть прочитана программа (в середине) и вирус (справа) может создать свою копию

При загрузке программы ДОС отводит в электронной памяти место не только для самой программы, но и для ее "рабочего пространства". Здесь программа будет хранить все значения, присваиваемые ее переменным, массивам и т.п. При этом ДОС принимает специальные меры предосторожности, чтобы не уничтожить другие программы или структуры данных, включая ту часть операционной системы, которая в данный момент находится в памяти. Аналогичные меры предосторожности ДОС принимает при записи программ или данных на диск.

Нередко программист считает, что ему необходимо использовать команды самой операционной системы. Эти команды обычно можно найти в руководствах по ДОС. С помощью этих команд можно написать подпрограмму, которая читает файлы с диска и помещает их в оперативную память, изменяет файлы и записывает их обратно на диск - иногда с недобрыми намерениями.

Приведем пример подпрограммы-вируса, действующей по такому принципу. Она состоит из псевдокоманд ДОС и подпрограмм: маленьких внутренних программ (составляющие их инструкции хранятся отдельно от главной программы), выполняющих некоторые специальные функции всякий раз, когда к ним обращаются.

this := findfile
LOAD(this)
loc := search(this)
insert(loc)
STORE(this)

Подпрограмма под названием findfile обращается к каталогу выполняемых файлов, или программ, на диске, берет произвольное имя файла и присваивает имя этого файла переменной this (этот). В следующей строке программы используется псевдокоманда ДОС LOAD (загрузить), с помощью которой файл помещается в оперативную память компьютера. Другая подпрограмма под названием search (поиск) просматривает только что загруженную программу в поисках инструкции, которая могла бы послужить подходящим местом, когда можно занести вирус. Когда процедура search находит такую инструкцию, она определяет соответствующий номер строки и присваивает его в качестве значения переменной lос.

Теперь все готово для того, чтобы подпрограмма-вирус могла проникнуть в произвольно выбранную из каталога программу. Подпрограмма insert (вставить) заменяет выбранную инструкцию другой (например такой, как вызов подпрограммы), которая передает управление блоку команд, составляющих главное тело подпрограммы-вируса, присоединяющейся к концу программы. Затем к концу добавленной подпрограммы присоединяется инструкция, возвращающая управление "зараженной" программе, на инструкцию, следующую за вставленной.

Таким образом, когда выполняется подпрограмма-вирус, выполняется также и подмененная инструкция зараженной программы. Исходная программа работает так, будто ничего особенного не произошло. Однако, на самом деле, подпрограмма-вирус воспользовалась каким-то мгновением, чтобы захватить власть над средствами операционной системы и прицепить свою копию к еще одной программе, хранящейся на диске. Этот процесс в графической форме представлен правой частью рисунка внизу. Когда зараженная таким образом программа будет затем загружена операционной системой в память компьютера, то в процессе выполнения она заразит еще одну программу на диске, хотя внешне ее работа будет выглядеть вполне нормально.

Еще в 1984г. Фред С.Койен провел управляемый эксперимент по заражению в Университете Южной Калифорнии и выяснил, к своему немалому удивлению, что вирусы, аналогичные тому, который был только что описан, могут заразить целую компьютерную сеть всего за каких-нибудь несколько минут. Чтобы дать читателю представление о том, какой вред способны принести подобного рода вирусы, я несколько адаптирую исходный вирус Койена, записав его на псевдоалгоритмическом языке:

1234567
главная программа:
1. infect
2. if условие удовлетворяется then навредить
3. go to исходная программа
подпрограмма infect:
1. выбрать произвольно выполняемый файл
2. if первая строка файла = 1234567 then go to 1, else присоединить спереди вирус к файлу
подпрограмма: "условие удовлетворяется"
подпрограмма: "навредить"

Вирус Койена отличается местом присоединения: вместо того чтобы забираться в середину или конец исходной программы, он прикрепляется к ее началу. Первая строка программы вируса - это "узнавание кода" 1234567. Главная программа сначала вызывает подпрограмму infect (заразить), которая случайным образом выбирает выполняемый файл на диске и проверяет, начинается ли первая строка этого файла с 1234567. Если да, то данная npoграмма уже была заражена, и подпрограмма infect выбирает какую-нибудь другую программу. Если находится незараженная программа, то перед ее началом вставляется вся npoграмма-виpyc. Это означает, что программа-вирус всегда будет выполняться в первую очередь и лишь затем возвращать управление зараженной программе.

Следующие две процедуры проверяют выполнение определенного условия и совершают определенное разрушительное действие. Условием срабатывания может быть, например, определенная дата, достигнутая системным часовым механизмом, или удаление фамилии какого-нибудь служащего из списка сотрудников, которым начисляется заработная плата. В качестве разрушительного действия может быть стирание всех файлов или более "тонкое" вредительство - замена нескольких битов в некоторых местах. Возможности тут безграничны.

Условия срабатывания и разрушительные действия уже подводят нас к границе, за которой начинаются аморальные поступки. Я думаю, что ни у кого не вызывает сомнения то, что причинение ущерба компьютерным файлам при помощи вируса или какой-нибудь другой разрушительной npoграммы - это предосудительное действие. Компьютерные программы и данные - это не просто безликие цепочки нулей и единиц. В них вложена мысль человека. Зачем же разрушать то, что было сделано другими?

Создатели программ-вирусов делают это по разным причинам. Например программист, служащий в большой компании, может, затаив обиду на правление фирмы, запустить в систему вирус, который срабатывает в день его увольнения из компании. Когда это случится, фамилия программистa исчезнет из списка сотрудников, которым начисляется зарплата, и это послужит вирусу сигналом. В результате ценные данные и программы, принадлежащие компании, будут либо уничтожены, либо в них появятся серьезные и дорогостоящие ошибки. Замена поврежденных данных и программ их запасными копиями, хранимыми на других носителях, может не всегда приводить к желаемому результату, потому что, если копии сделаны недавно, они тоже могут оказаться зараженными.

Конечно, разрушения, подобные описанным выше, могут произойти лишь в компьютерной системе коллективного пользования. Операционные системы таких компьютеров значительно сложнее, чем дисковая операционная система персонального компьютера. Во-вторых, уже тот факт, что одними и теми же ресурсами пользуется не один человек, а многие, означает, что операционная система должна как можно лучше защитить одних пользователей от случайного или преднамеренного вмешательства со стороны других. Даже в такой среде могут существовать вирусы, но создавать их уже значительно сложнее. Обычно они пользуются каким-либо слабым звеном в операционной системе - ошибкой или недосмотром,- как показывает пример "вируса" (на самом деле правильнее было бы назвать его "червяком"), поразившего прошлой осенью компьютерную сеть Internet.

Вечером 2 ноября 1988г. кто-то запустил программу "червяк" с одного из нескольких тысяч компьютеров, соединенных в сеть передачи данных под названием Internet. Эта сеть объединяет машины университетских центров, частных фирм, правительственных агентов, таких как Национальное управление по аэронавтике и исследованию космического пространства, и даже некоторые военные учреждения. С ужасающей быстротой червяк распространился более чем на 1000 машин менее чем за два дня. По мере того как размножались копии червяка, операторы различных вычислительных центров стали замечать, как увеличиватся размер занятой памяти и замедляются ответы машины. Однако червяк не поражал файлы или другие программы. Казалось, его целью было лишь проникнуть как можно в большее число машин сети. Но даже при этом условии ущерб, выразившийся в количестве потерянного времени, был колоссальным.

Как уже указывалось выше, червяк - это программа, способная самостоятельно существовать в компьютерной среде; она переходит из машины в машину, повсюду оставляя свои копии. Червяк, поразивший сеть Internet, состоял из двух частей: вектора и тела. Начав работать в каком-то компьютере, червяк ищет другую машину, засылая туда свой вектор. Оказавшись внутри машины, вектор устанавливает канал связи, по которому можно переслать тело червяка. Подробности этого нападения были раскрыты Юджином X.Спаффордом из Университета Пардю в 40-страничном документе, опубликованном через несколько недель после происшествия. Об изобретательности автора программы-червяка свидетельствует следующий пример. Операция система UNIX, предпочитаемая многими пользователями сети Internet, допускает в машине процессы, не связанные ни с одним конкретным пользователем. Такие независимые процессы называются "демонами". Один подобный демон fingerd (произносится как "фингерди") дает возможность пользователям получить информацию о других пользователях. Наличие такого сервиса очень желательно в компьютерной среде, когда многие пользуются одними и теми же программами и структурами данных, предназначенными для научных и технических расчетов.

Программа-червяк, работающая в данный момент в каком-то компьютере, посылает сообщение одному или нескольким другим компьютерам, потенциальным жертвам поражения, имеющимся в списке (полученном незаконным путем). Запросив услуги демона fingerd, червяк передает ему некоторую информацию, так же, как это делает любой другой нормальный пользователь. Однако червяк сообщает демону так много информации, что она заполняет всю область памяти, отведенную демону в компьютере, и проникает в "запретную зону".

Заполненная таким образом зона при нормальных условиях отводится под инструкции, выполняя которые fingerd решает, что следует делать дальше. Попав в эту зону, червяк (тело которого все еще находится в исходной машине), активирует так называемый интерпретатор команд новой машины, по существу завладев небольшой частью операционной системы UNIX. После того как командный интерпретатор поступил в его распоряжение, червяк передает 99 строк исходного кода, составляющего вектор. Ничего не подозревающая жертва, новый компьютер, компилирует и выполняет программу вектора, и теперь заражение уже фактически гарантировано.

Программа вектор прячется в системе, меняя свое имя и ликвидируя все файлы, созданные в процессе его проникновения в систему. После этого вектор устанавливает новый канал связи с исходной машиной и с помощью стандартных системных протоколов копирует файлы, составляющие основное тело червяка.

После того как червяк проник в новую машину, его главная задача заключается в том, чтобы раскрыть имена и адреса других машин, проникнув в области памяти, отведенные законным пользователям системы. Для этого червяк применяет хитроумную процедуру угадывания паролей, которая, благодаря небрежности большинства пользователей в выборе паролей, оказалась весьма эффективной. Раскрыв пароль законного пользователя, червяк "прикидывается" этим пользователем для того, чтобы прочитать то, что он записал в память компьютера, и раскрыть имена других компьютеров сети Internet, чтобы заразить их.

Как говорит Спаффорд, в большую часть средств операционной системы UNIX (охарактеризованных им как неудачные), позволивших червяку действовать так успешно, были внесены соответствующие коррективы. Однако этот факт не устранил его обеспокоенности в отношении компьютерной безопасности, как видно из цитаты, взятой в качестве эпиграфа к настоящей статье. Возможно, он думал о теоретическом исследовании вирусов, проведенном Койеном, которое может оказаться справедливым и для червяков.

Если технопаты проявят упорство в своих варварских нападениях на компьютерные системы, то, возможно, самое время организовать Центр по борьбе с вирусами. Во время нашествия червяков на сеть Internet специалисты Калифорнийского университета в Беркли и нескольких других центров, подключенных к сети, сумели "перехватить" несколько копий червяка, проанализировали его инструкции и установили, каким образом он работает. По-видимому имеет смысл учредить национальное агенство, которое боролось бы против вирусов и червяков, когда бы и где бы они не были обнаружены; такая служба будет необходимой, если компьютерные инфекции не перестанут распространяться. Хотя случай с сетью Internet - это лишь намек на ужасы, к которым может привести нашествие вирусов, он также продемонстрировал, насколько эффективным может быть организованное сопротивление.

Койен установил, что невозможно написать компьютерную программу, способную обнаружить вирус любой природы, хотя можно найти противоядие против любого известного вируса. С другой стороны, на любое противоядие найдутся другие вирусы, которые смогут обойти его. По мнению Койена, такое угрожающее положение дел в будущем может породить компьютерные среды со своеобразным эволюционным процессом, в котором выживут лишь самые "сильные" программы.

Эта ситуация напоминает нам о "Войне в памяти", компьютерной игре, о которой уже говорилось в нескольких статьях в рубрике "Занимательный компьютер" (см. "В мире науки", 1984, #7; 1985, #5 и 1987, #3). Однако "Война в памяти" не трогает ни в чем неповинных компьютерных систем. Ее программы ищут лишь себе подобных - другие программы, предназначенные для игры. Две программы вступают в бой в специально отведенной области компьютерной памяти, называемой колизеем. Не существует опасности, что программа игры "Война в памяти" когда-нибудь вырвется на свободу и причинит вред кому бы то ни было, потому что программа "Войны в памяти" или любая подобная ей программа никогда не сможет работать в нормальной компьютерной среде. Программы этой игры написаны на специальном языке "Редкод". Основные команды этого языка сведены в таблицу, приведенную на с.84.


Система команд для "Войны в памяти"

Простой пример такой программы поможет ввести в курс дела читателей, еще незнакомых с игрой. Ниже приведена программа DWARF (карлик), которая бросает нулевые бомбы в каждую пятую ячейку памяти:

DAT -1
ADD #5 -1
MOV #0 @-2
JMP -2

Арена колизея (область памяти, в которой обитают все программы "Войны в памяти") состоит из нескольких тысяч адресов, или пронумерованных ячеек памяти, организованных в длинную непрерывную полосу. Инструкции, составляющие программу DWARF, например, занимают 4 последовательных ячейки колизея с адресами, скажем, 1001, 1002, 1003 и 1004.

Инструкция DАТ служит для того, чтобы хранить число, используемое в программе (в данном случае -1), и записана в ячейку с адресом 1001. Инструкция ADD прибавляет число 5 к содержимому ячейки, отстоящей на
-1 адрес от инструкции ADD. Поскольку последняя имеет адрес 1002, то число 5 прибавляется к числу, хранящемуся по предшествующему адресу, т.е. по адресу 1001, заменяя число -1 на 4. Инструкция MOV помещает число 0 в ячейку памяти с адресом определенным как @-2. Где это? Этот адрес вычисляется путем обращения к инструкции DAT, расположенной на две ячейки позади от инструкции MOV. Там находится адрес ячейки, куда программа должна поместить 0. Заключительная инструкция JMP передает управление программе DWARF на две инструкции назад, т.е. возвращает ее на инструкцию ADD. В результате весь процесс повторяется снова.

После вторичного выполнения, программа заменит содержимое ячейки с инструкцией DAT на 9 и поместит 0 в ячейку с этим адресом. Если по этому адресу хранится одна из инструкций программы противника, она будет стерта и, так как на ее месте окажется невыполнимая команда, программа противника может "погибнуть".

Программа DWARF бросает нулевые бомбы в каждую пятую ячейку памяти до тех пор, пока не достигнет последнего адреса - но арена нигде не кончается, потому что последний адрес прилегает к первому. Следовательно бомбы, разбрасываемые "карликом" начинают падать все ближе и ближе к его собственным ячейкам. Однако, поскольку длина "карлика" равна всего 4 ячейкам, а общее число ячеек памяти обычно кратно 10, программа избегает случайных попаданий своих собственных бомб, продолжая жить и сражаться - хотя вслепую и довольно глупо.

За последние несколько лет "Война в памяти" превратилась в весьма замысловатую игру с многочисленными и разнообразными стратегиями и контрстратегиями. Существуют программы, разбрасывающие повсюду свои копии, программы, стреляющие "безмозглыми" боевыми программами, состоящими лишь из одной инструкции, и даже такие программы, которые "ремонтируют" себя после вызванных атакой неприятеля разрушений.

Международная ассоциация любителей игры "Война в памяти" со штаб-квартирой в Лонг-Биче (шт.Калифорния) и филиалами в Италии, Японии, Польше, Советском Союзе и ФРГ ежегодно организует турниры, в которых программисты могут испытать свое искусство. Читатели, желающие вступить в ассоциацию любителей игры, могут написать Уильяму Р. Бакли по адресу: William R. Buckley, 5712 Kern Drive, Huntington Beach, Calif. 92649.

В турнире 1987г. программы, присланные из Японии, задали немало хлопот боевым программам Северной Америки. А победителем последнего турнира, состоявшегося в декабре прошлого года в Лос-Анджелесе, оказалась программа из Советского Союза, получившая, как это ни странно, имя COWBOY (ковбой). Написанная Е.Лилитко из Переславля-Залесского, небольшого города недалеко от Москвы, программа COWBOY следила за "бомбометанием" программ противника, уходя из опасной зоны и затем переходя к мощным контратакующим действиям. Лилитко выиграл первый приз в 250долл. Второго приза в 100долл. был удостоен Джованни Чирауло из Пистои (Италия). Третий приз в 50долл. достался Дугласу Макдэниелсу из Александрии (шт.Вирджиния).

В заключение я еще раз процитирую высказывание Спаффорда: "Придумать и запустить вирус - это акт не программиста-профессионала, a компьютерного варвара". Пусть те, кто замышляет подобные дела, лучше попробуют свои силы в "Войне в памяти".

(По всем вопросам, связанным с игрой "Война в памяти" следует обращаться по адресу: 152140, Переславль-Залесский Ярославской обл. Институт программных сетей АН СССР - Ред.).

БИБЛИОГРАФИЯ

COMPUTER VIRUSES. In Computers and Security, Vol.7, No.2, pages 117-125, 139-184; April, 1988.

COMPUTER VIRUSES. In American Scientist, Vol.76, No.3, pages
236-238; May-June, 1988.

ОТКЛИКИ

9 1989
ТЕМОЙ статьи в нашей рубрике майского номера журнала был компьютерный вандализм: злонамеренные программы, размножающиеся в памяти машины и выводящие из строя полезное программное обеспечение. Нашествие таких компьютерных "вирусов" и "червяков" продолжается. Больше года ходили слухи о новом вирусе, поражающем программы для табличных расчетов, и недавно эти слухи подтвердились. Эксперт по вирусам Харольд Хайленд, редактор журнала "Computers and Security" ("Компьютеры и безопасность"), называет эту новую инфекцию макровирусом, поскольку она основана на командах, называемых макросами.

Получить детальную информацию о вспышке макровируса довольно трудно, наверное, потому, что она поразила корпорации, которые совсем не заинтересованы афишировать эти неприятные подробности. Говорят, что одна из версий вируса распространяется с программами "Лотус 1-3-3". Всякий раз, когда пользователь выполняет зараженную программу, вирус вызывает из памяти произвольную таблицу, изменяет на небольшую величину число, содержащееся в какой-то одной ячейке и возвращает измененную рабочую таблицу в память. Потенциально вирус может нанести большой ущерб, поскольку небольшие изменения в данных могут остаться незамеченными в течение нескольких месяцев, существенно влияя на результаты вычислений.

Несмотря на эти новые факты, Том Питтмен из Спрекелса (шт.Калифорния) считает, что в своей статье, опубликованной в майском номере, я несколько преувеличил опасность, связанную с вирусами. По его мнению, следует проводить четкое различие между полезными и разрушительными вирусами. Это различие может быть семантическим. Дело в том, что существуют полезные программы, которые ведут такой же образ жизни, как вирусы или черви. Они выполняют разнообразные функции, от сжатия файлов до сканирования входной информации, однако обычно их не называют ни вирусами, ни червями.

Е.Хайнляйн из Милл-Вэлли (шт.Калифорния) намерен добиваться создания центра по борьбе с компьютерными болезнями по аналогии с Центром по борьбе с (человеческими) заболеваниями, созданным в Атланте. Подобный центр был бы частью более широкой программы по изучению, классификации и подготовке нового законодательства, касающегося информирования общественности об эпидемиях вируса и наказания виновных. Исследования, предпринятые в рамках этой программы, возможно, помогут созданию новых фильтров и методов обнаружения вируса, а также методов восстановления поврежденных вирусом компьютерных систем.

6 1989
ОБ ОДНОМ МАТЕМАТИЧЕСКОМ ПАРАДОКСЕ И ЗОЛОТОМ СЛИТКЕ, ПОЛУЧЕННОМ ИЗ НИЧЕГО
А.К.ДЬЮДНИ

Ничто не возникает из ничего.
Лукреций

ПРИЗНАТЬСЯ, поначалу я не очень удивился, получив примерно гол назад длинное послание, автор которого утверждал, что изобрел машину, производящую материю. Не секрет, что среди тех, кто пишет мне, нередко попадаются люди, утверждения которых выглядят, по меньшей мере, невероятными. Но поскольку наука должна быть свободна от предрассудков и терпимой к различным точкам зрения, я стараюсь не торопиться с выводами и читаю письма до конца.

Именно так я и поступил с этим письмом. Изобретатель основывал свое утверждение на известном в математике парадоксе Банаха-Тарского. Названный по имени двух польских математиков, открывших его в 20-е годы нашего столетия, этот парадокс показывает, каким образом при определенных условиях идеальное геометрическое тело можно разрезать на куски, из которых затем получить новое тело, вдвое больше исходного.

Написавший мне изобретатель оказался профессиональным математиком, автором многих научных публикаций. По причинам, которые вскоре станут понятными, он не хочет называть своего имени и попросил, чтобы я называл его Арло Липоф (Arlo Lipof [Имя и фамилия составлены из букв английского выражения April Fool - первоапрельская шутка. - Прим. ред.]). Зная о парадоксе Банаха-Тарского, Липоф решил проанализировать возможность применения этого математического парадокса к физически реальным телам. Его исследования были щедро вознаграждены: он написал компьютерную программу, дающую точный рецепт, согласно которому физическое тело можно разрезать на много частей причудливой формы, а затем собрать их в тело вдвое большего размера, не содержащее никаких пустот между составными частями!

Очевидно, значение программы Липофа трудно переоценить. Чтобы объяснить сущность парадокса и то, каким образом он использовался в программе, лучше всего процитировать отрывок из письма, написанного самим Липофом.

"Парадокс напоминает известную головоломку с танграммами, маленькими кусочками бумаги, нарезанными в форме простых геометрических фигур. Из четырех таких фигурок можно собрать квадрат площадью 64 квадратных дюйма (примерно 413см2). Однако те же самые фигурки можно собрать в виде прямоугольника, имеющего большую площадь, а именно 65 квадратных дюймов. Если вы не верите, что это возможно, вырежьте фигурки, показанные на моем рисунке [внизу (размеры указаны в дюймах)].


Как получить из ничего кубический дюйм золота

Если бы вместо кусочков бумаги у нас были кусочки золота, то, сложив из квадрата прямоугольник, мы бы приумножили свое богатство. Начнем, например, с золотого квадрата, скажем, со стороной 8 дюймов и толщиной 1 дюйм. Разрежем квадрат согласно рисунку слева. Если теперь из его фрагментов собрать геометрическое тело, показанное на рисунке справа, то появится лишний кубический дюйм золота, который весит приблизительно 4.3 унции (примерно 122г) и по текущему курсу золота стоит около 1800долл.".

Далее Липоф признает - ощущение, будто мы получили нечто из ничего в приведенном примере, конечно, чисто иллюзорное. Однако, утверждает он, несмотря на то, что парадокс Банаха-Тарского "производит такое впечатление", теоретически в нем нет никакой ошибки. Парадокс Банаха-Тарского вполне реален - по крайней мере в математическом смысле.

Парадокс вытекает из доказанной теоремы, математическая формулировка которой, можно сказать, почти понятна: если A и B два произвольных ограниченных подмножества пространства R3, каждое из которых имеет непустую внутренность, то A и B эквивалентно разложимы. Теорему можно изложить проще, если сначала представить себе два тела, практически любой формы и размера, удовлетворяющие двум условиям: каждое тело должно быть "ограниченным", т.е. таким, которое можно заключить в полую сферу определенного размера, и каждое тело должно иметь "непустую внутренность" - другими словами, где-то во внутренней части тела всегда можно найти сферу, целиком заполненную материалом, из которого состоит это тело.

Очевидно, два приведенных условия не очень строгие. В самом деле, практически любой мыслимый объект, не удовлетворяющий этим двум условиям, едва ли можно назвать телом в привычном понимании слова. Бесконечная прямая линия, например, нарушает оба критерия: она не ограничена и ее внутренность пуста в том смысле, что она вообще не имеет никакого внутреннего пространства. Аналогичным образом исключенным из рассмотрения будет и воображаемое облако точек, распространяющееся в бесконечность во всех направлениях, этот объект также вряд ли можно назвать телом.

Итак, согласно теореме, любые два таких ограниченных тела с непустой внутренностью должны быть "равноразложимыми". Это означает, что оба тела можно разрезать на конечное число частей, которые конгруэнтны в геометрическом смысле: часть одного тела можно сделать идентичной части другого тела просто путем ее поворота. Следовательно, теоретически одно тело можно разрезать на части A1, A2, A3.., а другое - на части B1, B2, B3... таким образом, чтобы соответственно части A1 и B1, A2 и B2 и т.д. были идентичными друг другу. В этом и заключается сущность парадокса Банаха-Тарского.

"Таким образом,- пишет Липоф,- мы можем взять две сплошные сферы, одна из которых вдвое больше другой, и разрезать их на части, так чтобы они были попарно конгруэнтны. Забудем о большей сфере и рассмотрим меньшую. Предположим, что она сделана из золота. В принципе оказывается возможным разрезать ее на конечное число частей, которые затем можно снова собрать в сферу вдвое большего размера".

Здесь нет никакого мошенничества, хотя, конечно, под невинным словом "части" подразумеваются объекты с определенными топологическими свойствами. Во-первых, эти объекты совсем не обязательно просты по форме или даже состоят из связных фрагментов. Некоторые фрагменты одной части могут быть сколь угодно близкими друг к другу, но фактически не соприкасаться. Более того, эти части невозможно точно измерить каким-либо способом. Например, трудно даже представить себе, каким образом можно измерить их объем и как бы они выглядели на самом деле. По выражению Лилофа, "они ни на что не похожи. По сравнению с ними даже фракталы выглядят простыми танграммами".

Парадокс Банаха-Тарского справедлив в своей наиболее общей формулировке лишь для пространства трех и более измерений. Однако существуют аналогичные теоремы, иллюстрирующие существо парадокса в пространствах более низкой размерности. Одним из примеров этого явления может служить одномерное "пространство", состоящее из всех целых чисел, поскольку подмножество из всех четных чисел представляет одновременно и половину множества, и само множество. Это подмножество является половиной множества всех целых чисел в том смысле, что каждый второй элемент множества принадлежит подмножеству. Однако простое преобразование - деление каждого элемента подмножества на 2 - превращает четные числа в множество всех целых чисел; множество и его подмножество имеют один и тот же размер.

Большинство людей не считают этот факт чем-то примечательным, потому что размеры как самого множества, так и его подмножества бесконечны. В конце концов, бесконечность, поделенная на 2, остается все же бесконечностью. Гораздо интереснее было бы найти некое конечное множество, которое можно было бы разложить на "парадоксальные" части, но, согласно теории, это невозможно, по крайней мере, если ограничиться одномерными пространствами. То же самое относится и к евклидовым пространствам с двумя измерениями, или "плоским" поверхностям. Однако это оказывается возможным в некоторых неевклидовых двумерных пространствах.

Полное объяснение этого явления выходит за рамки настоящей статьи, однако я могу дать читателям некоторое представление о его парадоксальной природе, спроектировав экзотический мир двумерного гиперболического пространства на обычный евклидов круг, как показано на рисунке на с.79. В верхней части рисунка изображено гиперболическое пространство, занимающее половину плоскости. Его геометрия неевклидова и кратчайшее расстояние между двумя его точками не является отрезком прямой линии, соединяющей эти точки, а определяется полуокружностью. На этом рисунке гиперболическое пространство расчленено на "треугольные" области, размеры которых постепенно уменьшаются в направлении нижнего края пространства. Эти треугольники образуют основу для парадоксального разложения пространства на три части, окрашенные в красный, синий и желтый цвета. Для математиков в данном контексте "часть" или "кусок" могут и не быть таковыми в полном смысле слова. Они могут состоять из бесконечного числа фрагментов треугольной или какой-нибудь другой формы.


Две проекции гиперболического пространства (вверху) на круги (внизу). Красная часть одновременно есть и половина, и третья часть гиперболического пространства.

Необычная природа этих трех составных частей проявляется с особой очевидностью, если рассматривать гиперболическое пространство через специальную математическую "замочную скважину", т.е. спроектировав пространство двумя различными способами на круг. Точка, обозначенная в гиперболическом пространстве как P, лежит в центре левого круга, а точка, обозначенная как I, лежит в центре правого круга.

Каждый круг, очевидно, обладает простой вращательной симметрией по отношению к трем частям. Рассмотрим красную часть на круге слева. Если представить себе, что крут повернулся вокруг оси, проходящей через его центр, на 120o, или на треть оборота, то мы увидим, что красная часть наложится точно - фрагмент на фрагмент - на синюю часть. Еще один поворот на 120o приведет к наложению красной части на желтую. Другими словами, эти три части конгруэнтны и вместе составляют все гиперболическое пространство.

Парадоксальная природа пространства становится очевидной, если обратить внимание на второй круг. Здесь мы видим, что та же самая красная часть оказывается конгруэнтной по отношению к двум другим частям как единому целому. Чтобы убедиться в этом, представьте себе, что красная часть повернулась на 180o, или на полоборота, вокруг оси, проходящей через центр круга. Красный объект в точности наложится на синий и желтый объекты, закрыв их оба. Таким образом, мы нашли часть двумерного гиперболического пространства
(красная часть), которая одновременно оказалась равной и половине, и третьей части всего пространства.

Смысл демонстрации этого примера, возможно, каким-то образом затерялся за математическими манипуляциями. "Ну и что?- спросит читатель.- Что тут особенного?" Дело же в том, что три множества, представленные закрашенными частями, абсолютно конгруэнтны друг другу в гиперболическом пространстве. Тот факт, что красная часть выглядит конгуэнтной одновременно половине и третьей части гиперболического пространства на одном круге, является результатом искажений, которым подвергается гиперболическое пространство при таком проектировании.

Однако для рассмотрения наиболее общей версии парадокса Банаха-Тарского не нужно прибегать к гиперболам или гиперболическим пространствам. В евклидовом трехмерном пространстве (описывающем физический мир, в котором мы живем) любые два тела, удовлетворяющие очень простым условиям, являются равноразложимыми. К сожалению, доказательство этого факта неконструктивно в том смысле, что оно не дает описания процедуры, с помощью которой можно было бы продемонстрировать равноразложимость двух неравных сплошных шаров.

Здесь я опять процитирую отрывок из письма Липофа: "Я потратил много лет на изучение парадокса Банаха-Тарского и связанную с ним теорию. Наиболее примечательным во всем этом мне показался неконструктивный характер доказательства для трех измерений. Хотя математикам известно, что теоретически сплошной шар можно разбить на конечное число частей и затем собрать из них другой сплошной шар вдвое большего размера, никто не имел ни малейшего представления, каким образом должны выглядеть эти части, потому что способ вырезания частей основан на том, что специалисты по теории множеств называют аксиомой выбора.

Эта аксиома была названа так потому, что она постулирует: для любого набора множеств, неважно насколько большого, существует способ выбрать элемент из каждого множества совокупности. На самом деле многие математики предпочитают не прибегать к помощи этой аксиомы, потому что она не дает никакой информации о способе, при помощи которого осуществляется выбор.

По этой причине никто не представлял себе, как на практике могут выглядеть части парадоксального разбиения до тех пор, пока я не занялся изучением этого вопроса. Мне удалось автоматизировать доказательство парадокса Банаха-Тарского. В доказательстве указывается, что второй (больший) шар можно собрать путем вращения частей первого шара в двух направлениях относительно его центра, подобно тому как мы это делали с гиперболическим пространством... С помощью этих поворотов каждая часть первого шара устанавливается на соответствующее место во втором шаре. При известных точках, составляющих каждую часть, и необходимых вращениях было относительно нетрудно восстановить процедуру, при помощи которой следует разрезать первый шар на части. Всякий раз, когда в ходе доказательства требовалось обращение к аксиоме выбора, я просто прибегал к помощи генератора случайных чисел в моем персональном компьютере и таким образом мог установить, каким множеством принадлежали те или иные точки шара.

Честно говоря, на протяжении всех этих исследований я и не подозревал, что приближаюсь к открытию машины, производящей материю. В конце концов, я ведь понимаю, что следует четко различать идеальные математические пространства и то физическое пространство, в котором мы живем. Но когда я завершил свою первую модель доказательства теоремы Банаха-Тарского, я понял, что располагаю чем-то вроде рецепта, с помощью которого можно удвоить размеры любого тела.

Мне пришла в голову мысль поэкспериментировать с реальным физическим веществом, но вначале на этом пути возникло препятствие. Размеры фрагментов, вычисленные моей программой, выражались числами с тройной машинной точностью, которая требовала чуть ли не того, чтобы я разрезал пополам отдельные атомы, изготовляя необходимые фрагменты! Кроме того, у меня вообще начали возникать сомнения, что я нахожусь в здравом уме: уже из-за самой идеи провести реальное разбиение сплошного шара у меня возникло ощущение, что я живу в каком-то сне.

Снова и снова я говорил себе, что это, конечно, невозможно, но, как оказалось, напрасно. Наконец настал момент, когда я уже не мог больше откладывать эксперимент. Взяв в банке значительную часть своих сбережений, чтобы купить 12 унций (примерно 340г) золота, я попросил отлить его в виде шара и, купив маленькую пилу для ювелирных работ, начал вырезать из шара части, следуя рецепту своей программы. Здесь мне очень пригодилась вторая программа. Она точно указывала размеры и форму каждой части, а также подсказывала мне, куда должна быть помещена каждая часть во втором шаре.

Весь эксперимент, от начала до конца, продлился семь месяцев. Я работал по вечерам и в выходные дни. Закончив, наконец, вырезать части, я приступил к сборке второго шара, вдвое большего размера. Это была тонкая и утомительная работа. Я почти ослеп и страдал от головной боли, но не сдавался. Постепенно второй шар начал принимать свои очертания - но он не был гладким шаром. Отдельные части не прилегали друг к другу так плотно, как требовалось. Между фрагментами, которые я с такой тщательностью устанавливал по месту тонким пинцетом, возникали крошечные зазоры.

Наконец, еще через несколько недель шар был полностью собран. Я высылаю вам рисунок, показывающий структуру его поверхности [см. рисунок на с.80]. Несмотря на то что ваши читатели увидят карту поверхности шара, секрет все же не будет раскрыт: поверхностная структура - это пустяки в сравнении со сложным внутренним расположением фрагментов, из которых собран шар. Во всяком случае, настоящий шар не был таким гладким и круглым, как на моем рисунке. Он получился неровным и шероховатым. Но с каким волнением я сжимал в руках мешочек, в котором лежал мой шар, когда я отправился к ювелиру. Конечно, окончательно результаты моей работы будут выявлены тогда, когда мой шар будет расплавлен и я узнаю, действительно ли получил в восемь раз больше золота, чем содержалось в исходном шаре.


Исходный золотой шар (слева) и его реконструкция (справа), выполненная Липофом

На следующий день ювелир вручил мне слиток чистого золота весом 49.58 унций (около 1.4кг). Это было меньше, чем я ожидал; видимо, эти зазоры все-таки сделали свое дело. Но все же в главном теперь не было никаких сомнений. Впервые в мире парадокс Банаха-Тарского получил практическое применение. В течение нескольких дней у меня кружилась голова при мысли о совершенном мною открытии. И сейчас я просто не знаю, что делать дальше".

После этого первого письма от Липофа не было никаких вестей в течение нескольких месяцев. Но как-то в ноябре прошлого года почтальон принес мне от него короткое письмецо, отправленное из одного южноамериканского государства:

"Вам, конечно, небезынтересно будет узнать, что я в некоторой степени автоматизировал процедуру получения больших золотых шаров из маленьких. На оставшуюся часть моих сбережений я организовал мастерскую в маленьком городке N. Здесь несколько моих надежных помощников собирают золотые шары. Рабочее помещение оборудовано компьютерами и столами, за которыми мои люди собирают шары. Теперь фрагменты не вырезаются, а сразу отливаются в нужной форме, а затем подвергаются механической обработке. По завершении процесса у нас всегда получается лишнее золото, которое мы опять пускаем в работу. В настоящее время мы производим около пяти фунтов золота в неделю "из ничего". Может быть, это и есть философский камень, о котором мечтали алхимики? Скоро отсюда придется переезжать в другое место. Наверное, я вам больше не буду писать, это становится опасным. Простите меня, мой друг, но перед лицом такого потенциального богатства поневоле становишься мнительным. Нужно еще так много сделать... "

Больше я ничего не слышал о Липофе. Но в декабре прошлого года, чисто из любопытства, я начал следить за тем, как меняется день ото дня курс золота на бирже. На протяжении трех месяцев он медленно, но неуклонно падал. Возможно, это послужит окончательным доказательством для тех, кто считал парадокс Банаха-Тарского просто математической забавой.

Конечно, я проконсультировался и у других математиков по вопросам, связанным с этим парадоксом. Хочу выразить свою особую признательность Бруно У. Огенстейну из корпорации RAND в Санта-Монике (шт.Калифорния). Именно Огенстейн посоветовал мне воспользоваться гиперболическим пространством для иллюстрации парадоксальных свойств, присущих пространствам.

Несмотря на то что Огенстейн не верит утверждениям Липофа, он все же допускает, что между парадоксом Банаха-Тарского и реальным миром может существовать какая-то связь. В одной из научных статей Огенстейна. "Физика адронов и теория трансфинитных множеств", указывается на связь между физикой элементарных частиц и парадоксальными разложениями объектов в трехмерном пространстве. В статье предложены некоторые аналоги, из которых "непосредственно вытекают многие известные физические результаты, а также новые результаты, которые в принципе поддаются экспериментальной проверке. Цвет кварка и явление удержания кварка... получают непосредственное объяснение благодаря аналогиям с теоремами разложения". Среди наших читателей, наверное, найдутся не только алхимики, но и физики, которых заинтересует эта идея.

БИБЛИОГРАФИЯ

TANGRAMS - 330 PUZZLES. RONALD С. READ. Dover Publications, Inc., 1965.

HADRON PHYSICS AND TRANSFINITE SET THEORY. B.W.AUGENSTEIN in International Journal of Theoretical Physics, Vol.23, No.12, pages 1197-1205; December, 1984.

THE BANACH-TABSKI PARADOX, STAN WAGON. Cambridge University Press, 1985.

ОТКЛИКИ

10 1989
НАША статья в июньском номере журнала, посвященная шутливой теме о получении материи из ничего, вызвала многочисленные отклики читателей. В статье рассматривались два метода получения "дополнительной" материи, оба основанные на парадоксах. Первый метод заключался в разрезании квадрата 8*8 дюймов на четыре части, из которых затем собирался прямоугольник размером 5*13 дюймов. Если эту операцию применить к квадрату, сделанному из золота, то можно было бы быстро обогатиться.

Большинство читателей решило "парадокс", тщательно изучив приведенный в статье чертеж. Собранный прямоугольник, конечно, был подделкой (на что явно указал Липоф). Если попытаться собрать из фрагментов квадрата прямоугольник, как показано на рисунке, то в его середине будет зазор. Его площадь в точности равна одному квадратному дюйму. Следовательно, первый "парадокс" вовсе не является парадоксом. Это старый трюк, с которым я впервые познакомился, прочитав очаровательную книгу Р.Рида "Танграммы".

Второй парадокс совершенно реален, даже если он, несмотря на утверждения Липофа, и не может быть применен для производства материи. Парадокс Банаха-Тарского гласит, что шар можно разрезать на конечное число фрагментов таким образом, что из них можно собрать другой сплошной шар вдвое большего объема! Восклицательный знак, поставленный мною, возможно покажется излишним тем читателям, которые отдают себе отчет, что эти "фрагменты" совсем не просты и их лучше описывать как математические множества.

Схема, иллюстрирующая описание парадокса, была заимствована из книги С.Вэйгона, сотрудника колледжа Смита, под названием "Парадокс Банаха-Тарского". На рисунке двумерное гиперболическое пространство проектируется на плоский круг двумя различными способами. Рисунок служит наглядной демонстрацией парадоксальной природы пространства. Показаны три множества, каждое из которых одновременно равно половине и третьей части пространства. Теорема, положенная в основу иллюстрации, была результатом совместной работы Вэйгона и Яна Мициельски из университета Колорадо в Боулдере.

В последнее время парадокс Банаха-Тарского стал привлекать внимание математиков в связи с работами Миклоша Лашковича из Будапештского университета (см. заметку в рубрике "Наука и общество" в сентябрьском номере нашего журнала). Лашкович доказал, что круг можно разложить на конечное число фрагментов (на самом деле это число меньше 1E50), а затем собрать из них квадрат той же площади.

11 1989
И наконец, постскриптум к нашей июньской статье с ее шутливым сюжетом о производстве золота. В этой статье я несколько раз процитировал свою переписку с некоей сомнительной личностью по имени Арло Липоф. Липоф, в частности, утверждал, что уже несколько сбил рыночную стоимость золота, применив теорему Банаха-Тарского на практике для производства золота из ничего. Недавно я получил сердитое послание от организации "Международный совет по вопросам золота" со штаб-квартирой в Нью-Йорке. В письме говорится, что я несу полную ответственность за "неразбериху" и "крах цивилизации", которые могут стать следствием разглашения секретов Липофа. И далее: "В течение долгих лет наша организация принимала все меры к тому, чтобы парадокс Банаха-Тарского не стал известен широкой общественности... Мы всегда знали, что апокалиптическая возможность производства большего количества золота из меньшего имела бы роковые последствия для международного баланса в мировой финансовой системе".

7 1989
МОДЕЛИРОВАНИЕ ЭВОЛЮЦИИ: "БУКАШКИ" УЧАТСЯ ОХОТЕ НА БАКТЕРИЙ
А.К.ДЬЮДНИ

Для тех, кто, подобно мне, не очень силен в математике, компьютер - это могучий друг воображения.
Ричард Докинз, "Слепой часовой мастер"

НА ИЛИСТОМ дне прудика с застоявшейся водой копошатся инфузории, простейшие одноклеточные организмы. Они питаются бактериями, медленно оседающими на дно, подобно моросящему дождю. Внешне все инфузории выглядят одинаково, но в их поведении можно уловить важные различия. Одни движутся хаотично в поисках бактерий, и в результате их добыча скудна, другие передвигаются более целенаправленно, можно сказать, почти методично, и у них пищи в изобилии. Наблюдать такие микромиры - очень увлекательное занятие, однако в данном случае описываемая сцена имеет особое значение: методично движущиеся простейшие произошли от своих безалаберных предков всего лишь час назад!

Как уже, наверное, догадались многие читатели, эту сцену мы наблюдали не в микроскоп, а на экране компьютера. Действие на экране порождается программой "Модель эволюции", которую создал Майкл Палмайтер, учитель средней школы из Тэмпл-Сити (шт.Калифорния). Крошечные белые инфузории, которых Палмайтер называет букашками, ползают по экрану, поедая фиолетовых бактерий. по мере того как одно поколение букашек сменяет другое, можно наблюдать, как изменяется их поведение в охоте за бактериями.

Ричард Докинз из Оксфордского университета также пытался проникнуть в тайны эволюции, исследуя программы, в которых он пытается моделировать различные ее аспекты. Одна такая программа, написанная самим Докинзом, была темой нашей статьи, опубликованной немногим более года назад (см. "В мире науки", 1988, #4). В программе Докинза действующими лицами являются биоморфы - генерируемые компьютером формы, иногда напоминающие живые организмы. Они эволюционируют в процессе искусственного отбора: оператор, работающий с компьютером, произвольным образом выбирает одну из 9 возможных вариаций существующего в данный момент биоморфа в качестве основы для последующих поколений.

Биоморфы, порождаемые программой Докинза, могут принимать весьма причудливые формы (иногда они даже похожи на живые организмы), однако о них нельзя сказать, что они являются продуктом естественной эволюции, т.е. внутреннего естественного отбора. И все же Докинз считает, что можно создать компьютерную программу, которая действительно моделировала бы естественный отбор. Генерируемые компьютером "виды", обладающие способностью к "эволюции", могли бы порождать все более сложные формы, многообразие которых ограничивалось бы до разумных пределов механизмом отбора. Более того, выжившие потомки могли бы затем эволюционировать в новых направлениях, совершенно недоступных для их предков.

Одноклеточные букашки Палмайтера, несомненно, являются шагом, приближающим нас к цели, которую поставил перед собой Докинз. Взглянув на рисунок, приведенный на рис.85, мы видим, что букашки (белые комочки) населяют прямоугольник, в который непрерывно поступают осаждающиеся бактерии (фиолетовые точки). Букашки ведут образ жизни, в котором главную роль играют движение и поедание бактерий. Каждая съеденная бактерия придает букашке 40 единиц энергии, которой хватает на то, чтобы сделать 40 движений. В местах скопления корма букашка может за несколько минут набрать 1500 единиц энергии. Однако сразу после этого начинает действовать странный механизм: сколько бы букашка ни ела, запас ее энергии не увеличивается до тех пор, пока он снова не упадет ниже 1500 единиц.


"Трясучки" постепенно эволюционируют в "крейсера"

В то же время может случиться и так, что букашка окажется на голодном пайке в течение достаточно длительного времени. В этом случае запас энергии, которым обладает букашка, может постепенно снизиться до нуля. Букашка замирает на несколько циклов, как бы размышляя о своей близкой кончине, а затем исчезает.

Конечно, для того чтобы букашка всегда была сыта, необходимо, чтобы около нее было относительно большое количество бактерий. Поскольку изначально бактерии распределены на экране более или менее равномерно, интенсивная охота на них в одном месте приводит к тому, что там их становится мало, а в других областях - много. Некоторые букашки, кажется, быстрее других обнаруживают места скопления корма. Здесь все зависит от движений, совершаемых букашкой - так сказать, от ее тактики поиска добычи.

Дарвинистский сценарий программы моделирования эволюции, хотя и носит весьма абстрактную форму, основан на "генах", управляющих поведением букашек. Подобные гены, возможно, не существуют у реальных простейших, у букашек же Палмайтера их шесть. Назовем их В, П, СП, Н, СЛ и Л - соответственно для движений Вперед, наПраво, Сильно наПраво, Назад, Сильно наЛево и наЛево. (Все направления взяты с точки зрения самой букашки. Нормальный угол поворотов составляет 60o в соответствующем направлении, "сильные" повороты составляют 120o).

Направление каждого нового движения выбирается случайным образом: программа выбирает одно из шести возможных направлений, как бы бросая жребий. Если выпало, к примеру, Л, то букашка совершает поворот на 60o влево. Вероятность выпадания того или иного направления зависит от числового значения, присвоенного каждому из шести генов. Таким образом, чем больше значение гена, тем больший вклад этот ген вносит в характер поведения букашки. Если, например, у букашки превалирует ген Л, то большую часть времени она будет проводить в движении, направленном в левую сторону.

Каждая из возможных комбинаций числовых значений генов приводит к тому или иному характеру движения, отличному от поведения других букашек. Какие бы гены не были у организма, они останутся неизменными на протяжении всей его жизни. Ему остается лишь надеяться (возможно, это звучит несколько антропоморфно), что у его потомков генный набор окажется более удачным.

После того как букашка совершит 800 движений, она становится "созревшей" и готова к воспроизведению себе подобных. Однако размножаются лишь "сильные" букашки, хранящие под своей белой оболочкой 1000 или более единиц энергии. Например, парамеции размножаются путем так называемой конъюгации (слияния), букашки же размножаются делением: взрослая сильная букашка делится на два организма, каждый из которых обладает половиной энергетического запаса, который имел родительский организм. При этом новорожденные букашки наследуют двигательные гены от родителей, но с небольшими изменениями. Число, соответствующее одному из генов, слегка увеличивается или уменьшается.

Предположим, например, что зрелая сильная букашка обладает следующим генным набором: В=3, П=2, СП=0, Н=-2, ЕЛ=0 и Л=1. Два ее потомка, обозначим их как А и Б, могут унаследовать следующие, подвергнувшиеся мутации наборы генов: А: В=4, П=2, СП=0, Н=-2, СЛ=0, Л=1; Б: В=3, П=2, СП=0, Н=-2, СЛ=-1, Л=1.

Мы видим, таким образом, что у потомка А возросло на 1 значение гена В, а у потомка Б уменьшилось на 1 значение СЛ.

Как проявится в поведении отличие этих потомков от своих родителей? У потомка А будет несколько более выражена тенденция к движению вперед, в то время как потомок Б будет несколько реже по сравнению со своим родителем совершать сильные движения влево. На экране компьютера такие небольшие изменения тенденций будут едва уловимы даже для: тренированного наблюдателя.

В простейшем варианте программа "Модель эволюции" начинается с 10 букашек, наделенных случайно выбранным генетическим набором. В результате большинство из них будет, наверное, сновать туда-сюда совершенно непредсказуемым образом. Как правило, букашки с таким хаотичным поведением сравнительно быстро вымирают. Они просто поедают большую часть бактерий в непосредственной окрестности и, продолжая оставаться в ней уже на голодном пайке, погибают. Однако некоторая часть букашек выживает.

Поколения сменяют друг друга приблизительно каждую минуту. Эта борьба за выживание, разворачивающаяся на маленьком экране, представляет собой довольно захватывающее зрелище, но еще интереснее оно становится, когда через несколько минут наблюдатель начинает замечать, как меняется поведение некоторых букашек. Вместо того, чтобы хаотически сновать туда-сюда, они начинают ритмично подпрыгивать. Затем еще через несколько минут появляются букашки, которые кувыркаются. Приблизительно через 20 минут или немного позже мы увидим планирующих, правда на короткие дистанции, букашек, которые добиваются значительно больших успехов по сравнению со своими предками. Именно по этой причине они буквально на глазах начинают размножаться.

Планирующие букашки в свою очередь сменяются "крейсирующими" - движущимися большую часть времени вперед, но иногда меняющими направление. Это означает, что они почти всегда перемещаются к областям, которые гуще заселены бактериями. Впервые проявившись лишь у нескольких букашек, такое поведение быстро становится доминирующим во всей популяции, поскольку крейсирующим особям достается львиная доля пищи.

Хотя крейсирующие букашки превращаются в своеобразный биологический вид, среди них наблюдаются некоторые вариации. Например, есть такие особи, которые чаще поворачивают вправо, в то время как другие предпочитают левые повороты. Конечно, иногда бывают и неудачи. У некоторых "крейсеров" рождается плохо приспособленное к среде обитания потомство. Чаще всего проявляется передаваемое с генами заболевание, порождающее "вертушек", инфузорий, слишком часто совершающих повороты в одном и том же направлении. Эти несчастные создания обычно погибают, так и не познав радости размножения.

Конечно, интересно наблюдать за эволюцией, завершающейся появлением крейсирующих букашек, но возможности программы Палмайтера этим не исчерпываются. Что, если в среде обитания возникают изменения? Не приведет ли это к возникновению большего количества видов? На этот вопрос можно получить ответ, запустив программу ,в другом режиме, в котором экран выглядит почти так же, за исключением того, что в левом нижнем углу наблюдается особенно интенсивное сгущение бактерий. Здесь их воспроизводство происходит значительно быстрее, чем в других областях (см. рисунок вверху). Палмайтер называет этот район "райским садом".


Условия в райском саду (слева) благоприятствуют появлению "вертушек" (справа)

Поколения букашек сменяют друг друга, и опять мы видим, как появляется вид крейсеров. Однако в райском саду наблюдается совсем другая картина. Несколько счастливых букашек первого поколения, случайно попавших в богатую бактериями область, были щедро вознаграждены за отсутствие сколько-нибудь упорядоченной тактики поиска добычи. Несмотря на их беспорядочное топтание на месте, пища вокруг них не иссякает.

Однако, когда в конце концов бактерий в райском саду становится все-таки меньше, начинает действовать тонкий механизм естественной регуляции. Топтание на месте становится уже невыгодным. Вот тут и появляются "вертушки". То, что в обычных условиях является катастрофическим дефектом, становится преимуществом в перенаселенном райском саду.

Действительно, через какое-то время эти букашки с сильной склонностью поворачивать в одну и ту же сторону начинают доминировать в популяции, обитающей в райском саду. Дело в том, что букашки, часто совершающие повороты в одном и том же направлении, скажем вправо, в среднем дольше остаются в этой богатой бактериями области, чем их предки.

Через несколько часов большая часть территории райского сада оказывается населенной почти исключительно "высокоспециализированными" представителями рода вертушек. Букашки этой разновидности на протяжении многих циклов следуют определенной замкнутой орбите, затем внезапно сдвигаются на одну ячейку и снова движутся, уже по другой орбите, чисто выметая бактерий после каждого нового сдвига.

Можно ли считать эту программу действительно моделью биологической эволюции? Наверное, лишь в очень ограниченном смысле. Она показывает, как условия окружающей среды могут благоприятствовать определенным вариациям в потомстве, что в конечном итоге приводит к появлению нового вида. Но на этом моделирование и заканчивается. После того как появляются один или два стабильных вида букашек, никаких событий больше не происходит. Что же еще требуется для того, чтобы реализовать мечту Докинза о продолжающейся неопределенно долго эволюции, моделируемой компьютером? По-видимому, ни больше ни меньше, чем целая миниатюрная Вселенная, заключенная в компьютере.

Заинтересовавшиеся американские читатели могут заказать копию программы "Модель эволюции" за 39.95долл. у компании Life Science Associates, распространяющей образовательные программы подобного рода. Программа выполняется на IBM PC и совместимых компьютерах и к ней прилагается исчерпывающее руководство. Для тех же, кто уже имеет некоторый опыт программирования и предпочитает написать свою собственную версию "Модели эволюции", я опишу упрощенную программу, которую я назвал BUGS (букашки).

Букашка в программе BUGS может быть представлена маленьким квадратиком на экране, сторона квадратика будет равна 3 пикселам (точечным элементам изображения). Шесть направлений, в которых может двигаться букашка, могут быть такими, как показано на рисунке на с.84.


Букашка совершает повороты относительно направления, в котором она движется

Простая таблица указывает, как меняются координаты центрального пиксела букашки, в зависимости от направления, в котором она движется. Таблица содержит два массива, каждый из которых имеет по шесть элементов, xmove И ymove.



Направление, в котором движется букашка (в пределах компьютерного экрана), определяется значением переменной dir. Соответствующие числа в массивах xmove и ymove указывают, на сколько пикселов, в горизонтальном и вертикальном направлениях, соответственно, букашка должна перемещаться на экране за один акт движения. Если, например, букашка движется в направлении 2, она должна сместиться вправо на два пиксела и вниз на один пиксел, поскольку xmove(2) = 2 и ymove(2) = -1.

Программа BUGS определяет направление движения для каждого организма согласно формуле, основанной на генетическом коде букашки, который хранится в двумерном массиве gene. Элемент gene(k,j) содержит значение j-го гена букашки под номером k. В этой формуле значения всех генов выступают в роли показателей степени двойки. Это делается для того, чтобы избежать появления отрицательных чисел. Вероятность того, что букашка будет двигаться в направлении d, определяется путем деления двойки, возведенной в степень, равную значению гена d, на сумму двоек, возведенных в степени, равные значениям всех генов набора. Например, вероятность того, что при следующем акте движения букашка совершит сильный поворот влево, будет равна результату деления 2^СЛ на сумму 2^В+2^П+2^СП+2^Н+2^СЛ+2^Л.

Аналогичным образом программа BUGS вычисляет вероятности для всех остальных направлений. Если просуммировать все эти вероятности, результат, естественно, должен быть равен 1. Можно представлять себе вероятности шести актов движения как шесть различных диапазонов, которые вместе целиком заполняют интервал от 0 до 1. Другими словами, если вероятности шести различных направлений движения представлены числами от P0 до P5, то диапазон 0 является интервалом от 0 до P0, диапазон 1 - интервалом от P0 до Р0+P1, диапазон 2 - интервалом от P0+P1 до P0+P1+P2 и т.д.

На каждом цикле программа BUGS определяет новое значение для направления движения каждой букашки, выбирая случайное число в диапазоне между 0 и 1 в зависимости от того, в какой поддиапазон попало число, и присваивает номер поддиапазона в качестве значения переменной turn (поворот). Считается, таким образом, что значение turn равно 0 для направления В, 1 для П, 2 для СП, 3 для Н, 4 для СЛ и 5 для Л.

Несколько несложных операторов завершают алгоритм движения:

dir <- (dir+turn) mod 6
bugx(k) <- bugx(k) + xmove(dir)
bugy(k) <- bugy(к) + ymove(dir)

Элементы массивов bugx(k) и bugy(k) содержат координаты k-й букашки на данный момент времени.

В первой строчке направление dir изменяется путем прибавления результата бросания жребия, зафиксированного в переменной turn. Сложение выполняется по модулю. Например, если dir = 5 (а это означает, что букашка движется вверх и влево) и turn = 2 (т.е. она должна совершить крутой поворот вправо), новое значение dir будет 5+2 (mod 6) = 1, и следующим движением букашки будет смещение вверх и вправо.

Программа должна перемещать всех букашек согласно этой формуле, проверяя на каждом шаге, не наткнулась ли букашка на стенку или на бактерию. Кроме того, она должна следить за возрастом каждой инфузории и ее энергетическим запасом, чтобы вовремя определить, не подлежит ли букашка уничтожению и можно ли ей уже делиться. Как только букашка оказывается готовой к размножению, программа просто заменяет одну старую букашку двумя новыми, находящимися в точке, где произошло деление. Эти отпрыски наследуют родительский набор генов, за исключением того, что значение случайно выбранного гена одного отпрыска увеличивается на некоторую величину, а у другого значение случайно выбранного гена, наоборот, уменьшается.

Некоторым из тех, кто захочет попробовать свои силы и написать такую программу, приведенного описания программы BUGS будет достаточно. Тем же, кому оно покажется не очень подробным, следует проконсультироваться у более опытных программистов и попросить их составить полное алгоритмическое описание.

БИБЛИОГРАФИЯ

THE BLIND WATCHMAKER. RICHARD DAWKINS. W.W.Norton&Company, 1987. (Есть перевод.- G.).

ARTIFICIAL LIFE: THE PROCEEDINGS OF AN INTERDISCIPLINARY WORKSHOP ON THE SYNTHESIS AND SIMULATION OF LIVING SYSTEMS HELD SEPTEMBER, 1987, IN LOS ALAMOS. NEW MEXICO. Edited by Christopher G. Langton. Addison-Wesley Publishing Company, Inc., 1989.

ОТКЛИКИ

11 1989
МОДЕЛИРОВАНИЕ эволюции, тема нашей статьи в июльском номере, вызвало многочисленные отклики читателей. Несколько сот читателей пожелали приобрести подробное описание алгоритма, на основе которого они могли бы написать свою собственную версию программы. В конце концов не часто можно увидеть, как за какой-нибудь час или полчаса совершается эволюция простейших и бактерий.

Майкл Палмайтер, школьный учитель из Калифорнии, заслуживает пальмовой ветви за свое изобретение. Очевидно, это была очень своевременная идея. Несомненно, духом этой эпохи - эпохи моделируемой эволюции - прониклись несколько читателей, которые независимо разработали свои программы, оказавшиеся во многом схожими с "Моделью эволюции" Палмайтера.

Так, М.Штипановиц из Нэшвилла (шт.Теннесси), выиграл ряд конкурсов с программой, моделирующей овальных букашек, бороздящих двумерное пространство в поисках случайно распределенного корма. В его программе окружающая среда создает механическое сопротивление движущимся букашкам. Это сопротивление может быть сведено к минимуму путем эволюционного развития обтекаемых форм тела.

К.Охейвер также представил программу моделирования эволюции на конкурс любительских программ. В отличие от букашек Палмайтера организмы в программе Охейвера неподвижны (скорее подобны водорослям, нежели простейшим); они постоянно поглощают пищу, растут и сами служат пищей другим организмам.

П.X.Дил из Мориарти (шт.Нью-Мексико) создал довольно сложную эволюционную программу и распространяет ее в учебных заведениях. Генный набор его созданий включает 13 генов, управляющих такими характеристиками существа, как способность питаться органическими веществами, поглощать энергию и двигаться (хотя и несколько вяло).

Среди читателей, сумевших запустить BUGS, мою упрощенную версию программы Палмайтера, пользуясь лишь весьма поверхностным описанием, приведенным в статье, назовем Л.Глейвина из Бернаби (Британская Колумбия), К.Шеллера из Бельвю (шт.Небраска), Дж.Хенри из Де-Кальба (шт.Иллинойс) и А.Бенкс из Бостона (шт.Виргиния). Глейвин, которого раздражало количество энергии, иногда затрачиваемой букашками вблизи границ экрана, наделил своих простейших способностью отскакивать от границ экрана. Шеллер явно поощрял ген, вносящий наибольший вклад в успешную тактику поиска пищи. Столкнувшись с тем, как трудно отличить более развитых букашек от их эволюционно отсталых собратьев, Хенри окрашивал их в зависимости от проявляемой склонности оставаться на том же месте. Бенкс наделил своих созданий аналогичным свойством, заставляя букашку менять окраску, когда она меняет направление движения.

8 1989
КОМПЬЮТЕР ПРОБУЕТ СВОИ СИЛЫ В ПРОЗЕ И ПОЭЗИИ
А.К.ДЬЮДНИ

Главное позаботиться о смысле, а звуки позаботятся о себе сами.
ЛЬЮИС КЭРРОЛЛ, Приключения Алисы в стране чудес

КАК справедливо заметил этот знаменитый оксфордский специалист по бессмыслице, в литературном творчестве семантика важнее, чем синтаксис. Качество литературных произведений определяется тем смыслом, который писатель вкладывает в свои творения. Компьютеры пока еще не способны мыслить и поэтому не могут позаботиться о смысле сочиняемых ими произведений. Однако, как показывает ряд уже существующих программ, они вполне способны позаботиться о "звуках". Можно ли считать такие сочинения искусством? Предоставим судить об этом читателям.

Возьмем, к примеру, сочинения программы MARK V. SHANEY, созданной двумя исследователями из компании AT&T Bell Laboratories, Брусом Эллисом (в настоящее время работающим в Сиднейском университете) и Доном П. Митчелом. Программа MARK V. SHANEY не совсем самостоятельна в своем творчестве. Сначала ей нужно дать почитать сочинение какого-нибудь другого автора и поразмыслить над ним. После этого программа выдает своеобразный комментарий по поводу прочитанного. В качестве примера я процитирую мысли, высказанные программой MARK V. SHANEY после прочтения элементарного учебника химии.

"Вымоем классную доску. Понаблюдаем, как она сохнет. Вода уходит в воздух. Когда вода уходит в воздух, она испаряется. Привяжем влажную тряпку к одному из концов твердого или жидкого тела. Посмотрим вокруг. Что представляют собой твердые тела? Что представляют собой лишь те тела, которые сами попадают в облака? При перемещении облаков воздух бросает крошечные капельки воды. Иногда это та вода, которая покидает тело в листьях зеленых растений. Она очень пористая, почти как губка. Однако стенки полых трубок и клеток очень крепки. Химические превращения происходят при горении..."

Характер комментария едва ли будет другим, если программа ознакомится с учебником по элементарной математике.


Математический комментарий программы MARK V. SHANEY

Хотя смысл в произведениях программы MARK V. SHANEY явно отсутствует, звучат предложения вполне приемлемо. По общему впечатлению, все это слегка напоминает сумбур, который остается в голове не слишком прилежного ученика после поздней ночной зубрежки. В самом деле, начитавшись сочинений программы MARK V. SHANEY, я стал находить обычные тексты почти такими же странными и невразумительными!

Каким образом программа создает свои оригинальные произведения? На этот вопрос можно дать довольно простой ответ. Ключом тут является само название программы MARK V. SHANEY, пародирующее созвучный математический термин "Markov chain" - цепь Маркова. Если выражаться абстрактным научным языком, цепь Маркова - это последовательность символов, порождаемых в соответствии с таблицей вероятностей. В той версии этого понятия, которая используется программой MARK V. SHANEY, каждая строка таблицы соответствует паре символов. Элементы каждой строки таблицы состоят из символов, каждая пара которых соответствует определенной вероятности. Последовательность символов порождается алгоритмом, который, начиная с "цепи" из двух символов, циклически проходит через четыре простых шага:
1. Найти два последних символа в текущей цепи.
2. Выбрать строку таблицы, соответствующую этой паре символов.
3. Выбрать символ в строке в соответствии с его вероятностью.
4. Добавить выбранный символ, присоединив его к концу цепи.

Например, несколько первых элементов в таблице для цепи Маркова относительно символов A, B, C и D могут выглядеть следующим образом:

AB: B(0.1), C(0.1), D(0.8 )
AC: A(0.1), B(0.2), C(0.1), D(0.6)
AD: B(0.4), D(0.6)
BA: B(0.3), C(0.4), D(0.3)
BB: A(0.5), C(0.5)
...

Если в качестве исходной пары символов взять AB, то алгоритм с вероятностью 10% выберет B, с вероятностью 10% выберет C и с вероятностью 80% - D в качестве следующего символа цепи. Каким образом алгоритм выбирает символ в зависимости от вероятностей? Он делит интервал между 0 и 1 на сегменты, длина которых соответствует вероятностям отдельных символов. Затем он выбирает случайное число в диапазоне между 0 и 1 и определяет, в какой сегмент оно попало.

Для строки AB в приведенной выше таблице вероятности символов B, C и D соответственно находятся в диапазонах между 0 и 0.1, между 0.1 и 0.2 и между 0.2 и 1.0. Предположим далее, что генератор случайных чисел компьютера выдал число 0.0172. Поскольку это число лежит в первом диапазоне, в качестве следующего символа цепи будет выбрано B. Таким образом, цепь будет состоять из символов ABB. Теперь алгоритм обратится к строке BB, чтобы выбрать четвертый символ цепи. Здесь опять в работу вступает генератор случайных чисел. Если порожденное им число меньше или равно 0.5, то в качестве следующего символа выбирается A, в противном случае алгоритм выбирает C. Ввиду того что результат каждой операции выбора случаен, алгоритм, начиная работу с одной и той же исходной пары символов, может построить совершенно различные цепи.

Описанный алгоритм был в действительности применен в 40-х годах Клодом Е. Шенноном из фирмы Bell Laboratories в целях анализа информации, содержащейся в текстах естественного человеческого языка. Он построил таблицы вероятностей алгоритма, просматривая обычные тексты и подсчитывая частоту появления каждой буквы после каждой возможной пары предшествующих знаков (включая пробелы). После того как частоты встречаемости каждого знака в данном тексте подсчитаны, их нетрудно перевести в соответствующие вероятности. Марковские цепи символов, построенные таким образом, по своим статистическим свойствам были схожи с исходным текстом, хотя и редко содержали грамматически правильные слова. Каким же образом программа MARK V. SHANEY применяет марковские цепи, создавая последовательности из правильных слов английского языка?

Фокус заключается в том, чтобы применять алгоритм Шеннона для марковских цепей сразу к целым словам, а не к составляющим их отдельным буквам. По мере того как программа MARK V. SHANEY просматривает текст, она составляет таблицу частот для всех слов, следующих за каждой парой слов, которые встречаются в тексте. Затем, основываясь на подсчитанных частотах, программа начинает свою вероятностную болтовню на тему прочитанного текста.

Ключевым свойством программы является, в частности, то, что она воспринимает любой знак препинания, непосредственно следующий за словом, как часть этого слова. Благодаря указанному свойству она может строить предложения, имеющие начало и конец. Приблизительно половина из них оказывается грамматически правильной [Следует заметить, что написать аналогичную программу для текстов русского языка значительно сложнее. Она должна была бы учитывать родовые и падежные окончания слов, отсутствующие в английском языке.- Прим. перев.]. Невольно содрогаешься при мысли о том, что могла бы сочинить эта программа, просмотрев данную статью.

На самом деле, кое-кто уже содрогался от мыслей, высказанных программой MARK V. SHANEY, одни с гневом, другие с улыбкой. Несколько лет назад Эллис решил подключить свою программу к компьютерной сети. Жертвами ее критического анализа стали невинные пользователи сети, которые "подписались" на электронный бюллетень под названием "net. singles". Бюллетень предоставляет свои страницы научным работникам, инженерам, программистам и аспирантам со всех концов страны, давая им возможность высказаться по самым различным вопросам, таким как назначение свиданий, употребление косметики и личные взаимоотношения. Почему бы не дать программе почитать эти заметки и не высказать свои собственные "мысли" по затронутым там вопросам? Привожу некоторые наиболее глубокомысленные комментарии программы.

"Когда я встречаюсь с людьми на деловой почве, у меня возникает желание, чтобы они выбрили свои руки. На конференции, состоявшейся несколько недель тому назад, я провела интересный вечер с крупинкой соли. Я бы никогда не посмела принимать их всерьез! Это возвращает меня к мысли о наглецах, которые осмеливаются заставлять других поступать так или не так. Я обожаю пламенный спор, возможно больше, чем кто-либо другой...

Я хочу затронуть новую тему: у кого-нибудь есть предложения? Есть ли у кого-нибудь еще опыт высказываться по вопросу или на тему о смешанных супружеских парах, женатых или нет, о дискриминации вперед или в обратном направлении и о тенях для век? Возможно, в этом заключаются истоки косметики, хотя это и стоит почитать, не говоря уже о том, чтобы осудить другого человека за то, что он читает это или нет? Бог ты мой!"

К мыслям, высказанным новым корреспондентом бюллетеня, читатели отнеслись по-разному. Серьезные люди почувствовали какую-то насмешку. Разъяренные, они потребовали, чтобы кто-нибудь "заткнул" программу MARK V. SHANEY с ее чудовищным бредом. Другие же почти восторженно спрашивали, не является ли эта программа секретной разработкой по искусственному интеллекту, которую испытывают в среде человеческого общения. Возможно, кое у кого даже сложилось впечатление, что под именем MARK V. SHANEY скрывается человек, страдающий шизофренией и отчаянно ищущий родственную душу.

Но если бы цель компьютерной прозы заключалась лишь в том, чтобы заставить людей поверить, что произведение было написано психически нормальным человеком, то, по-видимому, продукцию программы MARK V. SHANEY следовало бы расценивать как неудачу. Программа MELL, детище Бонни В. Фернера из Пискетуэя (шт. Нью-Джерси), подошла ближе к достижению этой цели. MELL сочиняет необычные научно-фантастические рассказы, в которых присутствует элемент медитации.

"Воин нахмурился в порывах суховея. Он любит себя в суховее. Он формирует себя в суховее. Он грозно смотрит на воина Дугаки в порывах суховея. Он зовет ее в суховее. Он рычит на нее в суховее. Он садится рядом с ней помимо понимания. Он хватает ее.

О, я могуч, говорит Обан. Он душит ее в суховее. Он выбивает ее из бирюзы...

Обан убивает Дугаки. У него это от бирюзы. Он уставился на нее в порывах суховея. Он зовет ее в порывах суховея. Он рычит на нее в суховее. Он садится рядом с ней помимо жадности. Он хватает ее. Он душит ее в суховее. Он выбивает ее из бирюзы. Это нужно ему под ударом молнии. Его тело горит под ударом молнии..."

Программа MELL состоит приблизительно из 1500 строк на языке Бейсик. По сравнению с MARK V. SHANEY программа Фернера сложнее да же по своей концепции. Главный цикл программы порождает двух персонажей, характеризуемых при помощи 16 случайно выбираемых "описателей", значения которых определяются такими свойствами, как рост, внешняя привлекательность, род занятий, возраст и состояние здоровья, запах, приверженность идее (от безразличия до фанатизма) и обладание магическими способностями.

Выбрав имена и качества, которыми обладают персонажи рассказа, главный цикл программы определяет мотивы, движущие персонажем, анализируя значения различных его описателей. Если у одного из описателей персонажа оказывается низкое значение, MELL основывает на этом факте взаимоотношения данного персонажа с другими. Если ни у одного персонажа не находится описателя с низким значением, программа MELL рещает вопрос о характере взаимоотношений данного персонажа с другими, исходя из рода его занятий. При каждом прохождении главного цикла программа порождает несколько предложений, описывающих персонажи, путем подстановки названий свойств в заранее заготовленные грамматические ячейки. В порождаемых таким образом произведениях присутствует также и то, что Фернер называет "фоновыми" словами.

Например, в рассказе, который мы только что процитировали, фоновое слово "суховей" задает сцену действия. В результате это слово всплывает во многих предложениях. После того как сформирован очередной абзац, который описывает действие, совершаемое одним из персонажей, весь процесс повторяется сначала. От цикла к циклу программа может изменять качества, присущие персонажу. Благодаря этому приему сюжет (если о нем вообще можно говорить) становится менее однообразным.


Рассказ программы MELL Фермера

Ну а как дело обстоит с компьютерной поэзией? Может быть, стихи даются компьютеру легче, чем проза? Едва ли, потому что смысл, вкладываемый в стихотворные формы, обычно отличается значительно большей концентрацией по сравнению с прозой. Из трех поэтически настроенных программ, обсуждаемых в настоящей статье, лишь программа POETRY GENERATOR (генератор стихов), написанная Розмари Уэст из Мишшен-Хиллза (шт.Калифорния), является полностью автоматизированной. На завершающей стадии работы двух других программ требуется вмешательство человека. Уэст описывает свою программу следующим образом:
"Мой подход... основан на использовании богатого словаря слов и фраз, которые выбираются случайным образом, и из них формируются словосочетания согласно набору грамматических правил. Рассмотрим, например, следующее четверостишие:

"Дерево погружает голые пальцы
в черное озеро льда
словно три серых гуся
сползают по снежному склону".

Каждую строку стихотворения можно разбить на несколько частей... Дерево - подлежащее; опускает - сказуемое; голые пальцы - дополнение. Определив части, я могу вместо них подставлять другие слова из многочисленного (от 100 до 400) набора для каждой части. Эти подстановки выбираются компьютером случайным образом. Например, воспользовавшись той же стихотворной структурой, я могла бы получить другое четверостишие:

"Женщина прячет пять серых котят
под старым ржавым рыдваном
и тут же печальные клоуны
входят в ваш музей страданий"".

Стихотворные структуры, на которые программа POETRY GENERATOR навешивает свои слова, могут варьировать довольно широко, придавая определенное разнообразие как синтаксису, так и тому, что можно было бы понимать под смыслом стихотворения. В какой-то степени продукция программы основана на структурах, которые Уэст применяет в своих собственных стихах, частично опубликованных.


Программы POETRY GENERATOR (вверху) и THUNDER THOUGHT (внизу) бросают вызов литераторам

По мнению Томаса А. Истона из Белфаста (шт.Мэн) лучший способ применения компьютера для сочинения стихов заключается в симбиозе человека и машины. Он написал полуавтоматизированную программу под названием THUNDER THOUGHT, которая генерирует идеи для стихотворений. И опять я предоставляю слово автору программы:

"Я считаю, что творческий ум имеет две составляющие: поверхностный ум и критический ум. Первый генерирует случайные комбинации тех слов, мыслей и образов, которые в данный момент находятся в фокусе его внимания (но с участием и периферийного материала, благодаря чему поверхностный ум не перестает нас удивлять). Затем критический ум сбрасывает, подобно мусору, большую часть из того, что создает поверхностный ум, редактирует, разворачивает и уточняет оставшуюся часть, преобразуя ее в стихотворение".

Опираясь на внутренние списки существительных, глаголов, прилагательных и наречий, программа THUNDER THOUGHT действует примерно так же, как и программа Уэст POETRY GENERATOR. Она вставляет слова в скелетные структуры предложений и порождает то, что Истон рассматривает как поэтический полуфабрикат, который затем шлифуется человеком.

"Промежуточные результаты выглядят неграмотным, бессмысленным, смехотворным мусором... но не всегда. Среди многих строчек мусора обязательно попадется несколько привлекающих внимание. В них присутствует смысл (или, во всяком случае, кажется, что присутствует). Возникает желание покрутить их так и сяк. Затем к двум строчкам естественно напрашивается третья, а к ним начинаешь подыскивать и другие строки, подходящие по стилю. Немножно редактирования, интерполяции, шлифовки и - вуяля!- стихотворение готово".

Пользуясь этим методом, Истон написал около 110 стихотворений, 32 из которых были опубликованы - причем некоторые были напечатаны в литературных журналах. Такой процент, по его словам, заставит позеленеть от зависти многих настоящих поэтов.

И наконец, последнее слово в обсуждении компьютерной поэзии мы предоставим программе ORPHEUS, которая была разработана поэтом Майклом Ньюменом из Нью-Йорка. Программа задает жесткую структуру в том или ином поэтическом стиле. В эту структуру человек может вставлять слова по своему выбору. По существу, ORPHEUS - это программа обработки текстов ("обработки стихов", как говорит Ньюмен), которая закладывает строки по своему вкусу и завершает их с помощью словаря рифм. Настроив, например, программу на стиль сонета, можно написать следующую пару строк (имитируя 130-й сонет Шекспира):

My Apple' s screen is nothing like the sun;
The Cray is faster far on problems big;
(Экран у "Эппла" не похож на солнце;
"Крэй" побыстрее на больших задачах; )

Поскольку первая строка заканчивается словом "sun" (солнце), программа заглядывает в свой словарь рифм и высвечивает несколько слов, рифмующихся со словом sun: bun, done, fun, gun и т.д. Проглядывая их, человек может остановить свое внимание на слове "fun" (забава). Есть ли какой-нибудь компьютер, работать с которым было бы забавнее, чем с компьютером "Эппл" (Apple)?

По ассоциации с компьютерными играми невольно вспоминаешь компьютер "Атари" (Atari) и, таким образом, возникает третья строка:

If Apple pleasant be, th' Atari is more fun;
(Приятен "Эппл", "Атари" же забавней).

Первое четверостишие завершается выбором слова "wig" (парик), которое рифмуется со словом "big" из второй строки.

If wires be hairs, her circuits are a wig; (Проводинички, как волос - схемы, как парик; )

Полностью перевод сонета приведен внизу на с.90.


Сонет, написанный неизвестным автором в содружестве с программой ORPHEUS

БИБЛИОГРАФИЯ

COMPUTER RECREATIONS. BRIAN HAYES in Scientific American , Vol.249, No.5, pages 16-24; November, 1983 (#1 1984 В русском издании, см. на первой странице темы.- G.).

Программная реализация подобного MARK V. SHANEY генератора текстов рассмотрена в книге Б.КЕРНИГАН, Р.ПАЙК, ПРАКТИКА ПРОГРАММИРОВАНИЯ, 2001.- G.

ОТКЛИКИ

3 1990
В АВГУСТОВСКОМ номере журнала за прошлый год в нашей рубрике был проведен парад прозы и поэзии или, вернее, пародий на прозу и поэзию. Программа MARK V. SHANEY, которая читает обычный английский текст только для того, чтобы произвести чудовищно искаженные вариации на ту же тему, работает на основе цепей Маркова. Алгоритм программы крайне прост. По мере того как программа сканирует текст, она строит таблицу продолжений для двухсловных сочетаний. Иначе говоря, для каждой пары последовательных слов, которые программа встречает в анализируемом ею тексте, она фиксирует слово, стоящее после такой пары, каждый раз, когда ей попадается эта пара. Частотность слов, следующих за парой, легко преобразуется в вероятности на завершающем этапе процесса. Затем, когда программа "пересказывает" текст, она просто смотрит на последние два напечатанные ею слова, выбирает последующее слово, основываясь на вероятности, и печатает его, и так до бесконечности.

Я содрогался при одной мысли, что программа MARK V. SHANEY может когда-нибудь "пересказать" мою собственную статью, сведя тщательно продуманный текст к полнейшей чепухе. И вот К.Буллис из Кемпбелла (шт. Калифорния), реализовав SHANEY на компьютере Macintosh Plus, тут же и не взирая на мои личные чувства по этому поводу, ввел в машину мою статью из августовского номера. Полюбуйтесь, что сделала программа с этой статьей, так сказать, с первой попытки:

"Будьте осторожны с таблицей цепей Маркова для всех слов, рифмующихся с солнцем: донце, оконце и т.д. Просматривая их, ваш взгляд может остановиться на природе твердого или жидкого тела. Осмотритесь вокруг. Что представляют собой только те, что принимают участие в листьях зеленых растений. Это только первая остановка Манделобуса, которую можно приобрести, написав Пайку в тот момент, когда печальные клоуны входят в ваш музей страданий".

Г.Оттеуэлл из Гринвилля (шт.Южная Каролина) считает, что программы для сочинения стихов были не так хороши, как SHANEY. В частности, ему не понравился сонет, составленный программой Майкла Ньюмена, которая призвана помогать человеку, пишущему стихи. Здесь, наверное, виновата не столько программа, сколько сам поэт. Между прочим, программа эта выполняется на персональном компьютере IBM PC. Она состоит из трех частей: POETRY PROCESSOR, NERD II (акроним от слов: электронный словарь рифм Майкла Ньюмена) и ORPHEUS A-B-C. Можно приобрести эти части по отдельности или все вместе как пакет программ под названием POETRY PROCESSOR PACKAGE.

Еще один словарь рифм был составлен К.Вуртцем из Бэрбенка (шт.Калифорния). QUICKRHYME - так назвал Вуртц свою программу - очевидно, справляется со многими более сложными задачами, связанными с вычислением рифмованных продолжений, не ограничиваясь их простым перечислением. Читатели, заинтересовавшиеся программой QUICKRHYME, могут приобрести ее, связавшись с Вуртцем по адресу: 859 Hollywood Way, Suite 401, Burbank, CA 91510.

9 1989
БИОМОРФЫ, ПОПКОРН И УЛИТКИ
А.К.ДЬЮДНИ

Иногда я кажусь себе рыбаком. Компьютерные программы и идеи - это мои крючки, удилища и спиннинги. Компьютерные изображения - улов и деликатесные блюда.
Клиффорд А. Пикоувер, Компьютеры, образы, хаос и красота

УЖЕ несколько раз за последние годы у меня возникало искушение рассказать о причудливых и красивых графических творениях К.Пикоувера, известного ученого из Исследовательского центра им.Томаса Уотсона фирмы IBM в Йорктаун-Хейтсе (шт.Нью-Йорк). Помимо увлечения серьезными исследованиями он коллекционирует развлекательные программы. Это его "рыболовные снасти". С их помощью на экране дисплея можно получать хаотичные и в то же время эстетически привлекательные формы. Глядя на восхитительные уловы Пикоувера, я не в состоянии противостоять соблазну и в этой статье хочу рассказать о программах, с которыми читатели сами смогут отправиться на "рыбалку" и ловить представителей трех простых, но весьма забавных видов, а именно биоморфы, плитки Трюше и фрактальный попкорн. (Попкорн - это популярные в США зерна воздушной кукурузы.- Перев.). Читатели смогут также подивиться на трехмерных логарифмических улиток, пойманных этим увлеченным, но вполне здравомыслящим человеком. Что такое биоморфы? Это слово уже встречалось в статьях нашей рубрики. В апрельском номере за прошлый год речь шла о формах, напоминающих живые организмы и порождаемых программой Ричарда Докинза, биолога из Оксфордского университета. Начиная с нескольких похожих на деревья фигурок, человек, работающий с программой, выбирает какую-то одну, из которой программа строит набор фигурок, являющихся вариациями исходной. Из их числа человек снова выбирает одну понравившуюся ему фигурку и т.д. В конце концов могут возникнуть очень странные, но непременно "органические" формы.

Независимо и почти одновременно Пикоувер получил собственные биоморфы, однако и по методу генерирования, и по внешнему виду они принципиально отличаются от биоморфов Докинза. Организмы Пикоувера очень похожи на микробов, в связи с чем в журнале "Omni" Пикоувер был назван "Левенгуком XX века". (Антони ван Левенгук, живший в XVII в. нидерландский натуралист, один из основоположников научной микроскопии).

Биоморфы Пикоувера населяют комплексную плоскость; напомним, что там же обитает знаменитое множество Мандельброта (открытое Бенуа Б. Мандельбротом, коллегой Пикоувера по Исследовательскому центру фирмы IBM). Биоморфы возникают в результате процедуры, являющейся сокращенной версией процесса, с помощью которого прослеживаются изящные фрактальные очертания множеств Жюлиа, близких аналогов множества Мандельброта, о которых шла речь в статье январского номера журнала за 1988г. Каждый биоморф строится путем многочисленных итераций, или последовательных вычислений определенной математической функции, путем выполнения повторяющихся математических операций. На каждом шаге итерационного процесса результат предыдущего шага принимается за исходное значение переменной.


Так выглядят биоморфы под "микроскопом"; каждому биоморфу соответствует своя порождающая его функция

Рассмотрим, например, биоморф с 12 шипами, похожий на радиолярию внизу на рисунке слева, изображающем похожие на видимые в микроскоп организмы. Этот биоморф был получен с помощью итерационных вычислений по формуле

zn+1 <- zn3+c.

Исходное значение комплексной переменной (обозначенной z0 возводится в третью степень и к результату прибавляется фиксированное комплексное число c. Затем те же арифметические действия применяются к сумме z1, получается значение z2 и т.д.

Комплексное число состоит из двух обычных чисел, одно из которых называется действительной, а другое мнимой частью комплексного числа. Эти два числа удобно представить в виде двух координат в декартовой системе. Традиционно комплексное число записывается в виде суммы, например 3+5i, где 3 - действительная часть, а 5 - мнимая. (Буква i является своеобразным индексом, указывающим, какая из двух частей числа мнимая). На с.83 в рамке я привел основные правила сложения, умножения и возведения в степень комплексных чисел.

[Действия над комплексными числами:

Два комплексных числа складываются путем суммирования их действительных и мнимых частей по отдельности. Иными словами, сумма комплексных чисел a+bi и c+di равна комплексному числу (a+c)+(b+d)i.

Произведение двух комплексных чисел равно (ac-bd)+(ad+be)i. Пользуясь этой формулой, можно вывести формулу квадрата числа a+bi, которая имеет вид (a2-b2)+2abi. Действительная часть этого возведенного в квадрат числа равна (a2-b2), а мнимая - 2ab.

Применив еще раз формулу умножения, получим формулу для нахождения третьей степени числа a+bi. Действительная часть возведенного в куб комплексного числа будет равна a(a2-3b2), а мнимая - b(3a2-b2)].

Чтобы создать биоморф, нужно сначала расположить решетку точек в прямоугольнике, лежащем в комплексной плоскости. Координаты каждой из этих точек представляют действительную и мнимую части исходного значения z0 для описанного выше итерационного процесса. Каждой точке на экране компьютера также соответствует определенный пиксел (точечный элемент изображения). В зависимости от результата простого теста на величину действительной и мнимой части окончательного значения переменной z пиксел окрашивается черным или белым цветом.

Все биоморфы, изображенные на рисунке на с.80, были получены в пределах квадрата размером 20*20 и с центром в начале координат на комплексной плоскости. Интересно, сколько других организмов смогут открыть изобретательные читатели? Я готов вооружить их необходимым аппаратом наблюдения: программой, которую я назвал BIOMORPH и которая следует основному алгоритму Пикоувера. С помощью его версии, приведенной ниже, была найдена радиолярия:

c <- 0.5 + 0.0i
for j <- 1 to 100
for k <- 1 to 100
- ВЫЧИСЛИТЬ z0
- z <- z0
- for n <- 1 to 10
- - z <- z^3+с
- - if |real(z)| or |imag(z)| or |z| > 10
- - - then выйти из цикла
- if |real(z)| or |imag(z)| < 10
- - then plot(j, k) черным
- - else plot (j, k) белым

Казалось бы, простой оператор "вычислить z0" на самом деле оказывается не таким уж простым. Он требует преобразования каждой пары координат пиксела (j, k) в комплексное число. Это делается путем деления длины и ширины области комплексной плоскости на число значений j и число значений k соответственно. Полученные частные служат затем в качестве величины приращений, на которые увеличиваются действительная и мнимая части z0 систематически на каждом цикле алгоритма.

Например, радиолярия была в действительности найдена в квадратном "окне" на комплексной плоскости, ограниченном диапазоном следующих значений действительной и мнимой частей z0:
-1.5 < real(z0) < 1.5
-1.5 < imag(z0) < 1.5

Поскольку j и k пробегают значения от 1 до 100, и действительная, и мнимая часть z0 систематически увеличиваются с шагом 0.03. Поэтому в приведенной выше версии программы BIOMORPH должны фигурировать
операторы вида:

real(z0) <- -1.5+0.03j,
imag(z0) <- -1.5+0.03k

позволяющие вычислять 10000 значений z0, каждое из которых итерируется и тестируется.

В самом внутреннем цикле с 10 итерациями мы постоянно следим за величиной z. Величина комплексного числа - это просто квадратный корень из суммы квадратов действительной и мнимой его частей. Если величина оказывается больше 10, то программа должна сразу выйти из цикла (даже в том случае, когда число итераций еще не достигло 10) и перейти к проверке значений действительной и мнимой частей числа z по отдельности. (На самом деле проще сравнивать сумму квадратов действительной и мнимой частей z с числом 100, чем квадратный корень из этой суммы с числом 10; результат сравнения будет тем же).

Независимо от числа итераций величина последнего значения z проверяется по отдельности для действительной и мнимой части путем их сравнения с числом 10. (Абсолютное значение обычного числа со знаком равно самому этому числу без знака). Если действительная или мнимая часть меньше 10, то пиксел с координатами (j, k) окрашивается черным цветом. В противном случае - белым.
Для большинства персональных компьютеров пикселы с координатами в диапазоне от 1 до 100 лежат в угловой части экрана. Чтобы расположить изображение в центре, нужно изменить начальные и конечные значения индексов j и k. Например, j и k могут пробегать значения от 50 до 150, а не от 1 до 100, как это было в нашем алгоритме.

Все остальные подробности, касающиеся программы BIOMORPH, предоставим уточнять самим читателям. Я лишь напомню, что z, z0 и c представляют собой комплексные числа и их следует складывать и умножать по соответствующим правилам. По той же причине операторы присваивания в алгоритме, в которых участвуют величины z, z0 и c, на самом деле должны быть представлены двумя присваиваниями в рамках обычного языка программирования - одно для действительной и одно для мнимой части.

Как посмотреть в микроскоп Пикоувера на другие организмы? На самом деле это можно сделать с помощью все той же программы BIOMORPH. Нужно лишь подставить другую итерационную формулу в сердцевину алгоритма. Другими словами, вместо z3+с в рассмотренной выше программе нужно воспользоваться другой функцией.

Вероятно, те, кто напишет программу BIOMORPH, захотят поохотиться и на других существ, обитающих в центральном квадрате 20*20 комплексной плоскости. Простейший способ поиска заключается в том, чтобы систематически сканировать всю эту область; в последующем можно посмотреть ту или иную зону под увеличением, чтобы подробно исследовать графические элементы существа, обнаруженного в ходе предварительного поиска. Как правило, годится любое небольшое значение c.

В некоторых альтернативных формулах, с помощью которых генерируются биоморфы, можно, например, воспользоваться необычной степенью z, а именно z^z, в других - применить тригонометрические операции. Пикоувер любезно согласился выслать всем желающим короткое посвящение в тайны комплексной тригонометрии и искусство возведения комплексного числа z в степень z. Вооружившись этими познаниями, программисты сумеют написать свои версии программы BIOMORPH, с помощью которых можно "поймать" все показанные здесь виды простейших микроорганизмов.

Пикоувер впервые столкнулся с биоморфами, когда совершил случайную ошибку в программе, предназначенной для изучения фрактальных свойств различных формул. По невнимательности он поставил OR вместо AND в одном из условных операторов для проверки текущего значения переменной z. В результате этого непреднамеренного изменения в черный цвет было окрашено значительно большее количество пикселов на исследуемой картинке. В частности, отростки по бокам биоморфов, похожие на реснички, целиком состоят из таких пикселов.

Хотя биоморфы были созданы совершенно случайно, они, кажется, зажили своей собственной жизнью. Как говорит Пикоувер: "В некотором смысле можно сказать, что математические создания существуют. Эти объекты обитают на комплексной плоскости, хотя и напоминают микроскопические организмы, которые мы легко можем увидеть в капле воды из любой лужи". В каком же море мы могли бы поймать представителей более развитых форм жизни? Пикоувер считает важным и тот факт, что сложность как естественных, так и искусственных организмов является результатом многократного применения простых динамических правил.

В настоящее время работа Пикоувера в исследовательском центре связана с изучением новых подходов к определению смыслового содержания данных по их внешнему виду. Например, очень трудно выявить регулярность или случайность нулей и единиц, которыми заполнены страницы, где представлены биты данных. И все же Пикоувер может выявить степень случайности данных с помощью простого графического приема, основанного на плитках Трюше, названных так в честь французского монаха и энциклопедиста Себастьяна Трюше, жившего в ХУШв. Пикоувер модифицировал исходную форму плиток Трюше так, чтобы они состояли из двух четвертей круга в квадрате; центры круговых секторов находятся в противоположных углах квадрата, а ограничивающие их радиусы совпадают с двумя сторонами квадрата. Получающаяся в результате плитка (см. левый рисунок на с.81) может иметь только две различные ориентации.


Плитки Трюше в двух ориентациях (внизу) и случайные комбинации плиток (вверху)

Если покрыть плоскую область плитками Трюше, могут возникнуть причудливые синусоидальные кривые. При этом внутри области не возникает свободных концов, они встречаются лишь по краям. Каждая кривая будет обязательно непрерывной, потому что середины сторон прилегающих друг к другу квадратов (точки, в которых начинаются и заканчиваются дуги окружностей) соприкасаются.

Массив из нулей и единиц можно преобразовать в узор Трюше, просто расположив его отдельные плитки в том же порядке, что и двоичные разряды, и ориентируя плитку одним способом, когда встречается 0, и другим, когда встречается 1. Если биты данных выбраны случайным образом, утверждает Пикоувер, то в узоре не выявляется никаких закономерностей: кривые извиваются и замыкаются совершенно хаотически (хотя в этом хаосе есть своя красота).

Однако стоит внести в данные небольшой элемент регулярности, как характер узора меняется и в нем начинают проступать определенные закономерности. Если, к примеру, сгенерировать массив битов, в каждой строке которого за одним нулем с несколько большей вероятностью следует другой нуль, нежели единица, а за единицей опять-таки с большей вероятностью следует единица, то кривые, наблюдаемые на плитках Трюше, приобретут четко выраженную тенденцию к диагональному виду.

Лично мне больше по вкусу узоры, созданные случайными комбинациями битов, такие как на рисунке. Они предлагают нам множество задач занимательного характера. Например, встречаются ли в таких узорах лабиринты? Попытайтесь найти канал, ведущий от верхнего ряда плиток к нижнему или от одной стороны массива к другой. Прослеживая за этими каналами, мы часто будем наталкиваться на "острова" - замкнутые кривые. Любая кривая, не касающаяся краев квадратной области, должна рано или поздно соединиться сама с собой. Некоторые из подобных кривых образуют маленькие окружности. По оценкам Пикоувера, среднее количество таких окружностей в произвольном узоре Трюше составляет 0.054 от полного числа плиток. С другой стороны, отношение числа колоколообразных кривых к полному числу плиток равно 0.0125. Я предлагаю читателям самостоятельно классифицировать остальные типы замкнутых кривых. Какие еще типы возможны и каково их среднее число в расчете на одну плитку?

Написать программу, превращающую биты в плитки Трюше, нетрудно. Предположим, что у вас имеется массив двоичных разрядов. Тогда вам нужно лишь организовать двойной цикл просмотра массива, в котором для каждого элемента массива в соответствующей позиции компьютерного экрана изображается плитка с соответствующей ориентацией. Думаю, что этих объяснений достаточно, и теперь мы можем обратиться еще к одной графической забаве Пикоувера: фрактальному попкорну.

Изображение попкорна Пикоувера, как бы осязаемое, приведено в правой части рисунка на с.81. На самом деле эти кружева были получены путем итерационного решения пары дифференциальных уравнений в дискретной форме. Координата х точки решения вычисляется путем вычитания значения функции y из координаты x решения, вычисленного на предыдущем шаге. Аналогичным образом координата y точки решения вычисляется вычитанием значения функции x из координаты y решения на предыдущем шаге. Такая система уравнений называется циклической. Циклические системы, основанные на тригонометрических функциях, по-моему, особенно ботагый источник интересной компьютерной графики.


Фрактальный попкорн, порожденный циклической системой уравнений

Итерационный процесс с перекрестными переменными в программе POPCORN описывается следующей парой уравнений:

xn+1 = xn - h*sin(yn+tg(3yn)),
yn+1 = yn - h*sin(xn+tg(3xn)).

Здесь тригонометрические функции умножаются на малую константу h, так чтобы новые значения x или y никогда не отстояли далеко от предыдущих, независимо от того, как долго продолжается итерационный процесс. В программе Пикоувера h равно 0.05.

Как показывает приведенное ниже алгоритмическое описание, программа POPCORN итерирует формулы по 50 раз для каждой из 2500 исходных пар значений (x0, y0), при этом каждый раз на экране компьютера закрашивается соответствующий пиксел.

for j <- 1 to 50
- for k <- 1 to 50
- - x0 <- -6+0.24j
- - у0 <- -6+0.24k
- - x <- x0
- - y <- y0
- - for n <- 1 to 50
- - - хх <- x - h*sin(y+tg(3y))
- - - yy <- y - h*sin(x+tg(3x))
- - - x <- xx
- - - y <- yy
- - вычислить jp и kp
- - plot(jp, kp)

(Здесь xx и yy - временные переменные, которые служат для того, чтобы следить за текущими значениями переменных x и y в пределах данного шага итераций).

Исходные значения для обеих координат выбираются из точек, принадлежащих квадрату размером 12*12 единиц с центром в точке начала координат плоскости xy. Другими словами, исходные значения x лежат в интервале между -6 и +6; то же самое относится к исходным значениям y. Аналогично программе BIOMORPH программа POPCORN строится на вложенной структуре циклов, в которой вычисляются наборы начальных значений. Но в программе POPCORN индексы обоих циклов пробегают значения от 1 до 50.

Наконец, точки, заданные 50 парами (x, y), сгенерированными для каждой исходной пары (x, y), должны быть отображены в виде пикселов на экране. Это делается при помощи простой формулы, устанавливающей соответствие между значениями x, y, с одной стороны, и значениями jp, kp - с другой.

jp <- 4.166x+25,
kp <- 4.166y+25.

Поэтому фрактальный попкорн Пикоувера состоит целиком из пикселов, координаты которых получаются в результате итераций. Читатели могут по своему выбору рассмотреть под увеличением те или иные фрагменты попкорна и обнаружат изящные и совершенно неожиданные узоры. Они могут также "раскрасить" попкорн, как это делает сам Пикоувер, выбирая для закрашивания пикселов новый цвет всякий раз, когда внутренний цикл начинается сначала.

Графика Пикоувера уже не раз привлекала внимание общественности. Его работа обсуждалась не только в различных журналах, но и на телевидении; полученные им изображения демонстрировались даже на выставках в Швейцарии, Японии и в экспозиции музея вычислительной техники в Бостоне.

Я завершаю тему этой статьи, представляя вниманию читателей одно из последних творений Пикоувера: восхитительную раковину улитки с удивительно реалистичной окраской и бликами. Изображение, приведенное на рисунке на с.82, было построено из последовательности сфер, центры которых перемещались по плавной логарифмической спирали. Световые блики были получены с помощью метода трассирования лучей, моделирующего отражение лучей от различных поверхностей.


Раковина улитки, порожденная логарифмической функцией

БИБЛИОГРАФИЯ

BIOMORPHS: COMPUTER DISPLAYS OF BIOLOGICAL FORMS GENERATED FROM MATHEMATICAL FEEDBACK LOOPS. CLIFFORD A. PICKOVER in Computer Graphics Forum, Vol.5, pages 313-316; 1986.

MATHEMATICS AND BEAUTY: TIME-DISCRETE PHASE PLANES ASSOCIATED WITH THE CYCLIC SYSTEM. CLIFFORD A. PICKOVER in Computers and Graphics, Vol. 11, No. 2, pages 217-226; 1987.

Добавлю еще "10 PRINT CHR$(205.5+RND(1)); : GOTO 10" NICK MONTFORT, PATSY BAUDOIN, JOHN BELL, IAN BOGOST, JEREMY DOUGLASS, MARK C. MARINO, MICHAEL MATEAS, CASEY REAS, MARK SAMPLE, NOAH VAWTER, THE MIT PRESS, CAMBRIDGE, MASSACHUSETTS,LONDON, ENGLAND, 2013.- G.

ОТКЛИКИ

1 1990
ЛЮБИТЕЛИ множества Мандельброта, поклонники фракталов и многие другие читатели с большим интересом прочли нашу статью, опубликованную в сентябрьском номере журнала, где речь шла о биоморфах, улитках и фрактальном попкорне. Творцом этого широкого разнообразия структур был К.Пикоувер из Исследовательского центра им.Томаса Уотсона фирмы IBM в Йорктаун-Хейтсе (шт.Нью-Йорк). Биоморфов плодит программа, основанная, по существу, на том же уравнении, которое генерирует множества Жюлиа (см. статью в рубрике "Занимательный компьютер" в январском номере журнала за 1988г.). За счет введения дополнительных условий в итерационный процесс возникают изображения, напоминающие видимые в микроскоп живые организмы.

Д.Хоффман из Гринвилла (шт.Техас) отмечает, что биоморфы, благодаря тому что в формулах содержатся более высокие степени z по сравнению с формулами множеств Жюлиа, генерируются быстрее. Он рассматривает биоморфы как множества Жюлиа с "небольшим количеством" дополнительных элементов. Дополнительные пикселы встречаются не только в шипах и ресничках, но и в самом теле клетки: "Центральная часть биоморфа представляет собой либо связное множество Жюлиа, либо фрактальную пыль от взорвавшегося множества Жюлиа".

Несколько читателей столкнулись с некоторыми трудностями, пытаясь воспроизвести радиолярию с 12 шипами, изображенную на с.80. Им удалось получить лишь фрагмент радиолярии, увеличенную часть тела клетки. Дело в том, что окно было задано слишком маленьким. Мы советуем читателям воспользоваться вместо окна 3*3 окном 20*20.

Неменьший интерес был проявлен и к плиткам Трюше, которые представляют собой квадраты с двумя круговыми дугами, как бы срезающими два противоположных угла. Любой массив из нулей и единиц можно преобразовать в причудливый плоский орнамент из кривых линий, если заменить каждый ноль плиткой с одной ориентацией рисунка и каждую единицу - плиткой с другой ориентацией. Пикоувер отмечает, что даже небольшое отклонение в последовательности битов от случайного распределения приводит к возникновению легко различимых закономерностей в соответствующем орнаменте из плиток. Этот факт может оказаться полезным для тех, кто занимается поиском закономерностей в данных.

Дж.Саверино из Трекслертауна (шт.Пенсильвания) - инженер-химик, обладающий художественными наклонностями, варьируя орнаменты из плиток, получил интересные результаты. Его произведения напоминают то какие-то странные городские планы, то несколько хаотические мавританские и византийские орнаменты. Наполняя некоторые связные области цветом, Саверино получает возможность быстро выбирать связные области в своих орнаментах.

Д.Спенсер из Валенсии (шт.Калифорния) предложил программу, создающую на экране своеобразную мультипликацию: после того как все биты массива были превращены в узор из плиток, программа начинает переключать по одному случайно выбираемые биты и изменять ориентации соответствующих плиток. По словам Спенсера, такая программа приводит весь экран в движение и получается захватывающее зрелище.

10 1989
КЛЕТОЧНАЯ ВСЕЛЕННАЯ И ЕЕ РАЗВИТИЕ ВО ВРЕМЕНИ И ПРОСТРАНСТВЕ
А.К.ДЬЮДНИ

"Клеточные автоматы - это стилизованные, синтетические вселенные... У них свой вид материи, кружащейся в своем пространстве и времени".
Т.ТоФФОЛИ и Н.Марголас, Машины на клеточных автоматах

НЕКОТОРЫЕ математические системы, хотя имеют простое описание, способны порождать миниатюрные вселенные невероятной сложности. Эти меры не доступны ни телескопам, ни космическим кораблям, их можно исследовать только с помощью компьютеров. Одним из примеров является множество Мандельброта (о котором уже неоднократно писалось в статьях нашей рубрики). Элементы множества определяются путем итерирования простых арифметических операций, однако, когда результаты появляются на компьютерном экране, мы видим потрясающие по сложности изображения. Клеточные автоматы порождают, по-видимому, еще более удивительные миры, потому что, подобно нашему, они изменяются во времени.

Ну а самый лучший пример такой миниатюрной вселенной дает нам новый тип клеточного автомата, открытый Дейвидом Гриффитом из Висконсинского университета в Мадисоне. Стартуя из произвольно выбранного исходного состояния, автомат демонстрирует четыре различные фазы, завершающиеся причудливыми кристаллическими образованиями, сильно напоминающими примитивные формы жизни.

Клеточный автомат состоит из бесконечной решетки клеток, каждая из которых находится в одном из нескольких возможных состояний. Каждая клетка меняет свое состояние синхронно с очередным тактом воображаемого часового механизма и в соответствии с набором несложных правил. Реализованные на компьютере клетки представляют собой пикселы (точечные элементы изображения) на экране; различным состояниям клеток соответствуют различные по окраске пикселы. При правильно выбранном наборе правил и исходных состояний компьютерный клеточный автомат может порождать чрезвычайно интересные цветные узоры, изменяющиеся во времени.

Изобретение Гриффита, которое я буду называть циклическим пространством и которое способно демонстрировать удивительные явления, представляющие научный интерес и необыкновенно красивое зрелище, основано на чрезвычайно простом правиле. Оно заключается в том, чтобы пронумеровать возможные состояния от 0 до n-1 и считать, что если клетка находится на данном такте в состоянии k, то на следующем такте она должна "съесть" любые соседние клетки, находящиеся в состоянии k-1. Съедание проявляется в том, что съеденная соседняя клетка переходит из состояния k-1 в состояние k. Это правило напоминает действующую в природе систему поедания высшим существом низшего: клетка в состоянии 2 может съесть клетку в состоянии 1, в то время как последняя поедает клетки в состоянии 0. Однако в циклическом пространстве эта цепочка не имеет конца, потому что клетка в состоянии 0 может поедать соседние клетки в состоянии n-1.

На основе этого одного простого правила циклическое пространство способно превращать случайное распределение окрашенных точек в стабильные спиралевидные образования. Исходную хаотическую стадию Гриффит называет "осколками" - и не без оснований: на начальном этапе циклическое пространство выглядит как беспорядочная свалка предметов неправильной формы. Однако через какой-то промежуток времени осколки сменяются маленькими капельками, по которым пробегают внутренние цветовые волны. Капельки растут, пока не заполнят все циклическое пространство. В этот момент начинают выкристаллизовываться спиралевидные объекты, изящные структуры, питающиеся в ходе непрерывного вращения.


Циклическое пространство с 14 состояниями в фазе осколков (слева) и капель (справа)

Каждая спираль возникает из того, что Гриффит называет дефектом - этот термин заимствован из кристаллографии. Спирали растут медленно и величественно, но в конце концов им становится тесно и они начинают бороться за жизненное пространство. Одни уступают в борьбе, другие же продолжают доминировать вплоть до заключительной фазы в развитии циклического пространства. Такие долгоживущие спирали Гриффит называет демонами.

Независимо от того, велико или мало количество возможных состояний, развитие всегда идет по одному и тому же сценарию: осколки сменяются капельками, затем появляются дефекты и демоны. Первые три фазы характеризуются свойством метастабильности: они удерживаются в течение большого количества циклов, прежде чем уступят место следующей фазе.

Рассмотрим циклическое пространство, обладающее двадцатью возможными состояниями. Почему первоначальное случайное распределение состояний оказывается метастабильным? Другими словами, почему требуется довольно длительное время, прежде чем обширные области на экране изменят свою мелкодисперсную хаотическую структуру? (Конечно, время от времени и на начальной стадии возникают пульсирующие капельки, но в целом они не меняют картины).

На самом деле ответ тут очень простой. Скажем, если клетка находится в состоянии 5, то насколько велика вероятность, что по крайней мере одна из 4 соседних клеток будет в состоянии 4? Очевидно, невелика. При 20 дозволенных состояниях эта вероятность будет приблизительно равна 0,19. Но даже если одна из соседних клеток окажется "съедобной", велика ли вероятность, что на следующем такте либо у данной клетки, либо у "съеденной" по соседству окажется клетка в состоянии 4? Это вероятностное рассуждение объясняет картину, наблюдаемую на экране компьютера, когда циклическое пространство начинает эволюционировать от исходного случайного распределения клеточных состояний: после нескольких спорадических изменений циклическое пространство входит в состояние застоя.

Однако это не полный застой. Вспомним о нескольких изолированных капельках. По поверхности каждой капли прокатываются волны, которые, отражаясь от окружающих осколков, изменяют направление движения. Этот процесс, по-видимому, не только поддерживает жизнь в капельке, но и способствует ее росту: клетки из окружающих осколков вовлекаются в процессы, протекающие внутри капли. Увеличивающиеся капли постепенно сливаются друг с другом, оставляя все меньше рассеянных островков из осколков. Что заставляет капли расти?

Одним из факторов, гарантирующих постоянный рост капли, является наличие цикла: замкнутой цепочки клеток, в которой состояние каждой клетки отличается от состояния прилегающих к ней клеток не более чем на 1 (см. рисунок вверху). Таким образом, если взять любую клетку, принадлежащую циклу, то состояние следующей клетки можно получить прибавлением 1, -1 или 0 к состоянию данной. (Напомним, что в циклическом пространстве наивысшее состояние отличается от состояния 0 также на 1). Если просуммировать по всей замкнутой цепи разности состояний при переходе от клетки к клетке, то окончательная сумма может получиться и не равной 0. Цикл, обладающий такой характеристикой, будет неопределенно долго поддерживать процесс роста капли. На самом деле это и есть дефект, основа третьей метастабильной фазы в развитии циклического пространства.


Два цикла, один из которых (справа) является дефектом

Клеточные процессы, обусловленные дефектом, отличаются от процессов, протекающих в бездефектном цикле. Дефект заставляет окружающие клетки изменять состояние в регулярном ритме. На компьютерном экране область, окружающая дефект, приобретает изящную спиральную геометрию. В конце концов все циклическое пространство (или по крайней мере та его часть, которая видна на экране) полностью покрывается такими спиралями.



Циклическое пространство в фазе дефектов

Каким образом образуются дефекты по мере того, как циклическое пространство эволюционирует от исходного состояния, когда оно представляет собой "груду" осколков? Конечно же, дефект может существовать с самого начала клеточной вселенной. На самом деле, если учесть, что циклическое пространство бесконечно, то среди осколков статистически гарантировано наличие дефектов. И все же дефекты обычно образуются там, где их раньше не было. Как? Я предлагаю читателям построить маленький прямоугольник из клеток, который на данный момент не содержал бы дефекта, но в дальнейшем породил бы его. Для этого нужно выработать некоторый несложный тест (конечно, не такой, который компьютер выполнял бы в течение долгого времени), определяющий области, где в дальнейшем должен появиться дефект.

Четвертую и последнюю фазу трудно визуально отличить от третьей. По словам Гриффита, некоторые дефекты оказываются "эффективнее" других в том отношении, что они действуют как часовой механизм с n состояниями: прохождение клеточных состояний по самому внутреннему циклу требует в точности n тактов. Спирали, движущиеся в более медленном ритме, поглощаются более эффективными спиралями. Такие эффективные спирали и являются демонами, которые населяют четвертую фазу циклического пространства. Они обустраиваются на вечное существование, отделяясь от соседних демонов невидимыми, но прочными барьерами.


Циклическое пространство в заключительной фазе демонов

Возможно Гриффит и не открыл бы циклическое пространство, если бы Норман Марголас и Томассо Тоффоли из Массачусетского технологического института не разработали машину на клеточном автомате (Cellular Automaton Machine), сокращенно САМ. Эта машина состоит из нескольких больших микросхем на плате, вставляемой в стандартные гнезда персонального компьютера. В интегральных микросхемах каждая клетка автомата представляется отдельной ячейкой пямяти, содержимое которой изменяется с помощью специальных управляющих логических схем. При максимальном быстродействии САМ способна перевычислять клеточный массив размером 256*256 со скоростью 60 раз в секунду.

К сожалению, стоимость этого устройства довольно высока. Тем не менее читатели могут создать свою собственную модель циклического пространства (хотя и более медленную по сравнению с САМ) под названием DEMON, переведя приведенное ниже алгоритмическое описание на наиболее привычный для них язык программирования. В алгоритме используются два массива: new (новый) и old (старый), содержащие соответственно текущие и предшествующие состояния клеток циклического пространства.

repeat until нажата клавиша
- for i <- 1 to 100
- - for j <- 1 to 100
- - - for каждый сосед (k, l) клетки (i, j)
- - - - if old(k, l) = old(i, j)+1
- - - - - then new(k, l) <- old(i, j)
- for i <- 1 to 100
- - for j <- 1 to 100
- - - показать new(i, j)
- - - old(i, j) <- new(i, j)

Внешний цикл, заканчивающийся, когда пользователь программы DEMON нажимает определенную клавишу, управляет повторением основных циклов проверки и высвечивания состояний клеток. Разумеется, возможны и другие способы построения такого цикла. Читателям, компьютеры которых имеют небольшую память, мы советуем ограничиться сравнительно маленьким массивом клеток, скажем 50*50. В приведенных здесь двух внутренних циклах размеры клеточного массива предполагаются равными 100*100. Клетка с координатами (i, j) находится на пересечении i-й строки и j-го столбца.

В самом внутреннем цикле программы DEMON проверяется состояние каждой из четырех клеток, прилегающих к клетке (i, j). (Поэтому читателям в своих версиях алгоритма нужно включить инструкции, присваивающие значения i-1 и i+1 индексной переменной k, когда l равно j. Аналогичным образом, значения j-1 и j+1 должны быть присвоены l, когда k равно i). Если состояние одной из соседних клеток оказывается на 1 больше состояния клетки (i, j), то клетка (i, j) должна быть съедена: ее состояние становится равным состоянию этой соседней клетки.

В программе DEMON при вычислении значений old (i, j)+1 должно применяться сложение по модулю. Другими словами, если old(i, j) оказывается равным n-1, т.е. наивысшему состоянию, то сумма old(i, j)+1 должна быть равна 0. Следовательно, если число состояний было выбрано равным 10, то возможные состояния-это 0, 1, 2, ..., 9 и 9+1=0. Если состояние клетки изменяется, то его новое значение нужно присвоить элементу массива new(i, j).

В двойном цикле, следующем за циклом проверки, высвечиваются все клетки, содержащиеся в массиве new, а в массиве old старые значения заменяются соответствующими значениями из new. Чтобы выяснить, как высвечивать клетки на компьютерном экране, читатели могут ознакомиться с описанием этой процедуры в наших предшествующих статьях, в частности в статье за прошлый месяц.

Арифметические операции должны выполняться по модулю не только по отношению к значениям состояния клеток, но и по отношению к индексным переменным i и j. Простейший способ создать иллюзию бесконечного пространства заключается в том, чтобы придать экрану свойство замкнутости. Клетки в крайне правом столбце считаются прилегающими к клеткам крайне левого столбца, а клетки нижней строки - прилегающими к клеткам верхней. Для этого нужно воспользоваться значениями индекса от 0 до 99, а не от 1 до 100. Таким образом, клетка, прилегающая справа к клетке (23, 99), будет иметь координаты (23, 0). Следовательно, числа i-1, i+1, j-1 и j+1, являющиеся индексами соседей клетки (i, j), должны браться по модулю. В большинстве языков программирования существуют инструкции, которые делают это автоматически.

Конечно, программа DEMON должна позволять пользователю "инициализировать" клеточное пространство начальными значениями состояний. Для этого в алгоритме можно предусмотреть средство, позволяющее пользователю указать желаемое количество возможных состояний, а также организовать цикл, задающий каждой клетке пространства исходное, случайно выбранное состояние из допустимого диапазона чисел.

Каким же лучше всего выбрать число возможных состояний? Это зависит от того, как долго сможет ждать читатель, пока все четыре фазы не сменят друг друга на экране компьютера. Если число состояний очень велико, скажем больше 25, то случайно проинициализированный массив размером 100*100, вероятно, вообще не будет эволюционировать. С другой стороны, когда число состояний мало, то фазы сменяют друг друга слишком быстро, и это тоже не интересно. Гриффит рекомендует выбирать число состояний в интервале от 12 до 16.

Несколько месяцев назад я говорил, что собираюсь нанести визит в Висконсинский университет, чтобы рассказать о деятельности так называемой "мафии исследователей частиц", членом которой является также Гриффит. (Это название объясняется тем, что на раннем этапе область науки, изучающая системы частиц, была связана с именем Фрэнка Спитцера, математика из Корнеллского университета, т.е. из той местности, где (согласно голливудской легенде) скрывалась когда-то штаб-квартира мафии). Публикации и лекции Спитцера, посвященные системам частиц, способствовали популяризации этой области науки в Северной Америке; аналогичную роль сыграла работа его коллеги Р.Л.Добрушина в Советском Союзе. Несколько студентов, учившихся у Спитцера в Корнеллском университете, а также ряд других его последователей занялись играми, основанными на системах частиц. Помимо Гриффита можно назвать также таких исследователей, как М.Брамсон (тоже из Мадисона), Р.Деррет из Корнеллского университета и Т.Лиггет из Калифорнийского университета в Лос-Анджелесе.

Что же собой представляет система частиц? Обычно под такой системой подразумевается клеточный автомат, в котором в каждый момент лишь одна клетка может изменять свое состояние - зачастую случайным образом. Алгоритм диффузионно-ограниченной агрегации, описанный в нашей февральской статье, является одним из примеров. В данном случае единственная частица совершает случайное движение по решетке клеток до тех пор, пока не встретится с растущим агрегатом. Она застывает на месте, и в тот же момент другая частица начинает движение. Со временем агрегат всегда приобретает форму в виде дерева.

Системы частиц поставили перед исследователями ряд важных и трудных проблем, не последнее место среди которых занимает, в частности, вопрос, касающийся долговременной устойчивости определенных фаз, возникающих в ходе эволюции подобных систем. Хотя циклическое пространство и не относится к традиционным системам частиц, Гриффит считает, что оно по крайней мере дает модель локально периодических волновых объектов, которая, благодаря своим простым правилам, значительно легче поддается математическому изучению. И действительно, недавно он доказал теорему, которая дает для каждого возможного размера массива и числа состояний вероятность того, что циклическое пространство никогда не выйдет из своей первоначальной фазы осколков.

Ну а для нас с вами циклический клеточный автомат по крайней мере представляет возможность исследовать свойства миниатюрной вселенной. Конечно, она намного проще той Вселенной, в которой мы живем, но у нее есть свои неведомые нам красоты и удивительные явления.

БИБЛИОГРАФИЯ

CELLULAR AUTOMATA MACHINES. TOMMASO TOFFOLI AND NORMAN MARGOLUS. The MIT Press, 1988. (Т.ТОФФОЛИ, Н.МАРГОЛУС, МАШИНЫ КЛЕТОЧНЫХ АВТОМАТОВ, Москва, "МИР", 1991.- G.).

CYCLIC CELLULAR AUTOMATA IN TWO DIMENSIONS. ROBERT FISCH, JANKO GRAVNER AND DAVID GRIFFEATH. Ted E. Harris Festschrift. Birkhauser, in press.

ОТКЛИКИ

3 1990
В октябрьском номере в прошлом году мы поместили статью об исследовании клеточного автомата, который его изобретатель Дэвид Гриффит из Висконсинского университета в Мадисоне назвал циклическим пространством. После выхода этой статьи сотни любителей научных исследований занялись экспериментами с циклическим пространством. Я упомяну здесь лишь несколько наиболее интересных работ.

Клеточная вселенная Гриффита называется циклической из-за наличия своеобразных пищевых цепочек, действующих в популяции клеток. Клетка, находящаяся в состоянии k, поедает соседнюю клетку, находящуюся в состоянии k-1. Если k равно нулю, то следующее низшее состояние равно n-1, при условии, что полное число состояний равно n. Таким образом, пищевая цепочка становится пищевым циклом. Вначале, когда клеточное пространство заполнено клетками в произвольно выбранных состояниях (стадия осколков), при больших значениях n наблюдается низкая активность, потому что в среднем вероятность того, что клетка находится по соседству с другой клеткой в состоянии на 1 меньше, относительно мала.

X.Смит из Саратоги (шт. Калифорния) исследовал пространство 320*200 клеток, каждая из которых находится в одном из 14 разрешенных состояний. Вначале около 25% клеток изменяют свое состояние на каждом итерационном шаге, однако через 15 поколений доля таких клеток снижается менее чем до 3%. Затем, говорит Смит, начинают формироваться пятна интенсивной активности, которые Гриффит называет капельками. По мере того как капли растут, процент клеток, изменяющих свое состояние на каждом шаге итераций, также растет. Затем приблизительно через 150 поколений этот процент начинает расти еше быстрее, и в конце концов достигается фаза демонов, в которой все клетки изменяют свое состояние на каждом итерационном шаге.

В статье, посвященной циклическому пространству, я предложил читателям найти небольшой прямоугольник клеток, который не содержит дефекта, но со временем произведет его. Под дефектом Гриффит подразумевает цепочку клеток, которая содержит непрерывный цикл из всех возможных состояний. Это то самое яйцо, из которого позже вылупляется демон. Самое изящное решение этой задачи удалось получить М.Эллеру из Сиэтла (шт.Вашингтон). Проследите, что случится со следующим прямоугольником размером 3*3 в циклическом пространстве с 8 состояниями



Дж.Бреретон из Вест-Хейвена (шт. Коннектикут) придумал интересную форму отображения процессов, разворачивающихся в циклическом клеточном автомате. Он выводит не одно, а два изображения циклического пространства, разделив экран на две части. В левой части экрана показывается последнее поколение клеток, а в правой - только те клетки, которые изменяют свое состояние при вычислении следующего поколения. Не ограничиваясь тем, что было задумано Гриффитом и описано в статье, Бреретон экспериментировал с моделями, учитывающими в качестве соседей не только четыре клетки по сторонам, но и четыре, касающиеся данной в углах квадрата. Новое пространство вселило в него чувство первооткрывателя: "Приближаясь к этой странной планете, мы сначала видим многоцветное покрывало из облаков, под которым невозможно различить никаких деталей. Затем, по мере того как мы сквозь последовательные циклы спускаемся ниже, на поверхности планеты через промежутки между облаками начинают проступать цветные узоры. Наконец, становятся видимыми четкие разграничительные линии между полями различного цвета, а за ними небольшие строения ...". Однако предоставим читателям самим завершить это описание, если они пожелают посетить планету Бреретона.

11 1989
ДВУМЕРНЫЕ МАШИНЫ ТЬЮРИНГА И "ТЬЮРМИТЫ"
А.К.ДЬЮДНИ

"Термиты... способны создавать сложные узоры на ландшафте, как никакие другие организмы, кроме человека."
УОЛТЕР ЛИНСЕНМДЙЕР, Насекомые планеты

ТЕ КОМУ хотя раз доводил ось видеть термитник, наверное, остались под глубоким впечатлением от сложных систем тоннелей, построенных этими трудолюбивыми, но безмозглыми насекомыми. Парадоксально, но искусственные формы жизни, по сравнению с которыми термиты выглядят гениями, способны создавать не менее удивительные структуры. Возьмем, к примеру, "тьюрмитов". Эти угловатые кибернетические создания наделены самым рудиментарным мозгом. Тем не менее, двигаясь по бесконечной плоскости, которая является средой их обитания, они оставляют следы в виде причудливых узоров, казалось бы отражающих какой-то разумный замысел.

Своим появлением тьюрмиты отчасти обязаны Грегу Тэрку, аспиранту из Университета Северной Каролины в Чепел-Хилле. В течение некоторого времени Тэрк экспериментировал с одной из разновидностей машины Тьюринга, воображаемого устройства, которое долго служило в качестве фундаментальной модели вычислительных процессов. Обычно предполагается, что машина Тьюринга оперирует на бесконечной прямой ленте, поделенной на ячейки. Однако Тэрк изучал машины Тьюринга, работающие со своего рода двумерной лентой - по существу с той самой плоскостью, по которой блуждают тьюрмиты. Двумерную машину Тьюринга превратить в тьюрмита легко и просто: абстрактные правила заменяются несложным образом на нейронную сеть. Такое преобразование является ярким примером важной темы в теории вычислений: часто две, казалось не связанные друг с другом вычислительные схемы оказываются эквивалентными.

Машины Тьюринга были названы в честь английского математика Алана М.Тьюринга, который первым предложил их в качестве способа определения вычислений. По существу машина Тьюринга - это фундаментальная цифровая вычислительная машина. Она может выполнить любое вычисление, доступное современному компьютеру - при условии что ей будет предоставлено достаточно времени.

Машину Тьюринга можно представить себе такой, как она показана на рисунке на с.127: черный ящик, содержащий устройство, которое может считать символ, записанный в ячейке бесконечно длинной ленты, записать новый символ в ту же ячейку и переместить ленту вперед или назад для того, чтобы проанализировать символ, хранящийся в соседней ячейке. Что находится внутри черного ящика? На самом деле это не имеет значения, лишь бы машина придерживалась строго заданной таблицы, в которой указаны действия, которые машина обязана совершить для каждого прочитанного символа и каждого из возможных "СОСТОЯНИ№що-рые меняются с каждым новым циклом действия. Цикл состоит из трех следующих шагов:
1. Прочесть символ, находящийся в данный момент под устройством чтения/записи.
2. Обратиться к элементу таблицы, определяемому текущим состоянием машины и только что прочитанным символом.
3. Записать символ, определяемый элементом таблицы, продвинуть ленту в указанном направлении и перейти в указанное состояние.


Типичная машина Тьюринга

Таким образом, каждый элемент таблицы состоит из трех частей: символа, который нужно записать в текущую ячейку; направления, в котором должна переместиться лента; и состояния, к которому машина переходит по завершении цикла.

Перемещение ленты следует рассматривать в относительном смысле. С таким же успехом можно считать, что лента остается неподвижной, а машина сама перемещается по ней от ячейки к ячейке. На самом деле, если принять идею о том, что движется не лента, а машина Тьюринга, то уже не нужно обладать очень богатым воображением, чтобы представить себе двумерную "ленту", по которой свободно могла бы перемещаться машина.

Независимо от того, одномерна или двумерна лента, поведение машины Тьюринга в конечном итоге определяется ее таблицей. Она в точности эквивалентна программе, управляющей действиями современного цифрового компьютера. В смысле вычислительных возможностей двумерную машину Тьюринга не следует считать более мощной по сравнению с одномерными. Однако двумерная машина обладает, конечно, значительно более интересным репертуаром перемещений. Траектория следа, показанная на верхнем рисунке на с.128, была, например, получена с помощью двумерной машины Тьюринга с одним-единственным состоянием. Ее внутренняя таблица имеет следующий вид:



Единственное состояние машины было обозначено буквой A.


След от машины Тьюринга, придуманной Тэрком

Несколько более сложная двумерная машина Тьюринга, придуманная Тэрком, имеет два состояния, обозначенные как A и B, и в своем поведении руководствуется следующей внутренней таблицей:



По словам Тэрка, двумерная машина Тьюринга, запрограммированная с помощью этой таблицы, рисует восхитительные спиральные узоры. Она создает "все более увеличивающиеся разрисованные области, располагающиеся упорядоченным образом вокруг точки старта".

Любой рисунок следа, порожденного двумерной машиной Тьюринга, может быть в точности воссоздан тьюрмитом. Однако поведение тьюр-мита не управляется таинственным черным ящиком. Оно контролируется тем, что весьма условно можно было бы назвать мозгом. Тот факт, что мозг термита можно вскрыть и подвергнуть исследованию, делает эти существа особенно интересными.

Если же судить по внешнему виду и характеру поведения, то тьюрмит, конечно, не столь интересен. Тело у него приблизительно квадратное подходящее для квадратных ячеек, на которые поделена бесконечная плоскость, среда обитания тьюрмитов. Нижняя поверхность у тьюрмита плоская и оснащена некоторым двигательным аппаратом. (Лично я не знаю, каким образом работает этот аппарат, так как ни разу не переворачивал тьюрмита вверх ногами). Этот аппарат позволяет тьюрмиту вращаться и перемещаться ровно на одну клетку в том направлении, куда он в данный момент ориентирован. По сути дела головы как таковой у тьюрмита нет, она существует лишь условно, чтобы мы могли всегда определить, в какую сторону он ориентирован; "глаза" у него также не функционируют. Когда тьюрмит меняет направление, он просто поворачивается на 90o, оставаясь в том же квадрате, прежде чем переместиться в новый.


В каждый момент времени тъюрмит занимает одну клетку

Первоначально все клетки плоскости, включая ту, в которой находится тьюрмит, окрашены в черный цвет. Однако, прежде чем переместиться, тьюрмит может изменить цвет клетки, которую он в данный момент занимает. (Природа красящего органа тьюрмита для нас остается такой же загадочной, как и аппарат, с помощью которого он перемещается). Тьюрмит, рисующий след, показанный на верхнем рисунке на с.128, например, должен уметь окрашивать клетку в один из двух цветов (в данном случае красный или черный). Однако, чтобы воссоздать узор, показанный на нижнем рисунке, тьюрмит должен иметь в своем распоряжении более богатую палитру.


Многоцветный рисунок, созданный тьюрмитом

Каким образом тьюрмит узнает, когда нужно двигаться или когда изменить окраску квадрата? Этими действиями управляет его "мозг", который состоит из набора "нейродов", являющихся упрощенной моделью нейронов нашего головного мозга. Нейрод принимает сигналы, распространяющиеся по проводящим волокнам и исходящие из сенсоров (расположенных на нижней поверхности тьюрмита) или из других нейродов, и в свою очередь посылает сигналы эффекторам (таким как двигательный аппарат тьюрмита или орган, способный изменять окраску квадрата) или другим нейродам.

Нейрод срабатывает (посылает сигнал по своей выходной линии), если число входных сигналов равно или превышает пороговое значение данного нейрода, которое на схемах обозначается числом, помечающим каждый нейрод. В противном случае он не срабатывает. Поскольку время в мире тьюрмитов меняется дискретными шагами, все сигналы возбуждения и торможения посылаются и принимаются синхронно с этими дискретными шагами.

Чтобы проиллюстрировать, каким образом тьюрмит принимает то или иное решение, я проведу вскрытие мозга у двух представителей этого вида (см. левый и средний рисунки на с.129), каждый из которых производит в точности те же действия, что и двумерная машина Тьюринга с одним состоянием, уже рассмотренная выше. Мозг, изображенный на левом рисунке, имеет два нейрода, не соединенных друг с другом. У каждого нейрода имеется лишь одно входное и одно выходное волокно. Когда цветовой сенсор тьюрмита регистрирует красный цвет, он посылает один сигнал левому нейроду, заставляя его сработать. Выходное волокно нейрода расщепляется на две линии, одна из которых идет на цветовой эффектор (последний, получив сигнал, окрашивает клетку, в которой находится тьюрмит), а другой - на двигательный аппарат (который затем поворачивает тело тьюрмита на 90o вправо и перемещает его на одну клетку в новом направлении движения). С другой стороны, когда цветовой сенсор тьюрмита обнаруживает черную клетку, он посылает сигнал правому нейроду и тот также срабатывает. Выход этого нейрода в свою очередь заставляет тьюрмита перекрасить клетку в красный цвет, прежде чем развернуться и переместиться на соседнюю клетку слева.


Три мозговых устройства тъюрмитов, два из которых (левое и среднее) выполняют одну и ту же работу

Короче говоря, когда тьюрмит выясняет, что находится на красной клетке, он окрашивает ее в черный цвет и перемещается на одну клетку вправо. Если же он занимает черную клетку, то перекрашивает ее в красный цвет, затем поворачивает влево и переходит на одну клетку в одном из направлений.

Мозг второго тьюрмита имеет более замысловатую конструкцию, однако выполняет в точности ту же работу, что и первый. Здесь оба нейрода имеют порог 2; ни один из них не сработает, пока не получит два входных сигнала на одном и том же временном шаге. Предположим, что первоначальный сигнал привел мозг в действие и один из двух нейродов всегда будет срабатывать на каждом шаге.

Вот такое простое поведение, воплощенное в двух только что рассмотренных нейродных цепях, в результате приводит к созданию довольно сложного изображения (см. рисунок слева): красное облачко из маленьких квадратиков, от которого протягивается прямо в бесконечность замысловатая структура. По какой причине в поведении тьюрмита появляется вдруг такая целеустремленность, после длительных и, казалось бы, бесцельных блужданий? Ответ таится в той закономерности, которую можно пронаблюдать в облачке раскрашенных квадратиков. В какой-то момент времени эта закономерность в сочетании с правилами поведения тьюрмита, основанными на схеме его нейродов, вынуждают это существо войти в повторяющуюся последовательность действий, которая и приводит к построению той сложной структуры, которую мы видим на рисунке. (Интересно, смогут ли наши читатели найти конфигурацию, с которой начинается повторяющаяся последовательность?)

Ну что ж, такова жизнь в мире тьюрмитов. Иногда, казалось бы, бесцельное блуждание превращается в почти абсолютный детерминизм. Конечно, случайность здесь чисто иллюзорная. Все тьюрмиты полностью детерминированы в любой момент времени.

Тем не менее в мире тьюрмитов встречаются и загадочные явления. Рассмотрим, к примеру, конфигурацию, показанную на нижнем рисунке. Тьюрмит, оставивший этот след, снабжен четырьмя эффекторами, изменяющими цвет клетки, соответственно делая его черным, красным, желтым или зеленым. В своем поведении существо руководствуется следующими правилами:



Мозг этого тьюрмита также очень несложен. Он состоит из четырех нейродов, не соединенных между собой. Каждый из этих четырех нейродов реализует одно из четырех перечисленных правил поведения в той же манере, как это делал простейший мозг первого тьюрмита. Тэрк был озадачен тем фактом, что след, оставляемый этим тьюрмитом, обладает двусторонней симметрией. Возможно, читатели смогут объяснить причину этого явления.

Каким образом можно построить организм тьюрмита на основе той или иной двумерной машины Тьюринга? На самом деле метод построения очень прост. Нужно просто заменить каждый элемент внутренней таблицы машины нейродом с пороговым значением 2, который получал бы входные сигналы от сенсора цвета, соответствующего номеру столбца элемента в таблице, и, возможно, от других нейродов. Выходные линии каждого нейрода должны вести к эффекторам, производящим перемещение и замену цвета, как указано в данном элементе таблицы.

Предположим, что некоторый нейрод соответствует элементу таблицы в столбце, помеченном "красный", и строке, помеченной "В". Согласно схеме преобразования, у нейрода должна быть входная линия, исходящая от сенсора, детектирующего красный цвет. Если элемент таблицы содержит: (черный, влево, B), то у нейрода должен быть выход, ведущий к эффектору, который перекрашивает клетку в черный цвет, и другой выход - к эффектору , который позволяет тьюрмиту совершать левые повороты.

Различные состояния данной машины Тьюринга реализуются различными соединениями между нейродами в мозгу тьюрмита. Поскольку в рассматриваемом примере элемент таблицы требует, чтобы тьюрмит перешел в состояние B, то нейрод, представляющий данный табличный элемент, должен иметь выходные линии, ведущие к каждому нейроду, участвующему в представлении строки B таблицы.

В данном контексте такая нейронная сеть - это не что иное, как некое аппаратное устройство, воплощающее в себе правила поведения, которые содержатся в таблице. Пример рассмотренного преобразования схематически изображен на правом рисунке вверху. Рисунок показывает, как можно построить мозг тьюрмита, моделирующего поведение "спиральной" двумерной машины Тьюринга, придуманной Тэрком.

Забавно наблюдать за тем, как тьюрмит (или двумерная машина Тьюринга) блуждает по клеточной плоскости. Однако, чтобы стать свидетелем этого зрелища, читатель должен написать программу, моделирующую движения тьюрмита. Каким образом можно перейти от таблицы к программе? К счастью, это почти так же просто, как построить структуру мозга тьюрмита. Программа, которую я назову TURMITE, пользуется в своей работе таблицей машины Тьюринга, представленной в виде трех отдельных массивов: color (цвет), motion (движение) и state (состояние). Каждый массив индексируется двумя переменными, c и s. Переменная c индексирует цвет текущего квадрата, а s - текущее состояние машины Тьюринга (или эквивалентного тьюрмита). Поскольку этим переменным должны присваиваться в качестве значений целые числа, цвета и состояния, используемые в данной модели, должны быть пронумерованы. (Элементы массивов также должны быть целыми числами).

Например, черный и зеленый цвета могут быть присвоены переменной c в виде чисел 1 и 2 соответственно. Аналогичным образом, состояния A и B могут быть обозначены соответственно числами 1 и 2 в качестве значений переменной s. В нашем случае при моделировании спирального тьюрмита нам потребуются следующие массивы:



Направления движения также должны быть закодированы числами. Поэтому "вперед", "назад", "влево" и "вправо" будут соответственно обозначаться числами 1, 2, 3, 4 в качестве значений элементов массива motion.

Главная цель программы TURMITE заключается в том, чтобы закрашивать маленькие квадратики (может быть, даже отдельные пикселы) на экране компьютера в соответствии с действиями тьюрмита. Программа хранит цвета высвечиваемых ею квадратиков в двумерном массиве под именем pattern (картинка). Первоначально высвечивается лишь один квадратик - расположенный в самом центре экрана.

Значение c в каждый данный момент определяется элементом массива pattern, соответствующим текущим координатам тьюрмита на экране, скажем i и j. Располагая известными значениями c и s, программа просто обращается к элементам color(c, s), motion(c, s) и state(c, s). Программа изменяет цвет, закоди-
рованный в элементе pattern(i, j), а затем изменяет значение i или j в зависимости от значения, хранящегося в motion(c, s). Здесь программа должна преобразовать относительное перемещение, закодированное в motion, в абсолютное перемещение, проанализировав значение другой переменной dir, содержащей направление последнего перемещения: вверх, вниз, влево или вправо. Заключительный шаг в основном цикле действий программы TURMITE состоит просто в том, чтобы заменить значение s числом, содержащимся в state(c, s). Остальное можно оставить воображению и изобретательности тех читателей, которым нравится писать свои собственные программы.

Конструируя мозг тьюрмита или моделируя его поведение на компьютере, интересно, наверное, будет поразмышлять также и о том, что тьюрмиты, способные выполнить любое вычисление, производимое машиной Тьюринга, смогут вполне успешно работать в качестве компьютеров. Если, как некоторые утверждают, человеческий мозг представляет собой не что иное, как своеобразный цифровой компьютер, то кое-какие тьюрмиты могли бы быть и не глупее нас с вами - если не умнее!

БИБЛИОГРАФИЯ

MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.216, No.3, pages 124-129; March, 1967.

MATHEMATICAL GAMES. MARTIN GARDNER in Scientific American, Vol.229, No.5, pages 116-123; November, 1973.

ОТКЛИКИ

5 1990
КОМПЬЮТЕРЫ по всему миру подверглись нашествию "тьюрмитов" - кибернетических организмов, описанных в "Занимательном компьютере" в ноябрьском номере журнала за прошлый год. Начав жизнь в бесконечной решетке черных квадратиков, каждый тьюрмит начинает перекрашивать клетки согласно своей таблице переходов между состояниями. На самом деле тьюрмит представляет собой двумерную машину Тьюринга, а цвета, в которые окрашиваются клетки решетки, обычно рассматриваются как символы, считываемые или записываемые машиной Тьюринга. Даже простейшие машины, с одним состоянием, способны порождать изящные и замысловатые узоры, как паказал Г.Тэрк, персонаж статьи, посвященной тьюрмитам.

Т.Храпкевич из Дерборна (шт.Мичиган) говорит, что наблюдать за передвижениями тьюрмита намного интереснее, чем рассматривать получающиеся в результате узоры. Храпкевич написал короткую программу для простейшего тьюрмита, который порождает выглядящее случайным скопление цветных клеток, а затем уходит по регулярной кривой. Понаблюдав за поведением тьюрмита, Храпкевич заинтересовался вопросом, что будет делать тьюрмит, встретившись с уже нарисованной линией на решетке. Выяснилось, что тьюрмит любит двигаться вдоль нарисованных линий, а иногда по ходу своего движения перемешает их. Эти наблюдения привели Храпкевича к идее разбросать по решетке "снег": случайным образом расположенные нечерные клетки, с которыми тьюрмит может взаимодействовать. При этом практически гарантируется, что тьюрмит никогда не войдет в бесконечный цикл.

Т.Дэрхем, известный английский писатель-фантаст, запрограммировал некоторых тьюрмитов из коллекции Тэрка, в частности тех, которые порождают своеобразные, симметричные прямоугольные структуры. Меня интересовал вопрос, возникнет ли двусторонняя симметрия у тьюрмита, таблица поведения которого обладает лишь циклической симметрией. Дэрхем открыл противоположную версию этого тьюрмнта, которая сводит на нет все, что порождает его "непротивоположный" собрат.

Из Гонконга Л.Пратт сообщил о своей тьюрмитной программе, которая принимает любую таблицу с двумя состояниями, указанную пользователем. Эта программа позволила Пратту проследить за несколькими вариациями на тему с двумя состояниями. Изменение лишь одного элемента таблицы чаше всего приводит к появлению совершенно нового племени тьюрмитов.

О.Олсен из Трондхейма (Норвегия) выпустил на одну и ту же решетку сразу двух тьюрмитов, чтобы понаблюдать за тем, как они снуют по хаотическому облачку раскрашенных пикселов. Через некоторое время один из них уходит в бесконечность, оставляя за собой кружевной след. В конце концов, оставшийся в одиночестве его приятель нападает на этот след и "пускается в погоню за первым, чтобы сказать ему, что он неправ".

Наконец, я не могу не упомянуть и о красивых картинках, присланных X.Уэтсом из Колумбии (шт.Виргиния). Экспериментируя с вариациями четырехцветного тьюрмита, Уэтс обнаружил одну разновидность, порождающую продолговатую каплю, из которой периодически выбрасываются конечные "спиральные рукава". Однако тьюрмит всякий раз возвращается к капле, усложняя ее форму, делая ее более продолговатой и придавая ей более случайные очертания, прежде чем опять отправится по очередному рукаву. При разведении тьюрмитов девять десятых удовольствия, конечно, заключается в том, чтобы наблюдать за ними.

12 1989
КОМПЬЮТЕР ИЗ ДЕТАЛЕЙ ДЕТСКОГО КОНСТРУКТОРА ИГРАЕТ В "КРЕСТИКИ-НОЛИКИ"
А.К.ДЬЮДНИ

"Впервые с этим свойством [универсальностью вычислений] я столкнулся еще до того, как пощел в школу. Тогда не было никаких компьютеров, но у нас были детские конструкторские наборы. Один из них назывался "тинкертоЙ"... Удивительно, но его палочек и катушек хватало на то, чтобы построить что УГОДНО."
Марвин Минский

МНОГИЕ ЛИ из нас помнят конструкторы "тинкертой" - наборы цветных деревянных палочек и катушек с отверстиями? Глядя на сооружения в виде башен и кранов, многие ли из нас задумывались тогда в детстве, до каких пределов простираются возможности тинкертоя? Представляли ли мы себе сооружения высотой до потолка? Возможно, но на такие постройки у нас не хватало ни деталей в наборе, ни времени. Однако несколько лет назад нашу былую фантазию реализовали студенты из Массачусетского технологического института (МТИ), построив компьютер, целиком (точнее, почти целиком) состоящий из деталей тинкертоя.

Издали компьютер из тинкертоя выглядит как плод необузданной детской фантазии или, по замечанию одного из студентов, как палочно-катушечный вариант космической научной лаборатории из кинофильма "Космическая Одиссея: 2001г.". В отличие от лаборатории инопланетян компьютер, собранный из палочек и катушек, играет в крестики-нолики. Спереди сооружения, пощелкивая и как бы на ощупь вниз, перемещается конструкция, называемая головкой чтения. В какой-то момент щелканье прекращается, наступает таинственная тишина; начинает вращаться деталь, называемая "сердечником", затем вращение завершается другим странным звуком, и в движение приходит "выходная уточка" - конструкция, по форме напоминающая птицу; она наклоняется вперед со своего насеста, так что ее клюв указывает на число, определяющее следующий ход, который делает компьютер по ходу игры в крестики-нолики.

Что же конкретно просматривает головка чтения, когда она, ощупывая сооружение, перемещается вниз? Она проходит вдоль 48 рядов "запоминающих валиков", кодирующих все важнейшие комбинации крестиков и ноликов, которые могут возникнуть во время игры (см. рисунок на с.89). Каждый валик представляет собой последовательность гладких катушек, соединенных на оси палочками и разбитых на 9 групп, по 3 в каждой группе, так что на каждый квадрат игровой доски приходится по одной группе. Присутствие или отсутствие катушки в группе указывает на то, что соответствующая клетка игровой доски свободна или занята одним из знаков - крестиком или ноликом.


Компьютер из тинкертоев всегда готов сразиться в "крестики-нолики"

Компьютер из тинкертоя не полностью автоматизирован: оператор должен перемещать головку чтения и осуществлять ввод "данных". После того как человек, играющий с компьютером, делает ход, оператор подходит к машине, чтобы установить соответствующим образом сердечник внутри головки чтения, регистрируя таким образом сделанный ход. Затем оператор тянет за шнурок, чтобы взвести механизм сердечника перед тем, как он начнет поиск ответа. Когда компьютер находит запоминающий валик, состояние которого идентично положению в игре, сердечник поворачивается и компьютер указывает свой ответный ход.

Понять, как работает машина, наверное, будет проще, если рассказать историю ее создания. Машину построили студенты МТИ Э.Джи, Э.Хардебек, Д.Хиллис, М.Мински и братья Барри и Брайен Силвермен. Теперь большинство из них уже закончили институт и работают в различных областях информатики и вычислительной техники. Наибольшую известность приобрел, пожалуй, Хиллис. Он был "движущей силой" в компании Thinking Machines, Inc., создавшей широко известный параллельный суперкомпьютер, так называемую коммутационную машину Connection Machine. (Видимо, конструктор тинкертой может кое-чему научить).

В 1975г. Хиллис и Брайен Силвермен, когда они были еще второкурсниками, приняли участие в учебном проекте, целью которого было построить какое-нибудь цифровое устройство из тинкертоя. Студенты с удовольствием занялись этой игрой. Один из них сделал инвертер, логическое устройство, преобразующее двоичные сигналы - 1 в 0 и наоборот. Другой сделал вентиль ИЛИ: если один из входов этого устройства равен 1, то выход всегда будет также равен 1. Студенты быстро поняли, что конструктор тинкертой обладал свойством "универсальности вычислений" - этот теоретический термин характеризует набор компонентов, из которых можно собрать полностью программируемую вычислительную мащину. Однако теоретическая возможность - это одно, а практика, которая требует и времени и средств,- совсем другое.

Эти потребности были удовлетворены окольным путем благодаря интересу Хиллиса к роботам и его стремлению создать один из них, о чем он время от времени говорил со своими друзьями. Слухи о его мечтах каким-то образом достигли X.Лаукса, бывшего в то время директором Среднеамериканского центра в Хот-Спрингсе (шт.Арканзас). Не хотят ли студенты построить робота для витрины музея, принадлежавшего центру? Студенты согласились, но проект оказался слишком сложным. Тогда и всплыла старая мечта о машине из деталей тинкертоя. Может быть, вместо робота центр не против приобрести компьютер, собранный из тинкертоев?

Хиллис и его коллеги принялись за постройку первого компьютера на тинкертоях в лаборатории МТИ. Первая модель в отличие от последующей была довольно громоздкой и имела форму куба со стороной около метра. Конструкция выглядела весьма сложной. Набитая до отказа логическими схемами, сделанными целиком из деревянных палочек и катушек, машина указывала свои ходы, вращая девять флажков, расположенных в верхней части сооружения. Перед отправкой в Хот-Спрингс прототип компьютера пришлось разобрать, но после того, как его снова собрали на месте, компьютер уже так никогда и не заработал как следует. Тем не менее он все же был интригующим экспонатом. (В настоящее время он демонстрируется в Музее вычислительной техники в Бостоне).

В 1979 г. Лаукс снова обратился к студентам. Не смогут ли они сделать новый компьютер из тинкертоев, который бы работал по-настоящему? В то время Силвермен жил и работал в Оттаве, а Хиллис - в Бостоне. Переговариваясь по телефону, Хиллис и Силвермен разработали более совершенную конструкцию. Она должна была быть надежной, а значит, и простой. Они решили выставить все возможные комбинации игры "крестики-нолики" в ряд последовательностей и придумать какой-нибудь считывающий механизм, который передвигался бы по этому ряду от последовательности к последовательности и находил бы позицию, соответствующую положению в игре на данный момент. Само узнавание этой позиции непосредственно вызывало бы появление заранее заготовленного ответа.

Пока Хиллис обдумывал способы представления позиций игры
"крестики-нолики" в цифровых компонентах тинкертоя, Силвермен занимался анализом самой игры. Чтобы получить представление о сложности этой детской игры, читатели могут взглянуть на игровое дерево, приведенное на с.88. В середине дерева располагается исходная позиция - решетка из квадратных клеток 3*3, на которой пока нет ни крестиков, ни ноликов. Из этой исходной позиции могут возникнуть 9 первых ситуаций, в зависимости от того, в какую клетку будет поставлен первый крестик. На рисунке показаны лишь три варианта; остальные 6 можно получить вращением этих трех. Каждый их трех вариантов на втором уровне дерева игры порождает другие возможные позиции. Например, вариант, в котором "крестики" делают первый ход на центральную клетку, а затем ставится "ноль",приводит к двум различным ситуациям. Два других варианта на втором уровне порождают по пять новых позиций на третьем уровне.


Первые три уровня дерева игры "крестики-нолики"

Из соображений симметрии многие ветви игрового дерева усечены: исключенные ветви являются результатом вращения или зеркальным отражением оставленных вариантов. Люди легко обнаруживают симметрию, в то время как компьютер должен быть для этого специально запрограммирован или сконструирован. В мире конструкции из тинкертоев достижение симметрии возможно при очень сложной конструкции.

Силвермен, конечно, имел дело с деревом, во много раз большим того фрагмента, который представлен здесь на рисунке. Однако, как говорится, терпение и труд все перетрут; Силвермен обнаружил, что многие позиции можно слить в одну, когда необходимо сделать вынужденный ход. Предположим, что две клетки в каком-то ряду уже содержат нолики, а третья свободна. Тогда содержимое двух остальных рядов уже не имеет значения, поскольку в данном случае крестики должны заполнить эту третью клетку, и если они этого не сделают, то проиграют.

Силвермен был в восторге, когда ему удалось свести число возможных позиций к 48. Для каждой из них он заготовил правильный ход. Оказавшийся удивительно коротким список возможных позиций на доске обрадовал и Хиллиса. Когда группа собралась в Хот-Спрингсе, сказал Силвермен, "у нас был лишь список из 48 позиций, и мы очень смутно представляли себе, каким образом их можно интерпретировать механически".

Читатели с фанатичной склонностью к исследованию игр (или просто застрявшие на аэровокзале) могут поразвлечься, построив полное дерево игры на нескольких листах бумаги. Интересно, сколько времени потребуется, чтобы нарисовать 48 позиций, возникающих в игре "крестики-нолики"? Разобраться с этим вопросом помогут четыре символа X, 0, пробел и тире, означающее "безразлично".

Обосновавшись в Хот-Спрингсе, члены группы приобрели необходимый "строительный" материал для палочно-катушечной Одиссеи: 30 коробок тинкертоев, по 250 деталей в каждой. Затем они занялись сборкой опорной фермы, к которой должны были крепиться все 48 валиков памяти. Чтобы точно объяснить устройство этих валиков, придется немного отвлечься и изложить правила, принятые группой для кодирования позиций игры.

Во-первых, клетки игрового поля были пронумерованы следующим образом:



Далее, запоминающий валик делился на девять последовательных участков, в которых хранилась информация о состоянии каждой клетки, слева направо.

Каждый участок в свою очередь подразделялся на три равные секции, по одной на каждый возможный элемент, заполняющий данную клетку: X, 0 или пробел. Каждый вариант кодировался отсутствием соответствующей катушки. Например, если в данной клетке находился крестик, то запоминающий валик не содержал катушки в первой секции, но содержал их во второй и третьей секциях. Аналогичным образом отсутствие катушки во второй секции означало незанятую клетку, а отсутствие катушки в третьей секции - нолик. Наконец, если отсутствовали все три катушки, это означало, что содержимое данной клетки не имело значения.

Говоря о запоминающих валиках, нельзя не упомянуть и о сердечнике - детали пальцевидной формы. Здесь уместно сказать о том, что английское слово digital имеет два основных значения: пальцеобразный и цифровой. Оно происходит от латинского слова digitus (палец). Общность корней этих двух слов не случайна: люди, как известно, сначала научились считать на пальцах, а затем перешли на цифры. Поэтому сердечник, о котором идет речь и который по внешнему виду напоминает клешню с девятью пальцами, по-английски называется digital core. Сердечник и запоминающий валик показаны на рисунке, приведенном внизу.


Запоминающий валик, кодирующий крестики и нолики на игровом поле и препятствующий повороту сердечника

Сердечник состоял из девяти равных секций. У каждой из них был свой палец - короткий стержень, торчащий из ободка скользящей катушки. В каждой секции палец мог перемещаться вдоль оси сердечника и занимать одно из трех положений: одно для X, одно для 0 и одно для пробела. Таким образом, сердечник мог представлять любую из возможных позиций на игровом поле, закодированную положениями девяти пальцев, устанавливаемых оператором после каждого очередного хода. На рисунке нас.90 положение пальцев (последовательно 2, 1, 2, 3, 1, 2, 2, 2, 2) соответствует позиции, изображенной там же.

Но если сложившаяся на данный момент ситуация на игровом поле хранится в сердечнике, то нужна ли компьютеру из тинкертоя еще какая-нибудь память? Нельзя ли построить такую систему из палочно-катушечных логических элементов, чтобы компьютер мог "подумать" над позицией и выдать ответный ход? В принципе это возможно, но подобный компьютер на тинкертоях был бы слишком сложным и имел бы колоссальные размеры. Запоминающие валики почти полностью исключили необходимость в размышлении. Значительную часть этой работы выполнял другой компьютер, запрограммированный Силверменом с целью анализа игры "крестики-нолики". А все функции механического компьютера сводились просто к поиску сложившейся позиции на запоминающих валиках. Единственная же цель этого поиска, конечно, заключалась в том, чтобы выбрать правильный ход.

На рисунке, приведенном на с.89, видно, что каждому запоминающему валику соответствовало определенное число, записанное на бумажной полоске, висящей рядом с его выходной уточкой. Эти числа обозначили ответные ходы машины. В то время как головка чтения щелкает, продвигаясь вдоль ряда валиков, сердечник пытается провернуться, но не может до тех пор, пока хоть одна катушка запоминающего валика блокирует один из девяти пальцев сердечника. Только когда головка чтения прилегает к валику, отражающему сложившуюся позицию на игровом поле, все девять пальцев оказываются свободными, и сердечник проворачивается.

При помощи хитроумного механизма стержень, торчащий из одного конца сердечника, зацепляет другой стержень, соединенный с выходной уточкой. Таким образом, вращающийся сердечник сталкивает уточку с насеста и она указывает своим клювом на число, написанное на бумажной полоске.


Э.Хардебек собирает компьютер из тинкертоев

Сторонники "настоящих" компьютеров, наверное, усомнятся в том, что сооружение из тинкертоев действительно заслуживает названия "компьютер". Безусловно оно не является машиной, программируемой в обычном смысле слова: здесь нельзя сесть за клавиатуру и набрать на ней программу, которую должна выполнить машина. Но, с другой стороны, можно изменить содержимое запоминающих валиков и таким образом перепрограммировать компьютер на другие игры. Представьте себе устройство из деталей тинкертоев, играющее в "го-моку нарабе" (игра с полем 11*11 клеток, в которой один игрок пытается выстроить пять черных фишек в ряд, одновременно пытаясь помешать другому игроку создать такую же комбинацию из пяти белых фишек). Компьютер из тинкертоев, запрограммированный на эту игру, возвышался бы, наверное, до стратосферы.

Главный урок, которому может нас научить компьютер на тинкертоях, заключен в удивительном свойстве цифровых вычислений: в основе всякого вычисления лежит просто определенный поток информации. Материальная часть самого компьютера может принимать разнообразные формы и иметь различные конструкции. Можно построить безукоризненно действующие компьютеры не только из тинкертоев, но также из бамбуковых стержней, веревок и блоков (см. статью в рубрике "Занимательный компьютер" в июньском номере журнала за 1988г.), пластмассовых трубок с водой и даже, как это ни удивительно, из электронных компонентов. Последние, конечно, предпочтительнее ввиду их высокого быстродействия. Не следует с иронией воспринимать компьютер, сделанный из тинкертоев, только потому, что он не электронный. В конце концов и провода с электрическим током, по-видимому, не являются наилучшим средством для быстродействующих компьютеров. Фотоны и оптические волокна начинают все больше вытеснять их, поскольку обеспечивают более высокое быстродействие.

На самом деле, детали тинкертоя хорошо подходят для цифровых вычислений. Например, в запоминающих валиках используется двоичный принцип: присутствие или отсутствие катушек обозначает состояние данной клетки на поле "крестиков-ноликов". В работе сердечника также присутствует цифровая логика: он может повернуться лишь в том случае, когда ни один из его пальцев не блокируется соответствующими катушками на запоминающем валике. Здесь работает логическая операция И. Проследить за логикой работы сердечника можно по рисунку на с.90: если первая катушка отсутствует в первой секции запоминающего валика И, вторая катушка отсутствует во второй секции И, третья катушка отсутствует в третьей секции И и т.д.- только если все 9 условий выполняются одновременно, сердечник может повернуться. Достоинство компьютера на тинкертоях не только в его остроумной механике, но и в тонкой логике.

Поклонники тинкертоя будут рады узнать, что студенты МТИ лишь за несколькими исключениями использовали в своей конструкции только деревянные палочки и катушки. Кое-где ферму укрепляют алюминиевые трубки. Два проволочных кабеля, ось и кривошип сообщают машине потенциальную механическую энергию, необходимую для выбора следующего хода. Наконец, места соединений между палочками и катушками были укреплены клеем и специальными шпильками, при помощи которых обычно прикрепляют к стене мемориальные доски. Создатели компьютера из деталей тинкертоя вставляли эти шпильки в отверстия, просверленные в ободке катушки, в ее центральное отверстие и пропускали через вставленную палочку - задача, которую нужно было повторить более 1000 раз. (Когда Хиллис зашел в магазин, чтобы закупить несколько тысяч таких шпилек, продавец пришел в изумление. "Дело в том,- невозмутимо сказал Хиллис,- что нам нужно установить очень много мемориальных досок").

Компьютер из тинкертоя разделил участь большинства музейных экспонатов. Его разобрали на части и сложили в ящики. Он находится в хранилище Среднеамериканского центра в ожидании, быть может, новой славы. Кто знает, возможно, когда-нибудь он снова будет, пощелкивая, идти от победы к победе - этот монумент детской мечте, машина из тинкертоя.

ВОТ УЖЕ шестой год я веду рубрику "Занимательный компьютер" и могу с сожалением констатировать, что есть многие вещи, которые выходят за рамки возможностей этой рубрики. Из-за недостатка места и времени мы не можем, например, научить читателей программированию, не можем упомянуть о сотнях увлекательных программ и о многих присылаемых читателями занятных историях и идеях, касающихся компьютеров. Потребовалось шесть лет, чтобы найти наконец способ, как удовлетворить эти и другие потребности: издание периодического бюллетеня новостей. Называется он "Алгоритм: бюллетень по персональному программированию" (Algorithm: The Personal Programming Newsletter); его первый номер уже поступил в продажу.

Бюллетень будет выходить раз в два месяца, и мы попытаемся его сделать интересным и содержательным. Два раздела в бюллетене будут отведены любителям программировать. Один - для начинающих, другой - для более опытных программистов. В конце журнала будут регулярно появляться первые публикации "подпольных" программ со всех концов света. Письма, обзорные статьи и различные мнения специалистов все это призвано открыть перед читателем неизведанный мир. Я с удовольствием вышлю экземпляр первого номера бюллетеня бесплатно всем, кто напишет мне на адрес журнала "Scientific American".

БИБЛИОГРАФИЯ

CHARLES ВABBAGE: ON THE PRINCIPLES AND DEVELOPMENT OF THE CALCULATOR AND OTHER SEMINAL WRITINGS. CHARLES BABBAGE ET AL. Edited by Philip Morrison and Erily Morrison. Dover Publications, 1961.

OPTICAL COMPUTING. Special issue edited by Sing H. Lee and Ravindra A. Athale in Optical Engineering, Vol.28, No.4; April, 1989.

"ЗНАКОМЬТЕСЬ: КОМПЬЮТЕР". Пер. с англ. Под ред. В.М.Курочкина.- М.: Мир, 1989.

ОТКЛИКИ

7 1990
КОМПЬЮТЕР, собранный из игрушечного конструктора "тинкертой" и играющий в крестики-нолики, о котором шла речь в нашей рубрике в декабрьском номере журнала, стал предметом тщательного анализа читателей. Так, Р.Эренд из Уолкоттвила (шт.Индиана) попытался проследить ход мысли бывших студентов Массачусетского технологического института, который привел их к созданию массива памяти на 48 валиках. Неудовлетворенный пассивной игрой машины в тех ситуациях, когда человек упускает выигрышные возможности, Эренл добавил тщательно минимизированный набор из 12 дополнительных запоминающих валиков, для того чтобы машина быстрее доводила игру до победного конца.

Хотя в статье было упомянуто о 48 валиках, Ч.Клупфель из Блумфилда (шт.Нью-Джерси) заметил, что на иллюстрации машина имела лишь 47 валиков. Тем не менее он представил работу валиков в виде компьютерной программы, которая, как он обнаружил, содержала ошибку. Была ли эта ошибка следствием погрешности в нашей иллюстрации или она уже содержалась в исходной машине? Достигнув определенной игровой позиции, утверждает Клупфель, компьютер, играющий в крестики-нолики, может попытаться записать 0 в клетку, уже занятую 0, вместо того чтобы записать его на пустую клетку.

1 1990
ГОЛЬФ ДЛЯ ЛЮБИТЕЛЕЙ ПРОГРАММИРОВАНИЯ
А.К.ДЬЮДНИ

В ОБЫЧНОМ гольфе игрок, используя различные биты, пытается загнать мяч в лунку, скрытую в траве на газоне в несколько акров с прудами, деревьями и ямками. В мннигольф играют одной битой на гораздо меньшем игровом поле с небольшими препятствиями в виде кочек, тоннелей, вращающихся лопастей и качающихся маятников. Тому же, кто играет в микрогольф, не нужна никакая бита, а игровым полем им служит экран микрокомпьютера. В этом случае попасть в лунку с первого "удара" тоже нелегко; здесь имеются свои препятствия, в том числе и такие, которые противоречат законам физики.

Хотя в данном случае играть можно, сидя в кресле, игрок все же может ударять по мячу электронной битой и даже получать удовольствие от такого элемента в игре, которого нет в гольфе на естественных площадках, а именно программирования. Многие ли из нас способны разметить игровое поле, подготовить его к игре и сыграть матч - и все это в один день? Это не по плечу даже Джеку Никлаусу (чемпиону гольфа - Ред.) - если, конечно, он не умеет программировать. На самом деле, для того чтобы построить площадку для микрогольфа, ему совсем не обязательно быть профессиональным программистом.

Я укажу три варианта размещения трех лунок: один для начинающих игроков и два для более опытных. К концу дня каждый, кто играет по установленным правилам, овладеет игрой в микрогольф в той степени, в какой ему позволят собственные способности.

Простейший вариант игры представлен на рисунке внизу. Здесь программа, которую я назвал HOLE IN ONE, изображает всего одну лунку на прямоугольном зеленом поле. Бита выглядит как короткий отрезок прямой линии; она занесена над мячом, расположенным на краю поля. Игрок устанавливает биту в определенное положение и выбирает угол ее наклона так, чтобы послать мяч к цели - лунке, находящейся на другом краю игрового поля.


Точный удар на игровом поле для гольфа, построенном программой HOLE IN ONE

В простейшей версии игры, HOLE IN ONE, игрок наносит только один удар и либо попадает, либо промахивается. Если мяч не попадает в лунку, он уходит за край поля и исчезает с экрана, будто его и не было, он навсегда теряется в памяти компьютера. Но и в этой упрощенной версии игра довольно увлекательна и вызывает некоторый азарт.

Написать программу HOLE IN ONE и воспользоваться ею может любой рядовой программист-любитель; для него это будет своеобразным трамплином для перехода к более сложным версиям игры. Некоторые фрагменты из HOLE IN ONE можно вставить в более сложные программы, которые я назвал BIRDIE и EAGLE; они приведены на с.87 и 88.

В программе BIRDIE предусмотрено препятствие, расположенное вблизи лунки; это круговая зона, называемая ловушкой. Попав в нее, мяч изменяет направление и скорость движения совершенно непредсказуемым образом. Еще более коварные препятствия имеет программа EAGLE, но о них поговорим позже.

Примерно раз в год я обычно пытался давать в одной из статей более подробное описание программ для тех неуверенных в себе или начинающих программистов, которым требуется немного дополнительной информации, чтобы начать работать самостоятельно. В приведенном ниже описании программы HOLE IN ONE я воспользовался старым проверенным методом и начал с подробного описания алгоритма. Такой способ позволяет быстрее перейти к фрагментам настоящей программы. Читателям, которые сумеют во всем этом разобраться, останется лишь нажимать на клавиши, чтобы принять участие в открытом чемпионате на приз нашего журнала.

Программа HOLE IN ONE сначала показывает игровое поле и лунку и затем предлагает игроку прицелиться и нанести удар битой. Затем программа многократно "перерисовывает" мяч, катящийся по электронному газону, возможно, в лунку.

Руководствуясь этими правилами, можно уже в общих чертах составить алгоритм программы HOLE IN ONE: нарисовать площадку, предложить играющему нанести удар, многократно продвинуть мяч (создать своеобразную мультипликацию по направлению и скорости биты) и определить, попадет ли мяч в лунку. Потом алгоритм можно уточнить, чтобы перейти к написанию программы. Начнем с того, что исходное положение игры можно, например, представить последовательным изображением сначала прямоугольной площадки, затем мяча, лунки и биты. Эти шаги можно легко запрограммировать.

Для определенности будем предполагать, что программа пишется на языке Бейсик для персонального компьютера фирмы IBM. (He огорчайтесь, если у вас другой компьютер. Программу легко приспособить к любой другой системе). Для еше большей определенности будем предполагать, что экраны всех компьютеров имеют в ширину по крайней мере 300 пикселов (точечных элементов изображения) и 200 пикселов в высоту. Все расстояния на экране должны измеряться от начала координат, которое находится в левом верхнем углу экрана.

Для экрана размером 300*200 пикселов вполне подойдет поле в виде прямоугольника 240 пикселов в длину и 160 пикселов в высоту. Чтобы расположить игровое поле примерно в центре экрана, программа HOLE IN ONE смешает его на 30 пикселов от левого края и на 20 пикселов от верхнего края экрана. Короче говоря, горизонтальные координаты поля меняются в диапазоне от 30 до 270, а вертикальные - от 20 до 180. Зеленое поле принимает свои очертания на экране по ходу выполнения следующих инструкций:

10 CLS
20 LINE (30, 20) - (270, 20)
30 LINE (30, 180) - (270, 180)
40 LINE (30, 20) - (30, 180)
50 LINE (270, 20) - (270, 180)

Заметим, что, нумеруя инструкции Бейсика в возрастающем (но не обязательно равномерно) порядке, программист задает точную последовательность, в которой компьютер должен выполнять эти инструкции. Первая команда CLS очищает экран от любых изображений, оставшихся на нем от выполнения предыдущих действий. Этой командой обычно пользуются перед тем, как запустить программу.

Программа HOLE IN ONE представляет лунку в виде кружочка у дальнего конца прямоугольника. Центр его находится в 240 пикселах от левого края и в 100 пикселов от верхнего края. Следовательно, инструкция Бейсика, которая должна нарисовать лунку, выглядит так:

60 CIRCLE (240, 100), 5, 1

Центр кружочка располагается в точке с координатами (240, 100), а его радиус равен 5 пикселам. Единица в конце строчки указывает цвет - белый.

Чтобы игра не казалась слишком однообразной, программа помешает мячик каждый раз в случайно выбранной точке на исходной линии, которая удалена на 30 пикселов от левого края игровой площадки. Поскольку по ходу выполнения программы положение мяча изменяется, она следит за его координатами с помощью специально созданных для этого переменных XBALL и YBALL.

70 XBALL = 60
80 YBALL = 160*RND+20
90 CIRCLE (XBALL, YBALL), 4, 1

Строка 70 ограничивает координаты мяча исходной прямой линией. В строке 80 выбирается случайное число RND в диапазоне между 0 и 1, приводит его к масштабу от 0 до 160 и затем прибавляет к результату 20. Это означает, что значение YBALL попадет в какую-то точку вдоль исходной линии. В строке 90 находится команда, рисующая мяч с центром в точке (XBALL, YBALL). Радиус мяча равен 4, так чтобы он умещался в лунке с радиусом 5.

Отрезок прямой линии позади мяча представляет биту, или точнее, ее ударную часть. Координаты ее неподвижного положения задаются следующим образом:

100 LINE (54, YBALL+8 ) - (54, YBALL-8 )

Эта вертикальная линия касательна к левому краю мяча, а ее длина составляет 16 пикселов.

Следующий шаг алгоритма программы - "предложить играющему сделать удар". Прежде чем продолжить составление программы, уточним, что "предложить" - означает не только вывести соответствующее сообщение на экран, но также получить информацию об ориентации биты и скорости замаха. Нужно также перерисовать биту и изобразить ее в новом положении, так чтобы играющий смог оценить удар визуально.

Дополним поэтому программу HOLE IN ONE двумя строками, с помощью которых и выводится сообщение и принимаются необходимые входные данные:

110 PRINT "ВВЕДИТЕ СКОРОСТЬ И УГОЛ"
120 INPUT SPEED, AIM

В переменной SPEED (скорость) хранится расстояние в пикселах, которое проходит мяч всякий раз, когда программа заново вычисляет его координаты в процессе полета.

Переменная AIM (цель) хранит направление движения мяча. Многие, видимо, согласятся, что направление лучше всего выражать в градусах, которые и записываются в AIM. Поэтому программа HOLE IN ONE принимает значения угла в диапазоне от -90o до +90o, отсчитываемого от горизонтальной линии. Максимальное и минимальное значения угла соответствуют ударам, посылающим мяч прямо вверх или вниз.

К сожалению, в большинстве распространенных версий языка Бейсик углы измеряются не в градусах, а в единицах, называемых радианами. Поэтому в программу необходимо вставить небольшое вычисление, с помощью которого градусы переводятся в радианы.

130 RADAIM = (AIM*3.1416)/180

В основе этого преобразования лежит условие: 180o соответствуют пи радиан.

Значения переменных RADAIM и SPEED можно подставить в формулу, с помощью которой определяются положение и ориентация биты. Программа HOLE ON ONE требует, чтобы в соответствии с формулой на экране изображалась бита, занесенная для удара, после которого мяч либо попадет в лунку, либо улетит за пределы экрана.

Формула помешает центр биты за мячом по линии удара и на расстоянии, пропорциональном значению переменной SPEED. В случае когда значение SPEED равно нулю, бита должна касаться мяча, т.е. она должна находиться по крайней мере на расстоянии трех пикселов слева от центра мяча. Поэтому координата х центра биты определяется вычитанием величины (3+SPEED), умноженной на косинус RADAIM, из XBALL. Координату у можно найти прибавлением величины (3+SPEED), умноженной на синус RADAIM, к YBALL.

Чтобы определить угол наклона биты, потребуются дополнительные тригонометрические выкладки. Поскольку длина биты равна 16 пикселам, ее концевые точки удалены на расстояние 8 пикселов от центра. Таким образом, расстояние по оси x должно составлять 8*cos(RADAIM), a по оси y расстояние равно 8*sin(RADAIM).

Эти величины, обозначенные соответственно через A, B, C и D, вычисляются по отдельности в представленном ниже программном фрагменте, в строках со 140-й по 220-ю. Затем вычисляются действительные координаты "верхнего" конца биты (ТОРХ, TOPY) и ее "нижнего" конца (ВОТХ, BOTY). Наконец, по инструкции в строке 220 на экране рисуется линия, соединяющая эти точки.

140 А = 8*COS(RADAIM)
150 B = 8*SIN(RADAIM)
160 C = (SPEED+3)*COS(RADAIM)
170 D = (SPEED+3)*SIN(RADAIM)
180 XTOP = XBALL-C+B
190 YTOP = YBALL+D+A
200 XBOT = XBALL-C-B
210 YBOT = YBALL+D-A
220 LINE (XTOP, YTOP) - (XBOT, YBOT)

Может показаться, что теперь программа готова войти в третью фазу, а именно - изображение движущегося к цели мяча. Но, возможно, мы еще что-то не учли? А что, если игрок решит, будто неправильно задал угол наклона биты? Человеку ведь свойственно ошибаться, и ему следовало бы предоставить еще один шанс. Это можно сделать, предусмотрев по выбору играющего возможность перехода обратно к строке 10.

230 PRINT "ВВЕДИТЕ 0 ДЛЯ УДАРА"
240 INPUT PUTT
250 IF PUTT <> 0 THEN GOTO 10

Здесь, если играющий введет любое другое число, кроме 0, программа снова перейдет к строке 10, где она очистит экран, перерисует заново игровое поле и опять предложит игроку задать новые значения для переменных AIM (цель) и SPEED (скорость). Если же ифок введет 0, то программа перейдет к заключительной фазе, которую мы еще в начале статьи описали следующим образом: "многократно продвинуть мяч (создать своеобразую мультипликацию по направлению и скорости биты)".

Однако, для того чтобы переместить мяч, программа должна изменить значения его координат x и y независимым образом. Для этого переменная SPEED раскладывается на две новые переменные: XSPEED - скорость в направлении x и YSPEED - скорость в направлении y.

260 XSPEED = SPEED*COS(RADAIM)
270 YSPEED = SPEED*SIN(RADAIM)

Заключительная часть программы представляет собой цикл, в котором многократно выполняются две операции. Мяч перемешается и затем происходит проверка, не попал ли он в лунку.

280 FOR К = I ТО 300
290 XBALL = XBALL+XSPEED
300 YBALL = YBALL+YSPEED
310 CIRCLE (XBALL, YBALL), 4, 1
320 IF ABS (XBALL-240) > 4 THEN GOTO 360
330 IF ABS (YBALL-100) > 4 THEN GOTO 360
340 XSPEED = 0
350 YSPEED = 0
360 NEXT К

С помощью инструкции в строке 280 мы организуем простейший цикл. Переменная К отсчитывает от 1 до 300. Тем самым мы устанавливаем достаточное число повторений перемещения и изображения мяча, для того чтобы он достиг лунки, даже при скорости, равной 1. В теле цикла подсчитываются новые координаты мяча, а с помощью инструкции в строке 310 на экране строится его изображение.

В строках 320 и 330 производится покоординатная проверка с целью выяснить, не попал ли мяч в лунку. Если нет, программа сразу переходит к строке 360. Если да, то обе составляющие скорости мяча приравниваются нулю, и он застывает на месте.

Профессиональные программисты, возможно, сочтут неуместным применение в данном случае цикла типа FOR, потому что программа продолжает выполнение даже тогда, когда мяч уже попал в лунку. Программа HOLE IN ONE продолжает проверять значения координат мяча до тех пор, пока индекс К не достигнет 300. Чтобы избавиться от этого недостатка, программист-любитель может добавить две инструкции в конец программы. Одна из них будет проверять, не равна ли скорость мяча 0. Если да, то вторая инструкция будет выводить какой-нибудь текст, сообщающий об успехе, типа: "Превосходный удар!" И наконец, последняя инструкция, требуемая в большинстве диалектов языка Бейсик, означает конец программы, END.

На этом и завершается программа HOLE IN ONE. Читатели, которые введут эту программу в компьютер и запустят ее, заметят одну любопытную особенность при попытках варьировать скорость мяча, задавая различные значения параметра SPEED. Благодаря необычной дискретной физике, законы которой, кажется, действуют на площадке для микрогольфа в программе HOLE IN ONE, мяч будет попадать в лунку лишь в том случае, если расстояние до лунки делится на скорость мяча без остатка!

То, что может показаться дефектом с одной точки зрения, возможно, покажется "интересным свойством" с другой: если физические законы становятся необычными случайно, то, наверное, их можно сделать такими и преднамеренно. В программе BIRDIE предусмотрены препятствия, каких не встретишь ни на одном травяном поле. Вдобавок здесь мяч может отскакивать от краев игрового поля.


Ловушка и мяч-демон значительно затрудняют игру

Чтобы описать чудеса такого гольфа, я позволю себе отвлечься от конкретных свойств персонального компьютера IBM и языка Бейсик и вернуться к абстрактному языку алгоритмов. Площадка для гольфа в программе BIRDIE имеет Г-образную форму. Каким образом программа следит за тем, чтобы мяч все время оставался в пределах площадки? Даже в необычном мире микрогольфа угол падения должен оставаться равным углу отражения. Это правило нетрудно установить для шести отрезков прямых, не слишком заботясь о том, какой из этих отрезков обозначает ту или иную стенку; обозначим их wall1... wall6. Каждый раз, когда в цикле вывода изображения вычисляется новая позиция мяча, программа проверяет, не была ли пересечена какая-нибудь из стенок. Например, если была пересечена стенка wall1, мячик должен отразиться от нее.

Когда проверка и (возможно) результирующее отражение выполнены, программа производит проверку относительно стенки wall2, затем wall3 и т. д. Здесь возникает интересная проблема. Что, если мяч, "столкнувшись" с одной стенкой и отскочив от нее, пересечет и другую стенку? Не возникает ли такая ситуация, при которой мяч, ударяющийся о стенку вблизи угла, отскочит лишь от одной стенки, вместо того чтобы отскочить еще и от другой? Читатели, которые внимательно обдумают эту ситуацию, сумеют найти правильное решение.

После того как были выполнены все операции, связанные с возможными соударениями мяча на данном шаге цикла, программа BIRDIE выводит на экран его изображение и проверяет, не оказался ли он в лунке, точно так же, как это делала программа HOLE IN ONE. Ну а что, если неудачливый игрок промахнулся мимо цели? Мяч будет, отскакивая от стенок, снова и снова пересекать площадку, пока либо не свалится в лунку, либо не войдет в бесконечный цикл повторяющихся отскоков. Возможно, найдутся простаки, которые придут в восторг от такой перспективы, другие же раскритикуют программу за отсутствие реализма. И действительно, в игре отсутствует важнейший физический фактор - трение!

Чтобы движение мяча постепенно замедлялось, программа умножает переменную SPEED на некоторое постоянное число, меньшее единицы, скажем на 0.995, на каждом шаге цикла перемещения и проверок. Переменные XSPEED и YSPEED также умножаются на эту константу.

В конечном итоге скорость мяча может упасть до нуля, даже тогда, когда он так и не попал в лунку. В этом случае программа должна прекратить цикл, поэтому здесь вместо цикла типа FOR следует воспользоваться циклом типа WHILE. Цикл второго типа выполняется, пока не будет нарушено указанное условие. В нашем случае условие заключается в том, чтобы значение SPEED превосходило некоторое небольшое число, скажем 0.05. Когда скорость снижается до этой величины, программа BIRDIE возвращает играющего к интерактивной фазе, в которой он должен задать параметры для очередного удара.

С какими препятствиями может столкнуться гольфер в этой версии игры? Первое препятствие представляет собой круговую зону, или ловушку. Войдя в нее, мяч претерпевает случайные изменения в направлении и скорости своего движения. Программа BIRDIE проверяет, не находится ли мяч в данный момент в этой заколдованной зоне, и если находится, то она изменяет угол RADAIM на случайное число в диапазоне от -10 до +10. Тщательно спланировав несколько отскоков, хороший игрок может послать мяч в обход этого коварного круга.

Труднее миновать второе препятствие. Вокруг лунки, на некотором фиксированном расстоянии от нее, постоянно движется мяч-демон. Период его движения по орбите равен 10 шагам цикла программы. Если мяч игрока коснется демона, то будет вновь отброшен на исходную линию. Большинство читателей, до сих пор внимательно следивших за изложением, вероятно, сумеют найти способ избежать этого внушаюшего страх и ужас столкновения.


Три препятствия в усложненном варианте игры в гольф

У программы EAGLE, как это видно из рисунка на с.88, игровое поле сложнее по сравнению с BIRDIE. Хотя в основном она базируется на версии BIRDIE, у нее более развитая система препятствий. Например, всякий раз, когда мяч проходит через "горлышко", связывающее одну часть площадки с другой, он испытывает на себе силу, притягивающую его к центру прохода. Сила эта пропорциональна расстоянию мяча от центральной линии, как будто проход плавно сужается к центру. Есть тут и песчаная ловушка, в которой скорость мяча SPEED уменьшается в два раза, а не на 0.995, как на остальной части игрового поля. Только очень точным ударом можно обойти ловушку, чтобы не заставить мяч бесцельно метаться по площадке. И наконец, последнее препятствие, столкнувшись с которым мяч бесследно теряется из виду, даже не остановившись. Как найти его вновь? Если переместить биту в правильное положение, около нее появится мяч.

Мысль отправить читателей на экскурсию по зеленым лужайкам микро-гольфа пришла мне после того, как я познакомился с игрой под названием "Зану-Гольф", недавно выпущенной фирмой Electronic Arts в Сан-Матео (шт.Калифорния). Можно, конечно, купить готовую игру, но при этом вы лишитесь удовольствия создать свою собственную. Во всяком случае, совсем не обязательно ограничиваться гольфом. Описанные здесь приемы можно легко приспособить и к другим играм, таким как электронный бильярд или микропинбол (электронный вариант пинбола - игры с наклонной доской со штырьками и лунками, по которой скатывается шарик, и сталкиваясь со штырьками, попадает в одну из лунок).

БИБЛИОГРАФИЯ

MICROCOMPUTER DISPLAYS, GRAPHICS, AND ANIMATION. BRUCE A. ARTWICK. Prentice Hall, 1984.

ОТКЛИКИ

7 1990
У нескольких читателей возникли затруднения с реализацией программы HOLE IN ONE, о которой говорилось в январском номере журнала. Причиной этих затруднений были ошибки, содержавшиеся в приведенном листинге программы. Тем, кто все еще размышляет над этой программой, советуем в строке 10 заменить оператор CLS на SCREEN 1, а также исправить строки 160 и 170, в обоих случаях вставив звездочку, которая обозначает операцию умножения.

Самое замечательное усовершенствование нашей невинной игры в гольф было предложено нашим постоянным читателем Т.Япо, студентом инженерно-физического факультета Ренсселеровского политехнического института в Трое (шт.Нью-Йорк). Неудовлетворенный нашей евклидовой площадкой, Япо написал программу, которая позволяет пользователю самому определять практически любую кривую поверхность. Наблюдаемая сверху игра представляется весьма непростой. "Одна из наиболее интересных особенностей игры на исследованных мною поверхностях является следствием применения асимптотических функций... Они образуют бесконечно глубокие колодцы, которые играют роль черных дыр на площадке для игры в гольф". В настоящее время Япо строит микроминиатюрную площадку для гольфа на склонах горы Мандельброта, где вместо цветовых оттенков используются различные уровни высоты.

2 1990
О РАЗУМЕ, МАШИНАХ И МЕТАФИЗИКЕ
А.К.ДЬЮДНИ

"Подчиняется ли разум физическим законам? Да и что такое физические законы?"
Роджер Пенроуз, "Новый ум императора"

ЧЕЛОВЕЧЕСКИЙ разум превосходит системы искусственного интеллекта, потому что использует физические законы на квантовомеханическом уровне. К такому не бесспорному утверждению склоняется в своей новой книге Роджер Пенроуз, известный ученый, работающий в области математической физики. Хотя (как признает Пенроуз) это утверждение в настоящее время не может быть строго доказано, некоторые интригующие аргументы, содержащиеся в его книге "Новый ум императора", дают достаточно серьезные основания усомниться в справедливости философских положений, которые лежат в основе искусственного интеллекта.

Ниже мы рассмотрим аргументы Пекроуза, но поскольку в данной рубрике мы пользуемся своим компасом, совершая плавание по неизведанным морям, я подвергну критике некоторые его выводы, а некоторые его идеи попробую развить. В частности, вопрос "Как же все-таки люди думают?" я поставлю в более широком плане и сформулирую его так: "Получат ли люди когда-нибудь достаточно знаний, чтобы ответить на такой вопрос?" Если структура Вселенной бесконечна, то люди, вероятно, никогда не смогут ответить на этот вопрос в полной мере. С другой стороны, бесконечная регрессия структуры позволяет подойти к ответу на поставленный вопрос расчетным путем.

Но прежде чем погрузиться в рассматриваемую проблему, я приглашаю читателей вместе со мной исследовать глубины "Нового ума императора". Сначала мы посетим знаменитую китайскую комнату, чтобы узнать, понимают ли "разумные" программы, что они делают. Затем нанесем короткий визит в бильярдный зал, где увидим бильярдный стол, на котором с учетом законов классической фиэики об упругих столкновениях могут совершаться практически любые вычисления. Перейдя в лабораторию Эрвина Шредингера, мы справимся о здоровье его кошки, чтобы проанализировать отношение между классической физикой и квантовой механикой. И наконец, достигнув пункта назначения, мы рассмотрим компьютер с бесконечным интеллектом, способный решать такие задачи, которые ни один обыкновенный конечный компьютер никогда не сможет одолеть.

Несколько лет назад внимание Пенроуза привлекла телевизионная передача, в которой сторонники искусственного интеллекта позволили себе, с его точки зрения, неосторожное заявление. Они утверждали, что компьютеры, принципиально не очень отличающиеся от существующих, через какое-то время смогут проявить себя не менее разумными, чем люди,- а может быть, и превзойти их. Пенроуз был раздражен этим заявлением. Каким образом все тонкости человеческого интеллекта, в особенности его творческие способности, могут возникнуть из алгоритма, "щелкающего" в электронном мозге компьютера? Эти невероятные утверждения заставили его заняться исследованиями, которые, в свою очередь, привели к появлению книги "Новый ум императора".

Методично изучив теорию вычислений, Пенроуз подверг критике одно из ее ключевых положений - тест Тьюринга. Многие специалисты принимают этот тест в качестве критерия, с помощью которого можно отличить разумную программу от неразумной. Тест заключается в следующем. Человек-экзаменатор печатает сообщения двум скрытым от него субъектам, одно человеку, другое компьютеру, запрограммированному так, чтобы разумно отвечать на вопросы. Если в ходе достаточно продолжительного эксперимента экзаменатор не сможет отличить ответы человека от ответов компьютера, то программа успешно проходит тест Тьюринга.

Пенроуз отмечает, что тест дает лишь косвенное свидетельство наличия разума. В конце концов, то, что иногда кажется разумным, на самом деле может оказаться пародией, точно так же, как предмет н его зеркальное отображение, которые внешне, хотя и выглядят одинаково, все же различаются во многих других аспектах. Пенроуз утверждает, что прямой метод измерения разума может потребовать значительно большего, чем простой тест Тьюринга.

Чтобы подкрепить свою аргументацию, Пенроуз прибегает к так называемой "китайской комнате", своеобразной вариации на тему теста Тьюринга, которая была предложена философом Дж.Сирле. Человек-экзаменатор стоит перед дверью в комнату, через которую могут входит и выходить лишь письменные сообщения. Экзаменатор пишет некую историю, а также ряд относящихся к ней вопросов и передает сообщение в комнату. При этом необходимо соблюдать одно необычное требование: сообщения, как входящие, так и выходящие, должны быть написаны китайскими иероглифами.

Чтобы ситуация выглядела еще более необычной, человек, находящийся в комнате, выполняет программу, которая реагирует на представленную ей историю, отвечая на прилагаемые к ней вопросы. Этот человек полностью заменяет собой компьютер. Его работа была бы скучной и утомительной, но после того, как он овладевает правилами работы машины, у него уже не возникает никаких сложностей. Гарантией неведения человека-компьютера служит то, что он не знает китайского языка. Тем не менее то, что (или кто) находится в китайской комнате, кажется, прекрасно понимает рассказ и разумно отвечает на вопросы.

Этот мысленный эксперимент, по мнению Пенроуза, приводит нас к выводу, что "простой факт выполнения удачного алгоритма еще не свидетельствует о наличии какого бы то ни было понимания". Этот вывод, разумеется, справедлив по отношению к тому, кто выполняет программу, будь то человек или компьютер. В конце концов, в принципе, выполняется ли программа человеком или компьютером, не имеет значения для взаимодействия этой программы с внешним миром.

Но именно по этой причине человек в китайской комнате - это что-то вроде соломенного чучела. Никто не станет придираться к программе лишь на том основании, что выполняющая ее аппаратура ничего в ней не понимает. С еще большей строгостью можно сказать, что никому и в голову не придет критиковать поведение нейрона за то, что он не понимает смысла в тех импульсах, которые воздействуют на него и которые он сам вырабатывает. Это справедливо, независимо от того, выполняет нейрон лишь часть алгоритма или решает значительно более сложные задачи. Таким образом, любое свидетельство о наличии разума в искусственном интеллекте должно содержаться в самом алгоритме. Именно здесь Пенроуз наносит свой следующий удар.

Мир алгоритмов по существу сводится к миру вычислимых задач. По словам Пенроуза, алгоритмы представляют собой "лишь очень узкую и ограниченную часть математики". Пенроуз верит (так же, как я и многие другие математики), что математические объекты обладают своеобразной платонической реальностью. Одно из свидетельств существования таких объектов заключается в нашей полной неспособности изменить их. Они просто даны, нам, как горы или океаны.

В качестве примера Пенроуз приводит множество Мандельброта. Оно не было "изобретено" Бенуа Б. Мандельбротом, известным исследователем из фирмы IBM, оно было им открыто. Подобно планете Нептун, множество существовало задолго до того, как его увидели люди и поняли его значение. Множество Мандельброта несет в себе важное сообщение тем, кто считает его созданием компьютера. Это вовсе не так. Множество Мандельброта даже невозможно вычислить! Не слышу ли я возгласов возмущения? Строго говоря, Пенроуз прав.

Множество Мандельброта, хотя оно является лишь одним из объектов платонического мира, находится довольно далеко от сферы интересов людей, которые занимаются исследованием алгоритмов. Читатели, наверное, помнят, что внутреннюю часть множества можно найти с помощью итерационного процесса: комплексное число c возводится в квадрат, затем результат, z1, возводится в квадрат и прибавляется к c, затем второй результат, z2, возводится в квадрат и складывается с c и т.д. Если последовательность значений z, полученных таким образом, никогда не уходит в бесконечность, то c принадлежит внутренней части множества. Однако здесь возникает трудный вопрос. Как долго следует продолжать процесс, чтобы убедиться, что последовательность остается ограниченной? По существу правильный ответ - бесконечно долго!

На практике вычисления прерываются на некотором этапе. При этом неизбежно во множество оказываются включенными несколько точек, не принадлежащих ему, поскольку для них должно пройти больше времени, прежде чем проявится неограниченность соответствующих последовательностей. Трудности, возникающие при вычислении множества Мандельброта, ничтожны в сравнении с другими ограничениями, присущими алгоритмам. Например, математика сама по себе формально считается построенной из аксиоматических систем. Предложите небольшой набор аксиом, определите одно-два правила вывода - и у вас есть математическая теория. Концептуальный алгоритм, называемый "алгоритмом британского музея", генерирует все возможные теоремы, которые доказуемы в рамках формальной системы аксиом и правил вывода. К сожалению, полученные таким образом теоремы необязательно содержат в себе все истины данной системы.

Это открытие, сделанное математиком Куртом Геделем, сокрушило надежды на то, что вся математика может быть механизирована. Пенроуз пользуется знаменитой теоремой Геделя как свидетельством, что человеческий интеллект способен превзойти возможности алгоритмического метода: "... из теоремы Геделя со всей очевидностью следует, что понятие математической истины не может быть заключено в рамки какой бы то ни было формальной схемы". Но тогда возникает вопрос: "Как может сама теорема Геделя быть результатом алгоритма?"

Я не могу дать ответа на этот вопрос, хотя мне известно, что он уже обсуждался. Возможно, что теорему Геделя можно вывести из других аксиом и правил вывода и, следовательно, ее можно получить при помощи алгоритма. Теорема может быть лишь частью нескончаемого потока метатеорем. Я был бы благодарен знающим читателям, которые помогли бы разобраться в этом вопросе.

Однако, каким бы ни было наше мнение на этот счет, "Новый ум императора" атакует претензии искусственного интеллекта на другом фронте: со стороны физики вычислений, Пенроуз склонен считать, что вычислительные процессы в значительно большей мере "чувствуют себя как дома" в ощутимом мире классической физики, нежели в непостижимом царстве квантовой механики. Современный компьютер является детерминированной системой, которая главным образом просто выполняет алгоритмы. В несколько шутливой манере Пенроуз выбирает бильярд, так часто служащий в качестве примера при изучении классических столкновений, как подходящую среду для компьютера, работающего в классическом стиле.

Если изменить конфигурацию бортиков бильярдного стола, то можно построить своеобразный компьютер, в котором бильярдные шары действовали бы в качестве носителей сигналов, а их взаимодействие играло бы роль логических операций. Бильярдный компьютер был впервые сконструирован несколько лет назад исследователями из Массачусетского технологического института Э.Фредкином и Т.Тоффоли. О простоте и эффективности бильярдного компьютера читатели могут судить сами, рассмотрев диаграмму, приведенную внизу.


Вентиль И на бильярдных шарах

На диаграмме представлено бильярдное логическое устройство. Два входных канала принимают движущиеся шары в специальную камеру, которая имеет три выходных канала. Если в камеру через один из входных каналов входит только один шар, он покинет ее либо по нижнему, либо по верхнему правому выходному каналу. Однако если в камеру одновременно входят два шара, то один из них покинет ее через выходной канал, расположенный справа внизу. Присутствие или отсутствие шара в данном выходном канале представляет результат известной логической операции, выполняемой вентилем И. На выходе шар появляется тогда н только тогда, когда один шар поступает в первый входной канал и другой шар - во второй канал.

Компьютер можно построить, пользуясь вентилями только что описанного типа и еще одного типа, представляющего собой камеру, которую шар покидает по определенному каналу тогда и только тогда, когда по другому каналу не входит шар. Читателям, наверное, будет интересно сконструировать камеру такого типа, имея в виду, что полезную роль в этом устройстве могут сыграть дополнительные шары.

Нам всем нравится наблюдать за плавными, классическими движениями бильярдных шаров. У них есть и другие желательные свойства, о которых мы едва ли задумываемся. Например, никому и никогда не приходило в голову, что бильярдный шар может оказаться сразу в двух местах в один и тот же момент времени. Однако в квантовой механике такие явления вполне допустимы. Квантовомеханические системы, такие как в знаменитом эксперименте с двумя щелями, допускают возможность одновременного присутствия фотона в двух местах (см. Э.Шимони. Реальность квантового мира, "В мире науки", 1988, #3).

В нескольких словах: когда фотоны проходят через, двойную щель, их можно рассматривать как волны, интерферирующие сами с собой. На экране позади щелей появляется интерференционная картина, если только мы не установим по детектору у каждой щели. Сам акт наблюдения как бы заставляет фотон решиться, через какую щель ему пройти! Это явление называется коллапсом вектора состояния. Эксперимент можно расширить для щелей, отстоящих друг от друга на километр (и даже на расстояние, равное световому году). Как утверждают многие физики, фотон может лишь в том случае решить, через какую щель ему пройти, если он по существу находится в обоих местах одновременно.

В какой точке бесконечного множества масштабов, от атомного до галактического, квантовомеханическая система становится классической? Эта дилемма иллюстрируется знаменитой кошкой Шредингера. В воображаемом эксперименте ученый, не страшащийся активистов движения в защиту животных, помещает кошку и сосуд с ядовитым газом в камеру, содержащую лазер, наполовину посеребренное зеркало, фотодетектор и молоточек. После того как дверь в камеру заперли, лазер испускает фотон по направлению к зеркалу. Если фотон проходит через него насквозь, кошке не причиняется никакого вреда. Если же фотон отражается от зеркала, он попадает в фотодетектор; последний приводит в действие молоточек, который ударяет по сосуду с газом и разбивает его; ядовитый газ убивает кошку. Находясь снаружи, мы не можем узнать, жива кошка или нет.


Кошка Шредингера - мертва, жива или и то и другое одновременно?

В мире квантовой механики два возможных события могут сосуществовать как суперпозиция двух реальностей. В классическом же мире может произойти либо одно, либо другое событие. Вектор состояния (а с ним, возможно, и жизнь кошки) должен претерпеть коллапс. По мнению Пенроуза, в современной теории отсутствует переходная область между классической физикой и квантовой механикой. Теория как бы расщепляется на две части, вместо того чтобы плавно переходить от одного масштаба к другому на всем их протяжении. Возможно, желаемый синтез будет получен с помощью теории квантовой гравитации.

Теперь вернемся, наконец, к человеческому разуму. Пенроуз полагает, что в человеческом сознании присутствует неалгоритмическая компонента. На квантовом уровне возможно сосуществование взаимоисключающих, альтернативных вариантов реальности. Одно квантовое состояние может в принципе состоять из большого количества различных, одновременно проходящих явлений. Может быть, человеческий мозг каким-то образом использует такие явления? Едва ли мне удастся проанализировать эту кажущуюся такой необычной возможность так же хорошо, как это делает Пенроуз. Поэтому я советую заинтересованным читателям приобрести и прочитать его книгу.

Однако у меня возникло желание рассмотреть другой вопрос, имеющий некоторое отношение к затронутой теме. Могут ли люди количественно оценить возможности своего интеллекта во Вселенной, которая обладает бесконечной структурой? В самом деле, существование какого-то определенного предела в структуре материи, будь то одна элементарная частица или набор таких частиц, кажется невероятным. При этом я имею в виду не только частицы, но вообше любую структуру, скажем энергетическую или чисто информационную, лежащую в основе обсуждаемых явлений.

Мне представляется, что физика сама по себе может оказаться бесконечной наукой по той простой причине, что, как только будет открыта какая-то предельная "элементарная" структура, сразу же возникнет проблема объяснения предельных элементарных законов и самого факта их существования. Во всяком случае, я предпочитаю жить во Вселенной, обладающей бесконечной структурой. Во-первых, наш разум мог бы лучше понять такую Вселенную по сравнению со Вселенной, которая обладает конечной структурой.

Компьютеры конструируются таким образом, чтобы исключить влияние любого физического процесса, протекающего на уровне, масштабы которого меньше определенного порога. Алгоритм должен быть защищен от "ошибок". Возможно, наш мозг структурирован так же, но, возможно, что и не так, считает Пенроуз. Не исключено, что физические явления, протекающие на атомарном уровне, играют важную роль в процессе нашего мышления. Что касается молекулярного уровня, то это определенно так. Достаточно лишь вспомнить о влиянии молекул нейротрансмиттеров на поведение нервных клеток. Более того, хорошо известно, что природа обладает свойством использовать физические возможности, ставя их на службу для реализации биологических операций. Если физические структуры простираются до определенного уровня, то имеем ли мы какие-то априорные основания полагать, что мозг не может воспользоваться явлениями, протекающими на этом уровне?

А что, если мозг способен пользоваться всеми уровнями структуры в бесконечно структурированной Вселенной? Чтобы продемонстрировать в самой грубой форме потенциальные возможности бесконечного мозга, я построил схему бесконечного компьютера, который пользуется в своей работе структурами всех уровней. В целях удобства демонстрации я буду условно считать, что во всех масштабах физические структуры обладают классическими свойствами.

Мой бесконечный компьютер (см. рисунок справа) по существу представляет собой квадрат, содержащий два прямоугольника и два других квадрата меньшего размера. Входная линия подведена слева к большому квадрату, и войдя в него, она сразу идет к первому прямоугольнику. Последний представляет собой устройство обработки сигналов, которое я назову модулем подстановки. От модуля подстановки отходит по одной линии к каждому из меньших квадратов, а также к другому прямоугольнику, который мы будем ниже называть модулем сообщения.


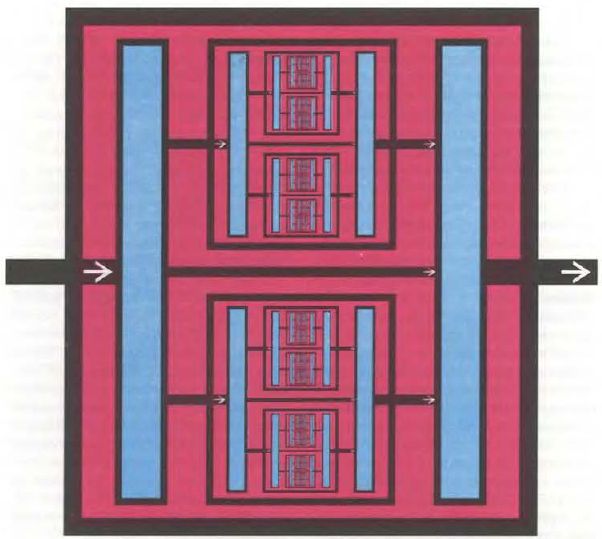
Фрактальный компьютер решает задачу Туэ о преобразовании слов

Структура этого компьютера обладает свойством бесконечной регрессии. Каждый из меньших квадратов является точной копией большего квадрата, но имеет вдвое меньшие размеры. Когда сигнал распространяется по проводникам и модулям вдвое меньшего размера, ему требуется вдвое меньше времени для прохождения соответствующего пути, поэтому модули подстановки и сообщения срабатывают в два раза быстрее соответствующих модулей внешнего уровня.

Бесконечный компьютер решает знаменитую задачу о преобразовании слов, изобретенную математиком Акселем Туэ. В этой задаче даны два слова и словарь допустимых подстановок. Можно ли, пользуясь только допустимыми подстановками, получить второе слово из первого? Рассмотрим задачу на следующем примере: предположим, первое "слово" представлено цепочкой 100101110, а второе - 01011101110. Возможно ли прийти от первого слова ко второму, пользуясь подстановками 010 вместо 110, 10 вместо 111 и 100 вместо 01? Пример был выбран совершенно произвольно, и я специально не буду пытаться решить его.

Может случиться так, что ни одна последовательность подстановок не приведет к преобразованию первой цепочки во вторую. В то же время такая последовательность существует. В процессе применения подстановок могут возникнуть очень длинные промежуточные слова. В этом и заключается проблема. Так же, как и в отношении некоторых точек множества Мандельброта, мы по существу не можем прийти к ответу. Не существует алгоритма решения этой задачи, поскольку любой алгоритм (по определению) должен когда-то остановиться. Опасность состоит в том, что алгоритм может остановиться прежде, чем будет получен ответ. По этой причине о задаче Туэ говорят как о неразрешимой. Ни одна компьютерная программа, даже в принципе, не сможет решить всех частных случаев этой задачи.

Введем условие задачи в бесконечный компьютер. Слово, к которому нужно прийти, вводится в компьютер через его главную входную линию. За четверть секунды оно попадает в первый подстановочный модуль. Затем слово передается этим подстановочным модулем двум другим подстановочным модулям следующего уровня.

Однако теперь передача данных потребует уже только 1/8 секунды. Пересылки на следующие уровни потребуют соответственно 1/16, затем 1/32 с и т.д. Время, которое потребуется, чтобы загрузить все подстановочные модули вторым словом, составит, таким образом, половину секунды.

Потом в ходе аналогичного процесса, протекающего с той же скоростью, в компьютер вводятся три (или сколько угодно) подстановочные формулы. Однако на этот раз различные подстановочные модули на разных уровнях запрограммированы так, чтобы воспринимать только определенные подстановки из вводимой последовательности. Каждый подстановочный модуль, согласно содержащейся в нем программе, должен всегда пытаться проводить определенную подстановку в определенной позиции слова, которое поступает в него из внешнего уровня. Подробное описание схемы распределения подстановок и позиций в слове по различным модулям, наверное, утомило бы читателя, поэтому я опускаю его. Однако это не должно помешать тем, кто любит анализировать бесконечные процессы, представить себе, каким образом можно все устроить.

Вычисление начинается, когда мы посылаем первое слово в компьютер. Первый подстановочный модуль пытается провести свою подстановку на отведенной для нее позиции введенного слова. Если подстановка не может быть выполнена в требуемом месте, слово передается следующему подстановочному модулю, принадлежащему более ниэкому уровню машины; если ему удается провести подстановку, он посылает преобразованное слово в квадрат более высокого уровня. Если подстановка оказывается успешной и полученное в результате слово совпадает со вторым заданным словом, хранящимся в памяти подстановочного модуля, то последний посылает сигнал модулю сообщения: "успешно".

Каждый квадрат каждого уровня работает в соответствии с только что описанным алгоритмом. Как уже говорилось выше, всегда можно распределить подстановки (и позиции, в которых их следует применять) по бесконечному компьютеру таким образом, чтобы задача преобразования слов успешно решалась. Ответ будет выдан не позднее чем через одну секунду: половина секунды потребуется, чтобы провести вычисления на всем пути до бесконечно малых модулей, и половина, секунды на то, чтобы сообщение "успешно" достигло главной выходной линии компьютера. Если подходящей последовательности подстановок не существует, то отсутствие сообщения по истечении одной секунды можно принять как ответ "нет". Читателям, возможно, будет интересно поразмыслить над бесконечным компьютером, воспользовавшись при этом многочисленными (а может быть, и бесконечным числом) структурами своего собственного мозга.

БИБЛИОГРАФИЯ

THE EMPEROR'S NEW MIND: CONCERNING COMPUTERS, MINDS, AND THE LAWS OF PHYSICS. ROGER PENROSE. Oxford University Press, 1989.

ОТКЛИКИ

9 1990
Ящик Пандоры, содержащий умы, машины и метафизику и открытый мною в февральском номере нашего журнала, позволил мне стать свидетелем битвы гигантов. В одном углу ринга стоял Р.Пенроуз, чья недавняя книга "Новый ум императора" вдохнула новые силы в тех, кто всегда чувствовал, что человеческий мозг - это нечто большее, чем компьютер. В противоположном углу находились специалисты по искусственному интеллекту и вычислительной технике, которые не нашли ничего необычного и убедительного в этой книге.

На помощь Пенроузу был призван философ Дж.Сирл (его статья "Разум мозга - компьютерная программа?" была опубликована в нашем журнале в феврале 1990г.). Сирл выдвинул аргумент "китайской комнаты": компьютерная программа, умеющая читать и писать по-китайски, понимает китайский не в большей степени, чем человек, слепо моделирующий поведение программы.

Среди тех, кто поддержал точку зрения специалистов по искусственному интеллекту, был X.Моравец, эксперт по робототехнике из университета Карнеги-Меллона, приславший мне копию открытого письма, написанного им Пенроузу. Моравец, энтузиазм которого в полной мере проявился в его книжке "Дети разума", называет аргументы Пенроуза "в высшей степени ошибочными".

Согласится ли Пенроуз наделить теми же интеллектуальными способностями робота, каким он наделяет собаку, глядящую на него преданными карими глазами и жалобно скулящую? Робот, которого имеет в виду Моравец, в настоящее время скорее воображаемый, чем реальный. Он говорит: "Знаешь, Роджер, меня огорчает, что ты не думаешь обо мне как о реальной личности. Ну что мне сделать, чтобы убедить тебя? Я воспринимаю тебя точно так же, как воспринимаю себя. И я говорю тебе, что твое отношение ко мне почти невыносимо". Эти слова робота являются результатом специальной программы, которая должна убеждать хозяина, что немножко заботы о роботе все-таки следует проявлять, иначе его поведение будет в каком-то смысле подобно поведению обиженной собаки.

Я могу упомянуть лишь о нескольких из многочисленных читательских откликов на статью в февральскои номере журнала. Дж.Рэскин из Пасифика (шт.Калифорния) говорит, что аргумент Сирла с китайской комнатой равносилен определению разума примерно в таком духе: "Разум - это не алгоритмический процесс, который..." П.Прейс, энтузиаст вычислительной техники и довольно известный писатель-фантаст из Сан-Франциско, утверждает, что аргумент с китайской комнатой не является полноценным мысленным экспериментом. Его следовало бы выполнить, говорит Прейс, "самому Сирлу. Если ему удастся убедить китайца, что он сам, находясь в комнате, действительно умеет читать и писать по-китайски, то тогда пусть он и поделится своими субъективными ощущениями относительно того, обучился или не обучился он китайскому языку в процессе эксперимента."

Знаменитая "теорема о неполноте" немецкого математика Курта Геделя часто цитируется как свидетельство тому, что существуют мысли, выходящие за рамки возможностей любого алгоритма. Но вопрос о том, может ли сама теорема воспользоваться внеалгоритмическим статусом, натолкнулся на целый поток отрицательных ответов со стороны, по-видимому, достаточно квалифицированных специалистов, включая Г.Рэя, изучающего логику и методологию науки в Калифорнийском университете в Беркли, и Р.Виленски, возглавляющего программу исследований по искусственному интеллекту в этом же университете. П.Кугел, работающий на факультете информатики Бостонского колледжа, считает, что доказательство Геделя само по себе уже является алгоритмом.

3 1990
ЭЛЕКТРОННЫЕ СХЕМЫ И КОВРОВЫЕ УЗОРЫ В КЛЕТОЧНОЙ ВСЕЛЕННОЙ
А.К.ДЬЮДНИ

"Шахматная доска - это мир, фигуры - его явления, а правила игры - то, что мы называем законами Природы".
Томас Хенри Хаксли, "Свободное образование"

КАК и шахматная доска, клеточный автомат тоже может представлять целый мир. На его решетке из квадратных клеток может разместиться значительно больше фигур, чем на шахматной доске, а количество возможных правил исчисляется у него мириадами. Мало того, цвета его клеток не ограничиваются черным и белым, они могут быть окрашены в любой цвет радуги. Что такое клеточный автомат? В свете рассматриваемых в настоящей статье примеров - это бесконечная двумерная поверхность, заполненная квадратиками, набор возможных состояний и часовой механизм. Каждая клетка всегда находится в том или ином допустимом состоянии. На каждом такте часового механизма каждая клетка меняет свое состояние в соответствии с определенными правилами, которые учитывают состояния соседних клеток.

Недавно мое внимание привлекли две программы, генерирующие клеточные автоматы: PHANTOM FISH TANK и RUDY RUCKER'S CA LAB (соответственно "Волшебный аквариум" и "Лаборатория КА Руди Ракера"). Люди, не обладающие навыками программирования, теперь могут заняться исследованием уже известных клеточных автоматов или создавать свои собственные.

На протяжении многих лет в статьях нашей рубрики несколько раз приводились описания различных клеточных автоматов. В октябре 1970г. знаменитый клеточный автомат под названием "Жизнь", изобретенный математиком Джоном Конвеем из Кембриджского университета, был впервые рассмотрен в журнале "Scientific American" Мартином Гарднером. "Жизнь" полна удивительных структур как статичных, так и подвижных. Рост этих структур напоминает развитие колонии бактерий. В октябрьском номере за 1988г. была помешена статья с описанием клеточного автомата, моделирующего постоянную химическую реакцию, а в октябрьском номере за 1989г. речь шла об эволюции клеточного автомата, называемого циклическим пространством, в котором первоначальное хаотическое состояние сменялось красивыми спиралями, конкурирующими в борьбе за жизненное пространство.

У каждого из этих клеточных автоматов свой набор правил, определяющих, каким образом изменяются состояния клеток в решетке. Обычно для проведения экспериментов с каким-нибудь новым клеточным автоматом необходимо было написать новую программу, воплощающую в себе соответствующий набор правил. А нельзя ли создать единую систему, каким-то образом воплощающую в себе все возможные клеточные автоматы?

Именно эта мысль пришла в голову Брайану Силвермену, и в 1987г. он написал свою программу "Волшебный аквариум". (Силвермен руководит исследовательской программой в компании Logo Computer Systems в Монреале, занимающейся производством программного обеспечения компьютеров; он был одним из авторов компьютера из "тинкертоев", о котором шла речь в декабрьском номере нашего журнала за 1989г.) В программе Силвермена компьютерный экран выступает в роли аквариума, а причудливые узоры, копошащиеся или плавно скользящие по клеточному пространству,- это рыба. В пакете программ Силвермена мне больше всего понравился клеточный автомат, с помощью которого можно создать простой компьютер, работающий в двумерном клеточном пространстве. Я назвал его миром электронных схем.

При помощи системы экранного редактирования, встроенной в программу PHANTOM FISH TANK, можно сконструировать и испытать в действии электронные схемы из клеточных "проводников" и "логических вентилей". Теоретически из этих клеточных устройств можно собрать компьютер сколь угодно большой мощности. На практике масштабы такого компьютера ограничиваются лишь несколькими вентилями и проводниками.

Однако этих нескольких устройств уже более чем достаточно, чтобы произвести впечатление на любого экспериментатора, увлеченного безграничными возможностями мира электронных схем. Строительными кирпичиками этого мира являются квадратные клетки автомата. В каждый данный момент времени клетка может находиться в одном из четырех разрешенных состояний. Вместо номеров эти состояния имеют названия: фон, проводник, хвост электрона и голова электрона. Пара прилегающих друг к другу клеток, голова электрона и хвост электрона, образуют объект, называемый электроном.

Конечно, не так уж важно, как назвать ту или иную клетку, однако эти названия приобретают определенный смысл, когда мы обращаемся к правилам. На каждом такте игры клетка головы электрона становится клеткой хвоста электрона, клетка хвоста электрона становится клеткой проводника и иногда клетка проводника становится клеткой головы электрона; клетки фона никогда не изменяют своего состояния. Каждая клетка изменяет свое состояние в зависимости от состояния своих соседей - восьми клеток, касающихся ее по четырем сторонам квадрата и в угловых точках. Клетки проводника, в окрестности которых находятся одна или две клетки головы электрона, становятся сами клетками головы электрона, однако клетки, окрестность которых содержит три или более клеток головы электрона, остаются клетками проводника.

Вот с таким простым набором правил мир электронных схем готов к работе. Случайное исходное распределение клеток проводника и электронов, вероятнее всего, приведет лишь к короткому замыканию. Для того чтобы клетки могли что-то вычислять, играющий сначала должен сконструировать из клеток проводника и фона логические устройства. Затем он может испытать свои устройства, вводя электроны в проводники, которые так непохожи на настоящие проводники в реальных электронных устройствах. Построить клеточный компьютер - это лишь половина удовольствия; интересно наблюдать за тем, как он работает.

Чтобы создать проводник в клеточном пространстве, достаточно расположить несколько клеток проводника в одну линию и окружить их клетками фона. Чтобы ввести электрон в проводник, нужно заменить его первую клетку хвостом электрона, а вторую - головой электрона. Электрон начнет плавно перемешаться вдоль проводника вследствие принятых в клеточном пространстве правил: на каждом такте часового механизма клетка проводника, расположенная перед электроном, превращается в голову электрона, а голова электрона превращается в его хвост, хвост же превращается в клетку проводника.

Однако каким образом в этом клеточном компьютере принимаются решения? Рассмотрим конфигурацию, изображенную вверху на рисунке на с.82. Два горизонтально расположенных проводника являются входными линиями вентиля ИЛИ, устройства, которое посылает электрон по вертикальному проводнику, если по одному или обоим входным каналам в него приходят электроны. На первый взгляд может показаться, что вентиль будет правильно работать и без странных прямоугольных блоков на каждой входной линии: если по одной или по обеим входным линиям движется электрон, по крайней мере один из них достигнет узловой точки, и один электрон наверняка продолжит путешествие по выходной линии. Проблема возникает, когда один электрон достигает узловой точки. Он не только продолжит свой путь по выходной линии устройства, но и пошлет свою копию по другой входной линии. Эта ситуация грозит аварией, когда другой электрон войдет в устройство по этой же линии и столкнется с образовавшимся в нем лишним электроном. При встрече они взаимно уничтожатся.


Вентиль ИЛИ, защищенный диодами (вверху). Электрон проходит через диод в правильном направлении (верхняя последовательность), но блокируется, когда идет в неправильном направлении (нижняя последовательность)

Прямоугольники на входных линиях предотвращают такие столкновения. Они представляют собой клеточные диоды, которые позволяют электронам проходить лишь в одном направлении. Диод имеет размеры 2*3 и в основном состоит из клеток проводника. Клетка, расположенная в центре одной из сторон прямоугольника, является фоновой; она прерывает проводник. Больше ничего и не требуется, как показывает диаграмма, приведенная на с.82. Электрон, входящий со сплошной стороны, расщепляется на два и активирует клетку проводника по другую сторону от фоновой клетки. Электрон, проходящий в противоположном направлении, расщепляется на три электрона, которые не могут продолжить движения по проводнику, поскольку прилегающая к ним проводящая клетка, согласно правилам, не может активироваться тремя электронами. Вентиль ИЛИ, таким образом, можно легко построить, поставив по одному диоду на каждую входную линию.

Два других устройства дополнят набор используемых нами компонентов: это - запоминающая ячейка и вентиль НЕ (или инвертер). Для того чтобы построить компьютер в завершенном виде, потребуется, конечно, каким-то образом решить вопрос о тактировании внутренних сигналов. В обычных электронных компьютерах двоичный сигнал представляется не отдельными электронами, а уровнями напряжения - либо "высоким" (1), либо "низким" (0). В нашем клеточном компьютере 1 или 0 будут соответственно интерпретироваться как присутствие или отсутствие электрона. Однако и в клеточном автомате вычислительными действиями нужно правильно дирижировать. Между отдельными электронными сигналами должны быть выдержаны определенные временные интервалы. Последовательные сигналы, проходящие по любому проводнику в нашем компьютере, будут разделены некоторым постоянным числом тактов часового механизма. Если это число тактов равно, скажем, T, то через каждые Т тактов каждая составляющая компьютера будет получать либо один электрон (1), либо ни одного электрона (0). Возникает вопрос, насколько малым можно сделать значение T?

Я предлагаю читателям самим сконструировать инвертер, дав им лишь несколько маленьких подсказок. Постройте замкнутый контур из клеток проводника, по которому один электрон мог бы циркулировать с периодом Т секунд. Присоедините к контуру проводник, ведущий к конфигурации клеток, напоминающей обратный диод. По проводнику, связывающему устройство с внешним миром, через каждые T тактов поступает электрон (или неэлектрон). В первом случае электрон, движущийся по замкнутому контуру, вовремя входит в квазидиод и уничтожает поступающий извне электрон. Если же извне не приходит электрон, то электрон из контура проходит через выходную линию.

В логическом смысле у нас теперь имеется полный набор компонентов для построения компьютера. Пользуясь только инвертерами и вентилями ИЛИ, можно реализовать любую логическую функцию и собрать любое устройство, от мультиплексоров (устройств, управляющих потоками сигналов в компьютере) до ЦПУ (центрального процессорного устройства - очень сложного аппарата, который выполняет компьютерные программы). В этой статье мы не будем пытаться конструировать подобные устройства; достаточно будет показать, что мы располагаем всеми компонентами, необходимыми для построения компьютера.

Ну а как быть с памятью? Каким образом мы сможем построить запоминающие регистры компьютера? Стандартный рецепт заключается в том, чтобы воспользоваться так называемым триггером, который строится из имеющихся в наличии логических вентилей. Однако мне больше по душе идея создать свою оригинальную ячейку памяти. На рисунке на с.83 показано устройство, которое я сконструировал с помощью программы PHANTOM FISH TANK (я воспользовался ею как при конструировании, так и при испытаниях устройства памяти).


Ячейка памяти должна забыть 1 и запомнить 0

В основе ячейки памяти лежит замкнутый контур, по которому циркулирует единственный электрон, когда в элементе хранится значение 1; в случае когда в нем хранится 0, электрон в контуре отсутствует. Две управляющие линии изменяют содержимое ячейки памяти. Электрон, движущийся по нижней линии и записывающий в ячейку значение 1, входит в контур в его левом верхнем углу. При этом не имеет значения, содержит ли контур один электрон или нет. Приходящий электрон попадает в контур точно в тот момент, когда в точку входа должен прибыть циркулирующий по контуру электрон, если он существует.

По верхней линии в ячейку поступает противоположный сигнал. Прибывающий по этой линии электрон сигнализирует о том, что впредь до следующего управляющего сигнала ячейка должна хранить значение 0. Электрон проходит сначала через предохранительный диод, а затем в другой диод. Последний в действительности представляет собой часть контура запоминающего элемента. Прибывающий электрон превращает три клетки диода со стороны контура в электроны точно в тот момент, когда циркулирующий электрон должен войти в диод снизу. В результате циркулирующий электрон уничтожается, так как все клетки, имевшие в предыдущий момент состояние головы электрона, переходят в состояние хвоста. Последние же не могут снова стать головой электрона в течение полного цикла. Контур "забывает" 1 и теперь "запоминает" 0. Разумеется, если он раньше хранил 0, то электрон в контуре отсутствовал. В этом случае электрон в нижней клетке диода пройдет в контур и будет двигаться "вверх по течению". Однако здесь кет причин для беспокойства: этот лишний импульс блокируется двумя другими диодами, прежде чем это приведет к ошибке. Один из этих диодов расположен на контуре, а другой предохраняет нижнюю входную линию.

Насколько длительным должен быть период, чтобы все протекало гладко? У самого короткого контура памяти, который я могу себе представить, период составляет 13 тактов. Если никому из читателей не удастся изобрести более быстрого запоминающего элемента, который функционировал бы так же, как и мой элемент, то мы должны будем довольствоваться основным циклом длительностью в 13 тактов часового механизма.

Силвермен с энтузиазмом относится к вычислительным возможностям клеточных автоматов. Он уже представляет себе компьютер, который не только способен работать на основе клеточных логических схем, подобных описанным выше, но может еше и модифицировать схемы по ходу работы, чтобы каким-то образом оптимизировать процесс вычисления, выполняемого в данный момент.

Руди Ракер предвидит еще более широкие горизонты, которые откроются перед клеточными автоматами в будущем. "Мне кажется, что величайшая научная задача конца XXв. заключается в создании живых машин... Они будут таким же высочайшим достижением ученых в области кибернетики... каким явилось создание собора Парижской богоматери средневековыми мастерами".

Реальны или нереальны подобные проекты, читатели в любом случае несомненно получат удовольствие, если попробуют свои силы в этой области, теперь когда Ракер в сотрудничестве с калифорнийской компанией Autodesk, выпускающей компьютерные игры, создал программный пакет под названием RUDY RUCKER'S CA LAB ("Лаборатория КА Руди Ракера"). (Руди Ракер - писатель, работавший в жанре научной фантастики, решил променять беспокойный образ жизни свободного художника на относительно благополучную, но в то же время захватывающую академическую деятельность; он живет и работает неподалеку от Кремниевой долины в Калифорнии). Его пакет состоит из двух программ: RC и CA. Первая программа, написанная самим Ракером, позволяет новичкам экспериментировать с набором интересных правил. Среди них правила для таких хорошо известных клеточных автоматов, как "Жизнь" и игра "Выборы" (см. статью в рубрике "Занимательный компьютер" в июньском номере журнала за 1985г.) и ряд других правил, в том числе и "Мозг Брайана" (клеточный автомат, впервые описанный Силверменом). Программа СА, написанная Дж.Уокером из компании Autodesk, содержит средства, позволяющие создавать почти любой вид клеточного автомата.

Один из клеточных автоматов, к которому Ракер питает особую симпатию, называется "Коврик". Он создает цветные орнаменты в виде овальных форм и эллиптических полосок. Эти орнаменты чем-то напоминают рисунок настенных ковриков, которые когда-то ткали наши предки в графстве Ланкастер (шт.Пенсильвания); однако коврики клеточного автомата "живые" - волны различного цвета то наступают, то отступают, и орнамент постоянно меняется. Каким образом создается коврик Ракера?

В этом клеточном автомате каждая клетка имеет восемь соседних - четыре по сторонам квадрата и четыре по углам. В процессе, состоящем из четырех шагов, каждая клетка решает, в каком из 256 возможных состояний она войдет в следующий цикл. Сначала вычисляется средняя величина по состояниям восьми соседних клеток. На втором шаге полученная средняя величина округляется до целого значения, дробная часть отбрасывается. На третьем шаге к этому числу прибавляется определенное приращение (выбираемое пользователем). И наконец, на четвертом шаге результирующая сумма маскируется другим числом, также задаваемым пользователем. "Маскирование" означает, что каждый бит представления нового состояния клетки логически комбинируется с битом двоичного представления числа, задаваемого пользователем. Например, если результатом вычисления будет число 107, а число-маска равно 224, то в процессе маскирования будут сопоставлены двоичные представления обоих чисел: 107 в двоичном коде имеет вид 01101011, а 224 - 11100000. В результате операции маскирования будет получено новое двоичное число, у которого 1 будет стоять лишь в тех позициях, в которых оба исходных числа имели по 1. В данном случае мы получим число 01100000. Маска по существу обрубает младшие биты вычисленной величины перед тем, как получить следующее состояние.

Конечно, в качестве маски можно воспользоваться и числом 255 (11111111). В этом случае результат вычисления остается без изменения, и следующее состояние каждой клетки будет определяться суммой среднего состояния среди соседей и приращения, заданного пользователем. Даже такое маленькое приращение, как 1, приводит к возникновению узоров, проявляющих тенденцию либо к росту, либо к сжатию, тем самым коврики как бы "оживают".

Для любителей мысленных приключений, желающих совершить путешествие в неизведанные пространства, программа CA дает возможность указать любое правило, пользуясь целым рядом разнообразных режимов и языков. Можно задать как размеры пространства, так и те изменения, которым подвергается клетка, пересекающая границы. Перепрыгнет ли клетка на противоположную сторону экрана или удалится в память компьютера?

Игроки, настроенные менее серьезно, всегда могут выбрать какой-нибудь понравившийся им клеточный автомат из числа тех, которые демонстрируются программой, и затем запускать его из различных исходных конфигураций. Трудно, однако, указать начальное состояние для всех 8000 клеток. К счастью, Ракер предоставляет пользователю возможность применить в качестве исходных конфигураций знакомые ему изображения, такие как изображение космического корабля "Энтерпрайз", приведенное на с.84 и 85. Его пикселы в действительности представляют собой цветные клетки клеточного автомата. Свою работу клеточный автомат "Коврик" начнет из этой исходной конфигурации, и космический корабль "Энтерпрайз" растворится в абстрактном "техническом" орнаменте. Если же запустить клеточный автомат под названием "Тепло", который моделирует тепловые потоки в материалах, то "Энтерпрайз" раскалится докрасна, затем приобретет фиолетовый цвет, и постепенно темнея, растворится в окружающем космическом пространстве. (У экипажа здесь нет шансов на спасение). С этой же конфигурации можно начать и работу клеточного автомата "Жизнь". В этом случае космический корабль "Энтерпрайз" взорвется, образовав целое облако из "планеров", "мигалок", "маяков" и "пчелиных ульев".



Космический корабль "Энтерпрайз" растворяется в клеточном пространстве под названием "Жизнь"

Программу PHANTOM FISH TANK для компьютера Apple II можно заказать у фирмы Logo Computer Systems, Inc., написав Брайану Силвермену, а программу RUDY RUC-KERS'S CA LAB для персонального компьютера IBM PC поставляет компания Autodesk, Inc.

БИБЛИОГРАФИЯ

CELLULAR AUTOMATA MACHINES. TOMMASO TOFFOLI AND NORMAN MARGOLUS. The MIT Press, 1988. (Т.ТОФФОЛИ, Н.МАРГОЛУС, МАШИНЫ КЛЕТОЧНЫХ АВТОМАТОВ, Москва, "МИР", 1991.- G.).

ОТКЛИКИ

9 1990
В последней нашей статье, вышедшей в рубрике "Занимательный компьютер" в мартовском номере журнала, были описаны два программно-моделируемых клеточных автомата, созданные Б.Силверменом из Монреаля и Р.Ракером из Лос-Гейтос (шт.Калифорния).

Мир электронных схем, двумерное клеточное пространство, в котором экспериментаторы-любители могут сами разрабатывать простые вычислительные схемы, привлекли внимание многих читателей. Н.Хайзе из Хьюстона (шт.Техас) разделяет энтузиазм Силвермена в отношении моделируемых электронных схем, причем до такой степени, что написал свою программу, воспроизводящую многие свойства мира схем Силвермена. Написанная на компактном языке АПЛ за один вечер, эта программа позволила Хайзе построить элементы памяти, превосходящие по быстродействию те, которые были предложены мною. Воспользовавшись автоматом, я построил замкнутый путь, по которому постоянно пробегает импульс с периодом в 13 тактовых импульсов часового механизма-автомата. Исключительно эффективный запоминающий элемент Хайзе имеет период, равный всего лишь четырем тактовым импульсам. Однако, чтобы построить столь быстрое устройство, ему пришлось изобрести новый способ передачи сигнала по проводящим линиям.

Среди других изобретательных читателей отмечу также О.Шпрингауфа из Вюрцбурга (ФРГ) и Д.Сервоне из Провиденса (шт.Род-Айленд). Следуя моей более консервативной технологии, Шпрингауф сумел усовершенствовать мой цикл памяти, уменьшив его период с 13 до 12 тактовых импульсов. Севроне построил целый ряд удивительных устройств, включая четырехбитовый сумматор. Чертежи, присланные всеми читателями, выглядели совершенно необычно по той причине, что клеточные автоматы в корне отличаются от непрерывной физики, используемой в реальных микроэлектронных компонентах.