01.03. ЭТО КОТ?
Страница 1 из 1
 01.03. ЭТО КОТ?
01.03. ЭТО КОТ?
ГЛАВА ТРЕТЬЯ. ЭТО КОТ?
10 OPTION BASE 1: DIM D$(1023): D$(1)="ЭТО КОТ": I=1: ON ERROR GOTO 80
20 PRINT D$(I);: INPUT O$: O$=LEFT$(O$,1)
30 IF I<512 THEN IF D$(I*2)<>"" GOTO 70
40 IF O$="Д" OR O$="д" THEN PRINT "УРРА-А!": I=1: GOTO 20
50 D$(I*2+1)=D$(I): INPUT "А КТО ЭТО";O$: D$(I*2)="ЭТО "+O$
60 INPUT "ЧЕМ ОТЛИЧАЕТСЯ";D$(I): I=1: GOTO 20
70 IF O$="Д" OR O$="д" THEN I=I*2: GOTO 20: ELSE I=I*2+1: GOTO 20
80 PRINT "НЕ ХВАТАЕТ МОЗГОВ!": END
Одна из самых коротких известных мне игровых программ. Суть проста: по ответам пользователя строится бинарное дерево, исполняющее функции простейшей базы знаний. Однажды во время учебы, я выдал вариант этой программы за некую экспертную систему.
Несмотря на простоту, игрушка довольно забавная, если играть толпой. Очень быстро классификация животных перерастает в остроумное обсуждение общих знакомых.
***
Это одна из привлекательных черт программирования: очень часто что-то очень простое выглядит в глазах непосвященных чем-то сакральным и обладающим чуть ли не искусственным интеллектом. Я здесь не оригинален. Вышла даже специальная книжка, посвященная "философским" проблемам BASIC-программы, состоящей из единственной строки, которая так и называется
10 PRINT CHR$(205.5+RND(1)); : GOTO 10
Хитрость там в том, что символы с номерами 205 и 206 на том компьютере - прямая и обратная косые черточки. Т.о. эта программа рисует на экране бесконечный узор-лабиринт:

К сожалению, уже эти примеры слишком уж машинно-зависимы, точнее, BASIS-зависимы. Попробуйте, например, переписать их на классическом PASCAL. Жуть.
***
Нас будут интересовать другие способы имитации разумного поведения - те, которые можно без труда воспроизвести на других языках.
В качестве примера рассмотрим книжку: Р.Левин, Д.Дранг, Б.Эдельсон (ЛДЭ), Практическое введение в технологию искусственного интеллекта и экспертных систем с иллюстрациями на Бейсике ( DJVU, 3.09Мб
DJVU, 3.09Мб ). Правда, чем дальше, тем меньше здесь будет оттуда и все больше - из других источников и отсебятины.
). Правда, чем дальше, тем меньше здесь будет оттуда и все больше - из других источников и отсебятины.
ОТКРОВЕННОЕ ЖУЛЬНИЧЕСТВО ЛДЭ
К сожалению, первая хитрость, к которой прибегли авторы книги - обман читателя. Их программы, мягко говоря, не совсем работают.
Например, используется имитация ввода:
340 REM ВВОД ПЕРЕМЕННЫХ, ВХОДЯЩИХ В УСЛОВНЫЕ ЧАСТИ ПРАВИЛ В
350 REM НУЖНОМ ПОРЯДКЕ (НЕ БОЛЬШЕ 3 ПЕРЕМЕННЫХ НА ПРАВИЛО)
360 REM ИМЕНА ПЕРЕМЕННЫХ НЕ ДОЛЖНЫ ПОВТОРЯТСЯ
365 REM КОГДА ВВЕДЕНЫ ВСЕ ИМЕНА, НУЖНО НАЖАТЬ КЛАВИШУ ВК
367 V$(1)="DO": V$(2)="FT": V$(3)="FM": V$(4)="IN": V$(5)="ST"
368 PRINT"*** СПИСОК ПЕРЕМЕННЫХ ***"
370 FOR I=1 TO 10
380 PRINT"ВВЕДИТЕ ПЕРЕМЕННУЮ";I;
385 PRINT V$(I)
395 NEXT I
396 INPUT"ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ";I
Большое количество слов маскирует тот факт, что все пять значений вводятся присваиванием, а цикл - простое украшение, дающее "правильную" распечатку.
Далее еще более наглая ложь - оператор ввода, на который опирается запуск "логического вывода" просто закомментарен, а примеры "частных примеров вывода" запускаются путем небольшого "взлома" программы.
***
Более тонкий случай. В программе есть символьный массив "имен переменных" (упомянутый выше V$(10)) и даже символьный массив CV$, в котором те же имена сгруппированы "по правилам" (ввод последнего авторы даже не пытаются имитировать). Однако, в алгоритмах самих правил используются не эти символьные имена, а сами переменные! Хотя, всем, конечно, понятно, что строка "DO" и переменная с именем DO$ - это вещи, совершенно друг с другом не связанные.
"Связь" осуществляется путем использования переключателей типа:
367 V$(1)="DO": ...
...
2430 IF V$=V$(I) THEN ...
...
2470 ON I GOSUB 1700, 1705, ...
...
1700 INPUT"КУРС ДОЛЛАРА ПАДАЕТ ИЛИ РАСТЕТ";DO$: RETURN
А обратно - исключительно "на словах":
1510 ST$="РАСТЕТ": PRINT "ST=РАСТЕТ": $V="ST": ...
***
Трудно решить, что в программах на BASIC является ошибкой, а что - недокументированной возможностью. Ведь, исходный текст предоставляется пользователю и можно не предусматривать все возможные случаи использования программы, вместо этого объяснив, "где что лежит".
Например, авторы вполне могли лишь обозначить комментариями места, где пользователь может, если захочет, ввести переменные, а совсем не хотели его обмануть. А совпадение имен одних переменных со значениями других переменных - лишь способ сделать программу понятнее.
***
Кроме того, мы сталкиваемся с хитрым приемом BASIC-программирования: оставление в своей программе места для пользовательского кода. Как в описываемом примере: по адресам 1500, 1520,.. 1600 пользователь ставит некоторые условные операторы, проверяющие "переменные правил" из "кадров" массива CV$(1-4), CV$(5-8 ),.. CV$(21-25). А по адресам 1510, 1530,.. 1610 - присвоения значения переменным других правил.
В одной из популярных BASIC-программ работы с базами данных, например, пользователю предлагалась команда: "Выполнить операцию со всеми записями",- а операцию надо было вписать по некоторым адресам BASIC-программы (этакий "call back").
Конечно, прием был не особенно удобен - мало того, что приходится править код программы, так еще и специфика редакторов тех версий BASIC способствовала появлению в этих перезаписываемых кусках мусорных строк. (Вообще, на "специфику BASIC-редакторов" можно списать очень много).
Продолжениями этого приема (уже машинно-зависимыми) служили разного рода оверлеи, вставка в BASIC-программу машинных кодов, и, даже, сброс участка памяти на экран в виде картинки. Суть везде одна - хакинг программы в специально оставленных открытых точках доступа.
10 OPTION BASE 1: DIM D$(1023): D$(1)="ЭТО КОТ": I=1: ON ERROR GOTO 80
20 PRINT D$(I);: INPUT O$: O$=LEFT$(O$,1)
30 IF I<512 THEN IF D$(I*2)<>"" GOTO 70
40 IF O$="Д" OR O$="д" THEN PRINT "УРРА-А!": I=1: GOTO 20
50 D$(I*2+1)=D$(I): INPUT "А КТО ЭТО";O$: D$(I*2)="ЭТО "+O$
60 INPUT "ЧЕМ ОТЛИЧАЕТСЯ";D$(I): I=1: GOTO 20
70 IF O$="Д" OR O$="д" THEN I=I*2: GOTO 20: ELSE I=I*2+1: GOTO 20
80 PRINT "НЕ ХВАТАЕТ МОЗГОВ!": END
Одна из самых коротких известных мне игровых программ. Суть проста: по ответам пользователя строится бинарное дерево, исполняющее функции простейшей базы знаний. Однажды во время учебы, я выдал вариант этой программы за некую экспертную систему.

Несмотря на простоту, игрушка довольно забавная, если играть толпой. Очень быстро классификация животных перерастает в остроумное обсуждение общих знакомых.
***
Это одна из привлекательных черт программирования: очень часто что-то очень простое выглядит в глазах непосвященных чем-то сакральным и обладающим чуть ли не искусственным интеллектом. Я здесь не оригинален. Вышла даже специальная книжка, посвященная "философским" проблемам BASIC-программы, состоящей из единственной строки, которая так и называется
10 PRINT CHR$(205.5+RND(1)); : GOTO 10
Хитрость там в том, что символы с номерами 205 и 206 на том компьютере - прямая и обратная косые черточки. Т.о. эта программа рисует на экране бесконечный узор-лабиринт:

К сожалению, уже эти примеры слишком уж машинно-зависимы, точнее, BASIS-зависимы. Попробуйте, например, переписать их на классическом PASCAL. Жуть.
***
Нас будут интересовать другие способы имитации разумного поведения - те, которые можно без труда воспроизвести на других языках.
В качестве примера рассмотрим книжку: Р.Левин, Д.Дранг, Б.Эдельсон (ЛДЭ), Практическое введение в технологию искусственного интеллекта и экспертных систем с иллюстрациями на Бейсике (
 DJVU, 3.09Мб
DJVU, 3.09Мб ). Правда, чем дальше, тем меньше здесь будет оттуда и все больше - из других источников и отсебятины.
). Правда, чем дальше, тем меньше здесь будет оттуда и все больше - из других источников и отсебятины.ОТКРОВЕННОЕ ЖУЛЬНИЧЕСТВО ЛДЭ
К сожалению, первая хитрость, к которой прибегли авторы книги - обман читателя. Их программы, мягко говоря, не совсем работают.
Например, используется имитация ввода:
340 REM ВВОД ПЕРЕМЕННЫХ, ВХОДЯЩИХ В УСЛОВНЫЕ ЧАСТИ ПРАВИЛ В
350 REM НУЖНОМ ПОРЯДКЕ (НЕ БОЛЬШЕ 3 ПЕРЕМЕННЫХ НА ПРАВИЛО)
360 REM ИМЕНА ПЕРЕМЕННЫХ НЕ ДОЛЖНЫ ПОВТОРЯТСЯ
365 REM КОГДА ВВЕДЕНЫ ВСЕ ИМЕНА, НУЖНО НАЖАТЬ КЛАВИШУ ВК
367 V$(1)="DO": V$(2)="FT": V$(3)="FM": V$(4)="IN": V$(5)="ST"
368 PRINT"*** СПИСОК ПЕРЕМЕННЫХ ***"
370 FOR I=1 TO 10
380 PRINT"ВВЕДИТЕ ПЕРЕМЕННУЮ";I;
385 PRINT V$(I)
395 NEXT I
396 INPUT"ДЛЯ ПРОДОЛЖЕНИЯ НАЖМИТЕ";I
Большое количество слов маскирует тот факт, что все пять значений вводятся присваиванием, а цикл - простое украшение, дающее "правильную" распечатку.
Далее еще более наглая ложь - оператор ввода, на который опирается запуск "логического вывода" просто закомментарен, а примеры "частных примеров вывода" запускаются путем небольшого "взлома" программы.
***
Более тонкий случай. В программе есть символьный массив "имен переменных" (упомянутый выше V$(10)) и даже символьный массив CV$, в котором те же имена сгруппированы "по правилам" (ввод последнего авторы даже не пытаются имитировать). Однако, в алгоритмах самих правил используются не эти символьные имена, а сами переменные! Хотя, всем, конечно, понятно, что строка "DO" и переменная с именем DO$ - это вещи, совершенно друг с другом не связанные.
"Связь" осуществляется путем использования переключателей типа:
367 V$(1)="DO": ...
...
2430 IF V$=V$(I) THEN ...
...
2470 ON I GOSUB 1700, 1705, ...
...
1700 INPUT"КУРС ДОЛЛАРА ПАДАЕТ ИЛИ РАСТЕТ";DO$: RETURN
А обратно - исключительно "на словах":
1510 ST$="РАСТЕТ": PRINT "ST=РАСТЕТ": $V="ST": ...
***
Трудно решить, что в программах на BASIC является ошибкой, а что - недокументированной возможностью. Ведь, исходный текст предоставляется пользователю и можно не предусматривать все возможные случаи использования программы, вместо этого объяснив, "где что лежит".
Например, авторы вполне могли лишь обозначить комментариями места, где пользователь может, если захочет, ввести переменные, а совсем не хотели его обмануть. А совпадение имен одних переменных со значениями других переменных - лишь способ сделать программу понятнее.
***
Кроме того, мы сталкиваемся с хитрым приемом BASIC-программирования: оставление в своей программе места для пользовательского кода. Как в описываемом примере: по адресам 1500, 1520,.. 1600 пользователь ставит некоторые условные операторы, проверяющие "переменные правил" из "кадров" массива CV$(1-4), CV$(5-8 ),.. CV$(21-25). А по адресам 1510, 1530,.. 1610 - присвоения значения переменным других правил.
В одной из популярных BASIC-программ работы с базами данных, например, пользователю предлагалась команда: "Выполнить операцию со всеми записями",- а операцию надо было вписать по некоторым адресам BASIC-программы (этакий "call back").
Конечно, прием был не особенно удобен - мало того, что приходится править код программы, так еще и специфика редакторов тех версий BASIC способствовала появлению в этих перезаписываемых кусках мусорных строк. (Вообще, на "специфику BASIC-редакторов" можно списать очень много).
Продолжениями этого приема (уже машинно-зависимыми) служили разного рода оверлеи, вставка в BASIC-программу машинных кодов, и, даже, сброс участка памяти на экран в виде картинки. Суть везде одна - хакинг программы в специально оставленных открытых точках доступа.
Последний раз редактировалось: Gudleifr (Пн Янв 23, 2023 12:23 am), всего редактировалось 3 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ПРЯМАЯ ЦЕПОЧКА РАССУЖДЕНИЙ ПО ЛДЭ
В программах используются не только "параллельные" массивы (V$(10) - имена переменных, IN(10) - признаки готовности переменных) и массивы, разделенные на "кадры" (CV$(1..4) - первое правило, CV$(5..8 ) - второе,...), но и более сложные структуры: стеки и очереди. Впрочем, эти структуры реализуются просто добавлением специальных переменных-указателей, содержащих номер текущего элемента в списке. По идее, применение этих структур должно обеспечивать работу с "неименованными данными" - т.е. операции над тем, что является "текущим" с переходом к "следующему", с гарантией того, что дважды одно и то же обработано не будет. Что не мешает авторам постоянно перелопачивать эти структуры от начала до конца и ничуть не заботиться об их переполнении, что, конечно, очень и очень плохо, даже для BASIC.
***
БЛОК ПЕРЕМЕННЫХ
- Массивы V$(10) и IN(10) - переменные. Первый - имен переменных, второй - признаков их готовности. Ввод в массив V$ лишь имитируется, на самом деле он заполняется именами переменных - "DO", "FT", "FM", "IN", "ST" - путем присваивания. IN(10) изначально обнуляется. Сами значения переменных, хранятся в одноименных переменных программы: DO$, FT$, FM$, IN$, ST$. Дополнительно имеется блок для ввода значений этих переменных пользователем.
- Массив CV$(40) - правила. Первые три элемента каждой четверки - имена переменных, использующихся в правиле, четвертый - всегда "", чтобы обозначить конец правила.
- Массив Q(10) - очередь. В нее заносятся имена переменных, которые вычислены, и она здесь нафиг не нужна. Переменные FP и BP - указывают, соответственно, первый занятый и первый свободный элементы очереди. Постановка элемента в очередь (со сводящим весь смысл "на нет" перелопачиванием всего массива и исправленными мной ошибками):
3117 IF V$=V$(I) THEN GOTO 3125
3120 NEXT I: RETURN
3125 IN(I)=1
3135 FOR I=1 ТО 10: IF V$=Q$(I) THEN RETURN
3140 NEXT I
3160 Q$(BP)=V$: BP=BP+1
3180 RETURN
Обработка текущего элемента (поиск текущей переменной в правилах).
3115 FOR 1=1 ТО 10
3025 FOR SN=F TO 10
3030 FOR CN=1 ТО 4
3035 K=(SN-1)*4+CN
3040 IF CV$(K)=Q$(FP) THEN RETURN
3045 NEXT CN
3050 NEXT SN
3055 SN=0: RETURN
Переход к следующему:
725 FP=FP+1
730 IF FP=BP THEN STOP
- База условных частей правил. Начинаются со строки 1500 (номера, кратные 20). Адресуются по номеру правила (SN). Проверяют значения переменных. Устанавливают признак выполнения (S).
585 S=0: ON SN GOSUB 1500,1520,1540,1560,1580,1600
...
1500 IF IN$="ПАДАЕТ" THEN S=1
1502 RETURN
...
1520 IF IN$="PACTET" THEN S=1
1522 RETURN
...
Видно, что ввиду не вычисления результирующей переменной, а только установки флага успеха, вынуждены "ходить парами" - для обоих альтернатив.
- База результирующих частей правил. Со смещением на 10 от условных частей (1510 и далее через 20). Вычисляют результирующую переменную и ставят ее в очередь. (Очередь здесь, в принципе может быть нужна, если за раз вычисляется больше одной переменной).
635 ON SN GOSUB 1510,1530,1550,1570,1590,1610
...
1510 ST$="PACTET": PRINT"ST=PACTET": V$="ST": GOSUB 3115: RETURN
...
1530 SТ$="ПАДАЕТ": PRINT"ST=ПАДАЕТ": V$="ST": GOSUB 3115: RETURN
***
ЧТО ПРОГРАММА ДОЛЖНА БЫЛА БЫ ДЕЛАТЬ НА САМОМ ДЕЛЕ?
Программа, очевидно, должна пробегать все правила и искать среди них те, все переменные которых вычислены. Если такое происходит, правило должно исполняться, устанавливая значение новой переменной. Попутно печатаются победные реляции об "открытии новых фактов". Затем правила (в идеале, только те, в которые входит данная переменная) должны быть просмотрены снова. И так - до тех пор, пока новых выводов нельзя будет сделать. Процесс можно слегка подтолкнуть, запросив значение особо необходимой переменной у пользователя.
***
МОЖНО ЛИ ЗАСТАВИТЬ ПРОГРАММУ ЭТО ДЕЛАТЬ?
Очевидное решение: вставить эти вычисления "по месту", отказавшись от всех этих "имен переменных" и "номеров правил". На самом деле, все программисты занимаются этим постоянно, только "они об этом не знают". Взять, хотя бы переменные, управляющие разруливающими блоками из "БОМБЕРА", ведь, там мы именно делаем выводы, результаты которых используем в дальнейшем.
Однако, интереснее, когда заранее неизвестно, что и как будет рассчитано. И такое встречается. Вспомним блок перемещения из "TANKTICS" ( ТЕМА #41
ТЕМА #41 ). Всем гексам вокруг танка присваиваются некие веса (первое правило - чем ближе к цели, тем лучше), а затем начинают применяться остальные правила: если есть укрытие, его лучше занять, если участок плохопроходим, лучше обойти и т.д. Понятно, в зависимости от обстановки (например, при отсутствии рядом врага) некоторые правила "не работают". Когда правила кончатся, танк переходит в самый выгодный гекс.
). Всем гексам вокруг танка присваиваются некие веса (первое правило - чем ближе к цели, тем лучше), а затем начинают применяться остальные правила: если есть укрытие, его лучше занять, если участок плохопроходим, лучше обойти и т.д. Понятно, в зависимости от обстановки (например, при отсутствии рядом врага) некоторые правила "не работают". Когда правила кончатся, танк переходит в самый выгодный гекс.
Можно ли из приведенной авторами книги программы сделать нечто работающее? Сначала надо добавить к массивам V$(10) и IN(10) массив значений переменных, например, VL$(10). Сразу уйдут все согласования имен и строк, которые могут запутать кого угодно.
Во-вторых, правила можно привести в нормальную логическую форму, позволяющую записывать их не в виде кода, а в том же массиве CV$(10) (только его проще сделать числовым - CV(40)). И тогда мы получим честный решатель силлогизмов. Как в замечательной книге Льюиса Кэррола "Как решать силлогизмы".
В-третьих, самое сложное, как перевести с человеческого языка на язык логических переменных? Если не придумать здесь какого-либо специального языка, все наши старания будут напрасными, придется опять руками править программу. Кэррол, кстати, предложил очень хороший способ подобной формализации.
***
А ЕСЛИ В АБСОЛЮТЕ?
А если довести до абсолюта, т.е. всякий полученный новый факт вставлять в некую систему правил и ожидать вывода? Получится человеческий мозг, только его правила чаще называют ассоциациями.
В программах используются не только "параллельные" массивы (V$(10) - имена переменных, IN(10) - признаки готовности переменных) и массивы, разделенные на "кадры" (CV$(1..4) - первое правило, CV$(5..8 ) - второе,...), но и более сложные структуры: стеки и очереди. Впрочем, эти структуры реализуются просто добавлением специальных переменных-указателей, содержащих номер текущего элемента в списке. По идее, применение этих структур должно обеспечивать работу с "неименованными данными" - т.е. операции над тем, что является "текущим" с переходом к "следующему", с гарантией того, что дважды одно и то же обработано не будет. Что не мешает авторам постоянно перелопачивать эти структуры от начала до конца и ничуть не заботиться об их переполнении, что, конечно, очень и очень плохо, даже для BASIC.
***
БЛОК ПЕРЕМЕННЫХ
- Массивы V$(10) и IN(10) - переменные. Первый - имен переменных, второй - признаков их готовности. Ввод в массив V$ лишь имитируется, на самом деле он заполняется именами переменных - "DO", "FT", "FM", "IN", "ST" - путем присваивания. IN(10) изначально обнуляется. Сами значения переменных, хранятся в одноименных переменных программы: DO$, FT$, FM$, IN$, ST$. Дополнительно имеется блок для ввода значений этих переменных пользователем.
- Массив CV$(40) - правила. Первые три элемента каждой четверки - имена переменных, использующихся в правиле, четвертый - всегда "", чтобы обозначить конец правила.
- Массив Q(10) - очередь. В нее заносятся имена переменных, которые вычислены, и она здесь нафиг не нужна. Переменные FP и BP - указывают, соответственно, первый занятый и первый свободный элементы очереди. Постановка элемента в очередь (со сводящим весь смысл "на нет" перелопачиванием всего массива и исправленными мной ошибками):
3117 IF V$=V$(I) THEN GOTO 3125
3120 NEXT I: RETURN
3125 IN(I)=1
3135 FOR I=1 ТО 10: IF V$=Q$(I) THEN RETURN
3140 NEXT I
3160 Q$(BP)=V$: BP=BP+1
3180 RETURN
Обработка текущего элемента (поиск текущей переменной в правилах).
3115 FOR 1=1 ТО 10
3025 FOR SN=F TO 10
3030 FOR CN=1 ТО 4
3035 K=(SN-1)*4+CN
3040 IF CV$(K)=Q$(FP) THEN RETURN
3045 NEXT CN
3050 NEXT SN
3055 SN=0: RETURN
Переход к следующему:
725 FP=FP+1
730 IF FP=BP THEN STOP
- База условных частей правил. Начинаются со строки 1500 (номера, кратные 20). Адресуются по номеру правила (SN). Проверяют значения переменных. Устанавливают признак выполнения (S).
585 S=0: ON SN GOSUB 1500,1520,1540,1560,1580,1600
...
1500 IF IN$="ПАДАЕТ" THEN S=1
1502 RETURN
...
1520 IF IN$="PACTET" THEN S=1
1522 RETURN
...
Видно, что ввиду не вычисления результирующей переменной, а только установки флага успеха, вынуждены "ходить парами" - для обоих альтернатив.
- База результирующих частей правил. Со смещением на 10 от условных частей (1510 и далее через 20). Вычисляют результирующую переменную и ставят ее в очередь. (Очередь здесь, в принципе может быть нужна, если за раз вычисляется больше одной переменной).
635 ON SN GOSUB 1510,1530,1550,1570,1590,1610
...
1510 ST$="PACTET": PRINT"ST=PACTET": V$="ST": GOSUB 3115: RETURN
...
1530 SТ$="ПАДАЕТ": PRINT"ST=ПАДАЕТ": V$="ST": GOSUB 3115: RETURN
***
ЧТО ПРОГРАММА ДОЛЖНА БЫЛА БЫ ДЕЛАТЬ НА САМОМ ДЕЛЕ?
Программа, очевидно, должна пробегать все правила и искать среди них те, все переменные которых вычислены. Если такое происходит, правило должно исполняться, устанавливая значение новой переменной. Попутно печатаются победные реляции об "открытии новых фактов". Затем правила (в идеале, только те, в которые входит данная переменная) должны быть просмотрены снова. И так - до тех пор, пока новых выводов нельзя будет сделать. Процесс можно слегка подтолкнуть, запросив значение особо необходимой переменной у пользователя.
***
МОЖНО ЛИ ЗАСТАВИТЬ ПРОГРАММУ ЭТО ДЕЛАТЬ?
Очевидное решение: вставить эти вычисления "по месту", отказавшись от всех этих "имен переменных" и "номеров правил". На самом деле, все программисты занимаются этим постоянно, только "они об этом не знают". Взять, хотя бы переменные, управляющие разруливающими блоками из "БОМБЕРА", ведь, там мы именно делаем выводы, результаты которых используем в дальнейшем.
Однако, интереснее, когда заранее неизвестно, что и как будет рассчитано. И такое встречается. Вспомним блок перемещения из "TANKTICS" (
 ТЕМА #41
ТЕМА #41 ). Всем гексам вокруг танка присваиваются некие веса (первое правило - чем ближе к цели, тем лучше), а затем начинают применяться остальные правила: если есть укрытие, его лучше занять, если участок плохопроходим, лучше обойти и т.д. Понятно, в зависимости от обстановки (например, при отсутствии рядом врага) некоторые правила "не работают". Когда правила кончатся, танк переходит в самый выгодный гекс.
). Всем гексам вокруг танка присваиваются некие веса (первое правило - чем ближе к цели, тем лучше), а затем начинают применяться остальные правила: если есть укрытие, его лучше занять, если участок плохопроходим, лучше обойти и т.д. Понятно, в зависимости от обстановки (например, при отсутствии рядом врага) некоторые правила "не работают". Когда правила кончатся, танк переходит в самый выгодный гекс.Можно ли из приведенной авторами книги программы сделать нечто работающее? Сначала надо добавить к массивам V$(10) и IN(10) массив значений переменных, например, VL$(10). Сразу уйдут все согласования имен и строк, которые могут запутать кого угодно.
Во-вторых, правила можно привести в нормальную логическую форму, позволяющую записывать их не в виде кода, а в том же массиве CV$(10) (только его проще сделать числовым - CV(40)). И тогда мы получим честный решатель силлогизмов. Как в замечательной книге Льюиса Кэррола "Как решать силлогизмы".
В-третьих, самое сложное, как перевести с человеческого языка на язык логических переменных? Если не придумать здесь какого-либо специального языка, все наши старания будут напрасными, придется опять руками править программу. Кэррол, кстати, предложил очень хороший способ подобной формализации.
***
А ЕСЛИ В АБСОЛЮТЕ?
А если довести до абсолюта, т.е. всякий полученный новый факт вставлять в некую систему правил и ожидать вывода? Получится человеческий мозг, только его правила чаще называют ассоциациями.
Последний раз редактировалось: Gudleifr (Ср Дек 06, 2017 2:08 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ПРЕРЕВОД С ЧЕЛОВЕЧЕСКОГО НА ЛОГИЧЕСКИЙ
Вспомним известную задачу:
1. Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть "мистер" (м-р).
2. М-р Робинсон живет в Лос-Анджелесе.
3. Кондуктор живет в Омахе.
4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже.
5. Пассажир - однофамилец кондуктора живет в Чикаго.
6. Кондуктор и один из пассажиров, известный специалист по математической физике, ходят в одну церковь.
7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд.
Как фамилия машиниста?
***
Введем переменные:
1. 9 логических переменных служащий-специальность - см, ск, сч, рм, рк, рч, дм, дк, дч. Из них истинны только 3 (точка - "и", плюс - "или", апостроф - "отрицание"):
см.рк.дч+см.рч.дк+ск.рм.дч+ск.рч.дм+сч.рм.дк+сч.рк.дм
см.ск'.сч'+см'.ск.сч'+см'.ск'.сч
рм.рк'.рч'+рм'.рк.рч'+рм'.рк'.рч
дм.дк'.дч'+дм'.дк.сч'+дм'.дк'.дч
С 9 переменными пассажир-город немого проще: пассажир проживает в одном из упомянутых городов или в каком-то другом (а вдруг):
СЛ.СО'.СЧ'+СЛ'.СО.СЧ'+СЛ'.СО'.СЧ+СЛ'.СО'.СЧ'
РЛ.РО'.РЧ'+РЛ'.РО.РЧ'+РЛ'.РО'.РЧ+РЛ'.РО'.РЧ'
ДЛ.ДО'.ДЧ'+ДЛ'.ДО.ДЧ'+ДЛ'.ДО'.ДЧ+ДЛ'.ДО'.ДЧ'
Конечно, из первого условия не следует необходимость наличия "пассажирских" переменных, но тут я пошел на поводу "классического" решения задачи раньше, чем подумал, что можно вводить их по мере ввода остальных правил.
2. РЛ - удачненько!
3. Еще три переменные: кО - истинна, кЛ и кЧ - ложны.
4. И еще три (знание пассажирами математики): Дт - ложна, а Ст+Рт - неизвестно.
5. ск.СЧ+рк.РЧ+дк.ДЧ.
6. кЛ.СЛ.Ст+кO.СO.Ст+кЧ.СЧ.Ст+кЛ.РЛ.Pт+кO.РO.Рт+кЧ.РЧ.Рт+кЛ.ДЛ.Дт+кO.ДO.Дт+кЧ.ДЧ.Дт - вот мы и увязали город кондуктора и математика.
7. сч - ложна, см+ск - истинно.
Проверяем, получится ли у нас? Правила (1) буду применять автоматически.
Истинность РЛ (2) превращает (5) в ск.СЧ+дк.ДЧ, а (6) в кO.СO.Ст+кЧ.СЧ.Ст+кЛ.Pт+кO.ДO.Дт+кЧ.ДЧ.Дт.
Истинность кО (3) - (6) в СO.Ст+ДO.Дт.
Добиваем (6) мы ложностью Дт (4) - СО.Ст, следовательно СО.
Тогда в (5) остается дк.ДЧ, следовательно, дк.
Ноконец дк и (7) дает см!
Смит - машинист.
***
Попробуем на BASIC.
10 DIM V$(24),IN(24),LV(13,2),CV$(43,3)
20 FOR V=1 TO 24: READ V$(V): IN(V)=0: NEXT V
30 DATA "см", "ск", "сч", "рм", "рк", "рч", "дм", "дк", "дч"
40 DATA "СЛ", "СО", "СЧ", "РЛ", "РО", "РЧ", "ДЛ", "ДО", "ДЧ"
50 DATA "кЛ", "кО", "кЧ", "Ст", "Рт", "Дт"
60 C = 1
70 FOR S=1 TO 13: LV(S,1) = C: READ LV(S,2)
80 FOR N=1 TO LV(S,2): READ CV$(C,1),CV$(C,2),CV$(C,3): C=C+1
90 DATA 6, "см","рк","дч", "см","рч","дк", "ск","рм","дч"
100 DATA "ск","рч","дм", "сч","рм","дк", "сч","рк","дм"
110 DATA 3, "см","ск-","сч-", "см-","ск","сч-", "см-","ск-","сч"
120 DATA 3, "рм","рк-","рч-", "рм-","рк","рч-", "рм-","рк-","рч"
130 DATA 3, "дм","дк-","дч-", "дм-","дк","дч-", "дм-","дк-","дч"
140 DATA 4, "СЛ","СО-","СЧ-", "СЛ-","СО","СЧ-", "СЛ-","СО-","СЧ"
150 DATA "СЛ-","СО-","СЧ-"
160 DATA 4, "РЛ","РО-","РЧ-", "РЛ-","РО","РЧ-", "РЛ-","РО-","РЧ"
170 DATA "РЛ-","РО-","РЧ-"
180 DATA 4, "ДЛ","ДО-","ДЧ-", "ДЛ-","ДО","ДЧ-", "ДЛ-","ДО-","ДЧ"
190 DATA "ДЛ-","ДО-","ДЧ-"
200 DATA 1, "РЛ","",""
210 DATA 1, "кЛ-","кО","кЧ-"
220 DATA 1, "Дт-","",""
230 DATA 3, "ск","СЧ","", "рк","РЧ","", "дк","ДЧ",""
240 DATA 9, "кЛ","СЛ","Ст", "кО","СО","Ст", "кЧ","СЧ","Ст"
250 DATA "кЛ","РЛ","Рт", "кО","РО","Рт", "кЧ","РЧ","Рт"
260 DATA "кЛ","ДЛ","Дт", "кО","ДО","Дт", "кЧ","ДЧ","Дт"
270 DATA 1, "сч-","",""
280 NEXT N,S
290 REM ПЕРЕБОР ПРАВИЛ
300 FOR S=1 TO 13: IF LV(S,2)=0 THEN GOTO 320
310 IF LV(S,2)=1 THEN GOSUB 1150 ELSE GOSUB 1200
320 NEXT S
330 V$="см": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: СМИТ": GOTO 370
340 V$="дм": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: ДЖОНС": GOTO 370
350 V$="рм": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: РОБИНСОН": GOTO 370
360 GOTO 300
370 END
1000 REM ПОИСК ПЕРЕМЕННОЙ
1010 FOR V=1 TO 24: IF LEFT$(V$,2)=V$(V) THEN RETURN
1020 NEXT V
1050 REM ОТБРАСЫВАНИЕ ЛОЖНОЙ КОНЬЮНКЦИИ
1060 CV$(C,1)="": CV$(C,2)="": CV$(C,3)=""
1070 LV(S,2)=LV(S,2)-1: RETURN
1100 REM ПРОПУСК ПУСТЫХ КОНЬЮНКЦИЙ
1110 T=0: FOR I=1 TO 3: IF LEN(CV$(C,I))=0 THEN T=T+1
1120 NEXT I: IF T=3 THEN C=C+1: GOTO 1110
1130 RETURN
1150 REM УСТАНОВКА ПЕРЕМЕННЫХ
1160 C=LV(S,1): GOSUB 1100
1170 FOR I=1 TO 3: V$=CV$(C,I): IF LEN(V$)=0 GOTO 1190
1180 GOSUB 1000: IN(V)=LEN(V$): PRINT V$, "ИСТИННО"
1190 NEXT I: LV(S,2)=0: RETURN
1200 REM ПОДСТАНОВКА ПЕРЕМЕННЫХ В ПРАВИЛО
1210 C=LV(S,1): L=LV(S,2): FOR N=1 TO L: GOSUB 1100: T=0
1220 FOR I=1 TO 3: V$=CV$(C,I)
1230 IF LEN(V$)=0 THEN T=T+1: GOTO 1270
1240 GOSUB 1000: IF IN(V)=0 THEN GOTO 1270
1250 IF LEN(V$)<>IN(V) THEN GOSUB 1050: GOTO 1280
1260 CV$(C,I)="": T=T+1
1270 NEXT I: IF T=3 THEN LV(S,2)=LV(S,2)-1
1280 C=C+1: NEXT N: RETURN
Работает!
***
Видно, что это задача уже не для BASIC: данные, занимающие больше половины программы, и отдельные счетчики для каждого вида данных намекают на изначальную структурность задачи.
Никаких проверок не предусмотрено потому, что когда я кое-как отладил программу, я с ней уже и наигрался. Конечно, если применять подобную механику для решения других задач (см. книги Смаллиана), то проверки, например, на противоречивость правил понадобятся.
Вообще же это фокус: программа очень проста, но может обработать только данный набор данных. Придумать другой, столь же интересный, набор данных достаточно сложно. Да и к тому времени, когда этот набор удастся засунуть в программу, программист, скорее всего, уже решит задачу в уме.
***
Так что, такое применение метода прямой цепочки рассуждений вряд ли может пригодиться где-либо, кроме разработки машинного интеллекта. Частные случаи - сложные цепочки условий, приводящих к неожиданным для игрока выводам вполне же востребованы (например, в тех же книгах-играх).
Вспомним известную задачу:
1. Смит, Джонс и Робинсон работают в одной поездной бригаде машинистом, кондуктором и кочегаром. Профессии их названы не обязательно в том же порядке, что и фамилии. В поезде, который обслуживает бригада, едут трое пассажиров с теми же фамилиями. В дальнейшем каждого пассажира мы будем почтительно называть "мистер" (м-р).
2. М-р Робинсон живет в Лос-Анджелесе.
3. Кондуктор живет в Омахе.
4. М-р Джонс давно позабыл всю алгебру, которой его учили в колледже.
5. Пассажир - однофамилец кондуктора живет в Чикаго.
6. Кондуктор и один из пассажиров, известный специалист по математической физике, ходят в одну церковь.
7. Смит всегда выигрывает у кочегара, когда им случается встречаться за партией в бильярд.
Как фамилия машиниста?
***
Введем переменные:
1. 9 логических переменных служащий-специальность - см, ск, сч, рм, рк, рч, дм, дк, дч. Из них истинны только 3 (точка - "и", плюс - "или", апостроф - "отрицание"):
см.рк.дч+см.рч.дк+ск.рм.дч+ск.рч.дм+сч.рм.дк+сч.рк.дм
см.ск'.сч'+см'.ск.сч'+см'.ск'.сч
рм.рк'.рч'+рм'.рк.рч'+рм'.рк'.рч
дм.дк'.дч'+дм'.дк.сч'+дм'.дк'.дч
С 9 переменными пассажир-город немого проще: пассажир проживает в одном из упомянутых городов или в каком-то другом (а вдруг):
СЛ.СО'.СЧ'+СЛ'.СО.СЧ'+СЛ'.СО'.СЧ+СЛ'.СО'.СЧ'
РЛ.РО'.РЧ'+РЛ'.РО.РЧ'+РЛ'.РО'.РЧ+РЛ'.РО'.РЧ'
ДЛ.ДО'.ДЧ'+ДЛ'.ДО.ДЧ'+ДЛ'.ДО'.ДЧ+ДЛ'.ДО'.ДЧ'
Конечно, из первого условия не следует необходимость наличия "пассажирских" переменных, но тут я пошел на поводу "классического" решения задачи раньше, чем подумал, что можно вводить их по мере ввода остальных правил.
2. РЛ - удачненько!
3. Еще три переменные: кО - истинна, кЛ и кЧ - ложны.
4. И еще три (знание пассажирами математики): Дт - ложна, а Ст+Рт - неизвестно.
5. ск.СЧ+рк.РЧ+дк.ДЧ.
6. кЛ.СЛ.Ст+кO.СO.Ст+кЧ.СЧ.Ст+кЛ.РЛ.Pт+кO.РO.Рт+кЧ.РЧ.Рт+кЛ.ДЛ.Дт+кO.ДO.Дт+кЧ.ДЧ.Дт - вот мы и увязали город кондуктора и математика.
7. сч - ложна, см+ск - истинно.
Проверяем, получится ли у нас? Правила (1) буду применять автоматически.
Истинность РЛ (2) превращает (5) в ск.СЧ+дк.ДЧ, а (6) в кO.СO.Ст+кЧ.СЧ.Ст+кЛ.Pт+кO.ДO.Дт+кЧ.ДЧ.Дт.
Истинность кО (3) - (6) в СO.Ст+ДO.Дт.
Добиваем (6) мы ложностью Дт (4) - СО.Ст, следовательно СО.
Тогда в (5) остается дк.ДЧ, следовательно, дк.
Ноконец дк и (7) дает см!
Смит - машинист.
***
Попробуем на BASIC.
10 DIM V$(24),IN(24),LV(13,2),CV$(43,3)
20 FOR V=1 TO 24: READ V$(V): IN(V)=0: NEXT V
30 DATA "см", "ск", "сч", "рм", "рк", "рч", "дм", "дк", "дч"
40 DATA "СЛ", "СО", "СЧ", "РЛ", "РО", "РЧ", "ДЛ", "ДО", "ДЧ"
50 DATA "кЛ", "кО", "кЧ", "Ст", "Рт", "Дт"
60 C = 1
70 FOR S=1 TO 13: LV(S,1) = C: READ LV(S,2)
80 FOR N=1 TO LV(S,2): READ CV$(C,1),CV$(C,2),CV$(C,3): C=C+1
90 DATA 6, "см","рк","дч", "см","рч","дк", "ск","рм","дч"
100 DATA "ск","рч","дм", "сч","рм","дк", "сч","рк","дм"
110 DATA 3, "см","ск-","сч-", "см-","ск","сч-", "см-","ск-","сч"
120 DATA 3, "рм","рк-","рч-", "рм-","рк","рч-", "рм-","рк-","рч"
130 DATA 3, "дм","дк-","дч-", "дм-","дк","дч-", "дм-","дк-","дч"
140 DATA 4, "СЛ","СО-","СЧ-", "СЛ-","СО","СЧ-", "СЛ-","СО-","СЧ"
150 DATA "СЛ-","СО-","СЧ-"
160 DATA 4, "РЛ","РО-","РЧ-", "РЛ-","РО","РЧ-", "РЛ-","РО-","РЧ"
170 DATA "РЛ-","РО-","РЧ-"
180 DATA 4, "ДЛ","ДО-","ДЧ-", "ДЛ-","ДО","ДЧ-", "ДЛ-","ДО-","ДЧ"
190 DATA "ДЛ-","ДО-","ДЧ-"
200 DATA 1, "РЛ","",""
210 DATA 1, "кЛ-","кО","кЧ-"
220 DATA 1, "Дт-","",""
230 DATA 3, "ск","СЧ","", "рк","РЧ","", "дк","ДЧ",""
240 DATA 9, "кЛ","СЛ","Ст", "кО","СО","Ст", "кЧ","СЧ","Ст"
250 DATA "кЛ","РЛ","Рт", "кО","РО","Рт", "кЧ","РЧ","Рт"
260 DATA "кЛ","ДЛ","Дт", "кО","ДО","Дт", "кЧ","ДЧ","Дт"
270 DATA 1, "сч-","",""
280 NEXT N,S
290 REM ПЕРЕБОР ПРАВИЛ
300 FOR S=1 TO 13: IF LV(S,2)=0 THEN GOTO 320
310 IF LV(S,2)=1 THEN GOSUB 1150 ELSE GOSUB 1200
320 NEXT S
330 V$="см": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: СМИТ": GOTO 370
340 V$="дм": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: ДЖОНС": GOTO 370
350 V$="рм": GOSUB 1000: IF IN(V)=2 THEN PRINT "ОТВЕТ: РОБИНСОН": GOTO 370
360 GOTO 300
370 END
1000 REM ПОИСК ПЕРЕМЕННОЙ
1010 FOR V=1 TO 24: IF LEFT$(V$,2)=V$(V) THEN RETURN
1020 NEXT V
1050 REM ОТБРАСЫВАНИЕ ЛОЖНОЙ КОНЬЮНКЦИИ
1060 CV$(C,1)="": CV$(C,2)="": CV$(C,3)=""
1070 LV(S,2)=LV(S,2)-1: RETURN
1100 REM ПРОПУСК ПУСТЫХ КОНЬЮНКЦИЙ
1110 T=0: FOR I=1 TO 3: IF LEN(CV$(C,I))=0 THEN T=T+1
1120 NEXT I: IF T=3 THEN C=C+1: GOTO 1110
1130 RETURN
1150 REM УСТАНОВКА ПЕРЕМЕННЫХ
1160 C=LV(S,1): GOSUB 1100
1170 FOR I=1 TO 3: V$=CV$(C,I): IF LEN(V$)=0 GOTO 1190
1180 GOSUB 1000: IN(V)=LEN(V$): PRINT V$, "ИСТИННО"
1190 NEXT I: LV(S,2)=0: RETURN
1200 REM ПОДСТАНОВКА ПЕРЕМЕННЫХ В ПРАВИЛО
1210 C=LV(S,1): L=LV(S,2): FOR N=1 TO L: GOSUB 1100: T=0
1220 FOR I=1 TO 3: V$=CV$(C,I)
1230 IF LEN(V$)=0 THEN T=T+1: GOTO 1270
1240 GOSUB 1000: IF IN(V)=0 THEN GOTO 1270
1250 IF LEN(V$)<>IN(V) THEN GOSUB 1050: GOTO 1280
1260 CV$(C,I)="": T=T+1
1270 NEXT I: IF T=3 THEN LV(S,2)=LV(S,2)-1
1280 C=C+1: NEXT N: RETURN
Работает!
***
Видно, что это задача уже не для BASIC: данные, занимающие больше половины программы, и отдельные счетчики для каждого вида данных намекают на изначальную структурность задачи.
Никаких проверок не предусмотрено потому, что когда я кое-как отладил программу, я с ней уже и наигрался. Конечно, если применять подобную механику для решения других задач (см. книги Смаллиана), то проверки, например, на противоречивость правил понадобятся.
Вообще же это фокус: программа очень проста, но может обработать только данный набор данных. Придумать другой, столь же интересный, набор данных достаточно сложно. Да и к тому времени, когда этот набор удастся засунуть в программу, программист, скорее всего, уже решит задачу в уме.
***
Так что, такое применение метода прямой цепочки рассуждений вряд ли может пригодиться где-либо, кроме разработки машинного интеллекта. Частные случаи - сложные цепочки условий, приводящих к неожиданным для игрока выводам вполне же востребованы (например, в тех же книгах-играх).

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ОБРАТНАЯ ЦЕПОЧКА РАССУЖДЕНИЙ ПО ЛДЭ
Авторы книги предлагают собирать программу обратной цепочки рассуждений из тех же элементов, что и для прямой. Только, вместо очереди готовых переменных используется стек переменных, подлежащих вычислению (а, заодно - и стек правил, которые следует вычислить).
Попутно была показана возможность смешивать в условных частях правил (блока 1500) логические операции с операциями арифметического сравнения. Это просто авторам, т.к. правила вписываются в программу руками, но может добавить мороки тем, кто попытается организовать табличное хранение правил.
Т.е. системе задается вопрос: "А не правда ли, что...?" А система ищет в своей базе правила, способные пролить свет на этот вопрос. Найденные правила могут сработать только при вычислении входящих в них переменных, а вычисление переменных ставит новые вопросы. Погружение продолжается до тех пор, пока не упрется в переменные, значения которых могут быть получены от пользователя. (В общем, вылитый юристконслульт с таксой $100 за вопрос. Только умнее).
***
К программе добавился еще один символьный массив GL$(8 ) - переменных, соответствующих правилам. Когда вводится переменная, подлежащая исполнению, ее имя ищется в этом массиве.
2200 FOR SN=F ТО 8
2210 IF V$=GL$(SN) THEN RETURN
2220 NEXT SN: SN=0: RETURN
Номер в массиве равен номеру правила в операторе ON ... GOSUB. Если переменной нет в этом списке она ищется в массиве переменных (как в первой программе), и если еще не известна, вводится пользователем. И опять - номер в списке равен номеру ввода в операторе ON ... GOSUB.
2400 FOR I=1 TO 10
2430 IF V$=V$(I) THEN GOTO 2450
2440 NEXT I: STOP
2450 IF IN(I)=1 THEN RETURN
2460 IN(I)=1
2470 ON I GOSUB 1700,1705,1710,1715
2480 RETURN
...
1700 INPUT "ПОСЕТИТЕЛЬ ИМЕЕТ УЧЕНОЕ ЗВАНИЕ ?";DE$: RETURN
...
В случае нахождения правила, в стек заносится его номер и номер первой входящей переменной (опять из кадра правила в массиве CV$(40)):
2000 SP=SP-1: SS(SP)=SN: CS(SP)=1
2010 RETURN
После чего начинается работа с 1-й переменной правила.
После обработки переменной CS(SP) увеличивается на единицу.
Когда кадр в CV$(40) кончается (помните, там был обязательный пустой элемент), правило вычисляется. Если оно срабатывает (S=1), выполняется его результируящая часть (т.е. вычисляется нужная переменная) и из стека удаяетя последний элемент (SP=SP+1), и уже старый CS(SP) увеличивается на единицу. Если правило не срабатывает (S=0), то последний элемент все равно удаляется, и происходит поиск имени переменной правила SS(SP) в остатке GL$(8 ), т.е. другое, более подходящее правило для нее.
505 INPUT"** ВВЕДИТЕ ИМЯ ПЕРЕМЕННОЙ ЛОГИЧЕСКОГО ВЫВОДА";V$
520 F=1: GOSUB 2200: REM ПОИСК V$ В GL$(8 ) (С ПОЗИЦИИ F)
525 IF SN THEN STOP: ЕСЛИ ПРАВИЛА ДЛЯ V$ КОНЧИЛИСЬ
540 GOSUB 2000: REM ВСТАВКА В СТЕК (СМ. ВЫШЕ)
550 I=(SS(SP)-1)*4+CS(SP)
555 V$=CV$(I)
565 IF V$="" THEN GOTO 582
568 F=1: GOSUB 2200: IF SN>0 THEN GOTO 540
570 GOSUB 2400: REM ВВОД ПЕРЕМЕННОЙ, ЕСЛИ ОНА ЕЩЕ НЕ ВВЕДЕНА
575 CS(SP)=CS(SP)+1: GOTO 550: REM СЛЕДУЮЩАЯ ПЕРЕМЕННАЯ
582 SN=SS(SP): REM ВСЕ ПЕРЕМЕННЫЕ ГОТОВЫ
585 S=0: ON SN GOSUB 1500,1520,1540,1560,1580,1600
600 IF S=1 THEN GOTO 635: REM СРАБОТАЛО ЛИ ПРАВИЛО?
610 I=SS(SP): V$=GL$(I): REM НЕ СРАБОТАЛО, ВСПОМИНАЕМ ИМЯ
620 F=SS(SP)+1: GOSUB 2200: ИЩЕМ СЛЕДУЮЩЕЕ ПРАВИЛО
625 SP=SP+1: GOTO 540: ПЕРЕВСТАВЛЯЕМ ЕГО В СТЕК
635 ON SN GOSUB 1510,1530,1550,1570,1590,1610: СРАБОТАЛО
660 SP=SP+1: ПРАВИЛО БОЛЬШЕ НЕ НУЖНО, УДАЛЯЕМ ИЗ СТЕКА
670 IF SP<11 THEN GOTO 695: REM А НЕ ПУСТ ЛИ СТЕК?
680 PRINT"*** НОРМАЛЬНОЕ ЗАВЕРШЕНИЕ"
685 STOP
695 CS(SP)=CS(SP)+1: GOTO 550: REM СЛЕДУЮЩАЯ ПЕРЕМЕННАЯ
В целом, программа кажется более проработанной, чем для прямой цепочки, и после исправления в ней ошибок (я удалил почти все) даже может заработать. Видимо, первую программу делали из второй путем закомментаривания ненужного и наложения заплаток - исключительно для книги.
Хитрость этой конструкции состоит в том, что тут параллельно существует две схемы вложенности управления: одна нормальная программная, вторая по стеку правил (т.е. положение процесса определяется не только текущей позицией в тексте программы, но и глубиной вложения в стеке). Необходимо ли это?
***
Поведение программы напоминает Ивана Царевича. Пришел за яблоками к Яге - укради сначала коня у Кащея. Пришел за конем к Кащею - достань Василису у Змея. Победил Змея - пошел проходить цепочку обратно, меняя предметы на нужные у тех же самых персонажей.
Или еще проще: надо найти значение переменной - для этого вызываем процедуру, переменные, нужные этой процедуре она получает у других процедур... Любой программист скажет, что всю жизнь это программировал и не заморачивался никакой "обратной цепочкой". По крайней мере, вполне хватает одного обычного программного стека (о котором BASIC-программист не всегда и знает). Например, приведенный выше страхолюдный кусок на "нормальном" языке записывается так.
FUNCTION ПЕРЕМЕННАЯ(ИМЯ)
- LOCAL ПРАВИЛО, НОМЕР, ЗНАЧЕНИЕ;
- WHILE ПРАВИЛО=GL-ПОИСК(ИМЯ)
- - ЗНАЧЕНИЕ=ПРАВИЛО(ПРАВИЛО);
- - IF ЗНАЧЕНИЕ
- - - RETURN ЗНАЧЕНИЕ;
- НОМЕР=V-ПОИСК(ИМЯ);
- IF НОМЕР
- - ЗНАЧЕНИЕ=IN-POISK(НОМЕР);
- - IF ЗНАЧЕНИЕ
- - - RETURN ЗНАЧЕНИЕ;
- - ELSE
- - - RETURN ВВОД(НОМЕР);
- RETURN ОТКАЗ;
FUNCTION ПРАВИЛО(НОМЕР)
- LOCAL ПОЗИЦИЯ, УСПЕХ;
- FOR ПОЗИЦИЯ=ПЕРВЫЙ(НОМЕР) ТО ПОСЛЕДНИЙ(НОМЕР)
- - ЗНАЧЕНИЕ(ПОЗИЦИЯ)=ПЕРЕМЕННАЯ(ИМЯ(ПОЗИЦИЯ));
- - IF ОТКАЗ
- - - RETURN ОТКАЗ;
- УСПЕХ=ВЫПОЛНИТЬ-УСЛОВНУЮ-ЧАСТЬ(НОМЕР);
- IF УСПЕХ
- - RETURN ВЫПОЛНИТЬ-РЕЗУЛЬТИРУЮЩУЮ-ЧАСТЬ(НОМЕР);
- ELSE
- - RETURN ОТКАЗ;
И стек здесь реализовался автоматически - путем использования привычного программисту механизма локальных переменных. Т.е. суть обратной цепочки рассуждений - суть программирования в том виде, каким его знаем. Этот метод присутствует в каждой нашей программе, независимо от нашего желания.
Так в чем тут суть? В написании программой самой себя? Или в решении задачи с конца?
***
Конечно, этот пример можно использовать просто как демонстрацию использования стека. На BASIC, где нет локальных переменных, такое бывает нужно.
***
По большому счету, умение подбирать для программы правильное соотношение прямой и обратной цепочки рассуждений - это основное требование к программисту ( ТЕМА #15, АБЗАЦ #389
ТЕМА #15, АБЗАЦ #389 ).
).
Авторы книги предлагают собирать программу обратной цепочки рассуждений из тех же элементов, что и для прямой. Только, вместо очереди готовых переменных используется стек переменных, подлежащих вычислению (а, заодно - и стек правил, которые следует вычислить).
Попутно была показана возможность смешивать в условных частях правил (блока 1500) логические операции с операциями арифметического сравнения. Это просто авторам, т.к. правила вписываются в программу руками, но может добавить мороки тем, кто попытается организовать табличное хранение правил.
Т.е. системе задается вопрос: "А не правда ли, что...?" А система ищет в своей базе правила, способные пролить свет на этот вопрос. Найденные правила могут сработать только при вычислении входящих в них переменных, а вычисление переменных ставит новые вопросы. Погружение продолжается до тех пор, пока не упрется в переменные, значения которых могут быть получены от пользователя. (В общем, вылитый юристконслульт с таксой $100 за вопрос. Только умнее).
***
К программе добавился еще один символьный массив GL$(8 ) - переменных, соответствующих правилам. Когда вводится переменная, подлежащая исполнению, ее имя ищется в этом массиве.
2200 FOR SN=F ТО 8
2210 IF V$=GL$(SN) THEN RETURN
2220 NEXT SN: SN=0: RETURN
Номер в массиве равен номеру правила в операторе ON ... GOSUB. Если переменной нет в этом списке она ищется в массиве переменных (как в первой программе), и если еще не известна, вводится пользователем. И опять - номер в списке равен номеру ввода в операторе ON ... GOSUB.
2400 FOR I=1 TO 10
2430 IF V$=V$(I) THEN GOTO 2450
2440 NEXT I: STOP
2450 IF IN(I)=1 THEN RETURN
2460 IN(I)=1
2470 ON I GOSUB 1700,1705,1710,1715
2480 RETURN
...
1700 INPUT "ПОСЕТИТЕЛЬ ИМЕЕТ УЧЕНОЕ ЗВАНИЕ ?";DE$: RETURN
...
В случае нахождения правила, в стек заносится его номер и номер первой входящей переменной (опять из кадра правила в массиве CV$(40)):
2000 SP=SP-1: SS(SP)=SN: CS(SP)=1
2010 RETURN
После чего начинается работа с 1-й переменной правила.
После обработки переменной CS(SP) увеличивается на единицу.
Когда кадр в CV$(40) кончается (помните, там был обязательный пустой элемент), правило вычисляется. Если оно срабатывает (S=1), выполняется его результируящая часть (т.е. вычисляется нужная переменная) и из стека удаяетя последний элемент (SP=SP+1), и уже старый CS(SP) увеличивается на единицу. Если правило не срабатывает (S=0), то последний элемент все равно удаляется, и происходит поиск имени переменной правила SS(SP) в остатке GL$(8 ), т.е. другое, более подходящее правило для нее.
505 INPUT"** ВВЕДИТЕ ИМЯ ПЕРЕМЕННОЙ ЛОГИЧЕСКОГО ВЫВОДА";V$
520 F=1: GOSUB 2200: REM ПОИСК V$ В GL$(8 ) (С ПОЗИЦИИ F)
525 IF SN THEN STOP: ЕСЛИ ПРАВИЛА ДЛЯ V$ КОНЧИЛИСЬ
540 GOSUB 2000: REM ВСТАВКА В СТЕК (СМ. ВЫШЕ)
550 I=(SS(SP)-1)*4+CS(SP)
555 V$=CV$(I)
565 IF V$="" THEN GOTO 582
568 F=1: GOSUB 2200: IF SN>0 THEN GOTO 540
570 GOSUB 2400: REM ВВОД ПЕРЕМЕННОЙ, ЕСЛИ ОНА ЕЩЕ НЕ ВВЕДЕНА
575 CS(SP)=CS(SP)+1: GOTO 550: REM СЛЕДУЮЩАЯ ПЕРЕМЕННАЯ
582 SN=SS(SP): REM ВСЕ ПЕРЕМЕННЫЕ ГОТОВЫ
585 S=0: ON SN GOSUB 1500,1520,1540,1560,1580,1600
600 IF S=1 THEN GOTO 635: REM СРАБОТАЛО ЛИ ПРАВИЛО?
610 I=SS(SP): V$=GL$(I): REM НЕ СРАБОТАЛО, ВСПОМИНАЕМ ИМЯ
620 F=SS(SP)+1: GOSUB 2200: ИЩЕМ СЛЕДУЮЩЕЕ ПРАВИЛО
625 SP=SP+1: GOTO 540: ПЕРЕВСТАВЛЯЕМ ЕГО В СТЕК
635 ON SN GOSUB 1510,1530,1550,1570,1590,1610: СРАБОТАЛО
660 SP=SP+1: ПРАВИЛО БОЛЬШЕ НЕ НУЖНО, УДАЛЯЕМ ИЗ СТЕКА
670 IF SP<11 THEN GOTO 695: REM А НЕ ПУСТ ЛИ СТЕК?
680 PRINT"*** НОРМАЛЬНОЕ ЗАВЕРШЕНИЕ"
685 STOP
695 CS(SP)=CS(SP)+1: GOTO 550: REM СЛЕДУЮЩАЯ ПЕРЕМЕННАЯ
В целом, программа кажется более проработанной, чем для прямой цепочки, и после исправления в ней ошибок (я удалил почти все) даже может заработать. Видимо, первую программу делали из второй путем закомментаривания ненужного и наложения заплаток - исключительно для книги.
Хитрость этой конструкции состоит в том, что тут параллельно существует две схемы вложенности управления: одна нормальная программная, вторая по стеку правил (т.е. положение процесса определяется не только текущей позицией в тексте программы, но и глубиной вложения в стеке). Необходимо ли это?
***
Поведение программы напоминает Ивана Царевича. Пришел за яблоками к Яге - укради сначала коня у Кащея. Пришел за конем к Кащею - достань Василису у Змея. Победил Змея - пошел проходить цепочку обратно, меняя предметы на нужные у тех же самых персонажей.
Или еще проще: надо найти значение переменной - для этого вызываем процедуру, переменные, нужные этой процедуре она получает у других процедур... Любой программист скажет, что всю жизнь это программировал и не заморачивался никакой "обратной цепочкой". По крайней мере, вполне хватает одного обычного программного стека (о котором BASIC-программист не всегда и знает). Например, приведенный выше страхолюдный кусок на "нормальном" языке записывается так.
FUNCTION ПЕРЕМЕННАЯ(ИМЯ)
- LOCAL ПРАВИЛО, НОМЕР, ЗНАЧЕНИЕ;
- WHILE ПРАВИЛО=GL-ПОИСК(ИМЯ)
- - ЗНАЧЕНИЕ=ПРАВИЛО(ПРАВИЛО);
- - IF ЗНАЧЕНИЕ
- - - RETURN ЗНАЧЕНИЕ;
- НОМЕР=V-ПОИСК(ИМЯ);
- IF НОМЕР
- - ЗНАЧЕНИЕ=IN-POISK(НОМЕР);
- - IF ЗНАЧЕНИЕ
- - - RETURN ЗНАЧЕНИЕ;
- - ELSE
- - - RETURN ВВОД(НОМЕР);
- RETURN ОТКАЗ;
FUNCTION ПРАВИЛО(НОМЕР)
- LOCAL ПОЗИЦИЯ, УСПЕХ;
- FOR ПОЗИЦИЯ=ПЕРВЫЙ(НОМЕР) ТО ПОСЛЕДНИЙ(НОМЕР)
- - ЗНАЧЕНИЕ(ПОЗИЦИЯ)=ПЕРЕМЕННАЯ(ИМЯ(ПОЗИЦИЯ));
- - IF ОТКАЗ
- - - RETURN ОТКАЗ;
- УСПЕХ=ВЫПОЛНИТЬ-УСЛОВНУЮ-ЧАСТЬ(НОМЕР);
- IF УСПЕХ
- - RETURN ВЫПОЛНИТЬ-РЕЗУЛЬТИРУЮЩУЮ-ЧАСТЬ(НОМЕР);
- ELSE
- - RETURN ОТКАЗ;
И стек здесь реализовался автоматически - путем использования привычного программисту механизма локальных переменных. Т.е. суть обратной цепочки рассуждений - суть программирования в том виде, каким его знаем. Этот метод присутствует в каждой нашей программе, независимо от нашего желания.
Так в чем тут суть? В написании программой самой себя? Или в решении задачи с конца?
***
Конечно, этот пример можно использовать просто как демонстрацию использования стека. На BASIC, где нет локальных переменных, такое бывает нужно.
***
По большому счету, умение подбирать для программы правильное соотношение прямой и обратной цепочки рассуждений - это основное требование к программисту (
 ТЕМА #15, АБЗАЦ #389
ТЕМА #15, АБЗАЦ #389 ).
).Последний раз редактировалось: Gudleifr (Пн Янв 23, 2023 12:25 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
Типичным примером "обратной разработки" является решение задачи о "наливании бочек" из книги Броуди  ТЕМА #24, АБЗАЦ #2133
ТЕМА #24, АБЗАЦ #2133 .
.
Или, даже,- тот этап обобщенного алгоритма разработки программ, который Д.Кнут называет проходом "сверху вниз" - разбиения большой задачи на мелкие подзадачи.
Рассмотрим, например решение одной из задач о "переправе" ТЕМА #32, АБЗАЦ #243
ТЕМА #32, АБЗАЦ #243 , решаемых там "прямым методом".
, решаемых там "прямым методом".
Возьмем задачу HELP THE SAIL:
ЛОДОЧНИКИ: папа, мама, коп;
ПАССАЖИРЫ: 2 сына, 2 дочери, бандит;
ВМЕСТИМОСТЬ ЛОДКИ: 2 человека;
ЗАПРЕТЫ: папа без мамы обижает дочерей, мама - сыновей, бандит без копа - всех.
Можно ли ее разбить на подзадачи? Т.к. все операции перевозки обратимы, а набор участников симметричен, то хочется считать правдоподобной средней операцией перевоз бандита копом, когда уже перевезены все остальные мужчины (или дамы). До и после нее, очевидно, будет два совершенно зеркальных действия - перевоз пол-семьи. (Обозначим: МДД>КБ - на правом берегу, очевидно, ПСС).
Как же нам перевезти мужскую половину семьи (МДД>ПСС)?
Очевидно (правдоподобно), удобнее считать по сыновьям: сначала перевезем первого (МДДПС>С), затем - второго (МДД>С). Эти задачи уже стоь малы, что их можно решить перебором:
МДДПС>С ::= МДДПСС>КБ, МДДПСС<К, МДДПС>КС, МДДПС<КБ;
МДД>С ::= КБМДД>ПС, КБМДД<П, КБДД>МП, КБДД<М. (Здесь три последние операции - просто перегон лодки).
Можно ли подобным рассуждениям научить BASIC?
Работать в вышеуказанных обозначениях он, конечно может и даже пересчитывать перевозки (<, >) в их результат. Можно в каком-то виде задать и проверку допустимости позиций. Но как заставить его выбирать правдоподобные решения?
Просто искать операции "с конца", как мы искали их "с начала" в "прямой цепочке", совершенно не интересно. Хочется "разделять и властвовать". Значит, надо как-то заранее ввести более общие операции:
ПЕРЕВОЗ ПЕРВОГО: X>КБ, X<К, >КX, <КБ;
ПЕРЕГОН ЛОДКИ: X<Y, >XY, <X.
Или заставить BASIC вычислить и их? Но для этого придется еще более расширить схему обозначений.
А чтобы поделить "пополам" надо будет ввести "вес позиции". Тогда средней операцией может быть любая допустимая типа "XYZ>VW".
Все, в принципе, считаемо.
 ТЕМА #24, АБЗАЦ #2133
ТЕМА #24, АБЗАЦ #2133 .
.Или, даже,- тот этап обобщенного алгоритма разработки программ, который Д.Кнут называет проходом "сверху вниз" - разбиения большой задачи на мелкие подзадачи.
Рассмотрим, например решение одной из задач о "переправе"
 ТЕМА #32, АБЗАЦ #243
ТЕМА #32, АБЗАЦ #243 , решаемых там "прямым методом".
, решаемых там "прямым методом".Возьмем задачу HELP THE SAIL:
ЛОДОЧНИКИ: папа, мама, коп;
ПАССАЖИРЫ: 2 сына, 2 дочери, бандит;
ВМЕСТИМОСТЬ ЛОДКИ: 2 человека;
ЗАПРЕТЫ: папа без мамы обижает дочерей, мама - сыновей, бандит без копа - всех.
Можно ли ее разбить на подзадачи? Т.к. все операции перевозки обратимы, а набор участников симметричен, то хочется считать правдоподобной средней операцией перевоз бандита копом, когда уже перевезены все остальные мужчины (или дамы). До и после нее, очевидно, будет два совершенно зеркальных действия - перевоз пол-семьи. (Обозначим: МДД>КБ - на правом берегу, очевидно, ПСС).
Как же нам перевезти мужскую половину семьи (МДД>ПСС)?
Очевидно (правдоподобно), удобнее считать по сыновьям: сначала перевезем первого (МДДПС>С), затем - второго (МДД>С). Эти задачи уже стоь малы, что их можно решить перебором:
МДДПС>С ::= МДДПСС>КБ, МДДПСС<К, МДДПС>КС, МДДПС<КБ;
МДД>С ::= КБМДД>ПС, КБМДД<П, КБДД>МП, КБДД<М. (Здесь три последние операции - просто перегон лодки).
Можно ли подобным рассуждениям научить BASIC?
Работать в вышеуказанных обозначениях он, конечно может и даже пересчитывать перевозки (<, >) в их результат. Можно в каком-то виде задать и проверку допустимости позиций. Но как заставить его выбирать правдоподобные решения?
Просто искать операции "с конца", как мы искали их "с начала" в "прямой цепочке", совершенно не интересно. Хочется "разделять и властвовать". Значит, надо как-то заранее ввести более общие операции:
ПЕРЕВОЗ ПЕРВОГО: X>КБ, X<К, >КX, <КБ;
ПЕРЕГОН ЛОДКИ: X<Y, >XY, <X.
Или заставить BASIC вычислить и их? Но для этого придется еще более расширить схему обозначений.
А чтобы поделить "пополам" надо будет ввести "вес позиции". Тогда средней операцией может быть любая допустимая типа "XYZ>VW".
Все, в принципе, считаемо.
Последний раз редактировалось: Gudleifr (Пн Янв 23, 2023 12:28 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ВЕРОЯТНОСТЬ И НЕЧЕТКАЯ ЛОГИКА В ЭКСПЕРТНЫХ СИСТЕМАХ (БАЙЕСОВСКОЕ ОЦЕНИВАНИЕ) ПО ЛДЭ
Вставили эту заумь в свою книгу авторы простейшим способом - добавлением "примеров на Байеса" в результирующие части правил "обратной цепочки" (строки 1510 и далее). Чем так провинился Байес?
По идее - это единственная формула теории вероятностей. Правило гласит: пусть событие A имеет вероятность a, а событие B - вероятность b1, если A происходит, и b2 - если нет. Тогда полная вероятность B есть b = a*b1 + (1-a)*b2. И все.
***
Зачем это надо? Допустим, читаем у одного из моих любимых российских авторов что-то вроде: "По американскому гаду было выпущено две ракеты. Каждая поражала цель с вероятностью 0.9. Супостат был обречен - вероятность его поражения была 1.8!"
Понятно, что-то тут не так. Пусть, событие A - поражение цели первым пуском (a=0.9). Тогда b1=1 (куда вторую ракету не пускай, цель уже сбита), а b2=0.9 (промах первой ракеты никакой роли в поведении второй ракеты не играет). Итого, b = 0.9*1 + (1 - 0.9)*0.9 = 0.99. Т.е. как ни крути, каждый сотый враг при таком раскладе выживает.
***
Вот и все. Зачем авторы во все свои "выводы" добавили по диалогу: "Введите a, b1, b2, - Получите b!", без всякой связи с остальной программой и, опять, и с таким количеством ошибок - совершенно непонятно. Наверное, просто НАДА!
***
На самом деле, если, при получении искомого значения путем обратной цепочки рассуждений, значение и/или его достоверность зависят от того пути, которым идешь, там не только Байеса вспомнишь. Но, это совсем друга история.
В игровом же программировании Байеса можно применять двояко:
1. упрощая сложные игровые алгоритмы. Я на своих страничках уже неоднократно замечал, что, то там, то сям, горсть кубиков может совершенно безболезненно заменить одним броском.
2. для огульной оценки результатов игры. Например, рассчитываю, что вероятность успешного прохождения этапа игры - 50%, а в игре 10 этапов. Какова вероятность ее пройти? На сколько должен игрок улучшить свое мастерство (поднять вероятность прохождения одного этапа), чтобы вероятность пройти игру стала ощутимой? Или, все равно, надо добавлять между этапами реанимационные пункты?
Вставили эту заумь в свою книгу авторы простейшим способом - добавлением "примеров на Байеса" в результирующие части правил "обратной цепочки" (строки 1510 и далее). Чем так провинился Байес?
По идее - это единственная формула теории вероятностей. Правило гласит: пусть событие A имеет вероятность a, а событие B - вероятность b1, если A происходит, и b2 - если нет. Тогда полная вероятность B есть b = a*b1 + (1-a)*b2. И все.
***
Зачем это надо? Допустим, читаем у одного из моих любимых российских авторов что-то вроде: "По американскому гаду было выпущено две ракеты. Каждая поражала цель с вероятностью 0.9. Супостат был обречен - вероятность его поражения была 1.8!"
Понятно, что-то тут не так. Пусть, событие A - поражение цели первым пуском (a=0.9). Тогда b1=1 (куда вторую ракету не пускай, цель уже сбита), а b2=0.9 (промах первой ракеты никакой роли в поведении второй ракеты не играет). Итого, b = 0.9*1 + (1 - 0.9)*0.9 = 0.99. Т.е. как ни крути, каждый сотый враг при таком раскладе выживает.
***
Вот и все. Зачем авторы во все свои "выводы" добавили по диалогу: "Введите a, b1, b2, - Получите b!", без всякой связи с остальной программой и, опять, и с таким количеством ошибок - совершенно непонятно. Наверное, просто НАДА!
***
На самом деле, если, при получении искомого значения путем обратной цепочки рассуждений, значение и/или его достоверность зависят от того пути, которым идешь, там не только Байеса вспомнишь. Но, это совсем друга история.
В игровом же программировании Байеса можно применять двояко:
1. упрощая сложные игровые алгоритмы. Я на своих страничках уже неоднократно замечал, что, то там, то сям, горсть кубиков может совершенно безболезненно заменить одним броском.
2. для огульной оценки результатов игры. Например, рассчитываю, что вероятность успешного прохождения этапа игры - 50%, а в игре 10 этапов. Какова вероятность ее пройти? На сколько должен игрок улучшить свое мастерство (поднять вероятность прохождения одного этапа), чтобы вероятность пройти игру стала ощутимой? Или, все равно, надо добавлять между этапами реанимационные пункты?

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ЭКСПЕРТНЫЕ СИСТЕМЫ ПО ЛДЭ
С точки зрения программирования здесь нет ничего интересного. Всего лишь метод наукообразной маркетоидной лабуды. Якобы заинтересованному лицу задаются несколько групп вопросов. Каждый вопрос имеет некоторую ценность. Суммы ценностей положительных ответов складываются (по группам). Считаются отношения сумм по группам к общей группе - трактуются, как вероятность отношения опрашиваемого к определенному типу. Определяется тип ситуации, в которую вовлечены несколько субъектов - как распределение вероятностей принадлежностей их к определенным типам. Трактуются превышения сумм в группах. Трактуются ответы на особо важные вопросы.
***
Пример достижения максимума заумности самым деревенским способом? Однажды меня попросили взломать программу теста Сонди. (Там испытуемого просят определить свое отношение к предъявляемым фотографиям). Расковырял. Переписал, кстати, на BASIC. Провел кое-какой анализ программы и обомлел: получить результат "психика без отклонений" практически невозможно.
Не интересуют авторов подобных программ "нормальные результаты".
***
Конечно, методы весовых коэффициентов и сбора разнообразных статистик в игростроениии применяются постоянно. Например, в случайном-прочем блоке "ОРЕГОНСКОЙ ТРОПЫ" разные неприятности вызывали разные траты ресурсов (кто-то же эти цифры придумал)? И кто решил, сколько времени тратит "БОМБЕР" на выполнение команды?
Вопрос об конкретных значениях коэффициентов и трактовке результатов всегда решается одним и тем же методом: пригласим эксперта, он знает. Потому и называют эти системы экспертными.
***
Было бы интересно применить какие-либо компьютерные методы для оценки правдоподобия подобных систем. Но они слишком математические (см. например, статью Егорова из нашей библиотеки - ТЕМА #16, АБЗАЦ #1221
ТЕМА #16, АБЗАЦ #1221 ). Все, что нам остается - Байесовское оценивание вероятность события "Бить будут!"
). Все, что нам остается - Байесовское оценивание вероятность события "Бить будут!"
С точки зрения программирования здесь нет ничего интересного. Всего лишь метод наукообразной маркетоидной лабуды. Якобы заинтересованному лицу задаются несколько групп вопросов. Каждый вопрос имеет некоторую ценность. Суммы ценностей положительных ответов складываются (по группам). Считаются отношения сумм по группам к общей группе - трактуются, как вероятность отношения опрашиваемого к определенному типу. Определяется тип ситуации, в которую вовлечены несколько субъектов - как распределение вероятностей принадлежностей их к определенным типам. Трактуются превышения сумм в группах. Трактуются ответы на особо важные вопросы.
***
Пример достижения максимума заумности самым деревенским способом? Однажды меня попросили взломать программу теста Сонди. (Там испытуемого просят определить свое отношение к предъявляемым фотографиям). Расковырял. Переписал, кстати, на BASIC. Провел кое-какой анализ программы и обомлел: получить результат "психика без отклонений" практически невозможно.
Не интересуют авторов подобных программ "нормальные результаты".
***
Конечно, методы весовых коэффициентов и сбора разнообразных статистик в игростроениии применяются постоянно. Например, в случайном-прочем блоке "ОРЕГОНСКОЙ ТРОПЫ" разные неприятности вызывали разные траты ресурсов (кто-то же эти цифры придумал)? И кто решил, сколько времени тратит "БОМБЕР" на выполнение команды?
Вопрос об конкретных значениях коэффициентов и трактовке результатов всегда решается одним и тем же методом: пригласим эксперта, он знает. Потому и называют эти системы экспертными.
***
Было бы интересно применить какие-либо компьютерные методы для оценки правдоподобия подобных систем. Но они слишком математические (см. например, статью Егорова из нашей библиотеки -
 ТЕМА #16, АБЗАЦ #1221
ТЕМА #16, АБЗАЦ #1221 ). Все, что нам остается - Байесовское оценивание вероятность события "Бить будут!"
). Все, что нам остается - Байесовское оценивание вероятность события "Бить будут!"Последний раз редактировалось: Gudleifr (Сб Июн 15, 2019 9:50 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ОБЪЕКТНО-ОРИЕНТИРОВАННОЕ ПРОГРАММИРОВАНИЕ ПО ЛДЭ
Это еще один пример того, как невозможность BASIC работать с некоторыми структурами данных компенсируется внесением изменений в программу руками. И, наоборот, как желание создать видимость работающей программы затрудняет этот процесс.
***
Начинается программа с меню "Введите номер операции: создать структуру (класс), создать объект (экземпляр)...". Эа меню следует очевидный ON номер GOSUB с переходом на исполнитель команд. На самом деле эти исполнители состоят только из ввода параметров и вызова реальных исполнителей. Некоторые реальные исполнители отсутствуют - их пользователь должен придумать и дописать в программу сам.
5 PRINT "ВВЕДИТЕ НУЖНЫЙ НОМЕР"
10 PRINT "1 - СОЗДАТЬ СТРУКТУРУ"
15 PRINT "2 - СОЗДАТЬ ОБЪЕКТ"
20 PRINT "3 - ВЫВЕСТИ ИМЕНА ВСЕХ СТРУКТУР"
...
55 INPUT N
60 ON N GOSUB 100,200,300,400,500,600,700,800,900
65 GOTO 5
100 REM **** СОЗДАНИЕ СТРУКТУРЫ ****
105 INPUT "ВВЕДИТЕ ИМЯ СТРУКТУРЫ"Т$(1)
110 INPUT "ВВЕДИТЕ ЧИСЛО АТРИБУТОВ";Т$(2)
115 N=VAL(T$(2)): E=3+N-1
120 FOR I=1 ТО Е
125 PRINT "АТРИБУТ"; I-2; "-";
130 INPUT T$(l)
135 NEXT I
140 REM ВЫЗОВ ПРОЦЕДУРЫ СОЗДАНИЯ СТРУКТУРЫ
145 GOSUB 3000
150 RETURN
...
2999 REM ***** СИСТЕМНЫЕ ПОДПРОГРАММЫ *********
3000 REM ***** СОЗДАНИЕ СТРУКТУРЫ
...
ООП-наполнение программы самоочевидно: тот же самый, знакомый по первым главам символьный массив с именами, на этот раз, не переменных, а атрибутов. К некоторым именам приписываются звездочки, обозначающие метод, но т.к. методов BASIC не понимает, то пользователь должен в соответствующий "распознаватель методов" (просто еще один ON ... GOSUB, а как иначе в BASIC можно вызвать "не знаю что"?) дописать свой код, проверяющий допустимость параметров, блюдущий целостность базы, делающий что-то полезное...
***
Это, как мне кажется, третий путь использования ООП.
- Первый путь - классический. Представления мира, в котором живет программа, в виде строгой иерархии "объектов". Если один объект является частью другого, считается, что в реальном мире этому соответствует связь "part_of" - "крыло - часть птицы", если же объект наследуется от другого - "is_a" - "аист тоже птица" (и значит, у него тоже есть крылья). По идее, такой подход должен давать возможность программе свободно ориентироваться в сложном мире и писаться на естественном языке.
Но, ловушка здесь в прилагательном "строгая" в первой строке. Допустим, я построил эту самую иерархию и написал нужную мне программу. И тут, как обычно, мне понадобилось ее изменить. Фигушки!
Во-первых, т.к моя иерархия изначально "глубоко продуманная", то как я заставлю себя ее перекроить? Не то, чтобы жалко, но просто мозги так не повернуть, чтоб "систему мира" переделать.
Во-вторых, во всех существующих системах ООП, переделка "мира" вещь практически неосуществимая, вызывающая лавинообразный рост ошибок.
Поэтому первый путь, столь любимый классиками, в дикой природе практически не встречается.
- Второй путь - быдлокодерский. Как "современный программист" решает задачу? Он ищет подходящую библиотеку. А для удобства применения сложных библиотек тупыми кодерами, первые естественно снабдить этой самой, описанной выше "иерархией".
"Найти в окне X кнопочку Y и запретить ее нажатие" == X.Y.ЗАПРЕТИТЬ().
"Сделать еще такую же кнопочку, но разместить левее" == Z-КЛАСС УНАСЛЕДОВАТЬ-ОТ Y-КЛАСС; Z-КЛАСС:РИСОВАТЬ()={ПРЕДОК.РИСОВАТЬ(); ПРЕДОК.СДВИНУТЬ-ВЛЕВО();}; Z=НОВЫЙ-ОБЪЕКТ Z-КЛАСС;"
Как-то так...
И многие "современные бейсики" этот механизм в себе имеют. Еще один стимул применения подобной схемы: вся привычная визуальная фигня - окошки, рамочки, кнопочки, прокрутки и менюшки - еще в 70-е годы прошлого века была создана объектно-ориентированной. И остается такой по настоящее время.
- Третий путь - обфускационный - "чтоб как у людей". Просто группирование разнообразных данных, а, если поднапрячься, и кода, в одном месте. Чтоб было! Именно его мы здесь и имеем.
Это еще один пример того, как невозможность BASIC работать с некоторыми структурами данных компенсируется внесением изменений в программу руками. И, наоборот, как желание создать видимость работающей программы затрудняет этот процесс.
***
Начинается программа с меню "Введите номер операции: создать структуру (класс), создать объект (экземпляр)...". Эа меню следует очевидный ON номер GOSUB с переходом на исполнитель команд. На самом деле эти исполнители состоят только из ввода параметров и вызова реальных исполнителей. Некоторые реальные исполнители отсутствуют - их пользователь должен придумать и дописать в программу сам.
5 PRINT "ВВЕДИТЕ НУЖНЫЙ НОМЕР"
10 PRINT "1 - СОЗДАТЬ СТРУКТУРУ"
15 PRINT "2 - СОЗДАТЬ ОБЪЕКТ"
20 PRINT "3 - ВЫВЕСТИ ИМЕНА ВСЕХ СТРУКТУР"
...
55 INPUT N
60 ON N GOSUB 100,200,300,400,500,600,700,800,900
65 GOTO 5
100 REM **** СОЗДАНИЕ СТРУКТУРЫ ****
105 INPUT "ВВЕДИТЕ ИМЯ СТРУКТУРЫ"Т$(1)
110 INPUT "ВВЕДИТЕ ЧИСЛО АТРИБУТОВ";Т$(2)
115 N=VAL(T$(2)): E=3+N-1
120 FOR I=1 ТО Е
125 PRINT "АТРИБУТ"; I-2; "-";
130 INPUT T$(l)
135 NEXT I
140 REM ВЫЗОВ ПРОЦЕДУРЫ СОЗДАНИЯ СТРУКТУРЫ
145 GOSUB 3000
150 RETURN
...
2999 REM ***** СИСТЕМНЫЕ ПОДПРОГРАММЫ *********
3000 REM ***** СОЗДАНИЕ СТРУКТУРЫ
...
ООП-наполнение программы самоочевидно: тот же самый, знакомый по первым главам символьный массив с именами, на этот раз, не переменных, а атрибутов. К некоторым именам приписываются звездочки, обозначающие метод, но т.к. методов BASIC не понимает, то пользователь должен в соответствующий "распознаватель методов" (просто еще один ON ... GOSUB, а как иначе в BASIC можно вызвать "не знаю что"?) дописать свой код, проверяющий допустимость параметров, блюдущий целостность базы, делающий что-то полезное...
***
Это, как мне кажется, третий путь использования ООП.
- Первый путь - классический. Представления мира, в котором живет программа, в виде строгой иерархии "объектов". Если один объект является частью другого, считается, что в реальном мире этому соответствует связь "part_of" - "крыло - часть птицы", если же объект наследуется от другого - "is_a" - "аист тоже птица" (и значит, у него тоже есть крылья). По идее, такой подход должен давать возможность программе свободно ориентироваться в сложном мире и писаться на естественном языке.
Но, ловушка здесь в прилагательном "строгая" в первой строке. Допустим, я построил эту самую иерархию и написал нужную мне программу. И тут, как обычно, мне понадобилось ее изменить. Фигушки!
Во-первых, т.к моя иерархия изначально "глубоко продуманная", то как я заставлю себя ее перекроить? Не то, чтобы жалко, но просто мозги так не повернуть, чтоб "систему мира" переделать.
Во-вторых, во всех существующих системах ООП, переделка "мира" вещь практически неосуществимая, вызывающая лавинообразный рост ошибок.
Поэтому первый путь, столь любимый классиками, в дикой природе практически не встречается.
- Второй путь - быдлокодерский. Как "современный программист" решает задачу? Он ищет подходящую библиотеку. А для удобства применения сложных библиотек тупыми кодерами, первые естественно снабдить этой самой, описанной выше "иерархией".
"Найти в окне X кнопочку Y и запретить ее нажатие" == X.Y.ЗАПРЕТИТЬ().
"Сделать еще такую же кнопочку, но разместить левее" == Z-КЛАСС УНАСЛЕДОВАТЬ-ОТ Y-КЛАСС; Z-КЛАСС:РИСОВАТЬ()={ПРЕДОК.РИСОВАТЬ(); ПРЕДОК.СДВИНУТЬ-ВЛЕВО();}; Z=НОВЫЙ-ОБЪЕКТ Z-КЛАСС;"
Как-то так...
И многие "современные бейсики" этот механизм в себе имеют. Еще один стимул применения подобной схемы: вся привычная визуальная фигня - окошки, рамочки, кнопочки, прокрутки и менюшки - еще в 70-е годы прошлого века была создана объектно-ориентированной. И остается такой по настоящее время.
- Третий путь - обфускационный - "чтоб как у людей". Просто группирование разнообразных данных, а, если поднапрячься, и кода, в одном месте. Чтоб было! Именно его мы здесь и имеем.
Последний раз редактировалось: Gudleifr (Чт Июл 22, 2021 1:32 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
КЛАССИЧЕСКИЙ ПУТЬ ООП
Все полезное, что ожидает нас на первом пути ООП, называется фреймами по Минскому. Т.е. плюем на строгость иерархии и акцентируемся на распознавании типов фреймов (чтобы понять, что с ним делать) и порождение ими друг друга (не столько в смысле наследования, сколько в смысле записи в виде некого нового фрейма результата действия над исходным).
Это может оказаться полезным, например, в играх имеющих сложный сценарий. В игре "HIGN HOON" мы видели, что состояние игры практически полностью описывается нашим положением в тексте программы. Помните, мы даже пометили особо важные точки: "ХОД ИГРОКА", "ХОД БАРТА" и т.д... Допустим, игра не заканчивается по окончании одной дуэли: мы покидаем Додж-Сити, чтобы, когда нам вновь захочется пострелять, снова туда вернуться. Ситуацию мы просто запоминаем: "Состояние Барта, Настроение Барта..." В зависимости от ситуации, Барт может "помнить" последнюю сказанную вами фразу или число ваших промахов... Т.е. требуется как можно более полное запоминание ситуации. Настолько полное, что универсальное запоминание невозможно.
Конечно, можно и без этого. Например, забегая вперед, мы можем видеть как в "STAR TREK", запоминаются только самые общие параметры ситуации, а остальные, при возвращении сюда генерируются случайным образом. И, ничего, играть можно.
***
Запоминать ситуацию в смысле обычно-реализуемого ООП или, тем более, реляционной базы данных скучно. Заполнять каждый раз фиксированный набор полей? Мы же видели выше, что "объект" представляет из себя кадр массива. А содержимое и размер кадра никого не интересует. Т.о. в виде такого массива гораздо проще организовать модель, в которой число и тип атрибутов каждого массива может варьироваться от объекта к объекту.
Это удобно для баз данных, но не для игр. На примере задачки про машиниста мы видели, что, хотя, программа, управляемая данными, упрощается, но сами данные замучаешься вводить.
В большинстве программ мы все-таки предпочитаем "откомпилировать модель". Например, в том же "БОМБЕРЕ": я могу рассматривать команды как фреймы: каждая из них описывает некоторую ситуацию, имеет свои атрибуты и т.п. И создавать обобщенный объект "команда" мне нет никакого проку.
Поэтому пример ЛДЭ, где объекты-процедуры пытаются взаимодействовать с объектами-массивами, это пример фантиков, завернутых в другие фантики.
***
Можно ли придумать какую-либо ситуацию, где объекты должны присутствовать "в сыром" виде, чтобы как-то взаимодействовать друг с другом?

Вспомнил задачку из детской книжки про компьютеры. Там робот путешествовал в мире драконов. Драконы были разные: разного цвета и формы, и обитающие в разных местах. Только некоторые драконы относились к роботу благосклонно - давали ему золото.
Задачка состояла в определении типа добрых драконов, причем этот тип мог был быть обобщенным: например, добрыми драконами могли оказаться как синие драконы, так и просто темные или, даже, драконы любого цвета.
Авторам задачи "повезло": встретив всего четырех драконов им удалось догадаться, какие драконы не кусаются.
Я написал простенькую программку:
100 DIM DR$(26), DN(26), DI(26), DZ(20)
110 FOR I=1 TO 26: READ DR$(I), DN(I): DI(I)=0: NEXT I
120 DATA "ТОЛСТЫЙ", 18, "ЗМЕЕВИДНЫЙ", 18
130 DATA "СИНИЙ", 19, "ЗЕЛЕНЫЙ", 19, "ПУРПУРНЫЙ", 19
140 DATA "РОЗОВЫЙ", 20, "ЖЕЛТЫЙ", 20, "ОРАНЖЕВЫЙ", 20
150 DATA "МОРСКОЙ", 21, "РЕЧНОЙ", 21, "БОЛОТНЫЙ", 21
160 DATA "ГОРНЫЙ", 22, "ПУСТЫННЫЙ", 22, "ПЕЩЕРНЫЙ", 22
170 DATA "ЗВЕЗДНЫЙ", 23, "ЛУННЫЙ", 23, "ОБЛАЧНЫЙ", 23
180 DATA "ЛЮБОЙ ФОРМЫ", 0, "ТЕМНЫЙ", 24, "СВЕТЛЫЙ", 24
190 DATA "ВОДЯНОЙ", 25, "СУХОПУТНЫЙ", 25, "НЕБЕСНЫЙ", 26
200 DATA "ЛЮБОГО ЦВЕТА", 0, "ЗЕМНОЙ", 26
210 DATA "ЛЮБОЕ МЕСТО ОБИТАНИЯ", 0
220 PRINT "Pres any key when you're ready to go" : RN = -32768!
230 WHILE LEN(INKEY$) = 0: RN = RN + 1: WEND
240 WHILE RN>32767: RN = RN - 65535!: WEND: RANDOMIZE RN: CLS
300 Y=1: GOSUB 1000: DI(X1)=1: DI(X2)=1: DI(X3)=1
310 PRINT"ВИДИМ ДРАКОНА:"
320 Y=0: GOSUB 1000: PRINT DR$(X1);" ";DR$(X2);" ";DR$(X3)
330 INPUT"БУДЕМ ПРОСИТЬ ЗОЛОТА [Y/N]",A$
340 IF LEFT$(A$,1)="Y" OR LEFT$(A$,1)="y" THEN GOSUB 1100
350 INPUT"ГОТОВЫ ОПРЕДЕЛИТЬ ДРАКОНА [Y/N]",A$
360 IF LEFT$(A$,1)="Y" OR LEFT$(A$,1)="y" THEN GOSUB 1200 ELSE 310
370 IF X=1 THEN PRINT"УРРА-А!": END
380 PRINT"НЕУДАЧКА!": GOTO 310
1000 REM СОЗДАНИЕ ДРАКОНА
1010 I=1: J=2: GOSUB 1050: X1=X
1020 I=3: J=6: GOSUB 1050: X2=X
1030 I=9: J=9: GOSUB 1050: X3=X
1040 RETURN
1050 X=INT(I+RND(1)*J)
1060 IF Y=1 THEN IF DN(X)>0 THEN IF RND(1)>0.5 THEN X=DN(X): GOTO 1060
1070 RETURN
1100 REM ПРОСЬБА ЗОЛОТА
1110 X=X1: GOSUB 1160: IF X=0 THEN 1150
1120 X=X2: GOSUB 1160: IF X=0 THEN 1150
1130 X=X3: GOSUB 1160: IF X=0 THEN 1150
1140 PRINT"ДАЛ":RETURN
1150 PRINT"НЕ ДАЛ":RETURN
1160 IF X>0 THEN IF DI(X)=0 THEN X=DN(X): GOTO 1160
1170 RETURN
1200 REM ОПОЗНАНИЕ
1210 N=1: I=1: J=2: GOSUB 1330: I=18: J=18: GOSUB 1330
1220 INPUT"КАКОЙ ФОРМЫ ДРАКОН";X1: X1=DZ(X1)
1230 N=1: I=3: J=8: GOSUB 1330: I=19: J=20: GOSUB 1330
1240 I=24: J=24: GOSUB 1330
1250 INPUT"КАКОГО ЦВЕТА ДРАКОН";X2: X2=DZ(X2)
1260 N=1: I=9: J=17: GOSUB 1330: I=21: J=23: GOSUB 1330
1270 I=25: J=26: GOSUB 1330
1280 INPUT"ГДЕ ЖИВЕТ ДРАКОН";X3: X3=DZ(X3)
1290 X=0: IF DI(X1)=0 THEN RETURN
1300 IF DI(X2)=0 THEN RETURN
1310 IF DI(X3)=0 THEN RETURN
1320 X=1: RETURN
1330 FOR K=I TO J: DZ(N)=K: PRINT N;DR$(K): N=N+1
1340 NEXT K: RETURN
Подобное моделирование принесло свои плоды. Я понял, что играет роль не число опрошенных драконов, а, практически, только число встреченных добрых драконов. Поэтому я решил несколько упростить программу: опрашивать драконов автоматически, а останавливаться только после встречи с добрыми драконами. Строки 310-340 заменил на
310 Y=0: GOSUB 1000: PRINT DR$(X1);" ";DR$(X2);" ";DR$(X3);" - ";
320 GOSUB 1100: IF X=0 THEN 310
Оказалось, что на определение дракона влияет не только статистика опроса, но и само примерное число опрошенных злых драконов на одного доброго. Возникла даже идея выделить игровой момент "подсознательного определения вероятности" для дальнейшего применения в какой-нибудь игре.
Все полезное, что ожидает нас на первом пути ООП, называется фреймами по Минскому. Т.е. плюем на строгость иерархии и акцентируемся на распознавании типов фреймов (чтобы понять, что с ним делать) и порождение ими друг друга (не столько в смысле наследования, сколько в смысле записи в виде некого нового фрейма результата действия над исходным).
Это может оказаться полезным, например, в играх имеющих сложный сценарий. В игре "HIGN HOON" мы видели, что состояние игры практически полностью описывается нашим положением в тексте программы. Помните, мы даже пометили особо важные точки: "ХОД ИГРОКА", "ХОД БАРТА" и т.д... Допустим, игра не заканчивается по окончании одной дуэли: мы покидаем Додж-Сити, чтобы, когда нам вновь захочется пострелять, снова туда вернуться. Ситуацию мы просто запоминаем: "Состояние Барта, Настроение Барта..." В зависимости от ситуации, Барт может "помнить" последнюю сказанную вами фразу или число ваших промахов... Т.е. требуется как можно более полное запоминание ситуации. Настолько полное, что универсальное запоминание невозможно.
Конечно, можно и без этого. Например, забегая вперед, мы можем видеть как в "STAR TREK", запоминаются только самые общие параметры ситуации, а остальные, при возвращении сюда генерируются случайным образом. И, ничего, играть можно.
***
Запоминать ситуацию в смысле обычно-реализуемого ООП или, тем более, реляционной базы данных скучно. Заполнять каждый раз фиксированный набор полей? Мы же видели выше, что "объект" представляет из себя кадр массива. А содержимое и размер кадра никого не интересует. Т.о. в виде такого массива гораздо проще организовать модель, в которой число и тип атрибутов каждого массива может варьироваться от объекта к объекту.
Это удобно для баз данных, но не для игр. На примере задачки про машиниста мы видели, что, хотя, программа, управляемая данными, упрощается, но сами данные замучаешься вводить.
В большинстве программ мы все-таки предпочитаем "откомпилировать модель". Например, в том же "БОМБЕРЕ": я могу рассматривать команды как фреймы: каждая из них описывает некоторую ситуацию, имеет свои атрибуты и т.п. И создавать обобщенный объект "команда" мне нет никакого проку.
Поэтому пример ЛДЭ, где объекты-процедуры пытаются взаимодействовать с объектами-массивами, это пример фантиков, завернутых в другие фантики.
***
Можно ли придумать какую-либо ситуацию, где объекты должны присутствовать "в сыром" виде, чтобы как-то взаимодействовать друг с другом?

Вспомнил задачку из детской книжки про компьютеры. Там робот путешествовал в мире драконов. Драконы были разные: разного цвета и формы, и обитающие в разных местах. Только некоторые драконы относились к роботу благосклонно - давали ему золото.
Задачка состояла в определении типа добрых драконов, причем этот тип мог был быть обобщенным: например, добрыми драконами могли оказаться как синие драконы, так и просто темные или, даже, драконы любого цвета.
Авторам задачи "повезло": встретив всего четырех драконов им удалось догадаться, какие драконы не кусаются.
Я написал простенькую программку:
100 DIM DR$(26), DN(26), DI(26), DZ(20)
110 FOR I=1 TO 26: READ DR$(I), DN(I): DI(I)=0: NEXT I
120 DATA "ТОЛСТЫЙ", 18, "ЗМЕЕВИДНЫЙ", 18
130 DATA "СИНИЙ", 19, "ЗЕЛЕНЫЙ", 19, "ПУРПУРНЫЙ", 19
140 DATA "РОЗОВЫЙ", 20, "ЖЕЛТЫЙ", 20, "ОРАНЖЕВЫЙ", 20
150 DATA "МОРСКОЙ", 21, "РЕЧНОЙ", 21, "БОЛОТНЫЙ", 21
160 DATA "ГОРНЫЙ", 22, "ПУСТЫННЫЙ", 22, "ПЕЩЕРНЫЙ", 22
170 DATA "ЗВЕЗДНЫЙ", 23, "ЛУННЫЙ", 23, "ОБЛАЧНЫЙ", 23
180 DATA "ЛЮБОЙ ФОРМЫ", 0, "ТЕМНЫЙ", 24, "СВЕТЛЫЙ", 24
190 DATA "ВОДЯНОЙ", 25, "СУХОПУТНЫЙ", 25, "НЕБЕСНЫЙ", 26
200 DATA "ЛЮБОГО ЦВЕТА", 0, "ЗЕМНОЙ", 26
210 DATA "ЛЮБОЕ МЕСТО ОБИТАНИЯ", 0
220 PRINT "Pres any key when you're ready to go" : RN = -32768!
230 WHILE LEN(INKEY$) = 0: RN = RN + 1: WEND
240 WHILE RN>32767: RN = RN - 65535!: WEND: RANDOMIZE RN: CLS
300 Y=1: GOSUB 1000: DI(X1)=1: DI(X2)=1: DI(X3)=1
310 PRINT"ВИДИМ ДРАКОНА:"
320 Y=0: GOSUB 1000: PRINT DR$(X1);" ";DR$(X2);" ";DR$(X3)
330 INPUT"БУДЕМ ПРОСИТЬ ЗОЛОТА [Y/N]",A$
340 IF LEFT$(A$,1)="Y" OR LEFT$(A$,1)="y" THEN GOSUB 1100
350 INPUT"ГОТОВЫ ОПРЕДЕЛИТЬ ДРАКОНА [Y/N]",A$
360 IF LEFT$(A$,1)="Y" OR LEFT$(A$,1)="y" THEN GOSUB 1200 ELSE 310
370 IF X=1 THEN PRINT"УРРА-А!": END
380 PRINT"НЕУДАЧКА!": GOTO 310
1000 REM СОЗДАНИЕ ДРАКОНА
1010 I=1: J=2: GOSUB 1050: X1=X
1020 I=3: J=6: GOSUB 1050: X2=X
1030 I=9: J=9: GOSUB 1050: X3=X
1040 RETURN
1050 X=INT(I+RND(1)*J)
1060 IF Y=1 THEN IF DN(X)>0 THEN IF RND(1)>0.5 THEN X=DN(X): GOTO 1060
1070 RETURN
1100 REM ПРОСЬБА ЗОЛОТА
1110 X=X1: GOSUB 1160: IF X=0 THEN 1150
1120 X=X2: GOSUB 1160: IF X=0 THEN 1150
1130 X=X3: GOSUB 1160: IF X=0 THEN 1150
1140 PRINT"ДАЛ":RETURN
1150 PRINT"НЕ ДАЛ":RETURN
1160 IF X>0 THEN IF DI(X)=0 THEN X=DN(X): GOTO 1160
1170 RETURN
1200 REM ОПОЗНАНИЕ
1210 N=1: I=1: J=2: GOSUB 1330: I=18: J=18: GOSUB 1330
1220 INPUT"КАКОЙ ФОРМЫ ДРАКОН";X1: X1=DZ(X1)
1230 N=1: I=3: J=8: GOSUB 1330: I=19: J=20: GOSUB 1330
1240 I=24: J=24: GOSUB 1330
1250 INPUT"КАКОГО ЦВЕТА ДРАКОН";X2: X2=DZ(X2)
1260 N=1: I=9: J=17: GOSUB 1330: I=21: J=23: GOSUB 1330
1270 I=25: J=26: GOSUB 1330
1280 INPUT"ГДЕ ЖИВЕТ ДРАКОН";X3: X3=DZ(X3)
1290 X=0: IF DI(X1)=0 THEN RETURN
1300 IF DI(X2)=0 THEN RETURN
1310 IF DI(X3)=0 THEN RETURN
1320 X=1: RETURN
1330 FOR K=I TO J: DZ(N)=K: PRINT N;DR$(K): N=N+1
1340 NEXT K: RETURN
Подобное моделирование принесло свои плоды. Я понял, что играет роль не число опрошенных драконов, а, практически, только число встреченных добрых драконов. Поэтому я решил несколько упростить программу: опрашивать драконов автоматически, а останавливаться только после встречи с добрыми драконами. Строки 310-340 заменил на
310 Y=0: GOSUB 1000: PRINT DR$(X1);" ";DR$(X2);" ";DR$(X3);" - ";
320 GOSUB 1100: IF X=0 THEN 310
Оказалось, что на определение дракона влияет не только статистика опроса, но и само примерное число опрошенных злых драконов на одного доброго. Возникла даже идея выделить игровой момент "подсознательного определения вероятности" для дальнейшего применения в какой-нибудь игре.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
БЫДЛОКОДЕРСКИЙ ПУТЬ ООП
Казалось бы, какое отношение синтаксически удобное решение может иметь к языку с упрощенным синтаксисом?
Однако, само понятие замкнутых "калькуляторов объектов", как мы видели в программах на BASIC, часто не просто полезен, но, даже, необходим.
Более того, написание этого калькулятора в кодах, как в TANKTICS, позволяет еще один финт - дописывание пользовательских кусков кода без нужды заставлять пользователя изучать BASIC и заполнять на нем оставленные программистом дыры. Ведь, в большинстве, BASIC-ов работает метод: "считываем из DATA, записываем PEEK и исполняем CALL". А это может делать сама программа!
***
Идея кажется фантастической? Зачем изобретать кодовый конструктор в таких ограниченных условиях? Не проще ли написать простенький FORTH или выучить C?
Позвольте... А чем занимаются т.н. IDE (визуальные средства программирования, совмещающие в себе редакторы, средства управления проектом, настраиватели компилятора, отладчики)? Всякие Delphi и Visual Studio. Именно этим. А ведь, языком пользовательского программирования (написания макросов) в MS Visual C является Basic...
Т.е. когда начинаешь добавлять в свой FORTH средства управления проектированием программ, опыт BASIC стоит учитывать.
Казалось бы, какое отношение синтаксически удобное решение может иметь к языку с упрощенным синтаксисом?
Однако, само понятие замкнутых "калькуляторов объектов", как мы видели в программах на BASIC, часто не просто полезен, но, даже, необходим.
Более того, написание этого калькулятора в кодах, как в TANKTICS, позволяет еще один финт - дописывание пользовательских кусков кода без нужды заставлять пользователя изучать BASIC и заполнять на нем оставленные программистом дыры. Ведь, в большинстве, BASIC-ов работает метод: "считываем из DATA, записываем PEEK и исполняем CALL". А это может делать сама программа!
***
Идея кажется фантастической? Зачем изобретать кодовый конструктор в таких ограниченных условиях? Не проще ли написать простенький FORTH или выучить C?
Позвольте... А чем занимаются т.н. IDE (визуальные средства программирования, совмещающие в себе редакторы, средства управления проектом, настраиватели компилятора, отладчики)? Всякие Delphi и Visual Studio. Именно этим. А ведь, языком пользовательского программирования (написания макросов) в MS Visual C является Basic...
Т.е. когда начинаешь добавлять в свой FORTH средства управления проектированием программ, опыт BASIC стоит учитывать.
Последний раз редактировалось: Gudleifr (Чт Янв 05, 2023 10:49 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ТРЕТИЙ ПУТЬ: "ПРОСТО ОБЪЕКТЫ"
По идее, этот путь означает просто построение программы путем создания в ней Базы Данных.
А, с точки зрения, канонов BASIC - метод "компиляции" Базы Данных в операции над массивами. См. выше "про кота".
По идее, этот путь означает просто построение программы путем создания в ней Базы Данных.
А, с точки зрения, канонов BASIC - метод "компиляции" Базы Данных в операции над массивами. См. выше "про кота".

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
СЕМАНТИЧЕСКИЕ СЕТИ ПО ЛДЭ
Авторы не стали изобретать велосипед и просто "доработали" программу для работы с объектами. Объекты разделились на "сущности" и "связи". Т.е. нужны два массива, причем массив связей двумерный: связь адресуется номерами объектов, которые связывает.
Использовать для подобных вычислений BASIC вряд ли рационально, есть куча инструментов для работы с Базами Данных, легко справляющихся с подобными задачами (имеющими нужный инструментарий).
***
Можно только заметить, что "семантические сети", встречающиеся в программах бывают двух типов: ложащиеся на модель вычислений (на модель "сущности-связи" Баз Данных, на связи is_a и part_of объектов ООП...), провоцирующие программиста изобретать замысловатые абстрактные "семантические" конструкции; и ложащиеся на естественное представление данных, на их "географию"...
Авторы не стали изобретать велосипед и просто "доработали" программу для работы с объектами. Объекты разделились на "сущности" и "связи". Т.е. нужны два массива, причем массив связей двумерный: связь адресуется номерами объектов, которые связывает.
Использовать для подобных вычислений BASIC вряд ли рационально, есть куча инструментов для работы с Базами Данных, легко справляющихся с подобными задачами (имеющими нужный инструментарий).
***
Можно только заметить, что "семантические сети", встречающиеся в программах бывают двух типов: ложащиеся на модель вычислений (на модель "сущности-связи" Баз Данных, на связи is_a и part_of объектов ООП...), провоцирующие программиста изобретать замысловатые абстрактные "семантические" конструкции; и ложащиеся на естественное представление данных, на их "географию"...

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
В качестве примера программы на BASIC, с кучей трюков, подобных описанным; и "географической сетью":
СДЕЛАЙТЕ САМИ / ZX-РЕВЮ 9-12/1993
(C) Т.Д. Фрост (T.D. FROST),1986.
(C) Адаптация, Алексеев А.Г.,1993.
(С) Авторизованный перевод, редактирование, "ИНФОРКОМ". 1993г.
ADVENTURE GAMES
2 части:
 PDF, 0.5Мб
PDF, 0.5Мб
 PDF, 0.36Мб
PDF, 0.36Мб
 ТЕМА #20, АБЗАЦ #2145
ТЕМА #20, АБЗАЦ #2145
СДЕЛАЙТЕ САМИ / ZX-РЕВЮ 9-12/1993
(C) Т.Д. Фрост (T.D. FROST),1986.
(C) Адаптация, Алексеев А.Г.,1993.
(С) Авторизованный перевод, редактирование, "ИНФОРКОМ". 1993г.
ADVENTURE GAMES
2 части:
 PDF, 0.5Мб
PDF, 0.5Мб
 PDF, 0.36Мб
PDF, 0.36Мб
 ТЕМА #20, АБЗАЦ #2145
ТЕМА #20, АБЗАЦ #2145
Последний раз редактировалось: Gudleifr (Сб Май 01, 2021 1:20 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
КОЭФФИЦИЕНТЫ УВЕРЕННОСТИ ПО ЛДЭ
Похоже на Байеса: просто прицепляем к одной из наших программ еще один механизм и набор коэффициентов.
Коэффициенты цепляются к логическим переменным (фактам) и силлогизмам (правилам вывода).
А новый механизм авторы определяют так: уверенность в результате конъюнкции есть минимальная из уверенностей переменных, умноженная на уверенность в правилах.
Это позволит нам, например, не просто строить все факты подряд (методом прямой цепочки), но и время от времени отсеивать те из них, в которых мы "не уверены" (уверенность ниже порога).
***
Если мы проводим аналогии с человеческим мозгом, там действует аналогичный механизм, отфильтровывающий ассоциации со слишком дохлой энергетикой (затухание). Однако, в мозгу есть еще и механизм усиления самой активной ассоциации (прокручиваемой в сознании).
***
Нужно ли это программам? Например, шахматные программы таким образом пытаются рассмотреть "самые перспективные" ситуации.
Похоже на Байеса: просто прицепляем к одной из наших программ еще один механизм и набор коэффициентов.
Коэффициенты цепляются к логическим переменным (фактам) и силлогизмам (правилам вывода).
А новый механизм авторы определяют так: уверенность в результате конъюнкции есть минимальная из уверенностей переменных, умноженная на уверенность в правилах.
Это позволит нам, например, не просто строить все факты подряд (методом прямой цепочки), но и время от времени отсеивать те из них, в которых мы "не уверены" (уверенность ниже порога).
***
Если мы проводим аналогии с человеческим мозгом, там действует аналогичный механизм, отфильтровывающий ассоциации со слишком дохлой энергетикой (затухание). Однако, в мозгу есть еще и механизм усиления самой активной ассоциации (прокручиваемой в сознании).
***
Нужно ли это программам? Например, шахматные программы таким образом пытаются рассмотреть "самые перспективные" ситуации.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
"ОТКОМПИЛИРОВАННЫЕ КОЭФФИЦИЕНТЫ"
В случае, если механизм подобных коэффициентов оказывается полезным в каком-либо алгоритме, то почти наверняка удается выкинуть все эти "рассуждающие фрагменты", оставив простейшую арифметику.
***
Например рассмотрим программу Дмитрия Сухова "Жук" ( JPG/RAR, 0.24Мб
JPG/RAR, 0.24Мб ) из книги "В Лабиринтах игр и головоломок" (сост. В.Н.Белов, Лениздат, 1992). Цель игры: построить такой лабиринт, из которого жуку будет выбраться труднее всего (конечно, полностью перекрывать ему проход нельзя). Исходный лабиринт представлем массивом M(32,23), где 255 - стена, а 0 - проход. Крайние ряды лабиринта - сплошные стены. Задача жука из верхнего правого угла переползти в левый верхний.
) из книги "В Лабиринтах игр и головоломок" (сост. В.Н.Белов, Лениздат, 1992). Цель игры: построить такой лабиринт, из которого жуку будет выбраться труднее всего (конечно, полностью перекрывать ему проход нельзя). Исходный лабиринт представлем массивом M(32,23), где 255 - стена, а 0 - проход. Крайние ряды лабиринта - сплошные стены. Задача жука из верхнего правого угла переползти в левый верхний.
Алгоритм жука:
460 P(1,1)=0:P(1,2)=-1
470 P(2,1)=-1:P(2,2)=0
480 P(3,1)=0:P(3,2)=1
490 P(4,1)=1:P(4,2)=0
... НАЧАЛЬНАЯ ОТРИСОВКА, ЗАПУСК ТАЙМЕРА
510 P(1,0)=(X,Y-1)
520 P(2,0)=(X-1,Y)
530 P(3,0)=(X,Y+1)
540 P(4,0)=(X+1,Y1)
550 A=200:B=2
560 FORI=1TO4:IFP(I,0)<ATHEN=I:A=P(I,0)
570 NEXT
580 M(X,Y)=M(X,Y)+1
590 X=X+P(B,1):Y=Y+P(B,2)
... ОТРИСОВКА ПЕРЕМЕЩЕНИЯ
620 IF X=1 AND Y=l THEN 640
630 GOTO 510
... ПОДСЧЕТ ЗАТРАЧЕННОГО ВРЕМЕНИ
Видно, что роль коэффициента уверенности "что туда ходить не надо" играет счетчик того, сколько раз жук уже там побывал.
Конечно, если "B=2" в строке 550, означает наше желание идти преимущественно влево, то и A следовало бы приравнять P(2,0). А еще лучше было бы вставить туда генератор случайных чисел, чтобы нельзя было предсказать поведение жука.
В случае, если механизм подобных коэффициентов оказывается полезным в каком-либо алгоритме, то почти наверняка удается выкинуть все эти "рассуждающие фрагменты", оставив простейшую арифметику.
***
Например рассмотрим программу Дмитрия Сухова "Жук" (
 JPG/RAR, 0.24Мб
JPG/RAR, 0.24Мб ) из книги "В Лабиринтах игр и головоломок" (сост. В.Н.Белов, Лениздат, 1992). Цель игры: построить такой лабиринт, из которого жуку будет выбраться труднее всего (конечно, полностью перекрывать ему проход нельзя). Исходный лабиринт представлем массивом M(32,23), где 255 - стена, а 0 - проход. Крайние ряды лабиринта - сплошные стены. Задача жука из верхнего правого угла переползти в левый верхний.
) из книги "В Лабиринтах игр и головоломок" (сост. В.Н.Белов, Лениздат, 1992). Цель игры: построить такой лабиринт, из которого жуку будет выбраться труднее всего (конечно, полностью перекрывать ему проход нельзя). Исходный лабиринт представлем массивом M(32,23), где 255 - стена, а 0 - проход. Крайние ряды лабиринта - сплошные стены. Задача жука из верхнего правого угла переползти в левый верхний.Алгоритм жука:
460 P(1,1)=0:P(1,2)=-1
470 P(2,1)=-1:P(2,2)=0
480 P(3,1)=0:P(3,2)=1
490 P(4,1)=1:P(4,2)=0
... НАЧАЛЬНАЯ ОТРИСОВКА, ЗАПУСК ТАЙМЕРА
510 P(1,0)=(X,Y-1)
520 P(2,0)=(X-1,Y)
530 P(3,0)=(X,Y+1)
540 P(4,0)=(X+1,Y1)
550 A=200:B=2
560 FORI=1TO4:IFP(I,0)<ATHEN=I:A=P(I,0)
570 NEXT
580 M(X,Y)=M(X,Y)+1
590 X=X+P(B,1):Y=Y+P(B,2)
... ОТРИСОВКА ПЕРЕМЕЩЕНИЯ
620 IF X=1 AND Y=l THEN 640
630 GOTO 510
... ПОДСЧЕТ ЗАТРАЧЕННОГО ВРЕМЕНИ
Видно, что роль коэффициента уверенности "что туда ходить не надо" играет счетчик того, сколько раз жук уже там побывал.
Конечно, если "B=2" в строке 550, означает наше желание идти преимущественно влево, то и A следовало бы приравнять P(2,0). А еще лучше было бы вставить туда генератор случайных чисел, чтобы нельзя было предсказать поведение жука.
Последний раз редактировалось: Gudleifr (Ср Дек 06, 2017 2:18 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
САМООБУЧАЮЩАЯСЯ СИСТЕМА ПО ЛДЭ
Наконец, используя все эти ООП и цепочки выводов, авторы написали программу, работающую так:
ВВЕДИТЕ ИМЯ ОБЪЕКТА 1 ? АВТОМОБИЛЬ
ВВЕДИТЕ ИМЯ ОБЪЕКТА 2 ? ТАНК
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? ПУШКА
ВВЕДИТЕ АТРИБУТ 2 ? ЛЮК
ВВЕДИТЕ АТРИБУТ 3 ? КУЗОВ
ЭТО АВТОМОБИЛЬ
ВЕРНО ДА ИЛИ НЕТ ? НЕТ
АВТОМОБИЛЬ
ТАНК ПУШКА ЛЮК КУЗОВ
ОБЩИЙ СПИСОК
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? КУЗОВ
ВВЕДИТЕ АТРИБУТ 2 ? КОЛЕСА
ВВЕДИТЕ АТРИБУТ 3 ? ДВЕРЦЫ
ЭТО ТАНК
ВЕРНО ДА ИЛИ НЕТ ? НЕТ
АВТОМОБИЛЬ КОЛЕСА ДВЕРЦЫ
ТАНК ПУШКА ЛЮК
ОБЩИЙ СПИСОК КУЗОВ
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? КУЗОВ
ВВЕДИТЕ АТРИБУТ 2 ? ДВЕРЦЫ
ВВЕДИТЕ АТРИБУТ 3 ? ВК
ЭТО АВТОМОБИЛЬ
ВЕРНО ДА ИЛИ НЕТ ? ДА
АВТОМОБИЛЬ КОЛЕСА ДВЕРЦЫ
ТАНК ПУШКА ЛЮК
ОБЩИЙ СПИСОК КУЗОВ
И после этого разве удивительно, что "ЭТО КОТ?" сошел за экспертную систему?
Наконец, используя все эти ООП и цепочки выводов, авторы написали программу, работающую так:
ВВЕДИТЕ ИМЯ ОБЪЕКТА 1 ? АВТОМОБИЛЬ
ВВЕДИТЕ ИМЯ ОБЪЕКТА 2 ? ТАНК
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? ПУШКА
ВВЕДИТЕ АТРИБУТ 2 ? ЛЮК
ВВЕДИТЕ АТРИБУТ 3 ? КУЗОВ
ЭТО АВТОМОБИЛЬ
ВЕРНО ДА ИЛИ НЕТ ? НЕТ
АВТОМОБИЛЬ
ТАНК ПУШКА ЛЮК КУЗОВ
ОБЩИЙ СПИСОК
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? КУЗОВ
ВВЕДИТЕ АТРИБУТ 2 ? КОЛЕСА
ВВЕДИТЕ АТРИБУТ 3 ? ДВЕРЦЫ
ЭТО ТАНК
ВЕРНО ДА ИЛИ НЕТ ? НЕТ
АВТОМОБИЛЬ КОЛЕСА ДВЕРЦЫ
ТАНК ПУШКА ЛЮК
ОБЩИЙ СПИСОК КУЗОВ
ВВЕДИТЕ АТРИБУТЫ ЛЮБОГО ОБЪЕКТА И ВК В КОНЦЕ
ВВЕДИТЕ АТРИБУТ 1 ? КУЗОВ
ВВЕДИТЕ АТРИБУТ 2 ? ДВЕРЦЫ
ВВЕДИТЕ АТРИБУТ 3 ? ВК
ЭТО АВТОМОБИЛЬ
ВЕРНО ДА ИЛИ НЕТ ? ДА
АВТОМОБИЛЬ КОЛЕСА ДВЕРЦЫ
ТАНК ПУШКА ЛЮК
ОБЩИЙ СПИСОК КУЗОВ
И после этого разве удивительно, что "ЭТО КОТ?" сошел за экспертную систему?

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
НАРОДНАЯ МУДРОСТЬ ГЛАСИТ:
"Искусственным интеллектом занимаются те, кому не хватает естественного".
Есть ли в этой шутке доля истины? Если просуммировать что мы знает об устройстве человеческого мозга, то для "подобного ему" искусственного (например, такого, как предполагает Тест Тьюринга) будут очевидны два ограничения:
1. Такой мозг может существовать только внутри "некого подобия" человека, т.к. разумность человеческого мозга является лишь побочным эффектом его биологической функции - способности Homo Sapiens выживать. Отсюда следуют такие, например, неприятные мелочи, как невозможность копипастинга из одного мозга в другой, требование многолетнего обучения и т.п. С другой стороны, строя роботов, живущих в "более простой" вселенной, мы можем использовать "модели мозга" для их разумного поведения (т.е. выживания) без претензий на разумность "в общечеловеческом" или Тьюринговом смысле.
2. Т.к. мы сами люди, то до конца понять свой мозг не можем. Инструмент препарирования должен быть более твердым и острым, чем препарируемый орган. Мы можем моделировать, но не можем предсказывать поведение. Т.е. мы вполне можем наделить наших роботов "чувствами", "логикой", "обучаемостью", "верой", но не можем гарантировать их идентичность нашим.
***
Эти две аксиомы надо помнить всегда, тогда все последующие кибернетические и логические результаты, полученные "мозго-программистами" не будут казаться столь странными.
Какие же это результаты?
Самый главный: все, что мы можем запрограммировать, по своим возможностям не будет превышать возможности Машины Тьюринга.
Сколько бы мы не рассуждали о программах, которые сами себя пишут, содержат внутри себя обучающиеся нейронные сети или создают новые сущности, они своим поведением ничем не будут отличаться от "обычных программ". Как говаривал классик: "Машины не могут создавать прибавочной стоимости".
Не поможет даже столь модное ныне увлечение мультитредовыми и/или мутирующими программами: создать нечто они, возможно, смогут (ибо любая бесконечная неповторяющаяся последовательность дает все варианты всего сущего), но вот процесс выбора из астрономического количества неработающих вариантов одного работающего ровно столь же труден, сколь и написание "обычной программы", изначально делающей искомое. Другое дело, что наблюдение за коллективами программ может быть увлекательно само по себе. Особенно, если число параметров невелико. Слишком же сложные и излишне вариабельные процессы обычно в сумме дают скучно усредненный результат.
***
Что можно считать разумным поведением игровой программы?
Два варианта (и программист заранее должен решить, что ему надо):
1. игрок замечает, что не может заранее предсказать поведение программы; или
2. игрок замечает, что программа умеет/учится играть в игру.
Есть +100500 широко известных работающих способов достичь одной или другой из этих целей, и один неработающий: "я сделаю программу столь умной, что она поймет, что надо игроку, и так и сделает".
Все работающие сводятся к умелому дозированию адекватной и неадекватной реакций программы на поведение игрока. С точки зрения математики - голимая Теория Игр, с точки зрения кодинга - подбор весовых коэффициентов... Между - любые умствования про иерархии модели, нейронные сети, продукционные системы... Причем, ни одно из решений не работает без предварительного решения дифуров на бумажке. Именно по последней причине, а не в силу того, что "новые методы ИИ слишком инновационны", применимость разумного поведения программ сильно ограничена.
"Искусственным интеллектом занимаются те, кому не хватает естественного".
Есть ли в этой шутке доля истины? Если просуммировать что мы знает об устройстве человеческого мозга, то для "подобного ему" искусственного (например, такого, как предполагает Тест Тьюринга) будут очевидны два ограничения:
1. Такой мозг может существовать только внутри "некого подобия" человека, т.к. разумность человеческого мозга является лишь побочным эффектом его биологической функции - способности Homo Sapiens выживать. Отсюда следуют такие, например, неприятные мелочи, как невозможность копипастинга из одного мозга в другой, требование многолетнего обучения и т.п. С другой стороны, строя роботов, живущих в "более простой" вселенной, мы можем использовать "модели мозга" для их разумного поведения (т.е. выживания) без претензий на разумность "в общечеловеческом" или Тьюринговом смысле.
2. Т.к. мы сами люди, то до конца понять свой мозг не можем. Инструмент препарирования должен быть более твердым и острым, чем препарируемый орган. Мы можем моделировать, но не можем предсказывать поведение. Т.е. мы вполне можем наделить наших роботов "чувствами", "логикой", "обучаемостью", "верой", но не можем гарантировать их идентичность нашим.
***
Эти две аксиомы надо помнить всегда, тогда все последующие кибернетические и логические результаты, полученные "мозго-программистами" не будут казаться столь странными.
Какие же это результаты?
Самый главный: все, что мы можем запрограммировать, по своим возможностям не будет превышать возможности Машины Тьюринга.
Сколько бы мы не рассуждали о программах, которые сами себя пишут, содержат внутри себя обучающиеся нейронные сети или создают новые сущности, они своим поведением ничем не будут отличаться от "обычных программ". Как говаривал классик: "Машины не могут создавать прибавочной стоимости".
Не поможет даже столь модное ныне увлечение мультитредовыми и/или мутирующими программами: создать нечто они, возможно, смогут (ибо любая бесконечная неповторяющаяся последовательность дает все варианты всего сущего), но вот процесс выбора из астрономического количества неработающих вариантов одного работающего ровно столь же труден, сколь и написание "обычной программы", изначально делающей искомое. Другое дело, что наблюдение за коллективами программ может быть увлекательно само по себе. Особенно, если число параметров невелико. Слишком же сложные и излишне вариабельные процессы обычно в сумме дают скучно усредненный результат.
***
Что можно считать разумным поведением игровой программы?
Два варианта (и программист заранее должен решить, что ему надо):
1. игрок замечает, что не может заранее предсказать поведение программы; или
2. игрок замечает, что программа умеет/учится играть в игру.
Есть +100500 широко известных работающих способов достичь одной или другой из этих целей, и один неработающий: "я сделаю программу столь умной, что она поймет, что надо игроку, и так и сделает".
Все работающие сводятся к умелому дозированию адекватной и неадекватной реакций программы на поведение игрока. С точки зрения математики - голимая Теория Игр, с точки зрения кодинга - подбор весовых коэффициентов... Между - любые умствования про иерархии модели, нейронные сети, продукционные системы... Причем, ни одно из решений не работает без предварительного решения дифуров на бумажке. Именно по последней причине, а не в силу того, что "новые методы ИИ слишком инновационны", применимость разумного поведения программ сильно ограничена.
Последний раз редактировалось: Gudleifr (Пт Апр 05, 2024 12:34 pm), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
Об обучающейся машине из коробков пишут часто. Например, фантастический рассказ Сайберхэгена "Не задумываясь"  ТЕМА #129, АБЗАЦ #3304
ТЕМА #129, АБЗАЦ #3304 . Или статья Мартина Гарднера в "Математических досугах" - Самодельная самообучающаяся машина из спичечных коробков.
. Или статья Мартина Гарднера в "Математических досугах" - Самодельная самообучающаяся машина из спичечных коробков.
Я приведу более техническое описание:
Д.М.КОМСКИЙ, Б.М.ИГОШЕВ / ЭЛЕКТРОННЫЕ АВТОМАТЫ И ИГРЫ
Из Главы #5 - АВТОМАТЫ УЧАТСЯ ИГРАТЬ
Гроссмейстерами не рождаются. Как ни талантлив будущий чемпион, начинать ему всегда приходится "с нуля", а путь к пьедесталу почета долог и тернист. Знакомство с правилами игры, первые робкие шаги новичка, многочисленные встречи с такими же, как и он, любителями... Радость побед и - увы!- горечь поражений. Потом - изучение партий, сыгранных лучшими мастерами прошлого и современности, знакомство с теорией. Упорная и напряженная учеба, тренировка... И игры, игры, игры - в матчах, турнирах, состязаниях всех рангов и уровней... Опыт и мастерство приходят постепенно. Нередко лишь через многие годы начинающий любитель превращается в прославленного чемпиона.
Но если таков путь к мастерству человека, то почему бы не направить по этому же пути и играющую машину, запрограммировав у нее способность совершенствоваться по мере накопления опыта?
Эту мысль высказал еще Норберт Винер.
"Предположим,- писал он,- что после нескольким партий машина делает перерыв и использует свои возможности совсем для другой цели. В то время, когда она не играет со своим противником, она изучает все предыдущие партии, записанные в ее памяти, производит оценку фигур в зависимости от их положения, мобильности и т.д., анализирует наиболее выигрышные ситуации. Таким путем она изучает не только свои собственные ошибки, но и удачи своего противника. Теперь она заменяет свои предыдущие ходы новыми и продолжает игру как новая, улучшенная машина. Такая машина больше не будет проявлять прежнего упорства, и комбинации, которые раньше против нее удавались, потеряют свою ценность. Более того, со временем машина может изучить манеру игры своего противника".
***
Поскольку, вероятно, вряд ли кто-нибудь из читателей возьмется за изготовление самообучающейся машины, для которой требуется 300 спичечных коробок, мы предлагаем построить более простого "спичечного" робота - машину, обучающуюся играть в знакомую нам игру Баше в том ее варианте, который мы назвали "Последний проигрывает". Напомним, что в этой игре двое играющих по очереди берут предметы из кучки, содержащей вначале семь предметов, причем за один ход можно взять один или два предмета; проигравшим считается тот, кто возьмет последний. Чтобы построить машину, способную быстро научиться выигрывать в этой игре, нужно всего шесть пустых спичечных коробок и одиннадцать одинаковых бусинок двух цветовых оттенков: На каждой коробке изображают одну из схем, показанных на рис.49.

Рис.49. Варианты позиций перед ответным ходом "спичечного" робота в игре "Последний проигрывает".
Эти схемы соответствуют различным позициям, которые могут возникать во время игры перед ходом машины (начинать игру всегда должен ее противник). В верхней части каждой схемы кружком обведено число, показывающее, сколько предметов остается в кучке после хода человека, а стрелками обозначены варианты возможных ходов машины из данной позиции. Рядом с каждой стрелкой записано число предметов, которые "берет" своим ходом машина, а острие стрелки указывает, сколько предметов в кучке останется после этого. Римские цифры I-III в нижней части каждой схемы показывают, перед каким ответным ходом машины возможно возникновение позиции, изображенной на данной схеме. Первые две схемы (на рис.49, а и б) изображают позиции, возможные только после первого хода человека; схемы на рис.49, в и г соответствуют позициям, которые могут возникнуть после второго хода человека; позиции на рис.49, д и е возможны как после второго, так и после третьего хода противника машины.
В каждую коробку нужно положить по одной бусинке определенного цвета на каждый вид стрелки на схеме - и "спичечный" робот готов к игре. Его допустимые правилами ходы изображены на схемах стрелками; он может делать любой ход и при том только законный, но у него нет никакой предпочтительной стратегии - он еще не обучен выигрывающему алгоритму.
Процесс обучения робота происходит следующим образом. Сделав первый ход, выберите ту из коробок с цифрой I, на которой изображена возникшая позиция. Встряхните коробку и, закрыв глаза, вытащите из нее наугад одну бусинку. Затем посмотрите, какого цвета эта бусинка, и сделайте за машину ответный ход, взяв указанное соответствующей стрелкой число предметов из кучки. Теперь снова ваш ход. Сделав его, повторите указанную процедуру с одной из коробок, обозначенных цифрами II или II-III. Так следует поступать, пока партия не окончится.
Если выиграет машина, положите все вынутые бусинки на место и играйте снова. Если же машина проиграет, то "накажите" ее, забрав из коробки ту бусинку, которая представляла последний ход машины. Все остальные бусинки положите на место и продолжайте обучение - играйте снова. Если во время игры очередная коробка окажется пустой, то это значит, что все дальнейшие ходы робота ведут к его проигрышу и он сдается. В этом случае надо его "наказать", забрав бусинку из предыдущей коробки. В процессе игры наш робот быстро накапливает опыт и обучается, и чем лучше играет партнер, тем быстрее машина овладевает выигрышной стратегией.
Чтобы прочно усвоить алгоритм победы, нашему роботу нужно потерпеть поражение не более чем в семи партиях (при этом из всех коробок изымаются бусинки, соответствующие таким ходам, которые могут привести к поражению машины). Поэтому во всяком турнире, состоящем более чем из 14 партий, общий счет будет в пользу машины. Слабого игрока она может победить и при меньшем числе сыгранных в турнире партий, но гарантировать ее идеальное обучение при этом мы не можем.
На рис. 50 показаны в виде графика результаты типичного турнира из 17 партий между машиной и человеком. Участок ломаной, направленный вниз, означает поражение машины, а участок ломаной, напразленный вверх - ее выигрыш. Из графика видно, что сыграв 11 партий (и проиграв из них 7), машина в совершенстве овладела выигрышной стратегией.
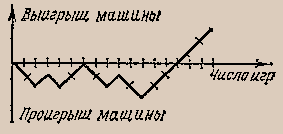
Рис.50. Результаты турнира человека и робота, обучающегося игре "Последний проигрывает".
***
После всего сказанного мы можем теперь сформулировать общий принцип обучения машины комбинаторным играм. Чтобы машина усвоила выигрывающий алгоритм, она должна, играя с противником, научиться отличать плохие ходы, ведущие к ее поражению, от хороших ходов, ведущих к выигрышу; потом, в следующих партиях игры в каждой позиции ей следует выбирать только хорошие ходы, избегая плохих. Перед началом обучения машине достаточно лишь знать правила игры. Впрочем, это последнее условие не является необходимым. Если засчитывать поражение машине всякий раз, когда она нарушает правила игры, то она будет относить все незаконные ходы к плохим и в дальнейшем станет их избегать. Не так ли и человек обучается комбинаторным играм?
***
Используя принцип обучения "спичечного" робота, предложенный Дональдом Мичи, можно построить несложный электронный автомат, обучающийся комбинаторной игре "Последний проигрывает". Как и в других описанных автоматах для игры Баше, здесь роль камешков играют выключаемые автоматом и ее партнером лампочки.

Рис. 53. Внешний вид обучающегося автомата для игры "Последний проигрывает".
На лицевой панели такого играющего автомата (рис.53) расположены в ряд семь горящих лампочек, снабженных выключателями, кнопки "Ход автомата", "Наказание", "Сброс", световые табло "Вы проиграли" и "Вы выиграли" и выключатель питания. Оба игрока (один из них автомат) по очереди отключают одну или две лампы. Проигравшим считается тот, кто своим очередным ходом должен будет выключить последнюю лампочку. Начинает игру всегда человек, после каждого своего хода он нажимает кнопку "Ход автомата". В случае проигрыша автомата он должен нажать кнопку "Наказание". Для подготовки автомата к следующей партии игры нажимается кнопка "Сброс" и все рычаги выключателей ламп возвращаются в исходное положение.

Рис. 54. Схема обучающегося автомата со случайным выбором стратегии.
Принципиальная электрическая схема автомата приведена на рис.54. Блок программы игры образуют реле Р1-Р6 с развязывающими диодами Д1-Д10. При срабатывании реле Р1 его контакты Р1.2 отключают лампу Л2 (автомат "берет" эту лампу), контакты Р2.2 отключают лампу Л3, контакты Р3.2 - лампу Л4, контакты Р4.2 - лампу Л5, контакты Р5.2 - лампу Л6, контакты Р6.2 - лампу Л7.
"Отключение" проигрышных вариантов игры автомата (вследствие его обучения) производит блок памяти, состоящий из реле Р7-Р11 с развязывающими диодами Д11-Д15. Реле этого блока "запоминают" проигрышные ходы и своими контактами отключают их, заменяя другими. Так, после срабатывания реле Р7 автомат в позиции 2 (в кучке осталось два предмета, очередной ход должен сделать автомат) будет всегда брать один предмет (лампу Л6), оставляя противнику выключение лампы Л7 и тем самым обеспечивая себе выигрыш; после срабатывания реле Р9 в позиции 4 - лампы Л4 и Л5; после срабатывания реле Р10 в позиции 6 - лампы Л2и Л3; после срабатывания реле Р11 в позиции 5 - лампу ЛЗ.
Случайный выбор одного из двух возможных вариантов хода автомата осуществляется контактами КР16.1 поляризованного реле КР16. При подключении обмотки этого реле к источнику переменного тока кнопкой Кн1.3 якорь будет вибрировать с частотой сети, отклоняясь поочередно то в одну, то в другую сторону. В момент отключения тока контакты КР16.1 могут оказаться замкнутыми или разомкнутыми. Если они замкнуты, то сработает реле Р13 и автомат в данной позиции "возьмет" две лампы, если разомкнуты, то реле Р13 не сработает и автомат отключит одну лампу.
Рассмотрим работу автомата на конкретных примерах. Допустим, человек первый ход сделал выключателем В1 - погасла лампа Л1. После нажатия кнопки Кн1 ("Ход автожата") контакты Кн1.3 замкнут цепь питания поляризованного реле КР16 и его якорь начнет вибрировать. Одновременно контакты Кн1.1 замкнут цепь питания реле Р12, которое сработает и контактами Р12.1 подключит к источнику питания реле Р13-Р15, причем реле Р15 сразу же сработает и контактами Р15.1 самоблокируется. При отпускании кнопки Кн1 сработает реле Р14 (контакты Р15.2 замкнуты) и его контакты Р14.2 подключат к источнику питания блок программы игры.
Предположим, что после отпускания кнопки Кн1 контакты КР16.1 поляризованного реле оказались замкнутыми, в результате чего реле Р13 сработало. Значит, после замыкания контактов Р14.2 сработают также реле Р1 и Р2 (контакты В 1.2 и Р13.1 замкнуты), контактами Р1.1 и Р2.1 они самоблокируются, а контактами Р1.2 и Р2.2 отключают лампы Л2 и Л3 - автомат сделает ответный ход. Необходимо отметить, что конденсатор С1 после отпускания кнопки Ход автомата разряжается через обмотку реле Р12 и таким образом задерживает его отпускание (а соответственно и отпускание реле Р13-Р15) для того, чтобы реле блока программы игры успели сработать и самоблокироваться. Время задержки определяется емкостью конденсатора С1 и должно быть около 0,4-0,5с.
Допустим далее, что человек при втором ходе выключателем В4.1 погасил лампу Л4. После нажатия кнопки "Ход автомата" (Кн1) устройство работает так же, как и при первом его ходе. Предположим, что на этот раз после отпускания кнопки Кн1 контакты КР16.1 оказались разомкнутыми и реле Р13 не сработало. В таком случае срабатывает реле Р4 (контакты В4.2 переключены), контактами Р4.1 оно самоблокируется, а контактами Р4.2 отключает лампу Л5 - автомат делает свой второй ход.
Далее человек делает третий ход - выключателем В6.1 гасит лампу Л6. Тогда после нажатия и отпускания кнопки Кн1 ("Ход автомата") срабатывает реле Р6, контактами Р6.1 оно самоблокируется, контактами Р6.2 отключает лампу Л7 и включает лампу Л8, подсвечивающую табло "Вы выиграли".
Поскольку автомат проиграл, надо нажать кнопку Кн2 ("Наказание"). При этом реле Р8 блока памяти сработает (контакты Р4.3 и Р6.3 замкнуты) и контактами Р8.1 самоблокируется. Контакты Р8.2 замыкаются - теперь в позиции 3 (возникающей, когда противник автомата делает ход выключателем В4 и ход должен сделать автомат) при нажатии кнопки "Ход автомата" будут срабатывать реле Р4 и Р5 и контактами Р4.2 и Р5.2 разрывать цепи питания ламп Л5 и Л6 независимо от того, какой выбор сделало реле КР16 - замкнуты или разомкнуты контакты P13.4. В последующих партиях игры автомат в этой позиции будет обеспечивать себе выигрыш.
Нажав кнопку Кн3 ("Сброс") - при этом отпускают все ранее сработавшие реле блока программы игры - и установив выключатели В1-В7 в исходное положение, противник автомата может начинать новую партию игры.
Предположим, что в следующей партии первым ходом человек выключателями В1 и В2 "берет" лампы Л1 и Л2. Пусть после нажатия и опускания кнопки "Ход автомата" контакты КР16.1 поляризованного реле КР16 будут разомкнуты. Сработает реле Р2, контактами Р2.1 оно самоблокируется, контактами Р2.2 отключит лампу Л3. Допустим, второй ход человек делает выключателем В4 - "берет" лампу Л4. Теперь при ходе автомата сработают реле Р4 и Р5 (контакты Р8.2 замкнуты),- самоблокируются контактами Р4.1 и Р5.1, а контактами Р4.2 и Р5.2 отключат лампы Л5 и Л6. Как видим, в этой партии игры автомат в позиции 3, в отличие от предыдущей партии, берет 2 предмета (автомат "обучился" и играет оптимально) и тем самым обеспечивает себе выигрыш, ибо следующим ходом человек вынужден выключить последнюю лампу Л7 (выключателем В7.1). При этом загорается лампа Л9, подсвечивающая табло "Вы проиграли".
Аналогично работает автомат при всех других вариантах игры. Чтобы пройти полный курс обучения и в дальнейшем играть безупречно, автомат должен проиграть пять партий (при этом в блоке памяти сработают реле Р7-Р11 и автомат "запомнит", как не следует играть).
В конструкции описанного автомата можно использовать: Л1-Л9 - лампы накаливания ЛН 3,5В х 0,28А; P1-P6 - реле РЭС-22 (паспорт РФ4.500.131); Р7-Р11, Р14 и Р15 - реле РЭС-9 (паспорт РС4.524.200); Р12 - реле РСМ-1 (паспорт Ю.171.81.37); Р13 - реле РС-13 (паспорт РС4.523.017); КР16 - реле РП-4; В1-В7 - выключатели ТП1-2; В8 - ТВ2-1. Кнопки могут быть самодельными, изготовленными из контактных пружин реле. Силовой трансформатор Тр намотан на сердечнике из пластин Ш32, толщина пакета 20мм (обмотка I содержит 1220 витков, обмотка II - 150 витков, обмотка III - 20 витков провода ПЭВ-1 или ПЭЛ-0,47).

Рис. 55. Схема обучающегося автомата с последовательным перебором стратегий.
В описанном играющем автомате выбор его стратегии (взять один или два предмета) определяется датчиком двух равновероятных стратегий - контактами поляризованного реле. Можно, однако, применить и другой принцип - последовательный перебор стратегий. Применительно к нашему автомату это будет выглядеть так: в любой позиции автомат своим ходом отключает одну лампочку; если он выиграет, то и в последующих партиях будет в этой позиции выключать одну лампочку; если же он проиграет, то меняет стратегию - в этой же позиции в следующий раз будет выключать две лампочки. Принципиальная схема такого автомата с последовательным перебором стратегий изображена на рис.55. После срабатывания реле Р7 блока памяти автомат будет выключать две лампочки в позиции 4, после срабатывания реле Р8 - две лампочки в позиции 6, после срабатывания реле Р9 - две лампочки в позиции 3. В остальном он работает так же, как первый автомат.
Используя рассмотренные принципы обучения, можно сконструировать обучающиеся автоматы для таких игр, как "Побеждает последний", "Набери чет", "Ход конем" и другие комбинаторные игры. Представляет большой интерес создание таких самообучающихся играющих автоматов, у которых процесс обучения осуществлялся бы не только отбрасыванием проигрышных стратегий, но и увеличением вероятности выбора выигрышных стратегий.
 ТЕМА #129, АБЗАЦ #3304
ТЕМА #129, АБЗАЦ #3304 . Или статья Мартина Гарднера в "Математических досугах" - Самодельная самообучающаяся машина из спичечных коробков.
. Или статья Мартина Гарднера в "Математических досугах" - Самодельная самообучающаяся машина из спичечных коробков.Я приведу более техническое описание:
Д.М.КОМСКИЙ, Б.М.ИГОШЕВ / ЭЛЕКТРОННЫЕ АВТОМАТЫ И ИГРЫ
Из Главы #5 - АВТОМАТЫ УЧАТСЯ ИГРАТЬ
Гроссмейстерами не рождаются. Как ни талантлив будущий чемпион, начинать ему всегда приходится "с нуля", а путь к пьедесталу почета долог и тернист. Знакомство с правилами игры, первые робкие шаги новичка, многочисленные встречи с такими же, как и он, любителями... Радость побед и - увы!- горечь поражений. Потом - изучение партий, сыгранных лучшими мастерами прошлого и современности, знакомство с теорией. Упорная и напряженная учеба, тренировка... И игры, игры, игры - в матчах, турнирах, состязаниях всех рангов и уровней... Опыт и мастерство приходят постепенно. Нередко лишь через многие годы начинающий любитель превращается в прославленного чемпиона.
Но если таков путь к мастерству человека, то почему бы не направить по этому же пути и играющую машину, запрограммировав у нее способность совершенствоваться по мере накопления опыта?
Эту мысль высказал еще Норберт Винер.
"Предположим,- писал он,- что после нескольким партий машина делает перерыв и использует свои возможности совсем для другой цели. В то время, когда она не играет со своим противником, она изучает все предыдущие партии, записанные в ее памяти, производит оценку фигур в зависимости от их положения, мобильности и т.д., анализирует наиболее выигрышные ситуации. Таким путем она изучает не только свои собственные ошибки, но и удачи своего противника. Теперь она заменяет свои предыдущие ходы новыми и продолжает игру как новая, улучшенная машина. Такая машина больше не будет проявлять прежнего упорства, и комбинации, которые раньше против нее удавались, потеряют свою ценность. Более того, со временем машина может изучить манеру игры своего противника".
***
Поскольку, вероятно, вряд ли кто-нибудь из читателей возьмется за изготовление самообучающейся машины, для которой требуется 300 спичечных коробок, мы предлагаем построить более простого "спичечного" робота - машину, обучающуюся играть в знакомую нам игру Баше в том ее варианте, который мы назвали "Последний проигрывает". Напомним, что в этой игре двое играющих по очереди берут предметы из кучки, содержащей вначале семь предметов, причем за один ход можно взять один или два предмета; проигравшим считается тот, кто возьмет последний. Чтобы построить машину, способную быстро научиться выигрывать в этой игре, нужно всего шесть пустых спичечных коробок и одиннадцать одинаковых бусинок двух цветовых оттенков: На каждой коробке изображают одну из схем, показанных на рис.49.

Рис.49. Варианты позиций перед ответным ходом "спичечного" робота в игре "Последний проигрывает".
Эти схемы соответствуют различным позициям, которые могут возникать во время игры перед ходом машины (начинать игру всегда должен ее противник). В верхней части каждой схемы кружком обведено число, показывающее, сколько предметов остается в кучке после хода человека, а стрелками обозначены варианты возможных ходов машины из данной позиции. Рядом с каждой стрелкой записано число предметов, которые "берет" своим ходом машина, а острие стрелки указывает, сколько предметов в кучке останется после этого. Римские цифры I-III в нижней части каждой схемы показывают, перед каким ответным ходом машины возможно возникновение позиции, изображенной на данной схеме. Первые две схемы (на рис.49, а и б) изображают позиции, возможные только после первого хода человека; схемы на рис.49, в и г соответствуют позициям, которые могут возникнуть после второго хода человека; позиции на рис.49, д и е возможны как после второго, так и после третьего хода противника машины.
В каждую коробку нужно положить по одной бусинке определенного цвета на каждый вид стрелки на схеме - и "спичечный" робот готов к игре. Его допустимые правилами ходы изображены на схемах стрелками; он может делать любой ход и при том только законный, но у него нет никакой предпочтительной стратегии - он еще не обучен выигрывающему алгоритму.
Процесс обучения робота происходит следующим образом. Сделав первый ход, выберите ту из коробок с цифрой I, на которой изображена возникшая позиция. Встряхните коробку и, закрыв глаза, вытащите из нее наугад одну бусинку. Затем посмотрите, какого цвета эта бусинка, и сделайте за машину ответный ход, взяв указанное соответствующей стрелкой число предметов из кучки. Теперь снова ваш ход. Сделав его, повторите указанную процедуру с одной из коробок, обозначенных цифрами II или II-III. Так следует поступать, пока партия не окончится.
Если выиграет машина, положите все вынутые бусинки на место и играйте снова. Если же машина проиграет, то "накажите" ее, забрав из коробки ту бусинку, которая представляла последний ход машины. Все остальные бусинки положите на место и продолжайте обучение - играйте снова. Если во время игры очередная коробка окажется пустой, то это значит, что все дальнейшие ходы робота ведут к его проигрышу и он сдается. В этом случае надо его "наказать", забрав бусинку из предыдущей коробки. В процессе игры наш робот быстро накапливает опыт и обучается, и чем лучше играет партнер, тем быстрее машина овладевает выигрышной стратегией.
Чтобы прочно усвоить алгоритм победы, нашему роботу нужно потерпеть поражение не более чем в семи партиях (при этом из всех коробок изымаются бусинки, соответствующие таким ходам, которые могут привести к поражению машины). Поэтому во всяком турнире, состоящем более чем из 14 партий, общий счет будет в пользу машины. Слабого игрока она может победить и при меньшем числе сыгранных в турнире партий, но гарантировать ее идеальное обучение при этом мы не можем.
На рис. 50 показаны в виде графика результаты типичного турнира из 17 партий между машиной и человеком. Участок ломаной, направленный вниз, означает поражение машины, а участок ломаной, напразленный вверх - ее выигрыш. Из графика видно, что сыграв 11 партий (и проиграв из них 7), машина в совершенстве овладела выигрышной стратегией.
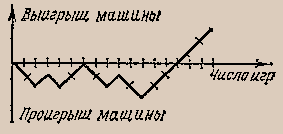
Рис.50. Результаты турнира человека и робота, обучающегося игре "Последний проигрывает".
***
После всего сказанного мы можем теперь сформулировать общий принцип обучения машины комбинаторным играм. Чтобы машина усвоила выигрывающий алгоритм, она должна, играя с противником, научиться отличать плохие ходы, ведущие к ее поражению, от хороших ходов, ведущих к выигрышу; потом, в следующих партиях игры в каждой позиции ей следует выбирать только хорошие ходы, избегая плохих. Перед началом обучения машине достаточно лишь знать правила игры. Впрочем, это последнее условие не является необходимым. Если засчитывать поражение машине всякий раз, когда она нарушает правила игры, то она будет относить все незаконные ходы к плохим и в дальнейшем станет их избегать. Не так ли и человек обучается комбинаторным играм?
***
Используя принцип обучения "спичечного" робота, предложенный Дональдом Мичи, можно построить несложный электронный автомат, обучающийся комбинаторной игре "Последний проигрывает". Как и в других описанных автоматах для игры Баше, здесь роль камешков играют выключаемые автоматом и ее партнером лампочки.

Рис. 53. Внешний вид обучающегося автомата для игры "Последний проигрывает".
На лицевой панели такого играющего автомата (рис.53) расположены в ряд семь горящих лампочек, снабженных выключателями, кнопки "Ход автомата", "Наказание", "Сброс", световые табло "Вы проиграли" и "Вы выиграли" и выключатель питания. Оба игрока (один из них автомат) по очереди отключают одну или две лампы. Проигравшим считается тот, кто своим очередным ходом должен будет выключить последнюю лампочку. Начинает игру всегда человек, после каждого своего хода он нажимает кнопку "Ход автомата". В случае проигрыша автомата он должен нажать кнопку "Наказание". Для подготовки автомата к следующей партии игры нажимается кнопка "Сброс" и все рычаги выключателей ламп возвращаются в исходное положение.

Рис. 54. Схема обучающегося автомата со случайным выбором стратегии.
Принципиальная электрическая схема автомата приведена на рис.54. Блок программы игры образуют реле Р1-Р6 с развязывающими диодами Д1-Д10. При срабатывании реле Р1 его контакты Р1.2 отключают лампу Л2 (автомат "берет" эту лампу), контакты Р2.2 отключают лампу Л3, контакты Р3.2 - лампу Л4, контакты Р4.2 - лампу Л5, контакты Р5.2 - лампу Л6, контакты Р6.2 - лампу Л7.
"Отключение" проигрышных вариантов игры автомата (вследствие его обучения) производит блок памяти, состоящий из реле Р7-Р11 с развязывающими диодами Д11-Д15. Реле этого блока "запоминают" проигрышные ходы и своими контактами отключают их, заменяя другими. Так, после срабатывания реле Р7 автомат в позиции 2 (в кучке осталось два предмета, очередной ход должен сделать автомат) будет всегда брать один предмет (лампу Л6), оставляя противнику выключение лампы Л7 и тем самым обеспечивая себе выигрыш; после срабатывания реле Р9 в позиции 4 - лампы Л4 и Л5; после срабатывания реле Р10 в позиции 6 - лампы Л2и Л3; после срабатывания реле Р11 в позиции 5 - лампу ЛЗ.
Случайный выбор одного из двух возможных вариантов хода автомата осуществляется контактами КР16.1 поляризованного реле КР16. При подключении обмотки этого реле к источнику переменного тока кнопкой Кн1.3 якорь будет вибрировать с частотой сети, отклоняясь поочередно то в одну, то в другую сторону. В момент отключения тока контакты КР16.1 могут оказаться замкнутыми или разомкнутыми. Если они замкнуты, то сработает реле Р13 и автомат в данной позиции "возьмет" две лампы, если разомкнуты, то реле Р13 не сработает и автомат отключит одну лампу.
Рассмотрим работу автомата на конкретных примерах. Допустим, человек первый ход сделал выключателем В1 - погасла лампа Л1. После нажатия кнопки Кн1 ("Ход автожата") контакты Кн1.3 замкнут цепь питания поляризованного реле КР16 и его якорь начнет вибрировать. Одновременно контакты Кн1.1 замкнут цепь питания реле Р12, которое сработает и контактами Р12.1 подключит к источнику питания реле Р13-Р15, причем реле Р15 сразу же сработает и контактами Р15.1 самоблокируется. При отпускании кнопки Кн1 сработает реле Р14 (контакты Р15.2 замкнуты) и его контакты Р14.2 подключат к источнику питания блок программы игры.
Предположим, что после отпускания кнопки Кн1 контакты КР16.1 поляризованного реле оказались замкнутыми, в результате чего реле Р13 сработало. Значит, после замыкания контактов Р14.2 сработают также реле Р1 и Р2 (контакты В 1.2 и Р13.1 замкнуты), контактами Р1.1 и Р2.1 они самоблокируются, а контактами Р1.2 и Р2.2 отключают лампы Л2 и Л3 - автомат сделает ответный ход. Необходимо отметить, что конденсатор С1 после отпускания кнопки Ход автомата разряжается через обмотку реле Р12 и таким образом задерживает его отпускание (а соответственно и отпускание реле Р13-Р15) для того, чтобы реле блока программы игры успели сработать и самоблокироваться. Время задержки определяется емкостью конденсатора С1 и должно быть около 0,4-0,5с.
Допустим далее, что человек при втором ходе выключателем В4.1 погасил лампу Л4. После нажатия кнопки "Ход автомата" (Кн1) устройство работает так же, как и при первом его ходе. Предположим, что на этот раз после отпускания кнопки Кн1 контакты КР16.1 оказались разомкнутыми и реле Р13 не сработало. В таком случае срабатывает реле Р4 (контакты В4.2 переключены), контактами Р4.1 оно самоблокируется, а контактами Р4.2 отключает лампу Л5 - автомат делает свой второй ход.
Далее человек делает третий ход - выключателем В6.1 гасит лампу Л6. Тогда после нажатия и отпускания кнопки Кн1 ("Ход автомата") срабатывает реле Р6, контактами Р6.1 оно самоблокируется, контактами Р6.2 отключает лампу Л7 и включает лампу Л8, подсвечивающую табло "Вы выиграли".
Поскольку автомат проиграл, надо нажать кнопку Кн2 ("Наказание"). При этом реле Р8 блока памяти сработает (контакты Р4.3 и Р6.3 замкнуты) и контактами Р8.1 самоблокируется. Контакты Р8.2 замыкаются - теперь в позиции 3 (возникающей, когда противник автомата делает ход выключателем В4 и ход должен сделать автомат) при нажатии кнопки "Ход автомата" будут срабатывать реле Р4 и Р5 и контактами Р4.2 и Р5.2 разрывать цепи питания ламп Л5 и Л6 независимо от того, какой выбор сделало реле КР16 - замкнуты или разомкнуты контакты P13.4. В последующих партиях игры автомат в этой позиции будет обеспечивать себе выигрыш.
Нажав кнопку Кн3 ("Сброс") - при этом отпускают все ранее сработавшие реле блока программы игры - и установив выключатели В1-В7 в исходное положение, противник автомата может начинать новую партию игры.
Предположим, что в следующей партии первым ходом человек выключателями В1 и В2 "берет" лампы Л1 и Л2. Пусть после нажатия и опускания кнопки "Ход автомата" контакты КР16.1 поляризованного реле КР16 будут разомкнуты. Сработает реле Р2, контактами Р2.1 оно самоблокируется, контактами Р2.2 отключит лампу Л3. Допустим, второй ход человек делает выключателем В4 - "берет" лампу Л4. Теперь при ходе автомата сработают реле Р4 и Р5 (контакты Р8.2 замкнуты),- самоблокируются контактами Р4.1 и Р5.1, а контактами Р4.2 и Р5.2 отключат лампы Л5 и Л6. Как видим, в этой партии игры автомат в позиции 3, в отличие от предыдущей партии, берет 2 предмета (автомат "обучился" и играет оптимально) и тем самым обеспечивает себе выигрыш, ибо следующим ходом человек вынужден выключить последнюю лампу Л7 (выключателем В7.1). При этом загорается лампа Л9, подсвечивающая табло "Вы проиграли".
Аналогично работает автомат при всех других вариантах игры. Чтобы пройти полный курс обучения и в дальнейшем играть безупречно, автомат должен проиграть пять партий (при этом в блоке памяти сработают реле Р7-Р11 и автомат "запомнит", как не следует играть).
В конструкции описанного автомата можно использовать: Л1-Л9 - лампы накаливания ЛН 3,5В х 0,28А; P1-P6 - реле РЭС-22 (паспорт РФ4.500.131); Р7-Р11, Р14 и Р15 - реле РЭС-9 (паспорт РС4.524.200); Р12 - реле РСМ-1 (паспорт Ю.171.81.37); Р13 - реле РС-13 (паспорт РС4.523.017); КР16 - реле РП-4; В1-В7 - выключатели ТП1-2; В8 - ТВ2-1. Кнопки могут быть самодельными, изготовленными из контактных пружин реле. Силовой трансформатор Тр намотан на сердечнике из пластин Ш32, толщина пакета 20мм (обмотка I содержит 1220 витков, обмотка II - 150 витков, обмотка III - 20 витков провода ПЭВ-1 или ПЭЛ-0,47).

Рис. 55. Схема обучающегося автомата с последовательным перебором стратегий.
В описанном играющем автомате выбор его стратегии (взять один или два предмета) определяется датчиком двух равновероятных стратегий - контактами поляризованного реле. Можно, однако, применить и другой принцип - последовательный перебор стратегий. Применительно к нашему автомату это будет выглядеть так: в любой позиции автомат своим ходом отключает одну лампочку; если он выиграет, то и в последующих партиях будет в этой позиции выключать одну лампочку; если же он проиграет, то меняет стратегию - в этой же позиции в следующий раз будет выключать две лампочки. Принципиальная схема такого автомата с последовательным перебором стратегий изображена на рис.55. После срабатывания реле Р7 блока памяти автомат будет выключать две лампочки в позиции 4, после срабатывания реле Р8 - две лампочки в позиции 6, после срабатывания реле Р9 - две лампочки в позиции 3. В остальном он работает так же, как первый автомат.
Используя рассмотренные принципы обучения, можно сконструировать обучающиеся автоматы для таких игр, как "Побеждает последний", "Набери чет", "Ход конем" и другие комбинаторные игры. Представляет большой интерес создание таких самообучающихся играющих автоматов, у которых процесс обучения осуществлялся бы не только отбрасыванием проигрышных стратегий, но и увеличением вероятности выбора выигрышных стратегий.
Последний раз редактировалось: Gudleifr (Ср Июл 26, 2023 12:37 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
Прежде чем перейти к шахматам, посмотрим на программирование старой игры OGRE (на гексовом поле компьютер управляет одним супертанком Ogre, а человек - большим количеством танков поменьше).
СТРАТЕГИИ ПРОГРАММИРОВАНИЯ OGRE (ОТ АВТОРА ИГРЫ)
ОСНОВЫ
Все нижеследуещее относится к игре в которой одиночный Ogre вторгается на вражескую территорию и должен, во-первых, обязательно уничтожить КП противника, во-вторых, если возможно, уничтожить вражеские танки и, в-третьих, если удасться, унести из зоны боя ноги.
Согласно такому распределению приоритетов, основным вопросом был и остается: "Как уничтожить КП?"
Понятное дело, огнем или гусеницами, но до этого еще нужно дожить.
В разгар же боя основной задачей является не дать себя отвлечь на второстепенные цели, пусть даже очень соблазнительные.
ОБОРОНИТЕЛЬНЫЕ СХЕМЫ ПРОТИВНИКА
Как уже говорилось выше, нет им числа, но все сводятся к трем основным типам, требующим разного подхода.
***
АРТИЛЛЕРИЙСКАЯ ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: суть этой стратегии в создании на изрядном расстоянии от КП защитного экрана из 3-х и более гаубиц. Их зоны поражения перекрываются таким образом, чтобы прорывающийся Ogre подвергался массированному обстрелу. Преодолев этот рубеж, он должен потерять все свое оружие и почти весь движитель, становясь легкой добычей для оставшихся сил обороны.
ОТВЕТНЫЕ МЕРЫ: кибертанк должен сразу определить, что имеет дело с этим родом обороны и начать маневр: попытаться уклониться в сторону, уменьшив плотность поражающего артиллерийского огня и сманить за собой большинство танков. Разделаться с последними вне досягаемости гаубиц и, вернувшись, прорвать поредевшую оборону.
Иногда удается нащупать слабое звено в стене гаубиц (непростреливаемый участок или слабо прикрытую краеугольную гаубицу), тогда - вперед туда на полных порах. Как можно быстрее и со всей силы.
***
GEV-ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: организуя оборонительные порядки исключительно или почти исключительно из GEV (маленькие юркие ховеркрафты), защитник поступает совершенно не так, как в первом варианте: вместо сосредоточенного огня нескольких танков - рассредоточенный огонь целого роя.
ОТВЕТНЫЕ МЕРЫ: зная начальное расположение GEV на поле, кибертанк выбирает точку вторжения в самом уязвимом месте - там, где их ряд самый тонкий. Затем надо перемещаться по полю сложным зигзагом, уничтожая группки зарвавшихся GEV. Идти прямо к КП в такой ситуации обычно не получается.
***
СТАНДАРТНАЯ ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: ею считается оборона, состоящая из смеси различных танков. Например против MkIII могут быть выставлены 20 отделений пехоты, 2 гаубицы, 2 тяжелых и 2 ракетных танка и 4 GEV. Стандартная оборона отличается гибкостью, и вторгающемуся кибертанку трудно заранее предугадать, какую именно часть ему постараются отстрелить в первую очередь. Кроме того, используя подобную смесь танков, обороняющиеся могут создать области с беспрецендентной плотностью огня.
ОТВЕТНЫЕ МЕРЫ: главная задача не попадать под огонь всех вражеских танков разом, но умелым маневром оттягивать на себя отдельные группы противника и уничтожать их поодиночке.
***
ВТОРЖЕНИЕ
Большинство командующих обороняющихся располагает КП посредине задней кромки поля. В этом случае кибертанку, чтобы сократить путь к нему, ничего не остается, кроме ответного вторжения по центру поля. Однако, возможны исключения. Иногда, например, используя стандартную оборонную стратегию, КП размещают в одном из углов поля. Тогда имеет смысл начать вторжение с противоположного угла, провоцируя танки обороны на выход из зоны наибольшей концентрации огня.
ПОЛЬЗОВАНИЕ РАКЕТАМИ
Бесспорно, ракеты - самое сильное и дальнобойное оружие в арсенале кибертанка, и некоторые программисты велят ему приберечь одну-две на черный день. Однако, как показывает опыт, такое решение слишком часто ведет к проигрышу. В большинстве случаев неиспользованные ракеты просто уничтожаются вражеским огнем. Рекомендуется беречь ракеты только тогда, когда с ближайшими танками обороняющихся можно спокойно разобраться при помощи пушек. Это не значит, что стоит тратить ракету на отделение пехоты, но КП, гаубица или танк, загораживающий путь,- вполне достойные цели. Как было сказано более ста лет назад создателями первого ядерного оружия: "Используете его, или потеряете".
ИСПОЛЬЗОВАНИЕ СВОЙСТВ МЕСТНОСТИ
Так как MkIII и MkV практически не чувствительны к местности, то во многих программах ей не уделяется никакого значения (кроме обхода кратеров и контроля за границами поля). Это неправильно. Горы щебня не задержат кибертанк, но препятствуют перемещениям его врагов - танков. Грешно этим не воспользоваться, чтобы облегчить себе отрыв от противника.
Некоторые программисты заставляют кибертанк красться вдоль самой кромки поля, считая, что так его можно атаковать только с одной стороны. Это отчасти верно, но опыт последних боев показывает, что жертвовать свободой маневра ради безопасности не имеет смысла. Рекомендуется прокладывать путь где-то между центром и краем зоны боя.
***
ИСКУССТВЕННЫЙ РАЗУМ OGRE
Задача разработчика киберразума (OAI - Ogre's Artificial Intelligence) - определить варианты действия Ogre в каждой ситуации. Для этого понадобились сложные исследования и разработки экспертов и многочасовое тестирование различных концепций поведения. Игра - вероятностная, результаты всех стрельб в общем случайны и просчет всех возможных исходов на каждом ходу представляется очень сложным.
Как говорилось выше, самая главная задача Ogre - уничтожить КП, и, если удасться, уцелеть. Для решения этой задачи Ogre должен по пути к КП уничтожить значительное число защитников и не получить при этом смертельных повреждений. Понятно, и вслепую ломиться сквозь строй, и пытаться перестрелять врагов с места бесполезно.
В мыслительных цепях Ogre можно выделить два контура: стратегический (выцеливание КП, гаубиц, отслеживание маршрута) и тактический (борьба с танками противника). Второй подчинен первому.
В каждый момент имеется несколько гексов, куда Ogre может переместиться в этом ходу.
Тактический блок Ogre пытается их оценить:
1. расстояние до стратегической цели (КП или гаубицы);
2. суммарная стоимость танков, поражаемых из данного гекса;
3. величина ущерба, которую Ogre получит на этом гексе.
Огре остается для каждого доступного гекса:
1. найти путь, ведущий к нему;
2. определить стоимость атакуемых оттуда танков (ATTACKVAL);
3. определить ущерб, который Ogre там получит (DAMAGEVAL);
4. определить, исходя из двух этих величин и расстояния до стратегической цели, ценность гекса
Остается выбрать самый "ценный" гекс.
Каждому танку мозг Ogre приписывает некоторую стоимость. Кроме того он определяет с какой вероятностью танк будет поражен (%HIT). Чем больше мощи оружия Ogre израсходует на цель, тем больше эта величина. После завершения целераспределения подсчитывается сумма относительных стоимостей целей (т.е. стоимостей, помноженных на %HIT), она и берется в качестве ATTACKVAL.
Подобным образом используются %HIT и для подсчета ущерба, грозящего Ogre на гексе - DAMAGEVAL.
Остаток главы будет посвящен более подробному освещению процедуры оценивания гексов.
***
СТРАТЕГИЧЕСКИЕ РАСЧЕТЫ
Чрезвычайная огневая мощь гаубиц не дает возможности пренебречь ими в стратегических расчетах. Если бы их не было можно было бы ограничиться прогнозированием партии только на 1 ход вперед (обеспечив только постоянное смещение в сторону КП). Однако, Ogre постоянно должен решать, следует ли считать следующей стратегической целью КП или особо опасную гаубицу (или их последовательный ряд).
Можно четко выделить две стратегические цели: 1) приближение к КП и 2) сокращение числа обстреливающих Ogre гаубиц.
Стратегия, выбираемая Ogre будет сильно зависеть от числа выставленных защитником гаубиц. Вариантов очень много, от выбора к качестве цели только КП до последовательного перебора всех гаубиц. Самым выгодным вариантом следует признать тот, который приведет Ogre к КП за минимальное число ходов и с минимальными потерями.
Как только (и не раньше) КП уничтожен, появляется новая стратегическая цель - покинуть зону боя. Чем раньше, тем лучше.
***
ТАКТИЧЕСКИЕ РАСЧЕТЫ
Рассматривается полное число доступных Ogre путей, ведущих из данного гекса - 58 для каждой из 6 его сторон.
ВЫБОР ПУТИ
Использовались следующие обозначения: исходный гекс пути - "S", конечный - "T". Стрелки отмечают направление каждого шага Ogre. Цифры показывают число шагов. Заштрихованные круги - кратеры (непроходимые места). На рис.1 иллюстрируется двухшажное перемещение Ogre.
Ogre должен рассмотреть все пути длиной от 1 до его максимально возможной скорости.
Некоторые пути - таранные (RPATH), т.е. такие, которые не ведут прямо к целевому гексу, расходуя ресурсы движителя для того, чтобы таранить танки врага (давить пехоту). На рис.2 показан такой путь с планируемой затратой лишего пункта скорости на повторный таран противника на целевом гексе.

Если при рассмотрении обходного RPATH не нашлось никакого врага, которого можно было бы протаранить, то дальше для него расчеты не производятся, так как ATTACKVAL и DAMAGEVAL целевого уже рассчитаны при рассмотрении соответствующего прямого пути.
Вклад таранов в ATTACKVAL следующий: подвижный танк имеет 50 %HIT (скорее, нужно учитывать 75 %HIT обездвиживания и 100 %HIT уничтожения обездвиженного или неподвижного). Численность пехоты уменьшится на 1 с 100%HIT.
При таране танков растет и DAMAGEVAL - по 1-2 единицы движителя за раз. Эта потеря может значительно повлиять на желание Ogre таранить.
После того, как расчет произведен и Ogre начал двигаться, имеет сиысл приостанавливаться и пересчитывать ценности гексов после уничтожения протараненного подвижного танка. Это важно, так как в силу незначительности (50 %HIT) шанса уничтожения подвижного танка в расчетах учитывались только 75 %HIT обездвиживания.
Ogre должен иметь не менее 3 единиц движителя для тарана тяжелого танка и не менее 2-х для тарана остальных (кроме КП), чтобы не остаться неподвижным.
РАСЧЕТ ATTACKVAL
При этом расчете, как говорилось выше, каждому виду танков защитника приписывалась некоторая базовая ATTACKVAL(защитник). Например, так:
Совокупная ATTACKVAL рассчитывается как их условная сумма (с учетом целераспределения и вероятности поражения). Целеуказание происходит в следующем порядке:
1. Противопехотные орудия
2. Дополнительные орудия
3. Основные орудия
4. Ракеты
Если все защитники не дальше 3-х гексов, то основные орудия рассматриваются раньше дополнительных, так как не нужно беречь их для более дальних целей.
Для начала, каждому защитнику вблизи гекса приписывается 0 %HIT, затем эта величина увеличивается по мере распределения ударов Ogre. Когда целераспределение закончено, остается перемножить ATTACKVALUE(защитник) на соответствующие %HIT и, просуммировав, получить суммарную ATTACKVALUE.
Для определения %HIT используется отношение силы удара Ogre к защите цели:
Отделение пехоты считается по столбцу поврежденных.
1. ПРОТИВОПЕХОТНЫЕ ОРУДИЯ (AP)
Так как на уничтожение каждого пехотного подразделения этим оружием отводится только одна попытка, воспользоваться ей надо с наибольшим эффектом. Приводимый ниже алгоритм рассчитан на поражение как можно большего числа целей. Поэтому начинает с соотношения сил 1/2.
Делается это так:
Составляется список пехоты в радиусе 1 гекса от Ogre в порядке убывания силы, далее распределяй удары, пока не кончаться силы:
- Ставь 1/2 снизу вверх по списку
- Ставь 1 сверху вниз
- Ставь 2 сверху вниз, кроме отдельных отделений
- Ставь 3 сверху вниз, кроме отдельных отделений
- Ставь 4 сверху вниз, кроме отдельных отделений
- Ставь 2 сверху вниз, включая отделения
- Ставь 3 сверху вниз, включая отделения
- Ставь 4 сверху вниз, включая отделения
- Добавь остаток сил к последней строчке
На рис.3 представлен пример целуказания противопехотных орудий против 9 отделений пехоты размещенных на 5 гексах. (D - число отделений, AP - сила удара.)
Понятно, что разместить 1/2 против отдельных отделений невозможно, и что на последем шаге AP на всех не хватит.
После размещения всех AP остается посчитать %HIT, так, например, выстрел силой 2 по взводу (соотношение сил 1/2) даст 25% .
2. ДОПОЛНИТЕЛЬНЫЕ ОРУДИЯ (SB)
Составляем список досягаемых целей.
Добавляем один выстрел для самой ценной цели с самым низким %HIT. Если выбор неоднозначен, выбираем танк ближайший к текущей стратегической цели.
Перерасчитываем %HIT цели. Повторяем процедуру, пока не кончаться орудия или пока все цели не будут иметь 100 %HIT.
3. ОСНОВНЫЕ ОРУДИЯ (MB)
Аналогично дополнительным.
4. РАКЕТЫ (MSL)
В принципе, тоже самое, но хотелось бы попридержать их для стратегических целей. Расходовать ракеты без оглядки можно только под угрозой их немедленного уничтожения.
После того, как все %HIT вычислены, находится и результирующая ATTACKVAL.
РАСЧЕТ DAMAGEVAL
В него вносят свой вклад все защитники, способные нанести удар по гексу.
Следует как-то соотнести рассчитанные величины ATTACKVAL и DAMAGEVAL, для чего вводится некоторый масштабный коэффициент.
Формула выглядит примерно так:
DAMAGEVAL = (сумма ударов защитников) * DAMAGECONSTANT
Изменение DAMAGECONSTANT сделает Ogre более агрессивным или, наоборот, осторожным.
Понятно, что при расчете возможности ударов защитников принимаются во внимание их дальнобойность, скорость перемещения и ландшафт. Сила затников уменьшается на соответствующие %HIT.
ВКЛЮЧЕНИЕ В РАСЧЕТЫ СТРАТЕГИЧЕСКИХ ЦЕЛЕЙ
TARGETVAL - переменная, учитывающая близость гекса к направлению на стратегическую цель.
Возможны три варианта.
1. Приближение (положительное значение)
2. Отсутствие приближения (отрицательное значение)
3. Удаление (большое отрицательное значение)
Когда Ogre движется к цели, кажется оптимальным делать это на полной скорости. Иногда же более выгодным будет сделать остановку для уничтожения большего числа защитников.
Техника расчета TARGETVAL состоит в делении некой константы на максимальную скорость Ogre и умножении результата на число гексов, приближающих Ogre к цели (удаляющих - со знаком минус), по достижении целевого гекса.
Возможно влияние некоторых факторов:
- Ogre желательно сделать крюк для уничтожения беззащитного защитника. Т.е. значительная величина разности ATTACKVAL и DAMAGEVAL должна перевесить TARGETVAL.
- Находящийся под обстрелам гаубицы Ogre может сделать ее текущей стратегической целью, чтобы побыстрее уничтожить.
- Если текущая цель уже имеет хотя бы 50 %HIT, имеет смысл переключится на следующую, а не подходить ближе.
- Чтобы удержать Ogre от кружения вокруг цели, отсутствие приближения должно иметь отрицательную ценность.
Как только все факторы оценены, дается окончательная оценка гексу.
Примерная формула выглядит так:
HEXVAL = ATTACKVAL - DAMAGEVAL + TARGETVAL
Остается повторить вычисления для всех доступных гексов и путей и выбрать самый выгодный.
СТРАТЕГИИ ПРОГРАММИРОВАНИЯ OGRE (ОТ АВТОРА ИГРЫ)
ОСНОВЫ
Все нижеследуещее относится к игре в которой одиночный Ogre вторгается на вражескую территорию и должен, во-первых, обязательно уничтожить КП противника, во-вторых, если возможно, уничтожить вражеские танки и, в-третьих, если удасться, унести из зоны боя ноги.
Согласно такому распределению приоритетов, основным вопросом был и остается: "Как уничтожить КП?"
Понятное дело, огнем или гусеницами, но до этого еще нужно дожить.
В разгар же боя основной задачей является не дать себя отвлечь на второстепенные цели, пусть даже очень соблазнительные.
ОБОРОНИТЕЛЬНЫЕ СХЕМЫ ПРОТИВНИКА
Как уже говорилось выше, нет им числа, но все сводятся к трем основным типам, требующим разного подхода.
***
АРТИЛЛЕРИЙСКАЯ ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: суть этой стратегии в создании на изрядном расстоянии от КП защитного экрана из 3-х и более гаубиц. Их зоны поражения перекрываются таким образом, чтобы прорывающийся Ogre подвергался массированному обстрелу. Преодолев этот рубеж, он должен потерять все свое оружие и почти весь движитель, становясь легкой добычей для оставшихся сил обороны.
ОТВЕТНЫЕ МЕРЫ: кибертанк должен сразу определить, что имеет дело с этим родом обороны и начать маневр: попытаться уклониться в сторону, уменьшив плотность поражающего артиллерийского огня и сманить за собой большинство танков. Разделаться с последними вне досягаемости гаубиц и, вернувшись, прорвать поредевшую оборону.
Иногда удается нащупать слабое звено в стене гаубиц (непростреливаемый участок или слабо прикрытую краеугольную гаубицу), тогда - вперед туда на полных порах. Как можно быстрее и со всей силы.
***
GEV-ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: организуя оборонительные порядки исключительно или почти исключительно из GEV (маленькие юркие ховеркрафты), защитник поступает совершенно не так, как в первом варианте: вместо сосредоточенного огня нескольких танков - рассредоточенный огонь целого роя.
ОТВЕТНЫЕ МЕРЫ: зная начальное расположение GEV на поле, кибертанк выбирает точку вторжения в самом уязвимом месте - там, где их ряд самый тонкий. Затем надо перемещаться по полю сложным зигзагом, уничтожая группки зарвавшихся GEV. Идти прямо к КП в такой ситуации обычно не получается.
***
СТАНДАРТНАЯ ОБОРОНА
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ: ею считается оборона, состоящая из смеси различных танков. Например против MkIII могут быть выставлены 20 отделений пехоты, 2 гаубицы, 2 тяжелых и 2 ракетных танка и 4 GEV. Стандартная оборона отличается гибкостью, и вторгающемуся кибертанку трудно заранее предугадать, какую именно часть ему постараются отстрелить в первую очередь. Кроме того, используя подобную смесь танков, обороняющиеся могут создать области с беспрецендентной плотностью огня.
ОТВЕТНЫЕ МЕРЫ: главная задача не попадать под огонь всех вражеских танков разом, но умелым маневром оттягивать на себя отдельные группы противника и уничтожать их поодиночке.
***
ВТОРЖЕНИЕ
Большинство командующих обороняющихся располагает КП посредине задней кромки поля. В этом случае кибертанку, чтобы сократить путь к нему, ничего не остается, кроме ответного вторжения по центру поля. Однако, возможны исключения. Иногда, например, используя стандартную оборонную стратегию, КП размещают в одном из углов поля. Тогда имеет смысл начать вторжение с противоположного угла, провоцируя танки обороны на выход из зоны наибольшей концентрации огня.
ПОЛЬЗОВАНИЕ РАКЕТАМИ
Бесспорно, ракеты - самое сильное и дальнобойное оружие в арсенале кибертанка, и некоторые программисты велят ему приберечь одну-две на черный день. Однако, как показывает опыт, такое решение слишком часто ведет к проигрышу. В большинстве случаев неиспользованные ракеты просто уничтожаются вражеским огнем. Рекомендуется беречь ракеты только тогда, когда с ближайшими танками обороняющихся можно спокойно разобраться при помощи пушек. Это не значит, что стоит тратить ракету на отделение пехоты, но КП, гаубица или танк, загораживающий путь,- вполне достойные цели. Как было сказано более ста лет назад создателями первого ядерного оружия: "Используете его, или потеряете".
ИСПОЛЬЗОВАНИЕ СВОЙСТВ МЕСТНОСТИ
Так как MkIII и MkV практически не чувствительны к местности, то во многих программах ей не уделяется никакого значения (кроме обхода кратеров и контроля за границами поля). Это неправильно. Горы щебня не задержат кибертанк, но препятствуют перемещениям его врагов - танков. Грешно этим не воспользоваться, чтобы облегчить себе отрыв от противника.
Некоторые программисты заставляют кибертанк красться вдоль самой кромки поля, считая, что так его можно атаковать только с одной стороны. Это отчасти верно, но опыт последних боев показывает, что жертвовать свободой маневра ради безопасности не имеет смысла. Рекомендуется прокладывать путь где-то между центром и краем зоны боя.
***
ИСКУССТВЕННЫЙ РАЗУМ OGRE
Задача разработчика киберразума (OAI - Ogre's Artificial Intelligence) - определить варианты действия Ogre в каждой ситуации. Для этого понадобились сложные исследования и разработки экспертов и многочасовое тестирование различных концепций поведения. Игра - вероятностная, результаты всех стрельб в общем случайны и просчет всех возможных исходов на каждом ходу представляется очень сложным.
Как говорилось выше, самая главная задача Ogre - уничтожить КП, и, если удасться, уцелеть. Для решения этой задачи Ogre должен по пути к КП уничтожить значительное число защитников и не получить при этом смертельных повреждений. Понятно, и вслепую ломиться сквозь строй, и пытаться перестрелять врагов с места бесполезно.
В мыслительных цепях Ogre можно выделить два контура: стратегический (выцеливание КП, гаубиц, отслеживание маршрута) и тактический (борьба с танками противника). Второй подчинен первому.
В каждый момент имеется несколько гексов, куда Ogre может переместиться в этом ходу.
Тактический блок Ogre пытается их оценить:
1. расстояние до стратегической цели (КП или гаубицы);
2. суммарная стоимость танков, поражаемых из данного гекса;
3. величина ущерба, которую Ogre получит на этом гексе.
Огре остается для каждого доступного гекса:
1. найти путь, ведущий к нему;
2. определить стоимость атакуемых оттуда танков (ATTACKVAL);
3. определить ущерб, который Ogre там получит (DAMAGEVAL);
4. определить, исходя из двух этих величин и расстояния до стратегической цели, ценность гекса
Остается выбрать самый "ценный" гекс.
Каждому танку мозг Ogre приписывает некоторую стоимость. Кроме того он определяет с какой вероятностью танк будет поражен (%HIT). Чем больше мощи оружия Ogre израсходует на цель, тем больше эта величина. После завершения целераспределения подсчитывается сумма относительных стоимостей целей (т.е. стоимостей, помноженных на %HIT), она и берется в качестве ATTACKVAL.
Подобным образом используются %HIT и для подсчета ущерба, грозящего Ogre на гексе - DAMAGEVAL.
Остаток главы будет посвящен более подробному освещению процедуры оценивания гексов.
***
СТРАТЕГИЧЕСКИЕ РАСЧЕТЫ
Чрезвычайная огневая мощь гаубиц не дает возможности пренебречь ими в стратегических расчетах. Если бы их не было можно было бы ограничиться прогнозированием партии только на 1 ход вперед (обеспечив только постоянное смещение в сторону КП). Однако, Ogre постоянно должен решать, следует ли считать следующей стратегической целью КП или особо опасную гаубицу (или их последовательный ряд).
Можно четко выделить две стратегические цели: 1) приближение к КП и 2) сокращение числа обстреливающих Ogre гаубиц.
Стратегия, выбираемая Ogre будет сильно зависеть от числа выставленных защитником гаубиц. Вариантов очень много, от выбора к качестве цели только КП до последовательного перебора всех гаубиц. Самым выгодным вариантом следует признать тот, который приведет Ogre к КП за минимальное число ходов и с минимальными потерями.
Как только (и не раньше) КП уничтожен, появляется новая стратегическая цель - покинуть зону боя. Чем раньше, тем лучше.
***
ТАКТИЧЕСКИЕ РАСЧЕТЫ
Рассматривается полное число доступных Ogre путей, ведущих из данного гекса - 58 для каждой из 6 его сторон.
ВЫБОР ПУТИ
Использовались следующие обозначения: исходный гекс пути - "S", конечный - "T". Стрелки отмечают направление каждого шага Ogre. Цифры показывают число шагов. Заштрихованные круги - кратеры (непроходимые места). На рис.1 иллюстрируется двухшажное перемещение Ogre.
Ogre должен рассмотреть все пути длиной от 1 до его максимально возможной скорости.
Некоторые пути - таранные (RPATH), т.е. такие, которые не ведут прямо к целевому гексу, расходуя ресурсы движителя для того, чтобы таранить танки врага (давить пехоту). На рис.2 показан такой путь с планируемой затратой лишего пункта скорости на повторный таран противника на целевом гексе.

Если при рассмотрении обходного RPATH не нашлось никакого врага, которого можно было бы протаранить, то дальше для него расчеты не производятся, так как ATTACKVAL и DAMAGEVAL целевого уже рассчитаны при рассмотрении соответствующего прямого пути.
Вклад таранов в ATTACKVAL следующий: подвижный танк имеет 50 %HIT (скорее, нужно учитывать 75 %HIT обездвиживания и 100 %HIT уничтожения обездвиженного или неподвижного). Численность пехоты уменьшится на 1 с 100%HIT.
При таране танков растет и DAMAGEVAL - по 1-2 единицы движителя за раз. Эта потеря может значительно повлиять на желание Ogre таранить.
После того, как расчет произведен и Ogre начал двигаться, имеет сиысл приостанавливаться и пересчитывать ценности гексов после уничтожения протараненного подвижного танка. Это важно, так как в силу незначительности (50 %HIT) шанса уничтожения подвижного танка в расчетах учитывались только 75 %HIT обездвиживания.
Ogre должен иметь не менее 3 единиц движителя для тарана тяжелого танка и не менее 2-х для тарана остальных (кроме КП), чтобы не остаться неподвижным.
РАСЧЕТ ATTACKVAL
При этом расчете, как говорилось выше, каждому виду танков защитника приписывалась некоторая базовая ATTACKVAL(защитник). Например, так:
| 1 | КП | 255 |
| 2 | Гаубица | 200 |
| 3 | GEV | 100 |
| 4 | Ракетный танк | 100 |
| 5 | Тяжелый танк | 100 |
| 6 | Взвод пехоты | 60 |
| 7 | 2 отделения пехоты | 40 |
| 8 | Отделение пехоты | 20 |
1. Противопехотные орудия
2. Дополнительные орудия
3. Основные орудия
4. Ракеты
Если все защитники не дальше 3-х гексов, то основные орудия рассматриваются раньше дополнительных, так как не нужно беречь их для более дальних целей.
Для начала, каждому защитнику вблизи гекса приписывается 0 %HIT, затем эта величина увеличивается по мере распределения ударов Ogre. Когда целераспределение закончено, остается перемножить ATTACKVALUE(защитник) на соответствующие %HIT и, просуммировав, получить суммарную ATTACKVALUE.
Для определения %HIT используется отношение силы удара Ogre к защите цели:
| Отношение сил | %HIT | |
| подвижных | поврежденных | |
| менее 1/2 | 0% | 0% |
| 1/2 | 25% | 33% |
| 1 | 50% | 67% |
| 2 | 67% | 83% |
| 3 | 83% | 100% |
| 4 | 92% | 100% |
| лучше | 100% | 100% |
1. ПРОТИВОПЕХОТНЫЕ ОРУДИЯ (AP)
Так как на уничтожение каждого пехотного подразделения этим оружием отводится только одна попытка, воспользоваться ей надо с наибольшим эффектом. Приводимый ниже алгоритм рассчитан на поражение как можно большего числа целей. Поэтому начинает с соотношения сил 1/2.
Делается это так:
Составляется список пехоты в радиусе 1 гекса от Ogre в порядке убывания силы, далее распределяй удары, пока не кончаться силы:
- Ставь 1/2 снизу вверх по списку
- Ставь 1 сверху вниз
- Ставь 2 сверху вниз, кроме отдельных отделений
- Ставь 3 сверху вниз, кроме отдельных отделений
- Ставь 4 сверху вниз, кроме отдельных отделений
- Ставь 2 сверху вниз, включая отделения
- Ставь 3 сверху вниз, включая отделения
- Ставь 4 сверху вниз, включая отделения
- Добавь остаток сил к последней строчке
На рис.3 представлен пример целуказания противопехотных орудий против 9 отделений пехоты размещенных на 5 гексах. (D - число отделений, AP - сила удара.)
| Сортируем | D | 3 | 2 | 2 | 1 | 1 |
| Размещаем 1/2 | D | 3 | 2 | 2 | 1 | 1 |
| AP | 2 | 1 | 1 | 1 | 1 | |
| Размещаем 1 | D | 3 | 2 | 2 | 1 | 1 |
| AP | 3 | 2 | 1 | 1 | 1 |
После размещения всех AP остается посчитать %HIT, так, например, выстрел силой 2 по взводу (соотношение сил 1/2) даст 25% .
2. ДОПОЛНИТЕЛЬНЫЕ ОРУДИЯ (SB)
Составляем список досягаемых целей.
Добавляем один выстрел для самой ценной цели с самым низким %HIT. Если выбор неоднозначен, выбираем танк ближайший к текущей стратегической цели.
Перерасчитываем %HIT цели. Повторяем процедуру, пока не кончаться орудия или пока все цели не будут иметь 100 %HIT.
3. ОСНОВНЫЕ ОРУДИЯ (MB)
Аналогично дополнительным.
4. РАКЕТЫ (MSL)
В принципе, тоже самое, но хотелось бы попридержать их для стратегических целей. Расходовать ракеты без оглядки можно только под угрозой их немедленного уничтожения.
После того, как все %HIT вычислены, находится и результирующая ATTACKVAL.
РАСЧЕТ DAMAGEVAL
В него вносят свой вклад все защитники, способные нанести удар по гексу.
Следует как-то соотнести рассчитанные величины ATTACKVAL и DAMAGEVAL, для чего вводится некоторый масштабный коэффициент.
Формула выглядит примерно так:
DAMAGEVAL = (сумма ударов защитников) * DAMAGECONSTANT
Изменение DAMAGECONSTANT сделает Ogre более агрессивным или, наоборот, осторожным.
Понятно, что при расчете возможности ударов защитников принимаются во внимание их дальнобойность, скорость перемещения и ландшафт. Сила затников уменьшается на соответствующие %HIT.
ВКЛЮЧЕНИЕ В РАСЧЕТЫ СТРАТЕГИЧЕСКИХ ЦЕЛЕЙ
TARGETVAL - переменная, учитывающая близость гекса к направлению на стратегическую цель.
Возможны три варианта.
1. Приближение (положительное значение)
2. Отсутствие приближения (отрицательное значение)
3. Удаление (большое отрицательное значение)
Когда Ogre движется к цели, кажется оптимальным делать это на полной скорости. Иногда же более выгодным будет сделать остановку для уничтожения большего числа защитников.
Техника расчета TARGETVAL состоит в делении некой константы на максимальную скорость Ogre и умножении результата на число гексов, приближающих Ogre к цели (удаляющих - со знаком минус), по достижении целевого гекса.
Возможно влияние некоторых факторов:
- Ogre желательно сделать крюк для уничтожения беззащитного защитника. Т.е. значительная величина разности ATTACKVAL и DAMAGEVAL должна перевесить TARGETVAL.
- Находящийся под обстрелам гаубицы Ogre может сделать ее текущей стратегической целью, чтобы побыстрее уничтожить.
- Если текущая цель уже имеет хотя бы 50 %HIT, имеет смысл переключится на следующую, а не подходить ближе.
- Чтобы удержать Ogre от кружения вокруг цели, отсутствие приближения должно иметь отрицательную ценность.
Как только все факторы оценены, дается окончательная оценка гексу.
Примерная формула выглядит так:
HEXVAL = ATTACKVAL - DAMAGEVAL + TARGETVAL
Остается повторить вычисления для всех доступных гексов и путей и выбрать самый выгодный.
Последний раз редактировалось: Gudleifr (Чт Окт 04, 2018 12:40 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
ШАХМАТНЫЕ АВТОМАТЫ
Во-первых, никаких коробков не хватит, во-вторых, самообучение путем полного перебора займет астрономическое время, поэтому применяются методы огульного оценивания. Конечно, можно выделить уровни абстракции, как в книгах Н.М.Амосова (человек, похоже, так и играет), но шахматному компьютеру "думать некогда, прыгать надо".
По сути, усложненный вариант расчетов OGRE.
Приведенный ниже фрагмент давно ходит по Сети и автора его, к сожалению, я не знаю.
***
АЛГОРИТМЫ ШАХМАТНЫХ ПРОГРАММ
ЧАСТЬ I. МИНИМАКС
Для начала рассмотрим более простую игру, например, крестики-нолики на доске 3*3. Рассмотрим начальную позицию. Тут у первого игрока (пусть это будут крестики) имеются 9 ходов (симметрию игнорируем). На каждый из них у соперника имеется 8 ответов, в свою очередь на каждый из них - по 7 ответов у крестиков и т.д. Максимальная длина игры - 9 полуходов (т.е. ходов одного из соперников), но она может кончиться и побыстрее, если кто-то выиграет. Возьмем листок бумаги и сверху нарисуем начальную позицию. Так как из нее возможно 9 ходов, проведем из нее 9 черточек (ветвей). В конце каждой ветви нарисуем позицию, которая получается после этого хода, и в свою очередь проведем из нее ветви - ходы, возможные из данной позиции. И так далее. Полученная структура называется деревом, ибо (1) у нее есть корень - начальная позиция, (2) у нее есть листья - позиции, из которых не идет ветвей, ибо один из игроков победил или случилась ничья, и (3) она отдаленно похоже на дерево, если лист бумаги перевернуть. Крестики-нолики - простая игра, ее дерево должно уместиться на (большом) листе бумаги, но можно себе представить так же нарисованное дерево для шахмат (вроде бы есть всего 10^50 или около того различных позиций, и правило 50 ходов ограничивает максимальную длину партии ~4000 ходов).
Разумеется, для такого листа бумаги не хватит всех атомов во вселенной, но представить такой лист все равно можно (я, во всяком случае, могу). Теперь припишем каждому листу его оценку. Пусть выигрыш крестиков будет -1, ноликов - плюс 1, а ничья будет нулем. Начнем "поднимать" оценку вверх по дереву - рассмотрим вершину, непосредственно стоящую над листом (терминальной позицией). Из нее ведет несколько ветвей (в крестиках-ноликах ровно одна, но это не важно). Представим, что ход сейчас - крестиков. Он заинтересован в получении -1, поэтому из нескольких вариантов он выберет вариант с минимальным значением (-1, если возможно, а если нет, то хотя бы 0). Таким образом, он выберет минимальную оценку из тех, какую имеют его "потомки", и припишет ее этой вершине. Уровнем выше - очередь хода "ноликов". Он, в свою очередь, заинтересован в получении +1, поэтому он будет максимизировать полученную снизу оценку.
В конце концов мы поднимем оценку до корня. В случае крестиков-ноликов это будет, разумеется, 0, ибо теоретическим результатом крестиков-ноликов при оптимальной игре обоих игроков является ничья. Что является теоретическим результатом шахмат науке неизвестно.
Разумеется, имея нарисованное дерево игры, играть очень легко - крестики должны выбирать ход, ведущий из текущей позиции в позицию с минимальной оценкой; нолики - в позицию с максимальной. Как легко понять, описанный алгоритм и есть обещанный минимакс.
***
ЧАСТЬ II. АЛЬФА-БЕТА
Внимательные читатели должны были догадаться что минимакс будет работать не только на деревьях с оценками плюс/минус один, но и на деревьях, листьям которых приписаны просто действительные числа. В дальнейшем мы будем рассматривать именно такие деревья (для объяснения основных алгоритмов я буду говорить о деревьях, забыв на время о собственно играх). Кроме того, я сосредоточусь именно на определении теоретического результата игры, т.е. на подъеме оценки вверх по дереву.
Минимакс - очень трудоемкий алгоритм. Для определения теоретического результата игры размечается абсолютно все дерево. Вопрос: нельзя ли, сохранив математическую корректность минимакса, обходить поменьше?
Оказывается, можно. Алгоритм называется альфа-бета. Легко доказать, что он дает те же результаты (не бойтесь, я этого делать не буду). Идея его, если объяснить на пальцах, такова:
Пусть есть корень, у него - 2 потомка, у каждого из них - по 3 потомка-листа. В корне - очередь хода мина, соответственно, в вершинах второго уровня - ход макса. Листам, которые потомки левого поддерева, приписаны оценки 0, 5, 10. Так как в вершинах второго подуровня мы максимизируем, левому поддереву припишем оценку 10.
Начинаем рассматривать правое поддерево. Пусть у самого левого листа оценка 100. А теперь - внимание! Мы знаем, что уровнем выше мы будем максимизировать. Это означает, что оценка "всего правого поддерева" будет уж не меньше 100, т.к. оставшиеся листья могут эту оценку только поднять. Кроме того мы знаем, что в начальной позиции мы будем минимизировать, и значит выберем левое поддерево, оценка которого 10.
Итого, мы получили оценку всего дерева, рассмотрев всего 4 позиции из 6. Шахматная аналогия - предположим, что я рассмотрел один из своих ходов, и обнаружил, что после всех ответов противника позиция равная. Я посмотрел, что происходит после другого моего хода, и обнаружил, что одним из своих ответов противник выигрывает коня. Рассматривать другие его ответы уже не имеет смысла - этот свой ход я уже не сделаю.
Просьба обратить внимание, что нам повезло, что в правом поддереве оценку 100 имеет самый левый лист. Будь он правым, и если при этом оба левых имеют оценку 7, нам пришлось бы обойти все 6 листьев. В наихудшем случае (мы всегда рассматриваем поддерево/лист с наилучшей оценкой в последнюю очередь) альфа-бета вырождается в минимакс. В наилучшем случае (наилучшее поддерево всегда рассматривается первым) рассматривается (очень грубо) 2*(sqrt(количества вершин, рассматриваемых минимаксом)).
Альфа-бета является строгим алгоритмом - ветвь отсекаются только после того, как хотя бы одного потомка оценили, и убедились, что значение этой ветви не повлияет на итоговый результат.
***
ЧАСТЬ III. ПРИМЕНЕНИЕ ТЕОРИИ К ПРАКТИКЕ
Разумеется, для реальных игр (шахмат, шашек, го) все дерево машина обойти не сможет. Поэтому идут на жульничество.
Во-первых, все дерево не строят - никакой памяти ни у какой машины не хватит. Хранят только текущую позицию и последовательность ходов, в нее приведшую. Идешь вглубь - сделай на доске (точнее, на ее аналоге в памяти) ход. Возвращаешься - возьми ход назад (это еще не жульничество, с теоретической точки зрения то, что мы явно дерево не строим, ничего не меняет).
Во-вторых и в главных, точная оценка заменяется на приближенную. А именно, после перебора на некоторую глубину, если не случилось мата или форсированной ничьи, вместо того, чтобы перебирать дальше, мы зовем оценочную функцию, которая приписывает текущей позиции (а точнее, всему поддереву, начинающемуся с текущей позиции), некоторую оценку. Как эта функция устроена - чуть позже, а пока главное: тут мы бесповоротно порвали с теорией, ибо оценочная функция есть нечто приближенное. Вот это и есть основное жульничество - альфа-бета была научно обоснована совсем в других условиях, и почему она после введения в нее оценочной функции работает в реальных играх, не совсем понятно (точнее говоря, есть сколько угодно работ на эту тему, но мне они представляются неубедительными). Более того, искусственно создан целый класс игр, где альфа-бета в таких условиях не работает.
Как устроена оценочная функция? Во-первых, надо просто сосчитать материал. Простейший вариант: пешка - 1, конь и слон - 3, ладья - 5, ферзь - 9.
Во-вторых, надо добавить позиционную оценку, и это есть самое сложное. Факторов много, в шахматных книжках приведены далеко не все, и главное - там сказано "это есть хорошо, а то плохо", а нам надо "это есть плюс половина, а то - минус три четверти". Соответственно, приходится сначала факторам приписывать веса с потолка, а потом отлаживать, вручную или пытаясь оптимизировать функцию в пространстве размерности несколько тысяч.
Вот несколько учитываемых факторов, с их ориентировочными весами (веса, разумеется, взяты с потолка, но за порядок величины ручаюсь):
- пара слонов - это плюс треть пешки,
- король прикрыт своими пешками - плюс пол-пешки,
- конь или ферзь близки к королю (своему или чужому) - плюс сотая пешки,
- слабая или отставшая пешка - минус четверть пешки,
- ладья на полуоткрытой вертикали - плюс пять сотых пешки,
- ладья на открытой вертикали - плюс одна десятая пешки,
- пара ладей на седьмой горизонтали - плюс пол-пешки,
- висящая фигура - минус четверть пешки, две висящих фигуры - минус пешка, три или больше - минус три пешки.
И так далее, и так далее. Кроме того, вес многих факторов может зависеть от ситуации на доске - например, пока ферзей не разменяли, прикрытость короля может оцениваться куда выше, чем после размена.
Таким образом, получаем позиционную оценку белых, складываем с материалом белых, делаем то же самое для черных, вычитаем одно из другого, и все сведено к одному числу. Красота!
К сожалению, не все так просто. Первые программы использовали только что описанный алгоритм - перебор на фиксированную глубину с вызовом там оценочной функции (если раньше мат не случился). И немедленно выяснилось, что мы можем прекратить перебор, например, в середине размена, или при "висящем" ферзе, или когда на доске стоит мат в один ход, и тот факт, что у атакующей стороны не хватает ладьи, не имеет никакого значения. Были попытки учитывать все это в оценочной функции, но она тогда становилась безумно сложной, и медленной. На каждый починенный таким образом случай начинало приходиться десять других, где замедление программы вследствие более медленной оценочной функции приводило к недостаточной глубине перебора и еще худшей игре. Кроме того, программа с маниакальным упорством пытается отсрочить свои неприятности, получая взамен худшие. "Ага, я перебираю на 7 полуходов, и вижу, что теряю слона. А вот отдам-ка я вот эту пешку, и тогда слона противник возьмет на 4 полухода позже, получится 11, я и не увижу. Итого минус 1, а не минус 3". Разумеется, при более глубоком переборе программа бы обнаружила, что в итоге у нее будет минус 4, но времени перебирать глубже нет. Это явление называется "эффектом горизонта", ибо программа стремится выпихнуть неприятности за горизонт видимости (или горизонт событий).
Попытки использовать селективные методы провалились с еще большим треском. Не удается понять, как человек играет в шахматы, и попытки сделать программы с "forward pruning" - отсечениями ветвей дерева без их предварительного рассмотрения, исходя из чисто шахматных принципов, проваливаются. Всегда находятся позиции, где программа отсекает нужный ход ("выплескивает воду месте с ребенком").
В конце концов стало понятно, что оценочную функцию можно звать только в спокойных позициях. Поэтому в конце основного перебора вставили еще один, упрощенный, где рассматриваются только взятия, превращения, и, возможно, шахи и ответы на шах. Так как таких ходов немного, "форсированный вариант" (так это называется) замедляет программу всего лишь на 20-50%, а сила игры резко увеличивается, т.к. программа не пытается оценить острые позиции.
Потом заметили, что серия ходов с разменом в конце будет рассмотрена на большую глубину, чем с разменом в середине, и сообразили, что некоторые варианты с разменом в середине тоже неплохо бы рассматривать поглубже. Возникла идея (не знаю, как по русски, пусть будет "углубление") - при переборе после некоторых ходов не уменьшать оставшуюся глубину перебора. Типичные углубления - после размена, при превращении пешки, при уходе от шаха. Идея та же, что и в форсированном варианте - ситуация на доске может кардинально измениться, этот вариант надо изучить поглубже.
Вот какова была ситуация в начале и середине 70-х.
***
ЧАСТЬ IV. УЛУЧШЕНИЯ
Как уже было сказано, за 40 лет никакой замены альфа-бете не найдено. В этом смысле наиболее печальна история Ботвинника. В течении 20 лет он занимался созданием шахматной программы. Он свято верил, что будучи чемпионом мира по шахматам и одновременно хорошо понимая программирование, он сумеет создать программу, которая будет играть на уровне чемпиона мира. Итог печален - программа так никогда не заиграла (по этому поводу кто-то хорошо сказал "Ботвинник только думает, что он знает, как он думает"). Что еще хуже, Ботвинник напечатал статью с описанием алгоритма в журнале International Computer Chess Association. Статья содержала результаты анализа нескольких позиций, якобы выполненных программой. Независимый анализ показал, что эти результаты являются фальсификацией - они не могли быть получены с использованием алгоритма Ботвинника.
Тем не менее, все эти годы качество игры шахматных программ улучшалось. Частично прогресс обьясняется быстрым развитием аппаратуры - персональные компьютеры по ряду параметров достигли уровня суперкомпьютеров конца 70-х (хотя по ряду параметров все еще серьезно отстают). Частично же "виновато" развитие алгоритмов - прорыва не было, но было множество эволюционных улучшений. Каковы главные из них?
(1) Использование библиотеки дебютов. Дебютная теория в шахматах хорошо разработана, и только естественно, что программы стали ее использовать. Более того, используют они ее лучше, чем гроссмейстеры, т.к. запомнить несколько миллионов позиций для машины проще простого.
(2) Использование баз данных с целиком просчитанными эндшпилями. Сейчас реальный предел для персонального компьютера - 5-фигурные эндшпили (считая королей). Используя такие базы данных, программы играют простые эндшпили безупречно. Более того, современные программы могут во время перебора вариантов "дотянуться" до базы данных из позднего миттельшпиля, когда на доске находится еще 10-15 фигур. Скромно замечу, что к созданию наиболее широко распространенных баз эндшпилей приложил руку я.
(3) Думанье во время хода противника. Мы сделали ход и теперь задумался противник. Зачем времени пропадать? Выберем наиболее разумный с нашей точки зрения ход, который он может сделать, и начнем думать над ответом на него. Если он сделает другой ход - ну и леший с ним, все равно не наше время было. Это - наиболее простой вариант использования времени противника, и он же наиболее эффективный, т.к. хорошие программы правильно предсказывают ~70% ходов противника.
(4) Различные эвристики, которые помогают отсортировать ходы в процессе перебора. Как уже отмечалось ранее, альфа-бета очень чувствительна к порядку, в котором анализируются ходы. При хорошем порядке она быстрее, причем быстрее принципиально. При этом алгоритм все равно остается экспоненциальным - перебор на N+1 полуходов работает в разы медленнее, чем на N полуходов, но по крайней мере возводимое в степень число ощутимо уменьшается. В типичной шахматной позиции возможно примерно 40 ходов, и для перебора на N полуходов минимаксу (он же альфа-бета с наихудшим упорядочением ходов) надо рассмотреть 40^N позиций. Альфа-бете с наилучшим упорядочением ходов надо рассмотреть примерно 6^N позиций - разница принципиальна. Эвристики применяются различные, например: первым делом попытаться съесть только что ходившую фигуру противника (она работает, т.к. большинство рассматриваемых ходов - полнейший идиотизм). Другая полезная эвристика (с меньшим приоритетом) - попытаться сделать ход, который был лучшим у соседа слева (она основана на том, что в похожих позициях наилучший ход часто один и тот же). Имеются еще несколько эвристик, но надеюсь, что идея в целом понятна.
(5) Итеративное углубление (iterative deepening). В реальной игре у программы имеется какое-то время на каждый ход, и им надо с умом распорядиться. Просто начинать перебор на фиксированную глубину, как делали ранние программы, неразумно - в сложной позиции с большим количеством разменов и/или шахов будет много вариантов, которые будут просчитываться очень глубока из-за "углублений", и программа может не успеть выполнить перебор. А одной из особенностей альфа-беты является то, что результатом незаконченного перебора воспользоваться нельзя - нет никакой гарантии, что найденный к моменту прерывания наилучший ход является хоть сколько-нибудь разумным. С другой стороны, в какой-нибудь закрытой позиции с малым количеством возможных ходов (branching factor) перебор может закончиться неожиданно быстро. Идея итеративного углубления состоит в том, что программа сначала производит перебор на глубину 1. Осталось время - перебираем на глубину 2. Осталось время - на глубину 3. И так далее. Разумеется, при этом приходится часть работы делать заново, но тут главное как раз экспоненциальный характер алгоритма. Следующий перебор занимает (грубо) в 6 раз больше времени, поэтому мы заново делаем максимум 1/6 работы. Зато у нас всегда есть ход от предыдущей итерации, которым мы можем воспользоваться, если нам придется прервать текущую. Возможны дальнейшие оптимизации - например, не начинать новую итерацию, если мы съели больше половины отведенного на думанье над этим ходом времени, ибо все равно почти наверняка не успеем.
(6) Хэш-таблицы (transposition tables). В шахматах мы имеем не дерево игры, а граф - очень часто после перестановки ходов мы получаем одну и ту же позицию. Возникла простая идея - занять всю память машины, которая иначе бы не использовалась, под запоминание уже рассмотренных позиций. Для каждой позиции надо хранить ее оценку (точнее, оценку поддерева под этой позицией), глубину перебора, наилучший ход, и некоторую служебную информацию. Теперь, начав разбирать позицию, надо взглянуть - а не встречали ли мы уже ее? Если не встречали, то поступаем как раньше. Если встречали, то смотрим, на какую глубину мы ее раньше разбирали. Если на такую же, как нам надо сейчас, или более глубокую, то можно воспользоваться старой оценкой и сэкономить время. Если же на меньшую, то мы все равно можем воспользоваться частью информации, а именно наилучшим ходом. Лучший ход для глубины N может оказаться лучшим и для глубины N+1. То есть, кроме своего изначального предназначения, хэаш-таблица оказывается полезна и для упорядочения ходов. Тут еще неожиданно помогает итеративное углубление - когда мы начинаем следующую итерацию, хэш-таблица оказывается заполнена информацией от предыдущей, и до какого-то момента (до глубины 1) все позиции просто есть в ней, с наилучшим ходом на глубину N-1. Программа, использующая итеративное углубление и хэш-таблицы, часто выполняет все итерации от 1 до N в несколько раз быстрее, чем если бы она сразу начала итерацию N, т.к. с вероятностью 75% она всегда первым выбирает наилучший ход, а с вероятностью ~90% наилучший ход оказывается в числе первых трех рассмотренных.
(7) Пустой ход (null move). В шахматах очередность хода очень важна, и тот игрок, который мог бы сделать два хода подряд, имел бы огромное преимущество. Возникла очень простая идея - пусть игрок A сделал свой ход и теперь очередь B. У него есть преимущество - например, лишний конь. Надо рассмотреть поддерево на глубину N. Игрок A говорит "я не буду делать ход, пусть B делает два хода подряд, зато поддерево после этого мы посмотрим до глубины N-2 а не N-1, как было бы после моего хода". Мы выполняем этот перебор на меньшую глубину, и если у A все равно преимущество, мы решаем "так как на самом деле он будет делать ход, наверное на самом деле его преимущество будет еще больше". То есть мы сэкономили, разобрав не настоящее поддерево до глубины N, а другое до глубины N-1 - напоминаю еще раз, что перебор экспоненциален, так что выигрыш очень значителен. Иногда оказывается, что игрок B, имея два хода подряд, может восстановить баланс - пустой ход не сработал, придется перебирать все честно до глубины N. Опять-таки, мы потеряли не очень много времени, т.к. перебирали до глубины N-1. Разумеется, пустой ход, являясь эвристикой, может и наврать - например, в цугцванге право хода лишь мешает. Но в реальной игре цугцванг встречается лишь в эндшпиле, а в эндшпиле пустой ход можно и не использовать. Пустой ход оказался очень серьезным улучшением, т.к. он позволяет сократить время перебора на глубину N с 6^N до (2.5-3)^N.
(8 ) Единственный ответ (singular extension). Стандартная альфа-бета прекращает анализ позиции, как только найден ход, который вызовет отсечение. Так как у нас не полное дерево игры, а мы используем оценочную функцию, может оказаться, что мы проврались, и никакого отсечения нет. Соответственно, мы думали, что в этой позиции у нас лучше, а на самом деле мы теряем ферзя. Идея единственного ответа состоит в том, что найдя один хороший ответ, мы не отсекаем сразу все поддерево, а продолжаем перебор, пока не найдем второй хороший ход. Если же мы его не нашли, то позиция анализируется заново, на сей раз на глубину N+1. Очень помогает в тактических позициях - программа начинает видеть комбинации на несколько ходов раньше, но резко замедляет перебор и поэтому используется только программами, работающими на суперкомпьютерах.
О текущем состоянии дел в компьютерных шахматах - в следующий раз.
***
ЧАСТЬ V. СОВРЕМЕННЫЕ ШАХМАТНЫЕ ПРОГРАММЫ
Сразу оговорюсь, что про наиболее известную программу (а точнее, машину+программу) - Deep Blue - я напишу в другой раз. Здесь же речь пойдет о типичных современных программах, работающих в основном на обычных компьютерах.
Итак, как они устроены внутри, мы уже разобрались. Тем не менее, продукты, построенные на одинаковых принципах, могут очень сильно друг от друга отличаться, и шахматные программы здесь не исключение.
Большую часть современных программ можно разбить на 3 категории:
Категория Fast searchers - идея состоит в том, что, упростив до предела оценочную функцию, и тщательно с оптимизировав всю программу в целом (что обычно достигается путем написания программы на ассемблере), можно довести количество позиций, рассматриваемых программой (nps - nodes per second) до астрономического числа, например, до 150-200k nps на P/200. То есть на каждую позицию программа тратит порядка одной-двух тысяч машинных команд. В это число входит делание хода из предыдущей позиции в эту, оценка позиции, генерация ходов из данной позиции, управляющая логика и т.д. На собственно оценочную функцию остаются вообще крохи - порядка сотни команд. Соответственно, она проста, как топор - перед началом перебора программа строит таблицы, где на каждой клетке нарисовано, какая фигура стоит хорошо, а какая - плохо. Например, вражеский король стоит на E8 - на клетках непосредственно рядом с ним нашему ферзю припишем +0.5 пешки, чуть подальше - +0.2, еще дальше - +0.1. Слабая пешка - на диагонали, откуда мы можем на нее давить, слону припишем +0.15, а ладье (разумеется, на вертикали или диагонали) - +0.2. И так далее. Для получения оценки достаточно для каждой фигуры слазить в ее таблицу, добавить разницу в материале - и оценка готова.
Проще всего, кстати, не выписывать оценочную функцию явно, а посчитать ее один раз перед началом перебора, а потом обновлять - сделали ход, вычли из нее оценку фигуры на старом месте и добавили на новом. Если кого-то сожрали, надо вычесть материальную и позиционную оценку для него.
Программы получаются безумно быстрыми и превосходно ведут себя в сложных тактических позициях, а также отлично решают комбинационные задачи. Разумеется, за все надо платить. Платой за тактическое умение становится слабая позиционная игра, особенно при нынешних скоростях машин. Длина рассматриваемого варианта может достичь 20 полуходов, и принятые в начале перебора решения оказываются далеки от истины. Например, подтянул я свои фигуры к E8, а вражеский король давно уже убежал и стоит на A3. Или появилась новая слабость в пешечной структуре, про которую программа ничего не знает. И так далее.
Соответственно, вторая категория - это так называемые knowledge-based программы. Тут все силы брошены на написание сложной оценочной функции. Учитывается и взаимодействие фигур друг с другом, и прикрытость короля, и контроль позиций, и чуть ли не фаза луны. В терминах nps программа работает в 10-100 раз медленнее, чем fast searches, но играет в хорошие позиционные шахматы. Точнее, хорошими эти шахматы являются только тогда, когда на доске нет глубокой тактики, или же контроль времени таков, что у программы есть достаточно времени, чтобы эту тактику просчитать. А еще одна стандартная беда - что-то не учтено в оценочной функции. Простейший (хотя и искусственный) пример - предположим, что программа не знает, что отставшая пешка - это плохо. Быстрая программа будет избегать позиций с отставшей пешкой, так как глубоко в дереве увидит "тактические" возможности противника - он подтянет свои фигуры и слопает несчастную пешку, т.е. сумеет перевести позиционное преимущество (о котором программа не знает) в материальное. Медленная же программа без такого знания обречена - что это позиционно плохо она не знает, а глубины перебора для нахождения выигрыша пешки противником не хватит.
Соответственно, большая часть современных программ есть некий гибрид между двумя крайностями. Они работают в 2-5 раза медленнее быстрых программ и имеют уже достаточно сложную оценочную функцию. Тем не менее они регулярно попадают впросак из-за слабой позиционной игры - впрочем, это же делают все программы, даже с самой лучшей оценочной функцией, ибо всегда оказывается, что какой-то фактор создатели программы просмотрели. Утверждается, что имеется очень много факторов, которые в явном виде нигде не записаны, но которые любой мастер (не говоря уж о гроссмейстере) считает самоочевидными.
Вокруг того, как должна быть устроена программа, идут непрекращающиеся споры. Все шахматисты, ровно как и большинство потребителей, очень любят knowledge-based программы. Стало даже модно писать "программа рассматривает всего 10000 позиций в секунду". Почему-то из этого делается вывод, что программа обладает немыслимо сложной оценочной функцией, как будто не бывает просто плохо написанных программ.
Программисты любят быстрые программы - хотя бы потому, что можно написать быструю программу, не будучи сильным шахматистом. Эта программа будет играть очень неплохо, во всяком случае, она сумеет обыграть своего автора, равно как и 99% игроков на Земле.
В какую силу играют сейчас лучшие программы на коммерческих машинах (например, на PIII/500)? Точного ответа вам никто не даст, ибо имеется очень мало статистики (гроссмейстеры не любят играть с программами в "серьезные" шахматы, в основном из-за того, что им за это не платят). Так что ниже есть моя личная точка зрения (хотя я могу подтвердить ее некоторой статистикой).
Все зависит от контроля времени:
(1) В блиц программы играют лучше любого игрока. Позиционная слабость программ более чем компенсируется тактическими ошибками человека, ибо в блице регулярно ошибаются самые лучшие гроссмейстеры.
(2) В активные шахматы (30 минут на партию) программы играют в силу лучших гроссмейстеров. За счет большего количества времени на обдумывание гроссмейстеры не делают особо грубых тактических ошибок и могут переиграть программу позиционно.
(3) В стандартные шахматы (2 часа на 40 ходов) программы играют в силу слабого гроссмейстера.
Разумеется, многое зависит и от любимого человеком стиля игры. Так, Каспарову особенно тяжело играть с компьютерами - он любит острую тактическую игру, а здесь компьютеры особенно сильны. Переиграть компьютер в тактике очень тяжело. А вот стиль игры Карпова, наоборот, тяжел для компьютера - он не знает, как надо играть в закрытой позиции, а Карпов тем временем потихоньку усиливает позицию. Есть и так называемый "антикомпьютерный" стиль - идея состоит в том, что современные программы недооценивают опасность атаки на короля, пока эта атака находится за их "горизонтом видимости". Хороший антикомпьютерный игрок потихоньку готовит атаку, подтаскивает фигуры, и дает тем временем возможность программе резвиться (заниматься пешкоедством) на другом фланге. Когда программа видит опасность - уже поздно, подтянуть застрявшего там ферзя (или кого-нибудь еще) она уже не успевает. Очень часто хорошие антикомпьютерные игроки с людьми играют плохо, так как человек видит опасность раньше.
***
ЧАСТЬ VI. ИСТОРИЯ DEEP BLUE
Отсутствие подробностей связано с маркетинговой политикой фирмы IBM. Отделу рекламы там нужно, чтобы средний американец знал, что "IBM сделала непобедимый шахматный компьютер". Он это и знает. Поэтому Deep Blue уже (похоже) никогда не будет играть в шахматы - выиграть от этого IBM ничего не выиграет, а проиграть (в случае выигрыша человека) есть чего.
Так что судить о Deep Blue (точнее, о Deep Blue II - последней машине из семейства) можно только по 6 сыгранным во втором матче с Каспаровым партиям, по редким публикациям в технических журналах, да по лекциям, которые иногда устраивают разработчики. Одна из таких лекций была года полтора назад в MS, я на ней присутствовал; ее читал Murray Campbell, который в Deep Blue отвечал за оценочную функцию. Очень интересна статья Feng Hsiung Hsu (автора специализированных шахматных процессоров) в IEEE Micro, #3 за этот год. По слухам, Joel Benjamin (гроссмейстер, работавший с командой Deep Blue; чемпион США) готовит книгу о Deep Blue, но я ее не видел. Интересная информация иногда проскакивает в rec.games.chess.computer, но там соотношение сигнал/шум очень мало.
Deep Blue - это не первая попытка создать специализированное "железо" для игры в шахматы. Можно вспомнить, например, что в конце 60-х - начале 70-х годов одна из отечественных машин М-20 была немного модернизирована, в нее были вставлены специальные шахматные команды (Россия - родина слонов; каких слонов я вчера видел в зоопарке... но мы отвлеклись от темы). Реальные же специализированные шахматные процессоры появились на Западе, в конце 70-х - начале 80-х годов. Самые известные разработки были сделаны Berliner HiTech и Ken Thompson (одним из авторов Unix) - Belle. В этих машинах реализован аппаратный генератор ходов, оценочная функция и альфа-бета перебор. Разработки были академические, и невзирая на то, что специализированное железо обычно на порядок быстрее, чем сопоставимое general purpose, о сопоставимости речи не было. Программа Cray Blitz на сверхсовременной тогда машине Cray (стоимостью $60млн) играла все равно лучше.
Deep Blue начинала как студенческая разработка - интересно было группе способных студентов попробовать свои силы, да и тема для диплома отличная. Прогресс технологии позволил сделать первую же версию процессоров (названную ChipTest) очень быстрыми. Последовала следующая, усовершенствованная версия, названная Deep Thought. В этот момент группу заметил маркетинговый департамент фирмы IBM и обратился к ней с предложением, от которого невозможно было отказаться. Результатом стали Deep Blue и Deep Blue II. Таким образом, Deep Blue II - это результат более чем 10 лет работы очень способной группы, в которой были как программисты/железячники, так и сильные гроссмейстеры (кроме уже упомянутого Бенджамина привлекались и другие гроссмейстеры, с хорошей оплатой). Финансировалась вся работа фирмой IBM, таким образом у группы были ресурсы, которые и не снились академическим организациям ("Бог на стороне больших батальонов").
***
ЧАСТЬ VII. КАК УСТРОЕНА DEEP BLUE
Deep Blue II сделана на основе мощного сервера RS/6000 фирмы IBM. В сервере имеется 31 обычных процессора; один объявлен главным, ему подчиняются 30 остальных. К каждому "рабочему" процессору подключено 16 специализированных шахматных процессора, таким образом всего имеется 480 шахматных процессоров. Они и являются "сердцем" системы, таким образом, утверждение IBM "Мы продаем сервер RS/6000, который обыграл в шахматы Каспарова", как бы это сказать... не совсем верно.
Первые несколько полуходов (4) перебираются на "главном" процессоре RS/6000. После 4-х полуходов он передает работу остальным 30-ти процессорам, и они рассматривают следующие 4 полухода. Программа здесь написана на обычном C, и не очень отличается от традиционных параллельных шахматных программ. Наиболее существенное отличие - при написании программы было известно, что система обладает огромной скоростью (т.к. в ней основную работу выполняют специализированные шахматные процессоры), соответственно, можно особо не экономить. Напомню - при написании шахматной программы всегда велико желание какие-то варианты рассмотреть поглубже ("углубиться"), но всегда приходится помнить, что если мы углубимся здесь, то останется меньше времени на рас смотр других вариантов. Соответственно, обычно приходится искать компромисс между более глубоким рассмотрением "тактических" вариантов (в которых только и работают классические углубления) и "тихих" вариантов (которые с точки зрения человека тоже могут быть тактическими, но только ходы не попадают под слишком узкое машинное определение тактических). Здесь же можно рассматривать более длинные варианты, не заботясь что другим времени не достанется - ресурсов хватит на всех. Так что формальные 4 полухода здесь легко могут превратиться в 30 полуходов. После этого работу перехватывают специализированные процессоры, и они делают ощутимо больше 99% всей работы системы - а именно, они перебирают еще на 4 полухода. Из-за того, что в них нет программы как таковой, а все, что надо сделать, зашито аппаратно (не микропрограммно!), при их проектировании приходилось серьезно думать, что надо в них делать, а что нет. В частности, в них не предусмотрено почти никакое углубление. Зато в них предусмотрена достаточно сложная оценочная функция - ведь то, что тяжело запрограммировать, часто очень легко сделать на аппаратном уровне. Например, детектор шахов работает один такт, т.к. одновременно проверяются все возможные варианты. Очень прост контроль X-rays (не знаю, как будет по-русски - это когда одна дальнобойная фигура стоит позади другой), вилок, перегрузки фигур и т.д. Вообще, оценочная функция в шахматном процессоре Deep Blue очень сложна - утверждается, что она соответствует примерно 40000 командам обычного процессора. В частности, там имеется около 8000 коэффициентов. Эти коэффициенты не прошиты намертво, а загружаются в процессор после включения. Таким образом можно было вести настройку процессора после его создания, и не бегать на фабрику для каждого изменения. Как решалась задача оптимизации в пространстве размерности 8000 - это отдельная история (и тоже опубликованная).
Шахматные процессоры были выполнены по устаревшей 0.6 микронной технологии и работают со скоростью 2-2.5млн позиций в секунду. Таким образом, весь монстр обрабатывает примерно миллиард шахматных позиций в секунду. Прошу обратить внимание, что general-purpose системе для этого потребовалось бы быстродействие порядка 40 триллионов операций в секунду.
(Процессоры были серьезно переработаны после первого матча с Каспаровым, когда стало ясно, что в предыдущей версии отсутствуют многие факторы, которые необходимы для игр на таком уровне; большая часть группы не верила, что это удастся сделать меньше чем за год, но Hsu совершил чудеса и управился в срок).
Разумеется, к.п.д. параллельного перебора всегда ниже 100% (раньше уже писалось, что альфа-бета распараллеливается очень тяжело). В данном случае удалось добиться к.п.д порядка 25%, что само по себе является очень большим достижением. То есть система работает как однопроцессорная, не векторная general-purpose машина со скоростью 10 триллионов операций в секунду. Таковых маши не бывает и в ближайшие годы не появится (а может, не появится никогда, т.к. технология упрется в размеры атома и квантовые эффекты).
Система в полном объеме в первый раз была собрана примерно за неделю до повторного матча с Каспаровым, когда были изготовлены все шахматные процессоры. Как протекал этот матч - в следующей главе...
Во-первых, никаких коробков не хватит, во-вторых, самообучение путем полного перебора займет астрономическое время, поэтому применяются методы огульного оценивания. Конечно, можно выделить уровни абстракции, как в книгах Н.М.Амосова (человек, похоже, так и играет), но шахматному компьютеру "думать некогда, прыгать надо".
По сути, усложненный вариант расчетов OGRE.
Приведенный ниже фрагмент давно ходит по Сети и автора его, к сожалению, я не знаю.
***
АЛГОРИТМЫ ШАХМАТНЫХ ПРОГРАММ
ЧАСТЬ I. МИНИМАКС
Для начала рассмотрим более простую игру, например, крестики-нолики на доске 3*3. Рассмотрим начальную позицию. Тут у первого игрока (пусть это будут крестики) имеются 9 ходов (симметрию игнорируем). На каждый из них у соперника имеется 8 ответов, в свою очередь на каждый из них - по 7 ответов у крестиков и т.д. Максимальная длина игры - 9 полуходов (т.е. ходов одного из соперников), но она может кончиться и побыстрее, если кто-то выиграет. Возьмем листок бумаги и сверху нарисуем начальную позицию. Так как из нее возможно 9 ходов, проведем из нее 9 черточек (ветвей). В конце каждой ветви нарисуем позицию, которая получается после этого хода, и в свою очередь проведем из нее ветви - ходы, возможные из данной позиции. И так далее. Полученная структура называется деревом, ибо (1) у нее есть корень - начальная позиция, (2) у нее есть листья - позиции, из которых не идет ветвей, ибо один из игроков победил или случилась ничья, и (3) она отдаленно похоже на дерево, если лист бумаги перевернуть. Крестики-нолики - простая игра, ее дерево должно уместиться на (большом) листе бумаги, но можно себе представить так же нарисованное дерево для шахмат (вроде бы есть всего 10^50 или около того различных позиций, и правило 50 ходов ограничивает максимальную длину партии ~4000 ходов).
Разумеется, для такого листа бумаги не хватит всех атомов во вселенной, но представить такой лист все равно можно (я, во всяком случае, могу). Теперь припишем каждому листу его оценку. Пусть выигрыш крестиков будет -1, ноликов - плюс 1, а ничья будет нулем. Начнем "поднимать" оценку вверх по дереву - рассмотрим вершину, непосредственно стоящую над листом (терминальной позицией). Из нее ведет несколько ветвей (в крестиках-ноликах ровно одна, но это не важно). Представим, что ход сейчас - крестиков. Он заинтересован в получении -1, поэтому из нескольких вариантов он выберет вариант с минимальным значением (-1, если возможно, а если нет, то хотя бы 0). Таким образом, он выберет минимальную оценку из тех, какую имеют его "потомки", и припишет ее этой вершине. Уровнем выше - очередь хода "ноликов". Он, в свою очередь, заинтересован в получении +1, поэтому он будет максимизировать полученную снизу оценку.
В конце концов мы поднимем оценку до корня. В случае крестиков-ноликов это будет, разумеется, 0, ибо теоретическим результатом крестиков-ноликов при оптимальной игре обоих игроков является ничья. Что является теоретическим результатом шахмат науке неизвестно.
Разумеется, имея нарисованное дерево игры, играть очень легко - крестики должны выбирать ход, ведущий из текущей позиции в позицию с минимальной оценкой; нолики - в позицию с максимальной. Как легко понять, описанный алгоритм и есть обещанный минимакс.
***
ЧАСТЬ II. АЛЬФА-БЕТА
Внимательные читатели должны были догадаться что минимакс будет работать не только на деревьях с оценками плюс/минус один, но и на деревьях, листьям которых приписаны просто действительные числа. В дальнейшем мы будем рассматривать именно такие деревья (для объяснения основных алгоритмов я буду говорить о деревьях, забыв на время о собственно играх). Кроме того, я сосредоточусь именно на определении теоретического результата игры, т.е. на подъеме оценки вверх по дереву.
Минимакс - очень трудоемкий алгоритм. Для определения теоретического результата игры размечается абсолютно все дерево. Вопрос: нельзя ли, сохранив математическую корректность минимакса, обходить поменьше?
Оказывается, можно. Алгоритм называется альфа-бета. Легко доказать, что он дает те же результаты (не бойтесь, я этого делать не буду). Идея его, если объяснить на пальцах, такова:
Пусть есть корень, у него - 2 потомка, у каждого из них - по 3 потомка-листа. В корне - очередь хода мина, соответственно, в вершинах второго уровня - ход макса. Листам, которые потомки левого поддерева, приписаны оценки 0, 5, 10. Так как в вершинах второго подуровня мы максимизируем, левому поддереву припишем оценку 10.
Начинаем рассматривать правое поддерево. Пусть у самого левого листа оценка 100. А теперь - внимание! Мы знаем, что уровнем выше мы будем максимизировать. Это означает, что оценка "всего правого поддерева" будет уж не меньше 100, т.к. оставшиеся листья могут эту оценку только поднять. Кроме того мы знаем, что в начальной позиции мы будем минимизировать, и значит выберем левое поддерево, оценка которого 10.
Итого, мы получили оценку всего дерева, рассмотрев всего 4 позиции из 6. Шахматная аналогия - предположим, что я рассмотрел один из своих ходов, и обнаружил, что после всех ответов противника позиция равная. Я посмотрел, что происходит после другого моего хода, и обнаружил, что одним из своих ответов противник выигрывает коня. Рассматривать другие его ответы уже не имеет смысла - этот свой ход я уже не сделаю.
Просьба обратить внимание, что нам повезло, что в правом поддереве оценку 100 имеет самый левый лист. Будь он правым, и если при этом оба левых имеют оценку 7, нам пришлось бы обойти все 6 листьев. В наихудшем случае (мы всегда рассматриваем поддерево/лист с наилучшей оценкой в последнюю очередь) альфа-бета вырождается в минимакс. В наилучшем случае (наилучшее поддерево всегда рассматривается первым) рассматривается (очень грубо) 2*(sqrt(количества вершин, рассматриваемых минимаксом)).
Альфа-бета является строгим алгоритмом - ветвь отсекаются только после того, как хотя бы одного потомка оценили, и убедились, что значение этой ветви не повлияет на итоговый результат.
***
ЧАСТЬ III. ПРИМЕНЕНИЕ ТЕОРИИ К ПРАКТИКЕ
Разумеется, для реальных игр (шахмат, шашек, го) все дерево машина обойти не сможет. Поэтому идут на жульничество.
Во-первых, все дерево не строят - никакой памяти ни у какой машины не хватит. Хранят только текущую позицию и последовательность ходов, в нее приведшую. Идешь вглубь - сделай на доске (точнее, на ее аналоге в памяти) ход. Возвращаешься - возьми ход назад (это еще не жульничество, с теоретической точки зрения то, что мы явно дерево не строим, ничего не меняет).
Во-вторых и в главных, точная оценка заменяется на приближенную. А именно, после перебора на некоторую глубину, если не случилось мата или форсированной ничьи, вместо того, чтобы перебирать дальше, мы зовем оценочную функцию, которая приписывает текущей позиции (а точнее, всему поддереву, начинающемуся с текущей позиции), некоторую оценку. Как эта функция устроена - чуть позже, а пока главное: тут мы бесповоротно порвали с теорией, ибо оценочная функция есть нечто приближенное. Вот это и есть основное жульничество - альфа-бета была научно обоснована совсем в других условиях, и почему она после введения в нее оценочной функции работает в реальных играх, не совсем понятно (точнее говоря, есть сколько угодно работ на эту тему, но мне они представляются неубедительными). Более того, искусственно создан целый класс игр, где альфа-бета в таких условиях не работает.
Как устроена оценочная функция? Во-первых, надо просто сосчитать материал. Простейший вариант: пешка - 1, конь и слон - 3, ладья - 5, ферзь - 9.
Во-вторых, надо добавить позиционную оценку, и это есть самое сложное. Факторов много, в шахматных книжках приведены далеко не все, и главное - там сказано "это есть хорошо, а то плохо", а нам надо "это есть плюс половина, а то - минус три четверти". Соответственно, приходится сначала факторам приписывать веса с потолка, а потом отлаживать, вручную или пытаясь оптимизировать функцию в пространстве размерности несколько тысяч.
Вот несколько учитываемых факторов, с их ориентировочными весами (веса, разумеется, взяты с потолка, но за порядок величины ручаюсь):
- пара слонов - это плюс треть пешки,
- король прикрыт своими пешками - плюс пол-пешки,
- конь или ферзь близки к королю (своему или чужому) - плюс сотая пешки,
- слабая или отставшая пешка - минус четверть пешки,
- ладья на полуоткрытой вертикали - плюс пять сотых пешки,
- ладья на открытой вертикали - плюс одна десятая пешки,
- пара ладей на седьмой горизонтали - плюс пол-пешки,
- висящая фигура - минус четверть пешки, две висящих фигуры - минус пешка, три или больше - минус три пешки.
И так далее, и так далее. Кроме того, вес многих факторов может зависеть от ситуации на доске - например, пока ферзей не разменяли, прикрытость короля может оцениваться куда выше, чем после размена.
Таким образом, получаем позиционную оценку белых, складываем с материалом белых, делаем то же самое для черных, вычитаем одно из другого, и все сведено к одному числу. Красота!
К сожалению, не все так просто. Первые программы использовали только что описанный алгоритм - перебор на фиксированную глубину с вызовом там оценочной функции (если раньше мат не случился). И немедленно выяснилось, что мы можем прекратить перебор, например, в середине размена, или при "висящем" ферзе, или когда на доске стоит мат в один ход, и тот факт, что у атакующей стороны не хватает ладьи, не имеет никакого значения. Были попытки учитывать все это в оценочной функции, но она тогда становилась безумно сложной, и медленной. На каждый починенный таким образом случай начинало приходиться десять других, где замедление программы вследствие более медленной оценочной функции приводило к недостаточной глубине перебора и еще худшей игре. Кроме того, программа с маниакальным упорством пытается отсрочить свои неприятности, получая взамен худшие. "Ага, я перебираю на 7 полуходов, и вижу, что теряю слона. А вот отдам-ка я вот эту пешку, и тогда слона противник возьмет на 4 полухода позже, получится 11, я и не увижу. Итого минус 1, а не минус 3". Разумеется, при более глубоком переборе программа бы обнаружила, что в итоге у нее будет минус 4, но времени перебирать глубже нет. Это явление называется "эффектом горизонта", ибо программа стремится выпихнуть неприятности за горизонт видимости (или горизонт событий).
Попытки использовать селективные методы провалились с еще большим треском. Не удается понять, как человек играет в шахматы, и попытки сделать программы с "forward pruning" - отсечениями ветвей дерева без их предварительного рассмотрения, исходя из чисто шахматных принципов, проваливаются. Всегда находятся позиции, где программа отсекает нужный ход ("выплескивает воду месте с ребенком").
В конце концов стало понятно, что оценочную функцию можно звать только в спокойных позициях. Поэтому в конце основного перебора вставили еще один, упрощенный, где рассматриваются только взятия, превращения, и, возможно, шахи и ответы на шах. Так как таких ходов немного, "форсированный вариант" (так это называется) замедляет программу всего лишь на 20-50%, а сила игры резко увеличивается, т.к. программа не пытается оценить острые позиции.
Потом заметили, что серия ходов с разменом в конце будет рассмотрена на большую глубину, чем с разменом в середине, и сообразили, что некоторые варианты с разменом в середине тоже неплохо бы рассматривать поглубже. Возникла идея (не знаю, как по русски, пусть будет "углубление") - при переборе после некоторых ходов не уменьшать оставшуюся глубину перебора. Типичные углубления - после размена, при превращении пешки, при уходе от шаха. Идея та же, что и в форсированном варианте - ситуация на доске может кардинально измениться, этот вариант надо изучить поглубже.
Вот какова была ситуация в начале и середине 70-х.
***
ЧАСТЬ IV. УЛУЧШЕНИЯ
Как уже было сказано, за 40 лет никакой замены альфа-бете не найдено. В этом смысле наиболее печальна история Ботвинника. В течении 20 лет он занимался созданием шахматной программы. Он свято верил, что будучи чемпионом мира по шахматам и одновременно хорошо понимая программирование, он сумеет создать программу, которая будет играть на уровне чемпиона мира. Итог печален - программа так никогда не заиграла (по этому поводу кто-то хорошо сказал "Ботвинник только думает, что он знает, как он думает"). Что еще хуже, Ботвинник напечатал статью с описанием алгоритма в журнале International Computer Chess Association. Статья содержала результаты анализа нескольких позиций, якобы выполненных программой. Независимый анализ показал, что эти результаты являются фальсификацией - они не могли быть получены с использованием алгоритма Ботвинника.
Тем не менее, все эти годы качество игры шахматных программ улучшалось. Частично прогресс обьясняется быстрым развитием аппаратуры - персональные компьютеры по ряду параметров достигли уровня суперкомпьютеров конца 70-х (хотя по ряду параметров все еще серьезно отстают). Частично же "виновато" развитие алгоритмов - прорыва не было, но было множество эволюционных улучшений. Каковы главные из них?
(1) Использование библиотеки дебютов. Дебютная теория в шахматах хорошо разработана, и только естественно, что программы стали ее использовать. Более того, используют они ее лучше, чем гроссмейстеры, т.к. запомнить несколько миллионов позиций для машины проще простого.
(2) Использование баз данных с целиком просчитанными эндшпилями. Сейчас реальный предел для персонального компьютера - 5-фигурные эндшпили (считая королей). Используя такие базы данных, программы играют простые эндшпили безупречно. Более того, современные программы могут во время перебора вариантов "дотянуться" до базы данных из позднего миттельшпиля, когда на доске находится еще 10-15 фигур. Скромно замечу, что к созданию наиболее широко распространенных баз эндшпилей приложил руку я.
(3) Думанье во время хода противника. Мы сделали ход и теперь задумался противник. Зачем времени пропадать? Выберем наиболее разумный с нашей точки зрения ход, который он может сделать, и начнем думать над ответом на него. Если он сделает другой ход - ну и леший с ним, все равно не наше время было. Это - наиболее простой вариант использования времени противника, и он же наиболее эффективный, т.к. хорошие программы правильно предсказывают ~70% ходов противника.
(4) Различные эвристики, которые помогают отсортировать ходы в процессе перебора. Как уже отмечалось ранее, альфа-бета очень чувствительна к порядку, в котором анализируются ходы. При хорошем порядке она быстрее, причем быстрее принципиально. При этом алгоритм все равно остается экспоненциальным - перебор на N+1 полуходов работает в разы медленнее, чем на N полуходов, но по крайней мере возводимое в степень число ощутимо уменьшается. В типичной шахматной позиции возможно примерно 40 ходов, и для перебора на N полуходов минимаксу (он же альфа-бета с наихудшим упорядочением ходов) надо рассмотреть 40^N позиций. Альфа-бете с наилучшим упорядочением ходов надо рассмотреть примерно 6^N позиций - разница принципиальна. Эвристики применяются различные, например: первым делом попытаться съесть только что ходившую фигуру противника (она работает, т.к. большинство рассматриваемых ходов - полнейший идиотизм). Другая полезная эвристика (с меньшим приоритетом) - попытаться сделать ход, который был лучшим у соседа слева (она основана на том, что в похожих позициях наилучший ход часто один и тот же). Имеются еще несколько эвристик, но надеюсь, что идея в целом понятна.
(5) Итеративное углубление (iterative deepening). В реальной игре у программы имеется какое-то время на каждый ход, и им надо с умом распорядиться. Просто начинать перебор на фиксированную глубину, как делали ранние программы, неразумно - в сложной позиции с большим количеством разменов и/или шахов будет много вариантов, которые будут просчитываться очень глубока из-за "углублений", и программа может не успеть выполнить перебор. А одной из особенностей альфа-беты является то, что результатом незаконченного перебора воспользоваться нельзя - нет никакой гарантии, что найденный к моменту прерывания наилучший ход является хоть сколько-нибудь разумным. С другой стороны, в какой-нибудь закрытой позиции с малым количеством возможных ходов (branching factor) перебор может закончиться неожиданно быстро. Идея итеративного углубления состоит в том, что программа сначала производит перебор на глубину 1. Осталось время - перебираем на глубину 2. Осталось время - на глубину 3. И так далее. Разумеется, при этом приходится часть работы делать заново, но тут главное как раз экспоненциальный характер алгоритма. Следующий перебор занимает (грубо) в 6 раз больше времени, поэтому мы заново делаем максимум 1/6 работы. Зато у нас всегда есть ход от предыдущей итерации, которым мы можем воспользоваться, если нам придется прервать текущую. Возможны дальнейшие оптимизации - например, не начинать новую итерацию, если мы съели больше половины отведенного на думанье над этим ходом времени, ибо все равно почти наверняка не успеем.
(6) Хэш-таблицы (transposition tables). В шахматах мы имеем не дерево игры, а граф - очень часто после перестановки ходов мы получаем одну и ту же позицию. Возникла простая идея - занять всю память машины, которая иначе бы не использовалась, под запоминание уже рассмотренных позиций. Для каждой позиции надо хранить ее оценку (точнее, оценку поддерева под этой позицией), глубину перебора, наилучший ход, и некоторую служебную информацию. Теперь, начав разбирать позицию, надо взглянуть - а не встречали ли мы уже ее? Если не встречали, то поступаем как раньше. Если встречали, то смотрим, на какую глубину мы ее раньше разбирали. Если на такую же, как нам надо сейчас, или более глубокую, то можно воспользоваться старой оценкой и сэкономить время. Если же на меньшую, то мы все равно можем воспользоваться частью информации, а именно наилучшим ходом. Лучший ход для глубины N может оказаться лучшим и для глубины N+1. То есть, кроме своего изначального предназначения, хэаш-таблица оказывается полезна и для упорядочения ходов. Тут еще неожиданно помогает итеративное углубление - когда мы начинаем следующую итерацию, хэш-таблица оказывается заполнена информацией от предыдущей, и до какого-то момента (до глубины 1) все позиции просто есть в ней, с наилучшим ходом на глубину N-1. Программа, использующая итеративное углубление и хэш-таблицы, часто выполняет все итерации от 1 до N в несколько раз быстрее, чем если бы она сразу начала итерацию N, т.к. с вероятностью 75% она всегда первым выбирает наилучший ход, а с вероятностью ~90% наилучший ход оказывается в числе первых трех рассмотренных.
(7) Пустой ход (null move). В шахматах очередность хода очень важна, и тот игрок, который мог бы сделать два хода подряд, имел бы огромное преимущество. Возникла очень простая идея - пусть игрок A сделал свой ход и теперь очередь B. У него есть преимущество - например, лишний конь. Надо рассмотреть поддерево на глубину N. Игрок A говорит "я не буду делать ход, пусть B делает два хода подряд, зато поддерево после этого мы посмотрим до глубины N-2 а не N-1, как было бы после моего хода". Мы выполняем этот перебор на меньшую глубину, и если у A все равно преимущество, мы решаем "так как на самом деле он будет делать ход, наверное на самом деле его преимущество будет еще больше". То есть мы сэкономили, разобрав не настоящее поддерево до глубины N, а другое до глубины N-1 - напоминаю еще раз, что перебор экспоненциален, так что выигрыш очень значителен. Иногда оказывается, что игрок B, имея два хода подряд, может восстановить баланс - пустой ход не сработал, придется перебирать все честно до глубины N. Опять-таки, мы потеряли не очень много времени, т.к. перебирали до глубины N-1. Разумеется, пустой ход, являясь эвристикой, может и наврать - например, в цугцванге право хода лишь мешает. Но в реальной игре цугцванг встречается лишь в эндшпиле, а в эндшпиле пустой ход можно и не использовать. Пустой ход оказался очень серьезным улучшением, т.к. он позволяет сократить время перебора на глубину N с 6^N до (2.5-3)^N.
(8 ) Единственный ответ (singular extension). Стандартная альфа-бета прекращает анализ позиции, как только найден ход, который вызовет отсечение. Так как у нас не полное дерево игры, а мы используем оценочную функцию, может оказаться, что мы проврались, и никакого отсечения нет. Соответственно, мы думали, что в этой позиции у нас лучше, а на самом деле мы теряем ферзя. Идея единственного ответа состоит в том, что найдя один хороший ответ, мы не отсекаем сразу все поддерево, а продолжаем перебор, пока не найдем второй хороший ход. Если же мы его не нашли, то позиция анализируется заново, на сей раз на глубину N+1. Очень помогает в тактических позициях - программа начинает видеть комбинации на несколько ходов раньше, но резко замедляет перебор и поэтому используется только программами, работающими на суперкомпьютерах.
О текущем состоянии дел в компьютерных шахматах - в следующий раз.
***
ЧАСТЬ V. СОВРЕМЕННЫЕ ШАХМАТНЫЕ ПРОГРАММЫ
Сразу оговорюсь, что про наиболее известную программу (а точнее, машину+программу) - Deep Blue - я напишу в другой раз. Здесь же речь пойдет о типичных современных программах, работающих в основном на обычных компьютерах.
Итак, как они устроены внутри, мы уже разобрались. Тем не менее, продукты, построенные на одинаковых принципах, могут очень сильно друг от друга отличаться, и шахматные программы здесь не исключение.
Большую часть современных программ можно разбить на 3 категории:
Категория Fast searchers - идея состоит в том, что, упростив до предела оценочную функцию, и тщательно с оптимизировав всю программу в целом (что обычно достигается путем написания программы на ассемблере), можно довести количество позиций, рассматриваемых программой (nps - nodes per second) до астрономического числа, например, до 150-200k nps на P/200. То есть на каждую позицию программа тратит порядка одной-двух тысяч машинных команд. В это число входит делание хода из предыдущей позиции в эту, оценка позиции, генерация ходов из данной позиции, управляющая логика и т.д. На собственно оценочную функцию остаются вообще крохи - порядка сотни команд. Соответственно, она проста, как топор - перед началом перебора программа строит таблицы, где на каждой клетке нарисовано, какая фигура стоит хорошо, а какая - плохо. Например, вражеский король стоит на E8 - на клетках непосредственно рядом с ним нашему ферзю припишем +0.5 пешки, чуть подальше - +0.2, еще дальше - +0.1. Слабая пешка - на диагонали, откуда мы можем на нее давить, слону припишем +0.15, а ладье (разумеется, на вертикали или диагонали) - +0.2. И так далее. Для получения оценки достаточно для каждой фигуры слазить в ее таблицу, добавить разницу в материале - и оценка готова.
Проще всего, кстати, не выписывать оценочную функцию явно, а посчитать ее один раз перед началом перебора, а потом обновлять - сделали ход, вычли из нее оценку фигуры на старом месте и добавили на новом. Если кого-то сожрали, надо вычесть материальную и позиционную оценку для него.
Программы получаются безумно быстрыми и превосходно ведут себя в сложных тактических позициях, а также отлично решают комбинационные задачи. Разумеется, за все надо платить. Платой за тактическое умение становится слабая позиционная игра, особенно при нынешних скоростях машин. Длина рассматриваемого варианта может достичь 20 полуходов, и принятые в начале перебора решения оказываются далеки от истины. Например, подтянул я свои фигуры к E8, а вражеский король давно уже убежал и стоит на A3. Или появилась новая слабость в пешечной структуре, про которую программа ничего не знает. И так далее.
Соответственно, вторая категория - это так называемые knowledge-based программы. Тут все силы брошены на написание сложной оценочной функции. Учитывается и взаимодействие фигур друг с другом, и прикрытость короля, и контроль позиций, и чуть ли не фаза луны. В терминах nps программа работает в 10-100 раз медленнее, чем fast searches, но играет в хорошие позиционные шахматы. Точнее, хорошими эти шахматы являются только тогда, когда на доске нет глубокой тактики, или же контроль времени таков, что у программы есть достаточно времени, чтобы эту тактику просчитать. А еще одна стандартная беда - что-то не учтено в оценочной функции. Простейший (хотя и искусственный) пример - предположим, что программа не знает, что отставшая пешка - это плохо. Быстрая программа будет избегать позиций с отставшей пешкой, так как глубоко в дереве увидит "тактические" возможности противника - он подтянет свои фигуры и слопает несчастную пешку, т.е. сумеет перевести позиционное преимущество (о котором программа не знает) в материальное. Медленная же программа без такого знания обречена - что это позиционно плохо она не знает, а глубины перебора для нахождения выигрыша пешки противником не хватит.
Соответственно, большая часть современных программ есть некий гибрид между двумя крайностями. Они работают в 2-5 раза медленнее быстрых программ и имеют уже достаточно сложную оценочную функцию. Тем не менее они регулярно попадают впросак из-за слабой позиционной игры - впрочем, это же делают все программы, даже с самой лучшей оценочной функцией, ибо всегда оказывается, что какой-то фактор создатели программы просмотрели. Утверждается, что имеется очень много факторов, которые в явном виде нигде не записаны, но которые любой мастер (не говоря уж о гроссмейстере) считает самоочевидными.
Вокруг того, как должна быть устроена программа, идут непрекращающиеся споры. Все шахматисты, ровно как и большинство потребителей, очень любят knowledge-based программы. Стало даже модно писать "программа рассматривает всего 10000 позиций в секунду". Почему-то из этого делается вывод, что программа обладает немыслимо сложной оценочной функцией, как будто не бывает просто плохо написанных программ.
Программисты любят быстрые программы - хотя бы потому, что можно написать быструю программу, не будучи сильным шахматистом. Эта программа будет играть очень неплохо, во всяком случае, она сумеет обыграть своего автора, равно как и 99% игроков на Земле.
В какую силу играют сейчас лучшие программы на коммерческих машинах (например, на PIII/500)? Точного ответа вам никто не даст, ибо имеется очень мало статистики (гроссмейстеры не любят играть с программами в "серьезные" шахматы, в основном из-за того, что им за это не платят). Так что ниже есть моя личная точка зрения (хотя я могу подтвердить ее некоторой статистикой).
Все зависит от контроля времени:
(1) В блиц программы играют лучше любого игрока. Позиционная слабость программ более чем компенсируется тактическими ошибками человека, ибо в блице регулярно ошибаются самые лучшие гроссмейстеры.
(2) В активные шахматы (30 минут на партию) программы играют в силу лучших гроссмейстеров. За счет большего количества времени на обдумывание гроссмейстеры не делают особо грубых тактических ошибок и могут переиграть программу позиционно.
(3) В стандартные шахматы (2 часа на 40 ходов) программы играют в силу слабого гроссмейстера.
Разумеется, многое зависит и от любимого человеком стиля игры. Так, Каспарову особенно тяжело играть с компьютерами - он любит острую тактическую игру, а здесь компьютеры особенно сильны. Переиграть компьютер в тактике очень тяжело. А вот стиль игры Карпова, наоборот, тяжел для компьютера - он не знает, как надо играть в закрытой позиции, а Карпов тем временем потихоньку усиливает позицию. Есть и так называемый "антикомпьютерный" стиль - идея состоит в том, что современные программы недооценивают опасность атаки на короля, пока эта атака находится за их "горизонтом видимости". Хороший антикомпьютерный игрок потихоньку готовит атаку, подтаскивает фигуры, и дает тем временем возможность программе резвиться (заниматься пешкоедством) на другом фланге. Когда программа видит опасность - уже поздно, подтянуть застрявшего там ферзя (или кого-нибудь еще) она уже не успевает. Очень часто хорошие антикомпьютерные игроки с людьми играют плохо, так как человек видит опасность раньше.
***
ЧАСТЬ VI. ИСТОРИЯ DEEP BLUE
Отсутствие подробностей связано с маркетинговой политикой фирмы IBM. Отделу рекламы там нужно, чтобы средний американец знал, что "IBM сделала непобедимый шахматный компьютер". Он это и знает. Поэтому Deep Blue уже (похоже) никогда не будет играть в шахматы - выиграть от этого IBM ничего не выиграет, а проиграть (в случае выигрыша человека) есть чего.
Так что судить о Deep Blue (точнее, о Deep Blue II - последней машине из семейства) можно только по 6 сыгранным во втором матче с Каспаровым партиям, по редким публикациям в технических журналах, да по лекциям, которые иногда устраивают разработчики. Одна из таких лекций была года полтора назад в MS, я на ней присутствовал; ее читал Murray Campbell, который в Deep Blue отвечал за оценочную функцию. Очень интересна статья Feng Hsiung Hsu (автора специализированных шахматных процессоров) в IEEE Micro, #3 за этот год. По слухам, Joel Benjamin (гроссмейстер, работавший с командой Deep Blue; чемпион США) готовит книгу о Deep Blue, но я ее не видел. Интересная информация иногда проскакивает в rec.games.chess.computer, но там соотношение сигнал/шум очень мало.
Deep Blue - это не первая попытка создать специализированное "железо" для игры в шахматы. Можно вспомнить, например, что в конце 60-х - начале 70-х годов одна из отечественных машин М-20 была немного модернизирована, в нее были вставлены специальные шахматные команды (Россия - родина слонов; каких слонов я вчера видел в зоопарке... но мы отвлеклись от темы). Реальные же специализированные шахматные процессоры появились на Западе, в конце 70-х - начале 80-х годов. Самые известные разработки были сделаны Berliner HiTech и Ken Thompson (одним из авторов Unix) - Belle. В этих машинах реализован аппаратный генератор ходов, оценочная функция и альфа-бета перебор. Разработки были академические, и невзирая на то, что специализированное железо обычно на порядок быстрее, чем сопоставимое general purpose, о сопоставимости речи не было. Программа Cray Blitz на сверхсовременной тогда машине Cray (стоимостью $60млн) играла все равно лучше.
Deep Blue начинала как студенческая разработка - интересно было группе способных студентов попробовать свои силы, да и тема для диплома отличная. Прогресс технологии позволил сделать первую же версию процессоров (названную ChipTest) очень быстрыми. Последовала следующая, усовершенствованная версия, названная Deep Thought. В этот момент группу заметил маркетинговый департамент фирмы IBM и обратился к ней с предложением, от которого невозможно было отказаться. Результатом стали Deep Blue и Deep Blue II. Таким образом, Deep Blue II - это результат более чем 10 лет работы очень способной группы, в которой были как программисты/железячники, так и сильные гроссмейстеры (кроме уже упомянутого Бенджамина привлекались и другие гроссмейстеры, с хорошей оплатой). Финансировалась вся работа фирмой IBM, таким образом у группы были ресурсы, которые и не снились академическим организациям ("Бог на стороне больших батальонов").
***
ЧАСТЬ VII. КАК УСТРОЕНА DEEP BLUE
Deep Blue II сделана на основе мощного сервера RS/6000 фирмы IBM. В сервере имеется 31 обычных процессора; один объявлен главным, ему подчиняются 30 остальных. К каждому "рабочему" процессору подключено 16 специализированных шахматных процессора, таким образом всего имеется 480 шахматных процессоров. Они и являются "сердцем" системы, таким образом, утверждение IBM "Мы продаем сервер RS/6000, который обыграл в шахматы Каспарова", как бы это сказать... не совсем верно.
Первые несколько полуходов (4) перебираются на "главном" процессоре RS/6000. После 4-х полуходов он передает работу остальным 30-ти процессорам, и они рассматривают следующие 4 полухода. Программа здесь написана на обычном C, и не очень отличается от традиционных параллельных шахматных программ. Наиболее существенное отличие - при написании программы было известно, что система обладает огромной скоростью (т.к. в ней основную работу выполняют специализированные шахматные процессоры), соответственно, можно особо не экономить. Напомню - при написании шахматной программы всегда велико желание какие-то варианты рассмотреть поглубже ("углубиться"), но всегда приходится помнить, что если мы углубимся здесь, то останется меньше времени на рас смотр других вариантов. Соответственно, обычно приходится искать компромисс между более глубоким рассмотрением "тактических" вариантов (в которых только и работают классические углубления) и "тихих" вариантов (которые с точки зрения человека тоже могут быть тактическими, но только ходы не попадают под слишком узкое машинное определение тактических). Здесь же можно рассматривать более длинные варианты, не заботясь что другим времени не достанется - ресурсов хватит на всех. Так что формальные 4 полухода здесь легко могут превратиться в 30 полуходов. После этого работу перехватывают специализированные процессоры, и они делают ощутимо больше 99% всей работы системы - а именно, они перебирают еще на 4 полухода. Из-за того, что в них нет программы как таковой, а все, что надо сделать, зашито аппаратно (не микропрограммно!), при их проектировании приходилось серьезно думать, что надо в них делать, а что нет. В частности, в них не предусмотрено почти никакое углубление. Зато в них предусмотрена достаточно сложная оценочная функция - ведь то, что тяжело запрограммировать, часто очень легко сделать на аппаратном уровне. Например, детектор шахов работает один такт, т.к. одновременно проверяются все возможные варианты. Очень прост контроль X-rays (не знаю, как будет по-русски - это когда одна дальнобойная фигура стоит позади другой), вилок, перегрузки фигур и т.д. Вообще, оценочная функция в шахматном процессоре Deep Blue очень сложна - утверждается, что она соответствует примерно 40000 командам обычного процессора. В частности, там имеется около 8000 коэффициентов. Эти коэффициенты не прошиты намертво, а загружаются в процессор после включения. Таким образом можно было вести настройку процессора после его создания, и не бегать на фабрику для каждого изменения. Как решалась задача оптимизации в пространстве размерности 8000 - это отдельная история (и тоже опубликованная).
Шахматные процессоры были выполнены по устаревшей 0.6 микронной технологии и работают со скоростью 2-2.5млн позиций в секунду. Таким образом, весь монстр обрабатывает примерно миллиард шахматных позиций в секунду. Прошу обратить внимание, что general-purpose системе для этого потребовалось бы быстродействие порядка 40 триллионов операций в секунду.
(Процессоры были серьезно переработаны после первого матча с Каспаровым, когда стало ясно, что в предыдущей версии отсутствуют многие факторы, которые необходимы для игр на таком уровне; большая часть группы не верила, что это удастся сделать меньше чем за год, но Hsu совершил чудеса и управился в срок).
Разумеется, к.п.д. параллельного перебора всегда ниже 100% (раньше уже писалось, что альфа-бета распараллеливается очень тяжело). В данном случае удалось добиться к.п.д порядка 25%, что само по себе является очень большим достижением. То есть система работает как однопроцессорная, не векторная general-purpose машина со скоростью 10 триллионов операций в секунду. Таковых маши не бывает и в ближайшие годы не появится (а может, не появится никогда, т.к. технология упрется в размеры атома и квантовые эффекты).
Система в полном объеме в первый раз была собрана примерно за неделю до повторного матча с Каспаровым, когда были изготовлены все шахматные процессоры. Как протекал этот матч - в следующей главе...
Последний раз редактировалось: Gudleifr (Вт Янв 30, 2018 1:25 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
Один из древнейших компьютерных игроков. Он был создан в те времена, когда ЭВМ были чем-то вроде конторских счетов с прицепленным мотором от стиральной машины, но при этом занимали десяток-другой огромных шкафов.
Обратите внмание, как тут переплетаются математические оценки вероятностей и правдоподобные рассуждения.
Ю.A.ПЕРВИН (ГОРЬКИЙ) / АЛГОРИТМИЗАЦИИ И ПРОГРАММИРОВАНИИ ИГРЫ В ДОМИНО / ПРОБЛЕМЫ КИБЕРНЕТИКИ #3. DJVU, 6.87Мб
DJVU, 6.87Мб
Игра в домино относится к классу игр с неполной информацией. Ее участники объединены в две коалиции, каждая из которых включает по два партнера. Неполная информация об игровом материале участников предопределяет основную трудность алгоритмизации: тривиальный подход к решению задачи - выбор стратегии путем оценки хода, используя перебор комбинаций всех возможных ответов участников - естественно, непригоден не столько в силу большого числа комбинаций, сколько в силу неполной информации об игровом материале участников.
Естественным подходом к решению задачи является вероятностный анализ игровой ситуации. По-видимому, это должно быть специфичным для всех игр с неполной информацией.
Алгоритм игры не является единственным и не претендует на звание лучшего. На пути к его улучшению наиболее заслуживающим внимания является вопрос о построении самосовершенствующейся программы игры.
Игровым материалом являются 28 камней, поровну распределенных между четырьмя участниками. На каждом камне отмечено две цифры от нуля до шести. Игроки выставляют поочередно камни на кон так, что одна из цифр выставляемого камня приставляется к уже поставленным на кон камням, а другая остается свободной.
Правила игры считаются общеизвестными и здесь не приводятся; при составлении алгоритма они не подвергались никаким идеализациям.
В игре участвуют четыре игрока:
- Iм - машина;
- I1 - противник машины, делающий ход после ее хода;
- I2 - партнер машины;
- I3 - противник машины, делающий ход перед ее ходом.
Возможна замена машиной любого числа участников от одного до всех четырех. Случай замены машиной одного игрока наиболее интересен в смысле сравнения способностей человека и программы, однако он не позволяет собрать достаточный статистический материал: велики потери машинного времени за счет неавтоматического ввода информации остальных игроков-людей. Случай замены всех четырех игроков машиной удобен в смысле сбора статистики, но требует учетверенной емкости накопителя, а главное, он интересен при наличии нескольких различных программ (или различных машин), так как, в противном случае, исход определится не стратегиями программ, а начальным раскладом камней. Этот случай (замены четырех игроков) особенно интересен при наличии самосовершенствующейся программы, программы, настраивающейся на стратегию враждебной коалиции и своего партнера. Так как, вообще говоря, машина может играть за любое число игроков (от единицы до четырех), то обозначение "Iм-машина" следует понимать как сокращенное, читаемое так: "Iм - игрок, за которого в данный момент играет машина".
Iм имеет полную информацию лишь о своих камнях и камнях, выставленных на кон. Каждому из остальных камней (s, t) игрок Iм приписывает вероятности p(s,t)I1, p(s,t)I2, p(s,t)I3 того, что данный камень принадлежит соответственно I1, I2, I3. Вероятности p(s,t)I1, p(s,t)I2, p(s,t)I3 служат основанием для выбора хода Iм. Для каждого (s, t), очевидно, имеет место
p(s,t)I1 + p(s,t)I2 + p(s,t)I3 = 1.
В начале игры p(s,t)I1 = p(s,t)I2 = p(s,t)I3 = 1/3 для любого камня. После каждого хода любого из участников, кроме Iм, следует пересчет соответствующих вероятностей.
Алгоритм выбора хода Iм разбит на четыре логически самостоятельных алгоритма, называемых "тактиками":
- тактика Iм - алгоритм, по которому работает программа, когда заходчиком является Iм;
- тактика I1 - алгоритм, по которому работает программа, когда заходчиком является I1;
- тактика I2 -алгоритм, по которому работает программа, когда заходчиком является I2;
- тактика I3 - алгоритм, по которому работает программа, когда заходчиком является I3.
Заходчиком называется игрок, который закончит игру при условии, что он ни разу не откажется от хода. Игрок обязан не отказываться от хода, если к моменту его хода (определяемому очередностью) у него на руках есть хоть один из камней, позволяющих сделать возможный ход [Если "крайними цифрами кона являются a и b, то возможным считается ход камнем (a, x) (соответственно (b, y)), если камень (a, x) (соответственно (b, y)) будет выставлен на конец с цифрой a (соответственно b), имея свободной цифру x (соответственно y)]. Заходчиком становится новый игрок, как только игрок, бывший до этого заходчиком, отказался от хода, кроме довольно редкого (конечно, учитываемого) случая, когда этому отказу предшествовали отказы всех остальных участников. Каждая из тактик позволяет однозначно выбрать ход Iм из нескольких возможностей.
Однако тактика - последний этап выборки хода. Ей предшествует ряд проверок, называемых предтактиковыми, которые работают перед каждым ходом Iм независимо от того, кто является заходчиком.

Рис.1.
Работа машины по выбору камней для хода Iм и наблюдение за ходами игроков I1, I2, I3 представлена на общей блок-схеме (рис.1). На этой блок-схеме стрелки x обозначают передачу управления подпрограмме реализации хода, если предтактиковые проверки однозначно выбрали камень для хода; стрелки М, 1, 2, 3 означают передачу управления соответствующим тактикам при неоднозначном выборе; стрелки I, II, III означают передачу управления блоку переключения тактик, если отказались от хода игроки I1, I2, I3 соответственно.
Первая проверка в программе: "Есть ли у Iм возможность хода?" В случае положительного ответа эта проверка отсылает к первой из предтактиковых проверок: "Есть ли возможность выбора хода?" В случае единственной возможности работает подпрограмма реализации хода. К этой же подпрограмме происходит обращение из любого другого участка программы, на котором однозначно определится камень, которым будет совершен ход. Подпрограмма реализации хода изменяет содержимое необходимых счетчиков и отмечает выставленный камень нужным индексом.
Если возможность не единственна, работают следующие предтактиковые проверки.
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "СТРАХОВКА I ДУПЛЯ". Специфической особенностью дупля - камня, имеющего две одинаковых цифры,- является его возможность быть "отсушенным": для дупля может сложиться ситуация (невозможная для любого другого камня), когда ход дуплем заведомо не станет возможным до конца кона. Если Iм имеет дупль, он должен опасаться такой ситуации. Для этого программа оценивает сложившуюся для дупля (x, x) опасность путем подсчета выставленных камней с цифрой х, оставшихся на руках Iм камней с цифрой x и ожидаемого числа камней с цифрой x, оставшихся у игроков I1, I2, I3. В зависимости от степени опасности Iм выставляет дупль (х, х) (оборонительная тактика) либо переходит к другой проверке, может быть, позволяющей сделать ход, меняющий ситуацию игры в пользу своей команды (наступательная тактика). Если программа находит возможным применить наступательную тактику, выставление (х, х) все же не запрещается (не блокируется), и, возможно, что дупль, не выставленный "страховкой I", будет все же выставлен, если это найдут необходимым следующие проверки.
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "СТРАХОВКА II ДУПЛЯ" учитывает возможность такой ситуации: Iм имеет камни (х, х) и (х, b) среди своих камней, на кону выставлены четыре камня с цифрой х, одна из концевых цифр кона есть b. В таком случае выставление (b, x) грозит тем, что до следующего кона камень (x, x) будет "засушен" выставлением любым из участников камня (x, a). Тогда программа блокирует (запрещает) выставление (b, x), и дальнейшие проверки ведутся с уменьшенным на единицу числом возможностей ((b, х) не может быть единственной возможностью, так как в противном случае раньше сработала бы программа реализации хода).
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "РЫБА". Возможна ситуация, при которой кон считается законченным, хотя у всех участников на руках остаются камни. Она возникает, когда выставлены все семь (или шесть без дупля) камней с x, причем цифра x стоит на обоих концах. Ситуация называется "рыбой". В этом случае подсчет очков производится особо: подсчитываются суммы Сум(М, 2) и Сум(1, 3) очков, оставшихся у игроков (Iм, I2) и (I1, I3) соответственно, и победителем оказывается команда с меньшей суммой.
Ход, которым делается "рыба", не может быть единственно возможным ходом, так как даже камень, которым делается "рыба", имеет две возможности - быть поставленным на оба конца. Выбор - делать или не делать рыбу (а если рыба неизбежна, на какой конец выгодней ставить камень)- осуществляет описываемая проверка. Прежде всего подсчитывается число очков на камнях, остающихся на руках у (Iм, I2) и (I1, I3). О принадлежности камня с цифрами s и t игроку I1, I2 или I3 судят по индексу, зависящему от вероятностей p(s,t)I1, p(s,t)I2, p(s,t)I3. Если p(s,t)I1 - наибольшая из вероятностей, относящихся к камню (s, t), то ставится индекс принадлежности (s, t) к I1 если pI1 = pI2 > pI3, то отмечается принадлежность (s, t) к I1 и I2, но не к I3. Если pI1 = pI2 = pI3, индекс ставится для всех трех игроков. Суждение о принадлежности камня игроку по этому индексу, конечно, условно, так как по мере развития игры вероятности будут пересчитываться, а индексы - меняться.
Для коалиции (Iм, I2) "рыба" выгодна, если Сум(М, 2) < Сум(1, 3). "Рыбу" иногда делают и при невыгодном результате сравнения сумм. Это делается в том случае, когда у (Iм, I2) мало шансов на окончание, т.е. игра идет на тактике I1 или I3 при незначительном числе оставшихся на руках камней. Тогда "рыба" делается, если это не ведет к проигрышному результату всей партии, так как это дает право начать следующий кон.
После хода на "рыбу" возможным может быть лишь один ход дуплем. Если этот дупль не выставлен раньше, то эта предтактиковая проверка проверяет еще, не принадлежит ли этот дупль I1 или I3. Это не опасно, если у I1 и I3 больше, чем по одному камню, если же это не так, "рыбу" делать не следует, так как после хода Iм на "рыбу" последует ход Iх или I3 дуплем, который будет естественным окончанием игры в пользу (I1, I3).
Число mIk (k = 1, 2, 3) индексов принадлежности, относящих камни к игроку Ik, можно назвать ожидаемым числом камней игрока Ik. Предварительный подсчет сумм очков по индексам принадлежности осложняется тем, что ожидаемое число mIk камней игрока Ik может и не быть равным истинному числу lIi его камней. Разность mIk - lТk , умноженная на среднее число очков на камне для данного игрока, вычитается из соответствующей суммы Сум(М, 2) или Сум(1, 3), чем компенсируется возможная ошибка при подсчете сумм очков.
Были запланированы и некоторые другие предтактиковые проверки, например, проверка возможности организовать "свой" конец кона, т.е. конец кона, на который не будет возможных ходов ни у одного из игроков, кроме Iм; проверка возможности предотвращения организации конца игроков I1 или I3. Однако для экономии места в накопителе эти проверки были исключены из программы за счет некоторого усложнения тактик.
Если ни одна из предтактиковых проверок не дала результата (уменьшения возможностей до единицы), включается необходимая тактика. Необходимость существования различных тактик видна хотя бы из следующего примера. Если заходчиком является Iм, предпочтение отдается в первую очередь тем из возможных ходов, которые обеспечат улучшение ситуации именно для Iм (так называемая "игра на себя"). Если заходчик I2, то Iм должен предпочитать ходы, улучшающие положение I2, "подыгрывать" ему (так называемая "игра на партнера").
В тактике I1 предпочитаются ходы, заставляющие "проехать" (отказаться от хода) игрока I1 или не допустить постановку камней, выгодных I1.
Если I3 выставляет камень (a, x), то Iм должен стремиться "забить" конец x, т.е. поставить какой-либо камень на этот конец. Проверка возможности такого "забивания" имеется в каждой тактике, однако в тактике I3 она перемещается ближе к началу последовательности предтактиковых проверок.
Когда остро встает вопрос об экономии места в накопителе, можно вместо тактик I1 и I3 в качестве приближения использовать тактики соответственно I2 и Iм. Если заходчиком является I3, то Iм вправе играть "на себя" (на тактике Iм), так как после отказа I3 от хода заходчиком станет Iм (если Iм не отказывался от хода раньше).
На рис.2 приведена блок-схема тактики Iм. a и b - цифры концов кона, хi - цифры, имеющие вторыми цифрами a или b, т.е. цифры камней возможных ходов. Для работы тактики необходим предварительный подсчет следующих чисел:
- Ky - сумма числа выставленных камней с цифрой y и числа оставшихся у Iм камней с цифрой y.
- Ly - число камней с цифрой y, принадлежавших Iм в начале игры.
- M2y - математическое ожидание числа камней с цифрой y, принадлежащих I2.
- M1y - математическое ожидание числа камней с цифрой y, принадлежащих I1.
Различаются два этапа работы тактики Iм. Этап I (см. рис.2) определяет, на какой из концов - a или b - следует ставить камень. Этап II выбирает вторую цифру выставляемого камня. На этом этапе число возможностей не превосходит пяти: по правилам игры участникам не разрешается иметь больше, чем пять камней с одинаковыми цифрами. Если a = b, то сразу работает этап II. Положительный ответ на одну из проверок второго ряда (см. рис.2) этапа I заставляет работать проверки этапа II лишь с камнями, выставление которых возможно только на конец a, аналогично, отрицательные ответы отсылают к возможностям выставления камней на конец b.
На втором этапе число сравниваемых величин может достигать пяти. Положительный ответ на проверки второго ряда дает возможность однозначно совершить ход. Возвращение из второго ряда в первый (наклонные стрелки в блок-схеме рис.2) связано с обязательным уменьшением не меньше чем на единицу числа возможностей (k >= l >= n >= m). Если ни одна из проверок не дала уменьшения возможностей до единицы, то ход совершается камнем (a, x) (или (b, x)), где x - наименьшая цифра из возможных. Тем самым Iм стремится предотвратить выставление игроком I1 большого числа очков. На тактике I2, когда Iм играет не на себя, в аналогичной ситуации выставляется камень с наибольшей цифрой, чтобы не оставить у себя на руках большого числа очков.


Рис.2.
Остальные тактики структурно выглядят так же, отличаясь лишь числом проверок, порядком их или знаками неравенств в проверках.
Приложением к тактике Iм является схема первого хода. Делая первый ход кона, игрок должен учитывать лишь качество своих собственных камней. Оценка качества камня производится так: каждой цифре от 0 до 6 приписывается число, называемое кратностью - число повторений этой цифры среди камней Iм. Каждый камень характеризуется суммой кратностей ее цифр. Ход совершается с камня, имеющего наибольшую сумму кратностей. Если таких камней несколько, выбирается камень, у которого есть наибольшее слагаемое в этой сумме. Например: если камню (a, x) соответствует пара кратностей (4, 1), а камню (b, y) - (3, 2), то предпочтение отдается камню (a, x), имеющему слагаемое 4.
Большое место в программе занимает так называемый блок наблюдений, занимающийся обработкой вводимой в машину информации о ходах I1, I2, I3. После каждого хода I1, I2, I3 проводится пересчет вероятностей камней, находящихся на руках у I1, I2, I3. В принципе, для каждой тактики и каждого из игроков должна существовать своя блок-схема анализа и обработки наблюдений. Однако некоторые из них в силу эквивалентности или полной или частичной симметрии взаимно заменяемы.
Каждый ход игроков должен давать такую информацию: "игрок Ik (k =1, 2, 3) поставил на конец с цифрой a камень (a, x)". Предполагается известным, что перед ходом этого игрока концевыми цифрами кона были a и b. Подсчет вероятностей ведется путем прибавления (или вычитания) некоторых определенных величин Dp к нужным вероятностям. Остальные вероятности должны пересчитываться для сохранения тождества
pI1 + pI2 + pI3 = 1.
Прибавки к вероятностям - величины Dp - условно разделены на слабые (от 0,05 до 0,10), средние (от 0,13 до 0,20) и сильные (от 0,25 до 0,40). Прибавление (вычитание) того или иного Dp производится в зависимости от сложившейся ситуации игры, от предшествующих ходов игроков и только что совершенного хода данного игрока. Анализом этой зависимости занимается блок наблюдений, схема которого не может быть приведена здесь ввиду своей громоздкости.
После прибавления (вычитания) Dp работает программа, роль которой предостеречь от получения вероятности вне интервала (0, 1) и определить значение двух других вероятностей, связанных с камнем (s, t). Если, например, сделано сложение p(s,t)I1нов = p(s,t)I1ст + Dp, то p(s,t)I2нов и p(s,t)I3нов вычисляются по формулам
p(s,t)I2нов = (1 - (p(s,t)I1ст + Dp)) * p(s,t)I2ст / (p(s,t)I2ст + p(s,t)I3ст);
p(s,t)I3нов = (1 - (p(s,t)I1ст + Dp)) * p(s,t)I3ст / (p(s,t)I2ст + p(s,t)I3ст).
По цифрам выставляемого на кон камня, учитывая сложившуюся игровую ситуацию, можно судить о распределении между игроками камней с определенными цифрами (например, камней с цифрами a, x, b, где a, x - цифры выставляемого камня, b -цифра противоположного конца кона). Поэтому Dp прибавляется (вычитается) сразу ко всем вероятностям, относящимся к камням с этими цифрами. Если, например, выставление какого-то камня позволяет говорить о том, что у I1 много камней с цифрой x, а у I2 - мало камней с цифрой y, то Dp1 прибавляется ко всем вероятностям р{s,x)I1, а Dр2 вычитается из всех вероятностей р(s,y)I2 где (s, x) и (s, y) - камни с цифрами x и y соответственно, не выставленные еще на кон и не принадлежащие Iм.
Блок наблюдений разделен на блок наблюдения "по забиванию" и "блок наблюдения по выставлению". Первый из них позволяет увеличить информацию о камнях игрока по тому, на какой конец он ставит свой камень, второй - по тому, какая цифра на выставляемом им камне свободна. При создании блока наблюдений описываемого варианта программы основой служили, главным образом, практический опыт игры и интуиция. Поэтому улучшение программы - это прежде всего улучшение блока наблюдений. Именно совершенствование этого блока представляет необъятное поле для экспериментов по самообучаемости машины и самонастраиванию на тактику враждебной коалиции. На первых порах это можно делать, выбирая разные Dp в зависимости от накопленного опыта. Более сложный этап - замена блоков и логических цепей программы в зависимости от накопленного опыта и тактики противника.
В некотором смысле обучаемость, самоорганизацию можно усмотреть в уже существующем блоке наблюдений. Следуя терминологии Фэрлея и Кларка [1], всю программу, кроме блока наблюдений, можно назвать преобразователем, а блок наблюдений - модификатором. Действительно, совершая после каждого хода пересчет вероятностей, модификатор осуществляет новые, измененные внутренние связи в программе - преобразователе. На протяжении кона происходит обучение в таком смысле: машина, наблюдая за ходами игроков, определяет принадлежность оставшихся камней игрокам I1, I2, I3 с уточняющейся, по мере развития игры, вероятностью.
Ясно, что это - обучаемость только "в некотором смысле", ибо накопление опыта происходит лишь на протяжении одного кона. С началом нового кона весь процесс начинается сначала, об использовании опыта, накопленного в предыдущих играх, здесь нет и речи.
Описание дополнительных программ - начала игры (определение заходчика), подсчета очков, определение победителей и других - не приводятся, так как все они строго определены правилами игры.
Программа игры в домино была выполнена в коде машины "Стрела". Структурная ячейка внутреннего накопителя очень удачно соответствует всем требованиям, предъявленным к кодировке камня.

Рис.3.
Каждый камень занимает отдельную ячейку в 43 двоичных разряда. В шести разрядах кода операции записываются цифры камня (рис.3). Для выставления на кон камня порядок цифр существен:
- (a, b) - камень, поставленный на конец a,
- (b, a) - камень, поставленный на конец b.
Разряд контрольного сигнала используется для признака дупля: 1 - дупль, 0 - обычный камень. Этот разряд вообще не необходим, но его наличие позволяет сократить некоторые участки программы.
Адреса I, II, III могут иметь разное значение.
Ячейки, в которых размещены камни Шм, не выставленные на кон и не заблокированные (блокировка - запрещение хода, дающего невыгодный исход), имеют все три адреса пустыми (рис.3, а).
Если камень Iм выставляется на левый (правый) конец кона, все разряды первого и второго (второго и третьего) адресов ячейки заполняются единицами [В коде машины "Стрела" при записи двоичных кодов в программе каждую тройку двоичных разрядов изображают одной восьмиричной цифрой. Поэтому единицы, стоящие во всех разрядах адреса на программном бланке, будут выглядеть как 7777 соответствующего адреса] (рис.3, б). Блокировка камня на левый (правый) конец отмечается единицами во всех разрядах первого (третьего) адреса.
В девяти младших разрядах каждого адреса тех ячеек, в которых размещены невыставленные камни игроков I1, I2, I3, записаны вероятности рI1, рI2, и рI3, соответственно в I, II, III адресах. Как видно, вероятность записывается тремя восьмеричными цифрами, что даже превосходит требуемую для задачи точность. Первый старший разряд предназначен для описанного выше индекса принадлежности. Если, например, pI2 > pI3 = pI1, то из старших разрядов адресов заполняется лишь первый старший разряд второго адреса. На рис.3, г представлена ячейка, в которой записаны вероятности:
p(0,2)I1 = 1/4, p(0,2)I2 = 1/2, p(0,2)I3 = 1/4.
Второй и третий разряды адресов для невыставленных камней I1, I2, I3 обычно пусты. Если в процессе пересчета вероятностей получится pIk >= 1 (соответственно pIk =< 0), это обнаружится по единице третьего разряда адреса. Тогда в девять младших разрядов данного адреса засылается вероятность 0,95 (соответственно 0,05).
Если камень выставлен I1, это отмечается единицами второго и третьего разрядов первого адреса, для I2 - второго адреса (рис.3, в), для I3 - третьего адреса. Остальные разряды адресов тогда чисты.
Описываемая программа была отлажена на машине "Стрела" и участвовала в практической игре, заменяя одного игрока. Анализ кона, сыгранного с участием машины, показал, что машина, имея перед каждым ходом по две - три возможности, выбирала лучшие из них. На семнадцатом ходе машина сделала "рыбу" и выиграла кон со счетом 40:24.
Ниже приводится сыгранный машиной кон. Надо отметить, что распределение камней между всеми четырьмя игроками было сделано обычным способом, т.е. совершенно случайно.
Перед началом игры участники получили такие камни:
- Iм: (1,1), (0,0), (4,0), (5,6), (6,2), (2,1), (6,3).
- I1: (1,0), (2,0), (4,4), (3,3), (4,3), (5,4), (0,3).
- I2: (2,5), (6,0), (6,4), (5,0), (5,5), (1,3), (5,1).
- I3: (5,3), (1,6), (6,6), (1,4), (2,2), (2,4), (3,2).
Ходы читаются так, как указывалось выше - (a, b) обозначает выставление на конец кона с цифрой а.
1.
- Iм - (1,1); машина делает первый ход, ибо находит у себя камень, с которого согласно правилам начинается игра.
- I1 - (1,0).
- I2 - (0,5).
- I3 - (1,4).
2.
- Iм - (5,6); машина стремится играть на своих "шестерках" (камнях с цифрой 6). Их у нее больше, чем камней с другими цифрами. Учитывая, что Iм сам является заходчиком, Iм не стоит перед дилеммой - забивать или не забивать "пятерку", выставленную I2: ходом (5,6) Iм "играет на себя".
- I1 - (4,4).
- I2 - (4,6). Естественно, что I2 подыгрывает Iм, а не ходит (6,4).
- I3 - (6,6).
3.
- Iм - (6,2). Есть две возможности: (6,3) и (6,2). Ни одной "двойки" или "тройки" на кону не выставлено, так что судить о наличии их у I1, I2, I3 с вероятностями, большими 1/3, невозможно. Машина выбирает именно этот камень, т.к. "двоек" у нее две, а "тройка" - одна.
- I1 - (2,0).
- I2 - (0,6).
- I3 - (6,1).
4.
- Iм - (1,2). Из имевшихся возможностей (1,2), (0,0) и (4,0) выбрана лучшая, так как выставление "четверки" подыграло бы игроку I1, а выставление (0,0) - игроку I3. Кроме того, этим ходом забивается "единица", выставленная игроком I3. Здесь не следует, конечно, усматривать тенденцию играть на "двойках".
- I1 не имеет возможности выставить ни одного из своих камней.
- I2 - (2,5).
- I3 - (5,3).
5.
- Iм - (3,6). Вряд ли стоило задумываться - делать ли "рыбу"? Достаточно взгляда на оставшиеся у Iм камни (0,0) и (0,4) и на число камней у прокатившегося игрока I1. К тому же, ходом (6,3) Iм передавал бы инициативу противникам.
Программы игры в домино не только лишний раз демонстрируют возможности электронных цифровых машин. После каждого хода игроков в машине фиксируется не только определенная информация, но и предположения машины о камнях игроков. Такие же предположения делаются и игроками-людьми. Действительное распределение камней, предположения, делаемые по этому поводу человеком и машиной - хороший материал для сравнения мыслительных способностей человека с оценивающими способностями алгоритма. Поэтому, может быть, в некоторой степени и к описываемой задаче могут быть отнесены слова К.Э.Шеннона [3]: "Мы надеемся, что исследования в области конструирования играющих машин приведут к пониманию работы человеческого мозга. Разумеется, было бы наивным ожидать, что мозг действует так же, как и машина, предназначенная для ведения игр, или сколько-нибудь аналогично ей, тем не менее несомненно, что создание любой обучающейся машины осветит путь к пониманию работы мозга".
ЛИТЕРАТУРА
[1] Farley В.G. а. Clаrk W.A., Simulation of self-organizing sistems by digital computer, Transaction IRE, 1954, RGTT-4, 9, 76.
[2] Штаркман В.С, Система команд быстродействующей электронной вычислительной машины "Стрела-1", М., 1956.
[3] Shannon С.Е., J. of the Franclin Inst. 260, 6, 1955.
Поступило в редакцию 3 II 1958.
***
ГЛАВНЫЕ ВЫВОДЫ
1. Для имитации сложного (разумного) поведения достаточно иногда простейших (случайных) механизмов.
2. Разумное поведение базируется на многоуровневости рассуждений. Подробнее см. в книгах Н.М.Амосова ТЕМА #148, АБЗАЦ #3309
ТЕМА #148, АБЗАЦ #3309 .
.
3. Расчет чего-либо не всегда является очевидно-логическим. И очень редко к оптимуму можно прийти путем правдоподобных рассуждений.
Обратите внмание, как тут переплетаются математические оценки вероятностей и правдоподобные рассуждения.
Ю.A.ПЕРВИН (ГОРЬКИЙ) / АЛГОРИТМИЗАЦИИ И ПРОГРАММИРОВАНИИ ИГРЫ В ДОМИНО / ПРОБЛЕМЫ КИБЕРНЕТИКИ #3.
 DJVU, 6.87Мб
DJVU, 6.87Мб
Игра в домино относится к классу игр с неполной информацией. Ее участники объединены в две коалиции, каждая из которых включает по два партнера. Неполная информация об игровом материале участников предопределяет основную трудность алгоритмизации: тривиальный подход к решению задачи - выбор стратегии путем оценки хода, используя перебор комбинаций всех возможных ответов участников - естественно, непригоден не столько в силу большого числа комбинаций, сколько в силу неполной информации об игровом материале участников.
Естественным подходом к решению задачи является вероятностный анализ игровой ситуации. По-видимому, это должно быть специфичным для всех игр с неполной информацией.
Алгоритм игры не является единственным и не претендует на звание лучшего. На пути к его улучшению наиболее заслуживающим внимания является вопрос о построении самосовершенствующейся программы игры.
Игровым материалом являются 28 камней, поровну распределенных между четырьмя участниками. На каждом камне отмечено две цифры от нуля до шести. Игроки выставляют поочередно камни на кон так, что одна из цифр выставляемого камня приставляется к уже поставленным на кон камням, а другая остается свободной.
Правила игры считаются общеизвестными и здесь не приводятся; при составлении алгоритма они не подвергались никаким идеализациям.
В игре участвуют четыре игрока:
- Iм - машина;
- I1 - противник машины, делающий ход после ее хода;
- I2 - партнер машины;
- I3 - противник машины, делающий ход перед ее ходом.
Возможна замена машиной любого числа участников от одного до всех четырех. Случай замены машиной одного игрока наиболее интересен в смысле сравнения способностей человека и программы, однако он не позволяет собрать достаточный статистический материал: велики потери машинного времени за счет неавтоматического ввода информации остальных игроков-людей. Случай замены всех четырех игроков машиной удобен в смысле сбора статистики, но требует учетверенной емкости накопителя, а главное, он интересен при наличии нескольких различных программ (или различных машин), так как, в противном случае, исход определится не стратегиями программ, а начальным раскладом камней. Этот случай (замены четырех игроков) особенно интересен при наличии самосовершенствующейся программы, программы, настраивающейся на стратегию враждебной коалиции и своего партнера. Так как, вообще говоря, машина может играть за любое число игроков (от единицы до четырех), то обозначение "Iм-машина" следует понимать как сокращенное, читаемое так: "Iм - игрок, за которого в данный момент играет машина".
Iм имеет полную информацию лишь о своих камнях и камнях, выставленных на кон. Каждому из остальных камней (s, t) игрок Iм приписывает вероятности p(s,t)I1, p(s,t)I2, p(s,t)I3 того, что данный камень принадлежит соответственно I1, I2, I3. Вероятности p(s,t)I1, p(s,t)I2, p(s,t)I3 служат основанием для выбора хода Iм. Для каждого (s, t), очевидно, имеет место
p(s,t)I1 + p(s,t)I2 + p(s,t)I3 = 1.
В начале игры p(s,t)I1 = p(s,t)I2 = p(s,t)I3 = 1/3 для любого камня. После каждого хода любого из участников, кроме Iм, следует пересчет соответствующих вероятностей.
Алгоритм выбора хода Iм разбит на четыре логически самостоятельных алгоритма, называемых "тактиками":
- тактика Iм - алгоритм, по которому работает программа, когда заходчиком является Iм;
- тактика I1 - алгоритм, по которому работает программа, когда заходчиком является I1;
- тактика I2 -алгоритм, по которому работает программа, когда заходчиком является I2;
- тактика I3 - алгоритм, по которому работает программа, когда заходчиком является I3.
Заходчиком называется игрок, который закончит игру при условии, что он ни разу не откажется от хода. Игрок обязан не отказываться от хода, если к моменту его хода (определяемому очередностью) у него на руках есть хоть один из камней, позволяющих сделать возможный ход [Если "крайними цифрами кона являются a и b, то возможным считается ход камнем (a, x) (соответственно (b, y)), если камень (a, x) (соответственно (b, y)) будет выставлен на конец с цифрой a (соответственно b), имея свободной цифру x (соответственно y)]. Заходчиком становится новый игрок, как только игрок, бывший до этого заходчиком, отказался от хода, кроме довольно редкого (конечно, учитываемого) случая, когда этому отказу предшествовали отказы всех остальных участников. Каждая из тактик позволяет однозначно выбрать ход Iм из нескольких возможностей.
Однако тактика - последний этап выборки хода. Ей предшествует ряд проверок, называемых предтактиковыми, которые работают перед каждым ходом Iм независимо от того, кто является заходчиком.

Рис.1.
Работа машины по выбору камней для хода Iм и наблюдение за ходами игроков I1, I2, I3 представлена на общей блок-схеме (рис.1). На этой блок-схеме стрелки x обозначают передачу управления подпрограмме реализации хода, если предтактиковые проверки однозначно выбрали камень для хода; стрелки М, 1, 2, 3 означают передачу управления соответствующим тактикам при неоднозначном выборе; стрелки I, II, III означают передачу управления блоку переключения тактик, если отказались от хода игроки I1, I2, I3 соответственно.
Первая проверка в программе: "Есть ли у Iм возможность хода?" В случае положительного ответа эта проверка отсылает к первой из предтактиковых проверок: "Есть ли возможность выбора хода?" В случае единственной возможности работает подпрограмма реализации хода. К этой же подпрограмме происходит обращение из любого другого участка программы, на котором однозначно определится камень, которым будет совершен ход. Подпрограмма реализации хода изменяет содержимое необходимых счетчиков и отмечает выставленный камень нужным индексом.
Если возможность не единственна, работают следующие предтактиковые проверки.
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "СТРАХОВКА I ДУПЛЯ". Специфической особенностью дупля - камня, имеющего две одинаковых цифры,- является его возможность быть "отсушенным": для дупля может сложиться ситуация (невозможная для любого другого камня), когда ход дуплем заведомо не станет возможным до конца кона. Если Iм имеет дупль, он должен опасаться такой ситуации. Для этого программа оценивает сложившуюся для дупля (x, x) опасность путем подсчета выставленных камней с цифрой х, оставшихся на руках Iм камней с цифрой x и ожидаемого числа камней с цифрой x, оставшихся у игроков I1, I2, I3. В зависимости от степени опасности Iм выставляет дупль (х, х) (оборонительная тактика) либо переходит к другой проверке, может быть, позволяющей сделать ход, меняющий ситуацию игры в пользу своей команды (наступательная тактика). Если программа находит возможным применить наступательную тактику, выставление (х, х) все же не запрещается (не блокируется), и, возможно, что дупль, не выставленный "страховкой I", будет все же выставлен, если это найдут необходимым следующие проверки.
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "СТРАХОВКА II ДУПЛЯ" учитывает возможность такой ситуации: Iм имеет камни (х, х) и (х, b) среди своих камней, на кону выставлены четыре камня с цифрой х, одна из концевых цифр кона есть b. В таком случае выставление (b, x) грозит тем, что до следующего кона камень (x, x) будет "засушен" выставлением любым из участников камня (x, a). Тогда программа блокирует (запрещает) выставление (b, x), и дальнейшие проверки ведутся с уменьшенным на единицу числом возможностей ((b, х) не может быть единственной возможностью, так как в противном случае раньше сработала бы программа реализации хода).
ПРЕДТАКТИКОВАЯ ПРОВЕРКА "РЫБА". Возможна ситуация, при которой кон считается законченным, хотя у всех участников на руках остаются камни. Она возникает, когда выставлены все семь (или шесть без дупля) камней с x, причем цифра x стоит на обоих концах. Ситуация называется "рыбой". В этом случае подсчет очков производится особо: подсчитываются суммы Сум(М, 2) и Сум(1, 3) очков, оставшихся у игроков (Iм, I2) и (I1, I3) соответственно, и победителем оказывается команда с меньшей суммой.
Ход, которым делается "рыба", не может быть единственно возможным ходом, так как даже камень, которым делается "рыба", имеет две возможности - быть поставленным на оба конца. Выбор - делать или не делать рыбу (а если рыба неизбежна, на какой конец выгодней ставить камень)- осуществляет описываемая проверка. Прежде всего подсчитывается число очков на камнях, остающихся на руках у (Iм, I2) и (I1, I3). О принадлежности камня с цифрами s и t игроку I1, I2 или I3 судят по индексу, зависящему от вероятностей p(s,t)I1, p(s,t)I2, p(s,t)I3. Если p(s,t)I1 - наибольшая из вероятностей, относящихся к камню (s, t), то ставится индекс принадлежности (s, t) к I1 если pI1 = pI2 > pI3, то отмечается принадлежность (s, t) к I1 и I2, но не к I3. Если pI1 = pI2 = pI3, индекс ставится для всех трех игроков. Суждение о принадлежности камня игроку по этому индексу, конечно, условно, так как по мере развития игры вероятности будут пересчитываться, а индексы - меняться.
Для коалиции (Iм, I2) "рыба" выгодна, если Сум(М, 2) < Сум(1, 3). "Рыбу" иногда делают и при невыгодном результате сравнения сумм. Это делается в том случае, когда у (Iм, I2) мало шансов на окончание, т.е. игра идет на тактике I1 или I3 при незначительном числе оставшихся на руках камней. Тогда "рыба" делается, если это не ведет к проигрышному результату всей партии, так как это дает право начать следующий кон.
После хода на "рыбу" возможным может быть лишь один ход дуплем. Если этот дупль не выставлен раньше, то эта предтактиковая проверка проверяет еще, не принадлежит ли этот дупль I1 или I3. Это не опасно, если у I1 и I3 больше, чем по одному камню, если же это не так, "рыбу" делать не следует, так как после хода Iм на "рыбу" последует ход Iх или I3 дуплем, который будет естественным окончанием игры в пользу (I1, I3).
Число mIk (k = 1, 2, 3) индексов принадлежности, относящих камни к игроку Ik, можно назвать ожидаемым числом камней игрока Ik. Предварительный подсчет сумм очков по индексам принадлежности осложняется тем, что ожидаемое число mIk камней игрока Ik может и не быть равным истинному числу lIi его камней. Разность mIk - lТk , умноженная на среднее число очков на камне для данного игрока, вычитается из соответствующей суммы Сум(М, 2) или Сум(1, 3), чем компенсируется возможная ошибка при подсчете сумм очков.
Были запланированы и некоторые другие предтактиковые проверки, например, проверка возможности организовать "свой" конец кона, т.е. конец кона, на который не будет возможных ходов ни у одного из игроков, кроме Iм; проверка возможности предотвращения организации конца игроков I1 или I3. Однако для экономии места в накопителе эти проверки были исключены из программы за счет некоторого усложнения тактик.
Если ни одна из предтактиковых проверок не дала результата (уменьшения возможностей до единицы), включается необходимая тактика. Необходимость существования различных тактик видна хотя бы из следующего примера. Если заходчиком является Iм, предпочтение отдается в первую очередь тем из возможных ходов, которые обеспечат улучшение ситуации именно для Iм (так называемая "игра на себя"). Если заходчик I2, то Iм должен предпочитать ходы, улучшающие положение I2, "подыгрывать" ему (так называемая "игра на партнера").
В тактике I1 предпочитаются ходы, заставляющие "проехать" (отказаться от хода) игрока I1 или не допустить постановку камней, выгодных I1.
Если I3 выставляет камень (a, x), то Iм должен стремиться "забить" конец x, т.е. поставить какой-либо камень на этот конец. Проверка возможности такого "забивания" имеется в каждой тактике, однако в тактике I3 она перемещается ближе к началу последовательности предтактиковых проверок.
Когда остро встает вопрос об экономии места в накопителе, можно вместо тактик I1 и I3 в качестве приближения использовать тактики соответственно I2 и Iм. Если заходчиком является I3, то Iм вправе играть "на себя" (на тактике Iм), так как после отказа I3 от хода заходчиком станет Iм (если Iм не отказывался от хода раньше).
На рис.2 приведена блок-схема тактики Iм. a и b - цифры концов кона, хi - цифры, имеющие вторыми цифрами a или b, т.е. цифры камней возможных ходов. Для работы тактики необходим предварительный подсчет следующих чисел:
- Ky - сумма числа выставленных камней с цифрой y и числа оставшихся у Iм камней с цифрой y.
- Ly - число камней с цифрой y, принадлежавших Iм в начале игры.
- M2y - математическое ожидание числа камней с цифрой y, принадлежащих I2.
- M1y - математическое ожидание числа камней с цифрой y, принадлежащих I1.
Различаются два этапа работы тактики Iм. Этап I (см. рис.2) определяет, на какой из концов - a или b - следует ставить камень. Этап II выбирает вторую цифру выставляемого камня. На этом этапе число возможностей не превосходит пяти: по правилам игры участникам не разрешается иметь больше, чем пять камней с одинаковыми цифрами. Если a = b, то сразу работает этап II. Положительный ответ на одну из проверок второго ряда (см. рис.2) этапа I заставляет работать проверки этапа II лишь с камнями, выставление которых возможно только на конец a, аналогично, отрицательные ответы отсылают к возможностям выставления камней на конец b.
На втором этапе число сравниваемых величин может достигать пяти. Положительный ответ на проверки второго ряда дает возможность однозначно совершить ход. Возвращение из второго ряда в первый (наклонные стрелки в блок-схеме рис.2) связано с обязательным уменьшением не меньше чем на единицу числа возможностей (k >= l >= n >= m). Если ни одна из проверок не дала уменьшения возможностей до единицы, то ход совершается камнем (a, x) (или (b, x)), где x - наименьшая цифра из возможных. Тем самым Iм стремится предотвратить выставление игроком I1 большого числа очков. На тактике I2, когда Iм играет не на себя, в аналогичной ситуации выставляется камень с наибольшей цифрой, чтобы не оставить у себя на руках большого числа очков.


Рис.2.
Остальные тактики структурно выглядят так же, отличаясь лишь числом проверок, порядком их или знаками неравенств в проверках.
Приложением к тактике Iм является схема первого хода. Делая первый ход кона, игрок должен учитывать лишь качество своих собственных камней. Оценка качества камня производится так: каждой цифре от 0 до 6 приписывается число, называемое кратностью - число повторений этой цифры среди камней Iм. Каждый камень характеризуется суммой кратностей ее цифр. Ход совершается с камня, имеющего наибольшую сумму кратностей. Если таких камней несколько, выбирается камень, у которого есть наибольшее слагаемое в этой сумме. Например: если камню (a, x) соответствует пара кратностей (4, 1), а камню (b, y) - (3, 2), то предпочтение отдается камню (a, x), имеющему слагаемое 4.
Большое место в программе занимает так называемый блок наблюдений, занимающийся обработкой вводимой в машину информации о ходах I1, I2, I3. После каждого хода I1, I2, I3 проводится пересчет вероятностей камней, находящихся на руках у I1, I2, I3. В принципе, для каждой тактики и каждого из игроков должна существовать своя блок-схема анализа и обработки наблюдений. Однако некоторые из них в силу эквивалентности или полной или частичной симметрии взаимно заменяемы.
Каждый ход игроков должен давать такую информацию: "игрок Ik (k =1, 2, 3) поставил на конец с цифрой a камень (a, x)". Предполагается известным, что перед ходом этого игрока концевыми цифрами кона были a и b. Подсчет вероятностей ведется путем прибавления (или вычитания) некоторых определенных величин Dp к нужным вероятностям. Остальные вероятности должны пересчитываться для сохранения тождества
pI1 + pI2 + pI3 = 1.
Прибавки к вероятностям - величины Dp - условно разделены на слабые (от 0,05 до 0,10), средние (от 0,13 до 0,20) и сильные (от 0,25 до 0,40). Прибавление (вычитание) того или иного Dp производится в зависимости от сложившейся ситуации игры, от предшествующих ходов игроков и только что совершенного хода данного игрока. Анализом этой зависимости занимается блок наблюдений, схема которого не может быть приведена здесь ввиду своей громоздкости.
После прибавления (вычитания) Dp работает программа, роль которой предостеречь от получения вероятности вне интервала (0, 1) и определить значение двух других вероятностей, связанных с камнем (s, t). Если, например, сделано сложение p(s,t)I1нов = p(s,t)I1ст + Dp, то p(s,t)I2нов и p(s,t)I3нов вычисляются по формулам
p(s,t)I2нов = (1 - (p(s,t)I1ст + Dp)) * p(s,t)I2ст / (p(s,t)I2ст + p(s,t)I3ст);
p(s,t)I3нов = (1 - (p(s,t)I1ст + Dp)) * p(s,t)I3ст / (p(s,t)I2ст + p(s,t)I3ст).
По цифрам выставляемого на кон камня, учитывая сложившуюся игровую ситуацию, можно судить о распределении между игроками камней с определенными цифрами (например, камней с цифрами a, x, b, где a, x - цифры выставляемого камня, b -цифра противоположного конца кона). Поэтому Dp прибавляется (вычитается) сразу ко всем вероятностям, относящимся к камням с этими цифрами. Если, например, выставление какого-то камня позволяет говорить о том, что у I1 много камней с цифрой x, а у I2 - мало камней с цифрой y, то Dp1 прибавляется ко всем вероятностям р{s,x)I1, а Dр2 вычитается из всех вероятностей р(s,y)I2 где (s, x) и (s, y) - камни с цифрами x и y соответственно, не выставленные еще на кон и не принадлежащие Iм.
Блок наблюдений разделен на блок наблюдения "по забиванию" и "блок наблюдения по выставлению". Первый из них позволяет увеличить информацию о камнях игрока по тому, на какой конец он ставит свой камень, второй - по тому, какая цифра на выставляемом им камне свободна. При создании блока наблюдений описываемого варианта программы основой служили, главным образом, практический опыт игры и интуиция. Поэтому улучшение программы - это прежде всего улучшение блока наблюдений. Именно совершенствование этого блока представляет необъятное поле для экспериментов по самообучаемости машины и самонастраиванию на тактику враждебной коалиции. На первых порах это можно делать, выбирая разные Dp в зависимости от накопленного опыта. Более сложный этап - замена блоков и логических цепей программы в зависимости от накопленного опыта и тактики противника.
В некотором смысле обучаемость, самоорганизацию можно усмотреть в уже существующем блоке наблюдений. Следуя терминологии Фэрлея и Кларка [1], всю программу, кроме блока наблюдений, можно назвать преобразователем, а блок наблюдений - модификатором. Действительно, совершая после каждого хода пересчет вероятностей, модификатор осуществляет новые, измененные внутренние связи в программе - преобразователе. На протяжении кона происходит обучение в таком смысле: машина, наблюдая за ходами игроков, определяет принадлежность оставшихся камней игрокам I1, I2, I3 с уточняющейся, по мере развития игры, вероятностью.
Ясно, что это - обучаемость только "в некотором смысле", ибо накопление опыта происходит лишь на протяжении одного кона. С началом нового кона весь процесс начинается сначала, об использовании опыта, накопленного в предыдущих играх, здесь нет и речи.
Описание дополнительных программ - начала игры (определение заходчика), подсчета очков, определение победителей и других - не приводятся, так как все они строго определены правилами игры.
Программа игры в домино была выполнена в коде машины "Стрела". Структурная ячейка внутреннего накопителя очень удачно соответствует всем требованиям, предъявленным к кодировке камня.

Рис.3.
Каждый камень занимает отдельную ячейку в 43 двоичных разряда. В шести разрядах кода операции записываются цифры камня (рис.3). Для выставления на кон камня порядок цифр существен:
- (a, b) - камень, поставленный на конец a,
- (b, a) - камень, поставленный на конец b.
Разряд контрольного сигнала используется для признака дупля: 1 - дупль, 0 - обычный камень. Этот разряд вообще не необходим, но его наличие позволяет сократить некоторые участки программы.
Адреса I, II, III могут иметь разное значение.
Ячейки, в которых размещены камни Шм, не выставленные на кон и не заблокированные (блокировка - запрещение хода, дающего невыгодный исход), имеют все три адреса пустыми (рис.3, а).
Если камень Iм выставляется на левый (правый) конец кона, все разряды первого и второго (второго и третьего) адресов ячейки заполняются единицами [В коде машины "Стрела" при записи двоичных кодов в программе каждую тройку двоичных разрядов изображают одной восьмиричной цифрой. Поэтому единицы, стоящие во всех разрядах адреса на программном бланке, будут выглядеть как 7777 соответствующего адреса] (рис.3, б). Блокировка камня на левый (правый) конец отмечается единицами во всех разрядах первого (третьего) адреса.
В девяти младших разрядах каждого адреса тех ячеек, в которых размещены невыставленные камни игроков I1, I2, I3, записаны вероятности рI1, рI2, и рI3, соответственно в I, II, III адресах. Как видно, вероятность записывается тремя восьмеричными цифрами, что даже превосходит требуемую для задачи точность. Первый старший разряд предназначен для описанного выше индекса принадлежности. Если, например, pI2 > pI3 = pI1, то из старших разрядов адресов заполняется лишь первый старший разряд второго адреса. На рис.3, г представлена ячейка, в которой записаны вероятности:
p(0,2)I1 = 1/4, p(0,2)I2 = 1/2, p(0,2)I3 = 1/4.
Второй и третий разряды адресов для невыставленных камней I1, I2, I3 обычно пусты. Если в процессе пересчета вероятностей получится pIk >= 1 (соответственно pIk =< 0), это обнаружится по единице третьего разряда адреса. Тогда в девять младших разрядов данного адреса засылается вероятность 0,95 (соответственно 0,05).
Если камень выставлен I1, это отмечается единицами второго и третьего разрядов первого адреса, для I2 - второго адреса (рис.3, в), для I3 - третьего адреса. Остальные разряды адресов тогда чисты.
Описываемая программа была отлажена на машине "Стрела" и участвовала в практической игре, заменяя одного игрока. Анализ кона, сыгранного с участием машины, показал, что машина, имея перед каждым ходом по две - три возможности, выбирала лучшие из них. На семнадцатом ходе машина сделала "рыбу" и выиграла кон со счетом 40:24.
Ниже приводится сыгранный машиной кон. Надо отметить, что распределение камней между всеми четырьмя игроками было сделано обычным способом, т.е. совершенно случайно.
Перед началом игры участники получили такие камни:
- Iм: (1,1), (0,0), (4,0), (5,6), (6,2), (2,1), (6,3).
- I1: (1,0), (2,0), (4,4), (3,3), (4,3), (5,4), (0,3).
- I2: (2,5), (6,0), (6,4), (5,0), (5,5), (1,3), (5,1).
- I3: (5,3), (1,6), (6,6), (1,4), (2,2), (2,4), (3,2).
Ходы читаются так, как указывалось выше - (a, b) обозначает выставление на конец кона с цифрой а.
1.
- Iм - (1,1); машина делает первый ход, ибо находит у себя камень, с которого согласно правилам начинается игра.
- I1 - (1,0).
- I2 - (0,5).
- I3 - (1,4).
2.
- Iм - (5,6); машина стремится играть на своих "шестерках" (камнях с цифрой 6). Их у нее больше, чем камней с другими цифрами. Учитывая, что Iм сам является заходчиком, Iм не стоит перед дилеммой - забивать или не забивать "пятерку", выставленную I2: ходом (5,6) Iм "играет на себя".
- I1 - (4,4).
- I2 - (4,6). Естественно, что I2 подыгрывает Iм, а не ходит (6,4).
- I3 - (6,6).
3.
- Iм - (6,2). Есть две возможности: (6,3) и (6,2). Ни одной "двойки" или "тройки" на кону не выставлено, так что судить о наличии их у I1, I2, I3 с вероятностями, большими 1/3, невозможно. Машина выбирает именно этот камень, т.к. "двоек" у нее две, а "тройка" - одна.
- I1 - (2,0).
- I2 - (0,6).
- I3 - (6,1).
4.
- Iм - (1,2). Из имевшихся возможностей (1,2), (0,0) и (4,0) выбрана лучшая, так как выставление "четверки" подыграло бы игроку I1, а выставление (0,0) - игроку I3. Кроме того, этим ходом забивается "единица", выставленная игроком I3. Здесь не следует, конечно, усматривать тенденцию играть на "двойках".
- I1 не имеет возможности выставить ни одного из своих камней.
- I2 - (2,5).
- I3 - (5,3).
5.
- Iм - (3,6). Вряд ли стоило задумываться - делать ли "рыбу"? Достаточно взгляда на оставшиеся у Iм камни (0,0) и (0,4) и на число камней у прокатившегося игрока I1. К тому же, ходом (6,3) Iм передавал бы инициативу противникам.
Программы игры в домино не только лишний раз демонстрируют возможности электронных цифровых машин. После каждого хода игроков в машине фиксируется не только определенная информация, но и предположения машины о камнях игроков. Такие же предположения делаются и игроками-людьми. Действительное распределение камней, предположения, делаемые по этому поводу человеком и машиной - хороший материал для сравнения мыслительных способностей человека с оценивающими способностями алгоритма. Поэтому, может быть, в некоторой степени и к описываемой задаче могут быть отнесены слова К.Э.Шеннона [3]: "Мы надеемся, что исследования в области конструирования играющих машин приведут к пониманию работы человеческого мозга. Разумеется, было бы наивным ожидать, что мозг действует так же, как и машина, предназначенная для ведения игр, или сколько-нибудь аналогично ей, тем не менее несомненно, что создание любой обучающейся машины осветит путь к пониманию работы мозга".
ЛИТЕРАТУРА
[1] Farley В.G. а. Clаrk W.A., Simulation of self-organizing sistems by digital computer, Transaction IRE, 1954, RGTT-4, 9, 76.
[2] Штаркман В.С, Система команд быстродействующей электронной вычислительной машины "Стрела-1", М., 1956.
[3] Shannon С.Е., J. of the Franclin Inst. 260, 6, 1955.
Поступило в редакцию 3 II 1958.
***
ГЛАВНЫЕ ВЫВОДЫ
1. Для имитации сложного (разумного) поведения достаточно иногда простейших (случайных) механизмов.
2. Разумное поведение базируется на многоуровневости рассуждений. Подробнее см. в книгах Н.М.Амосова
 ТЕМА #148, АБЗАЦ #3309
ТЕМА #148, АБЗАЦ #3309 .
.3. Расчет чего-либо не всегда является очевидно-логическим. И очень редко к оптимуму можно прийти путем правдоподобных рассуждений.
Последний раз редактировалось: Gudleifr (Пн Июл 31, 2023 12:57 am), всего редактировалось 5 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: 01.03. ЭТО КОТ?
Re: 01.03. ЭТО КОТ?
..
- Сказка, которую я расскажу вам, похожа на быль. Она называется "Рассказ о смеющемся Тюринге".
В наступившей тишине некоторое время еще слышались шаги обслуживающих автоматов. Потом утихли и они, а Калларла все еще не начинала, как бы ожидая чего-то. На ее губах блуждала легкая улыбка. Чего она ждала? Может быть, чтобы вернулось то настроение, которое охватило всех нас, когда в зале были дети?
Наконец она сказала:
- Слышала я этот рассказ от своей бабушки, женщины очень консервативной, которая... но, может быть, при сказках комментарии не нужны? Итак, я начинаю.
Она не смотрела на нас. Глаза ее, обращенные к искрящейся струе фонтана, стали неподвижными, а приглушенный голос смешивался со звуком воды, падающей в каменную чашу.
- Давным-давно, больше тысячи лет назад, мир делился на две части. В одной правили атлантиды. Они хотели уничтожить другую половину мира, которая не подчинялась их власти. Они накапливали яды, взрывчатые и радиоактивные вещества, при помощи которых можно было бы отравить воздух и воду. Но чем большие запасы таких веществ они делали, тем больший страх охватывал их.
Они покупали за золото ученых, чтобы те создавали самые совершенные машины для убийства. Однажды им стало известно, что на далеком острове за океаном живет ученый, по имени Тюринг, умеющий создавать автоматы. Тогда об автоматах знали еще очень мало и никто точно не представлял себе, какую пользу они могут приносить. Тюринг строил различные автоматы: одни делали машины, другие выпекали хлеб, третьи вычисляли и обладали способностью логически рассуждать. Он трудился сорок лет, пока не изобрел автомат, который мог делать все.
Этот автомат мог выплавлять металл из руды и шить сапоги, превращать один элемент в другой и строить дома, он мог и работать физически и думать обо всем. Он мог ответить на любой вопрос и решить любую задачу; не было дела, которого бы он не выполнил, если оно ему было поручено. Властители Атлантиды направили своих агентов с заданием купить Тюринга, но ученый не согласился на это. Тогда они заключили его в тюрьму и похитили чертежи его изобретений. Старший из атлантидов просмотрел эти чертежи, созвал других и сказал: "Если у нас будет такой автомат, спросим его, как уничтожить тех людей, которые хотят навсегда устранить войны". А другой властитель добавил: "Он, кроме того, скажет нам, как отучить наших подданных от мышления, потому что мыслящие люди неохотно умирают во славу нашего золота".
Все присутствующие, зааплодировали ему и решили: построим Большой Генеральный Автомат Тюринга, будем всемогущими, и никто в мире не сможет противостоять нам.
Затем собрали семь тысяч счетных работников (тогда люди еще считали в уме), чтобы те подсчитали, сколько золота понадобится на оплату строительства. Вслед за ними собрали семь тысяч инженеров и конструкторов, которые семь лет чертили проекты... Еще до того, как проекты были закончены, первые бригады рабочих отправились готовить строительную площадку.
В Аламогордо, в центре огромной песчаной пустыни Новой Мексики, было собрано семь раз по семи тысяч рабочих. Они жили в железных бараках, по ночам страдали от холода, а днем изнывали от страшной жары. Болезни истребляли их, но на смену умершим сгоняли все новых рабочих, которые копали огромные котлованы под фундаменты, пробивали шахты и галереи в скалах, а над ними возвышались землеройные машины, похожие на гадов, живших сто семьдесят миллионов лет назад.
Эта стройка длилась семь лет и еще семь лет, и через четырнадцать лет сто тысяч акров земли были покрыты металлическими башнями и домами и отгорожены от остального мира высокими стенами. Наступил день, когда ушли последние из тех, кто выполнил эту гигантскую работу, и ворота закрылись.
Строительные площадки опустели, кругом воцарилась тишина, и лишь ветер свистел высоко в натянутых проводах да по извилистым дорожкам шагали охранники с собаками. Так продолжалось семь дней, пока однажды темной, безлунной ночью у восточной стены не остановился экипаж, который назывался бронированным автомобилем. Из него вышли семь человек, управляющих Атлантидой. Первый был хозяином ее железа, второй - угля, третий - нефти, четвертый - дорог, пятый - хлеба и мяса, шестой - электричества, а седьмой - армии. С ними приехал восьмой, бледный юноша, сын одного из властителей.
Навстречу им из-под земли вышел главный инженер стройки и низко поклонился прибывшим. Властителя вышли из автомобиля и увидели раскачивающиеся высоко за стенами лампы, привешенные на проволочных канатах, а в их неспокойном свете - черные блоки и башни, стоящие рядом, как шеренги солдат: это была лишь видимая, находящаяся на поверхности земли, небольшая часть Генерального Автомата Тюринга, который уходил глубоко под землю, в галереи и залы, просверленные в скалах пустыни. Охранники с обеих сторон приблизились к черным дверям в стене, двери открылись, и посетители вошли внутрь, где их ожидала застекленная вагонетка, которая сейчас же двинулась в путь.
Они ехали по залам, залитым холодным синим светом, по зданиям, как бы перевернутым вверх ногами и вдавленным в скалу, а над их головами темнели лианы проводов, висевших на огромных грибообразных изоляторах. Они проезжали мимо вмонтированных в стены триггерных ячеек; миновали шахты, у которых стояли на страже бронированные автоматы; вагонетка углублялась все дальше, а инженер объяснял им все н говорил, что в подземельях одних лишь главных приборов больше, чем секунд в жизни человека. Они ехали дальше, спускаясь с одного этажа на другой; за стеклом извивались коридоры, взгляд терялся в лесу проводов. Вагонетка скользила под толстыми медными трубами. Иногда где-то в глубине сверкал рубиновый фонарик, мрак густел, а вагонетка с ритмическим стуком опускалась все ниже и ниже. И весь этот необъятный и неизмеримый лабиринт был мертв: ни один импульс тока еще не прошел через миллиарды километров проводов, оплетавших медный мозг машины.
Властители ехали долго, пока за стеклами не засверкали лампочки, осветившие влажные стены туннеля. Вагонетка затормозила и остановилась. Они были у цели. На самом нижнем этаже под этой гигантской стройкой находилась небольшая бронированная комната яйцевидной формы. Они вошли туда. На черных стенах виднелись контрольные часы - семьдесят семь часов. Посреди комнаты было возвышение. На нем стоял черный микрофон, а под бриллиантовым колпаком виднелась кнопка. И больше ничего. Отсюда надо было отдавать приказы Большому Генеральному Автомату Тюринга.
Инженер объяснил, что автомат может выращивать экзотические цветы, закладывать сады и уничтожать людей. Он не имел никаких предохранительных устройств, подобных тем, какие есть у современных автоматов, и вообще совершенно не был похож на них. Это был дикий, варварский автомат, своими размерами в миллионы раз превышавший пирамиды.
Они стали у возвышения. Наступила тишина. Хотя под сводами пылали семь люстр, черные стены поглощали свет. Пуск Автомата Тюринга должен был состояться позднее, но главный инженер, стремясь заслужить благоволение властителей, посоветовал произвести его испытание теперь. Уже несколько лет его самого мучило ожидание, и в глубине его сознания таилась сокровенная мысль: он понимал, что тот, кто станет у микрофона пущенного в ход Тюринга, будет самым сильным в мире человеком, сильнее ассирийских и вавилонских магов, которым служили демоны. И, когда первый властитель спросил: "А что нужно сделать, чтобы пустить автомат в ход?" - он ответил: "Нажмите вот эту черную кнопку, она поднимет затворы в плотинах, воды реки Святого Хуана устремятся на лопасти семидесяти семи турбин, возникнет ток, который насытит металлические внутренности Тюринга, и тогда в его органах забьется электрический пульс".
Властитель был немного взволнован: он любил великие и удивительные дела и, как бы нехотя, нажал кнопку. Вспыхнул свет, стрелки на всех циферблатах вздрогнули, лампы открыли свои красные глаза и взглянули на людей, а над их головами вздрогнуло и пришло в движение все пространство площадью в сто тысяч акров.
Вращались и пыхтели машины, тысячи вакуумных трубок раскалились докрасна, реле начали включаться и выключаться, и через все катушки, соленоиды и обмотки прошел ток. Но в черной комнате виднелись лишь неподвижные циферблаты часов, а в репродукторе слышался глухой шум: гигант, обладавший медным мозгом, был уже оживлен, но еще спал и, казалось, храпел.
Тогда властители поняли, что перед ними находится всемогущее существо, которое они сами создали и которое сделает все, что ему прикажут. Когда они вдумались в это, то в глубине души испугались, как бы заглянув в пропасть: они не привыкли к тому, что можно быть всемогущим.
Каждый подумал, что автомат по его приказу может уничтожить сокровища и лишить жизни шестерых других властителей, но отгонял эту назойливую мысль во имя интересов новой войны, которую они решили затеять.
Восьмому из них было всего восемнадцать лет, он был сыном хозяина железа, самого богатого из всех, потому что из железа производились все орудия истребления. Этот властитель умел как никто другой торговать кровью, на его заводах стучали тысячи стальных молотов для того, чтобы в далеких землях перестали биться тысячи живых сердец. А его сын был еще мальчиком, бледным и печальным. Он познал вкус всех плодов земли, всех ядов, возбуждающих расслабленные нервы, и все удовольствия, которые можно получить за золото. Поэтому мир казался ему полным безграничной скуки, и в поисках неизвестных ему волнений он охотно погружался в лабиринты темных философских учений.
Люди стояли неподвижно, подавленные собственным ничтожеством по сравнению с машиной, не пытались промолвить ни слова и лишь вслушивались в мерный гул, говоривший о том, что чуткий и покорный гигант замер в ожидании. Тогда бледный юноша неожиданно вышел вперед и задал вопрос:
- Зачем мы живем?
Охваченный ужасом, его отец хотел наказать юношу, но не успел открыть рот, как Тюринг пришел в движение. Лампочки начали мигать, свет ослабел, темные стены подползали к ним и снова отступали; из репродуктора вырвался железный вздох, за ним другой, третий, четвертый, с каждым разом все сильнее. Пол задрожал, с него поднялась пыль, у присутствующих, потрясенных ужасными толчками, подкосились ноги. Вдруг в грозовом скрежете и грохоте все бросились к двери, толкаясь и в панике сбивая друг друга с ног: они поняли, что машина смеялась...
/Станислав Лем, "Магелланово облако"/
- Сказка, которую я расскажу вам, похожа на быль. Она называется "Рассказ о смеющемся Тюринге".
В наступившей тишине некоторое время еще слышались шаги обслуживающих автоматов. Потом утихли и они, а Калларла все еще не начинала, как бы ожидая чего-то. На ее губах блуждала легкая улыбка. Чего она ждала? Может быть, чтобы вернулось то настроение, которое охватило всех нас, когда в зале были дети?
Наконец она сказала:
- Слышала я этот рассказ от своей бабушки, женщины очень консервативной, которая... но, может быть, при сказках комментарии не нужны? Итак, я начинаю.
Она не смотрела на нас. Глаза ее, обращенные к искрящейся струе фонтана, стали неподвижными, а приглушенный голос смешивался со звуком воды, падающей в каменную чашу.
- Давным-давно, больше тысячи лет назад, мир делился на две части. В одной правили атлантиды. Они хотели уничтожить другую половину мира, которая не подчинялась их власти. Они накапливали яды, взрывчатые и радиоактивные вещества, при помощи которых можно было бы отравить воздух и воду. Но чем большие запасы таких веществ они делали, тем больший страх охватывал их.
Они покупали за золото ученых, чтобы те создавали самые совершенные машины для убийства. Однажды им стало известно, что на далеком острове за океаном живет ученый, по имени Тюринг, умеющий создавать автоматы. Тогда об автоматах знали еще очень мало и никто точно не представлял себе, какую пользу они могут приносить. Тюринг строил различные автоматы: одни делали машины, другие выпекали хлеб, третьи вычисляли и обладали способностью логически рассуждать. Он трудился сорок лет, пока не изобрел автомат, который мог делать все.
Этот автомат мог выплавлять металл из руды и шить сапоги, превращать один элемент в другой и строить дома, он мог и работать физически и думать обо всем. Он мог ответить на любой вопрос и решить любую задачу; не было дела, которого бы он не выполнил, если оно ему было поручено. Властители Атлантиды направили своих агентов с заданием купить Тюринга, но ученый не согласился на это. Тогда они заключили его в тюрьму и похитили чертежи его изобретений. Старший из атлантидов просмотрел эти чертежи, созвал других и сказал: "Если у нас будет такой автомат, спросим его, как уничтожить тех людей, которые хотят навсегда устранить войны". А другой властитель добавил: "Он, кроме того, скажет нам, как отучить наших подданных от мышления, потому что мыслящие люди неохотно умирают во славу нашего золота".
Все присутствующие, зааплодировали ему и решили: построим Большой Генеральный Автомат Тюринга, будем всемогущими, и никто в мире не сможет противостоять нам.
Затем собрали семь тысяч счетных работников (тогда люди еще считали в уме), чтобы те подсчитали, сколько золота понадобится на оплату строительства. Вслед за ними собрали семь тысяч инженеров и конструкторов, которые семь лет чертили проекты... Еще до того, как проекты были закончены, первые бригады рабочих отправились готовить строительную площадку.
В Аламогордо, в центре огромной песчаной пустыни Новой Мексики, было собрано семь раз по семи тысяч рабочих. Они жили в железных бараках, по ночам страдали от холода, а днем изнывали от страшной жары. Болезни истребляли их, но на смену умершим сгоняли все новых рабочих, которые копали огромные котлованы под фундаменты, пробивали шахты и галереи в скалах, а над ними возвышались землеройные машины, похожие на гадов, живших сто семьдесят миллионов лет назад.
Эта стройка длилась семь лет и еще семь лет, и через четырнадцать лет сто тысяч акров земли были покрыты металлическими башнями и домами и отгорожены от остального мира высокими стенами. Наступил день, когда ушли последние из тех, кто выполнил эту гигантскую работу, и ворота закрылись.
Строительные площадки опустели, кругом воцарилась тишина, и лишь ветер свистел высоко в натянутых проводах да по извилистым дорожкам шагали охранники с собаками. Так продолжалось семь дней, пока однажды темной, безлунной ночью у восточной стены не остановился экипаж, который назывался бронированным автомобилем. Из него вышли семь человек, управляющих Атлантидой. Первый был хозяином ее железа, второй - угля, третий - нефти, четвертый - дорог, пятый - хлеба и мяса, шестой - электричества, а седьмой - армии. С ними приехал восьмой, бледный юноша, сын одного из властителей.
Навстречу им из-под земли вышел главный инженер стройки и низко поклонился прибывшим. Властителя вышли из автомобиля и увидели раскачивающиеся высоко за стенами лампы, привешенные на проволочных канатах, а в их неспокойном свете - черные блоки и башни, стоящие рядом, как шеренги солдат: это была лишь видимая, находящаяся на поверхности земли, небольшая часть Генерального Автомата Тюринга, который уходил глубоко под землю, в галереи и залы, просверленные в скалах пустыни. Охранники с обеих сторон приблизились к черным дверям в стене, двери открылись, и посетители вошли внутрь, где их ожидала застекленная вагонетка, которая сейчас же двинулась в путь.
Они ехали по залам, залитым холодным синим светом, по зданиям, как бы перевернутым вверх ногами и вдавленным в скалу, а над их головами темнели лианы проводов, висевших на огромных грибообразных изоляторах. Они проезжали мимо вмонтированных в стены триггерных ячеек; миновали шахты, у которых стояли на страже бронированные автоматы; вагонетка углублялась все дальше, а инженер объяснял им все н говорил, что в подземельях одних лишь главных приборов больше, чем секунд в жизни человека. Они ехали дальше, спускаясь с одного этажа на другой; за стеклом извивались коридоры, взгляд терялся в лесу проводов. Вагонетка скользила под толстыми медными трубами. Иногда где-то в глубине сверкал рубиновый фонарик, мрак густел, а вагонетка с ритмическим стуком опускалась все ниже и ниже. И весь этот необъятный и неизмеримый лабиринт был мертв: ни один импульс тока еще не прошел через миллиарды километров проводов, оплетавших медный мозг машины.
Властители ехали долго, пока за стеклами не засверкали лампочки, осветившие влажные стены туннеля. Вагонетка затормозила и остановилась. Они были у цели. На самом нижнем этаже под этой гигантской стройкой находилась небольшая бронированная комната яйцевидной формы. Они вошли туда. На черных стенах виднелись контрольные часы - семьдесят семь часов. Посреди комнаты было возвышение. На нем стоял черный микрофон, а под бриллиантовым колпаком виднелась кнопка. И больше ничего. Отсюда надо было отдавать приказы Большому Генеральному Автомату Тюринга.
Инженер объяснил, что автомат может выращивать экзотические цветы, закладывать сады и уничтожать людей. Он не имел никаких предохранительных устройств, подобных тем, какие есть у современных автоматов, и вообще совершенно не был похож на них. Это был дикий, варварский автомат, своими размерами в миллионы раз превышавший пирамиды.
Они стали у возвышения. Наступила тишина. Хотя под сводами пылали семь люстр, черные стены поглощали свет. Пуск Автомата Тюринга должен был состояться позднее, но главный инженер, стремясь заслужить благоволение властителей, посоветовал произвести его испытание теперь. Уже несколько лет его самого мучило ожидание, и в глубине его сознания таилась сокровенная мысль: он понимал, что тот, кто станет у микрофона пущенного в ход Тюринга, будет самым сильным в мире человеком, сильнее ассирийских и вавилонских магов, которым служили демоны. И, когда первый властитель спросил: "А что нужно сделать, чтобы пустить автомат в ход?" - он ответил: "Нажмите вот эту черную кнопку, она поднимет затворы в плотинах, воды реки Святого Хуана устремятся на лопасти семидесяти семи турбин, возникнет ток, который насытит металлические внутренности Тюринга, и тогда в его органах забьется электрический пульс".
Властитель был немного взволнован: он любил великие и удивительные дела и, как бы нехотя, нажал кнопку. Вспыхнул свет, стрелки на всех циферблатах вздрогнули, лампы открыли свои красные глаза и взглянули на людей, а над их головами вздрогнуло и пришло в движение все пространство площадью в сто тысяч акров.
Вращались и пыхтели машины, тысячи вакуумных трубок раскалились докрасна, реле начали включаться и выключаться, и через все катушки, соленоиды и обмотки прошел ток. Но в черной комнате виднелись лишь неподвижные циферблаты часов, а в репродукторе слышался глухой шум: гигант, обладавший медным мозгом, был уже оживлен, но еще спал и, казалось, храпел.
Тогда властители поняли, что перед ними находится всемогущее существо, которое они сами создали и которое сделает все, что ему прикажут. Когда они вдумались в это, то в глубине души испугались, как бы заглянув в пропасть: они не привыкли к тому, что можно быть всемогущим.
Каждый подумал, что автомат по его приказу может уничтожить сокровища и лишить жизни шестерых других властителей, но отгонял эту назойливую мысль во имя интересов новой войны, которую они решили затеять.
Восьмому из них было всего восемнадцать лет, он был сыном хозяина железа, самого богатого из всех, потому что из железа производились все орудия истребления. Этот властитель умел как никто другой торговать кровью, на его заводах стучали тысячи стальных молотов для того, чтобы в далеких землях перестали биться тысячи живых сердец. А его сын был еще мальчиком, бледным и печальным. Он познал вкус всех плодов земли, всех ядов, возбуждающих расслабленные нервы, и все удовольствия, которые можно получить за золото. Поэтому мир казался ему полным безграничной скуки, и в поисках неизвестных ему волнений он охотно погружался в лабиринты темных философских учений.
Люди стояли неподвижно, подавленные собственным ничтожеством по сравнению с машиной, не пытались промолвить ни слова и лишь вслушивались в мерный гул, говоривший о том, что чуткий и покорный гигант замер в ожидании. Тогда бледный юноша неожиданно вышел вперед и задал вопрос:
- Зачем мы живем?
Охваченный ужасом, его отец хотел наказать юношу, но не успел открыть рот, как Тюринг пришел в движение. Лампочки начали мигать, свет ослабел, темные стены подползали к ним и снова отступали; из репродуктора вырвался железный вздох, за ним другой, третий, четвертый, с каждым разом все сильнее. Пол задрожал, с него поднялась пыль, у присутствующих, потрясенных ужасными толчками, подкосились ноги. Вдруг в грозовом скрежете и грохоте все бросились к двери, толкаясь и в панике сбивая друг друга с ног: они поняли, что машина смеялась...
/Станислав Лем, "Магелланово облако"/

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
Страница 1 из 1
Права доступа к этому форуму:
Вы не можете отвечать на сообщения