02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Страница 1 из 5
Страница 1 из 5 • 1, 2, 3, 4, 5 
 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
НЕДОСТАТОК ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Придется начать конец второго тома заметок раньше середины. Уж слишком религиозным стало движение за внедрение того, что в 20-х годах XXI века начали вдруг называть "Искусственным Интеллектом". И, как всякая религия, оно базируется на вере, в ущерб пониманию.
Для запутывания вопроса были совмещены вместе две "технологии": "нейросетей" и "бредогенерации", что совершенно не обязательно. Зато, позволяет менять тему разговора и надувать щеки.
Попробуем разобраться.
Вопрос "нейросетей" - это вопрос теории вычислений, только там они называются конечными автоматами. Помните, как Бир встраивал их в цепочки управления - ТЕМА #112, АБЗАЦ #1634
ТЕМА #112, АБЗАЦ #1634 ? Как мы их обучали для имитации поведения игрока -
? Как мы их обучали для имитации поведения игрока -  ТЕМА #63, АБЗАЦ #696
ТЕМА #63, АБЗАЦ #696 ? Как они разбирали регулярные выражения -
? Как они разбирали регулярные выражения -  ТЕМА #74
ТЕМА #74 ?
?
Вопрос же бредогенерации - т.е. игры в тест Тьюринга - скорее, психологический - ТЕМА #63, АБЗАЦ #695
ТЕМА #63, АБЗАЦ #695 . Помните, как Растригин и Чачко (
. Помните, как Растригин и Чачко ( ТЕМА #144, АБЗАЦ #3233
ТЕМА #144, АБЗАЦ #3233 ) подбирали инструмент для диалога человек-машина? Не говоря уже о многочисленных игрушках, встреченных на страницах "В мире науки", или, даже, в виде простеньких примеров (
) подбирали инструмент для диалога человек-машина? Не говоря уже о многочисленных игрушках, встреченных на страницах "В мире науки", или, даже, в виде простеньких примеров ( ТЕМА #122, АБЗАЦ #2121
ТЕМА #122, АБЗАЦ #2121 ).
).
Начнем с теории "сетей". Обратите внимание на годы выхода этих работ.

Из книги "О чем размышляют роботы?" Жан-Пьера Пети
Придется начать конец второго тома заметок раньше середины. Уж слишком религиозным стало движение за внедрение того, что в 20-х годах XXI века начали вдруг называть "Искусственным Интеллектом". И, как всякая религия, оно базируется на вере, в ущерб пониманию.
Для запутывания вопроса были совмещены вместе две "технологии": "нейросетей" и "бредогенерации", что совершенно не обязательно. Зато, позволяет менять тему разговора и надувать щеки.
Попробуем разобраться.
Вопрос "нейросетей" - это вопрос теории вычислений, только там они называются конечными автоматами. Помните, как Бир встраивал их в цепочки управления -
 ТЕМА #112, АБЗАЦ #1634
ТЕМА #112, АБЗАЦ #1634 ? Как мы их обучали для имитации поведения игрока -
? Как мы их обучали для имитации поведения игрока -  ТЕМА #63, АБЗАЦ #696
ТЕМА #63, АБЗАЦ #696 ? Как они разбирали регулярные выражения -
? Как они разбирали регулярные выражения -  ТЕМА #74
ТЕМА #74 ?
? Вопрос же бредогенерации - т.е. игры в тест Тьюринга - скорее, психологический -
 ТЕМА #63, АБЗАЦ #695
ТЕМА #63, АБЗАЦ #695 . Помните, как Растригин и Чачко (
. Помните, как Растригин и Чачко ( ТЕМА #144, АБЗАЦ #3233
ТЕМА #144, АБЗАЦ #3233 ) подбирали инструмент для диалога человек-машина? Не говоря уже о многочисленных игрушках, встреченных на страницах "В мире науки", или, даже, в виде простеньких примеров (
) подбирали инструмент для диалога человек-машина? Не говоря уже о многочисленных игрушках, встреченных на страницах "В мире науки", или, даже, в виде простеньких примеров ( ТЕМА #122, АБЗАЦ #2121
ТЕМА #122, АБЗАЦ #2121 ).
).Начнем с теории "сетей". Обратите внимание на годы выхода этих работ.

Из книги "О чем размышляют роботы?" Жан-Пьера Пети
Последний раз редактировалось: Gudleifr (Ср Апр 03, 2024 12:45 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Из сб. АВТОМАТЫ, 1956  ТЕМА #135, АБЗАЦ #2819
ТЕМА #135, АБЗАЦ #2819
Сразу два замечания. Первое:
Как видно, эта статья вышла еще до того, как научились делать "настоящие ЭВМ". Позднее Н.Винер писал в своей "Кибернетике":
Т.е. это ЭВМ стали средством реализации сетевой модели, а не "сети отменили ЭВМ".
Второе замечание:
Конечно, тут не без некоторого жульничества. На протяжении всей этой темы под сетью подразумевается не честный кусок добытого из живого организма мыслящего вещества, а всего лишь некоторая математическая/электронная модель, "достаточная для имитации мыслепроцесса". Т.е. мы не гарантируем, что мозг работает именно так, но не можем найти разницы в работе мозга и машины.
Начало рассматриваемой статьи, как раз, посвящено выделению в нейронах разумного начала.
Т.о. авторы видят возможность упростить модель нейронной сети, отказавшись от рассмотрения сложных электрических переходных процессов. Впрочем, я знаю модель, в которой возбуждение "нейронов" было более "частотно-чувствительным" - ТЕМА #98, АБЗАЦ #1295
ТЕМА #98, АБЗАЦ #1295 .
.
Что дает нам способ расчета нервной активности по правилам обычной математической логики.
Большую часть формализмов я опускаю. Публикация 1956 года явно требует перевода на язык современной школьной мат.логики. Суть описываемых изысканий достаточно проста и интуитивно понятна из приведенных иллюстраций.
Первые две теоремы посвящены эквивалентности логических выражений и сетей. Для всякой сети найдется предикат и почти для каждого выражения - сеть без петель.
Выражения отличаются от обычных в двух отношениях. Во-первых, как отдельная операция (и как свойство других единичных операций) вводится задержка (синаптическая), позволяющая рассматривать вычисление в сети "пошагово" - от нейрона к нейрону. Понятие эквивалентности (реализуемости) т.о. становится вневременным - нам становится неважным, сколько шагов заняли два вычисления, важно, чтобы их результаты совпали.

Просто задержка. В статье порог нейрона обычно считается равным 2.

Простые логические операции с единичной задержкой.
Вторая тонкость - исключение из рассмотрения выражений являющихся истинными при отсутствии в их обозримом прошлом истинных входных значений (рецепторов, peripheral afferents). (Т.е. самовозбуждающихся сетей и сетей с бесконечной памятью).
Этому ограничению посвящена третья теорема.
Следующие четыре теоремы посвящены доказательству того, что дальнейшее "биологическое" усложнение сетей не дает новых вычислительных возможностей:
Т.е. относительное торможение - временное повышение порога чувствительности нейрона до его полной невозбудимости - вводить не нужно.
Т.е. обратная цепочка вполне позволяет нейрону "утомиться" - самому себя затормозить.
Т.е. вводить нейроны "переменных" свойств для изменения состояния сети нет никакой необходимости. Можно просто добавить нужные цепочки нейронов.
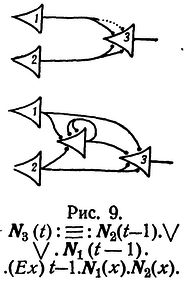
Замена изменяемого синапса петлей.
Последнее особенно печально для современных верующих в Исусственый Интеллект - обучение не может сделать сеть "умнее" сети, правильно запрограммированной изначально.
Формулы этой главы еще сложнее, но суть проста:
Проще говоря - ТЕМА #98, АБЗАЦ #1244
ТЕМА #98, АБЗАЦ #1244 .
.
Тут уж решайте сами, достаточно ли вам столь простых моделей, или вы считаете, что "настоящие мозги" устроены намного сложнее, а "современный искусственный интеллект" - и подавно.
 ТЕМА #135, АБЗАЦ #2819
ТЕМА #135, АБЗАЦ #2819
ЛОГИЧЕСКОЕ ИСЧИСЛЕНИЕ ИДЕЙ, ОТНОСЯЩИХСЯ К НЕРВНОЙ АКТИВНОСТИ
УОРРЕН С.МАК-КАЛЛОК И ВАЛЬТЕР ПИТТС
A logical calculus of the ideas immanent in nervous activity, W.S.McCulloch and W.Pitts, Bull. Math. Biophys., 5, 115-133 (1943)
Поскольку нервная активность подчиняется закону "все или ничего", то нейронные события и соотношения между ними можно изучать средствами логики предложений. Оказывается, что поведение любой сети может быть описано в этих терминах с привлечением более сложных логических средств для сетей, содержащих петли. Для всякого логического выражения, удовлетворяющего некоторым условиям, можно найти сеть, имеющую описываемое этим выражением поведение. Показывается, что различные выборы возможных нейрофизиологических предпосылок эквивалентны в том смысле, что для сети, действующей согласно одной предпосылке, существует другая сеть, действующая согласно другой и дающая те же результаты, хотя, быть может, не за то же самое время. Обсуждаются различные приложения исчисления.
Сразу два замечания. Первое:
Как видно, эта статья вышла еще до того, как научились делать "настоящие ЭВМ". Позднее Н.Винер писал в своей "Кибернетике":
Г-н Питтс был тогда основательно знаком с математической логикой и нейрофизиологией, но не имел случая сколько-нибудь близко соприкасаться с техникой. В частности, он не был знаком с работой д-ра Шеннона и недостаточно ясно представлял себе возможности электроники. Он очень заинтересовался, когда я показал ему образцы современных вакуумных ламп и объяснил, что они являются идеальным средством для реализации в металле эквивалентов рассматриваемых им нейронных сетей и систем. С этого времени нам стало ясно, что сверхбыстрая вычислительная машина, поскольку вся она строится на последовательном соединении переключательных устройств, является идеальной моделью для решения задач, возникающих при изучении нервной системы. Возбуждение нейронов по принципу "все или ничего" в точности подобно однократному выбору, производимому при определении разряда двоичного числа; а двоичная система счисления уже признавалась не одним из нас за наиболее удовлетворительную основу для проектирования вычислительных машин. Синапс есть не что иное, как механизм, определяющий, будет ли некоторая комбинация выходных сигналов от данных предыдущих элементов служить подходящим стимулом для возбуждения следующего элемента или нет; тем самым синапс в точности подобен устройствам вычислительной машины. Наконец, проблема объяснения природы и разновидностей памяти у животных находит параллель в задаче создания искусственных органов памяти для машин.
Т.е. это ЭВМ стали средством реализации сетевой модели, а не "сети отменили ЭВМ".
Второе замечание:
Конечно, тут не без некоторого жульничества. На протяжении всей этой темы под сетью подразумевается не честный кусок добытого из живого организма мыслящего вещества, а всего лишь некоторая математическая/электронная модель, "достаточная для имитации мыслепроцесса". Т.е. мы не гарантируем, что мозг работает именно так, но не можем найти разницы в работе мозга и машины.
Начало рассматриваемой статьи, как раз, посвящено выделению в нейронах разумного начала.
I. ВВЕДЕНИЕ
Теоретическая нейрофизиология базируется на нескольких основных предпосылках. Нервная система является сетью нейронов, каждый из которых имеет тело и аксон. Места контакта нейронов, или синапсы, находятся всегда между аксоном одного и телом другого нейрона. В каждый момент нейрон имеет известный порог, который должно превзойти раздражение, чтобы вызвать нервный импульс. Все это, если не считать самого факта и момента появления импульса, определено нейроном, а не раздражением. От точки раздражения импульс распространяется по всему нейрону. Скорость распространения импульса по аксону пропорциональна диаметру аксона и варьируется от менее 1м/сек в тонких аксонах, которые бывают обычно короткими, до более чем 150м/сек в толстых аксонах, обычно длинных. Время распространения импульса по аксону не играет, следовательно, большой роли при определении времени прибытия импульсов в точки, удаленные от одного и того же источника на разные расстояния. Возбуждение передается через синапсы преимущественно от окончания аксона к телу. Остается спорным вопрос, обусловлено ли это необратимостью отдельных синапсов или же преобладанием некоторых анатомических конфигураций. Последнее предположение не требует гипотез ad hoc и объясняет известные исключения; однако любое предположение о причине такого явления совместимо с нижеследующим исчислением. Не известно ни одного случая, когда возбуждение, приходящее через один синапс, вызвало бы импульс в каком-либо нейроне, тогда как любой нейрон может быть возбужден импульсами, приходящими через достаточное число соседних синапсов в течение латентного периода, который продолжается менее четверти миллисекунды. Наблюдаемая временная суммация импульсов в более длительных интервалах времени для отдельных нейронов невозможна и эмпирически зависит от структурных свойств сети. Между прибытием импульсов к нейрону и распространением собственного импульса нейрона имеется синаптическая задержка, большая половины миллисекунды. В начале нервного импульса нейрон абсолютно невозбудим. Затем его возбудимость быстро восстанавливается, достигая в некоторых случаях сверхнормального уровня, после чего она снова становится несколько ниже нормальной, а затем медленно возвращается к нормальному уровню. Частые возбуждения увеличивают понижение порога возбудимости ниже нормального уровня. Эти особенности связаны со временем и местом появления нервных импульсов и не связаны ни с какими другими особенностями действий нейронов. Из последних одно лишь явление торможения приводилось в качестве серьезного довода против этого тезиса. Торможение есть прекращение или предотвращение активности одной группы нейронов посредством одновременной или предшествующей активности другой группы. До последнего времени это могло быть объяснено предположением, что предшествующая активность нейронов второй группы может настолько повысить пороги вставочных нейронов (internuncial neurons), что последние будут не в состоянии возбудиться от нейронов первой группы, тогда как импульсы нейронов первой группы должны складываться с импульсами вставочных нейронов для возбуждения нейронов, теперь тормозимых.
В настоящее время показано, что в некоторых случаях, торможение происходит менее чем в одну миллисекунду. Это исключает участие вставочных нейронов и требует существования синапсов, импульсы через которые тормозят нейрон, возбуждаемый импульсами через другие синапсы. До сих пор эксперимент не обнаружил, является ли эта невозбудимость относительной или абсолютной. Мы предположим последнее и покажем, что разница несущественна для наших рассуждений. Каждый из видов невозбудимости может быть объяснен любым из двух способов: "тормозящий синапс" может обладать способностью вырабатывать вещество, повышающее порог нейрона, или же этот синапс может быть расположен таким образом, что локальное нарушение, производимое его возбуждением, препятствует изменению, вызываемому синапсами, которые в противном случае возбуждали бы нейрон. Поскольку в случае электрического раздражения уже известны условия, при которых подобный эффект имеет место, то первая гипотеза должна быть исключена, если и до тех пор пока она не будет подтверждена, ибо вторая не включает в себя никаких новых гипотез. Мы имеем тогда два объяснения торможения, основанных на одной и той же общей предпосылке и отличающихся только в отношении рассматриваемых нервных сетей и, следовательно, в отношении времени, потребного на торможение. В дальнейшем мы будем говорить о таких нервных сетях как об ЭКВИВАЛЕНТНЫХ В ШИРОКОМ СМЫСЛЕ. Поскольку мы рассматриваем свойства сетей, инвариантные по отношению к этой эквивалентности, мы можем делать физические допущения, наиболее удобные для нашего исчисления.
Т.о. авторы видят возможность упростить модель нейронной сети, отказавшись от рассмотрения сложных электрических переходных процессов. Впрочем, я знаю модель, в которой возбуждение "нейронов" было более "частотно-чувствительным" -
 ТЕМА #98, АБЗАЦ #1295
ТЕМА #98, АБЗАЦ #1295 .
.Много лет назад один из нас, путем смелого рассмотрения этой аргументации, пришел к пониманию реакции любого нейрона как фактического эквивалента предложения, изображающего соответствующее возбуждение. Вследствие этого он попытался описать поведение сложных сетей в терминах символической логики предложений. Закон нервной активности "все или ничего" достаточен для того, чтобы возбуждение любого нейрона могло быть представлено как некоторое предложение. Физиологические соотношения, существующие при нервной активности, соответствуют, конечно, соотношениям этих предложений. Полезность такого представления зависит от тождественности физиологических соотношений с соотношениями логики предложений. Для каждой реакции любого нейрона имеется соответствующее утверждение некоторого простого предложения. В свою очередь оно влечет или некоторое другое простое предложение, или дизъюнкцию, или конъюнкцию, с отрицанием или без отрицания, аналогичных предложений, согласно с конфигурацией синапсов и порогом данного нейрона.
Что дает нам способ расчета нервной активности по правилам обычной математической логики.
Появляются две трудности. Первая относится к явлениям облегчения и утомления (facilitation и extinction), при которых предшествующая активность временно изменяет реакцию одной и той же части сети на последующий стимул. Вторая трудность касается явления обучения, при котором одновременные активности в предшествующее время изменили сеть так, что стимул, прежде бывший недостаточным, становится теперь достаточным. Однако мы можем сети, подверженные обоим изменениям, заменить эквивалентными фиктивными сетями, составленными из нейронов с неизменяемыми связями и порогами. Однако один пункт должен быть сделан ясным: никто из нас не смешивает формальной эквивалентности с фактическим истолкованием. Per contra!- Мы рассматриваем облегчение и утомление как зависящие от непрерывных изменений порога, связанных с электрическими и химическими переменными, такими, как остаточные потенциалы (after potentials) и концентрации ионов; обучение же мы рассматриваем как длительное изменение, могущее перенести сон, анестезию, конвульсии и кому. Значение формальной эквивалентности состоит в следующем: изменения, фактически лежащие в основе облегчения, утомления и обучения, никоим образом не затрагивают выводов, следующих из формальной трактовки активности нервных сетей, и соотношения соответствующих предложений остаются соотношениями логики предложений.
Нервная система содержит много циклических путей. Их активность так регенерирует возбуждение всех участвующих в них нейронов, что связь с прошлым становится неопределенной, хотя при этом все же предполагается, что афферентная активность реализовала один из некоторого числа классов конфигураций во времени. Точная спецификация этих зависимостей посредством рекурсивных функций и определение тех из них, которые могут быть воплощены в активности нервных сетей, завершают теорию.
II. ТЕОРИЯ: СЕТИ БЕЗ ПЕТЕЛЬ
Примем следующие физические допущения для нашего исчисления.
1. Активность нейрона удовлетворяет принципу "все или ничего".
2. Возбуждению нейрона в какой-либо момент времени должен предшествовать латентный период накопления возбуждений определенного фиксированного числа синапсов. Это число не зависит от предыдущей активности и от расположения синапсов на нейроне.
3. Единственным запаздыванием в нервной системе, имеющим значение, является синаптическая задержка.
4. Активность какого-либо тормозящего синапса абсолютно исключает возбуждение данного нейрона в рассматриваемый момент времени.
5. С течением времени структура сети не изменяется.
Большую часть формализмов я опускаю. Публикация 1956 года явно требует перевода на язык современной школьной мат.логики. Суть описываемых изысканий достаточно проста и интуитивно понятна из приведенных иллюстраций.
Первые две теоремы посвящены эквивалентности логических выражений и сетей. Для всякой сети найдется предикат и почти для каждого выражения - сеть без петель.
Выражения отличаются от обычных в двух отношениях. Во-первых, как отдельная операция (и как свойство других единичных операций) вводится задержка (синаптическая), позволяющая рассматривать вычисление в сети "пошагово" - от нейрона к нейрону. Понятие эквивалентности (реализуемости) т.о. становится вневременным - нам становится неважным, сколько шагов заняли два вычисления, важно, чтобы их результаты совпали.

Просто задержка. В статье порог нейрона обычно считается равным 2.

Простые логические операции с единичной задержкой.
Вторая тонкость - исключение из рассмотрения выражений являющихся истинными при отсутствии в их обозримом прошлом истинных входных значений (рецепторов, peripheral afferents). (Т.е. самовозбуждающихся сетей и сетей с бесконечной памятью).
Этому ограничению посвящена третья теорема.
Следующие четыре теоремы посвящены доказательству того, что дальнейшее "биологическое" усложнение сетей не дает новых вычислительных возможностей:
Теорема 4. Относительное и абсолютное торможения эквивалентны в широком смысле.
Т.е. относительное торможение - временное повышение порога чувствительности нейрона до его полной невозбудимости - вводить не нужно.
Теорема 5. Утомление эквивалентно абсолютному торможению.
Т.е. обратная цепочка вполне позволяет нейрону "утомиться" - самому себя затормозить.
Теорема 6. Облегчение и временная суммация могут быть заменены пространственной суммацией.
Т.е. вводить нейроны "переменных" свойств для изменения состояния сети нет никакой необходимости. Можно просто добавить нужные цепочки нейронов.
Кажется, что явления обучения, имеющие устойчивый характер при большинстве физиологических изменений в нервной активности, требуют возможности постоянного изменения структуры сети. Простейшее изменение такого рода - образование новых синапсов или эквивалентное ему понижение порога. Предположим, что некоторые . окончания аксонов не могут сначала возбудить следующий нейрон, но если в ка-кой-нибудь момент нейрон возбуждается одновременно с этими окончаниями, то они превращаются в обычные синапсы, способные в дальнейшем возбуждать нейрон. Устранение тормозящего синапса дает совершенно эквивалентный результат.
Мы имеем теперь следующую теорему:
Теорема 7. Изменяемые синапсы могут быть заменены петлями.

Замена изменяемого синапса петлей.
Последнее особенно печально для современных верующих в Исусственый Интеллект - обучение не может сделать сеть "умнее" сети, правильно запрограммированной изначально.
III. ТЕОРИЯ: СЕТИ С ПЕТЛЯМИ
Формулы этой главы еще сложнее, но суть проста:
Легко показать, что, во-первых, каждая сеть, снабженная лентой, считывающим устройством, связанным с рецепторами, и подходящими эффекторами для выполнения необходимых моторных операций, может вычислять лишь такие числа, которые вычисляет машина Тьюринга; во-вторых, что каждое из последних чисел может быть вычислено такой сетью и что сети (без считывающего устройства и ленты) с петлями могут вычислять некоторые из вычислимых чисел и никакие другие, но не все из них. Это представляет интерес с точки зрения психологического оправдания тьюринговского определения вычислимости и его эквивалентов, черчевской А-опре-делимости и клинивской общерекурсивности: если какое-либо число может быть вычислено организмом, то оно вычислимо также по этим определениям, и обратно.
Проще говоря -
 ТЕМА #98, АБЗАЦ #1244
ТЕМА #98, АБЗАЦ #1244 .
.IV. СЛЕДСТВИЯ
Причинность, требующая описания состояний и закона необходимой связи между ними, проявляется в различных формах во многих науках, но нигде, за исключением статистики, она не является столь необратимой, как в теории нервной активности. Задание в произвольный момент времени рецепторных возбуждений и активности (удовлетворяющей принципу "все или ничего") всех составляющих нейронов определяет состояние. Задание нервной сети определяет закон необходимой связи, с помощью которого по описанию любого состояния можно вычислить следующее за ним состояние, однако включение дизъюнктивных соотношений не позволяет полностью определить предшествующее состояние. Кроме того, восстанавливающая активность входящих в сеть петель делает связь с прошлым неопределенной. Так, наше знание мира, включая нас самих, неполно в пространственном отношении и неопределенно в отношении времени. Это незнание, касающееся неявно всех наших умственных способностей, является обратной стороной абстракции, делающей наше знание полезным. Роль умственных способностей при определении эпистемологической связи наших теорий с нашими наблюдениями и наших наблюдений с фактами совершенно ясна, ибо очевидно, что каждая идея и каждое ощущение реализуются активностью внутри нервной сети и что действительные возбуждения рецепторов не определены полностью никакой такой активностью.
Не имеется никакой теории или наблюдения, которые могли бы сохранить нечто большее, кроме их дефектного отношения к фактам, если сеть изменяется. Появляются звон в ушах, мурашки, галлюцинации, иллюзии, смешение ощущений и дизориентация. Опыт, следовательно, подтверждает, что если наши сети не определены, то неопределенными являются и наши факты, и "реальности" мы не можем приписать ничего большего, чем одно качество или "форму". С определением сети непознаваемый объект знания, "вещь в себе", перестает быть непознаваемым.
В психологии, как бы она ни определялась, описание сети дало бы все, что может быть достигнуто в этой области, даже если анализ дошел бы до конечных психических единиц или "психонов", ибо психон не может быть ничем меньшим, чем активностью отдельного нейрона. Так как эта активность по своей природе пропозициональна, то все психические события имеют преднамеренный, или "семиотический", характер. Закон "все или ничего" этой активности и соответствие ее соотношений соотношениям логики предложений обеспечивают то, что соотношения психонов суть соотношения двузначной логики предложений. Следовательно, в психологии, интроспективной, бихэвиористской или физиологической, основными являются соотношения двузначной логики.
Отсюда возникают конструктивные решения холистических проблем, включающих в себя дифференцированный континуум чувственных ощущений и нормативные, совершенствующие и разрешающие свойства восприятия и исполнения. Из необратимости причинности следует, что, даже если сеть известна, то, хотя по настоящей активности мы можем предсказать будущее, мы не можем определить ни афферентное
по центральному, ни центральное по эфферентному, ни прошлое по настоящей активности. Эти заключения подкрепляются фактами существования противоречивых свидетельств очевидцев, трудностью дифференцированного диагностирования органических больных, истерики и симуляции, и сравнением памяти и воспоминаний с записями. Более того, системы, которые реагируют на различие между афферентами регенеративной сети и некоторой активностью в этой сети так, что уменьшают это различие, обнаруживают целевое поведение. Известно, что организмы обладают многими такими системами, обслуживающими гомеостазис, желание и внимание. Таким образом, как формальный, так и конечный аспекты этой активности, которую мы обычно называем умственной, строго выводимы из современной нейрофизиологии. Психиатр может найти утешение в очевидном заключении, касающемся причинности, именно, что для прогноза история никогда не необходима. Он может извлечь немногое из того равным образом справедливого вывода, что наблюдаемое им объяснимо лишь в терминах нервной активности, бывшей до последнего времени вне его кругозора. Центральным моментом этого незнания является неоднозначность перехода от произвольного образца видимого поведения к нервным сетям, тогда как из воображаемых сетей существует фактически только одна, и она может в любой момент обнаружить непредвиденную активность. Разумеется, для психиатра большее значение имеет то обстоятельство, что в таких системах "разум" уже не бродит "более призрачно, чем призрак". Напротив, расстройство ума можно изучать, без потери общности или строгости, в научных терминах нейрофизиологии.
В нейрологии теория нервных сетей заостряет различие между сетями, необходимыми или только достаточными для заданной активности, выясняя, таким образом, соотношения между нарушенной структурой и нарушенным функционированием. В собственной области этой теории различие между эквивалентными сетями и сетями, эквивалентными в- узком смысле, указывает на подходящее использование и на важность изучения нервной деятельности во времени.
Математической биофизике эта теория доставляет некоторый способ строгой символической трактовки известных сетей и легкий метод конструирования гипотетических сетей с требуемыми свойствами.
Тут уж решайте сами, достаточно ли вам столь простых моделей, или вы считаете, что "настоящие мозги" устроены намного сложнее, а "современный искусственный интеллект" - и подавно.
Последний раз редактировалось: Gudleifr (Пн Сен 18, 2023 2:49 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ПРЕДСТАВЛЕНИЕ СОБЫТИЙ В НЕРВНЫХ СЕТЯХ И КОНЕЧНЫХ АВТОМАТАХ
С.К.КЛИНИ
Тоже из сб. АВТОМАТЫ, 1956 ТЕМА #135, АБЗАЦ #2819
ТЕМА #135, АБЗАЦ #2819
Содержание этой статьи заимствовано из Project RAND Research Memorandum RM-704 (15 декабря 1951г., 101стр.) под тем же заглавием и того же автора. Это сочинение используется теперь с разрешения корпорации RAND. Первоначальная работа автора над этой проблемой поддерживалась корпорацией RAND в течение лета 1951г.
ВВЕДЕНИЕ
#1. СТИМУЛЫ И РЕАКЦИЯ
Организм или автомат получает стимулы (возбуждения) посредством своих воспринимающих органов и совершает действия посредством своих действующих органов. Утверждение, что некоторые действия являются реакцией (ответом) на известные стимулы, означает, в простейшем случае, что эти действия производятся тогда и только тогда, когда возникают эти стимулы.
В общем случае как стимулы, так и действия могут быть очень сложными.
Чтобы упростить наш анализ, мы для начала оставим в стороне сложность реакции. Мы будем считать, что любой вид возбуждения (или, короче, любое событие), который вызывает действие в том смысле, что различные действия возникают в соответствии с тем, имеет место возбуждение или нет, при некотором фиксированном множестве других обстоятельств должен иметь представление состоянием организма или автомата после того, как событие произошло, и до того, как наступило действие.
Мы спрашиваем, какого рода события могут быть представлены состоянием автомата.
Для объяснения действий как реакций на стимулы останется изучить, каким образом представления событий (разновидность внутренней реакции) приводят к явным реакциям.
Основным нашим результатом будет (в #7 и 9) доказательство того, что представимыми являются все события некоторого класса, называемые "регулярными событиями", и только они.
#2. Нервные сети и поведение
Мак-Каллок и Питтс [1943] в их фундаментальной статье о логическом анализе нервной деятельности сформулировали некоторые допущения, которые мы воспроизведем в #3.
При доказательстве того, что каждое регулярное событие представимо состоянием конечного автомата, мы будем пользоваться в качестве автомата нервной сетью Мак-Каллока-Питтса. Таким образом, их нейроны будут служить одним из примеров "универсальных элементов" для конечных автоматов.
Допущения Мак-Каллока-Питтса были предложены в качестве абстракции от нейрофизиологических данных. Мы не будем интересоваться вопросом, насколько точно их допущения согласуются с этими данными. Повидимому, они приблизительно согласуются, хотя один из результатов Мак-Каллока и Питтса гласит, что такое же поведение можно объяснить некоторыми другими допущениями. Нет сомнения, что, когда нейрофизиологические данные достигнут большей точности, внимание будет перенесено на то, в каких отношениях эти допущения не согласуются с данными.
Наша теоретическая установка не зависит от точного согласования. В науке обычен метод, состоящий в том, что при наличии совокупности данных, слишком сложной для того, чтобы овладеть ею в целом, выбираются некоторая ограниченная область опыта, некоторые простые ситуации и предпринимается построение модели, хотя бы приближенно соответствующей этой области.
Следующим шагом после построения такой модели является полное познание самой модели. Не следует ожидать, что все черты модели будут одинаково хорошо соответствовать действительности, из которой путем абстракции получена эта модель. Но, после того как модель изучена, нам легче изменить или приспособить ее, заставив лучше удовлетворять нашим ограниченным данным или более широкому кругу данных или же искать модель совершенно нового рода.
Мак-Каллок и Питтс в их оригинальной работе дали теорию нервных сетей без петель (часть II их работы) и теорию произвольных нервных сетей (часть III). Настоящая статья является отчасти изложением их результатов; но так как мы находим неясной ту часть их работы, которая связана с произвольными нервными сетями, то мы будем излагать эти вопросы независимо. Хотя нас больше интересует сама модель, чем ее применения, несколько замечаний о последних помогут предупредить недоразумения.
Например: как показывает рассмотрение модели, память можно объяснить на основе циркулирующих нервных импульсов. Это объяснение кажется правдоподобным для краткосрочной памяти. Для долгосрочной памяти оно неправдоподобно в связи с уставанием, а также ввиду того, что подсчет, учитывающий количество накопленного в памяти материала, приводит к слишком большому числу нейронов [Мак-Каллок, 1949], и ввиду того непосредственно экспериментального факта, что временное пресечение нервной деятельности не уничтожает памяти [Жерар, 1953].
Допущения Мак-Каллока-Питтса придают нервной сети характер цифрового автомата, в противоположность моделирующему механизму в обычном для теории вычислительных машин смысле. Некоторые регулирующие физиологические процессы являются, повидимому, моделирующими. Так же как в математике непрерывные процессы можно аппроксимировать дискретными, так и моделирующие механизмы можно аппроксимировать в их действии цифровыми. Несмотря на это, моделирующее или частично моделирующее урегулирование для некоторых целей может оказаться самым простым и самым экономным.
Одно из допущений излагаемой математической теории состоит в том, что в функционировании нейронов не бывает ошибок. Конечно, это допущение нереально как для живого нейрона, так и для соответствующих узлов механического автомата. Однако естественно начать с теории, основанной на допущении об отсутствии неправильного функционирования. Действительно, в нашей теории наступление события может быть представлено возбуждением единичного нейрона. Биологически неправдоподобно, чтобы важная информация была представлена в организме таким образом. Но при надлежащем дублировании и переплетении сетей можно надеяться обеспечить те же результаты с малой вероятностью ошибки в сетях, построенных из нейронов, подверженных ошибкам. Повторяем, что мы исследуем нервные сети Мак-Каллока-Питтса не только с целью получить упрощенную модель нервной деятельности, но и с целью иллюстрации общей теории автоматов, включая роботы, вычислительные машины и т.п. Проблема: что может и что не может делать конечный автомат - представляет, как нам кажется, самостоятельный математический интерес, и она может также содействовать лучшему пониманию задач, возникающих на практике.
С.К.КЛИНИ
Тоже из сб. АВТОМАТЫ, 1956
 ТЕМА #135, АБЗАЦ #2819
ТЕМА #135, АБЗАЦ #2819
Содержание этой статьи заимствовано из Project RAND Research Memorandum RM-704 (15 декабря 1951г., 101стр.) под тем же заглавием и того же автора. Это сочинение используется теперь с разрешения корпорации RAND. Первоначальная работа автора над этой проблемой поддерживалась корпорацией RAND в течение лета 1951г.
ВВЕДЕНИЕ
#1. СТИМУЛЫ И РЕАКЦИЯ
Организм или автомат получает стимулы (возбуждения) посредством своих воспринимающих органов и совершает действия посредством своих действующих органов. Утверждение, что некоторые действия являются реакцией (ответом) на известные стимулы, означает, в простейшем случае, что эти действия производятся тогда и только тогда, когда возникают эти стимулы.
В общем случае как стимулы, так и действия могут быть очень сложными.
Чтобы упростить наш анализ, мы для начала оставим в стороне сложность реакции. Мы будем считать, что любой вид возбуждения (или, короче, любое событие), который вызывает действие в том смысле, что различные действия возникают в соответствии с тем, имеет место возбуждение или нет, при некотором фиксированном множестве других обстоятельств должен иметь представление состоянием организма или автомата после того, как событие произошло, и до того, как наступило действие.
Мы спрашиваем, какого рода события могут быть представлены состоянием автомата.
Для объяснения действий как реакций на стимулы останется изучить, каким образом представления событий (разновидность внутренней реакции) приводят к явным реакциям.
Основным нашим результатом будет (в #7 и 9) доказательство того, что представимыми являются все события некоторого класса, называемые "регулярными событиями", и только они.
#2. Нервные сети и поведение
Мак-Каллок и Питтс [1943] в их фундаментальной статье о логическом анализе нервной деятельности сформулировали некоторые допущения, которые мы воспроизведем в #3.
При доказательстве того, что каждое регулярное событие представимо состоянием конечного автомата, мы будем пользоваться в качестве автомата нервной сетью Мак-Каллока-Питтса. Таким образом, их нейроны будут служить одним из примеров "универсальных элементов" для конечных автоматов.
Допущения Мак-Каллока-Питтса были предложены в качестве абстракции от нейрофизиологических данных. Мы не будем интересоваться вопросом, насколько точно их допущения согласуются с этими данными. Повидимому, они приблизительно согласуются, хотя один из результатов Мак-Каллока и Питтса гласит, что такое же поведение можно объяснить некоторыми другими допущениями. Нет сомнения, что, когда нейрофизиологические данные достигнут большей точности, внимание будет перенесено на то, в каких отношениях эти допущения не согласуются с данными.
Наша теоретическая установка не зависит от точного согласования. В науке обычен метод, состоящий в том, что при наличии совокупности данных, слишком сложной для того, чтобы овладеть ею в целом, выбираются некоторая ограниченная область опыта, некоторые простые ситуации и предпринимается построение модели, хотя бы приближенно соответствующей этой области.
Следующим шагом после построения такой модели является полное познание самой модели. Не следует ожидать, что все черты модели будут одинаково хорошо соответствовать действительности, из которой путем абстракции получена эта модель. Но, после того как модель изучена, нам легче изменить или приспособить ее, заставив лучше удовлетворять нашим ограниченным данным или более широкому кругу данных или же искать модель совершенно нового рода.
Мак-Каллок и Питтс в их оригинальной работе дали теорию нервных сетей без петель (часть II их работы) и теорию произвольных нервных сетей (часть III). Настоящая статья является отчасти изложением их результатов; но так как мы находим неясной ту часть их работы, которая связана с произвольными нервными сетями, то мы будем излагать эти вопросы независимо. Хотя нас больше интересует сама модель, чем ее применения, несколько замечаний о последних помогут предупредить недоразумения.
Например: как показывает рассмотрение модели, память можно объяснить на основе циркулирующих нервных импульсов. Это объяснение кажется правдоподобным для краткосрочной памяти. Для долгосрочной памяти оно неправдоподобно в связи с уставанием, а также ввиду того, что подсчет, учитывающий количество накопленного в памяти материала, приводит к слишком большому числу нейронов [Мак-Каллок, 1949], и ввиду того непосредственно экспериментального факта, что временное пресечение нервной деятельности не уничтожает памяти [Жерар, 1953].
Допущения Мак-Каллока-Питтса придают нервной сети характер цифрового автомата, в противоположность моделирующему механизму в обычном для теории вычислительных машин смысле. Некоторые регулирующие физиологические процессы являются, повидимому, моделирующими. Так же как в математике непрерывные процессы можно аппроксимировать дискретными, так и моделирующие механизмы можно аппроксимировать в их действии цифровыми. Несмотря на это, моделирующее или частично моделирующее урегулирование для некоторых целей может оказаться самым простым и самым экономным.
Одно из допущений излагаемой математической теории состоит в том, что в функционировании нейронов не бывает ошибок. Конечно, это допущение нереально как для живого нейрона, так и для соответствующих узлов механического автомата. Однако естественно начать с теории, основанной на допущении об отсутствии неправильного функционирования. Действительно, в нашей теории наступление события может быть представлено возбуждением единичного нейрона. Биологически неправдоподобно, чтобы важная информация была представлена в организме таким образом. Но при надлежащем дублировании и переплетении сетей можно надеяться обеспечить те же результаты с малой вероятностью ошибки в сетях, построенных из нейронов, подверженных ошибкам. Повторяем, что мы исследуем нервные сети Мак-Каллока-Питтса не только с целью получить упрощенную модель нервной деятельности, но и с целью иллюстрации общей теории автоматов, включая роботы, вычислительные машины и т.п. Проблема: что может и что не может делать конечный автомат - представляет, как нам кажется, самостоятельный математический интерес, и она может также содействовать лучшему пониманию задач, возникающих на практике.
Последний раз редактировалось: Gudleifr (Пт Июн 30, 2023 11:49 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ЧАСТЬ I. НЕРВНЫЕ СЕТИ
#3. НЕРВНЫЕ СЕТИ МАК-КАЛЛОКА-ПИТТСА
По допущениям Мак-Каллока и Питтса [1943], нервная клетка, или нейрон, состоит из тела (сомы), откуда нервные волокна (аксоны) ведут к одной или нескольким концевым пластинкам.
Нервная сеть является устройством из конечного числа нейронов, в котором каждая концевая пластинка любого нейрона соприкасается с телом не более чем одного нейрона (того же самого или другого), который она возбуждает; разделяющий промежуток называется синапсом. Каждая концевая пластинка является возбуждающей или тормозящей (и не может быть возбуждающей и тормозящей одновременно).
Мы будем называть нейроны, к которым не примыкают никакие концевые пластинки, входными нейронами (число их может равняться нулю); остальные нейроны мы будем называть внутренними.
В равноотстоящие моменты времени (которые мы будем рассматривать как целые числа на временной шкале, одни и те же для всех нейронов данной сети) каждый нейрон сети является возбужденным или невозбужденным (спокойным). Для входного нейрона возбужденность или невозбужденность в любой момент t определяется условиями, внешними по отношению к сети. Можно предположить, что к каждому из них примыкает чувственно воспринимающий орган, который при надлежащих условиях в окружающей среде вызывает возбуждение нейрона в момент t. Для внутреннего нейрона условие возбужденности в момент t состоит в том, что по меньшей мере h (h называется порогом этого нейрона) возбуждающих концевых пластинок действуют, а ни одна из тормозящих не действует в момент t-1).
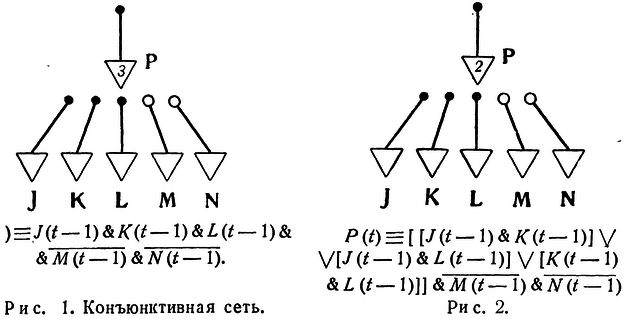
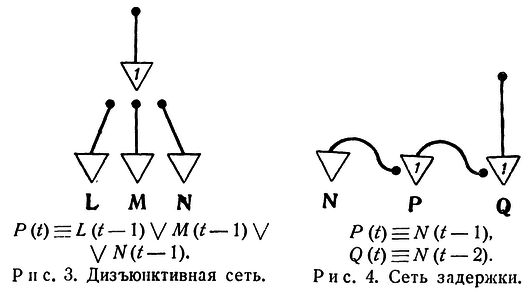
Для иллюстрации рассмотрим нервную сеть, показанную на рис.1, с входными нейронами J, К, L, М, N и внутренним нейроном Р. Возбуждающие концевые пластинки изображены жирными точками, а тормозящие - кружками. Порог Р равен 3, что указано числом, стоящим в треугольнике, представляющем тело этого нейрона. Формула, написанная под сетью, выражает в логической символике, что нейрон Р возбужден в момент t тогда и только тогда, когда все J, К, L возбуждены, но ни один из нейронов М и N не возбужден, в момент t-1. Мы пишем "P(t)" для указания, что нейрон Р возбужден в момент t; "J(t-1)" - для указания, что J возбужден в момент t-1, и т.д. Символ "=" означает "в том и только в том случае, если (или "эквивалентно"), "&" означает "и", "V" означает "или" (в неразделительном смысле), а "черта сверху" означает "не".
#4. ВХОД НЕРВНОЙ СЕТИ
Рассмотрим нервную сеть с k входными нейронами N1, ..., Nk. До пункта 6.3 мы будем считать, что k>=1. ВХОД (или ОПЫТ) всего прошлого до настоящего момента включительно можно описать таблицей с k столбцами, соответствующими входным нейронам, и строками, соответствующими моментам, отсчитываемым в обратном порядке от данного момента р) [Обозначение р от present - настоящее.- Прим. ред.]. Пересечения строк и столбцов заполняются нулями и единицами, причем 0 означает, что данный нейрон не возбужден, а 1 - что он возбужден в данный момент времени.
Например, при k = 2 таблица может иметь вид:

Цифра 1 в первой строке и первом столбце означает, что N1 возбужден в момент р; 0 в третьей строке и первом столбце - что N1 не возбужден в момент р-2, и т.д. Если эту таблицу продолжить вниз до бесконечности, мы получим представление опыта, мыслимого распространенным на все прошедшее время, которое мы считаем до настоящего момента бесконечным (в разделе 6 мы вернемся к рассмотрению этого вопроса).
Под СОБЫТИЕМ мы будем понимать любое свойство входа. Другими словами, любой подкласс класса всех возможных таблиц, описывающих вход всего прошлого (включая, если не оговорено противное, настоящий момент p), образует событие, которое НАСТУПАЕТ, если таблица, описывающая данный вход, принадлежит этому подклассу.
Примерами событий с двумя входными нейронами N1 и N2 являются:
(1) N1 возбужден в момент p.
(2) N2 не возбужден в момент p, a N1 возбужден в момент р-1.
(3) Один из нейронов, N1 или N2, возбужден в момент р.
(4) N1 и N2 оба возбуждены в момент р.
(5) N2 был возбужден в некоторый момент.
(6) N2 был возбужден в каждый момент, за исключением p.
В этих примерах вход, описанный табл.1, представляет наступление событий (1), (2), (3) и (5), но не (4), а для того, чтобы сказать, представляет ли он наступление события (6), мы должны знать продолжение таблицы.
#5. ОПРЕДЕЛЕННЫЕ СОБЫТИЯ
#5.1. ОПРЕДЕЛЕНИЕ "ОПРЕДЕЛЕННЫХ СОБЫТИЙ". Мы рассмотрим сначала события, которые относятся к фиксированному периоду времени, состоящему из некоторого числа l (>=1) последовательных моментов р-l+1, ..., p, оканчивающихся настоящим моментом. Мы будем называть такие события определенными событиями ДЛИНЫ (или ДЛИТЕЛЬНОСТИ) l. Среди предыдущих примеров определенными являются события (1)-(4), но не (5) и (6).
При этом в таблице такого вида, как табл.1, нам надо рассматривать только верхние l строк; например, при l=3 таблица 1 описывает событие, которое описывается также формулой
N1(p)&~N2(p) & N1(p-1)&N2(p-l) & ~N1(p-2)&N2(p-2).
Таблица, описывающая вход с k нейронами для l моментов р-l+1, ..., p, имеет ровно kl мест. Следовательно, возможно ровно 2**(kl) таких таблиц. Следовательно, имеется ровно 2**2**(kl) определенных событий длины с k входными нейронами, так как каждое из них определяется указанием того, какие из входов, описанных 2**(kl) k*l-таблицами, должны давать наступление события.
Определенное событие мы будем называть ПОЗИТИВНЫМ, если оно наступает только в том случае, когда хотя бы один из входных нейронов оказывается возбужденным хотя бы в один из моментов в продолжение периода, к которому это событие относится. Имеется ровно 2**(2**(kl)-1) позитивных определенных событий длины l с k входными нейронами, так как такие события определяются тем условием, что вход, описанный таблицей из одних нулей, не дает наступления события). [Эти выкладки показывают, что автор включает невозможное событие (т.е. событие, состоящее из пустого множества таблиц) в число позитивных, а значит, в частности, в число определенных событий.- Прим, ред.]
#5.2. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. ИЛЛЮСТРАЦИЯ. Рассмотрим определенное событие, которое наступает, когда конфигурация возбуждений совпадает с табл.1 (оборванной на трех строках) или с табл.2.
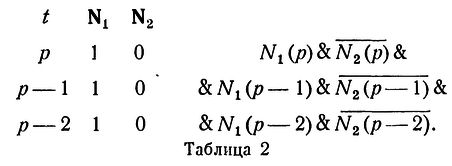
Это означает, что именно эти две (из 2**(2*3)=64) 2*3-таблицы, и только они, должны давать наступление события. Это событие описывается правой частью эквивалентности рис.5, получающейся путем дизъюнктивного сочетания конъюнкций, описывающих соответствующие таблицы в отдельности. В нервной сети рис.5 нейрон Р возбужден в момент p+2 в том и только в том случае, если наступает рассматриваемое событие, оканчивающееся в момент р, или, короче, сеть представляет это событие путем возбуждения нейрона Р с ЗАПАЗДЫВАНИЕМ 2. Нейроны N1, N'1, N''1 с указанными соединяющими их аксонами образуют "сеть задержки" (см. рис.4). Синапс нейрона M1, имеющий на себе шесть концевых пластинок, является "конъюнктивной сетью" (см. рис.1). Синапс нейрона Р является "дизъюнктивной сетью" (см. рис.3).

Метод этой иллюстрации применим к любому позитивному определенному событию, которое наступает для одной или нескольких таблиц.
Остается случай события, которое никогда не наступает. Этот случай представлен возбуждением нейрона Р, например с запаздыванием равным 2, в сети рис.6. Нейрон М2 вставлен с целью показать, что сеть можно выбрать связной (в очевидном смысле): иначе М2 можно опустить, тогда М1 совпадет с Р.

Мы, таким образом, уже доказали, что всякое позитивное определенное событие представимо посредством возбуждения нейрона с запаздыванием 2. Однако мы дадим ниже более гибкое рассуждение, в котором этот результат окажется частью следствия 1 теоремы 1.
#5.3. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ: ОБЩАЯ ТЕОРИЯ. Мы рассмотрим логические выражения, построенные с юмощью & и V из выражений, символизирующих возбужденность или невозбужденность одного из k входных нейронов N1, ..., Nk в один из l моментов р-l+1, ..., р. Такое выражение мы будем называть kl-ФОРМУЛОЙ и будем называть ее ГЛУБИНОЙ наибольшее число раз, которое знаки & или V используются последовательно в ее построении. При этом допускается любой способ расстановки скобок в конъюнкциях и дизъюнкциях, содержащих более двух членов; например
[[N1(р) & ~N2(p)] & N2(p-1)] V ~N1(p)
в таком виде имеет глубину 3, но эту формулу можно переписать в виде
[N1(p) & ~N2(p) & N2(p-1)] V ~N1(p)
с глубиной 2.
Эти определения можно следующим образом уточнить с помощью математической индукции по s:
1) Для каждых i и j (i=1,...,k; j=1,...,l) Ni(p-j+1) и ~Ni(p-j+1) являются kl-ФОРМУЛАМИ
ГЛУБИНЫ 0.
2) При s>0, если G1, ..., Gn(n>=2) - kl-формулы глубины <s и хотя бы одна из них имеет глубину s-1, то G1&...&Gn и G1V...VGn являются kl-ФОРМУЛАМИ ГЛУБИНЫ s (здесь каждое Ge глубины, отличной от 0, надлежит при записывании заключать в скобки).
Так как истинность или ложность kl-формулы F определяется логически только истинностью или ложностью формул Ni(p-j+1), входящих в нее в качестве ЭЛЕМЕНТАРНЫХ КОМПОНЕНТ, то каждая F выражает определенное событие E длины l с k входными нейронами.
Мы не теряем ничего существенного из-за того, что применяем символ ~ отрицания только непосредственно к элементарным компонентам. В самом деле, с помощью многократного применения логических тождеств
~~G = G
~(G1&...&Gn)=~G1V...V~Gn
~(G1V...VGn)=~G1&...&~Gn
символы отрицания, использованные другим способом, можно сдвинуть внутрь так, что они окажутся над элементарными компонентами и глубина формулы при этом не изменится. Две другие операции, обычно применяемые в двузначном исчислении высказываний, а именно -> (ВЛЕЧЕТ) и =, могут быть выражены в терминах ~, & и V следующим образом:
G->H = ~G V Н,
(G=H) = (G->H) & (H->G).
ПЕТЛЕЙ (ДЛИНЫ c) в нервной сети называется множество различных нейронов N1, ..., Nc (с>=1), таких, что Ni имеет концевую пластинку на N[i+1] для каждого i (i=1,...,c-1), a Nc имеет концевую пластинку на N1. Сети, рассмотренные нами до сих пор, в том числе конъюнктивная и дизъюнктивная сети и сеть задержки (см. рис.1, 3 и 4) и некоторые сети, составленные из них, не имеют петель.
ТЕОРЕМА 1. Пусть F - любая kl-формула глубины s и пусть Е - определенное событие длины l с k входными нейронами, выражаемое формулой F. Тогда имеется нервная сеть, структура которой соответствует F (и поэтому эта нервная сеть не имеет петель), причем эта сеть представляет E посредством возбужденности или невозбужденности (смотря по тому, позитивно или непозитивно E) некоторого нейрона P (внутреннего при s>0) в момент p+s.
Утверждение "структура нервной сети соответствует F" означает, что эта сеть составлена из конъюнктивных и дизъюнктивных сетей (а также сетей задержки), соответствующих, как будет указано в доказательстве, операциям, использованным при построении F.
ДОКАЗАТЕЛЬСТВО ИНДУКЦИЕЙ ПО s. По нашему определению kl-формулы, не обязательно все символы Ni (i=1,...,k) встречаются в F. Излагая индуктивное построение сети, соответствующей логической структуре F, мы будем принимать во внимание только те нейроны Ni, для которых Ni встречается в F. Остальные нейроны можно считать входящими фиктивно или же их можно связать с остальной цепью. При s>1 это можно сделать, например, так, как показано для N2 на рис.6.
БАЗИС: s=0. Тогда F есть Ni(p-j+1), или ~Ni(p-j+1) для некоторых i и j. Тогда Ni есть P, если j=1; если же j>1, то P есть нейрон, соединенный с Ni посредством надлежащей сети задержки (см. рис.4).
ИНДУКЦИОННЫЙ ШАГ: s>0. Тогда F есть G1&...&Gn или G1V...VGn. Для e= 1,...,n пусть Me будет Ge или ~Ge, в соответствии с тем, позитивно или нет событие, описанное посредством Ge. Тогда Ge (глубины se<s) эквивалентна Me или ~Me соответственно, и по индуктивному предположению имеется нервная сеть с нейроном Ge, возбужденность или, соответственно, невозбужденность которого в момент p+se представляет Ge. Далее мы получаем нейрон Me, возбужденность которого в момент p+s-1 представляет Me; этот нейрон Me есть сам Ge, если se=s-1, а в противном же случае Me получается из Ge при помощи надлежащей сети задержки. Теперь возможны четыре случая построения F из M1,...,Mn согласно построению F из
G1,...,Gn и эквивалентности каждой Ge одной из Me и ~Me.
СЛУЧАЙ 1. Конъюнкция, содержащая хоть один неотрицаемый сомножитель, например M1&M2&M3&~M4&~M5. В случае событие позитивно, значит, нам надлежит представить его возбуждением некоторого нейрона P в момент p+s. Конъюнктивная сеть (см. рис.1) дает нам этот нейрон.
СЛУЧАЙ 2. Конъюнкция, содержащая только отрицаемые сомножители, например ~M1&~M2&~M3. В этом случае событие непозитивно. Но его отрицание ~(~M1&~M2&~M3) позитивно. Оно эквивалентно М1VМ2VM3. Последнее представляется дизъюнктивной сетью (см. рис.3) с нейроном Р, возбужденным в момент p+s; полученная сеть представляет данное событие невозбуждением в момент p+s нейрона Р, как мы и хотели его представить.
СЛУЧАЙ 3. Дизъюнкция, содержащая по крайней мере oдин отрицаемый член, например ~M1V~M2V~M3VM4VM5. В этом случае событие непозитивно. Но его отрицание позитивно и эквивалентно M1&M2&M3&~M4&~M5. Конъюнктивная сеть представляет это событие возбуждением в момент p+s нейрона Р; данное событие представляется невозбуждением нейрона Р в момент p+s.
СЛУЧАЙ 4. Дизъюнкция, содержащая только неотрицаемые члены, например M1VM2VM3VM4VM5. Событие позитивно. Дизъюнктивная сеть представляет это событие, как и требуется, возбуждением в момент p+s нейрона Р.
ПРИМЕРЫ. Сеть рис.5 получена применением только что изложенного метода к написанной под рис.5 формуле. Другой пример дает рис.7. Рассмотрение трех формул N1(p)VN2(p)VN3(p), N1(p)V~N2(p)V~N3(p) и ~N1(p)VN2(p)VN3(p) дает нам соответственно нейроны М1, М2 и М3, которые представляют выражаемые этими формулами события; для первой формулы, когда событие позитивно,- возбуждением (случай 4), а для второй и третьей, когда событие непозитивно,- невозбуждением (случай 3) в момент p+1. Bee событие позитивно, и полученный нейрон Р представляет его, как и следует, возбуждением в момент p+2 (случай 1).

СЛЕДСТВИЕ 1. Для каждого позитивного (непозитивного) определенного события имеется нервная сеть без петель, которая представляет это событие возбуждением (невозбуждением) некоторого внутреннего нейрона в момент p+2.
Этот результат был высказан (для позитивных событий и без замечания о запаздывании) Мак-Каллоком и Питтсом [1943].
ДОКАЗАТЕЛЬСТВО. Чтобы получить это следствие из теоремы, достаточно заметить, что метод пункта 5.2 дает kl-формулу глубины <=2 для каждого определенного события длины l с k входными нейронами. (Если глубина <2, то с помощью задержки можно довести запаздывание до 2).
КОММЕНТАРИЙ. Читатель, знакомый с символической логикой, узнает в полученной таким образом [Подразумевается метод пункта 5.2.- Прим. ред.] kl-формуле СОВЕРШЕННУЮ ДИЗЪЮНКТИВНУЮ НОРМАЛЬНУЮ ФОРМУ (с.д.н.ф.) Гильберта и Аккермана [1928]. Она "совершенна" потому, что в каждом из ее членов встречается, отрицаемый или нет, любой из сомножителей N1(p),..., Nk(p-l+1) (за исключением случая, представленного на рис.6).
Формула рис.7 является СОВЕРШЕННОЙ КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ (с.к.н.ф.). Если с.д.н.ф. имеет n<2**(kl) членов, то с.к.н.ф. имеет 2**(kl)-n сомножителей (с.к.н.ф. получается вычислением отрицания с.д.н.ф. отрицания события).
Использование с.д.н.ф. упрощает доказательство представимости (см. 5.2) и дает результатом, что запаздывание можно свести к 2, но построенная при этом сеть может оказаться излишне усложненной. Событие может допускать более простое описание при помощи дизъюнктивной или конъюнктивной нормальной формы, не являющейся совершенной (причем запаздывание все еще может быть сделано <=2). Например (при k=2, l=3), [~N2(p)&N2(p-2)]VN2(p-1) есть д.н.ф., для которой с.д.н.ф. будет иметь 40 членов (а с.к.н.ф. 24 множителя). Могут иметься более простые эквиваленты, не являющиеся дизъюнктивной или конъюнктивной нормальными формами.
Ввиду того что теорема 1 дает представляющую сеть со структурой, соответствующей формуле, задача нахождения возможно более простых сетей для представления определенных событий связана с задачей нахождения наиболее простых эквивалентов выражений исчисления высказываний, которая недавно рассматривалась Куайном [1952].
В специальных случаях удается построить сеть, имеющую более простую структуру, чем та, которая соответствует формуле; например, если в рис.2 положить p=t-1, то сеть будет представлять событие с запаздыванием 1, хотя формула имеет глубину 3 и не существует никакой эквивалентной формулы глубины 1.
Сведение запаздывания к числу, меньшему 2, в общем случае невозможно. Например (при k=3, l=1), событие N1(p)&[~N2(p)V~N3(p)] не представимо с задержкой 1. В самом деле, легко видеть, что никакая сеть, состоящая из нейрона Р, возбуждаемого только концевыми пластинками, принадлежащими непосредственно нейронам N1, N2 и N3, не может представлять это событие.
Для сведения запаздывания к 2 может оказаться необходимым очень большое число концевых пластинок, исходящих из данного тела или соприкасающихся с ним.
СЛЕДСТВИЕ 2. Для каждого позитивного (непозитивного) определенного события имеется число s и нервная сеть без петель, каждый из нейронов которой имеет не более двух концевых пластинок и возбуждается не более чем двумя концевыми пластинками и имеет порог не более 2, представляющая это событие возбуждением (невозбуждением) некоторого нейрона в момент p+s.
ДОКАЗАТЕЛЬСТВО. Если в kl-формуле пользоваться символами & и V только как бинарными операциями, то в построенной согласно теореме сети ни один нейрон не будет юзбуждаться более чем двумя концевыми пластинками. Каждый внутренний нейрон, не входящий в сеть задержки, имеет только одну концевую пластинку. Каждый входной нейрон и сеть задержки можно при необходимости заменить (с увеличением запаздывания) "деревом" нейронов, каждый из соторых имеет не более двух концевых пластинок.
До сих пор мы рассматривали представление события, оканчивающегося в момент p, посредством возбуждения или невозбуждения некоторого нейрона в некоторый момент p+s (s>=0). Более общим образом можно рассматривать представление посредством свойства состояния сети (т.е. посредством возбуждения или невозбуждения каждого из ее нейронов) в момент p+s, т.е. состояние сети должно обладать или не обладать этим свойством в момент p+s в соответствии с тем, наступает или нет событие в момент р. В следующих лемме и следствии событие не предполагается определенным, а сеть - не имеющей петель.
ЛЕММА 1. Событие, представимое в нервной сети свойством состояния в момент p+s для данного s>0, представимо и свойством состояния той же самой сети в момент р.
ДОКАЗАТЕЛЬСТВО. Все, что происходит в моменты <=p, может влиять на состояние сети в момент p+s только посредством состояния всей сети, в том числе состояния k входных и всех, скажем m, внутренних нейронов в момент р.
СЛЕДСТВИЕ 3. Событие, представимое в нервной сети свойством состояния в момент p+s для данного s>=0, представимо также возбуждением или не возбуждением (в зависимости от природы этого свойства) некоторого внутреннего нейрона подходящей сети в момент р+2.
ДОКАЗАТЕЛЬСТВО. С целью применить следствие 1 будем рассматривать все k+m нейронов как входные. По лемме 1, рассматриваемое свойство эквивалентно некоторому свойству k+m нейронов в момент p. Последнее образует определенное событие длины 1 с k+m нейронами.
#5.4. НЕРВНЫЕ СЕТИ БЕЗ ПЕТЕЛЬ
ТЕОРЕМА 2. Для любой данной нервной сети без петель и любого данного внутреннего нейрона N этой сети возбужденность (невозбужденность) этого нейрона в момент р+1 эквивалентна наступлению некоторого позитивного (непозитивного) определенного события.
Эта теорема была высказана (для позитивных событий) Мак-Каллоком и Питтсом [1943].
ДОКАЗАТЕЛЬСТВО. Возбуждение или невозбуждение нейрона N в момент р+1 определяется полностью состоянием (возбужденностью или невозбужденностью) в момент p тех нейронов N'1,...,N'r, которые имеют концевые пластинки на N. Рассмотрим те из нейронов N'1,...,N'r, которые являются внутренними, и повторим это рассуждение. Так как петель нет, то любая начинающаяся с N цепь нейронов, каждый член которой возбуждается концевой пластинкой следующего члена, должна обрываться (на входном нейроне). Пусть l+1 - наибольшая из длин этих цепей; так как N - внутренний нейрон, то l>=1. После l шагов не остается подлежащих рассмотрению внутренних нейронов. Таким образом, возбужденность или невозбужденность нейрона N в момент р+1 полностью определяется состоянием некоторых входных нейронов в некоторые моменты между р-l+1 и р включительно, т.е. возбужденность N в момент р эквивалентна определенному событию длины l. Это событие позитивно, так как для внутренних нейронов возбуждение может только распространяться, но не порождаться.
ЗАМЕЧАНИЕ. Любое определенное событие выразимо логической формулой, например совершенной дизъюнктивной нормальной формой, как в 5.2. Таким образом, a priori имеется формула, выражающая событие теоремы 2. Используя условия для возбужденности на каждом синапсе, которые можно выразить логическими символами через пороги и числа и виды концевых пластинок (ср. рис.1-3 для нескольких рассмотренных примеров), можно построить формулу с помощью как раз l шагов, как указывают Мак-Каллок и Питтс.
СЛЕДСТВИЕ 1. Любое событие, представимое в нервной сети без петель возбужденностью (невозбужденностью) некоторого данного внутреннего нейрона N в момент p+s для некоторого данного s>=1, является позитивным (непозитивным) определенным.
ДОКАЗАТЕЛЬСТВО. Согласно теореме 2, возбужденность нейрона N в момент p+s эквивалентна наступлению некоторого позитивного определенного события, оканчивающегося в момент p+s-1. Но по условию возбуждение нейрона N в момент р+s представляет некоторое событие, подразумевается оканчивающееся в момент р (см. раздел 4), поэтому вход в моменты р+1,...,p+s-1 не оказывает влияния на возбужденность или невозбужденность N в момент p+s.
СЛЕДСТВИЕ 2. Любое событие, представимое в нервной сети без петель свойством состояния в момент p+s для данного s>=0, является определенным.
ДОКАЗАТЕЛЬСТВО. В силу следствия 1 и следствия 3 из теоремы 1 (это следствие не вводит петель).
#3. НЕРВНЫЕ СЕТИ МАК-КАЛЛОКА-ПИТТСА
По допущениям Мак-Каллока и Питтса [1943], нервная клетка, или нейрон, состоит из тела (сомы), откуда нервные волокна (аксоны) ведут к одной или нескольким концевым пластинкам.
Нервная сеть является устройством из конечного числа нейронов, в котором каждая концевая пластинка любого нейрона соприкасается с телом не более чем одного нейрона (того же самого или другого), который она возбуждает; разделяющий промежуток называется синапсом. Каждая концевая пластинка является возбуждающей или тормозящей (и не может быть возбуждающей и тормозящей одновременно).
Мы будем называть нейроны, к которым не примыкают никакие концевые пластинки, входными нейронами (число их может равняться нулю); остальные нейроны мы будем называть внутренними.
В равноотстоящие моменты времени (которые мы будем рассматривать как целые числа на временной шкале, одни и те же для всех нейронов данной сети) каждый нейрон сети является возбужденным или невозбужденным (спокойным). Для входного нейрона возбужденность или невозбужденность в любой момент t определяется условиями, внешними по отношению к сети. Можно предположить, что к каждому из них примыкает чувственно воспринимающий орган, который при надлежащих условиях в окружающей среде вызывает возбуждение нейрона в момент t. Для внутреннего нейрона условие возбужденности в момент t состоит в том, что по меньшей мере h (h называется порогом этого нейрона) возбуждающих концевых пластинок действуют, а ни одна из тормозящих не действует в момент t-1).
Для иллюстрации рассмотрим нервную сеть, показанную на рис.1, с входными нейронами J, К, L, М, N и внутренним нейроном Р. Возбуждающие концевые пластинки изображены жирными точками, а тормозящие - кружками. Порог Р равен 3, что указано числом, стоящим в треугольнике, представляющем тело этого нейрона. Формула, написанная под сетью, выражает в логической символике, что нейрон Р возбужден в момент t тогда и только тогда, когда все J, К, L возбуждены, но ни один из нейронов М и N не возбужден, в момент t-1. Мы пишем "P(t)" для указания, что нейрон Р возбужден в момент t; "J(t-1)" - для указания, что J возбужден в момент t-1, и т.д. Символ "=" означает "в том и только в том случае, если (или "эквивалентно"), "&" означает "и", "V" означает "или" (в неразделительном смысле), а "черта сверху" означает "не".


#4. ВХОД НЕРВНОЙ СЕТИ
Рассмотрим нервную сеть с k входными нейронами N1, ..., Nk. До пункта 6.3 мы будем считать, что k>=1. ВХОД (или ОПЫТ) всего прошлого до настоящего момента включительно можно описать таблицей с k столбцами, соответствующими входным нейронам, и строками, соответствующими моментам, отсчитываемым в обратном порядке от данного момента р) [Обозначение р от present - настоящее.- Прим. ред.]. Пересечения строк и столбцов заполняются нулями и единицами, причем 0 означает, что данный нейрон не возбужден, а 1 - что он возбужден в данный момент времени.
Например, при k = 2 таблица может иметь вид:

Цифра 1 в первой строке и первом столбце означает, что N1 возбужден в момент р; 0 в третьей строке и первом столбце - что N1 не возбужден в момент р-2, и т.д. Если эту таблицу продолжить вниз до бесконечности, мы получим представление опыта, мыслимого распространенным на все прошедшее время, которое мы считаем до настоящего момента бесконечным (в разделе 6 мы вернемся к рассмотрению этого вопроса).
Под СОБЫТИЕМ мы будем понимать любое свойство входа. Другими словами, любой подкласс класса всех возможных таблиц, описывающих вход всего прошлого (включая, если не оговорено противное, настоящий момент p), образует событие, которое НАСТУПАЕТ, если таблица, описывающая данный вход, принадлежит этому подклассу.
Примерами событий с двумя входными нейронами N1 и N2 являются:
(1) N1 возбужден в момент p.
(2) N2 не возбужден в момент p, a N1 возбужден в момент р-1.
(3) Один из нейронов, N1 или N2, возбужден в момент р.
(4) N1 и N2 оба возбуждены в момент р.
(5) N2 был возбужден в некоторый момент.
(6) N2 был возбужден в каждый момент, за исключением p.
В этих примерах вход, описанный табл.1, представляет наступление событий (1), (2), (3) и (5), но не (4), а для того, чтобы сказать, представляет ли он наступление события (6), мы должны знать продолжение таблицы.
#5. ОПРЕДЕЛЕННЫЕ СОБЫТИЯ
#5.1. ОПРЕДЕЛЕНИЕ "ОПРЕДЕЛЕННЫХ СОБЫТИЙ". Мы рассмотрим сначала события, которые относятся к фиксированному периоду времени, состоящему из некоторого числа l (>=1) последовательных моментов р-l+1, ..., p, оканчивающихся настоящим моментом. Мы будем называть такие события определенными событиями ДЛИНЫ (или ДЛИТЕЛЬНОСТИ) l. Среди предыдущих примеров определенными являются события (1)-(4), но не (5) и (6).
При этом в таблице такого вида, как табл.1, нам надо рассматривать только верхние l строк; например, при l=3 таблица 1 описывает событие, которое описывается также формулой
N1(p)&~N2(p) & N1(p-1)&N2(p-l) & ~N1(p-2)&N2(p-2).
Таблица, описывающая вход с k нейронами для l моментов р-l+1, ..., p, имеет ровно kl мест. Следовательно, возможно ровно 2**(kl) таких таблиц. Следовательно, имеется ровно 2**2**(kl) определенных событий длины с k входными нейронами, так как каждое из них определяется указанием того, какие из входов, описанных 2**(kl) k*l-таблицами, должны давать наступление события.
Определенное событие мы будем называть ПОЗИТИВНЫМ, если оно наступает только в том случае, когда хотя бы один из входных нейронов оказывается возбужденным хотя бы в один из моментов в продолжение периода, к которому это событие относится. Имеется ровно 2**(2**(kl)-1) позитивных определенных событий длины l с k входными нейронами, так как такие события определяются тем условием, что вход, описанный таблицей из одних нулей, не дает наступления события). [Эти выкладки показывают, что автор включает невозможное событие (т.е. событие, состоящее из пустого множества таблиц) в число позитивных, а значит, в частности, в число определенных событий.- Прим, ред.]
#5.2. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. ИЛЛЮСТРАЦИЯ. Рассмотрим определенное событие, которое наступает, когда конфигурация возбуждений совпадает с табл.1 (оборванной на трех строках) или с табл.2.
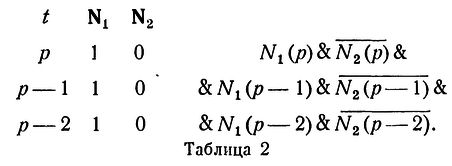
Это означает, что именно эти две (из 2**(2*3)=64) 2*3-таблицы, и только они, должны давать наступление события. Это событие описывается правой частью эквивалентности рис.5, получающейся путем дизъюнктивного сочетания конъюнкций, описывающих соответствующие таблицы в отдельности. В нервной сети рис.5 нейрон Р возбужден в момент p+2 в том и только в том случае, если наступает рассматриваемое событие, оканчивающееся в момент р, или, короче, сеть представляет это событие путем возбуждения нейрона Р с ЗАПАЗДЫВАНИЕМ 2. Нейроны N1, N'1, N''1 с указанными соединяющими их аксонами образуют "сеть задержки" (см. рис.4). Синапс нейрона M1, имеющий на себе шесть концевых пластинок, является "конъюнктивной сетью" (см. рис.1). Синапс нейрона Р является "дизъюнктивной сетью" (см. рис.3).

Метод этой иллюстрации применим к любому позитивному определенному событию, которое наступает для одной или нескольких таблиц.
Остается случай события, которое никогда не наступает. Этот случай представлен возбуждением нейрона Р, например с запаздыванием равным 2, в сети рис.6. Нейрон М2 вставлен с целью показать, что сеть можно выбрать связной (в очевидном смысле): иначе М2 можно опустить, тогда М1 совпадет с Р.

Мы, таким образом, уже доказали, что всякое позитивное определенное событие представимо посредством возбуждения нейрона с запаздыванием 2. Однако мы дадим ниже более гибкое рассуждение, в котором этот результат окажется частью следствия 1 теоремы 1.
#5.3. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ: ОБЩАЯ ТЕОРИЯ. Мы рассмотрим логические выражения, построенные с юмощью & и V из выражений, символизирующих возбужденность или невозбужденность одного из k входных нейронов N1, ..., Nk в один из l моментов р-l+1, ..., р. Такое выражение мы будем называть kl-ФОРМУЛОЙ и будем называть ее ГЛУБИНОЙ наибольшее число раз, которое знаки & или V используются последовательно в ее построении. При этом допускается любой способ расстановки скобок в конъюнкциях и дизъюнкциях, содержащих более двух членов; например
[[N1(р) & ~N2(p)] & N2(p-1)] V ~N1(p)
в таком виде имеет глубину 3, но эту формулу можно переписать в виде
[N1(p) & ~N2(p) & N2(p-1)] V ~N1(p)
с глубиной 2.
Эти определения можно следующим образом уточнить с помощью математической индукции по s:
1) Для каждых i и j (i=1,...,k; j=1,...,l) Ni(p-j+1) и ~Ni(p-j+1) являются kl-ФОРМУЛАМИ
ГЛУБИНЫ 0.
2) При s>0, если G1, ..., Gn(n>=2) - kl-формулы глубины <s и хотя бы одна из них имеет глубину s-1, то G1&...&Gn и G1V...VGn являются kl-ФОРМУЛАМИ ГЛУБИНЫ s (здесь каждое Ge глубины, отличной от 0, надлежит при записывании заключать в скобки).
Так как истинность или ложность kl-формулы F определяется логически только истинностью или ложностью формул Ni(p-j+1), входящих в нее в качестве ЭЛЕМЕНТАРНЫХ КОМПОНЕНТ, то каждая F выражает определенное событие E длины l с k входными нейронами.
Мы не теряем ничего существенного из-за того, что применяем символ ~ отрицания только непосредственно к элементарным компонентам. В самом деле, с помощью многократного применения логических тождеств
~~G = G
~(G1&...&Gn)=~G1V...V~Gn
~(G1V...VGn)=~G1&...&~Gn
символы отрицания, использованные другим способом, можно сдвинуть внутрь так, что они окажутся над элементарными компонентами и глубина формулы при этом не изменится. Две другие операции, обычно применяемые в двузначном исчислении высказываний, а именно -> (ВЛЕЧЕТ) и =, могут быть выражены в терминах ~, & и V следующим образом:
G->H = ~G V Н,
(G=H) = (G->H) & (H->G).
ПЕТЛЕЙ (ДЛИНЫ c) в нервной сети называется множество различных нейронов N1, ..., Nc (с>=1), таких, что Ni имеет концевую пластинку на N[i+1] для каждого i (i=1,...,c-1), a Nc имеет концевую пластинку на N1. Сети, рассмотренные нами до сих пор, в том числе конъюнктивная и дизъюнктивная сети и сеть задержки (см. рис.1, 3 и 4) и некоторые сети, составленные из них, не имеют петель.
ТЕОРЕМА 1. Пусть F - любая kl-формула глубины s и пусть Е - определенное событие длины l с k входными нейронами, выражаемое формулой F. Тогда имеется нервная сеть, структура которой соответствует F (и поэтому эта нервная сеть не имеет петель), причем эта сеть представляет E посредством возбужденности или невозбужденности (смотря по тому, позитивно или непозитивно E) некоторого нейрона P (внутреннего при s>0) в момент p+s.
Утверждение "структура нервной сети соответствует F" означает, что эта сеть составлена из конъюнктивных и дизъюнктивных сетей (а также сетей задержки), соответствующих, как будет указано в доказательстве, операциям, использованным при построении F.
ДОКАЗАТЕЛЬСТВО ИНДУКЦИЕЙ ПО s. По нашему определению kl-формулы, не обязательно все символы Ni (i=1,...,k) встречаются в F. Излагая индуктивное построение сети, соответствующей логической структуре F, мы будем принимать во внимание только те нейроны Ni, для которых Ni встречается в F. Остальные нейроны можно считать входящими фиктивно или же их можно связать с остальной цепью. При s>1 это можно сделать, например, так, как показано для N2 на рис.6.
БАЗИС: s=0. Тогда F есть Ni(p-j+1), или ~Ni(p-j+1) для некоторых i и j. Тогда Ni есть P, если j=1; если же j>1, то P есть нейрон, соединенный с Ni посредством надлежащей сети задержки (см. рис.4).
ИНДУКЦИОННЫЙ ШАГ: s>0. Тогда F есть G1&...&Gn или G1V...VGn. Для e= 1,...,n пусть Me будет Ge или ~Ge, в соответствии с тем, позитивно или нет событие, описанное посредством Ge. Тогда Ge (глубины se<s) эквивалентна Me или ~Me соответственно, и по индуктивному предположению имеется нервная сеть с нейроном Ge, возбужденность или, соответственно, невозбужденность которого в момент p+se представляет Ge. Далее мы получаем нейрон Me, возбужденность которого в момент p+s-1 представляет Me; этот нейрон Me есть сам Ge, если se=s-1, а в противном же случае Me получается из Ge при помощи надлежащей сети задержки. Теперь возможны четыре случая построения F из M1,...,Mn согласно построению F из
G1,...,Gn и эквивалентности каждой Ge одной из Me и ~Me.
СЛУЧАЙ 1. Конъюнкция, содержащая хоть один неотрицаемый сомножитель, например M1&M2&M3&~M4&~M5. В случае событие позитивно, значит, нам надлежит представить его возбуждением некоторого нейрона P в момент p+s. Конъюнктивная сеть (см. рис.1) дает нам этот нейрон.
СЛУЧАЙ 2. Конъюнкция, содержащая только отрицаемые сомножители, например ~M1&~M2&~M3. В этом случае событие непозитивно. Но его отрицание ~(~M1&~M2&~M3) позитивно. Оно эквивалентно М1VМ2VM3. Последнее представляется дизъюнктивной сетью (см. рис.3) с нейроном Р, возбужденным в момент p+s; полученная сеть представляет данное событие невозбуждением в момент p+s нейрона Р, как мы и хотели его представить.
СЛУЧАЙ 3. Дизъюнкция, содержащая по крайней мере oдин отрицаемый член, например ~M1V~M2V~M3VM4VM5. В этом случае событие непозитивно. Но его отрицание позитивно и эквивалентно M1&M2&M3&~M4&~M5. Конъюнктивная сеть представляет это событие возбуждением в момент p+s нейрона Р; данное событие представляется невозбуждением нейрона Р в момент p+s.
СЛУЧАЙ 4. Дизъюнкция, содержащая только неотрицаемые члены, например M1VM2VM3VM4VM5. Событие позитивно. Дизъюнктивная сеть представляет это событие, как и требуется, возбуждением в момент p+s нейрона Р.
ПРИМЕРЫ. Сеть рис.5 получена применением только что изложенного метода к написанной под рис.5 формуле. Другой пример дает рис.7. Рассмотрение трех формул N1(p)VN2(p)VN3(p), N1(p)V~N2(p)V~N3(p) и ~N1(p)VN2(p)VN3(p) дает нам соответственно нейроны М1, М2 и М3, которые представляют выражаемые этими формулами события; для первой формулы, когда событие позитивно,- возбуждением (случай 4), а для второй и третьей, когда событие непозитивно,- невозбуждением (случай 3) в момент p+1. Bee событие позитивно, и полученный нейрон Р представляет его, как и следует, возбуждением в момент p+2 (случай 1).

СЛЕДСТВИЕ 1. Для каждого позитивного (непозитивного) определенного события имеется нервная сеть без петель, которая представляет это событие возбуждением (невозбуждением) некоторого внутреннего нейрона в момент p+2.
Этот результат был высказан (для позитивных событий и без замечания о запаздывании) Мак-Каллоком и Питтсом [1943].
ДОКАЗАТЕЛЬСТВО. Чтобы получить это следствие из теоремы, достаточно заметить, что метод пункта 5.2 дает kl-формулу глубины <=2 для каждого определенного события длины l с k входными нейронами. (Если глубина <2, то с помощью задержки можно довести запаздывание до 2).
КОММЕНТАРИЙ. Читатель, знакомый с символической логикой, узнает в полученной таким образом [Подразумевается метод пункта 5.2.- Прим. ред.] kl-формуле СОВЕРШЕННУЮ ДИЗЪЮНКТИВНУЮ НОРМАЛЬНУЮ ФОРМУ (с.д.н.ф.) Гильберта и Аккермана [1928]. Она "совершенна" потому, что в каждом из ее членов встречается, отрицаемый или нет, любой из сомножителей N1(p),..., Nk(p-l+1) (за исключением случая, представленного на рис.6).
Формула рис.7 является СОВЕРШЕННОЙ КОНЪЮНКТИВНОЙ НОРМАЛЬНОЙ ФОРМОЙ (с.к.н.ф.). Если с.д.н.ф. имеет n<2**(kl) членов, то с.к.н.ф. имеет 2**(kl)-n сомножителей (с.к.н.ф. получается вычислением отрицания с.д.н.ф. отрицания события).
Использование с.д.н.ф. упрощает доказательство представимости (см. 5.2) и дает результатом, что запаздывание можно свести к 2, но построенная при этом сеть может оказаться излишне усложненной. Событие может допускать более простое описание при помощи дизъюнктивной или конъюнктивной нормальной формы, не являющейся совершенной (причем запаздывание все еще может быть сделано <=2). Например (при k=2, l=3), [~N2(p)&N2(p-2)]VN2(p-1) есть д.н.ф., для которой с.д.н.ф. будет иметь 40 членов (а с.к.н.ф. 24 множителя). Могут иметься более простые эквиваленты, не являющиеся дизъюнктивной или конъюнктивной нормальными формами.
Ввиду того что теорема 1 дает представляющую сеть со структурой, соответствующей формуле, задача нахождения возможно более простых сетей для представления определенных событий связана с задачей нахождения наиболее простых эквивалентов выражений исчисления высказываний, которая недавно рассматривалась Куайном [1952].
В специальных случаях удается построить сеть, имеющую более простую структуру, чем та, которая соответствует формуле; например, если в рис.2 положить p=t-1, то сеть будет представлять событие с запаздыванием 1, хотя формула имеет глубину 3 и не существует никакой эквивалентной формулы глубины 1.
Сведение запаздывания к числу, меньшему 2, в общем случае невозможно. Например (при k=3, l=1), событие N1(p)&[~N2(p)V~N3(p)] не представимо с задержкой 1. В самом деле, легко видеть, что никакая сеть, состоящая из нейрона Р, возбуждаемого только концевыми пластинками, принадлежащими непосредственно нейронам N1, N2 и N3, не может представлять это событие.
Для сведения запаздывания к 2 может оказаться необходимым очень большое число концевых пластинок, исходящих из данного тела или соприкасающихся с ним.
СЛЕДСТВИЕ 2. Для каждого позитивного (непозитивного) определенного события имеется число s и нервная сеть без петель, каждый из нейронов которой имеет не более двух концевых пластинок и возбуждается не более чем двумя концевыми пластинками и имеет порог не более 2, представляющая это событие возбуждением (невозбуждением) некоторого нейрона в момент p+s.
ДОКАЗАТЕЛЬСТВО. Если в kl-формуле пользоваться символами & и V только как бинарными операциями, то в построенной согласно теореме сети ни один нейрон не будет юзбуждаться более чем двумя концевыми пластинками. Каждый внутренний нейрон, не входящий в сеть задержки, имеет только одну концевую пластинку. Каждый входной нейрон и сеть задержки можно при необходимости заменить (с увеличением запаздывания) "деревом" нейронов, каждый из соторых имеет не более двух концевых пластинок.
До сих пор мы рассматривали представление события, оканчивающегося в момент p, посредством возбуждения или невозбуждения некоторого нейрона в некоторый момент p+s (s>=0). Более общим образом можно рассматривать представление посредством свойства состояния сети (т.е. посредством возбуждения или невозбуждения каждого из ее нейронов) в момент p+s, т.е. состояние сети должно обладать или не обладать этим свойством в момент p+s в соответствии с тем, наступает или нет событие в момент р. В следующих лемме и следствии событие не предполагается определенным, а сеть - не имеющей петель.
ЛЕММА 1. Событие, представимое в нервной сети свойством состояния в момент p+s для данного s>0, представимо и свойством состояния той же самой сети в момент р.
ДОКАЗАТЕЛЬСТВО. Все, что происходит в моменты <=p, может влиять на состояние сети в момент p+s только посредством состояния всей сети, в том числе состояния k входных и всех, скажем m, внутренних нейронов в момент р.
СЛЕДСТВИЕ 3. Событие, представимое в нервной сети свойством состояния в момент p+s для данного s>=0, представимо также возбуждением или не возбуждением (в зависимости от природы этого свойства) некоторого внутреннего нейрона подходящей сети в момент р+2.
ДОКАЗАТЕЛЬСТВО. С целью применить следствие 1 будем рассматривать все k+m нейронов как входные. По лемме 1, рассматриваемое свойство эквивалентно некоторому свойству k+m нейронов в момент p. Последнее образует определенное событие длины 1 с k+m нейронами.
#5.4. НЕРВНЫЕ СЕТИ БЕЗ ПЕТЕЛЬ
ТЕОРЕМА 2. Для любой данной нервной сети без петель и любого данного внутреннего нейрона N этой сети возбужденность (невозбужденность) этого нейрона в момент р+1 эквивалентна наступлению некоторого позитивного (непозитивного) определенного события.
Эта теорема была высказана (для позитивных событий) Мак-Каллоком и Питтсом [1943].
ДОКАЗАТЕЛЬСТВО. Возбуждение или невозбуждение нейрона N в момент р+1 определяется полностью состоянием (возбужденностью или невозбужденностью) в момент p тех нейронов N'1,...,N'r, которые имеют концевые пластинки на N. Рассмотрим те из нейронов N'1,...,N'r, которые являются внутренними, и повторим это рассуждение. Так как петель нет, то любая начинающаяся с N цепь нейронов, каждый член которой возбуждается концевой пластинкой следующего члена, должна обрываться (на входном нейроне). Пусть l+1 - наибольшая из длин этих цепей; так как N - внутренний нейрон, то l>=1. После l шагов не остается подлежащих рассмотрению внутренних нейронов. Таким образом, возбужденность или невозбужденность нейрона N в момент р+1 полностью определяется состоянием некоторых входных нейронов в некоторые моменты между р-l+1 и р включительно, т.е. возбужденность N в момент р эквивалентна определенному событию длины l. Это событие позитивно, так как для внутренних нейронов возбуждение может только распространяться, но не порождаться.
ЗАМЕЧАНИЕ. Любое определенное событие выразимо логической формулой, например совершенной дизъюнктивной нормальной формой, как в 5.2. Таким образом, a priori имеется формула, выражающая событие теоремы 2. Используя условия для возбужденности на каждом синапсе, которые можно выразить логическими символами через пороги и числа и виды концевых пластинок (ср. рис.1-3 для нескольких рассмотренных примеров), можно построить формулу с помощью как раз l шагов, как указывают Мак-Каллок и Питтс.
СЛЕДСТВИЕ 1. Любое событие, представимое в нервной сети без петель возбужденностью (невозбужденностью) некоторого данного внутреннего нейрона N в момент p+s для некоторого данного s>=1, является позитивным (непозитивным) определенным.
ДОКАЗАТЕЛЬСТВО. Согласно теореме 2, возбужденность нейрона N в момент p+s эквивалентна наступлению некоторого позитивного определенного события, оканчивающегося в момент p+s-1. Но по условию возбуждение нейрона N в момент р+s представляет некоторое событие, подразумевается оканчивающееся в момент р (см. раздел 4), поэтому вход в моменты р+1,...,p+s-1 не оказывает влияния на возбужденность или невозбужденность N в момент p+s.
СЛЕДСТВИЕ 2. Любое событие, представимое в нервной сети без петель свойством состояния в момент p+s для данного s>=0, является определенным.
ДОКАЗАТЕЛЬСТВО. В силу следствия 1 и следствия 3 из теоремы 1 (это следствие не вводит петель).
Последний раз редактировалось: Gudleifr (Пт Июн 30, 2023 11:50 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#6. НЕОПРЕДЕЛЕННЫЕ СОБЫТИЯ: ПРЕДВАРИТЕЛЬНЫЕ ЗАМЕЧАНИЯ
#6.1. ПРИМЕРЫ. Пусть "(Et)" означает "существует t... такое, что", "(t)" означает "для всех t" и "->" означает "влечет". Сеть на рис.8 имеет петлю длины 1. Если в некоторый момент t<=p входной нейрон N возбужден, то M будет возбужден в каждый последующий момент, в частности в момент p+1, как выражает формула. Но возбуждение M в момент p+1 не представляет неопределенного события (Et)[t<p]N(t) (т.е. мы не имеем M(p+1)=(Et)[t<=p]N(f)), если прошедшее время бесконечно, потому что возбужденность M в момент p+1 можно объяснить также тем, что M был возбужден в каждый прошлый момент, а N не был возбужден ни разу. Аналогичные примеры даны на рис.9 и 10.
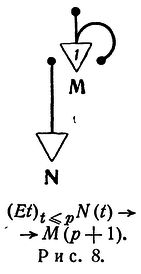
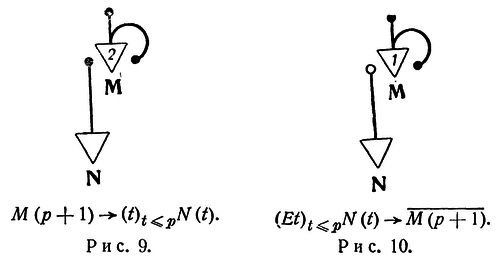
Этой трудности нельзя избежать, употребляя другие сети для представления этих событий или в других примерах неопределенных событий; она представляет общее правило в силу теоремы 6 в разделе 10 вместе с леммой 1.
Разумеется, всякий живой организм или построенный робот имеет только конечное прошлое. Теорема 6 показывает, что в теории мы должны принимать это во внимание, в противном случае мы могли бы попытаться упростить теорию при помощи фикции бесконечного прошлого, как мы это делали в разделе 5.
#6.2. НАЧАЛЬНОЕ СОСТОЯНИЕ. Поэтому в дальнейшем мы будем предполагать (если не оговорено противное), что прошлое для наших нервных сетей идет назад от р (настоящего момента) только на конечное число моментов, причем на нашей временной шкале первый момент есть 1. Областью изменения временной переменной в наших логических формулах будут целые числа начиная с 1 [Автор пренебрегает всем прошлым и начинает счет времени с момента 1.- Прим. ред.]).
Теперь, если в сети рис.8 M спокоен в момент 1, мы должны иметь M(p+1)=(Et)[t<=p]N(t); на рис.9, если M возбужден в момент 1, то M(p+1)=(t)[t<p]N(t), и на рис.10, если M возбужден в момент 1, то ~M(p+1)=(Et)[t<p]N(t). Таким образом, сети на рис.8 и 10 способны запомнить, что N был возбужден с момента начала их работы, путем изменения состояния M по сравнению с первоначальным состоянием этого нейрона; сеть рис.9 способна установить, что N был возбуждаем непрестанно, путем сохранения первоначального состояния нейрона М. Это отметили Хаусхолдер и Лэндал [1945, стр.109].
Рассматриваемые сети представляют указанные события только при условии, что внутренний нейрон M в момент 1 находился в указанном состоянии.
Это опять является общим правилом для неопределенных событий, в силу теоремы 7 и леммы 1. (Лемма 1 имеет место для конечного прошлого).
Для иллюстрации этого мы покажем сейчас, что для представления события (t)[t<p]N(t) хотя бы один внутренний нейрон должен быть возбужден в момент 1. В самом деле, допустим, что имеется представление этого события некоторым свойством состояния в момент p (лемма 1), т.е. свойством, зависящим только от самого этого состояния и не зависящим от значения p. Допустим, что N - единственный входной нейрон. Если бы все внутренние нейроны были спокойны в момент t=1, то при входе, указанном в табл.3, все внутренние нейроны были бы спокойными при t=2, так что состояние при t=2 было бы не отличимо от состояния, указанного в табл.4, в момент t=1. Следовательно, сеть при входе табл.3 имела бы при р=2,3,4,... те же состояния, что и при входе табл.4 при p=1,2,3,... соответственно, хотя в первом случае (t)st<pN(t) ложно, а во втором - истинно.
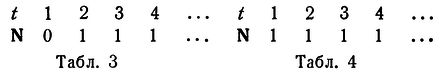
Поэтому при изучении представимости событий мы будем в дальнейшем выбирать не только подходящую сеть, но и состояние (возбужденность или невозбужденность) каждого внутреннего нейрона в момент 1.
Как показывает пример события (t)[t<=p]N(t) Для некоторых событий недостаточно будет иметь первоначально все внутренние нейроны спокойными.
Мы развиваем здесь теорию нервных сетей Мак-Каллока-Питтса как случай, иллюстрирующий теорию конечных автоматов. С точки зрения последней, каждое начальное состояние столь же приемлемо, как и любое другое. Исключать из класса представимых событий такие события, как (t)[t<=p]N(t), было бы не целесообразно.
Для тех, кто считает, что возбужденность внутренних нейронов в момент 1 требует объяснения с точки зрения, принятой Мак-Каллоком и Питтсом, достаточно будет просто сказать, что мы выделяем некоторые входные нейроны Ni,...,Nk и некоторую часть t=1,2,3,... времени в качестве входа для подлежащих представлению событий. Можно привлечь дополнительные нейроны и дополнительные моменты времени, чтобы осуществить любое заданное состояние наших внутренних нейронов в момент t=1. Проще всего этого можно достигнуть введением добавочного входного нейрона Nk+1, который должен быть возбужден при t=0 и только в этот момент и который должен иметь на каждом из тех внутренних нейронов, возбужденности которых при t=1 мы добиваемся, возбуждающие этот нейрон концевые пластинки в количестве, равном порогу этого внутреннего нейрона, и не иметь других концевых пластинок.
Более сложное устройство, для которого требуется добавочный входной нейрон K, но не требуется добавочного момента времени, изображено на рис.11 для события (t)[t<=p]N(t). Это событие представляется возбуждением P в момент t=p+2, если при t=1 нейрон K возбужден, а все внутренние нейроны спокойны. Можно считать, что K подвержен беспрерывному раздражению со стороны внешней среды, которое гарантирует его возбуждение при t=1; его возбуждение в последующие моменты не влияет на представление. Если К возбужден впервые не при t=1, а в более поздний момент времени t=u, то возбуждение P при t=р+2 будет представлять, что N был возбужден в каждый момент от u до p включительно.
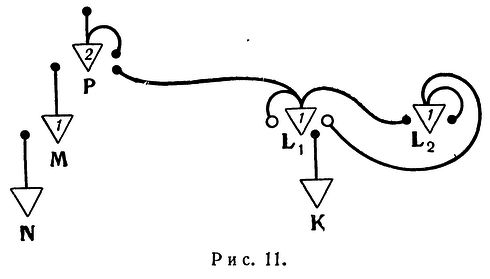
[Мак-Каллок и Питтс рассматривают задачу "решения" сетей, начальные состояния которых не заданы. При этом найти "решение" для данного внутреннего нейрона P, скажем, в момент р+1 означает найти, при каких входах в моменты 1,...,p и каких начальных состояниях внутренних нейронов нейрон P будет возбужден в момент р+1. В следующей сети необходимое и достаточное условие того, что P возбужден в момент p+1, состоит в том, что N возбужден во все моменты <=p, а P и Q оба возбуждены в момент 1. Повидимому, это служит противоречащим примером к той формуле, которая следует за (9) в статье Мак-Каллока-Питтса [1943] и доказательства которой мы не проследили; ибо, если мы правильно понимаем эту формулу, из нее следует, что условие для возбужденности Р требует только существования одного первоначально возбужденного нейрона (повидимому, их 0 играет роль 1 у нас). Этот очевидный контрпример охладил наше желание разобраться в части III статьи Мак-Каллока-Питтса [1943]]
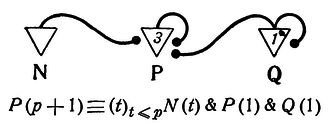
#6.3. НОВОЕ РАССМОТРЕНИЕ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. Событие - это разбиение класса всех возможных входов в прошлом (включая настоящее) на два подкласса: подкласс тех входов, для которых событие наступает, и подкласс тех входов, для которых событие не наступает. Возможные входы с k нейронами N1,...,Nk описываются k*p-таблицами из нулей и единиц со столбцами для N1,...,Nk и строками для t=p,...,1. Если p пробегает все целые положительные числа, то при этом получаются всевозможные таблицы из нулей и единиц с k столбцами и любым конечным числом строк.
В разделе 5 мы пользовались k*l-таблицами для описания входов за последние l моментов, кончая настоящим.
Теперь, когда наше время имеет начальный момент 1, мы должны позаботиться о том, чтобы при задании таблицы с k столбцами и, скажем, l строками, описывающей вход, было ясно, намерены ли мы описать вход за все прошлое время (так что р=l) или только за последние l моментов прошлого (так что р>=l). В первом случае мы будем называть таблицу ИЗНАЧАЛЬНОЙ, а во втором - НЕИЗНАЧАЛЬНОЙ. Можно считать, что таблица имеет на себе ярлык, на котором указано соответственно p=l или р>=l. В разделах 4 и 5 в этом не было необходимости, потому что там таблицы, относящиеся ко всему прошлому, были бесконечными [Отметим, что k*l-таблица - это матрица, состоящая из нулей и единиц, в которой p как таковое не фигурирует; l равно числу строк. Эти матрицы снабжены ярлыками "изначальная" или "неизначальная". В первом случае фиксируется, что р=l, а во втором p может быть любым числом >=l. Множества изначальных и неизначальных таблиц не пересекаются, несмотря на соотношения p>=l и р=l.- Прим. ред.].
Определенным событием длины l в разделе 5 было событие, у которого разбиение входов за все прошлое время было таким, что любые два входа, совпадавшие в l верхних строках их таблиц, попадали в один и тот же подкласс. Теперь, однако, при p<l в таблице, описывающей вход, окажется меньше, чем l строк. Может ли наступить событие для такого p? Мы примем соглашение, что событие в этом случае наступить не может. Итак, входы первого подкласса для определенного события длины l - это входы, описываемые множеством неизначальных k*l-таблиц. Если E1 - логическая формула, которую мы в разделе 5 употребляли для описания определенного события, то событие описывается теперь формулой E1&p>=l. Отрицанием этой формулы служит ~E1Vp<l, тогда как формулой для ДОПОЛНИТЕЛЬНОГО определенного события длины l является ~E1&p>=l, не эквивалентная предыдущей, за исключением случая l=1, когда "&p>=l" и "Vp<l" оказываются излишними.
ТОЖДЕСТВЕННОЕ событие (обозначаемое Ik или просто I), которое наступает при любом входе (так что второй подкласс разбиения пуст), является определенным событием длины 1; НЕСОБСТВЕННОЕ СОБЫТИЕ (обозначаемое ~Ik или ~I), которое никогда не наступает (так что первый подкласс пуст), можно рассматривать как определенное событие длины l для каждого l.
За единственным исключением несобственного события, данное событие может быть определенным длины l только для одного l и множество k*l-таблиц (все они неизначальны), описывающих это событие, единственно. Иначе обстояло дело в разделе 5, потому что там определенное событие длины l было в то же время определенным событием длины m для каждого m>l; теперь это было бы нелепостью (за исключением несобственного события), потому что добавочное условие p>m противоречит тому, что событие может наступить при р=l,...,m-1.
Только что описанные нами определенные события (которых при данных k и l имеется 2**2**(kl)) это те события, которые естественно возникают из определенных событий раздела 5, если принять во внимание, что теперь прошлое может не включать l моментов.
Теперь мы считаем целесообразным ввести также новый вид определенного события с k нейронами длины l путем замены для всех таблиц условия p>=l на p=l; к этим событиям мы не причисляем несобственного. Эти определенные события мы будем называть ИЗНАЧАЛЬНЫМИ. Для данных k и l их имеется 2**2**(kl)-1. Событие может быть изначальным определенным событием только для одного l, и множество k*l-таблиц (все они изначальны), описывающих это событие, единственно. Если Е1&p>=l - данное неизначальное определенное событие, отличное от несобственного, то E1&p=l - соответствующее изначальное определенное событие.
В разделе 5 p входило в формулы для событий только относительным образом, но теперь события могут быть связны и со значением p. Это может показаться несколько неестественным. Но если мы собираемся анализировать нервные сети в общем виде, отправляясь от произвольных начальных состояний, то, возвращаясь к точке зрения, послужившей основой для 6.1 и 6.2, мы вынуждены придать p абсолютное значение. Это изображено на рис.12-17, где для каждой сети формула дает "решение" для L1 т.е. условие для возбужденности этого нейрона. Знак "+" указывает на то, что соответствующий нейрон возбужден в начальном состоянии; внутренние нейроны, не помеченные знаком "+", в начальном состоянии спокойны.
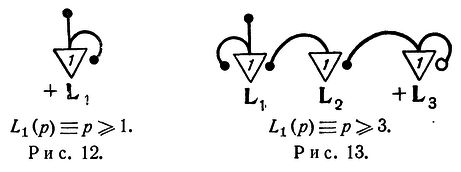
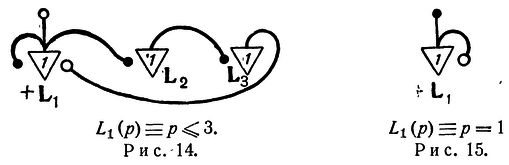
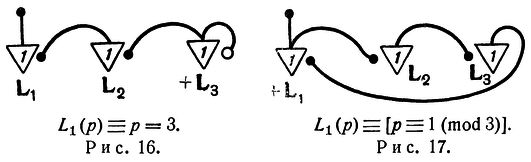
Теперь наша теория может охватить случай k=0. (В разделах 4 и 5 мы предполагали k>=1, что, конечно, необходимо для сетей без петель; лемма 1 и следствие 3 из теоремы 1 сохраняют силу для k=0). Для k=0 имеется ровно три определенных события данной длины l, а именно p=l, p>=l и p!=p; из них только p!=p позитивно. Сети рис.12-17 можно считать представляющими события для k=0.
#6.4. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. В разделе 5 мы показали, как строятся сети, представляющие определенные события длины l с k>0 входными нейронами при допущении бесконечного прошлого. Изложенное там доказательство того, что рассмотренные сети представляют события, остается в силе и для неизначальных (изначальных) определенных событий для значений p>=l(р=l), если все внутренние нейроны сетей спокойны в начальный момент t=1. Для общности дальнейших рассуждений мы будем считать, что представление дается свойством состояния сети при t=p (см. лемму 1).
Употребление этих сетей может теперь привести к "галлюцинации" в том смысле, что состояние сети в момент t=p будет обладать упомянутым свойством без наступления события. В силу рассуждения, аналогичного проведенному в 6.2 в связи с табл.3 и 4, это может произойти, при подходящих входах, когда p>l в случае изначального определенного события и когда p<l (так что l>1) в случае определенного события, могущего наступить без возбуждения входного нейрона в его первый момент t=p-l+1.
Обратно, это может произойти только в описанных случаях. В самом деле, рассмотрим произвольную нервную сеть, некоторое свойство которой в момент t=p правильно представляет неизначальное (изначальное) определенное событие для p>=l(p=l), если в начальный момент t=1 все внутренние нейроны сети спокойны. Для этой сети возникновение при p=m<l (так что l>1) галлюцинации означает, что для некоторого входа c1...cm за время t=1,...,m сеть принимает в момент t=m состояние, обладающее тем свойством, которое имеет место при наступлении события. Пусть теперь вход c1...cm связан вместо этого со временем t=l-m+1,...,l, а со временем t= 1,...,l-m связан вход, состоящий только из невозбуждений с'1...c'[l-m]. При входе c'1...c'[l-m] состояние внутренних нейронов должно включать одни невозбуждения, как прежде при t=1. Таким образом, при входе c'1...c'[l-m]c1...cm сеть будет иметь в момент t=l то же состояние, как прежде при t=m, а значит, c'1...c'[l-m]c1cm образует наступление события.
Определенное событие длины l мы будем называть ПРЕПОЗИТИВНЫМ, если это событие неизначально и притом или l=1, или событие наступает лишь в случае, когда некоторый входной нейрон возбужден в момент t=p-l+1. (Для k=0 препозитивны только р>=1 и р!=р). Препозитивность является необходимым и достаточным условием для представимости в нервной сети, все внутренние нейроны которой спокойны в начальный момент.
Этот результат подсказывает нам первый метод для построения сетей, представляющих непрепозитивные определенные события. Пусть сначала событие неизначально и l>1. Мы добавим нейрон L1 рис.12 и будем считать его k+1-м входным нейроном, который должен быть возбужденным в момент t=p-l+1 (а в остальном не принимается во внимание), и будем теперь рассматривать наше событие, как событие с k+l нейроном N1,...,Nk,L1. Это событие с k+1 нейроном является препозитивным, так что применимы наши прежние методы построения сетей (раздел 5).
Второй метод состоит в использовании сетей рис.13 или 14; например, если представление дается возбуждением внутреннего нейрона P (спокойного при t=1) в момент t=p+s, то тормозящая концевая пластинка нейрона L1 рис.14 будет воздействовать на P (рисунок соответствует случаю l+s=5). Если представление дается свойством состояния при t=р, то это свойство должно включать требование возбуждения (для l=3) нейрона L1 рис.13 или невозбуждения (для l=4) нейрона L1 рис.14.
Для изначальных определенных событий применяются соответственные методы с использованием рис.15 и 16 вместо рис.12 и 13.
Мы приходим к тому выводу, что лишь с помощью искусственно вызванного возбуждения внутренних нейронов в момент t=1 организм может констатировать полное отсутствие возбуждения данной длительности, которому не предшествовало возбуждение; другим способом он не сумеет узнать, отсутствовало ли возбуждение, или же оно возникло за это время.
Как уже было отмечено в 6.2, вместо первоначального возбуждения внутренних нейронов, как на рис.12-17, мы могли бы пользоваться дополнительным входным нейроном K, подверженным беспрерывному воздействию со стороны внешней среды.
Галлюцинация рассмотренного рода вряд ли может оказать серьезное длительное или запаздывающее воздействие на поведение; но когда определенные события используются при построении неопределенных, ее нельзя исключить из рассмотрения, не вдаваясь в дальнейшую проблему, каким образом представление событий переводится в явные реакции.
Для организмов картина нервной системы, приходящей в состояние полной активности в фиксированный момент t=1, во всяком случае неправдоподобна. Но это означает только, что организмы (по крайней мере жизнеспособные) справляются с задачей вхождения в состояние активности. Известно, что для искусственных автоматов или машин следует, вообще говоря, принимать во внимание начальные явления.
Разумеется, наш анализ не обязательно применим ко всему опыту и всей нервной системе организма, но t=1 может служить первым моментом ограниченной части его опыта, а рассматриваемая нервная сеть может быть подсетью всей его нервной системы.
#6.1. ПРИМЕРЫ. Пусть "(Et)" означает "существует t... такое, что", "(t)" означает "для всех t" и "->" означает "влечет". Сеть на рис.8 имеет петлю длины 1. Если в некоторый момент t<=p входной нейрон N возбужден, то M будет возбужден в каждый последующий момент, в частности в момент p+1, как выражает формула. Но возбуждение M в момент p+1 не представляет неопределенного события (Et)[t<p]N(t) (т.е. мы не имеем M(p+1)=(Et)[t<=p]N(f)), если прошедшее время бесконечно, потому что возбужденность M в момент p+1 можно объяснить также тем, что M был возбужден в каждый прошлый момент, а N не был возбужден ни разу. Аналогичные примеры даны на рис.9 и 10.


Этой трудности нельзя избежать, употребляя другие сети для представления этих событий или в других примерах неопределенных событий; она представляет общее правило в силу теоремы 6 в разделе 10 вместе с леммой 1.
Разумеется, всякий живой организм или построенный робот имеет только конечное прошлое. Теорема 6 показывает, что в теории мы должны принимать это во внимание, в противном случае мы могли бы попытаться упростить теорию при помощи фикции бесконечного прошлого, как мы это делали в разделе 5.
#6.2. НАЧАЛЬНОЕ СОСТОЯНИЕ. Поэтому в дальнейшем мы будем предполагать (если не оговорено противное), что прошлое для наших нервных сетей идет назад от р (настоящего момента) только на конечное число моментов, причем на нашей временной шкале первый момент есть 1. Областью изменения временной переменной в наших логических формулах будут целые числа начиная с 1 [Автор пренебрегает всем прошлым и начинает счет времени с момента 1.- Прим. ред.]).
Теперь, если в сети рис.8 M спокоен в момент 1, мы должны иметь M(p+1)=(Et)[t<=p]N(t); на рис.9, если M возбужден в момент 1, то M(p+1)=(t)[t<p]N(t), и на рис.10, если M возбужден в момент 1, то ~M(p+1)=(Et)[t<p]N(t). Таким образом, сети на рис.8 и 10 способны запомнить, что N был возбужден с момента начала их работы, путем изменения состояния M по сравнению с первоначальным состоянием этого нейрона; сеть рис.9 способна установить, что N был возбуждаем непрестанно, путем сохранения первоначального состояния нейрона М. Это отметили Хаусхолдер и Лэндал [1945, стр.109].
Рассматриваемые сети представляют указанные события только при условии, что внутренний нейрон M в момент 1 находился в указанном состоянии.
Это опять является общим правилом для неопределенных событий, в силу теоремы 7 и леммы 1. (Лемма 1 имеет место для конечного прошлого).
Для иллюстрации этого мы покажем сейчас, что для представления события (t)[t<p]N(t) хотя бы один внутренний нейрон должен быть возбужден в момент 1. В самом деле, допустим, что имеется представление этого события некоторым свойством состояния в момент p (лемма 1), т.е. свойством, зависящим только от самого этого состояния и не зависящим от значения p. Допустим, что N - единственный входной нейрон. Если бы все внутренние нейроны были спокойны в момент t=1, то при входе, указанном в табл.3, все внутренние нейроны были бы спокойными при t=2, так что состояние при t=2 было бы не отличимо от состояния, указанного в табл.4, в момент t=1. Следовательно, сеть при входе табл.3 имела бы при р=2,3,4,... те же состояния, что и при входе табл.4 при p=1,2,3,... соответственно, хотя в первом случае (t)st<pN(t) ложно, а во втором - истинно.
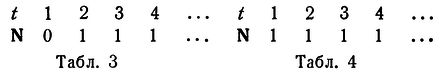
Поэтому при изучении представимости событий мы будем в дальнейшем выбирать не только подходящую сеть, но и состояние (возбужденность или невозбужденность) каждого внутреннего нейрона в момент 1.
Как показывает пример события (t)[t<=p]N(t) Для некоторых событий недостаточно будет иметь первоначально все внутренние нейроны спокойными.
Мы развиваем здесь теорию нервных сетей Мак-Каллока-Питтса как случай, иллюстрирующий теорию конечных автоматов. С точки зрения последней, каждое начальное состояние столь же приемлемо, как и любое другое. Исключать из класса представимых событий такие события, как (t)[t<=p]N(t), было бы не целесообразно.
Для тех, кто считает, что возбужденность внутренних нейронов в момент 1 требует объяснения с точки зрения, принятой Мак-Каллоком и Питтсом, достаточно будет просто сказать, что мы выделяем некоторые входные нейроны Ni,...,Nk и некоторую часть t=1,2,3,... времени в качестве входа для подлежащих представлению событий. Можно привлечь дополнительные нейроны и дополнительные моменты времени, чтобы осуществить любое заданное состояние наших внутренних нейронов в момент t=1. Проще всего этого можно достигнуть введением добавочного входного нейрона Nk+1, который должен быть возбужден при t=0 и только в этот момент и который должен иметь на каждом из тех внутренних нейронов, возбужденности которых при t=1 мы добиваемся, возбуждающие этот нейрон концевые пластинки в количестве, равном порогу этого внутреннего нейрона, и не иметь других концевых пластинок.
Более сложное устройство, для которого требуется добавочный входной нейрон K, но не требуется добавочного момента времени, изображено на рис.11 для события (t)[t<=p]N(t). Это событие представляется возбуждением P в момент t=p+2, если при t=1 нейрон K возбужден, а все внутренние нейроны спокойны. Можно считать, что K подвержен беспрерывному раздражению со стороны внешней среды, которое гарантирует его возбуждение при t=1; его возбуждение в последующие моменты не влияет на представление. Если К возбужден впервые не при t=1, а в более поздний момент времени t=u, то возбуждение P при t=р+2 будет представлять, что N был возбужден в каждый момент от u до p включительно.

[Мак-Каллок и Питтс рассматривают задачу "решения" сетей, начальные состояния которых не заданы. При этом найти "решение" для данного внутреннего нейрона P, скажем, в момент р+1 означает найти, при каких входах в моменты 1,...,p и каких начальных состояниях внутренних нейронов нейрон P будет возбужден в момент р+1. В следующей сети необходимое и достаточное условие того, что P возбужден в момент p+1, состоит в том, что N возбужден во все моменты <=p, а P и Q оба возбуждены в момент 1. Повидимому, это служит противоречащим примером к той формуле, которая следует за (9) в статье Мак-Каллока-Питтса [1943] и доказательства которой мы не проследили; ибо, если мы правильно понимаем эту формулу, из нее следует, что условие для возбужденности Р требует только существования одного первоначально возбужденного нейрона (повидимому, их 0 играет роль 1 у нас). Этот очевидный контрпример охладил наше желание разобраться в части III статьи Мак-Каллока-Питтса [1943]]
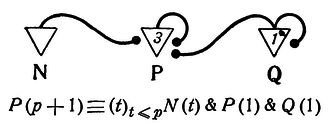
#6.3. НОВОЕ РАССМОТРЕНИЕ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. Событие - это разбиение класса всех возможных входов в прошлом (включая настоящее) на два подкласса: подкласс тех входов, для которых событие наступает, и подкласс тех входов, для которых событие не наступает. Возможные входы с k нейронами N1,...,Nk описываются k*p-таблицами из нулей и единиц со столбцами для N1,...,Nk и строками для t=p,...,1. Если p пробегает все целые положительные числа, то при этом получаются всевозможные таблицы из нулей и единиц с k столбцами и любым конечным числом строк.
В разделе 5 мы пользовались k*l-таблицами для описания входов за последние l моментов, кончая настоящим.
Теперь, когда наше время имеет начальный момент 1, мы должны позаботиться о том, чтобы при задании таблицы с k столбцами и, скажем, l строками, описывающей вход, было ясно, намерены ли мы описать вход за все прошлое время (так что р=l) или только за последние l моментов прошлого (так что р>=l). В первом случае мы будем называть таблицу ИЗНАЧАЛЬНОЙ, а во втором - НЕИЗНАЧАЛЬНОЙ. Можно считать, что таблица имеет на себе ярлык, на котором указано соответственно p=l или р>=l. В разделах 4 и 5 в этом не было необходимости, потому что там таблицы, относящиеся ко всему прошлому, были бесконечными [Отметим, что k*l-таблица - это матрица, состоящая из нулей и единиц, в которой p как таковое не фигурирует; l равно числу строк. Эти матрицы снабжены ярлыками "изначальная" или "неизначальная". В первом случае фиксируется, что р=l, а во втором p может быть любым числом >=l. Множества изначальных и неизначальных таблиц не пересекаются, несмотря на соотношения p>=l и р=l.- Прим. ред.].
Определенным событием длины l в разделе 5 было событие, у которого разбиение входов за все прошлое время было таким, что любые два входа, совпадавшие в l верхних строках их таблиц, попадали в один и тот же подкласс. Теперь, однако, при p<l в таблице, описывающей вход, окажется меньше, чем l строк. Может ли наступить событие для такого p? Мы примем соглашение, что событие в этом случае наступить не может. Итак, входы первого подкласса для определенного события длины l - это входы, описываемые множеством неизначальных k*l-таблиц. Если E1 - логическая формула, которую мы в разделе 5 употребляли для описания определенного события, то событие описывается теперь формулой E1&p>=l. Отрицанием этой формулы служит ~E1Vp<l, тогда как формулой для ДОПОЛНИТЕЛЬНОГО определенного события длины l является ~E1&p>=l, не эквивалентная предыдущей, за исключением случая l=1, когда "&p>=l" и "Vp<l" оказываются излишними.
ТОЖДЕСТВЕННОЕ событие (обозначаемое Ik или просто I), которое наступает при любом входе (так что второй подкласс разбиения пуст), является определенным событием длины 1; НЕСОБСТВЕННОЕ СОБЫТИЕ (обозначаемое ~Ik или ~I), которое никогда не наступает (так что первый подкласс пуст), можно рассматривать как определенное событие длины l для каждого l.
За единственным исключением несобственного события, данное событие может быть определенным длины l только для одного l и множество k*l-таблиц (все они неизначальны), описывающих это событие, единственно. Иначе обстояло дело в разделе 5, потому что там определенное событие длины l было в то же время определенным событием длины m для каждого m>l; теперь это было бы нелепостью (за исключением несобственного события), потому что добавочное условие p>m противоречит тому, что событие может наступить при р=l,...,m-1.
Только что описанные нами определенные события (которых при данных k и l имеется 2**2**(kl)) это те события, которые естественно возникают из определенных событий раздела 5, если принять во внимание, что теперь прошлое может не включать l моментов.
Теперь мы считаем целесообразным ввести также новый вид определенного события с k нейронами длины l путем замены для всех таблиц условия p>=l на p=l; к этим событиям мы не причисляем несобственного. Эти определенные события мы будем называть ИЗНАЧАЛЬНЫМИ. Для данных k и l их имеется 2**2**(kl)-1. Событие может быть изначальным определенным событием только для одного l, и множество k*l-таблиц (все они изначальны), описывающих это событие, единственно. Если Е1&p>=l - данное неизначальное определенное событие, отличное от несобственного, то E1&p=l - соответствующее изначальное определенное событие.
В разделе 5 p входило в формулы для событий только относительным образом, но теперь события могут быть связны и со значением p. Это может показаться несколько неестественным. Но если мы собираемся анализировать нервные сети в общем виде, отправляясь от произвольных начальных состояний, то, возвращаясь к точке зрения, послужившей основой для 6.1 и 6.2, мы вынуждены придать p абсолютное значение. Это изображено на рис.12-17, где для каждой сети формула дает "решение" для L1 т.е. условие для возбужденности этого нейрона. Знак "+" указывает на то, что соответствующий нейрон возбужден в начальном состоянии; внутренние нейроны, не помеченные знаком "+", в начальном состоянии спокойны.
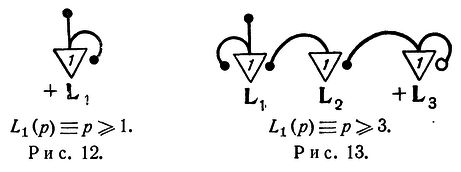

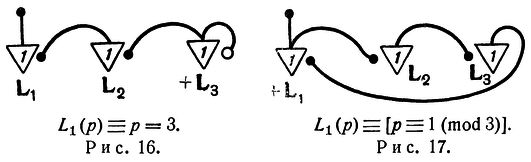
Теперь наша теория может охватить случай k=0. (В разделах 4 и 5 мы предполагали k>=1, что, конечно, необходимо для сетей без петель; лемма 1 и следствие 3 из теоремы 1 сохраняют силу для k=0). Для k=0 имеется ровно три определенных события данной длины l, а именно p=l, p>=l и p!=p; из них только p!=p позитивно. Сети рис.12-17 можно считать представляющими события для k=0.
#6.4. ПРЕДСТАВИМОСТЬ ОПРЕДЕЛЕННЫХ СОБЫТИЙ. В разделе 5 мы показали, как строятся сети, представляющие определенные события длины l с k>0 входными нейронами при допущении бесконечного прошлого. Изложенное там доказательство того, что рассмотренные сети представляют события, остается в силе и для неизначальных (изначальных) определенных событий для значений p>=l(р=l), если все внутренние нейроны сетей спокойны в начальный момент t=1. Для общности дальнейших рассуждений мы будем считать, что представление дается свойством состояния сети при t=p (см. лемму 1).
Употребление этих сетей может теперь привести к "галлюцинации" в том смысле, что состояние сети в момент t=p будет обладать упомянутым свойством без наступления события. В силу рассуждения, аналогичного проведенному в 6.2 в связи с табл.3 и 4, это может произойти, при подходящих входах, когда p>l в случае изначального определенного события и когда p<l (так что l>1) в случае определенного события, могущего наступить без возбуждения входного нейрона в его первый момент t=p-l+1.
Обратно, это может произойти только в описанных случаях. В самом деле, рассмотрим произвольную нервную сеть, некоторое свойство которой в момент t=p правильно представляет неизначальное (изначальное) определенное событие для p>=l(p=l), если в начальный момент t=1 все внутренние нейроны сети спокойны. Для этой сети возникновение при p=m<l (так что l>1) галлюцинации означает, что для некоторого входа c1...cm за время t=1,...,m сеть принимает в момент t=m состояние, обладающее тем свойством, которое имеет место при наступлении события. Пусть теперь вход c1...cm связан вместо этого со временем t=l-m+1,...,l, а со временем t= 1,...,l-m связан вход, состоящий только из невозбуждений с'1...c'[l-m]. При входе c'1...c'[l-m] состояние внутренних нейронов должно включать одни невозбуждения, как прежде при t=1. Таким образом, при входе c'1...c'[l-m]c1...cm сеть будет иметь в момент t=l то же состояние, как прежде при t=m, а значит, c'1...c'[l-m]c1cm образует наступление события.
Определенное событие длины l мы будем называть ПРЕПОЗИТИВНЫМ, если это событие неизначально и притом или l=1, или событие наступает лишь в случае, когда некоторый входной нейрон возбужден в момент t=p-l+1. (Для k=0 препозитивны только р>=1 и р!=р). Препозитивность является необходимым и достаточным условием для представимости в нервной сети, все внутренние нейроны которой спокойны в начальный момент.
Этот результат подсказывает нам первый метод для построения сетей, представляющих непрепозитивные определенные события. Пусть сначала событие неизначально и l>1. Мы добавим нейрон L1 рис.12 и будем считать его k+1-м входным нейроном, который должен быть возбужденным в момент t=p-l+1 (а в остальном не принимается во внимание), и будем теперь рассматривать наше событие, как событие с k+l нейроном N1,...,Nk,L1. Это событие с k+1 нейроном является препозитивным, так что применимы наши прежние методы построения сетей (раздел 5).
Второй метод состоит в использовании сетей рис.13 или 14; например, если представление дается возбуждением внутреннего нейрона P (спокойного при t=1) в момент t=p+s, то тормозящая концевая пластинка нейрона L1 рис.14 будет воздействовать на P (рисунок соответствует случаю l+s=5). Если представление дается свойством состояния при t=р, то это свойство должно включать требование возбуждения (для l=3) нейрона L1 рис.13 или невозбуждения (для l=4) нейрона L1 рис.14.
Для изначальных определенных событий применяются соответственные методы с использованием рис.15 и 16 вместо рис.12 и 13.
Мы приходим к тому выводу, что лишь с помощью искусственно вызванного возбуждения внутренних нейронов в момент t=1 организм может констатировать полное отсутствие возбуждения данной длительности, которому не предшествовало возбуждение; другим способом он не сумеет узнать, отсутствовало ли возбуждение, или же оно возникло за это время.
Как уже было отмечено в 6.2, вместо первоначального возбуждения внутренних нейронов, как на рис.12-17, мы могли бы пользоваться дополнительным входным нейроном K, подверженным беспрерывному воздействию со стороны внешней среды.
Галлюцинация рассмотренного рода вряд ли может оказать серьезное длительное или запаздывающее воздействие на поведение; но когда определенные события используются при построении неопределенных, ее нельзя исключить из рассмотрения, не вдаваясь в дальнейшую проблему, каким образом представление событий переводится в явные реакции.
Для организмов картина нервной системы, приходящей в состояние полной активности в фиксированный момент t=1, во всяком случае неправдоподобна. Но это означает только, что организмы (по крайней мере жизнеспособные) справляются с задачей вхождения в состояние активности. Известно, что для искусственных автоматов или машин следует, вообще говоря, принимать во внимание начальные явления.
Разумеется, наш анализ не обязательно применим ко всему опыту и всей нервной системе организма, но t=1 может служить первым моментом ограниченной части его опыта, а рассматриваемая нервная сеть может быть подсетью всей его нервной системы.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#7. РЕГУЛЯРНЫЕ СОБЫТИЯ
#7.1. РЕГУЛЯРНЫЕ МНОЖЕСТВА ТАБЛИЦ И РЕГУЛЯРНЫЕ СОБЫТИЯ. В этом разделе мы, как и в 6.3, будем пользоваться k*l-таблицами (с фиксированным k и различными l, причем каждая таблица снабжена ярлыком, указывающим на ее неизначальность или изначальность); эти таблицы будут служить для описания входа с k нейронами N1,...,Nk за время t= p-l+1,...,p, в течение которого должно наступить событие. Но мы не будем, как в 6.3, ограничивать наше внимание случаем, когда множество таблиц, описывающих, когда наступает событие, состоит только из к k*l-таблиц с одним и тем же l, причем или все они изначальны или все неизначальны.
Мы определим сначала три операции под множествами таблиц. Если E и F-множества таблиц, то EVF (их СУММОЙ, или ДИЗЪЮНКЦИЕЙ) будет множество таблиц, которому каждая таблица принадлежит в точности тогда, когда она принадлежит E или принадлежит F.
Если E и F - множества таблиц, то EF (их ПРОИЗВЕДЕНИЕМ) будет множество таблиц, которому некоторая таблица принадлежит в точности тогда, когда она является результатом приписывания какой-либо таблицы из F непосредственно снизу к какой-либо неизначальной таблице из E; если таблица из E имеет l1 строк, а таблица из F имеет l2 строк, то полученная таблица будет иметь l1+l2 строк и будет изначальной в точности тогда, когда таблица из F изначальна; эта таблица описывает наступление события, описанного множеством F, оканчивающегося в момент t=p-l1 и зависящего от входа за время t=p-l1-l2+1,...,p-l1 за которым следует событие E, оканчивающееся в момент t=p и зависящее от входа за время t=p-l1+1,...,p. Обозначение EF таково, что мы идем назад к прошлому при чтении слева направо.
Очевидно, что операции EVF и EF ассоциативны. Можно писать E**0F вместо F, E**1 вместо E, E**2 вместо EE, E**3 вместо EEE и т.д.
Если E и F - множества таблиц, то E*F (ИТЕРАЦИЕЙ E по F) будем называть бесконечную сумму множеств F,EF,EEF,..., или, в очевидных обозначениях, F V EF V EEF V..., СУММА[n=0,...,беск.](E**n)F
РЕГУЛЯРНЫЕ МНОЖЕСТВА (ТАБЛИЦ) будут, по определению, составлять наименьший класс множеств таблиц, включающий все единичные множества (т.е. множества, содержащие ровно одну таблицу) и пустое множество и замкнутый относительно операций перехода от E и F к EVF, EF и к E*F.
Событие мы будем называть РЕГУЛЯРНЫМ, если имеется регулярное множество таблиц, описывающее это событие в том смысле, что событие наступает или не наступает смотря по тому, описывается ли вход некоторой таблицей этого множества, или нет.
Чтобы охватить этими определениями случай k=0, мы условимся считать, что для k=0 и для каждого l>1 имеются две k*l-таблицы - изначальная и неизначальная [Мак-Каллок и Питтс [1943] пользуются термином "цепкий" ("prehensible"), введенным совсем другим способом, но, как нам кажется, связанным по значению с нашими рассуждениями. Так как мы не поняли их определения, то мы пользуемся другим терминам].
Очевидно, что регулярно любое конечное множество таблиц, в частности - пустое, и множества k*l-таблиц с данным l, в которых все таблицы неизначальны или изначальны. Следовательно, каждое определенное событие регулярно.
Выписывая выражения для регулярных множеств или описываемых ими событий, мы будем опускать скобки в соответствии с тремя ассоциативными законами [(3)-(5) в 7.2], а также в соответствии с соглашениями, принятыми в алгебре, причем EVF, EF и E*F мы будем рассматривать как аналоги для e+f, ef и СУММА[n=0,...,беск.](e**n)f. Например, NVNI*I означает NV(N(I*I)). Мы будем употреблять одну и ту же букву для обозначения определенного события и для его множества таблиц, а также для самой таблицы в случае единичного множества таблиц.
Мы будем писать E=F для обозначения того, что E и F совпадают как множества таблиц; E==F (E эквивалентно F) - для обозначения того, что они описывают одно и то же событие. Очевидно, E=F -> E==F. Обратное, вообще говоря, неверно, как мы сейчас покажем для регулярных множеств таблиц.
Так, при k=1, если N - неизначальная 1*1-таблица, состоящая из 1 (что описывает определенное событие, обозначенное в разделе 5 через N(p)), а I - множество всех неизначальных 1*1-таблиц (см.6.3), то NVNI*I есть множество всех неизначальных 1*l-таблиц (для всех l) с 1 в верхней строке. Теперь NVNI*I==N, но NVNI*I!=N.
Приведем также контрпримеры, в которых проявляется различие между неизначальными и изначальными таблицами. Если E - множество таблиц, то через Е^ мы обозначим множество таблиц, которые получаются из таблиц множества E, если переобозначить как изначальные те таблицы, которые таковыми не являются. Для любого E, E==EVЕ^, но, например, I!=IVI^.
Из E=F можно заключить, что EVG=FVG, GVE=GVF, EG=FG, GE=GF, E*G=F*G, G*E=G*F в силу общей теории замены для равенства, так как EVG, EG и E*G определены как однозначные операции над множествами таблиц. Если = заменить на ==, то третье и пятое из этих заключений, вообще говоря, отпадают, потому что в значение EG и E*G входят длины таблиц из E помимо события, описываемого этими таблицами. Так, например, NVNI*I==N но (NVNI*I)N!==NN и (NVNI*I)*N!==N*N.
Теперь имеются две системы обозначений для описания событий:
A) Логический символизм того типа, которым мы пользовались в разделе 5 для описания определенных событий (с добавленными в разделе 6 приставками p>=l или p==l), а также в некоторых примерах раздела 6, относившихся к неопределенным событиям.
B) Символизм, в котором мы, как правило, отправляемся от обозначения определенных событий заглавными буквами и посредством которого мы в этом разделе описываем регулярные события (с помощью регулярных множеств таблиц).
Вопрос о взаимной переводимости этих двух систем еще полностью не исследован. В силу теоремы 8 из раздела 12, для любого выражения "B" имеется логическое обозначение "A", коль скоро введен достаточный математический символизм. Конечно, мы не дали никакого четкого разграничения, характеризующего символизмы, относящиеся к "A", поэтому эта проблема переводимости не является точной. Во всяком случае, как мы увидим в разделе 13, посредством очень ограниченного математического символизма, относящегося к "A", можно выразить некоторое нерегулярное событие. Остается открытой проблема, существует ли простая характеристика регулярных событий непосредственно в терминах символизма "A".
Далее следуют некоторые примеры перевода из "A" в "B". В примерах, не содержащих N, k может иметь любое фиксированное значение >=0; при наличии только N, k>=1, при наличии также и K, k>=2. Множества неизначальных k*1-таблиц, выражающих, что N возбужден в момент p, что K возбужден в момент p и что K и N оба возбуждены в момент p, обозначаются соответственно через N, K и L. Кроме того, I есть множество всех неизначальных k*1-таблиц и для любого множества E неизначальных k*1-таблиц ~E является дополнительным множеством неизначальных k*1-таблиц, в частности ~I-пустое множество (см. 6.3).

#7.2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ РЕГУЛЯРНЫХ ВЫРАЖЕНИЙ. Перечислим некоторые равенства для множеств таблиц. (К изучению эквивалентностей мы лишь приступили).
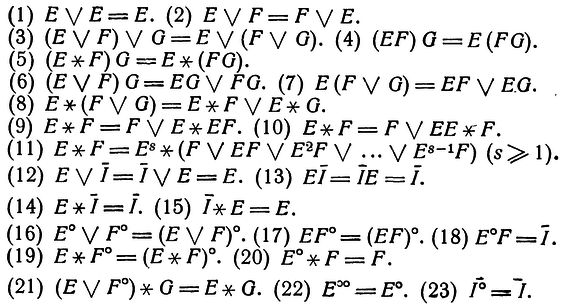
Для доказательства (11) мы имеем
E*F = СУММА[n=0...беск.](E**n)F = СУММА[q=0..беск.]СУММА[r=0...s-1](E**(sq+r))F = (СУММА[q=0...беск.](E**sq)F)СУММА[r=0...s-1](E**r)F.
В этом пункте мы будем иметь дело с конкретными способами выражения регулярного множества таблиц согласно определению из 7.1. Как мы уже видели в 7.1, можно отправляться с таким же успехом от любых множеств таблиц для определенных событий, а не только от единичных множеств и пустого множества. Под РЕГУЛЯРНЫМ ВЫРАЖЕНИЕМ мы будем подразумевать конкретный способ выражения регулярного множества таблиц с отправлением от множества таблиц для определенных событий и применением ноль или большее число раз трех известных операций (перехода от E и F к EVF, EF или E*F); те множества таблиц для определенных событий, с которых начинается построение, мы будем называть ЭЛЕМЕНТАМИ. Элемент имеет ДЛИНУ l, если он описывает определенное событие длины l, он называется изначальным, если это событие изначально. (Это почти равносильно тому, как если бы под "регулярным выражением" подразумевалось обозначение для регулярного множества таблиц, полученное из символов для определенных событий с помощью формальных операций, обозначаемых "EVF", "EF" и "E*F"; такое понимание пригодно для большей части наших утверждений. Но если мы говорим, что ~I не входит в регулярное выражение в качестве элемента, то в терминах обозначений это должно означать, что ни "~I", ни какой другой символ для пустого множества не входит в качестве элемента. Кроме того, пользуясь терминологией обозначений, мы должны отождествлять элементы, если не все из них являются единичными буквами).
ЛЕММА 2. Каждое регулярное выражение сводимо к ~I или к регулярному выражению, в которое ~I не входит в качестве элемента.
ДОКАЗАТЕЛЬСТВО. Применяем повторно (12)-(15).
ЛЕММА 3. Каждое регулярное выражение G приводимо к виду G1VG2^, где G1 не содержит изначальных элементов.
ДОКАЗАТЕЛЬСТВО. Применяем индукцию по числу n элементов в G.
Базис: n=1. В этом случае G - элемент. Если G не изначален, положим G1=G и применим (12) и (23). Если G изначален, положим G2^=G и применим (12).
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. По индуктивному предположению, E=Е1VЕ2^ и F=F1VF2^. Следовательно, в силу (2), (3) и (16), G=(E1VF1)V(E2VF2)^.
СЛУЧАЙ 2. G есть EF. Применяем индуктивное предположение, (6) и (7), (18 ) и (12) и (17). Тогда G=E1F1V(E1F2)^.
СЛУЧАЙ 3. G есть E*F. Применяем индуктивное предположение, (21), (8 ) и (19). Получаем: G=Е1*F1V(E1*F2)^.
Определим теперь рекурсивно "самые ранние элементы" регулярного выражения следующим образом:
1) Регулярное выражение, состоящее из одного только элемента, является своим САМЫМ РАННИМ ЭЛЕМЕНТОМ.
2) Самые ранние элементы для E и самые ранние элементы для F являются самыми ранними элементами для EVF.
3) Самые ранние элементы для F являются самыми ранними элементами для EF и для E*F.
ЛЕММА 4. Каждое регулярное выражение G приводимо
к виду ~I или к виду регулярного выражения, в которое ~I не входит как элемент и изначальными являются только самые ранние элементы.
ДОКАЗАТЕЛЬСТВО. Применим индукцию по числу n элементов в G.
БАЗИС: n=1. Тогда G есть ~I или отлично от ~I, но является элементом и, следовательно, самым ранним.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. Пользуемся индуктивным предположением.
СЛУЧАЙ 2. G есть EF. По лемме 3, E=E1VE2^. Следовательно, в силу (6), (18 ) и (12), G=E1F. Теперь остается применить к F индуктивное предположение.
СЛУЧАЙ 3. О есть E*F. С помощью леммы 3 и (21) получаем G=E1*F. Остается применить к F индуктивное предположение.
По ходу преобразования регулярных выражений мы можем заново образовывать элементы; например, если Е1 и Е2 - элементы длин l1 и l2, причем E1 неизначально и не совпадает с ~I, то E1E2 можно считать новым элементом, имеющим длину l1+l2, изначальным или нет - смотря по тому,
изначально или нет E2.
ЛЕММА 5. (Для любого s>=1). Всякое регулярное выражение приводимо или к виду ~I, или к регулярному выражению, не содержащему ~I в качестве элемента, содержащему изначальные элементы только в качестве самых ранних и имеющему вид дизъюнкции одного или нескольких членов двух типов: элемента длины <s или регулярного выражения, составленного из элементов, имеющих длину >=s.
Число членов второго рода всегда можно считать равным единице, так как дизъюнкция членов второго рода является членом второго рода (см. (2) и (3)).
ДОКАЗАТЕЛЬСТВО. Для s=1 лемма 5 совпадает с леммой 4. Возьмем теперь фиксированное s>=2 и предположим, что после применения леммы 4 мы получаем регулярное выражение G второго типа, указанного в этой лемме. Преобразования G посредством любого из равенств (1)-(11), которые содержат отдельные шаги используемых в дальнейшем преобразований, сохраняют этот тип. Это позволит нам ниже снова образовать E1E2...Em, где E1,...,Em - элементы, в качестве нового элемента. Теперь мы покажем посредством индукции по числу n элементов в G, что G можно преобразовать в дизъюнкцию членов двух родов, указанных в лемме 5.
БАЗИС: n=1. В этом случае G является членом первого или второго рода, смотря по тому, будет ли его длина <s или >=s.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. Тогда как E, так и F будут Членами второго типа в соответствии с леммой 4. Значит, по индуктивному предположению, E и F оба выразимы в виде дизъюнкции членов только двух наших родов. Сочетая обе эти дизъюнкции в одну, получаем такой же результат для EVF.
СЛУЧАЙ 2. G есть EF. Согласно индуктивному предположению, (6) и (7), EF равно в этом случае дизъюнкции членов, каждый из которых относится к одному из четырех типов
E'F', E''F'', E''F', E'F'',
где при помощи ' помечены множители первого рода (служащие первоначально членами дизъюнкции для E или для F), а при помощи '' - множители второго рода. Согласно рассуждению для случая 1, достаточно будет показать, что каждое из этих четырех типов произведений выразимо в виде дизъюнкции членов обоих родов.
Но E'F' можно рассматривать в качестве элемента, и в соответствии с тем, будет ли этот новый элемент иметь длину <s или >=s, E'F' будет выражением первого или второго рода.
Произведение E''F'' является выражением второго рода.
Рассмотрим теперь E''F'. Согласно (4)-(6), F' можно последовательно задвигать внутрь, пока, наконец, F' не будет входить только в части вида HF' где H - элемент длины >=s. Каждую такую часть можно перестроить в элемент длины >=s+1, так что E''F' оказывается выражением второго рода.
С E'F'' мы поступаем аналогично, применяя (4) (справа налево), (7) и (10), а затем (7) и (4).
СЛУЧАЙ 3. G есть E*F. Применяя к E*F последовательно (11) и (9), получаем
E*F = F V EF V (E**2)F V...V (E**(s-1))F V (E**s)*(E**s)(F V EF V (E**2)F V...V (E**(s-1))F).
Так как (E**2)F, ..., (E**(s-1))F являются просто многократными произведениями, то, применением метода случая 2 (в случае необходимости многократным), каждое из выражений F, EF, (E**2)F, ..., (E**(s-1))F можно представить в виде дизъюнкции членов обоих родов. Рассмотрим теперь E**s; выбрав, по индуктивному предположению, дизъюнкцию для E и выполнив умножение (6) и (7), мы получаем сумму произведений из s сомножителей каждое, подобно тому, как в случае 2 мы получили сумму произведений из двух сомножителей каждое. Произведение, в котором все сомножители первого рода, можно перестроить в элемент, который будет иметь длину >=s, так как число сомножителей есть s, а потому этот элемент будет выражением второго рода. Все остальные типы произведений, которые могут встретиться, содержат сомножитель второго рода, так что, при рассмотрении трех типов произведений E''F'', E''F' и E'F'' согласно методу случая 2 (в случае надобности примененному многократно), каждое из этих произведений оказывается выражением второго рода.
Поэтому E**s (после надлежащей перестройки элементов) становится выражением второго рода. Теперь, при рассмотрении обоих типов произведений E''F'' и E''F' согласно случаю 2, (E**s)(F V EF V (E**2)F V...V (E**(s-1))F) и, следовательно, также (E**s)*(E**s)(F V EF V (E**2)F V...V (E**(s-1))F) оказывается выражением второго рода.
ЛЕММА 6. Каждое регулярное выражение приводимо, без перестройки элементов, к дизъюнкции одного или нескольких членов вида EiFi, где каждое Ei является элементом, a Fi или пусто (тогда EiFi есть Ei), или регулярно (тогда Ei неизначально).
ДОКАЗАТЕЛЬСТВО. Для регулярного выражения G, относящегося ко второму типу, указанному в лемме 4, можно индукцией по числу n элементов в G убедиться в том, что G можно преобразовать (применяя только (4), (6), (10)) к виду дизъюнкции членов второго рода, указанному в лемме 6.
#7.3. ПРЕДСТАВИМОСТЬ РЕГУЛЯРНЫХ СОБЫТИЙ. k*l-таблицу мы будем называть ПРЕПОЗИТИВНОЙ (ПОЗИТИВНОЙ), если она описывает препозитивное определенное событие 6.4, т.е. если она неизначальна и либо l=1, либо в ее самой нижней строке встречается 1 (позитивное определенное событие 5.1, 6.3, т.е. если в ней встречается 1 в некоторой строке). Множество таблиц НАЗЫВАЕТСЯ ПРЕПОЗИТИВНЫМ (ПОЗИТИВНЫМ), если каждая таблица этого множества препозитивна (позитивна).
ТЕОРЕМА 3. Для каждого регулярного события имеется нервная сеть, которая представляет это событие возбуждением некоторого внутреннего нейрона в момент p+2 при условии, что в начальный момент 1 внутренние нейроны имеют надлежащие состояния. Если событие может быть описано препозитивным и позитивным регулярным множеством таблиц, то возможно представление в виде сети, все внутренние нейроны которой в начальный момент спокойны.
ДОКАЗАТЕЛЬСТВО. Докажем теорему сначала для регулярных событий, описываемых членом G второго рода, указанным в лемме 5, при s=2. Мы воспользуемся индукцией по числу n элементов в G.
Мы добьемся того, что нейрон (назовем его ВЫХОДНЫМ НЕЙРОНОМ), который должен быть возбужден в момент p+2 в том и только в том случае, если событие наступит, оканчиваясь в момент p, будет иметь порог 1 и будет возбуждаться только возбуждающими концевыми пластинками (как на рис.3), и не будет иметь аксонов, идущих обратно в сеть.
БАЗИС: n=1. Мы построим сеть, представляющую событие, описываемое выражением G, посредством метода доказательства следствия 1 теоремы 1, если G является препозитивным (и подавно, если G является позитивным, так как (l>=s>1), а в противном случае - при помощи первого метода из 6.4 (с нейроном, как на рис.12 или 15), благодаря чему событие, если его рассматривать как событие с k+1 входным нейроном, будет препозитивным (а значит, позитивным), так что в обоих случаях представление будет даваться возбуждением в момент p+2.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. По индуктивному предположению, имеются сети, представляющие E и F соответственно, каждая описанным выше образом; пусть P и Q - выходные нейроны этих сетей. Чтобы представить EVF, мы "отождествим" P и Q, т.е. мы заменим их одним нейроном (который будем обозначать через P), имеющим все концевые пластинки, которые соприкасались с P и Q в отдельности; и, разумеется, мы отождествляем аналогичным образом входные нейроны N1, ..., Nk. Диаграмма полученной сети изображена на рис.18. Прямоугольник, помеченный буквой E, обозначает сеть для E, за исключением ее входных и выходных нейронов. Жирная линия, ведущая от этого прямоугольника к P, представляет аксоны, которые прежде вели к выходному нейрону Р в сети для E.
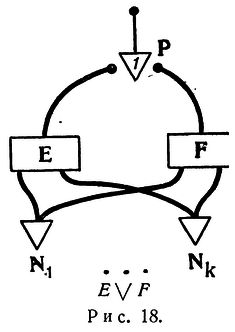
СЛУЧАЙ 2. G есть EF. Рассмотрим выражение E получающееся из E путем такого изменения каждого элемента, которое относит его к новому входному нейрону N[k+1], который должен быть возбужден во второй момент каждого самого раннего элемента (но которое в остальном не влияет на наступление или ненаступление соответствующих определенных событий); в силу допущения, что элементы имеют длину >=2, второй момент должен иметься. Тогда E' является выражением второго рода, указанным в лемме 5, с тем же самым числом элементов, что и E, так как наше изменение приводит к регулярному выражению с той же самой структурой соответствующих ему элементов относительно наших трех операций. Значит, в силу индуктивного предположения, мы можем представить E' и F сетями описанного рода. Мы, однако, упростим построение, опуская нейрон рис.12 в каждом случае самого раннего непрепозитивного элемента выражения E' (этот элемент должен быть неизначальным в силу одного из свойств G, вытекающих из леммы 5). Теперь сеть для EF получается отождествлением нового входного нейрона N[k+1] в сети для E' с выходным нейроном Q сети для F, наряду, разумеется, с отождествлением входных нейронов N1, ..., Nk для обеих сетей и выбором в качестве выходного того нейрона, который является выходным нейроном P для E' (рис.19). Событие E' является позитивным, так как в его второй момент требуется возбуждение N[k+1]. Никакая галлюцинация не может возникнуть в результате опускания нейронов рис.12 для самых ранних непрепозитивных элементов E' потому что нейрон N[k+1] (возбуждение которого требуется во второй момент этих элементов) не может быть возбужден раньше чем через два момента после наступления F, согласно построению сети для F. Эти опускания нейронов рис.12 приводят к последнему утверждению теоремы.
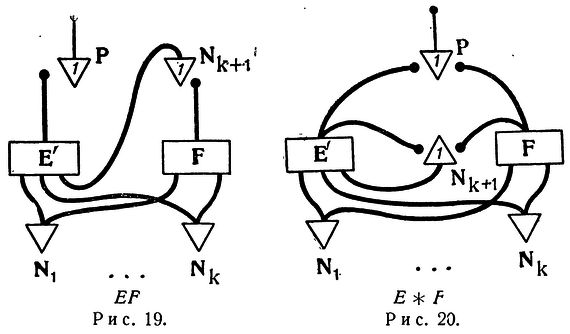
СЛУЧАЙ 3. G есть E*F. Сети для E' и F сочетаются, как на рис.20.
ЗАКЛЮЧЕНИЕ. Этим завершается индукция, показывающая представимость регулярного события, описываемого членом G второго рода, указанным в лемме 5, при s=2. Члены первого рода рассматриваются, как в базисе индукции (но с дополнительным использованием рис.12 в случае препозитивного непозитивного члена l=1), а дизъюнкция членов (если число последних больше единицы) - как в случае 1.
Случай, когда событие есть ~I, уже был рассмотрен в разделе 5 (см. рис.6).
КОММЕНТАРИЙ. Если первоначальное регулярное выражение для события уже дано в терминах элементов длины >=2, то доказательство теоремы проходит непосредственно и приводит к сетям, сложность которых находится в полном соответствии со сложностью регулярного выражения (об упрощении сетей, представляющих элементы, возможно, за счет увеличения запаздывания свыше 2, см. комментарий после следствия 1 теоремы 1). Трудность, которая приводит к употреблению усложненных формулировок, основанных на доказательстве леммы 5, появляется при попытке увязать последовательно представления событий, некоторые из которых имеют продолжительность меньшую, чем время, необходимое для сети, представляющей предыдущее событие возбуждением единственного нейрона; решение, даваемое леммой 5, состоит в рассмотрении более длительных событий до попытки увязать представления.
ТЕОРЕМА 4. Для каждого события, построенного из регулярных событий при полощи операций &, V, ~ найдется нервная сеть, которая представляет это событие возбуждением некоторого внутреннего нейрона в момент p+2, при надлежащих состояниях внутренних нейронов в начальный момент 1.
Доказательство сейчас будет приведено. В силу следствия из теоремы 5 (см. ниже), все представимые события регулярны. Поэтому, в силу обеих теорем 4 и 5, сочетания регулярных событий посредством &, V и ~ регулярны, что вместе с теоремой 3 содержит в себе теорему 4. Мы не определили & и ~ как операции над множествами таблиц, поэтому EF и E*F не могут быть использованы после применения & или ~.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 4. Рассмотрим регулярное выражение для каждого из регулярных событий, входящих в построение данного события при помощи &, V и ~. Применим лемму 5 при s=2 к этому выражению и лемму 6 к возникающим членам второго рода. Таким образом, мы для данного события получим выражение при помощи операций &, V и ~, примененных к компонентам E1F1, ..., EmFm, где каждое Ei является выражением для определенного события, a Fi является регулярным выражением или пусто (тогда определенное событие, выражаемое посредством Ei неизначально или имеет длину >=2). Пусть Ei' получено из Ei так же, как E' было получено из E в доказательстве случая 2 теоремы 3, если Fi регулярно, и возникает в результате введения дополнительного входного нейрона N[k+1], который должен быть возбужден в первый момент E'i, если Fi пусто. Рассмотрим теперь (в качестве события с k+m входными нейронами N1, ..., Nk, N[k+1], ..., N[k+m] комбинацию из E1', ..., Em', аналогичную той комбинации из E1F1, ..., EmFm, которая дает данное событие. Если эта комбинация из E1', ..., Em', рассматриваемая как определенное событие в смысле раздела 5 (но не раздела 6), имеет длину, равную наибольшей из длин E1', ..., Em' и не является позитивной, то мы сделаем ее позитивной путем добавления "&E[m+1]'", где E[m+1]' относится к возбуждению некоторого нейрона N[k+m+1] в момент p. Воспользуемся теперь методом построения сети в следствии 1 теоремы 1 для построения представляющей сети этого события с k+m или k+m+1 нейронами. Затем для каждого i, для которого Fi регулярно, отождествим N[k+1] с выходным нейроном сети, которую теорема 3 дает для представления Fi, для каждого i, для которого Fi пусто, сделаем N[k+i] внутренним нейроном, который должен быть возбужден в момент 1, как на рис.12, если Ei неизначально или i=m+1, и как на рис.15, если Ei изначально.
#7.4. ПРОБЛЕМЫ. Остаются нерешенными многочисленные задачи, которые мы не смогли рассмотреть за то ограниченное время, которое мы посвятили изучению этого вопроса, хотя, вероятно, некоторые из них могут быть решены быстро.
Существует ли обобщение следствия 2 теоремы 1 на все регулярные события?
Под ПОЛНЫМ МНОЖЕСТВОМ ТАБЛИЦ некоторого события будем понимать множество изначальных таблиц, описывающих это событие. Под МИНИМАЛЬНЫМ МНОЖЕСТВОМ ТАБЛИЦ события мы будем понимать множество таблиц, описывающих это событие и обладающих тем свойством, что никакой собственный верхний сегмент такой таблицы, ни она сама, если она изначальна, не описывает наступления этого события как неизначальная таблица. Полное множество таблиц для регулярного события регулярно в силу теоремы 3 и доказательства теоремы 5. Обязательно ли регулярно минимальное множество? Если да, то может ли регулярное выражение быть получено для него эффективно из регулярного выражения для полного множества?
Какого рода события, описанные первоначально в других терминах, регулярны? Мы имеем только несколько примеров перехода от "A" к "B" (см. конец 7.1) и один пример косвенно установленного свойства замкнутости регулярных событий (теоремы 4 и 5).
Если дано регулярное выражение для события, то может оказаться трудным усмотреть, в чем это событие состоит. Нам известны случаи, когда очень сложное регулярное выражение эквивалентно гораздо более простому, например это имеет место для некоторых выражений, возникающих при доказательстве теоремы 5. Существуют ли простые нормальные формы для регулярных выражений, такие, что каждое регулярное выражение равно или эквивалентно некоторому регулярному выражению в нормальной форме? Существует ли эффективное правило для распознавания того, являются ли равными (или эквивалентными) два данных регулярных выражения?
Соображением, которое привело нас к введению регулярных событий как таких, которые задаются регулярными множествами таблиц, описанными регулярными выражениями, послужила теорема 5, которую мы нашли раньше, чем теорему 3. Пользуясь понятием регулярного события, мы доказываем, что нервная сеть Мак-Каллока-Питтса годится для представления любого события, которое может быть представлено любым другим видом конечного цифрового автомата (в смысле, который будет изложен подробно в разделе 8 ). Это, конечно, содержит в себе некоторое число частных результатов, полученных Мак-Каллоком и Питтсом для других родов нервных сетей, но является более общим. Открыт путь для попыток установления аналогичных результатов для других родов "клеток" вместо нейронов и для поисков характеристики таких свойств клеток, чтобы образованные ими агрегаты обладали способностью представлять все представимые (т.е. все регулярные) события.
#7.1. РЕГУЛЯРНЫЕ МНОЖЕСТВА ТАБЛИЦ И РЕГУЛЯРНЫЕ СОБЫТИЯ. В этом разделе мы, как и в 6.3, будем пользоваться k*l-таблицами (с фиксированным k и различными l, причем каждая таблица снабжена ярлыком, указывающим на ее неизначальность или изначальность); эти таблицы будут служить для описания входа с k нейронами N1,...,Nk за время t= p-l+1,...,p, в течение которого должно наступить событие. Но мы не будем, как в 6.3, ограничивать наше внимание случаем, когда множество таблиц, описывающих, когда наступает событие, состоит только из к k*l-таблиц с одним и тем же l, причем или все они изначальны или все неизначальны.
Мы определим сначала три операции под множествами таблиц. Если E и F-множества таблиц, то EVF (их СУММОЙ, или ДИЗЪЮНКЦИЕЙ) будет множество таблиц, которому каждая таблица принадлежит в точности тогда, когда она принадлежит E или принадлежит F.
Если E и F - множества таблиц, то EF (их ПРОИЗВЕДЕНИЕМ) будет множество таблиц, которому некоторая таблица принадлежит в точности тогда, когда она является результатом приписывания какой-либо таблицы из F непосредственно снизу к какой-либо неизначальной таблице из E; если таблица из E имеет l1 строк, а таблица из F имеет l2 строк, то полученная таблица будет иметь l1+l2 строк и будет изначальной в точности тогда, когда таблица из F изначальна; эта таблица описывает наступление события, описанного множеством F, оканчивающегося в момент t=p-l1 и зависящего от входа за время t=p-l1-l2+1,...,p-l1 за которым следует событие E, оканчивающееся в момент t=p и зависящее от входа за время t=p-l1+1,...,p. Обозначение EF таково, что мы идем назад к прошлому при чтении слева направо.
Очевидно, что операции EVF и EF ассоциативны. Можно писать E**0F вместо F, E**1 вместо E, E**2 вместо EE, E**3 вместо EEE и т.д.
Если E и F - множества таблиц, то E*F (ИТЕРАЦИЕЙ E по F) будем называть бесконечную сумму множеств F,EF,EEF,..., или, в очевидных обозначениях, F V EF V EEF V..., СУММА[n=0,...,беск.](E**n)F
РЕГУЛЯРНЫЕ МНОЖЕСТВА (ТАБЛИЦ) будут, по определению, составлять наименьший класс множеств таблиц, включающий все единичные множества (т.е. множества, содержащие ровно одну таблицу) и пустое множество и замкнутый относительно операций перехода от E и F к EVF, EF и к E*F.
Событие мы будем называть РЕГУЛЯРНЫМ, если имеется регулярное множество таблиц, описывающее это событие в том смысле, что событие наступает или не наступает смотря по тому, описывается ли вход некоторой таблицей этого множества, или нет.
Чтобы охватить этими определениями случай k=0, мы условимся считать, что для k=0 и для каждого l>1 имеются две k*l-таблицы - изначальная и неизначальная [Мак-Каллок и Питтс [1943] пользуются термином "цепкий" ("prehensible"), введенным совсем другим способом, но, как нам кажется, связанным по значению с нашими рассуждениями. Так как мы не поняли их определения, то мы пользуемся другим терминам].
Очевидно, что регулярно любое конечное множество таблиц, в частности - пустое, и множества k*l-таблиц с данным l, в которых все таблицы неизначальны или изначальны. Следовательно, каждое определенное событие регулярно.
Выписывая выражения для регулярных множеств или описываемых ими событий, мы будем опускать скобки в соответствии с тремя ассоциативными законами [(3)-(5) в 7.2], а также в соответствии с соглашениями, принятыми в алгебре, причем EVF, EF и E*F мы будем рассматривать как аналоги для e+f, ef и СУММА[n=0,...,беск.](e**n)f. Например, NVNI*I означает NV(N(I*I)). Мы будем употреблять одну и ту же букву для обозначения определенного события и для его множества таблиц, а также для самой таблицы в случае единичного множества таблиц.
Мы будем писать E=F для обозначения того, что E и F совпадают как множества таблиц; E==F (E эквивалентно F) - для обозначения того, что они описывают одно и то же событие. Очевидно, E=F -> E==F. Обратное, вообще говоря, неверно, как мы сейчас покажем для регулярных множеств таблиц.
Так, при k=1, если N - неизначальная 1*1-таблица, состоящая из 1 (что описывает определенное событие, обозначенное в разделе 5 через N(p)), а I - множество всех неизначальных 1*1-таблиц (см.6.3), то NVNI*I есть множество всех неизначальных 1*l-таблиц (для всех l) с 1 в верхней строке. Теперь NVNI*I==N, но NVNI*I!=N.
Приведем также контрпримеры, в которых проявляется различие между неизначальными и изначальными таблицами. Если E - множество таблиц, то через Е^ мы обозначим множество таблиц, которые получаются из таблиц множества E, если переобозначить как изначальные те таблицы, которые таковыми не являются. Для любого E, E==EVЕ^, но, например, I!=IVI^.
Из E=F можно заключить, что EVG=FVG, GVE=GVF, EG=FG, GE=GF, E*G=F*G, G*E=G*F в силу общей теории замены для равенства, так как EVG, EG и E*G определены как однозначные операции над множествами таблиц. Если = заменить на ==, то третье и пятое из этих заключений, вообще говоря, отпадают, потому что в значение EG и E*G входят длины таблиц из E помимо события, описываемого этими таблицами. Так, например, NVNI*I==N но (NVNI*I)N!==NN и (NVNI*I)*N!==N*N.
Теперь имеются две системы обозначений для описания событий:
A) Логический символизм того типа, которым мы пользовались в разделе 5 для описания определенных событий (с добавленными в разделе 6 приставками p>=l или p==l), а также в некоторых примерах раздела 6, относившихся к неопределенным событиям.
B) Символизм, в котором мы, как правило, отправляемся от обозначения определенных событий заглавными буквами и посредством которого мы в этом разделе описываем регулярные события (с помощью регулярных множеств таблиц).
Вопрос о взаимной переводимости этих двух систем еще полностью не исследован. В силу теоремы 8 из раздела 12, для любого выражения "B" имеется логическое обозначение "A", коль скоро введен достаточный математический символизм. Конечно, мы не дали никакого четкого разграничения, характеризующего символизмы, относящиеся к "A", поэтому эта проблема переводимости не является точной. Во всяком случае, как мы увидим в разделе 13, посредством очень ограниченного математического символизма, относящегося к "A", можно выразить некоторое нерегулярное событие. Остается открытой проблема, существует ли простая характеристика регулярных событий непосредственно в терминах символизма "A".
Далее следуют некоторые примеры перевода из "A" в "B". В примерах, не содержащих N, k может иметь любое фиксированное значение >=0; при наличии только N, k>=1, при наличии также и K, k>=2. Множества неизначальных k*1-таблиц, выражающих, что N возбужден в момент p, что K возбужден в момент p и что K и N оба возбуждены в момент p, обозначаются соответственно через N, K и L. Кроме того, I есть множество всех неизначальных k*1-таблиц и для любого множества E неизначальных k*1-таблиц ~E является дополнительным множеством неизначальных k*1-таблиц, в частности ~I-пустое множество (см. 6.3).

#7.2. АЛГЕБРАИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ РЕГУЛЯРНЫХ ВЫРАЖЕНИЙ. Перечислим некоторые равенства для множеств таблиц. (К изучению эквивалентностей мы лишь приступили).
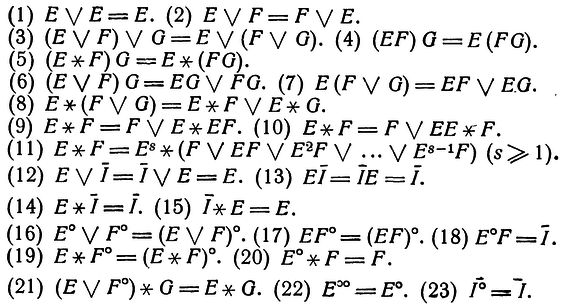
Для доказательства (11) мы имеем
E*F = СУММА[n=0...беск.](E**n)F = СУММА[q=0..беск.]СУММА[r=0...s-1](E**(sq+r))F = (СУММА[q=0...беск.](E**sq)F)СУММА[r=0...s-1](E**r)F.
В этом пункте мы будем иметь дело с конкретными способами выражения регулярного множества таблиц согласно определению из 7.1. Как мы уже видели в 7.1, можно отправляться с таким же успехом от любых множеств таблиц для определенных событий, а не только от единичных множеств и пустого множества. Под РЕГУЛЯРНЫМ ВЫРАЖЕНИЕМ мы будем подразумевать конкретный способ выражения регулярного множества таблиц с отправлением от множества таблиц для определенных событий и применением ноль или большее число раз трех известных операций (перехода от E и F к EVF, EF или E*F); те множества таблиц для определенных событий, с которых начинается построение, мы будем называть ЭЛЕМЕНТАМИ. Элемент имеет ДЛИНУ l, если он описывает определенное событие длины l, он называется изначальным, если это событие изначально. (Это почти равносильно тому, как если бы под "регулярным выражением" подразумевалось обозначение для регулярного множества таблиц, полученное из символов для определенных событий с помощью формальных операций, обозначаемых "EVF", "EF" и "E*F"; такое понимание пригодно для большей части наших утверждений. Но если мы говорим, что ~I не входит в регулярное выражение в качестве элемента, то в терминах обозначений это должно означать, что ни "~I", ни какой другой символ для пустого множества не входит в качестве элемента. Кроме того, пользуясь терминологией обозначений, мы должны отождествлять элементы, если не все из них являются единичными буквами).
ЛЕММА 2. Каждое регулярное выражение сводимо к ~I или к регулярному выражению, в которое ~I не входит в качестве элемента.
ДОКАЗАТЕЛЬСТВО. Применяем повторно (12)-(15).
ЛЕММА 3. Каждое регулярное выражение G приводимо к виду G1VG2^, где G1 не содержит изначальных элементов.
ДОКАЗАТЕЛЬСТВО. Применяем индукцию по числу n элементов в G.
Базис: n=1. В этом случае G - элемент. Если G не изначален, положим G1=G и применим (12) и (23). Если G изначален, положим G2^=G и применим (12).
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. По индуктивному предположению, E=Е1VЕ2^ и F=F1VF2^. Следовательно, в силу (2), (3) и (16), G=(E1VF1)V(E2VF2)^.
СЛУЧАЙ 2. G есть EF. Применяем индуктивное предположение, (6) и (7), (18 ) и (12) и (17). Тогда G=E1F1V(E1F2)^.
СЛУЧАЙ 3. G есть E*F. Применяем индуктивное предположение, (21), (8 ) и (19). Получаем: G=Е1*F1V(E1*F2)^.
Определим теперь рекурсивно "самые ранние элементы" регулярного выражения следующим образом:
1) Регулярное выражение, состоящее из одного только элемента, является своим САМЫМ РАННИМ ЭЛЕМЕНТОМ.
2) Самые ранние элементы для E и самые ранние элементы для F являются самыми ранними элементами для EVF.
3) Самые ранние элементы для F являются самыми ранними элементами для EF и для E*F.
ЛЕММА 4. Каждое регулярное выражение G приводимо
к виду ~I или к виду регулярного выражения, в которое ~I не входит как элемент и изначальными являются только самые ранние элементы.
ДОКАЗАТЕЛЬСТВО. Применим индукцию по числу n элементов в G.
БАЗИС: n=1. Тогда G есть ~I или отлично от ~I, но является элементом и, следовательно, самым ранним.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. Пользуемся индуктивным предположением.
СЛУЧАЙ 2. G есть EF. По лемме 3, E=E1VE2^. Следовательно, в силу (6), (18 ) и (12), G=E1F. Теперь остается применить к F индуктивное предположение.
СЛУЧАЙ 3. О есть E*F. С помощью леммы 3 и (21) получаем G=E1*F. Остается применить к F индуктивное предположение.
По ходу преобразования регулярных выражений мы можем заново образовывать элементы; например, если Е1 и Е2 - элементы длин l1 и l2, причем E1 неизначально и не совпадает с ~I, то E1E2 можно считать новым элементом, имеющим длину l1+l2, изначальным или нет - смотря по тому,
изначально или нет E2.
ЛЕММА 5. (Для любого s>=1). Всякое регулярное выражение приводимо или к виду ~I, или к регулярному выражению, не содержащему ~I в качестве элемента, содержащему изначальные элементы только в качестве самых ранних и имеющему вид дизъюнкции одного или нескольких членов двух типов: элемента длины <s или регулярного выражения, составленного из элементов, имеющих длину >=s.
Число членов второго рода всегда можно считать равным единице, так как дизъюнкция членов второго рода является членом второго рода (см. (2) и (3)).
ДОКАЗАТЕЛЬСТВО. Для s=1 лемма 5 совпадает с леммой 4. Возьмем теперь фиксированное s>=2 и предположим, что после применения леммы 4 мы получаем регулярное выражение G второго типа, указанного в этой лемме. Преобразования G посредством любого из равенств (1)-(11), которые содержат отдельные шаги используемых в дальнейшем преобразований, сохраняют этот тип. Это позволит нам ниже снова образовать E1E2...Em, где E1,...,Em - элементы, в качестве нового элемента. Теперь мы покажем посредством индукции по числу n элементов в G, что G можно преобразовать в дизъюнкцию членов двух родов, указанных в лемме 5.
БАЗИС: n=1. В этом случае G является членом первого или второго рода, смотря по тому, будет ли его длина <s или >=s.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. Тогда как E, так и F будут Членами второго типа в соответствии с леммой 4. Значит, по индуктивному предположению, E и F оба выразимы в виде дизъюнкции членов только двух наших родов. Сочетая обе эти дизъюнкции в одну, получаем такой же результат для EVF.
СЛУЧАЙ 2. G есть EF. Согласно индуктивному предположению, (6) и (7), EF равно в этом случае дизъюнкции членов, каждый из которых относится к одному из четырех типов
E'F', E''F'', E''F', E'F'',
где при помощи ' помечены множители первого рода (служащие первоначально членами дизъюнкции для E или для F), а при помощи '' - множители второго рода. Согласно рассуждению для случая 1, достаточно будет показать, что каждое из этих четырех типов произведений выразимо в виде дизъюнкции членов обоих родов.
Но E'F' можно рассматривать в качестве элемента, и в соответствии с тем, будет ли этот новый элемент иметь длину <s или >=s, E'F' будет выражением первого или второго рода.
Произведение E''F'' является выражением второго рода.
Рассмотрим теперь E''F'. Согласно (4)-(6), F' можно последовательно задвигать внутрь, пока, наконец, F' не будет входить только в части вида HF' где H - элемент длины >=s. Каждую такую часть можно перестроить в элемент длины >=s+1, так что E''F' оказывается выражением второго рода.
С E'F'' мы поступаем аналогично, применяя (4) (справа налево), (7) и (10), а затем (7) и (4).
СЛУЧАЙ 3. G есть E*F. Применяя к E*F последовательно (11) и (9), получаем
E*F = F V EF V (E**2)F V...V (E**(s-1))F V (E**s)*(E**s)(F V EF V (E**2)F V...V (E**(s-1))F).
Так как (E**2)F, ..., (E**(s-1))F являются просто многократными произведениями, то, применением метода случая 2 (в случае необходимости многократным), каждое из выражений F, EF, (E**2)F, ..., (E**(s-1))F можно представить в виде дизъюнкции членов обоих родов. Рассмотрим теперь E**s; выбрав, по индуктивному предположению, дизъюнкцию для E и выполнив умножение (6) и (7), мы получаем сумму произведений из s сомножителей каждое, подобно тому, как в случае 2 мы получили сумму произведений из двух сомножителей каждое. Произведение, в котором все сомножители первого рода, можно перестроить в элемент, который будет иметь длину >=s, так как число сомножителей есть s, а потому этот элемент будет выражением второго рода. Все остальные типы произведений, которые могут встретиться, содержат сомножитель второго рода, так что, при рассмотрении трех типов произведений E''F'', E''F' и E'F'' согласно методу случая 2 (в случае надобности примененному многократно), каждое из этих произведений оказывается выражением второго рода.
Поэтому E**s (после надлежащей перестройки элементов) становится выражением второго рода. Теперь, при рассмотрении обоих типов произведений E''F'' и E''F' согласно случаю 2, (E**s)(F V EF V (E**2)F V...V (E**(s-1))F) и, следовательно, также (E**s)*(E**s)(F V EF V (E**2)F V...V (E**(s-1))F) оказывается выражением второго рода.
ЛЕММА 6. Каждое регулярное выражение приводимо, без перестройки элементов, к дизъюнкции одного или нескольких членов вида EiFi, где каждое Ei является элементом, a Fi или пусто (тогда EiFi есть Ei), или регулярно (тогда Ei неизначально).
ДОКАЗАТЕЛЬСТВО. Для регулярного выражения G, относящегося ко второму типу, указанному в лемме 4, можно индукцией по числу n элементов в G убедиться в том, что G можно преобразовать (применяя только (4), (6), (10)) к виду дизъюнкции членов второго рода, указанному в лемме 6.
#7.3. ПРЕДСТАВИМОСТЬ РЕГУЛЯРНЫХ СОБЫТИЙ. k*l-таблицу мы будем называть ПРЕПОЗИТИВНОЙ (ПОЗИТИВНОЙ), если она описывает препозитивное определенное событие 6.4, т.е. если она неизначальна и либо l=1, либо в ее самой нижней строке встречается 1 (позитивное определенное событие 5.1, 6.3, т.е. если в ней встречается 1 в некоторой строке). Множество таблиц НАЗЫВАЕТСЯ ПРЕПОЗИТИВНЫМ (ПОЗИТИВНЫМ), если каждая таблица этого множества препозитивна (позитивна).
ТЕОРЕМА 3. Для каждого регулярного события имеется нервная сеть, которая представляет это событие возбуждением некоторого внутреннего нейрона в момент p+2 при условии, что в начальный момент 1 внутренние нейроны имеют надлежащие состояния. Если событие может быть описано препозитивным и позитивным регулярным множеством таблиц, то возможно представление в виде сети, все внутренние нейроны которой в начальный момент спокойны.
ДОКАЗАТЕЛЬСТВО. Докажем теорему сначала для регулярных событий, описываемых членом G второго рода, указанным в лемме 5, при s=2. Мы воспользуемся индукцией по числу n элементов в G.
Мы добьемся того, что нейрон (назовем его ВЫХОДНЫМ НЕЙРОНОМ), который должен быть возбужден в момент p+2 в том и только в том случае, если событие наступит, оканчиваясь в момент p, будет иметь порог 1 и будет возбуждаться только возбуждающими концевыми пластинками (как на рис.3), и не будет иметь аксонов, идущих обратно в сеть.
БАЗИС: n=1. Мы построим сеть, представляющую событие, описываемое выражением G, посредством метода доказательства следствия 1 теоремы 1, если G является препозитивным (и подавно, если G является позитивным, так как (l>=s>1), а в противном случае - при помощи первого метода из 6.4 (с нейроном, как на рис.12 или 15), благодаря чему событие, если его рассматривать как событие с k+1 входным нейроном, будет препозитивным (а значит, позитивным), так что в обоих случаях представление будет даваться возбуждением в момент p+2.
ИНДУКЦИОННЫЙ ШАГ: n>1.
СЛУЧАЙ 1. G есть EVF. По индуктивному предположению, имеются сети, представляющие E и F соответственно, каждая описанным выше образом; пусть P и Q - выходные нейроны этих сетей. Чтобы представить EVF, мы "отождествим" P и Q, т.е. мы заменим их одним нейроном (который будем обозначать через P), имеющим все концевые пластинки, которые соприкасались с P и Q в отдельности; и, разумеется, мы отождествляем аналогичным образом входные нейроны N1, ..., Nk. Диаграмма полученной сети изображена на рис.18. Прямоугольник, помеченный буквой E, обозначает сеть для E, за исключением ее входных и выходных нейронов. Жирная линия, ведущая от этого прямоугольника к P, представляет аксоны, которые прежде вели к выходному нейрону Р в сети для E.

СЛУЧАЙ 2. G есть EF. Рассмотрим выражение E получающееся из E путем такого изменения каждого элемента, которое относит его к новому входному нейрону N[k+1], который должен быть возбужден во второй момент каждого самого раннего элемента (но которое в остальном не влияет на наступление или ненаступление соответствующих определенных событий); в силу допущения, что элементы имеют длину >=2, второй момент должен иметься. Тогда E' является выражением второго рода, указанным в лемме 5, с тем же самым числом элементов, что и E, так как наше изменение приводит к регулярному выражению с той же самой структурой соответствующих ему элементов относительно наших трех операций. Значит, в силу индуктивного предположения, мы можем представить E' и F сетями описанного рода. Мы, однако, упростим построение, опуская нейрон рис.12 в каждом случае самого раннего непрепозитивного элемента выражения E' (этот элемент должен быть неизначальным в силу одного из свойств G, вытекающих из леммы 5). Теперь сеть для EF получается отождествлением нового входного нейрона N[k+1] в сети для E' с выходным нейроном Q сети для F, наряду, разумеется, с отождествлением входных нейронов N1, ..., Nk для обеих сетей и выбором в качестве выходного того нейрона, который является выходным нейроном P для E' (рис.19). Событие E' является позитивным, так как в его второй момент требуется возбуждение N[k+1]. Никакая галлюцинация не может возникнуть в результате опускания нейронов рис.12 для самых ранних непрепозитивных элементов E' потому что нейрон N[k+1] (возбуждение которого требуется во второй момент этих элементов) не может быть возбужден раньше чем через два момента после наступления F, согласно построению сети для F. Эти опускания нейронов рис.12 приводят к последнему утверждению теоремы.

СЛУЧАЙ 3. G есть E*F. Сети для E' и F сочетаются, как на рис.20.
ЗАКЛЮЧЕНИЕ. Этим завершается индукция, показывающая представимость регулярного события, описываемого членом G второго рода, указанным в лемме 5, при s=2. Члены первого рода рассматриваются, как в базисе индукции (но с дополнительным использованием рис.12 в случае препозитивного непозитивного члена l=1), а дизъюнкция членов (если число последних больше единицы) - как в случае 1.
Случай, когда событие есть ~I, уже был рассмотрен в разделе 5 (см. рис.6).
КОММЕНТАРИЙ. Если первоначальное регулярное выражение для события уже дано в терминах элементов длины >=2, то доказательство теоремы проходит непосредственно и приводит к сетям, сложность которых находится в полном соответствии со сложностью регулярного выражения (об упрощении сетей, представляющих элементы, возможно, за счет увеличения запаздывания свыше 2, см. комментарий после следствия 1 теоремы 1). Трудность, которая приводит к употреблению усложненных формулировок, основанных на доказательстве леммы 5, появляется при попытке увязать последовательно представления событий, некоторые из которых имеют продолжительность меньшую, чем время, необходимое для сети, представляющей предыдущее событие возбуждением единственного нейрона; решение, даваемое леммой 5, состоит в рассмотрении более длительных событий до попытки увязать представления.
ТЕОРЕМА 4. Для каждого события, построенного из регулярных событий при полощи операций &, V, ~ найдется нервная сеть, которая представляет это событие возбуждением некоторого внутреннего нейрона в момент p+2, при надлежащих состояниях внутренних нейронов в начальный момент 1.
Доказательство сейчас будет приведено. В силу следствия из теоремы 5 (см. ниже), все представимые события регулярны. Поэтому, в силу обеих теорем 4 и 5, сочетания регулярных событий посредством &, V и ~ регулярны, что вместе с теоремой 3 содержит в себе теорему 4. Мы не определили & и ~ как операции над множествами таблиц, поэтому EF и E*F не могут быть использованы после применения & или ~.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 4. Рассмотрим регулярное выражение для каждого из регулярных событий, входящих в построение данного события при помощи &, V и ~. Применим лемму 5 при s=2 к этому выражению и лемму 6 к возникающим членам второго рода. Таким образом, мы для данного события получим выражение при помощи операций &, V и ~, примененных к компонентам E1F1, ..., EmFm, где каждое Ei является выражением для определенного события, a Fi является регулярным выражением или пусто (тогда определенное событие, выражаемое посредством Ei неизначально или имеет длину >=2). Пусть Ei' получено из Ei так же, как E' было получено из E в доказательстве случая 2 теоремы 3, если Fi регулярно, и возникает в результате введения дополнительного входного нейрона N[k+1], который должен быть возбужден в первый момент E'i, если Fi пусто. Рассмотрим теперь (в качестве события с k+m входными нейронами N1, ..., Nk, N[k+1], ..., N[k+m] комбинацию из E1', ..., Em', аналогичную той комбинации из E1F1, ..., EmFm, которая дает данное событие. Если эта комбинация из E1', ..., Em', рассматриваемая как определенное событие в смысле раздела 5 (но не раздела 6), имеет длину, равную наибольшей из длин E1', ..., Em' и не является позитивной, то мы сделаем ее позитивной путем добавления "&E[m+1]'", где E[m+1]' относится к возбуждению некоторого нейрона N[k+m+1] в момент p. Воспользуемся теперь методом построения сети в следствии 1 теоремы 1 для построения представляющей сети этого события с k+m или k+m+1 нейронами. Затем для каждого i, для которого Fi регулярно, отождествим N[k+1] с выходным нейроном сети, которую теорема 3 дает для представления Fi, для каждого i, для которого Fi пусто, сделаем N[k+i] внутренним нейроном, который должен быть возбужден в момент 1, как на рис.12, если Ei неизначально или i=m+1, и как на рис.15, если Ei изначально.
#7.4. ПРОБЛЕМЫ. Остаются нерешенными многочисленные задачи, которые мы не смогли рассмотреть за то ограниченное время, которое мы посвятили изучению этого вопроса, хотя, вероятно, некоторые из них могут быть решены быстро.
Существует ли обобщение следствия 2 теоремы 1 на все регулярные события?
Под ПОЛНЫМ МНОЖЕСТВОМ ТАБЛИЦ некоторого события будем понимать множество изначальных таблиц, описывающих это событие. Под МИНИМАЛЬНЫМ МНОЖЕСТВОМ ТАБЛИЦ события мы будем понимать множество таблиц, описывающих это событие и обладающих тем свойством, что никакой собственный верхний сегмент такой таблицы, ни она сама, если она изначальна, не описывает наступления этого события как неизначальная таблица. Полное множество таблиц для регулярного события регулярно в силу теоремы 3 и доказательства теоремы 5. Обязательно ли регулярно минимальное множество? Если да, то может ли регулярное выражение быть получено для него эффективно из регулярного выражения для полного множества?
Какого рода события, описанные первоначально в других терминах, регулярны? Мы имеем только несколько примеров перехода от "A" к "B" (см. конец 7.1) и один пример косвенно установленного свойства замкнутости регулярных событий (теоремы 4 и 5).
Если дано регулярное выражение для события, то может оказаться трудным усмотреть, в чем это событие состоит. Нам известны случаи, когда очень сложное регулярное выражение эквивалентно гораздо более простому, например это имеет место для некоторых выражений, возникающих при доказательстве теоремы 5. Существуют ли простые нормальные формы для регулярных выражений, такие, что каждое регулярное выражение равно или эквивалентно некоторому регулярному выражению в нормальной форме? Существует ли эффективное правило для распознавания того, являются ли равными (или эквивалентными) два данных регулярных выражения?
Соображением, которое привело нас к введению регулярных событий как таких, которые задаются регулярными множествами таблиц, описанными регулярными выражениями, послужила теорема 5, которую мы нашли раньше, чем теорему 3. Пользуясь понятием регулярного события, мы доказываем, что нервная сеть Мак-Каллока-Питтса годится для представления любого события, которое может быть представлено любым другим видом конечного цифрового автомата (в смысле, который будет изложен подробно в разделе 8 ). Это, конечно, содержит в себе некоторое число частных результатов, полученных Мак-Каллоком и Питтсом для других родов нервных сетей, но является более общим. Открыт путь для попыток установления аналогичных результатов для других родов "клеток" вместо нейронов и для поисков характеристики таких свойств клеток, чтобы образованные ими агрегаты обладали способностью представлять все представимые (т.е. все регулярные) события.
Последний раз редактировалось: Gudleifr (Сб Июл 01, 2023 12:02 am), всего редактировалось 3 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ЧАСТЬ II КОНЕЧНЫЕ АВТОМАТЫ
#8. ПОНЯТИЕ КОНЕЧНОГО АВТОМАТА
#8.1. КЛЕТКИ. Время будет состоять из последовательности дискретных моментов, занумерованных целыми положительными числами, за исключением раздела 10, где будут использованы все числа.
Мы будем рассматривать автоматы, построенные из конечного числа частей, именуемых КЛЕТКАМИ, каждая из которых в любой момент находится в одном из конечного числа >=2 состояний.
Мы будем различать два вида клеток - ВХОДНЫЕ и ВНУТРЕННИЕ клетки.
Допускаются два состояния входной клетки, 0 и 1 ("спокойное* и "возбужденное"). Какое из них имеет место для входной клетки в любой данный момент, определяется внешней средой.
Благодаря тому, что число состояний входных клеток ограничено двумя, понятие входа для автомата совпадает с понятием входа для нервной сети, которое было сформулировано в разделе 4 и в пункте 6.3. Однако излагаемая теория будет также пригодна и для большего числа состояний. Но это не принесет никакой выгоды, потому что можно пользоваться p клетками, допускающими два состояния каждая, для замены одной клетки, допускающей любое число q (2<=q<=2**p) состояний 0, 1, ..., q-1, где при q<2**p можно или рассматривать только входы, в которых не встречаются состояния q, ..., 2**p-1, или отождествлять эти состояния с состоянием q-1 во всех действиях автомата.
Число состояний внутренней клетки не ограничено двумя, и различные внутренние клетки могут иметь различное число состояний.
Состояние каждой внутренней клетки в любой момент t>1 определяется состоянием всех клеток в момент t-1. Может, конечно, случиться, что нам не понадобится знать состояния всех клеток в момент t-1 для определения состояния данной внутренней клетки в момент t. Наша формулировка не фиксирует, какого рода закон используется для определения состояния, за исключением того, что, кроме состояний клеток в момент t-1, ничто не может иметь значения [Процессы такого типа называются марковскими процессами.- Прим. ред.].
Ввиду того, что счет времени ведется начиная с момента 1, состояние каждой из внутренних клеток в этот момент должно быть задано (исключение представляет раздел 11).
Конкретным примером конечного автомата служит нервная сеть Мак-Каллока-Питтса (часть I). Здесь все клетки допускают ровно два состояния. Другой пример связан с рассмотрением внутренних нейронов с "изменяемыми концевыми пластинками", которые не могут быть активными, если в некоторый предыдущий момент нейрон, имеющий такую пластинку, и нейрон, с которым эта пластинка соприкасается, не были одновременно возбуждены. Нейрон с r такими изменяемыми концевыми пластинками допускает 2**(r+1) состояний. Напрашиваются и многие другие возможности.
#8.2. СОСТОЯНИЕ. При k входных клетках N1, ..., Nk (k>=0) и m внутренних клетках M1, ..., Mm (m>=1) с соответствующими числами состояний s1, ..., sm имеется ровно 2**k*s1...sm возможных (полных) состояний автомата. Мы можем рассматривать каждое такое состояние как комбинацию ВНЕШНЕГО СОСТОЯНИЯ, для которого имеется 2**k возможностей, и ВНУТРЕННЕГО СОСТОЯНИЯ, для которого имеется
s1...sm возможностей.
Закон, по которому состояния внутренних клеток в момент t>1 определяются состояниями всех клеток в момент t-1, можно задать путем указания для каждого из полных состояний в момент t-1, какое из внутренних состояний последует за ним в момент t.
Мы могли бы всю совокупность внутренних клеток заменить единственной клеткой, допускающей s1...sm состояний. Но мы не воспользуемся этой возможностью, имея в виду применения теории конечных автоматов, в которых клетки обладают некоторыми простыми свойствами и связаны между собой некоторыми простыми способами.
Мы также могли бы обойтись (однако не будем этого делать) одной-единственной входной клеткой, считая, что входы с k первоначальными входными клетками образуют последовательно в некотором порядке новый вход, причем временная шкала меняется таким образом, что k моментов новой шкалы соответствуют одному моменту первоначальной шкалы. События, относящиеся к новой временной шкале, можно было бы интерпретировать в первоначальной шкале.
Обозначим теперь состояния через a1,...,ar, где r=2**k*s1...sm, а внутренние состояния - через b1, ..., bq, где q=s1...sm. Выберем обозначения таким образом, что внутренним состоянием в момент 1 будет b1.
При фиксированном внутреннем состоянии в момент 1, состояние в момент p является функцией входа за время 1, ..., p (включая значение p или, при k=0, только это значение).
Каждое из состояний a1, ..., ar представляет таким образом некоторое событие, которое наступает, оканчиваясь в момент p, в том и только в том случае, если вход за время 1, ..., p приводит в момент p к тому из а1, ..., аr, которое является этим состоянием. Таким образом, автомат может знать о своем прошлом, (включая настоящий момент) только то, что оно попадает в один из r попарно непересекающихся классов (некоторые из них могут быть пусты).
Аналогично, внутреннее состояние в момент p+1, или свойство полного состояния в момент p, или свойство внутреннего состояния в момент p+1 или свойство внутреннего состояния в момент p+s для некоторого s>1, не зависящее от входа за время p+1, ..., p+s-1, представляет событие. Таким образом, сказать, что состояние в момент p обладает некоторым свойством, означает сказать, что это состояние является элементом некоторого подкласса r возможных состояний, так что прошлое распадается в теоретико-множественную сумму (или дизъюнкцию) соответствующих классов прошлого, которые в отдельности представляются состояниями этого подкласса.
Какого рода события могут быть представлены? Поскольку под входом понимается то же, что и в части I, мы можем пользоваться понятием "регулярного события", введенным в разделе 7. Следующая теорема, которая, так же как и теорема 3, относится к специальному типу конечных автоматов, даст ответ на этот вопрос.
#9. РЕГУЛЯРНОСТЬ ПРЕДСТАВИМЫХ СОБЫТИЙ
ТЕОРЕМА 5. Для любого конечного автомата (в частности, для нервной сети Мак-Каллока-Питтса), отправляющегося в момент 1 от данного внутреннего состояния b1, событие, представленное данным состоянием, существующим в момент p, регулярно.
ДОКАЗАТЕЛЬСТВО. Так как начальное внутреннее состояние определено, то имеется 2**k возможных начальных состояний (получающихся путем сочетания данного начального внутреннего состояния b1 с каждым из 2**k возможных внешних состояний в момент 1).
Следовательно, если мы сумеем показать, что автомат, отправляясь в момент 1 от данного состояния, достигнет в момент p нужного состояния в том и только в том случае, если наступит некоторое регулярное событие, оканчивающееся в момент p, то для доказательства теоремы останется взять дизъюнкцию 2**k соответствующих регулярных событий, которая также является регулярным событием.
Если дано любое состояние а в момент t-1 (t>=2), то в момент t возможны ровно 2**k состояний, потому что внутренняя часть состояния в момент t определена состоянием a, для внешней же части имеется 2**k возможностей. Мы будем говорить, что каждое из этих 2**k состояний находится в ОТНОШЕНИИ R к a.
Следующая часть наших рассуждений будет применима к любому бинарному отношению R, определенному на данном множестве r>=1 объектов a1, ..., ar (называемых "состояниями"), независимо от того, получается оно или нет только что описанным образом.
Рассмотрим любые два состояния a и a', не обязательно различные. Мы будем изучать цепочки состояний dp d[p-1] ... d1 (p>=1), для которых dp есть a, d1 есть а' и для каждого t=2,...,p dt находится в отношении R к d[t-1] (символически dtRd[t-1]); мы будем говорить, что такие цепочки
связывают a с a'.
Для множества цепочек мы введем понятие "регулярности" посредством следующего определения (построенного аналогично определению "регулярных" множеств таблиц в 7.1).
Пустое множество и для каждого i(i=1,...,r) единичное множество {ai}, имеющее только один элемент аi, рассматриваемый как цепочка длины 1, РЕГУЛЯРНЫ. Если A и B регулярны, то регулярна и их сумма, обозначаемая через AVB. Если A и B регулярны, то регулярно и обозначаемое через AB множество цепочек, которые получаются приписыванием цепочки, принадлежащей A, слева к цепочке, принадлежащей B. Если A и B регулярны, то регулярна и обозначаемая через A*B сумма для n=0,1,2... множеств A...AB, где A стоит n раз перед B.
ЛЕММА 7. Цепочки dp...d1, связывающие a с a', образуют регулярное множество.
ДОКАЗАТЕЛЬСТВО. Применяем индукцию по r.
БАЗИС: r=1. Тогда a' есть a. Если ~aRa (т.е. если R - нерефлексивное отношение), то множество цепочек, связывающих a с a, является единичным множеством {a}, которое регулярно. Если aRa, то это множество есть {a, aa, aaa, ...} и, значит, оно регулярно, так как может быть записано в виде A*A, где A={a}.
ИНДУКЦИОННЫЙ ШАГ: r>1
СЛУЧАЙ 1. a=a'. В этом случае любая цепочка, связывающая a с a', имеет вид
a -> a -> a -> ... a -> a,
где число вхождений для "a ->" положительно или равно нулю и каждая -> представляет независимо пустую цепочку (что возможно только при aRa) или непустую цепочку, в которую не входит a. Пусть e1, ..., eg (g>=0) - такие состояния e, что aRe, но e!a, и f1, ..., fh (h>=0) - такие состояния f, что fRa, но f!=a. Тогда любая непустая цепочка, представленная посредством ->, должна начинаться с одного из e1, ..., eg и оканчиваться одним из f1, ..., fh. Для каждой пары ei fj, по индуктивному предположению, множество цепочек, связывающих ei с fj и не содержащих a, регулярно. Обозначим через B1, ..., Bgh эти регулярные множества, и пусть A есть {a}. Тогда если aRa, то множество возможных цепочек а -> есть AVA(B1 V ... V Bgh) (которое сводится к A, если gh=0 или если все B пусты); если же ~aRa, то это множество есть A(B1 V ... V Bgh) (которое пусто, если gh=0 или если все B пусты). Обозначим это множество через C. Тогда множество цепочек, ведущих от a к a, есть C*A (что сводится к A, если C пусто).
СЛУЧАЙ 2. a!=a'. Теперь вместо прежней мы имеем цепочку
a -> a -> a -> ... а -> a - - -> а',
где число вхождений "а ->" есть число >=0 и каждая -> и "- - ->" представляют независимо пустую цепочку или непустую цепочку, в которую не входит a. Если D - множество всех возможных цепочек "а - - ->" и E={a}, то множество цепочек,
связывающих a с a', есть C*DE. Это множество регулярно.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ (окончание). Мы должны показать, что для данного состояния a и для каждого из 2**k состояний a' состояние есть a в момент p и a' в момент 1 в том и только в том случае, если за время 1, ..., p наступает некоторое регулярное событие.
Согласно лемме, множество цепочек, соединяющих a с a', регулярно. Рассмотрим для этого регулярного множества выражение через пустое множество и множества {ai} в качестве элементов (см. 7.2). В этом выражении заменим каждый элемент {ai} на единичное множество, состоящее из k*l-таблицы (которая (при k>0) описывает внешнюю часть состояния ai), снабженной ярлыком "изначальная" или "неизначальная" смотря по тому, был ли этот элемент {ai} самым ранним или нет. Каждое пустое множество в качестве элемента заменим на его самого (но будем обозначать его ~I). Получится регулярное выражение. Состояние a' в момент 1 меняется на a в момент p в том и только в том случае, если событие, описанное этим регулярным выражением, наступает за время 1, ..., p.
СЛЕДСТВИЕ. Регулярно также событие, представленное каждым из следующих способов: внутренним состоянием в момент p+1, свойством состояния в момент p, свойством внутреннего состояния в момент p+1, свойством внутреннего состояния в момент p+s (для некоторого s>1), которое не зависит от входа за время p+1, ..., p+s-1.
ДОКАЗАТЕЛЬСТВО. Событие, представленное свойством состояния в момент p, является дизъюнкцией событий, представленных в момент p состояниями, которые обладают этим свойством. Остальные способы представления сводятся к этому посредством леммы 1 в 5.3 (которая применима здесь точно так же, как и в случае нервных сетей Мак-Каллока-Питтса).
КОММЕНТАРИЙ. Регулярные выражения, полученные при доказательстве теоремы 5, могут иметь только изначальные элементы или ~I в качестве самых ранних элементов и построены из элементов длины 1 (аналогично после упрощения, которое дается леммой 2). Во многих примерах ясно, что большие упрощения могут быть получены с помощью эквивалентностей (7.1); но мы не занимались изучением возможности систематического проведения таких упрощений.
Изучение структуры множества объектов a1, ..., ar с бинарным отношением R, составляющее суть изложенного доказательства, может оказаться полезным для какой-нибудь алгебраической теории.
Очевидно, для наших рассуждений существенно, чтобы число клеток и число состояний каждой клетки было конечным, так что число полных состояний заранее фиксировано. Машина Тьюринга [1936-1937] не является конечным автоматом, если лента рассматривается как часть машины, потому что, хотя в любой момент может быть заполнено знаками только конечное число квадратов ленты, для этого числа не имеется никакой предписанной границы. Если же ленту рассматривать как часть внешней среды, то машина Тьюринга оказывается конечным автоматом, который вдобавок может запасать информацию во внешней среде и пользоваться ею, впоследствии, так что настоящий вход не вполне независим от прошлого. Пока что неизвестно, может ли это сравнение привести к каким-либо полезным взглядам на машины Тьюринга или на конечные автоматы.
ДОБАВЛЕНИЯ
#10. ПРЕДСТАВИМОСТЬ В КОНЕЧНОМ АВТОМАТЕ С БЕСКОНЕЧНЫМ ПРОШЛЫМ
ТЕОРЕМА 6. Если событие E представило свойством состояния в момент p конечного автомата с бесконечным прошлым, то E является определенным событием.
ДОКАЗАТЕЛЬСТВО. Если число k входных клеток >0, то полный вход порождается выбором из конечного числа 2**k возможных входов в момент p, затем выбором из того же числа возможных входов в момент p-1 и т.д. до бесконечности.
По теореме Брауэра [1924] [Изложение Брауэра рассчитано на читателей, знакомых с интуиционистской теорией множеств, и его главное усилие направлено на интуиционистское доказательство этой теоремы], которую доказал также Кениг [1927], если для каждого входа определено на некоторой конечной стадии (т.е. в зависимости только от части входа, занимающей время p, ..., p-u, для некоторого u>=0), наступит ли событие или нет, то имеется такое число n>=0, что для любого входа наступление или ненаступление события определяется только частью входа, занимающей время p, ..., p-n. В этом случае событие будет определенным длины n+1.
Рассмотрим теперь неопределенное событие E. В силу контрапонированной теоремы Брауэра [Если данная теорема имеет вид A->B (A влечет B), то контрапонированной теоремой будет ~B->~A ("не B влечет не A").- Прим. ред.], имеется вход c0c1c2..., такой, что для каждого u>=0 частью этого входа c0...cu не определено, наступит E или нет.
СЛУЧАЙ 1. E не наступает для входа c0c1c2... Тогда для каждого u найдется вход cu0 cu1 cu2..., для которого E наступает, совпадающий с c0c1c2... во время p, ..., p-u и отличный от него в некоторый более ранний момент.
Допустим, что E представляется свойством состояния в момент p. Пусть состояния, обладающие этим свойством, будут a1, ..., a[r1], а состояния, не обладающие этим свойством, пусть будут a[r1+1], ..., ar.
Пусть S - множество всех последовательностей состояний d0d1d2..., совместимых с наличным состоянием, которое является одним из a1, ..., a[r1], т.е. d0 является одним из a1, ..., a[r1], и внутренняя часть каждого di является той, которая определена состоянием d[i+1] в непосредственно предшествующий момент. Имеется r1 возможностей для выбора d0, не более r для d1, не более r для d2 и т.д.
Любая последовательность состояний d0d1d2..., которую можно принять за вход cu0 cu1 cu2..., должна принадлежать S, потому что E наступает для cu0 cu1 cu2..., и в первых u+1 выбранных состояниях d0...du должна быть совместимой с c0c1c2... т.е. внешняя часть для d0...du должна быть входом c0...cu за последние u+1 моментов p, ..., p-u в последовательности c0c1c2...
По теореме Брауэра, если для каждой последовательности d0d1d2..., принадлежащей S, имелось u такое, что d0...du несовместимо с c0c1c2..., то имелось бы такое n> что для каждой d0d1d2..., принадлежащей S, часть d0...dn несовместима с c0c1c2..., что противоречит предыдущему замечанию при u>=n.
Следовательно, в S имеется бесконечная последовательность d0d1d2..., совместимая с c0c1c2... Но d0 - одно из состояний a1, ..., [ar1], хотя E не наступает для c0c1c2..., а это противоречит нашему допущению, что E представляется состоянием в момент p, которое является одним из a1, ..., a[r1].
СЛУЧАЙ 2. E наступает для входа c0c1c2... Применяя
к ~E рассуждение, примененное в случае 1 к E, приводим к противоречию допущение, что ~E представлено свойством состояния в момент p, и тем самым приводим к абсурду такое же допущение для E.
#11. ПРЕДСТАВИМОСТЬ ДЛЯ СЛУЧАЯ КОНЕЧНОГО ПРОШЛОГО, НО ПРИ ПРОИЗВОЛЬНОМ НАЧАЛЬНОМ ВНУТРЕННЕМ СОСТОЯНИИ
ТЕОРЕМА 7. Если событие E представило свойством состояния в момент p конечного автомата, отправляющегося от произвольного внутреннего состояния в момент 1, то E - неизначальное определенное событие длины 1.
ДОКАЗАТЕЛЬСТВО. Пусть E - событие, которое не является неизначальным определенным событием длины 1. Тогда найдется некоторый вход c для момента p, такой, что наступление или ненаступление E не определяется одним только входом c, т.е. различные выборы c1'...c[p'-1]' и c1''...с[p''-1]'' входа за время 1, ..., p-1 для p=p' и p=p'' вместе со входом c в момент p обеспечивают наступление или, соответственно, ненаступление события E. Допустим, что E представляется некоторым свойством состояния в момент p для данного начального внутреннего состояния b1. Рассмотрим внутренние состояния b' и b'' которые порождаются в моменты p' и p'' при начальном внутреннем состоянии b1 входами c1'...c[p'-1]' и c1''...c[p''-1]'' соответственно. Пусть далее в момент 1 вход будет c, а внутреннее состояние b' или, соответственно, b''. Тогда это состояние обладает или, соответственно, не обладает рассматриваемым свойством. Таким образом, это свойство не может представлять E как для b', так и для b'' в качестве начальных внутренних состояний: для одного из них оно дает ложный результат при p=1 и входе c.
#12. ПРИМИТИВНАЯ РЕКУРСИВНОСТЬ РЕГУЛЯРНЫХ СОБЫТИЙ
Для иллюстрации того, что выражение регулярных событий требует только того логического и математического символизма, который относится к области теории чисел, мы выскажем следующую теорему. Понятие относительной примитивной рекурсивности определено у Клини [1952]. В целях установления соответствия с принятыми там обозначениями, мы примем в этой теореме в качестве области изменения для временной переменной 0, 1, 2, ... вместо 1, 2, 3 ....
ТЕОРЕМА 8. Для любого регулярного события E, относящегося к входным нейронам N1, ..., Nk, предикат E(p) (== E наступает, оканчиваясь в момент p) примитивно-рекурсивен относительно предикатов N1(t), ..., Nk(t).
МЕТОД ДОКАЗАТЕЛЬСТВА. В силу теоремы 3, E(p) эквивалентно существованию некоторого рода цепочки состояний dp...d0 (см. раздел 9).
#13. ПРОСТОЙ ПРИМЕР НЕРЕГУЛЯРНОГО СОБЫТИЯ
Рассмотрим событие E, описанное следующим образом: N возбужден в момент u**2 для каждого u, такого, что u2<=p, и только в такие моменты. Символически
E(p) == (t)[t<=p](N(t)==(Eu)[u<=p](t=u2)).
Никакой конечный автомат не может представить E, и, следовательно, по теореме 3, событие E нерегулярно. В самом деле, допустим, что E представляется свойством состояния конечного автомата в момент p (автомат имеет состояния a1, ..., ar); пусть состояния, обладающие этим свойством, будут a1, ..., a[r1].
Рассмотрим любое число s, такое, что 2s>1. Допустим, что N возбужден в моменты 1, 4, 9, ..., s**2 и ни в какие последующие. Тогда E наступает для p=1,2,...,s+2s (=(s+1)**2-1) и ни для какого большего p.
Рассмотрим состояния d1, d2, d3, ... автомата в моменты s**2+1, s**2+2, s2**2+3... Начиная с момента s**2+1, N все время не возбужден, так что внешнее состояние постоянно. Таким образом, каждое из состояний d1, d2, d3, ..., начиная со второго, определяется непосредственно предшествующим. Так как всего имеется только r состояний, последовательность d1, d2, d3, ... оказывается в конце концов периодической.
Однако в течение времени s**2+1, ..., s**2+2s состояние должно быть одним из a1, ..., a[r1], потому что E наступает для этих значений p. Следовательно, ввиду 2s>r1, к моменту s**2+2s период должен обнаружиться (т.е. первое повторение в d1, d2, d3, ... должно уже произойти). Следовательно, состояние в момент (s+1)2 является одним из a1, ..., a[r1], хотя E не наступает для p=(s+1)**2.
Мы не хотим сказать, что это событие должно иметь какое-либо биологическое значение. Этот пример приведен для иллюстрации математических ограничений, налагаемых на представимые события.
#8. ПОНЯТИЕ КОНЕЧНОГО АВТОМАТА
#8.1. КЛЕТКИ. Время будет состоять из последовательности дискретных моментов, занумерованных целыми положительными числами, за исключением раздела 10, где будут использованы все числа.
Мы будем рассматривать автоматы, построенные из конечного числа частей, именуемых КЛЕТКАМИ, каждая из которых в любой момент находится в одном из конечного числа >=2 состояний.
Мы будем различать два вида клеток - ВХОДНЫЕ и ВНУТРЕННИЕ клетки.
Допускаются два состояния входной клетки, 0 и 1 ("спокойное* и "возбужденное"). Какое из них имеет место для входной клетки в любой данный момент, определяется внешней средой.
Благодаря тому, что число состояний входных клеток ограничено двумя, понятие входа для автомата совпадает с понятием входа для нервной сети, которое было сформулировано в разделе 4 и в пункте 6.3. Однако излагаемая теория будет также пригодна и для большего числа состояний. Но это не принесет никакой выгоды, потому что можно пользоваться p клетками, допускающими два состояния каждая, для замены одной клетки, допускающей любое число q (2<=q<=2**p) состояний 0, 1, ..., q-1, где при q<2**p можно или рассматривать только входы, в которых не встречаются состояния q, ..., 2**p-1, или отождествлять эти состояния с состоянием q-1 во всех действиях автомата.
Число состояний внутренней клетки не ограничено двумя, и различные внутренние клетки могут иметь различное число состояний.
Состояние каждой внутренней клетки в любой момент t>1 определяется состоянием всех клеток в момент t-1. Может, конечно, случиться, что нам не понадобится знать состояния всех клеток в момент t-1 для определения состояния данной внутренней клетки в момент t. Наша формулировка не фиксирует, какого рода закон используется для определения состояния, за исключением того, что, кроме состояний клеток в момент t-1, ничто не может иметь значения [Процессы такого типа называются марковскими процессами.- Прим. ред.].
Ввиду того, что счет времени ведется начиная с момента 1, состояние каждой из внутренних клеток в этот момент должно быть задано (исключение представляет раздел 11).
Конкретным примером конечного автомата служит нервная сеть Мак-Каллока-Питтса (часть I). Здесь все клетки допускают ровно два состояния. Другой пример связан с рассмотрением внутренних нейронов с "изменяемыми концевыми пластинками", которые не могут быть активными, если в некоторый предыдущий момент нейрон, имеющий такую пластинку, и нейрон, с которым эта пластинка соприкасается, не были одновременно возбуждены. Нейрон с r такими изменяемыми концевыми пластинками допускает 2**(r+1) состояний. Напрашиваются и многие другие возможности.
#8.2. СОСТОЯНИЕ. При k входных клетках N1, ..., Nk (k>=0) и m внутренних клетках M1, ..., Mm (m>=1) с соответствующими числами состояний s1, ..., sm имеется ровно 2**k*s1...sm возможных (полных) состояний автомата. Мы можем рассматривать каждое такое состояние как комбинацию ВНЕШНЕГО СОСТОЯНИЯ, для которого имеется 2**k возможностей, и ВНУТРЕННЕГО СОСТОЯНИЯ, для которого имеется
s1...sm возможностей.
Закон, по которому состояния внутренних клеток в момент t>1 определяются состояниями всех клеток в момент t-1, можно задать путем указания для каждого из полных состояний в момент t-1, какое из внутренних состояний последует за ним в момент t.
Мы могли бы всю совокупность внутренних клеток заменить единственной клеткой, допускающей s1...sm состояний. Но мы не воспользуемся этой возможностью, имея в виду применения теории конечных автоматов, в которых клетки обладают некоторыми простыми свойствами и связаны между собой некоторыми простыми способами.
Мы также могли бы обойтись (однако не будем этого делать) одной-единственной входной клеткой, считая, что входы с k первоначальными входными клетками образуют последовательно в некотором порядке новый вход, причем временная шкала меняется таким образом, что k моментов новой шкалы соответствуют одному моменту первоначальной шкалы. События, относящиеся к новой временной шкале, можно было бы интерпретировать в первоначальной шкале.
Обозначим теперь состояния через a1,...,ar, где r=2**k*s1...sm, а внутренние состояния - через b1, ..., bq, где q=s1...sm. Выберем обозначения таким образом, что внутренним состоянием в момент 1 будет b1.
При фиксированном внутреннем состоянии в момент 1, состояние в момент p является функцией входа за время 1, ..., p (включая значение p или, при k=0, только это значение).
Каждое из состояний a1, ..., ar представляет таким образом некоторое событие, которое наступает, оканчиваясь в момент p, в том и только в том случае, если вход за время 1, ..., p приводит в момент p к тому из а1, ..., аr, которое является этим состоянием. Таким образом, автомат может знать о своем прошлом, (включая настоящий момент) только то, что оно попадает в один из r попарно непересекающихся классов (некоторые из них могут быть пусты).
Аналогично, внутреннее состояние в момент p+1, или свойство полного состояния в момент p, или свойство внутреннего состояния в момент p+1 или свойство внутреннего состояния в момент p+s для некоторого s>1, не зависящее от входа за время p+1, ..., p+s-1, представляет событие. Таким образом, сказать, что состояние в момент p обладает некоторым свойством, означает сказать, что это состояние является элементом некоторого подкласса r возможных состояний, так что прошлое распадается в теоретико-множественную сумму (или дизъюнкцию) соответствующих классов прошлого, которые в отдельности представляются состояниями этого подкласса.
Какого рода события могут быть представлены? Поскольку под входом понимается то же, что и в части I, мы можем пользоваться понятием "регулярного события", введенным в разделе 7. Следующая теорема, которая, так же как и теорема 3, относится к специальному типу конечных автоматов, даст ответ на этот вопрос.
#9. РЕГУЛЯРНОСТЬ ПРЕДСТАВИМЫХ СОБЫТИЙ
ТЕОРЕМА 5. Для любого конечного автомата (в частности, для нервной сети Мак-Каллока-Питтса), отправляющегося в момент 1 от данного внутреннего состояния b1, событие, представленное данным состоянием, существующим в момент p, регулярно.
ДОКАЗАТЕЛЬСТВО. Так как начальное внутреннее состояние определено, то имеется 2**k возможных начальных состояний (получающихся путем сочетания данного начального внутреннего состояния b1 с каждым из 2**k возможных внешних состояний в момент 1).
Следовательно, если мы сумеем показать, что автомат, отправляясь в момент 1 от данного состояния, достигнет в момент p нужного состояния в том и только в том случае, если наступит некоторое регулярное событие, оканчивающееся в момент p, то для доказательства теоремы останется взять дизъюнкцию 2**k соответствующих регулярных событий, которая также является регулярным событием.
Если дано любое состояние а в момент t-1 (t>=2), то в момент t возможны ровно 2**k состояний, потому что внутренняя часть состояния в момент t определена состоянием a, для внешней же части имеется 2**k возможностей. Мы будем говорить, что каждое из этих 2**k состояний находится в ОТНОШЕНИИ R к a.
Следующая часть наших рассуждений будет применима к любому бинарному отношению R, определенному на данном множестве r>=1 объектов a1, ..., ar (называемых "состояниями"), независимо от того, получается оно или нет только что описанным образом.
Рассмотрим любые два состояния a и a', не обязательно различные. Мы будем изучать цепочки состояний dp d[p-1] ... d1 (p>=1), для которых dp есть a, d1 есть а' и для каждого t=2,...,p dt находится в отношении R к d[t-1] (символически dtRd[t-1]); мы будем говорить, что такие цепочки
связывают a с a'.
Для множества цепочек мы введем понятие "регулярности" посредством следующего определения (построенного аналогично определению "регулярных" множеств таблиц в 7.1).
Пустое множество и для каждого i(i=1,...,r) единичное множество {ai}, имеющее только один элемент аi, рассматриваемый как цепочка длины 1, РЕГУЛЯРНЫ. Если A и B регулярны, то регулярна и их сумма, обозначаемая через AVB. Если A и B регулярны, то регулярно и обозначаемое через AB множество цепочек, которые получаются приписыванием цепочки, принадлежащей A, слева к цепочке, принадлежащей B. Если A и B регулярны, то регулярна и обозначаемая через A*B сумма для n=0,1,2... множеств A...AB, где A стоит n раз перед B.
ЛЕММА 7. Цепочки dp...d1, связывающие a с a', образуют регулярное множество.
ДОКАЗАТЕЛЬСТВО. Применяем индукцию по r.
БАЗИС: r=1. Тогда a' есть a. Если ~aRa (т.е. если R - нерефлексивное отношение), то множество цепочек, связывающих a с a, является единичным множеством {a}, которое регулярно. Если aRa, то это множество есть {a, aa, aaa, ...} и, значит, оно регулярно, так как может быть записано в виде A*A, где A={a}.
ИНДУКЦИОННЫЙ ШАГ: r>1
СЛУЧАЙ 1. a=a'. В этом случае любая цепочка, связывающая a с a', имеет вид
a -> a -> a -> ... a -> a,
где число вхождений для "a ->" положительно или равно нулю и каждая -> представляет независимо пустую цепочку (что возможно только при aRa) или непустую цепочку, в которую не входит a. Пусть e1, ..., eg (g>=0) - такие состояния e, что aRe, но e!a, и f1, ..., fh (h>=0) - такие состояния f, что fRa, но f!=a. Тогда любая непустая цепочка, представленная посредством ->, должна начинаться с одного из e1, ..., eg и оканчиваться одним из f1, ..., fh. Для каждой пары ei fj, по индуктивному предположению, множество цепочек, связывающих ei с fj и не содержащих a, регулярно. Обозначим через B1, ..., Bgh эти регулярные множества, и пусть A есть {a}. Тогда если aRa, то множество возможных цепочек а -> есть AVA(B1 V ... V Bgh) (которое сводится к A, если gh=0 или если все B пусты); если же ~aRa, то это множество есть A(B1 V ... V Bgh) (которое пусто, если gh=0 или если все B пусты). Обозначим это множество через C. Тогда множество цепочек, ведущих от a к a, есть C*A (что сводится к A, если C пусто).
СЛУЧАЙ 2. a!=a'. Теперь вместо прежней мы имеем цепочку
a -> a -> a -> ... а -> a - - -> а',
где число вхождений "а ->" есть число >=0 и каждая -> и "- - ->" представляют независимо пустую цепочку или непустую цепочку, в которую не входит a. Если D - множество всех возможных цепочек "а - - ->" и E={a}, то множество цепочек,
связывающих a с a', есть C*DE. Это множество регулярно.
ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ (окончание). Мы должны показать, что для данного состояния a и для каждого из 2**k состояний a' состояние есть a в момент p и a' в момент 1 в том и только в том случае, если за время 1, ..., p наступает некоторое регулярное событие.
Согласно лемме, множество цепочек, соединяющих a с a', регулярно. Рассмотрим для этого регулярного множества выражение через пустое множество и множества {ai} в качестве элементов (см. 7.2). В этом выражении заменим каждый элемент {ai} на единичное множество, состоящее из k*l-таблицы (которая (при k>0) описывает внешнюю часть состояния ai), снабженной ярлыком "изначальная" или "неизначальная" смотря по тому, был ли этот элемент {ai} самым ранним или нет. Каждое пустое множество в качестве элемента заменим на его самого (но будем обозначать его ~I). Получится регулярное выражение. Состояние a' в момент 1 меняется на a в момент p в том и только в том случае, если событие, описанное этим регулярным выражением, наступает за время 1, ..., p.
СЛЕДСТВИЕ. Регулярно также событие, представленное каждым из следующих способов: внутренним состоянием в момент p+1, свойством состояния в момент p, свойством внутреннего состояния в момент p+1, свойством внутреннего состояния в момент p+s (для некоторого s>1), которое не зависит от входа за время p+1, ..., p+s-1.
ДОКАЗАТЕЛЬСТВО. Событие, представленное свойством состояния в момент p, является дизъюнкцией событий, представленных в момент p состояниями, которые обладают этим свойством. Остальные способы представления сводятся к этому посредством леммы 1 в 5.3 (которая применима здесь точно так же, как и в случае нервных сетей Мак-Каллока-Питтса).
КОММЕНТАРИЙ. Регулярные выражения, полученные при доказательстве теоремы 5, могут иметь только изначальные элементы или ~I в качестве самых ранних элементов и построены из элементов длины 1 (аналогично после упрощения, которое дается леммой 2). Во многих примерах ясно, что большие упрощения могут быть получены с помощью эквивалентностей (7.1); но мы не занимались изучением возможности систематического проведения таких упрощений.
Изучение структуры множества объектов a1, ..., ar с бинарным отношением R, составляющее суть изложенного доказательства, может оказаться полезным для какой-нибудь алгебраической теории.
Очевидно, для наших рассуждений существенно, чтобы число клеток и число состояний каждой клетки было конечным, так что число полных состояний заранее фиксировано. Машина Тьюринга [1936-1937] не является конечным автоматом, если лента рассматривается как часть машины, потому что, хотя в любой момент может быть заполнено знаками только конечное число квадратов ленты, для этого числа не имеется никакой предписанной границы. Если же ленту рассматривать как часть внешней среды, то машина Тьюринга оказывается конечным автоматом, который вдобавок может запасать информацию во внешней среде и пользоваться ею, впоследствии, так что настоящий вход не вполне независим от прошлого. Пока что неизвестно, может ли это сравнение привести к каким-либо полезным взглядам на машины Тьюринга или на конечные автоматы.
ДОБАВЛЕНИЯ
#10. ПРЕДСТАВИМОСТЬ В КОНЕЧНОМ АВТОМАТЕ С БЕСКОНЕЧНЫМ ПРОШЛЫМ
ТЕОРЕМА 6. Если событие E представило свойством состояния в момент p конечного автомата с бесконечным прошлым, то E является определенным событием.
ДОКАЗАТЕЛЬСТВО. Если число k входных клеток >0, то полный вход порождается выбором из конечного числа 2**k возможных входов в момент p, затем выбором из того же числа возможных входов в момент p-1 и т.д. до бесконечности.
По теореме Брауэра [1924] [Изложение Брауэра рассчитано на читателей, знакомых с интуиционистской теорией множеств, и его главное усилие направлено на интуиционистское доказательство этой теоремы], которую доказал также Кениг [1927], если для каждого входа определено на некоторой конечной стадии (т.е. в зависимости только от части входа, занимающей время p, ..., p-u, для некоторого u>=0), наступит ли событие или нет, то имеется такое число n>=0, что для любого входа наступление или ненаступление события определяется только частью входа, занимающей время p, ..., p-n. В этом случае событие будет определенным длины n+1.
Рассмотрим теперь неопределенное событие E. В силу контрапонированной теоремы Брауэра [Если данная теорема имеет вид A->B (A влечет B), то контрапонированной теоремой будет ~B->~A ("не B влечет не A").- Прим. ред.], имеется вход c0c1c2..., такой, что для каждого u>=0 частью этого входа c0...cu не определено, наступит E или нет.
СЛУЧАЙ 1. E не наступает для входа c0c1c2... Тогда для каждого u найдется вход cu0 cu1 cu2..., для которого E наступает, совпадающий с c0c1c2... во время p, ..., p-u и отличный от него в некоторый более ранний момент.
Допустим, что E представляется свойством состояния в момент p. Пусть состояния, обладающие этим свойством, будут a1, ..., a[r1], а состояния, не обладающие этим свойством, пусть будут a[r1+1], ..., ar.
Пусть S - множество всех последовательностей состояний d0d1d2..., совместимых с наличным состоянием, которое является одним из a1, ..., a[r1], т.е. d0 является одним из a1, ..., a[r1], и внутренняя часть каждого di является той, которая определена состоянием d[i+1] в непосредственно предшествующий момент. Имеется r1 возможностей для выбора d0, не более r для d1, не более r для d2 и т.д.
Любая последовательность состояний d0d1d2..., которую можно принять за вход cu0 cu1 cu2..., должна принадлежать S, потому что E наступает для cu0 cu1 cu2..., и в первых u+1 выбранных состояниях d0...du должна быть совместимой с c0c1c2... т.е. внешняя часть для d0...du должна быть входом c0...cu за последние u+1 моментов p, ..., p-u в последовательности c0c1c2...
По теореме Брауэра, если для каждой последовательности d0d1d2..., принадлежащей S, имелось u такое, что d0...du несовместимо с c0c1c2..., то имелось бы такое n> что для каждой d0d1d2..., принадлежащей S, часть d0...dn несовместима с c0c1c2..., что противоречит предыдущему замечанию при u>=n.
Следовательно, в S имеется бесконечная последовательность d0d1d2..., совместимая с c0c1c2... Но d0 - одно из состояний a1, ..., [ar1], хотя E не наступает для c0c1c2..., а это противоречит нашему допущению, что E представляется состоянием в момент p, которое является одним из a1, ..., a[r1].
СЛУЧАЙ 2. E наступает для входа c0c1c2... Применяя
к ~E рассуждение, примененное в случае 1 к E, приводим к противоречию допущение, что ~E представлено свойством состояния в момент p, и тем самым приводим к абсурду такое же допущение для E.
#11. ПРЕДСТАВИМОСТЬ ДЛЯ СЛУЧАЯ КОНЕЧНОГО ПРОШЛОГО, НО ПРИ ПРОИЗВОЛЬНОМ НАЧАЛЬНОМ ВНУТРЕННЕМ СОСТОЯНИИ
ТЕОРЕМА 7. Если событие E представило свойством состояния в момент p конечного автомата, отправляющегося от произвольного внутреннего состояния в момент 1, то E - неизначальное определенное событие длины 1.
ДОКАЗАТЕЛЬСТВО. Пусть E - событие, которое не является неизначальным определенным событием длины 1. Тогда найдется некоторый вход c для момента p, такой, что наступление или ненаступление E не определяется одним только входом c, т.е. различные выборы c1'...c[p'-1]' и c1''...с[p''-1]'' входа за время 1, ..., p-1 для p=p' и p=p'' вместе со входом c в момент p обеспечивают наступление или, соответственно, ненаступление события E. Допустим, что E представляется некоторым свойством состояния в момент p для данного начального внутреннего состояния b1. Рассмотрим внутренние состояния b' и b'' которые порождаются в моменты p' и p'' при начальном внутреннем состоянии b1 входами c1'...c[p'-1]' и c1''...c[p''-1]'' соответственно. Пусть далее в момент 1 вход будет c, а внутреннее состояние b' или, соответственно, b''. Тогда это состояние обладает или, соответственно, не обладает рассматриваемым свойством. Таким образом, это свойство не может представлять E как для b', так и для b'' в качестве начальных внутренних состояний: для одного из них оно дает ложный результат при p=1 и входе c.
#12. ПРИМИТИВНАЯ РЕКУРСИВНОСТЬ РЕГУЛЯРНЫХ СОБЫТИЙ
Для иллюстрации того, что выражение регулярных событий требует только того логического и математического символизма, который относится к области теории чисел, мы выскажем следующую теорему. Понятие относительной примитивной рекурсивности определено у Клини [1952]. В целях установления соответствия с принятыми там обозначениями, мы примем в этой теореме в качестве области изменения для временной переменной 0, 1, 2, ... вместо 1, 2, 3 ....
ТЕОРЕМА 8. Для любого регулярного события E, относящегося к входным нейронам N1, ..., Nk, предикат E(p) (== E наступает, оканчиваясь в момент p) примитивно-рекурсивен относительно предикатов N1(t), ..., Nk(t).
МЕТОД ДОКАЗАТЕЛЬСТВА. В силу теоремы 3, E(p) эквивалентно существованию некоторого рода цепочки состояний dp...d0 (см. раздел 9).
#13. ПРОСТОЙ ПРИМЕР НЕРЕГУЛЯРНОГО СОБЫТИЯ
Рассмотрим событие E, описанное следующим образом: N возбужден в момент u**2 для каждого u, такого, что u2<=p, и только в такие моменты. Символически
E(p) == (t)[t<=p](N(t)==(Eu)[u<=p](t=u2)).
Никакой конечный автомат не может представить E, и, следовательно, по теореме 3, событие E нерегулярно. В самом деле, допустим, что E представляется свойством состояния конечного автомата в момент p (автомат имеет состояния a1, ..., ar); пусть состояния, обладающие этим свойством, будут a1, ..., a[r1].
Рассмотрим любое число s, такое, что 2s>1. Допустим, что N возбужден в моменты 1, 4, 9, ..., s**2 и ни в какие последующие. Тогда E наступает для p=1,2,...,s+2s (=(s+1)**2-1) и ни для какого большего p.
Рассмотрим состояния d1, d2, d3, ... автомата в моменты s**2+1, s**2+2, s2**2+3... Начиная с момента s**2+1, N все время не возбужден, так что внешнее состояние постоянно. Таким образом, каждое из состояний d1, d2, d3, ..., начиная со второго, определяется непосредственно предшествующим. Так как всего имеется только r состояний, последовательность d1, d2, d3, ... оказывается в конце концов периодической.
Однако в течение времени s**2+1, ..., s**2+2s состояние должно быть одним из a1, ..., a[r1], потому что E наступает для этих значений p. Следовательно, ввиду 2s>r1, к моменту s**2+2s период должен обнаружиться (т.е. первое повторение в d1, d2, d3, ... должно уже произойти). Следовательно, состояние в момент (s+1)2 является одним из a1, ..., a[r1], хотя E не наступает для p=(s+1)**2.
Мы не хотим сказать, что это событие должно иметь какое-либо биологическое значение. Этот пример приведен для иллюстрации математических ограничений, налагаемых на представимые события.
Последний раз редактировалось: Gudleifr (Пн Сен 18, 2023 2:50 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Т.о. "нейронные сети" - всего лишь примитивный способ что-то посчитать, если соединить "нейроны" в нужном порядке. И никакими "самосовершенствованиями" нельзя выскочить за рамки, установленные безжалостной "теорией чисел". Дело, опять, оказывается не в программе, а в программисте.
И вопрос тут даже не в том, что "настоящие нейроны" умнее искусственных (и мы за прошедшие 70 лет, якобы, приблизились к их "настоящей сути", посрамив забытых классиков). Скорее, вопрос в том, как столь примитивным сетям, не будучи ни на гран умнее вышеописанных, удается обеспечить наш "умственный процесс"? Как нам удается думать, имея в своем распоряжении столь убогий инструмент? Дело снова в "программисте". Т.е. в том животном, которое этим инструментом пользуется для думания. Причем, пользуется бездумно, т.к. больше ему думать нечем.
И да, подобно приведенным выше статьям, всякая попытка программирования сетей начинается с построения некоторого математического аппарата. Конечно, в пределах указанного класса задач можно построить сетевую решалку вполне автоматически, но попробуйте доказать, что ваша задача принадлежит этому классу! Что построение (или обучение) будет в вашем случае успешным.
И вопрос тут даже не в том, что "настоящие нейроны" умнее искусственных (и мы за прошедшие 70 лет, якобы, приблизились к их "настоящей сути", посрамив забытых классиков). Скорее, вопрос в том, как столь примитивным сетям, не будучи ни на гран умнее вышеописанных, удается обеспечить наш "умственный процесс"? Как нам удается думать, имея в своем распоряжении столь убогий инструмент? Дело снова в "программисте". Т.е. в том животном, которое этим инструментом пользуется для думания. Причем, пользуется бездумно, т.к. больше ему думать нечем.
И да, подобно приведенным выше статьям, всякая попытка программирования сетей начинается с построения некоторого математического аппарата. Конечно, в пределах указанного класса задач можно построить сетевую решалку вполне автоматически, но попробуйте доказать, что ваша задача принадлежит этому классу! Что построение (или обучение) будет в вашем случае успешным.
Последний раз редактировалось: Gudleifr (Сб Июл 01, 2023 12:03 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
М.МИНСКИЙ, С.ПЕЙПЕРТ
ПЕРСЕПТРОНЫ
Перевод с английского Г.Л.ГИМЕЛЬФАРБА и В.М.ШАРЫПАНОВА
Под редакцией В.А.КОВАЛЕВСКОГО
1971
 DJVU, 1.87Мб
DJVU, 1.87Мб
#0. ВВЕДЕНИЕ
#0.0. О ЧИТАТЕЛЯХ
Создавая эту книгу, мы имели в виду три категории читателей. Во-первых, специалистов в области "распознавания образов", "обучающихся машин" и "пороговой логики", которым будут интересны полученные в книге новые результаты. Во-вторых, тех, кому будет приятно прочесть ее как своего рода этюд из области абстрактной математики, в особенности тех, кому хотелось бы увидеть возвращение геометрии в сферу топологии и алгебры. Мы относим себя к обеим этим категориям, но нам вряд ли удалось бы выполнить поставленную перед собой задачу, если бы мы не думали о третьей, менее определенной категории читателей.
Наша задача - помочь читателю достичь возможно более глубокого понимания основных представлений, являющихся, по нашему мнению, краеугольным камнем общей теории вычислений. Мы собираемся очень подробно изучить класс вычислений, в котором решения можно принять, лишь как следует взвесив данные опыта. Разумеется, такая задача представляет большой самостоятельный интерес; мы же надеемся на то, что понимание ее математической структуры поможет в конечном счете проникнуть в глубь почти неисследованной теории параллельных вычислительных машин.
Мы обращаемся главным образом к тем читателям, которых интересует такая общая теория вычислений. Мы надеемся, что в их число входят физиологи и биологи, которым хотелось бы знать, каким образом мозг "вычисляет" мысли и как генетическая программа "рассчитывает" организмы. Мы не претендуем ни на то, чтобы ответить на подобные вопросы, ни даже на то, чтобы предложить используемые нами простые устройства в качестве "моделей" таких процессов. Наша цель - а мы не знаем, является ли она более скромной или, наоборот, более честолюбивой,- показать, как могла бы возникнуть такая теория и какие направления исследований могли бы к ней привести.
Именно для этой третьей категории читателей написано наше введение. Тем из них, кто еще непосредственно не сталкивался с теорией распознавания образов, оно поможет осознать, что эту теорию стоит изучать и для других целей. В то же время мы хотим изложить упрощенный вариант теории для тех читателей, чья математическая подготовка не позволяет легко одолеть последующие главы. Остальная часть книги полностью самостоятельна, и тот, кому ненавистны введения, может перейти прямо к гл.1.
#0.1. РЕАЛЬНЫЕ, АБСТРАКТНЫЕ И МИФИЧЕСКИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
О наших вычислительных машинах и о выполняемых ими вычислениях мы знаем постыдно мало. Это кажется парадоксальным, поскольку и в физическом, и в логическом плане принципы работы вычислительных машин яснее ясного. Тем не менее даже школьник может задать вопросы, на которые современная "наука о вычислительных машинах" ответить не в состоянии. Например, очень мало известно о том, сколько может потребоваться вычислений для выполнения конкретного задания.
В качестве примера рассмотрим одну из наиболее часто встречающихся задач - РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. Решать такие системы необходимо, по сути дела, в любой научной работе. Для их решения существует множество стандартных программ, включающих сложение, умножение и деление. Казалось бы, столь простая и важная тема, давно разрабатываемая математиками, в настоящее время изучена до мельчайших подробностей. Зададим, однако, несколько вопросов. Какое количество арифметических шагов безусловно необходимо? Как оно зависит от объема памяти вычислительной машины? Сколько времени мы можем сэкономить, имея ДВЕ (или n) идентичные вычислительные машины? Любому специалисту по вычислительной технике "известно", что для решения системы из n уравнений потребуется что-то около n**3 умножений, но даже если это и так, никто не знает (к настоящему времени), с чего начать доказательство этого утверждения.
Ни дилетант, ни специалист-вычислитель, по-видимому, не осознают, насколько примитивно и эмпирично сейчас наше понимание такого рода проблем. Мы не знаем, насколько вообще можно ускорить вычисления, используя "параллельные" машины вместо "последовательных", "аналоговые" вместо "цифровых". У нас нет теории тех ситуаций, в которых "ассоциативная" память оправдывает свою более высокую по сравнению с "адресной" стоимость. Бытует множество легенд относительно такого рода противопоставлений, однако большая часть их основана просто на предубеждениях. В тех случаях, которые мы тщательно исследовали, широко распространенные ходячие представления оказывались не только "недоказанными" - они зачастую были попросту неверными.
Незрелость, которую демонстрирует наша неспособность ответить на такого рода вопросы, проявляется даже в языке, на котором вопросы формулируются. Пары противопоставляемых слов типа "параллельный" - "последовательный", "локальный" - "глобальный", "цифровой" - "аналоговый", используются так, как будто они относятся к четко определенным техническим понятиям, хотя даже в тех случаях, когда дело обстоит именно так, их технический смысл меняется от автора к автору и от контекста к контексту. Но обычно с ними обращаются настолько вольно, что классификация вычислительных машин, определяемая ими, относится скорее к области легенд, нежели к науке. Здесь мы отнюдь не стремимся навести читателя на мысль, что это простые псевдопроблемы, вызванные небрежным использованием языка (это не книга "лечебной семантики"!), ибо в этих интуитивных представлениях и различиях содержится глубокий смысл. Задача состоит в том, как объединить их в ясную, четкую теорию.
#0.2. МАТЕМАТИЧЕСКАЯ СТРАТЕГИЯ
Мы не убеждены, что настало время для попытки создать весьма общую теорию, достаточно всеобъемлющую, чтобы включить указанные нами понятия и им подобные. Хорошие теории редко развиваются не на основе хорошо понятых реальных задач и частных случаев. Без подобного фундамента получается либо бессмысленно общая теория с преобладанием определений над теоремами, либо теория, математически элегантная, но не имеющая никаких практических приложений.
Соответственно наилучшая линия нашего поведения должна, по всей видимости, состоять в том, чтобы ДОСКОНАЛЬНО разобраться в тщательно подобранных частных ситуациях, в которых встречаются основные понятия.
Действительно, мы решили изучать свойства самых простых (из тех, что сумели найти) машин, по праву называющихся "параллельными" (поскольку в них нет замкнутых контуров или линий обратной связи), но тем не менее способных выполнять вычисления, не тривиальные ни в практическом, ни в математическом смысле.
Прежде чем углубиться в детали, нам хотелось бы успокоить нематематиков, которые, возможно, напуганы тем, что промелькнуло перед их глазами при перелистывании последующих страниц. Математические методы, используемые нами, достаточно разнообразны, но редко требуют глубоких предварительных знаний. Большую часть того, что выходит за пределы элементарной алгебры и геометрии, мы объясняем. Иногда эти объяснения не рациональны; тогда разделы, требующие от читателей, на наш взгляд, больших математических усилий, чем это оправдано ролью соответствующей темы во всем изложении, мы выделяем как ФАКУЛЬТАТИВНЫЕ. Наша теория скорее похожа на ветвистое дерево, чем на узкую высокую башню из блоков; во многих случаях, если неожиданно возникнут трудности, можно перескочить к началу следующей главы.
Многие авторы современных математических книг заставляют читателя проделывать чрезмерно трудоемкую работу из-за стремления скрыть те пути мышления, которые привели их к открытию теорем. Мы старались оставлять на виду ход развития мысли. Нам бы хотелось пойти дальше и сохранить следы всех наших ложных путей. К несчастью, их было слишком много! Тем не менее мы иногда оставляли первоначальное доказательство, даже если потом находили "лучшее". В наши намерения входит не столько доказывать теоремы, сколько проникнуть в сущность методов и поощрить исследования. Мы надеемся, что все это будет читаться не как цепь логических умозаключений, а как математический роман, в котором действующие лица, раз возникнув, появляются вновь и вновь и совершенствуются.
#0.3. КИБЕРНЕТИКА И РОМАНТИКА
Машины, которые мы собираемся изучать, являются абстрактными вариантами класса устройств, известных под разными названиями Мы условились использовать термин "персептрон" в знак уважения к первой в этой области работе Фрэнка Розенблатта. Персептроны вырабатывают решения (определяют, соответствует ли событие данному "образу"), суммируя опытные данные, полученные из множества малых экспериментов. Эта простая и ясная концепция важна, поскольку многие, если не все, более сложные машины для принятия решений действуют в той или иной мере по такому же принципу, и пока мы не разберемся в нем досконально, нас могут подстерегать трудности в дальнейшем. В самом деле, мы считаем, что во многих областях науки и техники начало существенным достижениям было положено четкими определениями "линейных" систем, и именно такие машины мы выдвигаем кандидатами для первоначального изучения "параллельных" машин вообще.
В наших рассуждениях будет содержаться и довольно резкая критика предшествующих работ в этой области. Персептроны широко рекламировались как машины для "распознавания образов" или "обучающиеся машины" и как таковые обсуждались в многочисленных книгах, журнальных статьях и объемистых "отчетах". Большая часть этих творений лишена научной ценности, и мы обычно не станем ссылаться поименно на критикуемые нами работы. Наука о вычислениях и кибернетика начались - и это, по-видимому, совершенно правомерно - с шумной романтической рекламы. Они изобиловали волнующими и заманчивыми новыми идеями, уже принесшими богатые плоды. Тяжкие требования строгости и осторожности могли бы сильно затормозить темпы развития, только будущее могло бы показать, какие направления окажутся наилучшими. В самом деле, мы считаем, что маститые эксперты, наиболее активно выражавшие недовольство по поводу "неумеренных претензий" энтузиастов кибернетики, оказались в конечном итоге неправыми Но теперь наступило время зрелости, и мы должны противопоставить нашим рискованным начинаниям в равной мере впечатляющие образцы критического подхода
#0.4. ПАРАЛЛЕЛЬНОЕ ВЫЧИСЛЕНИЕ
Простейшее представление о параллельном вычислении дает схема на рис.0.1. Рисунок показывает, как можно вычислить функцию пси(X) в два этапа: сначала вычислить функции фи.1(X), фи.2(X), ...? фи.n(X) НЕЗАВИСИМО одну от другой, а затем объединить результаты при помощи функции ОМЕГА от n переменных и получить значение кси.

Чтобы такое определение имело смысл (или, точнее, было эффективным), необходимо наложить некоторые ограничения на функцию ОМЕГА и множество ФИ функций фи.1, фи.2, ... Если не ввести ограничений, не получится теории, любое вычисление функции пси можно представить как параллельное, причем самыми разнообразными тривиальными способами. Например, пусть пси будет одна из функций фи, a ОМЕГА просто передает ее результат. Мы рассмотрим целый ряд ограничений, но сначала приведем несколько конкретных примеров вида функций, которые нам бы хотелось принять в качестве пси.
#0.5. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ; ПРЕДИКАТЫ
Пусть R - обычная двумерная евклидова плоскость, X - геометрическая фигура, нарисованная на R. Например, X может быть окружностью, или парой окружностей, или черно-белым наброском лица. В общем случае мы будем представлять себе X просто как подмножество точек плоскости R (т.е. подмножество черных точек).
Пусть пси(X)- функция (от фигур X на R), принимающая только два значения. Обычно их считают равными нулю и единице. Если же считать их "ложью" и "истиной", то пси(X) можно рассматривать как предикат, т.е. переменное высказывание, истинность или ложность которого зависит от выбора X. Приведем несколько примеров предикатов, которые представят впоследствии особый интерес.
пси.ОКРУЖНОСТЬ(X) =
1, если X - окружность;
0, в противном случае.
пси.ВЫПУКЛОСТЬ(X) =
1, если X - выпуклая фигура;
0 в противном случае.
пси.СВЯЗНОСТЬ(X) =
1, если X - связная фигура;
0 в противном случае.
Мы будем также рассматривать и гораздо более простые предикаты [Мы будем обозначать фи (а не пси) те очень простые предикаты, которые затем будем объединять для получения более сложных. При этом мы не подразумеваем никаких абсолютных логических различий]. Самый простой предикат "распознает", принадлежит ли фигуре X данная единственная точка: допустим, что р - некоторая точка на плоскости, и положим
фи.p(X) =
1, если р принадлежит X;
0 в противном случае.
Наконец, нам понадобится предикат, указывающий, что некоторое множество A является подмножеством множества X:
фи.A(X) =
#1, если A подмножество X;
0 в противном случае.

#0.6. ПРОСТОЕ ПОНЯТИЕ "ЛОКАЛЬНОГО"
Начнем с изучения важного различия между предикатами пси.СВЯЗНОСТЬ и пси.ВЫПУКЛОСТЬ. Для того чтобы его выявить, определим, что такое выпуклость.
ОПРЕДЕЛЕНИЕ. Множество X НЕ ЯВЛЯЕТСЯ ВЫПУКЛЫМ тогда и только тогда, когда существуют такие три точки р, q и r, что q находится на отрезке прямой, соединяющем p и r, и
p принадлежит X,
q не принадлежит X,
r принадлежит X.
Итак, можно проверять выпуклость, изучая тройки точек. Если все возможные тройки выдержат такую проверку (т.е. не удовлетворят указанным выше условиям), то множество X выпукло; если хотя бы одна из них не выдержит проверки, то множество X не выпукло. Так как все эти испытания можно проводить независимо и окончательное решение задано столь простой логической процедурой - установлением единообразия результатов всех испытаний, - то мы предлагаем это в качестве первого проекта нашего определения "локального".
ОПРЕДЕЛЕНИЕ. Предикат пси называется КОНЪЮНКТИВНО ЛОКАЛЬНЫМ k-го ПОРЯДКА, если его можно вычислить, как и в #0.4, при помощи множества ФИ таких предикатов фи, что
каждый предикат фи зависит не более чем от k точек плоскости R;
пси(X)=
1, если фи(X)=1 для каждого предиката фи из ФИ;
0 в противном случае.
ПРИМЕР. пси.ВЫПУКЛОСТЬ является конъюнктивно локальным предикатом третьего порядка.
На первый взгляд может показаться, что свойство СВЯЗНОСТИ фигуры не очень отличается по характеру от свойства выпуклости. Однако мы докажем, что выполняется
ТЕОРЕМА 0.6.1. Предикат пси.СВЯЗНОСТЬ не является конъюнктивно локальным какого-либо порядка.
ДОКАЗАТЕЛЬСТВО. Предположим, что предикат при.СВЯЗНОСТЬ имеет порядок k. Тогда для того, чтобы можно было различить две фигуры
должен существовать некоторый предикат фи', принимающий на несвязной фигуре X.0 значение 0. Все предикаты фи на связной фигуре X.1 принимают значение 1. Так как фи' зависит не более чем от k точек, должен найтись по меньшей мере один средний квадрат, скажем Sj, не содержащий ни одной из них. Но тогда на связной фигуре
предикат фи' должен принимать то же самое нулевое значение, что и на X.0. Однако этого не может быть, так как все предикаты фи должны на Х.2 иметь значение 1.
Конечно, если некоторым предикатам фи разрешить просматривать ВСЕ точки плоскости R, то пси.СВЯЗНОСТЬ можно вычислить, что противоречит любому представлению о "локальности" функций фи.
#0.7. НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ ЛОКАЛЬНОГО
Мы уже привели ряд доводов в пользу того, что свойство "конъюнктивной локальности" предикатов имеет геометрический и вычислительный смысл. При более внимательном рассмотрении возникают сомнения, настолько ли это свойство широко, чтобы привести к достаточно плодотворной теории.
Читатели, знакомые с топологическими методами, должны заметить, что понятие "конъюнктивно локального" подобно понятию "локальности" в топологии. Однако, если точно следовать аналогии, нам нужно было бы ограничиться рассмотрением предикатов Фи, зависящих от всех точек, расположенных внутри малых окружностей, а не от фиксированного числа точек. Поэтому мы будем идти двумя параллельными путями. Один из них основан на ОГРАНИЧЕНИИ ЧИСЛА ТОЧЕК, и в этом случае мы будем говорить о предикатах ограниченного порядка. Второй основан на ОГРАНИЧЕНИИ РАССТОЯНИЙ между точками, и здесь мы будем говорить о предикатах, ОГРАНИЧЕННЫХ ПО ДИАМЕТРУ. Несмотря на аналогию с другими важными ситуациями, понятие локального, опирающееся на ограничения диаметра, в нашей теории, по-видимому, менее интересно (хотя можно было бы ожидать совершенно противоположного).
Узость требования "конъюнктивности", или "единогласия", вызывает более серьезные сомнения. В качестве следующего шага на пути к расширению нашего понятия ЛОКАЛЬНОГО попытаемся в определении КОНЪЮНКТИВНОЙ ЛОКАЛЬНОСТИ отделить существенные черты от остальных. По замыслу определения, вычисление предиката пси разделялось на два этапа.
ЭТАП I:
Нахождение множества функций фи.альфа, легко вычислимых либо из-за того, что каждая зависит лишь от небольшой части входного пространства R, либо из-за их простоты в каком-нибудь другом интересном смысле.
ЭТАП II:
Алгоритм решения ОМЕГА, который определяет пси, объединяя результаты вычислений, проведенных на этапе I. Для того чтобы это разделение на два этапа имело смысл, такая решающая функция также должна быть либо "отчетливо" однородной, либо легко программируемой, либо легко вычислимой.
Конкретный путь реализации этого замысла в нашем примере предиката пси.ВЫПУКЛОСТЬ был довольно произвольным. На этапе I мы обеспечили легкость вычисления предикатов фи.альфа, потребовав, чтобы каждый зависел только от нескольких точек из R. На этапе II мы использовали едва ли не самое простое правило, какое только можно себе представить: изображение принимается, если все предикаты фи "единогласны", и отвергается, если значение хотя бы одного предиката фи не совпадает с остальными.
Нам хотелось бы дать совершенно точное определение нашему интуитивному представлению о локальном как противоположности глобального, однако трудность заключается в том, что при попытке его сформулировать постоянно выплывают фразы типа "удобный для вычисления". Чтобы сделать их определенными, нужна какая-то схема сравнения сложности различных вычислительных методов. Пока не найдена такая интуитивно удовлетворяющая нас схема (а схема эта, по всей видимости, не лежит на поверхности), требования обоих этапов будут сохранять эвристический характер, что серьезно затрудняет формальное определение.
Перейдем теперь к рассмотрению частного случая этапа II - "взвешенного голосования", или "линейной комбинации" предикатов этапа I. Это так называемая схема ПЕРСЕПТРОНА, и сейчас мы дадим окончательное определение.
ПЕРСЕПТРОНЫ
Перевод с английского Г.Л.ГИМЕЛЬФАРБА и В.М.ШАРЫПАНОВА
Под редакцией В.А.КОВАЛЕВСКОГО
1971
 DJVU, 1.87Мб
DJVU, 1.87Мб
#0. ВВЕДЕНИЕ
#0.0. О ЧИТАТЕЛЯХ
Создавая эту книгу, мы имели в виду три категории читателей. Во-первых, специалистов в области "распознавания образов", "обучающихся машин" и "пороговой логики", которым будут интересны полученные в книге новые результаты. Во-вторых, тех, кому будет приятно прочесть ее как своего рода этюд из области абстрактной математики, в особенности тех, кому хотелось бы увидеть возвращение геометрии в сферу топологии и алгебры. Мы относим себя к обеим этим категориям, но нам вряд ли удалось бы выполнить поставленную перед собой задачу, если бы мы не думали о третьей, менее определенной категории читателей.
Наша задача - помочь читателю достичь возможно более глубокого понимания основных представлений, являющихся, по нашему мнению, краеугольным камнем общей теории вычислений. Мы собираемся очень подробно изучить класс вычислений, в котором решения можно принять, лишь как следует взвесив данные опыта. Разумеется, такая задача представляет большой самостоятельный интерес; мы же надеемся на то, что понимание ее математической структуры поможет в конечном счете проникнуть в глубь почти неисследованной теории параллельных вычислительных машин.
Мы обращаемся главным образом к тем читателям, которых интересует такая общая теория вычислений. Мы надеемся, что в их число входят физиологи и биологи, которым хотелось бы знать, каким образом мозг "вычисляет" мысли и как генетическая программа "рассчитывает" организмы. Мы не претендуем ни на то, чтобы ответить на подобные вопросы, ни даже на то, чтобы предложить используемые нами простые устройства в качестве "моделей" таких процессов. Наша цель - а мы не знаем, является ли она более скромной или, наоборот, более честолюбивой,- показать, как могла бы возникнуть такая теория и какие направления исследований могли бы к ней привести.
Именно для этой третьей категории читателей написано наше введение. Тем из них, кто еще непосредственно не сталкивался с теорией распознавания образов, оно поможет осознать, что эту теорию стоит изучать и для других целей. В то же время мы хотим изложить упрощенный вариант теории для тех читателей, чья математическая подготовка не позволяет легко одолеть последующие главы. Остальная часть книги полностью самостоятельна, и тот, кому ненавистны введения, может перейти прямо к гл.1.
#0.1. РЕАЛЬНЫЕ, АБСТРАКТНЫЕ И МИФИЧЕСКИЕ ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
О наших вычислительных машинах и о выполняемых ими вычислениях мы знаем постыдно мало. Это кажется парадоксальным, поскольку и в физическом, и в логическом плане принципы работы вычислительных машин яснее ясного. Тем не менее даже школьник может задать вопросы, на которые современная "наука о вычислительных машинах" ответить не в состоянии. Например, очень мало известно о том, сколько может потребоваться вычислений для выполнения конкретного задания.
В качестве примера рассмотрим одну из наиболее часто встречающихся задач - РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ. Решать такие системы необходимо, по сути дела, в любой научной работе. Для их решения существует множество стандартных программ, включающих сложение, умножение и деление. Казалось бы, столь простая и важная тема, давно разрабатываемая математиками, в настоящее время изучена до мельчайших подробностей. Зададим, однако, несколько вопросов. Какое количество арифметических шагов безусловно необходимо? Как оно зависит от объема памяти вычислительной машины? Сколько времени мы можем сэкономить, имея ДВЕ (или n) идентичные вычислительные машины? Любому специалисту по вычислительной технике "известно", что для решения системы из n уравнений потребуется что-то около n**3 умножений, но даже если это и так, никто не знает (к настоящему времени), с чего начать доказательство этого утверждения.
Ни дилетант, ни специалист-вычислитель, по-видимому, не осознают, насколько примитивно и эмпирично сейчас наше понимание такого рода проблем. Мы не знаем, насколько вообще можно ускорить вычисления, используя "параллельные" машины вместо "последовательных", "аналоговые" вместо "цифровых". У нас нет теории тех ситуаций, в которых "ассоциативная" память оправдывает свою более высокую по сравнению с "адресной" стоимость. Бытует множество легенд относительно такого рода противопоставлений, однако большая часть их основана просто на предубеждениях. В тех случаях, которые мы тщательно исследовали, широко распространенные ходячие представления оказывались не только "недоказанными" - они зачастую были попросту неверными.
Незрелость, которую демонстрирует наша неспособность ответить на такого рода вопросы, проявляется даже в языке, на котором вопросы формулируются. Пары противопоставляемых слов типа "параллельный" - "последовательный", "локальный" - "глобальный", "цифровой" - "аналоговый", используются так, как будто они относятся к четко определенным техническим понятиям, хотя даже в тех случаях, когда дело обстоит именно так, их технический смысл меняется от автора к автору и от контекста к контексту. Но обычно с ними обращаются настолько вольно, что классификация вычислительных машин, определяемая ими, относится скорее к области легенд, нежели к науке. Здесь мы отнюдь не стремимся навести читателя на мысль, что это простые псевдопроблемы, вызванные небрежным использованием языка (это не книга "лечебной семантики"!), ибо в этих интуитивных представлениях и различиях содержится глубокий смысл. Задача состоит в том, как объединить их в ясную, четкую теорию.
#0.2. МАТЕМАТИЧЕСКАЯ СТРАТЕГИЯ
Мы не убеждены, что настало время для попытки создать весьма общую теорию, достаточно всеобъемлющую, чтобы включить указанные нами понятия и им подобные. Хорошие теории редко развиваются не на основе хорошо понятых реальных задач и частных случаев. Без подобного фундамента получается либо бессмысленно общая теория с преобладанием определений над теоремами, либо теория, математически элегантная, но не имеющая никаких практических приложений.
Соответственно наилучшая линия нашего поведения должна, по всей видимости, состоять в том, чтобы ДОСКОНАЛЬНО разобраться в тщательно подобранных частных ситуациях, в которых встречаются основные понятия.
Действительно, мы решили изучать свойства самых простых (из тех, что сумели найти) машин, по праву называющихся "параллельными" (поскольку в них нет замкнутых контуров или линий обратной связи), но тем не менее способных выполнять вычисления, не тривиальные ни в практическом, ни в математическом смысле.
Прежде чем углубиться в детали, нам хотелось бы успокоить нематематиков, которые, возможно, напуганы тем, что промелькнуло перед их глазами при перелистывании последующих страниц. Математические методы, используемые нами, достаточно разнообразны, но редко требуют глубоких предварительных знаний. Большую часть того, что выходит за пределы элементарной алгебры и геометрии, мы объясняем. Иногда эти объяснения не рациональны; тогда разделы, требующие от читателей, на наш взгляд, больших математических усилий, чем это оправдано ролью соответствующей темы во всем изложении, мы выделяем как ФАКУЛЬТАТИВНЫЕ. Наша теория скорее похожа на ветвистое дерево, чем на узкую высокую башню из блоков; во многих случаях, если неожиданно возникнут трудности, можно перескочить к началу следующей главы.
Многие авторы современных математических книг заставляют читателя проделывать чрезмерно трудоемкую работу из-за стремления скрыть те пути мышления, которые привели их к открытию теорем. Мы старались оставлять на виду ход развития мысли. Нам бы хотелось пойти дальше и сохранить следы всех наших ложных путей. К несчастью, их было слишком много! Тем не менее мы иногда оставляли первоначальное доказательство, даже если потом находили "лучшее". В наши намерения входит не столько доказывать теоремы, сколько проникнуть в сущность методов и поощрить исследования. Мы надеемся, что все это будет читаться не как цепь логических умозаключений, а как математический роман, в котором действующие лица, раз возникнув, появляются вновь и вновь и совершенствуются.
#0.3. КИБЕРНЕТИКА И РОМАНТИКА
Машины, которые мы собираемся изучать, являются абстрактными вариантами класса устройств, известных под разными названиями Мы условились использовать термин "персептрон" в знак уважения к первой в этой области работе Фрэнка Розенблатта. Персептроны вырабатывают решения (определяют, соответствует ли событие данному "образу"), суммируя опытные данные, полученные из множества малых экспериментов. Эта простая и ясная концепция важна, поскольку многие, если не все, более сложные машины для принятия решений действуют в той или иной мере по такому же принципу, и пока мы не разберемся в нем досконально, нас могут подстерегать трудности в дальнейшем. В самом деле, мы считаем, что во многих областях науки и техники начало существенным достижениям было положено четкими определениями "линейных" систем, и именно такие машины мы выдвигаем кандидатами для первоначального изучения "параллельных" машин вообще.
В наших рассуждениях будет содержаться и довольно резкая критика предшествующих работ в этой области. Персептроны широко рекламировались как машины для "распознавания образов" или "обучающиеся машины" и как таковые обсуждались в многочисленных книгах, журнальных статьях и объемистых "отчетах". Большая часть этих творений лишена научной ценности, и мы обычно не станем ссылаться поименно на критикуемые нами работы. Наука о вычислениях и кибернетика начались - и это, по-видимому, совершенно правомерно - с шумной романтической рекламы. Они изобиловали волнующими и заманчивыми новыми идеями, уже принесшими богатые плоды. Тяжкие требования строгости и осторожности могли бы сильно затормозить темпы развития, только будущее могло бы показать, какие направления окажутся наилучшими. В самом деле, мы считаем, что маститые эксперты, наиболее активно выражавшие недовольство по поводу "неумеренных претензий" энтузиастов кибернетики, оказались в конечном итоге неправыми Но теперь наступило время зрелости, и мы должны противопоставить нашим рискованным начинаниям в равной мере впечатляющие образцы критического подхода
#0.4. ПАРАЛЛЕЛЬНОЕ ВЫЧИСЛЕНИЕ
Простейшее представление о параллельном вычислении дает схема на рис.0.1. Рисунок показывает, как можно вычислить функцию пси(X) в два этапа: сначала вычислить функции фи.1(X), фи.2(X), ...? фи.n(X) НЕЗАВИСИМО одну от другой, а затем объединить результаты при помощи функции ОМЕГА от n переменных и получить значение кси.

Чтобы такое определение имело смысл (или, точнее, было эффективным), необходимо наложить некоторые ограничения на функцию ОМЕГА и множество ФИ функций фи.1, фи.2, ... Если не ввести ограничений, не получится теории, любое вычисление функции пси можно представить как параллельное, причем самыми разнообразными тривиальными способами. Например, пусть пси будет одна из функций фи, a ОМЕГА просто передает ее результат. Мы рассмотрим целый ряд ограничений, но сначала приведем несколько конкретных примеров вида функций, которые нам бы хотелось принять в качестве пси.
#0.5. НЕКОТОРЫЕ ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ; ПРЕДИКАТЫ
Пусть R - обычная двумерная евклидова плоскость, X - геометрическая фигура, нарисованная на R. Например, X может быть окружностью, или парой окружностей, или черно-белым наброском лица. В общем случае мы будем представлять себе X просто как подмножество точек плоскости R (т.е. подмножество черных точек).
Пусть пси(X)- функция (от фигур X на R), принимающая только два значения. Обычно их считают равными нулю и единице. Если же считать их "ложью" и "истиной", то пси(X) можно рассматривать как предикат, т.е. переменное высказывание, истинность или ложность которого зависит от выбора X. Приведем несколько примеров предикатов, которые представят впоследствии особый интерес.
пси.ОКРУЖНОСТЬ(X) =
1, если X - окружность;
0, в противном случае.

пси.ВЫПУКЛОСТЬ(X) =
1, если X - выпуклая фигура;
0 в противном случае.

пси.СВЯЗНОСТЬ(X) =
1, если X - связная фигура;
0 в противном случае.

Мы будем также рассматривать и гораздо более простые предикаты [Мы будем обозначать фи (а не пси) те очень простые предикаты, которые затем будем объединять для получения более сложных. При этом мы не подразумеваем никаких абсолютных логических различий]. Самый простой предикат "распознает", принадлежит ли фигуре X данная единственная точка: допустим, что р - некоторая точка на плоскости, и положим
фи.p(X) =
1, если р принадлежит X;
0 в противном случае.
Наконец, нам понадобится предикат, указывающий, что некоторое множество A является подмножеством множества X:
фи.A(X) =
#1, если A подмножество X;
0 в противном случае.

#0.6. ПРОСТОЕ ПОНЯТИЕ "ЛОКАЛЬНОГО"
Начнем с изучения важного различия между предикатами пси.СВЯЗНОСТЬ и пси.ВЫПУКЛОСТЬ. Для того чтобы его выявить, определим, что такое выпуклость.
ОПРЕДЕЛЕНИЕ. Множество X НЕ ЯВЛЯЕТСЯ ВЫПУКЛЫМ тогда и только тогда, когда существуют такие три точки р, q и r, что q находится на отрезке прямой, соединяющем p и r, и
p принадлежит X,
q не принадлежит X,
r принадлежит X.
Итак, можно проверять выпуклость, изучая тройки точек. Если все возможные тройки выдержат такую проверку (т.е. не удовлетворят указанным выше условиям), то множество X выпукло; если хотя бы одна из них не выдержит проверки, то множество X не выпукло. Так как все эти испытания можно проводить независимо и окончательное решение задано столь простой логической процедурой - установлением единообразия результатов всех испытаний, - то мы предлагаем это в качестве первого проекта нашего определения "локального".
ОПРЕДЕЛЕНИЕ. Предикат пси называется КОНЪЮНКТИВНО ЛОКАЛЬНЫМ k-го ПОРЯДКА, если его можно вычислить, как и в #0.4, при помощи множества ФИ таких предикатов фи, что
каждый предикат фи зависит не более чем от k точек плоскости R;
пси(X)=
1, если фи(X)=1 для каждого предиката фи из ФИ;
0 в противном случае.
ПРИМЕР. пси.ВЫПУКЛОСТЬ является конъюнктивно локальным предикатом третьего порядка.
На первый взгляд может показаться, что свойство СВЯЗНОСТИ фигуры не очень отличается по характеру от свойства выпуклости. Однако мы докажем, что выполняется
ТЕОРЕМА 0.6.1. Предикат пси.СВЯЗНОСТЬ не является конъюнктивно локальным какого-либо порядка.
ДОКАЗАТЕЛЬСТВО. Предположим, что предикат при.СВЯЗНОСТЬ имеет порядок k. Тогда для того, чтобы можно было различить две фигуры

должен существовать некоторый предикат фи', принимающий на несвязной фигуре X.0 значение 0. Все предикаты фи на связной фигуре X.1 принимают значение 1. Так как фи' зависит не более чем от k точек, должен найтись по меньшей мере один средний квадрат, скажем Sj, не содержащий ни одной из них. Но тогда на связной фигуре

предикат фи' должен принимать то же самое нулевое значение, что и на X.0. Однако этого не может быть, так как все предикаты фи должны на Х.2 иметь значение 1.
Конечно, если некоторым предикатам фи разрешить просматривать ВСЕ точки плоскости R, то пси.СВЯЗНОСТЬ можно вычислить, что противоречит любому представлению о "локальности" функций фи.
#0.7. НЕКОТОРЫЕ ДРУГИЕ ПОНЯТИЯ ЛОКАЛЬНОГО
Мы уже привели ряд доводов в пользу того, что свойство "конъюнктивной локальности" предикатов имеет геометрический и вычислительный смысл. При более внимательном рассмотрении возникают сомнения, настолько ли это свойство широко, чтобы привести к достаточно плодотворной теории.
Читатели, знакомые с топологическими методами, должны заметить, что понятие "конъюнктивно локального" подобно понятию "локальности" в топологии. Однако, если точно следовать аналогии, нам нужно было бы ограничиться рассмотрением предикатов Фи, зависящих от всех точек, расположенных внутри малых окружностей, а не от фиксированного числа точек. Поэтому мы будем идти двумя параллельными путями. Один из них основан на ОГРАНИЧЕНИИ ЧИСЛА ТОЧЕК, и в этом случае мы будем говорить о предикатах ограниченного порядка. Второй основан на ОГРАНИЧЕНИИ РАССТОЯНИЙ между точками, и здесь мы будем говорить о предикатах, ОГРАНИЧЕННЫХ ПО ДИАМЕТРУ. Несмотря на аналогию с другими важными ситуациями, понятие локального, опирающееся на ограничения диаметра, в нашей теории, по-видимому, менее интересно (хотя можно было бы ожидать совершенно противоположного).
Узость требования "конъюнктивности", или "единогласия", вызывает более серьезные сомнения. В качестве следующего шага на пути к расширению нашего понятия ЛОКАЛЬНОГО попытаемся в определении КОНЪЮНКТИВНОЙ ЛОКАЛЬНОСТИ отделить существенные черты от остальных. По замыслу определения, вычисление предиката пси разделялось на два этапа.
ЭТАП I:
Нахождение множества функций фи.альфа, легко вычислимых либо из-за того, что каждая зависит лишь от небольшой части входного пространства R, либо из-за их простоты в каком-нибудь другом интересном смысле.
ЭТАП II:
Алгоритм решения ОМЕГА, который определяет пси, объединяя результаты вычислений, проведенных на этапе I. Для того чтобы это разделение на два этапа имело смысл, такая решающая функция также должна быть либо "отчетливо" однородной, либо легко программируемой, либо легко вычислимой.
Конкретный путь реализации этого замысла в нашем примере предиката пси.ВЫПУКЛОСТЬ был довольно произвольным. На этапе I мы обеспечили легкость вычисления предикатов фи.альфа, потребовав, чтобы каждый зависел только от нескольких точек из R. На этапе II мы использовали едва ли не самое простое правило, какое только можно себе представить: изображение принимается, если все предикаты фи "единогласны", и отвергается, если значение хотя бы одного предиката фи не совпадает с остальными.
Нам хотелось бы дать совершенно точное определение нашему интуитивному представлению о локальном как противоположности глобального, однако трудность заключается в том, что при попытке его сформулировать постоянно выплывают фразы типа "удобный для вычисления". Чтобы сделать их определенными, нужна какая-то схема сравнения сложности различных вычислительных методов. Пока не найдена такая интуитивно удовлетворяющая нас схема (а схема эта, по всей видимости, не лежит на поверхности), требования обоих этапов будут сохранять эвристический характер, что серьезно затрудняет формальное определение.
Перейдем теперь к рассмотрению частного случая этапа II - "взвешенного голосования", или "линейной комбинации" предикатов этапа I. Это так называемая схема ПЕРСЕПТРОНА, и сейчас мы дадим окончательное определение.
Последний раз редактировалось: Gudleifr (Вс Июл 02, 2023 12:30 am), всего редактировалось 3 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#0.8. ПЕРСЕПТРОНЫ
Пусть ФИ = {фи.1, фи.2, ..., ф.n} - семейство предикатов. Будем говорить, что
ПРЕДИКАТ ПСИ ЛИНЕЕН ОТНОСИТЕЛЬНО ФИ,
если существуют такие число тета и набор чисел {альфа.фи.1, альфа.фи.2, ..., альфа.фи.n}, что пси(X) = 1 тогда и только тогда, когда альфа.фи.1*фи.1(X)+...+альфа.фи.n*фи.n(X)>тета.
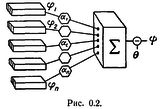
Число тета называется порогом, а числа альфа - коэффициентами, или весами (рис. 0.2). Обычно пишут сокращенно:
пси(X)=1 тогда и только тогда, когда СУММА[фи принадлежит ФИ]альфа.фи*фи(X)>тета.
Интуиция подсказывает нам следующее: можно считать, что каждый предикат из ФИ содержит определенные сведения о том, истинен ли предикат пси для какой-либо фигуры X. Если в целом фи(X) имеет положительную корреляцию с фи(X), то можно ожидать, что вес альфа.фи будет положительным, тогда как при отрицательной корреляции отрицательным будет и альфа.фи. Здесь идею корреляции следует воспринимать не буквально, а лишь как аналогию, наводящую на размышления.
ПРИМЕР. Любой конъюнктивно локальный предикат можно представить в такой форме, полагая тета=-1 и альфа.фи=-1 для каждого фи. Действительно, в этом случае
СУММА(-1)*фи(X)>-1
лишь при условии, что фи(X)=0 для каждого фи из ФИ. (Таким образом, для всех фи нужно переставить смысловые значения истина и ложь, но это несущественно).
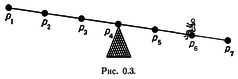
ПРИМЕР. Рассмотрим качели, изображенные на рис.0.3, и допустим, что X - расположение булыжников в некоторых из равноотстоящих точек {р.1, ..., р.7}. Здесь R состоит из семи точек. Пусть фи.i(X)=1 тогда и только тогда, когда булыжник находится в i-й точке. Тогда предикат
"Доска наклонится вправо"
можно выразить формулой
СУММА(i-4)фи.i(X)>0
где тета=0 и aльфа.i=(i-4).
При применении этого подхода для распознавания образов на евклидовой плоскости возникает множество проблем, связанных с возможностью появления бесконечных сумм и т.п. Такие вопросы широко обсуждаются в тексте, а здесь нам хочется только заверить математиков, что эти проблемы будут рассмотрены. Всюду, за исключением тех случаев, когда применение бесконечных сумм оправдано по техническим соображениям (а иногда дело обстоит именно так), мы будем сводить задачу к конечной при помощи двух общих методов. Один из них состоит в том, что плоскость R считается состоящей из дискретных малых квадратов (а не точек) и изображения, пересекающие одни и те же квадраты, считаются эквивалентными. При втором методе рассматривают только ограниченные изображения X и выбирают ФИ так, чтобы для любого ограниченного изображения X только конечное число предикатов фи были ненулевыми.
ОПРЕДЕЛЕНИЕ. ПЕРСЕПТРОНОМ называется устройство, способное вычислять все предикаты, линейные относительно некоторого заданного множества ФИ частных предикатов.
Иными словами, множество предикатов фи задано, а "веса" альфа и порог тета выбираются свободно. По причинам, которые станут ясны впоследствии, о персептронах вообще можно сказать очень мало. Но налагая определенные условия, можно получить интересные свойства некоторых семейств персептронов. К их числу относятся:
1. ПЕРСЕПТРОНЫ, ОГРАНИЧЕННЫЕ ПО ДИАМЕТРУ. Для каждого предиката фи из ФИ диаметр множества точек плоскости, от которых зависит фи, не превосходит некоторой фиксированной величины.
2. ПЕРСЕПТРОНЫ ОГРАНИЧЕННОГО ПОРЯДКА. Мы будем говорить, что персептрон имеет порядок <=n, если каждый элемент из ФИ зависит не более, чем от n точек.
3. ПЕРСЕПТРОНЫ ГАМБЫ. Каждый элемент из Ф может зависеть от всех точек, но должен быть "линейной пороговой функцией" (т.е. сам должен вычисляться персептроном первого порядка, определенным в предыдущем пункте).
4. СЛУЧАЙНЫЕ ПЕРСЕПТРОНЫ. Именно эта модель наиболее подробно изучалась группой Розенблатта; предикаты фи представляют собой случайно выбранные булевы функции. Иначе говоря, случайные персептроны являются персептронами ограниченного порядка, а множество ФИ порождается случайным процессом с определенной функцией распределения.
5. ОГРАНИЧЕННЫЕ ПЕРСЕПТРОНЫ. Множество ФИ предикатов фи бесконечно, а множество значений, принимаемых коэффициентами альфа.фи, конечно.
Чтобы дать предварительное представление о том, какого рода результаты мы собираемся получать, приведем простой пример теоремы о персептронах, ограниченных по диаметру.
ТЕОРЕМА 0.8. Никакой персептрон, ограниченный по диаметру, не в состоянии определить, связаны ли друг с другом все части какой-либо геометрической фигуры! Иными словами, никакой такой персептрон не позволяет вычислить предикат пси.СВЯЗНОСТЬ.
Для доказательства рассмотрим четыре фигуры

и такой персептрон пси, ограниченный по диаметру, что его носители [Множества точек, от которых зависят предикаты фи.- Прим. ред.] имеют диаметры, как у изображенных ниже окружностей:

Ясно, что сначала задается рассматриваемый диаметр, а уже потом выбираются фигуры X.ij так, чтобы их длина равнялась нескольким диаметрам. Допустим, что такой персептрон отличает несвязные фигуры (типа X.00 и X.11) от связных (типа X.01 и X.01) в соответствии с тем, выполняется ли условие
СУММА альфа.фи*фи(X) > тета,
т.е.
СУММА[группа 1]альфа.фи*фи(X) + СУММА[группа 2]альфа.фи*фи(X) + СУММА[группа 3]альфа.фи*фи(X) >тета
(здесь мы сгруппировали предикаты фи по расположению их носителей: у левого края, у правого края, не на краях фигуры). Тогда для X.00 общая сумма должна быть отрицательной. При переходе от X.00 к X.10 меняется только сумма СУММА[группа 1], причем ее величина должна ВОЗРАСТИ настолько, чтобы общая сумма стала положительной. При переходе от X.00 к X.01 возрастает сумма СУММА[группа 2]. Но если мы перейдем от X.00 к X.11, это приведет к такому же по величине возрастанию обеих сумм СУММА[группа 1] и СУММА[группа 2] , поскольку предикаты обеих групп отметят (локально!) те же самые изменения; сумма же СУММА[группа 3] во всех случаях остается постоянной. Следовательно, общее приращение суммы при переходе X.00->X.11 будет не только положительным, но даже большим по величине, чем прежде. Отсюда следует, что персептрон, принимающий правильные решения относительно X.00, X.01 и X.10, будет вынужден признать X.11 связной фигурой, а это не так! Поэтому искомый персептрон существовать не может.
Читатели, уже знакомые с персептронами, вероятно, отметят, что приведенное доказательство (устанавливающее, что персептроны, ограниченные по диаметру, не могут распознавать связность) не использует ни теорию "обучения", ни теорию вероятностей (ни даже геометрию гиперплоскостей в n-мерном пространстве). Оно полностью определяется геометрией образов и алгеброй взвешенных предикатов. Читатели, занимающиеся физиологией, несомненно, заметят, что, поскольку все известные сейчас функции рецепторных клеток ограничены по диаметру, от живого существа требуется нечто большее, чем нейросинаптическое "суммирование" эффектов, чтобы заставить эти клетки вычислять связность. В самом деле, столь сложное зрительное восприятие может быть лишь у наиболее высокоорганизованных животных. В гл.5 мы покажем, что эта теорема распространяется также и на персептроны ограниченного порядка.
#0.9. ПРИВЛЕКАТЕЛЬНЫЕ СТОРОНЫ ПЕРСЕПТРОНОВ
Наиболее отчетливое представление о персептроне как об устройстве для распознавания образов состоит в следующем.
Машина строится на основе фиксированного набора элементов, которые вычисляют частные функции фи, получаемые обычно при помощи случайного процесса. Чтобы заставить ее распознавать определенный образ (множество входных фигур), нужно просто придать подходящее значение коэффициентам альфа.фи. Тем самым "программирование" производится удобным единообразным способом. Более того, поскольку "программы" можно задать в виде точек (альфа.1 альфа.2, ..., альфа.n) в n-мерном пространстве, им присуща метрика, позволяющая легко представить себе некоторого рода автоматическое программирование, которое люди уже склонны называть ОБУЧЕНИЕМ: к управлению параметрами подключаются устройства обратной связи, и машину "программируют", представляя в ее распоряжение последовательность входных образов и "сигнал ошибки", вызывающий изменение коэффициентов в нужном направлении, когда машина принимает неверное решение. Теоремы о сходимости персептрона (см. гл.11) определяют условия, при которых такая процедура в конечном итоге наверняка приводит к правильному набору значений коэффициентов.
#0.9.1. ЕДИНООБРАЗНОЕ ПРОГРАММИРОВАНИЕ И ОБУЧЕНИЕ. Чтобы отделить действительное от желаемого, начнем с анализа некоторых наблюдений. Пусть ФИ - множество частных предикатов, а L(ФИ) - множество предикатов, линейных относительно ФИ. Таким образом, L(ФИ) - репертуар персептрона, или множество предикатов, которые он может вычислить, когда коэффициенты альфа.фи и порог тета пробегают всевозможные значения. В принципе L(ФИ) могло бы быть множеством ВСЕХ предикатов, но это практически неосуществимо, так как тогда ФИ должно было бы быть астрономически велико. Поэтому у любого физически реализуемого персептрона репертуар ограничен. Простота и единообразие программирования оплачены дорогой ценой! Мы утверждаем, что при традиционных исследованиях персептронов эта цена определяется нереалистично. В частности, не уделяется внимания следующим решающим моментам:
1. Идея представлять классы геометрических объектов (или программы, которые определяют или распознают их) в виде классов n-мерных векторов (альфа.1, ..., альфа.n) упускает из виду геометрическую индивидуальность образов и приводит только к такой теории, возможности которой лишь немногим перекрывают простой ПОДСЧЕТ числа предикатов в L(ФИ)! Подобные представления стали традиционными у тех, кто рассуждает о распознавании образов в направлениях, подсказанных классическими статистическими теориями. В результате, кажется, мало кто замечал или подозревал, что могли бы встретиться ОТДЕЛЬНЫЕ осмысленные и интуитивно простые предикаты, не принадлежащие НИ ОДНОМУ из практически реализуемых множеств L(ФИ). Мы предложим анализ предиката пси.СВЯЗНОСТЬ, чтобы показать, сколь глубокой может оказаться эта проблема. В то же время мы хотим продемонстрировать, как некоторые предикаты, которые могли бы интуитивно показаться трудными для такого рода устройств, на самом деле МОГУТ распознаваться персептронами низкого порядка: уже предикат пси.ВЫПУКЛОСТЬ демонстрирует такую возможность.
2. Мало внимания уделялось величине, или, точнее, информационному содержанию параметров альфа.1, ..., альфа.n. Мы дадим примеры (на наш взгляд, скорее типичные, чем исключительные), в которых отношение наибольшего коэффициента к наименьшему бессмысленно велико. В таких условиях то обстоятельство, что предикаты принадлежат L(ФИ), теряет свое практическое значение. В ряде случаев информационная емкость, требуемая для запоминания альфа.1, ..., альфа.n превышает даже емкость, необходимую, чтобы запомнить весь класс фигур, определенный как один образ!
#3. С предыдущим пунктом тесно связана проблема ВРЕМЕНИ СХОДИМОСТИ процесса "обучения". Практические персептроны, по сути дела, являются устройствами с конечным числом состояний (как показано в гл.11). Поэтому не имеет смысла ссылаться на "теорему о сходимости персептрона" как на гарантию того, что процесс обучения в конечном счете найдет правильный набор значений параметров персептрона (если таковой существует), так как этого можно было бы достичь тривиальным полным перебором всех его состояний, т.е. испытывая все возможные наборы коэффициентов. Важно знать, насколько быстрее обучается персептрон по сравнению с тем временем, которое занимает абсолютно случайная процедура, или процедура полного перебора. Мы покажем, что в некоторых ситуациях, представляющих определенный геометрический интерес, время сходимости растет даже быстрее, чем показательная функция от размера множества R.
Теоретики персептрона не одиноки в своем непонимании этих предостережений. Внимательно прочитав любой типичный сборник статей по "самоорганизующимся" системам, мы обычно обогащаемся превосходными примерами дискуссий по поводу "обучающихся", или "адаптивных", машин. Этим дискуссиям недостает даже той степени строгости и формальной определенности, которую можно найти в литературе о персептронах. Сторонники подобных схем редко проводят какой бы то ни было анализ диапазона способов поведения, которым может научиться машина, и не отдают себе отчета в том, какой ценой обычно достигается легкость некоторых методов обучения: они непреднамеренно ограничивают диапазон возможных способов поведения устройства, вводя неявные допущения относительно среды, в которой оно должно работать.
Эти критические замечания не следует воспринимать как намеки на то, что мы противимся созданию машин, могущих "обучаться". Совсем наоборот! Но мы абсолютно убеждены, что значительное обучение со значительной скоростью предполагает какую-то значительную предварительную организацию. Простые обучающиеся схемы, основанные на регулировании коэффициентов, могут действительно оказаться целесообразными и полезными, когда частные функции в достаточной мере соответствуют поставленной задаче, как, например, в случае с машиной для игр в шашки, предложенной Сэмюэлем. Персептрон, у которого предикаты фи должным образом приспособлены для различения и обладают достаточно низким порядком, имеет неплохие шансы адаптивным путем улучшить свои рабочие характеристики. Наша цель - объяснить, почему достижение достаточно хорошего результата маловероятно, если предикат высокого порядка предлагается реализовать квазиуниверсальному персептрону, при выборе частных функций которого не имелась в виду какая-либо конкретная задача.
Этому тезису можно противопоставить в качестве контрпримера тот довод, что люди являются универсальными обучающимися машинами. Но наш мозг устроен в достаточной степени сложно, чтобы программироваться в намного более общем смысле, чем персептрон, а наша КУЛЬТУРА достаточно многогранна, чтобы заготовить если не действительную программу, то по крайней мере довольно сложную систему взаимодействий, управляющих процессом самопрограммирования, каким бы ни был его характер. Кроме того, нам требуется определенное время, чтобы стать универсальными учениками: ряд переходов от младенчества к интеллектуальной зрелости служит до некоторой степени подтверждением тезиса о том, что скорость приобретения новой познавательной структуры (т.е. скорость обучения) очень сильно зависит от уровня существующей познавательной структуры.
#0.9.2. ПАРАЛЛЕЛЬНОЕ ВЫЧИСЛЕНИЕ. Персептрон понимался как параллельно действующее устройство в том физическом смысле, что частные предикаты вычисляются одновременно. (С формальной точки зрения важно, что они вычисляются независимо один от другого). Это оплачивается тем, что необходимо вычислять ВСЕ фи.i, хотя лишь небольшая их часть может фактически иметь отношение к каждому конкретному окончательному решению. ОБЩЕЕ КОЛИЧЕСТВО вычислений может намного превысить то количество, которое должно быть проведено при хорошо организованном последовательном процессе (использующем те же самые фи), когда решение о том, что вычислять далее, выносится на основе результата предыдущего вычисления. Поэтому в каждом конкретном случае выбор между параллельным и последовательным методами должен основываться на сопоставлении выигрыша от сокращения (общего затраченного) времени с затратами на вводимые добавочные вычисления.
Даже предикаты низкого порядка могут потребовать большого количества ненужных вычислений, без которых можно было бы обойтись при последовательном процессе. Соответствующий объем необходимого оборудования может иной раз остаться в пределах физической осуществимости, в особенности если допустима невысокая точность вычислений. Совершенно иное положение в случае персептронов высокого порядка. Поучительным примером служит предикат пси.СВЯЗНОСТЬ. Как показано в гл.5, для вычисления этого предиката на тороидальной сетчатке размером 100*100 ЛЮБОМУ персептрону ТРЕБУЮТСЯ частные функции, каждая из которых просматривает многие сотни точек! При этом понятие "локальной" функции становится почти неуместным: частные функции сами оказываются глобальными. Кроме того, фантастическое количество возможных частных функций с такими большими носителями гасит любую надежду на то, что полученное путем случайного выбора умеренно большое множество таких функций окажется достаточно плотным, чтобы охватить соответствующее пространство функций. Чтобы уточнить эту мысль, покажем, что для определенных предикатов и классов частных функций количество частных функций, которое нужно использовать (не говоря уже об аппаратуре, реализующей их коэффициенты), непременно превысит границы физической осуществимости.
Вывод, который необходимо сделать, состоит в том, что конкретную схему параллельного вычисления нельзя разумно оценить, если нет способа определить, в какой мере решаемая задача разлагается на локальные и глобальные компоненты. Отсутствие ОБЩЕЙ теории, указывающей, что считать глобальным и что - локальным, не может служить оправданием тому, чтобы уклоняться от решения этой задачи в конкретных случаях. В этой книге мы покажем, что для ограниченного, но важного класса задач разработка такой теории не представляет непреодолимых трудностей.
#0.9.3. ПРИМЕНЕНИЕ ПРОСТЫХ АНАЛОГОВЫХ УСТРОЙСТВ. Персептрон привлекает к себе внимание многих исследователей отчасти потому, что для вычисления линейных пороговых функций можно применить очень простые физические устройства - "аналоговые вычислительные машины". Принято считать, что полезность этой схемы ограничена тем, что среди ВСЕХ логических функций линейные пороговые функции встречаются редко. Однако не уделялось почти никакого внимания тому, что множество ПРАКТИЧЕСКИ осуществимых линейных функций может оказаться еще уже. Чтобы пояснить указанную проблему, мы вычислим (в гл.10) величины и пределы изменения коэффициентов линейных представлений отдельных предикатов. Мы покажем, что некоторые отношения коэффициентов могут расти быстрее, чем показательная функция числа точек, различаемых в R. Из этого следует, что для "больших" входных множеств (скажем, для множеств R, содержащих более 20 точек) нельзя создать простое аналоговое запоминающее устройство с информационной емкостью, достаточной для хранения всего набора коэффициентов!
Чтобы избежать неверного толкования, нам, быть может, следовало бы повторить те оговорки, которые мы сделали, критикуя персептрон как модель "обучающихся устройств". Мы ни в коей мере не сомневаемся в том, что аналоговые устройства такого рода играют свою роль в распознавании образов. Но МЫ НЕ ВИДИМ, КАКУЮ ПОЛЬЗУ МОЖНО БЫЛО БЫ ИЗВЛЕЧЬ ИЗ ЭКСПЕРИМЕНТОВ, НЕ УЧИТЫВАЮЩИХ ТЕ ОГРАНИЧИВАЮЩИЕ ФАКТОРЫ, КОТОРЫЕ ВСТУПАЮТ В СВОИ ПРАВА, КАК ТОЛЬКО МАСШТАБЫ МАЛОЙ МОДЕЛИ ВОЗРАСТАЮТ ДО ПРАКТИЧЕСКИХ РАЗМЕРОВ.
#0.9.4. МОДЕЛИ РАБОТЫ МОЗГА И ГЕШТАЛЬТПСИХОЛОГИЯ. Популярность персептрона как модели разумной универсальной обучающейся машины объясняется, по-видимому, существованием распространенного представления о том, что мозг является довольно слабо организованной системой сравнительно простых устройств, связанных случайным образом. Это представление, в свою очередь, частично основано на наших первоначальных впечатлениях от тех запутанных структур, которые наблюдаются при микроскопическом исследовании анатомии мозга (и, вероятно, также на наших все еще хаотических представлениях о психологических механизмах).
Так или иначе, мы представляем себе систему сравнительно простых элементов, соединенных друг с другом случайным способом, в которой может регулироваться степень легкости прохождения сигналов через соединения. Когда машина в чем-либо ведет себя плохо, мы стремимся "обучить" ее не поступать так опять, ослабляя соединения, участвовавшие в данном действии; вероятно, для поощрения нравящегося нам поведения мы станем делать обратное.
Машина типа "персептрон" - это один из особенно простых вариантов описанного выше более широкого класса систем; некоторые другие варианты уже также изучались экспериментально.
Мистический туман, окутывающий такого рода машины, частично держится на том, что при обучении подобной машины запоминаемая информация не локализуется в каком-то определенном месте, а, напротив, "распределяется по всей схеме машины". В первой половине двадцатого века эксперименты, не подтвердившие представлений девятнадцатого века о размещении памяти (или большинства других "способностей" человека) в сугубо локальных областях мозга, вызвали глубокое разочарование. Как бы точно ни интерпретировать эти отнюдь не решающие эксперименты, они, вне всякого сомнения, привели к поиску концепций, основанных на нелокальных функциях, реализуемых машинами. Этот поиск не увенчался заметными успехами. Были выдвинуты несколько схем, основанных на крупномасштабных полях, или на "интерференционных картинах" в глобальных волновых колебаниях, но они не привели к правдоподобным теориям. (Ближе к концу этой эпохи Хебб [1949] выдвинул более сложное и значительно менее глобальное понятие "клеточного ансамбля". Это понятие оказалось более плодотворным для теоретических построений. Хотя оно и не привело к какой-либо окончательной модели, его популярность с каждым днем возрастает). Здесь, однако, мы стремимся не столько оценить эти теории, сколько обрисовать тот интеллектуальный фон, на котором была воздвигнута идея персептрона. На этом фоне схемы Розенблатта [1958] быстро укоренились, и в скором времени буквально сотни групп, больших и малых, стали проводить опыты с этой моделью под видом либо "обучающейся машины", либо "адаптивной", т.е. "самоорганизующейся" системы, либо системы "автоматического управления".
Результаты этих сотен проектов и опытов, как правило, разочаровывали, а объяснения не убеждали. Машины обычно хорошо вели себя на очень простых задачах, но весьма быстро сдавали позиции, как только порученные им задания становились сложнее. При увеличении размеров и времени работы системы положение обычно почти не менялось к лучшему. Возникло подозрение, что даже тогда, когда обнаруживался некоторый успех, это достигалось за счет сравнительно небольшой части схемы, а не благодаря действительно глобальной деятельности системы в целом. Обоих авторов этой книги (сначала независимо друг от друга, а затем вместе) влекло в некотором смысле "врачебное" стремление: рассеять опасные призраки "холистских" (holistic), или "гештальтных" ложных представлений, угрожавших объявиться в области техники и искусственного интеллекта, как прежде в биологии и психологии. Поэтому и по многим другим, более практическим причинам, а также в теоретических целях мы стремились выяснить что-либо относительно возможностей персептронов и их ограничений.
И только впоследствии, когда теория была разработана, мы поняли, что знать подобные машины важно независимо от того, получит ли система практическое применение в конкретных ситуациях! Дело в том, что аналогичные задачи стали камнем преткновения на пути развития самой науки о вычислительных машинах.
Как уже отмечалось, мы недостаточно хорошо знаем, за счет чего некоторые алгоритмические процедуры становятся "по существу" последовательными и насколько (или, скорее, какой ценой) можно ускорить вычисления при помощи многочисленных перекрывающихся вычислений с использованием более крупных и более действенных запоминающих устройств.
#0.10. ОБЩИЙ ПЛАН КНИГИ
Теория персептронов естественным образом делится на три части. В части I изучаются весьма общие свойства семейств линейных предикатов. Теоремы в этой части относятся ко всем персептронам, независимо от вида рассматриваемых образов, так что здесь представлена скорее алгебраическая, чем геометрическая теория персептронов. В части II мы более внимательно рассматриваем интересные геометрические образы и получаем более четкие, но, естественно, менее общие теоремы о геометрических возможностях наших машин. В части III исследуется целый ряд вопросов, сконцентрированных вокруг потенциальных способностей персептронов как практических устройств для распознавания образов и обучения. В последней главе прослеживаются некоторые исторические пути развития этих идей и предлагаются вероятные направления дальнейших исследований.
Пусть ФИ = {фи.1, фи.2, ..., ф.n} - семейство предикатов. Будем говорить, что
ПРЕДИКАТ ПСИ ЛИНЕЕН ОТНОСИТЕЛЬНО ФИ,
если существуют такие число тета и набор чисел {альфа.фи.1, альфа.фи.2, ..., альфа.фи.n}, что пси(X) = 1 тогда и только тогда, когда альфа.фи.1*фи.1(X)+...+альфа.фи.n*фи.n(X)>тета.

Число тета называется порогом, а числа альфа - коэффициентами, или весами (рис. 0.2). Обычно пишут сокращенно:
пси(X)=1 тогда и только тогда, когда СУММА[фи принадлежит ФИ]альфа.фи*фи(X)>тета.
Интуиция подсказывает нам следующее: можно считать, что каждый предикат из ФИ содержит определенные сведения о том, истинен ли предикат пси для какой-либо фигуры X. Если в целом фи(X) имеет положительную корреляцию с фи(X), то можно ожидать, что вес альфа.фи будет положительным, тогда как при отрицательной корреляции отрицательным будет и альфа.фи. Здесь идею корреляции следует воспринимать не буквально, а лишь как аналогию, наводящую на размышления.
ПРИМЕР. Любой конъюнктивно локальный предикат можно представить в такой форме, полагая тета=-1 и альфа.фи=-1 для каждого фи. Действительно, в этом случае
СУММА(-1)*фи(X)>-1
лишь при условии, что фи(X)=0 для каждого фи из ФИ. (Таким образом, для всех фи нужно переставить смысловые значения истина и ложь, но это несущественно).

ПРИМЕР. Рассмотрим качели, изображенные на рис.0.3, и допустим, что X - расположение булыжников в некоторых из равноотстоящих точек {р.1, ..., р.7}. Здесь R состоит из семи точек. Пусть фи.i(X)=1 тогда и только тогда, когда булыжник находится в i-й точке. Тогда предикат
"Доска наклонится вправо"
можно выразить формулой
СУММА(i-4)фи.i(X)>0
где тета=0 и aльфа.i=(i-4).
При применении этого подхода для распознавания образов на евклидовой плоскости возникает множество проблем, связанных с возможностью появления бесконечных сумм и т.п. Такие вопросы широко обсуждаются в тексте, а здесь нам хочется только заверить математиков, что эти проблемы будут рассмотрены. Всюду, за исключением тех случаев, когда применение бесконечных сумм оправдано по техническим соображениям (а иногда дело обстоит именно так), мы будем сводить задачу к конечной при помощи двух общих методов. Один из них состоит в том, что плоскость R считается состоящей из дискретных малых квадратов (а не точек) и изображения, пересекающие одни и те же квадраты, считаются эквивалентными. При втором методе рассматривают только ограниченные изображения X и выбирают ФИ так, чтобы для любого ограниченного изображения X только конечное число предикатов фи были ненулевыми.
ОПРЕДЕЛЕНИЕ. ПЕРСЕПТРОНОМ называется устройство, способное вычислять все предикаты, линейные относительно некоторого заданного множества ФИ частных предикатов.
Иными словами, множество предикатов фи задано, а "веса" альфа и порог тета выбираются свободно. По причинам, которые станут ясны впоследствии, о персептронах вообще можно сказать очень мало. Но налагая определенные условия, можно получить интересные свойства некоторых семейств персептронов. К их числу относятся:
1. ПЕРСЕПТРОНЫ, ОГРАНИЧЕННЫЕ ПО ДИАМЕТРУ. Для каждого предиката фи из ФИ диаметр множества точек плоскости, от которых зависит фи, не превосходит некоторой фиксированной величины.
2. ПЕРСЕПТРОНЫ ОГРАНИЧЕННОГО ПОРЯДКА. Мы будем говорить, что персептрон имеет порядок <=n, если каждый элемент из ФИ зависит не более, чем от n точек.
3. ПЕРСЕПТРОНЫ ГАМБЫ. Каждый элемент из Ф может зависеть от всех точек, но должен быть "линейной пороговой функцией" (т.е. сам должен вычисляться персептроном первого порядка, определенным в предыдущем пункте).
4. СЛУЧАЙНЫЕ ПЕРСЕПТРОНЫ. Именно эта модель наиболее подробно изучалась группой Розенблатта; предикаты фи представляют собой случайно выбранные булевы функции. Иначе говоря, случайные персептроны являются персептронами ограниченного порядка, а множество ФИ порождается случайным процессом с определенной функцией распределения.
5. ОГРАНИЧЕННЫЕ ПЕРСЕПТРОНЫ. Множество ФИ предикатов фи бесконечно, а множество значений, принимаемых коэффициентами альфа.фи, конечно.
Чтобы дать предварительное представление о том, какого рода результаты мы собираемся получать, приведем простой пример теоремы о персептронах, ограниченных по диаметру.
ТЕОРЕМА 0.8. Никакой персептрон, ограниченный по диаметру, не в состоянии определить, связаны ли друг с другом все части какой-либо геометрической фигуры! Иными словами, никакой такой персептрон не позволяет вычислить предикат пси.СВЯЗНОСТЬ.
Для доказательства рассмотрим четыре фигуры

и такой персептрон пси, ограниченный по диаметру, что его носители [Множества точек, от которых зависят предикаты фи.- Прим. ред.] имеют диаметры, как у изображенных ниже окружностей:

Ясно, что сначала задается рассматриваемый диаметр, а уже потом выбираются фигуры X.ij так, чтобы их длина равнялась нескольким диаметрам. Допустим, что такой персептрон отличает несвязные фигуры (типа X.00 и X.11) от связных (типа X.01 и X.01) в соответствии с тем, выполняется ли условие
СУММА альфа.фи*фи(X) > тета,
т.е.
СУММА[группа 1]альфа.фи*фи(X) + СУММА[группа 2]альфа.фи*фи(X) + СУММА[группа 3]альфа.фи*фи(X) >тета
(здесь мы сгруппировали предикаты фи по расположению их носителей: у левого края, у правого края, не на краях фигуры). Тогда для X.00 общая сумма должна быть отрицательной. При переходе от X.00 к X.10 меняется только сумма СУММА[группа 1], причем ее величина должна ВОЗРАСТИ настолько, чтобы общая сумма стала положительной. При переходе от X.00 к X.01 возрастает сумма СУММА[группа 2]. Но если мы перейдем от X.00 к X.11, это приведет к такому же по величине возрастанию обеих сумм СУММА[группа 1] и СУММА[группа 2] , поскольку предикаты обеих групп отметят (локально!) те же самые изменения; сумма же СУММА[группа 3] во всех случаях остается постоянной. Следовательно, общее приращение суммы при переходе X.00->X.11 будет не только положительным, но даже большим по величине, чем прежде. Отсюда следует, что персептрон, принимающий правильные решения относительно X.00, X.01 и X.10, будет вынужден признать X.11 связной фигурой, а это не так! Поэтому искомый персептрон существовать не может.
Читатели, уже знакомые с персептронами, вероятно, отметят, что приведенное доказательство (устанавливающее, что персептроны, ограниченные по диаметру, не могут распознавать связность) не использует ни теорию "обучения", ни теорию вероятностей (ни даже геометрию гиперплоскостей в n-мерном пространстве). Оно полностью определяется геометрией образов и алгеброй взвешенных предикатов. Читатели, занимающиеся физиологией, несомненно, заметят, что, поскольку все известные сейчас функции рецепторных клеток ограничены по диаметру, от живого существа требуется нечто большее, чем нейросинаптическое "суммирование" эффектов, чтобы заставить эти клетки вычислять связность. В самом деле, столь сложное зрительное восприятие может быть лишь у наиболее высокоорганизованных животных. В гл.5 мы покажем, что эта теорема распространяется также и на персептроны ограниченного порядка.
#0.9. ПРИВЛЕКАТЕЛЬНЫЕ СТОРОНЫ ПЕРСЕПТРОНОВ
Наиболее отчетливое представление о персептроне как об устройстве для распознавания образов состоит в следующем.
Машина строится на основе фиксированного набора элементов, которые вычисляют частные функции фи, получаемые обычно при помощи случайного процесса. Чтобы заставить ее распознавать определенный образ (множество входных фигур), нужно просто придать подходящее значение коэффициентам альфа.фи. Тем самым "программирование" производится удобным единообразным способом. Более того, поскольку "программы" можно задать в виде точек (альфа.1 альфа.2, ..., альфа.n) в n-мерном пространстве, им присуща метрика, позволяющая легко представить себе некоторого рода автоматическое программирование, которое люди уже склонны называть ОБУЧЕНИЕМ: к управлению параметрами подключаются устройства обратной связи, и машину "программируют", представляя в ее распоряжение последовательность входных образов и "сигнал ошибки", вызывающий изменение коэффициентов в нужном направлении, когда машина принимает неверное решение. Теоремы о сходимости персептрона (см. гл.11) определяют условия, при которых такая процедура в конечном итоге наверняка приводит к правильному набору значений коэффициентов.
#0.9.1. ЕДИНООБРАЗНОЕ ПРОГРАММИРОВАНИЕ И ОБУЧЕНИЕ. Чтобы отделить действительное от желаемого, начнем с анализа некоторых наблюдений. Пусть ФИ - множество частных предикатов, а L(ФИ) - множество предикатов, линейных относительно ФИ. Таким образом, L(ФИ) - репертуар персептрона, или множество предикатов, которые он может вычислить, когда коэффициенты альфа.фи и порог тета пробегают всевозможные значения. В принципе L(ФИ) могло бы быть множеством ВСЕХ предикатов, но это практически неосуществимо, так как тогда ФИ должно было бы быть астрономически велико. Поэтому у любого физически реализуемого персептрона репертуар ограничен. Простота и единообразие программирования оплачены дорогой ценой! Мы утверждаем, что при традиционных исследованиях персептронов эта цена определяется нереалистично. В частности, не уделяется внимания следующим решающим моментам:
1. Идея представлять классы геометрических объектов (или программы, которые определяют или распознают их) в виде классов n-мерных векторов (альфа.1, ..., альфа.n) упускает из виду геометрическую индивидуальность образов и приводит только к такой теории, возможности которой лишь немногим перекрывают простой ПОДСЧЕТ числа предикатов в L(ФИ)! Подобные представления стали традиционными у тех, кто рассуждает о распознавании образов в направлениях, подсказанных классическими статистическими теориями. В результате, кажется, мало кто замечал или подозревал, что могли бы встретиться ОТДЕЛЬНЫЕ осмысленные и интуитивно простые предикаты, не принадлежащие НИ ОДНОМУ из практически реализуемых множеств L(ФИ). Мы предложим анализ предиката пси.СВЯЗНОСТЬ, чтобы показать, сколь глубокой может оказаться эта проблема. В то же время мы хотим продемонстрировать, как некоторые предикаты, которые могли бы интуитивно показаться трудными для такого рода устройств, на самом деле МОГУТ распознаваться персептронами низкого порядка: уже предикат пси.ВЫПУКЛОСТЬ демонстрирует такую возможность.
2. Мало внимания уделялось величине, или, точнее, информационному содержанию параметров альфа.1, ..., альфа.n. Мы дадим примеры (на наш взгляд, скорее типичные, чем исключительные), в которых отношение наибольшего коэффициента к наименьшему бессмысленно велико. В таких условиях то обстоятельство, что предикаты принадлежат L(ФИ), теряет свое практическое значение. В ряде случаев информационная емкость, требуемая для запоминания альфа.1, ..., альфа.n превышает даже емкость, необходимую, чтобы запомнить весь класс фигур, определенный как один образ!
#3. С предыдущим пунктом тесно связана проблема ВРЕМЕНИ СХОДИМОСТИ процесса "обучения". Практические персептроны, по сути дела, являются устройствами с конечным числом состояний (как показано в гл.11). Поэтому не имеет смысла ссылаться на "теорему о сходимости персептрона" как на гарантию того, что процесс обучения в конечном счете найдет правильный набор значений параметров персептрона (если таковой существует), так как этого можно было бы достичь тривиальным полным перебором всех его состояний, т.е. испытывая все возможные наборы коэффициентов. Важно знать, насколько быстрее обучается персептрон по сравнению с тем временем, которое занимает абсолютно случайная процедура, или процедура полного перебора. Мы покажем, что в некоторых ситуациях, представляющих определенный геометрический интерес, время сходимости растет даже быстрее, чем показательная функция от размера множества R.
Теоретики персептрона не одиноки в своем непонимании этих предостережений. Внимательно прочитав любой типичный сборник статей по "самоорганизующимся" системам, мы обычно обогащаемся превосходными примерами дискуссий по поводу "обучающихся", или "адаптивных", машин. Этим дискуссиям недостает даже той степени строгости и формальной определенности, которую можно найти в литературе о персептронах. Сторонники подобных схем редко проводят какой бы то ни было анализ диапазона способов поведения, которым может научиться машина, и не отдают себе отчета в том, какой ценой обычно достигается легкость некоторых методов обучения: они непреднамеренно ограничивают диапазон возможных способов поведения устройства, вводя неявные допущения относительно среды, в которой оно должно работать.
Эти критические замечания не следует воспринимать как намеки на то, что мы противимся созданию машин, могущих "обучаться". Совсем наоборот! Но мы абсолютно убеждены, что значительное обучение со значительной скоростью предполагает какую-то значительную предварительную организацию. Простые обучающиеся схемы, основанные на регулировании коэффициентов, могут действительно оказаться целесообразными и полезными, когда частные функции в достаточной мере соответствуют поставленной задаче, как, например, в случае с машиной для игр в шашки, предложенной Сэмюэлем. Персептрон, у которого предикаты фи должным образом приспособлены для различения и обладают достаточно низким порядком, имеет неплохие шансы адаптивным путем улучшить свои рабочие характеристики. Наша цель - объяснить, почему достижение достаточно хорошего результата маловероятно, если предикат высокого порядка предлагается реализовать квазиуниверсальному персептрону, при выборе частных функций которого не имелась в виду какая-либо конкретная задача.
Этому тезису можно противопоставить в качестве контрпримера тот довод, что люди являются универсальными обучающимися машинами. Но наш мозг устроен в достаточной степени сложно, чтобы программироваться в намного более общем смысле, чем персептрон, а наша КУЛЬТУРА достаточно многогранна, чтобы заготовить если не действительную программу, то по крайней мере довольно сложную систему взаимодействий, управляющих процессом самопрограммирования, каким бы ни был его характер. Кроме того, нам требуется определенное время, чтобы стать универсальными учениками: ряд переходов от младенчества к интеллектуальной зрелости служит до некоторой степени подтверждением тезиса о том, что скорость приобретения новой познавательной структуры (т.е. скорость обучения) очень сильно зависит от уровня существующей познавательной структуры.
#0.9.2. ПАРАЛЛЕЛЬНОЕ ВЫЧИСЛЕНИЕ. Персептрон понимался как параллельно действующее устройство в том физическом смысле, что частные предикаты вычисляются одновременно. (С формальной точки зрения важно, что они вычисляются независимо один от другого). Это оплачивается тем, что необходимо вычислять ВСЕ фи.i, хотя лишь небольшая их часть может фактически иметь отношение к каждому конкретному окончательному решению. ОБЩЕЕ КОЛИЧЕСТВО вычислений может намного превысить то количество, которое должно быть проведено при хорошо организованном последовательном процессе (использующем те же самые фи), когда решение о том, что вычислять далее, выносится на основе результата предыдущего вычисления. Поэтому в каждом конкретном случае выбор между параллельным и последовательным методами должен основываться на сопоставлении выигрыша от сокращения (общего затраченного) времени с затратами на вводимые добавочные вычисления.
Даже предикаты низкого порядка могут потребовать большого количества ненужных вычислений, без которых можно было бы обойтись при последовательном процессе. Соответствующий объем необходимого оборудования может иной раз остаться в пределах физической осуществимости, в особенности если допустима невысокая точность вычислений. Совершенно иное положение в случае персептронов высокого порядка. Поучительным примером служит предикат пси.СВЯЗНОСТЬ. Как показано в гл.5, для вычисления этого предиката на тороидальной сетчатке размером 100*100 ЛЮБОМУ персептрону ТРЕБУЮТСЯ частные функции, каждая из которых просматривает многие сотни точек! При этом понятие "локальной" функции становится почти неуместным: частные функции сами оказываются глобальными. Кроме того, фантастическое количество возможных частных функций с такими большими носителями гасит любую надежду на то, что полученное путем случайного выбора умеренно большое множество таких функций окажется достаточно плотным, чтобы охватить соответствующее пространство функций. Чтобы уточнить эту мысль, покажем, что для определенных предикатов и классов частных функций количество частных функций, которое нужно использовать (не говоря уже об аппаратуре, реализующей их коэффициенты), непременно превысит границы физической осуществимости.
Вывод, который необходимо сделать, состоит в том, что конкретную схему параллельного вычисления нельзя разумно оценить, если нет способа определить, в какой мере решаемая задача разлагается на локальные и глобальные компоненты. Отсутствие ОБЩЕЙ теории, указывающей, что считать глобальным и что - локальным, не может служить оправданием тому, чтобы уклоняться от решения этой задачи в конкретных случаях. В этой книге мы покажем, что для ограниченного, но важного класса задач разработка такой теории не представляет непреодолимых трудностей.
#0.9.3. ПРИМЕНЕНИЕ ПРОСТЫХ АНАЛОГОВЫХ УСТРОЙСТВ. Персептрон привлекает к себе внимание многих исследователей отчасти потому, что для вычисления линейных пороговых функций можно применить очень простые физические устройства - "аналоговые вычислительные машины". Принято считать, что полезность этой схемы ограничена тем, что среди ВСЕХ логических функций линейные пороговые функции встречаются редко. Однако не уделялось почти никакого внимания тому, что множество ПРАКТИЧЕСКИ осуществимых линейных функций может оказаться еще уже. Чтобы пояснить указанную проблему, мы вычислим (в гл.10) величины и пределы изменения коэффициентов линейных представлений отдельных предикатов. Мы покажем, что некоторые отношения коэффициентов могут расти быстрее, чем показательная функция числа точек, различаемых в R. Из этого следует, что для "больших" входных множеств (скажем, для множеств R, содержащих более 20 точек) нельзя создать простое аналоговое запоминающее устройство с информационной емкостью, достаточной для хранения всего набора коэффициентов!
Чтобы избежать неверного толкования, нам, быть может, следовало бы повторить те оговорки, которые мы сделали, критикуя персептрон как модель "обучающихся устройств". Мы ни в коей мере не сомневаемся в том, что аналоговые устройства такого рода играют свою роль в распознавании образов. Но МЫ НЕ ВИДИМ, КАКУЮ ПОЛЬЗУ МОЖНО БЫЛО БЫ ИЗВЛЕЧЬ ИЗ ЭКСПЕРИМЕНТОВ, НЕ УЧИТЫВАЮЩИХ ТЕ ОГРАНИЧИВАЮЩИЕ ФАКТОРЫ, КОТОРЫЕ ВСТУПАЮТ В СВОИ ПРАВА, КАК ТОЛЬКО МАСШТАБЫ МАЛОЙ МОДЕЛИ ВОЗРАСТАЮТ ДО ПРАКТИЧЕСКИХ РАЗМЕРОВ.
#0.9.4. МОДЕЛИ РАБОТЫ МОЗГА И ГЕШТАЛЬТПСИХОЛОГИЯ. Популярность персептрона как модели разумной универсальной обучающейся машины объясняется, по-видимому, существованием распространенного представления о том, что мозг является довольно слабо организованной системой сравнительно простых устройств, связанных случайным образом. Это представление, в свою очередь, частично основано на наших первоначальных впечатлениях от тех запутанных структур, которые наблюдаются при микроскопическом исследовании анатомии мозга (и, вероятно, также на наших все еще хаотических представлениях о психологических механизмах).
Так или иначе, мы представляем себе систему сравнительно простых элементов, соединенных друг с другом случайным способом, в которой может регулироваться степень легкости прохождения сигналов через соединения. Когда машина в чем-либо ведет себя плохо, мы стремимся "обучить" ее не поступать так опять, ослабляя соединения, участвовавшие в данном действии; вероятно, для поощрения нравящегося нам поведения мы станем делать обратное.
Машина типа "персептрон" - это один из особенно простых вариантов описанного выше более широкого класса систем; некоторые другие варианты уже также изучались экспериментально.
Мистический туман, окутывающий такого рода машины, частично держится на том, что при обучении подобной машины запоминаемая информация не локализуется в каком-то определенном месте, а, напротив, "распределяется по всей схеме машины". В первой половине двадцатого века эксперименты, не подтвердившие представлений девятнадцатого века о размещении памяти (или большинства других "способностей" человека) в сугубо локальных областях мозга, вызвали глубокое разочарование. Как бы точно ни интерпретировать эти отнюдь не решающие эксперименты, они, вне всякого сомнения, привели к поиску концепций, основанных на нелокальных функциях, реализуемых машинами. Этот поиск не увенчался заметными успехами. Были выдвинуты несколько схем, основанных на крупномасштабных полях, или на "интерференционных картинах" в глобальных волновых колебаниях, но они не привели к правдоподобным теориям. (Ближе к концу этой эпохи Хебб [1949] выдвинул более сложное и значительно менее глобальное понятие "клеточного ансамбля". Это понятие оказалось более плодотворным для теоретических построений. Хотя оно и не привело к какой-либо окончательной модели, его популярность с каждым днем возрастает). Здесь, однако, мы стремимся не столько оценить эти теории, сколько обрисовать тот интеллектуальный фон, на котором была воздвигнута идея персептрона. На этом фоне схемы Розенблатта [1958] быстро укоренились, и в скором времени буквально сотни групп, больших и малых, стали проводить опыты с этой моделью под видом либо "обучающейся машины", либо "адаптивной", т.е. "самоорганизующейся" системы, либо системы "автоматического управления".
Результаты этих сотен проектов и опытов, как правило, разочаровывали, а объяснения не убеждали. Машины обычно хорошо вели себя на очень простых задачах, но весьма быстро сдавали позиции, как только порученные им задания становились сложнее. При увеличении размеров и времени работы системы положение обычно почти не менялось к лучшему. Возникло подозрение, что даже тогда, когда обнаруживался некоторый успех, это достигалось за счет сравнительно небольшой части схемы, а не благодаря действительно глобальной деятельности системы в целом. Обоих авторов этой книги (сначала независимо друг от друга, а затем вместе) влекло в некотором смысле "врачебное" стремление: рассеять опасные призраки "холистских" (holistic), или "гештальтных" ложных представлений, угрожавших объявиться в области техники и искусственного интеллекта, как прежде в биологии и психологии. Поэтому и по многим другим, более практическим причинам, а также в теоретических целях мы стремились выяснить что-либо относительно возможностей персептронов и их ограничений.
И только впоследствии, когда теория была разработана, мы поняли, что знать подобные машины важно независимо от того, получит ли система практическое применение в конкретных ситуациях! Дело в том, что аналогичные задачи стали камнем преткновения на пути развития самой науки о вычислительных машинах.
Как уже отмечалось, мы недостаточно хорошо знаем, за счет чего некоторые алгоритмические процедуры становятся "по существу" последовательными и насколько (или, скорее, какой ценой) можно ускорить вычисления при помощи многочисленных перекрывающихся вычислений с использованием более крупных и более действенных запоминающих устройств.
#0.10. ОБЩИЙ ПЛАН КНИГИ
Теория персептронов естественным образом делится на три части. В части I изучаются весьма общие свойства семейств линейных предикатов. Теоремы в этой части относятся ко всем персептронам, независимо от вида рассматриваемых образов, так что здесь представлена скорее алгебраическая, чем геометрическая теория персептронов. В части II мы более внимательно рассматриваем интересные геометрические образы и получаем более четкие, но, естественно, менее общие теоремы о геометрических возможностях наших машин. В части III исследуется целый ряд вопросов, сконцентрированных вокруг потенциальных способностей персептронов как практических устройств для распознавания образов и обучения. В последней главе прослеживаются некоторые исторические пути развития этих идей и предлагаются вероятные направления дальнейших исследований.
Последний раз редактировалось: Gudleifr (Вс Июл 02, 2023 12:33 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
I. АЛГЕБРАИЧЕСКАЯ ТЕОРИЯ ЛИНЕЙНЫХ ПАРАЛЛЕЛЬНЫХ ПРЕДИКАТОВ
ПРЕДИСЛОВИЕ К ЧАСТИ I
В части I (гл.1-4) содержится ряд чисто алгебраических определений и общих теорем, которые впоследствии используются в части II. Прочитать этот материал будет значительно легче, если уже предварительно составить себе представление о роли, которую призван сыграть этот математический аппарат. С этой целью мы обрисуем в общих чертах, как будет доказана (в гл. 3) следующая теорема:
ТЕОРЕМА 3.1 (гл.3), НЕФОРМАЛЬНЫЙ ВАРИАНТ. Пусть сетчатка R содержит конечное число точек. Тогда персептрон СУММА альфа.фи*фи(X) >Q не может определить истинность или ложность предиката "число точек в X нечетно", если среди его частных предикатов фи не найдется ни одного, зависящего от всех точек сетчатки R.
Поэтому невозможно наложить никаких ограничений на ПОРЯДКИ персептронов, вычисляющих этот предикат для произвольно больших сетчаток. Чтобы его вычислить, в персептроне должен быть хотя бы один предикат фи, осматривающий всю картину в целом! Доказательство теоремы проводится в несколько этапов.
#1-Й ЭТАП. В #1.1-1.4 более точно определяются понятия "персептрон", "порядок" и др. и показывается, что некоторые слова в определениях можно изменить без каких-либо серьезных последствий.
#2-Й ЭТАП. В #1.4 определяются исключительно простые функции фи, называемые "масками". Для каждого подмножества A сетчатки R маска фи.A(X) полагается равной 1, если X содержит, или "покрывает", все подмножество A, и равной 0 в противном случае. Затем доказывается простая, но важная теорема (#1.5) о том, что если для ЛЮБОГО множества функций фи порядок некоторого предиката не превышает k (см. #1.3), то существует эквивалентный этому предикату персептрон, который использует только маски размера не выше k (см. #0.2).
#3-Й ЭТАП. Чтобы глубже понять свойство четности-нечетности, мы задаемся вопросом: КАКИЕ ПРЕОБРАЗОВАНИЯ ВХОДНОГО ПРОСТРАНСТВА R НЕ ВЛИЯЮТ НА ЭТО СВОЙСТВО? Другими словами, нас интересует группа преобразований фигуры, не меняющая четность. Подобный подход к задаче может показаться экзотическим, но поскольку он, по-видимому, необходим для решения более трудных задач, которыми мы займемся позже, полезно с самого начала привыкнуть к нему в этой простой ситуации. В данном случае группой преобразований служит группа всех перестановок на сетчатке R - множество ВСЕХ перегруппировок ее точек.
#4-Й ЭТАП. В гл.2 мы покажем, как использовать эту группу, чтобы упростить персептрон. С помощью ТЕОРЕМЫ ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП (#2.3) мы придем к выводу, что в персептроне, определяющем четность, ВСЕМ МАСКАМ, У КОТОРЫХ НОСИТЕЛИ ОДИНАКОВЫ ПО РАЗМЕРУ (т.е. тем, которые просматривают одно и то же число точек), МОЖНО ПРИСВОИТЬ ОДИНАКОВЫЕ КОЭФФИЦИЕНТЫ. Обозначим через бета.j вес, приписанный всем маскам, у которых размер носителя равен j.
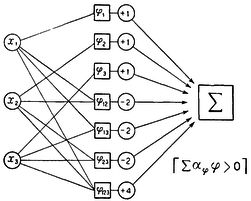
Инвариантные относительно группы коэффициенты предиката фи.ЧЕТНОСТЬ при |R|=3.
#5-Й ЭТАП. Затем мы докажем (в #3.1), что персептрон, определяющий четность, можно записать в виде
СУММА[0..k]бета.j*C(|X|.j)>0
где |X| - число точек множества X, k - наибольший размер носителя, C(|X|.j) - число подмножеств множества X, состоящих из j
элементов [Эта величина зависит от X и играет роль функции фи.j(X).- Прим. перев.].
#6-Й ЭТАП. Так как
C(n.k) = n!/(j!(n-j)!) = 1/j!*(n+1-1)(n+1-2)*(n+1-j),
т.е. C(n.j) можно представить в виде произведения j линейных членов, то это - многочлен от n степени j. Поэтому наш предикат можно записать в виде
P.k(|X|)>0,
где P.k - многочлен от |X|, алгебраическая степень которого не превышает k. Если |X| - нечетное число, то P.k(|J|)>0, а если |X| - четное число, то P.k(|X|)<=0. Следовательно, на отрезке 0<=|X|<=P многочлен P.k должен менять свой знак |R|-1 раз. Но для этого степень многочлена должна быть не меньше |R|, откуда следует, что k>=R. Доказательство на этом заканчивается (в точности, как в #3.1).

Приведенные рассуждения иллюстрируют, как в нашей теории действует алгебра. Для наиболее трудных теорем о связности из гл.5 нам потребуется что-то еще, кроме алгебры и теории групп. В гл.4 мы развиваем понятия геометрии алгебраических степеней, чтобы показать, что для реализации некоторых удивительно простых предикатов требуются персептроны неограниченного порядка Но на самом деле результаты гл.4 в дальнейшем не используются, и эту главу при первом чтении можно опустить.
За более простыми, но также характерными результатами читатель может обратиться непосредственно к гл.8, которая почти самостоятельна, так как не нуждается в алгебраической теории.
ГЛАВА 1. ТЕОРИЯ ЛИНЕЙНЫХ БУЛЕВЫХ НЕРАВЕНСТВ
#1.0
В этой главе изучается теория линейного представления предикатов. Мы обсудим свойства функций, определенных на абстрактном множестве точек, не обладающем никакой дополнительной математической структурой. Таким образом, эту главу можно рассматривать как развитие обычной булевой алгебры. Доказанные здесь теоремы мы применим потом к множествам, обладающим определенными геометрическими или топологическими свойствами, например к евклидовой плоскости. Итак, мы начнем с обсуждения множеств вообще, а потом рассмотрим хорошо знакомые объекты, такие, как "треугольники".
Начнем с предикатов, определенных для фиксированного базисного пространства R. В #1.1-1.5 мы будем предполагать, что R уже выбрано. В дальнейшем мы займемся "предикатами", определенными более широко: они либо вовсе не будут зависеть от выбора базисного пространства, либо не будут зависеть от выбора пространства из некоторого большого семейства пространств. Например, предикат
Множество X не пусто
может относиться к любому пространству R. Предикат
Множество X связно
имеет смысл, когда речь идет о множестве в пространстве, в котором существует понятие близости точек. Для такого более общего понятия "предиката" мы введем в #1.6 термин "предикатная схема". Главная наша цель состоит в том, чтобы дать общее определение ПОРЯДКА ПРЕДИКАТА (#1.5) и определение КОНЕЧНОГО ПОРЯДКА ПРЕДИКАТНОЙ СХЕМЫ (#1.6). В последних главах мы будем свободно использовать термин "предикат", подразумевая под этим также и предикатные схемы, а в #1.7 попытаемся сделать эти определения более точными и формальными. Однако советуем читателям не беспокоиться об этом до тех пор, пока главные результаты не станут интуитивно понятными.
#1.1. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ
Буква R будет обозначать произвольное множество точек. Для обозначения отдельных точек множества R мы будем обычно использовать строчные буквы a, b, c, ..., x, y, z, а для обозначения подмножества множества R - прописные A, B, C, ..., X, Y, Z. Переменные точки и подмножества будем обозначать через x и X.
Часто мы будем интересоваться особыми "семействами" подмножеств и обозначать их СЛОВАМИ, записанными прописными буквами. Таким образом, ОКРУЖНОСТЬ означает совокупность подмножеств множества R, образующих замкнутые окружности (как в #0.5). Абстрактное семейство подмножеств мы будем обозначать буквой F.
Естественно связывать с любым семейством множеств F предикат пси.F(X), принимающий значение истина тогда и только тогда, когда X принадлежит семейству F. Например, предикат пси.ВЫПУКЛОСТЬ принимает значение истина или ложь в зависимости от того, выпукло ли множество X. Разумеется, предикаты пси.ОКРУЖНОСТЬ и пси.ВЫПУКЛОСТЬ имеют смысл только для неабстрактных множеств R, в которых можно ввести эти геометрические понятия. Греческими буквами фи и пси всегда будут обозначаться предикаты. Буква пси обычно будет обозначать наиболее важный предикат, а через фи будут обозначаться предикаты из большого семейства легко вычисляемых функций; это семейство будет обозначаться буквой ФИ.
ПРЕДИКАТ - это функция (подмножеств множества R), принимающая лишь два значения. Иногда этими двумя значениями будут ИСТИНА и ЛОЖЬ, иногда полезно считать их равными 1 и 0. Так как существует некоторая опасность спутать эти два вида значений предикатов, то во избежание разнотолков вводится обозначение [пси.(X)]. Уголки всегда означают, что употребляются значения 1 и 0. Это дает возможность использовать значения предикатов как обыкновенные числа, а в нашей теории это важно, поскольку мы должны объединять полученные от предикатов данные (о чем уже говорилось в гл.0). Внутри уголков может стоять любое математическое утверждение. Зная, например, что 3 меньше 5, а 1 меньше 2, мы можем написать
[3<5] = 1,
[3<5]+[1<2] = 2,
[3<5]+[5<3] = 1
и даже
[3<[5=1]] = 0,
4*[3<5]+2*[6<2] = 4.
Иногда удобно считать, что точки множества R занумерованы в последовательность x.1, x.2, ..., x.i, ... В таком случае многие предикаты можно выразить в терминах традиционных представлений булевой алгебры. Например, два выражения
x.iVx.j, (x.i принадлежит X или x.j принадлежит X)
равнозначны, а именно они равны единице, если хотя бы одна из точек x.i и x.j принадлежит X, и равны нулю, если ни x.i, ни x.j не принадлежат X. Иными словами, выделение подмножества X из множества R состоит в присвоении значений 1 и 0 точкам x.i в зависимости от того, принадлежит ли i-я точка множеству X, так что x.i употребляется в двух смыслах: и для обозначения i-й точки, и для обозначения функции множества [x.i принадлежит X]. Это можно использовать для записи предикатов в АРИФМЕТИЧЕСКОЙ форме вместо ЛОГИЧЕСКОЙ, т.е. писать
[x.1+x.2+x.3>0] вместо х.1Vx.2Vx.3
или даже
[2*x.1*x.2-x.1-x.2>-1] вместо x.1==x.2,
где x.1==x.2 - предикат, принимающий значение ИСТИНА, когда либо обе точки x.1 и x.2 принадлежат X, либо ни одна из них не принадлежит X.
Нам понадобится в дальнейшем уметь выражать представление о том, что функция фи может зависеть только от какого-то определенного подмножества множества R. Обозначим такое подмножество через S(фи). Формально S(фи) - это такое наименьшее подмножество S множества R, что для каждого подмножества X множества R
фи(X) = фи(X пересечение S),
где (X пересечение S) - множество точек, принадлежащих и X, и S. Назовем S(фи) НОСИТЕЛЕМ предиката фи.
Если пространство R бесконечно, то для некоторых интересных предикатов S(ab) определить нельзя. Рассмотрим, например, предикат
фи(X) = [X содержит бесконечное множество точек]
Истинность предиката фи(X) можно было бы установить просмотром точек множества X, лежащих в любом множестве S, которое содержит все, кроме конечного числа точек множества R. Но "наименьшего" такого множества не существует!
#1.2. ФУНКЦИИ, ЛИНЕЙНЫЕ ОТНОСИТЕЛЬНО КЛАССА ПРЕДИКАТОВ
Пусть ФИ - семейство предикатов, определенных на множестве R. Мы говорим, что
кси - ЛИНЕЙНАЯ ПОРОГОВАЯ ФУНКЦИЯ относительно ФИ,
если существуют число тета и множество чисел альфа(фи), по одному на каждый предикат фи из ФИ, для которых
пси(X)=[СУММА[фи из ФИ]альфа(Фи)*фи(X)>тета].
Иными словами, значением пси(X) будет ИСТИНА, когда выполняется неравенство внутри уголков []. Часто записывают это менее формально в виде
пси = СУММА альфа(фи)*фи > тета
или даже в виде
пси = СУММА альфа.фи*фи > тета
Ради симметрии в класс линейных пороговых функций вместе с предикатом пси включим его отрицание
~пси(X) = СУММА альфа(фи)*фи <= тета
Множество всех предикатов, которое при заданном ФИ можно определить таким способом (т.е. выбором различных значений порога тета и чисел альфа), обозначим через L(ФИ).
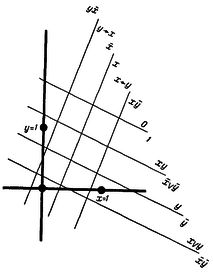
Для двухточечного пространства R={x,y} класс функций L({x,y}), линейных относительно одноточечных предикатов, включает 14 из 16=2**2**2 возможных булевых функций. Для большого числа точек доля функций, линейных относительно одноточечных предикатов, очень быстро снижается
#1.2.1. ДРУГИЕ ВОЗМОЖНЫЕ ОПРЕДЕЛЕНИЯ МНОЖЕСТВА L(ФИ). Так как определение множества L(ФИ) слишком общо для последующего изложения, его стоит пересмотреть и выяснить, что в этом определении существенно и что произвольно. Мы предлагаем несколько возможных изменений определения, не затрагивающих в значительной степени его характер. Действительно, для конечного пространства R (наиболее важный случай) все предлагаемые альтернативы приводят к строго эквивалентным определениям. В случае бесконечных пространств R некоторые определения приводят к различным смысловым значениям для L(ФИ), но не в такой мере, чтобы сколько-нибудь повлиять на наши последующие рассуждения.
ПРЕДЛОЖЕНИЕ. Следующие изменения в формальном определении L(ФИ) не затрагивают определяемые классы предикатов:
(1) Если допустить, что ФИ содержит постоянную функцию I(X)==1, то тета можно принять равным нулю.
(2) Знак неравенства > можно заменить на <, >= или <=.
(3) Если R конечно, то порог тета и все числа альфа(фи) можно выбрать целыми.
(4) Утверждения 1-3 можно применять независимо друг от друга.
Очевидно, что это предложение справедливо. Доказательство мы приведем главным образом для того, чтобы помочь читателям, желающим потренироваться в использовании наших обозначений.
ДОКАЗАТЕЛЬСТВО. (1) Положим альфа'(I) = альфа(I)-тета и альфа'(фи)=альфа(фи) для остальных фи. Тогда
[СУММА альфа(фи)*фи(X) > тета] = [СУММА альфа'(фи)*фи(X) > 0].
(2) Пусть альфа'(фи)=-альфа(фи) и тета'=тета. Тогда
[СУММА альфа(фи)*фи(X) < тета] = [СУММА альфа'(фи)*фи(X) > тета']
Утверждения об остальных заменах знака неравенства получатся, если заменить все предикаты их отрицаниями.
(3) Если R конечно, то и ФИ конечно, и можно допустить, что не существует множества X, для которого
СУММА альфа(фи)*фи(X) = тета.
В самом деле, если такое множество X существует, то положение можно исправить, заменив тета на тета+дельта, где дельта меньше, чем наименьшее ненулевое значение величины [СУММА альфа(фи)*фи(X) - тета] Предположим сначала, что все альфа(фи) - рациональные числа. Обозначим через D произведение всех их знаменателей и положим
альфа'(фи) = D*альфа(фи), тета' = D*тета.
Тогда все числа альфа' целые, и ясно, что
[СУММА альфа(фи)*фи(X) > тета] = [СУММА альфа'(фи)*фи(X) = тета'].
для всякого X. Предположим теперь, что среди чисел множества {альфа(фи)} есть иррациональные. Заменим каждое альфа(фи) некоторым рациональным числом альфа'(фи) из интервала
альфа(фи) < альфа'(фи) < альфа(фи) + дельта/2**2**|R|,
где величина дельта определена выше. Эта замена не может изменить сумму СУММА альфа(фи)*фи(X) больше чем на дельта, поэтому она не может повлиять на значение [СУММА альфа(фи)*фи(X) > тета], ибо существует самое большее 2**2**|R| различных предикатов фи.
#1.3. ПОНЯТИЕ ПОРЯДКА
Предикаты, носители которых невелики, чересчур локальны, а потому и не очень интересны сами по себе. Нас главным образом занимают предикаты, носителями которых служит все пространство R, но которые можно представить в виде линейных пороговых комбинаций предикатов с малыми носителями. Простой пример:
пси(X) = [X - непустое множество].
Ясно, что S(фи)=R. С другой стороны, если в качестве ФИ взять множество предикатов вида фи.p(X)=[р принадлежит X], то |S(фи.p)|=1 для всех фи из ФИ и пси(X) = [СУММА фи.p(X) > 0].
Эти два утверждения позволяют сказать, что ПОРЯДОК предиката пси равен 1. В общем случае порядок предиката пси есть наименьшее число k, для которого можно найти множество ФИ предикатов, удовлетворяющих условиям:
|S(фи)|<=k для всех фи из ФИ,
пси принадлежит L(ФИ).
Следует отметить, что порядок предиката пси является свойством самого предиката пси и не имеет отношения к какому-либо конкретному множеству ФИ. Именно это делает его важным "абсолютным" понятием. Те, кто знаком с соответствующей литературой, легко опознают в предикатах порядка 1 так называемые "линейные пороговые функции".
#1.4. МАСКИ И ДРУГИЕ ПРИМЕРЫ ЛИНЕЙНОГО ПРЕДСТАВЛЕНИЯ
Особую роль будут играть предикаты вида
фи.A(X)=[все элементы множества А принадлежат X]=[A включается в X].
В общепринятых обозначениях булевой алгебры эти предикаты оказываются конъюнкциями: если A={y.1, ..., y.n}, то фи.A(X)=(y.1 и y.2 и ... и y.n), или, как обычно пишут, фи.A(X)=y.1*y.2*...*y.n.
Назовем фи.A МАСКОЙ множества A. В частности, постоянный предикат I(X) служит маской пустого множества, а предикаты фи.p предыдущего параграфа - масками одноточечных множеств.

ПРЕДЛОЖЕНИЕ. Все маски имеют порядок 1.
ДОКАЗАТЕЛЬСТВО. Пусть A - любое конечное множество, состоящее из |A| точек. Для каждой точки x из A определим фи.x(X) как предикат [x принадлежит X]. Тогда
фи.A(X) = [СУММА[x из A]фи.x(X)>|A|]
ПРИМЕР 1. Среди 16 булевых функций двух переменных порядок 1 имеют все, кроме функции НЕРАВНОЗНАЧНОСТИ (x исключающее или y) и ее дополнения - функции ЛОГИЧЕСКОЙ ЭКВИВАЛЕНТНОСТИ x==y, порядок которых равен 2:
(x исключающее или y) = [x*~y+~x*y>0], x==y = [x*y+~x*~y>0]
где, например, x*~y - предикат с носителем, состоящим из двух точек, и его значением будет истина только тогда, когда x принадлежит X, а y нет.
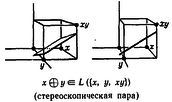
Можно считать, что линейное неравенство определяет поверхность, разделяющую точки пространства на два класса, и тем самым задает предикат. Мы рекомендуем воздержаться от подобного представления до части III.
(ЗАДАЧА: докажите, что порядок функции (x исключающее или y) не равен 1!) Вот еще примеры из булевой алгебры:
x импликация y = [~хVy] = [y-x>-1], ~x = [-x > -1].
Порядок любой маски равен 1:
(x и y и z) = [x+y+z>2],
то же справедливо и для любой дизъюнкции:
xVyVz = [x+y+z>0].
ПРИМЕР 2. Функцию x1==x2 можно представить в виде линейной комбинации масок:
x.1*x.2V~x.1*~x.2 = [x.1*x2+(1-x.1)(1-x.2)>0] =
= [2*x.1*x.2-x.1-x.2>-1].
Доказательство того, что порядок неравнозначности и логической эквивалентности не равен 1, мы приведем в #2.1.
ПРИМЕР 3. Пусть M - целое число, 0<=M<=|R|. Тогда "считающий предикат" фи.M, или [|X|=M], который определяет, что X СОДЕРЖИТ РОВНО М ТОЧЕК, имеет порядок 2.
ДОКАЗАТЕЛЬСТВО. Рассмотрим представление
[(2M-1)СУММА[все i]x.i + (-2)СУММА[i<j]x.i*x.j >= M**2].
Для любой фигуры X существует |X| членов x.i и 1/2*|X|*(|X|-1) членов x.1*y.1, значение которых равно 1. В таком случае предикатом служит выражение
[(2M-1)*|X|-|X|*(|X|-1)-M**2>=0]=[(|X|-M)**2<=0],
а единственным значением |X|, при котором это выражение истинно, является |X|=М. Заметим, что, повышая порог, можно получить предикат, истинный не для единственного значения |X|, а для значений, заполняющих некоторый интервал.
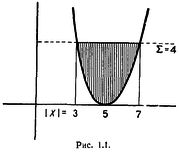
Мы уже показали, что порядок "считающего предиката" не больше 2; из теоремы 2.4 будет следовать, что он не равен 1. Заметим, что в линейной форме считающего предиката |R| в явном виде не содержится. Следовательно, этот предикат подходит также и для бесконечного пространства R.
ПРИМЕР 4. Порядок предикатов [|X|>=M] и [||X|<=M] равен 1, так как их можно представить в виде [СУММА x.i >= M] и [СУММА x.i <= M].
#1.5. ТЕОРЕМА О ПОЛОЖИТЕЛЬНОЙ НОРМАЛЬНОЙ ФОРМЕ
Порядок функции можно определить, представляя ее как линейную пороговую функцию относительно множества масок (теорема 1.5.3). Чтобы сделать это, докажем сначала следующую теорему.
ТЕОРЕМА 1.5.1. Каждый предикат пси является линейной пороговой функцией относительно множества всех масок, т.е. пси принадлежит L(вce маски).
ДОКАЗАТЕЛЬСТВО. Любую булеву функцию пси(x.1, ..., x.n) можно записать в дизъюнктивной нормальной форме
C.1(X) V C.2(X) V ... V C.p(X),
где Ci(X) - произведение (конъюнкция)
z.1*z.2*...*z.n
в котором каждое z есть x.i или ~x.i. Так как для любого X истинным может быть не более одного Cj(X), то, используя арифметическую сумму, можно переписать пси в виде
C.1(X)+C.2(X)+...+C.p(X).
Далее, к любому произведению, содержащему отрицание какой-либо буквы, можно применить следующую формулу: пусть B# и A# означают любые цепочки букв, тогда
B#*~x.i*A# = B#(1-x.i)A# = B#A#-B#*x.i*A#.
Если и дальше применять эту формулу, то можно уничтожить все отрицания, не увеличивая длины произведения.
Избавившись от отрицаний и сгруппировав подобные члены, мы получим ПОЛОЖИТЕЛЬНУЮ НОРМАЛЬНУЮ ФОРМУ
пси(X) = СУММА альфа.i*фи.i(X),
где каждый предикат фи, является маской, а каждое число альфа.i - целое. Поскольку сумма СУММА альфа.i*фи.i(X) равна нулю или единице, можно записать
пси(X) = [СУММА альфа.i*фи.i(X) > 0].
ПРИМЕР. [Сумма x.1+x.2+x.3 нечетна] = x.1+x.2+х.3-2*x.1*x.2-2*x.2*x.3-2*x.3*x.1+4*x.1*x.2*x.3.
ТЕОРЕМА 1.5.2 (факультативно). Положительная нормальная форма единственна.
Доказательство. Пусть {фи.i} - множество масок, а {гамма.i} - множество чисел, не равных нулю. Возьмем k, для которого S(фи.k) минимально, т.е. не существует такого j!=k, что S(фи.j) включается в S(фи.k). Тогда
фи.k(S(фи.k))=1,
фи.j(S(фи.k))=0, j!=k.
Отсюда следует, что сумма СУММА гамма.i*фи.i(X) не равна тождественно нулю, так как при X=S(фи.k) она принимает значение гамма.k.
Если теперь СУММА альфа.i*фи.i(X) = СУММА бета.i*фи.i(X) для всякого X, то СУММА(альфа.i-бета.i)*фи.i(X) = 0 для всякого X. Но
СУММА[все i](альфа.i-бета.i)*фи.i(X) = СУММА[0!=(альфа.i-бета.i)](альфа.i-бета.i)*фи.i(X),
откуда следует, что альфа.i=бета.i для всех i. Это доказывает единственность коэффициентов положительной нормальной формы предиката пси. Заметим, что положительная нормальная форма, будучи обычной арифметической суммой, всегда имеет нулевое или единичное значение и, таким образом, не нуждается в применении символа [ ]. предназначенного для интерпретации справедливости неравенства как предиката.
ТЕОРЕМА 1.5.3. Предикат пси имеет порядок k тогда и только тогда, когда k есть наименьшее число, для которого существует множество ФИ масок, удовлетворяющих условиям
||S(фи)| <= k для всех фи из ФИ,
пси принадлежит L(ФИ).
ДОКАЗАТЕЛЬСТВО. В выражении пси=[СУММА альфа.i*фи.i > 0] каждую функцию фи.i - заменяем ее положительной нормальной формой. Если |S(фи.i)| <= k, то аналогичное неравенство верно также и для масок, входящих в положительную нормальную форму [Для доказательства теоремы достаточно доказать два утверждения: а) всякий предикат порядка k можно представить в виде линейной комбинации таких масок фи, что |S(фи)| <= k; б) если для некоторого предиката пси число k является наименьшим, при котором существует множество ФИ масок фи, удовлетворяющих условиям, указанным в формулировке теоремы, то порядок предиката пси равен k. Утверждение а) доказано авторами. Для доказательства б) заметим, что порядок предиката пси не может быть выше указанного k по самому определению порядка. Если бы он был равен k'<k, то в силу а) существовала бы линейная комбинация масок, для которой |S(фи)| <= k' < k, что противоречит условию минимальности k. Теорема доказана.- Прим. ред.]
ПРИМЕР. Порядок "булевой формы" не превышает степени ее дизъюнктивной нормальной формы. Например,
СУММА альфа.ijk*x.i*x.j*~x.k = СУММА альфа.ijk*x.i*x.j - СУММА альфа.ijk*x.i*x.j*x.k
отсюда видно, как исключить отрицание, не повышая порядка. Эта частная форма порядка 3 появится позже (#6.3), в персептроне, распознающем выпуклые фигуры.
Естественно поинтересоваться порядком предикатов, которые представляют собой булевы функции других предикатов. Обнадеживающий результат дает
ТЕОРЕМА 1.5.4. Если предикат пси.1 имеет порядок П.1, а предикат пси.2 имеет порядок П.2, то порядки предикатов (пси.1 исключающее или пси.2) и пси.1==пси.2 не превышают П.1+П.2.
ДОКАЗАТЕЛЬСТВО. Пусть пси.1=[СУММА альфа.i*фи.1 > 0], пси.2=[СУММА альфа'.i*фи.1 > 0]. Предположим, что коэффициенты выбраны так, что суммы внутри уголков никогда не равны нулю. Тогда
пси.1==пси.2 = [(СУММА альфа.i*фи.i)(СУММА альфа'.i*фи.1i) > 0] = [СУММА[i,j] (альфа.i*альфа'.j)*фи.i*фи.j) > 0],
причем
|S(фи.i*фи.j)| <= |S(фи.i)|+|S(фи.j)|.
Утверждение о предикате (пси.1 исключающее или пси.2) следует из равенства
[пси.1 исключающее или пси.2] = 1 - [пси.1==пси.2].
ПРИМЕР. На основании равенства
пси.M(X) = [[M >= |X|]==[|X| >= M]]
заключаем, что порядок предиката пси.M не превышает 2. Это дает еще один способ получения результата, о котором говорилось в #1.4 (пример 3).
ВОПРОС: Что можно сказать о порядке предикатов [пси.1 и пси.2] и [пси.1 V пси.2]? Если принять во внимание простой результат теоремы 1.5.4, то ответ может показаться удивительным. В гл.4 мы докажем, что для любого порядка n можно найти такую пару предикатов пси.1 и пси.2 ПЕРВОГО ПОРЯДКА, что порядок предикатов [пси.1 и пси.2] и [пси.1 V пси.2] превышает n. В самом деле, пусть R = (A объединение В объединение С), где А, В, С - большие непересекающиеся подмножества множества R. Тогда каждый из предикатов пси.1 = [|X пересечение A| > |X пересечение C|] и [|X пересечение B| > |X пересечение C|] и ИМЕЕТ ПОРЯДОК 1, так как их можно представить в виде
[СУММА[x.i из A]x.i > СУММА[x.i из C]x.i] и [СУММА[x.i из B]x.i > СУММА[x.i из C]x.i].
В гл.4 мы увидим, что предикаты [пси.1 и пси.2] и [пси.1 V пси.2] не имеют даже КОНЕЧНОГО ПОРЯДКА в том смысле, как это будет описано в #1.6.
#1.6. ПРЕДИКАТЫ КОНЕЧНОГО ПОРЯДКА
Строго говоря, предикат определяется для конкретного множества R, и поэтому нельзя говорить ОБ ОДНОМ И ТОМ ЖЕ ПРЕДИКАТЕ для различных R. Но, как отмечено в #1.0, мы стремимся возможно больше узнать о "предикатах", определенных независимо от R - например, о предикатах, имеющих дело с числом элементов множества X или другими геометрическими свойствами тех фигур на вещественной евклидовой плоскости, для которых X и R служат простыми приближениями. Чтобы быть более точными, мы могли бы называть ПРЕДИКАТНОЙ СХЕМОЙ общую конструкцию, определяющую предикат для каждого множества из большого класса множеств R. Но это было бы слишком уж педантично, так что мы будем употреблять (исключая данный параграф) в этом более широком смысле также термин ПРЕДИКАТ.
Предположим, что нам задана предикатная схема пси, определяющая предикат пси.R для каждого множества R из некоторого семейства {R}. Будем говорить, что пси имеет КОНЕЧНЫЙ ПОРЯДОК (а именно <= k), если для всех R из этого семейства порядки предикатов пси.k равномерно ограничены числом k. Поясним это двумя примерами:
1. Пусть {R.i} - последовательность множеств, для которых |R.i|=i. Для каждого R.i - существует предикат пси.i определяемый предикатной схемой пси.ЧЕТНОСТЬ(X), который утверждает (для X включается в Ri), что |X| - НЕЧЕТНОЕ ЧИСЛО. Как мы увидим в #3.1, порядок любого такого предиката пси.i должен быть равен i. Следовательно, предикатная схема пси.ЧЕТНОСТЬ НЕ ИМЕЕТ конечного порядка.
2. Пусть пси.i - предикат, определяемый на Ri предикатной схемой пси.ДЕСЯТЬ:
пси.i(X)=[|X|=10].
В #1.4 мы уже показали, что пси.i - предикат порядка 2 для всякого R.i при i>10. Для R.1, ..., R.9 порядок этого предиката равен нулю (тривиально). Таким образом, предикатная схема пси.ДЕСЯТЬ имеет конечный порядок, а именно 2.
В обоих этих примерах подобные утверждения справедливы и для бесконечных R. На бесконечной сетчатке порядок предиката
пси.ДЕСЯТЬ(X)=[|X|=10]
конечен (и равен 2), а предикат
пси.ЧЕТНОСТЬ(X) = [|X| - нечетное число]
НЕ ИМЕЕТ порядка. Мы нередко будем рассматривать проблемы именно таким образом, так как часто легче представить себе одну машину, даже бесконечных размеров, чем бесконечную систему конечных машин. В гл.7 мы рассмотрим формализацию понятия бесконечного персептрона. Следует, однако, заметить, что использование бесконечных персептронов не охватывает всех случаев. Например, предикат
пси(X) = [|X| > 1/2*|R|]
полностью определен и имеет порядок 1 для любого конечного R. Для бесконечного R он лишен смысла, хотя нам хотелось бы считать, что соответствующая предикатная схема имеет конечный порядок.
ПРЕДИСЛОВИЕ К ЧАСТИ I
В части I (гл.1-4) содержится ряд чисто алгебраических определений и общих теорем, которые впоследствии используются в части II. Прочитать этот материал будет значительно легче, если уже предварительно составить себе представление о роли, которую призван сыграть этот математический аппарат. С этой целью мы обрисуем в общих чертах, как будет доказана (в гл. 3) следующая теорема:
ТЕОРЕМА 3.1 (гл.3), НЕФОРМАЛЬНЫЙ ВАРИАНТ. Пусть сетчатка R содержит конечное число точек. Тогда персептрон СУММА альфа.фи*фи(X) >Q не может определить истинность или ложность предиката "число точек в X нечетно", если среди его частных предикатов фи не найдется ни одного, зависящего от всех точек сетчатки R.
Поэтому невозможно наложить никаких ограничений на ПОРЯДКИ персептронов, вычисляющих этот предикат для произвольно больших сетчаток. Чтобы его вычислить, в персептроне должен быть хотя бы один предикат фи, осматривающий всю картину в целом! Доказательство теоремы проводится в несколько этапов.
#1-Й ЭТАП. В #1.1-1.4 более точно определяются понятия "персептрон", "порядок" и др. и показывается, что некоторые слова в определениях можно изменить без каких-либо серьезных последствий.
#2-Й ЭТАП. В #1.4 определяются исключительно простые функции фи, называемые "масками". Для каждого подмножества A сетчатки R маска фи.A(X) полагается равной 1, если X содержит, или "покрывает", все подмножество A, и равной 0 в противном случае. Затем доказывается простая, но важная теорема (#1.5) о том, что если для ЛЮБОГО множества функций фи порядок некоторого предиката не превышает k (см. #1.3), то существует эквивалентный этому предикату персептрон, который использует только маски размера не выше k (см. #0.2).
#3-Й ЭТАП. Чтобы глубже понять свойство четности-нечетности, мы задаемся вопросом: КАКИЕ ПРЕОБРАЗОВАНИЯ ВХОДНОГО ПРОСТРАНСТВА R НЕ ВЛИЯЮТ НА ЭТО СВОЙСТВО? Другими словами, нас интересует группа преобразований фигуры, не меняющая четность. Подобный подход к задаче может показаться экзотическим, но поскольку он, по-видимому, необходим для решения более трудных задач, которыми мы займемся позже, полезно с самого начала привыкнуть к нему в этой простой ситуации. В данном случае группой преобразований служит группа всех перестановок на сетчатке R - множество ВСЕХ перегруппировок ее точек.
#4-Й ЭТАП. В гл.2 мы покажем, как использовать эту группу, чтобы упростить персептрон. С помощью ТЕОРЕМЫ ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП (#2.3) мы придем к выводу, что в персептроне, определяющем четность, ВСЕМ МАСКАМ, У КОТОРЫХ НОСИТЕЛИ ОДИНАКОВЫ ПО РАЗМЕРУ (т.е. тем, которые просматривают одно и то же число точек), МОЖНО ПРИСВОИТЬ ОДИНАКОВЫЕ КОЭФФИЦИЕНТЫ. Обозначим через бета.j вес, приписанный всем маскам, у которых размер носителя равен j.

Инвариантные относительно группы коэффициенты предиката фи.ЧЕТНОСТЬ при |R|=3.
#5-Й ЭТАП. Затем мы докажем (в #3.1), что персептрон, определяющий четность, можно записать в виде
СУММА[0..k]бета.j*C(|X|.j)>0
где |X| - число точек множества X, k - наибольший размер носителя, C(|X|.j) - число подмножеств множества X, состоящих из j
элементов [Эта величина зависит от X и играет роль функции фи.j(X).- Прим. перев.].
#6-Й ЭТАП. Так как
C(n.k) = n!/(j!(n-j)!) = 1/j!*(n+1-1)(n+1-2)*(n+1-j),
т.е. C(n.j) можно представить в виде произведения j линейных членов, то это - многочлен от n степени j. Поэтому наш предикат можно записать в виде
P.k(|X|)>0,
где P.k - многочлен от |X|, алгебраическая степень которого не превышает k. Если |X| - нечетное число, то P.k(|J|)>0, а если |X| - четное число, то P.k(|X|)<=0. Следовательно, на отрезке 0<=|X|<=P многочлен P.k должен менять свой знак |R|-1 раз. Но для этого степень многочлена должна быть не меньше |R|, откуда следует, что k>=R. Доказательство на этом заканчивается (в точности, как в #3.1).

Приведенные рассуждения иллюстрируют, как в нашей теории действует алгебра. Для наиболее трудных теорем о связности из гл.5 нам потребуется что-то еще, кроме алгебры и теории групп. В гл.4 мы развиваем понятия геометрии алгебраических степеней, чтобы показать, что для реализации некоторых удивительно простых предикатов требуются персептроны неограниченного порядка Но на самом деле результаты гл.4 в дальнейшем не используются, и эту главу при первом чтении можно опустить.
За более простыми, но также характерными результатами читатель может обратиться непосредственно к гл.8, которая почти самостоятельна, так как не нуждается в алгебраической теории.
ГЛАВА 1. ТЕОРИЯ ЛИНЕЙНЫХ БУЛЕВЫХ НЕРАВЕНСТВ
#1.0
В этой главе изучается теория линейного представления предикатов. Мы обсудим свойства функций, определенных на абстрактном множестве точек, не обладающем никакой дополнительной математической структурой. Таким образом, эту главу можно рассматривать как развитие обычной булевой алгебры. Доказанные здесь теоремы мы применим потом к множествам, обладающим определенными геометрическими или топологическими свойствами, например к евклидовой плоскости. Итак, мы начнем с обсуждения множеств вообще, а потом рассмотрим хорошо знакомые объекты, такие, как "треугольники".
Начнем с предикатов, определенных для фиксированного базисного пространства R. В #1.1-1.5 мы будем предполагать, что R уже выбрано. В дальнейшем мы займемся "предикатами", определенными более широко: они либо вовсе не будут зависеть от выбора базисного пространства, либо не будут зависеть от выбора пространства из некоторого большого семейства пространств. Например, предикат
Множество X не пусто
может относиться к любому пространству R. Предикат
Множество X связно
имеет смысл, когда речь идет о множестве в пространстве, в котором существует понятие близости точек. Для такого более общего понятия "предиката" мы введем в #1.6 термин "предикатная схема". Главная наша цель состоит в том, чтобы дать общее определение ПОРЯДКА ПРЕДИКАТА (#1.5) и определение КОНЕЧНОГО ПОРЯДКА ПРЕДИКАТНОЙ СХЕМЫ (#1.6). В последних главах мы будем свободно использовать термин "предикат", подразумевая под этим также и предикатные схемы, а в #1.7 попытаемся сделать эти определения более точными и формальными. Однако советуем читателям не беспокоиться об этом до тех пор, пока главные результаты не станут интуитивно понятными.
#1.1. ОБОЗНАЧЕНИЯ И ОПРЕДЕЛЕНИЯ
Буква R будет обозначать произвольное множество точек. Для обозначения отдельных точек множества R мы будем обычно использовать строчные буквы a, b, c, ..., x, y, z, а для обозначения подмножества множества R - прописные A, B, C, ..., X, Y, Z. Переменные точки и подмножества будем обозначать через x и X.
Часто мы будем интересоваться особыми "семействами" подмножеств и обозначать их СЛОВАМИ, записанными прописными буквами. Таким образом, ОКРУЖНОСТЬ означает совокупность подмножеств множества R, образующих замкнутые окружности (как в #0.5). Абстрактное семейство подмножеств мы будем обозначать буквой F.
Естественно связывать с любым семейством множеств F предикат пси.F(X), принимающий значение истина тогда и только тогда, когда X принадлежит семейству F. Например, предикат пси.ВЫПУКЛОСТЬ принимает значение истина или ложь в зависимости от того, выпукло ли множество X. Разумеется, предикаты пси.ОКРУЖНОСТЬ и пси.ВЫПУКЛОСТЬ имеют смысл только для неабстрактных множеств R, в которых можно ввести эти геометрические понятия. Греческими буквами фи и пси всегда будут обозначаться предикаты. Буква пси обычно будет обозначать наиболее важный предикат, а через фи будут обозначаться предикаты из большого семейства легко вычисляемых функций; это семейство будет обозначаться буквой ФИ.
ПРЕДИКАТ - это функция (подмножеств множества R), принимающая лишь два значения. Иногда этими двумя значениями будут ИСТИНА и ЛОЖЬ, иногда полезно считать их равными 1 и 0. Так как существует некоторая опасность спутать эти два вида значений предикатов, то во избежание разнотолков вводится обозначение [пси.(X)]. Уголки всегда означают, что употребляются значения 1 и 0. Это дает возможность использовать значения предикатов как обыкновенные числа, а в нашей теории это важно, поскольку мы должны объединять полученные от предикатов данные (о чем уже говорилось в гл.0). Внутри уголков может стоять любое математическое утверждение. Зная, например, что 3 меньше 5, а 1 меньше 2, мы можем написать
[3<5] = 1,
[3<5]+[1<2] = 2,
[3<5]+[5<3] = 1
и даже
[3<[5=1]] = 0,
4*[3<5]+2*[6<2] = 4.
Иногда удобно считать, что точки множества R занумерованы в последовательность x.1, x.2, ..., x.i, ... В таком случае многие предикаты можно выразить в терминах традиционных представлений булевой алгебры. Например, два выражения
x.iVx.j, (x.i принадлежит X или x.j принадлежит X)
равнозначны, а именно они равны единице, если хотя бы одна из точек x.i и x.j принадлежит X, и равны нулю, если ни x.i, ни x.j не принадлежат X. Иными словами, выделение подмножества X из множества R состоит в присвоении значений 1 и 0 точкам x.i в зависимости от того, принадлежит ли i-я точка множеству X, так что x.i употребляется в двух смыслах: и для обозначения i-й точки, и для обозначения функции множества [x.i принадлежит X]. Это можно использовать для записи предикатов в АРИФМЕТИЧЕСКОЙ форме вместо ЛОГИЧЕСКОЙ, т.е. писать
[x.1+x.2+x.3>0] вместо х.1Vx.2Vx.3
или даже
[2*x.1*x.2-x.1-x.2>-1] вместо x.1==x.2,
где x.1==x.2 - предикат, принимающий значение ИСТИНА, когда либо обе точки x.1 и x.2 принадлежат X, либо ни одна из них не принадлежит X.
Нам понадобится в дальнейшем уметь выражать представление о том, что функция фи может зависеть только от какого-то определенного подмножества множества R. Обозначим такое подмножество через S(фи). Формально S(фи) - это такое наименьшее подмножество S множества R, что для каждого подмножества X множества R
фи(X) = фи(X пересечение S),
где (X пересечение S) - множество точек, принадлежащих и X, и S. Назовем S(фи) НОСИТЕЛЕМ предиката фи.
Если пространство R бесконечно, то для некоторых интересных предикатов S(ab) определить нельзя. Рассмотрим, например, предикат
фи(X) = [X содержит бесконечное множество точек]
Истинность предиката фи(X) можно было бы установить просмотром точек множества X, лежащих в любом множестве S, которое содержит все, кроме конечного числа точек множества R. Но "наименьшего" такого множества не существует!
#1.2. ФУНКЦИИ, ЛИНЕЙНЫЕ ОТНОСИТЕЛЬНО КЛАССА ПРЕДИКАТОВ
Пусть ФИ - семейство предикатов, определенных на множестве R. Мы говорим, что
кси - ЛИНЕЙНАЯ ПОРОГОВАЯ ФУНКЦИЯ относительно ФИ,
если существуют число тета и множество чисел альфа(фи), по одному на каждый предикат фи из ФИ, для которых
пси(X)=[СУММА[фи из ФИ]альфа(Фи)*фи(X)>тета].
Иными словами, значением пси(X) будет ИСТИНА, когда выполняется неравенство внутри уголков []. Часто записывают это менее формально в виде
пси = СУММА альфа(фи)*фи > тета
или даже в виде
пси = СУММА альфа.фи*фи > тета
Ради симметрии в класс линейных пороговых функций вместе с предикатом пси включим его отрицание
~пси(X) = СУММА альфа(фи)*фи <= тета
Множество всех предикатов, которое при заданном ФИ можно определить таким способом (т.е. выбором различных значений порога тета и чисел альфа), обозначим через L(ФИ).

Для двухточечного пространства R={x,y} класс функций L({x,y}), линейных относительно одноточечных предикатов, включает 14 из 16=2**2**2 возможных булевых функций. Для большого числа точек доля функций, линейных относительно одноточечных предикатов, очень быстро снижается
#1.2.1. ДРУГИЕ ВОЗМОЖНЫЕ ОПРЕДЕЛЕНИЯ МНОЖЕСТВА L(ФИ). Так как определение множества L(ФИ) слишком общо для последующего изложения, его стоит пересмотреть и выяснить, что в этом определении существенно и что произвольно. Мы предлагаем несколько возможных изменений определения, не затрагивающих в значительной степени его характер. Действительно, для конечного пространства R (наиболее важный случай) все предлагаемые альтернативы приводят к строго эквивалентным определениям. В случае бесконечных пространств R некоторые определения приводят к различным смысловым значениям для L(ФИ), но не в такой мере, чтобы сколько-нибудь повлиять на наши последующие рассуждения.
ПРЕДЛОЖЕНИЕ. Следующие изменения в формальном определении L(ФИ) не затрагивают определяемые классы предикатов:
(1) Если допустить, что ФИ содержит постоянную функцию I(X)==1, то тета можно принять равным нулю.
(2) Знак неравенства > можно заменить на <, >= или <=.
(3) Если R конечно, то порог тета и все числа альфа(фи) можно выбрать целыми.
(4) Утверждения 1-3 можно применять независимо друг от друга.
Очевидно, что это предложение справедливо. Доказательство мы приведем главным образом для того, чтобы помочь читателям, желающим потренироваться в использовании наших обозначений.
ДОКАЗАТЕЛЬСТВО. (1) Положим альфа'(I) = альфа(I)-тета и альфа'(фи)=альфа(фи) для остальных фи. Тогда
[СУММА альфа(фи)*фи(X) > тета] = [СУММА альфа'(фи)*фи(X) > 0].
(2) Пусть альфа'(фи)=-альфа(фи) и тета'=тета. Тогда
[СУММА альфа(фи)*фи(X) < тета] = [СУММА альфа'(фи)*фи(X) > тета']
Утверждения об остальных заменах знака неравенства получатся, если заменить все предикаты их отрицаниями.
(3) Если R конечно, то и ФИ конечно, и можно допустить, что не существует множества X, для которого
СУММА альфа(фи)*фи(X) = тета.
В самом деле, если такое множество X существует, то положение можно исправить, заменив тета на тета+дельта, где дельта меньше, чем наименьшее ненулевое значение величины [СУММА альфа(фи)*фи(X) - тета] Предположим сначала, что все альфа(фи) - рациональные числа. Обозначим через D произведение всех их знаменателей и положим
альфа'(фи) = D*альфа(фи), тета' = D*тета.
Тогда все числа альфа' целые, и ясно, что
[СУММА альфа(фи)*фи(X) > тета] = [СУММА альфа'(фи)*фи(X) = тета'].
для всякого X. Предположим теперь, что среди чисел множества {альфа(фи)} есть иррациональные. Заменим каждое альфа(фи) некоторым рациональным числом альфа'(фи) из интервала
альфа(фи) < альфа'(фи) < альфа(фи) + дельта/2**2**|R|,
где величина дельта определена выше. Эта замена не может изменить сумму СУММА альфа(фи)*фи(X) больше чем на дельта, поэтому она не может повлиять на значение [СУММА альфа(фи)*фи(X) > тета], ибо существует самое большее 2**2**|R| различных предикатов фи.
#1.3. ПОНЯТИЕ ПОРЯДКА
Предикаты, носители которых невелики, чересчур локальны, а потому и не очень интересны сами по себе. Нас главным образом занимают предикаты, носителями которых служит все пространство R, но которые можно представить в виде линейных пороговых комбинаций предикатов с малыми носителями. Простой пример:
пси(X) = [X - непустое множество].
Ясно, что S(фи)=R. С другой стороны, если в качестве ФИ взять множество предикатов вида фи.p(X)=[р принадлежит X], то |S(фи.p)|=1 для всех фи из ФИ и пси(X) = [СУММА фи.p(X) > 0].
Эти два утверждения позволяют сказать, что ПОРЯДОК предиката пси равен 1. В общем случае порядок предиката пси есть наименьшее число k, для которого можно найти множество ФИ предикатов, удовлетворяющих условиям:
|S(фи)|<=k для всех фи из ФИ,
пси принадлежит L(ФИ).
Следует отметить, что порядок предиката пси является свойством самого предиката пси и не имеет отношения к какому-либо конкретному множеству ФИ. Именно это делает его важным "абсолютным" понятием. Те, кто знаком с соответствующей литературой, легко опознают в предикатах порядка 1 так называемые "линейные пороговые функции".
#1.4. МАСКИ И ДРУГИЕ ПРИМЕРЫ ЛИНЕЙНОГО ПРЕДСТАВЛЕНИЯ
Особую роль будут играть предикаты вида
фи.A(X)=[все элементы множества А принадлежат X]=[A включается в X].
В общепринятых обозначениях булевой алгебры эти предикаты оказываются конъюнкциями: если A={y.1, ..., y.n}, то фи.A(X)=(y.1 и y.2 и ... и y.n), или, как обычно пишут, фи.A(X)=y.1*y.2*...*y.n.
Назовем фи.A МАСКОЙ множества A. В частности, постоянный предикат I(X) служит маской пустого множества, а предикаты фи.p предыдущего параграфа - масками одноточечных множеств.

ПРЕДЛОЖЕНИЕ. Все маски имеют порядок 1.
ДОКАЗАТЕЛЬСТВО. Пусть A - любое конечное множество, состоящее из |A| точек. Для каждой точки x из A определим фи.x(X) как предикат [x принадлежит X]. Тогда
фи.A(X) = [СУММА[x из A]фи.x(X)>|A|]
ПРИМЕР 1. Среди 16 булевых функций двух переменных порядок 1 имеют все, кроме функции НЕРАВНОЗНАЧНОСТИ (x исключающее или y) и ее дополнения - функции ЛОГИЧЕСКОЙ ЭКВИВАЛЕНТНОСТИ x==y, порядок которых равен 2:
(x исключающее или y) = [x*~y+~x*y>0], x==y = [x*y+~x*~y>0]
где, например, x*~y - предикат с носителем, состоящим из двух точек, и его значением будет истина только тогда, когда x принадлежит X, а y нет.

Можно считать, что линейное неравенство определяет поверхность, разделяющую точки пространства на два класса, и тем самым задает предикат. Мы рекомендуем воздержаться от подобного представления до части III.
(ЗАДАЧА: докажите, что порядок функции (x исключающее или y) не равен 1!) Вот еще примеры из булевой алгебры:
x импликация y = [~хVy] = [y-x>-1], ~x = [-x > -1].
Порядок любой маски равен 1:
(x и y и z) = [x+y+z>2],
то же справедливо и для любой дизъюнкции:
xVyVz = [x+y+z>0].
ПРИМЕР 2. Функцию x1==x2 можно представить в виде линейной комбинации масок:
x.1*x.2V~x.1*~x.2 = [x.1*x2+(1-x.1)(1-x.2)>0] =
= [2*x.1*x.2-x.1-x.2>-1].
Доказательство того, что порядок неравнозначности и логической эквивалентности не равен 1, мы приведем в #2.1.
ПРИМЕР 3. Пусть M - целое число, 0<=M<=|R|. Тогда "считающий предикат" фи.M, или [|X|=M], который определяет, что X СОДЕРЖИТ РОВНО М ТОЧЕК, имеет порядок 2.
ДОКАЗАТЕЛЬСТВО. Рассмотрим представление
[(2M-1)СУММА[все i]x.i + (-2)СУММА[i<j]x.i*x.j >= M**2].
Для любой фигуры X существует |X| членов x.i и 1/2*|X|*(|X|-1) членов x.1*y.1, значение которых равно 1. В таком случае предикатом служит выражение
[(2M-1)*|X|-|X|*(|X|-1)-M**2>=0]=[(|X|-M)**2<=0],
а единственным значением |X|, при котором это выражение истинно, является |X|=М. Заметим, что, повышая порог, можно получить предикат, истинный не для единственного значения |X|, а для значений, заполняющих некоторый интервал.

Мы уже показали, что порядок "считающего предиката" не больше 2; из теоремы 2.4 будет следовать, что он не равен 1. Заметим, что в линейной форме считающего предиката |R| в явном виде не содержится. Следовательно, этот предикат подходит также и для бесконечного пространства R.
ПРИМЕР 4. Порядок предикатов [|X|>=M] и [||X|<=M] равен 1, так как их можно представить в виде [СУММА x.i >= M] и [СУММА x.i <= M].
#1.5. ТЕОРЕМА О ПОЛОЖИТЕЛЬНОЙ НОРМАЛЬНОЙ ФОРМЕ
Порядок функции можно определить, представляя ее как линейную пороговую функцию относительно множества масок (теорема 1.5.3). Чтобы сделать это, докажем сначала следующую теорему.
ТЕОРЕМА 1.5.1. Каждый предикат пси является линейной пороговой функцией относительно множества всех масок, т.е. пси принадлежит L(вce маски).
ДОКАЗАТЕЛЬСТВО. Любую булеву функцию пси(x.1, ..., x.n) можно записать в дизъюнктивной нормальной форме
C.1(X) V C.2(X) V ... V C.p(X),
где Ci(X) - произведение (конъюнкция)
z.1*z.2*...*z.n
в котором каждое z есть x.i или ~x.i. Так как для любого X истинным может быть не более одного Cj(X), то, используя арифметическую сумму, можно переписать пси в виде
C.1(X)+C.2(X)+...+C.p(X).
Далее, к любому произведению, содержащему отрицание какой-либо буквы, можно применить следующую формулу: пусть B# и A# означают любые цепочки букв, тогда
B#*~x.i*A# = B#(1-x.i)A# = B#A#-B#*x.i*A#.
Если и дальше применять эту формулу, то можно уничтожить все отрицания, не увеличивая длины произведения.
Избавившись от отрицаний и сгруппировав подобные члены, мы получим ПОЛОЖИТЕЛЬНУЮ НОРМАЛЬНУЮ ФОРМУ
пси(X) = СУММА альфа.i*фи.i(X),
где каждый предикат фи, является маской, а каждое число альфа.i - целое. Поскольку сумма СУММА альфа.i*фи.i(X) равна нулю или единице, можно записать
пси(X) = [СУММА альфа.i*фи.i(X) > 0].
ПРИМЕР. [Сумма x.1+x.2+x.3 нечетна] = x.1+x.2+х.3-2*x.1*x.2-2*x.2*x.3-2*x.3*x.1+4*x.1*x.2*x.3.
ТЕОРЕМА 1.5.2 (факультативно). Положительная нормальная форма единственна.
Доказательство. Пусть {фи.i} - множество масок, а {гамма.i} - множество чисел, не равных нулю. Возьмем k, для которого S(фи.k) минимально, т.е. не существует такого j!=k, что S(фи.j) включается в S(фи.k). Тогда
фи.k(S(фи.k))=1,
фи.j(S(фи.k))=0, j!=k.
Отсюда следует, что сумма СУММА гамма.i*фи.i(X) не равна тождественно нулю, так как при X=S(фи.k) она принимает значение гамма.k.
Если теперь СУММА альфа.i*фи.i(X) = СУММА бета.i*фи.i(X) для всякого X, то СУММА(альфа.i-бета.i)*фи.i(X) = 0 для всякого X. Но
СУММА[все i](альфа.i-бета.i)*фи.i(X) = СУММА[0!=(альфа.i-бета.i)](альфа.i-бета.i)*фи.i(X),
откуда следует, что альфа.i=бета.i для всех i. Это доказывает единственность коэффициентов положительной нормальной формы предиката пси. Заметим, что положительная нормальная форма, будучи обычной арифметической суммой, всегда имеет нулевое или единичное значение и, таким образом, не нуждается в применении символа [ ]. предназначенного для интерпретации справедливости неравенства как предиката.
ТЕОРЕМА 1.5.3. Предикат пси имеет порядок k тогда и только тогда, когда k есть наименьшее число, для которого существует множество ФИ масок, удовлетворяющих условиям
||S(фи)| <= k для всех фи из ФИ,
пси принадлежит L(ФИ).
ДОКАЗАТЕЛЬСТВО. В выражении пси=[СУММА альфа.i*фи.i > 0] каждую функцию фи.i - заменяем ее положительной нормальной формой. Если |S(фи.i)| <= k, то аналогичное неравенство верно также и для масок, входящих в положительную нормальную форму [Для доказательства теоремы достаточно доказать два утверждения: а) всякий предикат порядка k можно представить в виде линейной комбинации таких масок фи, что |S(фи)| <= k; б) если для некоторого предиката пси число k является наименьшим, при котором существует множество ФИ масок фи, удовлетворяющих условиям, указанным в формулировке теоремы, то порядок предиката пси равен k. Утверждение а) доказано авторами. Для доказательства б) заметим, что порядок предиката пси не может быть выше указанного k по самому определению порядка. Если бы он был равен k'<k, то в силу а) существовала бы линейная комбинация масок, для которой |S(фи)| <= k' < k, что противоречит условию минимальности k. Теорема доказана.- Прим. ред.]
ПРИМЕР. Порядок "булевой формы" не превышает степени ее дизъюнктивной нормальной формы. Например,
СУММА альфа.ijk*x.i*x.j*~x.k = СУММА альфа.ijk*x.i*x.j - СУММА альфа.ijk*x.i*x.j*x.k
отсюда видно, как исключить отрицание, не повышая порядка. Эта частная форма порядка 3 появится позже (#6.3), в персептроне, распознающем выпуклые фигуры.
Естественно поинтересоваться порядком предикатов, которые представляют собой булевы функции других предикатов. Обнадеживающий результат дает
ТЕОРЕМА 1.5.4. Если предикат пси.1 имеет порядок П.1, а предикат пси.2 имеет порядок П.2, то порядки предикатов (пси.1 исключающее или пси.2) и пси.1==пси.2 не превышают П.1+П.2.
ДОКАЗАТЕЛЬСТВО. Пусть пси.1=[СУММА альфа.i*фи.1 > 0], пси.2=[СУММА альфа'.i*фи.1 > 0]. Предположим, что коэффициенты выбраны так, что суммы внутри уголков никогда не равны нулю. Тогда
пси.1==пси.2 = [(СУММА альфа.i*фи.i)(СУММА альфа'.i*фи.1i) > 0] = [СУММА[i,j] (альфа.i*альфа'.j)*фи.i*фи.j) > 0],
причем
|S(фи.i*фи.j)| <= |S(фи.i)|+|S(фи.j)|.
Утверждение о предикате (пси.1 исключающее или пси.2) следует из равенства
[пси.1 исключающее или пси.2] = 1 - [пси.1==пси.2].
ПРИМЕР. На основании равенства
пси.M(X) = [[M >= |X|]==[|X| >= M]]
заключаем, что порядок предиката пси.M не превышает 2. Это дает еще один способ получения результата, о котором говорилось в #1.4 (пример 3).
ВОПРОС: Что можно сказать о порядке предикатов [пси.1 и пси.2] и [пси.1 V пси.2]? Если принять во внимание простой результат теоремы 1.5.4, то ответ может показаться удивительным. В гл.4 мы докажем, что для любого порядка n можно найти такую пару предикатов пси.1 и пси.2 ПЕРВОГО ПОРЯДКА, что порядок предикатов [пси.1 и пси.2] и [пси.1 V пси.2] превышает n. В самом деле, пусть R = (A объединение В объединение С), где А, В, С - большие непересекающиеся подмножества множества R. Тогда каждый из предикатов пси.1 = [|X пересечение A| > |X пересечение C|] и [|X пересечение B| > |X пересечение C|] и ИМЕЕТ ПОРЯДОК 1, так как их можно представить в виде
[СУММА[x.i из A]x.i > СУММА[x.i из C]x.i] и [СУММА[x.i из B]x.i > СУММА[x.i из C]x.i].
В гл.4 мы увидим, что предикаты [пси.1 и пси.2] и [пси.1 V пси.2] не имеют даже КОНЕЧНОГО ПОРЯДКА в том смысле, как это будет описано в #1.6.
#1.6. ПРЕДИКАТЫ КОНЕЧНОГО ПОРЯДКА
Строго говоря, предикат определяется для конкретного множества R, и поэтому нельзя говорить ОБ ОДНОМ И ТОМ ЖЕ ПРЕДИКАТЕ для различных R. Но, как отмечено в #1.0, мы стремимся возможно больше узнать о "предикатах", определенных независимо от R - например, о предикатах, имеющих дело с числом элементов множества X или другими геометрическими свойствами тех фигур на вещественной евклидовой плоскости, для которых X и R служат простыми приближениями. Чтобы быть более точными, мы могли бы называть ПРЕДИКАТНОЙ СХЕМОЙ общую конструкцию, определяющую предикат для каждого множества из большого класса множеств R. Но это было бы слишком уж педантично, так что мы будем употреблять (исключая данный параграф) в этом более широком смысле также термин ПРЕДИКАТ.
Предположим, что нам задана предикатная схема пси, определяющая предикат пси.R для каждого множества R из некоторого семейства {R}. Будем говорить, что пси имеет КОНЕЧНЫЙ ПОРЯДОК (а именно <= k), если для всех R из этого семейства порядки предикатов пси.k равномерно ограничены числом k. Поясним это двумя примерами:
1. Пусть {R.i} - последовательность множеств, для которых |R.i|=i. Для каждого R.i - существует предикат пси.i определяемый предикатной схемой пси.ЧЕТНОСТЬ(X), который утверждает (для X включается в Ri), что |X| - НЕЧЕТНОЕ ЧИСЛО. Как мы увидим в #3.1, порядок любого такого предиката пси.i должен быть равен i. Следовательно, предикатная схема пси.ЧЕТНОСТЬ НЕ ИМЕЕТ конечного порядка.
2. Пусть пси.i - предикат, определяемый на Ri предикатной схемой пси.ДЕСЯТЬ:
пси.i(X)=[|X|=10].
В #1.4 мы уже показали, что пси.i - предикат порядка 2 для всякого R.i при i>10. Для R.1, ..., R.9 порядок этого предиката равен нулю (тривиально). Таким образом, предикатная схема пси.ДЕСЯТЬ имеет конечный порядок, а именно 2.
В обоих этих примерах подобные утверждения справедливы и для бесконечных R. На бесконечной сетчатке порядок предиката
пси.ДЕСЯТЬ(X)=[|X|=10]
конечен (и равен 2), а предикат
пси.ЧЕТНОСТЬ(X) = [|X| - нечетное число]
НЕ ИМЕЕТ порядка. Мы нередко будем рассматривать проблемы именно таким образом, так как часто легче представить себе одну машину, даже бесконечных размеров, чем бесконечную систему конечных машин. В гл.7 мы рассмотрим формализацию понятия бесконечного персептрона. Следует, однако, заметить, что использование бесконечных персептронов не охватывает всех случаев. Например, предикат
пси(X) = [|X| > 1/2*|R|]
полностью определен и имеет порядок 1 для любого конечного R. Для бесконечного R он лишен смысла, хотя нам хотелось бы считать, что соответствующая предикатная схема имеет конечный порядок.
Последний раз редактировалось: Gudleifr (Ср Июн 21, 2023 12:48 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 2. ИНВАРИАНТНОСТЬ БУЛЕВЫХ НЕРАВЕНСТВ ОТНОСИТЕЛЬНО ГРУПП
#2.0
В этой главе рассматриваются линейные пороговые неравенства, инвариантные относительно групп преобразований точек базисного пространства R. Цель этой главы - установить связь между геометрией пространства R и реализуемостью геометрических предикатов персептронами конечного порядка. Полностью эта цель достигается в части II.
#2.1. ПРИМЕР: КОЭФФИЦИЕНТЫ, УСРЕДНЕННЫЕ ПО СИММЕТРИИ
В качестве введения в изучаемые в этом разделе методы рассмотрим простой, почти тривиальный, пример. Пусть наше пространство R содержит две точки x и y. Докажем, что порядок предиката пси.== = [xyV~x~y] не равен 1. (Этот предикат утверждает, что X не состоит из одной единственной точки). Метод доказательства заключается в том, чтобы прийти к противоречию, предположив, что существуют такие числа альфа, бета и тета, для которых
пси.==(x,y) = xyV~x~y = [альфа*x+бета*y > тета].
Можно перейти непосредственно к доказательству, написав условия, налагаемые на альфа и бета:
пси.==(1,0) = 0 => альфа<=тета,
пси.==(0,1) = 0 => бета<=тета,
пси.==(1,1) = 1 => альфа+бета>тета,
пси.==(0,0) = 1 => 0>тета.
В этом простом случае получить противоречие довольно легко, так как сложение первых двух условий дает
альфа+бета <= 2*тета
а вместе с третьим условием приводит к
тета < 2*тета,
откуда следует, что число тета положительно, что противоречит четвертому условию.
Однако для более сложных случаев, при наличии большого числа переменных, подобные доказательства сложны. С другой стороны, приведенное ниже доказательство, хотя и чуть более сложное, позволяет гораздо глубже проникнуть в существо дела. Заметим вначале, что, переставляя x и y, т.е. меняя их местами, мы не изменяем значения предиката пси. Иначе говоря,
пси.==(x,y) = пси.==(y,x).
Таким образом, неравенства
альфа*x+бета*y > тета,
альфа*y+бета*x > тета
выполняются или не выполняются одновременно. Сложив их, получим
1/2(альфа+бета)x + 1/2(альфа+бета)y > тета.
Аналогично неравенства
альфа*x+бета*y <= тета,
альфа*y+бета*x <= тета
дают
1/2(альфа+бета)x + 1/2(альфа+бета)y <= тета.
Отсюда следует, что, заменив (альфа+бета)/2 на гамма. можно записать
пси.==(x,y) = [гамма*x+гамма*y > тета] = [гамма*(x+y) > тета].
Таким образом, можно построить новое линейное представление для пси в котором коэффициенты при x и y равны.
Следовательно,
пси.==(X) = [гамма*|X| > тета],
где |X|, как обычно, означает число точек в X.
Рассмотрим теперь три множества: X.0={}, X.1={x}, X.2={x,y}. Имеем
|X.0|=0 и гамма*0 > тета,
|X.1|=1 и гамма*1 <= тета,
|X.2|=2 и гамма*2 > тета.
Совершенно очевидно, что это невозможно. Таким образом, кое-что о пси можно узнать, "усредняя" его коэффициенты после перестановки, не меняющей предиката. (В разобранном примере гамма - это среднее арифметическое чисел альфа и бета.) В #2.3 мы точно определим введенное здесь понятие "среднее значение".
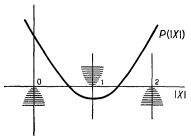
Рис.2.1. Функция P(|X|)=гамма|X|-тета не должна попадать в заштрихованные области, а для этого необходимо, чтобы она была многочленом не ниже второй степени.
#2.1.1. [Читатели, знакомые с основными определениями теории групп, могут этот раздел пропустить]. ГРУППЫ ПРЕОБРАЗОВАНИЙ И КЛАССЫ ЭКВИВАЛЕНТНОСТИ ПРЕДИКАТОВ. Обобщение описанной в #2.1 процедуры будет состоять в изучении произвольной группы преобразований на базисном пространстве R и в выяснении того, что подразумевается под независимостью предиката пси от любого из преобразований этой группы (так же, как предикат в #2.1 не зависел от перестановки двух точек). Именно на основе этого представления об "инвариантности относительно группы преобразований" мы сможем приступить к решению геометрических проблем; при этом мы заимствуем математическую точку зрения Феликса Клейна: всякое интересное геометрическое свойство является инвариантом некоторой группы преобразований.
Прекрасный пример группы преобразований дает множество всех переносов плоскости, т.е. таких преобразований, при которых каждая точка плоскости перемещается на место другой точки, причем все точки перемещаются на одно и то же расстояние в одном и том же направлении; иными словами, это жесткий параллельный сдвиг. Рисунок 2.2 иллюстрирует результат двух переносов g.1 и g.2 фигуры X. Он же служит иллюстрацией ряда определений и замечаний, которые мы хотим сейчас привести.
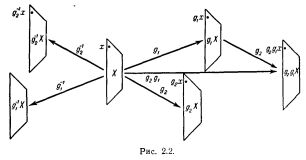
1. Мы определяем перенос как операцию, действующую на отдельные точки таким образом, что при действии операции g.1 на точку x получается другая точка g.1*x. Это "индуцирует" естественное представление о том, как воздействуют переносы g на фигуры в целом. Дадим определение. Если g - одно из преобразований из группы G, а X - некоторая фигура, т.е. подмножество множества R, то
g*X={g*x | x принадлежит X},
что читается так: g*X является (по определению) множеством точек g*x, полученных в результате действия преобразования g на все точки x, принадлежащие X.
2. Если к фигуре X применить сначала преобразование g.1, а затем g.2, то получим новую фигуру, которую можно обозначить g.2(g.1*X). Но ту же самую фигуру можно получить из X как результат одного преобразования - "композиции" преобразований g.1 и g.2. Обычно такую операцию обозначают g.2*g.1, а новое изображение обозначают g.2*g.1*X, как это показано на рис.2.2. Математическое определение группы требует, чтобы g.2*g.1 принадлежало G, если g.1 и и g.2 принадлежат G.
В случае переноса всегда справедливо равенство g.1*g.2*X = = g.2*gi.1*X, что можно проверить, достроив параллелограмм X, g.1*X, g.2*g.1*X, g.2*X. Но это равенство следует рассматривать как случайное стечение обстоятельств, ибо оно не всегда справедливо для других важных геометрических групп. Например, если G - группа всех поворотов вокруг всех точек плоскости, то для указанных на рис.2.3 преобразований g.1 и g.2 точки g.1*g.2*x и g.2*g.1*x различны.
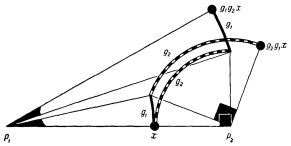
Рис.2.3. Здесь g.1 - небольшой поворот вокруг точки p.1 a g.2 - поворот на 90o вокруг p.2 Из этого рисунка видно, почему для группы вращений, вообще говоря, g.1*g.2*x!=g.2*g.l*x.
3. Последнее требование формального определения "группы преобразований" заключается в том, что группе G вместе с каждым g из G должно принадлежать обратное преобразование, т.е. такое преобразование g**-1, что (g**-1)*g*x=x для каждой точки x. На рис.2.2 показаны обратные преобразования для переносов g.1 и g.2. Обратное преобразование для g.2*g.1 можно получить, достроив параллелограмм на рис.2.2 слева от X. Несложным рассуждением легко показать, что (для любой группы!) всегда справедливо равенство (g.2*g.1)**-1 = g.1**-1 * g.2**-1.
Всегда подразумевается, что группа содержит тривиальное - тождественное - преобразование, т.е. такое преобразование e, что e*x=x для всякого x. Действительно, поскольку e является композицией g**-1*g любого преобразования g и его обратного g**-1, наличие e в G логически вытекает уже из требований 2 и 3. Нетрудно также видеть, что g*g**-1=e.
В учебниках по алгебре можно найти еще и другие требования к группам, например
(g.1*g.2)g.3 = g.1(g.2*g.3)
для любых g.1, g.2 и g.3 из G. Мы используем это требование для групп преобразований без дополнительных оговорок, поскольку оно входит в наше интуитивное представление о преобразовании. В справедливости ассоциативного закона в нашем случае мы убеждаемся, прослеживая просто, что же происходит с каждой отдельной точкой пространства R.
4. Если h - элемент группы G, то множество hG, определяемое формулой
h*G = {hg | g из G}
(т.е. множество, составленное из композиций элемента h со всеми элементами группы G), совпадает со всей группой G и каждый ее элемент входит в hG только один раз. В самом деле, любой элемент g этого множества есть композиция
h(h**-1*g) = (h*h**-1)g = e*g = g.
а потому h**-1*g входит в группу. Если бы, скажем, элемент g.0 встречался в группе дважды, т.е. для двух различных g.1 и g2 было бы
g.0 = h*g.2,
g.0 = h*g.2,
то мы получили бы
h**-1g.0 = h**-1*h*g.1 = g.1,
h**-1g.0 = h**-1*h*g.2 = g.2,
и тогда g.1 и g.2 не могли бы быть различными.
5. В большинстве из последующих разделов, в частности в #2.3, мы будем рассматривать группы G, содержащие лишь КОНЕЧНОЕ число преобразований. Но нам хотелось бы постичь характер обычных групп евклидовых преобразований, а они бесконечны. Например, число различных расстояний, на которые можно перенести фигуру в плоскости, бесконечно: если g!=e - любой нетривиальный перенос, то все переносы g, g*g, g*g*g, ... различны. В большинстве случаев мы сможем доказать нужные нам теоремы, заменив бесконечную группу конечной, изменив при этом, если необходимо, само пространство R! Например, рассматривая перенос, мы вместо евклидовой плоскости часто будем использовать тор (рис.2.4).

Тор разбит на квадраты, как показано на рисунке. Вместо бесконечного множества переносов в плоскости мы рассматриваем только такие преобразования тора, при которых каждая точка переносится на m квадратов вдоль большого экватора и на n квадратов вдоль малого экватора. Число таких "переносов" конечно. В большинстве практических случаев тор ведет себя как небольшая часть плоскости, так как его можно "разрезать" и развернуть (рис.2.5). Следовательно, для "небольших" фигур и "небольших" переносов нет существенной разницы между тором и плоскостью. Об этом мы еще будем говорить в введении к части II и в гл.7.
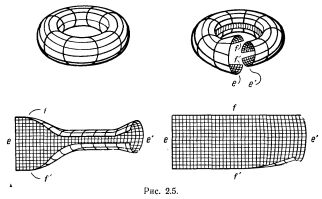
#2.2. КЛАССЫ ЭКВИВАЛЕНТНОСТИ ИЗОБРАЖЕНИЙ И ПРЕДИКАТОВ
Если задана группа G, то будем говорить, что фигуры X и Y являются G-эквивалентными (и писать X==Y в G), если в группе G найдется такой элемент g, что X=g*Y. Заметим, что
X==X в G, так как X=e*X,
X==Y в G влечет Y==X в G, так как если X=gY, то Y=g**-l*X,
X==Y в G и Y==Z в G влечет X==Z в G, так как если X=g*Y и Y=h*Z, то X=g*h*Z.
Выбирая некоторую группу, мы тем самым автоматически предполагаем, что фигуры разбиты на классы эквивалентности. Это будет важно в дальнейшем, когда окажется, что "образы" (или множества фигур), которые мы захотим распознать, подпадают под такие разбиения (классификации), если группы выбраны правильно.
ПРИМЕР. Пусть G - множество ВСЕХ перестановок конечного множества точек из R. (Перестановкой называется любое перемещение точек, при котором никакие две точки не сводятся в одну). В этом случае (теорема!) две фигуры X и Y будут G-эквивалентными тогда и только тогда, когда они обе будут содержать одинаковое число точек.
ПРИМЕР. Если требуется построить машину для чтения печатных букв или цифр, то возникает естественное желание, чтобы эта машина могла распознавать их независимо от их положения на странице:

т.е. чтобы на решение машины не оказывали влияния элементы группы переносов. Иными словами, восприятие машины должно быть "инвариантно относительно группы переносов", т.е. ее решение должно быть одним и тем же для каждого представителя какого-либо класса эквивалентности относительно группы переносов [Разумеется, на практике от машины требуется большее: желают знать не только, что находится на странице, но и где это находится. В противном случае вместо чтения страницы машина выдавала бы нам беспорядочный набор знаков!].
В #2.3 мы докажем важную теорему, из которой много узнаем о любом персептроне, инвариантном относительно некоторой группы G, т.е. о таком персептроне, предикат пси(X) которого зависит только от класса эквивалентности фигуры X. Прежде чем сформулировать эту теорему, нужно пояснить, что мы понимаем под G-эквивалентностью ПРЕДИКАТОВ.
Будем говорить, что два предиката фи и фи' ЭКВИВАЛЕНТНЫ относительно группы G, и записывать это в виде
фи==фи' в G, если существует такой элемент g из G, что фи(g*X) и фи'(X) СОВПАДАЮТ ДЛЯ КАЖДОГО X.
Нетрудно видеть, что это действительно есть отношение эквивалентности, т.е. что
фи==фи в Gдля любого ф,
фи==фи' в G влечет фи'==фи в G,
фи==фи' в G и фи'==фи'' в G влечет фи==фи'' в G.
Если нам даны предикат фи и элемент g некоторой группы, то определим фи*g как предикат, который для каждого X принимает значение фи(g*X). Таким образом, фи*g(X)=фи(g*X). Будем говорить, что множество ФИ ЗАМКНУТО ОТНОСИТЕЛЬНО G, если для любых фи из ФИ и g из G предикат фи*g принадлежит ФИ.
Три предиката фи, эквивалентные относительно группы вращений.
Сейчас, наконец, можно сформулировать и доказать нашу основную теорему. Из нее будет видно, что если предикат персептрона инвариантен относительно группы G, то его коэффициенты должны зависеть только от классов G-эквивалентности соответствующих им предикатов фи. В дальнейших исследованиях эта теорема будет наиболее мощным нашим орудием, так как она обобщает метод #1.2 и позволяет (как правило) преобразовывать сложные геометрические задачи в простые алгебраические.
#2.3. ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП
Пусть
(1) G - конечная группа преобразований конечного пространства R;
(2) ФИ - множество предикатов на R, замкнутое относительно G;
(3) предикат пси принадлежит L(ФИ) и инвариантен относительно G.
Тогда существует линейное представление предиката пси,
пси = [СУММА[фи из ФИ]бета.фи*фи > 0],
для которого коэффициенты бета.фи зависят только от класса G-эквивалентности предикатов фи, т.е.
если фи==фи' в G то бета.фи==бета.фи' в G.
Условия теоремы более строги, чем это необходимо. Разумеется, для бесконечных групп теорема, вообще говоря, неверна. Контрпример будет дан в #7.10. Но в некоторых случаях можно доказать теорему и для бесконечных групп. В #10.4 мы рассмотрим пример с интересными следствиями. Мы увидим, что можно несколько ослабить условие того, что G - группа.
Мы не исследовали возможности ослабления условия (2), а это было бы интересно. Однако это не препятствует тому, чтобы показать с помощью нашего метода, что определенные предикаты не являются предикатами конечного порядка. Действительно, когда теорема применяется для доказательства того, что конкретный предикат пси не принадлежит L(ФИ) для конкретного ФИ, то для этого доказывается нелинейность пси даже в G-замыкании множества ФИ. Напомним, что порядок предиката (#1.3) определен без ссылки на какое-либо конкретное множество ФИ предикатов фи! А замыкание множества ФИ относительно группы G не может изменить максимальный размер носителей предикатов, принадлежащих ФИ.
ДОКАЗАТЕЛЬСТВО. Пусть пси(X) имеет линейное представление СУММА[фи из ФИ] альфа(фи)фи(X) > 0]. Мы пишем альфа(фи) вместо альфа.фи, чтобы избежать сложных индексов. Любой элемент g из G определяет взаимно однозначное соответствие фи <-> фи*g, т.е. перестановку предикатов фи. Следовательно,
СУММА[фи из ФИ]альфа(фи)фи(X) = СУММА[фи из ФИ]альфа(фи*g)фи*g(X)
для всякого X, просто потому что в обеих суммах складываются одни и те же числа. Выберем теперь X, для которого пси(X)=1. Поскольку пси является G-инвариантным, a g**-1 - элемент из G, то
СУММА альфа(фи*g)фи*g(g**-1*X) > 0
Отсюда мы заключаем, что если пси(X)=1, то для любого g из G
СУММА альфа(фи*g)фи(X) > 0
Суммируя эти положительные величины по всем g из G, находим
СУММА[g из G]СУММА[фи из ФИ]альфа(фи*g)фи(X) > 0
Если сгруппировать коэффициенты для каждого фи, то получим выражение
СУММА[фи из ФИ]((СУММА[g из G]альфа(фи*g))фи(X) > 0
принадлежащее L(ФИ); его можно представить в виде
СУММА[фи из ФИ]бета(фи)фи(X) > 0
Напомним, что последнее неравенство получено в предположении, что пси(X)=l. Выберем теперь X, для которого фи(X)=0. Тогда те же рассуждения приводят к неравенству
СУММА[фи из ФИ]бета(фи)фи(X) <= 0
Объединив эти неравенства для пси=1 и пси=0, получим
пси(X)=[СУММА[фи из ФИ]бета(фи)фи(X) > 0].
Остается только показать, как мы и обещали, что
фи==фи' в G => бета(фи)=бета(фи').
Но фи==фи' в G означает, что существует такой элемент h, что фи==фи'*h, а потому
бета(фи) = СУММА[g из G]альфа(фи'*h*g) = СУММА[g из G]альфа(фи'*g) = бета(фи')
так как взаимно однозначное соответствие g <-> hg просто изменяет порядок суммирования, не изменяя самих чисел.
ДРУГОЕ ДОКАЗАТЕЛЬСТВО. Учитывая важность теоремы, дадим еще одно доказательство, которое для некоторых читателей может показаться интуитивно более ясным.
Выберем X, для которого пси(X)=1. Тогда для любого g из G будет пси(g*X)=1, и следовательно, каждая из сумм
СУММА альфа(фи)фи(g*X)
будет положительной, а потому положительной будет также и вся сумма
СУММА[фи из ФИ, g из G]альфа(фи)фи(g*X) = СУММА[фи из ФИ, g из G]альфа(фи)фи*g(X)
Члены этой суммы можно расположить в таблицу размера |ФИ|*|G|:
[ альфа(фи.1)фи.1*g.1 + альфа(фи.2)фи.2*g.1 + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.1
альфа(фи.1)фи.1*g.2 + альфа(фи.2)фи.2*g.2 + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.2
...
альфа(фи.1)фи.1*g.|G| + альфа(фи.2)фи.2*g.|G| + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.|G| ] (X)
Мы хотим записать эту сумму в виде бета.1*фи.1 + бета.2*фи.2 + ..., т.е. найти коэффициенты при каждом фи.i. Для этого необходимо при каждом фи.i, сгруппировать те члены
альфа(фи.j), для которых фи.j*g.k=фи.i.
Сумма таких членов равна, разумеется, бета.i. Но на самом деле наша цель состоит не в том, чтобы вычислять бета.i, а в том, чтобы показать, что
фи.a==фи.b в G => бета.a=бета.b.
Для этого предположим, что действительно фи.a==фи.b в G, а отсюда следует, что можно найти такой элемент g, что
фи.a==фи.b*g.
Используем это обстоятельство для того, чтобы установить взаимно однозначное соответствие между множествами тех элементов таблицы, которые суммируются для получения коэффициента бета.a, и тех элементов, которые в сумме дают бета.b. Назовем
g.j-вхождением предиката фи.k
выражение альфа(фи.i)фи.i*g.j, где i определяется условием фи.i*g.j=фи.k. Тогда для каждого j и k в массиве есть в точности одно g.j-вхождение предиката фи.k. (Существование НЕСКОЛЬКИХ различных элементов h из G, удовлетворяющих соотношению фи.i*h=фи.k, неважно. Нас интересует здесь лишь ПРИСУТСТВИЕ каждого вхождения в таблице, а не его значение).
Если теперь альфа(фи.i)фи.i*g.j является g.j-вхождением предиката фи.b, то
фи.i*g.j = фи.b,
и потому
фи.i*g.j*g = фи.b*g = фи.a,
Следовательно, альфа(фи.i)фи.i*g.i*g есть g.j*g-вхождение предиката фи.a. Если вспомнить, что
g.j <-> g.j*g
представляет собой взаимно однозначное соответствие между элементами группы, как показано в замечании 4 из #2.1.1 (рис.2.6), то можно сделать вывод, что соответствующие элементы в суммах бета.a и бета.b должны иметь Одинаковые коэффициенты. Поэтому суммы бета.a и бета.b должны быть равны.
Так как те же самые доводы справедливы и при пси(X)=0, то теорема доказана. В гл.7 и 10 эта теорема распространяется на некоторые бесконечные пространства.
Читателям, которым будет трудно воспринимать эти абстрактные представления, полезно разобрать конкретные примеры классов эквивалентности, скажем геометрические "спектры" из #5.2 и особенно из #6.2.
Доказанную теорему мы будем часто использовать в следующей формулировке.
СЛЕДСТВИЕ 1. Любой инвариантный относительно группы предикат пси (порядка k), удовлетворяющий условиям теоремы, можно представить в виде
пси = [СУММА[ФИ*]альфа.фи*фи > 0],
где ФИ* - множество масок (степени не более k), а альфа.фи=альфа.фи', если S(фи) можно преобразовать в S(фи') при помощи элемента группы G.
ДОКАЗАТЕЛЬСТВО. фи.A==фи.B в G для масок тогда и только тогда, когда A=B*g для некоторого g из G.
СЛЕДСТВИЕ 2. Пусть ФИ = ОБЪЕДИНЕНИЕ ФИ.1, ..., ФИ.m - разбиение множества ФИ на классы эквивалентности по отношению == в G. Тогда, если выполнены условия теоремы, то пси можно записать в виде
пси = [СУММА альфа.i*N.i(X) > 0],
где N.i(X) = |{фи | фи из Ф.i и фи(X)}|, т.е. N.i(X) есть число эквивалентных относительно группы предикатов фи i-го типа, которым удовлетворяет X.
ДОКАЗАТЕЛЬСТВО. В самом деле,
пси = [СУММА[фи из ФИ]альфа.фи*фи > 0] = [СУММА[i]СУММА[фи из ФИ.i]альфа.фи*фи > 0] = [СУММА[i](альфа.i*СУММА[фи из ФИ.i]фи) > 0] = [СУММА[i]альфа.i*N.i(X) > 0].
#2.4. ТРИВИАЛЬНОСТЬ ИНВАРИАНТНЫХ ПРЕДИКАТОВ ПОРЯДКА 1: ПЕРВОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП
ТЕОРЕМА 2.4. Пусть G - любая группа перестановок на R, обладающая следующим свойством [Это свойство, которым обладает большинство интересных геометрических групп, называют обычно "транзитивностью". Исключение составляют, например, чистые повороты вокруг фиксированного центра, а также все переносы, параллельные фиксированному направлению на плоскости. Но группа всех поворотов вокруг всех центров и группа всех переносов и т.д. транзитивны]: для каждой пары точек (р, q) пространства R существует по крайней мере один такой элемент g из G, что g*p=q. Тогда единственными предикатами порядка 1, инвариантными относительно G, будут предикаты (для некоторого числа m):
пси(X) = [|X| > m],
пси(X) = [|X| >= m],
пси(X) = [|X| < m],
пси(X) = [|X| <= m].
ДОКАЗАТЕЛЬСТВО. Так как все одноточечные предикаты фи.p эквивалентны, можно считать, что
пси(X) = [СУММА[p из X]альфа*фи.p > тета],
т.е. что коэффициенты альфа не зависят от p. Но
СУММА альфа*фи.p > тета равносильно СУММА фи.p > тета/альфа при альфа>0. (При альфа<0 знак неравенства нужно изменить на обратный). Далее,
СУММА[p из X]фи.p = |X|.
Таким образом, предикаты порядка 1, инвариантные относительно обычных геометрических групп, не могут делать ничего большего, кроме как определять простые неравенства типа >=m относительно размера, или "площади" фигур. В частности, рассматривая группу переносов G, мы видим, что никакой персептрон порядка 1 не может отличить буквы А, изображенные выше, от некоторого другого, инвариантного относительно переноса, множества фигур такой же площади.
#2.4.1. НЕИНВАРИАНТНЫЕ ПРЕДИКАТЫ ПОРЯДКА 1. Если отказаться от геометрической инвариантности относительно групп, то остаются еще некоторые простые, но полезные предикаты порядка 1, с помощью которых можно представить неравенства, относящиеся к обыкновенным интегралам. Пусть x.p и y.p обозначают координаты x и y точки p:
можно представить, например, следующие предикаты изображений на плоскости:
[Фигура X имеет в правой полуплоскости большую площадь, чем в левой] = [СУММА[правая половина]фи.p - СУММА[левая половина]фи.p > 0],
[Центр тяжести фигуры X находится справа от центральной точки] = [СУММА x.p*фи.p > 0],

[n-й центральный момент фигуры X относительно начала координат больше тета] = [СУММА фи.p(SQR(x.p**2+y.p**2)**n > 0]
и т.д. Но для таких предикатов "моментного типа" координаты точки, относительно которой вычисляется момент, непременно связаны с абсолютной плоскостью, а не с фигурой X. Например, НЕЛЬЗЯ представить при помощи выражения первого порядка предикат
[Второй момент фигуры X относительно собственного центра тяжести больше тета],
так как такой предикат инвариантен относительно (транзитивной) группы переносов.
МАТЕМАТИЧЕСКОЕ ПРИМЕЧАНИЕ. Эти результаты связаны с теоремой Хаара о единственности инвариантных мер (с точностью до постоянного множителя). Для конечных множеств и транзитивных групп единственной мерой Хаара является считающая функция мю(X)=|X|.
Функция множества, определенная формулой
мю(X) = СУММА альфа.i*x.i = СУММА[x.i из X]a.i,
удовлетворяет равенству мю(X)+мю(Y)=мю(объединение X и Y)+мю(пересечение X и Y). Если бы мы определили инвариантность как мю(X)=мю(g*X), то из теоремы Хаара немедленно следовало бы, что мю(X)=c|X|, где c - некоторая константа. Наше же предположение относительно мю несколько слабее, так как мы просто предполагаем, что
мю(X) > тета <=> мю(g*X) > тета
и получаем соответственно более слабый вывод, а именно
мю(X) > тета <=> c|X| > тета
В общем случае связь между теоремой об инвариантности и теорией меры Хаара менее очевидна, так как функция множества СУММА альфа.фи*фи(X), вообще говоря, не является мерой. Это наводит на мысль о некотором обобщении понятия меры, но мы не пытались этим заниматься. Читателям, интересующимся историей развития изложенных здесь идей, возможно, будет интересно проследить связь наших результатов с результатами Питтса и Маккаллока [1947].
#2.0
В этой главе рассматриваются линейные пороговые неравенства, инвариантные относительно групп преобразований точек базисного пространства R. Цель этой главы - установить связь между геометрией пространства R и реализуемостью геометрических предикатов персептронами конечного порядка. Полностью эта цель достигается в части II.
#2.1. ПРИМЕР: КОЭФФИЦИЕНТЫ, УСРЕДНЕННЫЕ ПО СИММЕТРИИ
В качестве введения в изучаемые в этом разделе методы рассмотрим простой, почти тривиальный, пример. Пусть наше пространство R содержит две точки x и y. Докажем, что порядок предиката пси.== = [xyV~x~y] не равен 1. (Этот предикат утверждает, что X не состоит из одной единственной точки). Метод доказательства заключается в том, чтобы прийти к противоречию, предположив, что существуют такие числа альфа, бета и тета, для которых
пси.==(x,y) = xyV~x~y = [альфа*x+бета*y > тета].
Можно перейти непосредственно к доказательству, написав условия, налагаемые на альфа и бета:
пси.==(1,0) = 0 => альфа<=тета,
пси.==(0,1) = 0 => бета<=тета,
пси.==(1,1) = 1 => альфа+бета>тета,
пси.==(0,0) = 1 => 0>тета.
В этом простом случае получить противоречие довольно легко, так как сложение первых двух условий дает
альфа+бета <= 2*тета
а вместе с третьим условием приводит к
тета < 2*тета,
откуда следует, что число тета положительно, что противоречит четвертому условию.
Однако для более сложных случаев, при наличии большого числа переменных, подобные доказательства сложны. С другой стороны, приведенное ниже доказательство, хотя и чуть более сложное, позволяет гораздо глубже проникнуть в существо дела. Заметим вначале, что, переставляя x и y, т.е. меняя их местами, мы не изменяем значения предиката пси. Иначе говоря,
пси.==(x,y) = пси.==(y,x).
Таким образом, неравенства
альфа*x+бета*y > тета,
альфа*y+бета*x > тета
выполняются или не выполняются одновременно. Сложив их, получим
1/2(альфа+бета)x + 1/2(альфа+бета)y > тета.
Аналогично неравенства
альфа*x+бета*y <= тета,
альфа*y+бета*x <= тета
дают
1/2(альфа+бета)x + 1/2(альфа+бета)y <= тета.
Отсюда следует, что, заменив (альфа+бета)/2 на гамма. можно записать
пси.==(x,y) = [гамма*x+гамма*y > тета] = [гамма*(x+y) > тета].
Таким образом, можно построить новое линейное представление для пси в котором коэффициенты при x и y равны.
Следовательно,
пси.==(X) = [гамма*|X| > тета],
где |X|, как обычно, означает число точек в X.
Рассмотрим теперь три множества: X.0={}, X.1={x}, X.2={x,y}. Имеем
|X.0|=0 и гамма*0 > тета,
|X.1|=1 и гамма*1 <= тета,
|X.2|=2 и гамма*2 > тета.
Совершенно очевидно, что это невозможно. Таким образом, кое-что о пси можно узнать, "усредняя" его коэффициенты после перестановки, не меняющей предиката. (В разобранном примере гамма - это среднее арифметическое чисел альфа и бета.) В #2.3 мы точно определим введенное здесь понятие "среднее значение".

Рис.2.1. Функция P(|X|)=гамма|X|-тета не должна попадать в заштрихованные области, а для этого необходимо, чтобы она была многочленом не ниже второй степени.
#2.1.1. [Читатели, знакомые с основными определениями теории групп, могут этот раздел пропустить]. ГРУППЫ ПРЕОБРАЗОВАНИЙ И КЛАССЫ ЭКВИВАЛЕНТНОСТИ ПРЕДИКАТОВ. Обобщение описанной в #2.1 процедуры будет состоять в изучении произвольной группы преобразований на базисном пространстве R и в выяснении того, что подразумевается под независимостью предиката пси от любого из преобразований этой группы (так же, как предикат в #2.1 не зависел от перестановки двух точек). Именно на основе этого представления об "инвариантности относительно группы преобразований" мы сможем приступить к решению геометрических проблем; при этом мы заимствуем математическую точку зрения Феликса Клейна: всякое интересное геометрическое свойство является инвариантом некоторой группы преобразований.
Прекрасный пример группы преобразований дает множество всех переносов плоскости, т.е. таких преобразований, при которых каждая точка плоскости перемещается на место другой точки, причем все точки перемещаются на одно и то же расстояние в одном и том же направлении; иными словами, это жесткий параллельный сдвиг. Рисунок 2.2 иллюстрирует результат двух переносов g.1 и g.2 фигуры X. Он же служит иллюстрацией ряда определений и замечаний, которые мы хотим сейчас привести.

1. Мы определяем перенос как операцию, действующую на отдельные точки таким образом, что при действии операции g.1 на точку x получается другая точка g.1*x. Это "индуцирует" естественное представление о том, как воздействуют переносы g на фигуры в целом. Дадим определение. Если g - одно из преобразований из группы G, а X - некоторая фигура, т.е. подмножество множества R, то
g*X={g*x | x принадлежит X},
что читается так: g*X является (по определению) множеством точек g*x, полученных в результате действия преобразования g на все точки x, принадлежащие X.
2. Если к фигуре X применить сначала преобразование g.1, а затем g.2, то получим новую фигуру, которую можно обозначить g.2(g.1*X). Но ту же самую фигуру можно получить из X как результат одного преобразования - "композиции" преобразований g.1 и g.2. Обычно такую операцию обозначают g.2*g.1, а новое изображение обозначают g.2*g.1*X, как это показано на рис.2.2. Математическое определение группы требует, чтобы g.2*g.1 принадлежало G, если g.1 и и g.2 принадлежат G.
В случае переноса всегда справедливо равенство g.1*g.2*X = = g.2*gi.1*X, что можно проверить, достроив параллелограмм X, g.1*X, g.2*g.1*X, g.2*X. Но это равенство следует рассматривать как случайное стечение обстоятельств, ибо оно не всегда справедливо для других важных геометрических групп. Например, если G - группа всех поворотов вокруг всех точек плоскости, то для указанных на рис.2.3 преобразований g.1 и g.2 точки g.1*g.2*x и g.2*g.1*x различны.

Рис.2.3. Здесь g.1 - небольшой поворот вокруг точки p.1 a g.2 - поворот на 90o вокруг p.2 Из этого рисунка видно, почему для группы вращений, вообще говоря, g.1*g.2*x!=g.2*g.l*x.
3. Последнее требование формального определения "группы преобразований" заключается в том, что группе G вместе с каждым g из G должно принадлежать обратное преобразование, т.е. такое преобразование g**-1, что (g**-1)*g*x=x для каждой точки x. На рис.2.2 показаны обратные преобразования для переносов g.1 и g.2. Обратное преобразование для g.2*g.1 можно получить, достроив параллелограмм на рис.2.2 слева от X. Несложным рассуждением легко показать, что (для любой группы!) всегда справедливо равенство (g.2*g.1)**-1 = g.1**-1 * g.2**-1.
Всегда подразумевается, что группа содержит тривиальное - тождественное - преобразование, т.е. такое преобразование e, что e*x=x для всякого x. Действительно, поскольку e является композицией g**-1*g любого преобразования g и его обратного g**-1, наличие e в G логически вытекает уже из требований 2 и 3. Нетрудно также видеть, что g*g**-1=e.
В учебниках по алгебре можно найти еще и другие требования к группам, например
(g.1*g.2)g.3 = g.1(g.2*g.3)
для любых g.1, g.2 и g.3 из G. Мы используем это требование для групп преобразований без дополнительных оговорок, поскольку оно входит в наше интуитивное представление о преобразовании. В справедливости ассоциативного закона в нашем случае мы убеждаемся, прослеживая просто, что же происходит с каждой отдельной точкой пространства R.
4. Если h - элемент группы G, то множество hG, определяемое формулой
h*G = {hg | g из G}
(т.е. множество, составленное из композиций элемента h со всеми элементами группы G), совпадает со всей группой G и каждый ее элемент входит в hG только один раз. В самом деле, любой элемент g этого множества есть композиция
h(h**-1*g) = (h*h**-1)g = e*g = g.
а потому h**-1*g входит в группу. Если бы, скажем, элемент g.0 встречался в группе дважды, т.е. для двух различных g.1 и g2 было бы
g.0 = h*g.2,
g.0 = h*g.2,
то мы получили бы
h**-1g.0 = h**-1*h*g.1 = g.1,
h**-1g.0 = h**-1*h*g.2 = g.2,
и тогда g.1 и g.2 не могли бы быть различными.
5. В большинстве из последующих разделов, в частности в #2.3, мы будем рассматривать группы G, содержащие лишь КОНЕЧНОЕ число преобразований. Но нам хотелось бы постичь характер обычных групп евклидовых преобразований, а они бесконечны. Например, число различных расстояний, на которые можно перенести фигуру в плоскости, бесконечно: если g!=e - любой нетривиальный перенос, то все переносы g, g*g, g*g*g, ... различны. В большинстве случаев мы сможем доказать нужные нам теоремы, заменив бесконечную группу конечной, изменив при этом, если необходимо, само пространство R! Например, рассматривая перенос, мы вместо евклидовой плоскости часто будем использовать тор (рис.2.4).

Тор разбит на квадраты, как показано на рисунке. Вместо бесконечного множества переносов в плоскости мы рассматриваем только такие преобразования тора, при которых каждая точка переносится на m квадратов вдоль большого экватора и на n квадратов вдоль малого экватора. Число таких "переносов" конечно. В большинстве практических случаев тор ведет себя как небольшая часть плоскости, так как его можно "разрезать" и развернуть (рис.2.5). Следовательно, для "небольших" фигур и "небольших" переносов нет существенной разницы между тором и плоскостью. Об этом мы еще будем говорить в введении к части II и в гл.7.

#2.2. КЛАССЫ ЭКВИВАЛЕНТНОСТИ ИЗОБРАЖЕНИЙ И ПРЕДИКАТОВ
Если задана группа G, то будем говорить, что фигуры X и Y являются G-эквивалентными (и писать X==Y в G), если в группе G найдется такой элемент g, что X=g*Y. Заметим, что
X==X в G, так как X=e*X,
X==Y в G влечет Y==X в G, так как если X=gY, то Y=g**-l*X,
X==Y в G и Y==Z в G влечет X==Z в G, так как если X=g*Y и Y=h*Z, то X=g*h*Z.
Выбирая некоторую группу, мы тем самым автоматически предполагаем, что фигуры разбиты на классы эквивалентности. Это будет важно в дальнейшем, когда окажется, что "образы" (или множества фигур), которые мы захотим распознать, подпадают под такие разбиения (классификации), если группы выбраны правильно.
ПРИМЕР. Пусть G - множество ВСЕХ перестановок конечного множества точек из R. (Перестановкой называется любое перемещение точек, при котором никакие две точки не сводятся в одну). В этом случае (теорема!) две фигуры X и Y будут G-эквивалентными тогда и только тогда, когда они обе будут содержать одинаковое число точек.
ПРИМЕР. Если требуется построить машину для чтения печатных букв или цифр, то возникает естественное желание, чтобы эта машина могла распознавать их независимо от их положения на странице:

т.е. чтобы на решение машины не оказывали влияния элементы группы переносов. Иными словами, восприятие машины должно быть "инвариантно относительно группы переносов", т.е. ее решение должно быть одним и тем же для каждого представителя какого-либо класса эквивалентности относительно группы переносов [Разумеется, на практике от машины требуется большее: желают знать не только, что находится на странице, но и где это находится. В противном случае вместо чтения страницы машина выдавала бы нам беспорядочный набор знаков!].
В #2.3 мы докажем важную теорему, из которой много узнаем о любом персептроне, инвариантном относительно некоторой группы G, т.е. о таком персептроне, предикат пси(X) которого зависит только от класса эквивалентности фигуры X. Прежде чем сформулировать эту теорему, нужно пояснить, что мы понимаем под G-эквивалентностью ПРЕДИКАТОВ.
Будем говорить, что два предиката фи и фи' ЭКВИВАЛЕНТНЫ относительно группы G, и записывать это в виде
фи==фи' в G, если существует такой элемент g из G, что фи(g*X) и фи'(X) СОВПАДАЮТ ДЛЯ КАЖДОГО X.
Нетрудно видеть, что это действительно есть отношение эквивалентности, т.е. что
фи==фи в Gдля любого ф,
фи==фи' в G влечет фи'==фи в G,
фи==фи' в G и фи'==фи'' в G влечет фи==фи'' в G.
Если нам даны предикат фи и элемент g некоторой группы, то определим фи*g как предикат, который для каждого X принимает значение фи(g*X). Таким образом, фи*g(X)=фи(g*X). Будем говорить, что множество ФИ ЗАМКНУТО ОТНОСИТЕЛЬНО G, если для любых фи из ФИ и g из G предикат фи*g принадлежит ФИ.

Три предиката фи, эквивалентные относительно группы вращений.
Сейчас, наконец, можно сформулировать и доказать нашу основную теорему. Из нее будет видно, что если предикат персептрона инвариантен относительно группы G, то его коэффициенты должны зависеть только от классов G-эквивалентности соответствующих им предикатов фи. В дальнейших исследованиях эта теорема будет наиболее мощным нашим орудием, так как она обобщает метод #1.2 и позволяет (как правило) преобразовывать сложные геометрические задачи в простые алгебраические.
#2.3. ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП
Пусть
(1) G - конечная группа преобразований конечного пространства R;
(2) ФИ - множество предикатов на R, замкнутое относительно G;
(3) предикат пси принадлежит L(ФИ) и инвариантен относительно G.
Тогда существует линейное представление предиката пси,
пси = [СУММА[фи из ФИ]бета.фи*фи > 0],
для которого коэффициенты бета.фи зависят только от класса G-эквивалентности предикатов фи, т.е.
если фи==фи' в G то бета.фи==бета.фи' в G.
Условия теоремы более строги, чем это необходимо. Разумеется, для бесконечных групп теорема, вообще говоря, неверна. Контрпример будет дан в #7.10. Но в некоторых случаях можно доказать теорему и для бесконечных групп. В #10.4 мы рассмотрим пример с интересными следствиями. Мы увидим, что можно несколько ослабить условие того, что G - группа.
Мы не исследовали возможности ослабления условия (2), а это было бы интересно. Однако это не препятствует тому, чтобы показать с помощью нашего метода, что определенные предикаты не являются предикатами конечного порядка. Действительно, когда теорема применяется для доказательства того, что конкретный предикат пси не принадлежит L(ФИ) для конкретного ФИ, то для этого доказывается нелинейность пси даже в G-замыкании множества ФИ. Напомним, что порядок предиката (#1.3) определен без ссылки на какое-либо конкретное множество ФИ предикатов фи! А замыкание множества ФИ относительно группы G не может изменить максимальный размер носителей предикатов, принадлежащих ФИ.
ДОКАЗАТЕЛЬСТВО. Пусть пси(X) имеет линейное представление СУММА[фи из ФИ] альфа(фи)фи(X) > 0]. Мы пишем альфа(фи) вместо альфа.фи, чтобы избежать сложных индексов. Любой элемент g из G определяет взаимно однозначное соответствие фи <-> фи*g, т.е. перестановку предикатов фи. Следовательно,
СУММА[фи из ФИ]альфа(фи)фи(X) = СУММА[фи из ФИ]альфа(фи*g)фи*g(X)
для всякого X, просто потому что в обеих суммах складываются одни и те же числа. Выберем теперь X, для которого пси(X)=1. Поскольку пси является G-инвариантным, a g**-1 - элемент из G, то
СУММА альфа(фи*g)фи*g(g**-1*X) > 0
Отсюда мы заключаем, что если пси(X)=1, то для любого g из G
СУММА альфа(фи*g)фи(X) > 0
Суммируя эти положительные величины по всем g из G, находим
СУММА[g из G]СУММА[фи из ФИ]альфа(фи*g)фи(X) > 0
Если сгруппировать коэффициенты для каждого фи, то получим выражение
СУММА[фи из ФИ]((СУММА[g из G]альфа(фи*g))фи(X) > 0
принадлежащее L(ФИ); его можно представить в виде
СУММА[фи из ФИ]бета(фи)фи(X) > 0
Напомним, что последнее неравенство получено в предположении, что пси(X)=l. Выберем теперь X, для которого фи(X)=0. Тогда те же рассуждения приводят к неравенству
СУММА[фи из ФИ]бета(фи)фи(X) <= 0
Объединив эти неравенства для пси=1 и пси=0, получим
пси(X)=[СУММА[фи из ФИ]бета(фи)фи(X) > 0].
Остается только показать, как мы и обещали, что
фи==фи' в G => бета(фи)=бета(фи').
Но фи==фи' в G означает, что существует такой элемент h, что фи==фи'*h, а потому
бета(фи) = СУММА[g из G]альфа(фи'*h*g) = СУММА[g из G]альфа(фи'*g) = бета(фи')
так как взаимно однозначное соответствие g <-> hg просто изменяет порядок суммирования, не изменяя самих чисел.

ДРУГОЕ ДОКАЗАТЕЛЬСТВО. Учитывая важность теоремы, дадим еще одно доказательство, которое для некоторых читателей может показаться интуитивно более ясным.
Выберем X, для которого пси(X)=1. Тогда для любого g из G будет пси(g*X)=1, и следовательно, каждая из сумм
СУММА альфа(фи)фи(g*X)
будет положительной, а потому положительной будет также и вся сумма
СУММА[фи из ФИ, g из G]альфа(фи)фи(g*X) = СУММА[фи из ФИ, g из G]альфа(фи)фи*g(X)
Члены этой суммы можно расположить в таблицу размера |ФИ|*|G|:
[ альфа(фи.1)фи.1*g.1 + альфа(фи.2)фи.2*g.1 + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.1
альфа(фи.1)фи.1*g.2 + альфа(фи.2)фи.2*g.2 + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.2
...
альфа(фи.1)фи.1*g.|G| + альфа(фи.2)фи.2*g.|G| + ... + альфа(фи.|ФИ|)фи.|ФИ|*g.|G| ] (X)
Мы хотим записать эту сумму в виде бета.1*фи.1 + бета.2*фи.2 + ..., т.е. найти коэффициенты при каждом фи.i. Для этого необходимо при каждом фи.i, сгруппировать те члены
альфа(фи.j), для которых фи.j*g.k=фи.i.
Сумма таких членов равна, разумеется, бета.i. Но на самом деле наша цель состоит не в том, чтобы вычислять бета.i, а в том, чтобы показать, что
фи.a==фи.b в G => бета.a=бета.b.
Для этого предположим, что действительно фи.a==фи.b в G, а отсюда следует, что можно найти такой элемент g, что
фи.a==фи.b*g.
Используем это обстоятельство для того, чтобы установить взаимно однозначное соответствие между множествами тех элементов таблицы, которые суммируются для получения коэффициента бета.a, и тех элементов, которые в сумме дают бета.b. Назовем
g.j-вхождением предиката фи.k
выражение альфа(фи.i)фи.i*g.j, где i определяется условием фи.i*g.j=фи.k. Тогда для каждого j и k в массиве есть в точности одно g.j-вхождение предиката фи.k. (Существование НЕСКОЛЬКИХ различных элементов h из G, удовлетворяющих соотношению фи.i*h=фи.k, неважно. Нас интересует здесь лишь ПРИСУТСТВИЕ каждого вхождения в таблице, а не его значение).
Если теперь альфа(фи.i)фи.i*g.j является g.j-вхождением предиката фи.b, то
фи.i*g.j = фи.b,
и потому
фи.i*g.j*g = фи.b*g = фи.a,
Следовательно, альфа(фи.i)фи.i*g.i*g есть g.j*g-вхождение предиката фи.a. Если вспомнить, что
g.j <-> g.j*g
представляет собой взаимно однозначное соответствие между элементами группы, как показано в замечании 4 из #2.1.1 (рис.2.6), то можно сделать вывод, что соответствующие элементы в суммах бета.a и бета.b должны иметь Одинаковые коэффициенты. Поэтому суммы бета.a и бета.b должны быть равны.

Так как те же самые доводы справедливы и при пси(X)=0, то теорема доказана. В гл.7 и 10 эта теорема распространяется на некоторые бесконечные пространства.
Читателям, которым будет трудно воспринимать эти абстрактные представления, полезно разобрать конкретные примеры классов эквивалентности, скажем геометрические "спектры" из #5.2 и особенно из #6.2.
Доказанную теорему мы будем часто использовать в следующей формулировке.
СЛЕДСТВИЕ 1. Любой инвариантный относительно группы предикат пси (порядка k), удовлетворяющий условиям теоремы, можно представить в виде
пси = [СУММА[ФИ*]альфа.фи*фи > 0],
где ФИ* - множество масок (степени не более k), а альфа.фи=альфа.фи', если S(фи) можно преобразовать в S(фи') при помощи элемента группы G.
ДОКАЗАТЕЛЬСТВО. фи.A==фи.B в G для масок тогда и только тогда, когда A=B*g для некоторого g из G.
СЛЕДСТВИЕ 2. Пусть ФИ = ОБЪЕДИНЕНИЕ ФИ.1, ..., ФИ.m - разбиение множества ФИ на классы эквивалентности по отношению == в G. Тогда, если выполнены условия теоремы, то пси можно записать в виде
пси = [СУММА альфа.i*N.i(X) > 0],
где N.i(X) = |{фи | фи из Ф.i и фи(X)}|, т.е. N.i(X) есть число эквивалентных относительно группы предикатов фи i-го типа, которым удовлетворяет X.
ДОКАЗАТЕЛЬСТВО. В самом деле,
пси = [СУММА[фи из ФИ]альфа.фи*фи > 0] = [СУММА[i]СУММА[фи из ФИ.i]альфа.фи*фи > 0] = [СУММА[i](альфа.i*СУММА[фи из ФИ.i]фи) > 0] = [СУММА[i]альфа.i*N.i(X) > 0].
#2.4. ТРИВИАЛЬНОСТЬ ИНВАРИАНТНЫХ ПРЕДИКАТОВ ПОРЯДКА 1: ПЕРВОЕ ПРИМЕНЕНИЕ ТЕОРЕМЫ ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП
ТЕОРЕМА 2.4. Пусть G - любая группа перестановок на R, обладающая следующим свойством [Это свойство, которым обладает большинство интересных геометрических групп, называют обычно "транзитивностью". Исключение составляют, например, чистые повороты вокруг фиксированного центра, а также все переносы, параллельные фиксированному направлению на плоскости. Но группа всех поворотов вокруг всех центров и группа всех переносов и т.д. транзитивны]: для каждой пары точек (р, q) пространства R существует по крайней мере один такой элемент g из G, что g*p=q. Тогда единственными предикатами порядка 1, инвариантными относительно G, будут предикаты (для некоторого числа m):
пси(X) = [|X| > m],
пси(X) = [|X| >= m],
пси(X) = [|X| < m],
пси(X) = [|X| <= m].
ДОКАЗАТЕЛЬСТВО. Так как все одноточечные предикаты фи.p эквивалентны, можно считать, что
пси(X) = [СУММА[p из X]альфа*фи.p > тета],
т.е. что коэффициенты альфа не зависят от p. Но
СУММА альфа*фи.p > тета равносильно СУММА фи.p > тета/альфа при альфа>0. (При альфа<0 знак неравенства нужно изменить на обратный). Далее,
СУММА[p из X]фи.p = |X|.
Таким образом, предикаты порядка 1, инвариантные относительно обычных геометрических групп, не могут делать ничего большего, кроме как определять простые неравенства типа >=m относительно размера, или "площади" фигур. В частности, рассматривая группу переносов G, мы видим, что никакой персептрон порядка 1 не может отличить буквы А, изображенные выше, от некоторого другого, инвариантного относительно переноса, множества фигур такой же площади.
#2.4.1. НЕИНВАРИАНТНЫЕ ПРЕДИКАТЫ ПОРЯДКА 1. Если отказаться от геометрической инвариантности относительно групп, то остаются еще некоторые простые, но полезные предикаты порядка 1, с помощью которых можно представить неравенства, относящиеся к обыкновенным интегралам. Пусть x.p и y.p обозначают координаты x и y точки p:

можно представить, например, следующие предикаты изображений на плоскости:
[Фигура X имеет в правой полуплоскости большую площадь, чем в левой] = [СУММА[правая половина]фи.p - СУММА[левая половина]фи.p > 0],
[Центр тяжести фигуры X находится справа от центральной точки] = [СУММА x.p*фи.p > 0],

[n-й центральный момент фигуры X относительно начала координат больше тета] = [СУММА фи.p(SQR(x.p**2+y.p**2)**n > 0]
и т.д. Но для таких предикатов "моментного типа" координаты точки, относительно которой вычисляется момент, непременно связаны с абсолютной плоскостью, а не с фигурой X. Например, НЕЛЬЗЯ представить при помощи выражения первого порядка предикат
[Второй момент фигуры X относительно собственного центра тяжести больше тета],
так как такой предикат инвариантен относительно (транзитивной) группы переносов.
МАТЕМАТИЧЕСКОЕ ПРИМЕЧАНИЕ. Эти результаты связаны с теоремой Хаара о единственности инвариантных мер (с точностью до постоянного множителя). Для конечных множеств и транзитивных групп единственной мерой Хаара является считающая функция мю(X)=|X|.
Функция множества, определенная формулой
мю(X) = СУММА альфа.i*x.i = СУММА[x.i из X]a.i,
удовлетворяет равенству мю(X)+мю(Y)=мю(объединение X и Y)+мю(пересечение X и Y). Если бы мы определили инвариантность как мю(X)=мю(g*X), то из теоремы Хаара немедленно следовало бы, что мю(X)=c|X|, где c - некоторая константа. Наше же предположение относительно мю несколько слабее, так как мы просто предполагаем, что
мю(X) > тета <=> мю(g*X) > тета
и получаем соответственно более слабый вывод, а именно
мю(X) > тета <=> c|X| > тета
В общем случае связь между теоремой об инвариантности и теорией меры Хаара менее очевидна, так как функция множества СУММА альфа.фи*фи(X), вообще говоря, не является мерой. Это наводит на мысль о некотором обобщении понятия меры, но мы не пытались этим заниматься. Читателям, интересующимся историей развития изложенных здесь идей, возможно, будет интересно проследить связь наших результатов с результатами Питтса и Маккаллока [1947].
Последний раз редактировалось: Gudleifr (Вс Июл 02, 2023 12:34 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 3. ПРЕДИКАТЫ "ЧЕТНОСТЬ" И "ОДИН-В-БЛОКЕ"
#3.0
В этой главе мы изучаем порядки двух особенно интересных предикатов. Ни один из них нельзя назвать геометрическим, так как их группы инвариантности слишком бесформенны. Но в #5.1 мы используем их для решения геометрических задач, подбирая соответствующие "подгруппы", имеющие нужные свойства инвариантности.
#3.1. ФУНКЦИЯ, ОПРЕДЕЛЯЮЩАЯ ЧЕТНОСТЬ
В этом параграфе мы довольно детально проанализируем очень простой предикат, определяемый формулой
пси.ЧЕТНОСТЬ(X) = [|X| - нечетное число].
Мы интересуемся предикатом пси.ЧЕТНОСТЬ по трем причинам: он интересен сам по себе; мы будем использовать его при анализе других, более важных функций; и, главным образом, потому что он иллюстрирует наши математические методы и род проблем, которые можно ими разрешать.
ТЕОРЕМА 3.1.1. Предикат пси.ЧЕТНОСТЬ имеет порядок |R|.
Иными словами, для вычисления этого предиката требуется по крайней мере один частный предикат, носителем которого служит ВСЕ ПРОСТРАНСТВО R.
ДОКАЗАТЕЛЬСТВО. Пусть G - группа всех перестановок точек пространства R. Очевидно, что предикат пси.ЧЕТНОСТЬ инвариантен относительно G (так как перемещение точек не может изменить их числа!).
Предположим теперь, что пси.ЧЕТНОСТЬ = [СУММА альфа.i*фи.i > 0], где фи.i - маски, удовлетворяющие неравенству |S(фи.i)|<=K. Теорема об инвариантности относительно групп гласит, что коэффициенты альфа можно выбрать так, чтобы они зависели только от классов эквивалентности, определенных отношением == в G.
Но тогда альфа.i зависит ТОЛЬКО от |S(фи.i)|. Чтобы показать это, заметим, что 1) все маски с одним и тем же носителем совпадают и 2) все множества с одним и тем же числом элементов можно преобразовать друг в друга с помощью элементов группы G, т.е.
фи.i==фи.j в G <=> |S(фи.i)|=|S(фи.j)|.
Таким образом, в силу следствия 2 из #2.3 предикат пси.ЧЕТНОСТЬ можно записать в виде
[СУММА[j=0..K](альфа.j(СУММА[ФИ.j]фи(X))) > 0] = [СУММА[j=0..K]альфа.j*N.j(X) > 0],
где {ФИ.j}- совокупность масок, носители которых содержат ровно j элементов. Теперь для произвольного подмножества X пространства R подсчитаем
N.j(X) = СУММА[фи из ФИ.j]ф(X).
Так как фи(X) равно 1, если S(фи) включается в X, и равно 0 в противном случае, то N.j(X) - это число подмножеств, состоящих из j точек фигуры X, т.е.
N.j(X) = C(|X|, j) = |X|(|X|-1)...(|X|-j+1)/j!,
а это есть многочлен от |X| степени j. Отсюда следует, что
СУММА[j=0..K]альфа.j*N.j(X)
есть многочлен от |X| степени не выше K; назовем его P(|X|)
Рассмотрим теперь такую последовательность множеств X.0, X.1, ..., X.|R|, что |X.i| = i. Так как Р(|X|) > 0 тогда и только тогда, когда |X| - нечетное число, то
P(|X.0|)<=0, P(|X.1|)>0, P(|X.2|)<=0, ...,
т.е. Р(|X|) по мере роста |X| от 0 до |R| меняет свое направление (т.е. знак производной) |R|-1 раз. Но Р - многочлен степени K, а потому (рис.3.1) K>=|R|. Теорема доказана.

Рис.3.1. Многочлен, изменяющий свое направление K-1 раз, должен иметь степень не менее, чем К.
Отсюда вытекает
ТЕОРЕМА 3.1.2. Если пси.ЧЕТНОСТЬ принадлежит L(ФИ) и ФИ содержит только маски, то ФИ содержит каждую возможную маску.
пси.ЧЕТНОСТЬ = [СУММА[фи из ФИ]альфа.фи*фи > 0]
даже тогда, когда ФИ содержит только маски, а маска с носителем A не принадлежит ФИ.
ДОКАЗАТЕЛЬСТВО. Допустим, что можно было бы записать
Определим для любого пси предикат пси.A(X) как пси(X пересечение А). Тогда пси.A.ЧЕТНОСТЬ - функция, определяющая четность подмножеств множества A, и по предыдущей теореме ее порядок равен |A|. Чтобы изучить представление этой функции в виде линейной комбинации масок подмножеств множества A, рассмотрим фи.А для фи из ФИ. Если S(фи) включается в A, то очевидно, что фи.A=фи; в противном случае фи.A тождественно равно нулю, так как
S(фи) не включается в A => S(фи) не включается в пересечение X и A => фи(X пересечение A)=0 => фи.A(X)=0.
Таким образом, либо S(фи.A) - СОБСТВЕННОЕ подмножество множества А, либо фи.A тождественно равно нулю. Пусть теперь ФИ.A будет совокупностью масок в ФИ, носителями которых служат подмножества множества A. Тогда
Фи.ЧЕТНОСТЬ = [СУММА[фи из ФИ.A]альфа.фи*фи > 0].
Но |S(фи)|<|A| для всех фи из ФИ.A (потому что по предположению маска A не принадлежит ФИ), а это противоречит теореме 3.1.1, так как означает, что порядок предиката пси.A.ЧЕТНОСТЬ меньше |A|. Таким образом, наше предположение невозможно, и теорема доказана.
СЛЕДСТВИЕ 1. Если пси.ЧЕТНОСТЬ принадлежит L(ФИ), то множество ФИ должно содержать по крайней мере один предикат фи, для которого |S(фи)|=|R|.
Следующее следствие, тоже непосредственно вытекающее из доказанной теоремы, представляет интерес для тех, кто изучает пороговую логику.
СЛЕДСТВИЕ 2. Пусть ФИ - совокупность всех предикатов пси.A.ЧЕТНОСТЬ для собственных подмножеств A пространства R. Тогда пси.ЧЕТНОСТЬ не принадлежит L(ФИ).
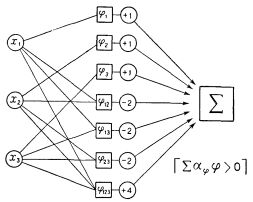
Инвариантные относительно группы коэффициенты предиката пси.ЧЕТНОСТЬ при |R|=3.
Из дальнейшего анализа предиката пси.ЧЕТНОСТЬ, проводимого в гл.10, мы увидим, что функции, которые в принципе можно было бы распознавать при помощи больших персептронов, фактически не могут быть реализованы на практике из-за чрезвычайно больших коэффициентов. Например, отношение наибольшего коэффициента к наименьшему в любом представлении предиката пси.ЧЕТНОСТЬ в виде выражения, линейного относительно множества масок, как будет показано далее, равно 2**(|R|-1).
#3.2. ТЕОРЕМА "ОДИН-В-БЛОКЕ"
[Эта теорема используется для доказательства теоремы в #5.1. Так как в #5.7 дается другое доказательство (опирающееся на теорему 3.1.1), данный параграф при первом чтении можно пропустить].
Другой очень интересный предикат ассоциируется с геометрическим свойством связности. Основную теорему о нем мы докажем сейчас, а применение и интерпретацию отложим до гл.5.
ТЕОРЕМА 3.2. Пусть A.1, ..., A.m - непересекающиеся подмножества пространства R. Зададим предикат
пси(X) = [|X пересечение Ai| > 0 для каждого A.i],
означающий, что в каждом множестве A.i имеется по крайней мере одна точка из X. Если |A.i|=4*m**2 для всякого i, то порядок предиката пси не менее m.
СЛЕДСТВИЕ. Если R = пересечение A.1, A.2, ..., A.m, то порядок предиката пси не менее |R|**(1/3)/4.
ДОКАЗАТЕЛЬСТВО. Для каждого i=1,...,m обозначим через G.i группу перестановок пространства R, изменяющих порядок элементов подмножества A.i но не влияющих на элементы его дополнения.
Пусть G - группа, порождаемая всеми элементами групп G.i. Ясно, что предикат пси инвариантен относительно G.
Пусть ФИ - множество масок степени не выше k. Для определения класса эквивалентности любого элемента фи из ФИ рассмотрим "числа замещений" [В оригинале occupancy numbers.- Прим. перев.]
|S(фи) пересечение A.i|.
Заметим, что фи.1==фи.2 в G тогда и только тогда, когда |S(фи.1) пересечение A.i|=|S(фи.2) пересечение A.i| для каждого i. Обозначим классы эквивалентности через ФИ.1, ФИ.2, ...
Рассмотрим произвольное множество X и класс эквивалентности ФИ.j. Мы хотим подсчитать число N.j(X) элементов класса ФИ.j, которым удовлетворяет X, т.е. число
N.j(X)=|{фи | фи из ФИ.j и S(фи) включается X}|.
С помощью простого рассуждения, использующего комбинаторные методы, получаем
N.j(X) = C(|X пересечение A.1|, |S(фи) пересечение A.1|)*C(|X пересечение A.2|, |S(фи) пересечение A.2|)*...*C(|X пересечение A.m|, |S(фи) пересечение A.m|),
где
C(y,n) = y(y-1)...(y-n+1)/n!,
а фи -произвольный элемент из ФИ.j. Поскольку числа |S(фи) пересечение A.i| зависят только от класса ФИ.2 [И не зависят от X.- Прим. ред.]), а их сумма не превосходит k [Подмножества A.i не пересекаются, а |S(фи)|<=k.- Прим. ред.], отсюда следует, что N.j(X) можно представить в виде многочлена степени не выше k от величин x.i=|пересечение X и A.i|:
N.i(X)=P.i(x.1, ..., x.m).
Пусть теперь [СУММА альфа.фи*фи >0] - представление предиката пси в виде линейной пороговой функции на множестве масок степени не выше k. С помощью рассуждений, которые мы уже неоднократно проводили, можно показать, что альфа.фи зависит только от класса эквивалентности предиката фи. Тогда сумма
СУММА альфа.фи*фи(X) = СУММА(бета.j*СУММА[фи из ФИ.j]фи(X)) = СУММА бета.j*N.j(X) = СУММА бета.j*P.j(x.1, ..., x.m),
будучи суммой многочленов степени не выше k, сама является многочленом. Следовательно, существует такой многочлен Q(x.1, ..., x.m) степени не выше k, что
пси(X) = [Q(x.1, ..., x.m) > 0].
Иными словами, если каждое число x.i=|X пересечение A.i| заключено в пределах
0<=x.i<=4*m**2.
то
Q(x.1, ..., x.m) > 0 <=> x.i для всех i.
Сделаем в Q(x.1, ..., x.m) замену переменных x.i=(t-(2*i-1))**2.
Тогда Q(x.1, ..., x.m) станет многочленом от t степени не выше 2*k. Пусть t принимает значения 0, 1, ..., 2*m. Тогда для нечетного t
x.i=0 при некотором i, а именно при i=1/2(t+1), а для четного t
x.i>0 при всех i.
Итак, по определению предиката пси значение Q должно быть положительным для четного t и отрицательным или равным нулю для нечетного t. На основании подсчета числа перемен знака заключаем, что 2*k>=2*m, т.е. k>=m. Теорема доказана.
ГЛАВА 4. ТЕОРЕМА "И/ИЛИ"
#4.0
В этой главе мы докажем сформулированную в #1.5 теорему "и/или".
ТЕОРЕМА 4.0. Существуют такие предикаты первого порядка пси.1 и пси.2, что пси.1 & пси.2 и пси.1 V пси.2 не являются предикатами конечного порядка.
Докажем это утверждение для пси.1 & пси.2. Утверждение для пси.1 V пси.2 доказывается аналогично. Методика, применяемая при доказательстве этой теоремы, в дальнейшем не используется; поэтому читатели, которые не знают или не любят алгебру подобного вида, могут пропустить оставшуюся часть главы.
#4.1. ЛЕММЫ
В #1.5 мы отмечали, что если R = пересечение A, B и C, то [|X пересечение A| > |X пересечение C|] - предикат порядка 1. Там же мы без доказательства утверждали, что если A, B и C не пересекаются (рис.4.1), то при росте |R| порядок предиката
[|X пересечение A| > |X пересечение C|] & [|X пересечение B| > |X пересечение C|]
не ограничен. Докажем теперь это утверждение. Не нарушая общности, можно считать, что все три части пространства R имеют одинаковую величину M=|A|=|B|=|C| и |R|=3*M. Мы рассмотрим предикаты указанного вида применительно к сетчаткам различного размера. Пусть пси.M(X) - предикат указанного вида и |R|=3*M. Докажем, что его порядок неограниченно возрастает при M->бесконечность.
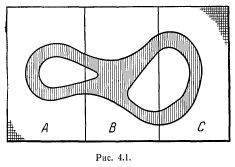
Доказательство повторяет схему доказательств, приведенных в гл.3. Предположим, что для всех M порядки предикатов {фи.M} ограничены фиксированным целым числом N. Мы получим противоречие, показав, что соответствующие многочлены удовлетворяют тогда несовместным условиям.
Определим сначала соответствующие многочлены для фиксированного M. Возьмем группу перестановок, сохраняющих множества A, B и C, но внутри каждого из этих множеств допускающих произвольные перемещения. Класс эквивалентности маски фи характеризуется в таком случае числами |A пересечение S(фи)|, |B пересечение S(фи)| и |C пересечение S(фи)|. Для любой данной маски фи и любого множества X число масок, эквивалентных фи, которым удовлетворяет X, равно
N.фи(X)=C(|A пересечение X|,|A пересечение S(фи)|)*C(|B пересечение X|,|B пересечение S(фи)|)*C(|B пересечение X|,|C пересечение S(фи)|).
Так как мы предположили, что |S(фи)|<=N, то можем быть уверены, что N.фи(X) - многочлен степени не выше N от
x=|A пересечение X|, y=|B пересечение X|, z=|C пересечение X|.
Пусть ФИ - множество масок, имеющих в своих носителях не более N элементов. Пронумеруем классы эквивалентности множества ФИ и обозначим через N.i(X) число масок i-го класса, которым удовлетворяет X. В силу теоремы об инвариантности относительно групп
пси.M(X) = [СУММА бета.i*N.i(X) > 0].
СУММА бета.i*N.i(X) представляет собой многочлен от x, y, z степени не выше N. Обозначим его P.M(x,y,z).
Тогда, по определению, для тех значений x, y, z, которые могут быть числами замещений, т.е. неотрицательными целыми числами, не превышающими М,
P.M(x,y,z) > 0 тогда и только тогда, когда x>z и y>z.
Покажем при помощи ряда лемм, что это Не может выполняться для любого M.
ЛЕММА 1. Пусть P.1(x,y,z), P.2(x,y,z), ... - бесконечная последовательность таких ненулевых многочленов степени не выше N, что для всех положительных целых чисел x, y, z, меньших М,
x>z и y>z влечет P.M(x,y,z) >= 0,
x<=z или y<=z влечет P.M(x,y,z) <= 0
(условия разделения).
Тогда существует единственный ненулевой многочлен Р(x,y,z) степени не выше N, для которого условия разделения выполняются при всех положительных целых значениях x, y, z.
Следует заметить, что нам пришлось ослабить условия разделения, разрешив в них знак равенства, ибо в пределе строгое неравенство не сохраняется. Последствия этого ослабления мы почувствуем при доказательстве леммы 2.
ДОКАЗАТЕЛЬСТВО. Представим многочлен
P.M(x,y,z) = СУММА[i=1..T]C.M.i*m.i(x,y,z)
в виде суммы одночленов m.i степени не выше N от x, y, z.
Так как условия на P.M сохраняются при умножении на положительный скалярный множитель, можно считать, что
СУММА C.M.i**2 = 1
Рассмотрим в T-мерном пространстве множество точек C.M={c.M.1, c.M.2, ..., c.M.T}, М=1,2...
Все они лежат в компактном [См. предметный указатель (см. также Б.3.Вулих, Введение в функциональный анализ, изд-во "Наука", 1967, #3.8.- Прим. перев.] множестве, а именно на единичной T-мерной сфере. Следовательно, существует подпоследовательность C.M.j, сходящаяся к пределу
C = (c.1, c.2, ..., c.T)
в том смысле, что для каждого i
lim[j->беск.]c.M.j.i = c.i.
Многочлен
P(x,y,z) = СУММА[i=1..T]c.i*m.i(x,y,z)
удовлетворяет условиям разделения для всех положительных целых значений x, y, z. Так как СУММА c.i**2 = 1, то он не равен тождественно нулю.
Для того чтобы доказать нашу основную теорему, получим сначала соответствующий результат для многочленов от двух переменных, а затем (лемма 3) приспособим его к P(x, y, z).
ЛЕММА 2. Если для всех целых значений альфа и бета многочлен f(альфа, бета) удовлетворяет условиям:
альфа>0 и бета>0 влечет f(альфа, бета)>=0,
альфа<=0 или бета<=0 влечет f(альфа, бета)<=0,
то он тождественно равен нулю.
ДОКАЗАТЕЛЬСТВО. Предположим, что многочлен f(альфа, бета) удовлетворяет указанным условиям, но не равен тождественно нулю. Тогда его можно записать в виде
f(альфа, бета) = бета**N*g(альфа)+r(альфа, бета),
где многочлен g(альфа) не равен тождественно нулю, а степень переменной бета в r(альфа, бета) меньше N [Здесь N обозначает не степень многочлена, а максимальную степень переменной бета.- Прим. ред.]. Возьмем теперь такое число альфа.0>0, что ни одно из значений g(+/-альфа.0) не равно нулю, а затем выберем такое большое число бета.0, что
|бета.0**N*g(+/-альфа.0)| > |r(+/-альфа.0, +/-бета.0)|.
При таком выборе значение r(+/-альфа.0, +/-бета.0) не будет влиять на знак числа f(+/-альфа.0, +/-бета.0). Далее, так как
f(-альфа.0, бета.0) < 0,
то
g(-альфа.0) < 0,
откуда
[Авторы здесь опустили часть доказательства. Полное доказательство таково:
f(альфа.0, бета.0) > 0 => (бета.0)**N*g(альфа.0) > 0,
f(-альфа.0, бета.0) < 0 => (бета.0)**N*g(-альфа.0) < 0 => g(-альфа.0) < 0,
f(альфа.0, -бета.0) < 0 => (-бета.0)**N*g(альфа.0) < 0 => (-бета.0) < 0,
откуда
(-бета.0)**N*g(альфа.0) > 0.- Прим. ред.]
(-бета.0)**N*g(-альфа.0) > 0
и, следовательно,
f(-альфа.0, -бета.0) > 0.
что противоречит условиям и тем самым доказывает лемму.
#4.2. ПРИМЕНЕНИЕ ТЕОРЕМЫ БЕЗУ
Читатели, знакомые с элементарной алгебраической геометрией [См., например, Уокер Р., Алгебраические кривые, ИЛ, М., 1952, Шафаревич И.Р., Основы алгебраической геометрии, УМН, 24, #6 (1969), 3-184. Плоской неприводимой алгебраической кривой называется множество всех точек плоскости с вещественными координатами (x,y), удовлетворяющими уравнению f(x,y)=0, где f(x,y) - неприводимый многочлен с вещественными коэффициентами. Если многочлен f(x,y) допускает разложение f=f.1*...*f.T на неприводимые множители f.1, ..., f.T, то система неприводимых кривых Y.1, ..., Y.T с уравнениями f.1(x,y)=0, ..., f.T(x,y)=0 называется приводимой алгебраической кривой Y, определяемой уравнением f(x,y)=0. Неприводимые кривые Y.1, ..., Y.T называются компонентами кривой Y. Степень уравнения кривой f(x,y) называется порядком кривой. Теорема Безу (ослабленный вариант): Если две кривые порядков N и M имеют более NM общих точек, то они имеют общую компоненту.- Прим. перев.], заметят, что лемма непосредственно вытекала бы из теоремы Безу, если бы указанные условия были справедливыми для всех вещественных значений альфа и бета. Тогда мы просто должны были бы доказать, что бесконечная в двух направлениях линия в виде буквы L на рис.4.2 не является алгебраической кривой.
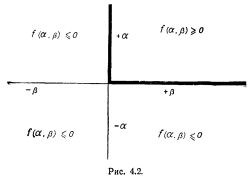
Теорема Безу гласит, что если пересечение алгебраической кривой L с неприводимой алгебраической кривой Y содержит бесконечное число точек, то оно должно содержать всю кривую Y. Кривая L на рис.4.2 содержит положительную полуось у. Так как прямые линии неприводимы, то L должна была бы содержать всю ось y, если бы она была алгебраической.
К сожалению, наши условия выполняются только для точек с целыми координатами; поэтому мы должны допускать возможность того, что кривая f(альфа, бета)=0 имеет более искривленную форму, как, например, на рис.4.3. Неприятное поведение этой кривой никак не связано с рассматриваемыми вопросами. Поскольку многочлен степени N пересекает прямую не более N раз, его вхождения внутрь квадрантов можно заключить в ограниченную область. Это означает, что кривая f(альфа, бета)=0 должна "асимптотически занимать" часть канала, показанного на рис.4.4.
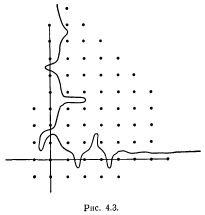
Наверное, можно было бы сформулировать обобщение теоремы Безу, из которого следовало бы, что кривая должна входить и в отрицательные части плоскости, и которое давало бы непосредственное и более иллюстративное доказательство нашей леммы. Однако нами это предположение не разрабатывалось.
ЛЕММА 3. Если для всех положительных целых значений x, y и z многочлен P(x,y,z) удовлетворяет условиям
x>z и y>z влечет P(x,y,z)>=0,
x<=z или y<=z влечет P(x,y,z)<=0,
то он тождественно равен нулю.
ДОКАЗАТЕЛЬСТВО. Предположим, что P(x,y,z) удовлетворяет этим условиям, но не равен тождественно нулю. Обозначим Q(альфа,бета,z)==P(z+альфа,z+бета,z) и запишем
Q(альфа,бета,z)=z**M*f(альфа,бета)+r(альфа,бета,z),
где степень переменной z в r меньше M, а многочлен f(альфа,бета) не равен тождественно нулю. Тогда можно показать, что f удовлетворяет условиям леммы 2. Действительно, возьмем такие альфа.0 и бета.0, что f(альфа.0,бета.0)!=0, и выберем число z.0 таким большим, что
z.0+альфа.0>0, z.0+бета.0>0 и |z.0**M*f(альфа.0,бета.0)|>|r(альфа.0,бета.0,z.0|.
Отсюда f(альфа.0,бета.0)>=0 <=> Q(альфа.0,бета.0,z.0)>=0, т.е. f(альфа.0,бета.0)>=0 тогда и только тогда, когда P(z.0+альфа.0,z.0+бета.0,z.0)>=0. Таким образом,
альфа.0>0 и бета.0>0 => z.0+альфа.0>z.0 и z.0+бета.0>z.0 => P(z.0+альфа.0,z.0+бета.0,z.0)>=0 => f(альфа.0,бета.0)>=0
и аналогично
альфа.0<0 и бета.0<0 => f(альфа.0,бета.0)<=0.
Но это справедливо для всех альфа.0 и бета.0. Поэтому по лемме 2 f(альфа,бета)==0. Отсюда следует, что P(x,y,z) имеет по z нулевую степень, что возможно только в том случае, если он тождественно равен нулю.
На этом доказательство теоремы "и/или" заканчивается.
#3.0
В этой главе мы изучаем порядки двух особенно интересных предикатов. Ни один из них нельзя назвать геометрическим, так как их группы инвариантности слишком бесформенны. Но в #5.1 мы используем их для решения геометрических задач, подбирая соответствующие "подгруппы", имеющие нужные свойства инвариантности.
#3.1. ФУНКЦИЯ, ОПРЕДЕЛЯЮЩАЯ ЧЕТНОСТЬ
В этом параграфе мы довольно детально проанализируем очень простой предикат, определяемый формулой
пси.ЧЕТНОСТЬ(X) = [|X| - нечетное число].
Мы интересуемся предикатом пси.ЧЕТНОСТЬ по трем причинам: он интересен сам по себе; мы будем использовать его при анализе других, более важных функций; и, главным образом, потому что он иллюстрирует наши математические методы и род проблем, которые можно ими разрешать.
ТЕОРЕМА 3.1.1. Предикат пси.ЧЕТНОСТЬ имеет порядок |R|.
Иными словами, для вычисления этого предиката требуется по крайней мере один частный предикат, носителем которого служит ВСЕ ПРОСТРАНСТВО R.
ДОКАЗАТЕЛЬСТВО. Пусть G - группа всех перестановок точек пространства R. Очевидно, что предикат пси.ЧЕТНОСТЬ инвариантен относительно G (так как перемещение точек не может изменить их числа!).
Предположим теперь, что пси.ЧЕТНОСТЬ = [СУММА альфа.i*фи.i > 0], где фи.i - маски, удовлетворяющие неравенству |S(фи.i)|<=K. Теорема об инвариантности относительно групп гласит, что коэффициенты альфа можно выбрать так, чтобы они зависели только от классов эквивалентности, определенных отношением == в G.
Но тогда альфа.i зависит ТОЛЬКО от |S(фи.i)|. Чтобы показать это, заметим, что 1) все маски с одним и тем же носителем совпадают и 2) все множества с одним и тем же числом элементов можно преобразовать друг в друга с помощью элементов группы G, т.е.
фи.i==фи.j в G <=> |S(фи.i)|=|S(фи.j)|.
Таким образом, в силу следствия 2 из #2.3 предикат пси.ЧЕТНОСТЬ можно записать в виде
[СУММА[j=0..K](альфа.j(СУММА[ФИ.j]фи(X))) > 0] = [СУММА[j=0..K]альфа.j*N.j(X) > 0],
где {ФИ.j}- совокупность масок, носители которых содержат ровно j элементов. Теперь для произвольного подмножества X пространства R подсчитаем
N.j(X) = СУММА[фи из ФИ.j]ф(X).
Так как фи(X) равно 1, если S(фи) включается в X, и равно 0 в противном случае, то N.j(X) - это число подмножеств, состоящих из j точек фигуры X, т.е.
N.j(X) = C(|X|, j) = |X|(|X|-1)...(|X|-j+1)/j!,
а это есть многочлен от |X| степени j. Отсюда следует, что
СУММА[j=0..K]альфа.j*N.j(X)
есть многочлен от |X| степени не выше K; назовем его P(|X|)
Рассмотрим теперь такую последовательность множеств X.0, X.1, ..., X.|R|, что |X.i| = i. Так как Р(|X|) > 0 тогда и только тогда, когда |X| - нечетное число, то
P(|X.0|)<=0, P(|X.1|)>0, P(|X.2|)<=0, ...,
т.е. Р(|X|) по мере роста |X| от 0 до |R| меняет свое направление (т.е. знак производной) |R|-1 раз. Но Р - многочлен степени K, а потому (рис.3.1) K>=|R|. Теорема доказана.

Рис.3.1. Многочлен, изменяющий свое направление K-1 раз, должен иметь степень не менее, чем К.
Отсюда вытекает
ТЕОРЕМА 3.1.2. Если пси.ЧЕТНОСТЬ принадлежит L(ФИ) и ФИ содержит только маски, то ФИ содержит каждую возможную маску.
пси.ЧЕТНОСТЬ = [СУММА[фи из ФИ]альфа.фи*фи > 0]
даже тогда, когда ФИ содержит только маски, а маска с носителем A не принадлежит ФИ.
ДОКАЗАТЕЛЬСТВО. Допустим, что можно было бы записать
Определим для любого пси предикат пси.A(X) как пси(X пересечение А). Тогда пси.A.ЧЕТНОСТЬ - функция, определяющая четность подмножеств множества A, и по предыдущей теореме ее порядок равен |A|. Чтобы изучить представление этой функции в виде линейной комбинации масок подмножеств множества A, рассмотрим фи.А для фи из ФИ. Если S(фи) включается в A, то очевидно, что фи.A=фи; в противном случае фи.A тождественно равно нулю, так как
S(фи) не включается в A => S(фи) не включается в пересечение X и A => фи(X пересечение A)=0 => фи.A(X)=0.
Таким образом, либо S(фи.A) - СОБСТВЕННОЕ подмножество множества А, либо фи.A тождественно равно нулю. Пусть теперь ФИ.A будет совокупностью масок в ФИ, носителями которых служат подмножества множества A. Тогда
Фи.ЧЕТНОСТЬ = [СУММА[фи из ФИ.A]альфа.фи*фи > 0].
Но |S(фи)|<|A| для всех фи из ФИ.A (потому что по предположению маска A не принадлежит ФИ), а это противоречит теореме 3.1.1, так как означает, что порядок предиката пси.A.ЧЕТНОСТЬ меньше |A|. Таким образом, наше предположение невозможно, и теорема доказана.
СЛЕДСТВИЕ 1. Если пси.ЧЕТНОСТЬ принадлежит L(ФИ), то множество ФИ должно содержать по крайней мере один предикат фи, для которого |S(фи)|=|R|.
Следующее следствие, тоже непосредственно вытекающее из доказанной теоремы, представляет интерес для тех, кто изучает пороговую логику.
СЛЕДСТВИЕ 2. Пусть ФИ - совокупность всех предикатов пси.A.ЧЕТНОСТЬ для собственных подмножеств A пространства R. Тогда пси.ЧЕТНОСТЬ не принадлежит L(ФИ).

Инвариантные относительно группы коэффициенты предиката пси.ЧЕТНОСТЬ при |R|=3.
Из дальнейшего анализа предиката пси.ЧЕТНОСТЬ, проводимого в гл.10, мы увидим, что функции, которые в принципе можно было бы распознавать при помощи больших персептронов, фактически не могут быть реализованы на практике из-за чрезвычайно больших коэффициентов. Например, отношение наибольшего коэффициента к наименьшему в любом представлении предиката пси.ЧЕТНОСТЬ в виде выражения, линейного относительно множества масок, как будет показано далее, равно 2**(|R|-1).
#3.2. ТЕОРЕМА "ОДИН-В-БЛОКЕ"
[Эта теорема используется для доказательства теоремы в #5.1. Так как в #5.7 дается другое доказательство (опирающееся на теорему 3.1.1), данный параграф при первом чтении можно пропустить].
Другой очень интересный предикат ассоциируется с геометрическим свойством связности. Основную теорему о нем мы докажем сейчас, а применение и интерпретацию отложим до гл.5.
ТЕОРЕМА 3.2. Пусть A.1, ..., A.m - непересекающиеся подмножества пространства R. Зададим предикат
пси(X) = [|X пересечение Ai| > 0 для каждого A.i],
означающий, что в каждом множестве A.i имеется по крайней мере одна точка из X. Если |A.i|=4*m**2 для всякого i, то порядок предиката пси не менее m.
СЛЕДСТВИЕ. Если R = пересечение A.1, A.2, ..., A.m, то порядок предиката пси не менее |R|**(1/3)/4.
ДОКАЗАТЕЛЬСТВО. Для каждого i=1,...,m обозначим через G.i группу перестановок пространства R, изменяющих порядок элементов подмножества A.i но не влияющих на элементы его дополнения.
Пусть G - группа, порождаемая всеми элементами групп G.i. Ясно, что предикат пси инвариантен относительно G.
Пусть ФИ - множество масок степени не выше k. Для определения класса эквивалентности любого элемента фи из ФИ рассмотрим "числа замещений" [В оригинале occupancy numbers.- Прим. перев.]
|S(фи) пересечение A.i|.
Заметим, что фи.1==фи.2 в G тогда и только тогда, когда |S(фи.1) пересечение A.i|=|S(фи.2) пересечение A.i| для каждого i. Обозначим классы эквивалентности через ФИ.1, ФИ.2, ...
Рассмотрим произвольное множество X и класс эквивалентности ФИ.j. Мы хотим подсчитать число N.j(X) элементов класса ФИ.j, которым удовлетворяет X, т.е. число
N.j(X)=|{фи | фи из ФИ.j и S(фи) включается X}|.
С помощью простого рассуждения, использующего комбинаторные методы, получаем
N.j(X) = C(|X пересечение A.1|, |S(фи) пересечение A.1|)*C(|X пересечение A.2|, |S(фи) пересечение A.2|)*...*C(|X пересечение A.m|, |S(фи) пересечение A.m|),
где
C(y,n) = y(y-1)...(y-n+1)/n!,
а фи -произвольный элемент из ФИ.j. Поскольку числа |S(фи) пересечение A.i| зависят только от класса ФИ.2 [И не зависят от X.- Прим. ред.]), а их сумма не превосходит k [Подмножества A.i не пересекаются, а |S(фи)|<=k.- Прим. ред.], отсюда следует, что N.j(X) можно представить в виде многочлена степени не выше k от величин x.i=|пересечение X и A.i|:
N.i(X)=P.i(x.1, ..., x.m).
Пусть теперь [СУММА альфа.фи*фи >0] - представление предиката пси в виде линейной пороговой функции на множестве масок степени не выше k. С помощью рассуждений, которые мы уже неоднократно проводили, можно показать, что альфа.фи зависит только от класса эквивалентности предиката фи. Тогда сумма
СУММА альфа.фи*фи(X) = СУММА(бета.j*СУММА[фи из ФИ.j]фи(X)) = СУММА бета.j*N.j(X) = СУММА бета.j*P.j(x.1, ..., x.m),
будучи суммой многочленов степени не выше k, сама является многочленом. Следовательно, существует такой многочлен Q(x.1, ..., x.m) степени не выше k, что
пси(X) = [Q(x.1, ..., x.m) > 0].
Иными словами, если каждое число x.i=|X пересечение A.i| заключено в пределах
0<=x.i<=4*m**2.
то
Q(x.1, ..., x.m) > 0 <=> x.i для всех i.
Сделаем в Q(x.1, ..., x.m) замену переменных x.i=(t-(2*i-1))**2.
Тогда Q(x.1, ..., x.m) станет многочленом от t степени не выше 2*k. Пусть t принимает значения 0, 1, ..., 2*m. Тогда для нечетного t
x.i=0 при некотором i, а именно при i=1/2(t+1), а для четного t
x.i>0 при всех i.
Итак, по определению предиката пси значение Q должно быть положительным для четного t и отрицательным или равным нулю для нечетного t. На основании подсчета числа перемен знака заключаем, что 2*k>=2*m, т.е. k>=m. Теорема доказана.
ГЛАВА 4. ТЕОРЕМА "И/ИЛИ"
#4.0
В этой главе мы докажем сформулированную в #1.5 теорему "и/или".
ТЕОРЕМА 4.0. Существуют такие предикаты первого порядка пси.1 и пси.2, что пси.1 & пси.2 и пси.1 V пси.2 не являются предикатами конечного порядка.
Докажем это утверждение для пси.1 & пси.2. Утверждение для пси.1 V пси.2 доказывается аналогично. Методика, применяемая при доказательстве этой теоремы, в дальнейшем не используется; поэтому читатели, которые не знают или не любят алгебру подобного вида, могут пропустить оставшуюся часть главы.
#4.1. ЛЕММЫ
В #1.5 мы отмечали, что если R = пересечение A, B и C, то [|X пересечение A| > |X пересечение C|] - предикат порядка 1. Там же мы без доказательства утверждали, что если A, B и C не пересекаются (рис.4.1), то при росте |R| порядок предиката
[|X пересечение A| > |X пересечение C|] & [|X пересечение B| > |X пересечение C|]
не ограничен. Докажем теперь это утверждение. Не нарушая общности, можно считать, что все три части пространства R имеют одинаковую величину M=|A|=|B|=|C| и |R|=3*M. Мы рассмотрим предикаты указанного вида применительно к сетчаткам различного размера. Пусть пси.M(X) - предикат указанного вида и |R|=3*M. Докажем, что его порядок неограниченно возрастает при M->бесконечность.

Доказательство повторяет схему доказательств, приведенных в гл.3. Предположим, что для всех M порядки предикатов {фи.M} ограничены фиксированным целым числом N. Мы получим противоречие, показав, что соответствующие многочлены удовлетворяют тогда несовместным условиям.
Определим сначала соответствующие многочлены для фиксированного M. Возьмем группу перестановок, сохраняющих множества A, B и C, но внутри каждого из этих множеств допускающих произвольные перемещения. Класс эквивалентности маски фи характеризуется в таком случае числами |A пересечение S(фи)|, |B пересечение S(фи)| и |C пересечение S(фи)|. Для любой данной маски фи и любого множества X число масок, эквивалентных фи, которым удовлетворяет X, равно
N.фи(X)=C(|A пересечение X|,|A пересечение S(фи)|)*C(|B пересечение X|,|B пересечение S(фи)|)*C(|B пересечение X|,|C пересечение S(фи)|).
Так как мы предположили, что |S(фи)|<=N, то можем быть уверены, что N.фи(X) - многочлен степени не выше N от
x=|A пересечение X|, y=|B пересечение X|, z=|C пересечение X|.
Пусть ФИ - множество масок, имеющих в своих носителях не более N элементов. Пронумеруем классы эквивалентности множества ФИ и обозначим через N.i(X) число масок i-го класса, которым удовлетворяет X. В силу теоремы об инвариантности относительно групп
пси.M(X) = [СУММА бета.i*N.i(X) > 0].
СУММА бета.i*N.i(X) представляет собой многочлен от x, y, z степени не выше N. Обозначим его P.M(x,y,z).
Тогда, по определению, для тех значений x, y, z, которые могут быть числами замещений, т.е. неотрицательными целыми числами, не превышающими М,
P.M(x,y,z) > 0 тогда и только тогда, когда x>z и y>z.
Покажем при помощи ряда лемм, что это Не может выполняться для любого M.
ЛЕММА 1. Пусть P.1(x,y,z), P.2(x,y,z), ... - бесконечная последовательность таких ненулевых многочленов степени не выше N, что для всех положительных целых чисел x, y, z, меньших М,
x>z и y>z влечет P.M(x,y,z) >= 0,
x<=z или y<=z влечет P.M(x,y,z) <= 0
(условия разделения).
Тогда существует единственный ненулевой многочлен Р(x,y,z) степени не выше N, для которого условия разделения выполняются при всех положительных целых значениях x, y, z.
Следует заметить, что нам пришлось ослабить условия разделения, разрешив в них знак равенства, ибо в пределе строгое неравенство не сохраняется. Последствия этого ослабления мы почувствуем при доказательстве леммы 2.
ДОКАЗАТЕЛЬСТВО. Представим многочлен
P.M(x,y,z) = СУММА[i=1..T]C.M.i*m.i(x,y,z)
в виде суммы одночленов m.i степени не выше N от x, y, z.
Так как условия на P.M сохраняются при умножении на положительный скалярный множитель, можно считать, что
СУММА C.M.i**2 = 1
Рассмотрим в T-мерном пространстве множество точек C.M={c.M.1, c.M.2, ..., c.M.T}, М=1,2...
Все они лежат в компактном [См. предметный указатель (см. также Б.3.Вулих, Введение в функциональный анализ, изд-во "Наука", 1967, #3.8.- Прим. перев.] множестве, а именно на единичной T-мерной сфере. Следовательно, существует подпоследовательность C.M.j, сходящаяся к пределу
C = (c.1, c.2, ..., c.T)
в том смысле, что для каждого i
lim[j->беск.]c.M.j.i = c.i.
Многочлен
P(x,y,z) = СУММА[i=1..T]c.i*m.i(x,y,z)
удовлетворяет условиям разделения для всех положительных целых значений x, y, z. Так как СУММА c.i**2 = 1, то он не равен тождественно нулю.
Для того чтобы доказать нашу основную теорему, получим сначала соответствующий результат для многочленов от двух переменных, а затем (лемма 3) приспособим его к P(x, y, z).
ЛЕММА 2. Если для всех целых значений альфа и бета многочлен f(альфа, бета) удовлетворяет условиям:
альфа>0 и бета>0 влечет f(альфа, бета)>=0,
альфа<=0 или бета<=0 влечет f(альфа, бета)<=0,
то он тождественно равен нулю.
ДОКАЗАТЕЛЬСТВО. Предположим, что многочлен f(альфа, бета) удовлетворяет указанным условиям, но не равен тождественно нулю. Тогда его можно записать в виде
f(альфа, бета) = бета**N*g(альфа)+r(альфа, бета),
где многочлен g(альфа) не равен тождественно нулю, а степень переменной бета в r(альфа, бета) меньше N [Здесь N обозначает не степень многочлена, а максимальную степень переменной бета.- Прим. ред.]. Возьмем теперь такое число альфа.0>0, что ни одно из значений g(+/-альфа.0) не равно нулю, а затем выберем такое большое число бета.0, что
|бета.0**N*g(+/-альфа.0)| > |r(+/-альфа.0, +/-бета.0)|.
При таком выборе значение r(+/-альфа.0, +/-бета.0) не будет влиять на знак числа f(+/-альфа.0, +/-бета.0). Далее, так как
f(-альфа.0, бета.0) < 0,
то
g(-альфа.0) < 0,
откуда
[Авторы здесь опустили часть доказательства. Полное доказательство таково:
f(альфа.0, бета.0) > 0 => (бета.0)**N*g(альфа.0) > 0,
f(-альфа.0, бета.0) < 0 => (бета.0)**N*g(-альфа.0) < 0 => g(-альфа.0) < 0,
f(альфа.0, -бета.0) < 0 => (-бета.0)**N*g(альфа.0) < 0 => (-бета.0) < 0,
откуда
(-бета.0)**N*g(альфа.0) > 0.- Прим. ред.]
(-бета.0)**N*g(-альфа.0) > 0
и, следовательно,
f(-альфа.0, -бета.0) > 0.
что противоречит условиям и тем самым доказывает лемму.
#4.2. ПРИМЕНЕНИЕ ТЕОРЕМЫ БЕЗУ
Читатели, знакомые с элементарной алгебраической геометрией [См., например, Уокер Р., Алгебраические кривые, ИЛ, М., 1952, Шафаревич И.Р., Основы алгебраической геометрии, УМН, 24, #6 (1969), 3-184. Плоской неприводимой алгебраической кривой называется множество всех точек плоскости с вещественными координатами (x,y), удовлетворяющими уравнению f(x,y)=0, где f(x,y) - неприводимый многочлен с вещественными коэффициентами. Если многочлен f(x,y) допускает разложение f=f.1*...*f.T на неприводимые множители f.1, ..., f.T, то система неприводимых кривых Y.1, ..., Y.T с уравнениями f.1(x,y)=0, ..., f.T(x,y)=0 называется приводимой алгебраической кривой Y, определяемой уравнением f(x,y)=0. Неприводимые кривые Y.1, ..., Y.T называются компонентами кривой Y. Степень уравнения кривой f(x,y) называется порядком кривой. Теорема Безу (ослабленный вариант): Если две кривые порядков N и M имеют более NM общих точек, то они имеют общую компоненту.- Прим. перев.], заметят, что лемма непосредственно вытекала бы из теоремы Безу, если бы указанные условия были справедливыми для всех вещественных значений альфа и бета. Тогда мы просто должны были бы доказать, что бесконечная в двух направлениях линия в виде буквы L на рис.4.2 не является алгебраической кривой.

Теорема Безу гласит, что если пересечение алгебраической кривой L с неприводимой алгебраической кривой Y содержит бесконечное число точек, то оно должно содержать всю кривую Y. Кривая L на рис.4.2 содержит положительную полуось у. Так как прямые линии неприводимы, то L должна была бы содержать всю ось y, если бы она была алгебраической.
К сожалению, наши условия выполняются только для точек с целыми координатами; поэтому мы должны допускать возможность того, что кривая f(альфа, бета)=0 имеет более искривленную форму, как, например, на рис.4.3. Неприятное поведение этой кривой никак не связано с рассматриваемыми вопросами. Поскольку многочлен степени N пересекает прямую не более N раз, его вхождения внутрь квадрантов можно заключить в ограниченную область. Это означает, что кривая f(альфа, бета)=0 должна "асимптотически занимать" часть канала, показанного на рис.4.4.


Наверное, можно было бы сформулировать обобщение теоремы Безу, из которого следовало бы, что кривая должна входить и в отрицательные части плоскости, и которое давало бы непосредственное и более иллюстративное доказательство нашей леммы. Однако нами это предположение не разрабатывалось.
ЛЕММА 3. Если для всех положительных целых значений x, y и z многочлен P(x,y,z) удовлетворяет условиям
x>z и y>z влечет P(x,y,z)>=0,
x<=z или y<=z влечет P(x,y,z)<=0,
то он тождественно равен нулю.
ДОКАЗАТЕЛЬСТВО. Предположим, что P(x,y,z) удовлетворяет этим условиям, но не равен тождественно нулю. Обозначим Q(альфа,бета,z)==P(z+альфа,z+бета,z) и запишем
Q(альфа,бета,z)=z**M*f(альфа,бета)+r(альфа,бета,z),
где степень переменной z в r меньше M, а многочлен f(альфа,бета) не равен тождественно нулю. Тогда можно показать, что f удовлетворяет условиям леммы 2. Действительно, возьмем такие альфа.0 и бета.0, что f(альфа.0,бета.0)!=0, и выберем число z.0 таким большим, что
z.0+альфа.0>0, z.0+бета.0>0 и |z.0**M*f(альфа.0,бета.0)|>|r(альфа.0,бета.0,z.0|.
Отсюда f(альфа.0,бета.0)>=0 <=> Q(альфа.0,бета.0,z.0)>=0, т.е. f(альфа.0,бета.0)>=0 тогда и только тогда, когда P(z.0+альфа.0,z.0+бета.0,z.0)>=0. Таким образом,
альфа.0>0 и бета.0>0 => z.0+альфа.0>z.0 и z.0+бета.0>z.0 => P(z.0+альфа.0,z.0+бета.0,z.0)>=0 => f(альфа.0,бета.0)>=0
и аналогично
альфа.0<0 и бета.0<0 => f(альфа.0,бета.0)<=0.
Но это справедливо для всех альфа.0 и бета.0. Поэтому по лемме 2 f(альфа,бета)==0. Отсюда следует, что P(x,y,z) имеет по z нулевую степень, что возможно только в том случае, если он тождественно равен нулю.
На этом доказательство теоремы "и/или" заканчивается.
Последний раз редактировалось: Gudleifr (Ср Июн 21, 2023 12:50 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
II. ГЕОМЕТРИЧЕСКАЯ ТЕОРИЯ ЛИНЕЙНЫХ НЕРАВЕНСТВ
ВВЕДЕНИЕ В ЧАСТЬ II
Анализ геометрических свойств персептронов начинается в гл.5 с изучения предиката пси.СВЯЗНОСТЬ, отвечающего на вопрос, связна ли фигура X, т.е. существует ли непрерывный путь между любыми двумя ее точками, целиком принадлежащий X (см. #0.5). Мы выбрали для изучения свойство СВЯЗНОСТИ в полной уверенности, что соответствующий предикат нелокален в некотором очень глубоком смысле, а потому должен бы оказаться твердым орешком для любого локального по своей сути параллельного способа вычислений. Сначала мы пытались доказать, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, основываясь на его повышенной чувствительности к малым изменениям фигуры (тонкий разрез или добавление изолированной точки легко превращает любую связную фигуру в несвязную), но нам так и не удалось провести настоящее доказательство.
К плодотворным методам, хотя и косвенным путем, привело использование теоремы об инвариантности относительно групп. Напомним, что в случае предиката пси.ЧЕТНОСТЬ мы начинали с определения наибольшей возможной группы преобразований пространства R, не изменяющих предикат пси (для предиката пси.ЧЕТНОСТЬ такой группой оказалась группа всех перестановок). Используя такую группу, мы затем объединяли предикаты фи в классы эквивалентности и в конечном итоге свели задачу о представлении предиката пси в L(ФИ) к задаче о многочленах от функций перечисления.
Однако любая попытка НЕПОСРЕДСТВЕННОГО применения подобного приема в случае предиката пси.СВЯЗНОСТЬ приводит к трудностям, связанным с представлением общего топологического преобразования на дискретной сетчатке. К счастью, оказалось, что задачу можно "привести" к более простой, в которой участвуют группы, легче поддающиеся исследованию. Действительно, в #5.1 мы покажем, что если бы персептрон мог различать хотя бы некоторые частные случаи связности, его можно было бы применить для моделирования предиката пси.ОДИН-В-БЛОКЕ из #3.2. Если бы это было возможно, то логически рассуждая, мы получили бы:
пси.СВЯЗНОСТЬ - предикат конечного порядка => частный случай связности - предикат конечного порядка => пси.ОДИН-В-БЛОКЕ - предикат конечного порядка,
а так как последнее неверно, то неверно и первое.
В конце гл.5 этот строго отрицательный результат, утверждающий, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, обобщается на все топологические предикаты за одним единственным исключением. Только ЭЙЛЕРОВУ ХАРАКТЕРИСТИКУ, наинизший и простейший из всех топологических инвариантов, можно распознать предикатной схемой конечного порядка.
В гл.6 мы получим ряд положительных результатов. Существуют предикаты, кроме упомянутых в #0.5 пси.ВЫПУКЛОСТЬ и пси.ОКРУЖНОСТЬ, отражающие геометрические свойства и весьма очевидным образом обладающие конечным (и даже довольно низким) порядком. К их числу относятся предикаты, различающие конфигурации типа треугольников, квадратов или букв алфавита. Некоторые из этих свойств образуют так называемые "геометрические спектры", которые можно рассматривать или как локальные геометрические свойства, или как простые статистические особенности образов. Тот факт, что персептроны могут распознавать образы, связанные с этими спектрами, породил, по всей вероятности, определенную долю ложного оптимизма по поводу способностей персептронов вообще. В конце гл.6 мы покажем, что даже когда персептрон распознает каждый из этих образов в отдельности, он не в состоянии обнаружить их в сложных сочетаниях.
Глава 7 ведет нас любопытным обходным путем. Оказывается, некоторые предикаты, на первый взгляд не обладающие конечным порядком (например, предикаты, указывающие на симметрию или подобие), в действительности можно реализовать предикатными схемами конечного порядка. Однако такие реализации неосуществимы в весьма специфическом смысле: их коэффициенты растут со столь астрономической скоростью, что теряют физический смысл. Это явление, по-видимому, служит серьезным уроком: даже в таком простом комбинаторном вопросе нужно быть начеку. Линейные формы, полученные методом "стратификации", описанным в гл. 7, чем-то напоминают числа Геделя в логике или "нестандартные модели" в математическом анализе. Наша интуиция в области вычислений все еще слаба, и здесь нас наверняка ждет немало сюрпризов.
В гл. 8 изучается персептрон, ограниченный по диаметру. Здесь все намного проще, и даже не нужно алгебраической теории, чтобы получить общие отрицательные результаты. Машины, ограниченные по диаметру, в большинстве своем подчиняются тем же требованиям, что и машины первого порядка. В некотором отношении они отличаются от последних: например, в способности аппроксимировать вычисления, подобные интегрированию. Это позволяет им с определенной точностью вычислять предикат пси.ОКРУЖНОСТЬ Кроме того, они могут вычислять узкий класс предикатов, связанных с эйлеровой характеристикой.
В нашем исследовании предикат пси.СВЯЗНОСТЬ будет играть столь большую роль, что мы посчитали целесообразным попытаться связать рабочие характеристики соответствующего персептрона с характеристиками других, существенно отличных вычислительных схем. Этот предикат изучается в гл.9 на фоне широкого многообразия моделей для геометрических вычислений. Мы с удивлением обнаружили, что для последовательных вычислительных машин требуется лишь весьма небольшой объем памяти.
ПРЕДСТАВЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ
Мы собираемся исследовать ряд интересных геометрических предикатов. В качестве первого шага нам нужно выбрать подходящее пространство R с топологическими и метрическими свойствами, необходимыми для определения геометрических фигур этого мы могли не делать в случае предикатов типа четности и других, имеющих дело с подсчетом, поскольку в действительности они не носят геометрического характера.
По-видимому, простейшая методика, в достаточной мере строгая, но еще не погрязшая в разного рода математических тонкостях, состоит в разбиении евклидовой плоскости E**2 на квадраты по типу бесконечной шахматной доски. Множество R задается тогда как МНОЖЕСТВО КВАДРАТОВ. Фигура X.E на E**2 отождествляется с подмножеством квадратов, в которых содержится по крайней мере одна точка из X.E. Таким образом, любому подмножеству X.E в E**2 соответствует подмножество X в R, определенное следующим образом:
x принадлежит X, если по крайней мере одна точка из X.E лежит в квадрате x.
Хотя по логике вещей X и X.E различны, их отождествление теперь не может вызвать никаких серьезных затруднений, и в дальнейшем мы будем их отождествлять. Поэтому, называя подмножества множества R "окружностями", "треугольниками" и т.п., мы будем иметь в виду, что они получаются из настоящих окружностей и треугольников с помощью отображения X.E->X. Это, разумеется, означает, что вблизи "пределов разрешающей способности" конечность размеров "ячейки" сетчатки R приводит к очевидным ошибкам классификации. Так, например, малая окружность не выглядит очень округлой.
Если бы возникла необходимость различать E**2 и R, мы бы сказали, что две фигуры X.E и X.E' из E**2 принадлежат одному и тому же классу R-ДОПУСТИМЫХ отклонений, если X=X'. Группы ПЕРЕНОСОВ, играющие основную роль в гл.6-8, не доставляют никаких трудностей. Серьезная проблема, связанная с допустимыми отклонениями, или допусками, возникает при обсуждении в #7.6 РАСТЯЖЕНИЙ и ВРАЩЕНИЙ. Любопытно, что при рассмотрении топологической эквивалентности в гл.5 эта проблема, по-видимому, не возникает, так как мы можем доказать все известные нам теоремы, не привлекая всю группу топологических преобразований.
ВВЕДЕНИЕ В ЧАСТЬ II
Анализ геометрических свойств персептронов начинается в гл.5 с изучения предиката пси.СВЯЗНОСТЬ, отвечающего на вопрос, связна ли фигура X, т.е. существует ли непрерывный путь между любыми двумя ее точками, целиком принадлежащий X (см. #0.5). Мы выбрали для изучения свойство СВЯЗНОСТИ в полной уверенности, что соответствующий предикат нелокален в некотором очень глубоком смысле, а потому должен бы оказаться твердым орешком для любого локального по своей сути параллельного способа вычислений. Сначала мы пытались доказать, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, основываясь на его повышенной чувствительности к малым изменениям фигуры (тонкий разрез или добавление изолированной точки легко превращает любую связную фигуру в несвязную), но нам так и не удалось провести настоящее доказательство.
К плодотворным методам, хотя и косвенным путем, привело использование теоремы об инвариантности относительно групп. Напомним, что в случае предиката пси.ЧЕТНОСТЬ мы начинали с определения наибольшей возможной группы преобразований пространства R, не изменяющих предикат пси (для предиката пси.ЧЕТНОСТЬ такой группой оказалась группа всех перестановок). Используя такую группу, мы затем объединяли предикаты фи в классы эквивалентности и в конечном итоге свели задачу о представлении предиката пси в L(ФИ) к задаче о многочленах от функций перечисления.
Однако любая попытка НЕПОСРЕДСТВЕННОГО применения подобного приема в случае предиката пси.СВЯЗНОСТЬ приводит к трудностям, связанным с представлением общего топологического преобразования на дискретной сетчатке. К счастью, оказалось, что задачу можно "привести" к более простой, в которой участвуют группы, легче поддающиеся исследованию. Действительно, в #5.1 мы покажем, что если бы персептрон мог различать хотя бы некоторые частные случаи связности, его можно было бы применить для моделирования предиката пси.ОДИН-В-БЛОКЕ из #3.2. Если бы это было возможно, то логически рассуждая, мы получили бы:
пси.СВЯЗНОСТЬ - предикат конечного порядка => частный случай связности - предикат конечного порядка => пси.ОДИН-В-БЛОКЕ - предикат конечного порядка,
а так как последнее неверно, то неверно и первое.
В конце гл.5 этот строго отрицательный результат, утверждающий, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, обобщается на все топологические предикаты за одним единственным исключением. Только ЭЙЛЕРОВУ ХАРАКТЕРИСТИКУ, наинизший и простейший из всех топологических инвариантов, можно распознать предикатной схемой конечного порядка.
В гл.6 мы получим ряд положительных результатов. Существуют предикаты, кроме упомянутых в #0.5 пси.ВЫПУКЛОСТЬ и пси.ОКРУЖНОСТЬ, отражающие геометрические свойства и весьма очевидным образом обладающие конечным (и даже довольно низким) порядком. К их числу относятся предикаты, различающие конфигурации типа треугольников, квадратов или букв алфавита. Некоторые из этих свойств образуют так называемые "геометрические спектры", которые можно рассматривать или как локальные геометрические свойства, или как простые статистические особенности образов. Тот факт, что персептроны могут распознавать образы, связанные с этими спектрами, породил, по всей вероятности, определенную долю ложного оптимизма по поводу способностей персептронов вообще. В конце гл.6 мы покажем, что даже когда персептрон распознает каждый из этих образов в отдельности, он не в состоянии обнаружить их в сложных сочетаниях.
Глава 7 ведет нас любопытным обходным путем. Оказывается, некоторые предикаты, на первый взгляд не обладающие конечным порядком (например, предикаты, указывающие на симметрию или подобие), в действительности можно реализовать предикатными схемами конечного порядка. Однако такие реализации неосуществимы в весьма специфическом смысле: их коэффициенты растут со столь астрономической скоростью, что теряют физический смысл. Это явление, по-видимому, служит серьезным уроком: даже в таком простом комбинаторном вопросе нужно быть начеку. Линейные формы, полученные методом "стратификации", описанным в гл. 7, чем-то напоминают числа Геделя в логике или "нестандартные модели" в математическом анализе. Наша интуиция в области вычислений все еще слаба, и здесь нас наверняка ждет немало сюрпризов.
В гл. 8 изучается персептрон, ограниченный по диаметру. Здесь все намного проще, и даже не нужно алгебраической теории, чтобы получить общие отрицательные результаты. Машины, ограниченные по диаметру, в большинстве своем подчиняются тем же требованиям, что и машины первого порядка. В некотором отношении они отличаются от последних: например, в способности аппроксимировать вычисления, подобные интегрированию. Это позволяет им с определенной точностью вычислять предикат пси.ОКРУЖНОСТЬ Кроме того, они могут вычислять узкий класс предикатов, связанных с эйлеровой характеристикой.
В нашем исследовании предикат пси.СВЯЗНОСТЬ будет играть столь большую роль, что мы посчитали целесообразным попытаться связать рабочие характеристики соответствующего персептрона с характеристиками других, существенно отличных вычислительных схем. Этот предикат изучается в гл.9 на фоне широкого многообразия моделей для геометрических вычислений. Мы с удивлением обнаружили, что для последовательных вычислительных машин требуется лишь весьма небольшой объем памяти.
ПРЕДСТАВЛЕНИЕ ГЕОМЕТРИЧЕСКИХ ОБРАЗОВ
Мы собираемся исследовать ряд интересных геометрических предикатов. В качестве первого шага нам нужно выбрать подходящее пространство R с топологическими и метрическими свойствами, необходимыми для определения геометрических фигур этого мы могли не делать в случае предикатов типа четности и других, имеющих дело с подсчетом, поскольку в действительности они не носят геометрического характера.
По-видимому, простейшая методика, в достаточной мере строгая, но еще не погрязшая в разного рода математических тонкостях, состоит в разбиении евклидовой плоскости E**2 на квадраты по типу бесконечной шахматной доски. Множество R задается тогда как МНОЖЕСТВО КВАДРАТОВ. Фигура X.E на E**2 отождествляется с подмножеством квадратов, в которых содержится по крайней мере одна точка из X.E. Таким образом, любому подмножеству X.E в E**2 соответствует подмножество X в R, определенное следующим образом:
x принадлежит X, если по крайней мере одна точка из X.E лежит в квадрате x.
Хотя по логике вещей X и X.E различны, их отождествление теперь не может вызвать никаких серьезных затруднений, и в дальнейшем мы будем их отождествлять. Поэтому, называя подмножества множества R "окружностями", "треугольниками" и т.п., мы будем иметь в виду, что они получаются из настоящих окружностей и треугольников с помощью отображения X.E->X. Это, разумеется, означает, что вблизи "пределов разрешающей способности" конечность размеров "ячейки" сетчатки R приводит к очевидным ошибкам классификации. Так, например, малая окружность не выглядит очень округлой.

Если бы возникла необходимость различать E**2 и R, мы бы сказали, что две фигуры X.E и X.E' из E**2 принадлежат одному и тому же классу R-ДОПУСТИМЫХ отклонений, если X=X'. Группы ПЕРЕНОСОВ, играющие основную роль в гл.6-8, не доставляют никаких трудностей. Серьезная проблема, связанная с допустимыми отклонениями, или допусками, возникает при обсуждении в #7.6 РАСТЯЖЕНИЙ и ВРАЩЕНИЙ. Любопытно, что при рассмотрении топологической эквивалентности в гл.5 эта проблема, по-видимому, не возникает, так как мы можем доказать все известные нам теоремы, не привлекая всю группу топологических преобразований.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 5. ПРЕДИКАТ ПСИ.СВЯЗНОСТЬ: ГЕОМЕТРИЧЕСКОЕ СВОЙСТВО НЕОГРАНИЧЕННОГО ПОРЯДКА
#5.0. ВВЕДЕНИЕ
В этой главе мы начинаем изучать свойство СВЯЗНОСТИ. Фигура X СВЯЗНА, если она не состоит из двух или более отдельных, несоприкасающихся частей. Хотя свойство связности интересно и само по себе, мы останавливаемся на нем в основном в надежде на то, что его изучение прольет свет на более фундаментальный, хотя и плохо определенный вопрос о противопоставлении локального и глобального. Дело в том, что связность вне всякого сомнения глобальна. На основе отдельных локальных опытов никогда нельзя заключить, что фигура связна. Разумеется, в случае фигуры
можно было бы обнаружить, что эта фигура несвязна, рассматривая только окрестность изолированной точки, расположенной в правом нижнем углу рисунка. Однако отсутствие такого локального свидетельства несвязности еще не позволяет сделать вывод, что фигура связна. Когда мы задаемся вопросом, которая из двух фигур на рис.5.1 связна, трудно представить себе какой-либо локальный результат, который мог бы склонить чашу весов в сторону того или другого заключения. Это легко ДОКАЗАТЬ, например, в узких рамках понятия ЛОКАЛЬНОГО как ОГРАНИЧЕННОГО по диаметру (см. #0.3 и гл.8 ). Труднее установить это же для структуры ограниченного порядка. Однако случай ограниченного диаметра подсказывает: рассматривая определенный подкласс фигур, мы могли бы показать, что эта задача эквивалентна распознаванию ЧЕТНОСТИ или чего-то с нею сходного. Мы и собираемся сейчас поступить именно так.
#5.1. ТЕОРЕМА О СВЯЗНОСТИ
[Мы дадим еще два других доказательства с различных точек зрения. Доказательство в #5.5, вероятно, легче всего понять само по себе, зато доказательство в #5.7 дает больше информации о том, каким образом возрастает порядок с ростом сетчатки R].
Две точки в R называются СМЕЖНЫМИ, если они являются квадратами с общей стороной [Мы не можем считать связью угловые касания, так как это позволило бы двум "кривым" пройти одна сквозь другую без "пересечения", и даже теорема о жордановых кривых не была бы верна. Но эту трудность можно обойти, разделив E**2 на шестиугольники, а не на квадраты!]. Фигура СВЯЗНА, если любые две ее точки (т.е. "квадраты") p.1, p.2 можно соединить путем, проходящим по смежным точкам.
ТЕОРЕМА 5.1. Предикат пси.СВЯЗНОСТЬ(X) = [X - связная фигура"] не имеет конечного порядка (#1.6), т.е. его порядок с ростом |R| неограниченно возрастает.
ДОКАЗАТЕЛЬСТВО. Допустим, что порядок предиката пси.СВЯЗНОСТЬ(X) меньше m. Расположим квадраты сетчатки R в 2*m+1 ряда по 4*m**2 квадратов в каждом (рис.5.2). Обозначим через Y.0 множество заштрихованных на рисунке квадратов, т.е. множество точек в нечетных рядах, а через Y.1 - множество оставшихся квадратов. Пусть F - семейство фигур, полученных добавлением к Y.0 подмножеств множества Y.1, т.е. X принадлежит F, если X имеет вид (Y.0 объединение X.1), где (X.1 включается в Y.1). Фигура X связна тогда и только тогда, когда X.1 содержит хотя бы по одному квадрату из каждого четного ряда, или, что то же, если множество X.1 удовлетворяет условию "один-в-блоке" из #3.2.
Чтобы разобраться в подробностях применения теоремы "один-в-блоке", если это еще не очевидно, рассмотрим фигуры семейства F как подмножество всех возможных фигур на R. Ясно, что если бы мы имели предикат k-то порядка пси.k.СВЯЗНОСТЬ, способный распознавать связность на R, то мы могли бы иметь и предикат, работающий на F: им был бы тот же самый предикат с постоянными нулевыми значениями для всех переменных, не принадлежащих (Y.0 объединение Y.1). А так как все точки нечетных рядов всегда принимают единичные значения для фигур в F, то это в свою очередь означает, что мы могли бы иметь предикат k-го порядка для принятия решения о свойстве "один-в-блоке" на множестве X.1: им был бы тот же самый предикат, но еще более ограниченный в том смысле, что точки в X.0 принимали бы постоянные единичные значения. Таким образом, каждая булева функция первоначального предиката пси.k.СВЯЗНОСТЬ заменяется функцией, полученной присвоением некоторым ее переменным фиксированных значений, равных нулю или единице; подобная операция никогда не может увеличить порядок функции. Но так как этот последний предикат существовать не может, то не может существовать и исходный предикат пси.k.СВЯЗНОСТЬ. Из нашего доказательства следует, что порядок предиката пси.СВЯЗНОСТЬ не менее C|R|**(1/3) В #5.7 мы покажем, что он не менее C|R|**(1/2).
#5.2. ПРИМЕР
Рассмотрим частный случай k=2 и эквивалентную задачу "один-в-блоке" для пространства вида
в котором m=3 и в каждом блоке ровно 4 квадрата. Далее, рассмотрим предикат пси порядка 2 и покажем, что он не может характеризовать связность такого рода фигур. Предположим, что пси = [СУММА альфа.i*фи.1 > тета], и рассмотрим эквивалентную форму, симметризированную относительно всей группы перестановок, переставляющих ряды и квадраты внутри рядов [Заметим, что это не та же самая группа, которая фигурировала в доказательстве теоремы из #3.2. Часть группы, переставляющая ряды, там не использовалась]. Тогда существуют только три класса эквивалентности масок порядка не выше 2, а именно:
отдельные точки фи.1.i = x.i;
пары точек фи.11.i.j = x.i*x.j (x.i и x.j в одном и том же ряду);
пары точек фи.12.i.j = x.i*x.j (x.i и x.j в разных рядах).
Следовательно, любой предикат порядка 2 должен иметь вид
пси = [альфа.1*N.1(X) + альфа.11*N.11(X) + альфа.12*N.12(X) > тета],
где N.1, N.11, N.12 - числа соответствующих точечных множеств в X. Теперь рассмотрим две фигуры:

В каждой
N.1=6, N.11=6, N.12=9,
так что значение пси одинаково для обеих фигур. Но фигура X.1 связна, а X.2 нет! Заметьте, что здесь m=3, и мы, предположив, что порядок меньше 3, получим противоречие уже при |A.i|=4, а общее доказательство требовало |A.i|=4*m**236. Тот же результат можно получить и при |A.i|=3, m=4, так как (3, 1, 1, 4) ~ (2, 2, 2, 0) [Эти цифры показывают, сколько черных квадратов в каждом из 4 блоков двух фигур, аналогичных изображенным выше. - Прим. ред.]. Известно также, что если m=6, то можно получить этот результат при |A.i|=16 (Д.Штраусс). Если m=3 и |A.i|=3, то налицо случай предиката порядка 2, так как
пси.СВЯЗНОСТЬ = |3*N.1(X)-2*N.11(X) > 8].
Приведенный выше метод доказательства служит примером использования так называемого "геометрического n-точечного спектра"; общий принцип развивается далее в гл.6.
#5.3. СВЯЗНОСТЬ НА ОСНОВЕ РАССЕЧЕНИЯ
Следует отметить, что доказательство в #5.1 проходит не только в случае свойства связности в его классическом смысле, но и применительно к более сильному предикату:
[Существует такая прямая L, что X не пересекает L и не лежит целиком по одну сторону от L].
В общем определении связности вместо "прямая L" должно быть "кривая L", и тогда можно ожидать, что для реализации общего определения потребуется более высокий порядок.
#5.4. СВЕДЕНИЕ ОДНОГО ПЕРСЕПТРОНА К ДРУГОМУ
Мы доказали, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, показав сначала, что этим свойством обладает другой (и притом более простой) предикат пси.ОДИН-В-БЛОКЕ, а затем, что НА ОПРЕДЕЛЕННОМ ПОДМНОЖЕСТВЕ ФИГУР с помощью предиката пси.СВЯЗНОСТЬ можно вычислить предикат пси.ОДИН-В-БЛОКЕ, и потому его порядок должен быть по крайней мере таким же высоким. Конечно, есть немало других фигур, которые должен классифицировать предикат пси.СВЯЗНОСТЬ (помимо тех, которые содержат все точки из Y.0; см. #5.1), но оказывается, что достаточно изучить поведение этого предиката только на рассмотренном в #5.1 подклассе фигур.
Мы будем еще много раз использовать эту идею, но положение будет усложняться. В рассмотренном только что случае оба предиката определялись для фигур НА ОДНОЙ И ТОЙ ЖЕ сетчатке, но в дальнейшем нам часто будет желательно установить взаимосвязь между двумя предикатами, определенными в разных пространствах. Возможность широкого применения этого приема устанавливается следующей простой теоремой.
#5.4.1. ТЕОРЕМА О СЖАТИИ. Эта теорема позволит нам оценить пределы, в которых лежит порядок предиката пси, заданного на множестве R, на основании сведений о порядке соответствующего ему предиката пси' на множестве R'.
Пусть F - функция, связывающая с любой фигурой X в R фигуру X'=F(X) в R'.
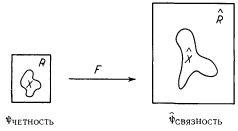
Пусть пси' - любой предикат на R'. Он ИНДУЦИРУЕТ предикат пси на R по формуле
пси(X)=пси'(F(X))=пси'(X').
ТЕОРЕМА 5.4.1. Порядок предиката пси' не меньше порядка предиката пси, если только каждая точка из R' зависит не более, чем от одной точки из R в том смысле, что для каждой точки x' из R' либо
x' принадлежит X' для всех X
или
x' не принадлежит X' для всех X,
либо найдется такая точка x, что
[x принадлежит X] == [x' принадлежит X'] для всех X
или
[x принадлежит X] == [x' не принадлежит X'] для всех X.
.
ДОКАЗАТЕЛЬСТВО. Предположим, что предикат пси' реализуется выражением K-го порядка:
[СУММА альфа.i*фи.i' > тета].
Тогда предикат фи имеет реализацию
[СУММА альфа.i*фи.i > тета].
где фи.i(X) = Фи.i'(F(X)). Чтобы проверить, что |S(фи.i)|<=K, вспомним, что фи.i' зависит не более, чем от K точек из R', а они в свою очередь зависят не более, чем от К точек из R. Таким образом, предикат фи.i(X)=фи.i'9F(X)) зависит не более, чем от К точек из R.
ПРИМЕР. Продемонстрируем типичное применение этого построения (рис.5.3). Множество R состоит из трех точек x.1, х.2, х.3. Множество R' состоит из 45 точек. На рисунке они подразделяются на три класса: 8 белых, 25 черных и 12 точек, обозначенных символами x.i или x.i'. Функция F определяется следующим образом. Для заданной фигуры X в R фигура F(X) должна содержать ВСЕ черные квадраты, НИ ОДНОГО белого квадрата, квадраты, обозначенные x.i только если x.i принадлежит X, и квадраты, обозначенные x.i', только если x.i не принадлежит X.
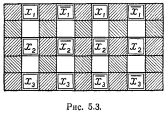
#5.5. ПОСТРОЕНИЕ ПРЕДИКАТА пси.СВЯЗНОСТЬ ПО ХАФФМЕНУ
Для иллюстрации применения изложенной выше концепции мы дадим другое доказательство того, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка. Это доказательство основано на построении, предложенном Д.Хаффменом.
Идея Хаффмена заключается в том, чтобы построить переключательную цепь, состоящую из n ключей, которая будет замкнута, если в положении "включено" находится нечетное число ключей. Тем самым проблема связности сведется к проблеме четности. Подобная схема для n = 3 показана на рис.5.3 при следующей интерпретации символов x.i и x.i' когда ключ x.i "включен", контакт замыкается всюду, где стоит символ x.i и разрывается там, где стоит x.i'; когда ключ x.i "выключен", замыкаются контакты x.i' и размыкаются контакты x.i. Нетрудно заметить, что вся цепь замкнута, а фигура связна, если включены один или три ключа. Обобщение на произвольное n очевидно:
1. Выписать члены конъюнктивной нормальной формы для предиката пси.ЧЕТНОСТЬ, рассматривая его как функцию точек, которая в данном случае имеет вид
(x.1 V х.2 V x.3) & (~x.1 V ~х.2 V x.3) & (x.1 V ~х.2 V ~x.3) & (~x.1 V х.2 V ~x.3).
#2. Перевести это булево выражение в форму переключательной схемы, интерпретируя конъюнкцию как последовательное соединение, а дизъюнкцию - как параллельное.
#3. Построить персептрон, "обозревающий" положение ключей.
Интуитивный смысл такого сведения одного предиката к другому заключается в следующем: переключательную схему Хаффмена можно рассматривать как определение класса F геометрических фигур, связных или нет в зависимости от четности определенного множества - множества включенных ключей. Таким образом, мы видим, как можно использовать персептрон для предиката пси.СВЯЗНОСТЬ, заданного на множестве R', в качестве персептрона для предиката пси.ЧЕТНОСТЬ, заданного на множестве R. Будучи персептроном для пси.ЧЕТНОСТЬ, он должен иметь порядок не менее |R|. Поэтому и порядок предиката пси.СВЯЗНОСТЬ должен быть не менее |R|. Для формализации этих рассуждений можно применить теорему о сжатии #5.4.1. Но сначала заметим, что их интуитивная простота стоит недешево: множество R' намного больше множества R; фактически величина |R'| должна быть порядка 2**|R|,так что наилучшим результатом этого построения служит вывод о том, что порядок предиката пси.СВЯЗНОСТЬ должен расти по меньшей мере как log|R'|. Это дает более слабую, чем в #5.1, нижнюю границу, а именно log|R'| вместо |R' |**(1/3).
Чтобы воспользоваться теоремой о сжатии, возьмем в качестве R трехточечное пространство, описанное в конце #5.4. Тогда предикат пси.ЧЕТНОСТЬ на R будет равносилен предикату пси.СВЯЗНОСТЬ для тех фигур на R, которые можно получить, применяя F к фигурам на R. Из теоремы о сжатии вытекает, что порядок предиката пси.ЧЕТНОСТЬ не превышает порядка предиката пси.СВЯЗНОСТЬ.
#5.6. СВЯЗНОСТЬ НА ТОРОИДАЛЬНОЙ СЕТЧАТКЕ
Самые первые наши попытки доказать, что связность обладает неограниченным порядком, привели к любопытному результату.
ТЕОРЕМА 5.6. Предикат пси.СВЯЗНОСТЬ на сетчатке размера 2**n*6, представляющей собой поверхность тора, имеет порядок не меньше n.
Доказательство. Рассмотрим пространство
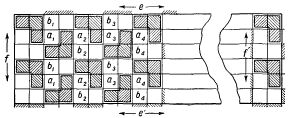
и отождествим в нем e с e' и f с f' (см. также рис.2.5). Рассмотрим далее семейство F подмножеств X из R, удовлетворяющих следующим условиям:
1. Все заштрихованные на рисунке квадраты принадлежат каждому X из F.
2. Для каждого X из F и каждого i либо обе точки a.i, либо обе точки b.i принадлежат X; никакие другие комбинации недопустимы.
Тогда можно показать, что каждое множество X из F либо имеет одну связную компоненту, либо подразделяется на две связные фигуры, причем это зависит лишь от четности числа пар точек a.i в X. А теперь из теоремы о сжатии и теоремы из #3.1.1 легко вытекает, что порядок предиката пси.СВЯЗНОСТЬ не менее |R|/12.
Идея теоремы 5.6 возникла из попытки свести СВЯЗНОСТЬ к ЧЕТНОСТИ непосредственно с помощью переключательной схемы, приведенной на рис.5.4. Если в нижнем положении находится четное число ключей, то x связан с x', а y с y'. Если число таких ключей нечетно, то x связан с y', а y с x'. Эту схему можно изобразить на плоскости, проводя вертикальные соединения вокруг конца (см. рис.5.11). Нетрудно найти тогда, что порядок предиката [x связан с x'] равен некоторой константе, умноженной на |R|**(1/2). Если ввести на R топологию тора, то (#5.6) порядок будет выше, чем альфа|R|, где альфа - константа, не превышающая 1; то же справедливо и для трехмерного евклидова пространства R. Все это решительно наводит на мысль, что наша граница для порядка предиката пси.СВЯЗНОСТЬ в случае плоскости чересчур низка.
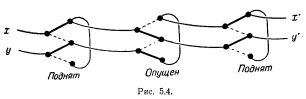
#5.0. ВВЕДЕНИЕ
В этой главе мы начинаем изучать свойство СВЯЗНОСТИ. Фигура X СВЯЗНА, если она не состоит из двух или более отдельных, несоприкасающихся частей. Хотя свойство связности интересно и само по себе, мы останавливаемся на нем в основном в надежде на то, что его изучение прольет свет на более фундаментальный, хотя и плохо определенный вопрос о противопоставлении локального и глобального. Дело в том, что связность вне всякого сомнения глобальна. На основе отдельных локальных опытов никогда нельзя заключить, что фигура связна. Разумеется, в случае фигуры

можно было бы обнаружить, что эта фигура несвязна, рассматривая только окрестность изолированной точки, расположенной в правом нижнем углу рисунка. Однако отсутствие такого локального свидетельства несвязности еще не позволяет сделать вывод, что фигура связна. Когда мы задаемся вопросом, которая из двух фигур на рис.5.1 связна, трудно представить себе какой-либо локальный результат, который мог бы склонить чашу весов в сторону того или другого заключения. Это легко ДОКАЗАТЬ, например, в узких рамках понятия ЛОКАЛЬНОГО как ОГРАНИЧЕННОГО по диаметру (см. #0.3 и гл.8 ). Труднее установить это же для структуры ограниченного порядка. Однако случай ограниченного диаметра подсказывает: рассматривая определенный подкласс фигур, мы могли бы показать, что эта задача эквивалентна распознаванию ЧЕТНОСТИ или чего-то с нею сходного. Мы и собираемся сейчас поступить именно так.

#5.1. ТЕОРЕМА О СВЯЗНОСТИ
[Мы дадим еще два других доказательства с различных точек зрения. Доказательство в #5.5, вероятно, легче всего понять само по себе, зато доказательство в #5.7 дает больше информации о том, каким образом возрастает порядок с ростом сетчатки R].
Две точки в R называются СМЕЖНЫМИ, если они являются квадратами с общей стороной [Мы не можем считать связью угловые касания, так как это позволило бы двум "кривым" пройти одна сквозь другую без "пересечения", и даже теорема о жордановых кривых не была бы верна. Но эту трудность можно обойти, разделив E**2 на шестиугольники, а не на квадраты!]. Фигура СВЯЗНА, если любые две ее точки (т.е. "квадраты") p.1, p.2 можно соединить путем, проходящим по смежным точкам.
ТЕОРЕМА 5.1. Предикат пси.СВЯЗНОСТЬ(X) = [X - связная фигура"] не имеет конечного порядка (#1.6), т.е. его порядок с ростом |R| неограниченно возрастает.
ДОКАЗАТЕЛЬСТВО. Допустим, что порядок предиката пси.СВЯЗНОСТЬ(X) меньше m. Расположим квадраты сетчатки R в 2*m+1 ряда по 4*m**2 квадратов в каждом (рис.5.2). Обозначим через Y.0 множество заштрихованных на рисунке квадратов, т.е. множество точек в нечетных рядах, а через Y.1 - множество оставшихся квадратов. Пусть F - семейство фигур, полученных добавлением к Y.0 подмножеств множества Y.1, т.е. X принадлежит F, если X имеет вид (Y.0 объединение X.1), где (X.1 включается в Y.1). Фигура X связна тогда и только тогда, когда X.1 содержит хотя бы по одному квадрату из каждого четного ряда, или, что то же, если множество X.1 удовлетворяет условию "один-в-блоке" из #3.2.
Чтобы разобраться в подробностях применения теоремы "один-в-блоке", если это еще не очевидно, рассмотрим фигуры семейства F как подмножество всех возможных фигур на R. Ясно, что если бы мы имели предикат k-то порядка пси.k.СВЯЗНОСТЬ, способный распознавать связность на R, то мы могли бы иметь и предикат, работающий на F: им был бы тот же самый предикат с постоянными нулевыми значениями для всех переменных, не принадлежащих (Y.0 объединение Y.1). А так как все точки нечетных рядов всегда принимают единичные значения для фигур в F, то это в свою очередь означает, что мы могли бы иметь предикат k-го порядка для принятия решения о свойстве "один-в-блоке" на множестве X.1: им был бы тот же самый предикат, но еще более ограниченный в том смысле, что точки в X.0 принимали бы постоянные единичные значения. Таким образом, каждая булева функция первоначального предиката пси.k.СВЯЗНОСТЬ заменяется функцией, полученной присвоением некоторым ее переменным фиксированных значений, равных нулю или единице; подобная операция никогда не может увеличить порядок функции. Но так как этот последний предикат существовать не может, то не может существовать и исходный предикат пси.k.СВЯЗНОСТЬ. Из нашего доказательства следует, что порядок предиката пси.СВЯЗНОСТЬ не менее C|R|**(1/3) В #5.7 мы покажем, что он не менее C|R|**(1/2).
#5.2. ПРИМЕР
Рассмотрим частный случай k=2 и эквивалентную задачу "один-в-блоке" для пространства вида

в котором m=3 и в каждом блоке ровно 4 квадрата. Далее, рассмотрим предикат пси порядка 2 и покажем, что он не может характеризовать связность такого рода фигур. Предположим, что пси = [СУММА альфа.i*фи.1 > тета], и рассмотрим эквивалентную форму, симметризированную относительно всей группы перестановок, переставляющих ряды и квадраты внутри рядов [Заметим, что это не та же самая группа, которая фигурировала в доказательстве теоремы из #3.2. Часть группы, переставляющая ряды, там не использовалась]. Тогда существуют только три класса эквивалентности масок порядка не выше 2, а именно:
отдельные точки фи.1.i = x.i;
пары точек фи.11.i.j = x.i*x.j (x.i и x.j в одном и том же ряду);
пары точек фи.12.i.j = x.i*x.j (x.i и x.j в разных рядах).
Следовательно, любой предикат порядка 2 должен иметь вид
пси = [альфа.1*N.1(X) + альфа.11*N.11(X) + альфа.12*N.12(X) > тета],
где N.1, N.11, N.12 - числа соответствующих точечных множеств в X. Теперь рассмотрим две фигуры:

В каждой
N.1=6, N.11=6, N.12=9,
так что значение пси одинаково для обеих фигур. Но фигура X.1 связна, а X.2 нет! Заметьте, что здесь m=3, и мы, предположив, что порядок меньше 3, получим противоречие уже при |A.i|=4, а общее доказательство требовало |A.i|=4*m**236. Тот же результат можно получить и при |A.i|=3, m=4, так как (3, 1, 1, 4) ~ (2, 2, 2, 0) [Эти цифры показывают, сколько черных квадратов в каждом из 4 блоков двух фигур, аналогичных изображенным выше. - Прим. ред.]. Известно также, что если m=6, то можно получить этот результат при |A.i|=16 (Д.Штраусс). Если m=3 и |A.i|=3, то налицо случай предиката порядка 2, так как
пси.СВЯЗНОСТЬ = |3*N.1(X)-2*N.11(X) > 8].
Приведенный выше метод доказательства служит примером использования так называемого "геометрического n-точечного спектра"; общий принцип развивается далее в гл.6.
#5.3. СВЯЗНОСТЬ НА ОСНОВЕ РАССЕЧЕНИЯ
Следует отметить, что доказательство в #5.1 проходит не только в случае свойства связности в его классическом смысле, но и применительно к более сильному предикату:
[Существует такая прямая L, что X не пересекает L и не лежит целиком по одну сторону от L].
В общем определении связности вместо "прямая L" должно быть "кривая L", и тогда можно ожидать, что для реализации общего определения потребуется более высокий порядок.
#5.4. СВЕДЕНИЕ ОДНОГО ПЕРСЕПТРОНА К ДРУГОМУ
Мы доказали, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка, показав сначала, что этим свойством обладает другой (и притом более простой) предикат пси.ОДИН-В-БЛОКЕ, а затем, что НА ОПРЕДЕЛЕННОМ ПОДМНОЖЕСТВЕ ФИГУР с помощью предиката пси.СВЯЗНОСТЬ можно вычислить предикат пси.ОДИН-В-БЛОКЕ, и потому его порядок должен быть по крайней мере таким же высоким. Конечно, есть немало других фигур, которые должен классифицировать предикат пси.СВЯЗНОСТЬ (помимо тех, которые содержат все точки из Y.0; см. #5.1), но оказывается, что достаточно изучить поведение этого предиката только на рассмотренном в #5.1 подклассе фигур.
Мы будем еще много раз использовать эту идею, но положение будет усложняться. В рассмотренном только что случае оба предиката определялись для фигур НА ОДНОЙ И ТОЙ ЖЕ сетчатке, но в дальнейшем нам часто будет желательно установить взаимосвязь между двумя предикатами, определенными в разных пространствах. Возможность широкого применения этого приема устанавливается следующей простой теоремой.
#5.4.1. ТЕОРЕМА О СЖАТИИ. Эта теорема позволит нам оценить пределы, в которых лежит порядок предиката пси, заданного на множестве R, на основании сведений о порядке соответствующего ему предиката пси' на множестве R'.
Пусть F - функция, связывающая с любой фигурой X в R фигуру X'=F(X) в R'.

Пусть пси' - любой предикат на R'. Он ИНДУЦИРУЕТ предикат пси на R по формуле
пси(X)=пси'(F(X))=пси'(X').
ТЕОРЕМА 5.4.1. Порядок предиката пси' не меньше порядка предиката пси, если только каждая точка из R' зависит не более, чем от одной точки из R в том смысле, что для каждой точки x' из R' либо
x' принадлежит X' для всех X
или
x' не принадлежит X' для всех X,
либо найдется такая точка x, что
[x принадлежит X] == [x' принадлежит X'] для всех X
или
[x принадлежит X] == [x' не принадлежит X'] для всех X.
.
ДОКАЗАТЕЛЬСТВО. Предположим, что предикат пси' реализуется выражением K-го порядка:
[СУММА альфа.i*фи.i' > тета].
Тогда предикат фи имеет реализацию
[СУММА альфа.i*фи.i > тета].
где фи.i(X) = Фи.i'(F(X)). Чтобы проверить, что |S(фи.i)|<=K, вспомним, что фи.i' зависит не более, чем от K точек из R', а они в свою очередь зависят не более, чем от К точек из R. Таким образом, предикат фи.i(X)=фи.i'9F(X)) зависит не более, чем от К точек из R.
ПРИМЕР. Продемонстрируем типичное применение этого построения (рис.5.3). Множество R состоит из трех точек x.1, х.2, х.3. Множество R' состоит из 45 точек. На рисунке они подразделяются на три класса: 8 белых, 25 черных и 12 точек, обозначенных символами x.i или x.i'. Функция F определяется следующим образом. Для заданной фигуры X в R фигура F(X) должна содержать ВСЕ черные квадраты, НИ ОДНОГО белого квадрата, квадраты, обозначенные x.i только если x.i принадлежит X, и квадраты, обозначенные x.i', только если x.i не принадлежит X.

#5.5. ПОСТРОЕНИЕ ПРЕДИКАТА пси.СВЯЗНОСТЬ ПО ХАФФМЕНУ
Для иллюстрации применения изложенной выше концепции мы дадим другое доказательство того, что предикат пси.СВЯЗНОСТЬ не имеет конечного порядка. Это доказательство основано на построении, предложенном Д.Хаффменом.
Идея Хаффмена заключается в том, чтобы построить переключательную цепь, состоящую из n ключей, которая будет замкнута, если в положении "включено" находится нечетное число ключей. Тем самым проблема связности сведется к проблеме четности. Подобная схема для n = 3 показана на рис.5.3 при следующей интерпретации символов x.i и x.i' когда ключ x.i "включен", контакт замыкается всюду, где стоит символ x.i и разрывается там, где стоит x.i'; когда ключ x.i "выключен", замыкаются контакты x.i' и размыкаются контакты x.i. Нетрудно заметить, что вся цепь замкнута, а фигура связна, если включены один или три ключа. Обобщение на произвольное n очевидно:
1. Выписать члены конъюнктивной нормальной формы для предиката пси.ЧЕТНОСТЬ, рассматривая его как функцию точек, которая в данном случае имеет вид
(x.1 V х.2 V x.3) & (~x.1 V ~х.2 V x.3) & (x.1 V ~х.2 V ~x.3) & (~x.1 V х.2 V ~x.3).
#2. Перевести это булево выражение в форму переключательной схемы, интерпретируя конъюнкцию как последовательное соединение, а дизъюнкцию - как параллельное.
#3. Построить персептрон, "обозревающий" положение ключей.
Интуитивный смысл такого сведения одного предиката к другому заключается в следующем: переключательную схему Хаффмена можно рассматривать как определение класса F геометрических фигур, связных или нет в зависимости от четности определенного множества - множества включенных ключей. Таким образом, мы видим, как можно использовать персептрон для предиката пси.СВЯЗНОСТЬ, заданного на множестве R', в качестве персептрона для предиката пси.ЧЕТНОСТЬ, заданного на множестве R. Будучи персептроном для пси.ЧЕТНОСТЬ, он должен иметь порядок не менее |R|. Поэтому и порядок предиката пси.СВЯЗНОСТЬ должен быть не менее |R|. Для формализации этих рассуждений можно применить теорему о сжатии #5.4.1. Но сначала заметим, что их интуитивная простота стоит недешево: множество R' намного больше множества R; фактически величина |R'| должна быть порядка 2**|R|,так что наилучшим результатом этого построения служит вывод о том, что порядок предиката пси.СВЯЗНОСТЬ должен расти по меньшей мере как log|R'|. Это дает более слабую, чем в #5.1, нижнюю границу, а именно log|R'| вместо |R' |**(1/3).
Чтобы воспользоваться теоремой о сжатии, возьмем в качестве R трехточечное пространство, описанное в конце #5.4. Тогда предикат пси.ЧЕТНОСТЬ на R будет равносилен предикату пси.СВЯЗНОСТЬ для тех фигур на R, которые можно получить, применяя F к фигурам на R. Из теоремы о сжатии вытекает, что порядок предиката пси.ЧЕТНОСТЬ не превышает порядка предиката пси.СВЯЗНОСТЬ.
#5.6. СВЯЗНОСТЬ НА ТОРОИДАЛЬНОЙ СЕТЧАТКЕ
Самые первые наши попытки доказать, что связность обладает неограниченным порядком, привели к любопытному результату.
ТЕОРЕМА 5.6. Предикат пси.СВЯЗНОСТЬ на сетчатке размера 2**n*6, представляющей собой поверхность тора, имеет порядок не меньше n.
Доказательство. Рассмотрим пространство

и отождествим в нем e с e' и f с f' (см. также рис.2.5). Рассмотрим далее семейство F подмножеств X из R, удовлетворяющих следующим условиям:
1. Все заштрихованные на рисунке квадраты принадлежат каждому X из F.
2. Для каждого X из F и каждого i либо обе точки a.i, либо обе точки b.i принадлежат X; никакие другие комбинации недопустимы.
Тогда можно показать, что каждое множество X из F либо имеет одну связную компоненту, либо подразделяется на две связные фигуры, причем это зависит лишь от четности числа пар точек a.i в X. А теперь из теоремы о сжатии и теоремы из #3.1.1 легко вытекает, что порядок предиката пси.СВЯЗНОСТЬ не менее |R|/12.
Идея теоремы 5.6 возникла из попытки свести СВЯЗНОСТЬ к ЧЕТНОСТИ непосредственно с помощью переключательной схемы, приведенной на рис.5.4. Если в нижнем положении находится четное число ключей, то x связан с x', а y с y'. Если число таких ключей нечетно, то x связан с y', а y с x'. Эту схему можно изобразить на плоскости, проводя вертикальные соединения вокруг конца (см. рис.5.11). Нетрудно найти тогда, что порядок предиката [x связан с x'] равен некоторой константе, умноженной на |R|**(1/2). Если ввести на R топологию тора, то (#5.6) порядок будет выше, чем альфа|R|, где альфа - константа, не превышающая 1; то же справедливо и для трехмерного евклидова пространства R. Все это решительно наводит на мысль, что наша граница для порядка предиката пси.СВЯЗНОСТЬ в случае плоскости чересчур низка.

Последний раз редактировалось: Gudleifr (Ср Июн 21, 2023 12:51 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#5.7. ЛУЧШАЯ ГРАНИЦА ДЛЯ ПОРЯДКА ПРЕДИКАТА пси.СВЯЗНОСТЬ НА ПЛОСКОСТИ
Мы покажем сейчас, что для двумерных фигур порядок предиката пси.СВЯЗНОСТЬ не ниже const*|R|**(1/2). Для этого мы так модифицируем рис.5.4, чтобы x и x' были связаны. Это легко сделать для тора, а для плоскости мы долго считали, что это выполнить невозможно.
Назовем 4-ключом пару фигур, изображенных на рис.5.5. Легко видеть, что в НИЖНЕМ положении
точка p.i, связана с q.(i+1)%4,
где j%4 - остаток при делении j на 4. В ВЕРХНЕМ положении
точка p.i связана с q.(i-l)%4.
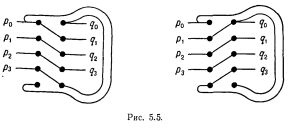
Рассмотрим теперь показанный на рис.5.6 результат последовательного соединения n таких ключей.

В этой схеме осуществляется простая итерация действия одного 4-ключа. Действительно, если d ключей ОПУЩЕНЫ, а u ключей ПОДНЯТЫ [Первые буквы английских слов down (здесь "опущен") и up (здесь "поднят").- Прим. перев.], то
точка p.i связана с q.(i+d-u)%4,
для всякого i. Так как каждый ключ либо ПОДНЯТ, либо ОПУЩЕН, то
d + u = n
и, следовательно,
q.(i+d-u)=q.i+2d-n)%4.
Заметим, что индексы у q зависят только от четности d. В самом деле,
(x+2(d+2))%4 = (x+2d+4)%4 = (x+2d)%4.
Добавим фиксированные связи, соединяющие точки
q.(1-n)%4, q.(2-n)%4, q.(3-n)%4.
Тогда, если d четно, то связаны p.1, p.2, p.3, а если d нечетно, то связаны p.3, p.0, p.1.
В каждом случае p.1 и p.3 связаны, так что можно пренебречь, скажем, p.3. Поэтому связность системы принимает одно из двух состояний в зависимости от четности числа ОПУЩЕННЫХ ключей. Эти состояния показаны на рис.5.7.
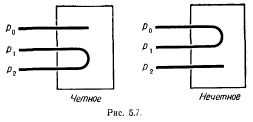
Чтобы доказать нашу теорему, свяжем p.1 и p.2 (рис.5.8 ).
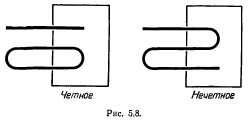
Остается только осуществить 4-ключи в деталях. На рис.5.9 показаны рассматриваемые конфигурации.
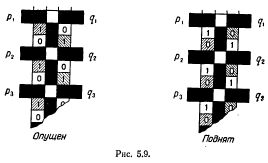
Напомним, что соединение клеток углами не является связью. Если выполнить полное построение схемы, состоящей из n ключей, то ее длина будет примерно 5n квадратов, а высота примерно 2n+12 квадратов, так что число ключей может расти пропорционально |R|**(1/2). Из этого следует, что порядок предиката пси.СВЯЗНОСТЬ растет по крайней мере так же быстро, как |R|**(1/2). Законченная конструкция для n=4 представлена на рис.5.10.
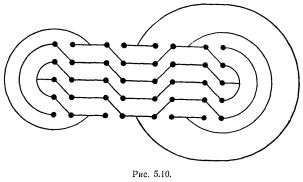
Теперь необходимо убедиться, что в схеме не осталось "заблудившихся" соединительных линий, не связанных в конце концов с p.0, p.1 или p.2. Это можно сделать, изучив рис.5.6. Кроме того, можно проверить, что не образовалось замкнутых контуров, кроме одного, указанного в левой части рис.5.8.
Замысел теоремы 5.6 возник из нашего наблюдения, что в плоском варианте рисунка 5.4 (см. рис.5.11) p.1<->q.1, p.2<->q.2 для одной четности и p.1<->q.2, p.2<->q.1 для другой. Если бы мы смогли ввести постоянную добавочную прямую связь между p.1 и q.1, то вся сеть была бы связна или несвязна в зависимости от этой четности. Но топологически это невозможно, и так как нам казалось, что нужное построение неосуществимо, мы избрали окольный путь, основанный на доказательстве и применении теоремы "один-в-блоке". И лишь позднее мы осознали, что связь p.1<->q.1 можно было бы осуществить если не непосредственно, то "динамически", при помощи конструкции, изображенной на рис.5.8.
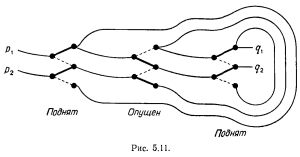
#5.7.2. ПОРЯДОК ПРЕДИКАТА пси.СВЯЗНОСТЬ КАК ФУНКЦИЯ ОТ |R|. Каков же порядок предиката пси.CBЯ3HOCTb на самом деле? Напомним, что в основе использованных нами методов доказательства лежит (#5.0) рассмотрение не всех фигур, а лишь особых подклассов с определенными комбинаторными свойствами. Поэтому даже величина |R|/12 (#5.6) является лишь нижней границей. Мы думаем, что порядок не может быть менее |R|/2. Что же касается числа требуемых предикатов фи, то теорема 3.1.2 и результаты на торе дают нам величину не менее 2**(|R|/12), но и она является только нижней границей, и можно подозревать, что необходимы почти все маски. Другое направление рассуждений наводит на мысль о том, что можно получить число порядка логарифма количества связных фигур, но это, по всей видимости, не намного уменьшает показатель степени.
Изучение построения на торе (#5.6) может вызвать подозрение, что результат "ПОРЯДОК ПРЕДИКАТА пси.СВЯЗНОСТЬ НЕ НИЖЕ |R|/12" искусствен, так как для его получения был использован длинный узкий тор. Разумеется, в случае "квадратного" тора мы не могли бы получить этот результат из-за той площади, которую должны были бы покрыть вспомогательные перемычки. Это несколько порочит полученный результат. С другой стороны, можно показать, что в случае ТРЕХМЕРНОГО пространства R для некоторой умеренной величины K порядок предиката пси.СВЯЗНОСТЬ не менее |R|/K. Трудно поверить, что такую большую роль играет различие в размерности.
#5.8. ТОПОЛОГИЧЕСКИЕ ПРЕДИКАТЫ
Мы уже видели, что предикат [фигура X связна] не имеет конечного порядка, а вскоре мы убедимся, что конечного порядка не имеет и предикат [X содержит дыру]. Довольно странно, но предикат
[фигура X связна или содержит дыру]
имеет конечный порядок, хотя по отдельности каждый из составляющих его предикатов этим не отличается - пример, полностью противоположный явлению "и/или". Мы докажем это с помощью конструкции, использующей эйлерову характеристику для ориентируемых геометрических фигур.
#5.8.1. ФОРМУЛА ЭЙЛЕРА ДЛЯ МНОГОГРАННИКОВ. Двумерные фигуры обладают топологическим инвариантом [Для наших целей под "топологическим инвариантом" подразумевается здесь предикат, не изменяющийся при деформациях фигуры с сохранением связности или свойства быть внешней или внутренней частью фигуры], который в случае многогранников задается формулой
B(X)=|грани(X)|-|ребра(X)|+|вершины(X)|.
Примеры, иллюстрирующие эту формулу, приведены на рис.5.12, где указаны соответствующие числа граней [Гранью двумерной фигуры называется здесь заштрихованная часть плоскости, ограниченная со всех сторон некоторыми ребрами и ие пересекаемая другими ребрами.- Прим. ред.], ребер и вершин. При использовании этой формулы заранее предполагается, что фигуру можно так рассечь на достаточно малые части, чтобы каждая "грань" оказалась ПРОСТОЙ, т.е. не содержала дыр. Интересно, что число B(X) будет одним и тем же для любого рассечения фигуры X, отвечающего этому условию.
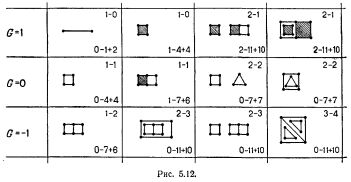
В нашем многообразии фигур, составленных из квадратов шахматной доски, B(X) можно вычислить при помощи линейной суммы G(X) низкого порядка, равной
G(X) = СУММА альфа.i*x.i + СУММА альфа.i.j*x.i*x.j + СУММА альфа.i.j.k.l*x.i*x.j*x.k*x.l, где
альфа.i = 1 для каждой точки (клетки) в R - вершины,
альфа.i.j = -1 для каждой смежной пары (вертикальной или горизонтальной, соседних клеток) - ребра,
альфа.i.j.k.l = 1 для каждого квадрата (из четырех смежных) клеток - грани.
На фигурах на шахматной доске значения G(X) и B(X) полностью совпадают, если только нет угловых касаний.
Когда в подобных случаях они различаются, наше определение связности требует знания величины G(X).
Важность величины G(X) в нашей теории объясняется тем, что, хотя эта величина в высшей степени ЛОКАЛЬНА (действительно, ограничена по диаметру и имеет конечный порядок), она эквивалентна глобальной формуле [Это формула Эйлера; величина Е(X) называется эйлеровой характеристикой.- Прим. ред.]
Е(X)=|компоненты(X)|-|дыры(X)|.
КОМПОНЕНТОЙ фигуры называется множество всех точек, связанных с данной точкой.
ДЫРОЙ фигуры называется компонента дополнения к фигуре.
Мы предполагаем, что расположенное вокруг фигуры "окружающее пространство" не является дырой. Кроме того, мы будем считать, что, когда речь идет о дополнении к фигуре, "угловое каcание" служит связью.
Теперь мы докажем, что локальная формула G(X) и глобальная формула Е(X) эквивалентны. Сначала дадим довольно прямое наглядное доказательство. Затем в # 5.8.2 приведем доказательство другого рода, в основе которого лежит деформация одной фигуры в другую; это позволит лучше понять доказательство основной теоремы в #5.9.
Начав с одного квадрата и добавляя квадраты последовательно друг за другом, можно получить любую фигуру X. Для единственного квадрата
G(X)=E(X)=1.
Добавление квадрата, не смежного ни с каким квадратом, принадлежащим X, прибавляет единицу к G(X) и (так как это новая компонента!) прибавляет единицу к E(X).
Добавление квадрата, смежного с одним и только одним квадратом, не может изменить E(X) и прибавляет ровно 1-1+0=0 к G(X).
Если добавляется квадрат, смежный с двумя другими, то возникают три возможности. Когда новый квадрат заполняет угол,
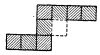
то к G прибавляется 1-2+1=0, так что G остается без изменения; не изменяется в этом случае и Е(X). Но если новый квадрат связывает два других, которые не были еще соединены,

то приращение к G равно 1-2+0=-1, причем E(X) тоже уменьшается на единицу, так как мы соединили две части, бывшие до этого разделенными. Если же добавляемый квадрат связывает два квадрата, уже соединенных каким-то путем,

то отсекается область пространства - образуется дыра, уменьшающая E на единицу, и G снова изменяется на 1-2+0=-1.
Наконец, случаи соседства с тремя и четырьмя квадратами: получаются фигуры типа

что прибавляет 1-3+2=0 и 1-4+4=1. Заметим, что в последнем случае G увеличивается на единицу, а дыра в конечном счете заполняется. Итак, в каждом случае либо G остается без изменения, либо изменяется топология фигуры X. (Все это соответствует рассуждениям в алгебраической топологии о добавлении ребер и клеток к цепным комплексам). Таким образом, доказана
Теорема 5.8.1. E(X)=G(X).
Из нее немедленно вытекает, что предикат [G(X)<n] реализуется выражением порядка не выше 4. Это приводит к некоторым любопытным замечаниям: если нам ЗАДАНО, что фигуры X могут быть только связными (т.е. однокомпонентными), то машина 4-го порядка может распознавать предикаты
[X не содержит дыр]=[G(X)>0]
и, например,
[X содержит менее 3 дыр]=[G(X)>-2].
Но, разумеется, отсюда не следует, что персептрон конечного порядка может распознавать эти предикаты НЕЗАВИСИМО ОТ КАКИХ-ЛИБО УСЛОВИЙ.
Этот топологический инвариант крайне "локален" по своей природе - в самом деле, все предикаты фи удовлетворяют весьма жестким ограничениям диаметра! Возвращаясь теперь к нашему первоначальному утверждению, заметим, что
[G(X)=n]=([G(X)<=n]==[G(X)>=n]).
Согласно теореме 1.5.4, порядок предиката [G(X)=N] не выше 8. Но при доказательстве этой теоремы строятся произведения предикатов фи, причем эти произведения НЕ ограничены по диаметру. В #8.4.3 мы покажем, что при помощи персептронов, ограниченных по диаметру, предикат [G(X)=N] реализовать нельзя.
#5.8.2. ДЕФОРМАЦИЯ ФИГУР В СТАНДАРТНЫЕ ФОРМЫ. В ходе доказательства теоремы #5.8.1 мы видели, что величина G одинакова для любых фигур X и Y, имеющих одно и то же значение Е=|компоненты|-|дыры|. Теперь мы покажем, что можно построить последовательность фигур X.1, ..., X.i, ..., Y с одним и тем же значением G=Е, каждая из которых получается из предыдущей некоторым локальным изменением [Авторы не дают точного определения этого понятия. По-видимому, имеется в виду изменение одной или нескольких соседних ячеек сетчатки.- Прим. ред.]. Легко понять, как можно "гладко" деформировать фигуры, не изменяя значения G или Е, т.е. не изменяя дыр и компонент. Например, последовательность

увеличивает дыру. Заметим, что компоненту C.0, лежащую внутри дыры H.1 другой компоненты C.1, можно вывести в окружающее пространство, не изменяя E(X) и G(X). Предположим для простоты, что C.1 соприкасается с окружающим пространством, а C.0 "просто" находится в H.1, т.е. никакая другая компонента, кроме C.1, не окружает C.0, как например, C' на фигуре
Тогда C.0 можно убрать из H.1 рядом деформаций, в ходе которых H.1 сначала оттягивается к периферии
а затем C.0 временно присоединяется к C.1:
Заметьте, что такая деформация не изменяет величины G(X). Точно так же, поскольку и C, и H уменьшаются на единицу, такая деформация не изменяет величины E(X)=C(X)-H(X) [C(X)=|компоненты(X)|, Н(X)=|дыры(X)|.- Прим. ред.]. Далее деформируем C.1 так, чтобы вывести C.0 в окружающее пространство
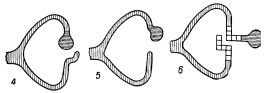
и отсоединить, получая при этом
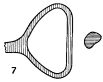
значения G(X) и E(X) не изменяются. Ясно, что в конце концов мы можем очистить все дыры, повторив эту процедуру для каждой внутренней компоненты и выведя ее таким образом в окружающее пространство. Выполнив это, мы получим некоторое число компонент, в каждой из которых может находиться несколько чистых дыр и которые можно деформировать в фигуры стандартного вида

Далее, обращая операцию перехода от фигуры 6 к фигуре 7, можно соединить любую компоненту, имеющую дыру, с любой другой компонентой:
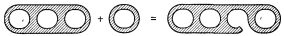
Так можно одновременно уменьшать и C, и H, пока H не станет равным нулю или С равным единице. Тогда получится либо
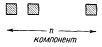
либо
и соответственно либо G(X)=E(X)=n, либо G(X)=E(X)=1-m. Мы будем использовать этот общеизвестный результат в следующем параграфе.
#5.9. ТОПОЛОГИЧЕСКИЕ ОГРАНИЧЕНИЯ ПЕРСЕПТРОНОВ
ТЕОРЕМА 5.9. Все топологически инвариантные предикаты конечного порядка являются функциями от эйлеровой характеристики E(X).
Мы уже доказали соответствующую теорему для персептрона, ограниченного по диаметру, и высказали предположение, что то же верно и в случае ограниченного порядка, но доказать последнее не сумели. Это было установлено М.Петерсоном; #5.9.1 целиком основан на его идее.
#5.9.1. ЗАПОЛНЕНИЕ ДЫР. Пусть C(X)>=2 и H(X)>=1. Возьмем дыру H.0 в компоненте C.0. Пусть C.1 - компонента, "доступная" для C.0, т.е. имеется путь P.01 от граничной точки фигуры C.0 до граничной точки фигуры C.1, не пересекающий X (в других точках.- Ред.). Пусть P.00 - путь ВНУТРИ C.0 от точки на границе дыры H.0 до точки на другой границе фигуры C.0, причем P.00 и P.01 связаны.
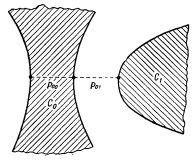
Такой путь P.00 всегда можно найти, даже если C.1 находится внутри H.0, или полностью вне C.0, или внутри какой-то другой дыры в C.0.
Если пси(X) - топологически инвариантный предикат, то его значение не меняется при деформациях типа
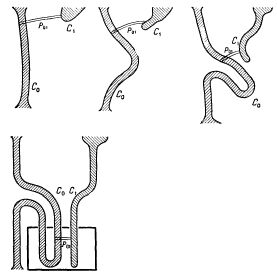
Предположим, что нам разрешено заменить следующим образом связи внутри прямоугольника:
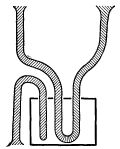
В сущности, это значит разрезать вдоль P.00, устранив дыру, и соединить вдоль одной стороны пути P.01, уменьшив на единицу число компонент. Таким образом, величина E(X) не изменится.
Покажем, что эти деформации не влияют на величину предиката пси!
Пусть пси имеет k-й порядок. Будем деформировать фигуру X до тех пор, пока в прямоугольнике не окажется каскад из k+1 4-ключей (см. рис.5.6 и 5.7). Это не изменяет топологии, так что пси остается тем же. Затем рассмотрим 2**(k+l) вариантов фигуры X, получаемых за счет 2**(k+1) состояний каскадного ключа. Если значение пси одинаково для всех них, то, очевидно, можно провести изменение тривиальным образом, не воздействуя на пси. Если два варианта дают РАЗНЫЕ значения, скажем пси(X')!=пси(X''), то они должны отвечать различным состояниям четности ключей, поскольку пси - топологический инвариант. Но коль скоро это так, то пси должен быть способен указывать четность этого ключа, так как все фигуры X данного класса четности топологически эквивалентны (подробности см. в #5.7). Но, как мы знаем, согласно теореме о сжатии, этого не может быть: при проверке четности предикат пси должен "сбиться", если порядок задачи превышает k. Поэтому все фигуры, полученные изменением позиций ключей, дают одно и то же значение пси, и можно применить преобразования, описанные в #5.8.2, не изменяя значений пси.
#5.9.2. КАНОНИЧЕСКАЯ ФОРМА. Используем метод #5.9.1 и #5.8.2, чтобы привести произвольную фигуру X к канонической форме, зависящей только от E(X). Будем повторять прием, описанный в #5.8.2, до тех пор, пока не исчерпаем все (лишние.- Ред.) дыры или компоненты. Должна остаться либо
(1) единственная компонента с одной или более дырами, либо
(2) одна или более простых сплошных компонент в зависимости от выполнения условия E(X)<=0.
В случае (1) окончательная фигура топологически эквивалентна фигуре типа

с 1-E(X) дырами, а в случае (2) она эквивалентна фигуре типа

с E(X) сплошными квадратами. Тогда очевидно, что для любых двух фигур X и X', для которых E(X)=E(X'), должно быть пси(X)=пси(X'). Это доказывает теорему 5.9, утверждающую, что предикат пси(X) зависит только от E(X).
ЗАМЕЧАНИЕ. Имеется одно исключение из правила, сформулированного в виде теоремы 5.9, поскольку каноническая форма не включает случай полностью пустого изображения! Дело в том, что предикат
[фигура X непустая]
ЯВЛЯЕТСЯ топологическим инвариантом, но не будет функцией от E(X). См. #8.1.1 и 8.4.
Кроме числа компонент фигуры X и величины G(X), существует много других ТОПОЛОГИЧЕСКИХ инвариантов, например
[компонента фигуры X находится внутри дыры в другой компоненте].
Из теоремы #5.9, таким образом, следует, что никакой предикат конечного порядка не в состоянии отличить фигуру, СОДЕРЖАЩУЮ ВНУТРИ СЕБЯ другую фигуру (левый рисунок), от фигуры, не содержащей других (правый рисунок).

ЗАДАЧА. Что даст подобный анализ топологических предикатов в пространствах большего числа измерений? Можно ли интерпретировать СУММА альфа.i*фи.i как коцепь на симплициальном комплексе, в котором пороговая операция как-то разумным образом определена?
Мы покажем сейчас, что для двумерных фигур порядок предиката пси.СВЯЗНОСТЬ не ниже const*|R|**(1/2). Для этого мы так модифицируем рис.5.4, чтобы x и x' были связаны. Это легко сделать для тора, а для плоскости мы долго считали, что это выполнить невозможно.
Назовем 4-ключом пару фигур, изображенных на рис.5.5. Легко видеть, что в НИЖНЕМ положении
точка p.i, связана с q.(i+1)%4,
где j%4 - остаток при делении j на 4. В ВЕРХНЕМ положении
точка p.i связана с q.(i-l)%4.

Рассмотрим теперь показанный на рис.5.6 результат последовательного соединения n таких ключей.

В этой схеме осуществляется простая итерация действия одного 4-ключа. Действительно, если d ключей ОПУЩЕНЫ, а u ключей ПОДНЯТЫ [Первые буквы английских слов down (здесь "опущен") и up (здесь "поднят").- Прим. перев.], то
точка p.i связана с q.(i+d-u)%4,
для всякого i. Так как каждый ключ либо ПОДНЯТ, либо ОПУЩЕН, то
d + u = n
и, следовательно,
q.(i+d-u)=q.i+2d-n)%4.
Заметим, что индексы у q зависят только от четности d. В самом деле,
(x+2(d+2))%4 = (x+2d+4)%4 = (x+2d)%4.
Добавим фиксированные связи, соединяющие точки
q.(1-n)%4, q.(2-n)%4, q.(3-n)%4.
Тогда, если d четно, то связаны p.1, p.2, p.3, а если d нечетно, то связаны p.3, p.0, p.1.
В каждом случае p.1 и p.3 связаны, так что можно пренебречь, скажем, p.3. Поэтому связность системы принимает одно из двух состояний в зависимости от четности числа ОПУЩЕННЫХ ключей. Эти состояния показаны на рис.5.7.

Чтобы доказать нашу теорему, свяжем p.1 и p.2 (рис.5.8 ).

Остается только осуществить 4-ключи в деталях. На рис.5.9 показаны рассматриваемые конфигурации.

Напомним, что соединение клеток углами не является связью. Если выполнить полное построение схемы, состоящей из n ключей, то ее длина будет примерно 5n квадратов, а высота примерно 2n+12 квадратов, так что число ключей может расти пропорционально |R|**(1/2). Из этого следует, что порядок предиката пси.СВЯЗНОСТЬ растет по крайней мере так же быстро, как |R|**(1/2). Законченная конструкция для n=4 представлена на рис.5.10.

Теперь необходимо убедиться, что в схеме не осталось "заблудившихся" соединительных линий, не связанных в конце концов с p.0, p.1 или p.2. Это можно сделать, изучив рис.5.6. Кроме того, можно проверить, что не образовалось замкнутых контуров, кроме одного, указанного в левой части рис.5.8.
Замысел теоремы 5.6 возник из нашего наблюдения, что в плоском варианте рисунка 5.4 (см. рис.5.11) p.1<->q.1, p.2<->q.2 для одной четности и p.1<->q.2, p.2<->q.1 для другой. Если бы мы смогли ввести постоянную добавочную прямую связь между p.1 и q.1, то вся сеть была бы связна или несвязна в зависимости от этой четности. Но топологически это невозможно, и так как нам казалось, что нужное построение неосуществимо, мы избрали окольный путь, основанный на доказательстве и применении теоремы "один-в-блоке". И лишь позднее мы осознали, что связь p.1<->q.1 можно было бы осуществить если не непосредственно, то "динамически", при помощи конструкции, изображенной на рис.5.8.

#5.7.2. ПОРЯДОК ПРЕДИКАТА пси.СВЯЗНОСТЬ КАК ФУНКЦИЯ ОТ |R|. Каков же порядок предиката пси.CBЯ3HOCTb на самом деле? Напомним, что в основе использованных нами методов доказательства лежит (#5.0) рассмотрение не всех фигур, а лишь особых подклассов с определенными комбинаторными свойствами. Поэтому даже величина |R|/12 (#5.6) является лишь нижней границей. Мы думаем, что порядок не может быть менее |R|/2. Что же касается числа требуемых предикатов фи, то теорема 3.1.2 и результаты на торе дают нам величину не менее 2**(|R|/12), но и она является только нижней границей, и можно подозревать, что необходимы почти все маски. Другое направление рассуждений наводит на мысль о том, что можно получить число порядка логарифма количества связных фигур, но это, по всей видимости, не намного уменьшает показатель степени.
Изучение построения на торе (#5.6) может вызвать подозрение, что результат "ПОРЯДОК ПРЕДИКАТА пси.СВЯЗНОСТЬ НЕ НИЖЕ |R|/12" искусствен, так как для его получения был использован длинный узкий тор. Разумеется, в случае "квадратного" тора мы не могли бы получить этот результат из-за той площади, которую должны были бы покрыть вспомогательные перемычки. Это несколько порочит полученный результат. С другой стороны, можно показать, что в случае ТРЕХМЕРНОГО пространства R для некоторой умеренной величины K порядок предиката пси.СВЯЗНОСТЬ не менее |R|/K. Трудно поверить, что такую большую роль играет различие в размерности.
#5.8. ТОПОЛОГИЧЕСКИЕ ПРЕДИКАТЫ
Мы уже видели, что предикат [фигура X связна] не имеет конечного порядка, а вскоре мы убедимся, что конечного порядка не имеет и предикат [X содержит дыру]. Довольно странно, но предикат
[фигура X связна или содержит дыру]
имеет конечный порядок, хотя по отдельности каждый из составляющих его предикатов этим не отличается - пример, полностью противоположный явлению "и/или". Мы докажем это с помощью конструкции, использующей эйлерову характеристику для ориентируемых геометрических фигур.
#5.8.1. ФОРМУЛА ЭЙЛЕРА ДЛЯ МНОГОГРАННИКОВ. Двумерные фигуры обладают топологическим инвариантом [Для наших целей под "топологическим инвариантом" подразумевается здесь предикат, не изменяющийся при деформациях фигуры с сохранением связности или свойства быть внешней или внутренней частью фигуры], который в случае многогранников задается формулой
B(X)=|грани(X)|-|ребра(X)|+|вершины(X)|.
Примеры, иллюстрирующие эту формулу, приведены на рис.5.12, где указаны соответствующие числа граней [Гранью двумерной фигуры называется здесь заштрихованная часть плоскости, ограниченная со всех сторон некоторыми ребрами и ие пересекаемая другими ребрами.- Прим. ред.], ребер и вершин. При использовании этой формулы заранее предполагается, что фигуру можно так рассечь на достаточно малые части, чтобы каждая "грань" оказалась ПРОСТОЙ, т.е. не содержала дыр. Интересно, что число B(X) будет одним и тем же для любого рассечения фигуры X, отвечающего этому условию.

В нашем многообразии фигур, составленных из квадратов шахматной доски, B(X) можно вычислить при помощи линейной суммы G(X) низкого порядка, равной
G(X) = СУММА альфа.i*x.i + СУММА альфа.i.j*x.i*x.j + СУММА альфа.i.j.k.l*x.i*x.j*x.k*x.l, где
альфа.i = 1 для каждой точки (клетки) в R - вершины,
альфа.i.j = -1 для каждой смежной пары (вертикальной или горизонтальной, соседних клеток) - ребра,
альфа.i.j.k.l = 1 для каждого квадрата (из четырех смежных) клеток - грани.
На фигурах на шахматной доске значения G(X) и B(X) полностью совпадают, если только нет угловых касаний.
Когда в подобных случаях они различаются, наше определение связности требует знания величины G(X).
Важность величины G(X) в нашей теории объясняется тем, что, хотя эта величина в высшей степени ЛОКАЛЬНА (действительно, ограничена по диаметру и имеет конечный порядок), она эквивалентна глобальной формуле [Это формула Эйлера; величина Е(X) называется эйлеровой характеристикой.- Прим. ред.]
Е(X)=|компоненты(X)|-|дыры(X)|.
КОМПОНЕНТОЙ фигуры называется множество всех точек, связанных с данной точкой.
ДЫРОЙ фигуры называется компонента дополнения к фигуре.
Мы предполагаем, что расположенное вокруг фигуры "окружающее пространство" не является дырой. Кроме того, мы будем считать, что, когда речь идет о дополнении к фигуре, "угловое каcание" служит связью.
Теперь мы докажем, что локальная формула G(X) и глобальная формула Е(X) эквивалентны. Сначала дадим довольно прямое наглядное доказательство. Затем в # 5.8.2 приведем доказательство другого рода, в основе которого лежит деформация одной фигуры в другую; это позволит лучше понять доказательство основной теоремы в #5.9.
Начав с одного квадрата и добавляя квадраты последовательно друг за другом, можно получить любую фигуру X. Для единственного квадрата
G(X)=E(X)=1.
Добавление квадрата, не смежного ни с каким квадратом, принадлежащим X, прибавляет единицу к G(X) и (так как это новая компонента!) прибавляет единицу к E(X).
Добавление квадрата, смежного с одним и только одним квадратом, не может изменить E(X) и прибавляет ровно 1-1+0=0 к G(X).
Если добавляется квадрат, смежный с двумя другими, то возникают три возможности. Когда новый квадрат заполняет угол,

то к G прибавляется 1-2+1=0, так что G остается без изменения; не изменяется в этом случае и Е(X). Но если новый квадрат связывает два других, которые не были еще соединены,

то приращение к G равно 1-2+0=-1, причем E(X) тоже уменьшается на единицу, так как мы соединили две части, бывшие до этого разделенными. Если же добавляемый квадрат связывает два квадрата, уже соединенных каким-то путем,

то отсекается область пространства - образуется дыра, уменьшающая E на единицу, и G снова изменяется на 1-2+0=-1.
Наконец, случаи соседства с тремя и четырьмя квадратами: получаются фигуры типа

что прибавляет 1-3+2=0 и 1-4+4=1. Заметим, что в последнем случае G увеличивается на единицу, а дыра в конечном счете заполняется. Итак, в каждом случае либо G остается без изменения, либо изменяется топология фигуры X. (Все это соответствует рассуждениям в алгебраической топологии о добавлении ребер и клеток к цепным комплексам). Таким образом, доказана
Теорема 5.8.1. E(X)=G(X).
Из нее немедленно вытекает, что предикат [G(X)<n] реализуется выражением порядка не выше 4. Это приводит к некоторым любопытным замечаниям: если нам ЗАДАНО, что фигуры X могут быть только связными (т.е. однокомпонентными), то машина 4-го порядка может распознавать предикаты
[X не содержит дыр]=[G(X)>0]
и, например,
[X содержит менее 3 дыр]=[G(X)>-2].
Но, разумеется, отсюда не следует, что персептрон конечного порядка может распознавать эти предикаты НЕЗАВИСИМО ОТ КАКИХ-ЛИБО УСЛОВИЙ.
Этот топологический инвариант крайне "локален" по своей природе - в самом деле, все предикаты фи удовлетворяют весьма жестким ограничениям диаметра! Возвращаясь теперь к нашему первоначальному утверждению, заметим, что
[G(X)=n]=([G(X)<=n]==[G(X)>=n]).
Согласно теореме 1.5.4, порядок предиката [G(X)=N] не выше 8. Но при доказательстве этой теоремы строятся произведения предикатов фи, причем эти произведения НЕ ограничены по диаметру. В #8.4.3 мы покажем, что при помощи персептронов, ограниченных по диаметру, предикат [G(X)=N] реализовать нельзя.
#5.8.2. ДЕФОРМАЦИЯ ФИГУР В СТАНДАРТНЫЕ ФОРМЫ. В ходе доказательства теоремы #5.8.1 мы видели, что величина G одинакова для любых фигур X и Y, имеющих одно и то же значение Е=|компоненты|-|дыры|. Теперь мы покажем, что можно построить последовательность фигур X.1, ..., X.i, ..., Y с одним и тем же значением G=Е, каждая из которых получается из предыдущей некоторым локальным изменением [Авторы не дают точного определения этого понятия. По-видимому, имеется в виду изменение одной или нескольких соседних ячеек сетчатки.- Прим. ред.]. Легко понять, как можно "гладко" деформировать фигуры, не изменяя значения G или Е, т.е. не изменяя дыр и компонент. Например, последовательность

увеличивает дыру. Заметим, что компоненту C.0, лежащую внутри дыры H.1 другой компоненты C.1, можно вывести в окружающее пространство, не изменяя E(X) и G(X). Предположим для простоты, что C.1 соприкасается с окружающим пространством, а C.0 "просто" находится в H.1, т.е. никакая другая компонента, кроме C.1, не окружает C.0, как например, C' на фигуре

Тогда C.0 можно убрать из H.1 рядом деформаций, в ходе которых H.1 сначала оттягивается к периферии

а затем C.0 временно присоединяется к C.1:

Заметьте, что такая деформация не изменяет величины G(X). Точно так же, поскольку и C, и H уменьшаются на единицу, такая деформация не изменяет величины E(X)=C(X)-H(X) [C(X)=|компоненты(X)|, Н(X)=|дыры(X)|.- Прим. ред.]. Далее деформируем C.1 так, чтобы вывести C.0 в окружающее пространство

и отсоединить, получая при этом

значения G(X) и E(X) не изменяются. Ясно, что в конце концов мы можем очистить все дыры, повторив эту процедуру для каждой внутренней компоненты и выведя ее таким образом в окружающее пространство. Выполнив это, мы получим некоторое число компонент, в каждой из которых может находиться несколько чистых дыр и которые можно деформировать в фигуры стандартного вида

Далее, обращая операцию перехода от фигуры 6 к фигуре 7, можно соединить любую компоненту, имеющую дыру, с любой другой компонентой:
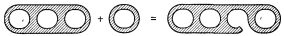
Так можно одновременно уменьшать и C, и H, пока H не станет равным нулю или С равным единице. Тогда получится либо

либо

и соответственно либо G(X)=E(X)=n, либо G(X)=E(X)=1-m. Мы будем использовать этот общеизвестный результат в следующем параграфе.
#5.9. ТОПОЛОГИЧЕСКИЕ ОГРАНИЧЕНИЯ ПЕРСЕПТРОНОВ
ТЕОРЕМА 5.9. Все топологически инвариантные предикаты конечного порядка являются функциями от эйлеровой характеристики E(X).
Мы уже доказали соответствующую теорему для персептрона, ограниченного по диаметру, и высказали предположение, что то же верно и в случае ограниченного порядка, но доказать последнее не сумели. Это было установлено М.Петерсоном; #5.9.1 целиком основан на его идее.
#5.9.1. ЗАПОЛНЕНИЕ ДЫР. Пусть C(X)>=2 и H(X)>=1. Возьмем дыру H.0 в компоненте C.0. Пусть C.1 - компонента, "доступная" для C.0, т.е. имеется путь P.01 от граничной точки фигуры C.0 до граничной точки фигуры C.1, не пересекающий X (в других точках.- Ред.). Пусть P.00 - путь ВНУТРИ C.0 от точки на границе дыры H.0 до точки на другой границе фигуры C.0, причем P.00 и P.01 связаны.

Такой путь P.00 всегда можно найти, даже если C.1 находится внутри H.0, или полностью вне C.0, или внутри какой-то другой дыры в C.0.
Если пси(X) - топологически инвариантный предикат, то его значение не меняется при деформациях типа

Предположим, что нам разрешено заменить следующим образом связи внутри прямоугольника:

В сущности, это значит разрезать вдоль P.00, устранив дыру, и соединить вдоль одной стороны пути P.01, уменьшив на единицу число компонент. Таким образом, величина E(X) не изменится.
Покажем, что эти деформации не влияют на величину предиката пси!
Пусть пси имеет k-й порядок. Будем деформировать фигуру X до тех пор, пока в прямоугольнике не окажется каскад из k+1 4-ключей (см. рис.5.6 и 5.7). Это не изменяет топологии, так что пси остается тем же. Затем рассмотрим 2**(k+l) вариантов фигуры X, получаемых за счет 2**(k+1) состояний каскадного ключа. Если значение пси одинаково для всех них, то, очевидно, можно провести изменение тривиальным образом, не воздействуя на пси. Если два варианта дают РАЗНЫЕ значения, скажем пси(X')!=пси(X''), то они должны отвечать различным состояниям четности ключей, поскольку пси - топологический инвариант. Но коль скоро это так, то пси должен быть способен указывать четность этого ключа, так как все фигуры X данного класса четности топологически эквивалентны (подробности см. в #5.7). Но, как мы знаем, согласно теореме о сжатии, этого не может быть: при проверке четности предикат пси должен "сбиться", если порядок задачи превышает k. Поэтому все фигуры, полученные изменением позиций ключей, дают одно и то же значение пси, и можно применить преобразования, описанные в #5.8.2, не изменяя значений пси.
#5.9.2. КАНОНИЧЕСКАЯ ФОРМА. Используем метод #5.9.1 и #5.8.2, чтобы привести произвольную фигуру X к канонической форме, зависящей только от E(X). Будем повторять прием, описанный в #5.8.2, до тех пор, пока не исчерпаем все (лишние.- Ред.) дыры или компоненты. Должна остаться либо
(1) единственная компонента с одной или более дырами, либо
(2) одна или более простых сплошных компонент в зависимости от выполнения условия E(X)<=0.
В случае (1) окончательная фигура топологически эквивалентна фигуре типа

с 1-E(X) дырами, а в случае (2) она эквивалентна фигуре типа

с E(X) сплошными квадратами. Тогда очевидно, что для любых двух фигур X и X', для которых E(X)=E(X'), должно быть пси(X)=пси(X'). Это доказывает теорему 5.9, утверждающую, что предикат пси(X) зависит только от E(X).
ЗАМЕЧАНИЕ. Имеется одно исключение из правила, сформулированного в виде теоремы 5.9, поскольку каноническая форма не включает случай полностью пустого изображения! Дело в том, что предикат
[фигура X непустая]
ЯВЛЯЕТСЯ топологическим инвариантом, но не будет функцией от E(X). См. #8.1.1 и 8.4.
Кроме числа компонент фигуры X и величины G(X), существует много других ТОПОЛОГИЧЕСКИХ инвариантов, например
[компонента фигуры X находится внутри дыры в другой компоненте].
Из теоремы #5.9, таким образом, следует, что никакой предикат конечного порядка не в состоянии отличить фигуру, СОДЕРЖАЩУЮ ВНУТРИ СЕБЯ другую фигуру (левый рисунок), от фигуры, не содержащей других (правый рисунок).

ЗАДАЧА. Что даст подобный анализ топологических предикатов в пространствах большего числа измерений? Можно ли интерпретировать СУММА альфа.i*фи.i как коцепь на симплициальном комплексе, в котором пороговая операция как-то разумным образом определена?

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 6. ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ МАЛОГО ПОРЯДКА: СПЕКТРЫ И КОНТЕКСТ
#6.0. ВВЕДЕНИЕ К ГЛАВАМ 6 И 7
В гл.6 и 7 исследуются предикаты, геометрические в более строгом смысле, чем связность. Типичным примером рассматриваемых задач служит распознавание всех ПЕРЕНОСОВ фигуры или класса фигур. В некотором смысле результаты получаются более положительными, чем в предыдущей главе. Многие подобные задачи можно решить с помощью персептронов низкого порядка, и стержневой осью этих двух глав будут два способа построения геометрических предикатов, порядок которых зачастую поразительно мал.
Некоторые специальные вопросы, излагаемые в настоящем введении, могут быть не до конца поняты до тех пор, пока не будет прочитана гл.7. Введение предназначено (если читать его в соответствующем настроении), чтобы создать атмосферу определенной взаимосвязи всех этих результатов и наблюдений.
Всякий раз, когда можно применить теорему об инвариантности относительно групп, изучение инвариантных предикатов малого порядка сводится к изучению нескольких типов элементарных локальных предикатов. Чем больше группа, тем меньше и проще этот набор элементарных предикатов. Поскольку предикат пси.ЧЕТНОСТЬ инвариантен относительно наибольшей возможной группы (группы всех перестановок), мы смогли использовать для соответствующих элементарных предикатов простые маски, рассортированные в соответствии с размерами их носителей. Геометрические предикаты, представляющие интерес, не выдержат подобных коренных преобразований. Такие группы, как ПЕРЕНОСЫ или ОБЩИЕ ПЕРЕМЕЩЕНИЯ ФИГУРЫ КАК ТВЕРДОГО ТЕЛА, ведут к более многочисленным типам эквивалентности частных предикатов. Фигуры, удовлетворяющие инвариантным предикатам, будут тем не менее полностью охарактеризованы наборами чисел, указывающих, какому количеству частных предикатов каждого типа эти фигуры удовлетворяют. Мы будем называть такие наборы СПЕКТРАМИ. В гл.6 мы покажем, как их применять.
Глава 7 посвящена совершенно иному способу построения геометрических предикатов. Всякий раз, когда можно подходящим образом упорядочить группу, можно выполнить стратификацию множества фигур, эквивалентных данной фигуре относительно этой группы, используя номер элемента группы, необходимого, чтобы осуществить преобразование. Поэтому мы можем (во многих интересных случаях) разделить задачу распознавания на две части: распознать страт, к которому принадлежит фигура, а затем употребить простое испытание, соответствующее этому страту). Внешне такое описание выглядит скорее как последовательное, а не параллельное вычисление, и действительно, оно вызывает интерес, в частности, тем, что предлагает по крайней мере один путь моделирования последовательного, или УСЛОВНОГО, процесса при помощи параллельной процедуры.
Естественно, за такое моделирование приходится расплачиваться. Предлагаемый метод ведет к исключительно большим коэффициентам получаемых линейных представлений. Само по себе это не исключает существования другой методики, позволяющей добиться того же самого результата меньшей ценой. Поэтому (в гл.10) мы приходим к новой области исследования - границам коэффициентов - и к ряду занимательных, хотя до конца еще не понятых, результатов.
Напомним, что, доказывая теорему об инвариантности относительно групп, мы предполагали, что группа конечна. Упорядочение, используемое нами при стратификации, предполагает бесконечность группы (например, переносы на бесконечной плоскости упорядочены очевидным образом), но если при помощи описанного в #5.6 построения на торе сделать группу конечно-циклической, то упорядочение станет невозможным. Когда мы впервые столкнулись с таким противоречием, мы сочли технику стратификации и технику, связанную с инвариантностью относительно групп (спектры и т.п.), нигде не пересекающимися направлениями исследований. Но дальнейшее изучение свело их вместе, по-видимому, в довольно глубоком смысле. Мы в самом деле можем в ряде бесконечных случаев спасти теорему об инвариантности относительно групп, полагая, что коэффициенты ограничены. Допустим, например, что пси(X) - предикат, определенный для КОНЕЧНЫХ ФИГУР X на бесконечной плоскости и инвариантный относительно группы переносов. Тогда его можно представить в виде бесконечной линейной формы, например
пси(X) = [СУММА[ФИ]альфа.фи*фи(X)>тета],
где ФИ - бесконечное множество (например, множество масок), выбранное так, чтобы для любой конечной фигуры X все слагаемые, кроме конечного числа, равнялись нулю. Далее, если коэффициенты альфа.фи ограничены, можно применить (согласно теореме 10.4.1) теорему об инвариантности относительно групп. В некоторых случаях получаемый при этом порядок ПРЕВЫШАЕТ порядок, получаемый на основе стратификации. Противоречие можно устранить, только придя к заключению, что нельзя ограничивать коэффициенты альфа.фи для ЛЮБОГО представителя низкого порядка. Поэтому огромная величина коэффициентов, которую дает наша методика стратификации, не следует просто из неудачного алгоритма (хотя, конечно, фактические значения коэффициентов могут быть любыми, поскольку не было доказано, что они минимальны).
Разумеется, нам было очень приятно обнаружить, что кажущееся на первый взгляд ограничение нашей излюбленной теоремы в действительности позволило получить ценный результат. Нам кажется, что это намного интереснее, чем сама проблема величины коэффициентов (и ее приложения). В этом нас убеждает устойчивое проявление ГЛОБАЛЬНОЙ СТРУКТУРЫ группы преобразований.
Долгое время мы были уверены, что распознавание всех переносов данной фигуры принадлежит к задачам высокого порядка. Стратификация показала, что мы ошибались. Но мы оказались не в состоянии найти предикаты низкого порядка для соответствующей задачи, когда группа содержит большие конечные циклические подгруппы, как, например, вращения или переносы на торе, и продолжаем вынашивать предположение, что такие задачи не являются задачами конечного порядка.
В дополнение к "положительным" результатам гл.6 мы докажем одну "отрицательную" теорему, имеющую большое практическое значение. Она относится к распознаванию фигур В КОНТЕКСТЕ. С помощью предиката низкого порядка легко решить, является ли данная фигура, скажем, прямоугольником. Задача нашего нового типа состоит в том, чтобы решить, содержит ли данная фигура прямоугольник и, быть может, что-то еще (рис.6.1).

Рис.6.1. Предикат пси.ПРЯМОУГОЛЬНИК не отвергает только фигуру 1. Предикат пси.ПРЯМОУГОЛЬНИК-В-КОНТЕКСТЕ отвергает только фигуру 6.
Кажется очевидным, что распознавание в контексте должно быть до некоторой степени более трудной задачей, требующей, быть может, более высокого порядка. Мы покажем (#6.6), что дело обстоит еще хуже: такое распознавание не обладает даже конечным порядком!
Наконец, следует отметить, что нам снова удалось обойти необходимость применения теории допустимых отклонений и избежать ограничений, которые дает использование массивов квадратных ячеек. В случае группы переносов эта проблема не возникает. Она возникает в случае группы вращений; однако мы излагаем все, что необходимо, в рамках поворотов на 90o. Более серьезные затруднения вызывает группа подобия: растянуть фигуру довольно легко, но как сжать малую фигуру? Оказалось, что мы об этой группе не можем сказать ничего интересного. Мы призываем будущих исследователей быть менее малодушными.
В #6.1-6.4 мы покажем, что определенные образы имеют порядок 1, другие 2, порядок третьих не превышает 3 и соответственно 4. Нижняя граница порядков для большинства случаев еще не установлена, и у нас нет для этого систематических методов.
#6.1. ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ ПОРЯДКА 1
Когда мы говорим "геометрическое свойство", мы имеем в виду что-то инвариантное относительно переноса, или вращения, или растяжения. Сочетание первых двух инвариантностей определяет "конгруэнтную" группу преобразований, а наличие всех трех дает фигуры, "подобные" в евклидовой геометрии. Мы уже знаем, что для первого порядка все коэффициенты можно считать равными [Во всех теоремах этой главы предполагается, что теорему об инвариантности относительно групп применить можно, даже несмотря на то, что группа переносов не является конечной. На самом деле эту теорему можно применить, если (теорема 10.4.1) коэффициенты ограничены, а для первого порядка ее можно применять всегда. Кроме того, есть немало других достаточных условий. В #7.10 мы обнаружим, что теорема эта не всегда пригодна. Хорошего общего метода проверки возможности ее применения у нас нет, но, конечно, в любой физической машине коэффициенты будут ограничены!]. Поэтому единственные образы порядка 1 это те, которые определены с помощью ОДНОГО сечения интервала значений мощности множества, т.е. площади фигуры X:
пси=[|X|>A] или пси=[|X|<A].
ЗАМЕЧАНИЕ. Если инвариантность относительно переносов НЕ требуется, то персептроны порядка 1 могут, разумеется, вычислять и другие свойства, например, связанные с МОМЕНТАМИ относительно ДАННЫХ точек или осей (#2.4.1). Но эти свойства не "геометричны" в том смысле, что не обладают нужной инвариантностью. Поэтому, несмотря на возможную практическую значимость этих свойств, мы в дальнейшем не будем их рассматривать [См., например, работу Питтса и Маккаллока [1947] о следящей системе центрирования глава, использующей, в сущности, предикат первого порядка].
#6.2. ОБРАЗЫ ПОРЯДКА 2, СПЕКТРЫ РАССТОЯНИЙ
При k=2 положение усложняется. Как показано в #1.4, пример 3, можно определять двойное сечение, или сегмент A.1<A<A.2, для площади множества и распознавать фигуры, удовлетворяющие предикату
пси=[A.1<|X|<A.2].
Действительно, в общем случае всегда можно найти функцию 2k-го порядка, распознающую множество, величина площади которого заключена в любом из k интервалов. Но вернемся к образам, имеющим геометрическое значение. Рассмотрим сначала только группу переносов и маски второго порядка. Здесь две маски х.1*х.2 и x.1'*x.2' эквивалентны тогда и только тогда, когда ВЕКТОРЫ
x.1-x.2 и x.1'-x.2'
равны по величине (знаки могут быть любые). Таким образом, по отношению к группе переносов любой предикат порядка 2 может зависеть только от "спектра разности векторов", определяемого как последовательность чисел эквивалентных пар точек, причем каждой паре значений длины вектора и угла наклона соответствует некоторое множество эквивалентных пар точек. Две фигуры

обладают одними и теми же спектрами разности векторов, а именно:
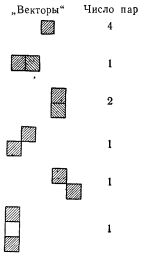
Следовательно, никакой предикат порядка 2 не может выполнить классификацию, инвариантную относительно переносов, при которой бы эти две фигуры различались. Действительно, из теоремы об инвариантности относительно групп непосредственно следует
ТЕОРЕМА 6.2. Пусть пси(X) - предикат второго порядка, инвариантный относительно переносов. Обозначим через n.ню(X) число пар точек в X, разность которых равна вектору ню. Тогда предикат пси(X) можно записать в виде
пси(X)=[СУММА[ню]альфа.ню*n.ню(X)>тета].
ДОКАЗАТЕЛЬСТВО. n.ню предикатов в классе ФИ.ню удовлетворяются при любом переносе фигуры X. По теореме 2.3 всем им можно присвоить один и тот же коэффициент.
СЛЕДСТВИЕ. Две фигуры с одинаковым спектром переносов [Авторы употребляют термины "спектр переносов" и "спектр разности векторов" для обозначения одного и того же понятия.- Прим. ред.] n.ню нельзя отличить одну от другой при помощи инвариантного относительно переносов персептрона второго порядка. (См., однако, примечание к #6.1).
И обратно, если спектры различны, например, n.ню.1(A) < n.ню.1(B), то при помощи предиката [n.ню.1(X) < n.ню.1(B)] можно различить переносы обеих фигур. Но КЛАССЫ, составленные из разных фигур, таким способом различить нельзя.
ПРИМЕР. Предикаты порядка 2 не способны отличить фигуры
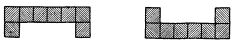
тогда как фигуры
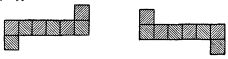
обладающие различными спектрами разности векторов, можно отличить друг от друга. Если мы потребуем еще и инвариантность относительно вращений, то последнюю пару фигур также нельзя будет различить, поскольку классы эквивалентности объединяют теперь все разности одной длины вне зависимости от их ориентации.
Заметим, что мы НЕ допускали отражений, и все же зеркально противоположные фигуры попали в один класс! В подобных вопросах полагаться на "интуицию" можно лишь с большой осторожностью. Теория общей инвариантности относительно вращений требует особого внимания к эффекту дискретной аппроксимации на сетчатке, но эту теорию можно, по-видимому, сделать состоятельной при помощи подходящей теории допустимых отклонений. Что же касается "группы" растяжений, то здесь возникают серьезные трудности. (Для группы, порождаемой поворотами на 90o, приведенный выше пример не годится, но зато хорошо работает следующий пример).
Интересным примером фигур, различных с точки зрения вращений, но тем не менее неразличимых при k=2, служат фигуры

характеризуемые одинаковыми (не зависящими от направления) спектрами расстояний между парами точек (для второго порядка), а именно:
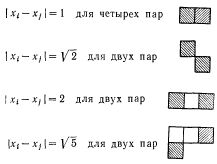
Каждая фигура содержит по 5 точек (спектр первого порядка).
Теорема об инвариантности относительно групп (#2.3) гласит, что любой персептрон, инвариантный относительно группы, должен зависеть только от "чисел замещения" образа, т.е. как раз от рассмотренных здесь "геометрических спектров". Множество других проектов "машин для распознавания образов" (не персептронов и соответственно не выражающихся просто в виде линейных форм) тоже можно лучше понять, изучив их взаимосвязь с теорией таких геометрических спектров. Однако маловероятно, чтобы подобный анализ внес ощутимый вклад в изучение более "описательных", или, как иногда говорят, "синтаксических", систем анализа окружающей действительности, в защиту которых втайне выступают авторы.
Еще один пример предиката порядка 2 дает предикат
[фигура X лежит в пределах одной строки или столбца и содержит не более n отрезков],
который определяется как
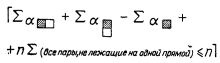
#6.3. ОБРАЗЫ ПОРЯДКА 3
#6.3.1. ВЫПУКЛОСТЬ. Особый интерес представляет предикат
пси.ВЫПУКЛОСТЬ(X) = [X - одна сплошная выпуклая фигура].
Этот предикат имеет порядок не выше 3, что следует из самого определения "выпуклости": фигура X выпукла тогда и только тогда, когда каждый отрезок, концы которого принадлежат X, целиком принадлежит X. В самом деле, из определения выпуклости следует, что фигура X выпукла тогда и только тогда, когда
a принадлежит X и b принадлежит X => (внутренняя точка отрезка [a, b]) принадлежит X,
а потому предикат
пси.ВЫПУКЛОСТЬ(X) = [СУММА[a, b из X][внутренняя точка отрезка [a, b] не принадлежит X] < 1]
имеет порядок не выше 3, и, по всей вероятности, равный 3. Это конъюнктивно локальное условие; такие условия были подробно рассмотрены в #0.2.
Если СВЯЗНАЯ фигура не Выпукла, то можно показать, что в ней содержится по крайней мере одна "локальная" вогнутость, сосредоточенная на трех как угодно близких точках, например
Поэтому, если дано, что фигура X связна, то выпуклость можно реализовать в виде ОГРАНИЧЕННОГО ПО ДИАМЕТРУ предиката порядка 3. Если нет уверенности, что фигура X связна, то для случая ограниченного диаметра предыдущее рассуждение неверно, поскольку ПАРА очень отдаленных друг от друга выпуклых фигур не отвергается.
При дополнительном ограничении на величину диаметра предикат пси.ВЫПУКЛОСТЬ скорее всего не будет иметь порядок 3, но отсюда не следует делать поспешный вывод о том, что при любом порядке этот предикат не будет ограниченным по диаметру. Такой вывод делать нельзя, учитывая следующее практическое соображение.
Даже если связность фигуры задана, ее выпуклость можно определить только с точностью до допустимых отклонений. Вдобавок размеры фигуры должны быть равномерно ограничены, иначе малые локальные допустимые отклонения станут глобально гибельными. Но при таком ограничении можно ПРИБЛИЖЕННО ОЦЕНИТЬ кривизну и определить выпуклость с помощью неравенства
ИНТЕГРАЛ |кривизна| ds<=2*пи.
Мы обсудим это в # 8.3 и 9.3.
#6.3.2. ПРЯМОУГОЛЬНИКИ. Рассматривая фигуры, составленные только из квадратиков сетчатки, можно с помощью предикатов порядка 3 задать множество сплошных прямоугольников со сторонами, параллельными осям координат. (На рис.6.2 показаны примеры "полых" прямоугольников).
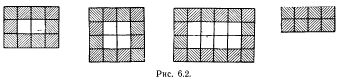
Этого можно добиться даже с помощью лишь предикатов фи, ограниченных по диаметру, а именно:
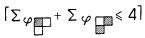
Сюда входят все предикаты фи, эквивалентные относительно поворота на 90o. Полые прямоугольники выявляются предикатом
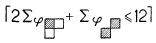
где коэффициенты подобраны так, чтобы исключить случай двух и более изолированных точек. Примеры такого рода, конечно, слабы из-за их зависимости от выбранной сетки квадратов. Но они обладают тем незаметным на первый взгляд достоинством, что рассматриваемые образы могут быть определены как прямолинейные фигуры с числом углов не более 4. Мы обсудим этот несколько более чем конъюнктивно локальный способ определения в гл.8.
Можно было бы ожидать, что множества полых и сплошных КВАДРАТОВ окажутся порядка 4 или еще выше, поскольку по меньшей мере такой порядок должно было бы потребовать сравнение длин сторон. Поэтому удивительно, что их порядок оказался равным 3. Построение явно не конъюнктивно локально, и мы его отложим до гл.7.
#6.3.3. СПЕКТРЫ ПЕРЕНОСА ВЫСШЕГО ПОРЯДКА. Определим ТРЕХВЕКТОРНЫЙ СПЕКТР фигуры как множество наборов чисел, выражающих количество трехточечных масок, удовлетворяемых в каждом классе эквивалентности относительно переносов. Интересно отметить следующее обстоятельство (относящееся скорее к геометрии, а не к линейному разделению).
ТЕОРЕМА 6.3.3. Фигуры однозначно характеризуются (с точностью до переноса) своими трехвекторными спектрами даже в случае пространства высокой размерности.
ДОКАЗАТЕЛЬСТВО. Пусть X - некоторая фигура и максимальное расстояние между ее точками равно D. Выберем пару (a, b) точек в X с этим расстоянием и рассмотрим множество ФИ.a.b = {фи.a.b.x} масок с трехточечными носителями, содержащими a, b и любую третью точку x из X. Коэффициент при каждой такой маске в спектре переноса должен равняться единице, так как если бы в X было две маски, эквивалентные относительно переносов:
фи.a.b.x и фи.ga.gb.gx
то длина одного из отрезков [a, gb] или [ga, b] была бы больше D, поскольку эти отрезки совпадают с диагоналями параллелограмма со стороной D (рис.6.3).
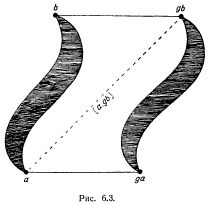
Таким образом, любой перенос фигуры X должен содержать ЕДИНСТВЕННЫЙ перенос пары (a, b), и часть спектра фигуры, соответствующая ФИ.a.b, позволяет полностью воспроизвести всю фигуру (рис.6.4).
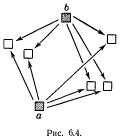
Тот факт, что фигура ОПРЕДЕЛЯЕТСЯ своим трехвекторным спектром, конечно же, не означает, что распознавание классов фигур имеет порядок 3. (Он свидетельствует только о том, что можно различить переносы двух разных фигур. На самом деле, как показывает метод #7.9, их можно различать даже с помощью второго порядка, но только если снять ограничение на величины коэффициентов).
#6.4. ОБРАЗЫ ПОРЯДКА 4 И ВЫШЕ
Известно, что любые три точки определяют окружность. Это обстоятельство можно использовать для построения персептрона порядка 4, реализующего предикат
[X - периметр полной окружности]
с помощью формы
[СУММА[d не из C.a.b.c]x.a*x.b*x.c*x.d + СУММА[d из C.a.b.c]x.a*x.b*x.c*~x.d],
где C.a.b.c - окружность [Здесь опять встает проблема допустимых отклонений: что считать окружностью на дискретной сетчатке? См.#8 3.], проходящая через точки x.a, x.b, x.c. Аналогично можно показать, что много других любопытных и интересных предикатов имеют низкий порядок. Нужно соблюдать осторожность в выводах отсюда практических следствий и учитывать следующие факты:
1. Для приведенных выше примеров может потребоваться большое число (порядка |R|**(k-1)) предикатов фи.
2. Пороговые условия выражены настолько резко, что по инженерным соображениям могут возникнуть трудности в реализации линейного суммирования, особенно при наличии какого-либо шума. При k=3 и выше простой квадратичный шум растет быстрее, чем размер сетчатки. Значения коэффициентов зачастую убийственно велики (см. гл.10).
3. Часто малейшее изменение в определении образа [Наша формула не отвергает нуль- и одномерных "окружностей" Этого не избежать при любой размерности, если используется конъюнктивно локальный предикат] совершенно меняет порядок предиката, способного распознавать этот образ. При низких значениях порядков невозможно определить такие допустимые отклонения, при которых предикат будет работать удовлетворительно.
#6.5. ТЕОРЕМЫ О СПЕКТРАЛЬНОМ РАСПОЗНАВАНИИ
Некоторые из предыдущих примеров являются частными случаями теорем. (Вводимые здесь понятия далее не используются). Из теоремы об инвариантности относительно группы (# 2.3) вытекает, что инвариантный относительно группы G предикат пси, принадлежащий L(ФИ) Для некоторого множества ФИ, можно представить в виде
пси = [СУММА[i]бета.i*N.i(X)>0],
где Ni - число предикатов фи в i-м классе эквивалентности, которым фигура X удовлетворяет. В #6.2 (в случае группы переносов на плоскости) мы столкнулись со "спектром разности векторов" геометрических фигур. Для нулевого, первого и второго порядков такими спектрами действительно служат числа N.i(X). Если G-инвариантный предикат пси при заданном ФИ нельзя описать для ЛЮБОГО условия на числа N.i, то очевидно, что пси не принадлежит L(ФИ). Следующие результаты дают условия на N.i, влекущие за собой конечность порядка предиката пси.
Допустим, что пси определяется одновременно m равенствами:
пси(X) == [N.1(X)=n.1 и N.2(X)=n.2 и ... N.m(X)=n.m],
где n.1, ..., n.m - конечная последовательность целых чисел. Покажем, что порядок предиката пси не более чем в два раза превышает максимальный из порядков предикатов фи, связанных с числами N.i. Сформулируем утверждение более точно.
ТЕОРЕМА 6.5. Пусть ФИ = объединение ФИ.1, ФИ.2, ..., ФИ.m и
N.i(X) = |{фи|фи из ФИ.i фи(X)=1}| = СУММА[фи из ФИ.i]фи(X).
Тогда порядок предиката
пси(X) = [N.i(X)=n.i для всех 1<=i<=m]
не превышает удвоенной величины max{|S(фи)|: фи из ФИ}.
Замысел доказательства заключается в том, чтобы показать, что предикат пси можно задать с помощью линейного порогового выражения:
пси(X) = [СУММА(N.i(X)-n.i)**2 < 1]
В таком виде это выражение НЕ является линейной пороговой комбинацией предикатов. Для придания ему желаемой формы введем СПЕЦИАЛЬНОЕ соглашение, которое нигде больше использоваться не будет. Для любого заданного множества ФИ предикатов фи.i построим новое множество ФИ2 предикатов фи.i.j, полагая
фи.i.j(X) = фи.i(X) & фи.j(X)
для любой пары (фи.i, фи.j) предикатов из ФИ. Многие из построенных таким образом предикатов окажутся логически эквивалентными, например фи.i.j=фи.j.i, однако мы условимся считать их различными элементами множества ФИ2. (Это означает, что в очень строгом смысле ФИ2 есть скорее множество "предикатных форм", а не предикатов).
В результате такого соглашения упрощаются арифметические действия и логические соображения при подсчете числа предикатов. Пусть X - фигура, удовлетворяющая в точности N предикатам из Ф. Очевидно, в ФИ2 фигура X будет удовлетворять N**2 предикатам, т.е.
СУММА[ФИ2]фи(X) = N**2.
Пусть теперь ФИ.1, ФИ.2... - классы эквивалентности множества ФИ. Так как
N.i(X) = СУММА[ФИ.i]фи(X)
- число предикатов из ФИ.i, удовлетворяемых фигурой X, то, как мы уже видели,
СУММА[ФИ2.i]фи(X) = N.i**2(X).
Таким образом,
СУММА[i](СУММА[ФИ2.i]фи(X) - 2*n.i*СУММА[ФИ.i]фи(X) + n.i**2) = СУММА[i](N.i(X)-n.i)**2.
Чтобы представить левую часть этого равенства в стандартной форме линейного порогового предиката, положим ФИ' = объединение ФИ2, ФИ и {постоянный предикат} и запишем
пси(X) = [СУММА[ФИ']альфа(фи)*фи(X) < 1],
где
альфа(фи) = 1 для фи иs ФИ2,
альфа(фи) = -2 для фи из Ф.i,
альфа(постоянный предикат) = СУММА n.i**2.
Для завершения доказательства теоремы нам осталось только заметить, что
|S(фи.i.j)| = |объединение S(фи.i) и S(фи.j)| <= |S(фи.i)|+|S(фи.j)| <= 2*(max|S(фи)|).
#6.5.1. РАСШИРЕННОЕ ТОЧНОЕ СООТВЕТСТВИЕ. Очевидно, что теорема 6.5 допускает следующее обобщение. Пусть предикат пси определяется формулой
пси(X) == V[i=1..n] &[j=1..m] N.i(X)=n.i.j,
т.е. удовлетворяется любым условием из множества точных условий, наложенных на N.i. Тогда порядок предиката пси конечен, поскольку полином
ПРОИЗВЕДЕНИЕ[i=1..n] СУММА[j=1..m] (N.i(X)-n.i.j)**2
можно реализовать при помощи методов, подобных применявшимся в предыдущем параграфе. Для обобщения потребуются булевы произведения предикатов разных классов эквивалентности, и максимальный порядок будет не более 2*n*max|S(фи)|.
Заметим, что, не зная явления "и/или", можно было бы невольно попытаться вывести результат #6.5.1 из #6.5 на основе неверного предположения о том, что порядок предиката
V[i=1..n](предикаты k-vo порядка)
не превосходит n*k.
#6.5.2. СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ. Если для предикатов, о которых шла речь в #6.5.1, увеличить значение порога тета, то система
[СУММА(N.i-n.i)**2 < тета]
будет удовлетворяться как раз теми фигурами, для которых СУММА КВАДРАТОВ разностей между величинами N.i и n.i меньше тета. Любое устройство классификации образов будет чувствительно к определенного рода искажениям, и это наводит на мысль, что, вероятно, полезно изучать такие устройства, в частности персептроны, в терминах их чувствительности к искажению спектра. К сожалению, у нас нет хороших идей о геометрической сути подобных искажений. Геометрическая природа "инвариантного шума" такого вида представляет благодатную тему для размышлений, но мы еще не занимались ее исследованием.
#6.6. ФИГУРЫ В КОНТЕКСТЕ
По практическим и теоретическим соображениям интересно изучить распознавание фигур в "контексте", т.е. предикаты вида:
пси(X) = [подмножество множества X - квадрат],
пси(X) = [связная компонента множества X - квадрат],
а чтобы приступить к рассмотрению проблемы проекций в трехмерном пространстве, интересно изучить предикат
пси(X) = [содержит значительную часть контура частично невидимого квадрата].

Эти примеры показывают, что интуитивным понятиям, связанным с распознаванием образов, находящихся в контексте, можно дать более чем одно естественное толкование. Нам не известно ни одного общего определения, охватывающего все естественные представления,, и поэтому мы не имеем возможности формулировать общие теоремы. Тем не менее мы утверждаем, что ДЛЯ ВСЕХ ПРЕДИКАТОВ НИЗКОГО ПОРЯДКА СВОЙСТВЕННА УТРАТА ИМИ КОНЕЧНОСТИ ПОРЯДКА ПРИ ЛЮБОМ ЕСТЕСТВЕННОМ СПОСОБЕ ПОМЕЩЕНИЯ ОБЪЕКТОВ РАСПОЗНАВАНИЯ В КОНТЕКСТ. Для иллюстрации этого положения выберем наиболее общую и, очевидно, безобидную интерпретацию: для любого предиката пси(X) определим новый предикат
пси.В-КОНТЕКСТЕ(X) = [пси(X) для некоторой связной компоненты фигуры X].
Мы увидим, что используемую нами методику можно тривиальным образом приспособить для множества других определений.
Интуитивно следовало бы ожидать, что предикат пси.В-КОНТЕКСТЕ окажется гораздо более трудным для персептрона, поскольку контекст каждой компоненты действует как шум, а параллельность работы устройства дает мало шансов на то, что подобный шум удастся отделить и не учитывать. Это становится особенно ясным в тех случаях, когда предикат пси использует правила отбрасывания, которые по вполне очевидным причинам нельзя передать в предикат пси.В-КОНТЕКСТЕ. Аналогично пропадут методы стратификации из гл.7 и, разумеется, большая часть технических уловок, с помощью которых мы получали представления предикатов низкого порядка. Следующие две теоремы показывают, как эту интуитивную идею можно выразить в строгой форме. Заметим, однако, что невозможно никакое простое обобщение взаимосвязи предикатов пси и пси.В-КОНТЕКСТЕ, поскольку некоторые предикаты пси в контексте вырождаются. Например, вырождается предикат пси.СВЯЗНОСТЬ, так как любое множество содержит связную компоненту!
ТЕОРЕМА 6.6.1. Пусть R - конечная квадратная сетчатка, а пси(X) - предикат
[X является единственной горизонтальной линией, пересекающей сетчатку].
Тогда порядок предиката пси равен 2, а предикат пси.В-КОНТЕКСТЕ не имеет конечного порядка.
ДОКАЗАТЕЛЬСТВО. Предоставляем читателю доказать в качестве упражнения, что порядок предиката пси равен 2. Чтобы показать, что предикат пси.В-КОНТЕКСТЕ не имеет конечного порядка, заметим просто, что он служит отрицанием негатива предиката пси.1=пси.ОДИН-В-БЛОКЕ т.е. предиката, утверждающего, что через сетчатку не проходит ни одной горизонтальной белой линии. Его негатив (в фотографическом смысле) утверждает, что через сетчатку не проходит ни одной горизонтальной черной линии. Далее, предикат пси.1 не имеет конечного порядка, а в общем случае можно показать, что этим свойством обладает любой негатив такого предиката. Наконец, обращая предикатное неравенство, получаем, что это справедливо и для искомого предиката
пси.В-КОНТЕКСТЕ = [X сoдержит горизонтальную линию, пересекающую сетчатку].
ТЕОРЕМА 6.6.2. Пусть пси(X) - предикат
[X - полый квадрат].
Тогда предикат пси.В-КОНТЕКСТЕ
[одна из компонент фигуры X - полый квадрат]
не имеет конечного порядка.

ДОКАЗАТЕЛЬСТВО. Доказательство подобно предыдущему, за тем исключением, что "блоки", или горизонтальные линии, изгибаются в квадраты и располагаются без перекрытий на большей сетчатке. Можно показать, что сам предикат пси имеет конечный порядок, в данном случае 3.
ЗАМЕЧАНИЕ. Другой метод доказательства состоит в изгибании линий переключательных элементов, использованных в построении Хаффмена для связности (#5.5).
Мы убеждены, что вырождение способности персептрона распознавать образы, если последние находятся в контексте других образов, служит серьезным предупреждением против использования его в реальных практических ситуациях. Конечно, этот недостаток можно смягчить, включая персептрон в некоторый последовательный процесс (такой, в котором интересующая нас фигура на предварительной стадии изолируется и отделяется от своего контекста). Однако это предполагает достаточную способность к распознаванию на этапе "предварительной обработки", чтобы можно было различить и устранить большинство обычно встречающихся контекстуальных помех. Иногда выполнить это гораздо труднее, чем провести собственно "основную обработку". Этот вопрос мы еще будем рассматривать в гл.13.
#6.0. ВВЕДЕНИЕ К ГЛАВАМ 6 И 7
В гл.6 и 7 исследуются предикаты, геометрические в более строгом смысле, чем связность. Типичным примером рассматриваемых задач служит распознавание всех ПЕРЕНОСОВ фигуры или класса фигур. В некотором смысле результаты получаются более положительными, чем в предыдущей главе. Многие подобные задачи можно решить с помощью персептронов низкого порядка, и стержневой осью этих двух глав будут два способа построения геометрических предикатов, порядок которых зачастую поразительно мал.
Некоторые специальные вопросы, излагаемые в настоящем введении, могут быть не до конца поняты до тех пор, пока не будет прочитана гл.7. Введение предназначено (если читать его в соответствующем настроении), чтобы создать атмосферу определенной взаимосвязи всех этих результатов и наблюдений.
Всякий раз, когда можно применить теорему об инвариантности относительно групп, изучение инвариантных предикатов малого порядка сводится к изучению нескольких типов элементарных локальных предикатов. Чем больше группа, тем меньше и проще этот набор элементарных предикатов. Поскольку предикат пси.ЧЕТНОСТЬ инвариантен относительно наибольшей возможной группы (группы всех перестановок), мы смогли использовать для соответствующих элементарных предикатов простые маски, рассортированные в соответствии с размерами их носителей. Геометрические предикаты, представляющие интерес, не выдержат подобных коренных преобразований. Такие группы, как ПЕРЕНОСЫ или ОБЩИЕ ПЕРЕМЕЩЕНИЯ ФИГУРЫ КАК ТВЕРДОГО ТЕЛА, ведут к более многочисленным типам эквивалентности частных предикатов. Фигуры, удовлетворяющие инвариантным предикатам, будут тем не менее полностью охарактеризованы наборами чисел, указывающих, какому количеству частных предикатов каждого типа эти фигуры удовлетворяют. Мы будем называть такие наборы СПЕКТРАМИ. В гл.6 мы покажем, как их применять.
Глава 7 посвящена совершенно иному способу построения геометрических предикатов. Всякий раз, когда можно подходящим образом упорядочить группу, можно выполнить стратификацию множества фигур, эквивалентных данной фигуре относительно этой группы, используя номер элемента группы, необходимого, чтобы осуществить преобразование. Поэтому мы можем (во многих интересных случаях) разделить задачу распознавания на две части: распознать страт, к которому принадлежит фигура, а затем употребить простое испытание, соответствующее этому страту). Внешне такое описание выглядит скорее как последовательное, а не параллельное вычисление, и действительно, оно вызывает интерес, в частности, тем, что предлагает по крайней мере один путь моделирования последовательного, или УСЛОВНОГО, процесса при помощи параллельной процедуры.
Естественно, за такое моделирование приходится расплачиваться. Предлагаемый метод ведет к исключительно большим коэффициентам получаемых линейных представлений. Само по себе это не исключает существования другой методики, позволяющей добиться того же самого результата меньшей ценой. Поэтому (в гл.10) мы приходим к новой области исследования - границам коэффициентов - и к ряду занимательных, хотя до конца еще не понятых, результатов.
Напомним, что, доказывая теорему об инвариантности относительно групп, мы предполагали, что группа конечна. Упорядочение, используемое нами при стратификации, предполагает бесконечность группы (например, переносы на бесконечной плоскости упорядочены очевидным образом), но если при помощи описанного в #5.6 построения на торе сделать группу конечно-циклической, то упорядочение станет невозможным. Когда мы впервые столкнулись с таким противоречием, мы сочли технику стратификации и технику, связанную с инвариантностью относительно групп (спектры и т.п.), нигде не пересекающимися направлениями исследований. Но дальнейшее изучение свело их вместе, по-видимому, в довольно глубоком смысле. Мы в самом деле можем в ряде бесконечных случаев спасти теорему об инвариантности относительно групп, полагая, что коэффициенты ограничены. Допустим, например, что пси(X) - предикат, определенный для КОНЕЧНЫХ ФИГУР X на бесконечной плоскости и инвариантный относительно группы переносов. Тогда его можно представить в виде бесконечной линейной формы, например
пси(X) = [СУММА[ФИ]альфа.фи*фи(X)>тета],
где ФИ - бесконечное множество (например, множество масок), выбранное так, чтобы для любой конечной фигуры X все слагаемые, кроме конечного числа, равнялись нулю. Далее, если коэффициенты альфа.фи ограничены, можно применить (согласно теореме 10.4.1) теорему об инвариантности относительно групп. В некоторых случаях получаемый при этом порядок ПРЕВЫШАЕТ порядок, получаемый на основе стратификации. Противоречие можно устранить, только придя к заключению, что нельзя ограничивать коэффициенты альфа.фи для ЛЮБОГО представителя низкого порядка. Поэтому огромная величина коэффициентов, которую дает наша методика стратификации, не следует просто из неудачного алгоритма (хотя, конечно, фактические значения коэффициентов могут быть любыми, поскольку не было доказано, что они минимальны).
Разумеется, нам было очень приятно обнаружить, что кажущееся на первый взгляд ограничение нашей излюбленной теоремы в действительности позволило получить ценный результат. Нам кажется, что это намного интереснее, чем сама проблема величины коэффициентов (и ее приложения). В этом нас убеждает устойчивое проявление ГЛОБАЛЬНОЙ СТРУКТУРЫ группы преобразований.
Долгое время мы были уверены, что распознавание всех переносов данной фигуры принадлежит к задачам высокого порядка. Стратификация показала, что мы ошибались. Но мы оказались не в состоянии найти предикаты низкого порядка для соответствующей задачи, когда группа содержит большие конечные циклические подгруппы, как, например, вращения или переносы на торе, и продолжаем вынашивать предположение, что такие задачи не являются задачами конечного порядка.
В дополнение к "положительным" результатам гл.6 мы докажем одну "отрицательную" теорему, имеющую большое практическое значение. Она относится к распознаванию фигур В КОНТЕКСТЕ. С помощью предиката низкого порядка легко решить, является ли данная фигура, скажем, прямоугольником. Задача нашего нового типа состоит в том, чтобы решить, содержит ли данная фигура прямоугольник и, быть может, что-то еще (рис.6.1).

Рис.6.1. Предикат пси.ПРЯМОУГОЛЬНИК не отвергает только фигуру 1. Предикат пси.ПРЯМОУГОЛЬНИК-В-КОНТЕКСТЕ отвергает только фигуру 6.
Кажется очевидным, что распознавание в контексте должно быть до некоторой степени более трудной задачей, требующей, быть может, более высокого порядка. Мы покажем (#6.6), что дело обстоит еще хуже: такое распознавание не обладает даже конечным порядком!
Наконец, следует отметить, что нам снова удалось обойти необходимость применения теории допустимых отклонений и избежать ограничений, которые дает использование массивов квадратных ячеек. В случае группы переносов эта проблема не возникает. Она возникает в случае группы вращений; однако мы излагаем все, что необходимо, в рамках поворотов на 90o. Более серьезные затруднения вызывает группа подобия: растянуть фигуру довольно легко, но как сжать малую фигуру? Оказалось, что мы об этой группе не можем сказать ничего интересного. Мы призываем будущих исследователей быть менее малодушными.
В #6.1-6.4 мы покажем, что определенные образы имеют порядок 1, другие 2, порядок третьих не превышает 3 и соответственно 4. Нижняя граница порядков для большинства случаев еще не установлена, и у нас нет для этого систематических методов.
#6.1. ГЕОМЕТРИЧЕСКИЕ ОБРАЗЫ ПОРЯДКА 1
Когда мы говорим "геометрическое свойство", мы имеем в виду что-то инвариантное относительно переноса, или вращения, или растяжения. Сочетание первых двух инвариантностей определяет "конгруэнтную" группу преобразований, а наличие всех трех дает фигуры, "подобные" в евклидовой геометрии. Мы уже знаем, что для первого порядка все коэффициенты можно считать равными [Во всех теоремах этой главы предполагается, что теорему об инвариантности относительно групп применить можно, даже несмотря на то, что группа переносов не является конечной. На самом деле эту теорему можно применить, если (теорема 10.4.1) коэффициенты ограничены, а для первого порядка ее можно применять всегда. Кроме того, есть немало других достаточных условий. В #7.10 мы обнаружим, что теорема эта не всегда пригодна. Хорошего общего метода проверки возможности ее применения у нас нет, но, конечно, в любой физической машине коэффициенты будут ограничены!]. Поэтому единственные образы порядка 1 это те, которые определены с помощью ОДНОГО сечения интервала значений мощности множества, т.е. площади фигуры X:
пси=[|X|>A] или пси=[|X|<A].
ЗАМЕЧАНИЕ. Если инвариантность относительно переносов НЕ требуется, то персептроны порядка 1 могут, разумеется, вычислять и другие свойства, например, связанные с МОМЕНТАМИ относительно ДАННЫХ точек или осей (#2.4.1). Но эти свойства не "геометричны" в том смысле, что не обладают нужной инвариантностью. Поэтому, несмотря на возможную практическую значимость этих свойств, мы в дальнейшем не будем их рассматривать [См., например, работу Питтса и Маккаллока [1947] о следящей системе центрирования глава, использующей, в сущности, предикат первого порядка].
#6.2. ОБРАЗЫ ПОРЯДКА 2, СПЕКТРЫ РАССТОЯНИЙ
При k=2 положение усложняется. Как показано в #1.4, пример 3, можно определять двойное сечение, или сегмент A.1<A<A.2, для площади множества и распознавать фигуры, удовлетворяющие предикату
пси=[A.1<|X|<A.2].
Действительно, в общем случае всегда можно найти функцию 2k-го порядка, распознающую множество, величина площади которого заключена в любом из k интервалов. Но вернемся к образам, имеющим геометрическое значение. Рассмотрим сначала только группу переносов и маски второго порядка. Здесь две маски х.1*х.2 и x.1'*x.2' эквивалентны тогда и только тогда, когда ВЕКТОРЫ
x.1-x.2 и x.1'-x.2'
равны по величине (знаки могут быть любые). Таким образом, по отношению к группе переносов любой предикат порядка 2 может зависеть только от "спектра разности векторов", определяемого как последовательность чисел эквивалентных пар точек, причем каждой паре значений длины вектора и угла наклона соответствует некоторое множество эквивалентных пар точек. Две фигуры

обладают одними и теми же спектрами разности векторов, а именно:

Следовательно, никакой предикат порядка 2 не может выполнить классификацию, инвариантную относительно переносов, при которой бы эти две фигуры различались. Действительно, из теоремы об инвариантности относительно групп непосредственно следует
ТЕОРЕМА 6.2. Пусть пси(X) - предикат второго порядка, инвариантный относительно переносов. Обозначим через n.ню(X) число пар точек в X, разность которых равна вектору ню. Тогда предикат пси(X) можно записать в виде
пси(X)=[СУММА[ню]альфа.ню*n.ню(X)>тета].
ДОКАЗАТЕЛЬСТВО. n.ню предикатов в классе ФИ.ню удовлетворяются при любом переносе фигуры X. По теореме 2.3 всем им можно присвоить один и тот же коэффициент.
СЛЕДСТВИЕ. Две фигуры с одинаковым спектром переносов [Авторы употребляют термины "спектр переносов" и "спектр разности векторов" для обозначения одного и того же понятия.- Прим. ред.] n.ню нельзя отличить одну от другой при помощи инвариантного относительно переносов персептрона второго порядка. (См., однако, примечание к #6.1).
И обратно, если спектры различны, например, n.ню.1(A) < n.ню.1(B), то при помощи предиката [n.ню.1(X) < n.ню.1(B)] можно различить переносы обеих фигур. Но КЛАССЫ, составленные из разных фигур, таким способом различить нельзя.
ПРИМЕР. Предикаты порядка 2 не способны отличить фигуры
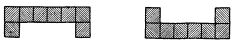
тогда как фигуры

обладающие различными спектрами разности векторов, можно отличить друг от друга. Если мы потребуем еще и инвариантность относительно вращений, то последнюю пару фигур также нельзя будет различить, поскольку классы эквивалентности объединяют теперь все разности одной длины вне зависимости от их ориентации.
Заметим, что мы НЕ допускали отражений, и все же зеркально противоположные фигуры попали в один класс! В подобных вопросах полагаться на "интуицию" можно лишь с большой осторожностью. Теория общей инвариантности относительно вращений требует особого внимания к эффекту дискретной аппроксимации на сетчатке, но эту теорию можно, по-видимому, сделать состоятельной при помощи подходящей теории допустимых отклонений. Что же касается "группы" растяжений, то здесь возникают серьезные трудности. (Для группы, порождаемой поворотами на 90o, приведенный выше пример не годится, но зато хорошо работает следующий пример).
Интересным примером фигур, различных с точки зрения вращений, но тем не менее неразличимых при k=2, служат фигуры

характеризуемые одинаковыми (не зависящими от направления) спектрами расстояний между парами точек (для второго порядка), а именно:

Каждая фигура содержит по 5 точек (спектр первого порядка).
Теорема об инвариантности относительно групп (#2.3) гласит, что любой персептрон, инвариантный относительно группы, должен зависеть только от "чисел замещения" образа, т.е. как раз от рассмотренных здесь "геометрических спектров". Множество других проектов "машин для распознавания образов" (не персептронов и соответственно не выражающихся просто в виде линейных форм) тоже можно лучше понять, изучив их взаимосвязь с теорией таких геометрических спектров. Однако маловероятно, чтобы подобный анализ внес ощутимый вклад в изучение более "описательных", или, как иногда говорят, "синтаксических", систем анализа окружающей действительности, в защиту которых втайне выступают авторы.
Еще один пример предиката порядка 2 дает предикат
[фигура X лежит в пределах одной строки или столбца и содержит не более n отрезков],
который определяется как
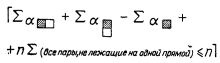
#6.3. ОБРАЗЫ ПОРЯДКА 3
#6.3.1. ВЫПУКЛОСТЬ. Особый интерес представляет предикат
пси.ВЫПУКЛОСТЬ(X) = [X - одна сплошная выпуклая фигура].
Этот предикат имеет порядок не выше 3, что следует из самого определения "выпуклости": фигура X выпукла тогда и только тогда, когда каждый отрезок, концы которого принадлежат X, целиком принадлежит X. В самом деле, из определения выпуклости следует, что фигура X выпукла тогда и только тогда, когда
a принадлежит X и b принадлежит X => (внутренняя точка отрезка [a, b]) принадлежит X,
а потому предикат
пси.ВЫПУКЛОСТЬ(X) = [СУММА[a, b из X][внутренняя точка отрезка [a, b] не принадлежит X] < 1]
имеет порядок не выше 3, и, по всей вероятности, равный 3. Это конъюнктивно локальное условие; такие условия были подробно рассмотрены в #0.2.
Если СВЯЗНАЯ фигура не Выпукла, то можно показать, что в ней содержится по крайней мере одна "локальная" вогнутость, сосредоточенная на трех как угодно близких точках, например

Поэтому, если дано, что фигура X связна, то выпуклость можно реализовать в виде ОГРАНИЧЕННОГО ПО ДИАМЕТРУ предиката порядка 3. Если нет уверенности, что фигура X связна, то для случая ограниченного диаметра предыдущее рассуждение неверно, поскольку ПАРА очень отдаленных друг от друга выпуклых фигур не отвергается.
При дополнительном ограничении на величину диаметра предикат пси.ВЫПУКЛОСТЬ скорее всего не будет иметь порядок 3, но отсюда не следует делать поспешный вывод о том, что при любом порядке этот предикат не будет ограниченным по диаметру. Такой вывод делать нельзя, учитывая следующее практическое соображение.
Даже если связность фигуры задана, ее выпуклость можно определить только с точностью до допустимых отклонений. Вдобавок размеры фигуры должны быть равномерно ограничены, иначе малые локальные допустимые отклонения станут глобально гибельными. Но при таком ограничении можно ПРИБЛИЖЕННО ОЦЕНИТЬ кривизну и определить выпуклость с помощью неравенства
ИНТЕГРАЛ |кривизна| ds<=2*пи.
Мы обсудим это в # 8.3 и 9.3.
#6.3.2. ПРЯМОУГОЛЬНИКИ. Рассматривая фигуры, составленные только из квадратиков сетчатки, можно с помощью предикатов порядка 3 задать множество сплошных прямоугольников со сторонами, параллельными осям координат. (На рис.6.2 показаны примеры "полых" прямоугольников).

Этого можно добиться даже с помощью лишь предикатов фи, ограниченных по диаметру, а именно:
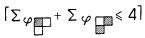
Сюда входят все предикаты фи, эквивалентные относительно поворота на 90o. Полые прямоугольники выявляются предикатом
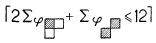
где коэффициенты подобраны так, чтобы исключить случай двух и более изолированных точек. Примеры такого рода, конечно, слабы из-за их зависимости от выбранной сетки квадратов. Но они обладают тем незаметным на первый взгляд достоинством, что рассматриваемые образы могут быть определены как прямолинейные фигуры с числом углов не более 4. Мы обсудим этот несколько более чем конъюнктивно локальный способ определения в гл.8.
Можно было бы ожидать, что множества полых и сплошных КВАДРАТОВ окажутся порядка 4 или еще выше, поскольку по меньшей мере такой порядок должно было бы потребовать сравнение длин сторон. Поэтому удивительно, что их порядок оказался равным 3. Построение явно не конъюнктивно локально, и мы его отложим до гл.7.
#6.3.3. СПЕКТРЫ ПЕРЕНОСА ВЫСШЕГО ПОРЯДКА. Определим ТРЕХВЕКТОРНЫЙ СПЕКТР фигуры как множество наборов чисел, выражающих количество трехточечных масок, удовлетворяемых в каждом классе эквивалентности относительно переносов. Интересно отметить следующее обстоятельство (относящееся скорее к геометрии, а не к линейному разделению).
ТЕОРЕМА 6.3.3. Фигуры однозначно характеризуются (с точностью до переноса) своими трехвекторными спектрами даже в случае пространства высокой размерности.
ДОКАЗАТЕЛЬСТВО. Пусть X - некоторая фигура и максимальное расстояние между ее точками равно D. Выберем пару (a, b) точек в X с этим расстоянием и рассмотрим множество ФИ.a.b = {фи.a.b.x} масок с трехточечными носителями, содержащими a, b и любую третью точку x из X. Коэффициент при каждой такой маске в спектре переноса должен равняться единице, так как если бы в X было две маски, эквивалентные относительно переносов:
фи.a.b.x и фи.ga.gb.gx
то длина одного из отрезков [a, gb] или [ga, b] была бы больше D, поскольку эти отрезки совпадают с диагоналями параллелограмма со стороной D (рис.6.3).

Таким образом, любой перенос фигуры X должен содержать ЕДИНСТВЕННЫЙ перенос пары (a, b), и часть спектра фигуры, соответствующая ФИ.a.b, позволяет полностью воспроизвести всю фигуру (рис.6.4).

Тот факт, что фигура ОПРЕДЕЛЯЕТСЯ своим трехвекторным спектром, конечно же, не означает, что распознавание классов фигур имеет порядок 3. (Он свидетельствует только о том, что можно различить переносы двух разных фигур. На самом деле, как показывает метод #7.9, их можно различать даже с помощью второго порядка, но только если снять ограничение на величины коэффициентов).
#6.4. ОБРАЗЫ ПОРЯДКА 4 И ВЫШЕ
Известно, что любые три точки определяют окружность. Это обстоятельство можно использовать для построения персептрона порядка 4, реализующего предикат
[X - периметр полной окружности]
с помощью формы
[СУММА[d не из C.a.b.c]x.a*x.b*x.c*x.d + СУММА[d из C.a.b.c]x.a*x.b*x.c*~x.d],
где C.a.b.c - окружность [Здесь опять встает проблема допустимых отклонений: что считать окружностью на дискретной сетчатке? См.#8 3.], проходящая через точки x.a, x.b, x.c. Аналогично можно показать, что много других любопытных и интересных предикатов имеют низкий порядок. Нужно соблюдать осторожность в выводах отсюда практических следствий и учитывать следующие факты:
1. Для приведенных выше примеров может потребоваться большое число (порядка |R|**(k-1)) предикатов фи.
2. Пороговые условия выражены настолько резко, что по инженерным соображениям могут возникнуть трудности в реализации линейного суммирования, особенно при наличии какого-либо шума. При k=3 и выше простой квадратичный шум растет быстрее, чем размер сетчатки. Значения коэффициентов зачастую убийственно велики (см. гл.10).
3. Часто малейшее изменение в определении образа [Наша формула не отвергает нуль- и одномерных "окружностей" Этого не избежать при любой размерности, если используется конъюнктивно локальный предикат] совершенно меняет порядок предиката, способного распознавать этот образ. При низких значениях порядков невозможно определить такие допустимые отклонения, при которых предикат будет работать удовлетворительно.
#6.5. ТЕОРЕМЫ О СПЕКТРАЛЬНОМ РАСПОЗНАВАНИИ
Некоторые из предыдущих примеров являются частными случаями теорем. (Вводимые здесь понятия далее не используются). Из теоремы об инвариантности относительно группы (# 2.3) вытекает, что инвариантный относительно группы G предикат пси, принадлежащий L(ФИ) Для некоторого множества ФИ, можно представить в виде
пси = [СУММА[i]бета.i*N.i(X)>0],
где Ni - число предикатов фи в i-м классе эквивалентности, которым фигура X удовлетворяет. В #6.2 (в случае группы переносов на плоскости) мы столкнулись со "спектром разности векторов" геометрических фигур. Для нулевого, первого и второго порядков такими спектрами действительно служат числа N.i(X). Если G-инвариантный предикат пси при заданном ФИ нельзя описать для ЛЮБОГО условия на числа N.i, то очевидно, что пси не принадлежит L(ФИ). Следующие результаты дают условия на N.i, влекущие за собой конечность порядка предиката пси.
Допустим, что пси определяется одновременно m равенствами:
пси(X) == [N.1(X)=n.1 и N.2(X)=n.2 и ... N.m(X)=n.m],
где n.1, ..., n.m - конечная последовательность целых чисел. Покажем, что порядок предиката пси не более чем в два раза превышает максимальный из порядков предикатов фи, связанных с числами N.i. Сформулируем утверждение более точно.
ТЕОРЕМА 6.5. Пусть ФИ = объединение ФИ.1, ФИ.2, ..., ФИ.m и
N.i(X) = |{фи|фи из ФИ.i фи(X)=1}| = СУММА[фи из ФИ.i]фи(X).
Тогда порядок предиката
пси(X) = [N.i(X)=n.i для всех 1<=i<=m]
не превышает удвоенной величины max{|S(фи)|: фи из ФИ}.
Замысел доказательства заключается в том, чтобы показать, что предикат пси можно задать с помощью линейного порогового выражения:
пси(X) = [СУММА(N.i(X)-n.i)**2 < 1]
В таком виде это выражение НЕ является линейной пороговой комбинацией предикатов. Для придания ему желаемой формы введем СПЕЦИАЛЬНОЕ соглашение, которое нигде больше использоваться не будет. Для любого заданного множества ФИ предикатов фи.i построим новое множество ФИ2 предикатов фи.i.j, полагая
фи.i.j(X) = фи.i(X) & фи.j(X)
для любой пары (фи.i, фи.j) предикатов из ФИ. Многие из построенных таким образом предикатов окажутся логически эквивалентными, например фи.i.j=фи.j.i, однако мы условимся считать их различными элементами множества ФИ2. (Это означает, что в очень строгом смысле ФИ2 есть скорее множество "предикатных форм", а не предикатов).
В результате такого соглашения упрощаются арифметические действия и логические соображения при подсчете числа предикатов. Пусть X - фигура, удовлетворяющая в точности N предикатам из Ф. Очевидно, в ФИ2 фигура X будет удовлетворять N**2 предикатам, т.е.
СУММА[ФИ2]фи(X) = N**2.
Пусть теперь ФИ.1, ФИ.2... - классы эквивалентности множества ФИ. Так как
N.i(X) = СУММА[ФИ.i]фи(X)
- число предикатов из ФИ.i, удовлетворяемых фигурой X, то, как мы уже видели,
СУММА[ФИ2.i]фи(X) = N.i**2(X).
Таким образом,
СУММА[i](СУММА[ФИ2.i]фи(X) - 2*n.i*СУММА[ФИ.i]фи(X) + n.i**2) = СУММА[i](N.i(X)-n.i)**2.
Чтобы представить левую часть этого равенства в стандартной форме линейного порогового предиката, положим ФИ' = объединение ФИ2, ФИ и {постоянный предикат} и запишем
пси(X) = [СУММА[ФИ']альфа(фи)*фи(X) < 1],
где
альфа(фи) = 1 для фи иs ФИ2,
альфа(фи) = -2 для фи из Ф.i,
альфа(постоянный предикат) = СУММА n.i**2.
Для завершения доказательства теоремы нам осталось только заметить, что
|S(фи.i.j)| = |объединение S(фи.i) и S(фи.j)| <= |S(фи.i)|+|S(фи.j)| <= 2*(max|S(фи)|).
#6.5.1. РАСШИРЕННОЕ ТОЧНОЕ СООТВЕТСТВИЕ. Очевидно, что теорема 6.5 допускает следующее обобщение. Пусть предикат пси определяется формулой
пси(X) == V[i=1..n] &[j=1..m] N.i(X)=n.i.j,
т.е. удовлетворяется любым условием из множества точных условий, наложенных на N.i. Тогда порядок предиката пси конечен, поскольку полином
ПРОИЗВЕДЕНИЕ[i=1..n] СУММА[j=1..m] (N.i(X)-n.i.j)**2
можно реализовать при помощи методов, подобных применявшимся в предыдущем параграфе. Для обобщения потребуются булевы произведения предикатов разных классов эквивалентности, и максимальный порядок будет не более 2*n*max|S(фи)|.
Заметим, что, не зная явления "и/или", можно было бы невольно попытаться вывести результат #6.5.1 из #6.5 на основе неверного предположения о том, что порядок предиката
V[i=1..n](предикаты k-vo порядка)
не превосходит n*k.
#6.5.2. СРЕДНЕКВАДРАТИЧНОЕ ОТКЛОНЕНИЕ. Если для предикатов, о которых шла речь в #6.5.1, увеличить значение порога тета, то система
[СУММА(N.i-n.i)**2 < тета]
будет удовлетворяться как раз теми фигурами, для которых СУММА КВАДРАТОВ разностей между величинами N.i и n.i меньше тета. Любое устройство классификации образов будет чувствительно к определенного рода искажениям, и это наводит на мысль, что, вероятно, полезно изучать такие устройства, в частности персептроны, в терминах их чувствительности к искажению спектра. К сожалению, у нас нет хороших идей о геометрической сути подобных искажений. Геометрическая природа "инвариантного шума" такого вида представляет благодатную тему для размышлений, но мы еще не занимались ее исследованием.
#6.6. ФИГУРЫ В КОНТЕКСТЕ
По практическим и теоретическим соображениям интересно изучить распознавание фигур в "контексте", т.е. предикаты вида:
пси(X) = [подмножество множества X - квадрат],
пси(X) = [связная компонента множества X - квадрат],
а чтобы приступить к рассмотрению проблемы проекций в трехмерном пространстве, интересно изучить предикат
пси(X) = [содержит значительную часть контура частично невидимого квадрата].

Эти примеры показывают, что интуитивным понятиям, связанным с распознаванием образов, находящихся в контексте, можно дать более чем одно естественное толкование. Нам не известно ни одного общего определения, охватывающего все естественные представления,, и поэтому мы не имеем возможности формулировать общие теоремы. Тем не менее мы утверждаем, что ДЛЯ ВСЕХ ПРЕДИКАТОВ НИЗКОГО ПОРЯДКА СВОЙСТВЕННА УТРАТА ИМИ КОНЕЧНОСТИ ПОРЯДКА ПРИ ЛЮБОМ ЕСТЕСТВЕННОМ СПОСОБЕ ПОМЕЩЕНИЯ ОБЪЕКТОВ РАСПОЗНАВАНИЯ В КОНТЕКСТ. Для иллюстрации этого положения выберем наиболее общую и, очевидно, безобидную интерпретацию: для любого предиката пси(X) определим новый предикат
пси.В-КОНТЕКСТЕ(X) = [пси(X) для некоторой связной компоненты фигуры X].
Мы увидим, что используемую нами методику можно тривиальным образом приспособить для множества других определений.
Интуитивно следовало бы ожидать, что предикат пси.В-КОНТЕКСТЕ окажется гораздо более трудным для персептрона, поскольку контекст каждой компоненты действует как шум, а параллельность работы устройства дает мало шансов на то, что подобный шум удастся отделить и не учитывать. Это становится особенно ясным в тех случаях, когда предикат пси использует правила отбрасывания, которые по вполне очевидным причинам нельзя передать в предикат пси.В-КОНТЕКСТЕ. Аналогично пропадут методы стратификации из гл.7 и, разумеется, большая часть технических уловок, с помощью которых мы получали представления предикатов низкого порядка. Следующие две теоремы показывают, как эту интуитивную идею можно выразить в строгой форме. Заметим, однако, что невозможно никакое простое обобщение взаимосвязи предикатов пси и пси.В-КОНТЕКСТЕ, поскольку некоторые предикаты пси в контексте вырождаются. Например, вырождается предикат пси.СВЯЗНОСТЬ, так как любое множество содержит связную компоненту!
ТЕОРЕМА 6.6.1. Пусть R - конечная квадратная сетчатка, а пси(X) - предикат
[X является единственной горизонтальной линией, пересекающей сетчатку].
Тогда порядок предиката пси равен 2, а предикат пси.В-КОНТЕКСТЕ не имеет конечного порядка.
ДОКАЗАТЕЛЬСТВО. Предоставляем читателю доказать в качестве упражнения, что порядок предиката пси равен 2. Чтобы показать, что предикат пси.В-КОНТЕКСТЕ не имеет конечного порядка, заметим просто, что он служит отрицанием негатива предиката пси.1=пси.ОДИН-В-БЛОКЕ т.е. предиката, утверждающего, что через сетчатку не проходит ни одной горизонтальной белой линии. Его негатив (в фотографическом смысле) утверждает, что через сетчатку не проходит ни одной горизонтальной черной линии. Далее, предикат пси.1 не имеет конечного порядка, а в общем случае можно показать, что этим свойством обладает любой негатив такого предиката. Наконец, обращая предикатное неравенство, получаем, что это справедливо и для искомого предиката
пси.В-КОНТЕКСТЕ = [X сoдержит горизонтальную линию, пересекающую сетчатку].
ТЕОРЕМА 6.6.2. Пусть пси(X) - предикат
[X - полый квадрат].
Тогда предикат пси.В-КОНТЕКСТЕ
[одна из компонент фигуры X - полый квадрат]
не имеет конечного порядка.

ДОКАЗАТЕЛЬСТВО. Доказательство подобно предыдущему, за тем исключением, что "блоки", или горизонтальные линии, изгибаются в квадраты и располагаются без перекрытий на большей сетчатке. Можно показать, что сам предикат пси имеет конечный порядок, в данном случае 3.
ЗАМЕЧАНИЕ. Другой метод доказательства состоит в изгибании линий переключательных элементов, использованных в построении Хаффмена для связности (#5.5).
Мы убеждены, что вырождение способности персептрона распознавать образы, если последние находятся в контексте других образов, служит серьезным предупреждением против использования его в реальных практических ситуациях. Конечно, этот недостаток можно смягчить, включая персептрон в некоторый последовательный процесс (такой, в котором интересующая нас фигура на предварительной стадии изолируется и отделяется от своего контекста). Однако это предполагает достаточную способность к распознаванию на этапе "предварительной обработки", чтобы можно было различить и устранить большинство обычно встречающихся контекстуальных помех. Иногда выполнить это гораздо труднее, чем провести собственно "основную обработку". Этот вопрос мы еще будем рассматривать в гл.13.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 7. СТРАТИФИКАЦИЯ И НОРМАЛИЗАЦИЯ
#7.1. ЭКВИВАЛЕНТНОСТЬ ФИГУР
В предыдущих главах мы рассмотрели распознавание образов - классов фигур, замкнутых относительно преобразований некоторой группы. Теперь мы займемся родственным вопросом распознавания ЭКВИВАЛЕНТНОСТИ относительно группы произвольной пары фигур. Приведенные ниже результаты нас в свое время удивили, так как мы думали, что эти задачи, вообще говоря, не бывают конечного порядка. Многие вопросы остаются открытыми, и внешне позитивный характер последующих построений омрачается необычайно большими коэффициентами, которые для них требуются, и характером роста коэффициентов при возрастании размеров сетчатки.
Типичная задача такова: сетчатка [Все теоремы этой главы применяются непосредственно к персептронам на бесконечных сетчатках, поэтому нет необходимости рассматривать предельные процессы на последовательностях конечных сетчаток, как это предлагалось в #1.6. Группы преобразований также бесконечны, а теорема об инвариантности относительно групп не используется. Так как этот материал несколько более специализирован, чем все остальное, мы немного отступим от нашего способа изложения и перейдем к общепринятому и пренеприятному математическому стилю, когда теоремы сначала формулируются и доказываются, а потом уж объясняется, для чего они нужны] задается в виде двух одинаковых частей A и B, и спрашивается, можно ли фигуру, находящуюся в части B, получить одним лишь переносом фигуры, находящейся в части A. Более общо: существует ли в заданной группе преобразований G такой элемент g, что фигура в B есть результат его воздействия на фигуру в A? Какой порядок предикатов требуется для решения этой задачи?
Все теоремы настоящей главы получены при помощи методики, названной нами СТРАТИФИКАЦИЕЙ. При определенных условиях стратификация позволяет моделировать последовательный процесс таким параллельным процессом, в котором результатам вычислений придаются настолько различные веса, что при выполнении определенных условий один из результатов перевешивает сумму всех остальных. Методика основывается на следующей теореме.
#7.2. ТЕОРЕМА О СТРАТИФИКАЦИИ
Пусть ПИ = {пи.1, пи.2, ..., пи.j, ...} - последовательность различных масок. Зададим последовательность C.1, ..., C.j, ... классов соответствием
X принадлежит C <=> [пи.j(X) и (k>j ~пи.k(X))],
где знак ~ означает отрицание.
Таким образом, X принадлежит классу C.j, если j - самый высокий индекс, для которого пи.j - истина. Пример таких классов показан на рис 7.1.
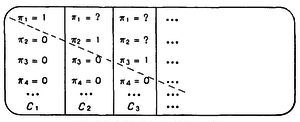
Рис.7.1. Разбиение на классы C.j.
Пусть ФИ = {фи.i} - семейство предикатов, и пусть пси.1, ..., пси.j, ...- упорядоченная последовательность предикатов в L(ФИ), ОГРАНИЧЕННЫХ в следующем смысле. Для каждого пси.j найдутся такая линейная форма СУММА.j с целыми коэффициентами, что
СУММА.j=СУММА[i]альфа.i.j*фи.i-тета.j и пси.j=[СУММА.j>0],
и такое число B.j, что
|СУММА.j(X)|<B.j
для всякого конечного множества X. (На самом деле для доказательства требуется лишь ограниченность функции |СУММА.j(X)| на каждом классе C.k).
ТЕОРЕМА 7.2. Предикат пси(X)=[X принадлежит C.j => пси.j(X)], принимающий на каждом классе C.j значения соответствующего предиката пси.j, принадлежит множеству L(ФИ*ПИ), т.е. его можно представить в виде [Здесь коэффициенты альфа.j.k, разумеется, отличны от коэффициентов в определении СУММА.j.- Прим. ред.]
пси(X)=[СУММА альфа.j.k(пи.j & фи.k)>тета].
ДОКАЗАТЕЛЬСТВО. Легко заметить, что каждая конечная фигура X принадлежит лишь одному из классов C.j. Положим
S.1=пи.1*СУММА.1
и для j>1 определим по индукции
M.j = max[C.j]|S.[j-1]| и
S.j = S.[j-1] - пи.j*M.j +(2M.j+1)*пи.j*СУММА.j.
Границы B.j гарантируют существование величин M.j. Далее, запишем формальную сумму, порожденную этим бесконечным процессом, в виде
S = СУММА альфа.j.k*(пи.j&фи.k)
и покажем, что пси(X)=[S(X)>0]. Сумма S определена корректно, поскольку для любой конечной фигуры X в любом классе C.j - найдется только конечное число отличных от нуля членов пи.j&фи.k. Применим индукцию. Если X принадлежит классу C.1, то очевидно, что S.i=СУММА.i, так что пси(X)=[S.i(X)>0]. Допустим, что если X принадлежит классу C.[j-1], то пси(X)=[S.[j-i](X)>0]. Так как коэффициенты линейной формы СУММА.j целые, то при X из C.j, и пи.j=1
пси(X) => СУММА.j>=1 => S.j>=-M.j-M.j+2M.j+1=1 и
~пси(X) => СУММА.j<=0 => S.j<=M.j-M.j=0,
и теорема доказана.
СЛЕДСТВИЕ 7.2. Порядок предиката пси(X) не превосходит суммы максимального числа элементов носителя в ФИ и максимального числа элементов носителя в ПИ.
Это следует из того, что предикаты из ФИ выступают только в конъюнкции с предикатами из ПИ. Идея доказательства состоит в разбиении области определения предиката пси(X) на непересекающиеся классы, или "страты", C.j. В пределах каждого страта член -пи.j*M.j настолько велик, что перевешивает (в сторону отрицательных значений) все решения, принятые на низших стратах, если только не удовлетворяется предикат пси.j. Во всех нижеследующих приложениях страты в большей или меньшей степени представляют собой различные возможные отклонения фигуры от "нормального" положения. Поэтому возможность построения "стратифицированных" предикатов тесно связана с принятым в "распознавании образов" представлением об идентификации фигуры сначала путем ее нормализации, а затем сравнения нормализованного изображения с эталоном. Разумеется, обычно это происходит последовательно.
Следует отметить, что у предикатов, полученных при помощи этой теоремы, коэффициенты огромны и с ростом индекса стратификации j растут экспоненциально или даже еще быстрее. Поэтому не надо рассматривать результаты этой главы с точки зрения практических применений. Они представляют скорее теоретический интерес, наглядно демонстрируя взаимосвязь структуры групп преобразований с порядками определенных предикатов, инвариантных относительно этих групп.
#7.3. ПРИЛОЖЕНИЕ 1. СИММЕТРИЯ НА ПРЯМОЙ
Пусть R = ..., x.s, ...,- бесконечная прямолинейная сетчатка, т.е. -беск.<s<беск. Удобно выбрать произвольное начало Хо и занумеровать квадраты так:

Предположим, что X - фигура на R, состоящая из конечного числа |X| точек. Спрашивается, конечен ли порядок предиката
пси.СИММЕТРИЯ = [X обладает зеркальной симметрией].
Заметим, что этот предикат будет тривиальным предикатом порядка 2, если центр симметрии фиксировать заранее. Но в общем случае предиката пси.СИММЕТРИЯ центр может находиться в любом месте бесконечной прямой.
Мы хотим стратифицировать предикат пси.СИММЕТРИЯ, найдя последовательности пи.1, ... и пси.1, ..., которые позволят нам проверять симметрию при помощи следующего приема: пи.i "найдут" две "крайние точки" фигуры X, а соответствующие предикаты пси.j проверят ее симметрию. Поэтому пи.i должны быть такими, чтобы каждый страт C.j оказался классом фигур с определенной парой крайних точек. Для этого нам нужно, чтобы последовательность пи.1,... была перечислением всех отрезков [x.s, x.[s+d]] для каждого s и каждого d>=0, причем при 0<=а<=b<=d отрезок [x.s, x.[s+d]] должен следовать за [x.[s+a], x.[s+b]]. Такие последовательности действительно существуют, например
пи.1=[x.0, x.0], пи.2=[x.1, x.1], пи.3=[x.0, x.1], пи.4=[x.-1, x.-1], пи.5=[x.-1, x.0], пи.6=[x.-1, x.1], пи.7=[x.2, x.2], пи.8=[x.1, x.2], ...:

Легко заметить, что
1) каждый отрезок в конечном итоге попадет в последовательность;
2) ни один отрезок, лежащий внутри другого отрезка, не следует за последним.
Поэтому, если х.s, x.[s+d] - соответственно крайние левая и правая точки фигуры X, то X принадлежит тому страту C.j, который соответствует отрезку [x.s, x.s+d]. Определим теперь пси.j формулой
пси.j = [x.[s+i]=x.[s+d-i], i=0..d],
или, что то же самое,
пси.j = [СУММА[i=0..d](x.[s+i])(1-x.[s+d-i])<=0].
Отсюда видно, что это предикат порядка 2, ограниченный числом B.j=d+1. (Мы удержались от соблазна написать B.j=d/2).
Таким образом, применяя теорему о стратификации, получаем, что порядок предиката пси.СИММЕТРИЯ не выше 4, поскольку порядок предикатов пси.j не выше 2, а носители функций пи содержат не более двух элементов.
#7.4. ПРИЛОЖЕНИЕ 2. КОНГРУЭНТНОСТЬ ПРИ ПЕРЕНОСЕ ВДОЛЬ ПРЯМОЙ
Пусть ..., x.s, ... и ..., y.t, ...- точки двух бесконечных прямолинейных сетчаток А я В, т.е. -беск.<s<беск. и -беск.<t<беск.:

Пусть фигура X состоит из множества X.A левой сетчатки и множества X.B правой сетчатки. Мы хотим построить предикат
пси.ПЕРЕНОС(X) = [(конечный) образ в A является переносом образа в B].
Чтобы стратифицировать этот предикат, нужно найти последовательность {пи.i}, которая вместе с соответствующими предикатами пси.i позволит проверить, конгруэнтны ли множества X.A и X.B. Мы будем осуществлять это методом, аналогичным использованному в #7.3, но теперь будем иметь дело сразу с двумя отрезками. Это значит, что нам надо построить последовательность {пи.j}, перечисляющую все четверки точек так, что фигура лежит в страте C.j тогда и только тогда, когда крайними точками ее частей в A и B служат как раз соответствующие значения x.s, x.[s+d.x], y.t и y.[t+d.y]. Такая последовательность действительно существует (!). Ее можно получить из последовательности {пи.j} #7.3 следующим образом (советуем читателю сначала попытаться найти ее самостоятельно).
Пусть пи.j.k будет четырехточечной маской, определенной формулой
пи.j.k(X)=пи.j(X.A)*пи.k(X.B),
т.е. выбором двух точек из A, соответствующих j, и двух точек из B, соответствующих k. Мы должны перечислить все маски пи.j.k, удовлетворяющие условию: четверка пи.a.b не может предшествовать четверке пи.c.d, если одновременно a>=c и b>=d.
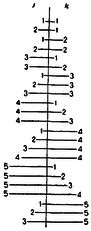
Решением служит последовательность
пи.1.1; пи.2.1, пи.1.2, пи.2.2; пи.3.1, пи.3.2, пи.1.3, пи.2.3, пи.3.3; пи.4.1, пи.4.2, пи.4.3, пи.1.4, пи.2.4, ...;
для члена пи.j.k соответствующим предикатом пси.j.k является предикат
пси.j.k = [отрезки, определяемые при помощи пи.j и пи.k, равны, а x и y на них имеют в соответствующих точках одинаковые значения].
Это предикат порядка 2 и ограниченный (длинами отрезков). Носители функций пи.j состоят из 4 элементов, так что порядок предиката пси.ПЕРЕНОС(X) не превышает 6. На самом же деле, найдя крайние точки множества X.A, мы должны будем найти лишь один конец множества X.B, и поэтому, проведя несколько иное построение, использующее метод #7.9, мы могли бы убедиться, что порядок предиката пси.ПЕРЕНОС не превышает даже 5.
#7.5. ПРИЛОЖЕНИЕ 3. ПЕРЕНОС НА ПЛОСКОСТИ
Метод, изложенный в #7.4, можно применить к задаче двумерных переносов ограниченных кусков плоскости. Пусть каждый экземпляр сетчатки имеет размер m*m. Расположим квадраты в последовательность {x.i} так, чтобы квадрат (a, b) был на {m*a+b)-м месте. Фактически мы считаем сетчатку цилиндром и нумеруем ее квадраты следующим способом:
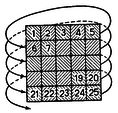
При этом каждая половина сетчатки отображается на прямую (типа той, которая встречалась в приложении 2) таким образом, что переносы на плоскости эквивалентны переносам вдоль прямой ПРИ УСЛОВИИ, что ПЕРЕНОСЫ НЕ ВЫВОДЯТ ФИГУРУ ЗА КРАЯ СЕТЧАТКИ. Тогда можно построить предикат порядка 5. В #7.6 мы покажем, как обойти это неприятное условие!
ПРИЛОЖЕНИЕ 4. Поворот на 180o относительно произвольной точки плоскости.
При тех же условиях и тем же самым способом, каким было получено приложение 3 из приложения 2, можно построить этот предикат порядка 4. Аналогичные построения можно провести и для отражения относительно любых вертикальных осей.
#7.6. ПОВТОРНАЯ СТРАТИФИКАЦИЯ
В теореме о стратификации на предикаты пси.j наложено единственное условие, чтобы они были подходящим образом ограничены. В некоторых приложениях сами эти предикаты можно получить с помощью стратификации. Это особенно легко сделать, когда носитель предиката пси.j конечен, так как тогда ограниченность получается непосредственно. Чтобы пояснить эту повторную стратификацию, покажем, как избавиться от условия, наложенного в конце приложения 3.
Занумеруем каким-нибудь способом (например, как на рис.7.2) все точки каждой из двух бесконечных плоских сетчаток A и B и расположим их соответственно в последовательности x.1, ..., x.s, ... и y.1, ..., y.t, ...
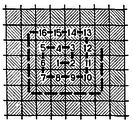
Рассмотрим затем последовательность пи.j.k, описанную в #7.4, но теперь определенную формулой
пи.j.k = (x.j из X.A и y.k из X.B) = x.j*y.k.
Тогда C.j.k будет классом пар (X.A, X.B), для которых
j = max{s|x.s из X.A},
k = max{t|y.t из X.B}
(рис.7.3). Нам нужен только (ограниченный) предикат пси.j.k, решающий, является ли X.A результатом переноса множества X.B для фигур из C.j.k. Но все фигуры из C.j.k расположены внутри ограниченных кусков плоскостей, а именно внутри квадратов со сторонами [max(j, k)]**(1/2) и с центрами в начальных точках. Внутри такого квадрата (или, еще лучше, внутри вдвое большего квадрата, чтобы избежать "краевых эффектов") мы можем применить результат приложения 3 и получить предикат пси.j.k с конечным носителем, обладающий нужным нам свойством. Порядок не будет превышать 5+2=7. Этот предикат можно построить и другим способом, дающим порядок не выше 5. Аналогично можно избавиться от условий, наложенных в приложении 4 #7.5.

#7.7. ПРИЛОЖЕНИЕ 5. КВАДРАТЫ СО СТОРОНАМИ, ПАРАЛЛЕЛЬНЫМИ ОСЯМ КООРДИНАТ
Отвлечемся на минуту и покажем методом, изложенным в #7.6, что порядок предиката
пси.КВАДРАТ(X) = [X - сплошной (полый) квадрат
со сторонами, параллельными осям],
где X может находиться в любом месте бесконечной плоскости, не выше 3.

(Мы считаем этот факт удивительным, поскольку неформальные рассуждения о сравнении по длине двух сторон с одновременной проверкой внутренних точек приводят к порядку не менее 4. Сформулированный только что результат обнаружил и доказал другим способом наш студент Джон Уайт).
Пронумеруем точки x.1, ... одной плоской сетчатки, как в #7.6, и положим пи.j=x.j. Тогда C.j будет множеством фигур, для которых x.j - "наибольшая" точка. Если X - квадрат, то ситуация совпадает с одним из случаев, изображенных на рис.7.4. Построим предикаты пси.j методом стратификации.
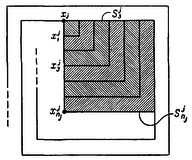
Пусть x.1**j, x.2**j, ..., x.n.j**j - конечная последовательность, образованная точками пересечения спиральной фигуры перпендикуляром к стороне квадрата, восставленным в точке x.j. Положим пи.i**j=x.i**j, так что C.i**j содержит все квадраты со стороной i, которые "упираются" в точку x.j. Но такой квадрат найдется только один, назовем его S.i**j. Теперь чтобы закончить двойную стратификацию, нам нужно иметь только предикаты пси.i**j для распознавания квадратов S.i**j. Для этой цели можно использовать предикат
пси.i**j = [СУММА альфа.k*x.k > i**2],
где
альфа.k =
1, если x.k принадлежит S.i**j или
-1, x.k не принадлежит S.i**j & (k<j) или
0 в остальных случаях.
Порядок предиката пси.i**j равен 1, так что порядок предиката пси.КВАДРАТ не выше 3, что и требовалось доказать!
#7.8. ПРИЛОЖЕНИЕ 6. ФИГУРЫ, ЭКВИВАЛЕНТНЫЕ ОТНОСИТЕЛЬНО ПЕРЕНОСА И РАСТЯЖЕНИЯ
Может ли система конечного порядка распознавать эквивалентность двух произвольных фигур относительно переноса и изменения размера?

Поразмыслив немного над методами #7.6 и 7.7 и над полученными результатами, мы придем к заключению, что имеем все необходимые данные: в #7.6 показано, как обращаться с переносами, а в #7.7, как распознавать все переносы и растяжения КОНКРЕТНОЙ фигуры. При РАСТЯЖЕНИИ возникают серьезные трудности с допустимыми отклонениями и пределами разрешающей способности, поскольку все наши построения проводятся на фиксированной дискретной сетчатке. Однако нам решительно не хочется столкнуться с этими трудностями. Интересно тем не менее, что нужное свойство можно по крайней мере аппроксимировать предикатом конечного порядка, причем интуитивно разумным образом. (Мы не думаем, что такую аппроксимацию можно выполнить в случае инвариантности относительно вращения, так как здесь возникают трудности иного рода, не связанные с дискретностью сетчатки. Скорее они вызваны тем, что преобразования группы вращений нельзя упорядочить простым способом, а это "преграждает путь" методам стратификации).
Наш метод начинается приемом, использованным в #7.6 для нахождения предикатов пи.j.k, которые "улавливали" две фигуры и заключали их в квадраты. После этого, как и в #7.6, задача сводится к нахождению предикатов пси.j.k, от которых требуется действовать только внутри квадратов, показанных на рис.7.3. Мы строим предикаты пси.j.k весьма грубым способом: в каждом квадрате нумеруем точки простейшим способом, как описано в #7.5. Затем проводим стратификацию 4 раза (!) подряд относительно
x, наивысшей и крайней левой точки множества A,
y, наивысшей и крайней левой точки множества B, x', наинизшей и крайней правой точки множества A, y', наинизшей и крайней правой точки множества В.
Для этого нам нужно задать предикаты пси.x.y.[x'].[y']**(j*k). Если направления векторов x-x' и y-y' не совпадают, мы полагаем пси=0; в противном случае нам нужно, чтобы предикат пси проверял, выполняется ли для каждого вектора ню условие
y+ню = x+(x-x')/(y-y')*ню,
а это предикат порядка 2, так что общий порядок не превышает 2+4+2=8. Конечно, на дискретной сетчатке указанные операции над векторами определены некорректно, но, по-видимому, ясно, что полученный результат вовсе не бессодержателен: например, мы можем распознать, является ли фигура X.B результатом переноса фигуры X.A и ее целым кратным, причем каждый черный квадрат фигуры X.A должен отображаться на соответственно больший квадрат фигуры X.B. Мы можем построить этот предикат и другим способом, дающим порядок не выше 6.
#7.9. ПРИЛОЖЕНИЕ 7. ЭКВИВАЛЕНТЫ ДАННОЙ ФИГУРЫ
Строя в приложении 5 предикат пси, мы отмечали, что всегда можно найти предикат порядка 1 для обнаружения одной-единственной фигуры X.0, если использовать выражение
[СУММА[x из X0]~x + СУММА [x не из X0]x >= 1]
Отсюда следует, что, построив стратификацию {пи.i} для группы G, удовлетворяющую условию
X принадлежит C.i и g*X принадлежит C.i => (g*X=X),
можно точно распознать G-эквиваленты заданной фигуры X.0 (с помощью предиката, порядок которого на единицу превышает порядок стратификации пи). Это наводит на мысль о машине, которая на первом этапе процесса распознавания приводит фигуры к некоторому нормальному виду. Для этого случая наш общий метод построения принимает следующую исключительно простую форму. Возьмем в качестве X.0 упорядоченную последовательность точек {x.i.1, ..., x.i.p} полупрямой

Положим пи.j(X)[x.j из X] и зададим пси.j(X) формулой
пси.j(X) = [СУММА [x.[k-j+i.p] принадлежит X.0]*~x.k + СУММА [x.[k-j+i.p] не принадлежит X.0 и k<j]*x.k < 1];
точки с отрицательными индексами пока рассматривать не будем. Тогда, если не обращать внимания на "краевые эффекты", мы получим предикат порядка 2, распознающий переносы фигуры X.0. Заметим, что на самом деле не представляет труда распространить это на бесконечную в обе стороны прямую, так как можно задать последовательность {пи.i} в виде

Если фигура оканчивается в классе C.[2*j], мы будем искать ее крайнюю левую точку х.-j, а если в классе C.[2*j+1], то крайнюю правую точку x.j. В любом случае можно построить соответствующий предикат пси. Итак, для любой заданной фигуры X.0 существует предикат порядка 2, распознающий ее линейные переносы, и при этом не возникает проблем ограниченности, ибо носители всех предикатов пси конечны.
#7.10. КАЖУЩИЙСЯ ПАРАДОКС
Рассмотрим фигуру

Мы только что показали, что существует предикат gcb порядка 2, распознающий переносы этой фигуры. Следовательно, этот предикат должен отклонить неэквивалентную ей фигуру

Но у этих фигур один и тот же спектр n-точечного распределения (#6.2 и 6.5) до второго порядка включительно! Каждая из них содержит три точки, одну смежную пару, одну пару с расстоянием в два элемента и одну пару с расстоянием в три элемента. Поэтому, если бы все предикаты фи, эквивалентные относительно группы, имели одинаковые веса, то для различения указанных фигур потребовался бы персептрон порядка не менее 3. Таким образом, если бы мы смогли применить теорему об инвариантности относительно групп, мы бы доказали, что НИКАКОЙ персептрон порядка 2 их различить не может. Это явилось бы противоречием! В чем же дело? Ответ состоит в том, что теорема об инвариантности относительно групп вообще неприменима в случае бесконечных групп. Когда группа конечна (например, группа циклического переноса на тороидальных сетчатках, которую мы иногда рассматриваем), теорему об инвариантности относительно групп всегда можно применить и уравнять коэффициенты эквивалентных предикатов фи. Но построить методом стратификации предикат на бесконечных группах с ее помощью нельзя.
В случае бесконечных групп можно использовать стратификацию для нормализации, но тогда в пределах подмножества эквивалентных предикатов фи могут получиться неограниченные коэффициенты, и операции усреднения по группе в общем случае не будут сходиться. Мы докажем соответствующую теорему в #10.4.
Мы предполагаем, что предикаты типа "близнецов" из #7.5 не являются предикатами конечного порядка с ограниченными коэффициентами. Во всяком случае было бы интересно узнать, существуют ли вообще такие предикаты.
#7.11. ПРОБЛЕМЫ
Укажем некоторые направления дальнейших исследований, которые нам кажутся интересными: Какова взаимосвязь между возможными стратификациями, включая повторные, и алгебраическими разложениями группы на разного рода подгруппы? При какого рода предикатах теорему об инвариантности относительно групп можно распространить на бесконечные группы? Для каких предикатов коэффициенты ограничены - для каждого класса эквивалентности? При каких условиях существуют "стратификации нормального вида" из приложения 7? Например, мы ПРЕДПОЛАГАЕМ, ЧТО НА ОКРУЖНОСТЯХ И НА ТОРАХ НЕ СУЩЕСТВУЕТ ГРАНИЦЫ ДЛЯ ПОРЯДКА ПРЕДИКАТОВ пси, ВЫДЕЛЯЮЩИХ ЕДИНСТВЕННУЮ ФИГУРУ "НОРМАЛЬНОЙ ФОРМЫ" [Из каждого класса эквивалентности.- Прим. ред.] В СЛУЧАЕ ГРУППЫ ВРАЩЕНИЙ:
пси(X) и пси(g*X) => X=g*X.
Мы подозреваем, что именно по этой причине мы не можем распространить метод приложения 6 на группу всех подобий, включая вращения.
Заметим, что требование теоремы 7.2, чтобы предикаты {пи.j} были масками, по всей вероятности, излишне строго. Мы не стали пока искать лучшей теоремы.
Стратифицированные предикаты, вероятно, физически нереализуемы вследствие их огромных коэффициентов. Представляло бы большую ценность получить вариант теоремы 7.2, позволяющий установить нижние границы для коэффициентов.
Стратификация, по-видимому, соответствует машине, которая последовательно воздействует на фигуру элементами группы преобразований до тех пор, пока не произойдет некоторое особое событие, устанавливающее принадлежность данной фигуры классу C.j, а затем применяет "проверку на совпадение" с помощью предиката пси.j. Предикаты пси.j должны давать информацию о фигуре во всех ее положениях, отвечающих всем преобразованиям данной группы. Поэтому возможность существования персептрона, выполняющего такое распознавание, не должна создавать впечатления, что машина обладает какой-либо особой способностью к обобщению по отношению к рассматриваемой группе; это скорее говорит о противоположном! Бесспорная громадность иерархий коэффициентов вызывает сомнения в целесообразности формирования коэффициентов стратификации при помощи поощрения, ибо поощрение не действует на фигуру из класса C.j, пока соответствующие члены суммы не подавят дискриминирующий эффект всех остальных членов, относящихся к предшествующим стратам. Это обсуждается далее в гл. 10 и 11.
#7.1. ЭКВИВАЛЕНТНОСТЬ ФИГУР
В предыдущих главах мы рассмотрели распознавание образов - классов фигур, замкнутых относительно преобразований некоторой группы. Теперь мы займемся родственным вопросом распознавания ЭКВИВАЛЕНТНОСТИ относительно группы произвольной пары фигур. Приведенные ниже результаты нас в свое время удивили, так как мы думали, что эти задачи, вообще говоря, не бывают конечного порядка. Многие вопросы остаются открытыми, и внешне позитивный характер последующих построений омрачается необычайно большими коэффициентами, которые для них требуются, и характером роста коэффициентов при возрастании размеров сетчатки.
Типичная задача такова: сетчатка [Все теоремы этой главы применяются непосредственно к персептронам на бесконечных сетчатках, поэтому нет необходимости рассматривать предельные процессы на последовательностях конечных сетчаток, как это предлагалось в #1.6. Группы преобразований также бесконечны, а теорема об инвариантности относительно групп не используется. Так как этот материал несколько более специализирован, чем все остальное, мы немного отступим от нашего способа изложения и перейдем к общепринятому и пренеприятному математическому стилю, когда теоремы сначала формулируются и доказываются, а потом уж объясняется, для чего они нужны] задается в виде двух одинаковых частей A и B, и спрашивается, можно ли фигуру, находящуюся в части B, получить одним лишь переносом фигуры, находящейся в части A. Более общо: существует ли в заданной группе преобразований G такой элемент g, что фигура в B есть результат его воздействия на фигуру в A? Какой порядок предикатов требуется для решения этой задачи?

Все теоремы настоящей главы получены при помощи методики, названной нами СТРАТИФИКАЦИЕЙ. При определенных условиях стратификация позволяет моделировать последовательный процесс таким параллельным процессом, в котором результатам вычислений придаются настолько различные веса, что при выполнении определенных условий один из результатов перевешивает сумму всех остальных. Методика основывается на следующей теореме.
#7.2. ТЕОРЕМА О СТРАТИФИКАЦИИ
Пусть ПИ = {пи.1, пи.2, ..., пи.j, ...} - последовательность различных масок. Зададим последовательность C.1, ..., C.j, ... классов соответствием
X принадлежит C <=> [пи.j(X) и (k>j ~пи.k(X))],
где знак ~ означает отрицание.
Таким образом, X принадлежит классу C.j, если j - самый высокий индекс, для которого пи.j - истина. Пример таких классов показан на рис 7.1.

Рис.7.1. Разбиение на классы C.j.
Пусть ФИ = {фи.i} - семейство предикатов, и пусть пси.1, ..., пси.j, ...- упорядоченная последовательность предикатов в L(ФИ), ОГРАНИЧЕННЫХ в следующем смысле. Для каждого пси.j найдутся такая линейная форма СУММА.j с целыми коэффициентами, что
СУММА.j=СУММА[i]альфа.i.j*фи.i-тета.j и пси.j=[СУММА.j>0],
и такое число B.j, что
|СУММА.j(X)|<B.j
для всякого конечного множества X. (На самом деле для доказательства требуется лишь ограниченность функции |СУММА.j(X)| на каждом классе C.k).
ТЕОРЕМА 7.2. Предикат пси(X)=[X принадлежит C.j => пси.j(X)], принимающий на каждом классе C.j значения соответствующего предиката пси.j, принадлежит множеству L(ФИ*ПИ), т.е. его можно представить в виде [Здесь коэффициенты альфа.j.k, разумеется, отличны от коэффициентов в определении СУММА.j.- Прим. ред.]
пси(X)=[СУММА альфа.j.k(пи.j & фи.k)>тета].
ДОКАЗАТЕЛЬСТВО. Легко заметить, что каждая конечная фигура X принадлежит лишь одному из классов C.j. Положим
S.1=пи.1*СУММА.1
и для j>1 определим по индукции
M.j = max[C.j]|S.[j-1]| и
S.j = S.[j-1] - пи.j*M.j +(2M.j+1)*пи.j*СУММА.j.
Границы B.j гарантируют существование величин M.j. Далее, запишем формальную сумму, порожденную этим бесконечным процессом, в виде
S = СУММА альфа.j.k*(пи.j&фи.k)
и покажем, что пси(X)=[S(X)>0]. Сумма S определена корректно, поскольку для любой конечной фигуры X в любом классе C.j - найдется только конечное число отличных от нуля членов пи.j&фи.k. Применим индукцию. Если X принадлежит классу C.1, то очевидно, что S.i=СУММА.i, так что пси(X)=[S.i(X)>0]. Допустим, что если X принадлежит классу C.[j-1], то пси(X)=[S.[j-i](X)>0]. Так как коэффициенты линейной формы СУММА.j целые, то при X из C.j, и пи.j=1
пси(X) => СУММА.j>=1 => S.j>=-M.j-M.j+2M.j+1=1 и
~пси(X) => СУММА.j<=0 => S.j<=M.j-M.j=0,
и теорема доказана.
СЛЕДСТВИЕ 7.2. Порядок предиката пси(X) не превосходит суммы максимального числа элементов носителя в ФИ и максимального числа элементов носителя в ПИ.
Это следует из того, что предикаты из ФИ выступают только в конъюнкции с предикатами из ПИ. Идея доказательства состоит в разбиении области определения предиката пси(X) на непересекающиеся классы, или "страты", C.j. В пределах каждого страта член -пи.j*M.j настолько велик, что перевешивает (в сторону отрицательных значений) все решения, принятые на низших стратах, если только не удовлетворяется предикат пси.j. Во всех нижеследующих приложениях страты в большей или меньшей степени представляют собой различные возможные отклонения фигуры от "нормального" положения. Поэтому возможность построения "стратифицированных" предикатов тесно связана с принятым в "распознавании образов" представлением об идентификации фигуры сначала путем ее нормализации, а затем сравнения нормализованного изображения с эталоном. Разумеется, обычно это происходит последовательно.
Следует отметить, что у предикатов, полученных при помощи этой теоремы, коэффициенты огромны и с ростом индекса стратификации j растут экспоненциально или даже еще быстрее. Поэтому не надо рассматривать результаты этой главы с точки зрения практических применений. Они представляют скорее теоретический интерес, наглядно демонстрируя взаимосвязь структуры групп преобразований с порядками определенных предикатов, инвариантных относительно этих групп.
#7.3. ПРИЛОЖЕНИЕ 1. СИММЕТРИЯ НА ПРЯМОЙ
Пусть R = ..., x.s, ...,- бесконечная прямолинейная сетчатка, т.е. -беск.<s<беск. Удобно выбрать произвольное начало Хо и занумеровать квадраты так:

Предположим, что X - фигура на R, состоящая из конечного числа |X| точек. Спрашивается, конечен ли порядок предиката
пси.СИММЕТРИЯ = [X обладает зеркальной симметрией].
Заметим, что этот предикат будет тривиальным предикатом порядка 2, если центр симметрии фиксировать заранее. Но в общем случае предиката пси.СИММЕТРИЯ центр может находиться в любом месте бесконечной прямой.
Мы хотим стратифицировать предикат пси.СИММЕТРИЯ, найдя последовательности пи.1, ... и пси.1, ..., которые позволят нам проверять симметрию при помощи следующего приема: пи.i "найдут" две "крайние точки" фигуры X, а соответствующие предикаты пси.j проверят ее симметрию. Поэтому пи.i должны быть такими, чтобы каждый страт C.j оказался классом фигур с определенной парой крайних точек. Для этого нам нужно, чтобы последовательность пи.1,... была перечислением всех отрезков [x.s, x.[s+d]] для каждого s и каждого d>=0, причем при 0<=а<=b<=d отрезок [x.s, x.[s+d]] должен следовать за [x.[s+a], x.[s+b]]. Такие последовательности действительно существуют, например
пи.1=[x.0, x.0], пи.2=[x.1, x.1], пи.3=[x.0, x.1], пи.4=[x.-1, x.-1], пи.5=[x.-1, x.0], пи.6=[x.-1, x.1], пи.7=[x.2, x.2], пи.8=[x.1, x.2], ...:

Легко заметить, что
1) каждый отрезок в конечном итоге попадет в последовательность;
2) ни один отрезок, лежащий внутри другого отрезка, не следует за последним.
Поэтому, если х.s, x.[s+d] - соответственно крайние левая и правая точки фигуры X, то X принадлежит тому страту C.j, который соответствует отрезку [x.s, x.s+d]. Определим теперь пси.j формулой
пси.j = [x.[s+i]=x.[s+d-i], i=0..d],
или, что то же самое,
пси.j = [СУММА[i=0..d](x.[s+i])(1-x.[s+d-i])<=0].
Отсюда видно, что это предикат порядка 2, ограниченный числом B.j=d+1. (Мы удержались от соблазна написать B.j=d/2).
Таким образом, применяя теорему о стратификации, получаем, что порядок предиката пси.СИММЕТРИЯ не выше 4, поскольку порядок предикатов пси.j не выше 2, а носители функций пи содержат не более двух элементов.
#7.4. ПРИЛОЖЕНИЕ 2. КОНГРУЭНТНОСТЬ ПРИ ПЕРЕНОСЕ ВДОЛЬ ПРЯМОЙ
Пусть ..., x.s, ... и ..., y.t, ...- точки двух бесконечных прямолинейных сетчаток А я В, т.е. -беск.<s<беск. и -беск.<t<беск.:

Пусть фигура X состоит из множества X.A левой сетчатки и множества X.B правой сетчатки. Мы хотим построить предикат
пси.ПЕРЕНОС(X) = [(конечный) образ в A является переносом образа в B].
Чтобы стратифицировать этот предикат, нужно найти последовательность {пи.i}, которая вместе с соответствующими предикатами пси.i позволит проверить, конгруэнтны ли множества X.A и X.B. Мы будем осуществлять это методом, аналогичным использованному в #7.3, но теперь будем иметь дело сразу с двумя отрезками. Это значит, что нам надо построить последовательность {пи.j}, перечисляющую все четверки точек так, что фигура лежит в страте C.j тогда и только тогда, когда крайними точками ее частей в A и B служат как раз соответствующие значения x.s, x.[s+d.x], y.t и y.[t+d.y]. Такая последовательность действительно существует (!). Ее можно получить из последовательности {пи.j} #7.3 следующим образом (советуем читателю сначала попытаться найти ее самостоятельно).
Пусть пи.j.k будет четырехточечной маской, определенной формулой
пи.j.k(X)=пи.j(X.A)*пи.k(X.B),
т.е. выбором двух точек из A, соответствующих j, и двух точек из B, соответствующих k. Мы должны перечислить все маски пи.j.k, удовлетворяющие условию: четверка пи.a.b не может предшествовать четверке пи.c.d, если одновременно a>=c и b>=d.

Решением служит последовательность
пи.1.1; пи.2.1, пи.1.2, пи.2.2; пи.3.1, пи.3.2, пи.1.3, пи.2.3, пи.3.3; пи.4.1, пи.4.2, пи.4.3, пи.1.4, пи.2.4, ...;
для члена пи.j.k соответствующим предикатом пси.j.k является предикат
пси.j.k = [отрезки, определяемые при помощи пи.j и пи.k, равны, а x и y на них имеют в соответствующих точках одинаковые значения].
Это предикат порядка 2 и ограниченный (длинами отрезков). Носители функций пи.j состоят из 4 элементов, так что порядок предиката пси.ПЕРЕНОС(X) не превышает 6. На самом же деле, найдя крайние точки множества X.A, мы должны будем найти лишь один конец множества X.B, и поэтому, проведя несколько иное построение, использующее метод #7.9, мы могли бы убедиться, что порядок предиката пси.ПЕРЕНОС не превышает даже 5.
#7.5. ПРИЛОЖЕНИЕ 3. ПЕРЕНОС НА ПЛОСКОСТИ
Метод, изложенный в #7.4, можно применить к задаче двумерных переносов ограниченных кусков плоскости. Пусть каждый экземпляр сетчатки имеет размер m*m. Расположим квадраты в последовательность {x.i} так, чтобы квадрат (a, b) был на {m*a+b)-м месте. Фактически мы считаем сетчатку цилиндром и нумеруем ее квадраты следующим способом:

При этом каждая половина сетчатки отображается на прямую (типа той, которая встречалась в приложении 2) таким образом, что переносы на плоскости эквивалентны переносам вдоль прямой ПРИ УСЛОВИИ, что ПЕРЕНОСЫ НЕ ВЫВОДЯТ ФИГУРУ ЗА КРАЯ СЕТЧАТКИ. Тогда можно построить предикат порядка 5. В #7.6 мы покажем, как обойти это неприятное условие!
ПРИЛОЖЕНИЕ 4. Поворот на 180o относительно произвольной точки плоскости.
При тех же условиях и тем же самым способом, каким было получено приложение 3 из приложения 2, можно построить этот предикат порядка 4. Аналогичные построения можно провести и для отражения относительно любых вертикальных осей.
#7.6. ПОВТОРНАЯ СТРАТИФИКАЦИЯ
В теореме о стратификации на предикаты пси.j наложено единственное условие, чтобы они были подходящим образом ограничены. В некоторых приложениях сами эти предикаты можно получить с помощью стратификации. Это особенно легко сделать, когда носитель предиката пси.j конечен, так как тогда ограниченность получается непосредственно. Чтобы пояснить эту повторную стратификацию, покажем, как избавиться от условия, наложенного в конце приложения 3.
Занумеруем каким-нибудь способом (например, как на рис.7.2) все точки каждой из двух бесконечных плоских сетчаток A и B и расположим их соответственно в последовательности x.1, ..., x.s, ... и y.1, ..., y.t, ...

Рассмотрим затем последовательность пи.j.k, описанную в #7.4, но теперь определенную формулой
пи.j.k = (x.j из X.A и y.k из X.B) = x.j*y.k.
Тогда C.j.k будет классом пар (X.A, X.B), для которых
j = max{s|x.s из X.A},
k = max{t|y.t из X.B}
(рис.7.3). Нам нужен только (ограниченный) предикат пси.j.k, решающий, является ли X.A результатом переноса множества X.B для фигур из C.j.k. Но все фигуры из C.j.k расположены внутри ограниченных кусков плоскостей, а именно внутри квадратов со сторонами [max(j, k)]**(1/2) и с центрами в начальных точках. Внутри такого квадрата (или, еще лучше, внутри вдвое большего квадрата, чтобы избежать "краевых эффектов") мы можем применить результат приложения 3 и получить предикат пси.j.k с конечным носителем, обладающий нужным нам свойством. Порядок не будет превышать 5+2=7. Этот предикат можно построить и другим способом, дающим порядок не выше 5. Аналогично можно избавиться от условий, наложенных в приложении 4 #7.5.

#7.7. ПРИЛОЖЕНИЕ 5. КВАДРАТЫ СО СТОРОНАМИ, ПАРАЛЛЕЛЬНЫМИ ОСЯМ КООРДИНАТ
Отвлечемся на минуту и покажем методом, изложенным в #7.6, что порядок предиката
пси.КВАДРАТ(X) = [X - сплошной (полый) квадрат
со сторонами, параллельными осям],
где X может находиться в любом месте бесконечной плоскости, не выше 3.

(Мы считаем этот факт удивительным, поскольку неформальные рассуждения о сравнении по длине двух сторон с одновременной проверкой внутренних точек приводят к порядку не менее 4. Сформулированный только что результат обнаружил и доказал другим способом наш студент Джон Уайт).
Пронумеруем точки x.1, ... одной плоской сетчатки, как в #7.6, и положим пи.j=x.j. Тогда C.j будет множеством фигур, для которых x.j - "наибольшая" точка. Если X - квадрат, то ситуация совпадает с одним из случаев, изображенных на рис.7.4. Построим предикаты пси.j методом стратификации.

Пусть x.1**j, x.2**j, ..., x.n.j**j - конечная последовательность, образованная точками пересечения спиральной фигуры перпендикуляром к стороне квадрата, восставленным в точке x.j. Положим пи.i**j=x.i**j, так что C.i**j содержит все квадраты со стороной i, которые "упираются" в точку x.j. Но такой квадрат найдется только один, назовем его S.i**j. Теперь чтобы закончить двойную стратификацию, нам нужно иметь только предикаты пси.i**j для распознавания квадратов S.i**j. Для этой цели можно использовать предикат
пси.i**j = [СУММА альфа.k*x.k > i**2],
где
альфа.k =
1, если x.k принадлежит S.i**j или
-1, x.k не принадлежит S.i**j & (k<j) или
0 в остальных случаях.
Порядок предиката пси.i**j равен 1, так что порядок предиката пси.КВАДРАТ не выше 3, что и требовалось доказать!
#7.8. ПРИЛОЖЕНИЕ 6. ФИГУРЫ, ЭКВИВАЛЕНТНЫЕ ОТНОСИТЕЛЬНО ПЕРЕНОСА И РАСТЯЖЕНИЯ
Может ли система конечного порядка распознавать эквивалентность двух произвольных фигур относительно переноса и изменения размера?

Поразмыслив немного над методами #7.6 и 7.7 и над полученными результатами, мы придем к заключению, что имеем все необходимые данные: в #7.6 показано, как обращаться с переносами, а в #7.7, как распознавать все переносы и растяжения КОНКРЕТНОЙ фигуры. При РАСТЯЖЕНИИ возникают серьезные трудности с допустимыми отклонениями и пределами разрешающей способности, поскольку все наши построения проводятся на фиксированной дискретной сетчатке. Однако нам решительно не хочется столкнуться с этими трудностями. Интересно тем не менее, что нужное свойство можно по крайней мере аппроксимировать предикатом конечного порядка, причем интуитивно разумным образом. (Мы не думаем, что такую аппроксимацию можно выполнить в случае инвариантности относительно вращения, так как здесь возникают трудности иного рода, не связанные с дискретностью сетчатки. Скорее они вызваны тем, что преобразования группы вращений нельзя упорядочить простым способом, а это "преграждает путь" методам стратификации).
Наш метод начинается приемом, использованным в #7.6 для нахождения предикатов пи.j.k, которые "улавливали" две фигуры и заключали их в квадраты. После этого, как и в #7.6, задача сводится к нахождению предикатов пси.j.k, от которых требуется действовать только внутри квадратов, показанных на рис.7.3. Мы строим предикаты пси.j.k весьма грубым способом: в каждом квадрате нумеруем точки простейшим способом, как описано в #7.5. Затем проводим стратификацию 4 раза (!) подряд относительно
x, наивысшей и крайней левой точки множества A,
y, наивысшей и крайней левой точки множества B, x', наинизшей и крайней правой точки множества A, y', наинизшей и крайней правой точки множества В.
Для этого нам нужно задать предикаты пси.x.y.[x'].[y']**(j*k). Если направления векторов x-x' и y-y' не совпадают, мы полагаем пси=0; в противном случае нам нужно, чтобы предикат пси проверял, выполняется ли для каждого вектора ню условие
y+ню = x+(x-x')/(y-y')*ню,
а это предикат порядка 2, так что общий порядок не превышает 2+4+2=8. Конечно, на дискретной сетчатке указанные операции над векторами определены некорректно, но, по-видимому, ясно, что полученный результат вовсе не бессодержателен: например, мы можем распознать, является ли фигура X.B результатом переноса фигуры X.A и ее целым кратным, причем каждый черный квадрат фигуры X.A должен отображаться на соответственно больший квадрат фигуры X.B. Мы можем построить этот предикат и другим способом, дающим порядок не выше 6.
#7.9. ПРИЛОЖЕНИЕ 7. ЭКВИВАЛЕНТЫ ДАННОЙ ФИГУРЫ
Строя в приложении 5 предикат пси, мы отмечали, что всегда можно найти предикат порядка 1 для обнаружения одной-единственной фигуры X.0, если использовать выражение
[СУММА[x из X0]~x + СУММА [x не из X0]x >= 1]
Отсюда следует, что, построив стратификацию {пи.i} для группы G, удовлетворяющую условию
X принадлежит C.i и g*X принадлежит C.i => (g*X=X),
можно точно распознать G-эквиваленты заданной фигуры X.0 (с помощью предиката, порядок которого на единицу превышает порядок стратификации пи). Это наводит на мысль о машине, которая на первом этапе процесса распознавания приводит фигуры к некоторому нормальному виду. Для этого случая наш общий метод построения принимает следующую исключительно простую форму. Возьмем в качестве X.0 упорядоченную последовательность точек {x.i.1, ..., x.i.p} полупрямой

Положим пи.j(X)[x.j из X] и зададим пси.j(X) формулой
пси.j(X) = [СУММА [x.[k-j+i.p] принадлежит X.0]*~x.k + СУММА [x.[k-j+i.p] не принадлежит X.0 и k<j]*x.k < 1];
точки с отрицательными индексами пока рассматривать не будем. Тогда, если не обращать внимания на "краевые эффекты", мы получим предикат порядка 2, распознающий переносы фигуры X.0. Заметим, что на самом деле не представляет труда распространить это на бесконечную в обе стороны прямую, так как можно задать последовательность {пи.i} в виде

Если фигура оканчивается в классе C.[2*j], мы будем искать ее крайнюю левую точку х.-j, а если в классе C.[2*j+1], то крайнюю правую точку x.j. В любом случае можно построить соответствующий предикат пси. Итак, для любой заданной фигуры X.0 существует предикат порядка 2, распознающий ее линейные переносы, и при этом не возникает проблем ограниченности, ибо носители всех предикатов пси конечны.
#7.10. КАЖУЩИЙСЯ ПАРАДОКС
Рассмотрим фигуру

Мы только что показали, что существует предикат gcb порядка 2, распознающий переносы этой фигуры. Следовательно, этот предикат должен отклонить неэквивалентную ей фигуру

Но у этих фигур один и тот же спектр n-точечного распределения (#6.2 и 6.5) до второго порядка включительно! Каждая из них содержит три точки, одну смежную пару, одну пару с расстоянием в два элемента и одну пару с расстоянием в три элемента. Поэтому, если бы все предикаты фи, эквивалентные относительно группы, имели одинаковые веса, то для различения указанных фигур потребовался бы персептрон порядка не менее 3. Таким образом, если бы мы смогли применить теорему об инвариантности относительно групп, мы бы доказали, что НИКАКОЙ персептрон порядка 2 их различить не может. Это явилось бы противоречием! В чем же дело? Ответ состоит в том, что теорема об инвариантности относительно групп вообще неприменима в случае бесконечных групп. Когда группа конечна (например, группа циклического переноса на тороидальных сетчатках, которую мы иногда рассматриваем), теорему об инвариантности относительно групп всегда можно применить и уравнять коэффициенты эквивалентных предикатов фи. Но построить методом стратификации предикат на бесконечных группах с ее помощью нельзя.
В случае бесконечных групп можно использовать стратификацию для нормализации, но тогда в пределах подмножества эквивалентных предикатов фи могут получиться неограниченные коэффициенты, и операции усреднения по группе в общем случае не будут сходиться. Мы докажем соответствующую теорему в #10.4.
Мы предполагаем, что предикаты типа "близнецов" из #7.5 не являются предикатами конечного порядка с ограниченными коэффициентами. Во всяком случае было бы интересно узнать, существуют ли вообще такие предикаты.
#7.11. ПРОБЛЕМЫ
Укажем некоторые направления дальнейших исследований, которые нам кажутся интересными: Какова взаимосвязь между возможными стратификациями, включая повторные, и алгебраическими разложениями группы на разного рода подгруппы? При какого рода предикатах теорему об инвариантности относительно групп можно распространить на бесконечные группы? Для каких предикатов коэффициенты ограничены - для каждого класса эквивалентности? При каких условиях существуют "стратификации нормального вида" из приложения 7? Например, мы ПРЕДПОЛАГАЕМ, ЧТО НА ОКРУЖНОСТЯХ И НА ТОРАХ НЕ СУЩЕСТВУЕТ ГРАНИЦЫ ДЛЯ ПОРЯДКА ПРЕДИКАТОВ пси, ВЫДЕЛЯЮЩИХ ЕДИНСТВЕННУЮ ФИГУРУ "НОРМАЛЬНОЙ ФОРМЫ" [Из каждого класса эквивалентности.- Прим. ред.] В СЛУЧАЕ ГРУППЫ ВРАЩЕНИЙ:
пси(X) и пси(g*X) => X=g*X.
Мы подозреваем, что именно по этой причине мы не можем распространить метод приложения 6 на группу всех подобий, включая вращения.
Заметим, что требование теоремы 7.2, чтобы предикаты {пи.j} были масками, по всей вероятности, излишне строго. Мы не стали пока искать лучшей теоремы.
Стратифицированные предикаты, вероятно, физически нереализуемы вследствие их огромных коэффициентов. Представляло бы большую ценность получить вариант теоремы 7.2, позволяющий установить нижние границы для коэффициентов.
Стратификация, по-видимому, соответствует машине, которая последовательно воздействует на фигуру элементами группы преобразований до тех пор, пока не произойдет некоторое особое событие, устанавливающее принадлежность данной фигуры классу C.j, а затем применяет "проверку на совпадение" с помощью предиката пси.j. Предикаты пси.j должны давать информацию о фигуре во всех ее положениях, отвечающих всем преобразованиям данной группы. Поэтому возможность существования персептрона, выполняющего такое распознавание, не должна создавать впечатления, что машина обладает какой-либо особой способностью к обобщению по отношению к рассматриваемой группе; это скорее говорит о противоположном! Бесспорная громадность иерархий коэффициентов вызывает сомнения в целесообразности формирования коэффициентов стратификации при помощи поощрения, ибо поощрение не действует на фигуру из класса C.j, пока соответствующие члены суммы не подавят дискриминирующий эффект всех остальных членов, относящихся к предшествующим стратам. Это обсуждается далее в гл. 10 и 11.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 8. ПЕРСЕПТРОН, ОГРАНИЧЕННЫЙ ПО ДИАМЕТРУ
#8.0
В этой главе обсуждаются сильные стороны и пределы возможностей персептронов, ограниченных по диаметру, т.е. таких, в которых каждый предикат фи может обозревать только ограниченный участок сетчатки R.
Мы рассматриваем машину, суммирующую взвешенные данные о фигуре, полученные в результате экспериментов фи.i, характеризующих ситуацию в ограниченной области, ДИАМЕТР КОТОРОЙ НЕ ПРЕВОСХОДИТ НЕКОТОРОЙ ДЛИНЫ D; символически diam(S(фи))<=D.
Можно прийти к двум различным теориям, если при изучении ограниченных по диаметру предикатных схем брать в качестве D
(1) абсолютную длину,
(2) фиксированную часть размера сетчатки R.
Как правило, для получения положительных результатов лучше выбирать случай (1). Для отрицательных результатов (1) является частным случаем теории персептронов ограниченного порядка, а (2) приводит к другим и подчас более сильным результатам. По-видимому, эта теория недостаточно глубока, чтобы оправдать попытки получить в каждом случае наилучший возможный результат. С практической точки зрения величина D должна быть настолько мала, чтобы ни один из предикатов фи не видел целиком всей фигуры (иначе мы не имели бы никакой теории), и в то же время достаточно велика, чтобы можно было заметить представляющие интерес признаки.
#8.1. ПОЛОЖИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
Рассмотрим сначала объекты, которые персептрон, ограниченный по диаметру, может распознать, а затем такие, которые он распознать не может.
#8.1.1. ОДНОРОДНЫЙ РИСУНОК. Персептрон, ограниченный по диаметру, может различить, является ли рисунок полностью черным или полностью белым: возьмем предикаты фи.i, НАКРЫВАЮЩИЕ сетчатку по областям (которые могут перекрываться), и положим фи.i=0 в том и только том случае, когда все просматриваемые точки белые. Тогда
СУММА фи.i > 0,
если в рисунке содержится хотя бы одна черная точка, и
СУММА фи.i <= 0,
если рисунок пуст. Точно так же можно задать предикаты фи.i, отличающие абсолютно черный рисунок от всех остальных.
Эти образы можно распознавать, поскольку они носят "конъюнктивно локальный" характер (#0.6): ни один предикат фи на самом деле не в состоянии привести убедительные доводы в пользу того, что фигура полностью белая (поскольку он весьма слабо с этим связан), но любой предикат фи может с полной определенностью утверждать, что имеются исчерпывающие опытные данные, свидетельствующие о том, что рисунок НЕ полностью белый. Подобным свойством обладают и другие интересные образы. Это свойство позволяет ОТБРОСИТЬ все рисунки, не принадлежащие данному классу, после проверки наличия в каком-нибудь месте рисунка локального признака, который является определяющим и может быть обнаружен на основании того, что происходит внутри области диаметра D.
#8.1.2. СЕЧЕНИЯ, ОСНОВАННЫЕ НА ВЕЛИЧИНЕ ПЛОЩАДИ. При любом числе S можно распознать класс фигур, площадь которых не превышает S. Для каждой точки p положим фи.p=1, если точка черная, и фи.p=0 в противном случае. Тогда неравенство
СУММА фи.p > S
служит для распознавания рассматриваемого класса.
#8.1.3. ТРЕУГОЛЬНИКИ И ПРЯМОУГОЛЬНИКИ. Персептрон, ограниченный по диаметру, можно заставить распознавать фигуры, состоящие только из одного треугольника (сплошного или контурного), используя следующий прием.
Применим предикаты фи двух типов: предикат фи.i, равный 1, если в его поле зрения находится вершина (два прямолинейных отрезка, образующие угол), и 0 в противном случае, и предикат фи.i', равный 0, если его поле зрения пусто или содержит прямолинейный отрезок, или сплошную зачерненную площадь, или вершину, и равный 1, если в поле зрения находится что-либо иное, включая и конец прямолинейного отрезка. Заготовим столько этих предикатов фи, чтобы можно было покрыть сетчатку предикатами обоих типов полностью и без перекрытий. Разумеется, такая система не сработает, если вершина попадает на край носителя предиката фи. С помощью подходящего перекрытия и присваивания весов систему можно усовершенствовать, однако она всегда останется некоторого рода приближением. Это относится как к определению "прямолинейного отрезка" и т.д., так и к определению "вершины" (#8.3). Наконец, первому типу предикатов мы припишем единичный вес, а второму типу - очень большой положительный вес W. Тогда неравенство
СУММА фи.i + W(СУММА фи.i') < 4
будет специфическим предикатом для распознавания треугольников. (Оно, однако, с таким же успехом будет воспринимать и пустой рисунок). Аналогично настраивая предикаты фи на распознавание только прямых углов, можно различить класс прямоугольников, проверяя выполнение неравенства
СУММА фи.i + W(СУММА фи.i') < 5
Такого рода приемами можно охватить и другие геометрические классы, но успех зависит от странных случайностей. Прямоугольник характеризуется наличием четырех прямых углов и отсутствием исключений, обнаруживаемых предикатами фи.i. В #6.3.2 мы построили соответствующие предикаты для прямоугольников со сторонами, параллельными осям координат. Очевидно, что для остальных прямоугольников возникают более серьезные трудности, связанные с разрешающей способностью и допустимыми отклонениями. Однако способа распознавания квадратов даже со сторонами, параллельными осям, с помощью предикатов фи, ограниченных по диаметру, не существует; метод из #7.7 никак нельзя для этого приспособить.
#8.1.4. АБСОЛЮТНОЕ СООТВЕТСТВИЕ ШАБЛОНУ. Допустим, требуется, чтобы машина распознавала только определенную фигуру X.0 и ничего более. Это можно осуществить с помощью ограниченной по диаметру машины, если разделить сетчатку на такие области, что в каждой из них фи=0, если эта область полностью соответствует отвечающей ей части фигуры X.0, и фи=1 в противном случае. Здесь
СУММА фи < 1
тогда и только тогда, когда рисунок представляет собой именно X.0.
Заметим, однако, что такая система срабатывает только при конкретном объекте в конкретном положении. Ее нельзя обобщить на распознавание конкретного объекта в ЛЮБОМ положении. Действительно, в следующем параграфе мы покажем, что даже простейшую фигуру, состоящую из одной-единственной точки, невозможно распознать независимо от положения!
#8.2. ОТРИЦАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
#8.2.1. ФИГУРА, СОДЕРЖАЩАЯ ЕДИНСТВЕННУЮ ЧЕРНУЮ ТОЧКУ. Это основной контрпример. Нам хочется, чтобы машина
СУММА альфа.фи*фи >= тета
принимала фигуры с площадью 1 и отвергала те, у которых площадь равна 0 или больше 1. Чтобы убедиться, что это невозможно выполнить при помощи персептрона, ограниченного по диаметру, предположим, что {фи}, {альфа} и тета уже выбраны. Предъявим сначала совершенно чистый рисунок X.0. Тогда, если f(X) = СУММА альфа.i*фи.i(X), то f(X.0) < тета. Затем предъявим фигуру X.1, содержащую только одну точку x.1. Мы должны тогда получить
f(X.1) >= тета.
Изменение суммы должно произойти за счет изменения значений некоторых предикатов фи. Фактически его должны вызвать изменения только тех предикатов фи, для которых x.1 принадлежит S(фи), поскольку в рисунке больше ничего не изменилось. В любом случае
f(X.1)-f(X.0)>0.
Теперь возьмем точку х.2, отстоящую от x.1 дальше, чем на D. Тогда никакой носитель S(фи) не может содержать одновременно и x.1 и х.2. Для фигуры X.2, состоящей только из точки х.2, мы должны также получить
f(X.2) = СУММА альфа.i*фи.i(X) >= тета.
Рассмотрим фигуру X.12, содержащую обе точки x.1 и х.2. Добавление точки x.1 к X.2 может оказать влияние только на те фи, для которых X.1 принадлежит S(фи), и вызовет точно такое же их изменение, как в случае перехода от абсолютно чистого рисунка Х.0 к рисунку X.1. Поэтому
f(X.12) = f (X.2) + (f(X.1)-f(X.0)),
откуда в силу двух предыдущих неравенств
f(X.12) > тета,
что противоречит требованию
f(X.12) < тета.
Разумеется, это то же самое явление, которое отмечалось уже в #0.8 и 2.1, и оно дает метод доказательства последнего утверждения из #8.1.3.
#8.2.2. ИНТЕРВАЛЫ ЗНАЧЕНИЙ ПЛОЩАДИ. Персептрон, ограниченный по диаметру, не может распознать класс фигур, площадь A которых заключена в пределах A.1 <= A <= A.2.
ДОКАЗАТЕЛЬСТВО. Это следует из метода #8.2.1, где рассматривается по существу частный случай нашего утверждения (A.1=A.2=1). Напомним, что такое распознавание можно выполнить при помощи предиката порядка 2, если снять ограничение диаметра и использовать метод #1.4, пример 3.
#8.2.3. СВЯЗНОСТЬ. Персептрон, ограниченный по диаметру, не в состоянии решить, представляет ли рисунок единое целое или состоит из двух и более разъединенных частей. Сейчас уже читателю нетрудно понять формальную корректность доказательства, проведенного нами в #0.8.
#8.3. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ, ОГРАНИЧЕННЫЕ ПО ДИАМЕТРУ
В #6.3.1 мы отмечали, что выпуклость имеет порядок 3, но выражение, которое мы там использовали, неприменимо в случае персептронов, ограниченных по диаметру, поскольку оно не отвергает фигуру, состоящую из двух сильно разнесенных выпуклых компонент. С другой стороны, в #8.1.3 показано, каким образом может персептрон, ограниченный по диаметру, различать некоторые выпуклые фигуры. Построение, которое мы сейчас проведем, можно обобщить, но возникнут серьезные проблемы, связанные с допустимыми отклонениями, и вопросы относительно дифференциалов.
Допустим, что мы определяем семейство предикатов ФИ, ограниченных по диаметру, используя следующую идею. Возьмем e>0 и разобьем R на малые клетки C.j. Для каждого целого числа k положим фи.j.k=1, если C.j пересечение X содержит "край", на котором изменение направления превышает k.e, и фи.j.k=0 в противном случае.
Рассмотрим "интеграл"
СУММА[j.k]e*фи.j.k.
Вклад каждого отрезка кривой в сумму равен e*c/e=c, где с - величина изменения направления отрезка; следовательно, вся сумма представляет собой "суммарную кривизну". Наконец, мы утверждаем, что можем "реализовать" предикат пси.ВЫПУКЛОСТЬ в виде
[СУММА[j.k]e*фи.j.k <= 2пи],
поскольку суммарная кривизна (точнее, сумма абсолютных величин кривизны.- Ред.) любой фигуры должна быть больше или равна 2пи, а равенство достигается лишь на выпуклых фигурах и притом на всех. Фигурами, доходящими до края сетчатки, и им подобными мы пренебрегаем.
Аналогично можно построить предикат, использующий кривизну С УЧЕТОМ ЗНАКА, для реализации функций от эйлеровой характеристики вида G(X)<n, так как этот инвариант и есть как раз суммарная кривизна со знаком, деленная на 2пи. Разумеется, на КВАНТОВАННОЙ плоскости ограниченному по диаметру предикату из #5.8.1 выполнить это проще.
Можно было бы перейти далее к описанию более сложных предикатов, классифицирующих фигуры в соответствии со свойствами их "дифференциальных спектров".
Мы, однако, не преследуем таких целей, так как у нас и так уже возникло много серьезных вопросов, связанных с допустимыми отклонениями и приближениями. Среди них задачи, связанные с размерами ограниченных по диаметру клеток C.j, величиной e, и проблемы накопления ошибок при суммировании малых приближенных величин. Вне всякого сомнения, в рамках отображения E**2->R, описанного в гл.5, или любого ему подобного, все такие предикаты приведут к специфическим результатам всякий раз, когда диаметр клеток невелик по сравнению с ячейками сетчатки или мал в сравнении с размерами соответствующих характерных признаков фигур X. В #9.3 при анализе предиката пси.ВЫПУКЛОСТЬ Делается попытка рассмотреть эти проблемы.
Например, распознавание прямоугольников, проведенное в #6.3.2, можно в связи со сказанным выше считать сугубо искусственным явлением, поскольку оно сильно зависит от размера ячеек сетчатки. Другая форма того же предиката описана в #8.1.3 таким образом, что уже МОЖНО БЫЛО бы провести разумную аппроксимацию в пределах разумного диапазона размеров.
#8.4. ДОКАЗАТЕЛЬСТВО ЕДИНСТВЕННОСТИ ЭЙЛЕРОВЫХ ИНВАРИАНТОВ ДЛЯ ПЕРСЕПТРОНОВ, ОГРАНИЧЕННЫХ ПО ДИАМЕТРУ
В этом параграфе мы покажем, как обещали в конце гл.5, что справедлива
ТЕОРЕМА 8.4. Персептроны, ограниченные по диаметру, не могут распознавать нетривиальные топологические свойства, за исключением эйлеровых предикатов [E{X)>n] и [E(X)<n].
ДОКАЗАТЕЛЬСТВО. Из рассуждений #5.8 следует, что предикат пси(X) должен быть функцией от E(X). Это непосредственно относится к ограничению абсолютной величины диаметра, что является частным случаем ограничения порядка. С соответствующими модификациями указанные рассуждения переносятся и на ограничения относительной величины диаметра. Рассмотрим две фигуры А и В, отличающиеся только одним внутренним квадратом:
Окружность на рисунке указывает диапазон ограничения диаметра. Допустим, что пси(X)=[СУММА альфа.фи*фи(X)>тета], и рассмотрим разность
ДЕЛЬТА = СУММА альфа.фи*фи(B) - СУММА альфа.фи*фи(A).
Если ДЕЛЬТА >= 0, то
пси(B) >= пси(A),
и потому устранение дыры не может уменьшить пси. В силу топологической эквивалентности добавление компоненты оказывает такое же воздействие на E(X), а потому и на пси(X). Таким образом, если ДЕЛЬТА>=0, то
E(B)>E(A) => пси(B)>=пси(A),
и аналогично, если ДЕЛЬТА<=0, то
E(B)>E(A) => пси(B)<=пси(A).
Отсюда следует, что всегда должно существовать такое n, что (если ДЕЛЬТА>=0)
пси(X)=[E(X)>n],
или (если ДЕЛЬТА<=0)
пси(X)=[E(X)<n],
или пси - константа.
Тривиальные исключения составляют постоянные предикаты и "однородные" предикаты из #8.1.1, которые являются исключениями по отношению к канонической форме #5.8.
#8.0
В этой главе обсуждаются сильные стороны и пределы возможностей персептронов, ограниченных по диаметру, т.е. таких, в которых каждый предикат фи может обозревать только ограниченный участок сетчатки R.
Мы рассматриваем машину, суммирующую взвешенные данные о фигуре, полученные в результате экспериментов фи.i, характеризующих ситуацию в ограниченной области, ДИАМЕТР КОТОРОЙ НЕ ПРЕВОСХОДИТ НЕКОТОРОЙ ДЛИНЫ D; символически diam(S(фи))<=D.
Можно прийти к двум различным теориям, если при изучении ограниченных по диаметру предикатных схем брать в качестве D
(1) абсолютную длину,
(2) фиксированную часть размера сетчатки R.
Как правило, для получения положительных результатов лучше выбирать случай (1). Для отрицательных результатов (1) является частным случаем теории персептронов ограниченного порядка, а (2) приводит к другим и подчас более сильным результатам. По-видимому, эта теория недостаточно глубока, чтобы оправдать попытки получить в каждом случае наилучший возможный результат. С практической точки зрения величина D должна быть настолько мала, чтобы ни один из предикатов фи не видел целиком всей фигуры (иначе мы не имели бы никакой теории), и в то же время достаточно велика, чтобы можно было заметить представляющие интерес признаки.
#8.1. ПОЛОЖИТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
Рассмотрим сначала объекты, которые персептрон, ограниченный по диаметру, может распознать, а затем такие, которые он распознать не может.
#8.1.1. ОДНОРОДНЫЙ РИСУНОК. Персептрон, ограниченный по диаметру, может различить, является ли рисунок полностью черным или полностью белым: возьмем предикаты фи.i, НАКРЫВАЮЩИЕ сетчатку по областям (которые могут перекрываться), и положим фи.i=0 в том и только том случае, когда все просматриваемые точки белые. Тогда
СУММА фи.i > 0,
если в рисунке содержится хотя бы одна черная точка, и
СУММА фи.i <= 0,
если рисунок пуст. Точно так же можно задать предикаты фи.i, отличающие абсолютно черный рисунок от всех остальных.
Эти образы можно распознавать, поскольку они носят "конъюнктивно локальный" характер (#0.6): ни один предикат фи на самом деле не в состоянии привести убедительные доводы в пользу того, что фигура полностью белая (поскольку он весьма слабо с этим связан), но любой предикат фи может с полной определенностью утверждать, что имеются исчерпывающие опытные данные, свидетельствующие о том, что рисунок НЕ полностью белый. Подобным свойством обладают и другие интересные образы. Это свойство позволяет ОТБРОСИТЬ все рисунки, не принадлежащие данному классу, после проверки наличия в каком-нибудь месте рисунка локального признака, который является определяющим и может быть обнаружен на основании того, что происходит внутри области диаметра D.
#8.1.2. СЕЧЕНИЯ, ОСНОВАННЫЕ НА ВЕЛИЧИНЕ ПЛОЩАДИ. При любом числе S можно распознать класс фигур, площадь которых не превышает S. Для каждой точки p положим фи.p=1, если точка черная, и фи.p=0 в противном случае. Тогда неравенство
СУММА фи.p > S
служит для распознавания рассматриваемого класса.
#8.1.3. ТРЕУГОЛЬНИКИ И ПРЯМОУГОЛЬНИКИ. Персептрон, ограниченный по диаметру, можно заставить распознавать фигуры, состоящие только из одного треугольника (сплошного или контурного), используя следующий прием.
Применим предикаты фи двух типов: предикат фи.i, равный 1, если в его поле зрения находится вершина (два прямолинейных отрезка, образующие угол), и 0 в противном случае, и предикат фи.i', равный 0, если его поле зрения пусто или содержит прямолинейный отрезок, или сплошную зачерненную площадь, или вершину, и равный 1, если в поле зрения находится что-либо иное, включая и конец прямолинейного отрезка. Заготовим столько этих предикатов фи, чтобы можно было покрыть сетчатку предикатами обоих типов полностью и без перекрытий. Разумеется, такая система не сработает, если вершина попадает на край носителя предиката фи. С помощью подходящего перекрытия и присваивания весов систему можно усовершенствовать, однако она всегда останется некоторого рода приближением. Это относится как к определению "прямолинейного отрезка" и т.д., так и к определению "вершины" (#8.3). Наконец, первому типу предикатов мы припишем единичный вес, а второму типу - очень большой положительный вес W. Тогда неравенство
СУММА фи.i + W(СУММА фи.i') < 4
будет специфическим предикатом для распознавания треугольников. (Оно, однако, с таким же успехом будет воспринимать и пустой рисунок). Аналогично настраивая предикаты фи на распознавание только прямых углов, можно различить класс прямоугольников, проверяя выполнение неравенства
СУММА фи.i + W(СУММА фи.i') < 5
Такого рода приемами можно охватить и другие геометрические классы, но успех зависит от странных случайностей. Прямоугольник характеризуется наличием четырех прямых углов и отсутствием исключений, обнаруживаемых предикатами фи.i. В #6.3.2 мы построили соответствующие предикаты для прямоугольников со сторонами, параллельными осям координат. Очевидно, что для остальных прямоугольников возникают более серьезные трудности, связанные с разрешающей способностью и допустимыми отклонениями. Однако способа распознавания квадратов даже со сторонами, параллельными осям, с помощью предикатов фи, ограниченных по диаметру, не существует; метод из #7.7 никак нельзя для этого приспособить.
#8.1.4. АБСОЛЮТНОЕ СООТВЕТСТВИЕ ШАБЛОНУ. Допустим, требуется, чтобы машина распознавала только определенную фигуру X.0 и ничего более. Это можно осуществить с помощью ограниченной по диаметру машины, если разделить сетчатку на такие области, что в каждой из них фи=0, если эта область полностью соответствует отвечающей ей части фигуры X.0, и фи=1 в противном случае. Здесь
СУММА фи < 1
тогда и только тогда, когда рисунок представляет собой именно X.0.
Заметим, однако, что такая система срабатывает только при конкретном объекте в конкретном положении. Ее нельзя обобщить на распознавание конкретного объекта в ЛЮБОМ положении. Действительно, в следующем параграфе мы покажем, что даже простейшую фигуру, состоящую из одной-единственной точки, невозможно распознать независимо от положения!
#8.2. ОТРИЦАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ
#8.2.1. ФИГУРА, СОДЕРЖАЩАЯ ЕДИНСТВЕННУЮ ЧЕРНУЮ ТОЧКУ. Это основной контрпример. Нам хочется, чтобы машина
СУММА альфа.фи*фи >= тета
принимала фигуры с площадью 1 и отвергала те, у которых площадь равна 0 или больше 1. Чтобы убедиться, что это невозможно выполнить при помощи персептрона, ограниченного по диаметру, предположим, что {фи}, {альфа} и тета уже выбраны. Предъявим сначала совершенно чистый рисунок X.0. Тогда, если f(X) = СУММА альфа.i*фи.i(X), то f(X.0) < тета. Затем предъявим фигуру X.1, содержащую только одну точку x.1. Мы должны тогда получить
f(X.1) >= тета.
Изменение суммы должно произойти за счет изменения значений некоторых предикатов фи. Фактически его должны вызвать изменения только тех предикатов фи, для которых x.1 принадлежит S(фи), поскольку в рисунке больше ничего не изменилось. В любом случае
f(X.1)-f(X.0)>0.
Теперь возьмем точку х.2, отстоящую от x.1 дальше, чем на D. Тогда никакой носитель S(фи) не может содержать одновременно и x.1 и х.2. Для фигуры X.2, состоящей только из точки х.2, мы должны также получить
f(X.2) = СУММА альфа.i*фи.i(X) >= тета.
Рассмотрим фигуру X.12, содержащую обе точки x.1 и х.2. Добавление точки x.1 к X.2 может оказать влияние только на те фи, для которых X.1 принадлежит S(фи), и вызовет точно такое же их изменение, как в случае перехода от абсолютно чистого рисунка Х.0 к рисунку X.1. Поэтому
f(X.12) = f (X.2) + (f(X.1)-f(X.0)),
откуда в силу двух предыдущих неравенств
f(X.12) > тета,
что противоречит требованию
f(X.12) < тета.
Разумеется, это то же самое явление, которое отмечалось уже в #0.8 и 2.1, и оно дает метод доказательства последнего утверждения из #8.1.3.
#8.2.2. ИНТЕРВАЛЫ ЗНАЧЕНИЙ ПЛОЩАДИ. Персептрон, ограниченный по диаметру, не может распознать класс фигур, площадь A которых заключена в пределах A.1 <= A <= A.2.
ДОКАЗАТЕЛЬСТВО. Это следует из метода #8.2.1, где рассматривается по существу частный случай нашего утверждения (A.1=A.2=1). Напомним, что такое распознавание можно выполнить при помощи предиката порядка 2, если снять ограничение диаметра и использовать метод #1.4, пример 3.
#8.2.3. СВЯЗНОСТЬ. Персептрон, ограниченный по диаметру, не в состоянии решить, представляет ли рисунок единое целое или состоит из двух и более разъединенных частей. Сейчас уже читателю нетрудно понять формальную корректность доказательства, проведенного нами в #0.8.
#8.3. ИНТЕГРАЛЬНЫЕ ИНВАРИАНТЫ, ОГРАНИЧЕННЫЕ ПО ДИАМЕТРУ
В #6.3.1 мы отмечали, что выпуклость имеет порядок 3, но выражение, которое мы там использовали, неприменимо в случае персептронов, ограниченных по диаметру, поскольку оно не отвергает фигуру, состоящую из двух сильно разнесенных выпуклых компонент. С другой стороны, в #8.1.3 показано, каким образом может персептрон, ограниченный по диаметру, различать некоторые выпуклые фигуры. Построение, которое мы сейчас проведем, можно обобщить, но возникнут серьезные проблемы, связанные с допустимыми отклонениями, и вопросы относительно дифференциалов.
Допустим, что мы определяем семейство предикатов ФИ, ограниченных по диаметру, используя следующую идею. Возьмем e>0 и разобьем R на малые клетки C.j. Для каждого целого числа k положим фи.j.k=1, если C.j пересечение X содержит "край", на котором изменение направления превышает k.e, и фи.j.k=0 в противном случае.

Рассмотрим "интеграл"
СУММА[j.k]e*фи.j.k.
Вклад каждого отрезка кривой в сумму равен e*c/e=c, где с - величина изменения направления отрезка; следовательно, вся сумма представляет собой "суммарную кривизну". Наконец, мы утверждаем, что можем "реализовать" предикат пси.ВЫПУКЛОСТЬ в виде
[СУММА[j.k]e*фи.j.k <= 2пи],
поскольку суммарная кривизна (точнее, сумма абсолютных величин кривизны.- Ред.) любой фигуры должна быть больше или равна 2пи, а равенство достигается лишь на выпуклых фигурах и притом на всех. Фигурами, доходящими до края сетчатки, и им подобными мы пренебрегаем.
Аналогично можно построить предикат, использующий кривизну С УЧЕТОМ ЗНАКА, для реализации функций от эйлеровой характеристики вида G(X)<n, так как этот инвариант и есть как раз суммарная кривизна со знаком, деленная на 2пи. Разумеется, на КВАНТОВАННОЙ плоскости ограниченному по диаметру предикату из #5.8.1 выполнить это проще.
Можно было бы перейти далее к описанию более сложных предикатов, классифицирующих фигуры в соответствии со свойствами их "дифференциальных спектров".
Мы, однако, не преследуем таких целей, так как у нас и так уже возникло много серьезных вопросов, связанных с допустимыми отклонениями и приближениями. Среди них задачи, связанные с размерами ограниченных по диаметру клеток C.j, величиной e, и проблемы накопления ошибок при суммировании малых приближенных величин. Вне всякого сомнения, в рамках отображения E**2->R, описанного в гл.5, или любого ему подобного, все такие предикаты приведут к специфическим результатам всякий раз, когда диаметр клеток невелик по сравнению с ячейками сетчатки или мал в сравнении с размерами соответствующих характерных признаков фигур X. В #9.3 при анализе предиката пси.ВЫПУКЛОСТЬ Делается попытка рассмотреть эти проблемы.
Например, распознавание прямоугольников, проведенное в #6.3.2, можно в связи со сказанным выше считать сугубо искусственным явлением, поскольку оно сильно зависит от размера ячеек сетчатки. Другая форма того же предиката описана в #8.1.3 таким образом, что уже МОЖНО БЫЛО бы провести разумную аппроксимацию в пределах разумного диапазона размеров.
#8.4. ДОКАЗАТЕЛЬСТВО ЕДИНСТВЕННОСТИ ЭЙЛЕРОВЫХ ИНВАРИАНТОВ ДЛЯ ПЕРСЕПТРОНОВ, ОГРАНИЧЕННЫХ ПО ДИАМЕТРУ
В этом параграфе мы покажем, как обещали в конце гл.5, что справедлива
ТЕОРЕМА 8.4. Персептроны, ограниченные по диаметру, не могут распознавать нетривиальные топологические свойства, за исключением эйлеровых предикатов [E{X)>n] и [E(X)<n].
ДОКАЗАТЕЛЬСТВО. Из рассуждений #5.8 следует, что предикат пси(X) должен быть функцией от E(X). Это непосредственно относится к ограничению абсолютной величины диаметра, что является частным случаем ограничения порядка. С соответствующими модификациями указанные рассуждения переносятся и на ограничения относительной величины диаметра. Рассмотрим две фигуры А и В, отличающиеся только одним внутренним квадратом:

Окружность на рисунке указывает диапазон ограничения диаметра. Допустим, что пси(X)=[СУММА альфа.фи*фи(X)>тета], и рассмотрим разность
ДЕЛЬТА = СУММА альфа.фи*фи(B) - СУММА альфа.фи*фи(A).
Если ДЕЛЬТА >= 0, то
пси(B) >= пси(A),
и потому устранение дыры не может уменьшить пси. В силу топологической эквивалентности добавление компоненты оказывает такое же воздействие на E(X), а потому и на пси(X). Таким образом, если ДЕЛЬТА>=0, то
E(B)>E(A) => пси(B)>=пси(A),
и аналогично, если ДЕЛЬТА<=0, то
E(B)>E(A) => пси(B)<=пси(A).
Отсюда следует, что всегда должно существовать такое n, что (если ДЕЛЬТА>=0)
пси(X)=[E(X)>n],
или (если ДЕЛЬТА<=0)
пси(X)=[E(X)<n],
или пси - константа.
Тривиальные исключения составляют постоянные предикаты и "однородные" предикаты из #8.1.1, которые являются исключениями по отношению к канонической форме #5.8.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 9. ГЕОМЕТРИЧЕСКИЕ ПРЕДИКАТЫ И ПОСЛЕДОВАТЕЛЬНЫЕ АЛГОРИТМЫ
#9.0. СВЯЗНОСТЬ И ПОСЛЕДОВАТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ
По-видимому, интуитивно ясно, что персептрон конечного порядка не может выявить связность по той причине, что ей внутренне присущи черты последовательной процедуры: никакое простое неупорядоченное сочетание простых испытаний не позволяет сделать вывод, что фигура связна. То же самое справедливо и для гораздо более простого свойства ЧЕТНОСТИ. В последнем случае следует указать на значительный контраст между "наихудшим" результатом, полученным для машин конечного порядка (#3.1, #10.1), и приведенным ниже "наилучшим" результатом для ПОСЛЕДОВАТЕЛЬНОГО вычисления четности. Пусть x.1, x.2, ..., x.n - любая нумерация точек сетчатки R. Рассмотрим следующий алгоритм определения четности числа |X|.
НАЧАЛО: Положить i=0.
ЧЕТ: Прибавить 1 к i.
Если i = |R|, то ОСТАНОВ; пси.ЧЕТНОСТЬ=0.
Если x.i=0, перейти к ЧЕТ, иначе перейти к НЕЧЕТ.
НЕЧЕТ: Прибавить 1 к i.
Если i = |R|, то ОСТАНОВ; пси.четность=1.
Если x.i=0, перейти к НЕЧЕТ, иначе перейти к ЧЕТ.
Итак, эта программа минимальна в двух отношениях: во-первых, по количеству вычислительных шагов на каждую точку, но что более существенно, программа не требует никакой памяти для хранения промежуточной информации, накапливаемой в процессе вычислений, кроме той, которая нужна для переменной i. (В некотором смысле этому процессу требуется одна двоичная единица текущей информации, но ее можно, как сделано выше, внести в структуру алгоритма).
Сказанное наводит на мысль, что в случае связности многое мог бы прояснить вопрос: какого объема память нужна для наилучшего последовательного алгоритма? Как показано ниже, ответ гласит, что потребуется не более чем удвоенный объем памяти, необходимой для запоминания самой переменной i. По-видимому, наиболее просто и естественно изучать эту задачу в рамках машины Тьюринга из-за того единообразия, с которым эта машина осуществляет накопление информации.
#9.1. ПОСЛЕДОВАТЕЛЬНЫЙ АЛГОРИТМ ПРОВЕРКИ СВЯЗНОСТИ
Связность геометрической фигуры X характеризуется тем, что любую пару (р, q) ее точек связывает путь, целиком лежащий в X. Дадим равносильное определение, в котором используется произвольная нумерация x.1, ..., x.|R| точек пространства R: ФИГУРА X СВЯЗНА, ЕСЛИ ОТ КАЖДОЙ ЕЕ ТОЧКИ x.i КРОМЕ ПЕРВОЙ, СУЩЕСТВУЕТ ПУТЬ К НЕКОТОРОЙ ДРУГОЙ ЕЕ ТОЧКЕ x.j, ПРИЧЕМ i>j. (Доказательство: очевидно, что каждая точка фигуры X связана с ПЕРВОЙ ее точкой). Используя это определение, можно описать красивый алгоритм проверки связности фигуры. Мы будем рассматривать только "достаточно регулярные" фигуры - точнее, мы предполагаем, что для каждой граничной точки x.i однозначно определена "следующая точка" x.i' на этой границе. Определим x.i' как граничную точку справа от x.i, если смотреть из x.i на дополнение к X. Будем предполагать, что ПОСЛЕДОВАТЕЛЬНЫЕ точки x.i и x.[i+i] являются СМЕЖНЫМИ всюду, за исключением краев пространства R. Наконец, будем рассматривать только те фигуры X, которые не касаются краев пространства R.
НАЧАЛО: Положить i=0 и перейти к ПОИСК.
ПОИСК: Прибавить 1 к i. Если i=|R|, остановиться и напечатать "X - пустая фигура".
Если x.i принадлежит X, перейти к ПРОСМОТР, иначе перейти к ПОИСК.
ПРОСМОТР: Прибавить 1 к i. Если i=|R|, остановиться и напечатать "X - связная фигура".
Если x.[i-1] не принадлежит X и x.i принадлежит к X, положить j=i и перейти к КРАЙ, иначе перейти к ПРОСМОТР.
КРАЙ: Положить j=j' (следующая точка для j).
Если j=i, остановиться и напечатать "X - несвязная фигура".
Если j>i, перейти к КРАЙ.
Если j<i, перейти к ПРОСМОТР.
Заметим, что на любой стадии вычислений достаточно хранить два целых числа i и j; мы увидим, что для запоминания величины |R| не потребуется никакой дополнительной памяти.
ПРОСМОТР завершается после обнаружения замкнутой петли при движении по подпрограмме КРАЙ вдоль границы внутренней компоненты.
АНАЛИЗ. ПОИСК попросту находит первую точку фигуры X среди пронумерованных точек пространства R. Как только такая точка найдена, просмотр пробегает по всем точкам пространства, проверяя таким образом каждую точку фигуры X. Это происходит следующим образом: если x.i не принадлежит X, то никакого испытания больше не требуется и ПРОСМОТР переходит к x.[i+l]. Если предыдущая точка x.[i-1] принадлежит X (и прошла проверку), то точка x.i, принадлежащая X, связана с x.[i-i] в силу их смежности. Наконец, если x.i принадлежит X и x.[i-1] не принадлежит X, то x.i - граничная точка, т.е. лежит на граничной кривой B. КРАЙ осуществляет обход вдоль этой граничной кривой. При этом возможны 3 случая: либо (1) B совпадает с внешней границей уже встречавшейся части фигуры X, и тогда некоторая точка, лежащая на В, должна была встретиться раньше, либо (2) B является внутренней границей и тогда некоторая ее точка должна была встретиться до точки x.[i-1] лежащей с ВНУТРЕННЕЙ стороны от В, либо (3) B совпадает с внешней границей еще не встречавшейся части фигуры X. Последний случай - единственный, когда КРАЙ вернется к x.i, не встретив точек x.j, для которых j<i. Поэтому ПРОСМОТР дойдет до i=|R| тогда и только тогда, когда X состоит из единственной непустой связной компоненты (рис.9.1).

Рис.9.1. a - граничные точки, считываемые подпрограммой КРАЙ; b - граничные точки, считываемые подпрограммой ПРОСМОТР.
#9.2. ВАРИАНТ АЛГОРИТМА ПРОВЕРКИ СВЯЗНОСТИ ДЛЯ МАШИНЫ ТЬЮРИНГА
Удобно принять, что R - квадратный массив размера 2**n*2**n. Пусть x.1, ..., x.|R| - точки этого массива, пронумерованные следующим образом:
1, 2**n+1, ... , (2**n-1)2**n+1,
2, 2**n+2, ... , (2**n-1)2**n+2,
...
2**n, 2**n+2**2n, ... , (2**n-1)2**n+2**n.
При таком выборе размеров и нумерации ситуацию можно легко представить в машине Тьюринга. Машина Тьюринга должна обладать способностью выделять точку x.i пространства R, выяснять, принадлежит ли она X, и если x.i - граничная точка фигуры X, находить индекс i' ее "правой соседки". Лента машины Тьюринга будет иметь вид

где ...n... обозначает промежуток, состоящий из n пустых квадратов. Тогда в промежутки справа от I.x и I.y можно поместить координаты x и y точки из R.
Будем считать, что машину Тьюринга с внешним миром, т.е. с фигурой X, соединяет "оракул", действующий по схеме: когда машина переходит в определенное внутреннее состояние, следующее результирующее состояние зависит от того, являются ли числа в I (или J) координатами точки фигуры X. Можно проверить, хотя детали весьма утомительны, что все описанные в алгоритме операции можно выполнить с помощью определенной машины Тьюринга, которая не использует никаких других квадратов ленты, кроме тех, что находятся в промежутках ...n... Например, i=|R| тогда и только тогда, когда промежутки ...n..., следующие за I.x и I.y, содержат одни нули. "Прибавить 1 к i" эквивалентно "начать в J.x и, передвигаясь влево, заменять единицы нулями до тех пор, пока не встретится (и не будет заменен единицей) нуль или пока не встретится I.y" [Такая операция сложения соответствует нумерации i=2**n(y-1)+x, а не i=2**n(x-1)+y, указанной в начале параграфа.- Прим. ред.]. Единственная нетривиальная операция - вычисление j' при заданном j. Но для этого нужно лишь обследовать точки, соседние с x.j, добавляя/вычитая 1 к J.x и J.y и учитывая указания оракула.
Так как машина Тьюринга может следить за тем, в каком из промежутков ...n... она находится, то фактически нам для пунктуации нужен только один символ, так что машина Тьюринга может быть трехсимвольной. Если использовать блочное кодирование, то машина может даже быть двухсимвольной, так что, опуская подробности, мы получаем следующий результат:
ТЕОРЕМА 9.2. При любом e существует двухсимвольная машина Тьюринга, которой для проверки связности фигуры X на любом прямоугольном массиве R требуется менее (2+e)log2|R| квадратов ленты.
Мы абсолютно уверены, что этот алгоритм проверки связности минимален в части использования им ленты, но доказательства у нас нет. (В самом деле, мы очень мало знаем о методах, с помощью которых можно показать, что некоторый алгоритм минимален по объему памяти; этот вопрос будет рассматриваться в гл.12.) Между прочим, нетрудно показать, что предикат [|X| - простое число] требует не более (2+e)log2|R| квадратов (и, предположительно, более (2-e)log2|R| квадратов).
Мы не знаем почти ничего определенного о геометрических предикатах, для которых требуется больший объем памяти, но подозреваем, что число ячеек памяти, необходимое для распознавания топологической эквивалентности двух фигур (например, двух компонент фигуры X) имеет порядок скорее |R|, а не log|R|. Разумеется, в теории функций существуют рекурсивные предикаты, требующие произвольно больших объемов памяти, но не известно, чтобы какой-нибудь из них поддавался прямой геометрической интерпретации.
#9.2.1. АВТОМАТЫ "С КАМЕШКОМ". Вариант этой модели вычислений изучали Блюм и Хьюитт. Машина Тьюринга заменяется здесь конечным автоматом, передвигающимся взад и вперед по сетчатке, считывая "черноту" той клетки, в которой он в данный момент находится. Автомат определяет свое следующее состояние и один из четырех возможных переходов (на север, восток, юг, запад) как функцию этого входного сигнала и своего текущего состояния. Правильно сконструированный автомат должен действовать на произвольной, сколь угодно большой сетчатке, при условии что задан способ обнаружения края массива. Подобный автомат следует признать весьма подходящим для воплощения идеи предикатной схемы.
Положение автомата на сетчатке играет роль ОДНОГО из двух напечатанных на ленте индексов I или J, запоминаемых машиной Тьюринга. Чтобы осуществить в машине запоминание второго индекса точки, ее можно снабдить камешком, который можно поместить в любом месте сетчатки, а потом забрать. Мы предлагаем читателям исключительно сложное самостоятельное упражнение: привести алгоритм машины Тьюринга к виду, пригодному для автомата с одним камешком. Можно ли распознать связность без помощи камешка? Конечно, нет, но доказательства мы не знаем.
#9.3. ТРЕБОВАНИЯ К ЛЕНТОЧНОЙ ПАМЯТИ В СЛУЧАЕ ПРЕДИКАТА пси.ВЫПУКЛОСТЬ
В случае предиката пси.ВЫПУКЛОСТЬ для объема ленточной памяти также можно установить границу. Однако в силу того, что выпуклость - метрическое свойство, необходимо рассмотреть проблему соответствия точности измерений и разрешающей способности конечной сетчатки R. По-видимому, разумно спросить: имеет ли фигура извилины, превышающие порядок размера квадрата сетчатки. Один из способов ответить на этот вопрос - проверить наличие таких извилин для каждой пары (a, b) граничных точек:
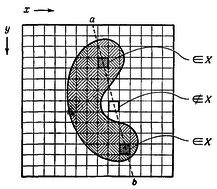
Для выполнения такой проверки требуется нечто эквивалентное просмотру всех квадратов, прилегающих к прямой, соединяющей a и b; кроме того, нужна некоторая память, чтобы оставаться в достаточной близости от задаваемого этой прямой наклона. Для каждого приращения, скажем величины y, необходимо вычислить и принять в качестве x наибольшее целое число, содержащееся в величине
a+y(b-a)/n,
a log2n разрядов остатка нужно сохранить для следующего шага вычислений. Поэтому можно выполнить вычисления, запоминая по log2n разрядов для каждого из чисел a, b, x, y и r, где
r(y)=(r(y-1)+b-a)%n,
который можно получить из регистра, содержащего x и r, прибавляя b-a на каждом шаге:

Таким образом, для проверки выпуклости достаточно примерно 5/2log2|R| квадратов. Избыточность здесь очевидна, поскольку, например, a можно получить, зная остальные 4 числа (b, x, y, r), а это наводит на мысль, что при некоторой изобретательности можно было бы обойтись всего лишь (2+e)log2|R| квадратами.
Что касается нижней границы, то у нас нет никаких идей по поводу того, как ее установить. Хотя выпуклость, будучи КОНЪЮНКТИВНО ЛОКАЛЬНОЙ, проще, чем связность, для машины Тьюринга, хорошо приспособленной для рекурсивных вычислений, это не является особым преимуществом, и вполне возможно, что указанная простота компенсируется сложностью вычислений, связанных с метрикой. Поэтому мы склонны считать, что для реализации как пси.ВЫПУКЛОСТЬ, так и пси.СВЯЗНОСТЬ в фoрме машин Тьюринга требуется порядка 2log2|R| квадратов ленты. Нашу неспособность найти достоверную нижнюю границу мы считаем еще одним признаком общей слабости тех средств современной теории вычислений, которые должны давать оценки минимальной вычислительной сложности конкретных алгоритмов.
#9.4. СВЯЗНОСТЬ И ПАРАЛЛЕЛЬНАЯ ТЕХНИКА
Мы уже видели, что существует машина Тьюринга, которой для вычисления предиката пси.СВЯЗНОСТЬ нужен небольшой объем вспомогательной ленточной памяти. Вычисление требует значительного времени, или числа рабочих шагов машины. Для "хороших" фигур этих шагов будет примерно |R|log|R| (для "плохих" фигур их может быть примерно |R|**2*log|R|). С другой стороны, для машины Тьюринга нужно необычайно мало физического оборудования, поскольку оно в ходе вычислений используется многократно.
Имея в распоряжении больше оборудования, можно, вероятно, уменьшить число рабочих шагов, но мы очень мало знаем о сущности таких замен. При реализации предиката пси.СВЯЗНОСТЬ можно сэкономить время, деля пространство на участки и вычисляя свойство связности одновременно на всех этих участках. Предположим, что у нас есть машины, которым для вычисления "матрицы связей" для точек пересечения границы фигуры с линиями деления пространства на участки требуется меньше времени, чем для вычисления предиката пси.СВЯЗНОСТЬ на всей сетчатке. Например, для фигуры
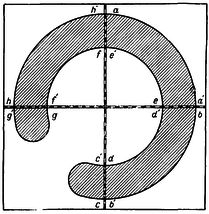
эта матрица дает информацию о связи точек a и a', b и b' и т.д. Заключение о связности всей фигуры можно получить с помощью алгоритма, "сшивающего" вместе эти края.
Если делить пространство на более мелкие участки, то вычисления внутри каждого участка проходят быстрее, но "сшивать" становится сложнее. С другой стороны, вполне вероятно, что к операции сшивания тоже можно рекурсивно применить разбиение, но возможных изменений мы еще не изучали. Мы можем установить интересную верхнюю границу для одного крайнего случая. Допустим, что машина составлена целиком из булевых функций двух аргументов. Сколько времени нужно такой машине, чтобы вычислить предикат пси.СВЯЗНОСТЬ, при условии что каждая булева операция занимает одну единицу времени?
Для удобства примем, что R содержит |R|=2**n квадратов (точек). Определенные пары точек предполагаются "смежными". Можно описать предикат пси.СВЯЗНОСТЬ, считая это отношение смежности цепным и используя компактное индуктивное определение (1):
С1.ij(X) = [x.i & x.j & (x.i смежна с x.j)]
и
С[m+1].ij(X) = V[k=1..|R|] (Сm.ik(X) & Сm.kj(X)).
Считается, что каждая точка x.i связана сама с собой, так что С1.ii=[x.i принадлежит X]. Тогда по индукции можно показать, что предикат Cm.ij(X) истинен тогда и только тогда, когда x.i и x.j, связаны цепью, состоящей не более чем из 2**m смежных точек, причем все они принадлежат X. Вся фигура связна, т.е. пси.СВЯЗНОСТЬ(X)=1 если Cn.ij(X)=1 для каждой пары, в которой x.i принадлежит X и x.j принадлежит X. Следовательно (2),
пси.СВЯЗНОСТЬ = [x.i & x.j => Cn.ij(X)] = &[i=1..|R|] &[k=1..|R|] [~x.i V ~x.j V Cn.ij(X)].
Такую функцию можно осуществить в машине, имеющей отдельный слой для каждого уровня предикатов Cm.ij. Чтобы связать предикаты C[m+1].ij(X) с соответствующими предикатами Cm.ij(X) требуется, согласно (1), осуществить логическое сложение |R| членов, а для этого необходимо дерево из элементов ИЛИ, содержащее не более n=log2|R| каскадов в глубину.
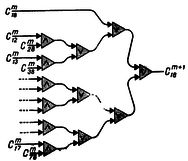
Поскольку таких слоев n (в каждом из них n каскадов), общее время вычисления Cn.ij будет порядка n**2. Согласно соотношению (2), комбинационная схема, реализующая выход системы, потребует еще около 2n слоев, поэтому
ВРЕМЯ(пси.СВЯЗНОСТЬ) <= (lоg|R|)**2 + k*log|R|,
где k - малая константа [Это построение предложили нам Р.Флойд и А.Мейер].
Мы сомневаемся в том, чтобы вычисления можно было провести намного меньше, чем за (log|R|)**2 шагов, как бы ни были расположены и каким бы способом ни были упорядочены составные части вычислительной машины. Заметьте, что мы предусмотрительно учли задержку, вызываемую операцией ИЛИ. Если этим пренебречь, то для вычислений потребуется только log|R| шагов, но для больших |R| это физически нереально. В самом деле, мы должны были бы запретить беспредельное "ветвление", или размножение, ВЫХОДОВ элементов; если принимать во внимание усилители, физически необходимые для этих целей, то вместо нашей оценки мы должны были бы взять 3(log|R|)**2. Как обычно, у нас нет надежного метода для установления нижней границы. Однако представляется уместным следующее псевдодоказательство:
1. ИСПОЛЬЗОВАНИЕ БОЛЬШЕГО ОБЪЕМА "ПАМЯТИ", ПО-ВИДИМОМУ, НЕ ПОМОГАЕТ. Может ли машина повысить скорость за счет запоминания библиотеки связных фигур и их идентификации вместо того, чтобы вырабатывать всякий раз определение связности? В пределе: построить библиотеку ВСЕХ связных фигур на сетчатке R. Можно построить дерево двоичных булевых операторов, позволяющее определять соответствие любому образу как раз за log|R| шагов. Это в значительной степени ускоряет работу аналога приведенной выше части 1 [По-видимому, имеется в виду часть машины, реализующая соотношение (1).- Прим. ред.]. Но существует так много различных связных фигур, что теперь нужно объединить операцией ИЛИ около 2**(тета*|R|) членов (где тета - некоторая дробь 2/3<=тета<=1), так что работа аналога части 2 потребует log(2**(тета*|R|))=тета*|R| шагов, что для больших сетчаток R гораздо хуже, чем (log|R|)**2. Это, конечно, не доказательство, но оно весьма симптоматично.
2. ИСПОЛЬЗОВАНИЕ ПЕТЕЛЬ ТИПА ОБРАТНОЙ СВЯЗИ НЕ МОЖЕТ ПОВЫСИТЬ СКОРОСТЬ. Машина с временем работы порядка (log|R|)**2 представляет собой иерархию булевых функций без петель: она не обладает иной способностью вычислять "последовательно", кроме той, которая заключена в ее слоистом строении.
Можно было бы значительно уменьшить количество ее частей (а их всего порядка |R|**3*log|R}), строя схему с замкнутыми контурами: фактически мы могли бы построить машину Тьюринга, содержащую только k*log|R| частей при некотором умеренном k. Однако для заданных вычислений ограниченной длины самая быстродействующая машина с замкнутыми контурами НЕ МОЖЕТ работать быстрее, чем самая быстродействующая машина без петель (если пренебречь стоимостью ветвления), так как всегда можно построить эквивалентную машину без петель, размножая первоначальную (по экземпляру на каждый шаг вычислений), причем аргументы всех функций берутся из предыдущих экземпляров.

3. СХЕМУ МАТРИЦЫ СВЯЗЕЙ, ПО-ВИДИМОМУ, ТРУДНО УСОВЕРШЕНСТВОВАТЬ. Существуют фигуры, в которых непересекающиеся пути имеют длину порядка |R|. По всей видимости, для любой процедуры распознавания (связности.- Ред.), использующей функции двух аргументов, требуется по крайней мере log|R| шагов, так как трудно сделать что-либо лучшее, чем удваивать длину пути на каждом шаге, как это делает наш метод матрицы связей C.ij. На каждом таком шаге должно оказаться порядка |R| возможных связей, которые должны быть объединены операцией ИЛИ. Вероятно, можно было бы завершить доказательство, показав, что откладывание "на потом" этих операций или (чтобы каждой из них требовалось log|R| логических уровней [В оригинале logic levels.- Прим. перев.]) не дает никакого выигрыша во времени.
#9.5. СВЯЗНОСТЬ В ИТЕРАТИВНЫХ МАССИВАХ
Т.Бейер выполнила исследование времени, необходимого для вычисления предиката пси.СВЯЗНОСТЬ с помoщью иной и, быть может, более естественной модели параллельных геометрических процедур. Допустим, что в каждом квадрате сетчатки находится автомат, связанный только с четырьмя своими соседями. Он также может сообщать о состоянии своего квадрата (черный или белый). Окончательное решение о связности фигуры должно выноситься некоторым фиксированным автоматом, скажем, тем, который расположен в верхнем левом углу. Предполагая, что состояния сетчатки меняются только в фиксированные промежутки времени, зададим вопрос: сколько единиц времени должно пройти до принятия окончательного решения? Очевидно, что на сетчатке размера n*n это потребует по меньшей мере 2n единиц времени, так как столько времени занимает продвижение любой информации от нижнего правого угла к верхнему левому. Не представляет труда сконструировать массивы автоматов, которые вынесут решение за время порядка n**2 (т.е. |R|) единиц. Замечательный результат Бейер состоит в том, что достаточно (2+е)sqr|R| единиц, где e можно выбрать как угодно малым, если число состояний автомата достаточно велико.
Таким образом, порядок величины времени, затрачиваемого массивом, пропорционален sqr|R|, что (естественно) находится в промежутке между временем, необходимым для одной последовательной машины (|R|), и временем, требуемым параллельной машиной, построенной без ограничений, которая, как известно, тратит не более (log|R|)**2 единиц времени.
Дальнейшее служит образной иллюстрацией (неопубликованного) алгоритмического процесса, предложенного Т.Бейер. Его действие заключается в том, что какая-нибудь компонента вписывается, как показано ниже, в треугольник, который затем медленно сжимается в северо-западном направлении за счет передвижения гипотенузы внутрь треугольника.
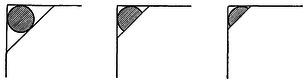
Каждая компонента, перед тем как исчезнуть, сжимается в одну изолированную точку. Всякий раз, когда происходит такое событие, его можно локально распознать и передать информацию о нем через элементы схемы в угол. Таким образом, выбор положительного или отрицательного решения о связности зависит от того, встречается такое событие один раз или больше. Процесс сжатия, если описать его подробнее, начинается с нахождения всех "юго-восточных" углов фигуры

Центральный квадрат служит ЮВ углом, если квадраты Юг и Восток белые. Все остальные квадраты на рисунке могут быть либо черными, либо белыми.
Операция сжатия Т удаляет каждый ЮВ угол и, если необходимо сохранить связность, вводит взамен
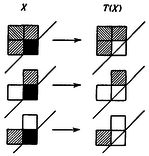
новый квадрат

так как переход к конфигурации

нарушил бы связность.
Диагональные линии показывают, каким образом при неоднократном повторении этого локального процесса фигура сжимается в северо-западном направлении.
Повторные применения операции Т в конечном счете сводят каждую компоненту в одну-единственную точку. На примере фигуры

видно, как (узконаправленно, зато эффективно) эта операция избегает соединения двух компонент.
Ясно, что компонента, расположенная внутри дыры, исчезнет (и будет учтена) как раз вовремя, чтобы позволить окружающей ее компоненте сжаться полностью. Эквивалентный процесс в трех измерениях мы не знаем. (Необходимо принимать во внимание узлы!)
#9.0. СВЯЗНОСТЬ И ПОСЛЕДОВАТЕЛЬНЫЕ ВЫЧИСЛЕНИЯ
По-видимому, интуитивно ясно, что персептрон конечного порядка не может выявить связность по той причине, что ей внутренне присущи черты последовательной процедуры: никакое простое неупорядоченное сочетание простых испытаний не позволяет сделать вывод, что фигура связна. То же самое справедливо и для гораздо более простого свойства ЧЕТНОСТИ. В последнем случае следует указать на значительный контраст между "наихудшим" результатом, полученным для машин конечного порядка (#3.1, #10.1), и приведенным ниже "наилучшим" результатом для ПОСЛЕДОВАТЕЛЬНОГО вычисления четности. Пусть x.1, x.2, ..., x.n - любая нумерация точек сетчатки R. Рассмотрим следующий алгоритм определения четности числа |X|.
НАЧАЛО: Положить i=0.
ЧЕТ: Прибавить 1 к i.
Если i = |R|, то ОСТАНОВ; пси.ЧЕТНОСТЬ=0.
Если x.i=0, перейти к ЧЕТ, иначе перейти к НЕЧЕТ.
НЕЧЕТ: Прибавить 1 к i.
Если i = |R|, то ОСТАНОВ; пси.четность=1.
Если x.i=0, перейти к НЕЧЕТ, иначе перейти к ЧЕТ.
Итак, эта программа минимальна в двух отношениях: во-первых, по количеству вычислительных шагов на каждую точку, но что более существенно, программа не требует никакой памяти для хранения промежуточной информации, накапливаемой в процессе вычислений, кроме той, которая нужна для переменной i. (В некотором смысле этому процессу требуется одна двоичная единица текущей информации, но ее можно, как сделано выше, внести в структуру алгоритма).
Сказанное наводит на мысль, что в случае связности многое мог бы прояснить вопрос: какого объема память нужна для наилучшего последовательного алгоритма? Как показано ниже, ответ гласит, что потребуется не более чем удвоенный объем памяти, необходимой для запоминания самой переменной i. По-видимому, наиболее просто и естественно изучать эту задачу в рамках машины Тьюринга из-за того единообразия, с которым эта машина осуществляет накопление информации.
#9.1. ПОСЛЕДОВАТЕЛЬНЫЙ АЛГОРИТМ ПРОВЕРКИ СВЯЗНОСТИ
Связность геометрической фигуры X характеризуется тем, что любую пару (р, q) ее точек связывает путь, целиком лежащий в X. Дадим равносильное определение, в котором используется произвольная нумерация x.1, ..., x.|R| точек пространства R: ФИГУРА X СВЯЗНА, ЕСЛИ ОТ КАЖДОЙ ЕЕ ТОЧКИ x.i КРОМЕ ПЕРВОЙ, СУЩЕСТВУЕТ ПУТЬ К НЕКОТОРОЙ ДРУГОЙ ЕЕ ТОЧКЕ x.j, ПРИЧЕМ i>j. (Доказательство: очевидно, что каждая точка фигуры X связана с ПЕРВОЙ ее точкой). Используя это определение, можно описать красивый алгоритм проверки связности фигуры. Мы будем рассматривать только "достаточно регулярные" фигуры - точнее, мы предполагаем, что для каждой граничной точки x.i однозначно определена "следующая точка" x.i' на этой границе. Определим x.i' как граничную точку справа от x.i, если смотреть из x.i на дополнение к X. Будем предполагать, что ПОСЛЕДОВАТЕЛЬНЫЕ точки x.i и x.[i+i] являются СМЕЖНЫМИ всюду, за исключением краев пространства R. Наконец, будем рассматривать только те фигуры X, которые не касаются краев пространства R.
НАЧАЛО: Положить i=0 и перейти к ПОИСК.
ПОИСК: Прибавить 1 к i. Если i=|R|, остановиться и напечатать "X - пустая фигура".
Если x.i принадлежит X, перейти к ПРОСМОТР, иначе перейти к ПОИСК.
ПРОСМОТР: Прибавить 1 к i. Если i=|R|, остановиться и напечатать "X - связная фигура".
Если x.[i-1] не принадлежит X и x.i принадлежит к X, положить j=i и перейти к КРАЙ, иначе перейти к ПРОСМОТР.
КРАЙ: Положить j=j' (следующая точка для j).
Если j=i, остановиться и напечатать "X - несвязная фигура".
Если j>i, перейти к КРАЙ.
Если j<i, перейти к ПРОСМОТР.
Заметим, что на любой стадии вычислений достаточно хранить два целых числа i и j; мы увидим, что для запоминания величины |R| не потребуется никакой дополнительной памяти.

ПРОСМОТР завершается после обнаружения замкнутой петли при движении по подпрограмме КРАЙ вдоль границы внутренней компоненты.
АНАЛИЗ. ПОИСК попросту находит первую точку фигуры X среди пронумерованных точек пространства R. Как только такая точка найдена, просмотр пробегает по всем точкам пространства, проверяя таким образом каждую точку фигуры X. Это происходит следующим образом: если x.i не принадлежит X, то никакого испытания больше не требуется и ПРОСМОТР переходит к x.[i+l]. Если предыдущая точка x.[i-1] принадлежит X (и прошла проверку), то точка x.i, принадлежащая X, связана с x.[i-i] в силу их смежности. Наконец, если x.i принадлежит X и x.[i-1] не принадлежит X, то x.i - граничная точка, т.е. лежит на граничной кривой B. КРАЙ осуществляет обход вдоль этой граничной кривой. При этом возможны 3 случая: либо (1) B совпадает с внешней границей уже встречавшейся части фигуры X, и тогда некоторая точка, лежащая на В, должна была встретиться раньше, либо (2) B является внутренней границей и тогда некоторая ее точка должна была встретиться до точки x.[i-1] лежащей с ВНУТРЕННЕЙ стороны от В, либо (3) B совпадает с внешней границей еще не встречавшейся части фигуры X. Последний случай - единственный, когда КРАЙ вернется к x.i, не встретив точек x.j, для которых j<i. Поэтому ПРОСМОТР дойдет до i=|R| тогда и только тогда, когда X состоит из единственной непустой связной компоненты (рис.9.1).

Рис.9.1. a - граничные точки, считываемые подпрограммой КРАЙ; b - граничные точки, считываемые подпрограммой ПРОСМОТР.
#9.2. ВАРИАНТ АЛГОРИТМА ПРОВЕРКИ СВЯЗНОСТИ ДЛЯ МАШИНЫ ТЬЮРИНГА
Удобно принять, что R - квадратный массив размера 2**n*2**n. Пусть x.1, ..., x.|R| - точки этого массива, пронумерованные следующим образом:
1, 2**n+1, ... , (2**n-1)2**n+1,
2, 2**n+2, ... , (2**n-1)2**n+2,
...
2**n, 2**n+2**2n, ... , (2**n-1)2**n+2**n.
При таком выборе размеров и нумерации ситуацию можно легко представить в машине Тьюринга. Машина Тьюринга должна обладать способностью выделять точку x.i пространства R, выяснять, принадлежит ли она X, и если x.i - граничная точка фигуры X, находить индекс i' ее "правой соседки". Лента машины Тьюринга будет иметь вид

где ...n... обозначает промежуток, состоящий из n пустых квадратов. Тогда в промежутки справа от I.x и I.y можно поместить координаты x и y точки из R.
Будем считать, что машину Тьюринга с внешним миром, т.е. с фигурой X, соединяет "оракул", действующий по схеме: когда машина переходит в определенное внутреннее состояние, следующее результирующее состояние зависит от того, являются ли числа в I (или J) координатами точки фигуры X. Можно проверить, хотя детали весьма утомительны, что все описанные в алгоритме операции можно выполнить с помощью определенной машины Тьюринга, которая не использует никаких других квадратов ленты, кроме тех, что находятся в промежутках ...n... Например, i=|R| тогда и только тогда, когда промежутки ...n..., следующие за I.x и I.y, содержат одни нули. "Прибавить 1 к i" эквивалентно "начать в J.x и, передвигаясь влево, заменять единицы нулями до тех пор, пока не встретится (и не будет заменен единицей) нуль или пока не встретится I.y" [Такая операция сложения соответствует нумерации i=2**n(y-1)+x, а не i=2**n(x-1)+y, указанной в начале параграфа.- Прим. ред.]. Единственная нетривиальная операция - вычисление j' при заданном j. Но для этого нужно лишь обследовать точки, соседние с x.j, добавляя/вычитая 1 к J.x и J.y и учитывая указания оракула.
Так как машина Тьюринга может следить за тем, в каком из промежутков ...n... она находится, то фактически нам для пунктуации нужен только один символ, так что машина Тьюринга может быть трехсимвольной. Если использовать блочное кодирование, то машина может даже быть двухсимвольной, так что, опуская подробности, мы получаем следующий результат:
ТЕОРЕМА 9.2. При любом e существует двухсимвольная машина Тьюринга, которой для проверки связности фигуры X на любом прямоугольном массиве R требуется менее (2+e)log2|R| квадратов ленты.
Мы абсолютно уверены, что этот алгоритм проверки связности минимален в части использования им ленты, но доказательства у нас нет. (В самом деле, мы очень мало знаем о методах, с помощью которых можно показать, что некоторый алгоритм минимален по объему памяти; этот вопрос будет рассматриваться в гл.12.) Между прочим, нетрудно показать, что предикат [|X| - простое число] требует не более (2+e)log2|R| квадратов (и, предположительно, более (2-e)log2|R| квадратов).
Мы не знаем почти ничего определенного о геометрических предикатах, для которых требуется больший объем памяти, но подозреваем, что число ячеек памяти, необходимое для распознавания топологической эквивалентности двух фигур (например, двух компонент фигуры X) имеет порядок скорее |R|, а не log|R|. Разумеется, в теории функций существуют рекурсивные предикаты, требующие произвольно больших объемов памяти, но не известно, чтобы какой-нибудь из них поддавался прямой геометрической интерпретации.
#9.2.1. АВТОМАТЫ "С КАМЕШКОМ". Вариант этой модели вычислений изучали Блюм и Хьюитт. Машина Тьюринга заменяется здесь конечным автоматом, передвигающимся взад и вперед по сетчатке, считывая "черноту" той клетки, в которой он в данный момент находится. Автомат определяет свое следующее состояние и один из четырех возможных переходов (на север, восток, юг, запад) как функцию этого входного сигнала и своего текущего состояния. Правильно сконструированный автомат должен действовать на произвольной, сколь угодно большой сетчатке, при условии что задан способ обнаружения края массива. Подобный автомат следует признать весьма подходящим для воплощения идеи предикатной схемы.
Положение автомата на сетчатке играет роль ОДНОГО из двух напечатанных на ленте индексов I или J, запоминаемых машиной Тьюринга. Чтобы осуществить в машине запоминание второго индекса точки, ее можно снабдить камешком, который можно поместить в любом месте сетчатки, а потом забрать. Мы предлагаем читателям исключительно сложное самостоятельное упражнение: привести алгоритм машины Тьюринга к виду, пригодному для автомата с одним камешком. Можно ли распознать связность без помощи камешка? Конечно, нет, но доказательства мы не знаем.
#9.3. ТРЕБОВАНИЯ К ЛЕНТОЧНОЙ ПАМЯТИ В СЛУЧАЕ ПРЕДИКАТА пси.ВЫПУКЛОСТЬ
В случае предиката пси.ВЫПУКЛОСТЬ для объема ленточной памяти также можно установить границу. Однако в силу того, что выпуклость - метрическое свойство, необходимо рассмотреть проблему соответствия точности измерений и разрешающей способности конечной сетчатки R. По-видимому, разумно спросить: имеет ли фигура извилины, превышающие порядок размера квадрата сетчатки. Один из способов ответить на этот вопрос - проверить наличие таких извилин для каждой пары (a, b) граничных точек:

Для выполнения такой проверки требуется нечто эквивалентное просмотру всех квадратов, прилегающих к прямой, соединяющей a и b; кроме того, нужна некоторая память, чтобы оставаться в достаточной близости от задаваемого этой прямой наклона. Для каждого приращения, скажем величины y, необходимо вычислить и принять в качестве x наибольшее целое число, содержащееся в величине
a+y(b-a)/n,
a log2n разрядов остатка нужно сохранить для следующего шага вычислений. Поэтому можно выполнить вычисления, запоминая по log2n разрядов для каждого из чисел a, b, x, y и r, где
r(y)=(r(y-1)+b-a)%n,
который можно получить из регистра, содержащего x и r, прибавляя b-a на каждом шаге:

Таким образом, для проверки выпуклости достаточно примерно 5/2log2|R| квадратов. Избыточность здесь очевидна, поскольку, например, a можно получить, зная остальные 4 числа (b, x, y, r), а это наводит на мысль, что при некоторой изобретательности можно было бы обойтись всего лишь (2+e)log2|R| квадратами.
Что касается нижней границы, то у нас нет никаких идей по поводу того, как ее установить. Хотя выпуклость, будучи КОНЪЮНКТИВНО ЛОКАЛЬНОЙ, проще, чем связность, для машины Тьюринга, хорошо приспособленной для рекурсивных вычислений, это не является особым преимуществом, и вполне возможно, что указанная простота компенсируется сложностью вычислений, связанных с метрикой. Поэтому мы склонны считать, что для реализации как пси.ВЫПУКЛОСТЬ, так и пси.СВЯЗНОСТЬ в фoрме машин Тьюринга требуется порядка 2log2|R| квадратов ленты. Нашу неспособность найти достоверную нижнюю границу мы считаем еще одним признаком общей слабости тех средств современной теории вычислений, которые должны давать оценки минимальной вычислительной сложности конкретных алгоритмов.
#9.4. СВЯЗНОСТЬ И ПАРАЛЛЕЛЬНАЯ ТЕХНИКА
Мы уже видели, что существует машина Тьюринга, которой для вычисления предиката пси.СВЯЗНОСТЬ нужен небольшой объем вспомогательной ленточной памяти. Вычисление требует значительного времени, или числа рабочих шагов машины. Для "хороших" фигур этих шагов будет примерно |R|log|R| (для "плохих" фигур их может быть примерно |R|**2*log|R|). С другой стороны, для машины Тьюринга нужно необычайно мало физического оборудования, поскольку оно в ходе вычислений используется многократно.
Имея в распоряжении больше оборудования, можно, вероятно, уменьшить число рабочих шагов, но мы очень мало знаем о сущности таких замен. При реализации предиката пси.СВЯЗНОСТЬ можно сэкономить время, деля пространство на участки и вычисляя свойство связности одновременно на всех этих участках. Предположим, что у нас есть машины, которым для вычисления "матрицы связей" для точек пересечения границы фигуры с линиями деления пространства на участки требуется меньше времени, чем для вычисления предиката пси.СВЯЗНОСТЬ на всей сетчатке. Например, для фигуры

эта матрица дает информацию о связи точек a и a', b и b' и т.д. Заключение о связности всей фигуры можно получить с помощью алгоритма, "сшивающего" вместе эти края.
Если делить пространство на более мелкие участки, то вычисления внутри каждого участка проходят быстрее, но "сшивать" становится сложнее. С другой стороны, вполне вероятно, что к операции сшивания тоже можно рекурсивно применить разбиение, но возможных изменений мы еще не изучали. Мы можем установить интересную верхнюю границу для одного крайнего случая. Допустим, что машина составлена целиком из булевых функций двух аргументов. Сколько времени нужно такой машине, чтобы вычислить предикат пси.СВЯЗНОСТЬ, при условии что каждая булева операция занимает одну единицу времени?
Для удобства примем, что R содержит |R|=2**n квадратов (точек). Определенные пары точек предполагаются "смежными". Можно описать предикат пси.СВЯЗНОСТЬ, считая это отношение смежности цепным и используя компактное индуктивное определение (1):
С1.ij(X) = [x.i & x.j & (x.i смежна с x.j)]
и
С[m+1].ij(X) = V[k=1..|R|] (Сm.ik(X) & Сm.kj(X)).
Считается, что каждая точка x.i связана сама с собой, так что С1.ii=[x.i принадлежит X]. Тогда по индукции можно показать, что предикат Cm.ij(X) истинен тогда и только тогда, когда x.i и x.j, связаны цепью, состоящей не более чем из 2**m смежных точек, причем все они принадлежат X. Вся фигура связна, т.е. пси.СВЯЗНОСТЬ(X)=1 если Cn.ij(X)=1 для каждой пары, в которой x.i принадлежит X и x.j принадлежит X. Следовательно (2),
пси.СВЯЗНОСТЬ = [x.i & x.j => Cn.ij(X)] = &[i=1..|R|] &[k=1..|R|] [~x.i V ~x.j V Cn.ij(X)].
Такую функцию можно осуществить в машине, имеющей отдельный слой для каждого уровня предикатов Cm.ij. Чтобы связать предикаты C[m+1].ij(X) с соответствующими предикатами Cm.ij(X) требуется, согласно (1), осуществить логическое сложение |R| членов, а для этого необходимо дерево из элементов ИЛИ, содержащее не более n=log2|R| каскадов в глубину.

Поскольку таких слоев n (в каждом из них n каскадов), общее время вычисления Cn.ij будет порядка n**2. Согласно соотношению (2), комбинационная схема, реализующая выход системы, потребует еще около 2n слоев, поэтому
ВРЕМЯ(пси.СВЯЗНОСТЬ) <= (lоg|R|)**2 + k*log|R|,
где k - малая константа [Это построение предложили нам Р.Флойд и А.Мейер].
Мы сомневаемся в том, чтобы вычисления можно было провести намного меньше, чем за (log|R|)**2 шагов, как бы ни были расположены и каким бы способом ни были упорядочены составные части вычислительной машины. Заметьте, что мы предусмотрительно учли задержку, вызываемую операцией ИЛИ. Если этим пренебречь, то для вычислений потребуется только log|R| шагов, но для больших |R| это физически нереально. В самом деле, мы должны были бы запретить беспредельное "ветвление", или размножение, ВЫХОДОВ элементов; если принимать во внимание усилители, физически необходимые для этих целей, то вместо нашей оценки мы должны были бы взять 3(log|R|)**2. Как обычно, у нас нет надежного метода для установления нижней границы. Однако представляется уместным следующее псевдодоказательство:
1. ИСПОЛЬЗОВАНИЕ БОЛЬШЕГО ОБЪЕМА "ПАМЯТИ", ПО-ВИДИМОМУ, НЕ ПОМОГАЕТ. Может ли машина повысить скорость за счет запоминания библиотеки связных фигур и их идентификации вместо того, чтобы вырабатывать всякий раз определение связности? В пределе: построить библиотеку ВСЕХ связных фигур на сетчатке R. Можно построить дерево двоичных булевых операторов, позволяющее определять соответствие любому образу как раз за log|R| шагов. Это в значительной степени ускоряет работу аналога приведенной выше части 1 [По-видимому, имеется в виду часть машины, реализующая соотношение (1).- Прим. ред.]. Но существует так много различных связных фигур, что теперь нужно объединить операцией ИЛИ около 2**(тета*|R|) членов (где тета - некоторая дробь 2/3<=тета<=1), так что работа аналога части 2 потребует log(2**(тета*|R|))=тета*|R| шагов, что для больших сетчаток R гораздо хуже, чем (log|R|)**2. Это, конечно, не доказательство, но оно весьма симптоматично.
2. ИСПОЛЬЗОВАНИЕ ПЕТЕЛЬ ТИПА ОБРАТНОЙ СВЯЗИ НЕ МОЖЕТ ПОВЫСИТЬ СКОРОСТЬ. Машина с временем работы порядка (log|R|)**2 представляет собой иерархию булевых функций без петель: она не обладает иной способностью вычислять "последовательно", кроме той, которая заключена в ее слоистом строении.
Можно было бы значительно уменьшить количество ее частей (а их всего порядка |R|**3*log|R}), строя схему с замкнутыми контурами: фактически мы могли бы построить машину Тьюринга, содержащую только k*log|R| частей при некотором умеренном k. Однако для заданных вычислений ограниченной длины самая быстродействующая машина с замкнутыми контурами НЕ МОЖЕТ работать быстрее, чем самая быстродействующая машина без петель (если пренебречь стоимостью ветвления), так как всегда можно построить эквивалентную машину без петель, размножая первоначальную (по экземпляру на каждый шаг вычислений), причем аргументы всех функций берутся из предыдущих экземпляров.

3. СХЕМУ МАТРИЦЫ СВЯЗЕЙ, ПО-ВИДИМОМУ, ТРУДНО УСОВЕРШЕНСТВОВАТЬ. Существуют фигуры, в которых непересекающиеся пути имеют длину порядка |R|. По всей видимости, для любой процедуры распознавания (связности.- Ред.), использующей функции двух аргументов, требуется по крайней мере log|R| шагов, так как трудно сделать что-либо лучшее, чем удваивать длину пути на каждом шаге, как это делает наш метод матрицы связей C.ij. На каждом таком шаге должно оказаться порядка |R| возможных связей, которые должны быть объединены операцией ИЛИ. Вероятно, можно было бы завершить доказательство, показав, что откладывание "на потом" этих операций или (чтобы каждой из них требовалось log|R| логических уровней [В оригинале logic levels.- Прим. перев.]) не дает никакого выигрыша во времени.
#9.5. СВЯЗНОСТЬ В ИТЕРАТИВНЫХ МАССИВАХ
Т.Бейер выполнила исследование времени, необходимого для вычисления предиката пси.СВЯЗНОСТЬ с помoщью иной и, быть может, более естественной модели параллельных геометрических процедур. Допустим, что в каждом квадрате сетчатки находится автомат, связанный только с четырьмя своими соседями. Он также может сообщать о состоянии своего квадрата (черный или белый). Окончательное решение о связности фигуры должно выноситься некоторым фиксированным автоматом, скажем, тем, который расположен в верхнем левом углу. Предполагая, что состояния сетчатки меняются только в фиксированные промежутки времени, зададим вопрос: сколько единиц времени должно пройти до принятия окончательного решения? Очевидно, что на сетчатке размера n*n это потребует по меньшей мере 2n единиц времени, так как столько времени занимает продвижение любой информации от нижнего правого угла к верхнему левому. Не представляет труда сконструировать массивы автоматов, которые вынесут решение за время порядка n**2 (т.е. |R|) единиц. Замечательный результат Бейер состоит в том, что достаточно (2+е)sqr|R| единиц, где e можно выбрать как угодно малым, если число состояний автомата достаточно велико.
Таким образом, порядок величины времени, затрачиваемого массивом, пропорционален sqr|R|, что (естественно) находится в промежутке между временем, необходимым для одной последовательной машины (|R|), и временем, требуемым параллельной машиной, построенной без ограничений, которая, как известно, тратит не более (log|R|)**2 единиц времени.
Дальнейшее служит образной иллюстрацией (неопубликованного) алгоритмического процесса, предложенного Т.Бейер. Его действие заключается в том, что какая-нибудь компонента вписывается, как показано ниже, в треугольник, который затем медленно сжимается в северо-западном направлении за счет передвижения гипотенузы внутрь треугольника.

Каждая компонента, перед тем как исчезнуть, сжимается в одну изолированную точку. Всякий раз, когда происходит такое событие, его можно локально распознать и передать информацию о нем через элементы схемы в угол. Таким образом, выбор положительного или отрицательного решения о связности зависит от того, встречается такое событие один раз или больше. Процесс сжатия, если описать его подробнее, начинается с нахождения всех "юго-восточных" углов фигуры

Центральный квадрат служит ЮВ углом, если квадраты Юг и Восток белые. Все остальные квадраты на рисунке могут быть либо черными, либо белыми.
Операция сжатия Т удаляет каждый ЮВ угол и, если необходимо сохранить связность, вводит взамен

новый квадрат

так как переход к конфигурации

нарушил бы связность.
Диагональные линии показывают, каким образом при неоднократном повторении этого локального процесса фигура сжимается в северо-западном направлении.
Повторные применения операции Т в конечном счете сводят каждую компоненту в одну-единственную точку. На примере фигуры

видно, как (узконаправленно, зато эффективно) эта операция избегает соединения двух компонент.
Ясно, что компонента, расположенная внутри дыры, исчезнет (и будет учтена) как раз вовремя, чтобы позволить окружающей ее компоненте сжаться полностью. Эквивалентный процесс в трех измерениях мы не знаем. (Необходимо принимать во внимание узлы!)
Последний раз редактировалось: Gudleifr (Ср Июл 19, 2023 11:25 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
III. ТЕОРИЯ ОБУЧЕНИЯ
ПРЕДИСЛОВИЕ К ЧАСТИ III
В заключительных главах нашей книги исследуются темы, которые на языке кибернетиков объединяются под общим названием "обучение". До сих пор линейные представления рассматривались вне всякой связи со временем. Сейчас нас интересует вопрос, как их вычислять, сколько нужно для этого времени, как велики они и насколько эффективны как средство хранения информации В гл.10 мы покажем, что коэффициенты персептрона могут расти значительно быстрее, чем показательная функция от |R|. Этот вывод имеет серьезные последствия, как практические, так и принципиальные: для запоминания коэффициентов нужна память большая, чем для записи всех изображений. Это ломает представление о том, что такая машина способна в некотором смысле абстрагировать.
В гл.11 объясняется замечательная ТЕОРЕМА О СХОДИМОСТИ ПЕРСЕПТРОНА и показывается ее связь с известными явлениями из области конечных автоматов, теории оптимизации и использования обратной связи в качестве средства для вычислений.
В гл.12 мы отказываемся от строгого определения персептрона, что дает возможность изучать более обширное семейство алгоритмов, основанных на использовании локальных частных предикатов. Эти алгоритмы включают методы (типа байесовских решений), используемые статистиками, а также понятия (как, например, смешанное кодирование), известные только программистам. Цель гл.12 - очертить область вычислительной техники, охватывающую эти явно разнородные процессы. Мы специально подчеркиваем необходимость такой теории, для чего выбираем просто формулируемую, но нерешенную задачу о более прямых, чем обычно пропагандируемые, способах хранения и поиска информации.
ГЛАВА 10. ВЕЛИЧИНА КОЭФФИЦИЕНТОВ
#10.1. КОЭФФИЦИЕНТЫ ПРЕДИКАТА, ОПРЕДЕЛЯЮЩЕГО ЧЕТНОСТЬ
В #3.1 мы рассмотрели предикат пси.ЧETH0CTb(X)=[|X|-нечетное число] и показали, что если ФИ - множество масок, то любое выражение предиката пси.ЧETH0CTb, принадлежащее L(ФИ), должно содержать все маски. Вот одно из таких выражений
пси.ЧETH0CTb(X) = [СУММА (-2)**|S(фи)| * фи(X) < -1],
содержащее все маски множества ФИ, причем коэффициенты этих масок растут экспоненциально с ростом мощности носителей масок. Покажем теперь, что КОЭФФИЦИЕНТЫ НЕИЗБЕЖНО ДОЛЖНЫ РАСТИ С ТАКОЙ СКОРОСТЬЮ, так как знакопеременный характер свойства четности требует, чтобы величина коэффициента при каждой маске была достаточно большой, чтобы свести на нет влияние множества коэффициентов подмасок этой маски. Фактически мы показываем, что на множестве масок предикат пси.ЧETH0CTb можно осуществить только при помощи методики, подобной стратификации! Итак, пусть задан предикат пси.ЧETH0CTb = [СУММА альфа.i*фи.i > 0]. Предположим, что, применив теорему об инвариантности относительно групп, мы уравняли коэффициенты альфа для всех масок фи, носители которых содержат одно и то же число элементов. Предположим, наконец, что предикат пси.ЧETH0CTb дает "достоверное" различение, например СУММА альфа.i*фи.i >= 1, если число точек фигуры X нечетное, и СУММА альфа.i*фи.i <= 0, если это число четное. Раскрывая линейную форму СУММА альфа.i*фи.i для фигур, имеющих 1, 2, 3, ... точки, получаем (1):
альфа.1 >= 1,
альфа.2 + 2альфа.1 <= 0,
альфа.3 + 3альфа.2 + 3альфа.1 >= 0,
альфа.4 + 4альфа.3 + 6альфа.2 + 4альфа.1 <= 0.
Общую формулу легко найти, если обратить внимание на то, что коэффициенты в неравенствах (1) биномиальные, и по индукции доказать, что (2)
СУММА[i=1..n] C(n i) * альфа.i
>= 1, если n нечетно,
<= 0 если n четно.
Последовательное вычитание неравенств (2) дает
D.n =
СУММА[i=1..n+1] C(n+1 i) * альфа.i - СУММА[1..n] C(n i) * альфа.i =
альфа.[n+1] + СУММА[1..n] (C(n+1 i) - C(n i)) * альфа.i =
альфа.[n+1] + СУММА[1..n] C(n i-1) * альфа.i =
СУММА[0..n] C(n i) * альфа.[i+1],
так что для всех n = 0, 1, 2, ... (3)
(-1)**n * D.n >= 1.
Просуммировав неравенства (3) с некоторыми положительными весами, получим границу для коэффициентов альфа.i. Возьмем любое число M>0 и рассмотрим сумму
СУММА[0..M] C(M i) (-1)**i * D.i >= СУММА[0..M] C(n i) = 2**M.
Левая часть равна
СУММА[i=0..M] СУММА[k=0..i] (-1)**i * альфа.[k+1] * C(i k) * C(M i) =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * C(i k) * C(M i) =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * i!/k!/(i-k)! * M!/i!/(M-i)! =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * M!/k!/(M-k)! * (M-k)!/(i-k)!/(M-i)! =
СУММА[k=0..M] альфа.[k+1] * C(M k) * (-1)**k * СУММА[j=0..M-k] (M-k)!/j!/(M-k-j)! * (-1)**j =
СУММА[k=0..M] альфа.[k+1] * C(M k) * (-1)**k * (-1)**(M-k) =
альфа.[M+1] * (-1)**M,
откуда
альфа.[M+1] >= 2**M.
ТЕОРЕМА 10.1. В любой "достоверной" реализации предиката пси.ЧЕТНОСТЬ являющейся пороговой линейной функцией на множестве масок, коэффициенты растут не медленнее, чем 2**(|S(фи)|-1).
Эта оценка справедлива для средних значений коэффициентов, так что если коэффициенты при масках каждого типа не одинаковы, то некоторые из них должны расти еще быстрее! Этот вывод показывает, что для распознавания функций, аналогичных определению четности, нецелесообразно использовать предикаты, подобные маскам: даже если бы можно было осуществить огромное число необходимых масок фи, то пришлось бы еще как-то охватить громадный диапазон их коэффициентов!
ЗАМЕЧАНИЕ. Для обучающихся машин данный вывод практически является роковым. Чтобы "выучить" наибольший коэффициент, необходимо по крайней мере 2**|R| примеров изображений, имеющих максимальное число точек. Фактически дело обстоит еще хуже из-за неприятных взаимодействий с коэффициентами более низкого порядка (#11.4). Кроме того, отсюда следует, что для запоминания коэффициентов альфа.i емкость памяти должна быть такой, какая потребовалась бы для хранения всего множества изображений, распознаваемых предикатом пси.ЧЕТНОСТЬ, т.е. нечетных подмножеств множества R. В самом деле, так как для любого единообразного представления коэффициентов альфа.i необходимо по |R|-1 бит на каждый, а коэффициентов всего 2**|R|, то потребуется (|R|-1)*2**|R| бит. С другой стороны, число нечетных подмножеств множества R равно 2(|R|-1), на каждое из них необходимо по |R| бит, так что для представления всех указанных подмножеств достаточно |R|*2**|R| бит. А для хранения коэффициентов предиката, описанного в #10.2, потребовалась бы память значительно большей емкости.
Заметим, что в этом отношении предикат пси.ЧЕТНОСТь не составляет никакого исключения, ибо по теореме о положительной нормальной форме все возможные 2**2**|R| булевы функции являются линейными пороговыми функциями на множестве масок. Таким образом, детальное описание функции требует В СРЕДНЕМ 2**|R| БИТ информации, а из-за разброса величин коэффициентов эта оценка может быть существенно больше.
#10.2. КОЭФФИЦИЕНТЫ МОГУТ РАСТИ С РОСТОМ |R| ДАЖЕ БЫСТРЕЕ, ЧЕМ ЭКСПОНЕНЦИАЛЬНО
Можно было бы подумать, что пси.ЧЕТН0СТЬ - наихудший предикат, так как, во-первых, четность - самая плохая функция, а, во-вторых, маски образуют наихудшее множество ФИ. На самом же деле маски образуют довольно хороший базис, потому что коэффициенты масок никогда не могут превышать |альфа.i|=2**|S(фи.i)|, в чем легко убедиться, приведя произвольный предикат к положительной нормальной форме. Рассмотрим теперь новый предикат пси.РАВЕНСТВО и весьма неприятное множество ФИ, которое приводит к худшим коэффициентам. Пусть R - множество точек y.1, ..., y.n, z.1, ..., z.n. Обозначим через {Y.i} и {Z.i} - последовательности, составленные из 2**n подмножеств точек y и z соответственно. Тогда для любой фигуры X включается в R существует единственное разложение X = Y.j объединение Z.k.
Пусть предикат пси.РАВЕНСТВО имеет простой вид
пси.РАВЕНСТВО (Y.j объединение Z.k) = [j=k].
Этот предикат для любого X проверяет, одинаковы ли номера его частей Y и Z в соответствующих последовательностях. Простой геометрический пример дает случай, когда обе половины пространства R имеют одинаковую форму, а Y.i и Z.i - множества точек y и z.
Построим весьма специфическое множество ФИ таких предикатов, при котором пси.РАВЕНСТВО принадлежит L(ФИ) и покажем, что любая реализация предиката пси.РАВЕНСТВО из L(ФИ) должна содержать невероятно большие коэффициенты!
С самого начала укажем на то, что это множество ФИ мы будем использовать исключительно для данной цели. При исследовании предиката пси.ЧЕТНОСТЬ мы видели, что коэффициенты могут расти с ростом |R| экспоненциально; там ФИ было естественным множеством масок, представляющим интерес независимо от проблемы коэффициентов. Здесь же мы создаем множество ФИ только ради того, что оно дает неудачные коэффициенты. Тем самым мы покажем, что существуют еще худшие ситуации.
Определим ФИ так, чтобы оно содержало два типа предикатов:
пси.i(Y.j объединение Z.k) = [j=k],
хи.i(Y.j объединение Z.k) = [(j=k & i=k) & (j=k-1 & i<k)],
где i = 1, ..., 2**n. Заметим, что |S(пси.i)|=n и |S(хи.i)|=2n. Докажем, что пси.РАВЕНСТВО принадлежит L(ФИ). Рассмотрим формулу
пси.РАВЕНСТВО = [СУММА 2**i (пси.i-хи.i) < 1].
СЛУЧАЙ 1: j=k. Тогда пси.k=1 и хи.k=1, откуда пси.РАВЕНСТВО=[2**k (1-1) < 1] принимает значение ИСТИНА.
СЛУЧАЙ 2: j!=k и j!=k-1. Тогда только пси.k=1 и пси.РАВЕНСТВО=[2**k < 1] принимает значение ЛОЖЬ.
СЛУЧАЙ 3: j=k-1. Тогда пси.k=1 и хи.k=1 для i=1, ..., k-1. Поэтому предикат
пси.РАВЕНСТВО = [2**k - СУММА[i=1..k-1] 2**i < 1] = [2<1] принимает значение ЛОЖЬ, и, следовательно, он истинен только для j=k, как и должно быть. Таким образом, предикат пси.РАВЕНСТВО действительно принадлежит L(ФИ).
Найдем теперь границы коэффициентов. Рассмотрим предикат
пси.РАВЕНСТВО = [СУММА альфа.i*хи.i + СУММА бета.i*пси.i > тета].
Тогда для множеств Y.[k+i] объединение Z.k будет бета.k<=тета, для множеств Y.k объединение Z.k будет альфа.k+бета.k>=тета+1 (СИЛЬНОЕ РАЗДЕЛЕНИЕ), для множеств Y.[k-1] объединение Z.k будет альфа.1+...+альфа.[k-1]+бета.k<тета.
Мы можем считать тета=0 - его можно вычесть из каждого бета, поскольку в каждом неравенстве бета содержится только один раз. Таким образом, бета.1<=0, альфа.1>=1. Но
альфа.k >= 1 + альфа.1 + ... + альфа.[k+1],
и потому мы немедленно получаем альфа.2>=2, альфа.3>=4, ..., альфа.j>=2**(j-1). Так как индекс j пробегает значения от 1 до 2**n, то наибольший коэффициент альфа должен быть по крайней мере в 2**2**(n-1) раз больше, чем начальный разделяющий член (альфа.1+бета.1)-бета.1=альфа.1. Эта невероятная скорость роста коэффициентов частично основана на математической шутке: отметим, что выражение j=k, равнозначное выражению для предиката пси.РАВЕНСТВ0> Уже присутствует в определениях предикатов хи.1 и введено оно туда как раз для того, чтобы свести почти на нет их роль в L(ФИ).
Самое смешное, что в терминах масок предикат пси.РАВЕНСТВ0 имеет вид
пси.РАВЕНСТВО = [СУММА(y.i+z.i-2*y.i*z.i) <1],
и коэффициенты в действительности очень малы!
ЗАДАЧИ. Найти такое множество ФИ, которое заставляет коэффициенты федиката пси.ЧЕТНОСТЬ расти, как 2**2**(|R|*const) . Решение дается в #10.3. В #10.1 множество ФИ состоит из 2**|R| элементов и коэффициенты предиката пси.ЧЕТНОСТЬ имеют величину порядка 2**|R|. В #10.2 ФИ содержит 2**(|R|/2) элементов, но его коэффициенты достигают величины 2**2**|R|. Число элементов множества ФИ можно
увеличить вплоть до 2**2**|R|. Означает ли это, что существуют множества ФИ и предикаты пси, приводящие к коэффициентам порядка 2**2**2**|R|? (Мы думаем, что этого не может быть. См. #10.3).
Можно ли доказать, что при любом ФИ отношения коэффициентов никогда не превысят 2**|ФИ|? Можно ли установить более точные зависимости между коэффициентами и их отношениями? Можно ли доказать, что оценки коэффициентов, найденные при условии их целочисленности, ограничивают точность, требуемую от произвольных вещественных коэффициентов? Можно ли установить линейные границы для коэффициентов предикатов, о которых говорилось в гл.7?
Линейный пороговый предикат
пси.РАВЕНСТВО = [СУММА 2**i * (пси.i-хи.i) > тета]
очень похож на предикаты, полученные методом стратификации. В этих предикатах коэффициент на каждом уровне i выбирается так, чтобы он превышал наихудший результат суммирования коэффициентов предыдущих уровней. Для таких предикатов, как следует из теорем #10.1-10.2, нет никаких линейных форм с меньшими коэффициентами. Это наводит на мысль, что некоторым предикатам, возможно, в некотором смысле внутренне присуща стратификация (по отношению к заданным множествам ФИ). В этом направлении у нас нет никаких определенных идей, кроме простой констатации факта, что ощущается пугающая нехватка приемлемых для ЭВМ методов распознавания образов. Для большей части случаев, рассмотренных в гл.7, неизвестно, в каких из них действительно требуется такой рост коэффициентов, какой наблюдается при стратификации. Иными словами, у нас нет общего метода, чтобы обнаружить "внутренне присущее разделение на страты".
#10.3. ПРЕДИКАТ С МАКСИМАЛЬНО ВОЗМОЖНЫМИ КОЭФФИЦИЕНТАМИ
Обозначим через ||X|| номер подмножества X в упорядоченной последовательности всех подмножеств пространства R. Рассмотрим простой предикат пси.||ЧЕТНОСТЬ||=[||X|| - нечетное число] и множество ФИ предикатов
фи.i =
0, если ||X||<i,
1, если ||X||=i,
(||X||-i)%2, если ||X||>i.
Тогда предикат пси.||ЧЕТНОСТЬ|| принадлежит L(ФИ) и реализуется в виде
пси.||ЧЕТНОСТЬ|| = [СУММА (-1)**i * f.i*фи.i < 0],
где f.i есть i-е число Фибоначчи (f.n=f.[n-i]+f.[n-2])):
{f.i} = {1, 1, 2, 3, 5, 8, 13, ...}.
ТЕОРЕМА 10.3. Коэффициенты любой формы предиката пси.||ЧЕТНОСТЬ||, принадлежащей L(ФИ), должны быть не меньше чисел Фибоначчи f.i. Так как f.i растут приближенно как
1/sqr(5) * ((sqr(5)+1)/2)**i,
то наибольший коэффициент имеет порядок ~2**(альфа*2**n), где альфа=log2((sqr(5)+1)/2).
Теорему нетрудно доказать, проанализировав таблицу

Легко видеть, что если альфа.1<0, а коэффициенты целые, то
альфа.[2i+1] < -СУММА[j=1..i] альфа.[2j],
альфа.[2i] >= -СУММА[j=1..i] альфа.[2j-1].
Это означает (читатель может проверить сам), что для всех альфа.i
|альфа.[i+1]| >= |альфа.i| + |альфа.[i-1]|;
следовательно, |альфа.i|>=f.i.
ОБСУЖДЕНИЕ И ПРЕДПОЛОЖЕНИЕ. Этот предикат и его множество ФИ обладают точно таким же свойством, как предикат пси.РАВЕНСТВО и его ФИ из #10.2: каждая из масок фи сама является почти искомым предикатом. Заметим также, что подходящим упорядочением подмножеств можно добиться равенства
пси.||ЧЕТНОСТЬ|| = пси.ЧЕТНОСТЬ.
Мы предполагаем, что этот пример - наихудший, т.е. если ФИ содержит |ФИ| элементов, то рост коэффициентов не может происходить быстрее, чем
2**((sqr(5)+1)/2)**|ФИ|,
где постоянная в показателе степени равна отношению Фибоначчи, или отношению "золотого прямоугольника". Наше предположение опирается на аргументы [Например, на факт из теории рациональных приближений и геометрии чисел, что в верхних границах фигурирует число sqr(5)], недостаточно обоснованные для того, чтобы излагать их письменно.
#10.4. ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП И ОГРАНИЧЕННЫЕ КОЭФФИЦИЕНТЫ НА БЕСКОНЕЧНОЙ ПЛОСКОСТИ
В #7.10 мы упоминали о примере, опровергающем возможность распространения теоремы об инвариантности относительно групп (#2.3) на бесконечные сетчатки. Трудность вызвана применением бесконечной стратификации, приводящей к неограниченным коэффициентам. В свою очередь это создает проблемы сходимости для суммирования по симметрии, используемого при доказательстве равенства коэффициентов в пределах одного класса эквивалентности. Если коэффициенты ограничены, а группа содержит все переносы, то соответствующую теорему МОЖНО доказать. (Более сильные результаты нам неизвестны: по-видимому, если наложить какие-то условия на суммируемость коэффициентов и на структуру группы, можно сформулировать лучшую теорему). В доказательстве используется известный из геометрии факт: при одинаковом увеличении радиусов для одинаковых кругов с фиксированными центрами относительная величина общей площади стремится к 1.

#10.4.1. ОГРАНИЧЕННЫЕ КОЭФФИЦИЕНТЫ И ИНВАРИАНТНОСТЬ ОТНОСИТЕЛЬНО ГРУПП. Пусть пси - предикат, инвариантный относительно переноса на бесконечной плоскости.
ТЕОРЕМА 10.4.1. Если в каждом классе эквивалентности коэффициенты при предикатах фи ограничены, то существует эквивалентный персептрон, у которого в каждом классе эквивалентности коэффициенты равны.
ДОКАЗАТЕЛЬСТВО. Обозначим через T.C множество переносов на расстояния, не превышающие некоторой величины C. Пусть пси=[СУММА альфа(фи)фи>=тета]. Определим предикат пси.C формулой
пси.C(X)=[СУММА[g из T.C] (СУММА[фи из ФИ] альфа(фи)фи(gX)-тета) >=0].
Так как под действием обратного элемента группы множество T.C переводится само в себя, то
пси.C(X) =
[СУММА[ФИ] фи(X) СУММА[T.C] альфа(фи*g**-1) >= СУММА[T.C] тета] =
[СУММА[ФИ] фи(X) СУММА[T.C] альфа(фи*g) >= СУММА[T.C] тета].
В силу приведенного в #2.3 доказательства каждый предикат пси.C эквивалентен пси. Докажем, что можно выбрать такую неубывающую последовательность радиусов R.1, R.2, ..., что предел
lim [i->беск.] [1/(пи*R.i**2) СУММА [g из T.R.i] альфа(фи*g)]
в каждом классе эквивалентности имеет постоянное значение, не зависящее от фи.
ЛЕММА. Пусть функция f(x) в пространстве E**2 ограничена, т.е. |f(x)|<M Тогда найдется такая неубывающая последовательность радиусов R.i, что для любой системы концентрических окружностей с этими радиусами предел
lim [i->беск.] 1/(пи*R.i**2) ИНТЕГРАЛ [|y-p|<R.i] f(y)dA
не зависит от выбора общего центра p, если он вообще существует для какого-нибудь центра.
ДОКАЗАТЕЛЬСТВО. Возьмем любую неограниченно возрастающую последовательность радиусов R.i, а в качестве центра - начало координат. Тогда для каждого i
|1/(пи*R.i**2) ИНТЕГРАЛ [|y|<R.i] f(y)dA| < M
Если нам задан другой центр р, то
|ИНТЕГРАЛ [|y|<R.i] f(y)dA - ИНТЕГРАЛ [|y|-R.i] f(p+y)dA| < 2M ДЕЛЬТА.i(p),
где ДЕЛЬТА.i(p) - площадь симметрической разности [Симметрической разностью двух множеств A и B называется множество (A объединение B) \ (A пересечение B). - Прим. ред.] двух кругов |y|<R.i и |y-p|<R.i. Но при увеличении радиуса для любого центра p
lim [i->беск.] ДЕЛЬТА.i(p)/R.i**2 = 0,
так что обе последовательности стремятся к одному и тому же пределу (если он существует).
Для доказательства основной теоремы просто выбираем из любого класса эквивалентности в качестве представителя некоторый предикат фи и полагаем f(g)=альфа(фи*g), считая g переносом из начала координат.
Таким образом, полученный в #7.4 персептрон должен иметь неограниченные коэффициенты, и в L(ФИ) не существует эквивалентного представления с ограниченными коэффициентами.
Фигурирующий в лемме предел может и не существовать - контрпримеры привести легко. Это означает, что теорема 10.4.1, по-видимому, не всегда справедлива без дополнительных условий, но мы считаем, что эти дополнительные условия не так уж важны. Соответствующий контрпример мы не знаем.
ПРИМЕЧАНИЕ. Методы #10.2 и 10.3 сходны с теми, которыми Майхилл и Котц [1961] находили максимальные коэффициенты в случае предикатов порядка 1. Майхилл и Котц показали, что существует предикат порядка 1 с целыми коэффициентами, у которого один из коэффициентов превышает 2/e*1/п*2**n.
ПРЕДИСЛОВИЕ К ЧАСТИ III
В заключительных главах нашей книги исследуются темы, которые на языке кибернетиков объединяются под общим названием "обучение". До сих пор линейные представления рассматривались вне всякой связи со временем. Сейчас нас интересует вопрос, как их вычислять, сколько нужно для этого времени, как велики они и насколько эффективны как средство хранения информации В гл.10 мы покажем, что коэффициенты персептрона могут расти значительно быстрее, чем показательная функция от |R|. Этот вывод имеет серьезные последствия, как практические, так и принципиальные: для запоминания коэффициентов нужна память большая, чем для записи всех изображений. Это ломает представление о том, что такая машина способна в некотором смысле абстрагировать.
В гл.11 объясняется замечательная ТЕОРЕМА О СХОДИМОСТИ ПЕРСЕПТРОНА и показывается ее связь с известными явлениями из области конечных автоматов, теории оптимизации и использования обратной связи в качестве средства для вычислений.
В гл.12 мы отказываемся от строгого определения персептрона, что дает возможность изучать более обширное семейство алгоритмов, основанных на использовании локальных частных предикатов. Эти алгоритмы включают методы (типа байесовских решений), используемые статистиками, а также понятия (как, например, смешанное кодирование), известные только программистам. Цель гл.12 - очертить область вычислительной техники, охватывающую эти явно разнородные процессы. Мы специально подчеркиваем необходимость такой теории, для чего выбираем просто формулируемую, но нерешенную задачу о более прямых, чем обычно пропагандируемые, способах хранения и поиска информации.
ГЛАВА 10. ВЕЛИЧИНА КОЭФФИЦИЕНТОВ
#10.1. КОЭФФИЦИЕНТЫ ПРЕДИКАТА, ОПРЕДЕЛЯЮЩЕГО ЧЕТНОСТЬ
В #3.1 мы рассмотрели предикат пси.ЧETH0CTb(X)=[|X|-нечетное число] и показали, что если ФИ - множество масок, то любое выражение предиката пси.ЧETH0CTb, принадлежащее L(ФИ), должно содержать все маски. Вот одно из таких выражений
пси.ЧETH0CTb(X) = [СУММА (-2)**|S(фи)| * фи(X) < -1],
содержащее все маски множества ФИ, причем коэффициенты этих масок растут экспоненциально с ростом мощности носителей масок. Покажем теперь, что КОЭФФИЦИЕНТЫ НЕИЗБЕЖНО ДОЛЖНЫ РАСТИ С ТАКОЙ СКОРОСТЬЮ, так как знакопеременный характер свойства четности требует, чтобы величина коэффициента при каждой маске была достаточно большой, чтобы свести на нет влияние множества коэффициентов подмасок этой маски. Фактически мы показываем, что на множестве масок предикат пси.ЧETH0CTb можно осуществить только при помощи методики, подобной стратификации! Итак, пусть задан предикат пси.ЧETH0CTb = [СУММА альфа.i*фи.i > 0]. Предположим, что, применив теорему об инвариантности относительно групп, мы уравняли коэффициенты альфа для всех масок фи, носители которых содержат одно и то же число элементов. Предположим, наконец, что предикат пси.ЧETH0CTb дает "достоверное" различение, например СУММА альфа.i*фи.i >= 1, если число точек фигуры X нечетное, и СУММА альфа.i*фи.i <= 0, если это число четное. Раскрывая линейную форму СУММА альфа.i*фи.i для фигур, имеющих 1, 2, 3, ... точки, получаем (1):
альфа.1 >= 1,
альфа.2 + 2альфа.1 <= 0,
альфа.3 + 3альфа.2 + 3альфа.1 >= 0,
альфа.4 + 4альфа.3 + 6альфа.2 + 4альфа.1 <= 0.
Общую формулу легко найти, если обратить внимание на то, что коэффициенты в неравенствах (1) биномиальные, и по индукции доказать, что (2)
СУММА[i=1..n] C(n i) * альфа.i
>= 1, если n нечетно,
<= 0 если n четно.
Последовательное вычитание неравенств (2) дает
D.n =
СУММА[i=1..n+1] C(n+1 i) * альфа.i - СУММА[1..n] C(n i) * альфа.i =
альфа.[n+1] + СУММА[1..n] (C(n+1 i) - C(n i)) * альфа.i =
альфа.[n+1] + СУММА[1..n] C(n i-1) * альфа.i =
СУММА[0..n] C(n i) * альфа.[i+1],
так что для всех n = 0, 1, 2, ... (3)
(-1)**n * D.n >= 1.
Просуммировав неравенства (3) с некоторыми положительными весами, получим границу для коэффициентов альфа.i. Возьмем любое число M>0 и рассмотрим сумму
СУММА[0..M] C(M i) (-1)**i * D.i >= СУММА[0..M] C(n i) = 2**M.
Левая часть равна
СУММА[i=0..M] СУММА[k=0..i] (-1)**i * альфа.[k+1] * C(i k) * C(M i) =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * C(i k) * C(M i) =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * i!/k!/(i-k)! * M!/i!/(M-i)! =
СУММА[k=0..M] СУММА[i=k..M] (-1)**i * альфа.[k+1] * M!/k!/(M-k)! * (M-k)!/(i-k)!/(M-i)! =
СУММА[k=0..M] альфа.[k+1] * C(M k) * (-1)**k * СУММА[j=0..M-k] (M-k)!/j!/(M-k-j)! * (-1)**j =
СУММА[k=0..M] альфа.[k+1] * C(M k) * (-1)**k * (-1)**(M-k) =
альфа.[M+1] * (-1)**M,
откуда
альфа.[M+1] >= 2**M.
ТЕОРЕМА 10.1. В любой "достоверной" реализации предиката пси.ЧЕТНОСТЬ являющейся пороговой линейной функцией на множестве масок, коэффициенты растут не медленнее, чем 2**(|S(фи)|-1).
Эта оценка справедлива для средних значений коэффициентов, так что если коэффициенты при масках каждого типа не одинаковы, то некоторые из них должны расти еще быстрее! Этот вывод показывает, что для распознавания функций, аналогичных определению четности, нецелесообразно использовать предикаты, подобные маскам: даже если бы можно было осуществить огромное число необходимых масок фи, то пришлось бы еще как-то охватить громадный диапазон их коэффициентов!
ЗАМЕЧАНИЕ. Для обучающихся машин данный вывод практически является роковым. Чтобы "выучить" наибольший коэффициент, необходимо по крайней мере 2**|R| примеров изображений, имеющих максимальное число точек. Фактически дело обстоит еще хуже из-за неприятных взаимодействий с коэффициентами более низкого порядка (#11.4). Кроме того, отсюда следует, что для запоминания коэффициентов альфа.i емкость памяти должна быть такой, какая потребовалась бы для хранения всего множества изображений, распознаваемых предикатом пси.ЧЕТНОСТЬ, т.е. нечетных подмножеств множества R. В самом деле, так как для любого единообразного представления коэффициентов альфа.i необходимо по |R|-1 бит на каждый, а коэффициентов всего 2**|R|, то потребуется (|R|-1)*2**|R| бит. С другой стороны, число нечетных подмножеств множества R равно 2(|R|-1), на каждое из них необходимо по |R| бит, так что для представления всех указанных подмножеств достаточно |R|*2**|R| бит. А для хранения коэффициентов предиката, описанного в #10.2, потребовалась бы память значительно большей емкости.
Заметим, что в этом отношении предикат пси.ЧЕТНОСТь не составляет никакого исключения, ибо по теореме о положительной нормальной форме все возможные 2**2**|R| булевы функции являются линейными пороговыми функциями на множестве масок. Таким образом, детальное описание функции требует В СРЕДНЕМ 2**|R| БИТ информации, а из-за разброса величин коэффициентов эта оценка может быть существенно больше.
#10.2. КОЭФФИЦИЕНТЫ МОГУТ РАСТИ С РОСТОМ |R| ДАЖЕ БЫСТРЕЕ, ЧЕМ ЭКСПОНЕНЦИАЛЬНО
Можно было бы подумать, что пси.ЧЕТН0СТЬ - наихудший предикат, так как, во-первых, четность - самая плохая функция, а, во-вторых, маски образуют наихудшее множество ФИ. На самом же деле маски образуют довольно хороший базис, потому что коэффициенты масок никогда не могут превышать |альфа.i|=2**|S(фи.i)|, в чем легко убедиться, приведя произвольный предикат к положительной нормальной форме. Рассмотрим теперь новый предикат пси.РАВЕНСТВО и весьма неприятное множество ФИ, которое приводит к худшим коэффициентам. Пусть R - множество точек y.1, ..., y.n, z.1, ..., z.n. Обозначим через {Y.i} и {Z.i} - последовательности, составленные из 2**n подмножеств точек y и z соответственно. Тогда для любой фигуры X включается в R существует единственное разложение X = Y.j объединение Z.k.
Пусть предикат пси.РАВЕНСТВО имеет простой вид
пси.РАВЕНСТВО (Y.j объединение Z.k) = [j=k].
Этот предикат для любого X проверяет, одинаковы ли номера его частей Y и Z в соответствующих последовательностях. Простой геометрический пример дает случай, когда обе половины пространства R имеют одинаковую форму, а Y.i и Z.i - множества точек y и z.
Построим весьма специфическое множество ФИ таких предикатов, при котором пси.РАВЕНСТВО принадлежит L(ФИ) и покажем, что любая реализация предиката пси.РАВЕНСТВО из L(ФИ) должна содержать невероятно большие коэффициенты!
С самого начала укажем на то, что это множество ФИ мы будем использовать исключительно для данной цели. При исследовании предиката пси.ЧЕТНОСТЬ мы видели, что коэффициенты могут расти с ростом |R| экспоненциально; там ФИ было естественным множеством масок, представляющим интерес независимо от проблемы коэффициентов. Здесь же мы создаем множество ФИ только ради того, что оно дает неудачные коэффициенты. Тем самым мы покажем, что существуют еще худшие ситуации.
Определим ФИ так, чтобы оно содержало два типа предикатов:
пси.i(Y.j объединение Z.k) = [j=k],
хи.i(Y.j объединение Z.k) = [(j=k & i=k) & (j=k-1 & i<k)],
где i = 1, ..., 2**n. Заметим, что |S(пси.i)|=n и |S(хи.i)|=2n. Докажем, что пси.РАВЕНСТВО принадлежит L(ФИ). Рассмотрим формулу
пси.РАВЕНСТВО = [СУММА 2**i (пси.i-хи.i) < 1].
СЛУЧАЙ 1: j=k. Тогда пси.k=1 и хи.k=1, откуда пси.РАВЕНСТВО=[2**k (1-1) < 1] принимает значение ИСТИНА.
СЛУЧАЙ 2: j!=k и j!=k-1. Тогда только пси.k=1 и пси.РАВЕНСТВО=[2**k < 1] принимает значение ЛОЖЬ.
СЛУЧАЙ 3: j=k-1. Тогда пси.k=1 и хи.k=1 для i=1, ..., k-1. Поэтому предикат
пси.РАВЕНСТВО = [2**k - СУММА[i=1..k-1] 2**i < 1] = [2<1] принимает значение ЛОЖЬ, и, следовательно, он истинен только для j=k, как и должно быть. Таким образом, предикат пси.РАВЕНСТВО действительно принадлежит L(ФИ).
Найдем теперь границы коэффициентов. Рассмотрим предикат
пси.РАВЕНСТВО = [СУММА альфа.i*хи.i + СУММА бета.i*пси.i > тета].
Тогда для множеств Y.[k+i] объединение Z.k будет бета.k<=тета, для множеств Y.k объединение Z.k будет альфа.k+бета.k>=тета+1 (СИЛЬНОЕ РАЗДЕЛЕНИЕ), для множеств Y.[k-1] объединение Z.k будет альфа.1+...+альфа.[k-1]+бета.k<тета.
Мы можем считать тета=0 - его можно вычесть из каждого бета, поскольку в каждом неравенстве бета содержится только один раз. Таким образом, бета.1<=0, альфа.1>=1. Но
альфа.k >= 1 + альфа.1 + ... + альфа.[k+1],
и потому мы немедленно получаем альфа.2>=2, альфа.3>=4, ..., альфа.j>=2**(j-1). Так как индекс j пробегает значения от 1 до 2**n, то наибольший коэффициент альфа должен быть по крайней мере в 2**2**(n-1) раз больше, чем начальный разделяющий член (альфа.1+бета.1)-бета.1=альфа.1. Эта невероятная скорость роста коэффициентов частично основана на математической шутке: отметим, что выражение j=k, равнозначное выражению для предиката пси.РАВЕНСТВ0> Уже присутствует в определениях предикатов хи.1 и введено оно туда как раз для того, чтобы свести почти на нет их роль в L(ФИ).
Самое смешное, что в терминах масок предикат пси.РАВЕНСТВ0 имеет вид
пси.РАВЕНСТВО = [СУММА(y.i+z.i-2*y.i*z.i) <1],
и коэффициенты в действительности очень малы!
ЗАДАЧИ. Найти такое множество ФИ, которое заставляет коэффициенты федиката пси.ЧЕТНОСТЬ расти, как 2**2**(|R|*const) . Решение дается в #10.3. В #10.1 множество ФИ состоит из 2**|R| элементов и коэффициенты предиката пси.ЧЕТНОСТЬ имеют величину порядка 2**|R|. В #10.2 ФИ содержит 2**(|R|/2) элементов, но его коэффициенты достигают величины 2**2**|R|. Число элементов множества ФИ можно
увеличить вплоть до 2**2**|R|. Означает ли это, что существуют множества ФИ и предикаты пси, приводящие к коэффициентам порядка 2**2**2**|R|? (Мы думаем, что этого не может быть. См. #10.3).
Можно ли доказать, что при любом ФИ отношения коэффициентов никогда не превысят 2**|ФИ|? Можно ли установить более точные зависимости между коэффициентами и их отношениями? Можно ли доказать, что оценки коэффициентов, найденные при условии их целочисленности, ограничивают точность, требуемую от произвольных вещественных коэффициентов? Можно ли установить линейные границы для коэффициентов предикатов, о которых говорилось в гл.7?
Линейный пороговый предикат
пси.РАВЕНСТВО = [СУММА 2**i * (пси.i-хи.i) > тета]
очень похож на предикаты, полученные методом стратификации. В этих предикатах коэффициент на каждом уровне i выбирается так, чтобы он превышал наихудший результат суммирования коэффициентов предыдущих уровней. Для таких предикатов, как следует из теорем #10.1-10.2, нет никаких линейных форм с меньшими коэффициентами. Это наводит на мысль, что некоторым предикатам, возможно, в некотором смысле внутренне присуща стратификация (по отношению к заданным множествам ФИ). В этом направлении у нас нет никаких определенных идей, кроме простой констатации факта, что ощущается пугающая нехватка приемлемых для ЭВМ методов распознавания образов. Для большей части случаев, рассмотренных в гл.7, неизвестно, в каких из них действительно требуется такой рост коэффициентов, какой наблюдается при стратификации. Иными словами, у нас нет общего метода, чтобы обнаружить "внутренне присущее разделение на страты".
#10.3. ПРЕДИКАТ С МАКСИМАЛЬНО ВОЗМОЖНЫМИ КОЭФФИЦИЕНТАМИ
Обозначим через ||X|| номер подмножества X в упорядоченной последовательности всех подмножеств пространства R. Рассмотрим простой предикат пси.||ЧЕТНОСТЬ||=[||X|| - нечетное число] и множество ФИ предикатов
фи.i =
0, если ||X||<i,
1, если ||X||=i,
(||X||-i)%2, если ||X||>i.
Тогда предикат пси.||ЧЕТНОСТЬ|| принадлежит L(ФИ) и реализуется в виде
пси.||ЧЕТНОСТЬ|| = [СУММА (-1)**i * f.i*фи.i < 0],
где f.i есть i-е число Фибоначчи (f.n=f.[n-i]+f.[n-2])):
{f.i} = {1, 1, 2, 3, 5, 8, 13, ...}.
ТЕОРЕМА 10.3. Коэффициенты любой формы предиката пси.||ЧЕТНОСТЬ||, принадлежащей L(ФИ), должны быть не меньше чисел Фибоначчи f.i. Так как f.i растут приближенно как
1/sqr(5) * ((sqr(5)+1)/2)**i,
то наибольший коэффициент имеет порядок ~2**(альфа*2**n), где альфа=log2((sqr(5)+1)/2).
Теорему нетрудно доказать, проанализировав таблицу

Легко видеть, что если альфа.1<0, а коэффициенты целые, то
альфа.[2i+1] < -СУММА[j=1..i] альфа.[2j],
альфа.[2i] >= -СУММА[j=1..i] альфа.[2j-1].
Это означает (читатель может проверить сам), что для всех альфа.i
|альфа.[i+1]| >= |альфа.i| + |альфа.[i-1]|;
следовательно, |альфа.i|>=f.i.
ОБСУЖДЕНИЕ И ПРЕДПОЛОЖЕНИЕ. Этот предикат и его множество ФИ обладают точно таким же свойством, как предикат пси.РАВЕНСТВО и его ФИ из #10.2: каждая из масок фи сама является почти искомым предикатом. Заметим также, что подходящим упорядочением подмножеств можно добиться равенства
пси.||ЧЕТНОСТЬ|| = пси.ЧЕТНОСТЬ.
Мы предполагаем, что этот пример - наихудший, т.е. если ФИ содержит |ФИ| элементов, то рост коэффициентов не может происходить быстрее, чем
2**((sqr(5)+1)/2)**|ФИ|,
где постоянная в показателе степени равна отношению Фибоначчи, или отношению "золотого прямоугольника". Наше предположение опирается на аргументы [Например, на факт из теории рациональных приближений и геометрии чисел, что в верхних границах фигурирует число sqr(5)], недостаточно обоснованные для того, чтобы излагать их письменно.
#10.4. ТЕОРЕМА ОБ ИНВАРИАНТНОСТИ ОТНОСИТЕЛЬНО ГРУПП И ОГРАНИЧЕННЫЕ КОЭФФИЦИЕНТЫ НА БЕСКОНЕЧНОЙ ПЛОСКОСТИ
В #7.10 мы упоминали о примере, опровергающем возможность распространения теоремы об инвариантности относительно групп (#2.3) на бесконечные сетчатки. Трудность вызвана применением бесконечной стратификации, приводящей к неограниченным коэффициентам. В свою очередь это создает проблемы сходимости для суммирования по симметрии, используемого при доказательстве равенства коэффициентов в пределах одного класса эквивалентности. Если коэффициенты ограничены, а группа содержит все переносы, то соответствующую теорему МОЖНО доказать. (Более сильные результаты нам неизвестны: по-видимому, если наложить какие-то условия на суммируемость коэффициентов и на структуру группы, можно сформулировать лучшую теорему). В доказательстве используется известный из геометрии факт: при одинаковом увеличении радиусов для одинаковых кругов с фиксированными центрами относительная величина общей площади стремится к 1.

#10.4.1. ОГРАНИЧЕННЫЕ КОЭФФИЦИЕНТЫ И ИНВАРИАНТНОСТЬ ОТНОСИТЕЛЬНО ГРУПП. Пусть пси - предикат, инвариантный относительно переноса на бесконечной плоскости.
ТЕОРЕМА 10.4.1. Если в каждом классе эквивалентности коэффициенты при предикатах фи ограничены, то существует эквивалентный персептрон, у которого в каждом классе эквивалентности коэффициенты равны.
ДОКАЗАТЕЛЬСТВО. Обозначим через T.C множество переносов на расстояния, не превышающие некоторой величины C. Пусть пси=[СУММА альфа(фи)фи>=тета]. Определим предикат пси.C формулой
пси.C(X)=[СУММА[g из T.C] (СУММА[фи из ФИ] альфа(фи)фи(gX)-тета) >=0].
Так как под действием обратного элемента группы множество T.C переводится само в себя, то
пси.C(X) =
[СУММА[ФИ] фи(X) СУММА[T.C] альфа(фи*g**-1) >= СУММА[T.C] тета] =
[СУММА[ФИ] фи(X) СУММА[T.C] альфа(фи*g) >= СУММА[T.C] тета].
В силу приведенного в #2.3 доказательства каждый предикат пси.C эквивалентен пси. Докажем, что можно выбрать такую неубывающую последовательность радиусов R.1, R.2, ..., что предел
lim [i->беск.] [1/(пи*R.i**2) СУММА [g из T.R.i] альфа(фи*g)]
в каждом классе эквивалентности имеет постоянное значение, не зависящее от фи.
ЛЕММА. Пусть функция f(x) в пространстве E**2 ограничена, т.е. |f(x)|<M Тогда найдется такая неубывающая последовательность радиусов R.i, что для любой системы концентрических окружностей с этими радиусами предел
lim [i->беск.] 1/(пи*R.i**2) ИНТЕГРАЛ [|y-p|<R.i] f(y)dA
не зависит от выбора общего центра p, если он вообще существует для какого-нибудь центра.
ДОКАЗАТЕЛЬСТВО. Возьмем любую неограниченно возрастающую последовательность радиусов R.i, а в качестве центра - начало координат. Тогда для каждого i
|1/(пи*R.i**2) ИНТЕГРАЛ [|y|<R.i] f(y)dA| < M
Если нам задан другой центр р, то
|ИНТЕГРАЛ [|y|<R.i] f(y)dA - ИНТЕГРАЛ [|y|-R.i] f(p+y)dA| < 2M ДЕЛЬТА.i(p),
где ДЕЛЬТА.i(p) - площадь симметрической разности [Симметрической разностью двух множеств A и B называется множество (A объединение B) \ (A пересечение B). - Прим. ред.] двух кругов |y|<R.i и |y-p|<R.i. Но при увеличении радиуса для любого центра p
lim [i->беск.] ДЕЛЬТА.i(p)/R.i**2 = 0,
так что обе последовательности стремятся к одному и тому же пределу (если он существует).
Для доказательства основной теоремы просто выбираем из любого класса эквивалентности в качестве представителя некоторый предикат фи и полагаем f(g)=альфа(фи*g), считая g переносом из начала координат.
Таким образом, полученный в #7.4 персептрон должен иметь неограниченные коэффициенты, и в L(ФИ) не существует эквивалентного представления с ограниченными коэффициентами.
Фигурирующий в лемме предел может и не существовать - контрпримеры привести легко. Это означает, что теорема 10.4.1, по-видимому, не всегда справедлива без дополнительных условий, но мы считаем, что эти дополнительные условия не так уж важны. Соответствующий контрпример мы не знаем.
ПРИМЕЧАНИЕ. Методы #10.2 и 10.3 сходны с теми, которыми Майхилл и Котц [1961] находили максимальные коэффициенты в случае предикатов порядка 1. Майхилл и Котц показали, что существует предикат порядка 1 с целыми коэффициентами, у которого один из коэффициентов превышает 2/e*1/п*2**n.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 11. ОБУЧЕНИЕ
#11.0. ВВЕДЕНИЕ
В предыдущих главах у нас не было никакой систематической методики представления предиката как элемента множества L(ФИ). Наоборот, мы строили коэффициенты на основе специального математического анализа самого предиката и множества элементарных предикатов фи. Эти исследования проводились СПЕЦИАЛЬНО для каждого предиката. В настоящей главе мы изучаем ситуации, в которых множества коэффициентов можно найти при помощи более систематизированной процедуры, легко воплотимой в автоматическом устройстве. Именно эта возможность и создала персептрону славу "обучающейся машины".
Принципиальную схему процесса "обучения", как он понимается здесь, можно представить себе в виде машины, состоящей из канала ввода изображений, двух выходных индикаторов да и нет и ПОДКРЕПЛЯЮЩЕЙ, или "поощряющей", кнопки, при помощи которой оператор машины может одобрять или не одобрять ее поведение (рис.11.1). Оператор имеет два набора F+ и F- изображений и хотел бы, чтобы машина отвечала ДА на каждое изображение из набора F+ и НЕТ на каждое изображение из F-. Если реакция машины верна, то свое одобрение оператор выражает, скажем, нажатием кнопки. Машина обязана изменять свое внутреннее состояние, чтобы приспосабливаться к желаниям ее хозяина.

Существует множество способов построения такой машины. Наиболее очевидная схема должна иметь какое нибудь записывающее усгройство для запоминания вводимых изображений в двух накопителях, отдельно для F+ и для F-. Такая машина никогда не сделает ошибки на изображении, которое она видела раньше, но наряду со способностью никогда ничего не забывать она бывает весьма неуклюжей. Другая машина, построенная на совершенно иных принципах, попыталась бы найти описательные характеристики, различные для изображений двух классов, и использовать новые изображения для уточнения и совершенствования этих описаний. Такая машина потребовала бы при длительной работе меньшей памяти, но ее устройство и теория значительно более сложные. Если классы F+ и F- очень велики, то первая машина работать не сможет, а если для встречающегося на практике репертуара изображений описания не существует, то потерпит неудачу машина второго вида.
Персептрон как машина, умеющая различать образы, лежит между этими двумя крайностями. Он не ищет соответствия с хранящимися в памяти изображениями, так как не запоминает самих изображений. При выработке описаний возможности персептрона, как мы видели в предыдущих главах, ограничены тем, чего можно достичь, используя лишь "локальные" отличительные свойства образов и только линейные пороговые отношения между этими свойствами. Существование описанных ниже простых процедур обучения следует из этого ограничения, наложенного на способность машины строить описание (и могло бы рассматриваться как частичная компенсация этого ограничения).
Предположим, что обучающейся машиной является персептрон с фиксированным множеством ФИ и регулируемыми коэффициентами. При подаче на вход персептрона изображения X вычисляется сумма
СУММА альфа.фи*фи(X).
Если X принадлежит F+ и эта сумма положительна, то машина отвечает ДА и все хорошо. Если X принадлежит F+, а сумма отрицательна, то машина отвечает НЕТ. Это плохо, и нужно что-то предпринимать. Что может служить простейшей процедурой коррекции?
Первое, что приходит в голову, особенно людям, воспитанным на идее обратной связи, это увеличить коэффициенты слагаемых, поскольку сумма оказалась слишком малой. Если бы она оказалась слишком большой (а именно ответ ДА на изображение из F-), у нас возникло бы желание уменьшить коэффициенты.
Но коэффициенты нужно регулировать разумно, чтобы должным образом направлять действие обратной связи.
Предположим, что для какого-то изображения X из F+ сумма СУММА альфа.фи*фи(X) получилась отрицательной. Вообще говоря, для некоторых предикатов фи значение фи(X) равно 0, и совершенно ясно, что их коэффициенты не отвечают за неверный результат. На самом деле изменение этих коэффициентов может даже нанести вред другим изображениям и уже во всяком случае не принесет никакой пользы для данного X. Поэтому будем увеличивать альфа.фи только в том случае, если фи(X)=1. Мы хотели бы иметь для этого такую процедуру, математическая форма которой достаточно ясна и поддается простому анализу, а ее способность добиться определенного успеха достаточно велика. Приведенная в #11.1 процедура удовлетворяет обоим этим требованиям, но, прежде чем перейти к ее описанию, сделаем несколько предварительных замечаний.
#11.0.1. КОЭФФИЦИЕНТЫ И ВЕКТОРЫ. Множество коэффициентов {альфа.фи}, упорядоченных произвольным, но фиксированным образом, удобно представить в виде вектора в |ФИ|-мерном пространстве. Обозначим этот вектор через A. Точно так же множество {фи(X)}, упорядоченное таким же образом, можно рассматривать как вектор, координатами которого служат значения предикатов фи(X). Обозначим этот вектор через Ф(X). Теперь увеличение коэффициентов, соответствующих ненулевым значениям фи(X), изящно осуществляется простым прибавлением вектора Ф(X) к вектору A. Если бы для X и F- сумма оказалась положительной, то следовало бы вычесть Ф(X) из А.
Любая подобная процедура с самого начала таит в себе опасность возникновения сильных колебаний. Регулировка в соответствующем направлении коэффициентов для одного изображения могла бы расстроить предыдущую регулировку для другого. Таким образом, наше интуитивное представление о работоспособности подобной процедуры подвержено влиянию двух противоречивых идей, почерпнутых из опыта кибернетики: простая обратная связь, корректирующая ошибки, часто оказывается вполне работоспособной; с другой стороны, процесс включает в себя поиск в |ФИ|-мерном пространстве, а наш опыт с другими системами типа "подъема на холм" заставляет нас остро сознавать опасности, которые грозят подобным процедурам. Необходим строгий анализ.
Этот вопрос о пригодности простой обратной связи можно изложить другими словами, тесно связанными с нашей главной темой. Условие, которому должны удовлетворять коэффициенты альфа.фи, определяется ГЛОБАЛЬНО по отношению ко всему множеству изображений. В то же время "корректирующая" процедура в высшей степени локальна в том смысле, что каждое изменение текущих значений коэффициентов основано на рассмотрении только одного изображения. Таким образом, проблема нахождения условий, при которых процедура заставит коэффициенты альфа.фи, сходиться к глобально удовлетворительным значениям, связана с изучением соотношений между явно глобальными и явно локальными вычислениями.
В настоящей главе мы покажем, что очень небольшие усовершенствования превращают простой принцип обратной связи в работоспособную процедуру "тренировки", или исправления ошибок. Основные теоремы об этом уже известны довольно хорошо. Главная наша забота - понять, почему эта процедура действует. Механизм процедуры и ее логические основы станут ясными и понятными в результате разностороннего анализа.
При рассмотрении возможности распознавания тех или иных классов фигур мы старались заменить неопределенные формулировки вопросов о том, являются ли персептроны "хорошими" или "плохими" распознающими устройствами, аналитической теорией, показывающей, почему в некоторых случаях персептроны работают успешно, а в других должны потерпеть неудачу. Несмотря на то что у нас нет так же хорошо разработанной теории обучения, мы можем по крайней мере показать, что в тех случаях, когда "обучение", или "адаптация", или "самоорганизация" все-таки происходит, это явление вполне объяснимо и не содержит ни малейшего намека на таинственные и малопонятные принципы поведения сложных систем. Действуют ли здесь такие принципы, мы не можем знать. Персептрон никаких доказательств этому не дает, а наш успешный анализ персептрона представляет еще одно косвенное подтверждение тезиса о том, что работоспособные кибернетические процессы понять можно, а те, которые нельзя понять, весьма подозрительны.
#11.1. ТЕОРЕМА О СХОДИМОСТИ ПЕРСЕПТРОНА
Рассмотрим следующую программу, в которой наша обычная сумма СУММА альфа.фи*фи(X) интерпретируется как скалярное произведение A*Ф.
НАЧАЛО: Выбрать любое значение для A.
ИСПЫТАНИЕ: Выбрать какое-нибудь изображение X из F+ объединение F-.
Если X принадлежит F+ и A*Ф>0, перейти к ИСПЫТАНИЕ.
Если X принадлежит F+ и A*Ф<=0, перейти к СЛОЖЕНИЕ.
Если X принадлежит F- и A*Ф<0, перейти к ИСПЫТАНИЕ.
Если X принадлежит F- и A*Ф>=0, перейти к ВЫЧИТАНИЕ.
СЛОЖЕНИЕ: Заменить A на A+Ф(X).
Перейти к ИСПЫТАНИЕ.
ВЫЧИТАНИЕ: Заменить A на A-Ф(X).
Перейти к ИСПЫТАНИЕ.
Впредь до последующего указания мы предполагаем, что существует такой вектор A", что А"*Ф(X)>0 для X из F+ и А"*Ф(X)<0 для X из F-. Теорема о сходимости персептрона утверждает, что при любом выборе в блоке НАЧАЛО и любой функции выбора в блоке ИСПЫТАНИЕ вектор А будет изменяться только конечное число раз. Другими словами, вектор А в результате примет значение А0, при котором А0*Ф(X) будет иметь надлежащий знак, т.е.
пси = [A0*Ф>0]
будет обладать свойством
X принадлежит F+ влечет пси(X)=1,
X принадлежит F- влечет пси(X)=0.
Часто по поводу этого свойства говорят, что предикат пси(X) разделяет множества F+ и F-. Теорему о сходимости можно сформулировать тогда так: если множества разделимы (т.е. существует вектор "решения" А"), то программа разделит их (т.е. найдет вектор решения А0, который может и не совпадать с А").
Так как сейчас нас больше интересуют множества коэффициентов {альфа.i}, а не характер множества ФИ и не геометрия изображений на R, то удобно связывать функции из L(ФИ) с множествами {альфа.i}, рассматриваемыми как векторы пространства, базис которого образуют предикаты фи из ФИ. Предостережение: базис векторного пространства образуют частные предикаты фи, а не точки сетчатки R! Хотя формы СУММА альфа.i*фи.i в этой главе будут считаться элементами векторного пространства, следует помнить, что множество L(ФИ) предикатов пси НЕ ЯВЛЯЕТСЯ векторным пространством и что каждый предикат пси принадлежит L(ФИ) можно представить с помощью многих различных векторов А [Отметим, что в этой книге теория векторных пространств встречается только здесь и в гл.12. Обычно в литературе о персептронах теория векторных пространств была основным математическим аппаратом, а второе место занимала статистика, играющая в наших изысканиях тоже незначительную роль. Если бы нам предложили назвать главную причину того, что о персептронах известно так мало, несмотря на целое десятилетие их изучения, мы указали бы именно на применение теории векторных пространств! Ибо в связи с тем, что формы СУММА альфа.i*фи.i рассматривались как скалярные произведения, отношения между образами (X) и предикатами из L(ФИ) стали совершенно неясными. Векторы A не являются линейными операторами, действующими на сами изображения; это "ко-операторы", т.е. они действуют в пространствах функциональных операторов, которые уже в свою очередь действуют на изображения. Поскольку базисы (ФИ-классы) этих векторных пространств произвольны, нет надежды использовать их для того, чтобы узнать многое о типах предикатов, принадлежащих L(ФИ). Важны не линейные свойства совокупностей L(ФИ), а степень сложности вычисления характеристик образов по информации, заключенной в самом множестве {фи(X)}].
С точки зрения теории векторных пространств классы F+ и F- отображаются на классы векторов, которые мы будем также обозначать F+ и F-. Разумеется, такое отображение может быть вырожденным, так как могут найтись два изображения X!=X', для которых ФИ(X)=ФИ(X'): персептрон "видит" исходные изображения только через посредство предикатов фи, и некоторые детали могут быть потеряны.
Отбросим теперь ограничение на функцию фи, согласно которому она могла равняться только 0 или 1. Пусть фи принимает любые вещественные (положительные и отрицательные) значения, и пусть для различных X каждая функция может иметь любое число различных значений. Таким образом, F+ и F- можно считать двумя произвольными множествами в пространстве ФИ.
Главная опасность, возникающая из-за такого обобщения, состоит в том, что слишком большие векторы могут испортить действие обратной связи, а слишком малые - замедлить его. Поэтому в дальнейшем будем прибавлять или вычитать не вектор Ф, а единичный вектор Ф' того же направления:
Ф' = Ф/|Ф|, откуда |Ф'| = 1.
Если множества F+ и F- бесконечны, то углы между векторами из разных множеств могут стремиться к нулю. В этом случае существует только один вектор решения, и программа может не найти его.
Условия теоремы 11.1 исключают эту возможность.
Блок ИСПЫТАНИЕ в описанной выше программе слишком сложен. Следующая программа работает точно так же:
НАЧАЛО: Выбрать любое значение А(!=0).
ИСПЫТАНИЕ: Выбрать вектор Ф из F+ объединение F-.
Если Ф принадлежит F+ и А*Ф>0, перейти к ИСПЫТАНИЕ.
Если Ф принадлежит F+ и А*Ф<=0, перейти к СЛОЖЕНИЕ.
Заменить Ф на -Ф.
Если Ф принадлежит F- и А*Ф>0, перейти к ИСПЫТАНИЕ.
Если Ф принадлежит F- и А*Ф<=0, перейти к СЛОЖЕНИЕ.
СЛОЖЕНИЕ: Заменить А на А+Ф.
Перейти к ИСПЫТАНИЕ.
Эта программа аналогична предыдущей, поскольку (1) изменен знак неравенства в той части блока ИСПЫТАНИЕ, которая следует за изменением Ф, так что все решения будут приниматься так же; (2) результат оператора "перейти к СЛОЖЕНИЕ" соответствует результату оператора "перейти к ВЫЧИТАНИЕ" при обратном знаке Ф. Далее, команда "заменить Ф на -Ф" выполняется тогда и только тогда, когда Ф принадлежит F-, а так как условия, выраженные неравенствами, имеют теперь одинаковые исходы, можно заменить эту программу другой, эквивалентной, программой:
НАЧАЛО: Выбрать любое значение A.
ИСПЫТАНИЕ: Выбрать вектор Ф из F+ объединение F-.
Если Ф принадлежит F-, изменить знак Ф.
Если A*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти к ИСПЫТАНИЕ.
СЛОЖЕНИЕ: Заменить A на A+Ф.
Перейти к ИСПЫТАНИЕ.
Другими словами, задача нахождения вектора A, разделяющего два данных множества F+ и F-, в действительности не отличается от задачи нахождения вектора А, удовлетворяющего условию
Ф принадлежит F => A*Ф>0
для одного заданного множества F, представляющего собой совокупность векторов из F+ и взятых с обратным знаком векторов из F-.
Учитывая эти замечания, упростим программу и формулировку теоремы о сходимости. Для простоты изложим вариант с единичными векторами.
ТЕОРЕМА 11.1 О СХОДИМОСТИ ПЕРСЕПТРОНА. Пусть F - множество единичных векторов Ф. Если существуют такие единичный вектор А* и число дельта>0, что A*Ф>дельта для всех Ф из F, то программа
НАЧАЛО: Выбрать произвольный вектор Ф из F в качестве A.
ИСПЫТАНИЕ: Выбрать вектор Ф из F и если А*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти к СЛОЖЕНИЕ.
СЛОЖЕНИЕ: Заменить А на А+Ф.
Перейти к ИСПЫТАНИЕ.
переходит к блоку СЛОЖЕНИЕ только конечное число раз.
Некоторые читатели, возможно, будут удивлены, заметив, что при доказательстве этой теоремы не используются никакие предположения о конечности множества F или размерности векторного пространства. В дальнейших разделах, где компактность единичной сферы играет существенную роль, такие предположения будут нужны.
СЛЕДСТВИЕ. Если программе представлена такая последовательность, в которой каждый вектор Ф принадлежит F повторяется как угодно много раз, то она в конце концов найдет вектор "решения", т.е. вектор A, для которого
A*Ф>0 для всех Ф принадлежит F.
Разумеется, он не обязательно должен быть вектором A", так как A" - ПРОИЗВОЛЬНЫЙ вектор решения. Все векторы решения образуют выпуклый конус, и программа прекратит изменение вектора A, как только он перейдет границу этого конуса. (Выпуклым конусом называется множество S векторов, для которых (1) альфа принадлежит S => k*aльфа принадлежит S для всех k>0, (2) альфа принадлежит S и бета принадлежит S => (альфа+бета) принадлежит S. Это не векторное подпространство, ибо k>0).
#11.2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О СХОДИМОСТИ 11.2.1. Обозначим
G(A)=A"*A/|A|,
т.е. G(A) - косинус угла между A и A". Так как |А"|=1, то
G(A)<=1.
Рассмотрим поведение G(A) при последовательных обращениях программы к блоку СЛОЖЕНИЕ:
А" * А.[t+1] = А" * (А.t + Ф) = А"*А.t + А"*Ф >= А"*А.t + дельта;
отсюда после n-го выполнения команды СЛОЖЕНИЕ получаем (ТЕЗИС)
А"*А.n >= n*дельта.
Таким образом, числитель дроби растет линейно с ростом числа n изменений вектора А, т.е. числа ошибок.
Теперь относительно знаменателя. Так как число A.t*Ф должно быть отрицательным (иначе программа не обратилась бы к блоку СЛОЖЕНИЕ), то
|А.[t+1]|**2 = A.[t+1]*A.[t+1] = (А.t+Ф)*(А.t+Ф) = |А.t|**2 + 2*А.t*Ф + |Ф|**2 < |А.t|**2 + 1
и после n-го выполнения команды СЛОЖЕНИЕ (АНТИТЕЗИС)
|А.n|**2 < n.
ТЕЗИС и АНТИТЕЗИС вместе дают
G(A.n) = A"*A.n/|A.n| > n*дельта/sqr(n),
но так как G(A.n)<=1, то это неравенство справедливо только для sqr(n)*дельта<=1, т.е. n<=1/дельта*2. Теорема доказана.
Некоторые аспекты геометрии скорости роста |A| представлены на рис.11.2 и 11.3. Эти рисунки особенно интересны для тех, кто хотел бы рассмотреть следующее диалектическое и, немного неверное, алгебраическое доказательство. Из неравенства АНТИТЕЗИС следует, что |A.n| растет медленнее, чем sqr(n). С другой стороны, из неравенства ТЕЗИС можно вывести (при помощи неравенства Коши-Шварца), что |A.n| растет пропорционально n. Это ведет к противоречию: величина |A.n| должна расти достаточно быстро, но не может
Рис.11.2. Увеличение радиуса должно равняться по меньшей мере дельта, однако новый вектор должен оставаться в заштрихованной области; это невозможно, если толщина этой области, меняющаяся обратно пропорционально |A|, становится меньше дельта.
Рис.11.3. Предельный случай, в котором граница |A.n|=sqr(n) достигается.
#11.3. ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО (ФАКУЛЬТАТИВНО)
Пусть нам задан такой (единичный) вектор A", что
А"*Ф > дельта для всех Ф из F.
Это значит, что cos(тета.Ф), где тета.Ф - угол, образованный вектором Ф из F с вектором А", больше дельта. Если выбрать угол тета">0 так, чтобы cos(тета") > cos(max(тета")), то для КАЖДОГО вектора V, отклоняющегося от A" на угол, не превышающий тета", будет
V*Ф>0 для всех Ф из F.
Поэтому любой вектор V внутри кругового конуса с осью A" и углом тета" будет вектором решения, который заставит программу прекратить изменение вектора A.
Рассмотрим теперь вектор А, вычисляемый программой. На каждой ступени вычислений A есть сумма элементов из F. Поэтому
A" * A = A" * (Ф.1+Ф.2+...) > 0.
Рассмотрим плоскость, в которой лежат векторы A" и A. Если в качестве А" взять вертикальный единичный вектор, то приведенное выше неравенство означает, что вектор A должен быть направлен в верхнюю полуплоскость:
Нам хотелось бы показать, что каждый раз, когда программа проходит через сложение, A приближается по направлению к A". К сожалению, это не ВСЕГДА так, но, как видно из рис.11.4, обычно это происходит. Разберемся в этом обычном случае, прежде чем погрузиться в детали строгого доказательства.
При выполнении команды СЛОЖЕНИЕ вектор Ф прибавляется к текущему значению вектора А, скажем A.t, и получается новое значение вектора A, скажем A.[t+1]=A.t+Ф. О векторе Ф нам известно два факта:
A" * Ф > 0,
A.t * Ф < 0.
Обозначим через Ф.N проекцию вектора Ф на плоскость, образованную векторами A" и A.t. Перенесем начало этой проекции в конец вектора A.t (для того чтобы получить геометрическую картину сложения векторов). В силу первого условия конец вектора Ф.N должен быть выше прямой p, а в силу второго - ниже прямой q. Таким образом, вектор Ф.N расположен, как на рис.11.4, и направлен из конца вектора A.t к вектору А".
Если рассмотреть конус, образованный вращением вектора A.t вокруг A", то легко обнаружить, что сам вектор Ф (проекцией которого служит Ф.N) заходит внутрь конуса. Доказательство теоремы было бы закончено, если бы не то обстоятельство, что Ф может снова выйти за пределы конуса, и тогда вектор A.[i+1] будет иметь большее угловое удаление от А", чем вектор А.t. Этот случай показан на рис.11.5.
Однако такой "прокол" конуса не является роковым, поскольку он может происходить только конечное число раз, зависящее от тета". В самом деле, рассмотрим конус, образованный вращением вектора A вокруг A". Так как Ф всегда имеет вертикальную составляющую Ф*А">дельта, то высота конуса растет всякий раз, когда изменяется A. Если угол между A и A" остается больше тета" (а если нет - доказательство закончено!), то радиус основания конуса становится неопределенно большим. Спроектируем все рассматриваемые векторы на основание конуса (рис.11.6). Обозначим через Ф" проекцию вектора Ф на это основание и покажем, что ее конец удален от касательной в точке A не менее чем на d и лежит по ту же сторону, что и A". Так как |Ф'| = 1, то этот конец должен лежать внутри единичного круга с центром в конце вектора А (рис.11.6).

Рис.11.6. a - единичная окружность вокруг конца вектора A; b - конец вектора; c - касательная к основанию конуса; e - основание конуса (малого); f - основание конуса (большого).
Итак, конец вектора Ф" должен лежать внутри заштрихованной области. Когда основание конуса станет достаточно большим, заштрихованная область целиком будет внутри конуса, а вместе с ней и ф". Тогда внутри конуса будет и конец вектора ф, так как он расположен непосредственно над Ф". Осталось только показать, откуда появилось магическое расстояние d.
Для этого спроектируем все на плоскость, перпендикулярную касательной (рис.11.7). Конец вектора Ф должен лежать внутри заштрихованной области, которая определяется плоскостью (1), перпендикулярной к A, и плоскостью (2), перпендикулярной к А" и расположенной на дельта выше A, поскольку A"*Ф>дельта. Таким образом, конец вектора ф должен быть удален от касательной не менее, чем на некоторое расстояние d. Нижнюю границу для d определяет тот факт, что вектор A образует с А" угол, не превышающий пи/2-тета", так как он является суммой векторов Ф. Итак, после конечного числа переходов к блоку СЛОЖЕНИЕ векторы A будут оставаться в вертикальном цилиндре, расположенном внутри конуса допустимых решений, имеющего своей осью вектор А".
Отсюда следует, что изменение вектора A должно прекратиться, и теорема 11.1, таким образом, доказана.
#11.0. ВВЕДЕНИЕ
В предыдущих главах у нас не было никакой систематической методики представления предиката как элемента множества L(ФИ). Наоборот, мы строили коэффициенты на основе специального математического анализа самого предиката и множества элементарных предикатов фи. Эти исследования проводились СПЕЦИАЛЬНО для каждого предиката. В настоящей главе мы изучаем ситуации, в которых множества коэффициентов можно найти при помощи более систематизированной процедуры, легко воплотимой в автоматическом устройстве. Именно эта возможность и создала персептрону славу "обучающейся машины".
Принципиальную схему процесса "обучения", как он понимается здесь, можно представить себе в виде машины, состоящей из канала ввода изображений, двух выходных индикаторов да и нет и ПОДКРЕПЛЯЮЩЕЙ, или "поощряющей", кнопки, при помощи которой оператор машины может одобрять или не одобрять ее поведение (рис.11.1). Оператор имеет два набора F+ и F- изображений и хотел бы, чтобы машина отвечала ДА на каждое изображение из набора F+ и НЕТ на каждое изображение из F-. Если реакция машины верна, то свое одобрение оператор выражает, скажем, нажатием кнопки. Машина обязана изменять свое внутреннее состояние, чтобы приспосабливаться к желаниям ее хозяина.

Существует множество способов построения такой машины. Наиболее очевидная схема должна иметь какое нибудь записывающее усгройство для запоминания вводимых изображений в двух накопителях, отдельно для F+ и для F-. Такая машина никогда не сделает ошибки на изображении, которое она видела раньше, но наряду со способностью никогда ничего не забывать она бывает весьма неуклюжей. Другая машина, построенная на совершенно иных принципах, попыталась бы найти описательные характеристики, различные для изображений двух классов, и использовать новые изображения для уточнения и совершенствования этих описаний. Такая машина потребовала бы при длительной работе меньшей памяти, но ее устройство и теория значительно более сложные. Если классы F+ и F- очень велики, то первая машина работать не сможет, а если для встречающегося на практике репертуара изображений описания не существует, то потерпит неудачу машина второго вида.
Персептрон как машина, умеющая различать образы, лежит между этими двумя крайностями. Он не ищет соответствия с хранящимися в памяти изображениями, так как не запоминает самих изображений. При выработке описаний возможности персептрона, как мы видели в предыдущих главах, ограничены тем, чего можно достичь, используя лишь "локальные" отличительные свойства образов и только линейные пороговые отношения между этими свойствами. Существование описанных ниже простых процедур обучения следует из этого ограничения, наложенного на способность машины строить описание (и могло бы рассматриваться как частичная компенсация этого ограничения).
Предположим, что обучающейся машиной является персептрон с фиксированным множеством ФИ и регулируемыми коэффициентами. При подаче на вход персептрона изображения X вычисляется сумма
СУММА альфа.фи*фи(X).
Если X принадлежит F+ и эта сумма положительна, то машина отвечает ДА и все хорошо. Если X принадлежит F+, а сумма отрицательна, то машина отвечает НЕТ. Это плохо, и нужно что-то предпринимать. Что может служить простейшей процедурой коррекции?
Первое, что приходит в голову, особенно людям, воспитанным на идее обратной связи, это увеличить коэффициенты слагаемых, поскольку сумма оказалась слишком малой. Если бы она оказалась слишком большой (а именно ответ ДА на изображение из F-), у нас возникло бы желание уменьшить коэффициенты.
Но коэффициенты нужно регулировать разумно, чтобы должным образом направлять действие обратной связи.
Предположим, что для какого-то изображения X из F+ сумма СУММА альфа.фи*фи(X) получилась отрицательной. Вообще говоря, для некоторых предикатов фи значение фи(X) равно 0, и совершенно ясно, что их коэффициенты не отвечают за неверный результат. На самом деле изменение этих коэффициентов может даже нанести вред другим изображениям и уже во всяком случае не принесет никакой пользы для данного X. Поэтому будем увеличивать альфа.фи только в том случае, если фи(X)=1. Мы хотели бы иметь для этого такую процедуру, математическая форма которой достаточно ясна и поддается простому анализу, а ее способность добиться определенного успеха достаточно велика. Приведенная в #11.1 процедура удовлетворяет обоим этим требованиям, но, прежде чем перейти к ее описанию, сделаем несколько предварительных замечаний.
#11.0.1. КОЭФФИЦИЕНТЫ И ВЕКТОРЫ. Множество коэффициентов {альфа.фи}, упорядоченных произвольным, но фиксированным образом, удобно представить в виде вектора в |ФИ|-мерном пространстве. Обозначим этот вектор через A. Точно так же множество {фи(X)}, упорядоченное таким же образом, можно рассматривать как вектор, координатами которого служат значения предикатов фи(X). Обозначим этот вектор через Ф(X). Теперь увеличение коэффициентов, соответствующих ненулевым значениям фи(X), изящно осуществляется простым прибавлением вектора Ф(X) к вектору A. Если бы для X и F- сумма оказалась положительной, то следовало бы вычесть Ф(X) из А.
Любая подобная процедура с самого начала таит в себе опасность возникновения сильных колебаний. Регулировка в соответствующем направлении коэффициентов для одного изображения могла бы расстроить предыдущую регулировку для другого. Таким образом, наше интуитивное представление о работоспособности подобной процедуры подвержено влиянию двух противоречивых идей, почерпнутых из опыта кибернетики: простая обратная связь, корректирующая ошибки, часто оказывается вполне работоспособной; с другой стороны, процесс включает в себя поиск в |ФИ|-мерном пространстве, а наш опыт с другими системами типа "подъема на холм" заставляет нас остро сознавать опасности, которые грозят подобным процедурам. Необходим строгий анализ.
Этот вопрос о пригодности простой обратной связи можно изложить другими словами, тесно связанными с нашей главной темой. Условие, которому должны удовлетворять коэффициенты альфа.фи, определяется ГЛОБАЛЬНО по отношению ко всему множеству изображений. В то же время "корректирующая" процедура в высшей степени локальна в том смысле, что каждое изменение текущих значений коэффициентов основано на рассмотрении только одного изображения. Таким образом, проблема нахождения условий, при которых процедура заставит коэффициенты альфа.фи, сходиться к глобально удовлетворительным значениям, связана с изучением соотношений между явно глобальными и явно локальными вычислениями.
В настоящей главе мы покажем, что очень небольшие усовершенствования превращают простой принцип обратной связи в работоспособную процедуру "тренировки", или исправления ошибок. Основные теоремы об этом уже известны довольно хорошо. Главная наша забота - понять, почему эта процедура действует. Механизм процедуры и ее логические основы станут ясными и понятными в результате разностороннего анализа.
При рассмотрении возможности распознавания тех или иных классов фигур мы старались заменить неопределенные формулировки вопросов о том, являются ли персептроны "хорошими" или "плохими" распознающими устройствами, аналитической теорией, показывающей, почему в некоторых случаях персептроны работают успешно, а в других должны потерпеть неудачу. Несмотря на то что у нас нет так же хорошо разработанной теории обучения, мы можем по крайней мере показать, что в тех случаях, когда "обучение", или "адаптация", или "самоорганизация" все-таки происходит, это явление вполне объяснимо и не содержит ни малейшего намека на таинственные и малопонятные принципы поведения сложных систем. Действуют ли здесь такие принципы, мы не можем знать. Персептрон никаких доказательств этому не дает, а наш успешный анализ персептрона представляет еще одно косвенное подтверждение тезиса о том, что работоспособные кибернетические процессы понять можно, а те, которые нельзя понять, весьма подозрительны.
#11.1. ТЕОРЕМА О СХОДИМОСТИ ПЕРСЕПТРОНА
Рассмотрим следующую программу, в которой наша обычная сумма СУММА альфа.фи*фи(X) интерпретируется как скалярное произведение A*Ф.
НАЧАЛО: Выбрать любое значение для A.
ИСПЫТАНИЕ: Выбрать какое-нибудь изображение X из F+ объединение F-.
Если X принадлежит F+ и A*Ф>0, перейти к ИСПЫТАНИЕ.
Если X принадлежит F+ и A*Ф<=0, перейти к СЛОЖЕНИЕ.
Если X принадлежит F- и A*Ф<0, перейти к ИСПЫТАНИЕ.
Если X принадлежит F- и A*Ф>=0, перейти к ВЫЧИТАНИЕ.
СЛОЖЕНИЕ: Заменить A на A+Ф(X).
Перейти к ИСПЫТАНИЕ.
ВЫЧИТАНИЕ: Заменить A на A-Ф(X).
Перейти к ИСПЫТАНИЕ.
Впредь до последующего указания мы предполагаем, что существует такой вектор A", что А"*Ф(X)>0 для X из F+ и А"*Ф(X)<0 для X из F-. Теорема о сходимости персептрона утверждает, что при любом выборе в блоке НАЧАЛО и любой функции выбора в блоке ИСПЫТАНИЕ вектор А будет изменяться только конечное число раз. Другими словами, вектор А в результате примет значение А0, при котором А0*Ф(X) будет иметь надлежащий знак, т.е.
пси = [A0*Ф>0]
будет обладать свойством
X принадлежит F+ влечет пси(X)=1,
X принадлежит F- влечет пси(X)=0.
Часто по поводу этого свойства говорят, что предикат пси(X) разделяет множества F+ и F-. Теорему о сходимости можно сформулировать тогда так: если множества разделимы (т.е. существует вектор "решения" А"), то программа разделит их (т.е. найдет вектор решения А0, который может и не совпадать с А").
Так как сейчас нас больше интересуют множества коэффициентов {альфа.i}, а не характер множества ФИ и не геометрия изображений на R, то удобно связывать функции из L(ФИ) с множествами {альфа.i}, рассматриваемыми как векторы пространства, базис которого образуют предикаты фи из ФИ. Предостережение: базис векторного пространства образуют частные предикаты фи, а не точки сетчатки R! Хотя формы СУММА альфа.i*фи.i в этой главе будут считаться элементами векторного пространства, следует помнить, что множество L(ФИ) предикатов пси НЕ ЯВЛЯЕТСЯ векторным пространством и что каждый предикат пси принадлежит L(ФИ) можно представить с помощью многих различных векторов А [Отметим, что в этой книге теория векторных пространств встречается только здесь и в гл.12. Обычно в литературе о персептронах теория векторных пространств была основным математическим аппаратом, а второе место занимала статистика, играющая в наших изысканиях тоже незначительную роль. Если бы нам предложили назвать главную причину того, что о персептронах известно так мало, несмотря на целое десятилетие их изучения, мы указали бы именно на применение теории векторных пространств! Ибо в связи с тем, что формы СУММА альфа.i*фи.i рассматривались как скалярные произведения, отношения между образами (X) и предикатами из L(ФИ) стали совершенно неясными. Векторы A не являются линейными операторами, действующими на сами изображения; это "ко-операторы", т.е. они действуют в пространствах функциональных операторов, которые уже в свою очередь действуют на изображения. Поскольку базисы (ФИ-классы) этих векторных пространств произвольны, нет надежды использовать их для того, чтобы узнать многое о типах предикатов, принадлежащих L(ФИ). Важны не линейные свойства совокупностей L(ФИ), а степень сложности вычисления характеристик образов по информации, заключенной в самом множестве {фи(X)}].
С точки зрения теории векторных пространств классы F+ и F- отображаются на классы векторов, которые мы будем также обозначать F+ и F-. Разумеется, такое отображение может быть вырожденным, так как могут найтись два изображения X!=X', для которых ФИ(X)=ФИ(X'): персептрон "видит" исходные изображения только через посредство предикатов фи, и некоторые детали могут быть потеряны.
Отбросим теперь ограничение на функцию фи, согласно которому она могла равняться только 0 или 1. Пусть фи принимает любые вещественные (положительные и отрицательные) значения, и пусть для различных X каждая функция может иметь любое число различных значений. Таким образом, F+ и F- можно считать двумя произвольными множествами в пространстве ФИ.
Главная опасность, возникающая из-за такого обобщения, состоит в том, что слишком большие векторы могут испортить действие обратной связи, а слишком малые - замедлить его. Поэтому в дальнейшем будем прибавлять или вычитать не вектор Ф, а единичный вектор Ф' того же направления:
Ф' = Ф/|Ф|, откуда |Ф'| = 1.
Если множества F+ и F- бесконечны, то углы между векторами из разных множеств могут стремиться к нулю. В этом случае существует только один вектор решения, и программа может не найти его.
Условия теоремы 11.1 исключают эту возможность.
Блок ИСПЫТАНИЕ в описанной выше программе слишком сложен. Следующая программа работает точно так же:
НАЧАЛО: Выбрать любое значение А(!=0).
ИСПЫТАНИЕ: Выбрать вектор Ф из F+ объединение F-.
Если Ф принадлежит F+ и А*Ф>0, перейти к ИСПЫТАНИЕ.
Если Ф принадлежит F+ и А*Ф<=0, перейти к СЛОЖЕНИЕ.
Заменить Ф на -Ф.
Если Ф принадлежит F- и А*Ф>0, перейти к ИСПЫТАНИЕ.
Если Ф принадлежит F- и А*Ф<=0, перейти к СЛОЖЕНИЕ.
СЛОЖЕНИЕ: Заменить А на А+Ф.
Перейти к ИСПЫТАНИЕ.
Эта программа аналогична предыдущей, поскольку (1) изменен знак неравенства в той части блока ИСПЫТАНИЕ, которая следует за изменением Ф, так что все решения будут приниматься так же; (2) результат оператора "перейти к СЛОЖЕНИЕ" соответствует результату оператора "перейти к ВЫЧИТАНИЕ" при обратном знаке Ф. Далее, команда "заменить Ф на -Ф" выполняется тогда и только тогда, когда Ф принадлежит F-, а так как условия, выраженные неравенствами, имеют теперь одинаковые исходы, можно заменить эту программу другой, эквивалентной, программой:
НАЧАЛО: Выбрать любое значение A.
ИСПЫТАНИЕ: Выбрать вектор Ф из F+ объединение F-.
Если Ф принадлежит F-, изменить знак Ф.
Если A*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти к ИСПЫТАНИЕ.
СЛОЖЕНИЕ: Заменить A на A+Ф.
Перейти к ИСПЫТАНИЕ.
Другими словами, задача нахождения вектора A, разделяющего два данных множества F+ и F-, в действительности не отличается от задачи нахождения вектора А, удовлетворяющего условию
Ф принадлежит F => A*Ф>0
для одного заданного множества F, представляющего собой совокупность векторов из F+ и взятых с обратным знаком векторов из F-.
Учитывая эти замечания, упростим программу и формулировку теоремы о сходимости. Для простоты изложим вариант с единичными векторами.
ТЕОРЕМА 11.1 О СХОДИМОСТИ ПЕРСЕПТРОНА. Пусть F - множество единичных векторов Ф. Если существуют такие единичный вектор А* и число дельта>0, что A*Ф>дельта для всех Ф из F, то программа
НАЧАЛО: Выбрать произвольный вектор Ф из F в качестве A.
ИСПЫТАНИЕ: Выбрать вектор Ф из F и если А*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти к СЛОЖЕНИЕ.
СЛОЖЕНИЕ: Заменить А на А+Ф.
Перейти к ИСПЫТАНИЕ.
переходит к блоку СЛОЖЕНИЕ только конечное число раз.
Некоторые читатели, возможно, будут удивлены, заметив, что при доказательстве этой теоремы не используются никакие предположения о конечности множества F или размерности векторного пространства. В дальнейших разделах, где компактность единичной сферы играет существенную роль, такие предположения будут нужны.
СЛЕДСТВИЕ. Если программе представлена такая последовательность, в которой каждый вектор Ф принадлежит F повторяется как угодно много раз, то она в конце концов найдет вектор "решения", т.е. вектор A, для которого
A*Ф>0 для всех Ф принадлежит F.
Разумеется, он не обязательно должен быть вектором A", так как A" - ПРОИЗВОЛЬНЫЙ вектор решения. Все векторы решения образуют выпуклый конус, и программа прекратит изменение вектора A, как только он перейдет границу этого конуса. (Выпуклым конусом называется множество S векторов, для которых (1) альфа принадлежит S => k*aльфа принадлежит S для всех k>0, (2) альфа принадлежит S и бета принадлежит S => (альфа+бета) принадлежит S. Это не векторное подпространство, ибо k>0).
#11.2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О СХОДИМОСТИ 11.2.1. Обозначим
G(A)=A"*A/|A|,
т.е. G(A) - косинус угла между A и A". Так как |А"|=1, то
G(A)<=1.
Рассмотрим поведение G(A) при последовательных обращениях программы к блоку СЛОЖЕНИЕ:
А" * А.[t+1] = А" * (А.t + Ф) = А"*А.t + А"*Ф >= А"*А.t + дельта;
отсюда после n-го выполнения команды СЛОЖЕНИЕ получаем (ТЕЗИС)
А"*А.n >= n*дельта.
Таким образом, числитель дроби растет линейно с ростом числа n изменений вектора А, т.е. числа ошибок.
Теперь относительно знаменателя. Так как число A.t*Ф должно быть отрицательным (иначе программа не обратилась бы к блоку СЛОЖЕНИЕ), то
|А.[t+1]|**2 = A.[t+1]*A.[t+1] = (А.t+Ф)*(А.t+Ф) = |А.t|**2 + 2*А.t*Ф + |Ф|**2 < |А.t|**2 + 1
и после n-го выполнения команды СЛОЖЕНИЕ (АНТИТЕЗИС)
|А.n|**2 < n.
ТЕЗИС и АНТИТЕЗИС вместе дают
G(A.n) = A"*A.n/|A.n| > n*дельта/sqr(n),
но так как G(A.n)<=1, то это неравенство справедливо только для sqr(n)*дельта<=1, т.е. n<=1/дельта*2. Теорема доказана.
Некоторые аспекты геометрии скорости роста |A| представлены на рис.11.2 и 11.3. Эти рисунки особенно интересны для тех, кто хотел бы рассмотреть следующее диалектическое и, немного неверное, алгебраическое доказательство. Из неравенства АНТИТЕЗИС следует, что |A.n| растет медленнее, чем sqr(n). С другой стороны, из неравенства ТЕЗИС можно вывести (при помощи неравенства Коши-Шварца), что |A.n| растет пропорционально n. Это ведет к противоречию: величина |A.n| должна расти достаточно быстро, но не может

Рис.11.2. Увеличение радиуса должно равняться по меньшей мере дельта, однако новый вектор должен оставаться в заштрихованной области; это невозможно, если толщина этой области, меняющаяся обратно пропорционально |A|, становится меньше дельта.

Рис.11.3. Предельный случай, в котором граница |A.n|=sqr(n) достигается.
#11.3. ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО (ФАКУЛЬТАТИВНО)
Пусть нам задан такой (единичный) вектор A", что
А"*Ф > дельта для всех Ф из F.
Это значит, что cos(тета.Ф), где тета.Ф - угол, образованный вектором Ф из F с вектором А", больше дельта. Если выбрать угол тета">0 так, чтобы cos(тета") > cos(max(тета")), то для КАЖДОГО вектора V, отклоняющегося от A" на угол, не превышающий тета", будет
V*Ф>0 для всех Ф из F.
Поэтому любой вектор V внутри кругового конуса с осью A" и углом тета" будет вектором решения, который заставит программу прекратить изменение вектора A.
Рассмотрим теперь вектор А, вычисляемый программой. На каждой ступени вычислений A есть сумма элементов из F. Поэтому
A" * A = A" * (Ф.1+Ф.2+...) > 0.
Рассмотрим плоскость, в которой лежат векторы A" и A. Если в качестве А" взять вертикальный единичный вектор, то приведенное выше неравенство означает, что вектор A должен быть направлен в верхнюю полуплоскость:

Нам хотелось бы показать, что каждый раз, когда программа проходит через сложение, A приближается по направлению к A". К сожалению, это не ВСЕГДА так, но, как видно из рис.11.4, обычно это происходит. Разберемся в этом обычном случае, прежде чем погрузиться в детали строгого доказательства.
При выполнении команды СЛОЖЕНИЕ вектор Ф прибавляется к текущему значению вектора А, скажем A.t, и получается новое значение вектора A, скажем A.[t+1]=A.t+Ф. О векторе Ф нам известно два факта:
A" * Ф > 0,
A.t * Ф < 0.
Обозначим через Ф.N проекцию вектора Ф на плоскость, образованную векторами A" и A.t. Перенесем начало этой проекции в конец вектора A.t (для того чтобы получить геометрическую картину сложения векторов). В силу первого условия конец вектора Ф.N должен быть выше прямой p, а в силу второго - ниже прямой q. Таким образом, вектор Ф.N расположен, как на рис.11.4, и направлен из конца вектора A.t к вектору А".

Если рассмотреть конус, образованный вращением вектора A.t вокруг A", то легко обнаружить, что сам вектор Ф (проекцией которого служит Ф.N) заходит внутрь конуса. Доказательство теоремы было бы закончено, если бы не то обстоятельство, что Ф может снова выйти за пределы конуса, и тогда вектор A.[i+1] будет иметь большее угловое удаление от А", чем вектор А.t. Этот случай показан на рис.11.5.

Однако такой "прокол" конуса не является роковым, поскольку он может происходить только конечное число раз, зависящее от тета". В самом деле, рассмотрим конус, образованный вращением вектора A вокруг A". Так как Ф всегда имеет вертикальную составляющую Ф*А">дельта, то высота конуса растет всякий раз, когда изменяется A. Если угол между A и A" остается больше тета" (а если нет - доказательство закончено!), то радиус основания конуса становится неопределенно большим. Спроектируем все рассматриваемые векторы на основание конуса (рис.11.6). Обозначим через Ф" проекцию вектора Ф на это основание и покажем, что ее конец удален от касательной в точке A не менее чем на d и лежит по ту же сторону, что и A". Так как |Ф'| = 1, то этот конец должен лежать внутри единичного круга с центром в конце вектора А (рис.11.6).

Рис.11.6. a - единичная окружность вокруг конца вектора A; b - конец вектора; c - касательная к основанию конуса; e - основание конуса (малого); f - основание конуса (большого).
Итак, конец вектора Ф" должен лежать внутри заштрихованной области. Когда основание конуса станет достаточно большим, заштрихованная область целиком будет внутри конуса, а вместе с ней и ф". Тогда внутри конуса будет и конец вектора ф, так как он расположен непосредственно над Ф". Осталось только показать, откуда появилось магическое расстояние d.
Для этого спроектируем все на плоскость, перпендикулярную касательной (рис.11.7). Конец вектора Ф должен лежать внутри заштрихованной области, которая определяется плоскостью (1), перпендикулярной к A, и плоскостью (2), перпендикулярной к А" и расположенной на дельта выше A, поскольку A"*Ф>дельта. Таким образом, конец вектора ф должен быть удален от касательной не менее, чем на некоторое расстояние d. Нижнюю границу для d определяет тот факт, что вектор A образует с А" угол, не превышающий пи/2-тета", так как он является суммой векторов Ф. Итак, после конечного числа переходов к блоку СЛОЖЕНИЕ векторы A будут оставаться в вертикальном цилиндре, расположенном внутри конуса допустимых решений, имеющего своей осью вектор А".

Отсюда следует, что изменение вектора A должно прекратиться, и теорема 11.1, таким образом, доказана.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#11.4. ДРУГИЕ ВАРИАНТЫ ТЕОРЕМЫ О СХОДИМОСТИ
Теорема о сходимости персептрона допускает массу других второстепенных формулировок. Наше доказательство легко приспособить к любому из видов, в которых эта теорема встречается в литературе о персептронах.
1) Вместо предположения о том, что множество F состоит из единичных векторов, можно допустить, что F - конечное множество или что его векторы ограничены по длине сверху и снизу, т.е. найдутся такие числа a и b, что 0<а<=|Ф|<=b для каждого Ф из F.
2) Вместо замены вектора А на А+Ф можно заменить его на А+kФ, где k - вещественное число, выбираемое по одному из следующих правил:
k - положительная константа;
k = 1/|Ф|, т.е. прибавляется единичный вектор;
k=c*A*Ф/|Ф|**2. Если c=1, то величина k вполне достаточна для вывода (А+kФ)-Ф из отрицательной области. Можно использовать любое значение c между 0 и 2 (Эгмон [1954]).
Эти и подобные им модификации не меняют теорему в том смысле, что после конечного числа переходов к блоку СЛОЖЕНИЕ вектор А все же станет вектором решения. Это число в каждом варианте теоремы будет своим. Интересно было бы сравнить относительную ЭФФЕКТИВНОСТЬ "локальной" программы сходимости персептрона с более "глобальными" аналитическими методами (например, с линейным программированием), которые можно применить для системы неравенств относительно А:
А*Ф>0 для всех Ф из F.
#11.4.1. СЛУЧАЙ БОЛЕЕ ЧЕМ ДВУХ КЛАССОВ. Обобщим теорему на случай, когда число классов входных изображений больше двух. Пусть F.i, F.2, ...- множества изображений, и пусть существуют такие векторы A.i" и число дельта>0, что
Ф принадлежит F.i влечет A.i"*Ф > A.j"*Ф + дельта для всех j!=i.
Тогда теорема о сходимости персептрона гласит, что векторы с тем же свойством можно найти, следуя обычному принципу обратной связи: всякий раз, когда в F.i - встречается изображение Ф, для которого А.i*Ф<A.j*Ф при некотором j, вектор A.i должен "увеличиваться", а А.j - "уменьшаться".
Более точно эта идея выражается в программе:
НАЧАЛО; Выбрать любые ненулевые значения A.1; A.2, ...
ИСПЫТАНИЕ: Выбрать i, j и Ф из F.i.
Если A.i*Ф>A.j*Ф, перейти к ИСПЫТАНИЕ; иначе перейти К ИЗМЕНЕНИЕ.
ИЗМЕНЕНИЕ: Заменить A.i на A.i+Ф.
Заменить A.j на A.j-Ф.
Перейти к ИСПЫТАНИЕ.
Обобщенная теорема утверждает, что эта программа будет обращаться к блоку ИЗМЕНЕНИЕ только конечное число раз. Но это возможно лишь в том случае, если машина в конце концов перестанет ошибаться, т.е. если для каждого вектора Ф из F.i в конце концов будет
A.i*Ф>A.j*Ф для всех j.
Для доказательства предположим, что векторы А.1", ..., A.i", ..., A.j", ..., A.m" удовлетворяют условию теоремы. Выпишем подряд координаты этих векторов и обозначим полученный вектор (в пространстве большей размерности) через А". Далее, для каждого Ф зададим (в этом новом пространстве) вектор Ф.ij, у которого i-й блок (т.е. место, отведенное для координат вектора A.i" в векторе А") заполнен координатами вектора Ф, j-й блок - координатами вектора -Ф, а все остальные блоки заполнены нулями. Теперь к этому большому пространству можно применить теорему 11.1.
#11.5. ПРИЛОЖЕНИЕ. ОБУЧЕНИЕ ПРЕДИКАТУ пси.ЧЕТН0СТЬ
В качестве примера, иллюстрирующего теорему о сходимости, оценим число шагов, необходимых для того, чтобы с помощью программы обучения определить коэффициенты предиката, проверяющего четность. В #10.1 мы показали, что вектор решения с наименьшими коэффициентами можно записать в виде
A = (
C(|R| 1) членов 2**(|R|-1),
...,
C(|R| j) членов 2**(|R|-j),
...,
1).
Длина этого вектора находится из равенства
|A|**2 = СУММА 2**(2*(|R|-j))*C(|R| j) = (1+2**2)**|R| = 5**|R|.
Соответствующий единичный вектор равен
A"=A/5**(|R|/2).
Проведенный в #10.1 анализ показывает, что произведение A*Ф равно 1 или -1. Так как вектор Ф имеет 2**|R| координат, каждая из которых равна либо 0, либо 1, то
|A"*Ф/|Ф|| >= 1/sqr(5**|R|*2**|R|) = 1/sqr(10**|R|).
Таким образом, в качестве дельта можно взять 1/sqr(10**|R|). Тогда число n коррекций ограничено величиной
n <= 1/дельта**2 <= 10**|R|.
Так как число |A.n| должно быть не менее 5**(|R|/2) и
|A.n| <= n,
то нижняя граница для n равна 5**|R|. Итак,
5**|R| <= n <= 10**|R|.
Заметим, что если бы в программе обучения вместо Ф" прибавлялся вектор Ф, то мы бы получили
5**|R|/max|Ф| <= n <= 10**|R|, т.е. (5/2)**|R| <= n <= 10**|R|.
Чтобы решить, действительно ли такая замена приведет к увеличению скорости обучения, требуется дополнительный анализ. Во всяком случае ясно, что время обучения должно расти экспоненциально с ростом |R|.
Эти неравенства определяют границы числа n коррекций, или, что то же самое, числа ошибок. При подсчете общего количества циклов программы (включая "пустые" циклы, в которых не наблюдается ошибка и, следовательно, не производится коррекция.- Ред.) нужно учитывать уменьшение числа ошибок в ходе обучения. Нетрудно, однако, видеть, что число M(r) циклов, необходимое для уменьшения относительного числа ошибок до величины r<1, должно удовлетворять неравенству M(r)<=n/r в предположении, что изображения подаются в машину в случайном порядке. Таким образом, для получения 1% ошибок необходимо немногим менее 10**(|R|+2) циклов.
#11.6. ПРОЦЕСС ОБУЧЕНИЯ, РАССМАТРИВАЕМЫЙ КАК ПОДЪЕМ НА ХОЛМ
Полезно рассмотреть, как связана процедура сходимости с общей проблемой "подъема на холм". Здесь также ищут глобальное решение (т.е. местонахождение абсолютной вершины) с помощью локальных операций (например, методом наискорейшего подъема). Эффективность таких методов зависит от того, в какой степени определение искомой вершины так глобально, как это могло бы показаться. В тех случаях, когда холм имеет сложную форму с большим количеством локальных пиков, гребней и т.д., процессы подъема на холм не всегда выгодны. Действительно, в таких ситуациях больше подходит случайный или систематический поиск, а не процесс, при котором с железной неумолимостью происходит подъем на каждый небольшой холмик.
В типичном случае подъема на холм ищут максимум функции G(A) от точек A некоторого n-мерного пространства. Простейшая процедура вычисляет значение функции "высоты" G для ряда точек A.i+Ф.i, в окрестности текущей точки А.i. На основании этих экспериментов выбирается величина Ф и сумма A.i+Ф принимается в качестве A.[t+i]. Алгоритм выбора Ф может быть различным. Например, в качестве Ф.i можно использовать единичные векторы, ориентированные в направлении осей, затем рассчитать направление наиболее крутого подъема и единичный вектор этого направления принять в качестве Ф. В более простой процедуре в качестве Ф можно взять первый же найденный единичный вектор, для которого G(A.i+Ф)>G(A.i). Выбор соответствующего алгоритма зависит от многих соображений. Однако если холм (т.е. поверхность, заданная функцией G) ведет себя достаточно хорошо, то подойдет любой алгоритм разумной сложности. Если же холм очень плохой, то даже самые остроумные локальные ухищрения будут бесполезны (рис.11.8 ).
Рис.11.8. Хороший холм, но плохой алгоритм (пример, предложенный О.Селфриджем). Подъем на холм вдоль обеих осей не срабатывает, так как для точки A, находящейся на гребне, оба значения G(A+Ф.1) и G(A+Ф.2) меньше, чем G(A). "Разрешающая способность" пробных векторов слишком груба для столь острого гребня.
Рассмотрим процесс обучения персептрона как алгоритм подъема на холм, заданный функцией
G(A)=A*A"/|A|.
Внешне он отличается от алгоритма обычного вида в двух отношениях. Во-первых, в нем нет процедуры систематического исследования результатов перемещения из текущей точки A.i во всех направлениях. Во-вторых, он фактически никогда не находит значение искомой функции G(A), так как вектор A" по определению неизвестен.
Тем не менее по логике действия он, в сущности, похож на более простой из двух упомянутых выше алгоритмов подъема на холм: переход от A.i к A.[i+1]+1 = А.i+Ф основывается на данных, показывающих (хотя и косвенным путем), что G(A.[i+1]) больше, чем G(A.i). Естественно ожидать, что эффективность алгоритма связана с формой поверхности G(A). Действительно, несложные рассуждения показывают, что эта поверхность не имеет ни одной из патологических особенностей, способных затруднить процесс подъема на холм: НЕТ ложных локальных максимумов, гребней, плато и т.д. Яснее всего это видно при рассмотрении функции G(A') на единичной сфере, где A'=A/|A|. Для векторов А, удовлетворяющих условию A*A">0 (а только такие нужно принимать во внимание), эта поверхность является n-мерным конусом. Он имеет единственную вершину при A=A", связные единообразные контуры, прямые линии наиболее крутого подъема; короче говоря, все свойства, которые можно пожелать для процедуры подъема на холм.
Таким образом, если посмотреть на теорему о сходимости с другой точки зрения, то описываемый ею процесс не будет казаться таким уже неожиданным, исключительным явлением.
#11.7. ПЕРСЕПТРОНЫ И ГОМЕОСГАТЫ
Значение теоремы о сходимости персептрона не должно сводиться (как это часто бывает в литературе) к простому утверждению: если два множества изображений линейно разделимы, то с помощью теоремы о сходимости можно найти разделяющий предикат. В самом деле, если бы все заключалось лишь в нахождении разделяющего предиката, то для этого вполне подошла бы и более простая процедура.
Заметим прежде всего, что если существует такой вектор A", что А"*Ф>дельта>0 для всех Ф из F, то существует вектор А', обладающий этим же свойством и имеющий целые координаты. Подходящее значение для А' дает простая программа:
НАЧАЛО: Положить A0 = 0.
ИСПЫТАНИЕ: Выбрать Ф из F.
Если A*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти
к ПОРОЖДЕНИЕ.
ПОРОЖДЕНИЕ: Заменить A на T(A), где T - такое преобразование, что ряд T(0), T(T(0)), T(T(T(0))), ... включает все возможные векторы с целыми координатами. Перейти к ИСПЫТАНИЕ.
Ясно, что эта процедура может сделать лишь конечное число ошибок, прежде чем наткнется на решение. Машине, которая так упорно игнорирует свой опыт, было бы трудно оправдать название "обучающаяся".
Итак, суть теоремы о сходимости персептрона состоит в том, что она дает лучший процесс обучения, чем этот простой гомеостат. Все же проблемой относительной скорости обучения персеп-тронов и других устройств почти полностью пренебрегают. Никакой общей теории этого вопроса пока еще не существует. В #11.5 рассматривались отдельные проблемы, возникающие при оценке времени обучения. Некоторые другие простые методы "обучения" мы исследуем в гл.12. Логическая теория гомеостатов, т.е. процедур перебора, подобных вышеупомянутой, изучается в книге Эшби [1962].
#11.8. СЛУЧАЙ НЕРАЗДЕЛИМОСТИ
Есть много причин, по которым следует изучать действие программы обучения персептрона, даже когда не существует такого вектора А", что А"*Ф>0 для всех Ф из F. Некоторые из этих мотивов чисто практические. Например, с помощью этой программы УЗНАТЬ, существует ли такой вектор А", или построить похожую обучающуюся машину и изучить влияние ошибок обратной связи или другого "шума". Другие причины носят теоретический характер. Никогда нельзя утверждать, что полностью ПОНИМАЕШЬ случай разделимости, если не обладаешь хотя бы какими-нибудь знаниями того, что происходит в других случаях.
Теперь совершенно очевидно, что теорема 11.1 в том виде, в каком она сформулирована, не может быть справедлива при таких более общих условиях. Вектор A должен иметь возможность меняться бесконечное число раз. Однако не ясно, что с ним произойдет: будет ли |A| неограниченно расти? Будет ли А принимать бесконечно много значений, или этот процесс зациклится, или же А еще каким-нибудь образом будет оставаться внутри фиксированного конечного множества значений?
В дальнейшем мы докажем, что величина |А| ограничена. Для большей точности изложения введем следующие определения. Пусть F - КОНЕЧНОЕ МНОЖЕСТВО ВЕКТОРОВ. Назовем F-цепью последовательность векторов A.1, A.2, ..., A.n, удовлетворяющую условиям:
A.[i+1] = A.i+Ф.i,
Ф.i*A.i <= 0,
Ф.i из F.
F-цепь называется ПРАВИЛЬНОЙ, если для всех i
|A.i| >= |А.1|.
Докажем, что элементы F-цепей, начинающихся большими векторами, не могут стать слишком большими.
#11.9. ТЕОРЕМА О "ЗАЦИКЛИВАНИИ" ПЕРСЕПТРОНА
Для любого e>0 существует такое число N=N(e,F), что если А, ..., А" - правильная F-цепь и |А|>N, то |А"|<|А|+е.
СЛЕДСТВИЕ 1. При данном множестве F и данном начальном векторе длины |A| векторов, получающихся в ходе работы программы, ограничены. Если к тому же координаты векторов, принадлежащих F, целые, то этот процесс имеет конечное число состояний.
Правдоподобность этих утверждений легко проверяется при изучении рис.11.10. По мере того как |A| увеличивается, становится труднее найти элемент F-цепи, удовлетворяющий одновременно условиям A*Ф<=0 и |A+Ф|>|A|. Формальное доказательство приведено в #11.10; оно использует индукцию по размерности векторов в F.
Впервые эту теорему (в форме следствия 1), по-видимому, сформулировал Нильсон и доказал Эфрон. Совершенно самостоятельно сформулировала это предложение Т.Бейер.
#11.10. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О "ЗАЦИКЛИВАНИИ"
Наше доказательство основано на фактах, связанных с изменением длины произвольно большого вектора A при добавлении к нему вектора C фиксированной малой длины.
#11.10.1. ЛЕММЫ [Через A' мы обозначаем единичный вектор направления A] Если C - произвольный вектор, а вектор A очень велик по сравнению с C, то
|A+C|-|A| ~ A'*С.
Чтобы точнее сформулировать это утверждение, введем обозначение: ДЕЛЬТА=|A+C|-|A|. Тогда если для любого e>0 взять |A|>|C|**(2/e), то разность между ДЕЛЬТА и A*C будет меньше e.
С помощью анализа бесконечно малых (рис.11.9) получаем
|A'-C-ДЕЛЬТА| < |B|*sin(тета) ~ |B|**2/|A| < |C|2/|A|, где |A| >> |C|.

Формальное доказательство вряд ли необходимо, но если угодно, можно положить x=|A+C|, y=|A|, и тогда в силу тождества
x**2 - y**2 = 2*y*(x-y)+(x-y)**2
имеем
2*A*C+|C|**2 = 2*|A|*ДЕЛЬТА + ДЕЛЬТА**2.
откуда
2*|A|*(A'*C-ДЕЛЬТА) = ДЕЛЬТА**2-|C|**2.
Так как |ДЕЛЬТА|<=|C|, то
|A'*C-ДЕЛЬТА| < |C|**2/|A|
Следовательно,
ДЕЛЬТА ~ A'*C
|A| >> |C|.
Из этого утверждения можно вывести ряд лемм.
ЛЕММА 1. Величину ДЕЛЬТА можно сделать как угодно малой, если выбрать подходящую нижнюю границу для |A| и подходящую верхнюю границу для A'*C', т.е. если взять вектор А достаточно большим и почти перпендикулярным к С.
ЛЕММА 2. Угол (A, A+C) можно сделать как угодно малым, придавая как угодно большие значения величине |A|, ибо sin(тета)<|C|/|A|.
ЛЕММА 3. Если сравнительно малый вектор C не перпендикулярен к очень большому вектору A и их скалярное произведение отрицательно, то величина ДЕЛЬТА всегда строго отрицательна.
Действительно, пусть A'*C'<-дельта<0 (рис.11.10). Возьмем |A|>(2/дельта)*|C|. Тогда, так как ДЕЛЬТА стремится к отрицательной величине A'*C'**|C|, то
A'*C'*|C| < ДЕЛЬТА < 1/2*A'*C'*|C| <0
и, следовательно,
ДЕЛЬТА < -1/2*дельта*|C|
Нам понадобится еще одна важная лемма.
ЛЕММА 4. Проекция правильной F-цепи А.1, ..., A.k на гиперплоскость, содержащую множество F, есть правильная F-цепь. Более того, разность |A.k|-|A.i| не превосходит соответствующей разности для цепи, полученной в результате проектирования.
ДОКАЗАТЕЛЬСТВО. Пусть A.1, ..., A.k - правильная цепь, H - гиперплоскость, содержащая F, и B' - нормаль к H. (Напомним, что B'*Ф=0 для всех Ф из F). Обозначим A.i=A.i'+x.i*B'. Чтобы показать, что A.1', ..., A.k' есть F-цепь, положим A.[i+1]=A.i+Ф, где A.i*Ф<=0. Тогда, с одной стороны,
A.[i+1] = A.[i+1]'+x.[i+1]*B',
а с другой стороны,
A.[i+1] = A.i'+x.i*B'+Ф = (A.i'+Ф)+x.i*B'.
В силу ортогональности вектора B' к векторам A,i', A.[i+1]' и Ф
x.[i+1]=x.i и A.[i+1]'=A.i'+Ф.
Полагая B=x.i*B', получаем
0 >= A.i*Ф = (A.i'+B)*Ф = A.i'*Ф+B*Ф = A.i*Ф.
Проверим теперь неравенство |A.i'|>=|A.1'|. Оно следует из соотношения
|A.i|**2 = |A.i'|**2+2*A.i'*B+|B|**2 = |A.i'|**2+|B|**2.
Таким образом, полученная в результате проектирования F-цепь является правильной.
Наконец,
|A.k|-|A.1| = sqr(|A.k|**2+|B|**2) - sqr(|A.1|**2+|B|**2) <= |A.k'|-|A.1'|,
и теорема доказана.
#11.10.2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О "ЗАЦИКЛИВАНИИ". Докажем теорему индукцией по размерности векторного пространства.
Для пространства E.1 т.е. для одномерного случая, справедливость теоремы очевидна, ибо векторами здесь будут вещественные числа и Ф*A<0 означает, что Ф и A имеют разные знаки. Если |A|>max|Ф|, то |Ф+A|<|A| при Ф-A<0, так что в конце концов будет |A.i|<max|Ф|.
Предположим, что теорема справедлива в пространстве E.[n-1]. Это означает, что существует такое число M.[n-1] что приращение длины вектора в любой F-цепи A.1, ..., A.m в E.[n-1] не может стать больше M.[n-1], т.е. |A.m|<|A.1|+M.[n+1].
Выберем в E.n любое направление A' (единичный вектор) и попытаемся построить на единичной сфере такую открытую окрестность V(A'), что длины векторов цепей, начинающихся с V(A'), возрастают ограниченно. Точнее, для любого e>0 найдется такое число N(A'), что при |B|>N(A') и B' принадлежит V(A) приращение длины векторов любой правильной F-цепи, начинающейся с B, не превышает e. Так как открытые множества V(A') покрывают единичную сферу, а сфера компактна, то вместо всех чисел N(A') можно найти единственное такое число N, и теорема будет доказана.
Обозначим через H(A') гиперплоскость, перпендикулярную к A', и через ~H(A') ее дополнение, т.е. ~H(A') = E.n - H(A').
Так как множество F конечно, то существует такое число дельта>0, что |Ф*A'|>2дельта для всех Ф из ~H(A') пересечние F. В силу непрерывности найдется такая окрестность V'(Ф'), что |Ф*B'|>дельта для Ф из ~H(A') пересечение F и B' из V'(A'). Кроме того, существует такое число b, что |Ф|<b для всех Ф из F. Согласно лемме 3, существуют такие числа дельта' и n(A'), что если
(1) |B|>n(A'),
(2) Ф принадлежит ~H(A') пересечение F,
(3) B' принадлежит V'(A'),
(4) Ф*B < 0,
то
(5) |B+Ф| < |B| - дельта'.
Условия (1)-(4) получаются из условий леммы 3, если в последней заменить A на B и C на Ф. В силу условия (2) вектор Ф не перпендикулярен к A', а в силу условия (4) Ф не перпендикулярен к B.
Рассмотрим правильную F-цепь B.1, ..., B.j, ..., где B.[j+i]=B.j+Ф.j, вектор B.1' очень близок к A' и |B.1|>n(A'). Обозначим через эта>0 такое число, что диаметр множества V'(A') превосходит эта. Возьмем в качестве окрестности V(A') такую окрестность точки A' на единичной сфере, у которой диаметр меньше эта/2, так что V(A') включается V'(A'). Выберем теперь вектор B.1' из V(A'), удовлетворяющий условию |B.1|>n(A') (скоро мы эту нижнюю границу для |B.1| изменим до нужной величины N(A')).
Согласно неравенству (5), цепь не может быть правильной, если Ф.1 не принадлежит H(A'). Таким образом, цепь должна начать рост с H(A'). Покажем, что не только Ф.1, но и все остальные векторы Ф принадлежат H(A').
Предположим, что
{Ф.1, ..., Ф.j} включается H(A') и Ф.[j+1] принадлежит ~H(A').
Тогда |B.[j+i]| меньше |B.1| по крайней мере на дельта'/2. Для доказательства этого утверждения воспользуемся леммами 1 и 2. Так как проекции B.1', ..., B.j' векторов цепи образуют правильную F-цепь в (n-1)-мерном пространстве H(A'), то
|B.j'| < |B.1'|+M.[n-1]
(по предположению индукции). Теперь, если число эта выбрано достаточно малым, а N(A') достаточно большим, то условия лемм 1 и 2 выполняются, если в качестве С взять Ф.1+...+Ф.j (так что |С|<M.[n-i]), вместо А взять В.1 а вместо e - число e'=min(e, дельта'/2).
В силу неравенства (5) и неравенств
|B.j| > |B.1| > N(A')
|B.[j+1]| < |B.j|-дельта' > |B.1|-дельта'/2,
так что при переходе от B.j к B.[j+1] длина вектора B уменьшается на величину большую, чем та, на которую она увеличилась за первые j шагов! Таким образом, цепь не может быть правильной, если не все векторы Ф принадлежат H(A'). Но так как наша цепь правильная, то Ф.k принадлежит H(A') для всех k = 1, 2, ... Итак, искомая окрестность V(A'), начиная от которой рост длины векторов всей цепи ограничен числом e, построена. Эти окрестности покрывают единичную сферу. Поскольку сфера компактна, из этого покрытия можно выделить конечное подпокрытие. Возьмем в качестве N максимальное из чисел N(A'). Тогда для ЛЮБОЙ правильной цепи В, ... , В'
|B|>N => |B'|<|B|+e.
Теорема о "зацикливании" доказана!
Теорема о сходимости персептрона допускает массу других второстепенных формулировок. Наше доказательство легко приспособить к любому из видов, в которых эта теорема встречается в литературе о персептронах.
1) Вместо предположения о том, что множество F состоит из единичных векторов, можно допустить, что F - конечное множество или что его векторы ограничены по длине сверху и снизу, т.е. найдутся такие числа a и b, что 0<а<=|Ф|<=b для каждого Ф из F.
2) Вместо замены вектора А на А+Ф можно заменить его на А+kФ, где k - вещественное число, выбираемое по одному из следующих правил:
k - положительная константа;
k = 1/|Ф|, т.е. прибавляется единичный вектор;
k=c*A*Ф/|Ф|**2. Если c=1, то величина k вполне достаточна для вывода (А+kФ)-Ф из отрицательной области. Можно использовать любое значение c между 0 и 2 (Эгмон [1954]).
Эти и подобные им модификации не меняют теорему в том смысле, что после конечного числа переходов к блоку СЛОЖЕНИЕ вектор А все же станет вектором решения. Это число в каждом варианте теоремы будет своим. Интересно было бы сравнить относительную ЭФФЕКТИВНОСТЬ "локальной" программы сходимости персептрона с более "глобальными" аналитическими методами (например, с линейным программированием), которые можно применить для системы неравенств относительно А:
А*Ф>0 для всех Ф из F.
#11.4.1. СЛУЧАЙ БОЛЕЕ ЧЕМ ДВУХ КЛАССОВ. Обобщим теорему на случай, когда число классов входных изображений больше двух. Пусть F.i, F.2, ...- множества изображений, и пусть существуют такие векторы A.i" и число дельта>0, что
Ф принадлежит F.i влечет A.i"*Ф > A.j"*Ф + дельта для всех j!=i.
Тогда теорема о сходимости персептрона гласит, что векторы с тем же свойством можно найти, следуя обычному принципу обратной связи: всякий раз, когда в F.i - встречается изображение Ф, для которого А.i*Ф<A.j*Ф при некотором j, вектор A.i должен "увеличиваться", а А.j - "уменьшаться".
Более точно эта идея выражается в программе:
НАЧАЛО; Выбрать любые ненулевые значения A.1; A.2, ...
ИСПЫТАНИЕ: Выбрать i, j и Ф из F.i.
Если A.i*Ф>A.j*Ф, перейти к ИСПЫТАНИЕ; иначе перейти К ИЗМЕНЕНИЕ.
ИЗМЕНЕНИЕ: Заменить A.i на A.i+Ф.
Заменить A.j на A.j-Ф.
Перейти к ИСПЫТАНИЕ.
Обобщенная теорема утверждает, что эта программа будет обращаться к блоку ИЗМЕНЕНИЕ только конечное число раз. Но это возможно лишь в том случае, если машина в конце концов перестанет ошибаться, т.е. если для каждого вектора Ф из F.i в конце концов будет
A.i*Ф>A.j*Ф для всех j.
Для доказательства предположим, что векторы А.1", ..., A.i", ..., A.j", ..., A.m" удовлетворяют условию теоремы. Выпишем подряд координаты этих векторов и обозначим полученный вектор (в пространстве большей размерности) через А". Далее, для каждого Ф зададим (в этом новом пространстве) вектор Ф.ij, у которого i-й блок (т.е. место, отведенное для координат вектора A.i" в векторе А") заполнен координатами вектора Ф, j-й блок - координатами вектора -Ф, а все остальные блоки заполнены нулями. Теперь к этому большому пространству можно применить теорему 11.1.
#11.5. ПРИЛОЖЕНИЕ. ОБУЧЕНИЕ ПРЕДИКАТУ пси.ЧЕТН0СТЬ
В качестве примера, иллюстрирующего теорему о сходимости, оценим число шагов, необходимых для того, чтобы с помощью программы обучения определить коэффициенты предиката, проверяющего четность. В #10.1 мы показали, что вектор решения с наименьшими коэффициентами можно записать в виде
A = (
C(|R| 1) членов 2**(|R|-1),
...,
C(|R| j) членов 2**(|R|-j),
...,
1).
Длина этого вектора находится из равенства
|A|**2 = СУММА 2**(2*(|R|-j))*C(|R| j) = (1+2**2)**|R| = 5**|R|.
Соответствующий единичный вектор равен
A"=A/5**(|R|/2).
Проведенный в #10.1 анализ показывает, что произведение A*Ф равно 1 или -1. Так как вектор Ф имеет 2**|R| координат, каждая из которых равна либо 0, либо 1, то
|A"*Ф/|Ф|| >= 1/sqr(5**|R|*2**|R|) = 1/sqr(10**|R|).
Таким образом, в качестве дельта можно взять 1/sqr(10**|R|). Тогда число n коррекций ограничено величиной
n <= 1/дельта**2 <= 10**|R|.
Так как число |A.n| должно быть не менее 5**(|R|/2) и
|A.n| <= n,
то нижняя граница для n равна 5**|R|. Итак,
5**|R| <= n <= 10**|R|.
Заметим, что если бы в программе обучения вместо Ф" прибавлялся вектор Ф, то мы бы получили
5**|R|/max|Ф| <= n <= 10**|R|, т.е. (5/2)**|R| <= n <= 10**|R|.
Чтобы решить, действительно ли такая замена приведет к увеличению скорости обучения, требуется дополнительный анализ. Во всяком случае ясно, что время обучения должно расти экспоненциально с ростом |R|.
Эти неравенства определяют границы числа n коррекций, или, что то же самое, числа ошибок. При подсчете общего количества циклов программы (включая "пустые" циклы, в которых не наблюдается ошибка и, следовательно, не производится коррекция.- Ред.) нужно учитывать уменьшение числа ошибок в ходе обучения. Нетрудно, однако, видеть, что число M(r) циклов, необходимое для уменьшения относительного числа ошибок до величины r<1, должно удовлетворять неравенству M(r)<=n/r в предположении, что изображения подаются в машину в случайном порядке. Таким образом, для получения 1% ошибок необходимо немногим менее 10**(|R|+2) циклов.
#11.6. ПРОЦЕСС ОБУЧЕНИЯ, РАССМАТРИВАЕМЫЙ КАК ПОДЪЕМ НА ХОЛМ
Полезно рассмотреть, как связана процедура сходимости с общей проблемой "подъема на холм". Здесь также ищут глобальное решение (т.е. местонахождение абсолютной вершины) с помощью локальных операций (например, методом наискорейшего подъема). Эффективность таких методов зависит от того, в какой степени определение искомой вершины так глобально, как это могло бы показаться. В тех случаях, когда холм имеет сложную форму с большим количеством локальных пиков, гребней и т.д., процессы подъема на холм не всегда выгодны. Действительно, в таких ситуациях больше подходит случайный или систематический поиск, а не процесс, при котором с железной неумолимостью происходит подъем на каждый небольшой холмик.
В типичном случае подъема на холм ищут максимум функции G(A) от точек A некоторого n-мерного пространства. Простейшая процедура вычисляет значение функции "высоты" G для ряда точек A.i+Ф.i, в окрестности текущей точки А.i. На основании этих экспериментов выбирается величина Ф и сумма A.i+Ф принимается в качестве A.[t+i]. Алгоритм выбора Ф может быть различным. Например, в качестве Ф.i можно использовать единичные векторы, ориентированные в направлении осей, затем рассчитать направление наиболее крутого подъема и единичный вектор этого направления принять в качестве Ф. В более простой процедуре в качестве Ф можно взять первый же найденный единичный вектор, для которого G(A.i+Ф)>G(A.i). Выбор соответствующего алгоритма зависит от многих соображений. Однако если холм (т.е. поверхность, заданная функцией G) ведет себя достаточно хорошо, то подойдет любой алгоритм разумной сложности. Если же холм очень плохой, то даже самые остроумные локальные ухищрения будут бесполезны (рис.11.8 ).

Рис.11.8. Хороший холм, но плохой алгоритм (пример, предложенный О.Селфриджем). Подъем на холм вдоль обеих осей не срабатывает, так как для точки A, находящейся на гребне, оба значения G(A+Ф.1) и G(A+Ф.2) меньше, чем G(A). "Разрешающая способность" пробных векторов слишком груба для столь острого гребня.
Рассмотрим процесс обучения персептрона как алгоритм подъема на холм, заданный функцией
G(A)=A*A"/|A|.
Внешне он отличается от алгоритма обычного вида в двух отношениях. Во-первых, в нем нет процедуры систематического исследования результатов перемещения из текущей точки A.i во всех направлениях. Во-вторых, он фактически никогда не находит значение искомой функции G(A), так как вектор A" по определению неизвестен.
Тем не менее по логике действия он, в сущности, похож на более простой из двух упомянутых выше алгоритмов подъема на холм: переход от A.i к A.[i+1]+1 = А.i+Ф основывается на данных, показывающих (хотя и косвенным путем), что G(A.[i+1]) больше, чем G(A.i). Естественно ожидать, что эффективность алгоритма связана с формой поверхности G(A). Действительно, несложные рассуждения показывают, что эта поверхность не имеет ни одной из патологических особенностей, способных затруднить процесс подъема на холм: НЕТ ложных локальных максимумов, гребней, плато и т.д. Яснее всего это видно при рассмотрении функции G(A') на единичной сфере, где A'=A/|A|. Для векторов А, удовлетворяющих условию A*A">0 (а только такие нужно принимать во внимание), эта поверхность является n-мерным конусом. Он имеет единственную вершину при A=A", связные единообразные контуры, прямые линии наиболее крутого подъема; короче говоря, все свойства, которые можно пожелать для процедуры подъема на холм.
Таким образом, если посмотреть на теорему о сходимости с другой точки зрения, то описываемый ею процесс не будет казаться таким уже неожиданным, исключительным явлением.
#11.7. ПЕРСЕПТРОНЫ И ГОМЕОСГАТЫ
Значение теоремы о сходимости персептрона не должно сводиться (как это часто бывает в литературе) к простому утверждению: если два множества изображений линейно разделимы, то с помощью теоремы о сходимости можно найти разделяющий предикат. В самом деле, если бы все заключалось лишь в нахождении разделяющего предиката, то для этого вполне подошла бы и более простая процедура.
Заметим прежде всего, что если существует такой вектор A", что А"*Ф>дельта>0 для всех Ф из F, то существует вектор А', обладающий этим же свойством и имеющий целые координаты. Подходящее значение для А' дает простая программа:
НАЧАЛО: Положить A0 = 0.
ИСПЫТАНИЕ: Выбрать Ф из F.
Если A*Ф>0, перейти к ИСПЫТАНИЕ; иначе перейти
к ПОРОЖДЕНИЕ.
ПОРОЖДЕНИЕ: Заменить A на T(A), где T - такое преобразование, что ряд T(0), T(T(0)), T(T(T(0))), ... включает все возможные векторы с целыми координатами. Перейти к ИСПЫТАНИЕ.
Ясно, что эта процедура может сделать лишь конечное число ошибок, прежде чем наткнется на решение. Машине, которая так упорно игнорирует свой опыт, было бы трудно оправдать название "обучающаяся".
Итак, суть теоремы о сходимости персептрона состоит в том, что она дает лучший процесс обучения, чем этот простой гомеостат. Все же проблемой относительной скорости обучения персеп-тронов и других устройств почти полностью пренебрегают. Никакой общей теории этого вопроса пока еще не существует. В #11.5 рассматривались отдельные проблемы, возникающие при оценке времени обучения. Некоторые другие простые методы "обучения" мы исследуем в гл.12. Логическая теория гомеостатов, т.е. процедур перебора, подобных вышеупомянутой, изучается в книге Эшби [1962].
#11.8. СЛУЧАЙ НЕРАЗДЕЛИМОСТИ
Есть много причин, по которым следует изучать действие программы обучения персептрона, даже когда не существует такого вектора А", что А"*Ф>0 для всех Ф из F. Некоторые из этих мотивов чисто практические. Например, с помощью этой программы УЗНАТЬ, существует ли такой вектор А", или построить похожую обучающуюся машину и изучить влияние ошибок обратной связи или другого "шума". Другие причины носят теоретический характер. Никогда нельзя утверждать, что полностью ПОНИМАЕШЬ случай разделимости, если не обладаешь хотя бы какими-нибудь знаниями того, что происходит в других случаях.
Теперь совершенно очевидно, что теорема 11.1 в том виде, в каком она сформулирована, не может быть справедлива при таких более общих условиях. Вектор A должен иметь возможность меняться бесконечное число раз. Однако не ясно, что с ним произойдет: будет ли |A| неограниченно расти? Будет ли А принимать бесконечно много значений, или этот процесс зациклится, или же А еще каким-нибудь образом будет оставаться внутри фиксированного конечного множества значений?
В дальнейшем мы докажем, что величина |А| ограничена. Для большей точности изложения введем следующие определения. Пусть F - КОНЕЧНОЕ МНОЖЕСТВО ВЕКТОРОВ. Назовем F-цепью последовательность векторов A.1, A.2, ..., A.n, удовлетворяющую условиям:
A.[i+1] = A.i+Ф.i,
Ф.i*A.i <= 0,
Ф.i из F.
F-цепь называется ПРАВИЛЬНОЙ, если для всех i
|A.i| >= |А.1|.
Докажем, что элементы F-цепей, начинающихся большими векторами, не могут стать слишком большими.
#11.9. ТЕОРЕМА О "ЗАЦИКЛИВАНИИ" ПЕРСЕПТРОНА
Для любого e>0 существует такое число N=N(e,F), что если А, ..., А" - правильная F-цепь и |А|>N, то |А"|<|А|+е.
СЛЕДСТВИЕ 1. При данном множестве F и данном начальном векторе длины |A| векторов, получающихся в ходе работы программы, ограничены. Если к тому же координаты векторов, принадлежащих F, целые, то этот процесс имеет конечное число состояний.
Правдоподобность этих утверждений легко проверяется при изучении рис.11.10. По мере того как |A| увеличивается, становится труднее найти элемент F-цепи, удовлетворяющий одновременно условиям A*Ф<=0 и |A+Ф|>|A|. Формальное доказательство приведено в #11.10; оно использует индукцию по размерности векторов в F.
Впервые эту теорему (в форме следствия 1), по-видимому, сформулировал Нильсон и доказал Эфрон. Совершенно самостоятельно сформулировала это предложение Т.Бейер.
#11.10. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О "ЗАЦИКЛИВАНИИ"
Наше доказательство основано на фактах, связанных с изменением длины произвольно большого вектора A при добавлении к нему вектора C фиксированной малой длины.
#11.10.1. ЛЕММЫ [Через A' мы обозначаем единичный вектор направления A] Если C - произвольный вектор, а вектор A очень велик по сравнению с C, то
|A+C|-|A| ~ A'*С.
Чтобы точнее сформулировать это утверждение, введем обозначение: ДЕЛЬТА=|A+C|-|A|. Тогда если для любого e>0 взять |A|>|C|**(2/e), то разность между ДЕЛЬТА и A*C будет меньше e.
С помощью анализа бесконечно малых (рис.11.9) получаем
|A'-C-ДЕЛЬТА| < |B|*sin(тета) ~ |B|**2/|A| < |C|2/|A|, где |A| >> |C|.

Формальное доказательство вряд ли необходимо, но если угодно, можно положить x=|A+C|, y=|A|, и тогда в силу тождества
x**2 - y**2 = 2*y*(x-y)+(x-y)**2
имеем
2*A*C+|C|**2 = 2*|A|*ДЕЛЬТА + ДЕЛЬТА**2.
откуда
2*|A|*(A'*C-ДЕЛЬТА) = ДЕЛЬТА**2-|C|**2.
Так как |ДЕЛЬТА|<=|C|, то
|A'*C-ДЕЛЬТА| < |C|**2/|A|
Следовательно,
ДЕЛЬТА ~ A'*C
|A| >> |C|.
Из этого утверждения можно вывести ряд лемм.
ЛЕММА 1. Величину ДЕЛЬТА можно сделать как угодно малой, если выбрать подходящую нижнюю границу для |A| и подходящую верхнюю границу для A'*C', т.е. если взять вектор А достаточно большим и почти перпендикулярным к С.
ЛЕММА 2. Угол (A, A+C) можно сделать как угодно малым, придавая как угодно большие значения величине |A|, ибо sin(тета)<|C|/|A|.
ЛЕММА 3. Если сравнительно малый вектор C не перпендикулярен к очень большому вектору A и их скалярное произведение отрицательно, то величина ДЕЛЬТА всегда строго отрицательна.

Действительно, пусть A'*C'<-дельта<0 (рис.11.10). Возьмем |A|>(2/дельта)*|C|. Тогда, так как ДЕЛЬТА стремится к отрицательной величине A'*C'**|C|, то
A'*C'*|C| < ДЕЛЬТА < 1/2*A'*C'*|C| <0
и, следовательно,
ДЕЛЬТА < -1/2*дельта*|C|
Нам понадобится еще одна важная лемма.
ЛЕММА 4. Проекция правильной F-цепи А.1, ..., A.k на гиперплоскость, содержащую множество F, есть правильная F-цепь. Более того, разность |A.k|-|A.i| не превосходит соответствующей разности для цепи, полученной в результате проектирования.
ДОКАЗАТЕЛЬСТВО. Пусть A.1, ..., A.k - правильная цепь, H - гиперплоскость, содержащая F, и B' - нормаль к H. (Напомним, что B'*Ф=0 для всех Ф из F). Обозначим A.i=A.i'+x.i*B'. Чтобы показать, что A.1', ..., A.k' есть F-цепь, положим A.[i+1]=A.i+Ф, где A.i*Ф<=0. Тогда, с одной стороны,
A.[i+1] = A.[i+1]'+x.[i+1]*B',
а с другой стороны,
A.[i+1] = A.i'+x.i*B'+Ф = (A.i'+Ф)+x.i*B'.
В силу ортогональности вектора B' к векторам A,i', A.[i+1]' и Ф
x.[i+1]=x.i и A.[i+1]'=A.i'+Ф.
Полагая B=x.i*B', получаем
0 >= A.i*Ф = (A.i'+B)*Ф = A.i'*Ф+B*Ф = A.i*Ф.
Проверим теперь неравенство |A.i'|>=|A.1'|. Оно следует из соотношения
|A.i|**2 = |A.i'|**2+2*A.i'*B+|B|**2 = |A.i'|**2+|B|**2.
Таким образом, полученная в результате проектирования F-цепь является правильной.
Наконец,
|A.k|-|A.1| = sqr(|A.k|**2+|B|**2) - sqr(|A.1|**2+|B|**2) <= |A.k'|-|A.1'|,
и теорема доказана.
#11.10.2. ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ О "ЗАЦИКЛИВАНИИ". Докажем теорему индукцией по размерности векторного пространства.
Для пространства E.1 т.е. для одномерного случая, справедливость теоремы очевидна, ибо векторами здесь будут вещественные числа и Ф*A<0 означает, что Ф и A имеют разные знаки. Если |A|>max|Ф|, то |Ф+A|<|A| при Ф-A<0, так что в конце концов будет |A.i|<max|Ф|.
Предположим, что теорема справедлива в пространстве E.[n-1]. Это означает, что существует такое число M.[n-1] что приращение длины вектора в любой F-цепи A.1, ..., A.m в E.[n-1] не может стать больше M.[n-1], т.е. |A.m|<|A.1|+M.[n+1].
Выберем в E.n любое направление A' (единичный вектор) и попытаемся построить на единичной сфере такую открытую окрестность V(A'), что длины векторов цепей, начинающихся с V(A'), возрастают ограниченно. Точнее, для любого e>0 найдется такое число N(A'), что при |B|>N(A') и B' принадлежит V(A) приращение длины векторов любой правильной F-цепи, начинающейся с B, не превышает e. Так как открытые множества V(A') покрывают единичную сферу, а сфера компактна, то вместо всех чисел N(A') можно найти единственное такое число N, и теорема будет доказана.
Обозначим через H(A') гиперплоскость, перпендикулярную к A', и через ~H(A') ее дополнение, т.е. ~H(A') = E.n - H(A').
Так как множество F конечно, то существует такое число дельта>0, что |Ф*A'|>2дельта для всех Ф из ~H(A') пересечние F. В силу непрерывности найдется такая окрестность V'(Ф'), что |Ф*B'|>дельта для Ф из ~H(A') пересечение F и B' из V'(A'). Кроме того, существует такое число b, что |Ф|<b для всех Ф из F. Согласно лемме 3, существуют такие числа дельта' и n(A'), что если
(1) |B|>n(A'),
(2) Ф принадлежит ~H(A') пересечение F,
(3) B' принадлежит V'(A'),
(4) Ф*B < 0,
то
(5) |B+Ф| < |B| - дельта'.
Условия (1)-(4) получаются из условий леммы 3, если в последней заменить A на B и C на Ф. В силу условия (2) вектор Ф не перпендикулярен к A', а в силу условия (4) Ф не перпендикулярен к B.
Рассмотрим правильную F-цепь B.1, ..., B.j, ..., где B.[j+i]=B.j+Ф.j, вектор B.1' очень близок к A' и |B.1|>n(A'). Обозначим через эта>0 такое число, что диаметр множества V'(A') превосходит эта. Возьмем в качестве окрестности V(A') такую окрестность точки A' на единичной сфере, у которой диаметр меньше эта/2, так что V(A') включается V'(A'). Выберем теперь вектор B.1' из V(A'), удовлетворяющий условию |B.1|>n(A') (скоро мы эту нижнюю границу для |B.1| изменим до нужной величины N(A')).
Согласно неравенству (5), цепь не может быть правильной, если Ф.1 не принадлежит H(A'). Таким образом, цепь должна начать рост с H(A'). Покажем, что не только Ф.1, но и все остальные векторы Ф принадлежат H(A').
Предположим, что
{Ф.1, ..., Ф.j} включается H(A') и Ф.[j+1] принадлежит ~H(A').
Тогда |B.[j+i]| меньше |B.1| по крайней мере на дельта'/2. Для доказательства этого утверждения воспользуемся леммами 1 и 2. Так как проекции B.1', ..., B.j' векторов цепи образуют правильную F-цепь в (n-1)-мерном пространстве H(A'), то
|B.j'| < |B.1'|+M.[n-1]
(по предположению индукции). Теперь, если число эта выбрано достаточно малым, а N(A') достаточно большим, то условия лемм 1 и 2 выполняются, если в качестве С взять Ф.1+...+Ф.j (так что |С|<M.[n-i]), вместо А взять В.1 а вместо e - число e'=min(e, дельта'/2).
В силу неравенства (5) и неравенств
|B.j| > |B.1| > N(A')
|B.[j+1]| < |B.j|-дельта' > |B.1|-дельта'/2,
так что при переходе от B.j к B.[j+1] длина вектора B уменьшается на величину большую, чем та, на которую она увеличилась за первые j шагов! Таким образом, цепь не может быть правильной, если не все векторы Ф принадлежат H(A'). Но так как наша цепь правильная, то Ф.k принадлежит H(A') для всех k = 1, 2, ... Итак, искомая окрестность V(A'), начиная от которой рост длины векторов всей цепи ограничен числом e, построена. Эти окрестности покрывают единичную сферу. Поскольку сфера компактна, из этого покрытия можно выделить конечное подпокрытие. Возьмем в качестве N максимальное из чисел N(A'). Тогда для ЛЮБОЙ правильной цепи В, ... , В'
|B|>N => |B'|<|B|+e.
Теорема о "зацикливании" доказана!

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
ГЛАВА 12. ЛИНЕЙНОЕ РАЗДЕЛЕНИЕ И ОБУЧЕНИЕ
#12.0. ВВЕДЕНИЕ
Персептрон и теоремы о сходимости из гл.11 родственны многим другим процедурам, которые исследуются в обширной и бессистемной литературе под такими названиями, как ОБУЧАЮЩИЕСЯ МАШИНЫ, МОДЕЛИ ОБУЧЕНИЯ, ИНФОРМАЦИОННЫЙ ПОИСК, ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ, РАСПОЗНАВАНИЕ ОБРАЗОВ и др. В настоящей главе мы рассмотрим некоторые из этих процедур, чтобы указать их точки соприкосновения с персептронами и выявить глубокие различия. Мы не можем привести ни полного и точного отчета, ни единой теории этих вопросов; это выходило бы очень далеко и за пределы наших знаний, и за пределы тематики этой книги. Глава 12 написана скорее для того, чтобы побудить читателей к исследованиям, а не предложить решения проблем.
#12.1. ИНФОРМАЦИОННЫЙ ПОИСК И ИНДУКТИВНЫЙ ВЫВОД
Процедуры обучения персептрона можно было бы использовать для создания устройства, действующего в соответствии со следующей схемой поведения:
В течение периода регистрации машине предъявляют множество данных в виде n-мерных векторов (их можно рассматривать как двоичные числа с n разрядами или точки в n-мерном пространстве). Позже, на стадии поиска, машина должна быть способной решить, какие векторы из множества вопросов принадлежат множеству данных. С целью обобщения этой модели мы будем употреблять символ А.РЕГИСТРАЦИЯ, когда речь будет идти об алгоритме, исследующем множество данных и в соответствии с этим исследованием Изменяющем Информацию в памяти. Алгоритм А.РЕГИСТРАЦИЯ предназначен для подготовки памяти к использованию ее при выполнении операции А.ПОИСК, которая на основе хранящейся в памяти информации принимает решения.
В настоящей главе мы рассмотрим несколько примеров этой общей схемы. Вначале сравним ПЕРСЕПТРОН с простейшей такой машиной: А.РЕГИСТРАЦИЯ в процедуре ПОЛНОЕ ЗАПОМИНАНИЕ просто записывает в память векторы исходных данных по мере их поступления. При поступлении вектора, который надо опознать, операция А.ПОИСК просматривает всю память и выясняет, записан ли в ней этот вектор.
#12.1.1. СРАВНЕНИЕ ПЕРСЕПТРОНА С ПОЛНЫМ ЗАПОМИНАНИЕМ. Перечислим вопросы, которые могут возникнуть при сравнении схем поиска в этом простейшем случае.
УНИВЕРСАЛЬНА ЛИ ПРОЦЕДУРА? ПЕРСЕПТРОН работает безупречно только при том условии, что множество исходных данных линейно разделимо, ПОЛНОЕ ЗАПОМИНАНИЕ универсально: оно работает на любом множестве данных.
КАКОВ ОБЪЕМ ПАМЯТИ ТРЕБУЕТСЯ? Для ПОЛНОГО ЗАПОМИНАНИЯ нужно хранить все множество данных, поэтому для него нужна довольно большая память. ПЕРСЕПТРОН (в тех случаях, когда он применим) иногда обладает способностью к обобщению, благодаря которой информационная емкость, требуемая для хранения его коэффициентов {альфа.i}, оказывается существенно меньшей, чем емкость, необходимая для хранения всего множества исходных данных. Мы уже видели (#10.2), что так бывает не всегда: для коэффициентов предиката пси.ЧЕТНОСТЬ может потребоваться значительно большая память, чем для множества приемлемых векторов.
КАКОВА СКОРОСТЬ ОПЕРАЦИИ А.ПОИСК? Характерная для ПОЛНОГО ЗАПОМИНАНИЯ схема поиска (полный перебор) имеет очень низкую скорость (обычно она ниже, чем скорость соответствующей операции у ПЕРСЕПТРОНА, при которой также должны выбираться из памяти все коэффициенты). С другой стороны, процессы, весьма сходные с указанными, могли бы проходить намного быстрее. Например, еСЛИ бы алгоритм А.РЕГИСТРАЦИЯ не только запоминэл множество данных в порядке их поступления, но и СОРТИРОВАЛ содержимое памяти, располагая векторы в порядке возрастания соответствующих чисел, то А.ПОИСК мог бы использовать двоичный поиск, снизив тем самым время ответа на вопрос до log2(|множество данных|) обращений к памяти. В #12.6 мы рассмотрим алгоритмы А.РЕГИСТРАЦИЯ, позволяющие ценой увеличения объема памяти достичь еще большего увеличения скорости (при помощи так называемого "смешанного кодирования").
Может ли машина работать достаточно успешно даже в том случае, когда алгоритм А.РЕГИСТРАЦИЯ ПРОСМАТРИВАЕТ ТОЛЬКО ЧАСТЬ МНОЖЕСТВА ИСХОДНЫХ ДАННЫХ; назовем эту часть "ВЫБОРКОЙ ДАННЫХ"? ПЕРСЕПТРОН мог бы, но ПОЛНОЕ ЗАПОМИНАНИЕ в том виде, как оно описано, не может прийти к разумному решению, если предъявляемый к опознанию вектор не встречался в выборке данных. Этот недостаток подсказывает важное усовершенствование процедуры полного запоминания: пусть А.ПОИСК вместо простой проверки, содержится ли предъявляемый к опознанию вектор в выборке данных, находит элемент выборки, НАИБОЛЕЕ БЛИЗКИЙ к этому вектору. При АПРИОРНОМ предположении о "непрерывности" исходных данных это усовершенствование привело бы к такой же степени обобщения, как и у персептрона. К сожалению, процедуры ускорения типа смешанного кодирования в этом случае непригодны, и мы предполагаем (в определенном смысле, который будет уточнен в #12.7.6), что эта потеря невосполнима.
Остальные рассматриваемые здесь вопросы касаются операции А.РЕГИСТРАЦИЯ. Заметим, что ПЕРСЕПТРОН и ПОЛНОЕ ЗАПОМИНАНИЕ обладают следующими общими свойствами:
Они действуют "по приращениям", т.е. понемногу изменяют содержимое памяти в зависимости от предъявляемого элемента из множества данных.
Они работают в "реальном масштабе времени", не используя больших массивов рабочей памяти.
Они могут воспринимать множество исходных данных в любом порядке и допускают повторения, которые только вызывают задержку, но не изменяют конечного состояния.
С другой стороны, они имеют по крайней мере одно, весьма существенное различие:
А.РЕГИСТРАЦИЯ ПЕРСЕПТРОНА является "поисковой процедурой", основанной на обратной связи со своими собственными результатами. Алгоритм регистрации ПОЛНОГО ЗАПОМИНАНИЯ пассивен. Преимущество персептрона в том, что при определенных условиях он находит экономное общее представление. Но за это ему приходится расплачиваться многократным просмотром некоторых точек.
#12.1.2. ПРОЦЕДУРЫ МНОЖЕСТВЕННОЙ КЛАССИФИКАЦИИ. Изложенные выше идеи можно слегка обобщить, если предположить, что множество данных разбито на классы F.1, ..., F.k. Как и прежде, алгоритму А.РЕГИСТРАЦИЯ предъявляются элементы множества данных, но при этом для каждого из них указывается соответствующий КЛАСС. Алгоритм формирует массив хранимой информации, предоставляемой затем в распоряжение алгоритма А.ПОИСК, задача которого состоит в том, чтобы с помощью этой информации отнести предъявляемые к опознанию точки к их классам.
ПРИМЕР. Мы уже видели (#11.4.1), как можно распространить идею персептрона на случай множественной классификации. Обучающий алгоритм А.РЕГИСТРАЦИЯ находит k векторов A.1, ..., A.k, а А.ПОИСК относит вектор Ф к F.j, если (скалярное произведение)
Ф*A.j > Ф*A.i (для всех i!=j).
ПРИМЕР. По-видимому, для многих читателей значительно более знакома следующая ситуация. Будем рассматривать каждый класс F.j как "комок", или "облако", или "кучу" точек в пространстве Ф и выделять в нем одну точку B.j, в каком-то смысле "типичную", или "среднюю". Например, точка B.j может быть ЦЕНТРОМ ТЯЖЕСТИ, т.е. СРЕДНИМ всех векторов из класса F.j (или, скажем, только тех, про которые уже выяснено, что они принадлежат F.j). Тогда знакомая уже процедура состоит в следующем: вектор Ф относим к тому классу F.j, для которого расстояние
|Ф-B.j|
НАИМЕНЬШЕЕ. Другими словами, каждый вектор Ф отождествляется с ближайшей к нему точкой B.j.
Хотя такая схема близости и схема скалярного произведения внешне выглядят совершенно различными, но по существу это одно и то же! Действительно, следует только заметить, что множество точек, расположенных ближе к точке B.1, чем к точке B.2, отделено от B.2 гиперплоскостью (рис.12.1), и, следовательно, его можно задать линейным неравенством. Аналогично точки, расположенные ближе к одной из нескольких точек B.j на плоскости, образуют (выпуклый) многоугольник (рис.12.2); это легко обобщить и на пространство большего числа измерений.

Формально эта эквивалентность получается из соотношения
|Ф-B.j|**2 = |Ф|**2 - 2*Ф*B.j + |B.j|**2.
Если все векторы Ф имеют одинаковую длину L, то расстояние |Ф-B.j| будет НАИМЕНЬШИМ, когда разность
Ф*B.j - 1/2*|B.j|**2 = Ф*B.j - тета.j
будет наибольшей. Если теперь, учитывая результаты #1.2.1 (1), удалить "порог" тета, то останется как раз скалярное произведение Ф*B.j. Требование равенства длин векторов Ф не умаляет общности. В самом деле, добавим еще одну ось координат и заменим каждый вектор Ф = (ф.1, ..., ф.n) вектором
Ф' = (ф.1, ..., ф.n, sqr(n - СУММА[1..n]ф.ш**2)),
так что все векторы Ф' имеют одну и ту же длину L=sqr(n). Для векторов B мы также должны были бы добавить еще одно измерение, но мы будем просто считать, что соответствующая координата равна нулю [На самом деле требование равенства длин векторов Ф даже излишне, поскольку неравенство |Ф-B.j|**2 < |Ф-B.i|**2 эквивалентно неравенству Ф*B.j-1/2*|B.j|**2>Ф*B.i-1/2*|B.i|**2 при любой величине |Ф|**2.- Прим. ред.].
#12.2. МНОГООБРАЗИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ
Из бесконечного многообразия схем, которые можно использовать для разбиения пространства на классы, выберем несколько моделей, иллюстрирующих различные стороны нашей основной темы - вычисление и линейное разделение. Каждой модели дадим краткую характеристику, а потом проведем сравнение некоторых сторон их алгоритмических структур, требований к памяти и ограничений, налагаемых на характер классов.
В каждой из наших моделей для операции А.ПОИСК используется один и тот же вид решающего алгоритма. В каждом случае за классом F.j закрепляется один или более векторов А.i; мы это будем выражать словами: вектор А.i соответствует классу F.[j(i)]. При заданном векторе Ф правило решения всегда состоит в выборе того класса F.[j(i)], для которого A.i>Ф принимает наибольшее значение. Как отмечалось в #12.1.2, оно с математической точки зрения эквивалентно правилу, минимизирующему |Ф-A.i|.
Для каждой модели следовало бы также описать операцию А.РЕГИСТРАЦИЯ, которая строит векторы A.i на основе прежнего опыта или АПРИОРНОЙ информации о классах. В приведенных ниже кратких набросках подробное описание этой операции не дается; мы займемся этим в следующих разделах.
#12.2.1. ПЕРСЕПТРОН. Здесь каждому классу F.j соответствует один вектор A.j. В качестве операции А.РЕГИСТРАЦИЯ можно использовать процедуру #11.1 для случая двух классов и процедуру #11.4.1 для случая многих классов.
#12.2.2. БАЙЕСОВСКАЯ ЛИНЕЙНАЯ СТАТИСТИЧЕСКАЯ ПРОЦЕДУРА. Каждому классу F.j здесь также соответствует один вектор A.j, а вот операция А.РЕГИСТРАЦИЯ совершенно другая. Для каждого класса F.j и каждого частного предиката фи.i положим
w.ij = log(p.ij/(1-p.ij)),
где p.ij - ВЕРОЯТНОСТЬ того, что фи.i=1, ПРИ УСЛОВИИ что Ф принадлежит F.j. Пусть
A.j = (тета.j, w.1j, w.2j, ...).
В #12.4.3 мы укажем условия, при которых эти "вероятности" имеют смысл, и опишем алгоритмы "обучения", с помощью которых можно будет оценить или аппроксимировать w.ij.
Если выполняются определенные статистические условия, то преимущество байесовской процедуры в том, что она дает хорошие результаты для классов, которые НЕ ЯВЛЯЮТСЯ линейно разделимыми [Правильнее было бы сказать "для пересекающихся классов", поскольку для классов, разделимых нелинейной поверхностью, но линейно не разделимых, описанная процедура не даст хороших результатов.- Прим. ред.]. Она фактически дает наинизшую возможную величину ошибки для процедур, в которых А.РЕГИСТРАЦИЯ зависит только от условных вероятностей, если предикаты фи.i статистически независимы в смысле #12.4.2. Просто поразительно, что это достигается с помощью линейной формулы.
#12.2.3. НАИЛУЧШИЕ ПЛОСКОСТИ. В различных ситуациях ПЕРСЕПТРОН и БАЙЕСОВСКАЯ процедура уступают друг другу. Но зачастую, когда классы F.j - линейно неразделимы, существует множество векторов A.j, дающее меньшие ошибки, чем любая из этих схем. Поэтому определим процедуру НАИЛУЧШИЕ ПЛОСКОСТИ как такую, при которой используется указанное множество векторов A.j. Это множество характеризуется здесь тем, что наибольшее скалярное произведение A.j*Ф приводит к наименьшей ошибке.
По определению НАИЛУЧШИЕ ПЛОСКОСТИ всегда по крайней мере не хуже, чем ПЕРСЕПТРОН или БАЙЕСОВСКАЯ процедура. Это не противоречит оптимальности БАЙЕСОВСКОЙ процедуры, поскольку поиск наилучшей плоскости использует иную информацию, чем условные вероятности. К сожалению, никакой практически действенный алгоритм А.РЕГИСТРАЦИЯ для выявления векторов A.j этой процедуры неизвестен. Как отмечается в #12.3, из-за проблемы локальных вершин подъем на холм не будет здесь работать успешно.
#12.2.4. ИЗОДЕЙТА. В описанных в #12.2.1-12.2.3 моделях каждому классу F соответствовал один вектор A. Если взглянуть на решаемую задачу с точки зрения минимизации расстояния, то станет ясно, что такие процедуры работают удовлетворительно только тогда, когда классы F "локализованы" в сравнительно изолированных, отдельных областях (их можно представлять себе в виде комков, куч или облаков). Естественно тогда задать вопрос: что же делать, если класс F хотя и не является четко очерченным сферическим образованием, но все же частично локализован в виде небольшого числа куч или, быть может, в виде змееподобной структуры? В таких ситуациях задачу можно решить с помощью алгоритма А.ПОИСК, вычисляющего кратчайшее расстояние, если закрепить за каждым скоплением,входящим в состав каждого класса F, свой вектор А или использовать много векторов А для задания "хребта змеи". Для реализации этой идеи потребуется операция А.РЕГИСТРАЦИЯ, обладающая некоторой способностью к анализу распределений в кучах. Одна такая схема под названием ИЗОДЕЙТА будет описана в #12.5.
#12.2.5. БЛИЖАЙШЕЕ СОСЕДСТВО. Наша простейшая и основная схема не налагает никаких ограничений на число векторов А. Алгоритм А.РЕГИСТРАЦИЯ хранит в памяти каждый просмотренный вектор Ф вместе с соответствующим ему классом F. Для каждого предъявляемого к опознанию вектора Ф.0 отыскивается в памяти ближайший к нему вектор Ф и выбирается класс F, соответствующий Ф.
Вообще говоря, это очень мощный метод: он весьма эффективен для многих разновидностей куч; он никогда не ошибается на уже просмотренной точке; в пределе он стремится к нулевой ошибке, за исключением довольно своеобразных случаев (один из которых рассматривается в следующем параграфе).
БЛИЖАЙШЕЕ СОСЕДСТВО имеет один очевидный недостаток - очень большой объем требуемой памяти, и другой, менее очевидный,- есть веские основания подозревать, что эта процедура приводит к большим и по существу неизбежным вычислительным затратам (последний вопрос рассматривается в #12.6).
#12.3. ЭВРИСТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ЛИНЕЙНОГО РАЗДЕЛЕНИЯ
В этом параграфе мы разберем несколько рисунков, чтобы лучше понять методы #12.4. Чтобы компенсировать нашу неспособность изображать многомерные конфигурации, будем пользоваться двумерными многозначными координатами. На первый взгляд может показаться, что эти чертежи внушают доверие, но на самом деле они очень несовершенны: в них нет даже намека на весь тот ужас, с которым можно столкнуться в пространстве многих измерений.
На этих наглядных рисунках мы представим два вида ситуаций, в каждой из которых попеременно проявляются преимущества БАЙЕСОВСКОЙ процедуры или ПЕРСЕПТРОНА (рис. 12.3). Прямая, соответствующая БАЙЕСОВСКОЙ процедуре, стремится пройти перпендикулярно к прямой, соединяющей "средние" точки множеств F+ и F-. Поэтому в ситуации рис.12.3(а) байесовская процедура допустит некоторые ошибки [Авторы, как и прежде, имеют в виду частный случай БАЙЕСОВСКОЙ процедуры, основанной на предположении о статистической независимости координат вектора Ф.БАЙЕСОВСКАЯ процедура общего вида, учитывающая действительные распределения вероятностей, даст по определению минимальную вероятность ошибки, т.е. безошибочное разделение в случае рис.12.3(а).- Прим. ред.]. Так как указанные здесь множества линейно разделимы, то ПЕРСЕПТРОН в конечном счете не ошибется. В случае рис.12.3(b) БАЙЕСОВСКАЯ процедура, как и на рис.12.3(а), приведет к небольшим ошибкам, а по поводу поведения ПЕРСЕПТРОНА в этом случае известно немного; ясно только, что в некоторых ситуациях он работает хуже БАЙЕСОВСКОЙ процедуры. Разумеется, НАИЛУЧШАЯ ПЛОСКОСТЬ по определению по меньшей мере так же хороша, как БАЙЕСОВСКАЯ процедура или как ПЕРСЕПТРОН.

Само по себе предположение о том, что любая из указанных процедур вообще окажется хоть сколько-нибудь хорошей, с самого начала равносильно АПРИОРНОМУ предположению, что классы F можно представить в виде простых "облаков", возможно, немного перекрывающихся (рис.12.4). Подобное допущение можно оправдать, если есть основания полагать, что различия между классами F+ и F- вызваны каким-то одним основным фактором, с которым суммируется множество разнообразных вторичных воздействий, гораздо меньших по величине. Вообще, похоже на то, что ПЕРСЕПТРОН чувствителен к внешним границам облаков и сравнительно нечувствителен к распределениям плотности внутри них, тогда как байесовская процедура взвешивает все векторы Ф одинаково [См. предыдущее замечание].

В случаях, когда условие единственности облака или условие небольшого перекрытия не удовлетворяются (рис.12.5), можно ожидать, что БАЙЕСОВСКАЯ процедура и, видимо, ПЕРСЕПТРОН будут работать плохо, НАИЛУЧШАЯ ПЛОСКОСТЬ может оказаться значительно лучше них, поскольку она не подвержена вредному влиянию симметрии. Однако, по всей видимости, нахождение наилучшей плоскости сопряжено с большими вычислительными трудностями, вызванными наличием множества локально оптимальных "холмов". На рис.12.6 показаны некоторые из локальных вершин для НАИЛУЧШЕЙ ПЛОСКОСТИ в плохой ситуации типа проверки четности. Здесь даже ИЗОДЕЙТА будет работать плохо, если не разрешить ей иметь по одному вектору А почти для каждого комка. Но для небольшого числа комков, в каждом из которых находится вектор A.k, ИЗОДЕЙТА действует вполне хорошо (#12.5). Вообще следует ожидать, что ПЕРСЕПТРОН окажется немного лучше БАЙЕСОВСКОЙ процедуры, поскольку в нем используется обратная связь, и немного хуже из-за его чрезмерной чувствительности к изолированным ошибкам.

Следует также ожидать, что БЛИЖАЙШЕЕ СОСЕДСТВО будет работать хорошо только при выполнении большого числа условий. В самом деле, в предельном случае записи всех векторов Ф с соответствующими им классами ближайшее соседство по меньшей мере так же хорошо, как и любая другая процедура. Но существуют условия, в которых БЛИЖАЙШЕЕ СОСЕДСТВО не показывает такой хорошей работы до тех пор, пока выборка не окажется равной почти всему пространству. В качестве примера рассмотрим пространство

Верхняя область характеризуется тем, что вероятность ее точки принадлежать классу F+ равна p, а для нижней эта вероятность равна 1-p=q. Для класса F- верхняя и нижняя области меняются ролями. Тогда если уже просмотрена небольшая часть точек, то вероятность того, что выбранная наудачу точка принадлежит тому же классу F, что и ближайшая к ней просмотренная точка, равна
p**2+q**2 = 1-2*p*q,
а вероятность правильного опознания при помощи БАЙЕСОВСКОЙ процедуры или НАИЛУЧШЕЙ ПЛОСКОСТИ равна p. Считая,что p>1/2 (иначе просто поменяем местами p и q), получаем
Ошибка.НАИЛУЧШАЯ-ПЛОСКОСТЬ < Ошибка.БЛИЖАЙШЕЕ-СОСЕДСТВО < 2*Ошибка.НАИЛУЧШАЯ-ПЛОСКОСТЬ.
Таким образом, БЛИЖАЙШЕЕ СОСЕДСТВО здесь хуже НАИЛУЧШЕЙ ПЛОСКОСТИ, но не сколь угодно хуже. Это явление сохраняется до тех пор, пока не будет выбрано так много точек, что появится заметная вероятность повторного выбора, т.е. пока не будет просмотрена значительная часть пространства.
С другой стороны, если классы F+ и F- не очень сильно "перемешаны" (рис.12.7), то БЛИЖАЙШЕЕ СОСЕДСТВО будет сходиться к очень хорошим результатам, как только появится реальный шанс найти одну выборочную точку в большинстве "микро-комков".

Очень плохим случаем является структура типа проверки четности; здесь БЛИЖАЙШЕЕ СОСЕДСТВО работает даже хуже, чем случайный выбор решения. Пусть Ф принадлежит F.i тогда и только тогда, когда фи.i=1 для четного числа индексов i. Тогда если предикатов фи всего n, то у каждой точки Ф окажется как раз n соседей, расстояния d до которых удовлетворяют условию 0<d<=l. Предположим, что векторы, которые уже прошли проверку, составляют (1-q)-ю часть всех возможных векторов Ф. Тогда ближайшее соседство ошибется на данном векторе Ф, если он еще не был осмотрен (вероятность последнего события равна q), а один из его непосредственных соседей уже осмотрен (эта вероятность равна 1-q**n). Поэтому вероятность ошибки будет не меньше q(1-q**n), что при больших значениях n практически не отличается от q.
Этот пример "патологический", как любят говорить математики, и, по всей вероятности, БЛИЖАЙШЕЕ СОСЕДСТВО хорошо работает во многих реальных ситуациях. Разумеется, качество работы зависит от формы, принятой для вычисления расстояния, так что многие из классических статистических методов посвящены оптимальному выбору координатных осей и масштабов измерений при использовании процедуры БЛИЖАЙШЕЕ СОСЕДСТВО.
Отметим, наконец, что из-за большого объема памяти и большого количества вычислений, требуемых для этой процедуры, с ней конкурируют более совершенные схемы, выходящие за рамки линейного разделения и, следовательно, за рамки этой книги.
#12.0. ВВЕДЕНИЕ
Персептрон и теоремы о сходимости из гл.11 родственны многим другим процедурам, которые исследуются в обширной и бессистемной литературе под такими названиями, как ОБУЧАЮЩИЕСЯ МАШИНЫ, МОДЕЛИ ОБУЧЕНИЯ, ИНФОРМАЦИОННЫЙ ПОИСК, ТЕОРИЯ СТАТИСТИЧЕСКИХ РЕШЕНИЙ, РАСПОЗНАВАНИЕ ОБРАЗОВ и др. В настоящей главе мы рассмотрим некоторые из этих процедур, чтобы указать их точки соприкосновения с персептронами и выявить глубокие различия. Мы не можем привести ни полного и точного отчета, ни единой теории этих вопросов; это выходило бы очень далеко и за пределы наших знаний, и за пределы тематики этой книги. Глава 12 написана скорее для того, чтобы побудить читателей к исследованиям, а не предложить решения проблем.
#12.1. ИНФОРМАЦИОННЫЙ ПОИСК И ИНДУКТИВНЫЙ ВЫВОД
Процедуры обучения персептрона можно было бы использовать для создания устройства, действующего в соответствии со следующей схемой поведения:

В течение периода регистрации машине предъявляют множество данных в виде n-мерных векторов (их можно рассматривать как двоичные числа с n разрядами или точки в n-мерном пространстве). Позже, на стадии поиска, машина должна быть способной решить, какие векторы из множества вопросов принадлежат множеству данных. С целью обобщения этой модели мы будем употреблять символ А.РЕГИСТРАЦИЯ, когда речь будет идти об алгоритме, исследующем множество данных и в соответствии с этим исследованием Изменяющем Информацию в памяти. Алгоритм А.РЕГИСТРАЦИЯ предназначен для подготовки памяти к использованию ее при выполнении операции А.ПОИСК, которая на основе хранящейся в памяти информации принимает решения.
В настоящей главе мы рассмотрим несколько примеров этой общей схемы. Вначале сравним ПЕРСЕПТРОН с простейшей такой машиной: А.РЕГИСТРАЦИЯ в процедуре ПОЛНОЕ ЗАПОМИНАНИЕ просто записывает в память векторы исходных данных по мере их поступления. При поступлении вектора, который надо опознать, операция А.ПОИСК просматривает всю память и выясняет, записан ли в ней этот вектор.
#12.1.1. СРАВНЕНИЕ ПЕРСЕПТРОНА С ПОЛНЫМ ЗАПОМИНАНИЕМ. Перечислим вопросы, которые могут возникнуть при сравнении схем поиска в этом простейшем случае.
УНИВЕРСАЛЬНА ЛИ ПРОЦЕДУРА? ПЕРСЕПТРОН работает безупречно только при том условии, что множество исходных данных линейно разделимо, ПОЛНОЕ ЗАПОМИНАНИЕ универсально: оно работает на любом множестве данных.
КАКОВ ОБЪЕМ ПАМЯТИ ТРЕБУЕТСЯ? Для ПОЛНОГО ЗАПОМИНАНИЯ нужно хранить все множество данных, поэтому для него нужна довольно большая память. ПЕРСЕПТРОН (в тех случаях, когда он применим) иногда обладает способностью к обобщению, благодаря которой информационная емкость, требуемая для хранения его коэффициентов {альфа.i}, оказывается существенно меньшей, чем емкость, необходимая для хранения всего множества исходных данных. Мы уже видели (#10.2), что так бывает не всегда: для коэффициентов предиката пси.ЧЕТНОСТЬ может потребоваться значительно большая память, чем для множества приемлемых векторов.
КАКОВА СКОРОСТЬ ОПЕРАЦИИ А.ПОИСК? Характерная для ПОЛНОГО ЗАПОМИНАНИЯ схема поиска (полный перебор) имеет очень низкую скорость (обычно она ниже, чем скорость соответствующей операции у ПЕРСЕПТРОНА, при которой также должны выбираться из памяти все коэффициенты). С другой стороны, процессы, весьма сходные с указанными, могли бы проходить намного быстрее. Например, еСЛИ бы алгоритм А.РЕГИСТРАЦИЯ не только запоминэл множество данных в порядке их поступления, но и СОРТИРОВАЛ содержимое памяти, располагая векторы в порядке возрастания соответствующих чисел, то А.ПОИСК мог бы использовать двоичный поиск, снизив тем самым время ответа на вопрос до log2(|множество данных|) обращений к памяти. В #12.6 мы рассмотрим алгоритмы А.РЕГИСТРАЦИЯ, позволяющие ценой увеличения объема памяти достичь еще большего увеличения скорости (при помощи так называемого "смешанного кодирования").
Может ли машина работать достаточно успешно даже в том случае, когда алгоритм А.РЕГИСТРАЦИЯ ПРОСМАТРИВАЕТ ТОЛЬКО ЧАСТЬ МНОЖЕСТВА ИСХОДНЫХ ДАННЫХ; назовем эту часть "ВЫБОРКОЙ ДАННЫХ"? ПЕРСЕПТРОН мог бы, но ПОЛНОЕ ЗАПОМИНАНИЕ в том виде, как оно описано, не может прийти к разумному решению, если предъявляемый к опознанию вектор не встречался в выборке данных. Этот недостаток подсказывает важное усовершенствование процедуры полного запоминания: пусть А.ПОИСК вместо простой проверки, содержится ли предъявляемый к опознанию вектор в выборке данных, находит элемент выборки, НАИБОЛЕЕ БЛИЗКИЙ к этому вектору. При АПРИОРНОМ предположении о "непрерывности" исходных данных это усовершенствование привело бы к такой же степени обобщения, как и у персептрона. К сожалению, процедуры ускорения типа смешанного кодирования в этом случае непригодны, и мы предполагаем (в определенном смысле, который будет уточнен в #12.7.6), что эта потеря невосполнима.
Остальные рассматриваемые здесь вопросы касаются операции А.РЕГИСТРАЦИЯ. Заметим, что ПЕРСЕПТРОН и ПОЛНОЕ ЗАПОМИНАНИЕ обладают следующими общими свойствами:
Они действуют "по приращениям", т.е. понемногу изменяют содержимое памяти в зависимости от предъявляемого элемента из множества данных.
Они работают в "реальном масштабе времени", не используя больших массивов рабочей памяти.
Они могут воспринимать множество исходных данных в любом порядке и допускают повторения, которые только вызывают задержку, но не изменяют конечного состояния.
С другой стороны, они имеют по крайней мере одно, весьма существенное различие:
А.РЕГИСТРАЦИЯ ПЕРСЕПТРОНА является "поисковой процедурой", основанной на обратной связи со своими собственными результатами. Алгоритм регистрации ПОЛНОГО ЗАПОМИНАНИЯ пассивен. Преимущество персептрона в том, что при определенных условиях он находит экономное общее представление. Но за это ему приходится расплачиваться многократным просмотром некоторых точек.
#12.1.2. ПРОЦЕДУРЫ МНОЖЕСТВЕННОЙ КЛАССИФИКАЦИИ. Изложенные выше идеи можно слегка обобщить, если предположить, что множество данных разбито на классы F.1, ..., F.k. Как и прежде, алгоритму А.РЕГИСТРАЦИЯ предъявляются элементы множества данных, но при этом для каждого из них указывается соответствующий КЛАСС. Алгоритм формирует массив хранимой информации, предоставляемой затем в распоряжение алгоритма А.ПОИСК, задача которого состоит в том, чтобы с помощью этой информации отнести предъявляемые к опознанию точки к их классам.
ПРИМЕР. Мы уже видели (#11.4.1), как можно распространить идею персептрона на случай множественной классификации. Обучающий алгоритм А.РЕГИСТРАЦИЯ находит k векторов A.1, ..., A.k, а А.ПОИСК относит вектор Ф к F.j, если (скалярное произведение)
Ф*A.j > Ф*A.i (для всех i!=j).
ПРИМЕР. По-видимому, для многих читателей значительно более знакома следующая ситуация. Будем рассматривать каждый класс F.j как "комок", или "облако", или "кучу" точек в пространстве Ф и выделять в нем одну точку B.j, в каком-то смысле "типичную", или "среднюю". Например, точка B.j может быть ЦЕНТРОМ ТЯЖЕСТИ, т.е. СРЕДНИМ всех векторов из класса F.j (или, скажем, только тех, про которые уже выяснено, что они принадлежат F.j). Тогда знакомая уже процедура состоит в следующем: вектор Ф относим к тому классу F.j, для которого расстояние
|Ф-B.j|
НАИМЕНЬШЕЕ. Другими словами, каждый вектор Ф отождествляется с ближайшей к нему точкой B.j.
Хотя такая схема близости и схема скалярного произведения внешне выглядят совершенно различными, но по существу это одно и то же! Действительно, следует только заметить, что множество точек, расположенных ближе к точке B.1, чем к точке B.2, отделено от B.2 гиперплоскостью (рис.12.1), и, следовательно, его можно задать линейным неравенством. Аналогично точки, расположенные ближе к одной из нескольких точек B.j на плоскости, образуют (выпуклый) многоугольник (рис.12.2); это легко обобщить и на пространство большего числа измерений.

Формально эта эквивалентность получается из соотношения
|Ф-B.j|**2 = |Ф|**2 - 2*Ф*B.j + |B.j|**2.
Если все векторы Ф имеют одинаковую длину L, то расстояние |Ф-B.j| будет НАИМЕНЬШИМ, когда разность
Ф*B.j - 1/2*|B.j|**2 = Ф*B.j - тета.j
будет наибольшей. Если теперь, учитывая результаты #1.2.1 (1), удалить "порог" тета, то останется как раз скалярное произведение Ф*B.j. Требование равенства длин векторов Ф не умаляет общности. В самом деле, добавим еще одну ось координат и заменим каждый вектор Ф = (ф.1, ..., ф.n) вектором
Ф' = (ф.1, ..., ф.n, sqr(n - СУММА[1..n]ф.ш**2)),
так что все векторы Ф' имеют одну и ту же длину L=sqr(n). Для векторов B мы также должны были бы добавить еще одно измерение, но мы будем просто считать, что соответствующая координата равна нулю [На самом деле требование равенства длин векторов Ф даже излишне, поскольку неравенство |Ф-B.j|**2 < |Ф-B.i|**2 эквивалентно неравенству Ф*B.j-1/2*|B.j|**2>Ф*B.i-1/2*|B.i|**2 при любой величине |Ф|**2.- Прим. ред.].
#12.2. МНОГООБРАЗИЕ АЛГОРИТМОВ КЛАССИФИКАЦИИ
Из бесконечного многообразия схем, которые можно использовать для разбиения пространства на классы, выберем несколько моделей, иллюстрирующих различные стороны нашей основной темы - вычисление и линейное разделение. Каждой модели дадим краткую характеристику, а потом проведем сравнение некоторых сторон их алгоритмических структур, требований к памяти и ограничений, налагаемых на характер классов.
В каждой из наших моделей для операции А.ПОИСК используется один и тот же вид решающего алгоритма. В каждом случае за классом F.j закрепляется один или более векторов А.i; мы это будем выражать словами: вектор А.i соответствует классу F.[j(i)]. При заданном векторе Ф правило решения всегда состоит в выборе того класса F.[j(i)], для которого A.i>Ф принимает наибольшее значение. Как отмечалось в #12.1.2, оно с математической точки зрения эквивалентно правилу, минимизирующему |Ф-A.i|.
Для каждой модели следовало бы также описать операцию А.РЕГИСТРАЦИЯ, которая строит векторы A.i на основе прежнего опыта или АПРИОРНОЙ информации о классах. В приведенных ниже кратких набросках подробное описание этой операции не дается; мы займемся этим в следующих разделах.
#12.2.1. ПЕРСЕПТРОН. Здесь каждому классу F.j соответствует один вектор A.j. В качестве операции А.РЕГИСТРАЦИЯ можно использовать процедуру #11.1 для случая двух классов и процедуру #11.4.1 для случая многих классов.
#12.2.2. БАЙЕСОВСКАЯ ЛИНЕЙНАЯ СТАТИСТИЧЕСКАЯ ПРОЦЕДУРА. Каждому классу F.j здесь также соответствует один вектор A.j, а вот операция А.РЕГИСТРАЦИЯ совершенно другая. Для каждого класса F.j и каждого частного предиката фи.i положим
w.ij = log(p.ij/(1-p.ij)),
где p.ij - ВЕРОЯТНОСТЬ того, что фи.i=1, ПРИ УСЛОВИИ что Ф принадлежит F.j. Пусть
A.j = (тета.j, w.1j, w.2j, ...).
В #12.4.3 мы укажем условия, при которых эти "вероятности" имеют смысл, и опишем алгоритмы "обучения", с помощью которых можно будет оценить или аппроксимировать w.ij.
Если выполняются определенные статистические условия, то преимущество байесовской процедуры в том, что она дает хорошие результаты для классов, которые НЕ ЯВЛЯЮТСЯ линейно разделимыми [Правильнее было бы сказать "для пересекающихся классов", поскольку для классов, разделимых нелинейной поверхностью, но линейно не разделимых, описанная процедура не даст хороших результатов.- Прим. ред.]. Она фактически дает наинизшую возможную величину ошибки для процедур, в которых А.РЕГИСТРАЦИЯ зависит только от условных вероятностей, если предикаты фи.i статистически независимы в смысле #12.4.2. Просто поразительно, что это достигается с помощью линейной формулы.
#12.2.3. НАИЛУЧШИЕ ПЛОСКОСТИ. В различных ситуациях ПЕРСЕПТРОН и БАЙЕСОВСКАЯ процедура уступают друг другу. Но зачастую, когда классы F.j - линейно неразделимы, существует множество векторов A.j, дающее меньшие ошибки, чем любая из этих схем. Поэтому определим процедуру НАИЛУЧШИЕ ПЛОСКОСТИ как такую, при которой используется указанное множество векторов A.j. Это множество характеризуется здесь тем, что наибольшее скалярное произведение A.j*Ф приводит к наименьшей ошибке.
По определению НАИЛУЧШИЕ ПЛОСКОСТИ всегда по крайней мере не хуже, чем ПЕРСЕПТРОН или БАЙЕСОВСКАЯ процедура. Это не противоречит оптимальности БАЙЕСОВСКОЙ процедуры, поскольку поиск наилучшей плоскости использует иную информацию, чем условные вероятности. К сожалению, никакой практически действенный алгоритм А.РЕГИСТРАЦИЯ для выявления векторов A.j этой процедуры неизвестен. Как отмечается в #12.3, из-за проблемы локальных вершин подъем на холм не будет здесь работать успешно.
#12.2.4. ИЗОДЕЙТА. В описанных в #12.2.1-12.2.3 моделях каждому классу F соответствовал один вектор A. Если взглянуть на решаемую задачу с точки зрения минимизации расстояния, то станет ясно, что такие процедуры работают удовлетворительно только тогда, когда классы F "локализованы" в сравнительно изолированных, отдельных областях (их можно представлять себе в виде комков, куч или облаков). Естественно тогда задать вопрос: что же делать, если класс F хотя и не является четко очерченным сферическим образованием, но все же частично локализован в виде небольшого числа куч или, быть может, в виде змееподобной структуры? В таких ситуациях задачу можно решить с помощью алгоритма А.ПОИСК, вычисляющего кратчайшее расстояние, если закрепить за каждым скоплением,входящим в состав каждого класса F, свой вектор А или использовать много векторов А для задания "хребта змеи". Для реализации этой идеи потребуется операция А.РЕГИСТРАЦИЯ, обладающая некоторой способностью к анализу распределений в кучах. Одна такая схема под названием ИЗОДЕЙТА будет описана в #12.5.
#12.2.5. БЛИЖАЙШЕЕ СОСЕДСТВО. Наша простейшая и основная схема не налагает никаких ограничений на число векторов А. Алгоритм А.РЕГИСТРАЦИЯ хранит в памяти каждый просмотренный вектор Ф вместе с соответствующим ему классом F. Для каждого предъявляемого к опознанию вектора Ф.0 отыскивается в памяти ближайший к нему вектор Ф и выбирается класс F, соответствующий Ф.
Вообще говоря, это очень мощный метод: он весьма эффективен для многих разновидностей куч; он никогда не ошибается на уже просмотренной точке; в пределе он стремится к нулевой ошибке, за исключением довольно своеобразных случаев (один из которых рассматривается в следующем параграфе).
БЛИЖАЙШЕЕ СОСЕДСТВО имеет один очевидный недостаток - очень большой объем требуемой памяти, и другой, менее очевидный,- есть веские основания подозревать, что эта процедура приводит к большим и по существу неизбежным вычислительным затратам (последний вопрос рассматривается в #12.6).
#12.3. ЭВРИСТИЧЕСКОЕ ОПИСАНИЕ МЕТОДОВ ЛИНЕЙНОГО РАЗДЕЛЕНИЯ
В этом параграфе мы разберем несколько рисунков, чтобы лучше понять методы #12.4. Чтобы компенсировать нашу неспособность изображать многомерные конфигурации, будем пользоваться двумерными многозначными координатами. На первый взгляд может показаться, что эти чертежи внушают доверие, но на самом деле они очень несовершенны: в них нет даже намека на весь тот ужас, с которым можно столкнуться в пространстве многих измерений.
На этих наглядных рисунках мы представим два вида ситуаций, в каждой из которых попеременно проявляются преимущества БАЙЕСОВСКОЙ процедуры или ПЕРСЕПТРОНА (рис. 12.3). Прямая, соответствующая БАЙЕСОВСКОЙ процедуре, стремится пройти перпендикулярно к прямой, соединяющей "средние" точки множеств F+ и F-. Поэтому в ситуации рис.12.3(а) байесовская процедура допустит некоторые ошибки [Авторы, как и прежде, имеют в виду частный случай БАЙЕСОВСКОЙ процедуры, основанной на предположении о статистической независимости координат вектора Ф.БАЙЕСОВСКАЯ процедура общего вида, учитывающая действительные распределения вероятностей, даст по определению минимальную вероятность ошибки, т.е. безошибочное разделение в случае рис.12.3(а).- Прим. ред.]. Так как указанные здесь множества линейно разделимы, то ПЕРСЕПТРОН в конечном счете не ошибется. В случае рис.12.3(b) БАЙЕСОВСКАЯ процедура, как и на рис.12.3(а), приведет к небольшим ошибкам, а по поводу поведения ПЕРСЕПТРОНА в этом случае известно немного; ясно только, что в некоторых ситуациях он работает хуже БАЙЕСОВСКОЙ процедуры. Разумеется, НАИЛУЧШАЯ ПЛОСКОСТЬ по определению по меньшей мере так же хороша, как БАЙЕСОВСКАЯ процедура или как ПЕРСЕПТРОН.

Само по себе предположение о том, что любая из указанных процедур вообще окажется хоть сколько-нибудь хорошей, с самого начала равносильно АПРИОРНОМУ предположению, что классы F можно представить в виде простых "облаков", возможно, немного перекрывающихся (рис.12.4). Подобное допущение можно оправдать, если есть основания полагать, что различия между классами F+ и F- вызваны каким-то одним основным фактором, с которым суммируется множество разнообразных вторичных воздействий, гораздо меньших по величине. Вообще, похоже на то, что ПЕРСЕПТРОН чувствителен к внешним границам облаков и сравнительно нечувствителен к распределениям плотности внутри них, тогда как байесовская процедура взвешивает все векторы Ф одинаково [См. предыдущее замечание].

В случаях, когда условие единственности облака или условие небольшого перекрытия не удовлетворяются (рис.12.5), можно ожидать, что БАЙЕСОВСКАЯ процедура и, видимо, ПЕРСЕПТРОН будут работать плохо, НАИЛУЧШАЯ ПЛОСКОСТЬ может оказаться значительно лучше них, поскольку она не подвержена вредному влиянию симметрии. Однако, по всей видимости, нахождение наилучшей плоскости сопряжено с большими вычислительными трудностями, вызванными наличием множества локально оптимальных "холмов". На рис.12.6 показаны некоторые из локальных вершин для НАИЛУЧШЕЙ ПЛОСКОСТИ в плохой ситуации типа проверки четности. Здесь даже ИЗОДЕЙТА будет работать плохо, если не разрешить ей иметь по одному вектору А почти для каждого комка. Но для небольшого числа комков, в каждом из которых находится вектор A.k, ИЗОДЕЙТА действует вполне хорошо (#12.5). Вообще следует ожидать, что ПЕРСЕПТРОН окажется немного лучше БАЙЕСОВСКОЙ процедуры, поскольку в нем используется обратная связь, и немного хуже из-за его чрезмерной чувствительности к изолированным ошибкам.

Следует также ожидать, что БЛИЖАЙШЕЕ СОСЕДСТВО будет работать хорошо только при выполнении большого числа условий. В самом деле, в предельном случае записи всех векторов Ф с соответствующими им классами ближайшее соседство по меньшей мере так же хорошо, как и любая другая процедура. Но существуют условия, в которых БЛИЖАЙШЕЕ СОСЕДСТВО не показывает такой хорошей работы до тех пор, пока выборка не окажется равной почти всему пространству. В качестве примера рассмотрим пространство

Верхняя область характеризуется тем, что вероятность ее точки принадлежать классу F+ равна p, а для нижней эта вероятность равна 1-p=q. Для класса F- верхняя и нижняя области меняются ролями. Тогда если уже просмотрена небольшая часть точек, то вероятность того, что выбранная наудачу точка принадлежит тому же классу F, что и ближайшая к ней просмотренная точка, равна
p**2+q**2 = 1-2*p*q,
а вероятность правильного опознания при помощи БАЙЕСОВСКОЙ процедуры или НАИЛУЧШЕЙ ПЛОСКОСТИ равна p. Считая,что p>1/2 (иначе просто поменяем местами p и q), получаем
Ошибка.НАИЛУЧШАЯ-ПЛОСКОСТЬ < Ошибка.БЛИЖАЙШЕЕ-СОСЕДСТВО < 2*Ошибка.НАИЛУЧШАЯ-ПЛОСКОСТЬ.
Таким образом, БЛИЖАЙШЕЕ СОСЕДСТВО здесь хуже НАИЛУЧШЕЙ ПЛОСКОСТИ, но не сколь угодно хуже. Это явление сохраняется до тех пор, пока не будет выбрано так много точек, что появится заметная вероятность повторного выбора, т.е. пока не будет просмотрена значительная часть пространства.
С другой стороны, если классы F+ и F- не очень сильно "перемешаны" (рис.12.7), то БЛИЖАЙШЕЕ СОСЕДСТВО будет сходиться к очень хорошим результатам, как только появится реальный шанс найти одну выборочную точку в большинстве "микро-комков".

Очень плохим случаем является структура типа проверки четности; здесь БЛИЖАЙШЕЕ СОСЕДСТВО работает даже хуже, чем случайный выбор решения. Пусть Ф принадлежит F.i тогда и только тогда, когда фи.i=1 для четного числа индексов i. Тогда если предикатов фи всего n, то у каждой точки Ф окажется как раз n соседей, расстояния d до которых удовлетворяют условию 0<d<=l. Предположим, что векторы, которые уже прошли проверку, составляют (1-q)-ю часть всех возможных векторов Ф. Тогда ближайшее соседство ошибется на данном векторе Ф, если он еще не был осмотрен (вероятность последнего события равна q), а один из его непосредственных соседей уже осмотрен (эта вероятность равна 1-q**n). Поэтому вероятность ошибки будет не меньше q(1-q**n), что при больших значениях n практически не отличается от q.
Этот пример "патологический", как любят говорить математики, и, по всей вероятности, БЛИЖАЙШЕЕ СОСЕДСТВО хорошо работает во многих реальных ситуациях. Разумеется, качество работы зависит от формы, принятой для вычисления расстояния, так что многие из классических статистических методов посвящены оптимальному выбору координатных осей и масштабов измерений при использовании процедуры БЛИЖАЙШЕЕ СОСЕДСТВО.
Отметим, наконец, что из-за большого объема памяти и большого количества вычислений, требуемых для этой процедуры, с ней конкурируют более совершенные схемы, выходящие за рамки линейного разделения и, следовательно, за рамки этой книги.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
 Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
Re: 02.06. НЕХВАТКА ЕСТЕСТВЕННОГО ИНТЕЛЛЕКТА
#12.4. РЕШЕНИЯ, ОСНОВАННЫЕ НА ВЕРОЯТНОСТНЫХ ЗНАЧЕНИЯХ ПРЕДИКАТОВ
Некоторые из описанных в предыдущих параграфах процедур можно было бы назвать "статистическими" в том очень нестрогом смысле, что при их применении гарантируется лишь какая-то вероятность получения успешного результата. Процедуры, рассматриваемые в этом параграфе, являются статистическими в более строгом смысле: запоминаются не элементы МНОЖЕСТВА ДАННЫХ, а статистические параметры этого множества. Мы проведем подробный анализ системы, вычисляющей (или оценивающей) условные вероятности p.ij того, что для каждого класса F.j предикат фи.i равен 1. Система запоминает эти p.ij вместе с безусловными вероятностями p.j принадлежности вектора Ф классу F.j.
Если задан вектор Ф, то выбор класса F.j представляет собой типичную статистическую задачу, решаемую обычно методом "максимального правдоподобия" или методом Байеса. Интересно, что такого рода процедуры очень похожи на персептронные методы разделения. В самом деле, если можно предположить, что условные вероятности p.ij в подходящем смысле независимы (#12.4.2), то наилучшей процедурой оказывается линейное пороговое решение, которое в #12.2.2 было нами названо БАЙЕСОВСКОЙ процедурой. Покажем теперь, откуда эта процедура возникает.
#12.4.1. МАКСИМАЛЬНОЕ ПРАВДОПОДОБИЕ И ПРАВИЛО БАЙЕСА. В гл.11 мы изучали ситуации, в которых каждый вектор Ф соответствовал одному-единственному классу F.j. Сейчас рассмотрим несколько более общий случай, когда один и тот же вектор можно получить в результате событий, относящихся к различным классам. Тогда, если задан вектор Ф, то, вообще говоря, нельзя с уверенностью сказать, какой именно класс F.j ему отвечает; в лучшем случае мы знаем соответствующие вероятности.
Предположим, что нам встретился некоторый вектор Ф.0 и мы хотим узнать, какой класс F для него наиболее вероятен. Если вектору Ф.0 отвечает класс F.j, то произошло совместное событие F.j&Ф.0, вероятность которого обозначим через P(F.j&Ф.0). По определению условной вероятности (1)
F.j&Ф.0 = P(F.j)*P(Ф.0|F.j),
т.е. вероятность совместного появления F.j и Ф.0 равна произведению вероятности появления F.j и вероятности того, что ПРИ УСЛОВИИ ПОЯВЛЕНИЯ F.j ПОЯВЛЯЕТСЯ И Ф.0.
Мы должны выбрать тот класс F.j, при котором формула (1) дает наибольшее значение вероятности совместного события, ибо такой выбор соответствует выбору наиболее вероятного из событий, которые могли бы произойти [Этот выбор приводит к минимуму вероятности ошибки, равной P.ош=СУММА[Ф]СУММА[i]P(F.j&Ф)[i!=j(Ф)], где j(Ф) - правило выбора.- Прим. ред.]:
F.1&Ф.0, F.2&Ф.0, ..., F.k&Ф.0.
Формулу (1) трудно использовать непосредственно из-за серьезных практических недостатков. Если различных векторов Ф много, практически немыслимо хранить в памяти все возможные решения, не говоря уже о статистической оценке всех этих решений на основе экспериментальных наблюдений. Система не способна также строить догадки относительно векторов Ф, с которыми она ранее не сталкивалась [Если не делать априорных предположений о вероятностях P(F.j&&Ф). Это относится к любым системам, так как подобные догадки всегда строятся на априорных сведениях. Поэтому в этом отношении байесовский подход ничем не хуже других. - Прим. ред.]. Всех этих трудностей можно избежать, вводя одно существенное предположение (разумеется, при условии, что ситуация хорошо согласуется с данной моделью), а именно что частные предикаты, образующие Ф=(Фи.1, ..., фи.m), в подходящем смысле независимы.
#12.4.2 НЕЗАВИСИМОСТЬ. До сих пор мы умалчивали об изображениях X, рассматривавшихся в предыдущих главах, поскольку происхождение предикатов фи нас не заботило. Вспомним теперь об этих изображениях, чтобы можно было придать гипотезе о независимости естественную окраску.
Упомянутых в конце #12.4.1 проблем можно избежать, если допустить, что испытания фи.i(X) статистически независимы в пределах каждого класса F. Это означает, что для всех Ф(X)=(фи.1(X), ..., фи.m(X)) и всех j
P(Ф|F.j) = P(фи.1|F.j) ... P(фи.m|F.j).
Подчеркнем, что это условие очень сильное. Оно, например, эквивалентно следующему:
Если дано, что вектор Ф принадлежит конкретному классу F, то знание некоторых предикатов фи.i,- не дает никакой дополнительной информации об остальных предикатах фи.i.
В экспериментах обычно рассчитывают встретиться с независимостью тогда, когда значения предикатов фи изменяются за счет "шума", или неопределенности измерении в каждом отдельном устройстве, измеряющем величину фи.i (рис.12.8 ).
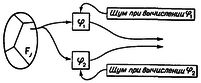
Независимость.
Действительно, поскольку причины помех различны, постольку нельзя надеяться, что знание одного из предикатов фи.i, поможет предсказать значение другого. Однако если вариации значений предикатов фи.i обусловлены выбором различных изображений X из одного и того же класса F, то обычно НЕЛЬЗЯ предполагать независимость, так как каждый предикат фи.i содержит какую-то информацию о том, какое именно изображение X из класса F было выбрано, и, следовательно, хотя бы частично должен помочь предсказать значения остальных предикатов фи.i (рис.12.9).
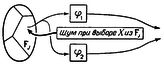
Отсутствие независимости.
Крайний случай отсутствия независимости иллюстрирует следующий пример. Пусть имеются два класса F.1 и F.2. Зададим предикаты фи.1 и фи.2: фи.1(X) пусть будет случайной величиной, причем Р(фи.1(X)=1)=1/2 (значение ее определяется бросанием монеты, а не изображением X), а
фи.2(X) =
фи.1(X), если X принадлежит F.1,
1-фи.1(X), если X принадлежит F.2.
Тогда
P(фи.1&ф.2|F.1) = 1/2,
P(фи.1|F.1)*P(фи.2|F.1) = 1/2*1/2.
Заметьте, что ни фи.1 ни фи.2 В ОТДЕЛЬНОСТИ не дают никакой информации о классе F! Каждый из этих предикатов определяется случайным бросанием монеты. А оба вместе они совершенно точно указывают, из какого класса F взята фигура:
если фи.1=фи.2, то из класса F.1,
если фи.1!=фи.2, то из класса F.2.
ЗАМЕЧАНИЕ. Независимость предполагается только В ПРЕДЕЛАХ каждого класса F.j. Поэтому если класс F.j не задан, то знание одного предиката фи, МОЖЕТ помочь предсказать значение другого. Например, пусть
фи.1 = фи.2 = 0, если X принадлежит F.1,
фи.1 = фи.2 = 1, если X принадлежит F.2.
Фактически в пределах каждого класса оба предиката независимы. Однако если ПРЕДВАРИТЕЛЬНО НЕ ДАНО, что X принадлежит F.1, но известно, что фи.1=0, то можно было бы, конечно, предсказать, что и фи.2=0, причем это не нарушает нашего допущения о независимости. (Если бы с самого начала знать, что X принадлежит F.1, то значение предиката фи.2 можно было бы предсказать СРАЗУ; в этом случае знание предиката фи.1, не влияет на наше предсказание значения фи.2).
#12.4.3. МАКСИМАЛЬНО ПРАВДОПОДОБНОЕ РЕШЕНИЕ ПРИ НЕЗАВИСИМЫХ ПРЕДИКАТАХ фи ЯВЛЯЕТСЯ ЛИНЕЙНЫМ ПОРОГОВЫМ ПРЕДИКАТОМ! Допустим, что для каждого класса F.j предикаты фи.j статистически независимы. Введем следующие обозначения (2):
p.j=P(F.j),
p.ij=P(фи.i=1|F.j),
q.ij=1-p.ij=P(фи.i=0|F.j).
Предположим, что мы только что просмотрели вектор Ф=(фи.1, ..., фи.m) и хотим узнать, какому классу F.j он соответствует с наибольшей вероятностью. Учитывая формулы (1) и (2), выберем индекс j, максимизирующий произведение
p.j * П[фи.i= 1]p.ij * П[фи.i=0]q.ij =
p.j * П[i]p.ij**фи.i*q.ij**(1-ф.i) =
p.j * П[i](p.ij/q.ij)**ф.i * П[i]q.ij.
Так как удобнее оперировать с суммами, чем с произведениями, то перейдем к логарифмам. Поскольку log(x) - возрастающая функция, мы должны максимизировать (3)
СУММА[i]фи.i*log(p.ij/q.ij) + (log(p.j) + СУММА[i]log(q.ij)[ф.i]).
Выражение в скобках зависит только от j и не зависит от векторов Ф, поэтому сумму (3) можно записать в виде (3')
СУММА w.ij*фи.i + тета.j.
ПРИМЕР 1. Если классов F всего два, то можно считать, что X принадлежит F.1 всякий раз, когда (4)
СУММА w.i1*фи.i + тета.1 > СУММА w.i2*фи.i + тета.2
т.е.
СУММА (w.i1-w.i2)*фи.i > тета.2 - тета.1,
и мы получаем линейный пороговый предикат
пси = [СУММА альфа.i*фи.i > тета].
Таким образом, гипотеза взаимной независимости предикатов фи в данном случае привела непосредственно к привычной нам тактике линейных решений.
ПРИМЕР 2 (вероятности ошибок). Пусть p.i1=q.i2 для всех i. Тогда p.i1 будет вероятностью события фи.i(X)=пси(X), a q.i1 - вероятностью события фи.i(X)!=пси(X), т.е. вероятностью того, что фи.i допускает ошибку в (индивидуальном) предсказании значения предиката пси=[X принадлежит F.i].
Неравенство (4) приобретает здесь вид (4')
СУММА[i]w.i1(2*фи.i-1) > log(p.2/p.1).
Множитель (2*фи.i-1) приводит к ПРИБАВЛЕНИЮ или ВЫЧИТАНИЮ w.i1 в зависимости от значения предиката фи.i. Поэтому величины w можно представлять себе как веса гирь, которые надо добавлять на правую или на левую чашу весов:
Величина log(p.2/p.1) является "априорным весом" в пользу F.2, а w.i1=log(p.i1/q.i1) - "весом признака", свидетельствующего в пользу F.1, если фи.i=1.
Заметим, что алгоритм оптимального разделения (при условии, что вероятности предикатов фи.i независимы) имеет вид линейного порогового предиката (неравенство (4)). Однако нужно, разумеется, понимать, что если [СУММА альфа.фи*фи > тета] - "оптимальный" предикат, полученный при условии независимости вероятностей, но не дающий точную реализацию искомого предиката пси, то это вовсе не означает, что не существует точного разделения [СУММА альфа.фи'*фи > тета'], полностью согласующегося с пси. (Подобная ситуация показана на рис.12.3(а)). Дело в том, что неравенство (4) "оптимально" лишь по отношению к тем алгоритмам А.РЕГИСТРАЦИЯ, которые НЕ ИСПОЛЬЗУЮТ НИКАКОЙ ИНФОРМАЦИИ, КРОМЕ УСЛОВНЫХ ВЕРОЯТНОСТЕЙ {p.j} и {p.ij}, в то время как персептрон вычисляет коэффициенты с помощью нестатистической поисковой процедуры, чувствительной к отдельным событиям [Это замечание авторов может создать у читателя впечатление о том, что возможности статистического решения задачи разделения двух множеств слабее, чем возможности персептрона. Это, конечно, неверно, поскольку метод Байеса дает точное решение задачи о минимуме вероятности ошибки. В рассматриваемой ситуации (рис.12.3(а)) плохие результаты статистического разделения объясняются тем, что алгоритм, предназначенный для случая независимых фи, применен для разделения множеств, характеризующихся резко выраженной зависимостью предикатов фи друг от друга. (В случае независимых фи множества должны изображаться на схемах, подобных рис.12.3(а), в виде прямоугольников со сторонами, параллельными координатным осям). Если использовать адекватное статистическое описание множеств, т.е. вероятности P(F.j&Ф), то БАЙЕСОВСКАЯ процедура даст результаты, по крайней мере не худшие, чем любая другая, включая и ПЕРСЕПТРОН. Поэтому нельзя согласиться с объяснением авторов, основанным на якобы "нестатистическон поисковой процедуре, чувствительной к отдельным событиям". Как БАЙЕСОВСКАЯ процедура, так и ПЕРСЕПТРОН обладают этим свойством в совершенно одинаковой мере.- Прим. ред.].
Так, например, если пси принадлежит L(Ф), то персептрон в конечном счете будет работать по крайней мере не хуже любой линейной статистической машины, имеющей преимущества лишь в следующих случаях:
1. Если пси не принадлежит L(Ф), то статистическая схема может осуществить хорошее приближенное разделение, а персептрон может дать большие флуктуации.
2. Время, необходимое для достижения приемлемого качества работы, для регистрирующего алгоритма персептрона может оказаться очень большим, поскольку этот алгоритм является в основном последовательной поисковой процедурой. Линейная статистическая машина в своей основе более параллельна, поскольку находит каждый коэффициент независимо от остальных и нуждается только в довольно большой выборке из классов F. (Хотя на первый взгляд кажется, что коэффициенты персептрона изменяются независимо один от другого, но на самом деле каждое решение об их изменении зависит от испытания, в котором участвуют все коэффициенты).
#12.4.4. МНОГОСЛОЙНЫЕ МАШИНЫ. Выражение (3') подсказывает следующую схему машины, вырабатывающей необходимое решение:
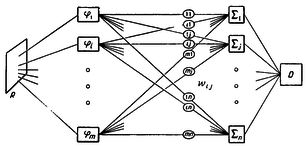
Устройство D решает, на каком из его входов наибольший сигнал. Каждое из устройств фи; при предъявлении изображения X вырабатывает импульс стандартной величины (если фи{X)=1). Импульсы умножаются на w.ij и суммируются в блоках СУММА[j]. Слагаемые тета.j можно считать поправками, характеризующими величину отклонения вероятностей p.ij от 1/2. Эти поправки объединены с АПРИОРНЫМИ смещениями, соответствующими каждому классу F.j.
Часто бывает нужно минимизировать СТОИМОСТЬ ошибок, а не вероятность ошибки. Если обозначить через C.jk стоимость решения в пользу F.k, когда в действительности изображение принадлежало классу F.j, то, как нетрудно показать, формулы (1) и (2) дадут значение k, минимизирующее
СУММА[j]C.jk*B.j*П[i](p.ij/q.ij)**фи.i.
где B.j=Пq.ij. Интересно, что эта более сложная процедура тоже сводится к многослойной структуре
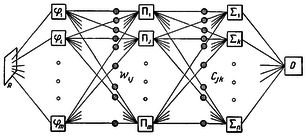
Для оптимизации весов w.ij в этой схеме можно, вероятно, предложить алгоритм обучения, в котором для сообщения схеме стоимости ошибки используется, скажем, величина сигнала поощрения. Этот вопрос мы не исследовали.
#12.4.5. ПРОЦЕДУРЫ ОЦЕНКИ ВЕРОЯТНОСТЕЙ. Алгоритм А.РЕГИСТРАЦИЯ для БАЙЕСОВСКОЙ линейной статистической процедуры должен вычислить или оценить вероятности p.ij и p.j, фигурирующие в сумме (3), или же другие статистические величины, как, например, отношения p/(1-p), характеризующие "веса признаков". Обычно подобные характеристики нельзя вычислить непосредственно (так как по определению они представляют собой пределы), и поэтому требуется находить оценки. Простейший способ оценить вероятность - это найти отношение H/N числа H "благоприятных" событий к числу N всех событий. Если фи[t] - значение предиката фи в t-м испытании, то вероятность Р(фи=1) после n испытаний можно оценить с помощью программы
НАЧАЛО: Положить альфа=0.
Положить n= 1.
ПОВТОРЕНИЕ: Присвоить альфа значение ((n-1)*альфа+фи.[n])/n.
Присвоить n значение n+1.
Перейти к ПОВТОРЕНИЕ.
Легко заметить, что после каждого события получается новое значение H/N.
Недостаток этой программы состоит в том, что при ее выполнении необходимо хранить в памяти число опытов n, которое неограниченно возрастает. Чтобы избежать этого, запишем значение альфа после n-го испытания в виде
альфа[n]=(1-1/n)альфа[n-1]+1/n*фи[n],
Тогда появляется возможность заменить эту программу более простой: пусть (5)
альфа[0] = 0
альфа[n] = (1-e)альфа[n-1]+e*фи[n],
где 0<e<1. С ростом n МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, или СРЕДНЕЕ функции альфа[n] (обозначим его <альфа[n]>) стремится к p=<фи>. В самом деле,
<альфа[1]> = (1-е)<а[0]>+е<фи[1]> = е*p = (1-(1-e))р,
<альфа[2]> = (1-е)(1-(1-e))p+e*p = (1-(1-p)**2)p
и вообще для всех n
<альфа[n]> = (1-(1-e)**n)p -> р при n->беск.
Итак, процесс (5) дает оценку вероятности того, что фи=1. При более детальном анализе можно было бы показать, как эта оценка зависит от последних событий, причем влияние давно прошедших событий падает по экспоненте (за счет коэффициентов вида (1-e)**(t.0-t)).
Поскольку процесс (5) "забывающий", он, разумеется, не использует свой накопленный опыт "оптимальным образом", но в некоторых обстоятельствах он может "приспосабливаться" к изменениям статистических свойств окружающей среды, что само по себе совсем неплохо. Как прямое следствие отмеченного выше спада влияния отдаленных событий, наша оценка приобретает своеобразное свойство: ее дисперсия сигма**2 не стремится к нулю. В самом деле, можно показать, что для процесса (5)
сигма**2 -> p(1-p)e/(2-e),
а это хотя и не равно нулю, но весьма мало, если мало e. Положение в этом случае в корне отличается от случая оценки H/N, дисперсия которой равна p(1-p)/n и стремится к нулю при n->беск.
Дисперсию можно использовать для сравнения указанных двух процессов. Будем считать, что дисперсии равны, т.е.
p(1-p)e/(2-e) ~ p(1-p)/n
Тогда
n ~ 2/e.
Это говорит о том, что процесс (5) обеспечивает почти такую же надежность оценки p, какую можно было бы получить при простом усреднении последних 2/e выборочных событий. Следовательно, можно считать, что число 1/e соответствует постоянной времени забывания.
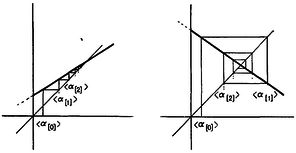
Сходимость к фиксированной точке.
Рассмотрим еще одну программу нахождения оценки:
НАЧАЛО: Присвоить альфа произвольное значение. ПОВТОРЕНИЕ: Если фи=1, то присвоить альфа значение альфа+1.
Если фи=0, то присвоить альфа значение (1-e)альфа.
Перейти к ПОВТОРЕНИЕ.
Здесь альфа[n] вычисляется по формуле
альфа[n] = (1-e)альфа[n-1] + e(1+е*альфа[n-1])фи[n].
Можно показать, что математическое ожидание <альфа[n]> этой оценки стремится к
1/e(p/(1-p))
Интересно, что отношение правдоподобия можно непосредственно оценить очень просто: ПРИБАВИТЬ 1, ЕСЛИ фи=1, И УМНОЖИТЬ НА (1-е) В ПРОТИВНОМ СЛУЧАЕ. Дисперсия здесь равна
сигма**2=p/(1-p)**2/(1-(1-e)**2).
#12.4.6. КОМПРОМИСС СЭМЮЭЛЯ. В своей классической статье 1959г. А.Л.Сэмюэль применяет остроумное сочетание методов оценки вероятностей. В его задаче время от времени ВВОДИТСЯ НОВЫЙ ПРИЗНАК фи.i (а старый отбрасывается, поскольку не оказывает заметного влияния на процесс решения). В этом случае необходимо предотвратить сильные колебания, вызванные тем, что после одного или нескольких испытаний дисперсия оценки вероятности этого нового признака будет гораздо больше, чем дисперсии для старых признаков, оценки которых построены на лучшем статистическом материале. Для "стабилизации" своей системы Сэмюэль использует следующий алгоритм: он присваивает альфа[0] значение 1/2 и строит оценку
где
альфа[n+1]=(1-1/N)альфа[n]+1/N*фи[n+1],
где
N =
16, если n<32,
2**m, если 2**m<=n<2**(m+1) и 32<=n<=256,
256, если n>=256.
Таким образом, для вероятности в самом начале выбирается значение 1/2, как будто бы оно получено на основе нескольких (порядка 16) испытаний. Затем в "средний" период алгоритм аппроксимирует равномерное взвешивание, а когда n становится порядка 256, наступает экспоненциальное затухание влияния отдаленных событий, при котором N фиксировано и недавний опыт может перевешивать прежние результаты. (Степени двойки здесь использованы из соображений удобства программирования на ЭВМ).
Признаки в системе Сэмюэля имеют вид, найденный нами при выводе неравенства (4') из #12.4.3, а именно 2*фи[t]-1, так что "оценка" изменяется в диапазоне -1<=ро[t]<=+1 и может рассматриваться как "коэффициент корреляции".
#12.4.7. ТЕОРИЯ ПРОСТОГО "СИНАПТИЧЕСКОГО" ПОДКРЕПЛЕНИЯ. В этом разделе мы построим простую "нейронную модель", которая должна будет оценить p.ij=P(фи.i|F.j) только на основе информации о событиях [фи.i=1] и [Ф принадлежит F.j]. "Анатомически" наша модель будет выглядеть так:

В пузырьках B.i и C.j содержится вещество E с очень высокой и постоянной концентрацией. Когда приходит нервный импульс от фи.i или от F.j, стенки соответствующих пузырьков B.i или C.j становятся в тот момент "проницаемыми" для вещества E. Если импульс приходит только от фи.i, то, в сущности, никаких изменений не происходит, поскольку пузырек B.i окружен тогда непроницаемым пузырьком C.j Если импульс приходит только от F.j, то за счет диффузии некоторая часть вещества E уходит из C.j в окружающее пространство. Если альфа - количество вещества E в Cj, то можно считать (согласно обычным законам диффузии и концентрации), что теряется некоторая доля е этого количества и остается
альфа' = (1-e)альфа,
если импульс пришел от F.j и фи.1=0. Если же импульсы приходят от фи.i и от F.j, то потеря вещества из пузырька C.j будет примерно такой же, как в предыдущем случае. Одновременно за счет диффузии из B.i в C.j попадет некоторое количество b вещества E. Поэтому
альфа' = (1-e)альфа+b,
если импульс пришел от F.j и фи.i=1. (Величину b можно считать постоянной, поскольку концентрация вещества Е в B.i очень высока по сравнению с концентрацией в C.j. Можно придумать множество аналогичных вариантов). В любом случае
альфа' = (1-e)альфа+b*фи,
так что в пределе среднее значение альфа стремится к b*p (как это можно видеть из анализа, проведенного в #12.4.5) и потому может служить оценкой вероятности p.ij= Р(фи.i|F.j).
Итак, эта простая схема с мембраной, которая становится проницаемой в момент прихода нервного импульса, дала возможность получить оценку соответствующей вероятности.
Каким же образом можно осуществить такое представление вероятности с помощью реального нейронного механизма? Нетрудно представить себе различные варианты схем: концентрации ионов (еще лучше - логарифмы этих концентраций!) могли бы превратиться в потенциалы мембран, или проводимости, или даже в вероятности других химических явлений Для получения отношений правдоподобия "анатомические" и "физиологические" особенности нашей модели можно непрерывно совершенствовать. Действительно, представить себе различные варианты настолько легко (описанный замысел очень нечувствителен к деталям), что мы не предлагаем эту модель всерьез. Мы просто считаем, что о подобном семействе простых и занимательных моделей нейротеоретикам следовало бы знать.
#12.5. АЛГОРИТМЫ A.РЕГИСТРАЦИЯ ДЛЯ ПРОЦЕДУРЫ ИЗОДЕЙТА
В этом параграфе мы опишем предложенную Боллом и Холлом процедуру нахождения куч в неоднородном распределении векторов. Поясним их идею на конкретном примере. Пусть дано двумерное множество точек {Ф}, которое очевидным образом распадается на кучи вида

Начнем с того, что в качестве некоторых "центров" выберем произвольные точки A[1].i скажем, расположенные вблизи начала координат. Затем разобьем все множество точек Ф на подмножества R.i, так, что Ф принадлежит R.i, если ближайшим к точке Ф центром является A[1].i.
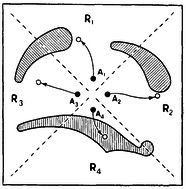
Заменим теперь каждый центр A[1].i новым центром A[2].i, который представляет собой СРЕДНЕЕ, или центр тяжести точек Ф из Ri, и обозначим через R[2].i множество точек Ф, ближайших к A[2].i:
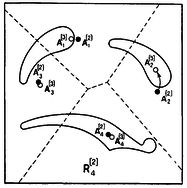
Повторяя этот процесс, получаем новый набор точек A.i и подмножеств R.i
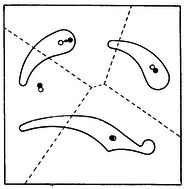
и далее
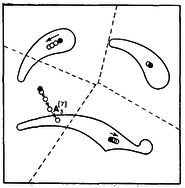
С некоторого момента изменения почти или полностью отсутствуют, что свидетельствует о том, что "центры нашли имеющиеся кучи".
Болл и Холл предложили целый ряд эвристических усовершенствований процедуры, заключающихся в устранении и добавлении центров; например, добавим один центр, если дисперсия множества R чересчур велика, и устраним одну точку, если два подмножества расположены слишком близко друг к другу. Разумеется, двумерные кучи обычно легко выявить на глаз, но ИЗОДЕЙТА может дать хорошие результаты и в n-мерных задачах, где о "визуальном наблюдении" не может быть и речи.
Чтобы использовать эту процедуру для решения рассматриваемых здесь задач, нужно как-то объединить ее способность к автоматической классификации с информацией о классах F. Очевидный первый шаг в этом направлении: применить процедуру к каждому классу F в отдельности и отнести все полученные точки A к этому же классу. Более утонченные схемы, которые могли бы привести к лучшим результатам на стадии А.ПОИСК, нам неизвестны.
#12.5.1. ТЕОРЕМА О СХОДИМОСТИ ИЗОДЕЙТЫ. Существует теорема (нам о ней сообщил Т.Кавер), из которой следует, что ИЗОДЕЙТА отыскивает некоторого рода локальный минимум. Для доказательства этой теоремы введем ряд обозначений:
A[n](Ф) - центр A[n].i, ближайший к точке Ф. (Если таких центров A[n].i несколько, возьмем центр с наименьшим индексом i).
R[n].i - множество точек Ф, для которых А[n](Ф)=А[n].i;
А[n+1].i - среднее <R[n].i>.
Введем, наконец, количественную характеристику разбиения:
s[n] = СУММА[все Ф]|Ф-A[n](Ф)|**2.
ТЕОРЕМА. Последовательность s[1], s[2], ..., s[n], ... убывает до тех пор, пока, начиная с некоторого n (для которого впервые A[n].i=A[n+1].i), она не стабилизируется.
ДОКАЗАТЕЛЬСТВО. В самом деле,
s[n] = СУММА[j]СУММА[R[n].j]|Ф-A[n].j|**2 > СУММА[j]СУММА[R[n].j]|Ф-A[n+1].j|**2
ибо среднее A[n+1].j множества R[n].j минимизирует сумму квадратов расстояний до всех его точек. Далее,
СУММА[j]СУММА[R[n].j]|Ф-A[n+1].j|**2 >= СУММА[i]СУММА[R[n+1].i]|Ф-A[n+1].i|**2 = s[n+1],
поскольку каждая точка Ф принадлежит тому множеству R[n+1].i, для которого расстояние |Ф-A[n+1].i| минимально, т.е. для каждого j
|Ф-A[n+1].j| >= |Ф-A[n+1].i|.
СЛЕДСТВИЕ. Будучи убывающей последовательностью положительных чисел, {s[n]} сходится. Если множество точек Ф конечно, то изменение центров А должно прекратиться за конечное число шагов.
Действительно, в этом случае число разбиений {Ri} конечное.
#12.5.2. МЕТОДЫ, ОСНОВАННЫЕ НА ПРИРАЩЕНИЯХ. По аналогии с методами "поощрения" из #12.4.5 процедуру ИЗОДЕЙТА можно аппроксимировать при помощи следующей программы [Этот алгоритм, как и процедура, описанная в #12.5, и теорема #12.5.1 (в более общем виде) были опубликованы М.И.Шлезингером в его статье "О самопроизвольном различении образов", сб. "Читающие автоматы", изд-во "Наукова думка", Киев, 1965, стр.38-45.- Прим. ред.]:
НАЧАЛО: Выбрать систему исходных точек А.i.
ПОВТОРЕНИЕ: Выбрать точку Ф.
Найти А(Ф), т.е. точку А.i ближайшую к Ф.
Заменить А(Ф) на (1-е)А(Ф)+е*Ф. Перейти к ПОВТОРЕНИЕ.
Ясно, что эта программа в качественном отношении ведет себя так же, как ИЗОДЕЙТА: точки А будут перемещаться по направлению к СРЕДНИМ своих R-областей. Однако, как и в #12.4, при таком процессе будет сохраняться некоторая дисперсия, вызванная появлением новых точек и забыванием старых. Следовательно, этому процессу присущи те же преимущества и недостатки. Фактически таким способом можно аппроксимировать все рассмотренные алгоритмы А.РЕГИСТРАЦИЯ: по-видимому, всегда имеется широкий диапазон выбора от очень локальных методов, основанных на приращениях, до более точных и в некоторой степени менее "адаптивных" глобальных схем. Итоги проведенного обсуждения мы подведем в #12.8.
Некоторые из описанных в предыдущих параграфах процедур можно было бы назвать "статистическими" в том очень нестрогом смысле, что при их применении гарантируется лишь какая-то вероятность получения успешного результата. Процедуры, рассматриваемые в этом параграфе, являются статистическими в более строгом смысле: запоминаются не элементы МНОЖЕСТВА ДАННЫХ, а статистические параметры этого множества. Мы проведем подробный анализ системы, вычисляющей (или оценивающей) условные вероятности p.ij того, что для каждого класса F.j предикат фи.i равен 1. Система запоминает эти p.ij вместе с безусловными вероятностями p.j принадлежности вектора Ф классу F.j.
Если задан вектор Ф, то выбор класса F.j представляет собой типичную статистическую задачу, решаемую обычно методом "максимального правдоподобия" или методом Байеса. Интересно, что такого рода процедуры очень похожи на персептронные методы разделения. В самом деле, если можно предположить, что условные вероятности p.ij в подходящем смысле независимы (#12.4.2), то наилучшей процедурой оказывается линейное пороговое решение, которое в #12.2.2 было нами названо БАЙЕСОВСКОЙ процедурой. Покажем теперь, откуда эта процедура возникает.
#12.4.1. МАКСИМАЛЬНОЕ ПРАВДОПОДОБИЕ И ПРАВИЛО БАЙЕСА. В гл.11 мы изучали ситуации, в которых каждый вектор Ф соответствовал одному-единственному классу F.j. Сейчас рассмотрим несколько более общий случай, когда один и тот же вектор можно получить в результате событий, относящихся к различным классам. Тогда, если задан вектор Ф, то, вообще говоря, нельзя с уверенностью сказать, какой именно класс F.j ему отвечает; в лучшем случае мы знаем соответствующие вероятности.
Предположим, что нам встретился некоторый вектор Ф.0 и мы хотим узнать, какой класс F для него наиболее вероятен. Если вектору Ф.0 отвечает класс F.j, то произошло совместное событие F.j&Ф.0, вероятность которого обозначим через P(F.j&Ф.0). По определению условной вероятности (1)
F.j&Ф.0 = P(F.j)*P(Ф.0|F.j),
т.е. вероятность совместного появления F.j и Ф.0 равна произведению вероятности появления F.j и вероятности того, что ПРИ УСЛОВИИ ПОЯВЛЕНИЯ F.j ПОЯВЛЯЕТСЯ И Ф.0.
Мы должны выбрать тот класс F.j, при котором формула (1) дает наибольшее значение вероятности совместного события, ибо такой выбор соответствует выбору наиболее вероятного из событий, которые могли бы произойти [Этот выбор приводит к минимуму вероятности ошибки, равной P.ош=СУММА[Ф]СУММА[i]P(F.j&Ф)[i!=j(Ф)], где j(Ф) - правило выбора.- Прим. ред.]:
F.1&Ф.0, F.2&Ф.0, ..., F.k&Ф.0.
Формулу (1) трудно использовать непосредственно из-за серьезных практических недостатков. Если различных векторов Ф много, практически немыслимо хранить в памяти все возможные решения, не говоря уже о статистической оценке всех этих решений на основе экспериментальных наблюдений. Система не способна также строить догадки относительно векторов Ф, с которыми она ранее не сталкивалась [Если не делать априорных предположений о вероятностях P(F.j&&Ф). Это относится к любым системам, так как подобные догадки всегда строятся на априорных сведениях. Поэтому в этом отношении байесовский подход ничем не хуже других. - Прим. ред.]. Всех этих трудностей можно избежать, вводя одно существенное предположение (разумеется, при условии, что ситуация хорошо согласуется с данной моделью), а именно что частные предикаты, образующие Ф=(Фи.1, ..., фи.m), в подходящем смысле независимы.
#12.4.2 НЕЗАВИСИМОСТЬ. До сих пор мы умалчивали об изображениях X, рассматривавшихся в предыдущих главах, поскольку происхождение предикатов фи нас не заботило. Вспомним теперь об этих изображениях, чтобы можно было придать гипотезе о независимости естественную окраску.
Упомянутых в конце #12.4.1 проблем можно избежать, если допустить, что испытания фи.i(X) статистически независимы в пределах каждого класса F. Это означает, что для всех Ф(X)=(фи.1(X), ..., фи.m(X)) и всех j
P(Ф|F.j) = P(фи.1|F.j) ... P(фи.m|F.j).
Подчеркнем, что это условие очень сильное. Оно, например, эквивалентно следующему:
Если дано, что вектор Ф принадлежит конкретному классу F, то знание некоторых предикатов фи.i,- не дает никакой дополнительной информации об остальных предикатах фи.i.
В экспериментах обычно рассчитывают встретиться с независимостью тогда, когда значения предикатов фи изменяются за счет "шума", или неопределенности измерении в каждом отдельном устройстве, измеряющем величину фи.i (рис.12.8 ).

Независимость.
Действительно, поскольку причины помех различны, постольку нельзя надеяться, что знание одного из предикатов фи.i, поможет предсказать значение другого. Однако если вариации значений предикатов фи.i обусловлены выбором различных изображений X из одного и того же класса F, то обычно НЕЛЬЗЯ предполагать независимость, так как каждый предикат фи.i содержит какую-то информацию о том, какое именно изображение X из класса F было выбрано, и, следовательно, хотя бы частично должен помочь предсказать значения остальных предикатов фи.i (рис.12.9).

Отсутствие независимости.
Крайний случай отсутствия независимости иллюстрирует следующий пример. Пусть имеются два класса F.1 и F.2. Зададим предикаты фи.1 и фи.2: фи.1(X) пусть будет случайной величиной, причем Р(фи.1(X)=1)=1/2 (значение ее определяется бросанием монеты, а не изображением X), а
фи.2(X) =
фи.1(X), если X принадлежит F.1,
1-фи.1(X), если X принадлежит F.2.
Тогда
P(фи.1&ф.2|F.1) = 1/2,
P(фи.1|F.1)*P(фи.2|F.1) = 1/2*1/2.
Заметьте, что ни фи.1 ни фи.2 В ОТДЕЛЬНОСТИ не дают никакой информации о классе F! Каждый из этих предикатов определяется случайным бросанием монеты. А оба вместе они совершенно точно указывают, из какого класса F взята фигура:
если фи.1=фи.2, то из класса F.1,
если фи.1!=фи.2, то из класса F.2.
ЗАМЕЧАНИЕ. Независимость предполагается только В ПРЕДЕЛАХ каждого класса F.j. Поэтому если класс F.j не задан, то знание одного предиката фи, МОЖЕТ помочь предсказать значение другого. Например, пусть
фи.1 = фи.2 = 0, если X принадлежит F.1,
фи.1 = фи.2 = 1, если X принадлежит F.2.
Фактически в пределах каждого класса оба предиката независимы. Однако если ПРЕДВАРИТЕЛЬНО НЕ ДАНО, что X принадлежит F.1, но известно, что фи.1=0, то можно было бы, конечно, предсказать, что и фи.2=0, причем это не нарушает нашего допущения о независимости. (Если бы с самого начала знать, что X принадлежит F.1, то значение предиката фи.2 можно было бы предсказать СРАЗУ; в этом случае знание предиката фи.1, не влияет на наше предсказание значения фи.2).
#12.4.3. МАКСИМАЛЬНО ПРАВДОПОДОБНОЕ РЕШЕНИЕ ПРИ НЕЗАВИСИМЫХ ПРЕДИКАТАХ фи ЯВЛЯЕТСЯ ЛИНЕЙНЫМ ПОРОГОВЫМ ПРЕДИКАТОМ! Допустим, что для каждого класса F.j предикаты фи.j статистически независимы. Введем следующие обозначения (2):
p.j=P(F.j),
p.ij=P(фи.i=1|F.j),
q.ij=1-p.ij=P(фи.i=0|F.j).
Предположим, что мы только что просмотрели вектор Ф=(фи.1, ..., фи.m) и хотим узнать, какому классу F.j он соответствует с наибольшей вероятностью. Учитывая формулы (1) и (2), выберем индекс j, максимизирующий произведение
p.j * П[фи.i= 1]p.ij * П[фи.i=0]q.ij =
p.j * П[i]p.ij**фи.i*q.ij**(1-ф.i) =
p.j * П[i](p.ij/q.ij)**ф.i * П[i]q.ij.
Так как удобнее оперировать с суммами, чем с произведениями, то перейдем к логарифмам. Поскольку log(x) - возрастающая функция, мы должны максимизировать (3)
СУММА[i]фи.i*log(p.ij/q.ij) + (log(p.j) + СУММА[i]log(q.ij)[ф.i]).
Выражение в скобках зависит только от j и не зависит от векторов Ф, поэтому сумму (3) можно записать в виде (3')
СУММА w.ij*фи.i + тета.j.
ПРИМЕР 1. Если классов F всего два, то можно считать, что X принадлежит F.1 всякий раз, когда (4)
СУММА w.i1*фи.i + тета.1 > СУММА w.i2*фи.i + тета.2
т.е.
СУММА (w.i1-w.i2)*фи.i > тета.2 - тета.1,
и мы получаем линейный пороговый предикат
пси = [СУММА альфа.i*фи.i > тета].
Таким образом, гипотеза взаимной независимости предикатов фи в данном случае привела непосредственно к привычной нам тактике линейных решений.
ПРИМЕР 2 (вероятности ошибок). Пусть p.i1=q.i2 для всех i. Тогда p.i1 будет вероятностью события фи.i(X)=пси(X), a q.i1 - вероятностью события фи.i(X)!=пси(X), т.е. вероятностью того, что фи.i допускает ошибку в (индивидуальном) предсказании значения предиката пси=[X принадлежит F.i].
Неравенство (4) приобретает здесь вид (4')
СУММА[i]w.i1(2*фи.i-1) > log(p.2/p.1).
Множитель (2*фи.i-1) приводит к ПРИБАВЛЕНИЮ или ВЫЧИТАНИЮ w.i1 в зависимости от значения предиката фи.i. Поэтому величины w можно представлять себе как веса гирь, которые надо добавлять на правую или на левую чашу весов:

Величина log(p.2/p.1) является "априорным весом" в пользу F.2, а w.i1=log(p.i1/q.i1) - "весом признака", свидетельствующего в пользу F.1, если фи.i=1.
Заметим, что алгоритм оптимального разделения (при условии, что вероятности предикатов фи.i независимы) имеет вид линейного порогового предиката (неравенство (4)). Однако нужно, разумеется, понимать, что если [СУММА альфа.фи*фи > тета] - "оптимальный" предикат, полученный при условии независимости вероятностей, но не дающий точную реализацию искомого предиката пси, то это вовсе не означает, что не существует точного разделения [СУММА альфа.фи'*фи > тета'], полностью согласующегося с пси. (Подобная ситуация показана на рис.12.3(а)). Дело в том, что неравенство (4) "оптимально" лишь по отношению к тем алгоритмам А.РЕГИСТРАЦИЯ, которые НЕ ИСПОЛЬЗУЮТ НИКАКОЙ ИНФОРМАЦИИ, КРОМЕ УСЛОВНЫХ ВЕРОЯТНОСТЕЙ {p.j} и {p.ij}, в то время как персептрон вычисляет коэффициенты с помощью нестатистической поисковой процедуры, чувствительной к отдельным событиям [Это замечание авторов может создать у читателя впечатление о том, что возможности статистического решения задачи разделения двух множеств слабее, чем возможности персептрона. Это, конечно, неверно, поскольку метод Байеса дает точное решение задачи о минимуме вероятности ошибки. В рассматриваемой ситуации (рис.12.3(а)) плохие результаты статистического разделения объясняются тем, что алгоритм, предназначенный для случая независимых фи, применен для разделения множеств, характеризующихся резко выраженной зависимостью предикатов фи друг от друга. (В случае независимых фи множества должны изображаться на схемах, подобных рис.12.3(а), в виде прямоугольников со сторонами, параллельными координатным осям). Если использовать адекватное статистическое описание множеств, т.е. вероятности P(F.j&Ф), то БАЙЕСОВСКАЯ процедура даст результаты, по крайней мере не худшие, чем любая другая, включая и ПЕРСЕПТРОН. Поэтому нельзя согласиться с объяснением авторов, основанным на якобы "нестатистическон поисковой процедуре, чувствительной к отдельным событиям". Как БАЙЕСОВСКАЯ процедура, так и ПЕРСЕПТРОН обладают этим свойством в совершенно одинаковой мере.- Прим. ред.].
Так, например, если пси принадлежит L(Ф), то персептрон в конечном счете будет работать по крайней мере не хуже любой линейной статистической машины, имеющей преимущества лишь в следующих случаях:
1. Если пси не принадлежит L(Ф), то статистическая схема может осуществить хорошее приближенное разделение, а персептрон может дать большие флуктуации.
2. Время, необходимое для достижения приемлемого качества работы, для регистрирующего алгоритма персептрона может оказаться очень большим, поскольку этот алгоритм является в основном последовательной поисковой процедурой. Линейная статистическая машина в своей основе более параллельна, поскольку находит каждый коэффициент независимо от остальных и нуждается только в довольно большой выборке из классов F. (Хотя на первый взгляд кажется, что коэффициенты персептрона изменяются независимо один от другого, но на самом деле каждое решение об их изменении зависит от испытания, в котором участвуют все коэффициенты).
#12.4.4. МНОГОСЛОЙНЫЕ МАШИНЫ. Выражение (3') подсказывает следующую схему машины, вырабатывающей необходимое решение:

Устройство D решает, на каком из его входов наибольший сигнал. Каждое из устройств фи; при предъявлении изображения X вырабатывает импульс стандартной величины (если фи{X)=1). Импульсы умножаются на w.ij и суммируются в блоках СУММА[j]. Слагаемые тета.j можно считать поправками, характеризующими величину отклонения вероятностей p.ij от 1/2. Эти поправки объединены с АПРИОРНЫМИ смещениями, соответствующими каждому классу F.j.
Часто бывает нужно минимизировать СТОИМОСТЬ ошибок, а не вероятность ошибки. Если обозначить через C.jk стоимость решения в пользу F.k, когда в действительности изображение принадлежало классу F.j, то, как нетрудно показать, формулы (1) и (2) дадут значение k, минимизирующее
СУММА[j]C.jk*B.j*П[i](p.ij/q.ij)**фи.i.
где B.j=Пq.ij. Интересно, что эта более сложная процедура тоже сводится к многослойной структуре

Для оптимизации весов w.ij в этой схеме можно, вероятно, предложить алгоритм обучения, в котором для сообщения схеме стоимости ошибки используется, скажем, величина сигнала поощрения. Этот вопрос мы не исследовали.
#12.4.5. ПРОЦЕДУРЫ ОЦЕНКИ ВЕРОЯТНОСТЕЙ. Алгоритм А.РЕГИСТРАЦИЯ для БАЙЕСОВСКОЙ линейной статистической процедуры должен вычислить или оценить вероятности p.ij и p.j, фигурирующие в сумме (3), или же другие статистические величины, как, например, отношения p/(1-p), характеризующие "веса признаков". Обычно подобные характеристики нельзя вычислить непосредственно (так как по определению они представляют собой пределы), и поэтому требуется находить оценки. Простейший способ оценить вероятность - это найти отношение H/N числа H "благоприятных" событий к числу N всех событий. Если фи[t] - значение предиката фи в t-м испытании, то вероятность Р(фи=1) после n испытаний можно оценить с помощью программы
НАЧАЛО: Положить альфа=0.
Положить n= 1.
ПОВТОРЕНИЕ: Присвоить альфа значение ((n-1)*альфа+фи.[n])/n.
Присвоить n значение n+1.
Перейти к ПОВТОРЕНИЕ.
Легко заметить, что после каждого события получается новое значение H/N.
Недостаток этой программы состоит в том, что при ее выполнении необходимо хранить в памяти число опытов n, которое неограниченно возрастает. Чтобы избежать этого, запишем значение альфа после n-го испытания в виде
альфа[n]=(1-1/n)альфа[n-1]+1/n*фи[n],
Тогда появляется возможность заменить эту программу более простой: пусть (5)
альфа[0] = 0
альфа[n] = (1-e)альфа[n-1]+e*фи[n],
где 0<e<1. С ростом n МАТЕМАТИЧЕСКОЕ ОЖИДАНИЕ, или СРЕДНЕЕ функции альфа[n] (обозначим его <альфа[n]>) стремится к p=<фи>. В самом деле,
<альфа[1]> = (1-е)<а[0]>+е<фи[1]> = е*p = (1-(1-e))р,
<альфа[2]> = (1-е)(1-(1-e))p+e*p = (1-(1-p)**2)p
и вообще для всех n
<альфа[n]> = (1-(1-e)**n)p -> р при n->беск.
Итак, процесс (5) дает оценку вероятности того, что фи=1. При более детальном анализе можно было бы показать, как эта оценка зависит от последних событий, причем влияние давно прошедших событий падает по экспоненте (за счет коэффициентов вида (1-e)**(t.0-t)).
Поскольку процесс (5) "забывающий", он, разумеется, не использует свой накопленный опыт "оптимальным образом", но в некоторых обстоятельствах он может "приспосабливаться" к изменениям статистических свойств окружающей среды, что само по себе совсем неплохо. Как прямое следствие отмеченного выше спада влияния отдаленных событий, наша оценка приобретает своеобразное свойство: ее дисперсия сигма**2 не стремится к нулю. В самом деле, можно показать, что для процесса (5)
сигма**2 -> p(1-p)e/(2-e),
а это хотя и не равно нулю, но весьма мало, если мало e. Положение в этом случае в корне отличается от случая оценки H/N, дисперсия которой равна p(1-p)/n и стремится к нулю при n->беск.
Дисперсию можно использовать для сравнения указанных двух процессов. Будем считать, что дисперсии равны, т.е.
p(1-p)e/(2-e) ~ p(1-p)/n
Тогда
n ~ 2/e.
Это говорит о том, что процесс (5) обеспечивает почти такую же надежность оценки p, какую можно было бы получить при простом усреднении последних 2/e выборочных событий. Следовательно, можно считать, что число 1/e соответствует постоянной времени забывания.

Сходимость к фиксированной точке.
Рассмотрим еще одну программу нахождения оценки:
НАЧАЛО: Присвоить альфа произвольное значение. ПОВТОРЕНИЕ: Если фи=1, то присвоить альфа значение альфа+1.
Если фи=0, то присвоить альфа значение (1-e)альфа.
Перейти к ПОВТОРЕНИЕ.
Здесь альфа[n] вычисляется по формуле
альфа[n] = (1-e)альфа[n-1] + e(1+е*альфа[n-1])фи[n].
Можно показать, что математическое ожидание <альфа[n]> этой оценки стремится к
1/e(p/(1-p))
Интересно, что отношение правдоподобия можно непосредственно оценить очень просто: ПРИБАВИТЬ 1, ЕСЛИ фи=1, И УМНОЖИТЬ НА (1-е) В ПРОТИВНОМ СЛУЧАЕ. Дисперсия здесь равна
сигма**2=p/(1-p)**2/(1-(1-e)**2).
#12.4.6. КОМПРОМИСС СЭМЮЭЛЯ. В своей классической статье 1959г. А.Л.Сэмюэль применяет остроумное сочетание методов оценки вероятностей. В его задаче время от времени ВВОДИТСЯ НОВЫЙ ПРИЗНАК фи.i (а старый отбрасывается, поскольку не оказывает заметного влияния на процесс решения). В этом случае необходимо предотвратить сильные колебания, вызванные тем, что после одного или нескольких испытаний дисперсия оценки вероятности этого нового признака будет гораздо больше, чем дисперсии для старых признаков, оценки которых построены на лучшем статистическом материале. Для "стабилизации" своей системы Сэмюэль использует следующий алгоритм: он присваивает альфа[0] значение 1/2 и строит оценку
где
альфа[n+1]=(1-1/N)альфа[n]+1/N*фи[n+1],
где
N =
16, если n<32,
2**m, если 2**m<=n<2**(m+1) и 32<=n<=256,
256, если n>=256.
Таким образом, для вероятности в самом начале выбирается значение 1/2, как будто бы оно получено на основе нескольких (порядка 16) испытаний. Затем в "средний" период алгоритм аппроксимирует равномерное взвешивание, а когда n становится порядка 256, наступает экспоненциальное затухание влияния отдаленных событий, при котором N фиксировано и недавний опыт может перевешивать прежние результаты. (Степени двойки здесь использованы из соображений удобства программирования на ЭВМ).
Признаки в системе Сэмюэля имеют вид, найденный нами при выводе неравенства (4') из #12.4.3, а именно 2*фи[t]-1, так что "оценка" изменяется в диапазоне -1<=ро[t]<=+1 и может рассматриваться как "коэффициент корреляции".
#12.4.7. ТЕОРИЯ ПРОСТОГО "СИНАПТИЧЕСКОГО" ПОДКРЕПЛЕНИЯ. В этом разделе мы построим простую "нейронную модель", которая должна будет оценить p.ij=P(фи.i|F.j) только на основе информации о событиях [фи.i=1] и [Ф принадлежит F.j]. "Анатомически" наша модель будет выглядеть так:

В пузырьках B.i и C.j содержится вещество E с очень высокой и постоянной концентрацией. Когда приходит нервный импульс от фи.i или от F.j, стенки соответствующих пузырьков B.i или C.j становятся в тот момент "проницаемыми" для вещества E. Если импульс приходит только от фи.i, то, в сущности, никаких изменений не происходит, поскольку пузырек B.i окружен тогда непроницаемым пузырьком C.j Если импульс приходит только от F.j, то за счет диффузии некоторая часть вещества E уходит из C.j в окружающее пространство. Если альфа - количество вещества E в Cj, то можно считать (согласно обычным законам диффузии и концентрации), что теряется некоторая доля е этого количества и остается
альфа' = (1-e)альфа,
если импульс пришел от F.j и фи.1=0. Если же импульсы приходят от фи.i и от F.j, то потеря вещества из пузырька C.j будет примерно такой же, как в предыдущем случае. Одновременно за счет диффузии из B.i в C.j попадет некоторое количество b вещества E. Поэтому
альфа' = (1-e)альфа+b,
если импульс пришел от F.j и фи.i=1. (Величину b можно считать постоянной, поскольку концентрация вещества Е в B.i очень высока по сравнению с концентрацией в C.j. Можно придумать множество аналогичных вариантов). В любом случае
альфа' = (1-e)альфа+b*фи,
так что в пределе среднее значение альфа стремится к b*p (как это можно видеть из анализа, проведенного в #12.4.5) и потому может служить оценкой вероятности p.ij= Р(фи.i|F.j).
Итак, эта простая схема с мембраной, которая становится проницаемой в момент прихода нервного импульса, дала возможность получить оценку соответствующей вероятности.
Каким же образом можно осуществить такое представление вероятности с помощью реального нейронного механизма? Нетрудно представить себе различные варианты схем: концентрации ионов (еще лучше - логарифмы этих концентраций!) могли бы превратиться в потенциалы мембран, или проводимости, или даже в вероятности других химических явлений Для получения отношений правдоподобия "анатомические" и "физиологические" особенности нашей модели можно непрерывно совершенствовать. Действительно, представить себе различные варианты настолько легко (описанный замысел очень нечувствителен к деталям), что мы не предлагаем эту модель всерьез. Мы просто считаем, что о подобном семействе простых и занимательных моделей нейротеоретикам следовало бы знать.
#12.5. АЛГОРИТМЫ A.РЕГИСТРАЦИЯ ДЛЯ ПРОЦЕДУРЫ ИЗОДЕЙТА
В этом параграфе мы опишем предложенную Боллом и Холлом процедуру нахождения куч в неоднородном распределении векторов. Поясним их идею на конкретном примере. Пусть дано двумерное множество точек {Ф}, которое очевидным образом распадается на кучи вида

Начнем с того, что в качестве некоторых "центров" выберем произвольные точки A[1].i скажем, расположенные вблизи начала координат. Затем разобьем все множество точек Ф на подмножества R.i, так, что Ф принадлежит R.i, если ближайшим к точке Ф центром является A[1].i.

Заменим теперь каждый центр A[1].i новым центром A[2].i, который представляет собой СРЕДНЕЕ, или центр тяжести точек Ф из Ri, и обозначим через R[2].i множество точек Ф, ближайших к A[2].i:

Повторяя этот процесс, получаем новый набор точек A.i и подмножеств R.i

и далее

С некоторого момента изменения почти или полностью отсутствуют, что свидетельствует о том, что "центры нашли имеющиеся кучи".
Болл и Холл предложили целый ряд эвристических усовершенствований процедуры, заключающихся в устранении и добавлении центров; например, добавим один центр, если дисперсия множества R чересчур велика, и устраним одну точку, если два подмножества расположены слишком близко друг к другу. Разумеется, двумерные кучи обычно легко выявить на глаз, но ИЗОДЕЙТА может дать хорошие результаты и в n-мерных задачах, где о "визуальном наблюдении" не может быть и речи.
Чтобы использовать эту процедуру для решения рассматриваемых здесь задач, нужно как-то объединить ее способность к автоматической классификации с информацией о классах F. Очевидный первый шаг в этом направлении: применить процедуру к каждому классу F в отдельности и отнести все полученные точки A к этому же классу. Более утонченные схемы, которые могли бы привести к лучшим результатам на стадии А.ПОИСК, нам неизвестны.
#12.5.1. ТЕОРЕМА О СХОДИМОСТИ ИЗОДЕЙТЫ. Существует теорема (нам о ней сообщил Т.Кавер), из которой следует, что ИЗОДЕЙТА отыскивает некоторого рода локальный минимум. Для доказательства этой теоремы введем ряд обозначений:
A[n](Ф) - центр A[n].i, ближайший к точке Ф. (Если таких центров A[n].i несколько, возьмем центр с наименьшим индексом i).
R[n].i - множество точек Ф, для которых А[n](Ф)=А[n].i;
А[n+1].i - среднее <R[n].i>.
Введем, наконец, количественную характеристику разбиения:
s[n] = СУММА[все Ф]|Ф-A[n](Ф)|**2.
ТЕОРЕМА. Последовательность s[1], s[2], ..., s[n], ... убывает до тех пор, пока, начиная с некоторого n (для которого впервые A[n].i=A[n+1].i), она не стабилизируется.
ДОКАЗАТЕЛЬСТВО. В самом деле,
s[n] = СУММА[j]СУММА[R[n].j]|Ф-A[n].j|**2 > СУММА[j]СУММА[R[n].j]|Ф-A[n+1].j|**2
ибо среднее A[n+1].j множества R[n].j минимизирует сумму квадратов расстояний до всех его точек. Далее,
СУММА[j]СУММА[R[n].j]|Ф-A[n+1].j|**2 >= СУММА[i]СУММА[R[n+1].i]|Ф-A[n+1].i|**2 = s[n+1],
поскольку каждая точка Ф принадлежит тому множеству R[n+1].i, для которого расстояние |Ф-A[n+1].i| минимально, т.е. для каждого j
|Ф-A[n+1].j| >= |Ф-A[n+1].i|.
СЛЕДСТВИЕ. Будучи убывающей последовательностью положительных чисел, {s[n]} сходится. Если множество точек Ф конечно, то изменение центров А должно прекратиться за конечное число шагов.
Действительно, в этом случае число разбиений {Ri} конечное.
#12.5.2. МЕТОДЫ, ОСНОВАННЫЕ НА ПРИРАЩЕНИЯХ. По аналогии с методами "поощрения" из #12.4.5 процедуру ИЗОДЕЙТА можно аппроксимировать при помощи следующей программы [Этот алгоритм, как и процедура, описанная в #12.5, и теорема #12.5.1 (в более общем виде) были опубликованы М.И.Шлезингером в его статье "О самопроизвольном различении образов", сб. "Читающие автоматы", изд-во "Наукова думка", Киев, 1965, стр.38-45.- Прим. ред.]:
НАЧАЛО: Выбрать систему исходных точек А.i.
ПОВТОРЕНИЕ: Выбрать точку Ф.
Найти А(Ф), т.е. точку А.i ближайшую к Ф.
Заменить А(Ф) на (1-е)А(Ф)+е*Ф. Перейти к ПОВТОРЕНИЕ.
Ясно, что эта программа в качественном отношении ведет себя так же, как ИЗОДЕЙТА: точки А будут перемещаться по направлению к СРЕДНИМ своих R-областей. Однако, как и в #12.4, при таком процессе будет сохраняться некоторая дисперсия, вызванная появлением новых точек и забыванием старых. Следовательно, этому процессу присущи те же преимущества и недостатки. Фактически таким способом можно аппроксимировать все рассмотренные алгоритмы А.РЕГИСТРАЦИЯ: по-видимому, всегда имеется широкий диапазон выбора от очень локальных методов, основанных на приращениях, до более точных и в некоторой степени менее "адаптивных" глобальных схем. Итоги проведенного обсуждения мы подведем в #12.8.

Gudleifr- Admin
- Сообщения : 3402
Дата регистрации : 2017-03-29
Страница 1 из 5 • 1, 2, 3, 4, 5 
 Похожие темы
Похожие темы» 02.03. СПОСОБНОСТЬ БОЛТАТЬ - ЕЩЕ НЕ ПРИЗНАК ИНТЕЛЛЕКТА
» Батальоны искусственного интеллекта - Battle Isle
» Батальоны искусственного интеллекта - Battle Isle
Страница 1 из 5
Права доступа к этому форуму:
Вы не можете отвечать на сообщения