Матчасть диванного танкиста
Страница 1 из 6
Страница 1 из 6 • 1, 2, 3, 4, 5, 6 
 Матчасть диванного танкиста
Матчасть диванного танкиста
По материалам журнала "Наука и жизнь" 80-х годов XX века.
Зачем нормальному человеку персональный компьютер? Как, по мере внедрения компьютеров упрощалась/усложнялась обработка персональной информации? Как обычные люди учились программировать?
Первые статьи о чем-то "персональном" появились в журнале еще в 70-е. Ходили вокруг больших ЭВМ и облизывались.
Данная статья шла как довесок к статье о пультах ТЕМА #34, АБЗАЦ #1233
ТЕМА #34, АБЗАЦ #1233 :
:
НАУКА И ЖИЗНЬ 8/75
ИНЖЕНЕР Р.СВОРЕНЬ. РОСЧЕРКОМ ЭЛЕКТРОННОГО ПЕРА
Многие машины обучены общению с человеком, умеют сообщать ему о своем состоянии, о своей работе. Перегрелся автомобильный двигатель - и перед водителем загорается яркая предупреждающая лампочка; десятки приборов в кабине пилота рассказывают ему, как идет полет; и даже часы научены в заказанное время безжалостно сигналить: "Пора вставать".
Но, конечно же, самого высокого совершенства в общении с человеком достигли вычислительные машины. Выдавать информацию - это просто основа их профессии. На бесконечных бумажных рулонах печатают они результаты своих расчетов и "размышлений". А вот дисплей - устройство, в котором на экране электронно-лучевой трубки ЭВМ быстрым электронным пером отображает все, что она должна поведать человеку: записывает колонки цифр и букв, целые фразы, рисует векторы, графики, чертежи.
Прежде, чем рассказывать о самом дисплее, напомним, как работает электронно-лучевая трубка (1). Выброшенные из накаленного катода электроны фокусируются электрическими или магнитными полями в острый электронный луч, который, попав в флюоресцирующий экран, заставляет светиться ту или иную его точку (на рисунках она обозначена красным цветом, хотя обычно свечение экрана зеленоватое или голубоватое). В трубке есть две системы управления лучом: его интенсивностью, а значит, в итоге яркостью светящейся точки, и его перемещением в пространстве.
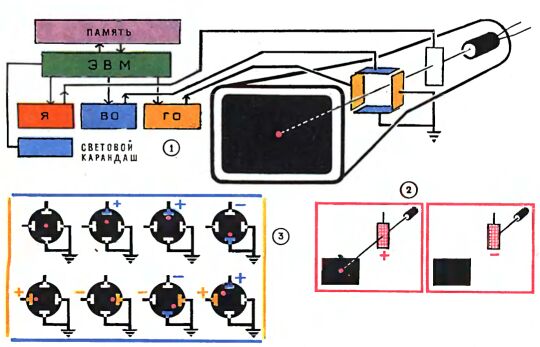
Яркость можно менять, изменяя напряжение на управляющем электроде. Он в принципе действует так же, как управляющая сетка в усилительной лампе: "плюс" на управляющем электроде ускоряет электроны, повышает яркость, "минус" тормозит электроны и даже может вообще оттолкнуть их назад, к катоду, то есть может полностью "запереть луч", погасить свечение экрана (2).
Перемещать луч в пространстве, двигать по экрану светящуюся точку можно с помощью электрических полей (их создают, подводя напряжение от блоков ВО и ГО К пластинам вертикального и горизонтального отклонения, или с помощью магнитных полей: они создаются отклоняющими катушками, которые прилегают к трубке снаружи). На рисунке 3 для наглядности показана трубка с электростатическим отклонением луча, хотя в дисплее, как правило, работают трубки с магнитным отклонением.
Если, меняя напряжение на отклоняющих пластинах, достаточно быстро двигать светящуюся точку по экрану, то можно создавать на нем светящиеся линии, рисовать "картинку", в частности цифры, буквы, векторы, геометрические фигуры. На рисунке 4 показано, как одновременным и согласованным изменением напряжений Uв и Uг, которые двигают луч "вверх - вниз" и "влево - вправо", можно нарисовать на экране несколько отрезков (а, б, в, г, д, е), составляющих букву Э.
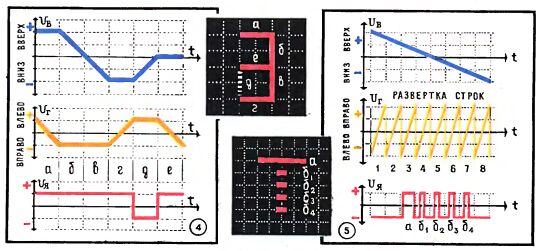
Обратите внимание на то, что, когда луч должен двигаться по участку д (чтобы перейти от отрезка г к отрезку е), светящаяся линия на экране не появляется. В этот момент на управляющий электрод вместо "плюса" подается "минус" - электронный луч в экран не попадает.
Извлекая из памяти машины "тройки" электрических сигналов (для управления яркостью, вертикальным и горизонтальным отклонением), можно рисовать на экране практически любые знаки и фигуры.
Другой способ рисования (5) более удобен для цифровых вычислительных машин, где цифры и буквы "живут" в виде серий электрических импульсов. При этом способе рисования луч непрерывно и быстро прочерчивает весь экран - напряжение Uв смещает его сверху вниз, напряжение Uг двигает луч слева направо, и он прочерчивает невидимые горизонтальные строки. Невидимые потому, что из блока управления яркостью на управляющий электрод подается "минус" и луч до экрана не доходит. Лишь в некоторые моменты времени (строго синхронизированные с отклоняющими напряжениями) из ЭВМ поступают команды "открыть путь лучу" и на экране появляются горизонтальные линии, короткие или. длинные, в зависимости от длительности отпирающего импульса. На рисунке (5) показано, как серия таких импульсов (а, б1, б2, б3, б4) рисует на экране букву Т. При достаточно большом числе "строк" (например, в дисплее ЕС-1064 Единой системы ЭВМ, луч прочерчивает по экрану 1024 строки, в полтора раза больше, чем в телевизоре) можно рисовать вполне четкие символы и фигуры.
С помощью светового карандаша (СК) оператор может вносить поправки в рисунок на экране, может сам рисовать на нем и вводить таким образом в машину свои "изменения и дополнения". Строго говоря, световой карандаш сам ничего не рисует - он лишь заставляет электронный луч провести на экране новую линию или не рисовать старую.
В одной из систем (6) светового карандаша он содержит только один светоприемник. Точки, образующие крестообразную метку, зажигаются в центре экрана последовательно, поочередно - создает эти точки серия (1, 2, 3, 4, 5, 6) импульсов напряжения на управляющем электроде, синхронизированная с движением луча. Точно такая же серия импульсов появится в цепи светоприемника СК, если он приставлен к центру экрана. При смещении СК некоторые импульсы будут выпадать, и это послужит для ЭВМ сигналом: луч нужно двигать по экрану.
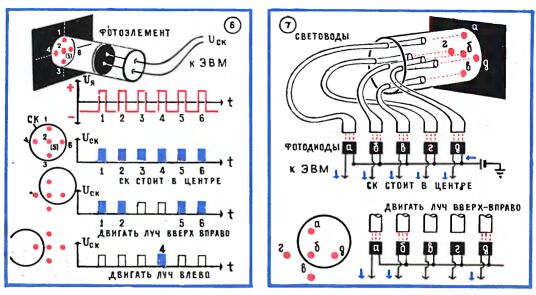
В другой системе (7) это делается так: луч ставит в самом центре экрана крестообразную светящуюся метку, на нашей схеме из пяти точек. В СК имеется пять точечных приемников света - это световоды, в конце которых закреплены фотодиоды, простейшие приборы, преобразующие свет в ток. СК начинает рисовать от центра экрана (как говорится, "от печки"), и в этом случае каждый фотодиод получает световой сигнал от "своей" светящейся точки - в машину идет сигнал: "СК находится в центре". Когда же оператор начнет двигать карандаш, то в цепи некоторых фотодиодов ток прекратится, и ЭВМ получит указание, куда нужно двигать луч (как всегда, с помощью блоков ВО и ГО), какую линию нужно рисовать или стирать (как всегда, "плюсом" или "минусом" на управляющем электроде). Метка движется по экрану вслед за карандашом.
Мы рассказали о дисплее коротко и, конечно, упрощенно. Создание дисплеев превратилось в самостоятельную область электронной техники, разработано и выпускается много разных и даже принципиально разных дисплеев, они непрерывно усложняются и совершенствуются, прочно удерживают позиции универсального средства отображения информации, удобного средства общения человека с машиной.
***
То же железо, но в профиль...
4/78

ДВА - НОЛЬ В ПОЛЬЗУ ТЕЛЕВИЗОРА
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Очень похоже, что телевизор - это размноженное миллионными тиражами чудо радиотехники и электроники, выигрывает еще один раунд в борьбе за наш досуг, освоив новый развлекательный жанр. Речь идет о домашних телевизионных играх, в которых экран телевизора, полностью отключившись от программ, прибывающих из эфира, становится ареной очень забавных состязаний - таких, например, как "теннис", "хоккей", "футбол". Играете вы в них со своим сидящим рядом партнером, и это развлечение чем-то напоминает настоящий теннис или настоящий хоккей. С той, конечно, разницей, что не нужно бегать и прыгать, ударять клюшкой или ракеткой, не нужно преодолевать усталость, утирать соленый пот с лица и в борьбе за победу выкладывать свои физические силы. Все атрибуты телевизионной игры - хоккейные ворота или теннисная сетка, мяч, шайба, клюшки, ракетки, границы поля - в виде некоторых условных фигурок и линий появляются на телевизионном экране, и, сражаясь с противником, вы ударяете "ракеткой" по "мячу", с легкостью двигая для этого рычажки или поворачивая ручки.
Мы отправляемся в гости и владельцу телевизионной игры и сами пробуем поработать ракеткой.
Чтобы читателю легче было представить себе, что такое домашние телевизионные игры, попробуем более или менее подробно описать одну из них - простейший теннис. (Мы, пожалуй, больше не будем употреблять кавычки, иначе они просто заполонят эти страницы; все называемые дальше спортивные игры и предметы спортивного инвентаря,- это не более чем условность).
Игра осуществляется с помощью небольшой, размером с книгу, приставки, от которой идет кусок кабеля со штекером на конце - этот штекер включается в антенное гнездо телевизора; сама телевизионная антенна при этом, конечно, вынимается из гнезда. На приставке несколько ручек управления, в том числе две ручки, поворотом которых игроки двигают по экрану свои ракетки.
Телевизор включен, нажата клавиша включения приставки, и на экране сразу же появляется большой, начерченный тонкими белыми линиями прямоугольник - это границы игровой площадки. В середине площадки проходит еще одна вертикальная светлая линия - это сетка. Справа, у самого края площадки, небольшой, длиной 3-4 сантиметра, вертикальный прямоугольник - это наша ракетка. А у левого края площадки такая же ракетка противника.

Вверху по обе стороны от сетки две цифры - это счет. Пока, конечно, счет 0:0, игра еще не начата.
Ну, что ж, начнем пожалуй... Нажимаем соответствующую клавишу приставки, и на экран выплывает яркая белая точка - мяч. Он быстро летит по прямой линии слева направо, перелетает сетку (точнее, проходит сквозь нее - все ведь происходит на плоскости) и движется уже по нашей половине поля куда-то вправо - вниз... Нам нужно быстрее повернуть ручку, переместить свою ракетку вниз, и отбить мяч (рисунок б)... Кажется, успели - мяч отбит и летит в сторону противника (рисунок в)... Теперь уже ему, противнику, нужно вовремя переместить ракетку в предполагаемую точку встречи с мячом... Но противник перестарался - он слишком высоко поднял ракетку, мяч проскочил мимо нее, ушел за пределы площадки (рисунок г), и индикатор счета сразу показал 1:0 в нашу пользу. Ура!
Мяч снова в игре, он влетает на площадку в направлении проигравшего... На этот раз противник успевает, отбивает мяч, и тот опять летит на нас, летит вправо вверх. Ситуация знакомая - быстро поднимаем ракетку (рисунок д)... Но что это? Мы, оказывается, просчитались - не учли, что мяч шел под очень большим углом и из-за этого ударился о верхнюю границу площадки... По правилам данной игры мяч отражается, отлетает от горизонтальных границ поля (обычно вертикальных границ вообще нет, и мяч может легко уйти, но только влево или вправо, а вверх или вниз не может), поэтому он прямо, под нашим носом резко поворачивает вниз, и мы уже не успеваем подставить ракетку (рисунок е)... Ничего не поделаешь - 1:1.
Вспоминая принципы телевидения, мы учимся рисовать на экране.
Современного человека окружает огромное множество самых разнообразных машин, приборов, аппаратов, и, конечно же, невозможно обо всех знать, как они устроены, как работают. Невозможно и не обязательно. Есть немало фотографов-любителей, которые делают прекрасные слайды, хотя и не знают, как образуется цветное изображение на обратимой пленке. И немало шоферов-любителей, которые прекрасно водят машину и при этом знать не хотят, что происходит, когда нога нажимает педаль сцепления. Ну, а без знания заэкранных секретов телевизионной игры наверняка можно прожить: чтобы точно двигать ракетку, совсем не обязательно понимать, как именно эта ракэтка нарисована на экране и как перемещается, как двигается мяч, ведется счет, зажигаются цифры.
И все же в расчете на пытливого читателя, на возможные вспышки любопытства мы уделим этим процессам немного внимания. Совсем немного. А попутно заметим: в телевизионных играх электроника использует свои классические методы и схемы, знакомство с ними может пригодиться при встрече с техникой, далекой от развлечений.
Начнем с описания двух простейших опытов. Один из них вы наверняка уже не раз наблюдали или даже непреднамеренно проделывали сами - если вблизи телевизора включить электробритву с моторчиком, например, "Харьков", то на экране замелькает множество черных и белых пятен и пятнышек. Второй опыт стоит проделать специально - он очень прост и совершенно безопасен. Вставьте в антенное гнездо телевизора кусок провода и набросьте его на включенный транзисторный приемник - на экране появятся замысловатые узоры, прямые и волнистые линии, темные и светлые пятна. Если поворачивать переключатель диапазонов или вращать ручку настройки приемника, то узоры эти придут в движение, а при некоторых положениях ручки настройки они остановятся и будут оставаться в сравнительно устойчивом состоянии.
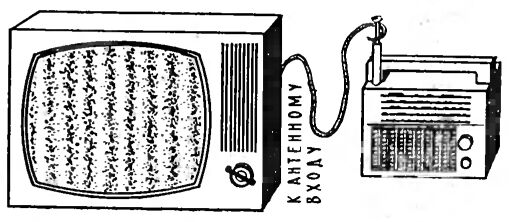
Простой и безопасный опыт убеждает, что с помощью электрических сигналов можно создать на экране телевизора "синтетическую картинку".
Теперь вывод: посторонний электрический сигнал, попав в телевизор, может создавать на экране какие-то элементы картинки. Почему мелькает экран, когда рядом работает бритва? Потому, что искрит коллектор ее моторчика, в процессе искрения в цепи резко меняется ток, резкие электрические всплески тока каким-то образом проникают в телевизор - либо через сеть, либо прямо через антенну,- и именно они, эти незваные электрические сигналы, поочередно создают на экране бессчетные блики. Примерно то, же самое происходит и в опыте с приемником. Практически все современные приемники - это супергетеродины, у них внутри имеется собственный вспомогательный генератор - маломощный гетеродин. Если приблизить приемник к антенне телевизора, то в нее пролезет сигнал гетеродина слабый меняющийся ток. Подобно трамвайному "зайцу", он доберется до конечной станции, до управляющего электрода кинескопа, а всякий сигнал на управляющем электроде - это светлое или темное пятнышко на экране: именно на этом основано создание картинки при нормальной телепередаче.
Рисование на телевизионном экране с помощью синтетических сигналов известно давно. Вспоминается, как лет 10 назад инженер В.Крапивников опубликовал в журнале "Радио" описание приставки, которая, используя оригинальный способ электрического рисования на экране, превращала телевизор в осциллограф. В этой приставке, кстати, уже в готовом виде были схемные решения, которые сейчас встречаются во всех телевизионных играх. Другой пример. Телецентры в паузах передают в эфир неподвижные картинки, заставки, например, задернутый занавес. Иногда такой занавес передается традиционным способом (телекамера смотрит на настоящий занавес и посылает его изображение нам), а иногда - от специального "генератора занавеса". Он вырабатывает определенные серии электрических сигналов, которые через телепередатчик приходят в телевизор и рисуют на его экране. Никакого настоящего занавеса и в помине нет, мы видим "полотнище", созданное виртуозом-генератором. И, наконец, еще один представитель электронной живописи - дисплей, устройство, где на телевизионном экране с помощью серии электрических импульсов рисует и пишет компьютер, сообщая результаты своих размышлений.
От проделанных простейших опытов до принципов рисования в телевизионной игре остается буквально несколько шагов. Прежде всего попробуем понять, чем определяется место появления светлых или темных точек на экране. Электронный луч кинескопа быстро прочерчивает экран горизонтальными строками и, медленно смещаясь вниз, заполняет в итоге весь кадр. Движением луча управляют два пилообразных напряжения - строчное и кадровое. Они меняются равномерно, линейно и постепенно подтягивают рисующий луч к своим отклоняющим пластинам (катушкам). Потом пила обрывается, и луч возвращается в исходное состояние. А еще есть в кинескопе управляющий электрод, он управляет интенсивностью электронного луча, то есть яркостью экрана. Если на управляющий электрод на мгновение подать "минус", то есть подать импульс отрицательного напряжения, то оно как бы оттолкнет электроны, ослабит луч, и на экране появится темная точка. Кратковременный "плюс", наоборот, ускорит электроны, электронный луч станет интенсивнее, и появится светлая точка. В каком месте экрана вспыхнет точка? Это зависит от того, в какой момент появится импульс. Если выпустить его на арену в начале кадровой пилы, то мы увидим точку вверху, а если в конце пилы - внизу; если импульс появится в начале строчной пилы, точка будет слева, если в конце строчной пилы - справа.
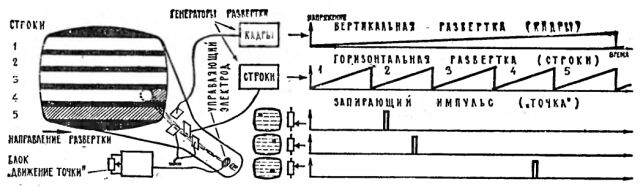
Электрические импульсы могут создавать на экране темные или светлые точки. Местоположение точки зависит от того, в какой момент появился импульс.
Следующий шаг - посмотрим, как можно поставить точку в нужном нам месте. Предположим, что у нас есть генератор импульсов, которым на равных управляют сразу два руководителя, противодействующих друг другу (в электронных схемах это осуществляется очень просто и протекает без эксцессов). Один из них - пилообразное напряжение строчной развертки, второй - постоянное напряжение, которое можно менять поворотом ручки переменного резистора (реостата). Схема построена так, что импульс появляется в момент, когда оба "руководителя" дают одинаковые указания - когда меняющееся напряжение строчной пилы становится равным установленному нами поворотом ручки постоянному напряжению. При этом, конечно, чем более высокий порог постоянного напряжения мы установим, тем позже пила достигнет этого порога, тем позже появится импульс и тем правее окажется на экране точка. Работу этой схемы можно проиллюстрировать такой аналогией. На одной чаше весов стоит гирька, на второй - стакан, который медленно наполняется водой. Наступит момент, когда вес воды превысит вес гирьки и весы "сработают". И, конечно, чем больше вес гирьки, тем позже произойдет такое срабатывание.
Пилообразное напряжение, которое помогает в нужный .момент выдать импульс (подобно тому, как будильник "выдает" звонок), может быть взято прямо от генераторов развертки или же должно быть жестко с ними синхронизировано - только в этих случаях точка на экране не будет дергаться. Чтобы точно разместить точку в любом месте экрана, обычно создают два импульса - один от строчной пилы, другой - от кадровой. Импульсы эти пропускают через схему совпадении (схема "И"), и точка появляется как бы на пересечении двух линий - вертикальной и горизонтальной. Ракетки в нашем теннисе двигаются только вверх-вниз, и поэтому к строчной пиле они намертво привязаны в одном месте. Чтобы управлять ракетками, достаточно менять время их появления, отсчитанное по кадровой пиле, то есть одним переменным резистором менять только одно постоянное напряжение. Намного сложнее управлять полетом мяча,- как правило, его нужно перемещать и вверх-вниз и влево-вправо. И при этом следить, чтобы, попав в точку, соприкасающуюся с ракеткой, мяч не пошел дальше. Чтобы он отскочил от ракетки. И притом под определенным углом. И чтобы он отскакивал также от горизонтальных границ площадки. И не отскакивал от вертикальных границ. Чтобы он проходил через них за пределы площадки. А потом возвращался. И опять под определенным углом...
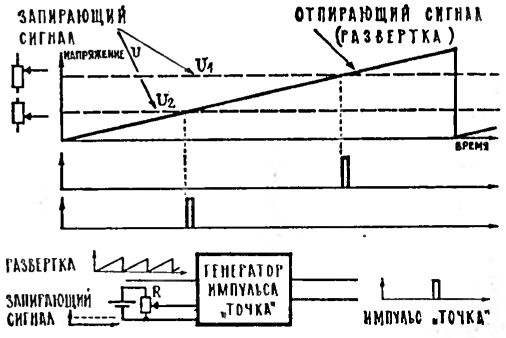
Одна из возможных систем перемещения точки: ее место на экране определится моментом появления импульса на выходе генератора; момент появления импульса, в свою очередь, зависит от того, когда пилообразное напряжение (отпирающее) сравняется с постоянным напряжением (запирающим), которое мы устанавливаем переменным резистором.
Ну и задачки... Кто может их решить? И каким образом?
Но позвольте - кто вообще двигает мяч по площадке? Ведь сами игроки управляют только ракетками...
Взглянув на схему телеигры, можно обнаружить ее сходство с компьютером.
Движение мяча, все его отскоки, исчезновения, появления, как и множество других важных дел, осуществляет самый главный блок телевизионной игры - вычисляющее устройство. Его работу в предельно упрощенном виде можно описать так. В этом блоке все начинается с дирижера. Это вспомогательный тактовый генератор, он выдает бесконечные пулеметные очереди импульсов высокой частоты - обычно миллион импульсов в секунду. Если бы все они попали на управляющий электрод кинескопа, то на экране появился бы монотонный "горошек" - тысячи точек, расположенных ровными рядами. (При существующем стандарте - 625 строк - на экране в принципе можно поставить около 50000 точек, но в простейшей телевизионной игре такая детализация картинки не нужна). На пути к кинескопу тактовые импульсы проходят через основные элементы вычисляющего устройства - счетчики импульсов, собранные из цепочек триггеров, и логические элементы, умеющие рассуждать таким примерно образом: "Если ко мне на вход придут одновременно 573-й и 826-й импульсы,- зажгу точку..." Или: "Если 128-й импульс появится вместе с 2593-м,- не зажгу точку..." Счетчики и логические элементы соединены между собой строго определенным образом, они точно работают по заданной программе. В итоге из ровного частокола импульсов остаются только те, которые в соответствии с правилами игры; и игровой обстановкой в нужном месте экрана высвечивают мячик. А в следующий момент, с учетом того, какие точки светились раньше, мячик передвигается в следующую точку траектории. Вычисляющее устройство, сформировав необходимые наборы импульсов, рисует границы площадки, ведет счет.
Все это, конечно, лишь просто сказывается: чтобы вести даже простейшую игру, нужны вычисляющие устройства с сотнями схемных узлов, состоящие из тысяч элементов - конденсаторов, транзисторов, резисторов, диодов. Если бы такой вычисляющий блок создавался лет двадцать назад и собирался из отдельных деталей, то он наверняка занял бы большой шкаф. Только интегральные схемы (см. "Наука и жизнь" 10/76 чуть далее) сделали телевизионную игру реальностью - все ее управляющее устройство вмещается сейчас в кремниевой пластинке размером с клеточку арифметической тетради.
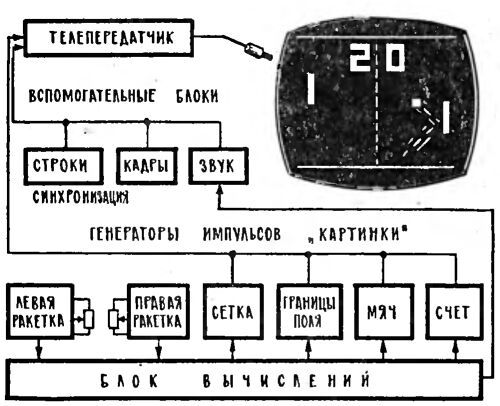
Блок-схема типичной телевизионной игры.
Просматривая технические журналы, мы узнаем, что телеигры осваивают массу новых профессий, что им предсказывают блестящее будущее.
Вычисляющее устройство телевизионной игры - это самый настоящий компьютер, хотя его и не принято так называть. Не принято скорее всего потому, что уже родилось новое поколение игр, в которых имеется программируемый процессор - главный вычисляющий блок ЭВМ. Процессор позволяет резко расширить ассортимент развлечений, усложнить условия игры и даже выполнять некоторые полезные работы. Так, в одной из моделей процессор дает возможность рисовать на экране цветными "карандашами" и даже сам рисует орнаменты и несложные мультипликации. В другой модели процессор вычисляет и записывает на экране оптимальную диету с учетом вашего веса - желаемого и реального. Программа вводится в игру (теперь ее уже и не очень удобно так называть) с магнитной пленки, со стандартной магнитофонной кассеты. Причем программ может быть огромное множество - как говорят, все зависит от фантазии разработчика. На смену простейшему теннису уже приходят автомобильные гонки, танковые и морские сражения. В волейболе мяч летит по сложной кривой и, подобно настоящему мячу, меняет скорость в процессе полета; появляется возможность давать противнику фору, уменьшая, например, размеры своей ракетки. Правда, и простейший теннис можно несколько разнообразить - уменьшать обе ракетки, увеличивать скорость мяча, менять угол его отражения, но это, конечно, и в сравнение не идет с возможностями, которые открывает программируемый процессор.
Телевизионные игры уже выпускаются и продаются - причем миллионными тиражами!- в некоторых странах, в частности, в США, Франции, Венгрии. Стоимость? Она примерно в том же диапазоне, что и цены на транзисторные приемники разного класса. В нашем радиолюбительском журнале "Радио" периодически появляются описания телеигр, сконструированных любителями. Судя по всему, отечественная промышленность уже намечает выпуск этой веселой продукции, так что вскоре, видимо, каждый из нас сможет приобщиться к домашнему телевизионному спорту. И, хочется верить, не в ущерб настоящему теннису или волейболу, не в ущерб общению с природой и друг с другом. Натуральному общению, без участия электроники...
Рисунок из журнала "Крокодил" 36/77:

- С трудом, но все-таки удалось их вытащить на свежий воздух...
Рис. Г.Андрианова
***
Надо заметить, что кроме основного направления развития видеоигр - улучшения картинки, было и другое - создание стильных игрушек, умеющих взаимодействовать с телевизором ТЕМА #91, АБЗАЦ #2912
ТЕМА #91, АБЗАЦ #2912 .
.
Зачем нормальному человеку персональный компьютер? Как, по мере внедрения компьютеров упрощалась/усложнялась обработка персональной информации? Как обычные люди учились программировать?
Первые статьи о чем-то "персональном" появились в журнале еще в 70-е. Ходили вокруг больших ЭВМ и облизывались.
Данная статья шла как довесок к статье о пультах
 ТЕМА #34, АБЗАЦ #1233
ТЕМА #34, АБЗАЦ #1233 :
:НАУКА И ЖИЗНЬ 8/75
ИНЖЕНЕР Р.СВОРЕНЬ. РОСЧЕРКОМ ЭЛЕКТРОННОГО ПЕРА
Многие машины обучены общению с человеком, умеют сообщать ему о своем состоянии, о своей работе. Перегрелся автомобильный двигатель - и перед водителем загорается яркая предупреждающая лампочка; десятки приборов в кабине пилота рассказывают ему, как идет полет; и даже часы научены в заказанное время безжалостно сигналить: "Пора вставать".
Но, конечно же, самого высокого совершенства в общении с человеком достигли вычислительные машины. Выдавать информацию - это просто основа их профессии. На бесконечных бумажных рулонах печатают они результаты своих расчетов и "размышлений". А вот дисплей - устройство, в котором на экране электронно-лучевой трубки ЭВМ быстрым электронным пером отображает все, что она должна поведать человеку: записывает колонки цифр и букв, целые фразы, рисует векторы, графики, чертежи.
Прежде, чем рассказывать о самом дисплее, напомним, как работает электронно-лучевая трубка (1). Выброшенные из накаленного катода электроны фокусируются электрическими или магнитными полями в острый электронный луч, который, попав в флюоресцирующий экран, заставляет светиться ту или иную его точку (на рисунках она обозначена красным цветом, хотя обычно свечение экрана зеленоватое или голубоватое). В трубке есть две системы управления лучом: его интенсивностью, а значит, в итоге яркостью светящейся точки, и его перемещением в пространстве.

Яркость можно менять, изменяя напряжение на управляющем электроде. Он в принципе действует так же, как управляющая сетка в усилительной лампе: "плюс" на управляющем электроде ускоряет электроны, повышает яркость, "минус" тормозит электроны и даже может вообще оттолкнуть их назад, к катоду, то есть может полностью "запереть луч", погасить свечение экрана (2).
Перемещать луч в пространстве, двигать по экрану светящуюся точку можно с помощью электрических полей (их создают, подводя напряжение от блоков ВО и ГО К пластинам вертикального и горизонтального отклонения, или с помощью магнитных полей: они создаются отклоняющими катушками, которые прилегают к трубке снаружи). На рисунке 3 для наглядности показана трубка с электростатическим отклонением луча, хотя в дисплее, как правило, работают трубки с магнитным отклонением.
Если, меняя напряжение на отклоняющих пластинах, достаточно быстро двигать светящуюся точку по экрану, то можно создавать на нем светящиеся линии, рисовать "картинку", в частности цифры, буквы, векторы, геометрические фигуры. На рисунке 4 показано, как одновременным и согласованным изменением напряжений Uв и Uг, которые двигают луч "вверх - вниз" и "влево - вправо", можно нарисовать на экране несколько отрезков (а, б, в, г, д, е), составляющих букву Э.

Обратите внимание на то, что, когда луч должен двигаться по участку д (чтобы перейти от отрезка г к отрезку е), светящаяся линия на экране не появляется. В этот момент на управляющий электрод вместо "плюса" подается "минус" - электронный луч в экран не попадает.
Извлекая из памяти машины "тройки" электрических сигналов (для управления яркостью, вертикальным и горизонтальным отклонением), можно рисовать на экране практически любые знаки и фигуры.
Другой способ рисования (5) более удобен для цифровых вычислительных машин, где цифры и буквы "живут" в виде серий электрических импульсов. При этом способе рисования луч непрерывно и быстро прочерчивает весь экран - напряжение Uв смещает его сверху вниз, напряжение Uг двигает луч слева направо, и он прочерчивает невидимые горизонтальные строки. Невидимые потому, что из блока управления яркостью на управляющий электрод подается "минус" и луч до экрана не доходит. Лишь в некоторые моменты времени (строго синхронизированные с отклоняющими напряжениями) из ЭВМ поступают команды "открыть путь лучу" и на экране появляются горизонтальные линии, короткие или. длинные, в зависимости от длительности отпирающего импульса. На рисунке (5) показано, как серия таких импульсов (а, б1, б2, б3, б4) рисует на экране букву Т. При достаточно большом числе "строк" (например, в дисплее ЕС-1064 Единой системы ЭВМ, луч прочерчивает по экрану 1024 строки, в полтора раза больше, чем в телевизоре) можно рисовать вполне четкие символы и фигуры.
С помощью светового карандаша (СК) оператор может вносить поправки в рисунок на экране, может сам рисовать на нем и вводить таким образом в машину свои "изменения и дополнения". Строго говоря, световой карандаш сам ничего не рисует - он лишь заставляет электронный луч провести на экране новую линию или не рисовать старую.
В одной из систем (6) светового карандаша он содержит только один светоприемник. Точки, образующие крестообразную метку, зажигаются в центре экрана последовательно, поочередно - создает эти точки серия (1, 2, 3, 4, 5, 6) импульсов напряжения на управляющем электроде, синхронизированная с движением луча. Точно такая же серия импульсов появится в цепи светоприемника СК, если он приставлен к центру экрана. При смещении СК некоторые импульсы будут выпадать, и это послужит для ЭВМ сигналом: луч нужно двигать по экрану.

В другой системе (7) это делается так: луч ставит в самом центре экрана крестообразную светящуюся метку, на нашей схеме из пяти точек. В СК имеется пять точечных приемников света - это световоды, в конце которых закреплены фотодиоды, простейшие приборы, преобразующие свет в ток. СК начинает рисовать от центра экрана (как говорится, "от печки"), и в этом случае каждый фотодиод получает световой сигнал от "своей" светящейся точки - в машину идет сигнал: "СК находится в центре". Когда же оператор начнет двигать карандаш, то в цепи некоторых фотодиодов ток прекратится, и ЭВМ получит указание, куда нужно двигать луч (как всегда, с помощью блоков ВО и ГО), какую линию нужно рисовать или стирать (как всегда, "плюсом" или "минусом" на управляющем электроде). Метка движется по экрану вслед за карандашом.
Мы рассказали о дисплее коротко и, конечно, упрощенно. Создание дисплеев превратилось в самостоятельную область электронной техники, разработано и выпускается много разных и даже принципиально разных дисплеев, они непрерывно усложняются и совершенствуются, прочно удерживают позиции универсального средства отображения информации, удобного средства общения человека с машиной.
***
То же железо, но в профиль...
4/78

ДВА - НОЛЬ В ПОЛЬЗУ ТЕЛЕВИЗОРА
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Очень похоже, что телевизор - это размноженное миллионными тиражами чудо радиотехники и электроники, выигрывает еще один раунд в борьбе за наш досуг, освоив новый развлекательный жанр. Речь идет о домашних телевизионных играх, в которых экран телевизора, полностью отключившись от программ, прибывающих из эфира, становится ареной очень забавных состязаний - таких, например, как "теннис", "хоккей", "футбол". Играете вы в них со своим сидящим рядом партнером, и это развлечение чем-то напоминает настоящий теннис или настоящий хоккей. С той, конечно, разницей, что не нужно бегать и прыгать, ударять клюшкой или ракеткой, не нужно преодолевать усталость, утирать соленый пот с лица и в борьбе за победу выкладывать свои физические силы. Все атрибуты телевизионной игры - хоккейные ворота или теннисная сетка, мяч, шайба, клюшки, ракетки, границы поля - в виде некоторых условных фигурок и линий появляются на телевизионном экране, и, сражаясь с противником, вы ударяете "ракеткой" по "мячу", с легкостью двигая для этого рычажки или поворачивая ручки.
Мы отправляемся в гости и владельцу телевизионной игры и сами пробуем поработать ракеткой.
Чтобы читателю легче было представить себе, что такое домашние телевизионные игры, попробуем более или менее подробно описать одну из них - простейший теннис. (Мы, пожалуй, больше не будем употреблять кавычки, иначе они просто заполонят эти страницы; все называемые дальше спортивные игры и предметы спортивного инвентаря,- это не более чем условность).
Игра осуществляется с помощью небольшой, размером с книгу, приставки, от которой идет кусок кабеля со штекером на конце - этот штекер включается в антенное гнездо телевизора; сама телевизионная антенна при этом, конечно, вынимается из гнезда. На приставке несколько ручек управления, в том числе две ручки, поворотом которых игроки двигают по экрану свои ракетки.
Телевизор включен, нажата клавиша включения приставки, и на экране сразу же появляется большой, начерченный тонкими белыми линиями прямоугольник - это границы игровой площадки. В середине площадки проходит еще одна вертикальная светлая линия - это сетка. Справа, у самого края площадки, небольшой, длиной 3-4 сантиметра, вертикальный прямоугольник - это наша ракетка. А у левого края площадки такая же ракетка противника.

Вверху по обе стороны от сетки две цифры - это счет. Пока, конечно, счет 0:0, игра еще не начата.
Ну, что ж, начнем пожалуй... Нажимаем соответствующую клавишу приставки, и на экран выплывает яркая белая точка - мяч. Он быстро летит по прямой линии слева направо, перелетает сетку (точнее, проходит сквозь нее - все ведь происходит на плоскости) и движется уже по нашей половине поля куда-то вправо - вниз... Нам нужно быстрее повернуть ручку, переместить свою ракетку вниз, и отбить мяч (рисунок б)... Кажется, успели - мяч отбит и летит в сторону противника (рисунок в)... Теперь уже ему, противнику, нужно вовремя переместить ракетку в предполагаемую точку встречи с мячом... Но противник перестарался - он слишком высоко поднял ракетку, мяч проскочил мимо нее, ушел за пределы площадки (рисунок г), и индикатор счета сразу показал 1:0 в нашу пользу. Ура!
Мяч снова в игре, он влетает на площадку в направлении проигравшего... На этот раз противник успевает, отбивает мяч, и тот опять летит на нас, летит вправо вверх. Ситуация знакомая - быстро поднимаем ракетку (рисунок д)... Но что это? Мы, оказывается, просчитались - не учли, что мяч шел под очень большим углом и из-за этого ударился о верхнюю границу площадки... По правилам данной игры мяч отражается, отлетает от горизонтальных границ поля (обычно вертикальных границ вообще нет, и мяч может легко уйти, но только влево или вправо, а вверх или вниз не может), поэтому он прямо, под нашим носом резко поворачивает вниз, и мы уже не успеваем подставить ракетку (рисунок е)... Ничего не поделаешь - 1:1.
Вспоминая принципы телевидения, мы учимся рисовать на экране.
Современного человека окружает огромное множество самых разнообразных машин, приборов, аппаратов, и, конечно же, невозможно обо всех знать, как они устроены, как работают. Невозможно и не обязательно. Есть немало фотографов-любителей, которые делают прекрасные слайды, хотя и не знают, как образуется цветное изображение на обратимой пленке. И немало шоферов-любителей, которые прекрасно водят машину и при этом знать не хотят, что происходит, когда нога нажимает педаль сцепления. Ну, а без знания заэкранных секретов телевизионной игры наверняка можно прожить: чтобы точно двигать ракетку, совсем не обязательно понимать, как именно эта ракэтка нарисована на экране и как перемещается, как двигается мяч, ведется счет, зажигаются цифры.
И все же в расчете на пытливого читателя, на возможные вспышки любопытства мы уделим этим процессам немного внимания. Совсем немного. А попутно заметим: в телевизионных играх электроника использует свои классические методы и схемы, знакомство с ними может пригодиться при встрече с техникой, далекой от развлечений.
Начнем с описания двух простейших опытов. Один из них вы наверняка уже не раз наблюдали или даже непреднамеренно проделывали сами - если вблизи телевизора включить электробритву с моторчиком, например, "Харьков", то на экране замелькает множество черных и белых пятен и пятнышек. Второй опыт стоит проделать специально - он очень прост и совершенно безопасен. Вставьте в антенное гнездо телевизора кусок провода и набросьте его на включенный транзисторный приемник - на экране появятся замысловатые узоры, прямые и волнистые линии, темные и светлые пятна. Если поворачивать переключатель диапазонов или вращать ручку настройки приемника, то узоры эти придут в движение, а при некоторых положениях ручки настройки они остановятся и будут оставаться в сравнительно устойчивом состоянии.

Простой и безопасный опыт убеждает, что с помощью электрических сигналов можно создать на экране телевизора "синтетическую картинку".
Теперь вывод: посторонний электрический сигнал, попав в телевизор, может создавать на экране какие-то элементы картинки. Почему мелькает экран, когда рядом работает бритва? Потому, что искрит коллектор ее моторчика, в процессе искрения в цепи резко меняется ток, резкие электрические всплески тока каким-то образом проникают в телевизор - либо через сеть, либо прямо через антенну,- и именно они, эти незваные электрические сигналы, поочередно создают на экране бессчетные блики. Примерно то, же самое происходит и в опыте с приемником. Практически все современные приемники - это супергетеродины, у них внутри имеется собственный вспомогательный генератор - маломощный гетеродин. Если приблизить приемник к антенне телевизора, то в нее пролезет сигнал гетеродина слабый меняющийся ток. Подобно трамвайному "зайцу", он доберется до конечной станции, до управляющего электрода кинескопа, а всякий сигнал на управляющем электроде - это светлое или темное пятнышко на экране: именно на этом основано создание картинки при нормальной телепередаче.
Рисование на телевизионном экране с помощью синтетических сигналов известно давно. Вспоминается, как лет 10 назад инженер В.Крапивников опубликовал в журнале "Радио" описание приставки, которая, используя оригинальный способ электрического рисования на экране, превращала телевизор в осциллограф. В этой приставке, кстати, уже в готовом виде были схемные решения, которые сейчас встречаются во всех телевизионных играх. Другой пример. Телецентры в паузах передают в эфир неподвижные картинки, заставки, например, задернутый занавес. Иногда такой занавес передается традиционным способом (телекамера смотрит на настоящий занавес и посылает его изображение нам), а иногда - от специального "генератора занавеса". Он вырабатывает определенные серии электрических сигналов, которые через телепередатчик приходят в телевизор и рисуют на его экране. Никакого настоящего занавеса и в помине нет, мы видим "полотнище", созданное виртуозом-генератором. И, наконец, еще один представитель электронной живописи - дисплей, устройство, где на телевизионном экране с помощью серии электрических импульсов рисует и пишет компьютер, сообщая результаты своих размышлений.
От проделанных простейших опытов до принципов рисования в телевизионной игре остается буквально несколько шагов. Прежде всего попробуем понять, чем определяется место появления светлых или темных точек на экране. Электронный луч кинескопа быстро прочерчивает экран горизонтальными строками и, медленно смещаясь вниз, заполняет в итоге весь кадр. Движением луча управляют два пилообразных напряжения - строчное и кадровое. Они меняются равномерно, линейно и постепенно подтягивают рисующий луч к своим отклоняющим пластинам (катушкам). Потом пила обрывается, и луч возвращается в исходное состояние. А еще есть в кинескопе управляющий электрод, он управляет интенсивностью электронного луча, то есть яркостью экрана. Если на управляющий электрод на мгновение подать "минус", то есть подать импульс отрицательного напряжения, то оно как бы оттолкнет электроны, ослабит луч, и на экране появится темная точка. Кратковременный "плюс", наоборот, ускорит электроны, электронный луч станет интенсивнее, и появится светлая точка. В каком месте экрана вспыхнет точка? Это зависит от того, в какой момент появится импульс. Если выпустить его на арену в начале кадровой пилы, то мы увидим точку вверху, а если в конце пилы - внизу; если импульс появится в начале строчной пилы, точка будет слева, если в конце строчной пилы - справа.

Электрические импульсы могут создавать на экране темные или светлые точки. Местоположение точки зависит от того, в какой момент появился импульс.
Следующий шаг - посмотрим, как можно поставить точку в нужном нам месте. Предположим, что у нас есть генератор импульсов, которым на равных управляют сразу два руководителя, противодействующих друг другу (в электронных схемах это осуществляется очень просто и протекает без эксцессов). Один из них - пилообразное напряжение строчной развертки, второй - постоянное напряжение, которое можно менять поворотом ручки переменного резистора (реостата). Схема построена так, что импульс появляется в момент, когда оба "руководителя" дают одинаковые указания - когда меняющееся напряжение строчной пилы становится равным установленному нами поворотом ручки постоянному напряжению. При этом, конечно, чем более высокий порог постоянного напряжения мы установим, тем позже пила достигнет этого порога, тем позже появится импульс и тем правее окажется на экране точка. Работу этой схемы можно проиллюстрировать такой аналогией. На одной чаше весов стоит гирька, на второй - стакан, который медленно наполняется водой. Наступит момент, когда вес воды превысит вес гирьки и весы "сработают". И, конечно, чем больше вес гирьки, тем позже произойдет такое срабатывание.
Пилообразное напряжение, которое помогает в нужный .момент выдать импульс (подобно тому, как будильник "выдает" звонок), может быть взято прямо от генераторов развертки или же должно быть жестко с ними синхронизировано - только в этих случаях точка на экране не будет дергаться. Чтобы точно разместить точку в любом месте экрана, обычно создают два импульса - один от строчной пилы, другой - от кадровой. Импульсы эти пропускают через схему совпадении (схема "И"), и точка появляется как бы на пересечении двух линий - вертикальной и горизонтальной. Ракетки в нашем теннисе двигаются только вверх-вниз, и поэтому к строчной пиле они намертво привязаны в одном месте. Чтобы управлять ракетками, достаточно менять время их появления, отсчитанное по кадровой пиле, то есть одним переменным резистором менять только одно постоянное напряжение. Намного сложнее управлять полетом мяча,- как правило, его нужно перемещать и вверх-вниз и влево-вправо. И при этом следить, чтобы, попав в точку, соприкасающуюся с ракеткой, мяч не пошел дальше. Чтобы он отскочил от ракетки. И притом под определенным углом. И чтобы он отскакивал также от горизонтальных границ площадки. И не отскакивал от вертикальных границ. Чтобы он проходил через них за пределы площадки. А потом возвращался. И опять под определенным углом...

Одна из возможных систем перемещения точки: ее место на экране определится моментом появления импульса на выходе генератора; момент появления импульса, в свою очередь, зависит от того, когда пилообразное напряжение (отпирающее) сравняется с постоянным напряжением (запирающим), которое мы устанавливаем переменным резистором.
Ну и задачки... Кто может их решить? И каким образом?
Но позвольте - кто вообще двигает мяч по площадке? Ведь сами игроки управляют только ракетками...
Взглянув на схему телеигры, можно обнаружить ее сходство с компьютером.
Движение мяча, все его отскоки, исчезновения, появления, как и множество других важных дел, осуществляет самый главный блок телевизионной игры - вычисляющее устройство. Его работу в предельно упрощенном виде можно описать так. В этом блоке все начинается с дирижера. Это вспомогательный тактовый генератор, он выдает бесконечные пулеметные очереди импульсов высокой частоты - обычно миллион импульсов в секунду. Если бы все они попали на управляющий электрод кинескопа, то на экране появился бы монотонный "горошек" - тысячи точек, расположенных ровными рядами. (При существующем стандарте - 625 строк - на экране в принципе можно поставить около 50000 точек, но в простейшей телевизионной игре такая детализация картинки не нужна). На пути к кинескопу тактовые импульсы проходят через основные элементы вычисляющего устройства - счетчики импульсов, собранные из цепочек триггеров, и логические элементы, умеющие рассуждать таким примерно образом: "Если ко мне на вход придут одновременно 573-й и 826-й импульсы,- зажгу точку..." Или: "Если 128-й импульс появится вместе с 2593-м,- не зажгу точку..." Счетчики и логические элементы соединены между собой строго определенным образом, они точно работают по заданной программе. В итоге из ровного частокола импульсов остаются только те, которые в соответствии с правилами игры; и игровой обстановкой в нужном месте экрана высвечивают мячик. А в следующий момент, с учетом того, какие точки светились раньше, мячик передвигается в следующую точку траектории. Вычисляющее устройство, сформировав необходимые наборы импульсов, рисует границы площадки, ведет счет.
Все это, конечно, лишь просто сказывается: чтобы вести даже простейшую игру, нужны вычисляющие устройства с сотнями схемных узлов, состоящие из тысяч элементов - конденсаторов, транзисторов, резисторов, диодов. Если бы такой вычисляющий блок создавался лет двадцать назад и собирался из отдельных деталей, то он наверняка занял бы большой шкаф. Только интегральные схемы (см. "Наука и жизнь" 10/76 чуть далее) сделали телевизионную игру реальностью - все ее управляющее устройство вмещается сейчас в кремниевой пластинке размером с клеточку арифметической тетради.

Блок-схема типичной телевизионной игры.
Просматривая технические журналы, мы узнаем, что телеигры осваивают массу новых профессий, что им предсказывают блестящее будущее.
Вычисляющее устройство телевизионной игры - это самый настоящий компьютер, хотя его и не принято так называть. Не принято скорее всего потому, что уже родилось новое поколение игр, в которых имеется программируемый процессор - главный вычисляющий блок ЭВМ. Процессор позволяет резко расширить ассортимент развлечений, усложнить условия игры и даже выполнять некоторые полезные работы. Так, в одной из моделей процессор дает возможность рисовать на экране цветными "карандашами" и даже сам рисует орнаменты и несложные мультипликации. В другой модели процессор вычисляет и записывает на экране оптимальную диету с учетом вашего веса - желаемого и реального. Программа вводится в игру (теперь ее уже и не очень удобно так называть) с магнитной пленки, со стандартной магнитофонной кассеты. Причем программ может быть огромное множество - как говорят, все зависит от фантазии разработчика. На смену простейшему теннису уже приходят автомобильные гонки, танковые и морские сражения. В волейболе мяч летит по сложной кривой и, подобно настоящему мячу, меняет скорость в процессе полета; появляется возможность давать противнику фору, уменьшая, например, размеры своей ракетки. Правда, и простейший теннис можно несколько разнообразить - уменьшать обе ракетки, увеличивать скорость мяча, менять угол его отражения, но это, конечно, и в сравнение не идет с возможностями, которые открывает программируемый процессор.
Телевизионные игры уже выпускаются и продаются - причем миллионными тиражами!- в некоторых странах, в частности, в США, Франции, Венгрии. Стоимость? Она примерно в том же диапазоне, что и цены на транзисторные приемники разного класса. В нашем радиолюбительском журнале "Радио" периодически появляются описания телеигр, сконструированных любителями. Судя по всему, отечественная промышленность уже намечает выпуск этой веселой продукции, так что вскоре, видимо, каждый из нас сможет приобщиться к домашнему телевизионному спорту. И, хочется верить, не в ущерб настоящему теннису или волейболу, не в ущерб общению с природой и друг с другом. Натуральному общению, без участия электроники...
Рисунок из журнала "Крокодил" 36/77:

- С трудом, но все-таки удалось их вытащить на свежий воздух...
Рис. Г.Андрианова
***
Надо заметить, что кроме основного направления развития видеоигр - улучшения картинки, было и другое - создание стильных игрушек, умеющих взаимодействовать с телевизором
 ТЕМА #91, АБЗАЦ #2912
ТЕМА #91, АБЗАЦ #2912 .
.Последний раз редактировалось: Gudleifr (Ср Дек 07, 2022 3:06 pm), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Появились калькуляторы...
10/76
ФАНТАСТИЧЕСКАЯ ЭЛЕКТРОНИКА
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Есть немало творений техники, которым выпала счастливая судьба непосредственно служить миллионам людей. Почти всегда они входят в нашу жизнь робко, но потом становятся не просто привычными - становятся необходимыми, и уже непонятно, как это раньше можно было без них.
Прыгающие кадры старинной кинохроники напоминают о первых самолетах - неуклюжих этажерках из ткани и дерева. В начале века полет на аэроплане был героическим событием, собирал огромные толпы зрителей. Сейчас только Аэрофлот перевозит 100 миллионов пассажиров ежегодно, и многие люди просто не представляют себе, как они будут добираться в Хабаровск или даже в Сочи поездом. Другой пример - телевидение. Вспоминается, как лет тридцать назад в витринах ленинградских магазинов стояли первые наши телевизоры и их цена была ниже себестоимости - нужно было помочь покупателям сделать трудный шаг в неизвестное. Но вскоре уже приходилось месяцами ждать очереди, чтобы купить телевизор, а сейчас в стране 60 миллионов телевизоров, они есть практически в каждой семье.
Сегодня в списке техники для миллионов - "... телефон, автомобили, часы, радио, книгопечатание, фотоаппараты и кинокамеры, электрическое освещение..." - появилась еще одна строка - "... электронная вычислительная техника...". Нет, нет, это не большие ЭВМ для научных исследований и управления производством, а малые, карманные вычислительные устройства, те, что принято называть микрокалькуляторами. Для первого знакомства с ними мы отправляемся в магазин #61 Москультторга (Москва, ул.Пушкина, дом 23/ , где в широкой продаже модели отечественных микрокалькуляторов. На правах покупателей заглядываем в инструкции по пользованию ими, где, как обычно, суховато, однако же достаточно подробно рассказывается о самих моделях, их возможностях и некоторых технических характеристиках, приводятся многочисленные примеры решения тех или иных видов вычислительных задач.
, где в широкой продаже модели отечественных микрокалькуляторов. На правах покупателей заглядываем в инструкции по пользованию ими, где, как обычно, суховато, однако же достаточно подробно рассказывается о самих моделях, их возможностях и некоторых технических характеристиках, приводятся многочисленные примеры решения тех или иных видов вычислительных задач.

Микрокалькулятор "Электроника Б3-18". Относится к так называемым инженерным вычислительным устройствам. Машина выполняет четыре действия арифметики над восьмиразрядными числами, то есть на ее цифровом табло может появляться восьмиразрядный результат - число до 100 миллионов (точнее, до 99999999). Операции с десятичными дробями ведутся с так называемой плавающей запятой: при вводе десятичной дроби вы ставите в нужном месте запятую, а затем калькулятор уже сам следит за ее положением, располагает запятую в нужном месте.
Сам ввод информации в калькулятор предельно прост. На передней панели имеются небольшие кнопки с цифрами от 0 до 9 и знаками арифметических действий. Последовательно нажимая на них, вы даете указание, с какими числами какое действие нужно произвести, и затем, нажав кнопку со знаком "=", практически мгновенно получаете результат.
Но этот калькулятор перешел Рубикон арифметики, его математическое образование шагнуло в тригонометрию и алгебру. "Электроника Б3-18" умеет мгновенно возводить в квадрат и извлекать квадратный корень, в два приема возводить в любую степень в пределах восьми разрядов, вычислять обратные величины, вычислять логарифмы и антилогарифмы (десятичные и натуральные), тригонометрические функции. Все это не обращение к памяти, не воспроизведение справочных данных. Так, например, для вычисления синуса калькулятор сам по своей внутренней программе производит десятки арифметических операций, пользуясь известным разложением в ряд Тейлора.
Косвенный показатель того, что некоторые задачи, решаемые инженерным калькулятором, довольно сложны,- это время, которое он затрачивает на вычисления. Так, например, если на сложение или вычитание двух восьмиразрядных чисел уходит около 50 миллисекунд (0.05 секунды), то на их умножение или деление затрачивается уже около 300 миллисекунд, на возведение в степень с высоким показателем - 1 секунда, а на вычисление арктангенса - 3 секунды. Когда видишь, как машина, которая только что мгновенно складывала огромные числа, тратит несколько секунд, чтобы выполнить какую-либо алгебраическую или тригонометрическую операцию, невольно задумываешься о той большой работе, которая идет внутри маленькой коробочки, прежде чем на ее индикаторе засветится результат.
Но об этом чуть позже. А пока отметим, что на индикаторе "Электроники Б3-18" светятся яркие зеленоватые цифры. Этот индикатор - некоторое подобие телевизионной трубки, изображение на нем создают электроны, бомбардирующие люминесцентный экран.
При продолжительной работе с микрокалькулятором пользуются небольшим, размером со спичечную коробку, внешним выпрямителем, который, кстати, подзаряжает внутренние аккумуляторы.
В памяти калькулятора помещается число "пи", и достаточно нажатия одной кнопки, чтобы ввести это число в какое-либо вычисление, скажем, умножить на "пи" или разделить. В памяти хранятся и два других восьмиразрядных числа, причем одно из них можно хранить как угодно долго, извлекая его в нужный момент.
Инженерные микрокалькуляторы прошли отличную школу математического сервиса, они используют любую возможность, чтобы предоставить своему владельцу дополнительные удобства. Так, например, в "Электронике Б3-18" при вычислении тригонометрических функций можно задавать угол в градусах или в радианах, как удобнее - для перехода от одной угловой меры к другой нужно лишь передвинуть небольшой переключатель; при извлечении какого-либо числа из памяти там остается копия этого числа на случай, если оно понадобится еще раз; в случае надобности можно мгновенно извлечь из памяти так называемый предыдущий оперант,- например, результат предыдущего вычисления, а затем вернуть его на место,- выполняя серию операций с постоянным коэффициентом, совсем не нужно каждый раз вводить его значение, повторение этого коэффициента может происходить автоматически; в случае, если калькулятор не может произвести действие над введенными числами, на индикаторе зажигается особый предупреждающий сигнал "переполнение"; калькулятор может суммировать результат нескольких вычислений, производить накопление произведений и частных; может по довольно простой процедуре вычислять средние значения нескольких величин, дисперсию, среднеквадратичное отклонение и погрешность среднеквадратичного отклонения; умеет находить гиперболические функции; вычислять сложные проценты; преобразовывать прямоугольные координаты в полярные...
Математические способности инженерного микрокалькулятора в какой-то мере отражают удивительные достижения современной "большой" вычислительной техники. Пока на страницах некоторых изданий шли утомительные дискуссии о том, может ли машина мыслить, инженеры и математики работали, создавали конкретные электронные системы, умеющие решать сложные логические и математические задачи. Торжественным словом "мыслить" нельзя, конечно, разбрасываться направо и налево, но то, что уже сегодня научились делать ЭВМ, бесспорно, раньше было монополией Человека Думающего.
Все, что делает ЭВМ, она делает, оперируя электрическими сигналами, оперируя сложными комбинациями импульсов тока, которые напоминают телеграфные точки и тире. В виде комбинаций электрических импульсов живут в машине цифры, команды, правила работы. Комбинации электрических импульсов рождаются, когда вы нажимаете кнопки ввода данных; комбинации электрических импульсов управляют работой индикатора вывода данных, зажигая на нем зеленые палочки-сегменты, из которых составляются нужные цифры. А между этими двумя событиями - вводом и выводом - стоят электронные схемы, которые производят с электрическими сигналами разные операции - складывают их и разделяют, пересылают из одного электронного блока в другой, сопоставляют с сигналами, записанными в память. И в этих действиях рождаются новые электрические сигналы, рождаются результаты вычислений, подобно тому, как они появляются при перебрасывании косточек на счетах. Хотя, конечно, электронные вычислительные машины, даже самые простые, настолько сложны и совершенны, что их сравнение со счетами требует не просто оговорок, но и извинений.
Упрощенная блок-схема "Электроники Б3-18" показана на первой странице цветной вкладки (рисунок вверху справа). Детальное знакомство с устройством отдельных узлов этой схемы - дело сложное и здесь вряд ли уместное. Можно лишь попытаться несколькими штрихами обрисовать блок-схему калькулятора с тем, чтобы получить самое общее представление о назначении его узлов и их взаимодействии.
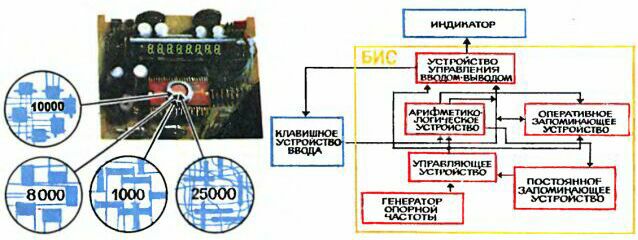
Каждая цифра восьмиразрядного числа и каждый символ команды представлены в калькуляторе комбинацией из четырех электрических импульсов или пауз. Скажем, комбинация "импульс - пауза - пауза - импульс" соответствует девятке, а комбинация "импульс - импульс - пауза - импульс" - тройке. Генератор опорной частоты ГОЧ дает непрерывную очередь импульсов, некоторые из них затем гасятся, и таким образом формируются нужные комбинации из импульсов и пауз. Формируются они прежде всего при нажатии тех или иных кнопок ввода - блок управления вводом-выводом УУВВ регулярно опрашивает кнопки, следит за тем, какая из них нажата.
Все введенные числа первым делом попадают в оперативную память, в ОЗУ (оперативное запоминающее устройство - тоже электронные схемы, их элементы могут находиться в одном из двух состояний - пропускать ток или не пропускать; это как раз и соответствует двум знакам машинного языка - импульсу и паузе), а оттуда на индикатор - так осуществляется контроль за правильностью ввода. Указание о нужной операции, которое также вводится нажатием кнопки, в итоге попадает в постоянную память - в ПЗУ, где определенными электрическими соединениями навеки записано, что нужно делать для выполнения той или иной операции. Это "что делать" из ПЗУ в виде длинной серии сигналов, длинной телеграммы, поступает в устройство управления УУ, где формируется руководящее указание "как делать". Например, такое: "Прочитать в первом секторе ОЗУ число; саму запись числа стереть; прибавить к нему число, записанное во втором секторе ОЗУ, саму запись числа оставить; результат сложения записать в освободившийся сектор ОЗУ; результат передать также на индикатор..." Такая телеграмма попадает в арифметико-логическое устройство АЛУ, где уже и реализуется "указание руководства", производятся необходимые операции с электрическими сигналами, то есть необходимые вычисления.
Наше ультракороткое описание блок-схемы калькулятора не должно создавать иллюзию ее простоты. Вот несколько цифр, которые в какой-то степени отражают сложность событий, происходящих в схеме: программы, записанные в ПЗУ, состоят из 1152 "слов" по 8 "букв", а каждая "буква" кодируется комбинацией из четырех импульсов-пауз; блок УУ может разослать другим блокам до 105 разных команд; при выполнении даже такой простой операции, как умножение двух восьмиразрядных чисел, отдельные блоки калькулятора обмениваются "телеграммами" в общей сложности из 10000 "слов".
А вот другие цифры: электронная схема калькулятора "Электроника Б3-18" содержит примерно 10 тысяч транзисторов, 8 тысяч резисторов, 1 тысячу конденсаторов и 25 тысяч соединительных проводников. Для сравнения заметим, что в транзисторном приемнике около 100 элементов, в телевизоре - около тысячи.
Как же разместилось такое огромное число компонентов - около 45 тысяч - в маленьком, размером чуть больше пачки сигарет, корпусе? Как удается упрятать в него сотни приемников или десятки телевизоров?
Ответ на эти вопросы в коротком слове "БИС" - так сокращенно называют большие интегральные схемы, это совершенно уже фантастическое творение современной электроники. Несколько лет назад автору этих строк случайно пришлось быть свидетелем того, как два бывалых радиоинженера из тех, которых объемным телевидением, наверное, не удивишь, впервые рассматривали большую интегральную схему и повторяли при этом одно слово: "Фантастика... Фантастика!.." Это слово, наверное, лучше всего выразит и наши чувства, когда, заглянув внутрь микрокалькулятора "Электроника Б3-18", вы увидите там лишь несколько детален. И узнаете, что все остальное, все эти "около 45000" транзисторов, резисторов, конденсаторов, проводников, разместились на тоненькой кремниевой пластинке размером 5*5.2мм. Вдумайтесь - полсотни телевизоров в одной клеточке арифметической тетради. Фантастика!
Прежде чем говорить о БИСах, несколько слов просто об интегральных схемах и даже, пожалуй, вообще о том, что есть схема в понимании специалистов по радиоэлектронике. Схема - это мир, где живут электрические сигналы, электрическая цепь, где они рождаются и умирают, усиливаются или ослабляются, суммируются или разделяются, словом, проходят самые различные виды обработки. Делают все это элементы схемы и их комплексы: транзисторы усиливают сигнал, резисторы ослабляют или выделяют, конденсатор реагирует на скорость изменения сигнала, двухтранзисторный комплекс - триггер - делит число сигналов на два. Несмотря на чрезвычайную сложность и огромное разнообразие, многие из схем, и прежде всего схемы вычислительных устройств, собираются всего из нескольких типов элементов. Скажем, из десятка типов транзисторов, двух-трех десятков типов конденсаторов и резисторов, двух-трех типов диодов. Это первая реальность, сделавшая возможным создание интегральных схем.
А вот и вторая.
Совершенно недвусмысленное, казалось бы, выражение "... изготовить электронный прибор..." с некоторого времени приобрело два совершенно разных значения. Еще недавно оно означало, что изготавливаются какие-то детали, скажем, детали электронной лампы - металлические цилиндры, спирали, сетки, трубки, стеклянный баллон, цоколь,- и затем эти детали собирают, соединяют, превращают в единое целое. Но вот лет тридцать назад физика твердого тела, академическая в общем-то наука, на основе глубокого исследования физических процессов в полупроводниках предложила практике новый вид усилительного электронного прибора - транзистор, аналог трех-электродной усилительной лампы. (Справедливость требует, чтобы, задумываясь об истории создания транзистора, мы первым вспоминали нижегородского радиоинженера Олега Лосева, который еще в 1926 году, примерно за 20 лет до появления транзисторов, построил первый полупроводниковый усилительный прибор - кристадин; один из американских радиотехнических журналов писал о работе Олега Лосева: "... генерирующий кристалл, как его назвал Лосев, призван совершать все то, что в настоящее время совершается катодной лампочкой"; к сожалению, работы О.Лосева не получили развития, физика еще не была готова к тому, чтобы понять процессы в полупроводниковом усилителе).
С точки зрения конструктора, транзистор - это только одна деталь - полупроводниковый кристалл. И лишь технолог знает, что в этом одном кристалле фактически есть три разные части: эмиттер, база и коллектор, или - в так называемых полевых транзисторах - исток, затвор и сток. Части эти могут создаваться разными способами, которые, однако, дают один и тот же результат - в полупроводниковый кристалл вводятся примеси, и в нем появляются отдельные участки с различными электрическими свойствами. Например, появляются зоны с разной концентрацией свободных электрических зарядов - отрицательных (это зоны n, от слова "negativus" - отрицательный) и положительных (это зоны p, от слова "positivns" - положительный). Вот такие зоны фактически представляют собой детали полупроводникового прибора, детали, созданные в целом, в одном кристалле, без его разрушения, без разделения на части.
Виртуозная технология, которой постепенно вооружалась электронная промышленность, сегодня позволяет формировать в кристалле почти все виды элементов электронных схем - диоды, транзисторы, проводники, конденсаторы (две примыкающие друг к другу зоны n и p, если подать на них определенное напряжение, становятся обкладками конденсатора), резисторы (точно дозируя количество примесей и размеры той области, куда они вводятся, можно создавать резисторы с самым разным сопротивлением). Вот это есть та вторая реальность, на основе которой выросла интегральная электроника.
Теперь о третьей, о тех причинах, которые заставили переходить к интегральным схемам, вдохновили науку и промышленность на решение этой чрезвычайно сложной задачи. Таких причин немало, но большинство из них связано с тем, что в радиоэлектронике часто называют "тиранией количеств". В двадцатые годы, когда детекторный приемник считался шедевром радиотехники, наиболее сложные электронные схемы состояли из десятков, максимум сотен элементов. Но постепенно радиоэлектронная аппаратура усложнялась и число элементов в одном аппарате резко увеличивалось - в среднем в 10 раз каждые 10 лет. Особенно быстро стало расти число элементов с появлением вычислительных машин, и сегодня схемы больших ЭВМ содержат многие миллионы элементов.
Увеличение числа элементов, если все они представлены в электронном приборе отдельными деталями, влечет за собой немало трагических последствий. Из-за ненадежности межэлементных соединений резко падает надежность всего прибора. Растет вес,- оказывается, например, что грузоподъемности самолета просто не хватает, чтобы поднять все необходимое ему современное электронное оборудование. Растут размеры и потребляемая мощность, страшно усложняется конструкция аппаратуры. Одним словом, если, опустив подробности, посмотреть на конечный результат, то окажется, что "тирания количеств" - это непреодолимое препятствие на пути прогресса радиоэлектроники, а вместе с ней и на пути прогресса многих областей современной техники.
Преодолеть это препятствие или по крайней мере заметно его отодвинуть позволили интегральные схемы.
Интегральная схема, как говорит само название,- это многоэлементный электронный блок, выполненный в виде единого целого. В частности, в виде полупроводникового кристалла, где последовательными технологическими операциями созданы и соединены друг с другом различные элементы схемы.
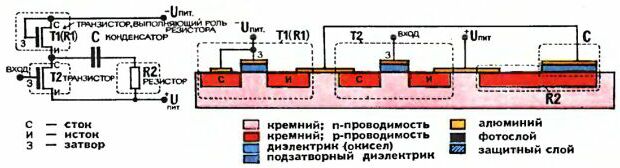
На рисунке очень упрощенно показана часть такой схемы. В нее входят транзистор Т1, два разных резистора R1 и R2, конденсатор С1 и несколько соединений, изображенных схематически. Перечислены основные этапы изготовления условной интегральной схемы; некоторые из этих этапов иллюстрируются упрощенными рисунками. После разработки самой электрической схемы следует создание топологии, то есть определение всех конфигураций и взаимного расположения тех зон кристалла, из которых будут образованы детали схемы, а также конфигурации соединительных целей. Работа эта весьма сложна, и ведется она с помощью ЭВМ, демонстрируя честному народу, как машина делает машину. Без ЭВМ не обходится и следующий этап - создание фотошаблонов, с помощью которых разработанная топология воплощается в кристалле. Воплощение это в общих чертах происходит так: на кристалл наносят светочувствительный слой, так называемый фоторезист, затем его засвечивают через фотошаблон, проявляют, удаляют засвеченные участки и в образовавшиеся окна либо вводят нужные примеси, либо убирают в глубине этих окон какой-нибудь ненужный слой и в нем вскрывают окна, либо, наконец, убирают участки алюминиевого покрытия, формируя таким образом соединительные цепи сложной конфигурации.
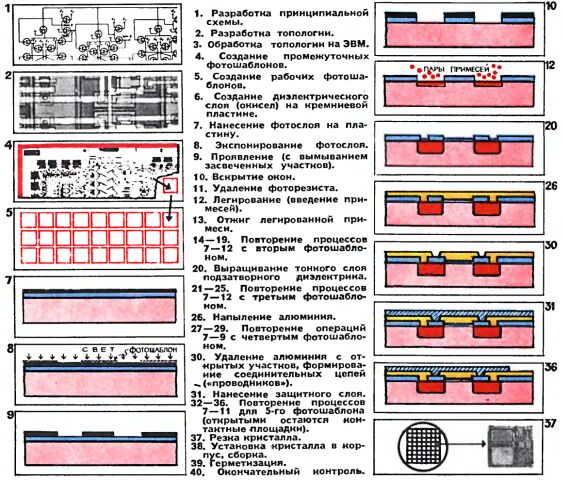
Вот и опять слишком короткое описание создает, по-видимому, иллюзию этакой простоты или, может быть, даже примитивности технологического процесса. Но это, конечно, не более чем иллюзия. В подтверждение - несколько цифр и фактов.
Если в первых интегральных схемах о одном кристалле создавали всего несколько элементов, то теперь степень интеграции резко возросла, создаются схемы, которые содержат тысячи и десятки тысяч элементов. Это и есть БИСы, большие интегральные схемы, в которых на один квадратный миллиметр поверхности (это поверхность булавочной головки) может приходиться более тысячи элементов. Размеры отдельного элемента при этом измеряются тысячными долями миллиметра, их, естественно, можно увидеть только в хороший микроскоп. Допустимые погрешности при создании определенных зон в кристалле - это вообще ангстремы, единицы измерения, до недавнего времени незнакомые технике. А количество вводимых примесей в этих процессах дозируется с точностью до миллиардных долей процента, здесь уже счет идет на атомы. С точностью до сотых долей процента поддерживаются тепловые режимы, малейшая ошибка здесь чревата серьезными последствиями. Потому что интегральные схемы не делают по одной, на кремниевой пластине их может разместиться несколько десятков. По окончании технологического цикла для каждой схемы производятся сотни контрольных замеров. Приведем еще одну цифру: на производственных участках фотолитографии допускается содержание в одном кубическом метре воздуха не более чем 3-4 пылинки диаметром до 0.5мкм.
Достоинства интегральных схем не требуют, по-видимому, пояснений: это высокая надежность, малые габариты и вес, малая потребляемая мощность. И еще одно парадоксальное на первый взгляд достоинство интегральных схем: эти уникальные по своей сложности и, по сути, невидимые изделия, сама их технология как будто бы специально созданы для автоматизированного производства.
В нашей стране серийно выпускается широкий ассортимент интегральных схем, в том числе БИСы. Все большими тиражами выпускаются и созданные на их основе микрокалькуляторы. Немного, наверное, пройдет времени, и миллионы этих электронных помощников инженера, исследователя, экономиста выйдут на скромную свою трудовую вахту, незаметно привнося в наши дела и планы точность, четкость, порядок, эффективность. Мы привыкнем к ним, забудем, что когда-то исписывали вычислениями листы бумаги, теряли миллионы из-за какой-то арифметической ошибки или из-за того, что прикидывали на глазок там, где надо считать точно...
Мы привыкнем к своим карманным компьютерам, как привыкли к телефону, к часам на руке, к яркому электрическому свету в квартире. Привыкнем и перестанем замечать... И это, если по-честному, будет несправедливо. Любуясь красками на экране цветного телевизора, или за час покрывая тысячу километров на десятикилометровой высоте, или нажимая клавиши электронного микрокалькулятора, мы должны хотя бы изредка вспомнить, какая изумительная техника и какой большой труд стоят за всем этим. И должны мысленно гордиться: "Велик человек!"
***
Шикарная строчка: "Пока на страницах некоторых изданий шли утомительные дискуссии о том, может ли машина мыслить, инженеры и математики работали, создавали конкретные электронные системы, умеющие решать сложные логические и математические задачи". Но мы же видели в "Тайной библиотеке", что без "дискуссий о мыслящей машине" не было бы и "конкретных электронных схем". Калькулятор - лишь перевод "в железо" малой части формул фундаментальной кибернетической науки. Технология - как полезные отходы чистой науки.
10/76
ФАНТАСТИЧЕСКАЯ ЭЛЕКТРОНИКА
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Есть немало творений техники, которым выпала счастливая судьба непосредственно служить миллионам людей. Почти всегда они входят в нашу жизнь робко, но потом становятся не просто привычными - становятся необходимыми, и уже непонятно, как это раньше можно было без них.
Прыгающие кадры старинной кинохроники напоминают о первых самолетах - неуклюжих этажерках из ткани и дерева. В начале века полет на аэроплане был героическим событием, собирал огромные толпы зрителей. Сейчас только Аэрофлот перевозит 100 миллионов пассажиров ежегодно, и многие люди просто не представляют себе, как они будут добираться в Хабаровск или даже в Сочи поездом. Другой пример - телевидение. Вспоминается, как лет тридцать назад в витринах ленинградских магазинов стояли первые наши телевизоры и их цена была ниже себестоимости - нужно было помочь покупателям сделать трудный шаг в неизвестное. Но вскоре уже приходилось месяцами ждать очереди, чтобы купить телевизор, а сейчас в стране 60 миллионов телевизоров, они есть практически в каждой семье.
Сегодня в списке техники для миллионов - "... телефон, автомобили, часы, радио, книгопечатание, фотоаппараты и кинокамеры, электрическое освещение..." - появилась еще одна строка - "... электронная вычислительная техника...". Нет, нет, это не большие ЭВМ для научных исследований и управления производством, а малые, карманные вычислительные устройства, те, что принято называть микрокалькуляторами. Для первого знакомства с ними мы отправляемся в магазин #61 Москультторга (Москва, ул.Пушкина, дом 23/

Микрокалькулятор "Электроника Б3-18". Относится к так называемым инженерным вычислительным устройствам. Машина выполняет четыре действия арифметики над восьмиразрядными числами, то есть на ее цифровом табло может появляться восьмиразрядный результат - число до 100 миллионов (точнее, до 99999999). Операции с десятичными дробями ведутся с так называемой плавающей запятой: при вводе десятичной дроби вы ставите в нужном месте запятую, а затем калькулятор уже сам следит за ее положением, располагает запятую в нужном месте.
Сам ввод информации в калькулятор предельно прост. На передней панели имеются небольшие кнопки с цифрами от 0 до 9 и знаками арифметических действий. Последовательно нажимая на них, вы даете указание, с какими числами какое действие нужно произвести, и затем, нажав кнопку со знаком "=", практически мгновенно получаете результат.
Но этот калькулятор перешел Рубикон арифметики, его математическое образование шагнуло в тригонометрию и алгебру. "Электроника Б3-18" умеет мгновенно возводить в квадрат и извлекать квадратный корень, в два приема возводить в любую степень в пределах восьми разрядов, вычислять обратные величины, вычислять логарифмы и антилогарифмы (десятичные и натуральные), тригонометрические функции. Все это не обращение к памяти, не воспроизведение справочных данных. Так, например, для вычисления синуса калькулятор сам по своей внутренней программе производит десятки арифметических операций, пользуясь известным разложением в ряд Тейлора.
Косвенный показатель того, что некоторые задачи, решаемые инженерным калькулятором, довольно сложны,- это время, которое он затрачивает на вычисления. Так, например, если на сложение или вычитание двух восьмиразрядных чисел уходит около 50 миллисекунд (0.05 секунды), то на их умножение или деление затрачивается уже около 300 миллисекунд, на возведение в степень с высоким показателем - 1 секунда, а на вычисление арктангенса - 3 секунды. Когда видишь, как машина, которая только что мгновенно складывала огромные числа, тратит несколько секунд, чтобы выполнить какую-либо алгебраическую или тригонометрическую операцию, невольно задумываешься о той большой работе, которая идет внутри маленькой коробочки, прежде чем на ее индикаторе засветится результат.
Но об этом чуть позже. А пока отметим, что на индикаторе "Электроники Б3-18" светятся яркие зеленоватые цифры. Этот индикатор - некоторое подобие телевизионной трубки, изображение на нем создают электроны, бомбардирующие люминесцентный экран.
При продолжительной работе с микрокалькулятором пользуются небольшим, размером со спичечную коробку, внешним выпрямителем, который, кстати, подзаряжает внутренние аккумуляторы.
В памяти калькулятора помещается число "пи", и достаточно нажатия одной кнопки, чтобы ввести это число в какое-либо вычисление, скажем, умножить на "пи" или разделить. В памяти хранятся и два других восьмиразрядных числа, причем одно из них можно хранить как угодно долго, извлекая его в нужный момент.
Инженерные микрокалькуляторы прошли отличную школу математического сервиса, они используют любую возможность, чтобы предоставить своему владельцу дополнительные удобства. Так, например, в "Электронике Б3-18" при вычислении тригонометрических функций можно задавать угол в градусах или в радианах, как удобнее - для перехода от одной угловой меры к другой нужно лишь передвинуть небольшой переключатель; при извлечении какого-либо числа из памяти там остается копия этого числа на случай, если оно понадобится еще раз; в случае надобности можно мгновенно извлечь из памяти так называемый предыдущий оперант,- например, результат предыдущего вычисления, а затем вернуть его на место,- выполняя серию операций с постоянным коэффициентом, совсем не нужно каждый раз вводить его значение, повторение этого коэффициента может происходить автоматически; в случае, если калькулятор не может произвести действие над введенными числами, на индикаторе зажигается особый предупреждающий сигнал "переполнение"; калькулятор может суммировать результат нескольких вычислений, производить накопление произведений и частных; может по довольно простой процедуре вычислять средние значения нескольких величин, дисперсию, среднеквадратичное отклонение и погрешность среднеквадратичного отклонения; умеет находить гиперболические функции; вычислять сложные проценты; преобразовывать прямоугольные координаты в полярные...
Математические способности инженерного микрокалькулятора в какой-то мере отражают удивительные достижения современной "большой" вычислительной техники. Пока на страницах некоторых изданий шли утомительные дискуссии о том, может ли машина мыслить, инженеры и математики работали, создавали конкретные электронные системы, умеющие решать сложные логические и математические задачи. Торжественным словом "мыслить" нельзя, конечно, разбрасываться направо и налево, но то, что уже сегодня научились делать ЭВМ, бесспорно, раньше было монополией Человека Думающего.
Все, что делает ЭВМ, она делает, оперируя электрическими сигналами, оперируя сложными комбинациями импульсов тока, которые напоминают телеграфные точки и тире. В виде комбинаций электрических импульсов живут в машине цифры, команды, правила работы. Комбинации электрических импульсов рождаются, когда вы нажимаете кнопки ввода данных; комбинации электрических импульсов управляют работой индикатора вывода данных, зажигая на нем зеленые палочки-сегменты, из которых составляются нужные цифры. А между этими двумя событиями - вводом и выводом - стоят электронные схемы, которые производят с электрическими сигналами разные операции - складывают их и разделяют, пересылают из одного электронного блока в другой, сопоставляют с сигналами, записанными в память. И в этих действиях рождаются новые электрические сигналы, рождаются результаты вычислений, подобно тому, как они появляются при перебрасывании косточек на счетах. Хотя, конечно, электронные вычислительные машины, даже самые простые, настолько сложны и совершенны, что их сравнение со счетами требует не просто оговорок, но и извинений.
Упрощенная блок-схема "Электроники Б3-18" показана на первой странице цветной вкладки (рисунок вверху справа). Детальное знакомство с устройством отдельных узлов этой схемы - дело сложное и здесь вряд ли уместное. Можно лишь попытаться несколькими штрихами обрисовать блок-схему калькулятора с тем, чтобы получить самое общее представление о назначении его узлов и их взаимодействии.

Каждая цифра восьмиразрядного числа и каждый символ команды представлены в калькуляторе комбинацией из четырех электрических импульсов или пауз. Скажем, комбинация "импульс - пауза - пауза - импульс" соответствует девятке, а комбинация "импульс - импульс - пауза - импульс" - тройке. Генератор опорной частоты ГОЧ дает непрерывную очередь импульсов, некоторые из них затем гасятся, и таким образом формируются нужные комбинации из импульсов и пауз. Формируются они прежде всего при нажатии тех или иных кнопок ввода - блок управления вводом-выводом УУВВ регулярно опрашивает кнопки, следит за тем, какая из них нажата.
Все введенные числа первым делом попадают в оперативную память, в ОЗУ (оперативное запоминающее устройство - тоже электронные схемы, их элементы могут находиться в одном из двух состояний - пропускать ток или не пропускать; это как раз и соответствует двум знакам машинного языка - импульсу и паузе), а оттуда на индикатор - так осуществляется контроль за правильностью ввода. Указание о нужной операции, которое также вводится нажатием кнопки, в итоге попадает в постоянную память - в ПЗУ, где определенными электрическими соединениями навеки записано, что нужно делать для выполнения той или иной операции. Это "что делать" из ПЗУ в виде длинной серии сигналов, длинной телеграммы, поступает в устройство управления УУ, где формируется руководящее указание "как делать". Например, такое: "Прочитать в первом секторе ОЗУ число; саму запись числа стереть; прибавить к нему число, записанное во втором секторе ОЗУ, саму запись числа оставить; результат сложения записать в освободившийся сектор ОЗУ; результат передать также на индикатор..." Такая телеграмма попадает в арифметико-логическое устройство АЛУ, где уже и реализуется "указание руководства", производятся необходимые операции с электрическими сигналами, то есть необходимые вычисления.
Наше ультракороткое описание блок-схемы калькулятора не должно создавать иллюзию ее простоты. Вот несколько цифр, которые в какой-то степени отражают сложность событий, происходящих в схеме: программы, записанные в ПЗУ, состоят из 1152 "слов" по 8 "букв", а каждая "буква" кодируется комбинацией из четырех импульсов-пауз; блок УУ может разослать другим блокам до 105 разных команд; при выполнении даже такой простой операции, как умножение двух восьмиразрядных чисел, отдельные блоки калькулятора обмениваются "телеграммами" в общей сложности из 10000 "слов".
А вот другие цифры: электронная схема калькулятора "Электроника Б3-18" содержит примерно 10 тысяч транзисторов, 8 тысяч резисторов, 1 тысячу конденсаторов и 25 тысяч соединительных проводников. Для сравнения заметим, что в транзисторном приемнике около 100 элементов, в телевизоре - около тысячи.
Как же разместилось такое огромное число компонентов - около 45 тысяч - в маленьком, размером чуть больше пачки сигарет, корпусе? Как удается упрятать в него сотни приемников или десятки телевизоров?
Ответ на эти вопросы в коротком слове "БИС" - так сокращенно называют большие интегральные схемы, это совершенно уже фантастическое творение современной электроники. Несколько лет назад автору этих строк случайно пришлось быть свидетелем того, как два бывалых радиоинженера из тех, которых объемным телевидением, наверное, не удивишь, впервые рассматривали большую интегральную схему и повторяли при этом одно слово: "Фантастика... Фантастика!.." Это слово, наверное, лучше всего выразит и наши чувства, когда, заглянув внутрь микрокалькулятора "Электроника Б3-18", вы увидите там лишь несколько детален. И узнаете, что все остальное, все эти "около 45000" транзисторов, резисторов, конденсаторов, проводников, разместились на тоненькой кремниевой пластинке размером 5*5.2мм. Вдумайтесь - полсотни телевизоров в одной клеточке арифметической тетради. Фантастика!
Прежде чем говорить о БИСах, несколько слов просто об интегральных схемах и даже, пожалуй, вообще о том, что есть схема в понимании специалистов по радиоэлектронике. Схема - это мир, где живут электрические сигналы, электрическая цепь, где они рождаются и умирают, усиливаются или ослабляются, суммируются или разделяются, словом, проходят самые различные виды обработки. Делают все это элементы схемы и их комплексы: транзисторы усиливают сигнал, резисторы ослабляют или выделяют, конденсатор реагирует на скорость изменения сигнала, двухтранзисторный комплекс - триггер - делит число сигналов на два. Несмотря на чрезвычайную сложность и огромное разнообразие, многие из схем, и прежде всего схемы вычислительных устройств, собираются всего из нескольких типов элементов. Скажем, из десятка типов транзисторов, двух-трех десятков типов конденсаторов и резисторов, двух-трех типов диодов. Это первая реальность, сделавшая возможным создание интегральных схем.
А вот и вторая.
Совершенно недвусмысленное, казалось бы, выражение "... изготовить электронный прибор..." с некоторого времени приобрело два совершенно разных значения. Еще недавно оно означало, что изготавливаются какие-то детали, скажем, детали электронной лампы - металлические цилиндры, спирали, сетки, трубки, стеклянный баллон, цоколь,- и затем эти детали собирают, соединяют, превращают в единое целое. Но вот лет тридцать назад физика твердого тела, академическая в общем-то наука, на основе глубокого исследования физических процессов в полупроводниках предложила практике новый вид усилительного электронного прибора - транзистор, аналог трех-электродной усилительной лампы. (Справедливость требует, чтобы, задумываясь об истории создания транзистора, мы первым вспоминали нижегородского радиоинженера Олега Лосева, который еще в 1926 году, примерно за 20 лет до появления транзисторов, построил первый полупроводниковый усилительный прибор - кристадин; один из американских радиотехнических журналов писал о работе Олега Лосева: "... генерирующий кристалл, как его назвал Лосев, призван совершать все то, что в настоящее время совершается катодной лампочкой"; к сожалению, работы О.Лосева не получили развития, физика еще не была готова к тому, чтобы понять процессы в полупроводниковом усилителе).
С точки зрения конструктора, транзистор - это только одна деталь - полупроводниковый кристалл. И лишь технолог знает, что в этом одном кристалле фактически есть три разные части: эмиттер, база и коллектор, или - в так называемых полевых транзисторах - исток, затвор и сток. Части эти могут создаваться разными способами, которые, однако, дают один и тот же результат - в полупроводниковый кристалл вводятся примеси, и в нем появляются отдельные участки с различными электрическими свойствами. Например, появляются зоны с разной концентрацией свободных электрических зарядов - отрицательных (это зоны n, от слова "negativus" - отрицательный) и положительных (это зоны p, от слова "positivns" - положительный). Вот такие зоны фактически представляют собой детали полупроводникового прибора, детали, созданные в целом, в одном кристалле, без его разрушения, без разделения на части.
Виртуозная технология, которой постепенно вооружалась электронная промышленность, сегодня позволяет формировать в кристалле почти все виды элементов электронных схем - диоды, транзисторы, проводники, конденсаторы (две примыкающие друг к другу зоны n и p, если подать на них определенное напряжение, становятся обкладками конденсатора), резисторы (точно дозируя количество примесей и размеры той области, куда они вводятся, можно создавать резисторы с самым разным сопротивлением). Вот это есть та вторая реальность, на основе которой выросла интегральная электроника.
Теперь о третьей, о тех причинах, которые заставили переходить к интегральным схемам, вдохновили науку и промышленность на решение этой чрезвычайно сложной задачи. Таких причин немало, но большинство из них связано с тем, что в радиоэлектронике часто называют "тиранией количеств". В двадцатые годы, когда детекторный приемник считался шедевром радиотехники, наиболее сложные электронные схемы состояли из десятков, максимум сотен элементов. Но постепенно радиоэлектронная аппаратура усложнялась и число элементов в одном аппарате резко увеличивалось - в среднем в 10 раз каждые 10 лет. Особенно быстро стало расти число элементов с появлением вычислительных машин, и сегодня схемы больших ЭВМ содержат многие миллионы элементов.
Увеличение числа элементов, если все они представлены в электронном приборе отдельными деталями, влечет за собой немало трагических последствий. Из-за ненадежности межэлементных соединений резко падает надежность всего прибора. Растет вес,- оказывается, например, что грузоподъемности самолета просто не хватает, чтобы поднять все необходимое ему современное электронное оборудование. Растут размеры и потребляемая мощность, страшно усложняется конструкция аппаратуры. Одним словом, если, опустив подробности, посмотреть на конечный результат, то окажется, что "тирания количеств" - это непреодолимое препятствие на пути прогресса радиоэлектроники, а вместе с ней и на пути прогресса многих областей современной техники.
Преодолеть это препятствие или по крайней мере заметно его отодвинуть позволили интегральные схемы.
Интегральная схема, как говорит само название,- это многоэлементный электронный блок, выполненный в виде единого целого. В частности, в виде полупроводникового кристалла, где последовательными технологическими операциями созданы и соединены друг с другом различные элементы схемы.

На рисунке очень упрощенно показана часть такой схемы. В нее входят транзистор Т1, два разных резистора R1 и R2, конденсатор С1 и несколько соединений, изображенных схематически. Перечислены основные этапы изготовления условной интегральной схемы; некоторые из этих этапов иллюстрируются упрощенными рисунками. После разработки самой электрической схемы следует создание топологии, то есть определение всех конфигураций и взаимного расположения тех зон кристалла, из которых будут образованы детали схемы, а также конфигурации соединительных целей. Работа эта весьма сложна, и ведется она с помощью ЭВМ, демонстрируя честному народу, как машина делает машину. Без ЭВМ не обходится и следующий этап - создание фотошаблонов, с помощью которых разработанная топология воплощается в кристалле. Воплощение это в общих чертах происходит так: на кристалл наносят светочувствительный слой, так называемый фоторезист, затем его засвечивают через фотошаблон, проявляют, удаляют засвеченные участки и в образовавшиеся окна либо вводят нужные примеси, либо убирают в глубине этих окон какой-нибудь ненужный слой и в нем вскрывают окна, либо, наконец, убирают участки алюминиевого покрытия, формируя таким образом соединительные цепи сложной конфигурации.

Вот и опять слишком короткое описание создает, по-видимому, иллюзию этакой простоты или, может быть, даже примитивности технологического процесса. Но это, конечно, не более чем иллюзия. В подтверждение - несколько цифр и фактов.
Если в первых интегральных схемах о одном кристалле создавали всего несколько элементов, то теперь степень интеграции резко возросла, создаются схемы, которые содержат тысячи и десятки тысяч элементов. Это и есть БИСы, большие интегральные схемы, в которых на один квадратный миллиметр поверхности (это поверхность булавочной головки) может приходиться более тысячи элементов. Размеры отдельного элемента при этом измеряются тысячными долями миллиметра, их, естественно, можно увидеть только в хороший микроскоп. Допустимые погрешности при создании определенных зон в кристалле - это вообще ангстремы, единицы измерения, до недавнего времени незнакомые технике. А количество вводимых примесей в этих процессах дозируется с точностью до миллиардных долей процента, здесь уже счет идет на атомы. С точностью до сотых долей процента поддерживаются тепловые режимы, малейшая ошибка здесь чревата серьезными последствиями. Потому что интегральные схемы не делают по одной, на кремниевой пластине их может разместиться несколько десятков. По окончании технологического цикла для каждой схемы производятся сотни контрольных замеров. Приведем еще одну цифру: на производственных участках фотолитографии допускается содержание в одном кубическом метре воздуха не более чем 3-4 пылинки диаметром до 0.5мкм.
Достоинства интегральных схем не требуют, по-видимому, пояснений: это высокая надежность, малые габариты и вес, малая потребляемая мощность. И еще одно парадоксальное на первый взгляд достоинство интегральных схем: эти уникальные по своей сложности и, по сути, невидимые изделия, сама их технология как будто бы специально созданы для автоматизированного производства.
В нашей стране серийно выпускается широкий ассортимент интегральных схем, в том числе БИСы. Все большими тиражами выпускаются и созданные на их основе микрокалькуляторы. Немного, наверное, пройдет времени, и миллионы этих электронных помощников инженера, исследователя, экономиста выйдут на скромную свою трудовую вахту, незаметно привнося в наши дела и планы точность, четкость, порядок, эффективность. Мы привыкнем к ним, забудем, что когда-то исписывали вычислениями листы бумаги, теряли миллионы из-за какой-то арифметической ошибки или из-за того, что прикидывали на глазок там, где надо считать точно...
Мы привыкнем к своим карманным компьютерам, как привыкли к телефону, к часам на руке, к яркому электрическому свету в квартире. Привыкнем и перестанем замечать... И это, если по-честному, будет несправедливо. Любуясь красками на экране цветного телевизора, или за час покрывая тысячу километров на десятикилометровой высоте, или нажимая клавиши электронного микрокалькулятора, мы должны хотя бы изредка вспомнить, какая изумительная техника и какой большой труд стоят за всем этим. И должны мысленно гордиться: "Велик человек!"
***
Шикарная строчка: "Пока на страницах некоторых изданий шли утомительные дискуссии о том, может ли машина мыслить, инженеры и математики работали, создавали конкретные электронные системы, умеющие решать сложные логические и математические задачи". Но мы же видели в "Тайной библиотеке", что без "дискуссий о мыслящей машине" не было бы и "конкретных электронных схем". Калькулятор - лишь перевод "в железо" малой части формул фундаментальной кибернетической науки. Технология - как полезные отходы чистой науки.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Однако, "железо" тех времен, это не самое интересное. "Деревяшки" и "картонки" были отработаны гораздо лучше:
3/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
Г.ГЕЦОВ
Если задуматься над тем, как мы работаем с книгой, как читаем газеты и журналы, то возникнет немало вопросов, требующих разрешения. Сейчас, например, модно говорить о скорочтении. Бесспорно, заманчиво убыстрить чтение, скажем, раз в пять. Но важно не только быстро усваивать тексты, но и уметь планировать чтение, вести его учет, быстро и точно фиксировать найденное в литературе, а затем сделать его легкодоступным в любой момент. Иначе просто немыслимо активно пользоваться большим объемом литературы. Для всего этого стоит овладеть соответствующей технологией.
РАБОТА СО СЛОВАРЕМ
Обычно при работе со словарем поиск идет по-разному. Читатель то забегает вперед, то возвращается назад, листает страницы словаря. Кроме нужной, приходится осмысливать и лишнюю информацию. По этой причине после нескольких часов работы притупляется внимание, снижается активность, труд становится малопроизводительным.
Читатели стремятся как-то облегчить работу со словарем. Скажем, избирают в качестве ориентира типографские метки на страницах. В таких случаях, удается быстро перелистывать книгу, почти не открывая ее, и это уже дает некоторый выигрыш времени. Но, скажем, в русско-французском словаре для слов с поисковым признаком ПРИ отведено 13 страниц, а слова на ПРО занимают 18 страниц.

Как видим, этот прием не очень существенно увеличивает скорость поиска, и читатели для облегчения своей работы пишут поисковые метки на обрезах книг, режут сбоку на книгах ступеньки, как в алфавитной записной книжке, приклеивают к страницам ярлыки с буквами.
Тем, кто решился таким способом усовершенствовать словарь, можно посоветовать сделать к нему дополнительные детализирующие "лесенки" снизу и сверху обреза книги. Тогда, открыв с помощью боковой метки нужный ряд слов, более детальные их признаки можно найти, "идя" по верхним или нижним ступеням. (Метки, написанные снизу книги, могут быть продолжением верхних). Правда, все эти усовершенствования хотя и облегчают поиск, наносят книгам определенный вред.
Но есть способ нанесения почти безвредных меток. Он легок в исполнении и доступен каждому. На одной из первых страниц, на обложке словаря, или, наконец, на листке, равном по высоте книге, размечают интервалы и озаглавливают их подряд буквами алфавита. Края всех страниц каждой части, метят в нужных местах (окрашивают или штрихуют горизонтальными линиями). Такие метки, сделанные на наружном боковом поле страниц, хорошо различимы, с обреза книги, причем они остаются видимыми даже в случае его чистки.
Можно ускорить и облегчить работу со словарем, заменив утомительный поиск по алфавитному признаку легким цифровым способом. Всегда легче найти число в ряду чисел, чем слово среди тысяч других, расположенных в алфавитной последовательности. Поэтому имеет смысл для облегчения работы со словарями создавать поисковые таблицы. С их помощью определяют страницы, на которых могут находиться искомые слова или понятия. При продолжительной работе таблица позволяет работать без усталости. Вместо обычного ориентирования по буквенным признакам в словаре сначала с помощью таблицы получают номера страниц, на которых может находиться искомое слово. Найти номер страницы в словаре куда легче, чем искать само слово. Кроме того, таблица указывает и на отсутствие в словаре того или иного слова.
Таблицу составляют следующим образом. В горизонтальную верхнюю строчку вписывают подряд буквы алфавита. Вертикальную алфавитную графу заполняют теми же буквами, какие расположены и на горизонтальной верхней строке, а также при необходимости слогами, например, MA, ME, МО, НА, НЕ, ПА, ПЕ, ПЕРЕ, ПО...

При составлении подобных таблиц надо не формально указывать страницы, в конце которых появляются первые слова из очередной группы, а те, куда отсылать можно с большей вероятностью. При использовании таблицы для поиска слов надо не забывать эту ее особенность.
Правомерно включать в поисковый ряд те сочетания признаков слов, встречи с которыми наиболее вероятны. Полезно добавлять к поисковому сочетанию букв третью, а то и четвертую букву. Именно так составлена поисковая таблица для Болгарско-русского словаря (М. "Сов. энциклопедия", 1966). К словам на ПР, занимающим в словаре 50 страниц, даны сочетания ПРЕ, ПРИ, ПРО. Более того, к имеющимся в словаре трем буквенным поисковым признакам ПРИ добавлены четвертые буквы. Образовался ряд: ПРИБ, ПРИГ, ПРИК, ПРИМ, ПРИС, ПРИУ. Таким образом, к словам на ПРИ получилось вместо одного шесть более
точных поисковых признаков.
Существует еще один способ активного словарного поиска. Замечено, что острие иглы, введенной между страницами закрытой книги параллельно их плоскостям, обеспечивает весьма точный быстрый поиск нужной страницы. При этом игла не накалывает торцов листов и не причиняет никакого вреда книге. Но для работы по этому методу потребуется механизм, ориентирующий иглу параллельно плоскостям страниц и перемещающий ее с нужной точностью поперек среза книги, а также кодировка словесных понятий. Найденная подобным образом страница придерживается поисковым элементом - иглой, и книга легко открывается в нужном месте.
1 - книга, 2 - поисковая планка, 3 - поисковые отверстия, 4 - игла.
Вот один из вариантов приспособления. Точный
поиск (+/-2стр.) обеспечивает булавка диаметром 0.63 миллиметра. В качестве матрицы для направления движения иглы используется планка из гетинакса, плексигласа и т.п. Длина ее равна высоте словаря, а ширина - толщине страничного блока. По диагоналям планки через 3-6 миллиметров сверлят сквозные отверстия. Они должны быть строго вертикальными и с выдержанным размером диаметра, чтобы булавка входила без перекоса. Для этого желательно иметь планку толщиной не менее 8-10 миллиметров, а отверстия сверлить коротким сверлом.
На планку с отверстиями с двух сторон наклеивают полоски бумаги, на которых временно нумеруют все отверстия подряд. Затем прикладывают поисковую планку к срезу книги и начинают калибровку. Вставив иглу в первое отверстие и затем открыв книгу, записывают на листке черновика номер найденной таким способом страницы рядом с номером отверстия. Так поступают со всеми отверстиями. Калибровку планки нужно провести несколько раз, чтобы устранить неточные попадания иглы. Если какое-то отверстие все же дает разброс номеров страниц, то нужно вычислить их среднее значение.
Поисковые алфавитные признаки с черновика переносят на планку вместо временных номеров, руководствуясь таблицей поисковых признаков, о которой говорилось выше. Она позволит рационально отбирать наиболее обоснованные буквенные сочетания и не давать на планке лишних, случайных.
Если нумеровать отверстия сверху вниз, то составляется ряд (отверстий на планке при длине ее 250 миллиметров получается около 80). Вот часть этого ряда: 1 - бав, 2 - бат, 3 - бла, 4 - бо, 5 - ва, 6 - ве, 7 - ви, 8 - во, 9 - ву, 10 - га, 11 - гл, 12 - го, 13 - гу, 14 - гь, 15 - де, 16 - ди, 17 - до, 18 - ду, 19 - е, 20 - ек, 21 - ен, 22 - же, 23 - зав, 24 - зак, 25 - зал, 26 - зам, 27 - зас, 28 - зат, 29 - зач, 30 - зи...
Одна сторона планки может быть предназначена только для половины книги. Тогда для того, чтобы работать с другой половиной, надо перевернуть планку. В этом случае увеличится точность поиска, так как возрастает длина поисковой прямой.
Для книг с очень тонкими страницами можно предложить еще один вариант разметки планки, будем говорить, четверной. Тогда поисковая прямая (в сравнении с одной диагональю через всю планку) удлиняется в четыре раза (считая и с оборотом планки). А это дает возможность сверлить отверстия, например, не через три, а через шесть и более миллиметров.
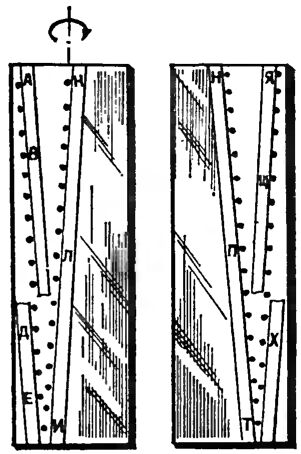
Заметим, что книга, не имеющая вкладок, позволяет сделать для нее поисковую шкалу равномерной. Если же в книге имеются вкладки (таблицы, иллюстрации), по толщине отличающиеся от страниц книги, то тогда при градуировке устройства нужно "обходить" вкладки, а затем продолжать метки с прежним "шагом".
И, наконец, для повышения точности поиска полезно срезать радиус у обреза книги.
ДЛЯ УДОБСТВА В РАБОТЕ
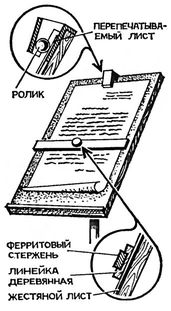
Перепечатывая на машинке текст, лежащий на столе, мы вынуждены часто склоняться к нему. Операция эта весьма утомительна. Чтобы ее облегчить, А.Пошивалов из Ленинграда предлагает усовершенствованный пюпитр с подвижной линейкой. Для удержания линейки лицевая плоскость пюпитра покрывается жестяным листом, в верхней части размещен зажим для рукописного текста.
Перепечатываемый текст накладывается на жестяной лист и прижимается линейкой с ферритовым магнитом, которая служит указателем строк. Магнит диаметром 18 миллиметров может удерживать одновременно до 25 листов рукописного текста. Линейка на плоскости пюпитра может находиться под любым углом, что очень важно для перепечатывания с рукописного текста.
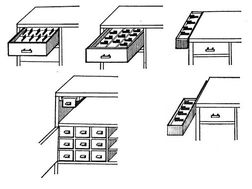
Хранение личной картотеки (особенно в тех случаях, когда размеры ее значительны) - далеко не простое дело, справедливо считает В.Федоров из Ленинграда. Сложность выбора форм хранения личных картотек определяется тем, что они должны удовлетворять ряду требований, в известной мере противоречивых. Картотеки должны располагаться на рабочем месте таким образом, чтобы постоянно находиться под рукой. Это, конечно, далеко не всегда возможно. Кроме того, они <не должны находиться на виду.
Какими же могут быть. импровизированные хранилища личных картотек? Как видно из рисунка, в одних случаях это отдельные хранилища. Возможен монтаж картотек в ящиках письменного стола или шкафа. Еще один вариант: подвеска каталожных ящиков возле стола на время работы. Следует постараться найти такой вариант размещения картотеки, который в наибольшей степени удовлетворял бы и характеру и условиям работы.
4/80
ОРИЕНТИРЫ В ПОТОКЕ ИНФОРМАЦИИ
О.МУРЫГИН, ведущий редактор отдела журнальной периодики Госкомиздата СССР
Тому, кто следит за публикациями определенной тематики, становится все труднее фиксировать нужную информацию. И не только потому, что нарастает поток публикаций. Сложность заключается и в том, что публикации по одной и той же проблеме (с определенным отраслевым преломлением) могут помещаться в самых различных по своему профилю научно-технических и производственных журналах.
Определенную помощь читателям в решении этой сложной задачи может оказать опережающая сигнальная информация о журнальных публикациях. Эксперимент подобного рода проводится Госкомиздатом СССР совместно с некоторыми изданиями: журналами "Советское государство и право", "Вестник сельскохозяйственной науки", "Лабораторное дело", "Механизация и автоматизация производства". Эти журналы с января 1980 года начали выпуск бюллетеней сигнальной информации, где печатаются рефераты статей, которые появятся в последующих номерах.
Итак, предположим, что вы интересуетесь кругом вопросов, связанных с гражданским правом, и решили ознакомиться с очередным, четвертым номером сигнальной информации "Советское государство и право". По внешнему виду он напомнит брошюру. В бюллетене сохранены все журнальные рубрики, под которыми публикуются рефераты тех статей, которые намечено напечатать в шестом номере журнала. Вот один из рефератов бюллетеня #1 "Советское государство и право":
"Н.В.Гудимов. Трудовая активность, дисциплина, поощрения за труд.
"Социалистическая дисциплина труда в социалистическом обществе обеспечивается методами убеждения и поощрения, а в необходимых случаях и методом принуждения в отношении недисциплинированных работников. В статье рассматриваются такие взаимосвязанные понятия, как трудовая активность и трудовая дисциплина; отмечается, что трудовая активность является обязательным условием не только повышения производительности труда, но и всестороннего развития личности, что постоянная трудовая активность работника выводит его в число передовиков производства; анализируется понятие социальной активности.
"Далее автор исследует соотношение трудовой активности и поощрений. В статье анализируется понятие первичной ячейки трудового коллектива - бригады, члены которой объединены общими целями и заняты решением конкретных производственных задач. В заключение автор высказывает предложение утвердить рекомендации о порядке и условиях применения мер морального и материального поощрения за успехи в работе".
Таким образом, заранее, а именно за два месяца до момента поступления журнала к подписчикам, и при минимальных затратах времени вы можете ознакомиться с кратким содержанием статей и определить, нужен или не нужен полный текст той или иной публикации для дальнейшей работы. Если такая необходимость возникнет, то вы можете послать заказ в редакцию журнала или в соответствующий орган научно технической информации, указав название статьи, авторов, номер журнала, в котором она будет опубликована. Копия нужной вам статьи окажется на вашем рабочем столе раньше, чем журнал получат подписчики.
Предлагаемая форма обслуживания читателей может найти очень много сторонников. И это понятно. Ведь годовой комплект любого из бюллетеней сигнальной информации практически содержит рефераты всех статей, помещенных за год в соответствующем журнале.
Эксперимент проводится и по второму варианту - заблаговременное информирование читателя о будущих статьях непосредственно на страницах журнала.
Ученый или специалист, взяв, например, в библиотеке журнал "Тракторы и сельхозмашины" #4 за 1980 год, найдет в нем раздел, в котором напечатаны рефераты статей, намеченных к публикации в июньском номере. Таким образом, за два месяца до выхода шестого номера журнала читатель знакомится не только с содержанием, но и с существом вопросов, изложенных в каждой статье. Примем на это затрачивается минимум времени. Вот один из рефератов, опубликованных в первом номере журнала "Тракторы и сельхозмашины".
"Борисов С.Г. и др. Вопросы долговечности муфт сцепления тракторов (С.Г.Борисов, С.А.Лапшин, В.Я.Юденко, В.Е. Захаров - Тракторы и сельхозмашины, 1980, #3).
"Изложены основные результаты комплексного изучения большинства условий нагружения тракторных муфт сцепления. Показано сильное влияние динамических нагрузок на надежность и долговечность их работы. Сформулированы рекомендации, позволяющие на стадии проектирования муфт сцепления заложить основы их повышенной долговечности. Библ. 10. УДК 629. 114. 2-233-192".
Если читателя заинтересовала какая-либо статья, то, сделав пометку в своей записной книжке, он может при поступлении журнала в библиотеку прочесть ее полный текст. Вместе с тем читатель имеет возможность, не дожидаясь выхода журнала, получить копию нужной ему статьи. Для этого необходимо сделать заказ в редакцию журнала или в ЦНИИТЭИ тракторосельхозмаш. Копию можно получить одновременно или даже раньше, чем журнал придет в библиотеку.
Периодичность бюллетеней сигнальной информации - 12 номеров в год. Цена одного экземпляра - 10коп., подписная цена на год - 1 рубль 20 копеек. Подписку можно оформить в любом отделении "Союзпечати".
Бюллетени имеют следующие индексы: "Советское государство и право" - 70348, "Вестник сельскохозяйственной науки" - 70345, "Механизация и автоматизация производства" - 70347, "Лабораторное дело" - 70346.
АДРЕСА РЕДАКЦИИ И ИНСТИТУТОВ. ПРИНИМАЮЩИХ ЗАКАЗЫ НА ИЗГОТОВЛЕНИЕ КОПИИ СТАТЕЙ
Редакция журнала : Орган научно-технической информации
Советское государство и право 119878, Москва, Г-19, ул.Фрунзе, 10 : Институт научной информации по общественным наукам АН СССР (ИНИОН АН СССР). Москва, ул.Красикова, 28/45
Вестник сельскохозяйственной науки 107807, ГСП, Москва, Садово-Спасская ул., 18 : Всесоюзный научно-исследовательский институт информации и технико-экономических исследований по сельскому хозяйству (ВНИИТЭИСХ). Москва, Орликов пер., 3
Лабораторное дело 117819, Москва, Научный проезд, 6 : Всесоюзный научно-исследовательский институт медицинской и медико-технической информации (ВНИИМИ). Москва, Москворецкая наб., 2а.
Механизация и автоматизация производства 103051, Москва, Трубная ул., 17 : Всесоюзный институт научной и технической информации (ВИНИТИ). 104010, г.Люберцы-10. Московская область, Октябрьский пер., 21, ком.31.
Журналы, публикующие рефераты статей
Журнал аналитической химии 117334, Москва, Воробьевское шоссе, д.47а : ВИНИТИ
Заводская лаборатория 119034, Москва, 2-й Обыдненский пер., 14 : ВИНИТИ
Известия высших учебных заведений Геология и разведка Москва, Проспект Маркса, 18, МГРИ : ВИНИТИ
Приборы и техника эксперимента 103717, ГСП, Москва, К-62, Подсосненский пер., 21, ком.31 : ВИНИТИ
Тракторы и сельхозмашины 103012, Москва, К-12, пр.Сапунова, 13/15, к.428 : Центральный научно-исследовательский институт информации и технико-экономических исследований по тракторному и сельскохозяйственному машиностроению (ЦНИИТЭИтракторосельхозмаш). 127247, Москва, Дмитровское шоссе, 165
Стоимость изготовления копии одной журнальной статьи - 3-5коп.
5/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РАБОТА С КНИГОЙ
Г.ГЕЦОВ
... Я усвоил себе привычку делать выписки из всех книг, какие я читал... мимоходом нанося на бумагу свои размышления.
Карл Маркс
Бессонный летит карандаш, кресты на полях остаются.
Лев Смирнов
Итак, библиотека, картотека, Наброски, сноски, выписки, мечты...
Валентин Берестов
... шелковинка - закладка.
Где остановился взором читатель.
Велимир Хлебников
Как будто сабли Первой Конной, Закладки - наискось и вверх!
Майя Борисова
... Я сразу же взял за правило заводить на каждую казавшуюся мне чем-либо примечательной книгу - карточку...
Н.П.Смирнов-Сокольский.
Первая встреча с книгой - дело едва ли не столь же серьезное, как знакомство с человеком: недаром истинному библиофилу свойственны подлинно человеческие пристрастия (симпатии и антипатии) к книгам.
Предварительный просмотр книги позволяет, кроме беглого знакомства с фактическим материалом, понять принцип и особенности построения издания. Многие книги имеют справочный и другой подсобный материал, который позволяет ориентироваться в содержании, а иногда вовремя отказаться от чтения или перенести его на будущее.
Знакомясь с книгой по теме, необходимой вам, следует заполнить на нее библиографическую карточку с такими (помимо основных, анкетных данных: автор, название, место и время издания) читательскими пометками на карточке:
1) о чем говорится в книге (с позиций ваших требований и запросов);
2) оценка книги с учетом ее дальнейшего использования.
Если вы решили прочесть книгу через какое-то время, то в таком случае поставьте ее библиографическую карточку в свой рабочий каталог с соответствующей пометкой, например: "прочесть после уяснения таких-то вопросов".
На всякий случай следует поинтересоваться, нет ли в книге списка опечаток, и, если он есть, перенести исправления в текст.
Чтобы отметить при чтении то, что нужно, читатели часто используют закладки из полосок бумаги. Можно усовершенствовать эти закладки так, чтобы они отмечали сразу два места в страничном блоке (рис.1).

Уже само положение закладок организует труд. Скажем, та видна сверху - отмечает место, где вы прервали чтение, закладка снизу - примечания, а помещенная сбоку дает возможность быстро обращаться к иллюстрациям, например, к картам, таблицам и тому подобному (рис.2).
На закладке можно написать номер отмечаемой страницы или пометить одну сторону закладки каким-либо значком, тогда она укажет читателю нужную страницу из двух смежных.
Существуют и более точные способы отметок нужных страниц и текстов. Например, подсчитав абзацы и строки, можно составить такой ключ: "название книги, стр.40, 3-5абз.св.". Между тем подсчитывать абзацы и строчки отнюдь не обязательно. Возьмите обычную 30-сантиметровую линейку с миллиметровой шкалой, край линейки установите на уровне верхней или нижней строки на странице. Теперь любую часть текста книги можно обозначить с помощью миллиметрового исчисления. Например, так: "110-185". Эти числа обозначат границу текста, расположенного между 110 и 185 миллиметрами линейки. Или с указанием номера страницы, вот так: "95.110-185".
Как обойтись без пометок в книге? Читатели часто задают себе этот вопрос. Ведь если не делать пометок, то работа с книгой замедлится, производительность чтения уменьшится. Между тем имеется прием, позволяющий делать записи какого угодно размера, не прикасаясь к книге карандашом. Сущность приема: при чтении вы закрываете соседнюю страницу чистым листком или полоской бумаги вровень с нижней строкой страницы и проводите черту на вкладном листке на уровне нужного отрывка (рис.3). Позже, приложив листок бумаги (разумеется, с номером страницы) к тексту, вы без труда прочтете или выпишете из книги найденный отрывок.

Вкладные листки позволяют весьма экономно и точно, лишь с помощью черточки, давать точный адрес цитат или отсылать личный комментарий к нужному месту текста источника, не требуя указания номеров абзацев ("снизу", "сверху"), подсчета строчек, "миллиметровых" пометок.
Этот прием известен, по существу, давно. К примеру, среди книг Стендаля (А.Бейля), Д.И.Менделеева имеются книги с вплетенными чистыми листками. Одна сторона таких листков предназначается для отметок, относящихся к левой, другая, оборотная,- к правой странице книги.
Читатель, желающий полнее использовать площадь вкладных листков, может сделать комментарии и отметки сразу к четырем страницам книги на одном листке. В этом случае делят листки пополам вертикальной чертой или хотя бы складывают: черта или изгиб покажут границу, за которую не должны переходить записи, относящиеся к разным страницам (рис.4).
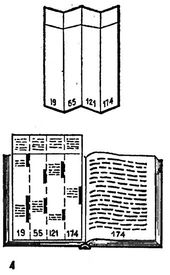
Прозрачные вкладные листки применяют для анализа карт, диаграмм и графиков. Это позволяет не только копировать элементы изображения, но и отмечать нужные детали, снабжая изображение в книге своими комментариями. Прозрачным листком можно накрыть страницу и на нем подчеркнуть нужные строчки книжного текста. Если затем вы приложите к странице листок, в тексте окажутся ваши подчеркивания.
Вкладные листки значительно упрощают сбор данных из книг (журналов). С их помощью - даже на одном листке!- можно вести параллельные и сопоставительные записи при работе с несколькими источниками, дополняя выписки из основной изучаемой книги примечаниями, взятыми из других, а также своими размышлениями. В дальнейшем вкладные листки объединяются, классифицируются. Если для удобства сортировки по темам потребуется размножить листки, то это сделать очень просто (рис.5).
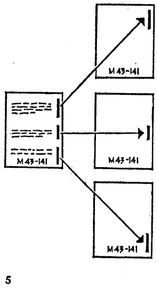
При проработке книги по ряду вопросов удобно пользоваться вкладными листками, заранее разграфленными на темы.
При заполнении таких разграфленных вкладных листков полезно сгибать их вдоль, приближая таким образом нужные вертикальные графы к тексту книги. Так же поступают и при работе с уже готовыми, заполненными вкладными листками, читая с их помощью "невыписаиные выписки".
Вы работали с литературой дома. Но вот вам понадобилось зайти в библиотеку. Вносить туда личные книги, как известно, строжайше запрещено. Но, взяв с собой вкладные листки, вы как бы проникаете в библиотеку со своими книгами. Или, встретив в библиотеке нужную книгу, читаете ее, делая пометки на вкладных листках. Дома вы сможете перенести пометки с листков на страницы собственной книги.
Оставлять все листки в книге после ее чтения не следует: книга разбухнет. По мере накопления листков их помещают в тематические картотеки, конверты, папки. Естественно, что на таких вкладных листках должен быть помечен источник. Чтобы не указывать названия книги, иногда очень длинного, и выходных данных, читатель может присвоить изданию произвольный шифр. Тогда на листках фиксируются только этот шифр и номера страниц. Предположим, книга имеет шифр 457; им помечают все листки и рядом проставляют номера страниц (457-34; 457-41; 457-169).
Если вы работаете над рядом источников или готовитесь выступить перед аудиторией, можно вкладные листки или обычные закладки пронумеровать. В планах к реферату, конспекту или устному выступлению указывают, в какой последовательности будут использоваться места, не отмеченные закладками. (При этом не важно, из какой книги и в какой очередности взяты материалы). Перед вами на столе или на кафедре лежат книги с пронумерованными закладками. Согласно своему плану, вы открываете книги в порядке нумерации закладок. Конечно, за первой книгой может следовать последняя, затем опять первая и так далее.
Вкладные листки не только не отвергают пометок на полях самих книг, но даже могут их существенно дополнить. Тут уже проявится способность листков к оперативной систематизации. В этом случае книжные отчеркивания просто копируют на вкладных листках, тем самым как бы вынимая пометки нз книг. На листках хотя бы коротко записывают тематические признаки взятых из книг извлечений или обозначают номерами сами темы. Получается набор листов, которые легко поддаются перетасовке и систематизации.

Московская фирма "Восход" уже выпускает пеналы с вкладными полосками ("Закладки для книг". Артикул МГ-087-01-285, ТУ-81-01-349-75, цена 20коп.).
Пеналы удобны тем, что их можно ставить на полках рядом с книгами.
Дополняют пометки в книгах также таблицы с перечнем тематических признаков в соответствующих графах. Пользуясь графами с номерами страниц, читатель всегда быстро найдет нужное место. Конечно, подобные таблицы могут отсылать не к одной, а к ряду книг.
Читая книгу, полезно четко разделять материал на освоенный и неосвоенный, на знакомый и незнакомый. А значит, нужен и учет пройденного и намеченного к проработке.
Как выделять прочтенное, отмечать особо важное, как планировать работу, ее тактику? Для регистрации и учета проработки книг полезно употреблять таблицы чисел. На обычной машинописной странице размещается 1000 порядковых номеров, которые будут обозначать страницы книги. Можно также воспользоваться таблицами, напечатанными на стандартных библиографических карточках, где умещаются сотни номеров страниц (рис.6). На бланке-таблице вы можете отмечать различными метками номера проработанных страниц. Кружок, скажем, будет означать, что эту страницу более читать не следует, подчеркнутый номер - что данная страница содержит особо нужный материал, и т.д. Вся эта гамма меток позволяет кратко и быстро вести разнообразную регистрацию работы и учет чтения.

Если к тому же на бланке вы пометите, с какой целью читалась книга, то, возвратившись к ней позже, всегда сможете понять, что именно уже было прочитано и какая работа вам еще предстоит.
3/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
Г.ГЕЦОВ
Если задуматься над тем, как мы работаем с книгой, как читаем газеты и журналы, то возникнет немало вопросов, требующих разрешения. Сейчас, например, модно говорить о скорочтении. Бесспорно, заманчиво убыстрить чтение, скажем, раз в пять. Но важно не только быстро усваивать тексты, но и уметь планировать чтение, вести его учет, быстро и точно фиксировать найденное в литературе, а затем сделать его легкодоступным в любой момент. Иначе просто немыслимо активно пользоваться большим объемом литературы. Для всего этого стоит овладеть соответствующей технологией.
РАБОТА СО СЛОВАРЕМ
Обычно при работе со словарем поиск идет по-разному. Читатель то забегает вперед, то возвращается назад, листает страницы словаря. Кроме нужной, приходится осмысливать и лишнюю информацию. По этой причине после нескольких часов работы притупляется внимание, снижается активность, труд становится малопроизводительным.
Читатели стремятся как-то облегчить работу со словарем. Скажем, избирают в качестве ориентира типографские метки на страницах. В таких случаях, удается быстро перелистывать книгу, почти не открывая ее, и это уже дает некоторый выигрыш времени. Но, скажем, в русско-французском словаре для слов с поисковым признаком ПРИ отведено 13 страниц, а слова на ПРО занимают 18 страниц.

Как видим, этот прием не очень существенно увеличивает скорость поиска, и читатели для облегчения своей работы пишут поисковые метки на обрезах книг, режут сбоку на книгах ступеньки, как в алфавитной записной книжке, приклеивают к страницам ярлыки с буквами.
Тем, кто решился таким способом усовершенствовать словарь, можно посоветовать сделать к нему дополнительные детализирующие "лесенки" снизу и сверху обреза книги. Тогда, открыв с помощью боковой метки нужный ряд слов, более детальные их признаки можно найти, "идя" по верхним или нижним ступеням. (Метки, написанные снизу книги, могут быть продолжением верхних). Правда, все эти усовершенствования хотя и облегчают поиск, наносят книгам определенный вред.
Но есть способ нанесения почти безвредных меток. Он легок в исполнении и доступен каждому. На одной из первых страниц, на обложке словаря, или, наконец, на листке, равном по высоте книге, размечают интервалы и озаглавливают их подряд буквами алфавита. Края всех страниц каждой части, метят в нужных местах (окрашивают или штрихуют горизонтальными линиями). Такие метки, сделанные на наружном боковом поле страниц, хорошо различимы, с обреза книги, причем они остаются видимыми даже в случае его чистки.

Можно ускорить и облегчить работу со словарем, заменив утомительный поиск по алфавитному признаку легким цифровым способом. Всегда легче найти число в ряду чисел, чем слово среди тысяч других, расположенных в алфавитной последовательности. Поэтому имеет смысл для облегчения работы со словарями создавать поисковые таблицы. С их помощью определяют страницы, на которых могут находиться искомые слова или понятия. При продолжительной работе таблица позволяет работать без усталости. Вместо обычного ориентирования по буквенным признакам в словаре сначала с помощью таблицы получают номера страниц, на которых может находиться искомое слово. Найти номер страницы в словаре куда легче, чем искать само слово. Кроме того, таблица указывает и на отсутствие в словаре того или иного слова.
Таблицу составляют следующим образом. В горизонтальную верхнюю строчку вписывают подряд буквы алфавита. Вертикальную алфавитную графу заполняют теми же буквами, какие расположены и на горизонтальной верхней строке, а также при необходимости слогами, например, MA, ME, МО, НА, НЕ, ПА, ПЕ, ПЕРЕ, ПО...

При составлении подобных таблиц надо не формально указывать страницы, в конце которых появляются первые слова из очередной группы, а те, куда отсылать можно с большей вероятностью. При использовании таблицы для поиска слов надо не забывать эту ее особенность.
Правомерно включать в поисковый ряд те сочетания признаков слов, встречи с которыми наиболее вероятны. Полезно добавлять к поисковому сочетанию букв третью, а то и четвертую букву. Именно так составлена поисковая таблица для Болгарско-русского словаря (М. "Сов. энциклопедия", 1966). К словам на ПР, занимающим в словаре 50 страниц, даны сочетания ПРЕ, ПРИ, ПРО. Более того, к имеющимся в словаре трем буквенным поисковым признакам ПРИ добавлены четвертые буквы. Образовался ряд: ПРИБ, ПРИГ, ПРИК, ПРИМ, ПРИС, ПРИУ. Таким образом, к словам на ПРИ получилось вместо одного шесть более
точных поисковых признаков.
Существует еще один способ активного словарного поиска. Замечено, что острие иглы, введенной между страницами закрытой книги параллельно их плоскостям, обеспечивает весьма точный быстрый поиск нужной страницы. При этом игла не накалывает торцов листов и не причиняет никакого вреда книге. Но для работы по этому методу потребуется механизм, ориентирующий иглу параллельно плоскостям страниц и перемещающий ее с нужной точностью поперек среза книги, а также кодировка словесных понятий. Найденная подобным образом страница придерживается поисковым элементом - иглой, и книга легко открывается в нужном месте.

1 - книга, 2 - поисковая планка, 3 - поисковые отверстия, 4 - игла.
Вот один из вариантов приспособления. Точный
поиск (+/-2стр.) обеспечивает булавка диаметром 0.63 миллиметра. В качестве матрицы для направления движения иглы используется планка из гетинакса, плексигласа и т.п. Длина ее равна высоте словаря, а ширина - толщине страничного блока. По диагоналям планки через 3-6 миллиметров сверлят сквозные отверстия. Они должны быть строго вертикальными и с выдержанным размером диаметра, чтобы булавка входила без перекоса. Для этого желательно иметь планку толщиной не менее 8-10 миллиметров, а отверстия сверлить коротким сверлом.
На планку с отверстиями с двух сторон наклеивают полоски бумаги, на которых временно нумеруют все отверстия подряд. Затем прикладывают поисковую планку к срезу книги и начинают калибровку. Вставив иглу в первое отверстие и затем открыв книгу, записывают на листке черновика номер найденной таким способом страницы рядом с номером отверстия. Так поступают со всеми отверстиями. Калибровку планки нужно провести несколько раз, чтобы устранить неточные попадания иглы. Если какое-то отверстие все же дает разброс номеров страниц, то нужно вычислить их среднее значение.
Поисковые алфавитные признаки с черновика переносят на планку вместо временных номеров, руководствуясь таблицей поисковых признаков, о которой говорилось выше. Она позволит рационально отбирать наиболее обоснованные буквенные сочетания и не давать на планке лишних, случайных.
Если нумеровать отверстия сверху вниз, то составляется ряд (отверстий на планке при длине ее 250 миллиметров получается около 80). Вот часть этого ряда: 1 - бав, 2 - бат, 3 - бла, 4 - бо, 5 - ва, 6 - ве, 7 - ви, 8 - во, 9 - ву, 10 - га, 11 - гл, 12 - го, 13 - гу, 14 - гь, 15 - де, 16 - ди, 17 - до, 18 - ду, 19 - е, 20 - ек, 21 - ен, 22 - же, 23 - зав, 24 - зак, 25 - зал, 26 - зам, 27 - зас, 28 - зат, 29 - зач, 30 - зи...
Одна сторона планки может быть предназначена только для половины книги. Тогда для того, чтобы работать с другой половиной, надо перевернуть планку. В этом случае увеличится точность поиска, так как возрастает длина поисковой прямой.
Для книг с очень тонкими страницами можно предложить еще один вариант разметки планки, будем говорить, четверной. Тогда поисковая прямая (в сравнении с одной диагональю через всю планку) удлиняется в четыре раза (считая и с оборотом планки). А это дает возможность сверлить отверстия, например, не через три, а через шесть и более миллиметров.

Заметим, что книга, не имеющая вкладок, позволяет сделать для нее поисковую шкалу равномерной. Если же в книге имеются вкладки (таблицы, иллюстрации), по толщине отличающиеся от страниц книги, то тогда при градуировке устройства нужно "обходить" вкладки, а затем продолжать метки с прежним "шагом".
И, наконец, для повышения точности поиска полезно срезать радиус у обреза книги.
ДЛЯ УДОБСТВА В РАБОТЕ

Перепечатывая на машинке текст, лежащий на столе, мы вынуждены часто склоняться к нему. Операция эта весьма утомительна. Чтобы ее облегчить, А.Пошивалов из Ленинграда предлагает усовершенствованный пюпитр с подвижной линейкой. Для удержания линейки лицевая плоскость пюпитра покрывается жестяным листом, в верхней части размещен зажим для рукописного текста.
Перепечатываемый текст накладывается на жестяной лист и прижимается линейкой с ферритовым магнитом, которая служит указателем строк. Магнит диаметром 18 миллиметров может удерживать одновременно до 25 листов рукописного текста. Линейка на плоскости пюпитра может находиться под любым углом, что очень важно для перепечатывания с рукописного текста.

Хранение личной картотеки (особенно в тех случаях, когда размеры ее значительны) - далеко не простое дело, справедливо считает В.Федоров из Ленинграда. Сложность выбора форм хранения личных картотек определяется тем, что они должны удовлетворять ряду требований, в известной мере противоречивых. Картотеки должны располагаться на рабочем месте таким образом, чтобы постоянно находиться под рукой. Это, конечно, далеко не всегда возможно. Кроме того, они <не должны находиться на виду.
Какими же могут быть. импровизированные хранилища личных картотек? Как видно из рисунка, в одних случаях это отдельные хранилища. Возможен монтаж картотек в ящиках письменного стола или шкафа. Еще один вариант: подвеска каталожных ящиков возле стола на время работы. Следует постараться найти такой вариант размещения картотеки, который в наибольшей степени удовлетворял бы и характеру и условиям работы.
4/80
ОРИЕНТИРЫ В ПОТОКЕ ИНФОРМАЦИИ
О.МУРЫГИН, ведущий редактор отдела журнальной периодики Госкомиздата СССР
Тому, кто следит за публикациями определенной тематики, становится все труднее фиксировать нужную информацию. И не только потому, что нарастает поток публикаций. Сложность заключается и в том, что публикации по одной и той же проблеме (с определенным отраслевым преломлением) могут помещаться в самых различных по своему профилю научно-технических и производственных журналах.
Определенную помощь читателям в решении этой сложной задачи может оказать опережающая сигнальная информация о журнальных публикациях. Эксперимент подобного рода проводится Госкомиздатом СССР совместно с некоторыми изданиями: журналами "Советское государство и право", "Вестник сельскохозяйственной науки", "Лабораторное дело", "Механизация и автоматизация производства". Эти журналы с января 1980 года начали выпуск бюллетеней сигнальной информации, где печатаются рефераты статей, которые появятся в последующих номерах.
Итак, предположим, что вы интересуетесь кругом вопросов, связанных с гражданским правом, и решили ознакомиться с очередным, четвертым номером сигнальной информации "Советское государство и право". По внешнему виду он напомнит брошюру. В бюллетене сохранены все журнальные рубрики, под которыми публикуются рефераты тех статей, которые намечено напечатать в шестом номере журнала. Вот один из рефератов бюллетеня #1 "Советское государство и право":
"Н.В.Гудимов. Трудовая активность, дисциплина, поощрения за труд.
"Социалистическая дисциплина труда в социалистическом обществе обеспечивается методами убеждения и поощрения, а в необходимых случаях и методом принуждения в отношении недисциплинированных работников. В статье рассматриваются такие взаимосвязанные понятия, как трудовая активность и трудовая дисциплина; отмечается, что трудовая активность является обязательным условием не только повышения производительности труда, но и всестороннего развития личности, что постоянная трудовая активность работника выводит его в число передовиков производства; анализируется понятие социальной активности.
"Далее автор исследует соотношение трудовой активности и поощрений. В статье анализируется понятие первичной ячейки трудового коллектива - бригады, члены которой объединены общими целями и заняты решением конкретных производственных задач. В заключение автор высказывает предложение утвердить рекомендации о порядке и условиях применения мер морального и материального поощрения за успехи в работе".
Таким образом, заранее, а именно за два месяца до момента поступления журнала к подписчикам, и при минимальных затратах времени вы можете ознакомиться с кратким содержанием статей и определить, нужен или не нужен полный текст той или иной публикации для дальнейшей работы. Если такая необходимость возникнет, то вы можете послать заказ в редакцию журнала или в соответствующий орган научно технической информации, указав название статьи, авторов, номер журнала, в котором она будет опубликована. Копия нужной вам статьи окажется на вашем рабочем столе раньше, чем журнал получат подписчики.
Предлагаемая форма обслуживания читателей может найти очень много сторонников. И это понятно. Ведь годовой комплект любого из бюллетеней сигнальной информации практически содержит рефераты всех статей, помещенных за год в соответствующем журнале.
Эксперимент проводится и по второму варианту - заблаговременное информирование читателя о будущих статьях непосредственно на страницах журнала.
Ученый или специалист, взяв, например, в библиотеке журнал "Тракторы и сельхозмашины" #4 за 1980 год, найдет в нем раздел, в котором напечатаны рефераты статей, намеченных к публикации в июньском номере. Таким образом, за два месяца до выхода шестого номера журнала читатель знакомится не только с содержанием, но и с существом вопросов, изложенных в каждой статье. Примем на это затрачивается минимум времени. Вот один из рефератов, опубликованных в первом номере журнала "Тракторы и сельхозмашины".
"Борисов С.Г. и др. Вопросы долговечности муфт сцепления тракторов (С.Г.Борисов, С.А.Лапшин, В.Я.Юденко, В.Е. Захаров - Тракторы и сельхозмашины, 1980, #3).
"Изложены основные результаты комплексного изучения большинства условий нагружения тракторных муфт сцепления. Показано сильное влияние динамических нагрузок на надежность и долговечность их работы. Сформулированы рекомендации, позволяющие на стадии проектирования муфт сцепления заложить основы их повышенной долговечности. Библ. 10. УДК 629. 114. 2-233-192".
Если читателя заинтересовала какая-либо статья, то, сделав пометку в своей записной книжке, он может при поступлении журнала в библиотеку прочесть ее полный текст. Вместе с тем читатель имеет возможность, не дожидаясь выхода журнала, получить копию нужной ему статьи. Для этого необходимо сделать заказ в редакцию журнала или в ЦНИИТЭИ тракторосельхозмаш. Копию можно получить одновременно или даже раньше, чем журнал придет в библиотеку.
Периодичность бюллетеней сигнальной информации - 12 номеров в год. Цена одного экземпляра - 10коп., подписная цена на год - 1 рубль 20 копеек. Подписку можно оформить в любом отделении "Союзпечати".
Бюллетени имеют следующие индексы: "Советское государство и право" - 70348, "Вестник сельскохозяйственной науки" - 70345, "Механизация и автоматизация производства" - 70347, "Лабораторное дело" - 70346.
АДРЕСА РЕДАКЦИИ И ИНСТИТУТОВ. ПРИНИМАЮЩИХ ЗАКАЗЫ НА ИЗГОТОВЛЕНИЕ КОПИИ СТАТЕЙ
Редакция журнала : Орган научно-технической информации
Советское государство и право 119878, Москва, Г-19, ул.Фрунзе, 10 : Институт научной информации по общественным наукам АН СССР (ИНИОН АН СССР). Москва, ул.Красикова, 28/45
Вестник сельскохозяйственной науки 107807, ГСП, Москва, Садово-Спасская ул., 18 : Всесоюзный научно-исследовательский институт информации и технико-экономических исследований по сельскому хозяйству (ВНИИТЭИСХ). Москва, Орликов пер., 3
Лабораторное дело 117819, Москва, Научный проезд, 6 : Всесоюзный научно-исследовательский институт медицинской и медико-технической информации (ВНИИМИ). Москва, Москворецкая наб., 2а.
Механизация и автоматизация производства 103051, Москва, Трубная ул., 17 : Всесоюзный институт научной и технической информации (ВИНИТИ). 104010, г.Люберцы-10. Московская область, Октябрьский пер., 21, ком.31.
Журналы, публикующие рефераты статей
Журнал аналитической химии 117334, Москва, Воробьевское шоссе, д.47а : ВИНИТИ
Заводская лаборатория 119034, Москва, 2-й Обыдненский пер., 14 : ВИНИТИ
Известия высших учебных заведений Геология и разведка Москва, Проспект Маркса, 18, МГРИ : ВИНИТИ
Приборы и техника эксперимента 103717, ГСП, Москва, К-62, Подсосненский пер., 21, ком.31 : ВИНИТИ
Тракторы и сельхозмашины 103012, Москва, К-12, пр.Сапунова, 13/15, к.428 : Центральный научно-исследовательский институт информации и технико-экономических исследований по тракторному и сельскохозяйственному машиностроению (ЦНИИТЭИтракторосельхозмаш). 127247, Москва, Дмитровское шоссе, 165
Стоимость изготовления копии одной журнальной статьи - 3-5коп.
5/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РАБОТА С КНИГОЙ
Г.ГЕЦОВ
... Я усвоил себе привычку делать выписки из всех книг, какие я читал... мимоходом нанося на бумагу свои размышления.
Карл Маркс
Бессонный летит карандаш, кресты на полях остаются.
Лев Смирнов
Итак, библиотека, картотека, Наброски, сноски, выписки, мечты...
Валентин Берестов
... шелковинка - закладка.
Где остановился взором читатель.
Велимир Хлебников
Как будто сабли Первой Конной, Закладки - наискось и вверх!
Майя Борисова
... Я сразу же взял за правило заводить на каждую казавшуюся мне чем-либо примечательной книгу - карточку...
Н.П.Смирнов-Сокольский.
Первая встреча с книгой - дело едва ли не столь же серьезное, как знакомство с человеком: недаром истинному библиофилу свойственны подлинно человеческие пристрастия (симпатии и антипатии) к книгам.
Предварительный просмотр книги позволяет, кроме беглого знакомства с фактическим материалом, понять принцип и особенности построения издания. Многие книги имеют справочный и другой подсобный материал, который позволяет ориентироваться в содержании, а иногда вовремя отказаться от чтения или перенести его на будущее.
Знакомясь с книгой по теме, необходимой вам, следует заполнить на нее библиографическую карточку с такими (помимо основных, анкетных данных: автор, название, место и время издания) читательскими пометками на карточке:
1) о чем говорится в книге (с позиций ваших требований и запросов);
2) оценка книги с учетом ее дальнейшего использования.
Если вы решили прочесть книгу через какое-то время, то в таком случае поставьте ее библиографическую карточку в свой рабочий каталог с соответствующей пометкой, например: "прочесть после уяснения таких-то вопросов".
На всякий случай следует поинтересоваться, нет ли в книге списка опечаток, и, если он есть, перенести исправления в текст.
Чтобы отметить при чтении то, что нужно, читатели часто используют закладки из полосок бумаги. Можно усовершенствовать эти закладки так, чтобы они отмечали сразу два места в страничном блоке (рис.1).

Уже само положение закладок организует труд. Скажем, та видна сверху - отмечает место, где вы прервали чтение, закладка снизу - примечания, а помещенная сбоку дает возможность быстро обращаться к иллюстрациям, например, к картам, таблицам и тому подобному (рис.2).
На закладке можно написать номер отмечаемой страницы или пометить одну сторону закладки каким-либо значком, тогда она укажет читателю нужную страницу из двух смежных.
Существуют и более точные способы отметок нужных страниц и текстов. Например, подсчитав абзацы и строки, можно составить такой ключ: "название книги, стр.40, 3-5абз.св.". Между тем подсчитывать абзацы и строчки отнюдь не обязательно. Возьмите обычную 30-сантиметровую линейку с миллиметровой шкалой, край линейки установите на уровне верхней или нижней строки на странице. Теперь любую часть текста книги можно обозначить с помощью миллиметрового исчисления. Например, так: "110-185". Эти числа обозначат границу текста, расположенного между 110 и 185 миллиметрами линейки. Или с указанием номера страницы, вот так: "95.110-185".
Как обойтись без пометок в книге? Читатели часто задают себе этот вопрос. Ведь если не делать пометок, то работа с книгой замедлится, производительность чтения уменьшится. Между тем имеется прием, позволяющий делать записи какого угодно размера, не прикасаясь к книге карандашом. Сущность приема: при чтении вы закрываете соседнюю страницу чистым листком или полоской бумаги вровень с нижней строкой страницы и проводите черту на вкладном листке на уровне нужного отрывка (рис.3). Позже, приложив листок бумаги (разумеется, с номером страницы) к тексту, вы без труда прочтете или выпишете из книги найденный отрывок.

Вкладные листки позволяют весьма экономно и точно, лишь с помощью черточки, давать точный адрес цитат или отсылать личный комментарий к нужному месту текста источника, не требуя указания номеров абзацев ("снизу", "сверху"), подсчета строчек, "миллиметровых" пометок.
Этот прием известен, по существу, давно. К примеру, среди книг Стендаля (А.Бейля), Д.И.Менделеева имеются книги с вплетенными чистыми листками. Одна сторона таких листков предназначается для отметок, относящихся к левой, другая, оборотная,- к правой странице книги.
Читатель, желающий полнее использовать площадь вкладных листков, может сделать комментарии и отметки сразу к четырем страницам книги на одном листке. В этом случае делят листки пополам вертикальной чертой или хотя бы складывают: черта или изгиб покажут границу, за которую не должны переходить записи, относящиеся к разным страницам (рис.4).

Прозрачные вкладные листки применяют для анализа карт, диаграмм и графиков. Это позволяет не только копировать элементы изображения, но и отмечать нужные детали, снабжая изображение в книге своими комментариями. Прозрачным листком можно накрыть страницу и на нем подчеркнуть нужные строчки книжного текста. Если затем вы приложите к странице листок, в тексте окажутся ваши подчеркивания.
Вкладные листки значительно упрощают сбор данных из книг (журналов). С их помощью - даже на одном листке!- можно вести параллельные и сопоставительные записи при работе с несколькими источниками, дополняя выписки из основной изучаемой книги примечаниями, взятыми из других, а также своими размышлениями. В дальнейшем вкладные листки объединяются, классифицируются. Если для удобства сортировки по темам потребуется размножить листки, то это сделать очень просто (рис.5).

При проработке книги по ряду вопросов удобно пользоваться вкладными листками, заранее разграфленными на темы.
При заполнении таких разграфленных вкладных листков полезно сгибать их вдоль, приближая таким образом нужные вертикальные графы к тексту книги. Так же поступают и при работе с уже готовыми, заполненными вкладными листками, читая с их помощью "невыписаиные выписки".
Вы работали с литературой дома. Но вот вам понадобилось зайти в библиотеку. Вносить туда личные книги, как известно, строжайше запрещено. Но, взяв с собой вкладные листки, вы как бы проникаете в библиотеку со своими книгами. Или, встретив в библиотеке нужную книгу, читаете ее, делая пометки на вкладных листках. Дома вы сможете перенести пометки с листков на страницы собственной книги.
Оставлять все листки в книге после ее чтения не следует: книга разбухнет. По мере накопления листков их помещают в тематические картотеки, конверты, папки. Естественно, что на таких вкладных листках должен быть помечен источник. Чтобы не указывать названия книги, иногда очень длинного, и выходных данных, читатель может присвоить изданию произвольный шифр. Тогда на листках фиксируются только этот шифр и номера страниц. Предположим, книга имеет шифр 457; им помечают все листки и рядом проставляют номера страниц (457-34; 457-41; 457-169).
Если вы работаете над рядом источников или готовитесь выступить перед аудиторией, можно вкладные листки или обычные закладки пронумеровать. В планах к реферату, конспекту или устному выступлению указывают, в какой последовательности будут использоваться места, не отмеченные закладками. (При этом не важно, из какой книги и в какой очередности взяты материалы). Перед вами на столе или на кафедре лежат книги с пронумерованными закладками. Согласно своему плану, вы открываете книги в порядке нумерации закладок. Конечно, за первой книгой может следовать последняя, затем опять первая и так далее.
Вкладные листки не только не отвергают пометок на полях самих книг, но даже могут их существенно дополнить. Тут уже проявится способность листков к оперативной систематизации. В этом случае книжные отчеркивания просто копируют на вкладных листках, тем самым как бы вынимая пометки нз книг. На листках хотя бы коротко записывают тематические признаки взятых из книг извлечений или обозначают номерами сами темы. Получается набор листов, которые легко поддаются перетасовке и систематизации.

Московская фирма "Восход" уже выпускает пеналы с вкладными полосками ("Закладки для книг". Артикул МГ-087-01-285, ТУ-81-01-349-75, цена 20коп.).
Пеналы удобны тем, что их можно ставить на полках рядом с книгами.
Дополняют пометки в книгах также таблицы с перечнем тематических признаков в соответствующих графах. Пользуясь графами с номерами страниц, читатель всегда быстро найдет нужное место. Конечно, подобные таблицы могут отсылать не к одной, а к ряду книг.
Читая книгу, полезно четко разделять материал на освоенный и неосвоенный, на знакомый и незнакомый. А значит, нужен и учет пройденного и намеченного к проработке.
Как выделять прочтенное, отмечать особо важное, как планировать работу, ее тактику? Для регистрации и учета проработки книг полезно употреблять таблицы чисел. На обычной машинописной странице размещается 1000 порядковых номеров, которые будут обозначать страницы книги. Можно также воспользоваться таблицами, напечатанными на стандартных библиографических карточках, где умещаются сотни номеров страниц (рис.6). На бланке-таблице вы можете отмечать различными метками номера проработанных страниц. Кружок, скажем, будет означать, что эту страницу более читать не следует, подчеркнутый номер - что данная страница содержит особо нужный материал, и т.д. Вся эта гамма меток позволяет кратко и быстро вести разнообразную регистрацию работы и учет чтения.

Если к тому же на бланке вы пометите, с какой целью читалась книга, то, возвратившись к ней позже, всегда сможете понять, что именно уже было прочитано и какая работа вам еще предстоит.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
7/80
РАБОТА ЗА ПИСЬМЕННЫМ СТОЛОМ
В.ФЕДОТОВ (г.Ленинград)
Письменный стол сам по себе лишь часть того, что понимается под рабочим местом в практике НОТ. В понятие рабочего места, помимо письменного стола, входят предметы мебели (книжные полки, шкафы для рабочих материалов).
Каким же образом совершенствовать рабочее место для умственного труда? В первую очередь это касается мебели: письменного стола, полок, шкафов. Размеры этой мебели должны соответствовать характеру выполняемой работы: величина поверхности стола - размеру рабочих материалов, емкость полок и ящиков - объему хранящихся книг, дел, каталогов и т.д. Самые несложные приемы помогут увеличить рабочую поверхность стола, более рационально использовать емкости полок и ящиков с целью раздельного хранения материалов.

Очень важно выяснить, как мебель рабочего места соответствует вашим антропометрическим данным. На это, как правило, мало обращают внимания. Между тем размеры выпускаемой мебели приблизительно соответствуют данным некоего "среднего" человека. Для полноценной работы этого недостаточно. Поэтому стоит соблюдать приведенные нормативы, чтобы повысить эффективность труда и сохранить здоровье.
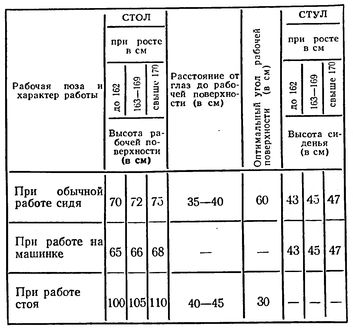
Совершенствуется рабочее место и за счет оснащения техническими средствами, различными приспособлениями. Практика показывает, что именно работники умственного труда используют мало средств из технического арсенала, позволяющего повысить эффективность труда. И это происходит совсем не потому, что эти средства не всегда доступны по своей стоимости или пока еще дефицитны. Основная причина в непонимании тех преимуществ, которые могут быть получены. Ведь почти не используется в работе и то, что вполне доступно: не так уж часто на письменном столе можно увидеть такие простейшие канцелярские принадлежности, как "дырокол", сшиватель для бумаг, машинка для точки карандашей. Тратится время на расчеты по бумажке, вместо того чтобы использовать микрокалькулятор. Имея фотоаппарат, почти никто не использует его для микрофильмирования.
Как это ни парадоксально, но многие вообще плохо представляют, какие технические средства и приспособления могут быть использованы в личной работе. Вот эти средства и приспособления.
КАНЦЕЛЯРСКИЕ ПРИНАДЛЕЖНОСТИ: набор шариковых ручек 2-3 цветов на подставке, цанговые и оформительские карандаши, перфоратор ("дырокол"), машинка для точки карандашей, сшиватель для бумаг, ложемент для мелких канцелярских принадлежностей, лотки для бумаги, пюпитр.
ПИШУЩАЯ МАШИНКА.
КАРТОТЕЧНАЯ ТЕХНИКА: перфокарты, рейтеркарты, блок каталожных ящиков, коробки для хранения перфокарт, селекторы для перфокарт.
АППАРАТУРА ДЛЯ МИКРОФИЛЬМИРОВАНИЯ И ЧТЕНИЯ МИКРОФИЛЬМОВ: фотоаппарат, настольная репродукционная установка, набор удлинительных колец, реле времени, микрофот (при отсутствии специального аппарата для чтения микрофильмов может быть использован фотоувеличитель или бытовой диапроектор), коробки для хранения микрофильмов.
ДИКТОФОН (вместо диктофоне можно использовать магнитофон).
СЧЕТНЫЕ ПРИСПОСОБЛЕНИЯ: логарифмическая линейка, микрокалькулятор.
ПРИНАДЛЕЖНОСТИ ДЛЯ ЧЕРЧЕНИЯ: чертежная доска с плавающей рейсшиной, приспособление для крепления чертежной доски, чертежные инструменты.
Здесь перечислены многие технические средства и приспособления. Конечно, не имеет смысла обзаводиться всеми ими без исключения. Выбор средств и приспособлений производится в соответствии с характером выполняемой работы.
К оснащению рабочего места относится упорядочение его электропитания и коммутация аппаратуры радиокомплекса. Этот вопрос возник сравнительно недавно, так как долгое время единственным потребителем тока на письменном столе была настольная лампа. Теперь же, в дополнение к ней, одновременно могут использоваться еще три-четыре прибора (установка для микрофильмирования, микрофот, магнитофон, монтажный столик). Всем знакома картина, когда стол загроможден проводами и для включения одного прибора другой надо отключить от сети, при этом, конечно, теряется время на поиски провода-удлинителя. Одним словом, возникает масса неудобств. Наилучший выход здесь в создании постоянной системы включения всех используемых приборов в сеть независимо один от другого.
Новым элементом совершенствования рабочего места стала также и коммутация радиокомплекса. Для многих профессий, чаще всего гуманитарных, радиоприемник, проигрыватель, магнитофон стали приборами, непосредственно связанными с работой. Постоянно возникает необходимость их взаимного использования: запись на магнитофон радиопередач, перезапись с одной магнитной пленки на другую и т.д. Но для этого приборы должны подсоединяться один к другому, на что уходит много времени. Процесс значительно ускоряется, если связать все используемые аппараты в единый блок с помощью специального переключателя, выпускаемого сейчас промышленностью.
Когда решены вопросы оснащения рабочего места, следует подумать о его планировке. Человек умственного труда не сидит в позе роденовского мыслителя: он пишет, печатает на машинке, ищет нужные материалы на книжных полках и в картотечных ящиках. Все это непрерывная цепь разнообразных движений, простых и сложных, однократных и часто повторяющихся, требующих внимания или выполняемых автоматически. Рациональны они или нет, над этим никто, как правило, не задумывается. Считается, что разговор о рациональности движений не заслуживает внимания, поскольку это не влияет на эффективность работы. На самом деле если проанализировать свои движения, то обнаруживается, что большая часть из них настолько часто повторяется, что даже небольшой выигрыш на каждом вырастает в ощутимую экономию рабочего времени. Для умственного труда продуманная планировка рабочего места имеет, кроме всего прочего, еще и то значение, что она несет с собой высвобождение внимания, обеспечивая известную "автоматичность" определенной части рабочих движений.
Итак, требованиями к планировке рабочего места следует считать: ДОСЯГАЕМОСТЬ всех рабочих материалов и их ОБОЗРЕВАЕМОСТЬ, а также ПОСТОЯННУЮ ГОТОВНОСТЬ к работе всех технических средств и приспособлений. При желании на сравнительно небольшом пространстве можно разместить гораздо больше материалов, чем это может показаться вначале. Для этого нужно только немного смелости, чтобы отказаться от привычного вида своего письменного стола и действительно позаботиться о создании удобств для работы.
Сделать все рабочие материалы досягаемыми можно также за счет рационального взаимного расположения различных предметов рабочей мебели. Наиболее идеальна такая их компоновка, когда они находятся в непосредственной близости один от другого, образуя как бы единое целое.
Необходимо взять за правило располагать материалы таким образом, чтобы каждый отдельный предмет был постоянно виден. Для этого используются коробки, лотки, ложементы, футляры, конверты, а в шкафах и на полках съемные или постоянные разделители. Для ускорения поиска все материалы нужно каким-то образом обозначать.
Есть еще одна особенность использования технических средств в процессе умственного труда. Она состоит в том, что ни одно из приспособлений никогда не находится в работе постоянно. Отсюда обычная картина, когда одно за другим что-то "свертывается" и убирается со стола, а другое приспособление достается и подготавливается к работе. Потери времени при этом значительны. Весьма наглядно это видно на примере с микрофильмированием: одно дело, когда репродукционная установка готова к работе, остается только положить материал для съемки под аппарат и нажать кнопку. На это уйдет 10-15 секунд. И совсем другое дело, когда нужно встать, достать аппарат, укрепить его, наладить освещение и т.д.; в этом случае для съемки потребуются уже не несколько секунд, а 15-20 минут. Определенные затраты времени связаны с подготовкой практически всех используемых предметов оргтехники. Поэтому очень важно, чтобы все технические средства, которыми оснащено рабочее место, находились в постоянной готовности. Достигается это различными путями. Главные из них - это монтаж (размещение) аппаратуры и приспособлений непосредственно на рабочем месте, устройство поворотных приспособлений, позволяющих приблизить к себе нужный предмет на время работы, коммутация электроприборов и радиокомплекса.
Совершенствование рабочего места всегда включает в себя создание благоприятных ГИГИЕНИЧЕСКИХ условий. Как правило, об этом мало кто думает, когда речь идет об умственном труде. Сложилось убеждение, что отклонения от норм здесь настолько невелики, что они не могут привести к каким-либо неприятным последствиям. Но это - заблуждение. При длительном воздействии неблагоприятные гигиенические условия могут сказаться и на работоспособности и на здоровье.
Подробные рекомендации по вопросам гигиены рабочих (помещений, в том числе и для умственного труда, содержатся во многих справочниках м руководствах. Упомянем лишь о нормах освещенности. Выражаются они в условных единицах - люксах и приводятся в большинстве случаев примерно в таком виде: чтение, письмо, печатание на машинке - 400 люксов, черчение - 700, работа с каталогами - 200, поиск материалов на полках - 100 люксов. Казалось бы, все ясно и просто: бери и пользуйся. Но оказывается, что эти нормы практически ничего не дают, так как замерить освещенность можно лишь с помощью специальных приборов. Для того, чтобы хотя бы ориентировочно судить об уровне освещенности, нами на основании соответствующих замеров была подготовлена таблица, которая дает представление о зависимости между освещенностью, силой источника света и расстоянием до него.

И, наконец, о тех ПСИХОЛОГИЧЕСКИХ условиях, которые должны быть созданы на рабочем месте. Из них главнейшим следует считать его изолированность. Степень изолированности - один из весьма существенных элементов оценки рабочего места для умственного труда. Разные люди относятся к этому по-разному: одни вообще не в состоянии работать "на виду", другие утверждают, что для них это совершенно безразлично. Фактически же это сказывается на состоянии и работоспособности любого человека, и тот, кто считает, что безразличен к окружающей его обстановке, просто не подозревает, сколько нервной энергии ему приходится затрачивать для компенсации неблагоприятных условий.
При работе в общей комнате возможно создать ощущение уединенности. Этот психологический эффект достигается самым несложным путем: за счет соответствующей расстановки мебели, обеспечивающей определенную изолированность рабочего места, использования небольших перегородок, ширм или занавесей, позволяющих как-то отгородить стол.
***
Пока еще скромно - "логарифмическая линейка, микрокалькулятор".
8/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РАБОТА С ЖУРНАЛОМ И ГАЗЕТОЙ
Г.ГЕЦОВ
При работе с журналами полезно использовать небольшие библиографические карточки двоякого рода. Одни - для учета самих номеров журналов и целеустремленного просмотра их годовых комплектов.
Карточки учета работы по отдельным статьям будут иметь иной вид. На их лицевую сторону заносят название статьи и тему. На обороте - сведения, раскрывающие содержание публикации, а также собственные замечания о предполагаемом использовании статьи.

Иногда при просмотре журналов приходится искать материалы только под углом зрения интересующей темы и проходить мимо других интересных в полезных публикаций. Конечно, в этот момент читать их совсем не обязательно, и все же такие публикации следует как-то фиксировать. Тут важен продуманный учет того, что прочитано, просмотрено и намечено к проработке. Организовать его просто: на карточках учета журналов следует регистрировать темы, интересующие вас. Но при этом важно всегда точно указать, с какой целью просматривается журнал. Проработка номеров отмечается значками. Так, на карточке ясно показано, какие из номеров журнала "Наука и жизнь" целиком просмотрены ("П"), в каких выделены материалы по теме "Охрана природы" ("О").
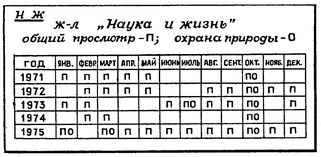
Название журнала на карточке учета так же, как и ссылки на вырезках и выписках из журналов, можно указывать с помощью шифров, образуемых из первых букв названий журналов, скажем, "НЖ" - "Наука и жизнь", "ТМ" - "Техника - молодежи" и так далее.
Если содержание той или иной статьи не раскрывается ее названием, то на карточке дают подзаголовок. Допустим, статья названа "Прорыв в будущее" (НЖ, 1979, 4). Всего два слова - "Первая пятилетка" приоткрывают тему.
Фиксируя данные об отдельных статьях, надо заранее представлять себе, что со временем эти карточки придется как-то рассортировывать по темам. Для этой цели, конечно, при большом объеме работы, потребуются ящики, а быть может, и целые блоки ящиков, а также и особая организация своего рабочего каталога (о ней мы расскажем в дальнейшем).
Уже в самом начале процесса организованной работы надо использовать элементарную оргтехническую оснастку. Карточки учета журналов и статей можно накапливать и хранить в конвертах. Конверты иногда наклеивают на плотное основание - бланк, чтобы удобнее устанавливать в ящик.
Теперь о работе с газетой. С нею мы встречаемся много раз на протяжении дня. Берем свежий номер рано утром из почтового ящика, просматриваем за завтраком. Заглядываем в газету во время поездки на работу. Иногда читаем материалы номера в обеденный перерыв. Вечером вновь раскрываем газету, пусть только с целью посмотреть программу телепередач.
Но чтобы не терять зря времени, не топтаться на месте, стоит научиться быстро удалять из поля своего зрения уже прочтенное. Поэтому при чтении газет, как и в любой работе, важны осознанная цель и использование приемов, делающих чтение целеустремленным.
Как же работают с газетами умудренные опытом читатели? Поэтапно. Первый этап - это беглый просмотр, по существу, только чтение заголовков. Его цель: быстро определить нужные и интересные материалы. Их отмечают разными значками и надписями. Конечно, при этом не только не исключается, но и обязательно подразумевается хотя бы частичное чтение отдельных публикаций.
Полезно научиться распознавать материал по заготовкам и рубрикам. Рубрики в сопоставлении с заголовками и подзаголовками еще до чтения помогают правильно схватывать суть публикации и вести убыстренный поиск нужной темы.
На газетных страницах легко тренировать свое умение отбирать главное, расчленять текст вехами на отдельные смысловые части. В отличие от книг в газетах всегда можно и нужно подчеркивать, отчеркивать, писать на полях, делать вырезки. Повседневные упражнения в схватывании сути газетного материала помогут выработать умение мгновенно видеть то, что нужно, быстро отбирать интересное, легко различать полезное в калейдоскопе газетной информации. Проверьте себя: если при попытке выделить в статье главное оказываются подчеркнутыми чуть ли не все строки - это значит, что статья не понята.
На втором этапе размеченную газету просматривают более тщательно. Здесь полезно пользоваться библиографической карточкой учета, похожей на ту, которая оформляется при работе с журналом. Только у газетной карточки 31 вертикальная колонка (по числу дней месяца) и 12 горизонтальных строчек по числу месяцев.

Стопки газет с отмеченными статьями громоздки. Подобранный материал трудно поддается классификации и распределению по темам. Иное дело вырезки. Они компактны, занимают мало места, их легко сортировать и классифицировать.
Особое значение имеют вырезки из еженедельника "Книжное обозрение". Они помогают накапливать библиографические сведения о литературе. Есть смысл подобные вырезки наклеивать на библиографические карточки.
Процесс подготовки вырезок можно "механизировать", используя вместо ножниц тонкую металлическую линейку или лезвие безопасной бритвы.
При распределении вырезок по темам могут быть использованы лотки для бумаг, а также картотеки для вертикального хранения документов.
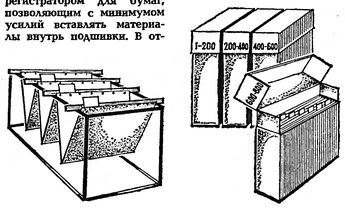
Для хранения вырезок можно использовать также разного рода коробки. Считается целесообразным приклеивать вырезки с особо нужными и часто используемыми материалами на листы плотной бумаги одного формата.
Мелкие вырезки помещают в конверты или коробки таких размеров, которые позволяют не нарушать заведенный порядок расположения вырезок. Листы бумаги с наклеенными на них вырезками имеет смысл в некоторых случаях скреплять скоросшивателем, правда, удобнее пользоваться регистратором для бумаг, позволяющим с минимумом усилий вставлять материалы внутрь подшивки. В отдельных случаях подборки вырезок переплетают, а иногда вклеивают в книги, дополняя их содержание новыми, свежими данными.
Но мыслимо ли найти в тысячах кусочков из разных газет то, что может потребоваться через месяц, год? Да, это возможно. Для этого используются определенные приемы.
Прежде всего с самого начала стоит позаботиться о систематизации вырезок по разделам. По мере роста массива вырезок следует уточнять их рубрики, вводить дополнительные рубрики для детализации, регистрировать номера вырезок в картотеках и в поисковых регистраторах - алфавитных, телефонных книжечках, где можно записывать названия тем и номера соответствующих вырезок.
Поисковая алфавитная картотека вырезок организуется просто, если вы пронумеровали все вырезки по порядку хотя бы независимо от тем. Тогда на карточках небольшого (скажем, 6*9 сантиметров) формата отмечают возможные тематические признаки той или иной вырезки, снабжают номером, под которым значится вырезка, и помещают в ящик по алфавиту признаков.

Предположим, вас давно интересует тема "Соединение металлов при помощи взрыва". Прежде всего стоит обратиться к журнальным публикациям. Вот одна из них: "Взрыв: энергия, машина, инструмент", "Наука и жизнь", 1973г. #4. Но вам хочется найти и последние газетные публикации по этой теме. Если металловедение - предмет вашего интереса и вы при чтении регистрируете тематические признаки статей в поисковой картотеке, то на каждую из тем - "сварка", "ковка", "упрочнение металлов" в ящике с алфавитным перечнем признаков найдете немало карточек. Первая ведущая тема "взрыв" конкретизирует поиск, так как в блоке с этой темой среди других карточек найдется искомая под номером, скажем, 4213, которую вы завели на вырезку статьи "Упрочняет... взрыв" ("Правда", 19.05. 80г.). Один и тот же номер - 4213 на тематических поисковых карточках других рубрик картотеки "сварка", "ковка" определит успех поиска и поможет уточнить содержание материала. Если вы вспомните, что одна из технологий сварки металла с помощью взрыва была разработана в Ташкенте, то сможете облегчить поиск, найдя карточку с признаком "Ташкент", даже не заглядывая в рубрики "сварка", "ковка". Подобная картотека помогает ценной информации не затеряться, продлевает ее жизнь.
На полях рядом с будущей вырезкой следует записать и ссылку на название газеты. Не следует указывать полное наименование газеты: "Правда", "Комсомольская правда", "Социалистическая индустрия". "П", "КП", "СИ" - это ваши шифры газет.
Такова техника самостоятельной работы с газетными вырезками. Нужно иметь в виду, что в крупных городах действуют специальные справочно-информационные службы - отделы газетно-журнальных вырезок. Подобный отдел при производственном объединении "Мосгорсправка" имеет тысячи абонентов и отправляет заказчикам в год миллионы вырезок.
БЮРО СПРАВОК
Службы газетно-журнальной информации работают в столицах республик, а также в крупных промышленных центрах страны, например, на территории РСФСР - в Ленинграде, Омске, Новосибирске, Свердловске, Хабаровске, Ярославле - всего в 32 городах.
За справками об условиях подписки и возможности абонирования можно обращаться в Главное управление непроизводственных бытовых услуг Министерства бытового обслуживания населения РСФСР по адресу: 103009, Москва, К-9, ул.Станиславского, 7.
Москвичей обслуживает отдел газетно-журнальной информации производственного объединения "Мосгорсправка". Его адрес: 103009, Москва, К-9, ул.Горького, 5/6.
Объединение справочно-информационных служб Московской области ("Мособлбытсправка", 109088, Москва, Шарикоподшипниковская ул., 40) обслуживает также Калининскую, Костромскую и Ярославскую области. Такие службы имеются также и в ряде других областей, например, в Ленинградской, Тульской, Белгородской, Саратовской, Горьковской, Томской, Омской, Хабаровской; в Башкирии и в Ставропольском, Красноярском, Алтайском краях.
Абоненты этого отдела могут заказывать вырезки по всем периодическим изданиям Советского Союза на год, месяц или использовать разовую подписку на одну тему. Нужно довольно точно определить тему своей подписки. Скажем, не вообще "Проблемы экономики", а "Эффективность", "Качество", "Производительность труда" и т.п.
Условия подписки зависят от тем. Вырезки высылаются подписчикам по почте три раза в месяц.
Отделы газетно-журнальной информации получают всю периодическую печать - центральную и областную, газеты краевых городов - приблизительно 250 наименований газет в необходимом количестве экземпляров, выписывают политические, социально - экономические, научно-технические и популярные журналы, экспресс-информацию - всего около 70 наименований.
Всего справочно-информационные службы РСФСР отправляют своим абонентам около 40 миллионов вырезок в год.
***
40млн. без Интернета!
3/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ? ВАШ РАБОЧИЙ КАТАЛОГ
Г.ГЕЦОВ
Когда приходится иметь дело с большим объемом литературы, трудно обойтись без собственного каталога - систематизированного перечня источников. Такой каталог организует и предельно облегчает каждодневное общение с литературой, делает работу с ней целеустремленной, быстрой и в то же время простой. В чем же специфика каталога для индивидуальной работы? Личный рабочий каталог преследует особые цели, и его карточки источников могут содержать много дополнительных данных по сравнению с библиотечными каталогами. Здесь могут быть сведения о степени пригодности источника для данной работы, о предполагаемых путях его использования, о номерах страниц, откуда следует сделать выписки. Здесь же отражаются и этапы чтения. На карточках записывают и отзывы о содержании источника. Это уже элементы аннотации. Если книга имеется в домашней библиотеке, на карточке делают пометки о месте ее хранения (шкаф, полка), о том, кому на время была отдана данная книга. Каталог может отражать не только книги личной библиотеки, но и те, что вас интересуют в общественных библиотеках, поэтому обязательно на таких карточках проставлять библиотечные шифры.
Иногда на карточки заносят полные имя и отчество автора, даже его адрес и телефон: читатель бывает заинтересован во встречах и переписке с автором.
Иные карточки вашего каталога будут фиксировать не сами книги или статьи, а только части их, скажем, главы или даже отдельные страницы. Одним словом, записи на карточках тематически разнородны и весьма индивидуальны.
Какие же источники следует использовать в каталоге? Пути поиска источников для разработки той или иной темы или знакомства с ней весьма разнообразны: тут и рекомендации специалиста, и библиографические справочники, и каталоги библиотек, и отдельные списки литературы, приводимые в статьях по изучаемой и смежным темам.
Если число источников велико и работа длится долго, то трудно сразу определить степень пригодности того или иного материала для работы. Поэтому, кроме нужных, в каталог включают и те источники, которые при первоначальном ознакомлении были признаны непригодными. Однако на подобных карточках должно быть отмечено ваше мнение об источниках - такая информация пригодится в дальнейшей работе. Например: "Слабо. Более не читать!", "Плохое повторение книги такой-то", "Проработать позднее, после уяснения вопроса". Как видите, характеристики должны быть определенными, мотивированными. Но в оценке литературы не нужно проявлять поспешность. Книга, сегодня как будто бы ненужная, со временем - после изучения других источников - подчас становится полезной.
По мере роста количества карточек и объема вашей работы каталог потребует определенной организации. Например, он может состоять из следующих отделов: тематического, алфавитного, вспомогательного.
Отделы каталога расчленяют рубриками (названиями, объединяющими группы карточек по какому-то общему для них признаку).
ТЕМАТИЧЕСКИЙ ОТДЕЛ. Этот отдел легко вместит любое количество рубрик, профессиональных и любительских. Тем самым появится возможность вести учет собственных книг, а также учебной, производственной и научной литературы, которую используете или хотели бы пока только зарегистрировать, имея в виду дальнейшую работу с ней. В последнем случае особенно важно уточнить на карточках содержание, отметить именно то, что вам может понадобиться. Например, подбирая литературу, на карточке книги авиаконструктора А.Яковлева "Записки конструктора" (М., Политиздат, 1979), вы укажете из сорока разделов книги на один, особенно интересующий вас раздел, "Испытатели".
Если вы, например, изучаете жизненный и творческий путь ученого, то картотеку удобнее составлять по датам его жизни. Когда же предметом ваших занятий становится тема более обширная, скажем, история техники, следует подчинить картотеку разделам этой большой темы (например, история техники в России, Польше, Чехословакии, возникновение в этих странах в том или ином веке отдельных направлений научной мысли, отраслей техники и т.д.).
Рубрики тематического отдела призваны организовать умственный труд. Часто в процессе систематизации литературных источников и материалов вырисовывается план будущей работы или, наоборот, изменяется намеченная последовательность изучения темы. Случается, что рубрики личного каталога помогают наметить основные главы будущей книги. Ведь изучение источников ведется под углом зрения темы, сформулированной рубрикой. В этом - значение, но и ответственность рубрик. Поэтому нельзя процесс организации рубрик выпускать из-под контроля.
Конечно, вначале, не зная еще глубоко материала и объема работы над темой, трудно провести наиболее логичную и точную систематизацию. Как правило, только в результате длительной работы рубрики становятся необходимым и естественным разделением общей темы.
Иногда в начале работы удается наметить лишь несколько основных рубрик, не прибегая к дробному членению, и только в процессе длительной работы над темой, когда материал будет усвоен, можно сделать более детальную разбивку. В это время рубрики обычно легко формулируются.
Как бы то ни было, но на всех этапах работы надо постоянно стремиться сблизить разбивку тематического отдела каталога с главными направлениями темы, постепенно добиваясь наиболее точных и отражающих существо вопроса формулировок.
Внутри каждой рубрики расположение карточек подчиняется определенному принципу, например, алфавитному. Карточки тематического отдела подвижны: их вынимают для работы и перегруппировок, их применение отражает ход работы над данным источником. Здесь же уточняется и местонахождение материала - проставляются страницы с чем-то важным. В карточке полезно указать, какие разделы (главы, параграфы, страницы и даже части их) и для какой цели надо будет проработать и когда.
Иногда карточки тематического отдела в процессе первоначальных этапов работы (просмотра литературы - подборе источников и предварительного их изучения) кочуют из одной рубрики в другую. Ведь по одному названию книги, статьи не всегда можно точно представить их содержание. Более того, иногда одну и ту же карточку приходится размножать в соответствии с главами или темами самой книги или статьи. Получившиеся таким образом дублетные карточки (кстати, они могут быть и не копиями основных, а лишь упрощенными - ссылочными) займут место в соответствующих рубриках.

Когда в процессе работы будут сформированы постоянные тематические рубрики каталога, их полезно пронумеровать. Номера рубрик проставляют и на карточках. Тогда карточки получат обратный адрес, их легко после работы возвратить в нужную рубрику.
АЛФАВИТНЫЙ ОТДЕЛ содержит карточки строго по алфавиту фамилий авторов или названий и позволяет быстро найти любой источник. На карточках этого отдела иногда делают пометки, указывающие, в каких рубриках следует искать тот или иной источник, поэтому карточки алфавитного отдела всегда должны быть на своих местах.
ВСПОМОГАТЕЛЬНЫЙ ОТДЕЛ. Здесь главная рубрика - шифровальная, где читатель фиксирует свои шифры источников. В других рубриках отражаются условные обозначения, принятые на короткий период, накапливаются и группируются карточки с различной целью: для работы в библиотеке, планирования, изучения источников или просто для дальнейшей обработки самих карточек.
В каталоге полезно регистрировать работу не только с книгами, но и со статьями из периодической печати. Поэтому в каталоге может появиться отдел "Периодические и продолжающиеся издания".
В следующей беседе мы продолжим рассказ о шифрах и вспомогательных средствах при работе с собственным каталогом.
[Рекомендуем читателям прочитать книгу Г.Гецова "Учиться работать с политической литературой" (Москва, "Московский рабочий". 1979). Эта работа отмечена Дипломом II степени и денежной премией на XVI Всесоюзном конкурсе на лучшее произведение научно-популярной литературы, который ежегодно проводится Всесоюзным обществом "Знание". В книге обобщается опыт работы пропагандистов, идет рассказ о методике и технических приемах работы с политической литературой].
РАБОТА ЗА ПИСЬМЕННЫМ СТОЛОМ
В.ФЕДОТОВ (г.Ленинград)
Письменный стол сам по себе лишь часть того, что понимается под рабочим местом в практике НОТ. В понятие рабочего места, помимо письменного стола, входят предметы мебели (книжные полки, шкафы для рабочих материалов).
Каким же образом совершенствовать рабочее место для умственного труда? В первую очередь это касается мебели: письменного стола, полок, шкафов. Размеры этой мебели должны соответствовать характеру выполняемой работы: величина поверхности стола - размеру рабочих материалов, емкость полок и ящиков - объему хранящихся книг, дел, каталогов и т.д. Самые несложные приемы помогут увеличить рабочую поверхность стола, более рационально использовать емкости полок и ящиков с целью раздельного хранения материалов.

Очень важно выяснить, как мебель рабочего места соответствует вашим антропометрическим данным. На это, как правило, мало обращают внимания. Между тем размеры выпускаемой мебели приблизительно соответствуют данным некоего "среднего" человека. Для полноценной работы этого недостаточно. Поэтому стоит соблюдать приведенные нормативы, чтобы повысить эффективность труда и сохранить здоровье.

Совершенствуется рабочее место и за счет оснащения техническими средствами, различными приспособлениями. Практика показывает, что именно работники умственного труда используют мало средств из технического арсенала, позволяющего повысить эффективность труда. И это происходит совсем не потому, что эти средства не всегда доступны по своей стоимости или пока еще дефицитны. Основная причина в непонимании тех преимуществ, которые могут быть получены. Ведь почти не используется в работе и то, что вполне доступно: не так уж часто на письменном столе можно увидеть такие простейшие канцелярские принадлежности, как "дырокол", сшиватель для бумаг, машинка для точки карандашей. Тратится время на расчеты по бумажке, вместо того чтобы использовать микрокалькулятор. Имея фотоаппарат, почти никто не использует его для микрофильмирования.
Как это ни парадоксально, но многие вообще плохо представляют, какие технические средства и приспособления могут быть использованы в личной работе. Вот эти средства и приспособления.
КАНЦЕЛЯРСКИЕ ПРИНАДЛЕЖНОСТИ: набор шариковых ручек 2-3 цветов на подставке, цанговые и оформительские карандаши, перфоратор ("дырокол"), машинка для точки карандашей, сшиватель для бумаг, ложемент для мелких канцелярских принадлежностей, лотки для бумаги, пюпитр.
ПИШУЩАЯ МАШИНКА.
КАРТОТЕЧНАЯ ТЕХНИКА: перфокарты, рейтеркарты, блок каталожных ящиков, коробки для хранения перфокарт, селекторы для перфокарт.
АППАРАТУРА ДЛЯ МИКРОФИЛЬМИРОВАНИЯ И ЧТЕНИЯ МИКРОФИЛЬМОВ: фотоаппарат, настольная репродукционная установка, набор удлинительных колец, реле времени, микрофот (при отсутствии специального аппарата для чтения микрофильмов может быть использован фотоувеличитель или бытовой диапроектор), коробки для хранения микрофильмов.
ДИКТОФОН (вместо диктофоне можно использовать магнитофон).
СЧЕТНЫЕ ПРИСПОСОБЛЕНИЯ: логарифмическая линейка, микрокалькулятор.
ПРИНАДЛЕЖНОСТИ ДЛЯ ЧЕРЧЕНИЯ: чертежная доска с плавающей рейсшиной, приспособление для крепления чертежной доски, чертежные инструменты.
Здесь перечислены многие технические средства и приспособления. Конечно, не имеет смысла обзаводиться всеми ими без исключения. Выбор средств и приспособлений производится в соответствии с характером выполняемой работы.
К оснащению рабочего места относится упорядочение его электропитания и коммутация аппаратуры радиокомплекса. Этот вопрос возник сравнительно недавно, так как долгое время единственным потребителем тока на письменном столе была настольная лампа. Теперь же, в дополнение к ней, одновременно могут использоваться еще три-четыре прибора (установка для микрофильмирования, микрофот, магнитофон, монтажный столик). Всем знакома картина, когда стол загроможден проводами и для включения одного прибора другой надо отключить от сети, при этом, конечно, теряется время на поиски провода-удлинителя. Одним словом, возникает масса неудобств. Наилучший выход здесь в создании постоянной системы включения всех используемых приборов в сеть независимо один от другого.
Новым элементом совершенствования рабочего места стала также и коммутация радиокомплекса. Для многих профессий, чаще всего гуманитарных, радиоприемник, проигрыватель, магнитофон стали приборами, непосредственно связанными с работой. Постоянно возникает необходимость их взаимного использования: запись на магнитофон радиопередач, перезапись с одной магнитной пленки на другую и т.д. Но для этого приборы должны подсоединяться один к другому, на что уходит много времени. Процесс значительно ускоряется, если связать все используемые аппараты в единый блок с помощью специального переключателя, выпускаемого сейчас промышленностью.
Когда решены вопросы оснащения рабочего места, следует подумать о его планировке. Человек умственного труда не сидит в позе роденовского мыслителя: он пишет, печатает на машинке, ищет нужные материалы на книжных полках и в картотечных ящиках. Все это непрерывная цепь разнообразных движений, простых и сложных, однократных и часто повторяющихся, требующих внимания или выполняемых автоматически. Рациональны они или нет, над этим никто, как правило, не задумывается. Считается, что разговор о рациональности движений не заслуживает внимания, поскольку это не влияет на эффективность работы. На самом деле если проанализировать свои движения, то обнаруживается, что большая часть из них настолько часто повторяется, что даже небольшой выигрыш на каждом вырастает в ощутимую экономию рабочего времени. Для умственного труда продуманная планировка рабочего места имеет, кроме всего прочего, еще и то значение, что она несет с собой высвобождение внимания, обеспечивая известную "автоматичность" определенной части рабочих движений.
Итак, требованиями к планировке рабочего места следует считать: ДОСЯГАЕМОСТЬ всех рабочих материалов и их ОБОЗРЕВАЕМОСТЬ, а также ПОСТОЯННУЮ ГОТОВНОСТЬ к работе всех технических средств и приспособлений. При желании на сравнительно небольшом пространстве можно разместить гораздо больше материалов, чем это может показаться вначале. Для этого нужно только немного смелости, чтобы отказаться от привычного вида своего письменного стола и действительно позаботиться о создании удобств для работы.

Сделать все рабочие материалы досягаемыми можно также за счет рационального взаимного расположения различных предметов рабочей мебели. Наиболее идеальна такая их компоновка, когда они находятся в непосредственной близости один от другого, образуя как бы единое целое.

Необходимо взять за правило располагать материалы таким образом, чтобы каждый отдельный предмет был постоянно виден. Для этого используются коробки, лотки, ложементы, футляры, конверты, а в шкафах и на полках съемные или постоянные разделители. Для ускорения поиска все материалы нужно каким-то образом обозначать.
Есть еще одна особенность использования технических средств в процессе умственного труда. Она состоит в том, что ни одно из приспособлений никогда не находится в работе постоянно. Отсюда обычная картина, когда одно за другим что-то "свертывается" и убирается со стола, а другое приспособление достается и подготавливается к работе. Потери времени при этом значительны. Весьма наглядно это видно на примере с микрофильмированием: одно дело, когда репродукционная установка готова к работе, остается только положить материал для съемки под аппарат и нажать кнопку. На это уйдет 10-15 секунд. И совсем другое дело, когда нужно встать, достать аппарат, укрепить его, наладить освещение и т.д.; в этом случае для съемки потребуются уже не несколько секунд, а 15-20 минут. Определенные затраты времени связаны с подготовкой практически всех используемых предметов оргтехники. Поэтому очень важно, чтобы все технические средства, которыми оснащено рабочее место, находились в постоянной готовности. Достигается это различными путями. Главные из них - это монтаж (размещение) аппаратуры и приспособлений непосредственно на рабочем месте, устройство поворотных приспособлений, позволяющих приблизить к себе нужный предмет на время работы, коммутация электроприборов и радиокомплекса.
Совершенствование рабочего места всегда включает в себя создание благоприятных ГИГИЕНИЧЕСКИХ условий. Как правило, об этом мало кто думает, когда речь идет об умственном труде. Сложилось убеждение, что отклонения от норм здесь настолько невелики, что они не могут привести к каким-либо неприятным последствиям. Но это - заблуждение. При длительном воздействии неблагоприятные гигиенические условия могут сказаться и на работоспособности и на здоровье.
Подробные рекомендации по вопросам гигиены рабочих (помещений, в том числе и для умственного труда, содержатся во многих справочниках м руководствах. Упомянем лишь о нормах освещенности. Выражаются они в условных единицах - люксах и приводятся в большинстве случаев примерно в таком виде: чтение, письмо, печатание на машинке - 400 люксов, черчение - 700, работа с каталогами - 200, поиск материалов на полках - 100 люксов. Казалось бы, все ясно и просто: бери и пользуйся. Но оказывается, что эти нормы практически ничего не дают, так как замерить освещенность можно лишь с помощью специальных приборов. Для того, чтобы хотя бы ориентировочно судить об уровне освещенности, нами на основании соответствующих замеров была подготовлена таблица, которая дает представление о зависимости между освещенностью, силой источника света и расстоянием до него.

И, наконец, о тех ПСИХОЛОГИЧЕСКИХ условиях, которые должны быть созданы на рабочем месте. Из них главнейшим следует считать его изолированность. Степень изолированности - один из весьма существенных элементов оценки рабочего места для умственного труда. Разные люди относятся к этому по-разному: одни вообще не в состоянии работать "на виду", другие утверждают, что для них это совершенно безразлично. Фактически же это сказывается на состоянии и работоспособности любого человека, и тот, кто считает, что безразличен к окружающей его обстановке, просто не подозревает, сколько нервной энергии ему приходится затрачивать для компенсации неблагоприятных условий.
При работе в общей комнате возможно создать ощущение уединенности. Этот психологический эффект достигается самым несложным путем: за счет соответствующей расстановки мебели, обеспечивающей определенную изолированность рабочего места, использования небольших перегородок, ширм или занавесей, позволяющих как-то отгородить стол.
***
Пока еще скромно - "логарифмическая линейка, микрокалькулятор".
8/80
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РАБОТА С ЖУРНАЛОМ И ГАЗЕТОЙ
Г.ГЕЦОВ
При работе с журналами полезно использовать небольшие библиографические карточки двоякого рода. Одни - для учета самих номеров журналов и целеустремленного просмотра их годовых комплектов.
Карточки учета работы по отдельным статьям будут иметь иной вид. На их лицевую сторону заносят название статьи и тему. На обороте - сведения, раскрывающие содержание публикации, а также собственные замечания о предполагаемом использовании статьи.

Иногда при просмотре журналов приходится искать материалы только под углом зрения интересующей темы и проходить мимо других интересных в полезных публикаций. Конечно, в этот момент читать их совсем не обязательно, и все же такие публикации следует как-то фиксировать. Тут важен продуманный учет того, что прочитано, просмотрено и намечено к проработке. Организовать его просто: на карточках учета журналов следует регистрировать темы, интересующие вас. Но при этом важно всегда точно указать, с какой целью просматривается журнал. Проработка номеров отмечается значками. Так, на карточке ясно показано, какие из номеров журнала "Наука и жизнь" целиком просмотрены ("П"), в каких выделены материалы по теме "Охрана природы" ("О").

Название журнала на карточке учета так же, как и ссылки на вырезках и выписках из журналов, можно указывать с помощью шифров, образуемых из первых букв названий журналов, скажем, "НЖ" - "Наука и жизнь", "ТМ" - "Техника - молодежи" и так далее.
Если содержание той или иной статьи не раскрывается ее названием, то на карточке дают подзаголовок. Допустим, статья названа "Прорыв в будущее" (НЖ, 1979, 4). Всего два слова - "Первая пятилетка" приоткрывают тему.
Фиксируя данные об отдельных статьях, надо заранее представлять себе, что со временем эти карточки придется как-то рассортировывать по темам. Для этой цели, конечно, при большом объеме работы, потребуются ящики, а быть может, и целые блоки ящиков, а также и особая организация своего рабочего каталога (о ней мы расскажем в дальнейшем).
Уже в самом начале процесса организованной работы надо использовать элементарную оргтехническую оснастку. Карточки учета журналов и статей можно накапливать и хранить в конвертах. Конверты иногда наклеивают на плотное основание - бланк, чтобы удобнее устанавливать в ящик.
Теперь о работе с газетой. С нею мы встречаемся много раз на протяжении дня. Берем свежий номер рано утром из почтового ящика, просматриваем за завтраком. Заглядываем в газету во время поездки на работу. Иногда читаем материалы номера в обеденный перерыв. Вечером вновь раскрываем газету, пусть только с целью посмотреть программу телепередач.
Но чтобы не терять зря времени, не топтаться на месте, стоит научиться быстро удалять из поля своего зрения уже прочтенное. Поэтому при чтении газет, как и в любой работе, важны осознанная цель и использование приемов, делающих чтение целеустремленным.
Как же работают с газетами умудренные опытом читатели? Поэтапно. Первый этап - это беглый просмотр, по существу, только чтение заголовков. Его цель: быстро определить нужные и интересные материалы. Их отмечают разными значками и надписями. Конечно, при этом не только не исключается, но и обязательно подразумевается хотя бы частичное чтение отдельных публикаций.
Полезно научиться распознавать материал по заготовкам и рубрикам. Рубрики в сопоставлении с заголовками и подзаголовками еще до чтения помогают правильно схватывать суть публикации и вести убыстренный поиск нужной темы.
На газетных страницах легко тренировать свое умение отбирать главное, расчленять текст вехами на отдельные смысловые части. В отличие от книг в газетах всегда можно и нужно подчеркивать, отчеркивать, писать на полях, делать вырезки. Повседневные упражнения в схватывании сути газетного материала помогут выработать умение мгновенно видеть то, что нужно, быстро отбирать интересное, легко различать полезное в калейдоскопе газетной информации. Проверьте себя: если при попытке выделить в статье главное оказываются подчеркнутыми чуть ли не все строки - это значит, что статья не понята.
На втором этапе размеченную газету просматривают более тщательно. Здесь полезно пользоваться библиографической карточкой учета, похожей на ту, которая оформляется при работе с журналом. Только у газетной карточки 31 вертикальная колонка (по числу дней месяца) и 12 горизонтальных строчек по числу месяцев.

Стопки газет с отмеченными статьями громоздки. Подобранный материал трудно поддается классификации и распределению по темам. Иное дело вырезки. Они компактны, занимают мало места, их легко сортировать и классифицировать.
Особое значение имеют вырезки из еженедельника "Книжное обозрение". Они помогают накапливать библиографические сведения о литературе. Есть смысл подобные вырезки наклеивать на библиографические карточки.
Процесс подготовки вырезок можно "механизировать", используя вместо ножниц тонкую металлическую линейку или лезвие безопасной бритвы.
При распределении вырезок по темам могут быть использованы лотки для бумаг, а также картотеки для вертикального хранения документов.

Для хранения вырезок можно использовать также разного рода коробки. Считается целесообразным приклеивать вырезки с особо нужными и часто используемыми материалами на листы плотной бумаги одного формата.
Мелкие вырезки помещают в конверты или коробки таких размеров, которые позволяют не нарушать заведенный порядок расположения вырезок. Листы бумаги с наклеенными на них вырезками имеет смысл в некоторых случаях скреплять скоросшивателем, правда, удобнее пользоваться регистратором для бумаг, позволяющим с минимумом усилий вставлять материалы внутрь подшивки. В отдельных случаях подборки вырезок переплетают, а иногда вклеивают в книги, дополняя их содержание новыми, свежими данными.
Но мыслимо ли найти в тысячах кусочков из разных газет то, что может потребоваться через месяц, год? Да, это возможно. Для этого используются определенные приемы.
Прежде всего с самого начала стоит позаботиться о систематизации вырезок по разделам. По мере роста массива вырезок следует уточнять их рубрики, вводить дополнительные рубрики для детализации, регистрировать номера вырезок в картотеках и в поисковых регистраторах - алфавитных, телефонных книжечках, где можно записывать названия тем и номера соответствующих вырезок.
Поисковая алфавитная картотека вырезок организуется просто, если вы пронумеровали все вырезки по порядку хотя бы независимо от тем. Тогда на карточках небольшого (скажем, 6*9 сантиметров) формата отмечают возможные тематические признаки той или иной вырезки, снабжают номером, под которым значится вырезка, и помещают в ящик по алфавиту признаков.

Предположим, вас давно интересует тема "Соединение металлов при помощи взрыва". Прежде всего стоит обратиться к журнальным публикациям. Вот одна из них: "Взрыв: энергия, машина, инструмент", "Наука и жизнь", 1973г. #4. Но вам хочется найти и последние газетные публикации по этой теме. Если металловедение - предмет вашего интереса и вы при чтении регистрируете тематические признаки статей в поисковой картотеке, то на каждую из тем - "сварка", "ковка", "упрочнение металлов" в ящике с алфавитным перечнем признаков найдете немало карточек. Первая ведущая тема "взрыв" конкретизирует поиск, так как в блоке с этой темой среди других карточек найдется искомая под номером, скажем, 4213, которую вы завели на вырезку статьи "Упрочняет... взрыв" ("Правда", 19.05. 80г.). Один и тот же номер - 4213 на тематических поисковых карточках других рубрик картотеки "сварка", "ковка" определит успех поиска и поможет уточнить содержание материала. Если вы вспомните, что одна из технологий сварки металла с помощью взрыва была разработана в Ташкенте, то сможете облегчить поиск, найдя карточку с признаком "Ташкент", даже не заглядывая в рубрики "сварка", "ковка". Подобная картотека помогает ценной информации не затеряться, продлевает ее жизнь.
На полях рядом с будущей вырезкой следует записать и ссылку на название газеты. Не следует указывать полное наименование газеты: "Правда", "Комсомольская правда", "Социалистическая индустрия". "П", "КП", "СИ" - это ваши шифры газет.
Такова техника самостоятельной работы с газетными вырезками. Нужно иметь в виду, что в крупных городах действуют специальные справочно-информационные службы - отделы газетно-журнальных вырезок. Подобный отдел при производственном объединении "Мосгорсправка" имеет тысячи абонентов и отправляет заказчикам в год миллионы вырезок.
БЮРО СПРАВОК
Службы газетно-журнальной информации работают в столицах республик, а также в крупных промышленных центрах страны, например, на территории РСФСР - в Ленинграде, Омске, Новосибирске, Свердловске, Хабаровске, Ярославле - всего в 32 городах.
За справками об условиях подписки и возможности абонирования можно обращаться в Главное управление непроизводственных бытовых услуг Министерства бытового обслуживания населения РСФСР по адресу: 103009, Москва, К-9, ул.Станиславского, 7.
Москвичей обслуживает отдел газетно-журнальной информации производственного объединения "Мосгорсправка". Его адрес: 103009, Москва, К-9, ул.Горького, 5/6.
Объединение справочно-информационных служб Московской области ("Мособлбытсправка", 109088, Москва, Шарикоподшипниковская ул., 40) обслуживает также Калининскую, Костромскую и Ярославскую области. Такие службы имеются также и в ряде других областей, например, в Ленинградской, Тульской, Белгородской, Саратовской, Горьковской, Томской, Омской, Хабаровской; в Башкирии и в Ставропольском, Красноярском, Алтайском краях.
Абоненты этого отдела могут заказывать вырезки по всем периодическим изданиям Советского Союза на год, месяц или использовать разовую подписку на одну тему. Нужно довольно точно определить тему своей подписки. Скажем, не вообще "Проблемы экономики", а "Эффективность", "Качество", "Производительность труда" и т.п.
Условия подписки зависят от тем. Вырезки высылаются подписчикам по почте три раза в месяц.
Отделы газетно-журнальной информации получают всю периодическую печать - центральную и областную, газеты краевых городов - приблизительно 250 наименований газет в необходимом количестве экземпляров, выписывают политические, социально - экономические, научно-технические и популярные журналы, экспресс-информацию - всего около 70 наименований.
Всего справочно-информационные службы РСФСР отправляют своим абонентам около 40 миллионов вырезок в год.
***
40млн. без Интернета!
3/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ? ВАШ РАБОЧИЙ КАТАЛОГ
Г.ГЕЦОВ
Когда приходится иметь дело с большим объемом литературы, трудно обойтись без собственного каталога - систематизированного перечня источников. Такой каталог организует и предельно облегчает каждодневное общение с литературой, делает работу с ней целеустремленной, быстрой и в то же время простой. В чем же специфика каталога для индивидуальной работы? Личный рабочий каталог преследует особые цели, и его карточки источников могут содержать много дополнительных данных по сравнению с библиотечными каталогами. Здесь могут быть сведения о степени пригодности источника для данной работы, о предполагаемых путях его использования, о номерах страниц, откуда следует сделать выписки. Здесь же отражаются и этапы чтения. На карточках записывают и отзывы о содержании источника. Это уже элементы аннотации. Если книга имеется в домашней библиотеке, на карточке делают пометки о месте ее хранения (шкаф, полка), о том, кому на время была отдана данная книга. Каталог может отражать не только книги личной библиотеки, но и те, что вас интересуют в общественных библиотеках, поэтому обязательно на таких карточках проставлять библиотечные шифры.
Иногда на карточки заносят полные имя и отчество автора, даже его адрес и телефон: читатель бывает заинтересован во встречах и переписке с автором.
Иные карточки вашего каталога будут фиксировать не сами книги или статьи, а только части их, скажем, главы или даже отдельные страницы. Одним словом, записи на карточках тематически разнородны и весьма индивидуальны.
Какие же источники следует использовать в каталоге? Пути поиска источников для разработки той или иной темы или знакомства с ней весьма разнообразны: тут и рекомендации специалиста, и библиографические справочники, и каталоги библиотек, и отдельные списки литературы, приводимые в статьях по изучаемой и смежным темам.
Если число источников велико и работа длится долго, то трудно сразу определить степень пригодности того или иного материала для работы. Поэтому, кроме нужных, в каталог включают и те источники, которые при первоначальном ознакомлении были признаны непригодными. Однако на подобных карточках должно быть отмечено ваше мнение об источниках - такая информация пригодится в дальнейшей работе. Например: "Слабо. Более не читать!", "Плохое повторение книги такой-то", "Проработать позднее, после уяснения вопроса". Как видите, характеристики должны быть определенными, мотивированными. Но в оценке литературы не нужно проявлять поспешность. Книга, сегодня как будто бы ненужная, со временем - после изучения других источников - подчас становится полезной.
По мере роста количества карточек и объема вашей работы каталог потребует определенной организации. Например, он может состоять из следующих отделов: тематического, алфавитного, вспомогательного.
Отделы каталога расчленяют рубриками (названиями, объединяющими группы карточек по какому-то общему для них признаку).
ТЕМАТИЧЕСКИЙ ОТДЕЛ. Этот отдел легко вместит любое количество рубрик, профессиональных и любительских. Тем самым появится возможность вести учет собственных книг, а также учебной, производственной и научной литературы, которую используете или хотели бы пока только зарегистрировать, имея в виду дальнейшую работу с ней. В последнем случае особенно важно уточнить на карточках содержание, отметить именно то, что вам может понадобиться. Например, подбирая литературу, на карточке книги авиаконструктора А.Яковлева "Записки конструктора" (М., Политиздат, 1979), вы укажете из сорока разделов книги на один, особенно интересующий вас раздел, "Испытатели".
Если вы, например, изучаете жизненный и творческий путь ученого, то картотеку удобнее составлять по датам его жизни. Когда же предметом ваших занятий становится тема более обширная, скажем, история техники, следует подчинить картотеку разделам этой большой темы (например, история техники в России, Польше, Чехословакии, возникновение в этих странах в том или ином веке отдельных направлений научной мысли, отраслей техники и т.д.).
Рубрики тематического отдела призваны организовать умственный труд. Часто в процессе систематизации литературных источников и материалов вырисовывается план будущей работы или, наоборот, изменяется намеченная последовательность изучения темы. Случается, что рубрики личного каталога помогают наметить основные главы будущей книги. Ведь изучение источников ведется под углом зрения темы, сформулированной рубрикой. В этом - значение, но и ответственность рубрик. Поэтому нельзя процесс организации рубрик выпускать из-под контроля.
Конечно, вначале, не зная еще глубоко материала и объема работы над темой, трудно провести наиболее логичную и точную систематизацию. Как правило, только в результате длительной работы рубрики становятся необходимым и естественным разделением общей темы.
Иногда в начале работы удается наметить лишь несколько основных рубрик, не прибегая к дробному членению, и только в процессе длительной работы над темой, когда материал будет усвоен, можно сделать более детальную разбивку. В это время рубрики обычно легко формулируются.
Как бы то ни было, но на всех этапах работы надо постоянно стремиться сблизить разбивку тематического отдела каталога с главными направлениями темы, постепенно добиваясь наиболее точных и отражающих существо вопроса формулировок.
Внутри каждой рубрики расположение карточек подчиняется определенному принципу, например, алфавитному. Карточки тематического отдела подвижны: их вынимают для работы и перегруппировок, их применение отражает ход работы над данным источником. Здесь же уточняется и местонахождение материала - проставляются страницы с чем-то важным. В карточке полезно указать, какие разделы (главы, параграфы, страницы и даже части их) и для какой цели надо будет проработать и когда.
Иногда карточки тематического отдела в процессе первоначальных этапов работы (просмотра литературы - подборе источников и предварительного их изучения) кочуют из одной рубрики в другую. Ведь по одному названию книги, статьи не всегда можно точно представить их содержание. Более того, иногда одну и ту же карточку приходится размножать в соответствии с главами или темами самой книги или статьи. Получившиеся таким образом дублетные карточки (кстати, они могут быть и не копиями основных, а лишь упрощенными - ссылочными) займут место в соответствующих рубриках.

Когда в процессе работы будут сформированы постоянные тематические рубрики каталога, их полезно пронумеровать. Номера рубрик проставляют и на карточках. Тогда карточки получат обратный адрес, их легко после работы возвратить в нужную рубрику.
АЛФАВИТНЫЙ ОТДЕЛ содержит карточки строго по алфавиту фамилий авторов или названий и позволяет быстро найти любой источник. На карточках этого отдела иногда делают пометки, указывающие, в каких рубриках следует искать тот или иной источник, поэтому карточки алфавитного отдела всегда должны быть на своих местах.
ВСПОМОГАТЕЛЬНЫЙ ОТДЕЛ. Здесь главная рубрика - шифровальная, где читатель фиксирует свои шифры источников. В других рубриках отражаются условные обозначения, принятые на короткий период, накапливаются и группируются карточки с различной целью: для работы в библиотеке, планирования, изучения источников или просто для дальнейшей обработки самих карточек.
В каталоге полезно регистрировать работу не только с книгами, но и со статьями из периодической печати. Поэтому в каталоге может появиться отдел "Периодические и продолжающиеся издания".
В следующей беседе мы продолжим рассказ о шифрах и вспомогательных средствах при работе с собственным каталогом.
[Рекомендуем читателям прочитать книгу Г.Гецова "Учиться работать с политической литературой" (Москва, "Московский рабочий". 1979). Эта работа отмечена Дипломом II степени и денежной премией на XVI Всесоюзном конкурсе на лучшее произведение научно-популярной литературы, который ежегодно проводится Всесоюзным обществом "Знание". В книге обобщается опыт работы пропагандистов, идет рассказ о методике и технических приемах работы с политической литературой].

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Еще про калькуляторы. Полезно попытаться понять, как их воспринимали в то время. Что было обязательным знать об их устройстве (т.е. о "ячейках" из Тайной Библиотеки)? Надо же как-то заткнуть дыру между первыми успехами микроэлектроники и дурацкими блогами об успехах "информационных технологий".

3-4/81

ПРИШЛА ПОРА ОСТАВИТЬ СЧЕТЫ
Размышления у прилавка магазина "Счетные машины"
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Специалисты утверждают, что человеческая история начинается с очень далеких времен - существа, которых мы сейчас именуем видом Homo habilis, человеком умелым, появились в семействе приматов чуть ли не полтора миллиона лет назад. Но вот что поразительно - природа посчитала нужным истратить эти годы в основном на подготовку к созданию своего шедевра: возраст человека разумного, Homo sapiens, определили в тридцать тысяч лет, а это всего лишь два процента от общего времени, пошедшего на сотворение чуда, всего лишь два процента от наших полутора миллионов лет.
Просто дух захватывает, когда пытаешься представить себе эволюцию разума, промелькнувшую за эти короткие тысячелетия. Приспособленный к решению совсем иных задач - к простейшей ориентировке, примитивному добыванию пищи, к нехитрой защите от стихий - человеческий мозг быстро осваивает компактные языки мышления, создает более точные модели мира, находит пути его активного освоения. Это разум привел голодного и замерзающего пещерного жителя в светлые теплые квартиры с горячей водой и цветными телевизорами. Продлил среднюю продолжительность человеческой жизни от примерно двадцати лет до примерно семидесяти. Разум вооружил человека станками и самолетами, рентгеном и рондомицином, ускорителем, ломающим атомные ядра, межпланетными станциями, моторами в сотни лошадиных сил. Разум обогатил нас поэзией, математикой, музыкой. Природа, начавшая свое главное дело всего тридцать тысяч лет назад и развернувшая его по-настоящему лишь в самые последние тысячелетия, может, видимо, быть довольна работой, проделанной за отчетный период. Во всяком случае, она, природа, много потрудилась над совершенствованием человека разумного и может, пожалуй, простить себе некоторые мелкие недоработки. В частности, такую - природа не научила нас считать в уме.
ЭКСКАВАТОРЫ ДЛЯ ЧИСЕЛ
Не то, чтобы человек в принципе не был способен к устному счету. В литературе, скажем, описан некий счетовод, который мог по просьбе сослуживца умножить в уме восемьсот тридцать шесть на четыреста двадцать три и выдать ответ, составляющий триста пятьдесят три тысячи шестьсот двадцать восемь, помедлив лишь самую малость. Известны люди, оперирующие в уме огромными числами настолько быстро, что они могут демонстрировать свое искусство на эстраде, как это делал, например, феноменальный счетчик Р.С.Арраго.
И все же это случаи редкие. Как правило, наш природный компьютер вычисляет очень плохо, хотя с легкостью решает чрезвычайно сложные задачи другого вида (такие, например, процессы, как узнавание лица знакомого человека или выбор направления и силы удара по волейбольному мячу, не удается пока смоделировать на лучших компьютерах мира). Не случайно в школьной программе на освоение четырех арифметических действий в пределах сотни отводится около 200 часов, почти в 20 раз больше, чем на весь переменный ток. Большинству людей, чтобы убедиться в своей счетной неспособности, достаточно всего лишь попробовать перемножить в уме два двухразрядных числа, например, умножить 27 на 39 или 43 на 96.
Убедились? Только, пожалуйста, не нужно огорчаться. Это не единственная из наших человеческих неспособностей и уж, во всяком случае, "зло не так большой руки". Как повел себя человек, обнаружив, что его физических сил не хватает для переноски очень тяжелых грузов? Он сначала, видимо, придумал волокушу, потом колесную повозку, научился запрягать в нее быков или лошадей, научился строить лодки, оснащать их парусом и, наконец, добрался до тысячетонных железнодорожных составов, супертанкеров и самолетов на полтысячи пассажиров. Что сделал человек, когда убедился, что руками или даже палкой глубокой ямы не выроешь? Он начал с изобретения лопаты и постепенно добрался до двадцатикубового экскаватора, который один может заменить несколько тысяч землекопов. И точно так же, убедившись в своей неспособности к умственным вычислениям, человек начал создавать, так сказать, продолжение своего мозга - счетные машины.
Первой такой машиной наверняка была рука. Пальцевый счет в чистом виде кое-где встречается и сейчас, о нем напоминает и сама наша десятичная система счисления, а также названия некоторых чисел - "пять", например, видимо, происходит от славянского "пясть", то есть кисть руки. От пальцевого счета лежал прямой путь к счетным палочкам, зарубкам на камне или дереве, к веревкам с узелками и, наконец, к абаку, некоторому подобию наших счетов. Прекрасная книга Р.Гутера и Ю.Полунова "От абака до компьютера",- рассказывающая об истории вычислительной техники, напоминает, что уже в V веке до нашей эры абак имел широкое распространение в Риме, Греции, Египте.
А потом два тысячелетия механизация вычислений сводилась лишь к некоторому совершенствованию древнего абака, к созданию китайского суанпаня, японского сорабана, популярной в средневековой Европе системы счета на линиях, к появлению 400 лет назад русских "счетов", которые благодаря их десятичной структуре, простоте и надежности благополучно дожили до наших дней.
Но все это, строго говоря, были не машины, а лишь приспособления - машина, по определению любого толкового словаря, должна что-то делать сама, что-то двигать, преобразовывать, перемещать. Изобретателей первых истинных машин для механизации вычислений было несколько, во всяком случае, трое хорошо известны. Это, во-первых, "французский Архимед" - выдающийся математик и физик Блез Паскаль, который, придумав счетную машину, по собственным его словам, "... не экономил ни времени, ни сил, ни труда... имел терпение сделать до 50 различных моделей: одни деревянные, другие из слоновой кости, из эбенового дерева, из меди...". Ему было восемнадцать, когда он начал это дело, и двадцать два, когда завершил,- в 1645 году "Паскалево колесо" заработало. Счетный механизм, упрятанный в небольшой латунный ящик, состоял в основном из зубчатых колес, колес со стержнями, линеек, защелок, вилок и рычагов. Для ввода чисел некоторые зубчатые колеса нужно было установить в определенное положение, при вычислениях механизм приводился в движение, разумеется, вручную, и на восьми круглых шкалах этой восьмиразрядной машины появлялся ответ.
Триста лет числился Блез Паскаль единственным первооткрывателем счетной машины, и лишь недавно, в 1957 году, обнаружились документы, из которых следовало, что за двадцать лет до "Паскалева колеса" аналогичную шестеренчатую машину, видимо, придумал и изготовил Вильгельм Шиккард, профессор кафедры восточных языков, а позже кафедры математики и астрономии Тюбингенского университета. И совсем уже в последние годы, немногим более десяти лет назад, были найдены эскизы суммирующей машины, которую придумал великий Леонардо чуть ли не за двести лет до двух
других изобретателей, действовавших, кстати, совершенно самостоятельно, независимо.

Арифмометр, придуманный немецким механиком Лейпольдом (1674-1727), где результат умножения (число до 9 разрядов) отображался на девяти отдельных внешних шкалах.
Фрагмент счетной машины Лейбница (1646-1716) - ребристый валик для умножения чисел в одном из разрядов.
Фрагмент счетной машины Паскаля (1623-1662) - устройство для выполнения операций в одном из разрядов.
Новейшая история вычислительной техники напоминает остросюжетный приключенческий роман - часто появляются новые идеи, конструкции, новые имена, в том числе и очень известные. Так, изобретателем интересного математического инструмента был сам Вильгельм Готфрид Лейбниц. Он ввел в машину ребристый цилиндр, на котором каждое из девяти ребер было несколько короче предыдущего, и, входя в зацепление со счетной шестеренкой разными своими частями, цилиндр производил умножение на разные числа - от нуля до девяти. Активность изобретателей привела к тому, что уже в начале прошлого века появились счетные машины, пригодные для серийного производства. А к нашему времени механический арифмометр, этот экскаватор для чисел, в десятки раз ускоряющий работу вычислителя, стал вообще рядовым прибором.
И тут оказалось, что огромное число людей, даже те, кому приходится считать довольно много - бухгалтеры, кассиры, продавцы,- предпочитают пользоваться не машиной, а приспособлением, не арифмометром, а обычными счетами. Почему? С чем связан такой консерватизм? Ответ простой: для несложных вычислений счеты удобнее, проще - не будешь же экскаватором рыть ямку для помидорной рассады или даже для саженцев яблони. Больше потеряешь на взаимодействии с машиной, чем выиграешь от помощи ее стальных мускулов.
А теперь смена жанра, маленькая фантастическая зарисовка. У вас в руках землеройная машина размером с лопату или даже с игрушечную детскую лопатку. На рукоятке несколько кнопок - нажимаешь на них, и лопатка тихо и быстро выполняет любое задание. Нажмешь на одну кнопку - и мгновенно в земле появляется траншея метровой глубины, нажмешь на другую - мелкая лунка для зернышек-семян.
Эта фантастическая картина введена в наш рассказ как аналогия хорошо известной реальности сегодняшнего дня - электронных счетных машин.
Вот мы стоим у прилавка московского магазина "Счетные машины", который прозаически торгует миниатюрными компьютерами примерно десяти разных типов. Нас несколько человек, потенциальных покупателей, людей совершенно незнакомых. Пока мы только листаем инструкции, рассматриваем образцы, нажимаем кнопки, сопровождая это приятное занятие самыми разными комментариями: "... восьми разрядов хватит... лучше взять за сорок, чем за тридцать... она и дома всегда нужна... у этой клавиши мелковаты... счеты надо припрятать, скоро будут цениться, как старые иконы... блок питания нужен обязательно... без машины как без рук... то ли брать ту, то ли эту...". Сейчас, видимо, колебания кончатся - каждый примет свое решение, совершит покупку, станет владельцем электронной счетной машины. Еще двадцать-тридцать лет назад сама эта ситуация показалась бы фантастикой.
ТЫСЯЧА КАЛЬКУЛЯТОРОВ, МИЛЛИОН ВОЗМОЖНОСТЕЙ
Хотя в части портативных, или, как еще говорят, карманных, электронных вычислительных машин существует немалая терминологическая путаница, чаще всего их все же именуют микрокалькуляторами. И делят на три большие группы - инженерные, программируемые и простейшие, или массовые. Последние иногда называют арифметическими машинами, а еще чаще просто микрокалькуляторами - если говорят "микрокалькулятор" без прибавления "инженерный" или "программируемый", то речь скорее всего идет о простейшей, массовой машине.
Слово "простейшая" в данном случае не должно огорчать. Такие счетные машины вполне могут быть использованы для разного рода бухгалтерских работ, экономических расчетов, решения многих технических задач, словом, во всех случаях, где нужно обрабатывать большие массивы числовой информации, умножать, делить, вычитать, складывать. Инженерные машины имеют, так сказать, более высокую квалификацию. Они быстро выдают значения синусов, косинусов и других прямых и обратных тригонометрических функций, быстро извлекают корни, оперируют с десятичными и натуральными логарифмами, решают некоторые виды уравнений, то есть делают много такого, что необходимо инженеру, ученому ну и, конечно же, студенту, связанному с точными науками.
А пот программируемый калькулятор, в отличие от простейшего и инженерного, имеет не только жесткие программы работы, такие, например, как "умножить" или "вычислить тангенс", но и позволяет пользователю самому формировать программы с тем, чтобы машина могла самостоятельно решать достаточно большое количество разнообразных задач. Ну, скажем, такую задачу: "Вычислить значение x=а**(2m)-b**m+c**2 для всех целочисленных a в интервале от 2 до 24, для b от 2 до 9, m от 1 до 3 при c, равном 8.5, и найти результат, наиболее близкий к числу 330". Подобную задачу можно в принципе решить и на любой другой счетной машине, затратив на это некоторое время, но программируемый калькулятор все сделает сам: вам останется только ввести в него задание, дать машине возможность спокойно поработать и через некоторое время подойти за результатами. Решая подобные задачи, программируемый микрокалькулятор уже чем-то напоминает большую вычислительную машину, которая вопреки своему названию не просто вычисляет, а выполняет более тонкую интеллектуальную работу - сопоставляет данные, ищет оптимальные значения каких-либо величин, составляет цепочки логических операций. Причем делается это настолько изящно и ловко, что даже маленький программируемый калькулятор, не говоря уже о больших компьютерах, нередко видится не мертвым инструментом, не "железкой", а умелым и инициативным помощником.
Но вернемся, однако, к самым простым микрокалькуляторам, которые, как показывает опыт сильно компьютеризованных стран, вполне могут удовлетворить миллионы пользователей.
У многих людей существует мнение, что простейший микрокалькулятор выполняет лишь четыре действия арифметики и ни на что большее не способен. В действительности это не так, и даже дважды не так. Во-первых, во многих простейших микрокалькуляторах, кроме традиционных клавиш "сложить" ("+"), "вычесть" ("-"), "делить" (":") и "умножить" ("*"), есть еще и другие операционные клавиши. В микрокалькуляторе Б3-23, например, имеется клавиша "процент" (%), и можно, взяв какое-нибудь 73724965, мгновенно найти, что 0.738 процента от него составляют 544090.24. В калькуляторе Б3-24Г клавиши процентов нет, но зато здесь есть дополнительный регистр, или, проще говоря, отдел памяти. Нажатием на клавишу "память+" ("П+") в эту дополнительную память можно загнать результат каких-либо предварительных вычислений, а затем в нужный момент извлечь его и вновь пустить в дело. Имеется в этой машине еще и клавиша "индикация памяти" ("ИП"), нажав на которую вы видите припрятанное число на светящемся цифровом табло, на этом маленьком дисплее микрокалькулятора. И, конечно, имеется клавиша "сброс памяти" ("СП"), позволяющая мгновенно забыть уже ненужное число и освободить место для другого.
Особенно много дополнительных клавиш, а значит, и дополнительных возможностей быстро проводить вычисления у настольных микрокалькуляторов, таких, как МК-44. Эти машины уже не рассчитаны на то, чтобы носить их в кармане,- слишком большой понадобился бы карман. Они имеют размеры книги и, как предполагается, будут стоять на столе у экономиста или бухгалтера, на прилавке у продавца. У настольных калькуляторов и клавиши крупнее, и цифры более крупные, и светятся эти цифры не красными, как у многих карманных машин, а более спокойным зеленоватым цветом. Словом, настольные микрокалькуляторы рассчитаны на то, что работать с ними будут целый день, и сделано многое, чтобы работа эта не утомляла. Кроме клавиш арифметических операций, извлечения корня и вычисления процентов, в настольных машинах обязательно есть дополнительная память, а иногда не один, а два или даже три регистра, каждый на свое число и со своими клавишами записи, индикации и сброса. Имеются часто и клавиши, меняющие знак у чисел, позволяющие быстро найти обратную величину и ряд других.
Итак, отличие простейших микрокалькуляторов от школяра, выполняющего лишь четыре действия арифметики, во-первых, состоит в том, что машины эти уже сами по себе умеют делать нечто большее. А вот и во-вторых: пользуясь некоторыми правилами, суховато изложенными в инструкции, можно с помощью арифметических машин делать многое такое, о чем даже не подумаешь, глядя на их клавиатуру. Иногда это предусмотренное конструктором некоторое дополнительное удобство, облегчающее вычисления. Так, например, на любом простейшем микрокалькуляторе можно любое число m (слово "любое" имеет одно ограничение - нужно, чтобы числа не переполняли индикатор, скажем, чтобы в восьмиразрядных машинах и числа и результат были бы до 100000000, а в двенадцатнразрядных машинах - до 1000000000000) возвести в любую целочисленную степень n. Для этого достаточно ввести в машину число m, а затем нажать клавишу "*" и n-1 раз нажать клавишу "=". Так, например, выполнив такое нажимание клавиш "5" "*" "=", "=", вы получите 5**3=625, а нажав "=" еще 7 раз, мгновенно получите 5**10=48828125.
Или другая очень удобная "мелочь": если вам нужно работать с постоянным числом, например, умножать различные величины T1, Т2, Т3... на постоянный коэффициент К, то достаточно сначала ввести одну из этих величин, например, Т, нажать клавишу "*" и ввести К. После этого можно будет выполнять умножение на К, не вводя ни самого К, ни знака умножения - достаточно будет ввести очередное Т и нажать на клавишу "=", как тут же появится результат умножения этого Т на К. Дело в том, что при умножении после нажатия клавиши "=", второй сомножитель, если его специально не убирать, автоматически становится постоянным коэффициентом. Точно так же становится постоянным коэффициентом второе слагаемое; вычитаемое или делитель. Если, скажем, вы хотите разделить ряд чисел 9, 27, 72, 126, 600... на какой-либо коэффициент, например, на 6, то достаточно полностью выполнить первое деление 9:6=1.5, а затем вводить лишь сами числа и знаки равенства: нажав клавиши "24", "=", вы увидите на индикаторе 4, так как автоматически произойдет деление, 24:6=4, нажав клавиши "72", "=", получите 12, будет выполнено деление 72:6=12 и т.д.
Простейшие микрокалькуляторы позволяют достаточно просто вычислять многое такое, что с первого взгляда не имеет прямого отношения к арифметике. Существует, в частности, довольно простой способ вычисления сложных процентов или нахождения корня любой степени из любого числа. Имеется возможность вычисления тригонометрических функций - синусов, косинусов, тангенсов.
"Так зачем же,- вправе поинтересоваться читатель,- переплачивать деньги за инженерные машины, если то, что делают они, можно осуществить и с помощью простейшего микрокалькулятора?"
Не имея возможности обсуждать финансовую сторону дела, напомним лишь о всем знакомой характеристике любого инструмента - об удобстве пользования. Ведь все то, что делает простейший микрокалькулятор, можно осуществить значительно более дешевыми средствами - с помощью карандаша и бумаги. Однако же миллионы людей предпочитают на этом не экономить, так как подобная экономия оборачивается невосполнимым перерасходом времени и нервной энергии. Инженерный микрокалькулятор значительно удобнее арифметической машины при выполнении большого числа алгебраических операций, при вычислениях с тригонометрическими функциями или логарифмами, при решении уравнений. То, что при работе с простейшим микрокалькулятором потребует десятков действий и многоступенчатых вычислений, в инженерной машине может быть сделано нажатием одной клавиши. И выбирая себе в помощники микрокалькулятор, нужно, видимо, прежде всего подумать о том, что он умеет делать и чем бы его хотел нагрузить хозяин. Словом, перефразируя известный стих, можно сказать: "Все машины хороши, выбирай на вкус".
МИКРОСЧЕТЫ С ЭЛЕКТРИЧЕСКИМИ КОСТЯШКАМИ
Ушли в прошлое времена, когда можно было всерьез декларировать: "Хочу все знать!" Сегодня это самое "все" настолько многопланово, настолько объемисто, что никакой индивидуальной памяти на него, конечно, не хватит. И уже нередко специалист не очень-то знает, что происходит в смежных областях, или даже не очень подробно знает, что делают зарубежные коллеги в его собственной области. Да что там подробности - в последнее время мы все чаще миримся с тем, что важнейшие фрагменты, уже прорисованные наукой в картине мира, незнакомы нам даже в самых общих чертах. Миримся с тем, что не знаем принципа действия машин и аппаратов, которые служат нам, с которыми мы регулярно общаемся. Это раньше для владельца приемника считалось неприличным не понимать, что делает радиолампа и какие бывают типы ламп. А шофер, или, как теперь говорят, водитель, просто обязан был разбираться в устройстве своей машины. Сегодня же человек, сдающий экзамен на водительские права, может вообще не знать, как устроен автомобиль,- в экзаменационных билетах даже нет вопросов об этом. И они, видимо, не нужны: можно виртуозно управлять автомобилем и не интересоваться тем, что делает карбюратор или откуда берется искра зажигания. Точно так же, любуясь яркими красками на экране телевизора, совсем не обязательно знать, как они приходят с телецентра в ваш дом.
Можно не интересоваться... Не обязательно знать... Но почему же, привычно нажимая клавиши микрокалькулятора, испытываешь какую-то неловкость, какое-то неудобство от того, что непонятно, как совершается это чудо мгновенного счета? Почему бухгалтер, давно привыкший к калькулятору, встретив специалиста по вычислительным машинам, отводит его в угол и осторожно пытается выведать, как же все-таки это делается, как она считает, эта небольшая коробочка? Кто знает, может быть, этим нашим любопытством движет какой-нибудь древнейший инстинкт - боязнь неизвестности, неясности. И поэтому нам неотвратимо хочется обо всем - именно обо всем - иметь представление, пусть даже самое общее, пусть только о существе дела. Человек по самой своей природе стремится к знанию, и в большинстве случаев дело сводится не к философическому "знать или не знать". Дело обычно сводится к простой житейской задаче: как конкретно, с минимальными затратами сил и времени ликвидировать "белое" пятно в своем мировоззрении, как конкретно представить себе ту или иную сложность, предельно упростив ее и не потеряв при этом существа дела.
Пытаясь ликвидировать в своих знаниях белое пятнышко, обозначенное надписью "Электронные счетные машины", мы, видимо, прежде всего должны вспомнить, что сам субстрат счета в таких машинах, само вещество, из которого формируются числа, это не что иное, как электрический ток. А конкретней - очень короткие, кратковременные всплески электрического тока, электрические импульсы. Энергию для них дает батарейка или электрическая сеть, а формируются такие импульсы с помощью внутренних генераторов и других электронных блоков машины. Когда вы нажимаете клавиши ввода чисел, то посылаете в сложный электрический мир калькулятора определенное количество импульсов тока, чередующихся в определенном порядке. А нажав клавишу операции, производите необходимые переключения в самой схеме машины с тем, чтобы импульсы-числа шли по определенным путям, складываясь, вычнтаясь или многократно складываясь и вычитаясь, что, как известно, эквивалентно умножению и делению. После такой переработки чисел-импульсов появится новая серия электрических всплесков, эквивалентная полученному результату. Этот записанный на электрическом языке результат будет направлен на цифровой индикатор, где зажжет определенные комбинации черточек, складывая из них нужные цифры,- в разных типах индикаторов используются различные физические процессы, но во всех случаях свечение сегментов, свечение черточек, из которых складывается цифра, происходит под действием электрического тока.
Познакомившись с этим веселым описанием, так и хочется, наверное, представить себе микрокалькулятор этакими канцелярскими счетами, где вместо деревянных костяшек двигаются по невидимым электрическим дорожкам невидимые электрические токи, собираясь группками, когда производится сложение, или разбегаясь при вычитании. Признаемся прямо: подобная картина должна быть приравнена, как сказали бы великие сатирики, к упрощенчеству со взломом. И все же эта недопустимо упрощенная модель электронного микрокалькулятора может быть допущена в качестве наглядного пособия для человека, у которого нет сил, чтобы знакомиться с предметом более подробно.
Ну, а если силы есть - попробуем продвинуться дальше.

3-4/81

ПРИШЛА ПОРА ОСТАВИТЬ СЧЕТЫ
Размышления у прилавка магазина "Счетные машины"
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"
Специалисты утверждают, что человеческая история начинается с очень далеких времен - существа, которых мы сейчас именуем видом Homo habilis, человеком умелым, появились в семействе приматов чуть ли не полтора миллиона лет назад. Но вот что поразительно - природа посчитала нужным истратить эти годы в основном на подготовку к созданию своего шедевра: возраст человека разумного, Homo sapiens, определили в тридцать тысяч лет, а это всего лишь два процента от общего времени, пошедшего на сотворение чуда, всего лишь два процента от наших полутора миллионов лет.
Просто дух захватывает, когда пытаешься представить себе эволюцию разума, промелькнувшую за эти короткие тысячелетия. Приспособленный к решению совсем иных задач - к простейшей ориентировке, примитивному добыванию пищи, к нехитрой защите от стихий - человеческий мозг быстро осваивает компактные языки мышления, создает более точные модели мира, находит пути его активного освоения. Это разум привел голодного и замерзающего пещерного жителя в светлые теплые квартиры с горячей водой и цветными телевизорами. Продлил среднюю продолжительность человеческой жизни от примерно двадцати лет до примерно семидесяти. Разум вооружил человека станками и самолетами, рентгеном и рондомицином, ускорителем, ломающим атомные ядра, межпланетными станциями, моторами в сотни лошадиных сил. Разум обогатил нас поэзией, математикой, музыкой. Природа, начавшая свое главное дело всего тридцать тысяч лет назад и развернувшая его по-настоящему лишь в самые последние тысячелетия, может, видимо, быть довольна работой, проделанной за отчетный период. Во всяком случае, она, природа, много потрудилась над совершенствованием человека разумного и может, пожалуй, простить себе некоторые мелкие недоработки. В частности, такую - природа не научила нас считать в уме.
ЭКСКАВАТОРЫ ДЛЯ ЧИСЕЛ
Не то, чтобы человек в принципе не был способен к устному счету. В литературе, скажем, описан некий счетовод, который мог по просьбе сослуживца умножить в уме восемьсот тридцать шесть на четыреста двадцать три и выдать ответ, составляющий триста пятьдесят три тысячи шестьсот двадцать восемь, помедлив лишь самую малость. Известны люди, оперирующие в уме огромными числами настолько быстро, что они могут демонстрировать свое искусство на эстраде, как это делал, например, феноменальный счетчик Р.С.Арраго.
И все же это случаи редкие. Как правило, наш природный компьютер вычисляет очень плохо, хотя с легкостью решает чрезвычайно сложные задачи другого вида (такие, например, процессы, как узнавание лица знакомого человека или выбор направления и силы удара по волейбольному мячу, не удается пока смоделировать на лучших компьютерах мира). Не случайно в школьной программе на освоение четырех арифметических действий в пределах сотни отводится около 200 часов, почти в 20 раз больше, чем на весь переменный ток. Большинству людей, чтобы убедиться в своей счетной неспособности, достаточно всего лишь попробовать перемножить в уме два двухразрядных числа, например, умножить 27 на 39 или 43 на 96.
Убедились? Только, пожалуйста, не нужно огорчаться. Это не единственная из наших человеческих неспособностей и уж, во всяком случае, "зло не так большой руки". Как повел себя человек, обнаружив, что его физических сил не хватает для переноски очень тяжелых грузов? Он сначала, видимо, придумал волокушу, потом колесную повозку, научился запрягать в нее быков или лошадей, научился строить лодки, оснащать их парусом и, наконец, добрался до тысячетонных железнодорожных составов, супертанкеров и самолетов на полтысячи пассажиров. Что сделал человек, когда убедился, что руками или даже палкой глубокой ямы не выроешь? Он начал с изобретения лопаты и постепенно добрался до двадцатикубового экскаватора, который один может заменить несколько тысяч землекопов. И точно так же, убедившись в своей неспособности к умственным вычислениям, человек начал создавать, так сказать, продолжение своего мозга - счетные машины.
Первой такой машиной наверняка была рука. Пальцевый счет в чистом виде кое-где встречается и сейчас, о нем напоминает и сама наша десятичная система счисления, а также названия некоторых чисел - "пять", например, видимо, происходит от славянского "пясть", то есть кисть руки. От пальцевого счета лежал прямой путь к счетным палочкам, зарубкам на камне или дереве, к веревкам с узелками и, наконец, к абаку, некоторому подобию наших счетов. Прекрасная книга Р.Гутера и Ю.Полунова "От абака до компьютера",- рассказывающая об истории вычислительной техники, напоминает, что уже в V веке до нашей эры абак имел широкое распространение в Риме, Греции, Египте.
А потом два тысячелетия механизация вычислений сводилась лишь к некоторому совершенствованию древнего абака, к созданию китайского суанпаня, японского сорабана, популярной в средневековой Европе системы счета на линиях, к появлению 400 лет назад русских "счетов", которые благодаря их десятичной структуре, простоте и надежности благополучно дожили до наших дней.
Но все это, строго говоря, были не машины, а лишь приспособления - машина, по определению любого толкового словаря, должна что-то делать сама, что-то двигать, преобразовывать, перемещать. Изобретателей первых истинных машин для механизации вычислений было несколько, во всяком случае, трое хорошо известны. Это, во-первых, "французский Архимед" - выдающийся математик и физик Блез Паскаль, который, придумав счетную машину, по собственным его словам, "... не экономил ни времени, ни сил, ни труда... имел терпение сделать до 50 различных моделей: одни деревянные, другие из слоновой кости, из эбенового дерева, из меди...". Ему было восемнадцать, когда он начал это дело, и двадцать два, когда завершил,- в 1645 году "Паскалево колесо" заработало. Счетный механизм, упрятанный в небольшой латунный ящик, состоял в основном из зубчатых колес, колес со стержнями, линеек, защелок, вилок и рычагов. Для ввода чисел некоторые зубчатые колеса нужно было установить в определенное положение, при вычислениях механизм приводился в движение, разумеется, вручную, и на восьми круглых шкалах этой восьмиразрядной машины появлялся ответ.
Триста лет числился Блез Паскаль единственным первооткрывателем счетной машины, и лишь недавно, в 1957 году, обнаружились документы, из которых следовало, что за двадцать лет до "Паскалева колеса" аналогичную шестеренчатую машину, видимо, придумал и изготовил Вильгельм Шиккард, профессор кафедры восточных языков, а позже кафедры математики и астрономии Тюбингенского университета. И совсем уже в последние годы, немногим более десяти лет назад, были найдены эскизы суммирующей машины, которую придумал великий Леонардо чуть ли не за двести лет до двух
других изобретателей, действовавших, кстати, совершенно самостоятельно, независимо.

Арифмометр, придуманный немецким механиком Лейпольдом (1674-1727), где результат умножения (число до 9 разрядов) отображался на девяти отдельных внешних шкалах.
Фрагмент счетной машины Лейбница (1646-1716) - ребристый валик для умножения чисел в одном из разрядов.
Фрагмент счетной машины Паскаля (1623-1662) - устройство для выполнения операций в одном из разрядов.
Новейшая история вычислительной техники напоминает остросюжетный приключенческий роман - часто появляются новые идеи, конструкции, новые имена, в том числе и очень известные. Так, изобретателем интересного математического инструмента был сам Вильгельм Готфрид Лейбниц. Он ввел в машину ребристый цилиндр, на котором каждое из девяти ребер было несколько короче предыдущего, и, входя в зацепление со счетной шестеренкой разными своими частями, цилиндр производил умножение на разные числа - от нуля до девяти. Активность изобретателей привела к тому, что уже в начале прошлого века появились счетные машины, пригодные для серийного производства. А к нашему времени механический арифмометр, этот экскаватор для чисел, в десятки раз ускоряющий работу вычислителя, стал вообще рядовым прибором.
И тут оказалось, что огромное число людей, даже те, кому приходится считать довольно много - бухгалтеры, кассиры, продавцы,- предпочитают пользоваться не машиной, а приспособлением, не арифмометром, а обычными счетами. Почему? С чем связан такой консерватизм? Ответ простой: для несложных вычислений счеты удобнее, проще - не будешь же экскаватором рыть ямку для помидорной рассады или даже для саженцев яблони. Больше потеряешь на взаимодействии с машиной, чем выиграешь от помощи ее стальных мускулов.
А теперь смена жанра, маленькая фантастическая зарисовка. У вас в руках землеройная машина размером с лопату или даже с игрушечную детскую лопатку. На рукоятке несколько кнопок - нажимаешь на них, и лопатка тихо и быстро выполняет любое задание. Нажмешь на одну кнопку - и мгновенно в земле появляется траншея метровой глубины, нажмешь на другую - мелкая лунка для зернышек-семян.
Эта фантастическая картина введена в наш рассказ как аналогия хорошо известной реальности сегодняшнего дня - электронных счетных машин.
Вот мы стоим у прилавка московского магазина "Счетные машины", который прозаически торгует миниатюрными компьютерами примерно десяти разных типов. Нас несколько человек, потенциальных покупателей, людей совершенно незнакомых. Пока мы только листаем инструкции, рассматриваем образцы, нажимаем кнопки, сопровождая это приятное занятие самыми разными комментариями: "... восьми разрядов хватит... лучше взять за сорок, чем за тридцать... она и дома всегда нужна... у этой клавиши мелковаты... счеты надо припрятать, скоро будут цениться, как старые иконы... блок питания нужен обязательно... без машины как без рук... то ли брать ту, то ли эту...". Сейчас, видимо, колебания кончатся - каждый примет свое решение, совершит покупку, станет владельцем электронной счетной машины. Еще двадцать-тридцать лет назад сама эта ситуация показалась бы фантастикой.
ТЫСЯЧА КАЛЬКУЛЯТОРОВ, МИЛЛИОН ВОЗМОЖНОСТЕЙ
Хотя в части портативных, или, как еще говорят, карманных, электронных вычислительных машин существует немалая терминологическая путаница, чаще всего их все же именуют микрокалькуляторами. И делят на три большие группы - инженерные, программируемые и простейшие, или массовые. Последние иногда называют арифметическими машинами, а еще чаще просто микрокалькуляторами - если говорят "микрокалькулятор" без прибавления "инженерный" или "программируемый", то речь скорее всего идет о простейшей, массовой машине.
Слово "простейшая" в данном случае не должно огорчать. Такие счетные машины вполне могут быть использованы для разного рода бухгалтерских работ, экономических расчетов, решения многих технических задач, словом, во всех случаях, где нужно обрабатывать большие массивы числовой информации, умножать, делить, вычитать, складывать. Инженерные машины имеют, так сказать, более высокую квалификацию. Они быстро выдают значения синусов, косинусов и других прямых и обратных тригонометрических функций, быстро извлекают корни, оперируют с десятичными и натуральными логарифмами, решают некоторые виды уравнений, то есть делают много такого, что необходимо инженеру, ученому ну и, конечно же, студенту, связанному с точными науками.
А пот программируемый калькулятор, в отличие от простейшего и инженерного, имеет не только жесткие программы работы, такие, например, как "умножить" или "вычислить тангенс", но и позволяет пользователю самому формировать программы с тем, чтобы машина могла самостоятельно решать достаточно большое количество разнообразных задач. Ну, скажем, такую задачу: "Вычислить значение x=а**(2m)-b**m+c**2 для всех целочисленных a в интервале от 2 до 24, для b от 2 до 9, m от 1 до 3 при c, равном 8.5, и найти результат, наиболее близкий к числу 330". Подобную задачу можно в принципе решить и на любой другой счетной машине, затратив на это некоторое время, но программируемый калькулятор все сделает сам: вам останется только ввести в него задание, дать машине возможность спокойно поработать и через некоторое время подойти за результатами. Решая подобные задачи, программируемый микрокалькулятор уже чем-то напоминает большую вычислительную машину, которая вопреки своему названию не просто вычисляет, а выполняет более тонкую интеллектуальную работу - сопоставляет данные, ищет оптимальные значения каких-либо величин, составляет цепочки логических операций. Причем делается это настолько изящно и ловко, что даже маленький программируемый калькулятор, не говоря уже о больших компьютерах, нередко видится не мертвым инструментом, не "железкой", а умелым и инициативным помощником.
Но вернемся, однако, к самым простым микрокалькуляторам, которые, как показывает опыт сильно компьютеризованных стран, вполне могут удовлетворить миллионы пользователей.
У многих людей существует мнение, что простейший микрокалькулятор выполняет лишь четыре действия арифметики и ни на что большее не способен. В действительности это не так, и даже дважды не так. Во-первых, во многих простейших микрокалькуляторах, кроме традиционных клавиш "сложить" ("+"), "вычесть" ("-"), "делить" (":") и "умножить" ("*"), есть еще и другие операционные клавиши. В микрокалькуляторе Б3-23, например, имеется клавиша "процент" (%), и можно, взяв какое-нибудь 73724965, мгновенно найти, что 0.738 процента от него составляют 544090.24. В калькуляторе Б3-24Г клавиши процентов нет, но зато здесь есть дополнительный регистр, или, проще говоря, отдел памяти. Нажатием на клавишу "память+" ("П+") в эту дополнительную память можно загнать результат каких-либо предварительных вычислений, а затем в нужный момент извлечь его и вновь пустить в дело. Имеется в этой машине еще и клавиша "индикация памяти" ("ИП"), нажав на которую вы видите припрятанное число на светящемся цифровом табло, на этом маленьком дисплее микрокалькулятора. И, конечно, имеется клавиша "сброс памяти" ("СП"), позволяющая мгновенно забыть уже ненужное число и освободить место для другого.
Особенно много дополнительных клавиш, а значит, и дополнительных возможностей быстро проводить вычисления у настольных микрокалькуляторов, таких, как МК-44. Эти машины уже не рассчитаны на то, чтобы носить их в кармане,- слишком большой понадобился бы карман. Они имеют размеры книги и, как предполагается, будут стоять на столе у экономиста или бухгалтера, на прилавке у продавца. У настольных калькуляторов и клавиши крупнее, и цифры более крупные, и светятся эти цифры не красными, как у многих карманных машин, а более спокойным зеленоватым цветом. Словом, настольные микрокалькуляторы рассчитаны на то, что работать с ними будут целый день, и сделано многое, чтобы работа эта не утомляла. Кроме клавиш арифметических операций, извлечения корня и вычисления процентов, в настольных машинах обязательно есть дополнительная память, а иногда не один, а два или даже три регистра, каждый на свое число и со своими клавишами записи, индикации и сброса. Имеются часто и клавиши, меняющие знак у чисел, позволяющие быстро найти обратную величину и ряд других.
Итак, отличие простейших микрокалькуляторов от школяра, выполняющего лишь четыре действия арифметики, во-первых, состоит в том, что машины эти уже сами по себе умеют делать нечто большее. А вот и во-вторых: пользуясь некоторыми правилами, суховато изложенными в инструкции, можно с помощью арифметических машин делать многое такое, о чем даже не подумаешь, глядя на их клавиатуру. Иногда это предусмотренное конструктором некоторое дополнительное удобство, облегчающее вычисления. Так, например, на любом простейшем микрокалькуляторе можно любое число m (слово "любое" имеет одно ограничение - нужно, чтобы числа не переполняли индикатор, скажем, чтобы в восьмиразрядных машинах и числа и результат были бы до 100000000, а в двенадцатнразрядных машинах - до 1000000000000) возвести в любую целочисленную степень n. Для этого достаточно ввести в машину число m, а затем нажать клавишу "*" и n-1 раз нажать клавишу "=". Так, например, выполнив такое нажимание клавиш "5" "*" "=", "=", вы получите 5**3=625, а нажав "=" еще 7 раз, мгновенно получите 5**10=48828125.
Или другая очень удобная "мелочь": если вам нужно работать с постоянным числом, например, умножать различные величины T1, Т2, Т3... на постоянный коэффициент К, то достаточно сначала ввести одну из этих величин, например, Т, нажать клавишу "*" и ввести К. После этого можно будет выполнять умножение на К, не вводя ни самого К, ни знака умножения - достаточно будет ввести очередное Т и нажать на клавишу "=", как тут же появится результат умножения этого Т на К. Дело в том, что при умножении после нажатия клавиши "=", второй сомножитель, если его специально не убирать, автоматически становится постоянным коэффициентом. Точно так же становится постоянным коэффициентом второе слагаемое; вычитаемое или делитель. Если, скажем, вы хотите разделить ряд чисел 9, 27, 72, 126, 600... на какой-либо коэффициент, например, на 6, то достаточно полностью выполнить первое деление 9:6=1.5, а затем вводить лишь сами числа и знаки равенства: нажав клавиши "24", "=", вы увидите на индикаторе 4, так как автоматически произойдет деление, 24:6=4, нажав клавиши "72", "=", получите 12, будет выполнено деление 72:6=12 и т.д.
Простейшие микрокалькуляторы позволяют достаточно просто вычислять многое такое, что с первого взгляда не имеет прямого отношения к арифметике. Существует, в частности, довольно простой способ вычисления сложных процентов или нахождения корня любой степени из любого числа. Имеется возможность вычисления тригонометрических функций - синусов, косинусов, тангенсов.
"Так зачем же,- вправе поинтересоваться читатель,- переплачивать деньги за инженерные машины, если то, что делают они, можно осуществить и с помощью простейшего микрокалькулятора?"
Не имея возможности обсуждать финансовую сторону дела, напомним лишь о всем знакомой характеристике любого инструмента - об удобстве пользования. Ведь все то, что делает простейший микрокалькулятор, можно осуществить значительно более дешевыми средствами - с помощью карандаша и бумаги. Однако же миллионы людей предпочитают на этом не экономить, так как подобная экономия оборачивается невосполнимым перерасходом времени и нервной энергии. Инженерный микрокалькулятор значительно удобнее арифметической машины при выполнении большого числа алгебраических операций, при вычислениях с тригонометрическими функциями или логарифмами, при решении уравнений. То, что при работе с простейшим микрокалькулятором потребует десятков действий и многоступенчатых вычислений, в инженерной машине может быть сделано нажатием одной клавиши. И выбирая себе в помощники микрокалькулятор, нужно, видимо, прежде всего подумать о том, что он умеет делать и чем бы его хотел нагрузить хозяин. Словом, перефразируя известный стих, можно сказать: "Все машины хороши, выбирай на вкус".
МИКРОСЧЕТЫ С ЭЛЕКТРИЧЕСКИМИ КОСТЯШКАМИ
Ушли в прошлое времена, когда можно было всерьез декларировать: "Хочу все знать!" Сегодня это самое "все" настолько многопланово, настолько объемисто, что никакой индивидуальной памяти на него, конечно, не хватит. И уже нередко специалист не очень-то знает, что происходит в смежных областях, или даже не очень подробно знает, что делают зарубежные коллеги в его собственной области. Да что там подробности - в последнее время мы все чаще миримся с тем, что важнейшие фрагменты, уже прорисованные наукой в картине мира, незнакомы нам даже в самых общих чертах. Миримся с тем, что не знаем принципа действия машин и аппаратов, которые служат нам, с которыми мы регулярно общаемся. Это раньше для владельца приемника считалось неприличным не понимать, что делает радиолампа и какие бывают типы ламп. А шофер, или, как теперь говорят, водитель, просто обязан был разбираться в устройстве своей машины. Сегодня же человек, сдающий экзамен на водительские права, может вообще не знать, как устроен автомобиль,- в экзаменационных билетах даже нет вопросов об этом. И они, видимо, не нужны: можно виртуозно управлять автомобилем и не интересоваться тем, что делает карбюратор или откуда берется искра зажигания. Точно так же, любуясь яркими красками на экране телевизора, совсем не обязательно знать, как они приходят с телецентра в ваш дом.
Можно не интересоваться... Не обязательно знать... Но почему же, привычно нажимая клавиши микрокалькулятора, испытываешь какую-то неловкость, какое-то неудобство от того, что непонятно, как совершается это чудо мгновенного счета? Почему бухгалтер, давно привыкший к калькулятору, встретив специалиста по вычислительным машинам, отводит его в угол и осторожно пытается выведать, как же все-таки это делается, как она считает, эта небольшая коробочка? Кто знает, может быть, этим нашим любопытством движет какой-нибудь древнейший инстинкт - боязнь неизвестности, неясности. И поэтому нам неотвратимо хочется обо всем - именно обо всем - иметь представление, пусть даже самое общее, пусть только о существе дела. Человек по самой своей природе стремится к знанию, и в большинстве случаев дело сводится не к философическому "знать или не знать". Дело обычно сводится к простой житейской задаче: как конкретно, с минимальными затратами сил и времени ликвидировать "белое" пятно в своем мировоззрении, как конкретно представить себе ту или иную сложность, предельно упростив ее и не потеряв при этом существа дела.
Пытаясь ликвидировать в своих знаниях белое пятнышко, обозначенное надписью "Электронные счетные машины", мы, видимо, прежде всего должны вспомнить, что сам субстрат счета в таких машинах, само вещество, из которого формируются числа, это не что иное, как электрический ток. А конкретней - очень короткие, кратковременные всплески электрического тока, электрические импульсы. Энергию для них дает батарейка или электрическая сеть, а формируются такие импульсы с помощью внутренних генераторов и других электронных блоков машины. Когда вы нажимаете клавиши ввода чисел, то посылаете в сложный электрический мир калькулятора определенное количество импульсов тока, чередующихся в определенном порядке. А нажав клавишу операции, производите необходимые переключения в самой схеме машины с тем, чтобы импульсы-числа шли по определенным путям, складываясь, вычнтаясь или многократно складываясь и вычитаясь, что, как известно, эквивалентно умножению и делению. После такой переработки чисел-импульсов появится новая серия электрических всплесков, эквивалентная полученному результату. Этот записанный на электрическом языке результат будет направлен на цифровой индикатор, где зажжет определенные комбинации черточек, складывая из них нужные цифры,- в разных типах индикаторов используются различные физические процессы, но во всех случаях свечение сегментов, свечение черточек, из которых складывается цифра, происходит под действием электрического тока.
Познакомившись с этим веселым описанием, так и хочется, наверное, представить себе микрокалькулятор этакими канцелярскими счетами, где вместо деревянных костяшек двигаются по невидимым электрическим дорожкам невидимые электрические токи, собираясь группками, когда производится сложение, или разбегаясь при вычитании. Признаемся прямо: подобная картина должна быть приравнена, как сказали бы великие сатирики, к упрощенчеству со взломом. И все же эта недопустимо упрощенная модель электронного микрокалькулятора может быть допущена в качестве наглядного пособия для человека, у которого нет сил, чтобы знакомиться с предметом более подробно.
Ну, а если силы есть - попробуем продвинуться дальше.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
ДЕЙСТВУЮЩИЕ ЛИЦА И ИСПОЛНИТЕЛИ
То, что происходит в микрокалькуляторе во время вычислений, очень напоминает спектакль со сложным сюжетом, с большим числом действующих лиц, частой сменой декораций, бесконечными выходами и исчезновением героев. Судите сами: в такой простой операции, как умножение двух трехзначных чисел, участвуют десятки тысяч импульсов. Они разными группами сотни раз появляются во всех участках машины, на время прячутся в памяти и вновь выходят на сцену, перестраиваются, производят новые тысячи импульсов, своими силами меняют декорацию, меняют состояние электрических схем машины, сходятся в общих электрических цепях или расходятся по разным участкам, в точном соответствии с указаниями автора - "... производит выстрел и выпрыгивает в окно...". Разбирать во всех подробностях подобные спектакли нет никакого смысла, но в самых общих чертах представить себе одну типичную вычислительную феерию мы все же попробуем. Только для того, чтобы ощутить атмосферу происходящего, почувствовать его масштабы, познакомиться с остроумнейшими методами технологии вычислений.
Начать, пожалуй, стоило бы со знакомства с действующими лицами, с героями спектакля. Или даже еще лучше со знакомства с актерами, с исполнителями - каждый из них "не одну играет роль" и многократно появляется в списке действующих лиц.
Взгляните на схему любого электронного прибора - из всех деталей чаще всего вы видите на ней транзисторы, полупроводниковые диоды, конденсаторы, резисторы и соединительные провода. Попробуем дать им всем короткую характеристику, начнем с конца.
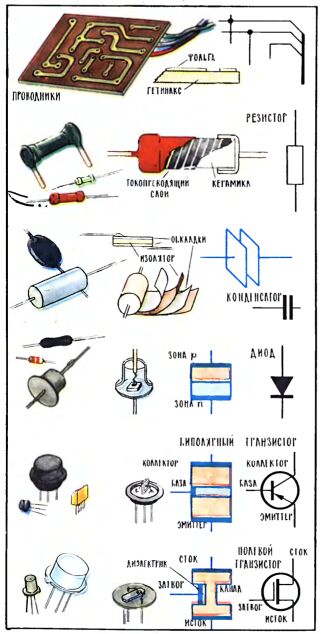
Что можно сказать о проводах? Их задача - беспрепятственно пропускать ток, направлять его из одного элемента схемы в другой. Пропускают ток и резисторы, ближайшие родственники школьного реостата, но они уже оказывают току определенное, дозированное сопротивление, ослабляют его в нужное число раз. Ток, проходя по резистору, выделяет на нем какую-то часть своей энергии, которая может быть использована для самых разных дел. Конденсатор - исполнитель со сложным характером, ему в электронных схемах поручают много разных ролей. Конденсатор, в частности, может накапливать и какое-то время хранить электрические заряды, может отделять импульсный ток от постоянного, участвовать в отделении коротких импульсов от длительных, вместе с резистором он может быть своего рода эталоном времени - чем больше емкость конденсатора, тем дольше он разряжается через резистор. Теперь полупроводниковые элементы - диод и транзистор. Диод, как и проводник, легко пропускает ток, но только в одну сторону. Его можно рассматривать как выключатель, учитывающий направление тока: если ток идет "туда" - выключатель замкнут, если "обратно" - разомкнут. Только в одну сторону пропускает ток и транзистор, но он в отличие от диода еще и усиливает слабые электрические токи, точнее, создает их мощную копию, используя энергию внешней батареи. Этот важнейший для всей радиоэлектроники процесс - усиление - можно представить себе, как управление мощным потоком воды с помощью легко перемещаемой заслонки. Такая аналогия, в свою очередь, помогает понять важное дело, которое поручают транзистору во многих схемах - он используется как управляемый выключатель. Под действием слабого управляющего сигнала (он подается на командный пункт транзистора, на электрод, названный базой, а у приборов другого типа, у полевых транзисторов - затвором) транзистор, как принято говорить, открывается и пропускает ток. А когда управляющий сигнал заканчивается, транзистор вновь закрывается и ведет себя уже как разомкнутый выключатель, тока не пропускает.
Из этих пяти основных элементов можно собрать много разнообразных блоков, позволяющих производить самые разные операции с электрическими импульсами. Вот некоторые из таких электронных схем.
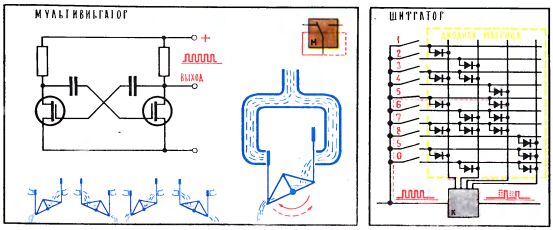
МУЛЬТИВИБРАТОР. Два транзистора соединены так, что каждый из них управляет работой другого. Конденсаторы создают некоторое запаздывание, несколько замедляют реакцию транзистора, на действие соседа, и в итоге транзисторы поочередно открывают и закрывают друг друга. А каждое такое открывание-закрывание создает импульс тока - начинает работать генератор, который, используя энергию батареи, создаст непрерывную очередь импульсов тока.

ТРИГГЕР. По начертанию эта схема похожа на мультивибратор, существенная разница в том, что транзисторы связаны друг с другом не через конденсатор, а непосредственно. В итоге один из транзисторов, открывшись, мгновенно закрывает второй прибор, и триггер замирает в этом устойчивом состоянии. Только внешний управляющий импульс ликвидирует сложившееся соотношение сил, и транзисторы меняются ролями - закрытый транзистор открывается и закрывает соседа, еще только что пропускавшего ток. Естественно, что внешние управляющие импульсы будут открывать транзисторы поочередно, то есть каждый из транзисторов будет открываться через такт и частота импульсов на его выходе будет в два раза меньше, чем на входе. А цепочка из двух последовательно включенных триггеров может делить частоту импульсов на 4, из трех триггеров - на 8 и так далее.

ПАМЯТЬ. Цепочки триггеров можно использовать как регистры памяти. В состоянии триггеров - левый транзистор открыт, правый закрыт или, наоборот,- зафиксируется (запомнится), сколько на вход было подано импульсов. А можно каждый триггер использовать как отдельный элемент памяти - он будет помнить, подавался на его вход управляющий импульс или нет. Записать в триггерную память новую информацию можно мгновенно, ее легко прочитать (проверив, какой из транзисторов пропускает ток) и стереть несложно, импульсом вернув триггер в исходное состояние.
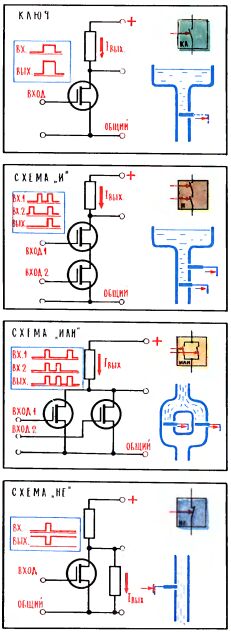
ЭЛЕМЕНТЫ ЛОГИКИ И, ИЛИ, НЕ. Можно подать на вход транзистора два управляющих сигнала так, чтобы он открывался от любого из них. В этом случае транзистор будет пропускать ток и выдавать импульс тока или под действием первого входного импульса, или под действием второго, схема будет выполнять логическую операцию ИЛИ. А можно построить схему так, чтобы усилий одного входного импульса не хватало для открывания транзистора, чтобы он открывался лишь при одновременном действии двух входных сигналов - и первого, и второго. Это схема для выполнения логической операции И. Наконец, можно так подвести входной импульс к транзистору, что он будет делать все наоборот - будет закрывать заранее открытый транзистор. Эта схема выполняет операцию НЕ - выдает выходной сигнал, когда нет входного, и наоборот, когда подается входной импульс, ток через транзистор не идет, на выходе импульс не появляется. Логические элементы И, ИЛИ, НЕ широко применяются в автоматике, из них собирают цепочки для выполнения более сложных логических операций. Такая цепочка, например, включает мотор лифта если И закрыта дверь шахты, И закрыта дверь кабины, НЕ включился датчик перегруза, И нажата кнопка ИЛИ второго, ИЛИ третьего, ИЛИ четвертого и т.д. этажа.
КОММУТАТОР. Объединив триггеры с логическими элементами, можно получить быстродействующий бесконтактный переключатель - непрерывную очередь импульсов он будет поочередно направлять по разным электрическим цепям. Например, первый импульс в один провод, второй - в другой и так далее.
ШИФРАТОР. Логические элементы в сочетании с коммутатором могут превратить однообразную последовательность одинаковых импульсов в шифровку из импульсов и пауз, чередующихся в заданном порядке. Можно, например, убрать третий импульс из каждой четверки - триггер посчитает импульсы, а логика в нужный момент закроет путь со входа на выход.
ДЕШИФРАТОР. Надежно решается и обратная задача - логические схемы из смеси импульсов и пауз отбирают и направляют по нужному адресу только строго определенные их комбинации. Например, только те пары импульсов, перед которыми была пара пауз.
ДИОДНАЯ МАТРИЦА. Перебрасывая диодные мостики от некоторых проводов одной группы к проводам другой группы, легко перераспределять сигналы, из одних потоков импульсов получать другие. Такие многомостиковые схемы - матрицы - можно рассматривать как постоянную ("запаянную") память.

СУММАТОР. Вычислительные машины работают с двоичными числами - ноль там 0, единица - 1, а вот двойка уже не привычный нам знак 2, а 10, тройка - 11, четверка 100, пятерка 101... Наши предки выбрали десятичный счет, видимо, потому, что на руках у человека десять пальцев и удобно переходить в следующий разряд, досчитав до десяти. Конструкторы электронных машин выбрали двоичный счет потому, что у основных электрических элементов схемы, грубо говоря, всего два пальца. Они могут находиться только в двух состояниях - выключатель, в частности, в состояниях "включено - выключено", триггер в состояниях "ток в правом транзисторе - ток в левом транзисторе", сам транзистор в состояниях "открыт - закрыт" и т.д. Этим элементам удобнее всего считать электрические сигналы, производить с ними вычислительные операции именно в двоичном коде.
Конструкторы механических вычислительных аппаратов, в частности Блез Паскаль, немало помучились, пока научились при сложении переносить числа в следующий разряд. Нетрудно сложить 4+5=9 с помощью двух простых зубчатых колес или линеек, а вот операция 4+8=12 требует дополнительных приспособлений - нужно проанализировать полученные двенадцать единиц, записать только две, а десять записать единицей в следующем разряде, в разряде десяток.
Подобная задача появляется и в электронной счетной машине, работающей с двоичными числами. Здесь при сложении должно получаться 0+0=0, 1+0=1, 0+1=1 и, наконец, 1+1=10. Первые три операции легко выполнить, если единицы отображать импульсами тока, нули паузами и два числа одновременно подавать на вход элемента ИЛИ. При обоих входных нулях (паузах) на выходе ИЛИ, конечно, ничего не будет - 0+0=0. При складывании нуля с единицей на выходе всегда будет единица - элемент ИЛИ одинаково хорошо сработает или от одного импульса (1+0=1), или от другого (0+1=1). Но что делать с операцией 1+1=10? Как, складывая две единицы, два импульса тока, получить ноль и сделать перенос - в нужный момент ввести единицу в следующий разряд?
Решается задача с помощью многоэлементной логической схемы - сумматора. Его остроумные действия сводятся к тому, чтобы операции 0+0, 1+0 и 0+1 осуществлять только в элементе ИЛИ а при операции 1+1 блокировать этот элемент и получать на выходе 0. Такое блокирование выполняет элемент И2. В первых трех случаях он срабатывает и пропускает импульс (единицу) из ИЛИ1 на выход СУММА; срабатывание И1 происходит под действием двух одновременных импульсов - и пришедшего с самого ИЛИ1, и пришедшего с элемента НЕ. Но когда на вход сумматора приходят сразу две складываемые единицы (1+1), два входных импульса, то от них срабатывает бездействовавший до этого элемент И2, тот приводит в действие элемент НЕ, а он, как и полагается этому путанику, получив входной импульс, прекращает подачу своих сигналов на вход И1 и тем самым, по сути, выключает его, прерывает подачу импульса на выход СУММА. Одновременно с выхода сработавшего И2 получают сигнал, который используется для переноса единицы в следующий разряд.
Сумматор, с которым мы познакомились в простейшем его варианте,- обязательный блок любой электронной вычислительной машины. Кроме того, его можно считать типичным блоком - на примере сумматора видно, как ловко обходятся электронные схемы с импульсами тока, какие интересные и тонкие операции с ними производят. Отметив этот приятный факт, мы вернемся к самому микрокалькулятору, где знакомые нам действующие лица начинают великолепный спектакль вычислений.

Перед тем как уйти с завода-изготовителя, микрокалькуляторы проходят суточный прогон: если в интегральной схеме есть скрытый дефект, то он, как правило, обнаруживается в первые часы работы.
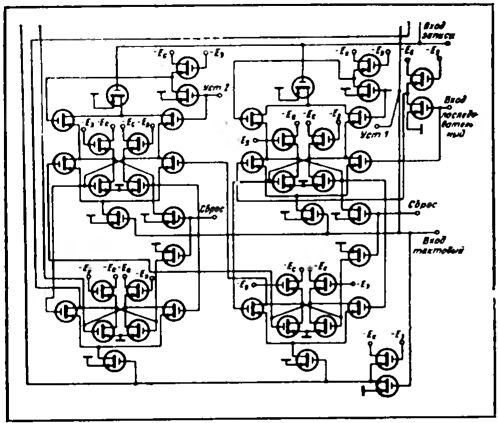
При первом знакомстве с электронным микрокалькулятором сильнейшее впечатление производят его безотказность, его доведенная до предела исполнительность. Машинка не рассуждает, любое ваше задание она выполняет с готовностью, мгновенно выбрасывая на табло результат. Посмотрев по сторонам, можно заметить, что все мы, стоящие у прилавка и выбирающие себе электронного помощника, делаем одно и то же: быстро нажимаем клавиши, вводим случайно пришедшие на ум числа, складываем их, умножаем, делим, любуясь ловкостью счетчика-виртуоза и почему-то подсознательно стараясь устроить ему экзамен потруднее. Но, оказывается, для калькулятора в пределах его квалификации трудных задач не существует. С одинаковой легкостью он сообщает, что 2*2=4 или что 0.65239:0.71263=0.915468. Машинка считает по житейским меркам с немыслимо высокой скоростью - не успеваешь нажать клавишу "=", как ответ уже готов. Иногда даже кажется, что все ответы в машине заготовлены заранее и в нужный момент просто подаются на табло. А вместе с тем каждое вычисление, как сообщают инструкции, длится вполне определенное время - у большинства микрокалькуляторов около 0.1 секунды. И если вдуматься, то любая операция, выполняемая калькулятором,- это огромная работа, которую мы лишь в погоне за легкостью описания назвали спектаклем вычислений.
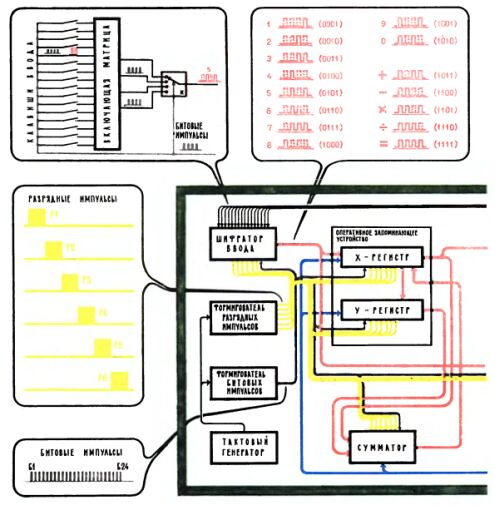
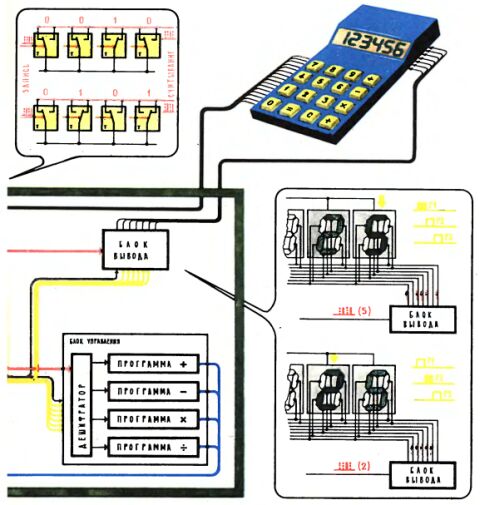
ПЬЕСА В 5 ДЕЙСТВИЯХ, 8 КАРТИНАХ
Поднимается занавес, и мы видим сцену, на которой будут разворачиваться события: упрощенная функциональная схема шестиразрядного калькулятора. "Функциональная" (иногда говорят "скелетная" или "блок-схема") означает, что на схеме показаны лишь самые основные блоки машины и основные линии их соединения. На полной схеме в квадратах блоков были бы изображены замысловатые орнаменты из многих тысяч деталей - транзисторов, конденсаторов, диодов, и такая схема, даже мелко начерченная, получилась бы в несколько метров длиной. Схема, по которой мы будем знакомиться с ходом вычислительных операций, не относится к какому-либо конкретному калькулятору, хотя в основных чертах она близка к реальности.
Итак, занавес поднят, и спектакль начинается.
ДЕЙСТВИЕ ПЕРВОЕ - ВКЛЮЧЕНИЕ КАЛЬКУЛЯТОРА. Миниатюрным выключателем мы подаем питание, включаем батареи. Карманному микрокалькулятору, кстати, мало тех 4.5 вольта, которые дают три гальванических элемента, и поэтому в нем есть преобразователи этого напряжения, они дают 5-15 вольт для питания триггеров, усилителей, коммутаторов и других "действующих лиц" и 15-20 вольт для питания цифровых индикаторов. Настольные калькуляторы питаются только от сети, так как батарей им хватило бы ненадолго.
Как только включилось питание, начал работать тактовый генератор. Он дает бесконечную очередь коротких импульсов, из которых потом формируются два основных вида импульсов, необходимых машине,- специалисты фамильярно называют их разрядными (Р) и битовыми (Б). Эти импульсы подаются во все блоки, они дирижируют всем спектаклем, всей работой калькулятора, синхронизируют взаимодействие его блоков. А битовые импульсы к тому же еще представляют собой сырье, из которого формируются двоичные числа и команды управления.
ДЕЙСТВИЕ ВТОРОЕ - ВВОД ПЕРВОГО ЧИСЛА. Любая клавиша ввода - это всего лишь простейший выключатель, и, нажав какую-либо клавишу, вы просто открываете путь для битовых импульсов на один из входов шифратора. Получив импульсы именно с этого своего входа, шифратор сделает из них строго определенную последовательность сигналов и пауз. Так, при нажатии на клавишу "2" шифратор выдаст серию "пауза - пауза - импульс - пауза", при нажатии на клавишу "5" появится серия "пауза - импульс - пауза - импульс", то есть 2 и 5 превратятся в двоичные числа, записанные в виде импульсов и пауз.
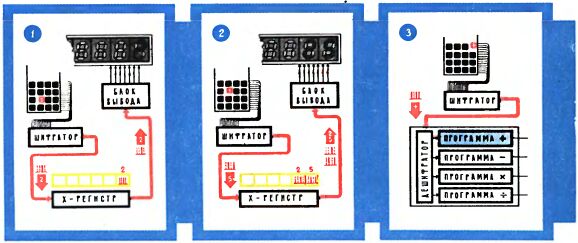
Здесь настал момент объявить - дальше уже тянуть невозможно,- что микрокалькуляторы работают не в двоичном коде, а в двоично-десятичном. Грубо говоря, это означает, что машина работает с многоразрядными десятичными числами, а каждый их разряд, каждая десятичная цифра записана в двоичном коде четверкой импульсов-пауз. Запись при этом получается несколько более громоздкой, чем при чисто двоичном коде, но зато проще становятся блоки перевода из одной системы счисления в другую - из десятичной (язык человека) в двоичную (язык машины) и обратно. А для миниатюрных машин упрощение каких-либо блоков - достоинство решающее.
Итак, нажата первая клавиша, и из очереди битовых импульсов родился код первой введенной цифры, первая четверка импульсов-пауз. Она сразу отправляется на хранение в один из двух блоков оперативной памяти, в так называемый х-регистр и там ждет момента, когда начнутся сами вычисления. Комплект триггеров x-регистра запомнит эту четверку импульсов-пауз и копию ее направит в цифровой индикатор - вы увидите, какая цифра введена в машину, сможете проконтролировать, правильно ли была нажата клавиша.
На этом дело бы и кончилось, если бы машина работала с одноразрядными числами - от 0 до 9. В действительности же мы вводим в машину числа многоразрядные, а это требует некоторых дополнительных приспособлений. Одно из них - формирователь разрядных импульсов. Каждый из них длится в 4 раза больше битового, и за время одного разрядного импульса успевает пройти целая четверка импульсов-пауз, соответствующая одной десятичной цифре. Сами же разрядные импульсы коммутатор поочередно рассылает по шести разным проводам, и по этим шести дорожкам импульсы приходят во все блоки калькулятора. Здесь каждый из шести разрядных импульсов управляет работой элементов, которые обслуживают закрепленный за ними разряд. Так, например, импульс Р1 включает элементы памяти для записи единиц, импульс Р2 включает элементы для записи десятков, импульс Р3 - для записи сотен и т.д. Аналогично импульсы Р1, Р2, Р3 из следующих серий включают нужные элементы памяти при считывании единиц, десятков, сотен. Или включают ячейки индикатора для высвечивания единиц, десятков, сотен. Одним словом, каждый разрядный импульс заставляет машину работать только с тем разрядом, который за этим импульсом закреплен. А потом появляется следующий разрядный импульс, и вся машина занимается уже следующим разрядом. Когда поочередно пройдут первые шесть разрядных импульсов от Р1 до Р6, машина первый раз обработает все имеющиеся в ней шестиразрядные десятичные числа. Потом появится новая серия импульсов Р1-Р6, и начнется следующий цикл поразрядной обработки.
Кстати, мы ограничились шестью разрядами в нашей схеме только для ее упрощения. И еще одно примечание. Многоразрядные числа вводятся в машину так, как мы привыкли их называть,- чтобы ввести число 25, мы сначала нажимаем клавишу 2, потом 5. В калькуляторе этот порядок ввода чисел учитывается так: первая введенная цифра - в нашем примере двойка - сначала занимает место первого разряда (единицы): машина ведь пока не знает, что должно быть - 2, 20, 200 или 2000 и на всякий случай для начала записывает 2 в разряд единиц. А затем при появлении следующей цифры - пятерки - двойка с помощью разрядного импульса сдвигается на один шаг влево, на место десятков. Если появится еще одна цифра - двойка сместится в разряд сотен. Такое смещение цифр происходит и в ячейках памяти и в цифровом индикаторе.
ДЕЙСТВИЕ ТРЕТЬЕ - ВВОД ОПЕРАЦИИ. Каждая операция, которую может выполнить наша машина, так же как и сами числа, зашифрована в определенной четверке импульсов-пауз. При нажатии, например, на клавишу "+" шифратор выдаст четверку "импульс - пауза - импульс - импульс" и направит ее уже не в оперативную память, а в блок управления. Здесь дешифратор, распознав прибывшую депешу, включит с ее помощью матрицу "Программа сложения" ("Программа +"). В этой матрице, если пустить в нее тактовые и разрядные импульсы, сформируются все необходимые последовательности включений и выключений блоков машины, и строго согласованное взаимодействие этих блоков осуществит все, что нужно для сложения. Но пока матрица только подготовлена к работе и ждет сигнала.
ДЕЙСТВИЕ ЧЕТВЕРТОЕ - ввод второго числа. Все, казалось бы, должно произойти точно так же, как и при вводе первого числа - в оперативной памяти есть второй регистр, y-регистр, и туда после нажатия соответствующей клавиши шифратор ввода должен направить второе число. Но вот оказывается, что при вводе второго числа происходит неожиданный сюжетный поворот - в y-регистр переводится первое число, а второе записывается в освободившийся x-регистр. Для чего нужно это дополнительное перемещение? Опять-таки для того, чтобы упростить схему калькулятора: x-регистр связан с цифровым индикатором, а y-регистр не связан. Поэтому, чтобы для контроля высветить на индикаторе второе число, его нужно поместить именно в x-регистр: это проще, чем создавать систему индикации чисел, хранящихся в y-регистре.
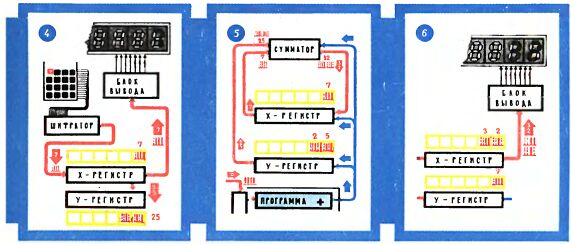
ДЕЙСТВИЕ ПЯТОЕ - ВЫЧИСЛЕНИЯ. Сами вычисления начинаются после нажатия клавиши "=". При этом в машине происходит несколько самостоятельных операции, как сказали бы в театре, пятое действие пьесы состоит из нескольких картин. Даже при самом простом вычислении - при сложении - таких "картин" четыре.
Прежде всего в блок управления пойдет команда "начать счет", а из него в x-регистр и y-регистр пойдут команды, по которым оба слагаемых одновременно и поразрядно двинутся из регистров в сумматор. Сам сумматор получит из блока управления команду, в каком режиме ему нужно работать, и при сложении, естественно, он просто поразрядно сложит оба числа. Из сумматора полученный результат попадает в x-регистр, а из него на цифровой индикатор. Этот результат будет храниться в x-регистре до особых указаний, на случай, если он понадобится для дальнейших вычислений. Точно так же в y-регнстре будет храниться второе слагаемое, оно может понадобиться при работе с постоянным числом, о чем мы уже говорили раньше.
Вот и все - на индикаторе появился результат вычислений, спектакль окончен. Но в самом конце, как говорится, под занавес, хочется сделать три коротких примечания.
Во-первых, отметим оригинальную систему высвечивания цифр на индикаторе. Каждая его ячейка, каждый разряд состоит из восьми сегментов - семь для самой цифры и один для запятой, которая зажигается при работе с десятичными дробями или когда получается дробный результат (например, 7:2-3.5). На индикатор работает его собственный преобразователь кода - получив четверку импульсов-пауз, в которой зашифрована некоторая десятичная цифра, он с помощью коммутаторов и матриц формирует комбинацию из семи раздельных токов - они зажгут комбинацию сегментов, из которых сложится эта цифра. Например, при появлении шифровки "пауза - пауза - импульс - пауза" токи пойдут к сегментам, из которых на индикаторе сложится двойка. Теперь простейший расчет, его можно выполнить и без калькулятора: для высвечивания числа на восьмиразрядном индикаторе может понадобиться в самых разных комбинациях переключать 64 контакта - восемь цифр по восемь (с учетом запятой) сегментов в каждой. Чтобы избежать столь сложной коммутации, принята такая система: комбинации токов, зажигающих цифры, подаются параллельно на сегменты всех ячеек, и при этом нужно переключать не 64, а всего 8 контактов. Комбинации токов, соответствующие разным цифрам, подводятся к индикатору поочередно. Так, при высвечивании числа 25 сначала на все сегменты индикатора подаются токи, которые зажгли бы цифру 5, а потом токи, которые зажгли бы цифру 2. Сослагательное наклонение, то есть глагол с частицей "бы", мы применили здесь не случайно - токи, поступающие на сегменты индикатора, сами по себе не могут зажечь цифру, для ее зажигания нужно еще подать напряжение на общий электрод, общий для всех сегментов данной ячейки (разряда). А напряжение на этот общий электрод подается в виде разрядных импульсов Р1-Р6, и каждый из них подходит только к одной ячейке, только к своему разряду. Причем подходит именно в тот момент, когда на сегменты подается комбинация токов для зажигания цифры именно этого разряда. Так, в нашем примере при появлении токов, которые на всех индикаторах зажгли бы цифру 5, разрядный импульс Р1 подходит только к общему электроду первой (справа) ячейки индикатора, и цифра 5 появляется только в первой (справа) ячейке; при появлении токов, соответствующих цифре 2, разрядный импульс Р2 разрешает зажигание только цифры во второй ячейке. При такой системе цифры на индикаторе, конечно, горят не все время, а поочередно, каждая вспыхивает только при появлении своего разрядного импульса. Однако серии разрядных импульсов появляются так часто, что мелькания цифр мы не замечаем.
Этот подробный рассказ о работе цифрового индикатора появился здесь совсем не для того, чтобы читатель, уже уставший, видимо, от напряженного сюжета, запоминал в деталях всю описанную процедуру. Рассказ этот - всего лишь еще одна иллюстрация виртуозных методов работы с электрическим сигналом, которыми с такой легкостью пользуется электроника.
Второе примечание связано с тем, что в качестве примера, иллюстрирующего работу калькулятора, было выбрано сложение. Если мы захотим умножить два числа или разделить их, то спектакль несколько затянется - в нем уже будет не 8 картин, а как минимум больше десятка, а то и несколько десятков. Потому что умножение выполняется как последовательное сложение, программа должна много раз посылать в сумматор один из сомножителей и много раз суммировать его. При этом нужно одновременно считать, сколько всего раз происходит суммирование и для этого, например, при каждом складывании первого сомножителя уменьшать на единицу второй сомножитель, пока он не превратится в ноль. Вот как с учетом всего этого может вестись в калькуляторе умножение 25*5:
0+25=25, 5-1=4;
25+25=50, 4-1=3;
50+25=75, 3-1=2;
75+25=100, 2-1=1;
100+25=125, 1-1=0.
Когда в контрольном вычитании получается ноль, вычисления прекращаются и последняя сумма 125 выдается как результат умножения. Поскольку одно сложение, по самым скромным подсчетам, требует четырех последовательных операций, которые мы в нашей условной пьесе назвали картинами, то можно подсчитать, что подобная пьеса уже при умножении 25*5 будет состоять из 20 картин. Особенно много операций приходится выполнять при умножении на большие числа. Правда, умножая, например, на 3752, машина выполняет не 3752 сложения, а всего 2+5+7+3=17 сложений, так как умножение ведется поразрядно, по школьной терминологии, "в столбик". И все же при умножении на число 99999999 машине приходится произвести 9*8=72 поочередных сложения и столько же контрольных вычитаний. И вот здесь начинаешь ощущать одно из достоинств электронного счета. Даже в самых медленных калькуляторах серии разрядных импульсов выстреливаются примерно 300 раз в секунду, битовые импульсы длятся меньше тысячной доли секунды, триггеры, элементы логики, дешифраторы срабатывают за миллионные доли секунды, и самое громоздкое вычисление происходит практически мгновенно. Лишь в инженерных машинах есть вычисления с таким большим числом промежуточных операций, что между нажатием клавиши "=" и выдачей результата проходит ощутимое время - что-то около секунды.
Итак, при нажатии на клавишу "=" в калькуляторе начинается невидимая нам электронная буря - длинные очереди импульсов проносятся из регистров памяти в сумматор или из сумматора в регистры, блок управления, этот генеральный штаб машины, одну за другой шлет на места ультимативные депеши - "... сумматору начать сложение... число из x-регистра - в сумматор... число из сумматора - в x-регистр... сдвинуть на один разряд число в y-регистре...- и в заключение - ... число из x-регистра - на индикатор". Все эти приказы составляются, прочитываются и исполняются с помощью транзисторных схем-триггеров, мультивибраторов, логических элементов, коммутаторов - которые, по сути, представляют собой управляемые выключатели. Обычно в калькуляторе несколько тысяч таких транзисторных выключателей, во время одного вычисления они могут произвести несколько миллионов включений-выключений.
"Дело плохо!" - только так может прореагировать на это человек, имеющий опыт общения с переключателем диапазонов в приемнике, переключателем телевизионных программ или даже просто с выключателем настольной лампы. Все это - элементы, мягко говоря, не слишком надежные. Особенно страшно, когда выключатели собираются тысячами, когда неисправность любого выводит из строя всю систему и к ненадежности самих коммутирующих элементов прибавляется еще ненадежность их соединений: отошел один из бесчисленных соединительных проводков - и все пропало. С этих позиций от микрокалькулятора, казалось бы, ничего хорошего ждать нельзя: один раз он сработает точно, два соврет или вообще откажется считать - шуточное ли дело, тысячи сложным образом соединенных выключателей!
В действительности же дело обстоит совсем иначе - из всей радиоэлектронной аппаратуры, обслуживающей рядового человека (или, как часто говорят, бытовой электроники), микрокалькуляторы наверняка могут быть признаны чемпионами надежности. Микрокалькулятор годами работает, не допуская ошибок, и в принципе не видно почти никаких возможностей, чтобы эта маленькая, но весьма сложная вычислительная машинка или во всяком случае ее основная, считающая часть вышла из строя. Этому как раз и посвящается третье примечание, несколько более подробное, чем два предыдущих.


То, что происходит в микрокалькуляторе во время вычислений, очень напоминает спектакль со сложным сюжетом, с большим числом действующих лиц, частой сменой декораций, бесконечными выходами и исчезновением героев. Судите сами: в такой простой операции, как умножение двух трехзначных чисел, участвуют десятки тысяч импульсов. Они разными группами сотни раз появляются во всех участках машины, на время прячутся в памяти и вновь выходят на сцену, перестраиваются, производят новые тысячи импульсов, своими силами меняют декорацию, меняют состояние электрических схем машины, сходятся в общих электрических цепях или расходятся по разным участкам, в точном соответствии с указаниями автора - "... производит выстрел и выпрыгивает в окно...". Разбирать во всех подробностях подобные спектакли нет никакого смысла, но в самых общих чертах представить себе одну типичную вычислительную феерию мы все же попробуем. Только для того, чтобы ощутить атмосферу происходящего, почувствовать его масштабы, познакомиться с остроумнейшими методами технологии вычислений.
Начать, пожалуй, стоило бы со знакомства с действующими лицами, с героями спектакля. Или даже еще лучше со знакомства с актерами, с исполнителями - каждый из них "не одну играет роль" и многократно появляется в списке действующих лиц.
Взгляните на схему любого электронного прибора - из всех деталей чаще всего вы видите на ней транзисторы, полупроводниковые диоды, конденсаторы, резисторы и соединительные провода. Попробуем дать им всем короткую характеристику, начнем с конца.

Что можно сказать о проводах? Их задача - беспрепятственно пропускать ток, направлять его из одного элемента схемы в другой. Пропускают ток и резисторы, ближайшие родственники школьного реостата, но они уже оказывают току определенное, дозированное сопротивление, ослабляют его в нужное число раз. Ток, проходя по резистору, выделяет на нем какую-то часть своей энергии, которая может быть использована для самых разных дел. Конденсатор - исполнитель со сложным характером, ему в электронных схемах поручают много разных ролей. Конденсатор, в частности, может накапливать и какое-то время хранить электрические заряды, может отделять импульсный ток от постоянного, участвовать в отделении коротких импульсов от длительных, вместе с резистором он может быть своего рода эталоном времени - чем больше емкость конденсатора, тем дольше он разряжается через резистор. Теперь полупроводниковые элементы - диод и транзистор. Диод, как и проводник, легко пропускает ток, но только в одну сторону. Его можно рассматривать как выключатель, учитывающий направление тока: если ток идет "туда" - выключатель замкнут, если "обратно" - разомкнут. Только в одну сторону пропускает ток и транзистор, но он в отличие от диода еще и усиливает слабые электрические токи, точнее, создает их мощную копию, используя энергию внешней батареи. Этот важнейший для всей радиоэлектроники процесс - усиление - можно представить себе, как управление мощным потоком воды с помощью легко перемещаемой заслонки. Такая аналогия, в свою очередь, помогает понять важное дело, которое поручают транзистору во многих схемах - он используется как управляемый выключатель. Под действием слабого управляющего сигнала (он подается на командный пункт транзистора, на электрод, названный базой, а у приборов другого типа, у полевых транзисторов - затвором) транзистор, как принято говорить, открывается и пропускает ток. А когда управляющий сигнал заканчивается, транзистор вновь закрывается и ведет себя уже как разомкнутый выключатель, тока не пропускает.
Из этих пяти основных элементов можно собрать много разнообразных блоков, позволяющих производить самые разные операции с электрическими импульсами. Вот некоторые из таких электронных схем.

МУЛЬТИВИБРАТОР. Два транзистора соединены так, что каждый из них управляет работой другого. Конденсаторы создают некоторое запаздывание, несколько замедляют реакцию транзистора, на действие соседа, и в итоге транзисторы поочередно открывают и закрывают друг друга. А каждое такое открывание-закрывание создает импульс тока - начинает работать генератор, который, используя энергию батареи, создаст непрерывную очередь импульсов тока.

ТРИГГЕР. По начертанию эта схема похожа на мультивибратор, существенная разница в том, что транзисторы связаны друг с другом не через конденсатор, а непосредственно. В итоге один из транзисторов, открывшись, мгновенно закрывает второй прибор, и триггер замирает в этом устойчивом состоянии. Только внешний управляющий импульс ликвидирует сложившееся соотношение сил, и транзисторы меняются ролями - закрытый транзистор открывается и закрывает соседа, еще только что пропускавшего ток. Естественно, что внешние управляющие импульсы будут открывать транзисторы поочередно, то есть каждый из транзисторов будет открываться через такт и частота импульсов на его выходе будет в два раза меньше, чем на входе. А цепочка из двух последовательно включенных триггеров может делить частоту импульсов на 4, из трех триггеров - на 8 и так далее.

ПАМЯТЬ. Цепочки триггеров можно использовать как регистры памяти. В состоянии триггеров - левый транзистор открыт, правый закрыт или, наоборот,- зафиксируется (запомнится), сколько на вход было подано импульсов. А можно каждый триггер использовать как отдельный элемент памяти - он будет помнить, подавался на его вход управляющий импульс или нет. Записать в триггерную память новую информацию можно мгновенно, ее легко прочитать (проверив, какой из транзисторов пропускает ток) и стереть несложно, импульсом вернув триггер в исходное состояние.

ЭЛЕМЕНТЫ ЛОГИКИ И, ИЛИ, НЕ. Можно подать на вход транзистора два управляющих сигнала так, чтобы он открывался от любого из них. В этом случае транзистор будет пропускать ток и выдавать импульс тока или под действием первого входного импульса, или под действием второго, схема будет выполнять логическую операцию ИЛИ. А можно построить схему так, чтобы усилий одного входного импульса не хватало для открывания транзистора, чтобы он открывался лишь при одновременном действии двух входных сигналов - и первого, и второго. Это схема для выполнения логической операции И. Наконец, можно так подвести входной импульс к транзистору, что он будет делать все наоборот - будет закрывать заранее открытый транзистор. Эта схема выполняет операцию НЕ - выдает выходной сигнал, когда нет входного, и наоборот, когда подается входной импульс, ток через транзистор не идет, на выходе импульс не появляется. Логические элементы И, ИЛИ, НЕ широко применяются в автоматике, из них собирают цепочки для выполнения более сложных логических операций. Такая цепочка, например, включает мотор лифта если И закрыта дверь шахты, И закрыта дверь кабины, НЕ включился датчик перегруза, И нажата кнопка ИЛИ второго, ИЛИ третьего, ИЛИ четвертого и т.д. этажа.
КОММУТАТОР. Объединив триггеры с логическими элементами, можно получить быстродействующий бесконтактный переключатель - непрерывную очередь импульсов он будет поочередно направлять по разным электрическим цепям. Например, первый импульс в один провод, второй - в другой и так далее.
ШИФРАТОР. Логические элементы в сочетании с коммутатором могут превратить однообразную последовательность одинаковых импульсов в шифровку из импульсов и пауз, чередующихся в заданном порядке. Можно, например, убрать третий импульс из каждой четверки - триггер посчитает импульсы, а логика в нужный момент закроет путь со входа на выход.
ДЕШИФРАТОР. Надежно решается и обратная задача - логические схемы из смеси импульсов и пауз отбирают и направляют по нужному адресу только строго определенные их комбинации. Например, только те пары импульсов, перед которыми была пара пауз.
ДИОДНАЯ МАТРИЦА. Перебрасывая диодные мостики от некоторых проводов одной группы к проводам другой группы, легко перераспределять сигналы, из одних потоков импульсов получать другие. Такие многомостиковые схемы - матрицы - можно рассматривать как постоянную ("запаянную") память.

СУММАТОР. Вычислительные машины работают с двоичными числами - ноль там 0, единица - 1, а вот двойка уже не привычный нам знак 2, а 10, тройка - 11, четверка 100, пятерка 101... Наши предки выбрали десятичный счет, видимо, потому, что на руках у человека десять пальцев и удобно переходить в следующий разряд, досчитав до десяти. Конструкторы электронных машин выбрали двоичный счет потому, что у основных электрических элементов схемы, грубо говоря, всего два пальца. Они могут находиться только в двух состояниях - выключатель, в частности, в состояниях "включено - выключено", триггер в состояниях "ток в правом транзисторе - ток в левом транзисторе", сам транзистор в состояниях "открыт - закрыт" и т.д. Этим элементам удобнее всего считать электрические сигналы, производить с ними вычислительные операции именно в двоичном коде.
Конструкторы механических вычислительных аппаратов, в частности Блез Паскаль, немало помучились, пока научились при сложении переносить числа в следующий разряд. Нетрудно сложить 4+5=9 с помощью двух простых зубчатых колес или линеек, а вот операция 4+8=12 требует дополнительных приспособлений - нужно проанализировать полученные двенадцать единиц, записать только две, а десять записать единицей в следующем разряде, в разряде десяток.
Подобная задача появляется и в электронной счетной машине, работающей с двоичными числами. Здесь при сложении должно получаться 0+0=0, 1+0=1, 0+1=1 и, наконец, 1+1=10. Первые три операции легко выполнить, если единицы отображать импульсами тока, нули паузами и два числа одновременно подавать на вход элемента ИЛИ. При обоих входных нулях (паузах) на выходе ИЛИ, конечно, ничего не будет - 0+0=0. При складывании нуля с единицей на выходе всегда будет единица - элемент ИЛИ одинаково хорошо сработает или от одного импульса (1+0=1), или от другого (0+1=1). Но что делать с операцией 1+1=10? Как, складывая две единицы, два импульса тока, получить ноль и сделать перенос - в нужный момент ввести единицу в следующий разряд?
Решается задача с помощью многоэлементной логической схемы - сумматора. Его остроумные действия сводятся к тому, чтобы операции 0+0, 1+0 и 0+1 осуществлять только в элементе ИЛИ а при операции 1+1 блокировать этот элемент и получать на выходе 0. Такое блокирование выполняет элемент И2. В первых трех случаях он срабатывает и пропускает импульс (единицу) из ИЛИ1 на выход СУММА; срабатывание И1 происходит под действием двух одновременных импульсов - и пришедшего с самого ИЛИ1, и пришедшего с элемента НЕ. Но когда на вход сумматора приходят сразу две складываемые единицы (1+1), два входных импульса, то от них срабатывает бездействовавший до этого элемент И2, тот приводит в действие элемент НЕ, а он, как и полагается этому путанику, получив входной импульс, прекращает подачу своих сигналов на вход И1 и тем самым, по сути, выключает его, прерывает подачу импульса на выход СУММА. Одновременно с выхода сработавшего И2 получают сигнал, который используется для переноса единицы в следующий разряд.
Сумматор, с которым мы познакомились в простейшем его варианте,- обязательный блок любой электронной вычислительной машины. Кроме того, его можно считать типичным блоком - на примере сумматора видно, как ловко обходятся электронные схемы с импульсами тока, какие интересные и тонкие операции с ними производят. Отметив этот приятный факт, мы вернемся к самому микрокалькулятору, где знакомые нам действующие лица начинают великолепный спектакль вычислений.

Перед тем как уйти с завода-изготовителя, микрокалькуляторы проходят суточный прогон: если в интегральной схеме есть скрытый дефект, то он, как правило, обнаруживается в первые часы работы.

При первом знакомстве с электронным микрокалькулятором сильнейшее впечатление производят его безотказность, его доведенная до предела исполнительность. Машинка не рассуждает, любое ваше задание она выполняет с готовностью, мгновенно выбрасывая на табло результат. Посмотрев по сторонам, можно заметить, что все мы, стоящие у прилавка и выбирающие себе электронного помощника, делаем одно и то же: быстро нажимаем клавиши, вводим случайно пришедшие на ум числа, складываем их, умножаем, делим, любуясь ловкостью счетчика-виртуоза и почему-то подсознательно стараясь устроить ему экзамен потруднее. Но, оказывается, для калькулятора в пределах его квалификации трудных задач не существует. С одинаковой легкостью он сообщает, что 2*2=4 или что 0.65239:0.71263=0.915468. Машинка считает по житейским меркам с немыслимо высокой скоростью - не успеваешь нажать клавишу "=", как ответ уже готов. Иногда даже кажется, что все ответы в машине заготовлены заранее и в нужный момент просто подаются на табло. А вместе с тем каждое вычисление, как сообщают инструкции, длится вполне определенное время - у большинства микрокалькуляторов около 0.1 секунды. И если вдуматься, то любая операция, выполняемая калькулятором,- это огромная работа, которую мы лишь в погоне за легкостью описания назвали спектаклем вычислений.


ПЬЕСА В 5 ДЕЙСТВИЯХ, 8 КАРТИНАХ
Поднимается занавес, и мы видим сцену, на которой будут разворачиваться события: упрощенная функциональная схема шестиразрядного калькулятора. "Функциональная" (иногда говорят "скелетная" или "блок-схема") означает, что на схеме показаны лишь самые основные блоки машины и основные линии их соединения. На полной схеме в квадратах блоков были бы изображены замысловатые орнаменты из многих тысяч деталей - транзисторов, конденсаторов, диодов, и такая схема, даже мелко начерченная, получилась бы в несколько метров длиной. Схема, по которой мы будем знакомиться с ходом вычислительных операций, не относится к какому-либо конкретному калькулятору, хотя в основных чертах она близка к реальности.
Итак, занавес поднят, и спектакль начинается.
ДЕЙСТВИЕ ПЕРВОЕ - ВКЛЮЧЕНИЕ КАЛЬКУЛЯТОРА. Миниатюрным выключателем мы подаем питание, включаем батареи. Карманному микрокалькулятору, кстати, мало тех 4.5 вольта, которые дают три гальванических элемента, и поэтому в нем есть преобразователи этого напряжения, они дают 5-15 вольт для питания триггеров, усилителей, коммутаторов и других "действующих лиц" и 15-20 вольт для питания цифровых индикаторов. Настольные калькуляторы питаются только от сети, так как батарей им хватило бы ненадолго.
Как только включилось питание, начал работать тактовый генератор. Он дает бесконечную очередь коротких импульсов, из которых потом формируются два основных вида импульсов, необходимых машине,- специалисты фамильярно называют их разрядными (Р) и битовыми (Б). Эти импульсы подаются во все блоки, они дирижируют всем спектаклем, всей работой калькулятора, синхронизируют взаимодействие его блоков. А битовые импульсы к тому же еще представляют собой сырье, из которого формируются двоичные числа и команды управления.
ДЕЙСТВИЕ ВТОРОЕ - ВВОД ПЕРВОГО ЧИСЛА. Любая клавиша ввода - это всего лишь простейший выключатель, и, нажав какую-либо клавишу, вы просто открываете путь для битовых импульсов на один из входов шифратора. Получив импульсы именно с этого своего входа, шифратор сделает из них строго определенную последовательность сигналов и пауз. Так, при нажатии на клавишу "2" шифратор выдаст серию "пауза - пауза - импульс - пауза", при нажатии на клавишу "5" появится серия "пауза - импульс - пауза - импульс", то есть 2 и 5 превратятся в двоичные числа, записанные в виде импульсов и пауз.

Здесь настал момент объявить - дальше уже тянуть невозможно,- что микрокалькуляторы работают не в двоичном коде, а в двоично-десятичном. Грубо говоря, это означает, что машина работает с многоразрядными десятичными числами, а каждый их разряд, каждая десятичная цифра записана в двоичном коде четверкой импульсов-пауз. Запись при этом получается несколько более громоздкой, чем при чисто двоичном коде, но зато проще становятся блоки перевода из одной системы счисления в другую - из десятичной (язык человека) в двоичную (язык машины) и обратно. А для миниатюрных машин упрощение каких-либо блоков - достоинство решающее.
Итак, нажата первая клавиша, и из очереди битовых импульсов родился код первой введенной цифры, первая четверка импульсов-пауз. Она сразу отправляется на хранение в один из двух блоков оперативной памяти, в так называемый х-регистр и там ждет момента, когда начнутся сами вычисления. Комплект триггеров x-регистра запомнит эту четверку импульсов-пауз и копию ее направит в цифровой индикатор - вы увидите, какая цифра введена в машину, сможете проконтролировать, правильно ли была нажата клавиша.
На этом дело бы и кончилось, если бы машина работала с одноразрядными числами - от 0 до 9. В действительности же мы вводим в машину числа многоразрядные, а это требует некоторых дополнительных приспособлений. Одно из них - формирователь разрядных импульсов. Каждый из них длится в 4 раза больше битового, и за время одного разрядного импульса успевает пройти целая четверка импульсов-пауз, соответствующая одной десятичной цифре. Сами же разрядные импульсы коммутатор поочередно рассылает по шести разным проводам, и по этим шести дорожкам импульсы приходят во все блоки калькулятора. Здесь каждый из шести разрядных импульсов управляет работой элементов, которые обслуживают закрепленный за ними разряд. Так, например, импульс Р1 включает элементы памяти для записи единиц, импульс Р2 включает элементы для записи десятков, импульс Р3 - для записи сотен и т.д. Аналогично импульсы Р1, Р2, Р3 из следующих серий включают нужные элементы памяти при считывании единиц, десятков, сотен. Или включают ячейки индикатора для высвечивания единиц, десятков, сотен. Одним словом, каждый разрядный импульс заставляет машину работать только с тем разрядом, который за этим импульсом закреплен. А потом появляется следующий разрядный импульс, и вся машина занимается уже следующим разрядом. Когда поочередно пройдут первые шесть разрядных импульсов от Р1 до Р6, машина первый раз обработает все имеющиеся в ней шестиразрядные десятичные числа. Потом появится новая серия импульсов Р1-Р6, и начнется следующий цикл поразрядной обработки.
Кстати, мы ограничились шестью разрядами в нашей схеме только для ее упрощения. И еще одно примечание. Многоразрядные числа вводятся в машину так, как мы привыкли их называть,- чтобы ввести число 25, мы сначала нажимаем клавишу 2, потом 5. В калькуляторе этот порядок ввода чисел учитывается так: первая введенная цифра - в нашем примере двойка - сначала занимает место первого разряда (единицы): машина ведь пока не знает, что должно быть - 2, 20, 200 или 2000 и на всякий случай для начала записывает 2 в разряд единиц. А затем при появлении следующей цифры - пятерки - двойка с помощью разрядного импульса сдвигается на один шаг влево, на место десятков. Если появится еще одна цифра - двойка сместится в разряд сотен. Такое смещение цифр происходит и в ячейках памяти и в цифровом индикаторе.
ДЕЙСТВИЕ ТРЕТЬЕ - ВВОД ОПЕРАЦИИ. Каждая операция, которую может выполнить наша машина, так же как и сами числа, зашифрована в определенной четверке импульсов-пауз. При нажатии, например, на клавишу "+" шифратор выдаст четверку "импульс - пауза - импульс - импульс" и направит ее уже не в оперативную память, а в блок управления. Здесь дешифратор, распознав прибывшую депешу, включит с ее помощью матрицу "Программа сложения" ("Программа +"). В этой матрице, если пустить в нее тактовые и разрядные импульсы, сформируются все необходимые последовательности включений и выключений блоков машины, и строго согласованное взаимодействие этих блоков осуществит все, что нужно для сложения. Но пока матрица только подготовлена к работе и ждет сигнала.
ДЕЙСТВИЕ ЧЕТВЕРТОЕ - ввод второго числа. Все, казалось бы, должно произойти точно так же, как и при вводе первого числа - в оперативной памяти есть второй регистр, y-регистр, и туда после нажатия соответствующей клавиши шифратор ввода должен направить второе число. Но вот оказывается, что при вводе второго числа происходит неожиданный сюжетный поворот - в y-регистр переводится первое число, а второе записывается в освободившийся x-регистр. Для чего нужно это дополнительное перемещение? Опять-таки для того, чтобы упростить схему калькулятора: x-регистр связан с цифровым индикатором, а y-регистр не связан. Поэтому, чтобы для контроля высветить на индикаторе второе число, его нужно поместить именно в x-регистр: это проще, чем создавать систему индикации чисел, хранящихся в y-регистре.

ДЕЙСТВИЕ ПЯТОЕ - ВЫЧИСЛЕНИЯ. Сами вычисления начинаются после нажатия клавиши "=". При этом в машине происходит несколько самостоятельных операции, как сказали бы в театре, пятое действие пьесы состоит из нескольких картин. Даже при самом простом вычислении - при сложении - таких "картин" четыре.
Прежде всего в блок управления пойдет команда "начать счет", а из него в x-регистр и y-регистр пойдут команды, по которым оба слагаемых одновременно и поразрядно двинутся из регистров в сумматор. Сам сумматор получит из блока управления команду, в каком режиме ему нужно работать, и при сложении, естественно, он просто поразрядно сложит оба числа. Из сумматора полученный результат попадает в x-регистр, а из него на цифровой индикатор. Этот результат будет храниться в x-регистре до особых указаний, на случай, если он понадобится для дальнейших вычислений. Точно так же в y-регнстре будет храниться второе слагаемое, оно может понадобиться при работе с постоянным числом, о чем мы уже говорили раньше.
Вот и все - на индикаторе появился результат вычислений, спектакль окончен. Но в самом конце, как говорится, под занавес, хочется сделать три коротких примечания.
Во-первых, отметим оригинальную систему высвечивания цифр на индикаторе. Каждая его ячейка, каждый разряд состоит из восьми сегментов - семь для самой цифры и один для запятой, которая зажигается при работе с десятичными дробями или когда получается дробный результат (например, 7:2-3.5). На индикатор работает его собственный преобразователь кода - получив четверку импульсов-пауз, в которой зашифрована некоторая десятичная цифра, он с помощью коммутаторов и матриц формирует комбинацию из семи раздельных токов - они зажгут комбинацию сегментов, из которых сложится эта цифра. Например, при появлении шифровки "пауза - пауза - импульс - пауза" токи пойдут к сегментам, из которых на индикаторе сложится двойка. Теперь простейший расчет, его можно выполнить и без калькулятора: для высвечивания числа на восьмиразрядном индикаторе может понадобиться в самых разных комбинациях переключать 64 контакта - восемь цифр по восемь (с учетом запятой) сегментов в каждой. Чтобы избежать столь сложной коммутации, принята такая система: комбинации токов, зажигающих цифры, подаются параллельно на сегменты всех ячеек, и при этом нужно переключать не 64, а всего 8 контактов. Комбинации токов, соответствующие разным цифрам, подводятся к индикатору поочередно. Так, при высвечивании числа 25 сначала на все сегменты индикатора подаются токи, которые зажгли бы цифру 5, а потом токи, которые зажгли бы цифру 2. Сослагательное наклонение, то есть глагол с частицей "бы", мы применили здесь не случайно - токи, поступающие на сегменты индикатора, сами по себе не могут зажечь цифру, для ее зажигания нужно еще подать напряжение на общий электрод, общий для всех сегментов данной ячейки (разряда). А напряжение на этот общий электрод подается в виде разрядных импульсов Р1-Р6, и каждый из них подходит только к одной ячейке, только к своему разряду. Причем подходит именно в тот момент, когда на сегменты подается комбинация токов для зажигания цифры именно этого разряда. Так, в нашем примере при появлении токов, которые на всех индикаторах зажгли бы цифру 5, разрядный импульс Р1 подходит только к общему электроду первой (справа) ячейки индикатора, и цифра 5 появляется только в первой (справа) ячейке; при появлении токов, соответствующих цифре 2, разрядный импульс Р2 разрешает зажигание только цифры во второй ячейке. При такой системе цифры на индикаторе, конечно, горят не все время, а поочередно, каждая вспыхивает только при появлении своего разрядного импульса. Однако серии разрядных импульсов появляются так часто, что мелькания цифр мы не замечаем.
Этот подробный рассказ о работе цифрового индикатора появился здесь совсем не для того, чтобы читатель, уже уставший, видимо, от напряженного сюжета, запоминал в деталях всю описанную процедуру. Рассказ этот - всего лишь еще одна иллюстрация виртуозных методов работы с электрическим сигналом, которыми с такой легкостью пользуется электроника.
Второе примечание связано с тем, что в качестве примера, иллюстрирующего работу калькулятора, было выбрано сложение. Если мы захотим умножить два числа или разделить их, то спектакль несколько затянется - в нем уже будет не 8 картин, а как минимум больше десятка, а то и несколько десятков. Потому что умножение выполняется как последовательное сложение, программа должна много раз посылать в сумматор один из сомножителей и много раз суммировать его. При этом нужно одновременно считать, сколько всего раз происходит суммирование и для этого, например, при каждом складывании первого сомножителя уменьшать на единицу второй сомножитель, пока он не превратится в ноль. Вот как с учетом всего этого может вестись в калькуляторе умножение 25*5:
0+25=25, 5-1=4;
25+25=50, 4-1=3;
50+25=75, 3-1=2;
75+25=100, 2-1=1;
100+25=125, 1-1=0.
Когда в контрольном вычитании получается ноль, вычисления прекращаются и последняя сумма 125 выдается как результат умножения. Поскольку одно сложение, по самым скромным подсчетам, требует четырех последовательных операций, которые мы в нашей условной пьесе назвали картинами, то можно подсчитать, что подобная пьеса уже при умножении 25*5 будет состоять из 20 картин. Особенно много операций приходится выполнять при умножении на большие числа. Правда, умножая, например, на 3752, машина выполняет не 3752 сложения, а всего 2+5+7+3=17 сложений, так как умножение ведется поразрядно, по школьной терминологии, "в столбик". И все же при умножении на число 99999999 машине приходится произвести 9*8=72 поочередных сложения и столько же контрольных вычитаний. И вот здесь начинаешь ощущать одно из достоинств электронного счета. Даже в самых медленных калькуляторах серии разрядных импульсов выстреливаются примерно 300 раз в секунду, битовые импульсы длятся меньше тысячной доли секунды, триггеры, элементы логики, дешифраторы срабатывают за миллионные доли секунды, и самое громоздкое вычисление происходит практически мгновенно. Лишь в инженерных машинах есть вычисления с таким большим числом промежуточных операций, что между нажатием клавиши "=" и выдачей результата проходит ощутимое время - что-то около секунды.
Итак, при нажатии на клавишу "=" в калькуляторе начинается невидимая нам электронная буря - длинные очереди импульсов проносятся из регистров памяти в сумматор или из сумматора в регистры, блок управления, этот генеральный штаб машины, одну за другой шлет на места ультимативные депеши - "... сумматору начать сложение... число из x-регистра - в сумматор... число из сумматора - в x-регистр... сдвинуть на один разряд число в y-регистре...- и в заключение - ... число из x-регистра - на индикатор". Все эти приказы составляются, прочитываются и исполняются с помощью транзисторных схем-триггеров, мультивибраторов, логических элементов, коммутаторов - которые, по сути, представляют собой управляемые выключатели. Обычно в калькуляторе несколько тысяч таких транзисторных выключателей, во время одного вычисления они могут произвести несколько миллионов включений-выключений.
"Дело плохо!" - только так может прореагировать на это человек, имеющий опыт общения с переключателем диапазонов в приемнике, переключателем телевизионных программ или даже просто с выключателем настольной лампы. Все это - элементы, мягко говоря, не слишком надежные. Особенно страшно, когда выключатели собираются тысячами, когда неисправность любого выводит из строя всю систему и к ненадежности самих коммутирующих элементов прибавляется еще ненадежность их соединений: отошел один из бесчисленных соединительных проводков - и все пропало. С этих позиций от микрокалькулятора, казалось бы, ничего хорошего ждать нельзя: один раз он сработает точно, два соврет или вообще откажется считать - шуточное ли дело, тысячи сложным образом соединенных выключателей!
В действительности же дело обстоит совсем иначе - из всей радиоэлектронной аппаратуры, обслуживающей рядового человека (или, как часто говорят, бытовой электроники), микрокалькуляторы наверняка могут быть признаны чемпионами надежности. Микрокалькулятор годами работает, не допуская ошибок, и в принципе не видно почти никаких возможностей, чтобы эта маленькая, но весьма сложная вычислительная машинка или во всяком случае ее основная, считающая часть вышла из строя. Этому как раз и посвящается третье примечание, несколько более подробное, чем два предыдущих.


Последний раз редактировалось: Gudleifr (Сб Окт 15, 2022 12:11 pm), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
ТЕХНОЛОГИЯ ПРОТИВ ТИРАНИИ
То, что происходит в микрокалькуляторе, в принципе происходит в любом другом электронном аппарате - вся его работа сводится к переработке электрических сигналов. В приемнике обрабатываются чрезвычайно слабые токи, которые наводит в антенне радиоволна: эти токи усиливаются, и из них извлекается информация, которая затем используется для создания звука. В телевизоре аналогичным способом извлекается зашифрованная в электрических сигналах информация о картинке, ее цветах, извлекаются "врезанные" в сигнал синхронизирующие импульсы, которые управляют процессом рисования на экране, подобно тому, как разрядные импульсы дирижируют счетом в калькуляторе. Процессы обработки электрических сигналов во всех случаях разные, но все они очень похожи по существу: ток обрабатывается (усиливается, ослабляется, разделяется на составляющие, складывается с другими токами) в сложных электрических цепях, в электронных схемах, собранных все из тех же основных элементов,- из транзисторов, резисторов, конденсаторов, диодов и ряда других деталей.
Во все времена конструкторы электронной аппаратуры стирались упростить схемы, уменьшить число деталей в них. И когда разработчик новой модели телевизора рассказывал о ее достоинствах, он с особой гордостью отмечал, что ему удалось "сэкономить два баллона", то есть удалось построить несколько более простую схему телевизора, и в нем на две электронные лампы меньше, чем в предыдущей модели. Уменьшать количество элементов в электронном аппарате имело смысл по многим причинам: упрощение схемы - это меньший вес и объем, более высокая надежность и, наконец, просто снижение себестоимости.
В толстых папках, заполнивших стеллажи Государственной патентной библиотеки, отражена многолетняя борьба радиоинженеров за создание совершенных электронных схем, за то, чтобы обработка электрических сигналов производилась в них минимальными средствами.
Но вот наступает время резко увеличивать число элементов в схемах. Это время сложных электронных систем, прежде всего таких, как электронные вычислительные машины. Уже в первых больших ЭВМ не тысячи, а сотни тысяч деталей (в цветном телевизоре их примерно 2-3 тысячи, в приемнике около 100), в том числе огромное число радиоламп (транзисторов тогда еще не было), из которых собраны триггеры, коммутаторы, элементы логики. Машины занимают большие помещения, потребляют много энергии, сильно греются и, что особо неприятно, часто выходят из строя. Все это вместе взятое видится главным препятствием на пути совершенствования больших электронных систем, препятствием роковым, непреодолимым. И в лексиконе инженеров появляется выражение в несвойственных для них драматических тонах - "Тирания количеств".
Однако неодолимая, казалось, "тирания количеств" не смогла остановить прогресс электроники. В конце пятидесятых годов, то есть примерно лет двадцать назад, происходит событие, повернувшее электронику на совершенно новый путь: начинается эпоха монолитных интегральных схем, монолитных полупроводниковых ИСов - маленьких, миллиметровых размеров кристаллических пластинок, внутри которых виртуозная технология создала законченные блоки из многих транзисторов, конденсаторов, резисторов, диодов, соединительных цепей. Заметьте: все это не отдельные, не дискретные детали, а лишь сформированные в едином кристалле области с разными электрическими свойствами.
Проходит еще несколько лет, растет, как выражаются специалисты, степень интеграции, и появляется большая интегральная схема - БИС. Большая не по размерам; обычно БИС - это квадратная пластинка со стороной 3-5 миллиметров. Но по числу элементов БИС даже не большая, а огромная схема, она состоит из многих тысяч деталей, каждая размером в несколько микрометров, несколько тысячных долей миллиметра. Причем все эти тысячи транзисторов, конденсаторов и т.п. делают, так сказать, одним заходом - сотня-другая последовательных технологических операций и большая интегральная схема готова, завершено изготовление сразу всех ее деталей, и все они нужным образом соединены друг с другом. Более того - за один технологический цикл на кремниевой пластине получается несколько десятков интегральных схем, и автоматизированную линию, "печатающую" БИСы, можно сравнить с фантастическим прессом, который из металлических слитков, листов стекла, резины, ткани одним ударом штампует целые колонны автомобилей, причем законченных, готовых - заводи и езжай.
Исключительная технологичность БИСов определила одно из решающих их достоинств - монолитные интегральные схемы, а значит, и аппараты, созданные на их основе, получаются сравнительно дешевыми, доступными. Продавец напоминает покупателю, размышляющему "брать или не брать?", что микрокалькулятор стоимостью в 30-40 рублей, если бы в нем использовалась не БИС, а схема, собранная из дискретных деталей, стоил бы, видимо, в 20, а то и в 50 раз дороже. Кроме того, он потреблял бы значительно больше энергии, весил бы несколько килограммов и размерами наверняка был бы с добрый чемодан.
Наконец, еще одно достоинство БИСов - ему и посвящено это третье примечание под занавес. Многие элементы интегральной схемы соединяются друг с другом, так сказать, путем личных контактов - они просто соприкасаются своими "телами" внутри кристалла. Остальные соединения осуществляет замысловатая металлическая паутинка, напыленная на поверхность кристалла. Все это очень надежные соединения, в БИСах практически не бывает отказов из-за плохих контактов, а именно этот вид неисправностей, как утверждает статистика, в основном и нарушает работу аппаратов, собранных из дискретных деталей.
ШЕДЕВРЫ НА КОНВЕЙЕРЕ
Говорят, что идею монолитных интегральных схем подсказало само производство транзисторов - на одной кремниевой или германиевой пластине сразу создается несколько десятков транзисторных структур, затем пластину разрезают, получая отдельные кристаллики-транзисторы. "Несомненно,- пишет американский журнал "Электроника",- многие исследователи отмечали бессмысленность такого вырезания отдельных транзисторов из общей пластины, сборку каждого из них в отдельном корпусе и затем соединение с помощью проводов в электронную схему".
Идея соединения транзисторов внутри кристалла без его разрезания, то есть идея создания интегральной схемы, как говорится, носилась в воздухе. И неудивительно, что она была независимо и почти одновременно реализована разными людьми - американскими инженерами Д.Килби и Р.Нойсом.
Но нельзя, конечно, считать, что интегральные схемы, особенно БИСы, есть результат нескольких изобретений. Вся нынешняя фантастическая микроэлектроника (в том числе микрокалькулятор, который мы сейчас спокойно рассматриваем на прилавке, собираясь купить его с такой же легкостью, как пару туфель) начинается с абстрактных на первый взгляд теоретических построений Планка, Эйнштейна, Шредингера, с глубоких исследований полупроводников, выполненных, в частности, такими физиками, как Невил Мотт, Борис Иосифович Давыдов, Абрам Федорович Иоффе, Вальтер Шотки, Яков Ильич Френкель, Вильям Шокли. К этому великолепному списку историки науки наверняка захотят добавить имена, известные пока, так сказать, лишь в узком кругу. Это ученые и инженеры, проложившие десятки путей от Большой Физики к Большой Технологии, создавшие все многообразие и совершенство современной полупроводниковой микроэлектроники.
Можно попытаться несколькими штрихами обозначить то, что стоит за словами "многообразие" и "совершенство", назвав некоторые термины микроэлектроники, устоявшиеся, кстати, уже настолько, что специалисты, как правило, употребляют их в сокращении, в виде аббревиатур:
СТРУКТУРА МДП - МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК. Кроме наиболее распространенных пока биполярных транзисторов, напоминающих слоеный пирог из трех чисто полупроводниковых "деталей" - эмиттера, базы и коллектора, все чище применяют сейчас полевые транзисторы. Их основная "деталь" - полупроводниковый канал, в котором двигаются заряды между двумя малыми областями - истоком и стоком. Управляющий электрод - металлический затвор - отделен от полупроводникового канала тончайшим слоем изолятора, диэлектрика. Через этот диэлектрик затвор своим электрическим полем воздействует на заряды, движущиеся в канале, управляет током. Металлический затвор, полупроводниковый канал и диэлектрический слой между ним и затвором определили структуру полевого транзистора - это МДП-структура. Полевые транзисторы очень широко используются в БИСах, и в этих случаях они тоже имеют структуру МДП.
СТРУКТУРА МОП - металл-окисел-полупроводник. Частный случай структуры МДП, где в качестве диэлектрика используются окислы самого, полупроводника, конкретно кремния. Существует и разрабатывается большое многообразие МОП-структур, в частности p-МОП, n-МОП, V-МОП, D-МОП, H-МОП, H-МОП-II, K-МОП, K-МОП (КНС) и другие. У каждого вида структур свои физические и технологические особенности (например, K-МОП - комплементарные структуры, где совместно работают полупроводниковые приборы с электронной и дырочной проводимостью, K-МОП (КНС) - комплементарные структуры, основа которых кремний на сапфире и т.д.). И у каждой структуры свои особенности в части плотности упаковки, быстродействия, надежности, стоимости.
ЦМД - ЦИЛИНДРИЧЕСКИЕ МАГНИТНЫЕ ДОМЕНЫ. Эти микроскопические "магнитики" внутри кристалла с помощью внешних полей можно индивидуально перемещать или перемагничивать, записывая и считывая таким образом "единицы" и "нули" двоичного кода. На ЦМД создают чрезвычайно компактную оперативную память, где каждый магнитный домен, по сути дела, заменяет целый триггер.
ПЗС - ПРИБОРЫ С ЗАРЯДОВОЙ СВЯЗЬЮ. Они могут использоваться в оперативной памяти в виде кристаллов с очень большим числом микроскопических электродов на поверхности. Каждый из них, запоминая "единицу", удерживает малую порцию электрического заряда; при необходимости эти заряды внутри кристалла быстро перекатывают к считывающему электроду.
СБИС - СВЕРХБОЛЬШАЯ ИНТЕГРАЛЬНАЯ СХЕМА. Здесь на плоском кристаллике - обычно это квадрат со стороной 5-6 миллиметров - размещаются десятки тысяч элементов и даже сотни тысяч.
ССИС - СВЕРХСКОРОСТНЫЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ. Одна из основных характеристик вычислительного устройства - быстродействие. Для микрокалькулятора оно не столь важно, но может иметь первостепенное значение для микроэлектронных устройств автоматики или для БИСов, используемых в больших ЭВМ. У разных структур различное быстродействие. Например, переключающие элементы в МОП-структурах срабатывают примерно за 0.04мкс, в биполярных - примерно за 0.01мкс.
ППЭ, ПТУП и ПТУГП, приборы с передачей электронов; полевые транзисторы с управляемым переходом и управляемым гетеропереходом. Все это новые полупроводниковые приборы, применение которых в БИСах должно заметно поднять их быстродействие.
ЗУПВ - ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПРОИЗВОЛЬНОЙ ВЫБОРКОЙ. Система оперативной памяти, позволяющая маневрировать свободными запоминающими элементами и тем самым более эффективно использовать участки БИСов, предназначенные для хранения информации.
РТЛ - РЕЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА. Это схемы, где логические элементы должны быть образованы из традиционных деталей - резисторов, конденсаторов, транзисторов. Поэтому в РТЛ БИСах приходится создавать все эти детали, разными способами меняя свойства полупроводникового кристалла в определенных микрообластях.
ТТЛ - ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА. А здесь во всех логических элементах и многих других узлах - только один тип деталей: транзисторы. Многие из них работают в таком режиме, что заменяют резистор или конденсатор. Так, например, для ТТЛ созданы триггеры, где вместо двух транзисторов используются восемь, но зато нет ни одного конденсатора или резистора.
И2Л - ИНЖЕКЦИОННАЯ ИНТЕГРАЛЬНАЯ ЛОГИКА. Разновидность ТТЛ, где элементы, в частности транзисторы, расположены и параллельно поверхности кристалла и перпендикулярно, что делает БИСы более компактными.
И3Л - ИЗОПЛАНАРНАЯ ИНЖЕКЦИОНИАЯ ЛОГИКА. Разновидность ТТЛ, выполненная по технологии, которая формирует очень тонкие плоские "детали" БИСа, а это повышает компактность и надежность схемы.
ТТЛ С ДИОДАМИ ШОТКИ. Разновидность ТТЛ, в несколько раз повышающая быстродействие БИСов.
В прежние времена характерное для ТТЛ усложнение схемы - восемь транзисторов вместо двух!- считалось бы недопустимой расточительностью. Но БИС на одинаковых элементах настолько технологична, что за нее можно с легкостью переплатить тысячу-другую транзисторов. Тем более, что технология БИСов не просто пресекла "тиранию количеств", а создала, так сказать, невиданное количественное изобилие. Огромные шкафы с аппаратурой превратились в миниатюрные кристаллические пластинки, выпускаемые к тому же массовыми тиражами на автоматизированных линиях, и специалисты по электронной технике с легкостью оперируют теперь схемами из сотен тысяч и миллионов деталей. С новой технологией приходит и новая психология создания электронной аппаратуры. А может быть, даже новая психология взаимоотношений с электроникой.
ЗА ТЕХНОЛОГИЕЙ - ПСИХОЛОГИЯ
Уже в БИСе микрокалькулятора видны черты большой вычислительной машины. Здесь есть оперативное запоминающее устройство - ОЗУ, есть вычисляющий блок - сумматор, есть набор программ - "сложить", "вычесть", "умножить" и т.п. Если значительно расширить ОЗУ, сделать в нем большое число "полок", куда можно раскладывать вводимые или полученные в процессе вычислений числа, если создать систему адресов (это "прикрепленные" к числам личные метки в виде обычных комбинаций импульсов-пауз), по которым число можно положить на определенную "полку", а затем найти его по известному адресу, если, наконец, создать широкий ассортимент программ, предусмотреть сборку больших программных последовательностей и позволить самой программе участвовать в их формировании, если сделать все это, естественно усложнив БИС, то можно получить в одном кристалле законченный процессор, основную действующую систему компьютера.
Из таких однокристалльных процессоров, нацеленных на решение разных классов задач, создаются многопроцессорные ЭВМ, где переход с одной задачи на другую может сводиться к простому переключению кристаллов. Уже проектируются многопроцессорные компьютеры, считающие со скоростью 500 и даже 800 миллионов операций в секунду. А ведь еще несколько лет назад быстродействие миллион операций в секунду считалось непревзойденным достижением. Микропроцессоры - их в этом случае называют микроконтроллерами - могут управлять машинами, открывая тем самым невиданные ранее возможности широкой автоматизации производства. Малые габариты и невысокая стоимость (в сравнении с приборами-шкафами эпохи дискретных схем) открыли микропроцессорам путь даже в бытовую аппаратуру.
Создается, например, телевизор, который запоминает все ваши пожелания касательно недельной программы передач, в нужный момент включает нужный телевизионный канал, заранее напомнив, что в такой-то час вас ждет наконец веселая музыкальная передача. Создается кухонный комбайн, который, получив задание в самом общем виде: "Хотелось бы съесть пироги с грибами...", - сначала сообщает, что и как подготовить, сам в нужной последовательности включает кухонное оборудование, а затем, управляя тепловым режимом плиты, готовит блюда по всем правилам, введенным в микропроцессор по проводам прямо из кулинарного техникума. А вот еще один домашний работник с микропроцессором - телефон. Дублируя записную книжку, он держит в памяти основные нужные вам номера, по первой просьбе соединяет с абонентом "несмотря ни на что", (повторяя, в частности, набор, если номер занят), сам коротко отвечает на звонок, если вас нет дома, умеет набирать номер "с голоса", а кроме того, по совместительству в назначенное время будит вас по утрам, напоминает о программе дня, о приближающихся днях рождения знакомых и предстоящих праздниках.
В последнее время к кристаллам вычисляющим и управляющим прибавились еще н кристаллы развлекающие - обрадованные возможностью крупными сериями производить тысячеэлементные электронные блоки, инженеры уже вводят их даже в игры и игрушки. В ассортименте развлекательной электроники, которой занимаются сейчас многие фирмы, в том числе и очень известные, есть, например, выполняющий 20 команд маленький электрический вездеход, играя с которым ребенок получает первые навыки программирования. Есть небольшие, размером с микрокалькулятор, игровые автоматы, где на экране из жидких кристаллов не без вашего участия, конечно, сражаются за шайбу хоккеисты. Есть даже портативные машины, с которыми можно сыграть в шахматы, причем в одной из моделей машина сама передвигает свои фигуры механической "рукой". Все эти простые игрушки на самом деле не так, конечно, просты, каждому их действию предшествует детальный анализ обстановки, громоздкие вычисления, выполняемые электронными схемами. Причем все их умения и способности формируются один раз и навсегда - при разработке алгоритмов, схемы и технологии изготовления микропроцессора. После этого полупроводниковый шедевр размножают, так сказать, типографским способом, не занимаясь уже ни наладкой, ни регулировкой.


Выпускаемые различными фирмами игровые и обучающие электронные машины. Автоматы для игры в шахматы (фото 1 и 5); ответ "противника" (машины) может высвечиваться на индикаторе, а может завершаться перемещением фигуры (5). Машины, с которыми можно играть в "футбол" (2), "хоккей" (3), нарды (4), "бейсбол" (6), "боулинг" и другие игры (9). Машина для лингвистических игр (7) и аналог карманного словаря (8 ). Обучающая машина "Спик энд спэлл" (10).
Особое место среди микропроцессорных игрушек занимает уже весьма распространенная в англоязычных странах игра-машина "Спик энд спэлл" ("Speak and Spell"), что в вольном переводе означает "Говори и пиши". Игра помогает освоить написание примерно двухсот английских слов, причем уже, кажется, появились машинки со сменными словарными блоками. Подобная помощь полезна при изучении любого языка, но особенно английского: в нем произношение и написание различаются настолько, что сами англичане шутят: "У нас пишется Манчестер, а читается Ливерпуль".
Одна из замечательных особенностей игры-машины "Спик энд спэлл" состоит в том, что она сама произносит слова, причем без помощи миниатюрного магнитофона или мини-проигрывателя. Слова и отдельные их слоги синтезируются из электрических сигналов по описаниям, которые в виде двоичных чисел хранятся в памяти микропроцессора. Для такого синтеза речи нужны настолько сложные схемы, что до появления БИСов говорящие машины считались непозволительной роскошью. И вот теперь, пожалуйста,- непозволительная роскошь в рядовой и не очень дорогой игрушке.
С машиной играют так: она произносит слово, и вы, нажимая клавиши с буквами, пишете это слово на небольшом световом табло. Если слово написано верно, то машина произносит "Вы правы" и засчитывает вам очко, а если написано с ошибкой, просит: "Попробуйте еще раз". После третьей попытки электронный репетитор, не рассчитывая больше на ваши знания, пишет слово сам, а вам, извините, ставит двойку - на машинном языке это минус очко. После каждого десятка слов подводится итог: и на экране появляется счет, скажем +7, -3. Машина называет слова в разном порядке, но все они сгруппированы по степени сложности - сначала идут десятки самых простых слов, а затем все более сложных.
Играть с такой машиной, кстати, довольно интересно. И полезно - быстро входишь в азарт и, сам того не замечая, начинаешь грамотно писать. И уже как-то более оптимистично относишься к известным проектам использования микрокомпьютеров в системе образования. Один из проектов, например, предполагает широко применять микрокомпьютеры для обучения во всех 7200 школах Франции. В Соединенных Штатах уже сейчас компьютеры используются примерно в пятой части муниципальных школ, и количество таких компьютеризованных школ предполагается вскоре резко увеличить.
Всерьез поговаривают и о системах самообразования на основе микрокомпьютеров. И о том, что массовое применение считающих, обучающих, информирующих, развлекающих, управляющих и иных микромашин в сочетании с изобилием каналов связи (французы уже придумали для такого компьютерно-коммуникационного альянса отдельный термин - телематика) может резко изменить сам образ жизни человека, формы общения и даже психологию. Возможно ли это? Нужно ли? И целесообразно ли само обсуждение проблемы? Не окажется ли электронное обогащение человечества процессом стихийным, неотвратимым? Пока подобные вопросы очень робко обсуждаются лишь в технических журналах и остается ждать - теперь уже, видимо, недолго,- когда темой заинтересуются профессиональные спорщики и прогнозисты. Пока же каждый может индивидуально оценить для себя целесообразность союза с электроникой в каждом конкретном случае.
Машинка для игры в шахматы? Поиграть любопытно, но нельзя же, чтобы эта "железка" отняла такую житейскую радость, как шахматная партия с приятелем где-нибудь в летнем скверике на скамейке.
Электронная автоматика? А вот здесь двух мнений быть не может. Когда, приняв пятачок, электронный автомат пропускает вас в метро, вспомните - еще не так давно эту изнурительную однообразную работу делали сотни симпатичных девушек. Лучшее творение природы - человеческий интеллект - расходовалось на то, чтобы бездумно надрывать бумажные билетики. Только в Москве нужно было надорвать 8-10 миллионов этих бумажек в день.
Электронный педагог? В какой-то мере да... Он может, видимо, чему-то подучить нас, но научить - это дело человека, учителя.
Электронный информатор? Вещь, видимо, полезная. Но только пусть не посягает на книгу, на ничем не заменяемое удовольствие чтения.
Электронный калькулятор? Да. И без каких-либо оговорок. Потому что глупо тратить бесценные часы жизни, или даже минуты на чисто машинную перетасовку чисел. Потребность в личной счетной машинке ощущают, видимо, многие люди. Во всяком случае, все, кто только что стоял у прилавка и рассматривал микрокалькуляторы, через какое-то время отправились в кассу. Все, кроме одного, кроме автора этих заметок, для которого посещение магазина "Счетные машины", консультации со специалистами, знакомство с ассортиментом калькуляторов, с запросами и настроением покупателей было лишь одним из пунктов в плане подготовки заказанного многими читателями рассказа об электронных счетных машинках личного пользования. Что же касается микрокалькулятора, то я приобрел его давно, когда он, к сожалению, стоил значительно дороже. И даже несмотря на это, очень доволен, что не принял тогда главный аргумент скептиков - в жизни рядовому человеку, мол, не так-то уж много приходится считать. Молотком и отверткой мы тоже пользуемся не каждый день, но они вместе с тем есть в каждом доме. Что это за дом без молотка и отвертки? И что это за современный дом без электронного микрокалькулятора...
***
Где-то мы про это уже слышали ТЕМА #41, АБЗАЦ #397
ТЕМА #41, АБЗАЦ #397 .
.
То, что происходит в микрокалькуляторе, в принципе происходит в любом другом электронном аппарате - вся его работа сводится к переработке электрических сигналов. В приемнике обрабатываются чрезвычайно слабые токи, которые наводит в антенне радиоволна: эти токи усиливаются, и из них извлекается информация, которая затем используется для создания звука. В телевизоре аналогичным способом извлекается зашифрованная в электрических сигналах информация о картинке, ее цветах, извлекаются "врезанные" в сигнал синхронизирующие импульсы, которые управляют процессом рисования на экране, подобно тому, как разрядные импульсы дирижируют счетом в калькуляторе. Процессы обработки электрических сигналов во всех случаях разные, но все они очень похожи по существу: ток обрабатывается (усиливается, ослабляется, разделяется на составляющие, складывается с другими токами) в сложных электрических цепях, в электронных схемах, собранных все из тех же основных элементов,- из транзисторов, резисторов, конденсаторов, диодов и ряда других деталей.
Во все времена конструкторы электронной аппаратуры стирались упростить схемы, уменьшить число деталей в них. И когда разработчик новой модели телевизора рассказывал о ее достоинствах, он с особой гордостью отмечал, что ему удалось "сэкономить два баллона", то есть удалось построить несколько более простую схему телевизора, и в нем на две электронные лампы меньше, чем в предыдущей модели. Уменьшать количество элементов в электронном аппарате имело смысл по многим причинам: упрощение схемы - это меньший вес и объем, более высокая надежность и, наконец, просто снижение себестоимости.
В толстых папках, заполнивших стеллажи Государственной патентной библиотеки, отражена многолетняя борьба радиоинженеров за создание совершенных электронных схем, за то, чтобы обработка электрических сигналов производилась в них минимальными средствами.
Но вот наступает время резко увеличивать число элементов в схемах. Это время сложных электронных систем, прежде всего таких, как электронные вычислительные машины. Уже в первых больших ЭВМ не тысячи, а сотни тысяч деталей (в цветном телевизоре их примерно 2-3 тысячи, в приемнике около 100), в том числе огромное число радиоламп (транзисторов тогда еще не было), из которых собраны триггеры, коммутаторы, элементы логики. Машины занимают большие помещения, потребляют много энергии, сильно греются и, что особо неприятно, часто выходят из строя. Все это вместе взятое видится главным препятствием на пути совершенствования больших электронных систем, препятствием роковым, непреодолимым. И в лексиконе инженеров появляется выражение в несвойственных для них драматических тонах - "Тирания количеств".
Однако неодолимая, казалось, "тирания количеств" не смогла остановить прогресс электроники. В конце пятидесятых годов, то есть примерно лет двадцать назад, происходит событие, повернувшее электронику на совершенно новый путь: начинается эпоха монолитных интегральных схем, монолитных полупроводниковых ИСов - маленьких, миллиметровых размеров кристаллических пластинок, внутри которых виртуозная технология создала законченные блоки из многих транзисторов, конденсаторов, резисторов, диодов, соединительных цепей. Заметьте: все это не отдельные, не дискретные детали, а лишь сформированные в едином кристалле области с разными электрическими свойствами.
Проходит еще несколько лет, растет, как выражаются специалисты, степень интеграции, и появляется большая интегральная схема - БИС. Большая не по размерам; обычно БИС - это квадратная пластинка со стороной 3-5 миллиметров. Но по числу элементов БИС даже не большая, а огромная схема, она состоит из многих тысяч деталей, каждая размером в несколько микрометров, несколько тысячных долей миллиметра. Причем все эти тысячи транзисторов, конденсаторов и т.п. делают, так сказать, одним заходом - сотня-другая последовательных технологических операций и большая интегральная схема готова, завершено изготовление сразу всех ее деталей, и все они нужным образом соединены друг с другом. Более того - за один технологический цикл на кремниевой пластине получается несколько десятков интегральных схем, и автоматизированную линию, "печатающую" БИСы, можно сравнить с фантастическим прессом, который из металлических слитков, листов стекла, резины, ткани одним ударом штампует целые колонны автомобилей, причем законченных, готовых - заводи и езжай.
Исключительная технологичность БИСов определила одно из решающих их достоинств - монолитные интегральные схемы, а значит, и аппараты, созданные на их основе, получаются сравнительно дешевыми, доступными. Продавец напоминает покупателю, размышляющему "брать или не брать?", что микрокалькулятор стоимостью в 30-40 рублей, если бы в нем использовалась не БИС, а схема, собранная из дискретных деталей, стоил бы, видимо, в 20, а то и в 50 раз дороже. Кроме того, он потреблял бы значительно больше энергии, весил бы несколько килограммов и размерами наверняка был бы с добрый чемодан.
Наконец, еще одно достоинство БИСов - ему и посвящено это третье примечание под занавес. Многие элементы интегральной схемы соединяются друг с другом, так сказать, путем личных контактов - они просто соприкасаются своими "телами" внутри кристалла. Остальные соединения осуществляет замысловатая металлическая паутинка, напыленная на поверхность кристалла. Все это очень надежные соединения, в БИСах практически не бывает отказов из-за плохих контактов, а именно этот вид неисправностей, как утверждает статистика, в основном и нарушает работу аппаратов, собранных из дискретных деталей.
ШЕДЕВРЫ НА КОНВЕЙЕРЕ
Говорят, что идею монолитных интегральных схем подсказало само производство транзисторов - на одной кремниевой или германиевой пластине сразу создается несколько десятков транзисторных структур, затем пластину разрезают, получая отдельные кристаллики-транзисторы. "Несомненно,- пишет американский журнал "Электроника",- многие исследователи отмечали бессмысленность такого вырезания отдельных транзисторов из общей пластины, сборку каждого из них в отдельном корпусе и затем соединение с помощью проводов в электронную схему".
Идея соединения транзисторов внутри кристалла без его разрезания, то есть идея создания интегральной схемы, как говорится, носилась в воздухе. И неудивительно, что она была независимо и почти одновременно реализована разными людьми - американскими инженерами Д.Килби и Р.Нойсом.
Но нельзя, конечно, считать, что интегральные схемы, особенно БИСы, есть результат нескольких изобретений. Вся нынешняя фантастическая микроэлектроника (в том числе микрокалькулятор, который мы сейчас спокойно рассматриваем на прилавке, собираясь купить его с такой же легкостью, как пару туфель) начинается с абстрактных на первый взгляд теоретических построений Планка, Эйнштейна, Шредингера, с глубоких исследований полупроводников, выполненных, в частности, такими физиками, как Невил Мотт, Борис Иосифович Давыдов, Абрам Федорович Иоффе, Вальтер Шотки, Яков Ильич Френкель, Вильям Шокли. К этому великолепному списку историки науки наверняка захотят добавить имена, известные пока, так сказать, лишь в узком кругу. Это ученые и инженеры, проложившие десятки путей от Большой Физики к Большой Технологии, создавшие все многообразие и совершенство современной полупроводниковой микроэлектроники.
Можно попытаться несколькими штрихами обозначить то, что стоит за словами "многообразие" и "совершенство", назвав некоторые термины микроэлектроники, устоявшиеся, кстати, уже настолько, что специалисты, как правило, употребляют их в сокращении, в виде аббревиатур:
СТРУКТУРА МДП - МЕТАЛЛ-ДИЭЛЕКТРИК-ПОЛУПРОВОДНИК. Кроме наиболее распространенных пока биполярных транзисторов, напоминающих слоеный пирог из трех чисто полупроводниковых "деталей" - эмиттера, базы и коллектора, все чище применяют сейчас полевые транзисторы. Их основная "деталь" - полупроводниковый канал, в котором двигаются заряды между двумя малыми областями - истоком и стоком. Управляющий электрод - металлический затвор - отделен от полупроводникового канала тончайшим слоем изолятора, диэлектрика. Через этот диэлектрик затвор своим электрическим полем воздействует на заряды, движущиеся в канале, управляет током. Металлический затвор, полупроводниковый канал и диэлектрический слой между ним и затвором определили структуру полевого транзистора - это МДП-структура. Полевые транзисторы очень широко используются в БИСах, и в этих случаях они тоже имеют структуру МДП.
СТРУКТУРА МОП - металл-окисел-полупроводник. Частный случай структуры МДП, где в качестве диэлектрика используются окислы самого, полупроводника, конкретно кремния. Существует и разрабатывается большое многообразие МОП-структур, в частности p-МОП, n-МОП, V-МОП, D-МОП, H-МОП, H-МОП-II, K-МОП, K-МОП (КНС) и другие. У каждого вида структур свои физические и технологические особенности (например, K-МОП - комплементарные структуры, где совместно работают полупроводниковые приборы с электронной и дырочной проводимостью, K-МОП (КНС) - комплементарные структуры, основа которых кремний на сапфире и т.д.). И у каждой структуры свои особенности в части плотности упаковки, быстродействия, надежности, стоимости.
ЦМД - ЦИЛИНДРИЧЕСКИЕ МАГНИТНЫЕ ДОМЕНЫ. Эти микроскопические "магнитики" внутри кристалла с помощью внешних полей можно индивидуально перемещать или перемагничивать, записывая и считывая таким образом "единицы" и "нули" двоичного кода. На ЦМД создают чрезвычайно компактную оперативную память, где каждый магнитный домен, по сути дела, заменяет целый триггер.
ПЗС - ПРИБОРЫ С ЗАРЯДОВОЙ СВЯЗЬЮ. Они могут использоваться в оперативной памяти в виде кристаллов с очень большим числом микроскопических электродов на поверхности. Каждый из них, запоминая "единицу", удерживает малую порцию электрического заряда; при необходимости эти заряды внутри кристалла быстро перекатывают к считывающему электроду.
СБИС - СВЕРХБОЛЬШАЯ ИНТЕГРАЛЬНАЯ СХЕМА. Здесь на плоском кристаллике - обычно это квадрат со стороной 5-6 миллиметров - размещаются десятки тысяч элементов и даже сотни тысяч.
ССИС - СВЕРХСКОРОСТНЫЕ ИНТЕГРАЛЬНЫЕ СХЕМЫ. Одна из основных характеристик вычислительного устройства - быстродействие. Для микрокалькулятора оно не столь важно, но может иметь первостепенное значение для микроэлектронных устройств автоматики или для БИСов, используемых в больших ЭВМ. У разных структур различное быстродействие. Например, переключающие элементы в МОП-структурах срабатывают примерно за 0.04мкс, в биполярных - примерно за 0.01мкс.
ППЭ, ПТУП и ПТУГП, приборы с передачей электронов; полевые транзисторы с управляемым переходом и управляемым гетеропереходом. Все это новые полупроводниковые приборы, применение которых в БИСах должно заметно поднять их быстродействие.
ЗУПВ - ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО С ПРОИЗВОЛЬНОЙ ВЫБОРКОЙ. Система оперативной памяти, позволяющая маневрировать свободными запоминающими элементами и тем самым более эффективно использовать участки БИСов, предназначенные для хранения информации.
РТЛ - РЕЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА. Это схемы, где логические элементы должны быть образованы из традиционных деталей - резисторов, конденсаторов, транзисторов. Поэтому в РТЛ БИСах приходится создавать все эти детали, разными способами меняя свойства полупроводникового кристалла в определенных микрообластях.
ТТЛ - ТРАНЗИСТОРНО-ТРАНЗИСТОРНАЯ ЛОГИКА. А здесь во всех логических элементах и многих других узлах - только один тип деталей: транзисторы. Многие из них работают в таком режиме, что заменяют резистор или конденсатор. Так, например, для ТТЛ созданы триггеры, где вместо двух транзисторов используются восемь, но зато нет ни одного конденсатора или резистора.
И2Л - ИНЖЕКЦИОННАЯ ИНТЕГРАЛЬНАЯ ЛОГИКА. Разновидность ТТЛ, где элементы, в частности транзисторы, расположены и параллельно поверхности кристалла и перпендикулярно, что делает БИСы более компактными.
И3Л - ИЗОПЛАНАРНАЯ ИНЖЕКЦИОНИАЯ ЛОГИКА. Разновидность ТТЛ, выполненная по технологии, которая формирует очень тонкие плоские "детали" БИСа, а это повышает компактность и надежность схемы.
ТТЛ С ДИОДАМИ ШОТКИ. Разновидность ТТЛ, в несколько раз повышающая быстродействие БИСов.
В прежние времена характерное для ТТЛ усложнение схемы - восемь транзисторов вместо двух!- считалось бы недопустимой расточительностью. Но БИС на одинаковых элементах настолько технологична, что за нее можно с легкостью переплатить тысячу-другую транзисторов. Тем более, что технология БИСов не просто пресекла "тиранию количеств", а создала, так сказать, невиданное количественное изобилие. Огромные шкафы с аппаратурой превратились в миниатюрные кристаллические пластинки, выпускаемые к тому же массовыми тиражами на автоматизированных линиях, и специалисты по электронной технике с легкостью оперируют теперь схемами из сотен тысяч и миллионов деталей. С новой технологией приходит и новая психология создания электронной аппаратуры. А может быть, даже новая психология взаимоотношений с электроникой.
ЗА ТЕХНОЛОГИЕЙ - ПСИХОЛОГИЯ
Уже в БИСе микрокалькулятора видны черты большой вычислительной машины. Здесь есть оперативное запоминающее устройство - ОЗУ, есть вычисляющий блок - сумматор, есть набор программ - "сложить", "вычесть", "умножить" и т.п. Если значительно расширить ОЗУ, сделать в нем большое число "полок", куда можно раскладывать вводимые или полученные в процессе вычислений числа, если создать систему адресов (это "прикрепленные" к числам личные метки в виде обычных комбинаций импульсов-пауз), по которым число можно положить на определенную "полку", а затем найти его по известному адресу, если, наконец, создать широкий ассортимент программ, предусмотреть сборку больших программных последовательностей и позволить самой программе участвовать в их формировании, если сделать все это, естественно усложнив БИС, то можно получить в одном кристалле законченный процессор, основную действующую систему компьютера.
Из таких однокристалльных процессоров, нацеленных на решение разных классов задач, создаются многопроцессорные ЭВМ, где переход с одной задачи на другую может сводиться к простому переключению кристаллов. Уже проектируются многопроцессорные компьютеры, считающие со скоростью 500 и даже 800 миллионов операций в секунду. А ведь еще несколько лет назад быстродействие миллион операций в секунду считалось непревзойденным достижением. Микропроцессоры - их в этом случае называют микроконтроллерами - могут управлять машинами, открывая тем самым невиданные ранее возможности широкой автоматизации производства. Малые габариты и невысокая стоимость (в сравнении с приборами-шкафами эпохи дискретных схем) открыли микропроцессорам путь даже в бытовую аппаратуру.
Создается, например, телевизор, который запоминает все ваши пожелания касательно недельной программы передач, в нужный момент включает нужный телевизионный канал, заранее напомнив, что в такой-то час вас ждет наконец веселая музыкальная передача. Создается кухонный комбайн, который, получив задание в самом общем виде: "Хотелось бы съесть пироги с грибами...", - сначала сообщает, что и как подготовить, сам в нужной последовательности включает кухонное оборудование, а затем, управляя тепловым режимом плиты, готовит блюда по всем правилам, введенным в микропроцессор по проводам прямо из кулинарного техникума. А вот еще один домашний работник с микропроцессором - телефон. Дублируя записную книжку, он держит в памяти основные нужные вам номера, по первой просьбе соединяет с абонентом "несмотря ни на что", (повторяя, в частности, набор, если номер занят), сам коротко отвечает на звонок, если вас нет дома, умеет набирать номер "с голоса", а кроме того, по совместительству в назначенное время будит вас по утрам, напоминает о программе дня, о приближающихся днях рождения знакомых и предстоящих праздниках.
В последнее время к кристаллам вычисляющим и управляющим прибавились еще н кристаллы развлекающие - обрадованные возможностью крупными сериями производить тысячеэлементные электронные блоки, инженеры уже вводят их даже в игры и игрушки. В ассортименте развлекательной электроники, которой занимаются сейчас многие фирмы, в том числе и очень известные, есть, например, выполняющий 20 команд маленький электрический вездеход, играя с которым ребенок получает первые навыки программирования. Есть небольшие, размером с микрокалькулятор, игровые автоматы, где на экране из жидких кристаллов не без вашего участия, конечно, сражаются за шайбу хоккеисты. Есть даже портативные машины, с которыми можно сыграть в шахматы, причем в одной из моделей машина сама передвигает свои фигуры механической "рукой". Все эти простые игрушки на самом деле не так, конечно, просты, каждому их действию предшествует детальный анализ обстановки, громоздкие вычисления, выполняемые электронными схемами. Причем все их умения и способности формируются один раз и навсегда - при разработке алгоритмов, схемы и технологии изготовления микропроцессора. После этого полупроводниковый шедевр размножают, так сказать, типографским способом, не занимаясь уже ни наладкой, ни регулировкой.


Выпускаемые различными фирмами игровые и обучающие электронные машины. Автоматы для игры в шахматы (фото 1 и 5); ответ "противника" (машины) может высвечиваться на индикаторе, а может завершаться перемещением фигуры (5). Машины, с которыми можно играть в "футбол" (2), "хоккей" (3), нарды (4), "бейсбол" (6), "боулинг" и другие игры (9). Машина для лингвистических игр (7) и аналог карманного словаря (8 ). Обучающая машина "Спик энд спэлл" (10).
Особое место среди микропроцессорных игрушек занимает уже весьма распространенная в англоязычных странах игра-машина "Спик энд спэлл" ("Speak and Spell"), что в вольном переводе означает "Говори и пиши". Игра помогает освоить написание примерно двухсот английских слов, причем уже, кажется, появились машинки со сменными словарными блоками. Подобная помощь полезна при изучении любого языка, но особенно английского: в нем произношение и написание различаются настолько, что сами англичане шутят: "У нас пишется Манчестер, а читается Ливерпуль".
Одна из замечательных особенностей игры-машины "Спик энд спэлл" состоит в том, что она сама произносит слова, причем без помощи миниатюрного магнитофона или мини-проигрывателя. Слова и отдельные их слоги синтезируются из электрических сигналов по описаниям, которые в виде двоичных чисел хранятся в памяти микропроцессора. Для такого синтеза речи нужны настолько сложные схемы, что до появления БИСов говорящие машины считались непозволительной роскошью. И вот теперь, пожалуйста,- непозволительная роскошь в рядовой и не очень дорогой игрушке.
С машиной играют так: она произносит слово, и вы, нажимая клавиши с буквами, пишете это слово на небольшом световом табло. Если слово написано верно, то машина произносит "Вы правы" и засчитывает вам очко, а если написано с ошибкой, просит: "Попробуйте еще раз". После третьей попытки электронный репетитор, не рассчитывая больше на ваши знания, пишет слово сам, а вам, извините, ставит двойку - на машинном языке это минус очко. После каждого десятка слов подводится итог: и на экране появляется счет, скажем +7, -3. Машина называет слова в разном порядке, но все они сгруппированы по степени сложности - сначала идут десятки самых простых слов, а затем все более сложных.
Играть с такой машиной, кстати, довольно интересно. И полезно - быстро входишь в азарт и, сам того не замечая, начинаешь грамотно писать. И уже как-то более оптимистично относишься к известным проектам использования микрокомпьютеров в системе образования. Один из проектов, например, предполагает широко применять микрокомпьютеры для обучения во всех 7200 школах Франции. В Соединенных Штатах уже сейчас компьютеры используются примерно в пятой части муниципальных школ, и количество таких компьютеризованных школ предполагается вскоре резко увеличить.
Всерьез поговаривают и о системах самообразования на основе микрокомпьютеров. И о том, что массовое применение считающих, обучающих, информирующих, развлекающих, управляющих и иных микромашин в сочетании с изобилием каналов связи (французы уже придумали для такого компьютерно-коммуникационного альянса отдельный термин - телематика) может резко изменить сам образ жизни человека, формы общения и даже психологию. Возможно ли это? Нужно ли? И целесообразно ли само обсуждение проблемы? Не окажется ли электронное обогащение человечества процессом стихийным, неотвратимым? Пока подобные вопросы очень робко обсуждаются лишь в технических журналах и остается ждать - теперь уже, видимо, недолго,- когда темой заинтересуются профессиональные спорщики и прогнозисты. Пока же каждый может индивидуально оценить для себя целесообразность союза с электроникой в каждом конкретном случае.
Машинка для игры в шахматы? Поиграть любопытно, но нельзя же, чтобы эта "железка" отняла такую житейскую радость, как шахматная партия с приятелем где-нибудь в летнем скверике на скамейке.
Электронная автоматика? А вот здесь двух мнений быть не может. Когда, приняв пятачок, электронный автомат пропускает вас в метро, вспомните - еще не так давно эту изнурительную однообразную работу делали сотни симпатичных девушек. Лучшее творение природы - человеческий интеллект - расходовалось на то, чтобы бездумно надрывать бумажные билетики. Только в Москве нужно было надорвать 8-10 миллионов этих бумажек в день.
Электронный педагог? В какой-то мере да... Он может, видимо, чему-то подучить нас, но научить - это дело человека, учителя.
Электронный информатор? Вещь, видимо, полезная. Но только пусть не посягает на книгу, на ничем не заменяемое удовольствие чтения.
Электронный калькулятор? Да. И без каких-либо оговорок. Потому что глупо тратить бесценные часы жизни, или даже минуты на чисто машинную перетасовку чисел. Потребность в личной счетной машинке ощущают, видимо, многие люди. Во всяком случае, все, кто только что стоял у прилавка и рассматривал микрокалькуляторы, через какое-то время отправились в кассу. Все, кроме одного, кроме автора этих заметок, для которого посещение магазина "Счетные машины", консультации со специалистами, знакомство с ассортиментом калькуляторов, с запросами и настроением покупателей было лишь одним из пунктов в плане подготовки заказанного многими читателями рассказа об электронных счетных машинках личного пользования. Что же касается микрокалькулятора, то я приобрел его давно, когда он, к сожалению, стоил значительно дороже. И даже несмотря на это, очень доволен, что не принял тогда главный аргумент скептиков - в жизни рядовому человеку, мол, не так-то уж много приходится считать. Молотком и отверткой мы тоже пользуемся не каждый день, но они вместе с тем есть в каждом доме. Что это за дом без молотка и отвертки? И что это за современный дом без электронного микрокалькулятора...
***
Где-то мы про это уже слышали
 ТЕМА #41, АБЗАЦ #397
ТЕМА #41, АБЗАЦ #397 .
.
Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Вернемся к "картонкам"...
4/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ВАШ РАБОЧИЙ КАТАЛОГ
Г.ГЕЦОВ
Сегодня мы продолжим рассказ о личном каталоге. Речь пойдет о шифровальной технике, а также об элементах технологии.
СОБСТВЕННЫЕ ШИФРЫ
Источникам рекомендуется присваивать условные номера-цифры. Их используют как ссылки на книгу или статью. Номер фиксируется на карточке источника и в особой шифровальной рубрике вспомогательного отдела. На выписке вы проставляете этот условный номер источника вместо выходных данных книги, журнала, газеты. Рядом с шифром указываете страницу источника, а иногда номера абзацев и даже строк.
Конечно, подобрав книги и статьи, не следует автоматически присваивать им шифры: согласитесь, что если будет сделана всего одна выписка из источника, то разумнее рядом с выпиской зафиксировать адресные данные этого источника, нежели давать шифр.
Для нумерации шифровки источников используют таблицу с порядковыми номерами от 0 до, например, 500. При большом объеме работы делают несколько подобных таблиц, но дополнительно индексируют их буквами. Первая таблица будет иметь индекс "А" (ее шифры - А0, A1, A2, A3... А499, А500), вторая - индекс "Б" и т. д. Присваивая номер источнику, зачеркните его в таблице. Этим вы избежите повторов шифров. Сам же шифр фиксируется на карточках источника в алфавитном, тематическом и вспомогательных отделах каталога.
Буквенные индексы - это дополнительные поисковые признаки. Можно шифру придать букву, кратко обозначающую фамилию автора или название книги. Если к тому же выбрать и числа, которые легко запоминаются, скажем, такие: 1, 11, 111; 22, 222; 5, 15, 25; 10, 100, 200..., то такие шифры хорошо сохраняются в памяти. Например, индекс "П-100" шифрует книгу профессора П.Т.Приходько "Пути в науку. Беседы по организации труда начинающих исследователей", (М., Знание, 1973г.), "Щ-400" - монографию А.И.Щербакова "Социально-экономические проблемы эффективности научного труда" ("Наука", Новосибирск, 1975г.).
Обратим внимание на приведенные примеры. Если вам потребовалось собрать материал о методах организации научного труда (рациональный режим умственной работы, совершенствование памяти и внимания...); об использовании научных результатов в народном хозяйстве, то обратитесь в соответствующую рубрику тематического отдела своего каталога. Там вы легко найдете, в частности, карточки с шифрами П-100 и Щ-400.
Для определения источника по таким шифрам можно не обращаться к шифровальной рубрике, а в алфавитном отделе каталога, если он не очень велик, среди карточек на "П", "Щ" уже бегло по номерам 100 и 400 легко найти нужное. При необходимости вы возьмете карточки с отметками для дальнейшей работы над источниками.
Шифровальная техника позволяет облегчить не только работу с источниками (например, быстрее делать выписки), но и пользование самим каталогом. Шифры своего каталога используют и для того, чтобы иметь возможность, не копируя текстов карточек, ставить их шифровальные "копии" в ряд рубрик (в том случае, когда тот или иной источник должен быть представлен в нескольких рубриках тематического отдела каталога).
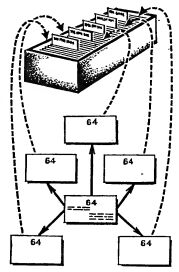
Как зашифровать отдельные журнальные и газетные статьи? Шифры журналов и газет регистрируют на карточках отдела "Периодические и продолжающиеся издания". Мы знаем, что ссылки на журнальные и газетные статьи можно делать, используя условные обозначения журналов и газет. Однако отдельные статьи иногда кодируются как самостоятельные источники - по типу книжных шифров, то есть условным номерам, без сокращенного упоминания журнала или газеты. Поясним сказанное примером.
В седьмом номере журнала "Наука и жизнь" за 1980 год на страницах 6-12 помещена статья академика Н.Федоренко "Лоция технического прогресса". Ссылка на статью, например, в вашей выписке может быть дана шифром, скажем, таким - "Ф-19". Легко догадаться, статья обозначается шифром "Ф-19", если же указать и ее объем, то индекс будет выглядеть так: "Ф-19-6-12". В этом случае Можно узнать автора статьи, полное ее название, место, где она напечатана и степень ее проработки вами с помощью каталога и все это без привлечения журнала, подчас не имеющегося под рукой.
Для этой цели нужно будет обратиться прежде всего к шифровальной рубрике вспомогательного отдела своего каталога. Там в группе индексированных буквами карточек с общим цифровым адресом "19" будет найдена карточка с индексом "Ф-19", которая укажет источник, а именно - статью академика Н.Федоренко со всеми выходными данными. Чтобы вспомнить, что именно вы почерпнули из этой статьи, какие ассоциации возникли при ее чтении, вам следует обратиться к карточке этой статьи в соответствующей рубрике тематического отдела ("Комплексная программа научно-технического прогресса"). Если вы сразу не вспомните названия этой рубрики, то ссылка на нее имеется на карточке данной статьи в алфавитном отделе каталога (на фамилию Н.Федоренко).
ЭЛЕМЕНТЫ ТЕХНОЛОГИИ
Для индивидуального применения практично иметь карточки из обычной писчей бумаги. Тонкая бумага обеспечит компактность каталогов и картотек, вдвое-втрое сократит объем, позволит "под копирку" делать нужное число копий (напомним, что в вашей работе могут потребоваться карточки в нескольких экземплярах).
Идентичные карточки разумнее скреплять скобками с помощью сшивателя бумаг. При работе в библиотеке есть смысл пользоваться сфальцованными карточками. Продублировав текст под копирку, вы, кроме основной карточки, тотчас же получите ее "ссылочную" копию. Когда потребуется, сдвоенные карточки разъединяются. Карточки могут постоянно оставаться удлиненными - двойными, тройными... Как же их помещать в каталог? Просто сложить, выдерживая при этом размер обычной стандартной карточки.
Полезно изготовить карточки, специально предназначенные для объединения массивов каталога или их частей. Для этого на карточках делают выступы или, наоборот, вырезы. Если карточка с выступом или с вырезом стоит не в своей группе, это будет заметно. Выступы и вырезы помогают сохранять порядок в ящиках, позволяя быстро помещать ту или иную карточку по этим признакам в их родные рубрики.
Когда во время работы приходится вынимать целиком отдельные рубрики из ящиков каталога, то карточки помещают в специальные держатели, в обложку, в коробки или в конверты.
Если вы постоянно имеете дело с одними и теми же карточками и заинтересованы в их сохранности, то полезно воспользоваться прозрачными чехлами.
Особую роль в каталогах и картотеках играют разделители. Они облегчают расстановку карточек, убыстряют поиск. Сверху на разделителях делают выступы. На выступах буквами отмечают разделы каталога, куда помещаются карточки с общими для них алфавитными признаками. Разделители могут нести и цифровые индексы, скажем, в шифровальной рубрике.
Материалом для разделителей обычно служат плотная бумага или картон. Временные рубрики каталога часто меняют свое название. Для них удобно использовать пластмассовые разделители, матированная поверхность которых позволяет наносить легко стирающиеся надписи.
"Наездники" (рейтеры) - металлические или пластмассовые пластинки с зажимами позволяют обозначать сами карточки, обходясь без разделителей или заменять, таким образом, некоторые разделители. Наездники иногда снабжаются специальными оконцами, в которые можно вставлять написанные на бумаге сведения или признаки. Применяются и пластмассовые пластинки, позволяющие делать карандашные надписи, а в необходимых случаях стирать их. Наездники окрашиваются в яркие цвета, что облегчает поиск карточек. Для сортировки карточек по алфавитному признаку используются сортировочные ящики, полки с ячейками. Ячейки используют для разных целей: с одной стороны пишут, например, буквы алфавита, с другой - порядковые номера для сортировки карточек каталога, имеющих номерные шифры.
Не возникает особых проблем, если, скажем, ваш каталог умещается в одном ящике. Но когда требуется уже несколько ящиков, то полезно использовать специальные блоки, изготавливаемые промышленностью, или хотя бы пластмассовые ящики с крышками (они могут быть установлены один на другой, образуя блоки).
Библиографические карточки из плотной бумаги, а также картонные и пластмассовые, каталожные разделители продаются в магазинах библиотечных коллекторов. Цена 250 карточек - 65коп.
Для карточек можно использовать листки для заметок, которые продаются в магазинах канцелярских товаров. Однако формат этих листков не очень удобен для работы с каталогом.
По просьбе журнала "Наука и жизнь" Московское производственное объединение бумажных изделий "Восход" в настоящее время разрабатывает образцы и вскоре приступит к выпуску карточек для личных каталогов. Набор карточек состоит из 100 и 150 листков тонкой бумаги стандартного размера (75*125мм). Фирме было бы полезно знать, какова потребность в библиографических карточках из тонкой бумаги. Просим сообщать об этом в письмах по адресу: Москва, центр, ул.Кирова, 15, фирме "Восход". На конвертах сделайте условную пометку "Каталог".
Пластмассовые н картонные ящики для каталогов также поступают в магазины библиотечных коллекторов. Если вы используете карточки нестандартных размеров, то картонные коробки нужного размера можно заказывать на переплетно-картонажных фабриках или в мастерских. Приводим эскизы возможных конструкций ящиков.
5/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ВЫПИСКИ
Г.ГЕЦОВ
Работая с книгами, трудно обойтись без выписок. Выписки нужны, чтобы выбирать из книг наиболее существенное, они помогают накопить нужные сведения по тем или иным вопросам, облегчают запоминание. Наконец, они особенно удобны в том случае, когда требуется собрать материал из разных источников на одну тему.
Выписки могут быть дословные (цитаты) и свободные, когда мысли автора излагаются своими словами. Однако в этом случае необходимо приобрести умение кратко и не в ущерб содержанию формулировать мысли. При чтении на страницах, например, с помощью вкладных листков отмечаются те места, которые предполагается выписать.
Выписки полезно делать на карточках. Работать с ними удобно, их легко подобрать и по темам и сформировать по фамилиям авторов. Над каждой выпиской указывается ее тема, под ней - фамилия автора, название книги, год издания, страница с цитатой. Целесообразнее все это делать с помощью шифров.
Но шифры позволяют фиксировать нужные места из литературы и без выписок. В этом случае на карточку заносят шифр источника, а рядом пишут номер страницы и указывают нужные абзацы. Такую "невыписанную выписку" полезно для большей определенности озаглавить. Со временем па карточку может быть перенесен и текст.
Карточки раскладываются по определенным рубрикам картотеки. Разделители с названием рубрик помогают систематизировать имеющийся материал. Рубрикам иногда присваивают определенные номера, ими метят и выписки - это дает возможность использовать для работы любую выписку, не рискуя потерять ее обратный адрес. Выписки можно хранить в ящиках, в конвертах, папках, на которых обозначены темы.
Иногда целесообразно завести указатель будущих выписок по тому или иному источнику. В таких указателях фиксируются нужные номера страниц и абзацев - снизу, сверху или в миллиметровом исчислении.
Приведем пример. Изучая книгу "Горький и советские писатели" (Литературное наследство, т.70, М., АН СССР, 1963г.), литературовед прежде всего сформулировал темы найденных отрывков, сделал пометки на карточках и составил из них указатель, скажем, в виде плоской картотеки. С такой карманной картотекой удобно работать в библиотеке.
Иногда сведения по выпискам заносят не на карточки, а на разделители картотеки, которые в данном случае несут соответствующие тематические признаки.
Еще один способ систематизации - использование тетрадей с пронумерованными страницами, где на специально отведенных полях записывают темы. Каждая выписка сопровождается фамилией автора, названием работы и т.д., подобно тому как это делается на карточках. В тетради отводится место алфавитному указателю тем - своеобразному оглавлению. Делая какую-нибудь выписку, отмечают в указателе ее тему и страницу.
Человек почти молниеносно воспринимает текст книги, быстро, под нужным углом зрения его оценивает, выбирает необходимое. Но вот процесс переписки требует подчас куда больше времени, чем отбор нужного. Как освободиться от этой трудной и неинтересной работы?
Можно прибегнуть к помощи магнитофона. Тексты наговаривают на магнитофон, а затем, воспринимая на слух, перепечатывают на машинке. Это очень ускоряет процесс работы над выписками. Известно, что человек говорит в шесть раз быстрее, чем записывает, а печатать на машинке может в шесть раз быстрее, чем писать рукой.
Существенную помощь оказывают также фотографии и ксерокопии, фоторепродукции из книг можно сделать и самим. Для этого используют стол увеличителя, на штангу закрепляют фотоаппарат (желательно "зеркалку"), чтобы наводка на резкость была сделана возможно точнее. Специальная приставка позволяет использовать другие малоформатные камеры. Можно обойтись и без фотоаппарата, применяя увеличитель, заряженный неэкспонированной пленкой.
Наконец, можно фотографировать вообще и без оптических устройств с помощью рефлексной (прямой или обратимой) фотобумаги. Достаточно такую фотобумагу прижать стеклом к тексту книги, осветить сверху, а затем проявить, чтобы получить изображение. Если приходится снимать "с рук", то в этом случае лучше работать с помощью фотоаппаратов, определяющих экспозицию через объектив.
Уже негативы сами по себе надежные и долговечные носители информации. Их можно просматривать с помощью лупы или проекционной аппаратуры - фотоувеличителей, диапроекторов, некоторых фильмоскопов. Негативы хранят не только в рулончиках, но и в виде отдельных кадров в конвертах, наконец, в бумажных карманах, приклеенных к карточкам с выписками.
И все же удобнее всего в работе отпечатки, которые не требуют для чтения аппаратуры, легко комбинируются, позволяют делать пометки.
Фотокопию можно сделать лишь с нужной части текста, закрыв остальное чистой бумагой. Но лучше фотографировать всю страницу, отметив узкими полосками черной бумаги, положенными на поля, нужные места текста.

Полезно заранее, еще при съемке, пометить негативы. Для этой цели удобно иметь набор из крупных цифр и букв. При репродуцировании в кадр помещают номер страницы, составленный из цифр. Сюда же можно поместить и шифр источника. Этот шифр при съемке соответствующей книги будет постоянным, а номера страниц наборными. Эти символы легко различимы на экране увеличителя и хорошо видны при просмотре негативов.
На готовых фотовыписках полезно проставить полные метки и рассортировать по номерам страниц текста книги и источникам. Отпечатки наклеиваются на отдельные листки писчей бумаги одинакового формата (например, в половину стандартного машинописного листа). С такими одинаковыми листами легче будет работать в дальнейшем.
При ксерографировании ("электрокопировании") страницы с выписками, как правило, снимают полностью. От лишних строк текста в копиях избавляться не стоит. Можно хранить отснятые страницы целиком. Тогда не тратится время на вырезание и наклеивание, поля страниц используют для пометок.
При фото- и электрографировании можно использовать вкладные листки, о которых уже говорилось. Они с необходимыми отметками подкладываются под страницы источников так, чтобы эти отметки были видны сбоку от текста. При увеличении с микропленки номера страниц источника будут четко видны, что позволит до экспонирования записать эти номера на обороте листков фотобумаги.
Электрографические копии текстов, сделанные в масштабе 1:1, полезно наклеивать непосредственно на вкладные листки с отметками. При этом сохраняются ранее сделанные пометки и отчеркивания.
6/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ПЛАНЫ
Г.ГЕЦОВ
Можно без преувеличения утверждать, что чтение обычно сопровождается составлением - в уме или на бумаге - плана, когда определяются опорные логические пункты, отражающие содержание, логику и последовательность изложения. Это способствует более углубленному пониманию прочитанного, выборке нужного материала, его запоминанию и освоению.
Таким образом, план - весьма важное средство организации умственного труда. Примером плана, правда, очень общего, отмечающего лишь узловые разделы, служит обычное оглавление. Просматривая его, без чтения самой книги можно получить представление о ее содержании и схеме построения. План же, как форма записи, более подробно передает содержание, чем оглавление книги.
План - это самая краткая запись. Поэтому его легко переделывать, совершенствуя как по существу, так и по форме, продумывая при этом вновь содержание текста. План в легко обозримой форме отражает последовательность изложения и обобщает его. Эта запись, составляемая в процессе чтения, помогает легче уяснить содержание прочитанного и способствует ускоренной проработке книг и статей. Руководствуясь планом и обратившись к подлиннику, можно составить более подробные и обстоятельные записи - конспекты и тезисы, причем совершенно не обязательно готовить их одновременно с планом. Иногда подробно составленный план может на время заменять такие виды записей.
Если вы готовите какой-либо текст (лекцию, статью, большое деловое письмо и т.д.), то составление плана в процессе этой работы помогает легко и быстро выявлять повторения и непоследовательность и в целом улучшать текст.
И еще одно. План помогает сосредоточиваться при рассеивании внимания и умственном утомлении. Если, например, вы устали н работа над материалом не ладится, идет вяло, то сделайте подробный план к двум-трем страницам текста - это поможет снять утомление и ускорить процесс работы.
Каковы же принципы составления плана? План способствует активизации чтения. Поэтому в отличие от конспектов и тезисов, которые готовятся, как правило, только после полного ознакомления с материалом, пункты плана можно и должно фиксировать немедленно в процессе первоначального чтения. В дальнейшем план может исправляться и уточняться.
Составляя план при чтении, прежде всего стараются определить те места, где кончается одна мысль и начинается другая. Эти места в книге следует отмечать на вкладных листках.
Подзаголовки в книге, деление текста на абзацы облегчают формирование плана. Можно при его составлении (особенно когда план предназначен для подготовки тезисов) не обращать внимания на подзаголовки и абзацы. В этом случае следует стараться оценивать высказывания автора книги по существу и отображать их в плане, причем последовательность пунктов не обязательно должна совпадать с порядком изложения. Поэтому полезно рядом с пунктами плана фиксировать нужные номера страниц источника.
Планы могут быть простыми и сложными. Сложный план в отличие от простого имеет, кроме основных пунктов, еще и подпункты, которые детализируют, разъясняют содержание.
Сложный план не следует составлять в один прием, без черновика. Составляя сложный план, объединяют часть пунктов под одним заголовком или, наоборот, детализируют некоторые пункты, разбивая их на части.
Другими словами, возможны два способа работы: а) составляется подробнейший простой план, а далее он преобразуется в сложный за счет группировки части пунктов под общими заголовками; б) составляется краткий простой план, а затем при повторном чтении формируется сложный план с детализирующими частями. Такой метод приемлем лишь при продолжительной работе над фундаментальными источниками, так как требует много времени.
В общем случае целесообразно составлять подробный план к тексту книги при первом же ее чтении. Такой план легко превратить в сложный, объединяя те или иные пункты. Сам процесс обработки детального простого плана помогает лучше разобраться в содержании: ведь, объединяя, обобщают, а выбрасывая, выделяют главное, фильтруют его в своем сознании. Пункты плана частично или полностью могут текстуально совпадать с отдельными фразами источника. От этого план лишь выигрывает.
Чтобы избежать нерационального переписывания, главные заголовки сложного плана выделяются. Если это сделать нельзя, заголовки выписывают в отдельные графы - слева или справа от текста простого плана. При уплотненной записи заголовки приходится выносить на поля и отсылать стрелкой к нужному месту. Вот почему опытные читатели стараются вести запись планов с большими интервалами между пунктами и с достаточными для дополнений полями.
Запись планов желательно делать так, чтобы ее легко можно было увидеть в целом. Для этого используют один большой лист бумаги или несколько листов, но запись ведут лишь с одной их стороны. Можно сразу увидеть все пункты, раскладывая листки один под другим. При составлении сложного плана полезно отдельно выписать основные его пункты.
Планы накапливают и хранят в отдельных тетрадях, в конвертах, в самом источнике (скажем, на полях газеты или на вкладных листах), в каталоге - на карточках или на листках, сложенных "гармошкой".
Такая форма записи, как план, имеет и свои недостатки. Он, например, не передает фактического содержания, а лишь упоминает о нем и о схеме его расположения. Отсюда вывод: планом можно пользоваться, чтобы оживить в памяти хорошо знакомый текст или воспроизвести в памяти текст вскоре после составления плана.
7/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ТЕЗИСЫ
Г.ГЕЦОВ
"Заключение должно повторить дело трактата и в сокращеньи обнять его снова, чтобы читатель мог повторить самому себе". В этих словах Н.В.Гоголя хорошо передана суть тезисов. Они действительно повторяют, сжато формулируют и заключают прочитанное. Это положения, вбирающие в себя существо значительной части текста, то, что доказывает или опровергает автор, в чем он стремится убедить читателя. В отличие от выписок, содержащих только иллюстративный или фактический материал, тезисы всегда имеют доказательства.
Тезисы, как никакая другая запись, позволяют обобщить изучаемый материал, выразить его суть в кратких формулировках. И если план заставляет читателя неотступно следовать за автором книги, то тезисы дают возможность раскрыть содержание книги, активно разобраться в нем. Процесс их составления позволяет продумать, изучить тот или иной вопрос, используя несколько книг и статей. Важно и то, что ни одна другая форма записи не помогает так хорошо составить доклад, выпукло представляя основную точку зрения автора. Наконец, тезисы ценны, а часто совершенно необходимы для критического анализа книги, статьи или доклада. При их использовании акцентируется, заостряется суть вопроса. Тезисы облегчают возможность противопоставить свои мысли мыслям и убеждениям исследуемых авторов. Обратите внимание - именно убеждениям. Ведь порою автор может незаметно, четко не формулируя, проводить определенную мысль. Цель исследователя - выявить суть суждений и сделать нужные выводы, хотя бы они явно и не были сформулированы автором.
О тезисах говорят в двух смыслах, имея в виду и способ выражения собственных размышлений и способ изложения содержания какого-либо литературного источника. Нас интересует последняя форма записи, для которой возможны три типа.
ОСНОВНЫЕ ТЕЗИСЫ - это принципиально важные, главные положения, обобщающие содержание источника, которые в своей совокупности иногда носят характер главных выводов. Они могут составить отдельную самостоятельную запись, отображающую содержание всего материала при необходимости под тем или иным углом зрения (тематическая запись). Основные тезисы составляются, как правило, по крупным законченным разделам или же целиком по всему произведению, если автор дает вывод в конце книги.
ПРОСТЫЕ тезисы, напротив, удается выделить из многих частей произведения вне зависимости от его общей направленности. Причем это можно сделать уже при первоначальном ознакомлении. Основные тезисы, наоборот, можно успешно составить лишь после уяснения сути всего произведения в целом. К каждому основному тезису может быть составлено несколько простых, разъясняющих тезисов. Если тезисы составляются к сложному плану, то главным пунктам такого плана могут соответствовать основные, подпунктам - простые тезисы.
Таким образом, мы подошли к определению третьего типа. Запись, включающая два вида тезисов (простые и основные), называется СЛОЖНЫМИ тезисами.
Как в сложном плане за основными пунктами следуют подпункты, так и в сложных тезисах за основными будут следовать простые, раскрывая и поясняя их содержание.
Сложные тезисы в сочетании с планом и выписками, иллюстрирующими, раскрывающими детали, могут составить прекрасный конспект.
В самих тезисах не приводятся обосновывающие факты, примеры. Но тезисы сами по себе всегда должны быть обоснованны, доказаны. Поэтому полезно в записи отсылать к обоснованиям, доказательствам, остающимся в проработанной книге или статье. Самобытная форма высказывания, оригинальность авторитетного суждения могут быть сохранены, иначе тезисы рискуют потерять свою документальность, снизится острота восприятия материала.
Часть тезисов может быть записана в виде цитат. Этот метод применяют при подготовке рецензий и аннотаций для сравнения разных точек зрения, а также в тех случаях, когда необходима особая "осторожность в выводах. Но тезисы-цитаты иной раз могут быть очень длинными. Поэтому полезно составлять в дополнение к ним план. Для ускорения подготовки материалов можно пользоваться вкладными листками, шифрами и копиями текстов.
Тезисы, зафиксированные в виде шифров, скажем:
13-11-4в, 13-14-2н (в - строка вверху, н - строка внизу), или отчеркнутые с помощью вкладных листков, не потребуют переписывания. Тогда в необходимых источниках (не только в одном, но и одновременно в нескольких) можно будет открыть нужные места и сравнить положения, отобранные с помощью шифров-цитат или отчеркиваний на вкладных листках.
В противоположность простым тезисам, которые в большинстве случаев могут быть составлены из цитат, основные тезисы чаще всего формулируют самостоятельно. После предварительного ознакомления текст необходимо прочитать вторично. При этом следует разбить его (с помощью плана или без него - отчеркиванием и подчеркиванием) на ряд логически завершенных частей. В этих частях определяют, а затем выписывают главные идеи или временно просто отмечают их с помощью вкладных листков или полосок бумаги. Затем, хорошо продумав выделенное, уяснив его суть, формулируют отдельные положения. Это и будут тезисы.
Умело составленные тезисы вытекают один из другого. Первый, открывающий записи, или последний, завершающий их (наиболее общие в той или иной мере), определяет содержание остальных тезисов или подытоживает все предыдущие. Не исключено, что ряд положений потребуется объединить не в порядке изложения, а в их логической связи, важной для того, кто составляет тезисы. Чтобы не осложнять при этом поиск, полезно связывать тезисы с текстом источника с помощью ссылочных страниц, шифров или вкладных листков, отсылающих к нужному абзацу и даже к отдельным строкам.
Предварительно составленный план оказывает существенную помощь в подготовке тезисов, в частности при совершенствовании формулировок. Его делают не очень подробным. Если подробный план уже есть, его предельно сокращают, исключая второстепенные пункты, отражающие отдельные факты, примеры и т.д.
Но не следует думать, что план остается лишь вспомогательным орудием. Это весьма нужное пособие в дальнейшей работе над тезисом и с помощью тезисов. Его можно использовать для раскрытия тезисов при подготовке лекций, докладов или при повторении пройденного к экзаменам. Вспомогательные пункты плана, которые при составлении тезисов не были приняты во внимание, теперь помогут обосновать, проиллюстрировать тезисы. Все это окажется важным и тогда, когда на их основе потребуется составить конспект.
Тезисы, составленные вчерне, нелишне тщательно сверить с содержанием источника и после этого переписать начисто. Этому поможет подробный план, связанный с текстом источника ссылочными страницами.
В окончательном виде тезисы нумеруют по порядку. Рациональная последовательность позволяет сделать их краткими, избежав повторений. Все это, как правило, ведет к коренной переработке записей, к их совершенствованию, другими словами, к улучшению восприятия материала, его глубокому изучению, анализу и к проверке усвоения пройденного.

[Вы видите на фотографии карточки 125*75мм для индивидуальных домашних каталогов и картотек. Они будут продаваться блоками в футлярах. Это новая продукция Московского производственного объединения бумажных изделий "Восход", разработанная по рекомендации журнала "Наука и жизнь". Объединение "Восход" продолжает разработку новых товаров в помощь читателям, активно работающим с различной литературой. Информация об этих новинках будет публиковаться в журнале].
4/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ВАШ РАБОЧИЙ КАТАЛОГ
Г.ГЕЦОВ
Сегодня мы продолжим рассказ о личном каталоге. Речь пойдет о шифровальной технике, а также об элементах технологии.
СОБСТВЕННЫЕ ШИФРЫ
Источникам рекомендуется присваивать условные номера-цифры. Их используют как ссылки на книгу или статью. Номер фиксируется на карточке источника и в особой шифровальной рубрике вспомогательного отдела. На выписке вы проставляете этот условный номер источника вместо выходных данных книги, журнала, газеты. Рядом с шифром указываете страницу источника, а иногда номера абзацев и даже строк.
Конечно, подобрав книги и статьи, не следует автоматически присваивать им шифры: согласитесь, что если будет сделана всего одна выписка из источника, то разумнее рядом с выпиской зафиксировать адресные данные этого источника, нежели давать шифр.
Для нумерации шифровки источников используют таблицу с порядковыми номерами от 0 до, например, 500. При большом объеме работы делают несколько подобных таблиц, но дополнительно индексируют их буквами. Первая таблица будет иметь индекс "А" (ее шифры - А0, A1, A2, A3... А499, А500), вторая - индекс "Б" и т. д. Присваивая номер источнику, зачеркните его в таблице. Этим вы избежите повторов шифров. Сам же шифр фиксируется на карточках источника в алфавитном, тематическом и вспомогательных отделах каталога.
Буквенные индексы - это дополнительные поисковые признаки. Можно шифру придать букву, кратко обозначающую фамилию автора или название книги. Если к тому же выбрать и числа, которые легко запоминаются, скажем, такие: 1, 11, 111; 22, 222; 5, 15, 25; 10, 100, 200..., то такие шифры хорошо сохраняются в памяти. Например, индекс "П-100" шифрует книгу профессора П.Т.Приходько "Пути в науку. Беседы по организации труда начинающих исследователей", (М., Знание, 1973г.), "Щ-400" - монографию А.И.Щербакова "Социально-экономические проблемы эффективности научного труда" ("Наука", Новосибирск, 1975г.).
Обратим внимание на приведенные примеры. Если вам потребовалось собрать материал о методах организации научного труда (рациональный режим умственной работы, совершенствование памяти и внимания...); об использовании научных результатов в народном хозяйстве, то обратитесь в соответствующую рубрику тематического отдела своего каталога. Там вы легко найдете, в частности, карточки с шифрами П-100 и Щ-400.
Для определения источника по таким шифрам можно не обращаться к шифровальной рубрике, а в алфавитном отделе каталога, если он не очень велик, среди карточек на "П", "Щ" уже бегло по номерам 100 и 400 легко найти нужное. При необходимости вы возьмете карточки с отметками для дальнейшей работы над источниками.
Шифровальная техника позволяет облегчить не только работу с источниками (например, быстрее делать выписки), но и пользование самим каталогом. Шифры своего каталога используют и для того, чтобы иметь возможность, не копируя текстов карточек, ставить их шифровальные "копии" в ряд рубрик (в том случае, когда тот или иной источник должен быть представлен в нескольких рубриках тематического отдела каталога).

Как зашифровать отдельные журнальные и газетные статьи? Шифры журналов и газет регистрируют на карточках отдела "Периодические и продолжающиеся издания". Мы знаем, что ссылки на журнальные и газетные статьи можно делать, используя условные обозначения журналов и газет. Однако отдельные статьи иногда кодируются как самостоятельные источники - по типу книжных шифров, то есть условным номерам, без сокращенного упоминания журнала или газеты. Поясним сказанное примером.
В седьмом номере журнала "Наука и жизнь" за 1980 год на страницах 6-12 помещена статья академика Н.Федоренко "Лоция технического прогресса". Ссылка на статью, например, в вашей выписке может быть дана шифром, скажем, таким - "Ф-19". Легко догадаться, статья обозначается шифром "Ф-19", если же указать и ее объем, то индекс будет выглядеть так: "Ф-19-6-12". В этом случае Можно узнать автора статьи, полное ее название, место, где она напечатана и степень ее проработки вами с помощью каталога и все это без привлечения журнала, подчас не имеющегося под рукой.
Для этой цели нужно будет обратиться прежде всего к шифровальной рубрике вспомогательного отдела своего каталога. Там в группе индексированных буквами карточек с общим цифровым адресом "19" будет найдена карточка с индексом "Ф-19", которая укажет источник, а именно - статью академика Н.Федоренко со всеми выходными данными. Чтобы вспомнить, что именно вы почерпнули из этой статьи, какие ассоциации возникли при ее чтении, вам следует обратиться к карточке этой статьи в соответствующей рубрике тематического отдела ("Комплексная программа научно-технического прогресса"). Если вы сразу не вспомните названия этой рубрики, то ссылка на нее имеется на карточке данной статьи в алфавитном отделе каталога (на фамилию Н.Федоренко).
ЭЛЕМЕНТЫ ТЕХНОЛОГИИ
Для индивидуального применения практично иметь карточки из обычной писчей бумаги. Тонкая бумага обеспечит компактность каталогов и картотек, вдвое-втрое сократит объем, позволит "под копирку" делать нужное число копий (напомним, что в вашей работе могут потребоваться карточки в нескольких экземплярах).
Идентичные карточки разумнее скреплять скобками с помощью сшивателя бумаг. При работе в библиотеке есть смысл пользоваться сфальцованными карточками. Продублировав текст под копирку, вы, кроме основной карточки, тотчас же получите ее "ссылочную" копию. Когда потребуется, сдвоенные карточки разъединяются. Карточки могут постоянно оставаться удлиненными - двойными, тройными... Как же их помещать в каталог? Просто сложить, выдерживая при этом размер обычной стандартной карточки.
Полезно изготовить карточки, специально предназначенные для объединения массивов каталога или их частей. Для этого на карточках делают выступы или, наоборот, вырезы. Если карточка с выступом или с вырезом стоит не в своей группе, это будет заметно. Выступы и вырезы помогают сохранять порядок в ящиках, позволяя быстро помещать ту или иную карточку по этим признакам в их родные рубрики.
Когда во время работы приходится вынимать целиком отдельные рубрики из ящиков каталога, то карточки помещают в специальные держатели, в обложку, в коробки или в конверты.

Если вы постоянно имеете дело с одними и теми же карточками и заинтересованы в их сохранности, то полезно воспользоваться прозрачными чехлами.
Особую роль в каталогах и картотеках играют разделители. Они облегчают расстановку карточек, убыстряют поиск. Сверху на разделителях делают выступы. На выступах буквами отмечают разделы каталога, куда помещаются карточки с общими для них алфавитными признаками. Разделители могут нести и цифровые индексы, скажем, в шифровальной рубрике.
Материалом для разделителей обычно служат плотная бумага или картон. Временные рубрики каталога часто меняют свое название. Для них удобно использовать пластмассовые разделители, матированная поверхность которых позволяет наносить легко стирающиеся надписи.
"Наездники" (рейтеры) - металлические или пластмассовые пластинки с зажимами позволяют обозначать сами карточки, обходясь без разделителей или заменять, таким образом, некоторые разделители. Наездники иногда снабжаются специальными оконцами, в которые можно вставлять написанные на бумаге сведения или признаки. Применяются и пластмассовые пластинки, позволяющие делать карандашные надписи, а в необходимых случаях стирать их. Наездники окрашиваются в яркие цвета, что облегчает поиск карточек. Для сортировки карточек по алфавитному признаку используются сортировочные ящики, полки с ячейками. Ячейки используют для разных целей: с одной стороны пишут, например, буквы алфавита, с другой - порядковые номера для сортировки карточек каталога, имеющих номерные шифры.

Не возникает особых проблем, если, скажем, ваш каталог умещается в одном ящике. Но когда требуется уже несколько ящиков, то полезно использовать специальные блоки, изготавливаемые промышленностью, или хотя бы пластмассовые ящики с крышками (они могут быть установлены один на другой, образуя блоки).
Библиографические карточки из плотной бумаги, а также картонные и пластмассовые, каталожные разделители продаются в магазинах библиотечных коллекторов. Цена 250 карточек - 65коп.
Для карточек можно использовать листки для заметок, которые продаются в магазинах канцелярских товаров. Однако формат этих листков не очень удобен для работы с каталогом.
По просьбе журнала "Наука и жизнь" Московское производственное объединение бумажных изделий "Восход" в настоящее время разрабатывает образцы и вскоре приступит к выпуску карточек для личных каталогов. Набор карточек состоит из 100 и 150 листков тонкой бумаги стандартного размера (75*125мм). Фирме было бы полезно знать, какова потребность в библиографических карточках из тонкой бумаги. Просим сообщать об этом в письмах по адресу: Москва, центр, ул.Кирова, 15, фирме "Восход". На конвертах сделайте условную пометку "Каталог".
Пластмассовые н картонные ящики для каталогов также поступают в магазины библиотечных коллекторов. Если вы используете карточки нестандартных размеров, то картонные коробки нужного размера можно заказывать на переплетно-картонажных фабриках или в мастерских. Приводим эскизы возможных конструкций ящиков.

5/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ВЫПИСКИ
Г.ГЕЦОВ
Работая с книгами, трудно обойтись без выписок. Выписки нужны, чтобы выбирать из книг наиболее существенное, они помогают накопить нужные сведения по тем или иным вопросам, облегчают запоминание. Наконец, они особенно удобны в том случае, когда требуется собрать материал из разных источников на одну тему.
Выписки могут быть дословные (цитаты) и свободные, когда мысли автора излагаются своими словами. Однако в этом случае необходимо приобрести умение кратко и не в ущерб содержанию формулировать мысли. При чтении на страницах, например, с помощью вкладных листков отмечаются те места, которые предполагается выписать.
Выписки полезно делать на карточках. Работать с ними удобно, их легко подобрать и по темам и сформировать по фамилиям авторов. Над каждой выпиской указывается ее тема, под ней - фамилия автора, название книги, год издания, страница с цитатой. Целесообразнее все это делать с помощью шифров.
Но шифры позволяют фиксировать нужные места из литературы и без выписок. В этом случае на карточку заносят шифр источника, а рядом пишут номер страницы и указывают нужные абзацы. Такую "невыписанную выписку" полезно для большей определенности озаглавить. Со временем па карточку может быть перенесен и текст.
Карточки раскладываются по определенным рубрикам картотеки. Разделители с названием рубрик помогают систематизировать имеющийся материал. Рубрикам иногда присваивают определенные номера, ими метят и выписки - это дает возможность использовать для работы любую выписку, не рискуя потерять ее обратный адрес. Выписки можно хранить в ящиках, в конвертах, папках, на которых обозначены темы.
Иногда целесообразно завести указатель будущих выписок по тому или иному источнику. В таких указателях фиксируются нужные номера страниц и абзацев - снизу, сверху или в миллиметровом исчислении.
Приведем пример. Изучая книгу "Горький и советские писатели" (Литературное наследство, т.70, М., АН СССР, 1963г.), литературовед прежде всего сформулировал темы найденных отрывков, сделал пометки на карточках и составил из них указатель, скажем, в виде плоской картотеки. С такой карманной картотекой удобно работать в библиотеке.

Иногда сведения по выпискам заносят не на карточки, а на разделители картотеки, которые в данном случае несут соответствующие тематические признаки.
Еще один способ систематизации - использование тетрадей с пронумерованными страницами, где на специально отведенных полях записывают темы. Каждая выписка сопровождается фамилией автора, названием работы и т.д., подобно тому как это делается на карточках. В тетради отводится место алфавитному указателю тем - своеобразному оглавлению. Делая какую-нибудь выписку, отмечают в указателе ее тему и страницу.
Человек почти молниеносно воспринимает текст книги, быстро, под нужным углом зрения его оценивает, выбирает необходимое. Но вот процесс переписки требует подчас куда больше времени, чем отбор нужного. Как освободиться от этой трудной и неинтересной работы?
Можно прибегнуть к помощи магнитофона. Тексты наговаривают на магнитофон, а затем, воспринимая на слух, перепечатывают на машинке. Это очень ускоряет процесс работы над выписками. Известно, что человек говорит в шесть раз быстрее, чем записывает, а печатать на машинке может в шесть раз быстрее, чем писать рукой.
Существенную помощь оказывают также фотографии и ксерокопии, фоторепродукции из книг можно сделать и самим. Для этого используют стол увеличителя, на штангу закрепляют фотоаппарат (желательно "зеркалку"), чтобы наводка на резкость была сделана возможно точнее. Специальная приставка позволяет использовать другие малоформатные камеры. Можно обойтись и без фотоаппарата, применяя увеличитель, заряженный неэкспонированной пленкой.

Наконец, можно фотографировать вообще и без оптических устройств с помощью рефлексной (прямой или обратимой) фотобумаги. Достаточно такую фотобумагу прижать стеклом к тексту книги, осветить сверху, а затем проявить, чтобы получить изображение. Если приходится снимать "с рук", то в этом случае лучше работать с помощью фотоаппаратов, определяющих экспозицию через объектив.
Уже негативы сами по себе надежные и долговечные носители информации. Их можно просматривать с помощью лупы или проекционной аппаратуры - фотоувеличителей, диапроекторов, некоторых фильмоскопов. Негативы хранят не только в рулончиках, но и в виде отдельных кадров в конвертах, наконец, в бумажных карманах, приклеенных к карточкам с выписками.
И все же удобнее всего в работе отпечатки, которые не требуют для чтения аппаратуры, легко комбинируются, позволяют делать пометки.
Фотокопию можно сделать лишь с нужной части текста, закрыв остальное чистой бумагой. Но лучше фотографировать всю страницу, отметив узкими полосками черной бумаги, положенными на поля, нужные места текста.

Полезно заранее, еще при съемке, пометить негативы. Для этой цели удобно иметь набор из крупных цифр и букв. При репродуцировании в кадр помещают номер страницы, составленный из цифр. Сюда же можно поместить и шифр источника. Этот шифр при съемке соответствующей книги будет постоянным, а номера страниц наборными. Эти символы легко различимы на экране увеличителя и хорошо видны при просмотре негативов.
На готовых фотовыписках полезно проставить полные метки и рассортировать по номерам страниц текста книги и источникам. Отпечатки наклеиваются на отдельные листки писчей бумаги одинакового формата (например, в половину стандартного машинописного листа). С такими одинаковыми листами легче будет работать в дальнейшем.
При ксерографировании ("электрокопировании") страницы с выписками, как правило, снимают полностью. От лишних строк текста в копиях избавляться не стоит. Можно хранить отснятые страницы целиком. Тогда не тратится время на вырезание и наклеивание, поля страниц используют для пометок.
При фото- и электрографировании можно использовать вкладные листки, о которых уже говорилось. Они с необходимыми отметками подкладываются под страницы источников так, чтобы эти отметки были видны сбоку от текста. При увеличении с микропленки номера страниц источника будут четко видны, что позволит до экспонирования записать эти номера на обороте листков фотобумаги.

Электрографические копии текстов, сделанные в масштабе 1:1, полезно наклеивать непосредственно на вкладные листки с отметками. При этом сохраняются ранее сделанные пометки и отчеркивания.
6/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ПЛАНЫ
Г.ГЕЦОВ
Можно без преувеличения утверждать, что чтение обычно сопровождается составлением - в уме или на бумаге - плана, когда определяются опорные логические пункты, отражающие содержание, логику и последовательность изложения. Это способствует более углубленному пониманию прочитанного, выборке нужного материала, его запоминанию и освоению.
Таким образом, план - весьма важное средство организации умственного труда. Примером плана, правда, очень общего, отмечающего лишь узловые разделы, служит обычное оглавление. Просматривая его, без чтения самой книги можно получить представление о ее содержании и схеме построения. План же, как форма записи, более подробно передает содержание, чем оглавление книги.
План - это самая краткая запись. Поэтому его легко переделывать, совершенствуя как по существу, так и по форме, продумывая при этом вновь содержание текста. План в легко обозримой форме отражает последовательность изложения и обобщает его. Эта запись, составляемая в процессе чтения, помогает легче уяснить содержание прочитанного и способствует ускоренной проработке книг и статей. Руководствуясь планом и обратившись к подлиннику, можно составить более подробные и обстоятельные записи - конспекты и тезисы, причем совершенно не обязательно готовить их одновременно с планом. Иногда подробно составленный план может на время заменять такие виды записей.
Если вы готовите какой-либо текст (лекцию, статью, большое деловое письмо и т.д.), то составление плана в процессе этой работы помогает легко и быстро выявлять повторения и непоследовательность и в целом улучшать текст.
И еще одно. План помогает сосредоточиваться при рассеивании внимания и умственном утомлении. Если, например, вы устали н работа над материалом не ладится, идет вяло, то сделайте подробный план к двум-трем страницам текста - это поможет снять утомление и ускорить процесс работы.
Каковы же принципы составления плана? План способствует активизации чтения. Поэтому в отличие от конспектов и тезисов, которые готовятся, как правило, только после полного ознакомления с материалом, пункты плана можно и должно фиксировать немедленно в процессе первоначального чтения. В дальнейшем план может исправляться и уточняться.
Составляя план при чтении, прежде всего стараются определить те места, где кончается одна мысль и начинается другая. Эти места в книге следует отмечать на вкладных листках.
Подзаголовки в книге, деление текста на абзацы облегчают формирование плана. Можно при его составлении (особенно когда план предназначен для подготовки тезисов) не обращать внимания на подзаголовки и абзацы. В этом случае следует стараться оценивать высказывания автора книги по существу и отображать их в плане, причем последовательность пунктов не обязательно должна совпадать с порядком изложения. Поэтому полезно рядом с пунктами плана фиксировать нужные номера страниц источника.
Планы могут быть простыми и сложными. Сложный план в отличие от простого имеет, кроме основных пунктов, еще и подпункты, которые детализируют, разъясняют содержание.
Сложный план не следует составлять в один прием, без черновика. Составляя сложный план, объединяют часть пунктов под одним заголовком или, наоборот, детализируют некоторые пункты, разбивая их на части.
Другими словами, возможны два способа работы: а) составляется подробнейший простой план, а далее он преобразуется в сложный за счет группировки части пунктов под общими заголовками; б) составляется краткий простой план, а затем при повторном чтении формируется сложный план с детализирующими частями. Такой метод приемлем лишь при продолжительной работе над фундаментальными источниками, так как требует много времени.
В общем случае целесообразно составлять подробный план к тексту книги при первом же ее чтении. Такой план легко превратить в сложный, объединяя те или иные пункты. Сам процесс обработки детального простого плана помогает лучше разобраться в содержании: ведь, объединяя, обобщают, а выбрасывая, выделяют главное, фильтруют его в своем сознании. Пункты плана частично или полностью могут текстуально совпадать с отдельными фразами источника. От этого план лишь выигрывает.
Чтобы избежать нерационального переписывания, главные заголовки сложного плана выделяются. Если это сделать нельзя, заголовки выписывают в отдельные графы - слева или справа от текста простого плана. При уплотненной записи заголовки приходится выносить на поля и отсылать стрелкой к нужному месту. Вот почему опытные читатели стараются вести запись планов с большими интервалами между пунктами и с достаточными для дополнений полями.
Запись планов желательно делать так, чтобы ее легко можно было увидеть в целом. Для этого используют один большой лист бумаги или несколько листов, но запись ведут лишь с одной их стороны. Можно сразу увидеть все пункты, раскладывая листки один под другим. При составлении сложного плана полезно отдельно выписать основные его пункты.
Планы накапливают и хранят в отдельных тетрадях, в конвертах, в самом источнике (скажем, на полях газеты или на вкладных листах), в каталоге - на карточках или на листках, сложенных "гармошкой".
Такая форма записи, как план, имеет и свои недостатки. Он, например, не передает фактического содержания, а лишь упоминает о нем и о схеме его расположения. Отсюда вывод: планом можно пользоваться, чтобы оживить в памяти хорошо знакомый текст или воспроизвести в памяти текст вскоре после составления плана.
7/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ТЕЗИСЫ
Г.ГЕЦОВ
"Заключение должно повторить дело трактата и в сокращеньи обнять его снова, чтобы читатель мог повторить самому себе". В этих словах Н.В.Гоголя хорошо передана суть тезисов. Они действительно повторяют, сжато формулируют и заключают прочитанное. Это положения, вбирающие в себя существо значительной части текста, то, что доказывает или опровергает автор, в чем он стремится убедить читателя. В отличие от выписок, содержащих только иллюстративный или фактический материал, тезисы всегда имеют доказательства.
Тезисы, как никакая другая запись, позволяют обобщить изучаемый материал, выразить его суть в кратких формулировках. И если план заставляет читателя неотступно следовать за автором книги, то тезисы дают возможность раскрыть содержание книги, активно разобраться в нем. Процесс их составления позволяет продумать, изучить тот или иной вопрос, используя несколько книг и статей. Важно и то, что ни одна другая форма записи не помогает так хорошо составить доклад, выпукло представляя основную точку зрения автора. Наконец, тезисы ценны, а часто совершенно необходимы для критического анализа книги, статьи или доклада. При их использовании акцентируется, заостряется суть вопроса. Тезисы облегчают возможность противопоставить свои мысли мыслям и убеждениям исследуемых авторов. Обратите внимание - именно убеждениям. Ведь порою автор может незаметно, четко не формулируя, проводить определенную мысль. Цель исследователя - выявить суть суждений и сделать нужные выводы, хотя бы они явно и не были сформулированы автором.
О тезисах говорят в двух смыслах, имея в виду и способ выражения собственных размышлений и способ изложения содержания какого-либо литературного источника. Нас интересует последняя форма записи, для которой возможны три типа.
ОСНОВНЫЕ ТЕЗИСЫ - это принципиально важные, главные положения, обобщающие содержание источника, которые в своей совокупности иногда носят характер главных выводов. Они могут составить отдельную самостоятельную запись, отображающую содержание всего материала при необходимости под тем или иным углом зрения (тематическая запись). Основные тезисы составляются, как правило, по крупным законченным разделам или же целиком по всему произведению, если автор дает вывод в конце книги.
ПРОСТЫЕ тезисы, напротив, удается выделить из многих частей произведения вне зависимости от его общей направленности. Причем это можно сделать уже при первоначальном ознакомлении. Основные тезисы, наоборот, можно успешно составить лишь после уяснения сути всего произведения в целом. К каждому основному тезису может быть составлено несколько простых, разъясняющих тезисов. Если тезисы составляются к сложному плану, то главным пунктам такого плана могут соответствовать основные, подпунктам - простые тезисы.
Таким образом, мы подошли к определению третьего типа. Запись, включающая два вида тезисов (простые и основные), называется СЛОЖНЫМИ тезисами.
Как в сложном плане за основными пунктами следуют подпункты, так и в сложных тезисах за основными будут следовать простые, раскрывая и поясняя их содержание.
Сложные тезисы в сочетании с планом и выписками, иллюстрирующими, раскрывающими детали, могут составить прекрасный конспект.
В самих тезисах не приводятся обосновывающие факты, примеры. Но тезисы сами по себе всегда должны быть обоснованны, доказаны. Поэтому полезно в записи отсылать к обоснованиям, доказательствам, остающимся в проработанной книге или статье. Самобытная форма высказывания, оригинальность авторитетного суждения могут быть сохранены, иначе тезисы рискуют потерять свою документальность, снизится острота восприятия материала.
Часть тезисов может быть записана в виде цитат. Этот метод применяют при подготовке рецензий и аннотаций для сравнения разных точек зрения, а также в тех случаях, когда необходима особая "осторожность в выводах. Но тезисы-цитаты иной раз могут быть очень длинными. Поэтому полезно составлять в дополнение к ним план. Для ускорения подготовки материалов можно пользоваться вкладными листками, шифрами и копиями текстов.
Тезисы, зафиксированные в виде шифров, скажем:
13-11-4в, 13-14-2н (в - строка вверху, н - строка внизу), или отчеркнутые с помощью вкладных листков, не потребуют переписывания. Тогда в необходимых источниках (не только в одном, но и одновременно в нескольких) можно будет открыть нужные места и сравнить положения, отобранные с помощью шифров-цитат или отчеркиваний на вкладных листках.
В противоположность простым тезисам, которые в большинстве случаев могут быть составлены из цитат, основные тезисы чаще всего формулируют самостоятельно. После предварительного ознакомления текст необходимо прочитать вторично. При этом следует разбить его (с помощью плана или без него - отчеркиванием и подчеркиванием) на ряд логически завершенных частей. В этих частях определяют, а затем выписывают главные идеи или временно просто отмечают их с помощью вкладных листков или полосок бумаги. Затем, хорошо продумав выделенное, уяснив его суть, формулируют отдельные положения. Это и будут тезисы.
Умело составленные тезисы вытекают один из другого. Первый, открывающий записи, или последний, завершающий их (наиболее общие в той или иной мере), определяет содержание остальных тезисов или подытоживает все предыдущие. Не исключено, что ряд положений потребуется объединить не в порядке изложения, а в их логической связи, важной для того, кто составляет тезисы. Чтобы не осложнять при этом поиск, полезно связывать тезисы с текстом источника с помощью ссылочных страниц, шифров или вкладных листков, отсылающих к нужному абзацу и даже к отдельным строкам.
Предварительно составленный план оказывает существенную помощь в подготовке тезисов, в частности при совершенствовании формулировок. Его делают не очень подробным. Если подробный план уже есть, его предельно сокращают, исключая второстепенные пункты, отражающие отдельные факты, примеры и т.д.
Но не следует думать, что план остается лишь вспомогательным орудием. Это весьма нужное пособие в дальнейшей работе над тезисом и с помощью тезисов. Его можно использовать для раскрытия тезисов при подготовке лекций, докладов или при повторении пройденного к экзаменам. Вспомогательные пункты плана, которые при составлении тезисов не были приняты во внимание, теперь помогут обосновать, проиллюстрировать тезисы. Все это окажется важным и тогда, когда на их основе потребуется составить конспект.
Тезисы, составленные вчерне, нелишне тщательно сверить с содержанием источника и после этого переписать начисто. Этому поможет подробный план, связанный с текстом источника ссылочными страницами.
В окончательном виде тезисы нумеруют по порядку. Рациональная последовательность позволяет сделать их краткими, избежав повторений. Все это, как правило, ведет к коренной переработке записей, к их совершенствованию, другими словами, к улучшению восприятия материала, его глубокому изучению, анализу и к проверке усвоения пройденного.

[Вы видите на фотографии карточки 125*75мм для индивидуальных домашних каталогов и картотек. Они будут продаваться блоками в футлярах. Это новая продукция Московского производственного объединения бумажных изделий "Восход", разработанная по рекомендации журнала "Наука и жизнь". Объединение "Восход" продолжает разработку новых товаров в помощь читателям, активно работающим с различной литературой. Информация об этих новинках будет публиковаться в журнале].

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Какое отношение "картонки" имеют к "современным информационным технологиям"?
Во-первых, все эти метОды слишком удобны для работы и не всегда очевидны, т.е. их стоит примерить на свой органайзер. Я даже хотел составить списочек удобств и выложить его в виде анкеты, мол, кто чем пользуется. От этого, всяко, должно быть больше проку, чем от обычного перечисления общепринятых способов машинного индексирования.
Во-вторых, слишком много из удачных решений не нашли своего компьютерного воплощения. Причем, это не только те удобства, которые реализовать трудно, но и просто забытые за первоначальной эйфорией "безбумажной информатики".
И, да, чтобы полнее прочувствовать "запах картона", я выкладываю даже те попутные статьи, которые не про "информацию", а про "оч.умелые ручки".
***
9/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
КОНСПЕКТЫ
Г.ГЕЦОВ
Как ни странно, но далеко не каждый знает, что такое конспект. Обычно так называют любую краткую запись. Между тем понятие "конспект" подразумевает объединение плана, выписок, тезисов или по крайней мере двух любых этих форм. Главное требование к конспекту - запись должна быть систематической, логически связной, чтобы ею можно было пользоваться не только составителю, но и другим читателям. По этой же причине к правильно составленному конспекту можно с успехом обратиться через несколько лет после его подготовки. Одним словом, конспект - это наиболее универсальный вид записей по сравнению с другими их формами. При работе с ним меньше риска заблудиться в чужих мыслях, чем при использовании выписок, планов и даже тезисов, не говоря уже о набросках "для себя".
Каковы же особенности составления конспектов? Прежде всего нужно стремиться к форме связного пересказа, но не в ущерб другим, более важным качествам конспекта - ясности и краткости. И тут важно заметить, что связующим звеном при составлении конспекта должна быть внутренняя логика изложения, которую не следует заменять пространными словесными переходами.
С другой стороны, конспекты при своей обязательной краткости содержат не только основные положения и выводы, но и факты, доказательства, примеры. Ведь утверждение, не подкрепленное фактом или примером, не будет убедительным и трудно запоминается.
Поэтому при составлении конспекта записывают отнюдь не только основные положения. Не следует даже избегать повторений, если они по-иному подводят к вопросу или дополнительно, более выразительно освещают его. Это тот "аромат стиля", который помогает глубже разобраться в материале и лучше его запомнить.
На страницах конспекта может быть отражено отношение составителя к самому материалу. Но при этом следует организовать текст таким образом, чтобы, можно было впоследствии легко разобраться, где авторское, а где ваше личное, читательское понимание вопроса.
Конспекты можно условно подразделить на четыре типа: плановые, текстуальные, свободные, тематические.
ПЛАНОВЫЙ КОНСПЕКТ составляется с помощью предварительного плана произведения. Каждому вопросу плана в такой записи отвечает определенная часть конспекта. Но если какой-то пункт плана не требует дополнений и разъяснений, его не следует сопровождать текстом. Это одна из особенностей короткого плана-конспекта, помогающего лучше усвоить материал еще в процессе его изучения. Составление такого конспекта приучает последовательно и четко излагать свои мысли, работать над книгой, обобщая ее содержание в формулировках плана. Краткий, простой, ясный по своей форме план-конспект - незаменимое пособие при необходимости быстро подготовить доклад, выступление.
Однако работать с таким конспектом спустя какое-то время после составления довольно трудно - не всегда легко удается восстановить в памяти содержание источников. Существенную помощь здесь могут оказать вкладные листки или отметки в книге, сделанные в процессе чтения.
Самый простой плановый конспект составляется в виде ответов на пункты плана, выраженные в вопросительной форме. В процессе подготовки, а иногда и при последующей переделке плановый конспект может отразить логическую структуру и взаимосвязь отдельных положений.
ТЕКСТУАЛЬНЫЙ КОНСПЕКТ составляется в основном из цитат. Выписки связываются друг с другом цепью логических переходов. Они могут быть снабжены планом и включать отдельные тезисы в изложении составителя или автора. Текстуальный конспект - прекрасный источник дословных высказываний автора. Он помогает выявить спорные моменты. Особенно целесообразно использовать этот вид конспектирования при изучении материалов для сравнительного анализа положений, высказанных рядом авторов.
Текстуальный конспект в большинстве случаев - пособие, используемое длительное время. Иногда он составляется и как временное пособие для ускоренной проработки произведений. Хотя при его подготовке требуется определенное умение быстро и правильно выбирать основные цитаты, этот тип конспекта не трудно составлять.
Существенный недостаток текстуального конспекта заключается в том, что он недостаточно активизирует внимание и память. Этот недостаток особенно проявляется, если конспект составлен на основе выписок, сделанных давно, а также без глубокой проработки материала, без его усвоения. Поэтому следует вовремя привлекать в помощь ссылочные страницы и вкладные листки.
Текстуальный конспект при последующей его разработке или даже в процессе составления может превратиться в свободный конспект, который представляет собой сочетание выписок, цитат, иногда тезисов. Причем часть текста иногда снабжается планом.
СВОБОДНЫЙ КОНСПЕКТ требует умения самостоятельно четко и кратко формулировать основные положения. Для этого необходимо глубокое осмысление материала, большой и активный запас слов. Само составление такого конспекта успешно развивает эти качества. Свободный конспект, пожалуй, наиболее полноценный, но он достаточно трудоемок.
ТЕМАТИЧЕСКИЙ КОНСПЕКТ дает более или менее исчерпывающий ответ (в зависимости от числа привлеченных источников, в том числе и своих же записей) на поставленный вопрос - тему. Специфика этого конспекта заключается в том, что, разрабатывая определенную тему по ряду источников, он не отображает всего содержания используемых произведений. Составление тематического конспекта помогает всесторонне обдумывать тему, анализировать различные точки зрения на один и тот же вопрос, мобилизовывать свои знания. Собственный рабочий каталог, картотеки, наконец, те же конспекты и другие записи будут способствовать этому.
ОБЗОРНЫЙ ТЕМАТИЧЕСКИЙ КОНСПЕКТ. Это тематический обзор на определенную тему с использованием одного или чаще нескольких источников.
К обзорному тематическому конспекту можно отнести и ХРОНОЛОГИЧЕСКИЙ КОНСПЕКТ. Как говорит само название, основное, чему подчинена запись, это хронологическая последовательность событий на фоне отражения самих событий. В отличие от обзорного конспекта на ту же тему хронологический конспект более краткий.
Конечно, чтобы в полной мере освоить работу над конспектами, первоначально следует овладеть методикой подготовки выписок, затем составлением планов, а в дальнейшем - тезисов. И все же можно не проходить последовательно всей цепочки. В принципе конспекты - эти синтетические записи - помогают использовать в нужном объеме различные формы работы над текстом, подходящие для каждого конкретного случая.
10/81
БЛОК-ПАПКА ДЛЯ ВЫРЕЗОК
А.ПОПОВ, г.Липецк
Рано или поздно в ящиках вашего письменного стола скапливается такое количество вырезок из газет, журнальных статей, старых брошюр, конспектов, что надо принимать решение, что с ними делать дальше. Существует, конечно, радикальный способ - отдать все это в переплет и потом поставить на книжные полки. Но такая возможность имеется не везде и не у всех. Есть другой вариант: сложить вырезки в папки с завязками и убрать в закрытую часть шкафа. В закрытую потому, что эти папки в квартире выглядят не очень красиво. Но, упрятав их туда, вы потеряете эти материалы из вида, что не всегда желательно. Да и жалко бывает роман, который вам нравится и который вы собрали из многих журналов, убирать с глаз долой.
Блок-папка на шесть корешков. 1 - верхняя крышка, 2 - боковые крылья верхние, 3 - боковые крылья нижние, 4 - нижняя крышка, 5 - корешки наружного переплета, 6 - боковые крышки, 7 - передняя стенка.
Между тем существует еще один способ хранения вырезок, который многие, вероятно, найдут для себя приемлемым. Речь идет о специальных блок-папках, представляющих собой складную картонную коробку, в которую вкладывают брошюры или вырезки. Коробку ставят на книжную полку, а чтобы она вписывалась в ряды книг, та ее сторона, которая обращена наружу, оформляется, как книжные корешки. Размеры блок-папки выбираются такими, чтобы в нее вмещались страницы журнала, вырезки из которого вы собираете. В ней можно хранить и целые журналы. За рубежом некоторые издательства изготовляют такого типа папки-футляры типографским способом. Они рассчитаны на годовую подписку журналов. Высылают их подписчикам по заказам.
Изготовить блок-папку нетрудно самому. Для этого необходимо иметь картон, цветную бумагу, однотонную хлопчатобумажную или льняную ткань (можно и бывшую в употреблении). Вместо листового картона годятся старые картонные крышки скоросшивателей, папок и альбомов. Если картон тонкий, его надо склеить в 2-3 слоя.
Конструкция блок-папки складная. Развертка ее приведена на рисунке. На переднюю стенку переплета наклеивают несколько корешков, подобных книжным, на которых проставляют название содержащейся литературы. В верхних и нижних боковых крыльях стальной трубкой с острыми краями пробивают по два отверстия. После сборки отверстия совмещают друг с другом, продевают в них шнур и завязывают. Так фиксируется объемная форма блок-папки. Для прочности в отверстия вставляют металлические пистоны. Если их нет, края оклеивают хлопчатобумажной лентой.
Развертка блок-папки. Развертка блок-папки с закрытой задней стенкой.
Когда блок-папка предназначается для хранения мелких вырезок, изготовлять ее лучше с закрытой задней частью, тогда развертка ее будет иметь несколько иную форму.
Как уже говорилось, размеры блок-папки выбираются в зависимости от размеров издания, которое будет в ней храниться. Большинство литературных журналов имеет формат 165*260мм (таков же формат журнала "Наука и жизнь"). Исходя из этого, ширина верхней и нижней части, а также боковых крыльев (глубина блока) должна быть примерно 170мм, высота боковых крыльев в наложенном друг на друге положении (при совпадении отверстий) - 260мм. Корешки и боковые крышки должны быть на несколько миллиметров выше самого блока.
Пользуясь этими расчетами, из картона вырезают заготовки. В местах перегиба детали соединяются хлопчатобумажной лентой. Чтобы все части легко складывались, стыки должны иметь зазор 1-2мм. Обе поверхности каждой детали оклеивают цветной бумагой. Для верхней крышки блока больше подходит белая или кремовая бумага. Тканевую ленту не следует полностью закрывать бумагой: нужно оставить кант шириной в несколько миллиметров.
Изготовление корешков. 1 - картонная подложка, 2 - облицовочный материал. Для фиксации выпуклости корешков облицовочный материал склеивается внахлест.
Особое внимание уделяется отделке наружной части блок-папки. Для того, чтобы она по внешнему виду была похожа на плотно сложенные книги, каждый корешок изготавливается отдельно. Для корешковой части переплета вырезают две картонные заготовки. Одна (передняя стенка), шириной в нашем примере 260мм, является основой для крепления корешков и всех других элементов. Другая - на 20% длиннее и на 3мм выше. Увеличение длины необходимо для того, чтобы корешки получились выпуклыми. Вторая заготовка разрезается на 6 равных частей. Корешки оклеивают тканью (что предпочтительнее) или цветной бумагой. Можно использовать и другие материалы, например, гранитоль или дерматин.
Для склеивания бумаги, картона и ткани можно использовать конторский казеиновый клей, клей ПВА и столярный. Не следует пользоваться силикатным клеем: от него желтеет бумага. Крайние корешки оклеивают заодно с крышкой переплета. Некоторые корешки можно оклеить материалом другого цвета. Затем на них наносят названия. Это может быть вырезанное с первой страницы название журнала, заголовок романа, графическое изображение серии брошюр, название газеты и т.д. В качестве декоративных элементов можно использовать орнаменты.
Окончательная сборка блок-папки состоит в том, что к передней стенке приклеивают свободные кромки лент от всех остальных деталей, с внутренней стороны наклеивают цветную бумагу, а снаружи темную бумагу или темную ткань. Затем приклеивают корешки, сначала крайние, а потом остальные. Аккуратно изготовленные блок-папки украсят вашу домашнюю библиотеку.
12/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РЕФЕРАТЫ
Г.ГЕЦОВ
Слово "реферат" в переводе с латинского буквально означает "пусть он доложит". Реферат при индивидуальной работе с литературой представляет собой краткую запись идей, содержащихся в одном пли нескольких источниках. Зачастую рефераты готовят для того, чтобы передать эти идеи аудитории.
Реферат требует глубокого изучения первоисточников, умения связывать теоретические положения с условиями современности, проводить глубокие анализы, делать практические выводы, наконец, учит вести дискуссии.
Для этого надо иметь свое собственное твердое мнение на определенную тему, то есть требуется не только хорошо знать материал, но и быть готовым передать его содержание. Рассмотрим частный случай реферата, предназначенного для защиты его идей перед аудиторией.
При подготовке и защите рефератов особенно важно определить четкое предназначение работы, установить задания самому себе. Излагаемое должно быть полностью осознано составителем. Если можно мириться с неясными местами в конспекте, то в реферате этого допускать нельзя. В случае, если неясные места все же остаются, то их преднамеренно выносят на обсуждение. Реферат зачастую - плод коллективного творчества, потому что его идеи нередко формулируются не только автором, но и аудиторией.
Поэтому полезно, чтобы коллектив слушателей и оппоненты были бы заранее подготовленными. Другими словами, к реферату должны готовиться не только референт, но и аудитория и, что особенно важно, готовиться в контакте друг с другом.
Итак, повторим, реферат пишут для себя, чтобы иметь возможность с его помощью осмыслить и передать идеи, мысли, обобщения другим, совместно их обсудить. Реферат может стать пособием для устного выступления с элементами импровизации или же будет дословно зачитан вслух. В последнем случае особое внимание следует обращать на стиль изложения (недаром некоторые рефераты иногда рекомендуют тиражировать, настолько их содержание ясно и понятно). И еще раз подчеркнем, что одна из главных задач реферата - это умение доложить, довести идеи до аудитории. Для совершенствования этого умения в помощь привлекается обширная литература о лекторском мастерстве и ораторском искусстве.
Написать хороший реферат, а тем более эффективно выступить с ним может лишь тот, кто овладел азбукой работы с книгой. Мы надеемся, что изучение цикла статей "Умеете ли вы читать?" вооружит референтов и оппонентов необходимым умением.
Проще организовать подготовку, когда на тему реферата имеется всего несколько источников. Сложнее работать с большим количеством книг и статей. Во всех случаях дело облегчит рационально организованный предварительный просмотр литературы. Во время просмотра нужное фиксируют на карточках своего рабочего каталога, делают отдельные выписки - текстовые или же лишь со ссылкой на источник. При подготовке реферата удобно воспользоваться своими указателями содержания и картотеками выписок. Кстати, вспомним, что не обязательно делать выписки, чтобы ввести их в реферат. Нужные отрывки отмечают закладками (более точно, вкладными листами) и приносят эти книги или журналы на защиту реферата.
В тексте реферата или в плане своего выступления указывают, в какой момент и к каким именно страницам источника следует обратиться. При использовании источников вкладные листки могут информировать не только о поисковых признаках (отчеркиваниях), по также дать и текстовые дополнения, обозначить логические связки. Таким образом, во время выступления можно будет зачитывать тексты из книг, без обращения к самому реферату.
При работе с многочисленными источниками их необходимо регистрировать в собственном рабочем каталоге (хотя бы в процессе быстрого поискового чтения), тогда из каталога легко можно будет почерпнуть нужные сведения. Уже сами рубрики каталога помогут организовать будущий реферат. Переходя от одних карточек и рубрик к другим, вы будете уточнять и расширять содержание реферата.
Если тема вас интересует постоянно, то следует перед составлением реферата заглянуть в личный архив. Особенно помогают в этой работе конспекты. При рациональном ведении архива поиску помогут регистраторы и поисковые алфавитные картотеки. Определенную помощь в ускорении сбора материалов может оказать магнитофон. Когда вы подберете накопленные извлечения из книг и газет, то полезно для полноты картины обратиться к самим первоисточникам. При составлении реферата желательно просматривать новые книги и брошюры, свежие номера журналов и газет, чтобы учесть последние публикации по интересующей теме. Мы уже знаем, как организовать процесс рационального поиска, уметь читать заголовки, бегло знакомиться с отдельными публикациями.
Для облегчения поиска газетных и журнальных публикаций можно воспользоваться услугами специальных служб, которые действуют в столицах республик и в ряде крупных городов страны. В этих службах подбираются вырезки по различным темам из газет и журналов. Вырезки периодически высылаются подписчикам (индивидуальным и коллективным). При подготовке рефератов можно также воспользоваться хранилищами вырезок, которые организованы учреждениями, организациями и отдельными лицами.
2/82
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ОФОРМЛЕНИЕ ЗАПИСЕЙ
Г.ГЕЦОВ
Казалось бы, самое простое - вести свои записи при чтении. Тем не менее существуют определенные приемы для рациональной организации текста таких записей, чтобы лучше усвоить прочитанное, обозначить, заострить логику изложения.
Прежде всего нужно сказать, что планы, выписки, тезисы, а также рефераты удобнее готовить на отдельных листках-карточках, затем их можно соединить скрепкой. Для подготовки. конспекта в большинстве случаев используют тетради.
Записи должны быть убористыми, компактными, чтобы на страницах разместилось как можно больше текста: он становится более обозримым. Записи полезно расчленить разными способами. Интервалы между строками должны быть достаточными для того, чтобы вписывать дополнения. Рекомендуется вести записи только чернилами, а карандашами пользоваться только для отметок и выделений при последующей работе. Наконец, полезно датировать записи.
Выделения и разграничения можно и нужно делать на всех этапах подготовки текста, когда он готовится как самостоятельное пособие, чтобы заменить впоследствии источники, а также когда возникает необходимость вновь обратиться к источнику. Обычно выделяется взаимосвязь положений и частей самого текста, а также связь между текстом и источником.
Отсутствие выделений и разграничений мешает быстро улавливать логические связи при чтении записи. Пока вы пишете конспект или тезисы, логика изложения держится в памяти, но впоследствии может легко ускользнуть, а это заставит снова и снова обращаться к источнику.
Существуют определенные приемы выделений и разграничений текста. АБЗАЦНЫЕ ОТСТУПЫ сигнализируют о переходе к новой микротеме. Полезно использовать "ПРОБЕЛЬНЫЕ СТРОКИ", подобные книжным, отделяющим заголовки и формулы от основного текста. Это способствует удобству чтения записи и организует страницы.
Тезисы, пункты плана или главы следует НУМЕРОВАТЬ. Иногда делают сплошную (сквозную) нумерацию, продолжая ее в нескольких тетрадях или на листах-карточках. Такая сквозная нумерация облегчает ссылки. Номера в отдельных случаях выносят на поля.
Правильно ПОДЧЕРКНУТЬ или ОТЧЕРКНУТЬ - значит найти в тексте главное, нужное, полезное. Это умение приобретается после определенной тренировки. Проявите скупость: иначе подчеркнутым окажется весь текст, что равносильно отсутствию всякого выделения.
Самим подчеркиваниям можно придать особый смысл, например, ввести для себя правило: одно карандашное подчеркивание означает трудное место, требующее выяснения (впоследствии пометка может быть стерта), волнистая черта помечает сомнительные утверждения. Можно не только подчеркивать горизонтально, но и отчеркивать текст вертикально, если, например, надо выделить несколько строк или целый абзац.
Иногда отдельные ключевые слова выносят на поля или выделяют другим цветом, чтобы привлечь к ним внимание. Можно с этой же целью выносить ключевые слова в начало предложения.
Полезно также обозначить важные части текста, проставляя на полях ГОРИЗОНТАЛЬНЫЕ ЧЕРТОЧКИ - вехи, разделяющие текст по смыслу. В РАМКИ обычно заключают символические выражения, формулы, зависимости, реже - законы, правила.
В большинстве случаев в процессе первой записи все выделения лучше делать такими же чернилами, которыми пишется текст. При последующей его проработке новые выделения обозначаются другим цветом. Это существенно, так как, работая непосредственно над записью уже без оригинала, вы можете отойти от источника, делать выводы, основываясь на собственных формулировках.
Все перечисленные способы расчленения текста применяются комбинированно. Любое из выделений в каждом отдельном случае можно усилить. Например, заголовок написать прописными буквами и подчеркнуть, формулы заключить в цветные рамки и пронумеровать.
Но использовать выделения, особенно цветные, надо разумно, не превращая записи в пестрые картинки. Рамки, краски, стрелки не должны отвлекать внимания. Назначение цветных обозначений полезно оговорить на заглавном листе, чтобы со временем не забыть их первоначального смысла.
Полезно также выработать для себя неизменную систему выделений. Уже в школе никто не пишет "треугольник", "угол", "параллельно", "перпендикулярно" а употребляет очевидные значки-символы. Символы можно широко использовать во многих записях с целью их сокращения и более образного, выразительного восприятия.
Иной раз может быть принята временная символика (полезная для определенной работы). Чтобы не спутать свои краткие буквенные обозначения слов, понятий, терминов с обычными буквами, скажем, с предлогами, эти буквенные обозначения можно записывать особым образом. Например, студенты Куйбышевского авиационного института обводят буквы-символы в кружок. Можно класть букву-символ набок или переворачивать.
Для уточнения замечаний, сделанных на полях, удобно пользоваться значками (<, >), символизирующими начало и конец отрывка. Замечания на полях и выделенную часть текста можно связать стрелкой.
В текстах планов, выписок, тезисов и конспектов стрелками полезно фиксировать взаимосвязь положений. Связь же между своею записью и книгой фиксируется с помощью указания номеров страниц прорабатываемого источника на специальных узких вертикальных полях.
Обычно страница тетради или карточка делятся по вертикали на две части. Одна ее треть (например, с левой стороны) отводится для пометок, а остальные две трети становятся рабочей частью, где автор ведет запись. Для полей, где ведутся пометки, следует использовать правую или левую сторону, а не чередовать их, как это, например, делается в школьных тетрадях.
Открывает конспект (тезисы) заглавный лист, на котором указывается лишь название источника и его выходные данные. В начале и в конце тетради полезно оставлять несколько чистых страниц для оглавления и тематических указателей содержания.
9/82
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
НОВОЕ ПОСОБИЕ
Г.ГЕЦОВ
В издательстве "Политическая литература" вышло в свет пособие "Как самостоятельно изучать политическую книгу" (М., 1982, 240стр., тираж 200000экз.).
В книге, подготовленной редакцией журнала ЦК КПСС "Политическое самообразование", даны рекомендации о том, как ориентироваться в общественно-политической литературе, рассказывается о формах и методах индивидуальной работы с нею, культуре чтения, организации личной библиотеки и о других вопросах политического самообразования.
Книга рассчитана на пропагандистов и слушателей системы марксистско-ленинской учебы, на всех самостоятельно изучающих теорию и политику партии.
Наряду со специальными методическими рекомендациями в пособии даются и практические советы по культуре чтения, записи прочитанного, составлению рефератов. Мы знакомим читателей журнала с некоторыми советами.
РЕФЕРАТЫ
Подготовка реферата способствует всестороннему знакомству с литературой по избранной теме, создает возможность комплексно использовать приобретенные навыки работы с книгой, развивает самостоятельность мышления, умение на научной основе анализировать различные явления.
Нередко читатели не отличают запись в виде тематического конспекта от реферата. Поэтому было бы неправильно ограничить работу только объединением положений в нечто целое из разных источников. В подобном случае получится тематический конспект, а не реферат. Правда, для многих читателей, не имеющих серьезных навыков литературной работы, тематический конспект может стать промежуточным звеном в создании реферата, ибо, безусловно, способствует выработке активного, творческого мышления, умения выявлять главные проблемы, строить композиционно сложную, завершенную работу на основе многочисленных источников.
Тематический конспект составляется обычно для того, чтобы глубже изучить определенный вопрос, подготовиться к докладу, лекции или выступлению на семинарском занятии. Такой конспект по своему содержанию приближается к реферату, докладу по избранной теме, особенно в том случае, если включает собственный, пусть маленький вклад читателя в изучение избранной им проблемы. Под таким вкладом понимается не только пересказ изучаемого материала, но и выводы, сделанные и сформулированные читателем самостоятельно. Конспект призван способствовать работе мысли, а не подменять ее.
В отличие от тематического конспекта реферат требует несравненно большей творческой активности, самостоятельности в обобщении изученной литературы, умения логически стройно изложить материал, оценить различные точки зрения на исследуемую проблему, высказать о ней собственное мнение.
Следует не забывать о необходимости особой целеустремленности в работе, об организации активного чтения. Полезнее всего изучать источники под углом зрения уже намеченной проблематики. Это экономит время, будит мысль читателя, позволяет составлять реферат в ходе работы с литературой.
Каждый проработанный источник прибавляет что-то новое к имеющимся у нас знаниям - и именно это новое мы стремимся вычленить, усвоить, зафиксировать - или же вносит серьезную корректировку в сложившуюся у нас систему представлений. Такое активное чтение, усвоение и обработка источников и собственное литературное творчество не могут не привести к некоторым, порой существенным изменениям в плане реферата. Не нужно бояться дополнить его новыми пунктами или отказаться от того или иного пункта, некоторые частные вопросы объединить в более крупные.
Если при изучении литературы главной задачей читателя было расчленение материала, выявление центральных идей, положений, то в период подготовки реферата идет другой процесс - синтез, обобщение положений, примеров, фактов, систематизация того ценного, важного, что мы поняли в результате усвоения темы.
Изученный материал в нашем изложении преобразуется, предстает в новой литературной форме, по-новому группируется, систематизируется. Искусство собственных формулировок, составленных на основе всевозможных выписок, естественно, приходит к человеку, который хорошо усвоил прочитанное, включил новое в общую сумму своих знаний.
КАК ПОЛЬЗОВАТЬСЯ МБА
... Большинство читателей, переступая порог библиотеки, не подозревают о том, что в этот момент они становятся потенциальными абонентами огромной системы источников информации. Особенность современных библиотек - их расширяющееся взаимодействие друг с другом, особенно в области обмена библиографической информацией и межбиблиотечного абонемента.
Порой нужного вам издания в библиотеке не оказывается. Тогда можно через межбиблиотечный абонемент (МБА) получить книгу из другой местной библиотеки или из другого города. Общегосударственная система МБА позволяет читателям библиотеки любого населенного пункта пользоваться в случае необходимости фондами крупнейших научных библиотек.
Но следует учесть некоторые ограничения: 1) художественная и учебная литература высылается только для научной и производственной работы; 2) редкие и особо ценные издания предоставляются только в виде микрофильмов и копий; 3) не высылаются подшивки газет, поэтому по МБА следует заказывать только фотокопии отдельных газетных статей.
Во-первых, все эти метОды слишком удобны для работы и не всегда очевидны, т.е. их стоит примерить на свой органайзер. Я даже хотел составить списочек удобств и выложить его в виде анкеты, мол, кто чем пользуется. От этого, всяко, должно быть больше проку, чем от обычного перечисления общепринятых способов машинного индексирования.
Во-вторых, слишком много из удачных решений не нашли своего компьютерного воплощения. Причем, это не только те удобства, которые реализовать трудно, но и просто забытые за первоначальной эйфорией "безбумажной информатики".
И, да, чтобы полнее прочувствовать "запах картона", я выкладываю даже те попутные статьи, которые не про "информацию", а про "оч.умелые ручки".
***
9/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
КОНСПЕКТЫ
Г.ГЕЦОВ
Как ни странно, но далеко не каждый знает, что такое конспект. Обычно так называют любую краткую запись. Между тем понятие "конспект" подразумевает объединение плана, выписок, тезисов или по крайней мере двух любых этих форм. Главное требование к конспекту - запись должна быть систематической, логически связной, чтобы ею можно было пользоваться не только составителю, но и другим читателям. По этой же причине к правильно составленному конспекту можно с успехом обратиться через несколько лет после его подготовки. Одним словом, конспект - это наиболее универсальный вид записей по сравнению с другими их формами. При работе с ним меньше риска заблудиться в чужих мыслях, чем при использовании выписок, планов и даже тезисов, не говоря уже о набросках "для себя".
Каковы же особенности составления конспектов? Прежде всего нужно стремиться к форме связного пересказа, но не в ущерб другим, более важным качествам конспекта - ясности и краткости. И тут важно заметить, что связующим звеном при составлении конспекта должна быть внутренняя логика изложения, которую не следует заменять пространными словесными переходами.
С другой стороны, конспекты при своей обязательной краткости содержат не только основные положения и выводы, но и факты, доказательства, примеры. Ведь утверждение, не подкрепленное фактом или примером, не будет убедительным и трудно запоминается.
Поэтому при составлении конспекта записывают отнюдь не только основные положения. Не следует даже избегать повторений, если они по-иному подводят к вопросу или дополнительно, более выразительно освещают его. Это тот "аромат стиля", который помогает глубже разобраться в материале и лучше его запомнить.
На страницах конспекта может быть отражено отношение составителя к самому материалу. Но при этом следует организовать текст таким образом, чтобы, можно было впоследствии легко разобраться, где авторское, а где ваше личное, читательское понимание вопроса.
Конспекты можно условно подразделить на четыре типа: плановые, текстуальные, свободные, тематические.
ПЛАНОВЫЙ КОНСПЕКТ составляется с помощью предварительного плана произведения. Каждому вопросу плана в такой записи отвечает определенная часть конспекта. Но если какой-то пункт плана не требует дополнений и разъяснений, его не следует сопровождать текстом. Это одна из особенностей короткого плана-конспекта, помогающего лучше усвоить материал еще в процессе его изучения. Составление такого конспекта приучает последовательно и четко излагать свои мысли, работать над книгой, обобщая ее содержание в формулировках плана. Краткий, простой, ясный по своей форме план-конспект - незаменимое пособие при необходимости быстро подготовить доклад, выступление.
Однако работать с таким конспектом спустя какое-то время после составления довольно трудно - не всегда легко удается восстановить в памяти содержание источников. Существенную помощь здесь могут оказать вкладные листки или отметки в книге, сделанные в процессе чтения.
Самый простой плановый конспект составляется в виде ответов на пункты плана, выраженные в вопросительной форме. В процессе подготовки, а иногда и при последующей переделке плановый конспект может отразить логическую структуру и взаимосвязь отдельных положений.
ТЕКСТУАЛЬНЫЙ КОНСПЕКТ составляется в основном из цитат. Выписки связываются друг с другом цепью логических переходов. Они могут быть снабжены планом и включать отдельные тезисы в изложении составителя или автора. Текстуальный конспект - прекрасный источник дословных высказываний автора. Он помогает выявить спорные моменты. Особенно целесообразно использовать этот вид конспектирования при изучении материалов для сравнительного анализа положений, высказанных рядом авторов.
Текстуальный конспект в большинстве случаев - пособие, используемое длительное время. Иногда он составляется и как временное пособие для ускоренной проработки произведений. Хотя при его подготовке требуется определенное умение быстро и правильно выбирать основные цитаты, этот тип конспекта не трудно составлять.
Существенный недостаток текстуального конспекта заключается в том, что он недостаточно активизирует внимание и память. Этот недостаток особенно проявляется, если конспект составлен на основе выписок, сделанных давно, а также без глубокой проработки материала, без его усвоения. Поэтому следует вовремя привлекать в помощь ссылочные страницы и вкладные листки.
Текстуальный конспект при последующей его разработке или даже в процессе составления может превратиться в свободный конспект, который представляет собой сочетание выписок, цитат, иногда тезисов. Причем часть текста иногда снабжается планом.
СВОБОДНЫЙ КОНСПЕКТ требует умения самостоятельно четко и кратко формулировать основные положения. Для этого необходимо глубокое осмысление материала, большой и активный запас слов. Само составление такого конспекта успешно развивает эти качества. Свободный конспект, пожалуй, наиболее полноценный, но он достаточно трудоемок.
ТЕМАТИЧЕСКИЙ КОНСПЕКТ дает более или менее исчерпывающий ответ (в зависимости от числа привлеченных источников, в том числе и своих же записей) на поставленный вопрос - тему. Специфика этого конспекта заключается в том, что, разрабатывая определенную тему по ряду источников, он не отображает всего содержания используемых произведений. Составление тематического конспекта помогает всесторонне обдумывать тему, анализировать различные точки зрения на один и тот же вопрос, мобилизовывать свои знания. Собственный рабочий каталог, картотеки, наконец, те же конспекты и другие записи будут способствовать этому.
ОБЗОРНЫЙ ТЕМАТИЧЕСКИЙ КОНСПЕКТ. Это тематический обзор на определенную тему с использованием одного или чаще нескольких источников.
К обзорному тематическому конспекту можно отнести и ХРОНОЛОГИЧЕСКИЙ КОНСПЕКТ. Как говорит само название, основное, чему подчинена запись, это хронологическая последовательность событий на фоне отражения самих событий. В отличие от обзорного конспекта на ту же тему хронологический конспект более краткий.
Конечно, чтобы в полной мере освоить работу над конспектами, первоначально следует овладеть методикой подготовки выписок, затем составлением планов, а в дальнейшем - тезисов. И все же можно не проходить последовательно всей цепочки. В принципе конспекты - эти синтетические записи - помогают использовать в нужном объеме различные формы работы над текстом, подходящие для каждого конкретного случая.
10/81
БЛОК-ПАПКА ДЛЯ ВЫРЕЗОК
А.ПОПОВ, г.Липецк
Рано или поздно в ящиках вашего письменного стола скапливается такое количество вырезок из газет, журнальных статей, старых брошюр, конспектов, что надо принимать решение, что с ними делать дальше. Существует, конечно, радикальный способ - отдать все это в переплет и потом поставить на книжные полки. Но такая возможность имеется не везде и не у всех. Есть другой вариант: сложить вырезки в папки с завязками и убрать в закрытую часть шкафа. В закрытую потому, что эти папки в квартире выглядят не очень красиво. Но, упрятав их туда, вы потеряете эти материалы из вида, что не всегда желательно. Да и жалко бывает роман, который вам нравится и который вы собрали из многих журналов, убирать с глаз долой.

Блок-папка на шесть корешков. 1 - верхняя крышка, 2 - боковые крылья верхние, 3 - боковые крылья нижние, 4 - нижняя крышка, 5 - корешки наружного переплета, 6 - боковые крышки, 7 - передняя стенка.
Между тем существует еще один способ хранения вырезок, который многие, вероятно, найдут для себя приемлемым. Речь идет о специальных блок-папках, представляющих собой складную картонную коробку, в которую вкладывают брошюры или вырезки. Коробку ставят на книжную полку, а чтобы она вписывалась в ряды книг, та ее сторона, которая обращена наружу, оформляется, как книжные корешки. Размеры блок-папки выбираются такими, чтобы в нее вмещались страницы журнала, вырезки из которого вы собираете. В ней можно хранить и целые журналы. За рубежом некоторые издательства изготовляют такого типа папки-футляры типографским способом. Они рассчитаны на годовую подписку журналов. Высылают их подписчикам по заказам.
Изготовить блок-папку нетрудно самому. Для этого необходимо иметь картон, цветную бумагу, однотонную хлопчатобумажную или льняную ткань (можно и бывшую в употреблении). Вместо листового картона годятся старые картонные крышки скоросшивателей, папок и альбомов. Если картон тонкий, его надо склеить в 2-3 слоя.
Конструкция блок-папки складная. Развертка ее приведена на рисунке. На переднюю стенку переплета наклеивают несколько корешков, подобных книжным, на которых проставляют название содержащейся литературы. В верхних и нижних боковых крыльях стальной трубкой с острыми краями пробивают по два отверстия. После сборки отверстия совмещают друг с другом, продевают в них шнур и завязывают. Так фиксируется объемная форма блок-папки. Для прочности в отверстия вставляют металлические пистоны. Если их нет, края оклеивают хлопчатобумажной лентой.

Развертка блок-папки. Развертка блок-папки с закрытой задней стенкой.
Когда блок-папка предназначается для хранения мелких вырезок, изготовлять ее лучше с закрытой задней частью, тогда развертка ее будет иметь несколько иную форму.
Как уже говорилось, размеры блок-папки выбираются в зависимости от размеров издания, которое будет в ней храниться. Большинство литературных журналов имеет формат 165*260мм (таков же формат журнала "Наука и жизнь"). Исходя из этого, ширина верхней и нижней части, а также боковых крыльев (глубина блока) должна быть примерно 170мм, высота боковых крыльев в наложенном друг на друге положении (при совпадении отверстий) - 260мм. Корешки и боковые крышки должны быть на несколько миллиметров выше самого блока.
Пользуясь этими расчетами, из картона вырезают заготовки. В местах перегиба детали соединяются хлопчатобумажной лентой. Чтобы все части легко складывались, стыки должны иметь зазор 1-2мм. Обе поверхности каждой детали оклеивают цветной бумагой. Для верхней крышки блока больше подходит белая или кремовая бумага. Тканевую ленту не следует полностью закрывать бумагой: нужно оставить кант шириной в несколько миллиметров.

Изготовление корешков. 1 - картонная подложка, 2 - облицовочный материал. Для фиксации выпуклости корешков облицовочный материал склеивается внахлест.
Особое внимание уделяется отделке наружной части блок-папки. Для того, чтобы она по внешнему виду была похожа на плотно сложенные книги, каждый корешок изготавливается отдельно. Для корешковой части переплета вырезают две картонные заготовки. Одна (передняя стенка), шириной в нашем примере 260мм, является основой для крепления корешков и всех других элементов. Другая - на 20% длиннее и на 3мм выше. Увеличение длины необходимо для того, чтобы корешки получились выпуклыми. Вторая заготовка разрезается на 6 равных частей. Корешки оклеивают тканью (что предпочтительнее) или цветной бумагой. Можно использовать и другие материалы, например, гранитоль или дерматин.
Для склеивания бумаги, картона и ткани можно использовать конторский казеиновый клей, клей ПВА и столярный. Не следует пользоваться силикатным клеем: от него желтеет бумага. Крайние корешки оклеивают заодно с крышкой переплета. Некоторые корешки можно оклеить материалом другого цвета. Затем на них наносят названия. Это может быть вырезанное с первой страницы название журнала, заголовок романа, графическое изображение серии брошюр, название газеты и т.д. В качестве декоративных элементов можно использовать орнаменты.
Окончательная сборка блок-папки состоит в том, что к передней стенке приклеивают свободные кромки лент от всех остальных деталей, с внутренней стороны наклеивают цветную бумагу, а снаружи темную бумагу или темную ткань. Затем приклеивают корешки, сначала крайние, а потом остальные. Аккуратно изготовленные блок-папки украсят вашу домашнюю библиотеку.
12/81
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
РЕФЕРАТЫ
Г.ГЕЦОВ
Слово "реферат" в переводе с латинского буквально означает "пусть он доложит". Реферат при индивидуальной работе с литературой представляет собой краткую запись идей, содержащихся в одном пли нескольких источниках. Зачастую рефераты готовят для того, чтобы передать эти идеи аудитории.
Реферат требует глубокого изучения первоисточников, умения связывать теоретические положения с условиями современности, проводить глубокие анализы, делать практические выводы, наконец, учит вести дискуссии.
Для этого надо иметь свое собственное твердое мнение на определенную тему, то есть требуется не только хорошо знать материал, но и быть готовым передать его содержание. Рассмотрим частный случай реферата, предназначенного для защиты его идей перед аудиторией.
При подготовке и защите рефератов особенно важно определить четкое предназначение работы, установить задания самому себе. Излагаемое должно быть полностью осознано составителем. Если можно мириться с неясными местами в конспекте, то в реферате этого допускать нельзя. В случае, если неясные места все же остаются, то их преднамеренно выносят на обсуждение. Реферат зачастую - плод коллективного творчества, потому что его идеи нередко формулируются не только автором, но и аудиторией.
Поэтому полезно, чтобы коллектив слушателей и оппоненты были бы заранее подготовленными. Другими словами, к реферату должны готовиться не только референт, но и аудитория и, что особенно важно, готовиться в контакте друг с другом.
Итак, повторим, реферат пишут для себя, чтобы иметь возможность с его помощью осмыслить и передать идеи, мысли, обобщения другим, совместно их обсудить. Реферат может стать пособием для устного выступления с элементами импровизации или же будет дословно зачитан вслух. В последнем случае особое внимание следует обращать на стиль изложения (недаром некоторые рефераты иногда рекомендуют тиражировать, настолько их содержание ясно и понятно). И еще раз подчеркнем, что одна из главных задач реферата - это умение доложить, довести идеи до аудитории. Для совершенствования этого умения в помощь привлекается обширная литература о лекторском мастерстве и ораторском искусстве.
Написать хороший реферат, а тем более эффективно выступить с ним может лишь тот, кто овладел азбукой работы с книгой. Мы надеемся, что изучение цикла статей "Умеете ли вы читать?" вооружит референтов и оппонентов необходимым умением.
Проще организовать подготовку, когда на тему реферата имеется всего несколько источников. Сложнее работать с большим количеством книг и статей. Во всех случаях дело облегчит рационально организованный предварительный просмотр литературы. Во время просмотра нужное фиксируют на карточках своего рабочего каталога, делают отдельные выписки - текстовые или же лишь со ссылкой на источник. При подготовке реферата удобно воспользоваться своими указателями содержания и картотеками выписок. Кстати, вспомним, что не обязательно делать выписки, чтобы ввести их в реферат. Нужные отрывки отмечают закладками (более точно, вкладными листами) и приносят эти книги или журналы на защиту реферата.
В тексте реферата или в плане своего выступления указывают, в какой момент и к каким именно страницам источника следует обратиться. При использовании источников вкладные листки могут информировать не только о поисковых признаках (отчеркиваниях), по также дать и текстовые дополнения, обозначить логические связки. Таким образом, во время выступления можно будет зачитывать тексты из книг, без обращения к самому реферату.
При работе с многочисленными источниками их необходимо регистрировать в собственном рабочем каталоге (хотя бы в процессе быстрого поискового чтения), тогда из каталога легко можно будет почерпнуть нужные сведения. Уже сами рубрики каталога помогут организовать будущий реферат. Переходя от одних карточек и рубрик к другим, вы будете уточнять и расширять содержание реферата.
Если тема вас интересует постоянно, то следует перед составлением реферата заглянуть в личный архив. Особенно помогают в этой работе конспекты. При рациональном ведении архива поиску помогут регистраторы и поисковые алфавитные картотеки. Определенную помощь в ускорении сбора материалов может оказать магнитофон. Когда вы подберете накопленные извлечения из книг и газет, то полезно для полноты картины обратиться к самим первоисточникам. При составлении реферата желательно просматривать новые книги и брошюры, свежие номера журналов и газет, чтобы учесть последние публикации по интересующей теме. Мы уже знаем, как организовать процесс рационального поиска, уметь читать заголовки, бегло знакомиться с отдельными публикациями.
Для облегчения поиска газетных и журнальных публикаций можно воспользоваться услугами специальных служб, которые действуют в столицах республик и в ряде крупных городов страны. В этих службах подбираются вырезки по различным темам из газет и журналов. Вырезки периодически высылаются подписчикам (индивидуальным и коллективным). При подготовке рефератов можно также воспользоваться хранилищами вырезок, которые организованы учреждениями, организациями и отдельными лицами.
2/82
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
ОФОРМЛЕНИЕ ЗАПИСЕЙ
Г.ГЕЦОВ
Казалось бы, самое простое - вести свои записи при чтении. Тем не менее существуют определенные приемы для рациональной организации текста таких записей, чтобы лучше усвоить прочитанное, обозначить, заострить логику изложения.
Прежде всего нужно сказать, что планы, выписки, тезисы, а также рефераты удобнее готовить на отдельных листках-карточках, затем их можно соединить скрепкой. Для подготовки. конспекта в большинстве случаев используют тетради.
Записи должны быть убористыми, компактными, чтобы на страницах разместилось как можно больше текста: он становится более обозримым. Записи полезно расчленить разными способами. Интервалы между строками должны быть достаточными для того, чтобы вписывать дополнения. Рекомендуется вести записи только чернилами, а карандашами пользоваться только для отметок и выделений при последующей работе. Наконец, полезно датировать записи.
Выделения и разграничения можно и нужно делать на всех этапах подготовки текста, когда он готовится как самостоятельное пособие, чтобы заменить впоследствии источники, а также когда возникает необходимость вновь обратиться к источнику. Обычно выделяется взаимосвязь положений и частей самого текста, а также связь между текстом и источником.
Отсутствие выделений и разграничений мешает быстро улавливать логические связи при чтении записи. Пока вы пишете конспект или тезисы, логика изложения держится в памяти, но впоследствии может легко ускользнуть, а это заставит снова и снова обращаться к источнику.
Существуют определенные приемы выделений и разграничений текста. АБЗАЦНЫЕ ОТСТУПЫ сигнализируют о переходе к новой микротеме. Полезно использовать "ПРОБЕЛЬНЫЕ СТРОКИ", подобные книжным, отделяющим заголовки и формулы от основного текста. Это способствует удобству чтения записи и организует страницы.
Тезисы, пункты плана или главы следует НУМЕРОВАТЬ. Иногда делают сплошную (сквозную) нумерацию, продолжая ее в нескольких тетрадях или на листах-карточках. Такая сквозная нумерация облегчает ссылки. Номера в отдельных случаях выносят на поля.
Правильно ПОДЧЕРКНУТЬ или ОТЧЕРКНУТЬ - значит найти в тексте главное, нужное, полезное. Это умение приобретается после определенной тренировки. Проявите скупость: иначе подчеркнутым окажется весь текст, что равносильно отсутствию всякого выделения.
Самим подчеркиваниям можно придать особый смысл, например, ввести для себя правило: одно карандашное подчеркивание означает трудное место, требующее выяснения (впоследствии пометка может быть стерта), волнистая черта помечает сомнительные утверждения. Можно не только подчеркивать горизонтально, но и отчеркивать текст вертикально, если, например, надо выделить несколько строк или целый абзац.
Иногда отдельные ключевые слова выносят на поля или выделяют другим цветом, чтобы привлечь к ним внимание. Можно с этой же целью выносить ключевые слова в начало предложения.
Полезно также обозначить важные части текста, проставляя на полях ГОРИЗОНТАЛЬНЫЕ ЧЕРТОЧКИ - вехи, разделяющие текст по смыслу. В РАМКИ обычно заключают символические выражения, формулы, зависимости, реже - законы, правила.
В большинстве случаев в процессе первой записи все выделения лучше делать такими же чернилами, которыми пишется текст. При последующей его проработке новые выделения обозначаются другим цветом. Это существенно, так как, работая непосредственно над записью уже без оригинала, вы можете отойти от источника, делать выводы, основываясь на собственных формулировках.
Все перечисленные способы расчленения текста применяются комбинированно. Любое из выделений в каждом отдельном случае можно усилить. Например, заголовок написать прописными буквами и подчеркнуть, формулы заключить в цветные рамки и пронумеровать.
Но использовать выделения, особенно цветные, надо разумно, не превращая записи в пестрые картинки. Рамки, краски, стрелки не должны отвлекать внимания. Назначение цветных обозначений полезно оговорить на заглавном листе, чтобы со временем не забыть их первоначального смысла.
Полезно также выработать для себя неизменную систему выделений. Уже в школе никто не пишет "треугольник", "угол", "параллельно", "перпендикулярно" а употребляет очевидные значки-символы. Символы можно широко использовать во многих записях с целью их сокращения и более образного, выразительного восприятия.
Иной раз может быть принята временная символика (полезная для определенной работы). Чтобы не спутать свои краткие буквенные обозначения слов, понятий, терминов с обычными буквами, скажем, с предлогами, эти буквенные обозначения можно записывать особым образом. Например, студенты Куйбышевского авиационного института обводят буквы-символы в кружок. Можно класть букву-символ набок или переворачивать.
Для уточнения замечаний, сделанных на полях, удобно пользоваться значками (<, >), символизирующими начало и конец отрывка. Замечания на полях и выделенную часть текста можно связать стрелкой.
В текстах планов, выписок, тезисов и конспектов стрелками полезно фиксировать взаимосвязь положений. Связь же между своею записью и книгой фиксируется с помощью указания номеров страниц прорабатываемого источника на специальных узких вертикальных полях.

Обычно страница тетради или карточка делятся по вертикали на две части. Одна ее треть (например, с левой стороны) отводится для пометок, а остальные две трети становятся рабочей частью, где автор ведет запись. Для полей, где ведутся пометки, следует использовать правую или левую сторону, а не чередовать их, как это, например, делается в школьных тетрадях.
Открывает конспект (тезисы) заглавный лист, на котором указывается лишь название источника и его выходные данные. В начале и в конце тетради полезно оставлять несколько чистых страниц для оглавления и тематических указателей содержания.
9/82
УМЕЕТЕ ЛИ ВЫ ЧИТАТЬ?
НОВОЕ ПОСОБИЕ
Г.ГЕЦОВ
В издательстве "Политическая литература" вышло в свет пособие "Как самостоятельно изучать политическую книгу" (М., 1982, 240стр., тираж 200000экз.).
В книге, подготовленной редакцией журнала ЦК КПСС "Политическое самообразование", даны рекомендации о том, как ориентироваться в общественно-политической литературе, рассказывается о формах и методах индивидуальной работы с нею, культуре чтения, организации личной библиотеки и о других вопросах политического самообразования.
Книга рассчитана на пропагандистов и слушателей системы марксистско-ленинской учебы, на всех самостоятельно изучающих теорию и политику партии.
Наряду со специальными методическими рекомендациями в пособии даются и практические советы по культуре чтения, записи прочитанного, составлению рефератов. Мы знакомим читателей журнала с некоторыми советами.
РЕФЕРАТЫ
Подготовка реферата способствует всестороннему знакомству с литературой по избранной теме, создает возможность комплексно использовать приобретенные навыки работы с книгой, развивает самостоятельность мышления, умение на научной основе анализировать различные явления.
Нередко читатели не отличают запись в виде тематического конспекта от реферата. Поэтому было бы неправильно ограничить работу только объединением положений в нечто целое из разных источников. В подобном случае получится тематический конспект, а не реферат. Правда, для многих читателей, не имеющих серьезных навыков литературной работы, тематический конспект может стать промежуточным звеном в создании реферата, ибо, безусловно, способствует выработке активного, творческого мышления, умения выявлять главные проблемы, строить композиционно сложную, завершенную работу на основе многочисленных источников.
Тематический конспект составляется обычно для того, чтобы глубже изучить определенный вопрос, подготовиться к докладу, лекции или выступлению на семинарском занятии. Такой конспект по своему содержанию приближается к реферату, докладу по избранной теме, особенно в том случае, если включает собственный, пусть маленький вклад читателя в изучение избранной им проблемы. Под таким вкладом понимается не только пересказ изучаемого материала, но и выводы, сделанные и сформулированные читателем самостоятельно. Конспект призван способствовать работе мысли, а не подменять ее.
В отличие от тематического конспекта реферат требует несравненно большей творческой активности, самостоятельности в обобщении изученной литературы, умения логически стройно изложить материал, оценить различные точки зрения на исследуемую проблему, высказать о ней собственное мнение.
Следует не забывать о необходимости особой целеустремленности в работе, об организации активного чтения. Полезнее всего изучать источники под углом зрения уже намеченной проблематики. Это экономит время, будит мысль читателя, позволяет составлять реферат в ходе работы с литературой.
Каждый проработанный источник прибавляет что-то новое к имеющимся у нас знаниям - и именно это новое мы стремимся вычленить, усвоить, зафиксировать - или же вносит серьезную корректировку в сложившуюся у нас систему представлений. Такое активное чтение, усвоение и обработка источников и собственное литературное творчество не могут не привести к некоторым, порой существенным изменениям в плане реферата. Не нужно бояться дополнить его новыми пунктами или отказаться от того или иного пункта, некоторые частные вопросы объединить в более крупные.
Если при изучении литературы главной задачей читателя было расчленение материала, выявление центральных идей, положений, то в период подготовки реферата идет другой процесс - синтез, обобщение положений, примеров, фактов, систематизация того ценного, важного, что мы поняли в результате усвоения темы.
Изученный материал в нашем изложении преобразуется, предстает в новой литературной форме, по-новому группируется, систематизируется. Искусство собственных формулировок, составленных на основе всевозможных выписок, естественно, приходит к человеку, который хорошо усвоил прочитанное, включил новое в общую сумму своих знаний.
КАК ПОЛЬЗОВАТЬСЯ МБА
... Большинство читателей, переступая порог библиотеки, не подозревают о том, что в этот момент они становятся потенциальными абонентами огромной системы источников информации. Особенность современных библиотек - их расширяющееся взаимодействие друг с другом, особенно в области обмена библиографической информацией и межбиблиотечного абонемента.
Порой нужного вам издания в библиотеке не оказывается. Тогда можно через межбиблиотечный абонемент (МБА) получить книгу из другой местной библиотеки или из другого города. Общегосударственная система МБА позволяет читателям библиотеки любого населенного пункта пользоваться в случае необходимости фондами крупнейших научных библиотек.
Но следует учесть некоторые ограничения: 1) художественная и учебная литература высылается только для научной и производственной работы; 2) редкие и особо ценные издания предоставляются только в виде микрофильмов и копий; 3) не высылаются подшивки газет, поэтому по МБА следует заказывать только фотокопии отдельных газетных статей.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
10/82
КАК ХРАНИТЬ КНИГИ
Г.ГЕЦОВ
В этом материале говорится о некоторых вариантах книжной мебели, которую можно изготовить своими руками. Мы не приводим подробностей конструирования, рисунки и подписи следует рассматривать как начальный импульс к дальнейшему творчеству.
Полки для папок, коробок, каталожных и картотечных ящиков далеко не обязательно изготавливать целиком из досок. Можно отдать предпочтение решетчатым (деревянным или металлическим) полкам, так как на них меньше задерживается пыль. Интересные конструкции полок легко создаются из проволоки, прутков и трубок.

Стеллажи могут быть выполнены из дерева или металла. Если на стеллаже десять полок толщиной по полтора-два сантиметра, то легко подсчитать, что по объему одну из десяти полок стеллажа занимают не книги, а само дерево. Поэтому полки можно делать решетчатыми и вставлять их одну в другую.
Стеллажи бывают двухсторонними. Книги на них расставляют в два ряда. Доступ
к книгам возможен с двух сторон стеллажа. Такие стеллажи могут делить комнаты на части.
Такая полка, нагруженная книгами, выглядит легко и изящно. Она целиком изготавливается из тонкой (3мм) фанеры. Для того, чтобы фанера не прогибалась под тяжестью книг, ее надо снизу поддержать рейками, которые вставляются в прорези боковых стенок так, чтобы концы реек выходили наружу. Во избежание коробления в фанерных полках делают выступы, которые также вставляются в соответствующие прорези стенок и закрепляются фиксаторами. Собирается и разбирается такая полка моментально. В сложенном виде занимает очень мало места: это всего лишь листы фанеры, несколько реек (или брусочков), крошечные фиксаторы.
Стенки-полки можно собирать из одинаковых секционных ящиков, имеющих отношение высоты к ширине, равное 1:2. Такой модуль дает особое преимущество. Из рисунка видно, каких интересных результатов можно достичь, комбинируя набором таких ящиков.
На декоративных цепях, канатах или шнурах легко соорудить подвесные полки. По их краям иногда с декоративной целью оставляют древесную кору.
В хозяйственных магазинах можно приобрести кронштейны разных типов, которые с успехом используются для сборки книжных полок из досок нужных размеров. Один из кронштейнов мы показываем на рисунке.

Книжные полки, стеллажи и шкафы размещаются в любом уголке квартиры - в углу, вокруг дверного проема или на месте закрытого дверного проема, причем мебель при этом поможет не только рационально использовать помещение, но и украсить его.
Имеется несколько способов упорядочивания книг на полках. Книги, лежащие горизонтально - в стопках, по мере использования сами занимают нужную последовательность. Сверху оказываются те книги, которыми чаще пользовались, то есть самые нужные, внизу - к которым обращались реже. Как видим, в таком положении книги сами себя организуют.
Стопки книг могут быть полезны особенно в тех случаях, когда полка не вся заполнена и книги рассыпаются. Этому помогут и угловые книгодержатели. В отличие от полок, имеющих фиксированное расстояние между стенками, держатели позволяют легко его менять, образуя удобную раздвижную полку.
Книгодержатели довольно просто изготовить: согнуть под прямым углом кусок металла - и держатель готов. Их мастерят также из дерева и пластмасс.
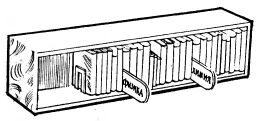
Тематические разделители помогают организовать ряды книг, облегчить поиск нужных тем.
1/84
КАК ПИСАТЬ ОБЗОРЫ
Г.ГЕЦОВ
Издательство "Металлургия" выпустило книгу М.А.Штремеля "Инженер в лаборатории (организация труда)" (М., 1983, 128с.). В книге рассказывается о рациональных приемах работы инженера-исследователя, в том числе о подготовке технического задания, работе с литературой, о выборе и создании методики исследования.
Книга предназначена для молодых инженеров, работающих в различных отраслях промышленности.
Наряду со специальными рекомендациями в книге даются практические советы по поиску источников, чтению и составлению записей, которые будут полезны широкому кругу читателей.
ПЛАН
План, написанный наспех, иногда можно уточнять весь год. Поэтому вряд ли стоит сожалеть о времени, потраченном на составление подобного плана, даже для единично выполняемой поисковой работы. Только обозначив по порядку все действия, можно убедиться, что работа имеет конец, и он достижим за разумное время.
ОБЗОР ЛИТЕРАТУРЫ
Обзор литературы - обязательная часть любого отчета об исследовании. По обзору можно также судить об уровне знаний и общей культуре исследователя (очень плохой признак - обзор, составленный после завершения работы, чтобы сдать отчет). Труд окупается, если обзор помог уяснить необходимость, цель и метод исследования - в начале пути и понять смысл и место собственных результатов в общем ряду - в конце.
Из анализа литературы должно быть видно, что в том или ином вопросе известно вполне достоверно и что сомнительно, спорно. Хороший обзор - это труд не менее сложный, чем оригинальное исследование. Нельзя научиться писать хорошие обзоры, читая инструкцию,- нужен собственный опыт.
Затраты времени на обзор складываются примерно так: выписки из справочников, чтение и конспектирование основных монографий - 3-5 процентов; составление рабочего плана обзора - 1-2; поиск периодики (и составление картотеки) - 5-8; чтение и конспектирование периодики - 30-40; отбор материала из конспектов, его сопоставление и анализ - 20-30; написание обзора - 10-20; правка текста - 10-15; переписка и подготовка рисунков - 5-6 процентов.
ПОИСК ИСТОЧНИКОВ
Приступая к совсем новому для себя вопросу, надо взять из наиболее известных монографий и справочников основные сведения о нем и ссылки на основные статьи. Библиография в книге обрывается за 2-3 года до выхода в свет. Все, что было опубликовано позже, надо искать в периодических изданиях.
Во многих журналах статьи снабжены рефератами. Уяснив по реферату, аннотациям, рисункам, выводам, что работа полезна, ее фиксируют в картотеке. Картотека много удобнее, чем тетрадь для ссылок, потому что карточки легко сортировать, отбирать, сравнивать. На карточке обязательно пишут фамилии и инициалы всех авторов, название журнала, год, том, номер, страницу. Некоторая избыточность информации здесь полезна. Не стоит ограничивать список первыми тремя авторами (как это заведено у библиографов): иногда чтобы судить, одной ли школы эта работа, какого она плана (и качества), надо выделить главу коллектива (или единственного известного мне автора), а он может оказаться по алфавиту пятым...
Нет единого правила, что писать в карточке. Для личной картотеки выгоднее фиксировать не название работы, а суть интересующего результата и метода. Выбрав круг чтения, просматривают хотя бы несколько журналов постоянно, из номера в номер, и заносят в карточки наиболее ценное. Никакие автоматизированные поисковые системы не заменяют личного архива, где материал регистрируется лишь после оценки по надежности, полезности, перспективности.
Закончив просмотр, сортируют карточки и планируют чтение. Читают "с конца к началу": в первую очередь - обзоры и наиболее свежие работы. В начале их обычно говорится о предыдущих работах. Отсюда можно понять, что стоит прочитать. Если сгруппировать карточки по пунктам плана обзора и читать родственные работы в один день, легче их сопоставлять. В прочитанном есть ссылка на другие интересные работы, о которых не знал раньше. Они составят второй круг чтения. Можно надеяться, что основная литература изучена, если "круг ссылок" замкнулся: в новых статьях уже не встречаются новые источники.
СОДЕРЖАНИЕ КОНСПЕКТА
Цель конспектирования не только записать, но и предварительно обработать, проанализировать основные факты и аргументы автора.
Чтобы иметь возможность критически сравнивать работы и отбирать верное, все обоснование выводов фактами должно сохраниться в конспекте. Надо записать не вывод, а его логическую схему со своими замечаниями.
Многие недоразумения и сомнения всплывут при сравнении одной работы с другими. Конспект полезен только тогда, когда по нему можно сличить работы, не перечитывая их целиком.
ТЕХНИКА КОНСПЕКТИРОВАНИЯ
Статью читают целиком, до конца. Изучая для экономии отдельные куски, можно потерять где-нибудь в примечании такую подробность, которая ставит крест на всей работе. Только монографии можно читать выборочно - отдельными главами и параграфами (выяснив общие позиции автора по введению и заключению).
При чтении делают пометки, что выписать. Выписывать что-то сразу, по мере чтения неэкономно (трудно выделить важное, не зная, чем дело кончится, одни и те же мысли повторяются: сначала намеком, потом более стройно). Прочитав и разметив текст, не откладывая, пока вся статья свежа в памяти, готовят конспект.
Выгоднее писать конспект полными словами, приемлемы только сокращенные обозначения терминов, если их одинаково используешь во всех конспектах. Тогда при их чтении быстро схватываешь суть дела, не отвлекаясь на расшифровку своих "иероглифов". Использование конспекта - более напряженная работа, чем его составление, поэтому сокращение слов - дорогая "экономия на спичках".
Пропорции между объемами статьи и конспекта зависят, конечно, от сложности содержания, но в среднем, при некотором опыте, удается сжимать материал в пропорции 1:10. Если интересен только какой-то частный результат или методика, можно конспектировать не всю статью, но прочесть ее нужно целиком.
Обязательно следует записать словами смысл всех буквенных обозначений. То, что само собой разумеется при чтении, со временем забудется.
2/84
КАРАНДАШ? ПЕРО? ДИСПЛЕЙ?
К.БАРЫКИН, заместитель председателя Всесоюзной комиссии по НОТ при Правлении Союза журналистов СССР


Позвольте сразу же напомнить об одном ленинском пожелании: "нормализацию БУМАЖНОЙ работы мы должны выработать, и ее потом применять всюду". Тогда же, а было это осенью 1922 года, Ленин расшифровал понятие "бумажная работа", сказав, что это порядок обмена бумажек, формы, контроль, переписка на машинке, запросы и ответы. Но не только, поэтому следует расширяющее границы темы добавление, "и т.д. и т.п.".
Бумажные потоки с той поры возросли многократно; не на порядок и не на два - на величины заметно большие. Входит в жизнь и в практику так называемая безбумажная информатика, но долго еще бумага останется главным носителем информации, будь то небольшая записка или доклад на научном симпозиуме. Недавно снова мелькнула цифра: ежегодно в стране составляется более 800 миллиардов различных документов. Понятно, они не могут напрочь обойти ваш рабочий стол, вовсе не коснуться его. Да и домашнее бумаготворчество тоже велико: письма либо почтовая открытка, кипы свежих газет, из которых предстоит сделать выписки (или вырезки), рефераты либо курсовые работы, заметки для памяти. На многих письменных столах уже появились рабочие картотеки: небольшие, на 2-2.5 тысячи карточек, но они, эти мини-банки информации, требуют ежедневного внимания.
Стоит и у меня на столе пластмассовый короб для картотеки, сделанный заводом по переработке пластмасс, что в латвийском городе Олайне. Много месяцев шла переписка между Всесоюзной комиссией по НОТ при Правлении Союза журналистов СССР и Министерством химической промышленности - комиссия доказывала надобность картотек, химики не отвергали их полезности, но все тянули, как я теперь понимаю,- надеялись или на забывчивость комиссии, либо на то, что комиссии просто-напросто надоест просить-напоминать. Однако все же начали делать простейшее оборудование: картотечные ящики, ложементы, лотки в три этажа, такие особенно удобны, да и экономят площадь столешницы.
Недавно удалось приобрести по случаю блок картотечных карточек - добротных, из плотной бумаги (хотя не все карточки делаются на уровне; иногда в ход идет даже тетрадная линованная бумага - и это недопустимо!). Такие карточки выпускаются фирмой "Восход" по рекомендации журнала "Наука и жизнь", что и отмечено на упаковке. Увидел эту надпись, порадовался настойчивости коллег из журнала и подумал о том, что хорошо бы в журнале публиковать описания и рисунки различных оргтехнических новшеств. И пусть самые удачные из них войдут в производственные планы предприятии, пусть появятся на прилавках, как произошло с картотечными листочками... Таково пожелание и просьба нашей комиссии по НОТ.
Размеры поверхности стола не безграничны, использовать столешницу следует разумно. И относиться к ней, как хороший рабочий относится к станку, как добросовестный оператор - к пульту управления, как хозяйка - к кухонному столу, если позволите такое сравнение, то есть как к рабочему месту, требующему определенной организации, продуманности, четкости.
Письменный стол - место занятий пишущего, а пишут-то все, это, убежден, "самое массовое занятие". Даже для того, чтобы опровергнуть такое мое утверждение, кому-то придется сесть за письменный стол...
В организации письменного стола есть свои резоны и свои правила. Резоны в том, что работа за таким столом - процесс творческий, жесткой регламентации не поддающийся. Но это вовсе не противоречит определенным правилам. И нужно стремиться к тому, чтобы такая работа не была в тягость, рационализировать ее. Правда, разговор о рационализации начат не сегодня. Крупнейший ученый-экономист Станислав Густавович Струмилин отметил в свое время: "О рационализации, или, как теперь принято говорить, о научной организации труда, у нас теперь довольно много думают и говорят. К сожалению, говорят больше, чем делают".
Понятно, любые заметки по этому поводу можно отнести к категории "разговоры", но тут есть одна существенная разница. Во-первых, хотелось бы, чтобы эти строки стали толчком к действию. Наши фабрики бумажно-беловых товаров, заводы оргтехники и местная промышленность как-то неохотно и неумело решают проблемы выпуска добротного инструментария для тех, кто работает за письменным столом,- от удобного пюпитра и хорошей авторучки до современной пишущей машинки и диктофона. Поэтому мы предполагаем публиковать краткие описания (со схемами и чертежами) разумных и простых оргтехнических поделок - к их массовому выпуску промышленность, мы полагаем, рано или поздно приступит. Второй раздел - идеи и предложения, самые смелые и неожиданные проекты: кто знает, может быть, они тоже послужат делу развития оргтехники. Поэтому присылайте в редакцию разработки и предложения, делитесь замечаниями и идеями, наблюдениями - всем тем, что поможет сделать работу за письменным столом более удобной, комфортной. Отнесем комфорт к рабочим понятиям, ведь комфорт - не помеха деловитости. Письменный стол оказался настолько неразработанным "станком", что изобретателям, рационализаторам, людям с воображением он даст возможность применить и свои знания и свою энергию.
Ведь если к токарному станку или слесарному верстаку отношение однозначное (он должен быть оснащен современным инструментарием, отвечать известной формуле А.К.Гастева: с плохим инструментом не работа, а суета), то к письменному столу мы относимся почти снисходительно, даже с пренебрежением: что это, дескать, за работа, бумажку написать? Вместе с тем есть свод определенных правил, которые при всей их несложности заметно повышают кпд работающего за письменным столом.
Хорошо организованный стол экономит наше время и нашу квалификацию, не распыляя их на мелочи - на поиск вдруг затерявшейся авторучки ("я ищу" - работа в принципе мнимая), на то, чтобы погасить раздражение, возникающее, когда садишься за неудобный, плохо оборудованный стол.
В ГДР, в институте, занимающемся вопросами организации канцелярского труда, который находится в Лейпциге, я не без удивления выяснил, что здесь есть целое направление по проблемам стола ("целое" - не значит многочисленное, два научных сотрудника справляются со всей программой). Из института я и привез доклад экономиста X.-И.Рэ "Функциональный рабочий стол - основной элемент рациональной организации рабочего места". Нет тут возможности и надобности пересказать весь доклад, приведу одну фразу: "Функциональный письменный стол лишь в том случае выполняет свои задачи, если правильно оснащен оргтехникой...". Все новейшие работы по эргономике, по социологии труда, по его разумной организации, все авторитеты отмечают: проблема письменного стола сложнее, чем предполагалось поначалу.

Автопортрет Г.Дж.Уэллса за письменным столом.
1892г.
Впрочем, она ие была бы внове, эта проблема, если бы прислушались к голосу, который слышен уже не первый десяток лет; если бы, не забираясь в эргономические сложности, обратились к писателям, к ученым. И для начала вспомнили бы Марину Цветаеву, сказавшую: "Мой письменный вьючный мул!". Из этой строчки проектант, специалист по оргтехнике мог бы при желании вывести программу работы, которую я назову так: "Письменный стол. Функциональность. Нагрузки. Оснащение инструментарием"...
Мой письменный верный стол!
Спасибо за то, что шел
Со мною по всем путям.
Меня охранял...
Так писала Марина Цветаева...
Алексей Толстой с заметным уважением к предмету рассказал: "Я люблю процесс писания: чисто убранный стол, изящные вещи на нем, изящные и удобные письменные принадлежности, хорошую бумагу. Каждый мастер должен любить орудия своего производства. Цинизм в работе невозможен".
А разве не показателен тот факт, что Олег Константинович Антонов сам разработал конструкцию своего стола? Многие яркие личности не обходили вниманием свое рабочее письменное место.
Хорошо организованный и оснащенный письменный стол платит сторицей: повышением работоспособности, минутами творческого порыва (определишь ли им цену?). Поэтому-то даже большие затраты - внимания и средств - на письменный стол окупаются.
4/84
НАСТОЛЬНАЯ КАРТОТЕКА

Московский второй электромеханический завод начал выпуск настольной картотеки. На вытянутом алюминиевом лотке - карточки, закрепленные на двух металлических шинках. Пластмассовые разделители позволяют быстро найти нужную букву, а форма лотка и откидная ножка под ним обеспечивают устойчивость всего информационного массива на любой карточке: если вы открыли нужное место, не требуется придерживать карточку рукой или вставлять импровизированную закладку, картотека не закроется. Изготовители поставили на каждую букву около двух десятков карточек, но их можно пересортировать по-своему.
Разнообразны возможности нового предмета оргтехники: можно разнести на карточки свою телефонную книжку, зафиксировать сведения о книгах домашней библиотеки, о собрании вырезок из газет и журналов, об экспонатах любой коллекции.
Справедливости ради отметим и некоторые недостатки в целом полезного устройства: картотека будет пылиться на столе, так как футляр для нее не предусмотрен; кроме того, размещение в футляре позволило бы ставить такие комплекты один на другой, экономя место на рабочем столе. Досадно и то, что в картотеке использованы нестандартные библиографические карточки, что делает затруднительным ее пополнение (карточки придется вырезать самому из плотной бумаги). Цена настольной картотеки - 6 рублей.
7/84
БАНК ИНФОРМАЦИИ. ЧТО МОЖЕТ КАРТОТЕКА
В.ЛАВРЕНТЬЕВ (г.Арзамас).
Системно хранить и вести оперативный поиск различных записей, выписок и вырезок можно с помощью личной информационной картотеки (банка информации). Вот один из ее вариантов.
Картотека представляет собой несколько десятков ячеек, например, сорок. Эти ячейки объединены в секции: календарную (дни, недели и месяцы года), тематическую и алфавитную.

Картотека размещается в картонном или деревянном ящике (размеры 420*160*80мм). Внутреннее пространство делится на ячейки. Для этого можно использовать перегородки из органического стекла. Переменные темы (в данном случае - ячейки 10-13) фиксируются на карточке. Она находится в кармашке из прозрачного оргстекла на лицевой стороне ящика.
Календарные ячейки представляют собой, по сути дела, настольный перекидной календарь, но они удобнее тем, что позволяют оперативно просматривать необходимую информацию. Помещая карточки в соответствующие ячейки, мы тем самым планируем работу на текущий день или на любой день недели или на месяц и т.д. В случае невыполнения работы или переноса ее срока соответствующая карточка перекладывается в ячейку другого дня или месяца. Ячейку "Текущий день" лучше заполнять накануне вечером или утром того же дня.
Карточки с записями срочных и важных дел рекомендуем ставить в ячейки вертикально, чтобы они сами сигнализировали о своей первоочередности.
Тематическая секция используется для хранения карточек с записями и вырезок по вопросам, охватывающим круг ваших интересов или служебных обязанностей. Например, моя домашняя картотека содержит 13 тематических ячеек, из которых 9 отведено для постоянной тематики, составляющей круг основных интересов, а 5 ячеек - для переменных тем, над которыми требуется работать лишь определенное время.
Когда по какому-то конкретному вопросу накапливается достаточный объем информации, карточки с записями и вырезки перекладываются в специальную папку, а ячейка картотеки освобождается для новых оперативных записей по той же или другой теме.
Алфавитная секция в основном используется для записи адресов, телефонов, а также для накопления другой информации, поиск которой наиболее удобен в алфавитном порядке. Чтобы ограничить размеры секции, рекомендуем на каждую ее ячейку отнести несколько букв.
Подобная картотека позволяет активно работать с информацией, подбирать, располагать и сосредоточивать необходимую информацию из разных ячеек по тематическому, алфавитному или временному (сроки исполнения) признакам.
Кстати, картотека такого рода может стать большим подспорьем и при решении различных производственных вопросов. Так, при поручении или получении какого-то задания оно фиксируется на карточке, которая закладывается в календарную ячейку соответственно срокам выполнения. Содержание задания или темы можно поместить в тематическую ячейку. А карточки, на которых фиксируются мнения, решения и другая информация по содержанию и способам выполнения задания, закладываются в соответствующие тематические ячейки. Таким образом, по каждой теме накапливается информация, необходимая и для планирования и для выполнения работы.
Картотека благодаря своей универсальности значительно облегчает творческую и рутинную работу, помогает памяти, а также экономит огромное количество времени. Даже само наличие картотеки стимулирует процесс работы.
Правда, чтобы добиться этого, нужно обязательно выполнить два условия. Прежде всего следует так "запрограммировать" картотеку (продумать содержание и расположение ячеек информации), чтобы ее емкость, "ввод" и "вывод" информации полностью отвечали вашим потребностям и занимали минимум времени на поиск того, что нужно. И еще необходимо соблюдать пунктуальность, точность, аккуратность в ведении картотеки.
Для ведения карточек можно приобрести "Бумагу для заметок" (формат 90*130мм), которая продается в пачках, или же воспользоваться чертежной бумагой (формат 105*148мм). Из одного листа ватмана получается 32 карточки.
1/85
СКОРОСТНОЕ КОНСПЕКТИРОВАНИЕ
Л.ШТЕРНБЕРГ (г.Куйбышев)
Сравним три фрагмента одного и того же конспекта. Первый - это обычная запись. Второй - стенографический текст. Третий - обработанная и подготовленная для восприятия запись.

Теперь представим себе людей в момент конспектирования. Почти не поднимая головы, с бешеной скоростью строчит автор первого варианта: опускаются окончания, иногда целые слова, при этом некогда осознать смысл - процесс записи поглощает все время. Несколько лучше обстоят дела у автора второго варианта: запись отнимает меньше времени, можно осознать смысл того, о чем говорит лектор. А вот у автора третьего варианта ни во время подготовки конспекта, ни тогда, когда придет время им пользоваться, не возникает никаких проблем. Если текст "дан прямоугольный треугольник" звучит три секунды, то на обдумывание, как записать фразу, уходит секунда, еще одна - на изображение треугольника, и секунда остается в резерве.
А теперь произведем эксперимент. Посмотрите на карточку с первым вариантом и скажите, что там написано. Ответ будет готов через несколько секунд - ведь надо прочесть и осознать текст. Тот же текст на второй карточке доступен лишь тому, кто знает стенографию. В этом случае ответ получим не ранее чем через полминуты - ведь запись требуется расшифровать. А вот по третьей карточке ответ получим моментальный: "Теорема Пифагора", потому что видим ие слова, а готовые образы. Кстати, третий вариант и легче запоминается, потому что он уже осмыслен в процессе записи, и, кроме того, зрительные образы (рисунок треугольника) лучше фиксируются в памяти, чем описательный текст.
Итак, как видим, тому, кто использует третий вариант, легче всех записывать, читать, запоминать. Но чтобы конспектировать подобным образом, нужна определенная тренировка. Во-первых, требуется овладеть некоторыми техническими приемами такого конспектирования, а во-вторых, прежде чем записать, надо подумать, как это сделать. Последнее условие соблюсти совсем несложно, не надо забывать, что человек думает примерно в десять раз быстрее, чем пишет, и затраченное время иа осмысление окупается с лихвой.
СЛОВА, СЛОВОСОЧЕТАНИЯ, ТЕРМИНЫ. О КАНТОРЕ И КВАНТОРЕ
Кантор придумал кванторы. Это не каламбур, а исторический факт: немецкий математик Георг Кантор ввел знаки, получившие название кванторов: "перевернутое A" - каждый (всякий), для каждого и "обратное E" - существует.
Эти значки представляют собой перевернутые буквы немецких слов Аllе - все и Existieren - существовать.
Воспользуемся приемом Кантора для часто встречающихся слов. В любом научном тексте неоднократно употребляются слова "рассмотрим" и "получим". Для них введем первые сокращения: "перевернутое Р" или "обратное P" - рассмотрим, "перевернутое П" - получим.
Эти символы легко записать и отличить от букв. А что делать, например, со словом "построим" - буква "П" уже использована? Положим ее набок, на тот или другой.
Какие еще слова можно сократить подобным образом? Это зависит от того, с какими текстами приходится иметь дело: надо только выбрать наиболее часто употребляющиеся понятия и ввести для них сокращения.
В отличие от стенографии, которая использует общие (одинаковые для всех) и универсальные (пригодные для любых текстов) методы скоростной записи, предлагаемый способ индивидуален и специализирован. Даются только идеи, на основе которых каждый может самостоятельно создать самостоятельную систему записи, в соответствии с особенностями тех текстов, с которыми ему приходится иметь дело, с учетом своего вкуса и даже почерка. Подобная специализация позволит вести записи быстрее, чем при стенографировании. Приводимые примеры относятся к области математики и техники программирования, тем не менее любой читатель, не знакомый с этими областями, сможет понять примеры.
БУКВА В "ОБЕРТКЕ"
На клавиатуре подсоединенных к ЭВМ пишущих машинок в нижнем ряду справа есть символ @ - так называемое "коммерческое at". Используем эту идею: "обернем" линией, не отрывая пера от бумаги, первую букву наиболее часто употребляемого термина. В программировании наиболее часто употребляемый термин "идентификатор" - вот его и сократим до (и).
Обратите внимание: пишется быстрее, чем произносится, и ни с чем не спутаешь. Но как поступить, если несколько слов начинаются с одной и той же буквы? В этом случае можно использовать большие и малые буквы, скажем, (А) - алгоритм, @ - анализ.
Можно брать группу начальных букв: (инф) - информация. Наконец, поможет и латинский алфавит: (p) - реакция, (s) - раствор (от англ. или франц. solution).
Подобные сокращения воспринимаются легче, чем, скажем, "р-р", ибо из каждой минуты чтения 58 секунд уходит на считывание промежутков между символами.
ВОСПОЛЬЗУЕМСЯ ИЕРОГЛИФАМИ
Иероглифами мы пользуемся давно, особенно в математических текстах, только не замечаем этого. Запись "а+б" читается "а плюс б". Крестик здесь - самый настоящий иероглиф. Математики договорились обозначать им сложение и читать "плюс".
Изобретите себе несколько иероглифов, чтобы их можно было легко писать, желательно без изломов линий, и отличать от букв. Например: "L готическое" - может означать все, что вам будет угодно (его можно, скажем, использовать для сокращения слова "удовлетворяет"). Вот еще несколько удобных иероглифов: "молния вверх" - противоречие, "ломаная стрелка вверх" - "пусть противное", / - "такой что".
Последний подсказан обычным математическим текстом: A={х/х...}, который читается: "А есть множество иксов, таких, что...".
Вводить иероглифы следует постепенно (так же, впрочем, как и остальные сокращения).
КАК ХРАНИТЬ КНИГИ
Г.ГЕЦОВ
В этом материале говорится о некоторых вариантах книжной мебели, которую можно изготовить своими руками. Мы не приводим подробностей конструирования, рисунки и подписи следует рассматривать как начальный импульс к дальнейшему творчеству.

Полки для папок, коробок, каталожных и картотечных ящиков далеко не обязательно изготавливать целиком из досок. Можно отдать предпочтение решетчатым (деревянным или металлическим) полкам, так как на них меньше задерживается пыль. Интересные конструкции полок легко создаются из проволоки, прутков и трубок.

Стеллажи могут быть выполнены из дерева или металла. Если на стеллаже десять полок толщиной по полтора-два сантиметра, то легко подсчитать, что по объему одну из десяти полок стеллажа занимают не книги, а само дерево. Поэтому полки можно делать решетчатыми и вставлять их одну в другую.
Стеллажи бывают двухсторонними. Книги на них расставляют в два ряда. Доступ
к книгам возможен с двух сторон стеллажа. Такие стеллажи могут делить комнаты на части.

Такая полка, нагруженная книгами, выглядит легко и изящно. Она целиком изготавливается из тонкой (3мм) фанеры. Для того, чтобы фанера не прогибалась под тяжестью книг, ее надо снизу поддержать рейками, которые вставляются в прорези боковых стенок так, чтобы концы реек выходили наружу. Во избежание коробления в фанерных полках делают выступы, которые также вставляются в соответствующие прорези стенок и закрепляются фиксаторами. Собирается и разбирается такая полка моментально. В сложенном виде занимает очень мало места: это всего лишь листы фанеры, несколько реек (или брусочков), крошечные фиксаторы.

Стенки-полки можно собирать из одинаковых секционных ящиков, имеющих отношение высоты к ширине, равное 1:2. Такой модуль дает особое преимущество. Из рисунка видно, каких интересных результатов можно достичь, комбинируя набором таких ящиков.

На декоративных цепях, канатах или шнурах легко соорудить подвесные полки. По их краям иногда с декоративной целью оставляют древесную кору.

В хозяйственных магазинах можно приобрести кронштейны разных типов, которые с успехом используются для сборки книжных полок из досок нужных размеров. Один из кронштейнов мы показываем на рисунке.


Книжные полки, стеллажи и шкафы размещаются в любом уголке квартиры - в углу, вокруг дверного проема или на месте закрытого дверного проема, причем мебель при этом поможет не только рационально использовать помещение, но и украсить его.

Имеется несколько способов упорядочивания книг на полках. Книги, лежащие горизонтально - в стопках, по мере использования сами занимают нужную последовательность. Сверху оказываются те книги, которыми чаще пользовались, то есть самые нужные, внизу - к которым обращались реже. Как видим, в таком положении книги сами себя организуют.
Стопки книг могут быть полезны особенно в тех случаях, когда полка не вся заполнена и книги рассыпаются. Этому помогут и угловые книгодержатели. В отличие от полок, имеющих фиксированное расстояние между стенками, держатели позволяют легко его менять, образуя удобную раздвижную полку.
Книгодержатели довольно просто изготовить: согнуть под прямым углом кусок металла - и держатель готов. Их мастерят также из дерева и пластмасс.

Тематические разделители помогают организовать ряды книг, облегчить поиск нужных тем.
1/84
КАК ПИСАТЬ ОБЗОРЫ
Г.ГЕЦОВ
Издательство "Металлургия" выпустило книгу М.А.Штремеля "Инженер в лаборатории (организация труда)" (М., 1983, 128с.). В книге рассказывается о рациональных приемах работы инженера-исследователя, в том числе о подготовке технического задания, работе с литературой, о выборе и создании методики исследования.
Книга предназначена для молодых инженеров, работающих в различных отраслях промышленности.
Наряду со специальными рекомендациями в книге даются практические советы по поиску источников, чтению и составлению записей, которые будут полезны широкому кругу читателей.
ПЛАН
План, написанный наспех, иногда можно уточнять весь год. Поэтому вряд ли стоит сожалеть о времени, потраченном на составление подобного плана, даже для единично выполняемой поисковой работы. Только обозначив по порядку все действия, можно убедиться, что работа имеет конец, и он достижим за разумное время.
ОБЗОР ЛИТЕРАТУРЫ
Обзор литературы - обязательная часть любого отчета об исследовании. По обзору можно также судить об уровне знаний и общей культуре исследователя (очень плохой признак - обзор, составленный после завершения работы, чтобы сдать отчет). Труд окупается, если обзор помог уяснить необходимость, цель и метод исследования - в начале пути и понять смысл и место собственных результатов в общем ряду - в конце.
Из анализа литературы должно быть видно, что в том или ином вопросе известно вполне достоверно и что сомнительно, спорно. Хороший обзор - это труд не менее сложный, чем оригинальное исследование. Нельзя научиться писать хорошие обзоры, читая инструкцию,- нужен собственный опыт.
Затраты времени на обзор складываются примерно так: выписки из справочников, чтение и конспектирование основных монографий - 3-5 процентов; составление рабочего плана обзора - 1-2; поиск периодики (и составление картотеки) - 5-8; чтение и конспектирование периодики - 30-40; отбор материала из конспектов, его сопоставление и анализ - 20-30; написание обзора - 10-20; правка текста - 10-15; переписка и подготовка рисунков - 5-6 процентов.
ПОИСК ИСТОЧНИКОВ
Приступая к совсем новому для себя вопросу, надо взять из наиболее известных монографий и справочников основные сведения о нем и ссылки на основные статьи. Библиография в книге обрывается за 2-3 года до выхода в свет. Все, что было опубликовано позже, надо искать в периодических изданиях.
Во многих журналах статьи снабжены рефератами. Уяснив по реферату, аннотациям, рисункам, выводам, что работа полезна, ее фиксируют в картотеке. Картотека много удобнее, чем тетрадь для ссылок, потому что карточки легко сортировать, отбирать, сравнивать. На карточке обязательно пишут фамилии и инициалы всех авторов, название журнала, год, том, номер, страницу. Некоторая избыточность информации здесь полезна. Не стоит ограничивать список первыми тремя авторами (как это заведено у библиографов): иногда чтобы судить, одной ли школы эта работа, какого она плана (и качества), надо выделить главу коллектива (или единственного известного мне автора), а он может оказаться по алфавиту пятым...
Нет единого правила, что писать в карточке. Для личной картотеки выгоднее фиксировать не название работы, а суть интересующего результата и метода. Выбрав круг чтения, просматривают хотя бы несколько журналов постоянно, из номера в номер, и заносят в карточки наиболее ценное. Никакие автоматизированные поисковые системы не заменяют личного архива, где материал регистрируется лишь после оценки по надежности, полезности, перспективности.
Закончив просмотр, сортируют карточки и планируют чтение. Читают "с конца к началу": в первую очередь - обзоры и наиболее свежие работы. В начале их обычно говорится о предыдущих работах. Отсюда можно понять, что стоит прочитать. Если сгруппировать карточки по пунктам плана обзора и читать родственные работы в один день, легче их сопоставлять. В прочитанном есть ссылка на другие интересные работы, о которых не знал раньше. Они составят второй круг чтения. Можно надеяться, что основная литература изучена, если "круг ссылок" замкнулся: в новых статьях уже не встречаются новые источники.
СОДЕРЖАНИЕ КОНСПЕКТА
Цель конспектирования не только записать, но и предварительно обработать, проанализировать основные факты и аргументы автора.
Чтобы иметь возможность критически сравнивать работы и отбирать верное, все обоснование выводов фактами должно сохраниться в конспекте. Надо записать не вывод, а его логическую схему со своими замечаниями.
Многие недоразумения и сомнения всплывут при сравнении одной работы с другими. Конспект полезен только тогда, когда по нему можно сличить работы, не перечитывая их целиком.
ТЕХНИКА КОНСПЕКТИРОВАНИЯ
Статью читают целиком, до конца. Изучая для экономии отдельные куски, можно потерять где-нибудь в примечании такую подробность, которая ставит крест на всей работе. Только монографии можно читать выборочно - отдельными главами и параграфами (выяснив общие позиции автора по введению и заключению).
При чтении делают пометки, что выписать. Выписывать что-то сразу, по мере чтения неэкономно (трудно выделить важное, не зная, чем дело кончится, одни и те же мысли повторяются: сначала намеком, потом более стройно). Прочитав и разметив текст, не откладывая, пока вся статья свежа в памяти, готовят конспект.
Выгоднее писать конспект полными словами, приемлемы только сокращенные обозначения терминов, если их одинаково используешь во всех конспектах. Тогда при их чтении быстро схватываешь суть дела, не отвлекаясь на расшифровку своих "иероглифов". Использование конспекта - более напряженная работа, чем его составление, поэтому сокращение слов - дорогая "экономия на спичках".
Пропорции между объемами статьи и конспекта зависят, конечно, от сложности содержания, но в среднем, при некотором опыте, удается сжимать материал в пропорции 1:10. Если интересен только какой-то частный результат или методика, можно конспектировать не всю статью, но прочесть ее нужно целиком.
Обязательно следует записать словами смысл всех буквенных обозначений. То, что само собой разумеется при чтении, со временем забудется.
2/84
КАРАНДАШ? ПЕРО? ДИСПЛЕЙ?
К.БАРЫКИН, заместитель председателя Всесоюзной комиссии по НОТ при Правлении Союза журналистов СССР


Позвольте сразу же напомнить об одном ленинском пожелании: "нормализацию БУМАЖНОЙ работы мы должны выработать, и ее потом применять всюду". Тогда же, а было это осенью 1922 года, Ленин расшифровал понятие "бумажная работа", сказав, что это порядок обмена бумажек, формы, контроль, переписка на машинке, запросы и ответы. Но не только, поэтому следует расширяющее границы темы добавление, "и т.д. и т.п.".
Бумажные потоки с той поры возросли многократно; не на порядок и не на два - на величины заметно большие. Входит в жизнь и в практику так называемая безбумажная информатика, но долго еще бумага останется главным носителем информации, будь то небольшая записка или доклад на научном симпозиуме. Недавно снова мелькнула цифра: ежегодно в стране составляется более 800 миллиардов различных документов. Понятно, они не могут напрочь обойти ваш рабочий стол, вовсе не коснуться его. Да и домашнее бумаготворчество тоже велико: письма либо почтовая открытка, кипы свежих газет, из которых предстоит сделать выписки (или вырезки), рефераты либо курсовые работы, заметки для памяти. На многих письменных столах уже появились рабочие картотеки: небольшие, на 2-2.5 тысячи карточек, но они, эти мини-банки информации, требуют ежедневного внимания.
Стоит и у меня на столе пластмассовый короб для картотеки, сделанный заводом по переработке пластмасс, что в латвийском городе Олайне. Много месяцев шла переписка между Всесоюзной комиссией по НОТ при Правлении Союза журналистов СССР и Министерством химической промышленности - комиссия доказывала надобность картотек, химики не отвергали их полезности, но все тянули, как я теперь понимаю,- надеялись или на забывчивость комиссии, либо на то, что комиссии просто-напросто надоест просить-напоминать. Однако все же начали делать простейшее оборудование: картотечные ящики, ложементы, лотки в три этажа, такие особенно удобны, да и экономят площадь столешницы.
Недавно удалось приобрести по случаю блок картотечных карточек - добротных, из плотной бумаги (хотя не все карточки делаются на уровне; иногда в ход идет даже тетрадная линованная бумага - и это недопустимо!). Такие карточки выпускаются фирмой "Восход" по рекомендации журнала "Наука и жизнь", что и отмечено на упаковке. Увидел эту надпись, порадовался настойчивости коллег из журнала и подумал о том, что хорошо бы в журнале публиковать описания и рисунки различных оргтехнических новшеств. И пусть самые удачные из них войдут в производственные планы предприятии, пусть появятся на прилавках, как произошло с картотечными листочками... Таково пожелание и просьба нашей комиссии по НОТ.
Размеры поверхности стола не безграничны, использовать столешницу следует разумно. И относиться к ней, как хороший рабочий относится к станку, как добросовестный оператор - к пульту управления, как хозяйка - к кухонному столу, если позволите такое сравнение, то есть как к рабочему месту, требующему определенной организации, продуманности, четкости.
Письменный стол - место занятий пишущего, а пишут-то все, это, убежден, "самое массовое занятие". Даже для того, чтобы опровергнуть такое мое утверждение, кому-то придется сесть за письменный стол...
В организации письменного стола есть свои резоны и свои правила. Резоны в том, что работа за таким столом - процесс творческий, жесткой регламентации не поддающийся. Но это вовсе не противоречит определенным правилам. И нужно стремиться к тому, чтобы такая работа не была в тягость, рационализировать ее. Правда, разговор о рационализации начат не сегодня. Крупнейший ученый-экономист Станислав Густавович Струмилин отметил в свое время: "О рационализации, или, как теперь принято говорить, о научной организации труда, у нас теперь довольно много думают и говорят. К сожалению, говорят больше, чем делают".
Понятно, любые заметки по этому поводу можно отнести к категории "разговоры", но тут есть одна существенная разница. Во-первых, хотелось бы, чтобы эти строки стали толчком к действию. Наши фабрики бумажно-беловых товаров, заводы оргтехники и местная промышленность как-то неохотно и неумело решают проблемы выпуска добротного инструментария для тех, кто работает за письменным столом,- от удобного пюпитра и хорошей авторучки до современной пишущей машинки и диктофона. Поэтому мы предполагаем публиковать краткие описания (со схемами и чертежами) разумных и простых оргтехнических поделок - к их массовому выпуску промышленность, мы полагаем, рано или поздно приступит. Второй раздел - идеи и предложения, самые смелые и неожиданные проекты: кто знает, может быть, они тоже послужат делу развития оргтехники. Поэтому присылайте в редакцию разработки и предложения, делитесь замечаниями и идеями, наблюдениями - всем тем, что поможет сделать работу за письменным столом более удобной, комфортной. Отнесем комфорт к рабочим понятиям, ведь комфорт - не помеха деловитости. Письменный стол оказался настолько неразработанным "станком", что изобретателям, рационализаторам, людям с воображением он даст возможность применить и свои знания и свою энергию.
Ведь если к токарному станку или слесарному верстаку отношение однозначное (он должен быть оснащен современным инструментарием, отвечать известной формуле А.К.Гастева: с плохим инструментом не работа, а суета), то к письменному столу мы относимся почти снисходительно, даже с пренебрежением: что это, дескать, за работа, бумажку написать? Вместе с тем есть свод определенных правил, которые при всей их несложности заметно повышают кпд работающего за письменным столом.
Хорошо организованный стол экономит наше время и нашу квалификацию, не распыляя их на мелочи - на поиск вдруг затерявшейся авторучки ("я ищу" - работа в принципе мнимая), на то, чтобы погасить раздражение, возникающее, когда садишься за неудобный, плохо оборудованный стол.
В ГДР, в институте, занимающемся вопросами организации канцелярского труда, который находится в Лейпциге, я не без удивления выяснил, что здесь есть целое направление по проблемам стола ("целое" - не значит многочисленное, два научных сотрудника справляются со всей программой). Из института я и привез доклад экономиста X.-И.Рэ "Функциональный рабочий стол - основной элемент рациональной организации рабочего места". Нет тут возможности и надобности пересказать весь доклад, приведу одну фразу: "Функциональный письменный стол лишь в том случае выполняет свои задачи, если правильно оснащен оргтехникой...". Все новейшие работы по эргономике, по социологии труда, по его разумной организации, все авторитеты отмечают: проблема письменного стола сложнее, чем предполагалось поначалу.

Автопортрет Г.Дж.Уэллса за письменным столом.
1892г.
Впрочем, она ие была бы внове, эта проблема, если бы прислушались к голосу, который слышен уже не первый десяток лет; если бы, не забираясь в эргономические сложности, обратились к писателям, к ученым. И для начала вспомнили бы Марину Цветаеву, сказавшую: "Мой письменный вьючный мул!". Из этой строчки проектант, специалист по оргтехнике мог бы при желании вывести программу работы, которую я назову так: "Письменный стол. Функциональность. Нагрузки. Оснащение инструментарием"...
Мой письменный верный стол!
Спасибо за то, что шел
Со мною по всем путям.
Меня охранял...
Так писала Марина Цветаева...
Алексей Толстой с заметным уважением к предмету рассказал: "Я люблю процесс писания: чисто убранный стол, изящные вещи на нем, изящные и удобные письменные принадлежности, хорошую бумагу. Каждый мастер должен любить орудия своего производства. Цинизм в работе невозможен".
А разве не показателен тот факт, что Олег Константинович Антонов сам разработал конструкцию своего стола? Многие яркие личности не обходили вниманием свое рабочее письменное место.
Хорошо организованный и оснащенный письменный стол платит сторицей: повышением работоспособности, минутами творческого порыва (определишь ли им цену?). Поэтому-то даже большие затраты - внимания и средств - на письменный стол окупаются.
4/84
НАСТОЛЬНАЯ КАРТОТЕКА

Московский второй электромеханический завод начал выпуск настольной картотеки. На вытянутом алюминиевом лотке - карточки, закрепленные на двух металлических шинках. Пластмассовые разделители позволяют быстро найти нужную букву, а форма лотка и откидная ножка под ним обеспечивают устойчивость всего информационного массива на любой карточке: если вы открыли нужное место, не требуется придерживать карточку рукой или вставлять импровизированную закладку, картотека не закроется. Изготовители поставили на каждую букву около двух десятков карточек, но их можно пересортировать по-своему.
Разнообразны возможности нового предмета оргтехники: можно разнести на карточки свою телефонную книжку, зафиксировать сведения о книгах домашней библиотеки, о собрании вырезок из газет и журналов, об экспонатах любой коллекции.
Справедливости ради отметим и некоторые недостатки в целом полезного устройства: картотека будет пылиться на столе, так как футляр для нее не предусмотрен; кроме того, размещение в футляре позволило бы ставить такие комплекты один на другой, экономя место на рабочем столе. Досадно и то, что в картотеке использованы нестандартные библиографические карточки, что делает затруднительным ее пополнение (карточки придется вырезать самому из плотной бумаги). Цена настольной картотеки - 6 рублей.
7/84
БАНК ИНФОРМАЦИИ. ЧТО МОЖЕТ КАРТОТЕКА
В.ЛАВРЕНТЬЕВ (г.Арзамас).
Системно хранить и вести оперативный поиск различных записей, выписок и вырезок можно с помощью личной информационной картотеки (банка информации). Вот один из ее вариантов.
Картотека представляет собой несколько десятков ячеек, например, сорок. Эти ячейки объединены в секции: календарную (дни, недели и месяцы года), тематическую и алфавитную.

Картотека размещается в картонном или деревянном ящике (размеры 420*160*80мм). Внутреннее пространство делится на ячейки. Для этого можно использовать перегородки из органического стекла. Переменные темы (в данном случае - ячейки 10-13) фиксируются на карточке. Она находится в кармашке из прозрачного оргстекла на лицевой стороне ящика.
Календарные ячейки представляют собой, по сути дела, настольный перекидной календарь, но они удобнее тем, что позволяют оперативно просматривать необходимую информацию. Помещая карточки в соответствующие ячейки, мы тем самым планируем работу на текущий день или на любой день недели или на месяц и т.д. В случае невыполнения работы или переноса ее срока соответствующая карточка перекладывается в ячейку другого дня или месяца. Ячейку "Текущий день" лучше заполнять накануне вечером или утром того же дня.
Карточки с записями срочных и важных дел рекомендуем ставить в ячейки вертикально, чтобы они сами сигнализировали о своей первоочередности.
Тематическая секция используется для хранения карточек с записями и вырезок по вопросам, охватывающим круг ваших интересов или служебных обязанностей. Например, моя домашняя картотека содержит 13 тематических ячеек, из которых 9 отведено для постоянной тематики, составляющей круг основных интересов, а 5 ячеек - для переменных тем, над которыми требуется работать лишь определенное время.
Когда по какому-то конкретному вопросу накапливается достаточный объем информации, карточки с записями и вырезки перекладываются в специальную папку, а ячейка картотеки освобождается для новых оперативных записей по той же или другой теме.
Алфавитная секция в основном используется для записи адресов, телефонов, а также для накопления другой информации, поиск которой наиболее удобен в алфавитном порядке. Чтобы ограничить размеры секции, рекомендуем на каждую ее ячейку отнести несколько букв.
Подобная картотека позволяет активно работать с информацией, подбирать, располагать и сосредоточивать необходимую информацию из разных ячеек по тематическому, алфавитному или временному (сроки исполнения) признакам.
Кстати, картотека такого рода может стать большим подспорьем и при решении различных производственных вопросов. Так, при поручении или получении какого-то задания оно фиксируется на карточке, которая закладывается в календарную ячейку соответственно срокам выполнения. Содержание задания или темы можно поместить в тематическую ячейку. А карточки, на которых фиксируются мнения, решения и другая информация по содержанию и способам выполнения задания, закладываются в соответствующие тематические ячейки. Таким образом, по каждой теме накапливается информация, необходимая и для планирования и для выполнения работы.
Картотека благодаря своей универсальности значительно облегчает творческую и рутинную работу, помогает памяти, а также экономит огромное количество времени. Даже само наличие картотеки стимулирует процесс работы.
Правда, чтобы добиться этого, нужно обязательно выполнить два условия. Прежде всего следует так "запрограммировать" картотеку (продумать содержание и расположение ячеек информации), чтобы ее емкость, "ввод" и "вывод" информации полностью отвечали вашим потребностям и занимали минимум времени на поиск того, что нужно. И еще необходимо соблюдать пунктуальность, точность, аккуратность в ведении картотеки.
Для ведения карточек можно приобрести "Бумагу для заметок" (формат 90*130мм), которая продается в пачках, или же воспользоваться чертежной бумагой (формат 105*148мм). Из одного листа ватмана получается 32 карточки.
1/85
СКОРОСТНОЕ КОНСПЕКТИРОВАНИЕ
Л.ШТЕРНБЕРГ (г.Куйбышев)
Сравним три фрагмента одного и того же конспекта. Первый - это обычная запись. Второй - стенографический текст. Третий - обработанная и подготовленная для восприятия запись.

Теперь представим себе людей в момент конспектирования. Почти не поднимая головы, с бешеной скоростью строчит автор первого варианта: опускаются окончания, иногда целые слова, при этом некогда осознать смысл - процесс записи поглощает все время. Несколько лучше обстоят дела у автора второго варианта: запись отнимает меньше времени, можно осознать смысл того, о чем говорит лектор. А вот у автора третьего варианта ни во время подготовки конспекта, ни тогда, когда придет время им пользоваться, не возникает никаких проблем. Если текст "дан прямоугольный треугольник" звучит три секунды, то на обдумывание, как записать фразу, уходит секунда, еще одна - на изображение треугольника, и секунда остается в резерве.
А теперь произведем эксперимент. Посмотрите на карточку с первым вариантом и скажите, что там написано. Ответ будет готов через несколько секунд - ведь надо прочесть и осознать текст. Тот же текст на второй карточке доступен лишь тому, кто знает стенографию. В этом случае ответ получим не ранее чем через полминуты - ведь запись требуется расшифровать. А вот по третьей карточке ответ получим моментальный: "Теорема Пифагора", потому что видим ие слова, а готовые образы. Кстати, третий вариант и легче запоминается, потому что он уже осмыслен в процессе записи, и, кроме того, зрительные образы (рисунок треугольника) лучше фиксируются в памяти, чем описательный текст.
Итак, как видим, тому, кто использует третий вариант, легче всех записывать, читать, запоминать. Но чтобы конспектировать подобным образом, нужна определенная тренировка. Во-первых, требуется овладеть некоторыми техническими приемами такого конспектирования, а во-вторых, прежде чем записать, надо подумать, как это сделать. Последнее условие соблюсти совсем несложно, не надо забывать, что человек думает примерно в десять раз быстрее, чем пишет, и затраченное время иа осмысление окупается с лихвой.
СЛОВА, СЛОВОСОЧЕТАНИЯ, ТЕРМИНЫ. О КАНТОРЕ И КВАНТОРЕ
Кантор придумал кванторы. Это не каламбур, а исторический факт: немецкий математик Георг Кантор ввел знаки, получившие название кванторов: "перевернутое A" - каждый (всякий), для каждого и "обратное E" - существует.
Эти значки представляют собой перевернутые буквы немецких слов Аllе - все и Existieren - существовать.
Воспользуемся приемом Кантора для часто встречающихся слов. В любом научном тексте неоднократно употребляются слова "рассмотрим" и "получим". Для них введем первые сокращения: "перевернутое Р" или "обратное P" - рассмотрим, "перевернутое П" - получим.
Эти символы легко записать и отличить от букв. А что делать, например, со словом "построим" - буква "П" уже использована? Положим ее набок, на тот или другой.
Какие еще слова можно сократить подобным образом? Это зависит от того, с какими текстами приходится иметь дело: надо только выбрать наиболее часто употребляющиеся понятия и ввести для них сокращения.
В отличие от стенографии, которая использует общие (одинаковые для всех) и универсальные (пригодные для любых текстов) методы скоростной записи, предлагаемый способ индивидуален и специализирован. Даются только идеи, на основе которых каждый может самостоятельно создать самостоятельную систему записи, в соответствии с особенностями тех текстов, с которыми ему приходится иметь дело, с учетом своего вкуса и даже почерка. Подобная специализация позволит вести записи быстрее, чем при стенографировании. Приводимые примеры относятся к области математики и техники программирования, тем не менее любой читатель, не знакомый с этими областями, сможет понять примеры.
БУКВА В "ОБЕРТКЕ"
На клавиатуре подсоединенных к ЭВМ пишущих машинок в нижнем ряду справа есть символ @ - так называемое "коммерческое at". Используем эту идею: "обернем" линией, не отрывая пера от бумаги, первую букву наиболее часто употребляемого термина. В программировании наиболее часто употребляемый термин "идентификатор" - вот его и сократим до (и).
Обратите внимание: пишется быстрее, чем произносится, и ни с чем не спутаешь. Но как поступить, если несколько слов начинаются с одной и той же буквы? В этом случае можно использовать большие и малые буквы, скажем, (А) - алгоритм, @ - анализ.
Можно брать группу начальных букв: (инф) - информация. Наконец, поможет и латинский алфавит: (p) - реакция, (s) - раствор (от англ. или франц. solution).
Подобные сокращения воспринимаются легче, чем, скажем, "р-р", ибо из каждой минуты чтения 58 секунд уходит на считывание промежутков между символами.
ВОСПОЛЬЗУЕМСЯ ИЕРОГЛИФАМИ
Иероглифами мы пользуемся давно, особенно в математических текстах, только не замечаем этого. Запись "а+б" читается "а плюс б". Крестик здесь - самый настоящий иероглиф. Математики договорились обозначать им сложение и читать "плюс".
Изобретите себе несколько иероглифов, чтобы их можно было легко писать, желательно без изломов линий, и отличать от букв. Например: "L готическое" - может означать все, что вам будет угодно (его можно, скажем, использовать для сокращения слова "удовлетворяет"). Вот еще несколько удобных иероглифов: "молния вверх" - противоречие, "ломаная стрелка вверх" - "пусть противное", / - "такой что".
Последний подсказан обычным математическим текстом: A={х/х...}, который читается: "А есть множество иксов, таких, что...".
Вводить иероглифы следует постепенно (так же, впрочем, как и остальные сокращения).

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
2/85
СКОРОСТНОЕ КОНСПЕКТИРОВАНИЕ
Кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт)
ПОМОГУТ ПИКТОГРАММЫ
Пиктограммы - упрощенные стилизованные рисунки - мы встречаем часто. Это, например, дорожные знаки, разъясняющие, что можно и что нельзя делать на этом месте улицы. Пиктограммы Московской олимпиады говорили без слов об определенном виде спорта.

Пиктограммы можно с успехом использовать и для сокращенной записи. Они отличное средство для запоминания: ведь самая прочная память у человека - зрительная. Пример простейших пиктограмм:

Пример более сложных пиктограмм:

Графики каких-то зависимостей для этих двух типов самолетов можно записать двумя способами. Но первая запись выглядит нейтрально. Вторая же создает образ: самолетик с треугольным крылом "летит" выше. Подобную пиктограмму можно использовать в конспекте.
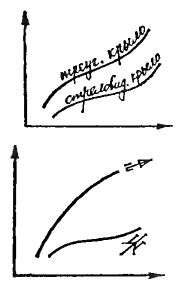
Внизу - первый рисунок представляет собой график скорости самолетов двух типов (в зависимости от какого-то параметра), второй - график скороподъемности (скорость набора высоты), третий - график потолка (максимальной высоты).

Пиктограммы не только ускоряют запись, они заставляют работать зрительную память, дают возможность воспринимать не слова, а образы. А это значительно ускоряет и улучшает восприятие конспекта и запоминание материала.
Придумать точные, выразительные пиктограммы не так-то просто. Но посмотрите вокруг себя. На панели домашнего телевизора вы обнаружите удобные пиктограммы для конспектирования лекций по оптике, акустике, охране труда.
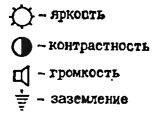
Фрагмент электронной схемы тоже легко "разбирается" на пиктограммы. Вообще различные обозначения на любых схемах почти всегда можно использовать в этом качестве.

Запишем с помощью пиктограмм электронной схемы следующую фразу: "Если на потенциальный вход подать положительный потенциал, то схема вырабатывает импульс, который...". Запись будет выглядеть так:

Наконец, в качестве пиктограммы можно использовать рисунок какого-то предмета, если его проще нарисовать, чем написать название. Химикам предлагаем пиктограммы такого рода.

Оговоримся, что пиктограммой "пробирка" можно пользоваться, если латинская буква "U" в вашем почерке четко отличима от рисунка пробирки. Если же нет, то для сокращения слова "пробирка" надо придумывать что-то другое.
ПРИСТАВКИ, СУФФИКСЫ, ОКОНЧАНИЯ
При конспектировании без приставок обойтись невозможно: они меняют смысл слов. Чаще опускают суффиксы или окончания, которые можно восстановить по контексту. Но иногда после таких сокращений текст превращается в головоломку.
Эти части слов можно добавлять к сокращениям следующим образом:

Можно для записи суффиксов воспользоваться простыми стенографическими обозначениями типовых концовок слов. Например:

Применяются эти "хвостики" как в обычном тексте, так и с разными видами сокращений:

Часто нам нужно не конкретное окончание, а какой-то признак части речи: существительного, глагола, прилагательного. Для таких признаков можно использовать те же стенографические "хвостики", только надо расширить их функции. Например:

СМЕСЬ ЯЗЫКОВ
При конспектировании можно использовать более короткие слова других языков. Прием этот хорошо известен и достаточно распространен. Например, "англоязычные" студенты очень часто пишут if вместо "если" и use вместо "использовать". Интересно, что даже в математических книгах прижилось довольно удачное английское слово-сокращение iff, означающее "тогда и только тогда".
Легкость чтения конспекта с такой смесью, по-видимому, зависит от индивидуальных особенностей восприятия.
КАК ПОЛЬЗОВАТЬСЯ СОКРАЩЕНИЯМИ
Приемы сокращения записи, о которых говорилось выше, чисто технические, они не требуют мыслительной работы и после небольшой тренировки выполняются автоматически. Если полностью освоить эти приемы, то можно достичь примерно двух-, а то и трехкратного ускорения записи. Причем качество ее восприятия не ухудшается, наоборот, даже улучшается.
При использовании сокращений надо выработать собственную систему. Иероглифами злоупотреблять не стоит - этот прием годен только тогда, когда не подходят другие. А вот пиктограммы рекомендуем использовать везде, где только можно; прием дает отличные результаты в процессе самой записи, а также при ее запоминании и чтении.
Опыт показывает, что на различные виды конспектируемых текстов достаточно 50 сокращений всех типов: десяток кванторов, 20 букв "в обертке" и т.д.
Если выбрать 50 сокращений и тут же попытаться их немедленно и полностью использовать, то ничего хорошего не получится. Сокращения следует вводить постепенно: по одному-два в неделю, чтобы без труда к ним привыкнуть.
Создание собственной системы записи требует затрат умственного труда. Если же преподаватель вуза или школьный учитель преподносит готовые сокращения, то обычно одного их показа достаточно для того, чтобы сокращения приняли на вооружение 95 процентов слушателей. Если же преподаватель сам пользуется на доске сокращениями, то их без всякого труда осваивают все слушатели. Кстати, показ конкретных сокращений полезен и тем, что все ученики в классе или студенты на курсе осваивают одинаковую систему записи.
11/85
"ГАРМОШКА" БЕРЕЖЕТ ВРЕМЯ
Миниатюрный еженедельник экспресс-записей для памяти и исполнения.
Ю.ОРЛОВ, преподаватель (г.Ленинград)
Хотелось бы поделиться опытом использования простой и удобной формы записей. Она уже более тридцати лет помогает четко планировать, рационально использовать, а также контролировать выполнение намеченных дел.
Для миниатюрного еженедельника пригоден любой стандартный лист плотной писчей бумаги. Он складывается сначала втрое по длинной стороне, а затем еще раз втрое - по короткой стороне. В результате получается квадратик-гармошка, он легко помещается в кармане пиджака и всегда бывает при себе. В сложенном виде квадратик обладает достаточной жесткостью, это позволяет вести записи даже на ладони.
В сложенной указанным способом заготовке шесть небольших, но довольно вместительных полосок (три - на одной стороне листа и три - на обороте). В верхней части каждой полоски указывается фломастером или цветной авторучкой дата и день недели - от понедельника до пятницы (например: "вторник, 9 февраля"), затем фиксируются дела на каждый день. Оставшаяся свободной шестая полоска предназначается для планов на субботу и воскресенье, а также для накопившихся за неделю хозяйственно-бытовых дел.
Квадратик непременно должен быть сложен таким образом, чтобы на одной стороне всегда была дата сегодняшнего дня, а на обороте - полоска на завтра: это даст возможность иметь под рукой записи первостепенных дел на ближайшее время.
Каждое утро я внимательно просматриваю гармошку, чтобы уяснить, как выполнялись дела вчера. Затем переворачиваю очередную полоску-страничку и корректирую планы на сегодня и на следующие дни.
На полоске каждый день разграничивается благодаря сгибам на три равных отрезка: "утро" (верх полосы), "день" (средняя часть), "вечер" (нижняя часть).
Соответственно распределяются и предстоящие дела.
В понедельник утром анализирую запланированные и выполненные (или невыполненные) дела, оцениваю затраченное время и после этого "конструирую" гармошку на следующую неделю.
Весьма разумно и целесообразно готовить сразу четыре квадратика - на полный месяц по неделям: в этом случае больше возможностей для перспективно-целевого планирования.
Целесообразно завести также папку для хранения отработанных гармошек - пятьдесят две недели-странички полного года займут немного места. Возможность же критически оценить свои действия в течение года часто оказывается весьма необходимой и полезной.
Было бы небезынтересно знать, какими способами записей для памяти вы пользуетесь. Обзор писем и рекомендаций на эту тему надеемся напечатать.
***
Невзирая на обещания, регулярные публикации об организации личного офиса в журнале после 85-го года прекратились. Все силы были брошены на калькуляторно-компьютерный фронт. Попробуем проследить, как и что пытались считать в те времена.
5/83
ЛЕГКОМЫСЛЕННЫЙ ШАХ И "ЭЛЕКТРОНИКА БЗ-34"
Кандидат технических наук Р.ВАССЕЛЬ
Электронные микрокалькуляторы вошли в наш повседневный быт столь же прочно, как электробритва и междугородная телефонная связь, как бег трусцой и кубик Рубина. С помощью этой миниатюрной машинки школьник уверенно рассчитывает путь пешехода из пункта А в пункт В, инженер успешно решает дифференциальные уравнения, а домохозяйка с подлинно научной строгостью оптимизирует домашний бюджет. Как свидетельствует публикуемая здесь статья, микрокалькулятор порою приводит своих приверженцев к задачам, лежащим несколько в стороне от его основных применений, бесполезных на первый взгляд... Но это только на первый взгляд! Такие задачи, изящные, отмеченные смекалкой и юмором, особенно наглядно демонстрируют богатые возможности наших маленьких электронных помощников. Редакция надеется, что подобные заметки найдут плодотворный отклик у читателей журнала.
Вероятно, каждому любителю шахматной игры известна легенда об изобретателе шахмат и восточном владыке, который в порыве щедрости позволил изобретателю просить любую награду за его интересное изобретение. Изобретатель запросил весьма "скромную" плату зерном (очевидно, в те времена хлеб умели ценить): за первую клетку шахматной доски - 1 зернышко, за вторую клетку - 2 зернышка, за третью клетку - 4 зернышка, за четвертую клетку - 8 зернышек... и так далее до 64-й клетки.
Восточный владыка легкомысленно согласился, и напрасно: плата оказалась настолько высокой, что была не по карману даже ему.
Тем, кто знаком с этой историей, известно, что количество зерна исчислялось астрономической цифрой. Ну, а конкретно?.. И решил я заняться подсчетом зерна, причитающегося изобретателю.
В журнале НиЖ 3-4/81 я прочел статью о-микрокалькуляторах и пошел в магазин, ибо счетами в таком деле не обойдешься. Купил микрокалькулятор "Электроника Б3-34", который, как оказалось, может считать по заданной программе.
Математическая постановка задачи была для меня понятна: надо взвесить зернышко пшеницы и умножить на общее количество зерен.
На математическом языке количество зерен, запрошенное изобретателем, выражается формулой:
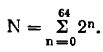
За данными о среднем весе пшеничного зерна я обратился к энциклопедии (БСЭ. 3-е изд., т.21, с.266) и принял его равным
g = 0.04г = 4e-8т
Изучив инструкцию по пользованию микрокалькулятором, приложенную к нему, я иаписал программу вычислений - см. ниже. В правой колонке программы сжато описано содержание каждой операции; ради краткости не отмечается, что при занесении какого-либо числа в регистр "x" его прежнее содержание автоматически пересылается в регистр "y", а результат вычислительной операции заносится в "x". Количество зерен, выраженное формулой, подсчитывается последовательным суммированием слагаемых и накапливается в регистре памяти "5", счетный индекс n хранится в регистре "1" (оба регистра к началу вычислений пусты). Число сложений (64) заранее заносится в регистр "0", вес зерна - в регистр "2".
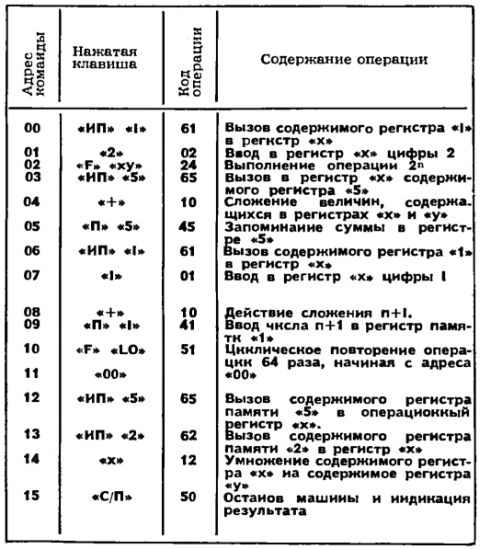
Я человек пунктуальный, поэтому решил зафиксировать время, затраченное на проведение вычислений. Отмечу, что за 6.5 минуты счета машина произвела 772 действия, то есть на каждую команду затратила в среднем 0.505 секунды.
Ввел программу в машину, нажимая соответствующие клавиши; затем нажал клавишу "Пуск" и через 6.5 минуты прочел на индикаторе: 7.378688e11 тонн!
А количество зерен - 1.844672e19 штук!
Ого! Изобретатель умел ценить свой труд и излишней скромностью не страдал. Получилось больше 7.3e11 тонн, или, выражаясь языком современного ядерного века, почти миллион мегатонн! Цифра даже для нас, привыкших слышать о мегатоннах, весьма внушительная.
Этот шутливый расчет, в котором все верно (кроме, может быть, исторического факта), я привел как небольшую иллюстрацию возможностей современных мини-ЭВМ.
Хочется выразить благодарность создателям этой весьма интересной машины и пожелать успехов в ее дальнейшем совершенствовании. В частности, было бы полезным увеличить объем памяти и количество выполняемых команд.
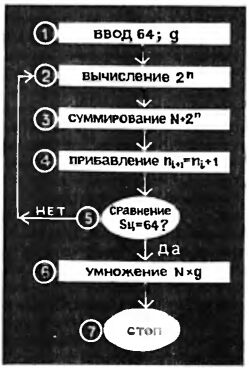
***
Первый блин комом. Ненужные вычисления, дурацкий результат. Неинтересная программа. В чем замануха?
В следующем выпуске это попробовали исправить, добавив околокалькуляторных врезок.
8/83
ЧЕЛОВЕК С МИКРОКАЛЬКУЛЯТОРОМ
Завоевывая все большую популярность, микрокалькуляторы находят все новые применения. Они обосновываются в кабине водителя автобуса и в кабинете театрального администратора, становятся предметом забавных детских игр и хитроумных головоломок для любителей математики, художнику они подсказывают темы для юмористических рисунков, а среди коллекционеров уже появились такие, кто собирает любопытные факты, связанные с миниатюрными компьютерами. Обо всем этом рассказывают письма читателей нашего журнала, легшие в основу публикуемых здесь заметок.
[КСТАТИ...
Шутка, игра вовсе не чужды вычислительной технике - напротив, симпатия к ним написана компьютерам на роду: Чарлз Бэббидж, изобретатель первой автоматической вычислительной машины, намеревался написать исследование о юморе. Видимо, не случайно...]
КАРМАННАЯ ИГРОТЕКА
Я работаю преподавателем в филиале Ставропольского политехнического института в городе Черкесске. В научной работе большую помощь мне оказывает микрокалькулятор "Электроника Б3-21".
Однажды моя восьмилетняя дочь попросила научить ее считать на микрокалькуляторе. Когда я стал объяснять ей принцип его работы, у меня возникла идея "научить" микрокалькулятор играть в какую-нибудь простую игру.
Я запрограммировал игру Баше (подробнее о ней ниже), и дочь стала играть в нее с калькулятором. Надо было видеть, с каким упорством неискушенный в математике ребенок пытался добиться выигрыша! Все напрасно: крохотная, но умная машинка неизменно добивалась успеха.
Поединки с электронным партнером понравились и нашим знакомым. Теперь мой микрокалькулятор частенько демонстрирует свои способности, а от меня требуют программировать все новые игры. К настоящему времени таких программ у меня скопилось достаточно много, так что микрокалькулятор превратился в своеобразную игротеку.
Разберем, каким же образом микрокалькулятор может играть. Обратимся ради этого к простому примеру - к все той же игре Баше. Сущность ее заключается в следующем. Из кучи, содержащей определенное количество камней, двое играющих берут поочередно каждый раз по произвольному числу камней, но не меньше одного и не больше n за один ход. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся камни.
Выигрышный алгоритм игры очень прост. Неблагоприятным для игрока, делающего очередной ход, будет число камней в куче, кратное (n+1). Действительно, когда камней всего (n+1), то при любом ходе игрока противник может сразу забрать все оставшиеся камни и выиграть. Если же число камней кратно (n+1), то после любого хода игрока противник, сделав соответствующий ход, может оставить в куче число камней, опять же кратное (n+1), и так при каждом ходе, доведя наконец число камней в куче до (n+1), что обеспечивает ему выигрыш. Во всех остальных исходных положениях (когда число камней равно p(n+1)+m, где р произвольно, 1<=m<=n) начинающий игру, взяв m камней, обречет своего противника на проигрыш.
Таким образом, выигрышный алгоритм сводится к следующему:
1) уступать право первого хода противнику, если исходное число камней кратно (n+1);
2) начинать игру самому в случае, если это число не кратно (n+1);
3) своим очередным ходом оставлять в куче число камней, кратное (n+1).
Предположим, что в куче 17 камней, а брать из нее разрешается не более трех за один ход. Тогда партия между знатоком выигрышного алгоритма А (он ходит первым) и не знающим ее игроком В может протекать, например, так (после двоеточия указывается оставшееся в куче после очередного хода число камней) - А:16, В:13, А:12, В:10, А:8, В:7, А:4, В:3, А:0.
Как видно, алгоритм достаточно прост и доступен такому микрокалькулятору, как "Электроника Б3-21". Но еще надо составить программу, по которой он будет работать, и начинать надо, как всегда, с разработки блок-схемы программы.
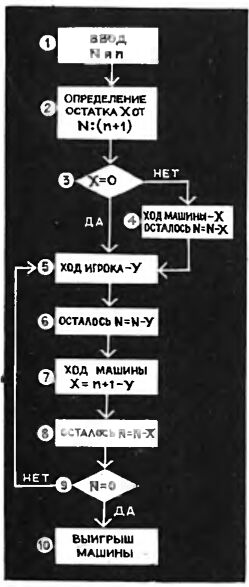
1. Ввод в регистр 2 числа N камней в куче (оно высвечивается на индикаторе), в регистр 3 - предельного числа n камней за один ход, в регистр 5 - условного числа, обозначающего выигрыш машины, например, 777.
2. Определение величины остатка от деления числа камней в куче N на (n+1).
3. Логический блок, определяющий равенство остатка нулю. В случае неравенства машина переходит к следующему блоку, в случае равенства - к блоку 5; при этом число на индикаторе остается прежним; это означает, что машина предлагает первый ход своему партнеру.
4. Машина берет число камней, равное величине остатка, и определяет число камней, оставшихся в куче (высвечивается на индикаторе) .
5. Ход игрока. Ввод числа камней, "взятых" игроком, в регистр 4.
6. Определение оставшегося числа камней (высвечивается на индикаторе).
7. Ход машины в соответствии с выигрышным алгоритмом.
8. Определение оставшегося числа камней (высвечивается на индикаторе).
9. Логический блок, определяющий равенство числа камней в куче нулю. В случае неравенства машина переходит к блоку 5, в случае равенства - к блоку 10.
10. На индикаторе высвечивается число 777: выигрыш машины.
Приведенный алгоритм я реализовал в программе для микрокалькулятора "Электроника БЗ-21". Для калькуляторов других марок читатель сможет составить свою программу согласно описанной блок-схеме.
Изложенная программа предполагает честную игру партнера машины. Если же он будет делать заведомо неверные ходы (например, брать больше камней, чем условлено), то машина проиграет.
Читатели могут усовершенствовать программу, введя в нее логические блоки для определения корректности ходов партнера.
В.БУДОВСКИЙ (г.Черкесск).
[МИКРОЗАДАЧНИК
Возьмите произвольное число, большее нуля и меньшее единицы. Представьте, что это радианная мера некоторого угла. Вычислите синус этого угла, нажав соответствующую клавишу микрокалькулятора. От полученного числа вновь возьмите синус, с полученным на сей раз проделайте ту же операцию... и так далее. Числа, загорающиеся на табло микрокалькулятора, будут постепенно приближаться к нулю. Почему?
Снова возьмите произвольное число между нулем и единицей и проведите с ним вычисления по той же схеме, но нажимая всякий раз на клавишу "косинус". Получающиеся последовательные результаты теперь будут стремиться к ненулевому числу, вполне определенному, не зависящему от исходного. Что это за число?
А.ВАСИН (г.Долгопрудный, МФТИ)].
УСЛОЖНЕННАЯ ИГРА УВЛЕКАТЕЛЬНЕЕ
Игра Баше представляет собой частный случай игры "ним". Правила этой игры таковы.
Имеется произвольное количество куч, в каждой из которых содержится произвольное количество камней. Играют двое. Каждый берет за один ход произвольную (обязательно ненулевую!) порцию камней, но только из одной кучи. Выигрывает тот, кто своим очередным ходом забирает последние камни.
Известен выигрышный алгоритм игры "ним". Прежде чем его излагать, надо напомнить о двоичной системе счисления. В общеупотребительной десятичной системе цифры некоторого числа, если их перебирать справа налево, от младших разрядов к старшим, указывают, сколько содержится в числе единиц, десятков, сотен, тысяч и более высоких степеней десятки. Например: 1983 = 1*10**3 + 9*10**2 + 8*10 + 3*1. В двоичной системе запись числа указывает количество содержащихся в нем степеней двойки (как говорят, двойка служит основанием системы). Например, число 83 в двоичной системе изображается так: 101011 = 1*2**6 + 0*2**5 + 1*2*4 + 0*2**3 + 1*2 + 1. В подобных системах, называемых позиционными, количество единиц в каждом разряде не превышает основания. Поэтому в двоичной записи чисел фигурируют лишь нули и единицы.
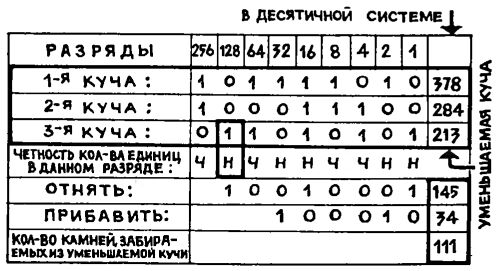
Вернемся к выигрышному алгоритму игры "ним" (см. таблицу; куч для простоты взято всего три). Количество камней в каждой куче выразим в двоичной системе. Подсчитаем количество единиц в каждом разряде полученных двоичных чисел. Выигрышный алгоритм заключается в том, чтобы после каждого очередного хода игрока количество единиц в каждом разряде становилось четным.
Пусть после очередного хода противника в некоторых разрядах оно стало нечетным. Отметим эти разряды (в таблице - буквой Н в четвертой снизу строке) и отыщем кучу, где в старшем из этих разрядов стоит единица (в таблице это третья куча). Из этой кучи и следует взять камни очередным ходом, уменьшая ее.
В двоичной записи числа камней в этой куче просмотрим все отмеченные разряды, выделим те, где стоит единица, и составим двоичное число из таких единиц, оставляя их в своих разрядах, а в прочие разряды поставим нули. Если из кучи взять количество камней, выражаемое этим числом, в отмеченных разрядах исчезнет по единице, и общее по всем кучам количество единиц в этих разрядах станет четным.
Теперь в двоичной записи количества камней в уменьшаемой куче выделим среди отмеченных разрядов те, где стоят нули. Составим двоичное число, где в таких разрядах стоят единицы, а в прочих - нули. Если добавить к куче количество камней, выражаемое составленным на сей раз числом, то в соответствующих разрядах появятся единицы и общее по всем кучам количество единиц в этих разрядах также станет четным.
Сравним оба составленных нами числа, выражающих изымаемое из кучи и добавляемое к ней количество камней. Первое больше второго, как содержащее больше разрядов. Алгебраическая сумма обоих чисел, взятых со знаками минус и плюс соответственно, указывает количество камней, которое игрок своим очередным ходом должен забрать из кучи.
Из какой бы кучи своим ответным ходом ни взял камни противник, в двоичной записи количества камней в этой куче нули кое-где сменятся единицами, а единицы - нулями. В каждом из таких разрядов суммарное по всем кучам количество единиц станет нечетным, так что выигрышный алгоритм оказывается применимым вновь.
Количество камней уменьшается с каждым ходом, и для того, кто придерживается выигрышного алгоритма, рано или поздно создастся единственная возможность добиться четного количества единиц во всех разрядах: взять последние камни. А это означает выигрыш.
Если принять условие, что своим очередным ходом каждый игрок может взять не более n камней, то желающий выиграть перед каждым своим ходом должен разделить число камней в каждой куче на (n+1), и к остаткам применить вышеописанный выигрышный алгоритм. Когда в каждой куче останется менее (n+1) камней, выигрышный алгоритм применяется без только что сделанной оговорки, ведя к победному концу.
Ю.ПОБОЖИЙ.

ДОПОЛНЕНИЕ К МАТЕРИАЛАМ ПРЕДЫДУЩИХ НОМЕРОВ
Журнальная рубрика, привлекшая к себе широкое внимание читателей, вскоре становится похожей на клуб, где время от времени люди собираются поговорить о предмете своего общего увлечения. Такие разговоры замечательны, в частности, тем, что в них не бывает последнего слова: сказанное одним получает развитие в реплике другого, одобрительной или критической; слово за слово - и затронутая тема вырисовывается яснее, понимается глубже... Важно ли при этом, насколько прав был высказавшийся первым? Бывает, что и неудачное на чей-то взгляд высказывание оказывается плодотворным, дает повод к содержательной беседе.
Многие из тех, кто прочел статью Р.Васселя "Легкомысленный шах. и "Электроника БЗ-34" (НИЖ 5/83), упрекнули автора в незнании элементарной математики: мол, можно было бы воспользоваться формулой суммы геометрической прогрессии
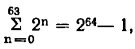
и тогда расчеты на микрокалькуляторе длились бы не минуты, а секунды.
Стоит прежде всего заметить, что, судя по статье, подсчет громадной суммы был для автора не самоцелью, а средством освоить азы счета на карманном калькуляторе. Что же касается соображений об экономии времени, о значении математической эрудиции в вычислительной работе, они несомненны.
Уместно привести здесь выдержку из книги профессора Л. Д. Кудрявцева "Современная математика и ее преподавание", где рассказывается поучительный случай, произошедший однажды с членом-корреспондентом АН СССР Л.А Люстерником:
"Несколько лет назад он был приглашен консультантом в один институт, и первая задача, с которой он столкнулся, состояла в табулировании значений одного трехкратного интеграла от функции, зависящей еще от нескольких параметров. Были уже составлены программы для вычисления соответствующих таблиц, осуществление счета по которым должно было занять около полугода работы на ЭВМ типа "Стрела".
"Л.А.Люстернику показалось, что рассматриваемый интеграл напоминает ему что-то встречавшееся в теории функций Бесселя. Через два-три дня ему действительно удалось, используя аналогии с преобразованиями интегралов в указанной теории, свести злополучный интеграл к однократному, вычисление нужных значений которого на той же "Стреле" потребовало меньше суток!
"Этот случай является, конечно, красноречивым примером важности математического мастерства и общей математической культуры, примером того, как много может дать правильное использование аналитических методов, примером настоящего математического образования, наконец, убедительным примером пользы от владения чистой математикой для прикладной математики в век компьютеров".
Надеемся, что в каждом новом выпуске рубрики "Человек с микрокалькулятором" читатели станут находить нечто такое, что хотелось бы поддержать или опровергнуть, развить или оспорить своим откликом. Рассчитываем, что в своих письмах читатели будут сообщать о все новых применениях микрокомпьютеров. Так, разговор о микрокомпьютерах, об этой самой массовой разновидности вычислительной техники, будет продолжаться на страницах журнала, способствуя все более широкому ее освоению. Редакция со своей стороны станет помещать комментарии специалистов по принципиальным и спорным вопросам, вызывавшим дискуссии читателей.
["Всякую программу можно сократить по крайней мере на одну команду".
Из старинной рукописи "Заповеди программиста"].


На этих снимках - два микрокалькулятора, выпускаемые в нашей стране. Простейший "Электроника Б3-39" и программируемый "Электроника Б3-34". Перечислим марки микрокалькуляторов, выпускаемых советской промышленностью. Программируемые: Б3-21, Б3-34 Инженерные: С3-15, Б3-18А, Б3-18М, Б3-37, Б3-19М, Б3-32, Б3-35, Б3-36, Б3-38. Простейшие: Б3-14, Б3-23, Б3-24Г, Б3-26, С3-33, Б3-30, Б3-39. Их характеристики указаны в справочной статье "Микрокалькуляторы "Электроника", опубликованной в нашем журнале 9/81.
[В ФРГ выдано авторское свидетельство на устройство, в котором микрокалькулятор соединен с широкоформатным табло, демонстрирующим результаты расчетов. Предполагается, что новшество будет полезно водителям автобусов для передачи путевой информации пассажирам, администраторам учреждений для оповещения клиентов, собравшихся в зале ожидания.
Гибрид микрокалькулятора и рулетки, разработанный в Японии, содержит в качестве мерного шнура полую пластмассовую трубку с магнитными и немагнитными шариками внутри. По мере вытягивания шнура из щели установленный близ нее датчик отсчитывает число прошедших мимо него магнитных шариков. Определенная таким способом длина вводится в память калькулятора и может быть использована в дальнейших вычислениях.
Э.Веттер из Техаса (США) запатентовал способ предохранить микрокомпьютер от нежелательных пользователей: калькулятор не работает и автоматически отключается, если предварительно не набрать на его клавиатуре комбинацию цифр, известную лишь хозяину.
Подборку этих фактов, подтвержденных ссылками на достоверные источники, прислал в редакцию Л.СИНЕЛЬНИКОВ (г.Гомель)].
СКОРОСТНОЕ КОНСПЕКТИРОВАНИЕ
Кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт)
ПОМОГУТ ПИКТОГРАММЫ
Пиктограммы - упрощенные стилизованные рисунки - мы встречаем часто. Это, например, дорожные знаки, разъясняющие, что можно и что нельзя делать на этом месте улицы. Пиктограммы Московской олимпиады говорили без слов об определенном виде спорта.

Пиктограммы можно с успехом использовать и для сокращенной записи. Они отличное средство для запоминания: ведь самая прочная память у человека - зрительная. Пример простейших пиктограмм:

Пример более сложных пиктограмм:

Графики каких-то зависимостей для этих двух типов самолетов можно записать двумя способами. Но первая запись выглядит нейтрально. Вторая же создает образ: самолетик с треугольным крылом "летит" выше. Подобную пиктограмму можно использовать в конспекте.

Внизу - первый рисунок представляет собой график скорости самолетов двух типов (в зависимости от какого-то параметра), второй - график скороподъемности (скорость набора высоты), третий - график потолка (максимальной высоты).

Пиктограммы не только ускоряют запись, они заставляют работать зрительную память, дают возможность воспринимать не слова, а образы. А это значительно ускоряет и улучшает восприятие конспекта и запоминание материала.
Придумать точные, выразительные пиктограммы не так-то просто. Но посмотрите вокруг себя. На панели домашнего телевизора вы обнаружите удобные пиктограммы для конспектирования лекций по оптике, акустике, охране труда.

Фрагмент электронной схемы тоже легко "разбирается" на пиктограммы. Вообще различные обозначения на любых схемах почти всегда можно использовать в этом качестве.

Запишем с помощью пиктограмм электронной схемы следующую фразу: "Если на потенциальный вход подать положительный потенциал, то схема вырабатывает импульс, который...". Запись будет выглядеть так:

Наконец, в качестве пиктограммы можно использовать рисунок какого-то предмета, если его проще нарисовать, чем написать название. Химикам предлагаем пиктограммы такого рода.

Оговоримся, что пиктограммой "пробирка" можно пользоваться, если латинская буква "U" в вашем почерке четко отличима от рисунка пробирки. Если же нет, то для сокращения слова "пробирка" надо придумывать что-то другое.
ПРИСТАВКИ, СУФФИКСЫ, ОКОНЧАНИЯ
При конспектировании без приставок обойтись невозможно: они меняют смысл слов. Чаще опускают суффиксы или окончания, которые можно восстановить по контексту. Но иногда после таких сокращений текст превращается в головоломку.
Эти части слов можно добавлять к сокращениям следующим образом:

Можно для записи суффиксов воспользоваться простыми стенографическими обозначениями типовых концовок слов. Например:

Применяются эти "хвостики" как в обычном тексте, так и с разными видами сокращений:

Часто нам нужно не конкретное окончание, а какой-то признак части речи: существительного, глагола, прилагательного. Для таких признаков можно использовать те же стенографические "хвостики", только надо расширить их функции. Например:

СМЕСЬ ЯЗЫКОВ
При конспектировании можно использовать более короткие слова других языков. Прием этот хорошо известен и достаточно распространен. Например, "англоязычные" студенты очень часто пишут if вместо "если" и use вместо "использовать". Интересно, что даже в математических книгах прижилось довольно удачное английское слово-сокращение iff, означающее "тогда и только тогда".
Легкость чтения конспекта с такой смесью, по-видимому, зависит от индивидуальных особенностей восприятия.
КАК ПОЛЬЗОВАТЬСЯ СОКРАЩЕНИЯМИ
Приемы сокращения записи, о которых говорилось выше, чисто технические, они не требуют мыслительной работы и после небольшой тренировки выполняются автоматически. Если полностью освоить эти приемы, то можно достичь примерно двух-, а то и трехкратного ускорения записи. Причем качество ее восприятия не ухудшается, наоборот, даже улучшается.
При использовании сокращений надо выработать собственную систему. Иероглифами злоупотреблять не стоит - этот прием годен только тогда, когда не подходят другие. А вот пиктограммы рекомендуем использовать везде, где только можно; прием дает отличные результаты в процессе самой записи, а также при ее запоминании и чтении.
Опыт показывает, что на различные виды конспектируемых текстов достаточно 50 сокращений всех типов: десяток кванторов, 20 букв "в обертке" и т.д.
Если выбрать 50 сокращений и тут же попытаться их немедленно и полностью использовать, то ничего хорошего не получится. Сокращения следует вводить постепенно: по одному-два в неделю, чтобы без труда к ним привыкнуть.
Создание собственной системы записи требует затрат умственного труда. Если же преподаватель вуза или школьный учитель преподносит готовые сокращения, то обычно одного их показа достаточно для того, чтобы сокращения приняли на вооружение 95 процентов слушателей. Если же преподаватель сам пользуется на доске сокращениями, то их без всякого труда осваивают все слушатели. Кстати, показ конкретных сокращений полезен и тем, что все ученики в классе или студенты на курсе осваивают одинаковую систему записи.
11/85
"ГАРМОШКА" БЕРЕЖЕТ ВРЕМЯ
Миниатюрный еженедельник экспресс-записей для памяти и исполнения.
Ю.ОРЛОВ, преподаватель (г.Ленинград)
Хотелось бы поделиться опытом использования простой и удобной формы записей. Она уже более тридцати лет помогает четко планировать, рационально использовать, а также контролировать выполнение намеченных дел.
Для миниатюрного еженедельника пригоден любой стандартный лист плотной писчей бумаги. Он складывается сначала втрое по длинной стороне, а затем еще раз втрое - по короткой стороне. В результате получается квадратик-гармошка, он легко помещается в кармане пиджака и всегда бывает при себе. В сложенном виде квадратик обладает достаточной жесткостью, это позволяет вести записи даже на ладони.
В сложенной указанным способом заготовке шесть небольших, но довольно вместительных полосок (три - на одной стороне листа и три - на обороте). В верхней части каждой полоски указывается фломастером или цветной авторучкой дата и день недели - от понедельника до пятницы (например: "вторник, 9 февраля"), затем фиксируются дела на каждый день. Оставшаяся свободной шестая полоска предназначается для планов на субботу и воскресенье, а также для накопившихся за неделю хозяйственно-бытовых дел.
Квадратик непременно должен быть сложен таким образом, чтобы на одной стороне всегда была дата сегодняшнего дня, а на обороте - полоска на завтра: это даст возможность иметь под рукой записи первостепенных дел на ближайшее время.
Каждое утро я внимательно просматриваю гармошку, чтобы уяснить, как выполнялись дела вчера. Затем переворачиваю очередную полоску-страничку и корректирую планы на сегодня и на следующие дни.
На полоске каждый день разграничивается благодаря сгибам на три равных отрезка: "утро" (верх полосы), "день" (средняя часть), "вечер" (нижняя часть).
Соответственно распределяются и предстоящие дела.
В понедельник утром анализирую запланированные и выполненные (или невыполненные) дела, оцениваю затраченное время и после этого "конструирую" гармошку на следующую неделю.
Весьма разумно и целесообразно готовить сразу четыре квадратика - на полный месяц по неделям: в этом случае больше возможностей для перспективно-целевого планирования.
Целесообразно завести также папку для хранения отработанных гармошек - пятьдесят две недели-странички полного года займут немного места. Возможность же критически оценить свои действия в течение года часто оказывается весьма необходимой и полезной.
Было бы небезынтересно знать, какими способами записей для памяти вы пользуетесь. Обзор писем и рекомендаций на эту тему надеемся напечатать.
***
Невзирая на обещания, регулярные публикации об организации личного офиса в журнале после 85-го года прекратились. Все силы были брошены на калькуляторно-компьютерный фронт. Попробуем проследить, как и что пытались считать в те времена.
5/83
ЛЕГКОМЫСЛЕННЫЙ ШАХ И "ЭЛЕКТРОНИКА БЗ-34"
Кандидат технических наук Р.ВАССЕЛЬ
Электронные микрокалькуляторы вошли в наш повседневный быт столь же прочно, как электробритва и междугородная телефонная связь, как бег трусцой и кубик Рубина. С помощью этой миниатюрной машинки школьник уверенно рассчитывает путь пешехода из пункта А в пункт В, инженер успешно решает дифференциальные уравнения, а домохозяйка с подлинно научной строгостью оптимизирует домашний бюджет. Как свидетельствует публикуемая здесь статья, микрокалькулятор порою приводит своих приверженцев к задачам, лежащим несколько в стороне от его основных применений, бесполезных на первый взгляд... Но это только на первый взгляд! Такие задачи, изящные, отмеченные смекалкой и юмором, особенно наглядно демонстрируют богатые возможности наших маленьких электронных помощников. Редакция надеется, что подобные заметки найдут плодотворный отклик у читателей журнала.
Вероятно, каждому любителю шахматной игры известна легенда об изобретателе шахмат и восточном владыке, который в порыве щедрости позволил изобретателю просить любую награду за его интересное изобретение. Изобретатель запросил весьма "скромную" плату зерном (очевидно, в те времена хлеб умели ценить): за первую клетку шахматной доски - 1 зернышко, за вторую клетку - 2 зернышка, за третью клетку - 4 зернышка, за четвертую клетку - 8 зернышек... и так далее до 64-й клетки.
Восточный владыка легкомысленно согласился, и напрасно: плата оказалась настолько высокой, что была не по карману даже ему.
Тем, кто знаком с этой историей, известно, что количество зерна исчислялось астрономической цифрой. Ну, а конкретно?.. И решил я заняться подсчетом зерна, причитающегося изобретателю.
В журнале НиЖ 3-4/81 я прочел статью о-микрокалькуляторах и пошел в магазин, ибо счетами в таком деле не обойдешься. Купил микрокалькулятор "Электроника Б3-34", который, как оказалось, может считать по заданной программе.
Математическая постановка задачи была для меня понятна: надо взвесить зернышко пшеницы и умножить на общее количество зерен.
На математическом языке количество зерен, запрошенное изобретателем, выражается формулой:
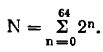
За данными о среднем весе пшеничного зерна я обратился к энциклопедии (БСЭ. 3-е изд., т.21, с.266) и принял его равным
g = 0.04г = 4e-8т
Изучив инструкцию по пользованию микрокалькулятором, приложенную к нему, я иаписал программу вычислений - см. ниже. В правой колонке программы сжато описано содержание каждой операции; ради краткости не отмечается, что при занесении какого-либо числа в регистр "x" его прежнее содержание автоматически пересылается в регистр "y", а результат вычислительной операции заносится в "x". Количество зерен, выраженное формулой, подсчитывается последовательным суммированием слагаемых и накапливается в регистре памяти "5", счетный индекс n хранится в регистре "1" (оба регистра к началу вычислений пусты). Число сложений (64) заранее заносится в регистр "0", вес зерна - в регистр "2".

Я человек пунктуальный, поэтому решил зафиксировать время, затраченное на проведение вычислений. Отмечу, что за 6.5 минуты счета машина произвела 772 действия, то есть на каждую команду затратила в среднем 0.505 секунды.
Ввел программу в машину, нажимая соответствующие клавиши; затем нажал клавишу "Пуск" и через 6.5 минуты прочел на индикаторе: 7.378688e11 тонн!
А количество зерен - 1.844672e19 штук!
Ого! Изобретатель умел ценить свой труд и излишней скромностью не страдал. Получилось больше 7.3e11 тонн, или, выражаясь языком современного ядерного века, почти миллион мегатонн! Цифра даже для нас, привыкших слышать о мегатоннах, весьма внушительная.
Этот шутливый расчет, в котором все верно (кроме, может быть, исторического факта), я привел как небольшую иллюстрацию возможностей современных мини-ЭВМ.
Хочется выразить благодарность создателям этой весьма интересной машины и пожелать успехов в ее дальнейшем совершенствовании. В частности, было бы полезным увеличить объем памяти и количество выполняемых команд.

***
Первый блин комом. Ненужные вычисления, дурацкий результат. Неинтересная программа. В чем замануха?
В следующем выпуске это попробовали исправить, добавив околокалькуляторных врезок.
8/83
ЧЕЛОВЕК С МИКРОКАЛЬКУЛЯТОРОМ
Завоевывая все большую популярность, микрокалькуляторы находят все новые применения. Они обосновываются в кабине водителя автобуса и в кабинете театрального администратора, становятся предметом забавных детских игр и хитроумных головоломок для любителей математики, художнику они подсказывают темы для юмористических рисунков, а среди коллекционеров уже появились такие, кто собирает любопытные факты, связанные с миниатюрными компьютерами. Обо всем этом рассказывают письма читателей нашего журнала, легшие в основу публикуемых здесь заметок.
[КСТАТИ...
Шутка, игра вовсе не чужды вычислительной технике - напротив, симпатия к ним написана компьютерам на роду: Чарлз Бэббидж, изобретатель первой автоматической вычислительной машины, намеревался написать исследование о юморе. Видимо, не случайно...]
КАРМАННАЯ ИГРОТЕКА
Я работаю преподавателем в филиале Ставропольского политехнического института в городе Черкесске. В научной работе большую помощь мне оказывает микрокалькулятор "Электроника Б3-21".
Однажды моя восьмилетняя дочь попросила научить ее считать на микрокалькуляторе. Когда я стал объяснять ей принцип его работы, у меня возникла идея "научить" микрокалькулятор играть в какую-нибудь простую игру.
Я запрограммировал игру Баше (подробнее о ней ниже), и дочь стала играть в нее с калькулятором. Надо было видеть, с каким упорством неискушенный в математике ребенок пытался добиться выигрыша! Все напрасно: крохотная, но умная машинка неизменно добивалась успеха.
Поединки с электронным партнером понравились и нашим знакомым. Теперь мой микрокалькулятор частенько демонстрирует свои способности, а от меня требуют программировать все новые игры. К настоящему времени таких программ у меня скопилось достаточно много, так что микрокалькулятор превратился в своеобразную игротеку.
Разберем, каким же образом микрокалькулятор может играть. Обратимся ради этого к простому примеру - к все той же игре Баше. Сущность ее заключается в следующем. Из кучи, содержащей определенное количество камней, двое играющих берут поочередно каждый раз по произвольному числу камней, но не меньше одного и не больше n за один ход. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся камни.
Выигрышный алгоритм игры очень прост. Неблагоприятным для игрока, делающего очередной ход, будет число камней в куче, кратное (n+1). Действительно, когда камней всего (n+1), то при любом ходе игрока противник может сразу забрать все оставшиеся камни и выиграть. Если же число камней кратно (n+1), то после любого хода игрока противник, сделав соответствующий ход, может оставить в куче число камней, опять же кратное (n+1), и так при каждом ходе, доведя наконец число камней в куче до (n+1), что обеспечивает ему выигрыш. Во всех остальных исходных положениях (когда число камней равно p(n+1)+m, где р произвольно, 1<=m<=n) начинающий игру, взяв m камней, обречет своего противника на проигрыш.
Таким образом, выигрышный алгоритм сводится к следующему:
1) уступать право первого хода противнику, если исходное число камней кратно (n+1);
2) начинать игру самому в случае, если это число не кратно (n+1);
3) своим очередным ходом оставлять в куче число камней, кратное (n+1).
Предположим, что в куче 17 камней, а брать из нее разрешается не более трех за один ход. Тогда партия между знатоком выигрышного алгоритма А (он ходит первым) и не знающим ее игроком В может протекать, например, так (после двоеточия указывается оставшееся в куче после очередного хода число камней) - А:16, В:13, А:12, В:10, А:8, В:7, А:4, В:3, А:0.
Как видно, алгоритм достаточно прост и доступен такому микрокалькулятору, как "Электроника Б3-21". Но еще надо составить программу, по которой он будет работать, и начинать надо, как всегда, с разработки блок-схемы программы.

1. Ввод в регистр 2 числа N камней в куче (оно высвечивается на индикаторе), в регистр 3 - предельного числа n камней за один ход, в регистр 5 - условного числа, обозначающего выигрыш машины, например, 777.
2. Определение величины остатка от деления числа камней в куче N на (n+1).
3. Логический блок, определяющий равенство остатка нулю. В случае неравенства машина переходит к следующему блоку, в случае равенства - к блоку 5; при этом число на индикаторе остается прежним; это означает, что машина предлагает первый ход своему партнеру.
4. Машина берет число камней, равное величине остатка, и определяет число камней, оставшихся в куче (высвечивается на индикаторе) .
5. Ход игрока. Ввод числа камней, "взятых" игроком, в регистр 4.
6. Определение оставшегося числа камней (высвечивается на индикаторе).
7. Ход машины в соответствии с выигрышным алгоритмом.
8. Определение оставшегося числа камней (высвечивается на индикаторе).
9. Логический блок, определяющий равенство числа камней в куче нулю. В случае неравенства машина переходит к блоку 5, в случае равенства - к блоку 10.
10. На индикаторе высвечивается число 777: выигрыш машины.
Приведенный алгоритм я реализовал в программе для микрокалькулятора "Электроника БЗ-21". Для калькуляторов других марок читатель сможет составить свою программу согласно описанной блок-схеме.
Изложенная программа предполагает честную игру партнера машины. Если же он будет делать заведомо неверные ходы (например, брать больше камней, чем условлено), то машина проиграет.
Читатели могут усовершенствовать программу, введя в нее логические блоки для определения корректности ходов партнера.
В.БУДОВСКИЙ (г.Черкесск).
[МИКРОЗАДАЧНИК
Возьмите произвольное число, большее нуля и меньшее единицы. Представьте, что это радианная мера некоторого угла. Вычислите синус этого угла, нажав соответствующую клавишу микрокалькулятора. От полученного числа вновь возьмите синус, с полученным на сей раз проделайте ту же операцию... и так далее. Числа, загорающиеся на табло микрокалькулятора, будут постепенно приближаться к нулю. Почему?
Снова возьмите произвольное число между нулем и единицей и проведите с ним вычисления по той же схеме, но нажимая всякий раз на клавишу "косинус". Получающиеся последовательные результаты теперь будут стремиться к ненулевому числу, вполне определенному, не зависящему от исходного. Что это за число?
А.ВАСИН (г.Долгопрудный, МФТИ)].
УСЛОЖНЕННАЯ ИГРА УВЛЕКАТЕЛЬНЕЕ
Игра Баше представляет собой частный случай игры "ним". Правила этой игры таковы.
Имеется произвольное количество куч, в каждой из которых содержится произвольное количество камней. Играют двое. Каждый берет за один ход произвольную (обязательно ненулевую!) порцию камней, но только из одной кучи. Выигрывает тот, кто своим очередным ходом забирает последние камни.
Известен выигрышный алгоритм игры "ним". Прежде чем его излагать, надо напомнить о двоичной системе счисления. В общеупотребительной десятичной системе цифры некоторого числа, если их перебирать справа налево, от младших разрядов к старшим, указывают, сколько содержится в числе единиц, десятков, сотен, тысяч и более высоких степеней десятки. Например: 1983 = 1*10**3 + 9*10**2 + 8*10 + 3*1. В двоичной системе запись числа указывает количество содержащихся в нем степеней двойки (как говорят, двойка служит основанием системы). Например, число 83 в двоичной системе изображается так: 101011 = 1*2**6 + 0*2**5 + 1*2*4 + 0*2**3 + 1*2 + 1. В подобных системах, называемых позиционными, количество единиц в каждом разряде не превышает основания. Поэтому в двоичной записи чисел фигурируют лишь нули и единицы.

Вернемся к выигрышному алгоритму игры "ним" (см. таблицу; куч для простоты взято всего три). Количество камней в каждой куче выразим в двоичной системе. Подсчитаем количество единиц в каждом разряде полученных двоичных чисел. Выигрышный алгоритм заключается в том, чтобы после каждого очередного хода игрока количество единиц в каждом разряде становилось четным.
Пусть после очередного хода противника в некоторых разрядах оно стало нечетным. Отметим эти разряды (в таблице - буквой Н в четвертой снизу строке) и отыщем кучу, где в старшем из этих разрядов стоит единица (в таблице это третья куча). Из этой кучи и следует взять камни очередным ходом, уменьшая ее.
В двоичной записи числа камней в этой куче просмотрим все отмеченные разряды, выделим те, где стоит единица, и составим двоичное число из таких единиц, оставляя их в своих разрядах, а в прочие разряды поставим нули. Если из кучи взять количество камней, выражаемое этим числом, в отмеченных разрядах исчезнет по единице, и общее по всем кучам количество единиц в этих разрядах станет четным.
Теперь в двоичной записи количества камней в уменьшаемой куче выделим среди отмеченных разрядов те, где стоят нули. Составим двоичное число, где в таких разрядах стоят единицы, а в прочих - нули. Если добавить к куче количество камней, выражаемое составленным на сей раз числом, то в соответствующих разрядах появятся единицы и общее по всем кучам количество единиц в этих разрядах также станет четным.
Сравним оба составленных нами числа, выражающих изымаемое из кучи и добавляемое к ней количество камней. Первое больше второго, как содержащее больше разрядов. Алгебраическая сумма обоих чисел, взятых со знаками минус и плюс соответственно, указывает количество камней, которое игрок своим очередным ходом должен забрать из кучи.
Из какой бы кучи своим ответным ходом ни взял камни противник, в двоичной записи количества камней в этой куче нули кое-где сменятся единицами, а единицы - нулями. В каждом из таких разрядов суммарное по всем кучам количество единиц станет нечетным, так что выигрышный алгоритм оказывается применимым вновь.
Количество камней уменьшается с каждым ходом, и для того, кто придерживается выигрышного алгоритма, рано или поздно создастся единственная возможность добиться четного количества единиц во всех разрядах: взять последние камни. А это означает выигрыш.
Если принять условие, что своим очередным ходом каждый игрок может взять не более n камней, то желающий выиграть перед каждым своим ходом должен разделить число камней в каждой куче на (n+1), и к остаткам применить вышеописанный выигрышный алгоритм. Когда в каждой куче останется менее (n+1) камней, выигрышный алгоритм применяется без только что сделанной оговорки, ведя к победному концу.
Ю.ПОБОЖИЙ.

ДОПОЛНЕНИЕ К МАТЕРИАЛАМ ПРЕДЫДУЩИХ НОМЕРОВ
Журнальная рубрика, привлекшая к себе широкое внимание читателей, вскоре становится похожей на клуб, где время от времени люди собираются поговорить о предмете своего общего увлечения. Такие разговоры замечательны, в частности, тем, что в них не бывает последнего слова: сказанное одним получает развитие в реплике другого, одобрительной или критической; слово за слово - и затронутая тема вырисовывается яснее, понимается глубже... Важно ли при этом, насколько прав был высказавшийся первым? Бывает, что и неудачное на чей-то взгляд высказывание оказывается плодотворным, дает повод к содержательной беседе.
Многие из тех, кто прочел статью Р.Васселя "Легкомысленный шах. и "Электроника БЗ-34" (НИЖ 5/83), упрекнули автора в незнании элементарной математики: мол, можно было бы воспользоваться формулой суммы геометрической прогрессии
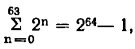
и тогда расчеты на микрокалькуляторе длились бы не минуты, а секунды.
Стоит прежде всего заметить, что, судя по статье, подсчет громадной суммы был для автора не самоцелью, а средством освоить азы счета на карманном калькуляторе. Что же касается соображений об экономии времени, о значении математической эрудиции в вычислительной работе, они несомненны.
Уместно привести здесь выдержку из книги профессора Л. Д. Кудрявцева "Современная математика и ее преподавание", где рассказывается поучительный случай, произошедший однажды с членом-корреспондентом АН СССР Л.А Люстерником:
"Несколько лет назад он был приглашен консультантом в один институт, и первая задача, с которой он столкнулся, состояла в табулировании значений одного трехкратного интеграла от функции, зависящей еще от нескольких параметров. Были уже составлены программы для вычисления соответствующих таблиц, осуществление счета по которым должно было занять около полугода работы на ЭВМ типа "Стрела".
"Л.А.Люстернику показалось, что рассматриваемый интеграл напоминает ему что-то встречавшееся в теории функций Бесселя. Через два-три дня ему действительно удалось, используя аналогии с преобразованиями интегралов в указанной теории, свести злополучный интеграл к однократному, вычисление нужных значений которого на той же "Стреле" потребовало меньше суток!
"Этот случай является, конечно, красноречивым примером важности математического мастерства и общей математической культуры, примером того, как много может дать правильное использование аналитических методов, примером настоящего математического образования, наконец, убедительным примером пользы от владения чистой математикой для прикладной математики в век компьютеров".
Надеемся, что в каждом новом выпуске рубрики "Человек с микрокалькулятором" читатели станут находить нечто такое, что хотелось бы поддержать или опровергнуть, развить или оспорить своим откликом. Рассчитываем, что в своих письмах читатели будут сообщать о все новых применениях микрокомпьютеров. Так, разговор о микрокомпьютерах, об этой самой массовой разновидности вычислительной техники, будет продолжаться на страницах журнала, способствуя все более широкому ее освоению. Редакция со своей стороны станет помещать комментарии специалистов по принципиальным и спорным вопросам, вызывавшим дискуссии читателей.
["Всякую программу можно сократить по крайней мере на одну команду".
Из старинной рукописи "Заповеди программиста"].


На этих снимках - два микрокалькулятора, выпускаемые в нашей стране. Простейший "Электроника Б3-39" и программируемый "Электроника Б3-34". Перечислим марки микрокалькуляторов, выпускаемых советской промышленностью. Программируемые: Б3-21, Б3-34 Инженерные: С3-15, Б3-18А, Б3-18М, Б3-37, Б3-19М, Б3-32, Б3-35, Б3-36, Б3-38. Простейшие: Б3-14, Б3-23, Б3-24Г, Б3-26, С3-33, Б3-30, Б3-39. Их характеристики указаны в справочной статье "Микрокалькуляторы "Электроника", опубликованной в нашем журнале 9/81.
[В ФРГ выдано авторское свидетельство на устройство, в котором микрокалькулятор соединен с широкоформатным табло, демонстрирующим результаты расчетов. Предполагается, что новшество будет полезно водителям автобусов для передачи путевой информации пассажирам, администраторам учреждений для оповещения клиентов, собравшихся в зале ожидания.
Гибрид микрокалькулятора и рулетки, разработанный в Японии, содержит в качестве мерного шнура полую пластмассовую трубку с магнитными и немагнитными шариками внутри. По мере вытягивания шнура из щели установленный близ нее датчик отсчитывает число прошедших мимо него магнитных шариков. Определенная таким способом длина вводится в память калькулятора и может быть использована в дальнейших вычислениях.
Э.Веттер из Техаса (США) запатентовал способ предохранить микрокомпьютер от нежелательных пользователей: калькулятор не работает и автоматически отключается, если предварительно не набрать на его клавиатуре комбинацию цифр, известную лишь хозяину.
Подборку этих фактов, подтвержденных ссылками на достоверные источники, прислал в редакцию Л.СИНЕЛЬНИКОВ (г.Гомель)].

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
10/83
НАТУРАЛЬНЫЙ РЯД - КЛАДЕЗЬ ОТКРЫТИЙ
Микрокалькулятор - это ЭВМ в кармане. И хотя по своим возможностям он не сравнится с мощными современными вычислительными машинами, он способен существенно облегчить труд инженера и научного работника, а любителю математики позволит сделать немало интересных открытий.
В этом номере - находки наших читателей, подсказанные работой с микрокалькуляторами; приводятся также отклики на предыдущие публикации.
Математик Николо Тарталья, живший в XVI веке в Италии, известен тем, что построил формулу для решения кубических уравнений. Среди менее знаменитых его находок есть такая: оказывается, числа натурального ряда в порядке их следования можно разбить на пары равных сумм:
1+2=3, 4+5+6=7+8, 9+10+11+12=13+14+15,..
Можно ли иначе разбить натуральный ряд на такие суммы? Можно ли провести подобное разбиение, начиная не с единицы, а с какого-то другого числа?
Чтобы ответить на эти вопросы, запишем в общем виде какую-либо пару равных сумм:
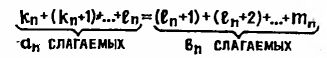
Назовем kn, ln, mn параметрами суммы. Прослеживая с помощью микрокалькулятора то разбиение натурального ряда, которое произвел Тарталья, можно в порядке гипотезы сформулировать некоторые соотношения, связывающие эти параметры. Например: разность an-bn есть величина постоянная. Назовем эту разность характеристикой и обозначим ее Q. По свойству арифметической прогрессии получаем: Q=(2*ln+1)-kn-mn.
Далее, замечаем: an=bn+i и kn+i=mn+l.
После этого можно установить следующие три зависимости между параметрами пар:
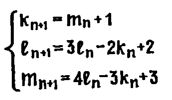
Полученная система из трех уравнений, где индекс n - переменный, разворачивается в цепочку систем, причем неизвестные каждой последующей тройки уравнений входят также и в предыдущую. Такие уравнения и системы называются возвратными. Их решение заключается в выражении неизвестных с произвольным индексом n через неизвестные с единичным индексом k1, l1, m1.
Способы решения подобных систем приводятся в книге А.А.Маркова "Исчисление конечных разностей" (2-е изд., Одесса, 1910г.).
Ответ можно записать в виде:
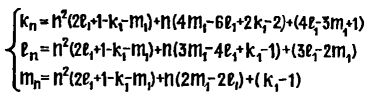
Найденное решение позволяет сделать вывод: чтобы построить новый ряд парных сумм, достаточно отыскать первую пару сумм, не совпадающую с 1+2=3. Как же ее искать?
Возьмем произвольную пару сумм, начинающуюся с некоторого числа k, и добавим слева все целые положительные числа, меньшие k, а также равные им по абсолютной величине отрицательные числа и нуль. Равенство от этого не нарушится:
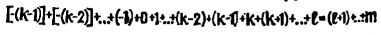
На основе расширенной описанным способом пары можно построить новый ряд парных сумм.
Любопытно, что первая пара сумм 1+2=3 из уже известного нам разбиения натурального ряда, для которого Q=1, расширяется в новую пару добавлением одного лишь нуля: 0+1+2=3. В новом равенстве Q уже равна двум. Новый ряд парных сумм отсюда получается таким:
0+1+2=3, 4+5+6+7+8=9+10+11, 12+13+14+15+16+17+18=19+20+21+22+23.
Аналогично можем получить новый ряд из пары 4+5+6=7+8:
(-3)+(-2)+(-1)+0+1+2+3+4+5+6=7+8, 9+10+...+25+26=27+28+...+35+36, 37+38+...+61+62=63+...+79+80 и так далее; здесь Q=8.
Итак, от одной известной пары равных сумм мы пришли к бесчисленному множеству бесконечных рядов таких пар.
Назовем базовой такую пару, для которой нельзя построить предыдущую с той же характеристикой. Это нельзя сделать, например, для пары 1+2=3, а для пары 4+5+6=7+8 можно.
Существуют ли еще базовые пары, кроме 1+2=3? Полагаю, что любителям математических головоломок будет небезынтересно подумать над этим вопросом и микрокалькулятор будет им в этом хорошим подспорьем.
В.СТОЛЯР (Москва).
СНАЧАЛА ПОДОЗРЕВАЛИ ОШИБКУ...
... В Государственном реестре Госкомитета СССР по делам изобретений и открытий под номером 55 значится открытие нового физического эффекта - Т-слоя. О том, как было сделано открытие, рассказывает один из его авторов, доктор физико-математических наук Ю.П.ПОПОВ, в ту пору аспирант Московского физико-технического института.
Рассказ об открытии, идею которого "подсказала" ЭВМ в ходе вычислительного эксперимента, вероятно, будет интересен тем, кто мечтает об открытии, экспериментируя над числами с помощью карманной ЭВМ - микрокалькулятора.
Это было в конце 60-х годов, когда оживленно обсуждалась идея МГД генератора. (Буквы МГД в его названии расшифровываются как "магнитногидродинамический": это прилагательное употребляют, когда говорят о течениях плазмы в магнитном поле).
Известно, что если проводник движется в магнитном поле, пересекая магнитные силовые линии, то в нем возникает электродвижущая сила. При этом проводник не обязательно должен быть твердым, металлическим. Это может быть проводящий газ - плазма. Пусть в канале, по которому она течет, магнитные силовые линии направлены сверху вниз. Если боковые стенки канала снабдить электродами, с них можно снимать ток, возникающий в плазме.
Даже из этого предельно грубого описания понятны выгоды такого генератора. В его конструкции нет движущихся деталей (как в турбогенераторе), за трение между ноторыми приходилось бы расплачиваться уменьшением кпд.
Такой генератор тем эффективнее, чем выше проводимость газа. А она растет с температурой. Но температуру нельзя наращивать беспредельно: тогда ее не выдержит никакой канал. С другой стороны, если она упадет ниже некоторого порогового значения, плазма перестанет взаимодействовать с магнитным полем.
Как быть в столь противоречивой ситуации?
Наш научный коллектив тоже участвовал в исследованиях, связанных с разработкой МГД-генератора. Нашим оружием был вычислительный эксперимент (НиЖ 2/79).
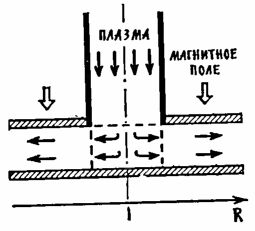
Один из процессов, которые рассчитывались на ЭВМ, мыслился так. В пространство между двумя проводящими дисками по осевому каналу впрыскивается порция плотной горячей плазмы, затем она растекается между дисками в радиальных направлениях. Схематизируя явление, можно представить, что в некоторый момент сгусток плазмы приобрел конфигурацию цилиндра (на рисунке очерчен пунктиром), а тот далее расширяется в пустоту. По мере расширения плазма будет остывать, и картина распределения температуры в ее объеме, вероятно, станет изменяться так, как показано на графике.
Начали счет. Его результаты поначалу вполне согласовывались с ожиданиями. И вдруг на температурном графике, на самом его хвосте появился небольшой всплеск. Он рос и рос.

Первая мысль была такая: может быть, это дефект вычислительного алгоритма, разностной схемы, по которой ведется счет? Стали совершенствовать ее, чтобы устранить ошибку. Всплеск упрямо появлялся все снова и снова. И чем аккуратнее мы вели расчеты, тем отчетливее вырисовывалась все та же странная картина. И в конце концов стало ясно, что перед нами не случайная погрешность вычислений, а математическая модель реального физического явления.
Это был интереснейший момент исследования: круто изменился наш взгляд на происходящее, резко поменялась психология наших действий. Теперь мы старались доказать, что обнаруженный нами феномен должен возникать непременно, выясняли условия его появления.
Проводимость плазмы по мере роста температуры вначале растет по экспоненциальному закону, затем график этой зависимости описывается степенной функцией с показателем 3/2. Диапазон наиболее крутого роста проводимости приходится на довольно низкие температуры (порядка пороговой), но именно в этом диапазоне разогрев плазмы протекает лавинообразно: небольшой прирост температуры вызывает резкий скачок проводимости, текущий по плазме ток усиливается, обусловленное им джоулево тепло разогревает плазму сильнее, ее проводимость вновь прирастает... Высокая температура, таким образом, подхлестывает сама себя, развивается, как говорят радиотехники, в режиме с положительной обратной связью.
Вникая в природу необычного феномена, мы вводили в расчеты все более тонкие детали, уточняющие физическую картину явления,- учли излучение, поточнее задали график роста проводимости с температурой. Результаты счета говорили, что в некоторых вариантах процесса эти тонкости могут подавить развитие эффекта, а в некоторых - лишь стабилизируют его рост.
Правда, говорить о новом эффекте, располагал расчетами лишь одного довольно специфического процесса, было рановато. Хотелось понять, насколько распространено необычное явление, обнаружить его в других магнитогидродинамических процессах. Примеры такого рода нашлись.
И тогда была подана заявка на открытие. В плазме, взаимодействующей с магнитным полем, говорилось в заявке, при определенных условиях могут возникать устойчивые зоны относительно высокой температуры. Температурные, токовые слои или кратко Т-слои - так были названы эти зоны.
Заявка вызвала бурные дебаты среди экспертов. Еще бы: эффект еще никем не наблюдался в физическом эксперименте, он обнаружил себя лишь в расчетах, в эксперименте вычислительном. Видимо, кое-кого это даже задевало: мол, математики должны лишь уточнять расчетами то, что выявлено в реальной действительности. "Такого не может быть!" - говорили, прочитав заявку, наши оппоненты - физики. Но расчеты говорили сами за себя - и физики меняли тон возражений: "Это давно известно!" - и пытались все свести к эффектам давно исследованным (перегревной неустойчивости, скин-эффекту...). Пришлось доказывать, что ими обнаруженный феномен не исчерпывается.
В марте 1967 года Госкомитет СССР по делам изобретений н открытий признал эффект Т-слоя открытием. Некоторое время спустя его независимо друг от друга зарегистрировали три различных научных коллектива в Москве, Новосибирске и Сухуми. А сейчас уже намечается практическое использование Т-слоя.
Представьте: в канал МГД-генератора подается газ, обладающий достаточно низкой температурой, чтобы не разрушить канал, и неспособный эффективно взаимодействовать с магнитным полем, но имеющий достаточный запас тепловой энергии, чтобы совершить полезную работу. В нем создаются высокотемпературные Т-слои. Они-то и взаимодействуют с магнитным полем, в них-то и рождается электрический ток. Быстро проходя по каналу, они не успевают его разогреть. Так мыслится решение каверзной проблемы, от которой начинался путь к открытию.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Своим микрокалькулятором я пользуюсь не часто. Когда он бездействует, я вынимаю из него батарейки и кладу их в холодильник: так они служат гораздо дольше гарантийного срока.
А.КЛЕМАНОВ (г. Курск)].
В ПОИСКАХ ЛУЧШЕЙ ПРОГРАММЫ
Как выбрать наилучшую среди нескольких программ, составленных для решения одной и той же задачи? Этот важный вопрос затрагивается в публикуемом ниже отклике Г.Ионова на статью Р.Васселя "Легкомысленный шах и "Электроника Б3-34" (НИЖ 5/83) и анализируется далее в статье И.Данилова.
Предложенная Р.Васселем программа для подсчета суммы 2**N (N от 0 до 63) и веса зерна, полученного изобретателем шахмат, показалась мне нерациональной, и я составил взамен две новых. Первая реализует тот же алгоритм, что и у Р.Васселя: слагаемые суммы вычисляются возведением в степень. Во второй каждое последующее слагаемое получается из предыдущего умножением на два. Первая из этих программ короче и требует меньшего объема памяти.
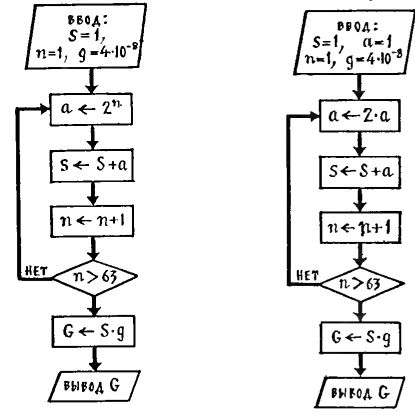

Вторая считает быстрее и с большей точностью. Это и понятно: время экономится за счет того, что на очередном этапе вычислении используются результаты предшествующего этапа, а меньшее количество выполняемых операций - это и меньшая погрешность. К тому же операции сложения и умножения, которые лишь и применяются во второй программе, выполняются в микрокалькуляторе точнее, нежели операция возведения в степень.
Г.ИОНОВ (г.Балашов).
[ ИЗ АННАЛОВ КИБЕРНЕТИКИ
Программа для вычисления чисел Бсрнулли (первая в истории программа для вычислительной машины!) была составлена в июле 1813 года Адой Лавлейс, дочерью поэта Байрона. Ее размышления о будущем вычислительной техники интересны и сегодня. Вот что, в частности, она писала: "Аналитическая машина не претендует на то, чтобы создать что-либо. Она может делать все то, что мы знаем, как приказать ей делать... Она не в состоянии предугадать какие-либо соотношения или истины. Сфера ее деятельности - помочь нам сделать то, с чем мы уже знакомы".
Сегодняшний уровень применения ЭВМ в научных исследованиях позволяет, однако, утверждать, что вычислительная машина способна быть достойным соавтором ученого, первооткрывателя неведомых ранее истин].
ДЛИНА, БЫСТРОТА ИЛИ ТОЧНОСТЬ?
"Все зависит от каждого индивидуума в отдельности. Например, вой тот блондинчик в третьем ряду. Положим, ои играет хорошо... А вон тот брюнет, допустим, хуже... Что же мы видим, товарищи? Мы видим, что блондин играет хорошо, а брюнет играет плохо".
Так говорил Остап Бендер шахматистам-любителям из Васюков. Что такое хорошо и что такое плохо, Остап не пояснил: в шахматном искусстве этот вопрос решается очень не однозначно. В искусстве программирования - тоже.
Допустим, на чей-то взгляд, программа А лучше программы В. Почему? Она короче? Или считает быстрее? Или точнее? Или понятнее написана? Если все сразу, то очень хорошо. Но, увы, нет в мире совершенства. Приходится выбирать.
Критерии оценки зависят от целей и назначения программы и сами меняются со временем. На заре программирования каждая программа рассматривалась как законченное произведение искусства, где "ни убавить, ни прибавить". Такую программу нелегко написать, еще сложнее отлаживать, а о модернизации и говорить нечего. Однако в связи с появлением сложных программных комплексов и необходимостью частых их модернизаций требования простоты ("структурное программирование") вышли на первое место.
Правда, относится это прежде всего к программным модулям, составным частям больших комплексов. При анализе сравнительно небольших программ, к которым, в частности, относятся программы для программируемых микрокалькуляторов, структурность можно не включать в критерии оценки.
О точности, погрешностях и ошибках при расчетах на ЭВМ - разговор особый. Договоримся, что будем сравнивать программы, решающие определенную задачу с точностью не ниже заданной. Таким образом остаются два критерия: длина программы и скорость счета по ней. В той или иной ситуации на первый план может выйти любой из них.
Длина (точнее, объем памяти) - это не только количество ячеек, в которых записана программа, но и количество ячеек, в которых хранятся исходные, промежуточные и выходные данные. Иными словами, имеется в виду вся память, нужная для выполнения программы. Этот параметр важен прежде всего для программ, которые должны находиться в машине одновременно. Да и для одной программы, если она велика, может просто не хватить места в памяти машины. Если задача решается на ЭВМ, работающей в мультипрограммном режиме, то чем меньше она требует памяти, тем больше у нее шансов проскочить быстрее на фоне других задач.
Скорость - это, пожалуй, самый важный критерий для задач, по которым проводятся массовые расчеты. Очень важна она и для задач, решаемых, как говорят, в реальном масштабе времени. Это задачи управления технологическими процессами, информационно-поисковые задачи (например, системы для продажи авиа- и железнодорожных билетов) и т.д.
К сожалению, скорость и длина программы находятся в обратно пропорциональной зависимости. Опытный программист знает: чем меньше машинного времени требует программа, тем она, как правило, длиннее.
Поясним это на паре простых примеров.
Пусть по некоторой программе вычисляется значение функции
y = a sin x + b sin2 x.
Выражение в правой части равенства можно записать так:
y = a sin x + b (sin x )2.
можно так:
z = sin x;
y = a z + b z2.
Вторая запись длиннее, используется дополнительная ячейка памяти (z), но вычисления в этом случае идут в несколько раз быстрее. Дело в том, что вычисление синуса по любой машинной подпрограмме - операция медленная. Во всяком случае, во много раз более медленная, чем считывание числа из ячейки памяти. А во второй записи значение синуса вычисляется лишь раз (z = sin x), далее из памяти извлекается число z. За счет этого достигается большее быстродействие.
Пример того же рода демонстрируется и в письме Г.Ионова. Вторая программа и тут длиннее первой и занимает дополнительную ячейку памяти. И опять скорость во втором случае выше. Это достигается заменой операции возведения в степень операцией более быстрой - умножением. (Обратим внимание, что время выполнения различных операций в ЭВМ неодинаково. Это дает определенный резерв программисту для повышения быстродействия программ).
Вернемся к вопросу, поставленному в заголовке. Какая же программа лучше? Если сравниваются программы для микрокалькулятора и если они решают задачу с точностью не ниже заданной и, наконец, если они не превосходят максимально допустимой длины, то лучше та, счет по которой выполняется быстрее.
И.ДАНИЛОВ.
[ УЗЕЛКИ НА ПАМЯТЬ
Из углов, для которых известны точные значения тригонометрических функций, наиболее употребительны, пожалуй, следующие: 0o, 30o, 45o. 60o, 90o. Если вы забыли эти значения, не отчаивайтесь. Под строчкой из названных углов напишите числа 0, 1, 2, 3, 4. Из каждого числа извлеките квадратный корень и каждый корень поделите на два. Получатся синусы соответствующих углов. Остальные функции найдутся по формулам тригонометрии.
К.ИЛЮШИН (г.Воронеж)].
МЕТОД ИТЕРАЦИЙ
Сначала наберем на клавишах микрокалькулятора какое-то число, большее нуля и меньшее единицы (например, одну вторую), а затем станем раз за разом нажимать на клавишу "синус". Число на табло все уменьшается. Почему? Затем, начав с произвольного аргумента (хотя бы с той же одной второй), станем нажимать клавишу "косинус". На сей раз мы придем к некоторому ненулевому числу. Какому?
Такие вопросы поставлены были в прошлом выпуске рубрики "Человек с микрокалькулятором" (НИЖ 8/83). Читатель И.Ефанов из Звенигорода прислал решения обеих задач вместе с графическим пояснением.
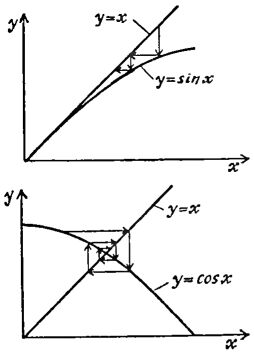
Разберем вторую (первая разбирается аналогично). На графике каждая вертикальная стрелочка, соответствующая n-му шагу вычислительного процесса, означает: вычисляется значение cos х в точке x[n-1]. Горизонтальная: полученное число принимается за новое значение аргумента x[n]. Процесс сходится к корню уравнения x = cos x. Вот как протекает он, если за начальное приближение взять семь десятых:
x0 = 0.70000000
x1 = 0.76484222
x2 = 0.72149167
x11 = 0.73958447
x12 = 0.73874869.
В пределе x = 0.7390851.
Метод, по которому в этих задачах отыскивается корень уравнения типа x = f(x), называется методом итераций. Примеры его применения нетрудно умножить. Еще в Древнем Вавилоне так отыскивались квадратные корни. Пусть требуется извлечь корень из некоторого положительного числа a. Зададимся некоторым начальным приближением x[0], а следующие станем вычислять по формуле
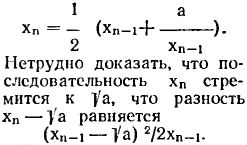
x[n] = 1/2 (х[n-1] + a/x[n-1]).
Нетрудно доказать, что последовательность x[n] стремится к sqr(a), что разность х[п]-sqr(a) равняется
(x[n-1] - sqr(a))**2/(2x[n-1]).
Тот, кому в своей вычислительной практике приходится решать итерационные уравнения x = f(x), обычно предварительно не доказывает и не оценивает сходимость возникающей последовательности (дело это трудоемкое), считая сближение членов последовательности непреложным свидетельством ее сходимости и оценивая разностью соседних членов нх близость к пределу. При таком подходе возможны заблуждения (например, два случайно совпавших приближения полагаются равными корню, хотя на самом деле это не так), не говоря уже о том, что отнюдь не при всякой функции f(x) процесс сходится: скажем, при f(x) = tg(x) он расходится (см. график). Напротив, если производная функции f(x) по абсолютной величине не превышает единицы, процесс сходится.
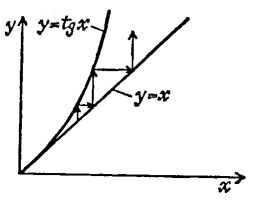
Вид уравнения x = f(x) может показаться искусственным, редко встречающимся на практике. К нему, однако, удается сводить многие задачи поиска корней уравнений ф(x)=0. Сходным образом можно найти решение дифференциального уравнения

y' = f(x, y),
подчиненное условию
y0 = f(x0)
пишут интегральное уравнение, равносильное исходному дифференциальному
y(x) = y0 + Интеграл [X0..X] f(x; y(x))dx,
выбирают y[0](х) - начальное приближение к искомому решению - и применяют метод итераций:
y[n](x) = y0 + Интеграл [X0..X] f(x; y[n-1](x))dx
Ю.ПОБОЖИЙ.

Рис. М.Сагатова.
***
А где про пользу калькуляторов-то? Приписать к статейке про цифровые методы слово "калькулятор", и готово? Они собираются начинать говорить по делу?
НАТУРАЛЬНЫЙ РЯД - КЛАДЕЗЬ ОТКРЫТИЙ
Микрокалькулятор - это ЭВМ в кармане. И хотя по своим возможностям он не сравнится с мощными современными вычислительными машинами, он способен существенно облегчить труд инженера и научного работника, а любителю математики позволит сделать немало интересных открытий.
В этом номере - находки наших читателей, подсказанные работой с микрокалькуляторами; приводятся также отклики на предыдущие публикации.
Математик Николо Тарталья, живший в XVI веке в Италии, известен тем, что построил формулу для решения кубических уравнений. Среди менее знаменитых его находок есть такая: оказывается, числа натурального ряда в порядке их следования можно разбить на пары равных сумм:
1+2=3, 4+5+6=7+8, 9+10+11+12=13+14+15,..
Можно ли иначе разбить натуральный ряд на такие суммы? Можно ли провести подобное разбиение, начиная не с единицы, а с какого-то другого числа?
Чтобы ответить на эти вопросы, запишем в общем виде какую-либо пару равных сумм:
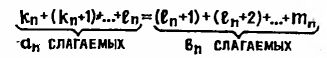
Назовем kn, ln, mn параметрами суммы. Прослеживая с помощью микрокалькулятора то разбиение натурального ряда, которое произвел Тарталья, можно в порядке гипотезы сформулировать некоторые соотношения, связывающие эти параметры. Например: разность an-bn есть величина постоянная. Назовем эту разность характеристикой и обозначим ее Q. По свойству арифметической прогрессии получаем: Q=(2*ln+1)-kn-mn.
Далее, замечаем: an=bn+i и kn+i=mn+l.
После этого можно установить следующие три зависимости между параметрами пар:
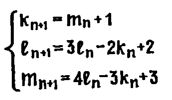
Полученная система из трех уравнений, где индекс n - переменный, разворачивается в цепочку систем, причем неизвестные каждой последующей тройки уравнений входят также и в предыдущую. Такие уравнения и системы называются возвратными. Их решение заключается в выражении неизвестных с произвольным индексом n через неизвестные с единичным индексом k1, l1, m1.
Способы решения подобных систем приводятся в книге А.А.Маркова "Исчисление конечных разностей" (2-е изд., Одесса, 1910г.).
Ответ можно записать в виде:
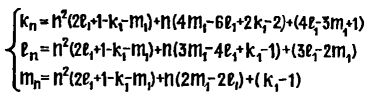
Найденное решение позволяет сделать вывод: чтобы построить новый ряд парных сумм, достаточно отыскать первую пару сумм, не совпадающую с 1+2=3. Как же ее искать?
Возьмем произвольную пару сумм, начинающуюся с некоторого числа k, и добавим слева все целые положительные числа, меньшие k, а также равные им по абсолютной величине отрицательные числа и нуль. Равенство от этого не нарушится:
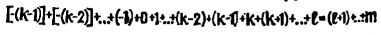
На основе расширенной описанным способом пары можно построить новый ряд парных сумм.
Любопытно, что первая пара сумм 1+2=3 из уже известного нам разбиения натурального ряда, для которого Q=1, расширяется в новую пару добавлением одного лишь нуля: 0+1+2=3. В новом равенстве Q уже равна двум. Новый ряд парных сумм отсюда получается таким:
0+1+2=3, 4+5+6+7+8=9+10+11, 12+13+14+15+16+17+18=19+20+21+22+23.
Аналогично можем получить новый ряд из пары 4+5+6=7+8:
(-3)+(-2)+(-1)+0+1+2+3+4+5+6=7+8, 9+10+...+25+26=27+28+...+35+36, 37+38+...+61+62=63+...+79+80 и так далее; здесь Q=8.
Итак, от одной известной пары равных сумм мы пришли к бесчисленному множеству бесконечных рядов таких пар.
Назовем базовой такую пару, для которой нельзя построить предыдущую с той же характеристикой. Это нельзя сделать, например, для пары 1+2=3, а для пары 4+5+6=7+8 можно.
Существуют ли еще базовые пары, кроме 1+2=3? Полагаю, что любителям математических головоломок будет небезынтересно подумать над этим вопросом и микрокалькулятор будет им в этом хорошим подспорьем.
В.СТОЛЯР (Москва).
СНАЧАЛА ПОДОЗРЕВАЛИ ОШИБКУ...
... В Государственном реестре Госкомитета СССР по делам изобретений и открытий под номером 55 значится открытие нового физического эффекта - Т-слоя. О том, как было сделано открытие, рассказывает один из его авторов, доктор физико-математических наук Ю.П.ПОПОВ, в ту пору аспирант Московского физико-технического института.
Рассказ об открытии, идею которого "подсказала" ЭВМ в ходе вычислительного эксперимента, вероятно, будет интересен тем, кто мечтает об открытии, экспериментируя над числами с помощью карманной ЭВМ - микрокалькулятора.
Это было в конце 60-х годов, когда оживленно обсуждалась идея МГД генератора. (Буквы МГД в его названии расшифровываются как "магнитногидродинамический": это прилагательное употребляют, когда говорят о течениях плазмы в магнитном поле).
Известно, что если проводник движется в магнитном поле, пересекая магнитные силовые линии, то в нем возникает электродвижущая сила. При этом проводник не обязательно должен быть твердым, металлическим. Это может быть проводящий газ - плазма. Пусть в канале, по которому она течет, магнитные силовые линии направлены сверху вниз. Если боковые стенки канала снабдить электродами, с них можно снимать ток, возникающий в плазме.
Даже из этого предельно грубого описания понятны выгоды такого генератора. В его конструкции нет движущихся деталей (как в турбогенераторе), за трение между ноторыми приходилось бы расплачиваться уменьшением кпд.
Такой генератор тем эффективнее, чем выше проводимость газа. А она растет с температурой. Но температуру нельзя наращивать беспредельно: тогда ее не выдержит никакой канал. С другой стороны, если она упадет ниже некоторого порогового значения, плазма перестанет взаимодействовать с магнитным полем.
Как быть в столь противоречивой ситуации?
Наш научный коллектив тоже участвовал в исследованиях, связанных с разработкой МГД-генератора. Нашим оружием был вычислительный эксперимент (НиЖ 2/79).

Один из процессов, которые рассчитывались на ЭВМ, мыслился так. В пространство между двумя проводящими дисками по осевому каналу впрыскивается порция плотной горячей плазмы, затем она растекается между дисками в радиальных направлениях. Схематизируя явление, можно представить, что в некоторый момент сгусток плазмы приобрел конфигурацию цилиндра (на рисунке очерчен пунктиром), а тот далее расширяется в пустоту. По мере расширения плазма будет остывать, и картина распределения температуры в ее объеме, вероятно, станет изменяться так, как показано на графике.

Начали счет. Его результаты поначалу вполне согласовывались с ожиданиями. И вдруг на температурном графике, на самом его хвосте появился небольшой всплеск. Он рос и рос.

Первая мысль была такая: может быть, это дефект вычислительного алгоритма, разностной схемы, по которой ведется счет? Стали совершенствовать ее, чтобы устранить ошибку. Всплеск упрямо появлялся все снова и снова. И чем аккуратнее мы вели расчеты, тем отчетливее вырисовывалась все та же странная картина. И в конце концов стало ясно, что перед нами не случайная погрешность вычислений, а математическая модель реального физического явления.
Это был интереснейший момент исследования: круто изменился наш взгляд на происходящее, резко поменялась психология наших действий. Теперь мы старались доказать, что обнаруженный нами феномен должен возникать непременно, выясняли условия его появления.

Проводимость плазмы по мере роста температуры вначале растет по экспоненциальному закону, затем график этой зависимости описывается степенной функцией с показателем 3/2. Диапазон наиболее крутого роста проводимости приходится на довольно низкие температуры (порядка пороговой), но именно в этом диапазоне разогрев плазмы протекает лавинообразно: небольшой прирост температуры вызывает резкий скачок проводимости, текущий по плазме ток усиливается, обусловленное им джоулево тепло разогревает плазму сильнее, ее проводимость вновь прирастает... Высокая температура, таким образом, подхлестывает сама себя, развивается, как говорят радиотехники, в режиме с положительной обратной связью.
Вникая в природу необычного феномена, мы вводили в расчеты все более тонкие детали, уточняющие физическую картину явления,- учли излучение, поточнее задали график роста проводимости с температурой. Результаты счета говорили, что в некоторых вариантах процесса эти тонкости могут подавить развитие эффекта, а в некоторых - лишь стабилизируют его рост.
Правда, говорить о новом эффекте, располагал расчетами лишь одного довольно специфического процесса, было рановато. Хотелось понять, насколько распространено необычное явление, обнаружить его в других магнитогидродинамических процессах. Примеры такого рода нашлись.
И тогда была подана заявка на открытие. В плазме, взаимодействующей с магнитным полем, говорилось в заявке, при определенных условиях могут возникать устойчивые зоны относительно высокой температуры. Температурные, токовые слои или кратко Т-слои - так были названы эти зоны.
Заявка вызвала бурные дебаты среди экспертов. Еще бы: эффект еще никем не наблюдался в физическом эксперименте, он обнаружил себя лишь в расчетах, в эксперименте вычислительном. Видимо, кое-кого это даже задевало: мол, математики должны лишь уточнять расчетами то, что выявлено в реальной действительности. "Такого не может быть!" - говорили, прочитав заявку, наши оппоненты - физики. Но расчеты говорили сами за себя - и физики меняли тон возражений: "Это давно известно!" - и пытались все свести к эффектам давно исследованным (перегревной неустойчивости, скин-эффекту...). Пришлось доказывать, что ими обнаруженный феномен не исчерпывается.
В марте 1967 года Госкомитет СССР по делам изобретений н открытий признал эффект Т-слоя открытием. Некоторое время спустя его независимо друг от друга зарегистрировали три различных научных коллектива в Москве, Новосибирске и Сухуми. А сейчас уже намечается практическое использование Т-слоя.
Представьте: в канал МГД-генератора подается газ, обладающий достаточно низкой температурой, чтобы не разрушить канал, и неспособный эффективно взаимодействовать с магнитным полем, но имеющий достаточный запас тепловой энергии, чтобы совершить полезную работу. В нем создаются высокотемпературные Т-слои. Они-то и взаимодействуют с магнитным полем, в них-то и рождается электрический ток. Быстро проходя по каналу, они не успевают его разогреть. Так мыслится решение каверзной проблемы, от которой начинался путь к открытию.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Своим микрокалькулятором я пользуюсь не часто. Когда он бездействует, я вынимаю из него батарейки и кладу их в холодильник: так они служат гораздо дольше гарантийного срока.
А.КЛЕМАНОВ (г. Курск)].
В ПОИСКАХ ЛУЧШЕЙ ПРОГРАММЫ
Как выбрать наилучшую среди нескольких программ, составленных для решения одной и той же задачи? Этот важный вопрос затрагивается в публикуемом ниже отклике Г.Ионова на статью Р.Васселя "Легкомысленный шах и "Электроника Б3-34" (НИЖ 5/83) и анализируется далее в статье И.Данилова.
Предложенная Р.Васселем программа для подсчета суммы 2**N (N от 0 до 63) и веса зерна, полученного изобретателем шахмат, показалась мне нерациональной, и я составил взамен две новых. Первая реализует тот же алгоритм, что и у Р.Васселя: слагаемые суммы вычисляются возведением в степень. Во второй каждое последующее слагаемое получается из предыдущего умножением на два. Первая из этих программ короче и требует меньшего объема памяти.


Вторая считает быстрее и с большей точностью. Это и понятно: время экономится за счет того, что на очередном этапе вычислении используются результаты предшествующего этапа, а меньшее количество выполняемых операций - это и меньшая погрешность. К тому же операции сложения и умножения, которые лишь и применяются во второй программе, выполняются в микрокалькуляторе точнее, нежели операция возведения в степень.
Г.ИОНОВ (г.Балашов).
[ ИЗ АННАЛОВ КИБЕРНЕТИКИ
Программа для вычисления чисел Бсрнулли (первая в истории программа для вычислительной машины!) была составлена в июле 1813 года Адой Лавлейс, дочерью поэта Байрона. Ее размышления о будущем вычислительной техники интересны и сегодня. Вот что, в частности, она писала: "Аналитическая машина не претендует на то, чтобы создать что-либо. Она может делать все то, что мы знаем, как приказать ей делать... Она не в состоянии предугадать какие-либо соотношения или истины. Сфера ее деятельности - помочь нам сделать то, с чем мы уже знакомы".
Сегодняшний уровень применения ЭВМ в научных исследованиях позволяет, однако, утверждать, что вычислительная машина способна быть достойным соавтором ученого, первооткрывателя неведомых ранее истин].
ДЛИНА, БЫСТРОТА ИЛИ ТОЧНОСТЬ?
"Все зависит от каждого индивидуума в отдельности. Например, вой тот блондинчик в третьем ряду. Положим, ои играет хорошо... А вон тот брюнет, допустим, хуже... Что же мы видим, товарищи? Мы видим, что блондин играет хорошо, а брюнет играет плохо".
Так говорил Остап Бендер шахматистам-любителям из Васюков. Что такое хорошо и что такое плохо, Остап не пояснил: в шахматном искусстве этот вопрос решается очень не однозначно. В искусстве программирования - тоже.
Допустим, на чей-то взгляд, программа А лучше программы В. Почему? Она короче? Или считает быстрее? Или точнее? Или понятнее написана? Если все сразу, то очень хорошо. Но, увы, нет в мире совершенства. Приходится выбирать.
Критерии оценки зависят от целей и назначения программы и сами меняются со временем. На заре программирования каждая программа рассматривалась как законченное произведение искусства, где "ни убавить, ни прибавить". Такую программу нелегко написать, еще сложнее отлаживать, а о модернизации и говорить нечего. Однако в связи с появлением сложных программных комплексов и необходимостью частых их модернизаций требования простоты ("структурное программирование") вышли на первое место.
Правда, относится это прежде всего к программным модулям, составным частям больших комплексов. При анализе сравнительно небольших программ, к которым, в частности, относятся программы для программируемых микрокалькуляторов, структурность можно не включать в критерии оценки.
О точности, погрешностях и ошибках при расчетах на ЭВМ - разговор особый. Договоримся, что будем сравнивать программы, решающие определенную задачу с точностью не ниже заданной. Таким образом остаются два критерия: длина программы и скорость счета по ней. В той или иной ситуации на первый план может выйти любой из них.
Длина (точнее, объем памяти) - это не только количество ячеек, в которых записана программа, но и количество ячеек, в которых хранятся исходные, промежуточные и выходные данные. Иными словами, имеется в виду вся память, нужная для выполнения программы. Этот параметр важен прежде всего для программ, которые должны находиться в машине одновременно. Да и для одной программы, если она велика, может просто не хватить места в памяти машины. Если задача решается на ЭВМ, работающей в мультипрограммном режиме, то чем меньше она требует памяти, тем больше у нее шансов проскочить быстрее на фоне других задач.
Скорость - это, пожалуй, самый важный критерий для задач, по которым проводятся массовые расчеты. Очень важна она и для задач, решаемых, как говорят, в реальном масштабе времени. Это задачи управления технологическими процессами, информационно-поисковые задачи (например, системы для продажи авиа- и железнодорожных билетов) и т.д.
К сожалению, скорость и длина программы находятся в обратно пропорциональной зависимости. Опытный программист знает: чем меньше машинного времени требует программа, тем она, как правило, длиннее.
Поясним это на паре простых примеров.
Пусть по некоторой программе вычисляется значение функции
y = a sin x + b sin2 x.
Выражение в правой части равенства можно записать так:
y = a sin x + b (sin x )2.
можно так:
z = sin x;
y = a z + b z2.
Вторая запись длиннее, используется дополнительная ячейка памяти (z), но вычисления в этом случае идут в несколько раз быстрее. Дело в том, что вычисление синуса по любой машинной подпрограмме - операция медленная. Во всяком случае, во много раз более медленная, чем считывание числа из ячейки памяти. А во второй записи значение синуса вычисляется лишь раз (z = sin x), далее из памяти извлекается число z. За счет этого достигается большее быстродействие.
Пример того же рода демонстрируется и в письме Г.Ионова. Вторая программа и тут длиннее первой и занимает дополнительную ячейку памяти. И опять скорость во втором случае выше. Это достигается заменой операции возведения в степень операцией более быстрой - умножением. (Обратим внимание, что время выполнения различных операций в ЭВМ неодинаково. Это дает определенный резерв программисту для повышения быстродействия программ).
Вернемся к вопросу, поставленному в заголовке. Какая же программа лучше? Если сравниваются программы для микрокалькулятора и если они решают задачу с точностью не ниже заданной и, наконец, если они не превосходят максимально допустимой длины, то лучше та, счет по которой выполняется быстрее.
И.ДАНИЛОВ.
[ УЗЕЛКИ НА ПАМЯТЬ
Из углов, для которых известны точные значения тригонометрических функций, наиболее употребительны, пожалуй, следующие: 0o, 30o, 45o. 60o, 90o. Если вы забыли эти значения, не отчаивайтесь. Под строчкой из названных углов напишите числа 0, 1, 2, 3, 4. Из каждого числа извлеките квадратный корень и каждый корень поделите на два. Получатся синусы соответствующих углов. Остальные функции найдутся по формулам тригонометрии.
К.ИЛЮШИН (г.Воронеж)].
МЕТОД ИТЕРАЦИЙ
Сначала наберем на клавишах микрокалькулятора какое-то число, большее нуля и меньшее единицы (например, одну вторую), а затем станем раз за разом нажимать на клавишу "синус". Число на табло все уменьшается. Почему? Затем, начав с произвольного аргумента (хотя бы с той же одной второй), станем нажимать клавишу "косинус". На сей раз мы придем к некоторому ненулевому числу. Какому?
Такие вопросы поставлены были в прошлом выпуске рубрики "Человек с микрокалькулятором" (НИЖ 8/83). Читатель И.Ефанов из Звенигорода прислал решения обеих задач вместе с графическим пояснением.

Разберем вторую (первая разбирается аналогично). На графике каждая вертикальная стрелочка, соответствующая n-му шагу вычислительного процесса, означает: вычисляется значение cos х в точке x[n-1]. Горизонтальная: полученное число принимается за новое значение аргумента x[n]. Процесс сходится к корню уравнения x = cos x. Вот как протекает он, если за начальное приближение взять семь десятых:
x0 = 0.70000000
x1 = 0.76484222
x2 = 0.72149167
x11 = 0.73958447
x12 = 0.73874869.
В пределе x = 0.7390851.
Метод, по которому в этих задачах отыскивается корень уравнения типа x = f(x), называется методом итераций. Примеры его применения нетрудно умножить. Еще в Древнем Вавилоне так отыскивались квадратные корни. Пусть требуется извлечь корень из некоторого положительного числа a. Зададимся некоторым начальным приближением x[0], а следующие станем вычислять по формуле
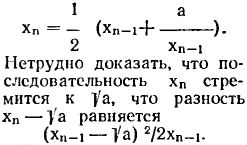
x[n] = 1/2 (х[n-1] + a/x[n-1]).
Нетрудно доказать, что последовательность x[n] стремится к sqr(a), что разность х[п]-sqr(a) равняется
(x[n-1] - sqr(a))**2/(2x[n-1]).
Тот, кому в своей вычислительной практике приходится решать итерационные уравнения x = f(x), обычно предварительно не доказывает и не оценивает сходимость возникающей последовательности (дело это трудоемкое), считая сближение членов последовательности непреложным свидетельством ее сходимости и оценивая разностью соседних членов нх близость к пределу. При таком подходе возможны заблуждения (например, два случайно совпавших приближения полагаются равными корню, хотя на самом деле это не так), не говоря уже о том, что отнюдь не при всякой функции f(x) процесс сходится: скажем, при f(x) = tg(x) он расходится (см. график). Напротив, если производная функции f(x) по абсолютной величине не превышает единицы, процесс сходится.

Вид уравнения x = f(x) может показаться искусственным, редко встречающимся на практике. К нему, однако, удается сводить многие задачи поиска корней уравнений ф(x)=0. Сходным образом можно найти решение дифференциального уравнения

y' = f(x, y),
подчиненное условию
y0 = f(x0)
пишут интегральное уравнение, равносильное исходному дифференциальному
y(x) = y0 + Интеграл [X0..X] f(x; y(x))dx,
выбирают y[0](х) - начальное приближение к искомому решению - и применяют метод итераций:
y[n](x) = y0 + Интеграл [X0..X] f(x; y[n-1](x))dx
Ю.ПОБОЖИЙ.

Рис. М.Сагатова.
***
А где про пользу калькуляторов-то? Приписать к статейке про цифровые методы слово "калькулятор", и готово? Они собираются начинать говорить по делу?

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
12/83
Этот выпуск рубрики "Человек с микрокалькулятором", как и прежние, составлен на основе читательских писем.
Читатель С.Морозов из Краснодара сообщает в своем письме неожиданные факты: оказывается, при расчетах на микрокалькуляторе могут не выполняться классические законы математики: переместительный, сочетательный... Примеры, приводимые в письме, позволяют легко вскрыть источник парадоксов: все дело в округлении чисел, производимом по ходу вычислений.
Эти примеры интересны не только сами по себе - они удобны для иллюстрации некоторых важных вопросов, связанных с погрешностями вычислений. Интересные соображения на эту тему высказал в своем письме читатель И.Вязовский. Его мы и попросили дать обстоятельный комментарий сообщению С.Морозова.
ОТ ПЕРЕМЕНЫ МЕСТ...
Волга впадает в Каспийское море. Все тела падают на Землю с одинаковым ускорением. От перемены мест слагаемых сумма не меняется.
Все это прописные истины. Но всегда ли они верны? Что касается Волги, то тут сомнений нет. С переменой мест слагаемых, дело сложнее, если складываются они на вычислительной машине.
Предположим, машина оперирует четырьмя десятичными разрядами и что значение первого отбрасываемого разряда (в нашей машине пятого) учитывается при округлении последнего значащего. Сложим на нашей ЭВМ пять чисел подряд, каждый раз округляя результат:
1.326e1 + 4.624 + 5.432e-1 + 4.365e-2 + 3.416e-2
Получим 18.48. Теперь изменим порядок слагаемых: будем складывать их с конца. Получим 18.51. Сумма изменилась!
Парадоксы и с другими законами. Распределительный закон, например, тоже не выполняется.
4*(2.873-2.872) = 0.004
4*2.873 - 4*2.872 = 0
Еще пример. Сложим на нашей ЭВМ четыре числа:
6.824 + 6.778 + 6.793 + 6.814 = 27.20
А теперь будем складывать те же числа, объединяя попарно:
(6.824+6.778 ) + (6.793+6.814) = 27.21
Результаты не совпадают!
Для любой ЭВМ существуют наибольшее и наименьшее по абсолютной величине числа. Это оборачивает ся новыми парадоксами. Например, a*b*c != c*a*b. Каково? Покажем это на примере, допустив, что максимальное число в нашей ЭВМ - это 1e16.
Вычисляем 2e9 * 5e-8 * 6.5e6 и получаем: 6.5e8.
А теперь 6.5e6 * 2e9 * 5e-8. Получаем... Ничего не получаем. Первое умножение не может быть выполнено, так как результат его (1.3e16) представляет число, большее допустимого предела. "Авост",- говорят в таких случаях те, кто работает на "больших" ЭВМ
[Сейчас трудно выяснить, как раскрывалась эта аббревиатура первоначально. Большинство программистов интерпретирует ее как "аварийный останов". В этом есть доля истины - в программе произошла авария. Но, с точки зрения обслуживающего персонала ЭВМ. это "автоматический останов". Ведь с машиной-то все в порядке!].
Микрокалькулятор на такую ситуацию реагирует малоприятным для программиста сообщением: ERROR (ошибка).
С подобными парадоксами всегда приходится считаться, работая на вычислительных машинах - и на мощных ЭВМ и на крошечных микрокалькуляторах.
С.МОРОЗОВ (г.Краснодар).
СЧЕТ И ТОЧНОСТЬ
Различают погрешности абсолютные и относительные. Абсолютная погрешность - это разность между истинным и измеренным значением величины. Если ее поделить на саму величину, то получим относительную погрешность. Понятно, что одинаковым абсолютным погрешностям не всегда соответствуют одинаковые относительные - и наоборот.
Точно так же, как несовершенство, точнее, неидеальность измерительных приборов приводит к ошибкам измерений, неидеальность вычислительных машин приводит к ошибкам вычислений. Дело осложняется тем, что результат всякого вычисления заранее неизвестен. Потому и оценить ошибку трудно.
Существуют различные способы оценок. Возьмем для примера задачу нахождения определенного интеграла. Решать ее можно по-разному, но всякий раз это связано с разбиением промежутка интегрирования на небольшие, как правило, одинаковые отрезки, длина которых называется шагом интегрирования. Задавшись некоторым разбиением, вычисляют интеграл; потом дробят промежуток мельче (скажем, в два раза), повторяют ту же вычислительную процедуру с новым шагом и получают новый результат - а разность между ним и предыдущим принимают за абсолютную ошибку вычисления. (Ясно, что прием небезупречен).
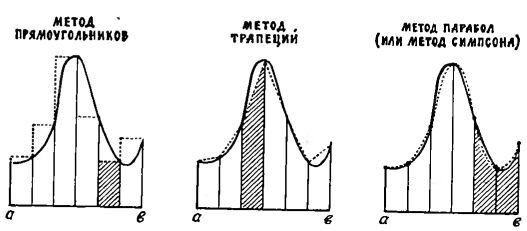
Различные методы аппроксимации интегрируемых функций.
При расчетах на ЭВМ ошибки бывают двух типов: ошибки ограничения и ошибки округления. Первые определяются используемыми алгоритмами. Их причина, грубо говоря,- замена бесконечного конечным. Например, отыскивая определенный интеграл от некоторой функции, то есть площадь, очерченную графиком функции, мы заменяем этот график конечной последовательностью отрезков прямых или парабол. Их столько, сколько отрезков, на которые разбит промежуток интегрирования. Между тем определение интеграла требует дробить этот промежуток до бесконечности, устремляя шаг интегрирования к нулю. Производные, то есть отношения приращений функции к бесконечно малым приращениям аргумента, в численных расчетах рассматриваются при конечных приращениях. Ряды, суммы бесконечного числа членов заменяются конечными суммами начальных слагаемых.
В принципе такого рода ошибки можно сделать сколь угодно малыми. Чем мельче шаг интегрирования, тем ближе вычисляемая площадь к истинной. Чем меньше интервал, на котором вычисляется приращение функции, подставляемое далее в приближенную формулу для производной, тем точнее эта формула позволит вычислить значение производной. Чем больше взято членов ряда, тем точнее будет определена его сумма.
Другой тип ошибок - ошибки округления. Возникают они из-за того, что каждая машина оперирует конечным количеством разрядов в представлении десятичных чисел, говоря образно, "держит в голове" ограниченное число знаков после запятой. Для ЭВМ каждого типа это число свое, но оно всегда конечно. Чтобы втиснуть числа в это прокрустово ложе, их приходится округлять при каждом акте вычисления.
Но... не таится ли здесь парадокс? Разбирая задачу интегрирования функции, мы отмечали: чем меньше шаг, тем меньше ошибка отбрасывания. Вместе с тем, чем меньше шаг, тем на большее число отрезков дробится промежуток интегрирования, тем больше операций необходимо выполнить, вычисляя интеграл, тем больше ошибка округления. Выходит, и большой шаг плохо и слишком маленький не очень хорошо!
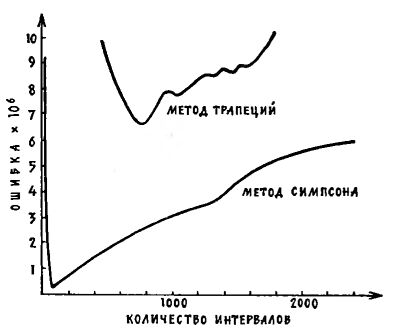
Зависимость суммарной ошибки (ограничения и округления) от количества интервалов при интегрировании синуса по полупериоду, выполненном по методам трапеций и парабол (Симпсона). Как подсказывают графики, при численном нахождении интеграла существует оптимальное количество интервалов, на которые разбивается промежуток интегрирования.
На практике не стремятся делать шаги разбиения слишком малыми, так как это не только приводит к возрастанию ошибок округления, но и резко увеличивает время счета, а часто еще и объем используемой памяти. Программист стремится обычно выбрать такой алгоритм, который позволил бы получить наивысшую точность при ограниченном объеме вычислительной работы. Часто точность вычислений можно увеличивать довольно простыми приемами.
Рассмотрим некоторые из них, относящиеся к самой простой операции - сложению. Если слагаемые x1 и x2 заданы с относительными погрешностями e1 и e2 соответственно, а относительная ошибка округления равна r, то относительная погрешность суммы равна
ey/y = x1e1/(x1+x2) + x2e2/(x1+x2) + r
Если слагаемые x1 и x2 заданы точно, то остается лишь относительная ошибка округления r, а абсолютная погрешность, с которой вычисляется сумма, согласно формуле, равна (x1+x2)r. Будем складывать последователыю четыре числа
y = (((x1 + x2) + x3) + x4).
Поскольку при каждом суммировании набегает ошибка округления, то аналогично предыдущему получим, что абсолютная погрешность итоговой суммы равна (3x1 + 3x2 + 2x3 + x4)r.
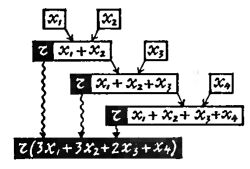
Значения слагаемых входят в это выражение с разными коэффициентами. Если x1 по абсолютной величине намного превосходит остальные слагаемые, то можно приближенно считать ey = 3x1r. Поменяем местами слагаемые, поставив самое большое в конце. Ошибка в этом случае будет ey = x1r, то есть в три раза меньше, чем раньше! Вот и первый простой рецепт по увеличению точности: при сложении чисел разных порядков начинайте с малых и заканчивайте большими.
Теперь положим, что числа близки друг другу по величине. Только что данный рецепт здесь не годится. Попробуем складывать числа попарно:
y = ((x1 + x2) + (x3 + x4)).
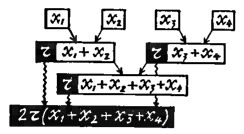
Полная ошибка, подсчитанная прежним приемом, такова: ey =2(x1 + x2 + x3 + x4)r. В предположении, что все числа близки друг другу, можно положить каждое равным одной величине x. Что же получается? При последовательном сложении ошибка составит 9xr, а при попарном - 8xr, то есть будет несколько меньше. Если же слагаемых не четыре, а больше, ошибка уменьшится сильнее. Итак, второй рецепт: при сложении примерно одинаковых чисел точность возрастает, если складывать их группами.
Опытный программист, как правило, знает множество приемов, увеличивающих точность счета. Но знает он и другое: точность не самоцель. Главное - получить требуемый результат с точностью не ниже заданной за возможно более короткое время. Это и должно быть путеводной звездой при составлении любых программ.
И.ВЯЗОВСКИЙ (г.Люберцы).
["... Для прикладных вопросов нет надобности производить вычисления... с совершенною точностью... лишь бы была уверенность, что происходящая от этого погрешность не превышает тех пределов, которые в данном вопросе допускаются... В приложениях обыкновенно интересен не процесс вычисления, а результат его: поэтому и стараются получить этот результат при наименьшей затрате труда и времени".
А.Н.КРЫЛОВ]
["Недостатки математического образования с наибольшей отчетливостью проявляются в чрезмерной точности численных расчетов".
К.Ф.ГАУСС]
ВНИМАНИЕ КОНКУРС
Каждая программа - это своего рода художественное произведение. И трудно ожидать, что два программиста написали бы одинаковые программы. Это все равно, как если бы два поэта написали одинаковые стихи на заданную тему. А какое стихотворение лучше, решает конкурс.
С предложением объявлять конкурсы на лучшую программу для решения той или иной задачи на микрокалькуляторе обращаются к нам читатели С.Конин из Ленинграда, Л.Яковлев из Старой Русы, А.Киба из Ростова-на-Дону, А.Лернер из Москвы и другие. Редакция поддерживает это предложение, надеясь, что подобные конкурсы позволят не только выявить наиболее искусных программистов, но и наладить между участниками обмен опытом.
Для конкурса предлагается две задачи:
1) поиск простых чисел и их естественной последовательности: 1, 2, 3, 5, 7, 11 и т.д.;
2) выделение целой части числа.
Решение каждой задачи должно содержать, кроме программы, словесное описание алгоритма и его блок-схему. Можно послать решение одной задачи. Срок отправки - до 1.02.84.
Наиболее интересные решения будут опубликованы.
ЕЩЕ ОДНА ЦИФРА
О резервах микрокалькулятора, позволяющих добавлять к результатам некоторых вычислений несколько цифр сверх тех, что высвечиваются на индикаторе, пишет читатель С.Мельников. Его письмо комментирует инженер Е.Кузнецов - один из тех, кто разрабатывает отечественные микрокалькуляторы.
Если нажать клавишу "пи" микрокалькулятора "Электроника Б3-38", на световом табло появятся восемь цифр: 3.1415926. Но все ли это, что может дать микрокалькулятор? Я вычел из пи число 3.1415926, набрав его на клавиатуре, и получил 5e-8. Таким образом, из микрокалькулятора извлечена еще одна цифра!
Вычислим теперь e**1 и из полученного результата вычтем 2.7182818 - то есть то, что высветилось на индикаторе. Разность равна 3e-8. В точном представлении числа e после восьмой цифры следует 28... Значит, полученная нами девятая цифра верна лишь округленно.
Но самое главное - она имеется в микрокалькуляторе и ее можно оттуда извлечь!
Знание этого факта позволяет получать на 8-разрядной "Электронике Б3-38" точные произведения пятизначных чисел. Например, 78979*55555. Микрокалькулятор дает 4.38767e9. Сверх этих шести цифр в памяти микрокалькулятора существуют еще несколько. Извлечем их описанным способом, вычитая из результата умножения число, появившееся на индикаторе. Получим 8350. Третья цифра разности, очевидно, округлена, а последнюю нетрудно уточнить, перемножив последние цифры сомножителей. 9 и 5, - это пятерка. Итак, искомое произведение равно 4.387678345e9.
Еще пример: 88888**2 = 7.90107e9. Такой ответ читаем на индикаторе. Недостающее получим привычным вычитанием: 6540, последнюю цифру уточним перемножением последних цифр сомножителей: 4. Искомое произведение: 7.901076544e9.
С.МЕЛЬНИКОВ.
(г.Буденновск Ставропольского края).
Рис. М.САГАТОВА
(г.Ташкент).
ИЗБЫТОЧНЫЕ РАЗРЯДЫ НЕОБХОДИМЫ
Суть дела, затронутого в письме С.Мельникова, разберем сначала на простом примере. Предположим, что требуется перемножить три числа: 1.13*1.14*1.15. Все эти числа - трехзначные. Условимся выразить искомое произведение также трехзначным числом. Тому же условию подчиним и промежуточные результаты вычислений. Таким результатом в нашем примере будет произведение первых двух сомножителей. Точное его значение 1.2882. Согласно принятому условию округлим его до сотых долей единицы.
Классическое правило округления, с которым знакомят школьников, таково: если в разряде, следующем за последним из сохраняемых, стоит число, меньшее пяти, то число в последнем сохраняемом разряде остается неизменным; в противном случае к нему прибавляют единицу. В простейших микрокалькуляторах применяется более простой способ округления: сохраняемые разряды остаются неизменными, каким бы ни было содержимое отбрасываемых.
Так поступим и мы: примем произведение первых двух сомножителей равным 1.28. Умножая это число на заключительный сомножитель и обрезая результат прежним приемом, получаем в итоге 1.47.
Вычислим теперь для сравнения точное произведение наших трех сомножителей: 1.48143. Округленное до трех значащих цифр любым из вышеописанных способов, оно равно 1.48. То есть не совпадает с тем, что мы получили ранее.
Итак, если по ходу промежуточных выкладок сохранять в получающихся числах ровно столько знаков, сколько требуется в ответе, нельзя гарантировать, что все значащие цифры ответа окажутся верными.
Приняв во внимание это соображение, перемножим вновь наши три сомножителя. Но на сей раз оставим в промежуточном результате не три, а четыре значащих цифры: 1.288. Умножим это число на 1.15 и получим 1.4812; после отбрасывания лишних знаков оно будет таким же, что было получено округлением точного результата.
Итак, округляя числа простым отбрасыванием лишних разрядов, мы сможем гарантировать безошибочность всех значащих цифр ответа, если в промежуточных выкладках станем удерживать больше разрядов, нежели требуется иметь в ответе.
В калькуляторах различных марок число избыточных разрядов неодинаково, но, как правило, невелико - от одного до трех. Этого бывает недостаточно, чтобы гарантировать точность всех выводимых на индикатор цифр при выполнении каждой из процедур, обозначенных на клавишах микрокалькулятора. Для каждой из них в инструкции, приложенной к калькулятору, указано, сколько верных знаков гарантированно содержит ее результат, высвечиваемый на индикаторе.
(Напомним, что все значащие цифры результата выводятся лишь в системах индикации с плавающей запятой - это обеспечивает принципиально более высокую точность, чем при фиксированной запятой).
Вспомним теперь про классический способ округления и применим его к промежуточным результатам разобранного вначале примера с перемножением трех чисел. Точный ответ получается здесь без использования избыточных разрядов: 1.13*1.14 = 1.29; 1.29*1.15 = 1.48.
Отечественные микрокалькуляторы "Электроника Б3-38" и "Электроника МК-51" оперируют одним-двумя (в зависимости от характера конкретного вычисления) избыточными разрядами, причем последний из них округляется по описанной классической методике. Любая вычислительная процедура, выполняемая на этих микрокалькуляторах, дает ответ, который отличается от точного лишь на плюс-минус единицу в последнем из выводимых на индикатор, восьмом разряде. Обеспечивается это, в частности, еще и тем, что элементарные функции вычисляются здесь новым способом "цифра за цифрой". Микрокалькулятор "Электроника С3-15" позволяет пользователю сокращать число выводимых на индикатор разрядов; при этом содержимое последнего из них округляется по классическому правилу.
Е.КУЗНЕЦОВ
СТАТИСТИКА НА МИКРОКАЛЬКУЛЯТОРЕ
Говорят, статистика знает все. Сегодня эту поговорку можно было бы переиначить: статистику знают все. Действительно, ее нынче используют инженеры и агрономы, медики и геологи...
Наиболее широко используемые статистические параметры - это среднее значение величины, среднеквадратическое отклонение и коэффициент вариации. Для набора n величин xi они вычисляются по формулам:
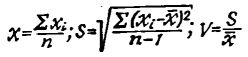
Среднеквадратическое отклонение s характеризует абсолютный разброс величины вокруг среднего значения x, а коэффициент вариации v, величина безразмерная, дает относительное отклонение, степень изменчивости процесса. По коэффициенту вариации можно судить об устойчивости и однообразии протекающих процессов, о состоянии наладки оборудования и т.п. Количественные характеристики изменчивости имеют большое экономическое значение. Известно, например, что при производстве бетона уменьшение коэффициента вариации до 5 процентов вместо исходных 13 снижает расход цемента на 10-15 процентов: чем однороднее смесь, тем меньше цемента нужно для достижения требуемой прочности. Аналогичные примеры можно привести и из других областей техники.
Конечно, статистические расчеты лучше всего проводить на ЭВМ. Но, к сожалению, они имеются еще не везде. Поэтому часто вычисления проводят вручную при помощи счетных машин. Запись в таблицы, ввод промежуточных чисел в счетную машину требуют немалых затрат времени и чреваты ошибками. Применение программируемых калькуляторов резко повышает эффективность вычислений. Микрокалькулятор доступен всем, прост в обращении, считает автоматически, не устает и не ошибается. Вероятность вычислительных ошибок и затраты времени снижаются в несколько раз. Но для работы с микрокалькулятором надо располагать программой, рационально составленной и отлаженной.
Если вести расчет по вышеприведенным формулам, то полный цикл вычислений нужно проводить дважды: сначала получить
среднее x, а потом вновь ввести все данные и вычислить среднеквадратическое отклонение s. Этого можно избежать, преобразовав соответствующую формулу так:

(При этом использованы соотношения:
(a - b)2 = a2 - 2ab + b2;
Sum(xi) = nx).
Теперь все вычисления можно проводить в одни цикл. Блок-схема вычислительного алгоритма показана на рисунке.
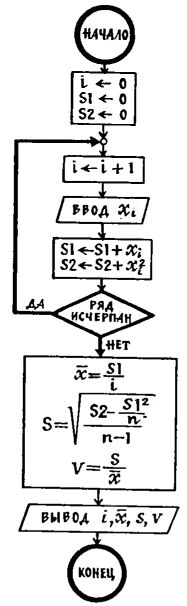
Приведена программа для микрокалькулятора "Электроника Б3-34". Цифры с двоеточиями - номера команд, цифры в скобках - коды команд, команды, не имеющие номеров, выполняются вручную. Дан контрольный пример, позволяющий проверить, правильно ли введена программа. Сделав такую проверку и убедившись в отсутствии ошибок ввода, можно переходить к расчету. Опыт показывает, что ввод и обработка ряда из 60-70 трехзначных чисел занимает 12-13 минут.
Тем, кто возьмет на вооружение предложенный мною алгоритм, советую выработать привычку: после ввода очередного числа проверьте по индикатору, правильно ли оно введено, и только после этого начинайте счет.
Н.БОГИН (г.Москва).
ПРОГРАММА. В/О, с/п. 00: Сх (ОГ). 01: П3 (43). 02: П4 (44). 03: П5 (45). 04: П6 (46). 05: П7 (47). 06: с/п (50; на индикаторе 0). Ввод значений xi - каждое вводится после высвечивания числа i, номера ранее введенного значения; с/п. 07: П8 (48 ). 08: ИП3 (63). 09: + (10). 10: П3 (43). 11: ИП8 (68 ). 12: Fx2 (22). 13: ИП4 (64). 14: + (10). 15: П7 (44). 16: ИП7 (67). 17: 1 (01). 18: + (10). 19: П7 (47). 20: БП (51). 21: 06 (06; на инд. i). БП 22; с/п; команду ввести после окончания ввода всех чисел. 22: ИП3 (63). 23: Fx2 (22). 24: ИП7 (67). 25: / (13). 26: /-/ (0L). 27: ИП4 (64). 28: + (10). 29: П5 (48 ). 30: ИП7 (67). 31: 1 (01). 32: - (11). 33: F1/x (23). 34: ИП8 (68 ). 35: * (12). 36: Fsqrx (21). 37: П5 (45). 38: с/п (50; на инд. s); с/п. 39: ИП3 (63). 40: ИП7 (67). 41: / (13). 42: П6 (46). 43: с/п (50; на инд. x); с/п. 44: ИП5 (65). 45: ИП6 (66). 46: / (13). 47: П8 (48 ). 48: с/п (50; на инд. V); с/п. 49: ИП7 (67). 50: с/п (50; на инд. n - конец счета).
КОНТРОЛЬНЫЙ ПРИМЕР. x1 = 2, x2 = 3, x3 = 4. Результаты: x = 3; s = 1; V = 3.33333e-1; ИП3 = 9; ИП4 = 29; ИП7 = 3.
Этот выпуск рубрики "Человек с микрокалькулятором", как и прежние, составлен на основе читательских писем.
Читатель С.Морозов из Краснодара сообщает в своем письме неожиданные факты: оказывается, при расчетах на микрокалькуляторе могут не выполняться классические законы математики: переместительный, сочетательный... Примеры, приводимые в письме, позволяют легко вскрыть источник парадоксов: все дело в округлении чисел, производимом по ходу вычислений.
Эти примеры интересны не только сами по себе - они удобны для иллюстрации некоторых важных вопросов, связанных с погрешностями вычислений. Интересные соображения на эту тему высказал в своем письме читатель И.Вязовский. Его мы и попросили дать обстоятельный комментарий сообщению С.Морозова.
ОТ ПЕРЕМЕНЫ МЕСТ...
Волга впадает в Каспийское море. Все тела падают на Землю с одинаковым ускорением. От перемены мест слагаемых сумма не меняется.
Все это прописные истины. Но всегда ли они верны? Что касается Волги, то тут сомнений нет. С переменой мест слагаемых, дело сложнее, если складываются они на вычислительной машине.
Предположим, машина оперирует четырьмя десятичными разрядами и что значение первого отбрасываемого разряда (в нашей машине пятого) учитывается при округлении последнего значащего. Сложим на нашей ЭВМ пять чисел подряд, каждый раз округляя результат:
1.326e1 + 4.624 + 5.432e-1 + 4.365e-2 + 3.416e-2
Получим 18.48. Теперь изменим порядок слагаемых: будем складывать их с конца. Получим 18.51. Сумма изменилась!
Парадоксы и с другими законами. Распределительный закон, например, тоже не выполняется.
4*(2.873-2.872) = 0.004
4*2.873 - 4*2.872 = 0
Еще пример. Сложим на нашей ЭВМ четыре числа:
6.824 + 6.778 + 6.793 + 6.814 = 27.20
А теперь будем складывать те же числа, объединяя попарно:
(6.824+6.778 ) + (6.793+6.814) = 27.21
Результаты не совпадают!
Для любой ЭВМ существуют наибольшее и наименьшее по абсолютной величине числа. Это оборачивает ся новыми парадоксами. Например, a*b*c != c*a*b. Каково? Покажем это на примере, допустив, что максимальное число в нашей ЭВМ - это 1e16.
Вычисляем 2e9 * 5e-8 * 6.5e6 и получаем: 6.5e8.
А теперь 6.5e6 * 2e9 * 5e-8. Получаем... Ничего не получаем. Первое умножение не может быть выполнено, так как результат его (1.3e16) представляет число, большее допустимого предела. "Авост",- говорят в таких случаях те, кто работает на "больших" ЭВМ
[Сейчас трудно выяснить, как раскрывалась эта аббревиатура первоначально. Большинство программистов интерпретирует ее как "аварийный останов". В этом есть доля истины - в программе произошла авария. Но, с точки зрения обслуживающего персонала ЭВМ. это "автоматический останов". Ведь с машиной-то все в порядке!].
Микрокалькулятор на такую ситуацию реагирует малоприятным для программиста сообщением: ERROR (ошибка).
С подобными парадоксами всегда приходится считаться, работая на вычислительных машинах - и на мощных ЭВМ и на крошечных микрокалькуляторах.
С.МОРОЗОВ (г.Краснодар).
СЧЕТ И ТОЧНОСТЬ
Различают погрешности абсолютные и относительные. Абсолютная погрешность - это разность между истинным и измеренным значением величины. Если ее поделить на саму величину, то получим относительную погрешность. Понятно, что одинаковым абсолютным погрешностям не всегда соответствуют одинаковые относительные - и наоборот.
Точно так же, как несовершенство, точнее, неидеальность измерительных приборов приводит к ошибкам измерений, неидеальность вычислительных машин приводит к ошибкам вычислений. Дело осложняется тем, что результат всякого вычисления заранее неизвестен. Потому и оценить ошибку трудно.
Существуют различные способы оценок. Возьмем для примера задачу нахождения определенного интеграла. Решать ее можно по-разному, но всякий раз это связано с разбиением промежутка интегрирования на небольшие, как правило, одинаковые отрезки, длина которых называется шагом интегрирования. Задавшись некоторым разбиением, вычисляют интеграл; потом дробят промежуток мельче (скажем, в два раза), повторяют ту же вычислительную процедуру с новым шагом и получают новый результат - а разность между ним и предыдущим принимают за абсолютную ошибку вычисления. (Ясно, что прием небезупречен).

Различные методы аппроксимации интегрируемых функций.
При расчетах на ЭВМ ошибки бывают двух типов: ошибки ограничения и ошибки округления. Первые определяются используемыми алгоритмами. Их причина, грубо говоря,- замена бесконечного конечным. Например, отыскивая определенный интеграл от некоторой функции, то есть площадь, очерченную графиком функции, мы заменяем этот график конечной последовательностью отрезков прямых или парабол. Их столько, сколько отрезков, на которые разбит промежуток интегрирования. Между тем определение интеграла требует дробить этот промежуток до бесконечности, устремляя шаг интегрирования к нулю. Производные, то есть отношения приращений функции к бесконечно малым приращениям аргумента, в численных расчетах рассматриваются при конечных приращениях. Ряды, суммы бесконечного числа членов заменяются конечными суммами начальных слагаемых.
В принципе такого рода ошибки можно сделать сколь угодно малыми. Чем мельче шаг интегрирования, тем ближе вычисляемая площадь к истинной. Чем меньше интервал, на котором вычисляется приращение функции, подставляемое далее в приближенную формулу для производной, тем точнее эта формула позволит вычислить значение производной. Чем больше взято членов ряда, тем точнее будет определена его сумма.
Другой тип ошибок - ошибки округления. Возникают они из-за того, что каждая машина оперирует конечным количеством разрядов в представлении десятичных чисел, говоря образно, "держит в голове" ограниченное число знаков после запятой. Для ЭВМ каждого типа это число свое, но оно всегда конечно. Чтобы втиснуть числа в это прокрустово ложе, их приходится округлять при каждом акте вычисления.
Но... не таится ли здесь парадокс? Разбирая задачу интегрирования функции, мы отмечали: чем меньше шаг, тем меньше ошибка отбрасывания. Вместе с тем, чем меньше шаг, тем на большее число отрезков дробится промежуток интегрирования, тем больше операций необходимо выполнить, вычисляя интеграл, тем больше ошибка округления. Выходит, и большой шаг плохо и слишком маленький не очень хорошо!

Зависимость суммарной ошибки (ограничения и округления) от количества интервалов при интегрировании синуса по полупериоду, выполненном по методам трапеций и парабол (Симпсона). Как подсказывают графики, при численном нахождении интеграла существует оптимальное количество интервалов, на которые разбивается промежуток интегрирования.
На практике не стремятся делать шаги разбиения слишком малыми, так как это не только приводит к возрастанию ошибок округления, но и резко увеличивает время счета, а часто еще и объем используемой памяти. Программист стремится обычно выбрать такой алгоритм, который позволил бы получить наивысшую точность при ограниченном объеме вычислительной работы. Часто точность вычислений можно увеличивать довольно простыми приемами.
Рассмотрим некоторые из них, относящиеся к самой простой операции - сложению. Если слагаемые x1 и x2 заданы с относительными погрешностями e1 и e2 соответственно, а относительная ошибка округления равна r, то относительная погрешность суммы равна
ey/y = x1e1/(x1+x2) + x2e2/(x1+x2) + r
Если слагаемые x1 и x2 заданы точно, то остается лишь относительная ошибка округления r, а абсолютная погрешность, с которой вычисляется сумма, согласно формуле, равна (x1+x2)r. Будем складывать последователыю четыре числа
y = (((x1 + x2) + x3) + x4).
Поскольку при каждом суммировании набегает ошибка округления, то аналогично предыдущему получим, что абсолютная погрешность итоговой суммы равна (3x1 + 3x2 + 2x3 + x4)r.

Значения слагаемых входят в это выражение с разными коэффициентами. Если x1 по абсолютной величине намного превосходит остальные слагаемые, то можно приближенно считать ey = 3x1r. Поменяем местами слагаемые, поставив самое большое в конце. Ошибка в этом случае будет ey = x1r, то есть в три раза меньше, чем раньше! Вот и первый простой рецепт по увеличению точности: при сложении чисел разных порядков начинайте с малых и заканчивайте большими.
Теперь положим, что числа близки друг другу по величине. Только что данный рецепт здесь не годится. Попробуем складывать числа попарно:
y = ((x1 + x2) + (x3 + x4)).

Полная ошибка, подсчитанная прежним приемом, такова: ey =2(x1 + x2 + x3 + x4)r. В предположении, что все числа близки друг другу, можно положить каждое равным одной величине x. Что же получается? При последовательном сложении ошибка составит 9xr, а при попарном - 8xr, то есть будет несколько меньше. Если же слагаемых не четыре, а больше, ошибка уменьшится сильнее. Итак, второй рецепт: при сложении примерно одинаковых чисел точность возрастает, если складывать их группами.
Опытный программист, как правило, знает множество приемов, увеличивающих точность счета. Но знает он и другое: точность не самоцель. Главное - получить требуемый результат с точностью не ниже заданной за возможно более короткое время. Это и должно быть путеводной звездой при составлении любых программ.
И.ВЯЗОВСКИЙ (г.Люберцы).
["... Для прикладных вопросов нет надобности производить вычисления... с совершенною точностью... лишь бы была уверенность, что происходящая от этого погрешность не превышает тех пределов, которые в данном вопросе допускаются... В приложениях обыкновенно интересен не процесс вычисления, а результат его: поэтому и стараются получить этот результат при наименьшей затрате труда и времени".
А.Н.КРЫЛОВ]
["Недостатки математического образования с наибольшей отчетливостью проявляются в чрезмерной точности численных расчетов".
К.Ф.ГАУСС]
ВНИМАНИЕ КОНКУРС
Каждая программа - это своего рода художественное произведение. И трудно ожидать, что два программиста написали бы одинаковые программы. Это все равно, как если бы два поэта написали одинаковые стихи на заданную тему. А какое стихотворение лучше, решает конкурс.
С предложением объявлять конкурсы на лучшую программу для решения той или иной задачи на микрокалькуляторе обращаются к нам читатели С.Конин из Ленинграда, Л.Яковлев из Старой Русы, А.Киба из Ростова-на-Дону, А.Лернер из Москвы и другие. Редакция поддерживает это предложение, надеясь, что подобные конкурсы позволят не только выявить наиболее искусных программистов, но и наладить между участниками обмен опытом.
Для конкурса предлагается две задачи:
1) поиск простых чисел и их естественной последовательности: 1, 2, 3, 5, 7, 11 и т.д.;
2) выделение целой части числа.
Решение каждой задачи должно содержать, кроме программы, словесное описание алгоритма и его блок-схему. Можно послать решение одной задачи. Срок отправки - до 1.02.84.
Наиболее интересные решения будут опубликованы.
ЕЩЕ ОДНА ЦИФРА
О резервах микрокалькулятора, позволяющих добавлять к результатам некоторых вычислений несколько цифр сверх тех, что высвечиваются на индикаторе, пишет читатель С.Мельников. Его письмо комментирует инженер Е.Кузнецов - один из тех, кто разрабатывает отечественные микрокалькуляторы.
Если нажать клавишу "пи" микрокалькулятора "Электроника Б3-38", на световом табло появятся восемь цифр: 3.1415926. Но все ли это, что может дать микрокалькулятор? Я вычел из пи число 3.1415926, набрав его на клавиатуре, и получил 5e-8. Таким образом, из микрокалькулятора извлечена еще одна цифра!
Вычислим теперь e**1 и из полученного результата вычтем 2.7182818 - то есть то, что высветилось на индикаторе. Разность равна 3e-8. В точном представлении числа e после восьмой цифры следует 28... Значит, полученная нами девятая цифра верна лишь округленно.
Но самое главное - она имеется в микрокалькуляторе и ее можно оттуда извлечь!
Знание этого факта позволяет получать на 8-разрядной "Электронике Б3-38" точные произведения пятизначных чисел. Например, 78979*55555. Микрокалькулятор дает 4.38767e9. Сверх этих шести цифр в памяти микрокалькулятора существуют еще несколько. Извлечем их описанным способом, вычитая из результата умножения число, появившееся на индикаторе. Получим 8350. Третья цифра разности, очевидно, округлена, а последнюю нетрудно уточнить, перемножив последние цифры сомножителей. 9 и 5, - это пятерка. Итак, искомое произведение равно 4.387678345e9.
Еще пример: 88888**2 = 7.90107e9. Такой ответ читаем на индикаторе. Недостающее получим привычным вычитанием: 6540, последнюю цифру уточним перемножением последних цифр сомножителей: 4. Искомое произведение: 7.901076544e9.
С.МЕЛЬНИКОВ.
(г.Буденновск Ставропольского края).

Рис. М.САГАТОВА
(г.Ташкент).
ИЗБЫТОЧНЫЕ РАЗРЯДЫ НЕОБХОДИМЫ
Суть дела, затронутого в письме С.Мельникова, разберем сначала на простом примере. Предположим, что требуется перемножить три числа: 1.13*1.14*1.15. Все эти числа - трехзначные. Условимся выразить искомое произведение также трехзначным числом. Тому же условию подчиним и промежуточные результаты вычислений. Таким результатом в нашем примере будет произведение первых двух сомножителей. Точное его значение 1.2882. Согласно принятому условию округлим его до сотых долей единицы.
Классическое правило округления, с которым знакомят школьников, таково: если в разряде, следующем за последним из сохраняемых, стоит число, меньшее пяти, то число в последнем сохраняемом разряде остается неизменным; в противном случае к нему прибавляют единицу. В простейших микрокалькуляторах применяется более простой способ округления: сохраняемые разряды остаются неизменными, каким бы ни было содержимое отбрасываемых.
Так поступим и мы: примем произведение первых двух сомножителей равным 1.28. Умножая это число на заключительный сомножитель и обрезая результат прежним приемом, получаем в итоге 1.47.
Вычислим теперь для сравнения точное произведение наших трех сомножителей: 1.48143. Округленное до трех значащих цифр любым из вышеописанных способов, оно равно 1.48. То есть не совпадает с тем, что мы получили ранее.
Итак, если по ходу промежуточных выкладок сохранять в получающихся числах ровно столько знаков, сколько требуется в ответе, нельзя гарантировать, что все значащие цифры ответа окажутся верными.
Приняв во внимание это соображение, перемножим вновь наши три сомножителя. Но на сей раз оставим в промежуточном результате не три, а четыре значащих цифры: 1.288. Умножим это число на 1.15 и получим 1.4812; после отбрасывания лишних знаков оно будет таким же, что было получено округлением точного результата.
Итак, округляя числа простым отбрасыванием лишних разрядов, мы сможем гарантировать безошибочность всех значащих цифр ответа, если в промежуточных выкладках станем удерживать больше разрядов, нежели требуется иметь в ответе.
В калькуляторах различных марок число избыточных разрядов неодинаково, но, как правило, невелико - от одного до трех. Этого бывает недостаточно, чтобы гарантировать точность всех выводимых на индикатор цифр при выполнении каждой из процедур, обозначенных на клавишах микрокалькулятора. Для каждой из них в инструкции, приложенной к калькулятору, указано, сколько верных знаков гарантированно содержит ее результат, высвечиваемый на индикаторе.
(Напомним, что все значащие цифры результата выводятся лишь в системах индикации с плавающей запятой - это обеспечивает принципиально более высокую точность, чем при фиксированной запятой).
Вспомним теперь про классический способ округления и применим его к промежуточным результатам разобранного вначале примера с перемножением трех чисел. Точный ответ получается здесь без использования избыточных разрядов: 1.13*1.14 = 1.29; 1.29*1.15 = 1.48.
Отечественные микрокалькуляторы "Электроника Б3-38" и "Электроника МК-51" оперируют одним-двумя (в зависимости от характера конкретного вычисления) избыточными разрядами, причем последний из них округляется по описанной классической методике. Любая вычислительная процедура, выполняемая на этих микрокалькуляторах, дает ответ, который отличается от точного лишь на плюс-минус единицу в последнем из выводимых на индикатор, восьмом разряде. Обеспечивается это, в частности, еще и тем, что элементарные функции вычисляются здесь новым способом "цифра за цифрой". Микрокалькулятор "Электроника С3-15" позволяет пользователю сокращать число выводимых на индикатор разрядов; при этом содержимое последнего из них округляется по классическому правилу.
Е.КУЗНЕЦОВ
СТАТИСТИКА НА МИКРОКАЛЬКУЛЯТОРЕ
Говорят, статистика знает все. Сегодня эту поговорку можно было бы переиначить: статистику знают все. Действительно, ее нынче используют инженеры и агрономы, медики и геологи...
Наиболее широко используемые статистические параметры - это среднее значение величины, среднеквадратическое отклонение и коэффициент вариации. Для набора n величин xi они вычисляются по формулам:
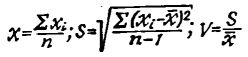
Среднеквадратическое отклонение s характеризует абсолютный разброс величины вокруг среднего значения x, а коэффициент вариации v, величина безразмерная, дает относительное отклонение, степень изменчивости процесса. По коэффициенту вариации можно судить об устойчивости и однообразии протекающих процессов, о состоянии наладки оборудования и т.п. Количественные характеристики изменчивости имеют большое экономическое значение. Известно, например, что при производстве бетона уменьшение коэффициента вариации до 5 процентов вместо исходных 13 снижает расход цемента на 10-15 процентов: чем однороднее смесь, тем меньше цемента нужно для достижения требуемой прочности. Аналогичные примеры можно привести и из других областей техники.
Конечно, статистические расчеты лучше всего проводить на ЭВМ. Но, к сожалению, они имеются еще не везде. Поэтому часто вычисления проводят вручную при помощи счетных машин. Запись в таблицы, ввод промежуточных чисел в счетную машину требуют немалых затрат времени и чреваты ошибками. Применение программируемых калькуляторов резко повышает эффективность вычислений. Микрокалькулятор доступен всем, прост в обращении, считает автоматически, не устает и не ошибается. Вероятность вычислительных ошибок и затраты времени снижаются в несколько раз. Но для работы с микрокалькулятором надо располагать программой, рационально составленной и отлаженной.
Если вести расчет по вышеприведенным формулам, то полный цикл вычислений нужно проводить дважды: сначала получить
среднее x, а потом вновь ввести все данные и вычислить среднеквадратическое отклонение s. Этого можно избежать, преобразовав соответствующую формулу так:

(При этом использованы соотношения:
(a - b)2 = a2 - 2ab + b2;
Sum(xi) = nx).
Теперь все вычисления можно проводить в одни цикл. Блок-схема вычислительного алгоритма показана на рисунке.

Приведена программа для микрокалькулятора "Электроника Б3-34". Цифры с двоеточиями - номера команд, цифры в скобках - коды команд, команды, не имеющие номеров, выполняются вручную. Дан контрольный пример, позволяющий проверить, правильно ли введена программа. Сделав такую проверку и убедившись в отсутствии ошибок ввода, можно переходить к расчету. Опыт показывает, что ввод и обработка ряда из 60-70 трехзначных чисел занимает 12-13 минут.
Тем, кто возьмет на вооружение предложенный мною алгоритм, советую выработать привычку: после ввода очередного числа проверьте по индикатору, правильно ли оно введено, и только после этого начинайте счет.
Н.БОГИН (г.Москва).
ПРОГРАММА. В/О, с/п. 00: Сх (ОГ). 01: П3 (43). 02: П4 (44). 03: П5 (45). 04: П6 (46). 05: П7 (47). 06: с/п (50; на индикаторе 0). Ввод значений xi - каждое вводится после высвечивания числа i, номера ранее введенного значения; с/п. 07: П8 (48 ). 08: ИП3 (63). 09: + (10). 10: П3 (43). 11: ИП8 (68 ). 12: Fx2 (22). 13: ИП4 (64). 14: + (10). 15: П7 (44). 16: ИП7 (67). 17: 1 (01). 18: + (10). 19: П7 (47). 20: БП (51). 21: 06 (06; на инд. i). БП 22; с/п; команду ввести после окончания ввода всех чисел. 22: ИП3 (63). 23: Fx2 (22). 24: ИП7 (67). 25: / (13). 26: /-/ (0L). 27: ИП4 (64). 28: + (10). 29: П5 (48 ). 30: ИП7 (67). 31: 1 (01). 32: - (11). 33: F1/x (23). 34: ИП8 (68 ). 35: * (12). 36: Fsqrx (21). 37: П5 (45). 38: с/п (50; на инд. s); с/п. 39: ИП3 (63). 40: ИП7 (67). 41: / (13). 42: П6 (46). 43: с/п (50; на инд. x); с/п. 44: ИП5 (65). 45: ИП6 (66). 46: / (13). 47: П8 (48 ). 48: с/п (50; на инд. V); с/п. 49: ИП7 (67). 50: с/п (50; на инд. n - конец счета).
КОНТРОЛЬНЫЙ ПРИМЕР. x1 = 2, x2 = 3, x3 = 4. Результаты: x = 3; s = 1; V = 3.33333e-1; ИП3 = 9; ИП4 = 29; ИП7 = 3.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
2/84
Для нашей новой рубрики "Человек с микрокалькулятором" становятся традиционными рассказы о том, как карманные ЭВМ помогают в работе специалистам самых разнообразных профессий. В прошлом выпуске Н.Богин писал о статистических расчетах на микрокалькуляторе. На этот раз о выполняемых на нем геодезических вычислениях сообщает В.Молчанов.
В недавних откликах на новую рубрику есть такие письма, где речь идет о применении микрокалькуляторов в целях обучения: от первых уроков устного счета для дошкольников до вузовских лабораторных работ. С рассказов об этом и начинается очередной выпуск рубрики.
В опубликованных далее статьях и заметках читатели, увлеченные работой на микрокалькуляторах, делятся своими находками, советами. Особого внимания заслуживает выступление П.Эпьясберга, который предостерегает от "компьютерной эйфории", от дилетантской переоценки роли и возможностей вычислительной техники.
СНАЧАЛА В УМЕ, ПОТОМ НА КЛАВИШАХ
Скептики утверждают, что калькуляторы отучат людей считать в уме. Я с этим не согласен. Программа, которую я написал, наоборот, учит устному счету. Работа с калькулятором при этом очень проста. После ввода программы обучаемый вводит в машину два числа, а потом подсчитанную в уме их сумму. Калькулятор проверяет результат, и если он правилен, то на индикаторе появляется оценка 5, в противном случае высвечивается ERROR (ошибка). Моя пятилетняя дочь освоила работу с этой программой очень быстро (правда, ввожу программу я сам), и теперь калькулятор стал ее учителем. Он не только обучает устному счету, но еще развивает у детей внимательность, аккуратность, координацию движений.
ПРОГРАММА. 00. ИП1 (61) 01. ИП2 (62) 02. + (10) 03. ИП3 (63) 04. - (11) 05. Fx=0 (5Е) 06. 09 (09) 07. 05 (05) 08. с/п (50) 09. 00 (00) 10. F1/x (23) 11. с/п (50)
Слагаемые вводятся в регистры 1 и 2, а результат - в регистр 3. Затем следует нажать клавиши "в/о" и "с/п". Через 3-5 секунд на индикаторе появится оценка.
Программу можно изменить так, чтобы использовать ее для обучения не только сложению, но и любому другому арифметическому действию, потренироваться в устном вычислении корней, факториалов, тригонометрических функций и т.д.
А.ЛЮДИН (г.Выборг).
ЭЛЕКТРОННЫЙ ТОПОГРАФ
В топографии часто приходится решать так называемую обратную геодезическую задачу, когда по прямоугольным координатам двух точек на плоскости нужно определить расстояние между ними и дирекционный угол, то есть направление прямой линии, соединяющей эти точки. Дирекционный угол отсчитывается по часовой стрелке от направления на север и измеряется в градусах. Он может принимать значения от 0o до 360o. Если вычислить этот угол на микрокалькуляторе по стандартной формуле
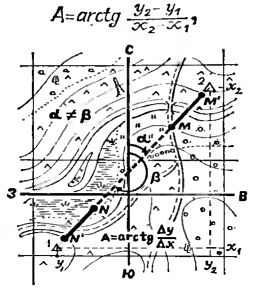
Если вычислять дирекционный угол по приведенной формуле, то отмеченные на карте углы получатся одинаковыми.
то правильные результаты будут получаться только для углов в северо-восточном направлении. Ведь на индикаторе значения арктангенса выдаются в пределах от -90o до 90o. Поэтому углы в северо-восточном и юго-западном направлениях будут неразличимы, так же, как и углы в юго-восточном и северо-западном направлениях. Последние к тому же будут отрицательными, и, чтобы не перепутать север с югом, необходимо вносить коррективы и вычисления, анализируя знаки разностей Dx = x2-x1 и Dy = y2-y1. Кроме того, микрокалькулятор вычисляет значение дирекционного угла в градусах и десятичных долях градуса в то время, как топографы привыкли иметь дело с минутами и секундами.
И все-таки можно заставить микрокалькулятор преодолеть обе эти трудности. "Электроника Б3-34" за 20 секунд вычисляет точную величину днрекционного угла, переводя десятичные доли градуса в минуты и секунды. На индикатор результат выводится в форме ГГГ.ММССД. Это значит, что если высветилось, например, число 218.26372, то нужно читать 218o 26' 37", 2.
Перед началом работы нужно занести в память следующие постоянные величины: число 100 в регистр 0, число 0.55555555 (1/1.8 ) в регистр 1, 10000000 (1e7) в регистр 2, числа 0.6; 180; 360; 17; 26 соответственно в регистры 3, 4, 5, А, В. Координаты x1, y1, x2, 2 вводятся в регистры 6, 7, 8, 0.
Случай Dx = 0 в программе не рассматривается. Но в этом случае калькулятор и не нужен. Угол равен 90o или 270o в зависимости от знака Dy.
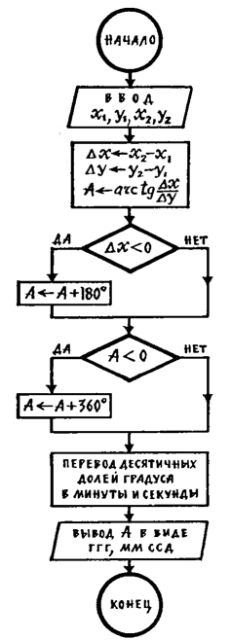
ПРОГРАММА. 00. ИП9 (69) 01. ИП7 (67) 02. - (11; считывание y2, y1 и вычисление Dy) 03. ИП8 (68 ) 04. ИП6 (66) 05. - (11; считывание x2, x1 и вычисление Dx) 06. ИПС (6С; запись Dx в регистр C) 07. / (13) 08. Farctg (1L; вычисление А = arctg Dy/Dy) 09. ИПС (6С) 10. Fx<0 (5C) 11. 16 (16; переход к адресу 16 при Dx>0) 12. FO (25) 13. ИП4 (64) 14. + (10; увеличение А на 180o) 15. КБПА (8-) 16. FО (25) 17.Fx<0 (5С) 18. 21 (21; переход к адресу 21 при А>0) 19. ИП5 (65) 20. + (10; увеличение А на 360o) 21. КППВ (-L) 22. * (12; отделение долей минуты от целых минут) 23. КППВ (-L) 24. / (13; отделение градусов от минут и секунд) 25. с/п (50; индикация результата).
Подпрограмма для перевода десятичных долей градуса в минуты и секунды. 26. ^ (ОЕ) 27. ^ (ОЕ) 28. ИП1 (61) 29. - (11) 30. ИП2 (62) 31. + (10) 32. FBx (0) 33. - (11) 34. - (11) 35. FBx (0) 36. х-у (14) 37. ИП3 (63) 38. * (12) 39. + (10) 40. ИП0 (60) 41. в/о (52).
В.МОЛЧАНОВ (г.Воронеж).
[ В подпрограмме перевода долей градуса в минуты и секунды, предложенной В.Молчановым, происходит выделение целой части числа, объявленное темой конкурса в предыдущем выпуске рубрики "Человек с микрокалькулятором" (12/83). Вероятно, этого же заслуживает и вся задача, для которой составлена программа. Итак, очередное задание нашего конкурса: перевод десятичных долей градуса в минуты, секунды и десятичные доли секунды.
И еще одно задание: вычисление факториала натурального числа. Задача несложна, и реализующая ее программа будет короткой и простой. Однако среди различных вариантов программы наверняка окажется особенно лаконичный и изящный. ]
ОТМЕТКУ СТАВИТ КАЛЬКУЛЯТОР
Хочу рассказать о том, как учитель начальных классов может использовать микрокалькулятор, чтобы быстро и беспристрастно проставить школьникам оценки за скорость чтения. Оценивается она по числу слов, прочитанных за минуту. Нормы скорости предусмотрены учебной программой: 30-40 слов в минуту для первого класса, 60-70 слов - для второго и 80-90 - для третьего.
Подсчитываем заранее количество знаков в тексте. Длина текста может быть любой, например, один абзац. Потом включаем секундомер и засекаем время, за которое ученик прочтет текст. Всю остальную работу делает за нас калькулятор. А сводится она к вычислениям по формуле:
число знаков * 60 * 3 / (длина слова * время * норма).
Среднюю длину слова можно принять равной семи
буквам. Время подставляем в секундах.
Например, 290 знаков третьеклассник прочитал за 48 секунд. Вычисляем на микрокалькуляторе:
290*60*5/(7*48*80) = 3.2
Ученик получает тройку.
Видно, что меняются в этой формуле только число знаков и время. Поэтому постоянную часть формулы достаточно вычислить один раз. При такой методике один учитель может свободно провести проверку скорости чтения у 25-30 учеников за урок, а дома кто-нибудь из взрослых может оценить навыки ребенка в чтении за 2-3 минуты.
В.АКСЕЛЬРУД, учитель школы-интерната (с.Затока Овидиопольского района Одесской области).
МИКРО-ВЦ В НАШЕМ ОБЩЕЖИТИИ
Программируемые микрокалькуляторы лишь недавно появились в учебных лабораториях Московского института инженеров железнодорожного транспорта, но уже убедительно продемонстрировали свои богатые и широкие возможности.
На кафедре "Измерительная техника" они используются в 16 лабораторных работах. На кафедре "Физика-1" - для контроля знаний студентов. Кафедра "Электрическая тяга" создала в общежитии МИИТа студенческий "микро-ВЦ" для курсового и дипломного проектирования. Все руководства для этого ВЦ написаны студентами.
Как показывает опыт, микрокалькуляторы с программной памятью на несколько десятков команд едва ли не оптимальны в учебном процессе. Ведь из 90 минут, обычно отводимых на занятие, программирование не должно занимать слишком много времени.
Когда студент освобожден от необходимости многократно повторять одну и ту же цепочку вычислений, атмосфера занятия меняется в корне, делается более творческой, позволяя сосредоточиться на сущности исследования. Работы, считавшиеся раньше скучными и однообразными, вдруг превратились в увлекательные и интересные. "Студентов невозможно выгнать из аудитории",- говорит доцент Ю.В.Темлякова.
Программируемый микрокалькулятор - идеальный инструмент для не слишком сложного (но все-таки достаточно сложного!) математического эксперимента. Конечно, он никогда не заменит классических средств исследования функций. Но вспомним: ведь даже "чистый математик" Шарль Эрмит подчеркивал роль "наблюдения фактов" в математике. А в прикладных исследованиях роль такого эксперимента (пусть простого, но зато оперативного) несомненна. И овладеть этим средством надо, конечно, еще в вузе.
Ф.ГОРЮШЕВ, младший научный сотрудник (МИИТ).

[ Этот снимок сделай в одной из учебных лабораторий Московского физико-технического института. Определяя отношение заряда электрона к его массе по методу Милликена, студент должен проделать обширные статистические расчеты. Их облегчает микрокалькулятор, встроенный в пульт управления экспериментальным прибором.
Фото В.БЕЗДУДНОГО. ]
КАК РЕШИТЬ НЕРАЗРЕШИМОЕ УРАВНЕНИЕ
Давние читатели журнала, возможно, помнят "загадку жрецов бога Ра" ("Наука и жизнь" 1/66). Глубина воды в цилиндрическом колодце - 1 локоть, две тростинки длиной 2 и 3 локтя опущены в колодец, как показано на рисунке. От кандидатов на замещение вакантной должности жреца требовалось определить диаметр колодца.
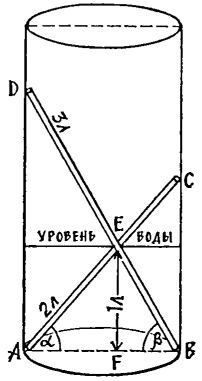
Обозначим длины тростинок L и l, глубину воды в колодце - h, неизвестный диаметр колодца - x. Все эти величины несложно связать уравнением:
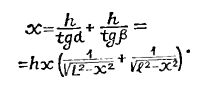
Полученное уравнение неразрешимо - по крайней мере, средствами школьной математики: оно сводится к уравнению четвертой степени, решение которого дается далеко не в каждом справочнике. Но, к счастью, оно имеет вид x = f(x), удобный для применения метода итераций (10/83). По этому методу решение уравнения отыскивается как предел последовательности приближений xn, каждый член которой определяется через предыдущий: x[n+1] = f(xn). Надо лишь задаться начальным приближением x0.
Из условия задачи ясно, что искомый x больше 0 и меньше 2. Вот и возьмем начальное приближение посередине: x=1. Подставив это значение в правую часть нашего уравнения, получим x1=0.931 (надеясь, что точность до тысячной доли локтя жрецов удовлетворяла, будем указывать только три знака после запятой), и далее x2=0.852; x3=0.767; ... x9=0.315; x10=0.205... Что-то узковатый колодец получается... Непохоже, что эта последовательность сходится к решению.
Может, изменить начальное значение? Меньше единицы его брать бесполезно, этот участок мы уже "прошагали", возьмем число поближе к другому концу интервала: x0=1.5. Находим x1=1.711; х2=2.348. Опять неудача - ведь х не может быть больше двух.
Выходит, к нашему уравнению с методом итераций и не подступишься? Нет, отчаиваться рано: к виду x=f(x) его можно привести и иначе - например, преобразовав так:
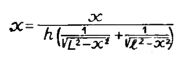
Начнем опять с x0=1. Первые итерации - x1= 1.074; x2=1.131; х3=1.171. Последовательность пошла в сторону увеличения х, а не уменьшения, как в первом случае, и это уже обнадеживает. Но не стремится ли она к правому концу интервала, как раньше к левому? Возьмем x0=1.5. Имеем х1=1.315; x2=1.271; x3= 1.252... Вот теперь, похоже, можно закричать, как кот Матроскин из известного мультфильма: "Ура! Заработало!"
Но сначала вглядимся в формулу критическим взглядом: нельзя ли видоизменить се так, чтобы реализующая ее программа оказалась наилучшей?
Должен сказать, что в критериях оценки программ для микрокалькуляторов я не согласен с И.Даниловым (10/83), который соображения быстроты выдвигает на первый план, а насчет объема программы замечает вскользь: лишь бы она вмешалась в память микрокалькулятора. Владельцы микрокалькуляторов, как правило, имеют достаточно времени для своих вычислений и могут им распоряжаться: не успел утром, можно закончить вечером. Но если уж программа чрезмерно длинна, то так оно будет и вечером и на следующий день. Подобные неприятности гарантированы тому, кто не старается постоянно упражнять себя в искусстве лаконичного программирования. Чтобы их избежать, следует, на мой взгляд, в первую очередь соблюдать принцип экономии памяти и только во вторую - экономии времени. Если микрокалькулятор выполняет действия с запоминанием константы, целесообразно преобразовать наше уравнение еще раз:

Теперь в правой части неизвестное x присутствует лишь в квадрате, который достаточно вычислить лишь однажды, да и сам х лишь однажды придется вызывать из памяти. Все это - в пользу краткости программы, да и скорости вычислений тоже.
Заметим еще, что в нашей формуле используются только квадраты величин L и l. Их сразу и запишем в память. На этом мы сэкономим еще две строки программы и время, затрачиваемое на возведение в квадрат.
Возьмем начальное приближение x0=1 и получим ответ 1.231, достигнув заданную точность в третьем знаке за одиннадцать итерации.
А.РАЗДОБРЕЕВ (г.Владимир].
[ Многие из тех, кто имеет солидный опыт работы с микрокалькуляторами, сталкивались с необходимостью вписать громоздкую программу в небольшую память карманной ЭВМ и могли бы поделиться остроумными уловками, позволявшими выйти из затруднительного положения.
Ждем писем на эту немаловажную тему. ]
ОСТОРОЖНО-КОМПЬЮТЕРЫ!
Быстрое внедрение компьютеров в различные области науки и техники, появление миллионов специалистов, владеющих машинными методами вычислений, достигнутые в результате большие успехи - все это привело к известной переоценке возможностей ЭВМ. Многие забывают, что ЭВМ - это всего лишь инструмент в руках человека, инструмент очень совершенный, но с ограниченными возможностями. И часто значительно лучше пользоваться не им, а старыми, хорошо отработанными методами математических и логических исследований.
Компьютер всегда работает по заданной программе. А человек (по крайней мере творчески мыслящий человек), руководствуясь опытом и интуицией, сам определяет порядок своей работы. В этом его громадное преимущество перед любым самым совершенным компьютером.
И вот человек получает в руки компьютер. Пользоваться этим инструментом непросто. Нужно сначала овладеть его "языком", изучить его возможности, научиться подготавливать для него программы, приобрести опыт работы с ним... Наконец, все трудности позади. И тогда многими овладевает своеобразная эйфория. Какая красота! Компьютер все может! Не надо ломать голову над методами решения задач. Можно все решать "в лоб" численными методами. Тем более что соответствующие программы расчета обычно имеются в математическом обеспечении ЭВМ.
Начинается вакханалия численных расчетов - первый признак "компьютерной" болезни. В результате теряется присущая аналитическим методам наглядность и общность исследований, вместо выигрыша имеет место потеря времени, теряется точность, чрезвычайно затрудняется решение "обратных" задач.
Остановимся на еще одной опасности, подстерегающей пользователя ЭВМ. Она связана с использованием чужих программ. Их делают по заказу, дарят, продают за деньги... Все это очень хорошо и существенно облегчает работу. Но... любая программа в действительности соответствует не реальному явлению, а его математической модели, которая верна лишь с определенной точностью, при некоторых условиях и допущениях, в известных пространственных и временных пределах. Кроме того, для решения математических задач, как правило, используются приближенные методы, а это вносит дополнительные ошибки. Поэтому к любому результату расчета на ЭВМ следует относиться критически, помня о пределах, в которых ими можно пользоваться. А это не всегда просто, особенно при работе с чужой программой: если составитель не снабдил ее соответствующими пояснениями, то ее внутренняя структура, пределы применимости и т.п. остаются неизвестными пользователю. Человеку свойственно стремление к экономии сил. Поэтому, приобретя чужую программу, пользователь зачастую не затрудняет себя ее длительным изучением и начинает эксплуатировать программу, что называется, "в хвост и в гриву". При этом он рискует выйти за пределы применимости программы и получить грубо ошибочный результат.
Все это может случиться даже при отсутствии ошибок программирования. А ведь они не исключены. Недаром говорят: "Б каждой отлаженной программе есть по крайней мере две ошибки". Причем ошибки могут находиться в программах, успешно работающих в течение длительного времени. Это связано с тем, что обычно используются не все возможности данной программы. Поэтому некоторые ошибки долго могут находиться в скрытом состоянии и проявятся лишь при переходе к новому варианту расчета. В качестве примера можно указать на известные случаи, когда машины, занятые исчислением налогов и других выплат, предъявляли некоторым людям совершенно необоснованные и непомерные требования.
В заключение хочу привести цитату из еженедельника "За рубежом" 29/83. "Наш мозг недостаточно упражняется, по мнению профессора Т.Мацузавы из Токийского университета.
"Главное противодействие процессам сокращения некоторых участков мозга - это использование его психической мощи. Риск уменьшается у юристов, ученых, врачей, но максимален у людей, занятых монотонной работой.
"Чтобы поддержать нормальное питание клеток мозга, необходима сильная циркуляция крови,- говорит профессор Мацузава,- а лучший путь обеспечить это - напряженная работа мозга. Не полагайтесь на карманные калькуляторы..."
Полностью согласен с уважаемым профессором. Но я несколько уточнил бы его последнюю фразу и сказал бы: не полагайтесь только на компьютеры. Старайтесь побольше загружать свой мозг. Это полезно и для дела и для мозга!
Доктор технических наук П.ЭЛЬЯСБЕРГ (г.Москва).
[ УЗЕЛКИ НА ПАМЯТЬ
На основании своего опыта работы с микрокалькулятором "Электроника Б3-21" могу сказать:
- в режиме программирования не стоит использовать питание от внутреннего источнина - калькулятор работает слишком медленно;
- после ввода программы необходимо сделать проверку - при помощи нлавиши ШГ "прогнать" записанную в память программу, сверяя ее с текстом.
Д.РАТНИКОВ (г.Ленинград). ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Некоторые микрокалькуляторы "Электроника Б3-34" иногда дают ошибки при использовании клавиши Fxy (т.е. при возведении чисел в степень). Оказывается, эти ошибки пропадают, если перед нажатием клавиши Fxy два раза нажать клавишу F1/x.
Б.ГРИГОРЬЕВ (г.Ростов-на-Дону).
ГАРМОНИЯ СФЕР
Рациональные числа - это, как известно, дроби, отношения целых чисел. Будем изображать положительные рациональные числа точками на координатной плоскости: знаменатель - абсцисса, числитель - ордината. Ограничимся для начала дробями, у которых числители и знаменатели не превосходят некоторого n. Нанеся соответствующие точки yа плоскость, выбросим те, которые представляют сократимые дроби (на рисунке 1 - светлые кружки). Вычислим отношение числа оставшихся точек (темные кружки) к общему их числу и посмотрим, как ведет себя это отношение при неограниченном возрастании n.
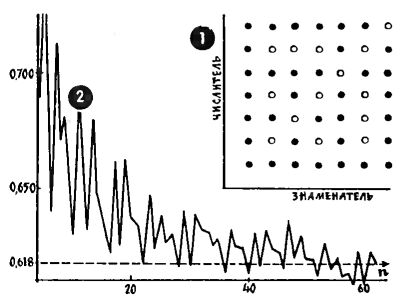
Расчеты на микрокалькуляторе (выборочно мы проводили их для n, достигавших триллиона; см. рис.2) позволяют предположить, что это отношение стремится к знаменитому отношению золотого сечения (sqr(5)-1)/2 = 0.618...
Представленные точками на координатной плоскости рациональные числа располагаются весьма неравномерно. А как распределяются они на числовой оси? Например, на единичном отрезке? Известно, что множество рациональных чисел всюду плотно: между любыми двумя найдется еще одно. Но всюду ли эта плотность одинакова?
Известно, что каждое положительное рациональное число, меньшее единицы, можно представить цепной дробью вида

Здесь a1, a2, a3...- натуральные числа. Ограничимся для начала однозвенными дробями (то есть положим все ak, начиная с a2, равными нулю) и, придавая ak всевозможные натуральные значения, отметим получающиеся при этом числа на единичном отрезке. Потом нанесем на него точки, соответствующие двухзвенным и трехзвенным дробям (3).

Видно, что нанесенные точки сгущаются у отметок, соответствующих элементарным дробям вида 1/n, а на некоторых участках единичного отрезка эти точки располагаются весьма разреженно. Чтобы сделать их распределение нагляднее, над каждым отрезочком, образованным нанесенными точками, проведем горизонтальную линию на высоте, обратно пропорциональной длине отрезочка (4).
Получившиеся ступенчатые линии обнаруживают поразительное сходство с записью показаний вольтметра на выходе активного электрического фильтра - резонансного усилителя, на вход которого подается сигнал постоянного напряжения, но меняющейся частоты (5). Пики графика, уходящие за пределы чертежа, находятся в тех точках, которые соответствуют некоторой основной частоте (правый конец интервала), ее половине, трети, четверти и так далее - при этом в усилителе возникает резонанс.
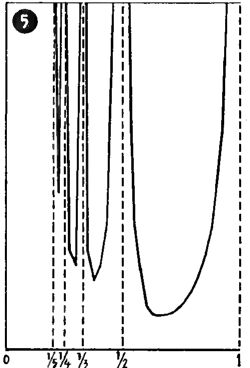
Естественно поинтересоваться: а при каких соотношениях частот система особенно далека от резонанса? Снова обратимся к теории цепных дробей. В ней утверждается, что цепные дроби с ограниченным числом звеньев с наибольшей погрешностью аппроксимируют иррациональные числа, выраженные периодическими бесконечными цепными дробями вида
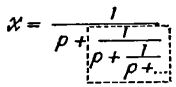
и аппроксимируют тем хуже, чем меньше p.
Нетрудно заметить, что число, обведенное пунктирной рамкой, равно x, и вывести отсюда уравнение x2+px-1=0, а далее определить положительный корень уравнения x: он равен (sqr(p2 + 4)-p)/2. При p=1 получаем известное отношение золотого сечения, дальнейшие значения х указаны в таблице (6). Они приходятся как раз на минимумы графика, снятого с выхода резонансного усилителя.
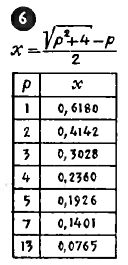
Можно утверждать: если частоты двух колебаний находятся в одном из отношений вида (sqr(p2+4)-p)/2, то колебания наиболее далеки от резонанса по сравнению с другими близлежащими соотношениями частот.
Отсутствие резонанса характеризует устойчивость колебательной системы. Рассмотрим для примера нашу Солнечную систему, периоды обращения ее планет - от Меркурия до Юпитера. Сформулированный критерий устойчивости предписывает определенные соотношения этих периодов, а поскольку периоды обращения T связаны с радиусами орбит R третьим законом Кеплера (квадраты периодов пропорциональны кубам радиусов), то отсюда можно вывести соотношения радиусов орбит, обеспечивающие устойчивость всей системы (рис.7; период обращения и радиус орбиты Юпитера в таком сравнении примем за единицу).

Замечательно, что периоды обращения планет Солнечной системы и радиусы их орбит находятся в соотношениях, весьма близких к выведенным, среднее отклонение составляет около трех процентов (8 ).

Не в этом ли следует усматривать ту "гармонию сфер", которую так настойчиво искал Пифагор в семье планет?
Выведенные соотношения, на наш взгляд, могли бы найти применение в технике. Можно предположить, например, что лопатки турбины будут наименее подвержены риску резонансного разрушения, если их собственные частоты и частота возмущающих колебаний находятся в отношении (sqr(5)-1)/2=0.618...
К.ДОМБРОВСКИЙ, К.СТАНЮКОВИЧ (г.Москва).
Для нашей новой рубрики "Человек с микрокалькулятором" становятся традиционными рассказы о том, как карманные ЭВМ помогают в работе специалистам самых разнообразных профессий. В прошлом выпуске Н.Богин писал о статистических расчетах на микрокалькуляторе. На этот раз о выполняемых на нем геодезических вычислениях сообщает В.Молчанов.
В недавних откликах на новую рубрику есть такие письма, где речь идет о применении микрокалькуляторов в целях обучения: от первых уроков устного счета для дошкольников до вузовских лабораторных работ. С рассказов об этом и начинается очередной выпуск рубрики.
В опубликованных далее статьях и заметках читатели, увлеченные работой на микрокалькуляторах, делятся своими находками, советами. Особого внимания заслуживает выступление П.Эпьясберга, который предостерегает от "компьютерной эйфории", от дилетантской переоценки роли и возможностей вычислительной техники.
СНАЧАЛА В УМЕ, ПОТОМ НА КЛАВИШАХ
Скептики утверждают, что калькуляторы отучат людей считать в уме. Я с этим не согласен. Программа, которую я написал, наоборот, учит устному счету. Работа с калькулятором при этом очень проста. После ввода программы обучаемый вводит в машину два числа, а потом подсчитанную в уме их сумму. Калькулятор проверяет результат, и если он правилен, то на индикаторе появляется оценка 5, в противном случае высвечивается ERROR (ошибка). Моя пятилетняя дочь освоила работу с этой программой очень быстро (правда, ввожу программу я сам), и теперь калькулятор стал ее учителем. Он не только обучает устному счету, но еще развивает у детей внимательность, аккуратность, координацию движений.
ПРОГРАММА. 00. ИП1 (61) 01. ИП2 (62) 02. + (10) 03. ИП3 (63) 04. - (11) 05. Fx=0 (5Е) 06. 09 (09) 07. 05 (05) 08. с/п (50) 09. 00 (00) 10. F1/x (23) 11. с/п (50)
Слагаемые вводятся в регистры 1 и 2, а результат - в регистр 3. Затем следует нажать клавиши "в/о" и "с/п". Через 3-5 секунд на индикаторе появится оценка.
Программу можно изменить так, чтобы использовать ее для обучения не только сложению, но и любому другому арифметическому действию, потренироваться в устном вычислении корней, факториалов, тригонометрических функций и т.д.
А.ЛЮДИН (г.Выборг).
ЭЛЕКТРОННЫЙ ТОПОГРАФ
В топографии часто приходится решать так называемую обратную геодезическую задачу, когда по прямоугольным координатам двух точек на плоскости нужно определить расстояние между ними и дирекционный угол, то есть направление прямой линии, соединяющей эти точки. Дирекционный угол отсчитывается по часовой стрелке от направления на север и измеряется в градусах. Он может принимать значения от 0o до 360o. Если вычислить этот угол на микрокалькуляторе по стандартной формуле

Если вычислять дирекционный угол по приведенной формуле, то отмеченные на карте углы получатся одинаковыми.
то правильные результаты будут получаться только для углов в северо-восточном направлении. Ведь на индикаторе значения арктангенса выдаются в пределах от -90o до 90o. Поэтому углы в северо-восточном и юго-западном направлениях будут неразличимы, так же, как и углы в юго-восточном и северо-западном направлениях. Последние к тому же будут отрицательными, и, чтобы не перепутать север с югом, необходимо вносить коррективы и вычисления, анализируя знаки разностей Dx = x2-x1 и Dy = y2-y1. Кроме того, микрокалькулятор вычисляет значение дирекционного угла в градусах и десятичных долях градуса в то время, как топографы привыкли иметь дело с минутами и секундами.
И все-таки можно заставить микрокалькулятор преодолеть обе эти трудности. "Электроника Б3-34" за 20 секунд вычисляет точную величину днрекционного угла, переводя десятичные доли градуса в минуты и секунды. На индикатор результат выводится в форме ГГГ.ММССД. Это значит, что если высветилось, например, число 218.26372, то нужно читать 218o 26' 37", 2.
Перед началом работы нужно занести в память следующие постоянные величины: число 100 в регистр 0, число 0.55555555 (1/1.8 ) в регистр 1, 10000000 (1e7) в регистр 2, числа 0.6; 180; 360; 17; 26 соответственно в регистры 3, 4, 5, А, В. Координаты x1, y1, x2, 2 вводятся в регистры 6, 7, 8, 0.
Случай Dx = 0 в программе не рассматривается. Но в этом случае калькулятор и не нужен. Угол равен 90o или 270o в зависимости от знака Dy.

ПРОГРАММА. 00. ИП9 (69) 01. ИП7 (67) 02. - (11; считывание y2, y1 и вычисление Dy) 03. ИП8 (68 ) 04. ИП6 (66) 05. - (11; считывание x2, x1 и вычисление Dx) 06. ИПС (6С; запись Dx в регистр C) 07. / (13) 08. Farctg (1L; вычисление А = arctg Dy/Dy) 09. ИПС (6С) 10. Fx<0 (5C) 11. 16 (16; переход к адресу 16 при Dx>0) 12. FO (25) 13. ИП4 (64) 14. + (10; увеличение А на 180o) 15. КБПА (8-) 16. FО (25) 17.Fx<0 (5С) 18. 21 (21; переход к адресу 21 при А>0) 19. ИП5 (65) 20. + (10; увеличение А на 360o) 21. КППВ (-L) 22. * (12; отделение долей минуты от целых минут) 23. КППВ (-L) 24. / (13; отделение градусов от минут и секунд) 25. с/п (50; индикация результата).
Подпрограмма для перевода десятичных долей градуса в минуты и секунды. 26. ^ (ОЕ) 27. ^ (ОЕ) 28. ИП1 (61) 29. - (11) 30. ИП2 (62) 31. + (10) 32. FBx (0) 33. - (11) 34. - (11) 35. FBx (0) 36. х-у (14) 37. ИП3 (63) 38. * (12) 39. + (10) 40. ИП0 (60) 41. в/о (52).
В.МОЛЧАНОВ (г.Воронеж).
[ В подпрограмме перевода долей градуса в минуты и секунды, предложенной В.Молчановым, происходит выделение целой части числа, объявленное темой конкурса в предыдущем выпуске рубрики "Человек с микрокалькулятором" (12/83). Вероятно, этого же заслуживает и вся задача, для которой составлена программа. Итак, очередное задание нашего конкурса: перевод десятичных долей градуса в минуты, секунды и десятичные доли секунды.
И еще одно задание: вычисление факториала натурального числа. Задача несложна, и реализующая ее программа будет короткой и простой. Однако среди различных вариантов программы наверняка окажется особенно лаконичный и изящный. ]
ОТМЕТКУ СТАВИТ КАЛЬКУЛЯТОР
Хочу рассказать о том, как учитель начальных классов может использовать микрокалькулятор, чтобы быстро и беспристрастно проставить школьникам оценки за скорость чтения. Оценивается она по числу слов, прочитанных за минуту. Нормы скорости предусмотрены учебной программой: 30-40 слов в минуту для первого класса, 60-70 слов - для второго и 80-90 - для третьего.
Подсчитываем заранее количество знаков в тексте. Длина текста может быть любой, например, один абзац. Потом включаем секундомер и засекаем время, за которое ученик прочтет текст. Всю остальную работу делает за нас калькулятор. А сводится она к вычислениям по формуле:
число знаков * 60 * 3 / (длина слова * время * норма).
Среднюю длину слова можно принять равной семи
буквам. Время подставляем в секундах.
Например, 290 знаков третьеклассник прочитал за 48 секунд. Вычисляем на микрокалькуляторе:
290*60*5/(7*48*80) = 3.2
Ученик получает тройку.
Видно, что меняются в этой формуле только число знаков и время. Поэтому постоянную часть формулы достаточно вычислить один раз. При такой методике один учитель может свободно провести проверку скорости чтения у 25-30 учеников за урок, а дома кто-нибудь из взрослых может оценить навыки ребенка в чтении за 2-3 минуты.
В.АКСЕЛЬРУД, учитель школы-интерната (с.Затока Овидиопольского района Одесской области).
МИКРО-ВЦ В НАШЕМ ОБЩЕЖИТИИ
Программируемые микрокалькуляторы лишь недавно появились в учебных лабораториях Московского института инженеров железнодорожного транспорта, но уже убедительно продемонстрировали свои богатые и широкие возможности.
На кафедре "Измерительная техника" они используются в 16 лабораторных работах. На кафедре "Физика-1" - для контроля знаний студентов. Кафедра "Электрическая тяга" создала в общежитии МИИТа студенческий "микро-ВЦ" для курсового и дипломного проектирования. Все руководства для этого ВЦ написаны студентами.
Как показывает опыт, микрокалькуляторы с программной памятью на несколько десятков команд едва ли не оптимальны в учебном процессе. Ведь из 90 минут, обычно отводимых на занятие, программирование не должно занимать слишком много времени.
Когда студент освобожден от необходимости многократно повторять одну и ту же цепочку вычислений, атмосфера занятия меняется в корне, делается более творческой, позволяя сосредоточиться на сущности исследования. Работы, считавшиеся раньше скучными и однообразными, вдруг превратились в увлекательные и интересные. "Студентов невозможно выгнать из аудитории",- говорит доцент Ю.В.Темлякова.
Программируемый микрокалькулятор - идеальный инструмент для не слишком сложного (но все-таки достаточно сложного!) математического эксперимента. Конечно, он никогда не заменит классических средств исследования функций. Но вспомним: ведь даже "чистый математик" Шарль Эрмит подчеркивал роль "наблюдения фактов" в математике. А в прикладных исследованиях роль такого эксперимента (пусть простого, но зато оперативного) несомненна. И овладеть этим средством надо, конечно, еще в вузе.
Ф.ГОРЮШЕВ, младший научный сотрудник (МИИТ).

[ Этот снимок сделай в одной из учебных лабораторий Московского физико-технического института. Определяя отношение заряда электрона к его массе по методу Милликена, студент должен проделать обширные статистические расчеты. Их облегчает микрокалькулятор, встроенный в пульт управления экспериментальным прибором.
Фото В.БЕЗДУДНОГО. ]
КАК РЕШИТЬ НЕРАЗРЕШИМОЕ УРАВНЕНИЕ
Давние читатели журнала, возможно, помнят "загадку жрецов бога Ра" ("Наука и жизнь" 1/66). Глубина воды в цилиндрическом колодце - 1 локоть, две тростинки длиной 2 и 3 локтя опущены в колодец, как показано на рисунке. От кандидатов на замещение вакантной должности жреца требовалось определить диаметр колодца.

Обозначим длины тростинок L и l, глубину воды в колодце - h, неизвестный диаметр колодца - x. Все эти величины несложно связать уравнением:
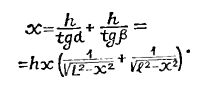
Полученное уравнение неразрешимо - по крайней мере, средствами школьной математики: оно сводится к уравнению четвертой степени, решение которого дается далеко не в каждом справочнике. Но, к счастью, оно имеет вид x = f(x), удобный для применения метода итераций (10/83). По этому методу решение уравнения отыскивается как предел последовательности приближений xn, каждый член которой определяется через предыдущий: x[n+1] = f(xn). Надо лишь задаться начальным приближением x0.
Из условия задачи ясно, что искомый x больше 0 и меньше 2. Вот и возьмем начальное приближение посередине: x=1. Подставив это значение в правую часть нашего уравнения, получим x1=0.931 (надеясь, что точность до тысячной доли локтя жрецов удовлетворяла, будем указывать только три знака после запятой), и далее x2=0.852; x3=0.767; ... x9=0.315; x10=0.205... Что-то узковатый колодец получается... Непохоже, что эта последовательность сходится к решению.
Может, изменить начальное значение? Меньше единицы его брать бесполезно, этот участок мы уже "прошагали", возьмем число поближе к другому концу интервала: x0=1.5. Находим x1=1.711; х2=2.348. Опять неудача - ведь х не может быть больше двух.
Выходит, к нашему уравнению с методом итераций и не подступишься? Нет, отчаиваться рано: к виду x=f(x) его можно привести и иначе - например, преобразовав так:
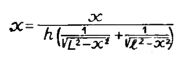
Начнем опять с x0=1. Первые итерации - x1= 1.074; x2=1.131; х3=1.171. Последовательность пошла в сторону увеличения х, а не уменьшения, как в первом случае, и это уже обнадеживает. Но не стремится ли она к правому концу интервала, как раньше к левому? Возьмем x0=1.5. Имеем х1=1.315; x2=1.271; x3= 1.252... Вот теперь, похоже, можно закричать, как кот Матроскин из известного мультфильма: "Ура! Заработало!"
Но сначала вглядимся в формулу критическим взглядом: нельзя ли видоизменить се так, чтобы реализующая ее программа оказалась наилучшей?
Должен сказать, что в критериях оценки программ для микрокалькуляторов я не согласен с И.Даниловым (10/83), который соображения быстроты выдвигает на первый план, а насчет объема программы замечает вскользь: лишь бы она вмешалась в память микрокалькулятора. Владельцы микрокалькуляторов, как правило, имеют достаточно времени для своих вычислений и могут им распоряжаться: не успел утром, можно закончить вечером. Но если уж программа чрезмерно длинна, то так оно будет и вечером и на следующий день. Подобные неприятности гарантированы тому, кто не старается постоянно упражнять себя в искусстве лаконичного программирования. Чтобы их избежать, следует, на мой взгляд, в первую очередь соблюдать принцип экономии памяти и только во вторую - экономии времени. Если микрокалькулятор выполняет действия с запоминанием константы, целесообразно преобразовать наше уравнение еще раз:

Теперь в правой части неизвестное x присутствует лишь в квадрате, который достаточно вычислить лишь однажды, да и сам х лишь однажды придется вызывать из памяти. Все это - в пользу краткости программы, да и скорости вычислений тоже.
Заметим еще, что в нашей формуле используются только квадраты величин L и l. Их сразу и запишем в память. На этом мы сэкономим еще две строки программы и время, затрачиваемое на возведение в квадрат.
Возьмем начальное приближение x0=1 и получим ответ 1.231, достигнув заданную точность в третьем знаке за одиннадцать итерации.
А.РАЗДОБРЕЕВ (г.Владимир].
[ Многие из тех, кто имеет солидный опыт работы с микрокалькуляторами, сталкивались с необходимостью вписать громоздкую программу в небольшую память карманной ЭВМ и могли бы поделиться остроумными уловками, позволявшими выйти из затруднительного положения.
Ждем писем на эту немаловажную тему. ]
ОСТОРОЖНО-КОМПЬЮТЕРЫ!
Быстрое внедрение компьютеров в различные области науки и техники, появление миллионов специалистов, владеющих машинными методами вычислений, достигнутые в результате большие успехи - все это привело к известной переоценке возможностей ЭВМ. Многие забывают, что ЭВМ - это всего лишь инструмент в руках человека, инструмент очень совершенный, но с ограниченными возможностями. И часто значительно лучше пользоваться не им, а старыми, хорошо отработанными методами математических и логических исследований.
Компьютер всегда работает по заданной программе. А человек (по крайней мере творчески мыслящий человек), руководствуясь опытом и интуицией, сам определяет порядок своей работы. В этом его громадное преимущество перед любым самым совершенным компьютером.
И вот человек получает в руки компьютер. Пользоваться этим инструментом непросто. Нужно сначала овладеть его "языком", изучить его возможности, научиться подготавливать для него программы, приобрести опыт работы с ним... Наконец, все трудности позади. И тогда многими овладевает своеобразная эйфория. Какая красота! Компьютер все может! Не надо ломать голову над методами решения задач. Можно все решать "в лоб" численными методами. Тем более что соответствующие программы расчета обычно имеются в математическом обеспечении ЭВМ.
Начинается вакханалия численных расчетов - первый признак "компьютерной" болезни. В результате теряется присущая аналитическим методам наглядность и общность исследований, вместо выигрыша имеет место потеря времени, теряется точность, чрезвычайно затрудняется решение "обратных" задач.
Остановимся на еще одной опасности, подстерегающей пользователя ЭВМ. Она связана с использованием чужих программ. Их делают по заказу, дарят, продают за деньги... Все это очень хорошо и существенно облегчает работу. Но... любая программа в действительности соответствует не реальному явлению, а его математической модели, которая верна лишь с определенной точностью, при некоторых условиях и допущениях, в известных пространственных и временных пределах. Кроме того, для решения математических задач, как правило, используются приближенные методы, а это вносит дополнительные ошибки. Поэтому к любому результату расчета на ЭВМ следует относиться критически, помня о пределах, в которых ими можно пользоваться. А это не всегда просто, особенно при работе с чужой программой: если составитель не снабдил ее соответствующими пояснениями, то ее внутренняя структура, пределы применимости и т.п. остаются неизвестными пользователю. Человеку свойственно стремление к экономии сил. Поэтому, приобретя чужую программу, пользователь зачастую не затрудняет себя ее длительным изучением и начинает эксплуатировать программу, что называется, "в хвост и в гриву". При этом он рискует выйти за пределы применимости программы и получить грубо ошибочный результат.
Все это может случиться даже при отсутствии ошибок программирования. А ведь они не исключены. Недаром говорят: "Б каждой отлаженной программе есть по крайней мере две ошибки". Причем ошибки могут находиться в программах, успешно работающих в течение длительного времени. Это связано с тем, что обычно используются не все возможности данной программы. Поэтому некоторые ошибки долго могут находиться в скрытом состоянии и проявятся лишь при переходе к новому варианту расчета. В качестве примера можно указать на известные случаи, когда машины, занятые исчислением налогов и других выплат, предъявляли некоторым людям совершенно необоснованные и непомерные требования.
В заключение хочу привести цитату из еженедельника "За рубежом" 29/83. "Наш мозг недостаточно упражняется, по мнению профессора Т.Мацузавы из Токийского университета.
"Главное противодействие процессам сокращения некоторых участков мозга - это использование его психической мощи. Риск уменьшается у юристов, ученых, врачей, но максимален у людей, занятых монотонной работой.
"Чтобы поддержать нормальное питание клеток мозга, необходима сильная циркуляция крови,- говорит профессор Мацузава,- а лучший путь обеспечить это - напряженная работа мозга. Не полагайтесь на карманные калькуляторы..."
Полностью согласен с уважаемым профессором. Но я несколько уточнил бы его последнюю фразу и сказал бы: не полагайтесь только на компьютеры. Старайтесь побольше загружать свой мозг. Это полезно и для дела и для мозга!
Доктор технических наук П.ЭЛЬЯСБЕРГ (г.Москва).
[ УЗЕЛКИ НА ПАМЯТЬ
На основании своего опыта работы с микрокалькулятором "Электроника Б3-21" могу сказать:
- в режиме программирования не стоит использовать питание от внутреннего источнина - калькулятор работает слишком медленно;
- после ввода программы необходимо сделать проверку - при помощи нлавиши ШГ "прогнать" записанную в память программу, сверяя ее с текстом.
Д.РАТНИКОВ (г.Ленинград). ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Некоторые микрокалькуляторы "Электроника Б3-34" иногда дают ошибки при использовании клавиши Fxy (т.е. при возведении чисел в степень). Оказывается, эти ошибки пропадают, если перед нажатием клавиши Fxy два раза нажать клавишу F1/x.
Б.ГРИГОРЬЕВ (г.Ростов-на-Дону).
ГАРМОНИЯ СФЕР
Рациональные числа - это, как известно, дроби, отношения целых чисел. Будем изображать положительные рациональные числа точками на координатной плоскости: знаменатель - абсцисса, числитель - ордината. Ограничимся для начала дробями, у которых числители и знаменатели не превосходят некоторого n. Нанеся соответствующие точки yа плоскость, выбросим те, которые представляют сократимые дроби (на рисунке 1 - светлые кружки). Вычислим отношение числа оставшихся точек (темные кружки) к общему их числу и посмотрим, как ведет себя это отношение при неограниченном возрастании n.

Расчеты на микрокалькуляторе (выборочно мы проводили их для n, достигавших триллиона; см. рис.2) позволяют предположить, что это отношение стремится к знаменитому отношению золотого сечения (sqr(5)-1)/2 = 0.618...
Представленные точками на координатной плоскости рациональные числа располагаются весьма неравномерно. А как распределяются они на числовой оси? Например, на единичном отрезке? Известно, что множество рациональных чисел всюду плотно: между любыми двумя найдется еще одно. Но всюду ли эта плотность одинакова?
Известно, что каждое положительное рациональное число, меньшее единицы, можно представить цепной дробью вида

Здесь a1, a2, a3...- натуральные числа. Ограничимся для начала однозвенными дробями (то есть положим все ak, начиная с a2, равными нулю) и, придавая ak всевозможные натуральные значения, отметим получающиеся при этом числа на единичном отрезке. Потом нанесем на него точки, соответствующие двухзвенным и трехзвенным дробям (3).

Видно, что нанесенные точки сгущаются у отметок, соответствующих элементарным дробям вида 1/n, а на некоторых участках единичного отрезка эти точки располагаются весьма разреженно. Чтобы сделать их распределение нагляднее, над каждым отрезочком, образованным нанесенными точками, проведем горизонтальную линию на высоте, обратно пропорциональной длине отрезочка (4).
Получившиеся ступенчатые линии обнаруживают поразительное сходство с записью показаний вольтметра на выходе активного электрического фильтра - резонансного усилителя, на вход которого подается сигнал постоянного напряжения, но меняющейся частоты (5). Пики графика, уходящие за пределы чертежа, находятся в тех точках, которые соответствуют некоторой основной частоте (правый конец интервала), ее половине, трети, четверти и так далее - при этом в усилителе возникает резонанс.

Естественно поинтересоваться: а при каких соотношениях частот система особенно далека от резонанса? Снова обратимся к теории цепных дробей. В ней утверждается, что цепные дроби с ограниченным числом звеньев с наибольшей погрешностью аппроксимируют иррациональные числа, выраженные периодическими бесконечными цепными дробями вида
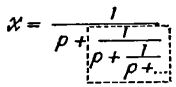
и аппроксимируют тем хуже, чем меньше p.
Нетрудно заметить, что число, обведенное пунктирной рамкой, равно x, и вывести отсюда уравнение x2+px-1=0, а далее определить положительный корень уравнения x: он равен (sqr(p2 + 4)-p)/2. При p=1 получаем известное отношение золотого сечения, дальнейшие значения х указаны в таблице (6). Они приходятся как раз на минимумы графика, снятого с выхода резонансного усилителя.

Можно утверждать: если частоты двух колебаний находятся в одном из отношений вида (sqr(p2+4)-p)/2, то колебания наиболее далеки от резонанса по сравнению с другими близлежащими соотношениями частот.
Отсутствие резонанса характеризует устойчивость колебательной системы. Рассмотрим для примера нашу Солнечную систему, периоды обращения ее планет - от Меркурия до Юпитера. Сформулированный критерий устойчивости предписывает определенные соотношения этих периодов, а поскольку периоды обращения T связаны с радиусами орбит R третьим законом Кеплера (квадраты периодов пропорциональны кубам радиусов), то отсюда можно вывести соотношения радиусов орбит, обеспечивающие устойчивость всей системы (рис.7; период обращения и радиус орбиты Юпитера в таком сравнении примем за единицу).

Замечательно, что периоды обращения планет Солнечной системы и радиусы их орбит находятся в соотношениях, весьма близких к выведенным, среднее отклонение составляет около трех процентов (8 ).

Не в этом ли следует усматривать ту "гармонию сфер", которую так настойчиво искал Пифагор в семье планет?
Выведенные соотношения, на наш взгляд, могли бы найти применение в технике. Можно предположить, например, что лопатки турбины будут наименее подвержены риску резонансного разрушения, если их собственные частоты и частота возмущающих колебаний находятся в отношении (sqr(5)-1)/2=0.618...
К.ДОМБРОВСКИЙ, К.СТАНЮКОВИЧ (г.Москва).
Последний раз редактировалось: Gudleifr (Ср Дек 07, 2022 12:46 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
4/84
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
СЕКРЕТЫ МИКРОКАЛЬКУЛЯТОРА
Рубрика "Человек с микрокалькулятором", недавно появившаяся в нашем журнале, вскоре приобрела характер бесед за круглым столом. Публикуемые под нею заметки читателей - словно выступления в широкой дискуссии о разнообразных применениях карманных ЭВМ, о вычислительных "секретах", повышающих эффективность этих применений.
Так обстоит дело и с письмами, поступившими в редакцию за последнее время: мысль, высказанная в одном письме, подхватывается в другом и развивается в третьем... При подготовке к печати очередного выпуска рубрики было решено не нарушать qyx такой связной последовательности и объединить фрагменты писем в слитный текст своеобразной беседы.
В ней участвуют: А.БОЙКО (студент, г.Москва), В. ДЬЯКОНОВ (доктор технических наук, г.Смоленск), Л.МИЛЕХИН (кандидат технических наук, г.Ленинград, Д.МЫСЛИН (кандидат технических наук, г.Новосибирск), С.КОНИН (студент, г.Ленинград).
В.Дьяконов. К ЭВМ мне приходится обращаться частенько. Но встречаются, и нередко, задачи, решать которые на больших ЭВМ - все равно, что стрелять из пушки по воробьям. Однажды мне понадобилось срочно вычислить несколько значении функции f(x)=ln((exp(x)+1)/(x+1)).
Вычислять их вручную утомительно. И я решил обратиться за помощью к "Электронике Б3-34".
Что за чудо-машина! Экспоненциальные, логарифмические, тригонометрические и целый ряд других функции вычисляет при нажатии всего двух клавиш, на первой из которых проставлено F, а на второй - название функции, имеет 14 регистров памяти, стек из 4 ячеек. А главное, в микрокалькулятор можно вводить программы длиной до 98 команд.
Д.Мыслин. Возникает вопрос: в каких случаях использовать программы? С одной стороны, автоматический счет быстрее ручного, но с другой - программу каждый раз нужно вводить с клавиатуры. Использование внешних носителей - магнитных карт и лент, перфолент и т.д. - для микрокалькулятора не предусмотрено.
Ввод программы требует такого же времени, как и набор последовательности операций в "ручном случае". Кроме того, время составления и отладки программы измеряется часами, а сам расчет секундами. Поэтому составление программы для проведения расчета, пусть и очень трудоемкого, но единственного, вряд ли целесообразно. Очевидно, стоит разрабатывать программы для расчетов, которые систематически встречаются и работе, или и ситуациях, когда число операций, выполняемых при вводе программы, меньше числа операции, необходимых для выполнения расчета. Это бывает в двух случаях: во-первых, когда используются циклы н, во-вторых, при использовании подпрограмм. Сюда же примыкают случаи, когда по одной и той же формуле (или формулам) нужно провести вычисления для различных значений исходных параметров. Во всех этих ситуациях программа дает выигрыш во времени при расчетах и обеспечивает большую надежность результатов по сравнению с ручными вычислениями.
В.Дьяконов. Программа для микрокалькулятора - это последовательность команд, записанная па специальном языке. У "Электроники "Б3-34" этот язык элементарно прост. Текст на нем указывает символы и порядок нажатия клавиш. Каждая команда имеет свои помер - адрес, по которому она записывается в памяти. Программа для вычисления функции, о которой я упомянул выше, может быть записана так:
00. П9 01. Fexp 02. 1 03. + 04. ИП9 05. 1 06. + 07. / 08. Fln 09. С/П 10. БП 11. 00.
Размещается она в памяти, начиная с адреса 00. Значение x берется из 9-го регистра. Команда С/П (стоп-пуск) задает остановку вычислений, а команда БП 00 организует безусловный переход на шаг 00, то есть к началу программы.
Теперь можно считать. Ввожу программу, нажимаю клавиши F, АВТ и В/О (возврат к пулевому адресу), набираю на клавиатуре значение x=1 и, нажав клавишу С/П, через несколько секунд получаю результат: f(1)=0.6201145. Набрав другое значение x, получаю новый результат и т.д.
Кроме безусловных переходоп, есть еще и условные. Например, если в программе написано Fх!=0 23, то при равенстве содержимого регистра x нулю управление передается на адрес 23. В противном случае эта команда игнорируется и выполняется следующая за ней.
Существуют два тина адресации: прямая и косвенная. В первом случае адрес, если он стоит после команды перехода, или регистр, содержимое которого нужно использовать, указываются непосредственно. Косвенная адресация вводится клавишей "К". Что достигается с ее помощью? Например, в регистре 8 записано число 2, а в регистре 2 - число 10. Если использовать прямую адресацию и выполнить команду считывания ИП8, то из памяти будет вызвано содержимое регистра 8, то есть число 2. Если же используется адресация косвенная, по команде КИП8, то из памяти будет вызвано не число 2, а содержимое регистра 2, то есть число 10. Косвенные адреса могут меняться и процессе вычислений. Это называется модификацией адреса.
С.Конин. Итак, позади первые радости. Вы узнали, что означают те или иные команды, что модификация адреса - это просто его изменение, написали несколько простеньких программ и хотите перейти к более сложным. Для начала два методических совета: во-первых, заведите общую тетрадь, в которую записывайте тексты отлаженных программ, и, во-вторых, систематизируйте таблицу кодов, приведенную в инструкции. К сожалению, они разбросаны по разным ее разделам, что сильно затрудняет дешифровку команд при отладке программ.
Д.Мыслин. Так как расчеты по одной программе проводятся неоднократно, лучше использовать для записи программ специальные бланки, куда следует вписать и соответствующие контрольные примеры.
С.Конин. При написании разных программ часто встречаются одинаковые проблемы, поэтому знание отдельных программистских приемов, "маленьких хитростей" программиста, может значительно облегчить процесс составления сложных программ.
В.Дьяконов. Одна из таких хитростей - использование модификации адреса, о которой я уже упоминал. Если адрес задан в регистрах 0, 1, 2 или 3, то адрес этот (содержимое регистра) при каждом обращении к нему уменьшается на 1; если обращаться к регистрам 4, 5 или 6, то адрес увеличивается на 1. Содержимое остальных регистров не меняется при обращении.
Поясним это примером. Необходимо, скажем, вычислить значение многочлена:
P(x)=a0+a1*x+a2*x**2+...an*x**n
Это можно сделать, используя схему Горнера:
P(x)=((...(an*x+a[n-1])x+a[n-2])x+...+al)x+a0.
Берем вначале коэффициент an и умножаем на x, к произведению прибавляем a[n-1], результат снова умножаем на x и т.д. Чтобы реализовать этот алгоритм, нужно научиться программными средствами извлекать из памяти значения коэффициентов. Здесь-то и пригодится модификация адреса. Ограничимся значением n=9 и запишем a1 в регистр Р1, a2 - в P2... a9 - в P9. Коэффициент a0 занесем в регистр C. Программу для вычисления значений полинома запишем так:
00 ПД 01. 9. 02. П0 03. ИП9 04. ^ 05. x-y 06. ИПД 07. * 08. КИПО 09. + 10. ИП0 11. Fx=0 12. 05 13. x-y 14. ИПС 15. + 16. С/П 17. БП 18. 00.
Читатели сами могут проверить работу программы. Циклически повторяется часть программы с 5 по 12 адрес. Поочередный вызов коэффициентов организован командой косвенной адресации КИП0 с адресным регистром Р0, содержимое которого на каждом цикле уменьшается на 1. Как только оно станет нулевым, циклы прекращаются и к результату прибавляется a0 (содержимое регистра C).
А.Бойко. Еще одни интересный прием, обогащающий возможности микрокалькулятора,- использование стека.
Стек состоит из четырех регистров: X, Y, Z, Т, которые заполняются числами, словно пистолетная обойма патронами: когда в регистр X вводится новое число, то находившееся в нем прежде перемещается в регистр Y, содержимое регистра Y - в Z и т.д. Числа при этом, образце говоря, движутся "снизу вверх", и каждый раз содержимое регистра T теряется.
Есть команды, по которым в стеке идет движение "сверху вниз". Содержимое регистра X при этом перемещается в регистр XI. Он может быть причислен к стеку. Его содержимое при перемещении "снизу вверх" по команде FВх поступает в регистр X; когда же содержимое регистра X используется в качестве аргумента при вычислении функций и выполнении двухместных операций, а результат направляется опять-таки в регистр X, прежнее его содержимое передается в регистр XI.
Д.Мыслин. Движение информации по стеку при выполнении различных операций удобно выразить диаграммой:
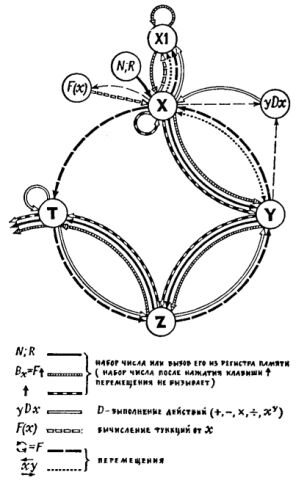
(При возведении в степень содержимое регистров Y, Z, T не меняется).
Л.Милехин. Простейший пример применения стековой памяти - суммирование последовательности чисел. Фрагмент программы, ответственный за эту процедуру, может быть записан всего одним символом: +. Перед началом суммирования следует очистить все стековые регистры. Если ввести в калькулятор первое слагаемое (при вводе оно попадает в регистр X) и выполнить команду суммирования, то она сложит содержимое регистров X и Y, а результат запишет в X (так оно происходит при пыполнении любой двухместной операции). При введении очередного слагаемого вычисленная сумма попадает в регистр Y. С каждым повторением этих операций (ввод, суммирование) к ней будут прибавляться псе новые и новые слагаемые.
A.Бойко. Использование стека значительно повышает быстродействие. Например, программа для вычисления факториала без использования стека па подсчет 69! потратила 115 секунд, а программа с использованием стека - 70 секунд.
С.Конин. Экономить время работы можно не только за счет улучшения программ. Представьте себе, что вы работаете целый день с одной программой. Для того чтобы пустить ее на счет, нужно нажать дне клавиши: В/О и С/П. Но можно сократить время запуска ровно вдвое, если по нулевому адресу записать КНОП и после С/П занести В/О. Первый раз придется все-таки нажать обе клавиши (В/О и С/П), зато каждый следующий достаточно нажимать одну (С/П). Следует отметить, что использовать эту рекомендацию можно лишь для программ, в которчх нет подпрограмм.
B.Дьяконов. Микрокалькуляторы хранят в себе немало секретов. Каждый раз садясь за эту маленькую машинку, ощущаешь себя в положении исследователя, который может открыть что-то новое. И в этом, наверное, еще одно достоинство микрокалькулятора.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Длительное ожидание результатов вычислений на микрокалькуляторе при использовании сложных программ утомительно. Заполнить это время другими делами помогает звуковой индикатор, подающий сигнал об окончании счета. Роль такого индикатора может пыполнить обычный радиоприемник, принимающий и диапазоне средних волн. Работающий микрокалькулятор нужно положить рядом с ним. Оказывается, при появлении каждой комбинации цифр на индикаторе калькулятор излучает определенный спектр электромагнитных ноли. Завершив программу выводом некоторого числа и "настроив" на него приемник, молено пустить программу, заняться другим делом и ждать сигнала о завершении счета.
Я проверил свою идею на микрокалькуляторах марок Б3-21 и Б3-34. Во втором случае сигнал мощнее.
В.БОГАТКО (г.Ленинград). ]
ЗНАКОМЬТЕСЬ: "ПРОМИК"
"Запись программ для микрокалькуляторов на языке команд страдает целым рядом недостатков. Она громоздка, не отличается наглядностью. Кроме того, для разных микрокалькуляторов некоторые одинаковые по смыслу команды записываются по-разному. Это затрудняет использование программ, написанных для калькуляторов одного типа, на других. Наконец, и это самое важное, задачи на калькуляторах решаются в полуавтоматическом режиме, и человек является при этом полноправной составной частью вычислительной системы. Поэтому программа должна содержать инструкции и для него".
Так начинает свое письмо в редакцию кандидат технических наук Л.Н.МИЛЕХИН. Проблема, поставленная читателем, весьма насущна. В письме предлагается одно из возможных ее решений. Комментирует его в статье, помещенной далее, член-корреспондент АН СССР А.П.ЕРШОВ.
Итак, нужен специальный язык для записи программ, предназначенных для микрокалькулятора. Придя к этому выводу, я попытался создать такой язык. Называется он "Промик" - ПРОграммирование для МИКрокалькуляторов. Наряду с ним я предлагаю стандарт для оформления отлаженных программ, чтобы облегчить обмен ими.
Чтобы уяснить, как выглядит программа, написанная в соответствии с предложенным стандартом на языке "Промик", опишем на нем алгоритм численного решения уравнения f(x)=0.
ПРОГРАММА. Вычисления кория уравнения методом половинного деления.
1. МОДЕЛЬ. Вычисляется корень уравнения f(x)=0 на отрезке [a,b].
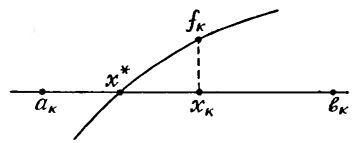
Обозначения: xk, x*, xe - значения корня соответственно на k-том шаге вычислений, точное, вычисленное с заданной точностью; ak, bk - границы интервала на k-том шаге; e - допустимая погрешность; fk - значение функции в точке xk.
2. ФОРМУЛЫ.
Пункты 1 и 2 описывают постановку задачи и алгоритм, по которому она решается.
x = (ak+bk)/2
a[k+1]=ak, b[x+1]=xk, если fk>=0
a[k+1]=xk, b[x+1]=bk, если fk,0
Пункты 1 и 2 описывают постанову задачи и алгоритм, по которому она решается.
3. РАСПРЕДЕЛЕНИЕ ПАМЯТИ.
R7=xk, R9=2e, RA=ak, RB=bk
Здесь показано, какие величины должны храниться в регистрах или вводиться в них. Регистры обозначаются буквой R с соответствующим индексом.
4. ОПИСАНИЕ ПРОЦЕДУР И ПОД-ПРОЦЕДУР.
Процедуры и подпроцедуры - это последовательности команд, заносимых в память микрокалькулятора. В записи они ограждаются фигурными скобками. Различаются они тем, что обращение к процедуре осуществляется с клавиатуры, а обращение к подпроцедуре - автоматическое, с помощью команд. Каждая команда состоит из названий клавиш, которые нужно нажать для ее выполнения, и обрамляется точками. Смежные точки позволяется "сливать" в одну. Двойные стрелки используются вместо имен клавиш П и ИП, то есть для показа записи и чтения, что делает команды более наглядными. Остальные обозначения соответствуют надписям на клавишах микрокалькулятора. Над командой записывается ее порядковый номер (адрес). Выше адреса и ниже команды допускается комментарий, который облегчает чтение команды. Например:
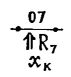
Это команда по адресу 07, чтение содержимого 7-го регистра, где записана величина xk.
Кроме команд, в записи программы допускается использование идентификаторов - имен, значения которым приписываются лишь при решении конкретных задач. В нашей программе, например, Aпв - это адрес, начиная с которого записана подпроцедура вычисления значений функции f(x).
Вот как записывается процедура отыскания корня:
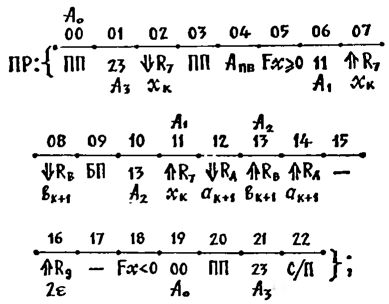
В надстрочном комментарии для лучшей ориентации заглавными буквами А с индексами отмечены некоторые "ключевые" адреса, в подстрочном - переходы к этим адресам, а также заносимые и выводимые в ходе счета значения xk, ak, bk, 2e.
А вот как выглядят подпроцедуры для вычисления xk (середины очередного отрезка деления) и значения функции f(х):
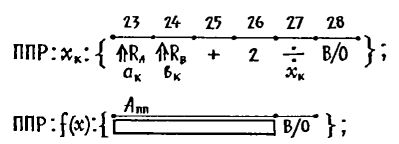
Процедуры и подпроцедуры - две разновидности операторов. Кроме этих двух, в "Промике" есть еще две разновидности.
Условный оператор. Он начинается с буквы Е, далее в круглых скобках пишется условие, затем в фигурных скобках - последовательность команд, которая либо выполняется (если условие соблюдается), либо пропускается (если условие не соблюдается).
Оператор цикла. Он начинается с буквы Ц, далее в круглых скобках указывается параметр цикла и список значений, которые он должен принять, затем в фигурных скобках - последовательность команд, которая должна быть выполнена для всех значений параметра.
5. ДИРЕКТИВА.

Директива - это часть программы, адресуемая для выполнения человеку. Здесь мы встречаемся с предписаниями. Прямоугольник означает: "ждать окончания работы процедуры". Ломаная стрелка: "прочитать число с индикатора и присвоить это значение переменной, написанной в подстрочном комментарии" или "выполнить указание, стоящее в подстрочном комментарии". Идентификатор в скобках, например (2e). означает, что в этом месте нужно набрать на клавиатуре числовое значение идентификатора для ввода его в память.
6. УКАЗАНИЯ ПО ПРИМЕНЕНИЮ. Выбрать знак перед f(x) так, чтобы производная f(x) в окрестности точки х* была положительной.
7. КОНТРОЛЬНЫЙ ПРИМЕР.
В этом разделе описывается пример использования программы.
Л. МИЛЕХИН, кандидат технических наук (г.Ленинград).
ЯЗЫК ИЛИ ЛЕКСИКОН?
Осповная задача, стоящая перед пашнм обществом сегодня,- подъем производительности труда. Нужно создавать условия, при которых она поднимается. Одно из таких условий - творческая атмосфера, привычка к творческому труду. Широкое внедрение ЭВМ способствует этому. ЭВМ в руках инженера резко расширяет сферу посильпых для него творческих задач.
До последнего времени бытовало мнение, что ЭВМ - это удел избранных, посвященных. Освоить машину нелегко. При этом, образпо говоря, человек должен идти навстречу машине. Теперь направление движения меняется. Машина идет навстречу человеку, современные ЭВМ все более удобны в работе.
В числе таких машин - программируемые калькуляторы. Но и они не сегодня-завтра уступят место на столе инженера персональным ЭВМ, которые возьмут на себя огромную часть рутинной работы - расчеты, оформлепие документов, упростят поиск информации и т.д.
Готовиться к этому процессу нужно заранее. Считаю, что большую роль в этом может сыграть постоянная рубрика "Человек с микрокалькулятором", цель которой привить читателям журнала вкус к работе с ЭВМ, собирать и распространять опыт по использованию вычислительной техники. В этой связи, пожалуй, первоочередным является вопрос о языке, на котором было бы удобпо записывать программы для программируемых микрокалькуляторов.
Язык программирования - это язык для описания данных (информации) и алгоритмов (программ) их обработки на ЭВМ. Это замкнутая совокупность определенных символов и правил, диктующих, как с помощью этих символов записывать алгоритмы для ЭВМ.
Число существующих языков программирования перевалило за несколько тысяч и, наверное, скоро будет сравнимо с количеством человеческих языков. Но программистов не покидает мечта об общем языке программирования, на котором можно было бы не только учить программированию, но и описывать программы, годные для использования на любых типах ЭВМ.
Главные вехи развития этой мечты - языки "Алгол-60", "Кобол", "ПЛ/1". Сейчас появился еще один - "Ада". Каждый из этих языков имеет много достоинств, но, увы, и много недостатков.
"Алгол-60", например, может претендовать па роль латыни в алгоритмическом мире. Строгий и одновременно удобный, наглядпый, он наложил отпечаток практически на все появившиеся после него языки. Основной его недостаток - оторванность от машины. Трудности учета требований на конкретных ЭВМ ограничивают его употребление.
Напор вавилонского столпотворепия в алгоритмическом мнре сегодня сдерживают "Фортран" и "Бейсик". Живучесть их объясняется хорошей реализацией на наиболее распространенных типах машин и простотой. Но простота эта сродни простоте языка человека каменного века.
Создатели каждого из языков программирования сталкиваются с диалектическим противоречием. Обусловлено оно тем, что всякий язык программирования имеет две стороны. С одной стороны, он должен быть максимально понятен человеку и удобен для записи алгоритмов. Очень хорошо, если этот язык включает обширную математическую символику, широкий набор алгоритмических конструкций. Короче говоря, идеальным представляется язык, используемый математиками и дополненный еще целым рядом понятий из других наук, задачи которых решаются с его помощью: физики, химии, экономики и т.д.
С другой стороны, язык должен быть максимально "понятен" машине. Ведь программы-то мы пишем для нее! С этой точки зрения чем он экономичней, чем меньше в нем символов и понятий, тем лучше. Идеальным здесь представляется язык команд - единственный, который машина понимает без перевода.
Вот мы и подошли к камню преткновения. Для того чтобы машина понимала какой-нибудь другой язык, кроме своего, нужен переводчик. Переводчик, или, как его называют, транслятор,- программа, написанная на машинном языке и переводящая тексты другого языка в машинные команды.
Представьте себе для сравнения англо-русский словарь, в который включены еще все допустимые сочетания слов. С помощью такого словаря человек, владеющий только русским языком, смог бы прочесть (и понять!) любую английскую книгу. Роль такого словаря и выполняет транслятор.
Понятно, что составить такой словарь - дело безнадежное. Вот если бы язык, для перевода с которого он нужен, был не английский, а какой-либо другой, попроще, насчитывающий мало слов и немного словосочетаний,- тогда создание описанного словаря было бы делом реальным и книги, написанные на нем, мы читали бы без труда. Но... на таком языке вряд ли мог быть написан "Гамлет".
Постоянное стремление разрешить эти противоречия порождает все новые языки программирования. Один из них обладают широким набором средств для записи алгоритмов, но трансляторы с них очень сложны, транслированные программы громоздки и малоэффективны. Другие языки, наоборот, позволяют создавать простые трансляторы и эффективные транслированные программы, но достигается это за счет резкого обеднения языка.
Кстати, языки программирования для микрокалькуляторов, состоящие просто-напросто из команд,- наглядное тому подтверждение. Удовлетворительные со второй стороны, они не выдерживают никакой критики с точки зрения первой.
Противоречивость требований, которым должен удовлетворять универсальный язык, приводит к важному выводу: создание такого языка невозможно. Мы и дальше вряд ли сможем повлиять на языковое разнообразие. И отсюда второй вывод: универсальная методология программирования не может ориентироваться на конкретный язык.
Каков же выход из этого положения? В качестве альтернативы единому языку мы выдвигаем понятие о языковой среде, которую называем лексиконом программирования.
В отличие от языка программирования лексикон - открытая система, которая может развиваться и дополняться подобно языку, на котором мы общаемся. Лексикон должен содержать стандартную математическую символику алгебры, теории множеств, математической логики. Он должен позволять не только записывать программы, но и давать характеристики их функциональных свойств. С этой точки зрения он будет максимально приближен к человеческому языку. С другой стороны, он должен иметь четкую структуру и систему обозначений, не допускающую неоднозначного толкования его конструкций. И с этой точки зрения он будет приближаться к языку программирования. Лексикон должен допускать формальное преобразование программы в конструкции любого языка программирования.
Публикуемая статья Л.Милехина может рассматриваться как попытка создать систему обозначений для составления и записи программ для микрокалькулятора. С лексиконом ее роднит то, что она предназначена для употребления человеком, который тут же играет роль транслятора. Подобно лексикону, эта система открыта для расширений и новых обозначений.
"Промик" далек от идеала-неудачна нотация, употребляются символы, отсутствующие как в программировании, так и в математике, смешиваются названия клавиш и операторов, нечетка терминология. Тем не менее он представляет безусловный интерес в качестве первого опыта. Кроме того, автор уже пользуется им на практике, обосновывая его право на существование.
Мы в Вычислительном центре СО АН СССР собираемся приступить к созданию "Микролексикона", ориентируя его в первую очередь на владельцев программируемых микрокалькуляторов. Надеемся, что он окажется полезным всем, кто по роду своей работы связан с программированием.
Член-корреспондент АН СССР А.ЕРШОВг (г.Новосибирск)
[ Так как создание алгоритмического языка для микрокалькуляторов - насущная необходимость, редакция предлагает читателям очередной конкурс, тема которого-создание языка программирования для программируемого микрокалькулятора. Ждем не только завершенные проекты, но и любые соображения по его структуре и особенностям.
Все предложения будут рассмотрены редакцией и лабораторией информатики ВЦ СО АН СССР. Лучшие из них будут опубликованы. ]
ПОЧЕМУ ВЫИГРЫВАЕТ КАЛЬКУЛЯТОР?
Игра в "чет-нечет" очень Проста. Один из участников что-то загадывает, а другой отгадывает. Нужно только, чтобы "что-то" имело два равновероятных варианта (четное число - нечетное число, орел-решка, 0-1 и т.д.).
"Обучить" микрокалькулятор играть в эту игру просто. Нужно занести в регистры X и Y числа 0 и 1 и ввести "микропрограмму": X-Y X-Y В/O, которая циклически меняет содержимое регистров. Вот и все.
Теперь загадайте ход микрокалькулятора (0 или 1) и запускайте программу (клавиши В/О и С/П). Остановив программу в любой случайный момент времени (клавиша С/П), вы получаете на индикаторе ответ калькулятора. Если он не совпал с вашим - выиграл калькулятор, если совпал - вы.
Сыграв с микрокалькулятором несколько партий, вы убеждаетесь: чем дольше длится игра, тем устойчивее выигрыш вашего соперника. В чем же дело? Может быть, калькулятор обучается в процессе игры? Нет. Программа этого не предусматривает. Просто оказывается, что ваш соперник играет по наилучшей стратегии. В игре "чет-нечет" таковой для обоих участников является чисто случайный выбор с равной вероятностью. Потому калькулятор и выигрывает.
Я.ТРОХИМЕНКО (г.Киев).
Любит?.. Не любит?.. Рис. Ю.ПОБОЖИЯ.
МИКРОКАЛЬКУЛЯТОР ОБРАЩАЕТ МАТРИЦУ
Система линейных алгебраических уравнений. Их столько же, сколько неизвестных. Как решить систему!
Знатокам математики известен такой способ. Выпишем в таблицу, называемую матрицей (обозначим ее А), коэффициенты при неизвестных, сохраняя их расстановку в системе. Выпишем в столбец неизвестные (x) и правые части системы (c). Тогда ее левую часть можно записать в виде произведения: Ax=с. Теперь надо отыскать матрицу, обратную к А, обозначаемую А'. Определяется она тем, что ее умножение на A дает единичную матрицу E, произведение которой на любой столбец не меняет этого столбца. И тогда систему можно считать решенной. Умножим обе ее части слева на A'. В правой части получим А'c, в левой А'Ах=Ех=х. Столбец неизвестных выразился в виде произведения А'с.
Но как искать матрицу, обратную к данной! Дело это важное (обращать матрицы приходится при решении многих задач), но непростое. Уместится ли в небольшой памяти микрокалькулятора выполняющая его программа! Здесь необходимо искусство лаконичного программирования, о котором в предыдущем выпуске рубрики писал А.Раздобреев (2/84).
Алгоритмов для обращения матриц известно немало. Из них наиболее лаконичную программу для микрокалькулятора, на мой взгляд, позволяет составить тот, который приведен в книге Ф.Р.Гантмахера "Теория матриц" (М., 1954, стр.46-47).
На основе матрицы, подлежащей обращению, составляется расширенная матрица со вдвое большим числом строк и столбцов, как показано на рисунке. Далее по алгоритму Гаусса обращаются в нуль элементы первого, затем второго и, наконец, третьего столбцов, расположенные ниже главной диагонали. В результате в правом нижнем углу матрицы, где вначале стояли нули, возникает матрица, обратная по отношению к исходной.
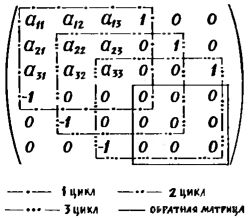
Казалось бы, на микрокалькуляторе такой алгоритм неосуществим даже для матриц третьего порядка. В самом деле: в этом случае для размещения исходной матрицы требуется 9 регистров памяти, для размещения обратной - еще 9, где-то нужно еще хранить промежуточные результаты... А память "Электроники Б3-34" насчитывает всего 14 регистров, программа же не может содержать более 98 адресов.
Тем не менее выход из положения мною был найден. Внимательный анализ приведенного алгоритма приводит к выводу, что его можно применить сначала к минору четвертого порядка, расположенному в левом верхнем углу матрицы (на рисунке обведен штрих-пунктиром), затем к минору, лежащему строкой ниже и столбцом правее, и наконец к минору, лежащему еще строкой ниже и столбцом правее. Таким образом, программе вычислений удается придать циклический характер, отчего она и получается весьма короткой. Она состоит всего лишь из 59 команд.
Элементы исходной матрицы вводятся в память, как указано ниже, стек перед пуском программы очищается, в регистр X заносится число 3. Элементы искомой обратной матрицы по окончании вычислений располагаются там же, где и элементы исходной:

Поскольку программа получилась короткой, я дополнил ее до программы решения системы линейных алгебраических уравнений с помощью обратной матрицы (команды 59-91). После того как найдена матрица, обратная по отношению к матрице системы, программа останавливается и элементы столбца правых частей вводятся в регистры А, В, С. Затем нажатием кнопок БП 59 С/П программа вновь переводится в автоматический режим для вычисления столбца неизвестных. Значение первого из них по окончании счета находится в нулевом регистре, второго - в регистре D, третьего выводится на индикатор: его следует выписать ь первую очередь, чтобы случайно не утерять.
ПРОГРАММА. 00. ПО 01. ИП4 02. ИП1 О3. / 04. ПD 05. ИПD 06. /-/ 07. ПС 08. ИП5 09. ИПD 10. ИП2 ll. * 12. - 13. ПА 14. ИП6 15. ИПD 16. ИП3 17. * 18. - 19. ПВ 20. ИП7 21. ИП1 22. / 23. ПD 24. ИПD 25. /-/ 26 П6 27. ИП8 28. ИПD 29. ИП2 30. * 31. - 32. П4 33 ИП9 34. ИПD 35. ИП3 36. * 37. - 38. П5 39. ИП2 40. ИП1 41. / 42. П7 43. ИП3 44. ИП1 45. / 46. П8 47. ИП1 48. F1/x 49. П9 50. ИПА 51. П1 52. ИПВ 53. П2 54. ИПС 55. П3 56. FL0 57. 01 58. С/П (матрица обращена, дальнейшее - решение системы линейных уравнений) 59. ПП 60. 80 61. ПО 62. ИП4 63. П1 64. ИП5 65. П2 66. ИП6 67. П3 68. ПП 69. 80 70. ПD 71. ИП7 72. П1 73. ИП8 74. П2 75. ИП9 76. П3 77. ПП 78. 80 79. С/П 80. ИП1 81. ИПА 82. * 83. ИП2 84. ИПВ 85. * 86. + 87. ИП3 88. ИПС 89. * 90. + 91. В/О.
А.ТУЛАЙКОВ. (г.Долгопрудный).
***
До кучи. Мой язык для Б3-34 тех времен.

(Кликнуть для увеличения).
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
СЕКРЕТЫ МИКРОКАЛЬКУЛЯТОРА
Рубрика "Человек с микрокалькулятором", недавно появившаяся в нашем журнале, вскоре приобрела характер бесед за круглым столом. Публикуемые под нею заметки читателей - словно выступления в широкой дискуссии о разнообразных применениях карманных ЭВМ, о вычислительных "секретах", повышающих эффективность этих применений.
Так обстоит дело и с письмами, поступившими в редакцию за последнее время: мысль, высказанная в одном письме, подхватывается в другом и развивается в третьем... При подготовке к печати очередного выпуска рубрики было решено не нарушать qyx такой связной последовательности и объединить фрагменты писем в слитный текст своеобразной беседы.
В ней участвуют: А.БОЙКО (студент, г.Москва), В. ДЬЯКОНОВ (доктор технических наук, г.Смоленск), Л.МИЛЕХИН (кандидат технических наук, г.Ленинград, Д.МЫСЛИН (кандидат технических наук, г.Новосибирск), С.КОНИН (студент, г.Ленинград).
В.Дьяконов. К ЭВМ мне приходится обращаться частенько. Но встречаются, и нередко, задачи, решать которые на больших ЭВМ - все равно, что стрелять из пушки по воробьям. Однажды мне понадобилось срочно вычислить несколько значении функции f(x)=ln((exp(x)+1)/(x+1)).
Вычислять их вручную утомительно. И я решил обратиться за помощью к "Электронике Б3-34".
Что за чудо-машина! Экспоненциальные, логарифмические, тригонометрические и целый ряд других функции вычисляет при нажатии всего двух клавиш, на первой из которых проставлено F, а на второй - название функции, имеет 14 регистров памяти, стек из 4 ячеек. А главное, в микрокалькулятор можно вводить программы длиной до 98 команд.
Д.Мыслин. Возникает вопрос: в каких случаях использовать программы? С одной стороны, автоматический счет быстрее ручного, но с другой - программу каждый раз нужно вводить с клавиатуры. Использование внешних носителей - магнитных карт и лент, перфолент и т.д. - для микрокалькулятора не предусмотрено.
Ввод программы требует такого же времени, как и набор последовательности операций в "ручном случае". Кроме того, время составления и отладки программы измеряется часами, а сам расчет секундами. Поэтому составление программы для проведения расчета, пусть и очень трудоемкого, но единственного, вряд ли целесообразно. Очевидно, стоит разрабатывать программы для расчетов, которые систематически встречаются и работе, или и ситуациях, когда число операций, выполняемых при вводе программы, меньше числа операции, необходимых для выполнения расчета. Это бывает в двух случаях: во-первых, когда используются циклы н, во-вторых, при использовании подпрограмм. Сюда же примыкают случаи, когда по одной и той же формуле (или формулам) нужно провести вычисления для различных значений исходных параметров. Во всех этих ситуациях программа дает выигрыш во времени при расчетах и обеспечивает большую надежность результатов по сравнению с ручными вычислениями.
В.Дьяконов. Программа для микрокалькулятора - это последовательность команд, записанная па специальном языке. У "Электроники "Б3-34" этот язык элементарно прост. Текст на нем указывает символы и порядок нажатия клавиш. Каждая команда имеет свои помер - адрес, по которому она записывается в памяти. Программа для вычисления функции, о которой я упомянул выше, может быть записана так:
00. П9 01. Fexp 02. 1 03. + 04. ИП9 05. 1 06. + 07. / 08. Fln 09. С/П 10. БП 11. 00.
Размещается она в памяти, начиная с адреса 00. Значение x берется из 9-го регистра. Команда С/П (стоп-пуск) задает остановку вычислений, а команда БП 00 организует безусловный переход на шаг 00, то есть к началу программы.
Теперь можно считать. Ввожу программу, нажимаю клавиши F, АВТ и В/О (возврат к пулевому адресу), набираю на клавиатуре значение x=1 и, нажав клавишу С/П, через несколько секунд получаю результат: f(1)=0.6201145. Набрав другое значение x, получаю новый результат и т.д.
Кроме безусловных переходоп, есть еще и условные. Например, если в программе написано Fх!=0 23, то при равенстве содержимого регистра x нулю управление передается на адрес 23. В противном случае эта команда игнорируется и выполняется следующая за ней.
Существуют два тина адресации: прямая и косвенная. В первом случае адрес, если он стоит после команды перехода, или регистр, содержимое которого нужно использовать, указываются непосредственно. Косвенная адресация вводится клавишей "К". Что достигается с ее помощью? Например, в регистре 8 записано число 2, а в регистре 2 - число 10. Если использовать прямую адресацию и выполнить команду считывания ИП8, то из памяти будет вызвано содержимое регистра 8, то есть число 2. Если же используется адресация косвенная, по команде КИП8, то из памяти будет вызвано не число 2, а содержимое регистра 2, то есть число 10. Косвенные адреса могут меняться и процессе вычислений. Это называется модификацией адреса.
С.Конин. Итак, позади первые радости. Вы узнали, что означают те или иные команды, что модификация адреса - это просто его изменение, написали несколько простеньких программ и хотите перейти к более сложным. Для начала два методических совета: во-первых, заведите общую тетрадь, в которую записывайте тексты отлаженных программ, и, во-вторых, систематизируйте таблицу кодов, приведенную в инструкции. К сожалению, они разбросаны по разным ее разделам, что сильно затрудняет дешифровку команд при отладке программ.
Д.Мыслин. Так как расчеты по одной программе проводятся неоднократно, лучше использовать для записи программ специальные бланки, куда следует вписать и соответствующие контрольные примеры.
С.Конин. При написании разных программ часто встречаются одинаковые проблемы, поэтому знание отдельных программистских приемов, "маленьких хитростей" программиста, может значительно облегчить процесс составления сложных программ.
В.Дьяконов. Одна из таких хитростей - использование модификации адреса, о которой я уже упоминал. Если адрес задан в регистрах 0, 1, 2 или 3, то адрес этот (содержимое регистра) при каждом обращении к нему уменьшается на 1; если обращаться к регистрам 4, 5 или 6, то адрес увеличивается на 1. Содержимое остальных регистров не меняется при обращении.
Поясним это примером. Необходимо, скажем, вычислить значение многочлена:
P(x)=a0+a1*x+a2*x**2+...an*x**n
Это можно сделать, используя схему Горнера:
P(x)=((...(an*x+a[n-1])x+a[n-2])x+...+al)x+a0.
Берем вначале коэффициент an и умножаем на x, к произведению прибавляем a[n-1], результат снова умножаем на x и т.д. Чтобы реализовать этот алгоритм, нужно научиться программными средствами извлекать из памяти значения коэффициентов. Здесь-то и пригодится модификация адреса. Ограничимся значением n=9 и запишем a1 в регистр Р1, a2 - в P2... a9 - в P9. Коэффициент a0 занесем в регистр C. Программу для вычисления значений полинома запишем так:
00 ПД 01. 9. 02. П0 03. ИП9 04. ^ 05. x-y 06. ИПД 07. * 08. КИПО 09. + 10. ИП0 11. Fx=0 12. 05 13. x-y 14. ИПС 15. + 16. С/П 17. БП 18. 00.
Читатели сами могут проверить работу программы. Циклически повторяется часть программы с 5 по 12 адрес. Поочередный вызов коэффициентов организован командой косвенной адресации КИП0 с адресным регистром Р0, содержимое которого на каждом цикле уменьшается на 1. Как только оно станет нулевым, циклы прекращаются и к результату прибавляется a0 (содержимое регистра C).
А.Бойко. Еще одни интересный прием, обогащающий возможности микрокалькулятора,- использование стека.
Стек состоит из четырех регистров: X, Y, Z, Т, которые заполняются числами, словно пистолетная обойма патронами: когда в регистр X вводится новое число, то находившееся в нем прежде перемещается в регистр Y, содержимое регистра Y - в Z и т.д. Числа при этом, образце говоря, движутся "снизу вверх", и каждый раз содержимое регистра T теряется.
Есть команды, по которым в стеке идет движение "сверху вниз". Содержимое регистра X при этом перемещается в регистр XI. Он может быть причислен к стеку. Его содержимое при перемещении "снизу вверх" по команде FВх поступает в регистр X; когда же содержимое регистра X используется в качестве аргумента при вычислении функций и выполнении двухместных операций, а результат направляется опять-таки в регистр X, прежнее его содержимое передается в регистр XI.
Д.Мыслин. Движение информации по стеку при выполнении различных операций удобно выразить диаграммой:

(При возведении в степень содержимое регистров Y, Z, T не меняется).
Л.Милехин. Простейший пример применения стековой памяти - суммирование последовательности чисел. Фрагмент программы, ответственный за эту процедуру, может быть записан всего одним символом: +. Перед началом суммирования следует очистить все стековые регистры. Если ввести в калькулятор первое слагаемое (при вводе оно попадает в регистр X) и выполнить команду суммирования, то она сложит содержимое регистров X и Y, а результат запишет в X (так оно происходит при пыполнении любой двухместной операции). При введении очередного слагаемого вычисленная сумма попадает в регистр Y. С каждым повторением этих операций (ввод, суммирование) к ней будут прибавляться псе новые и новые слагаемые.
A.Бойко. Использование стека значительно повышает быстродействие. Например, программа для вычисления факториала без использования стека па подсчет 69! потратила 115 секунд, а программа с использованием стека - 70 секунд.
С.Конин. Экономить время работы можно не только за счет улучшения программ. Представьте себе, что вы работаете целый день с одной программой. Для того чтобы пустить ее на счет, нужно нажать дне клавиши: В/О и С/П. Но можно сократить время запуска ровно вдвое, если по нулевому адресу записать КНОП и после С/П занести В/О. Первый раз придется все-таки нажать обе клавиши (В/О и С/П), зато каждый следующий достаточно нажимать одну (С/П). Следует отметить, что использовать эту рекомендацию можно лишь для программ, в которчх нет подпрограмм.
B.Дьяконов. Микрокалькуляторы хранят в себе немало секретов. Каждый раз садясь за эту маленькую машинку, ощущаешь себя в положении исследователя, который может открыть что-то новое. И в этом, наверное, еще одно достоинство микрокалькулятора.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Длительное ожидание результатов вычислений на микрокалькуляторе при использовании сложных программ утомительно. Заполнить это время другими делами помогает звуковой индикатор, подающий сигнал об окончании счета. Роль такого индикатора может пыполнить обычный радиоприемник, принимающий и диапазоне средних волн. Работающий микрокалькулятор нужно положить рядом с ним. Оказывается, при появлении каждой комбинации цифр на индикаторе калькулятор излучает определенный спектр электромагнитных ноли. Завершив программу выводом некоторого числа и "настроив" на него приемник, молено пустить программу, заняться другим делом и ждать сигнала о завершении счета.
Я проверил свою идею на микрокалькуляторах марок Б3-21 и Б3-34. Во втором случае сигнал мощнее.
В.БОГАТКО (г.Ленинград). ]
ЗНАКОМЬТЕСЬ: "ПРОМИК"
"Запись программ для микрокалькуляторов на языке команд страдает целым рядом недостатков. Она громоздка, не отличается наглядностью. Кроме того, для разных микрокалькуляторов некоторые одинаковые по смыслу команды записываются по-разному. Это затрудняет использование программ, написанных для калькуляторов одного типа, на других. Наконец, и это самое важное, задачи на калькуляторах решаются в полуавтоматическом режиме, и человек является при этом полноправной составной частью вычислительной системы. Поэтому программа должна содержать инструкции и для него".
Так начинает свое письмо в редакцию кандидат технических наук Л.Н.МИЛЕХИН. Проблема, поставленная читателем, весьма насущна. В письме предлагается одно из возможных ее решений. Комментирует его в статье, помещенной далее, член-корреспондент АН СССР А.П.ЕРШОВ.
Итак, нужен специальный язык для записи программ, предназначенных для микрокалькулятора. Придя к этому выводу, я попытался создать такой язык. Называется он "Промик" - ПРОграммирование для МИКрокалькуляторов. Наряду с ним я предлагаю стандарт для оформления отлаженных программ, чтобы облегчить обмен ими.
Чтобы уяснить, как выглядит программа, написанная в соответствии с предложенным стандартом на языке "Промик", опишем на нем алгоритм численного решения уравнения f(x)=0.
ПРОГРАММА. Вычисления кория уравнения методом половинного деления.
1. МОДЕЛЬ. Вычисляется корень уравнения f(x)=0 на отрезке [a,b].

Обозначения: xk, x*, xe - значения корня соответственно на k-том шаге вычислений, точное, вычисленное с заданной точностью; ak, bk - границы интервала на k-том шаге; e - допустимая погрешность; fk - значение функции в точке xk.
2. ФОРМУЛЫ.
Пункты 1 и 2 описывают постановку задачи и алгоритм, по которому она решается.
x = (ak+bk)/2
a[k+1]=ak, b[x+1]=xk, если fk>=0
a[k+1]=xk, b[x+1]=bk, если fk,0
Пункты 1 и 2 описывают постанову задачи и алгоритм, по которому она решается.
3. РАСПРЕДЕЛЕНИЕ ПАМЯТИ.
R7=xk, R9=2e, RA=ak, RB=bk
Здесь показано, какие величины должны храниться в регистрах или вводиться в них. Регистры обозначаются буквой R с соответствующим индексом.
4. ОПИСАНИЕ ПРОЦЕДУР И ПОД-ПРОЦЕДУР.
Процедуры и подпроцедуры - это последовательности команд, заносимых в память микрокалькулятора. В записи они ограждаются фигурными скобками. Различаются они тем, что обращение к процедуре осуществляется с клавиатуры, а обращение к подпроцедуре - автоматическое, с помощью команд. Каждая команда состоит из названий клавиш, которые нужно нажать для ее выполнения, и обрамляется точками. Смежные точки позволяется "сливать" в одну. Двойные стрелки используются вместо имен клавиш П и ИП, то есть для показа записи и чтения, что делает команды более наглядными. Остальные обозначения соответствуют надписям на клавишах микрокалькулятора. Над командой записывается ее порядковый номер (адрес). Выше адреса и ниже команды допускается комментарий, который облегчает чтение команды. Например:

Это команда по адресу 07, чтение содержимого 7-го регистра, где записана величина xk.
Кроме команд, в записи программы допускается использование идентификаторов - имен, значения которым приписываются лишь при решении конкретных задач. В нашей программе, например, Aпв - это адрес, начиная с которого записана подпроцедура вычисления значений функции f(x).
Вот как записывается процедура отыскания корня:
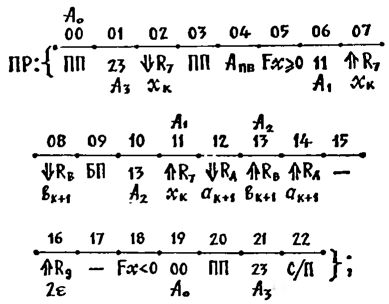
В надстрочном комментарии для лучшей ориентации заглавными буквами А с индексами отмечены некоторые "ключевые" адреса, в подстрочном - переходы к этим адресам, а также заносимые и выводимые в ходе счета значения xk, ak, bk, 2e.
А вот как выглядят подпроцедуры для вычисления xk (середины очередного отрезка деления) и значения функции f(х):

Процедуры и подпроцедуры - две разновидности операторов. Кроме этих двух, в "Промике" есть еще две разновидности.
Условный оператор. Он начинается с буквы Е, далее в круглых скобках пишется условие, затем в фигурных скобках - последовательность команд, которая либо выполняется (если условие соблюдается), либо пропускается (если условие не соблюдается).
Оператор цикла. Он начинается с буквы Ц, далее в круглых скобках указывается параметр цикла и список значений, которые он должен принять, затем в фигурных скобках - последовательность команд, которая должна быть выполнена для всех значений параметра.
5. ДИРЕКТИВА.

Директива - это часть программы, адресуемая для выполнения человеку. Здесь мы встречаемся с предписаниями. Прямоугольник означает: "ждать окончания работы процедуры". Ломаная стрелка: "прочитать число с индикатора и присвоить это значение переменной, написанной в подстрочном комментарии" или "выполнить указание, стоящее в подстрочном комментарии". Идентификатор в скобках, например (2e). означает, что в этом месте нужно набрать на клавиатуре числовое значение идентификатора для ввода его в память.
6. УКАЗАНИЯ ПО ПРИМЕНЕНИЮ. Выбрать знак перед f(x) так, чтобы производная f(x) в окрестности точки х* была положительной.
7. КОНТРОЛЬНЫЙ ПРИМЕР.
В этом разделе описывается пример использования программы.
Л. МИЛЕХИН, кандидат технических наук (г.Ленинград).
ЯЗЫК ИЛИ ЛЕКСИКОН?
Осповная задача, стоящая перед пашнм обществом сегодня,- подъем производительности труда. Нужно создавать условия, при которых она поднимается. Одно из таких условий - творческая атмосфера, привычка к творческому труду. Широкое внедрение ЭВМ способствует этому. ЭВМ в руках инженера резко расширяет сферу посильпых для него творческих задач.
До последнего времени бытовало мнение, что ЭВМ - это удел избранных, посвященных. Освоить машину нелегко. При этом, образпо говоря, человек должен идти навстречу машине. Теперь направление движения меняется. Машина идет навстречу человеку, современные ЭВМ все более удобны в работе.
В числе таких машин - программируемые калькуляторы. Но и они не сегодня-завтра уступят место на столе инженера персональным ЭВМ, которые возьмут на себя огромную часть рутинной работы - расчеты, оформлепие документов, упростят поиск информации и т.д.
Готовиться к этому процессу нужно заранее. Считаю, что большую роль в этом может сыграть постоянная рубрика "Человек с микрокалькулятором", цель которой привить читателям журнала вкус к работе с ЭВМ, собирать и распространять опыт по использованию вычислительной техники. В этой связи, пожалуй, первоочередным является вопрос о языке, на котором было бы удобпо записывать программы для программируемых микрокалькуляторов.
Язык программирования - это язык для описания данных (информации) и алгоритмов (программ) их обработки на ЭВМ. Это замкнутая совокупность определенных символов и правил, диктующих, как с помощью этих символов записывать алгоритмы для ЭВМ.
Число существующих языков программирования перевалило за несколько тысяч и, наверное, скоро будет сравнимо с количеством человеческих языков. Но программистов не покидает мечта об общем языке программирования, на котором можно было бы не только учить программированию, но и описывать программы, годные для использования на любых типах ЭВМ.
Главные вехи развития этой мечты - языки "Алгол-60", "Кобол", "ПЛ/1". Сейчас появился еще один - "Ада". Каждый из этих языков имеет много достоинств, но, увы, и много недостатков.
"Алгол-60", например, может претендовать па роль латыни в алгоритмическом мире. Строгий и одновременно удобный, наглядпый, он наложил отпечаток практически на все появившиеся после него языки. Основной его недостаток - оторванность от машины. Трудности учета требований на конкретных ЭВМ ограничивают его употребление.
Напор вавилонского столпотворепия в алгоритмическом мнре сегодня сдерживают "Фортран" и "Бейсик". Живучесть их объясняется хорошей реализацией на наиболее распространенных типах машин и простотой. Но простота эта сродни простоте языка человека каменного века.
Создатели каждого из языков программирования сталкиваются с диалектическим противоречием. Обусловлено оно тем, что всякий язык программирования имеет две стороны. С одной стороны, он должен быть максимально понятен человеку и удобен для записи алгоритмов. Очень хорошо, если этот язык включает обширную математическую символику, широкий набор алгоритмических конструкций. Короче говоря, идеальным представляется язык, используемый математиками и дополненный еще целым рядом понятий из других наук, задачи которых решаются с его помощью: физики, химии, экономики и т.д.
С другой стороны, язык должен быть максимально "понятен" машине. Ведь программы-то мы пишем для нее! С этой точки зрения чем он экономичней, чем меньше в нем символов и понятий, тем лучше. Идеальным здесь представляется язык команд - единственный, который машина понимает без перевода.
Вот мы и подошли к камню преткновения. Для того чтобы машина понимала какой-нибудь другой язык, кроме своего, нужен переводчик. Переводчик, или, как его называют, транслятор,- программа, написанная на машинном языке и переводящая тексты другого языка в машинные команды.
Представьте себе для сравнения англо-русский словарь, в который включены еще все допустимые сочетания слов. С помощью такого словаря человек, владеющий только русским языком, смог бы прочесть (и понять!) любую английскую книгу. Роль такого словаря и выполняет транслятор.
Понятно, что составить такой словарь - дело безнадежное. Вот если бы язык, для перевода с которого он нужен, был не английский, а какой-либо другой, попроще, насчитывающий мало слов и немного словосочетаний,- тогда создание описанного словаря было бы делом реальным и книги, написанные на нем, мы читали бы без труда. Но... на таком языке вряд ли мог быть написан "Гамлет".
Постоянное стремление разрешить эти противоречия порождает все новые языки программирования. Один из них обладают широким набором средств для записи алгоритмов, но трансляторы с них очень сложны, транслированные программы громоздки и малоэффективны. Другие языки, наоборот, позволяют создавать простые трансляторы и эффективные транслированные программы, но достигается это за счет резкого обеднения языка.
Кстати, языки программирования для микрокалькуляторов, состоящие просто-напросто из команд,- наглядное тому подтверждение. Удовлетворительные со второй стороны, они не выдерживают никакой критики с точки зрения первой.
Противоречивость требований, которым должен удовлетворять универсальный язык, приводит к важному выводу: создание такого языка невозможно. Мы и дальше вряд ли сможем повлиять на языковое разнообразие. И отсюда второй вывод: универсальная методология программирования не может ориентироваться на конкретный язык.
Каков же выход из этого положения? В качестве альтернативы единому языку мы выдвигаем понятие о языковой среде, которую называем лексиконом программирования.
В отличие от языка программирования лексикон - открытая система, которая может развиваться и дополняться подобно языку, на котором мы общаемся. Лексикон должен содержать стандартную математическую символику алгебры, теории множеств, математической логики. Он должен позволять не только записывать программы, но и давать характеристики их функциональных свойств. С этой точки зрения он будет максимально приближен к человеческому языку. С другой стороны, он должен иметь четкую структуру и систему обозначений, не допускающую неоднозначного толкования его конструкций. И с этой точки зрения он будет приближаться к языку программирования. Лексикон должен допускать формальное преобразование программы в конструкции любого языка программирования.
Публикуемая статья Л.Милехина может рассматриваться как попытка создать систему обозначений для составления и записи программ для микрокалькулятора. С лексиконом ее роднит то, что она предназначена для употребления человеком, который тут же играет роль транслятора. Подобно лексикону, эта система открыта для расширений и новых обозначений.
"Промик" далек от идеала-неудачна нотация, употребляются символы, отсутствующие как в программировании, так и в математике, смешиваются названия клавиш и операторов, нечетка терминология. Тем не менее он представляет безусловный интерес в качестве первого опыта. Кроме того, автор уже пользуется им на практике, обосновывая его право на существование.
Мы в Вычислительном центре СО АН СССР собираемся приступить к созданию "Микролексикона", ориентируя его в первую очередь на владельцев программируемых микрокалькуляторов. Надеемся, что он окажется полезным всем, кто по роду своей работы связан с программированием.
Член-корреспондент АН СССР А.ЕРШОВг (г.Новосибирск)
[ Так как создание алгоритмического языка для микрокалькуляторов - насущная необходимость, редакция предлагает читателям очередной конкурс, тема которого-создание языка программирования для программируемого микрокалькулятора. Ждем не только завершенные проекты, но и любые соображения по его структуре и особенностям.
Все предложения будут рассмотрены редакцией и лабораторией информатики ВЦ СО АН СССР. Лучшие из них будут опубликованы. ]
ПОЧЕМУ ВЫИГРЫВАЕТ КАЛЬКУЛЯТОР?
Игра в "чет-нечет" очень Проста. Один из участников что-то загадывает, а другой отгадывает. Нужно только, чтобы "что-то" имело два равновероятных варианта (четное число - нечетное число, орел-решка, 0-1 и т.д.).
"Обучить" микрокалькулятор играть в эту игру просто. Нужно занести в регистры X и Y числа 0 и 1 и ввести "микропрограмму": X-Y X-Y В/O, которая циклически меняет содержимое регистров. Вот и все.
Теперь загадайте ход микрокалькулятора (0 или 1) и запускайте программу (клавиши В/О и С/П). Остановив программу в любой случайный момент времени (клавиша С/П), вы получаете на индикаторе ответ калькулятора. Если он не совпал с вашим - выиграл калькулятор, если совпал - вы.
Сыграв с микрокалькулятором несколько партий, вы убеждаетесь: чем дольше длится игра, тем устойчивее выигрыш вашего соперника. В чем же дело? Может быть, калькулятор обучается в процессе игры? Нет. Программа этого не предусматривает. Просто оказывается, что ваш соперник играет по наилучшей стратегии. В игре "чет-нечет" таковой для обоих участников является чисто случайный выбор с равной вероятностью. Потому калькулятор и выигрывает.
Я.ТРОХИМЕНКО (г.Киев).

Любит?.. Не любит?.. Рис. Ю.ПОБОЖИЯ.
МИКРОКАЛЬКУЛЯТОР ОБРАЩАЕТ МАТРИЦУ
Система линейных алгебраических уравнений. Их столько же, сколько неизвестных. Как решить систему!
Знатокам математики известен такой способ. Выпишем в таблицу, называемую матрицей (обозначим ее А), коэффициенты при неизвестных, сохраняя их расстановку в системе. Выпишем в столбец неизвестные (x) и правые части системы (c). Тогда ее левую часть можно записать в виде произведения: Ax=с. Теперь надо отыскать матрицу, обратную к А, обозначаемую А'. Определяется она тем, что ее умножение на A дает единичную матрицу E, произведение которой на любой столбец не меняет этого столбца. И тогда систему можно считать решенной. Умножим обе ее части слева на A'. В правой части получим А'c, в левой А'Ах=Ех=х. Столбец неизвестных выразился в виде произведения А'с.
Но как искать матрицу, обратную к данной! Дело это важное (обращать матрицы приходится при решении многих задач), но непростое. Уместится ли в небольшой памяти микрокалькулятора выполняющая его программа! Здесь необходимо искусство лаконичного программирования, о котором в предыдущем выпуске рубрики писал А.Раздобреев (2/84).
Алгоритмов для обращения матриц известно немало. Из них наиболее лаконичную программу для микрокалькулятора, на мой взгляд, позволяет составить тот, который приведен в книге Ф.Р.Гантмахера "Теория матриц" (М., 1954, стр.46-47).
На основе матрицы, подлежащей обращению, составляется расширенная матрица со вдвое большим числом строк и столбцов, как показано на рисунке. Далее по алгоритму Гаусса обращаются в нуль элементы первого, затем второго и, наконец, третьего столбцов, расположенные ниже главной диагонали. В результате в правом нижнем углу матрицы, где вначале стояли нули, возникает матрица, обратная по отношению к исходной.

Казалось бы, на микрокалькуляторе такой алгоритм неосуществим даже для матриц третьего порядка. В самом деле: в этом случае для размещения исходной матрицы требуется 9 регистров памяти, для размещения обратной - еще 9, где-то нужно еще хранить промежуточные результаты... А память "Электроники Б3-34" насчитывает всего 14 регистров, программа же не может содержать более 98 адресов.
Тем не менее выход из положения мною был найден. Внимательный анализ приведенного алгоритма приводит к выводу, что его можно применить сначала к минору четвертого порядка, расположенному в левом верхнем углу матрицы (на рисунке обведен штрих-пунктиром), затем к минору, лежащему строкой ниже и столбцом правее, и наконец к минору, лежащему еще строкой ниже и столбцом правее. Таким образом, программе вычислений удается придать циклический характер, отчего она и получается весьма короткой. Она состоит всего лишь из 59 команд.
Элементы исходной матрицы вводятся в память, как указано ниже, стек перед пуском программы очищается, в регистр X заносится число 3. Элементы искомой обратной матрицы по окончании вычислений располагаются там же, где и элементы исходной:

Поскольку программа получилась короткой, я дополнил ее до программы решения системы линейных алгебраических уравнений с помощью обратной матрицы (команды 59-91). После того как найдена матрица, обратная по отношению к матрице системы, программа останавливается и элементы столбца правых частей вводятся в регистры А, В, С. Затем нажатием кнопок БП 59 С/П программа вновь переводится в автоматический режим для вычисления столбца неизвестных. Значение первого из них по окончании счета находится в нулевом регистре, второго - в регистре D, третьего выводится на индикатор: его следует выписать ь первую очередь, чтобы случайно не утерять.
ПРОГРАММА. 00. ПО 01. ИП4 02. ИП1 О3. / 04. ПD 05. ИПD 06. /-/ 07. ПС 08. ИП5 09. ИПD 10. ИП2 ll. * 12. - 13. ПА 14. ИП6 15. ИПD 16. ИП3 17. * 18. - 19. ПВ 20. ИП7 21. ИП1 22. / 23. ПD 24. ИПD 25. /-/ 26 П6 27. ИП8 28. ИПD 29. ИП2 30. * 31. - 32. П4 33 ИП9 34. ИПD 35. ИП3 36. * 37. - 38. П5 39. ИП2 40. ИП1 41. / 42. П7 43. ИП3 44. ИП1 45. / 46. П8 47. ИП1 48. F1/x 49. П9 50. ИПА 51. П1 52. ИПВ 53. П2 54. ИПС 55. П3 56. FL0 57. 01 58. С/П (матрица обращена, дальнейшее - решение системы линейных уравнений) 59. ПП 60. 80 61. ПО 62. ИП4 63. П1 64. ИП5 65. П2 66. ИП6 67. П3 68. ПП 69. 80 70. ПD 71. ИП7 72. П1 73. ИП8 74. П2 75. ИП9 76. П3 77. ПП 78. 80 79. С/П 80. ИП1 81. ИПА 82. * 83. ИП2 84. ИПВ 85. * 86. + 87. ИП3 88. ИПС 89. * 90. + 91. В/О.
А.ТУЛАЙКОВ. (г.Долгопрудный).
***
До кучи. Мой язык для Б3-34 тех времен.

(Кликнуть для увеличения).

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
6/84
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Многие заметки, опубликованные в прежних выпусках рубрики "Человек с микрокалькулятором", вызвали оживленные, зачастую критические отклики читателей. Некоторые из них публикуются в нынешнем выпуске. Надеемся, что подобные дискуссии еще не раз развернутся под нашей рубрикой, помогая ее читателям совершенствовать навыки работы с вычислительной техникой.
ЦЕНА ЭКОНОМИИ
То, что микрокалькулятор экономит время, очевидно. Но, оказывается, он может и "расширять" его! По крайней мере такой вывод можно сделать после прочтения статьи А.Раздобреева "Как решить неразрешимое уравнение" (2/84). "Владельцы микрокалькуляторов,- пишет автор статьи,- как правило, имеют достаточно времени для своих вычислений: не успел утром, можно закончить вечером". Выходит, что ученые, инженеры, домохозяйки - все жалуются на недостаток времени, а вот владельцы микрокалькуляторов имеют его в избытке.
Не будем обсуждать этот парадоксальный тезис - лучше посмотрим, какие выводы делает из него автор. "Следует в первую очередь соблюдать принцип экономии памяти и, только во-вторых, экономии времени". Любопытно, что, оптимизируя программу для решения "уравнения жрецов бога Ра", автор делает ее не только более короткой, но и более быстрой, однако тут же подчеркивает, что это чуть ли не побочный эффект от экономии памяти. Не лучше ли сказать, что оптимизировать программу - значит стремиться сделать ее и короче и быстрее?
Правда, эти два требования могут оказаться альтернативными. И тогда надо учитывать аспект, без которого рассуждать о качестве программы нельзя,- назначение программы.
Если она создается для одноразового решения единичной задачи, как, например, "загадки жрецов бога Ра", то на первый план должно выступить общее время от постановки задачи до получения результата, и вряд ли целесообразно тратить часы на оптимизацию программы, чтобы добиться ускорения ее работы на секунды и сокращения на одну-две команды. Лишь бы она справлялась с задачей за достижимо короткое время и умещалась в память!
Если же программируется задача, расчеты по которой проводятся часто,- например, статистический анализ или другие задачи, постоянно решаемые с разными входными данными,- то, по-моему, здесь важнее всего быстрота работы программы, пусть даже достигаемая ценой некоторого ее удлинения.
Иное дело - подпрограммы. Здесь критерии быстроты и краткости выступают на равных. Но это тема особого разговора.
... Стремление к экономии памяти как к самоцели я сравнил бы с рекомендацией писать романы на рисовых зернах. Это, безусловно, интересно, даже красиво и бумагу экономит, но вряд ли целесообразно рекомендовать такой метод писателям.
И.ДАНИЛОВ (Москва)
НА ОШИБКАХ УЧИМСЯ
Программа для вычисления статистических характеристик, помещенная в статье Н.Богина "Статистика на микрокалькуляторе" (12/83), вызвала много нареканий у читателей как изобилующая погрешностями. Признавая их, заметим: свою задачу программа решает. Что же касается совершенства...
Говорят, на ошибках учатся. Поговорка убеждает, что в деле обучения разбор ошибок иной раз лучше, чем демонстрация безупречных примеров.
На основе писем С.Дорофеева (Грозный), Я.Закина, В.Козлова, А.Орлова (Ленинград), Я.Кирпичева (Москва), И.Обухова (Киев), Ю. и Я.Пашковых (Ворошиловград), В.Шеина (Харьков) и других такой разбор по просьбе редакции провел А.Бойко (Москва).
Итак, окинем программу Н. Богина критическим взглядом. В самом ее начале замечаем излишние операции: регистры Р5 и Р6 очищать незачем - их исходное содержание не влияет на ход программы.
Не стоит заносить в регистры и промежуточные результаты - лучше использовать возможности стека. Команды 07 и 11 можно заменить соответственно командами "^" и "x-y".
Во фрагменте 16-19 неудачно примечен в качестве счетчика регистр Р7. Здесь упущены возможности косвенной адресации, при которой во время обращения к регистрам Р0-Р3 их содержимое каждый раз уменьшается на единицу, а во время обращения к регистрам Р4-Р6 увеличивается. Указанный фрагмент лучше заменить командами КИП4-ИП4.
Некорректна в анализируемой программе последовательность операций / /-/, поскольку это вызывает ошибки счета в калькуляторах ранних выпусков (см. инструкцию). Ошибки исчезнут, если начать со смены знака и лишь после этого выполнить необходимое действие. Впрочем, не стоит сначала менять знак (26), а затем складывать (28 ), когда проще вычесть. Для этого вместо команд 22-28 следует написать ИП4 ИП3 Fx2 ИП7 / -. Не следует брать и обратную величину для того, чтобы умножить на нее результат. Проще разделить, то есть вместо 29-35 написать ИП7 1 - /. (Тот, кто усмехнется над такими оплошностями, пусть вспомнит свои первые шаги в программировании). Наконец, не стоит заносить результат сложения в регистр Р8 (29) только для того, чтобы один-единственный раз его вызвать (34): достаточно помнить, что он содержится в регистре Y стека.
Совершенно справедливо замечание, что необходимость набора БП, 2, 2, С/П - это дополнительный источник ошибок. Удобнее при соответствующем построении программы лишь нажать на клавишу ШГ со стрелкой вправо и пустить программу командой С/П.
Потенциальная возможность ошибок - обилие остановов в ходе программы. Уменьшить их число можно, например, используя стек как "магазин", заполненный к моменту останова результатами расчета.
Можно отметить и другие слабые места программы Н.Богина (сложность исправления допущенной ошибки ввода данных и т.п.), но в отличие от описанных выше недочетов здесь трудно дать общие рекомендации.
Не будем касаться возможностей, связанных с априорным знанием длины массива обрабатываемых данных, так как это повлекло бы радикальные изменения в структуре исходной программы, что не соответствует цели настоящей статьи.
Приняв за основу версию программы Н.Богина, данную В.Козловым, можно предложить такой вариант, где устранены отмеченные недостатки.
Программа. 00. ^ 01. Сх 02. П4 03. П5 04. П6 05. F() 06. ^ 07. ИП4 08.+ 09. П4 10. x-y 11. Fx2 12. ИП5 13. + 14. П5 15. КИП6 16. ИП6 17. С/П 18. БП 19. 06 20. F() 21. ИП5 22. ИП4 23. Fx2 24. ИП6 25. / 26. - 27. ИП6 28. 1 29. - 30. / 31. Fsqr 32. П5 33. ИП4 34. ИП6 35. / 36. / 37. FBx 38. ИП5 39. С/П.
Нажав клавишу В/О, вводим первое число из обрабатываемого массива; клавишей С/П пускаем программу; после останова вводим новое число и вновь нажимаем С/П - суммируем (адреса 06-17) вводимые числа и их квадраты. Прекратив на любом из остановов ввод чисел, видим на индикаторе их количество. Нажал клавиши ШГ и С/П, пускаем программу далее (адреса 21-38 ) и получаем статистические характеристики массива: на индикаторе - среднеквадратическое отклонение S, в регистре Y - среднее X, в регистре Z - коэффициент вариации V.
[ Под рубрикой "Человек с микрокалькулятором" и впредь будут публиковаться программы, составленные нашими читателями для решения различных производственных и учебных задач. Возможные несовершенства программ должны служить для их авторов не тормозом, а стимулом к обнародованию. Ведь вынесенные на суд товарищей по увлечению ошибки будут устранены надежнее, чем наедине. Обмен опытом, повышение культуры программирования - таков выигрыш, в котором окажутся все участники обсуждения. А главное - оно будет служить важной цели: внедрению вычислительных методов всюду, где к этому имеются предпосылки.
Итак, ждем новых писем от наших читателей, сделавших микрокалькулятор своим помощником в решении вставших перед ними проблем. ]
НЕ БОЙТЕСЬ КОМПЬЮТЕРОВ
Прочитав в 2/83 статью П.Эльясберга "Осторожно - компьютеры!", я подумал: а ведь что-то подобное уже было! Лет тридцать тому назад лозунг "Осторожно - авторучки!" буквально не сходил с уст педагогов. Авторучки, мол, испортят почерк, и посему никаких авторучек!
Прошло время, об этих призывах все забыли. Почерк у детей, может быть, и стал хуже. (Правда, и во времена стальных да и гусиных перьев не все были каллиграфами). Но зато писать стало удобнее, и тетради стали явно чище.
В чем же надо проявлять осторожность сейчас? П.Эльясберг предостерегает от "переоценки возможностей ЭВМ". Что ж, она действительно встречается, но только у тех, кто не имеет дела с машиной. Те же, кто их использует, оценивают возможности ЭВМ достаточно трезво и прекрасно понимают, что машина может сделать лишь то, что в нее заложили.
"Компьютер всегда работает по заданной программе. А человек... сам определяет порядок своей работы. И в этом его громадное преимущество перед любым компьютером". Наверное, следуя такой логике, можно сказать, что преимущество человека перед автомобилем в том, что человек может повернуться на месте, а автомобиль нет. Но, наверное, преимущество человека в том, что он создал и автомобиль и компьютер. Автомобиль - чтобы увеличить скорость передвижения, а компьютер - чтобы увеличить скорость вычислений. А что касается программ, то и человек и компьютер работают по программе. Только в одном случае человек составляет ее для себя и сам выполняет, а во втором пишет для компьютера, перекладывая на его плечи утомительную, рутинную работу.
Автор совершенно прав, предостерегая от увлечения компьютерами. Только лучше сказать "от бездумного увлечения". К сожалению, это бывает. Наглядный пример тому - публикация в 5/83 программы для решения задачи о "легкомысленном шахе". Для иллюстрации возможностей микрокалькулятора лучше было бы выбрать другой пример. То, что искомый результат удалось выразить простенькой формулой, напоминает: сначала анализ, а уж потом программирование.
А вот с противопоставлением аналитических и численных методов решения я не согласен. Думаю, что не противопоставлять их нужно, а комбинировать. Где есть возможность, доводить до формул, а где нет - считать численно. Машина полезна и при расчетах по формулам. Ведь иногда они настолько сложны, что о наглядности говорить не приходится. Чтобы получить по ним, скажем, графические зависимости, удобнее обратиться к ЭВМ.
Еще одна важная проблема, поднимаемая автором,- использование чужих программ. Вряд ли стоит сетовать по поводу того, что "любая программа соответствует не реальному явлению, а его математической модели". Ведь то же самое можно сказать и о любой формуле и о любом методе решения технической задачи. Совершенно естественно, что, обращаясь к чужим программам, нужно выбрать из них ту, которая наиболее подходит для решения поставленной задачи. Если же составитель программы не снабдил ее соответствующими пояснениями, то ею просто нельзя пользоваться, как нельзя пользоваться электроутюгом, если ма нем не указано, на какое напряжение он рассчитан.
Ошибки в программах. Избежать их полностью трудно, хотя стремиться к этому надо. Но почему-то об ошибке компьютера, неправильно начислившего налог, знают все, а о такой же ошибке, допущенной бухгалтером,- разве что сам "обиженный". Не потому ли, что ошибка компьютера - явление уникальное, а ошибка бухгалтера - заурядное?
И, наконец, последнее. Не приведет ли компьютер к "атрофии мозга"? Не отучит ли он человека думать? В свое время У.Р.Эшби назвал машину "усилителем мозга". Усилителем, а не заменителем! Применение ЭВМ не освобождает от умственного труда. Оно делает его более производительным, творческим и интересным.
Осваивайте программирование! Тогда машина превратится для вас в полезного, дельного помощника.
И.ВЯЗОВСКИЙ (г.Люберцы).
ПОДВЕДЕМ ИТОГИ КОНКУРСА
Наш журнал 12/83 объявил конкурс на лучшую программу для решения двух задач: поиск простых чисел в их естественной последовательности и нахождение целой части числа. В конкурсе приняло участие 445 человек. Среди них представители самых различных профессий: рабочий М.Говжеев из города Ново-Ждановка Донецкой области и биохимик И.Ионтов из Одессы, учитель И.Калужских из села Пищалье Кировской области и зимовщик Г.Хохорин со станции "Северный полюс-25"... Этот поистине всеобъемлющий диапазон специальностей убедительно свидетельствует, что вычислительная техника проникает во все сферы деятельности.
Большинство же участников конкурса - инженеры, преподаватели, студенты технических вузов. Наряду с ними хотелось бы отметить еще одну группу - не столь многочисленную, но дающую повод к отрадным прогнозам. Это школьники: шестиклассники М.Барановский (Ленинград) и К.Максимов (Иваново), семиклассники С.Белых (Свердловск) и А.Черных (Краснодар)... Справившись с заданиями конкурса, ребята косвенно поддержали мнение тех, кто считает своевременным и даже необходимым введение в школьную программу факультативного курса по основам электронно-вычислительной техники.
Львиная доля участников - мужчины. Это удивляет: ведь среди программистов довольно много женщин. Может быть, микрокалькулятор стал домашним развлечением сильного пола!
По первой задаче лучшей признана программа В.Илюхина, студента Московского института инженеров железнодорожного транспорта. Отмечены также программы Д.Богданова (Москва), Л.Добрынина (Воронеж), П.Калехмана (Оренбург), В.Линиса (Рига), Г.Натансона (Ленинград). Они, как и подавляющее большинство участников конкурса, работают с калькулятором "Электроника Б3-34". Для "Электроники Б3-21" лучшие программы прислали А.Пушкарев (Душанбе) и Г.Тютюма (Киев). По второй задаче отмечено 13 программ (о них ниже).
Программы для решения обеих задач на весьма высоком уровне составили В.Пендюра (Киев), О.Гречникова и Г.Сварчевский (Львов). Москвичи Д.Богданов и С.Бутырин прислали программы для обоих калькуляторов.
Программы победителей с комментариями будут опубликованы в одном из следующих выпусков рубрики "Человек с микрокалькулятором". В нынешнем ее выпуске разбираются типичные недочеты, допущенные участниками конкурса. Тому, кто встретит в этом разборе свои ошибки, вероятно, будет интересно заново и лучшим образом составить программы для решения конкурсных задач, чтобы затем сравнить их с работами победителей и успешнее выступить в последующих конкурсах.
Оценка качества работ оказалась вопреки ожиданиям делом несложным. И не потому, что правильных программ мало. По первой задаче их больше 90 процентов; самые быстрые из них, как правило, компактны, оптимально используют память, реализуют наиболее интересные алгоритмы и наилучшим образом учитывают специфику микрокалькуляторов.
Тем не менее по примеру чемпионатов по фигурному катанию было решено отдельно оценивать "технику" и "артистичность", вернее, совершенство алгоритма, использование специфики конкретного микрокалькулятора и культуру программирования.
Говоря о поиске простых чисел, следует напомнить, что простое число - это целое положительное число, большее единицы, не имеющее никаких делителей, кроме единицы и самого себя. Формулы, позволяющей последовательно вычислять простые числа, не существует. Поэтому приходится каждое число проверять "на простоту", то есть непосредственно убеждаться в отсутствии у него делителей. С выбора способа проверки и начинается построение алгоритма.
К сожалению, больше половины участников пошло по самому простому и отнюдь не оптимальному пути. Они перебирали все натуральные числа подряд и делители "примеряли" к ним тоже подряд. Программы, составленные по этому алгоритму, работают слишком медленно. (Одна из них, по оценке самого автора, числа порядка 1e7 проверяет на простоту примерно... 10 лет).
Многие участники конкурса (около 80 работ) правильно заметили, что четные числа явно не простые. Их и проверять не надо. Программы, где проверяются только нечетные числа и делители рассматриваются только нечетные, существенно быстрее программ, где числа анализируются подряд. При этом они не сложнее. Какая разница - увеличивать число в цикле на единицу или на двойку? Из этой когорты участников рекордно короткую (26 шагов) и притом достаточно быструю программу прислал В.Федотов из Красноярска.
Кстати, на каком наибольшем делителе нужно прекращать исследование на делимость? Увы, очень многие читатели для каждого проверяемого числа испытывали делители вплоть до n/2 или n/3, хотя известно, что достаточно ограничиться величинами, не превосходящими sqr(n).
Вернемся к алгоритму перебора. Несколько читателей заранее исключали не только четные числа, но и числа, кратные трем. Их программы еще более эффективны. Так поступили Д.Богданов (Москва), О.Гречникова и Г.Сверчевский (Львов), В.Клейзит (Кишинев), А.Копылов (Подольск), В.Тюрин (Москва), А.Черных (Краснодар).
Наконец, лучший, по мнению жюри (по крайней мере для используемого класса микрокалькуляторов), алгоритм, где заранее исключаются числа, кратные 2, 3 и 5, предложили и реализовали В.Илюхин (Москва) и А.Сельский (Сумы). В.Илюхин к тому же заметил и остроумно использовал периодическую повторяемость разностей между членами анализируемого ряда чисел, а именно: 6, 4, 2, 4, 2, 4, 6, 2. Использование этих разностей, записанных в регистры калькулятора, позволило ему достаточно быстро перебирать как проверяемые числа, так и потенциальные делители.
Теперь о культуре программирования. Большинство огрехов здесь связано с неаккуратным составлением циклов. Вряд ли стоит пояснять, сколь целесообразно выносить за пределы цикла те операции, результат которых в нем не меняется. В программах, о которых идет речь, многократно "прокручивается" цикл, где перебираются возможные делители. Следовало особенно тщательно следить, не попали ли в него лишние операции. Многие, к примеру, вычисляли в нем величину sqr(n), хотя это вычисление можно безболезненно вынести за пределы цикла. Это хоть и удлинит программу на команду-другую, но значительно сократит время ее работы.
Некоторые читатели сравнивали величину делителя с целой частью sqr(n). Между тем достаточно было сравнить его просто с sqr(n).
Еще один недостаток, довольно распространенный. В ряде программ выделение целой части числа было оформлено в виде подпрограммы. Конечно, подпрограммы - одно из мощных средств программирования. Но когда к подпрограмме обращаются всего один раз, то она превращается в своего рода архитектурное излишество. Она и удлиняет программу, и замедляет ее за счет выполнения команд перехода.
Нельзя забывать, что программа должна быть не только быстрой, но и удобной. Только очень немногие читатели (в основном уже упоминавшиеся) делали программы, позволяющие получать последовательность простых чисел, начиная с любого наперед заданного натурального. Киевлянин В.Пендюра сделал очень удобным и вывод информации. Его программа считает простые числа дюжинами и записывает их в регистры. После получения очередной дюжины она останавливается. Можно прочесть числа (кстати, как тут не пожалеть об отсутствии печатающего устройства!) и продолжить счет. Это не только удобно, но и сокращает общее время счета: меньше остановок.
Прекрасный пример культурного оформления программы дан в книге Г.Славина "Прикладные программы для программируемого микрокалькулятора "Электроника Б3-34": когда в калькулятор вводится число, проверяемое на простоту, он оценивает и указывает на индикаторе ориентировочное время проверки.
Специфические особенности калькулятора - модификации адресов при косвенной адресации и использование этого факта для выделения целой части числа, а иногда и для замены операций суммирования - применялись многими участниками конкурса. Оригинальный способ проверки величины на целочисленность предложили Е.Левина и Е.Налимов (Москва) и С.Беляков (Горький). Они умножают число на 180 и берут синус от произведения. Если результат равен нулю, то число целое. (Заметим, что при умножении на пи и интерпретации произведения в виде радианной меры угла этот способ может не пройти, поскольку калькулятор "держит в памяти" приближенное значение величины пи). По числу команд это, пожалуй, самый короткий способ. Но по времени он довольно длинен за счет обращения к "медленной" операции взятия синуса.
Теперь перейдем ко второй задаче - выделению целой части числа. Как это ни парадоксально, исчерпывающего решения она не нашла у подавляющего большинства участников конкурса. Многие забыли, что целая часть бывает не только у положительных, но и у отрицательных чисел. Те же, кто вспомнил об этом, в большинстве случаев неправильно ее указывали. По определению целая часть числа a (обозначается [a]) есть наибольшее целое число, не превосходящее а. Поэтому [3.4]=3, а [-3.4]=-4, а не -3, как полагают некоторые читатели.
Многие решили использовать операцию КИПX, где X - номер одного из регистров 7-9, А-Д. Если там записано дробное число большее единицы, то после выполнения этой операции в регистре остается целая часть числа. Некоторые пробовали распространить такой прием на числа между нулем и единицей, сдвигая диапазон аргументов на -1, однако при этом редко кто смог избежать ошибок.
Для всех чисел без исключения предлагалось округление за счет переполнения разрядной сетки. Для этого число складывалось с 1e7, а затем из суммы вычиталось 1e7. К сожалению, некоторые из применивших такую возможность не учли, что округление при этом может произойти и в большую сторону. Из тех, кто предвидел это, некоторые неверно выбирали "антиокруглитель" - слагаемое, нейтрализующее округление в нежелательную сторону. В качестве такого слагаемого нужно брать 5.5555555e-1, число из восьми пятерок, иначе ошибки неизбежны.
Программы, свободные от перечисленных недостатков, прислали в срок Г.Артюх (Рустави), А.Бармак (Одесса), А.Басов, Д.Довженко, А. и Л.Лериеры, Д.Малиновский, В. Нестеров, Л.Финк (Ленинград), С.Еремин (Новокузнецк), Ю. Кошельский (Томск), Б.Скубаренко (Калинин), Ю.Тертычный (Северодонецк), Е.Хрулев (Даугавпилс). Все они не лучше тех, что опубликованы в книгах Я.Трохименко и Ф.Любича "Радиотехнические расчеты на микрокалькуляторах:", А.Цветкова "Прикладные программы для микроЭВМ "Электроника Б3-21". В помощь самообразованию наших читателей завершаем обзор кратким списком литературы о микрокалькуляторах. Он будет продолжен в дальнейших выпусках рубрики.
ЛИТЕРАТУРА
Белый Ю.А. Считающая микроэлентроника. М., "Наука". 1983.
Белый Ю.А. Электронные микрокалькуляторы и техника вычислений. М., "Знание", 1981.
Блох А.Ш., Павловский А.И., Пенкрат В.В. Программирование на микрокалькуляторах. Минск, "Вышэйшая школа". 1981.
Гильде В., Альтрихтер З. С микрокалькулятором в руках. М., "Мир", 1980.
Кройль Г. Что умеет мой микрокалькулятор. М., "Мир", 1981.
Петров М.И. Техника вычислений иа микрокалькуляторе "Электроника Б3-19М". М., "Финансы и статистика", 1981.
Петров М.И. Технико-экономические расчеты на электронной микромашине "Электроника Б3-38". М., "Статистика", 1979.
Трохименко Я.К., Любич Ф.Д. Инженерные расчеты на мнкрокалькуляторах. Киев, "Техника". 1980.
Трохименко Я.К., Любич Ф.Д. Радиотехнические расчеты ка микрокалькуляторах. М., "Радио и связь", 1983.
Цветков А.Н. Прикладные программы для мииро-ЭВМ "Электроника Б3-21". М., "Финансы н статистика", 1982.
Цветков А.Н., Епанечников В.А. Прикладные программы для мннроЭВМ "Электроника Б3-34" и "Электроника МК-56".
Чакань А. Что умеет карманная ЭВМ. М., "Радио и связь", 1982.
Рис. Ю.Побожия
ПОВЕРКА С МИКРОКАЛЬКУЛЯТОРОМ
По профессии я учитель. Преподаю в учебном производственном комбинате курс "Контрольно-измерительные приборы и автоматика". Тема одного из практических занятии моих учеников - поверка измерительных приборов. По ходу занятия школьники контролируют правильность показаний термометра сопротивления. Прибор представляет собой катушку из тонкой платиновой или медной проволоки. При изменении температуры сопротивление проволоки меняется. Изменения фиксируются так называемым вторичным прибором, который преобразует величину сопротивления в значение температуры.
Если сам термометр работает весьма надежно, то вторичные приборы, более сложные но конструкции, могут иногда ошибаться. Поэтому их периодически поверяют. Подключают на вход прибора вместо термометра магазин сопротивлений и смотрят, насколько отклоняются его показания от тех, которые соответствуют эталонным сопротивлениям.
Непосредственные измерения при этом занимают не более получаса. Вычисления, связанные с их обработкой, отнимают в несколько раз больше времени.
Чтобы облегчить труд, мы применили "малую механизацию" - простые, непрограммируемые микрокалькуляторы. Однако, работая с ними, приходилось многократно сверяться с таблицами, да и ввод данных создавал лазейку для ошибок.
Тогда мы решили полностью автоматизировать расчеты, перейти на программируемые микрокалькуляторы и заставить их вычислять табличные величины, а потом рассчитывать абсолютную и относительную погрешности.
Зависимость сопротивления платины и меди от температуры известна. Для платины она определяется формулой: R=R0(1+At+Bt2) при 0<=t<=650oC; R=R0(1+At+Bt2+Ct3(t-100)) при -200<=t<=0oC.
Величина R0 определяет градуировку прибора. Она может быть равна 10, 46 или 100 Ом. А = 3.96847e-3 1/oС, В = -5.847e-7 1/oС2, С = -4.22e-12 1/oС3.
Для меди в диапазоне температур от -50oС до 150oС зависимость проще: R=R0(l+at), где a = 0.00426 1/oС, а R0 принимает значения 53 или 100 Ом.
От идеи до исполнения часа три работы. И вот программа готова. Остается ввести в нее константы. А потом брать из таблиц всего две величины - сопротивления для начальной н конечной точек диапазона измерений, да еще вводить величину сопротивления, полученную экспериментально. 15 секунд работы (включая ввод сопротивления), и расчет готов.
С нетерпением дождался очередного занятия и предложил школьникам провести расчеты по-новому. Несмотря иа то, что с непривычки они довольно долго вводили программу в калькулятор, удалось сэкономить не менее часа.
Замечу, что мне известны учителя физики, которые запрещают применять калькуляторы при расчетах даже в десятом классе. Полагают, что учащиеся должны проводить все расчеты на бумажке. И это при современном дефиците времени!
Ниже приводится программа для поверки платинового термометра. Сделать аналогичную для медного значительно проще. Думаю, что эти программы окажут пользу не только преподавателям, но и многочисленным работникам лабораторий контрольно-измерительных приборов.
Г.ДАВЫДОВИЧ (г.Красноярск)
Программа. 00. С/П 01. П0 02. ИПD 03. Fx>=0 04. 10. 05. ИП6 06. ПП 07. 38 08. БП 09. 21 10. ИПD 11. ИП3 12. - 13. ИП7 14. * 15. ИПD 16. * 17. ИП6 18. + 19. ПП 20. 38 21. ИП0 22. ИПА 23. - 24. Fx2 25. Fsqr 26. ПВ 27. ИП8 28. / 29. ИП3 30. * 31. ПС 32. ИПD 33. ИП2 34. + 35. ПD 36. БП 37. 00 38. ИПD 39. * 40. ИП5 41. + 42. ИПD 43. * 44. 1 45. + 46. ИП4 47. * 48. ПА 49. В/О.
Перед началом работы регистры нужно заполнить так: шаг шкалы прибора - в Р2, цифра 100 - в Р3, R0 - в Р4, коэффициент А - в Р5, В - в Р6, С - в Р7. Разность сопротивлений между начальной и конечной точками шкалы (она берется из таблиц и в расчете используется для определения относительной погрешности) - в Р8, начальное значение температуры - в PD. Измеренное значение сопротивления - в Р0. Результаты расчета распределяются по регистрам так: табличное значение сопротивления R - в РА, абсолютная погрешность - в РВ, относительная (в процентах) - в PC.
Oт редакции. Программа не свободна от недостатков. Тем, кто ради упражнения возьмется улучшить ее, советуем обратить внимание на слишком частое обращение к регистру PD (почему бы не использовать стек?), возможность сэкономить регистр Р3, если применить команды F10X и ВП, не лучшее расположение команды С/П.
[ УЗЕЛКИ НА ПАМЯТЬ
Набрать число 1eM на индикаторе н сложить с ним содержимое регистра N быстрее и проще всего так: ИПN M F1eX +.
Если число, извлеченное нз регистра N. необходимо помножить на 1eM, то короче будет: ИПN ВП M.
Б.АЛЕКСЕЕВ (г.Москва). ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Секреты есть не только у программируемых калькуляторов. Микрокалькулятор "Электроника Б3-36", к примеру, запоминает значение (точнее, код) предыдущей операции. Это позволяет сократить количество нажимаемых в процессе вычислений клавиш. Мне удалось довести программу перевода комплексного числа из алгебраической формы в тригонометрическую до обращеиня всего к семи клавишам.
Реализованы формулы: В=arctg(y/x); А=x/cosВ.
А вот программа: (->y) / (->x) / ARC tg (В->) Fcos = (A->). Обозначения: (->y) - ввод числа с клавиатуры, (А->) - чтение величины на индикаторе.
А.ХОДАКСВ (г.Москва). ]
ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
"Секреты микрокалькулятора" - так называлась подборка читательских писем, посвященных особенностям вычислений на "Электронике Б3-34" 4/84). В своих откликах на нее читатели предлагают устроить это своеобразное "заседание за круглым столом" еще раз. Предложение принимается. Для последующих заседаний предлагаются такие темы:
- метод наименьших квадратов;
- удобство программ, приемы сервиса.
Ждем писем с конкретными примерами, обобщающими рассуждениями, находками, советами и т.п.
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Многие заметки, опубликованные в прежних выпусках рубрики "Человек с микрокалькулятором", вызвали оживленные, зачастую критические отклики читателей. Некоторые из них публикуются в нынешнем выпуске. Надеемся, что подобные дискуссии еще не раз развернутся под нашей рубрикой, помогая ее читателям совершенствовать навыки работы с вычислительной техникой.
ЦЕНА ЭКОНОМИИ
То, что микрокалькулятор экономит время, очевидно. Но, оказывается, он может и "расширять" его! По крайней мере такой вывод можно сделать после прочтения статьи А.Раздобреева "Как решить неразрешимое уравнение" (2/84). "Владельцы микрокалькуляторов,- пишет автор статьи,- как правило, имеют достаточно времени для своих вычислений: не успел утром, можно закончить вечером". Выходит, что ученые, инженеры, домохозяйки - все жалуются на недостаток времени, а вот владельцы микрокалькуляторов имеют его в избытке.
Не будем обсуждать этот парадоксальный тезис - лучше посмотрим, какие выводы делает из него автор. "Следует в первую очередь соблюдать принцип экономии памяти и, только во-вторых, экономии времени". Любопытно, что, оптимизируя программу для решения "уравнения жрецов бога Ра", автор делает ее не только более короткой, но и более быстрой, однако тут же подчеркивает, что это чуть ли не побочный эффект от экономии памяти. Не лучше ли сказать, что оптимизировать программу - значит стремиться сделать ее и короче и быстрее?
Правда, эти два требования могут оказаться альтернативными. И тогда надо учитывать аспект, без которого рассуждать о качестве программы нельзя,- назначение программы.
Если она создается для одноразового решения единичной задачи, как, например, "загадки жрецов бога Ра", то на первый план должно выступить общее время от постановки задачи до получения результата, и вряд ли целесообразно тратить часы на оптимизацию программы, чтобы добиться ускорения ее работы на секунды и сокращения на одну-две команды. Лишь бы она справлялась с задачей за достижимо короткое время и умещалась в память!
Если же программируется задача, расчеты по которой проводятся часто,- например, статистический анализ или другие задачи, постоянно решаемые с разными входными данными,- то, по-моему, здесь важнее всего быстрота работы программы, пусть даже достигаемая ценой некоторого ее удлинения.
Иное дело - подпрограммы. Здесь критерии быстроты и краткости выступают на равных. Но это тема особого разговора.
... Стремление к экономии памяти как к самоцели я сравнил бы с рекомендацией писать романы на рисовых зернах. Это, безусловно, интересно, даже красиво и бумагу экономит, но вряд ли целесообразно рекомендовать такой метод писателям.
И.ДАНИЛОВ (Москва)
НА ОШИБКАХ УЧИМСЯ
Программа для вычисления статистических характеристик, помещенная в статье Н.Богина "Статистика на микрокалькуляторе" (12/83), вызвала много нареканий у читателей как изобилующая погрешностями. Признавая их, заметим: свою задачу программа решает. Что же касается совершенства...
Говорят, на ошибках учатся. Поговорка убеждает, что в деле обучения разбор ошибок иной раз лучше, чем демонстрация безупречных примеров.
На основе писем С.Дорофеева (Грозный), Я.Закина, В.Козлова, А.Орлова (Ленинград), Я.Кирпичева (Москва), И.Обухова (Киев), Ю. и Я.Пашковых (Ворошиловград), В.Шеина (Харьков) и других такой разбор по просьбе редакции провел А.Бойко (Москва).
Итак, окинем программу Н. Богина критическим взглядом. В самом ее начале замечаем излишние операции: регистры Р5 и Р6 очищать незачем - их исходное содержание не влияет на ход программы.
Не стоит заносить в регистры и промежуточные результаты - лучше использовать возможности стека. Команды 07 и 11 можно заменить соответственно командами "^" и "x-y".
Во фрагменте 16-19 неудачно примечен в качестве счетчика регистр Р7. Здесь упущены возможности косвенной адресации, при которой во время обращения к регистрам Р0-Р3 их содержимое каждый раз уменьшается на единицу, а во время обращения к регистрам Р4-Р6 увеличивается. Указанный фрагмент лучше заменить командами КИП4-ИП4.
Некорректна в анализируемой программе последовательность операций / /-/, поскольку это вызывает ошибки счета в калькуляторах ранних выпусков (см. инструкцию). Ошибки исчезнут, если начать со смены знака и лишь после этого выполнить необходимое действие. Впрочем, не стоит сначала менять знак (26), а затем складывать (28 ), когда проще вычесть. Для этого вместо команд 22-28 следует написать ИП4 ИП3 Fx2 ИП7 / -. Не следует брать и обратную величину для того, чтобы умножить на нее результат. Проще разделить, то есть вместо 29-35 написать ИП7 1 - /. (Тот, кто усмехнется над такими оплошностями, пусть вспомнит свои первые шаги в программировании). Наконец, не стоит заносить результат сложения в регистр Р8 (29) только для того, чтобы один-единственный раз его вызвать (34): достаточно помнить, что он содержится в регистре Y стека.
Совершенно справедливо замечание, что необходимость набора БП, 2, 2, С/П - это дополнительный источник ошибок. Удобнее при соответствующем построении программы лишь нажать на клавишу ШГ со стрелкой вправо и пустить программу командой С/П.
Потенциальная возможность ошибок - обилие остановов в ходе программы. Уменьшить их число можно, например, используя стек как "магазин", заполненный к моменту останова результатами расчета.
Можно отметить и другие слабые места программы Н.Богина (сложность исправления допущенной ошибки ввода данных и т.п.), но в отличие от описанных выше недочетов здесь трудно дать общие рекомендации.
Не будем касаться возможностей, связанных с априорным знанием длины массива обрабатываемых данных, так как это повлекло бы радикальные изменения в структуре исходной программы, что не соответствует цели настоящей статьи.
Приняв за основу версию программы Н.Богина, данную В.Козловым, можно предложить такой вариант, где устранены отмеченные недостатки.
Программа. 00. ^ 01. Сх 02. П4 03. П5 04. П6 05. F() 06. ^ 07. ИП4 08.+ 09. П4 10. x-y 11. Fx2 12. ИП5 13. + 14. П5 15. КИП6 16. ИП6 17. С/П 18. БП 19. 06 20. F() 21. ИП5 22. ИП4 23. Fx2 24. ИП6 25. / 26. - 27. ИП6 28. 1 29. - 30. / 31. Fsqr 32. П5 33. ИП4 34. ИП6 35. / 36. / 37. FBx 38. ИП5 39. С/П.
Нажав клавишу В/О, вводим первое число из обрабатываемого массива; клавишей С/П пускаем программу; после останова вводим новое число и вновь нажимаем С/П - суммируем (адреса 06-17) вводимые числа и их квадраты. Прекратив на любом из остановов ввод чисел, видим на индикаторе их количество. Нажал клавиши ШГ и С/П, пускаем программу далее (адреса 21-38 ) и получаем статистические характеристики массива: на индикаторе - среднеквадратическое отклонение S, в регистре Y - среднее X, в регистре Z - коэффициент вариации V.
[ Под рубрикой "Человек с микрокалькулятором" и впредь будут публиковаться программы, составленные нашими читателями для решения различных производственных и учебных задач. Возможные несовершенства программ должны служить для их авторов не тормозом, а стимулом к обнародованию. Ведь вынесенные на суд товарищей по увлечению ошибки будут устранены надежнее, чем наедине. Обмен опытом, повышение культуры программирования - таков выигрыш, в котором окажутся все участники обсуждения. А главное - оно будет служить важной цели: внедрению вычислительных методов всюду, где к этому имеются предпосылки.
Итак, ждем новых писем от наших читателей, сделавших микрокалькулятор своим помощником в решении вставших перед ними проблем. ]
НЕ БОЙТЕСЬ КОМПЬЮТЕРОВ
Прочитав в 2/83 статью П.Эльясберга "Осторожно - компьютеры!", я подумал: а ведь что-то подобное уже было! Лет тридцать тому назад лозунг "Осторожно - авторучки!" буквально не сходил с уст педагогов. Авторучки, мол, испортят почерк, и посему никаких авторучек!
Прошло время, об этих призывах все забыли. Почерк у детей, может быть, и стал хуже. (Правда, и во времена стальных да и гусиных перьев не все были каллиграфами). Но зато писать стало удобнее, и тетради стали явно чище.
В чем же надо проявлять осторожность сейчас? П.Эльясберг предостерегает от "переоценки возможностей ЭВМ". Что ж, она действительно встречается, но только у тех, кто не имеет дела с машиной. Те же, кто их использует, оценивают возможности ЭВМ достаточно трезво и прекрасно понимают, что машина может сделать лишь то, что в нее заложили.
"Компьютер всегда работает по заданной программе. А человек... сам определяет порядок своей работы. И в этом его громадное преимущество перед любым компьютером". Наверное, следуя такой логике, можно сказать, что преимущество человека перед автомобилем в том, что человек может повернуться на месте, а автомобиль нет. Но, наверное, преимущество человека в том, что он создал и автомобиль и компьютер. Автомобиль - чтобы увеличить скорость передвижения, а компьютер - чтобы увеличить скорость вычислений. А что касается программ, то и человек и компьютер работают по программе. Только в одном случае человек составляет ее для себя и сам выполняет, а во втором пишет для компьютера, перекладывая на его плечи утомительную, рутинную работу.
Автор совершенно прав, предостерегая от увлечения компьютерами. Только лучше сказать "от бездумного увлечения". К сожалению, это бывает. Наглядный пример тому - публикация в 5/83 программы для решения задачи о "легкомысленном шахе". Для иллюстрации возможностей микрокалькулятора лучше было бы выбрать другой пример. То, что искомый результат удалось выразить простенькой формулой, напоминает: сначала анализ, а уж потом программирование.
А вот с противопоставлением аналитических и численных методов решения я не согласен. Думаю, что не противопоставлять их нужно, а комбинировать. Где есть возможность, доводить до формул, а где нет - считать численно. Машина полезна и при расчетах по формулам. Ведь иногда они настолько сложны, что о наглядности говорить не приходится. Чтобы получить по ним, скажем, графические зависимости, удобнее обратиться к ЭВМ.
Еще одна важная проблема, поднимаемая автором,- использование чужих программ. Вряд ли стоит сетовать по поводу того, что "любая программа соответствует не реальному явлению, а его математической модели". Ведь то же самое можно сказать и о любой формуле и о любом методе решения технической задачи. Совершенно естественно, что, обращаясь к чужим программам, нужно выбрать из них ту, которая наиболее подходит для решения поставленной задачи. Если же составитель программы не снабдил ее соответствующими пояснениями, то ею просто нельзя пользоваться, как нельзя пользоваться электроутюгом, если ма нем не указано, на какое напряжение он рассчитан.
Ошибки в программах. Избежать их полностью трудно, хотя стремиться к этому надо. Но почему-то об ошибке компьютера, неправильно начислившего налог, знают все, а о такой же ошибке, допущенной бухгалтером,- разве что сам "обиженный". Не потому ли, что ошибка компьютера - явление уникальное, а ошибка бухгалтера - заурядное?
И, наконец, последнее. Не приведет ли компьютер к "атрофии мозга"? Не отучит ли он человека думать? В свое время У.Р.Эшби назвал машину "усилителем мозга". Усилителем, а не заменителем! Применение ЭВМ не освобождает от умственного труда. Оно делает его более производительным, творческим и интересным.
Осваивайте программирование! Тогда машина превратится для вас в полезного, дельного помощника.
И.ВЯЗОВСКИЙ (г.Люберцы).
ПОДВЕДЕМ ИТОГИ КОНКУРСА
Наш журнал 12/83 объявил конкурс на лучшую программу для решения двух задач: поиск простых чисел в их естественной последовательности и нахождение целой части числа. В конкурсе приняло участие 445 человек. Среди них представители самых различных профессий: рабочий М.Говжеев из города Ново-Ждановка Донецкой области и биохимик И.Ионтов из Одессы, учитель И.Калужских из села Пищалье Кировской области и зимовщик Г.Хохорин со станции "Северный полюс-25"... Этот поистине всеобъемлющий диапазон специальностей убедительно свидетельствует, что вычислительная техника проникает во все сферы деятельности.
Большинство же участников конкурса - инженеры, преподаватели, студенты технических вузов. Наряду с ними хотелось бы отметить еще одну группу - не столь многочисленную, но дающую повод к отрадным прогнозам. Это школьники: шестиклассники М.Барановский (Ленинград) и К.Максимов (Иваново), семиклассники С.Белых (Свердловск) и А.Черных (Краснодар)... Справившись с заданиями конкурса, ребята косвенно поддержали мнение тех, кто считает своевременным и даже необходимым введение в школьную программу факультативного курса по основам электронно-вычислительной техники.
Львиная доля участников - мужчины. Это удивляет: ведь среди программистов довольно много женщин. Может быть, микрокалькулятор стал домашним развлечением сильного пола!
По первой задаче лучшей признана программа В.Илюхина, студента Московского института инженеров железнодорожного транспорта. Отмечены также программы Д.Богданова (Москва), Л.Добрынина (Воронеж), П.Калехмана (Оренбург), В.Линиса (Рига), Г.Натансона (Ленинград). Они, как и подавляющее большинство участников конкурса, работают с калькулятором "Электроника Б3-34". Для "Электроники Б3-21" лучшие программы прислали А.Пушкарев (Душанбе) и Г.Тютюма (Киев). По второй задаче отмечено 13 программ (о них ниже).
Программы для решения обеих задач на весьма высоком уровне составили В.Пендюра (Киев), О.Гречникова и Г.Сварчевский (Львов). Москвичи Д.Богданов и С.Бутырин прислали программы для обоих калькуляторов.
Программы победителей с комментариями будут опубликованы в одном из следующих выпусков рубрики "Человек с микрокалькулятором". В нынешнем ее выпуске разбираются типичные недочеты, допущенные участниками конкурса. Тому, кто встретит в этом разборе свои ошибки, вероятно, будет интересно заново и лучшим образом составить программы для решения конкурсных задач, чтобы затем сравнить их с работами победителей и успешнее выступить в последующих конкурсах.
Оценка качества работ оказалась вопреки ожиданиям делом несложным. И не потому, что правильных программ мало. По первой задаче их больше 90 процентов; самые быстрые из них, как правило, компактны, оптимально используют память, реализуют наиболее интересные алгоритмы и наилучшим образом учитывают специфику микрокалькуляторов.
Тем не менее по примеру чемпионатов по фигурному катанию было решено отдельно оценивать "технику" и "артистичность", вернее, совершенство алгоритма, использование специфики конкретного микрокалькулятора и культуру программирования.
Говоря о поиске простых чисел, следует напомнить, что простое число - это целое положительное число, большее единицы, не имеющее никаких делителей, кроме единицы и самого себя. Формулы, позволяющей последовательно вычислять простые числа, не существует. Поэтому приходится каждое число проверять "на простоту", то есть непосредственно убеждаться в отсутствии у него делителей. С выбора способа проверки и начинается построение алгоритма.
К сожалению, больше половины участников пошло по самому простому и отнюдь не оптимальному пути. Они перебирали все натуральные числа подряд и делители "примеряли" к ним тоже подряд. Программы, составленные по этому алгоритму, работают слишком медленно. (Одна из них, по оценке самого автора, числа порядка 1e7 проверяет на простоту примерно... 10 лет).
Многие участники конкурса (около 80 работ) правильно заметили, что четные числа явно не простые. Их и проверять не надо. Программы, где проверяются только нечетные числа и делители рассматриваются только нечетные, существенно быстрее программ, где числа анализируются подряд. При этом они не сложнее. Какая разница - увеличивать число в цикле на единицу или на двойку? Из этой когорты участников рекордно короткую (26 шагов) и притом достаточно быструю программу прислал В.Федотов из Красноярска.
Кстати, на каком наибольшем делителе нужно прекращать исследование на делимость? Увы, очень многие читатели для каждого проверяемого числа испытывали делители вплоть до n/2 или n/3, хотя известно, что достаточно ограничиться величинами, не превосходящими sqr(n).
Вернемся к алгоритму перебора. Несколько читателей заранее исключали не только четные числа, но и числа, кратные трем. Их программы еще более эффективны. Так поступили Д.Богданов (Москва), О.Гречникова и Г.Сверчевский (Львов), В.Клейзит (Кишинев), А.Копылов (Подольск), В.Тюрин (Москва), А.Черных (Краснодар).
Наконец, лучший, по мнению жюри (по крайней мере для используемого класса микрокалькуляторов), алгоритм, где заранее исключаются числа, кратные 2, 3 и 5, предложили и реализовали В.Илюхин (Москва) и А.Сельский (Сумы). В.Илюхин к тому же заметил и остроумно использовал периодическую повторяемость разностей между членами анализируемого ряда чисел, а именно: 6, 4, 2, 4, 2, 4, 6, 2. Использование этих разностей, записанных в регистры калькулятора, позволило ему достаточно быстро перебирать как проверяемые числа, так и потенциальные делители.
Теперь о культуре программирования. Большинство огрехов здесь связано с неаккуратным составлением циклов. Вряд ли стоит пояснять, сколь целесообразно выносить за пределы цикла те операции, результат которых в нем не меняется. В программах, о которых идет речь, многократно "прокручивается" цикл, где перебираются возможные делители. Следовало особенно тщательно следить, не попали ли в него лишние операции. Многие, к примеру, вычисляли в нем величину sqr(n), хотя это вычисление можно безболезненно вынести за пределы цикла. Это хоть и удлинит программу на команду-другую, но значительно сократит время ее работы.
Некоторые читатели сравнивали величину делителя с целой частью sqr(n). Между тем достаточно было сравнить его просто с sqr(n).
Еще один недостаток, довольно распространенный. В ряде программ выделение целой части числа было оформлено в виде подпрограммы. Конечно, подпрограммы - одно из мощных средств программирования. Но когда к подпрограмме обращаются всего один раз, то она превращается в своего рода архитектурное излишество. Она и удлиняет программу, и замедляет ее за счет выполнения команд перехода.
Нельзя забывать, что программа должна быть не только быстрой, но и удобной. Только очень немногие читатели (в основном уже упоминавшиеся) делали программы, позволяющие получать последовательность простых чисел, начиная с любого наперед заданного натурального. Киевлянин В.Пендюра сделал очень удобным и вывод информации. Его программа считает простые числа дюжинами и записывает их в регистры. После получения очередной дюжины она останавливается. Можно прочесть числа (кстати, как тут не пожалеть об отсутствии печатающего устройства!) и продолжить счет. Это не только удобно, но и сокращает общее время счета: меньше остановок.
Прекрасный пример культурного оформления программы дан в книге Г.Славина "Прикладные программы для программируемого микрокалькулятора "Электроника Б3-34": когда в калькулятор вводится число, проверяемое на простоту, он оценивает и указывает на индикаторе ориентировочное время проверки.
Специфические особенности калькулятора - модификации адресов при косвенной адресации и использование этого факта для выделения целой части числа, а иногда и для замены операций суммирования - применялись многими участниками конкурса. Оригинальный способ проверки величины на целочисленность предложили Е.Левина и Е.Налимов (Москва) и С.Беляков (Горький). Они умножают число на 180 и берут синус от произведения. Если результат равен нулю, то число целое. (Заметим, что при умножении на пи и интерпретации произведения в виде радианной меры угла этот способ может не пройти, поскольку калькулятор "держит в памяти" приближенное значение величины пи). По числу команд это, пожалуй, самый короткий способ. Но по времени он довольно длинен за счет обращения к "медленной" операции взятия синуса.
Теперь перейдем ко второй задаче - выделению целой части числа. Как это ни парадоксально, исчерпывающего решения она не нашла у подавляющего большинства участников конкурса. Многие забыли, что целая часть бывает не только у положительных, но и у отрицательных чисел. Те же, кто вспомнил об этом, в большинстве случаев неправильно ее указывали. По определению целая часть числа a (обозначается [a]) есть наибольшее целое число, не превосходящее а. Поэтому [3.4]=3, а [-3.4]=-4, а не -3, как полагают некоторые читатели.
Многие решили использовать операцию КИПX, где X - номер одного из регистров 7-9, А-Д. Если там записано дробное число большее единицы, то после выполнения этой операции в регистре остается целая часть числа. Некоторые пробовали распространить такой прием на числа между нулем и единицей, сдвигая диапазон аргументов на -1, однако при этом редко кто смог избежать ошибок.
Для всех чисел без исключения предлагалось округление за счет переполнения разрядной сетки. Для этого число складывалось с 1e7, а затем из суммы вычиталось 1e7. К сожалению, некоторые из применивших такую возможность не учли, что округление при этом может произойти и в большую сторону. Из тех, кто предвидел это, некоторые неверно выбирали "антиокруглитель" - слагаемое, нейтрализующее округление в нежелательную сторону. В качестве такого слагаемого нужно брать 5.5555555e-1, число из восьми пятерок, иначе ошибки неизбежны.
Программы, свободные от перечисленных недостатков, прислали в срок Г.Артюх (Рустави), А.Бармак (Одесса), А.Басов, Д.Довженко, А. и Л.Лериеры, Д.Малиновский, В. Нестеров, Л.Финк (Ленинград), С.Еремин (Новокузнецк), Ю. Кошельский (Томск), Б.Скубаренко (Калинин), Ю.Тертычный (Северодонецк), Е.Хрулев (Даугавпилс). Все они не лучше тех, что опубликованы в книгах Я.Трохименко и Ф.Любича "Радиотехнические расчеты на микрокалькуляторах:", А.Цветкова "Прикладные программы для микроЭВМ "Электроника Б3-21". В помощь самообразованию наших читателей завершаем обзор кратким списком литературы о микрокалькуляторах. Он будет продолжен в дальнейших выпусках рубрики.
ЛИТЕРАТУРА
Белый Ю.А. Считающая микроэлентроника. М., "Наука". 1983.
Белый Ю.А. Электронные микрокалькуляторы и техника вычислений. М., "Знание", 1981.
Блох А.Ш., Павловский А.И., Пенкрат В.В. Программирование на микрокалькуляторах. Минск, "Вышэйшая школа". 1981.
Гильде В., Альтрихтер З. С микрокалькулятором в руках. М., "Мир", 1980.
Кройль Г. Что умеет мой микрокалькулятор. М., "Мир", 1981.
Петров М.И. Техника вычислений иа микрокалькуляторе "Электроника Б3-19М". М., "Финансы и статистика", 1981.
Петров М.И. Технико-экономические расчеты на электронной микромашине "Электроника Б3-38". М., "Статистика", 1979.
Трохименко Я.К., Любич Ф.Д. Инженерные расчеты на мнкрокалькуляторах. Киев, "Техника". 1980.
Трохименко Я.К., Любич Ф.Д. Радиотехнические расчеты ка микрокалькуляторах. М., "Радио и связь", 1983.
Цветков А.Н. Прикладные программы для мииро-ЭВМ "Электроника Б3-21". М., "Финансы н статистика", 1982.
Цветков А.Н., Епанечников В.А. Прикладные программы для мннроЭВМ "Электроника Б3-34" и "Электроника МК-56".
Чакань А. Что умеет карманная ЭВМ. М., "Радио и связь", 1982.

Рис. Ю.Побожия
ПОВЕРКА С МИКРОКАЛЬКУЛЯТОРОМ
По профессии я учитель. Преподаю в учебном производственном комбинате курс "Контрольно-измерительные приборы и автоматика". Тема одного из практических занятии моих учеников - поверка измерительных приборов. По ходу занятия школьники контролируют правильность показаний термометра сопротивления. Прибор представляет собой катушку из тонкой платиновой или медной проволоки. При изменении температуры сопротивление проволоки меняется. Изменения фиксируются так называемым вторичным прибором, который преобразует величину сопротивления в значение температуры.
Если сам термометр работает весьма надежно, то вторичные приборы, более сложные но конструкции, могут иногда ошибаться. Поэтому их периодически поверяют. Подключают на вход прибора вместо термометра магазин сопротивлений и смотрят, насколько отклоняются его показания от тех, которые соответствуют эталонным сопротивлениям.
Непосредственные измерения при этом занимают не более получаса. Вычисления, связанные с их обработкой, отнимают в несколько раз больше времени.
Чтобы облегчить труд, мы применили "малую механизацию" - простые, непрограммируемые микрокалькуляторы. Однако, работая с ними, приходилось многократно сверяться с таблицами, да и ввод данных создавал лазейку для ошибок.
Тогда мы решили полностью автоматизировать расчеты, перейти на программируемые микрокалькуляторы и заставить их вычислять табличные величины, а потом рассчитывать абсолютную и относительную погрешности.
Зависимость сопротивления платины и меди от температуры известна. Для платины она определяется формулой: R=R0(1+At+Bt2) при 0<=t<=650oC; R=R0(1+At+Bt2+Ct3(t-100)) при -200<=t<=0oC.
Величина R0 определяет градуировку прибора. Она может быть равна 10, 46 или 100 Ом. А = 3.96847e-3 1/oС, В = -5.847e-7 1/oС2, С = -4.22e-12 1/oС3.
Для меди в диапазоне температур от -50oС до 150oС зависимость проще: R=R0(l+at), где a = 0.00426 1/oС, а R0 принимает значения 53 или 100 Ом.
От идеи до исполнения часа три работы. И вот программа готова. Остается ввести в нее константы. А потом брать из таблиц всего две величины - сопротивления для начальной н конечной точек диапазона измерений, да еще вводить величину сопротивления, полученную экспериментально. 15 секунд работы (включая ввод сопротивления), и расчет готов.
С нетерпением дождался очередного занятия и предложил школьникам провести расчеты по-новому. Несмотря иа то, что с непривычки они довольно долго вводили программу в калькулятор, удалось сэкономить не менее часа.
Замечу, что мне известны учителя физики, которые запрещают применять калькуляторы при расчетах даже в десятом классе. Полагают, что учащиеся должны проводить все расчеты на бумажке. И это при современном дефиците времени!
Ниже приводится программа для поверки платинового термометра. Сделать аналогичную для медного значительно проще. Думаю, что эти программы окажут пользу не только преподавателям, но и многочисленным работникам лабораторий контрольно-измерительных приборов.
Г.ДАВЫДОВИЧ (г.Красноярск)
Программа. 00. С/П 01. П0 02. ИПD 03. Fx>=0 04. 10. 05. ИП6 06. ПП 07. 38 08. БП 09. 21 10. ИПD 11. ИП3 12. - 13. ИП7 14. * 15. ИПD 16. * 17. ИП6 18. + 19. ПП 20. 38 21. ИП0 22. ИПА 23. - 24. Fx2 25. Fsqr 26. ПВ 27. ИП8 28. / 29. ИП3 30. * 31. ПС 32. ИПD 33. ИП2 34. + 35. ПD 36. БП 37. 00 38. ИПD 39. * 40. ИП5 41. + 42. ИПD 43. * 44. 1 45. + 46. ИП4 47. * 48. ПА 49. В/О.
Перед началом работы регистры нужно заполнить так: шаг шкалы прибора - в Р2, цифра 100 - в Р3, R0 - в Р4, коэффициент А - в Р5, В - в Р6, С - в Р7. Разность сопротивлений между начальной и конечной точками шкалы (она берется из таблиц и в расчете используется для определения относительной погрешности) - в Р8, начальное значение температуры - в PD. Измеренное значение сопротивления - в Р0. Результаты расчета распределяются по регистрам так: табличное значение сопротивления R - в РА, абсолютная погрешность - в РВ, относительная (в процентах) - в PC.
Oт редакции. Программа не свободна от недостатков. Тем, кто ради упражнения возьмется улучшить ее, советуем обратить внимание на слишком частое обращение к регистру PD (почему бы не использовать стек?), возможность сэкономить регистр Р3, если применить команды F10X и ВП, не лучшее расположение команды С/П.
[ УЗЕЛКИ НА ПАМЯТЬ
Набрать число 1eM на индикаторе н сложить с ним содержимое регистра N быстрее и проще всего так: ИПN M F1eX +.
Если число, извлеченное нз регистра N. необходимо помножить на 1eM, то короче будет: ИПN ВП M.
Б.АЛЕКСЕЕВ (г.Москва). ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Секреты есть не только у программируемых калькуляторов. Микрокалькулятор "Электроника Б3-36", к примеру, запоминает значение (точнее, код) предыдущей операции. Это позволяет сократить количество нажимаемых в процессе вычислений клавиш. Мне удалось довести программу перевода комплексного числа из алгебраической формы в тригонометрическую до обращеиня всего к семи клавишам.
Реализованы формулы: В=arctg(y/x); А=x/cosВ.
А вот программа: (->y) / (->x) / ARC tg (В->) Fcos = (A->). Обозначения: (->y) - ввод числа с клавиатуры, (А->) - чтение величины на индикаторе.
А.ХОДАКСВ (г.Москва). ]
ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
"Секреты микрокалькулятора" - так называлась подборка читательских писем, посвященных особенностям вычислений на "Электронике Б3-34" 4/84). В своих откликах на нее читатели предлагают устроить это своеобразное "заседание за круглым столом" еще раз. Предложение принимается. Для последующих заседаний предлагаются такие темы:
- метод наименьших квадратов;
- удобство программ, приемы сервиса.
Ждем писем с конкретными примерами, обобщающими рассуждениями, находками, советами и т.п.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
8/84
Раздел ведет кандидат физико-математических наук Ю. ПУХНАЧЕВ.
Тот, кто давно работает с микрокалькулятором, наверняка знает за своим электронным помощником некоторые странности, объяснить которые можно, пишь глубоко разобравшись в его устройстве и принципах действия. И каждое такое "микроисследование" так или иначе повышает мастерство программирования.
Ленинградец X.Смолицкий заметил: если вычислять косинус на калькуляторах разных марок, то результаты получаются неодинаковые. Для подобной проверки он взял однажды в качестве аргумента ни много ни мало... 12345678.
Результаты вычислений получились поистине ошеломляющими и побудили читателя к плодотворным размышлениям. Мы помещаем их вместе с комментарием инженера Е.Кузнецова, рассказывающего, как карманные ЭВМ вычисляют элементарные функции.
КАКОМУ РЕЗУЛЬТАТУ ВЕРИТЬ?
Вычисление тригонометрических функций на микрокалькуляторе - операция довольно частая. Но какую она обеспечивает точность? Я вычислил на трех калькуляторах - Б3-34. Б3-21 и С3-15 - одну и ту же величину cos(12345678 ) и получил соответственно -0.23015689, -0.585271 и -0.42850134. О таких числах трудно поставить вопрос, сколько верных знаков они содержат. Не совпадают уже первые цифры результатов. (Как выяснилось впоследствии, С3-15 дает правильный ответ: в третьем из приведенных чисел верны все восемь знаков).
Не зная, по какому алгоритму карманные ЭВМ вычисляют тригонометрические функции, я предположил следующее. Прежде всего заданный аргумент x приводится к числу e, абсолютная величина которого не превышает пи/4. Делается это, например, так. Вычисляется частное от деления x/(пи/2) и выбирается ближайшее к результату целое число n. Тогда e=x-n(пи/2). Пусть k - остаток от деления n на 4, равный 0, 1, 2, 3. По свойствам тригонометрических функций в зависимости от величины k получим, что cos(x) соответственно равен cos(e), -sin(e), -cos(e), sin(e). В нашем примере k=3, так что cos(x)=sin(e).
Очевидно, величина e зависит от точности представления числа пи в том или ином микрокалькуляторе. Это число в С3-15 представлено 24 знаками, а в Б3-34 и Б3-21 - восемью и равно соответственно 3.1415926 и 3.1415927. Различаются они лишь на единичку в последнем знаке, но это может привести к резкому расхождению в значениях e: в нашем примере они равны соответственно -0.2322389 для Б3-34, -0.62521405 для Б3-21 и -0.44283470 для С3-15. Вычисление sin в для этих значений дает как раз те числа, которые приведены в начале заметки. Следовательно, моя гипотеза об алгоритме вычисления косинуса верна, и все дело в точности задания пи.
Сделав такой вывод, я попытался увеличить точность получения косинуса иа микрокалькуляторе. Я изменил алгоритм вычисления e. Положим пи/2=Pi/2+q, где Pi - это значение пи для того или иного микрокалькулятора, и вычислим для каждого "расхождение" q. Эта величина равна 2.6794897e-8 для Б3-34 и -2.3205101e-8 для Б3-21. Теперь можно определить уточненное e: его новое значение равно старому минус nq. По этой формуле новые значения e для Б3-34 и Б3-21 оказались почти равными: -0.4428347 и -0.4428349. То есть расхождение наблюдается лишь в последнем знаке, что вполне приемлемо. Соответственно и значения косинуса теперь получаются с семью верными цифрами.
Кстати, ошибки бывают и при небольших значениях x. Я проверил вычисления косинуса для калькуляторов Б3-34 и Б3-21 при х=1.5708. Для этого аргумента, близкого к пи/2, получилось лишь по два правильных знака. По уточненному алгоритму мне удалось получить все восемь правильных цифр для обоих типов калькуляторов.
X.СМОЛИЦКИЙ (г.Ленинград)
СТОИТ ТОЛЬКО НАЖАТЬ КЛАВИШУ...
Если спросить у владельца микрокалькулятора, в чем основное достоинство его машинки, то в ответ мы услышим и о быстроте вычислений и об их высокой точности... Но, наверное, при этом все единодушно отметили бы также возможность быстро вычислять элементарные функции. Именно она принципиально отличает электронные микрокалькуляторы от их предшественников - электрических счетных машин. Те такой возможности не предоставляли, и в случае необходимости приходилось обращаться к специальным таблицам, делать утомительные прикидки... А тут нажал одну-две клавиши, подождал несколько секунд, иногда и того меньше, и значение логарифма или косинуса - на индикаторе.
Что же происходит, пока мы ждем?
Есть в любом микрокалькуляторе область памяти, недоступная пользователю. Это ПЗУ - постоянное запоминающее устройство. Там хранятся программы, отвечающие за работу машины. Они расшифровывают и выполняют команды, вводимые нажатием клавиш, организуют различные режимы работы. Там же хранятся программы, вычисляющие значения элементарных функций - логарифмических, тригонометрических, степенных. Функции, значения которых машина вычисляет по собственным программам, называются стандартными. Программы их вычисления, хранящиеся в ПЗУ калькулятора, принципиально отличаются от тех, которые пишут пользователи. Записываются они раз и навсегда, замене не подлежат. Кроме того, от них требуется повышенное быстродействие.
Когда микрокалькулятор работает по программе пользователя, каждая команда, записанная в памяти, порождает последовательность микрокоманд - элементарных операций, выполняемых за один такт работы машины. Если же речь идет о вычислении стандартных функций, то в этом случае программа "зашита" в памяти намертво и оперирует непосредственно микрокомандами - поразрядным сложением, сдвигом и т.д. Составлять такую программу намного сложнее, но и работает она намного быстрее.
Независимо от способа реализации, качество программы определяется алгоритмом, заложенным в ее основу. Существует довольно много способов вычисления стандартных функций. В цифровой вычислительной технике нашли применение следующие: разложение в ряд Тейлора, аппроксимации с помощью различного рода многочленов, рациональные приближения, приближения с помощью цепных дробей, табличные методы, итерационные методы. Такое многообразие объясняется просто: идеального метода на все случаи жизни нет. Каждый из способов имеет свои достоинства и недостатки. Однако до последнего времени в микрокалькуляторах использовался только один из них - метод разложения в ряд Тейлора. Память у микрокалькуляторов очень маленькая, а он самый экономичный. Основное достоинство тейлоровского разложения - возможность вычислять каждый следующий член ряда через предыдущий, используя минимальный набор констант. А ведь их тоже приходится хранить в драгоценной памяти.
Поясним специфику ряда Тейлора на примере вычисления синуса. Ряд для этой функции таков (x - в радианах):
sin х = х - x3/3! + x5/5! - ...
Видно, что первый член ряда равен x, а каждый следующий равен предыдущему, умноженному на выражение - x2/(2i(2i+1)), где i - номер слагаемого. Подобные соотношения можно получить и для других функций.
На примере синуса отчетливо виден и основной недостаток метода - медленная сходимость и накопление ошибок. Многим программистам известен "парадокс синуса". Если вычислять эту функцию по описанному методу для больших аргументов, то можно получить все, что угодно, только не синус. Ошибки округления становятся настолько большими, что до неузнаваемости маскируют истинное значение функции. Это убедительно продемонстрировал своим примером читатель X.Смолицкий. Поэтому, как он правильно установил, приходится приводить аргумент функции к узкой области значений, проводить вычисления, а потом восстанавливать аргумент. Но все равно для таких функций, как логарифм, арктангенс, арксинус, ряды сходятся очень медленно. (Интересующиеся подробностями могут обратиться к книге В.Д.Байкова и С.А.Селютина "Вычисление элементарных функций в ЭКВМ", М., "Радио и связь", 1982; кстати: в книге - богатая библиография).
Тем не менее до последнего времени альтернативы этому методу не было. Все остальные требовали значительной памяти. Сейчас ситуация меняется, и виной тому новый метод, известный под названием "цифра за цифрой". Он носит итерационный характер; при этом используются только операции сложения и сдвига.
Первоначально метод "цифра за цифрой" был разработан для двоичной системы счисления. В микрокалькуляторах же применяется двоично-десятичная система: каждая десятичная цифра представляется двоичной тетрадой - четырьмя разрядами. Сейчас проблема реализации нового метода для такого представления решена. Он уже использован на микрокалькуляторах "Электроника Б3-38" и "Электроника МК-51". Во всех новых моделях также будет использоваться этот метод. О нем будет рассказано в одном из ближайших выпусков рубрики "Человек с микрокалькулятором".
Е.КУЗНЕЦОВ

- Так... Главному инженеру - один микрокалькулятор, в отдел снабжения - четыре, в плановый -
шесть...
Рис. Ю.ПОБОЖИЯ.
[ УЗЕЛКИ НА ПАМЯТЬ
Часто инженерные проблемы сводятся к решению ряда задач, программы которых последовательно вводятся в память и каждая последующая использует результаты предыдущих. Программы при этом надо составлять так, чтобы уменьшать объем информации, вводимой вручную, то есть хранить промежуточные результаты в регистрах.
В.ХОХЛОВ (г.Днепропетровск) ]
ПРЕДСТАВЛЯЕМ ЛУЧШИХ
В предыдущем выпуске рубрики (6/84) были подведены итоги "Конкурс программистов". Лучшую программу для построения последовательности простых чисел составил москвич В.Илюхин. Для изложения выигрышного алгоритма предоставляем слово автору одной из отмеченных программ ленинградцу Г.Натансону, сопроводившему свое решение интересным и поучительным комментарием.
При составлении экономичных программ, пишет в своем комментарии профессор Г.Натансон, необходимо максимальным образом использовать все возможности микрокалькулятора, в том числе достаточно тонкие.
Чтобы установить простоту натурального числа m, надо проверить, что оно не делится на все натуральные числа, не превосходящие sqr(т). Разумеется, вовсе не нужно испытывать все такие числа. При их переборе целесообразно заранее исключить числа четные (это совсем просто: стоит лишь вести перебор с шагом, равным двум), числа, кратные 3 (это лишь немногим сложнее) и делящиеся на 5. Исключение последних значительно усложняет программу, однако экономит примерно 25 процентов времени, так что игра стоит свеч.
Можно заметить, что числа, не кратные двум, трем и пяти, образуют последовательность, состоящую из групп по восемь чисел, начиная с семерки, причем разности между соседями в этих группах одинаковы: 6, 4, 2, 4, 2, 4, 6, 2. Длина каждой группы тоже одинакова: 30. Отсюда и проистекает идея алгоритма, по которому можно находить простые числа одно за другим, начиная с любого назначенного n.
Делим назначенное число на 30 и запоминаем остаток. Затем составляем сумму из единицы и последовательных вышеуказанных разностей до тех пор, пока сумма эта не превзойдет остатка. Потом вычитаем из испытуемого числа остаток и прибавляем сумму. Таким образом получаем число m, не меньшее исходного и к тому же не делящееся на 2, 3 и 5. Запоминаем его номер в группе, то есть количество разностей, использованных при составлении суммы, и начинаем проверку его на простоту. Делители выбираем на основе той же последовательности разностей, перебирая числа 7=1+6, 11=7+4, 13=11+2 и так далее до 31; при этом смотрим, не "перескочил" ли восьмой делитель через sqr(m). Если нет, то строим новую восьмерку 37=31+6, 41=37+4... и снова проверяем, не превышен ли sqr(m). При его превышении процесс оканчивается. Если ни на одном шаге испытуемое число m не разделилось нацело на перебираемые делители, заключаем: m - простое число. Высвечиваем его на экране, выбираем следующее число из ряда и проверяем его.
(Сравнение с sqr(m) лишь каждого восьмого из потенциальных делителей оказывается в данном алгоритме эффективнее при исследовании чисел больших 10000).
Если испытуемое число разделилось на какой-нибудь делитель без остатка, сразу переходим к следующему числу и повторяем цикл, пока не будет найдено очередное простое число.
Блок-схема программы Г.Натансона, реализующая этот алгоритм:
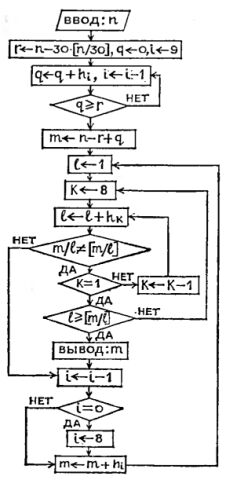
Вот сама программа: 00. ПA 01. 3 02. 0 03. / 04. ПD 05. КИПD 06. 1 07. 0 08. П0 09. 1 10. П9 11. ИПD 12. FBx 13. * 14. ИПA 15. - 16. КИП0 17. + 18. Fx>=0 19. 16 20. ИПА 21. + 22. ПС 23. ИП0 24. ПВ 25. 8 26. П0 27. ИПС 28. ИП9 29. КИП^ 30. + 31. П9 32. / 33. ПD 34. КИПD 35. x-y 36. ИПD 37. - 38. Fx!=0 39. 49. 40. FL0 41. 27 42. ИП9 43. ИПD 44. - 45. Fx>=0 46. 25 47. ИПС 48. С/П 49. ИПВ 50. 1 51. П9 52. - 53. Fx=0 54. 56 55. 8 56. ПВ 57. КИПВ 58. ИПС 59. + 60. ПС 61. БП 62. 25.
После ввода программы нужно записать в регистры 1-8 числа: 2, 6, 4, 2, 4, 2, 4, 6, (на блок-схеме обозначены hi). Величина п вводится с клавиатуры. Программа запускается нажатием клавиш В/О, С/П. После останова и считывания простого числа следует нажать С/П и т.д.
Отметим некоторые особенности программы.
Команда 05. КИПD - это команда косвенной адресации. Если при этом в PD находится нецелое число a, большее единицы, то оно заменяется на его целую часть [a]. В данном случае в PD появляется [n/30]. Ограничение на величину a заставляет брать начальное n лишь большим тридцати.
Команда 12. FBx восстанавливает предыдущий результат. Последним действием было деление на 30 (команда 03), команды 04-11 (запись в память, вызов из памяти, ввод с клавиатуры) содержимое регистра предыдущего результата не меняют. Поэтому команда 12 вызовет в РХ число 30. Таким приемом экономится одна команда.
16. КИП0. Команда КИПN при N=0, 1, 2, 3 сначала уменьшает содержимое регистра на 1, а затем извлекает число из регистра с получившимся номером. Таким образом, последовательно извлекаются разности между соседями в группах испытуемых делителей.
Команды 27-32. Здесь используется стековая память. Это позволяет экономить команды, регистры памяти. При подробной записи команд 27-30 с содержимым регистров стека X, Y, Z (регистр Т здесь не используется), они будут выглядеть так (в скобках - содержимое регистров): 27. ИПС (m) 28. ИП9 (l, m) 29. КИП^ (hi, l, m) 30. + (l, m). Теперь все готово для деления m на l.
29. КИП^. Такой команды в инструкции к микрокалькулятору почему-то нет. Это, так сказать, "черный ход" в Р0. В отличие от команды КИП0, "парадного входа" она не меняет содержимого Р0. Аналогично, кстати, работают и команды КП^, КПП^ и другие, им подобные: по каждой из них происходит обращение по адресу, указанному в нулевом регистре, содержимое которого при этом не уменьшается, как при использовании команд КП0, КПП0 и т.д. Возможность обращаться к РО двумя способами чрезвычайно полезна.
Переходим к программе победителя конкурса, московского студента В.Илюхина. В ней заложена та же идея - исключение чисел, кратных 2, 3 и 5. Но реализована она в более компактной и более быстродействующей программе. Программа его настолько оптимизирована, что даже блок-схема дает не совсем полное представление о ней.
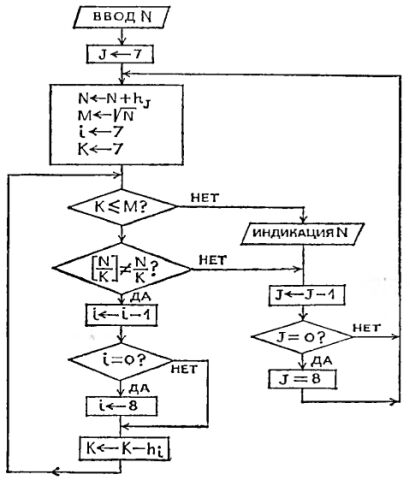
Мы решили привести ее без комментариев, чтобы дать возможность читателям самостоятельно разобрать ее работу.
00. ПD 01. 7 02. ПА 03. КИПА 04. ИПD 05. + 06. ПD 07. Fsqr 08. ПС 09. 7 10. ПО 11. ПВ 12. ИПС 13. ИПВ 14. - 15. Fx>=0 16. 34 17. ИПD 18. ИПВ 19. / 20. П9 21. КИП9 22. x-y 23. ИП9 24. - 25. Fx!!=0 26. 36 27. КИП0 28. Fx!=0 29. 44 30. ИПВ 31. + 32. БП 33. 11 34. ИПD 35. С/П 36. ИПА 37. 1 38. - 39. Fx=0 40. 02 41. 8 42. БП 43. 02 44. 9 45. П0 46. БП 47. 27.
Порядок работы с программой таков. После ввода программы в регистры 7, 6, ..., 1, 8 заносятся числа 6, 4, 2, 4, 2, 4, 6, 2. Начальное исследуемое число вводится с клавиатуры. Оно должно иметь вид 30n+l, где n - целое (специальная форма вводимого числа - плата за быстроту и краткость программы). Клавиши В/О, С/П запускают программу. После вывода очередного простого числа нужно снова нажать клавишу С/П, и поиск будет продолжен.
Что касается программ для выделения целой части, то ни один из участников конкурса, как уже отмечалось в предыдущем выпуске рубрики, не предложил решения лучше приведенных в книге Я.Трохименко и Ф.Любича "Радиотехнические расчеты на микрокалькуляторах". Перепечатываем их здесь.
Для "Электроники Б3-34", фрагмент программы 71/34: 00. 5 01. ^ 02. 9 03. / 04. - 05. ^ 06. 1 07. ВП 08. 7 09. + 10. Вх 11. -.
Для "Электроники Б3-21", программа 70/21: 00. 1 01. ВП 02. 7 03. ^ 04. + 05. x-y. 06. -.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Если регистр X очищен, то есть в нем содержится 0, то в программном режиме заслать и него единицу быстрее командой F10X.
Б.АЛЕКСЕЕВ (г.Москва) ]
ЕСЛИ НУЖНО ПОСТРОИТЬ ГРАФИК...
... Закончено исследование, и его результаты выразились в строчках формул, колонках цифр. Хочется придать им наглядный вид - построить график, гистограмму. Микрокалькулятор и тут может оказать свои успуги.
Графики строят люди многих профессий. Хорошо, когда для этого есть специальные графопостроители. Но если их нет, то строят графики вручную, на миллиметровке. При этом нередко, при заданных размерах графика, масштабы по осям оказываются неудобными. Допустим, требуется нанести на координатную ось некоторую величину. Сколько для этого нужно отложить миллиметров? Расчеты, поиск нужной точки занимают значительное время и к тому же ведут к увеличению ошибок. Это особенно проявляется при необходимости строить график в том же темпе, в котором снимаются данные, и при использовании нелинейных масштабов.
Микрокалькулятор по разработанной мной программе автоматизирует этот процесс и позволяет для любого масштаба определять целое число миллиметров, которые нужно откладывать по той или иной оси.
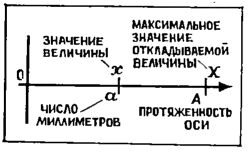
Программа имеет две модификации: для линейно-линейного и логарифмически-линейного масштабов. Перед началом работы первой из них в регистры Р1 и Р2 вводятся величины А/Х и B/Y - отношения протяженности горизонтальной и вертикальной осей графика к максимальным значениям величин, откладываемых по этим осям. Перед началом работы второй программы величина B/Y вводится также в регистр Р2, lgX0 - в Р4, A/lg(X/X0) - в Р3. Здесь Хо - значение параметра, откладываемого в начальной точке логарифмической оси.
Программа для линейно-линейного масштаба: 00. ИП2 01. * 02. БП 03. 06 04. ИП1 05. * 06. 7 07. F10X 08. + 09. FBx 10. - 11. С/П 12. БП 13. 04.
Программа для логарифмически-линейного масштаба: 00. ИП2 01. * 02. БП 03. 09 04. Flg 05. ИП4 06. - 07. ИП3 08. * 09. 7 10. F10X 11. + 12. FBx 13. - 14. С/П 15. БП 16. 04.
Перед первым пуском программ необходимо нажать на клавиши БП 04. Величину, наносимую на ту или другую координатную ось, следует набрать на клавиатуре. Если речь идет об оси X, нажимается клавиша С/П, и калькулятор сообщает, сколько миллиметров следует отложить, на этой оси, если об оси Y - нажимаются две клавиши: В/О и С/П, и калькулятор определяет, сколько миллиметров следует отложить на ней.
П.ПОЛЯНСКИЙ (г.Москва)
... ИЛИ ГИСТОГРАММУ
Гистограмма - один из видов графического представления экспериментальных данных. Гистограмма строится так. Весь диапазон изменения исследуемой величины (м, М) делится на несколько равных интервалов. Подсчитывается число наблюдений Mi, приходящееся на каждый i-тый интервал, и определяется
частота Hi = Mi/n, где n - общее число наблюдений. По горизонтальной оси откладываются равные интервалы, которые принимаются за основания прямоугольников с высотами пропорциональными Mi или Hi.
Калькулятор "Электроника Б3-34" легко справится с сортировкой данных по 12 накопительным регистрам. Останется только нарисовать саму гистограмму. Программа выглядит так: 00. - 01. 01 02. 02 03. x-y 04. / 05. ПС 06. С/П 07. ИПС 08. * 09. ПD 10. КИПD 11. 1 12. + 13. KПD 14. БП 15. 06. Чтобы подготовить программу к работе, необходимо набрать М, ^, м, нажать клавиши В/О и С/П. Программа остановится, готовая к работе. Набираем начальное значение исследуемой величины и нажимаем С/П, набираем следующее значение, снова нажимаем С/П и так далее до тех пор, пока это необходимо. В любой момент мы можем посмотреть содержимое накопителей Р0-Р9, РА, РВ. В них записаны количества точек, попавших в тот или иной интервал - высоты будущих прямоугольников гистограммы.
Этот метод построения гистограмм был использован автором, чтобы исследовать распределение псевдослучайной величины, вычисляемой следующим образом: ее начальное значение х0 принимается равным нулю, а каждое последующее x[i+i] определяется через xi как дробная часть выражения (пи+xi)**5.
Программа: 00. 5 01. ИПС 02. Fпи 03. + 04. FxY 05. ^ 06. ПD 07. КИПD 08. F() 09. ИПD 10. - 11. ПС 12. 1 13. 0 14. * 15. 1 16. + 17. ПD 18. КИПD 19. 1 20. + 21. KПD 22. FL0 23. 00 24. С/П.
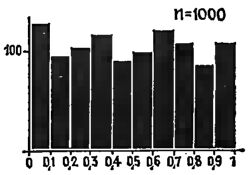
Перед пуском программы в регистры с 1 по 9, А, С засылались нули, а в Р0 заносилось n - число экспериментов. Программа была запущена нажатием клавиш В/О, С/П. После ее останова по результатам исследования строилась гистограмма, отражающая характер распределения псевдослучайной величины х по диапазону 0..1. Ясно видно, сколь отличается оно от равномерного.
А.БОЙКО (г.Москва)
КАЛЬКУЛЯТОР В НЕОБЫЧНЫХ АМПЛУА
Каждая операция калькулятора требует определенного времени - вот принцип программ-секундомеров.
Автор одной нз них (см. ниже), С.Бармин из Тольятти, предвидел, что время выполнения операций для разных экземпляров калькулятора будет неодинаковым, и советует перед началом работы настроить "секундомер". Нужно записать в Р2 число 1 и запустить микрокалькулятор на 10 секунд, после остановки считать число на индикаторе и разделить на него 10. Это и будет "постоянная времени" вашего калькулятора. Введите ее в регистр Р2, нажмите клавиши В/О, С/П - и "секундомер" готов работать по команде С/П. Его погрешность - 2 процента.
Тот же принцип использовал читатель Л.Борисов из Москвы. Засылается знак + в ячейки с 00 по 10, затем записывается В/О в ячейки 11 и 12. Перед началом работы "секундомер" также требует настройки. Единица засылается во все регистры стека (1 ^ ^ ^). затем надо очистить индикатор клавишей Сх и, нажав В/О, С/П, запустить программу на 100 секунд. После остановки делим 100 на число на индикаторе, засылаем результат во все регистры стека, нажимаем Сх, В/О. Включается "секундомер" клавишей С/П, останавливается той же клавишей. Точность хода - порядка 0.3 процента!
Читатель Г.Ионов из г.Балашова (Саратовская обл.) перед пуском своей программы заносит в регистр Р7 величину 1/120 (для каждого экземпляра калькулятора ее следует подобрать более точно), нажимает В/О, набирает требуемое число минут на индикаторе. Запущенная клавишей С/П программа останавливается через заданное число минут, которое и высвечивается на индикаторе.
Программа-таймер С.Конина и А.Шарапова (г.Ленинград) чуть короче, с ней проще работать, но точность ее ниже. В регистр Р9 заносится отмеряемый промежуток времени в секундах, в Р8 - какое-либо условное число, которое будет высвечиваться после конца счета. Авторы рекомендуют "яркое" число, например, 8.8888888e-88. Программа запускается клавишами В/О, С/П.
Другая программа С.Конина и А.Шарапова превращает микрокалькулятор в электронные часы, на индикаторе которых высвечивается точное время. Перед началом работы часы, естественно, устанавливаются. Текущее время вводится в Р8 (часы) и Р9 (минуты). Нужные для работы константы заносятся в регистры: в РА - 10, в Р2 - 11, в Р4 - 24, в Р6 - 60, в Р7 - 100. Часы можно подстраивать, повышая точность хода. Делается это варьированием числа, заносимого в РА (у авторов - 10).
Проделав все эти манипуляции, можно запускать часы (клавиши В/О, С/П). В левом углу индикатора высвечивается текущее время: две последние цифры - минуты, две (или одна) первые - часы. Единственный недостаток часов - в момент "передвижения стрелок" вместо времени мелькают различные числа, но вот "стрелки передвинулись" - и снова на индикаторе часы и минуты.
Программа-секундомер С.Бармина: 00. F2 01. ^ 02. Сх 03. ВП 04. С/П 05. + 10. БП 11. ^.
Программа-таймер Г.Ионова: 00. П8 01. ИП7 02. / 03. П1 04. FL1 05. 04 06. ИП8 07. С/П 08. БП 09. 00.
Программа-таймер С.Конина и А.Шарапова: 00. ИП9 01. П0 02. Fпи 03. F1/x 04. F1/x 05. FL0 06. 02 07. ИП8 08. С/П.
Программа-часы С.Конина и А.Шарапова: 00. ИП4 01. ИП8 02. - 03. П3 04. ИП6 05. ИП9 06. - 07. П0 08. ИП8 09. ИП7 10. * 11. ИП9 12. + 13. П5 14. ИП2 15. П1 16. ИП5 17. ^ 18. ^ 19. ^ 20. ^ 21. ^ 22. ^ 23. ^ 24. ^ 25. ^ 26. ^ 27. ^ 28 ^ 29. FL1 30. 17 31. 1 32. ИПА 33. FxY 34. Fx2 35. КИП5 36. FLO 37. 14 38. ИП6 39. П0 40. ИП5 41. ИП7 42. / 43. П5 44. 1 45. - 46. Fx<0 47. 50 48. Cx 49. П5 50. КИП5 51. ИП5 52. ИП7 53. * 54. П5 55. FL3 56. 14 57. ИП4 58. П3 59. Cx 60. П5 61. БП 62. 14.
Первая программа составлена для микрокалькулятора Б3-21, остальные - для Б3-34.
[ КНИГА ЗА КНИГОЙ
В прошлом выпуске нашей рубрики (6/84) был помещен список книг о микрокалькуляторах, вышедших до последнего времени. Он, конечно, неполон - за его рамками осталась литература, выпускаемая в областных и специализированных издательствах, в вузах. Авторы этих книг любезно присылают их нам. Мы будем представлять их читателю отдельными интересными фрагментами.
Вот взятая из книги профессора В.П.Дьяконова "Методы расчета электронных схем на микроЭВМ" (Москва, МЭИ, 1983г., 94стр.) программа для калькулятора "Электроника Б3-34", по которой вычисляется определитель третьего порядка. Она убедительно демонстрирует возможности стека: все вычисления ведутся по ней лишь с помощью стековых регистров; регистры памяти при этом используются лишь для хранения элементов определителя согласно схеме:

00. ИП4 01. ИП2 02. * 03. ИП1 04. ИП5 05. * 06. - 07. ИП9 08. * 09. ИП1 10. ИП8 11. * 12. ИП7 13. ИП2 14. * 15. - 16. ИП6 17. * 18. + 19. ИП7 20. ИП5 21. * 22. ИП4 23. ИП8 24. * 25. - 26. ИП3 27. * 28. + 29. С/П.
В книге В.П.Дьяконова описаны микроЭВМ марок Б3-21, Б3-34, МК-46, МК-56, Д3-28; изложены и пояснены примерами методы анализа и расчета электронных схем на этих вычислительных машинах.
Раздел ведет кандидат физико-математических наук Ю. ПУХНАЧЕВ.
Тот, кто давно работает с микрокалькулятором, наверняка знает за своим электронным помощником некоторые странности, объяснить которые можно, пишь глубоко разобравшись в его устройстве и принципах действия. И каждое такое "микроисследование" так или иначе повышает мастерство программирования.
Ленинградец X.Смолицкий заметил: если вычислять косинус на калькуляторах разных марок, то результаты получаются неодинаковые. Для подобной проверки он взял однажды в качестве аргумента ни много ни мало... 12345678.
Результаты вычислений получились поистине ошеломляющими и побудили читателя к плодотворным размышлениям. Мы помещаем их вместе с комментарием инженера Е.Кузнецова, рассказывающего, как карманные ЭВМ вычисляют элементарные функции.
КАКОМУ РЕЗУЛЬТАТУ ВЕРИТЬ?
Вычисление тригонометрических функций на микрокалькуляторе - операция довольно частая. Но какую она обеспечивает точность? Я вычислил на трех калькуляторах - Б3-34. Б3-21 и С3-15 - одну и ту же величину cos(12345678 ) и получил соответственно -0.23015689, -0.585271 и -0.42850134. О таких числах трудно поставить вопрос, сколько верных знаков они содержат. Не совпадают уже первые цифры результатов. (Как выяснилось впоследствии, С3-15 дает правильный ответ: в третьем из приведенных чисел верны все восемь знаков).
Не зная, по какому алгоритму карманные ЭВМ вычисляют тригонометрические функции, я предположил следующее. Прежде всего заданный аргумент x приводится к числу e, абсолютная величина которого не превышает пи/4. Делается это, например, так. Вычисляется частное от деления x/(пи/2) и выбирается ближайшее к результату целое число n. Тогда e=x-n(пи/2). Пусть k - остаток от деления n на 4, равный 0, 1, 2, 3. По свойствам тригонометрических функций в зависимости от величины k получим, что cos(x) соответственно равен cos(e), -sin(e), -cos(e), sin(e). В нашем примере k=3, так что cos(x)=sin(e).
Очевидно, величина e зависит от точности представления числа пи в том или ином микрокалькуляторе. Это число в С3-15 представлено 24 знаками, а в Б3-34 и Б3-21 - восемью и равно соответственно 3.1415926 и 3.1415927. Различаются они лишь на единичку в последнем знаке, но это может привести к резкому расхождению в значениях e: в нашем примере они равны соответственно -0.2322389 для Б3-34, -0.62521405 для Б3-21 и -0.44283470 для С3-15. Вычисление sin в для этих значений дает как раз те числа, которые приведены в начале заметки. Следовательно, моя гипотеза об алгоритме вычисления косинуса верна, и все дело в точности задания пи.
Сделав такой вывод, я попытался увеличить точность получения косинуса иа микрокалькуляторе. Я изменил алгоритм вычисления e. Положим пи/2=Pi/2+q, где Pi - это значение пи для того или иного микрокалькулятора, и вычислим для каждого "расхождение" q. Эта величина равна 2.6794897e-8 для Б3-34 и -2.3205101e-8 для Б3-21. Теперь можно определить уточненное e: его новое значение равно старому минус nq. По этой формуле новые значения e для Б3-34 и Б3-21 оказались почти равными: -0.4428347 и -0.4428349. То есть расхождение наблюдается лишь в последнем знаке, что вполне приемлемо. Соответственно и значения косинуса теперь получаются с семью верными цифрами.
Кстати, ошибки бывают и при небольших значениях x. Я проверил вычисления косинуса для калькуляторов Б3-34 и Б3-21 при х=1.5708. Для этого аргумента, близкого к пи/2, получилось лишь по два правильных знака. По уточненному алгоритму мне удалось получить все восемь правильных цифр для обоих типов калькуляторов.
X.СМОЛИЦКИЙ (г.Ленинград)
СТОИТ ТОЛЬКО НАЖАТЬ КЛАВИШУ...
Если спросить у владельца микрокалькулятора, в чем основное достоинство его машинки, то в ответ мы услышим и о быстроте вычислений и об их высокой точности... Но, наверное, при этом все единодушно отметили бы также возможность быстро вычислять элементарные функции. Именно она принципиально отличает электронные микрокалькуляторы от их предшественников - электрических счетных машин. Те такой возможности не предоставляли, и в случае необходимости приходилось обращаться к специальным таблицам, делать утомительные прикидки... А тут нажал одну-две клавиши, подождал несколько секунд, иногда и того меньше, и значение логарифма или косинуса - на индикаторе.
Что же происходит, пока мы ждем?
Есть в любом микрокалькуляторе область памяти, недоступная пользователю. Это ПЗУ - постоянное запоминающее устройство. Там хранятся программы, отвечающие за работу машины. Они расшифровывают и выполняют команды, вводимые нажатием клавиш, организуют различные режимы работы. Там же хранятся программы, вычисляющие значения элементарных функций - логарифмических, тригонометрических, степенных. Функции, значения которых машина вычисляет по собственным программам, называются стандартными. Программы их вычисления, хранящиеся в ПЗУ калькулятора, принципиально отличаются от тех, которые пишут пользователи. Записываются они раз и навсегда, замене не подлежат. Кроме того, от них требуется повышенное быстродействие.
Когда микрокалькулятор работает по программе пользователя, каждая команда, записанная в памяти, порождает последовательность микрокоманд - элементарных операций, выполняемых за один такт работы машины. Если же речь идет о вычислении стандартных функций, то в этом случае программа "зашита" в памяти намертво и оперирует непосредственно микрокомандами - поразрядным сложением, сдвигом и т.д. Составлять такую программу намного сложнее, но и работает она намного быстрее.
Независимо от способа реализации, качество программы определяется алгоритмом, заложенным в ее основу. Существует довольно много способов вычисления стандартных функций. В цифровой вычислительной технике нашли применение следующие: разложение в ряд Тейлора, аппроксимации с помощью различного рода многочленов, рациональные приближения, приближения с помощью цепных дробей, табличные методы, итерационные методы. Такое многообразие объясняется просто: идеального метода на все случаи жизни нет. Каждый из способов имеет свои достоинства и недостатки. Однако до последнего времени в микрокалькуляторах использовался только один из них - метод разложения в ряд Тейлора. Память у микрокалькуляторов очень маленькая, а он самый экономичный. Основное достоинство тейлоровского разложения - возможность вычислять каждый следующий член ряда через предыдущий, используя минимальный набор констант. А ведь их тоже приходится хранить в драгоценной памяти.
Поясним специфику ряда Тейлора на примере вычисления синуса. Ряд для этой функции таков (x - в радианах):
sin х = х - x3/3! + x5/5! - ...
Видно, что первый член ряда равен x, а каждый следующий равен предыдущему, умноженному на выражение - x2/(2i(2i+1)), где i - номер слагаемого. Подобные соотношения можно получить и для других функций.
На примере синуса отчетливо виден и основной недостаток метода - медленная сходимость и накопление ошибок. Многим программистам известен "парадокс синуса". Если вычислять эту функцию по описанному методу для больших аргументов, то можно получить все, что угодно, только не синус. Ошибки округления становятся настолько большими, что до неузнаваемости маскируют истинное значение функции. Это убедительно продемонстрировал своим примером читатель X.Смолицкий. Поэтому, как он правильно установил, приходится приводить аргумент функции к узкой области значений, проводить вычисления, а потом восстанавливать аргумент. Но все равно для таких функций, как логарифм, арктангенс, арксинус, ряды сходятся очень медленно. (Интересующиеся подробностями могут обратиться к книге В.Д.Байкова и С.А.Селютина "Вычисление элементарных функций в ЭКВМ", М., "Радио и связь", 1982; кстати: в книге - богатая библиография).
Тем не менее до последнего времени альтернативы этому методу не было. Все остальные требовали значительной памяти. Сейчас ситуация меняется, и виной тому новый метод, известный под названием "цифра за цифрой". Он носит итерационный характер; при этом используются только операции сложения и сдвига.
Первоначально метод "цифра за цифрой" был разработан для двоичной системы счисления. В микрокалькуляторах же применяется двоично-десятичная система: каждая десятичная цифра представляется двоичной тетрадой - четырьмя разрядами. Сейчас проблема реализации нового метода для такого представления решена. Он уже использован на микрокалькуляторах "Электроника Б3-38" и "Электроника МК-51". Во всех новых моделях также будет использоваться этот метод. О нем будет рассказано в одном из ближайших выпусков рубрики "Человек с микрокалькулятором".
Е.КУЗНЕЦОВ

- Так... Главному инженеру - один микрокалькулятор, в отдел снабжения - четыре, в плановый -
шесть...
Рис. Ю.ПОБОЖИЯ.
[ УЗЕЛКИ НА ПАМЯТЬ
Часто инженерные проблемы сводятся к решению ряда задач, программы которых последовательно вводятся в память и каждая последующая использует результаты предыдущих. Программы при этом надо составлять так, чтобы уменьшать объем информации, вводимой вручную, то есть хранить промежуточные результаты в регистрах.
В.ХОХЛОВ (г.Днепропетровск) ]
ПРЕДСТАВЛЯЕМ ЛУЧШИХ
В предыдущем выпуске рубрики (6/84) были подведены итоги "Конкурс программистов". Лучшую программу для построения последовательности простых чисел составил москвич В.Илюхин. Для изложения выигрышного алгоритма предоставляем слово автору одной из отмеченных программ ленинградцу Г.Натансону, сопроводившему свое решение интересным и поучительным комментарием.
При составлении экономичных программ, пишет в своем комментарии профессор Г.Натансон, необходимо максимальным образом использовать все возможности микрокалькулятора, в том числе достаточно тонкие.
Чтобы установить простоту натурального числа m, надо проверить, что оно не делится на все натуральные числа, не превосходящие sqr(т). Разумеется, вовсе не нужно испытывать все такие числа. При их переборе целесообразно заранее исключить числа четные (это совсем просто: стоит лишь вести перебор с шагом, равным двум), числа, кратные 3 (это лишь немногим сложнее) и делящиеся на 5. Исключение последних значительно усложняет программу, однако экономит примерно 25 процентов времени, так что игра стоит свеч.
Можно заметить, что числа, не кратные двум, трем и пяти, образуют последовательность, состоящую из групп по восемь чисел, начиная с семерки, причем разности между соседями в этих группах одинаковы: 6, 4, 2, 4, 2, 4, 6, 2. Длина каждой группы тоже одинакова: 30. Отсюда и проистекает идея алгоритма, по которому можно находить простые числа одно за другим, начиная с любого назначенного n.
Делим назначенное число на 30 и запоминаем остаток. Затем составляем сумму из единицы и последовательных вышеуказанных разностей до тех пор, пока сумма эта не превзойдет остатка. Потом вычитаем из испытуемого числа остаток и прибавляем сумму. Таким образом получаем число m, не меньшее исходного и к тому же не делящееся на 2, 3 и 5. Запоминаем его номер в группе, то есть количество разностей, использованных при составлении суммы, и начинаем проверку его на простоту. Делители выбираем на основе той же последовательности разностей, перебирая числа 7=1+6, 11=7+4, 13=11+2 и так далее до 31; при этом смотрим, не "перескочил" ли восьмой делитель через sqr(m). Если нет, то строим новую восьмерку 37=31+6, 41=37+4... и снова проверяем, не превышен ли sqr(m). При его превышении процесс оканчивается. Если ни на одном шаге испытуемое число m не разделилось нацело на перебираемые делители, заключаем: m - простое число. Высвечиваем его на экране, выбираем следующее число из ряда и проверяем его.
(Сравнение с sqr(m) лишь каждого восьмого из потенциальных делителей оказывается в данном алгоритме эффективнее при исследовании чисел больших 10000).
Если испытуемое число разделилось на какой-нибудь делитель без остатка, сразу переходим к следующему числу и повторяем цикл, пока не будет найдено очередное простое число.
Блок-схема программы Г.Натансона, реализующая этот алгоритм:

Вот сама программа: 00. ПA 01. 3 02. 0 03. / 04. ПD 05. КИПD 06. 1 07. 0 08. П0 09. 1 10. П9 11. ИПD 12. FBx 13. * 14. ИПA 15. - 16. КИП0 17. + 18. Fx>=0 19. 16 20. ИПА 21. + 22. ПС 23. ИП0 24. ПВ 25. 8 26. П0 27. ИПС 28. ИП9 29. КИП^ 30. + 31. П9 32. / 33. ПD 34. КИПD 35. x-y 36. ИПD 37. - 38. Fx!=0 39. 49. 40. FL0 41. 27 42. ИП9 43. ИПD 44. - 45. Fx>=0 46. 25 47. ИПС 48. С/П 49. ИПВ 50. 1 51. П9 52. - 53. Fx=0 54. 56 55. 8 56. ПВ 57. КИПВ 58. ИПС 59. + 60. ПС 61. БП 62. 25.
После ввода программы нужно записать в регистры 1-8 числа: 2, 6, 4, 2, 4, 2, 4, 6, (на блок-схеме обозначены hi). Величина п вводится с клавиатуры. Программа запускается нажатием клавиш В/О, С/П. После останова и считывания простого числа следует нажать С/П и т.д.
Отметим некоторые особенности программы.
Команда 05. КИПD - это команда косвенной адресации. Если при этом в PD находится нецелое число a, большее единицы, то оно заменяется на его целую часть [a]. В данном случае в PD появляется [n/30]. Ограничение на величину a заставляет брать начальное n лишь большим тридцати.
Команда 12. FBx восстанавливает предыдущий результат. Последним действием было деление на 30 (команда 03), команды 04-11 (запись в память, вызов из памяти, ввод с клавиатуры) содержимое регистра предыдущего результата не меняют. Поэтому команда 12 вызовет в РХ число 30. Таким приемом экономится одна команда.
16. КИП0. Команда КИПN при N=0, 1, 2, 3 сначала уменьшает содержимое регистра на 1, а затем извлекает число из регистра с получившимся номером. Таким образом, последовательно извлекаются разности между соседями в группах испытуемых делителей.
Команды 27-32. Здесь используется стековая память. Это позволяет экономить команды, регистры памяти. При подробной записи команд 27-30 с содержимым регистров стека X, Y, Z (регистр Т здесь не используется), они будут выглядеть так (в скобках - содержимое регистров): 27. ИПС (m) 28. ИП9 (l, m) 29. КИП^ (hi, l, m) 30. + (l, m). Теперь все готово для деления m на l.
29. КИП^. Такой команды в инструкции к микрокалькулятору почему-то нет. Это, так сказать, "черный ход" в Р0. В отличие от команды КИП0, "парадного входа" она не меняет содержимого Р0. Аналогично, кстати, работают и команды КП^, КПП^ и другие, им подобные: по каждой из них происходит обращение по адресу, указанному в нулевом регистре, содержимое которого при этом не уменьшается, как при использовании команд КП0, КПП0 и т.д. Возможность обращаться к РО двумя способами чрезвычайно полезна.
Переходим к программе победителя конкурса, московского студента В.Илюхина. В ней заложена та же идея - исключение чисел, кратных 2, 3 и 5. Но реализована она в более компактной и более быстродействующей программе. Программа его настолько оптимизирована, что даже блок-схема дает не совсем полное представление о ней.

Мы решили привести ее без комментариев, чтобы дать возможность читателям самостоятельно разобрать ее работу.
00. ПD 01. 7 02. ПА 03. КИПА 04. ИПD 05. + 06. ПD 07. Fsqr 08. ПС 09. 7 10. ПО 11. ПВ 12. ИПС 13. ИПВ 14. - 15. Fx>=0 16. 34 17. ИПD 18. ИПВ 19. / 20. П9 21. КИП9 22. x-y 23. ИП9 24. - 25. Fx!!=0 26. 36 27. КИП0 28. Fx!=0 29. 44 30. ИПВ 31. + 32. БП 33. 11 34. ИПD 35. С/П 36. ИПА 37. 1 38. - 39. Fx=0 40. 02 41. 8 42. БП 43. 02 44. 9 45. П0 46. БП 47. 27.
Порядок работы с программой таков. После ввода программы в регистры 7, 6, ..., 1, 8 заносятся числа 6, 4, 2, 4, 2, 4, 6, 2. Начальное исследуемое число вводится с клавиатуры. Оно должно иметь вид 30n+l, где n - целое (специальная форма вводимого числа - плата за быстроту и краткость программы). Клавиши В/О, С/П запускают программу. После вывода очередного простого числа нужно снова нажать клавишу С/П, и поиск будет продолжен.
Что касается программ для выделения целой части, то ни один из участников конкурса, как уже отмечалось в предыдущем выпуске рубрики, не предложил решения лучше приведенных в книге Я.Трохименко и Ф.Любича "Радиотехнические расчеты на микрокалькуляторах". Перепечатываем их здесь.
Для "Электроники Б3-34", фрагмент программы 71/34: 00. 5 01. ^ 02. 9 03. / 04. - 05. ^ 06. 1 07. ВП 08. 7 09. + 10. Вх 11. -.
Для "Электроники Б3-21", программа 70/21: 00. 1 01. ВП 02. 7 03. ^ 04. + 05. x-y. 06. -.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Если регистр X очищен, то есть в нем содержится 0, то в программном режиме заслать и него единицу быстрее командой F10X.
Б.АЛЕКСЕЕВ (г.Москва) ]
ЕСЛИ НУЖНО ПОСТРОИТЬ ГРАФИК...
... Закончено исследование, и его результаты выразились в строчках формул, колонках цифр. Хочется придать им наглядный вид - построить график, гистограмму. Микрокалькулятор и тут может оказать свои успуги.
Графики строят люди многих профессий. Хорошо, когда для этого есть специальные графопостроители. Но если их нет, то строят графики вручную, на миллиметровке. При этом нередко, при заданных размерах графика, масштабы по осям оказываются неудобными. Допустим, требуется нанести на координатную ось некоторую величину. Сколько для этого нужно отложить миллиметров? Расчеты, поиск нужной точки занимают значительное время и к тому же ведут к увеличению ошибок. Это особенно проявляется при необходимости строить график в том же темпе, в котором снимаются данные, и при использовании нелинейных масштабов.
Микрокалькулятор по разработанной мной программе автоматизирует этот процесс и позволяет для любого масштаба определять целое число миллиметров, которые нужно откладывать по той или иной оси.

Программа имеет две модификации: для линейно-линейного и логарифмически-линейного масштабов. Перед началом работы первой из них в регистры Р1 и Р2 вводятся величины А/Х и B/Y - отношения протяженности горизонтальной и вертикальной осей графика к максимальным значениям величин, откладываемых по этим осям. Перед началом работы второй программы величина B/Y вводится также в регистр Р2, lgX0 - в Р4, A/lg(X/X0) - в Р3. Здесь Хо - значение параметра, откладываемого в начальной точке логарифмической оси.
Программа для линейно-линейного масштаба: 00. ИП2 01. * 02. БП 03. 06 04. ИП1 05. * 06. 7 07. F10X 08. + 09. FBx 10. - 11. С/П 12. БП 13. 04.
Программа для логарифмически-линейного масштаба: 00. ИП2 01. * 02. БП 03. 09 04. Flg 05. ИП4 06. - 07. ИП3 08. * 09. 7 10. F10X 11. + 12. FBx 13. - 14. С/П 15. БП 16. 04.
Перед первым пуском программ необходимо нажать на клавиши БП 04. Величину, наносимую на ту или другую координатную ось, следует набрать на клавиатуре. Если речь идет об оси X, нажимается клавиша С/П, и калькулятор сообщает, сколько миллиметров следует отложить, на этой оси, если об оси Y - нажимаются две клавиши: В/О и С/П, и калькулятор определяет, сколько миллиметров следует отложить на ней.
П.ПОЛЯНСКИЙ (г.Москва)
... ИЛИ ГИСТОГРАММУ
Гистограмма - один из видов графического представления экспериментальных данных. Гистограмма строится так. Весь диапазон изменения исследуемой величины (м, М) делится на несколько равных интервалов. Подсчитывается число наблюдений Mi, приходящееся на каждый i-тый интервал, и определяется
частота Hi = Mi/n, где n - общее число наблюдений. По горизонтальной оси откладываются равные интервалы, которые принимаются за основания прямоугольников с высотами пропорциональными Mi или Hi.
Калькулятор "Электроника Б3-34" легко справится с сортировкой данных по 12 накопительным регистрам. Останется только нарисовать саму гистограмму. Программа выглядит так: 00. - 01. 01 02. 02 03. x-y 04. / 05. ПС 06. С/П 07. ИПС 08. * 09. ПD 10. КИПD 11. 1 12. + 13. KПD 14. БП 15. 06. Чтобы подготовить программу к работе, необходимо набрать М, ^, м, нажать клавиши В/О и С/П. Программа остановится, готовая к работе. Набираем начальное значение исследуемой величины и нажимаем С/П, набираем следующее значение, снова нажимаем С/П и так далее до тех пор, пока это необходимо. В любой момент мы можем посмотреть содержимое накопителей Р0-Р9, РА, РВ. В них записаны количества точек, попавших в тот или иной интервал - высоты будущих прямоугольников гистограммы.
Этот метод построения гистограмм был использован автором, чтобы исследовать распределение псевдослучайной величины, вычисляемой следующим образом: ее начальное значение х0 принимается равным нулю, а каждое последующее x[i+i] определяется через xi как дробная часть выражения (пи+xi)**5.
Программа: 00. 5 01. ИПС 02. Fпи 03. + 04. FxY 05. ^ 06. ПD 07. КИПD 08. F() 09. ИПD 10. - 11. ПС 12. 1 13. 0 14. * 15. 1 16. + 17. ПD 18. КИПD 19. 1 20. + 21. KПD 22. FL0 23. 00 24. С/П.

Перед пуском программы в регистры с 1 по 9, А, С засылались нули, а в Р0 заносилось n - число экспериментов. Программа была запущена нажатием клавиш В/О, С/П. После ее останова по результатам исследования строилась гистограмма, отражающая характер распределения псевдослучайной величины х по диапазону 0..1. Ясно видно, сколь отличается оно от равномерного.
А.БОЙКО (г.Москва)
КАЛЬКУЛЯТОР В НЕОБЫЧНЫХ АМПЛУА
Каждая операция калькулятора требует определенного времени - вот принцип программ-секундомеров.
Автор одной нз них (см. ниже), С.Бармин из Тольятти, предвидел, что время выполнения операций для разных экземпляров калькулятора будет неодинаковым, и советует перед началом работы настроить "секундомер". Нужно записать в Р2 число 1 и запустить микрокалькулятор на 10 секунд, после остановки считать число на индикаторе и разделить на него 10. Это и будет "постоянная времени" вашего калькулятора. Введите ее в регистр Р2, нажмите клавиши В/О, С/П - и "секундомер" готов работать по команде С/П. Его погрешность - 2 процента.
Тот же принцип использовал читатель Л.Борисов из Москвы. Засылается знак + в ячейки с 00 по 10, затем записывается В/О в ячейки 11 и 12. Перед началом работы "секундомер" также требует настройки. Единица засылается во все регистры стека (1 ^ ^ ^). затем надо очистить индикатор клавишей Сх и, нажав В/О, С/П, запустить программу на 100 секунд. После остановки делим 100 на число на индикаторе, засылаем результат во все регистры стека, нажимаем Сх, В/О. Включается "секундомер" клавишей С/П, останавливается той же клавишей. Точность хода - порядка 0.3 процента!
Читатель Г.Ионов из г.Балашова (Саратовская обл.) перед пуском своей программы заносит в регистр Р7 величину 1/120 (для каждого экземпляра калькулятора ее следует подобрать более точно), нажимает В/О, набирает требуемое число минут на индикаторе. Запущенная клавишей С/П программа останавливается через заданное число минут, которое и высвечивается на индикаторе.
Программа-таймер С.Конина и А.Шарапова (г.Ленинград) чуть короче, с ней проще работать, но точность ее ниже. В регистр Р9 заносится отмеряемый промежуток времени в секундах, в Р8 - какое-либо условное число, которое будет высвечиваться после конца счета. Авторы рекомендуют "яркое" число, например, 8.8888888e-88. Программа запускается клавишами В/О, С/П.
Другая программа С.Конина и А.Шарапова превращает микрокалькулятор в электронные часы, на индикаторе которых высвечивается точное время. Перед началом работы часы, естественно, устанавливаются. Текущее время вводится в Р8 (часы) и Р9 (минуты). Нужные для работы константы заносятся в регистры: в РА - 10, в Р2 - 11, в Р4 - 24, в Р6 - 60, в Р7 - 100. Часы можно подстраивать, повышая точность хода. Делается это варьированием числа, заносимого в РА (у авторов - 10).
Проделав все эти манипуляции, можно запускать часы (клавиши В/О, С/П). В левом углу индикатора высвечивается текущее время: две последние цифры - минуты, две (или одна) первые - часы. Единственный недостаток часов - в момент "передвижения стрелок" вместо времени мелькают различные числа, но вот "стрелки передвинулись" - и снова на индикаторе часы и минуты.
Программа-секундомер С.Бармина: 00. F2 01. ^ 02. Сх 03. ВП 04. С/П 05. + 10. БП 11. ^.
Программа-таймер Г.Ионова: 00. П8 01. ИП7 02. / 03. П1 04. FL1 05. 04 06. ИП8 07. С/П 08. БП 09. 00.
Программа-таймер С.Конина и А.Шарапова: 00. ИП9 01. П0 02. Fпи 03. F1/x 04. F1/x 05. FL0 06. 02 07. ИП8 08. С/П.
Программа-часы С.Конина и А.Шарапова: 00. ИП4 01. ИП8 02. - 03. П3 04. ИП6 05. ИП9 06. - 07. П0 08. ИП8 09. ИП7 10. * 11. ИП9 12. + 13. П5 14. ИП2 15. П1 16. ИП5 17. ^ 18. ^ 19. ^ 20. ^ 21. ^ 22. ^ 23. ^ 24. ^ 25. ^ 26. ^ 27. ^ 28 ^ 29. FL1 30. 17 31. 1 32. ИПА 33. FxY 34. Fx2 35. КИП5 36. FLO 37. 14 38. ИП6 39. П0 40. ИП5 41. ИП7 42. / 43. П5 44. 1 45. - 46. Fx<0 47. 50 48. Cx 49. П5 50. КИП5 51. ИП5 52. ИП7 53. * 54. П5 55. FL3 56. 14 57. ИП4 58. П3 59. Cx 60. П5 61. БП 62. 14.
Первая программа составлена для микрокалькулятора Б3-21, остальные - для Б3-34.
[ КНИГА ЗА КНИГОЙ
В прошлом выпуске нашей рубрики (6/84) был помещен список книг о микрокалькуляторах, вышедших до последнего времени. Он, конечно, неполон - за его рамками осталась литература, выпускаемая в областных и специализированных издательствах, в вузах. Авторы этих книг любезно присылают их нам. Мы будем представлять их читателю отдельными интересными фрагментами.
Вот взятая из книги профессора В.П.Дьяконова "Методы расчета электронных схем на микроЭВМ" (Москва, МЭИ, 1983г., 94стр.) программа для калькулятора "Электроника Б3-34", по которой вычисляется определитель третьего порядка. Она убедительно демонстрирует возможности стека: все вычисления ведутся по ней лишь с помощью стековых регистров; регистры памяти при этом используются лишь для хранения элементов определителя согласно схеме:

00. ИП4 01. ИП2 02. * 03. ИП1 04. ИП5 05. * 06. - 07. ИП9 08. * 09. ИП1 10. ИП8 11. * 12. ИП7 13. ИП2 14. * 15. - 16. ИП6 17. * 18. + 19. ИП7 20. ИП5 21. * 22. ИП4 23. ИП8 24. * 25. - 26. ИП3 27. * 28. + 29. С/П.
В книге В.П.Дьяконова описаны микроЭВМ марок Б3-21, Б3-34, МК-46, МК-56, Д3-28; изложены и пояснены примерами методы анализа и расчета электронных схем на этих вычислительных машинах.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
10/84
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
"Уважаемая редакция!- пишет нам читательница Т.Орлова из Петропавловска-Камчатского.- Я часто читаю в вашем журнале рубрику "Человек с микрокалькулятором". Очень интересная и увлекательная рубрика остается для меня пустым звуком! Я не умею программировать, то есть составлять программы. Не могли бы вы открыть на страницах журнала школу, в которой читатели учились бы приемам программирования!"
О том, как предполагается наладить такую школу, речь пойдет ниже. Принять участие в обучении тех, кто не умеет программировать, мы призываем читателей, уже освоивших это искусство.
Программирование - вторая грамотность. Практической реализацией этого лозунга должно стать широкое общественное движение за ликвидацию программистской неграмотности.
Вспомним двадцатые годы. Кружки ликбеза организовывались тогда по всей стране. Газеты пестрели сообщениями: такой-то рабочий научил читать и писать своих товарищей по цеху, такой-то красноармеец ликвидировал безграмотность солдат своего взвода.
Важная задача стоит сегодня перед нашим обществом: широчайшее внедрение вычислительной техники в производственную, научную, управленческую деятельность. Успех в решении этой задачи будет особенно прочным, если каждый, кто владеет искусством программирования (пусть даже на микрокалькуляторах!), передаст его хотя бы нескольким своим товарищам, коллегам.
Человек учится грамоте не для того лишь, чтобы разбирать вывески. Книги открывают перед ним огромный мир культуры. И программистская грамотность полезна не только для того, чтобы проводить расчеты. Она прививает особую, характерную для века компьютеров культуру мышления, которая способна сделать эффективнее всякую деятельность человека, своеобразно заострить его мысль.
ЗАВЕДИТЕ БИБЛИОТЕЧКУ ПОДПРОГРАММ
Польза от нее очевидна. Владелец такой библиотеки, будь то программист со стажем или новичок, сможет использовать в своих программах готовые отлаженные модули, не утруждая себя каждый раз их "изобретением".
Основным требованием к подпрограммам должна стать, на мой взгляд, минимальная длина. Ведь выполняют онн вспомогательные функции, и нужно "втискивать" их в любые программы. Но нельзя укорачивать подпрограмму за счет использования многих регистров памяти.
Противоречие это можно разрешить, если хранить в библиотеке две-три модификации каждой из подпрограмм. Одна - минимальной длины, другая - пусть и более длинная, но с минимальным использованием памяти, наконец, третья - оптимальная с точки зрения автора.
Нумерация операторов подпрограммы, на мой взгляд, должна быть относительной, чтобы любой пользователь мог применить ее как внутри, так и вне основной программы.
Вот как может быть оформлена подпрограмма отделения целой части числа, лежащего в пределах от 1 до 99999999. А1: 1. ПР0 2. КИПР0 3. ИПР0. Запись А1 - это метка. Она показывает, что адреса подпрограммы, начиная с первого, при включении в основную программу должны приобретать другие (каждый раз конкретные) последовательные значения. Р0 - обозначение регистров 7-9, А-Д, содержание которых при обращении к ним ие меняется (отбрасывание дробной части не в счет). Подобным образом предлагаю обозначать через Р- регистры 0-3, содержимое которых при косвенном обращении к ним уменьшается на единицу, через Р+ - регистры 4-6, содержимое которых в аналогичных случаях возрастает на единицу; если же свойства используемого регистра безразличны, то просто Р.
Команда В/О отсутствует в конце не случайно. Ведь если подпрограмма будет включена непосредственно в тело программы, как последовательность операторов, то команда эта и не нужна. Так вообще, по-моему, следует поступать с короткими подпрограммами из 3-4 операторов, используемыми в программе достаточно редко. Лишь когда подпрограмма вызывается многократно и имеет длину 7-14 операторов, ее целесообразно дополнить командой В/О и вынести за пределы основной программы.
Приведу еще один пример, связанный с адресацией внутри подпрограммы (предназначена она для вычисления функции n!!): А1: 1. П0 2. 1 А3: 3. ИП0 4. * 5. FL0 6. А2 А2: 7. FL0 8. A3 9. В/О. Если мы хотим записать ее с 98-9=89 шага, то она примет вид: 89. П0 90. 1 91. ИП0 92. * 93. FL0 94. 95 95. FL0 96. 91 97. В/О. Теперь 89 можно занести в Р0 и вызывать подпрограмму оператором КППР0.
Какие же задачи следует прежде всего иметь в виду, составляя библиотеку подпрограмм? Это, на мой взгляд, отделение целой и дробной части числа, округление числа до любого количества значащих цифр, генераторы псевдослучайных последовательностей с различными распределениями, нахождение абсолютного значения числа, вычисление факториала, расчет среднеквадратического отклонения; еще, может быть, вычисление гиперболических функций, переход от декартовых координат к полярным и обратно, перевод десятичных долей градуса в минуты.
А.БОЙКО (г.Москва)
[ МИКРОЗАДАЧНИК
Я набрал на моем микрокалькуляторе трехзначное число. Мой сын, сидевший напротив, сказал:
- Я тоже вижу трехзначное число, и оно меньше твоего.
Я прибавил к моему числу 12.
- Я и сейчас вижу число и опять меньше твоего,- сказал сын.
Тогда я умножил последнее число на 6.
- Теперь мое число больше твоего. Тогда я прибавил 11.
- Теперь... меньше,- сказал сын к моему удивлению, и мы оба рассмеялись. Каким было исходное число?
Перевел из журнала "Нью сайентист" Ю.ФЛОРЕНСКИЙ (г.Рязань)
ЦИФРА ЗА ЦИФРОЙ
Когда разработчик микрокалькулятора выбирает алгоритмы для вычисления элементарных функций, ему приходится исходить прежде всего из того, что все связанное с этими алгоритмами должно быть "микро": память, время работы... Точность, хоть и говорим мы о ней в последнюю очередь, играет тоже далеко не последнюю роль.
Итерационный метод "цифра за цифрой" появился сравнительно недавно, но сразу привлек внимание разработчиков: он счастливым образом объединяет в себе все три достоинства. И, кроме того, обладает еще одним: алгоритмы вычисления всех функций очень похожи друг на друга и могут быть реализованы с помощью одних и тех же блоков, а это для аппаратурной реализации очень важно.
Первоначально этот метод был разработан для двоичной системы счисления. При этом он действительно на каждом итерационном шаге вычислял одну верную цифру результата. Для десятичной системы название утратило буквальность: теперь нельзя сказать, что на каждом шаге вычисляется одна верная цифра, но суть метода и основные достоинства сохранились.
Вычисление любой элементарной функции методом "цифра за цифрой" происходит в два этапа. На первом аргумент функции представляется в виде суммы или произведения ряда членов определенного вида. На втором, с помощью коэффициентов, полученных при членах ряда, строится значение функции. Выбор разложения определяется свойствами функции. Например, известно, что ln(xy)=ln(x)+ln(y). Поэтому аргумент логарифмической функции удобно представить в виде произведения; при этом результат получится в виде суммы. Для показательной функции exp(x+y)=exp(x)*exp(y). Здесь, наоборот, аргумент удобнее представить в виде суммы, тогда результат получится в виде произведения.
Рассмотрим подробнее, как вычисляется показательная функция. Аргумент представляется в виде:

Десятичные цифры qj составляют предмет вычислений на первом этапе. Для их определения используется процесс, называемый псевдоделением. Запоминаются цифры qj в одном числе z, на разных позициях, образуя как бы представление числа x в новой системе счисления. Да и сам процесс напоминает алгоритм перевода числа из одной системы счисления в другую. Только эта другая система имеет "плавающее" основание.
Состоит первый этап из n шагов (n - это количество значащих цифр, с которыми проводятся вычисления; величина n по их ходу не меняется) и реализуется с помощью формул:
y[i+1]=y1-1ej*ln(1+1e-j)
z[i+1]=zi+1e-n
где j = 0, 1,... n; y0 = x; z0 = 0.
Переход от j-го шага к [l+1]-му происходит после выполнения условия y<1ej*ln(1+1e-j) - иными словами, когда следующий yi получился бы уже отрицательным. При этом полученная на j-ом шаге цифра числа z - это и есть очередное qj. После перехода достигнутые значения y и z увеличиваются в 10 раз.
Из формул видно, что фактически деления-то и нет - оно заменяется вычитанием и сдвигом влево, который равносилен умножению на 10. Первому этапу соответствует верхняя часть приведенной блок-схемы.
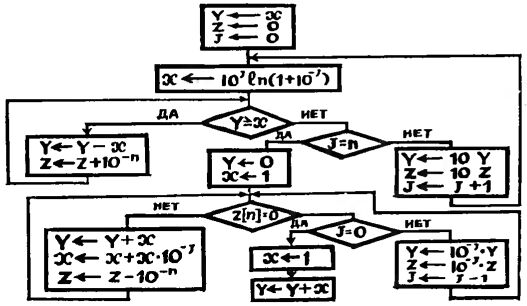
Второй этап - собственно вычисление функции. Он называется псевдоумножеиием. Ему соответствует нижняя часть блок-схемы. Вычисления здесь проходят по формулам:
y[i+1]=yi+xi
x[i+1]=xi+xi*1e-j
z[i+1]=zi-1e-j
где j = n, n-1, ..., y0=0; x0=1; z0 - величина z, полученная на первом этапе.
На втором этапе цифры числа z отрабатываются в обратном порядке. Как только очередной разряд отработан, то есть последняя цифра числа z стала равной нулю, происходит переход к следующему шагу. При этом достигнутые величины y и z уменьшаются в 10 раз. Так происходит до тех пор, пока не будут исчерпаны все цифры числа z, то есть все qj. И здесь, так же как и на первом этапе, используются только элементарные операции: сложение и сдвиг вправо (деление на 10). После окончания вычислений величина y равна exp(x)-1. Сложив ее с единицей, мы получаем искомый результат.
Для вычисления других функций используются процессы, похожие на описанный. Метод "цифра за цифрой" благодаря минимуму различных операций довольно легко реализуется аппаратурно. Быстродействие его раза в 1.5-2 выше, чем у ранее применявшегося тейлоровского метода, точность выше, места для хранения программ требуется меньше. А это значит, что без увеличения ПЗУ можно реализовать в микрокалькуляторах дополнительные функции.
И.ДАНИЛОВ (г.Москва)
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
Школа будет открыта в одном из ближайших выпусков рубрики "Человек с микрокалькулятором". В ее программу намечается включить следующие статьи-лекции:
1. Какие задачи и как целесообразно решать на программируемых микрокалькуляторах.
2. Алгоритмы и способы их записи (блок-схемы и т.п.).
3. Основные команды программируемого микрокалькулятора. Использование стека. Распределение памяти.
4. Ввод и вывод информации.
5. Ветви и циклы в программах. Подпрограммы.
6. Специфические приемы программирования. Оптимизация программ.
Читателей, желающих поделиться своим опытом в пользу начинающих, просим высказываться по предложенным пунктам. Высказывания могут касаться лишь какой-то частности разбираемой темы. На основе присланных писем будет строиться каждая статья-лекция, наподобие того, как в 4/84 год была составлена подборка "Секреты микрокалькулятора".
Удачное письмо будет давать читателю право стать основным лектором по теме и подбирать себе "ассистентов" из числа тех, кто высказался в своем письме на эту тему. Список тем можно дополнять.
Слушатели, то есть читатели, могут задавать вопросы лекторам: ответы углубят затронутую тему. Дополнять лекторов тоже можно.
Некоторые читатели в своих письмах укоряют нас в том, что в нашей рубрике слишком много места уделяется азбучным истинам. Наверное, будут такие письма и сейчас. И правда: зачем эти лекции? Ведь, не говоря об инструкциях к калькуляторам, уже существуют хорошие пособия по программированию на них - Я.К.Трохименко и Ф.Д.Любича, А.Н.Цветкова и В.А.Епанечникова.
Но, во-первых, существование пособий никогда не заменяло лекций. К тому же названные книги изданы слишком малым для многомиллионной армии пользователей тиражом. Во-вторых, мы надеемся на участие авторов этих пособий в наших лекциях.
Конкретные программы-примеры просим приводить для калькулятора Б3-34.
НАСЛЕДСТВО ЛЕДИ ЛАВЛЕЙС
ЛИРИЧЕСКОЕ ОТСТУПЛЕНИЕ
"Мой мозг - нечто большее, чем просто смертная субстанция, я надеюсь, время покажет это.
"Клянусь дьяволом, что не пройдет и десяти лет, как я высосу некоторое количество жизненной крови из загадок Вселенной, причем так, как этого не смогли бы сделать обычные смертные умы и губы.
"Никто не знает, какая ужасающая энергия и сила лежат еще не использованными в моем маленьком гибком существе".
Эти слова написала дочь Байрона Ада Лавлейс.
Она исполнила клятву.
В 1843 году была опубликована статья Л.Ф.Менабреа "Описание аналитической машины, изобретенной Ч.Бэббиджем. С примечаниями переводчика".
Машина Бэббиджа - прообраз современной ЭВМ, содержащий многие ее особенности. Переводчик - Ада Лавлейс. В примечаниях, превышающих по объему статью, встречаются термины и понятия, используемые в современном программировании, приведены примеры первых в мире программ, обрисованы перспективы развития вычислительной техники.
Все это погрузилось в забвение и воскресло только в наше время.
Не странно ли: 150 лет назад мир был охвачен модой на Джорджа Байрона, а в наше время все стороны жизни людей так же охвачены программированием, у истоков которого - дочь поэта, Ада.
Она ушла в тридцать семь лет - в возрасте Моцарта, Рафаэля, Пушкина и Байрона. Родилась Ада Лавлейс 10 декабря 1815 года. Не пора ли программистской общественности отмечать эту дату как один из своих профессиональных праздников?
Итак, первый программист - женщина. А сейчас?
Армия программистов - это женская армия. Роль мужчин в этой армии - командиры, снайперы, интенданты...
Отношения Ады Лавлейс с Чарлзом Бэббиджем - это отношения разработчика и научного руководителя. Примерно такими остаются и сейчас типичные отношения между программистом-женщиной и руководителем-мужчиной. В роли разработчика женщина с успехом может реализовать такие сильные стороны своей личности, как реализм и прилежность.
А умение ладить с управленцами? Вундеркинды-мужчины - сложный объект управления, а покладистые женщины, подобно океану в "Солярисе", легко имитируют реализацию фантазий быстро меняющегося руководства вычислительных центров. Не потому ли их хрупкие плечи несут основную часть плановой работы?
Программирование - одна из массовых профессий, дающих практичному и переимчивому уму современной гражданки с высшим образованием интересную возможность самоутверждения в профессиональной сфере, неплохо оплачиваемую и способную приемлемо сочетаться с личной и общественной жизнью.
Разработка программ, создание искусственного интеллекта чем-то импонирует материнскому инстинкту: надо вдохнуть жизнь, надо поставить на ноги, и сделать это надо срочно, не откладывая - все расчислено по календарю.
Легендарный доктор Фауст мечтал вырастить гомункулуса в реторте. Что сказал бы искатель счастья и новых технических решений, изучив и испытав на деле искусственный интеллект, взлелеянный в кельях современных информационно-вычислительных центров? Смог бы Гете представить свою Маргариту в роли инженера-программиста?
Л.ПОПЕЛЬ (г.Москва).
ПО АЛГОРИТМУ ЖЮЛЯ ВЕРНА
"Когда после достаточно долгого периода хорошей погоды барометр начинает быстро и непрерывно падать - это верный признак дождя". Ж.Верн "Пятнадцатилетний капитан"
Точный прогноз погоды - дело исключительно сложное. Увы, даже Гидрометцентр дает его далеко не всегда. А вот приблизительный особого искусства не требует. Если ломит кости, то это к дождю; если хорошо видны звезды, то день будет ясный.
То, что мы предлагаем, лежит, наверное, посередине между прогнозом, даваемым Гидрометцентром, и прогнозом по "чистоте неба".
Программа "Прогноз погоды". 00. Сх 01. 4 02. 6 03. ПD 04. 5 05. П0 06. 1 07. П6 08. ИП6 09. ВП 10. 5 11. С/П 12. КП6 13. FL0 14. 08 15. ИП4 16. 2 17. - 18. Fx=0 19. 24 20. 1 21. ПВ 22. БП 23. 43 24. ИП3 25. Fx!=0 26. 28 27. 1 28. ИП5 29. + 30. ПB 31. ИП4 32. Fx=0 33. 64 34. ИП5 35. Fx=0 36. 43 37. ИП6 38. Fx=0 39. 55 40. ИП2 41. Fx!=0 42. 53 43. 1 44. ИП2 45. + 46. ПА 47.2 48. F10X 49. * 50. ИПВ 51. + 52. С/П 53. 3 54. КБПD 55. ИП6 56. 2 57. - 58.Fx>=0 59. 62 60. 4 61. КБПD 62. 5 63.КБПD 64. ИП6 65. 3 66. - 67. Fx=0 68. 72 69. ИП2 70. Fx=0 71. 76 72. 2 73. ИП2 74. - 75. КБПD 76. 6 77. КБПD.
После ввода программы следует нажать клавиши В/О, С/П и сообщить калькулятору информацию, на основе которой он будет формировать прогноз. Нужно ввести пять чисел.
1. Состояние погоды: 0 - хорошая погода, 1 - плохая.
2. Давно ли стоит такая погода: 0 - недавно, 1 - давно.
3. Показания барометра: 0 - падают, 1 - растут, 2 - не изменяются.
4. Меняются эти показания: 0 - быстро, 1 - медленно, 2 - вообще не меняются.
5. Время года: 0 - лето, 1 - зима, 2 - весна, 3 - осень.
Каждое из этих сообщений вводится в ответ на очередной запрос микрокалькулятора, высвечиваемый на индикаторе в виде пятизначного числа. Например, 20000 - запрос #2.
Каждый ввод завершается нажатием клавиши С/П. После пятого ввода калькулятор высвечивает прогноз в виде трехзначного числа А0В. Цифра А указывает характер погоды, В - ее продолжительность. Расшифровываются цифры так. А: 1 - плохая погода, 2 - хорошая, 3 - ливень, гроза, 4 - сильный ветер, 5 - оттепель, снегопад, 6 - северный ветер, мороз. В: 0 - продержится совсем недолго (меньше суток), 1 - несколько дней, 2 - будет стоять долго.
Например, в калькулятор была введена такая информация: хорошая погода (0) стояла долго (1); барометр падает (0) и притом быстро (0); на дворе весна (2). Калькулятор выдает прогноз: 401, то есть сильный ветер в течение нескольких дней.
После получения прогноза включите радио или телевизор и послушайте, какую погоду обещают на завтра. Если информация диктора не совпадет с выданной калькулятором, значит, кто-то из них неправ.
Г.СЛАВИН (г.Тарту)
КСТАТИ...
К слову, о пользе глубоких знаний математики. Они порою помогают в самых неожиданных ситуациях.
Однажды ректор одного института потребовал сведения о том, много ли аспирантов института защищают кандидатские диссертации к окончанию аспирантуры.
Принесенный ему график выглядел неутешительно: он то взлетал над осью абсцисс, то прямо-таки прижимался к ней.
И тут присутствовавший в кабинете проректор произнес спасительную фразу: "Интеграл с переменным верхним пределом от неотрицательной функции есть функция неубывающая!" И пояснил: "Надо показывать на графике число защитившихся в срок не в данном году, а к данному году".

Перестроенная кривая уверенно ползла ввысь. Где бы ректор впоследствии ни показывал эту диаграмму, она неизменно вызывала самое благосклонное отношение.
М.СЕМЕНОВ (г.Новосибирск)
[ СОВЕТЫ
При записи программы обязательно фиксируйте комментарии. Без них не только посторонний, но и вы сами через неделю не сможете разобраться в собственной программе. Часто понять программу без комментариев труднее, чем написать новую.
В.ПУХОВОЙ (г.Харьков) ]
ВВОД ЧИСЕЛ БЕЗ ОШИБОК
Ввод исходных данных непосредственно в регистры памяти часто приводит к ошибкам из-за необходимости нажимать много клавиш. Риск ошибки значительно уменьшится, если перед текстом программы разместить команды вида ПР, где Р - соответствующий регистр Например: 00. П2 01. П4 02. П6 03. С/П. В автоматическом режиме набираем на индикаторе число, которое требуется заслать в регистр 2, нажимаем клавишу ПП, набираем содержимое регистра 4, снова ПП, набираем содержимое регистра 6 и снова ПП... Калькулятор сам безошибочно разместит данные по регистрам и по команде С/П начнет выполнение программы.
Таким же путем, но уже с помощью команд вида ИПР, можно облегчить и вывод результатов счета.
С.КОМИССАРОВ (г.Москва)
В недавно вышедшей книге В.П.Дьяконова "Расчет нелинейных импульсных устройств на программируемых микрокалькуляторах" (Москва, "Радио и связь", 1984) на стр.11 приводится программа для ввода чисел в регистры памяти калькулятора Б3-34. Возможности способа, данного В.П.Дьяконовым, можно расширить. Для этой цели предлагается программа: 00. КП4 01. FL3 02. 00 03. С/П 04. КП4 05. БП 06. 03. С помощью ее фрагмента 03-06 в память микрокалькулятора можно внести 11 чисел, а не 8, как указано у В.П.Дьяконова.
Вносим число 4 в регистр Р4 и нажимаем клавиши БП, 0, 3, С/П. Калькулятор готов к работе. Набираем на индикаторе первое из вносимых чисел и нажимаем клавишу С/П. После останова вносим второе число, опять С/П и так далее. Набираемые числа расположатся в порядке их введения в регистрах Р5, Р6, ... Р9, РА. ... РД. РО. Р1. В оставшиеся регистры (второй, третий и четвертый) числа можно ввести обычным способом.
Фрагмент 00-03 служит для ввода одного и того же числа в несколько регистров памяти. Такая необходимость возникает при решении задач интерполяции, расчетах квадратичных приближений и т.д.
Возможности программы проиллюстрируем на примере такой задачи: даны числа a, b, c, d, e; требуется ввести а в пять регистров, b - в три и с, d, e по одному в три регистра. Для решения задачи вводим программу и переходим в автоматический режим. Вводим 4 в Р4, 5 - в Р3, a набираем на индикаторе, нажимаем В/О и С/П. После останова вводим 3 в РЗ3, b набираем на индикаторе, снова нажимаем В/О и С/П. Затем после останова набираем на индикаторе с и нажимаем только С/П; так же поступаем для ввода d и е. Число a окажется в регистрах Р5-Р9, b - в регистрах РА-PC, с - в РД, d - в Р0, е - в Р1.
Конечно, можно использовать и меньшее число регистров памяти, прекратив в нужном месте ввод чисел нлн внеся в регистр Р4 число, большее четырех (последним из регистров, куда можно вносить числа вторым из этих способов, будет по-прежнему Р1).
А.ТУЛАЙКОВ (г.Долгопрудный)
[ УЗЕЛКИ НА ПАМЯТЬ
Программу отладить тем легче, чем больше в ней уже испытанных подпрограмм.
И.ГРИЦЕНКО (с.Иванковцы Знаменского р-на Кировоградской обл.) ]
[ ОТВЕТ НА ЗАДАЧУ
Исходное число - 909, последнее - 5537, что при чтении "вверх ногами" дает английское LESS (меньше) ]
РАССЧИТЫВАЕМ ПЛАВКУ
Судя по статьям, публикуемым под рубрикой "Человек с микрокалькулятором", возможности микрокалькуляторов далеко не в полной мере используются в практике промышленного производства. Возьму на себя смелость утверждать, что это объясняется не столько ограниченными возможностями калькуляторов, сколько косностью некоторых производственников.
Возьмем, к примеру, задачу расчета добавок по ходу плавки сталей высоколегированных марок. Расчет достаточно несложен, чтобы выполнить его на микрокалькуляторе. Вооружившись им, плавильный мастер получит нужные числа за полминуты.
Задача ставится так. В определенный момент плавки отбирается проба жидкого металла, в которой методами химического и спектрального анализа устанавливается содержание легирующих элементов в весовых процентах. Обозначим эти количества Вi.
Содержание легирующих элементов в сплаве, который должен быть получен, обозначим Аi. Эти значения достигаются путем добавления в металл ферросплавов, в каждый из которых наряду с железом входит соответствующий элемент с процентным содержанием Ci. Требуется вычислить вес добавки каждого ферросплава. Обозначим эти искомые величины Pi, а вес металла при отборе пробы Р0. Теперь достижение заданного химического состава по каждому элементу нетрудно выразить равенствами:
Р0Вi + РiСi = (Р0 + sum2Pi)Ai.
Получилась система линейных уравнений. Если решать ее на калькуляторе и использовать для этого какой-либо стандартный алгоритм, то, сопоставляя его с возможностями калькулятора, мы тем самым ограничим порядок системы, то есть число легирующих добавок, охватываемое расчетом. Но стоит ли связывать себя заведомыми ограничениями? Весьма стройный вид системы позволяет надеяться, что у нее есть аналитическое решение. И оно действительно существует:
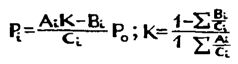
Теперь все определяется объемом памяти микрокалькулятора: в каком количестве сможет она вместить числа А, В, С? Делу помогает такое обстоятельство: некоторые элементы вносятся в металл плавки лишь с добавкой ферросплавов, так что соответствующие Bi равны нулю и не требуют места в памяти.
Рассмотрим в качестве примера плавку стали марки 06х23н27м3д3т. Вот исходные данные, сведенные в таблицы:

Пусть вес плавки Р0 равен 23000кг. Отметим, что титан в металле плавки отсутствует (В5=0). Поэтому все необходимые данные удается занести в память "Электроники Б3-34".

Программа. 00. ИПД 01. / 02. ИП1 03. ИП0 04. / 05. + 06. ИП2 07. ИПА 08. / 09. + 10. ИП3 11. ИПВ 12. / 13. + 14. ИП4 15. ИПС 16. / 17. + 18. 1 19. - 20. ИП6 21. ИП0 22. / 23. ИП7 24. ИПА 25. / 26. + 27. ИП8 28. ИПВ 29. / 30. + 31. ИП9 32. ИПС 33. / 34. + 35. 1 36. - 37. x-y 38. / 39. ПД 40. ИП1 41. * 42. ИП6 43. - 44. ИП0 45. / 46. ИП5 47. * 48. П6 49. ИПД 50. ИП2 51. * 52. ИП7 53. - 54. ИПА 55. / 56. ИП5 57. * 58. П7 59. + 60. ИПД 61. ИП3 62. * 63. ИП8 64. - 65. ИПВ 66. / 67. ИП5 68. * 69. П8 70. + 71. ИПД 72. ИП4 73. * 74. ИП9 75. - 76. ИПС 77. / 78. ИП5 79. * 80. П9 81. + 82. ИП5 83. + 84. /-/ 85. ИПД 86. ИП5 87. * 88. ПД 89. + 90. П0 91. С/П 92. ИП6 93. ИП7 94. ИП8 95. ИП9 96. ИПД
Заносим А5 в регистр X, нажимаем клавиши В/О, С/П и получаем значения искомых величин в килограммах (здесь округлены):
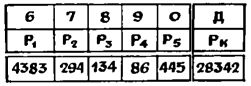
Pк = P0+sum(Pi) - конечный вес плавки. Таким образом можно рассчитать плавку стали любой марки с числом легирующих элементов до пяти.
Одно плохо: "Электроникой Б3-34" трудно пользоваться в условиях цеха. Его автономная работа ограничена двумя часами, а оставлять его на подзарядке рискованно. Неудобна и "Электроника МК-56".
Металлургов устроил бы микрокалькулятор, который по размеру и по возможностям был бы идентичен "Электронике Б3-34", но к тому же имел бы приставку для хранения нескольких (скажем, пяти) программ по 98 шагов в выключенном состоянии, действовал бы автономно в продолжение смены.
Ю.ВОЛОВИЧ, заместитель директора завода "Днепроспецсталь" (г.Запорожье)
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
"Уважаемая редакция!- пишет нам читательница Т.Орлова из Петропавловска-Камчатского.- Я часто читаю в вашем журнале рубрику "Человек с микрокалькулятором". Очень интересная и увлекательная рубрика остается для меня пустым звуком! Я не умею программировать, то есть составлять программы. Не могли бы вы открыть на страницах журнала школу, в которой читатели учились бы приемам программирования!"
О том, как предполагается наладить такую школу, речь пойдет ниже. Принять участие в обучении тех, кто не умеет программировать, мы призываем читателей, уже освоивших это искусство.
Программирование - вторая грамотность. Практической реализацией этого лозунга должно стать широкое общественное движение за ликвидацию программистской неграмотности.
Вспомним двадцатые годы. Кружки ликбеза организовывались тогда по всей стране. Газеты пестрели сообщениями: такой-то рабочий научил читать и писать своих товарищей по цеху, такой-то красноармеец ликвидировал безграмотность солдат своего взвода.
Важная задача стоит сегодня перед нашим обществом: широчайшее внедрение вычислительной техники в производственную, научную, управленческую деятельность. Успех в решении этой задачи будет особенно прочным, если каждый, кто владеет искусством программирования (пусть даже на микрокалькуляторах!), передаст его хотя бы нескольким своим товарищам, коллегам.
Человек учится грамоте не для того лишь, чтобы разбирать вывески. Книги открывают перед ним огромный мир культуры. И программистская грамотность полезна не только для того, чтобы проводить расчеты. Она прививает особую, характерную для века компьютеров культуру мышления, которая способна сделать эффективнее всякую деятельность человека, своеобразно заострить его мысль.
ЗАВЕДИТЕ БИБЛИОТЕЧКУ ПОДПРОГРАММ
Польза от нее очевидна. Владелец такой библиотеки, будь то программист со стажем или новичок, сможет использовать в своих программах готовые отлаженные модули, не утруждая себя каждый раз их "изобретением".
Основным требованием к подпрограммам должна стать, на мой взгляд, минимальная длина. Ведь выполняют онн вспомогательные функции, и нужно "втискивать" их в любые программы. Но нельзя укорачивать подпрограмму за счет использования многих регистров памяти.
Противоречие это можно разрешить, если хранить в библиотеке две-три модификации каждой из подпрограмм. Одна - минимальной длины, другая - пусть и более длинная, но с минимальным использованием памяти, наконец, третья - оптимальная с точки зрения автора.
Нумерация операторов подпрограммы, на мой взгляд, должна быть относительной, чтобы любой пользователь мог применить ее как внутри, так и вне основной программы.
Вот как может быть оформлена подпрограмма отделения целой части числа, лежащего в пределах от 1 до 99999999. А1: 1. ПР0 2. КИПР0 3. ИПР0. Запись А1 - это метка. Она показывает, что адреса подпрограммы, начиная с первого, при включении в основную программу должны приобретать другие (каждый раз конкретные) последовательные значения. Р0 - обозначение регистров 7-9, А-Д, содержание которых при обращении к ним ие меняется (отбрасывание дробной части не в счет). Подобным образом предлагаю обозначать через Р- регистры 0-3, содержимое которых при косвенном обращении к ним уменьшается на единицу, через Р+ - регистры 4-6, содержимое которых в аналогичных случаях возрастает на единицу; если же свойства используемого регистра безразличны, то просто Р.
Команда В/О отсутствует в конце не случайно. Ведь если подпрограмма будет включена непосредственно в тело программы, как последовательность операторов, то команда эта и не нужна. Так вообще, по-моему, следует поступать с короткими подпрограммами из 3-4 операторов, используемыми в программе достаточно редко. Лишь когда подпрограмма вызывается многократно и имеет длину 7-14 операторов, ее целесообразно дополнить командой В/О и вынести за пределы основной программы.
Приведу еще один пример, связанный с адресацией внутри подпрограммы (предназначена она для вычисления функции n!!): А1: 1. П0 2. 1 А3: 3. ИП0 4. * 5. FL0 6. А2 А2: 7. FL0 8. A3 9. В/О. Если мы хотим записать ее с 98-9=89 шага, то она примет вид: 89. П0 90. 1 91. ИП0 92. * 93. FL0 94. 95 95. FL0 96. 91 97. В/О. Теперь 89 можно занести в Р0 и вызывать подпрограмму оператором КППР0.
Какие же задачи следует прежде всего иметь в виду, составляя библиотеку подпрограмм? Это, на мой взгляд, отделение целой и дробной части числа, округление числа до любого количества значащих цифр, генераторы псевдослучайных последовательностей с различными распределениями, нахождение абсолютного значения числа, вычисление факториала, расчет среднеквадратического отклонения; еще, может быть, вычисление гиперболических функций, переход от декартовых координат к полярным и обратно, перевод десятичных долей градуса в минуты.
А.БОЙКО (г.Москва)
[ МИКРОЗАДАЧНИК
Я набрал на моем микрокалькуляторе трехзначное число. Мой сын, сидевший напротив, сказал:
- Я тоже вижу трехзначное число, и оно меньше твоего.
Я прибавил к моему числу 12.
- Я и сейчас вижу число и опять меньше твоего,- сказал сын.
Тогда я умножил последнее число на 6.
- Теперь мое число больше твоего. Тогда я прибавил 11.
- Теперь... меньше,- сказал сын к моему удивлению, и мы оба рассмеялись. Каким было исходное число?
Перевел из журнала "Нью сайентист" Ю.ФЛОРЕНСКИЙ (г.Рязань)
ЦИФРА ЗА ЦИФРОЙ
Когда разработчик микрокалькулятора выбирает алгоритмы для вычисления элементарных функций, ему приходится исходить прежде всего из того, что все связанное с этими алгоритмами должно быть "микро": память, время работы... Точность, хоть и говорим мы о ней в последнюю очередь, играет тоже далеко не последнюю роль.
Итерационный метод "цифра за цифрой" появился сравнительно недавно, но сразу привлек внимание разработчиков: он счастливым образом объединяет в себе все три достоинства. И, кроме того, обладает еще одним: алгоритмы вычисления всех функций очень похожи друг на друга и могут быть реализованы с помощью одних и тех же блоков, а это для аппаратурной реализации очень важно.
Первоначально этот метод был разработан для двоичной системы счисления. При этом он действительно на каждом итерационном шаге вычислял одну верную цифру результата. Для десятичной системы название утратило буквальность: теперь нельзя сказать, что на каждом шаге вычисляется одна верная цифра, но суть метода и основные достоинства сохранились.
Вычисление любой элементарной функции методом "цифра за цифрой" происходит в два этапа. На первом аргумент функции представляется в виде суммы или произведения ряда членов определенного вида. На втором, с помощью коэффициентов, полученных при членах ряда, строится значение функции. Выбор разложения определяется свойствами функции. Например, известно, что ln(xy)=ln(x)+ln(y). Поэтому аргумент логарифмической функции удобно представить в виде произведения; при этом результат получится в виде суммы. Для показательной функции exp(x+y)=exp(x)*exp(y). Здесь, наоборот, аргумент удобнее представить в виде суммы, тогда результат получится в виде произведения.
Рассмотрим подробнее, как вычисляется показательная функция. Аргумент представляется в виде:

Десятичные цифры qj составляют предмет вычислений на первом этапе. Для их определения используется процесс, называемый псевдоделением. Запоминаются цифры qj в одном числе z, на разных позициях, образуя как бы представление числа x в новой системе счисления. Да и сам процесс напоминает алгоритм перевода числа из одной системы счисления в другую. Только эта другая система имеет "плавающее" основание.
Состоит первый этап из n шагов (n - это количество значащих цифр, с которыми проводятся вычисления; величина n по их ходу не меняется) и реализуется с помощью формул:
y[i+1]=y1-1ej*ln(1+1e-j)
z[i+1]=zi+1e-n
где j = 0, 1,... n; y0 = x; z0 = 0.
Переход от j-го шага к [l+1]-му происходит после выполнения условия y<1ej*ln(1+1e-j) - иными словами, когда следующий yi получился бы уже отрицательным. При этом полученная на j-ом шаге цифра числа z - это и есть очередное qj. После перехода достигнутые значения y и z увеличиваются в 10 раз.
Из формул видно, что фактически деления-то и нет - оно заменяется вычитанием и сдвигом влево, который равносилен умножению на 10. Первому этапу соответствует верхняя часть приведенной блок-схемы.

Второй этап - собственно вычисление функции. Он называется псевдоумножеиием. Ему соответствует нижняя часть блок-схемы. Вычисления здесь проходят по формулам:
y[i+1]=yi+xi
x[i+1]=xi+xi*1e-j
z[i+1]=zi-1e-j
где j = n, n-1, ..., y0=0; x0=1; z0 - величина z, полученная на первом этапе.
На втором этапе цифры числа z отрабатываются в обратном порядке. Как только очередной разряд отработан, то есть последняя цифра числа z стала равной нулю, происходит переход к следующему шагу. При этом достигнутые величины y и z уменьшаются в 10 раз. Так происходит до тех пор, пока не будут исчерпаны все цифры числа z, то есть все qj. И здесь, так же как и на первом этапе, используются только элементарные операции: сложение и сдвиг вправо (деление на 10). После окончания вычислений величина y равна exp(x)-1. Сложив ее с единицей, мы получаем искомый результат.
Для вычисления других функций используются процессы, похожие на описанный. Метод "цифра за цифрой" благодаря минимуму различных операций довольно легко реализуется аппаратурно. Быстродействие его раза в 1.5-2 выше, чем у ранее применявшегося тейлоровского метода, точность выше, места для хранения программ требуется меньше. А это значит, что без увеличения ПЗУ можно реализовать в микрокалькуляторах дополнительные функции.
И.ДАНИЛОВ (г.Москва)
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
Школа будет открыта в одном из ближайших выпусков рубрики "Человек с микрокалькулятором". В ее программу намечается включить следующие статьи-лекции:
1. Какие задачи и как целесообразно решать на программируемых микрокалькуляторах.
2. Алгоритмы и способы их записи (блок-схемы и т.п.).
3. Основные команды программируемого микрокалькулятора. Использование стека. Распределение памяти.
4. Ввод и вывод информации.
5. Ветви и циклы в программах. Подпрограммы.
6. Специфические приемы программирования. Оптимизация программ.
Читателей, желающих поделиться своим опытом в пользу начинающих, просим высказываться по предложенным пунктам. Высказывания могут касаться лишь какой-то частности разбираемой темы. На основе присланных писем будет строиться каждая статья-лекция, наподобие того, как в 4/84 год была составлена подборка "Секреты микрокалькулятора".
Удачное письмо будет давать читателю право стать основным лектором по теме и подбирать себе "ассистентов" из числа тех, кто высказался в своем письме на эту тему. Список тем можно дополнять.
Слушатели, то есть читатели, могут задавать вопросы лекторам: ответы углубят затронутую тему. Дополнять лекторов тоже можно.
Некоторые читатели в своих письмах укоряют нас в том, что в нашей рубрике слишком много места уделяется азбучным истинам. Наверное, будут такие письма и сейчас. И правда: зачем эти лекции? Ведь, не говоря об инструкциях к калькуляторам, уже существуют хорошие пособия по программированию на них - Я.К.Трохименко и Ф.Д.Любича, А.Н.Цветкова и В.А.Епанечникова.
Но, во-первых, существование пособий никогда не заменяло лекций. К тому же названные книги изданы слишком малым для многомиллионной армии пользователей тиражом. Во-вторых, мы надеемся на участие авторов этих пособий в наших лекциях.
Конкретные программы-примеры просим приводить для калькулятора Б3-34.
НАСЛЕДСТВО ЛЕДИ ЛАВЛЕЙС
ЛИРИЧЕСКОЕ ОТСТУПЛЕНИЕ
"Мой мозг - нечто большее, чем просто смертная субстанция, я надеюсь, время покажет это.
"Клянусь дьяволом, что не пройдет и десяти лет, как я высосу некоторое количество жизненной крови из загадок Вселенной, причем так, как этого не смогли бы сделать обычные смертные умы и губы.
"Никто не знает, какая ужасающая энергия и сила лежат еще не использованными в моем маленьком гибком существе".
Эти слова написала дочь Байрона Ада Лавлейс.
Она исполнила клятву.
В 1843 году была опубликована статья Л.Ф.Менабреа "Описание аналитической машины, изобретенной Ч.Бэббиджем. С примечаниями переводчика".
Машина Бэббиджа - прообраз современной ЭВМ, содержащий многие ее особенности. Переводчик - Ада Лавлейс. В примечаниях, превышающих по объему статью, встречаются термины и понятия, используемые в современном программировании, приведены примеры первых в мире программ, обрисованы перспективы развития вычислительной техники.
Все это погрузилось в забвение и воскресло только в наше время.
Не странно ли: 150 лет назад мир был охвачен модой на Джорджа Байрона, а в наше время все стороны жизни людей так же охвачены программированием, у истоков которого - дочь поэта, Ада.
Она ушла в тридцать семь лет - в возрасте Моцарта, Рафаэля, Пушкина и Байрона. Родилась Ада Лавлейс 10 декабря 1815 года. Не пора ли программистской общественности отмечать эту дату как один из своих профессиональных праздников?
Итак, первый программист - женщина. А сейчас?
Армия программистов - это женская армия. Роль мужчин в этой армии - командиры, снайперы, интенданты...
Отношения Ады Лавлейс с Чарлзом Бэббиджем - это отношения разработчика и научного руководителя. Примерно такими остаются и сейчас типичные отношения между программистом-женщиной и руководителем-мужчиной. В роли разработчика женщина с успехом может реализовать такие сильные стороны своей личности, как реализм и прилежность.
А умение ладить с управленцами? Вундеркинды-мужчины - сложный объект управления, а покладистые женщины, подобно океану в "Солярисе", легко имитируют реализацию фантазий быстро меняющегося руководства вычислительных центров. Не потому ли их хрупкие плечи несут основную часть плановой работы?
Программирование - одна из массовых профессий, дающих практичному и переимчивому уму современной гражданки с высшим образованием интересную возможность самоутверждения в профессиональной сфере, неплохо оплачиваемую и способную приемлемо сочетаться с личной и общественной жизнью.
Разработка программ, создание искусственного интеллекта чем-то импонирует материнскому инстинкту: надо вдохнуть жизнь, надо поставить на ноги, и сделать это надо срочно, не откладывая - все расчислено по календарю.
Легендарный доктор Фауст мечтал вырастить гомункулуса в реторте. Что сказал бы искатель счастья и новых технических решений, изучив и испытав на деле искусственный интеллект, взлелеянный в кельях современных информационно-вычислительных центров? Смог бы Гете представить свою Маргариту в роли инженера-программиста?
Л.ПОПЕЛЬ (г.Москва).
ПО АЛГОРИТМУ ЖЮЛЯ ВЕРНА
"Когда после достаточно долгого периода хорошей погоды барометр начинает быстро и непрерывно падать - это верный признак дождя". Ж.Верн "Пятнадцатилетний капитан"
Точный прогноз погоды - дело исключительно сложное. Увы, даже Гидрометцентр дает его далеко не всегда. А вот приблизительный особого искусства не требует. Если ломит кости, то это к дождю; если хорошо видны звезды, то день будет ясный.
То, что мы предлагаем, лежит, наверное, посередине между прогнозом, даваемым Гидрометцентром, и прогнозом по "чистоте неба".
Программа "Прогноз погоды". 00. Сх 01. 4 02. 6 03. ПD 04. 5 05. П0 06. 1 07. П6 08. ИП6 09. ВП 10. 5 11. С/П 12. КП6 13. FL0 14. 08 15. ИП4 16. 2 17. - 18. Fx=0 19. 24 20. 1 21. ПВ 22. БП 23. 43 24. ИП3 25. Fx!=0 26. 28 27. 1 28. ИП5 29. + 30. ПB 31. ИП4 32. Fx=0 33. 64 34. ИП5 35. Fx=0 36. 43 37. ИП6 38. Fx=0 39. 55 40. ИП2 41. Fx!=0 42. 53 43. 1 44. ИП2 45. + 46. ПА 47.2 48. F10X 49. * 50. ИПВ 51. + 52. С/П 53. 3 54. КБПD 55. ИП6 56. 2 57. - 58.Fx>=0 59. 62 60. 4 61. КБПD 62. 5 63.КБПD 64. ИП6 65. 3 66. - 67. Fx=0 68. 72 69. ИП2 70. Fx=0 71. 76 72. 2 73. ИП2 74. - 75. КБПD 76. 6 77. КБПD.
После ввода программы следует нажать клавиши В/О, С/П и сообщить калькулятору информацию, на основе которой он будет формировать прогноз. Нужно ввести пять чисел.
1. Состояние погоды: 0 - хорошая погода, 1 - плохая.
2. Давно ли стоит такая погода: 0 - недавно, 1 - давно.
3. Показания барометра: 0 - падают, 1 - растут, 2 - не изменяются.
4. Меняются эти показания: 0 - быстро, 1 - медленно, 2 - вообще не меняются.
5. Время года: 0 - лето, 1 - зима, 2 - весна, 3 - осень.
Каждое из этих сообщений вводится в ответ на очередной запрос микрокалькулятора, высвечиваемый на индикаторе в виде пятизначного числа. Например, 20000 - запрос #2.
Каждый ввод завершается нажатием клавиши С/П. После пятого ввода калькулятор высвечивает прогноз в виде трехзначного числа А0В. Цифра А указывает характер погоды, В - ее продолжительность. Расшифровываются цифры так. А: 1 - плохая погода, 2 - хорошая, 3 - ливень, гроза, 4 - сильный ветер, 5 - оттепель, снегопад, 6 - северный ветер, мороз. В: 0 - продержится совсем недолго (меньше суток), 1 - несколько дней, 2 - будет стоять долго.
Например, в калькулятор была введена такая информация: хорошая погода (0) стояла долго (1); барометр падает (0) и притом быстро (0); на дворе весна (2). Калькулятор выдает прогноз: 401, то есть сильный ветер в течение нескольких дней.
После получения прогноза включите радио или телевизор и послушайте, какую погоду обещают на завтра. Если информация диктора не совпадет с выданной калькулятором, значит, кто-то из них неправ.
Г.СЛАВИН (г.Тарту)
КСТАТИ...
К слову, о пользе глубоких знаний математики. Они порою помогают в самых неожиданных ситуациях.
Однажды ректор одного института потребовал сведения о том, много ли аспирантов института защищают кандидатские диссертации к окончанию аспирантуры.
Принесенный ему график выглядел неутешительно: он то взлетал над осью абсцисс, то прямо-таки прижимался к ней.

И тут присутствовавший в кабинете проректор произнес спасительную фразу: "Интеграл с переменным верхним пределом от неотрицательной функции есть функция неубывающая!" И пояснил: "Надо показывать на графике число защитившихся в срок не в данном году, а к данному году".

Перестроенная кривая уверенно ползла ввысь. Где бы ректор впоследствии ни показывал эту диаграмму, она неизменно вызывала самое благосклонное отношение.
М.СЕМЕНОВ (г.Новосибирск)
[ СОВЕТЫ
При записи программы обязательно фиксируйте комментарии. Без них не только посторонний, но и вы сами через неделю не сможете разобраться в собственной программе. Часто понять программу без комментариев труднее, чем написать новую.
В.ПУХОВОЙ (г.Харьков) ]
ВВОД ЧИСЕЛ БЕЗ ОШИБОК
Ввод исходных данных непосредственно в регистры памяти часто приводит к ошибкам из-за необходимости нажимать много клавиш. Риск ошибки значительно уменьшится, если перед текстом программы разместить команды вида ПР, где Р - соответствующий регистр Например: 00. П2 01. П4 02. П6 03. С/П. В автоматическом режиме набираем на индикаторе число, которое требуется заслать в регистр 2, нажимаем клавишу ПП, набираем содержимое регистра 4, снова ПП, набираем содержимое регистра 6 и снова ПП... Калькулятор сам безошибочно разместит данные по регистрам и по команде С/П начнет выполнение программы.
Таким же путем, но уже с помощью команд вида ИПР, можно облегчить и вывод результатов счета.
С.КОМИССАРОВ (г.Москва)
В недавно вышедшей книге В.П.Дьяконова "Расчет нелинейных импульсных устройств на программируемых микрокалькуляторах" (Москва, "Радио и связь", 1984) на стр.11 приводится программа для ввода чисел в регистры памяти калькулятора Б3-34. Возможности способа, данного В.П.Дьяконовым, можно расширить. Для этой цели предлагается программа: 00. КП4 01. FL3 02. 00 03. С/П 04. КП4 05. БП 06. 03. С помощью ее фрагмента 03-06 в память микрокалькулятора можно внести 11 чисел, а не 8, как указано у В.П.Дьяконова.
Вносим число 4 в регистр Р4 и нажимаем клавиши БП, 0, 3, С/П. Калькулятор готов к работе. Набираем на индикаторе первое из вносимых чисел и нажимаем клавишу С/П. После останова вносим второе число, опять С/П и так далее. Набираемые числа расположатся в порядке их введения в регистрах Р5, Р6, ... Р9, РА. ... РД. РО. Р1. В оставшиеся регистры (второй, третий и четвертый) числа можно ввести обычным способом.
Фрагмент 00-03 служит для ввода одного и того же числа в несколько регистров памяти. Такая необходимость возникает при решении задач интерполяции, расчетах квадратичных приближений и т.д.
Возможности программы проиллюстрируем на примере такой задачи: даны числа a, b, c, d, e; требуется ввести а в пять регистров, b - в три и с, d, e по одному в три регистра. Для решения задачи вводим программу и переходим в автоматический режим. Вводим 4 в Р4, 5 - в Р3, a набираем на индикаторе, нажимаем В/О и С/П. После останова вводим 3 в РЗ3, b набираем на индикаторе, снова нажимаем В/О и С/П. Затем после останова набираем на индикаторе с и нажимаем только С/П; так же поступаем для ввода d и е. Число a окажется в регистрах Р5-Р9, b - в регистрах РА-PC, с - в РД, d - в Р0, е - в Р1.
Конечно, можно использовать и меньшее число регистров памяти, прекратив в нужном месте ввод чисел нлн внеся в регистр Р4 число, большее четырех (последним из регистров, куда можно вносить числа вторым из этих способов, будет по-прежнему Р1).
А.ТУЛАЙКОВ (г.Долгопрудный)
[ УЗЕЛКИ НА ПАМЯТЬ
Программу отладить тем легче, чем больше в ней уже испытанных подпрограмм.
И.ГРИЦЕНКО (с.Иванковцы Знаменского р-на Кировоградской обл.) ]
[ ОТВЕТ НА ЗАДАЧУ
Исходное число - 909, последнее - 5537, что при чтении "вверх ногами" дает английское LESS (меньше) ]
РАССЧИТЫВАЕМ ПЛАВКУ
Судя по статьям, публикуемым под рубрикой "Человек с микрокалькулятором", возможности микрокалькуляторов далеко не в полной мере используются в практике промышленного производства. Возьму на себя смелость утверждать, что это объясняется не столько ограниченными возможностями калькуляторов, сколько косностью некоторых производственников.
Возьмем, к примеру, задачу расчета добавок по ходу плавки сталей высоколегированных марок. Расчет достаточно несложен, чтобы выполнить его на микрокалькуляторе. Вооружившись им, плавильный мастер получит нужные числа за полминуты.
Задача ставится так. В определенный момент плавки отбирается проба жидкого металла, в которой методами химического и спектрального анализа устанавливается содержание легирующих элементов в весовых процентах. Обозначим эти количества Вi.
Содержание легирующих элементов в сплаве, который должен быть получен, обозначим Аi. Эти значения достигаются путем добавления в металл ферросплавов, в каждый из которых наряду с железом входит соответствующий элемент с процентным содержанием Ci. Требуется вычислить вес добавки каждого ферросплава. Обозначим эти искомые величины Pi, а вес металла при отборе пробы Р0. Теперь достижение заданного химического состава по каждому элементу нетрудно выразить равенствами:
Р0Вi + РiСi = (Р0 + sum2Pi)Ai.
Получилась система линейных уравнений. Если решать ее на калькуляторе и использовать для этого какой-либо стандартный алгоритм, то, сопоставляя его с возможностями калькулятора, мы тем самым ограничим порядок системы, то есть число легирующих добавок, охватываемое расчетом. Но стоит ли связывать себя заведомыми ограничениями? Весьма стройный вид системы позволяет надеяться, что у нее есть аналитическое решение. И оно действительно существует:
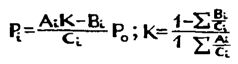
Теперь все определяется объемом памяти микрокалькулятора: в каком количестве сможет она вместить числа А, В, С? Делу помогает такое обстоятельство: некоторые элементы вносятся в металл плавки лишь с добавкой ферросплавов, так что соответствующие Bi равны нулю и не требуют места в памяти.
Рассмотрим в качестве примера плавку стали марки 06х23н27м3д3т. Вот исходные данные, сведенные в таблицы:

Пусть вес плавки Р0 равен 23000кг. Отметим, что титан в металле плавки отсутствует (В5=0). Поэтому все необходимые данные удается занести в память "Электроники Б3-34".

Программа. 00. ИПД 01. / 02. ИП1 03. ИП0 04. / 05. + 06. ИП2 07. ИПА 08. / 09. + 10. ИП3 11. ИПВ 12. / 13. + 14. ИП4 15. ИПС 16. / 17. + 18. 1 19. - 20. ИП6 21. ИП0 22. / 23. ИП7 24. ИПА 25. / 26. + 27. ИП8 28. ИПВ 29. / 30. + 31. ИП9 32. ИПС 33. / 34. + 35. 1 36. - 37. x-y 38. / 39. ПД 40. ИП1 41. * 42. ИП6 43. - 44. ИП0 45. / 46. ИП5 47. * 48. П6 49. ИПД 50. ИП2 51. * 52. ИП7 53. - 54. ИПА 55. / 56. ИП5 57. * 58. П7 59. + 60. ИПД 61. ИП3 62. * 63. ИП8 64. - 65. ИПВ 66. / 67. ИП5 68. * 69. П8 70. + 71. ИПД 72. ИП4 73. * 74. ИП9 75. - 76. ИПС 77. / 78. ИП5 79. * 80. П9 81. + 82. ИП5 83. + 84. /-/ 85. ИПД 86. ИП5 87. * 88. ПД 89. + 90. П0 91. С/П 92. ИП6 93. ИП7 94. ИП8 95. ИП9 96. ИПД
Заносим А5 в регистр X, нажимаем клавиши В/О, С/П и получаем значения искомых величин в килограммах (здесь округлены):

Pк = P0+sum(Pi) - конечный вес плавки. Таким образом можно рассчитать плавку стали любой марки с числом легирующих элементов до пяти.
Одно плохо: "Электроникой Б3-34" трудно пользоваться в условиях цеха. Его автономная работа ограничена двумя часами, а оставлять его на подзарядке рискованно. Неудобна и "Электроника МК-56".
Металлургов устроил бы микрокалькулятор, который по размеру и по возможностям был бы идентичен "Электронике Б3-34", но к тому же имел бы приставку для хранения нескольких (скажем, пяти) программ по 98 шагов в выключенном состоянии, действовал бы автономно в продолжение смены.
Ю.ВОЛОВИЧ, заместитель директора завода "Днепроспецсталь" (г.Запорожье)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
А тем временем уже начали появляться персоналки...
В том же 10/84.
НУЖЕН ЛИ ПЕРСОНАЛЬНО ВАМ ПЕРСОНАЛЬНЫЙ КОМПЬЮТЕР?
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь".
Когда мы прибыли на место, в институт, где должны были увидеть "Агат", то выяснилось, что вся команда, разрабатывавшая его электронные схемы, работает здесь же и есть возможность не только потрогать машину, не только просмотреть красивые проспекты, которые обычно готовят для международных выставок и высокого начальства, но еще и получить информацию об "Агате" от самих его разработчиков, из первых рук. Большинству читателей нужно, видимо, сообщить, что "Агат" - это одна из многих отечественных микроЭВМ и в то же время первая наша машина, которую без оговорок можно отнести к классу персональных компьютеров (персональных ЭВМ) или сокращенно ПК (ПЭВМ).
Всю малогабаритную вычислительную технику до недавнего времени делили на миниЭВМ и микроЭВМ, машины, как правило, совершенно разные, и по назначению и по возможностям. Появившиеся несколько лет назад персональные компьютеры внешне похожи на некоторые микроЭВМ, однако по существу отличаются от всех малых машин настолько, что даже в спокойных и сдержанных технических журналах их появление было отмечено такими, например, эмоциональными всплесками: "Феномен ПК", "Новый этап информационной технологии" и даже "Массовый психоз приобщения к ПК".
Что дает основания для столь сильных оценок? Специалисты объясняют все четко и обстоятельно, но можно рискнуть и пересказать суть дела в двух словах: персональные компьютеры могут постепенно и бескровно приобщить к современной вычислительной технике огромные массы людей, открыть им великолепный инструмент, имя которому ЭВМ. Слово "постепенно" в данном случае означает, что начинающим пользователям персональных ЭВМ не нужно особо сильно напрягаться, бросать свою основную профессию и переучиваться на программистов. Более того - начать работу с персональным компьютером, получить от него первую помощь может человек, не имеющий вообще никакой компьютерной подготовки. То, что все это действительно так, надежно подтверждается спросом на персональные компьютеры - в мире их уже выпущено и продано несколько миллионов, спрос растет, причем очень часто машины покупаются не за казенный счет, не "по перечислению", а за свои собственные деньги, за наличные.
В связи с планируемым серийным выпуском "Агата" журнал еще не раз будет обращаться к теме персональных компьютеров. А сейчас в качестве первого знакомства коротко (точнее, очень коротко) об устройстве этого ПК. Говорят, что пользователю знать устройство ЭВМ совсем не обязательно, подобно тому, как машине не нужно знать устройство человека. Но уместно ли такое сравнение? Человеку, во-первых, хочется знать (на то он и человек), а во-вторых, нужно знать, конечно, в общих чертах, компьютер, с которым он работает: это поможет снять чувство неуверенности, повысит коэффициент раскованности в общении с машиной.
Чтобы наше описание "Агата" не показалось утомительным, автор позволит себе прерывать его извлеченными из записной книжки фрагментами бесед с людьми, уже знающими ПК. Всем им для начала предлагался один и тот же вопрос: "Нужен ли вам персональный компьютер?"
- Персонально мне? Нет, не нужен. Эта вычислительная машина - велосипед, а уже есть ЭВМ автомобили и самолеты. Мне же лично нужна ранета.
- Ну а другим инженерам вашего КБ?
- Это совсем иное дело: вам нужно отредактировать свой вопрос. Есть масса специалистов, которым ПК позволит работать за двоих, а то и за троих. Прн этом работать лучше и легче. Думаю, что в стране несколько миллионов потенциальных пользователей ПК, имею в виду тех, ному машина нужна для дела, а не для фасона.
Как ни старайся уйти от деталей и сжать рассказ об устройстве ЭВМ, начинать приходится с того, что вся электроника машины работает в двоичном коде. Или скажем иначе: машине удобно использовать только два вида знаков - электрический импульс и паузу, как их называют 1 и 0. При этом все сотни тысяч или миллионы элементов машины работают в простом и четком ключевом режиме: "пропускаю ток - не пропускаю", "зарядился - разрядился", "включено - выключено", и все это может иметь только одно толкование - единица или нуль. Правда, двоичный код влечет за собой некоторую громоздкость записей - вместо 2 приходится писать 10, вместо 5 - 101, вместо 55 - 110111. Но это громоздкость, принятая, как говорят врачи, по жизненным показаниям,- гигантские схемы современных ЭВМ могут быть надежными, работая только в двоичном коде.
Двоичным кодом выражаются также буквы и иные знаки. В "Агате", например, 74 клавиши, на большинстве два обозначения, например, русская и латинская буквы (переход с одного значения на другое, как и в пишущей машинке, осуществляется нажатием клавиши "Регистр", есть также переключение больших и малых букв), а всего с клавиатуры может вводиться в машину 192 знака. Каждый из них имеет свой код - свою комбинацию из восьми импульсов-пауз. Легко посчитать, что таких комбинаций может быть 2**8=256, то есть еще есть резерв на 64 кода - резерв конструктора и программиста. Напомним, что один знак в двоичном коде, один импульс или пауза - это наименьшая единица информации, один бит. Ну а 8 бит - узаконенная более крупная единица, байт. Если для передачи буквы тратить 1 байт, то для передачи страницы машинописного текста понадобится около 1800 байт, или примерно 1.8 килобайт, сокращенно 1.8 кбайт (точно 1кбайт = 2**10 бит = 1024 бит). На этой журнальной странице примерно около 6 кбайт; во всем номере журнала (если бы он был без картинок, с одним текстом) почти 1000 кбайт, или иначе почти 1 мегабайт, сокращенно Мбайт; в тридцати томах Большой Советской Энциклопедии - примерно 300 Мбайт. К единицам измерения информации хорошо было бы постепенно привыкнуть, как мы привыкли к метрам или килограммам и без пояснений чувствуем, что такое 0.5м или 20кг.
- Я уже года два работаю на ПК, с удовольствием купил бы такую машину себе домой. Интересно, снолько она будет стоить?
- Где-то между стоимостью цветного телевизора и автомобиля...
- Если будет цена телевизора или даже двух - куплю, если автомобиля - пока воздержусь.
"Агат" построен на основе восьмиразрядного микропроцессора, это, в частности, значит, что цифры, буквы, команды живут в машине в виде восьмибитовых слов, они передаются по восьми параллельным линиям - по каждой линии-проводу идет импульс или пауза передаваемой восьмерки. Все восемь бит одновременно обрабатываются, имеют общий адрес, по которому их, опять-таки одновременно, записывают в память или извлекают из нее.
Появление в нашем рассказе слов "процессор", "адрес", "память" напоминает, что уже пора назвать с суперкороткими пояснениями важнейшие узлы "Агата".
ТАКТОВЫЙ ГЕНЕРАТОР. Это метроном, отбивающий такт, синхронизирующий все процессы в ЭВМ и к тому же главный поставщик сырья для изготовления двоичных чисел, команд, адресов: генератор дает нескончаемые серии импульсов, любой из них можно развести по восьми каналам, в некоторых каналах прервать ток, погасить импульс и создать паузу. Так получают необходимую комбинацию из импульсов и пауз, например, при нажатии клавиши А - рождается 11001001, клавиши Б - 10000101, В - 00100101 и так далее. В "Агате" частота тактового генератора 2МГц (мегагерц), то есть в секунду выстреливается 2 миллиона импульсов. В этой цифре в какой-то мере отражено быстродействие машины - операцию средней сложности она выполняет за 6 тактов, то есть выполняет примерно 300 тысяч таких операций в секунду.
АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО, АЛУ. Именно здесь и проводится обработка байтов (восьмибитовых сигналов), здесь, в АЛУ, их можно складывать, вычитать, умножать и т.д. Можно проводить такие важные для компьютера операции, как сравнение байтов - если, например, 10011011-10011011=0, то эти байты равны. А когда машина умеет сравнивать, то она сама (именно сама, автоматически!), работая циклами ("Сравнить, если А>В, начать сначала...") и перемалывая тонны цифр и знаков, может не просто вычислять, а искать наивыгоднейшие формы металлоконструкций, маршруты перевозок или дозировку лекарств.
- Я пока прекрасно обхожусь ежедневником и записной книжкой.
- А если нужно решить какую-ннбудь сложную производственную задачу?
- Шевелю мозгами и умножаю на бумажке столбиком. Вполне хватает.
ПОСТОЯННОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО, ПЗУ. Его "вечные" (созданные при изготовлении машины) электрические соединения определяют порядок операций, заданных машине раз и навсегда, например, а**5=а*а*а*а*а или sin(x)=х-х**3/3+х**5/5-х**7/7+х**9/9... Емкость ПЗУ "Агата" - 32 килобайта, то есть инструкции, которые он запомнил, заняли бы 20 машинописных страниц. И вот еще что - "вечные" записи в ПЗУ в принципе можно менять, ориентируя "Агат" на определенный класс проблем.
ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО, ОЗУ. Сюда байты попадают на время, например, при вводе информации, с тем чтобы из ОЗУ в нужный момент отправиться на обработку в АЛУ. В ОЗУ (его еще называют запоминающим устройством с произвольной выборкой - ЗУПВ) попадают результаты промежуточных вычислений и команды, которые в нужном порядке пойдут в АЛУ и включат его на нужный режим, например, на сложение чисел. Каждый конкретный байт имеет свой ярлык, свой адрес. А как же иначе? Только по точному ярлыку, по точному адресу можно найти и вызвать конкретную букву или число, данную конкретную команду - чтобы взять именно то, что хочешь, надо точно знать, куда положил. А поскольку в ОЗУ должны одновременно храниться тысячи байтов и у всех у них, естественно, должны быть разные адреса, то адрес, как правило, получается длиннее самого информационного байта. Так, в "Агате" сам информационный сигнал - это 8 бит, а адрес - 16 бит, по 16 параллельным линиям он сопровождает свой информационный байт. Шестнадцатибитовая комбинация позволяет иметь 2**16=65536 разных адресов, то есть разместить в ОЗУ 65536 информационных байтов, 64 килобайта. В "Агате" ОЗУ собрано на одной плате и, устанавливая дополнительные платы - а это предусмотрено,- можно поднять емкость ОЗУ (она в сильной степени определяет возможности машин в решении сложных задач) до 128 и 256 килобайт.
- А почему вы не спрашиваете, нужны ли строителю экскаватор или столяру пила? Персональный компьютер - это инструмент, он берет на себя массу тяжкой, рутинной работы. Вы внесли в таблицу одно изменение, а ПК с учетом этого мгновенно пересчитал все данные в других столбцах. Вы сменили номер рисунка, а ПК сразу же сдвинул всю последующую нумерацию. Но это все мелочи - ПК позволит инженеру, агроному, хозяйственнику быть точным там, где сегодня еще прикидывают на глазок, и поэтому многое теряют.
- Но для этого нужно программировать...
- Ну и что? Немножко программировать должен каждый, и это не так уж сложно. Не сложнее, чем выучить небольшой набор слов и фраз на иностранном языке. Мы обязательно придем к всеобщей компьютерной грамотности, именно в этом, думаю, будет главная миссия ПК.
Трудно удержаться, чтобы не упомянуть две интересные детали. В ЭВМ можно встретить разные виды памяти, в ОЗУ это, как правило, быстродействующая память на электронных приборах. Типичным элементом для запоминания одного бита много десятилетий был триггер - схема на двух взаимосвязанных электронных лампах, а позднее на двух транзисторах: если ток идет в первом транзисторе (или лампе), значит, триггер запомнил 1, если ток во втором транзисторе - запомнился 0. В ОЗУ "Агата" тоже транзисторная память, но на каждый бит "тратится" уже не два транзистора, а один. Это ключ, через который заряжают или разряжают конденсатор - в первом случае записывают 1, во втором- 0. Конденсатор, как известно, постепенно разряжается, и чтобы в ОЗУ не развился склероз, всем заряженным конденсаторам 200 раз в секунду добавляется порция энергии - происходит восстановление информации. И это усложнение оказывается выгодным, так как экономит десятки тысяч транзисторов.
- Нужна ли нашему отделу персональная вычислительная машина? Это не тот вопрос. Спросите лучше, нужны ли ей мы со своей неорганизованностью, расхлябанностью, нечеткостью?
- Но машина дисциплинирует, подтягивает.
- Ничего не выйдет. Машина подсчитает одно, а директор прикажет другое...
Второе, что хотелось бы сказать, завершая знакомство с ОЗУ, связано с личными воспоминаниями о не столь уж далеких временах. Лет тридцать тому назад ламповое ОЗУ на 64 килобайта занимало бы несколько больших шкафов, 128 тысяч электронных ламп (в триггере - две лампы) энергию потребляли бы сотнями киловатт и каждые несколько часов какая-нибудь лампа выходила бы из строя. Потом лампы заменил транзистор, аппаратура стала значительно компактней, экономичней и надежней, транзисторная память на 64 кбайта уже, пожалуй, могла бы разместиться в тумбах письменного стола. И вот теперь - оперативная память "Агата", 32 черных прямоугольника размером с почтовую марку, каждый соединился с печатным монтажом платы большим числом ножек-выводов, чем-то напоминая сороконожку. Это интегральная схема К565РУ6, запрессованный в пластмассу кремниевый кристалл (НиЖ 10/76), внутри которого создано 16 тысяч запоминающих конденсаторов, каждый с транзисторным ключом. Проще говоря, каждая микросхема имеет 16 тысяч отдельных "ящиков" для хранения одного бита, а 32 микросхемы (в комплектах по 8 штук), работая одновременно, запоминают 65536 восьмибитовых комбинаций, то есть 64 килобайта. И не просто запоминают. На восьмерку микросхем одновременно подается адрес данного байта, по этому адресу байт попадает в строго определенные элементы памяти, откуда его легко достать, сообщив микросхемам тот же адрес. Все это происходит внутри микросхем. Всего в "Агате" 86 микросхем, их эквивалент - миллионы транзисторов, диодов, конденсаторов, резисторов и других элементов.
Что ни говори, а людям старшего поколения, заставшим эпоху ламповой электроники, трудно привыкнуть к фантастической компактности интегральных схем, встречи с ними, скажу прямо, всегда волнуют, заставляют о многом задумываться.
- Любой, кто поработал с ПК, скажет вам: через десять-двадцать лет эти машины будут на рабочем месте каждого специалиста, а у многих и дома. У нас так много дел и часто очень сложных, иметь такого помощника, как ПК,- просто счастье.
- Но многим понадобятся большие машины...
- Скорее сети ЭВМ, чтобы я по телефонному кабелю мог подключиться к большому банку данных, например, заглянуть в книги большой библиотеки. Или подключиться к большой машине для решения сложных задач.
УСТРОЙСТВО УПРАВЛЕНИЯ. Это дирижер, который строго в соответствии с партитурой, с программой, записанной в ПЗУ и ОЗУ, управляет работой всей машины - дает указания направить тот или иной байт в память, в нужный момент извлечь его оттуда, направить в АЛУ, переключить АЛУ для проведения определенной операции, записать в ОЗУ промежуточный результат, завершить вычисления, запросить из ОЗУ результат, направить его для отображения на дисплей и т.д.
ПРОЦЕССОР. Названные узлы - АЛУ, небольшая "для служебных целей" оперативная память и устройство управления - образуют основу ЭВМ, ее процессор. В "Агате" микропроцессор, как уже говорилось, восьмиразрядный и реализован в виде трех интегральных схем - одной К588ВС2 и двух К588ВУ2. Электронная промышленность выпускает и однокристальные микропроцессоры - в одной интегральной схеме практически целая ЭВМ.
КОММУТАТОРЫ И ДЕШИФРАТОРЫ. Это главные работники компьютера, в машинах их тысячи, и делают они все то, что скрыто за словами "записать в память", "запросить по заданному адресу", "изменить режим АЛУ" и т.д. Дешифратор - это несложное транзисторное устройство (в интегральной схеме все оно умещается в микроскопическом участке кристалла), которое распознает комбинации нулей и управляет транзисторным коммутатором-переключателем. Если, например, придет команда 10110110 - включится одна схема, если 10110111 -другая; разбираясь в адресах, дешифраторы с коммутаторами могут подключаться к разным хранилищам ОЗУ, извлекая из них только те байты, которые заданы адресом.
- Я, признаться, начал с игровых программ, целыми вечерами гонял по экрану красных и синих футболистов за желтым мячом. Благодаря играм привык к машине. Уже имею неплохую библиотеку магнитных дисков с деловыми программами.
- Больше не играете?
- Играю, и еще как! Я экономист, вся моя деятельность - игра с хаосом. Выигрываю для предприятия деньги, фонды. Официально это называется повышением эффективности производства.
НАКОПИТЕЛЬ НА ГИБКИХ МАГНИТНЫХ ДИСКАХ, НГМД. Разработав какую-либо программу, не нужно каждый раз вводить ее в "Агат", нажимая клавиши, программу записывают на гибком пластиковом диске с тонким ферромагнитным слоем, как у магнитофонной ленты. По команде машина считает информацию с диска и запишет ее в ОЗУ. Во внешней магнитной памяти можно хранить в большом объеме справочную информацию - на диске диаметром 133мм записано как минимум около 125кбайт (шахматная программа "средней квалификации" занимает 10кбайт), запись ведется по кольцеобразным дорожкам. Шаговый двигатель точно смещает считывающую магнитную головку с дорожки на дорожку, и можно, не просматривая всей записи, сразу попасть в нужный массив информации. Управляет работой накопителя электронный автомат, его скромно называют контроллером. Кстати, внешней памятью для "Агата" может служить и обычный магнитофон.
- Все только и говорят о персональных компьютерах, можно подумать, что это какая-то вершина вычислительной техники. А ведь наша промышленность выпускает целые семейства прекрасных машин - больших, средних и малых. Не за горами сверхбольшие машины. У создателей ЭВМ давние традиции и очень интересные планы.
- И в них отдельная строка для ПК...
- Для промышленности это одна из многих строк в планах.
УСТРОЙСТВО ОТОБРАЖЕНИЯ ИНФОРМАЦИИ, ДИСПЛЕЙ. Его роль может исполнять цветной телевизор, существует приставка, позволяющая вводить сигнал в телевизор прямо в гнездо "Антенна". Но буквы и картинки получаются более четкими, если использовать специальный дисплейный блок (в габаритах того же телевизора). Чтобы писать или рисовать на экране, нужно достаточно сложное управление электронными лучами, делает это контроллер дисплея. На экране размещается 32 строки текста; цифры, рисунки могут появляться в 8 или 16 цветах. Картинка может иметь 256*256 элементов, четкость не на много хуже, чем на газетной фотографии.
ПЕЧАТАЮЩЕЕ УСТРОЙСТВО, ПРИНТЕР. Печатающий элемент - управляемые электромагнитами иголочки (НиЖ 10/80), различные их комбинации формируют нужную букву или цифру. Системой управляет контроллер принтера.
- Детей к ПК надо приучать, школьников. Я в свои 57 лет научился программировать на языке Бейсик за неделю, детям все дается легче и быстрее.
- Но не сделает ли компьютер детей сухими, слишком расчетливыми?
- Если нас телевизор не сломил, то компьютера бояться нечего. Он в личную жизнь не вторгается, голубое небо не перекрашивает и запах полыни не забивает. А работать действительно надо четко, расчетливо.
Нынешний "Агат" (конструкция машины предусматривает ее совершенствование, установку новых плат) скорее всего будет массовым нашим персональным компьютером, но наверняка не единственным. Уже создаются ПК, в которых, например, будет 16- и даже 32-разрядный микропроцессор, то есть информация за каждый такт будет обрабатываться большими порциями. И к тому же эта обработка будет идти быстрее - высокое быстродействие элементов в микросхемах позволит поднять частоту тактового генератора до 5-10 мегагерц. Все это обеспечит машине важные достоинства, она, в частности, будет активнее, быстрее общаться с пользователем.
- Персональный компьютер - хороший секретарь, большой микрокалькулятор, записная книжка, педагог, картотека, шахматный партнер, редактор. Но главное не в этом.
- А в чем?
- Главное в том, что человек, работающий с компьютером,- это совсем другой человек. Другой по стилю, по характеру мышления, по самому подходу к тем задачам, которые он решает. И в итоге по умению обозначить проблему и найти правильное решение. Это касается всех: врачей, экономистов, строителей, транспортников, педагогов. Одним словом, всех.
И вот здесь мы подошли к самой интересной особенности ПК, к тому, с чего и начали. Читатель, мало-мальски знакомый с устройством ЭВМ, прочитав наш микрорассказ об "Агате", скорее всего удивится - все названные узлы есть и в других вычислительных машинах. В чем же тогда состоит "феномен ПК"? Он скорее всего в совершенно новой технологии общения пользователя и ЭВМ. Когда-то это делалось так - программист скрупулезно выписывал машине все предписания, из какой ячейки памяти взять число, какой код команды задействовать, в какую ячейку направить результат и т.д. Потом появились языки программирования, более простые, компактные и логичные способы описания инструкций для машины, их перевод на язык, понятный машине ("из такой-то ячейки взять"... "такую-то команду включить"), поручили программе, зашитой в ПЗУ,- транслятору.
А теперь технология взаимодействия с персональным компьютером: простыми словами, в некоторых языках программирования (Бейсик, Паскаль и др.) английскими, в других (Рапира, Робик и др.) - русскими, вы, человек, только что освоивший клавиатуру, сообщаете машине задание, а она выписывает на экране дисплея набор возможных ваших действий или отмечает вашу ошибку. Вы даете следующее указание или делаете запрос, машина вновь вам отвечает и в диалоговом режиме, при высоком, как говорят специалисты, уровне интерактивности, или, проще, взаимодействия, вы общаетесь с машиной, решаете нужную вам задачу или извлекаете нужную вам конкретную информацию. Именно поэтому пишут о дружественном программировании в персональном компьютере и считают ПК наиболее удобным информационно-вычислительным устройством для "непрограммирующих специалистов".
Но об этом, как говорится, в следующий раз.

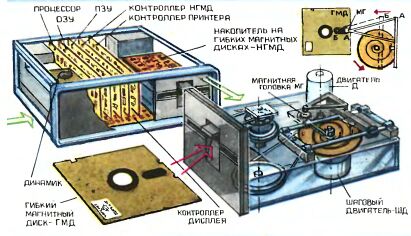
ПРОФЕССИИ ПЕРСОНАЛЬНОГО КОМПЬЮТЕРА
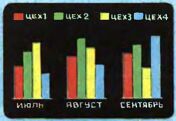
Помощник руководителя: оперативные справки (в том числе в виде графиков и гистограмм); архив совещаний: личный деловой архив; контроль за исполнением поручений; напоминание о деловых планах; обработка экономической информации.
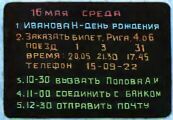
Личный секретарь: контроль за перепиской; подготовка типовых писем, ведение архива; справки (адреса, телефоны, расписания поездов и т.п.): напоминание о назначенных встречах, предстоящих событиях.
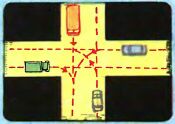
Профессиональная ориентация и подготовка, профессиональный отбор, трудоустройство: тесты на пригодность для работы летчиком, водителем автомобиля, монтажником; проверка квалификации специалиста; обучение профессии; рекомендации по трудоустройству.
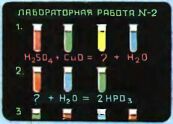
Образование и обучение: обучение основам программирования, применение машины при решении задач, геометрических преобразованиях, редактировании текстов и т.д., лабораторные работы на моделях, справки (формулы, даты, факты).
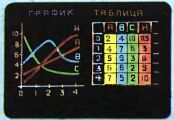
Помощник исследователя, инженера: предварительное моделирование эксперимента; обработка данных; редактирование текстов и рисунков; выборки данных: библиографические справки; типовые инженерные и экономические расчеты; построение таблиц, графиков; работа в сети больших ЭВМ.
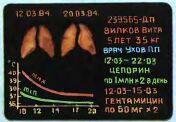
Помощник врача, медицинского работника: подбор лекарств, назначение процедур и прогнозирование хирургических операции с учетом данных больного: ведение истории, болезни: сбор и обработка данных для профилактической диагностики; контроль психофизиологического состояния.

Игры: шахматы, шашки, кубик Рубина, "морской бой", "хоккей", "футбол", "автогонки", "приключения в лабиринте", рисование и раскрашивание картинок на экране, синтез музыки.

Домашнее хозяйство: моделирование одежды; расчет программ вязания; подсчет калорийности блюд; составление меню; контроль коммунальных платежей; учет книг в домашней библиотеке; справки о телевизионных и радиопрограммах.
***
Вроде за 40 лет, все это мы получили... Однако, маленький нюанс, оказалось, что честные программы слишком дороги для пользователя. В любой из перечисленной областей применения поставлен непроходимый барьер между информационным миром и реальностью. Даже "программы руководителя" уже не имеют ничего общего с реальным руководством, а служат генераторами отписок и фальсификаторами результатов. Просто потому, что ее писал не "руководитель", а "программист". Все цепочки передачи информации проходят не "по умным компьютерам и кибернетическим фильтрам", а через руки равнодушных, а часто и злонамеренных "информационных специалистов".
В том же 10/84.
НУЖЕН ЛИ ПЕРСОНАЛЬНО ВАМ ПЕРСОНАЛЬНЫЙ КОМПЬЮТЕР?
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь".
Когда мы прибыли на место, в институт, где должны были увидеть "Агат", то выяснилось, что вся команда, разрабатывавшая его электронные схемы, работает здесь же и есть возможность не только потрогать машину, не только просмотреть красивые проспекты, которые обычно готовят для международных выставок и высокого начальства, но еще и получить информацию об "Агате" от самих его разработчиков, из первых рук. Большинству читателей нужно, видимо, сообщить, что "Агат" - это одна из многих отечественных микроЭВМ и в то же время первая наша машина, которую без оговорок можно отнести к классу персональных компьютеров (персональных ЭВМ) или сокращенно ПК (ПЭВМ).
Всю малогабаритную вычислительную технику до недавнего времени делили на миниЭВМ и микроЭВМ, машины, как правило, совершенно разные, и по назначению и по возможностям. Появившиеся несколько лет назад персональные компьютеры внешне похожи на некоторые микроЭВМ, однако по существу отличаются от всех малых машин настолько, что даже в спокойных и сдержанных технических журналах их появление было отмечено такими, например, эмоциональными всплесками: "Феномен ПК", "Новый этап информационной технологии" и даже "Массовый психоз приобщения к ПК".
Что дает основания для столь сильных оценок? Специалисты объясняют все четко и обстоятельно, но можно рискнуть и пересказать суть дела в двух словах: персональные компьютеры могут постепенно и бескровно приобщить к современной вычислительной технике огромные массы людей, открыть им великолепный инструмент, имя которому ЭВМ. Слово "постепенно" в данном случае означает, что начинающим пользователям персональных ЭВМ не нужно особо сильно напрягаться, бросать свою основную профессию и переучиваться на программистов. Более того - начать работу с персональным компьютером, получить от него первую помощь может человек, не имеющий вообще никакой компьютерной подготовки. То, что все это действительно так, надежно подтверждается спросом на персональные компьютеры - в мире их уже выпущено и продано несколько миллионов, спрос растет, причем очень часто машины покупаются не за казенный счет, не "по перечислению", а за свои собственные деньги, за наличные.
В связи с планируемым серийным выпуском "Агата" журнал еще не раз будет обращаться к теме персональных компьютеров. А сейчас в качестве первого знакомства коротко (точнее, очень коротко) об устройстве этого ПК. Говорят, что пользователю знать устройство ЭВМ совсем не обязательно, подобно тому, как машине не нужно знать устройство человека. Но уместно ли такое сравнение? Человеку, во-первых, хочется знать (на то он и человек), а во-вторых, нужно знать, конечно, в общих чертах, компьютер, с которым он работает: это поможет снять чувство неуверенности, повысит коэффициент раскованности в общении с машиной.
Чтобы наше описание "Агата" не показалось утомительным, автор позволит себе прерывать его извлеченными из записной книжки фрагментами бесед с людьми, уже знающими ПК. Всем им для начала предлагался один и тот же вопрос: "Нужен ли вам персональный компьютер?"
- Персонально мне? Нет, не нужен. Эта вычислительная машина - велосипед, а уже есть ЭВМ автомобили и самолеты. Мне же лично нужна ранета.
- Ну а другим инженерам вашего КБ?
- Это совсем иное дело: вам нужно отредактировать свой вопрос. Есть масса специалистов, которым ПК позволит работать за двоих, а то и за троих. Прн этом работать лучше и легче. Думаю, что в стране несколько миллионов потенциальных пользователей ПК, имею в виду тех, ному машина нужна для дела, а не для фасона.
Как ни старайся уйти от деталей и сжать рассказ об устройстве ЭВМ, начинать приходится с того, что вся электроника машины работает в двоичном коде. Или скажем иначе: машине удобно использовать только два вида знаков - электрический импульс и паузу, как их называют 1 и 0. При этом все сотни тысяч или миллионы элементов машины работают в простом и четком ключевом режиме: "пропускаю ток - не пропускаю", "зарядился - разрядился", "включено - выключено", и все это может иметь только одно толкование - единица или нуль. Правда, двоичный код влечет за собой некоторую громоздкость записей - вместо 2 приходится писать 10, вместо 5 - 101, вместо 55 - 110111. Но это громоздкость, принятая, как говорят врачи, по жизненным показаниям,- гигантские схемы современных ЭВМ могут быть надежными, работая только в двоичном коде.
Двоичным кодом выражаются также буквы и иные знаки. В "Агате", например, 74 клавиши, на большинстве два обозначения, например, русская и латинская буквы (переход с одного значения на другое, как и в пишущей машинке, осуществляется нажатием клавиши "Регистр", есть также переключение больших и малых букв), а всего с клавиатуры может вводиться в машину 192 знака. Каждый из них имеет свой код - свою комбинацию из восьми импульсов-пауз. Легко посчитать, что таких комбинаций может быть 2**8=256, то есть еще есть резерв на 64 кода - резерв конструктора и программиста. Напомним, что один знак в двоичном коде, один импульс или пауза - это наименьшая единица информации, один бит. Ну а 8 бит - узаконенная более крупная единица, байт. Если для передачи буквы тратить 1 байт, то для передачи страницы машинописного текста понадобится около 1800 байт, или примерно 1.8 килобайт, сокращенно 1.8 кбайт (точно 1кбайт = 2**10 бит = 1024 бит). На этой журнальной странице примерно около 6 кбайт; во всем номере журнала (если бы он был без картинок, с одним текстом) почти 1000 кбайт, или иначе почти 1 мегабайт, сокращенно Мбайт; в тридцати томах Большой Советской Энциклопедии - примерно 300 Мбайт. К единицам измерения информации хорошо было бы постепенно привыкнуть, как мы привыкли к метрам или килограммам и без пояснений чувствуем, что такое 0.5м или 20кг.
- Я уже года два работаю на ПК, с удовольствием купил бы такую машину себе домой. Интересно, снолько она будет стоить?
- Где-то между стоимостью цветного телевизора и автомобиля...
- Если будет цена телевизора или даже двух - куплю, если автомобиля - пока воздержусь.
"Агат" построен на основе восьмиразрядного микропроцессора, это, в частности, значит, что цифры, буквы, команды живут в машине в виде восьмибитовых слов, они передаются по восьми параллельным линиям - по каждой линии-проводу идет импульс или пауза передаваемой восьмерки. Все восемь бит одновременно обрабатываются, имеют общий адрес, по которому их, опять-таки одновременно, записывают в память или извлекают из нее.
Появление в нашем рассказе слов "процессор", "адрес", "память" напоминает, что уже пора назвать с суперкороткими пояснениями важнейшие узлы "Агата".
ТАКТОВЫЙ ГЕНЕРАТОР. Это метроном, отбивающий такт, синхронизирующий все процессы в ЭВМ и к тому же главный поставщик сырья для изготовления двоичных чисел, команд, адресов: генератор дает нескончаемые серии импульсов, любой из них можно развести по восьми каналам, в некоторых каналах прервать ток, погасить импульс и создать паузу. Так получают необходимую комбинацию из импульсов и пауз, например, при нажатии клавиши А - рождается 11001001, клавиши Б - 10000101, В - 00100101 и так далее. В "Агате" частота тактового генератора 2МГц (мегагерц), то есть в секунду выстреливается 2 миллиона импульсов. В этой цифре в какой-то мере отражено быстродействие машины - операцию средней сложности она выполняет за 6 тактов, то есть выполняет примерно 300 тысяч таких операций в секунду.
АРИФМЕТИКО-ЛОГИЧЕСКОЕ УСТРОЙСТВО, АЛУ. Именно здесь и проводится обработка байтов (восьмибитовых сигналов), здесь, в АЛУ, их можно складывать, вычитать, умножать и т.д. Можно проводить такие важные для компьютера операции, как сравнение байтов - если, например, 10011011-10011011=0, то эти байты равны. А когда машина умеет сравнивать, то она сама (именно сама, автоматически!), работая циклами ("Сравнить, если А>В, начать сначала...") и перемалывая тонны цифр и знаков, может не просто вычислять, а искать наивыгоднейшие формы металлоконструкций, маршруты перевозок или дозировку лекарств.
- Я пока прекрасно обхожусь ежедневником и записной книжкой.
- А если нужно решить какую-ннбудь сложную производственную задачу?
- Шевелю мозгами и умножаю на бумажке столбиком. Вполне хватает.
ПОСТОЯННОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО, ПЗУ. Его "вечные" (созданные при изготовлении машины) электрические соединения определяют порядок операций, заданных машине раз и навсегда, например, а**5=а*а*а*а*а или sin(x)=х-х**3/3+х**5/5-х**7/7+х**9/9... Емкость ПЗУ "Агата" - 32 килобайта, то есть инструкции, которые он запомнил, заняли бы 20 машинописных страниц. И вот еще что - "вечные" записи в ПЗУ в принципе можно менять, ориентируя "Агат" на определенный класс проблем.
ОПЕРАТИВНОЕ ЗАПОМИНАЮЩЕЕ УСТРОЙСТВО, ОЗУ. Сюда байты попадают на время, например, при вводе информации, с тем чтобы из ОЗУ в нужный момент отправиться на обработку в АЛУ. В ОЗУ (его еще называют запоминающим устройством с произвольной выборкой - ЗУПВ) попадают результаты промежуточных вычислений и команды, которые в нужном порядке пойдут в АЛУ и включат его на нужный режим, например, на сложение чисел. Каждый конкретный байт имеет свой ярлык, свой адрес. А как же иначе? Только по точному ярлыку, по точному адресу можно найти и вызвать конкретную букву или число, данную конкретную команду - чтобы взять именно то, что хочешь, надо точно знать, куда положил. А поскольку в ОЗУ должны одновременно храниться тысячи байтов и у всех у них, естественно, должны быть разные адреса, то адрес, как правило, получается длиннее самого информационного байта. Так, в "Агате" сам информационный сигнал - это 8 бит, а адрес - 16 бит, по 16 параллельным линиям он сопровождает свой информационный байт. Шестнадцатибитовая комбинация позволяет иметь 2**16=65536 разных адресов, то есть разместить в ОЗУ 65536 информационных байтов, 64 килобайта. В "Агате" ОЗУ собрано на одной плате и, устанавливая дополнительные платы - а это предусмотрено,- можно поднять емкость ОЗУ (она в сильной степени определяет возможности машин в решении сложных задач) до 128 и 256 килобайт.
- А почему вы не спрашиваете, нужны ли строителю экскаватор или столяру пила? Персональный компьютер - это инструмент, он берет на себя массу тяжкой, рутинной работы. Вы внесли в таблицу одно изменение, а ПК с учетом этого мгновенно пересчитал все данные в других столбцах. Вы сменили номер рисунка, а ПК сразу же сдвинул всю последующую нумерацию. Но это все мелочи - ПК позволит инженеру, агроному, хозяйственнику быть точным там, где сегодня еще прикидывают на глазок, и поэтому многое теряют.
- Но для этого нужно программировать...
- Ну и что? Немножко программировать должен каждый, и это не так уж сложно. Не сложнее, чем выучить небольшой набор слов и фраз на иностранном языке. Мы обязательно придем к всеобщей компьютерной грамотности, именно в этом, думаю, будет главная миссия ПК.
Трудно удержаться, чтобы не упомянуть две интересные детали. В ЭВМ можно встретить разные виды памяти, в ОЗУ это, как правило, быстродействующая память на электронных приборах. Типичным элементом для запоминания одного бита много десятилетий был триггер - схема на двух взаимосвязанных электронных лампах, а позднее на двух транзисторах: если ток идет в первом транзисторе (или лампе), значит, триггер запомнил 1, если ток во втором транзисторе - запомнился 0. В ОЗУ "Агата" тоже транзисторная память, но на каждый бит "тратится" уже не два транзистора, а один. Это ключ, через который заряжают или разряжают конденсатор - в первом случае записывают 1, во втором- 0. Конденсатор, как известно, постепенно разряжается, и чтобы в ОЗУ не развился склероз, всем заряженным конденсаторам 200 раз в секунду добавляется порция энергии - происходит восстановление информации. И это усложнение оказывается выгодным, так как экономит десятки тысяч транзисторов.
- Нужна ли нашему отделу персональная вычислительная машина? Это не тот вопрос. Спросите лучше, нужны ли ей мы со своей неорганизованностью, расхлябанностью, нечеткостью?
- Но машина дисциплинирует, подтягивает.
- Ничего не выйдет. Машина подсчитает одно, а директор прикажет другое...
Второе, что хотелось бы сказать, завершая знакомство с ОЗУ, связано с личными воспоминаниями о не столь уж далеких временах. Лет тридцать тому назад ламповое ОЗУ на 64 килобайта занимало бы несколько больших шкафов, 128 тысяч электронных ламп (в триггере - две лампы) энергию потребляли бы сотнями киловатт и каждые несколько часов какая-нибудь лампа выходила бы из строя. Потом лампы заменил транзистор, аппаратура стала значительно компактней, экономичней и надежней, транзисторная память на 64 кбайта уже, пожалуй, могла бы разместиться в тумбах письменного стола. И вот теперь - оперативная память "Агата", 32 черных прямоугольника размером с почтовую марку, каждый соединился с печатным монтажом платы большим числом ножек-выводов, чем-то напоминая сороконожку. Это интегральная схема К565РУ6, запрессованный в пластмассу кремниевый кристалл (НиЖ 10/76), внутри которого создано 16 тысяч запоминающих конденсаторов, каждый с транзисторным ключом. Проще говоря, каждая микросхема имеет 16 тысяч отдельных "ящиков" для хранения одного бита, а 32 микросхемы (в комплектах по 8 штук), работая одновременно, запоминают 65536 восьмибитовых комбинаций, то есть 64 килобайта. И не просто запоминают. На восьмерку микросхем одновременно подается адрес данного байта, по этому адресу байт попадает в строго определенные элементы памяти, откуда его легко достать, сообщив микросхемам тот же адрес. Все это происходит внутри микросхем. Всего в "Агате" 86 микросхем, их эквивалент - миллионы транзисторов, диодов, конденсаторов, резисторов и других элементов.
Что ни говори, а людям старшего поколения, заставшим эпоху ламповой электроники, трудно привыкнуть к фантастической компактности интегральных схем, встречи с ними, скажу прямо, всегда волнуют, заставляют о многом задумываться.
- Любой, кто поработал с ПК, скажет вам: через десять-двадцать лет эти машины будут на рабочем месте каждого специалиста, а у многих и дома. У нас так много дел и часто очень сложных, иметь такого помощника, как ПК,- просто счастье.
- Но многим понадобятся большие машины...
- Скорее сети ЭВМ, чтобы я по телефонному кабелю мог подключиться к большому банку данных, например, заглянуть в книги большой библиотеки. Или подключиться к большой машине для решения сложных задач.
УСТРОЙСТВО УПРАВЛЕНИЯ. Это дирижер, который строго в соответствии с партитурой, с программой, записанной в ПЗУ и ОЗУ, управляет работой всей машины - дает указания направить тот или иной байт в память, в нужный момент извлечь его оттуда, направить в АЛУ, переключить АЛУ для проведения определенной операции, записать в ОЗУ промежуточный результат, завершить вычисления, запросить из ОЗУ результат, направить его для отображения на дисплей и т.д.
ПРОЦЕССОР. Названные узлы - АЛУ, небольшая "для служебных целей" оперативная память и устройство управления - образуют основу ЭВМ, ее процессор. В "Агате" микропроцессор, как уже говорилось, восьмиразрядный и реализован в виде трех интегральных схем - одной К588ВС2 и двух К588ВУ2. Электронная промышленность выпускает и однокристальные микропроцессоры - в одной интегральной схеме практически целая ЭВМ.
КОММУТАТОРЫ И ДЕШИФРАТОРЫ. Это главные работники компьютера, в машинах их тысячи, и делают они все то, что скрыто за словами "записать в память", "запросить по заданному адресу", "изменить режим АЛУ" и т.д. Дешифратор - это несложное транзисторное устройство (в интегральной схеме все оно умещается в микроскопическом участке кристалла), которое распознает комбинации нулей и управляет транзисторным коммутатором-переключателем. Если, например, придет команда 10110110 - включится одна схема, если 10110111 -другая; разбираясь в адресах, дешифраторы с коммутаторами могут подключаться к разным хранилищам ОЗУ, извлекая из них только те байты, которые заданы адресом.
- Я, признаться, начал с игровых программ, целыми вечерами гонял по экрану красных и синих футболистов за желтым мячом. Благодаря играм привык к машине. Уже имею неплохую библиотеку магнитных дисков с деловыми программами.
- Больше не играете?
- Играю, и еще как! Я экономист, вся моя деятельность - игра с хаосом. Выигрываю для предприятия деньги, фонды. Официально это называется повышением эффективности производства.
НАКОПИТЕЛЬ НА ГИБКИХ МАГНИТНЫХ ДИСКАХ, НГМД. Разработав какую-либо программу, не нужно каждый раз вводить ее в "Агат", нажимая клавиши, программу записывают на гибком пластиковом диске с тонким ферромагнитным слоем, как у магнитофонной ленты. По команде машина считает информацию с диска и запишет ее в ОЗУ. Во внешней магнитной памяти можно хранить в большом объеме справочную информацию - на диске диаметром 133мм записано как минимум около 125кбайт (шахматная программа "средней квалификации" занимает 10кбайт), запись ведется по кольцеобразным дорожкам. Шаговый двигатель точно смещает считывающую магнитную головку с дорожки на дорожку, и можно, не просматривая всей записи, сразу попасть в нужный массив информации. Управляет работой накопителя электронный автомат, его скромно называют контроллером. Кстати, внешней памятью для "Агата" может служить и обычный магнитофон.
- Все только и говорят о персональных компьютерах, можно подумать, что это какая-то вершина вычислительной техники. А ведь наша промышленность выпускает целые семейства прекрасных машин - больших, средних и малых. Не за горами сверхбольшие машины. У создателей ЭВМ давние традиции и очень интересные планы.
- И в них отдельная строка для ПК...
- Для промышленности это одна из многих строк в планах.
УСТРОЙСТВО ОТОБРАЖЕНИЯ ИНФОРМАЦИИ, ДИСПЛЕЙ. Его роль может исполнять цветной телевизор, существует приставка, позволяющая вводить сигнал в телевизор прямо в гнездо "Антенна". Но буквы и картинки получаются более четкими, если использовать специальный дисплейный блок (в габаритах того же телевизора). Чтобы писать или рисовать на экране, нужно достаточно сложное управление электронными лучами, делает это контроллер дисплея. На экране размещается 32 строки текста; цифры, рисунки могут появляться в 8 или 16 цветах. Картинка может иметь 256*256 элементов, четкость не на много хуже, чем на газетной фотографии.
ПЕЧАТАЮЩЕЕ УСТРОЙСТВО, ПРИНТЕР. Печатающий элемент - управляемые электромагнитами иголочки (НиЖ 10/80), различные их комбинации формируют нужную букву или цифру. Системой управляет контроллер принтера.
- Детей к ПК надо приучать, школьников. Я в свои 57 лет научился программировать на языке Бейсик за неделю, детям все дается легче и быстрее.
- Но не сделает ли компьютер детей сухими, слишком расчетливыми?
- Если нас телевизор не сломил, то компьютера бояться нечего. Он в личную жизнь не вторгается, голубое небо не перекрашивает и запах полыни не забивает. А работать действительно надо четко, расчетливо.
Нынешний "Агат" (конструкция машины предусматривает ее совершенствование, установку новых плат) скорее всего будет массовым нашим персональным компьютером, но наверняка не единственным. Уже создаются ПК, в которых, например, будет 16- и даже 32-разрядный микропроцессор, то есть информация за каждый такт будет обрабатываться большими порциями. И к тому же эта обработка будет идти быстрее - высокое быстродействие элементов в микросхемах позволит поднять частоту тактового генератора до 5-10 мегагерц. Все это обеспечит машине важные достоинства, она, в частности, будет активнее, быстрее общаться с пользователем.
- Персональный компьютер - хороший секретарь, большой микрокалькулятор, записная книжка, педагог, картотека, шахматный партнер, редактор. Но главное не в этом.
- А в чем?
- Главное в том, что человек, работающий с компьютером,- это совсем другой человек. Другой по стилю, по характеру мышления, по самому подходу к тем задачам, которые он решает. И в итоге по умению обозначить проблему и найти правильное решение. Это касается всех: врачей, экономистов, строителей, транспортников, педагогов. Одним словом, всех.
И вот здесь мы подошли к самой интересной особенности ПК, к тому, с чего и начали. Читатель, мало-мальски знакомый с устройством ЭВМ, прочитав наш микрорассказ об "Агате", скорее всего удивится - все названные узлы есть и в других вычислительных машинах. В чем же тогда состоит "феномен ПК"? Он скорее всего в совершенно новой технологии общения пользователя и ЭВМ. Когда-то это делалось так - программист скрупулезно выписывал машине все предписания, из какой ячейки памяти взять число, какой код команды задействовать, в какую ячейку направить результат и т.д. Потом появились языки программирования, более простые, компактные и логичные способы описания инструкций для машины, их перевод на язык, понятный машине ("из такой-то ячейки взять"... "такую-то команду включить"), поручили программе, зашитой в ПЗУ,- транслятору.
А теперь технология взаимодействия с персональным компьютером: простыми словами, в некоторых языках программирования (Бейсик, Паскаль и др.) английскими, в других (Рапира, Робик и др.) - русскими, вы, человек, только что освоивший клавиатуру, сообщаете машине задание, а она выписывает на экране дисплея набор возможных ваших действий или отмечает вашу ошибку. Вы даете следующее указание или делаете запрос, машина вновь вам отвечает и в диалоговом режиме, при высоком, как говорят специалисты, уровне интерактивности, или, проще, взаимодействия, вы общаетесь с машиной, решаете нужную вам задачу или извлекаете нужную вам конкретную информацию. Именно поэтому пишут о дружественном программировании в персональном компьютере и считают ПК наиболее удобным информационно-вычислительным устройством для "непрограммирующих специалистов".
Но об этом, как говорится, в следующий раз.


ПРОФЕССИИ ПЕРСОНАЛЬНОГО КОМПЬЮТЕРА

Помощник руководителя: оперативные справки (в том числе в виде графиков и гистограмм); архив совещаний: личный деловой архив; контроль за исполнением поручений; напоминание о деловых планах; обработка экономической информации.

Личный секретарь: контроль за перепиской; подготовка типовых писем, ведение архива; справки (адреса, телефоны, расписания поездов и т.п.): напоминание о назначенных встречах, предстоящих событиях.

Профессиональная ориентация и подготовка, профессиональный отбор, трудоустройство: тесты на пригодность для работы летчиком, водителем автомобиля, монтажником; проверка квалификации специалиста; обучение профессии; рекомендации по трудоустройству.

Образование и обучение: обучение основам программирования, применение машины при решении задач, геометрических преобразованиях, редактировании текстов и т.д., лабораторные работы на моделях, справки (формулы, даты, факты).

Помощник исследователя, инженера: предварительное моделирование эксперимента; обработка данных; редактирование текстов и рисунков; выборки данных: библиографические справки; типовые инженерные и экономические расчеты; построение таблиц, графиков; работа в сети больших ЭВМ.

Помощник врача, медицинского работника: подбор лекарств, назначение процедур и прогнозирование хирургических операции с учетом данных больного: ведение истории, болезни: сбор и обработка данных для профилактической диагностики; контроль психофизиологического состояния.

Игры: шахматы, шашки, кубик Рубина, "морской бой", "хоккей", "футбол", "автогонки", "приключения в лабиринте", рисование и раскрашивание картинок на экране, синтез музыки.

Домашнее хозяйство: моделирование одежды; расчет программ вязания; подсчет калорийности блюд; составление меню; контроль коммунальных платежей; учет книг в домашней библиотеке; справки о телевизионных и радиопрограммах.
***
Вроде за 40 лет, все это мы получили... Однако, маленький нюанс, оказалось, что честные программы слишком дороги для пользователя. В любой из перечисленной областей применения поставлен непроходимый барьер между информационным миром и реальностью. Даже "программы руководителя" уже не имеют ничего общего с реальным руководством, а служат генераторами отписок и фальсификаторами результатов. Просто потому, что ее писал не "руководитель", а "программист". Все цепочки передачи информации проходят не "по умным компьютерам и кибернетическим фильтрам", а через руки равнодушных, а часто и злонамеренных "информационных специалистов".

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
12/84
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
Мне нравится клубный характер рубрики "Человек с микрокалькулятором", возможность бесед и даже споров",- так начинает свое письмо в редакцию читатель Е.Федорец из Владивостока. Новая рубрика так и задумывалась: она существует, питаясь, как живой водой, читательской почтой.
За год жизни "Человек с микрокалькулятором" получил свыше тысячи писем (не считая ответов на конкурсные задачи). Пишут инженеры и рабочие, астрономы и музыканты, пишут студенты и домохозяйки, школьники и пенсионеры... В одних письмах - слова благодарности, в других - нелицеприятная критика. Нам одинаково дороги и те и другие. Первые - как признание полезности нашей работы, вторые - как рекомендации для ее улучшения.
Характер рубрики таков, что ни одна публикация под нею не может претендовать на роль истины в последней инстанции. Каждая затронутая проблема остается открытой для дальнейшей разработки. В спорах читателей рождается их мастерство программирования.
Редкое письмо не содержит ту или иную программу. И здесь, уважаемые читатели, позвольте познакомить вас с небольшой статистикой. Анализ случайной выборки из 200 писем (сделанный, естественно, с помощью микрокалькулятора) дал такие результаты.
64 процента программ - игровые. Первенство здесь делят разновидности игр "Ним" и "Морской бой" (по 20 процентов). Участвующие в этих "боях" корабли, пожалуй, уже сравнимы по численности с военно-морскими силами всех стран мира.
Столько же, то есть 20 процентов писем, содержит описание "вечного календаря" и связанных с ним проблем "биоритмов" и "гороскопов". Теперь все сотрудники редакции, а заодно их родные и близкие могут узнавать свою судьбу, пользуясь индивидуальными программами.
10 процентов - серьезные математические программы: решение алгебраических и дифференциальных уравнений, интегрирование, статистика.
Наконец, 6 процентов - прикладные программы, призванные облегчить труд геодезистов и металлургов, строителей и преподавателей. Хотелось бы, чтобы таких программ присылалось побольше и чтобы их спектр был пошире. Ждем писем от врачей и филологов, спортивных тренеров и архитекторов.
Понятно, что далеко не все программы мы можем опубликовать. Тем более что изрядная их часть не лучше приведенных в книгах А.Цветкова и В.Епанечникова, Я.Трохименко и Ф.Любича (библиография была дана в 6/84).
Тем не менее мы стараемся всесторонне отражать читательские интересы. Так, в этом номере журнала К.Ткачук из г.Апатиты Мурманской области излагает свою концепцию "нежестких" программ, А.Раздобреев из г.Владимира рассказывает о методе Ньютона для решения уравнений, москвич А.Бойко предлагает звуковой индикатор для микрокалькулятора "Электроника Б3-34", по предложению Д.Мыслина из г.Новосибирска дается таблица кодов. Как всегда, есть и "маленькие хитрости". Мы надеемся, что читатели будут чаще присылать нам эти крупицы программистского опыта.
Верстая очередной выпуск рубрики, мы каждый раз отдаем предпочтение тем письмам, где либо ставятся новые, оригинальные проблемы, либо по-новому решаются старые. "Да иначе, наверное, и нельзя из-за большого разнообразия специальностей, представленных в вашем, простите, в нашем клубе",- пишет уже упомянутый Е.Федорец.
МЕТОД НЬЮТОНА
Корень уравнения ф(x)=0 бывает удобно отыскивать итерационным методом, приводя уравнение к виду x=f(x) и выполняя итерации по правилу x[n+i]=f(xn). Из уравнения, которое нужно решить, можно получить множество итерационных уравнений с разными правыми частями. Твердых правил по выбору подходящей функции f(x) нет, поэтому сходимость процесса, тем более быстрая сходимость, часто бывает делом случая. Можно ли улучшить сходимость, меняя вид функции f(x)?
Каждое последующее итерационное приближение отличается от предыдущего на поправку дn=f(xn)-xn, и итерационное уравнение можно записать так: x[n+i]=хn+дn. Вспомним уравнение х=cos(x) с начальным приближением х0=0.7 (10/83). Получалось
д0=0.0648422
д1=-0.0433505
д2=0.0293297
д3=-0.0196926
...
Как видим, величины дn не так уж малы. Чтобы все семь цифр после запятой стали нулями, требуется 35 приближений, при этом х=0.7390851.
Быть может, стоит на каждом шагу уменьшать поправку д - брать вместо нее некоторую ее долю а, то есть модифицировать уравнение так: x[n+i]=xn+a[f(хn)-хn]? Возьмем а=0.5, и тогда ответ с семью верными знаками после запятой получается всего за восемь итераций. Существенное уменьшение! Если взять а=0.6, то хватит всего трех итераций. Можно ли уменьшить их число?
Известно, что сходимость итерационного метода для уравнения х=f(x) обеспечивается неравенством |f'(x)|<1, причем сходимость тем быстрее, чем меньше абсолютная величина производной. В модифицированном уравнении будем выбирать коэффициент а таким, чтобы производная правой части на каждом шагу равнялась 0. Так мы приходим к методу Ньютона для поиска корня уравнения
ф(х)=0;
к стандартному виду оно приводится заменой
f(x)=Ф(х)+х.
Смысл метода ясен из графика, а итерационная формула такова:
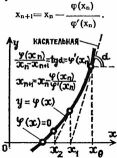
Здесь для получения следующего приближения требуется вычислять не только значение функции ф(х), но и ее производной ф'(х), что усложняет расчеты. Зато условия сходимости для этого метода менее жесткие, чем для метода итераций.
Владельцам программируемых микрокалькуляторов лучше запрограммировать формулу, оформив вычисление функции ф(х) как подпрограмму. Производную можно вычислять приближенно:
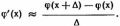
Чем меньше приращение дельта, тем точнее значение производной. При программировании итерационных процессов в один из регистров заносится величина, определяющая заданную точность нахождения корня. Именно ее удобно использовать в качестве дельты. Программа уточнения корня должна быть как можно короче, чтобы в программной памяти осталось достаточно места для вычисления функции. С этой точки зрения наиболее удобной записью итерационного уравнения будет

которая получается из исходного уравнения элементарными преобразованиями. Применим метод Ньютона для решения уравнения, к которому привела "загадка жрецов бога Ра" (2/84). Запишем его так:
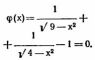
Принимая Дельта=0.001 и x0=1, по последней из форм итерационного уравнения получим x1=1.292, х2=1.235, х3=1.231, x4=1.231.
Чтобы найти ответ, потребовалось четыре приближения. Метод итераций требовал 11, причем сначала надо было подобрать подходящий вид функции.
Какой же метод лучше? Для микрокалькулятора с весьма жесткими ограничениями на объем памяти больше подходит метод итераций: программа получается короче. Но могут возникнуть значительные трудности при подборе функции, обеспечивающей сходимость.
Метод Ньютона, хотя реализуется более громоздкой программой, как правило, обеспечивает более быструю (по числу шагов) сходимость, но выигрыш во времени невелик, так как за каждый цикл функция вычисляется дважды.
Так что, если можно применить метод итераций, надо остановиться на нем. Правда, с методом Ньютона трудно конкурировать, если требуется найти несколько корней. Например, уравнение х2-х-2=0 имеет корни x1=2, х2=-1. Методом Ньютона при разных начальных приближениях легко находятся оба. Чтобы найти эти корни методом итераций, надо использовать два разных уравнения, например, x=sqr(x+2) и х=2/(x-1).
Еще сложней обстоит дело с трансцендентными уравнениями. Например, уравнение tg(x)=3/4х имеет бесконечное число решений, и методом Ньютона можно нх найти столько, сколько нужно. А с помощью метода итераций искать их непросто.
В общем, готовых рецептов нет, каждая новая задача требует творческого подхода. Тем больше удовлетворение, когда ее удается решить.
А.РАЗДОБРЕЕВ (г.Владимир)
[ УЗЕЛКИ НА ПАМЯТЬ
Желательно избегать команды ^. В программном режиме она, как правило, лишняя. Правильное использование стека практически реализует ее функции.
В.ХОХЛОВ (г.Днепропетровск) ]
"НЕЖЕСТКИЕ" ПРОГРАММЫ
Многие владельцы микрокалькуляторов не представляют всех тех возможностей, которые заложены в этих машинах.
Программа для калькулятора составляется, как правило, для решения конкретной задачи. Варьируются лишь исходные данные. Я инженер-строитель и ради примера приведу типичную задачу из сопромата: определение моментов инерции J и J' прямоугольного сечения балки соответственно относительно оси хх, проходящей через центр тяжести и произвольной оси х'х'.
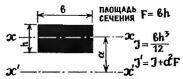
Нетрудно составить программу для вычисления J' и использовать ее в неизменном виде, каждый раз вводя значения a, b, h. Но допустим, сечение балки имеет более замысловатый вид:

Составлять для каждой конфигурации свою программу? Нецелесообразно! Имеет смысл разбить сечение на прямоугольники, затем, опираясь на это разбиение, определить центр тяжести сечения, вычислить момент инерцин Ji' каждого прямоугольника относительно проходящей через этот центр оси и подсчитать момент инерции всего сечения в виде суммы: J=sum(Ji').
Суммирование предполагается также и при нахождении центра тяжести сечения, точнее, его расстояния у от некоторой выбранной вначале оси: F=sum(Fi), S=SUM(Fi*ai), y=S/F. Число слагаемых для сечений различных конфигураций будет изменяться в широких пределах, памяти калькулятора может не хватить для хранения исходных данных. Поэтому управление суммированием владельцу калькулятора приходится взять на себя. Но зато в таком "нежестком" режиме удается рассчитывать весьма разнообразные профили!
Рассмотрим соответствующий пример (размеры в сантиметрах).
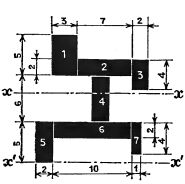
Требуется определить момент инерции сечения относительно оси хх, проходящей через его центр тяжести. Разбиваем сечение на семь прямоугольников, как указано на схеме; вспомогательную ось х'х' проводим по нижней его грани.
Вводим в калькулятор программу; заносим нуль в регистры 4, В, С; проводим вычисления 1-го этапа программы (адреса 00-13). Ширину отдельного прямоугольника bi каждый раз заносим в регистр y, высоту hi - в x (bi ^ hi c/п), расстояние аi' от оси симметрии прямоугольника до вспомогательной оси х'х' - в регистр х (аi' с/п). Результаты: в Р4 - площадь сечения F=83см2, в PC и на индикаторе - статический момент сечения относительно вспомогательной оси S=671.5см3.
Чтобы провести вычисления 2-го этапа (адреса 14-18 ), нажимаем клавишу ШГ со стрелкой вправо, затем С/П. В Р5 и на индикаторе - ордината центра тяжести y=8.09см. В автоматическом режиме вычисляем расстояния ai от центров тяжести отдельных прямоугольников до осн хх, проходящей через центр тяжести сечения (четвертый столбец таблицы).
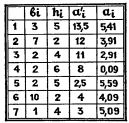
Проводим вычисления 3-го этапа (адреса 19-47). Ширину каждого прямоугольника bi заносим в регистр z, высоту hi - в y, расстояние ai от его центра тяжести до оси хх - в x (bi ^ hi ^ ai c/n). В итоге в РВ и на индикаторе - момент инерции сечения: J=1586,99см4.
ПРОГРАММА. 00. * 01. П6 02. ИП4 03. + 04. П4 05. С/П 06. ИП6 07. * 08. ИПС 09. + 10. ПС 11. С/П 12. БП 13. 00 14. ИПС 15. ИП4 16. / 17. П5 18. С/П 19. П2 20. F() 21. П1 22. F() 23. П0 24. 3 25. ИП1 26. FxY 27. ИП0 28. * 29. 1 30. 2 31. / 32. П3 33. ИП0 34. ИП1 35. * 36. ИП2 37. Fx2 38. * 39. ИП3 40. + 41. ПА 42. ИПВ 43. + 44. ПВ 45. С/П 46. БП 47. 19.
К.ТКАЧУК (г.Апатиты Мурманской обл.)
ОТ РЕДАКЦИИ. Программа не свободна от недостатков. Ее улучшения могут стать упражнением для читателей и вкладом в объявленную ранее (6/84) дискуссию за круглым столом о приемах сервиса. Ждем новых писем на эту тему.
[ КСТАТИ
Во время работы с калькулятором часто замечаешь ту или иную интересную закономерность, которая позже позволяет проводить устные расчеты без калькулятора с большей скоростью и точностью. Как это ни парадоксально, калькулятор помогает считать без калькулятора.
В.ХАРЧЕНКО (г.Киев) ]
ВЫЧИСЛЯЕМ ФАКТОРИАЛ
ИТОГИ КОНКУРСА
На предложение принять участие в конкурсе на лучшую программу для вычисления факториала данного натурального числа откликнулось около 250 человек из самых различных районов страны. Здесь и крупные центры - Москва, Ленинград, Киев, Рига, Новосибирск, Томск, Одесса, Норильск и такие города, как Абакан, Урюпинск, Буй. Из заказника "Предуралье" Пермской области ответ прислал В.Демидов, из латвийского города Лимбежи - К.Лайва, из г.Назыма Тюменской области - В.Лукашев. Военнослужащий В.Кенарский составил программу, находясь в море. Правильные ответы прислали инженеры, студенты, рабочие... Как всегда, радуют ответы школьников - семиклассников А.Кроонмаа и Г.Хилвра (Таллин), С.Виницкого (Москва), восьмиклассников Б.Игнатьева из Ленинграда и В.Черемушкина из Чеховского района Московской области.
Задача была нетрудной, и ее решения в подавляющем большинстве правильны. Причем программы практически одинаковы. Они, как выразился О.Фомичев из Грозного, "действительно несложные и очень простые". О.Рыбаков из Куйбышева был еще более категоричным - после текста программы он написал: "А других и не пришлют", выбрать лучшие работы поэтому было сложно. Тем не менее жюри решило отметить С.Кузнецова, приславшего программу еще до объявления конкурса, программы В.Власова (Нурек), Ю.Тертычного (Северодонецк), Б.Кайсинова (Московская область), использовавших для обработки информации только стековые регистры, программу Е.Атавина (Омск), которая позволяет получать все цифры результата для значений аргумента, не превосходящих 47.
К сожалению, большинство читателей прислали программы, с помощью которых можно вычислять лишь факториалы чисел от 1 до 69, причем некоторые даже не отметили это и не обратили внимание, что результаты расчетов для больших чисел не "влезают" в разрядную сетку микрокалькулятора. Программы для работы с большими аргументами прислали Л.Тихомиров, В.Козлов (Ленинград), А.Сельский (Сумы), П.Якубович (Днепропетровск) и некоторые другие.
Из всех присланных писем одно содержало наиболее полный и интересный анализ проблемы. Автор этого письма - ленинградский профессор Л.Финк и был объявлен победителем нашего конкурса. Соображения его представляются настолько поучительными, что мы решили познакомить с ними читателей.
Составляя программу, пишет Л.Финк, важно представлять область ее применения. Программа вычисления факториала для "Электроники Б3-34" может содержать лишь 7 шагов: 00. П1 01. 1 02. ИП1 03. * 04. FL1 05. 2 06. С/П. Значение n вводится с клавиатуры, результат n! высвечивается на индикаторе. Эта программа, вероятно, рекордна по своей компактности [Можно, правда, получить программу еще короче (5 шагов). Многие читатели прислали такие варианты. Вот один из них: 00. ИП2 01. * 02. FL2 03. 00 04. С/П. Но перед выполнением этой программы нужно занести в соответствующий регистр аргумент и затем набрать на клавиатуре число 1. Пожалуй, такие сложности вряд ли оправдывают сокращение на две команды] и работает достаточно быстро: 5! вычисляется за 8 секунд, 69! - за 95 секунд. При больших числах происходит переполнение разрядной сетки калькулятора, так как результат превосходит 1e100. Однако 0! по этой программе получить также не удается. Она зацикливается. Можно, конечно, сказать: мы и так знаем, что 0!=1, и незачем вводить такой аргумент в программу. А если такую программу нужно использовать в качестве подпрограммы или фрагмента другой программы? При этом приходится вычислять факториалы промежуточных результатов, среди которых может встретиться и ноль. В этом случае необходимо дополнить программу, пожертвовав ее краткостью, например, так: 00. П1 01. Fx=0 02. 9 03. 1 04. ИП1 05. * 06. FL1 07. 4 08. С/П 09. 1 10. С/П. (Еще лучший путь указан далее в заметке "Книга за книгой").
Работа с этой программой не отличается от описанной выше. На продолжительности вычислений удлинение практически не сказывается, зато теперь можно вычислять факториалы чисел, начиная с нуля. Ну, а если число больше 69? Конечно, на индикаторе нельзя получить число с трехзначным показателем степени. Но можно придумать другой способ индикации. Например, отдельно выводить мантиссу числа и его порядок.
Прежде, чем составлять новую программу, преобразуем формулу для вычисления факториала, записав ее в виде:
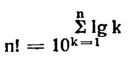
Программа для расчета по этой формуле
00. П1 O1. Cx 02. ИП1 03. lg 04. + 05. FL1 06. 02 07. П9 08. КИП9 09. x-y 10. ИП9 11. - 12. 10X 13. ИП9 14. x-y 15. С/П.
Величина n по-прежнему вводится с клавиатуры. После окончания работы на индикаторе - мантисса, а в регистре y - порядок. Так для 100! получаем Х=9.3319, Y=157. Это значит, что 100!~9.332e157.
Продолжительность вычислений по такой программе примерно пропорциональна n. Так, вычисление 1000!~4.0235e2567 заняло около 55 минут.
Можно вычислять и быстрее. Для этого надо использовать формулу Стирлинга:
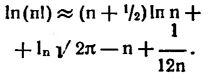
Программа, составленная на основании этого разложения, несколько длиннее предыдущей, точность ее пониже, зато для любого n она вычисляет факториал за 20 секунд:
00. П1 01. ln 02. ИП1 03. 2 04. 1/х 05. + 06. * 07. 2 08. пи 09. * 10. sqr 11. ln 12. + 13. ИП1 14. - 15. ИП1 16. 1 17. 2 18. * 19. 1/х 20. + 21. 1 22. 0 23. ln 24. / 25. П9 26. КИП9 27. x-y 28. ИП9 29. - 30. 10X 31. ИП9 32. x-y 33. С/П
Ввод и вывод происходят как в предыдущей программе.
Кстати, при работе этой программы мы сталкиваемся со спецификой машинных вычислений. Казалось бы, чем больше n, тем большую точность обеспечивает формула Стирлинга. Однако при больших n ошибки округления опережают рост точности формулы. Поэтому наименьшая относительная погрешность (1e-4..5) будет для значений n примерно от 30 до 1000. Дальше при n не превосходящих 1e6, можно гарантировать лишь два правильных знака результата; при значениях аргумента свыше 1e7 правильно будет вычисляться только порядок величины.
Теперь о программе для перевода долей градуса в минуты и секунды. Естественно предположить, что исходное число находится в регистре X, причем оно является результатом выполнения какой-либо предыдущей операции. Это следует из назначения программы. Результат также получается в регистре X. В какой же форме лучше его представить? В подавляющем большинстве присланных программ он выводится на индикатор в слитном виде (Г)ММССД(Д), где Г -градусы, ММ - минуты, ССД- секунды и их доли; символ, заключенный в круглые скобки, может повториться несколько раз или не появиться вовсе, а положение запятой не определено и зависит от величины исходного числа. Считывать результат в такой форме не всегда удобно. Легко понять, например, что 12.34567 означает 12o34'56,7". Однако, как только исходный угол уменьшится до долей градуса, начинаются неприятности. Попробуйте быстро сообразить, что 7.24445-02 это 0o7,24,445", а 4.4444-03 - это 0o44,444".
Все дело в том, что в диапазоне 0<Х<1 калькулятор начинает представлять числа в форме с плавающей запятой, что в данном случае совершенно неприемлемо.
Прекрасный выход предложил инженер Э.Балуянц (г.Баку), благодаря своей находке признанный победителем конкурса. Если дополнить показания градусов ничего не означающей единичкой слева, то ценой потери одного разряда существенно упрощается считывание показаний. Результат теперь выглядит так: 1ГГГ.ММСС. Показания индикатора 1085,4253 надо понимать как 85o42'53", а 1000,0541 как 0o05'41".
Алгоритм перевода десятичных долей градуса в минуты и секунды достаточно прост. У угла выделяется целая и дробная части, дробная умножается на 0.6 (это число вводится заранее в регистр РВ) и суммируется с целой частью. Полученное число умножается на 100, и повторяется операция выделения целой и дробной части. И сно. ва умножение на 0.6 и суммирование. Чтобы восстановить положение запятой, отделяющей градусы от минут с секундами, надо разделить результат на 100.
По этому алгоритму работает программа, составленная в редакции на основе программы Э.Балуянца:
00. 3 01. 10X 02. + 03. ПП 04. 10 05. * 06. ПП 07. 10 08. / 09. С/П 10. ПА 11. КИПА 12. x-y 13. ИПА 14. - 15. ИПВ 16. * 17. ИПА 18. + 19. 2 20. 10X 21. В/О.
Ее фрагмент 00-02 создает фиксированный формат представления результата, необходимый для удобства работы с программой. Команды 03-04 и 06-07 соответственно передают управление подпрограмме для преобразования: первый раз десятичных долей градуса в минуты и десятичные доли минут и второй раз десятичных долей минут в секунды. Команды 10-13 выделяют целую часть, а команда 14 - дробную часть. Так как преобразования ведутся с числом, большим единицы, для такого выделения допустимо использование команды КИПА.
Команды 17-20, 05, 08 в первый раз подготавливают обрабатываемый результат для повторного преобразования, во второй раз - приводят его к формату, принятому для вывода результата на индикатор.
Хочется отметить тех читателей, чьи программы наиболее экономичны. Это В.Власов из Нурека, А.Хоменко из Киева, А.Карповский из Ленинграда и И.Федотов из г.Иваново. Как и на прошлом конкурсе, лучшую программу для "Электроники Б3-21" прислал Г.Тютюма из Киева.
Стоит поговорить о типичных ошибках. Может быть, некоторые участники конкурса увидят в них и свои?
8о многих программах встречаются повторяющиеся фрагменты, которые стоило бы выделить в виде подпрограммы. О целесообразности такого выделения позволяет судить предложенное Я.К.Трохименко и Ф.Д.Любичем неравенство mn>m+1+2n, где n - число одинаковых фрагментов из m операторов. Если неравенство выполняется, то при вынесении фрагмента в подпрограмму произойдет сокращение длины программы. На случай использования команд косвенной адресации, то есть, когда имеются свободные регистры, а длина вспомогательной программы должна быть предельно сокращена, неравенство принимает вид: mn>m+n+1.
Некоторые программы предполагают вывод результатов последовательно: С/П - на индикаторе градусы, С/П - минуты, С/П - секунды. Представьте теперь, что вам необходимо обработать массив из 100 или более результатов. Сколько раз придется нажать на клавишу С/П? И уж совершенно неприемлемо это решение, если у микрокалькулятора есть печатающее устройство.
"ЭЛЕКТРОНИКА БЗ-34" ОБРЕТАЕТ ГОЛОС
Во время счета на индикатор микрокалькулятора подаются лишь короткие и сравнительно редкие импульсы тока. Когда счет прекращается, импульсы начинают следовать друг за другом с частотой 2-5 тысяч в секунду. Человеческое ухо особо чувствительно к такой частоте колебаний. Токовые импульсы нетрудно превратить в звуковые сигналы, которыми калькулятор доложит, что заданная ему работа выполнена. Снимите заднюю крышку калькулятора и подключите цепочку, показанную на схеме:
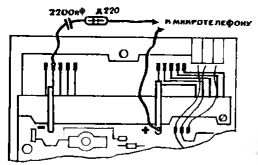
Емкость конденсатора - порядка 2200пФ, диод подойдет почти любой, например, Д220, микротелефон - марки ТМ-2А.
Если вы не впервые держите в руках паяльник, то можете предпринять еще одно усовершенствование. В описанном звуковом индикаторе замените микротелефон схемой, показанной на следующем рисунке,- и сигнал останова будет услышан вами даже из соседней комнаты.

Схема экономична: громкость звука регулируется в цепи питания, обычной батарейки от карманного фонарика хватит на несколько месяцев работы. Транзисторы - любые маломощные кремниевые, например, КТ502, КТ503. Диод - также кремниевый Д220, как и в первом случае. Конденсатор С2 - электролитический, типа К50-6 емкостью 10мкФ.
А.БОЙКО (г.Москаа)
[ Интересно? Некоторые команды можно задать разными сочетаниями клавиш. Для того чтобы заслать число в регистры 0, 1, 2, 3 или 4, обычно нажимают клавиши П0, П1 и т.д. Но можно это сделать и по-другому. Нажатие после клавиши П клавиш + или ^ заносит число в регистр 0, клавиши - в Р1, * в Р2, / в Р3, x-y в Р4. Аналогично можно организовать и вызов.
С.СОБИНЕВСКИЙ (г.Запорожье) ]
[ КНИГА ЗА КНИГОЙ
Издательство "Финансы и статистика" выпустило в нынешнем году книгу А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для микроЭВМ "Электроника Б3-34", "Электроника MK-56", "Электроника MK-54"".
Цель книги - очертить круг задач, которые целесообразно решать на программируемых микрокалькуляторах и дать читателю конкретные программы их решения в различных областях прикладной математики. Приведены очень интересные и необходимые сведения об особенностях выполнения некоторых операций. Так, авторам удалось заметить, что операции Fexp при Х<-231 и F10X при х<=-100 вместо машинного нуля дают ERROR на индикаторе. При аварийном останове одну команду микрокалькулятор пропускает. Если содержимое регистров 0-6 лежит в пределах 1e-2<=X<=9,9999998e-2, исполнение команд КП0-КП3' и КИП0-КИП3 уменьшает, а КП4-КП6 и КИП4-КИП6 увеличивает содержимое соответствующего регистра на величину 1e-9.
Есть в книге программа вычисления факториала: 00. ВП 01. П0 02. 1 03. ИП0 04. * 05. FL0 06. 03 07. С/П. ]
КАК ОТРЕДАКТИРОВАТЬ ПРОГРАММУ!
Вы набрали программу, но вот беда - контрольный пример дает неверный результат. Что же делать, набирать программу заново? Не торопитесь - программу можно отредактировать. В этом вам поможет таблица.

Переход в режим редактирования осуществляется последовательным нажатием клавиш В/О, F ПРГ. На индикаторе, там, где в счетном режиме расположена мантисса, высвечиваются двузначные коды трех введенных последними операторов программы. На месте порядка - адрес следующего по тексту программы оператора.
Код любого оператора, считанный с индикатора в виде двузначного числа АВ, сверяем с таблицей, понимая А как номер строки, В - как номер столбца.
Например, на индикаторе высвечивается 08 42 01 03. Как это расшифровать? 03 - адрес следующего оператора, значит, оператор, код которого 08, записан по адресу 02. По таблице на пересечении строки 0 и столбца 8 находим соответствующую команду. Так с помощью таблицы убеждаемся, что на индикаторе - фрагмент программы 00. 1 01. П2 02. 8. Читаем программу далее, нажимая клавишу ШГ со стрелкой вправо. Если на левом краю индикатора появился ошибочный код, то нажатием клавиши ШГ со стрелкой влево возвращаемся на шаг назад и засылаем верную команду нажатием нужной клавиши. "Парные" команды, связанные с условными переходами, адресацией и т.д., следует исправлять целиком, возвращаясь на два шага, если необходимо.
Многие владельцы "Электроники Б3-34", чтобы лучше запомнить назначение отдельных клавиш, составляют схемы, сходные по своей структуре с клавиатурой калькулятора. В правом нижнем углу таблицы - одна из таких схем, присланная Т.Эйхлером (Берлин, ГДР).
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
Мне нравится клубный характер рубрики "Человек с микрокалькулятором", возможность бесед и даже споров",- так начинает свое письмо в редакцию читатель Е.Федорец из Владивостока. Новая рубрика так и задумывалась: она существует, питаясь, как живой водой, читательской почтой.
За год жизни "Человек с микрокалькулятором" получил свыше тысячи писем (не считая ответов на конкурсные задачи). Пишут инженеры и рабочие, астрономы и музыканты, пишут студенты и домохозяйки, школьники и пенсионеры... В одних письмах - слова благодарности, в других - нелицеприятная критика. Нам одинаково дороги и те и другие. Первые - как признание полезности нашей работы, вторые - как рекомендации для ее улучшения.
Характер рубрики таков, что ни одна публикация под нею не может претендовать на роль истины в последней инстанции. Каждая затронутая проблема остается открытой для дальнейшей разработки. В спорах читателей рождается их мастерство программирования.
Редкое письмо не содержит ту или иную программу. И здесь, уважаемые читатели, позвольте познакомить вас с небольшой статистикой. Анализ случайной выборки из 200 писем (сделанный, естественно, с помощью микрокалькулятора) дал такие результаты.
64 процента программ - игровые. Первенство здесь делят разновидности игр "Ним" и "Морской бой" (по 20 процентов). Участвующие в этих "боях" корабли, пожалуй, уже сравнимы по численности с военно-морскими силами всех стран мира.
Столько же, то есть 20 процентов писем, содержит описание "вечного календаря" и связанных с ним проблем "биоритмов" и "гороскопов". Теперь все сотрудники редакции, а заодно их родные и близкие могут узнавать свою судьбу, пользуясь индивидуальными программами.
10 процентов - серьезные математические программы: решение алгебраических и дифференциальных уравнений, интегрирование, статистика.
Наконец, 6 процентов - прикладные программы, призванные облегчить труд геодезистов и металлургов, строителей и преподавателей. Хотелось бы, чтобы таких программ присылалось побольше и чтобы их спектр был пошире. Ждем писем от врачей и филологов, спортивных тренеров и архитекторов.
Понятно, что далеко не все программы мы можем опубликовать. Тем более что изрядная их часть не лучше приведенных в книгах А.Цветкова и В.Епанечникова, Я.Трохименко и Ф.Любича (библиография была дана в 6/84).
Тем не менее мы стараемся всесторонне отражать читательские интересы. Так, в этом номере журнала К.Ткачук из г.Апатиты Мурманской области излагает свою концепцию "нежестких" программ, А.Раздобреев из г.Владимира рассказывает о методе Ньютона для решения уравнений, москвич А.Бойко предлагает звуковой индикатор для микрокалькулятора "Электроника Б3-34", по предложению Д.Мыслина из г.Новосибирска дается таблица кодов. Как всегда, есть и "маленькие хитрости". Мы надеемся, что читатели будут чаще присылать нам эти крупицы программистского опыта.
Верстая очередной выпуск рубрики, мы каждый раз отдаем предпочтение тем письмам, где либо ставятся новые, оригинальные проблемы, либо по-новому решаются старые. "Да иначе, наверное, и нельзя из-за большого разнообразия специальностей, представленных в вашем, простите, в нашем клубе",- пишет уже упомянутый Е.Федорец.
МЕТОД НЬЮТОНА
Корень уравнения ф(x)=0 бывает удобно отыскивать итерационным методом, приводя уравнение к виду x=f(x) и выполняя итерации по правилу x[n+i]=f(xn). Из уравнения, которое нужно решить, можно получить множество итерационных уравнений с разными правыми частями. Твердых правил по выбору подходящей функции f(x) нет, поэтому сходимость процесса, тем более быстрая сходимость, часто бывает делом случая. Можно ли улучшить сходимость, меняя вид функции f(x)?
Каждое последующее итерационное приближение отличается от предыдущего на поправку дn=f(xn)-xn, и итерационное уравнение можно записать так: x[n+i]=хn+дn. Вспомним уравнение х=cos(x) с начальным приближением х0=0.7 (10/83). Получалось
д0=0.0648422
д1=-0.0433505
д2=0.0293297
д3=-0.0196926
...
Как видим, величины дn не так уж малы. Чтобы все семь цифр после запятой стали нулями, требуется 35 приближений, при этом х=0.7390851.
Быть может, стоит на каждом шагу уменьшать поправку д - брать вместо нее некоторую ее долю а, то есть модифицировать уравнение так: x[n+i]=xn+a[f(хn)-хn]? Возьмем а=0.5, и тогда ответ с семью верными знаками после запятой получается всего за восемь итераций. Существенное уменьшение! Если взять а=0.6, то хватит всего трех итераций. Можно ли уменьшить их число?
Известно, что сходимость итерационного метода для уравнения х=f(x) обеспечивается неравенством |f'(x)|<1, причем сходимость тем быстрее, чем меньше абсолютная величина производной. В модифицированном уравнении будем выбирать коэффициент а таким, чтобы производная правой части на каждом шагу равнялась 0. Так мы приходим к методу Ньютона для поиска корня уравнения
ф(х)=0;
к стандартному виду оно приводится заменой
f(x)=Ф(х)+х.
Смысл метода ясен из графика, а итерационная формула такова:

Здесь для получения следующего приближения требуется вычислять не только значение функции ф(х), но и ее производной ф'(х), что усложняет расчеты. Зато условия сходимости для этого метода менее жесткие, чем для метода итераций.
Владельцам программируемых микрокалькуляторов лучше запрограммировать формулу, оформив вычисление функции ф(х) как подпрограмму. Производную можно вычислять приближенно:
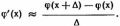
Чем меньше приращение дельта, тем точнее значение производной. При программировании итерационных процессов в один из регистров заносится величина, определяющая заданную точность нахождения корня. Именно ее удобно использовать в качестве дельты. Программа уточнения корня должна быть как можно короче, чтобы в программной памяти осталось достаточно места для вычисления функции. С этой точки зрения наиболее удобной записью итерационного уравнения будет

которая получается из исходного уравнения элементарными преобразованиями. Применим метод Ньютона для решения уравнения, к которому привела "загадка жрецов бога Ра" (2/84). Запишем его так:
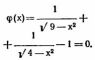
Принимая Дельта=0.001 и x0=1, по последней из форм итерационного уравнения получим x1=1.292, х2=1.235, х3=1.231, x4=1.231.
Чтобы найти ответ, потребовалось четыре приближения. Метод итераций требовал 11, причем сначала надо было подобрать подходящий вид функции.
Какой же метод лучше? Для микрокалькулятора с весьма жесткими ограничениями на объем памяти больше подходит метод итераций: программа получается короче. Но могут возникнуть значительные трудности при подборе функции, обеспечивающей сходимость.
Метод Ньютона, хотя реализуется более громоздкой программой, как правило, обеспечивает более быструю (по числу шагов) сходимость, но выигрыш во времени невелик, так как за каждый цикл функция вычисляется дважды.
Так что, если можно применить метод итераций, надо остановиться на нем. Правда, с методом Ньютона трудно конкурировать, если требуется найти несколько корней. Например, уравнение х2-х-2=0 имеет корни x1=2, х2=-1. Методом Ньютона при разных начальных приближениях легко находятся оба. Чтобы найти эти корни методом итераций, надо использовать два разных уравнения, например, x=sqr(x+2) и х=2/(x-1).
Еще сложней обстоит дело с трансцендентными уравнениями. Например, уравнение tg(x)=3/4х имеет бесконечное число решений, и методом Ньютона можно нх найти столько, сколько нужно. А с помощью метода итераций искать их непросто.
В общем, готовых рецептов нет, каждая новая задача требует творческого подхода. Тем больше удовлетворение, когда ее удается решить.
А.РАЗДОБРЕЕВ (г.Владимир)
[ УЗЕЛКИ НА ПАМЯТЬ
Желательно избегать команды ^. В программном режиме она, как правило, лишняя. Правильное использование стека практически реализует ее функции.
В.ХОХЛОВ (г.Днепропетровск) ]
"НЕЖЕСТКИЕ" ПРОГРАММЫ
Многие владельцы микрокалькуляторов не представляют всех тех возможностей, которые заложены в этих машинах.
Программа для калькулятора составляется, как правило, для решения конкретной задачи. Варьируются лишь исходные данные. Я инженер-строитель и ради примера приведу типичную задачу из сопромата: определение моментов инерции J и J' прямоугольного сечения балки соответственно относительно оси хх, проходящей через центр тяжести и произвольной оси х'х'.

Нетрудно составить программу для вычисления J' и использовать ее в неизменном виде, каждый раз вводя значения a, b, h. Но допустим, сечение балки имеет более замысловатый вид:

Составлять для каждой конфигурации свою программу? Нецелесообразно! Имеет смысл разбить сечение на прямоугольники, затем, опираясь на это разбиение, определить центр тяжести сечения, вычислить момент инерцин Ji' каждого прямоугольника относительно проходящей через этот центр оси и подсчитать момент инерции всего сечения в виде суммы: J=sum(Ji').
Суммирование предполагается также и при нахождении центра тяжести сечения, точнее, его расстояния у от некоторой выбранной вначале оси: F=sum(Fi), S=SUM(Fi*ai), y=S/F. Число слагаемых для сечений различных конфигураций будет изменяться в широких пределах, памяти калькулятора может не хватить для хранения исходных данных. Поэтому управление суммированием владельцу калькулятора приходится взять на себя. Но зато в таком "нежестком" режиме удается рассчитывать весьма разнообразные профили!
Рассмотрим соответствующий пример (размеры в сантиметрах).

Требуется определить момент инерции сечения относительно оси хх, проходящей через его центр тяжести. Разбиваем сечение на семь прямоугольников, как указано на схеме; вспомогательную ось х'х' проводим по нижней его грани.
Вводим в калькулятор программу; заносим нуль в регистры 4, В, С; проводим вычисления 1-го этапа программы (адреса 00-13). Ширину отдельного прямоугольника bi каждый раз заносим в регистр y, высоту hi - в x (bi ^ hi c/п), расстояние аi' от оси симметрии прямоугольника до вспомогательной оси х'х' - в регистр х (аi' с/п). Результаты: в Р4 - площадь сечения F=83см2, в PC и на индикаторе - статический момент сечения относительно вспомогательной оси S=671.5см3.
Чтобы провести вычисления 2-го этапа (адреса 14-18 ), нажимаем клавишу ШГ со стрелкой вправо, затем С/П. В Р5 и на индикаторе - ордината центра тяжести y=8.09см. В автоматическом режиме вычисляем расстояния ai от центров тяжести отдельных прямоугольников до осн хх, проходящей через центр тяжести сечения (четвертый столбец таблицы).

Проводим вычисления 3-го этапа (адреса 19-47). Ширину каждого прямоугольника bi заносим в регистр z, высоту hi - в y, расстояние ai от его центра тяжести до оси хх - в x (bi ^ hi ^ ai c/n). В итоге в РВ и на индикаторе - момент инерции сечения: J=1586,99см4.
ПРОГРАММА. 00. * 01. П6 02. ИП4 03. + 04. П4 05. С/П 06. ИП6 07. * 08. ИПС 09. + 10. ПС 11. С/П 12. БП 13. 00 14. ИПС 15. ИП4 16. / 17. П5 18. С/П 19. П2 20. F() 21. П1 22. F() 23. П0 24. 3 25. ИП1 26. FxY 27. ИП0 28. * 29. 1 30. 2 31. / 32. П3 33. ИП0 34. ИП1 35. * 36. ИП2 37. Fx2 38. * 39. ИП3 40. + 41. ПА 42. ИПВ 43. + 44. ПВ 45. С/П 46. БП 47. 19.
К.ТКАЧУК (г.Апатиты Мурманской обл.)
ОТ РЕДАКЦИИ. Программа не свободна от недостатков. Ее улучшения могут стать упражнением для читателей и вкладом в объявленную ранее (6/84) дискуссию за круглым столом о приемах сервиса. Ждем новых писем на эту тему.
[ КСТАТИ
Во время работы с калькулятором часто замечаешь ту или иную интересную закономерность, которая позже позволяет проводить устные расчеты без калькулятора с большей скоростью и точностью. Как это ни парадоксально, калькулятор помогает считать без калькулятора.
В.ХАРЧЕНКО (г.Киев) ]
ВЫЧИСЛЯЕМ ФАКТОРИАЛ
ИТОГИ КОНКУРСА
На предложение принять участие в конкурсе на лучшую программу для вычисления факториала данного натурального числа откликнулось около 250 человек из самых различных районов страны. Здесь и крупные центры - Москва, Ленинград, Киев, Рига, Новосибирск, Томск, Одесса, Норильск и такие города, как Абакан, Урюпинск, Буй. Из заказника "Предуралье" Пермской области ответ прислал В.Демидов, из латвийского города Лимбежи - К.Лайва, из г.Назыма Тюменской области - В.Лукашев. Военнослужащий В.Кенарский составил программу, находясь в море. Правильные ответы прислали инженеры, студенты, рабочие... Как всегда, радуют ответы школьников - семиклассников А.Кроонмаа и Г.Хилвра (Таллин), С.Виницкого (Москва), восьмиклассников Б.Игнатьева из Ленинграда и В.Черемушкина из Чеховского района Московской области.
Задача была нетрудной, и ее решения в подавляющем большинстве правильны. Причем программы практически одинаковы. Они, как выразился О.Фомичев из Грозного, "действительно несложные и очень простые". О.Рыбаков из Куйбышева был еще более категоричным - после текста программы он написал: "А других и не пришлют", выбрать лучшие работы поэтому было сложно. Тем не менее жюри решило отметить С.Кузнецова, приславшего программу еще до объявления конкурса, программы В.Власова (Нурек), Ю.Тертычного (Северодонецк), Б.Кайсинова (Московская область), использовавших для обработки информации только стековые регистры, программу Е.Атавина (Омск), которая позволяет получать все цифры результата для значений аргумента, не превосходящих 47.
К сожалению, большинство читателей прислали программы, с помощью которых можно вычислять лишь факториалы чисел от 1 до 69, причем некоторые даже не отметили это и не обратили внимание, что результаты расчетов для больших чисел не "влезают" в разрядную сетку микрокалькулятора. Программы для работы с большими аргументами прислали Л.Тихомиров, В.Козлов (Ленинград), А.Сельский (Сумы), П.Якубович (Днепропетровск) и некоторые другие.
Из всех присланных писем одно содержало наиболее полный и интересный анализ проблемы. Автор этого письма - ленинградский профессор Л.Финк и был объявлен победителем нашего конкурса. Соображения его представляются настолько поучительными, что мы решили познакомить с ними читателей.
Составляя программу, пишет Л.Финк, важно представлять область ее применения. Программа вычисления факториала для "Электроники Б3-34" может содержать лишь 7 шагов: 00. П1 01. 1 02. ИП1 03. * 04. FL1 05. 2 06. С/П. Значение n вводится с клавиатуры, результат n! высвечивается на индикаторе. Эта программа, вероятно, рекордна по своей компактности [Можно, правда, получить программу еще короче (5 шагов). Многие читатели прислали такие варианты. Вот один из них: 00. ИП2 01. * 02. FL2 03. 00 04. С/П. Но перед выполнением этой программы нужно занести в соответствующий регистр аргумент и затем набрать на клавиатуре число 1. Пожалуй, такие сложности вряд ли оправдывают сокращение на две команды] и работает достаточно быстро: 5! вычисляется за 8 секунд, 69! - за 95 секунд. При больших числах происходит переполнение разрядной сетки калькулятора, так как результат превосходит 1e100. Однако 0! по этой программе получить также не удается. Она зацикливается. Можно, конечно, сказать: мы и так знаем, что 0!=1, и незачем вводить такой аргумент в программу. А если такую программу нужно использовать в качестве подпрограммы или фрагмента другой программы? При этом приходится вычислять факториалы промежуточных результатов, среди которых может встретиться и ноль. В этом случае необходимо дополнить программу, пожертвовав ее краткостью, например, так: 00. П1 01. Fx=0 02. 9 03. 1 04. ИП1 05. * 06. FL1 07. 4 08. С/П 09. 1 10. С/П. (Еще лучший путь указан далее в заметке "Книга за книгой").
Работа с этой программой не отличается от описанной выше. На продолжительности вычислений удлинение практически не сказывается, зато теперь можно вычислять факториалы чисел, начиная с нуля. Ну, а если число больше 69? Конечно, на индикаторе нельзя получить число с трехзначным показателем степени. Но можно придумать другой способ индикации. Например, отдельно выводить мантиссу числа и его порядок.
Прежде, чем составлять новую программу, преобразуем формулу для вычисления факториала, записав ее в виде:
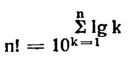
Программа для расчета по этой формуле
00. П1 O1. Cx 02. ИП1 03. lg 04. + 05. FL1 06. 02 07. П9 08. КИП9 09. x-y 10. ИП9 11. - 12. 10X 13. ИП9 14. x-y 15. С/П.
Величина n по-прежнему вводится с клавиатуры. После окончания работы на индикаторе - мантисса, а в регистре y - порядок. Так для 100! получаем Х=9.3319, Y=157. Это значит, что 100!~9.332e157.
Продолжительность вычислений по такой программе примерно пропорциональна n. Так, вычисление 1000!~4.0235e2567 заняло около 55 минут.
Можно вычислять и быстрее. Для этого надо использовать формулу Стирлинга:
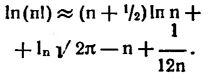
Программа, составленная на основании этого разложения, несколько длиннее предыдущей, точность ее пониже, зато для любого n она вычисляет факториал за 20 секунд:
00. П1 01. ln 02. ИП1 03. 2 04. 1/х 05. + 06. * 07. 2 08. пи 09. * 10. sqr 11. ln 12. + 13. ИП1 14. - 15. ИП1 16. 1 17. 2 18. * 19. 1/х 20. + 21. 1 22. 0 23. ln 24. / 25. П9 26. КИП9 27. x-y 28. ИП9 29. - 30. 10X 31. ИП9 32. x-y 33. С/П
Ввод и вывод происходят как в предыдущей программе.
Кстати, при работе этой программы мы сталкиваемся со спецификой машинных вычислений. Казалось бы, чем больше n, тем большую точность обеспечивает формула Стирлинга. Однако при больших n ошибки округления опережают рост точности формулы. Поэтому наименьшая относительная погрешность (1e-4..5) будет для значений n примерно от 30 до 1000. Дальше при n не превосходящих 1e6, можно гарантировать лишь два правильных знака результата; при значениях аргумента свыше 1e7 правильно будет вычисляться только порядок величины.
Теперь о программе для перевода долей градуса в минуты и секунды. Естественно предположить, что исходное число находится в регистре X, причем оно является результатом выполнения какой-либо предыдущей операции. Это следует из назначения программы. Результат также получается в регистре X. В какой же форме лучше его представить? В подавляющем большинстве присланных программ он выводится на индикатор в слитном виде (Г)ММССД(Д), где Г -градусы, ММ - минуты, ССД- секунды и их доли; символ, заключенный в круглые скобки, может повториться несколько раз или не появиться вовсе, а положение запятой не определено и зависит от величины исходного числа. Считывать результат в такой форме не всегда удобно. Легко понять, например, что 12.34567 означает 12o34'56,7". Однако, как только исходный угол уменьшится до долей градуса, начинаются неприятности. Попробуйте быстро сообразить, что 7.24445-02 это 0o7,24,445", а 4.4444-03 - это 0o44,444".
Все дело в том, что в диапазоне 0<Х<1 калькулятор начинает представлять числа в форме с плавающей запятой, что в данном случае совершенно неприемлемо.
Прекрасный выход предложил инженер Э.Балуянц (г.Баку), благодаря своей находке признанный победителем конкурса. Если дополнить показания градусов ничего не означающей единичкой слева, то ценой потери одного разряда существенно упрощается считывание показаний. Результат теперь выглядит так: 1ГГГ.ММСС. Показания индикатора 1085,4253 надо понимать как 85o42'53", а 1000,0541 как 0o05'41".
Алгоритм перевода десятичных долей градуса в минуты и секунды достаточно прост. У угла выделяется целая и дробная части, дробная умножается на 0.6 (это число вводится заранее в регистр РВ) и суммируется с целой частью. Полученное число умножается на 100, и повторяется операция выделения целой и дробной части. И сно. ва умножение на 0.6 и суммирование. Чтобы восстановить положение запятой, отделяющей градусы от минут с секундами, надо разделить результат на 100.
По этому алгоритму работает программа, составленная в редакции на основе программы Э.Балуянца:
00. 3 01. 10X 02. + 03. ПП 04. 10 05. * 06. ПП 07. 10 08. / 09. С/П 10. ПА 11. КИПА 12. x-y 13. ИПА 14. - 15. ИПВ 16. * 17. ИПА 18. + 19. 2 20. 10X 21. В/О.
Ее фрагмент 00-02 создает фиксированный формат представления результата, необходимый для удобства работы с программой. Команды 03-04 и 06-07 соответственно передают управление подпрограмме для преобразования: первый раз десятичных долей градуса в минуты и десятичные доли минут и второй раз десятичных долей минут в секунды. Команды 10-13 выделяют целую часть, а команда 14 - дробную часть. Так как преобразования ведутся с числом, большим единицы, для такого выделения допустимо использование команды КИПА.
Команды 17-20, 05, 08 в первый раз подготавливают обрабатываемый результат для повторного преобразования, во второй раз - приводят его к формату, принятому для вывода результата на индикатор.
Хочется отметить тех читателей, чьи программы наиболее экономичны. Это В.Власов из Нурека, А.Хоменко из Киева, А.Карповский из Ленинграда и И.Федотов из г.Иваново. Как и на прошлом конкурсе, лучшую программу для "Электроники Б3-21" прислал Г.Тютюма из Киева.
Стоит поговорить о типичных ошибках. Может быть, некоторые участники конкурса увидят в них и свои?
8о многих программах встречаются повторяющиеся фрагменты, которые стоило бы выделить в виде подпрограммы. О целесообразности такого выделения позволяет судить предложенное Я.К.Трохименко и Ф.Д.Любичем неравенство mn>m+1+2n, где n - число одинаковых фрагментов из m операторов. Если неравенство выполняется, то при вынесении фрагмента в подпрограмму произойдет сокращение длины программы. На случай использования команд косвенной адресации, то есть, когда имеются свободные регистры, а длина вспомогательной программы должна быть предельно сокращена, неравенство принимает вид: mn>m+n+1.
Некоторые программы предполагают вывод результатов последовательно: С/П - на индикаторе градусы, С/П - минуты, С/П - секунды. Представьте теперь, что вам необходимо обработать массив из 100 или более результатов. Сколько раз придется нажать на клавишу С/П? И уж совершенно неприемлемо это решение, если у микрокалькулятора есть печатающее устройство.
"ЭЛЕКТРОНИКА БЗ-34" ОБРЕТАЕТ ГОЛОС
Во время счета на индикатор микрокалькулятора подаются лишь короткие и сравнительно редкие импульсы тока. Когда счет прекращается, импульсы начинают следовать друг за другом с частотой 2-5 тысяч в секунду. Человеческое ухо особо чувствительно к такой частоте колебаний. Токовые импульсы нетрудно превратить в звуковые сигналы, которыми калькулятор доложит, что заданная ему работа выполнена. Снимите заднюю крышку калькулятора и подключите цепочку, показанную на схеме:

Емкость конденсатора - порядка 2200пФ, диод подойдет почти любой, например, Д220, микротелефон - марки ТМ-2А.
Если вы не впервые держите в руках паяльник, то можете предпринять еще одно усовершенствование. В описанном звуковом индикаторе замените микротелефон схемой, показанной на следующем рисунке,- и сигнал останова будет услышан вами даже из соседней комнаты.

Схема экономична: громкость звука регулируется в цепи питания, обычной батарейки от карманного фонарика хватит на несколько месяцев работы. Транзисторы - любые маломощные кремниевые, например, КТ502, КТ503. Диод - также кремниевый Д220, как и в первом случае. Конденсатор С2 - электролитический, типа К50-6 емкостью 10мкФ.
А.БОЙКО (г.Москаа)
[ Интересно? Некоторые команды можно задать разными сочетаниями клавиш. Для того чтобы заслать число в регистры 0, 1, 2, 3 или 4, обычно нажимают клавиши П0, П1 и т.д. Но можно это сделать и по-другому. Нажатие после клавиши П клавиш + или ^ заносит число в регистр 0, клавиши - в Р1, * в Р2, / в Р3, x-y в Р4. Аналогично можно организовать и вызов.
С.СОБИНЕВСКИЙ (г.Запорожье) ]
[ КНИГА ЗА КНИГОЙ
Издательство "Финансы и статистика" выпустило в нынешнем году книгу А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для микроЭВМ "Электроника Б3-34", "Электроника MK-56", "Электроника MK-54"".
Цель книги - очертить круг задач, которые целесообразно решать на программируемых микрокалькуляторах и дать читателю конкретные программы их решения в различных областях прикладной математики. Приведены очень интересные и необходимые сведения об особенностях выполнения некоторых операций. Так, авторам удалось заметить, что операции Fexp при Х<-231 и F10X при х<=-100 вместо машинного нуля дают ERROR на индикаторе. При аварийном останове одну команду микрокалькулятор пропускает. Если содержимое регистров 0-6 лежит в пределах 1e-2<=X<=9,9999998e-2, исполнение команд КП0-КП3' и КИП0-КИП3 уменьшает, а КП4-КП6 и КИП4-КИП6 увеличивает содержимое соответствующего регистра на величину 1e-9.
Есть в книге программа вычисления факториала: 00. ВП 01. П0 02. 1 03. ИП0 04. * 05. FL0 06. 03 07. С/П. ]
КАК ОТРЕДАКТИРОВАТЬ ПРОГРАММУ!
Вы набрали программу, но вот беда - контрольный пример дает неверный результат. Что же делать, набирать программу заново? Не торопитесь - программу можно отредактировать. В этом вам поможет таблица.

Переход в режим редактирования осуществляется последовательным нажатием клавиш В/О, F ПРГ. На индикаторе, там, где в счетном режиме расположена мантисса, высвечиваются двузначные коды трех введенных последними операторов программы. На месте порядка - адрес следующего по тексту программы оператора.
Код любого оператора, считанный с индикатора в виде двузначного числа АВ, сверяем с таблицей, понимая А как номер строки, В - как номер столбца.
Например, на индикаторе высвечивается 08 42 01 03. Как это расшифровать? 03 - адрес следующего оператора, значит, оператор, код которого 08, записан по адресу 02. По таблице на пересечении строки 0 и столбца 8 находим соответствующую команду. Так с помощью таблицы убеждаемся, что на индикаторе - фрагмент программы 00. 1 01. П2 02. 8. Читаем программу далее, нажимая клавишу ШГ со стрелкой вправо. Если на левом краю индикатора появился ошибочный код, то нажатием клавиши ШГ со стрелкой влево возвращаемся на шаг назад и засылаем верную команду нажатием нужной клавиши. "Парные" команды, связанные с условными переходами, адресацией и т.д., следует исправлять целиком, возвращаясь на два шага, если необходимо.
Многие владельцы "Электроники Б3-34", чтобы лучше запомнить назначение отдельных клавиш, составляют схемы, сходные по своей структуре с клавиатурой калькулятора. В правом нижнем углу таблицы - одна из таких схем, присланная Т.Эйхлером (Берлин, ГДР).

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
2/85
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Рубрика "Человек с микрокалькулятором" вступает в новый год своего существования. Многие направления раздела стали традиционными: конкурсы и дискуссии за круглым столом, "маленькие хитрости" и прикладные программы, присылаемые читателями. Почта раздела содержит также и письма, в которых обсуждается его будущее. В публикуемом ниже отрывке из письма И.Вязовского (г.Люберцы Московской области) речь идет о персональных ЭВМ. Предлагается уделить им место в рамках раздела.
Ждем читательских откликов на это предложение. Несомненно, персональные ЭВМ заслуживают серьезного, углубленного разговора. Следует заранее продумать, как вести его в разделе "Человек с микрокалькулятором" |а быть может, и в отдельных крупных статьях журнала). Провести дискуссию о том, как лучше использовать первые, пока еще немногочисленные персональные ЭВМ? Разобрать устройство этих машин? Дать краткий курс языков "бейсик", "рапира"? Надеемся на активное участие читателей в обсуждении этой темы и, что особенно важно,- в обсуждении подходов к ее освещению в журнале.
НА РАЗНЫХ ПОЛЮСАХ?
Каковы различия между типичными программируемыми микрокалькуляторами (ПМК) и персональными электронными вычислительными машинами (ПЭВМ)?
Что касается быстродействия, объема памяти, то это дело наживное. На этих чисто количественных различиях останавливаться не будем. Поговорим о различиях качественных, принципиальных. С точки зрения пользователя, это прежде всего языки программирования.
Язык микрокалькулятора близок к так называемым автокодам [Автокод - язык программирования, ориентированный на конкретную ЭВМ. Отличается от машинного языка заменой кодов команд их мнемоническими обозначениями и возможностью использовать относительные адреса]. Запись любой программной конструкции, например, арифметического выражения, распадается на ряд элементарных команд, в каждой из которых записывается либо операция, либо операнд (число, над которым совершается операция), либо адрес. Каждая команда заносится в конкретную ячейку памяти. Возможность редактирования программ очень ограничена. Можно заменить какую-то команду, но вставить новую команду в середину программы нельзя. Для нее нет места. Да и набор команд очень мал.
Владелец ПЭВМ оперирует языком высокого уровня. Это "бэйсик" или "рапира" (язык, специально разработанный новосибирскими учеными, которым будут оснащены отечественные ПЭВМ). Программировать на этих языках значительно удобнее, чем в автокодах. Запись выражений почти не отличается от обычной, принятой в математике. Очень широк набор операторов, особенно в "рапире". Там есть возможность работать не только с числами, но и с текстами, рисунками. Практически не ограничены возможности редактирования. Есть еще один аспект, облегчающий работу на ПЭВМ: богатое математическое обеспечение, пользоваться которым может любой человек, даже не умеющий программировать.
С точки зрения программирования, ПМК и ПЭВМ находятся на разных полюсах. Микрокалькулятор как бы возвращает нас к "древней" машинной культуре, когда автокоды были единственными языками программирования. Перефразируя остроумное замечание академика А.П.Ершова, можно сказать, что ПМК - это разновидность искусственно выведенного комнатного динозавра, а ПЭВМ - представитель отряда высших млекопитающих в мире ЭВМ. Смысл этой метафоры станет еще более ясным, если мы сравним структуры микрокалькулятора и персональной ЭВМ.
В ПМК области хранения чисел и команд разделены. Так было и в первых ЭВМ. Выдвинутый американским математиком Дж. фон Нейманом принцип единой области памяти, каждый элемент которой можно трактовать или как число или как команду, привел к современным ЭВМ. Так что и с этой точки зрения ПМК и ПЭВМ на разных полюсах.
И все-таки можно утверждать, что оба этих вычислительных устройства - братья. Роднит их важное качество: и то и другое - машины индивидуального пользования. Владелец каждой из них - одновременно и постановщик задач, и программист, и оператор, и пользователь. Короче, он хозяин машины. Может считать на ней что хочет и когда хочет, может использовать ее как партнера в игре, может беспредельно экспериментировать на ней. Ему не нужно днями, а то и неделями ждать очереди, чтобы выйти на ЭВМ, нервно сидеть за пультом, боясь потерять минуты драгоценного времени. Его ЭВМ всегда доступна. Благодаря этому процесс отладки и получения результатов резко сокращается. В государственном аспекте это означает большую эффективность решения задач с помощью ЭВМ.
Как же поведут себя "братья" дальше? Будут ли микрокалькуляторы вытеснены персональными ЭВМ подобно тому, как трамвай вытеснил конку? Или они будут мирно сосуществовать, как, скажем, лампы накаливания и люминесцентные трубки?
Конечно, возможности персональной ЭВМ много выше. Она может служить и картотекой, и запиской книжкой, и большим калькулятором, и универсальной ЭВМ. Работать на ней легче и удобнее. Но место ее - на рабочем столе. Из дома на работу ее не возьмешь, в командировку с ней не поедешь. Микрокалькулятор же легко умещается в портфеле или даже в кармане. Это по сути своей - переносная машина. Нельзя сбрасывать со счетов и цены на машины того и другого класса: конечно, по мере развития технологии они будут снижаться, но соотношение между ними вряд ли скоро изменится. Не за горами и увеличение возможностей ПМК - расширение набора команд, увеличение быстродействия, дополнительные блоки памяти, магнитные карты и т.д. Все это, естественно, без существенного изменения цен и габаритов.
Вообще ПМК постепенно догоняют ПЭВМ не только по количественным показателям, но и по качественным, поэтому со временем различие между ними, наверное, исчезнет. Скорее всего, эти два типа вычислительных устройств будут сосуществовать долго. И, пожалуй, еще одно. Опыт работы с ПМК, где постоянно приходится учитывать специфику машины, идти на разные ухищрения, чтобы втиснуть сложный алгоритм в малую память, безусловно, даст себя знать при переходе на ПЭВМ или другую универсальную машину. Тот, кто прошел школу ПМК, наверняка значительно лучше сможет использовать ресурсы и возможности другой ЭВМ, нежели "человек с улицы".
... Дружные родственники всегда стремятся жить поближе друг к другу. Не отвести ли братьям из большой семьи вычислительных устройств единую "жилплощадь" на страницах журнала "Наука и жизнь"? Думаю, что персональные ЭВМ должны найти свое место под рубрикой "Человек с микрокалькулятором".
И.ВЯЗОВСКИЙ (г.Люберцы)
[ ИЗ ПИСЕМ
Считаю крайне важным и необходимым делом использование ЭВМ в школах и вузах. Самое удивительное, что в своем большинстве наши преподаватели полностью игнорируют возможность применения ЭВМ у нас в институте, не говоря уже о том, чтобы готовить нас к будущей работе в школе с микрокалькуляторами и персональными ЭВМ. Доходит до смешного. На практических занятиях по статистической физике наша преподавательница, кандидат физико-математических наук, весьма недвусмысленно высказалась об использовании нами микрокалькуляторов для вычислений. Она утверждает, что так мы теряем "чувство числа" и получаем "немыслимые результаты". Я не отрицаю, что можно ошибиться, считая на калькуляторе, но ведь еще легче ошибиться, считая в уме или на бумаге.
Г.БЕЛЫЙ, студент пединститута (г.Ставрополь) ]
[ Я учусь в физико-математической школе, в 10 классе. С необходимостью приобрести программируемый микрокалькулятор я столкнулся при выполнении работ физического практикума. На обработку результатов измерений мне приходилось тратить по нескольку часов. Я составил для микрокалькулятора программу анализа погрешностей, и теперь на обработку сотни результатов у меня уходит около 20 минут. С помощью микрокалькулятора также очень удобно решать численные задачи по физике и химии, строить графики различных функций.
Я считаю, что овладение навыками элементарного программирования необходимо всем старшеклассникам. Хорошо бы ввести курс программирования в средней школе, хотя бы факультативно.
С.КАДУЛИН, ученик школы #145 (г.Киев) ]
[ ИЗ ГАЗЕТ
Факультативный курс электроники для школьников 9-10 классов, читаемый в общеобразовательных школах ГДР с 1970/71 учебного года, в новом учебном году будет существенно обновлен и обогащен с учетом достижений микроэлектроники, в частности, оптоэлектроники и т.д.
Новый курс даст школьникам основу для дальнейшего самообразования в этой области и позволит осваивать будущие новинки электроники. Вместе с тем учащиеся закрепят знания, полученные ими в курсах физики и ВСП ["Введение в социалистическое производство", учебная дисциплина об основах социалистической экономики, преподаваемая в школах ГДР].
Переработанная программа курса будет утверждена после тщательного опробования, в котором примут участие и сами школьники. Сейчас педагоги на курсах усовершенствования знакомятся с нею, чтобы быть готовыми к началу работы по ней ("Берлинер Цайтунг", 6 марта 1984г.) ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Отладка длинных программ на микрокалькуляторе - дело трудоемкое. Останавливать вычисления клавишей С/П нельзя - может нарушиться работа программы. Использовать программный останов, например, по состоянию счетчика, тоже не всегда удобно, особенно, если длительность цикла вычислений заранее неизвестна.
Предлагаю управлять работой микрокалькулятора в таких случаях с помощью переключателя Р-Г. Для этого надо ввести в нужное место программы последовательность команд вида: 3 Fcos Fx<0 А С/П, где А-номер команды, следующей за С/П. Если переключатель находится в положении Г (градусы), то cos(3o)>0, и команда останова обходится. При переключении в режим Р (радианы) cos(3)<0, и решение прерывается. Введя вместо С/П команду передачи управления, можно с пульта менять логику выполнения программы.
И.ПЯТАК (г.Днепропетровск) ]
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
В июньском выпуске рубрики "Человек с микрокалькулятором" за прошлый год читатели приглашались на дискуссию за круглым столом о методе наименьших квадратов. В ней приняли участие 25 человек. Публикуем выдержки из выступлений некоторых участников. Это В.Адриан (г.Химки Московской обл.), Е.Атавин (г.Омск), Д.Богданов (г.Москва), Ю.Каптелов (г.Ивано-Франковск), С.Кулибаба (г. Донецк), А. Тулайков (г.Долгопрудный Московской обл.), Б.Ходов (г.Москва), И.Шмаков (г.Новосибирск).
Д.Богданов. Метод наименьших квадратов - один из наиболее распространенных методов математической обработки данных. Рассмотрим простейший пример его применения, когда изучается зависимость одной величины от другой - например, силы тока в цепи от напряжения. По данным опыта наносим точки на график. Они выстраиваются почти по прямой. Естественно желание провести такую сглаживающую прямую. Определим ее требованием, чтобы сумма квадратов вертикальных отклонений всех n точек от прямой sum(h[i]2) была минимальной. Вслед за этим воспользуемся необходимым условием минимума функции двух переменных, в данном случае - суммы
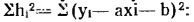
приравняем нулю ее частные производные по а и b . В итоге получим систему для определения параметров искомой прямой, так называемой линии регрессии:
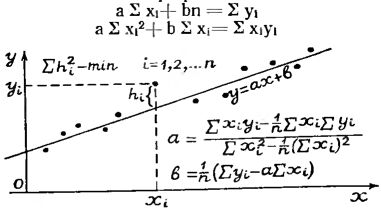
В.Адриан. Предлагаю программу для вычисления a и b, а также среднеквадратичного отклонения точек от построенной прямой.
00. Сх 01. П1 02. П2 03. П3 04. П4 05. П5 06. П6 07. С/П 08. ПВ 09. x-y 10. ПА 11. 7 12. П0 13. ИПА 14. КППD 15. ИПВ 16. КППD 17. ИПА 18. Fx2 19. КППD 20. ИПВ 21. Fx2 22. КППD 23. ИПА 24. ИПВ 25. * 26. КППD 27. 1 28. КППD 29. ИП1 30. С/П 31. БП 32. 08 33. ИП5 34. ИП6 35. ИП1 36. / 37. ИП5 38. * 39. ИП2 40. - 41. ИП6 42. Fx2 43. ИП1 44. / 45. ИП4 46. - 47. / 48. ПА 49. ИП6 50. * 51. - 52. ИП1 53. / 54. ПВ 55. ИП3 56. ИПВ 57. ИП5 58. * 59. - 60. ИПА 61. ИП2 62. * 63. - 64. ИП1 65. / 66. ПС 67. С/П 68. /-/ 69. КИПО 70. + 71. КП^ 72. В/О.
После ввода программы набрать В/О С/П 69 ПD x1 ^ y1 С/П ... xn ^ yn ШГ> (со стрелкой вправо) С/П. Результаты: a в PA, b в РВ, сигма2 в PC и на индикаторе. Для продолжения ввода исходных данных набрать БП 08 x[n+i] ^ y[n+1] С/П...
Программа допускает исправление ошибок ввода. Допустим, неверно введена очередная пара чисел. Проделайте операции:
4 П0 68 ПД С/П. затем заново зашлите 69 в РД, и все готово к повторному вводу той же пары. Если ошибка обнаружена не в последней паре (xi,yi), исключите образованные ею слагаемые из всех накопленных сумм. Для этого наберите 68 ПВ xi ^ yi С/П 69 ПВ и продолжайте счет.
Д. Богданов. Часто необходимо знать, насколько сильна связь между переменными, насколько велик разброс опытных данных. Для этого необходимо вычислить коэффициент корреляции r и среднее отклонение сигма:
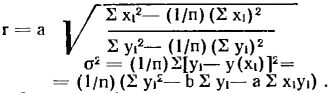
Знак коэффициента корреляции соответствует наклону сглаживающей прямой, по абсолютной величине он не может превышать единицу, и чем он ближе к ней, тем теснее точки группируются около линии регрессии. Однако если коэффициент корреляции близок к нулю, это еще не означает, что исследуемые величины никак ие связаны. Можно лишь утверждать, что отсутствует линейная связь, переменные же могут иметь тесную нелинейную зависимость. Надо попытаться "угадать" ее по расположению точек на графике - например, проведя сглаживающую их линию от руки.
Ю.Каптелов. Иногда в подобных случаях удается так преобразовать координаты, что линия регрессии представляется уже прямолинейной и ее можно строить описанными выше простыми приемами.
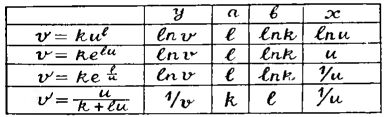
С.Кулибаба. В таких случаях в программу целесообразно включить фрагмент, где будет проводиться линеаризирующее преобразование исходных величии u и v, а затем искать параметры прямой y=ax+b.
И.Шмаков. Но если при этом рассчитывать коэффициент корреляции и среднее отклонение, то следует помнить, что они соответствуют преобразованным величинам н не равны тем же характеристикам исходных величин. Минимизируя линеаризованную зависимость, иногда можно проиграть в величине среднего квадрата ошибки в несколько раз. Подход оказывается спорным. Оптимума иногда можно достичь путем последовательных приближений. В приложении к микрокалькуляторам он рассмотрен в книге А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для микро-ЭВМ "Б3-34", "МК-56", "МК-54".
Б.Ходов. Если линеаризирующее преобразование отыскать не удается, можно попытаться строить линию регрессии в виде многочлена. Правда, объем вычислений при этом резко возрастает. Для построения сглаживающего многочлена n-ной степени приходится решать систему линейных уравнений порядка n+1. На основании своего опыта могу с уверенностью сказать, что на практике в 70 процентах случаев удовлетворительное приближение достигается с помощью линейного сглаживания, а две трети остальных задач допускают приемлемое сглаживание с помощью параболы y=ax2+bx+c. Вот система уравнений для отыскания ее параметров:
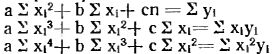
Программа (А.Цветков, В.Епанечников). 00. КНОП 01. С/П 02. П2 03. x-y 04. П3 05. 1 06. 2 07. П0 08. КИП4 09. 4 10. П1 11. ИП3 12. ПП 13. 14 14. ^ 15. КИП0 16. + 17. КП ^ 18. x-y 19. ИП3 20. * 21. FL1 22. 14 23. 3 24. П1 25. ИП2 26. В/О 27. 8 28. 6 29. ПD 30. ИПА 31. ИП9 32. ИП9 33. ИП8 34. / 35. П2 36. КППD 37. П1 38. ИП4 39. ИПВ 40. ИП2 41. ИПА 42. КППD 43.ПВ 44. Fx2 45. ИП1 46. / 47. - 48. ИПA 49. ИПА 50. ИП8 51. / 52. П3 53. КППD 54. П4 55. ИП6 56. ИП2 57. ИП5 58. КППD 59. П6 60. ИП7 61. ИП3 62. ИП5 63. КППD 64. ИП6 65. ИПВ 66. * 67. ИП1 68. / 69. - 70. ИП4 71. / 72. П0 73. ИПВ 74. КППD 75. ИП1 76. / 77. П1 78. ИП5 79. ИП8 80. / 81. ИП2 82. ИП1 83. КППD 84. ИП3 85. ИП0 86. * 87. - 88. ПС 89. В/О 90. 1 91. 2 92. П0 93. Сх 94. КП^ 95. FL0 96. 94 97. С/П.
После ввода программы набрать БП 90 С/П В/О С/П x1 ^ y1 С/П... xn ^ yn С/П БП 27 С/П. Результаты: а в PC и на индикаторе, b в Р1, c в Р0.
Е.Атавин. Для периодических процессов удобно сглаживание тригонометрическими рядами - например, для нечетных функций
y=sum(ak*sin(k*x));
число слагаемых определяется требованиями конкретной задачи. Для точек xi, равностоящих на отрезке [0,2пи] с шагом 2пи/(n-1), метод наименьших квадратов дает: (n-1)ak=2sum(yi*sin(k*xi)).
А.Тулайков. Если значения xi можно задавать по произволу, то поиск сглаживающего многочлена существенно упрощается с помощью полиномов Чебышева Tk(x). В силу их ортогональности на некоторых системах точек (их и следует брать в качестве xi), коэффициенты разложения сглаживающего многочлена по чебышевским полиномам вычисляются независимо друг от друга. Предварительно интервал изменения аргумента x простым линейным преобразованием приводится к интервалу [-1,1]. На нем берем х1=cos((2i+1)пи/(2m+2)). i=0, 1, ... m, и строим сглаживающий многочлен Р(х)=а0+sum(ak*Tk(x)), где (m+1)ak=2sum(y1*cos((2i+1)k*пи/(2m+2))), k= 1, ... n; (m+1)an=sum(yi).
Длина суммы n не должна превышать m, число точек xi.
00. 4 01. П4 02. С/П 03. КП4 04. БП 05. 02 06. 4 07. П4 08. Сх 09. Fпи 10. ИП2 11. * 12. A1 13. А2 14. / 15. ИП1 16. 2 17. + 18. П1 19. * 20. Fcos 21. КИП4 22. * 23. + 24. FL3 25. 09 26. 2 27. * 28. А3 29. / 30. С/П 31. БП 32. 06.
Задавшись конкретным m<=9, находим фигурирующие в программе (адреса 12, 13, 28 ) однозначные числа А1 и А2 из равенства 10А1+А2=2(m+1); A3=m+1, но если m=9, то окончание программы: 26. 5 27. / 28. С/П 29. БП 30. 06. После ввода программы набрать: -1 П1 0 П2 (m + 1) П3 В/О С/П y1 С/П... ym; БП 06 С/П. Получаем 2ас. Затем набираем: -1 П1 k П2 (m + 1) ПЗ С/П. На индикаторе: ak . Программу можно использовать и при m>9. Она позволяет последовательно наращивать степень сглаживающего полинома и остановиться на приемлемой степени.
И.Шмаков. Метод наименьших квадратов весьма универсален, но это лишь метод обработки результатов исследования, он не может подменить всестороннего изучения исследуемых процессов. Порою точки графика почти с одинаковым успехом удается сгладить кривыми, совершенно различными по функциональной природе. Пренебрежение этими соображениями чревато грубыми ошибками в выводах. Выбор сглаживающей функции должен диктоваться физическим смыслом задачи, при анализе которой получены экспериментальные точки, а ие математическим аппаратом, всегда играющим лишь служебную роль.
ОТ РЕДАКЦИИ. к сожалению, никому из тех читателей, кто брался за задачу сглаживания функции, зависящей от двух переменных, не удалось свести решение к одной программе, умещающейся в памяти "Электроники Б3-34". Тем не менее это возможно - см. уже упоминавшуюся книгу А.Н.Цветкова и В.А.Епанечникова. Методу наименьших квадратов в ней уделяется значительное внимание: рассматривается общая задача сглаживания функциями вида af(x)+bg(x), степенной и экспоненциальной функциями и т.д.
Некоторые читатели затрагивают в своих письмах вычисление на микрокалькуляторе дисперсии коэффициентов регрессии (1), построение доверительных интервалов для них и коэффициента корреляции (2), численную оценку точности сглаживания по критерию Фишера (3), вопросы использования полиномов Чебышева (4). Авторы некоторых этих писем любезно согласились опубликовать свои адреса в нашем журнале, чтобы обменяться опытом с коллегами.
644077 Омск, просп.Мира, 55а, университет, химический факультет. Атавин Е.Г. (1).
410026 Саратов, ул.Астраханская, 83, кор.1. НИИ химии СГУ. отдел физической химии. лаб. 1.2. Камнев А.А. (1, 2).
150051 Ярославль до востребования. Москвин А.Ф. (1,2).
650027 Кемерово, пр.Ленина. 46. кв.19. Мурышкин Д.Л. (1,2).
141700 Московская обл., г.Долгопрудный, Лихачевское шоссе. 21. кв.128. Тулайков А.Н. (4).
127562 Москва, ул.Санникова, 17, кв.217, Ходов Б.Н. (3).
ЛИТЕРАТУРА
Линник Ю. В. Метод наименьших квадратов и основы теории обработки данных. М., Физматгиз. 1958.
Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. М.. "Наука". 1968.
Фeрстер Э., Ренц В. Методы корреляционного и регрессионного анализа (пер. с нем.). М., "Финансы и статистика". 1983.
Цветков А.Н. Анализ и интерпретация экспериментальных данных. Известия вузов MB и ССО СССР. Радиоэлектроника, т.27, #8. 1984.
ВЕДЕМ СЛУЧАЙНЫЙ ПОИСК
Суть любой задачи оптимизации состоит в нахождении максимума или минимума функции, зависящей и общем случае от нескольких аргументов.
В предлагаемой программе реализован алгоритм решения безусловной трехмерной оптимизационной задачи методом случайного поиска. Суть метода поясним для наглядности на примере функции всего лишь двух переменных, для которой можно построить зримый график в виде некоторой поверхности. Пусть требуется найти минимум функции. Выбираем произвольную точку из области аргументов и в ней вычисляем значение функции. Затем в окрестности некоторого радиуса вокруг начальной точки случайным образом берем несколько других точек. Если в какой-то из них значение функции меньше, чем в исходной, то принимаем ее за центр новой окрестности. Если такой точки не нашлось, то сужаем радиус окрестности для уточнения координат минимума.
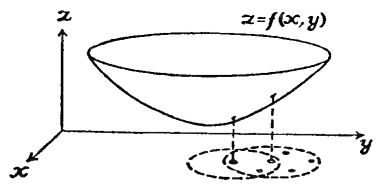
Метод не безупречен, но во многих случаях удовлетворителен. Конечно, он требует большого объема вычислений, что удлиняет счет, но при этом ие выдвигается никаких специальных требований к виду функции. Ее не приходится дифференцировать, как при использовании других алгоритмов - здесь сравниваются сами значения функции.
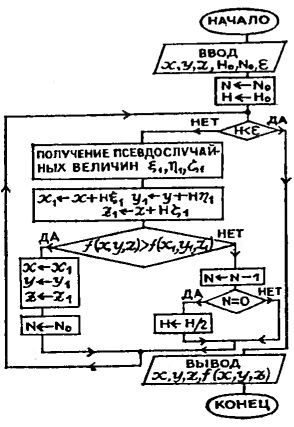
Блок-схема алгоритма приведена на рисунке (е - погрешность). Генератор псевдослучайных чисел реализован с помощью простого приема. Задается произвольное число а0 между нулем и единицей, и затем каждое новое значение случайной величины вычисляется через предыдущее по формуле a[k+1]=10**ak-[10**ak]. где квадратные скобки означают целую часть. Так как в программе удобнее пользоваться числами, лежащими в пределах от -0.5 до 0.5, то последовательность заменяется другой: кси=ak-0.5. Она не дает идеального равномерного распределения, но зато каждый ее член генерируется достаточно быстро.
В программе предусмотрен автоматический останов после "неудачных" сравнений (когда все новые значения функции больше старого). Пользователь имеет возможность оперативно просмотреть полученные результаты и, если они устраивают его, закончить счет, а если нет, то продолжить, нажав клавишу С/П. При этом вычисления повторяются, но уже с уменьшенным вдвое шагом. Рекомендуется сравнить результаты двух циклов и при их расхождении, не превышающем нужной пользователю точности, прекращать вычисления.
Программа. 00. ПП 01. 47 02. x-y 03. ПА 04. ИП1 05. П2 06. ИП4 07. П5 08. ИП7 09. П8 10. ИПД 11. П3 12. 9 13. П0 14. ИПС 15. F10X 16. ПС 17. КИПС 18. x-y 19. ИПС 20. - 21. ПС 22. 2 23. F1/x 24. - 25. ИП6 26. * 27. КИП0 28. + 29. КП0 30. FL0 31. 14 32. ПП 33. 47 34. ИПА 35. - 36. Fx>=0 37. 02 38. FL3 39. 12 40. ИП6 41. 2 42. / 43. П6 44. С/П 45. БП 46. 10.
Подпрограмма контрольного примера. 47. ИП7 48. Fx2 49. ИП4 50. Fx2 51. 2 52. * 53. + 54. ИП1 55. Fx2 56. 4 57. * 58. + 59. ИП1 60. 1 61. - 62. ИП4 63. * 64. ИП7 65. + 66. + 67. ^ 68. В/О.
Поясню порядок работы с программой. После ввода ее текста набрать, начиная с адреса 47, подпрограмму вычисления значений оптимизирующей функции. Текущие значения переменных для нее выбирать из регистров: X из Р7, Y из Р4 и Z из Р1. Подпрограмма должна заканчиваться командой ^. Начальные значения переменных Хо, Yo и Zo записываются в те же регистры, Р7, Р4 и Р1 соответственно, число повторений N - в PD. Я считаю, что брать N больше 10 нецелесообразно. Начальное значение шага Н0 - в Р6, a0 - в PC. После ввода начальных данных запустить программу, нажав клавиши В/О, С/П.
Контрольный пример: f(x,y,z)=х2+2у2+4z2+х+y(z-1). Начальные значения: X0=Y0=Z0=l, H0=l, a0=0.4, N=10. Первый останов наступает минут через 20. На экране: 5e-1. Это значение нового шага. Текущие значения X, Y, Z, f находятся в регистрах Р8, Р5, Р2 и РА и равны соответственно -0.4388439, 0.3597393, 0.0417096, -0.32521117. Точное решение: Х=-0.5; Y=0.25806451; Z=-0.032258064; f=-0.37903227. Приближение, обеспечивающее четыре верных знака, получается при Н=3.90625e-3, то есть на восьмом шаге итераций.
Е.ПЕТРАКОВ (г.Москва)
ВСЕ НАЧАЛОСЬ С МИКРОКАЛЬКУЛЯТОРА
На рисунке - фрагмент плана Москвы, составленного в 1767 году. Бросается в глаза, что у Большой Садовнической улицы (ныне улица Осипенко; на плане отмечена стрелкой), идущей вдоль южного берега Москвы-реки, застроена преимущественно южная сторона. Казалось бы, для застройки предпочтительнее другая, противоположная сторона - ведь она обращена к солнцу. Но, быть может, определяющими здесь были интересы видовой ориентации зданий? Южная сторона Большой Садовнической улицы глядела иа Кремль, его соборы, на храмы, стоявшие восточнее него. С помощью микрокалькулятора было подсчитано число домов на разных сторонах улиц, идущих вдоль Москвы-реки на Замоскворецком и Кремлевском берегах. Подсчет подтвердил гипотезу и тем самым дал основание для того, чтобы с помощью уже "большой" ЭВМ проанализировать всю застройку Москвы в границах того времени. Результаты расчета вошли в научную публикацию иа эту тему. Они позволили уверенно говорить о тенденции московских градостроителей прошлого ориентировать здания преимущественно на значительные архитектурные сооружения - Кремль, соборы, монастыри.
Р.ГАРЯЕВ, архитектор (г.Москва)
НА КЛАВИШАХ - РЕЛЬЕФНЫЕ ЦИФРЫ
Слепым недоступна логарифмическая линейка, а таблицы Брадиса, изданные по Брайлю, занимают так много томов, что поиск необходимых данных малопродуктивен и чрезвычайно утомителен. Нужен эффективный вычислительный инструмент для людей с ослабленным зрением. Мы решили создать микрокалькулятор для слепых.
Первый и основной вопрос, который необходимо было решить,- как отображать информацию микрокалькулятора? Кодированными сигналами типа азбуки Морзе? Речевым произношением цифр? Индикацией по системе Брайля?
Первые два способа ориентируются на слуховое восприятие и, как показали эксперименты, малоэффективны, хотя и принципиально возможны. Мы остановились на системе Брайля. Были разработаны специальные электромеханические индикаторы с электронными схемами управления. Важно было обеспечить надежность индикатора, потому что при выбранном способе практически невозможно исправить ошибочно отображенную информацию.
Второй вопрос - это выбор базового микрокалькулятора. На основании эргономических и инженерно-психологических исследований был выбран калькулятор МК-46. На клавиатуре дополнительно были нанесены рельефные обозначения, что облегчает поиск нужных клавиш.
Наконец, третий вопрос, который пришлось решать, касается некоторых специальных методических приемов вычислений, облегчающих работу слепых. Один из таких приемов заключается, например, в максимальном использовании регистров памяти, чтобы сократить запись промежуточных результатов.
Какова же эффективность работы на таком микрокалькуляторе? В сравнительном эксперименте приняли участие слепой математик-программист и один из авторов статьи. Эксперимент заключался в вычислении значений многочлена по схеме Горнера. Время, затраченное обоими на решение поставленной задачи, практически одинаково.
Сейчас по заказу Института дефектологии АПН СССР мы готовим опытную партию микрокалькуляторов с брайлевской индикацией.
В.ВОРОНИН, В.ИВАНОВСКИЙ (г.Свердловск)
ВНИМАНИЕ, ЭНТУЗИАСТЫ!
Желая принять участие в "Школе начинающего программиста" (см. 10/84), киевлянин В.Бардадым прислал в редакцию подробный конспект занятий, которые он вел в одной из школ г.Киева. Такие материалы существенно помогут становлению школы. Предлагаем тем, кто вел кружки, читал лекции, проводил занятия по программированию на калькуляторах, последовать примеру В. Бардадыма.
"Хотелось бы поучаствовать в школе,- пишет нам С.Карпов из Орла,- но все как-то не могу определиться с темой и формой". Время между тем не ждет. Предлагаем каждому из желающих немедля прислать законченное выступление по любому пункту программы, опубликованной в 10/84 в любой форме,- за редактированием дело не станет.
***
Тем временем в большом мире...
ЗРИТЕЛЬНАЯ ПАМЯТЬ ЭВМ
В крупных современных учреждениях роль архива нередко поручают электронно-вычислительным машинам, которые хранят документы в своей памяти в виде последовательности импульсов, записанных на магнитный диск или ленту. Набрав на пульте ЭВМ номер документа, иногда очень сложный и многозначный, можно практически мгновенно получить его текст на экране специального телевизора-дисплея или положить на стол в отпечатанном виде. Такой способ хранения информации удобен во всем, кроме одного: люди, работающие с документами, с трудом запоминают, а зачастую и вообще не знают их номера и, стоя перед ЭВМ, с тоской вспоминают те времена, когда было твердо известно, что искомая бумага находится "в четвертой комнате, во втором шкафу слева, в синей папке на третьей полке снизу". Зрительный образ места хранения запоминается гораздо легче комбинации цифр.
Но, оказывается, современная электронная техника способна держать в своей памяти даже такие сведения о документе, как цвет папки, в которой он лежит, и специалисты японской фирмы "Тосиба" создали подобное устройство специально для хранения архивной информации. Его дисплей имеет два экрана - цветной и черно-белый. Набрав соответствующий код, оператор выводит на экран... цветное изображение хранилища документов со множеством шкафов и полок. Экран дисплея чувствует прикосновения, и команду "нарисовать" во весь экран нужный шкаф оператор дает, просто коснувшись пальцем его изображения на общем плане. Таким образом оператор выводит на цветной экран отдельно нужную полку с папками, а содержимое той или иной папки быстро "перелистывает" на черно-белом экране, пока не увидит требуемый документ.
Так можно найти документ только по его визуальным признакам, не имея других характеристик, скажем, можно отыскать личное дело сотрудника по фотографии, не помня его фамилии, но зная в лицо.
Разумеется, весь интерьер хранилища со всеми его шкафами и разноцветными папками в них существует только в самой ЭВМ в виде программы, формирующей изображение на экране.
Для ее хранения нужен огромный объем памяти, который способен обеспечить только новый, недавно разработанный способ записи информации при помощи лазера. Мощный лазерный луч проплавляет в металлизированном пластмассовом диске отверстия диаметром около микрометра (0.001мм). Получается нечто вроде перфокарты микроскопических размеров, информация с которой считывается также лазерным лучом. На диске диаметром 30см можно записать более 1 гигабайта, то есть 1e9 байт информации (байт - "слог" машинного языка, составляющий 8 бит - двоичных единиц) или 2500 страниц текста. Это в 10-15 раз больше, чем на магнитном диске такого же размера.
Огромный объем оптической памяти позволяет использовать ее не только для хранения информации, но и для других целей. На ее основе, например, предполагается сделать тренажер для обучения пилотов. В существующих устройствах применяются видеомагнитофоны и кинопроекторы, которые могут воспроизводить практически только идеальные условия полета. Оптические диски могут хранить самые различные виды окружающего ландшафта и ситуаций и мгновенно выдавать их на экран в соответствии с движением рукояток управления в руках курсанта, имитируя любые мыслимые перипетии, возникающие при взлете, полете и посадке.
(По материалам иностранной печати)
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Рубрика "Человек с микрокалькулятором" вступает в новый год своего существования. Многие направления раздела стали традиционными: конкурсы и дискуссии за круглым столом, "маленькие хитрости" и прикладные программы, присылаемые читателями. Почта раздела содержит также и письма, в которых обсуждается его будущее. В публикуемом ниже отрывке из письма И.Вязовского (г.Люберцы Московской области) речь идет о персональных ЭВМ. Предлагается уделить им место в рамках раздела.
Ждем читательских откликов на это предложение. Несомненно, персональные ЭВМ заслуживают серьезного, углубленного разговора. Следует заранее продумать, как вести его в разделе "Человек с микрокалькулятором" |а быть может, и в отдельных крупных статьях журнала). Провести дискуссию о том, как лучше использовать первые, пока еще немногочисленные персональные ЭВМ? Разобрать устройство этих машин? Дать краткий курс языков "бейсик", "рапира"? Надеемся на активное участие читателей в обсуждении этой темы и, что особенно важно,- в обсуждении подходов к ее освещению в журнале.
НА РАЗНЫХ ПОЛЮСАХ?
Каковы различия между типичными программируемыми микрокалькуляторами (ПМК) и персональными электронными вычислительными машинами (ПЭВМ)?
Что касается быстродействия, объема памяти, то это дело наживное. На этих чисто количественных различиях останавливаться не будем. Поговорим о различиях качественных, принципиальных. С точки зрения пользователя, это прежде всего языки программирования.
Язык микрокалькулятора близок к так называемым автокодам [Автокод - язык программирования, ориентированный на конкретную ЭВМ. Отличается от машинного языка заменой кодов команд их мнемоническими обозначениями и возможностью использовать относительные адреса]. Запись любой программной конструкции, например, арифметического выражения, распадается на ряд элементарных команд, в каждой из которых записывается либо операция, либо операнд (число, над которым совершается операция), либо адрес. Каждая команда заносится в конкретную ячейку памяти. Возможность редактирования программ очень ограничена. Можно заменить какую-то команду, но вставить новую команду в середину программы нельзя. Для нее нет места. Да и набор команд очень мал.
Владелец ПЭВМ оперирует языком высокого уровня. Это "бэйсик" или "рапира" (язык, специально разработанный новосибирскими учеными, которым будут оснащены отечественные ПЭВМ). Программировать на этих языках значительно удобнее, чем в автокодах. Запись выражений почти не отличается от обычной, принятой в математике. Очень широк набор операторов, особенно в "рапире". Там есть возможность работать не только с числами, но и с текстами, рисунками. Практически не ограничены возможности редактирования. Есть еще один аспект, облегчающий работу на ПЭВМ: богатое математическое обеспечение, пользоваться которым может любой человек, даже не умеющий программировать.
С точки зрения программирования, ПМК и ПЭВМ находятся на разных полюсах. Микрокалькулятор как бы возвращает нас к "древней" машинной культуре, когда автокоды были единственными языками программирования. Перефразируя остроумное замечание академика А.П.Ершова, можно сказать, что ПМК - это разновидность искусственно выведенного комнатного динозавра, а ПЭВМ - представитель отряда высших млекопитающих в мире ЭВМ. Смысл этой метафоры станет еще более ясным, если мы сравним структуры микрокалькулятора и персональной ЭВМ.
В ПМК области хранения чисел и команд разделены. Так было и в первых ЭВМ. Выдвинутый американским математиком Дж. фон Нейманом принцип единой области памяти, каждый элемент которой можно трактовать или как число или как команду, привел к современным ЭВМ. Так что и с этой точки зрения ПМК и ПЭВМ на разных полюсах.
И все-таки можно утверждать, что оба этих вычислительных устройства - братья. Роднит их важное качество: и то и другое - машины индивидуального пользования. Владелец каждой из них - одновременно и постановщик задач, и программист, и оператор, и пользователь. Короче, он хозяин машины. Может считать на ней что хочет и когда хочет, может использовать ее как партнера в игре, может беспредельно экспериментировать на ней. Ему не нужно днями, а то и неделями ждать очереди, чтобы выйти на ЭВМ, нервно сидеть за пультом, боясь потерять минуты драгоценного времени. Его ЭВМ всегда доступна. Благодаря этому процесс отладки и получения результатов резко сокращается. В государственном аспекте это означает большую эффективность решения задач с помощью ЭВМ.
Как же поведут себя "братья" дальше? Будут ли микрокалькуляторы вытеснены персональными ЭВМ подобно тому, как трамвай вытеснил конку? Или они будут мирно сосуществовать, как, скажем, лампы накаливания и люминесцентные трубки?
Конечно, возможности персональной ЭВМ много выше. Она может служить и картотекой, и запиской книжкой, и большим калькулятором, и универсальной ЭВМ. Работать на ней легче и удобнее. Но место ее - на рабочем столе. Из дома на работу ее не возьмешь, в командировку с ней не поедешь. Микрокалькулятор же легко умещается в портфеле или даже в кармане. Это по сути своей - переносная машина. Нельзя сбрасывать со счетов и цены на машины того и другого класса: конечно, по мере развития технологии они будут снижаться, но соотношение между ними вряд ли скоро изменится. Не за горами и увеличение возможностей ПМК - расширение набора команд, увеличение быстродействия, дополнительные блоки памяти, магнитные карты и т.д. Все это, естественно, без существенного изменения цен и габаритов.
Вообще ПМК постепенно догоняют ПЭВМ не только по количественным показателям, но и по качественным, поэтому со временем различие между ними, наверное, исчезнет. Скорее всего, эти два типа вычислительных устройств будут сосуществовать долго. И, пожалуй, еще одно. Опыт работы с ПМК, где постоянно приходится учитывать специфику машины, идти на разные ухищрения, чтобы втиснуть сложный алгоритм в малую память, безусловно, даст себя знать при переходе на ПЭВМ или другую универсальную машину. Тот, кто прошел школу ПМК, наверняка значительно лучше сможет использовать ресурсы и возможности другой ЭВМ, нежели "человек с улицы".
... Дружные родственники всегда стремятся жить поближе друг к другу. Не отвести ли братьям из большой семьи вычислительных устройств единую "жилплощадь" на страницах журнала "Наука и жизнь"? Думаю, что персональные ЭВМ должны найти свое место под рубрикой "Человек с микрокалькулятором".
И.ВЯЗОВСКИЙ (г.Люберцы)
[ ИЗ ПИСЕМ
Считаю крайне важным и необходимым делом использование ЭВМ в школах и вузах. Самое удивительное, что в своем большинстве наши преподаватели полностью игнорируют возможность применения ЭВМ у нас в институте, не говоря уже о том, чтобы готовить нас к будущей работе в школе с микрокалькуляторами и персональными ЭВМ. Доходит до смешного. На практических занятиях по статистической физике наша преподавательница, кандидат физико-математических наук, весьма недвусмысленно высказалась об использовании нами микрокалькуляторов для вычислений. Она утверждает, что так мы теряем "чувство числа" и получаем "немыслимые результаты". Я не отрицаю, что можно ошибиться, считая на калькуляторе, но ведь еще легче ошибиться, считая в уме или на бумаге.
Г.БЕЛЫЙ, студент пединститута (г.Ставрополь) ]
[ Я учусь в физико-математической школе, в 10 классе. С необходимостью приобрести программируемый микрокалькулятор я столкнулся при выполнении работ физического практикума. На обработку результатов измерений мне приходилось тратить по нескольку часов. Я составил для микрокалькулятора программу анализа погрешностей, и теперь на обработку сотни результатов у меня уходит около 20 минут. С помощью микрокалькулятора также очень удобно решать численные задачи по физике и химии, строить графики различных функций.
Я считаю, что овладение навыками элементарного программирования необходимо всем старшеклассникам. Хорошо бы ввести курс программирования в средней школе, хотя бы факультативно.
С.КАДУЛИН, ученик школы #145 (г.Киев) ]
[ ИЗ ГАЗЕТ
Факультативный курс электроники для школьников 9-10 классов, читаемый в общеобразовательных школах ГДР с 1970/71 учебного года, в новом учебном году будет существенно обновлен и обогащен с учетом достижений микроэлектроники, в частности, оптоэлектроники и т.д.
Новый курс даст школьникам основу для дальнейшего самообразования в этой области и позволит осваивать будущие новинки электроники. Вместе с тем учащиеся закрепят знания, полученные ими в курсах физики и ВСП ["Введение в социалистическое производство", учебная дисциплина об основах социалистической экономики, преподаваемая в школах ГДР].
Переработанная программа курса будет утверждена после тщательного опробования, в котором примут участие и сами школьники. Сейчас педагоги на курсах усовершенствования знакомятся с нею, чтобы быть готовыми к началу работы по ней ("Берлинер Цайтунг", 6 марта 1984г.) ]
[ МАЛЕНЬКИЕ ХИТРОСТИ
Отладка длинных программ на микрокалькуляторе - дело трудоемкое. Останавливать вычисления клавишей С/П нельзя - может нарушиться работа программы. Использовать программный останов, например, по состоянию счетчика, тоже не всегда удобно, особенно, если длительность цикла вычислений заранее неизвестна.
Предлагаю управлять работой микрокалькулятора в таких случаях с помощью переключателя Р-Г. Для этого надо ввести в нужное место программы последовательность команд вида: 3 Fcos Fx<0 А С/П, где А-номер команды, следующей за С/П. Если переключатель находится в положении Г (градусы), то cos(3o)>0, и команда останова обходится. При переключении в режим Р (радианы) cos(3)<0, и решение прерывается. Введя вместо С/П команду передачи управления, можно с пульта менять логику выполнения программы.
И.ПЯТАК (г.Днепропетровск) ]
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
В июньском выпуске рубрики "Человек с микрокалькулятором" за прошлый год читатели приглашались на дискуссию за круглым столом о методе наименьших квадратов. В ней приняли участие 25 человек. Публикуем выдержки из выступлений некоторых участников. Это В.Адриан (г.Химки Московской обл.), Е.Атавин (г.Омск), Д.Богданов (г.Москва), Ю.Каптелов (г.Ивано-Франковск), С.Кулибаба (г. Донецк), А. Тулайков (г.Долгопрудный Московской обл.), Б.Ходов (г.Москва), И.Шмаков (г.Новосибирск).
Д.Богданов. Метод наименьших квадратов - один из наиболее распространенных методов математической обработки данных. Рассмотрим простейший пример его применения, когда изучается зависимость одной величины от другой - например, силы тока в цепи от напряжения. По данным опыта наносим точки на график. Они выстраиваются почти по прямой. Естественно желание провести такую сглаживающую прямую. Определим ее требованием, чтобы сумма квадратов вертикальных отклонений всех n точек от прямой sum(h[i]2) была минимальной. Вслед за этим воспользуемся необходимым условием минимума функции двух переменных, в данном случае - суммы
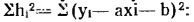
приравняем нулю ее частные производные по а и b . В итоге получим систему для определения параметров искомой прямой, так называемой линии регрессии:
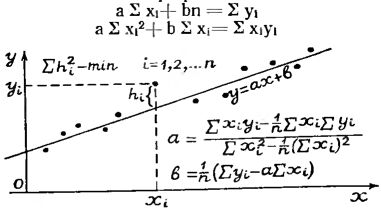
В.Адриан. Предлагаю программу для вычисления a и b, а также среднеквадратичного отклонения точек от построенной прямой.
00. Сх 01. П1 02. П2 03. П3 04. П4 05. П5 06. П6 07. С/П 08. ПВ 09. x-y 10. ПА 11. 7 12. П0 13. ИПА 14. КППD 15. ИПВ 16. КППD 17. ИПА 18. Fx2 19. КППD 20. ИПВ 21. Fx2 22. КППD 23. ИПА 24. ИПВ 25. * 26. КППD 27. 1 28. КППD 29. ИП1 30. С/П 31. БП 32. 08 33. ИП5 34. ИП6 35. ИП1 36. / 37. ИП5 38. * 39. ИП2 40. - 41. ИП6 42. Fx2 43. ИП1 44. / 45. ИП4 46. - 47. / 48. ПА 49. ИП6 50. * 51. - 52. ИП1 53. / 54. ПВ 55. ИП3 56. ИПВ 57. ИП5 58. * 59. - 60. ИПА 61. ИП2 62. * 63. - 64. ИП1 65. / 66. ПС 67. С/П 68. /-/ 69. КИПО 70. + 71. КП^ 72. В/О.
После ввода программы набрать В/О С/П 69 ПD x1 ^ y1 С/П ... xn ^ yn ШГ> (со стрелкой вправо) С/П. Результаты: a в PA, b в РВ, сигма2 в PC и на индикаторе. Для продолжения ввода исходных данных набрать БП 08 x[n+i] ^ y[n+1] С/П...
Программа допускает исправление ошибок ввода. Допустим, неверно введена очередная пара чисел. Проделайте операции:
4 П0 68 ПД С/П. затем заново зашлите 69 в РД, и все готово к повторному вводу той же пары. Если ошибка обнаружена не в последней паре (xi,yi), исключите образованные ею слагаемые из всех накопленных сумм. Для этого наберите 68 ПВ xi ^ yi С/П 69 ПВ и продолжайте счет.
Д. Богданов. Часто необходимо знать, насколько сильна связь между переменными, насколько велик разброс опытных данных. Для этого необходимо вычислить коэффициент корреляции r и среднее отклонение сигма:
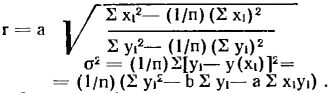
Знак коэффициента корреляции соответствует наклону сглаживающей прямой, по абсолютной величине он не может превышать единицу, и чем он ближе к ней, тем теснее точки группируются около линии регрессии. Однако если коэффициент корреляции близок к нулю, это еще не означает, что исследуемые величины никак ие связаны. Можно лишь утверждать, что отсутствует линейная связь, переменные же могут иметь тесную нелинейную зависимость. Надо попытаться "угадать" ее по расположению точек на графике - например, проведя сглаживающую их линию от руки.
Ю.Каптелов. Иногда в подобных случаях удается так преобразовать координаты, что линия регрессии представляется уже прямолинейной и ее можно строить описанными выше простыми приемами.

С.Кулибаба. В таких случаях в программу целесообразно включить фрагмент, где будет проводиться линеаризирующее преобразование исходных величии u и v, а затем искать параметры прямой y=ax+b.
И.Шмаков. Но если при этом рассчитывать коэффициент корреляции и среднее отклонение, то следует помнить, что они соответствуют преобразованным величинам н не равны тем же характеристикам исходных величин. Минимизируя линеаризованную зависимость, иногда можно проиграть в величине среднего квадрата ошибки в несколько раз. Подход оказывается спорным. Оптимума иногда можно достичь путем последовательных приближений. В приложении к микрокалькуляторам он рассмотрен в книге А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для микро-ЭВМ "Б3-34", "МК-56", "МК-54".
Б.Ходов. Если линеаризирующее преобразование отыскать не удается, можно попытаться строить линию регрессии в виде многочлена. Правда, объем вычислений при этом резко возрастает. Для построения сглаживающего многочлена n-ной степени приходится решать систему линейных уравнений порядка n+1. На основании своего опыта могу с уверенностью сказать, что на практике в 70 процентах случаев удовлетворительное приближение достигается с помощью линейного сглаживания, а две трети остальных задач допускают приемлемое сглаживание с помощью параболы y=ax2+bx+c. Вот система уравнений для отыскания ее параметров:
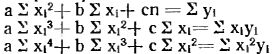
Программа (А.Цветков, В.Епанечников). 00. КНОП 01. С/П 02. П2 03. x-y 04. П3 05. 1 06. 2 07. П0 08. КИП4 09. 4 10. П1 11. ИП3 12. ПП 13. 14 14. ^ 15. КИП0 16. + 17. КП ^ 18. x-y 19. ИП3 20. * 21. FL1 22. 14 23. 3 24. П1 25. ИП2 26. В/О 27. 8 28. 6 29. ПD 30. ИПА 31. ИП9 32. ИП9 33. ИП8 34. / 35. П2 36. КППD 37. П1 38. ИП4 39. ИПВ 40. ИП2 41. ИПА 42. КППD 43.ПВ 44. Fx2 45. ИП1 46. / 47. - 48. ИПA 49. ИПА 50. ИП8 51. / 52. П3 53. КППD 54. П4 55. ИП6 56. ИП2 57. ИП5 58. КППD 59. П6 60. ИП7 61. ИП3 62. ИП5 63. КППD 64. ИП6 65. ИПВ 66. * 67. ИП1 68. / 69. - 70. ИП4 71. / 72. П0 73. ИПВ 74. КППD 75. ИП1 76. / 77. П1 78. ИП5 79. ИП8 80. / 81. ИП2 82. ИП1 83. КППD 84. ИП3 85. ИП0 86. * 87. - 88. ПС 89. В/О 90. 1 91. 2 92. П0 93. Сх 94. КП^ 95. FL0 96. 94 97. С/П.
После ввода программы набрать БП 90 С/П В/О С/П x1 ^ y1 С/П... xn ^ yn С/П БП 27 С/П. Результаты: а в PC и на индикаторе, b в Р1, c в Р0.
Е.Атавин. Для периодических процессов удобно сглаживание тригонометрическими рядами - например, для нечетных функций
y=sum(ak*sin(k*x));
число слагаемых определяется требованиями конкретной задачи. Для точек xi, равностоящих на отрезке [0,2пи] с шагом 2пи/(n-1), метод наименьших квадратов дает: (n-1)ak=2sum(yi*sin(k*xi)).
А.Тулайков. Если значения xi можно задавать по произволу, то поиск сглаживающего многочлена существенно упрощается с помощью полиномов Чебышева Tk(x). В силу их ортогональности на некоторых системах точек (их и следует брать в качестве xi), коэффициенты разложения сглаживающего многочлена по чебышевским полиномам вычисляются независимо друг от друга. Предварительно интервал изменения аргумента x простым линейным преобразованием приводится к интервалу [-1,1]. На нем берем х1=cos((2i+1)пи/(2m+2)). i=0, 1, ... m, и строим сглаживающий многочлен Р(х)=а0+sum(ak*Tk(x)), где (m+1)ak=2sum(y1*cos((2i+1)k*пи/(2m+2))), k= 1, ... n; (m+1)an=sum(yi).
Длина суммы n не должна превышать m, число точек xi.
00. 4 01. П4 02. С/П 03. КП4 04. БП 05. 02 06. 4 07. П4 08. Сх 09. Fпи 10. ИП2 11. * 12. A1 13. А2 14. / 15. ИП1 16. 2 17. + 18. П1 19. * 20. Fcos 21. КИП4 22. * 23. + 24. FL3 25. 09 26. 2 27. * 28. А3 29. / 30. С/П 31. БП 32. 06.
Задавшись конкретным m<=9, находим фигурирующие в программе (адреса 12, 13, 28 ) однозначные числа А1 и А2 из равенства 10А1+А2=2(m+1); A3=m+1, но если m=9, то окончание программы: 26. 5 27. / 28. С/П 29. БП 30. 06. После ввода программы набрать: -1 П1 0 П2 (m + 1) П3 В/О С/П y1 С/П... ym; БП 06 С/П. Получаем 2ас. Затем набираем: -1 П1 k П2 (m + 1) ПЗ С/П. На индикаторе: ak . Программу можно использовать и при m>9. Она позволяет последовательно наращивать степень сглаживающего полинома и остановиться на приемлемой степени.
И.Шмаков. Метод наименьших квадратов весьма универсален, но это лишь метод обработки результатов исследования, он не может подменить всестороннего изучения исследуемых процессов. Порою точки графика почти с одинаковым успехом удается сгладить кривыми, совершенно различными по функциональной природе. Пренебрежение этими соображениями чревато грубыми ошибками в выводах. Выбор сглаживающей функции должен диктоваться физическим смыслом задачи, при анализе которой получены экспериментальные точки, а ие математическим аппаратом, всегда играющим лишь служебную роль.
ОТ РЕДАКЦИИ. к сожалению, никому из тех читателей, кто брался за задачу сглаживания функции, зависящей от двух переменных, не удалось свести решение к одной программе, умещающейся в памяти "Электроники Б3-34". Тем не менее это возможно - см. уже упоминавшуюся книгу А.Н.Цветкова и В.А.Епанечникова. Методу наименьших квадратов в ней уделяется значительное внимание: рассматривается общая задача сглаживания функциями вида af(x)+bg(x), степенной и экспоненциальной функциями и т.д.
Некоторые читатели затрагивают в своих письмах вычисление на микрокалькуляторе дисперсии коэффициентов регрессии (1), построение доверительных интервалов для них и коэффициента корреляции (2), численную оценку точности сглаживания по критерию Фишера (3), вопросы использования полиномов Чебышева (4). Авторы некоторых этих писем любезно согласились опубликовать свои адреса в нашем журнале, чтобы обменяться опытом с коллегами.
644077 Омск, просп.Мира, 55а, университет, химический факультет. Атавин Е.Г. (1).
410026 Саратов, ул.Астраханская, 83, кор.1. НИИ химии СГУ. отдел физической химии. лаб. 1.2. Камнев А.А. (1, 2).
150051 Ярославль до востребования. Москвин А.Ф. (1,2).
650027 Кемерово, пр.Ленина. 46. кв.19. Мурышкин Д.Л. (1,2).
141700 Московская обл., г.Долгопрудный, Лихачевское шоссе. 21. кв.128. Тулайков А.Н. (4).
127562 Москва, ул.Санникова, 17, кв.217, Ходов Б.Н. (3).
ЛИТЕРАТУРА
Линник Ю. В. Метод наименьших квадратов и основы теории обработки данных. М., Физматгиз. 1958.
Пустыльник Е.И. Статистические методы анализа и обработки наблюдений. М.. "Наука". 1968.
Фeрстер Э., Ренц В. Методы корреляционного и регрессионного анализа (пер. с нем.). М., "Финансы и статистика". 1983.
Цветков А.Н. Анализ и интерпретация экспериментальных данных. Известия вузов MB и ССО СССР. Радиоэлектроника, т.27, #8. 1984.
ВЕДЕМ СЛУЧАЙНЫЙ ПОИСК
Суть любой задачи оптимизации состоит в нахождении максимума или минимума функции, зависящей и общем случае от нескольких аргументов.
В предлагаемой программе реализован алгоритм решения безусловной трехмерной оптимизационной задачи методом случайного поиска. Суть метода поясним для наглядности на примере функции всего лишь двух переменных, для которой можно построить зримый график в виде некоторой поверхности. Пусть требуется найти минимум функции. Выбираем произвольную точку из области аргументов и в ней вычисляем значение функции. Затем в окрестности некоторого радиуса вокруг начальной точки случайным образом берем несколько других точек. Если в какой-то из них значение функции меньше, чем в исходной, то принимаем ее за центр новой окрестности. Если такой точки не нашлось, то сужаем радиус окрестности для уточнения координат минимума.

Метод не безупречен, но во многих случаях удовлетворителен. Конечно, он требует большого объема вычислений, что удлиняет счет, но при этом ие выдвигается никаких специальных требований к виду функции. Ее не приходится дифференцировать, как при использовании других алгоритмов - здесь сравниваются сами значения функции.

Блок-схема алгоритма приведена на рисунке (е - погрешность). Генератор псевдослучайных чисел реализован с помощью простого приема. Задается произвольное число а0 между нулем и единицей, и затем каждое новое значение случайной величины вычисляется через предыдущее по формуле a[k+1]=10**ak-[10**ak]. где квадратные скобки означают целую часть. Так как в программе удобнее пользоваться числами, лежащими в пределах от -0.5 до 0.5, то последовательность заменяется другой: кси=ak-0.5. Она не дает идеального равномерного распределения, но зато каждый ее член генерируется достаточно быстро.
В программе предусмотрен автоматический останов после "неудачных" сравнений (когда все новые значения функции больше старого). Пользователь имеет возможность оперативно просмотреть полученные результаты и, если они устраивают его, закончить счет, а если нет, то продолжить, нажав клавишу С/П. При этом вычисления повторяются, но уже с уменьшенным вдвое шагом. Рекомендуется сравнить результаты двух циклов и при их расхождении, не превышающем нужной пользователю точности, прекращать вычисления.
Программа. 00. ПП 01. 47 02. x-y 03. ПА 04. ИП1 05. П2 06. ИП4 07. П5 08. ИП7 09. П8 10. ИПД 11. П3 12. 9 13. П0 14. ИПС 15. F10X 16. ПС 17. КИПС 18. x-y 19. ИПС 20. - 21. ПС 22. 2 23. F1/x 24. - 25. ИП6 26. * 27. КИП0 28. + 29. КП0 30. FL0 31. 14 32. ПП 33. 47 34. ИПА 35. - 36. Fx>=0 37. 02 38. FL3 39. 12 40. ИП6 41. 2 42. / 43. П6 44. С/П 45. БП 46. 10.
Подпрограмма контрольного примера. 47. ИП7 48. Fx2 49. ИП4 50. Fx2 51. 2 52. * 53. + 54. ИП1 55. Fx2 56. 4 57. * 58. + 59. ИП1 60. 1 61. - 62. ИП4 63. * 64. ИП7 65. + 66. + 67. ^ 68. В/О.
Поясню порядок работы с программой. После ввода ее текста набрать, начиная с адреса 47, подпрограмму вычисления значений оптимизирующей функции. Текущие значения переменных для нее выбирать из регистров: X из Р7, Y из Р4 и Z из Р1. Подпрограмма должна заканчиваться командой ^. Начальные значения переменных Хо, Yo и Zo записываются в те же регистры, Р7, Р4 и Р1 соответственно, число повторений N - в PD. Я считаю, что брать N больше 10 нецелесообразно. Начальное значение шага Н0 - в Р6, a0 - в PC. После ввода начальных данных запустить программу, нажав клавиши В/О, С/П.
Контрольный пример: f(x,y,z)=х2+2у2+4z2+х+y(z-1). Начальные значения: X0=Y0=Z0=l, H0=l, a0=0.4, N=10. Первый останов наступает минут через 20. На экране: 5e-1. Это значение нового шага. Текущие значения X, Y, Z, f находятся в регистрах Р8, Р5, Р2 и РА и равны соответственно -0.4388439, 0.3597393, 0.0417096, -0.32521117. Точное решение: Х=-0.5; Y=0.25806451; Z=-0.032258064; f=-0.37903227. Приближение, обеспечивающее четыре верных знака, получается при Н=3.90625e-3, то есть на восьмом шаге итераций.
Е.ПЕТРАКОВ (г.Москва)
ВСЕ НАЧАЛОСЬ С МИКРОКАЛЬКУЛЯТОРА

На рисунке - фрагмент плана Москвы, составленного в 1767 году. Бросается в глаза, что у Большой Садовнической улицы (ныне улица Осипенко; на плане отмечена стрелкой), идущей вдоль южного берега Москвы-реки, застроена преимущественно южная сторона. Казалось бы, для застройки предпочтительнее другая, противоположная сторона - ведь она обращена к солнцу. Но, быть может, определяющими здесь были интересы видовой ориентации зданий? Южная сторона Большой Садовнической улицы глядела иа Кремль, его соборы, на храмы, стоявшие восточнее него. С помощью микрокалькулятора было подсчитано число домов на разных сторонах улиц, идущих вдоль Москвы-реки на Замоскворецком и Кремлевском берегах. Подсчет подтвердил гипотезу и тем самым дал основание для того, чтобы с помощью уже "большой" ЭВМ проанализировать всю застройку Москвы в границах того времени. Результаты расчета вошли в научную публикацию иа эту тему. Они позволили уверенно говорить о тенденции московских градостроителей прошлого ориентировать здания преимущественно на значительные архитектурные сооружения - Кремль, соборы, монастыри.
Р.ГАРЯЕВ, архитектор (г.Москва)
НА КЛАВИШАХ - РЕЛЬЕФНЫЕ ЦИФРЫ
Слепым недоступна логарифмическая линейка, а таблицы Брадиса, изданные по Брайлю, занимают так много томов, что поиск необходимых данных малопродуктивен и чрезвычайно утомителен. Нужен эффективный вычислительный инструмент для людей с ослабленным зрением. Мы решили создать микрокалькулятор для слепых.
Первый и основной вопрос, который необходимо было решить,- как отображать информацию микрокалькулятора? Кодированными сигналами типа азбуки Морзе? Речевым произношением цифр? Индикацией по системе Брайля?
Первые два способа ориентируются на слуховое восприятие и, как показали эксперименты, малоэффективны, хотя и принципиально возможны. Мы остановились на системе Брайля. Были разработаны специальные электромеханические индикаторы с электронными схемами управления. Важно было обеспечить надежность индикатора, потому что при выбранном способе практически невозможно исправить ошибочно отображенную информацию.
Второй вопрос - это выбор базового микрокалькулятора. На основании эргономических и инженерно-психологических исследований был выбран калькулятор МК-46. На клавиатуре дополнительно были нанесены рельефные обозначения, что облегчает поиск нужных клавиш.
Наконец, третий вопрос, который пришлось решать, касается некоторых специальных методических приемов вычислений, облегчающих работу слепых. Один из таких приемов заключается, например, в максимальном использовании регистров памяти, чтобы сократить запись промежуточных результатов.
Какова же эффективность работы на таком микрокалькуляторе? В сравнительном эксперименте приняли участие слепой математик-программист и один из авторов статьи. Эксперимент заключался в вычислении значений многочлена по схеме Горнера. Время, затраченное обоими на решение поставленной задачи, практически одинаково.
Сейчас по заказу Института дефектологии АПН СССР мы готовим опытную партию микрокалькуляторов с брайлевской индикацией.
В.ВОРОНИН, В.ИВАНОВСКИЙ (г.Свердловск)
ВНИМАНИЕ, ЭНТУЗИАСТЫ!
Желая принять участие в "Школе начинающего программиста" (см. 10/84), киевлянин В.Бардадым прислал в редакцию подробный конспект занятий, которые он вел в одной из школ г.Киева. Такие материалы существенно помогут становлению школы. Предлагаем тем, кто вел кружки, читал лекции, проводил занятия по программированию на калькуляторах, последовать примеру В. Бардадыма.
"Хотелось бы поучаствовать в школе,- пишет нам С.Карпов из Орла,- но все как-то не могу определиться с темой и формой". Время между тем не ждет. Предлагаем каждому из желающих немедля прислать законченное выступление по любому пункту программы, опубликованной в 10/84 в любой форме,- за редактированием дело не станет.
***
Тем временем в большом мире...
ЗРИТЕЛЬНАЯ ПАМЯТЬ ЭВМ
В крупных современных учреждениях роль архива нередко поручают электронно-вычислительным машинам, которые хранят документы в своей памяти в виде последовательности импульсов, записанных на магнитный диск или ленту. Набрав на пульте ЭВМ номер документа, иногда очень сложный и многозначный, можно практически мгновенно получить его текст на экране специального телевизора-дисплея или положить на стол в отпечатанном виде. Такой способ хранения информации удобен во всем, кроме одного: люди, работающие с документами, с трудом запоминают, а зачастую и вообще не знают их номера и, стоя перед ЭВМ, с тоской вспоминают те времена, когда было твердо известно, что искомая бумага находится "в четвертой комнате, во втором шкафу слева, в синей папке на третьей полке снизу". Зрительный образ места хранения запоминается гораздо легче комбинации цифр.
Но, оказывается, современная электронная техника способна держать в своей памяти даже такие сведения о документе, как цвет папки, в которой он лежит, и специалисты японской фирмы "Тосиба" создали подобное устройство специально для хранения архивной информации. Его дисплей имеет два экрана - цветной и черно-белый. Набрав соответствующий код, оператор выводит на экран... цветное изображение хранилища документов со множеством шкафов и полок. Экран дисплея чувствует прикосновения, и команду "нарисовать" во весь экран нужный шкаф оператор дает, просто коснувшись пальцем его изображения на общем плане. Таким образом оператор выводит на цветной экран отдельно нужную полку с папками, а содержимое той или иной папки быстро "перелистывает" на черно-белом экране, пока не увидит требуемый документ.
Так можно найти документ только по его визуальным признакам, не имея других характеристик, скажем, можно отыскать личное дело сотрудника по фотографии, не помня его фамилии, но зная в лицо.
Разумеется, весь интерьер хранилища со всеми его шкафами и разноцветными папками в них существует только в самой ЭВМ в виде программы, формирующей изображение на экране.
Для ее хранения нужен огромный объем памяти, который способен обеспечить только новый, недавно разработанный способ записи информации при помощи лазера. Мощный лазерный луч проплавляет в металлизированном пластмассовом диске отверстия диаметром около микрометра (0.001мм). Получается нечто вроде перфокарты микроскопических размеров, информация с которой считывается также лазерным лучом. На диске диаметром 30см можно записать более 1 гигабайта, то есть 1e9 байт информации (байт - "слог" машинного языка, составляющий 8 бит - двоичных единиц) или 2500 страниц текста. Это в 10-15 раз больше, чем на магнитном диске такого же размера.
Огромный объем оптической памяти позволяет использовать ее не только для хранения информации, но и для других целей. На ее основе, например, предполагается сделать тренажер для обучения пилотов. В существующих устройствах применяются видеомагнитофоны и кинопроекторы, которые могут воспроизводить практически только идеальные условия полета. Оптические диски могут хранить самые различные виды окружающего ландшафта и ситуаций и мгновенно выдавать их на экран в соответствии с движением рукояток управления в руках курсанта, имитируя любые мыслимые перипетии, возникающие при взлете, полете и посадке.
(По материалам иностранной печати)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
4/85
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
В ближайшее время обучение навыкам работы с вычислительной техникой станет неотъемлемой частью школьной программы. Как лучше организовать такое обучение! Приглашаем читателей раздела "Человек с микрокалькулятором" принять активное участие в обсуждении этой проблемы. Открываем дискуссию по ней выступлением академика В.С.МИХАЛЕВИЧА, директора Института кибернетики имени В.М.Глушкова АН УССР, и В.Б.РАСПОПОВА, члена бюро Республиканского совета молодых ученых и специалистов при ЦК ЛКСМ Украины и Президиуме АН УССР.
ШКОЛЬНЫЙ КОМПЬЮТЕР - ПРОПУСК В XXI ВЕК
В памяти промышленных роботов можно быстро закодировать профессиональный опыт, который у квалифицированного рабочего вырабатывается годами. Становятся реальностью безлюдные технологии; появляются заводы-автоматы, способные по предписанной программе обрабатывать сырье и выпускать готовую продукцию.
Возможности "умных" машин поражают человека, слабо сведущего в технике. Для него ЭВМ выступает уже не как мощное орудие труда, а, наоборот, вызывает чувство растерянности и безволия.
Чтобы выпускник школы был психологически подготовлен к общению со столь сложной техникой и смог овладеть ею, ему нужно привить особый стиль мышления, который предполагает умение продумывать способы достижения поставленной цели, расчленять их на элементарные действия и планировать требуемые для их выполнения ресурсы. Такой стиль мышления называется операционным, алгоритмическим. Выработать его можно только в результате теоретического анализа и синтеза алгоритмов решения задач на уроках математики, через изучение и применение программирования, практику общения с компьютерами.
Будут ли наши дети подготовлены к тому, чтобы успешно развивать советскую науку и обеспечивать дальнейший рост экономики и оборонного могущества Родины - это в значительной степени зависит от уровня их грамотности в области информатики. Поэтому реформа школы поставила задачу "... вооружать учащихся знаниями и навыками использования современной вычислительной техники, обеспечить широкое применение компьютеров в учебном процессе, создавать для этого специальные школьные и межшкольные кабинеты".
Раннее общение с компьютерами поможет сформировать операционное мышление у учащихся общеобразовательных школ. ЭВМ позволят учителю вести углубленное преподавание естественнонаучных предметов для тех учащихся, которые склонны к инженерному и исследовательскому труду и продолжат обучение в физико-математических классах. На базе межшкольных вычислительных центров будет совершенствоваться профессиональное обучение по специальностям "оператор ЭВМ и станков с числовым программным управлением", "мастер по ремонту вычислительной техники".
В соответствии с уровнями сложности этих трех задач и с учетом экономических возможностей определены три типа технических средств обучения основам информатики: обычные и программируемые микрокалькуляторы, персональные компьютеры и современные вычислительные учебно-производственные центры базовых предприятий.
В 1985-1990 годах сотни тысяч электронных помощников учителя займут свое место на школьных партах. Сегодня учителя ряда школ уже используют на уроках разработанный в 1979 году школьный микрокалькулятор МКШ-2. Но этот калькулятор не программируемый. С его помощью в лучшем случае можно повысить лишь вычислительную культуру учащихся. Сформировать у выпускников алгоритмическое мышление позволят именно программируемые калькуляторы (ПМК) и компьютеры.
В некоторых школах уже нашли применение ПМК "Электроника Б3-21", "Б3-34", "МК-54", "МК-56". Практика показала, что они эффективны в том случае, когда вычисления носят рутинный (в строгом смысле - повторяющийся) характер. Таковы многократные расчеты по одной и той же формуле, которые приходится выполнять школьнику при заполнении таблиц, построении графиков функций и т.п. Именно эти вычислительные школьные задачи наиболее трудоемки, а однообразие повторяющихся вычислений делает их скучными. Располагая программируемым калькулятором, учащийся подготавливает его к рутинным вычислениям по определенной программе, а затем на протяжении оставшегося времени с удовольствием "пожинает плоды" программирования - численные результаты. Так ПМК органически вписывается в традиционные разделы школьного курса математики.
Программируемые микрокалькуляторы предоставляют возможность ознакомить старшеклассника с идеологией современной прикладной математики, численными методами решения сложных задач на ЭВМ. Как известно, применение компьютеров сделало возможным и полет человека в космос, и освоение морских глубин, и укрощение атомной энергии. К сожалению, машинные методы математики еще не нашли должного отражения в школьном курсе. Современный выпускник школы имеет весьма смутное представление и о том, как устроена ЭВМ и о характере решаемых с ее помощью математических задач.
Время покажет, какие новые разделы современной прикладной математики придут в школу. Но некоторые соображения по этому поводу можно высказать уже сегодня.
Во многих комбинаторных и логических головоломках подкупающая простота формулировок часто уживается с необычайной трудностью их решения. "Серьезные" аналоги этих задач возникают при математической формализации важных народнохозяйственных проблем, которые затем удается решить только с помощью компьютера. Подобные комбинаторные игры, если их алгоритмизировать и "втиснуть" в память программируемого микрокалькулятора, познакомят школьника с подходами к решению экономических задач на ЭВМ.
На уроках математики программируемый калькулятор сделает наглядными, позволит воплотить в числах многие отвлеченные теоретические построения - продемонстрировать сходимость последовательности к пределу, численно проверить возникающие у учащихся гипотезы о свойствах геометрических фигур и т.п.
На уроках физики программируемые микрокалькуляторы эффективны при обработке результатов лабораторных работ, поскольку тут вычисления носят явно рутинный характер. Принципиально новые возможности при изучении физики открываются, если использовать ПМК как инструмент в так называемом вычислительном эксперименте. Ведь тогда можно учесть в исследуемой физической модели и силу сопротивления, и нелинейность уравнений движения, и многие другие эффекты. Иными словами, программируемые микрокалькуляторы позволят на конкретных примерах познакомить старшеклассника с более адекватными, чем это принято сегодня в школе, моделями окружающей действительности.
Необходимо, однако, предостеречь от чрезмерного увлечения в школе программируемыми микрокалькуляторами в ущерб современным персональным и "большим" ЭВМ. Ведь программирование на калькуляторе сродни лишь "ручному" программированию на ЭВМ первого поколения. Кроме того, микрокалькулятор оперирует только числами, тогда как компьютер может обрабатывать текст, рисовать, исполнять мелодии.
Со временем в среднюю школу придут микрокалькуляторы с внешней магнитной памятью, автоматической печатью, более выразительными средствами отображения информации. Их программная совместимость со школьными персональными компьютерами позволит создавать локальные вычислительные сети.
Учащиеся старших классов получат возможность работать на персональных компьютерах. Первые персональные ЭВМ типа "Агат" уже установлены в одной из школ Новосибирска. В частности, такие компьютеры позволят учителю автоматизировать контроль за успеваемостью учащихся. С этой целью в дополнение к существующим школьным учебникам можно разработать для персональных ЭВМ контрольные вопросы, чтобы ученик с их помощью сам проверял свои знания. Думается, в этом деле пригодится опыт по созданию так называемых программированных пособий (см., например, недавно изданную в Киеве книгу "ФОРТРАН" под редакцией Е.Л.Ющенко).
Сегодня в научных лабораториях разрабатываются автоматизированные обучающие системы, наделяемые чертами искусственного интеллекта. Подобная экспериментальная система "СПОК" создана специалистами Института кибернетики имени В.М.Глушкова АН УССР под руководством доктора технических наук А.М.Довгялло. В 132-й средней школе г.Киева с ее помощью старшеклассники обучаются искусству программирования. Порции теоретического материала тут же закрепляются практической работой школьника за дисплеем ЭВМ. При этом компьютер настраивается на индивидуальные особенности ученика. Если тот сделал ошибку при составлении своей программы, ЭВМ поправит его и предложит выполнить новое упражнение для закрепления материала.
Реформа школы предусматривает дальнейшее сближение обучения подростков с их производительным трудом. Думается, что в тех регионах, где ощущается острая потребность в операторах, техниках-программистах и мастерах для работы на станках с числовым программным управлением, целесообразно создавать хозрасчетные межшкольные учебно-производственные вычислительные центры или же размещать ВЦ базовых предприятий непосредственно в учебно-производственных комбинатах района. Юридическим основанием для создания таких ВЦ может служить недавно утвержденное Советом Министров СССР положение о базовом предприятии общеобразовательной школы. Дополнительно нужно решить такие специфические для вычислительного центра вопросы, как распределение машинного времени, материально-техническое обслуживание и снабжение, поскольку эти вопросы сегодня лихорадят многие межшкольные ВЦ. В частности, нужно предусмотреть в штате ВЦ должности инженерно-технического персонала, в обязанности которого входят исключительно ремонт и обслуживание вычислительной техники. Машинное время таких центров днем следует использовать для учебных целей, вечерами - для кружковой работы, а ночью - сдавать в аренду на условиях хозрасчета или использовать для нужд базовых предприятий. Средства, получаемые ВЦ за счет аренды машинного времени, могут идти на оплату труда обслуживающих технику специалистов и на приобретение более современного оборудования. Со временем межшкольные ВЦ станут центрами повышения квалификации педагогов в вопросах информатики, а учащихся этих ВЦ можно привлекать в качестве операторов даже к выполнению хоздоговорной тематики, к ремонту школьных калькуляторов и персональных компьютеров, к обслуживанию станков с числовым и программным управлением и иного электронного оборудования.
Когда речь заходит о путях компьютеризации школы, сегодня еще довольно часто можно услышать, что общеобразовательная школа пока "не доросла" до программируемых микрокалькуляторов и предел интеллектуальных возможностей ученика со средними способностями - освоение непрограммируемого калькулятора. Мы убеждены, что придерживаться этой точки зрения - значит противиться естественному развитию отечественного научно-технического прогресса.
Задача на ближайшие годы - совместными усилиями ученых и педагогов разработать качественные учебники и методические пособия по применению программируемых микрокалькуляторов на уроках математики, физики, химии. Разрешить эту важную общественно значимую задачу вполне по силам молодым энтузиастам компьютеризации школы.
Академик В.МИХАЛЕВИЧ, кандидат физико-математических наук В.РАСПОПОВ
ПСИХОЛОГИЧЕСКИЙ ПРАКТИКУМ
Как вы к себе относитесь? Умеете ли оценивать себя по справедливости? Несложный тест, проведенный с помощью микрокалькулятора, разрешит сомнения.
Взгляните на список. В нем в алфавитном порядке приведены двадцать различных качеств личности: 1 - аккуратность, 2 - активность, 3 - бережливость, 4 - вдумчивость, 5 - вежливость, 6 - гордость, 7 - доброта, 8 - жизнерадостность, 9 - искренность, 10 - настойчивость, 11-нежность, 12 - отзывчивость, 13 - приветливость, 14 - принципиальность, 15 - решительность, 16 - самостоятельность, 17 - скромность, 18 - терпеливость, 19 - увлеченность, 20 - целеустремленность.
Теперь заполните таблицу. В первом ее столбце запишите сверху вниз по порядку числа от 1 до 20. Во втором расположите номера всех качеств из вышеприведенного списка в таком порядке, который соответствует вашему понятию об идеале человека. Первым здесь должно стоять качество, которое вы более других цените в людях, последним - то, которое вы считаете наименее необходимым. Готово? Заполните третий столбец: расположите там номера тех же качеств в том порядке, который характеризует лично вас, каким вы себя считаете.
Составленная таблица позволяет провести эксперимент, численно выражающий вашу способность к объективной самооценке. Он детально описан в книге Б.А.Сосновского "Лабораторный практикум по общей психологии" (М., "Просвещение", 1979). Его математическая сущность состоит в том, что вычисляются коэффициенты ранговой корреляции, определяется теснота связи между парами одинаковых чисел в двух числовых последовательностях. Необходимые для этого расчеты выполняет микрокалькулятор "Электроника Б3-34" по программе:
00. ИП4 01. - 02. Х2 03. ИПД 04. + 05. ПД 06. КИП4 07. Сх 08. С/П 09. БП 10. 00 11. 1 12. ИПД 13. 1 14. 3 15. 3 16. 0 17. / 18. - 19. ПД 20. ИПА 21. - 22. Fx<0 23. 25 24. К+ 25. ИПД 26. С/П
Заносим 0 в РД, 1 в Р4, 0.45 в РА, нажимаем В/О. Во втором столбце ("идеал") находим качество, стоящее первым, определяем, под каким порядковым номером записано это качество в третий столбец ("Я") и вводим этот номер в регистр X, затем нажимаем С/П. Нуль, появившийся вскоре на индикаторе, сигнализирует, что калькулятор готов к следующему вводу. На этот раз разыскиваем в третьем столбце качество, стоящее вторым в столбце "идеал", и вводим в калькулятор найденный порядковый номер, нажимаем С/П... Так поступаем до тех пор, пока список исходных данных не окажется исчерпанным. Остается лишь нажать клавишу ШГ (со стрелкой вправо), С/П, чтобы получить коэффициент, характеризующий степень самооценки.
Если его значение больше 0.7, то самооценка явно завышена. Если же вами получено число, меньшее 0.7, то вас можно поздравить - вам доступен самоанализ, вы умеете по заслугам оценить себя. Если же на индикаторе появилось сообщение ЕГГОГ - самооценка занижена, вы слишком самокритичны.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Углы измеряют и градусах, в радианах, а существует еще один, менее распространенный способ измерения - в градах, сотых долях прямого угла. Оказывается. "Электроника Б3-34" может вычислять тригонометрические функции, аргументы которых заданы в градах. Для этого нужно установить переключатель "Р-Г" в среднее положение.
Б.КОГАН (г.Москва) ]
У КНИЖНОЙ ПОЛКИ
Увлекательный и очень доходчивый стиль изложения, обилие ярких примеров и сравнений, краткость и ясность, то есть все то, что принято называть мастерством популяризации,- вот основные достоинства недавно вышедшей книги Г.В.Славина "Программирование на программируемых микрокалькуляторах типа "Электроника Б3-34" (Таллин, Валгус, 1984).
В книге нашли отражение и азы работы с "Электроникой Б3-34" и сложные приемы, которые заинтересуют знатоков. Читатель знакомится с устройством стековой памяти и получает рекомендации по отладке программ, прослеживает пути алгоритмизации задач и вникает в тонкости применения косвенной адресации - а в заключительном разделе его ждет набор полезных советов по части программирования.
Есть в книге и недостатки. Объясняя подчас весьма элементарные вещи, автор ни слова не говорит о специфике обратной бесскобочной записи - а ведь освоить ее не так уж просто для начинающего. В книге очень мало иллюстраций, элементы блок-схем отличаются от рекомендуемых ГОСТом.
Недостатки, конечно, не заслоняют основного достоинства книги: это практически первое учебное (именно учебное!) пособие по программированию на ПМК. При последующих изданиях книги нетрудно будет устранить ее слабые стороны - и прежде всего самую досадную: тираж книги - всего 2000 экземпляров, то есть по одному на каждые полтысячи сегодняшних владельцев программируемых микрокалькуляторов.
Книга Т.Б.Романовского "Микрокалькуляторы в рассказах и играх" выпущена в 1984 году рижским издательством "Зинатне". Цикл рассказов начинается описанием первого советского микрокалькулятора и знакомит читателя со всеми тремя поколениями отечественных вычислительных машин этого класса. Особое внимание автор уделяет опыту внедрения калькуляторов в средней школе. Приводятся беседы на эту тему с зарубежными специалистами, статистика экспериментов, сведения о калькуляторах социалистических стран. Особенно интересны данные о том, что распространенность и частота использования карманных вычислителей не сказываются отрицательно на формировании и сохранении навыков счета. Притом повседневное общение с электронным помощником приучает концентрировать внимание, координировать движение рук, развивает алгоритмическое мышление.
Часть книги посвящена решению познавательных задач и играм с программируемыми калькуляторами (такими, как "Угадай число", "Календарь", "Мягкая посадка на Луну" и другие). Для некоторых игр приведены готовые программы.
Серия "Электроника" из обширного цикла книг "Массовая библиотека инженера" пополнилась 40-м выпуском: Е.Ю.Кузнецов, Б.В.Острецов, Л.К.Минкин, Ю.И.Егорова. "Микрокалькуляторы: технические и конструктивные характеристики" (М., Радио и связь, 1984). В книге содержатся сведения о многих отечественных и зарубежных микрокалькуляторах: конструктивные особенности, принципы ввода и вывода информации, вопросы проектирования интегральных микросхем и т.д. Более подробно описаны 24 модели, среди которых хочется отметить хорошо зарекомендовавшие себя МК-53, МК-40, МК-51, Б3-38, Б3-34, МК-54, НР-41С, TI-59.
Привлекает внимание глава, посвященная специализированным калькуляторам, тесно смыкающимся с персональными ЭВМ. В ней рассмотрены отечественный электронный словарь-переводчик "Электроника СП" и японская карманная ЭВМ "PC-1211".
ВСЕГО ОДИН ДИОД
- Ну что ты опять прилип к своему калькулятору?! Ведь за полночь уже!
- Дорогая, но мне обязательно нужно досчитать...
- Тогда марш на кухню! И немедленно!
Отсоединить "Электронику Б3-34" от сети, переключить ее на питание от внутренней батареи нельзя, предварительно не выключив, а при этом утрачивается, стирается введенная в калькулятор программа.
Между тем подобные неприятности легко устранимы: стоит лишь установить в калькуляторе всего один диод, как показано на упрощенной схеме.
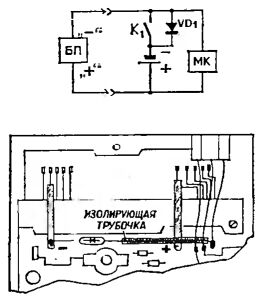
Когда калькулятор работает от аккумуляторной батареи, то при подключении блока питания диод закрывается и отсоединяет батарею. Если напряжение от блока питания по какой-либо причине пропадет (например, мы его выключим), диод откроется, и калькулятор автоматически перейдет к работе от аккумуляторов. Таким образом, диод играет роль безынерционного переключателя. Расположить его удобно так, как показано на рисунке. Диод должен быть германиевым, например, Д310.
Теперь вы сможете, не выключая калькулятора, в любой момент изменять режим питания. Даже случайный перебой в подаче электроэнергии не прервет ваших расчетов.
А.БОЙКО, А.ПОТАШОВ (г.Москва)
ВНИМАНИЕ-КОНКУРС!
"Почему вы не печатаете программы для игр с микрокалькуляторами?- спрашивает нас девятиклассник Арсений Цаплев из Ленинграда.- Разве вам их не присылают?"
Присылают. И в немалом количестве. Вот, к примеру, игра "Ним". Не проходит недели, чтобы почта не принесла письма с программой для этой игры. Между тем о ней (и ее упрощенном варианте - игре Баше] писалось под нашей рубрикой еще в позапрошлом году (8/83). Нетрудно запрограммировать выигрышную стратегию для "Нима". Но что за интерес играть с партнером, который никогда не проигрывает! Что за удовольствие, если на определенную последовательность ваших ходов всегда следуют одни и те же ответы! И так ли уж увлекательна эта игре! Неужели "Электроника БЗ-34" не дает возможности сыграть во что-то более захватывающее!
Те же вопросы вызывают и другие игровые программы, присланные до сих пор в редакцию и предназначенные для игр "Крестики-нолики", "Морской бой" (она же "Порази цель", она же "Танкодром"), "Посадка на Луну", "Быки и коровы" (она же "Угадай число"), "Одинокий ферзь".
Нам очень хотелось бы порадовать читателей игровыми программами, но такими, чтобы игра по ним не наскучила после первых же проб, увлекала бы нетривиальными, а порою совсем неожиданными ответами электронного партнера, заставляла бы продумывать хитроумные пути к победе, короче, доставляла бы удовольствие, а вместе, с тем (что тоже немаловажно) побуждала бы вникать в тонкости устройства и работы микрокалькулятора.
Объявляем конкурс на лучшую игру как для непрограммируемого микрокалькулятора (подобно описанной иа этой Странице игре "Упрямые числа"), так и для программируемого (в этом случае просьба составить программу для "Электроники Б3-34"). Единственное условие: игра не должна повторять собою ни одну из вышеназванных.
И еще один конкурс. Его задание относится ко вполне деловой проблематике. При обработке экспериментальных данных часто возникает потребность упорядочить по величине совокупность чисел, расположить их в порядке возрастания или убывания - как говорят, построить вариационный рад или ранжировать массив. Делая это вручную, пишут, например, каждое число на отдельной карточке, а затем вставляют эти карточки по одной в общий пакет.
Существует немало алгоритмов, позволяющих программировать этот процесс. Однако они, как правило, требуют больших объемов памяти для хранения результатов.
Предлагается составить программу для "Электроники Б3-34", решающую аналогичную задачу. Интересно выяснить, каково максимальное число элементов массива, который можно ранжировать на микрокалькуляторе, и как, сочетая ручной труд с машинным, получить вариационный ряд для большого числа элементов.
УПРЯМЫЕ ЧИСЛА
Возьмите любое двузначное число от 11 до 99. Прибавьте к нему зеркальное число, то есть исходное число, прочитанное справа налево - например, 39+93=132. К результату прибавьте его зеркальное число: 132+231=363. Вы получили симметричное число, то есть такое, чье зеркальное число равно ему самому. В нашем примере для его получения потребовалось два сложения.
Таким способом можно получить симметричное число из любого от 11 до 99. В большинстве случаев для этого потребуется от одного до четырех сложений. Четыре числа в этом диапазоне несколько более упрямы: чтобы получить из них симметричные числа, нужно 6 сложений. А два числа очень упорны - каждое из них превращается в симметричное лишь после 24 сложений! В результате получается симметричное число, насчитывающее 13 знаков.
Разумеется, эту игру можно вести и с трехзначными или даже более длинными числами, надеясь рано или поздно достичь симметрии. Впрочем, и тут есть несколько крепких орешков. Самое маленькое из чисел, не поддающихся никаким усилиям, - 196.
Еще никому не удалось установить, для всех ли чисел можно получить симметричный итог путем конечного числа сложений, или существуют такие числа, которые для этой игры не годятся.
"Нойес Дойчланд". 17/18 ноября 1984г. (перевел Ю.ФЛОРЕНСКИЙ, г.Рязань)
БЕЗ ТАБЛИЦ
Современный микрокалькулятор позволяет нажатием одной-двух клавиш получить значение синуса и косинуса, логарифма и арктангенса - общим счетом около десятка функций. Еще большими возможностями наверняка будут обладать карманные вычислители завтрашнего дня. Но вряд ли появятся когда-нибудь калькуляторы, в которые будут заложены программы вычисления всех функций - слишком их много.
А что если владельцу калькулятора понадобилось значение, скажем, функции Бесселя с точностью до восьмого знака? Что, если его электронный помощник не умеет вычислить даже синус и логарифм?
Преодолеть подобные затруднения поможет "Справочник по специальным функциям" под редакцией М.Абрамовича и И.Стиган (М. "Наука", 1979). Там приведены приближенные представления многочленами многих элементарных и специальных функций. В комплекте с микрокалькулятором (самым простым!) книга заменит и многотомные таблицы и большую ЭВМ.
Например, вам требуется определить величину arctg(0.5). В вашем распоряжении микрокалькулятор "Электроника Б3-26", не имеющая клавиши "arctg". Вот формула из справочника, дающая погрешность не более 2e-8 при 0<x<1:
arctg(x)=x(a16*x**16-a14*x**14+a12*x1**12-...+a4*x**4-a2*x2**2+1).
a16=0.0028662
a14=0.0161657
a12=0.0429096
a10=0.0752896
a8=0.1065626
a6=0.1420890
a4=0.1999355
a2=0.3333315
Вычисления удобно вести по схеме Горнера. Вносим в ПI+ величину х**2=0.25, далее следуем программе:
a16 * ИП - a14 * ИП + a12 * ИП - a10 * ИП + a8 * ИП - a6 * ИП + a4 * ИП - a2 * ИП + 1 * 0.5
Ответ: arct(0.5) = 0.4636476. Здесь все знаки - верные.
А.ТУЛАЙКОВ (г.Долгопрудный)
КАЛЬКУЛЯЦИЯ НА КАЛЬКУЛЯТОРЕ
"И, внимая моторному лаю.., ни за что я теперь не желаю слушать песню тележных колес!" - воскликнул некогда поэт, приветствуя технический прогресс. Времена меняются - мы предпочитаем сегодня бесшумные машины (разумеется, к тому же и более производительные). Причем не только на полях. Лязг арифмометра раздражает не меньше, чем перестук костяшек на счетах. Электронные микрокалькуляторы выполняют арифметические действия, повинуясь легкому прикосновению к клавишам. Но и эта работа может быть неприятной, если ее приходится повторять помногу раз каждый день. Не лучше ли поручить ее программируемому калькулятору и запускать каждый очередной расчет одним нажатием на клавишу?
Я работаю инженером-технологом на заводе по ремонту вычислительной техники. По долгу службы мне часто приходится рассчитывать калькуляции. Для этих целей я разработал простую программу для "Электроники Б3-34". Она приспособлена к условиям нашего завода. Однако по такому же принципу можно составить программу для любого другого предприятия, изменив должным образом процентное содержание одних статей по отношению к другим. Несмотря на простоту программы, польза от ее внедрения достаточно велика: ведь она автоматизирует расчеты, до сих пор проводившиеся вручную.
Так как программа занимает мало места в памяти, я решил не записывать константы в адресуемые регистры, а формировать их по ходу выполнения программы (см. ее фрагменты 01-05, 10-13, 17-21, 33-35). Мне кажется, что в этом случае уменьшается вероятность ошибки при вводе программы.
Исходными данными для расчета калькуляции являются стоимость материалов (М) и величина основной заработной платы (З0), выраженные в рублях. Остальные величины определяются из формул: дополнительная заработная плата Зд=З0*10.8%, отчисления на соцстрахование Ос=(З0+Зд)*7%, общезаводские расходы Р0=З0*57.4%, производственная себестоимость С=М+З0+Ос+Р0+Зд, прибыль П=С*20% и оптовая цена Оц=С+П. Перед запуском программы величины М и З0 вводятся соответственно в регистры 1 и 2. После запуска программы во время первого останова на индикаторе появляется Зд. Списав эту величину, вновь нажимаем клавишу С/П и получаем Ос. Продолжая расчет, последовательно получаем Р0, С, П, Оц.
Программа. 00. ^ 01. 0 02. ,
03. 0 04. 7 05. ИП2 06. 0 07. ,
08. 1 09. 0 10. 8 11. * 12. С/П 13. ИП2 14. + 15. * 16. С/П 17. Вх 18. + 19. 0 20. , 21. 5 22. 7 23. 4 24. ИП2 25. * 26. С/П 27. + 28. ИП1 29. + 30. ^ 31. С/П 32. 5 33. / 34. С/П 35. + 36. С/П 37. В/О
Для повторного расчета с теми же данными нажать С/П. Для расчета с новыми исходными данными ввести их в регистры 1 и 2, затем нажать С/П.
Контрольный пример: М=10, З0=20. Результаты: Зд=2.16, Ос=1.5512, Р0=11.48, С=45.1912, П=9.03824, Оц=54.22944.
С.ЧУЧАНОВ (г.Дружковка Донецкой обл.)
АНКЕТА ЧИТАТЕЛЕЙ РАЗДЕЛА
Обсудить прошлые выпуски раздела "Человек с микрокалькулятором", наметить планы на будущее - таковы цели публикации анкеты.
1. Считаете ли вы раздел "Человек с микрокалькулятором" нужным, полезным?
2. Ваша профессия, возраст.
3. Каким микрокалькулятором вы пользуетесь и как долго?
4. Какие выпуски раздела "Человек с микрокалькулятором" и какие отдельные статьи наиболее понравились вам?
5. О чем вы хотели бы прочесть на страницах раздела?
6. Какие новые постоянные темы раздела вы можете предложить?
7. О чем хотели бы вы спросить разработчиков микрокалькуляторов и что хотели бы им пожелать?
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
В ближайшее время обучение навыкам работы с вычислительной техникой станет неотъемлемой частью школьной программы. Как лучше организовать такое обучение! Приглашаем читателей раздела "Человек с микрокалькулятором" принять активное участие в обсуждении этой проблемы. Открываем дискуссию по ней выступлением академика В.С.МИХАЛЕВИЧА, директора Института кибернетики имени В.М.Глушкова АН УССР, и В.Б.РАСПОПОВА, члена бюро Республиканского совета молодых ученых и специалистов при ЦК ЛКСМ Украины и Президиуме АН УССР.
ШКОЛЬНЫЙ КОМПЬЮТЕР - ПРОПУСК В XXI ВЕК
В памяти промышленных роботов можно быстро закодировать профессиональный опыт, который у квалифицированного рабочего вырабатывается годами. Становятся реальностью безлюдные технологии; появляются заводы-автоматы, способные по предписанной программе обрабатывать сырье и выпускать готовую продукцию.
Возможности "умных" машин поражают человека, слабо сведущего в технике. Для него ЭВМ выступает уже не как мощное орудие труда, а, наоборот, вызывает чувство растерянности и безволия.
Чтобы выпускник школы был психологически подготовлен к общению со столь сложной техникой и смог овладеть ею, ему нужно привить особый стиль мышления, который предполагает умение продумывать способы достижения поставленной цели, расчленять их на элементарные действия и планировать требуемые для их выполнения ресурсы. Такой стиль мышления называется операционным, алгоритмическим. Выработать его можно только в результате теоретического анализа и синтеза алгоритмов решения задач на уроках математики, через изучение и применение программирования, практику общения с компьютерами.
Будут ли наши дети подготовлены к тому, чтобы успешно развивать советскую науку и обеспечивать дальнейший рост экономики и оборонного могущества Родины - это в значительной степени зависит от уровня их грамотности в области информатики. Поэтому реформа школы поставила задачу "... вооружать учащихся знаниями и навыками использования современной вычислительной техники, обеспечить широкое применение компьютеров в учебном процессе, создавать для этого специальные школьные и межшкольные кабинеты".
Раннее общение с компьютерами поможет сформировать операционное мышление у учащихся общеобразовательных школ. ЭВМ позволят учителю вести углубленное преподавание естественнонаучных предметов для тех учащихся, которые склонны к инженерному и исследовательскому труду и продолжат обучение в физико-математических классах. На базе межшкольных вычислительных центров будет совершенствоваться профессиональное обучение по специальностям "оператор ЭВМ и станков с числовым программным управлением", "мастер по ремонту вычислительной техники".
В соответствии с уровнями сложности этих трех задач и с учетом экономических возможностей определены три типа технических средств обучения основам информатики: обычные и программируемые микрокалькуляторы, персональные компьютеры и современные вычислительные учебно-производственные центры базовых предприятий.
В 1985-1990 годах сотни тысяч электронных помощников учителя займут свое место на школьных партах. Сегодня учителя ряда школ уже используют на уроках разработанный в 1979 году школьный микрокалькулятор МКШ-2. Но этот калькулятор не программируемый. С его помощью в лучшем случае можно повысить лишь вычислительную культуру учащихся. Сформировать у выпускников алгоритмическое мышление позволят именно программируемые калькуляторы (ПМК) и компьютеры.
В некоторых школах уже нашли применение ПМК "Электроника Б3-21", "Б3-34", "МК-54", "МК-56". Практика показала, что они эффективны в том случае, когда вычисления носят рутинный (в строгом смысле - повторяющийся) характер. Таковы многократные расчеты по одной и той же формуле, которые приходится выполнять школьнику при заполнении таблиц, построении графиков функций и т.п. Именно эти вычислительные школьные задачи наиболее трудоемки, а однообразие повторяющихся вычислений делает их скучными. Располагая программируемым калькулятором, учащийся подготавливает его к рутинным вычислениям по определенной программе, а затем на протяжении оставшегося времени с удовольствием "пожинает плоды" программирования - численные результаты. Так ПМК органически вписывается в традиционные разделы школьного курса математики.
Программируемые микрокалькуляторы предоставляют возможность ознакомить старшеклассника с идеологией современной прикладной математики, численными методами решения сложных задач на ЭВМ. Как известно, применение компьютеров сделало возможным и полет человека в космос, и освоение морских глубин, и укрощение атомной энергии. К сожалению, машинные методы математики еще не нашли должного отражения в школьном курсе. Современный выпускник школы имеет весьма смутное представление и о том, как устроена ЭВМ и о характере решаемых с ее помощью математических задач.
Время покажет, какие новые разделы современной прикладной математики придут в школу. Но некоторые соображения по этому поводу можно высказать уже сегодня.
Во многих комбинаторных и логических головоломках подкупающая простота формулировок часто уживается с необычайной трудностью их решения. "Серьезные" аналоги этих задач возникают при математической формализации важных народнохозяйственных проблем, которые затем удается решить только с помощью компьютера. Подобные комбинаторные игры, если их алгоритмизировать и "втиснуть" в память программируемого микрокалькулятора, познакомят школьника с подходами к решению экономических задач на ЭВМ.
На уроках математики программируемый калькулятор сделает наглядными, позволит воплотить в числах многие отвлеченные теоретические построения - продемонстрировать сходимость последовательности к пределу, численно проверить возникающие у учащихся гипотезы о свойствах геометрических фигур и т.п.
На уроках физики программируемые микрокалькуляторы эффективны при обработке результатов лабораторных работ, поскольку тут вычисления носят явно рутинный характер. Принципиально новые возможности при изучении физики открываются, если использовать ПМК как инструмент в так называемом вычислительном эксперименте. Ведь тогда можно учесть в исследуемой физической модели и силу сопротивления, и нелинейность уравнений движения, и многие другие эффекты. Иными словами, программируемые микрокалькуляторы позволят на конкретных примерах познакомить старшеклассника с более адекватными, чем это принято сегодня в школе, моделями окружающей действительности.
Необходимо, однако, предостеречь от чрезмерного увлечения в школе программируемыми микрокалькуляторами в ущерб современным персональным и "большим" ЭВМ. Ведь программирование на калькуляторе сродни лишь "ручному" программированию на ЭВМ первого поколения. Кроме того, микрокалькулятор оперирует только числами, тогда как компьютер может обрабатывать текст, рисовать, исполнять мелодии.
Со временем в среднюю школу придут микрокалькуляторы с внешней магнитной памятью, автоматической печатью, более выразительными средствами отображения информации. Их программная совместимость со школьными персональными компьютерами позволит создавать локальные вычислительные сети.
Учащиеся старших классов получат возможность работать на персональных компьютерах. Первые персональные ЭВМ типа "Агат" уже установлены в одной из школ Новосибирска. В частности, такие компьютеры позволят учителю автоматизировать контроль за успеваемостью учащихся. С этой целью в дополнение к существующим школьным учебникам можно разработать для персональных ЭВМ контрольные вопросы, чтобы ученик с их помощью сам проверял свои знания. Думается, в этом деле пригодится опыт по созданию так называемых программированных пособий (см., например, недавно изданную в Киеве книгу "ФОРТРАН" под редакцией Е.Л.Ющенко).
Сегодня в научных лабораториях разрабатываются автоматизированные обучающие системы, наделяемые чертами искусственного интеллекта. Подобная экспериментальная система "СПОК" создана специалистами Института кибернетики имени В.М.Глушкова АН УССР под руководством доктора технических наук А.М.Довгялло. В 132-й средней школе г.Киева с ее помощью старшеклассники обучаются искусству программирования. Порции теоретического материала тут же закрепляются практической работой школьника за дисплеем ЭВМ. При этом компьютер настраивается на индивидуальные особенности ученика. Если тот сделал ошибку при составлении своей программы, ЭВМ поправит его и предложит выполнить новое упражнение для закрепления материала.
Реформа школы предусматривает дальнейшее сближение обучения подростков с их производительным трудом. Думается, что в тех регионах, где ощущается острая потребность в операторах, техниках-программистах и мастерах для работы на станках с числовым программным управлением, целесообразно создавать хозрасчетные межшкольные учебно-производственные вычислительные центры или же размещать ВЦ базовых предприятий непосредственно в учебно-производственных комбинатах района. Юридическим основанием для создания таких ВЦ может служить недавно утвержденное Советом Министров СССР положение о базовом предприятии общеобразовательной школы. Дополнительно нужно решить такие специфические для вычислительного центра вопросы, как распределение машинного времени, материально-техническое обслуживание и снабжение, поскольку эти вопросы сегодня лихорадят многие межшкольные ВЦ. В частности, нужно предусмотреть в штате ВЦ должности инженерно-технического персонала, в обязанности которого входят исключительно ремонт и обслуживание вычислительной техники. Машинное время таких центров днем следует использовать для учебных целей, вечерами - для кружковой работы, а ночью - сдавать в аренду на условиях хозрасчета или использовать для нужд базовых предприятий. Средства, получаемые ВЦ за счет аренды машинного времени, могут идти на оплату труда обслуживающих технику специалистов и на приобретение более современного оборудования. Со временем межшкольные ВЦ станут центрами повышения квалификации педагогов в вопросах информатики, а учащихся этих ВЦ можно привлекать в качестве операторов даже к выполнению хоздоговорной тематики, к ремонту школьных калькуляторов и персональных компьютеров, к обслуживанию станков с числовым и программным управлением и иного электронного оборудования.
Когда речь заходит о путях компьютеризации школы, сегодня еще довольно часто можно услышать, что общеобразовательная школа пока "не доросла" до программируемых микрокалькуляторов и предел интеллектуальных возможностей ученика со средними способностями - освоение непрограммируемого калькулятора. Мы убеждены, что придерживаться этой точки зрения - значит противиться естественному развитию отечественного научно-технического прогресса.
Задача на ближайшие годы - совместными усилиями ученых и педагогов разработать качественные учебники и методические пособия по применению программируемых микрокалькуляторов на уроках математики, физики, химии. Разрешить эту важную общественно значимую задачу вполне по силам молодым энтузиастам компьютеризации школы.
Академик В.МИХАЛЕВИЧ, кандидат физико-математических наук В.РАСПОПОВ
ПСИХОЛОГИЧЕСКИЙ ПРАКТИКУМ
Как вы к себе относитесь? Умеете ли оценивать себя по справедливости? Несложный тест, проведенный с помощью микрокалькулятора, разрешит сомнения.
Взгляните на список. В нем в алфавитном порядке приведены двадцать различных качеств личности: 1 - аккуратность, 2 - активность, 3 - бережливость, 4 - вдумчивость, 5 - вежливость, 6 - гордость, 7 - доброта, 8 - жизнерадостность, 9 - искренность, 10 - настойчивость, 11-нежность, 12 - отзывчивость, 13 - приветливость, 14 - принципиальность, 15 - решительность, 16 - самостоятельность, 17 - скромность, 18 - терпеливость, 19 - увлеченность, 20 - целеустремленность.
Теперь заполните таблицу. В первом ее столбце запишите сверху вниз по порядку числа от 1 до 20. Во втором расположите номера всех качеств из вышеприведенного списка в таком порядке, который соответствует вашему понятию об идеале человека. Первым здесь должно стоять качество, которое вы более других цените в людях, последним - то, которое вы считаете наименее необходимым. Готово? Заполните третий столбец: расположите там номера тех же качеств в том порядке, который характеризует лично вас, каким вы себя считаете.
Составленная таблица позволяет провести эксперимент, численно выражающий вашу способность к объективной самооценке. Он детально описан в книге Б.А.Сосновского "Лабораторный практикум по общей психологии" (М., "Просвещение", 1979). Его математическая сущность состоит в том, что вычисляются коэффициенты ранговой корреляции, определяется теснота связи между парами одинаковых чисел в двух числовых последовательностях. Необходимые для этого расчеты выполняет микрокалькулятор "Электроника Б3-34" по программе:
00. ИП4 01. - 02. Х2 03. ИПД 04. + 05. ПД 06. КИП4 07. Сх 08. С/П 09. БП 10. 00 11. 1 12. ИПД 13. 1 14. 3 15. 3 16. 0 17. / 18. - 19. ПД 20. ИПА 21. - 22. Fx<0 23. 25 24. К+ 25. ИПД 26. С/П
Заносим 0 в РД, 1 в Р4, 0.45 в РА, нажимаем В/О. Во втором столбце ("идеал") находим качество, стоящее первым, определяем, под каким порядковым номером записано это качество в третий столбец ("Я") и вводим этот номер в регистр X, затем нажимаем С/П. Нуль, появившийся вскоре на индикаторе, сигнализирует, что калькулятор готов к следующему вводу. На этот раз разыскиваем в третьем столбце качество, стоящее вторым в столбце "идеал", и вводим в калькулятор найденный порядковый номер, нажимаем С/П... Так поступаем до тех пор, пока список исходных данных не окажется исчерпанным. Остается лишь нажать клавишу ШГ (со стрелкой вправо), С/П, чтобы получить коэффициент, характеризующий степень самооценки.
Если его значение больше 0.7, то самооценка явно завышена. Если же вами получено число, меньшее 0.7, то вас можно поздравить - вам доступен самоанализ, вы умеете по заслугам оценить себя. Если же на индикаторе появилось сообщение ЕГГОГ - самооценка занижена, вы слишком самокритичны.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Углы измеряют и градусах, в радианах, а существует еще один, менее распространенный способ измерения - в градах, сотых долях прямого угла. Оказывается. "Электроника Б3-34" может вычислять тригонометрические функции, аргументы которых заданы в градах. Для этого нужно установить переключатель "Р-Г" в среднее положение.
Б.КОГАН (г.Москва) ]
У КНИЖНОЙ ПОЛКИ
Увлекательный и очень доходчивый стиль изложения, обилие ярких примеров и сравнений, краткость и ясность, то есть все то, что принято называть мастерством популяризации,- вот основные достоинства недавно вышедшей книги Г.В.Славина "Программирование на программируемых микрокалькуляторах типа "Электроника Б3-34" (Таллин, Валгус, 1984).
В книге нашли отражение и азы работы с "Электроникой Б3-34" и сложные приемы, которые заинтересуют знатоков. Читатель знакомится с устройством стековой памяти и получает рекомендации по отладке программ, прослеживает пути алгоритмизации задач и вникает в тонкости применения косвенной адресации - а в заключительном разделе его ждет набор полезных советов по части программирования.
Есть в книге и недостатки. Объясняя подчас весьма элементарные вещи, автор ни слова не говорит о специфике обратной бесскобочной записи - а ведь освоить ее не так уж просто для начинающего. В книге очень мало иллюстраций, элементы блок-схем отличаются от рекомендуемых ГОСТом.
Недостатки, конечно, не заслоняют основного достоинства книги: это практически первое учебное (именно учебное!) пособие по программированию на ПМК. При последующих изданиях книги нетрудно будет устранить ее слабые стороны - и прежде всего самую досадную: тираж книги - всего 2000 экземпляров, то есть по одному на каждые полтысячи сегодняшних владельцев программируемых микрокалькуляторов.
Книга Т.Б.Романовского "Микрокалькуляторы в рассказах и играх" выпущена в 1984 году рижским издательством "Зинатне". Цикл рассказов начинается описанием первого советского микрокалькулятора и знакомит читателя со всеми тремя поколениями отечественных вычислительных машин этого класса. Особое внимание автор уделяет опыту внедрения калькуляторов в средней школе. Приводятся беседы на эту тему с зарубежными специалистами, статистика экспериментов, сведения о калькуляторах социалистических стран. Особенно интересны данные о том, что распространенность и частота использования карманных вычислителей не сказываются отрицательно на формировании и сохранении навыков счета. Притом повседневное общение с электронным помощником приучает концентрировать внимание, координировать движение рук, развивает алгоритмическое мышление.
Часть книги посвящена решению познавательных задач и играм с программируемыми калькуляторами (такими, как "Угадай число", "Календарь", "Мягкая посадка на Луну" и другие). Для некоторых игр приведены готовые программы.
Серия "Электроника" из обширного цикла книг "Массовая библиотека инженера" пополнилась 40-м выпуском: Е.Ю.Кузнецов, Б.В.Острецов, Л.К.Минкин, Ю.И.Егорова. "Микрокалькуляторы: технические и конструктивные характеристики" (М., Радио и связь, 1984). В книге содержатся сведения о многих отечественных и зарубежных микрокалькуляторах: конструктивные особенности, принципы ввода и вывода информации, вопросы проектирования интегральных микросхем и т.д. Более подробно описаны 24 модели, среди которых хочется отметить хорошо зарекомендовавшие себя МК-53, МК-40, МК-51, Б3-38, Б3-34, МК-54, НР-41С, TI-59.
Привлекает внимание глава, посвященная специализированным калькуляторам, тесно смыкающимся с персональными ЭВМ. В ней рассмотрены отечественный электронный словарь-переводчик "Электроника СП" и японская карманная ЭВМ "PC-1211".
ВСЕГО ОДИН ДИОД
- Ну что ты опять прилип к своему калькулятору?! Ведь за полночь уже!
- Дорогая, но мне обязательно нужно досчитать...
- Тогда марш на кухню! И немедленно!
Отсоединить "Электронику Б3-34" от сети, переключить ее на питание от внутренней батареи нельзя, предварительно не выключив, а при этом утрачивается, стирается введенная в калькулятор программа.
Между тем подобные неприятности легко устранимы: стоит лишь установить в калькуляторе всего один диод, как показано на упрощенной схеме.

Когда калькулятор работает от аккумуляторной батареи, то при подключении блока питания диод закрывается и отсоединяет батарею. Если напряжение от блока питания по какой-либо причине пропадет (например, мы его выключим), диод откроется, и калькулятор автоматически перейдет к работе от аккумуляторов. Таким образом, диод играет роль безынерционного переключателя. Расположить его удобно так, как показано на рисунке. Диод должен быть германиевым, например, Д310.
Теперь вы сможете, не выключая калькулятора, в любой момент изменять режим питания. Даже случайный перебой в подаче электроэнергии не прервет ваших расчетов.
А.БОЙКО, А.ПОТАШОВ (г.Москва)
ВНИМАНИЕ-КОНКУРС!
"Почему вы не печатаете программы для игр с микрокалькуляторами?- спрашивает нас девятиклассник Арсений Цаплев из Ленинграда.- Разве вам их не присылают?"
Присылают. И в немалом количестве. Вот, к примеру, игра "Ним". Не проходит недели, чтобы почта не принесла письма с программой для этой игры. Между тем о ней (и ее упрощенном варианте - игре Баше] писалось под нашей рубрикой еще в позапрошлом году (8/83). Нетрудно запрограммировать выигрышную стратегию для "Нима". Но что за интерес играть с партнером, который никогда не проигрывает! Что за удовольствие, если на определенную последовательность ваших ходов всегда следуют одни и те же ответы! И так ли уж увлекательна эта игре! Неужели "Электроника БЗ-34" не дает возможности сыграть во что-то более захватывающее!
Те же вопросы вызывают и другие игровые программы, присланные до сих пор в редакцию и предназначенные для игр "Крестики-нолики", "Морской бой" (она же "Порази цель", она же "Танкодром"), "Посадка на Луну", "Быки и коровы" (она же "Угадай число"), "Одинокий ферзь".
Нам очень хотелось бы порадовать читателей игровыми программами, но такими, чтобы игра по ним не наскучила после первых же проб, увлекала бы нетривиальными, а порою совсем неожиданными ответами электронного партнера, заставляла бы продумывать хитроумные пути к победе, короче, доставляла бы удовольствие, а вместе, с тем (что тоже немаловажно) побуждала бы вникать в тонкости устройства и работы микрокалькулятора.
Объявляем конкурс на лучшую игру как для непрограммируемого микрокалькулятора (подобно описанной иа этой Странице игре "Упрямые числа"), так и для программируемого (в этом случае просьба составить программу для "Электроники Б3-34"). Единственное условие: игра не должна повторять собою ни одну из вышеназванных.
И еще один конкурс. Его задание относится ко вполне деловой проблематике. При обработке экспериментальных данных часто возникает потребность упорядочить по величине совокупность чисел, расположить их в порядке возрастания или убывания - как говорят, построить вариационный рад или ранжировать массив. Делая это вручную, пишут, например, каждое число на отдельной карточке, а затем вставляют эти карточки по одной в общий пакет.
Существует немало алгоритмов, позволяющих программировать этот процесс. Однако они, как правило, требуют больших объемов памяти для хранения результатов.
Предлагается составить программу для "Электроники Б3-34", решающую аналогичную задачу. Интересно выяснить, каково максимальное число элементов массива, который можно ранжировать на микрокалькуляторе, и как, сочетая ручной труд с машинным, получить вариационный ряд для большого числа элементов.
УПРЯМЫЕ ЧИСЛА
Возьмите любое двузначное число от 11 до 99. Прибавьте к нему зеркальное число, то есть исходное число, прочитанное справа налево - например, 39+93=132. К результату прибавьте его зеркальное число: 132+231=363. Вы получили симметричное число, то есть такое, чье зеркальное число равно ему самому. В нашем примере для его получения потребовалось два сложения.
Таким способом можно получить симметричное число из любого от 11 до 99. В большинстве случаев для этого потребуется от одного до четырех сложений. Четыре числа в этом диапазоне несколько более упрямы: чтобы получить из них симметричные числа, нужно 6 сложений. А два числа очень упорны - каждое из них превращается в симметричное лишь после 24 сложений! В результате получается симметричное число, насчитывающее 13 знаков.
Разумеется, эту игру можно вести и с трехзначными или даже более длинными числами, надеясь рано или поздно достичь симметрии. Впрочем, и тут есть несколько крепких орешков. Самое маленькое из чисел, не поддающихся никаким усилиям, - 196.
Еще никому не удалось установить, для всех ли чисел можно получить симметричный итог путем конечного числа сложений, или существуют такие числа, которые для этой игры не годятся.
"Нойес Дойчланд". 17/18 ноября 1984г. (перевел Ю.ФЛОРЕНСКИЙ, г.Рязань)
БЕЗ ТАБЛИЦ
Современный микрокалькулятор позволяет нажатием одной-двух клавиш получить значение синуса и косинуса, логарифма и арктангенса - общим счетом около десятка функций. Еще большими возможностями наверняка будут обладать карманные вычислители завтрашнего дня. Но вряд ли появятся когда-нибудь калькуляторы, в которые будут заложены программы вычисления всех функций - слишком их много.
А что если владельцу калькулятора понадобилось значение, скажем, функции Бесселя с точностью до восьмого знака? Что, если его электронный помощник не умеет вычислить даже синус и логарифм?
Преодолеть подобные затруднения поможет "Справочник по специальным функциям" под редакцией М.Абрамовича и И.Стиган (М. "Наука", 1979). Там приведены приближенные представления многочленами многих элементарных и специальных функций. В комплекте с микрокалькулятором (самым простым!) книга заменит и многотомные таблицы и большую ЭВМ.
Например, вам требуется определить величину arctg(0.5). В вашем распоряжении микрокалькулятор "Электроника Б3-26", не имеющая клавиши "arctg". Вот формула из справочника, дающая погрешность не более 2e-8 при 0<x<1:
arctg(x)=x(a16*x**16-a14*x**14+a12*x1**12-...+a4*x**4-a2*x2**2+1).
a16=0.0028662
a14=0.0161657
a12=0.0429096
a10=0.0752896
a8=0.1065626
a6=0.1420890
a4=0.1999355
a2=0.3333315
Вычисления удобно вести по схеме Горнера. Вносим в ПI+ величину х**2=0.25, далее следуем программе:
a16 * ИП - a14 * ИП + a12 * ИП - a10 * ИП + a8 * ИП - a6 * ИП + a4 * ИП - a2 * ИП + 1 * 0.5
Ответ: arct(0.5) = 0.4636476. Здесь все знаки - верные.
А.ТУЛАЙКОВ (г.Долгопрудный)
КАЛЬКУЛЯЦИЯ НА КАЛЬКУЛЯТОРЕ
"И, внимая моторному лаю.., ни за что я теперь не желаю слушать песню тележных колес!" - воскликнул некогда поэт, приветствуя технический прогресс. Времена меняются - мы предпочитаем сегодня бесшумные машины (разумеется, к тому же и более производительные). Причем не только на полях. Лязг арифмометра раздражает не меньше, чем перестук костяшек на счетах. Электронные микрокалькуляторы выполняют арифметические действия, повинуясь легкому прикосновению к клавишам. Но и эта работа может быть неприятной, если ее приходится повторять помногу раз каждый день. Не лучше ли поручить ее программируемому калькулятору и запускать каждый очередной расчет одним нажатием на клавишу?
Я работаю инженером-технологом на заводе по ремонту вычислительной техники. По долгу службы мне часто приходится рассчитывать калькуляции. Для этих целей я разработал простую программу для "Электроники Б3-34". Она приспособлена к условиям нашего завода. Однако по такому же принципу можно составить программу для любого другого предприятия, изменив должным образом процентное содержание одних статей по отношению к другим. Несмотря на простоту программы, польза от ее внедрения достаточно велика: ведь она автоматизирует расчеты, до сих пор проводившиеся вручную.
Так как программа занимает мало места в памяти, я решил не записывать константы в адресуемые регистры, а формировать их по ходу выполнения программы (см. ее фрагменты 01-05, 10-13, 17-21, 33-35). Мне кажется, что в этом случае уменьшается вероятность ошибки при вводе программы.
Исходными данными для расчета калькуляции являются стоимость материалов (М) и величина основной заработной платы (З0), выраженные в рублях. Остальные величины определяются из формул: дополнительная заработная плата Зд=З0*10.8%, отчисления на соцстрахование Ос=(З0+Зд)*7%, общезаводские расходы Р0=З0*57.4%, производственная себестоимость С=М+З0+Ос+Р0+Зд, прибыль П=С*20% и оптовая цена Оц=С+П. Перед запуском программы величины М и З0 вводятся соответственно в регистры 1 и 2. После запуска программы во время первого останова на индикаторе появляется Зд. Списав эту величину, вновь нажимаем клавишу С/П и получаем Ос. Продолжая расчет, последовательно получаем Р0, С, П, Оц.
Программа. 00. ^ 01. 0 02. ,
03. 0 04. 7 05. ИП2 06. 0 07. ,
08. 1 09. 0 10. 8 11. * 12. С/П 13. ИП2 14. + 15. * 16. С/П 17. Вх 18. + 19. 0 20. , 21. 5 22. 7 23. 4 24. ИП2 25. * 26. С/П 27. + 28. ИП1 29. + 30. ^ 31. С/П 32. 5 33. / 34. С/П 35. + 36. С/П 37. В/О
Для повторного расчета с теми же данными нажать С/П. Для расчета с новыми исходными данными ввести их в регистры 1 и 2, затем нажать С/П.
Контрольный пример: М=10, З0=20. Результаты: Зд=2.16, Ос=1.5512, Р0=11.48, С=45.1912, П=9.03824, Оц=54.22944.
С.ЧУЧАНОВ (г.Дружковка Донецкой обл.)
АНКЕТА ЧИТАТЕЛЕЙ РАЗДЕЛА
Обсудить прошлые выпуски раздела "Человек с микрокалькулятором", наметить планы на будущее - таковы цели публикации анкеты.
1. Считаете ли вы раздел "Человек с микрокалькулятором" нужным, полезным?
2. Ваша профессия, возраст.
3. Каким микрокалькулятором вы пользуетесь и как долго?
4. Какие выпуски раздела "Человек с микрокалькулятором" и какие отдельные статьи наиболее понравились вам?
5. О чем вы хотели бы прочесть на страницах раздела?
6. Какие новые постоянные темы раздела вы можете предложить?
7. О чем хотели бы вы спросить разработчиков микрокалькуляторов и что хотели бы им пожелать?

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Итак, в 85-м году НиЖ открыла "Школу программиста". Менее, чем за десять лет преподавание сменилось с "осторожно включите калькулятор в сеть" на "внесите изменения и скомпилируйте". А через 10 лет все закончилось полным развалом всех систем преподавания вместе со страной.
Зачем теперь это вспоминать? Наверное, только затем, что сейчас каждый может без проблем иметь свой калькулятор на любой вкус ТЕМА #14, АБЗАЦ #379
ТЕМА #14, АБЗАЦ #379 , написав его программу на том сверхмощном компьютере, что ныне заменяет ему телефон. И главное к этому препятствие - не незнание того, как это делается, а просто благоговение перед "прогрессом", олицетворяемым профессионально написанными программами. Вы видели последнюю версию MS Excel? Так куда же вы со своей самодельной таблицей? Лучше знать пару кнопок в "правильной программе", чем уметь писать свои "неправильные"... И т.д. и т.п.
, написав его программу на том сверхмощном компьютере, что ныне заменяет ему телефон. И главное к этому препятствие - не незнание того, как это делается, а просто благоговение перед "прогрессом", олицетворяемым профессионально написанными программами. Вы видели последнюю версию MS Excel? Так куда же вы со своей самодельной таблицей? Лучше знать пару кнопок в "правильной программе", чем уметь писать свои "неправильные"... И т.д. и т.п.
Так что, эта "школа", сама сначала учившая знать "пару модных кнопок", оказалась не удел, когда "кнопки" стали слишком уж коммерческими...
Отсюда первый интерес. Как увеличение мощности калькуляторов отразилось на способности среднего человека что-то посчитать? В какой момент наши потребности сократились настолько, что стало хватать покупных программ?
Так что, читая первый урок - "О числах" (хотя и обратите внимание, на требование решать задачу несколько формальнее, чем мы привыкли, считая на бумажке), задавайтесь больше вопросом: что бы вы хотели считать на своем супер-пупер калькуляторе: может, телефонные номера или сетевые адреса, может, иностранные слова или абзацы договоров, может фотографии? За время существования ЭВМ появилось огромное количество алгоритмов обработки чего попало и еще больше "языков программирования".
И, да, об обратной польской записи. Причина ее популярности в ПМК - не какая-то злокозненность производителей, а только лишь удобство реализации. Ведь, все же запомнили, что двоичные числа железякам удобнее десятичных, так запомните, что обратная польская запись - самая удобная форма языка для программ. По сути, вы на ней пишете, когда в каком-нибудь окошке сначала вводите все нужные данные, и только потом нажимаете кнопку OK.
***
6/85
В принятом недавно постановлении ЦК КПСС и Совета Министров СССР предусматривается введение с нового учебного года во всех средних учебных заведениях страны курса "Основы информатики и вычислительной техники", проведение широкого эксперимента по использованию ЭВМ в преподавании школьных предметов. Подчеркнуто, что всестороннее и глубокое овладение молодежью вычислительной техникой должно стать важным фактором ускорения научно-технического прогресса в стране.
Электронно-вычислительная техника в наши дни стремительно проникает во все новые сферы человеческой деятельности, так что навыки программирования становятся насущно необходимыми людям самых разнообразных специальностей и всех возрастов. Помочь овладению этими навыками - цель новой рубрики "Семинар по информатике", в который войдет и ставший уже традиционным раздел "Человек с микрокалькулятором".
Его нынешняя ориентация на программируемые микрокалькуляторы небезосновательна. Как невозможно научиться музыке, не имея музыкального инструмента, так программирование нельзя освоить, не располагая вычислительным устройством, способным работать по программе. Среди таких устройств сейчас наиболее доступны именно программируемые микрокалькуляторы.
Наша рубрика и впредь будет опираться на наиболее доступные и распространенные вычислительные машины, в ближайшем будущем - на персональные компьютеры. Приобретая массовость, они займут прочное место и на наших страницах.
А сейчас - карманные ЭВМ: "Электроника Б3-34" и ей подобные. При всей ограниченности своих возможностей, умелому владельцу они позволяют достичь многого, о чем свидетельствуют наши публикации.
Многие читатели, желающие научиться программировать на "Электронике Б3-34", просят опубликовать серию учебных статей на эту тему. Откликаясь на просьбы читателей, мы открываем наш "Семинар по информатике" циклом занятий "Школа начинающего программиста". Ее уроки будут полезны также владельцам микрокалькуляторов других марок, отличающихся от "Б3-34" лишь некоторыми обозначениями на клавишах.
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ПЕРВОЕ, ознакомительное, где читатель узнает, как включать и выключать микрокалькулятор, учится вводить в него числа и считывать их с индикатора, переводит углы из градусной меры в радианную и обратно, осваивает простейшие операции с числами и проводит несложные цепочные вычисления.
Ведет занятие Г.СЛАВИН (Тартуский государственный университет)
Искусством программирования невозможно овладеть за один присест. Чтобы сохранить калькулятор для следующих занятий и дальнейшей работы, надо строго соблюдать правила обращения с ним, оговоренные в инструкции, и прежде всего порядок его включения и выключения.
Необходимое ему для работы питание калькулятор может получать либо от размешенных внутри него аккумуляторов, либо от сети 220 вольт. В первом случае особой в обратной осторожности не требуется: чтобы включить калькулятор, переведите в крайнее правое положение тумблер в левом верхнем углу его панели, под индикатором. Тотчас на индикаторе загорится ноль с точкой: калькулятор готов к работе (если загорятся запятые, это значит, что аккумуляторы разряжены).
Если же вы намереваетесь пользоваться электроэнергией от сети, то тщательно следите за последовательностью своих действий: вначале к калькулятору подключается блок питания, затем блок питания включается в сеть, и уже потом включается сам калькулятор.
Выключение калькулятора производится в обратной последовательности: сначала выключается он сам, потом от розетки отсоединяется блок питания, потом, если требуется, он отсоединяется от калькулятора. Промежуток времени между выключением и повторным включением калькулятора должен составлять не менее 10 секунд.
На панели калькулятора тридцать клавиш. На каждой проставлено свое обозначение. Кроме того, обозначения есть и над клавишами, а в нижнем ряду клавиатуры - и под ними. Такое обилие связано с тем, что наш калькулятор может выполнять довольно много разных операций (около двухсот). Поэтому каждая клавиша предназначена для выполнения двух, а то и трех действий. Однако это не приводит к путанице. Опыт различения "что есть что" придет очень быстро.
Если нажать на клавишу, то будет выполняться действие, обозначенное на ней. Если же нажать сначала клавишу F (от слова Function - функция) и затем какую-то другую клавишу [Работающие на вычислительных машинах обычно говорят "нажать клавишу", а не "нажать на клавишу"], то будет выполнена операция, обозначенная над клавишей.
Например, если надо вычислить sqr(5), то нажимаем клавиши
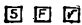
На индикаторе загорается значение корня: 2.2360679. (Обратите внимание: числа, выводимые на индикатор вашего калькулятора, могут содержать до восьми разрядов).
Отметим, что последняя из нажатых вами клавиш несет на себе символ "минус". Но вы, вероятно, не обратили на это внимание. Символ квадратного корня, написанный над нею, однозначно указал, что нажимать нужно было именно ее. Стало быть, вы уже приобретаете верную ориентацию в обозначениях на клавишах вашего калькулятора. В дальнейшем мы всегда будем называть требуемую по смыслу операцию независимо от того, обозначена она на самой клавише, сверху или снизу от нее.
Отметим и то, что для вычисления корня калькулятору сначала было сообщено подкоренное выражение, пять, а уже потом указано требуемое действие (хотя, казалось бы, традиционная запись корня sqr(5) диктует иначе: сначала sqr, потом 5). Такой обратный порядок характерен для команд, отдаваемых микрокалькулятору. К этому надо привыкнуть.
И еще примечание: действие клавиши F распространяется лишь на одну операцию, клавиша которой нажата сразу вслед. Для повторного выполнения "надклавишной" операции (только что выполненной или любой другой) необходимо снова нажать клавишу F, а уже затем требуемую, скажем, lg или sin.
При вычислении тригонометрических функций надо отчетливо представлять себе, в каких единицах выражен угол - в радианах или в градусах. Соответственно надо устанавливать и переключатель Р-Г. При градусном измерении минуты и секунды передаются на индикаторе десятичной дробью. Например, 17o45' будет выражено так: 17.75 - ведь 45 минут составляют 0.75 от одного градуса.
С помощью переключателя Р-Г можно переходить от градусной меры к радианной и наоборот. Например, переведем в раднаны угол 37o30'. Чтобы ввести эти величины в калькулятор, превратим минуты в десятичную дробь: 37.5. Установив переключатель в положение Г, вводим это число последовательным нажатием клавиш.
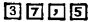
Заметьте: если число содержит не более восьми знаков, то ввести его проще всего именно так, как мы только что поступили - набирая на клавиатуре его последовательные цифры и не забывая своевременно нажать на клавишу "запятая", если это нужно.
Возьмем от введенного числа функцию "синус", нажав клавиши

На индикаторе читаем значение синуса: 0.60876144.
Переставим переключатель в положение Р и от результата предыдущей выкладки возьмем арксинус:

На индикаторе читаем радианную меру нашего угла: 0.65449853.
Впрочем, так прочтет показания индикатора лишь тот, кто обладает известной сноровкой в обращении с числами. На самом деле индикатор показывал сначала
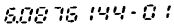
а потом

Это связано с тем, что числа, по абсолютной величине меньшие 1 и большие 99999999, в микрокалькуляторе представляются в так называемом нормализованном виде (как еще говорят, с плавающей запятой). Такой вид числам придается с помощью степеней десятки: 1e1=10, 1e3=1000, 1e7=10000000, 1e-1=0.1, 1e-3=0.001, 1e-7= 0.0000001 и т.д.
Любое число, как бы мало или велико оно ни было, можно представить в виде произведения двух сомножителей. В одном из них - те же цифры, что и в исходном числе, но запятая стоит сразу после первой ненулевой его цифры. Этот сомножитель называется мантиссой. Другой сомножитель - это 10 в некоторой степени (она называется порядком). Например: 23790000=2.379*10000000=2,.379e7, 0.00002379=2.379*(1/100000)=2.379e-5.
Использование такого представления, кроме чисто технических соображений, удобно во многих отношениях: благодаря этому калькулятор может работать воистину с гигантским диапазоном чисел - от 1e-99 до почти 1e100. (Напомним, что масса протона - около 1e-24г, а масса Вселенной оценивается в 1e55г.)
На индикаторе порядок числа представлен двумя крайними правыми цифрами со знаком перед ними ("+" не показывается). Все, что левее,- мантисса. Полученное в предыдущем примере число радиан перепишем с индикатора так:
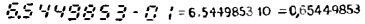
К такому представлению чисел привыкнуть совсем нетрудно. Для начала можно пользоваться таким советом: если знак порядка отрицательный, то перед первой цифрой мантиссы напишите столько нулей, сколько указано в порядке, и поставьте запятую после первого нуля; если же порядок задан положительным числом, то на такое число цифр переносите запятую вправо - по исчерпании цифр мантиссы добавляйте нули:
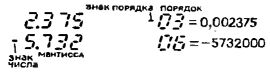
Определить мантиссу и порядок числа для его ввода можно, используя наш совет "наоборот".
Если число начинается с нулей, то его порядок отрицательный и равен количеству нулей. Мантиссу получаем, смещая запятую вправо, чтобы она оказалась после первой ненулевой цифры, и отбрасывая нули. В остальных случаях получаем мантиссу, сдвигая запятую влево, чтобы она стояла после первой значащей цифры. Количество десятичных разрядов, пройденное запятой при таком сдвиге, даст порядок числа - разумеется, неотрицательный. Он равен нулю, если запятая с самого начала стоит после первой значащей цифры.
При вводе числа в калькулятор действуют так: вводят мантиссу, нажимают клавишу ВП (ввод порядка; при этом справа появляются два нуля) и вводят порядок. Если число отрицательное, то после набора мантиссы нажимают клавишу /-/. Если порядок отрицательный, то клавишу /-/ нажимают после ввода порядка.
Ради тренировки введем в калькулятор числа 0.00002375,-237500 и -0,00002375. Нажатые клавиши указываем, как и прежде, символами в квадратных рамках, показания индикатора - записью, окруженной рамкой в форме параллелограмма.

Отметим, что вводить числа в нормализованном виде приходится только тогда, когда без этого не обойтись. Например, если требуется ввести число 0.000034655789, то обычным образом можно ввести только 0,0000346: цифры, вводимые после восьми начальных, восприняты не будут. Представленное же в виде 3.465789e-5 оно вводится полностью.
Потренируйтесь сами в вводе чисел в нормализованной форме и умении их легко читать. Для этого используйте клавишу ^ она автоматически нормализует набранное на клавиатуре число, меньшее единицы:

Вернемся к примеру с переводом угла из градусной меры в радианную. Мы уже выяснили, что 37.5o=0.654449853 радиана. Теперь посмотрим, как совершается перевод из радианной меры в градусную. Установив переключатель в положение Р, наберем 0.65449853 и нажмем клавиши F sin. На индикаторе читаем 0.60876151. Установим затем переключатель в положение Г и нажмем клавиши F arcsin. На индикаторе читаем 37.500009.
Тот факт, что значения синуса, вычисленные нами прежде и теперь, совпадают не полностью и что исходный угол получен обратно с маленькой "добавкой", обычен для вычислительной техники и не должен смущать.
Любой ЭВМ свойственно делать ничтожные ошибки. Это происходит из-за целого ряда причин; например, в нашем случае из-за того, что функции sin x и arcsin x подсчитываются по довольно сложным программам, заложенным в машину. Каждая из этих программ допускает ошибку в вычислениях, нередко достигающую шестого знака после запятой. Но заметьте: мы четыре раза использовали эти программы, да еще два раза делали перевод из одной меры в другую, что влечет за собой умножение и деление. Остается только удивляться, что после таких "приключений" исходное число возвратилось назад с завидной точностью.
Машинные ошибки такого рода столь малы, что не оказывают никакого вреда в практической работе, тем более что при необходимости можно избавиться и от них, внося некоторые усложнения в программы вычислений.
Процесс работы микрокалькулятора, вычислявшего синус и арксинус, был хорошо заметен: в это время на индикаторе около секунды ничего не было. Если бы мы взялись вручную повторить все то, что делала наша миниатюрная вычислительная машина, по таким же формулам и с такой же точностью, нам потребовалось бы не менее рабочего дня!
Наш калькулятор, как и любая другая вычислительная машина, оперирует с числами. Важно понять, что при выполнении любого действия используемые числа не могут находиться в калькуляторе иным образом, как только записанными в память.
Числа запоминаются машиной в отведенных для этого ячейках, регистрах памяти.
Каждый регистр памяти в калькуляторе имеет свое обозначение в виде цифры или буквы. Десять из них обозначаются начальными натуральными числами, от 0 до 9 включительно, еще четыре - начальными буквами латинского алфавита (А, В, С, D) и еще пять - латинскими буквами X, Y, Z, Т, XI. Группа последних регистров существенно отличается от остальных, и об этом мы поговорим подробнее на следующем занятии.
В дальнейшем для краткости мы будем обозначать регистры сокращенно: РХ, Р4 или РА.
При вводе в калькулятор число заносится в регистр X. От всех прочих он отличается тем, что его содержимое (то есть записанное в него число) всегда видно на индикаторе. И наоборот: если на индикаторе видно какое-то число, то оно находится в PX. Для прочного запоминания, скажем, допуская некоторое огрубление: индикатор и регистр X - это одно и то же.
Все операции, при помощи которых вычисляются функции от некоторого числа, выполняются в нашем калькуляторе таким образом, что в качестве аргумента берется число из РХ и туда же помещается результат. Так было и с sqr(5): после нажатия клавишш 5 и sqr значение корня было занесено в РХ, то есть появилось на индикаторе.
Каждая такая операция (извлечение квадратного корня, возведение числа в квадрат, получение обратной величины от числа; вычисление синуса, косинуса, тангенса и обратных к ним функций; возведение в степень чисел 10 и е; вычисление логарифмов, десятичного и натурального) выполняется над одним числом, и потому все они называются одноместными. Сложнее структура у арифметических операций - сложения и вычитания, умножения и деления. Все они двуместные, каждая выполняется над двумя числами. Порядок построения команд и в этом случае обратный: сначала калькулятору сообщают оба числа, а потом символ операции, которую требуется над ними совершить.
Каким бы странным ни казался такой порядок, у него есть определенные преимущества по сравнению с привычной для нас записью арифметических операций. Записывая их, мы не можем обойтись без скобок. Уберите их, например, в выражении 3.5*(2.5-1) и оно превратится в 3.5*2.5-1, что приведет к другому результату. А команды для нашего калькулятора, как мы увидим чуть позже, в подобных случаях можно отдавать, не прибегая к скобкам.
Используемая в калькуляторных выкладках бесскобочная запись называется также польской, потому что впервые ее предложил польский ученый А.Лукасевич.
Числа, над которыми нужно совершить ту или иную арифметическую операцию, должны находиться в двух регистрах - РХ и PY. Ход в первый из них нам уже знаком: вводимое в него число набирается на клавиатуре. В PY можно попасть только из РХ. Делается это нажатием клавиши ^. При этом копня переданного числа остается в РХ. Затем туда записывается второе число; бывшее там прежде автоматически стирается.
Порядок расположения обоих чисел в регистрах РХ и PY неважен, если их предстоит сложить или перемножить. В случае вычитания уменьшаемое должно находиться в PY, вычитаемое - в РХ. В случае деления в PY должно располагаться делимое, в, РХ - делитель.
Введя числа в оба регистра, можно нажать клавишу выбранной операции. Результат ее будет помещен в РХ. То, что было прежде в PY, не сохранится.
Ради примера вычислим арифметические выражения, встретившиеся нам тремя абзацами выше. Итак, 3.5*(2.5-1). Начнем с выражения в скобках. Набираем на клавиатуре уменьшаемое 2.5 и нажимаем клавишу ^. Число на индикаторе "мигнуло": теперь оно переслано в PY, а его копия осталась в РХ. Вводим вычитаемое, единицу, и нажимаем клавишу "минус". Результат вычитания читаем на индикаторе: 1.5. Казалось бы, для выполнения умножения его нужно переслать в PY при помощи все той же клавиши ^. Эту операцию, однако, можно сэкономить благодаря интересному свойству нашего калькулятора. Оказывается, если число на индикаторе является результатом некоторой операции, то оно передвигается в PY, когда в РХ вводится новое число.
Набираем на клавиатуре 3.5. Теперь все готово для умножения: в PY находится 1.5 и в РХ записано 3.5. Нажимаем клавишу со знаком умножения и читаем на индикаторе окончательный результат: 5.25.
Выполним вторую выкладку: 3.5*2.5-1. Продумайте последовательность нажатия клавиш и сравните ее с приведенной здесь:
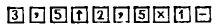
Совершите все эти действия и сверьте результат с истинным: 7.75.
Вдумаемся в только что отмечавшуюся особенность нашего калькулятора: если в РХ ввести очередное число, то результат предыдущей операции перейдет в PY. Вслед за этим можно выполнить действие с введенным в РХ числом н предыдущим результатом, находящимся в PY. Получившийся результат опять перейдет в PY при наборе нового числа и так далее. Такие действия называются цепочечными.
В качестве иллюстрации рассмотрим суммирование нескольких чисел: 11, 12, 13... Набираем число 11 и нажатием клавиши переводим его в PY; вводим 12, нажимаем клавишу "плюс" и читаем на индикаторе результат: 23. Набираем число 13. При этом предыдущий результат 23 сразу переходит в PY, и при нажатии клавиши "плюс" читаем сумму: 36. Теперь вводим 14... и так далее.

Возьмем формулу посложнее:
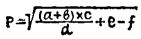
Советуем и на сей раз самостоятельно предложить порядок действий и уже затем проверить себя по приведенному здесь:
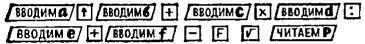
Вычислите значение Р при таких исходных данных: а=10, b=11, с=12, d=-156, е=15.2 и f=-348.3. Проверьте, получилось ли Р=19.023265.
На результаты промежуточных вычислений можно не обращать особого внимания, ограничившись лишь быстрым контролем. Например, если выполнялось деление положительного и отрицательного чисел и частное получилось положительным, значит, при вводе не был установлен знак числа. Напомним: он устанавливается после того, как введены все цифры числа.
Неверно введенное число можно ввести заново: стираем его нажатием клавиши Сх, набираем его вновь и продолжаем работу.
В отличие от результата арифметического действия результат одноместной операции не изменяет содержимого PY. Если над этим результатом, находящимся в РХ, опять провести одноместную операцию, то содержимое PY опять не испортится. И так будет продолжаться до задания арифметической, двухместной операции.
Этот факт существенно облегчает проведение расчета по сложным формулам. Пусть, например, нам требуется вычислить гипотенузу прямоугольного треугольника c, у которого известны катеты a и b. Воспользуемся хорошо известной из геометрии теоремой Пифагора:

Вычисления на калькуляторе по этой формуле сводятся к короткой цепочке действий:
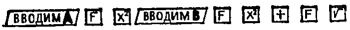
Проверьте, что при a=3 и b=4 получается c=5.
Теперь немного тригонометрии. Вот формула:

Порядок вычисления здесь может быть таким:

Для заключительной иллюстрации обратимся к пропорции золотого сечения, сыгравшей большую роль в истории математики и архитектуры. Выражающее ее число Ф равно (1+sqr(5))/2. Вычислите его на калькуляторе. Должно получиться 1.6180339.
Известно несколько приближений к этому числу:
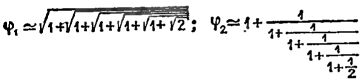
Мы ограничимся конечным количеством корней и дробей. Вычислите оба выражения. Сравните, насколько они отличаются друг от друга и от самого числа ф. Небольшая подсказка: начинайте вычисления с конца формул.
Повторите вычисления еще и еще раз, каждый раз удлиняя формулы для ф1 и ф2. Как видите, результаты все менее отличаются от ф.
Метод последовательных приближений широко и разнообразно применяется в вычислительной математике. На будущих занятиях мы еще встретимся с соответствующими примерами.
Зачем теперь это вспоминать? Наверное, только затем, что сейчас каждый может без проблем иметь свой калькулятор на любой вкус
 ТЕМА #14, АБЗАЦ #379
ТЕМА #14, АБЗАЦ #379 , написав его программу на том сверхмощном компьютере, что ныне заменяет ему телефон. И главное к этому препятствие - не незнание того, как это делается, а просто благоговение перед "прогрессом", олицетворяемым профессионально написанными программами. Вы видели последнюю версию MS Excel? Так куда же вы со своей самодельной таблицей? Лучше знать пару кнопок в "правильной программе", чем уметь писать свои "неправильные"... И т.д. и т.п.
, написав его программу на том сверхмощном компьютере, что ныне заменяет ему телефон. И главное к этому препятствие - не незнание того, как это делается, а просто благоговение перед "прогрессом", олицетворяемым профессионально написанными программами. Вы видели последнюю версию MS Excel? Так куда же вы со своей самодельной таблицей? Лучше знать пару кнопок в "правильной программе", чем уметь писать свои "неправильные"... И т.д. и т.п.Так что, эта "школа", сама сначала учившая знать "пару модных кнопок", оказалась не удел, когда "кнопки" стали слишком уж коммерческими...
Отсюда первый интерес. Как увеличение мощности калькуляторов отразилось на способности среднего человека что-то посчитать? В какой момент наши потребности сократились настолько, что стало хватать покупных программ?
Так что, читая первый урок - "О числах" (хотя и обратите внимание, на требование решать задачу несколько формальнее, чем мы привыкли, считая на бумажке), задавайтесь больше вопросом: что бы вы хотели считать на своем супер-пупер калькуляторе: может, телефонные номера или сетевые адреса, может, иностранные слова или абзацы договоров, может фотографии? За время существования ЭВМ появилось огромное количество алгоритмов обработки чего попало и еще больше "языков программирования".
И, да, об обратной польской записи. Причина ее популярности в ПМК - не какая-то злокозненность производителей, а только лишь удобство реализации. Ведь, все же запомнили, что двоичные числа железякам удобнее десятичных, так запомните, что обратная польская запись - самая удобная форма языка для программ. По сути, вы на ней пишете, когда в каком-нибудь окошке сначала вводите все нужные данные, и только потом нажимаете кнопку OK.
***
6/85
В принятом недавно постановлении ЦК КПСС и Совета Министров СССР предусматривается введение с нового учебного года во всех средних учебных заведениях страны курса "Основы информатики и вычислительной техники", проведение широкого эксперимента по использованию ЭВМ в преподавании школьных предметов. Подчеркнуто, что всестороннее и глубокое овладение молодежью вычислительной техникой должно стать важным фактором ускорения научно-технического прогресса в стране.
Электронно-вычислительная техника в наши дни стремительно проникает во все новые сферы человеческой деятельности, так что навыки программирования становятся насущно необходимыми людям самых разнообразных специальностей и всех возрастов. Помочь овладению этими навыками - цель новой рубрики "Семинар по информатике", в который войдет и ставший уже традиционным раздел "Человек с микрокалькулятором".
Его нынешняя ориентация на программируемые микрокалькуляторы небезосновательна. Как невозможно научиться музыке, не имея музыкального инструмента, так программирование нельзя освоить, не располагая вычислительным устройством, способным работать по программе. Среди таких устройств сейчас наиболее доступны именно программируемые микрокалькуляторы.
Наша рубрика и впредь будет опираться на наиболее доступные и распространенные вычислительные машины, в ближайшем будущем - на персональные компьютеры. Приобретая массовость, они займут прочное место и на наших страницах.
А сейчас - карманные ЭВМ: "Электроника Б3-34" и ей подобные. При всей ограниченности своих возможностей, умелому владельцу они позволяют достичь многого, о чем свидетельствуют наши публикации.
Многие читатели, желающие научиться программировать на "Электронике Б3-34", просят опубликовать серию учебных статей на эту тему. Откликаясь на просьбы читателей, мы открываем наш "Семинар по информатике" циклом занятий "Школа начинающего программиста". Ее уроки будут полезны также владельцам микрокалькуляторов других марок, отличающихся от "Б3-34" лишь некоторыми обозначениями на клавишах.
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ПЕРВОЕ, ознакомительное, где читатель узнает, как включать и выключать микрокалькулятор, учится вводить в него числа и считывать их с индикатора, переводит углы из градусной меры в радианную и обратно, осваивает простейшие операции с числами и проводит несложные цепочные вычисления.
Ведет занятие Г.СЛАВИН (Тартуский государственный университет)
Искусством программирования невозможно овладеть за один присест. Чтобы сохранить калькулятор для следующих занятий и дальнейшей работы, надо строго соблюдать правила обращения с ним, оговоренные в инструкции, и прежде всего порядок его включения и выключения.
Необходимое ему для работы питание калькулятор может получать либо от размешенных внутри него аккумуляторов, либо от сети 220 вольт. В первом случае особой в обратной осторожности не требуется: чтобы включить калькулятор, переведите в крайнее правое положение тумблер в левом верхнем углу его панели, под индикатором. Тотчас на индикаторе загорится ноль с точкой: калькулятор готов к работе (если загорятся запятые, это значит, что аккумуляторы разряжены).
Если же вы намереваетесь пользоваться электроэнергией от сети, то тщательно следите за последовательностью своих действий: вначале к калькулятору подключается блок питания, затем блок питания включается в сеть, и уже потом включается сам калькулятор.
Выключение калькулятора производится в обратной последовательности: сначала выключается он сам, потом от розетки отсоединяется блок питания, потом, если требуется, он отсоединяется от калькулятора. Промежуток времени между выключением и повторным включением калькулятора должен составлять не менее 10 секунд.
На панели калькулятора тридцать клавиш. На каждой проставлено свое обозначение. Кроме того, обозначения есть и над клавишами, а в нижнем ряду клавиатуры - и под ними. Такое обилие связано с тем, что наш калькулятор может выполнять довольно много разных операций (около двухсот). Поэтому каждая клавиша предназначена для выполнения двух, а то и трех действий. Однако это не приводит к путанице. Опыт различения "что есть что" придет очень быстро.
Если нажать на клавишу, то будет выполняться действие, обозначенное на ней. Если же нажать сначала клавишу F (от слова Function - функция) и затем какую-то другую клавишу [Работающие на вычислительных машинах обычно говорят "нажать клавишу", а не "нажать на клавишу"], то будет выполнена операция, обозначенная над клавишей.
Например, если надо вычислить sqr(5), то нажимаем клавиши
На индикаторе загорается значение корня: 2.2360679. (Обратите внимание: числа, выводимые на индикатор вашего калькулятора, могут содержать до восьми разрядов).
Отметим, что последняя из нажатых вами клавиш несет на себе символ "минус". Но вы, вероятно, не обратили на это внимание. Символ квадратного корня, написанный над нею, однозначно указал, что нажимать нужно было именно ее. Стало быть, вы уже приобретаете верную ориентацию в обозначениях на клавишах вашего калькулятора. В дальнейшем мы всегда будем называть требуемую по смыслу операцию независимо от того, обозначена она на самой клавише, сверху или снизу от нее.
Отметим и то, что для вычисления корня калькулятору сначала было сообщено подкоренное выражение, пять, а уже потом указано требуемое действие (хотя, казалось бы, традиционная запись корня sqr(5) диктует иначе: сначала sqr, потом 5). Такой обратный порядок характерен для команд, отдаваемых микрокалькулятору. К этому надо привыкнуть.
И еще примечание: действие клавиши F распространяется лишь на одну операцию, клавиша которой нажата сразу вслед. Для повторного выполнения "надклавишной" операции (только что выполненной или любой другой) необходимо снова нажать клавишу F, а уже затем требуемую, скажем, lg или sin.
При вычислении тригонометрических функций надо отчетливо представлять себе, в каких единицах выражен угол - в радианах или в градусах. Соответственно надо устанавливать и переключатель Р-Г. При градусном измерении минуты и секунды передаются на индикаторе десятичной дробью. Например, 17o45' будет выражено так: 17.75 - ведь 45 минут составляют 0.75 от одного градуса.
С помощью переключателя Р-Г можно переходить от градусной меры к радианной и наоборот. Например, переведем в раднаны угол 37o30'. Чтобы ввести эти величины в калькулятор, превратим минуты в десятичную дробь: 37.5. Установив переключатель в положение Г, вводим это число последовательным нажатием клавиш.
Заметьте: если число содержит не более восьми знаков, то ввести его проще всего именно так, как мы только что поступили - набирая на клавиатуре его последовательные цифры и не забывая своевременно нажать на клавишу "запятая", если это нужно.
Возьмем от введенного числа функцию "синус", нажав клавиши

На индикаторе читаем значение синуса: 0.60876144.
Переставим переключатель в положение Р и от результата предыдущей выкладки возьмем арксинус:

На индикаторе читаем радианную меру нашего угла: 0.65449853.
Впрочем, так прочтет показания индикатора лишь тот, кто обладает известной сноровкой в обращении с числами. На самом деле индикатор показывал сначала
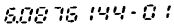
а потом

Это связано с тем, что числа, по абсолютной величине меньшие 1 и большие 99999999, в микрокалькуляторе представляются в так называемом нормализованном виде (как еще говорят, с плавающей запятой). Такой вид числам придается с помощью степеней десятки: 1e1=10, 1e3=1000, 1e7=10000000, 1e-1=0.1, 1e-3=0.001, 1e-7= 0.0000001 и т.д.
Любое число, как бы мало или велико оно ни было, можно представить в виде произведения двух сомножителей. В одном из них - те же цифры, что и в исходном числе, но запятая стоит сразу после первой ненулевой его цифры. Этот сомножитель называется мантиссой. Другой сомножитель - это 10 в некоторой степени (она называется порядком). Например: 23790000=2.379*10000000=2,.379e7, 0.00002379=2.379*(1/100000)=2.379e-5.
Использование такого представления, кроме чисто технических соображений, удобно во многих отношениях: благодаря этому калькулятор может работать воистину с гигантским диапазоном чисел - от 1e-99 до почти 1e100. (Напомним, что масса протона - около 1e-24г, а масса Вселенной оценивается в 1e55г.)
На индикаторе порядок числа представлен двумя крайними правыми цифрами со знаком перед ними ("+" не показывается). Все, что левее,- мантисса. Полученное в предыдущем примере число радиан перепишем с индикатора так:
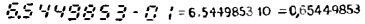
К такому представлению чисел привыкнуть совсем нетрудно. Для начала можно пользоваться таким советом: если знак порядка отрицательный, то перед первой цифрой мантиссы напишите столько нулей, сколько указано в порядке, и поставьте запятую после первого нуля; если же порядок задан положительным числом, то на такое число цифр переносите запятую вправо - по исчерпании цифр мантиссы добавляйте нули:
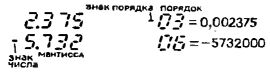
Определить мантиссу и порядок числа для его ввода можно, используя наш совет "наоборот".
Если число начинается с нулей, то его порядок отрицательный и равен количеству нулей. Мантиссу получаем, смещая запятую вправо, чтобы она оказалась после первой ненулевой цифры, и отбрасывая нули. В остальных случаях получаем мантиссу, сдвигая запятую влево, чтобы она стояла после первой значащей цифры. Количество десятичных разрядов, пройденное запятой при таком сдвиге, даст порядок числа - разумеется, неотрицательный. Он равен нулю, если запятая с самого начала стоит после первой значащей цифры.
При вводе числа в калькулятор действуют так: вводят мантиссу, нажимают клавишу ВП (ввод порядка; при этом справа появляются два нуля) и вводят порядок. Если число отрицательное, то после набора мантиссы нажимают клавишу /-/. Если порядок отрицательный, то клавишу /-/ нажимают после ввода порядка.
Ради тренировки введем в калькулятор числа 0.00002375,-237500 и -0,00002375. Нажатые клавиши указываем, как и прежде, символами в квадратных рамках, показания индикатора - записью, окруженной рамкой в форме параллелограмма.

Отметим, что вводить числа в нормализованном виде приходится только тогда, когда без этого не обойтись. Например, если требуется ввести число 0.000034655789, то обычным образом можно ввести только 0,0000346: цифры, вводимые после восьми начальных, восприняты не будут. Представленное же в виде 3.465789e-5 оно вводится полностью.
Потренируйтесь сами в вводе чисел в нормализованной форме и умении их легко читать. Для этого используйте клавишу ^ она автоматически нормализует набранное на клавиатуре число, меньшее единицы:

Вернемся к примеру с переводом угла из градусной меры в радианную. Мы уже выяснили, что 37.5o=0.654449853 радиана. Теперь посмотрим, как совершается перевод из радианной меры в градусную. Установив переключатель в положение Р, наберем 0.65449853 и нажмем клавиши F sin. На индикаторе читаем 0.60876151. Установим затем переключатель в положение Г и нажмем клавиши F arcsin. На индикаторе читаем 37.500009.
Тот факт, что значения синуса, вычисленные нами прежде и теперь, совпадают не полностью и что исходный угол получен обратно с маленькой "добавкой", обычен для вычислительной техники и не должен смущать.
Любой ЭВМ свойственно делать ничтожные ошибки. Это происходит из-за целого ряда причин; например, в нашем случае из-за того, что функции sin x и arcsin x подсчитываются по довольно сложным программам, заложенным в машину. Каждая из этих программ допускает ошибку в вычислениях, нередко достигающую шестого знака после запятой. Но заметьте: мы четыре раза использовали эти программы, да еще два раза делали перевод из одной меры в другую, что влечет за собой умножение и деление. Остается только удивляться, что после таких "приключений" исходное число возвратилось назад с завидной точностью.
Машинные ошибки такого рода столь малы, что не оказывают никакого вреда в практической работе, тем более что при необходимости можно избавиться и от них, внося некоторые усложнения в программы вычислений.
Процесс работы микрокалькулятора, вычислявшего синус и арксинус, был хорошо заметен: в это время на индикаторе около секунды ничего не было. Если бы мы взялись вручную повторить все то, что делала наша миниатюрная вычислительная машина, по таким же формулам и с такой же точностью, нам потребовалось бы не менее рабочего дня!
Наш калькулятор, как и любая другая вычислительная машина, оперирует с числами. Важно понять, что при выполнении любого действия используемые числа не могут находиться в калькуляторе иным образом, как только записанными в память.
Числа запоминаются машиной в отведенных для этого ячейках, регистрах памяти.
Каждый регистр памяти в калькуляторе имеет свое обозначение в виде цифры или буквы. Десять из них обозначаются начальными натуральными числами, от 0 до 9 включительно, еще четыре - начальными буквами латинского алфавита (А, В, С, D) и еще пять - латинскими буквами X, Y, Z, Т, XI. Группа последних регистров существенно отличается от остальных, и об этом мы поговорим подробнее на следующем занятии.
В дальнейшем для краткости мы будем обозначать регистры сокращенно: РХ, Р4 или РА.
При вводе в калькулятор число заносится в регистр X. От всех прочих он отличается тем, что его содержимое (то есть записанное в него число) всегда видно на индикаторе. И наоборот: если на индикаторе видно какое-то число, то оно находится в PX. Для прочного запоминания, скажем, допуская некоторое огрубление: индикатор и регистр X - это одно и то же.
Все операции, при помощи которых вычисляются функции от некоторого числа, выполняются в нашем калькуляторе таким образом, что в качестве аргумента берется число из РХ и туда же помещается результат. Так было и с sqr(5): после нажатия клавишш 5 и sqr значение корня было занесено в РХ, то есть появилось на индикаторе.
Каждая такая операция (извлечение квадратного корня, возведение числа в квадрат, получение обратной величины от числа; вычисление синуса, косинуса, тангенса и обратных к ним функций; возведение в степень чисел 10 и е; вычисление логарифмов, десятичного и натурального) выполняется над одним числом, и потому все они называются одноместными. Сложнее структура у арифметических операций - сложения и вычитания, умножения и деления. Все они двуместные, каждая выполняется над двумя числами. Порядок построения команд и в этом случае обратный: сначала калькулятору сообщают оба числа, а потом символ операции, которую требуется над ними совершить.
Каким бы странным ни казался такой порядок, у него есть определенные преимущества по сравнению с привычной для нас записью арифметических операций. Записывая их, мы не можем обойтись без скобок. Уберите их, например, в выражении 3.5*(2.5-1) и оно превратится в 3.5*2.5-1, что приведет к другому результату. А команды для нашего калькулятора, как мы увидим чуть позже, в подобных случаях можно отдавать, не прибегая к скобкам.
Используемая в калькуляторных выкладках бесскобочная запись называется также польской, потому что впервые ее предложил польский ученый А.Лукасевич.
Числа, над которыми нужно совершить ту или иную арифметическую операцию, должны находиться в двух регистрах - РХ и PY. Ход в первый из них нам уже знаком: вводимое в него число набирается на клавиатуре. В PY можно попасть только из РХ. Делается это нажатием клавиши ^. При этом копня переданного числа остается в РХ. Затем туда записывается второе число; бывшее там прежде автоматически стирается.
Порядок расположения обоих чисел в регистрах РХ и PY неважен, если их предстоит сложить или перемножить. В случае вычитания уменьшаемое должно находиться в PY, вычитаемое - в РХ. В случае деления в PY должно располагаться делимое, в, РХ - делитель.
Введя числа в оба регистра, можно нажать клавишу выбранной операции. Результат ее будет помещен в РХ. То, что было прежде в PY, не сохранится.
Ради примера вычислим арифметические выражения, встретившиеся нам тремя абзацами выше. Итак, 3.5*(2.5-1). Начнем с выражения в скобках. Набираем на клавиатуре уменьшаемое 2.5 и нажимаем клавишу ^. Число на индикаторе "мигнуло": теперь оно переслано в PY, а его копия осталась в РХ. Вводим вычитаемое, единицу, и нажимаем клавишу "минус". Результат вычитания читаем на индикаторе: 1.5. Казалось бы, для выполнения умножения его нужно переслать в PY при помощи все той же клавиши ^. Эту операцию, однако, можно сэкономить благодаря интересному свойству нашего калькулятора. Оказывается, если число на индикаторе является результатом некоторой операции, то оно передвигается в PY, когда в РХ вводится новое число.
Набираем на клавиатуре 3.5. Теперь все готово для умножения: в PY находится 1.5 и в РХ записано 3.5. Нажимаем клавишу со знаком умножения и читаем на индикаторе окончательный результат: 5.25.
Выполним вторую выкладку: 3.5*2.5-1. Продумайте последовательность нажатия клавиш и сравните ее с приведенной здесь:
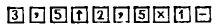
Совершите все эти действия и сверьте результат с истинным: 7.75.
Вдумаемся в только что отмечавшуюся особенность нашего калькулятора: если в РХ ввести очередное число, то результат предыдущей операции перейдет в PY. Вслед за этим можно выполнить действие с введенным в РХ числом н предыдущим результатом, находящимся в PY. Получившийся результат опять перейдет в PY при наборе нового числа и так далее. Такие действия называются цепочечными.
В качестве иллюстрации рассмотрим суммирование нескольких чисел: 11, 12, 13... Набираем число 11 и нажатием клавиши переводим его в PY; вводим 12, нажимаем клавишу "плюс" и читаем на индикаторе результат: 23. Набираем число 13. При этом предыдущий результат 23 сразу переходит в PY, и при нажатии клавиши "плюс" читаем сумму: 36. Теперь вводим 14... и так далее.

Возьмем формулу посложнее:
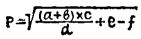
Советуем и на сей раз самостоятельно предложить порядок действий и уже затем проверить себя по приведенному здесь:
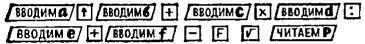
Вычислите значение Р при таких исходных данных: а=10, b=11, с=12, d=-156, е=15.2 и f=-348.3. Проверьте, получилось ли Р=19.023265.
На результаты промежуточных вычислений можно не обращать особого внимания, ограничившись лишь быстрым контролем. Например, если выполнялось деление положительного и отрицательного чисел и частное получилось положительным, значит, при вводе не был установлен знак числа. Напомним: он устанавливается после того, как введены все цифры числа.
Неверно введенное число можно ввести заново: стираем его нажатием клавиши Сх, набираем его вновь и продолжаем работу.
В отличие от результата арифметического действия результат одноместной операции не изменяет содержимого PY. Если над этим результатом, находящимся в РХ, опять провести одноместную операцию, то содержимое PY опять не испортится. И так будет продолжаться до задания арифметической, двухместной операции.
Этот факт существенно облегчает проведение расчета по сложным формулам. Пусть, например, нам требуется вычислить гипотенузу прямоугольного треугольника c, у которого известны катеты a и b. Воспользуемся хорошо известной из геометрии теоремой Пифагора:

Вычисления на калькуляторе по этой формуле сводятся к короткой цепочке действий:
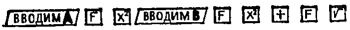
Проверьте, что при a=3 и b=4 получается c=5.
Теперь немного тригонометрии. Вот формула:

Порядок вычисления здесь может быть таким:

Для заключительной иллюстрации обратимся к пропорции золотого сечения, сыгравшей большую роль в истории математики и архитектуры. Выражающее ее число Ф равно (1+sqr(5))/2. Вычислите его на калькуляторе. Должно получиться 1.6180339.
Известно несколько приближений к этому числу:
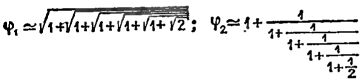
Мы ограничимся конечным количеством корней и дробей. Вычислите оба выражения. Сравните, насколько они отличаются друг от друга и от самого числа ф. Небольшая подсказка: начинайте вычисления с конца формул.
Повторите вычисления еще и еще раз, каждый раз удлиняя формулы для ф1 и ф2. Как видите, результаты все менее отличаются от ф.
Метод последовательных приближений широко и разнообразно применяется в вычислительной математике. На будущих занятиях мы еще встретимся с соответствующими примерами.

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
6/85
ЧЕЛОВЕК С МИКРОКАЛЬКУЛЯТОРОМ
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Многие читатели спрашивают, какие новые микрокалькуляторы будут выпускаться в нашей стране в ближайшее время. Корреспондент журнала "Наука и жизнь" Л.БОЙКО побывал в научно-производственном объединении "Кристалл" (г.Киев) и задал этот вопрос сотрудникам объединения Л.ЖИЖКО, Ю.ПОЛЬСКОМУ, Н.РОМАШКО, А.ШЕРЕВЕНЕ. Речь шла не только о разработке будущих, но и совершенствовании старых моделей программируемых микрокалькуляторов.

Новые программируемые микрокалькуляторы "Электроника МК-52" и "Электроника МК-61".
ДВЕ НОВЫЕ МАРКИ: "МК-61" и "МК-52"
- Прежде чем говорить о новых марках программируемых микрокалькуляторов, хотелось бы уделить внимание старым. Вот, к примеру, "Электроника МК-54". Репутация у этого калькулятора неплохая, однако среди благодарных отзывов о нем встречаются н критические замечания о недостатках, обнаруживаемых при работе с ним. Например, из-за ненадежной работы кнопки "переключатель питания" микрокалькулятор может самопроизвольно отключаться.
- Замечание справедливое. Такие критические отзывы очень ценны разработчикам микрокалькуляторов, поскольку позволяют быстрее выявить огрехи и устранить их в последующих партиях изделия. Что касается злополучной кнопки, то в микрокалькуляторы новых выпусков устанавливается унифицированный переключатель, обладающий повышенной надежностью.
- Есть претензии к вычислению логарифмической функции на "Электронике Б3-34". Например, читатель В.Богатко из Ленинграда отмечает, что последовательность команд 1. ИП1 2. ИП2 3. Fln 4. / 5. С/П при единице в регистре Р1 и z в регистре Р2, где exp(-1)<z<l, вызывает в "Электронике Б3-34" сигнал ошибки при работе в автоматическом режиме.
- Этот дефект был обнаружен вскоре после того, как начался выпуск названного калькулятора. Сейчас он устранен и в "Электронике Б3-34" и в ее аналогах марок "МК-54" и "МК-56". В интегральные микросхемы, которые у всех трех калькуляторов одни и те же, внесены необходимые изменения. Для калькуляторов прежних выпусков в таких случаях рекомендуется последовательность команд 1. ИП2 2. Fln 3. ИП1 4. / 5. F1/x 6. С/П.
Исправлена команда FxY, вызывавшая много нареканий. Владельцам микрокалькуляторов прежних выпусков лучше пользоваться вместо нее цепочкой команд Fln Fexp.
К ошибкам приводил программный фрагмент вида 1. Fx2 2. /-/ 3. С/П, например, когда х=1e-40 набрано с клавиатуры. Тем читателям, чьи калькуляторы в таком случае дают неверный результат 1e40, рекомендуется дополнить фрагмент командой ^ непосредственно перед командой Fx2.
- Микрокалькуляторы марок "Б3-34", "МК-54", "МК-56" страдают еще таким недостатком: выполнение операций Fexp при х<-230.26 и F10X при х<-100 вместо машинного нуля дает аварийный останов.
- Ликвидация этого дефекта труднее, чем устранение названных до этого недостатков, требует дополнительных разработок. Здесь, чтобы аргумент не попал в нежелательную область, надо обходиться программными средствами.
- Теперь хотелось бы услышать о новых программируемых микрокалькуляторах.
- Новый программируемый микрокалькулятор "Электроника МК-61" конструктивно выполнен в однотипном с "МК-54" корпусе. У нового микрокалькулятора "Электроника "МК-52", также программируемого,- горизонтальная компоновка, размеры корпуса несколько больше, чем у "МК-54".
- Какова система команд, принятая для новых моделей? Если она принципиально нова, то пользователям придется перерабатывать программное обеспечение, накопленное для прежних моделей.
- Эти соображения учитывались при разработке "Электроники МК-61" и "Электроники МК-52". Было решено взять за основу систему команд "Электроники Б3-34", "МК-54", "МК-56" и расширять ее. Так, помимо всех возможностей, предоставляемых "Электроникой Б3-34" и ее аналогами, микрокалькулятор марки "МК-61" позволяет выделять целую или дробную часть числа, определять знак числа и его абсолютную величину, определять максимальное из двух произвольных чисел, выполнять над двумя двоичными числами поразрядные логические операции "и", "или", "не", "исключающее или". Каждая из этих операций выполняется одной командой. Время, заданное в часах, минутах и секундах, можно будет выразить в часах и десятичных долях часа; угол, выраженный в градусах, минутах и секундах,- перевести в градусы и десятичные доли градуса. Предусмотрен и обратный перевод соответствующих величин. Общее число автоматически выполняемых операций достигло таким образом 65. Есть в новом калькуляторе и датчик псевдослучайных чисел.
В меньшей степени учтены в этой модели пожелания увеличить объем программной памяти и количество регистров. Появился лишь один дополнительный регистр РЕ, пятнадцатый по счету. На семь шагов, то есть до 105, расширилась программная память. Впрочем, об эффективном расширении памяти нельзя судить лишь по этой семерке. То, что раньше требовало нескольких команд, сейчас выполняется в одно действие. В среднем программа, которая займет в "МК-61" все 105 шагов программной памяти и 15 регистров, по своим возможностям будет эквивалентна примерно 140-150 шагам и 18 регистрам программы, написанной в системе команд "Б3-34".
Таковы же соответствующие характеристики микрокалькулятора "Электроника МК-52", выпуск которого ожидается уже в этом году.
- А быстродействие? Увеличилось ли оно у новых микрокалькуляторов по сравнению со старыми?
- В целом на существенное повышение быстродействия рассчитывать пока не приходится. Ограничения накладывают и малые объемы памяти и скромные ресурсы первичных источников питания - батареек. Еще одна причина: те схемы, на основе которых строятся микрокалькуляторы в настоящее время, обладают очень высокой помехоустойчивостью. Это существенное достижение разработчиков, поскольку даже в домашних условиях микровычислительной технике приходится испытывать на себе воздействие значительных помех от радиостанции и всевозможных электроприборов. С этой точки зрения применяемые в "МК-54", "БЗ-34", "МК-56" и в "МК-61", "МК-52" схемы - вне конкуренции. Обратной стороной медали является невысокое быстродействие. Тем не менее расширенная система команд двух последних моделей микрокалькуляторов в некоторой мере обеспечивает относительное увеличение быстродействия. В дальнейшем предполагается существенное (может быть, в 100 раз) увеличение скорости вычислений, однако это окажется возможным лишь при переходе к новой технологии изготовления электронных схем.
Кстати, не следует забывать, что программируемый
микрокалькулятор - принципиально диалоговая система и, как всякая диалоговая система, значительное время работает в режиме ожидания, где быстродействие не имеет значения и экономически невыгодно.
- Осталось поговорить о дополнительных ресурсах программной памяти новых микрокалькуляторов. Посмотрим, что предлагают читатели. Увеличить общий объем программной памяти до 200-400 шагов. Сделать так, чтобы введенная в калькулятор программа не стиралась при отключении питания. Встроить в микрокалькулятор программы для статистических или экономических расчетов. Облегчить повторный ввод программ с помощью, например, магнитных карточек. Обеспечить возможность подключения микрокалькулятора к бытовому магнитофону как библиотеке программ и к телевизору как дисплею.
- Два последних пожелания следует скорее относить к персональным ЭВМ. Остальные успешно учтены в программируемом микрокалькуляторе "Электроника МК-52". Особенность этой модели - наличие встроенного полупостоянного запоминающего устройства (ППЗУ), которое в отличие от оперативного запоминающего устройства (ОЗУ) способно длительно (не менее 5000 часов) хранить информацию при отключении или отказе основного источника питания. Емкость ППЗУ - 512 шагов. Говоря иначе, таково число команд, способных там разместиться. В любой момент из него можно считать в ОЗУ микрокалькулятора одну из ранее записанных программ. Записывать их в ППЗУ можно, начиная с произвольного адреса. Возможна и пакетная обработка информации, то есть режим, когда результаты вычислений по одной программе, помещенные в регистрах данных, используются как исходные данные для других программ.
На одном торце микрокалькулятора размещаются электрические контакты - разъемы для подключения постоянных запоминающих устройств (ПЗУ) большой емкости. Они будут выпускаться в виде этаких пластмассовых коробочек - модулей с ответной частью разъема. В каждой такой коробочке разместится множество программ - например, по статистике. Модуль программируется раз навсегда на предприятии-изготовителе, причем в каждом сможет уместиться около ста программ различной сложности. Каждый пользователь будет приобретать модули с тем набором программ, которые ему нужны. Из модулей можно будет создавать тематические или универсальные библиотеки программ.
Возможность подключения к бытовому магнитофону и телевизору будет реализована в разрабатываемом сейчас микрокалькуляторе "Электроника МК-72". Эта модель по своим возможностям может быть отнесена к портативным персональным микрокомпьютерам.

Программируемый микрокалькулятор "Электроника Б3-34".
[ МАЛЕНЬКИЕ ХИТРОСТИ
Бывает, что две подпрограммы имеют одинаковые окончания, но разные начала или середины. В таком случае можно использовать команду безусловного перехода с одной подпрограммы на другую. Команда В/О всегда обеспечит возврат на верное место.
В.КОВАЛЕНКО (г.Подольск) ]
С МИКРОКАЛЬКУЛЯТОРОМ НА РЫНОК
Когда на рынке много товаров, сделать покупку не просто. У разных продавцов товары сильно различаются по качеству и цене. Качество мы оцениваем по нескольким признакам - размеру, сочности) чистоте и так далее, причем каждый оцениваем по сравнению с другими, зачастую иначе, нежели продавец. Поэтому наша оценка товара и цена, назначенная продавцом, могут не совпадать.
Как выбрать товар получше и подешевле? Предположим, мы выбираем яблоки и оцениваем их по размеру и сочности. Разложим цену товара на составляющие, зависящие от этих признаков, плюс еще одна, от качества не зависящая,- скажем, расходы на транспортировку и хранение. Примем ради простоты, что каждая из первых двух составляющих прямо пропорциональна уровню соответствующего качественного признака, причем коэффициент пропорциональности зависит от другого признака и тоже линейно:
Ц(x,y)=А+(В+by)x+(C+cx)y=А+Вх+Су+Dxy,
где x,y - уровни качественных признаков. Цены, назначаемые продавцами за товары разного качества, помогут нам определить коэффициенты А, В, С, D. Тогда, оценивая яблоки каждого отдельного продавца по их качественным признакам x и y, мы будем рассчитывать цену товара по формуле и сравнивать с назначенной продавцом. Яблоки мы купим у того, чья цена наиболее отступает вниз от рассчитанной нами: в этом случае за удовлетворяющее нас качество мы заплатим самую низкую цену.
Как же отыскать коэффициенты формулы? Можно методом наименьших квадратов (2/85), номы поступим иначе, проще. Выберем товары, отличающиеся предельными значениями уровней качественных признаков, оцениваемых, допустим, по пятибалльной шкале:

Под таблицей помещены определения величин, которые нужно ввести в указанные регистры перед запуском программы. Вот сама программа; она решает (адреса 07-31) систему линейных уравнений, которая получается после подстановки нормированных центрированных чисел x в формулу, затем (адреса 32-69) решения пересчитываются в соответствии с исходными ненормированными значениями качественных признаков.
00. 4 01. П0 02. С/П 03. КП^ 04. F() 05. FL0 06. 03 07. + 08. + 09. + 10. 1 11. 4 12.П0 13. F() 14. ПП 15. 90 16. ИП2 17. + 18. ИП3 19. ПП 20. 87 21. ИП3 22. + 23. ИП2 24. ПП
25. 87 26. ИП1 27. + 28. ИП3 29. ИП2 30. ПП
31. 88 32. ИПД 33. ИП7 34. ИП9 35. / 36. ИПС 37. * 38. ИПВ 39. + 40. ИПА 41. ИП7 42. * 43. - 44. ИП9 45. * 46. - 47. П2 48. ИПС 49. ИПА 50. ИП9 51. * 52. - 53. ИП6 54. / 55. П3 56. ИПВ 57. ИПА 58. ИП7 59. * 60. - 61. ИП8 62. / 63. П4 64. ИПА 65. ИП6 66. / 67. ИП8 68. / 69. П5 70. С/П 71. ^ 72. ИП4 73. * 74. F() 75. * 76. ИП5 77. * 78. x-y 79. ИП3 80. * 81. + 82. + 83. ИП2 84. + 85. БП 86. 70 87. ИП1 88. + 89. - 90. 4 91. / 92. КП0 93. ИП4 94. В/О.
Набираем на клавиатуре В/О С/П Ц(1.1) ^ Ц(5.1) ^ Ц(l.5) ^ Ц(5.5) Ц(5,5), С/П. Для расчета цены по заданным признакам x и y набираем после останова x ^ y С/П. После непродолжительной: счета (адреса 70-86) считываем с индикатора цену.
Допустим, нас устраивает качество яблок у двух продавцов. Оба запрашивают 1.30 рубля за килограмм, но яблоки первого мы оценили по качеству в 4 и 3 балла, второго - 3 н 4 балла. Формула дает для яблок первого продавца 1.35руб/кг, для яблок второго - 1.23руб/кг. Яблоки первого следует предпочесть яблокам второго, поскольку первый недооценил свои яблоки на 0.05руб/кг, второй же переоценил на 0.07руб/кг.
Теперь отвлечемся от рыночной ситуации и обратим внимание на следующее. Сложную и неизвестную нам функцию нескольких аргументов мы заменили полиномом, в определенных точках получили опытные значения функции, рассчитали довольно просто коэффициенты полинома, а затем использовали формулу для требуемых целей. Такой подход к экспериментальным исследованиям - проведение опытов при определенных сочетаниях значений измеряемых величин, описание неизвестной функции полиномом, перевод размерных значений аргументов в нормированные центрированные - позволяет сократить число опытов и упростить обработку наблюдений. Основа такого подхода - математическая теория планирования эксперимента. Ею-то мы и воспользовались, выбирая яблоки. Как мы при этом убедились, предписываемые теорией расчеты даже в довольно сложных случаях можно выполнить на микрокалькуляторе. Как это делается с помощью теории - предмет особого разговора.
Б.ХОДОВ (г.Москва)
[ Дополняем список литературы, опубликованный в 6/84.
Алимов В.И. Вычисления на микрокалькуляторе "Электроника Б3-21". Томск, изд-во Томского политехнического института, 1981.
Андреев Н.А., Герштсйн Г.Б. Инструкции по применению микрокалькулятора "Электроника Б3-21" в клинической кардиологии. Рига, изд-во Рижского медицинского института, 1978.
Варламов Р.Г. Эксплуатация и ремонт современных микрокалькуляторов. М.. "Легкая и пищевая промышленность", 1983.
Воробьев С.А.. Шваров Ю.В. Программы для обработки геохимических данных на микрокалькуляторах. М., "Финансы и статистика", 1984.
Дьяконов В.П. Расчет нелинейных и импульсных устройств на программируемых микрокалькуляторах, М., "Радио и связь", 1984.
Кузнецов Б.Ю. и др. Микрокалькуляторы: технические и конструктивные характеристики ("Массовая библиотека инженера", вып.40). М., "Радио и связь", 1984.
Поснов Н.Н., Поснова М. Ф. Микрокалькуляторы "Электроника Б3" в учебной лаборатории. Минск, изд-во БГУ. 1981.
Романовский Т.Б. Микрокалькуляторы в рассказах и играх, Рига, "Зинатне", 1984.
Славин Г.В. Программирование на программируемых микрокалькуляторах типа "Электроника Б3-34". Таллин, "Валгус", 1984.
Трохименко Я.К., Любич Ф.Д. Искусство программирования программируемых микрокалькуляторов (серия статей). "Известия вузов. Радиоэлектроника", 1983, #7 и далее.
Трохимеико Я.К., Любич Ф.Д. Инженерные расчеты на программируемых микрокалькуляторах. Киев, "Техника", 1985.
Францевич Л.И. Обработка результатов биологических экспериментов на микро-ЭВМ "Б3-21". Киев, "Наукова думка", 1979.
Цветков А.Н., Епанечников В.А. Прикладные программы для микроЭВМ "Электроника БЗ-34", "Электроника МК-54", "Электроника МК-56". М., "Финансы и статистика", 1984.
Цимринг Ш.Б. Специальные функции. Программы для микрокалькулятора "Электроника Б3-21". М., "Радио и связь", 1983 ]
МЕТОД СЕКУЩИХ
Итерационные методы решения уравнений (см. выпуски рубрики в 2 и 12/84 год) продолжают оставаться темой многих читательских писем. Профессор Г.И.НАТАНСОН (г.Ленинград) посвящает свое выступление методу секущих.
Чтобы решить уравнение f(х)=0, часто поступают так. Находят значения функции в каких-нибудь двух точках x0 и x1, затем проводят прямую через точки плоскости (x0, f(x0)) и (x1, f(x1)). Абсциссу x2 точки пересечения этой прямой с горизонтальной осью координат считают приближенным решением уравнения. Обычно начальные точки x0 и x1 выбирают так, чтобы значения функции f(x0) и f(x1) имели разные знаки. Тогда для непрерывной функции обязательно найдется хотя бы один корень уравнения между x0 и x1 (обозначим его х*). На втором шаге берут точку х2 н ту из точек х0, x1, в которой значение функции противоположно по знаку f(x2). Процесс продолжают, пока не достигнут требуемой точности.

Таков метод хорд. Скорость сходимости у него невелика. Чтобы ее повысить, на каждом шаге берут две последние точки, х[n-1] и х[n]. Этот метод и называется методом секущих. Вот его расчетная формула:

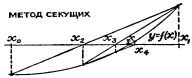
В подавляющем большинстве случаев метод обеспечивает сходимость и не ведет к зацикливанию (относительно условий сходимости см. А.М.Островский. "Решение уравнений и систем уравнений". М., 1963). Более того, если хn достаточно близко к х*, то на каждом следующем шаге достигнутое число верных знаков увеличивается примерно в а раз, где а=(1+sqr(5))/2= 1.618... Например, получив 2 верных знака, через 3 шага будем иметь 2*l.618**3 ~ 8 верных знаков - то есть все, что может дать микрокалькулятор.
Начальные значения x0 и x1 могут находиться по одну сторону от корня х*. и чем они ближе к нему, тем быстрее сойдется процесс.
При заданной точности е счет надо прекращать по достижении неравенства |х*-xn|<е. Но х* нам неизвестно (иначе зачем считать!). Поэтому неравенство заменяют: |хn-х[n-1]|<е. В предлагаемой ниже программе счет продолжается, пока калькулятор перестанет различать x[n-1] и хn или, что почти то же самое, f(xn) и f(х[n-1]). Величина f(xn)-f(x[n-1]) фигурирует в качестве делителя, и в случае обращения ее в нуль калькулятор остановится.
Интересно сравнить метод секущих с методом Ньютона (12/84), в котором считают по формуле x[n+1]=xn-f(xn)/f'(xn). Известно, что каждый достаточно далекий шаг метода Ньютона удваивает число верных знаков. Но для осуществления этого шага надо вычислять два значения: f(xn) и f'(xn) - Таким образом, на одно значение в методе Ньютона приходится увеличение числа верных знаков в sqr(2)=1.414 раз, что меньше числа 1.618, даваемого методом секущих. Это замечание относится и к тому варианту метода Ньютона, в котором производная f'(xn) заменяется на (f(хn+D)-f(xn))/D: скорость сходимости здесь не больше, а на каждом шаге также вычисляются два значения: f(xn) и f(хn+D).
Программа, реализующая метод секущих на "Электронике Б3-34" выглядит так:
00. П8 01. ПП 02. 18 03. ИП9 04. ИП7 05. ИП8 06. - 07. F() 08. - 09. x-y 10. П9 11. / 12. / 13. ИП8 14. П7 15. + 16. БП 17. 00.
Подпрограмма вычисления функции размещается, начиная с адреса 18. Аргумент x берется из регистров X и С, результат размещается в регистре X.
После ввода программы и перехода в автоматический режим надо очистить Р9 (заслать туда 0), набрать x1 и заслать в Р7, набрать х0 и нажать клавиши В/О, С/П. Когда калькулятор остановится, на индикаторе загорится ERROR. Это значит, что произошло деление на 0 из-за того, что f(xn-1)=f(xn) или f(xn)=0. Найденное решение хn находится в Р8, a f(xn) - в Р9.
Для иллюстрации решим уравнение (см. 2/84):
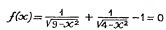
Подпрограмма, вычисляющая f(x) здесь может быть, например, такой: 18. Fx2 19. 4 20. x-y 21. - 22. 9 23. FBx 24. - 25. Fsqr 26. F1/x 27. x-y 28. Fsqr 29. F1/x 30. + 31. 1 32. - 33. В/О.
Взяв х0 = 1, x1 = 1.5 через 1 минуту 10 секунд получим хn=1.2311858, f(xn)=0. Калькулятор сделает для этого 7 итераций (то есть n=6). При х0=0 и x1=1, а также при х0=1.6 и х1=1.9 (начальные значения по одну сторону от корня) тот же ответ получается за 9 итераций. В таблице показано, сколько требуется итераций для достижения той же точности другими методами.

* См. 2 и 12/84, начальное приближение - единица.
[ ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
Он будет посвящен вычислению определенных интегралов на микрокалькуляторе "Электроника Б3-34". Просим читателей присылать свои соображения на эту тему, программы, полезные советы по работе с ними и т.п. Просим также сообщать при этом о своем согласии или несогласии на публикацию в журнале своих адресов (домашних, служебных или до востребования) ]
[ ВНИМАНИЕ, ЮМОРИСТЫ!
Ждем от вас юмористические рисунки без слов и юмористические рассказы (объем - не более машинописной страницы) на темы из вычислительного дела ]
УЗОРЫ ПРЕДЛАГАЕТ МИКРОКАЛЬКУЛЯТОР
Как часто любительницы вышивания стоят перед проблемой выбора узоров! Наверное, многие из них с завистью вспоминают про детский калейдоскоп: богатство появляющихся в нем орнаментов поистине неисчерпаемо! И в то же время они строго симметричны, потому что получаются многократным отражением в зеркалах той картинки, которая складывается из цветных стеклышек в центральном поле. Но эти узоры так трудно зарисовать! Малейшее движение - и только что сложившаяся картинка заменилась новой.
Дело может поправить электронный калейдоскоп-программа, по которой "Электроника Б3-34" предлагает узоры в виде, наиболее удобном для вышивания.
Правда, микрокалькулятор дает лишь рисунок центрального поля. В роли зеркал будем выступать мы сами. Мы должны будем научиться этой интересной работе. Цвета будем обозначать цифрами, причем пустое место (пробел) также обозначает некоторый цвет и используется для наглядности всей картины. Итак, берем основной элемент - прямоугольник размером 8 на 4.

Если на вертикальную штрих-пунктирную линию поставить зеркало, то вместе с самим элементом и его отражением мы увидим картину, как на рисунке ниже. С полученным прямоугольником проделаем точно такое же отражение, но уже вверх, и получим картину, как на рисунке правее.
Количество цветов (до восьми) выбираем мы сами, помня, что истинная красота проста. Лучшие результаты получаются при выборе от двух до четырех цветов. По окончании работы программы из регистра P1 читаются и записываются 8 цифр первой строки основного элемента, из Р2 - второй, из Р3 - третьей, из Р4 - четвертой строки.
В программе работает датчик случайных чисел ak (адреса 31-42; a[k+1]={11ak+пи}). Он требует ввода начального случайного числа a0. Для этой цели удобно использовать комбинацию таких трех чисел: дата, час и минута ввода программы. Например, сейчас 15 июля (месяц не играет роли), 18 часов 38 минут. В калькулятор вводим: 15 ^ 18 ^ 38. Сформировав первую строку чисел, программа определенным образом переставляет ее числа и тем самым составляет вторую, третью и четвертую строки.
Количество получаемых узоров весьма велико: для двух цветов - 256, для четырех - более 65000, для шести - более полутора миллионов. Правда, если заказан орнамент с шестью или более цветами, то все они могут не быть использованы в одной картине. Тогда нажмите на клавишу С/П - и калькулятор выдаст новый орнамент.
Замена цифр цветами - дело вашего творчества. Время работы программы - примерно 2 минуты 20 секунд. Появление во всех строках одних лишь единиц показывает, что в регистр Р6 не было занесено требуемое число цветов.
00. + 01. / 02. П9 О3. Сх 04. П1 05. П2 06. П3 07. П4 08. ПП 09. 24 10. 4 11. П0 12. КИП^ 13. ВП 14. 4 15. КП^ 16. FL0 17. 12 18. ПП 19. 24 20. 1 21. С/П 22. БП 23. 03 24. 4 25. П0 26. 9 27. П5 28. 1 29. 0 30. П8 31. ИП9 32. 1 33. 1 34. * 35. Fпи 36. + 37. П9 38. КИП9 39. x-y 40. ИП9 41. - 42. П9 43. ИП6 44. * 45. 1 46. + 47. КП5 48. FL0 49. 31. 50. КИПА 51. КИПВ 52. КИПС 53. КИПD 54. 5 55. П0 56. ИПВ 57. ИПС 58. ИПD 59. ИПА 60. ПП 61. 78 62. ИПС 63. ИПD 64. ИПА 65. ИПВ 66. ПП 67. 78 68. ИПD 69. ИПС 70. ИПВ 71. ИПА 72. ПП 73. 78 74. ИПС 75. ИПВ 76. ИПА 77. ИПD 78. П7 79. F() 80. ИП8 81. * 82. + 83. ИП8 84. * 85. + 86. ИП8 87. * 88. ИП7 89. + 90. КИП0 91. + 92. КП^ 93. В/О.
Введя программу, заносим в Р6 требуемое число цветов, набираем на клавиатуре В/О дату ^ час ^ минуты С/П. После останова берем из Р1-Р4 строки основного элемента. Для получения нового орнамента нажимаем С/П, предварительно занеся, если это нужно, новое число цветов в Р6.
Надеемся, что программа, предложенная "Человеком с микрокалькулятором", сослужит добрую службу "для тех, кто вяжет".
С.ГЕТА (г.Таллин)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Работа любого аккумулятора сопровождается выделением газа. Не составляет исключения и аккумулятор для "Электроники-Б3-34" Д-0, 55C-VI.I. На его кольцевом уплотнении под воздействием газа со временем образуется белый налет. Поскольку он проводит ток, аккумулятор саморазряжается, его приходится заряжать все чаще, он раньше выходит из строя.
Избавиться от этого легко. Достаточно нанести на кольцевое уплотнение тонкий слой технического вазелина. Теперь выделяющийся газ не будет иметь контакта с металлом, не появится и налет. В качестве защитной смазки годятся еще солидол, литол, фиол, ЦИАТИМ и т.п. А вот эпоксидный и другие клеи использовать недопустимо: газ станет скапливаться в аккумуляторе и выведет его из строя.
Перед тем, как наносить защитную смазку, поверхность аккумулятора необходимо зачистить. Если аккумулятор новый, то достаточно воспользоваться стирательной резинкой. Старый аккумулятор протирают кусочком ткани, кольцевое уплотнение прочищают спичкой или подходящей по размеру щепкой (но не металлическим предметом: возможно короткое замыкание). Непосредственно перед тем, как наносить защитную смазку, следует зачистить резинкой всю поверхность аккумулятора.
Б.АЛЕКСЕЕВ, В.СТОЛЯРОВ (г.Москва) ]
ЧЕЛОВЕК С МИКРОКАЛЬКУЛЯТОРОМ
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Многие читатели спрашивают, какие новые микрокалькуляторы будут выпускаться в нашей стране в ближайшее время. Корреспондент журнала "Наука и жизнь" Л.БОЙКО побывал в научно-производственном объединении "Кристалл" (г.Киев) и задал этот вопрос сотрудникам объединения Л.ЖИЖКО, Ю.ПОЛЬСКОМУ, Н.РОМАШКО, А.ШЕРЕВЕНЕ. Речь шла не только о разработке будущих, но и совершенствовании старых моделей программируемых микрокалькуляторов.

Новые программируемые микрокалькуляторы "Электроника МК-52" и "Электроника МК-61".
ДВЕ НОВЫЕ МАРКИ: "МК-61" и "МК-52"
- Прежде чем говорить о новых марках программируемых микрокалькуляторов, хотелось бы уделить внимание старым. Вот, к примеру, "Электроника МК-54". Репутация у этого калькулятора неплохая, однако среди благодарных отзывов о нем встречаются н критические замечания о недостатках, обнаруживаемых при работе с ним. Например, из-за ненадежной работы кнопки "переключатель питания" микрокалькулятор может самопроизвольно отключаться.
- Замечание справедливое. Такие критические отзывы очень ценны разработчикам микрокалькуляторов, поскольку позволяют быстрее выявить огрехи и устранить их в последующих партиях изделия. Что касается злополучной кнопки, то в микрокалькуляторы новых выпусков устанавливается унифицированный переключатель, обладающий повышенной надежностью.
- Есть претензии к вычислению логарифмической функции на "Электронике Б3-34". Например, читатель В.Богатко из Ленинграда отмечает, что последовательность команд 1. ИП1 2. ИП2 3. Fln 4. / 5. С/П при единице в регистре Р1 и z в регистре Р2, где exp(-1)<z<l, вызывает в "Электронике Б3-34" сигнал ошибки при работе в автоматическом режиме.
- Этот дефект был обнаружен вскоре после того, как начался выпуск названного калькулятора. Сейчас он устранен и в "Электронике Б3-34" и в ее аналогах марок "МК-54" и "МК-56". В интегральные микросхемы, которые у всех трех калькуляторов одни и те же, внесены необходимые изменения. Для калькуляторов прежних выпусков в таких случаях рекомендуется последовательность команд 1. ИП2 2. Fln 3. ИП1 4. / 5. F1/x 6. С/П.
Исправлена команда FxY, вызывавшая много нареканий. Владельцам микрокалькуляторов прежних выпусков лучше пользоваться вместо нее цепочкой команд Fln Fexp.
К ошибкам приводил программный фрагмент вида 1. Fx2 2. /-/ 3. С/П, например, когда х=1e-40 набрано с клавиатуры. Тем читателям, чьи калькуляторы в таком случае дают неверный результат 1e40, рекомендуется дополнить фрагмент командой ^ непосредственно перед командой Fx2.
- Микрокалькуляторы марок "Б3-34", "МК-54", "МК-56" страдают еще таким недостатком: выполнение операций Fexp при х<-230.26 и F10X при х<-100 вместо машинного нуля дает аварийный останов.
- Ликвидация этого дефекта труднее, чем устранение названных до этого недостатков, требует дополнительных разработок. Здесь, чтобы аргумент не попал в нежелательную область, надо обходиться программными средствами.
- Теперь хотелось бы услышать о новых программируемых микрокалькуляторах.
- Новый программируемый микрокалькулятор "Электроника МК-61" конструктивно выполнен в однотипном с "МК-54" корпусе. У нового микрокалькулятора "Электроника "МК-52", также программируемого,- горизонтальная компоновка, размеры корпуса несколько больше, чем у "МК-54".
- Какова система команд, принятая для новых моделей? Если она принципиально нова, то пользователям придется перерабатывать программное обеспечение, накопленное для прежних моделей.
- Эти соображения учитывались при разработке "Электроники МК-61" и "Электроники МК-52". Было решено взять за основу систему команд "Электроники Б3-34", "МК-54", "МК-56" и расширять ее. Так, помимо всех возможностей, предоставляемых "Электроникой Б3-34" и ее аналогами, микрокалькулятор марки "МК-61" позволяет выделять целую или дробную часть числа, определять знак числа и его абсолютную величину, определять максимальное из двух произвольных чисел, выполнять над двумя двоичными числами поразрядные логические операции "и", "или", "не", "исключающее или". Каждая из этих операций выполняется одной командой. Время, заданное в часах, минутах и секундах, можно будет выразить в часах и десятичных долях часа; угол, выраженный в градусах, минутах и секундах,- перевести в градусы и десятичные доли градуса. Предусмотрен и обратный перевод соответствующих величин. Общее число автоматически выполняемых операций достигло таким образом 65. Есть в новом калькуляторе и датчик псевдослучайных чисел.
В меньшей степени учтены в этой модели пожелания увеличить объем программной памяти и количество регистров. Появился лишь один дополнительный регистр РЕ, пятнадцатый по счету. На семь шагов, то есть до 105, расширилась программная память. Впрочем, об эффективном расширении памяти нельзя судить лишь по этой семерке. То, что раньше требовало нескольких команд, сейчас выполняется в одно действие. В среднем программа, которая займет в "МК-61" все 105 шагов программной памяти и 15 регистров, по своим возможностям будет эквивалентна примерно 140-150 шагам и 18 регистрам программы, написанной в системе команд "Б3-34".
Таковы же соответствующие характеристики микрокалькулятора "Электроника МК-52", выпуск которого ожидается уже в этом году.
- А быстродействие? Увеличилось ли оно у новых микрокалькуляторов по сравнению со старыми?
- В целом на существенное повышение быстродействия рассчитывать пока не приходится. Ограничения накладывают и малые объемы памяти и скромные ресурсы первичных источников питания - батареек. Еще одна причина: те схемы, на основе которых строятся микрокалькуляторы в настоящее время, обладают очень высокой помехоустойчивостью. Это существенное достижение разработчиков, поскольку даже в домашних условиях микровычислительной технике приходится испытывать на себе воздействие значительных помех от радиостанции и всевозможных электроприборов. С этой точки зрения применяемые в "МК-54", "БЗ-34", "МК-56" и в "МК-61", "МК-52" схемы - вне конкуренции. Обратной стороной медали является невысокое быстродействие. Тем не менее расширенная система команд двух последних моделей микрокалькуляторов в некоторой мере обеспечивает относительное увеличение быстродействия. В дальнейшем предполагается существенное (может быть, в 100 раз) увеличение скорости вычислений, однако это окажется возможным лишь при переходе к новой технологии изготовления электронных схем.
Кстати, не следует забывать, что программируемый
микрокалькулятор - принципиально диалоговая система и, как всякая диалоговая система, значительное время работает в режиме ожидания, где быстродействие не имеет значения и экономически невыгодно.
- Осталось поговорить о дополнительных ресурсах программной памяти новых микрокалькуляторов. Посмотрим, что предлагают читатели. Увеличить общий объем программной памяти до 200-400 шагов. Сделать так, чтобы введенная в калькулятор программа не стиралась при отключении питания. Встроить в микрокалькулятор программы для статистических или экономических расчетов. Облегчить повторный ввод программ с помощью, например, магнитных карточек. Обеспечить возможность подключения микрокалькулятора к бытовому магнитофону как библиотеке программ и к телевизору как дисплею.
- Два последних пожелания следует скорее относить к персональным ЭВМ. Остальные успешно учтены в программируемом микрокалькуляторе "Электроника МК-52". Особенность этой модели - наличие встроенного полупостоянного запоминающего устройства (ППЗУ), которое в отличие от оперативного запоминающего устройства (ОЗУ) способно длительно (не менее 5000 часов) хранить информацию при отключении или отказе основного источника питания. Емкость ППЗУ - 512 шагов. Говоря иначе, таково число команд, способных там разместиться. В любой момент из него можно считать в ОЗУ микрокалькулятора одну из ранее записанных программ. Записывать их в ППЗУ можно, начиная с произвольного адреса. Возможна и пакетная обработка информации, то есть режим, когда результаты вычислений по одной программе, помещенные в регистрах данных, используются как исходные данные для других программ.
На одном торце микрокалькулятора размещаются электрические контакты - разъемы для подключения постоянных запоминающих устройств (ПЗУ) большой емкости. Они будут выпускаться в виде этаких пластмассовых коробочек - модулей с ответной частью разъема. В каждой такой коробочке разместится множество программ - например, по статистике. Модуль программируется раз навсегда на предприятии-изготовителе, причем в каждом сможет уместиться около ста программ различной сложности. Каждый пользователь будет приобретать модули с тем набором программ, которые ему нужны. Из модулей можно будет создавать тематические или универсальные библиотеки программ.
Возможность подключения к бытовому магнитофону и телевизору будет реализована в разрабатываемом сейчас микрокалькуляторе "Электроника МК-72". Эта модель по своим возможностям может быть отнесена к портативным персональным микрокомпьютерам.

Программируемый микрокалькулятор "Электроника Б3-34".
[ МАЛЕНЬКИЕ ХИТРОСТИ
Бывает, что две подпрограммы имеют одинаковые окончания, но разные начала или середины. В таком случае можно использовать команду безусловного перехода с одной подпрограммы на другую. Команда В/О всегда обеспечит возврат на верное место.
В.КОВАЛЕНКО (г.Подольск) ]
С МИКРОКАЛЬКУЛЯТОРОМ НА РЫНОК
Когда на рынке много товаров, сделать покупку не просто. У разных продавцов товары сильно различаются по качеству и цене. Качество мы оцениваем по нескольким признакам - размеру, сочности) чистоте и так далее, причем каждый оцениваем по сравнению с другими, зачастую иначе, нежели продавец. Поэтому наша оценка товара и цена, назначенная продавцом, могут не совпадать.
Как выбрать товар получше и подешевле? Предположим, мы выбираем яблоки и оцениваем их по размеру и сочности. Разложим цену товара на составляющие, зависящие от этих признаков, плюс еще одна, от качества не зависящая,- скажем, расходы на транспортировку и хранение. Примем ради простоты, что каждая из первых двух составляющих прямо пропорциональна уровню соответствующего качественного признака, причем коэффициент пропорциональности зависит от другого признака и тоже линейно:
Ц(x,y)=А+(В+by)x+(C+cx)y=А+Вх+Су+Dxy,
где x,y - уровни качественных признаков. Цены, назначаемые продавцами за товары разного качества, помогут нам определить коэффициенты А, В, С, D. Тогда, оценивая яблоки каждого отдельного продавца по их качественным признакам x и y, мы будем рассчитывать цену товара по формуле и сравнивать с назначенной продавцом. Яблоки мы купим у того, чья цена наиболее отступает вниз от рассчитанной нами: в этом случае за удовлетворяющее нас качество мы заплатим самую низкую цену.
Как же отыскать коэффициенты формулы? Можно методом наименьших квадратов (2/85), номы поступим иначе, проще. Выберем товары, отличающиеся предельными значениями уровней качественных признаков, оцениваемых, допустим, по пятибалльной шкале:

Под таблицей помещены определения величин, которые нужно ввести в указанные регистры перед запуском программы. Вот сама программа; она решает (адреса 07-31) систему линейных уравнений, которая получается после подстановки нормированных центрированных чисел x в формулу, затем (адреса 32-69) решения пересчитываются в соответствии с исходными ненормированными значениями качественных признаков.
00. 4 01. П0 02. С/П 03. КП^ 04. F() 05. FL0 06. 03 07. + 08. + 09. + 10. 1 11. 4 12.П0 13. F() 14. ПП 15. 90 16. ИП2 17. + 18. ИП3 19. ПП 20. 87 21. ИП3 22. + 23. ИП2 24. ПП
25. 87 26. ИП1 27. + 28. ИП3 29. ИП2 30. ПП
31. 88 32. ИПД 33. ИП7 34. ИП9 35. / 36. ИПС 37. * 38. ИПВ 39. + 40. ИПА 41. ИП7 42. * 43. - 44. ИП9 45. * 46. - 47. П2 48. ИПС 49. ИПА 50. ИП9 51. * 52. - 53. ИП6 54. / 55. П3 56. ИПВ 57. ИПА 58. ИП7 59. * 60. - 61. ИП8 62. / 63. П4 64. ИПА 65. ИП6 66. / 67. ИП8 68. / 69. П5 70. С/П 71. ^ 72. ИП4 73. * 74. F() 75. * 76. ИП5 77. * 78. x-y 79. ИП3 80. * 81. + 82. + 83. ИП2 84. + 85. БП 86. 70 87. ИП1 88. + 89. - 90. 4 91. / 92. КП0 93. ИП4 94. В/О.
Набираем на клавиатуре В/О С/П Ц(1.1) ^ Ц(5.1) ^ Ц(l.5) ^ Ц(5.5) Ц(5,5), С/П. Для расчета цены по заданным признакам x и y набираем после останова x ^ y С/П. После непродолжительной: счета (адреса 70-86) считываем с индикатора цену.
Допустим, нас устраивает качество яблок у двух продавцов. Оба запрашивают 1.30 рубля за килограмм, но яблоки первого мы оценили по качеству в 4 и 3 балла, второго - 3 н 4 балла. Формула дает для яблок первого продавца 1.35руб/кг, для яблок второго - 1.23руб/кг. Яблоки первого следует предпочесть яблокам второго, поскольку первый недооценил свои яблоки на 0.05руб/кг, второй же переоценил на 0.07руб/кг.
Теперь отвлечемся от рыночной ситуации и обратим внимание на следующее. Сложную и неизвестную нам функцию нескольких аргументов мы заменили полиномом, в определенных точках получили опытные значения функции, рассчитали довольно просто коэффициенты полинома, а затем использовали формулу для требуемых целей. Такой подход к экспериментальным исследованиям - проведение опытов при определенных сочетаниях значений измеряемых величин, описание неизвестной функции полиномом, перевод размерных значений аргументов в нормированные центрированные - позволяет сократить число опытов и упростить обработку наблюдений. Основа такого подхода - математическая теория планирования эксперимента. Ею-то мы и воспользовались, выбирая яблоки. Как мы при этом убедились, предписываемые теорией расчеты даже в довольно сложных случаях можно выполнить на микрокалькуляторе. Как это делается с помощью теории - предмет особого разговора.
Б.ХОДОВ (г.Москва)
[ Дополняем список литературы, опубликованный в 6/84.
Алимов В.И. Вычисления на микрокалькуляторе "Электроника Б3-21". Томск, изд-во Томского политехнического института, 1981.
Андреев Н.А., Герштсйн Г.Б. Инструкции по применению микрокалькулятора "Электроника Б3-21" в клинической кардиологии. Рига, изд-во Рижского медицинского института, 1978.
Варламов Р.Г. Эксплуатация и ремонт современных микрокалькуляторов. М.. "Легкая и пищевая промышленность", 1983.
Воробьев С.А.. Шваров Ю.В. Программы для обработки геохимических данных на микрокалькуляторах. М., "Финансы и статистика", 1984.
Дьяконов В.П. Расчет нелинейных и импульсных устройств на программируемых микрокалькуляторах, М., "Радио и связь", 1984.
Кузнецов Б.Ю. и др. Микрокалькуляторы: технические и конструктивные характеристики ("Массовая библиотека инженера", вып.40). М., "Радио и связь", 1984.
Поснов Н.Н., Поснова М. Ф. Микрокалькуляторы "Электроника Б3" в учебной лаборатории. Минск, изд-во БГУ. 1981.
Романовский Т.Б. Микрокалькуляторы в рассказах и играх, Рига, "Зинатне", 1984.
Славин Г.В. Программирование на программируемых микрокалькуляторах типа "Электроника Б3-34". Таллин, "Валгус", 1984.
Трохименко Я.К., Любич Ф.Д. Искусство программирования программируемых микрокалькуляторов (серия статей). "Известия вузов. Радиоэлектроника", 1983, #7 и далее.
Трохимеико Я.К., Любич Ф.Д. Инженерные расчеты на программируемых микрокалькуляторах. Киев, "Техника", 1985.
Францевич Л.И. Обработка результатов биологических экспериментов на микро-ЭВМ "Б3-21". Киев, "Наукова думка", 1979.
Цветков А.Н., Епанечников В.А. Прикладные программы для микроЭВМ "Электроника БЗ-34", "Электроника МК-54", "Электроника МК-56". М., "Финансы и статистика", 1984.
Цимринг Ш.Б. Специальные функции. Программы для микрокалькулятора "Электроника Б3-21". М., "Радио и связь", 1983 ]
МЕТОД СЕКУЩИХ
Итерационные методы решения уравнений (см. выпуски рубрики в 2 и 12/84 год) продолжают оставаться темой многих читательских писем. Профессор Г.И.НАТАНСОН (г.Ленинград) посвящает свое выступление методу секущих.
Чтобы решить уравнение f(х)=0, часто поступают так. Находят значения функции в каких-нибудь двух точках x0 и x1, затем проводят прямую через точки плоскости (x0, f(x0)) и (x1, f(x1)). Абсциссу x2 точки пересечения этой прямой с горизонтальной осью координат считают приближенным решением уравнения. Обычно начальные точки x0 и x1 выбирают так, чтобы значения функции f(x0) и f(x1) имели разные знаки. Тогда для непрерывной функции обязательно найдется хотя бы один корень уравнения между x0 и x1 (обозначим его х*). На втором шаге берут точку х2 н ту из точек х0, x1, в которой значение функции противоположно по знаку f(x2). Процесс продолжают, пока не достигнут требуемой точности.

Таков метод хорд. Скорость сходимости у него невелика. Чтобы ее повысить, на каждом шаге берут две последние точки, х[n-1] и х[n]. Этот метод и называется методом секущих. Вот его расчетная формула:


В подавляющем большинстве случаев метод обеспечивает сходимость и не ведет к зацикливанию (относительно условий сходимости см. А.М.Островский. "Решение уравнений и систем уравнений". М., 1963). Более того, если хn достаточно близко к х*, то на каждом следующем шаге достигнутое число верных знаков увеличивается примерно в а раз, где а=(1+sqr(5))/2= 1.618... Например, получив 2 верных знака, через 3 шага будем иметь 2*l.618**3 ~ 8 верных знаков - то есть все, что может дать микрокалькулятор.
Начальные значения x0 и x1 могут находиться по одну сторону от корня х*. и чем они ближе к нему, тем быстрее сойдется процесс.
При заданной точности е счет надо прекращать по достижении неравенства |х*-xn|<е. Но х* нам неизвестно (иначе зачем считать!). Поэтому неравенство заменяют: |хn-х[n-1]|<е. В предлагаемой ниже программе счет продолжается, пока калькулятор перестанет различать x[n-1] и хn или, что почти то же самое, f(xn) и f(х[n-1]). Величина f(xn)-f(x[n-1]) фигурирует в качестве делителя, и в случае обращения ее в нуль калькулятор остановится.
Интересно сравнить метод секущих с методом Ньютона (12/84), в котором считают по формуле x[n+1]=xn-f(xn)/f'(xn). Известно, что каждый достаточно далекий шаг метода Ньютона удваивает число верных знаков. Но для осуществления этого шага надо вычислять два значения: f(xn) и f'(xn) - Таким образом, на одно значение в методе Ньютона приходится увеличение числа верных знаков в sqr(2)=1.414 раз, что меньше числа 1.618, даваемого методом секущих. Это замечание относится и к тому варианту метода Ньютона, в котором производная f'(xn) заменяется на (f(хn+D)-f(xn))/D: скорость сходимости здесь не больше, а на каждом шаге также вычисляются два значения: f(xn) и f(хn+D).
Программа, реализующая метод секущих на "Электронике Б3-34" выглядит так:
00. П8 01. ПП 02. 18 03. ИП9 04. ИП7 05. ИП8 06. - 07. F() 08. - 09. x-y 10. П9 11. / 12. / 13. ИП8 14. П7 15. + 16. БП 17. 00.
Подпрограмма вычисления функции размещается, начиная с адреса 18. Аргумент x берется из регистров X и С, результат размещается в регистре X.
После ввода программы и перехода в автоматический режим надо очистить Р9 (заслать туда 0), набрать x1 и заслать в Р7, набрать х0 и нажать клавиши В/О, С/П. Когда калькулятор остановится, на индикаторе загорится ERROR. Это значит, что произошло деление на 0 из-за того, что f(xn-1)=f(xn) или f(xn)=0. Найденное решение хn находится в Р8, a f(xn) - в Р9.
Для иллюстрации решим уравнение (см. 2/84):
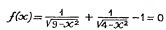
Подпрограмма, вычисляющая f(x) здесь может быть, например, такой: 18. Fx2 19. 4 20. x-y 21. - 22. 9 23. FBx 24. - 25. Fsqr 26. F1/x 27. x-y 28. Fsqr 29. F1/x 30. + 31. 1 32. - 33. В/О.
Взяв х0 = 1, x1 = 1.5 через 1 минуту 10 секунд получим хn=1.2311858, f(xn)=0. Калькулятор сделает для этого 7 итераций (то есть n=6). При х0=0 и x1=1, а также при х0=1.6 и х1=1.9 (начальные значения по одну сторону от корня) тот же ответ получается за 9 итераций. В таблице показано, сколько требуется итераций для достижения той же точности другими методами.

* См. 2 и 12/84, начальное приближение - единица.
[ ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
Он будет посвящен вычислению определенных интегралов на микрокалькуляторе "Электроника Б3-34". Просим читателей присылать свои соображения на эту тему, программы, полезные советы по работе с ними и т.п. Просим также сообщать при этом о своем согласии или несогласии на публикацию в журнале своих адресов (домашних, служебных или до востребования) ]
[ ВНИМАНИЕ, ЮМОРИСТЫ!
Ждем от вас юмористические рисунки без слов и юмористические рассказы (объем - не более машинописной страницы) на темы из вычислительного дела ]
УЗОРЫ ПРЕДЛАГАЕТ МИКРОКАЛЬКУЛЯТОР
Как часто любительницы вышивания стоят перед проблемой выбора узоров! Наверное, многие из них с завистью вспоминают про детский калейдоскоп: богатство появляющихся в нем орнаментов поистине неисчерпаемо! И в то же время они строго симметричны, потому что получаются многократным отражением в зеркалах той картинки, которая складывается из цветных стеклышек в центральном поле. Но эти узоры так трудно зарисовать! Малейшее движение - и только что сложившаяся картинка заменилась новой.
Дело может поправить электронный калейдоскоп-программа, по которой "Электроника Б3-34" предлагает узоры в виде, наиболее удобном для вышивания.
Правда, микрокалькулятор дает лишь рисунок центрального поля. В роли зеркал будем выступать мы сами. Мы должны будем научиться этой интересной работе. Цвета будем обозначать цифрами, причем пустое место (пробел) также обозначает некоторый цвет и используется для наглядности всей картины. Итак, берем основной элемент - прямоугольник размером 8 на 4.

Если на вертикальную штрих-пунктирную линию поставить зеркало, то вместе с самим элементом и его отражением мы увидим картину, как на рисунке ниже. С полученным прямоугольником проделаем точно такое же отражение, но уже вверх, и получим картину, как на рисунке правее.
Количество цветов (до восьми) выбираем мы сами, помня, что истинная красота проста. Лучшие результаты получаются при выборе от двух до четырех цветов. По окончании работы программы из регистра P1 читаются и записываются 8 цифр первой строки основного элемента, из Р2 - второй, из Р3 - третьей, из Р4 - четвертой строки.
В программе работает датчик случайных чисел ak (адреса 31-42; a[k+1]={11ak+пи}). Он требует ввода начального случайного числа a0. Для этой цели удобно использовать комбинацию таких трех чисел: дата, час и минута ввода программы. Например, сейчас 15 июля (месяц не играет роли), 18 часов 38 минут. В калькулятор вводим: 15 ^ 18 ^ 38. Сформировав первую строку чисел, программа определенным образом переставляет ее числа и тем самым составляет вторую, третью и четвертую строки.
Количество получаемых узоров весьма велико: для двух цветов - 256, для четырех - более 65000, для шести - более полутора миллионов. Правда, если заказан орнамент с шестью или более цветами, то все они могут не быть использованы в одной картине. Тогда нажмите на клавишу С/П - и калькулятор выдаст новый орнамент.
Замена цифр цветами - дело вашего творчества. Время работы программы - примерно 2 минуты 20 секунд. Появление во всех строках одних лишь единиц показывает, что в регистр Р6 не было занесено требуемое число цветов.
00. + 01. / 02. П9 О3. Сх 04. П1 05. П2 06. П3 07. П4 08. ПП 09. 24 10. 4 11. П0 12. КИП^ 13. ВП 14. 4 15. КП^ 16. FL0 17. 12 18. ПП 19. 24 20. 1 21. С/П 22. БП 23. 03 24. 4 25. П0 26. 9 27. П5 28. 1 29. 0 30. П8 31. ИП9 32. 1 33. 1 34. * 35. Fпи 36. + 37. П9 38. КИП9 39. x-y 40. ИП9 41. - 42. П9 43. ИП6 44. * 45. 1 46. + 47. КП5 48. FL0 49. 31. 50. КИПА 51. КИПВ 52. КИПС 53. КИПD 54. 5 55. П0 56. ИПВ 57. ИПС 58. ИПD 59. ИПА 60. ПП 61. 78 62. ИПС 63. ИПD 64. ИПА 65. ИПВ 66. ПП 67. 78 68. ИПD 69. ИПС 70. ИПВ 71. ИПА 72. ПП 73. 78 74. ИПС 75. ИПВ 76. ИПА 77. ИПD 78. П7 79. F() 80. ИП8 81. * 82. + 83. ИП8 84. * 85. + 86. ИП8 87. * 88. ИП7 89. + 90. КИП0 91. + 92. КП^ 93. В/О.
Введя программу, заносим в Р6 требуемое число цветов, набираем на клавиатуре В/О дату ^ час ^ минуты С/П. После останова берем из Р1-Р4 строки основного элемента. Для получения нового орнамента нажимаем С/П, предварительно занеся, если это нужно, новое число цветов в Р6.
Надеемся, что программа, предложенная "Человеком с микрокалькулятором", сослужит добрую службу "для тех, кто вяжет".
С.ГЕТА (г.Таллин)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Работа любого аккумулятора сопровождается выделением газа. Не составляет исключения и аккумулятор для "Электроники-Б3-34" Д-0, 55C-VI.I. На его кольцевом уплотнении под воздействием газа со временем образуется белый налет. Поскольку он проводит ток, аккумулятор саморазряжается, его приходится заряжать все чаще, он раньше выходит из строя.
Избавиться от этого легко. Достаточно нанести на кольцевое уплотнение тонкий слой технического вазелина. Теперь выделяющийся газ не будет иметь контакта с металлом, не появится и налет. В качестве защитной смазки годятся еще солидол, литол, фиол, ЦИАТИМ и т.п. А вот эпоксидный и другие клеи использовать недопустимо: газ станет скапливаться в аккумуляторе и выведет его из строя.
Перед тем, как наносить защитную смазку, поверхность аккумулятора необходимо зачистить. Если аккумулятор новый, то достаточно воспользоваться стирательной резинкой. Старый аккумулятор протирают кусочком ткани, кольцевое уплотнение прочищают спичкой или подходящей по размеру щепкой (но не металлическим предметом: возможно короткое замыкание). Непосредственно перед тем, как наносить защитную смазку, следует зачистить резинкой всю поверхность аккумулятора.
Б.АЛЕКСЕЕВ, В.СТОЛЯРОВ (г.Москва) ]

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Попутно. Сказав "обратная польская запись", мы говорим "Стек!". (Правда, мы говорим "Стек!" и говоря "рекурсия", но - шепотом). О стеке -  ТЕМА #31
ТЕМА #31 .
.
7/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ВТОРОЕ, на котором читатель составит несколько небольших программ, в процессе их составления освоит почти все команды "Электроники Б3-34", познакомится со стеком и порядком передвижения чисел по его регистрам, узнает ряд важных понятий: "цикл", "подпрограмма", "модификация адреса" и т.д.
Занятие ведет кандидат технических наук И.К.ВЯЗОВСКИЙ (Московский физико-технический институт)
Команд, о которых говорилось на прошлом занятии, достаточно, чтобы приняться за составление какой-нибудь несложной программы. Например, такой, по которой калькулятор вычислит площадь круга с диаметром D.
Формула для площади круга хорошо известна: S=пи*D2/4. Необходимые для расчета числа пи и 4 имеются в калькуляторе, и их можно будет вызвать по ходу вычислений. Величину D надо ввести в регистр X заранее. Пусть, например, она равна 3.
Нажата клавиша 3, н то же число - на индикаторе, а значит, и в регистре X.
Если вести расчет по формуле вручную, то для этого, очевидно, далее надо нажать такие клавиши:

На индикаторе читаем результат: 7.0685832.
Те же клавиши и в той же последовательности нужно будет нажать, когда мы станем вводить в калькулятор программу для вычисления площади круга. В таком естественном порядке, воспроизводящем ход расчетов вручную, в калькулятор вводится любая программа для прямых вычислений по формулам, включающим выполнимые на нем математические операции. В этом заключается значительное удобство.
Программа не может располагаться в калькуляторе иначе, как в виде отдельных команд, каждая из которых занимает свою ячейку программной памяти (а некоторые команды - даже две ячейки). Всего таких ячеек 98. Им присвоены номера, называемые адресами,- от 00 до 97.
Чтобы ввести программу в калькулятор, надо перевести его в состояние, называемое режимом программирования. Делается это нажатием двух клавиш:

Тотчас же в правом углу индикатора загорится 00. Это значит, что счетчик адресов установлен на нулевую отметку и команда, которую мы сейчас введем, займет адрес 00.
Ввод каждой новой команды станет увеличивать на единицу содержимое счетчика адресов, отображаемое в правом углу индикатора.
Нажимаем клавишу F. На индикаторе ничего не изменилось. Нажимаем клавишу х2. В левом углу загорается 22. Это код операции возведения в квадрат. Его появление на индикаторе означает, что команда занесена в программную память. Одновременно сменилось число в правом углу: сейчас там горит 01. По такому адресу разместится следующая введенная нами команда.

Нажимаем еще раз клавишу F, и вновь это не вызывает никаких перемен на индикаторе: клавиша F самостоятельного значения не имеет и образует команду лишь тогда, когда вслед за ней нажата еще одна клавиша.
Нажимаем клавишу пи. Код 22 сдвинулся вправо, а на его месте появилось число 20 - код засылки числа пи в регистр X. В правом углу - 02. По этому адресу разместится следующая команда, "умножить". Нажав соответствующую клавишу, замечаем: в левом углу оба кода разом сместились вправо, а на освободившемся месте загорелся код операции умножения: 12.
Три кода горят в левой стороне индикатора. Ввод каждой новой команды теперь будет приводить к тому, что левый и средний из этой тройки кодов сместятся на одну позицию вправо, стирая правый, а на освобождаемом ими месте появится код только что введенной операции. В правом же углу при этом загорится адрес, который будет занят командой, введенной вслед.
Вот как это происходит, когда мы вводим команды, по которым заканчивается вычисление площади круга:

В ячейки памяти калькулятора программа записывается как последовательность кодов операций.
Когда калькулятор выполнит первую команду введенной в него программы, содержимое счетчика адресов автоматически увеличится на единицу, и калькулятор приступит к выполнению второй команды; выполнив ее, перейдет к следующей... По исполнении команды, дающей окончательный результат вычислений, машину нужно остановить. Для этого в программе ставится команда С/П.
Нажав на клавишу с таким обозначением, завершаем ввод нашей программы. Текст ее запишем, указывая перед каждой командой ее адрес с точкой между ними:
00. Fх2 01. Fпи 02. * 03. 4 04. / 05. С/П.
У клавиши С/П два назначения. Одно из них мы уже выяснили: если нажать ее в режиме программирования, то в программе появится команда останова. Чтобы познакомиться с другим назначением клавиши, вернем калькулятор в состояние, в котором он был сразу после включения.
Это состояние мы будем называть режимом вычислений. Находясь в нем, калькулятор либо выполняет отдельные команды, отдаваемые ему нажатием клавиш (режим ручных вычислений), либо автоматически вычисляет по имеющейся в его памяти программе (автоматический режим). Запуск калькулятора на автоматический счет и производится клавишей С/П. Отсюда ее обозначение, расшифровываемое как "Стоп/ Пуск".
Чтобы вернуть калькулятор в режим вычислений из режима программирования, надо нажать клавиши:

Калькулятор готов к работе по программе. Но прежде чем запускать его, надо еще сообщить ему, с какой команды он должен начать вычисления.
Начальная команда введенной нами программы располагается по адресу 00. Калькулятор снабжен клавишей В/0, по сигналу которой счетчик адресов в режиме ручных вычислений возвращается на нулевую отметку - как говорят программисты, управление передается на адрес 00. Отсюда и обозначение В/0 ("Возврат на 0").
(Это не единственное назначение клавиши В/0 - в свое время мы познакомимся и с другими).
Итак, установим счетчик адресов на отметку 00. Введем в регистр X диаметр круга (пусть он по-прежнему равен трем). Запускаем калькулятор клавишей С/П - и он за несколько секунд выполнит одну за другой все команды нашей крохотной программы. На индикаторе - площадь круга с диаметром 3, уже известная нам: 7.0685832.
Подсчитав на калькуляторе площадь круга вручную и по программе, иной читатель может разочарованно подумать, что никаких выгод по сравнению с ручным счетом программирование нам не принесло. Чтобы ввести программу, потребовалось нажать не только те же восемь клавиш, что и при работе вручную, но еще и семь "лишних": F и ПРГ, чтобы перейти в режим программирования; С/П, чтобы калькулятор знал, где остановиться; F и АВТ, чтобы вернуться в режим вычислений; В/0 и С/П, чтобы запустить программу на счет.
15 нажатий против 8. Конечно, такое сопоставление не в пользу программирования, если речь идет о единичном расчете по заданной формуле. Но представьте, что вам нужно определить площадь нескольких кругов - скажем, с целочисленными диаметрами от 1 до 20 включительно. При ручном счете для этого потребуется нажать на клавиши 171 раз. А при счете по программе - всего 83 раза. В самом деле, 15 нажатий уйдет на то, чтобы получить первый результат. Но для получения каждого следующего нужно лишь после очередного останова вводить новое значение диаметра (одно нажатие, если число однозначное, два - если двузначное) и запускать программу на новый счет клавишами В/0 и С/П. Программа, записанная в память калькулятора, сохраняется неизменной, покуда он не выключен. Для нового использования ее не нужно вводить заново.
83 против 171 - в таком сопоставлении выигрыш от программных расчетов налицо.
Он заметен тем отчетливее, чем больше программа и чем чаще приходится проводить по ней повторяющиеся вычисления. Так оно бывает, например, при составлении таблиц. А методы последовательных приближений, столь характерные для вычислительной математики? В них каждое приближение выполняется одной и той же последовательностью команд.
Большие программы отличаются еще и тем, что в вычислениях по ним, как правило, используется много исходных данных (а не одно-единственное число, как в нашем учебном примере с площадью круга). Хранят их в так называемых адресуемых регистрах памяти, обозначаемых цифрами (от 0 до 9) и буквами (А, В, С, D). Нетрудно подсчитать, что всего их 14.
Числа направляются на хранение в эти регистры командами засылки. Перед выполнением такой команды засылаемое в память число сначала должно оказаться в регистре X (в результате набора на клавиатуре, вызова или выполнения какой-либо операции), и уже оттуда оно направляется в адресуемый регистр. Извлечь число из адресуемого регистра можно командой вызова; при этом оно направляется опять-таки в регистр X.
Команда засылки выполняется с помощью клавиши П (от слова "Память"), команда вызова - с помощью клавиши ИП ("Из Памяти").
Освоим обе команды сначала в ручном исполнении. Наберем на клавиатуре какое-нибудь число - например, 3. Оно тотчас появляется на индикаторе и, стало быть, находится сейчас в регистре X.
Допустим, мы хотим поместить его в регистр 4. Нажимаем клавишу П и затем - клавишу 4. Число на индикаторе мигнуло: теперь оно и в регистре X и в регистре 4. То, что было раньше в регистре 4, пропадает.
Очистим регистр X, нажав клавишу Сх. На индикаторе - нуль. Затем нажимаем клавиши ИП и 4. На индикаторе - снова 3: число переписано из регистра 4. Но и там оио не пропало: в этом можно убедиться, вторично очистив индикатор и нажав клавиши ИП 4.
Опробуем теперь те же операции в программном варианте. Предположим, что в некоторой большой программе по ходу расчета потребовалось вычислить площадь круга. Его диаметр берется из регистра 4 (напомним, что мы уже поместили туда число три), а найденная площадь засылается в регистр 5. Допустим, что цепочка команд, выполняющих этот расчет, должна размещаться в программе, начиная с адреса 60.
Устанавливаем счетчик адресов на нужный адрес в режиме ручных вычислений с помощью клавиши БП ("Безусловный Переход"). Нажимаем сначала ее, а потом набираем на клавиатуре 60. Это число будет гореть в правом углу индикатора, когда нажатием клавиш F ПРГ мы переведем калькулятор в режим программирования. Именно по 60-му адресу запишется команда, которую мы введем первой.
Ею, очевидно, диаметр круга должен вызываться из регистра 4 в регистр X. Речь, стало быть, идет о команде ИП4.
Нажимаем клавишу ИП. На индикаторе - никаких перемен. Нажимаем клавишу 4. В левом углу загорается 64. Это код операции вызова в регистр X содержимого регистра 4. То, что он загорелся лишь после нажатия второй клавиши, свидетельствует: клавиша ИП самостоятельного значения не имеет и образует команду вызова лишь в сочетании с другой клавишей, обозначающей номер регистра, содержимое которого вызывается в регистр X.
Вводим далее команды, по которым определяется площадь круга. Затем нажимаем клавиши П и 5: ими в программу вводится команда засылки результата в регистр 5. Наблюдая в это время за индикатором, можно убедиться, что клавиша П также не имеет самостоятельного значения и образует команду засылки в сочетании с нажимаемой далее клавишей, цифровой или буквенной.
Завершим ввод нажатием клавиши С/П. Вот текст введенной нами программы:
60. ИП4 61. Fx2 62. Fпи 63. * 64. 4 65. / 66. П5 67. С/П.
Клавишами F АВТ возвращаем калькулятор в режим вычислений. Клавишами БП 60 устанавливаем счетчик адресов на 60-й адрес. Клавишей С/П запускаем программу. Через несколько мгновений вычисления заканчиваются и на индикаторе загорается знакомое нам число 7.0685832. Нажав клавиши ИП5, можно убедиться, что оно размещается в регистре 5. А заодно и в том, что в момент останова по команде С/П в регистре X находится результат выполнения предыдущей команды.
Выгоды от программирования мы могли оценить уже на примере, где требовалось провести многократные однотипные расчеты при меняющихся исходных данных. Такие задачи на практике встречаются нередко. Но при этом часто требуется не только получить ряд результатов, но и подвергнуть их статистической обработке - например, вычислить их среднее арифметическое.
Предположим, что подобным требованием дополнена наша задача о вычислении площади кругов с целочисленными диаметрами от 1 до 10: в довершение расчетов нужно определить среднюю площадь. Программу придется расширить: вычислив площадь очередного круга, следует прибавить ее к сумме площадей; попутно надо подсчитывать количество кругов, а когда все они будут перебраны, полученную сумму нужно будет поделить на это количество.
Обе эти величины можно шаг за шагом накапливать в адресуемых регистрах: скажем, количество кругов - в нулевом, сумму их площадей - в первом. Получив по составленной нами программе площадь очередного круга в регистре X, можно вызвать туда из регистра 1 накопленную на этот момент сумму площадей. Содержимое регистра X при этом сдвинется в регистр Y. Затем остается выполнить сложение - так к сумме площадей прибавится новое слагаемое. Результат сложения, как мы знаем, получится в регистре X. Оттуда его нужно отослать в регистр 1. Подобным же образом, вызвав содержимое регистра 0, затем единицу и сложив оба числа, получим пополнившееся количество кругов и отошлем его обратно в регистр 0.
К этой цепочке команд надо приписать еще команду останова и команду возврата на нулевой адрес. Когда счет остановится по первой из них, надо ввести в калькулятор диаметр нового круга и нажать клавишу С/П. Программа перейдет к следующей команде, совершит по ней возврат на адрес 00 и проведет расчет для нового круга.
Чтобы рассчитать среднее арифметическое, надо приписать к нашей программе еще четыре команды: вызов содержимого регистра 1 (сумма площадей), вызов содержимого регистра 0 (количество кругов), деление (оно даст интересующую нас среднюю площадь) и останов (на индикаторе будет светиться результат предыдущей операции, то есть ответ на поставленную задачу). На первую из этих команд мы передадим управление с помощью клавиши БП, когда переберем все круги, и после останова считаем искомый ответ с индикатора.
Это описание нетрудно перевести на язык команд. Но прежде надо решить, как организовать возврат на нулевой адрес. Дело в том, что команда В/0 передает управление на первый адрес только в режиме ручных вычислений. Стало быть, вместо нее в программе придется использовать команду безусловного перехода - ту самую, которую мы уже исполняли недавно с помощью клавиши БП.
У этой команды - своя тонкость. Когда мы станем вводить ее в программу (забегая вперед, скажем, что счетчик адресов к этому моменту будет показывать 16) и нажмем клавишу БП, содержимое счетчика адресов тотчас же увеличится на единицу: 17. Когда же мы наберем адрес перехода, содержимое счетчика адресов увеличится еще раз: 18. Это означает, что команда безусловного перехода - "двойная", то есть занимает в программе два адреса. В первом из них записывается операция безусловного перехода БП, во втором - адрес перехода.
Отказавшись от команды В/0, мы свободны в выборе этого адреса. Учтем, что перед запуском программы следует очистить регистры 0 и 1, предназначенные для накопления сумм. Очистку можно произвести вручную, нажав клавиши Сх П0 П1. Но лучше, чтобы это сделал калькулятор, и вызов из памяти, притом с самого начала: 00. Сх 01. П0 02. П1 03. С/П.
Команда останова здесь не лишняя, да и в дальнейшем пригодится: на нее-то мы и станем передавать управление, вычислив площадь очередного круга, и покуда калькулятор стоит, будем вводить диаметр следующего круга.
С учетом высказанных соображений программа примет такой вид:
00. Сх 01. П0 02. П1 03. С/П 04. Fx2 05. Fпи 06. * 07. 4 08. / 09. ИП1 10. * 11. П1 12. ИП0 13. 1 14. + 15. П0 16. БП 17. 03 18. ИП1 19. ИП0 20. / 21. С/П.
Программа получилась объемистая - будем внимательны при ее вводе. Введя, нажмем клавиши В/0, С/П. Очистив за три первые команды регистры 0 и 1, калькулятор остановится. Введем диаметр первого круга, единицу, запустим программу, после останова введем диаметр второго круга, двойку, запустим программу вновь... и так будем продолжать, пока не будет вычислена площадь последнего круга, чей диаметр равен десяти. Передадим управление на адрес 18 и вскоре после нового пуска получим на индикаторе искомую среднюю площадь кругов. 30.237829.
Тот, кто знакомится с программированием на наших занятиях, вряд ли представит себе, что ответ на поставленную нами задачу можно получить по более короткой программе. Между тем программисты не зря говорят: всякую программу можно сократить по крайней мере на одну команду. Сейчас мы докажем это на примере нашей задачи. Правда, для этого нам придется освоить несколько новых команд.
Когда на прошлом занятии, поговорив об одноместных операциях, мы перешли к рассмотрению двуместных, мы сразу отметили, что для их выполнения необходимы два операционных регистра - X и Y. Мы узнали, как с помощью клавиши ^ в них вводятся участники арифметических действий и где размещается результат.
Ради простоты мы умолчали тогда, что перемещение чисел охватывает при этом не только регистры X и У, но также Z и Т. Эти четыре регистра находятся в тесной взаимосвязи и объединяются названием стек (английское слово, означающее "охапка, стопка"). К ним примыкает регистр X1, куда после выполнения многих операций направляется прежнее содержимое регистра X.
То, что мы узнали на прошлом занятии, дополним здесь до завершенной картины всевозможных перемещений чисел по стеку.
...
 ТЕМА #31
ТЕМА #31 .
. 7/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ВТОРОЕ, на котором читатель составит несколько небольших программ, в процессе их составления освоит почти все команды "Электроники Б3-34", познакомится со стеком и порядком передвижения чисел по его регистрам, узнает ряд важных понятий: "цикл", "подпрограмма", "модификация адреса" и т.д.
Занятие ведет кандидат технических наук И.К.ВЯЗОВСКИЙ (Московский физико-технический институт)
Команд, о которых говорилось на прошлом занятии, достаточно, чтобы приняться за составление какой-нибудь несложной программы. Например, такой, по которой калькулятор вычислит площадь круга с диаметром D.
Формула для площади круга хорошо известна: S=пи*D2/4. Необходимые для расчета числа пи и 4 имеются в калькуляторе, и их можно будет вызвать по ходу вычислений. Величину D надо ввести в регистр X заранее. Пусть, например, она равна 3.
Нажата клавиша 3, н то же число - на индикаторе, а значит, и в регистре X.
Если вести расчет по формуле вручную, то для этого, очевидно, далее надо нажать такие клавиши:

На индикаторе читаем результат: 7.0685832.
Те же клавиши и в той же последовательности нужно будет нажать, когда мы станем вводить в калькулятор программу для вычисления площади круга. В таком естественном порядке, воспроизводящем ход расчетов вручную, в калькулятор вводится любая программа для прямых вычислений по формулам, включающим выполнимые на нем математические операции. В этом заключается значительное удобство.
Программа не может располагаться в калькуляторе иначе, как в виде отдельных команд, каждая из которых занимает свою ячейку программной памяти (а некоторые команды - даже две ячейки). Всего таких ячеек 98. Им присвоены номера, называемые адресами,- от 00 до 97.
Чтобы ввести программу в калькулятор, надо перевести его в состояние, называемое режимом программирования. Делается это нажатием двух клавиш:

Тотчас же в правом углу индикатора загорится 00. Это значит, что счетчик адресов установлен на нулевую отметку и команда, которую мы сейчас введем, займет адрес 00.
Ввод каждой новой команды станет увеличивать на единицу содержимое счетчика адресов, отображаемое в правом углу индикатора.
Нажимаем клавишу F. На индикаторе ничего не изменилось. Нажимаем клавишу х2. В левом углу загорается 22. Это код операции возведения в квадрат. Его появление на индикаторе означает, что команда занесена в программную память. Одновременно сменилось число в правом углу: сейчас там горит 01. По такому адресу разместится следующая введенная нами команда.

Нажимаем еще раз клавишу F, и вновь это не вызывает никаких перемен на индикаторе: клавиша F самостоятельного значения не имеет и образует команду лишь тогда, когда вслед за ней нажата еще одна клавиша.
Нажимаем клавишу пи. Код 22 сдвинулся вправо, а на его месте появилось число 20 - код засылки числа пи в регистр X. В правом углу - 02. По этому адресу разместится следующая команда, "умножить". Нажав соответствующую клавишу, замечаем: в левом углу оба кода разом сместились вправо, а на освободившемся месте загорелся код операции умножения: 12.
Три кода горят в левой стороне индикатора. Ввод каждой новой команды теперь будет приводить к тому, что левый и средний из этой тройки кодов сместятся на одну позицию вправо, стирая правый, а на освобождаемом ими месте появится код только что введенной операции. В правом же углу при этом загорится адрес, который будет занят командой, введенной вслед.
Вот как это происходит, когда мы вводим команды, по которым заканчивается вычисление площади круга:

В ячейки памяти калькулятора программа записывается как последовательность кодов операций.
Когда калькулятор выполнит первую команду введенной в него программы, содержимое счетчика адресов автоматически увеличится на единицу, и калькулятор приступит к выполнению второй команды; выполнив ее, перейдет к следующей... По исполнении команды, дающей окончательный результат вычислений, машину нужно остановить. Для этого в программе ставится команда С/П.
Нажав на клавишу с таким обозначением, завершаем ввод нашей программы. Текст ее запишем, указывая перед каждой командой ее адрес с точкой между ними:
00. Fх2 01. Fпи 02. * 03. 4 04. / 05. С/П.
У клавиши С/П два назначения. Одно из них мы уже выяснили: если нажать ее в режиме программирования, то в программе появится команда останова. Чтобы познакомиться с другим назначением клавиши, вернем калькулятор в состояние, в котором он был сразу после включения.
Это состояние мы будем называть режимом вычислений. Находясь в нем, калькулятор либо выполняет отдельные команды, отдаваемые ему нажатием клавиш (режим ручных вычислений), либо автоматически вычисляет по имеющейся в его памяти программе (автоматический режим). Запуск калькулятора на автоматический счет и производится клавишей С/П. Отсюда ее обозначение, расшифровываемое как "Стоп/ Пуск".
Чтобы вернуть калькулятор в режим вычислений из режима программирования, надо нажать клавиши:

Калькулятор готов к работе по программе. Но прежде чем запускать его, надо еще сообщить ему, с какой команды он должен начать вычисления.
Начальная команда введенной нами программы располагается по адресу 00. Калькулятор снабжен клавишей В/0, по сигналу которой счетчик адресов в режиме ручных вычислений возвращается на нулевую отметку - как говорят программисты, управление передается на адрес 00. Отсюда и обозначение В/0 ("Возврат на 0").
(Это не единственное назначение клавиши В/0 - в свое время мы познакомимся и с другими).
Итак, установим счетчик адресов на отметку 00. Введем в регистр X диаметр круга (пусть он по-прежнему равен трем). Запускаем калькулятор клавишей С/П - и он за несколько секунд выполнит одну за другой все команды нашей крохотной программы. На индикаторе - площадь круга с диаметром 3, уже известная нам: 7.0685832.
Подсчитав на калькуляторе площадь круга вручную и по программе, иной читатель может разочарованно подумать, что никаких выгод по сравнению с ручным счетом программирование нам не принесло. Чтобы ввести программу, потребовалось нажать не только те же восемь клавиш, что и при работе вручную, но еще и семь "лишних": F и ПРГ, чтобы перейти в режим программирования; С/П, чтобы калькулятор знал, где остановиться; F и АВТ, чтобы вернуться в режим вычислений; В/0 и С/П, чтобы запустить программу на счет.
15 нажатий против 8. Конечно, такое сопоставление не в пользу программирования, если речь идет о единичном расчете по заданной формуле. Но представьте, что вам нужно определить площадь нескольких кругов - скажем, с целочисленными диаметрами от 1 до 20 включительно. При ручном счете для этого потребуется нажать на клавиши 171 раз. А при счете по программе - всего 83 раза. В самом деле, 15 нажатий уйдет на то, чтобы получить первый результат. Но для получения каждого следующего нужно лишь после очередного останова вводить новое значение диаметра (одно нажатие, если число однозначное, два - если двузначное) и запускать программу на новый счет клавишами В/0 и С/П. Программа, записанная в память калькулятора, сохраняется неизменной, покуда он не выключен. Для нового использования ее не нужно вводить заново.
83 против 171 - в таком сопоставлении выигрыш от программных расчетов налицо.
Он заметен тем отчетливее, чем больше программа и чем чаще приходится проводить по ней повторяющиеся вычисления. Так оно бывает, например, при составлении таблиц. А методы последовательных приближений, столь характерные для вычислительной математики? В них каждое приближение выполняется одной и той же последовательностью команд.
Большие программы отличаются еще и тем, что в вычислениях по ним, как правило, используется много исходных данных (а не одно-единственное число, как в нашем учебном примере с площадью круга). Хранят их в так называемых адресуемых регистрах памяти, обозначаемых цифрами (от 0 до 9) и буквами (А, В, С, D). Нетрудно подсчитать, что всего их 14.
Числа направляются на хранение в эти регистры командами засылки. Перед выполнением такой команды засылаемое в память число сначала должно оказаться в регистре X (в результате набора на клавиатуре, вызова или выполнения какой-либо операции), и уже оттуда оно направляется в адресуемый регистр. Извлечь число из адресуемого регистра можно командой вызова; при этом оно направляется опять-таки в регистр X.
Команда засылки выполняется с помощью клавиши П (от слова "Память"), команда вызова - с помощью клавиши ИП ("Из Памяти").
Освоим обе команды сначала в ручном исполнении. Наберем на клавиатуре какое-нибудь число - например, 3. Оно тотчас появляется на индикаторе и, стало быть, находится сейчас в регистре X.
Допустим, мы хотим поместить его в регистр 4. Нажимаем клавишу П и затем - клавишу 4. Число на индикаторе мигнуло: теперь оно и в регистре X и в регистре 4. То, что было раньше в регистре 4, пропадает.
Очистим регистр X, нажав клавишу Сх. На индикаторе - нуль. Затем нажимаем клавиши ИП и 4. На индикаторе - снова 3: число переписано из регистра 4. Но и там оио не пропало: в этом можно убедиться, вторично очистив индикатор и нажав клавиши ИП 4.
Опробуем теперь те же операции в программном варианте. Предположим, что в некоторой большой программе по ходу расчета потребовалось вычислить площадь круга. Его диаметр берется из регистра 4 (напомним, что мы уже поместили туда число три), а найденная площадь засылается в регистр 5. Допустим, что цепочка команд, выполняющих этот расчет, должна размещаться в программе, начиная с адреса 60.
Устанавливаем счетчик адресов на нужный адрес в режиме ручных вычислений с помощью клавиши БП ("Безусловный Переход"). Нажимаем сначала ее, а потом набираем на клавиатуре 60. Это число будет гореть в правом углу индикатора, когда нажатием клавиш F ПРГ мы переведем калькулятор в режим программирования. Именно по 60-му адресу запишется команда, которую мы введем первой.
Ею, очевидно, диаметр круга должен вызываться из регистра 4 в регистр X. Речь, стало быть, идет о команде ИП4.
Нажимаем клавишу ИП. На индикаторе - никаких перемен. Нажимаем клавишу 4. В левом углу загорается 64. Это код операции вызова в регистр X содержимого регистра 4. То, что он загорелся лишь после нажатия второй клавиши, свидетельствует: клавиша ИП самостоятельного значения не имеет и образует команду вызова лишь в сочетании с другой клавишей, обозначающей номер регистра, содержимое которого вызывается в регистр X.
Вводим далее команды, по которым определяется площадь круга. Затем нажимаем клавиши П и 5: ими в программу вводится команда засылки результата в регистр 5. Наблюдая в это время за индикатором, можно убедиться, что клавиша П также не имеет самостоятельного значения и образует команду засылки в сочетании с нажимаемой далее клавишей, цифровой или буквенной.
Завершим ввод нажатием клавиши С/П. Вот текст введенной нами программы:
60. ИП4 61. Fx2 62. Fпи 63. * 64. 4 65. / 66. П5 67. С/П.
Клавишами F АВТ возвращаем калькулятор в режим вычислений. Клавишами БП 60 устанавливаем счетчик адресов на 60-й адрес. Клавишей С/П запускаем программу. Через несколько мгновений вычисления заканчиваются и на индикаторе загорается знакомое нам число 7.0685832. Нажав клавиши ИП5, можно убедиться, что оно размещается в регистре 5. А заодно и в том, что в момент останова по команде С/П в регистре X находится результат выполнения предыдущей команды.
Выгоды от программирования мы могли оценить уже на примере, где требовалось провести многократные однотипные расчеты при меняющихся исходных данных. Такие задачи на практике встречаются нередко. Но при этом часто требуется не только получить ряд результатов, но и подвергнуть их статистической обработке - например, вычислить их среднее арифметическое.
Предположим, что подобным требованием дополнена наша задача о вычислении площади кругов с целочисленными диаметрами от 1 до 10: в довершение расчетов нужно определить среднюю площадь. Программу придется расширить: вычислив площадь очередного круга, следует прибавить ее к сумме площадей; попутно надо подсчитывать количество кругов, а когда все они будут перебраны, полученную сумму нужно будет поделить на это количество.
Обе эти величины можно шаг за шагом накапливать в адресуемых регистрах: скажем, количество кругов - в нулевом, сумму их площадей - в первом. Получив по составленной нами программе площадь очередного круга в регистре X, можно вызвать туда из регистра 1 накопленную на этот момент сумму площадей. Содержимое регистра X при этом сдвинется в регистр Y. Затем остается выполнить сложение - так к сумме площадей прибавится новое слагаемое. Результат сложения, как мы знаем, получится в регистре X. Оттуда его нужно отослать в регистр 1. Подобным же образом, вызвав содержимое регистра 0, затем единицу и сложив оба числа, получим пополнившееся количество кругов и отошлем его обратно в регистр 0.
К этой цепочке команд надо приписать еще команду останова и команду возврата на нулевой адрес. Когда счет остановится по первой из них, надо ввести в калькулятор диаметр нового круга и нажать клавишу С/П. Программа перейдет к следующей команде, совершит по ней возврат на адрес 00 и проведет расчет для нового круга.
Чтобы рассчитать среднее арифметическое, надо приписать к нашей программе еще четыре команды: вызов содержимого регистра 1 (сумма площадей), вызов содержимого регистра 0 (количество кругов), деление (оно даст интересующую нас среднюю площадь) и останов (на индикаторе будет светиться результат предыдущей операции, то есть ответ на поставленную задачу). На первую из этих команд мы передадим управление с помощью клавиши БП, когда переберем все круги, и после останова считаем искомый ответ с индикатора.
Это описание нетрудно перевести на язык команд. Но прежде надо решить, как организовать возврат на нулевой адрес. Дело в том, что команда В/0 передает управление на первый адрес только в режиме ручных вычислений. Стало быть, вместо нее в программе придется использовать команду безусловного перехода - ту самую, которую мы уже исполняли недавно с помощью клавиши БП.
У этой команды - своя тонкость. Когда мы станем вводить ее в программу (забегая вперед, скажем, что счетчик адресов к этому моменту будет показывать 16) и нажмем клавишу БП, содержимое счетчика адресов тотчас же увеличится на единицу: 17. Когда же мы наберем адрес перехода, содержимое счетчика адресов увеличится еще раз: 18. Это означает, что команда безусловного перехода - "двойная", то есть занимает в программе два адреса. В первом из них записывается операция безусловного перехода БП, во втором - адрес перехода.
Отказавшись от команды В/0, мы свободны в выборе этого адреса. Учтем, что перед запуском программы следует очистить регистры 0 и 1, предназначенные для накопления сумм. Очистку можно произвести вручную, нажав клавиши Сх П0 П1. Но лучше, чтобы это сделал калькулятор, и вызов из памяти, притом с самого начала: 00. Сх 01. П0 02. П1 03. С/П.
Команда останова здесь не лишняя, да и в дальнейшем пригодится: на нее-то мы и станем передавать управление, вычислив площадь очередного круга, и покуда калькулятор стоит, будем вводить диаметр следующего круга.
С учетом высказанных соображений программа примет такой вид:
00. Сх 01. П0 02. П1 03. С/П 04. Fx2 05. Fпи 06. * 07. 4 08. / 09. ИП1 10. * 11. П1 12. ИП0 13. 1 14. + 15. П0 16. БП 17. 03 18. ИП1 19. ИП0 20. / 21. С/П.
Программа получилась объемистая - будем внимательны при ее вводе. Введя, нажмем клавиши В/0, С/П. Очистив за три первые команды регистры 0 и 1, калькулятор остановится. Введем диаметр первого круга, единицу, запустим программу, после останова введем диаметр второго круга, двойку, запустим программу вновь... и так будем продолжать, пока не будет вычислена площадь последнего круга, чей диаметр равен десяти. Передадим управление на адрес 18 и вскоре после нового пуска получим на индикаторе искомую среднюю площадь кругов. 30.237829.
Тот, кто знакомится с программированием на наших занятиях, вряд ли представит себе, что ответ на поставленную нами задачу можно получить по более короткой программе. Между тем программисты не зря говорят: всякую программу можно сократить по крайней мере на одну команду. Сейчас мы докажем это на примере нашей задачи. Правда, для этого нам придется освоить несколько новых команд.
Когда на прошлом занятии, поговорив об одноместных операциях, мы перешли к рассмотрению двуместных, мы сразу отметили, что для их выполнения необходимы два операционных регистра - X и Y. Мы узнали, как с помощью клавиши ^ в них вводятся участники арифметических действий и где размещается результат.
Ради простоты мы умолчали тогда, что перемещение чисел охватывает при этом не только регистры X и У, но также Z и Т. Эти четыре регистра находятся в тесной взаимосвязи и объединяются названием стек (английское слово, означающее "охапка, стопка"). К ним примыкает регистр X1, куда после выполнения многих операций направляется прежнее содержимое регистра X.
То, что мы узнали на прошлом занятии, дополним здесь до завершенной картины всевозможных перемещений чисел по стеку.
...
Последний раз редактировалось: Gudleifr (Пн Дек 26, 2022 12:58 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3399
Дата регистрации : 2017-03-29
Страница 1 из 6 • 1, 2, 3, 4, 5, 6 
Страница 1 из 6
Права доступа к этому форуму:
Вы не можете отвечать на сообщения