Матчасть диванного танкиста
Страница 2 из 6
Страница 2 из 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
...
Посмотрим сначала, что происходит в нем, когда в регистр X засылается новое число. Пусть оно вызывается туда из какого-то адресуемого регистра (командами ИП1, ИПА и т.п.) или из ячейки, где хранится число "пи" (командой Fn). Тогда прежнее содержимое РX смещается в РY, содержимое РY - в PZ, содержимое PZ - в РТ, прежнее содержимое регистра Т пропадет. И если представить регистры стека один над другим, то описанное перемещение удобно назвать движением снизу вверх. Содержимое регистра X1 при этом не меняется.
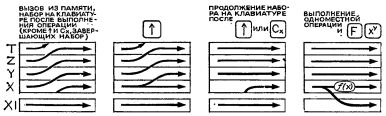
Когда новое число вводится в регистр X с клавиатуры, числа в стеке тоже перемещаются снизу вверх, за исключением случаев, когда перед этим с клавиатуры вводилось какое-то число и вслед за его набором были выполнены команды ^ или Сх. Тогда при вводе нового числа в РХ с остальными регистрами стека и с регистром РХ1 ничего не происходит.
Если после набора числа на клавиатуре не нажать клавишу ^, то при дальнейшем нажатии цифровых клавиш все будет происходить так, как если бы мы продолжали вводить цифры предыдущего числа.
Кстати сказать, аналогичным образом можно ввести число в регистр X и в режиме автоматических вычислений по программе. Например, цепочка команд 00. 3 01. , 02. 1 03. 4 запишет в регистр X число 3.14.
По команде ^ числа, находившиеся в стеке, сдвигаются по его регистрам снизу вверх, причем в РХ остается копия числа, находившегося там прежде.
По команде Сх содержимое регистра X стирается (точнее, заменяется нулем), а в прочих регистрах стека и в регистре X1 все остается по-прежнему.
Когда над числом, находящимся в регистре X, совершается какая-либо одноместная операция, в регистрах Y, Z, Т также ничего не происходит, а в регистр X1 отправляется прежнее содержимое регистра X. Таким же образом выполняется и операция FхY.
Каждая арифметическая операция выполняется так: ее участники берутся из регистров X и Y, результат направляется в регистр X. Прежнее содержимое регистра X отсылается в регистр X1, прежнее содержимое регистра Y утрачивается - туда спускается содержимое PZ. Содержимое РТ, в свою очередь, смещается в PZ, оставляя на прежнем месте свою копию.
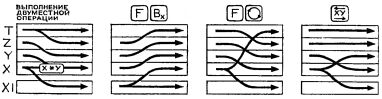
При засылке числа из регистра X в любой адресуемый регистр сохраняется прежнее содержимое и регистра X, и всех других регистров стека, и регистра X1.
Вот еще три команды, по которым движутся числа по регистрам стека.
Команда Вх вызывает содержимое регистра X1 в регистр X. Числа в регистрах стека при этом сдвигаются снизу вверх. В регистре X1 остается копия находившегося там прежде числа.
По команде x-y содержимое РY переходит в РХ, содержимое РХ - в РY и РХ1. С ее помощью удобно выводить на индикатор содержимое регистра Y.
Команда () осуществляет круговое движение чисел по стеку: из РY - в РХ, из PZ - в РY, из РТ - в PZ, из РX - в РТ н РХ1. С ее помощью можно просмотреть на индикаторе содержимое всех регистров стека.
Научившись управлять движением чисел по стеку, мы сможем сократить последнюю из составленных нами программ на целых четыре, команды:
00. Сх O1. ^ 02. С/П 03. Fx2 04. Fпи 05. * 06. 4 07. / 08. + 09. x-y 10. 1 11. + 12. x-y 13. БП 14. 02 15. x-y 16. / 17. С/П.
Здесь начальные команды Сх и ^ очищают регистры X и Y перед последующим накоплением количества кругов и суммы их площадей. После останова в регистр X вводится диаметр первого круга, калькулятор запускается вновь, после останова вводится диаметр следующего круга и снова нажимается клавиша С/П...
К моменту очередного останова в регистре X находится сумма площадей кругов с первого по некоторый k-тый (обозначим ее сигма-k), в регистре Y - их количество k. В этом нетрудно убедиться с помощью таблицы, в последовательных столбцах которой указаны адреса, команды, коды операций, а также содержимое регистров стека после выполнения каждой команды.
Первые два столбца заполним по тексту программы. Ручные операции ввода (когда в РХ заносится диаметр нового круга) и последующего пуска программы клавишей С/П запишем в таблицу без адресов.
Проходя по строчкам таблицы сверху вниз, заполняйте остальные столбцы в соответствии с результатами выполнения команд - и при вычислении площади [k+1]-го круга она примет вид, подтверждающий, что программа работает так, как мы предполагали:
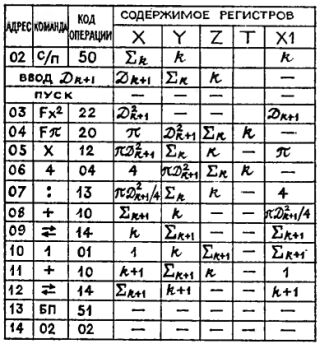
(Прочерк означает, что содержимое регистра сохранилось неизменным).
Попробуйте продолжить эту таблицу до завершающего адреса 17, проверьте, что к моменту останова по этому адресу в регистре X (и на индикаторе) находится искомое среднее арифметическое.
Введите программу в калькулятор, проведите расчет с теми же исходными данными, что прежде, и убедитесь, что результат получается тот же: 30.237829.
Заметим, что подобные таблицы очень облегчают разбор программ - и своих, и особенно составленных другими.
Попытаемся теперь переделать нашу последнюю программу так, чтобы уменьшить количество ручных операций. Ведь чем их больше, тем выше риск ошибки.
Программа распадается на две части. В первой (адреса 00-14) вычисляется площадь очередного круга, подсчитывается сумма всех до сих пор перебранных кругов и их количество. Во второй части (адреса 15-17) вычисляется среднее арифметическое площадей. По какой цепочке команд пойти, определяем мы сами, в первом случае - просто запуская программу после очередного останова, во втором - совершая безусловный переход на адрес 15.
Нельзя ли поручить выбор пути самому калькулятору?
Вопросы такого рода могут возникнуть при составлении многих программ, даже весьма несложных. Например, при решении квадратного уравнения: если его дискриминант положительный или равен нулю, то корни отыскиваются по одним формулам, если отрицательный - то по другим. Или возьмем пример из тригонометрии: при положительном аргументе арккосинус связан с арксинусом одним соотношением, при отрицательном - другим. И если по ходу работы программы может возникнуть любая из двух каких-то альтернативных возможностей, программа должна содержать фрагменты для расчета каждого варианта и работать по тому или другому в зависимости от выполнения или невыполнения некоторого условия. Фрагменты такого характера называют ветвями.
На эти случаи в нашем калькуляторе предусмотрены команды условного перехода. Они вводятся в программу с помощью клавиш, над которыми написаны соотношения: х<0, х=0, х>=0, x!=0. Судя по этим обозначениям, проверка любого альтернативного условия должна быть сведена к сравнению с нулем содержимого регистра X.
В силу "надклавишного" расположения надписей ввод команд условного перехода в программу предваряется нажатием клавиши F. Нажав вслед за ней клавишу, помеченную выбранным соотношением (скажем, х!=0), замечаем, что счетчик адресов увеличился на единицу. Он вновь увеличится на единицу, когда затем мы введем адрес перехода. Как видим, каждая команда условного перехода - двойная, занимает в программе два адреса. Например: 03. Fx!=0 04. 17.
На указанный в такой команде адрес перехода управление передается, если условие не выполняется. Так в нашем примере, если содержимое регистра X равно нулю и неравенство x!=0 не соблюдается, совершается переход иа адрес 17. Если же условие выполняется, то есть x!=0, управление передается на адрес, следующий за командой условного перехода, в нашем примере - на адрес 05.
Для иллюстрации подобных переходов мы не случайно привели фрагмент 03. Fx!=0 04. 17. Оказывается, если вставить его в нашу программу, она будет гораздо удобнее.
00. Сх 01. ^ 02. С/П 03. Fx!=0 04. 17 05. Fx2 06. Fпи 07. * 08. 4 09. / 10. + 11. x-y 12. 1 13. + 14. x-y 15. БП 16. 02 17. F() 18. x-y 19. / 20. С/П.
(Исправлена опечатка согласно 9/85).
Покуда мы будем вводить в калькулятор одни за другим диаметры кругов - выраженные, разумеется, ненулевыми числами,- команда условного перехода будет передавать управление на адрес 05, начальный адрес первой части программы, где вычисляются и суммируются площади кругов, подсчитывается их количество. А когда расчет этих величии закончится, введем нуль. Поскольку условие х!=0 теперь не выполнено, программа перейдет на адрес 17, начальный адрес второй части, где будет вычислена средняя площадь кругов.
Теперь для перехода к заключительной стадии расчета надо нажимать всего две клавиши, 0 и С/П, вместо четырех - БП, две цифры адреса перехода, С/П. Не нужно вспоминать или сверяться по инструкции к программе, каков этот адрес. Заботы об этом калькулятор берет на себя.
Наш учебный пример с определением средней площади круга, конечно, слишком прост, чтобы иметь самостоятельное значение. Но вполне может статься, что подобный расчет придется выполнить по ходу решения какой-то крупной задачи. И тогда в программу для ее решения цепочка команд, вычисляющих среднюю площадь, войдет в качестве фрагмента.
Допустим, он должен разместиться в большой программе, начиная с 60-го адреса. Предположим, что к началу его работы диаметры кругов уже находятся в адресуемых регистрах: D1 - в PD, D2 - в PC, D3 - в РВ, D4 - в PA, D5 - в Р9, D6 - в Р8 и так далее. (Такой "обратный" порядок обнаружит свой смысл позже). Предположим еще, что длина массива заполненных регистров известна и ие превышает 12, так что регистр 1 остается свободным, а выражающее эту длину число кругов находится в регистре 0.
(Эти облегчающие предположения не поблажка читателю, они естественны для программ, составленных опытным программистом, который всегда думает об удобствах своей работы).
Подсчет средней площади кругов теперь представляется совсем простым: вызывать один за другим диаметры кругов из последовательных регистров, вычислять по ним и суммировать площади кругов, а затем поделить сумму иа число слагаемых. Но для такой процедуры нужны соответствующие команды. Во-первых, такая команда условного перехода, по которой он совершается заданное число раз. Во-вторых, такая команда вызова, которая при многократном ее исполнении вызывает в регистр X числа из последовательных адресуемых регистров.
Нужные нам команды условного перехода вводятся в программу с помощью клавиш FL0, FL1, FL2, FL3. Будем объединять эти пары клавиш обозначением FLM. Как и при вводе всякой команды условного перехода, нажав такую пару, мы должны далее ввести адрес перехода. В программе такая команда займет два адреса: в первом - операция FLM, во втором - две цифры, означающие адрес перехода.
Допустим, он меньше того, под которым записана операция FLM, а в регистре М находится целое число N, большее единицы. Выполнив цепочку команд, предшествующих операции FLM, программа приступает к выполнению команды условного перехода. Операцией FLM из содержимого регистра М вычитается единица и полученная разность сравнивается с нулем. Если она не равна нулю, то засылается в регистр М, а управление передается по адресу перехода. Цепочка тех же команд выполняется еще раз, снова из содержимого регистра М вычитается единица... Так продолжается до тех пор, пока результат вычитания ие окажется равным нулю. В таком случае он не засылается в регистр М, и там остается единица; управление же передается на команду, следующую за командой условного перехода, то есть через адрес от операции FLM.
Это происходит, как нетрудно установить, после N-кратного прохождения цепочки. Засылая в регистр М нужное число, мы можем задавать количество таких прохождений.
Фрагмент программы, выполняемый многократно,- с первой до последней команды и далее вновь с первой - называется циклом. Поэтому операция FLM, образующая только что описанную команду условного перехода, именуется операцией организации цикла.
Есть среди команд нашего калькулятора и нужная нам команда вызова чисел из последовательных регистров. В программу она вводится нажатием трех клавиш: сначала К, затем ИП, затем той, что указывает номер одного из адресуемых регистров. Условно обозначим этот номер М и предположим, что в нем находится целое число.
Несмотря на обилие клавиш, требуемых для ее ввода, эта команда занимает в программе один адрес и записывается слитно: КИПМ. Работает она по-разному в зависимости от значения М.
Пусть М равно одному из чисел от 0 до 3 включительно. Тогда по команде КИПМ содержимое регистра М уменьшается иа единицу н в РХ вызывается содержимое того регистра, номер которого равен получившейся разности.
Пусть М равно одному из чисел от 4 до 6 включительно. Тогда по команде КИПМ содержимое регистра М увеличивается на единицу и в РХ вызывается содержимое того регистра, номер которого равен получившейся сумме.
Пусть М представляет собой число от 7 до 9 или букву от А до D, Тогда по команде КИПМ в РХ вызывается содержимое того регистра, номер которого равен числу, находящемуся в регистре М.
Это число может превышать 9. Скажем, если оно равно 10, то калькулятор поймет его как обозначение регистра А, 11 - как В, 12 - как С, 13 - как D. Именно 13 получится, например, в регистре 1 при первом выполнении команды КИП1, если до того там находилось 14.
Команды вида КИПМ называются командами косвенного вызова. Есть у нашего калькулятора и сходные с ними по структуре команды косвенной засылки. Набираются они нажатием клавиши К, П и еще одной, указывающей номер некоторого регистра М. Каждая занимает в программе один адрес.
Работают они аналогично командам косвенного вызова и тоже в предположении, что в регистре М находится целое число. Вот, скажем, что происходит по команде КП1: из содержимого регистра 1 вычитается единица, и в регистр, номер которого равен получившейся разности, направляется содержимое регистра X.
Кстати, приведем соответствующий термин: уменьшение или увеличение содержимого каких-либо регистров при использовании команд косвенного вызова и косвенной засылки называется модификацией адреса.
Располагая командами косвенного вызова и организации циклов, нетрудно составить задуманный нами фрагмент:
60. ИП0 61. 1 62. 4 63. П1 64. Сх 65. КИП1 66. Fx2 67. Fпи 68. * 69. 4 70. / 71. + 72. FL0 73. 65 74. x-y 75. /
Начертите таблицу, с помощью которой можно следить за движением чисел по стеку, и пронаблюдайте по ней, как "работает" только что составленная нами цепочка команд.
Команда ИП0 вызывает из регистра 0 в регистр X количество кругов: оно понадобится в самом конце для нахождения среднего арифметического. Три дальнейшие команды засылают в регистр 1 число 14, используемое в работе следующей команды КИП1, и очищают регистр X: в нем далее будет накапливаться сумма площадей. При первом выполнении команды КИП1 из начального содержимого регистра 1, то есть из числа 14, вычтется единица и получится 13 - номер регистра D. Из него-то и будет вызвано значение первого диаметра. Цикл команд, записанных под адресами 65-71, в первый раз вычислит площадь первого круга, во второй раз - уже площадь второго круга: ведь при втором исполнении команды КИП1 из содержимого ячейки 1 вновь вычтется единица и получится 12, номер регистра С. Там находится значение второго диаметра - его-то и вызовет на сей раз команда КИП1 в регистр X. Команда FL0 65 (адреса 72-73) будет вновь и вновь передавать управление на начало цикла, и каждый раз из содержимого регистра 0, куда вначале было записано количество кругов, будет вычитаться по единице. Сколько кругов, столько раз н будет пройден цикл. По выходе из него в регистре X - сумма площадей кругов, в регистре Y - их количество. Их надо вначале переставить (адрес 74), чтобы затем поделить (адрес 75) и получить тем самым искомую среднюю площадь.
В разобранном нами фрагменте программы нет команды останова. Можно предположить, что полученный результат будет незамедлительно использован в следующей части программы. Но возможно и другое толкование: расчет, производимый этим фрагментом, требуется проводить в различных местах "большой" программы. Писать его в тексте программы несколько раз неэкономно. Лучше каждый раз передавать на него управление и возвращаться обратно.
Для организации таких переходов с возвратом служит клавиша ПП ("Переход к Подпрограмме"). Вслед за ее нажатием нужно ввести в программу начальный адрес фрагмента, на который нужно передать управление. Такой фрагмент и называется подпрограммой. Команда перехода к нему, как нетрудно понять из нашего описания, занимает два адреса. На следующий за ними адрес произойдет возврат, если в конце подпрограммы поставить команду В/О.
Судя по сказанному до сих пор, система команд у "Электроники Б3-34" весьма богатая: мы сумели выполнить все свои замыслы при составлении и совершенствовании задуманных программ. Некоторые возможности нашего микрокалькулятора при этом даже остались неиспользованными и неописанными.
Разумеется, в одной статье невозможно описать все секреты нашего калькулятора. Их знание придет с опытом работы по составлению и совершенствованию программ.
Посмотрим сначала, что происходит в нем, когда в регистр X засылается новое число. Пусть оно вызывается туда из какого-то адресуемого регистра (командами ИП1, ИПА и т.п.) или из ячейки, где хранится число "пи" (командой Fn). Тогда прежнее содержимое РX смещается в РY, содержимое РY - в PZ, содержимое PZ - в РТ, прежнее содержимое регистра Т пропадет. И если представить регистры стека один над другим, то описанное перемещение удобно назвать движением снизу вверх. Содержимое регистра X1 при этом не меняется.

Когда новое число вводится в регистр X с клавиатуры, числа в стеке тоже перемещаются снизу вверх, за исключением случаев, когда перед этим с клавиатуры вводилось какое-то число и вслед за его набором были выполнены команды ^ или Сх. Тогда при вводе нового числа в РХ с остальными регистрами стека и с регистром РХ1 ничего не происходит.
Если после набора числа на клавиатуре не нажать клавишу ^, то при дальнейшем нажатии цифровых клавиш все будет происходить так, как если бы мы продолжали вводить цифры предыдущего числа.
Кстати сказать, аналогичным образом можно ввести число в регистр X и в режиме автоматических вычислений по программе. Например, цепочка команд 00. 3 01. , 02. 1 03. 4 запишет в регистр X число 3.14.
По команде ^ числа, находившиеся в стеке, сдвигаются по его регистрам снизу вверх, причем в РХ остается копия числа, находившегося там прежде.
По команде Сх содержимое регистра X стирается (точнее, заменяется нулем), а в прочих регистрах стека и в регистре X1 все остается по-прежнему.
Когда над числом, находящимся в регистре X, совершается какая-либо одноместная операция, в регистрах Y, Z, Т также ничего не происходит, а в регистр X1 отправляется прежнее содержимое регистра X. Таким же образом выполняется и операция FхY.
Каждая арифметическая операция выполняется так: ее участники берутся из регистров X и Y, результат направляется в регистр X. Прежнее содержимое регистра X отсылается в регистр X1, прежнее содержимое регистра Y утрачивается - туда спускается содержимое PZ. Содержимое РТ, в свою очередь, смещается в PZ, оставляя на прежнем месте свою копию.

При засылке числа из регистра X в любой адресуемый регистр сохраняется прежнее содержимое и регистра X, и всех других регистров стека, и регистра X1.
Вот еще три команды, по которым движутся числа по регистрам стека.
Команда Вх вызывает содержимое регистра X1 в регистр X. Числа в регистрах стека при этом сдвигаются снизу вверх. В регистре X1 остается копия находившегося там прежде числа.
По команде x-y содержимое РY переходит в РХ, содержимое РХ - в РY и РХ1. С ее помощью удобно выводить на индикатор содержимое регистра Y.
Команда () осуществляет круговое движение чисел по стеку: из РY - в РХ, из PZ - в РY, из РТ - в PZ, из РX - в РТ н РХ1. С ее помощью можно просмотреть на индикаторе содержимое всех регистров стека.
Научившись управлять движением чисел по стеку, мы сможем сократить последнюю из составленных нами программ на целых четыре, команды:
00. Сх O1. ^ 02. С/П 03. Fx2 04. Fпи 05. * 06. 4 07. / 08. + 09. x-y 10. 1 11. + 12. x-y 13. БП 14. 02 15. x-y 16. / 17. С/П.
Здесь начальные команды Сх и ^ очищают регистры X и Y перед последующим накоплением количества кругов и суммы их площадей. После останова в регистр X вводится диаметр первого круга, калькулятор запускается вновь, после останова вводится диаметр следующего круга и снова нажимается клавиша С/П...
К моменту очередного останова в регистре X находится сумма площадей кругов с первого по некоторый k-тый (обозначим ее сигма-k), в регистре Y - их количество k. В этом нетрудно убедиться с помощью таблицы, в последовательных столбцах которой указаны адреса, команды, коды операций, а также содержимое регистров стека после выполнения каждой команды.
Первые два столбца заполним по тексту программы. Ручные операции ввода (когда в РХ заносится диаметр нового круга) и последующего пуска программы клавишей С/П запишем в таблицу без адресов.
Проходя по строчкам таблицы сверху вниз, заполняйте остальные столбцы в соответствии с результатами выполнения команд - и при вычислении площади [k+1]-го круга она примет вид, подтверждающий, что программа работает так, как мы предполагали:

(Прочерк означает, что содержимое регистра сохранилось неизменным).
Попробуйте продолжить эту таблицу до завершающего адреса 17, проверьте, что к моменту останова по этому адресу в регистре X (и на индикаторе) находится искомое среднее арифметическое.
Введите программу в калькулятор, проведите расчет с теми же исходными данными, что прежде, и убедитесь, что результат получается тот же: 30.237829.
Заметим, что подобные таблицы очень облегчают разбор программ - и своих, и особенно составленных другими.
Попытаемся теперь переделать нашу последнюю программу так, чтобы уменьшить количество ручных операций. Ведь чем их больше, тем выше риск ошибки.
Программа распадается на две части. В первой (адреса 00-14) вычисляется площадь очередного круга, подсчитывается сумма всех до сих пор перебранных кругов и их количество. Во второй части (адреса 15-17) вычисляется среднее арифметическое площадей. По какой цепочке команд пойти, определяем мы сами, в первом случае - просто запуская программу после очередного останова, во втором - совершая безусловный переход на адрес 15.
Нельзя ли поручить выбор пути самому калькулятору?
Вопросы такого рода могут возникнуть при составлении многих программ, даже весьма несложных. Например, при решении квадратного уравнения: если его дискриминант положительный или равен нулю, то корни отыскиваются по одним формулам, если отрицательный - то по другим. Или возьмем пример из тригонометрии: при положительном аргументе арккосинус связан с арксинусом одним соотношением, при отрицательном - другим. И если по ходу работы программы может возникнуть любая из двух каких-то альтернативных возможностей, программа должна содержать фрагменты для расчета каждого варианта и работать по тому или другому в зависимости от выполнения или невыполнения некоторого условия. Фрагменты такого характера называют ветвями.
На эти случаи в нашем калькуляторе предусмотрены команды условного перехода. Они вводятся в программу с помощью клавиш, над которыми написаны соотношения: х<0, х=0, х>=0, x!=0. Судя по этим обозначениям, проверка любого альтернативного условия должна быть сведена к сравнению с нулем содержимого регистра X.
В силу "надклавишного" расположения надписей ввод команд условного перехода в программу предваряется нажатием клавиши F. Нажав вслед за ней клавишу, помеченную выбранным соотношением (скажем, х!=0), замечаем, что счетчик адресов увеличился на единицу. Он вновь увеличится на единицу, когда затем мы введем адрес перехода. Как видим, каждая команда условного перехода - двойная, занимает в программе два адреса. Например: 03. Fx!=0 04. 17.
На указанный в такой команде адрес перехода управление передается, если условие не выполняется. Так в нашем примере, если содержимое регистра X равно нулю и неравенство x!=0 не соблюдается, совершается переход иа адрес 17. Если же условие выполняется, то есть x!=0, управление передается на адрес, следующий за командой условного перехода, в нашем примере - на адрес 05.
Для иллюстрации подобных переходов мы не случайно привели фрагмент 03. Fx!=0 04. 17. Оказывается, если вставить его в нашу программу, она будет гораздо удобнее.
00. Сх 01. ^ 02. С/П 03. Fx!=0 04. 17 05. Fx2 06. Fпи 07. * 08. 4 09. / 10. + 11. x-y 12. 1 13. + 14. x-y 15. БП 16. 02 17. F() 18. x-y 19. / 20. С/П.
(Исправлена опечатка согласно 9/85).
Покуда мы будем вводить в калькулятор одни за другим диаметры кругов - выраженные, разумеется, ненулевыми числами,- команда условного перехода будет передавать управление на адрес 05, начальный адрес первой части программы, где вычисляются и суммируются площади кругов, подсчитывается их количество. А когда расчет этих величии закончится, введем нуль. Поскольку условие х!=0 теперь не выполнено, программа перейдет на адрес 17, начальный адрес второй части, где будет вычислена средняя площадь кругов.
Теперь для перехода к заключительной стадии расчета надо нажимать всего две клавиши, 0 и С/П, вместо четырех - БП, две цифры адреса перехода, С/П. Не нужно вспоминать или сверяться по инструкции к программе, каков этот адрес. Заботы об этом калькулятор берет на себя.
Наш учебный пример с определением средней площади круга, конечно, слишком прост, чтобы иметь самостоятельное значение. Но вполне может статься, что подобный расчет придется выполнить по ходу решения какой-то крупной задачи. И тогда в программу для ее решения цепочка команд, вычисляющих среднюю площадь, войдет в качестве фрагмента.
Допустим, он должен разместиться в большой программе, начиная с 60-го адреса. Предположим, что к началу его работы диаметры кругов уже находятся в адресуемых регистрах: D1 - в PD, D2 - в PC, D3 - в РВ, D4 - в PA, D5 - в Р9, D6 - в Р8 и так далее. (Такой "обратный" порядок обнаружит свой смысл позже). Предположим еще, что длина массива заполненных регистров известна и ие превышает 12, так что регистр 1 остается свободным, а выражающее эту длину число кругов находится в регистре 0.
(Эти облегчающие предположения не поблажка читателю, они естественны для программ, составленных опытным программистом, который всегда думает об удобствах своей работы).
Подсчет средней площади кругов теперь представляется совсем простым: вызывать один за другим диаметры кругов из последовательных регистров, вычислять по ним и суммировать площади кругов, а затем поделить сумму иа число слагаемых. Но для такой процедуры нужны соответствующие команды. Во-первых, такая команда условного перехода, по которой он совершается заданное число раз. Во-вторых, такая команда вызова, которая при многократном ее исполнении вызывает в регистр X числа из последовательных адресуемых регистров.
Нужные нам команды условного перехода вводятся в программу с помощью клавиш FL0, FL1, FL2, FL3. Будем объединять эти пары клавиш обозначением FLM. Как и при вводе всякой команды условного перехода, нажав такую пару, мы должны далее ввести адрес перехода. В программе такая команда займет два адреса: в первом - операция FLM, во втором - две цифры, означающие адрес перехода.
Допустим, он меньше того, под которым записана операция FLM, а в регистре М находится целое число N, большее единицы. Выполнив цепочку команд, предшествующих операции FLM, программа приступает к выполнению команды условного перехода. Операцией FLM из содержимого регистра М вычитается единица и полученная разность сравнивается с нулем. Если она не равна нулю, то засылается в регистр М, а управление передается по адресу перехода. Цепочка тех же команд выполняется еще раз, снова из содержимого регистра М вычитается единица... Так продолжается до тех пор, пока результат вычитания ие окажется равным нулю. В таком случае он не засылается в регистр М, и там остается единица; управление же передается на команду, следующую за командой условного перехода, то есть через адрес от операции FLM.
Это происходит, как нетрудно установить, после N-кратного прохождения цепочки. Засылая в регистр М нужное число, мы можем задавать количество таких прохождений.
Фрагмент программы, выполняемый многократно,- с первой до последней команды и далее вновь с первой - называется циклом. Поэтому операция FLM, образующая только что описанную команду условного перехода, именуется операцией организации цикла.
Есть среди команд нашего калькулятора и нужная нам команда вызова чисел из последовательных регистров. В программу она вводится нажатием трех клавиш: сначала К, затем ИП, затем той, что указывает номер одного из адресуемых регистров. Условно обозначим этот номер М и предположим, что в нем находится целое число.
Несмотря на обилие клавиш, требуемых для ее ввода, эта команда занимает в программе один адрес и записывается слитно: КИПМ. Работает она по-разному в зависимости от значения М.
Пусть М равно одному из чисел от 0 до 3 включительно. Тогда по команде КИПМ содержимое регистра М уменьшается иа единицу н в РХ вызывается содержимое того регистра, номер которого равен получившейся разности.
Пусть М равно одному из чисел от 4 до 6 включительно. Тогда по команде КИПМ содержимое регистра М увеличивается на единицу и в РХ вызывается содержимое того регистра, номер которого равен получившейся сумме.
Пусть М представляет собой число от 7 до 9 или букву от А до D, Тогда по команде КИПМ в РХ вызывается содержимое того регистра, номер которого равен числу, находящемуся в регистре М.
Это число может превышать 9. Скажем, если оно равно 10, то калькулятор поймет его как обозначение регистра А, 11 - как В, 12 - как С, 13 - как D. Именно 13 получится, например, в регистре 1 при первом выполнении команды КИП1, если до того там находилось 14.
Команды вида КИПМ называются командами косвенного вызова. Есть у нашего калькулятора и сходные с ними по структуре команды косвенной засылки. Набираются они нажатием клавиши К, П и еще одной, указывающей номер некоторого регистра М. Каждая занимает в программе один адрес.
Работают они аналогично командам косвенного вызова и тоже в предположении, что в регистре М находится целое число. Вот, скажем, что происходит по команде КП1: из содержимого регистра 1 вычитается единица, и в регистр, номер которого равен получившейся разности, направляется содержимое регистра X.
Кстати, приведем соответствующий термин: уменьшение или увеличение содержимого каких-либо регистров при использовании команд косвенного вызова и косвенной засылки называется модификацией адреса.
Располагая командами косвенного вызова и организации циклов, нетрудно составить задуманный нами фрагмент:
60. ИП0 61. 1 62. 4 63. П1 64. Сх 65. КИП1 66. Fx2 67. Fпи 68. * 69. 4 70. / 71. + 72. FL0 73. 65 74. x-y 75. /
Начертите таблицу, с помощью которой можно следить за движением чисел по стеку, и пронаблюдайте по ней, как "работает" только что составленная нами цепочка команд.
Команда ИП0 вызывает из регистра 0 в регистр X количество кругов: оно понадобится в самом конце для нахождения среднего арифметического. Три дальнейшие команды засылают в регистр 1 число 14, используемое в работе следующей команды КИП1, и очищают регистр X: в нем далее будет накапливаться сумма площадей. При первом выполнении команды КИП1 из начального содержимого регистра 1, то есть из числа 14, вычтется единица и получится 13 - номер регистра D. Из него-то и будет вызвано значение первого диаметра. Цикл команд, записанных под адресами 65-71, в первый раз вычислит площадь первого круга, во второй раз - уже площадь второго круга: ведь при втором исполнении команды КИП1 из содержимого ячейки 1 вновь вычтется единица и получится 12, номер регистра С. Там находится значение второго диаметра - его-то и вызовет на сей раз команда КИП1 в регистр X. Команда FL0 65 (адреса 72-73) будет вновь и вновь передавать управление на начало цикла, и каждый раз из содержимого регистра 0, куда вначале было записано количество кругов, будет вычитаться по единице. Сколько кругов, столько раз н будет пройден цикл. По выходе из него в регистре X - сумма площадей кругов, в регистре Y - их количество. Их надо вначале переставить (адрес 74), чтобы затем поделить (адрес 75) и получить тем самым искомую среднюю площадь.
В разобранном нами фрагменте программы нет команды останова. Можно предположить, что полученный результат будет незамедлительно использован в следующей части программы. Но возможно и другое толкование: расчет, производимый этим фрагментом, требуется проводить в различных местах "большой" программы. Писать его в тексте программы несколько раз неэкономно. Лучше каждый раз передавать на него управление и возвращаться обратно.
Для организации таких переходов с возвратом служит клавиша ПП ("Переход к Подпрограмме"). Вслед за ее нажатием нужно ввести в программу начальный адрес фрагмента, на который нужно передать управление. Такой фрагмент и называется подпрограммой. Команда перехода к нему, как нетрудно понять из нашего описания, занимает два адреса. На следующий за ними адрес произойдет возврат, если в конце подпрограммы поставить команду В/О.
Судя по сказанному до сих пор, система команд у "Электроники Б3-34" весьма богатая: мы сумели выполнить все свои замыслы при составлении и совершенствовании задуманных программ. Некоторые возможности нашего микрокалькулятора при этом даже остались неиспользованными и неописанными.
Разумеется, в одной статье невозможно описать все секреты нашего калькулятора. Их знание придет с опытом работы по составлению и совершенствованию программ.
Последний раз редактировалось: Gudleifr (Ср 28 Дек 2022 - 13:41), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Тут, как назло, в журнале оказался и пример "калькулятора", позволяющего программировать автоматическое управление.
7/85
РЕМИКОНТ: РЕГУЛИРОВАНИЕ СТАНОВИТСЯ МИКРОПРОЦЕССОРНЫМ
Доктор технических наук, профессор Г.ИОРДАН, директор Государственного научно-исследовательского института теплоэнергетического приборостроения (НИИ теплоприбор), и кандидат технических наук В.ПЕВЗНЕР, заведующий лабораторией института
Двести лет назад была изобретена паровая машина. Это событие ознаменовало начало первой промышленной революции. Примечательно, что у ее истоков стоял и регулятор. С тех пор оснащение механизмов и агрегатов регуляторами стало характерной чертой развития техники. Различные по назначению, конструкции, принципу действия, размерам, они работают на суше, на воде и в воздухе, на производстве и в быту, используются поодиночке или объединяются в группы. Они участвуют в управлении работой тепловых и атомных электростанций, прокатных цехов и домен, газоперекачивающих станций и нефтеперерабатывающих заводов...
Без регуляторов немыслимо существование современной индустрии. Лишь предприятия нашей отрасли ежегодно выпускают более 150 тысяч регулирующих приборов для автоматизации технологических процессов.
В последнее время в мировом приборостроении сформировалось новое, перспективное направление. Оно связано с использованием микропроцессоров. Именно они позволили существенно снизить габариты, вес и стоимость технических средств управления, повысить их универсальность, надежность и точность. Однако одновременно обострилась далеко не простая проблема программирования.
Созданный недавно нашими специалистами регулирующий контроллер - ремиконт, используя все преимущества микропроцессорной техники, вместе с тем не требует от тех, кто его применяет, каких-пибо навыков в области традиционных методов программирования. Открывается широкая возможность внедрения высокоэффективной микропроцессорной регулирующей техники в народное хозяйство.
Министр приборостроения, средств автоматизации и систем управления СССР доктор технических наук М.С.ШКАБАРДНЯ.
Опережающими темпами развивать производство... электронных устройств регулирования и телемеханики, исполнительных механизмов, приборов и датчиков систем комплексной автоматизации сложных технологических процессов, агрегатов, машин и оборудования.
Основные направления экономического и социального развития СССР на 1981-1985 годы и на период до 1990 года.
СТРАТЕГИЯ РЕГУЛЯТОРА
Сегодня в мире эксплуатируются миллионы промышленных регуляторов, а с учетом бытовой сферы счет идет на миллиарды.
Какие же задачи решает этот гигантский парк приборов? Если не говорить о небольшом числе специальных регуляторов, то ответ на поставленный вопрос будет достаточно простым: независимо от того, где установлен регулятор, он должен поддерживать заданную величину какого-либо параметра или изменять ее в соответствии с программой. Отсюда и происхождение термина "регулятор": латинское regulare означает "приводить в порядок".
Выполнять эту "хозяйственную" роль регулятор может, только если удается измерять интересующий нас параметр. Но одного этого недостаточно - надо еще иметь возможность воздействовать на этот параметр, то есть в зависимости от обстоятельств увеличивать его или уменьшать. Оба эти условия кратко формулируются так: объект должен быть наблюдаемым и управляемым.
Службу наблюдения несут различные датчики. Они преобразуют регулируемую величину, например, давление, разрежение, расход, уровень, температуру, в электрические или пневматические сигналы (в зависимости от того, используются ли электрические, или пневматические регуляторы).
Для выполнения второго условия, то есть для управления объектом, в состав регулятора включают исполнительный механизм. Он приводит в действие регулирующий орган, который непосредственно воздействует на процесс, скажем, меняет расход жидкости или газа, тягу, подводимую электрическую мощность, и т.п.
Датчик, исполнительный механизм и задающее устройство, с помощью которого устанавливается нужное значение параметра (постоянное или изменяющееся в соответствии с программой),- все это "периферия" регулятора. Она связывает его с объектом управления и оператором.
В центральной части регулятора, где сосредоточен его "интеллект", сигнал, поступающий от датчика, сравнивается с сигналом задающего устройства. Выделенный разностный сигнал - его называют "рассогласование" - подвергается обработке, с тем чтобы сформировать управляющее воздействие.

Пример системы автоматического регулирования.
В особенностях этой обработки, ее алгоритме и заключается своеобразие регулятора. Вопрос о том, каков должен быть алгоритм в каждом конкретном случае,- один из центральных в теории и практике автоматического управления. В некоторых случаях, когда требуемая точность регулирования невелика, например, при поддержании заданной температуры в холодильной камере, алгоритм этот достаточно прост: холодильный агрегат включается, если, допустим, температура поднимается выше 4oC, и выключается, когда она понизится до 2oC.
Однако при автоматизации сложного промышленного оборудования, такого, например, как ректификационные колонны или прокатные станы, управлять ими методом включения-выключения недопустимо: возникнут ударные нагрузки и оборудование быстро выйдет из строя, да и точность регулирования будет недостаточной. Как же должен вести себя регулятор в подобных случаях?
Чтобы составить себе представление об этой далеко не простой проблеме, обратимся к бытовому примеру.
Вы стоите под душем и манипулируете кранами холодной и горячей воды. Чтобы сделать ее теплее, открываете кран горячей воды, но если будете делать это слишком быстро, наверняка проскочите желаемую точку и придется срочно кран закрывать. Однако вскоре вода станет холоднее требуемой и кран надо будет вновь открывать. Жизненный опыт подсказывает, как избежать подобных температурных стрессов: воду следует прибавлять или убавлять небольшими порциями, каждый раз оценивая результат и медленно доводя температуру до желаемой. Это уже своеобразная стратегия регулятора, роль которого выполняет человек.
Что же мешает человеку мгновенно установить желаемую температуру воды? Ему, как и любому регулятору, противодействует запаздывание. Оно проявляется в том, что реакция на управляющее воздействие наступает не сразу: проходит какое-то время, пока интересующий нас параметр, то есть физическая величина, которая характеризует процесс (в примере с душем - температура воды), примет новое значение. Запаздывание может быть следствием, скажем, тепловой инерции (металлических труб) и транспортных перемещений (воды по трубам). Его характер и величина у различных объектов существенно разнятся: при регулировании, например, разрежения в топке котла оно не превышает 2-3 секунды, а при регулировании уровня воды в мелиоративных каналах достигает нескольких часов.
Автоматический регулятор должен учитывать все эти факторы и осуществлять такую стратегию управления - ее называют законом регулирования,- которая обеспечивала бы нормальное, в пределах допустимых отклонений, протекание технологического процесса.
ЗАКОН ЕСТЬ ЗАКОН
Важнейшие характеристики регулятора, которые определяют качество его работы,- это точность и быстродействие. Создавать для управления каждой системой, каждым процессом, каждой машиной, каждым агрегатом свой регулятор, осуществляющий свою стратегию управления, просто невозможно из соображений экономических: велики были бы затраты на конструирование и слишком часто приходилось бы заводам осваивать новую продукцию. Конечно, в ряде случаев, когда требуется особое качество регулирования, скажем, при управлении синхрофазотроном или стартовым комплексом космодрома, именно так и поступают.
Однако для массового промышленного применения - в энергетике, металлургической, химической, цементной, пищевой и многих других отраслях промышленности - важно не только качество регулирования, но и технико-экономические показатели приборов: их стоимость, габариты, вес, удобство и простота обслуживания, конструктивная унификация, надежность. Поэтому приходится искать компромисс между этими противоречивыми факторами.
Поиски такого компромисса привели к двум так называемым стандартным законам регулирования. О наиболее простом из них - позиционном (включено-выключено) - мы уже говорили. Второй, значительно более совершенный, связанный с непрерывным управлением, получил наименование пропорционально-интегрально-дифференциального (ПИД) закона.
Стратегия ПИД-регулятора, который содержит усилитель, интегратор и дифференциатор, выглядит следующим образом. Обнаружив на своем входе рассогласование, усилитель регулятора в первый момент перемещает исполнительный механизм быстро, но строго дозированно, компенсируя значительную часть рассогласования. Затем в работу вступает интегратор, который медленно, чтобы не проскочить желаемую точку, приближает регулируемый параметр к заданному значению. Дифференциатор, реагирующий на скорость изменения рассогласования, форсирует работу прибора в тех случаях, когда параметр начинает быстро отклоняться от требуемой величины.

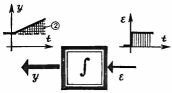

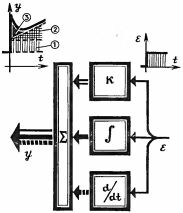
На схемах показано, как меняется выходной сигнал (y) при скачкообразном изменении сигнала рассогласования (e) для регуляторов: пропорционального, интегрального, пропорционально-интегрального и пропорционально-интегрально-дифференциального. 1, 2, 3 - соответственно пропорциональная, интегральная и дифференциальная составляющая сигнала y; K - усилитель; f - интегратор; d/dt - дифференциатор; Сигма - сумматор.
Успехи электроники позволили создать компактные и дешевые усилители, интеграторы и дифференциаторы, на базе которых в 60-х годах и начался массовый выпуск промышленных электронных ПИД-регуляторов. Был достигнут настолько удачный компромисс между качеством управления и сложностью, а одновременно и ценой приборов, что в мире автоматического регулирования ПИД-регулятор стал своеобразной "классикой".
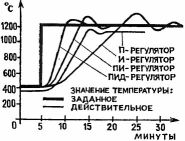
Поступила команда на изменение температуры в печи с 400 до 1200oC. Кривые показывают, как изменяется действительная температура при использовании регуляторов различного типа. Видно, что наиболее эффективен ПИД-регулятор.
ПИД-регулятор легко приспособить для автоматизации самых разнообразных процессов путем простой манипуляции тремя потенциометрами, изменяющими удельный вес П-, И-, Д- составляющих в законе регулирования (здесь можно проследить определенную аналогию с регулировкой радиоприемника, где с помощью трех потенциометров устанавливают желаемые громкость и тембр звучания по низким и высоким частотам).
ПО ВЗАИМНОМУ СОГЛАСОВАНИЮ
В таких объектах, как, например, электрические печи, мы имеем дело с одним регулируемым параметром и одним исполнительным механизмом. Подобные системы - их называют одноконтурными - хорошо управляются одним ПИД-регулятором. Ситуация, однако, осложняется, если приходится управлять многоконтурной системой.
Некоторое представление о возникающих здесь проблемах может дать небольшая вариация нашего "домашнего" примера. Если вы принимаете душ, а жена как раз в это время начинает мыть на кухне посуду и открывает кран горячей воды, у вас наступает резкое похолодание. Допустим, вы знакомы с ПИД-законом регулирования и, руководствуясь предписанной им стратегией, начинаете соответствующим образом вращать краны, ожидая быстрого эффекта. Однако эти действия меняют температуру воды не только у вас, но и на кухне, что вызывает там ответную реакцию. В результате двое людей, пытаясь добиться своих целей, будут долго вращать краны то горячей, то холодной воды и, возможно, так и не достигнут желаемых результатов, пока каким-либо образом не скоординируют свои действия.
Примерно так выглядят трудности двухконтурного регулирования. Можно представить, какие проблемы возникают, допустим, на тепловой электростанции, где необходимо одновременно управлять несколькими десятками параметров: температурой и давлением пара в котле, расходом воды и ее уровнем, разрежением в топке котла, содержанием кислорода в отходящих газах и т.д. И все эти параметры взаимосвязаны. Автономные ПИД регуляторы не в состоянии справиться со столь сложной задачей.
Как поступать в подобных ситуациях? Идти на дальнейшее усложнение закона регулирования малоперспективно: сложность и стоимость приборов будут расти гораздо быстрее, чем экономический эффект от повышения качества регулирования.
Специалистами по управлению был найден иной путь: сохранить ПИД-закон, но сделать действия ПИД-регуляторов согласованными. Для этого сигналы от датчиков подаются не только на "свои", но и (после ряда преобразований) на другие регуляторы, информируя их о процессах, происходящих в смежных взаимосвязанных контурах управления.
Сегодня для координации действий ПИД-регуляторов промышленность выпускает набор специальных так называемых функциональных приборов. Опыт автоматизации наиболее сложных с точки зрения управления промышленных объектов, таких, например, как мощные энергоблоки тепловых и атомных электростанций, показал, что для их регулирования требуется порядка 100-200 приборов. Это ПИД-регуляторы и функциональные приборы 10-15 наименований - сумматоры, дифференциаторы, фильтры, умножители, программаторы и т.д. Соединяясь по определенным правилам друг с другом и с датчиками, они образуют многосвязную систему автоматического регулирования, в которой все действия приборов оказываются согласованными.
АНАЛОГОВЫЕ ИЛИ ЦИФРОВЫЕ?
До середины 60-х годов в промышленных регуляторах использовался в основном аналоговый, то есть непрерывный, способ преобразования получаемой от датчиков информации в управляющее воздействие.
Аналоговые приборы хорошо себя зарекомендовали главным образом благодаря высокой "живучести": функции отдельно взятого устройства относительно просты и при отказе одного прибора, а выход из строя сразу группы приборов маловероятен, его временно в состоянии подменить оператор. Однако для автоматизации крупных объектов, сложных технологических процессов приходится устанавливать несколько сотен соединенных между собой аналоговых приборов, причем для их монтажа нужны панели длиной до полусотни метров.
Когда задачи автоматического регулирования заметно усложнились, возникла идея поручить их электронной цифровой вычислительной машине. В тот период многие специалисты (и неспециалисты) находились под влиянием "компьютерной эйфории": считалось, что вот-вот будет создан чуть ли не искусственный разум, ну, а проведение вычислений, необходимых для управления технологическими процессами,- задача для ЭВМ совсем уж простая.
Тем не менее при использовании ЭВМ для прямого управления технологическими процессами появились серьезные препятствия. И дело было не в недостаточной изученности предмета и не в том, что "интеллект" машин был слаб. Все свелось к проблеме надежности. Даже выполненные на интегральных микросхемах современные крупные ЭВМ (о машинах на лампах или транзисторах и говорить не приходится) содержат десятки тысяч элементов и раз в месяц, а то и чаще, хотя бы один из них отказывает. Если такое случается в вычислительном центре, работу прерывают, машину ремонтируют и задачу начинают решать сначала. Ситуация неприятная, но не критическая: дело все равно будет сделано, только несколько позже.
При автоматическом регулировании промышленных агрегатов все выглядит по-другому. Здесь ЭВМ должна работать в реальном времени. Технологический процесс течет непрерывно, и нельзя ждать, пока починят ЭВМ. Спасительная помощь оператора, который на период ремонта может подменить отказавшую аппаратуру, в данном случае неэффективна: попробуйте одновременно следить за сотней меняющихся взаимосвязанных параметров и воздействовать на такое же число исполнительных устройств! А ведь именно это пришлось бы делать на многих объектах при отказе ЭВМ. Поэтому вслед за ней приходится останавливать и оборудование, иначе авария, часто с катастрофическими последствиями, неизбежна.

Внешний вид традиционного ПИД-регулятора (кожух снят). Один ремиконт Р-100 заменяет до 64 таких приборов.
...
7/85
РЕМИКОНТ: РЕГУЛИРОВАНИЕ СТАНОВИТСЯ МИКРОПРОЦЕССОРНЫМ
Доктор технических наук, профессор Г.ИОРДАН, директор Государственного научно-исследовательского института теплоэнергетического приборостроения (НИИ теплоприбор), и кандидат технических наук В.ПЕВЗНЕР, заведующий лабораторией института
Двести лет назад была изобретена паровая машина. Это событие ознаменовало начало первой промышленной революции. Примечательно, что у ее истоков стоял и регулятор. С тех пор оснащение механизмов и агрегатов регуляторами стало характерной чертой развития техники. Различные по назначению, конструкции, принципу действия, размерам, они работают на суше, на воде и в воздухе, на производстве и в быту, используются поодиночке или объединяются в группы. Они участвуют в управлении работой тепловых и атомных электростанций, прокатных цехов и домен, газоперекачивающих станций и нефтеперерабатывающих заводов...
Без регуляторов немыслимо существование современной индустрии. Лишь предприятия нашей отрасли ежегодно выпускают более 150 тысяч регулирующих приборов для автоматизации технологических процессов.
В последнее время в мировом приборостроении сформировалось новое, перспективное направление. Оно связано с использованием микропроцессоров. Именно они позволили существенно снизить габариты, вес и стоимость технических средств управления, повысить их универсальность, надежность и точность. Однако одновременно обострилась далеко не простая проблема программирования.
Созданный недавно нашими специалистами регулирующий контроллер - ремиконт, используя все преимущества микропроцессорной техники, вместе с тем не требует от тех, кто его применяет, каких-пибо навыков в области традиционных методов программирования. Открывается широкая возможность внедрения высокоэффективной микропроцессорной регулирующей техники в народное хозяйство.
Министр приборостроения, средств автоматизации и систем управления СССР доктор технических наук М.С.ШКАБАРДНЯ.
Опережающими темпами развивать производство... электронных устройств регулирования и телемеханики, исполнительных механизмов, приборов и датчиков систем комплексной автоматизации сложных технологических процессов, агрегатов, машин и оборудования.
Основные направления экономического и социального развития СССР на 1981-1985 годы и на период до 1990 года.
СТРАТЕГИЯ РЕГУЛЯТОРА
Сегодня в мире эксплуатируются миллионы промышленных регуляторов, а с учетом бытовой сферы счет идет на миллиарды.
Какие же задачи решает этот гигантский парк приборов? Если не говорить о небольшом числе специальных регуляторов, то ответ на поставленный вопрос будет достаточно простым: независимо от того, где установлен регулятор, он должен поддерживать заданную величину какого-либо параметра или изменять ее в соответствии с программой. Отсюда и происхождение термина "регулятор": латинское regulare означает "приводить в порядок".
Выполнять эту "хозяйственную" роль регулятор может, только если удается измерять интересующий нас параметр. Но одного этого недостаточно - надо еще иметь возможность воздействовать на этот параметр, то есть в зависимости от обстоятельств увеличивать его или уменьшать. Оба эти условия кратко формулируются так: объект должен быть наблюдаемым и управляемым.
Службу наблюдения несут различные датчики. Они преобразуют регулируемую величину, например, давление, разрежение, расход, уровень, температуру, в электрические или пневматические сигналы (в зависимости от того, используются ли электрические, или пневматические регуляторы).
Для выполнения второго условия, то есть для управления объектом, в состав регулятора включают исполнительный механизм. Он приводит в действие регулирующий орган, который непосредственно воздействует на процесс, скажем, меняет расход жидкости или газа, тягу, подводимую электрическую мощность, и т.п.
Датчик, исполнительный механизм и задающее устройство, с помощью которого устанавливается нужное значение параметра (постоянное или изменяющееся в соответствии с программой),- все это "периферия" регулятора. Она связывает его с объектом управления и оператором.
В центральной части регулятора, где сосредоточен его "интеллект", сигнал, поступающий от датчика, сравнивается с сигналом задающего устройства. Выделенный разностный сигнал - его называют "рассогласование" - подвергается обработке, с тем чтобы сформировать управляющее воздействие.

Пример системы автоматического регулирования.
В особенностях этой обработки, ее алгоритме и заключается своеобразие регулятора. Вопрос о том, каков должен быть алгоритм в каждом конкретном случае,- один из центральных в теории и практике автоматического управления. В некоторых случаях, когда требуемая точность регулирования невелика, например, при поддержании заданной температуры в холодильной камере, алгоритм этот достаточно прост: холодильный агрегат включается, если, допустим, температура поднимается выше 4oC, и выключается, когда она понизится до 2oC.
Однако при автоматизации сложного промышленного оборудования, такого, например, как ректификационные колонны или прокатные станы, управлять ими методом включения-выключения недопустимо: возникнут ударные нагрузки и оборудование быстро выйдет из строя, да и точность регулирования будет недостаточной. Как же должен вести себя регулятор в подобных случаях?
Чтобы составить себе представление об этой далеко не простой проблеме, обратимся к бытовому примеру.
Вы стоите под душем и манипулируете кранами холодной и горячей воды. Чтобы сделать ее теплее, открываете кран горячей воды, но если будете делать это слишком быстро, наверняка проскочите желаемую точку и придется срочно кран закрывать. Однако вскоре вода станет холоднее требуемой и кран надо будет вновь открывать. Жизненный опыт подсказывает, как избежать подобных температурных стрессов: воду следует прибавлять или убавлять небольшими порциями, каждый раз оценивая результат и медленно доводя температуру до желаемой. Это уже своеобразная стратегия регулятора, роль которого выполняет человек.
Что же мешает человеку мгновенно установить желаемую температуру воды? Ему, как и любому регулятору, противодействует запаздывание. Оно проявляется в том, что реакция на управляющее воздействие наступает не сразу: проходит какое-то время, пока интересующий нас параметр, то есть физическая величина, которая характеризует процесс (в примере с душем - температура воды), примет новое значение. Запаздывание может быть следствием, скажем, тепловой инерции (металлических труб) и транспортных перемещений (воды по трубам). Его характер и величина у различных объектов существенно разнятся: при регулировании, например, разрежения в топке котла оно не превышает 2-3 секунды, а при регулировании уровня воды в мелиоративных каналах достигает нескольких часов.
Автоматический регулятор должен учитывать все эти факторы и осуществлять такую стратегию управления - ее называют законом регулирования,- которая обеспечивала бы нормальное, в пределах допустимых отклонений, протекание технологического процесса.
ЗАКОН ЕСТЬ ЗАКОН
Важнейшие характеристики регулятора, которые определяют качество его работы,- это точность и быстродействие. Создавать для управления каждой системой, каждым процессом, каждой машиной, каждым агрегатом свой регулятор, осуществляющий свою стратегию управления, просто невозможно из соображений экономических: велики были бы затраты на конструирование и слишком часто приходилось бы заводам осваивать новую продукцию. Конечно, в ряде случаев, когда требуется особое качество регулирования, скажем, при управлении синхрофазотроном или стартовым комплексом космодрома, именно так и поступают.
Однако для массового промышленного применения - в энергетике, металлургической, химической, цементной, пищевой и многих других отраслях промышленности - важно не только качество регулирования, но и технико-экономические показатели приборов: их стоимость, габариты, вес, удобство и простота обслуживания, конструктивная унификация, надежность. Поэтому приходится искать компромисс между этими противоречивыми факторами.
Поиски такого компромисса привели к двум так называемым стандартным законам регулирования. О наиболее простом из них - позиционном (включено-выключено) - мы уже говорили. Второй, значительно более совершенный, связанный с непрерывным управлением, получил наименование пропорционально-интегрально-дифференциального (ПИД) закона.
Стратегия ПИД-регулятора, который содержит усилитель, интегратор и дифференциатор, выглядит следующим образом. Обнаружив на своем входе рассогласование, усилитель регулятора в первый момент перемещает исполнительный механизм быстро, но строго дозированно, компенсируя значительную часть рассогласования. Затем в работу вступает интегратор, который медленно, чтобы не проскочить желаемую точку, приближает регулируемый параметр к заданному значению. Дифференциатор, реагирующий на скорость изменения рассогласования, форсирует работу прибора в тех случаях, когда параметр начинает быстро отклоняться от требуемой величины.




На схемах показано, как меняется выходной сигнал (y) при скачкообразном изменении сигнала рассогласования (e) для регуляторов: пропорционального, интегрального, пропорционально-интегрального и пропорционально-интегрально-дифференциального. 1, 2, 3 - соответственно пропорциональная, интегральная и дифференциальная составляющая сигнала y; K - усилитель; f - интегратор; d/dt - дифференциатор; Сигма - сумматор.
Успехи электроники позволили создать компактные и дешевые усилители, интеграторы и дифференциаторы, на базе которых в 60-х годах и начался массовый выпуск промышленных электронных ПИД-регуляторов. Был достигнут настолько удачный компромисс между качеством управления и сложностью, а одновременно и ценой приборов, что в мире автоматического регулирования ПИД-регулятор стал своеобразной "классикой".

Поступила команда на изменение температуры в печи с 400 до 1200oC. Кривые показывают, как изменяется действительная температура при использовании регуляторов различного типа. Видно, что наиболее эффективен ПИД-регулятор.
ПИД-регулятор легко приспособить для автоматизации самых разнообразных процессов путем простой манипуляции тремя потенциометрами, изменяющими удельный вес П-, И-, Д- составляющих в законе регулирования (здесь можно проследить определенную аналогию с регулировкой радиоприемника, где с помощью трех потенциометров устанавливают желаемые громкость и тембр звучания по низким и высоким частотам).
ПО ВЗАИМНОМУ СОГЛАСОВАНИЮ
В таких объектах, как, например, электрические печи, мы имеем дело с одним регулируемым параметром и одним исполнительным механизмом. Подобные системы - их называют одноконтурными - хорошо управляются одним ПИД-регулятором. Ситуация, однако, осложняется, если приходится управлять многоконтурной системой.
Некоторое представление о возникающих здесь проблемах может дать небольшая вариация нашего "домашнего" примера. Если вы принимаете душ, а жена как раз в это время начинает мыть на кухне посуду и открывает кран горячей воды, у вас наступает резкое похолодание. Допустим, вы знакомы с ПИД-законом регулирования и, руководствуясь предписанной им стратегией, начинаете соответствующим образом вращать краны, ожидая быстрого эффекта. Однако эти действия меняют температуру воды не только у вас, но и на кухне, что вызывает там ответную реакцию. В результате двое людей, пытаясь добиться своих целей, будут долго вращать краны то горячей, то холодной воды и, возможно, так и не достигнут желаемых результатов, пока каким-либо образом не скоординируют свои действия.
Примерно так выглядят трудности двухконтурного регулирования. Можно представить, какие проблемы возникают, допустим, на тепловой электростанции, где необходимо одновременно управлять несколькими десятками параметров: температурой и давлением пара в котле, расходом воды и ее уровнем, разрежением в топке котла, содержанием кислорода в отходящих газах и т.д. И все эти параметры взаимосвязаны. Автономные ПИД регуляторы не в состоянии справиться со столь сложной задачей.
Как поступать в подобных ситуациях? Идти на дальнейшее усложнение закона регулирования малоперспективно: сложность и стоимость приборов будут расти гораздо быстрее, чем экономический эффект от повышения качества регулирования.
Специалистами по управлению был найден иной путь: сохранить ПИД-закон, но сделать действия ПИД-регуляторов согласованными. Для этого сигналы от датчиков подаются не только на "свои", но и (после ряда преобразований) на другие регуляторы, информируя их о процессах, происходящих в смежных взаимосвязанных контурах управления.
Сегодня для координации действий ПИД-регуляторов промышленность выпускает набор специальных так называемых функциональных приборов. Опыт автоматизации наиболее сложных с точки зрения управления промышленных объектов, таких, например, как мощные энергоблоки тепловых и атомных электростанций, показал, что для их регулирования требуется порядка 100-200 приборов. Это ПИД-регуляторы и функциональные приборы 10-15 наименований - сумматоры, дифференциаторы, фильтры, умножители, программаторы и т.д. Соединяясь по определенным правилам друг с другом и с датчиками, они образуют многосвязную систему автоматического регулирования, в которой все действия приборов оказываются согласованными.
АНАЛОГОВЫЕ ИЛИ ЦИФРОВЫЕ?
До середины 60-х годов в промышленных регуляторах использовался в основном аналоговый, то есть непрерывный, способ преобразования получаемой от датчиков информации в управляющее воздействие.
Аналоговые приборы хорошо себя зарекомендовали главным образом благодаря высокой "живучести": функции отдельно взятого устройства относительно просты и при отказе одного прибора, а выход из строя сразу группы приборов маловероятен, его временно в состоянии подменить оператор. Однако для автоматизации крупных объектов, сложных технологических процессов приходится устанавливать несколько сотен соединенных между собой аналоговых приборов, причем для их монтажа нужны панели длиной до полусотни метров.
Когда задачи автоматического регулирования заметно усложнились, возникла идея поручить их электронной цифровой вычислительной машине. В тот период многие специалисты (и неспециалисты) находились под влиянием "компьютерной эйфории": считалось, что вот-вот будет создан чуть ли не искусственный разум, ну, а проведение вычислений, необходимых для управления технологическими процессами,- задача для ЭВМ совсем уж простая.
Тем не менее при использовании ЭВМ для прямого управления технологическими процессами появились серьезные препятствия. И дело было не в недостаточной изученности предмета и не в том, что "интеллект" машин был слаб. Все свелось к проблеме надежности. Даже выполненные на интегральных микросхемах современные крупные ЭВМ (о машинах на лампах или транзисторах и говорить не приходится) содержат десятки тысяч элементов и раз в месяц, а то и чаще, хотя бы один из них отказывает. Если такое случается в вычислительном центре, работу прерывают, машину ремонтируют и задачу начинают решать сначала. Ситуация неприятная, но не критическая: дело все равно будет сделано, только несколько позже.
При автоматическом регулировании промышленных агрегатов все выглядит по-другому. Здесь ЭВМ должна работать в реальном времени. Технологический процесс течет непрерывно, и нельзя ждать, пока починят ЭВМ. Спасительная помощь оператора, который на период ремонта может подменить отказавшую аппаратуру, в данном случае неэффективна: попробуйте одновременно следить за сотней меняющихся взаимосвязанных параметров и воздействовать на такое же число исполнительных устройств! А ведь именно это пришлось бы делать на многих объектах при отказе ЭВМ. Поэтому вслед за ней приходится останавливать и оборудование, иначе авария, часто с катастрофическими последствиями, неизбежна.

Внешний вид традиционного ПИД-регулятора (кожух снят). Один ремиконт Р-100 заменяет до 64 таких приборов.
...

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
...
РЕМИКОНТЫ
Древние говорили: non multa, sed multum - немного, но многое. Это изречение могло бы стать девизом современной электроники.
Действительно, всего 37 лет назад был изобретен транзистор, а сегодня серийно производятся микросхемы, содержащие на пластине кремния размером с ноготь десятки и даже сотни тысяч транзисторов. Столь высокая степень интеграции позволила в одной микросхеме, получившей название "микропроцессор", разместить ядро вычислительной машины.
Специалисты по автоматизации быстро поняли, что микропроцессор - это как раз то, что позволит им объединить преимущества аналоговой техники и ЭВМ. Поскольку микропроцессоры малы по размерам и дешевы, можно автоматизированный агрегат оснастить не одним, а несколькими десятками (а то и сотнями) компьютерных устройств, разделив между ними функции и создав так называемую распределенную систему управления. Ее живучесть будет столь же высока, как и у аналоговых систем, а сосредоточенный в относительно малом объеме "интеллект" позволит резко сократить габариты приборов и снизить их стоимость.
Однако, прежде чем на практике реализовать столь заманчивую идею, необходимо было решить один принципиальный вопрос, связанный с программированием.
Английский философ Локк называл душу новорожденного tabula rasa - чистый лист. Это же можно сказать и о микропроцессорной ЭВМ, или, как теперь принято говорить, микро-ЭВМ. Как и любая другая вычислительная машина, она в состоянии выполнить полезную работу лишь после того, как будет составлена и введена в нее программа. Сделать это не так просто. Недаром этот род занятий сравнивают с искусством.
Программировать ЭВМ (или микро-ЭВМ) непосредственно на объекте управления - задача трудновыполнимая. Обычно для этих целей используется посредническая организация, которая ведет программирование у себя, "на дому", и затем передает программы производственному персоналу. Но что делать, если во время наладки на объекте или после пуска оборудования обнаружится, что в схему автоматизации нужно внести изменения: добавить каналы регулирования, скорректировать настройку регуляторов или установить между ними новые связи?
В НИИтеплоприборе начали искать пути, которые избавили бы потребителей промышленных регуляторов от "тирании" программирования.
Его учеными в содружестве с инженерами чебоксарского Специального конструкторского бюро систем промышленной автоматики (СКБ СПА) удалось в 1982 году создать первое в стране промышленное микропроцессорное устройство для автоматического регулирования технологических процессов. Авторы разработки назвали его "ремиконт" - сокращение слов "регулирующий микропроцессорный контроллер".

Регулирующий микропроцессорный контроллер - ремиконт Р-100; слева - пульт оператора.
Что же представляет собой ремиконт? Когда речь идет о программируемом изделии (а ремнконт принадлежит к этому классу устройств), нужно, с одной стороны, описать состав н назначение физических элементов, из которых состоит изделие, с другой - охарактеризовать возможности, средства и методы его программирования. Как говорят специалисты по компьютерам, надо показать твердый и мягкий товар.
"Твердая" часть ремиконта - это прежде всего процессор, выполненный на базе серийно выпускаемого электронной промышленностью 8-разрядного микропроцессора КР580ИК80А, а также память для хранения программ и данных, построенная на больших (с точки зрения числа элементов) интегральных схемах. Процессор и память дополнены устройствами связи с объектом управления - с датчиками и исполнительными механизмами; специализированный пульт связывает оператора с ремиконтом.

Один из модулей ремиконта; хорошо виден самый крупный элемент на плате - микропроцессор.
Главное, к чему стремились при создании "мягкой" части ремиконта - его программного обеспечения,- это устранить трудности программирования, которые испытывает каждый, кому приходится общаться с Э8М. Здесь разработчики как раз и учли, что задачу автоматического регулирования большинства технологических процессов в состоянии решить набор из ПИД-регуляторов и ограниченного (по номенклатуре) числа функциональных приборов. Значит, надо создать программы, моделирующие этот набор, то есть реализующие алгоритмы работы соответствующих приборов. Если поместить эти программы в память микропроцессорного регулирующего устройства и к тому же сделать так, чтобы оператор смог извлекать готовые алгоритмы управления и желаемым образом их соединять, то проблема программирования будет решена.
Это и удалось сделать создателям ремиконта. По существу, все трудности программирования они взяли на себя, создав программный продукт, превращающий аппаратуру компьютерного по своей природе ремиконта в привычные и понятные пользователю алгоритмы управления. Наладчикам средств автоматики теперь нет никакой необходимости взаимодействовать с процессором и памятью ЭВМ - элементами, которые сами по себе не могут управлять объектом. Он имеет дело лишь с алгоритмами, которые формируются в результате совместной работы процессора и памяти. Именно они и выполняют роль ПИД-регуляторов, интеграторов, сумматоров, таймеров, переключателей и других приборов, необходимых для построения системы автоматического регулирования. Все эти алгоритмы систематизированы и под своими номерами помещены в программную библиотеку.
Есть в ремиконте и "корпуса" - оболочки приборов, называемые алгоритмическими блоками. Как и начинки корпусов - алгоритмы, эти блоки реально (физически) не существуют, а опять-таки формируются соответствующими программами. А чтобы сформировать систему управления, в распоряжении оператора имеются программные средства соединения приборов в нужной последовательности, а также настройки их с учетом специфики конкретного технологического процесса.
Таким образом, в исходном состоянии в ремиконте приборы управления находятся в виде заготовок: начинок и отделенных от них оболочек.
8се программы, посредством которых создаются библиотека алгоритмов и алгоритмические блоки, "зашивают" в память ремиконта на заводе-изготовителе. Такой универсальный прибор готов к решению практически любой задачи, связанной с автоматическим регулированием разнообразных технологических процессов.
ПРОГРАММИРОВАНИЕ БЕЗ ПРОГРАММИСТОВ
Как же приспособить ремиконт для автоматизации конкретного процесса? Для этого к нему подключают датчики и исполнительные механизмы и тем самым связывают его с управляемым агрегатом. Затем подсоединяют специальный пульт; по внешнему виду он напоминает настольный микрокалькулятор, но отличается от него специфическими названиями клавиш, такими, как, например, "алгоритм", "конфигурация", "коэффициенты".
Теперь, пользуясь только этим пультом, можно начинать "сборку" системы регулирования.
Оператор сначала набирает номер соответствующего алгоритмического блока - корпуса будущего прибора, переводит пульт в режим "алгоритм", после чего набирает номер, под которым в библиотеке хранится требуемый алгоритм. В процессе такой манипуляции ранее пустой блок "начиняется" одним из алгоритмов и в функциональном отношении становится традиционным аналоговым прибором.
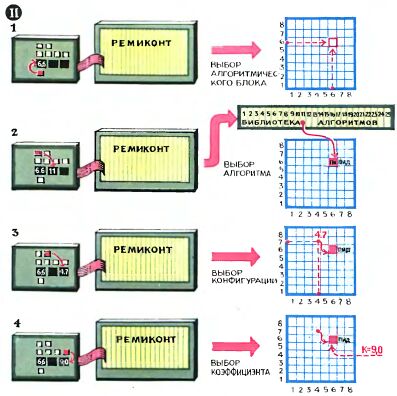
Технологическое программирование: 1, 2, 3 и 4 - последовательные операции формирования системы регулирования с помощью пульта.
Чтобы включить алгоритмический блок в систему управления, не нужны монтажники: достаточно нажать на пульте клавишу "конфигурация" и набрать номер цепи, с которой надо произвести соединение. В процессе такого беспроволочного монтажа формируется система автоматического регулирования, конфигурация которой соответствует особенностям данного объекта управления.
Последнее, что нужно сделать, это настроить приборы - алгоритмические блоки - для решения конкретной задачи. Напомним, что, скажем, в случае ПИД-алгоритма - это выбор соотношения между П-, И-, н Д-составляющими закона регулирования. Чтобы выполнить настройку, не нужны потенциометры - достаточно перевести пульт в режим "коэффициенты", выбрать по номеру требуемый коэффициент и по цифровому индикатору установить его значение.
Путем такого технологического программирования наладчик, двигаясь от одного алгоритмического блока к другому, создает нужное число ПИД-регуляторов, дополняет их координирующими функциональными преобразователями, формирует требуемую конфигурацию системы и настраивает ее параметры. Теперь ремиконт готов взять на себя автоматическое регулирование данного процесса.
Благодаря дружественному помогающему в работе программному обеспечению, все, кому приходится иметь с ремиконтом дело, избавлены от необходимости вникать в особенности его устройства. Более того, не нужно изучать и сами довольно сложные программы, зашитые в память,- достаточно лишь знать несколько простых правил манипулирования небольшим числом клавиш. А это под силу любому, кто был связан с традиционными регуляторами и незнаком даже с основами вычислительной техники. Сборка системы регулирования происходит непосредственно на объекте и занимает несколько часов, в то время как раньше на это уходили месяцы.
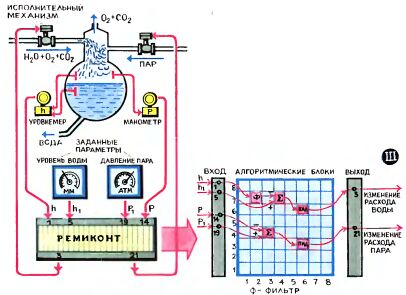
Автоматическое регулирование деаэратора - аппарата, используемого на тепловых электростанциях для очистки воды от растворенных в ней газов. Для этого в деаэраторе необходимо поддерживать заданные значения уровня воды и давления пара. Показана "собранная" с пульта алгоритмическая структура ремиконта для выполнения такой задачи.
Все, что запрограммировал оператор, запоминается и сохраняется в памяти ремиконта. Любые изменения в стратегии регулирования или расширение системы выполняются так же просто, как и ее первоначальная сборка.
А как быть, если в результате изменений в технологическом процессе, например, при смене вида топлива на тепловой электростанции или величины ее нагрузки требуется перейти на другую структуру системы регулирования, но перерывы в работе оборудования, даже кратковременные, недопустимы?
Разработчики позаботились о том, чтобы
ремнконт справлялся и с подобными ситуациями. Для этого лишь требуется прн технологическом программировании предусмотреть все необходимые конфигурации системы регулирования и переходы между ними. Поступает, скажем, команда оператора: в несколько раз увеличить мощность, вырабатываемую энергоблоком. Ремиконт, автоматически изменяя свою структуру и параметры настройки, плавно переведет паровой котел и турбину на новую нагрузку, после чего продолжит стабилизацию технологического процесса.

Автоматическое регулирование печи для нагрева металла. Задача состоит в поддержании требуемой температуры и оптимального соотношения расходов сжигаемого газа и воздуха. В зависимости от марки нагреваемого металла значение заданной температуры должно меняться с помощью переключателя. Показана сформированная с пульта структура ремиконта который решает эти задачи. Оператор печи имеет возможность по прибору, контролирующему рассогласование, следить за изменением температуры. Если она превысит максимально допустимую величину, ремиконт сообщит об этом световым сигналом.
Поскольку ремиконт решает ответственные задачи управления, нужно было подумать также о том, что же произойдет, если в нем возникнут неисправности. Важнейшее условие в такой ситуации - добиться, чтобы ремиконт не выдавал ложных команд. Ведь если такое случится, управляемый агрегат скорее всего придется останавливать, а это, как правило, связано с материальными убытками. Неправильному действию ремнконта, безусловно, следует предпочесть его бездействие. Но н оно не должно быть длительным - в противном случае слишком большая нагрузка ляжет на оператора, который не в состоянии долго и с нужной точностью поддерживать оставшиеся без присмотра ремиконта технологические параметры.
Чтобы минимизировать последствия неполадок, ремиконт наделен способностью самостоятельно ставить себе диагноз. Почувствовав "недомогание", он действует следующим образом: во-первых, перестает изменять (как говорят, замораживает) положение исполнительных механизмов и, во-вторых, с помощью специальной сигнализации не только оповещает оператора о неисправности, но и одновременно сообщает, какой узел в нем отказал. Благодаря такой самодиагностике работу ремиконта можно очень быстро восстановить путем простой замены неисправного узла. А в тех случаях, когда процесс управления нельзя задерживать даже на короткое время, сигнал об отказе можно использовать для автоматического включения другого ремиконта, работающего в "горячем" резерве.
ПЕРВЫЕ ПРИМЕНЕНИЯ И ПЕРСПЕКТИВЫ
Выпуск ремиконтов начало примерно год назад промышленное объединение "Промприбор" (г.Чебоксары). У первой в семье ремиконтов модели (Р-100) - 64 алгоритмических блока, а библиотека насчитывает 25 наименований алгоритмов. Любой из них можно поместить в какой угодно блок, входы которого могут соединяться с выходами любых других блоков или с любыми входами ремиконта, к которым подключаются датчики. Один н тот же алгоритм можно использовать многократно, помещая в различные блоки. Столь разнообразные возможности позволяют реализовать огромное число сочетаний различных функций и параметров управления. Один такой ремиконт заменяет в среднем 25-30, а в отдельных случаях до 100 аналоговых приборов.

Испытания ремиконта в одной из лабораторий НИИтеплоприбора.
Ремиконты уже нашли применение на таких промышленных объектах, как, например, крупнейшая в Европе машина непрерывной разливки стали Ново-Липецкого металлургического комбината, энергоблок мощностью 300тыс.кВт на Литовской ГРЭС, нагревательные печи прокатного стана 350/250 металлургического завода "Электросталь", закалочный агрегат московского завода "Серп и Молот", на ряде предприятий по производству белково-витаминных концентратов. На каждом из этих столь непохожих друг на друга объектов ремиконт был быстро и просто приспособлен для решения конкретных задач автоматизации. Нажаты несколько клавиш на пульте ремиконта - и стальная многометровая полоса, выходящая из кристаллизатора машины непрерывного литья, получает нужный режим охлаждения, при этом на каждом ее участке устанавливается своя оптимальная температура. Выбраны другой набор алгоритмов ремиконта, другая их конфигурация и настройка - и полторы сотни различных технологических параметров энергоблока жестко стабилизируются на требуемых значениях...
В течение двенадцатой пятилетки выпуск ремиконтов по сравнению с производством аналоговых промышленных регуляторов будет расти опережающими темпами. Микропроцессорные приборы станут регулировать сотни тысяч технологических параметров. Предполагается, что за счет меньшей стоимости, габаритов и веса ремиконтов, повышения точности, сокращения времени ввода в эксплуатацию экономический эффект от их внедрения составит за пятилетку десятки миллионов рублей.
Заглянем теперь несколько дальше и попробуем в самых общих чертах представить, какой будет техника регулирования в ближайшие 10-15 лет.
С большой вероятностью можно предположить, что практически все промышленные регуляторы будут выполняться на базе микропроцессоров. Повышение степени интеграции микросхем приведет к тому, что в управлении цифровые методы обработки информации повсеместно будут теснить аналоговые.
Но регуляторы неизбежно должны сосуществовать с аналоговым миром технологических процессов. Поэтому центральной проблемой станут не столько средства обработки информации, сколько средства сопряжения регуляторов с объектом автоматизации. Уже сейчас в ремиконте Р-100 этим занято более двух третей (по объему) аппаратуры. А если учесть, что аналоговые компоненты совершенствуются значительно медленнее цифровых, то при сохранении существующих методов сопряжения подобная диспропорция будет усугубляться.
Выход из затруднения в общем плане выглядит следующим образом. Если говорить об информации, идущей от датчика через регулятор к исполнительному механизму, то ее следует преобразовывать из аналоговой в цифровую форму как можно раньше, а из цифровой в аналоговую - как можно позже. Благодаря этому не только удастся сократить размеры аппаратуры и сделать ее более "интеллектуальной", но и заменить многие тысячи километров кабеля, идущего к датчикам и исполнительным механизмам, на компактную цифровую сеть. Подключаясь к ней, любой регулятор сможет связываться с любым датчиком, любым исполнительным механизмом, другими регуляторами или другими элементами системы управления. Возможно, что к концу 90-х годов появятся системы регулирования с беспроводной связью; это будет важное техническое достижение, которое позволит вообще избавиться от кабельных соединений.
Другое направление, где можно ждать больших изменений, связано со способом общения человека с регулятором.
Ремиконту Р-100, как и регуляторам предыдущих поколений, все команды отдаются руками - с помощью клавиатуры. Конечно, удобнее было бы приказывать голосом.
Уже разработаны микросхемы речевых анализаторов и синтезаторов. Когда они станут более компактными и будут легко сопрягаться с микропроцессором, а возможно, даже разместятся с ним на одном кристалле, такой метод общения войдет в обиход промышленной автоматики.
Однако все это в будущем. А пока в нашей промышленности накапливается опыт применения ремиконтов первого поколения. Совершенствуется их аппаратура, пополняется библиотека алгоритмов.
В лабораториях и конструкторских бюро создаются новые модели микропроцессорных регуляторов.
РЕМИКОНТЫ
Древние говорили: non multa, sed multum - немного, но многое. Это изречение могло бы стать девизом современной электроники.
Действительно, всего 37 лет назад был изобретен транзистор, а сегодня серийно производятся микросхемы, содержащие на пластине кремния размером с ноготь десятки и даже сотни тысяч транзисторов. Столь высокая степень интеграции позволила в одной микросхеме, получившей название "микропроцессор", разместить ядро вычислительной машины.
Специалисты по автоматизации быстро поняли, что микропроцессор - это как раз то, что позволит им объединить преимущества аналоговой техники и ЭВМ. Поскольку микропроцессоры малы по размерам и дешевы, можно автоматизированный агрегат оснастить не одним, а несколькими десятками (а то и сотнями) компьютерных устройств, разделив между ними функции и создав так называемую распределенную систему управления. Ее живучесть будет столь же высока, как и у аналоговых систем, а сосредоточенный в относительно малом объеме "интеллект" позволит резко сократить габариты приборов и снизить их стоимость.
Однако, прежде чем на практике реализовать столь заманчивую идею, необходимо было решить один принципиальный вопрос, связанный с программированием.
Английский философ Локк называл душу новорожденного tabula rasa - чистый лист. Это же можно сказать и о микропроцессорной ЭВМ, или, как теперь принято говорить, микро-ЭВМ. Как и любая другая вычислительная машина, она в состоянии выполнить полезную работу лишь после того, как будет составлена и введена в нее программа. Сделать это не так просто. Недаром этот род занятий сравнивают с искусством.
Программировать ЭВМ (или микро-ЭВМ) непосредственно на объекте управления - задача трудновыполнимая. Обычно для этих целей используется посредническая организация, которая ведет программирование у себя, "на дому", и затем передает программы производственному персоналу. Но что делать, если во время наладки на объекте или после пуска оборудования обнаружится, что в схему автоматизации нужно внести изменения: добавить каналы регулирования, скорректировать настройку регуляторов или установить между ними новые связи?
В НИИтеплоприборе начали искать пути, которые избавили бы потребителей промышленных регуляторов от "тирании" программирования.
Его учеными в содружестве с инженерами чебоксарского Специального конструкторского бюро систем промышленной автоматики (СКБ СПА) удалось в 1982 году создать первое в стране промышленное микропроцессорное устройство для автоматического регулирования технологических процессов. Авторы разработки назвали его "ремиконт" - сокращение слов "регулирующий микропроцессорный контроллер".

Регулирующий микропроцессорный контроллер - ремиконт Р-100; слева - пульт оператора.
Что же представляет собой ремиконт? Когда речь идет о программируемом изделии (а ремнконт принадлежит к этому классу устройств), нужно, с одной стороны, описать состав н назначение физических элементов, из которых состоит изделие, с другой - охарактеризовать возможности, средства и методы его программирования. Как говорят специалисты по компьютерам, надо показать твердый и мягкий товар.
"Твердая" часть ремиконта - это прежде всего процессор, выполненный на базе серийно выпускаемого электронной промышленностью 8-разрядного микропроцессора КР580ИК80А, а также память для хранения программ и данных, построенная на больших (с точки зрения числа элементов) интегральных схемах. Процессор и память дополнены устройствами связи с объектом управления - с датчиками и исполнительными механизмами; специализированный пульт связывает оператора с ремиконтом.

Один из модулей ремиконта; хорошо виден самый крупный элемент на плате - микропроцессор.
Главное, к чему стремились при создании "мягкой" части ремиконта - его программного обеспечения,- это устранить трудности программирования, которые испытывает каждый, кому приходится общаться с Э8М. Здесь разработчики как раз и учли, что задачу автоматического регулирования большинства технологических процессов в состоянии решить набор из ПИД-регуляторов и ограниченного (по номенклатуре) числа функциональных приборов. Значит, надо создать программы, моделирующие этот набор, то есть реализующие алгоритмы работы соответствующих приборов. Если поместить эти программы в память микропроцессорного регулирующего устройства и к тому же сделать так, чтобы оператор смог извлекать готовые алгоритмы управления и желаемым образом их соединять, то проблема программирования будет решена.
Это и удалось сделать создателям ремиконта. По существу, все трудности программирования они взяли на себя, создав программный продукт, превращающий аппаратуру компьютерного по своей природе ремиконта в привычные и понятные пользователю алгоритмы управления. Наладчикам средств автоматики теперь нет никакой необходимости взаимодействовать с процессором и памятью ЭВМ - элементами, которые сами по себе не могут управлять объектом. Он имеет дело лишь с алгоритмами, которые формируются в результате совместной работы процессора и памяти. Именно они и выполняют роль ПИД-регуляторов, интеграторов, сумматоров, таймеров, переключателей и других приборов, необходимых для построения системы автоматического регулирования. Все эти алгоритмы систематизированы и под своими номерами помещены в программную библиотеку.
Есть в ремиконте и "корпуса" - оболочки приборов, называемые алгоритмическими блоками. Как и начинки корпусов - алгоритмы, эти блоки реально (физически) не существуют, а опять-таки формируются соответствующими программами. А чтобы сформировать систему управления, в распоряжении оператора имеются программные средства соединения приборов в нужной последовательности, а также настройки их с учетом специфики конкретного технологического процесса.
Таким образом, в исходном состоянии в ремиконте приборы управления находятся в виде заготовок: начинок и отделенных от них оболочек.
8се программы, посредством которых создаются библиотека алгоритмов и алгоритмические блоки, "зашивают" в память ремиконта на заводе-изготовителе. Такой универсальный прибор готов к решению практически любой задачи, связанной с автоматическим регулированием разнообразных технологических процессов.
ПРОГРАММИРОВАНИЕ БЕЗ ПРОГРАММИСТОВ
Как же приспособить ремиконт для автоматизации конкретного процесса? Для этого к нему подключают датчики и исполнительные механизмы и тем самым связывают его с управляемым агрегатом. Затем подсоединяют специальный пульт; по внешнему виду он напоминает настольный микрокалькулятор, но отличается от него специфическими названиями клавиш, такими, как, например, "алгоритм", "конфигурация", "коэффициенты".
Теперь, пользуясь только этим пультом, можно начинать "сборку" системы регулирования.
Оператор сначала набирает номер соответствующего алгоритмического блока - корпуса будущего прибора, переводит пульт в режим "алгоритм", после чего набирает номер, под которым в библиотеке хранится требуемый алгоритм. В процессе такой манипуляции ранее пустой блок "начиняется" одним из алгоритмов и в функциональном отношении становится традиционным аналоговым прибором.

Технологическое программирование: 1, 2, 3 и 4 - последовательные операции формирования системы регулирования с помощью пульта.
Чтобы включить алгоритмический блок в систему управления, не нужны монтажники: достаточно нажать на пульте клавишу "конфигурация" и набрать номер цепи, с которой надо произвести соединение. В процессе такого беспроволочного монтажа формируется система автоматического регулирования, конфигурация которой соответствует особенностям данного объекта управления.
Последнее, что нужно сделать, это настроить приборы - алгоритмические блоки - для решения конкретной задачи. Напомним, что, скажем, в случае ПИД-алгоритма - это выбор соотношения между П-, И-, н Д-составляющими закона регулирования. Чтобы выполнить настройку, не нужны потенциометры - достаточно перевести пульт в режим "коэффициенты", выбрать по номеру требуемый коэффициент и по цифровому индикатору установить его значение.
Путем такого технологического программирования наладчик, двигаясь от одного алгоритмического блока к другому, создает нужное число ПИД-регуляторов, дополняет их координирующими функциональными преобразователями, формирует требуемую конфигурацию системы и настраивает ее параметры. Теперь ремиконт готов взять на себя автоматическое регулирование данного процесса.
Благодаря дружественному помогающему в работе программному обеспечению, все, кому приходится иметь с ремиконтом дело, избавлены от необходимости вникать в особенности его устройства. Более того, не нужно изучать и сами довольно сложные программы, зашитые в память,- достаточно лишь знать несколько простых правил манипулирования небольшим числом клавиш. А это под силу любому, кто был связан с традиционными регуляторами и незнаком даже с основами вычислительной техники. Сборка системы регулирования происходит непосредственно на объекте и занимает несколько часов, в то время как раньше на это уходили месяцы.

Автоматическое регулирование деаэратора - аппарата, используемого на тепловых электростанциях для очистки воды от растворенных в ней газов. Для этого в деаэраторе необходимо поддерживать заданные значения уровня воды и давления пара. Показана "собранная" с пульта алгоритмическая структура ремиконта для выполнения такой задачи.
Все, что запрограммировал оператор, запоминается и сохраняется в памяти ремиконта. Любые изменения в стратегии регулирования или расширение системы выполняются так же просто, как и ее первоначальная сборка.
А как быть, если в результате изменений в технологическом процессе, например, при смене вида топлива на тепловой электростанции или величины ее нагрузки требуется перейти на другую структуру системы регулирования, но перерывы в работе оборудования, даже кратковременные, недопустимы?
Разработчики позаботились о том, чтобы
ремнконт справлялся и с подобными ситуациями. Для этого лишь требуется прн технологическом программировании предусмотреть все необходимые конфигурации системы регулирования и переходы между ними. Поступает, скажем, команда оператора: в несколько раз увеличить мощность, вырабатываемую энергоблоком. Ремиконт, автоматически изменяя свою структуру и параметры настройки, плавно переведет паровой котел и турбину на новую нагрузку, после чего продолжит стабилизацию технологического процесса.

Автоматическое регулирование печи для нагрева металла. Задача состоит в поддержании требуемой температуры и оптимального соотношения расходов сжигаемого газа и воздуха. В зависимости от марки нагреваемого металла значение заданной температуры должно меняться с помощью переключателя. Показана сформированная с пульта структура ремиконта который решает эти задачи. Оператор печи имеет возможность по прибору, контролирующему рассогласование, следить за изменением температуры. Если она превысит максимально допустимую величину, ремиконт сообщит об этом световым сигналом.
Поскольку ремиконт решает ответственные задачи управления, нужно было подумать также о том, что же произойдет, если в нем возникнут неисправности. Важнейшее условие в такой ситуации - добиться, чтобы ремиконт не выдавал ложных команд. Ведь если такое случится, управляемый агрегат скорее всего придется останавливать, а это, как правило, связано с материальными убытками. Неправильному действию ремнконта, безусловно, следует предпочесть его бездействие. Но н оно не должно быть длительным - в противном случае слишком большая нагрузка ляжет на оператора, который не в состоянии долго и с нужной точностью поддерживать оставшиеся без присмотра ремиконта технологические параметры.
Чтобы минимизировать последствия неполадок, ремиконт наделен способностью самостоятельно ставить себе диагноз. Почувствовав "недомогание", он действует следующим образом: во-первых, перестает изменять (как говорят, замораживает) положение исполнительных механизмов и, во-вторых, с помощью специальной сигнализации не только оповещает оператора о неисправности, но и одновременно сообщает, какой узел в нем отказал. Благодаря такой самодиагностике работу ремиконта можно очень быстро восстановить путем простой замены неисправного узла. А в тех случаях, когда процесс управления нельзя задерживать даже на короткое время, сигнал об отказе можно использовать для автоматического включения другого ремиконта, работающего в "горячем" резерве.
ПЕРВЫЕ ПРИМЕНЕНИЯ И ПЕРСПЕКТИВЫ
Выпуск ремиконтов начало примерно год назад промышленное объединение "Промприбор" (г.Чебоксары). У первой в семье ремиконтов модели (Р-100) - 64 алгоритмических блока, а библиотека насчитывает 25 наименований алгоритмов. Любой из них можно поместить в какой угодно блок, входы которого могут соединяться с выходами любых других блоков или с любыми входами ремиконта, к которым подключаются датчики. Один н тот же алгоритм можно использовать многократно, помещая в различные блоки. Столь разнообразные возможности позволяют реализовать огромное число сочетаний различных функций и параметров управления. Один такой ремиконт заменяет в среднем 25-30, а в отдельных случаях до 100 аналоговых приборов.

Испытания ремиконта в одной из лабораторий НИИтеплоприбора.
Ремиконты уже нашли применение на таких промышленных объектах, как, например, крупнейшая в Европе машина непрерывной разливки стали Ново-Липецкого металлургического комбината, энергоблок мощностью 300тыс.кВт на Литовской ГРЭС, нагревательные печи прокатного стана 350/250 металлургического завода "Электросталь", закалочный агрегат московского завода "Серп и Молот", на ряде предприятий по производству белково-витаминных концентратов. На каждом из этих столь непохожих друг на друга объектов ремиконт был быстро и просто приспособлен для решения конкретных задач автоматизации. Нажаты несколько клавиш на пульте ремиконта - и стальная многометровая полоса, выходящая из кристаллизатора машины непрерывного литья, получает нужный режим охлаждения, при этом на каждом ее участке устанавливается своя оптимальная температура. Выбраны другой набор алгоритмов ремиконта, другая их конфигурация и настройка - и полторы сотни различных технологических параметров энергоблока жестко стабилизируются на требуемых значениях...
В течение двенадцатой пятилетки выпуск ремиконтов по сравнению с производством аналоговых промышленных регуляторов будет расти опережающими темпами. Микропроцессорные приборы станут регулировать сотни тысяч технологических параметров. Предполагается, что за счет меньшей стоимости, габаритов и веса ремиконтов, повышения точности, сокращения времени ввода в эксплуатацию экономический эффект от их внедрения составит за пятилетку десятки миллионов рублей.
Заглянем теперь несколько дальше и попробуем в самых общих чертах представить, какой будет техника регулирования в ближайшие 10-15 лет.
С большой вероятностью можно предположить, что практически все промышленные регуляторы будут выполняться на базе микропроцессоров. Повышение степени интеграции микросхем приведет к тому, что в управлении цифровые методы обработки информации повсеместно будут теснить аналоговые.
Но регуляторы неизбежно должны сосуществовать с аналоговым миром технологических процессов. Поэтому центральной проблемой станут не столько средства обработки информации, сколько средства сопряжения регуляторов с объектом автоматизации. Уже сейчас в ремиконте Р-100 этим занято более двух третей (по объему) аппаратуры. А если учесть, что аналоговые компоненты совершенствуются значительно медленнее цифровых, то при сохранении существующих методов сопряжения подобная диспропорция будет усугубляться.
Выход из затруднения в общем плане выглядит следующим образом. Если говорить об информации, идущей от датчика через регулятор к исполнительному механизму, то ее следует преобразовывать из аналоговой в цифровую форму как можно раньше, а из цифровой в аналоговую - как можно позже. Благодаря этому не только удастся сократить размеры аппаратуры и сделать ее более "интеллектуальной", но и заменить многие тысячи километров кабеля, идущего к датчикам и исполнительным механизмам, на компактную цифровую сеть. Подключаясь к ней, любой регулятор сможет связываться с любым датчиком, любым исполнительным механизмом, другими регуляторами или другими элементами системы управления. Возможно, что к концу 90-х годов появятся системы регулирования с беспроводной связью; это будет важное техническое достижение, которое позволит вообще избавиться от кабельных соединений.
Другое направление, где можно ждать больших изменений, связано со способом общения человека с регулятором.
Ремиконту Р-100, как и регуляторам предыдущих поколений, все команды отдаются руками - с помощью клавиатуры. Конечно, удобнее было бы приказывать голосом.
Уже разработаны микросхемы речевых анализаторов и синтезаторов. Когда они станут более компактными и будут легко сопрягаться с микропроцессором, а возможно, даже разместятся с ним на одном кристалле, такой метод общения войдет в обиход промышленной автоматики.
Однако все это в будущем. А пока в нашей промышленности накапливается опыт применения ремиконтов первого поколения. Совершенствуется их аппаратура, пополняется библиотека алгоритмов.
В лабораториях и конструкторских бюро создаются новые модели микропроцессорных регуляторов.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Вот тут большая ошибка, из-за которой большинство обычных людей отказались отрезанными от программирования.
Я постоянно пишу, что для того, чтобы "что-то закодировать", программист должен знать три вещи:
1. как решить задачу (математика);
2. как запрограммировать решение (язык программирования);
3. как написать/запустить программу (операционная система).
И задачи эти практически независимы в решении, но устанавливают друг для друга ограничения.
А здесь все подается путаным описанием общей математики и единичных образцов техники. Из-за этого пропадает понимание, как программировать в хоть чуть отличающихся условиях. Приведенные решения работают у автора, но не у вас.
8/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ТРЕТЬЕ, на котором, решая несложные системы линейных уравнений, читатель узнает, что решение всякой задачи на любой ЭВМ (в частности - на программируемом микрокалькуляторе) подразделяется на определенные этапы: постановка задачи и ее математическая формулировка, выбор метода и построение алгоритма решения.
Занятие ведут М.ПОСНОВА, кандидат физико-математических наук Н.ПОСНОВ (Белорусский государственный университет), кандидат технических наук И.ВЯЗОВСКИЙ (Московский физико-технический институт).
Микрокалькулятор - машина миниатюрная, и ее возможности ограниченны: мала емкость запоминающих устройств, невысока скорость вычислений, отсутствуют внешние устройства для автоматического ввода и вывода информации. Но тем не менее это современная электронная вычислительная машина, и потому решение любой задачи на ней можно подразделить на те же этапы, которые характерны для работы на всякой ЭВМ.
ПОСТАНОВКА ЗАДАЧИ. Описывается исходная информация об исследуемом объекте, явлении, ситуации, и ставится вопрос, ответ на который требуется получить путем надлежащей переработки этой информации.
Чтобы поначалу не осложнять дело чисто математическими трудностями, возьмем задачу попроще, например, из сборника загадок на смекалку: "У отца с матерью сыновей на два больше, чем дочерей, а всего мужчин в семье вдвое больше, чем женщин. Сколько у отца с матерью сыновей и сколько дочерей?"
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ. Взаимосвязи между данными и искомыми величинами выражаются в виде равенств, неравенств, уравнений. Все вместе они образуют математическую модель исследуемого объекта, явления, ситуации.
Обозначим в нашей шутливой задаче число сыновей через y, число дочерей - через z. Разность этих величин по условию равна двум:
y-z=2
Выразим далее соотношение между числом мужчин (y+1) и числом женщин (z+1) в семье:
y+1=2(z+1)
или иначе:
y-2z=1
Теперь уже нетрудно заключить: в семье три сына и одна дочь.
Наша задача, таким образом, свелась к системе двух линейных уравнений. При математической формулировке многих проблем возникают подобные системы, решить которые не так просто, как нашу шутливую задачу. Поэтому стоит рассмотреть общие подходы к их решению на микрокалькуляторе, заменив конкретные числа буквами:

ВЫБОР МЕТОДА РЕШЕНИЯ. На этом этапе с самого начала следует изыскивать возможности для упрощения работы. Например, может оказаться, что искомые величины явным образом выражаются через данные. Так дело обстоит с нашей системой - по методу Крамера каждое из неизвестных выражается отношением определителей второго порядка:

Если к тому же оказывается, что расчет несложен и его требуется провести одни раз, то разумнее всего выполнить его вручную, предварительно продумав наиболее экономный порядок действий. Так, решая нашу систему из двух линейных уравнений и вычислив z по второй из приведенных формул, y лучше всего вычислять не по первой формуле, а иначе: y=(D1-C1)/B1. В таком случае расчет потребует меньшего числа операций, и результат будет получен быстрее. (Забегая вперед, скажем, что реализующая такой подход программа для "Электроники Б3-34" насчитывает 26 команд. Без предпринятого нами упрощения она потребовала бы более тридцати команд).
Если явных зависимостей искомых величин от данных вывести не удалось, следует обратиться к математической литературе и там поискать метод аналитического или приближенного решения задачи. В первую очередь стоит заглянуть в книги, посвященные вычислениям на программируемых микрокалькуляторах: А.Н.Цветков и В.А.Епанечииков, "Прикладные программы для микро-ЭВМ "Электроника Б3-34", "МК-56", "МК-54"" (М., "Финансы и статистика", 1984); Я.К. Трохименко и Ф.Д.Любич, "Инженерные расчеты на микрокалькуляторах" (Киев, "Технiка", 1980); "Радиотехнические расчеты иа микрокалькуляторах" (М., "Радио и связь", 1983); "Инженерные расчеты на программируемых микрокалькуляторах" (Киев, "Технiка", 1985). Если там отыщется подходящая программа, проведите расчет по ней.
Правда, готовая программа, взятая из книг или полученная от коллег, требует известной осторожности: порою, относясь в принципе к интересующему вас классу задач, она может охватывать не все возможные варианты. Поэтому, прежде чем пользоваться ею, надо тщательно выяснить рамки ее применения.
Но, предположим, готовой программы не нашлось, а составить ее необходимо (так бывает, когда задачу приходится решать многократно при меняющихся исходных данных или когда ее решение требует сложной вычислительной работы). В таком случае все дальнейшие этапы решения, начиная с выбора метода, надо пройти самостоятельно.
В математической литературе может найтись даже не один метод, пригодный для решения стоящей перед вами задачи. Из них надо взять наиболее подходящий. Следует выбирать его так, чтобы он обеспечивал решение с заданной точностью при минимальных затратах времени на программирование и счет, допускал создание программы в границах числовой и программной памяти имеющегося у вас микрокалькулятора. Узость этих границ порой вынуждает разбить чрезмерно длинную программу на несколько небольших или вообще отказаться от программирования для микрокалькулятора и обратиться к более мощной ЭВМ.
Проиллюстрируем перипетии выбора на примере нашей задачи, несколько усложнив ее. Предположим, что нам предстоит решить систему не из двух, а из трех линейных уравнений:

Если решать систему по методу Крамера, надо будет вычислить четыре определителя третьего порядка. Каждый выражается алгебраической суммой шести произведений из трех сомножителей. Нетрудно подсчитать, что вычисление каждого такого произведения и его прибавление к общей сумме требует шести операций (вызов первого сомножителя, вызов второго, умножение, вызов третьего сомножителя, умножение, наконец, сложение или вычитание). Прямое вычисление неизвестных по методу Крамера требует, таким образом, более 140 операций. Включающая их программа не уместится в памяти "Электроники Б3-34".
Обратимся к методу Гаусса, согласно которому система решается после преобразований, исключающих неизвестные из уравнений и в итоге оставляющих в каждом уравнении по одному неизвестному. Если в нашей системе a3!=0, то из первых двух уравнений можно исключить x:
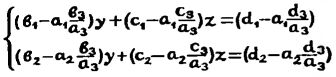
Пара этих уравнений приобрела вид системы, выписанной нами в самом начале занятия, и это позволяет сокращенно обозначить выражения в скобках:

Расчет каждого из шести новых коэффициентов требует семи операций (например, если речь идет о коэффициенте В1: вызов b1, вызов b3, вызов a3, деление, вызов a1, умножение, вычитание). Итого - 42 операции. Значения y и z можно определить тем же методом, который мы уже описывали (26 операций). Зная y и z, можно определить x из третьего уравнения (11 операций). Таким образом, программа для нахождения всех трех неизвестных будет насчитывать около 80 команд. Возможно, нам удастся ее сократить, когда дело дойдет до конкретной разработки. Короче говоря, есть надежда вписать ее в программную память нашего калькулятора.
Числовой памяти тоже должно хватить: ведь в ней надо разместить шесть коэффициентов системы для определения y и z, четыре - для определения x. На это потребуется 10 из 14 адресуемых регистров. Остальные четыре можно будет использовать для хранения промежуточных результатов.
Разумеется, эти прикидки уточнятся при составлении программы. Сейчас можно лишь сказать, что возможностей калькулятора для ее составления, по-видимому, достаточно.
ПОСТРОЕНИЕ АЛГОРИТМА, то есть последовательности конкретных действий, дающих в итоге ответ на поставленную задачу. Этот этап начинается с анализа расчетных формул. Их следует максимально упростить, а точнее - придать им такой вид, чтобы вычисления по ним были наиболее просты с точки зрения возможностей имеющейся машины. Желательно выделить в формулах повторяющиеся комбинации переменных и принять эти комбинации за промежуточные переменные. Их целесообразно вычислить однажды и потом использовать в готовом виде. Иногда стоит преобразовать формулы так, чтобы в них появились подобные повторяющиеся комбинации. Затем следует установить порядок выполнения операций, а попутно продумать, как разместить по адресуемым регистрам исходные данные, значения промежуточных переменных и окончательные результаты.
Как правило, для вычислений по одним и тем же формулам можно предложить несколько алгоритмов, притом далеко не равноценных. Соответствующий пример нетрудно усмотреть в стоящей перед нами задаче о решении системы из трех линейных уравнений. Исключая неизвестную x из первых двух уравнений, можно получить вариант системы. Уже приведенный выше (назовем его первым вариантом), а можно прийти и к. другому варианту, который условимся называть вторым.

Нетрудно усмотреть, что в обоих вариантах константы в левой и правой частях можно вычислить по однотипной схеме, в циклическом порядке, занося в стек сначала набор величин b1, b2, b3, затем c1, c2, c3, затем d1, d2, d3. Предположим, что величины a1, a2, a3 уже размещены перед этим в адресуемых регистрах так: a1 - в РВ, a2- в PC, a3 - в PD.
Если внести коэффициенты b1, b2, b3 в естественном порядке, с b1 по b3, то в регистрах стека они окажутся на таких местах: b1 - в PZ, b2 - в PY, b3 - в РХ. Если принять второй вариант преобразованной системы, то для вычисления разности (a3b1-a1b3) следует, очевидно, начать с таких операций:

А дальше? Надо перегнать величину b1 в регистр X. Это можно сделать командой F(), выполнив ее дважды. Но тогда величина b2 окажется в регистре Т. Когда она понадобится, опять придется прибегнуть к команде F(), причем использовать ее троекратно. Это уже очевидное излишество. Не легче подсчитать и разность (a3b2-a2bз).
Если же принять первый вариант, то тут сначала удобно вычислить дробь b3/a3, потом образовать выражение a2b3/a3 и вычесть его из коэффициента b2 - благо он к этому моменту (проследите за движением чисел по стеку!) - окажется рядом, в регистре Y. Получив в регистре X величину B2=b2-a2b3/a3 и переслав ее на нужное место, можно вычислять далее выражение B1=b1-a1b3/a3. Для этого b1 надо предварительно переместить в регистр X - а это можно сделать, использовав команду F() один-единственный раз. В цикле, где вычисляются величины b3/a3, B2=b2-a2b3/a3 и B1=b1-a1b3/a3, удобно использовать для их отсылки в адресуемые регистры команду вида КПМ (М=0, 1, 2 или 3). Тогда при следующих повторениях цикла с исходными данными c1, c2, c3, затем d1, d2, d3 образующиеся величины c3/a3, C2=c2-a2c3/a3, C1=c1-a1c3/a3, d3a3, D2=d2-a2d3/a3, D1=d1-a1d3/a3 встанут в адресуемые регистры одна за другой. Говоря точнее, если номер регистра-счетчика М будет иметь одно из указанных значений, названные выражения расположатся по адресуемым регистрам в порядке убывания их номеров (вспомните, как модифицируется адрес при выполнении команд вида КПМ).
Решение системы из двух линейных уравнений с неизвестными y и z можно отыскать точно так же, как мы это делали в начале занятия.

Получив y и z, останется вычислить x - например, по формуле:
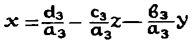
Здесь опять пригодятся дроби b3/a3, c3/a3, d3/a3, вычислявшиеся при образовании системы для y и z. На этом закончится решение исходной системы из трех линейных уравнений.
Чтобы завершить это схематическое описание алгоритма, следует сказать о том, что в начальной его части величины a1, a2, a3, вводимые в стек, соответствующими командами отсылаются на свои места (например, в регистры B, C, D, как мы оговаривали походя). Следует также упомянуть, что некоторые из регистров будут играть роль счетчиков. Таких счетчиков нам, очевидно, понадобится два. Один - для организации цикла, где вычисляются коэффициенты системы с неизвестными y и z. Пусть это будет, скажем, Р0. Поскольку цикл проходится троекратно, туда перед его прохождением надо заслать тройку. Другой регистр-счетчик (пусть это будет P1) потребуется для расстановки вычисленных коэффициентов системы по адресуемым регистрам. Туда перед прохождением того же цикла следует заслать 11. Тогда первая засылка произойдет в регистр 10, то есть в регистр A, и в процессе дальнейших вычислений адресуемые регистры заполнятся так:
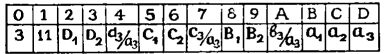
Как видим, их вполне должно хватить для реализации разработанного нами алгоритма. Некоторые регистры можно даже использовать дважды. Например, судя по формулам для неизвестных x, y и z, в их вычислении уже не участвуют непосредственно коэффициенты a1, a2, a3. В регистры В, С, D, где хранились эти коэффициенты, зашлем вычисленные значения неизвестных. Если по завершении счета возникнет подозрение, что они неточно считаны с индикатора, их можно будет вызвать командами ИПВ, ИПС, ИПD и списать повторно.
Теперь все готово для того, чтобы приняться за написание программы. Ведь она, говоря по существу, представляет собой перевод разработанного алгоритма на язык команд микрокалькулятора. Алгоритм же изложен достаточно подробно и полно.
Правда, в подобном изложении сложный алгоритм плохо обозрим. Поэтому, прежде чем приниматься за составление программы, его записывают на специальном алгоритмическом языке, а для большей наглядности - изображают в графической форме. В этом случае каждая стадия решения описывается словами и формулами, заключенными в замкнутую рамку. Такие фигуры называются блоками. Они соединяются линиями, указывающими последовательность стадий. Вся конструкция именуется блок-схемой алгоритма. Составить ее следует так, чтобы по каждому блоку можно было написать достаточно независимые и обозримые куски программы.
СОСТАВЛЕНИЕ БЛОК-СХЕМЫ АЛГОРИТМА. Всякая такая схема состоит из блоков четырех различных очертаний: овалов, параллелограммов, прямоугольников и ромбов. Форма блока соответствует характеру действий, в нем записываемых. В параллелограммах обозначаются ввод и вывод информации, в прямоугольниках - конкретные вычисления (если они выполняются в подпрограмме, то вертикальные стороны прямоугольника чертятся двойными), в ромбах - проверки условий (условные переходы). В овалах пишутся слова "начало" и "конец"; такие фигуры располагаются по концам блок-схемы.
Стоит заметить: если форма блоков закреплена нормами ГОСТа и должна соблюдаться неукоснительно, то содержание блоков, способы описания алгоритмов этими нормами не регламентируются - лишь бы было понятнее.
Блоки обычно размещаются сверху вниз и часто нумеруются. Соединительные линии рисуются в виде прямолинейных отрезков или ломаных с вертикальными и горизонтальными звеньями, иногда снабжаются стрелками. Если же на соединительных линиях стрелки отсутствуют, то предполагается, что по вертикальным прямым движение совершается сверху вниз, а по горизонтальным - слева направо. Из каждого ромба выходят две линии. Одна соответствует выполнению условия и помечается еловой "да", другая - невыполнению и помечается словом "нет".
Составим блок-схему разработанного нами алгоритма для решения системы из трех линейных уравнений.
Нарисовав овал с надписью "начало", поставим под ним параллелограмм, обозначающий ввод коэффициентов a1, a2, a3. Ниже поставим прямоугольник, где показано, что введенные коэффициенты рассылаются в регистры B, C, D соответственно. Еще ниже - прямоугольник, где описана организация счетчиков: засылка числа 3 в регистр 0 и числа 11 в регистр 1.
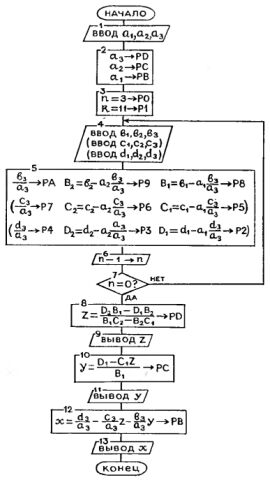
Затем поставим образующие цикл блоки, где указано, как вычисляются коэффициенты системы для отыскания неизвестных y и z. Сначала - параллелограмм, описывающий ввод величин b1, b2, b3 (при дальнейших прохождениях цикла - c1, c2, c3, затем d1, d2, d3). Ниже - прямоугольник, где собраны все формулы, выражающие величины B1, B2, C1, C2, D1, D2 через a1, a2, a3, b1, b2, b3. c1, c2, c3, d1, d2, d3. Детализация в подобных случаях вряд ли нужна: каждая формула довольно жестко определяет порядок вычислений по ней, а общая последовательность вычислительных действий в блоке задается порядком записи формул. В следующем прямоугольнике отражено уменьшение числа n, содержимого регистра 0, на единицу, а в замыкающем цикл ромбе - проверка: "n=0?". Невыполнение условия диктует возврат к началу цикла и его повторение, выполнение - выход из цикла.
Следующие прямоугольник и параллелограмм - это вычисление z, его засылка в регистр D и вывод на индикатор. Следующая пара того же вида - вычисление, засылка в PC и вывод y. Еще одна такая же пара - вычисление, засылка в РВ и вывод х. Замыкает блок-схему овал с надписью "конец".
Составив блок-схему, внимательно проверим ее. Она должна быть разработана так тщательно, чтобы превратить программирование в почти автоматическое расписывание команд программы по отдельным блокам.
[ ВНИМАНИЮ ВЛАДЕЛЬЦЕВ КОМПЬЮТЕРОВ "БК-0010" и "АГАТ"
Просим написать в редакцию, как вы их используете, какие задачи на них решаете, довольны ли ими, какие советы могли бы дать другим их владельцам ]
Я постоянно пишу, что для того, чтобы "что-то закодировать", программист должен знать три вещи:
1. как решить задачу (математика);
2. как запрограммировать решение (язык программирования);
3. как написать/запустить программу (операционная система).
И задачи эти практически независимы в решении, но устанавливают друг для друга ограничения.
А здесь все подается путаным описанием общей математики и единичных образцов техники. Из-за этого пропадает понимание, как программировать в хоть чуть отличающихся условиях. Приведенные решения работают у автора, но не у вас.
8/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ТРЕТЬЕ, на котором, решая несложные системы линейных уравнений, читатель узнает, что решение всякой задачи на любой ЭВМ (в частности - на программируемом микрокалькуляторе) подразделяется на определенные этапы: постановка задачи и ее математическая формулировка, выбор метода и построение алгоритма решения.
Занятие ведут М.ПОСНОВА, кандидат физико-математических наук Н.ПОСНОВ (Белорусский государственный университет), кандидат технических наук И.ВЯЗОВСКИЙ (Московский физико-технический институт).
Микрокалькулятор - машина миниатюрная, и ее возможности ограниченны: мала емкость запоминающих устройств, невысока скорость вычислений, отсутствуют внешние устройства для автоматического ввода и вывода информации. Но тем не менее это современная электронная вычислительная машина, и потому решение любой задачи на ней можно подразделить на те же этапы, которые характерны для работы на всякой ЭВМ.
ПОСТАНОВКА ЗАДАЧИ. Описывается исходная информация об исследуемом объекте, явлении, ситуации, и ставится вопрос, ответ на который требуется получить путем надлежащей переработки этой информации.
Чтобы поначалу не осложнять дело чисто математическими трудностями, возьмем задачу попроще, например, из сборника загадок на смекалку: "У отца с матерью сыновей на два больше, чем дочерей, а всего мужчин в семье вдвое больше, чем женщин. Сколько у отца с матерью сыновей и сколько дочерей?"
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ. Взаимосвязи между данными и искомыми величинами выражаются в виде равенств, неравенств, уравнений. Все вместе они образуют математическую модель исследуемого объекта, явления, ситуации.
Обозначим в нашей шутливой задаче число сыновей через y, число дочерей - через z. Разность этих величин по условию равна двум:
y-z=2
Выразим далее соотношение между числом мужчин (y+1) и числом женщин (z+1) в семье:
y+1=2(z+1)
или иначе:
y-2z=1
Теперь уже нетрудно заключить: в семье три сына и одна дочь.
Наша задача, таким образом, свелась к системе двух линейных уравнений. При математической формулировке многих проблем возникают подобные системы, решить которые не так просто, как нашу шутливую задачу. Поэтому стоит рассмотреть общие подходы к их решению на микрокалькуляторе, заменив конкретные числа буквами:

ВЫБОР МЕТОДА РЕШЕНИЯ. На этом этапе с самого начала следует изыскивать возможности для упрощения работы. Например, может оказаться, что искомые величины явным образом выражаются через данные. Так дело обстоит с нашей системой - по методу Крамера каждое из неизвестных выражается отношением определителей второго порядка:

Если к тому же оказывается, что расчет несложен и его требуется провести одни раз, то разумнее всего выполнить его вручную, предварительно продумав наиболее экономный порядок действий. Так, решая нашу систему из двух линейных уравнений и вычислив z по второй из приведенных формул, y лучше всего вычислять не по первой формуле, а иначе: y=(D1-C1)/B1. В таком случае расчет потребует меньшего числа операций, и результат будет получен быстрее. (Забегая вперед, скажем, что реализующая такой подход программа для "Электроники Б3-34" насчитывает 26 команд. Без предпринятого нами упрощения она потребовала бы более тридцати команд).
Если явных зависимостей искомых величин от данных вывести не удалось, следует обратиться к математической литературе и там поискать метод аналитического или приближенного решения задачи. В первую очередь стоит заглянуть в книги, посвященные вычислениям на программируемых микрокалькуляторах: А.Н.Цветков и В.А.Епанечииков, "Прикладные программы для микро-ЭВМ "Электроника Б3-34", "МК-56", "МК-54"" (М., "Финансы и статистика", 1984); Я.К. Трохименко и Ф.Д.Любич, "Инженерные расчеты на микрокалькуляторах" (Киев, "Технiка", 1980); "Радиотехнические расчеты иа микрокалькуляторах" (М., "Радио и связь", 1983); "Инженерные расчеты на программируемых микрокалькуляторах" (Киев, "Технiка", 1985). Если там отыщется подходящая программа, проведите расчет по ней.
Правда, готовая программа, взятая из книг или полученная от коллег, требует известной осторожности: порою, относясь в принципе к интересующему вас классу задач, она может охватывать не все возможные варианты. Поэтому, прежде чем пользоваться ею, надо тщательно выяснить рамки ее применения.
Но, предположим, готовой программы не нашлось, а составить ее необходимо (так бывает, когда задачу приходится решать многократно при меняющихся исходных данных или когда ее решение требует сложной вычислительной работы). В таком случае все дальнейшие этапы решения, начиная с выбора метода, надо пройти самостоятельно.
В математической литературе может найтись даже не один метод, пригодный для решения стоящей перед вами задачи. Из них надо взять наиболее подходящий. Следует выбирать его так, чтобы он обеспечивал решение с заданной точностью при минимальных затратах времени на программирование и счет, допускал создание программы в границах числовой и программной памяти имеющегося у вас микрокалькулятора. Узость этих границ порой вынуждает разбить чрезмерно длинную программу на несколько небольших или вообще отказаться от программирования для микрокалькулятора и обратиться к более мощной ЭВМ.
Проиллюстрируем перипетии выбора на примере нашей задачи, несколько усложнив ее. Предположим, что нам предстоит решить систему не из двух, а из трех линейных уравнений:

Если решать систему по методу Крамера, надо будет вычислить четыре определителя третьего порядка. Каждый выражается алгебраической суммой шести произведений из трех сомножителей. Нетрудно подсчитать, что вычисление каждого такого произведения и его прибавление к общей сумме требует шести операций (вызов первого сомножителя, вызов второго, умножение, вызов третьего сомножителя, умножение, наконец, сложение или вычитание). Прямое вычисление неизвестных по методу Крамера требует, таким образом, более 140 операций. Включающая их программа не уместится в памяти "Электроники Б3-34".
Обратимся к методу Гаусса, согласно которому система решается после преобразований, исключающих неизвестные из уравнений и в итоге оставляющих в каждом уравнении по одному неизвестному. Если в нашей системе a3!=0, то из первых двух уравнений можно исключить x:
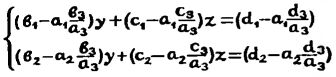
Пара этих уравнений приобрела вид системы, выписанной нами в самом начале занятия, и это позволяет сокращенно обозначить выражения в скобках:

Расчет каждого из шести новых коэффициентов требует семи операций (например, если речь идет о коэффициенте В1: вызов b1, вызов b3, вызов a3, деление, вызов a1, умножение, вычитание). Итого - 42 операции. Значения y и z можно определить тем же методом, который мы уже описывали (26 операций). Зная y и z, можно определить x из третьего уравнения (11 операций). Таким образом, программа для нахождения всех трех неизвестных будет насчитывать около 80 команд. Возможно, нам удастся ее сократить, когда дело дойдет до конкретной разработки. Короче говоря, есть надежда вписать ее в программную память нашего калькулятора.
Числовой памяти тоже должно хватить: ведь в ней надо разместить шесть коэффициентов системы для определения y и z, четыре - для определения x. На это потребуется 10 из 14 адресуемых регистров. Остальные четыре можно будет использовать для хранения промежуточных результатов.
Разумеется, эти прикидки уточнятся при составлении программы. Сейчас можно лишь сказать, что возможностей калькулятора для ее составления, по-видимому, достаточно.
ПОСТРОЕНИЕ АЛГОРИТМА, то есть последовательности конкретных действий, дающих в итоге ответ на поставленную задачу. Этот этап начинается с анализа расчетных формул. Их следует максимально упростить, а точнее - придать им такой вид, чтобы вычисления по ним были наиболее просты с точки зрения возможностей имеющейся машины. Желательно выделить в формулах повторяющиеся комбинации переменных и принять эти комбинации за промежуточные переменные. Их целесообразно вычислить однажды и потом использовать в готовом виде. Иногда стоит преобразовать формулы так, чтобы в них появились подобные повторяющиеся комбинации. Затем следует установить порядок выполнения операций, а попутно продумать, как разместить по адресуемым регистрам исходные данные, значения промежуточных переменных и окончательные результаты.
Как правило, для вычислений по одним и тем же формулам можно предложить несколько алгоритмов, притом далеко не равноценных. Соответствующий пример нетрудно усмотреть в стоящей перед нами задаче о решении системы из трех линейных уравнений. Исключая неизвестную x из первых двух уравнений, можно получить вариант системы. Уже приведенный выше (назовем его первым вариантом), а можно прийти и к. другому варианту, который условимся называть вторым.

Нетрудно усмотреть, что в обоих вариантах константы в левой и правой частях можно вычислить по однотипной схеме, в циклическом порядке, занося в стек сначала набор величин b1, b2, b3, затем c1, c2, c3, затем d1, d2, d3. Предположим, что величины a1, a2, a3 уже размещены перед этим в адресуемых регистрах так: a1 - в РВ, a2- в PC, a3 - в PD.
Если внести коэффициенты b1, b2, b3 в естественном порядке, с b1 по b3, то в регистрах стека они окажутся на таких местах: b1 - в PZ, b2 - в PY, b3 - в РХ. Если принять второй вариант преобразованной системы, то для вычисления разности (a3b1-a1b3) следует, очевидно, начать с таких операций:

А дальше? Надо перегнать величину b1 в регистр X. Это можно сделать командой F(), выполнив ее дважды. Но тогда величина b2 окажется в регистре Т. Когда она понадобится, опять придется прибегнуть к команде F(), причем использовать ее троекратно. Это уже очевидное излишество. Не легче подсчитать и разность (a3b2-a2bз).
Если же принять первый вариант, то тут сначала удобно вычислить дробь b3/a3, потом образовать выражение a2b3/a3 и вычесть его из коэффициента b2 - благо он к этому моменту (проследите за движением чисел по стеку!) - окажется рядом, в регистре Y. Получив в регистре X величину B2=b2-a2b3/a3 и переслав ее на нужное место, можно вычислять далее выражение B1=b1-a1b3/a3. Для этого b1 надо предварительно переместить в регистр X - а это можно сделать, использовав команду F() один-единственный раз. В цикле, где вычисляются величины b3/a3, B2=b2-a2b3/a3 и B1=b1-a1b3/a3, удобно использовать для их отсылки в адресуемые регистры команду вида КПМ (М=0, 1, 2 или 3). Тогда при следующих повторениях цикла с исходными данными c1, c2, c3, затем d1, d2, d3 образующиеся величины c3/a3, C2=c2-a2c3/a3, C1=c1-a1c3/a3, d3a3, D2=d2-a2d3/a3, D1=d1-a1d3/a3 встанут в адресуемые регистры одна за другой. Говоря точнее, если номер регистра-счетчика М будет иметь одно из указанных значений, названные выражения расположатся по адресуемым регистрам в порядке убывания их номеров (вспомните, как модифицируется адрес при выполнении команд вида КПМ).
Решение системы из двух линейных уравнений с неизвестными y и z можно отыскать точно так же, как мы это делали в начале занятия.

Получив y и z, останется вычислить x - например, по формуле:
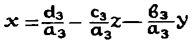
Здесь опять пригодятся дроби b3/a3, c3/a3, d3/a3, вычислявшиеся при образовании системы для y и z. На этом закончится решение исходной системы из трех линейных уравнений.
Чтобы завершить это схематическое описание алгоритма, следует сказать о том, что в начальной его части величины a1, a2, a3, вводимые в стек, соответствующими командами отсылаются на свои места (например, в регистры B, C, D, как мы оговаривали походя). Следует также упомянуть, что некоторые из регистров будут играть роль счетчиков. Таких счетчиков нам, очевидно, понадобится два. Один - для организации цикла, где вычисляются коэффициенты системы с неизвестными y и z. Пусть это будет, скажем, Р0. Поскольку цикл проходится троекратно, туда перед его прохождением надо заслать тройку. Другой регистр-счетчик (пусть это будет P1) потребуется для расстановки вычисленных коэффициентов системы по адресуемым регистрам. Туда перед прохождением того же цикла следует заслать 11. Тогда первая засылка произойдет в регистр 10, то есть в регистр A, и в процессе дальнейших вычислений адресуемые регистры заполнятся так:
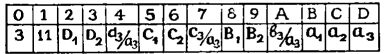
Как видим, их вполне должно хватить для реализации разработанного нами алгоритма. Некоторые регистры можно даже использовать дважды. Например, судя по формулам для неизвестных x, y и z, в их вычислении уже не участвуют непосредственно коэффициенты a1, a2, a3. В регистры В, С, D, где хранились эти коэффициенты, зашлем вычисленные значения неизвестных. Если по завершении счета возникнет подозрение, что они неточно считаны с индикатора, их можно будет вызвать командами ИПВ, ИПС, ИПD и списать повторно.
Теперь все готово для того, чтобы приняться за написание программы. Ведь она, говоря по существу, представляет собой перевод разработанного алгоритма на язык команд микрокалькулятора. Алгоритм же изложен достаточно подробно и полно.
Правда, в подобном изложении сложный алгоритм плохо обозрим. Поэтому, прежде чем приниматься за составление программы, его записывают на специальном алгоритмическом языке, а для большей наглядности - изображают в графической форме. В этом случае каждая стадия решения описывается словами и формулами, заключенными в замкнутую рамку. Такие фигуры называются блоками. Они соединяются линиями, указывающими последовательность стадий. Вся конструкция именуется блок-схемой алгоритма. Составить ее следует так, чтобы по каждому блоку можно было написать достаточно независимые и обозримые куски программы.
СОСТАВЛЕНИЕ БЛОК-СХЕМЫ АЛГОРИТМА. Всякая такая схема состоит из блоков четырех различных очертаний: овалов, параллелограммов, прямоугольников и ромбов. Форма блока соответствует характеру действий, в нем записываемых. В параллелограммах обозначаются ввод и вывод информации, в прямоугольниках - конкретные вычисления (если они выполняются в подпрограмме, то вертикальные стороны прямоугольника чертятся двойными), в ромбах - проверки условий (условные переходы). В овалах пишутся слова "начало" и "конец"; такие фигуры располагаются по концам блок-схемы.
Стоит заметить: если форма блоков закреплена нормами ГОСТа и должна соблюдаться неукоснительно, то содержание блоков, способы описания алгоритмов этими нормами не регламентируются - лишь бы было понятнее.
Блоки обычно размещаются сверху вниз и часто нумеруются. Соединительные линии рисуются в виде прямолинейных отрезков или ломаных с вертикальными и горизонтальными звеньями, иногда снабжаются стрелками. Если же на соединительных линиях стрелки отсутствуют, то предполагается, что по вертикальным прямым движение совершается сверху вниз, а по горизонтальным - слева направо. Из каждого ромба выходят две линии. Одна соответствует выполнению условия и помечается еловой "да", другая - невыполнению и помечается словом "нет".
Составим блок-схему разработанного нами алгоритма для решения системы из трех линейных уравнений.
Нарисовав овал с надписью "начало", поставим под ним параллелограмм, обозначающий ввод коэффициентов a1, a2, a3. Ниже поставим прямоугольник, где показано, что введенные коэффициенты рассылаются в регистры B, C, D соответственно. Еще ниже - прямоугольник, где описана организация счетчиков: засылка числа 3 в регистр 0 и числа 11 в регистр 1.

Затем поставим образующие цикл блоки, где указано, как вычисляются коэффициенты системы для отыскания неизвестных y и z. Сначала - параллелограмм, описывающий ввод величин b1, b2, b3 (при дальнейших прохождениях цикла - c1, c2, c3, затем d1, d2, d3). Ниже - прямоугольник, где собраны все формулы, выражающие величины B1, B2, C1, C2, D1, D2 через a1, a2, a3, b1, b2, b3. c1, c2, c3, d1, d2, d3. Детализация в подобных случаях вряд ли нужна: каждая формула довольно жестко определяет порядок вычислений по ней, а общая последовательность вычислительных действий в блоке задается порядком записи формул. В следующем прямоугольнике отражено уменьшение числа n, содержимого регистра 0, на единицу, а в замыкающем цикл ромбе - проверка: "n=0?". Невыполнение условия диктует возврат к началу цикла и его повторение, выполнение - выход из цикла.
Следующие прямоугольник и параллелограмм - это вычисление z, его засылка в регистр D и вывод на индикатор. Следующая пара того же вида - вычисление, засылка в PC и вывод y. Еще одна такая же пара - вычисление, засылка в РВ и вывод х. Замыкает блок-схему овал с надписью "конец".
Составив блок-схему, внимательно проверим ее. Она должна быть разработана так тщательно, чтобы превратить программирование в почти автоматическое расписывание команд программы по отдельным блокам.
[ ВНИМАНИЮ ВЛАДЕЛЬЦЕВ КОМПЬЮТЕРОВ "БК-0010" и "АГАТ"
Просим написать в редакцию, как вы их используете, какие задачи на них решаете, довольны ли ими, какие советы могли бы дать другим их владельцам ]

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
8/85
Раздел ведет кандидат физико-математичесних наук Ю.ПУХНАЧЕВ
Трудно предугадывать, какой из материалов раздела вызовет наибольший отклик у читателей. Порою небольшая заметка на узкоспециальную тему вовлекает десятки людей в широкую дискуссию об общих принципах составления программ для микрокалькулятора. Так случилось со статьей К.Ткачука "Нежесткие программы" (12/84). Хотя речь в ней шла о весьма частном расчете из области сопротивления материалов, соображения, высказанные по ее поводу в письмах читателей, по-видимому, будут интересны всем, кто решает задачи на программируемом микрокалькуляторе. Своими мнениями поделились В.Анисимов (г.Уфа), Ю.Газиев, Л.Горохов, В.Козлов (г.Ленинград), В.Кочетов (г.Хмельницкий), А.Маринкевич (пос.Татищево Саратовской области), Е.Новик (г.Ташкент), А.Новиков (г.Москва), И.Сонин (г.Саратов), И.Шериньш (г.Рига), Е.Шидловский (г.Тбилиси) и другие. Обзор читательской почты подготовил А.Бойко.
ИЩИТЕ УДАЧНЫЕ АЛГОРИТМЫ!
Вспомним суть проблемы, для решения которой составил свою программу К.Ткачук. Требуется вычислить момент инерции балки сложного профиля относительно оси, проходящей через центр тяжести. Профиль разбивается на прямоугольники - фигуры, для которых расчет момента инерции проводится по очень простой формуле. Общий момент подсчитывается суммированием. Сначала (первая часть программы) и он и положение центра тяжести профиля определяются относительно некоторой произвольной оси. Затем (вторая часть) вручную определяется положение отдельных прямоугольников относительно оси, проходящей через центр тяжести профиля. Наконец (третья часть), найденная ранее величина момента инерции пересчитывается для нового положения оси.
ПЕРВЫЙ ШАГ НА ПУТИ УЛУЧШЕНИЯ ЛЮБОЙ ПРОГРАММЫ - ИСКЛЮЧИТЬ ИЛИ СВЕСТИ К МИНИМУМУ РУЧНЫЕ ВЫЧИСЛЕНИЯ И ДЕЙСТВИЯ ПРИ ВВОДЕ И ВЫВОДЕ ДАННЫХ - в этом единодушны все, кто, совершенствуя программу К.Ткачука, сохранял предложенное им разбиение профиля иа прямоугольники.
А.НОВИКОВ (восьмиклассник). На первом этапе в программе К.Ткачука слишком много остановов, на последнем приходится заново вводить величины b1 и h1. Необходимо, по-моему, отказаться от деления процесса вычислений иа три этапа. Лучше начать с определения момента инерции какого-то одного прямоугольника относительно оси, проходящей через его центр тяжести, потом добавить еще один прямоугольник, найти центр тяжести пары и определить ее общий момент инерции относительно оси, проходящей через этот центр, а затем пересчитывать результаты с добавлением каждого нового прямоугольника, как показано с левого края на рисунке:


В.КОЗЛОВ. Предлагаю сузить область применения программы до случая, когда число прямоугольников, на которые разбито сечение, не превышает восьми. Пусть данные о каждом прямоугольнике запоминаются в регистрах как числа вида "ВВНН.АА", в которых соответствующие разряды выделены для записи bi, hi, ai. Работая с программой, оператор пользуется лишь одной клавишей С/П как при вводе исходных данных, так и при выводе результатов расчета. Если воспользоваться командами ИПР, можно контролировать данные, введенные раньше.
Сравнение программ, присланных читателями в ответ на опубликованную, с точки зрения удобства использования и вычислительных возможностей дает различные результаты.

Удобная для пользователя программа В.Козлова оказалась далеко не самой эффективной, как и программа А.Новикова. (Следует оговориться, что программы, предназначенные для решения более сложных задач, как у В.Кочетова, или более слабые, на схеме не представлены).
Программа А.Маринкевича, напротив, "подпрыгнула" на второе место по эффективности. Чем это объясняется?
ВЫБРАТЬ ИНОЙ АЛГОРИТМ РАСЧЕТОВ - ТОЛЬКО ТАК МОЖНО РАДИКАЛЬНО ПОВЫСИТЬ ЭФФЕКТИВНОСТЬ ПРОГРАММЫ. Одна из заповедей программирования недаром гласит: "Время, потраченное на подбор хорошего алгоритма, приносит гораздо больший выигрыш, чем время, потраченное на доводку плохой программы".
А.МАРИНКЕВИЧ. Моя программа позволяет вычислять геометрические характеристики плоских сечений более сложных форм, чем составленных из прямоугольников. Сечение произвольной формы - например, с внутренней полостью - вычерчивается на координатной плоскости, как показано на рисунке. Нумерацию угловых точек проводим по часовой стрелке, оставляя область сечения справа. По очереди вводим в микрокалькулятор координаты угловых точек, а после останова программы командами ИП0, ИПА-ИПД выводим на индикатор значения F, X0, Z0, Jz0, Jx0.

ВЫЧИСЛИТЕЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММЫ МОГУТ БЫТЬ РАСШИРЕНЫ БЛАГОДАРЯ ПОДПРОГРАММАМ.
И.СОНИН. Сечение можно разбивать на однотипные элементы, кодировать их и, в зависимости от кода, вести расчет по той или иной формуле. Сложное сечение разбивается на N элементарных фигур - прямоугольников, треугольников, кругов,- и расчет производится последовательным добавлением фрагментов сечения. Исходное сечение можно разбивать на фигуры не только действительные, но и "мнимые". Например, прямоугольный трубчатый профиль можно составить из четырех прямоугольников - стенок трубы, а можно из двух фигур: одной действительной (прямоугольник ABCD из рисунке) и мнимой (отверстие EFGH), для которой численные характеристики берутся со знаком минус. Очевидно, что второй способ проще.
Аналогичный способ применил и Е.Шидловский, хотя набор элементов разбиения у него иной:

Вернемся к схеме, где сопоставляются достоинства программ, присланных читателями. Обратим внимание: программа И.Шериньша оказалась на первом месте и по своим вычислительным возможностям и по удобству работы с нею. Об удобстве программы позволила позаботиться ее краткость. Но почему программа короче остальных?
"ЧЕЛОВЕЧЕСКИЕ" МЕТОДЫ РАСЧЕТА, РАЗРАБОТАННЫЕ ДЛЯ ВЫЧИСЛЕНИЙ ВРУЧНУЮ, ДАЛЕКО НЕ ВСЕГДА ОКАЗЫВАЮТСЯ ЭФФЕКТИВНЫМИ ПРИ ПЕРЕНОСЕ ИХ НА ЭВМ.
В.АНИСИМОВ. Наибольшие резервы улучшения программы заключаются порой в корректировке алгоритма с учетом специфики решения задач на ЭВМ. "Человеческие" методы, как правило, весьма экономичны по числу выполняемых операций, но если вычислительная машина действует, следуя тем же методам, это иногда оборачивается во вред пользователю: программы оказываются сложными, неудобными в работе.
И.ШЕРИНЬШ. Работать по готовым формулам было целесообразно при счете, например, на логарифмических линейках. С этой целью создавались формулы для отдельных часто встречающихся случаев - например, для момента инерции прямоугольника, круга и других фигур. В общем случае любое сечение эффективнее не разбивать на эти привычные элементарные фигуры, а рассчитывать сразу по общей формуле

Подсчитывать нужно три интеграла с одинаковыми пределами и переменными интегрирования. Это суммарная площадь F, статический момент S и вышеупомянутый интеграл. Интегралы можно заменить суммами, например
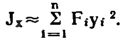
А поскольку в них содержатся одинаковые слагаемые, программу удается сократить за счет параллельного формирования всех трех сумм. Степень точности можно регулировать выбором числа n.
Решим задачу К.Ткачука. Для этого разделим площадь на 16 полос равной высоты, по одному сантиметру, как показано с правого края на первом рисунке. Ось Х'Х' разместим иа 0.5см ниже края сечения, чтобы расстояние центра тяжести каждой полоски до оси выражалось целым числом сантиметров, это упростит ввод. Различной остается ширина полосок bi. Только одну эту величину для каждого цикла счета понадобится вводить оператору. Результат: Jx=1580.07. Это менее чем на полпроцента отличается от результата К.Ткачука.
Подведем итог. ЕСЛИ ПРОГРАММА НЕУДОБНА В РАБОТЕ, ТО ЭТО СКОРЕЕ ВСЕГО СВИДЕТЕЛЬСТВУЕТ О НЕУДАЧНО ВЫБРАННОМ АЛГОРИТМЕ, НЕУМЕЛОМ ПРОГРАММИРОВАНИИ, А НЕ О ТОМ, ЧТО ВЫЧИСЛИТЕЛЬНЫЕ ВОЗМОЖНОСТИ МИКРОКАЛЬКУЛЯТОРА НЕ ПОЗВОЛЯЮТ ДОСТИЧЬ ЛУЧШЕГО. Хотелось бы познакомиться с мнением читателей рубрики иа этот счет.
Программа А.Новикова: 00. Сх 01. П7 02. П8 03. П9 04. С/П 05. С/П 06. С/П 07. * 08. П1 09. FBx 10. Fx2 11. * 12. 1 13. 2 14. / 15. x-y 16. П2 17. ИП1 18. * 19. ИП7 20. ИП8 21. * 22. + 23. ИП7 24. ИП1 25. + 26. П4 27. / 28. П5 29. ИП2 30. - 31. Fx2 32. ИП1 33. * 34. ИП8 35. ИП5 36. П8 37. - 38. Fx2 39. ИП7 40. * 41. + 42. ИП9 43. + 44. + 45. П9 46. ИП4 47. П7 48. x-y 49. БП 50. 04
Инструкция: В/0 С/П "О" a1 С/П b1 С/П h1 С/П "J1" a2 С/П ... "Jn" x-y "F" ИП8 "y".
Программа И.Шериньша: 00. Сх 01. П4 02. П5 03. П6 04. С/П 05. П2 06. С/П 07. П0 08. С/П 09. ИП2 10. * 11. П1 12. ИП3 13. + 14. П3 15. ИП2 16. ИП4 17. + 18. П4 19. ИП1 20. * 21. ИП5 22. + 23. П5 24. ИП1 25. ИП4 26. Fx2 27. * 28. ИП6 29. + 30. П6 31. FL0 32. 08 33. ИП5 34. ИП3 35. / 36. ПА 37. Fx2 38. ИП3 39. * 40. ИП6 41. x-y 42. - 43. С/П.
Инструкция: В/0 С/П "О" Dh С/П n С/П b1 С/П ... bn С/П "J" ИП3 "F" ИПА "а0" ИП5 "S".
Программа А.Маринкевича: 00. ИП9 01. ИП6 02. * 03. ИП8 04. ИП7 05. * 06. - 07. П2 08. 2 09. / 10. ИП0 11. + 12. П0 13. ИП9 14. ИП7 15. + 16. ^ 17. Fx2 18. ИП9 19. ИП7 20. * 21. - 22. ИП2 23. * 24. ИПС 25. + 26. ПС 27. x-y 28. ИП2 29. * 30. ИПА 31. + 32. ПА 33. ИП8 34. ИП6 35. + 36. ^ 37. Fx2 38. ИП8 39. ИП6 40. * 41. - 42. ИП2 43. * 44. ИПД 45. + 46. ПД 47. x-y 48. ИП2 49. * 50. ИПВ 51. + 52. ПВ 53. ИП9 54. П7 55. ИП8 56. П6 57. КИП5 58. ИП5 59. С/П 60. FL1 61. 00 62. ИПА 63. ИП0 64. 6 65. * 66. / 67. ПА 68. ИПВ 69. FBx 70. / 71. ПВ 72. ИПС 73. ПП 74. 90 75. ПС 76. ИПД 77. ПП 78. 90 79. ПД 80. ИПС 81. * 82. ИПД 83. FBx 84. + 85. / 86. 4 87. * 88. П1 89. С/П 90. ИП3 91. / 92. КИП4 93. Fx2 94. ИП0 95. * 96. - 97. В/0.
Инструкция: Сх П0 П5 ПА ПВ ПС ПД n П1 12 П3 9 П4 zk П6 хk П7 z1 П8 х1 П9 В/0 С/П "1" z2 П8 х2 П9 С/П ... zn П8 хn П9 С/П ИП0 "F" ИП1 "J" ИПА "х0" ИПВ
"z0" ИПС "Jz0" ИПД "Jx0".
Примечание: Во всех инструкциях кавычки означают - читай на индикаторе.
МИКРОКАЛЬКУЛЯТОР-СОВЕТЧИК ВРАЧА
В руках у врача листок с результатами обследования пациента, больного вирусным гепатитом. Множество цифр... Как свести их к одной характеристике, объективно оценивающей тяжесть заболевания и позволяющей назначить оптимальный режим лечения?
Алгоритм для выработки такой численной характеристики был предложен академиком Г.И.Марчуком, математическая модель разработана Вычислительным центром СО АН СССР и кафедрой детских болезней Московского медицинского института. Результаты применения модели оказались блестящими. Интересующийся найдет ее в книге Н.И.Нисевич и В.Ф.Учайкина "Тяжелые и злокачественные формы вирусного гепатита у детей" (М., "Медицина", 1982). Авторы книги сетуют на то, что ие всякая больница имеет ЭВМ для расчетов по этой модели. А между тем все расчеты по ней можно выполнить на "Электронике Б3-34".
Вычисляются три индекса:
фб - биохимический индекс, характеризующий степень функционального нарушения печени;
фк - клинический индекс, характеризующий клиническое состояние больного;
фт - совокупный индекс тяжести заболевания.
Интерпретируются эти индексы согласно графику:
Для расчета биохимического индекса фб в калькулятор вводятся четыре числа, взятых из анализа:
b - количество свободного билирубина в миллиграмм-процентах;
В - количество связанного билирубина в миллиграмм-процентах (если обе величины выражены в микромолях на литр, их надо разделить на 17.1);
бета - содержание бета-липопротеидов в условных единицах (по методу Бурштейна);
f - активность Ф-1-ФА (Фруктоза - 1 - фосфатальдолаза) в единицах экстинкции (метод Товарницкого в модификации Брагинского).
Программа вычисляет индекс фб по формулам:
P=b+3B
K1=2.2-0.12P
K2=2-K1
J1=1/100[10(P-1.5)+2(f-1.2)+1/2(бета-40)]
J2=20/бета+(b+B)/5f
фб=K1J1+K2J2
K1=К2=1 при Р>=10. Если величины, заключенные в круглые скобки в выражении для J1 отрицательны, то они заменяются нулями.
Для расчета клинического индекса фк вводятся оценки семи клинических симптомов: 1 - вялость; 2 - отсутствие аппетита; 3 - частота рвоты; 4 - желтушность кожных покровов; 5 - размеры печени; 6 - подкожные кровоизлияния; 7 - беспокойство (капризность, нарушение сна).
Каждый из этих симптомов оценивается в баллах по степени его выраженности: 0 - симптом отсутствует (то есть показатель в норме); 1 - симптом выражен слабо; 2 - выражен умеренно; 3 - выражен резко.
При вводе этих оценок в калькулятор программа работает в "диалоговом режиме", то есть перед вводом оценки на индикаторе показывается ее номер со знаком минус (для отличия номера вопроса от оценки). Оценки суммируются и делятся на четыре, давая величину фк.
Обобщающий индекс - индекс тяжести заболевания фт - вычисляется программой по формуле фт=0.25фк+0.75фб, где весовые коэффициенты 0.25 и 0.75 рассчитаны методом наименьших квадратов из условий наилучшего согласования фт с оценкой тяжести заболевания общепринятыми клиническими методами.
Введя программу, набрать на клавиатуре
0.12 П1 1.2 П2 1.5 П3 2.2 П4 40 П5. Далее записать в память биохимические показатели: b ПА В ПВ бета ПС f ПД. Нажать клавиши В/0, С/П. Далее в "диалоговом режиме" в ответ на появляющиеся на индикаторе числа -1, -2, ..., -7 ввести оценки симптомов. Нажать С/П, затем после останова ИПА, ИПВ - и считать с индикатора значения фт, фб, фк. Для нового расчета ввести новые значения b, В, бета, f.
Время расчета до появления минус единицы на индикаторе - около 25 секунд. Общее время получения трех индексов для одного больного - около минуты.
Контрольный пример. У больного биохимические исследования показали: b=2; В=4; бета=78; f=44. Клинические признаки получили такие оценки: 3, 3, 3, 3, 2, 2, 2. В результате расчета были подучены индексы: фт=3.06: фб=2.58: фк=4.5, что можно интерпретировать следующим образом: нарушение функционального состояния печени у данного больного соответствует среднетяжелой форме заболевания с переходом к тяжелой, клиническая картина соответствует тяжелой форме; обобщенный индекс фт расценивается как тяжелая форма вирусного гепатита.
Анализ полученных индексов помогает правильно и объективно оценить тяжесть заболевания, своевременно диагностировать тяжелую форму и принять решение о проведении интенсивной терапии. Весьма плодотворен анализ индексов в динамике, с помощью их графического изображения в зависимости от времени.
Г.СЛАВИН (г.Тарту)
00. ИПА 01. ИПВ 02. 3 03. * 04. + 05. П9 06. ИП3 07. ПП 08. 93 09. 1 10. 0 11. * 12. ИПD 13. ИП2 14. ПП 15. 93 16. 2 17. * 18. + 19. ИПС 20. ИП5 21. ПП 22. 93 23. 2 24. / 25. + 26. 2 27. F10X 28. / 29. П6 30. ИПА 31. ИПВ 32. + 33. ИПD 34. 5 35. * 36. / 37. 2 38. 0 39. ИПС 40. / 41. + 42. П8 43. ИП9 44. 1 45. 0 46. - 47. Fx>=0 48. 53 49. 1 50. П7 51. БП 52. 62 53. ИП4 54. ИП9 55. ИП1 56. * 57. - 58. П7 59. 2 60. x-y 61. - 62. ИП8 63. * 64. ИП7 65. ИП6 66. * 67. + 68. ПА 69. Сх 70. П6 71. П9 72. 7 73. П0 74. КИП6 75. ИП6 76. /-/ 77. С/П 78. ИП9 79. + 80. П9 81. FL0 82. 74 83. 4 84. / 85. ПВ 86. ИПА 87. 3 88. * 89. + 90. 4 91. / 92. С/П 93. - 94. Fx<0 95. 97 96. 0 97. В/0.
Адреса
00-05: вычисление Р и запись в Р9.
05-29: вычисление J1 и запись в Р6.
30-42: вычисление J2 н запись в Р8.
43-52: проверка р>10? и присваивание K1=К2=1.
53-61: вычисление K1 и запись в Р7, вычисление К2.
62-68: вычисление Фб и запись в РА.
69-77: подготовка к суммированию оценок симптомов и к показу номеров вопросов со знаком минус.
74-82: суммирование оценок в диалоговом режиме.
83-85: получение фк и запись в РВ.
86-92: вычисление и показ фт.
93-97: подпрограмма, не изменяющая положительное число и приравнивающая нулю отрицательное (для круглых скобок в выражении для J1).
КАК ВЫБРАТЬ АРБУЗ?
Десятиклассник Сергей Васюк из села Шаповаловка Борзянского района Черниговской области вывел простую эмпирическую формулу зависимости веса спелого арбуза от длины его обхвата: m~17e-6*L**3, где L - длина "экватора" арбуза в сантиметрах, m - масса в килограммах.
Вот программа расчета по этой формуле для "Электроники Б3-34". 00. 1 01. 0 02. 0 03. П0 04. 1 05. 7 06. ВП 07. 6 0В. /-/ 09. ^ 10. ИП0 11. ^ 12. Fx2 13. * 14. * 15. ^ 16. ВП 17. 5 18. + 19. FBx 20. - 21. С/П 22. F() 23. FL0 24. 10
После каждого нажатия на С/П вы будете получать очередное значение "критической массы" арбуза, определяющей границу спелости и неспелости, для значений L = 100, 99, 98см и т.д.
Выбор арбуза с помощью заполненной по программе таблицы или нарисованного по таблице графика становится несложным делом. Стоит лишь обмерить арбуз сантиметровой лентой, взвесить его и сравнить экспериментальные данные с табличными. Вес арбуза должен быть меньше, чем значится в таблице,- тогда арбуз окажется спелым. Однако важно не переусердствовать: "очень спелый" арбуз с весом, значительно меньшим табличного, скорее всего окажется просто гнилым.
А.БОРИСОВ (г.Москва)
Раздел ведет кандидат физико-математичесних наук Ю.ПУХНАЧЕВ
Трудно предугадывать, какой из материалов раздела вызовет наибольший отклик у читателей. Порою небольшая заметка на узкоспециальную тему вовлекает десятки людей в широкую дискуссию об общих принципах составления программ для микрокалькулятора. Так случилось со статьей К.Ткачука "Нежесткие программы" (12/84). Хотя речь в ней шла о весьма частном расчете из области сопротивления материалов, соображения, высказанные по ее поводу в письмах читателей, по-видимому, будут интересны всем, кто решает задачи на программируемом микрокалькуляторе. Своими мнениями поделились В.Анисимов (г.Уфа), Ю.Газиев, Л.Горохов, В.Козлов (г.Ленинград), В.Кочетов (г.Хмельницкий), А.Маринкевич (пос.Татищево Саратовской области), Е.Новик (г.Ташкент), А.Новиков (г.Москва), И.Сонин (г.Саратов), И.Шериньш (г.Рига), Е.Шидловский (г.Тбилиси) и другие. Обзор читательской почты подготовил А.Бойко.
ИЩИТЕ УДАЧНЫЕ АЛГОРИТМЫ!
Вспомним суть проблемы, для решения которой составил свою программу К.Ткачук. Требуется вычислить момент инерции балки сложного профиля относительно оси, проходящей через центр тяжести. Профиль разбивается на прямоугольники - фигуры, для которых расчет момента инерции проводится по очень простой формуле. Общий момент подсчитывается суммированием. Сначала (первая часть программы) и он и положение центра тяжести профиля определяются относительно некоторой произвольной оси. Затем (вторая часть) вручную определяется положение отдельных прямоугольников относительно оси, проходящей через центр тяжести профиля. Наконец (третья часть), найденная ранее величина момента инерции пересчитывается для нового положения оси.
ПЕРВЫЙ ШАГ НА ПУТИ УЛУЧШЕНИЯ ЛЮБОЙ ПРОГРАММЫ - ИСКЛЮЧИТЬ ИЛИ СВЕСТИ К МИНИМУМУ РУЧНЫЕ ВЫЧИСЛЕНИЯ И ДЕЙСТВИЯ ПРИ ВВОДЕ И ВЫВОДЕ ДАННЫХ - в этом единодушны все, кто, совершенствуя программу К.Ткачука, сохранял предложенное им разбиение профиля иа прямоугольники.
А.НОВИКОВ (восьмиклассник). На первом этапе в программе К.Ткачука слишком много остановов, на последнем приходится заново вводить величины b1 и h1. Необходимо, по-моему, отказаться от деления процесса вычислений иа три этапа. Лучше начать с определения момента инерции какого-то одного прямоугольника относительно оси, проходящей через его центр тяжести, потом добавить еще один прямоугольник, найти центр тяжести пары и определить ее общий момент инерции относительно оси, проходящей через этот центр, а затем пересчитывать результаты с добавлением каждого нового прямоугольника, как показано с левого края на рисунке:


В.КОЗЛОВ. Предлагаю сузить область применения программы до случая, когда число прямоугольников, на которые разбито сечение, не превышает восьми. Пусть данные о каждом прямоугольнике запоминаются в регистрах как числа вида "ВВНН.АА", в которых соответствующие разряды выделены для записи bi, hi, ai. Работая с программой, оператор пользуется лишь одной клавишей С/П как при вводе исходных данных, так и при выводе результатов расчета. Если воспользоваться командами ИПР, можно контролировать данные, введенные раньше.
Сравнение программ, присланных читателями в ответ на опубликованную, с точки зрения удобства использования и вычислительных возможностей дает различные результаты.

Удобная для пользователя программа В.Козлова оказалась далеко не самой эффективной, как и программа А.Новикова. (Следует оговориться, что программы, предназначенные для решения более сложных задач, как у В.Кочетова, или более слабые, на схеме не представлены).
Программа А.Маринкевича, напротив, "подпрыгнула" на второе место по эффективности. Чем это объясняется?
ВЫБРАТЬ ИНОЙ АЛГОРИТМ РАСЧЕТОВ - ТОЛЬКО ТАК МОЖНО РАДИКАЛЬНО ПОВЫСИТЬ ЭФФЕКТИВНОСТЬ ПРОГРАММЫ. Одна из заповедей программирования недаром гласит: "Время, потраченное на подбор хорошего алгоритма, приносит гораздо больший выигрыш, чем время, потраченное на доводку плохой программы".
А.МАРИНКЕВИЧ. Моя программа позволяет вычислять геометрические характеристики плоских сечений более сложных форм, чем составленных из прямоугольников. Сечение произвольной формы - например, с внутренней полостью - вычерчивается на координатной плоскости, как показано на рисунке. Нумерацию угловых точек проводим по часовой стрелке, оставляя область сечения справа. По очереди вводим в микрокалькулятор координаты угловых точек, а после останова программы командами ИП0, ИПА-ИПД выводим на индикатор значения F, X0, Z0, Jz0, Jx0.

ВЫЧИСЛИТЕЛЬНЫЕ ВОЗМОЖНОСТИ ПРОГРАММЫ МОГУТ БЫТЬ РАСШИРЕНЫ БЛАГОДАРЯ ПОДПРОГРАММАМ.
И.СОНИН. Сечение можно разбивать на однотипные элементы, кодировать их и, в зависимости от кода, вести расчет по той или иной формуле. Сложное сечение разбивается на N элементарных фигур - прямоугольников, треугольников, кругов,- и расчет производится последовательным добавлением фрагментов сечения. Исходное сечение можно разбивать на фигуры не только действительные, но и "мнимые". Например, прямоугольный трубчатый профиль можно составить из четырех прямоугольников - стенок трубы, а можно из двух фигур: одной действительной (прямоугольник ABCD из рисунке) и мнимой (отверстие EFGH), для которой численные характеристики берутся со знаком минус. Очевидно, что второй способ проще.
Аналогичный способ применил и Е.Шидловский, хотя набор элементов разбиения у него иной:

Вернемся к схеме, где сопоставляются достоинства программ, присланных читателями. Обратим внимание: программа И.Шериньша оказалась на первом месте и по своим вычислительным возможностям и по удобству работы с нею. Об удобстве программы позволила позаботиться ее краткость. Но почему программа короче остальных?
"ЧЕЛОВЕЧЕСКИЕ" МЕТОДЫ РАСЧЕТА, РАЗРАБОТАННЫЕ ДЛЯ ВЫЧИСЛЕНИЙ ВРУЧНУЮ, ДАЛЕКО НЕ ВСЕГДА ОКАЗЫВАЮТСЯ ЭФФЕКТИВНЫМИ ПРИ ПЕРЕНОСЕ ИХ НА ЭВМ.
В.АНИСИМОВ. Наибольшие резервы улучшения программы заключаются порой в корректировке алгоритма с учетом специфики решения задач на ЭВМ. "Человеческие" методы, как правило, весьма экономичны по числу выполняемых операций, но если вычислительная машина действует, следуя тем же методам, это иногда оборачивается во вред пользователю: программы оказываются сложными, неудобными в работе.
И.ШЕРИНЬШ. Работать по готовым формулам было целесообразно при счете, например, на логарифмических линейках. С этой целью создавались формулы для отдельных часто встречающихся случаев - например, для момента инерции прямоугольника, круга и других фигур. В общем случае любое сечение эффективнее не разбивать на эти привычные элементарные фигуры, а рассчитывать сразу по общей формуле

Подсчитывать нужно три интеграла с одинаковыми пределами и переменными интегрирования. Это суммарная площадь F, статический момент S и вышеупомянутый интеграл. Интегралы можно заменить суммами, например
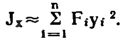
А поскольку в них содержатся одинаковые слагаемые, программу удается сократить за счет параллельного формирования всех трех сумм. Степень точности можно регулировать выбором числа n.
Решим задачу К.Ткачука. Для этого разделим площадь на 16 полос равной высоты, по одному сантиметру, как показано с правого края на первом рисунке. Ось Х'Х' разместим иа 0.5см ниже края сечения, чтобы расстояние центра тяжести каждой полоски до оси выражалось целым числом сантиметров, это упростит ввод. Различной остается ширина полосок bi. Только одну эту величину для каждого цикла счета понадобится вводить оператору. Результат: Jx=1580.07. Это менее чем на полпроцента отличается от результата К.Ткачука.
Подведем итог. ЕСЛИ ПРОГРАММА НЕУДОБНА В РАБОТЕ, ТО ЭТО СКОРЕЕ ВСЕГО СВИДЕТЕЛЬСТВУЕТ О НЕУДАЧНО ВЫБРАННОМ АЛГОРИТМЕ, НЕУМЕЛОМ ПРОГРАММИРОВАНИИ, А НЕ О ТОМ, ЧТО ВЫЧИСЛИТЕЛЬНЫЕ ВОЗМОЖНОСТИ МИКРОКАЛЬКУЛЯТОРА НЕ ПОЗВОЛЯЮТ ДОСТИЧЬ ЛУЧШЕГО. Хотелось бы познакомиться с мнением читателей рубрики иа этот счет.
Программа А.Новикова: 00. Сх 01. П7 02. П8 03. П9 04. С/П 05. С/П 06. С/П 07. * 08. П1 09. FBx 10. Fx2 11. * 12. 1 13. 2 14. / 15. x-y 16. П2 17. ИП1 18. * 19. ИП7 20. ИП8 21. * 22. + 23. ИП7 24. ИП1 25. + 26. П4 27. / 28. П5 29. ИП2 30. - 31. Fx2 32. ИП1 33. * 34. ИП8 35. ИП5 36. П8 37. - 38. Fx2 39. ИП7 40. * 41. + 42. ИП9 43. + 44. + 45. П9 46. ИП4 47. П7 48. x-y 49. БП 50. 04
Инструкция: В/0 С/П "О" a1 С/П b1 С/П h1 С/П "J1" a2 С/П ... "Jn" x-y "F" ИП8 "y".
Программа И.Шериньша: 00. Сх 01. П4 02. П5 03. П6 04. С/П 05. П2 06. С/П 07. П0 08. С/П 09. ИП2 10. * 11. П1 12. ИП3 13. + 14. П3 15. ИП2 16. ИП4 17. + 18. П4 19. ИП1 20. * 21. ИП5 22. + 23. П5 24. ИП1 25. ИП4 26. Fx2 27. * 28. ИП6 29. + 30. П6 31. FL0 32. 08 33. ИП5 34. ИП3 35. / 36. ПА 37. Fx2 38. ИП3 39. * 40. ИП6 41. x-y 42. - 43. С/П.
Инструкция: В/0 С/П "О" Dh С/П n С/П b1 С/П ... bn С/П "J" ИП3 "F" ИПА "а0" ИП5 "S".
Программа А.Маринкевича: 00. ИП9 01. ИП6 02. * 03. ИП8 04. ИП7 05. * 06. - 07. П2 08. 2 09. / 10. ИП0 11. + 12. П0 13. ИП9 14. ИП7 15. + 16. ^ 17. Fx2 18. ИП9 19. ИП7 20. * 21. - 22. ИП2 23. * 24. ИПС 25. + 26. ПС 27. x-y 28. ИП2 29. * 30. ИПА 31. + 32. ПА 33. ИП8 34. ИП6 35. + 36. ^ 37. Fx2 38. ИП8 39. ИП6 40. * 41. - 42. ИП2 43. * 44. ИПД 45. + 46. ПД 47. x-y 48. ИП2 49. * 50. ИПВ 51. + 52. ПВ 53. ИП9 54. П7 55. ИП8 56. П6 57. КИП5 58. ИП5 59. С/П 60. FL1 61. 00 62. ИПА 63. ИП0 64. 6 65. * 66. / 67. ПА 68. ИПВ 69. FBx 70. / 71. ПВ 72. ИПС 73. ПП 74. 90 75. ПС 76. ИПД 77. ПП 78. 90 79. ПД 80. ИПС 81. * 82. ИПД 83. FBx 84. + 85. / 86. 4 87. * 88. П1 89. С/П 90. ИП3 91. / 92. КИП4 93. Fx2 94. ИП0 95. * 96. - 97. В/0.
Инструкция: Сх П0 П5 ПА ПВ ПС ПД n П1 12 П3 9 П4 zk П6 хk П7 z1 П8 х1 П9 В/0 С/П "1" z2 П8 х2 П9 С/П ... zn П8 хn П9 С/П ИП0 "F" ИП1 "J" ИПА "х0" ИПВ
"z0" ИПС "Jz0" ИПД "Jx0".
Примечание: Во всех инструкциях кавычки означают - читай на индикаторе.
МИКРОКАЛЬКУЛЯТОР-СОВЕТЧИК ВРАЧА
В руках у врача листок с результатами обследования пациента, больного вирусным гепатитом. Множество цифр... Как свести их к одной характеристике, объективно оценивающей тяжесть заболевания и позволяющей назначить оптимальный режим лечения?
Алгоритм для выработки такой численной характеристики был предложен академиком Г.И.Марчуком, математическая модель разработана Вычислительным центром СО АН СССР и кафедрой детских болезней Московского медицинского института. Результаты применения модели оказались блестящими. Интересующийся найдет ее в книге Н.И.Нисевич и В.Ф.Учайкина "Тяжелые и злокачественные формы вирусного гепатита у детей" (М., "Медицина", 1982). Авторы книги сетуют на то, что ие всякая больница имеет ЭВМ для расчетов по этой модели. А между тем все расчеты по ней можно выполнить на "Электронике Б3-34".
Вычисляются три индекса:
фб - биохимический индекс, характеризующий степень функционального нарушения печени;
фк - клинический индекс, характеризующий клиническое состояние больного;
фт - совокупный индекс тяжести заболевания.
Интерпретируются эти индексы согласно графику:

Для расчета биохимического индекса фб в калькулятор вводятся четыре числа, взятых из анализа:
b - количество свободного билирубина в миллиграмм-процентах;
В - количество связанного билирубина в миллиграмм-процентах (если обе величины выражены в микромолях на литр, их надо разделить на 17.1);
бета - содержание бета-липопротеидов в условных единицах (по методу Бурштейна);
f - активность Ф-1-ФА (Фруктоза - 1 - фосфатальдолаза) в единицах экстинкции (метод Товарницкого в модификации Брагинского).
Программа вычисляет индекс фб по формулам:
P=b+3B
K1=2.2-0.12P
K2=2-K1
J1=1/100[10(P-1.5)+2(f-1.2)+1/2(бета-40)]
J2=20/бета+(b+B)/5f
фб=K1J1+K2J2
K1=К2=1 при Р>=10. Если величины, заключенные в круглые скобки в выражении для J1 отрицательны, то они заменяются нулями.
Для расчета клинического индекса фк вводятся оценки семи клинических симптомов: 1 - вялость; 2 - отсутствие аппетита; 3 - частота рвоты; 4 - желтушность кожных покровов; 5 - размеры печени; 6 - подкожные кровоизлияния; 7 - беспокойство (капризность, нарушение сна).
Каждый из этих симптомов оценивается в баллах по степени его выраженности: 0 - симптом отсутствует (то есть показатель в норме); 1 - симптом выражен слабо; 2 - выражен умеренно; 3 - выражен резко.
При вводе этих оценок в калькулятор программа работает в "диалоговом режиме", то есть перед вводом оценки на индикаторе показывается ее номер со знаком минус (для отличия номера вопроса от оценки). Оценки суммируются и делятся на четыре, давая величину фк.
Обобщающий индекс - индекс тяжести заболевания фт - вычисляется программой по формуле фт=0.25фк+0.75фб, где весовые коэффициенты 0.25 и 0.75 рассчитаны методом наименьших квадратов из условий наилучшего согласования фт с оценкой тяжести заболевания общепринятыми клиническими методами.
Введя программу, набрать на клавиатуре
0.12 П1 1.2 П2 1.5 П3 2.2 П4 40 П5. Далее записать в память биохимические показатели: b ПА В ПВ бета ПС f ПД. Нажать клавиши В/0, С/П. Далее в "диалоговом режиме" в ответ на появляющиеся на индикаторе числа -1, -2, ..., -7 ввести оценки симптомов. Нажать С/П, затем после останова ИПА, ИПВ - и считать с индикатора значения фт, фб, фк. Для нового расчета ввести новые значения b, В, бета, f.
Время расчета до появления минус единицы на индикаторе - около 25 секунд. Общее время получения трех индексов для одного больного - около минуты.
Контрольный пример. У больного биохимические исследования показали: b=2; В=4; бета=78; f=44. Клинические признаки получили такие оценки: 3, 3, 3, 3, 2, 2, 2. В результате расчета были подучены индексы: фт=3.06: фб=2.58: фк=4.5, что можно интерпретировать следующим образом: нарушение функционального состояния печени у данного больного соответствует среднетяжелой форме заболевания с переходом к тяжелой, клиническая картина соответствует тяжелой форме; обобщенный индекс фт расценивается как тяжелая форма вирусного гепатита.
Анализ полученных индексов помогает правильно и объективно оценить тяжесть заболевания, своевременно диагностировать тяжелую форму и принять решение о проведении интенсивной терапии. Весьма плодотворен анализ индексов в динамике, с помощью их графического изображения в зависимости от времени.
Г.СЛАВИН (г.Тарту)
00. ИПА 01. ИПВ 02. 3 03. * 04. + 05. П9 06. ИП3 07. ПП 08. 93 09. 1 10. 0 11. * 12. ИПD 13. ИП2 14. ПП 15. 93 16. 2 17. * 18. + 19. ИПС 20. ИП5 21. ПП 22. 93 23. 2 24. / 25. + 26. 2 27. F10X 28. / 29. П6 30. ИПА 31. ИПВ 32. + 33. ИПD 34. 5 35. * 36. / 37. 2 38. 0 39. ИПС 40. / 41. + 42. П8 43. ИП9 44. 1 45. 0 46. - 47. Fx>=0 48. 53 49. 1 50. П7 51. БП 52. 62 53. ИП4 54. ИП9 55. ИП1 56. * 57. - 58. П7 59. 2 60. x-y 61. - 62. ИП8 63. * 64. ИП7 65. ИП6 66. * 67. + 68. ПА 69. Сх 70. П6 71. П9 72. 7 73. П0 74. КИП6 75. ИП6 76. /-/ 77. С/П 78. ИП9 79. + 80. П9 81. FL0 82. 74 83. 4 84. / 85. ПВ 86. ИПА 87. 3 88. * 89. + 90. 4 91. / 92. С/П 93. - 94. Fx<0 95. 97 96. 0 97. В/0.
Адреса
00-05: вычисление Р и запись в Р9.
05-29: вычисление J1 и запись в Р6.
30-42: вычисление J2 н запись в Р8.
43-52: проверка р>10? и присваивание K1=К2=1.
53-61: вычисление K1 и запись в Р7, вычисление К2.
62-68: вычисление Фб и запись в РА.
69-77: подготовка к суммированию оценок симптомов и к показу номеров вопросов со знаком минус.
74-82: суммирование оценок в диалоговом режиме.
83-85: получение фк и запись в РВ.
86-92: вычисление и показ фт.
93-97: подпрограмма, не изменяющая положительное число и приравнивающая нулю отрицательное (для круглых скобок в выражении для J1).
КАК ВЫБРАТЬ АРБУЗ?
Десятиклассник Сергей Васюк из села Шаповаловка Борзянского района Черниговской области вывел простую эмпирическую формулу зависимости веса спелого арбуза от длины его обхвата: m~17e-6*L**3, где L - длина "экватора" арбуза в сантиметрах, m - масса в килограммах.
Вот программа расчета по этой формуле для "Электроники Б3-34". 00. 1 01. 0 02. 0 03. П0 04. 1 05. 7 06. ВП 07. 6 0В. /-/ 09. ^ 10. ИП0 11. ^ 12. Fx2 13. * 14. * 15. ^ 16. ВП 17. 5 18. + 19. FBx 20. - 21. С/П 22. F() 23. FL0 24. 10
После каждого нажатия на С/П вы будете получать очередное значение "критической массы" арбуза, определяющей границу спелости и неспелости, для значений L = 100, 99, 98см и т.д.

Выбор арбуза с помощью заполненной по программе таблицы или нарисованного по таблице графика становится несложным делом. Стоит лишь обмерить арбуз сантиметровой лентой, взвесить его и сравнить экспериментальные данные с табличными. Вес арбуза должен быть меньше, чем значится в таблице,- тогда арбуз окажется спелым. Однако важно не переусердствовать: "очень спелый" арбуз с весом, значительно меньшим табличного, скорее всего окажется просто гнилым.
А.БОРИСОВ (г.Москва)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
9/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ЧЕТВЕРТОЕ, тема которого - завершающие этапы решения задач на ЭВМ: составление программы, ее отладка и оформление, счет по ней.
Ведут занятие М.Ф.ПОСНОВА, кандидат физико-математических наук И.Н.ПОСНОВ (Белорусский государственный университет), кандидаты физико-математических наук В.Л.ЛЕОНТЬЕВ и Г.Н.БАКУНИН (Винницкий политехнический институт)
ПРОГРАММИРОВАНИЕ. Начнем его с "начала", хотя этот блок ни в каких командах не воплощается. Не находят отражения в программе и действия, записанные в параллелограммах: ввод информации производится вручную с клавиатуры, вывод заключается в считывании чисел с индикатора. Короче говоря, первые команды нашей программы отразят содержимое первого из прямоугольников блок-схемы, по командам которого введенные в калькулятор коэффициенты a1, a2, a3 расставляются по своим местам в числовой памяти.
Читателю, ознакомившемуся на предыдущем занятии с системой команд "Электроники Б3-34", по-видимому, не составит труда написать этот начальный фрагмент. Завершим его командой С/П, чтобы была возможность ввести следующую тройку: b1, b2, b3.
00. ПД 01. F() 02. ПС 03. F() 04. ПВ 05. 1 06. 1 07. П1 08.3 09. П0 10. С/П.
Переводить на язык команд следующий блок, пожалуй, будет уже посложнее. Здесь наверняка придется в полной мере использовать стек. Поэтому, составляя программу, будем указывать перемещения чисел по его регистрам с помощью уже привычной нам таблицы. Заполнять ее станем карандашом: если допустим ошибку, то сотрем неверные записи и впишем на их место исправленные.
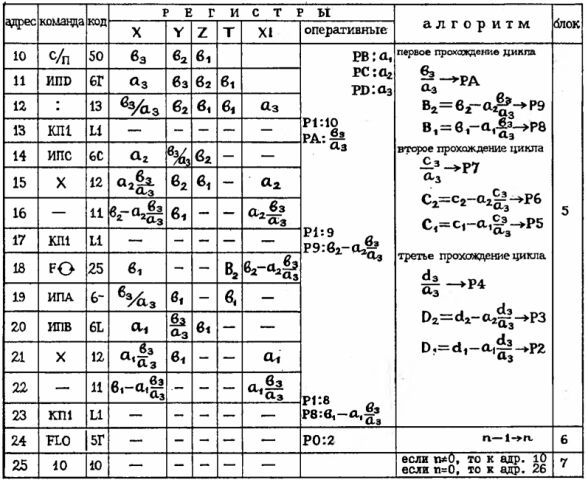
Предположим, фрагмент получился таким, каким он записан в первых трех столбцах таблицы. В следующих столбцах показано, как будут заполняться по ходу выполнения цикла регистры стека, если вначале в него были занесены величины b1, b2, b3.
Как видим, нынешняя таблица шире той, что составлялась нами на прежнем занятии. В последних двух колонках отмечен номер блока, которому соответствует данная цепочка команд, н приведен фрагмент алгоритма, переводом которого на командный язык она служит. Добавлена также колонка, где указано содержимое адресуемых регистров, упоминаемых в этом отрывке текста программы.
Проследив цикл от начала до конца, вернемся к его началу н мысленно введем следующую тройку чисел: c1, c2, c3. Сотрем содержимое колонок, соответствующих регистрам стека, и будем заполнять их заново, прослеживая новое прохождение цикла.
Добравшись до адреса 19. выполняем записанную там команду ИПА. Она вызовет в регистр X дробь b3/a3. Нам же нужна сейчас совсем другая дробь: c3/a3. Ошибка? Несомненно. Как же исправить ее? Очевидно, дроби b3/a3, c3/a3, d3/a3, после их вычисления надо засылать не только в регистры А, 7, 4, но и запасать еще где-то, откуда извлекать при необходимости. Но где? Все адресуемые регистры уже отведены под величины, участвующие или определяемые в процессе вычислений. Однако заполняются они не сразу. И тот из них, который заполняется последним (то есть Р2), можно привлечь для временного хранения нужных нам дробей.
Исправляем ошибочный фрагмент программы с учетом этого замечания: 10. С/П 11. ИПД 12. / 13. КП1 14. П2 15. ИПС 16. * 17. - 18. КП1 19. F() 20. ИП2 21. ИПВ 22. * 23. - 24. КП1 25. FL0 26. 10.
Составьте заново таблицу и убедитесь, что теперь вычисление коэффициентов B1, B2, C1, C2, D1, D2 протекает верно.
(Здесь следует заметить, что решению задач на ЭВМ вообще присущ подобный "циклический" характер, когда ошибка, обнаруженная на некотором этапе работы, возвращает программиста назад, к одному из уже пройденных этапов. Так, например, не найдя хорошего метода решения, приходится заново формулировать задачу; не сумев разработать алгоритм, выполнимый на имеющейся машине,- искать новый метод решения. При составлении блок-схемы, а затем и при программировании нередко вскрываются ошибки, допущенные при разработке алгоритма... И даже тогда, когда программа составлена окончательно и представляется безупречной, во время счета в ней может вскрыться не замеченная ранее ошибка, исправление которой заставит начать работу вновь с того или иного из предшествующих этапов, вплоть до того, где задаче еще только давалась математическая формулировка. Программист, особенно начинающий, должен быть готов к подобным неприятностям).
Попробуйте самостоятельно составить завершающий фрагмент программы, где вычисляются z, y и x. Не забудьте поставить команды останова там, где получается каждая из неизвестных: это нужно, чтобы считывать их значения с индикатора. Сравните полный текст программы с приведенным ниже.
ОТЛАДКА ПРОГРАММЫ. Так называется этап, начинающийся с ввода программы в калькулятор н заключающийся в проверке, действительно ли она выполняет алгоритм, который должна выполнить.
Итак, включаем калькулятор, устанавливаем его в режим программирования и вводим в него нашу программу. Как мы уже знаем, она хранится в калькуляторе в виде последовательности кодов операций, записанных в ячейки программной памяти. Если при вводе допущена ошибка, эта последовательность не совпадает с той, что находится в третьей колонке только что составленного нами текста программы.
Чтобы выяснить, так это или не так, возвращаемся в режим вычислений, передаем управление на начальный адрес программы с помощью клавиши В/0 и вновь переводим калькулятор в режим программирования. Затем раз за разом нажимаем клавишу "ШГ вправо". С каждым ее нажатием содержимое счетчика адресов, отображаемое в правой стороне индикатора, увеличивается на единицу, так что у левого края индикатора последовательно появляются коды, записанные в программную память. Адрес крайнего левого кода всегда на единицу меньше того, что в данный момент виден у правого края.
Так можно просмотреть всю программную память. Если после очередного нажима клавиши "ШГ вправо" слева на индикаторе появился не тот код. что записан в тексте программы, следует вернуться на адрес назад, нажав клавишу "ШГ влево", а потом заново набрать команду, которая должна стоять по адресу, высвечиваемому справа. Прежнее содержимое этого адреса сотрется и заменится кодом набранной операции.
Команды перехода, каждая из которых занимает два адреса, в ходе подобного исправления должны вводиться заново целиком. Пусть, например, просматривая составленную нами программу и добравшись до адреса 26, мы обнаружили, что в команде организации цикла неверно указан адрес перехода: 25. FL0 26. 20. Чтобы исправить ошибку, надо дважды нажать клавишу "ШГ влево", а затем заново ввести и операцию FL0 и верный адрес перехода 10. Если бы мы попытались поступить проще, ввести вновь одно лишь это число 10, калькулятор "не понял" бы, что речь идет об адресе перехода, и записал бы в две последовательные ячейки программной памяти 1 и 0 - а это совсем не то, что требуется.
Так, исправляя ошибку за ошибкой, можно добиться полного совпадения текстов - записанных в память калькулятора и на бумаге.
Окончательно убедившись, что программа правильно введена в калькулятор, проверим, правильно ли она работает, и исправим ошибки, если они были допущены при ее составлении.
Если программа невелика, проще всего это сделать так. В режиме ручных вычислений передаем управление на начальный адрес, а затем раз за разом нажимаем клавишу ПП. ("Потактовый Проход" - так раскрывается это обозначение, если вычисления выполняются вручную). С каждым ее нажатием последовательно выполняется по одной команде программы и результат выводится на индикатор. Особенно легко протекает такая проверка, если составить контрольный пример, для которого можно сказать, какие результаты должны получиться после выполнения каждой команды.
Обратимся к нашей программе для решения системы трех линейных уравнений. Пусть система такова:
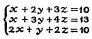
Циклический фрагмент программы, стоящий по адресам с 10 по 26, должен преобразовать первые два уравнения системы к виду:

Таким образом, B1=1.5; B2=2.5; C1=2; C2=3; D1=5; D2=8.
Предположим, что этот фрагмент содержит ошибку, допущенную нами при первой попытке составить его: 10. С/П 11. ИПД 12. / 13. КП1 14. ИПС 15. * 16. - 17. КП1 18. F() 19. ИПА 20. ИПВ 21. * 22. - 23. КП1 24. FL0 25. 10.
Передаем управление на нулевой адрес с помощью клавиши В/0 и вводим в калькулятор числа a1=1, a2=1, a3=2. С помощью клавиши ПП проходим первые девять команд и останавливаемся по адресу 10. Вводим b1=2, b2=3, b3=1 и, нажимая клавишу ПП, выполняем интересующий нас цикл в режиме потактового прохода. Дойдя до команды 17. КП1, мы видим, что она отсылает в Р9 верную величину B1=1.5. Продолжая проход, отмечаем, что команда 23. КП1 направляет в Р8 опять-такн верную величину В2=2.5. Наконец, по команде 24. FL0 25. 10 программа вернется на адрес 10 и остановится на нем (мы заметим при этом, что всякая команда перехода выполняется за одно нажатие клавиши ПП). Введем c1=3, c2=4, c3=2 и начнем второй потактовый проход цикла. И тут мы обнаружим, что команда 17. КП1 пошлет в Р6 неверно вычисленный коэффициент C1=2.5 (должно быть 2). Командой 23. КП1 в Р5 будет направлен также неверный результат C2=3.5 (должно получиться 3).
Как исправить ошибку, мы уже знаем: между командами КП1 и ИПС, стоящими по адресам 13 и 14, надо вставить команду П2. Однако вакантного адреса для нее нет. Исправленную программу, начиная с 14-го адреса, придется вводить заново.
Бывает, надо сказать, и так, что верный фрагмент оказывается короче неверного. Тогда при замене старого фрагмента исправленным можно не трогать остальной текст программы, а в освободившиеся адреса записать "пустую" операцию. Она заносится нажатием двух клавиш К и НОП ("Нет ОПерации") и занимает один адрес.
Начинающим программистам рекомендуется при составлении первого варианта программы записывать эту команду в сомнительные фрагменты, обеспечивая резервы программной памяти на тот случай, если исправление ошибочного фрагмента обернется его удлинением, как это только что произошло у нас.
Описанный способ потактового прохода очень удобен при отладке простых программ. Для более сложных он несколько трудоемок. В этом случае прибегают к поблочному проходу. После конечного адреса каждого блока или в другие ключевые места программы вставляют при ее составлении команду С/П. После запуска программа останавливается в этих местах, и в моменты останова на индикаторе появляются промежуточные результаты. Анализируя их, определяют ошибочный блок или фрагмент и проверяют его в режиме потактового прохода. Для этого программу вновь запускают с самого начала и, остановившись перед подозрительным фрагментом, проходят его с помощью клавиши ПП команда за командой. Прн появлении очевидно неверного результата можно, не нажимая в очередной раз клавишу ПП и перейдя в режим программирования (F ПРГ), увидеть слева код последней выполненной операции. В лучшем случае причина ошибки - неверно введенная команда (тогда надо лишь занести ее заново, предварительно нажав клавишу "ШГ влево"). В худшем - неправильно составленная программа (в таком случае ее порою приходится переделывать с самого начала).
Иногда по самому характеру неверного промежуточного результата удается определить ошибочные команды. Если их адреса близки к адресу, высвечиваемому справа на индикаторе после нажатия клавиши F ПРГ, до них можно добраться с помощью клавиши "ШГ вправо" или "ШГ влево". При большой разнице в адресах ошибочной н текущей команд надо перейти в режим вычислений (F АВТ) и далее передать управление на нужный адрес.
Случается, что при первом пуске программы или при поблочном ее проходе калькулятор останавливается, и на индикаторе появляется сообщение ЕГГОГ (ошибка) - сигнал так называемого аварийного останова. Он может означать, что неверно составленная программа поставила калькулятор перед необходимостью выполнить невыполнимую операцию (разделить число на нуль, извлечь квадратный корень из отрицательного числа, вычислить арксинус от числа, большего единицы, взять логарифм от х или выполнить команду х**y при неположительном х, вычислить тангенс от числа вида пи/2+пи*n). Если сразу после этого перейти в режим программирования, то вторым слева на индикаторе будет код операции, послужившей причиной аварийного останова. Адрес, по которому он записан, на два меньше того, что высвечивается на индикаторе справа. Если теперь вернуться в режим вычислений, на индикаторе появится и число - виновник останова. После этого надо выявить причину создавшейся ситуации.
Сообщение ЕГГОГ появляется и в том случае, если содержимое регистра X превышает по абсолютной величине
9*9999999e99 и потому не может быть выведено на индикатор. Надо заметить, что останов в подобных случаях происходит не всегда. Это зависит от того, какая последовательность команд привела к появлению чрезмерно большого числа.
Когда ошибка в программе устранена, можно продолжить решение контрольного примера, предварительно исправив содержимое регистров, искаженное вследствие ошибки. Но если сделать это трудно, отладку надо начать сначала.
Но вот отладка окончена. Чтобы окончательно убедиться в том, что программа не содержит ошибок, решение контрольного примера проводят вновь с самого начала, попутно отмечая, сколько времени требуется на получение каждого из искомых результатов (эти данные понадобятся при оформлении программы).
Как видим, при составлении качественной программы порой приходится тратить много времени на постановку задачи, выбор метода, разработку алгоритма, составление программы и ее отладку. Однако все эти усилия, как правило, окупаются при использовании программы. Использовать же ее можно лишь тогда, когда она отлажена окончательно, то есть верность выдаваемых ею результатов гарантируется.
Если пользоваться ею в будущем предполагается неоднократно, ее следует тщательно оформить.
ОФОРМЛЕНИЕ ПРОГРАММЫ должно быть очень аккуратным. Ведь достаточно одной неразборчиво написанной команды нлн кода - н использовать программу будет невозможно.
Для ее оформления лучше всего взять лист ватмана или плотной бумаги. В заголовке помещают название программы - несколько слов, кратко и точно поясняющих ее суть. Потом - достаточно подробное описание того, что делает программа, со всеми необходимыми формулами, с указанием области допустимых значений исходных данных. Желательно указать, как используются по ходу счета адресуемые регистры, сколько времени уходит на получение каждого результата, сообщить о существенных, но не очевидных особенностях программы. Без подобных комментариев даже ее составителю бывает трудно работать с нею некоторое время спустя, не говоря уже о тех, кто захочет воспользоваться этой программой.
Затем следует собственно текст программы: адреса, команды, коды по столбцам.
Сразу после текста пишется инструкция по пользованию данной программой. По пунктам, коротко и понятно описывается работа человека от ввода текста программы, начальных данных и констант до получения результата. Можно оформить инструкцию в виде таблицы (символы вводимых величин в графе "нажимаемые клавиши" означают, что указанные числа вводятся с клавиатуры).
Далее обязательно приводится контрольный пример с конкретными значениями начальных данных и получающихся результатов. Как бы тщательно ни вводилась программа, лишь точное решение контрольного примера дает уверенность, что она введена без ошибок.


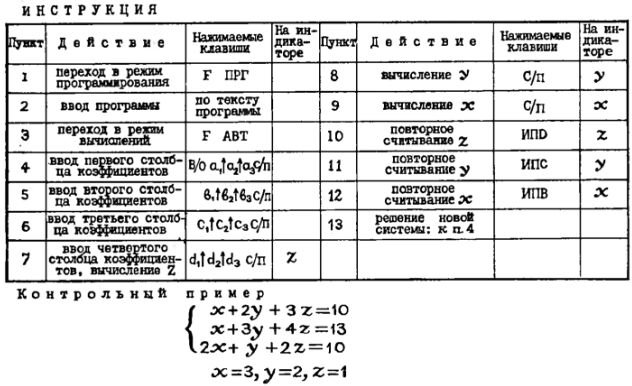
Для начинающего программиста нелишне прикладывать к оформленной таким образом программе блок-схему алгоритма и таблицы, показывающие движение чисел по стеку для тех участков программы, разработка которых вызвала особые затруднения. Подробный комментарий к таблице, записанный в графе "алгоритм", поможет избежать трудностей в дальнейшем, при работе с программой.
Различные программы лучше писать на листах одинакового формата. Со временем, когда их скопится много, нх нужно будет расклассифицировать по тематике, по характеру решаемых задач и хранить в добротной коробке.
Лист с только что составленной нами программой для решения системы трех линейных уравнений может выглядеть так, как показано (ср. А.Н.Цветков и В.А.Епанечннков "Прикладные программы для микроЭВМ "Электроника Б3-34", "МК-56", "МК-54"". М., "Финансы н статистика", 1984, стр.14-15).
Разумеется, оформлять программы можно и по-иному - так, как удобнее их предполагаемым и возможным пользователям.
СЧЕТ ПО ПРОГРАММЕ требует тщательной подготовки. Ведь при более или менее серьезных вычислениях приходится иметь дело с большим количеством чисел (исходные данные, промежуточные и окончательные результаты), многократно нажимать клавиши, считывать числа с индикатора и записывать на бумагу... Далеко ли тут до ошибки?
Поэтому перед началом вычислений нужно должным образом подготовить рабочее место: по возможности исключить внешние помехи, приготовить перечень исходных данных и бумагу для записи результатов, авторучку, карандаши, стирательную резинку.
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ЧЕТВЕРТОЕ, тема которого - завершающие этапы решения задач на ЭВМ: составление программы, ее отладка и оформление, счет по ней.
Ведут занятие М.Ф.ПОСНОВА, кандидат физико-математических наук И.Н.ПОСНОВ (Белорусский государственный университет), кандидаты физико-математических наук В.Л.ЛЕОНТЬЕВ и Г.Н.БАКУНИН (Винницкий политехнический институт)
ПРОГРАММИРОВАНИЕ. Начнем его с "начала", хотя этот блок ни в каких командах не воплощается. Не находят отражения в программе и действия, записанные в параллелограммах: ввод информации производится вручную с клавиатуры, вывод заключается в считывании чисел с индикатора. Короче говоря, первые команды нашей программы отразят содержимое первого из прямоугольников блок-схемы, по командам которого введенные в калькулятор коэффициенты a1, a2, a3 расставляются по своим местам в числовой памяти.
Читателю, ознакомившемуся на предыдущем занятии с системой команд "Электроники Б3-34", по-видимому, не составит труда написать этот начальный фрагмент. Завершим его командой С/П, чтобы была возможность ввести следующую тройку: b1, b2, b3.
00. ПД 01. F() 02. ПС 03. F() 04. ПВ 05. 1 06. 1 07. П1 08.3 09. П0 10. С/П.
Переводить на язык команд следующий блок, пожалуй, будет уже посложнее. Здесь наверняка придется в полной мере использовать стек. Поэтому, составляя программу, будем указывать перемещения чисел по его регистрам с помощью уже привычной нам таблицы. Заполнять ее станем карандашом: если допустим ошибку, то сотрем неверные записи и впишем на их место исправленные.

Предположим, фрагмент получился таким, каким он записан в первых трех столбцах таблицы. В следующих столбцах показано, как будут заполняться по ходу выполнения цикла регистры стека, если вначале в него были занесены величины b1, b2, b3.
Как видим, нынешняя таблица шире той, что составлялась нами на прежнем занятии. В последних двух колонках отмечен номер блока, которому соответствует данная цепочка команд, н приведен фрагмент алгоритма, переводом которого на командный язык она служит. Добавлена также колонка, где указано содержимое адресуемых регистров, упоминаемых в этом отрывке текста программы.
Проследив цикл от начала до конца, вернемся к его началу н мысленно введем следующую тройку чисел: c1, c2, c3. Сотрем содержимое колонок, соответствующих регистрам стека, и будем заполнять их заново, прослеживая новое прохождение цикла.
Добравшись до адреса 19. выполняем записанную там команду ИПА. Она вызовет в регистр X дробь b3/a3. Нам же нужна сейчас совсем другая дробь: c3/a3. Ошибка? Несомненно. Как же исправить ее? Очевидно, дроби b3/a3, c3/a3, d3/a3, после их вычисления надо засылать не только в регистры А, 7, 4, но и запасать еще где-то, откуда извлекать при необходимости. Но где? Все адресуемые регистры уже отведены под величины, участвующие или определяемые в процессе вычислений. Однако заполняются они не сразу. И тот из них, который заполняется последним (то есть Р2), можно привлечь для временного хранения нужных нам дробей.
Исправляем ошибочный фрагмент программы с учетом этого замечания: 10. С/П 11. ИПД 12. / 13. КП1 14. П2 15. ИПС 16. * 17. - 18. КП1 19. F() 20. ИП2 21. ИПВ 22. * 23. - 24. КП1 25. FL0 26. 10.
Составьте заново таблицу и убедитесь, что теперь вычисление коэффициентов B1, B2, C1, C2, D1, D2 протекает верно.
(Здесь следует заметить, что решению задач на ЭВМ вообще присущ подобный "циклический" характер, когда ошибка, обнаруженная на некотором этапе работы, возвращает программиста назад, к одному из уже пройденных этапов. Так, например, не найдя хорошего метода решения, приходится заново формулировать задачу; не сумев разработать алгоритм, выполнимый на имеющейся машине,- искать новый метод решения. При составлении блок-схемы, а затем и при программировании нередко вскрываются ошибки, допущенные при разработке алгоритма... И даже тогда, когда программа составлена окончательно и представляется безупречной, во время счета в ней может вскрыться не замеченная ранее ошибка, исправление которой заставит начать работу вновь с того или иного из предшествующих этапов, вплоть до того, где задаче еще только давалась математическая формулировка. Программист, особенно начинающий, должен быть готов к подобным неприятностям).
Попробуйте самостоятельно составить завершающий фрагмент программы, где вычисляются z, y и x. Не забудьте поставить команды останова там, где получается каждая из неизвестных: это нужно, чтобы считывать их значения с индикатора. Сравните полный текст программы с приведенным ниже.
ОТЛАДКА ПРОГРАММЫ. Так называется этап, начинающийся с ввода программы в калькулятор н заключающийся в проверке, действительно ли она выполняет алгоритм, который должна выполнить.
Итак, включаем калькулятор, устанавливаем его в режим программирования и вводим в него нашу программу. Как мы уже знаем, она хранится в калькуляторе в виде последовательности кодов операций, записанных в ячейки программной памяти. Если при вводе допущена ошибка, эта последовательность не совпадает с той, что находится в третьей колонке только что составленного нами текста программы.
Чтобы выяснить, так это или не так, возвращаемся в режим вычислений, передаем управление на начальный адрес программы с помощью клавиши В/0 и вновь переводим калькулятор в режим программирования. Затем раз за разом нажимаем клавишу "ШГ вправо". С каждым ее нажатием содержимое счетчика адресов, отображаемое в правой стороне индикатора, увеличивается на единицу, так что у левого края индикатора последовательно появляются коды, записанные в программную память. Адрес крайнего левого кода всегда на единицу меньше того, что в данный момент виден у правого края.
Так можно просмотреть всю программную память. Если после очередного нажима клавиши "ШГ вправо" слева на индикаторе появился не тот код. что записан в тексте программы, следует вернуться на адрес назад, нажав клавишу "ШГ влево", а потом заново набрать команду, которая должна стоять по адресу, высвечиваемому справа. Прежнее содержимое этого адреса сотрется и заменится кодом набранной операции.
Команды перехода, каждая из которых занимает два адреса, в ходе подобного исправления должны вводиться заново целиком. Пусть, например, просматривая составленную нами программу и добравшись до адреса 26, мы обнаружили, что в команде организации цикла неверно указан адрес перехода: 25. FL0 26. 20. Чтобы исправить ошибку, надо дважды нажать клавишу "ШГ влево", а затем заново ввести и операцию FL0 и верный адрес перехода 10. Если бы мы попытались поступить проще, ввести вновь одно лишь это число 10, калькулятор "не понял" бы, что речь идет об адресе перехода, и записал бы в две последовательные ячейки программной памяти 1 и 0 - а это совсем не то, что требуется.
Так, исправляя ошибку за ошибкой, можно добиться полного совпадения текстов - записанных в память калькулятора и на бумаге.
Окончательно убедившись, что программа правильно введена в калькулятор, проверим, правильно ли она работает, и исправим ошибки, если они были допущены при ее составлении.
Если программа невелика, проще всего это сделать так. В режиме ручных вычислений передаем управление на начальный адрес, а затем раз за разом нажимаем клавишу ПП. ("Потактовый Проход" - так раскрывается это обозначение, если вычисления выполняются вручную). С каждым ее нажатием последовательно выполняется по одной команде программы и результат выводится на индикатор. Особенно легко протекает такая проверка, если составить контрольный пример, для которого можно сказать, какие результаты должны получиться после выполнения каждой команды.
Обратимся к нашей программе для решения системы трех линейных уравнений. Пусть система такова:
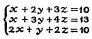
Циклический фрагмент программы, стоящий по адресам с 10 по 26, должен преобразовать первые два уравнения системы к виду:

Таким образом, B1=1.5; B2=2.5; C1=2; C2=3; D1=5; D2=8.
Предположим, что этот фрагмент содержит ошибку, допущенную нами при первой попытке составить его: 10. С/П 11. ИПД 12. / 13. КП1 14. ИПС 15. * 16. - 17. КП1 18. F() 19. ИПА 20. ИПВ 21. * 22. - 23. КП1 24. FL0 25. 10.
Передаем управление на нулевой адрес с помощью клавиши В/0 и вводим в калькулятор числа a1=1, a2=1, a3=2. С помощью клавиши ПП проходим первые девять команд и останавливаемся по адресу 10. Вводим b1=2, b2=3, b3=1 и, нажимая клавишу ПП, выполняем интересующий нас цикл в режиме потактового прохода. Дойдя до команды 17. КП1, мы видим, что она отсылает в Р9 верную величину B1=1.5. Продолжая проход, отмечаем, что команда 23. КП1 направляет в Р8 опять-такн верную величину В2=2.5. Наконец, по команде 24. FL0 25. 10 программа вернется на адрес 10 и остановится на нем (мы заметим при этом, что всякая команда перехода выполняется за одно нажатие клавиши ПП). Введем c1=3, c2=4, c3=2 и начнем второй потактовый проход цикла. И тут мы обнаружим, что команда 17. КП1 пошлет в Р6 неверно вычисленный коэффициент C1=2.5 (должно быть 2). Командой 23. КП1 в Р5 будет направлен также неверный результат C2=3.5 (должно получиться 3).
Как исправить ошибку, мы уже знаем: между командами КП1 и ИПС, стоящими по адресам 13 и 14, надо вставить команду П2. Однако вакантного адреса для нее нет. Исправленную программу, начиная с 14-го адреса, придется вводить заново.
Бывает, надо сказать, и так, что верный фрагмент оказывается короче неверного. Тогда при замене старого фрагмента исправленным можно не трогать остальной текст программы, а в освободившиеся адреса записать "пустую" операцию. Она заносится нажатием двух клавиш К и НОП ("Нет ОПерации") и занимает один адрес.
Начинающим программистам рекомендуется при составлении первого варианта программы записывать эту команду в сомнительные фрагменты, обеспечивая резервы программной памяти на тот случай, если исправление ошибочного фрагмента обернется его удлинением, как это только что произошло у нас.
Описанный способ потактового прохода очень удобен при отладке простых программ. Для более сложных он несколько трудоемок. В этом случае прибегают к поблочному проходу. После конечного адреса каждого блока или в другие ключевые места программы вставляют при ее составлении команду С/П. После запуска программа останавливается в этих местах, и в моменты останова на индикаторе появляются промежуточные результаты. Анализируя их, определяют ошибочный блок или фрагмент и проверяют его в режиме потактового прохода. Для этого программу вновь запускают с самого начала и, остановившись перед подозрительным фрагментом, проходят его с помощью клавиши ПП команда за командой. Прн появлении очевидно неверного результата можно, не нажимая в очередной раз клавишу ПП и перейдя в режим программирования (F ПРГ), увидеть слева код последней выполненной операции. В лучшем случае причина ошибки - неверно введенная команда (тогда надо лишь занести ее заново, предварительно нажав клавишу "ШГ влево"). В худшем - неправильно составленная программа (в таком случае ее порою приходится переделывать с самого начала).
Иногда по самому характеру неверного промежуточного результата удается определить ошибочные команды. Если их адреса близки к адресу, высвечиваемому справа на индикаторе после нажатия клавиши F ПРГ, до них можно добраться с помощью клавиши "ШГ вправо" или "ШГ влево". При большой разнице в адресах ошибочной н текущей команд надо перейти в режим вычислений (F АВТ) и далее передать управление на нужный адрес.
Случается, что при первом пуске программы или при поблочном ее проходе калькулятор останавливается, и на индикаторе появляется сообщение ЕГГОГ (ошибка) - сигнал так называемого аварийного останова. Он может означать, что неверно составленная программа поставила калькулятор перед необходимостью выполнить невыполнимую операцию (разделить число на нуль, извлечь квадратный корень из отрицательного числа, вычислить арксинус от числа, большего единицы, взять логарифм от х или выполнить команду х**y при неположительном х, вычислить тангенс от числа вида пи/2+пи*n). Если сразу после этого перейти в режим программирования, то вторым слева на индикаторе будет код операции, послужившей причиной аварийного останова. Адрес, по которому он записан, на два меньше того, что высвечивается на индикаторе справа. Если теперь вернуться в режим вычислений, на индикаторе появится и число - виновник останова. После этого надо выявить причину создавшейся ситуации.
Сообщение ЕГГОГ появляется и в том случае, если содержимое регистра X превышает по абсолютной величине
9*9999999e99 и потому не может быть выведено на индикатор. Надо заметить, что останов в подобных случаях происходит не всегда. Это зависит от того, какая последовательность команд привела к появлению чрезмерно большого числа.
Когда ошибка в программе устранена, можно продолжить решение контрольного примера, предварительно исправив содержимое регистров, искаженное вследствие ошибки. Но если сделать это трудно, отладку надо начать сначала.
Но вот отладка окончена. Чтобы окончательно убедиться в том, что программа не содержит ошибок, решение контрольного примера проводят вновь с самого начала, попутно отмечая, сколько времени требуется на получение каждого из искомых результатов (эти данные понадобятся при оформлении программы).
Как видим, при составлении качественной программы порой приходится тратить много времени на постановку задачи, выбор метода, разработку алгоритма, составление программы и ее отладку. Однако все эти усилия, как правило, окупаются при использовании программы. Использовать же ее можно лишь тогда, когда она отлажена окончательно, то есть верность выдаваемых ею результатов гарантируется.
Если пользоваться ею в будущем предполагается неоднократно, ее следует тщательно оформить.
ОФОРМЛЕНИЕ ПРОГРАММЫ должно быть очень аккуратным. Ведь достаточно одной неразборчиво написанной команды нлн кода - н использовать программу будет невозможно.
Для ее оформления лучше всего взять лист ватмана или плотной бумаги. В заголовке помещают название программы - несколько слов, кратко и точно поясняющих ее суть. Потом - достаточно подробное описание того, что делает программа, со всеми необходимыми формулами, с указанием области допустимых значений исходных данных. Желательно указать, как используются по ходу счета адресуемые регистры, сколько времени уходит на получение каждого результата, сообщить о существенных, но не очевидных особенностях программы. Без подобных комментариев даже ее составителю бывает трудно работать с нею некоторое время спустя, не говоря уже о тех, кто захочет воспользоваться этой программой.
Затем следует собственно текст программы: адреса, команды, коды по столбцам.
Сразу после текста пишется инструкция по пользованию данной программой. По пунктам, коротко и понятно описывается работа человека от ввода текста программы, начальных данных и констант до получения результата. Можно оформить инструкцию в виде таблицы (символы вводимых величин в графе "нажимаемые клавиши" означают, что указанные числа вводятся с клавиатуры).
Далее обязательно приводится контрольный пример с конкретными значениями начальных данных и получающихся результатов. Как бы тщательно ни вводилась программа, лишь точное решение контрольного примера дает уверенность, что она введена без ошибок.



Для начинающего программиста нелишне прикладывать к оформленной таким образом программе блок-схему алгоритма и таблицы, показывающие движение чисел по стеку для тех участков программы, разработка которых вызвала особые затруднения. Подробный комментарий к таблице, записанный в графе "алгоритм", поможет избежать трудностей в дальнейшем, при работе с программой.
Различные программы лучше писать на листах одинакового формата. Со временем, когда их скопится много, нх нужно будет расклассифицировать по тематике, по характеру решаемых задач и хранить в добротной коробке.
Лист с только что составленной нами программой для решения системы трех линейных уравнений может выглядеть так, как показано (ср. А.Н.Цветков и В.А.Епанечннков "Прикладные программы для микроЭВМ "Электроника Б3-34", "МК-56", "МК-54"". М., "Финансы н статистика", 1984, стр.14-15).
Разумеется, оформлять программы можно и по-иному - так, как удобнее их предполагаемым и возможным пользователям.
СЧЕТ ПО ПРОГРАММЕ требует тщательной подготовки. Ведь при более или менее серьезных вычислениях приходится иметь дело с большим количеством чисел (исходные данные, промежуточные и окончательные результаты), многократно нажимать клавиши, считывать числа с индикатора и записывать на бумагу... Далеко ли тут до ошибки?
Поэтому перед началом вычислений нужно должным образом подготовить рабочее место: по возможности исключить внешние помехи, приготовить перечень исходных данных и бумагу для записи результатов, авторучку, карандаши, стирательную резинку.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Немного разговоров...
10/85

"Ириша" - так называется новый школьный компьютер. На снимке: один из его ведущих разработчиков - научный сотрудник МГУ В.Романов знакомит с ним энтузиастов "дошкольной информатики".
ПЕРСОНАЛЬНЫЙ КОМПЬЮТЕР: ПЕРСПЕКТИВЫ БЛИЗКИЕ И ДАЛЕКИЕ
Академик Е.ВЕЛИХОВ, вице-президент Академии наук СССР, академик-секретарь Отделения информатики, вычислительной техники и автоматизации АН СССР.
ПРЕЖДЕ всего представлю участников "круглого стола", организованного журналом "Наука и жизнь":
- академик Андрей Петрович ЕРШОВ (г.Новосибирск), заведующий отделом Вычислительного центра Сибирского отделения АН СССР,
- член-корреспондент АН СССР Святослав Сергеевич ЛАВРОВ (г.Ленинград), директор Института теоретической астрономии АН СССР,
- старший научный сотрудник Научно-исследовательского вычислительного центра АН СССР (г.Пущино) Григорий Рафаилович ГРОМОВ.
Наш "круглый стол" посвящен феномену персонального компьютера (ПК), как иногда говорят, чтобы подчеркнуть огромный по размаху и скорости фронт проникновения таких ЭВМ во все сферы человеческой деятельности.
Электронные вычислительные машины появились сорок лет назад и представляли собой огромные, загадочно мигающие тысячами ламп электронные монстры. Вокруг них круглосуточно, в три смены, сновали люди в белых халатах, которые должны были вовремя припаять то, что отвалилось, сменить то, что перегорело, и, наконец, самое главное, перевести на понятный машине язык электрических "нулей" и "единиц" ту или иную важную математическую задачу - запрограммировать ее. Участвующий в беседе С.С.Лавров - один из первых советских программистов, в то время работал в коллективе ученых под руководством С.П.Королева, и он хорошо помнит, какие тогда были машины, как трудно было обеспечивать их работоспособность и весьма непросто программировать. Однако именно на первых наших ЭВМ удалось в то время решать важные задачи.
Ныне ЭВМ заметно большей мощности создаются на нескольких кристаллах размером с клеточку арифметической тетради, а с вычислительной машиной на "ты" уже многие наши школьники. Но сегодня этого мало. Нам надо стремиться к полной "компьютерной грамотности". Это одно из необходимых условий выполнения тех широкомасштабных задач, которые стоят перед нами по ускорению научно-технического прогресса, переводу экономики на интенсивный путь развития.
Поэтому потребовалось срочно издать к началу учебного года пособие по новой учебной дисциплине - школьной информатике. Один из авторов этого школьного пособия - академик А.П.Ершов. Замечу, что первая школьная "компьютерная книжка" издается тиражом даже большим, чем печатается такой массовый журнал, как "Наука и жизнь". Зачем это делается?
Микропроцессорная революция резко расширила границы использования вычислительной техники. Приближается то время, когда экономическая мощь общества решающим образом станет определяться арсеналом средств электронной обработки информации.
Первой "ласточкой" этого процесса, первым массовым инструментом электронной обработки информации стали персональные компьютеры - простые в управлении, компактные вычислительные машины.
Цель нашей беседы - рассказать о месте и роли персональных ЭВМ в решении многотрудных задач массовой компьютеризации.
Не стану предварять ход обсуждения, отмечу лишь, что сегодня мировой парк персональных ЭВМ уже превышает 20 миллионов действующих машин. В нашей стране выпускаются и профессиональные ПК и такие компьютеры, которые можно использовать дома, в учебе, в техническом творчестве школьников и студентов. Скажу прямо: этих машин у нас пока много меньше, чем хотелось бы. Перед промышленностью поставлены серьезные задачи, и, несомненно, имеющийся разрыв со временем удастся ликвидировать.
Вместе с тем следует подчеркнуть, что промышленное производство ПК - это лишь одна сторона проблемы. Дело в том, что массовое, эффективное их использование в народном хозяйстве потребует решительного отказа от сложившихся стереотипов профессионального мышления, причем не только миллионов непосвященных - тех, кто сегодня только еще постигает "азы" компьютерной грамотности, но и у многих ученых и специалистов, в том числе и ветеранов вычислительной техники. Замечу, что совсем не очевидно, кому при этом будет труднее перестраиваться...
Дискуссии и обсуждения, подобные нашей встрече, а они проводятся сейчас во многих институтах, конструкторских бюро и на предприятиях различных отраслей промышленности, очень нужны и полезны, ибо привлекают внимание миллионов людей к проблеме огромной важности.
Ученые, собравшиеся за "круглым столом", уже ряд лет принимают участие в таких обсуждениях, активно отстаивают свою точку зрения на страницах научной периодики и массовой печати. Мне представляется особенно уместным замечание, которым однажды начал свой доклад академик Ершов: "Мало иметь что сказать, надо еще быть услышанным..."
Предоставив свои страницы, журнал "Наука и жизнь" дал нам именно такую возможность, и первым воспользоваться ею я попрошу Андрея Петровича Ершова.
АКАДЕМИК А.ЕРШОВ
Хочу сразу сказать, что феномен персональной ЭВМ - ПЭМВ (мне лично этот термин кажется лучше, чем "персональный компьютер") больше всего напоминает "скандал в благородном семействе". Налицо потрясение основ, с таким трудом сформированных за последние 30 лет большой наукой программирования и промышленностью, производящей ЭВМ. И как скандал в благородном семействе вскрывает фальшь внешне благопристойных отношений, так и феномен ПЭВМ выявляет ряд назревших противоречий в развитии вычислительного дела и выводит на сцену новых действующих лиц, новые сущности в программировании и применении ЭВМ.
Позволю себе не углублять здесь этой констатации, многочисленные подтверждения которой можно найти на страницах технической периодики, а подробный анализ в недавно вышедшей книге Г.Р.Громова "Национальные информационные ресурсы: проблемы промышленной эксплуатации".
Отмечу лишь, что, с какой бы стороны и в какой форме ни пришла бы к каждому из нас новость о персональных ЭВМ, уже стало бесспорным одно: эти машины - неотъемлемая и одна из главных ветвей вычислительной техники, приближающая цель ее ускоренного развития: полную информатизацию - перевооружение народного хозяйства страны на основе вычислительной техники.
Полная информатизация общества наступит тогда, когда вся информация, в которой оно нуждается, будет возникать, храниться и циркулировать на машинных носителях и вся ее обработка, как внутренняя, так и во взаимодействии с человеком, будет осуществляться посредством ЭВМ. Революционная сторона перенесения информации на машинные носители состоит в создании предпосылок (а с развитием электросвязи и их реализации) к оперативному обмену всей информацией, к ее доставке в любое требуемое место со скоростью электрических сигналов для обработки и использования.
Не будем гадать, когда это наступит, но, считая полную информатизацию предвидимым будущим, например, лет через пятьдесят, можем оценить число активных членов нашего общества - работающих и учащихся - скажем, в 250 миллионов человек. Если глобальная сеть информационного обмена должна быть доведена до каждого человека, то с учетом его относительной подвижности число входов в такую сеть составит несколько сот миллионов, скажем, 300-400. Совершенно очевидно, что на конце каждого из этих входов нужно устройство, которое теперь никак иначе, кроме как персональной ЭВМ, не назовешь. Сделаем, однако, некоторую уступку экономической целесообразности, введя следующие виды персональных ЭВМ: бытовые, профессиональные и активные терминалы. Последнее - это нечто промежуточное между более скромной бытовой машиной и профессиональной, оснащенной всем, что нужно для эффективной работы.
Дополнительные предположения о числе и численности семей, о соотношении более и менее однородной профессиональной работы приводят к следующей оценке числа персональных вычислительных средств при полной информатизации: профессиональных - 50, бытовых - 200, активных терминалов - 100 миллионов.
Естественно, что персональная вычислительная техника составляет только часть вычислительных средств народного хозяйства. Мы не совершим большой ошибки, если предположим, что ко времени наступления полной информатизации на одного активного члена общества будет приходиться 8-10 машин (на производстве и в быту), в каждую из которых встроен микропроцессорный контроллер или микро-ЭВМ. Отсюда можно оценить общий объем встроенных вычислительных средств в 2 миллиарда.
Может ли такой парк универсальных и встроенных ЭВМ эффективно действовать без достижения в стране всеобщей компьютерной грамотности? Уверен, что нет.
Именно поэтому, например, в Новосибирском академгородке последние десять лет разрабатываются научные и методологические основы школьной информатики. Некоторые из положений созданного нами курса всеобщей "компьютерной грамотности" мы попытались изложить в пробном массовом учебном пособии, о котором здесь уже упоминал академик Е.П.Велихов.
Несколько лет назад я как-то обсуждал с коллегами тезисы своего доклада на конференции в г.Пущино: "Персональная ЭВМ - предок млекопитающих в динозавровом мире ВЦКП" (под ВЦКП имелись в виду вычислительные центры коллективного пользования). Один из участников сказал примерно следующее: "Не знаю, изведут ли твои млекопитающие динозавровые ВЦКП, но то, что они поглотят профессиональных программистов задолго до того, как их станет 600 тысяч,- это уже факт. Твоими же усилиями программирование станет второй грамотностью и человечество без всяких слуг по-хозяйски усядется за персональные ЭВМ и будет делать свое дело".
Я задумался, но потом успокоенно вспомнил, что имел похожий разговор 30 лет назад. Это было после исторического семинара 1955 года в Институте прикладной математики АН СССР у академика М.В.Келдыша. Там первые советские разработчики программирующих программ обсуждали перспективы автоматизации программирования. Воодушевленные происходящим, они философски констатировали, что, занимаясь уже третий год программированием и получая за это зарплату, в то же время рубят сук, на котором сидят.
И хотя с тех пор программистов стало гораздо больше, сук, на котором они устроились, еще достаточно крепок, и можно повторить вслед за другими, что честный ученый в любой данный момент подрывает условия своего существования, и лишь беспредельность человеческого познания позволяет ему не беспокоиться о будущем.
ЧЛЕН-КОРРЕСПОНДЕНТ АН СССР С.ЛАВРОВ
Если не заглядывать далеко вперед, когда, по А.П.Ершову, наступит эра всеобщей информатизации общества, то до той поры основными пользователями ПЭВМ будут оставаться люди из числа ведущих (не в административном, а в творческом плане) специалистов институтов, бюро и других организаций, прежде всего те, кто уже сейчас знаком с вычислительной техникой и прилично ею владеет.
Что больше всего нужно этим людям? Если спросить об этом инженера или научного сотрудника, то он наверняка ответит, что больше всего ему недостает (на работе - не в быту) хорошего помощника - техника, лаборанта, машинистки... Другими словами, ему хочется избавиться от рутинных операций, облегчить себе работу творческую. Такие операции - это прежде всего поиск нужных данных в различных справочниках, нормативных документах, архивных делах, поиск самих этих справочников и документов, нужной бумаги в собственном столе, составление шаблонных документов, содержание которых почти не меняется из года в год. Сюда относится и ведение дневника хронометража и прочих записей, фиксирующих ход и формальные итоги наших повседневных действий, и вообще выполнение типичных операций по привычной, хорошо отработанной схеме.
Даже если человек завоевал себе положение в коллективе, дающее ему возможность заниматься творческой работой, но не занял какой-нибудь административный пост, то в самой этой работе встречаются те же рутинные элементы, хотя и в другой пропорции и в ином контексте.
Поэтому, на наш взгляд, персональная вычислительная машина в первую очередь мощное средство оргтехники, единственное пока реальное средство, способное свести рутинную работу к ее совершенно необходимым элементам.
Вот как, исходя из этой посылки, представляются области использования персональной ЭВМ и ее возможности.
ЗАПИСНАЯ КНИЖКА. Машина хранит нужные адреса и телефоны, расписание постоянных и текущих обязанностей и т.п. При этом она может выполнять свою роль активно: при включении автоматически вывести на экран список неотложных дел, во время работы напомнить о приближающемся совещании или о необходимости позвонить по телефону.
ЛИЧНАЯ КАРТОТЕКА. Каждый заносит в нее то, что ему нужно: библиографический указатель прочитанных или, наоборот, интересных, но еще не прочитанных статей и книг, список полезных программ, каталог личной библиотеки книг и, разумеется, каталог всего содержимого архива, созданного на данной ПЭВМ.
РАБОЧАЯ ТЕТРАДЬ. В ней фиксируется разнообразная информация: конспекты прочитанных материалов и выписки из них, черновики писем, отчетов, статей, программ (до того, как они поступают на отладку), неформальные спецификации. Занимающийся научно-техническими расчетами может выполнить в рабочей тетради необходимые формульные выкладки и т.д.
ЛАБОРАТОРНЫЙ ЖУРНАЛ. Сюда регулярно и систематически заносится все, что относится к основной научно-производственной деятельности владельца персональной машины. В журнал (а не в рабочую тетрадь) полезно также записывать все мотивировки предпринимаемых действий - обоснование изменений или варианта исходных данных, экспресс-выводы из полученных результатов.
Сейчас следы многого из того, что делается на вычислительных машинах, утрачиваются безвозвратно-распечатки не сохраняются, а если и сохраняются, то их трудно бывает связать друг с другом. Поэтому желательно, чтобы ведение такого машинного журнала было в значительной степени автоматизировано.
БОЛЬШОЙ МИКРОКАЛЬКУЛЯТОР. В этом режиме персональная ЭВМ производит (по постоянным или редко меняющимся программам) операции, наиболее часто нужные ее владельцу. Можно также выполнять несложные композиции из таких операций.
МАЛЕНЬКАЯ УНИВЕРСАЛЬНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА. Не предполагается, что персональная ЭВМ будет конкурировать по вычислительной мощности с большими машинами (из-за ограниченной памяти, меньшей разрядности чисел и т.п.). Но сравнительно небольшие по объему расчеты по произвольной, составленной пользователем программе ей доступны.
ТЕКСТОВЫЙ ПРОЦЕССОР. Желательно, чтобы это был не традиционный "редактор текстов", используемый сегодня программистами, а нечто большее. Например, схема ссылок на фрагменты текста была бы более разнообразной и гибкой, так же как система операций по преобразованию текстов. Полезно, чтобы текстовый процессор мог использоваться и для аналитических (формульных) выкладок в режиме диалога.
СРЕДСТВО ВЫВОДА ИЗОБРАЖЕНИЙ. Кроме различных текстов, таблиц и графиков, система должна позволить, например, вывести официальное письмо для отправки адресату, рукопись статьи (рисунки на отдельных листах) для сдачи в издательство и т.п.
УПРАВЛЕНИЕ БАЗАМИ ДАННЫХ. Наряду с хранением готовых баз данных, в том числе, например, описывающих состав и возможности самой машины и ее программного обеспечения, целесообразно дать возможность пользователю создавать базы данных с разнообразной структурой и средствами доступа к ним.
БИБЛИОТЕКА ПРОГРАММ. В ней находятся необходимые владельцу машины программы, а также несложные средства организации их в пакеты.
В наши дни почти никто не работает в одиночку. Поэтому и персональные машины сотрудников одного коллектива (отдела, лаборатории, может быть, института) необходимо связать между собой. Наиболее гибкой представляется система связи, при которой любое отправление попадает в общий архив, а к адресату поступает только короткое извещение. Если в данный момент он не работает, то это произойдет в момент подключения машины, и он сам решает, когда получить отправление и как им распорядиться.
Кроме того, надо иметь возможность переслать разработанную на персональной машине большую программу на большую ЭВМ, а после окончания счета получить в свой архив результаты.
Но почему для всего этого нужна именно персональная ЭВМ, а, скажем, не дисплей обычной большой ЭВМ?
Образно говоря, разница между тем, у кого есть персональная ЭВМ, и пользователем общей ЭВМ, работающим на ней в режиме разделения времени, такая же, как между владельцем отдельной квартиры и проживающим в коммунальной, даже при наилучших отношениях с соседями.
Преимущества персональной ЭВМ неоспоримы.

Рост мирового парка ЭВМ (1) и численности программистов (2) (график из книги Г.Громова - см. литературу).
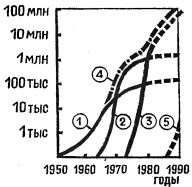
Изменение структуры мирового парка ЭВМ: 1 - большие ЭВМ; 2 - мини-ЭВМ; 3 - персональные ЭВМ; 4 - общий парк ЭВМ; 5 - новый тип ЭВМ образца 90-х гг. (график из книги Г.Громова).
СТАРШИЙ НАУЧНЫЙ СОТРУДНИК Г.ГРОМОВ
Можно, разумеется, сказать, что персональный компьютер - это вычислительная машина, которая умещается на письменном столе или даже в небольшом чемоданчике типа "дипломат". На одном из обсуждений А.П.Ершов заметил, что, по существу, такой подход и есть самый надежный способ закрыть глаза на проблему - рассматривать персональную ЭВМ просто как маленькую "большую" ЭВМ.
Главное для "феномена ПК" - это быстрое расширение уровня профессиональной доступности ЭВМ. В течение 30 лет, после появления на рубеже 50-х годов первых серийных ЭВМ, работать с ними могли только специалисты по вычислительной технике: инженеры-электронщики и программисты. Казалось бы, что же тут странного? Ведь с любой более или менее сложной и дорогостоящей техникой всегда имеют дело только специалисты. Мы же не требуем от всех умения, например, управлять экскаватором. Верно, но ЭВМ сама по себе ничего не производит. Она лишь преобразует информацию. Информация на входе машины, информация - на выходе. Работа ЭВМ имеет экономический смысл лишь в той степени, в которой она используется для целей автоматизации, то есть способствует повышению производительности труда людей, воздействующих на материальные объекты с помощью орудий и машин.
Но можно ли существенно расширять круг лиц, которым доступны "услуги" ЭВМ, если общаться с машиной только через представителей профессиональной касты "жрецов-посредников" - прикладных программистов?
В первые десятилетия эры ЭВМ, когда машины стоили очень дорого, для обеспечения их эффективной загрузки оправданно было держать в "обслуге" достаточное число инженеров и программистов. Однако электронная технология быстро развивалась, и вместе со снижением стоимости ЭВМ исчезала и экономическая целесообразность общения с машиной через "посредников" - программистов.
Поэтому вместо попыток, зачастую бесплодных, понять, что конкретно хочет тот или иной отраслевой специалист сделать на ЭВМ, профессиональные программисты начали переходить к решению более универсальных задач: создавать такие программы, которые позволяют ЭВМ в значительной степени самой понимать существо задач мало подготовленных к работе с ЭВМ пользователей.
Это, собственно, и привело наряду с быстрыми успехами в области миниатюризации электронной техники к появлению персональных компьютеров, то есть вычислительных машин, имеющих такой задел "дружественного" к пользователю программного обеспечения, которое позволяет почти любому из тысяч заинтересованных специалистов иметь при необходимости непосредственный доступ к ресурсам ЭВМ.
Может возникнуть вопрос: а не означает ли наметившаяся с появлением персональных ЭВМ тенденция повышения уровня "понятливости" ЭВМ, что соответственно отпадает необходимость прилагать встречные усилия для достижения всеобщей компьютерной грамотности?
Подобно тому как уровень грамотности человека определяет глубину проникновения его в сокровищницу накопленных человечеством знаний, так и уровень компьютерной грамотности определяет в конечном счете производственную эффективность использования принципиально нового, не имеющего исторических аналогов инструмента обработки информации.
Но, может быть, в эпоху всеобщей компьютерной грамотности и персональных ЭВМ окажется возможным несколько ослабить масштаб усилий по подготовке профессиональных программистов?
Разумеется, нет! Разница в объеме необходимых специальных знаний между человеком, овладевшим, например, наиболее популярным среди миллионов пользователей персональных ЭВМ языком программирования типа БЭЙСИК, и профессиональным программистом такая же, как между человеком, способным читать и писать без посторонней помощи, и дипломированным филологом. Всеобщая грамотность не только не отменяет, как известно, потребности общества в филологах, но, наоборот, ее повышает.
До появления "феномена ПК" типичный процесс составления прикладной программы развивался по принципу игры в "испорченный телефон". Специалист из той или иной области приложений ЭВМ нередко месяцами безуспешно пытался разъяснить программисту таинства своей профессии. Когда же через некоторое время программист с законной гордостью демонстрировал работу готовой программы, специалист-заказчик нередко убеждался, что, увы, его опять неправильно поняли: нужна было не совсем то или совсем не то. Причина: программист и заказчик неправильно поняли Друг друга на самом первом этапе формулировки задачи.
Удачными исключениями оставались лишь программы расчетного характера, условия которых можно было записать на точном языке математических формул. Но много ли в повседневной производственной деятельности выполняется работ, которые уже на этапе постановки задачи поддаются точному описанию? Чем дальше распространялась область приложений ЭВМ за пределы исторически первых, чисто математических (в своей исходной постановке) задач, тем труднее становилось работать прикладным программистам. Так в середине 70-х годов возник "кризис прикладного программирования".
Программист, будь он хоть "семи пядей...", не может, конечно же, быть специалистом сразу во всех областях приложений ЭВМ. Да и освоить пусть даже немногие области приложений во всех их тонкостях на предметном уровне отнюдь не просто. "То, что мастера действительно знают, не написано в учебниках для мастеров",- сокрушался один из зарубежных специалистов в области искусственного интеллекта.
Выход представляется только один: АВТОФОРМАЛИЗАЦИЯ профессиональных знаний. Это значит, что прикладные программы должен писать именно тот, кто лучше всех знает суть прикладной задачи,- профессионал в данной предметной области. Так вот, микроЭВМ, ориентированная на разработку и выполнение прикладных программ "непрограммирующим профессионалом", это и есть персональный компьютер. Такая ЭВМ имеет развитые средства самообучения пользователя-новичка работе за пультом, гибкие средства защиты от его ошибок. Но самое главное - все аппаратно-программные ресурсы подчинены одной сверхзадаче - обеспечить "дружественную реакцию" машины на любые, в том числе ошибочные, действия пользователя.
Основная задача персональных вычислений - формализация профессиональных задач - выполняется, как правило, полностью самостоятельно "непрограммирующим профессионалом" или при минимальной технической поддержке программиста. В последнем случае он имеет возможность включаться в процесс формализации знаний только на инструментальном уровне, оставляя наиболее трудную для его понимания содержательную часть задачи специалисту в данной области.
По возможному влиянию на темпы научно-технического прогресса феномен персональных вычислений сравнивают с изобретением книгопечатания. Подобно тому как книга - "источник знания" - вышла за пределы монастырских келий "в свет" после изобретения книгопечатания, персональные компьютеры выносят ресурсы ЭВМ и современные машинные методы обработки данных далеко за пределы "крепостных рвов" больших вычислительных центров. При этом ЭВМ постепенно превращается из "загадочного монстра", с которым люди могли общаться только через посредников-программистов, в простой и понятный индивидуальный инструмент, доступный для повседневной эксплуатации на работе, в учебной аудитории, в быту.
Е.ВЕЛИХОВ (заключение)
В этих коротких выступлениях, естественно, удалось только коснуться некоторых особенностей многогранного и сложного процесса проникновения персональных ЭВМ во все сферы профессиональной деятельности людей. По существу, сегодня на наших глазах еще только-только зарождается совершенно новая для человечества технологическая культура. Замечу, что чисто внешне она, быть может, наиболее заметно проявляется пока в компьютерных играх... Даже для короткого рассказа о направлениях развития персональных компьютеров, их роли в экономическом и социальном развитии нашего общества нужна не одна такая беседа, и я уверен, что журнал "Наука и жизнь" еще не раз будет возвращаться к этой теме.
Читателям, которые захотят более глубоко разобраться в предмете нашего сегодняшнего разговора, я рекомендую познакомиться непосредственно с работами выступавших здесь ученых.
В заключение хотелось бы еще раз подчеркнуть, что разработка и массовый выпуск персональных ЭВМ - одна из наиболее актуальных крупномасштабных проблем, которые нам предстоит решить в ближайшие годы.
ЛИТЕРАТУРА
Ершов А.П. Человек и машина. М., "Знание", 1985. Брошюра составлена по материалам выступлений автора на международных и всесоюзных конференциях. Объединяющая их идея: в условиях НТР человек все теснее связывает себя с ЭВМ, которая становится его постоянным партнером в учебе и на работе.
Лaвров С.С. Использование вычислительной техники и искусственный интеллект (перспективы развития). Статья в журнале "Микропроцессорные средства и системы", 1984. #3. На материале собственных исследований и анализа накопленного опыта автор обсуждает место и роль вычислительной техники в современном обществе, а также пути наиболее эффективного ее использования.
Громов Г.Р. Национальные информационные ресурсы: проблемы промышленной эксплуатации. М., "Наука", 1984. Это первая на русском языке книга, в которой дается целостная картина эволюции средств вычислительной техники за истекшие четыре десятилетия компьютерной эры. Приводятся результаты исследования феномена персональной" ЭВМ: разработка технологии автоформализации профессиональных знаний, обоснование роли "игровой компоненты" в стимулировании творчества. Показано растущее значение персональных компьютеров для формирования национальных информационных ресурсов.
Статьи, опубликованные в журнале "Наука и жизнь":
Сворень Р. Нужен ли персонально вам персональный компьютер? 10/84.
ЭВМ уходит в завтра. 8/85.
10/85

"Ириша" - так называется новый школьный компьютер. На снимке: один из его ведущих разработчиков - научный сотрудник МГУ В.Романов знакомит с ним энтузиастов "дошкольной информатики".
ПЕРСОНАЛЬНЫЙ КОМПЬЮТЕР: ПЕРСПЕКТИВЫ БЛИЗКИЕ И ДАЛЕКИЕ
Академик Е.ВЕЛИХОВ, вице-президент Академии наук СССР, академик-секретарь Отделения информатики, вычислительной техники и автоматизации АН СССР.
ПРЕЖДЕ всего представлю участников "круглого стола", организованного журналом "Наука и жизнь":
- академик Андрей Петрович ЕРШОВ (г.Новосибирск), заведующий отделом Вычислительного центра Сибирского отделения АН СССР,
- член-корреспондент АН СССР Святослав Сергеевич ЛАВРОВ (г.Ленинград), директор Института теоретической астрономии АН СССР,
- старший научный сотрудник Научно-исследовательского вычислительного центра АН СССР (г.Пущино) Григорий Рафаилович ГРОМОВ.
Наш "круглый стол" посвящен феномену персонального компьютера (ПК), как иногда говорят, чтобы подчеркнуть огромный по размаху и скорости фронт проникновения таких ЭВМ во все сферы человеческой деятельности.
Электронные вычислительные машины появились сорок лет назад и представляли собой огромные, загадочно мигающие тысячами ламп электронные монстры. Вокруг них круглосуточно, в три смены, сновали люди в белых халатах, которые должны были вовремя припаять то, что отвалилось, сменить то, что перегорело, и, наконец, самое главное, перевести на понятный машине язык электрических "нулей" и "единиц" ту или иную важную математическую задачу - запрограммировать ее. Участвующий в беседе С.С.Лавров - один из первых советских программистов, в то время работал в коллективе ученых под руководством С.П.Королева, и он хорошо помнит, какие тогда были машины, как трудно было обеспечивать их работоспособность и весьма непросто программировать. Однако именно на первых наших ЭВМ удалось в то время решать важные задачи.
Ныне ЭВМ заметно большей мощности создаются на нескольких кристаллах размером с клеточку арифметической тетради, а с вычислительной машиной на "ты" уже многие наши школьники. Но сегодня этого мало. Нам надо стремиться к полной "компьютерной грамотности". Это одно из необходимых условий выполнения тех широкомасштабных задач, которые стоят перед нами по ускорению научно-технического прогресса, переводу экономики на интенсивный путь развития.
Поэтому потребовалось срочно издать к началу учебного года пособие по новой учебной дисциплине - школьной информатике. Один из авторов этого школьного пособия - академик А.П.Ершов. Замечу, что первая школьная "компьютерная книжка" издается тиражом даже большим, чем печатается такой массовый журнал, как "Наука и жизнь". Зачем это делается?
Микропроцессорная революция резко расширила границы использования вычислительной техники. Приближается то время, когда экономическая мощь общества решающим образом станет определяться арсеналом средств электронной обработки информации.
Первой "ласточкой" этого процесса, первым массовым инструментом электронной обработки информации стали персональные компьютеры - простые в управлении, компактные вычислительные машины.
Цель нашей беседы - рассказать о месте и роли персональных ЭВМ в решении многотрудных задач массовой компьютеризации.
Не стану предварять ход обсуждения, отмечу лишь, что сегодня мировой парк персональных ЭВМ уже превышает 20 миллионов действующих машин. В нашей стране выпускаются и профессиональные ПК и такие компьютеры, которые можно использовать дома, в учебе, в техническом творчестве школьников и студентов. Скажу прямо: этих машин у нас пока много меньше, чем хотелось бы. Перед промышленностью поставлены серьезные задачи, и, несомненно, имеющийся разрыв со временем удастся ликвидировать.
Вместе с тем следует подчеркнуть, что промышленное производство ПК - это лишь одна сторона проблемы. Дело в том, что массовое, эффективное их использование в народном хозяйстве потребует решительного отказа от сложившихся стереотипов профессионального мышления, причем не только миллионов непосвященных - тех, кто сегодня только еще постигает "азы" компьютерной грамотности, но и у многих ученых и специалистов, в том числе и ветеранов вычислительной техники. Замечу, что совсем не очевидно, кому при этом будет труднее перестраиваться...
Дискуссии и обсуждения, подобные нашей встрече, а они проводятся сейчас во многих институтах, конструкторских бюро и на предприятиях различных отраслей промышленности, очень нужны и полезны, ибо привлекают внимание миллионов людей к проблеме огромной важности.
Ученые, собравшиеся за "круглым столом", уже ряд лет принимают участие в таких обсуждениях, активно отстаивают свою точку зрения на страницах научной периодики и массовой печати. Мне представляется особенно уместным замечание, которым однажды начал свой доклад академик Ершов: "Мало иметь что сказать, надо еще быть услышанным..."
Предоставив свои страницы, журнал "Наука и жизнь" дал нам именно такую возможность, и первым воспользоваться ею я попрошу Андрея Петровича Ершова.
АКАДЕМИК А.ЕРШОВ
Хочу сразу сказать, что феномен персональной ЭВМ - ПЭМВ (мне лично этот термин кажется лучше, чем "персональный компьютер") больше всего напоминает "скандал в благородном семействе". Налицо потрясение основ, с таким трудом сформированных за последние 30 лет большой наукой программирования и промышленностью, производящей ЭВМ. И как скандал в благородном семействе вскрывает фальшь внешне благопристойных отношений, так и феномен ПЭВМ выявляет ряд назревших противоречий в развитии вычислительного дела и выводит на сцену новых действующих лиц, новые сущности в программировании и применении ЭВМ.
Позволю себе не углублять здесь этой констатации, многочисленные подтверждения которой можно найти на страницах технической периодики, а подробный анализ в недавно вышедшей книге Г.Р.Громова "Национальные информационные ресурсы: проблемы промышленной эксплуатации".
Отмечу лишь, что, с какой бы стороны и в какой форме ни пришла бы к каждому из нас новость о персональных ЭВМ, уже стало бесспорным одно: эти машины - неотъемлемая и одна из главных ветвей вычислительной техники, приближающая цель ее ускоренного развития: полную информатизацию - перевооружение народного хозяйства страны на основе вычислительной техники.
Полная информатизация общества наступит тогда, когда вся информация, в которой оно нуждается, будет возникать, храниться и циркулировать на машинных носителях и вся ее обработка, как внутренняя, так и во взаимодействии с человеком, будет осуществляться посредством ЭВМ. Революционная сторона перенесения информации на машинные носители состоит в создании предпосылок (а с развитием электросвязи и их реализации) к оперативному обмену всей информацией, к ее доставке в любое требуемое место со скоростью электрических сигналов для обработки и использования.
Не будем гадать, когда это наступит, но, считая полную информатизацию предвидимым будущим, например, лет через пятьдесят, можем оценить число активных членов нашего общества - работающих и учащихся - скажем, в 250 миллионов человек. Если глобальная сеть информационного обмена должна быть доведена до каждого человека, то с учетом его относительной подвижности число входов в такую сеть составит несколько сот миллионов, скажем, 300-400. Совершенно очевидно, что на конце каждого из этих входов нужно устройство, которое теперь никак иначе, кроме как персональной ЭВМ, не назовешь. Сделаем, однако, некоторую уступку экономической целесообразности, введя следующие виды персональных ЭВМ: бытовые, профессиональные и активные терминалы. Последнее - это нечто промежуточное между более скромной бытовой машиной и профессиональной, оснащенной всем, что нужно для эффективной работы.
Дополнительные предположения о числе и численности семей, о соотношении более и менее однородной профессиональной работы приводят к следующей оценке числа персональных вычислительных средств при полной информатизации: профессиональных - 50, бытовых - 200, активных терминалов - 100 миллионов.
Естественно, что персональная вычислительная техника составляет только часть вычислительных средств народного хозяйства. Мы не совершим большой ошибки, если предположим, что ко времени наступления полной информатизации на одного активного члена общества будет приходиться 8-10 машин (на производстве и в быту), в каждую из которых встроен микропроцессорный контроллер или микро-ЭВМ. Отсюда можно оценить общий объем встроенных вычислительных средств в 2 миллиарда.
Может ли такой парк универсальных и встроенных ЭВМ эффективно действовать без достижения в стране всеобщей компьютерной грамотности? Уверен, что нет.
Именно поэтому, например, в Новосибирском академгородке последние десять лет разрабатываются научные и методологические основы школьной информатики. Некоторые из положений созданного нами курса всеобщей "компьютерной грамотности" мы попытались изложить в пробном массовом учебном пособии, о котором здесь уже упоминал академик Е.П.Велихов.
Несколько лет назад я как-то обсуждал с коллегами тезисы своего доклада на конференции в г.Пущино: "Персональная ЭВМ - предок млекопитающих в динозавровом мире ВЦКП" (под ВЦКП имелись в виду вычислительные центры коллективного пользования). Один из участников сказал примерно следующее: "Не знаю, изведут ли твои млекопитающие динозавровые ВЦКП, но то, что они поглотят профессиональных программистов задолго до того, как их станет 600 тысяч,- это уже факт. Твоими же усилиями программирование станет второй грамотностью и человечество без всяких слуг по-хозяйски усядется за персональные ЭВМ и будет делать свое дело".
Я задумался, но потом успокоенно вспомнил, что имел похожий разговор 30 лет назад. Это было после исторического семинара 1955 года в Институте прикладной математики АН СССР у академика М.В.Келдыша. Там первые советские разработчики программирующих программ обсуждали перспективы автоматизации программирования. Воодушевленные происходящим, они философски констатировали, что, занимаясь уже третий год программированием и получая за это зарплату, в то же время рубят сук, на котором сидят.
И хотя с тех пор программистов стало гораздо больше, сук, на котором они устроились, еще достаточно крепок, и можно повторить вслед за другими, что честный ученый в любой данный момент подрывает условия своего существования, и лишь беспредельность человеческого познания позволяет ему не беспокоиться о будущем.
ЧЛЕН-КОРРЕСПОНДЕНТ АН СССР С.ЛАВРОВ
Если не заглядывать далеко вперед, когда, по А.П.Ершову, наступит эра всеобщей информатизации общества, то до той поры основными пользователями ПЭВМ будут оставаться люди из числа ведущих (не в административном, а в творческом плане) специалистов институтов, бюро и других организаций, прежде всего те, кто уже сейчас знаком с вычислительной техникой и прилично ею владеет.
Что больше всего нужно этим людям? Если спросить об этом инженера или научного сотрудника, то он наверняка ответит, что больше всего ему недостает (на работе - не в быту) хорошего помощника - техника, лаборанта, машинистки... Другими словами, ему хочется избавиться от рутинных операций, облегчить себе работу творческую. Такие операции - это прежде всего поиск нужных данных в различных справочниках, нормативных документах, архивных делах, поиск самих этих справочников и документов, нужной бумаги в собственном столе, составление шаблонных документов, содержание которых почти не меняется из года в год. Сюда относится и ведение дневника хронометража и прочих записей, фиксирующих ход и формальные итоги наших повседневных действий, и вообще выполнение типичных операций по привычной, хорошо отработанной схеме.
Даже если человек завоевал себе положение в коллективе, дающее ему возможность заниматься творческой работой, но не занял какой-нибудь административный пост, то в самой этой работе встречаются те же рутинные элементы, хотя и в другой пропорции и в ином контексте.
Поэтому, на наш взгляд, персональная вычислительная машина в первую очередь мощное средство оргтехники, единственное пока реальное средство, способное свести рутинную работу к ее совершенно необходимым элементам.
Вот как, исходя из этой посылки, представляются области использования персональной ЭВМ и ее возможности.
ЗАПИСНАЯ КНИЖКА. Машина хранит нужные адреса и телефоны, расписание постоянных и текущих обязанностей и т.п. При этом она может выполнять свою роль активно: при включении автоматически вывести на экран список неотложных дел, во время работы напомнить о приближающемся совещании или о необходимости позвонить по телефону.
ЛИЧНАЯ КАРТОТЕКА. Каждый заносит в нее то, что ему нужно: библиографический указатель прочитанных или, наоборот, интересных, но еще не прочитанных статей и книг, список полезных программ, каталог личной библиотеки книг и, разумеется, каталог всего содержимого архива, созданного на данной ПЭВМ.
РАБОЧАЯ ТЕТРАДЬ. В ней фиксируется разнообразная информация: конспекты прочитанных материалов и выписки из них, черновики писем, отчетов, статей, программ (до того, как они поступают на отладку), неформальные спецификации. Занимающийся научно-техническими расчетами может выполнить в рабочей тетради необходимые формульные выкладки и т.д.
ЛАБОРАТОРНЫЙ ЖУРНАЛ. Сюда регулярно и систематически заносится все, что относится к основной научно-производственной деятельности владельца персональной машины. В журнал (а не в рабочую тетрадь) полезно также записывать все мотивировки предпринимаемых действий - обоснование изменений или варианта исходных данных, экспресс-выводы из полученных результатов.
Сейчас следы многого из того, что делается на вычислительных машинах, утрачиваются безвозвратно-распечатки не сохраняются, а если и сохраняются, то их трудно бывает связать друг с другом. Поэтому желательно, чтобы ведение такого машинного журнала было в значительной степени автоматизировано.
БОЛЬШОЙ МИКРОКАЛЬКУЛЯТОР. В этом режиме персональная ЭВМ производит (по постоянным или редко меняющимся программам) операции, наиболее часто нужные ее владельцу. Можно также выполнять несложные композиции из таких операций.
МАЛЕНЬКАЯ УНИВЕРСАЛЬНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА. Не предполагается, что персональная ЭВМ будет конкурировать по вычислительной мощности с большими машинами (из-за ограниченной памяти, меньшей разрядности чисел и т.п.). Но сравнительно небольшие по объему расчеты по произвольной, составленной пользователем программе ей доступны.
ТЕКСТОВЫЙ ПРОЦЕССОР. Желательно, чтобы это был не традиционный "редактор текстов", используемый сегодня программистами, а нечто большее. Например, схема ссылок на фрагменты текста была бы более разнообразной и гибкой, так же как система операций по преобразованию текстов. Полезно, чтобы текстовый процессор мог использоваться и для аналитических (формульных) выкладок в режиме диалога.
СРЕДСТВО ВЫВОДА ИЗОБРАЖЕНИЙ. Кроме различных текстов, таблиц и графиков, система должна позволить, например, вывести официальное письмо для отправки адресату, рукопись статьи (рисунки на отдельных листах) для сдачи в издательство и т.п.
УПРАВЛЕНИЕ БАЗАМИ ДАННЫХ. Наряду с хранением готовых баз данных, в том числе, например, описывающих состав и возможности самой машины и ее программного обеспечения, целесообразно дать возможность пользователю создавать базы данных с разнообразной структурой и средствами доступа к ним.
БИБЛИОТЕКА ПРОГРАММ. В ней находятся необходимые владельцу машины программы, а также несложные средства организации их в пакеты.
В наши дни почти никто не работает в одиночку. Поэтому и персональные машины сотрудников одного коллектива (отдела, лаборатории, может быть, института) необходимо связать между собой. Наиболее гибкой представляется система связи, при которой любое отправление попадает в общий архив, а к адресату поступает только короткое извещение. Если в данный момент он не работает, то это произойдет в момент подключения машины, и он сам решает, когда получить отправление и как им распорядиться.
Кроме того, надо иметь возможность переслать разработанную на персональной машине большую программу на большую ЭВМ, а после окончания счета получить в свой архив результаты.
Но почему для всего этого нужна именно персональная ЭВМ, а, скажем, не дисплей обычной большой ЭВМ?
Образно говоря, разница между тем, у кого есть персональная ЭВМ, и пользователем общей ЭВМ, работающим на ней в режиме разделения времени, такая же, как между владельцем отдельной квартиры и проживающим в коммунальной, даже при наилучших отношениях с соседями.
Преимущества персональной ЭВМ неоспоримы.

Рост мирового парка ЭВМ (1) и численности программистов (2) (график из книги Г.Громова - см. литературу).

Изменение структуры мирового парка ЭВМ: 1 - большие ЭВМ; 2 - мини-ЭВМ; 3 - персональные ЭВМ; 4 - общий парк ЭВМ; 5 - новый тип ЭВМ образца 90-х гг. (график из книги Г.Громова).
СТАРШИЙ НАУЧНЫЙ СОТРУДНИК Г.ГРОМОВ
Можно, разумеется, сказать, что персональный компьютер - это вычислительная машина, которая умещается на письменном столе или даже в небольшом чемоданчике типа "дипломат". На одном из обсуждений А.П.Ершов заметил, что, по существу, такой подход и есть самый надежный способ закрыть глаза на проблему - рассматривать персональную ЭВМ просто как маленькую "большую" ЭВМ.
Главное для "феномена ПК" - это быстрое расширение уровня профессиональной доступности ЭВМ. В течение 30 лет, после появления на рубеже 50-х годов первых серийных ЭВМ, работать с ними могли только специалисты по вычислительной технике: инженеры-электронщики и программисты. Казалось бы, что же тут странного? Ведь с любой более или менее сложной и дорогостоящей техникой всегда имеют дело только специалисты. Мы же не требуем от всех умения, например, управлять экскаватором. Верно, но ЭВМ сама по себе ничего не производит. Она лишь преобразует информацию. Информация на входе машины, информация - на выходе. Работа ЭВМ имеет экономический смысл лишь в той степени, в которой она используется для целей автоматизации, то есть способствует повышению производительности труда людей, воздействующих на материальные объекты с помощью орудий и машин.
Но можно ли существенно расширять круг лиц, которым доступны "услуги" ЭВМ, если общаться с машиной только через представителей профессиональной касты "жрецов-посредников" - прикладных программистов?
В первые десятилетия эры ЭВМ, когда машины стоили очень дорого, для обеспечения их эффективной загрузки оправданно было держать в "обслуге" достаточное число инженеров и программистов. Однако электронная технология быстро развивалась, и вместе со снижением стоимости ЭВМ исчезала и экономическая целесообразность общения с машиной через "посредников" - программистов.
Поэтому вместо попыток, зачастую бесплодных, понять, что конкретно хочет тот или иной отраслевой специалист сделать на ЭВМ, профессиональные программисты начали переходить к решению более универсальных задач: создавать такие программы, которые позволяют ЭВМ в значительной степени самой понимать существо задач мало подготовленных к работе с ЭВМ пользователей.
Это, собственно, и привело наряду с быстрыми успехами в области миниатюризации электронной техники к появлению персональных компьютеров, то есть вычислительных машин, имеющих такой задел "дружественного" к пользователю программного обеспечения, которое позволяет почти любому из тысяч заинтересованных специалистов иметь при необходимости непосредственный доступ к ресурсам ЭВМ.
Может возникнуть вопрос: а не означает ли наметившаяся с появлением персональных ЭВМ тенденция повышения уровня "понятливости" ЭВМ, что соответственно отпадает необходимость прилагать встречные усилия для достижения всеобщей компьютерной грамотности?
Подобно тому как уровень грамотности человека определяет глубину проникновения его в сокровищницу накопленных человечеством знаний, так и уровень компьютерной грамотности определяет в конечном счете производственную эффективность использования принципиально нового, не имеющего исторических аналогов инструмента обработки информации.
Но, может быть, в эпоху всеобщей компьютерной грамотности и персональных ЭВМ окажется возможным несколько ослабить масштаб усилий по подготовке профессиональных программистов?
Разумеется, нет! Разница в объеме необходимых специальных знаний между человеком, овладевшим, например, наиболее популярным среди миллионов пользователей персональных ЭВМ языком программирования типа БЭЙСИК, и профессиональным программистом такая же, как между человеком, способным читать и писать без посторонней помощи, и дипломированным филологом. Всеобщая грамотность не только не отменяет, как известно, потребности общества в филологах, но, наоборот, ее повышает.
До появления "феномена ПК" типичный процесс составления прикладной программы развивался по принципу игры в "испорченный телефон". Специалист из той или иной области приложений ЭВМ нередко месяцами безуспешно пытался разъяснить программисту таинства своей профессии. Когда же через некоторое время программист с законной гордостью демонстрировал работу готовой программы, специалист-заказчик нередко убеждался, что, увы, его опять неправильно поняли: нужна было не совсем то или совсем не то. Причина: программист и заказчик неправильно поняли Друг друга на самом первом этапе формулировки задачи.
Удачными исключениями оставались лишь программы расчетного характера, условия которых можно было записать на точном языке математических формул. Но много ли в повседневной производственной деятельности выполняется работ, которые уже на этапе постановки задачи поддаются точному описанию? Чем дальше распространялась область приложений ЭВМ за пределы исторически первых, чисто математических (в своей исходной постановке) задач, тем труднее становилось работать прикладным программистам. Так в середине 70-х годов возник "кризис прикладного программирования".
Программист, будь он хоть "семи пядей...", не может, конечно же, быть специалистом сразу во всех областях приложений ЭВМ. Да и освоить пусть даже немногие области приложений во всех их тонкостях на предметном уровне отнюдь не просто. "То, что мастера действительно знают, не написано в учебниках для мастеров",- сокрушался один из зарубежных специалистов в области искусственного интеллекта.
Выход представляется только один: АВТОФОРМАЛИЗАЦИЯ профессиональных знаний. Это значит, что прикладные программы должен писать именно тот, кто лучше всех знает суть прикладной задачи,- профессионал в данной предметной области. Так вот, микроЭВМ, ориентированная на разработку и выполнение прикладных программ "непрограммирующим профессионалом", это и есть персональный компьютер. Такая ЭВМ имеет развитые средства самообучения пользователя-новичка работе за пультом, гибкие средства защиты от его ошибок. Но самое главное - все аппаратно-программные ресурсы подчинены одной сверхзадаче - обеспечить "дружественную реакцию" машины на любые, в том числе ошибочные, действия пользователя.
Основная задача персональных вычислений - формализация профессиональных задач - выполняется, как правило, полностью самостоятельно "непрограммирующим профессионалом" или при минимальной технической поддержке программиста. В последнем случае он имеет возможность включаться в процесс формализации знаний только на инструментальном уровне, оставляя наиболее трудную для его понимания содержательную часть задачи специалисту в данной области.
По возможному влиянию на темпы научно-технического прогресса феномен персональных вычислений сравнивают с изобретением книгопечатания. Подобно тому как книга - "источник знания" - вышла за пределы монастырских келий "в свет" после изобретения книгопечатания, персональные компьютеры выносят ресурсы ЭВМ и современные машинные методы обработки данных далеко за пределы "крепостных рвов" больших вычислительных центров. При этом ЭВМ постепенно превращается из "загадочного монстра", с которым люди могли общаться только через посредников-программистов, в простой и понятный индивидуальный инструмент, доступный для повседневной эксплуатации на работе, в учебной аудитории, в быту.
Е.ВЕЛИХОВ (заключение)
В этих коротких выступлениях, естественно, удалось только коснуться некоторых особенностей многогранного и сложного процесса проникновения персональных ЭВМ во все сферы профессиональной деятельности людей. По существу, сегодня на наших глазах еще только-только зарождается совершенно новая для человечества технологическая культура. Замечу, что чисто внешне она, быть может, наиболее заметно проявляется пока в компьютерных играх... Даже для короткого рассказа о направлениях развития персональных компьютеров, их роли в экономическом и социальном развитии нашего общества нужна не одна такая беседа, и я уверен, что журнал "Наука и жизнь" еще не раз будет возвращаться к этой теме.
Читателям, которые захотят более глубоко разобраться в предмете нашего сегодняшнего разговора, я рекомендую познакомиться непосредственно с работами выступавших здесь ученых.
В заключение хотелось бы еще раз подчеркнуть, что разработка и массовый выпуск персональных ЭВМ - одна из наиболее актуальных крупномасштабных проблем, которые нам предстоит решить в ближайшие годы.
ЛИТЕРАТУРА
Ершов А.П. Человек и машина. М., "Знание", 1985. Брошюра составлена по материалам выступлений автора на международных и всесоюзных конференциях. Объединяющая их идея: в условиях НТР человек все теснее связывает себя с ЭВМ, которая становится его постоянным партнером в учебе и на работе.
Лaвров С.С. Использование вычислительной техники и искусственный интеллект (перспективы развития). Статья в журнале "Микропроцессорные средства и системы", 1984. #3. На материале собственных исследований и анализа накопленного опыта автор обсуждает место и роль вычислительной техники в современном обществе, а также пути наиболее эффективного ее использования.
Громов Г.Р. Национальные информационные ресурсы: проблемы промышленной эксплуатации. М., "Наука", 1984. Это первая на русском языке книга, в которой дается целостная картина эволюции средств вычислительной техники за истекшие четыре десятилетия компьютерной эры. Приводятся результаты исследования феномена персональной" ЭВМ: разработка технологии автоформализации профессиональных знаний, обоснование роли "игровой компоненты" в стимулировании творчества. Показано растущее значение персональных компьютеров для формирования национальных информационных ресурсов.
Статьи, опубликованные в журнале "Наука и жизнь":
Сворень Р. Нужен ли персонально вам персональный компьютер? 10/84.
ЭВМ уходит в завтра. 8/85.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
И еще...
10/85
УСТНЫЙ ВЫПУСК
13 июня 1985 года в Малом зале Центрального лектория Всесоюзного общества "Знание" состоялся устный выпуск журнала "Наука и жизнь", целиком посвященный разделу "Человек с микрокалькулятором".
Открывая эту встречу с читателями популярного раздела, главный редактор журнала "Наука и жизнь" И.К.Лаговский сказал: "Журнал всегда был чуток к перестройкам и нововведениям в народном образовании, старается помочь школе, когда какой-либо новый предмет школьной программы усваивается учащимися не так успешно, как ожидалось. Постоянным подписчикам "Науки и жизни", вероятно, помнится рубрика "Готовьтесь к конкурсным экзаменам". Абитуриенты (а люди этого возраста неизменно составляют немалый процент наших читателей) могли получить из материалов рубрики обстоятельную консультацию по многим вопросам, еще недавно включенным в школьный курс и уже взятым на вооружение экзаменаторами вузов. В этом году девятиклассники средних школ страны приступают к изучению "Основ информатики и вычислительной техники". В канун этого нововведения в журнале и появился раздел "Человек с микрокалькулятором". Выступая в нем, владельцы карманных ЭВМ делятся со своими товарищами по увлечению, как опытными, так и новичками секретами работы на этих чудесных машинках. Недавно появилась у нас и рубрика "Семинар по информатике": в ней публикуются уроки для тех, кто хотел бы освоить программируемые микрокалькуляторы".

Ведущий раздела "Человек с микрокалькулятором" кандидат физико-математических наук Ю.В.Пухначев поделился планами на будущее. "Судя по ответам читателей журнала на анкету, опубликованную в 4/85,- сказал он,- прочное признание завоевали такие направления раздела, как дискуссии за "круглым столом" о методах решения задач на программируемых микрокалькуляторах, конкурсы на лучшее решение задач с последующим разбором результатов, рассмотрение различных аспектов прикладной математики, усовершенствования калькулятора, сделанные своими руками, рассказы о нестандартных применениях калькулятора, "маленькие хитрости". Эти направления раздел сохранит и в дальнейшем. В нем по-прежнему будут публиковаться сообщения читателей о решенных ими прикладных задачах. При этом более подробно будут поясняться алгоритмы решения, будут даваться рекомендации для тех, кто намеревается решать аналогичные задачи. В своих письмах читатели просят публиковать игры на программируемом микрокалькуляторе, посвященные ему юмористические заметки и рисунки, материалы в помощь школьникам, работающим с калькуляторами, информацию о тенденциях развития отечественных микрокалькуляторов на фоне мирового уровня в этой области, статьи, демонстрирующие пределы возможного применения карманных ЭВМ. В скором времени эта тематика появится на страницах раздела. В перспективе видятся материалы о персональных компьютерах, приемах работы с ними. И еще одна важная тема: методы математической трактовки таких задач, к которым лишь недавно начали применяться численные подходы, о способах алгоритмизации решения проблем, встречающихся п практической деятельности специалистов самых различных направлении. Ждем от наших читателей писем на эти актуальные темы".

Кандидат физико-математических наук В.П.Захаров, начальник отдела производственного объединения "Кристалл" (г.Киев), продемонстрировал собравшимся программируемый микрокалькулятор "Электроника МК-52". о котором недавно писал наш журнал (6/85), ответил на вопросы.

"Культура и искусство программирования на микрокалькуляторах" - так озаглавил свое выступление кандидат технических наук А.Н.Цветков, автор известных сборников прикладных программ для микро-ЭВМ. Он обратил внимание своих слушателей на примечательный факт: в научных учреждениях, обладающих неплохим парком мощных ЭВМ, широкое применение находят также и программируемые микрокалькуляторы. Объясняется это, очевидно, тем, что и тому и другому классу вычислительных машин свойственны такие сферы применения, где они наиболее предпочтительны. Программируемый микрокалькулятор позволяет получить ответ на несложную задачу за достаточно короткий срок, чтобы не затормозить творческого процесса,- и в этом его основное преимущество. Критерий оптимальности программ для микрокалькуляторов, по мнению выступающего, зависит от их целевого назначения. Программы для астрономических расчетов требуют в первую очередь точности, программы для статистических расчетов - скорости и т.д.

"Программисты, свысока смотрящие на микрокалькуляторы.- сказал Г.В.Славин (Тартуский государственный университет) в своем выступлении, посвященном границам применения карманных ЭВМ,- любят говорить: да ведь на этой машинке нельзя решить систему из десяти линейных уравнений! Да, в самом деле, разочарованно соглашается с ними тот, кто заинтересовался было программируемыми микрокалькуляторами,- соглашается. забывая, что подобная задача перед ним вряд ли и встанет. А вот системы из трех уравнений ему приходится решать частенько. Между тем карманная ЭВМ, столь маломощная на первый взгляд, позволит ему решить за пару часов полсотни таких систем".
В дискуссии, развернувшейся вслед за этими выступлениями, приняли участие К.А.Лапинг (ВНИИ автоматизации управления в непромышленной сфере), Б.С.Мельников (Московский энергетический институт). И.Д.Данилов (объединение "Росгеофонд"), А.Б.Бойко (Всесоюзный заочный электротехнический институт связи), Д.Д.Богданов (Московский институт нефтехимической и газовой промышленности) и др.
10/85
УСТНЫЙ ВЫПУСК
13 июня 1985 года в Малом зале Центрального лектория Всесоюзного общества "Знание" состоялся устный выпуск журнала "Наука и жизнь", целиком посвященный разделу "Человек с микрокалькулятором".
Открывая эту встречу с читателями популярного раздела, главный редактор журнала "Наука и жизнь" И.К.Лаговский сказал: "Журнал всегда был чуток к перестройкам и нововведениям в народном образовании, старается помочь школе, когда какой-либо новый предмет школьной программы усваивается учащимися не так успешно, как ожидалось. Постоянным подписчикам "Науки и жизни", вероятно, помнится рубрика "Готовьтесь к конкурсным экзаменам". Абитуриенты (а люди этого возраста неизменно составляют немалый процент наших читателей) могли получить из материалов рубрики обстоятельную консультацию по многим вопросам, еще недавно включенным в школьный курс и уже взятым на вооружение экзаменаторами вузов. В этом году девятиклассники средних школ страны приступают к изучению "Основ информатики и вычислительной техники". В канун этого нововведения в журнале и появился раздел "Человек с микрокалькулятором". Выступая в нем, владельцы карманных ЭВМ делятся со своими товарищами по увлечению, как опытными, так и новичками секретами работы на этих чудесных машинках. Недавно появилась у нас и рубрика "Семинар по информатике": в ней публикуются уроки для тех, кто хотел бы освоить программируемые микрокалькуляторы".

Ведущий раздела "Человек с микрокалькулятором" кандидат физико-математических наук Ю.В.Пухначев поделился планами на будущее. "Судя по ответам читателей журнала на анкету, опубликованную в 4/85,- сказал он,- прочное признание завоевали такие направления раздела, как дискуссии за "круглым столом" о методах решения задач на программируемых микрокалькуляторах, конкурсы на лучшее решение задач с последующим разбором результатов, рассмотрение различных аспектов прикладной математики, усовершенствования калькулятора, сделанные своими руками, рассказы о нестандартных применениях калькулятора, "маленькие хитрости". Эти направления раздел сохранит и в дальнейшем. В нем по-прежнему будут публиковаться сообщения читателей о решенных ими прикладных задачах. При этом более подробно будут поясняться алгоритмы решения, будут даваться рекомендации для тех, кто намеревается решать аналогичные задачи. В своих письмах читатели просят публиковать игры на программируемом микрокалькуляторе, посвященные ему юмористические заметки и рисунки, материалы в помощь школьникам, работающим с калькуляторами, информацию о тенденциях развития отечественных микрокалькуляторов на фоне мирового уровня в этой области, статьи, демонстрирующие пределы возможного применения карманных ЭВМ. В скором времени эта тематика появится на страницах раздела. В перспективе видятся материалы о персональных компьютерах, приемах работы с ними. И еще одна важная тема: методы математической трактовки таких задач, к которым лишь недавно начали применяться численные подходы, о способах алгоритмизации решения проблем, встречающихся п практической деятельности специалистов самых различных направлении. Ждем от наших читателей писем на эти актуальные темы".

Кандидат физико-математических наук В.П.Захаров, начальник отдела производственного объединения "Кристалл" (г.Киев), продемонстрировал собравшимся программируемый микрокалькулятор "Электроника МК-52". о котором недавно писал наш журнал (6/85), ответил на вопросы.

"Культура и искусство программирования на микрокалькуляторах" - так озаглавил свое выступление кандидат технических наук А.Н.Цветков, автор известных сборников прикладных программ для микро-ЭВМ. Он обратил внимание своих слушателей на примечательный факт: в научных учреждениях, обладающих неплохим парком мощных ЭВМ, широкое применение находят также и программируемые микрокалькуляторы. Объясняется это, очевидно, тем, что и тому и другому классу вычислительных машин свойственны такие сферы применения, где они наиболее предпочтительны. Программируемый микрокалькулятор позволяет получить ответ на несложную задачу за достаточно короткий срок, чтобы не затормозить творческого процесса,- и в этом его основное преимущество. Критерий оптимальности программ для микрокалькуляторов, по мнению выступающего, зависит от их целевого назначения. Программы для астрономических расчетов требуют в первую очередь точности, программы для статистических расчетов - скорости и т.д.

"Программисты, свысока смотрящие на микрокалькуляторы.- сказал Г.В.Славин (Тартуский государственный университет) в своем выступлении, посвященном границам применения карманных ЭВМ,- любят говорить: да ведь на этой машинке нельзя решить систему из десяти линейных уравнений! Да, в самом деле, разочарованно соглашается с ними тот, кто заинтересовался было программируемыми микрокалькуляторами,- соглашается. забывая, что подобная задача перед ним вряд ли и встанет. А вот системы из трех уравнений ему приходится решать частенько. Между тем карманная ЭВМ, столь маломощная на первый взгляд, позволит ему решить за пару часов полсотни таких систем".
В дискуссии, развернувшейся вслед за этими выступлениями, приняли участие К.А.Лапинг (ВНИИ автоматизации управления в непромышленной сфере), Б.С.Мельников (Московский энергетический институт). И.Д.Данилов (объединение "Росгеофонд"), А.Б.Бойко (Всесоюзный заочный электротехнический институт связи), Д.Д.Богданов (Московский институт нефтехимической и газовой промышленности) и др.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
10/85
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
КАЛЬКУЛЯТОР НА ПРИЛАВКЕ
Наша промышленность выпускает несколько десятков типов микрокальнуляторов. Около двадцати различных моделей было представлено на выставке-продаже этих миниатюрных ЭВМ в московском ГУМе. Проходила выставка в апреле этого года. Среди покупателей распространялась анкета, итоги которой позволяют составить некоторое представление о ситуации в калькуляторном мире.
Прежде всего одна цифра: 2300. Столько калькуляторов было продано за 12 дней работы выставки. Это значит, что ежедневная продажа была почти в четыре раза выше обычной.
Калькулятор, как ни странно,- предмет сезонной продажи. Пик "раскупаемости" приходится на осень, а провал - на лето. Впрочем, странность эта легко объяснима: 41.7 процента покупателей - студенты, а 35 процентов - школьники или их родители. То есть, три четверти микрокалькуляторов попадают в руки учащихся, а они, как известно, летом отдыхают.
Устроители выставки обратили внимание на очень низкий процент учеников ПТУ среди покупателей: всего 3.2 процента. Выяснилось, однако, что большинство ПТУ покупает калькуляторы по безналичному расчету и бесплатно предоставляет их учащимся. Факт отрадный!
Какие калькуляторы пользуются наибольшим спросом? На первом месте стоят инженерные - их желают купить 40.9 процента опрошенных, за ними идут программируемые (36.6 процента) и замыкают ряд простейшие (22.5 процента).
Что касается конкретных моделей, то наибольшим спросом среди простейших пользуются "Б3-23" и "МК-33". Они самые дешевые, стоят по 25 рублей, и наиболее удобны для проведения несложных планово-экономических расчетов. Для начального обучения детей.
Из инженерных на первом месте идет "МК-51". Снабженный литиевым элементом питания, он рассчитан на работу без перезарядки в течение примерно полутора лет. Выполняет он 35 различных операций, среди которых и такие "экзотические", как статистические расчеты. Не исключено, правда, что скоро ему придется потесниться и пропустить вперед новую модель, "МК-71". Этот калькулятор самый мощный среди отечественных машин инженерного типа. Он имеет еще более широкий набор операций, чем "МК-51", питается от "вечного" источника - батарей солнечных элементов, которые могут заряжаться как при естественном, так и при искусственном освещении. Обе эти модели быстрые, точные и достаточно надежные в работе. Кстати, о "МК-51" реализованы алгоритмы вычисления элементарных функций по методу "Цифра за цифрой", описанному в 10/84.
Первое место, занимаемое инженерными калькуляторами, объясняется просто. Они не требуют никаких начальных навыков для работы, запись арифметических выражений на них прямая, как принято в математике; можно использовать скобки, причем на "МК-71" - пять уровней скобок.
И, наконец, элита калькуляторного мира - программируемые микрокалькуляторы. Здесь первое место безоговорочно принадлежит "МК-54". Обладая всеми достоинствами горячо любимого нами "Б3-34", этот калькулятор на 20 рублей дешевле (за счет источников питания другого типа), да и внешне более элегантен.
Две перспективные модели программируемых микрокалькуляторов "МК-52" и "МК-61", о которых уже писал наш журнал (6/85), скоро появятся в фирменных магазинах-салонах "Электроника".
Приятно отметить, что они полностью совместимы по системе команд со своими предшественниками, как говорят, снизу вверх. Это значит, что любая программа, написанная для "Б3-34" или "МК-54", может быть реализована на них, если в ней нет команд КП^, КИП^ и прочих, содержащих стрелку.
Теперь о последних цифрах анкеты, которые хотелось бы привести. Только 37.2 процента покупателей приобретают калькуляторы впервые. Остальные покупают новые модели взамен морально устаревших. О чем это говорит? Раз появившись в руках, маленькая ЭВМ становится спутником человека навсегда. Будут меняться модели, типы, но возврата к безкалькуляторной жизни не будет.
И.ДАНИЛОВ (г.Москва)
[ ДОПОЛНЕНИЯ К МАТЕРИАЛАМ ПРЕДЫДУЩИХ НОМЕРОВ
Микрокалькулятор "Электроника Б3-34", усовершенствованный примерно так, как это было описано в статье "Всего один диод" 4/85, мы используем для подсчета нагрузки за смену. Вот уже пять месяцев он нас не подводит, хотя работает круглосуточно. Не страшны даже кратковременные уменьшения напряжения в сети или ее отключения на незначительное время.
С.ПЕТРОВ, М.ВАХТЕРОВ (г.Москва) ]
НА ИНДИКАТОРЕ - СИГНАЛ АВОСТА
...Счет по программе внезапно остановился, и на индикаторе появилось: ЕГГОГ. Это слово (error - ошибка) служит сигналом аварийного останова или, как кратко говорят программисты, авоста. Причины подобного сбоя бывают двух типов: неудачно составленная программа либо привела к необходимости совершить некорректную операцию (деление на нуль, извлечение квадратного корня из отрицательного числа и т.д.), либо результат выполненной операции чрезмерно велик, превосходит 9.9999999e99 (программисты называют это переполнением).
Что же делать, если на индикаторе возникло сообщение ЕГГОГ? Многие читатели в своих письмах касаются этого вопроса.
А.НЕКЛЮДОВ (Одесса). Не торопитесь сбросить сообщение об ошибке. Если ЕГГОГ является результатом некорректной операции, то, нажав на клавишу ^ или КНОП, можно вызвать на табло число, действие с которым привело к авосту. Если же ЕГГОГ возникло в результате переполнения, то при нажатии клавиши оно остается на табло.
М.МАКСИМОВ (пос.Горелово Ленинградской области). Сообщение ЕГГОГ в этом случае появляется не из-за неспособности микрокалькулятора выполнить необходимое действие, а из-за невозможности вывести на табло результат. Его можно узнать, выполнив деление два раза на 1e50 и прибавив 100 к порядку получившегося на индикаторе числа. Если ЕГГОГ переполнения в ходе работы с большими числами возникает часто, то подобное понижение степени можно упростить: наберите на клавиатуре 1e50, умножьте это число само на себя и запишите результат умножения в одну из свободных ячеек памяти. (Пусть вас не смущает, что при этом на табло высвечивается ЕГГОГ). В дальнейшем для понижения порядка результата, превышающего 9.9999999e99, достаточно вызвать делитель 1e100 из памяти и выполнить деление один раз. Если результат вычислений получается в пределах от 1e200 до 1e299, то изменяется вид сообщения об ошибке: ЕГГОГ. В этом случае узнать результат можно двойным делением на 1e100; к порядку получившегося числа следует прибавить 200.
С числами, скрытыми под сообщением ЕГГОГ, можно производить арифметические действия, возводить их в квадрат командой Fx2, извлекать из них квадратный корень командой Fsqr. Других действий с ними делать нельзя. В ряде случаев результат, приводящий к сообщению ЕГГОГ, не вызывает останова. Возьмем, например, программу для вычисления факториала, рекомендуемую для чисел, больших 69:
00. ВП 01. П0 02. 1 03. ИП0 04. * 05. FL0 06. 03 07. С/П. По ней можно вычислять факториалы чисел до 166 (166!=9.0036828e297).
В.КОЗЛОВ (Ленинград). Записать сообщение ЕГГОГ в адресуемый регистр или передвигать его в регистрах стека можно только в том случае, если оно получено в результате переполнения. Сообщение ЕГГОГ, полученное благодаря некорректной операции, исчезает при нажатии почти что на любую клавишу. Когда результат лежит в пределах от 1e200 до 1e299 (на табло высвечивается ЕГГОГ), изменяется состояние счетчика шагов программы: управление передается на шаг, номер которого совпадает с первыми двумя цифрами показателя степени полученного числа. Например, если получено число 1.15e235, то произойдет переход на двадцать третий шаг. Если в результате действий будет получен ¦результат, превышающий 1e299, то микрокалькулятор перестает нормально работать: самопроизвольно переходит в режим программирования или запускается на счет, может погаснуть индикатор... Вернуть микрокалькулятор к нормальному состоянию в этом случае можно, лишь отключив его на некоторое время от питания.
Е.ЖУРАВЛЕВ (Москва). Остановится ли программа, когда произошло переполнение, или продолжит свою работу - это зависит от команд программы, выполняемых микрокалькулятором к моменту авоста переполнения и после него. Если переполнение возникло в результате арифметического действия (команды +, -, *, /, Fx2), то остановки вычислений по программе не будет. Число, по абсолютной величине большее 9,9999999e99, находящееся в регистре X, безостановочно обрабатывают команды ^, x-y, ПР, КПР, F(), Fx2, Fsqr, +, -, *, /. Наличие числа, вызвавшего сообщение ЕГГОГ, в одном из регистров стека или адресуемых регистрах не оказывает никакого влияния на выполнение команд по обработке других чисел, нормально выполняются все команды управления переходами.
Выполнение программы прерывается тогда, когда чрезмерно большое число появляется в регистре X в результате выполнения команд ИПР, КИПР, FBx. Программа останавливает вычисления и в том случае, если от чрезмерно большого числа попытаться взять стандартную функцию (за исключением Fx2 и Fsqr), причем ЕГГОГ переполнения сменится на ЕГГОГ от выполнения некорректной операции.
Вообще надо отметить, что у сигнала аварийного останова есть много особенностей, исследовать которые надо более внимательно.
А.МАТВЕЕВ (Чебоксары). Команда ИПР, вызывающая содержимое регистра, куда записано чрезмерно большое число, может быть преднамеренно проставлена в тексте программы для остановки счета с одновременным высвечиванием символа ЕГГОГ. Стоит отметить вот еще что: если на индикаторе загорелось сообщение ЕГГОГ от некорректной операции, а калькулятор затем пускается вновь, то он пропускает один шаг программы. Напротив, ЕГГОГ переполнения не вызывает пропуска шагов программы, когда калькулятор вновь запускается на счет.
К.ШИФФ (Ленинград). В некоторых задачах удобно выводить на индикатор служебные сообщения, отличающиеся по виду, от обычных цифр. Облечь эти сообщения в специальную форму можно с помощью ЕГГОГ. Сообщение строится в виде символа EN, где N некоторое целое многозначное число, и получается так: на индикаторе набирается число, в первой позиции которого стоит единица, в следующих позициях вписывается значение N. Нажмите теперь клавиши ВП 9 9 ВП ^ - на табло сформируется символ EN. Его можно записать в любой адресуемый регистр памяти микрокалькулятора и вызывать на табло в нужном месте программы перед командой С/П. Набрав 110, получаем описанным способом E10 и так далее.
В.НЕСТЕРОВ (Ленинград). На табло микрокалькулятора можно получить и символы Г, С
Г, С, L, -. Для этого сначала набираем 1 ВП 50 ^ * ВП ^, и на табло появляется Е. Запишем его в регистр 1 и выполним команды КИП1 и ИП1: на табло высветится символ Г. Его можно записать в любой регистр памяти. Теперь вновь выполним команды КИП1 и ИП1: на табло высветится С. Вновь КИП1 и ИП1 - микрокалькулятор выдаст символ L. Снова повторим команды и получим на табло символ -. И каждый такой символ, в свою очередь, можно записать в любой адресуемый регистр.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Пластмассовое окошко индикатора часто царапается. Чтобы избежать этого, я наклеиваю на него прозрачную клейкую ленту. Практически не затрудняя считывание результатов с индикатора, лента сохраняет его неповрежденным
В.БИЛЫК (г.Киев) ]
ЕСЛИ НЕ ХВАТАЕТ АДРЕСУЕМЫХ РЕГИСТРОВ
Часто приходится сталкиваться с проблемами, для решения которых не требуется сложных действий, однако необходим большой объем памяти. Оказывается, для таких случаев можно своеобразным способом размножить адресуемые регистры.
Каждый регистр разобьем на К секций по Ц разрядов в каждом.

Предположим, мы хотим вести учет товаров по 20 наименованиям. Объем хранения по каждому не превышает 999 единиц. Тогда Ц=3 (три знака в числе 999), К=2 (в регистре полностью помещаются 2 секции, секцию неполной емкости пока использовать не будем). Рассмотрим, как программа, приведенная в конце, ведет учет товаров (вместо Ц и К ввести их значения).
После ввода программы очистим регистры, набрав В/0, С/П. Теперь можно вводить значения прихода (+), а позже и расхода (-) по любому номеру наименования. Пусть к нам пришла партия товара в 200 единиц по 3-му наименованию. Введем эти данные, набрав 200 ^ 3 С/П.
Программа начнет работу. Сначала по ней определится номер регистра (деление на число секций в регистре, адреса 54-65), а затем номер секции в нем (вычитание общего числа секций, 65), расположенных в регистрах с первого до найденного (в нашем примере второго). Номер регистра (двойка) записывается в Р0, а номер секции (единица) остается в РХ и используется для смещения значения прихода в высшие разряды. Управление передается по адресу 81, где происходит умножение на 10, 100, 1000 и так далее, в нашем случае 200 умножается на 1000 и становится равным 200000. Теперь это число прибавляется к содержимому регистра (адреса 22-25) и для контроля выводится на индикатор. Можно вводить приход по другим наименованиям: скажем, 175 по четвертому, 578 по первому наименованию, далее расход - 35 по третьему наименованию (после каждого ввода нажимать клавишу С/П). Число 175 запишется во второй регистр на нулевое место, на индикаторе загорится 175, 578 запишется в первый регистр на первое место, на индикаторе будет 578000, после ввода - 35 на индикаторе увидим - 35000. Для того, чтобы узнать остаток товара, скажем, третьего наименования, наберем БП 29 (переход в режим считывания остатка) 3 С/П. После этого программа снова сначала найдет соответствующие регистр и номер секции (ПП54). Дальше, в соответствии с номером места, запятая в числе 165175 (содержимое второго регистра) перемещается влево (адреса 31-43) до границы секций (165, 175), после чего дробная часть отбрасывается (ПП71)
и остается 165. Однако это еще не все. Ведь наша секция могла оказаться не крайней левой, а, скажем, в центре. Тогда нам потребуется отбросить все цифры левее левой границы секции. Для этого исходное число сначала также обрабатывается переносом запятой вправо, но уже до места левой границы секции 0.165175 (адреса 38, 44-46), в результате отбрасывания дробной части получаем 0. Далее запятая снова переносится к правой границе секции, что равносильно приписыванию нулей справа (адреса 47-49, в нашем случае 0*1000=0 - результат не изменился). Наконец, получаем разность двух чисел: 165-0 =165, которая и выводится на индикатор: это и есть остаток товара третьего наименования. Чтобы найти остаток по другому наименованию, достаточно ввести его номер и нажать С/П. Для повторного возврата в режим ввода набрать БП09, а затем вводить данные, как ранее.
Чтобы использовать в регистрах крайние левые секции, значение К увеличьте на единицу. В нашем случае К станет равным 3. Число в дополнительной секции не должно превышать 99.
00.Сх 01. 1 02. 3 03. П9 04. Сх 05. КП^ 06. FL0 07. 05 08. С/П 09. ПП 10. 54 11. ИП0 12. ^ 13. F() 14. F() 15. Fx!=0 16. 21 17. ПП 18. 81 19. x-y 20. П0 21. F() 22. КИП^ 23. x-y 24. + 25. КП^ 26. FBx 27. БП 28. 08 29.ПП 30. 54 31. КИП^ 32. x-y 33. 1 34. x-y 35. ПП 36. 79 37. / 38. ^ 39. ПП 40. 91 41. * 42. ПП 43. 71 44. x-y 45. ПП 46. 71 47. ПП 48. 91 49. * 50. - 51. С/П 52. БП 53. 29 54. ^ 55. ^ 56. "К" 57. / 58. 2 59. ПП 60. 72 61. 1 62. - 63. "К" 64. * 65. - 66. Fx=0 67. 70 68. КИП0 69. F() 70. В/0 71. 1 72. + 73. П0 74. F() 75. КИП0 76. F() 77. ИПО 78. В/0 79. 1 80. + 81. П0 82. F() 83. ПП 84. 91 85. F() 86. FBx 87. * 88. FL0 89. 86 90. В/0 91. 1 92. ВП 93. "Ц" 94. В/0.
Работающий с программой должен следить за тем, чтобы ни по какому наименованию расход не превышал остатка, иначе остатки по другим наименованиям будут ошибочно изменены. Переложить предотвращение таких ошибок на программу затруднительно: ее длина тогда превзошла бы рамки памяти "Электроники Б3-34".
Б.ХОДОВ (г.Москва)
СЧИТАЕМ АККОРДЫ ДЛЯ ШЕСТИСТРУННОЙ ГИТАРЫ
Расчет аккордов для шестиструнной гитары в четырехголосном складе с заданным расположением звуков по голосам можно выполнить с помощью "Электроники Б3-34". Аккорд в микрокалькулятор записывается в регистры А (бас), В (тенор), С (альт), Д (сопрано).
Например, требуется рассчитать мажорное трезвучие. Представим его в виде последовательности из четырех цифр, каждая из которых обозначает (смотри рисунок) расстояние от баса, выраженное в полутонах, причем 12 заменяется нулем. Теперь мы можем расшифровать рисунок: 4 - это большая терция, 7 - квинта, 0 в сопрано - удвоение основного тона. Запишем 0 в РА, 4 в РВ, 7 в PC, 0 в РД. (Для секстаккорда соответствием было бы 4 0 7 0, для квартсекстаккорда 7 0 4 0). Результаты расчета - шесть вариантов расположения пальцев по струнам - хранятся в Р3-Р8. Выпишем содержимое этих регистров, снова запустим программу и получим вторые шесть вариантов. Так много их рассчитывается для того, чтобы для каждого конкретного случая выбрать наиболее удобную комбинацию.
Если проделать эти действия для нашего примера - мажорного трезвучия, то получится такая таблица:
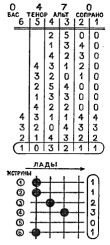
Цифры в комбинациях нумеруются справа налево и соответствуют положению пальцев на струнах. Расшифруем комбинацию 1 0 3 2 1 1. Первая единице, справа означает, что первую струну следует прижать пальцем на выбранном ладу. Остальные цифры 1 0 3 2 1 показывают номер лада, на котором нужно прижать соответствующую струну, как показано на рисунке; нуль означает, что струну прижимать не следует. Если в комбинации встретилась цифра, большая четырех,- это признак наложения звуков; струну не следует прижимать и в этом случае.
Программа: 00. 5 01. 8 02. П7 03. 1 04. 2 05. П8 06. 6 07. П9 08. 1 09. - 10. П9 11. Сx 12. КП9 13. ИПА 14. КПП7 15. ПП 16. 72 17. ИПА 18. КПП7 19. ИПВ 20. КПП7 21. ПП 22. 72 23. ИПА 24. КПП7 25. ИПВ 26. КПП7 27. ИПС 28. КПП7 29. ПП 30. 72 31. ИПВ 32. КПП7 33. ИПС 34. КПП7 35. ИПД 36. КПП7 37. ПП 38. 73 39. ИПС 40. КПП7 41. ИПД 42. КПП7 43. ПП 44. 72 45. ИПД 46. КПП7 47. КИП6 48. ИП9 49. Fx=0 50. 08 51. ИП5 52. С/П 53. ИП4 54. ИП3 55. ИП2 56. ИП1 57. ИП0 58. ИП6 59. - 60. ПП 61. 88 62. 5 63. - 64. Fx<0 65. 71 66. 5 67. + 68. КИП9 69. + 70. КП9 71. В/0 72. КИП6 73. 4 74. ИП6 75. + 76. ПП 77. 86 78. П6 79. КИП9 80. 1 81. 0 82. * 83. КП9 84. Сx 85. В/0 86. ИП8 87. - 88. Fx<0 89. 86 90. ИП8 91. + 92. Fx>=0 93. 90 94. В/0
Инструкция: Введите числа, соответствующие басу в РА, тенору - в РВ, альту - в PC, сопрано - в РД, В/0, С/П. На индикаторе первая возможная комбинация, ПП, вторая, ПП, третья, ПП, четвертая, ПП, пятая, ПП, шестая, В/0, С/П, седьмая, ПП, восьмая, ПП ... двенадцатая.
А.БАКУЛИН (пос. Черноголовка
Московской обл.)
ОСТАНОВИСЬ, МГНОВЕНИЕ!
... Микрокалькулятор вычисляет по программе очередной результат, выполнение программы останавливается, результат высвечивается на индикаторе, и одновременно раздается звуковой сигнал, привлекающий внимание оператора. Спустя некоторое время после останова (1-6 секунд) микрокалькулятор автоматически принимается за вычисление следующего результата.
Такой режим особенно удобен, например, для табулирования сложных функций, когда требуется пройти весь диапазон изменения аргумента, записывая значения функции в интересующих точках. Пяти-шести секунд вполне достаточно, чтобы записать результат.
Удобно это и при счете по программам, где требуется лишь контролировать изменение одного или нескольких параметров,- например, при решении дифференциальных уравнений или задач оптимизации. Контролируемый параметр выводится в регистр X перед командой С/П. Длительность паузы выбирается равной 1-2 секундам - вы получаете требуемую информацию и можете в любой момент остановить процесс вычисления.
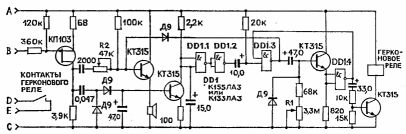
Устройство для реализации такого режима представлено схемой. Одновибратор формирует импульс, длительность которого определяет время паузы. Время индикации можно изменять переменным резистором R1. Громкость предупредительного сигнала регулируется переменным резистором R2. Ток, потребляемый устройством,- всего 15мА, так что можно смело использовать блок питания микрокалькулятора. Схема подключения устройства показана ниже. Точки, обозначенные одной и той же буквой, следует соединить между собой.

Устройство удобно подключать к микрокалькулятору с помощью разъема, который нетрудно разместить в левой верхней части корпуса.
А.БОЙКО, А.ПОТАШОВ. (г.Москва)
В #6 за текущий год мы обращались к юмористам присылать нам веселые рассказы и рисунки без слов на темы нэ вычислительного дела. Публикуем два рисунка из числа тех. что поступили первыми.

Рис. А.МАКАРЕНКО (г.Москва)

Рис. А.ШТЫРИНА (г.Калинин)
СТОИТ ЛИ ПРОГРАММИРОВАТЬ
Во всех руководствах по программируемым микрокалькуляторам предлагается для вычисления значений полинома вводить его коэффициенты в регистры памяти. Это имеет смысл, если приходится многократно вычислять значения одного и того же полинома при разных значениях аргумента х. Оправдана тогда и немалая длина программы. При однократном же вычислении для одного значения х (что, вероятно, случается чаще всего) целесообразнее вводить коэффициенты по ходу счета. Сама же программа, реализующая схему Горнера, при этом может быть сокращена до пяти адресов: 00. x-y 01. * 02. С/П 03. + 04. В/0. Без учета ввода аргумента х и коэффициентов ai здесь для получения результата требуется нажать на клавиши всего n+14 раз: F ПРГ x-y * С/П + В/0 F АВТ В/0 x ^ ^ ^ an С/П a[n-1] С/П ... a1 С/П а0 +. Если коэффициент при x**n равен единице, удобна программа 00. ^ 01. С/П 02. + 03. * 04. В/0, требующая n+12 нажатий на клавиши: F ПРГ ^ С/П + * В/0 F АВТ В/0 х ^ С/П а[n-1] С/П а[n-2] С/П ... а1 С/П а0 +.
Возможен и ультракороткий вариант 00. + 01. * 02.С/П, но он требует 2n+12 нажатий на клавиши.
Если же вычислять значения полинома по схеме Горнера вручную, то на клавиши нужно нажать 2n+3 раза: x ^ ^ ^ аn * a[n-1] + х * ... затем фрагмент из последних четырех команд повторяется с дальнейшими коэффициентами, пока очередь не дойдет до а0: нажав клавишу "плюс", получаем результат.
Какой же из подходов лучше, если значение полинома определяется для единственного х? Ответ дает решение неравенства n+14<2n+3, то есть n>11. Лишь для полиномов столь высокой степени стоит вводить в калькулятор программу. Но часто ли встречаются на практике такие полиномы?
В программировании, как во всякой работе, вредны трафареты мышления. Каждый раз с учетом конкретных особенностей задачи нужно отдавать себе отчет: какой порядок счета лучше? Как, например, вводить исходные данные - в регистры памяти перед вводом программы или по ходу счета в стек? И стоит ли вообще программировать, если можно быстрее получить результат вручную?
А.ТУЛАЙКОВ (г.Долгопрудный)
[ УЗЕЛКИ НА ПАМЯТЬ
Как происходит косвенное обращение к регистрам памяти по команде КИПР, если содержимое регистра Р по модулю больше или равно 10? Регистр, к которому производится обращение, тогда определяется цифрой в младшем разряде целой части абсолютной величины числа, хранящегося в регистре Р:
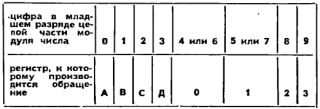
Если в регистре Р7 хранится, например, 1985.314, то при выполнении операции КИП7 произойдет обращение к регистру Р1, так как младший разряд целой части числа содержит 5. Знак числа, хранящегося в регистре P, не влияет на выбор регистра.
Н.КОНОПЛЕВ (г.Пермь) ]
[ МАЛЕНЬКИЕ РЕЦЕНЗИИ
В издательстве "Технiка" (Киев) вышла книга Я.К.Трохименко и Ф.Д.Любича "Инженерные расчеты на программируемых микрокалькуляторах".
В книге приведено более 200 программ для решения уравнений, численного интегрирования, статистической обработки данных, численной оптимизации. Но книга не справочник по прикладным программам. Здесь систематически изложена методика составления оптимальных программ, впервые подробно рассмотрены погрешности вычислений на микрокалькуляторах.
Авторами разработан язык управления заданиями для микрокалькуляторов Б3-21 и Б3-34, позволяющий заметно облегчить вычисления. К примеру, программа работы с комплексными числами на Б3-34 составлена так, что по "команде" ИП+ С/П комплексные числа складываются, по "команде" ИП* С/П - умножаются и т.д. Язык управления заданиями применяется также для вычисления гиперболических и обратных гиперболических функций. Впервые приведена программа решения системы из пяти линейных уравнений.
Специальная глава посвящена методам линейного и нелинейного программирования. Сколько и каких грузовиков нужно приобрести, если задано число водителей, выдана определенная сумма денег на эти цели и надо достичь максимальной производительности? Как найти путь к вершине, если на дороге гребни и овраги, а традиционные методы поиска отказывают? Оказывается, и здесь может помочь микрокалькулятор. Программы, методы их составления - в книге Я.К.Трохименко и Ф.Д.Любича ]
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
КАЛЬКУЛЯТОР НА ПРИЛАВКЕ
Наша промышленность выпускает несколько десятков типов микрокальнуляторов. Около двадцати различных моделей было представлено на выставке-продаже этих миниатюрных ЭВМ в московском ГУМе. Проходила выставка в апреле этого года. Среди покупателей распространялась анкета, итоги которой позволяют составить некоторое представление о ситуации в калькуляторном мире.
Прежде всего одна цифра: 2300. Столько калькуляторов было продано за 12 дней работы выставки. Это значит, что ежедневная продажа была почти в четыре раза выше обычной.
Калькулятор, как ни странно,- предмет сезонной продажи. Пик "раскупаемости" приходится на осень, а провал - на лето. Впрочем, странность эта легко объяснима: 41.7 процента покупателей - студенты, а 35 процентов - школьники или их родители. То есть, три четверти микрокалькуляторов попадают в руки учащихся, а они, как известно, летом отдыхают.
Устроители выставки обратили внимание на очень низкий процент учеников ПТУ среди покупателей: всего 3.2 процента. Выяснилось, однако, что большинство ПТУ покупает калькуляторы по безналичному расчету и бесплатно предоставляет их учащимся. Факт отрадный!
Какие калькуляторы пользуются наибольшим спросом? На первом месте стоят инженерные - их желают купить 40.9 процента опрошенных, за ними идут программируемые (36.6 процента) и замыкают ряд простейшие (22.5 процента).
Что касается конкретных моделей, то наибольшим спросом среди простейших пользуются "Б3-23" и "МК-33". Они самые дешевые, стоят по 25 рублей, и наиболее удобны для проведения несложных планово-экономических расчетов. Для начального обучения детей.
Из инженерных на первом месте идет "МК-51". Снабженный литиевым элементом питания, он рассчитан на работу без перезарядки в течение примерно полутора лет. Выполняет он 35 различных операций, среди которых и такие "экзотические", как статистические расчеты. Не исключено, правда, что скоро ему придется потесниться и пропустить вперед новую модель, "МК-71". Этот калькулятор самый мощный среди отечественных машин инженерного типа. Он имеет еще более широкий набор операций, чем "МК-51", питается от "вечного" источника - батарей солнечных элементов, которые могут заряжаться как при естественном, так и при искусственном освещении. Обе эти модели быстрые, точные и достаточно надежные в работе. Кстати, о "МК-51" реализованы алгоритмы вычисления элементарных функций по методу "Цифра за цифрой", описанному в 10/84.
Первое место, занимаемое инженерными калькуляторами, объясняется просто. Они не требуют никаких начальных навыков для работы, запись арифметических выражений на них прямая, как принято в математике; можно использовать скобки, причем на "МК-71" - пять уровней скобок.
И, наконец, элита калькуляторного мира - программируемые микрокалькуляторы. Здесь первое место безоговорочно принадлежит "МК-54". Обладая всеми достоинствами горячо любимого нами "Б3-34", этот калькулятор на 20 рублей дешевле (за счет источников питания другого типа), да и внешне более элегантен.
Две перспективные модели программируемых микрокалькуляторов "МК-52" и "МК-61", о которых уже писал наш журнал (6/85), скоро появятся в фирменных магазинах-салонах "Электроника".
Приятно отметить, что они полностью совместимы по системе команд со своими предшественниками, как говорят, снизу вверх. Это значит, что любая программа, написанная для "Б3-34" или "МК-54", может быть реализована на них, если в ней нет команд КП^, КИП^ и прочих, содержащих стрелку.
Теперь о последних цифрах анкеты, которые хотелось бы привести. Только 37.2 процента покупателей приобретают калькуляторы впервые. Остальные покупают новые модели взамен морально устаревших. О чем это говорит? Раз появившись в руках, маленькая ЭВМ становится спутником человека навсегда. Будут меняться модели, типы, но возврата к безкалькуляторной жизни не будет.
И.ДАНИЛОВ (г.Москва)
[ ДОПОЛНЕНИЯ К МАТЕРИАЛАМ ПРЕДЫДУЩИХ НОМЕРОВ
Микрокалькулятор "Электроника Б3-34", усовершенствованный примерно так, как это было описано в статье "Всего один диод" 4/85, мы используем для подсчета нагрузки за смену. Вот уже пять месяцев он нас не подводит, хотя работает круглосуточно. Не страшны даже кратковременные уменьшения напряжения в сети или ее отключения на незначительное время.
С.ПЕТРОВ, М.ВАХТЕРОВ (г.Москва) ]
НА ИНДИКАТОРЕ - СИГНАЛ АВОСТА
...Счет по программе внезапно остановился, и на индикаторе появилось: ЕГГОГ. Это слово (error - ошибка) служит сигналом аварийного останова или, как кратко говорят программисты, авоста. Причины подобного сбоя бывают двух типов: неудачно составленная программа либо привела к необходимости совершить некорректную операцию (деление на нуль, извлечение квадратного корня из отрицательного числа и т.д.), либо результат выполненной операции чрезмерно велик, превосходит 9.9999999e99 (программисты называют это переполнением).
Что же делать, если на индикаторе возникло сообщение ЕГГОГ? Многие читатели в своих письмах касаются этого вопроса.
А.НЕКЛЮДОВ (Одесса). Не торопитесь сбросить сообщение об ошибке. Если ЕГГОГ является результатом некорректной операции, то, нажав на клавишу ^ или КНОП, можно вызвать на табло число, действие с которым привело к авосту. Если же ЕГГОГ возникло в результате переполнения, то при нажатии клавиши оно остается на табло.
М.МАКСИМОВ (пос.Горелово Ленинградской области). Сообщение ЕГГОГ в этом случае появляется не из-за неспособности микрокалькулятора выполнить необходимое действие, а из-за невозможности вывести на табло результат. Его можно узнать, выполнив деление два раза на 1e50 и прибавив 100 к порядку получившегося на индикаторе числа. Если ЕГГОГ переполнения в ходе работы с большими числами возникает часто, то подобное понижение степени можно упростить: наберите на клавиатуре 1e50, умножьте это число само на себя и запишите результат умножения в одну из свободных ячеек памяти. (Пусть вас не смущает, что при этом на табло высвечивается ЕГГОГ). В дальнейшем для понижения порядка результата, превышающего 9.9999999e99, достаточно вызвать делитель 1e100 из памяти и выполнить деление один раз. Если результат вычислений получается в пределах от 1e200 до 1e299, то изменяется вид сообщения об ошибке: ЕГГОГ. В этом случае узнать результат можно двойным делением на 1e100; к порядку получившегося числа следует прибавить 200.
С числами, скрытыми под сообщением ЕГГОГ, можно производить арифметические действия, возводить их в квадрат командой Fx2, извлекать из них квадратный корень командой Fsqr. Других действий с ними делать нельзя. В ряде случаев результат, приводящий к сообщению ЕГГОГ, не вызывает останова. Возьмем, например, программу для вычисления факториала, рекомендуемую для чисел, больших 69:
00. ВП 01. П0 02. 1 03. ИП0 04. * 05. FL0 06. 03 07. С/П. По ней можно вычислять факториалы чисел до 166 (166!=9.0036828e297).
В.КОЗЛОВ (Ленинград). Записать сообщение ЕГГОГ в адресуемый регистр или передвигать его в регистрах стека можно только в том случае, если оно получено в результате переполнения. Сообщение ЕГГОГ, полученное благодаря некорректной операции, исчезает при нажатии почти что на любую клавишу. Когда результат лежит в пределах от 1e200 до 1e299 (на табло высвечивается ЕГГОГ), изменяется состояние счетчика шагов программы: управление передается на шаг, номер которого совпадает с первыми двумя цифрами показателя степени полученного числа. Например, если получено число 1.15e235, то произойдет переход на двадцать третий шаг. Если в результате действий будет получен ¦результат, превышающий 1e299, то микрокалькулятор перестает нормально работать: самопроизвольно переходит в режим программирования или запускается на счет, может погаснуть индикатор... Вернуть микрокалькулятор к нормальному состоянию в этом случае можно, лишь отключив его на некоторое время от питания.
Е.ЖУРАВЛЕВ (Москва). Остановится ли программа, когда произошло переполнение, или продолжит свою работу - это зависит от команд программы, выполняемых микрокалькулятором к моменту авоста переполнения и после него. Если переполнение возникло в результате арифметического действия (команды +, -, *, /, Fx2), то остановки вычислений по программе не будет. Число, по абсолютной величине большее 9,9999999e99, находящееся в регистре X, безостановочно обрабатывают команды ^, x-y, ПР, КПР, F(), Fx2, Fsqr, +, -, *, /. Наличие числа, вызвавшего сообщение ЕГГОГ, в одном из регистров стека или адресуемых регистрах не оказывает никакого влияния на выполнение команд по обработке других чисел, нормально выполняются все команды управления переходами.
Выполнение программы прерывается тогда, когда чрезмерно большое число появляется в регистре X в результате выполнения команд ИПР, КИПР, FBx. Программа останавливает вычисления и в том случае, если от чрезмерно большого числа попытаться взять стандартную функцию (за исключением Fx2 и Fsqr), причем ЕГГОГ переполнения сменится на ЕГГОГ от выполнения некорректной операции.
Вообще надо отметить, что у сигнала аварийного останова есть много особенностей, исследовать которые надо более внимательно.
А.МАТВЕЕВ (Чебоксары). Команда ИПР, вызывающая содержимое регистра, куда записано чрезмерно большое число, может быть преднамеренно проставлена в тексте программы для остановки счета с одновременным высвечиванием символа ЕГГОГ. Стоит отметить вот еще что: если на индикаторе загорелось сообщение ЕГГОГ от некорректной операции, а калькулятор затем пускается вновь, то он пропускает один шаг программы. Напротив, ЕГГОГ переполнения не вызывает пропуска шагов программы, когда калькулятор вновь запускается на счет.
К.ШИФФ (Ленинград). В некоторых задачах удобно выводить на индикатор служебные сообщения, отличающиеся по виду, от обычных цифр. Облечь эти сообщения в специальную форму можно с помощью ЕГГОГ. Сообщение строится в виде символа EN, где N некоторое целое многозначное число, и получается так: на индикаторе набирается число, в первой позиции которого стоит единица, в следующих позициях вписывается значение N. Нажмите теперь клавиши ВП 9 9 ВП ^ - на табло сформируется символ EN. Его можно записать в любой адресуемый регистр памяти микрокалькулятора и вызывать на табло в нужном месте программы перед командой С/П. Набрав 110, получаем описанным способом E10 и так далее.
В.НЕСТЕРОВ (Ленинград). На табло микрокалькулятора можно получить и символы Г, С
Г, С, L, -. Для этого сначала набираем 1 ВП 50 ^ * ВП ^, и на табло появляется Е. Запишем его в регистр 1 и выполним команды КИП1 и ИП1: на табло высветится символ Г. Его можно записать в любой регистр памяти. Теперь вновь выполним команды КИП1 и ИП1: на табло высветится С. Вновь КИП1 и ИП1 - микрокалькулятор выдаст символ L. Снова повторим команды и получим на табло символ -. И каждый такой символ, в свою очередь, можно записать в любой адресуемый регистр.
[ МАЛЕНЬКИЕ ХИТРОСТИ
Пластмассовое окошко индикатора часто царапается. Чтобы избежать этого, я наклеиваю на него прозрачную клейкую ленту. Практически не затрудняя считывание результатов с индикатора, лента сохраняет его неповрежденным
В.БИЛЫК (г.Киев) ]
ЕСЛИ НЕ ХВАТАЕТ АДРЕСУЕМЫХ РЕГИСТРОВ
Часто приходится сталкиваться с проблемами, для решения которых не требуется сложных действий, однако необходим большой объем памяти. Оказывается, для таких случаев можно своеобразным способом размножить адресуемые регистры.
Каждый регистр разобьем на К секций по Ц разрядов в каждом.

Предположим, мы хотим вести учет товаров по 20 наименованиям. Объем хранения по каждому не превышает 999 единиц. Тогда Ц=3 (три знака в числе 999), К=2 (в регистре полностью помещаются 2 секции, секцию неполной емкости пока использовать не будем). Рассмотрим, как программа, приведенная в конце, ведет учет товаров (вместо Ц и К ввести их значения).
После ввода программы очистим регистры, набрав В/0, С/П. Теперь можно вводить значения прихода (+), а позже и расхода (-) по любому номеру наименования. Пусть к нам пришла партия товара в 200 единиц по 3-му наименованию. Введем эти данные, набрав 200 ^ 3 С/П.
Программа начнет работу. Сначала по ней определится номер регистра (деление на число секций в регистре, адреса 54-65), а затем номер секции в нем (вычитание общего числа секций, 65), расположенных в регистрах с первого до найденного (в нашем примере второго). Номер регистра (двойка) записывается в Р0, а номер секции (единица) остается в РХ и используется для смещения значения прихода в высшие разряды. Управление передается по адресу 81, где происходит умножение на 10, 100, 1000 и так далее, в нашем случае 200 умножается на 1000 и становится равным 200000. Теперь это число прибавляется к содержимому регистра (адреса 22-25) и для контроля выводится на индикатор. Можно вводить приход по другим наименованиям: скажем, 175 по четвертому, 578 по первому наименованию, далее расход - 35 по третьему наименованию (после каждого ввода нажимать клавишу С/П). Число 175 запишется во второй регистр на нулевое место, на индикаторе загорится 175, 578 запишется в первый регистр на первое место, на индикаторе будет 578000, после ввода - 35 на индикаторе увидим - 35000. Для того, чтобы узнать остаток товара, скажем, третьего наименования, наберем БП 29 (переход в режим считывания остатка) 3 С/П. После этого программа снова сначала найдет соответствующие регистр и номер секции (ПП54). Дальше, в соответствии с номером места, запятая в числе 165175 (содержимое второго регистра) перемещается влево (адреса 31-43) до границы секций (165, 175), после чего дробная часть отбрасывается (ПП71)
и остается 165. Однако это еще не все. Ведь наша секция могла оказаться не крайней левой, а, скажем, в центре. Тогда нам потребуется отбросить все цифры левее левой границы секции. Для этого исходное число сначала также обрабатывается переносом запятой вправо, но уже до места левой границы секции 0.165175 (адреса 38, 44-46), в результате отбрасывания дробной части получаем 0. Далее запятая снова переносится к правой границе секции, что равносильно приписыванию нулей справа (адреса 47-49, в нашем случае 0*1000=0 - результат не изменился). Наконец, получаем разность двух чисел: 165-0 =165, которая и выводится на индикатор: это и есть остаток товара третьего наименования. Чтобы найти остаток по другому наименованию, достаточно ввести его номер и нажать С/П. Для повторного возврата в режим ввода набрать БП09, а затем вводить данные, как ранее.
Чтобы использовать в регистрах крайние левые секции, значение К увеличьте на единицу. В нашем случае К станет равным 3. Число в дополнительной секции не должно превышать 99.
00.Сх 01. 1 02. 3 03. П9 04. Сх 05. КП^ 06. FL0 07. 05 08. С/П 09. ПП 10. 54 11. ИП0 12. ^ 13. F() 14. F() 15. Fx!=0 16. 21 17. ПП 18. 81 19. x-y 20. П0 21. F() 22. КИП^ 23. x-y 24. + 25. КП^ 26. FBx 27. БП 28. 08 29.ПП 30. 54 31. КИП^ 32. x-y 33. 1 34. x-y 35. ПП 36. 79 37. / 38. ^ 39. ПП 40. 91 41. * 42. ПП 43. 71 44. x-y 45. ПП 46. 71 47. ПП 48. 91 49. * 50. - 51. С/П 52. БП 53. 29 54. ^ 55. ^ 56. "К" 57. / 58. 2 59. ПП 60. 72 61. 1 62. - 63. "К" 64. * 65. - 66. Fx=0 67. 70 68. КИП0 69. F() 70. В/0 71. 1 72. + 73. П0 74. F() 75. КИП0 76. F() 77. ИПО 78. В/0 79. 1 80. + 81. П0 82. F() 83. ПП 84. 91 85. F() 86. FBx 87. * 88. FL0 89. 86 90. В/0 91. 1 92. ВП 93. "Ц" 94. В/0.
Работающий с программой должен следить за тем, чтобы ни по какому наименованию расход не превышал остатка, иначе остатки по другим наименованиям будут ошибочно изменены. Переложить предотвращение таких ошибок на программу затруднительно: ее длина тогда превзошла бы рамки памяти "Электроники Б3-34".
Б.ХОДОВ (г.Москва)
СЧИТАЕМ АККОРДЫ ДЛЯ ШЕСТИСТРУННОЙ ГИТАРЫ
Расчет аккордов для шестиструнной гитары в четырехголосном складе с заданным расположением звуков по голосам можно выполнить с помощью "Электроники Б3-34". Аккорд в микрокалькулятор записывается в регистры А (бас), В (тенор), С (альт), Д (сопрано).
Например, требуется рассчитать мажорное трезвучие. Представим его в виде последовательности из четырех цифр, каждая из которых обозначает (смотри рисунок) расстояние от баса, выраженное в полутонах, причем 12 заменяется нулем. Теперь мы можем расшифровать рисунок: 4 - это большая терция, 7 - квинта, 0 в сопрано - удвоение основного тона. Запишем 0 в РА, 4 в РВ, 7 в PC, 0 в РД. (Для секстаккорда соответствием было бы 4 0 7 0, для квартсекстаккорда 7 0 4 0). Результаты расчета - шесть вариантов расположения пальцев по струнам - хранятся в Р3-Р8. Выпишем содержимое этих регистров, снова запустим программу и получим вторые шесть вариантов. Так много их рассчитывается для того, чтобы для каждого конкретного случая выбрать наиболее удобную комбинацию.
Если проделать эти действия для нашего примера - мажорного трезвучия, то получится такая таблица:

Цифры в комбинациях нумеруются справа налево и соответствуют положению пальцев на струнах. Расшифруем комбинацию 1 0 3 2 1 1. Первая единице, справа означает, что первую струну следует прижать пальцем на выбранном ладу. Остальные цифры 1 0 3 2 1 показывают номер лада, на котором нужно прижать соответствующую струну, как показано на рисунке; нуль означает, что струну прижимать не следует. Если в комбинации встретилась цифра, большая четырех,- это признак наложения звуков; струну не следует прижимать и в этом случае.
Программа: 00. 5 01. 8 02. П7 03. 1 04. 2 05. П8 06. 6 07. П9 08. 1 09. - 10. П9 11. Сx 12. КП9 13. ИПА 14. КПП7 15. ПП 16. 72 17. ИПА 18. КПП7 19. ИПВ 20. КПП7 21. ПП 22. 72 23. ИПА 24. КПП7 25. ИПВ 26. КПП7 27. ИПС 28. КПП7 29. ПП 30. 72 31. ИПВ 32. КПП7 33. ИПС 34. КПП7 35. ИПД 36. КПП7 37. ПП 38. 73 39. ИПС 40. КПП7 41. ИПД 42. КПП7 43. ПП 44. 72 45. ИПД 46. КПП7 47. КИП6 48. ИП9 49. Fx=0 50. 08 51. ИП5 52. С/П 53. ИП4 54. ИП3 55. ИП2 56. ИП1 57. ИП0 58. ИП6 59. - 60. ПП 61. 88 62. 5 63. - 64. Fx<0 65. 71 66. 5 67. + 68. КИП9 69. + 70. КП9 71. В/0 72. КИП6 73. 4 74. ИП6 75. + 76. ПП 77. 86 78. П6 79. КИП9 80. 1 81. 0 82. * 83. КП9 84. Сx 85. В/0 86. ИП8 87. - 88. Fx<0 89. 86 90. ИП8 91. + 92. Fx>=0 93. 90 94. В/0
Инструкция: Введите числа, соответствующие басу в РА, тенору - в РВ, альту - в PC, сопрано - в РД, В/0, С/П. На индикаторе первая возможная комбинация, ПП, вторая, ПП, третья, ПП, четвертая, ПП, пятая, ПП, шестая, В/0, С/П, седьмая, ПП, восьмая, ПП ... двенадцатая.
А.БАКУЛИН (пос. Черноголовка
Московской обл.)
ОСТАНОВИСЬ, МГНОВЕНИЕ!
... Микрокалькулятор вычисляет по программе очередной результат, выполнение программы останавливается, результат высвечивается на индикаторе, и одновременно раздается звуковой сигнал, привлекающий внимание оператора. Спустя некоторое время после останова (1-6 секунд) микрокалькулятор автоматически принимается за вычисление следующего результата.
Такой режим особенно удобен, например, для табулирования сложных функций, когда требуется пройти весь диапазон изменения аргумента, записывая значения функции в интересующих точках. Пяти-шести секунд вполне достаточно, чтобы записать результат.
Удобно это и при счете по программам, где требуется лишь контролировать изменение одного или нескольких параметров,- например, при решении дифференциальных уравнений или задач оптимизации. Контролируемый параметр выводится в регистр X перед командой С/П. Длительность паузы выбирается равной 1-2 секундам - вы получаете требуемую информацию и можете в любой момент остановить процесс вычисления.

Устройство для реализации такого режима представлено схемой. Одновибратор формирует импульс, длительность которого определяет время паузы. Время индикации можно изменять переменным резистором R1. Громкость предупредительного сигнала регулируется переменным резистором R2. Ток, потребляемый устройством,- всего 15мА, так что можно смело использовать блок питания микрокалькулятора. Схема подключения устройства показана ниже. Точки, обозначенные одной и той же буквой, следует соединить между собой.

Устройство удобно подключать к микрокалькулятору с помощью разъема, который нетрудно разместить в левой верхней части корпуса.
А.БОЙКО, А.ПОТАШОВ. (г.Москва)
В #6 за текущий год мы обращались к юмористам присылать нам веселые рассказы и рисунки без слов на темы нэ вычислительного дела. Публикуем два рисунка из числа тех. что поступили первыми.

Рис. А.МАКАРЕНКО (г.Москва)

Рис. А.ШТЫРИНА (г.Калинин)
СТОИТ ЛИ ПРОГРАММИРОВАТЬ
Во всех руководствах по программируемым микрокалькуляторам предлагается для вычисления значений полинома вводить его коэффициенты в регистры памяти. Это имеет смысл, если приходится многократно вычислять значения одного и того же полинома при разных значениях аргумента х. Оправдана тогда и немалая длина программы. При однократном же вычислении для одного значения х (что, вероятно, случается чаще всего) целесообразнее вводить коэффициенты по ходу счета. Сама же программа, реализующая схему Горнера, при этом может быть сокращена до пяти адресов: 00. x-y 01. * 02. С/П 03. + 04. В/0. Без учета ввода аргумента х и коэффициентов ai здесь для получения результата требуется нажать на клавиши всего n+14 раз: F ПРГ x-y * С/П + В/0 F АВТ В/0 x ^ ^ ^ an С/П a[n-1] С/П ... a1 С/П а0 +. Если коэффициент при x**n равен единице, удобна программа 00. ^ 01. С/П 02. + 03. * 04. В/0, требующая n+12 нажатий на клавиши: F ПРГ ^ С/П + * В/0 F АВТ В/0 х ^ С/П а[n-1] С/П а[n-2] С/П ... а1 С/П а0 +.
Возможен и ультракороткий вариант 00. + 01. * 02.С/П, но он требует 2n+12 нажатий на клавиши.
Если же вычислять значения полинома по схеме Горнера вручную, то на клавиши нужно нажать 2n+3 раза: x ^ ^ ^ аn * a[n-1] + х * ... затем фрагмент из последних четырех команд повторяется с дальнейшими коэффициентами, пока очередь не дойдет до а0: нажав клавишу "плюс", получаем результат.
Какой же из подходов лучше, если значение полинома определяется для единственного х? Ответ дает решение неравенства n+14<2n+3, то есть n>11. Лишь для полиномов столь высокой степени стоит вводить в калькулятор программу. Но часто ли встречаются на практике такие полиномы?
В программировании, как во всякой работе, вредны трафареты мышления. Каждый раз с учетом конкретных особенностей задачи нужно отдавать себе отчет: какой порядок счета лучше? Как, например, вводить исходные данные - в регистры памяти перед вводом программы или по ходу счета в стек? И стоит ли вообще программировать, если можно быстрее получить результат вручную?
А.ТУЛАЙКОВ (г.Долгопрудный)
[ УЗЕЛКИ НА ПАМЯТЬ
Как происходит косвенное обращение к регистрам памяти по команде КИПР, если содержимое регистра Р по модулю больше или равно 10? Регистр, к которому производится обращение, тогда определяется цифрой в младшем разряде целой части абсолютной величины числа, хранящегося в регистре Р:

Если в регистре Р7 хранится, например, 1985.314, то при выполнении операции КИП7 произойдет обращение к регистру Р1, так как младший разряд целой части числа содержит 5. Знак числа, хранящегося в регистре P, не влияет на выбор регистра.
Н.КОНОПЛЕВ (г.Пермь) ]
[ МАЛЕНЬКИЕ РЕЦЕНЗИИ
В издательстве "Технiка" (Киев) вышла книга Я.К.Трохименко и Ф.Д.Любича "Инженерные расчеты на программируемых микрокалькуляторах".
В книге приведено более 200 программ для решения уравнений, численного интегрирования, статистической обработки данных, численной оптимизации. Но книга не справочник по прикладным программам. Здесь систематически изложена методика составления оптимальных программ, впервые подробно рассмотрены погрешности вычислений на микрокалькуляторах.
Авторами разработан язык управления заданиями для микрокалькуляторов Б3-21 и Б3-34, позволяющий заметно облегчить вычисления. К примеру, программа работы с комплексными числами на Б3-34 составлена так, что по "команде" ИП+ С/П комплексные числа складываются, по "команде" ИП* С/П - умножаются и т.д. Язык управления заданиями применяется также для вычисления гиперболических и обратных гиперболических функций. Впервые приведена программа решения системы из пяти линейных уравнений.
Специальная глава посвящена методам линейного и нелинейного программирования. Сколько и каких грузовиков нужно приобрести, если задано число водителей, выдана определенная сумма денег на эти цели и надо достичь максимальной производительности? Как найти путь к вершине, если на дороге гребни и овраги, а традиционные методы поиска отказывают? Оказывается, и здесь может помочь микрокалькулятор. Программы, методы их составления - в книге Я.К.Трохименко и Ф.Д.Любича ]

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
11/85
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ПЯТОЕ, посвященное частным, на первый взгляд маловажным моментам в решении задач на программируемом микрокалькуляторе - вводу исходных данных и выводу полученных результатов.
Ведет занятие С.В.КОМИССАРОВ (Московский инженерно-строительный
институт)
Известно несколько основных способов ввода чисел в калькулятор. Выбор подходящего определяется при составлении конкретной программы ее особенностями, а те - ее назначением. Различные способы можно комбинировать в одной и той же программе. Однако не следует забывать, что считающему на калькуляторе удобнее единообразие. Неоправданное чередование клавиш, нажимаемых при вводе, может значительно затруднить работу, послужить причиной ошибок.
Идеалом начинающего программиста должна стать простота. А наиболее просто работать с калькулятором, когда все управление им сводится к нажатию в нужные моменты на одну-единственную клавишу.
Чтобы запустить программу на счет, то, какова бы оиа ни была, надо нажать клавишу С/П. Вот ею-то в лучшем случае и следует ограничиться, управляя калькулятором.
... Калькулятор включен, управление передано на начальный адрес программы, на клавиатуре набрано первое из вводимых чисел, нажата клавиша С/П, запущенная программа переслала введенное число в какой-либо из адресуемых регистров или вычислила от него какое-то выражение, выполнила последующие действия, для которых хватает введенного числа, и остановилась по команде останова, проставленной в программе. Пока калькулятор бездействует, на клавиатуре набрано следующее из вводимых чисел, снова нажата клавиша С/П, введенное число, в свою очередь, подвергнуто обработке, и вновь программа остановилась, готовая к приему и обработке другого, очередного числа...
Работать в таком порядке очень легко, а это очень важно, если за калькулятором новичок. Однако описанный порядок осуществим не всегда. Нередко приходится вводить исходные данные более или менее обширными группами. Способам группового ввода в основном и посвящен наш рассказ.
Руководство по эксплуатации, прилагаемое к "Электронике Б3-34", рекомендует вводить числа с помощью клавиши П, вызвать на индикатор - с помощью клавиши ИП. При вводе нужное число набирается на клавиатуре и отображается на индикаторе, а одновременно заносится в регистр X. Затем нажимается клавиша П и вслед за нею - клавиша с номером нужного адресуемого регистра. В нем тотчас копируется содержимое регистра X. При выводе результатов сначала нажимают клавишу ИП, затем клавишу нужного адресуемого регистра, после чего его содержимое копируется в регистре X и высвечивается на индикаторе.
Пусть нам требуется, например, заслать в регистр 5 число 3, а из регистра 6 вызвать хранящееся там число 4. Выразим это, прибегая к таким обозначениям:
Здесь над чертой пишутся числа, набираемые на цифровых клавишах и выводимые на индикатор, или их символы, а в кружках - команды, выполняемые для засылки и вызова.
Рассмотренный способ ввода и вывода информации будем для краткости именовать ПР-вводом и ИПР-выводом. С точки зрения человека, работающего с микрокалькулятором (назовем его оператором), это самый неудобный и медленный способ. Напрягая внимание, чтобы не ошибиться при нажатии нужных клавиш, оператор быстро утомляется, скорость его работы падает, он начинает допускать ошибки...
Вспомним, как действует клавиша потактового прохождения программы - ПП. Одно ее нажатие приводит к тому, что калькулятор выполняет лишь одну, очередную команду программы. Между двумя нажатиями клавиши ПП можно ввести новое число в регистр X.
Чтобы лучше понять, как протекает работа оператора в этом случае, рассмотрим ради примера небольшую программу: 00. ПС 01. ПВ 02. ПА 03. - 04. Fx2 05. x-y 06. / 07. С/П 08. ИПС 09. ИПВ 10. ИПА.
Набрав программу, выполните такие действия:

По команде В/0 счетчик команд настраивается на адрес 00. Затем на клавиатуре набирается число 16. Нажата клавиша ПП. Калькулятор выполняет команду, записанную по адресу 00,- то есть команду ПС, пересылая число 16 из регистра X в регистр С, и останавливается. Пока он стоит, сменим содержимое регистра X, набрав число 12. Вновь нажмем клавишу ПП. Число 12 окажется в регистре В в соответствии с командой по адресу 01. Далее аналогичным образом наберем и поместим в регистр А число 20.
Группа команд, записанная в нашем примере по адресам 00-02, служит для ввода исходной информации и называется программным блоком ввода данных или проще - блоком ввода.
Обратим внимание: после того, как введенное в регистр X число послано в какой-то адресуемый регистр, оно передвигается в регистр Y при вводе следующего числа. Так по ходу записи чисел в адресуемые регистры происходит и их размещение по регистрам стека. В нашем примере в регистре Z оказывается в итоге число 16, а в регистре Y - число 12, в регистре X - число 20. Это обстоятельство удобно использовать для организации последующих вычислений. Так и в нашем примере. После того, как ввод закончен и калькулятор стоит перед выполнением команды по адресу 03, его можно запустить на счет клавишей С/П. Выполнив команды по адресам 03-06, калькулятор остановится по адресу 07, где записана команда останова. Выполненные команды, как нетрудно проследить, вычислят дробь (20-12)**2/16=4. Четверка и высветится на индикаторе после останова.
Команды, записанные в нашей программе по адресам 08-10, образуют блок вывода. Они обеспечивают последовательный вызов на индикатор чисел, записанных в регистрах С, В, А. Для этого надо лишь три раза подряд нажать все ту же клавишу ПП.
Этот способ будем в дальнейшем называть ПП-вво-дом и соответственно ПП-выводом. Для оператора он удобен тем, что не нужно думать, в какие адресуемые регистры засылать и из каких регистров вызывать нужные числа. Просто нажимай клавишу ПП, и очередное число обрабатывается должным образом. Последовательность ввода чисел устанавливается инструкцией к программе.
Однако блоки ввода и вывода требуют места в программной памяти. Можно ли устранить этот недостаток? И в каких случаях?
Иногда вводимые числа не обязательно записывать в адресуемые регистры. Нужно лишь вычислить какое-то зависящее от них выражение, которое будет использоваться в дальнейших вычислениях по программе. Здесь опять можно обратиться к только что рассмотренной нами цепочке команд: из введенных в калькулятор чисел а=20, b=12, с=16 они сформировали величину (a-b)**2/с.
Если в подобном выражении участвует не более четырех чисел, их можно ввести в регистры стека с помощью клавиши ^, а затем клавишей С/П запустить программу, в самом начале которой должны, разумеется, стоять команды, вычисляющие нужное выражение.
Рассмотренная нами программа при таком способе ввода (назовем его СТ-вводом) выглядела бы короче: 00. - 01. Fx2 02. x-y 03. / 04. С/П.
Набираем на клавиатуре 16 ^ 12 ^ 20 В/0, нажимаем клавишу С/П - и через несколько секунд на индикаторе появится знакомое число 4.
Применяя СТ-ввод, программирование задачи лучше начинать с выяснения, в какой последовательности вводить исходные данные. В нашем примере она была такой: c, b, a. Но, допустим, с точки зрения оператора удобнее вводить числа в алфавитном порядке их символов: a, b, c. Если вы хотите, чтобы с вашими программами было легко работать, то возьмите за правило отдавать предпочтение в выборе последовательности вводимых чисел оператору. Раз ему удобнее последовательность a, b, c - так тому и быть. Набираем на клавиатуре 20 ^ 12 ^ 16, и числа помещаются в стеке в следующем порядке: a=20 в PZ, b=12 в PY, c=16 в РХ. В таком случае нашу программу нужно дополнить командами, переставляющими числа по регистрам стека так, как это требуется для подсчета дроби (a-b)**2/c. Например: 00. ^ 01. F() 02. F() 03. - 04. Fx2 05. x-y 06. / 07. С/П.
Наряду с СТ-вводом можно говорить и про СТ-вывод результатов. Назовем так способ, при котором числа из различных регистров стека перемещаются в регистр X и отображаются на индикаторе. Для такого вывода часто используют команду x-y. С ее помощью на индикаторе появляется содержимое регистра Y. А командой F() можно последовательно вывести на индикатор содержимое всех регистров стека.
При СТ-выводе программа составляется так, чтобы по окончании ее работы результаты располагались по стековым регистрам нужным образом.
В ряде случаев, когда вводится много чисел и потому СТ-ввод применять нельзя, а для ПП-ввода не хватает программной памяти, можно использовать команды косвенной засылки вида КПМ. Имея дело с ними, будем говорить о КП-вводе. В качестве регистра М выбирается один из тех, чье содержимое при косвенной засылке модифицируется - то есть регистры 0, 1, ..., 6. Выбор подходящего регистра зависит от особенностей решаемой задачи. В подобных случаях находит удачное применение команда КП^, не описанная инструкцией к "Электронике Б3-34". Вариант, где используется она и операция FL0, мы сейчас и рассмотрим.
Команда КП^ "работает" почти так же, как команда КП0: засылает содержимое регистра X в адресуемый регистр, номер которого есть содержимое регистра 0 (положим для простоты, что в регистре 0 находится целое неотрицательное число от 0 до 13 включительно). От команды КП0 (команда КП^ отличается тем, что перед своим выполнением не уменьшает на единицу содержимое Р0 - как говорят, не модифицирует адреса. Аналогичным образом команда КИП^ производит вызов так же, как команда КИП^, но без модификации адреса.
Программу, поясняющую КП-ввод, для большей наглядности изобразим рисунком, где команды располагаются в столбик и без указания адресов (между ними могут располагаться команды промежуточной обработки вводимых данных).
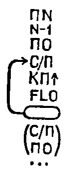
Такой блок позволяет вводить числа в адресуемые регистры в порядке убывания адресов - с некоторого N-ного по 1-й. Число N может равняться даже 13 (калькулятор "поймет" его как обозначение регистра D).
Разумеется, если число (N-1) двузначное, то его знаки записываются в программу по двум последовательным адресам. Программа "наберет" это число точно так же, как мы набирали бы его на цифровых клавишах вручную.
Положим, что перед началом ввода по этим командам калькулятор стоит, готовый к выполнению первой из них, ПN. Набираем на клавиатуре первое из вводимых чисел x1 и нажимаем клавишу С/П. Командой ПN оно отсылается в N-ный адресуемый регистр. Следующими двумя командами в регистр 0 направляется число (N-1). Калькулятор останавливается вновь. Набираем на клавиатуре второе из вводимых чисел x2 и запускаем машину клавишей С/П. Командой КП^ число x2 отсылается в (N-1)-й адресуемый регистр - тот самый, номер которого указан содержимым нулевого регистра.
Операция FL0 вычтет из содержимого этого регистра единицу (теперь там будет N-2) и сравнит результат с нулем. Если получившаяся разность не равна нулю, то она заносится в Р0 и управление передается на команду, адрес которой указан сразу за операцией FL0. Поскольку в нашем случае этот адрес не известен, мы обвели отведенное под него место рамкой, от которой провели стрелку-указатель на шаг, куда следует передать управление,- на команду С/П. После этой остановки наберем на клавиатуре число x3 - и команда КП^ направит его в регистр с номером N-3. При дальнейших повторениях цикла, охваченного на схеме стрелкой, вводимые далее числа будут размещаться в регистрах с убывающими номерами.
Сколь бы сложным ни казалось описание работы программы, действия оператора будут при этом предельно простыми: набрано x1, нажата клавиша С/П, набрано x2, вновь нажата клавиша С/П... и так далее.
Этот процесс записи будет продолжаться до тех пор, пока в регистре 0 не получится единица. В этом случае последнее из набранных на клавиатуре чисел будет направлено в регистр 1. Операция вычтет единицу из содержимого регистра 0 и, поскольку на сей раз результат равен нулю, управление не будет передано по стрелке, а программа будет выполняться далее - и остановится, судя по нашей схеме.
Команды, заключенные на ней в скобки, могут и отсутствовать. Поставить их нужно, если желательно ввести какое-то число еще и в регистр 0. Набрать это число следует, пока калькулятор стоит. Затем надо нажать клавишу С/П - и калькулятор приступит к выполнению команд, находящихся в программе далее: набранное число зашлется в Р0. Если же команды, заключенные на схеме в скобки, не писать, то программа начнет выполнение дальнейших команд после ввода числа, направленного в регистр 1.
В нашем разговоре давно назревала тема, связанная с исправлением ошибок ввода. Если оператор заметил ошибку по ходу набора, нужно нажать клавишу Сх и набрать число вновь. Сложнее исправить ошибку тогда, когда число уже заслано в память. Тут многое зависит от способа, с помощью которого вводятся исходные данные.
Проще всего исправлять ошибки при ПР-вводе: набранное заново число нужно отослать на свое место повторно. Чуть сложнее исправить ошибку при ПП-вводе: здесь следует вернуть программу на один шаг назад и лишь затем повторить ввод.

Однако если при ПП-вводе числа должны не только рассылаться по адресуемым регистрам, но и определенным образом размещаться по регистрам стека, то при исправлении ошибки надо восстановить и предыдущее расположение чисел в стеке:
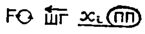
При СТ-вводе отдельное неверно введенное число вводится заново так:
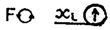
При КП-вводе исправление ошибок зависит от того, каков блок ввода. Для блока, приведенного выше в качестве примера, ошибка исправляется следующим образом:

К борьбе с ошибками ввода и вывода можно отнести целый набор специальных приемов, повышающих надежность работы оператора с программой. Например, до сих пор мы подразумевали, что введенное число сохраняется на индикаторе после ввода с клавиатуры, так что его можно прочесть и проконтролировать. Но так оно бывает не всегда, особенно если запись чисел сопровождается их обработкой. Следует учитывать и условия работы оператора. Представьте, что он ведет вычисления на палубе корабля. Качка, удар волны в любую минуту могут заставить его отвлечься. Здесь легко забыть, какие числа уже введены, какое должно вводиться следующим.
Хорошо сделать так, чтобы программа сама подсказывала оператору порядковый номер числа, которое должно быть введено. Вот, например, цепочка команд КИП4 ИП4 С/П. Команда косвенного вызова КИП4 перед своим выполнением увеличит на единицу содержимое регистра 4. Что она вызовет на индикатор, не очень-то важно. Следующей командой на индикатор будет вызвано содержимое регистра 4, после чего калькулятор остановится. С каждым повторением этой цепочки на индикаторе будут появляться последовательно нарастающие целые числа, под которыми можно понимать порядковые номера вводимых величин и в соответствии с такими подсказками эти величины и набирать на клавиатуре.
Может, правда, оказаться, что вводимые числа похожи на числа-подсказки. В таких случаях во избежание путаницы числам-подсказкам можно придавать особенный вид - скажем, 100, 200... Часто прибегают к более выразительным символам - E1, E2, Е100, Е200... [10/85] Впрочем, подготовка таких символов занимает и дополнительное время и программную память, так что не следует стремиться к излишним эффектам.
Рассмотрим для примера задачу определения заработной платы работника по числу отработанных им часов.
Зi=Чi*Тi
где Зi - величина заработной платы в рублях, Ti - отработанное время в часах, Чi - часовая тарифная ставка работника, соответствующая его квалификационному разряду, в рублях на час. Например, для строительных рабочих часовая ставка первого разряда равна 0.438 рубля, второго разряда - 0.493 рубля и т.д. Всего имеется шесть разрядов, и все возможные Чi в формуле определены этим набором.
Попробуем при определении Зi с помощью программы вводить не часовую ставку работника, а его разряд - это значительно проще для оператора. Помочь нам в этом может косвенная адресация. Занесем часовые ставки соответственно разрядам в первый, второй и так далее по шестой регистры памяти микрокалькулятора. Записав разряд работника Ri в один из неизменяемых при косвенной адресации регистров - допустим, в регистр Д,- можно вызвать Чi в программе одной командой КИПД. Таким образом, ставки при вычислении заработной платы будут набраны только один раз, в самом начале, а потом будут вызываться в регистр X с помощью служебных чисел, означающих разряд того или иного из работников.
Программа для определения заработной платы может иметь следующий вид: 00. ПД 01. С/П 02. КИПД 03. * 04. С/П 05. БП 06. 00
Инструкция по работе с программой:
1. Нажать клавиши В/0 F ПРГ, набрать текст программы, F АВТ.
2. Подготовить программу к работе, записав в память часовые ставки.
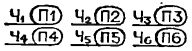
3. Нажать клавишу В/0.
4. Вычислить заработную плату работника по тарифу:
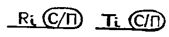
5. По окончании счета списать с табло величину Зi; для повторных вычислений действовать по п.4.
Чтобы рассчитать заработную плату для бригады из 30 человек по такой программе, потребуется 100-120 нажатий на клавиши, а вероятность ошибки при этом не так уж велика.
Рассмотренный пример дает повод поговорить о вещах, на первый взгляд далеких от программирования, но при внимательном рассмотрении оказывающихся очень важными. Предположим, что такую задачу часто решает наш знакомый. У него есть программируемый микрокалькулятор, но программировать он не умеет. Мы обещаем ему сделать маленькую программу, значительно облегчающую подобные вычисления, притом такую, что работать с нею совсем не сложно. И в самом деле: по предложенной нами программе все операции ввода выполняются одной клавишей С/П.
Спросим знакомого, что лучше вводить сначала - часы или разряд? Он объяснит нам, что последовательность данных о работнике задана в табеле: сначала идет списочный номер работника, фамилия, разряд, число отработанных часов. Естественно, писать программу так, чтобы при вводе исходной информации задавать сначала разряд, а затем число отработанных часов.
Учитывать общепринятые условности следует всегда, когда речь идет о составлении прикладных программ для широкого круга пользователей. Начинающий оператор, такой, как наш знакомый, похож yа неопытного велосипедиста, умеющего ездить только по прямой дорожке. Обеспечить ему эту прямую и должен программист при составлении программы.
В заключение стоит рассмотреть несколько специальных случаев ввода чисел. Константы, содержащие немного значащих цифр, проще занести в регистр X, не набирая на клавиатуре, а командами программы. Например, цепочка команд. 10. 1 11. , 12. 2 13. 5 запишет в регистр X число 1.25; его затем можно направить в любой адресуемый регистр - скажем, командой ПА в регистр А.
Довольно часто приходится засылать нули в некоторые регистры памяти (нулевыми, должны быть, например, начальные значения всевозможных сумм в программах математической статистики, аппроксимации и т.п.). Такого рода операция производится либо вручную способом ПР-ввода, либо автоматически, с помощью представленных здесь блоков:
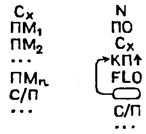
При выборе подходящего блока следует учитывать, что варианты типа ПП-ввода позволяют направлять нули в регистры с произвольными, а варианты типа КП-ввода - с упорядоченными номерами. Передав управление на первую из команд блока, оператор нажимает клавишу С/П, после чего во все нужные регистры нули засылаются автоматически, и затем программа останавливается, готовая к продолжению работы.
Навыки безошибочного ввода и вывода информации придут к начинающему программисту постепенно, по мере накопления опыта практической работы. Сделав первые программы и поработав с ними некоторое время, подумайте, что вам в них не нравится, каким образом можно улучшить процесс ввода-вывода данных, если к этому имеются возможности.
Однозначные рекомендации здесь дать сложно - слишком велико разнообразие решаемых задач. Но все же попытаемся дать краткие сравнительные характеристики рассмотренных выше способов ввода и вывода.
Для коротких и быстрых программ, когда вводится не более трех чисел и возможностей стековой памяти достаточно для вычислений по программе, можно уверенно рекомендовать СТ-ввод. СТ-вывод хорош для двух выводимых показателей, для большего числа выводимых данных он используется значительно реже. СТ-ввод с успехом может быть применен и в сложных программах для циклически повторяемого ввода небольших порций информации, которые сразу же перерабатываются и отсылаются в адресуемые регистры в переработанном виде.
В случаях, когда СТ-ввод по каким-либо причинам не может быть применен, а желательно, сохранить легкую и удобную форму ввода, можно успешно использовать ПП-ввод. При ПП-вводе одновременно происходит размещение вводимых чисел по стековым регистрам, что дает ему преимущество по сравнению с СТ-вводом в тех случаях, когда вводимую информацию нужно не только переслать в адресуемые регистры, но и определенным образом разместить в регистрах стека для последующей обработки. Если вводимых данных много, то их при ПП-способе лучше записывать в виде таблицы - как при вводе, так и при выводе. К недостаткам ПП-способа следует отнести повышенный расход программной памяти, а также то обстоятельство, что при его применении оператору всегда приходится отчетливо помнить, на каком адресе остановилась программа при вводе очередного числа.
КП-ввод исходных данных используется значительно чаще, чем КИП-вывод результатов. Этот способ становится целесообразным в том случае, если вводится много чисел и их можно разместить в упорядоченной последовательности по адресуемым регистрам. С учетом последнего обстоятельства применение КП-ввода становится эффективным по сравнению с ПП-вводом тогда, когда число вводимых показателей превышает число команд, затрачиваемых на организацию программного блока КП-ввода (его длина составляет обычно шесть-семь команд). КП-ввод лучше использовать тогда, когда в программе обрабатываются однотипные данные и для этой обработки не требуется большого количества адресуемых регистров памяти (например, суммирование какой-либо числовой последовательности).
Применение ПР-ввода не накладывает никаких ограничений на программирование задач, не удлиняет программу. Занести исходные данные этим способом можно еще до набора программы. Безразлична и последовательность записи чисел в регистры. Этот способ остается единственно возможным в случаях, когда программа занимает всю программную память. На его применение лучше ориентироваться также в сложных программах, когда вычисления происходят достаточно долго, когда любая ошибка при вводе показателей может перечеркнуть большую подготовительную работу. В этих случаях лучше сознательно идти на некоторые сложности при вводе, предусматривать проверку записи показателей, чтобы, потеряв несколько дополнительных минут, не терять часы из-за возможных ошибок.
В заключение представим тех, кто принимал участие в проведении этого занятия,- читателей рубрики. чьи письма во многом определяли его содержание. Это Б.Маминов (Горький), А.Неклюдов (Одесса), С.Чигирев (Симферополь), А.Волошин (Киев), Л.Ницецкий (Рига), А.Дринов (Волгоград), С.Камнев (Москва), А.Тулайков (Долгопрудный Московской области).
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ПЯТОЕ, посвященное частным, на первый взгляд маловажным моментам в решении задач на программируемом микрокалькуляторе - вводу исходных данных и выводу полученных результатов.
Ведет занятие С.В.КОМИССАРОВ (Московский инженерно-строительный
институт)
Известно несколько основных способов ввода чисел в калькулятор. Выбор подходящего определяется при составлении конкретной программы ее особенностями, а те - ее назначением. Различные способы можно комбинировать в одной и той же программе. Однако не следует забывать, что считающему на калькуляторе удобнее единообразие. Неоправданное чередование клавиш, нажимаемых при вводе, может значительно затруднить работу, послужить причиной ошибок.
Идеалом начинающего программиста должна стать простота. А наиболее просто работать с калькулятором, когда все управление им сводится к нажатию в нужные моменты на одну-единственную клавишу.
Чтобы запустить программу на счет, то, какова бы оиа ни была, надо нажать клавишу С/П. Вот ею-то в лучшем случае и следует ограничиться, управляя калькулятором.
... Калькулятор включен, управление передано на начальный адрес программы, на клавиатуре набрано первое из вводимых чисел, нажата клавиша С/П, запущенная программа переслала введенное число в какой-либо из адресуемых регистров или вычислила от него какое-то выражение, выполнила последующие действия, для которых хватает введенного числа, и остановилась по команде останова, проставленной в программе. Пока калькулятор бездействует, на клавиатуре набрано следующее из вводимых чисел, снова нажата клавиша С/П, введенное число, в свою очередь, подвергнуто обработке, и вновь программа остановилась, готовая к приему и обработке другого, очередного числа...
Работать в таком порядке очень легко, а это очень важно, если за калькулятором новичок. Однако описанный порядок осуществим не всегда. Нередко приходится вводить исходные данные более или менее обширными группами. Способам группового ввода в основном и посвящен наш рассказ.
Руководство по эксплуатации, прилагаемое к "Электронике Б3-34", рекомендует вводить числа с помощью клавиши П, вызвать на индикатор - с помощью клавиши ИП. При вводе нужное число набирается на клавиатуре и отображается на индикаторе, а одновременно заносится в регистр X. Затем нажимается клавиша П и вслед за нею - клавиша с номером нужного адресуемого регистра. В нем тотчас копируется содержимое регистра X. При выводе результатов сначала нажимают клавишу ИП, затем клавишу нужного адресуемого регистра, после чего его содержимое копируется в регистре X и высвечивается на индикаторе.
Пусть нам требуется, например, заслать в регистр 5 число 3, а из регистра 6 вызвать хранящееся там число 4. Выразим это, прибегая к таким обозначениям:
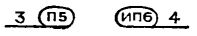
Здесь над чертой пишутся числа, набираемые на цифровых клавишах и выводимые на индикатор, или их символы, а в кружках - команды, выполняемые для засылки и вызова.
Рассмотренный способ ввода и вывода информации будем для краткости именовать ПР-вводом и ИПР-выводом. С точки зрения человека, работающего с микрокалькулятором (назовем его оператором), это самый неудобный и медленный способ. Напрягая внимание, чтобы не ошибиться при нажатии нужных клавиш, оператор быстро утомляется, скорость его работы падает, он начинает допускать ошибки...
Вспомним, как действует клавиша потактового прохождения программы - ПП. Одно ее нажатие приводит к тому, что калькулятор выполняет лишь одну, очередную команду программы. Между двумя нажатиями клавиши ПП можно ввести новое число в регистр X.
Чтобы лучше понять, как протекает работа оператора в этом случае, рассмотрим ради примера небольшую программу: 00. ПС 01. ПВ 02. ПА 03. - 04. Fx2 05. x-y 06. / 07. С/П 08. ИПС 09. ИПВ 10. ИПА.
Набрав программу, выполните такие действия:

По команде В/0 счетчик команд настраивается на адрес 00. Затем на клавиатуре набирается число 16. Нажата клавиша ПП. Калькулятор выполняет команду, записанную по адресу 00,- то есть команду ПС, пересылая число 16 из регистра X в регистр С, и останавливается. Пока он стоит, сменим содержимое регистра X, набрав число 12. Вновь нажмем клавишу ПП. Число 12 окажется в регистре В в соответствии с командой по адресу 01. Далее аналогичным образом наберем и поместим в регистр А число 20.
Группа команд, записанная в нашем примере по адресам 00-02, служит для ввода исходной информации и называется программным блоком ввода данных или проще - блоком ввода.
Обратим внимание: после того, как введенное в регистр X число послано в какой-то адресуемый регистр, оно передвигается в регистр Y при вводе следующего числа. Так по ходу записи чисел в адресуемые регистры происходит и их размещение по регистрам стека. В нашем примере в регистре Z оказывается в итоге число 16, а в регистре Y - число 12, в регистре X - число 20. Это обстоятельство удобно использовать для организации последующих вычислений. Так и в нашем примере. После того, как ввод закончен и калькулятор стоит перед выполнением команды по адресу 03, его можно запустить на счет клавишей С/П. Выполнив команды по адресам 03-06, калькулятор остановится по адресу 07, где записана команда останова. Выполненные команды, как нетрудно проследить, вычислят дробь (20-12)**2/16=4. Четверка и высветится на индикаторе после останова.
Команды, записанные в нашей программе по адресам 08-10, образуют блок вывода. Они обеспечивают последовательный вызов на индикатор чисел, записанных в регистрах С, В, А. Для этого надо лишь три раза подряд нажать все ту же клавишу ПП.
Этот способ будем в дальнейшем называть ПП-вво-дом и соответственно ПП-выводом. Для оператора он удобен тем, что не нужно думать, в какие адресуемые регистры засылать и из каких регистров вызывать нужные числа. Просто нажимай клавишу ПП, и очередное число обрабатывается должным образом. Последовательность ввода чисел устанавливается инструкцией к программе.
Однако блоки ввода и вывода требуют места в программной памяти. Можно ли устранить этот недостаток? И в каких случаях?
Иногда вводимые числа не обязательно записывать в адресуемые регистры. Нужно лишь вычислить какое-то зависящее от них выражение, которое будет использоваться в дальнейших вычислениях по программе. Здесь опять можно обратиться к только что рассмотренной нами цепочке команд: из введенных в калькулятор чисел а=20, b=12, с=16 они сформировали величину (a-b)**2/с.
Если в подобном выражении участвует не более четырех чисел, их можно ввести в регистры стека с помощью клавиши ^, а затем клавишей С/П запустить программу, в самом начале которой должны, разумеется, стоять команды, вычисляющие нужное выражение.
Рассмотренная нами программа при таком способе ввода (назовем его СТ-вводом) выглядела бы короче: 00. - 01. Fx2 02. x-y 03. / 04. С/П.
Набираем на клавиатуре 16 ^ 12 ^ 20 В/0, нажимаем клавишу С/П - и через несколько секунд на индикаторе появится знакомое число 4.
Применяя СТ-ввод, программирование задачи лучше начинать с выяснения, в какой последовательности вводить исходные данные. В нашем примере она была такой: c, b, a. Но, допустим, с точки зрения оператора удобнее вводить числа в алфавитном порядке их символов: a, b, c. Если вы хотите, чтобы с вашими программами было легко работать, то возьмите за правило отдавать предпочтение в выборе последовательности вводимых чисел оператору. Раз ему удобнее последовательность a, b, c - так тому и быть. Набираем на клавиатуре 20 ^ 12 ^ 16, и числа помещаются в стеке в следующем порядке: a=20 в PZ, b=12 в PY, c=16 в РХ. В таком случае нашу программу нужно дополнить командами, переставляющими числа по регистрам стека так, как это требуется для подсчета дроби (a-b)**2/c. Например: 00. ^ 01. F() 02. F() 03. - 04. Fx2 05. x-y 06. / 07. С/П.
Наряду с СТ-вводом можно говорить и про СТ-вывод результатов. Назовем так способ, при котором числа из различных регистров стека перемещаются в регистр X и отображаются на индикаторе. Для такого вывода часто используют команду x-y. С ее помощью на индикаторе появляется содержимое регистра Y. А командой F() можно последовательно вывести на индикатор содержимое всех регистров стека.
При СТ-выводе программа составляется так, чтобы по окончании ее работы результаты располагались по стековым регистрам нужным образом.
В ряде случаев, когда вводится много чисел и потому СТ-ввод применять нельзя, а для ПП-ввода не хватает программной памяти, можно использовать команды косвенной засылки вида КПМ. Имея дело с ними, будем говорить о КП-вводе. В качестве регистра М выбирается один из тех, чье содержимое при косвенной засылке модифицируется - то есть регистры 0, 1, ..., 6. Выбор подходящего регистра зависит от особенностей решаемой задачи. В подобных случаях находит удачное применение команда КП^, не описанная инструкцией к "Электронике Б3-34". Вариант, где используется она и операция FL0, мы сейчас и рассмотрим.
Команда КП^ "работает" почти так же, как команда КП0: засылает содержимое регистра X в адресуемый регистр, номер которого есть содержимое регистра 0 (положим для простоты, что в регистре 0 находится целое неотрицательное число от 0 до 13 включительно). От команды КП0 (команда КП^ отличается тем, что перед своим выполнением не уменьшает на единицу содержимое Р0 - как говорят, не модифицирует адреса. Аналогичным образом команда КИП^ производит вызов так же, как команда КИП^, но без модификации адреса.
Программу, поясняющую КП-ввод, для большей наглядности изобразим рисунком, где команды располагаются в столбик и без указания адресов (между ними могут располагаться команды промежуточной обработки вводимых данных).

Такой блок позволяет вводить числа в адресуемые регистры в порядке убывания адресов - с некоторого N-ного по 1-й. Число N может равняться даже 13 (калькулятор "поймет" его как обозначение регистра D).
Разумеется, если число (N-1) двузначное, то его знаки записываются в программу по двум последовательным адресам. Программа "наберет" это число точно так же, как мы набирали бы его на цифровых клавишах вручную.
Положим, что перед началом ввода по этим командам калькулятор стоит, готовый к выполнению первой из них, ПN. Набираем на клавиатуре первое из вводимых чисел x1 и нажимаем клавишу С/П. Командой ПN оно отсылается в N-ный адресуемый регистр. Следующими двумя командами в регистр 0 направляется число (N-1). Калькулятор останавливается вновь. Набираем на клавиатуре второе из вводимых чисел x2 и запускаем машину клавишей С/П. Командой КП^ число x2 отсылается в (N-1)-й адресуемый регистр - тот самый, номер которого указан содержимым нулевого регистра.
Операция FL0 вычтет из содержимого этого регистра единицу (теперь там будет N-2) и сравнит результат с нулем. Если получившаяся разность не равна нулю, то она заносится в Р0 и управление передается на команду, адрес которой указан сразу за операцией FL0. Поскольку в нашем случае этот адрес не известен, мы обвели отведенное под него место рамкой, от которой провели стрелку-указатель на шаг, куда следует передать управление,- на команду С/П. После этой остановки наберем на клавиатуре число x3 - и команда КП^ направит его в регистр с номером N-3. При дальнейших повторениях цикла, охваченного на схеме стрелкой, вводимые далее числа будут размещаться в регистрах с убывающими номерами.
Сколь бы сложным ни казалось описание работы программы, действия оператора будут при этом предельно простыми: набрано x1, нажата клавиша С/П, набрано x2, вновь нажата клавиша С/П... и так далее.
Этот процесс записи будет продолжаться до тех пор, пока в регистре 0 не получится единица. В этом случае последнее из набранных на клавиатуре чисел будет направлено в регистр 1. Операция вычтет единицу из содержимого регистра 0 и, поскольку на сей раз результат равен нулю, управление не будет передано по стрелке, а программа будет выполняться далее - и остановится, судя по нашей схеме.
Команды, заключенные на ней в скобки, могут и отсутствовать. Поставить их нужно, если желательно ввести какое-то число еще и в регистр 0. Набрать это число следует, пока калькулятор стоит. Затем надо нажать клавишу С/П - и калькулятор приступит к выполнению команд, находящихся в программе далее: набранное число зашлется в Р0. Если же команды, заключенные на схеме в скобки, не писать, то программа начнет выполнение дальнейших команд после ввода числа, направленного в регистр 1.
В нашем разговоре давно назревала тема, связанная с исправлением ошибок ввода. Если оператор заметил ошибку по ходу набора, нужно нажать клавишу Сх и набрать число вновь. Сложнее исправить ошибку тогда, когда число уже заслано в память. Тут многое зависит от способа, с помощью которого вводятся исходные данные.
Проще всего исправлять ошибки при ПР-вводе: набранное заново число нужно отослать на свое место повторно. Чуть сложнее исправить ошибку при ПП-вводе: здесь следует вернуть программу на один шаг назад и лишь затем повторить ввод.

Однако если при ПП-вводе числа должны не только рассылаться по адресуемым регистрам, но и определенным образом размещаться по регистрам стека, то при исправлении ошибки надо восстановить и предыдущее расположение чисел в стеке:
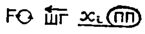
При СТ-вводе отдельное неверно введенное число вводится заново так:
При КП-вводе исправление ошибок зависит от того, каков блок ввода. Для блока, приведенного выше в качестве примера, ошибка исправляется следующим образом:

К борьбе с ошибками ввода и вывода можно отнести целый набор специальных приемов, повышающих надежность работы оператора с программой. Например, до сих пор мы подразумевали, что введенное число сохраняется на индикаторе после ввода с клавиатуры, так что его можно прочесть и проконтролировать. Но так оно бывает не всегда, особенно если запись чисел сопровождается их обработкой. Следует учитывать и условия работы оператора. Представьте, что он ведет вычисления на палубе корабля. Качка, удар волны в любую минуту могут заставить его отвлечься. Здесь легко забыть, какие числа уже введены, какое должно вводиться следующим.
Хорошо сделать так, чтобы программа сама подсказывала оператору порядковый номер числа, которое должно быть введено. Вот, например, цепочка команд КИП4 ИП4 С/П. Команда косвенного вызова КИП4 перед своим выполнением увеличит на единицу содержимое регистра 4. Что она вызовет на индикатор, не очень-то важно. Следующей командой на индикатор будет вызвано содержимое регистра 4, после чего калькулятор остановится. С каждым повторением этой цепочки на индикаторе будут появляться последовательно нарастающие целые числа, под которыми можно понимать порядковые номера вводимых величин и в соответствии с такими подсказками эти величины и набирать на клавиатуре.
Может, правда, оказаться, что вводимые числа похожи на числа-подсказки. В таких случаях во избежание путаницы числам-подсказкам можно придавать особенный вид - скажем, 100, 200... Часто прибегают к более выразительным символам - E1, E2, Е100, Е200... [10/85] Впрочем, подготовка таких символов занимает и дополнительное время и программную память, так что не следует стремиться к излишним эффектам.
Рассмотрим для примера задачу определения заработной платы работника по числу отработанных им часов.
Зi=Чi*Тi
где Зi - величина заработной платы в рублях, Ti - отработанное время в часах, Чi - часовая тарифная ставка работника, соответствующая его квалификационному разряду, в рублях на час. Например, для строительных рабочих часовая ставка первого разряда равна 0.438 рубля, второго разряда - 0.493 рубля и т.д. Всего имеется шесть разрядов, и все возможные Чi в формуле определены этим набором.
Попробуем при определении Зi с помощью программы вводить не часовую ставку работника, а его разряд - это значительно проще для оператора. Помочь нам в этом может косвенная адресация. Занесем часовые ставки соответственно разрядам в первый, второй и так далее по шестой регистры памяти микрокалькулятора. Записав разряд работника Ri в один из неизменяемых при косвенной адресации регистров - допустим, в регистр Д,- можно вызвать Чi в программе одной командой КИПД. Таким образом, ставки при вычислении заработной платы будут набраны только один раз, в самом начале, а потом будут вызываться в регистр X с помощью служебных чисел, означающих разряд того или иного из работников.
Программа для определения заработной платы может иметь следующий вид: 00. ПД 01. С/П 02. КИПД 03. * 04. С/П 05. БП 06. 00
Инструкция по работе с программой:
1. Нажать клавиши В/0 F ПРГ, набрать текст программы, F АВТ.
2. Подготовить программу к работе, записав в память часовые ставки.
3. Нажать клавишу В/0.
4. Вычислить заработную плату работника по тарифу:
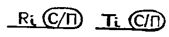
5. По окончании счета списать с табло величину Зi; для повторных вычислений действовать по п.4.
Чтобы рассчитать заработную плату для бригады из 30 человек по такой программе, потребуется 100-120 нажатий на клавиши, а вероятность ошибки при этом не так уж велика.
Рассмотренный пример дает повод поговорить о вещах, на первый взгляд далеких от программирования, но при внимательном рассмотрении оказывающихся очень важными. Предположим, что такую задачу часто решает наш знакомый. У него есть программируемый микрокалькулятор, но программировать он не умеет. Мы обещаем ему сделать маленькую программу, значительно облегчающую подобные вычисления, притом такую, что работать с нею совсем не сложно. И в самом деле: по предложенной нами программе все операции ввода выполняются одной клавишей С/П.
Спросим знакомого, что лучше вводить сначала - часы или разряд? Он объяснит нам, что последовательность данных о работнике задана в табеле: сначала идет списочный номер работника, фамилия, разряд, число отработанных часов. Естественно, писать программу так, чтобы при вводе исходной информации задавать сначала разряд, а затем число отработанных часов.
Учитывать общепринятые условности следует всегда, когда речь идет о составлении прикладных программ для широкого круга пользователей. Начинающий оператор, такой, как наш знакомый, похож yа неопытного велосипедиста, умеющего ездить только по прямой дорожке. Обеспечить ему эту прямую и должен программист при составлении программы.
В заключение стоит рассмотреть несколько специальных случаев ввода чисел. Константы, содержащие немного значащих цифр, проще занести в регистр X, не набирая на клавиатуре, а командами программы. Например, цепочка команд. 10. 1 11. , 12. 2 13. 5 запишет в регистр X число 1.25; его затем можно направить в любой адресуемый регистр - скажем, командой ПА в регистр А.
Довольно часто приходится засылать нули в некоторые регистры памяти (нулевыми, должны быть, например, начальные значения всевозможных сумм в программах математической статистики, аппроксимации и т.п.). Такого рода операция производится либо вручную способом ПР-ввода, либо автоматически, с помощью представленных здесь блоков:

При выборе подходящего блока следует учитывать, что варианты типа ПП-ввода позволяют направлять нули в регистры с произвольными, а варианты типа КП-ввода - с упорядоченными номерами. Передав управление на первую из команд блока, оператор нажимает клавишу С/П, после чего во все нужные регистры нули засылаются автоматически, и затем программа останавливается, готовая к продолжению работы.
Навыки безошибочного ввода и вывода информации придут к начинающему программисту постепенно, по мере накопления опыта практической работы. Сделав первые программы и поработав с ними некоторое время, подумайте, что вам в них не нравится, каким образом можно улучшить процесс ввода-вывода данных, если к этому имеются возможности.
Однозначные рекомендации здесь дать сложно - слишком велико разнообразие решаемых задач. Но все же попытаемся дать краткие сравнительные характеристики рассмотренных выше способов ввода и вывода.
Для коротких и быстрых программ, когда вводится не более трех чисел и возможностей стековой памяти достаточно для вычислений по программе, можно уверенно рекомендовать СТ-ввод. СТ-вывод хорош для двух выводимых показателей, для большего числа выводимых данных он используется значительно реже. СТ-ввод с успехом может быть применен и в сложных программах для циклически повторяемого ввода небольших порций информации, которые сразу же перерабатываются и отсылаются в адресуемые регистры в переработанном виде.
В случаях, когда СТ-ввод по каким-либо причинам не может быть применен, а желательно, сохранить легкую и удобную форму ввода, можно успешно использовать ПП-ввод. При ПП-вводе одновременно происходит размещение вводимых чисел по стековым регистрам, что дает ему преимущество по сравнению с СТ-вводом в тех случаях, когда вводимую информацию нужно не только переслать в адресуемые регистры, но и определенным образом разместить в регистрах стека для последующей обработки. Если вводимых данных много, то их при ПП-способе лучше записывать в виде таблицы - как при вводе, так и при выводе. К недостаткам ПП-способа следует отнести повышенный расход программной памяти, а также то обстоятельство, что при его применении оператору всегда приходится отчетливо помнить, на каком адресе остановилась программа при вводе очередного числа.
КП-ввод исходных данных используется значительно чаще, чем КИП-вывод результатов. Этот способ становится целесообразным в том случае, если вводится много чисел и их можно разместить в упорядоченной последовательности по адресуемым регистрам. С учетом последнего обстоятельства применение КП-ввода становится эффективным по сравнению с ПП-вводом тогда, когда число вводимых показателей превышает число команд, затрачиваемых на организацию программного блока КП-ввода (его длина составляет обычно шесть-семь команд). КП-ввод лучше использовать тогда, когда в программе обрабатываются однотипные данные и для этой обработки не требуется большого количества адресуемых регистров памяти (например, суммирование какой-либо числовой последовательности).
Применение ПР-ввода не накладывает никаких ограничений на программирование задач, не удлиняет программу. Занести исходные данные этим способом можно еще до набора программы. Безразлична и последовательность записи чисел в регистры. Этот способ остается единственно возможным в случаях, когда программа занимает всю программную память. На его применение лучше ориентироваться также в сложных программах, когда вычисления происходят достаточно долго, когда любая ошибка при вводе показателей может перечеркнуть большую подготовительную работу. В этих случаях лучше сознательно идти на некоторые сложности при вводе, предусматривать проверку записи показателей, чтобы, потеряв несколько дополнительных минут, не терять часы из-за возможных ошибок.
В заключение представим тех, кто принимал участие в проведении этого занятия,- читателей рубрики. чьи письма во многом определяли его содержание. Это Б.Маминов (Горький), А.Неклюдов (Одесса), С.Чигирев (Симферополь), А.Волошин (Киев), Л.Ницецкий (Рига), А.Дринов (Волгоград), С.Камнев (Москва), А.Тулайков (Долгопрудный Московской области).

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Параллельно "школе" в эти месяцы публиковались лекции академика А.Ершова по алгоритмам (а в начале года, еще более формально - Н.Нагорного). Но это был тупик: алгоритмы в те времена понимались "программистами" лишь как довесок к "главному знанию" - технической документации на машины и операционные системы. Зачем общая теория решения задач, если тогдашних готовых решений хватает и по сей день, сорок лет спустя? А документация обновляется чуть не ежемесячно. Думать некогда, прыгать надо.
Но вернемся в "калькуляторный клуб":
12/85
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ

Диаграмма показывает, из кого состоит круг читателей раздела "Человек с микрокалькулятором". Составлена она по результатам анкеты, опубликованной в 4/85.
Почти половина наших читателей - школьники, студенты, преподаватели; немало инженеров, включая программистов.
Кто же занимает следующее место по численности? Врачи. Факт отрадный, свидетельствующий о том, что методы точных наук все глубже проникают в медицину.
Врачам и предоставлено слово на первых страницах нынешнего выпуска раздела. Среди публикуемых писем - и такие, что касаются тонкостей программирования, и такие, где микрокалькулятор выступает советчиком по части здоровья.
ВРЕМЯ ДОРОЖЕ
Обработка серии опытных данных, полученных при любых экспериментах (физических, биологических, медицинских), всегда связана со статистическими расчетами.
У нас, в медицине, подобные задачи встречаются сплошь и рядом. Например, при обработке длительности кардиоинтервалов, то есть промежутков времени между сердечными сокращениями, вычислении корреляции между дозами лекарственного препарата и параметрами состояния больного (артериальное давление, частота пульса, температура и пр.). Почти всегда исходные данные приходится обрабатывать путем накопления сумм вида sum(xi**n * yi**m), где n и m обычно не больше 4.
В 2/85 напечатан очень интересный обзор "Метод наименьших квадратов", в котором программы накопления сумм построены с использованием косвенной адресации.
В компактной и изящной программе В.Адриана накопление сумм занимает 27 шагов и предусматривает возможность полуавтоматического исправления ошибок. В аналогичной программе, составленной мною, нет подпрограммы и косвенной адресации, и она занимает 32 шага. Проигрыш "пространства" - 5 шагов. Зато моя программа выполняет цикл обработки одной пары xi, yi за 10 секунд, а программа В.Адриана - за 17 секунд. Выигрыш времени - 7 секунд. Правда, нет у меня и полуавтоматического "вычеркивания" ошибочных пар данных, как у В.Адриана. Я их вычеркиваю вручную. Быть может, это "съедает" выигрыш во времеии? Нет, и это не так.
Известно, что при операторской работе одна ошибка приходится на 100-150 чисел. В программе В.Адриана для исключения ошибки требуется семь раз нажать на клавиши, выждать один цикл и еще три раза нажать на клавиши. Итого - не меньше 30 секунд. Алгоритм этой операции состоит из 28 команд или 18 нажатий на клавиши. Если выполнить "вычеркивание" неправильной пары данных из соответствующих регистров вручную, то это займет не больше 2 минут. Общий баланс времени на обработку 100 чисел с учетом одной ошибки, допущенной при вводе, в пользу моего варианта: выигрывается около 4 минут. При построении, допустим, автокорреляционных функций, когда один и тот же массив в 100 чисел приходится обрабатывать по 10-15 раз, выигрыш становится вполне заметным.
Бывает, конечно, что "пространство" даже в один шаг важнее времени. И тем не менее, если в программной памяти есть свободные ячейки (а у В.Адриана их оставалось 26), то я предпочитаю удлинить программу, чтобы сократить длительность обработки, то есть жертвую пространством во имя времени. Все-таки для нас, практиков, оно дороже всего. И потому, на мой взгляд, его экономия с лихвой окупает лишние команды.
С.ЧУРОВ (г.Москва)
БАЛЛЫ СТАВИТ КАЛЬКУЛЯТОР
В практике спортивного врача важное место занимают профилактические осмотры спортсменов, когда определяется уровень их физического развития (рост, вес, объем легких) и физическая работоспособность. Данные осмотра сравниваются с величинами, средними для спортсменом того же пола и возраста. Оценка выводится так. Из полученной при обследовании величины показателя a вычитают среднее значение a и делят разность Da на величину стандартного отклонения сигма. Результат показывает, на сколько сигм фактический параметр отличается от стандартного.
Для удобства оценок применяется десятибалльная шкала, позволяющая сделать результат более наглядным. Если он меньше -2, то ставится 1 балл, если больше -2, но меньше -1.5, то 2 балла и так далее, прибавляя каждый раз по 0.5 к значению Da/сигма и по 1 к оценке. Наконец, результат, больший 2, получает наивысшую оценку - 10 баллов. Запись дробных чисел, участвующих в подобных расчетах на "Электронике Б3-34", в адресуемые регистры потребовала бы сравнительно большего числа команд для ручных операций. Кстати, подобные проблемы типичны для задач классификации.
Чтобы обойти эту трудность, мы заменяли отклонение Da/сигма на величину 2(Da/сигма+2). Для этой величины границы классов стали целыми положительными числами 0, 1, 2..., и появилась возможность воспользоваться свойствами косвенной адресации. Программа. 00. КНОП 01. ПС 02. F() 03. - 04. ИПС 05. / 06. С/П 07. 2 08. + 09. FBx 10. * 11. Fx>=0 12. 29 13. 1 14. + 15. П6 16. КИП6 17. ИП6 18. 1 19. 0 20. - 21. Fx<0 22. 26 23. ИП6 24. С/П 25. В/0 26. FBx 27. С/П 28. В/0 29. 1 30. С/П 31. В/0.
Работа с программой проста. После того, как она введена, нажать клавиши F АВТ В/0 и ввести данные: a ^ a' ^ сигма С/П. Через несколько секунд на индикаторе - значение отклонения в сигмах. После повторного нажатия клавиши С/П выводится оценка в баллах. При этом калькулятор готов для приема следующего параметра. Просто и удобно.
Например, у лыжницы первого разряда при обследовании получены данные: рост - 163см, вес - 62кг, мышечная сила правой кисти - 36кг. Из таблицы, приведенной в книге "Спортивная медицина" (под редакцией В.Л.Карпмана), берем эталонные значения: рост - 161.5+/-3.8, вес - 60.3+/-2.2, сила - 41.2+/-6.0. В результате обработки данных получаем результаты: отклонение роста 0.39 или 6 баллов; отклонение веса - 0.77 или 7 баллов; отклонение силы равно - 0.87 и оценивается в 4 балла.
Расчет трех величин занимает не более двух минут. Если учесть, что для комплексной оценки состояния спортсмена иной раз требуется анализ нескольких десятков показателен, ясно, что без калькулятора врачу приходится очень трудно.
Думаю, что при наличии соответствующих таблиц программа может быть использована при оценке здоровья людей в ходе диспансеризации, в педиатрии и других отраслях медицины.
С.НАЗАРОВ, студент-медик (г.Иваново)
ЧИСЛА ЗДОРОВЬЯ
Предлагаемая программа позволяет контролировать рацион н сверять его с нормой, зависящей от веса человека и рода его занятий. Введя программу и клавишей В/0 установив счетчик адресов на нуль, следует набрать на цифровых клавишах свой рост (по нему определяется нормальный вес) и, нажав клавишу ^,- оценку труда по приложенному перечню. Запущенный клавишей С/П, калькулятор вычисляет необходимое и допустимое при повышенных энергозатратах суточное потребление килокалорий, белков, жиров и углеводов. Первое из этих чисел появляется на индикаторе после останова, а следующие выводятся с помощью клавиши ИП: "Kmin" ИПА, "Бmin" ИПВ "Жmin" ИПС "Уmin" С/П "Кmax" ИПА "Бmax" ИПВ "Жmax" ИПС "Уmax". Вновь нажимается клавиша С/П, и после останова с нулем на индикаторе вводятся по приложенной таблице шифры каждого съеденного блюда; числа разделяются нажатием клавиши ^. Запущенный вновь, калькулятор подсчитывает и выводит на индикатор калорийность всех уже учтенных блюд (в килокалориях). Нажатием клавиш ИПА, ИПВ, ИПС можно вызвать количество белков, жиров и углеводов соответственно, содержавшихся в этих блюдах (в граммах). Для нового подсчета следует вернуться на адрес 25 с помощью клавиши БП.
Программа. 00. П0 01. 7 02. + 03. 5 04. * 05. П0 06. x-y 07. 2 08. F10x 09. - 10. П1 11. ПП 12. 51 13. ИП2 14. С/П 15. ИП0 16. 1 17. 0 18. П3 19. + 20. ИП1 21. ПП 22. 51 23. ИП2 24. С/П 25. Сх 26. ПА 27. ПВ 28. ПС 29. ПД 30. С/П 31. П1 32. F() 33. ИП0 34. + 35. ПС 36. F() 37. ИПВ 38. + 39. ПВ 40. F() 41. ИПА 42. + 43. ПА 44. ИП1 45. ИП3 46. * 47. ИПД 48. + 49. БП 50. 29 51. * 52. П2 53. 0 54. , 55. 1 56. 5 57. * 58. ПС 59. ИП2 60. 3 61. 3 62. , 63. 3 64. / 65. 1 66. 0 67. + 68. ПА 69. ИП2 70. 3 71. 0 72. / 73. ПВ 74. В/0.
Контрольный пример: рост - 169см, оценка труда - 1. Минимальные К=2760, Б=93, Ж=92, У=414. Максимальные К=3450, Б=114, Ж=115, У=518. Съеденные блюда: рассольник, котлеты, кофе, бутерброд (вводятся их шифры). Результаты подсчета: К=940, Б=23, Ж=35, У=55.
Гороховый суп. 7. 6. 35. 23
Суп с фрикадельками. 16. 23. 0. 18
Рассольник. 6. 11. 27. 25
Солянка. 23. 30. 15. 40
Борщ. 10. 12. 35. 25
Щи. 5. 11. 14. 18
Тушеное мясо с картофелем. 18. 12. 35. 31
Котлеты. 7. 12. 45. 35
Яичница с колбасой. 15. 30. 1. 32
Гуляш. 15. 10. 6. 17
Шашлык. 20. 17. 0. 24
Пельмени. 20. 12. 40. 40
Голубцы. 30. 30. 25. 47
Рыбные блюда. 17. 11. 4. 18
Овощные блюда. 17. 11. 40. 30
Блинчики с мясом. 23. 15. 40. 85
Овсяная, манная каша. 15. 25. 60. 43
Рисовая, гречневая каша. 6. 14. 45. 30
Компот. 0. 5. 35. 18
Кофе, какао (1ст.). 5. 5. 30. 20
Стакан молока. 3. 6. 10. 12
Стакан кефира. 3. 10. 6. 12
Бутерброд. 5. 7. 15. 14
Сосиски. 11. 25. 0. 25
Колбаса копченая. 15. 33. 0. 36
Колбаса докторская. 14. 23. 0. 25
Яйцо. 11. 2. 0. 3
Курица (100г). 18. 13. 1. 20
Язык (100г). 13. 40. 0. 40
Говядина (100г). 20. 10. 0. 16
Спинина (100г). 13. 40. 0. 40
Хлеб (100г). 7. 1. 45. 22.
Печенье (100г). 7. 12. 23. 40
Шоколад (100г). 8. 35. 100. 55
Сметана (100г). 3. 5. 25. 25
Сыр (100г). 25. 27. 0. 35
Овощи, фрукты (100г). 2. 0. 10. 50
Ассортимент можно расширить. Шифр для каждого продукта определяется так: первое число - количество белков. второе - жиров. третье - углеводов (все в граммах), четвертое - калорийность в килокалориях, деленная на 10.
Желающим минимизировать стоимость оптимального рациона рекомендуем ознакомиться с книгой Я.К.Трохименко и Ф.Д.Любича "Микрокалькулятор, ваш ход!" (М., "Радио и связь", 1985) и в ней - с разделом "Подарок молодым хозяйкам".
Оценки труда. Работа, не связанная с физическим трудом (например, педагоги, служащие) - 1. Механизированный труд (токари, фрезеровщики) - 2. Частично механизированный труд (сталевары, строители) - 3. Тяжелый фнзический труд (землекопы) - 4.
С.ГЕТА (г.Таллин)
ПРОГРАММА-ЭКЗАМЕНАТОР
Многие преподаватели - М.Асанов (Уфа), Г.Горовой (Керчь), Г.Зайденберг (Калинин), Н.Мазур (Владивосток), В.Мищенко (Москва), А.Соколов (Рустави), Э.Федотова и В.Панченко (Ростов-на-Дону), П.Шоцкий (Киев) - пишут нам о том, что "Электроника Б3-34" позволяет оперативно контролировать знания учащихся, судить о наличии необходимого минимума знаний на пути к более серьезному экзамену, может даже выступать в роли экзаменатора.
Работа с любой из присланных нам программ-экзаменаторов протекает так: студент получает билет, где на поставленные вопросы даются несколько ответов, каждый из которых помечен цифровым кодом. Студент должен выбрать правильный ответ и набрать на клавиатуре его код. Калькулятор, сверяя вводимые числа с верными кодами, хранящимися в его памяти или генерируемыми программой, оценивает знания студента.
Здесь мы приводим с небольшими изменениями программу Г.Горового. Перед ее использованием преподаватель составляет билеты, в каждом из которых содержится 5 вопросов. Верный ответ на каждый вопрос оценивается в один балл. К каждому вопросу прилагается 3-5 ответов, среди которых только один верный. Цифровые коды ответов двузначные. Их вырабатывает включенный в программу генератор целых случайных чисел Zi. В качестве z0 используется номер билета. Для работы генератора нужны две константы, употребляемые при получении очередного числа: a и b, превышающее на единицу наибольший код. Если число билетов не превосходит 26, можно рекомендовать a=11, b=27, 29 или 31. Цифровые коды ответов лучше писать на билетах карандашом: если билеты использовались достаточно долго и возникает подозрение, что отвечающие не думают над ответами, а пользуются разгаданными сочетаниями цифровых кодов, то достаточно, изменив b, перекодировать ответы, стирая старые коды.
(Если же есть опасения, что учащиеся изменят введенную в калькулятор программу так, что она будет выставлять лишь положительные оценки, клавиатуру можно закрыть маской с прорезями для необходимых клавиш).
Программа может использоваться в двух режимах: в режиме кодировки при подготовке билетов и в режиме контроля ответов по билетам.
00. ПД 01. ПС 02. ИП9 03. П0 04. 5 05. П1 06. 6 07. ИП1 08. - 09. 2 10. F10x 11. * 12. С/П 13. ИПД 14. ИПА 15. * 16. ^ 17. ИПВ 18. / 19. 1 20. + 21. П2 22. F() 23. КИП2 24. F() 25. ИП2 26. ИПВ 27. * 28. - 29. ПД 30. - 31. Fx!=0 32. 37 33. КИП0 34. 2 35. БП 36. 39 37. 5 38. ^ 39. 6 40. ИП1 41. - 42. F10x 43. / 44. ИПС 45. + 46. ПС 47. FL1 48. 06. 49. ИП0 50. С/П 51. БП 52. 00.
Если предполагается работать с программой в режиме контроля, преподаватель вводит ее, затем набирает на клавиатуре F АВТ 1 5 ВП 9 9 ВП ^ П9 а ПА b ПВ Сх В/0. Студент должен набрать на табло номер билета N и нажать клавишу С/П. Через некоторое время на индикаторе высвечивается цифра 100, означающая, что следует отвечать на первый вопрос билета (номера вопросов выводятся с двумя нулями специально, чтобы их было легко отличить от кодов ответов и оценки). Отвечающий выбирает правильный, по его мнению, ответ, набирает на табло код этого ответа и нажимает клавишу С/П. На индикаторе - цифра 200, означающая, что надо отвечать на второй вопрос билета. Вновь набирается код и нажимается клавиша С/П... После ответа на пятый вопрос на индикаторе появляется оценка. Чтобы отличить ее от кодов, она выводится с символом Е, например Е5 - отлично. Хранится оценка в регистре 0. Можно узнать, на какие вопросы был дан неверный ответ: если нажать клавишу x-y, иа индикаторе высветится число вида N.qqnqn. Например 15.55252 означает, что были неправильно даны ответы на третий и пятый вопросы (цифры после запятой) 15-го билета (цифры до запятой). Это число хранится в PC.
Для того, чтобы закодировать верные ответы при составлении билетов, следует внести в текст программы следующие изменения: ... 12. КНОП... 30. С/П 31.БП 32.13... (если программа используется только для кодировки, то дальше текст набирать не нужно). Введя программу, надо затем ввести вручную число a в регистр А, число b в регистр В (эти же числа следует потом использовать и при работе в режиме контроля). Далее надо выписать коды верных ответов на билет, действуя следующим образом: набрать номер билета N В/0 С/П; на индикаторе высвечивается код правильного ответа на первый вопрос данного билета. Списав код, вновь нажимаем клавишу С/П, списываем код ответа на следующий вопрос билета, и так далее до последнего вопроса. Неверные ответы кодируются произвольным образом в рамках интервала 1-К.
Несколько слов о работе программы. Команды по адресам 00-12 заносят константы в соответствующие регистры, в частности сообщение Е5 в регистр 0, и выводят на индикатор номер вопроса, на который следует дать ответ. По адресам 13-29 размещается программа-генератор верных кодов, работающая согласно формуле zi=z[i-1]a-(z[i-1]a/b)b.
Если отвечающий выбрал верный код ответа, то при вычитании из него кода, сгенерированного программой, получается ноль (адреса 30-32) и начальное значение оценки остается без изменения, а в контрольном числе учета верных ответов (регистр С) в соответствующей позиции проставляется 5 (адреса 37-46). Если же набранный и выработанный программой коды не совпали, то оценка снижается на 1 балл и в соответствующей позиции контрольного числа проставляется 2 (адреса 33-36 и 39-46). Оператор цикла, размещенный по адресам 47-48, обеспечивает пятикратное выполнение указанных действий, что соответствует числу вопросов в билете. Выполнение программы заканчивается индикацией оценки; контрольное число при этом располагается в стековом регистре Y. Команда 51. БП 52. 00 передает управление на начальный адрес программы при новом цикле вычислений, то есть при ответе другого студента на иной билет.
В заключение читатели
могут с помощью данной программы проверить свои знания об "Электронике Б3-34", приняв a=11 и b=27. В скобках к ответам предлагаемого билета указаны коды ответов,- выбирайте правильный. Ни пуха ни пера!
Билет #1
1. С помощью какой команды (из числа предлагаемых) в регистр X вызывается предыдущий результат: F() (32); ^ (3); FBx (ll)
2. Каким образом отреагирует программа на команду В/0, помещенную вне подпрограммы? Остановится (17); передаст управление на адрес 00 (28 ); передаст управление на адрес 01 (13).
3. Какой результат появится на индикаторе при выполнении команд ВП 26 ^, если до этого там было число 3.56e12? 3.56e26 (18 ); 3.56e12 (4); 3.56e38 (8 ).
4. Что произойдет при выполнении программы: 00. 5 01. 0 02. F10x 03. ^ 04. * 05. П9 06. КНОП 07. ИП9 08. 7 09. С/П? Программа выполнится до конца, и на индикаторе высветится число 7 (2); произойдет останов программы на шаге 04, и высветится ЕГТОГ (25); произойдет останов программы на шаге 07, и высветится ЕГГОГ (7).
5. Какой результат получится при выполнении команд: 10 ВП 99 П7? ЕГГОГ (6); 1e10 (23); 0 (15).
С МИКРОКАЛЬКУЛЯТОРОМ В ГЛУБЬ ВЕКОВ
Подробности обстановки делают описания исторических событий гораздо более запоминающимися. Известно ли вам, светила ли Луна в Варфоломеевскую ночь? Это легко выяснить с помощью нехитрой программы, приведенной ниже. Число 15, полученное в результате,- это возраст полной Луны, какой она была 24 августа 1572 года. Представив ее себе, вы словно оказываетесь на месте тех трагических событий при зловеще ярком лунном свете.
Луна, как утверждали средневековые астрологи, влияет на жизнь человека ночью, но есть исключения, например, солнечные затмения. В начале похода князя Игоря на половцев, 1 мая 1185 года, наблюдалось солнечное затмение. Расчет по той же программе показывает возраст Луны: 29. Это естественно, так как солнечное затмение практически совпадает с новолунием. (Лунный цикл составляет 29.530588 дня).
В одной из научно-популярных книг по истории России я прочел цитату из "Летописной повести о побоище на Дону" (то есть о Куликовской битве): "В субботу рано 8 сентября, в самый праздник во время восхода солнца была тьма великая по всей земле, мгла, не было света от утра до третьего часа". Я подумал, что речь идет о солнечном затмении. Калькулятор не подтвердил это предположение: возраст Луны в День битвы оказывается равным 8. Таким образом, летописец передал свои впечатления о каком-то другом явлении, для меня оставшемся загадкой.
Привожу программу "Возраст Луны":
Программа. 00. П3 01. С/П 02. П1 03. С/П 04. П2 05. 3. 06. - 07. Fx<0 08. 13 09. КИП3 10. ИП2 11. 9 12. + 13. 4 14. + 15. 3 16. 0 17. , 18. 6 19. * 20. ПП 21. 54 22. 3 23. 6 24. 5 25. , 26. 2 27. 5 28. ИП3 29. * 30. + 31. ПП 32. 54 33. ИП1 34. + 35. 2 36. + 37. П5 38. 2 39. 9 40. , 41. 5 42. 3 43. 0 44. 5 45. 8 46. 8 47. П4 48. / 49. ПП 50. 54 51. ИП4 52. * 53. - 54. 1 55. + 56. П0 57. КИП0 58. ИП5 59. ИП0 60. В/0.
Программа составлена для юлианского летосчисления (старого стиля). Инструкция: набрать на клавиатуре В/0 год С/П число С/П месяц С/П. На индикаторе - возраст Луны.
В.АДРИАН (г.Химки).
[ ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
"Часто бывает нужно вывести на индикатор сообщение ЕГГОГ,- пишет нам инженер М.Хузмиев из г.Орджоникидзе.- Обычно в программах для этого используются команды К+, К5 и т.п. или сочетания команд Сх F1/х, - Fsqr и им подобные, приводящие к некорректным операциям. Однако желаемого сообщения при этом приходится ждать более 3 секунд. Оказывается, однако, что двумя командами, вводимыми последовательным нажатием клавиш "ВП" и "запятая", сообщение ЕГГОГ вызывается мгновенно.
Обнаружил это мой пятилетний сын, успешно осваивающий микрокалькулятор в рамках нашей семейной учебной программы "Программировать раньше, чем читать". Жаль, что эта программа не вписывается в рамки раздела "Человек с микрокалькулятором" - можно было бы поделиться интересным опытом".
Рамки раздела раздвинуть нетрудно. Объявляем предложение М.Хузмиева темой очередного "круглого стола". Просим тех, кто имеет успешный опыт ликвидации компьютерной неграмотности в собственной семье, рассказать в своих письмах об этом ]
[ НАШЕГО ПОЛКУ ПРИБЫЛО
Один за другим наши научно-популярные журналы включаются в борьбу за ликвидацию компьютерной неграмотности. Работе на микрокалькуляторе "Электроника Б3-34" учит "Школа программирования", которую вел в "Технике-молодежи" И.Данилов, и продолжающиеся в ней "Электронные игры" (консультант - летчик-космонавт СССР Ю.Глазков). О решении отдельных конкретных задач на том же калькуляторе обстоятельно рассказывает "Химия и жизнь". Цикл статей А.Когана "Программируйте с нами, программируйте сами" в журнале "Энергия" увлекательно и последовательно излагает общетеоретические основы программирования без привязки к какой-либо конкретной вычислительной машине.
Появление все новых циклов, рубрик, разделов такого рода становится привычным. Вместе с тем уже заявляет о себе другое направление пропаганды компьютерной грамотности, пока менее заметное, но открывающее большие возможности, поскольку оно не ограничено рамками никаких разделов и циклов.
В 2 журнала "Геодезия и картография" за 1985 год есть статья К.Лапинга "Гиперболическая засечка с трех исходных пунктов". Постановка задачи, формулы решения - и вслед за ними фраза: "Предлагаемые формулы удобны для программирования на микрокалькуляторе "Электроника Б3-34".
Это короткое примечание - знак нового качества исследовательской работы, которая с самого начала, с выбора метода решения предполагает машинное завершение. При таком подходе многие статьи, публикуемые в специальных журналах, могли бы стать конкретными уроками компьютеризации научных исследований. Пример "Геодезии и картографии" достоин подражания и развития ]
ЭТА ТАИНСТВЕННАЯ КОМАНДА ВП
Как пользоваться командой ВП по ее прямому назначению, знают все, кто работает с "Электроникой Б3-34". Однако есть у этой команды и другие возможности. Взять, к примеру, такую программу: ПР ВП С/П (Р - обозначение одного из регистров). Для аргумента X из интервала 1<=Х<10 эта программа выполняет функцию отделения дробной части. Если же говорить о более широком диапазоне изменения аргумента 0<Х<=9.9999999e99, то здесь калькулятор, работая по такой программе, будет отбрасывать первый разряд числа, соответственно уменьшая порядок результата на единицу. Другой вариант: ^ ПР ВП - С/П. Такая программа в "широком" диапазоне изменения аргумента будет отбрасывать все значащие разряды, кроме первого, сохраняя неизменным порядок числа. Если говорить об X, заключенном в 1<=Х<11, то программа отделяет целую часть числа.
Эти программы можно использовать и как подпрограммы, вызывая их, например, в цикле. Следует отметить, что в ряде случаев перед командами ПР ВП необходимо вставлять команду ^, например, при выделении второго разряда числа из интервала 10<=Х<=99. Цепочка команд ПР КИПР ИПР ^ ПР ВП в течение двух-трех секунд превратит число 65.432109 в 5. (Здесь Р - число от 7 до 9 или буква).
По-другому функционируют указанные последовательности команд в области отрицательных чисел. Каждый сам может исследовать это, поставив несложный численный эксперимент.
А.БОЙКО (г.Москва)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Знание кодов команд, или таблица кодов, например, та, что была опубликована в 12/84, поможет быстрее отредактировать программу с ошибками. Если ошибка обнаружена в адресе "парной" команды (команды цикла, условного или безусловного перехода, обращения к подпрограмме), не всегда следует, как рекомендуется в пояснении к таблице, исправлять команду целиком, отступая на два шага. Верный адрес можно набрать клавишами, определяющими команду, код которой совпадает с требуемым адресом. Часто при этом достаточно нажать лишь одну клавишу, например, для адреса 50 - клавишу С/П, для 13 - клавишу / (деление). Набор текста готовой программы можно ускорить, если вместо адресов 50 и 52 использовать команды С/П и В/0 и т.п.
А.БОРИСОВ (г.Москва) ]
[ УЗЕЛКИ НА ПАМЯТЬ
В 12/84 год описывалось устройство, подсоединяемое к "Электронике "Б3-34": оно подает звуковой сигнал, когда микрокалькулятор заканчивает вычисления по программе.

Озвучить можно и "Электронику МК-54". Удобно включить в цепочку диод Д220, микротелефон ТМ-2А и для регуляции громкости - переменный резистор 100кОм типа СПЗ-36. Все детали поместятся в корпусе микрокалькулятора. Под диск регулировки резистора и микротелефон необходимо вырезать окна в крышке калькулятора.
М.БАХМУТСКИЙ (г.Львов.) ]
ОХОТА НА "ЛИС"
Название позаимствовано от известной спортивной игры, детали которой узнаются п нижеследующем описании.
В памяти калькулятора хранится картина игрового поля размером 9*9 клеток. В пяти различных клетках располагаются пять "лис" - радиопередатчики, посылающие в эфир сигнал "я здесь". Передатчики могут занимать соседствующие клетки. Играющий очередным своим ходом вводит в калькулятор положение "охотника", набирая на клавиатуре дробное двузначное число вида Y.X - целая и дробная его части выражают координаты по вертикали и по горизонтали соответственно. "Охотник" вооружен приемником, имеющим направленную антенну, так что сигналы от "лис" принимаются лишь по восьми направлениям, как показано на рисунке. На индикатор выводится число "лис", расположенных по этим направлениям. Если на каком-то направлении оказались две "лисы", то считаются обе. Если координаты какой-либо "лисы" совпадают с положением "охотника", то на индикаторе появляется сообщение ЕГГОГ. Обнаруженная "лиса" не исчезает с игрового поля н продолжает посылать сигналы. Меняя ход за ходом положение "охотника" и анализируя информацию, выдаваемую калькулятором, играющий путем логических умозаключений или графических построений должен обнаружить всех "лис" за наименьшее число ходов. Играть в эту игру можно в одиночку, но можно проводить и соревнования.

Настало время вводить программу. Кратко прокомментируем назначение отдельных фрагментов (по адресам).
Программа. 00. ПД 01. 1 02. 0 03. П0 04. П3 05. 5 06. П1 07. ПП 08. 69 09. П2 10. ПП 11. 69 12. ИП3 13. / 14. ИП2 15. + 16. КП0 17. FL1 18. 07 19. Сх 20. С/П 21. ПД 22. 0 23. П4 24. ИП3 25. П0 26. 5 27. П1 28. ИПД 29. КИП0 30. - 31. ПС 32. Fx=0 33. 38 34. ВП 35. , 36. БП 37. 21 38. ИПД 39. ПА 40. КИПА 41. КИП^ 42. ПВ 43. КИПВ 44. ИПВ 45. ИПА 46. - 47. Fx!=0 48. 63 49. ПВ 50. ИПС 51. + 52. ИП3 53. * 54. Fx!=0 55. 63 56. ИПВ 57. / 58. Fx2 59. 1 60. - 61. Fx=0 62. 64 63. КИП4 64. FL1 65. 28 66. ИП4 67. БП 68. 20 69. ИПД 70. ВП 71. 9 72. Fcos 73. Farccos 74. Fпи 75. / 76. ПД 77. 9 78. * 79. 1 80. + 81. ПА 82. КИПА 83. ИПА 84. B/0.
00: запись исходного случайного числа. 01-06: запись констант, 07-15: формирование числа вида Y, X. 16: установка "лисы". 17-18: проверка "все ли лисы поставлены?" 19: сообщение о начале игры, "0". 20-21: запись координат "охотника". 22-23: очистка счетчика сигналов. 24-25: установка указателя на адрес первой "лисы". 26-27: начальная установка счетчика "лис". 28-35: проверка "лиса обнаружена?" 36-37: переход к индикации и запросу координат "охотника". 38-40: выделение координаты Yо "охотника". 41-43: выделение координаты Yл "лисы". 44-48: проверка "лиса пеленгуется по горизонтали?" 49-51: отделение дробной части разности Yo, Xо - Yл, Xл; результат - число 0.(Xо-Хл). 52-53: получение числа Xо-Xл . 54-55: проверка "лиса пеленгуется по вертикали?" 56-62: проверка "лиса пеленгуется по диагонали?" 63: добавление единицы к содержимому счетчика сигналов. 64-65: переход к очередной "лисе". 66-68: формирование сообщения о числе "лис". 69-84: генерация псевдослучайного числа по формуле e[i+i]=(1/пи)arccos(cos(1e8*ei)+D), где D - погрешность вычисления косинуса, и формирование целого числа [9e + 1] . Программа введена, и осталось лишь внимательно ознакомиться с инструкцией.
1. Нажмите В/0. Наберите случайное число от 0 до 1, например, 0.ЧЧММ; здесь ЧЧ и ММ - часы и минуты, в которые начата игра. Нажмите С/П - калькулятор примется распределять "лис" по игровому полю. Через пару минут на индикаторе появится сигнал готовности "0".
2. Введите координаты "охотника" Y.X С/П, где Y и X - целые числа от 1 до 9, разделенные запятой. Например, 7.6 - это позиция охотника на рисунке. На индикаторе появляется число "лис" по направлениям пеленга или- ЕГГОГ, если "лиса" найдена. В нашем случае получаем 2. Затем вводим следующие У, X.
3. Для повторения игры с иной расстановкой "лис" переходите к п.1.
А.НЕСЧЕТНЫЙ (г.Ленинград)

Рис. В.Торгашина (г.Жуковский Московской обл.)
"ВОЛЧЬИ ЯМЫ" ОКРУГЛЕНИЯ
Американский математик Уилкинсон исследовал уравнение
(х-1)(х-2)(х-3)... (х-20) = х**20 - 210*х**19 + ... + 20! = 0
Он заменил коэффициент -210 на -(210+2**-23), то есть увеличил его примерно на 1e-7. Ни один из корней нового уравнения не был близок к корням 11, 13, 15 старого, причем среди них оказались и комплексные корни.
Этот пример убеждает, какую каверзную роль может сыграть в расчетах изменение даже далеких от запятой значащих цифр. А ведь таким риском нередко чреваты вычисления на микрокалькуляторе. Все, что лежит за пределами его восьмиразрядного индикатора, отсекается, и возникают ошибки округления. Опыт вычислений на бумаге не воспитывает в нас осторожности по отношению к ним: эффекты округления видны воочию; опасаясь ошибки, можно менять число удерживаемых разрядов. При счете на калькуляторе приходится доверяться машине, и может случиться так, что основную часть полученного ответа составят ошибки округления, отчего ответ окажется весьма далеким от истинного.
Наиболее опасной в смысле потери точности операцией является вычитание близких друг к другу чисел.
Попробуем вычислить на микрокалькуляторе еxp(-10) согласно разложению
exp(-10) = 1 - 10 + 1e2/2! - 1e3/3! + ...
Вместо истинного результата 0.0000454 получается 0.0001112 - число, в 2.5 раза больше. Откуда же набежала погрешность? Покуда в слагаемых ряда рост факториала в знаменателе обгонит рост степени в числителе, они возрастают до десятого включительно, принимая значения, превосходящие 2000. А так как счет ведется только до восьми значащих цифр, то ответ получается с точностью лишь до 0.0001. Вот и набегают ошибки, значительно превосходящие искомый ответ. Чтобы получить верный результат, надо записать exp(-10) в виде 1/еxp(10), разложить знаменатель этой дроби в ряд
exp(10) = 1 + 10 + 1e2/2! + 1e3/51 + ...
а затем от найденной суммы ряда взять обратную величину.
Разумеется, нет смысла считать еxp(-10) на калькуляторе, имеющем клавишу exp. Но ведь иногда приходится вычислять значения и более экзотических функций, скажем, бесселевой или гипергеометрической, используя опять-таки степенные ряды, где подстерегают "волчьи ямы" округления.
Ошибки, вызванные вычитанием мало отличающихся друг от друга чисел, могут возникнуть и при такой простой операции, как нахождение корней квадратного уравнения: X1,2=(-b +/- sqr(b**2-4ас))/2а. Если b**2 значительно превосходит 4ас, то в числителе формулы приходится вычитать именно такие числа. Например, решая на микрокалькуляторе уравнение х**2-1e5*x+1=0, вместо одного из корней 0.0000100 мы получим нуль. Это уже никуда не годится.
Такие примеры напоминают: применение микрокалькулятора, как использование любого технического устройства, предъявляет свои требования к выбору методов работы и к ясности понимания того, что может и чего не может сделать данное устройство.
Н.ВИЛЕНКИН (г.Москва)
[ С увеличением адреса выполняемой команды быстродействие микрокалькулятора постепенно уменьшается. При этом разница во времени исполнения одних и тех же команд, расположенных по различным адресам, может достигать 30 процентов. Сравните время выполнения следующих двух программ. 00. FL0 01. 00 02.С/П и 95. FL0 96. 95 97. С/П. В регистр Р0 занесите число циклов, например, 600. Эту особенность следует, по-моему, использовать для убыстрения расчетов: подпрограммы следует размещать не в конце, а в начале программной памяти.
П.МОЛОДЧИК (г.Киев) ]
[ Как известно, микрокалькулятор Б3-34 не вычисляет корней с нечетными показателями из отрицательных чисел. Предлагаю программу, которая позволяет обойти этот недостаток. 00. Fx2 01 . Flg 02. M 03. / 04. F10x 05. Fsqr 06. С/П. Здесь М = 3, 5, 7, 9 - показатель корня. Если требуется вычислить корень большей степени, М принимает значения 11, 13 и т.д., а программа, начиная с адреса 03, выглядит так: 03. М 04. / 05. F1Ox 06. Fsqr 07. С/П
А.ЗАЙЦЕВ (г.Щигры Курской обл.) ]

Рис. А.Кузовкииа
(г.Березники Пермской обл.)
Но вернемся в "калькуляторный клуб":
12/85
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ

Диаграмма показывает, из кого состоит круг читателей раздела "Человек с микрокалькулятором". Составлена она по результатам анкеты, опубликованной в 4/85.
Почти половина наших читателей - школьники, студенты, преподаватели; немало инженеров, включая программистов.
Кто же занимает следующее место по численности? Врачи. Факт отрадный, свидетельствующий о том, что методы точных наук все глубже проникают в медицину.
Врачам и предоставлено слово на первых страницах нынешнего выпуска раздела. Среди публикуемых писем - и такие, что касаются тонкостей программирования, и такие, где микрокалькулятор выступает советчиком по части здоровья.
ВРЕМЯ ДОРОЖЕ
Обработка серии опытных данных, полученных при любых экспериментах (физических, биологических, медицинских), всегда связана со статистическими расчетами.
У нас, в медицине, подобные задачи встречаются сплошь и рядом. Например, при обработке длительности кардиоинтервалов, то есть промежутков времени между сердечными сокращениями, вычислении корреляции между дозами лекарственного препарата и параметрами состояния больного (артериальное давление, частота пульса, температура и пр.). Почти всегда исходные данные приходится обрабатывать путем накопления сумм вида sum(xi**n * yi**m), где n и m обычно не больше 4.
В 2/85 напечатан очень интересный обзор "Метод наименьших квадратов", в котором программы накопления сумм построены с использованием косвенной адресации.
В компактной и изящной программе В.Адриана накопление сумм занимает 27 шагов и предусматривает возможность полуавтоматического исправления ошибок. В аналогичной программе, составленной мною, нет подпрограммы и косвенной адресации, и она занимает 32 шага. Проигрыш "пространства" - 5 шагов. Зато моя программа выполняет цикл обработки одной пары xi, yi за 10 секунд, а программа В.Адриана - за 17 секунд. Выигрыш времени - 7 секунд. Правда, нет у меня и полуавтоматического "вычеркивания" ошибочных пар данных, как у В.Адриана. Я их вычеркиваю вручную. Быть может, это "съедает" выигрыш во времеии? Нет, и это не так.
Известно, что при операторской работе одна ошибка приходится на 100-150 чисел. В программе В.Адриана для исключения ошибки требуется семь раз нажать на клавиши, выждать один цикл и еще три раза нажать на клавиши. Итого - не меньше 30 секунд. Алгоритм этой операции состоит из 28 команд или 18 нажатий на клавиши. Если выполнить "вычеркивание" неправильной пары данных из соответствующих регистров вручную, то это займет не больше 2 минут. Общий баланс времени на обработку 100 чисел с учетом одной ошибки, допущенной при вводе, в пользу моего варианта: выигрывается около 4 минут. При построении, допустим, автокорреляционных функций, когда один и тот же массив в 100 чисел приходится обрабатывать по 10-15 раз, выигрыш становится вполне заметным.
Бывает, конечно, что "пространство" даже в один шаг важнее времени. И тем не менее, если в программной памяти есть свободные ячейки (а у В.Адриана их оставалось 26), то я предпочитаю удлинить программу, чтобы сократить длительность обработки, то есть жертвую пространством во имя времени. Все-таки для нас, практиков, оно дороже всего. И потому, на мой взгляд, его экономия с лихвой окупает лишние команды.
С.ЧУРОВ (г.Москва)
БАЛЛЫ СТАВИТ КАЛЬКУЛЯТОР
В практике спортивного врача важное место занимают профилактические осмотры спортсменов, когда определяется уровень их физического развития (рост, вес, объем легких) и физическая работоспособность. Данные осмотра сравниваются с величинами, средними для спортсменом того же пола и возраста. Оценка выводится так. Из полученной при обследовании величины показателя a вычитают среднее значение a и делят разность Da на величину стандартного отклонения сигма. Результат показывает, на сколько сигм фактический параметр отличается от стандартного.
Для удобства оценок применяется десятибалльная шкала, позволяющая сделать результат более наглядным. Если он меньше -2, то ставится 1 балл, если больше -2, но меньше -1.5, то 2 балла и так далее, прибавляя каждый раз по 0.5 к значению Da/сигма и по 1 к оценке. Наконец, результат, больший 2, получает наивысшую оценку - 10 баллов. Запись дробных чисел, участвующих в подобных расчетах на "Электронике Б3-34", в адресуемые регистры потребовала бы сравнительно большего числа команд для ручных операций. Кстати, подобные проблемы типичны для задач классификации.
Чтобы обойти эту трудность, мы заменяли отклонение Da/сигма на величину 2(Da/сигма+2). Для этой величины границы классов стали целыми положительными числами 0, 1, 2..., и появилась возможность воспользоваться свойствами косвенной адресации. Программа. 00. КНОП 01. ПС 02. F() 03. - 04. ИПС 05. / 06. С/П 07. 2 08. + 09. FBx 10. * 11. Fx>=0 12. 29 13. 1 14. + 15. П6 16. КИП6 17. ИП6 18. 1 19. 0 20. - 21. Fx<0 22. 26 23. ИП6 24. С/П 25. В/0 26. FBx 27. С/П 28. В/0 29. 1 30. С/П 31. В/0.
Работа с программой проста. После того, как она введена, нажать клавиши F АВТ В/0 и ввести данные: a ^ a' ^ сигма С/П. Через несколько секунд на индикаторе - значение отклонения в сигмах. После повторного нажатия клавиши С/П выводится оценка в баллах. При этом калькулятор готов для приема следующего параметра. Просто и удобно.
Например, у лыжницы первого разряда при обследовании получены данные: рост - 163см, вес - 62кг, мышечная сила правой кисти - 36кг. Из таблицы, приведенной в книге "Спортивная медицина" (под редакцией В.Л.Карпмана), берем эталонные значения: рост - 161.5+/-3.8, вес - 60.3+/-2.2, сила - 41.2+/-6.0. В результате обработки данных получаем результаты: отклонение роста 0.39 или 6 баллов; отклонение веса - 0.77 или 7 баллов; отклонение силы равно - 0.87 и оценивается в 4 балла.
Расчет трех величин занимает не более двух минут. Если учесть, что для комплексной оценки состояния спортсмена иной раз требуется анализ нескольких десятков показателен, ясно, что без калькулятора врачу приходится очень трудно.
Думаю, что при наличии соответствующих таблиц программа может быть использована при оценке здоровья людей в ходе диспансеризации, в педиатрии и других отраслях медицины.
С.НАЗАРОВ, студент-медик (г.Иваново)
ЧИСЛА ЗДОРОВЬЯ
Предлагаемая программа позволяет контролировать рацион н сверять его с нормой, зависящей от веса человека и рода его занятий. Введя программу и клавишей В/0 установив счетчик адресов на нуль, следует набрать на цифровых клавишах свой рост (по нему определяется нормальный вес) и, нажав клавишу ^,- оценку труда по приложенному перечню. Запущенный клавишей С/П, калькулятор вычисляет необходимое и допустимое при повышенных энергозатратах суточное потребление килокалорий, белков, жиров и углеводов. Первое из этих чисел появляется на индикаторе после останова, а следующие выводятся с помощью клавиши ИП: "Kmin" ИПА, "Бmin" ИПВ "Жmin" ИПС "Уmin" С/П "Кmax" ИПА "Бmax" ИПВ "Жmax" ИПС "Уmax". Вновь нажимается клавиша С/П, и после останова с нулем на индикаторе вводятся по приложенной таблице шифры каждого съеденного блюда; числа разделяются нажатием клавиши ^. Запущенный вновь, калькулятор подсчитывает и выводит на индикатор калорийность всех уже учтенных блюд (в килокалориях). Нажатием клавиш ИПА, ИПВ, ИПС можно вызвать количество белков, жиров и углеводов соответственно, содержавшихся в этих блюдах (в граммах). Для нового подсчета следует вернуться на адрес 25 с помощью клавиши БП.
Программа. 00. П0 01. 7 02. + 03. 5 04. * 05. П0 06. x-y 07. 2 08. F10x 09. - 10. П1 11. ПП 12. 51 13. ИП2 14. С/П 15. ИП0 16. 1 17. 0 18. П3 19. + 20. ИП1 21. ПП 22. 51 23. ИП2 24. С/П 25. Сх 26. ПА 27. ПВ 28. ПС 29. ПД 30. С/П 31. П1 32. F() 33. ИП0 34. + 35. ПС 36. F() 37. ИПВ 38. + 39. ПВ 40. F() 41. ИПА 42. + 43. ПА 44. ИП1 45. ИП3 46. * 47. ИПД 48. + 49. БП 50. 29 51. * 52. П2 53. 0 54. , 55. 1 56. 5 57. * 58. ПС 59. ИП2 60. 3 61. 3 62. , 63. 3 64. / 65. 1 66. 0 67. + 68. ПА 69. ИП2 70. 3 71. 0 72. / 73. ПВ 74. В/0.
Контрольный пример: рост - 169см, оценка труда - 1. Минимальные К=2760, Б=93, Ж=92, У=414. Максимальные К=3450, Б=114, Ж=115, У=518. Съеденные блюда: рассольник, котлеты, кофе, бутерброд (вводятся их шифры). Результаты подсчета: К=940, Б=23, Ж=35, У=55.
Гороховый суп. 7. 6. 35. 23
Суп с фрикадельками. 16. 23. 0. 18
Рассольник. 6. 11. 27. 25
Солянка. 23. 30. 15. 40
Борщ. 10. 12. 35. 25
Щи. 5. 11. 14. 18
Тушеное мясо с картофелем. 18. 12. 35. 31
Котлеты. 7. 12. 45. 35
Яичница с колбасой. 15. 30. 1. 32
Гуляш. 15. 10. 6. 17
Шашлык. 20. 17. 0. 24
Пельмени. 20. 12. 40. 40
Голубцы. 30. 30. 25. 47
Рыбные блюда. 17. 11. 4. 18
Овощные блюда. 17. 11. 40. 30
Блинчики с мясом. 23. 15. 40. 85
Овсяная, манная каша. 15. 25. 60. 43
Рисовая, гречневая каша. 6. 14. 45. 30
Компот. 0. 5. 35. 18
Кофе, какао (1ст.). 5. 5. 30. 20
Стакан молока. 3. 6. 10. 12
Стакан кефира. 3. 10. 6. 12
Бутерброд. 5. 7. 15. 14
Сосиски. 11. 25. 0. 25
Колбаса копченая. 15. 33. 0. 36
Колбаса докторская. 14. 23. 0. 25
Яйцо. 11. 2. 0. 3
Курица (100г). 18. 13. 1. 20
Язык (100г). 13. 40. 0. 40
Говядина (100г). 20. 10. 0. 16
Спинина (100г). 13. 40. 0. 40
Хлеб (100г). 7. 1. 45. 22.
Печенье (100г). 7. 12. 23. 40
Шоколад (100г). 8. 35. 100. 55
Сметана (100г). 3. 5. 25. 25
Сыр (100г). 25. 27. 0. 35
Овощи, фрукты (100г). 2. 0. 10. 50
Ассортимент можно расширить. Шифр для каждого продукта определяется так: первое число - количество белков. второе - жиров. третье - углеводов (все в граммах), четвертое - калорийность в килокалориях, деленная на 10.
Желающим минимизировать стоимость оптимального рациона рекомендуем ознакомиться с книгой Я.К.Трохименко и Ф.Д.Любича "Микрокалькулятор, ваш ход!" (М., "Радио и связь", 1985) и в ней - с разделом "Подарок молодым хозяйкам".
Оценки труда. Работа, не связанная с физическим трудом (например, педагоги, служащие) - 1. Механизированный труд (токари, фрезеровщики) - 2. Частично механизированный труд (сталевары, строители) - 3. Тяжелый фнзический труд (землекопы) - 4.
С.ГЕТА (г.Таллин)
ПРОГРАММА-ЭКЗАМЕНАТОР
Многие преподаватели - М.Асанов (Уфа), Г.Горовой (Керчь), Г.Зайденберг (Калинин), Н.Мазур (Владивосток), В.Мищенко (Москва), А.Соколов (Рустави), Э.Федотова и В.Панченко (Ростов-на-Дону), П.Шоцкий (Киев) - пишут нам о том, что "Электроника Б3-34" позволяет оперативно контролировать знания учащихся, судить о наличии необходимого минимума знаний на пути к более серьезному экзамену, может даже выступать в роли экзаменатора.
Работа с любой из присланных нам программ-экзаменаторов протекает так: студент получает билет, где на поставленные вопросы даются несколько ответов, каждый из которых помечен цифровым кодом. Студент должен выбрать правильный ответ и набрать на клавиатуре его код. Калькулятор, сверяя вводимые числа с верными кодами, хранящимися в его памяти или генерируемыми программой, оценивает знания студента.
Здесь мы приводим с небольшими изменениями программу Г.Горового. Перед ее использованием преподаватель составляет билеты, в каждом из которых содержится 5 вопросов. Верный ответ на каждый вопрос оценивается в один балл. К каждому вопросу прилагается 3-5 ответов, среди которых только один верный. Цифровые коды ответов двузначные. Их вырабатывает включенный в программу генератор целых случайных чисел Zi. В качестве z0 используется номер билета. Для работы генератора нужны две константы, употребляемые при получении очередного числа: a и b, превышающее на единицу наибольший код. Если число билетов не превосходит 26, можно рекомендовать a=11, b=27, 29 или 31. Цифровые коды ответов лучше писать на билетах карандашом: если билеты использовались достаточно долго и возникает подозрение, что отвечающие не думают над ответами, а пользуются разгаданными сочетаниями цифровых кодов, то достаточно, изменив b, перекодировать ответы, стирая старые коды.
(Если же есть опасения, что учащиеся изменят введенную в калькулятор программу так, что она будет выставлять лишь положительные оценки, клавиатуру можно закрыть маской с прорезями для необходимых клавиш).
Программа может использоваться в двух режимах: в режиме кодировки при подготовке билетов и в режиме контроля ответов по билетам.
00. ПД 01. ПС 02. ИП9 03. П0 04. 5 05. П1 06. 6 07. ИП1 08. - 09. 2 10. F10x 11. * 12. С/П 13. ИПД 14. ИПА 15. * 16. ^ 17. ИПВ 18. / 19. 1 20. + 21. П2 22. F() 23. КИП2 24. F() 25. ИП2 26. ИПВ 27. * 28. - 29. ПД 30. - 31. Fx!=0 32. 37 33. КИП0 34. 2 35. БП 36. 39 37. 5 38. ^ 39. 6 40. ИП1 41. - 42. F10x 43. / 44. ИПС 45. + 46. ПС 47. FL1 48. 06. 49. ИП0 50. С/П 51. БП 52. 00.
Если предполагается работать с программой в режиме контроля, преподаватель вводит ее, затем набирает на клавиатуре F АВТ 1 5 ВП 9 9 ВП ^ П9 а ПА b ПВ Сх В/0. Студент должен набрать на табло номер билета N и нажать клавишу С/П. Через некоторое время на индикаторе высвечивается цифра 100, означающая, что следует отвечать на первый вопрос билета (номера вопросов выводятся с двумя нулями специально, чтобы их было легко отличить от кодов ответов и оценки). Отвечающий выбирает правильный, по его мнению, ответ, набирает на табло код этого ответа и нажимает клавишу С/П. На индикаторе - цифра 200, означающая, что надо отвечать на второй вопрос билета. Вновь набирается код и нажимается клавиша С/П... После ответа на пятый вопрос на индикаторе появляется оценка. Чтобы отличить ее от кодов, она выводится с символом Е, например Е5 - отлично. Хранится оценка в регистре 0. Можно узнать, на какие вопросы был дан неверный ответ: если нажать клавишу x-y, иа индикаторе высветится число вида N.qqnqn. Например 15.55252 означает, что были неправильно даны ответы на третий и пятый вопросы (цифры после запятой) 15-го билета (цифры до запятой). Это число хранится в PC.
Для того, чтобы закодировать верные ответы при составлении билетов, следует внести в текст программы следующие изменения: ... 12. КНОП... 30. С/П 31.БП 32.13... (если программа используется только для кодировки, то дальше текст набирать не нужно). Введя программу, надо затем ввести вручную число a в регистр А, число b в регистр В (эти же числа следует потом использовать и при работе в режиме контроля). Далее надо выписать коды верных ответов на билет, действуя следующим образом: набрать номер билета N В/0 С/П; на индикаторе высвечивается код правильного ответа на первый вопрос данного билета. Списав код, вновь нажимаем клавишу С/П, списываем код ответа на следующий вопрос билета, и так далее до последнего вопроса. Неверные ответы кодируются произвольным образом в рамках интервала 1-К.
Несколько слов о работе программы. Команды по адресам 00-12 заносят константы в соответствующие регистры, в частности сообщение Е5 в регистр 0, и выводят на индикатор номер вопроса, на который следует дать ответ. По адресам 13-29 размещается программа-генератор верных кодов, работающая согласно формуле zi=z[i-1]a-(z[i-1]a/b)b.
Если отвечающий выбрал верный код ответа, то при вычитании из него кода, сгенерированного программой, получается ноль (адреса 30-32) и начальное значение оценки остается без изменения, а в контрольном числе учета верных ответов (регистр С) в соответствующей позиции проставляется 5 (адреса 37-46). Если же набранный и выработанный программой коды не совпали, то оценка снижается на 1 балл и в соответствующей позиции контрольного числа проставляется 2 (адреса 33-36 и 39-46). Оператор цикла, размещенный по адресам 47-48, обеспечивает пятикратное выполнение указанных действий, что соответствует числу вопросов в билете. Выполнение программы заканчивается индикацией оценки; контрольное число при этом располагается в стековом регистре Y. Команда 51. БП 52. 00 передает управление на начальный адрес программы при новом цикле вычислений, то есть при ответе другого студента на иной билет.
В заключение читатели
могут с помощью данной программы проверить свои знания об "Электронике Б3-34", приняв a=11 и b=27. В скобках к ответам предлагаемого билета указаны коды ответов,- выбирайте правильный. Ни пуха ни пера!
Билет #1
1. С помощью какой команды (из числа предлагаемых) в регистр X вызывается предыдущий результат: F() (32); ^ (3); FBx (ll)
2. Каким образом отреагирует программа на команду В/0, помещенную вне подпрограммы? Остановится (17); передаст управление на адрес 00 (28 ); передаст управление на адрес 01 (13).
3. Какой результат появится на индикаторе при выполнении команд ВП 26 ^, если до этого там было число 3.56e12? 3.56e26 (18 ); 3.56e12 (4); 3.56e38 (8 ).
4. Что произойдет при выполнении программы: 00. 5 01. 0 02. F10x 03. ^ 04. * 05. П9 06. КНОП 07. ИП9 08. 7 09. С/П? Программа выполнится до конца, и на индикаторе высветится число 7 (2); произойдет останов программы на шаге 04, и высветится ЕГТОГ (25); произойдет останов программы на шаге 07, и высветится ЕГГОГ (7).
5. Какой результат получится при выполнении команд: 10 ВП 99 П7? ЕГГОГ (6); 1e10 (23); 0 (15).
С МИКРОКАЛЬКУЛЯТОРОМ В ГЛУБЬ ВЕКОВ
Подробности обстановки делают описания исторических событий гораздо более запоминающимися. Известно ли вам, светила ли Луна в Варфоломеевскую ночь? Это легко выяснить с помощью нехитрой программы, приведенной ниже. Число 15, полученное в результате,- это возраст полной Луны, какой она была 24 августа 1572 года. Представив ее себе, вы словно оказываетесь на месте тех трагических событий при зловеще ярком лунном свете.
Луна, как утверждали средневековые астрологи, влияет на жизнь человека ночью, но есть исключения, например, солнечные затмения. В начале похода князя Игоря на половцев, 1 мая 1185 года, наблюдалось солнечное затмение. Расчет по той же программе показывает возраст Луны: 29. Это естественно, так как солнечное затмение практически совпадает с новолунием. (Лунный цикл составляет 29.530588 дня).
В одной из научно-популярных книг по истории России я прочел цитату из "Летописной повести о побоище на Дону" (то есть о Куликовской битве): "В субботу рано 8 сентября, в самый праздник во время восхода солнца была тьма великая по всей земле, мгла, не было света от утра до третьего часа". Я подумал, что речь идет о солнечном затмении. Калькулятор не подтвердил это предположение: возраст Луны в День битвы оказывается равным 8. Таким образом, летописец передал свои впечатления о каком-то другом явлении, для меня оставшемся загадкой.
Привожу программу "Возраст Луны":
Программа. 00. П3 01. С/П 02. П1 03. С/П 04. П2 05. 3. 06. - 07. Fx<0 08. 13 09. КИП3 10. ИП2 11. 9 12. + 13. 4 14. + 15. 3 16. 0 17. , 18. 6 19. * 20. ПП 21. 54 22. 3 23. 6 24. 5 25. , 26. 2 27. 5 28. ИП3 29. * 30. + 31. ПП 32. 54 33. ИП1 34. + 35. 2 36. + 37. П5 38. 2 39. 9 40. , 41. 5 42. 3 43. 0 44. 5 45. 8 46. 8 47. П4 48. / 49. ПП 50. 54 51. ИП4 52. * 53. - 54. 1 55. + 56. П0 57. КИП0 58. ИП5 59. ИП0 60. В/0.
Программа составлена для юлианского летосчисления (старого стиля). Инструкция: набрать на клавиатуре В/0 год С/П число С/П месяц С/П. На индикаторе - возраст Луны.
В.АДРИАН (г.Химки).
[ ПРИГЛАШАЕМ ЗА "КРУГЛЫЙ СТОЛ"
"Часто бывает нужно вывести на индикатор сообщение ЕГГОГ,- пишет нам инженер М.Хузмиев из г.Орджоникидзе.- Обычно в программах для этого используются команды К+, К5 и т.п. или сочетания команд Сх F1/х, - Fsqr и им подобные, приводящие к некорректным операциям. Однако желаемого сообщения при этом приходится ждать более 3 секунд. Оказывается, однако, что двумя командами, вводимыми последовательным нажатием клавиш "ВП" и "запятая", сообщение ЕГГОГ вызывается мгновенно.
Обнаружил это мой пятилетний сын, успешно осваивающий микрокалькулятор в рамках нашей семейной учебной программы "Программировать раньше, чем читать". Жаль, что эта программа не вписывается в рамки раздела "Человек с микрокалькулятором" - можно было бы поделиться интересным опытом".
Рамки раздела раздвинуть нетрудно. Объявляем предложение М.Хузмиева темой очередного "круглого стола". Просим тех, кто имеет успешный опыт ликвидации компьютерной неграмотности в собственной семье, рассказать в своих письмах об этом ]
[ НАШЕГО ПОЛКУ ПРИБЫЛО
Один за другим наши научно-популярные журналы включаются в борьбу за ликвидацию компьютерной неграмотности. Работе на микрокалькуляторе "Электроника Б3-34" учит "Школа программирования", которую вел в "Технике-молодежи" И.Данилов, и продолжающиеся в ней "Электронные игры" (консультант - летчик-космонавт СССР Ю.Глазков). О решении отдельных конкретных задач на том же калькуляторе обстоятельно рассказывает "Химия и жизнь". Цикл статей А.Когана "Программируйте с нами, программируйте сами" в журнале "Энергия" увлекательно и последовательно излагает общетеоретические основы программирования без привязки к какой-либо конкретной вычислительной машине.
Появление все новых циклов, рубрик, разделов такого рода становится привычным. Вместе с тем уже заявляет о себе другое направление пропаганды компьютерной грамотности, пока менее заметное, но открывающее большие возможности, поскольку оно не ограничено рамками никаких разделов и циклов.
В 2 журнала "Геодезия и картография" за 1985 год есть статья К.Лапинга "Гиперболическая засечка с трех исходных пунктов". Постановка задачи, формулы решения - и вслед за ними фраза: "Предлагаемые формулы удобны для программирования на микрокалькуляторе "Электроника Б3-34".
Это короткое примечание - знак нового качества исследовательской работы, которая с самого начала, с выбора метода решения предполагает машинное завершение. При таком подходе многие статьи, публикуемые в специальных журналах, могли бы стать конкретными уроками компьютеризации научных исследований. Пример "Геодезии и картографии" достоин подражания и развития ]
ЭТА ТАИНСТВЕННАЯ КОМАНДА ВП
Как пользоваться командой ВП по ее прямому назначению, знают все, кто работает с "Электроникой Б3-34". Однако есть у этой команды и другие возможности. Взять, к примеру, такую программу: ПР ВП С/П (Р - обозначение одного из регистров). Для аргумента X из интервала 1<=Х<10 эта программа выполняет функцию отделения дробной части. Если же говорить о более широком диапазоне изменения аргумента 0<Х<=9.9999999e99, то здесь калькулятор, работая по такой программе, будет отбрасывать первый разряд числа, соответственно уменьшая порядок результата на единицу. Другой вариант: ^ ПР ВП - С/П. Такая программа в "широком" диапазоне изменения аргумента будет отбрасывать все значащие разряды, кроме первого, сохраняя неизменным порядок числа. Если говорить об X, заключенном в 1<=Х<11, то программа отделяет целую часть числа.
Эти программы можно использовать и как подпрограммы, вызывая их, например, в цикле. Следует отметить, что в ряде случаев перед командами ПР ВП необходимо вставлять команду ^, например, при выделении второго разряда числа из интервала 10<=Х<=99. Цепочка команд ПР КИПР ИПР ^ ПР ВП в течение двух-трех секунд превратит число 65.432109 в 5. (Здесь Р - число от 7 до 9 или буква).
По-другому функционируют указанные последовательности команд в области отрицательных чисел. Каждый сам может исследовать это, поставив несложный численный эксперимент.
А.БОЙКО (г.Москва)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Знание кодов команд, или таблица кодов, например, та, что была опубликована в 12/84, поможет быстрее отредактировать программу с ошибками. Если ошибка обнаружена в адресе "парной" команды (команды цикла, условного или безусловного перехода, обращения к подпрограмме), не всегда следует, как рекомендуется в пояснении к таблице, исправлять команду целиком, отступая на два шага. Верный адрес можно набрать клавишами, определяющими команду, код которой совпадает с требуемым адресом. Часто при этом достаточно нажать лишь одну клавишу, например, для адреса 50 - клавишу С/П, для 13 - клавишу / (деление). Набор текста готовой программы можно ускорить, если вместо адресов 50 и 52 использовать команды С/П и В/0 и т.п.
А.БОРИСОВ (г.Москва) ]
[ УЗЕЛКИ НА ПАМЯТЬ
В 12/84 год описывалось устройство, подсоединяемое к "Электронике "Б3-34": оно подает звуковой сигнал, когда микрокалькулятор заканчивает вычисления по программе.

Озвучить можно и "Электронику МК-54". Удобно включить в цепочку диод Д220, микротелефон ТМ-2А и для регуляции громкости - переменный резистор 100кОм типа СПЗ-36. Все детали поместятся в корпусе микрокалькулятора. Под диск регулировки резистора и микротелефон необходимо вырезать окна в крышке калькулятора.
М.БАХМУТСКИЙ (г.Львов.) ]
ОХОТА НА "ЛИС"
Название позаимствовано от известной спортивной игры, детали которой узнаются п нижеследующем описании.
В памяти калькулятора хранится картина игрового поля размером 9*9 клеток. В пяти различных клетках располагаются пять "лис" - радиопередатчики, посылающие в эфир сигнал "я здесь". Передатчики могут занимать соседствующие клетки. Играющий очередным своим ходом вводит в калькулятор положение "охотника", набирая на клавиатуре дробное двузначное число вида Y.X - целая и дробная его части выражают координаты по вертикали и по горизонтали соответственно. "Охотник" вооружен приемником, имеющим направленную антенну, так что сигналы от "лис" принимаются лишь по восьми направлениям, как показано на рисунке. На индикатор выводится число "лис", расположенных по этим направлениям. Если на каком-то направлении оказались две "лисы", то считаются обе. Если координаты какой-либо "лисы" совпадают с положением "охотника", то на индикаторе появляется сообщение ЕГГОГ. Обнаруженная "лиса" не исчезает с игрового поля н продолжает посылать сигналы. Меняя ход за ходом положение "охотника" и анализируя информацию, выдаваемую калькулятором, играющий путем логических умозаключений или графических построений должен обнаружить всех "лис" за наименьшее число ходов. Играть в эту игру можно в одиночку, но можно проводить и соревнования.

Настало время вводить программу. Кратко прокомментируем назначение отдельных фрагментов (по адресам).
Программа. 00. ПД 01. 1 02. 0 03. П0 04. П3 05. 5 06. П1 07. ПП 08. 69 09. П2 10. ПП 11. 69 12. ИП3 13. / 14. ИП2 15. + 16. КП0 17. FL1 18. 07 19. Сх 20. С/П 21. ПД 22. 0 23. П4 24. ИП3 25. П0 26. 5 27. П1 28. ИПД 29. КИП0 30. - 31. ПС 32. Fx=0 33. 38 34. ВП 35. , 36. БП 37. 21 38. ИПД 39. ПА 40. КИПА 41. КИП^ 42. ПВ 43. КИПВ 44. ИПВ 45. ИПА 46. - 47. Fx!=0 48. 63 49. ПВ 50. ИПС 51. + 52. ИП3 53. * 54. Fx!=0 55. 63 56. ИПВ 57. / 58. Fx2 59. 1 60. - 61. Fx=0 62. 64 63. КИП4 64. FL1 65. 28 66. ИП4 67. БП 68. 20 69. ИПД 70. ВП 71. 9 72. Fcos 73. Farccos 74. Fпи 75. / 76. ПД 77. 9 78. * 79. 1 80. + 81. ПА 82. КИПА 83. ИПА 84. B/0.
00: запись исходного случайного числа. 01-06: запись констант, 07-15: формирование числа вида Y, X. 16: установка "лисы". 17-18: проверка "все ли лисы поставлены?" 19: сообщение о начале игры, "0". 20-21: запись координат "охотника". 22-23: очистка счетчика сигналов. 24-25: установка указателя на адрес первой "лисы". 26-27: начальная установка счетчика "лис". 28-35: проверка "лиса обнаружена?" 36-37: переход к индикации и запросу координат "охотника". 38-40: выделение координаты Yо "охотника". 41-43: выделение координаты Yл "лисы". 44-48: проверка "лиса пеленгуется по горизонтали?" 49-51: отделение дробной части разности Yo, Xо - Yл, Xл; результат - число 0.(Xо-Хл). 52-53: получение числа Xо-Xл . 54-55: проверка "лиса пеленгуется по вертикали?" 56-62: проверка "лиса пеленгуется по диагонали?" 63: добавление единицы к содержимому счетчика сигналов. 64-65: переход к очередной "лисе". 66-68: формирование сообщения о числе "лис". 69-84: генерация псевдослучайного числа по формуле e[i+i]=(1/пи)arccos(cos(1e8*ei)+D), где D - погрешность вычисления косинуса, и формирование целого числа [9e + 1] . Программа введена, и осталось лишь внимательно ознакомиться с инструкцией.
1. Нажмите В/0. Наберите случайное число от 0 до 1, например, 0.ЧЧММ; здесь ЧЧ и ММ - часы и минуты, в которые начата игра. Нажмите С/П - калькулятор примется распределять "лис" по игровому полю. Через пару минут на индикаторе появится сигнал готовности "0".
2. Введите координаты "охотника" Y.X С/П, где Y и X - целые числа от 1 до 9, разделенные запятой. Например, 7.6 - это позиция охотника на рисунке. На индикаторе появляется число "лис" по направлениям пеленга или- ЕГГОГ, если "лиса" найдена. В нашем случае получаем 2. Затем вводим следующие У, X.
3. Для повторения игры с иной расстановкой "лис" переходите к п.1.
А.НЕСЧЕТНЫЙ (г.Ленинград)

Рис. В.Торгашина (г.Жуковский Московской обл.)
"ВОЛЧЬИ ЯМЫ" ОКРУГЛЕНИЯ
Американский математик Уилкинсон исследовал уравнение
(х-1)(х-2)(х-3)... (х-20) = х**20 - 210*х**19 + ... + 20! = 0
Он заменил коэффициент -210 на -(210+2**-23), то есть увеличил его примерно на 1e-7. Ни один из корней нового уравнения не был близок к корням 11, 13, 15 старого, причем среди них оказались и комплексные корни.
Этот пример убеждает, какую каверзную роль может сыграть в расчетах изменение даже далеких от запятой значащих цифр. А ведь таким риском нередко чреваты вычисления на микрокалькуляторе. Все, что лежит за пределами его восьмиразрядного индикатора, отсекается, и возникают ошибки округления. Опыт вычислений на бумаге не воспитывает в нас осторожности по отношению к ним: эффекты округления видны воочию; опасаясь ошибки, можно менять число удерживаемых разрядов. При счете на калькуляторе приходится доверяться машине, и может случиться так, что основную часть полученного ответа составят ошибки округления, отчего ответ окажется весьма далеким от истинного.
Наиболее опасной в смысле потери точности операцией является вычитание близких друг к другу чисел.
Попробуем вычислить на микрокалькуляторе еxp(-10) согласно разложению
exp(-10) = 1 - 10 + 1e2/2! - 1e3/3! + ...
Вместо истинного результата 0.0000454 получается 0.0001112 - число, в 2.5 раза больше. Откуда же набежала погрешность? Покуда в слагаемых ряда рост факториала в знаменателе обгонит рост степени в числителе, они возрастают до десятого включительно, принимая значения, превосходящие 2000. А так как счет ведется только до восьми значащих цифр, то ответ получается с точностью лишь до 0.0001. Вот и набегают ошибки, значительно превосходящие искомый ответ. Чтобы получить верный результат, надо записать exp(-10) в виде 1/еxp(10), разложить знаменатель этой дроби в ряд
exp(10) = 1 + 10 + 1e2/2! + 1e3/51 + ...
а затем от найденной суммы ряда взять обратную величину.
Разумеется, нет смысла считать еxp(-10) на калькуляторе, имеющем клавишу exp. Но ведь иногда приходится вычислять значения и более экзотических функций, скажем, бесселевой или гипергеометрической, используя опять-таки степенные ряды, где подстерегают "волчьи ямы" округления.
Ошибки, вызванные вычитанием мало отличающихся друг от друга чисел, могут возникнуть и при такой простой операции, как нахождение корней квадратного уравнения: X1,2=(-b +/- sqr(b**2-4ас))/2а. Если b**2 значительно превосходит 4ас, то в числителе формулы приходится вычитать именно такие числа. Например, решая на микрокалькуляторе уравнение х**2-1e5*x+1=0, вместо одного из корней 0.0000100 мы получим нуль. Это уже никуда не годится.
Такие примеры напоминают: применение микрокалькулятора, как использование любого технического устройства, предъявляет свои требования к выбору методов работы и к ясности понимания того, что может и чего не может сделать данное устройство.
Н.ВИЛЕНКИН (г.Москва)
[ С увеличением адреса выполняемой команды быстродействие микрокалькулятора постепенно уменьшается. При этом разница во времени исполнения одних и тех же команд, расположенных по различным адресам, может достигать 30 процентов. Сравните время выполнения следующих двух программ. 00. FL0 01. 00 02.С/П и 95. FL0 96. 95 97. С/П. В регистр Р0 занесите число циклов, например, 600. Эту особенность следует, по-моему, использовать для убыстрения расчетов: подпрограммы следует размещать не в конце, а в начале программной памяти.
П.МОЛОДЧИК (г.Киев) ]
[ Как известно, микрокалькулятор Б3-34 не вычисляет корней с нечетными показателями из отрицательных чисел. Предлагаю программу, которая позволяет обойти этот недостаток. 00. Fx2 01 . Flg 02. M 03. / 04. F10x 05. Fsqr 06. С/П. Здесь М = 3, 5, 7, 9 - показатель корня. Если требуется вычислить корень большей степени, М принимает значения 11, 13 и т.д., а программа, начиная с адреса 03, выглядит так: 03. М 04. / 05. F1Ox 06. Fsqr 07. С/П
А.ЗАЙЦЕВ (г.Щигры Курской обл.) ]

Рис. А.Кузовкииа
(г.Березники Пермской обл.)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
1/86
Высокими темпами наращивать масштабы применения современных высокопроизводительных электронно-вычислительных машин всех классов.
Активнее внедрять информатику и электронно-вычислительную технику в учебный процесс.
Из проекта Основных направлений экономического и социального развития СССР на 1986-1990 годы и на период до 2000 года.
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
В большой семье электронно-вычислительных машин микрокалькуляторы на первый взгляд неприметны. Быстродействие у них невысокое, объем памяти ограничен. Но есть у них свои достоинства. Они портативны, просты в обращении. Владелец такой "карманной ЭВМ" может воспользоваться ею в любой момент, когда требуется провести посильный ей расчет. Необходимость в этом то и дело возникает у работников самых различных специальностей. Но для работы на программируемом микрокалькуляторе необходимы определенные знания и навыки. Помочь в их приобретении - задача цикла статей "Школа начинающего программиста", публикуемого в нашем журнале с 6/85.
ЗАНЯТИЕ ШЕСТОЕ, где речь пойдет о трех важных понятиях, уверенное владение которыми необходимо для составления сложных программ,- о ветвях, циклах, подпрограммах.
Занятие ведет кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт).
Самая первая программа, составленная нами для вычисления площади круга, была коротко" и простой:
00. Fx2 01. Fпи 02. * 03. 4 04. / 05. С/П.
Простота се заключается не только в краткости. Обратите внимание: все ее команды выполняются в том порядке, в котором они записаны. Программы, отличающиеся таким свойством, называются ЛИНЕЙНЫМИ. На практике они встречаются чрезвычайно редко. Для большинства программ характерно то, что порядок выполнения команд не совпадает с порядком их записи. Для того, чтобы изменить естественный порядок выполнения программ, применяются УПРАВЛЯЮЩИЕ КОНСТРУКЦИИ, которые подразделяются на три типа:
- ВЕТВЛЕНИЕ, когда в зависимости от соблюдения или несоблюдения некоторого условия надо выполнить либо одну, либо другую последовательность действий;
- ЦИКЛ, многократное выполнение каких-либо действий (записанная один раз в программе последовательность команд выполняется несколько раз подряд);
- ПОДПРОГРАММА, специальным образом оформленная последовательность команд, к котором можно обратиться, то есть потребовать прервать выполнение команд основной программы, выполнить нею последовательность команд подпрограммы, а затем продолжить выполнение команд основной программы.
О трех перечисленных конструкциях и пойдет сейчас речь. Как и ранее, будем иллюстрировать алгоритмы блок-схемами; записывать их станем на алгоритмическом языке, с которым с этого года начинают знакомиться школьники девятых классов.
Для изменения естественного порядка выполнения команд у калькулятора "Электроника Б3-34" имеется операция БЕЗУСЛОВНОГО ПЕРЕХОДА БП; четыре операции УСЛОВНЫХ ПЕРЕХОДОВ Fx=0, Fx!=0, Fx<0, Fx>=0, четыре операции ОРГАНИЗАЦИИ ЦИКЛОВ FL0, FL1, FL2, FL3, операция ПЕРЕХОДА К ПОДПРОГРАММЕ ПП и команда ВОЗВРАЩЕНИЯ К ОСНОВНОЙ ПРОГРАММЕ В/0 (есть еще команды косвенных безусловных и условных переходов, но они употребляются крайне редко и потому пока рассматриваться не будут).
Отметим характерную особенность операций условных переходов: все они основаны на сравнении содержимого регистра X с нулем. Правда, на нашем калькуляторе возможны не все такие проверки: нет операций х>0, х<=0 . Когда необходимо выполнить какую-либо из них, то у величин, подлежащих подобной проверке, меняют знак и проводят сравнения -х<0, -х<=0 соответственно.
ВЕТВЛЕНИЕ. Рассмотрим несложную задачу: взять максимальное из значений переменных a и b, хранящихся в РА и РВ соответственно, и присвоить взятое значение переменной c, хранящейся в PC. Нетрудно составить алгоритм требуемого действия: если a=>b, то положить c=a; в противном случае положить c=b. На алгоритмическом языке это можно записать так:
если а>=b то с:=а иначе с:=в все.
Составим соответствующую программу для нашего калькулятора. Будем рассматривать ее как фрагмент какой-то большой программы и потому станем записывать ее не с нулевого адреса, а с какого-то другого, скажем, с 10-го. (Так будем поступать и при записи дальнейших программ, играющих роль примера).
Сначала программируем условие а>=b. Видоизменяем его так, чтобы получилось выполняемое на калькуляторе сравнение с нулем: a-b>=0.
10. ИПА 11. ИПВ 12. - 13. Fx>0 14. []
Если условие не выполняется, то произойдет переход по адресу, указанному вслед за операцией сравнения. Начиная с этого адреса, мы будем программировать ветвь ИНАЧЕ. Но этот адрес мы пока не знаем, а потому место для него оставляем незаполненным и обводим рамкой, чтобы не забывать о необходимости выполнения его в свое время, когда станет ясно, где расположится вновь ИНАЧЕ.
Если же условие выполняется (a-b>=0, то есть a>=b), управление будет передано на следующий за операцией сравнения, 15-й адрес. Начиная с него, и следует запрограммировать ветвь ТО, записать команды пересылки в регистр С числа а, которое хранится в регистре А:
15. ИПА 16. ПС
Далее можно разместить ветвь иначе. Но писать ее команды сразу вслед за командами ветви ТО нельзя: в таком случае калькулятор выполнит подряд и те, и другие действия, смешает их. Закончив ветвь то, надо обойти ветвь ИНАЧЕ. Ставим команду безусловного перехода и опять оставляем пустым место для адреса перехода, так как пока не знаем, куда надо перейти:
17. БП 18. []
А затем программируем ветвь ИНАЧЕ, пересылку в регистр С числа b, которое хранится в регистре В:
19. ИПВ 20. ПС
Для лучшего понимания всю эту цепочку команд, записанных в строчку или в столбик, можно снабдить стрелками, как на рисунке. Там же приведена и блок-схема программируемого фрагмента.
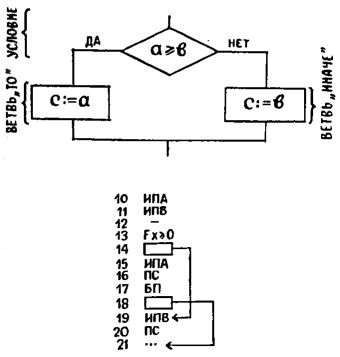
Теперь можно заполнить пропущенные ячейки. Чтобы обойти ветвь ТО (ветвь ДА на блок-схеме), по адресу 14, после операции сравнения записываем 19 - начальный адрес ветви ИНАЧЕ (ветви НЕТ на блок-схеме). Чтобы обойти ветвь ИНАЧЕ, по адресу 18, после операции безусловного перехода, записываем 21 - начальный адрес последующего фрагмента программы. Заметим: на этот адрес мы попадаем, пройдя и по той к по другой ветви.
Как видим, записанное на алгоритмическом языке или в виде блок-схемы ветвление переводится в программу для калькулятора по чисто формальным правилам:
1. Запрограммировать левую часть условия, предварительно преобразованного к сравнению с нулем.
2. Записать соответствующую команду условного перехода и оставить незаполненным адрес перехода.
3. Запрограммировать ветвь ТО.
4. Записать команду БП и оставить незаполненным адрес перехода.
5. Запрограммировать ветвь ИНАЧЕ.
6. В пропущенную на шаге 2 ячейку записать адрес начала ветви ИНАЧЕ; в пропущенную на шаге 4 ячейку записать адрес очередной еще не занятой ячейки.
Тщательная запись алгоритма на алгоритмическом языке превращает дальнейшее составление соответствующей программы в почти автоматический процесс. Однако наша программа получилась не совсем оптимальной из-за того, что школьный алгоритмический язык не отражает всех возможностей калькулятора. На ветви ТО (как на ветви ИНАЧЕ) можно запрограммировать лишь вызов величины a (соответственно b) в регистр X, а закончив ветвление, содержимое регистра X надо переслать в регистр С. Так мы получим более короткую программу.
10. ИПА 11. ИПВ 12. - 13. Fx>=0 14. 18 15. ИПА 16. БП 17. 19 18. ИПВ 19. ПС
Прослеживая перемещения чисел по регистрам X, A, В, С, убедитесь, что этот вариант программы дает те же результаты, что и предыдущий.
Если отказаться от "подстрочного" перевода нашей записи алгоритма на язык команд микрокалькулятора, то возможен еще более короткий вариант:
10. ИПА 11. ИПВ 12. ПС 13. - 14. Fx>=0 15. 18 16. ИПА 17. ПС.
Этот пример ставит нас перед вопросом: насколько полезны при составлении программы такие вспомогательные средства, как блок-схема алгоритма и его запись на алгоритмическом языке? И какое из этих средств предпочтительнее? Конечно, запись на алгоритмическом языке уступает блок-схеме в наглядности, но при своей построчечной структуре, подкрепленная строгими правилами ее перевода на язык команд, эта запись, пожалуй, надежнее позволяет получить работающую программу даже в сложных случаях, при наличии многих циклов и ветвлений. Это тем более верно, если в алгоритмическом языке имеются конструкции, отражающие существенные для программирования особенности микрокалькулятора. К сожалению, используемый нами язык не таков, блок-схема и в этом отношении превосходит его, способна оказать большую помощь при поиске оптимального варианта программы. Достигнет же оптимума тот, кто владеет всеми возможностями калькулятора (прежде всего - возможностями стека) и умело использует их, претворяя алгоритм в программу.
Перевод разветвляющегося алгоритма в программу упрощается, когда при невыполнении условия надо просто ничего не делать, то есть ветвь ИНАЧЕ оказывается пустой:
1. Запрограммировать проверку условия.
2. Записать команду условного перехода и оставить незаполненным адрес перехода.
3. Запрограммировать ветвь ТО.
4. В пропущенную на шаге 2 ячейку записать адрес очередной свободной ячейки.
Например, пусть надо получить абсолютную величину числа a, хранящегося в РА. (Забудем на время, что проще всего это делается командами Fx2 Fsqr). Иными словами, надо выполнить действие:
если a<0 то a:=-a все
Первой командой программы, реализующей этот алгоритм, вызовем в регистр X число a, которое предстоит сравнить с нулем: 10. ИПА. Пишем команду сравнения, оставляя пока не заполненным адрес перехода: ll. Fx<0 12... Программируем ветвь ТО,- изменяем знак у содержимого РХ и засылаем результат в РА: 13. /-/ 14. ПА. Начальный адрес последующего фрагмента - 15. Его и вписываем в пустующее место по адресу 12. Окончательно:
10. ИПА 11. Fx<0 12. 15 13. /-/ 14. ПА
ЦИКЛ. Напомним, что так называется предписание о многократном повторении подряд некоторого фрагмента программы. Сам этот фрагмент называется телом цикла. Очередное его повторение определяется проверкой некоторого условия.
Обычно выделяют два типа циклов, в зависимости от того, когда производится проверка условия:
- цикл "пока" (сначала проверяется условие, и если оно соблюдено, то выполняется тело цикла, опять проверяется условие и так далее - таким образом, тело цикла выполняется, пока соблюдается условие);
- цикл "до" (сначала выполняется тело цикла, затем проверяется условие, и если оно не соблюдено, тело цикла выполняется вновь и так далее - таким образом, тело цикла выполняется до тех пор, как становится истинным условие).
На алгоритмическом языке цикл "пока" записывается так:
пока (указать условие) цикл (описать действия) кц
Цикл "до" записывается так:
цикл (описать действия) до (указать условие) кц
(Здесь кц - служебное слово, означающее "конец цикла").
Поясним сказанное примером. При взлете самолета его вертикальная скорость v (скорость набора высоты) изменяется в зависимости от времени t по некоторому закону v(t). Надо определить, за какое время самолет достигнет заданной высоты Н. Высота S, набранная к моменту времени Т, выражается интегралом(0,T)v(t)dt . Оставив в стороне самолет и сосредоточившись на математической стороне дела, получаем задачу:
найти Т такое, что интеграл(0,T)v(t)dt=Н.
Для вычисления интеграла возьмем простейшую формулу прямоугольников (см. рисунок). Разобьем площадь под кривой v(t) на столбики шириной h и каждый из них заменим прямоугольником той же ширины с высотою, равной значению функции в левой точке отрезка. Суммарная площадь таких прямоугольников есть приближенное значение интеграла. Будем набирать прямоугольники, пока их суммарная площадь ие превосходит величину Н.
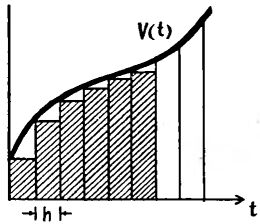
Отметим, что при Н=0 нам не надо брать ни одного прямоугольника. Таким образом, проверку, брать ли очередной прямоугольник, надо производить перед тем, как его взять. Вспоминая, что циклы бывают двух типов, мы можем сказать, что программируемый нами относится к типу цикл "пока".
Запишем лежащий в его основе алгоритм - назовем его ВЗЛЕТ. В заголовке алгоритма перечислим его аргументы (Н, h) и результаты (Т). Промежуточную переменную S укажем позже, сразу вслед за служебным словом нач (начало). Примем, что скорость нарастает как квадрат времени: v(t)=t**2.
В перечне промежуточных переменных, как видим, нет v и t, которые встречаются в программируемых нами формулах. Первое из этих обозначений излишне, поскольку мы установили явную зависимость v(t). Обозначение t можно объединить с Т. Так можно сократить запись алгоритма - избежать присваивания Т:=t, когда переменная S достигнет значения Н: при этом значение Т и будет давать ответ поставленной задачи.
Придадим величинам S и Т исходные нулевые значения (стартуем в нулевой момент с нулевой высоты). Приступим к программированию цикла. Прежде всего запишем условие, при выполнении которого тело цикла должно быть пройдено в очередной раз: пока S<Н. Пока это неравенство соблюдается, величине S при каждом очередном прохождении цикла надо присваивать значение S+T**2*h, а величине Т - значение Т+h. Перечень этих операций предварим служебным словом цикл, а завершим служебным словом кц (конец цикла).
Если неравенство S<Н не соблюдается, должен произойти выход из цикла. Текущее значение величины Т при этом и является результатом.
алг ВЗЛЕТ (вещ Н, h, T);
- арг Н, h; рез Т;
нач вещ S;
- S:=0; Т: =0;
- пока S<Н цикл
- - S:=S+T**2*h; Т=Т+h
- кц
кон
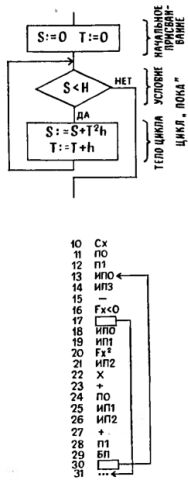
Запрограммируем разработанный алгоритм. Аргументы и результаты, указанные в первых строках его записи на алгоритмическом языке, и вспомогательные переменные, указанные далее, напоминают нам: перед составлением программы необходимо распределить адресуемые регистры под хранение величин, фигурирующих в алгоритме. Пусть величина S хранится в Р0, Т - в Р1, h - в Р2, Н - в Р3. Поскольку начальные значения S и Т должны равняться нулю, зашлем нули в Р0 и Р1.
10. Cx 11. П0 12. П1
Преобразуем условие S<H к сравнению с нулем S-Н<0 и запрограммируем это сравнение. Адрес перехода пока оставим незаполненным.
13. ИП0 14. ИП3 15. - 16. Fx<0 17. []
При соблюдении условия Fx<0 калькулятор передаст управление на команду, следующую за командой условного перехода. С этого места мы и запишем тело цикла.
Завершим его командой безусловного перехода: она должна передавать управление на команду, с которой начинается проверка условия, определяющего очередное прохождение цикла.
18. ИП0 19. ИП1 20. Fx2 21. ИП2 22. * 23. + 24. П0 25. ИП1 26. ИП2 27. + 28. П1 29. БП 30. 13
Внимательно разберите эту цепочку команд. Проверьте, что команды 18-24 вычисляют выражение S+T**2*h. Команда безусловного перехода (адреса 29-30), как и требуется от нее, передает управление на адрес 13, то есть на команду, с которой начинается проверка условия S-Н<0. Если оно выполняется вновь, тело цикла будет пройдено еще раз. Если не выполняется, надо передать управление на начало фрагмента, который должен выполняться по выходе из цикла,- то есть иа адрес 31. Его-то и нужно записать под адресом 17, пустующим до сих пор адресом команды условного перехода.
Проверьте, правильно ли составлена и верно ли работает программа. Введите ее в калькулятор, завершив набор командами 31. ИП1 32. С/П. Клавишами F АВТ верните калькулятор в режим вычислений; занесите в регистр 3 число 3, в регистр 2 - число 0.1; клавишами БП 10 передайте управление на адрес 10; клавишей С/П запустите калькулятор. Примерно через две минуты на индикаторе появится результат 2.2. Он сильно отличается от точного (2.08), так как ширина прямоугольников h=0.1 была выбрана нами довольно большой.
Если разбор приведенной программы покажется вам трудным, укажите переходы стрелками и сравните свой рисунок с помещенным здесь.
Рассмотренный нами пример позволяет сформулировать правила программирования цикла "пока".
1. Программируем условие, преобразованное к сравнению с нулем.
2. Записываем команду сравнения и оставляем незаполненным адрес перехода.
3. Программируем тело цикла.
4. Записываем операцию БП, за нею - адрес начала проверки условия.
5. В пропущенную на шаге 2 ячейку записываем первый еще не занятый адрес.
Строя только что разобранную программу по типу цикла "пока", мы поступали так лишь потому, что из чисто формальных соображений не захотели исключать из рассмотрения случай Н=0. Если же заведомо ясно, что величина Н не нулевая, то программу для решения той же задачи можно составить по типу цикл "до". В этом случае тот же интеграл, что и ранее, будет подсчитываться до наступления условия S>=H (то есть условия, противоположного тому, на проверке которого строилась предыдущая программа, построенная с помощью цикла "пока").
На сей раз тело цикла запишется так: сначала, после служебного слова цикл - повторяемые действия, затем, после слова до,- условие, затем - служебное слово кц.
цикл S:=S+T**2*h; T:=T+h
- до S>=Н кц
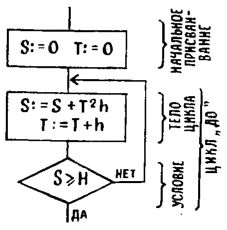
Предлагаем читателю самостоятельно составить программу, реализующую этот алгоритм, и сверить ее с помещенной ниже. Напомним лишь, что условие повторения цикла надо преобразовать к сравнению с нулем: S-Н>=0. Проверять его будем с помощью операции Fx>=0, которую проставим за телом цикла. А вслед за нею проставим начальный адрес тела цикла. Если неравенство ие выполняется, тело цикла будет пройдено еще раз. Если выполняется, произойдет выход из цикла.
10. Сх 11. П0 12. П1 13. ИП0 14. ИП1 15. Fx2 16. ИП2 17. * 18. + 19. П0 20. ИП1 21. ИП2 22. + 23. П1 24. ИП0 25. ИП3 26. - 27. Fx>=0 28. 13
(Чтобы испытать работу этого фрагмента, его следует дополнить командами 29. ИП5 30. С/П).
Как нетрудно усмотреть уже из этого примера, правила программирования цикла "до" несколько проще, чем цикла "пока":
1. Запрограммировать тело цикла.
2. Запрограммировать левую часть условия, преобразованного к сравнению с нулем.
3. Записать операцию сравнения и за нею - адрес начала тела цикла.
В обоих только что рассмотренных примерах к моменту начала выполнения цикла (к моменту входа в цикл) мы не могли сказать, сколько раз он будет пройден - это определяется по мере все новых его прохождений. Такие циклы называются итерационными. Но часто встречаются случаи, когда количество повторений цикла можно определить заранее. Например, если бы на до было вычислить интеграл(a b)f(x)dx описанным выше методом, цикл нужно было бы повторить столько раз, на сколько отрезков разбит промежуток интегрирования.
Поскольку подобные случаи весьма часто встречаются в практике программирования, для них имеется специальная форма записи на алгоритмическом языке:
цикл (указать число повторений) раз (описать действия) кц
Именно для организации таких циклов предназначены имеющиеся у "Электроники Б3-34" операции вида FLM (M - номер одного из первых адресуемых регистров, от нулевого до третьего включительно; его в подобных случаях называют счетчиком повторений цикла).
На предыдущих занятиях Мы уже не раз использовали эти операции (7/85, 9/85), знаем их свойства. Каждая из ннх образует команду в соединении с записанным сразу вслед за ней адресом перехода. Такая команда ставится в конце тела цикла и совершает два действия: уменьшает на единицу содержимое регистра М и, если это содержимое не равно единице к моменту выполнения команды, совершает переход на начальный адрес тела цикла. Если же к моменту выполнения команды содержимое регистра М равно единице, то, не уменьшая его, команда передает управление на следующий за нею адрес.
Зная все это, мы сможем сформулировать правила перевода конструкций, описанных выше на алгоритмическом языке, на язык команд "Электроники Б3-34":
1. Выбрать один из его регистров: Р0, Р1, Р2, Р3. Занести в него число повторений цикла.
2. Запрограммировать тело цикла.
3. Записать одну из операций: FL0, FL1, FL2, FL3 (в соответствии с тем, какой регистр был выбран на шаге 1) и за нею - начальный адрес тела цикла.
Чтобы не отступать от принятого порядка изложения, следовало бы разобрать здесь еще один пример на применение операции вида FLM. Попробуйте самостоятельно описать на алгоритмическом языке и затем запрограммировать для нашего калькулятора вычисление интеграла(a b)f(x)dx, положив по-прежнему f(х)=х**2. Обозначьте число отрезков, на которые разбит промежуток интегрирования, через n. Воспользуйтесь тем, что переменные величины в описаниях алгоритмов можно обозначить не только буквами, но и словами. Например, вычисляемый интеграл можно так и назвать: "интеграл".
Сравните свой вариант с приведенным здесь:
алг ИНТЕГРАЛ (вещ a, b, n, интеграл); арг а, b, n; рез интеграл;
нач вещ h, x
- h:=(b-а)/n;
- интеграл:=0; х:=а
- цикл n раз
- - интеграл:=интеграл+x**2*h;
- - х:=х+h;
- кц
кон
10. Сх 11. П5 12. ИП0 13. П4 14. ИП1 15. ИП0 16. - 17. ИП3 18. / 19. П2 20. ИП5 21. ИП4 22. Fx2 23. ИП2 24. * 25. + 26. П5 27. ИП4 28. ИП2 29. + 30. П4 31. FL3 32. 20
Распределение регистров тут таково: а - Р0, b - P1, h - Р2, n - Р3, х - Р4, интеграл - Р5. Адреса 10-19: очищаем Р5, заносим число а в Р4, вычисляем h=(b-а)/n и заносим в Р2. Адреса 20-30: тело цикла. Адреса 31-32: записанная здесь команда FL3 20 совершает переход на начальный адрес тела цикла до тех пор, когда содержимое регистра-счетчика Р3 станет равным единице. Тогда команда FL3 20 совершит выход из цикла - передаст управление на адрес 33, на последующий фрагмент, где будет использовано полученное значение интеграла.
Высокими темпами наращивать масштабы применения современных высокопроизводительных электронно-вычислительных машин всех классов.
Активнее внедрять информатику и электронно-вычислительную технику в учебный процесс.
Из проекта Основных направлений экономического и социального развития СССР на 1986-1990 годы и на период до 2000 года.
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
В большой семье электронно-вычислительных машин микрокалькуляторы на первый взгляд неприметны. Быстродействие у них невысокое, объем памяти ограничен. Но есть у них свои достоинства. Они портативны, просты в обращении. Владелец такой "карманной ЭВМ" может воспользоваться ею в любой момент, когда требуется провести посильный ей расчет. Необходимость в этом то и дело возникает у работников самых различных специальностей. Но для работы на программируемом микрокалькуляторе необходимы определенные знания и навыки. Помочь в их приобретении - задача цикла статей "Школа начинающего программиста", публикуемого в нашем журнале с 6/85.
ЗАНЯТИЕ ШЕСТОЕ, где речь пойдет о трех важных понятиях, уверенное владение которыми необходимо для составления сложных программ,- о ветвях, циклах, подпрограммах.
Занятие ведет кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт).
Самая первая программа, составленная нами для вычисления площади круга, была коротко" и простой:
00. Fx2 01. Fпи 02. * 03. 4 04. / 05. С/П.
Простота се заключается не только в краткости. Обратите внимание: все ее команды выполняются в том порядке, в котором они записаны. Программы, отличающиеся таким свойством, называются ЛИНЕЙНЫМИ. На практике они встречаются чрезвычайно редко. Для большинства программ характерно то, что порядок выполнения команд не совпадает с порядком их записи. Для того, чтобы изменить естественный порядок выполнения программ, применяются УПРАВЛЯЮЩИЕ КОНСТРУКЦИИ, которые подразделяются на три типа:
- ВЕТВЛЕНИЕ, когда в зависимости от соблюдения или несоблюдения некоторого условия надо выполнить либо одну, либо другую последовательность действий;
- ЦИКЛ, многократное выполнение каких-либо действий (записанная один раз в программе последовательность команд выполняется несколько раз подряд);
- ПОДПРОГРАММА, специальным образом оформленная последовательность команд, к котором можно обратиться, то есть потребовать прервать выполнение команд основной программы, выполнить нею последовательность команд подпрограммы, а затем продолжить выполнение команд основной программы.
О трех перечисленных конструкциях и пойдет сейчас речь. Как и ранее, будем иллюстрировать алгоритмы блок-схемами; записывать их станем на алгоритмическом языке, с которым с этого года начинают знакомиться школьники девятых классов.
Для изменения естественного порядка выполнения команд у калькулятора "Электроника Б3-34" имеется операция БЕЗУСЛОВНОГО ПЕРЕХОДА БП; четыре операции УСЛОВНЫХ ПЕРЕХОДОВ Fx=0, Fx!=0, Fx<0, Fx>=0, четыре операции ОРГАНИЗАЦИИ ЦИКЛОВ FL0, FL1, FL2, FL3, операция ПЕРЕХОДА К ПОДПРОГРАММЕ ПП и команда ВОЗВРАЩЕНИЯ К ОСНОВНОЙ ПРОГРАММЕ В/0 (есть еще команды косвенных безусловных и условных переходов, но они употребляются крайне редко и потому пока рассматриваться не будут).
Отметим характерную особенность операций условных переходов: все они основаны на сравнении содержимого регистра X с нулем. Правда, на нашем калькуляторе возможны не все такие проверки: нет операций х>0, х<=0 . Когда необходимо выполнить какую-либо из них, то у величин, подлежащих подобной проверке, меняют знак и проводят сравнения -х<0, -х<=0 соответственно.
ВЕТВЛЕНИЕ. Рассмотрим несложную задачу: взять максимальное из значений переменных a и b, хранящихся в РА и РВ соответственно, и присвоить взятое значение переменной c, хранящейся в PC. Нетрудно составить алгоритм требуемого действия: если a=>b, то положить c=a; в противном случае положить c=b. На алгоритмическом языке это можно записать так:
если а>=b то с:=а иначе с:=в все.
Составим соответствующую программу для нашего калькулятора. Будем рассматривать ее как фрагмент какой-то большой программы и потому станем записывать ее не с нулевого адреса, а с какого-то другого, скажем, с 10-го. (Так будем поступать и при записи дальнейших программ, играющих роль примера).
Сначала программируем условие а>=b. Видоизменяем его так, чтобы получилось выполняемое на калькуляторе сравнение с нулем: a-b>=0.
10. ИПА 11. ИПВ 12. - 13. Fx>0 14. []
Если условие не выполняется, то произойдет переход по адресу, указанному вслед за операцией сравнения. Начиная с этого адреса, мы будем программировать ветвь ИНАЧЕ. Но этот адрес мы пока не знаем, а потому место для него оставляем незаполненным и обводим рамкой, чтобы не забывать о необходимости выполнения его в свое время, когда станет ясно, где расположится вновь ИНАЧЕ.
Если же условие выполняется (a-b>=0, то есть a>=b), управление будет передано на следующий за операцией сравнения, 15-й адрес. Начиная с него, и следует запрограммировать ветвь ТО, записать команды пересылки в регистр С числа а, которое хранится в регистре А:
15. ИПА 16. ПС
Далее можно разместить ветвь иначе. Но писать ее команды сразу вслед за командами ветви ТО нельзя: в таком случае калькулятор выполнит подряд и те, и другие действия, смешает их. Закончив ветвь то, надо обойти ветвь ИНАЧЕ. Ставим команду безусловного перехода и опять оставляем пустым место для адреса перехода, так как пока не знаем, куда надо перейти:
17. БП 18. []
А затем программируем ветвь ИНАЧЕ, пересылку в регистр С числа b, которое хранится в регистре В:
19. ИПВ 20. ПС
Для лучшего понимания всю эту цепочку команд, записанных в строчку или в столбик, можно снабдить стрелками, как на рисунке. Там же приведена и блок-схема программируемого фрагмента.

Теперь можно заполнить пропущенные ячейки. Чтобы обойти ветвь ТО (ветвь ДА на блок-схеме), по адресу 14, после операции сравнения записываем 19 - начальный адрес ветви ИНАЧЕ (ветви НЕТ на блок-схеме). Чтобы обойти ветвь ИНАЧЕ, по адресу 18, после операции безусловного перехода, записываем 21 - начальный адрес последующего фрагмента программы. Заметим: на этот адрес мы попадаем, пройдя и по той к по другой ветви.
Как видим, записанное на алгоритмическом языке или в виде блок-схемы ветвление переводится в программу для калькулятора по чисто формальным правилам:
1. Запрограммировать левую часть условия, предварительно преобразованного к сравнению с нулем.
2. Записать соответствующую команду условного перехода и оставить незаполненным адрес перехода.
3. Запрограммировать ветвь ТО.
4. Записать команду БП и оставить незаполненным адрес перехода.
5. Запрограммировать ветвь ИНАЧЕ.
6. В пропущенную на шаге 2 ячейку записать адрес начала ветви ИНАЧЕ; в пропущенную на шаге 4 ячейку записать адрес очередной еще не занятой ячейки.
Тщательная запись алгоритма на алгоритмическом языке превращает дальнейшее составление соответствующей программы в почти автоматический процесс. Однако наша программа получилась не совсем оптимальной из-за того, что школьный алгоритмический язык не отражает всех возможностей калькулятора. На ветви ТО (как на ветви ИНАЧЕ) можно запрограммировать лишь вызов величины a (соответственно b) в регистр X, а закончив ветвление, содержимое регистра X надо переслать в регистр С. Так мы получим более короткую программу.
10. ИПА 11. ИПВ 12. - 13. Fx>=0 14. 18 15. ИПА 16. БП 17. 19 18. ИПВ 19. ПС
Прослеживая перемещения чисел по регистрам X, A, В, С, убедитесь, что этот вариант программы дает те же результаты, что и предыдущий.
Если отказаться от "подстрочного" перевода нашей записи алгоритма на язык команд микрокалькулятора, то возможен еще более короткий вариант:
10. ИПА 11. ИПВ 12. ПС 13. - 14. Fx>=0 15. 18 16. ИПА 17. ПС.
Этот пример ставит нас перед вопросом: насколько полезны при составлении программы такие вспомогательные средства, как блок-схема алгоритма и его запись на алгоритмическом языке? И какое из этих средств предпочтительнее? Конечно, запись на алгоритмическом языке уступает блок-схеме в наглядности, но при своей построчечной структуре, подкрепленная строгими правилами ее перевода на язык команд, эта запись, пожалуй, надежнее позволяет получить работающую программу даже в сложных случаях, при наличии многих циклов и ветвлений. Это тем более верно, если в алгоритмическом языке имеются конструкции, отражающие существенные для программирования особенности микрокалькулятора. К сожалению, используемый нами язык не таков, блок-схема и в этом отношении превосходит его, способна оказать большую помощь при поиске оптимального варианта программы. Достигнет же оптимума тот, кто владеет всеми возможностями калькулятора (прежде всего - возможностями стека) и умело использует их, претворяя алгоритм в программу.
Перевод разветвляющегося алгоритма в программу упрощается, когда при невыполнении условия надо просто ничего не делать, то есть ветвь ИНАЧЕ оказывается пустой:
1. Запрограммировать проверку условия.
2. Записать команду условного перехода и оставить незаполненным адрес перехода.
3. Запрограммировать ветвь ТО.
4. В пропущенную на шаге 2 ячейку записать адрес очередной свободной ячейки.
Например, пусть надо получить абсолютную величину числа a, хранящегося в РА. (Забудем на время, что проще всего это делается командами Fx2 Fsqr). Иными словами, надо выполнить действие:
если a<0 то a:=-a все
Первой командой программы, реализующей этот алгоритм, вызовем в регистр X число a, которое предстоит сравнить с нулем: 10. ИПА. Пишем команду сравнения, оставляя пока не заполненным адрес перехода: ll. Fx<0 12... Программируем ветвь ТО,- изменяем знак у содержимого РХ и засылаем результат в РА: 13. /-/ 14. ПА. Начальный адрес последующего фрагмента - 15. Его и вписываем в пустующее место по адресу 12. Окончательно:
10. ИПА 11. Fx<0 12. 15 13. /-/ 14. ПА
ЦИКЛ. Напомним, что так называется предписание о многократном повторении подряд некоторого фрагмента программы. Сам этот фрагмент называется телом цикла. Очередное его повторение определяется проверкой некоторого условия.
Обычно выделяют два типа циклов, в зависимости от того, когда производится проверка условия:
- цикл "пока" (сначала проверяется условие, и если оно соблюдено, то выполняется тело цикла, опять проверяется условие и так далее - таким образом, тело цикла выполняется, пока соблюдается условие);
- цикл "до" (сначала выполняется тело цикла, затем проверяется условие, и если оно не соблюдено, тело цикла выполняется вновь и так далее - таким образом, тело цикла выполняется до тех пор, как становится истинным условие).
На алгоритмическом языке цикл "пока" записывается так:
пока (указать условие) цикл (описать действия) кц
Цикл "до" записывается так:
цикл (описать действия) до (указать условие) кц
(Здесь кц - служебное слово, означающее "конец цикла").
Поясним сказанное примером. При взлете самолета его вертикальная скорость v (скорость набора высоты) изменяется в зависимости от времени t по некоторому закону v(t). Надо определить, за какое время самолет достигнет заданной высоты Н. Высота S, набранная к моменту времени Т, выражается интегралом(0,T)v(t)dt . Оставив в стороне самолет и сосредоточившись на математической стороне дела, получаем задачу:
найти Т такое, что интеграл(0,T)v(t)dt=Н.
Для вычисления интеграла возьмем простейшую формулу прямоугольников (см. рисунок). Разобьем площадь под кривой v(t) на столбики шириной h и каждый из них заменим прямоугольником той же ширины с высотою, равной значению функции в левой точке отрезка. Суммарная площадь таких прямоугольников есть приближенное значение интеграла. Будем набирать прямоугольники, пока их суммарная площадь ие превосходит величину Н.

Отметим, что при Н=0 нам не надо брать ни одного прямоугольника. Таким образом, проверку, брать ли очередной прямоугольник, надо производить перед тем, как его взять. Вспоминая, что циклы бывают двух типов, мы можем сказать, что программируемый нами относится к типу цикл "пока".
Запишем лежащий в его основе алгоритм - назовем его ВЗЛЕТ. В заголовке алгоритма перечислим его аргументы (Н, h) и результаты (Т). Промежуточную переменную S укажем позже, сразу вслед за служебным словом нач (начало). Примем, что скорость нарастает как квадрат времени: v(t)=t**2.
В перечне промежуточных переменных, как видим, нет v и t, которые встречаются в программируемых нами формулах. Первое из этих обозначений излишне, поскольку мы установили явную зависимость v(t). Обозначение t можно объединить с Т. Так можно сократить запись алгоритма - избежать присваивания Т:=t, когда переменная S достигнет значения Н: при этом значение Т и будет давать ответ поставленной задачи.
Придадим величинам S и Т исходные нулевые значения (стартуем в нулевой момент с нулевой высоты). Приступим к программированию цикла. Прежде всего запишем условие, при выполнении которого тело цикла должно быть пройдено в очередной раз: пока S<Н. Пока это неравенство соблюдается, величине S при каждом очередном прохождении цикла надо присваивать значение S+T**2*h, а величине Т - значение Т+h. Перечень этих операций предварим служебным словом цикл, а завершим служебным словом кц (конец цикла).
Если неравенство S<Н не соблюдается, должен произойти выход из цикла. Текущее значение величины Т при этом и является результатом.
алг ВЗЛЕТ (вещ Н, h, T);
- арг Н, h; рез Т;
нач вещ S;
- S:=0; Т: =0;
- пока S<Н цикл
- - S:=S+T**2*h; Т=Т+h
- кц
кон

Запрограммируем разработанный алгоритм. Аргументы и результаты, указанные в первых строках его записи на алгоритмическом языке, и вспомогательные переменные, указанные далее, напоминают нам: перед составлением программы необходимо распределить адресуемые регистры под хранение величин, фигурирующих в алгоритме. Пусть величина S хранится в Р0, Т - в Р1, h - в Р2, Н - в Р3. Поскольку начальные значения S и Т должны равняться нулю, зашлем нули в Р0 и Р1.
10. Cx 11. П0 12. П1
Преобразуем условие S<H к сравнению с нулем S-Н<0 и запрограммируем это сравнение. Адрес перехода пока оставим незаполненным.
13. ИП0 14. ИП3 15. - 16. Fx<0 17. []
При соблюдении условия Fx<0 калькулятор передаст управление на команду, следующую за командой условного перехода. С этого места мы и запишем тело цикла.
Завершим его командой безусловного перехода: она должна передавать управление на команду, с которой начинается проверка условия, определяющего очередное прохождение цикла.
18. ИП0 19. ИП1 20. Fx2 21. ИП2 22. * 23. + 24. П0 25. ИП1 26. ИП2 27. + 28. П1 29. БП 30. 13
Внимательно разберите эту цепочку команд. Проверьте, что команды 18-24 вычисляют выражение S+T**2*h. Команда безусловного перехода (адреса 29-30), как и требуется от нее, передает управление на адрес 13, то есть на команду, с которой начинается проверка условия S-Н<0. Если оно выполняется вновь, тело цикла будет пройдено еще раз. Если не выполняется, надо передать управление на начало фрагмента, который должен выполняться по выходе из цикла,- то есть иа адрес 31. Его-то и нужно записать под адресом 17, пустующим до сих пор адресом команды условного перехода.
Проверьте, правильно ли составлена и верно ли работает программа. Введите ее в калькулятор, завершив набор командами 31. ИП1 32. С/П. Клавишами F АВТ верните калькулятор в режим вычислений; занесите в регистр 3 число 3, в регистр 2 - число 0.1; клавишами БП 10 передайте управление на адрес 10; клавишей С/П запустите калькулятор. Примерно через две минуты на индикаторе появится результат 2.2. Он сильно отличается от точного (2.08), так как ширина прямоугольников h=0.1 была выбрана нами довольно большой.
Если разбор приведенной программы покажется вам трудным, укажите переходы стрелками и сравните свой рисунок с помещенным здесь.
Рассмотренный нами пример позволяет сформулировать правила программирования цикла "пока".
1. Программируем условие, преобразованное к сравнению с нулем.
2. Записываем команду сравнения и оставляем незаполненным адрес перехода.
3. Программируем тело цикла.
4. Записываем операцию БП, за нею - адрес начала проверки условия.
5. В пропущенную на шаге 2 ячейку записываем первый еще не занятый адрес.
Строя только что разобранную программу по типу цикла "пока", мы поступали так лишь потому, что из чисто формальных соображений не захотели исключать из рассмотрения случай Н=0. Если же заведомо ясно, что величина Н не нулевая, то программу для решения той же задачи можно составить по типу цикл "до". В этом случае тот же интеграл, что и ранее, будет подсчитываться до наступления условия S>=H (то есть условия, противоположного тому, на проверке которого строилась предыдущая программа, построенная с помощью цикла "пока").
На сей раз тело цикла запишется так: сначала, после служебного слова цикл - повторяемые действия, затем, после слова до,- условие, затем - служебное слово кц.
цикл S:=S+T**2*h; T:=T+h
- до S>=Н кц

Предлагаем читателю самостоятельно составить программу, реализующую этот алгоритм, и сверить ее с помещенной ниже. Напомним лишь, что условие повторения цикла надо преобразовать к сравнению с нулем: S-Н>=0. Проверять его будем с помощью операции Fx>=0, которую проставим за телом цикла. А вслед за нею проставим начальный адрес тела цикла. Если неравенство ие выполняется, тело цикла будет пройдено еще раз. Если выполняется, произойдет выход из цикла.
10. Сх 11. П0 12. П1 13. ИП0 14. ИП1 15. Fx2 16. ИП2 17. * 18. + 19. П0 20. ИП1 21. ИП2 22. + 23. П1 24. ИП0 25. ИП3 26. - 27. Fx>=0 28. 13
(Чтобы испытать работу этого фрагмента, его следует дополнить командами 29. ИП5 30. С/П).
Как нетрудно усмотреть уже из этого примера, правила программирования цикла "до" несколько проще, чем цикла "пока":
1. Запрограммировать тело цикла.
2. Запрограммировать левую часть условия, преобразованного к сравнению с нулем.
3. Записать операцию сравнения и за нею - адрес начала тела цикла.
В обоих только что рассмотренных примерах к моменту начала выполнения цикла (к моменту входа в цикл) мы не могли сказать, сколько раз он будет пройден - это определяется по мере все новых его прохождений. Такие циклы называются итерационными. Но часто встречаются случаи, когда количество повторений цикла можно определить заранее. Например, если бы на до было вычислить интеграл(a b)f(x)dx описанным выше методом, цикл нужно было бы повторить столько раз, на сколько отрезков разбит промежуток интегрирования.
Поскольку подобные случаи весьма часто встречаются в практике программирования, для них имеется специальная форма записи на алгоритмическом языке:
цикл (указать число повторений) раз (описать действия) кц
Именно для организации таких циклов предназначены имеющиеся у "Электроники Б3-34" операции вида FLM (M - номер одного из первых адресуемых регистров, от нулевого до третьего включительно; его в подобных случаях называют счетчиком повторений цикла).
На предыдущих занятиях Мы уже не раз использовали эти операции (7/85, 9/85), знаем их свойства. Каждая из ннх образует команду в соединении с записанным сразу вслед за ней адресом перехода. Такая команда ставится в конце тела цикла и совершает два действия: уменьшает на единицу содержимое регистра М и, если это содержимое не равно единице к моменту выполнения команды, совершает переход на начальный адрес тела цикла. Если же к моменту выполнения команды содержимое регистра М равно единице, то, не уменьшая его, команда передает управление на следующий за нею адрес.
Зная все это, мы сможем сформулировать правила перевода конструкций, описанных выше на алгоритмическом языке, на язык команд "Электроники Б3-34":
1. Выбрать один из его регистров: Р0, Р1, Р2, Р3. Занести в него число повторений цикла.
2. Запрограммировать тело цикла.
3. Записать одну из операций: FL0, FL1, FL2, FL3 (в соответствии с тем, какой регистр был выбран на шаге 1) и за нею - начальный адрес тела цикла.
Чтобы не отступать от принятого порядка изложения, следовало бы разобрать здесь еще один пример на применение операции вида FLM. Попробуйте самостоятельно описать на алгоритмическом языке и затем запрограммировать для нашего калькулятора вычисление интеграла(a b)f(x)dx, положив по-прежнему f(х)=х**2. Обозначьте число отрезков, на которые разбит промежуток интегрирования, через n. Воспользуйтесь тем, что переменные величины в описаниях алгоритмов можно обозначить не только буквами, но и словами. Например, вычисляемый интеграл можно так и назвать: "интеграл".
Сравните свой вариант с приведенным здесь:
алг ИНТЕГРАЛ (вещ a, b, n, интеграл); арг а, b, n; рез интеграл;
нач вещ h, x
- h:=(b-а)/n;
- интеграл:=0; х:=а
- цикл n раз
- - интеграл:=интеграл+x**2*h;
- - х:=х+h;
- кц
кон
10. Сх 11. П5 12. ИП0 13. П4 14. ИП1 15. ИП0 16. - 17. ИП3 18. / 19. П2 20. ИП5 21. ИП4 22. Fx2 23. ИП2 24. * 25. + 26. П5 27. ИП4 28. ИП2 29. + 30. П4 31. FL3 32. 20
Распределение регистров тут таково: а - Р0, b - P1, h - Р2, n - Р3, х - Р4, интеграл - Р5. Адреса 10-19: очищаем Р5, заносим число а в Р4, вычисляем h=(b-а)/n и заносим в Р2. Адреса 20-30: тело цикла. Адреса 31-32: записанная здесь команда FL3 20 совершает переход на начальный адрес тела цикла до тех пор, когда содержимое регистра-счетчика Р3 станет равным единице. Тогда команда FL3 20 совершит выход из цикла - передаст управление на адрес 33, на последующий фрагмент, где будет использовано полученное значение интеграла.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
А компьютеры тем временем грубой силой вытесняли из жизни все эти маленькие библиофильные и эпистолярные самоделки...
2/86
БУМАЖНЫЙ ДОКУМЕНТ В ВЕК БЕЗБУМАЖНОЙ ИНФОРМАТИКИ
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"

Картина уже довольно привычная - человек сидит за терминалом электронной вычислительной машины. Перед ним слегка приподнятый над столом элегантный дисплей, напоминающий средних размеров телевизор в пластмассовом корпусе, и прижавшийся к столу плоский блок клавиатуры, похожий на портативную пишущую машинку, но несколько более широкий и с большим числом клавишей. Скупой язык словаря определяет терминал (от латинского "терминус" - "граница", "конец") как "конечное устройство в составе вычислительной системы, предназначенное для ввода информации в систему и вывода информации из нее". Самый распространенный вариант терминала как раз и есть комплекс дисплей-клавиатура, столь часто мелькающий на газетных фотографиях,- нажимая клавиши, пользователь дает компьютеру задание, вводит в него данные, а свой ответ машина выводит на экран дисплея.
Человек, работающий за терминалом, пользующийся помощью компьютера, официально именуется "пользователь". Не стоит обсуждать, удачное ли это слово - в бурно развивающейся информатике термины мгновенно становятся общепринятыми.
Иногда дисплей-клавиатура - это терминал мощной вычислительной машины, у нее может быть несколько или даже несколько десятков таких терминалов, а значит, столько же пользователей, и машина умеет одновременно решать задачи, поступающие от всех. Точнее, компьютер решает эти задачи поочередно, он чаще всего разбивает их на части и по указанию своего внутреннего диспетчера переключается с одной задачи на другую, запоминая промежуточный результат. При этом, как правило, ни один из пользователей не замечает, что он не один: человек в сравнении с машиной работает очень медленно, и она просто простаивала бы, дожидаясь, пока пользователь прочтет на экране очередной результат или введет очередное уточнение. Вместо таких простоев машина и занимается решением других задач - никаких потерь времени, никаких "сижу куру".
Есть, правда, компьютеры, работающие всего на один терминал,- это небольшие машины, как их называют, микроЭВМ, самая распространенная разновидность которых - персональная ЭВМ (10/84 и 9/85). Нередко у микрокомпьютера самого компьютера внешне и не увидишь - он весь упрятан в корпус клавиатуры.
Взрывоподобный прогресс вычислительной техники обычно иллюстрируют цифрами: если вести отсчет от первых машин, то сегодня объемы внутренней памяти ЭВМ увеличились в сотни раз, а быстродействие - в сотни тысяч раз, в тысячи раз уменьшилось потребление энергии, и снизилась стоимость. Специалисты прикинули, что если бы такими темпами прогрессировало автомобилестроение, то машина класса "Волги" двигалась бы чуть ли не со скоростью света, потребляла бы несколько граммов бензина на сотню километров и стоила бы несколько рублей.
И еще один показатель прогресса - резко упростилось общение с машиной. Когда-то работа пользователя на ЭВМ была настоящим священнодействием с участием целой свиты диспетчеров, инженеров, программистов, операторов. А сегодня небольшой дисплейный терминал можно увидеть на рабочем столе ученого, инженера, финансиста, в диспетчерской завода, в институтской аудитории и школьном классе. По самым скромным подсчетам, в мире уже больше 10 миллионов таких терминалов (с учетом персональных компьютеров), и прогнозы говорят, что их будет во много раз больше - удобный вход в компьютер появится чуть ли не на каждом рабочем месте и в каждой квартире. А что тут удивительного? Техника создала полезный инструмент, вполне естественно, что каждый, кто может, старается его использовать. Так бывало уже много раз, скажем, с часами, радиоприемниками, телефоном.
Через 20 лет после изобретения телефона в таком большом городе, как Киев, работало 174 телефонных аппарата, сейчас их примерно полмиллиона, для полного удовлетворения спроса должно быть еще раза в два больше.
Растущий спрос на вычислительные машины... Всеобщая компьютеризация... Терминал в каждом доме... Для чего это нужно? Что конкретно может дать? Как повлияет на наш образ жизни? Может быть, оснащаясь компьютерами, мы идем к чрезмерному рационализму? К тому, чтобы производственные и житейские проблемы любых масштабов, вплоть до покупки моркови в овощном магазине, решать безошибочно, передав их компьютеру в виде системы уравнений. И, пользуясь своим личным терминалом, в любых ситуациях не размышлять, а вычислять.
Чтобы ответить на вопрос "Для чего?", нет нужды обсуждать эти интригующие проблемы. Во-первых, до чрезмерного рационализма еще, видимо, довольно далеко - сегодня не то что морковку, а дорогие станки, а бывает, и целые заводы покупают, не вычисляя, а размышляя. Ну а, во-вторых, интересуясь нынешним применением и тем более будущим электронных вычислительных машин, слово "вычислительная" не следует понимать в прямом смысле - очень часто оно не отражает существа дела.
Словосочетание "вычислительная машина" совсем не означает, что речь идет о машине, которая вычисляет, и здесь нет никакого парадокса. Просто вычисляющую машину обучили нескольким другим профессиям, одна из них, кстати, особенно сильно активизировала массовый спрос на ЭВМ. Речь идет о "языкознании" компьютера, о его умении работать с текстами.
Человек, пытающийся популярно описать сложное творение техники и разъяснить при этом суть дела, всегда рискует услышать упреки специалистов в том, что он утомляет читателя азбучными истинами и становится похожим на знаменитого гашековского полковника Фридриха Крауса фон Циллергута ("Похождения бравого солдата Швейка", глава XV, "Катастрофа"). Полковник изводил окружающих тем, что как некое откровение пояснял очевидные вещи: "Дорога, по обеим сторонам которой тянутся канавы, называется шоссе. Да-с, господа. Знаете ли вы что такое канава? Канава - это вырытое значительным числом рабочих углубление... Вот это, господа, окно. Да знаете ли вы, что такое окно?.. Известно ли вам, что такое кирка?.. Знаете ли вы, что такое клейстер?.." Автор этих заметок должен признаться, что над ним всегда витает, нагоняя безумный страх, тень нудного полковника Циллергута и немало "Известно ли вам?" было безжалостно вымарано и из этого текста. Но то, о чем хочется рассказать сейчас (многим читателям, разумеется, не более чем напомнить), было оставлено без всяких колебаний.
Известно ли вам, как работает электронная вычислительная машина?
Когда вычислительная машина вычисляет, то введенные в нее человеком привычные для него десятичные числа она прежде всего превращает в удобные для себя двоичные. Так, например, 2 превращается в 10, 3 - в 101, 5 - в 111, 50 - в 110010, 28679 - в 110000011011011 и т.д. Разница между десятичными и двоичными числами, так сказать, чисто техническая - одно и то же реальное количество каких-либо объектов (карандашей, яблок, звезд на небе) в десятичной системе записывают с помощью десяти разных знаков (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а в двоичной - с помощью всего лишь двух знаков (0, 1). Двоичный счет удобен для машины потому, что она, по сути дела, представляет собой сложнейший электрический орнамент, сотканный из сотен тысяч или даже из миллионов выключателей, а выключатель, как нетрудно убедиться в эксперименте с настольной лампой, может находиться лишь в одном из двух состояний - он либо замкнут и пропускает ток, либо разомкнут и тока не пропускает. Замкнутый выключатель - это записанная машинным знаком единица, разомкнутый - ноль. Роль выключателей в вычислительной машине выполняют полупроводниковые приборы, чаще всего микронных размеров транзисторы, работающие в так называемом ключевом режиме - "открыт-закрыт" или иначе "включен-выключен".
Компьютер - система динамичная, быстродействующая. Единицы отображаются здесь не застывшими, не постоянными токами, а очень короткими, обычно в миллионные или даже миллиардные доли секунды электрическими вспышками, импульсами, нули - такими же короткими паузами. Любое число живет, путешествует, обрабатывается в ЭВМ в виде определенной комбинации импульсов-пауз. В ЭВМ среднего быстродействия за секунду происходит много тысяч так называемых машинных тактов, и во время каждого такта в разных частях компьютера производятся разнообразные операции с комплектами импульсов-пауз. Эти операции сливаются в четко организованный многоступенчатый, многотактовый процесс, и компьютер быстро продвигается к решению задачи.
Комбинациями импульсов-пауз можно зашифровать не только количество предметов, не только числа, но также и буквы, а значит, слова и тексты. Если взять комплект из трех импульсов-пауз - будем, как принято, обозначать их через 1 и 0,- то можно получить 8 разных шифров, 8 разных комбинаций - 000, 001, 010, 011, 100, 101, 110 и 111. Этими комбинациями можно было бы зашифровать 8 букв алфавита. Четырехзначный код, то есть комплекты из четырех единиц и нулей, дает уже 16 комбинаций- 0000, 0001, 0010 и так далее до 1111. Число N возможных комбинаций из 1 и 0 подсчитывается довольно просто - N=2**n, где n число знаков, число 1 или 0 в каждом комплекте. В русском алфавите 33 буквы, если избавиться от одной, обойдясь, например, одной е, то можно было бы обойтись пятизначными комплектами для кодирования всего алфавита, так как 2**5=32. Но, чтобы писать нормальные тексты машинными кодами, то есть комплектами импульсов и пауз, мало иметь 32 шифра - нужно еще какого зашифровать знаки препинания, пробел между словами, наконец, нужно иметь отдельные шифры на прописные буквы, а для научных текстов еще и на латынь. Вот почему в машинах семи- и восьмизначные коды - в первом случае можно зашифровать 2**7=128, а во втором - 2**8=256 знакам. Этого вполне хватает и на буквы, и на цифры, и на разные служебные знаки, которыми удобно пользоваться машине. В типичном восьмиразрядном коде ДКОИ (двоичный код обработки информации) буква А кодируется, как 11000001, а - 10000001, щ - 10110101, г - 10001101, открытие скобок - 10001101, закрытие - 01011101, пробел - 01000000, ? - 01101111, кавычки - 01111111 и так далее. Когда пользователь вводит в машину, например, букву А, то он нажимает на клавиатуре соответствующую кнопку, она определенным образом переключает электронную схему шифратора, и он направляет в машину комбинацию импульсов-пауз, которую мы записали как 11000001. А если такая комбинация появится на выходе компьютера, то она включит электронную схему знакогенератора таким образом, что он заставит светиться на дисплее точки, сливающиеся в букву А.
Так что, работая с текстами, компьютер никаких текстов в нашем понимании и не видит, он имеет дело с такими же комбинациями импульсов-пауз, с такими же двоичными числами, как и при вычислениях. И то, что для нас "Я помню чудное мгновенье...", для компьютера всего лишь 01111111 11011101 01000000 10010101 10010110 10011100 10011101 10111000 01000000 10110110 10101000 10001010 10011101 10010110 10000101 01000000 0011100 10001101 10011101 10010110 10101111 10000101 10011101 10110000 10000101 01001011 01001011 01001011 01111111. Так что не стоит преувеличивать значение того факта, что вычислительная машина работает с текстами.
И еще такой штрих. Вы обращаетесь к машине с просьбой, набираете на клавиатуре "Печатать раздел 5", и через несколько секунд из печатающего устройства, из принтера, выползает лист бумаги с заказанным текстом. Это значит, что комбинация импульсов-пауз, которыми было зашифровано слово "Печатать", опознано дешифратором и произведены необходимые включения в принтере. А комбинация импульсов-пауз, в которой закодировано "раздел 5", привела в действие цепочку электронных схем, заставивших двигаться магнитный диск и считывающую головку, с тем чтобы найти на диске нужный кусок записи, нужный файл. Таким образом, ваш словесный приказ был выполнен только потому, что введенные в машину слова превратились в знакомые ей коды. Непримиримый автоматизм машины, ее неумение чувствовать свободность нашего естественного языка может проявиться в таком, например, факте: если, случайно нажав на клавишу, вы сделаете между словами "печатать" и "раздел" два пробела вместо одного, то машина команду не выполнит, так как она получит незнакомую ей шифровку с лишним знаком пробела 01000000.
Вычислительная машина виртуозно работает с двоичными числами, выполняет большой ассортимент математических операций - складывает, умножает, делит, извлекает корни, логарифмирует, вычисляет синусы и тангенсы, решает дифференциальные уравнения. Но что может сделать компьютер со словами? Какие операции может выполнить с ними, кроме заранее известного "Саша + Маша = любовь"? А если тексты не нужно вычислять, если нет надобности складывать или перемножать двоичные числа, в которых зашифрованы слова, то зачем тогда вообще затевать все это непростое дело? Зачем вводить в вычислительную машину текст, а затем выписывать его на экране дисплея?
В попытке ответить на это "Зачем вычислительной машине текст?" или, правильнее, "Зачем тексту вычислительная машина?" назовем несколько новых возможностей из числа тех, что открыл нам текстовый компьютер.
Первое - компактные хранилища текста. Восьмиразрядное двоичное число, которым кодируется одна буква,- это распространенная единица количества информации - байт. В этом номере журнала, если считать, что в нем только тексты, содержится примерно миллион букв, то есть примерно миллион байт информации, или иначе-один мегабайт, Мбайт. В устройствах внешней памяти компьютеров сейчас наиболее широко применяются магнитные диски размером с граммофонную пластинку, на которых мельчайшими точками разной намагниченности, расположенными по тонким спиральным дорожкам, записаны "единицы" в "нули", записаны байты информации. Типичная (далеко не рекордная!) ширина дорожки 0.1мм, на одном миллиметре ее длины можно поставить 500 магнитных точек, то есть размер точки 0.1*0.002мм, и, значит, на запись одной буквы (1 байт, 8 знаков) расходуется площадь диска 0.1мм(0.002*8 )мм=0.0016мм2. Нетрудно подсчитать, что на территории, которую в среднем занимает на этой странице каждая буква (примерно 4мм2), магнитный диск позволяет разместить 2500 букв, записанных восьмизначным двоичным кодом. С этого и начинается компактность компьютерных хранилищ текста.
На сравнительно недорогих, так называемых гибких дисках удается записать до 3Мбайт, то есть вместить в такой диск текст трех номеров нашего журнала. В более сложных жестких дисковых модулях ("винчестерский диск") записывают до 1000Мбайт ~ 1Гбайт (гигабайт), а это уже комплект подшивок журнала за 30 лет. Наконец, на диске с оптической записью двоичных чисел может храниться до 10 Гбайт информации, сотня таких видеодисков, разместившихся на небольшом стеллаже, это крупная библиотека, для которой нужны книжные полки длиной 20 километров.
Второе - снабдив часть текста цифровой меткой, его легко найти в большом массиве информации. В этом случае компьютер выполняет привычную для него работу: просмотрев хранящееся в памяти оглавление, он дает команду иа перемещение считывающей магнитной головки именно в то место диска, где находится нужный текст. За какие-то доли секунды машина может отыскать текст в записи, эквивалентной по объему многотомной энциклопедии.
Третье - созданы программы, позволяющие компьютеру находить тексты по ключевым словам в названиях статей или книг. Вот пример: введенное в вычислительную машину с заданием поиска слово "сон", это привычные для нее байты 10000011 10010110 10011101; перебирая хранящиеся в памяти слова названий статей или книг, машина будет сравнивать их с заданным ключевым словом и искать сходство; в принципе его обнаружить несложно, можно, например, вычитать код одного слова из другого, и если получится ноль, то, значит, шифры совпадают, слова одинаковы; обнаружив ключевое слово в заголовке, машина запомнит заголовок, его кодовую метку; если понадобится, по ней легко найти и саму статью. Можно отбирать заголовки по совпадению нескольких ключевых слов, скажем, в нашем примере искать статьи, посвященные летаргическому сну, электросну или дневному сну детей дошкольного возраста. Не так, конечно, просто дело делается, как сказка сказывается, нужно, например, предусмотреть появление ключевого слова в косвенном падеже или сделать так, чтобы пунктуальная машина, выискивая "сон", не попалась на "Карлсон". Многие трудности, однако, уже преодолены, и тысячи людей по ключевым словам сейчас находят нужные им документы в огромных компьютерных хранилищах информации.
Документом в информатике принято называть не только справку, отчет или техническое задание, но также и книгу, журнальную статью, рукопись, кинофильм, граммофонную пластинку, магнитный диск, одним словом, официально любой "материальный носитель записи с зафиксированной на нем информацией, предназначенной для передачи во времени и пространстве".
Четвертое - машина позволяет легко преобразовывать тексты. В какой-либо записанной на диске текст, например, в телефонный справочник, очень просто внести дополнение, сделать вставку. В упрощенном варианте (точнее, в усложненном, но более понятном) это выглядит так: текст с диска переписывают в оперативную память машины; туда же отдельно записывают вставку; затем вновь записывают весь текст на диске, поместив вставку в отведенное ей место. Пользователю достаточно лишь указать, где и какое дополнение нужно сделать, а всю техническую часть дела машина возьмет на себя. Аналогично можно корректировать текст, сокращать и менять его, раздвинуть два слова и вставить между ними еще одно, короче говоря, редактировать. Редактирование с помощью ЭВМ во многом очень удобно, во всяком случае, не нужно бессчетное число раз перепечатывать и вклеивать исправленные куски.
Пятое - машины могут очень быстро обмениваться документами, пересылая их на большие расстояния по линии связи, причем без каких-либо дополнительных преобразований - в виде обычных своих восьмерок "импульс-пауза". Это не требует, видимо, особых пояснений, хочется лишь напомнить, как не просто бывает получить из другого города какой-либо бумажный документ и что уходят на это не секунды, как при запросе у компьютера, а уходят на это дни, чаще всего в интервале от 3-5 дней до бесконечности.
Последние годы отмечены лавиной применения вычислительных машин в решении самых разных, так сказать, невычислительных задач - для хранения и поиска информации, обработки текстов, учета и распределения ресурсов, диспетчеризации, оформления деловых отношений. Рухнули многие бюрократические технологии, резко сократился обмен бумагами и бумажками, проходящими через руки человека, с помощью какого-нибудь не очень большого компьютера стали выполняться сложнейшие операции, которые раньше наверняка потребовали бы участия сотен симпатичных девушек, вооруженных шариковыми ручками и квитанционными книжками с фиолетовой копиркой.
Иллюстраций здесь можно привести очень много, черпая их не только в науке, но и в жизни. Так, например, в Москве, Ленинграде, Киеве и других городах компьютерам поручили учет всех международных телефонных разговоров, выписку счетов и последующий контроль за их оплатой. Компьютеру доверили держать в памяти все места и продавать билеты на все сто с лишним ежедневно уходящих из Москвы поездов. И кассиру в окошечке остается лишь ввести вашу просьбу в ЭВМ и получить деньги за билет или обреченно отказать - "В машине ничего нет". Компьютерная "Сирена" не только ежедневно распределяет десятки тысяч мест в вылетающих из Москвы самолетах, но также входит в контакт с компьютерами других аэропортов и аналогичными международными системами, которые вместе координируют продажу мест чуть ли не на все самолеты мира.
Перечисляя достоинства электронных текстов, нужно бы вспомнить такую мелочь, как возможность сопровождать цифровые потоки словесными дополнениями. Научив машину пользоваться не только цифрами, но и буквами, можно, например, в результатах расчета вместо "0.5...110" вывести на дисплей "0.5 миллиампера при сопротивлении 110 килоом" или вместо "235...18.30" отпечатать "235 тонн по 18 рублей 30 копеек за тонну". Одним словом, можно выводить из машины таблицы, планы, расписания, билеты, счета, квитанции, ведомости и другую насыщенную цифрами деловую документацию в привычном для человека виде.
Появились терминалы в издательских кабинетах, и редакторы забросили в далекий ящик свое грозное вооружение - карандаши, ножницы и клей. Короткие записи на магнитных дисках сильно потеснили бессчетные бумажки в конторах и на складах. Даже осторожные банковские работники кое-где доверили компьютеру выплату наличных денег без заполнения расходных ордеров, сличения подписей и каллиграфического выписывания суммы прописью - достаточно сунуть в щель простейшего терминала магнитную карточку с личным шифром и набрать клавиатурой нужную сумму, как по желобку к вам тут же вылетят наличные деньги (если, конечно, позволяет остаток на счете), а банковский компьютер внесет необходимые изменения в свои записи на магнитном диске.
Вместо библиотек, а вернее параллельно с ними, уже организованы тысячи огромных хранилищ информации на магнитных дисках, откуда с помощью компьютера можно быстро извлечь нужный текст к себе на дисплей. В ряде стран появились городские справочные компьютеры, от которых по телефонной линии можно получить на домашний терминал расписание автобусов, карту погоды, справку из словаря.
Одним словом, безбумажная информатика во многих конкретных областях уверенно доказала решающие свои достоинства - экономические, деловые, житейские. И уже появились прогнозы полного отстранения бумажного документа от всех его нынешних дел. Деловая переписка? Только электрическими сигналами, с терминала на терминал. Газеты и журналы? Только поступающие подписчику на дисплей. Домашняя библиотека? Только в виде магнитных дисков. В общем, никакой бумаги - безбумажное общество.
Дискуссии футурологов по этому поводу не угасают и по сей день, они дают оценки будущего в широких пределах - от "полностью электронная система изданий" до "безбумажное общество, где исчезнут любые коммуникации на бумаге,- это химера".
И все ж, тот, кто собирается всю жизнь сортировать накладные, перекладывать складские требования или набивать бумагами архивные папки, может оказаться в положении "ничейной бабушки", которая жгла у себя на антресолях керосиновую лампу, так как не верила в электричество.
Отдать вычислительным машинам все, что можно отдать! Отдать, не раздумывая и не откладывая,- массу дел они делают лучше нас, быстрее, четче. Эти машины умеют то, что нам вообще недоступно, без них уже невозможно управиться с работающим на нас огромным миром техники и технологий. Но нельзя же отдавать компьютеру книгу! Потерять возможность взять ее с полки и полистать перед сном. И вряд ли мерцающий зеленоватыми буквами дисплей заменит пахнущую краской свежую газету, которую ты сунул в карман до первой свободной минуты. Вряд ли он заменит и первые каракули внука в школьной тетради или письмо, написанное рукой друга,- слишком важное место занимает бумажный документ в нашей жизни, чтобы полностью отказаться от него. Это, видимо, значило бы стать совсем другим человеком, с иными ритмами жизни и даже с иной шкалой жизненных ценностей. Нужно ли это? И возможно ли с позиций психологии и даже физиологии? А потом, почему должно быть "или-или"? Ведь радиосвязь не отменила телефона и самолет не отучил нас перемещаться пешком.
Как ни интересны дискуссии футурологов о перспективах безбумажной информатики, как ни аргументированы их "за" и "против", будущее сформируется все-таки не из них. Будущее в руках людей, как правило, невидимых миру,- системных программистов, технологов, инженеров. Это они делают все, чтобы вытеснить бумажный документ оттуда, где он стал обузой, и это они же ищут пути состыковать ЭВМ с бумажным документом там, где от него отказаться нельзя. Такая стыковка, такое сосуществование позволят объединить достоинства безбумажной информатики, в частности компактность хранилищ, автоматизацию поиска, удобство редактирования, скорость пересылки и достоинства бумажного документа, в числе которых удобство пользования, простота транспортировки, независимость от электропитания и линий связи. Рисунки ниже иллюстрируют основные идеи и методы, используемые на таком важном участке взаимодействия компьютер-бумага, как вывод информации из ЭВМ на печатный лист. Все эти идеи уже реализованы в серийных установках, с помощью которых компьютер выдает десятки страниц печатного текста в минуту или с отредактированных на терминале и попавших на магнитный диск статей и заметок сразу формирует газетную полосу и без посредников готовит для нее печатную форму.
Техника эта быстро совершенствуется, позволяя надеяться, что бумажный документ не будет помехой на пути безбумажной информатики.
...
2/86
БУМАЖНЫЙ ДОКУМЕНТ В ВЕК БЕЗБУМАЖНОЙ ИНФОРМАТИКИ
Р.СВОРЕНЬ, специальный корреспондент журнала "Наука и жизнь"

Картина уже довольно привычная - человек сидит за терминалом электронной вычислительной машины. Перед ним слегка приподнятый над столом элегантный дисплей, напоминающий средних размеров телевизор в пластмассовом корпусе, и прижавшийся к столу плоский блок клавиатуры, похожий на портативную пишущую машинку, но несколько более широкий и с большим числом клавишей. Скупой язык словаря определяет терминал (от латинского "терминус" - "граница", "конец") как "конечное устройство в составе вычислительной системы, предназначенное для ввода информации в систему и вывода информации из нее". Самый распространенный вариант терминала как раз и есть комплекс дисплей-клавиатура, столь часто мелькающий на газетных фотографиях,- нажимая клавиши, пользователь дает компьютеру задание, вводит в него данные, а свой ответ машина выводит на экран дисплея.
Человек, работающий за терминалом, пользующийся помощью компьютера, официально именуется "пользователь". Не стоит обсуждать, удачное ли это слово - в бурно развивающейся информатике термины мгновенно становятся общепринятыми.
Иногда дисплей-клавиатура - это терминал мощной вычислительной машины, у нее может быть несколько или даже несколько десятков таких терминалов, а значит, столько же пользователей, и машина умеет одновременно решать задачи, поступающие от всех. Точнее, компьютер решает эти задачи поочередно, он чаще всего разбивает их на части и по указанию своего внутреннего диспетчера переключается с одной задачи на другую, запоминая промежуточный результат. При этом, как правило, ни один из пользователей не замечает, что он не один: человек в сравнении с машиной работает очень медленно, и она просто простаивала бы, дожидаясь, пока пользователь прочтет на экране очередной результат или введет очередное уточнение. Вместо таких простоев машина и занимается решением других задач - никаких потерь времени, никаких "сижу куру".
Есть, правда, компьютеры, работающие всего на один терминал,- это небольшие машины, как их называют, микроЭВМ, самая распространенная разновидность которых - персональная ЭВМ (10/84 и 9/85). Нередко у микрокомпьютера самого компьютера внешне и не увидишь - он весь упрятан в корпус клавиатуры.
Взрывоподобный прогресс вычислительной техники обычно иллюстрируют цифрами: если вести отсчет от первых машин, то сегодня объемы внутренней памяти ЭВМ увеличились в сотни раз, а быстродействие - в сотни тысяч раз, в тысячи раз уменьшилось потребление энергии, и снизилась стоимость. Специалисты прикинули, что если бы такими темпами прогрессировало автомобилестроение, то машина класса "Волги" двигалась бы чуть ли не со скоростью света, потребляла бы несколько граммов бензина на сотню километров и стоила бы несколько рублей.
И еще один показатель прогресса - резко упростилось общение с машиной. Когда-то работа пользователя на ЭВМ была настоящим священнодействием с участием целой свиты диспетчеров, инженеров, программистов, операторов. А сегодня небольшой дисплейный терминал можно увидеть на рабочем столе ученого, инженера, финансиста, в диспетчерской завода, в институтской аудитории и школьном классе. По самым скромным подсчетам, в мире уже больше 10 миллионов таких терминалов (с учетом персональных компьютеров), и прогнозы говорят, что их будет во много раз больше - удобный вход в компьютер появится чуть ли не на каждом рабочем месте и в каждой квартире. А что тут удивительного? Техника создала полезный инструмент, вполне естественно, что каждый, кто может, старается его использовать. Так бывало уже много раз, скажем, с часами, радиоприемниками, телефоном.
Через 20 лет после изобретения телефона в таком большом городе, как Киев, работало 174 телефонных аппарата, сейчас их примерно полмиллиона, для полного удовлетворения спроса должно быть еще раза в два больше.
Растущий спрос на вычислительные машины... Всеобщая компьютеризация... Терминал в каждом доме... Для чего это нужно? Что конкретно может дать? Как повлияет на наш образ жизни? Может быть, оснащаясь компьютерами, мы идем к чрезмерному рационализму? К тому, чтобы производственные и житейские проблемы любых масштабов, вплоть до покупки моркови в овощном магазине, решать безошибочно, передав их компьютеру в виде системы уравнений. И, пользуясь своим личным терминалом, в любых ситуациях не размышлять, а вычислять.
Чтобы ответить на вопрос "Для чего?", нет нужды обсуждать эти интригующие проблемы. Во-первых, до чрезмерного рационализма еще, видимо, довольно далеко - сегодня не то что морковку, а дорогие станки, а бывает, и целые заводы покупают, не вычисляя, а размышляя. Ну а, во-вторых, интересуясь нынешним применением и тем более будущим электронных вычислительных машин, слово "вычислительная" не следует понимать в прямом смысле - очень часто оно не отражает существа дела.
Словосочетание "вычислительная машина" совсем не означает, что речь идет о машине, которая вычисляет, и здесь нет никакого парадокса. Просто вычисляющую машину обучили нескольким другим профессиям, одна из них, кстати, особенно сильно активизировала массовый спрос на ЭВМ. Речь идет о "языкознании" компьютера, о его умении работать с текстами.
Человек, пытающийся популярно описать сложное творение техники и разъяснить при этом суть дела, всегда рискует услышать упреки специалистов в том, что он утомляет читателя азбучными истинами и становится похожим на знаменитого гашековского полковника Фридриха Крауса фон Циллергута ("Похождения бравого солдата Швейка", глава XV, "Катастрофа"). Полковник изводил окружающих тем, что как некое откровение пояснял очевидные вещи: "Дорога, по обеим сторонам которой тянутся канавы, называется шоссе. Да-с, господа. Знаете ли вы что такое канава? Канава - это вырытое значительным числом рабочих углубление... Вот это, господа, окно. Да знаете ли вы, что такое окно?.. Известно ли вам, что такое кирка?.. Знаете ли вы, что такое клейстер?.." Автор этих заметок должен признаться, что над ним всегда витает, нагоняя безумный страх, тень нудного полковника Циллергута и немало "Известно ли вам?" было безжалостно вымарано и из этого текста. Но то, о чем хочется рассказать сейчас (многим читателям, разумеется, не более чем напомнить), было оставлено без всяких колебаний.
Известно ли вам, как работает электронная вычислительная машина?
Когда вычислительная машина вычисляет, то введенные в нее человеком привычные для него десятичные числа она прежде всего превращает в удобные для себя двоичные. Так, например, 2 превращается в 10, 3 - в 101, 5 - в 111, 50 - в 110010, 28679 - в 110000011011011 и т.д. Разница между десятичными и двоичными числами, так сказать, чисто техническая - одно и то же реальное количество каких-либо объектов (карандашей, яблок, звезд на небе) в десятичной системе записывают с помощью десяти разных знаков (0, 1, 2, 3, 4, 5, 6, 7, 8, 9), а в двоичной - с помощью всего лишь двух знаков (0, 1). Двоичный счет удобен для машины потому, что она, по сути дела, представляет собой сложнейший электрический орнамент, сотканный из сотен тысяч или даже из миллионов выключателей, а выключатель, как нетрудно убедиться в эксперименте с настольной лампой, может находиться лишь в одном из двух состояний - он либо замкнут и пропускает ток, либо разомкнут и тока не пропускает. Замкнутый выключатель - это записанная машинным знаком единица, разомкнутый - ноль. Роль выключателей в вычислительной машине выполняют полупроводниковые приборы, чаще всего микронных размеров транзисторы, работающие в так называемом ключевом режиме - "открыт-закрыт" или иначе "включен-выключен".
Компьютер - система динамичная, быстродействующая. Единицы отображаются здесь не застывшими, не постоянными токами, а очень короткими, обычно в миллионные или даже миллиардные доли секунды электрическими вспышками, импульсами, нули - такими же короткими паузами. Любое число живет, путешествует, обрабатывается в ЭВМ в виде определенной комбинации импульсов-пауз. В ЭВМ среднего быстродействия за секунду происходит много тысяч так называемых машинных тактов, и во время каждого такта в разных частях компьютера производятся разнообразные операции с комплектами импульсов-пауз. Эти операции сливаются в четко организованный многоступенчатый, многотактовый процесс, и компьютер быстро продвигается к решению задачи.
Комбинациями импульсов-пауз можно зашифровать не только количество предметов, не только числа, но также и буквы, а значит, слова и тексты. Если взять комплект из трех импульсов-пауз - будем, как принято, обозначать их через 1 и 0,- то можно получить 8 разных шифров, 8 разных комбинаций - 000, 001, 010, 011, 100, 101, 110 и 111. Этими комбинациями можно было бы зашифровать 8 букв алфавита. Четырехзначный код, то есть комплекты из четырех единиц и нулей, дает уже 16 комбинаций- 0000, 0001, 0010 и так далее до 1111. Число N возможных комбинаций из 1 и 0 подсчитывается довольно просто - N=2**n, где n число знаков, число 1 или 0 в каждом комплекте. В русском алфавите 33 буквы, если избавиться от одной, обойдясь, например, одной е, то можно было бы обойтись пятизначными комплектами для кодирования всего алфавита, так как 2**5=32. Но, чтобы писать нормальные тексты машинными кодами, то есть комплектами импульсов и пауз, мало иметь 32 шифра - нужно еще какого зашифровать знаки препинания, пробел между словами, наконец, нужно иметь отдельные шифры на прописные буквы, а для научных текстов еще и на латынь. Вот почему в машинах семи- и восьмизначные коды - в первом случае можно зашифровать 2**7=128, а во втором - 2**8=256 знакам. Этого вполне хватает и на буквы, и на цифры, и на разные служебные знаки, которыми удобно пользоваться машине. В типичном восьмиразрядном коде ДКОИ (двоичный код обработки информации) буква А кодируется, как 11000001, а - 10000001, щ - 10110101, г - 10001101, открытие скобок - 10001101, закрытие - 01011101, пробел - 01000000, ? - 01101111, кавычки - 01111111 и так далее. Когда пользователь вводит в машину, например, букву А, то он нажимает на клавиатуре соответствующую кнопку, она определенным образом переключает электронную схему шифратора, и он направляет в машину комбинацию импульсов-пауз, которую мы записали как 11000001. А если такая комбинация появится на выходе компьютера, то она включит электронную схему знакогенератора таким образом, что он заставит светиться на дисплее точки, сливающиеся в букву А.
Так что, работая с текстами, компьютер никаких текстов в нашем понимании и не видит, он имеет дело с такими же комбинациями импульсов-пауз, с такими же двоичными числами, как и при вычислениях. И то, что для нас "Я помню чудное мгновенье...", для компьютера всего лишь 01111111 11011101 01000000 10010101 10010110 10011100 10011101 10111000 01000000 10110110 10101000 10001010 10011101 10010110 10000101 01000000 0011100 10001101 10011101 10010110 10101111 10000101 10011101 10110000 10000101 01001011 01001011 01001011 01111111. Так что не стоит преувеличивать значение того факта, что вычислительная машина работает с текстами.
И еще такой штрих. Вы обращаетесь к машине с просьбой, набираете на клавиатуре "Печатать раздел 5", и через несколько секунд из печатающего устройства, из принтера, выползает лист бумаги с заказанным текстом. Это значит, что комбинация импульсов-пауз, которыми было зашифровано слово "Печатать", опознано дешифратором и произведены необходимые включения в принтере. А комбинация импульсов-пауз, в которой закодировано "раздел 5", привела в действие цепочку электронных схем, заставивших двигаться магнитный диск и считывающую головку, с тем чтобы найти на диске нужный кусок записи, нужный файл. Таким образом, ваш словесный приказ был выполнен только потому, что введенные в машину слова превратились в знакомые ей коды. Непримиримый автоматизм машины, ее неумение чувствовать свободность нашего естественного языка может проявиться в таком, например, факте: если, случайно нажав на клавишу, вы сделаете между словами "печатать" и "раздел" два пробела вместо одного, то машина команду не выполнит, так как она получит незнакомую ей шифровку с лишним знаком пробела 01000000.
Вычислительная машина виртуозно работает с двоичными числами, выполняет большой ассортимент математических операций - складывает, умножает, делит, извлекает корни, логарифмирует, вычисляет синусы и тангенсы, решает дифференциальные уравнения. Но что может сделать компьютер со словами? Какие операции может выполнить с ними, кроме заранее известного "Саша + Маша = любовь"? А если тексты не нужно вычислять, если нет надобности складывать или перемножать двоичные числа, в которых зашифрованы слова, то зачем тогда вообще затевать все это непростое дело? Зачем вводить в вычислительную машину текст, а затем выписывать его на экране дисплея?
В попытке ответить на это "Зачем вычислительной машине текст?" или, правильнее, "Зачем тексту вычислительная машина?" назовем несколько новых возможностей из числа тех, что открыл нам текстовый компьютер.
Первое - компактные хранилища текста. Восьмиразрядное двоичное число, которым кодируется одна буква,- это распространенная единица количества информации - байт. В этом номере журнала, если считать, что в нем только тексты, содержится примерно миллион букв, то есть примерно миллион байт информации, или иначе-один мегабайт, Мбайт. В устройствах внешней памяти компьютеров сейчас наиболее широко применяются магнитные диски размером с граммофонную пластинку, на которых мельчайшими точками разной намагниченности, расположенными по тонким спиральным дорожкам, записаны "единицы" в "нули", записаны байты информации. Типичная (далеко не рекордная!) ширина дорожки 0.1мм, на одном миллиметре ее длины можно поставить 500 магнитных точек, то есть размер точки 0.1*0.002мм, и, значит, на запись одной буквы (1 байт, 8 знаков) расходуется площадь диска 0.1мм(0.002*8 )мм=0.0016мм2. Нетрудно подсчитать, что на территории, которую в среднем занимает на этой странице каждая буква (примерно 4мм2), магнитный диск позволяет разместить 2500 букв, записанных восьмизначным двоичным кодом. С этого и начинается компактность компьютерных хранилищ текста.
На сравнительно недорогих, так называемых гибких дисках удается записать до 3Мбайт, то есть вместить в такой диск текст трех номеров нашего журнала. В более сложных жестких дисковых модулях ("винчестерский диск") записывают до 1000Мбайт ~ 1Гбайт (гигабайт), а это уже комплект подшивок журнала за 30 лет. Наконец, на диске с оптической записью двоичных чисел может храниться до 10 Гбайт информации, сотня таких видеодисков, разместившихся на небольшом стеллаже, это крупная библиотека, для которой нужны книжные полки длиной 20 километров.
Второе - снабдив часть текста цифровой меткой, его легко найти в большом массиве информации. В этом случае компьютер выполняет привычную для него работу: просмотрев хранящееся в памяти оглавление, он дает команду иа перемещение считывающей магнитной головки именно в то место диска, где находится нужный текст. За какие-то доли секунды машина может отыскать текст в записи, эквивалентной по объему многотомной энциклопедии.
Третье - созданы программы, позволяющие компьютеру находить тексты по ключевым словам в названиях статей или книг. Вот пример: введенное в вычислительную машину с заданием поиска слово "сон", это привычные для нее байты 10000011 10010110 10011101; перебирая хранящиеся в памяти слова названий статей или книг, машина будет сравнивать их с заданным ключевым словом и искать сходство; в принципе его обнаружить несложно, можно, например, вычитать код одного слова из другого, и если получится ноль, то, значит, шифры совпадают, слова одинаковы; обнаружив ключевое слово в заголовке, машина запомнит заголовок, его кодовую метку; если понадобится, по ней легко найти и саму статью. Можно отбирать заголовки по совпадению нескольких ключевых слов, скажем, в нашем примере искать статьи, посвященные летаргическому сну, электросну или дневному сну детей дошкольного возраста. Не так, конечно, просто дело делается, как сказка сказывается, нужно, например, предусмотреть появление ключевого слова в косвенном падеже или сделать так, чтобы пунктуальная машина, выискивая "сон", не попалась на "Карлсон". Многие трудности, однако, уже преодолены, и тысячи людей по ключевым словам сейчас находят нужные им документы в огромных компьютерных хранилищах информации.
Документом в информатике принято называть не только справку, отчет или техническое задание, но также и книгу, журнальную статью, рукопись, кинофильм, граммофонную пластинку, магнитный диск, одним словом, официально любой "материальный носитель записи с зафиксированной на нем информацией, предназначенной для передачи во времени и пространстве".
Четвертое - машина позволяет легко преобразовывать тексты. В какой-либо записанной на диске текст, например, в телефонный справочник, очень просто внести дополнение, сделать вставку. В упрощенном варианте (точнее, в усложненном, но более понятном) это выглядит так: текст с диска переписывают в оперативную память машины; туда же отдельно записывают вставку; затем вновь записывают весь текст на диске, поместив вставку в отведенное ей место. Пользователю достаточно лишь указать, где и какое дополнение нужно сделать, а всю техническую часть дела машина возьмет на себя. Аналогично можно корректировать текст, сокращать и менять его, раздвинуть два слова и вставить между ними еще одно, короче говоря, редактировать. Редактирование с помощью ЭВМ во многом очень удобно, во всяком случае, не нужно бессчетное число раз перепечатывать и вклеивать исправленные куски.
Пятое - машины могут очень быстро обмениваться документами, пересылая их на большие расстояния по линии связи, причем без каких-либо дополнительных преобразований - в виде обычных своих восьмерок "импульс-пауза". Это не требует, видимо, особых пояснений, хочется лишь напомнить, как не просто бывает получить из другого города какой-либо бумажный документ и что уходят на это не секунды, как при запросе у компьютера, а уходят на это дни, чаще всего в интервале от 3-5 дней до бесконечности.
Последние годы отмечены лавиной применения вычислительных машин в решении самых разных, так сказать, невычислительных задач - для хранения и поиска информации, обработки текстов, учета и распределения ресурсов, диспетчеризации, оформления деловых отношений. Рухнули многие бюрократические технологии, резко сократился обмен бумагами и бумажками, проходящими через руки человека, с помощью какого-нибудь не очень большого компьютера стали выполняться сложнейшие операции, которые раньше наверняка потребовали бы участия сотен симпатичных девушек, вооруженных шариковыми ручками и квитанционными книжками с фиолетовой копиркой.
Иллюстраций здесь можно привести очень много, черпая их не только в науке, но и в жизни. Так, например, в Москве, Ленинграде, Киеве и других городах компьютерам поручили учет всех международных телефонных разговоров, выписку счетов и последующий контроль за их оплатой. Компьютеру доверили держать в памяти все места и продавать билеты на все сто с лишним ежедневно уходящих из Москвы поездов. И кассиру в окошечке остается лишь ввести вашу просьбу в ЭВМ и получить деньги за билет или обреченно отказать - "В машине ничего нет". Компьютерная "Сирена" не только ежедневно распределяет десятки тысяч мест в вылетающих из Москвы самолетах, но также входит в контакт с компьютерами других аэропортов и аналогичными международными системами, которые вместе координируют продажу мест чуть ли не на все самолеты мира.
Перечисляя достоинства электронных текстов, нужно бы вспомнить такую мелочь, как возможность сопровождать цифровые потоки словесными дополнениями. Научив машину пользоваться не только цифрами, но и буквами, можно, например, в результатах расчета вместо "0.5...110" вывести на дисплей "0.5 миллиампера при сопротивлении 110 килоом" или вместо "235...18.30" отпечатать "235 тонн по 18 рублей 30 копеек за тонну". Одним словом, можно выводить из машины таблицы, планы, расписания, билеты, счета, квитанции, ведомости и другую насыщенную цифрами деловую документацию в привычном для человека виде.
Появились терминалы в издательских кабинетах, и редакторы забросили в далекий ящик свое грозное вооружение - карандаши, ножницы и клей. Короткие записи на магнитных дисках сильно потеснили бессчетные бумажки в конторах и на складах. Даже осторожные банковские работники кое-где доверили компьютеру выплату наличных денег без заполнения расходных ордеров, сличения подписей и каллиграфического выписывания суммы прописью - достаточно сунуть в щель простейшего терминала магнитную карточку с личным шифром и набрать клавиатурой нужную сумму, как по желобку к вам тут же вылетят наличные деньги (если, конечно, позволяет остаток на счете), а банковский компьютер внесет необходимые изменения в свои записи на магнитном диске.
Вместо библиотек, а вернее параллельно с ними, уже организованы тысячи огромных хранилищ информации на магнитных дисках, откуда с помощью компьютера можно быстро извлечь нужный текст к себе на дисплей. В ряде стран появились городские справочные компьютеры, от которых по телефонной линии можно получить на домашний терминал расписание автобусов, карту погоды, справку из словаря.
Одним словом, безбумажная информатика во многих конкретных областях уверенно доказала решающие свои достоинства - экономические, деловые, житейские. И уже появились прогнозы полного отстранения бумажного документа от всех его нынешних дел. Деловая переписка? Только электрическими сигналами, с терминала на терминал. Газеты и журналы? Только поступающие подписчику на дисплей. Домашняя библиотека? Только в виде магнитных дисков. В общем, никакой бумаги - безбумажное общество.
Дискуссии футурологов по этому поводу не угасают и по сей день, они дают оценки будущего в широких пределах - от "полностью электронная система изданий" до "безбумажное общество, где исчезнут любые коммуникации на бумаге,- это химера".
И все ж, тот, кто собирается всю жизнь сортировать накладные, перекладывать складские требования или набивать бумагами архивные папки, может оказаться в положении "ничейной бабушки", которая жгла у себя на антресолях керосиновую лампу, так как не верила в электричество.
Отдать вычислительным машинам все, что можно отдать! Отдать, не раздумывая и не откладывая,- массу дел они делают лучше нас, быстрее, четче. Эти машины умеют то, что нам вообще недоступно, без них уже невозможно управиться с работающим на нас огромным миром техники и технологий. Но нельзя же отдавать компьютеру книгу! Потерять возможность взять ее с полки и полистать перед сном. И вряд ли мерцающий зеленоватыми буквами дисплей заменит пахнущую краской свежую газету, которую ты сунул в карман до первой свободной минуты. Вряд ли он заменит и первые каракули внука в школьной тетради или письмо, написанное рукой друга,- слишком важное место занимает бумажный документ в нашей жизни, чтобы полностью отказаться от него. Это, видимо, значило бы стать совсем другим человеком, с иными ритмами жизни и даже с иной шкалой жизненных ценностей. Нужно ли это? И возможно ли с позиций психологии и даже физиологии? А потом, почему должно быть "или-или"? Ведь радиосвязь не отменила телефона и самолет не отучил нас перемещаться пешком.
Как ни интересны дискуссии футурологов о перспективах безбумажной информатики, как ни аргументированы их "за" и "против", будущее сформируется все-таки не из них. Будущее в руках людей, как правило, невидимых миру,- системных программистов, технологов, инженеров. Это они делают все, чтобы вытеснить бумажный документ оттуда, где он стал обузой, и это они же ищут пути состыковать ЭВМ с бумажным документом там, где от него отказаться нельзя. Такая стыковка, такое сосуществование позволят объединить достоинства безбумажной информатики, в частности компактность хранилищ, автоматизацию поиска, удобство редактирования, скорость пересылки и достоинства бумажного документа, в числе которых удобство пользования, простота транспортировки, независимость от электропитания и линий связи. Рисунки ниже иллюстрируют основные идеи и методы, используемые на таком важном участке взаимодействия компьютер-бумага, как вывод информации из ЭВМ на печатный лист. Все эти идеи уже реализованы в серийных установках, с помощью которых компьютер выдает десятки страниц печатного текста в минуту или с отредактированных на терминале и попавших на магнитный диск статей и заметок сразу формирует газетную полосу и без посредников готовит для нее печатную форму.
Техника эта быстро совершенствуется, позволяя надеяться, что бумажный документ не будет помехой на пути безбумажной информатики.
...

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
...
Устройства, которые связывают компьютер с бумажным листом, можно разделить на две большие группы - аппараты для ввода печатной информации в ЭВМ прямо с бумажного листа и аппараты для вывода информации на бумагу, для получения бумажного документа. Системы ввода текста, как их называют, читающие автоматы, пока еще не стали распространенным явлением. Эти автоматы уже умеют читать типографский и машинописный тексты, но их не так-то просто перестроить при смене шрифта и научить чтению плохо пропечатавшейся буквы. Все еще далекой остается перспектива свободного чтения рукописных текстов.
Устройства вывода информации из ЭВМ на бумагу используются очень широко, можно сказать, повсеместно. Существует большое многообразие таких устройств, и классифицировать их принято по разным признакам. Можно, например, разделить устройства вывода текстов на две группы, объединив в одной все, что, подобно пишущей машинке, печатает буквы и цифры прямо на бумаге. Это принтеры, или, более строго, АЦПУ - алфавитно-цифровые печатающие устройства (10/80). Они выдают документ в одном экземпляре, но пользователю, как правило, больше и не нужно. А если понадобится, то можно дать принтеру команду "повторить" или снять нужное число копий на ксерографическом аппарате.
В другую группу войдут установки, которые фотоспособом воспроизводят тексты на светочувствительной пленке. После проявки с нее готовят печатную форму, с которой традиционными способами (офсетная печать) можно размножить документ любым необходимым тиражом. Этот метод вывода информации - его называют фотонабором - широко используется в современной полиграфии: наборщик, работая на клавиатуре терминала, записывает текст на магнитный диск в виде обычных кодов, а затем фотонаборный автомат превращает эту запись в буквы и цифры на пленке.
Некоторое промежуточное место между непосредственной печатью и фотонабором занимает перенос текста на селеновый барабан ксерографической установки (от греческого "ксерос" - "сухой", имеется в виду печать не жидкой, а сухой красной), а затем получение с него нужного числа ксерокопий.
Еще один важный принцип классификации - по способу получения знака. В одних устройствах знак имеется в готовом виде, и он просто тем или иным способом переводится, переносится на бумагу или на пленку. В устройствах другой группы знака в готовом, так сказать, вещественном виде нет, его каждый раз изготавливают заново, синтезируют по электрическому описанию, которое хранится в памяти одного из блоков машины (на рисунках - блок управления).
А теперь короткие заметки о некоторых типах устройств вывода печатной информации, которые в предельно упрощенном виде представлены на рисунках 1-8.
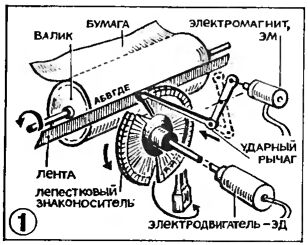
1. Печатающее устройство с лепестковым знаконосителем. Синхронный электродвигатель вращает "ромашку", на которой имеется весь необходимый набор знаков, ударный рычаг в нужный момент прижимает к бумаге один из лепестков, и на бумаге появляется оттиск заданной буквы. Импульс тока на электромагнит, который приводит в действие ударный рычаг, подается с электронного блока управления, а он получает информацию о положении "ромашки" и о том, какую букву нужно отпечатать. Этот печатающий блок можно встретить и в современных пишущих машинках, в том числе в машинках с памятью на магнитном диске (для автоматической печати повторяющихся или заранее подготовленных на терминале текстов).

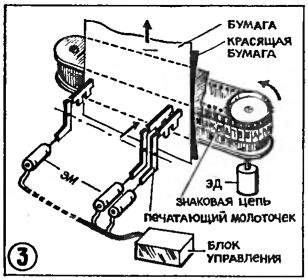
2, 3. Алфавитно-цифровое печатающее устройство с барабанным (2) и цепным (3) знаконосителями. Печатающие молоточки ударяют поочередно, формируя таким образом строку, причем удар происходит в момент, когда к молоточку подходит нужный для данного места (в строке) знак. Решает эту задачу, как всегда, блок управления.

4. Блок формирования печатных текстов в распространенных системах фотонабора. Лампа-вспышка, получая команду от блока управления, дает световой импульс именно в тот момент, когда в объектив попадает нужная цифра или буква. Меняя объективы, можно менять размеры знаков на светочувствительной пленке, а меняя саму пленку-знаконоситель - выбирать нужный шрифт. Фотопленка находится в светонепроницаемой насеете, имеющей лишь окно для ввода изображения одного знака.

5а. Знакосинтезирующая система, где буква или цифра появляется в результате удара определенной комбинации печатающих иголочек. Их приводят в движение электромагниты, получая команду от блока управления. Одновременно печатается лишь один вертикальный ряд точек, но каретка с бумагой смещается небольшими шагами слева направо, и после нескольких таких шагов появляется целиком буква или цифра. Она получается тем более четкой, чем больше иголочек в печатающей системе, то есть чем из большего числа элементов состоит растр одного знака. В простых системах чаще всего встречается растр 7*9 элементов (63 точки), в более совершенных - вплоть до 15*18 (270 точек).
5б. Аналогичный блок, но избавленный от недостатков элентромеханических печатающих систем. Изображение знака на фотопленке синтезируется из светящихся точек, их дают миниатюрные источники света - светодиоды, причем знак можно сделать меньше светодиодной линейки, передав свет с помощью сужающегося световолоконного пучка.

6. Струйная печать: наэлектризованные мельчайшие капельки чернил направлены на бумажный лист; электрическим или магнитным полем поток капель отклоняют, прочерчивая тончайшую горизонтальную нитку, а управляющий сигнал в определенные моменты прерывает поток капель. На листе образуются наборы точек, из которых и формируется знак. Существуют струйные установки для многоцветной печати.

7. На светочувствительную пленку изображение знака попадает с экрана ЭЛТ - электронно-лучевой трубки. Набор сигналов, необходимых для получения той или иной буквы, поступает из ЭВМ. По-разному управляя электронным лучом, можно легко менять шрифт и размеры знаков.
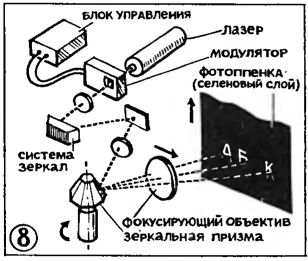
8. Лазерное печатающее устройство: тончайший луч строку за строкой быстро прочерчивает фотопленку, отклоняет его вращающееся зеркало (грань зеркальной призмы); твердотельный модулятор, управляемый компьютером, то прерывает световой луч, то открывает ему путь к пленке, формируя на ней таким образом изображение знаков. Размеры рисующей световой точки - несколько микрон, и знаки получаются очень четкими. Аналогично воспроизводятся рисунки и фотографии.
Последним двум методам - с использованием ЭЛТ и лазера - в последнее время уделяют особое внимание. Это, в частности, связано с их высокой производительностью, столь ценным качеством для стыковки с быстродействующими ЭВМ. Так, в частности, в печати сообщается о лазерных и электронных принтерах, печатающих многие тысячи знаков в секунду (десятки и сотни страниц в минуту), в то время как скорости, характерные для классических АЦПУ,- десятки и сотни знаков в секунду, то есть страница за время порядка минуты.

В Специальном конструкторском бюро Всесоюзного института научной и технической информации (СКБ ВИНИТИ) создано немало современных аппаратов для решения различных задач бумажной и безбумажной информатики (12/83). Одна из последних разработок - печатающее устройство "Принтер-Э512". Полученные из ЭВМ и записанные на магнитной пленке девятиразрядным кодом знаки преобразуются в сигналы, управляющие яркостью луча в электронно-лучевой трубке. На трубке формируется одна строка текста (четкость знака - 16*16 точек), она попадает на селеновый барабан ксерографической установки, и построчно сложившийся текст печатается на бумаге.
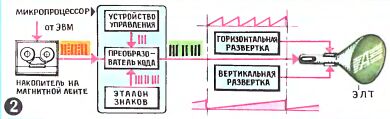
В памяти установки одновременно хранятся электрические эталоны 512 разных знаков, этот набор при необходимости можно легко заменить другим. "Принтер-Э512" воспроизводит тексты с учетом важных требований полиграфии, о выдает от 1 до 256 копий, в минуту может быть отпечатано до 40 страниц.
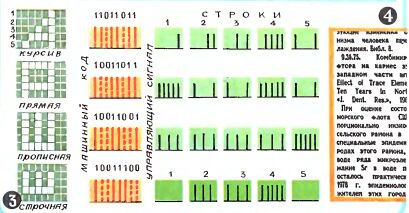
Устройства, которые связывают компьютер с бумажным листом, можно разделить на две большие группы - аппараты для ввода печатной информации в ЭВМ прямо с бумажного листа и аппараты для вывода информации на бумагу, для получения бумажного документа. Системы ввода текста, как их называют, читающие автоматы, пока еще не стали распространенным явлением. Эти автоматы уже умеют читать типографский и машинописный тексты, но их не так-то просто перестроить при смене шрифта и научить чтению плохо пропечатавшейся буквы. Все еще далекой остается перспектива свободного чтения рукописных текстов.
Устройства вывода информации из ЭВМ на бумагу используются очень широко, можно сказать, повсеместно. Существует большое многообразие таких устройств, и классифицировать их принято по разным признакам. Можно, например, разделить устройства вывода текстов на две группы, объединив в одной все, что, подобно пишущей машинке, печатает буквы и цифры прямо на бумаге. Это принтеры, или, более строго, АЦПУ - алфавитно-цифровые печатающие устройства (10/80). Они выдают документ в одном экземпляре, но пользователю, как правило, больше и не нужно. А если понадобится, то можно дать принтеру команду "повторить" или снять нужное число копий на ксерографическом аппарате.
В другую группу войдут установки, которые фотоспособом воспроизводят тексты на светочувствительной пленке. После проявки с нее готовят печатную форму, с которой традиционными способами (офсетная печать) можно размножить документ любым необходимым тиражом. Этот метод вывода информации - его называют фотонабором - широко используется в современной полиграфии: наборщик, работая на клавиатуре терминала, записывает текст на магнитный диск в виде обычных кодов, а затем фотонаборный автомат превращает эту запись в буквы и цифры на пленке.
Некоторое промежуточное место между непосредственной печатью и фотонабором занимает перенос текста на селеновый барабан ксерографической установки (от греческого "ксерос" - "сухой", имеется в виду печать не жидкой, а сухой красной), а затем получение с него нужного числа ксерокопий.
Еще один важный принцип классификации - по способу получения знака. В одних устройствах знак имеется в готовом виде, и он просто тем или иным способом переводится, переносится на бумагу или на пленку. В устройствах другой группы знака в готовом, так сказать, вещественном виде нет, его каждый раз изготавливают заново, синтезируют по электрическому описанию, которое хранится в памяти одного из блоков машины (на рисунках - блок управления).
А теперь короткие заметки о некоторых типах устройств вывода печатной информации, которые в предельно упрощенном виде представлены на рисунках 1-8.

1. Печатающее устройство с лепестковым знаконосителем. Синхронный электродвигатель вращает "ромашку", на которой имеется весь необходимый набор знаков, ударный рычаг в нужный момент прижимает к бумаге один из лепестков, и на бумаге появляется оттиск заданной буквы. Импульс тока на электромагнит, который приводит в действие ударный рычаг, подается с электронного блока управления, а он получает информацию о положении "ромашки" и о том, какую букву нужно отпечатать. Этот печатающий блок можно встретить и в современных пишущих машинках, в том числе в машинках с памятью на магнитном диске (для автоматической печати повторяющихся или заранее подготовленных на терминале текстов).


2, 3. Алфавитно-цифровое печатающее устройство с барабанным (2) и цепным (3) знаконосителями. Печатающие молоточки ударяют поочередно, формируя таким образом строку, причем удар происходит в момент, когда к молоточку подходит нужный для данного места (в строке) знак. Решает эту задачу, как всегда, блок управления.

4. Блок формирования печатных текстов в распространенных системах фотонабора. Лампа-вспышка, получая команду от блока управления, дает световой импульс именно в тот момент, когда в объектив попадает нужная цифра или буква. Меняя объективы, можно менять размеры знаков на светочувствительной пленке, а меняя саму пленку-знаконоситель - выбирать нужный шрифт. Фотопленка находится в светонепроницаемой насеете, имеющей лишь окно для ввода изображения одного знака.

5а. Знакосинтезирующая система, где буква или цифра появляется в результате удара определенной комбинации печатающих иголочек. Их приводят в движение электромагниты, получая команду от блока управления. Одновременно печатается лишь один вертикальный ряд точек, но каретка с бумагой смещается небольшими шагами слева направо, и после нескольких таких шагов появляется целиком буква или цифра. Она получается тем более четкой, чем больше иголочек в печатающей системе, то есть чем из большего числа элементов состоит растр одного знака. В простых системах чаще всего встречается растр 7*9 элементов (63 точки), в более совершенных - вплоть до 15*18 (270 точек).
5б. Аналогичный блок, но избавленный от недостатков элентромеханических печатающих систем. Изображение знака на фотопленке синтезируется из светящихся точек, их дают миниатюрные источники света - светодиоды, причем знак можно сделать меньше светодиодной линейки, передав свет с помощью сужающегося световолоконного пучка.

6. Струйная печать: наэлектризованные мельчайшие капельки чернил направлены на бумажный лист; электрическим или магнитным полем поток капель отклоняют, прочерчивая тончайшую горизонтальную нитку, а управляющий сигнал в определенные моменты прерывает поток капель. На листе образуются наборы точек, из которых и формируется знак. Существуют струйные установки для многоцветной печати.

7. На светочувствительную пленку изображение знака попадает с экрана ЭЛТ - электронно-лучевой трубки. Набор сигналов, необходимых для получения той или иной буквы, поступает из ЭВМ. По-разному управляя электронным лучом, можно легко менять шрифт и размеры знаков.

8. Лазерное печатающее устройство: тончайший луч строку за строкой быстро прочерчивает фотопленку, отклоняет его вращающееся зеркало (грань зеркальной призмы); твердотельный модулятор, управляемый компьютером, то прерывает световой луч, то открывает ему путь к пленке, формируя на ней таким образом изображение знаков. Размеры рисующей световой точки - несколько микрон, и знаки получаются очень четкими. Аналогично воспроизводятся рисунки и фотографии.
Последним двум методам - с использованием ЭЛТ и лазера - в последнее время уделяют особое внимание. Это, в частности, связано с их высокой производительностью, столь ценным качеством для стыковки с быстродействующими ЭВМ. Так, в частности, в печати сообщается о лазерных и электронных принтерах, печатающих многие тысячи знаков в секунду (десятки и сотни страниц в минуту), в то время как скорости, характерные для классических АЦПУ,- десятки и сотни знаков в секунду, то есть страница за время порядка минуты.

В Специальном конструкторском бюро Всесоюзного института научной и технической информации (СКБ ВИНИТИ) создано немало современных аппаратов для решения различных задач бумажной и безбумажной информатики (12/83). Одна из последних разработок - печатающее устройство "Принтер-Э512". Полученные из ЭВМ и записанные на магнитной пленке девятиразрядным кодом знаки преобразуются в сигналы, управляющие яркостью луча в электронно-лучевой трубке. На трубке формируется одна строка текста (четкость знака - 16*16 точек), она попадает на селеновый барабан ксерографической установки, и построчно сложившийся текст печатается на бумаге.

В памяти установки одновременно хранятся электрические эталоны 512 разных знаков, этот набор при необходимости можно легко заменить другим. "Принтер-Э512" воспроизводит тексты с учетом важных требований полиграфии, о выдает от 1 до 256 копий, в минуту может быть отпечатано до 40 страниц.


Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
2/86
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
Раздел "Человек с микрокалькулятором" сменил название. Отныне он будет именоваться "Человек и компьютер". Эта смена - логическое развитие нашей рубрики. В ответ на призыв редакции (8/85) читатели стали присылать свои рассказы о работе на персональных компьютерах. Два письма из тех, что пришли первыми, публикуются в нынешнем выпуске. Надеемся, что подобные письма будут приходить все чаще и станут занимать все большую часть раздела.
Эти письма, которых мы ждем в ближайшее время, зададут и направленность, и уровень дальнейших родственных им публикаций. Пусть же поспешат со своими корреспонденциями те, кому есть что рассказать о своем опыте работы с персональными компьютерами, те, кто желает видеть наш раздел ярким, содержательным, поучительным.
Что же касается микрокалькуляторов, то свое место в обновляющемся разделе сохранят и они: ведь они тоже принадлежат к большому семейству компьютеров.
Организовать массовый выпуск персональных компьютеров. Обеспечить рост производства вычислительной техники в 2-2.3 раза.
Из проекта Основных направлений экономического и социального развития СССР на 1986-1990 годы и на период до 2000 года
КАК Я ЗАВЕДОВАЛ СКЛАДОМ ХИМРЕАКТИВОВ
История эта началась, когда мне, младшему научному сотруднику НИИ химического профиля, поручили совмещать свои прямые обязанности с заведованием складом химреактивов нашей лаборатории.
Завел я себе общую тетрадь и решил вести записи по каждому реактиву - сколько его осталось, где он хранится и т.д. Записей становилось все больше, работать с тетрадью становилось все труднее. Произошел какой-то локальный информационный бум.
В конце концов стало ясно, что какую систему записей ни заводи - по алфавиту ли, по содержимому шкафов и полок, по степени чистоты реактивов,- так или иначе при поиске нужной упаковки часто приходится просматривать тетрадь от корки до корки. Информационный бум перерос в информационный кризис.
Тут произошло важное событие: наша лаборатория получила ЭВМ "Искра-226" с языком программирования "бейсик". Его я освоил быстро и понял, что наша "Искра" - идеальное средство для ведения учетной тетради реактивов.
Работать с электронной "тетрадью" - одно удовольствие. Ввожу программу, запускаю машину клавишей ВК. Машина начинает выполнять команды программы - строка за строкой. У каждой строки-свой номер, команды разделяются двоеточиями.

1-я строка. N=200. Это число страниц в тетради. Следующая команда начинается с буквы DIM. Это сокращенное английское слово dimension, размер. Язык "бейсик", которому обучена "Искра", использует слова английского языка. Своеобразный крестик, стоящий вслед за буквой A, указывает на то, что эта переменная не числовая, а литерная, то есть представляет собою сочетание букв, а не цифр. В скобках указано, что переменная А может принять 200 значений, после скобок - что она может содержать до 100 букв. Переменная К, указанная далее, будет кодировать информацию о требующихся реактивах, сообщаемую машине. В - переменная числовая. Судя по цифре в скобках, она может принимать два значения. Это признаки, по которым машина станет отыскивать в своей памяти нужную мне информацию. REM - ремарки, пояснения к программе. Они помогают разобраться в ней. Машина в ходе работы не обращает на них внимания. (Здесь прямая аналогия с ремарками в тексте пьесы - действующие лнца их не произносят, но они помогают успешно поставить спектакль).
Вслед за 1-й строкой машина переходит ко 2-й. INPUT - значит ввести. И дальше - текст в кавычках. Только такие тексты, содержащиеся в программе, выводятся на экран дисплея. В данном случае это так называемое меню, перечень возможных видов работы по программе "1 - новая запись, 2 - поиск информации, 3 - перелистывание, 4 - изменение, 5 - конец работы". В машину нужно ввести цифру, обозначающую желаемый режим. Сейчас мне нужно найти какую-нибудь соль соляной кислоты, причем чистую для анализа. Нажимаю клавишу 2 (поиск информации), а затем-клавишу ВК. Это буквосочетание - аналог слова "прием", который используют радисты, когда заканчивают свою фразу и ждут ответа собеседника. Значение 2 присваивается переменной A, которая в программе стоит сразу за текстом меню. В следующей команде есть слово GOTO - пойти к... и перечень переходов, зависящих от значения A. Второй (A=2) в этом перечне стоит цифра 5. На 5-ю строку и переходит машина.
На экране дисплея - надпись: "1-е ключевое слово, логическая связка (1 - И, 2 - ИЛИ, 3 - НЕ), 2-е слово". Названия всех солей соляной кислоты начинаются со слова "хлор". Начинаю набирать его на клавиатуре, предваряя пробелом. Пробел не даст тетради открыться на страницах со словами ЧЕТЫРЕХХЛОРИСТЫЙ, ДИХЛОР н т.п. Итак, набираю - ХЛОР, 1, ЧДА. И нажимаю клавишу В К.
Выполнив команды 5-й строки, машина переходит на 6-ю. FOR J = 1 TO N. Это предписание выполнить цикл, в котором переменная J, счетчик цикла, примет все значения от 1 до N. Иными словами, машина станет просматривать страницы тетради с 1-й по N-ную и будет выполнять при этом команды 7-й строки: ведь в шестой строке вслед за только что выполненной командой стоит такая: IF A=2 THEN 7 (если А=2, то 7).
7-я строка. Мы видим, что здесь двукратно выполняется цикл (FOR J=1 TO 2), в котором переменная В принимает два значения, В(1) и В (2); что, судя по обозначению Аx(1), здесь просматривается строка с номером 1 от первой ее буквы (Р=1) до той, которая определяется длиной записанного здесь текста (LEN - это сокращенное length, длина); что в ходе просмотра проверяется совпадение или несовпадение ключевого слова Кx(J) с фрагментом строки такой же длины LEN(Кx(J)), начинающегося с буквы под порядковым номером Р на странице под номером 1. Все эти приметы просматриваемого фрагмента указаны в обозначении STR(Аx(1)),Р,LEN(Kx(J)). STR - это сокращенное string, строка. Проверка несовпадения кодируется знаком <> (меньше или больше, то есть не равно, не совпадает), разделяющим символы Kx(J)) и STR. Если обнаружилось несовпадение, мы переходим к 8-й строке (THEN 8 ), согласно которой смещается "поле зрения" (NEXT P, следующий номер знака в тексте). Если же обнаружено совпадение, то произойдет переход на 9-ю строку (GOTO 9) - а предварительно признаку B(J) будет придано значение 1. Выполняя команды строк 9-11, машина по признакам В(1) и В(2) разберется, нужно ли печатать и выводить найденную информацию на экран дисплея.
Читаю появившуюся на нем надпись: "НАТРИИ ХЛОРИСТЫЙ, ЧДА, 0.2КГ, НОРМА 2КГ, МЕНЬШЕ НОРМЫ, 5 ШКАФ 3 ПОЛКА, 28.10.85". Поваренная соль, стало быть, хранится в пятом шкафу на третьей полке. Данные иа 28 октября 1985 года. Осталось ее всего 200 граммов, меньше нормального запаса.
Я не подозревал столь неприятной оказии. В таком случае реактив лучше не использовать, а постараться поискать ему замену, открыв тетрадь на страницах с фрагментом его названия, но там, где нет слов МЕНЬШЕ НОРМЫ. Тогда мой запрос должен выглядеть так: ХЛОР, 3, МЕНЬШЕ НОРМЫ. Однако нет худа без добра. Составлю заявку, отпечатаю на той же "Искре" и отнесу в отдел снабжения. Я заметил, что в последнее время получаю там меньше отказов - ведь заявки теперь составляет ЭВМ, существо точное и беспристрастное.
Но вернемся к программе. Я мог бы подробно разъяснить каждую ее команду, но это потребовало бы слишком много места. Мне кажется, что в журнале "Наука н жизнь" стоит напечатать рассказ о языке "бейсик" - наподобие "Школы начинающего программиста", где читатели обучались работе на микрокалькуляторе.
В.СОЛОВЬЕВ (г.Киев).
[ Предлагаем задание: составить и записать на языке "бейсик" (BASIC) алгоритмы перевода римских цифр в десятичную систему счисления и обратного перевода. Хотя такие алгоритмы и приводятся в некоторых книгах по "бейсику", можно разработать более совершенные их варианты. Просим указывать, для какой конкретной машины составлена программа.
Интересующимся языком "бейсик" советуем ознакомиться с книгами:
Кетков Ю.Л. Программирование на "бейсике". М., "Статистика", 1973.
Семик В.П. и др. Программирование на языке "бейсик-плюс" для СМ-4. М., "Финансы и статистика", 1982.
Уорт Т. Программирование на языке "бейсик" М., "Машиностроение", 1981 ]
ОТ КОНКУРСА К ВНЕДРЕНИЮ
Дан ряд чисел. Требуется ранжировать их, то есть расположить в порядке возрастания или убывания. Так ставилась конкурсная задача, опубликованная в 4/85. Вслед за постановкой задачи высказывался вопрос: какова максимальная длина массива, который можно ранжировать на микрокалькуляторе, и как, сочетая ручной труд с машинным, получить упорядоченный ряд для массива большей длины?
Свои решения прислали 63 человека. Среди них - немало скептиков. "Массивы, которые вмещает "Электроника Б3-34", быстрее ранжировать вручную,- пишет Г.Натансон (Ленинград).- Я не обнаружил возможности ускорить ранжирование массивов с помощью микрокалькулятора. Остается задача спортивного характера: составить программу, упорядочивающую массив возможно большего размера".
Г.Натансону удалось разработать программу, располагающую в порядке возрастания 16 чисел. Столько же чисел упорядочивает с помощью более быстрой программы И.Шестак (Киев); он также предлагает доказательство, что больший массив "Электронике Б3-34" не осилить. Программа Л.Габрида (Фрунзе) ранжирует массив такой же длины, однако она удобнее, чем у обоих названных авторов, и работает ненамного дольше программы И.Шестака - около 10 минут. Вот она:
00. ПД 01. 1 02. 2 03. П0 04. Сх 05. КП:^ 06. FL0 07. 05 08. F() 09. С/П 10. ^ 11. 1 12. 3 13. П0 14. F() 15. КИП^ 16. Fx!=0 17. 36 18. - 19. Fx<0 20. 30 21. FBx 22. + 23. FBx 24. x-y 25. КП^ 26. FL0 27. 14 28. БП 29. 08 3O. FBx 31. + 32. FL0 33. 15 34. БП 35. 09 36. F() 37. КП^ 38. БП 39. 08 40. 1 41. 3 42. П0 43. F() 44. КИП^ 45. С/П 46. FL0 47. 43 48. ПП 49. 62 50. П0 51. ПП 52. 62 53. ИП0 54. ПП 55. 63 56. С/П 57. F() 58. С/П 59. F() 60. С/П 61. К7 62. F() 63. - 64. Fx<0 65. 71 66. FBx 67. + 68. FBx 69. x-y 70. B/0 71. FBx 72. + 73. FBx 74. B/0
Инструкция.
1. Ввести программу.
2. Ввести первый член ряда: x1 В/0 С/П.
3. Ввести последующие члены ряда: х2 С/П ... x16 С/П. Нуль заменять числом на порядок ниже, чем точность задания вводимых чисел.
4. Подать команду БП 40 С/П и прочесть на индикаторе минимальный член ряда.
5. Командой С/П вызвать остальные члены.
6. Появление на индикаторе сигнала ЕГГОГ показывает, что вся информация выведена.
После вывода первые 13 членов ряда сохраняются в регистрах Д...1, последние 4 - в регистрах стека Y, Z, Т, X.
Если все члены ранжируемого массива положительны и содержат не более четырех знаков, то в каждый регистр можно вводить по два таких числа, разделяя их запятой. Например, 25 и 72 объединяются так: 25.0072. Подобный прием используют В.Козлов (Ленинград), Ю.Мильчаков (Владивосток), С.Носков (Родники Ивановской обл.). Эти программы работают медленно - 40 минут и более. Ограничившись двузначными числами, С.Носков и А.Соболь (Донецк) расширяют границы массива еще вдвое. А.Виноградов (Киев) предлагает размещать подобные числа (скажем, трехзначные) в программной памяти, завершая их ввод командой В/0; извлекаются они командой КПП^.
Авторы присланных на конкурс программ использовали в большинстве своем два алгоритма. Согласно первому, упорядочиваемые числа при их вводе в калькулятор заполняют адресуемые регистры в порядке поступления. Далее адресуемые регистры просматриваются попарно, и в каждой паре после ее просмотра большее число оказывается в регистре с большим номером (или с меньшим, смотря по тому, в каком порядке ранжируются числа). После первого просмотра всего массива наибольшее число оказывается в регистре с наибольшим номером, после второго следующее по величине число - в регистре с номером, на единицу меньшим, и т.д. Таков метод "пузырька" (перемещения чисел напоминают всплывание пузырька в воде; рис. слева). Согласно второму алгоритму, для очередного вводимого числа, начиная уже со второго, определяется его место среди введенных. Затем массив введенных чисел раздвигается так, чтобы вводимое число оказалось на найденном для него месте. Таков метод локальных максимумов (рис. справа).
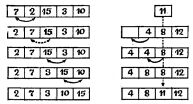
Что же делать, если в массиве, подлежащем ранжировке, больше чисел, чем единовременно упорядочивается программой? С.Носков предлагает на этот случай программу, которая ранжирует 14 чисел, а если ввести в калькулятор еще и 15-е, то из всех 15 наибольшее будет выведено на индикатор, 14 остальных выстроятся в порядке возрастания в адресуемых регистрах. После просмотра всего массива так будут отделены и упорядочены 14 наименьших чисел; большие следует списывать с индикатора и упорядочивать заново. В сущности, тот же метод излагают Н.Клименко (Челябинск), А.Коганцев (Москва), М.Корнилов и Е.Бережной (Киев), А.Куцеванов (Никополь), А.Соболь (Донецк), И.Шахнович (Кронштадт), а также А.Капцан (Ташкент), Т.Астахович и В.Новосельский (Ленинград).
А.Клейн (Балабаново, Калужской обл.) предлагает на глазок выделить в массиве среднюю величину и разделить его на две группы, состоящие из чисел либо меньших либо больших выделенного. Деление повторять, пока в каждой из полученных групп ие окажется столько чисел, что их можно ранжировать имеющейся программой.
A.Анашкин (Москва), В.Гавриленко (Харьков), С.Мусатов (Ногинск Московской обл.) считают целесообразным разбить весь массив иа группы, единовременно ранжируемые имеющейся программой, а полученные упорядоченные группы последовательно объединять попарно.
Все эти способы весьма трудоемки. Более эффективной представляется идея
B.Брауна (Волчанск Свердловской обл.), В.Захарова (Кемерово), А.Мержеевского (Житомир). Особенно четко излагает ее А.Мержеевский. Его программа позволяет располагать в порядке возрастания 13 чисел. Пусть это будут первые 13 чисел массива. Выписываем их в строчку, вводим в калькулятор следующие 13, упорядочиваем и выписываем их строчкой ниже и т.д. Если в последней группе меньше 13 чисел, то вместо недостающих вводим нули. Получив из выписанных строк таблицу, отчерчиваем слева направо (см. рисунок) группы чисел, заключенных в определенных пределах, следя, чтобы в каждой группе было ие более 13 чисел. Каждую из этих групп упорядочиваем повторно. В результате весь массив будет упорядочен в порядке возрастания.

Раздел таблицы на группы легко выполним, если количество строк не превышает количества чисел в строке. Иными словами, так удобно ранжировать массив из n**2 чисел, где n - размер группы, упорядочиваемой в калькуляторе единовременно.
Девятиклассник С.Нуднов (Минск) предлагает автоматизировать и процесс разбивки массива на группы. Для этого в калькулятор надо ввести наибольшее (А) и наименьшее (В) числа массива. Определяемый ими интервал программа разбивает на С равных по длине участков. Число С также надо ввести в калькулятор, вычислив его по формуле [N/12]+1, где N - количество чисел массива, а квадратные скобки означают целую часть заключенной в них величины. Если затем ввести какое-либо из ранжируемых чисел, то на индикатор будет выведен номер участка, в который попадает это число. Такой разбивкой на группы занимается первая часть программы С.Нуднова. Затем управление вручную передается на вторую часть программы, в калькулятор вводятся числа какой-либо группы и упорядочиваются программой. В группе не должно быть более 12 чисел.
00. / 01. 1 02. 3 03. П0 04. F() 05. + 06. КП^ 07. FBx 08. FL0 09. 05 10. Сх 11. П1 12. С/П 13. + 14. 1 15. 4 16. П0 17. КИП0 18. Fx!=0 19. 24 20. FBx 21. - 22. Fx>=0 23. 17 24. 1 25. 4 26. ИП0 27. - 28. БП 29. 12 30. 1 31. 3 32. П0 33. Сх 34. КП^ 35. FL0 36. 34 37. 1 38. 2 39. П1 40. Сх 41. С/П 42. + 43. 1 44. 4 45. П0 46. КИП0 47. Fx!=0 48. 90 49. FBx 50. - 51. Fx!=0 52. 40 53. Fx>=0 54. 46 55. FBx 56. 1 57. КИП0 58. Fx!=0 59. 65 60. F() 61. 1 62. + 63. БП 64. 57 65. F() 66. ИП1 67. x-y 68. П1 69. F() 70. КИП0 71. F() 72. ИП0 73. 3 74. + 75. П0 76. F() 77. КИП0 78. КП0 79. FL1 80. 71 81. F() 82. П1 83. x-y 84. ИП0 85. 1 86. + 87. П0 88. x-y 89. + 90. FBx 91. КП^ 92. FL1 93. 40 94. С/П
Инструкция.
1. Ввести программу.
2. Ввести B ^ (A - В) ^ С.
3. Нажать клавиши В/0 С/П.
4. Взять С карточек и пронумеровать их.
5. Ввести первое число массива и нажать клавишу С/П; занести это число в карточку с номером, который появится иа индикаторе; сделать это со всеми числами массива.
6. Нажать клавиши БП 30 С/П.
7. Выбрать первую карточку, ввести первое из записанных на нее чисел, нажать клавишу С/П. Сделать это со всеми числами карточки. Упорядоченные числа расположатся в порядке убывания в регистрах Р2, Р3, ... Р9, РА, ... РД. Вывести их на индикатор с помощью клавиши ИП и списать. Сделать это с каждой карточкой.
Аналогичный подход излагает в своем письме и С.Старченко (Истра Московской обл.).
Метод С. Нуднова особенно удобен в том благоприятном случае, если ранжируемые числа распределяются в массиве равномерно и на каждой из карточек оказывается по 12 чисел. Что же делать, если числа сгущаются в каких-то участках занимаемого ими интервала? С.Нуднов попытался составить программу, которая по первым 18 введенным числам оценивает подобные сгущения и разбивает интервал на соответственно неодинаковые по длине участки. Однако программа не уместилась в программной памяти "Электроники Б3-34".
Программы А.Мержеевского, В.Брауна, В.Захарова, С.Нуднова, С.Старченко производят весьма обнадеживающее впечатление. Сочетая автоматический счет с ручными операциями, удается упорядочивать столь часто встречающиеся на практике массивы порядка 100 чисел. Но чтобы описанные методы ранжировки могли конкурировать с чисто ручными, они должны быть достаточно быстрыми. Здесь все определяется средним временем обработки одного числа. С помощью программы С.Нуднова массив из 100 чисел упорядочивается за полтора часа. Желательно сократить это время втрое-вчетверо. Тогда на калькуляторе работать будет быстрее и удобнее, чем вручную. Мы обращаемся к читателям с призывом продолжить разработку ранжирующих программ, добиваясь результатов лучших, чем изложены здесь. Иными словами, конкурс вступает во второй тур, в итоге которого и будет определен победитель.
Количество чисел, обрабатываемых программой единовременно, может быть различным - лишь бы поменьше было среднее время обработки каждого числа. Но не следует забывать и о сервисе. Желательно, чтобы обработка каждого числа производилась нажатием клавиши С/П после его набора на клавиатуре; чтобы после обработки число светилось на индикаторе, не позволяя оператору сбиваться; чтобы при вводе массива, обрабатываемого единовременно, дальнейший ввод избыточных чисел блокировался появлением сигнала ЕГГОГ; чтобы на вводимые числа не налагалось никаких ограничений (некоторые из присланных программ - скажем, программа С.Нуднова - не допускают ввод нуля и повторяющихся чисел). Разумеется, эти пожелания не обязательны, но победитель будет определяться с их учетом.
Настоятельно просим подробно описывать алгоритм ранжировки, давать его блок-схему, указывать, какие фрагменты программы реализуют каждый блок, приводить инструкцию. Отсутствие подобных комментариев затрудняло разбор некоторых присланных программ и не позволило отметить их достоинства в этом обзоре. Для оценки скорости, с которой работает программа, просим указать, за какое время она упорядочивает массив, приведенный выше для иллюстрации метода А.Мержеевского.
Так удастся создать программу, которую с успехом можно будет внедрять в практическую работу исследователей, имеющих дело с задачами подобного рода.
НА СВАРКЕ ТРУБ
По роду моей работы иногда приходится врезать трубы в трубопроводы под заданным углом. Для этого предварительно нужно определенным образом обрезать трубы по специально вычерченным шаблонам. Получение шаблона - дело трудоемкое, сопряженное с вычислениями по громоздким формулам. Вот я и решил поручить эту задачу микрокалькулятору. Формы шаблонов показаны на рисунке, там же - формулы для вычисления координат А, В и С.

При программировании я столкнулся с проблемой измерения углов. Дело в том, что угол l/r определяется в радианах, а угол между свариваемыми трубами а привычнее задавать в градусах.
Разрешить проблему можно было тремя способами. Первый - самый простой: переводить значение угла из градусов в радианы вручную. Второй, более остроумный: разнести в программе вычисления с градусами и радианами по разным частям ее, и одну часть вычислений делать в режиме Г - градусы, а перед началом другой части переключаться на режим Р - радианы. Наконец, третий способ - переводить градусы в радианы программным путем и работать постоянно в радианном режиме.
Первый способ, при котором резко возрастает объем работы пользователя, я сразу признал неудовлетворительным. Второй более удобен, да и программа получается такой же длины, как и при первом способе. Однако постоянное переключение режимов работы хотя и не отражается на памяти машины, зато засоряет память пользователя. Поэтому, так как программная память при решении моей задачи была заполнена не до конца, я выбрал третий путь. Хотя программа н удлинилась на пяток команд, работать с ней стало удобнее. По этой же причине константа 180 записана непосредственно в программную память, а не в адресуемый регистр, куда ее нужно было бы вводить вручную.
00. П1 01. F() 02. П2 03. x-y 04. - 05. П3 06. ИП1 07. / 08. П4 09. x-y 10. 1 11. 8 12. 0 13. / 14. Fпи 15. * 16. Fsin 17. П5 18. FBx 19. Ftg 20. П6 21. ИП2 22. Fпи 23. * 24. П0 25. С/П 26. П8 27. ПД 28. ИПД 29. ИП2 30. / 31. Fcos 32. FBx 33. Fsin 34. ИП4 35. * 36. Farcsin 37. ПВ 38. Fcos 39. 1 40. - 41. ИП1 42. * 43. ПС 44. ИП6 45. / 46. x-y 47. 1 48. - 49. ИП3 50. * 51. П7 52. ИП5 53. / 54. - 55. ПА 56. ИПВ 57. ИП1 58. * 59. ИПС 60. ИП5 61. / 62. ИП7 63. ИП6 64. / 65. - 66. x-y 67. ИПА 68. ИПД 69. С/П 70. ИПО 71. ИП8 72. ИПД 73. + 74. ПД 75. - 76. Fx<0 77. 28 78. Fsqr 79. КНОП 80. ИПО 81. ПД 82. БП 83. 29
Работать с программой нужно так. После ее набора ввести начальные данные: В/0 a ^ b ^ r ^ R С/П. Через несколько секунд программа останавливается: на индикаторе - величина пи*r. Остается ввести шаг изменения координаты dl и нажать С/П. При остановках вся нужная информация будет в стеке в такой последовательности: l, А, В, С. Так как почти наверняка выбранный шаг изменения координаты не уложится целое число раз на отрезке пи*r, то, как только координата l превысит эту величину, калькулятор даст предупреждающее сообщение ЕГГОГ. Нажав снова клавишу С/П, вы получите значение искомых величин при l=пи*r.
При желании величину шага можно изменять во время работы вручную. Для этого при очередном останове нужно заслать новое значение шага в Р8.
ПРИМЕР РАСЧЕТА: а=30o, b=3.5, r=38, R=57; шаг dl=20.
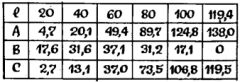
А.ТАЛАНКИН (г.Абакан)
ГОНКИ НА ЗИМНЕМ ОЗЕРЕ
В эту игру играют несколько человек, соревнуясь друг с другом. У каждого свой микрокалькулятор "Электроника Б3-34", который по введенной в него программе моделирует движение аэросаней по ледяной дорожке. Она расчищена в снегу, покрывающем замерзшее озеро. Справа дует порывистый ветер, который относит машину к обочине. Компенсировать снос можно поворотом руля от 90 до -90 градусов (во время игры переключатель "Р-Г" должен быть в положении "Г").
Ширина дорожки равна 6 единицам, и в момент старта сани находятся на осевой линии. Длина дорожки составляет 20-50 единиц, по соглашению соревнующихся, и вводится в каждый калькулятор перед началом игры. После нажатия клавиш В/0 С/П калькулятор останавливается, готовый принять информацию для очередного хода, соответствующего единице времени. В момент каждого последующего такого останова на индикаторе высвечивается расстояние от саней до левой обочины (зная ширину дорожки, нетрудно определить расстояние до правой). Нажав клавишу x-y, можно узнать скорость саней. С каждым ходом участник вводит приращение скорости саней Дv и угол поворота руля ф (как правило, положительный, поскольку ветер дует справа): Дv ^ ф. Величина Дv может равняться либо единице, либо нулю, либо минус единице - это условие игры.

Задача гонщика - достичь финиша за наименьшее время, то есть за наименьшее число ходов, заработав наименьшее число штрафных очков. Одно такое очко начисляется каждый раз, если скорость саней упала до нуля, если абсолютная величина приращения скорости больше единицы (в обоих случаях приращение надо ввести заново) или если сани пересекли левую или правую обочину (тогда скорость саней гасится до нуля, и дальнейшее движение начинается с осевой линии). О начислении штрафного очка говорит сигнал авоста ЕГГОГ на индикаторе, и к счетчику времени в любом из трех случаев прибавляется единица. Увидев сигнал авоста, следует нажать клавишу С/П. Если после этого на индикаторе загорается число пи - значит, слишком резко возросла скорость саней, если нуль - скорость упала до нуля, если число, меньше нуля или больше шести,- сани заехали на обочину. С/П - и игра продолжается. Если же во время останова на индикаторе высвечивается длина дистанции - значит, сани достигли финиша. Нажав клавиши ИП6, можно узнать, сколько времени t ушло на прохождение дистанции, ИП5 - сколько получено штрафных очков n.
Распределение остальных регистров: Р1 - длина дистанции L, P2 - пройденный путь S, Р3 - угол поворота руля ф, Р4 - приращение скорости Дv, P7 - случайное число e, используемое для расчета порывов ветра, Р8 - расстояние d от саней до левой обочины, Р9 - скорость саней v, P0 - счетчик.
Перед расчетом каждого очередного хода в регистр 0 заносится значение скорости v. Расчет происходит в циклическом порядке и с каждым из v прохождений цикла к d прибавляется
sin(ф)-(v/9)-(e/2)
к S прибавляется cos(ф). к t - единица, а также проверяется, не оказались ли сани на обочине.
00. П1 01. 3 02. П8 03. Сх 04. П2 05. П5 06. П6 07. П7 08. П9 09. КИП6 10. ИП9 11. ИП8 12. С/П 13. П3 14. x-y 15. П4 16. Fпи 17. ПД 18. 1 19. ИП4 20. Fx2 21. - 22. Fx>=0 23. 81 24. ИП4 25. ИП9 26. + 27. ПД 28. Fx!=0 29. 81 30. П9 31. П0 32. ИП1 33. ИП2 34. ИП3 35. Fcos 36. + 37. П2 38. - 39. Fх>=0 40. 84 41. ИП3 42. Fsin 43. ИП8 44. + 45. ИП9 46. 9 47. / 48. - 49. ИП7 50. 1 51. 1 52. * 53. Fпи 54. + 55. П7 56. КИП7 57. F() 58. ИП7 59. - 60. П7 61. 2 62. / 63. - 64. П8 65. ПД 66. Fx>=0 67. 77 68. 6 69. ИП8 70. - 71. Fx>=0 72. 77 73. FL0 74. 32 75. БП 76. 09 77. Сх 78. П9 79. 3 80. П8 81. КИП5 82. ИПД 83. К- 84. ИП1 85. С/П 86. БП 87.09.
Адреса 00-08: засылка введенного числа L в Р1, тройки - Р8, нулей - в Р2, Р5, Р6, Р7, Р9. 09-12: прибавление единицы к счетчику времени, вызов в регистры Y и X величин v и d для их демонстрации на индикаторе и останов, во время которого происходит ввод Д v f ф. а затем запуск калькулятора. 13-15: рассылка величин Ду и ф по своим местам. 16-23: проверка "соблюдено ли условие |Дv|<=1?". 24-29: вычисление и проверка "v=0?". 30-31: запись величины v в Р9 и Р0. 32-40: расчет продвижения саней вдоль дистанции v*cos(ф) и проверка "S-L<=0?". 41-44: расчет бокового сноса саней, вызванного отклонением от курса, v*sin(ф). 45-48: расчет постоянной составляющей ветрового сноса (v**2/9). 49-65: расчет случайной составляющей ветрового сноса, при котором к нему за каждое i-тое прохождение цикла прибавляется величина ei/2, рассчитываемая согласно формуле
ei={11*e[i-1]+пи},
где фигурные скобки означают дробную часть заключенного в них числа. 66-72: проверка "d<=0?", "d>=6?". 73-74: возврат к началу цикла. 75-76: возврат к началу расчета очередного хода. 77-80: уменьшение до нуля скорости саней, заехавших на обочину, возврат машины на середину дорожки. 81-87: блок начисления штрафных очков.
Порядок работы с программой ясен из вышесказанного. Приводим ради примера протокол одной из гонок. Длина дистанции - 20. Штрафное очко начислено на седьмом ходу из-за пересечения левой обочины (d=-0.01).

А.БОЙКО (г.Москва)
Публикуя один из множества поступивших в редакцию рисунков на неисчерпаемый сюжет "Микрокалькулятор и счеты", мы призываем читателей усилить поиски других, менее очевидных и потому более выигрышных юмористических тем.

Рис. И.Музыки (г.Жданов Донецкой обл.)
ЛУЧШИЙ РЕЖИМ - ДИАЛОГОВЫЙ
Тридцати студентам-четверокурсникам, будущим физикам и математикам, была предложена задача: найти шестизначное число с возрастающими слева направо цифрами, являющееся полным квадратом.
Ясно, что решение задачи вовсе не требует полного перебора всех шестизначных чисел. Минимальное из них, выражаемое возрастающими цифрами,- это 123456. Максимальное - 456789. Полный квадрат оканчивается цифрами 1, 4, 5, 6 или 9. В нашем случае цифры 1, 4 и 5 исключены: если бы они стояли на конце искомого числа, то левее их мы не смогли бы поставить пяти убывающих цифр. Шестеркой оканчивается единственное из допустимых чисел, а именно минимальное, 123456. Но это число - не квадрат: 351**2=123201; 352**2=123904. Следовательно, конечная цифра искомого числа - 9. Тогда третья цифра трехзначного основания квадрата - 3 или 7. Наименьшее основание - 317, наибольшее - 673.
Ограниченность множества допустимых чисел была объяснена студентам, решавшим задачу, и учтена при составлении программы для микрокалькулятора "Электроника Б3-34", строившей искомое число.
Свой ответ, число 134689, микрокалькулятор выдал через 6 минут. Полный перебор допустимых чисел, не давший других ответов, занял 45 минут. Основное время счета ушло на то, чтобы проверять, возрастают ли цифры в очередном анализируемом шестизначном числе.
Студенты решали задачу в два этапа.
Сначала им разрешалось пользоваться микрокалькулятором лишь для того, чтобы возводить числа в квадрат. Из 30 человек с задачей справились лишь 24. Среднее время, затраченное решавшим на нахождение искомого квадрата,- 30 минут. Трудности и ошибки решавших, как показал последующий опрос, были связаны с необходимостью держать в уме и записывать большое количество промежуточных данных, с монотонностью вычислений. Быстро наступало утомление, и интерес к задаче терялся.
На втором этапе задача решалась в диалоговом режиме. Калькулятор строил одно за другим допустимые основания и их квадраты выводил на индикатор. Человеку оставалось проверять, возрастают ли цифры в демонстрируемом ему числе. И с этим он справлялся быстрее калькулятора.
По этой методике ответ 134689 был получен за 45 секунд. Полный перебор вариантов, не обнаруживший других решений, потребовал 7 минут.
Человек и машина выгодно дополняли друг друга на этом самом коротком пути к ответу. Каждый выполнял ту работу, с которой он справляется наилучшим образом. Зрительный анализ информации, недоступный калькулятору, человеком производился мгновенно. А на долю калькулятора достались рутинные вычисления.
Диалоговый режим оказался эффективнее, чем независимое решение задачи человеком или микрокалькулятором.
С.ШАПИРО (г.Курск)
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
Раздел "Человек с микрокалькулятором" сменил название. Отныне он будет именоваться "Человек и компьютер". Эта смена - логическое развитие нашей рубрики. В ответ на призыв редакции (8/85) читатели стали присылать свои рассказы о работе на персональных компьютерах. Два письма из тех, что пришли первыми, публикуются в нынешнем выпуске. Надеемся, что подобные письма будут приходить все чаще и станут занимать все большую часть раздела.
Эти письма, которых мы ждем в ближайшее время, зададут и направленность, и уровень дальнейших родственных им публикаций. Пусть же поспешат со своими корреспонденциями те, кому есть что рассказать о своем опыте работы с персональными компьютерами, те, кто желает видеть наш раздел ярким, содержательным, поучительным.
Что же касается микрокалькуляторов, то свое место в обновляющемся разделе сохранят и они: ведь они тоже принадлежат к большому семейству компьютеров.
Организовать массовый выпуск персональных компьютеров. Обеспечить рост производства вычислительной техники в 2-2.3 раза.
Из проекта Основных направлений экономического и социального развития СССР на 1986-1990 годы и на период до 2000 года
КАК Я ЗАВЕДОВАЛ СКЛАДОМ ХИМРЕАКТИВОВ
История эта началась, когда мне, младшему научному сотруднику НИИ химического профиля, поручили совмещать свои прямые обязанности с заведованием складом химреактивов нашей лаборатории.
Завел я себе общую тетрадь и решил вести записи по каждому реактиву - сколько его осталось, где он хранится и т.д. Записей становилось все больше, работать с тетрадью становилось все труднее. Произошел какой-то локальный информационный бум.
В конце концов стало ясно, что какую систему записей ни заводи - по алфавиту ли, по содержимому шкафов и полок, по степени чистоты реактивов,- так или иначе при поиске нужной упаковки часто приходится просматривать тетрадь от корки до корки. Информационный бум перерос в информационный кризис.
Тут произошло важное событие: наша лаборатория получила ЭВМ "Искра-226" с языком программирования "бейсик". Его я освоил быстро и понял, что наша "Искра" - идеальное средство для ведения учетной тетради реактивов.
Работать с электронной "тетрадью" - одно удовольствие. Ввожу программу, запускаю машину клавишей ВК. Машина начинает выполнять команды программы - строка за строкой. У каждой строки-свой номер, команды разделяются двоеточиями.

1-я строка. N=200. Это число страниц в тетради. Следующая команда начинается с буквы DIM. Это сокращенное английское слово dimension, размер. Язык "бейсик", которому обучена "Искра", использует слова английского языка. Своеобразный крестик, стоящий вслед за буквой A, указывает на то, что эта переменная не числовая, а литерная, то есть представляет собою сочетание букв, а не цифр. В скобках указано, что переменная А может принять 200 значений, после скобок - что она может содержать до 100 букв. Переменная К, указанная далее, будет кодировать информацию о требующихся реактивах, сообщаемую машине. В - переменная числовая. Судя по цифре в скобках, она может принимать два значения. Это признаки, по которым машина станет отыскивать в своей памяти нужную мне информацию. REM - ремарки, пояснения к программе. Они помогают разобраться в ней. Машина в ходе работы не обращает на них внимания. (Здесь прямая аналогия с ремарками в тексте пьесы - действующие лнца их не произносят, но они помогают успешно поставить спектакль).
Вслед за 1-й строкой машина переходит ко 2-й. INPUT - значит ввести. И дальше - текст в кавычках. Только такие тексты, содержащиеся в программе, выводятся на экран дисплея. В данном случае это так называемое меню, перечень возможных видов работы по программе "1 - новая запись, 2 - поиск информации, 3 - перелистывание, 4 - изменение, 5 - конец работы". В машину нужно ввести цифру, обозначающую желаемый режим. Сейчас мне нужно найти какую-нибудь соль соляной кислоты, причем чистую для анализа. Нажимаю клавишу 2 (поиск информации), а затем-клавишу ВК. Это буквосочетание - аналог слова "прием", который используют радисты, когда заканчивают свою фразу и ждут ответа собеседника. Значение 2 присваивается переменной A, которая в программе стоит сразу за текстом меню. В следующей команде есть слово GOTO - пойти к... и перечень переходов, зависящих от значения A. Второй (A=2) в этом перечне стоит цифра 5. На 5-ю строку и переходит машина.
На экране дисплея - надпись: "1-е ключевое слово, логическая связка (1 - И, 2 - ИЛИ, 3 - НЕ), 2-е слово". Названия всех солей соляной кислоты начинаются со слова "хлор". Начинаю набирать его на клавиатуре, предваряя пробелом. Пробел не даст тетради открыться на страницах со словами ЧЕТЫРЕХХЛОРИСТЫЙ, ДИХЛОР н т.п. Итак, набираю - ХЛОР, 1, ЧДА. И нажимаю клавишу В К.
Выполнив команды 5-й строки, машина переходит на 6-ю. FOR J = 1 TO N. Это предписание выполнить цикл, в котором переменная J, счетчик цикла, примет все значения от 1 до N. Иными словами, машина станет просматривать страницы тетради с 1-й по N-ную и будет выполнять при этом команды 7-й строки: ведь в шестой строке вслед за только что выполненной командой стоит такая: IF A=2 THEN 7 (если А=2, то 7).
7-я строка. Мы видим, что здесь двукратно выполняется цикл (FOR J=1 TO 2), в котором переменная В принимает два значения, В(1) и В (2); что, судя по обозначению Аx(1), здесь просматривается строка с номером 1 от первой ее буквы (Р=1) до той, которая определяется длиной записанного здесь текста (LEN - это сокращенное length, длина); что в ходе просмотра проверяется совпадение или несовпадение ключевого слова Кx(J) с фрагментом строки такой же длины LEN(Кx(J)), начинающегося с буквы под порядковым номером Р на странице под номером 1. Все эти приметы просматриваемого фрагмента указаны в обозначении STR(Аx(1)),Р,LEN(Kx(J)). STR - это сокращенное string, строка. Проверка несовпадения кодируется знаком <> (меньше или больше, то есть не равно, не совпадает), разделяющим символы Kx(J)) и STR. Если обнаружилось несовпадение, мы переходим к 8-й строке (THEN 8 ), согласно которой смещается "поле зрения" (NEXT P, следующий номер знака в тексте). Если же обнаружено совпадение, то произойдет переход на 9-ю строку (GOTO 9) - а предварительно признаку B(J) будет придано значение 1. Выполняя команды строк 9-11, машина по признакам В(1) и В(2) разберется, нужно ли печатать и выводить найденную информацию на экран дисплея.
Читаю появившуюся на нем надпись: "НАТРИИ ХЛОРИСТЫЙ, ЧДА, 0.2КГ, НОРМА 2КГ, МЕНЬШЕ НОРМЫ, 5 ШКАФ 3 ПОЛКА, 28.10.85". Поваренная соль, стало быть, хранится в пятом шкафу на третьей полке. Данные иа 28 октября 1985 года. Осталось ее всего 200 граммов, меньше нормального запаса.
Я не подозревал столь неприятной оказии. В таком случае реактив лучше не использовать, а постараться поискать ему замену, открыв тетрадь на страницах с фрагментом его названия, но там, где нет слов МЕНЬШЕ НОРМЫ. Тогда мой запрос должен выглядеть так: ХЛОР, 3, МЕНЬШЕ НОРМЫ. Однако нет худа без добра. Составлю заявку, отпечатаю на той же "Искре" и отнесу в отдел снабжения. Я заметил, что в последнее время получаю там меньше отказов - ведь заявки теперь составляет ЭВМ, существо точное и беспристрастное.
Но вернемся к программе. Я мог бы подробно разъяснить каждую ее команду, но это потребовало бы слишком много места. Мне кажется, что в журнале "Наука н жизнь" стоит напечатать рассказ о языке "бейсик" - наподобие "Школы начинающего программиста", где читатели обучались работе на микрокалькуляторе.
В.СОЛОВЬЕВ (г.Киев).
[ Предлагаем задание: составить и записать на языке "бейсик" (BASIC) алгоритмы перевода римских цифр в десятичную систему счисления и обратного перевода. Хотя такие алгоритмы и приводятся в некоторых книгах по "бейсику", можно разработать более совершенные их варианты. Просим указывать, для какой конкретной машины составлена программа.
Интересующимся языком "бейсик" советуем ознакомиться с книгами:
Кетков Ю.Л. Программирование на "бейсике". М., "Статистика", 1973.
Семик В.П. и др. Программирование на языке "бейсик-плюс" для СМ-4. М., "Финансы и статистика", 1982.
Уорт Т. Программирование на языке "бейсик" М., "Машиностроение", 1981 ]
ОТ КОНКУРСА К ВНЕДРЕНИЮ
Дан ряд чисел. Требуется ранжировать их, то есть расположить в порядке возрастания или убывания. Так ставилась конкурсная задача, опубликованная в 4/85. Вслед за постановкой задачи высказывался вопрос: какова максимальная длина массива, который можно ранжировать на микрокалькуляторе, и как, сочетая ручной труд с машинным, получить упорядоченный ряд для массива большей длины?
Свои решения прислали 63 человека. Среди них - немало скептиков. "Массивы, которые вмещает "Электроника Б3-34", быстрее ранжировать вручную,- пишет Г.Натансон (Ленинград).- Я не обнаружил возможности ускорить ранжирование массивов с помощью микрокалькулятора. Остается задача спортивного характера: составить программу, упорядочивающую массив возможно большего размера".
Г.Натансону удалось разработать программу, располагающую в порядке возрастания 16 чисел. Столько же чисел упорядочивает с помощью более быстрой программы И.Шестак (Киев); он также предлагает доказательство, что больший массив "Электронике Б3-34" не осилить. Программа Л.Габрида (Фрунзе) ранжирует массив такой же длины, однако она удобнее, чем у обоих названных авторов, и работает ненамного дольше программы И.Шестака - около 10 минут. Вот она:
00. ПД 01. 1 02. 2 03. П0 04. Сх 05. КП:^ 06. FL0 07. 05 08. F() 09. С/П 10. ^ 11. 1 12. 3 13. П0 14. F() 15. КИП^ 16. Fx!=0 17. 36 18. - 19. Fx<0 20. 30 21. FBx 22. + 23. FBx 24. x-y 25. КП^ 26. FL0 27. 14 28. БП 29. 08 3O. FBx 31. + 32. FL0 33. 15 34. БП 35. 09 36. F() 37. КП^ 38. БП 39. 08 40. 1 41. 3 42. П0 43. F() 44. КИП^ 45. С/П 46. FL0 47. 43 48. ПП 49. 62 50. П0 51. ПП 52. 62 53. ИП0 54. ПП 55. 63 56. С/П 57. F() 58. С/П 59. F() 60. С/П 61. К7 62. F() 63. - 64. Fx<0 65. 71 66. FBx 67. + 68. FBx 69. x-y 70. B/0 71. FBx 72. + 73. FBx 74. B/0
Инструкция.
1. Ввести программу.
2. Ввести первый член ряда: x1 В/0 С/П.
3. Ввести последующие члены ряда: х2 С/П ... x16 С/П. Нуль заменять числом на порядок ниже, чем точность задания вводимых чисел.
4. Подать команду БП 40 С/П и прочесть на индикаторе минимальный член ряда.
5. Командой С/П вызвать остальные члены.
6. Появление на индикаторе сигнала ЕГГОГ показывает, что вся информация выведена.
После вывода первые 13 членов ряда сохраняются в регистрах Д...1, последние 4 - в регистрах стека Y, Z, Т, X.
Если все члены ранжируемого массива положительны и содержат не более четырех знаков, то в каждый регистр можно вводить по два таких числа, разделяя их запятой. Например, 25 и 72 объединяются так: 25.0072. Подобный прием используют В.Козлов (Ленинград), Ю.Мильчаков (Владивосток), С.Носков (Родники Ивановской обл.). Эти программы работают медленно - 40 минут и более. Ограничившись двузначными числами, С.Носков и А.Соболь (Донецк) расширяют границы массива еще вдвое. А.Виноградов (Киев) предлагает размещать подобные числа (скажем, трехзначные) в программной памяти, завершая их ввод командой В/0; извлекаются они командой КПП^.
Авторы присланных на конкурс программ использовали в большинстве своем два алгоритма. Согласно первому, упорядочиваемые числа при их вводе в калькулятор заполняют адресуемые регистры в порядке поступления. Далее адресуемые регистры просматриваются попарно, и в каждой паре после ее просмотра большее число оказывается в регистре с большим номером (или с меньшим, смотря по тому, в каком порядке ранжируются числа). После первого просмотра всего массива наибольшее число оказывается в регистре с наибольшим номером, после второго следующее по величине число - в регистре с номером, на единицу меньшим, и т.д. Таков метод "пузырька" (перемещения чисел напоминают всплывание пузырька в воде; рис. слева). Согласно второму алгоритму, для очередного вводимого числа, начиная уже со второго, определяется его место среди введенных. Затем массив введенных чисел раздвигается так, чтобы вводимое число оказалось на найденном для него месте. Таков метод локальных максимумов (рис. справа).

Что же делать, если в массиве, подлежащем ранжировке, больше чисел, чем единовременно упорядочивается программой? С.Носков предлагает на этот случай программу, которая ранжирует 14 чисел, а если ввести в калькулятор еще и 15-е, то из всех 15 наибольшее будет выведено на индикатор, 14 остальных выстроятся в порядке возрастания в адресуемых регистрах. После просмотра всего массива так будут отделены и упорядочены 14 наименьших чисел; большие следует списывать с индикатора и упорядочивать заново. В сущности, тот же метод излагают Н.Клименко (Челябинск), А.Коганцев (Москва), М.Корнилов и Е.Бережной (Киев), А.Куцеванов (Никополь), А.Соболь (Донецк), И.Шахнович (Кронштадт), а также А.Капцан (Ташкент), Т.Астахович и В.Новосельский (Ленинград).
А.Клейн (Балабаново, Калужской обл.) предлагает на глазок выделить в массиве среднюю величину и разделить его на две группы, состоящие из чисел либо меньших либо больших выделенного. Деление повторять, пока в каждой из полученных групп ие окажется столько чисел, что их можно ранжировать имеющейся программой.
A.Анашкин (Москва), В.Гавриленко (Харьков), С.Мусатов (Ногинск Московской обл.) считают целесообразным разбить весь массив иа группы, единовременно ранжируемые имеющейся программой, а полученные упорядоченные группы последовательно объединять попарно.
Все эти способы весьма трудоемки. Более эффективной представляется идея
B.Брауна (Волчанск Свердловской обл.), В.Захарова (Кемерово), А.Мержеевского (Житомир). Особенно четко излагает ее А.Мержеевский. Его программа позволяет располагать в порядке возрастания 13 чисел. Пусть это будут первые 13 чисел массива. Выписываем их в строчку, вводим в калькулятор следующие 13, упорядочиваем и выписываем их строчкой ниже и т.д. Если в последней группе меньше 13 чисел, то вместо недостающих вводим нули. Получив из выписанных строк таблицу, отчерчиваем слева направо (см. рисунок) группы чисел, заключенных в определенных пределах, следя, чтобы в каждой группе было ие более 13 чисел. Каждую из этих групп упорядочиваем повторно. В результате весь массив будет упорядочен в порядке возрастания.

Раздел таблицы на группы легко выполним, если количество строк не превышает количества чисел в строке. Иными словами, так удобно ранжировать массив из n**2 чисел, где n - размер группы, упорядочиваемой в калькуляторе единовременно.
Девятиклассник С.Нуднов (Минск) предлагает автоматизировать и процесс разбивки массива на группы. Для этого в калькулятор надо ввести наибольшее (А) и наименьшее (В) числа массива. Определяемый ими интервал программа разбивает на С равных по длине участков. Число С также надо ввести в калькулятор, вычислив его по формуле [N/12]+1, где N - количество чисел массива, а квадратные скобки означают целую часть заключенной в них величины. Если затем ввести какое-либо из ранжируемых чисел, то на индикатор будет выведен номер участка, в который попадает это число. Такой разбивкой на группы занимается первая часть программы С.Нуднова. Затем управление вручную передается на вторую часть программы, в калькулятор вводятся числа какой-либо группы и упорядочиваются программой. В группе не должно быть более 12 чисел.
00. / 01. 1 02. 3 03. П0 04. F() 05. + 06. КП^ 07. FBx 08. FL0 09. 05 10. Сх 11. П1 12. С/П 13. + 14. 1 15. 4 16. П0 17. КИП0 18. Fx!=0 19. 24 20. FBx 21. - 22. Fx>=0 23. 17 24. 1 25. 4 26. ИП0 27. - 28. БП 29. 12 30. 1 31. 3 32. П0 33. Сх 34. КП^ 35. FL0 36. 34 37. 1 38. 2 39. П1 40. Сх 41. С/П 42. + 43. 1 44. 4 45. П0 46. КИП0 47. Fx!=0 48. 90 49. FBx 50. - 51. Fx!=0 52. 40 53. Fx>=0 54. 46 55. FBx 56. 1 57. КИП0 58. Fx!=0 59. 65 60. F() 61. 1 62. + 63. БП 64. 57 65. F() 66. ИП1 67. x-y 68. П1 69. F() 70. КИП0 71. F() 72. ИП0 73. 3 74. + 75. П0 76. F() 77. КИП0 78. КП0 79. FL1 80. 71 81. F() 82. П1 83. x-y 84. ИП0 85. 1 86. + 87. П0 88. x-y 89. + 90. FBx 91. КП^ 92. FL1 93. 40 94. С/П
Инструкция.
1. Ввести программу.
2. Ввести B ^ (A - В) ^ С.
3. Нажать клавиши В/0 С/П.
4. Взять С карточек и пронумеровать их.
5. Ввести первое число массива и нажать клавишу С/П; занести это число в карточку с номером, который появится иа индикаторе; сделать это со всеми числами массива.
6. Нажать клавиши БП 30 С/П.
7. Выбрать первую карточку, ввести первое из записанных на нее чисел, нажать клавишу С/П. Сделать это со всеми числами карточки. Упорядоченные числа расположатся в порядке убывания в регистрах Р2, Р3, ... Р9, РА, ... РД. Вывести их на индикатор с помощью клавиши ИП и списать. Сделать это с каждой карточкой.
Аналогичный подход излагает в своем письме и С.Старченко (Истра Московской обл.).
Метод С. Нуднова особенно удобен в том благоприятном случае, если ранжируемые числа распределяются в массиве равномерно и на каждой из карточек оказывается по 12 чисел. Что же делать, если числа сгущаются в каких-то участках занимаемого ими интервала? С.Нуднов попытался составить программу, которая по первым 18 введенным числам оценивает подобные сгущения и разбивает интервал на соответственно неодинаковые по длине участки. Однако программа не уместилась в программной памяти "Электроники Б3-34".
Программы А.Мержеевского, В.Брауна, В.Захарова, С.Нуднова, С.Старченко производят весьма обнадеживающее впечатление. Сочетая автоматический счет с ручными операциями, удается упорядочивать столь часто встречающиеся на практике массивы порядка 100 чисел. Но чтобы описанные методы ранжировки могли конкурировать с чисто ручными, они должны быть достаточно быстрыми. Здесь все определяется средним временем обработки одного числа. С помощью программы С.Нуднова массив из 100 чисел упорядочивается за полтора часа. Желательно сократить это время втрое-вчетверо. Тогда на калькуляторе работать будет быстрее и удобнее, чем вручную. Мы обращаемся к читателям с призывом продолжить разработку ранжирующих программ, добиваясь результатов лучших, чем изложены здесь. Иными словами, конкурс вступает во второй тур, в итоге которого и будет определен победитель.
Количество чисел, обрабатываемых программой единовременно, может быть различным - лишь бы поменьше было среднее время обработки каждого числа. Но не следует забывать и о сервисе. Желательно, чтобы обработка каждого числа производилась нажатием клавиши С/П после его набора на клавиатуре; чтобы после обработки число светилось на индикаторе, не позволяя оператору сбиваться; чтобы при вводе массива, обрабатываемого единовременно, дальнейший ввод избыточных чисел блокировался появлением сигнала ЕГГОГ; чтобы на вводимые числа не налагалось никаких ограничений (некоторые из присланных программ - скажем, программа С.Нуднова - не допускают ввод нуля и повторяющихся чисел). Разумеется, эти пожелания не обязательны, но победитель будет определяться с их учетом.
Настоятельно просим подробно описывать алгоритм ранжировки, давать его блок-схему, указывать, какие фрагменты программы реализуют каждый блок, приводить инструкцию. Отсутствие подобных комментариев затрудняло разбор некоторых присланных программ и не позволило отметить их достоинства в этом обзоре. Для оценки скорости, с которой работает программа, просим указать, за какое время она упорядочивает массив, приведенный выше для иллюстрации метода А.Мержеевского.
Так удастся создать программу, которую с успехом можно будет внедрять в практическую работу исследователей, имеющих дело с задачами подобного рода.
НА СВАРКЕ ТРУБ
По роду моей работы иногда приходится врезать трубы в трубопроводы под заданным углом. Для этого предварительно нужно определенным образом обрезать трубы по специально вычерченным шаблонам. Получение шаблона - дело трудоемкое, сопряженное с вычислениями по громоздким формулам. Вот я и решил поручить эту задачу микрокалькулятору. Формы шаблонов показаны на рисунке, там же - формулы для вычисления координат А, В и С.

При программировании я столкнулся с проблемой измерения углов. Дело в том, что угол l/r определяется в радианах, а угол между свариваемыми трубами а привычнее задавать в градусах.
Разрешить проблему можно было тремя способами. Первый - самый простой: переводить значение угла из градусов в радианы вручную. Второй, более остроумный: разнести в программе вычисления с градусами и радианами по разным частям ее, и одну часть вычислений делать в режиме Г - градусы, а перед началом другой части переключаться на режим Р - радианы. Наконец, третий способ - переводить градусы в радианы программным путем и работать постоянно в радианном режиме.
Первый способ, при котором резко возрастает объем работы пользователя, я сразу признал неудовлетворительным. Второй более удобен, да и программа получается такой же длины, как и при первом способе. Однако постоянное переключение режимов работы хотя и не отражается на памяти машины, зато засоряет память пользователя. Поэтому, так как программная память при решении моей задачи была заполнена не до конца, я выбрал третий путь. Хотя программа н удлинилась на пяток команд, работать с ней стало удобнее. По этой же причине константа 180 записана непосредственно в программную память, а не в адресуемый регистр, куда ее нужно было бы вводить вручную.
00. П1 01. F() 02. П2 03. x-y 04. - 05. П3 06. ИП1 07. / 08. П4 09. x-y 10. 1 11. 8 12. 0 13. / 14. Fпи 15. * 16. Fsin 17. П5 18. FBx 19. Ftg 20. П6 21. ИП2 22. Fпи 23. * 24. П0 25. С/П 26. П8 27. ПД 28. ИПД 29. ИП2 30. / 31. Fcos 32. FBx 33. Fsin 34. ИП4 35. * 36. Farcsin 37. ПВ 38. Fcos 39. 1 40. - 41. ИП1 42. * 43. ПС 44. ИП6 45. / 46. x-y 47. 1 48. - 49. ИП3 50. * 51. П7 52. ИП5 53. / 54. - 55. ПА 56. ИПВ 57. ИП1 58. * 59. ИПС 60. ИП5 61. / 62. ИП7 63. ИП6 64. / 65. - 66. x-y 67. ИПА 68. ИПД 69. С/П 70. ИПО 71. ИП8 72. ИПД 73. + 74. ПД 75. - 76. Fx<0 77. 28 78. Fsqr 79. КНОП 80. ИПО 81. ПД 82. БП 83. 29
Работать с программой нужно так. После ее набора ввести начальные данные: В/0 a ^ b ^ r ^ R С/П. Через несколько секунд программа останавливается: на индикаторе - величина пи*r. Остается ввести шаг изменения координаты dl и нажать С/П. При остановках вся нужная информация будет в стеке в такой последовательности: l, А, В, С. Так как почти наверняка выбранный шаг изменения координаты не уложится целое число раз на отрезке пи*r, то, как только координата l превысит эту величину, калькулятор даст предупреждающее сообщение ЕГГОГ. Нажав снова клавишу С/П, вы получите значение искомых величин при l=пи*r.
При желании величину шага можно изменять во время работы вручную. Для этого при очередном останове нужно заслать новое значение шага в Р8.
ПРИМЕР РАСЧЕТА: а=30o, b=3.5, r=38, R=57; шаг dl=20.

А.ТАЛАНКИН (г.Абакан)
ГОНКИ НА ЗИМНЕМ ОЗЕРЕ
В эту игру играют несколько человек, соревнуясь друг с другом. У каждого свой микрокалькулятор "Электроника Б3-34", который по введенной в него программе моделирует движение аэросаней по ледяной дорожке. Она расчищена в снегу, покрывающем замерзшее озеро. Справа дует порывистый ветер, который относит машину к обочине. Компенсировать снос можно поворотом руля от 90 до -90 градусов (во время игры переключатель "Р-Г" должен быть в положении "Г").
Ширина дорожки равна 6 единицам, и в момент старта сани находятся на осевой линии. Длина дорожки составляет 20-50 единиц, по соглашению соревнующихся, и вводится в каждый калькулятор перед началом игры. После нажатия клавиш В/0 С/П калькулятор останавливается, готовый принять информацию для очередного хода, соответствующего единице времени. В момент каждого последующего такого останова на индикаторе высвечивается расстояние от саней до левой обочины (зная ширину дорожки, нетрудно определить расстояние до правой). Нажав клавишу x-y, можно узнать скорость саней. С каждым ходом участник вводит приращение скорости саней Дv и угол поворота руля ф (как правило, положительный, поскольку ветер дует справа): Дv ^ ф. Величина Дv может равняться либо единице, либо нулю, либо минус единице - это условие игры.

Задача гонщика - достичь финиша за наименьшее время, то есть за наименьшее число ходов, заработав наименьшее число штрафных очков. Одно такое очко начисляется каждый раз, если скорость саней упала до нуля, если абсолютная величина приращения скорости больше единицы (в обоих случаях приращение надо ввести заново) или если сани пересекли левую или правую обочину (тогда скорость саней гасится до нуля, и дальнейшее движение начинается с осевой линии). О начислении штрафного очка говорит сигнал авоста ЕГГОГ на индикаторе, и к счетчику времени в любом из трех случаев прибавляется единица. Увидев сигнал авоста, следует нажать клавишу С/П. Если после этого на индикаторе загорается число пи - значит, слишком резко возросла скорость саней, если нуль - скорость упала до нуля, если число, меньше нуля или больше шести,- сани заехали на обочину. С/П - и игра продолжается. Если же во время останова на индикаторе высвечивается длина дистанции - значит, сани достигли финиша. Нажав клавиши ИП6, можно узнать, сколько времени t ушло на прохождение дистанции, ИП5 - сколько получено штрафных очков n.
Распределение остальных регистров: Р1 - длина дистанции L, P2 - пройденный путь S, Р3 - угол поворота руля ф, Р4 - приращение скорости Дv, P7 - случайное число e, используемое для расчета порывов ветра, Р8 - расстояние d от саней до левой обочины, Р9 - скорость саней v, P0 - счетчик.
Перед расчетом каждого очередного хода в регистр 0 заносится значение скорости v. Расчет происходит в циклическом порядке и с каждым из v прохождений цикла к d прибавляется
sin(ф)-(v/9)-(e/2)
к S прибавляется cos(ф). к t - единица, а также проверяется, не оказались ли сани на обочине.
00. П1 01. 3 02. П8 03. Сх 04. П2 05. П5 06. П6 07. П7 08. П9 09. КИП6 10. ИП9 11. ИП8 12. С/П 13. П3 14. x-y 15. П4 16. Fпи 17. ПД 18. 1 19. ИП4 20. Fx2 21. - 22. Fx>=0 23. 81 24. ИП4 25. ИП9 26. + 27. ПД 28. Fx!=0 29. 81 30. П9 31. П0 32. ИП1 33. ИП2 34. ИП3 35. Fcos 36. + 37. П2 38. - 39. Fх>=0 40. 84 41. ИП3 42. Fsin 43. ИП8 44. + 45. ИП9 46. 9 47. / 48. - 49. ИП7 50. 1 51. 1 52. * 53. Fпи 54. + 55. П7 56. КИП7 57. F() 58. ИП7 59. - 60. П7 61. 2 62. / 63. - 64. П8 65. ПД 66. Fx>=0 67. 77 68. 6 69. ИП8 70. - 71. Fx>=0 72. 77 73. FL0 74. 32 75. БП 76. 09 77. Сх 78. П9 79. 3 80. П8 81. КИП5 82. ИПД 83. К- 84. ИП1 85. С/П 86. БП 87.09.
Адреса 00-08: засылка введенного числа L в Р1, тройки - Р8, нулей - в Р2, Р5, Р6, Р7, Р9. 09-12: прибавление единицы к счетчику времени, вызов в регистры Y и X величин v и d для их демонстрации на индикаторе и останов, во время которого происходит ввод Д v f ф. а затем запуск калькулятора. 13-15: рассылка величин Ду и ф по своим местам. 16-23: проверка "соблюдено ли условие |Дv|<=1?". 24-29: вычисление и проверка "v=0?". 30-31: запись величины v в Р9 и Р0. 32-40: расчет продвижения саней вдоль дистанции v*cos(ф) и проверка "S-L<=0?". 41-44: расчет бокового сноса саней, вызванного отклонением от курса, v*sin(ф). 45-48: расчет постоянной составляющей ветрового сноса (v**2/9). 49-65: расчет случайной составляющей ветрового сноса, при котором к нему за каждое i-тое прохождение цикла прибавляется величина ei/2, рассчитываемая согласно формуле
ei={11*e[i-1]+пи},
где фигурные скобки означают дробную часть заключенного в них числа. 66-72: проверка "d<=0?", "d>=6?". 73-74: возврат к началу цикла. 75-76: возврат к началу расчета очередного хода. 77-80: уменьшение до нуля скорости саней, заехавших на обочину, возврат машины на середину дорожки. 81-87: блок начисления штрафных очков.
Порядок работы с программой ясен из вышесказанного. Приводим ради примера протокол одной из гонок. Длина дистанции - 20. Штрафное очко начислено на седьмом ходу из-за пересечения левой обочины (d=-0.01).

А.БОЙКО (г.Москва)
Публикуя один из множества поступивших в редакцию рисунков на неисчерпаемый сюжет "Микрокалькулятор и счеты", мы призываем читателей усилить поиски других, менее очевидных и потому более выигрышных юмористических тем.

Рис. И.Музыки (г.Жданов Донецкой обл.)
ЛУЧШИЙ РЕЖИМ - ДИАЛОГОВЫЙ
Тридцати студентам-четверокурсникам, будущим физикам и математикам, была предложена задача: найти шестизначное число с возрастающими слева направо цифрами, являющееся полным квадратом.
Ясно, что решение задачи вовсе не требует полного перебора всех шестизначных чисел. Минимальное из них, выражаемое возрастающими цифрами,- это 123456. Максимальное - 456789. Полный квадрат оканчивается цифрами 1, 4, 5, 6 или 9. В нашем случае цифры 1, 4 и 5 исключены: если бы они стояли на конце искомого числа, то левее их мы не смогли бы поставить пяти убывающих цифр. Шестеркой оканчивается единственное из допустимых чисел, а именно минимальное, 123456. Но это число - не квадрат: 351**2=123201; 352**2=123904. Следовательно, конечная цифра искомого числа - 9. Тогда третья цифра трехзначного основания квадрата - 3 или 7. Наименьшее основание - 317, наибольшее - 673.
Ограниченность множества допустимых чисел была объяснена студентам, решавшим задачу, и учтена при составлении программы для микрокалькулятора "Электроника Б3-34", строившей искомое число.
Свой ответ, число 134689, микрокалькулятор выдал через 6 минут. Полный перебор допустимых чисел, не давший других ответов, занял 45 минут. Основное время счета ушло на то, чтобы проверять, возрастают ли цифры в очередном анализируемом шестизначном числе.
Студенты решали задачу в два этапа.
Сначала им разрешалось пользоваться микрокалькулятором лишь для того, чтобы возводить числа в квадрат. Из 30 человек с задачей справились лишь 24. Среднее время, затраченное решавшим на нахождение искомого квадрата,- 30 минут. Трудности и ошибки решавших, как показал последующий опрос, были связаны с необходимостью держать в уме и записывать большое количество промежуточных данных, с монотонностью вычислений. Быстро наступало утомление, и интерес к задаче терялся.
На втором этапе задача решалась в диалоговом режиме. Калькулятор строил одно за другим допустимые основания и их квадраты выводил на индикатор. Человеку оставалось проверять, возрастают ли цифры в демонстрируемом ему числе. И с этим он справлялся быстрее калькулятора.
По этой методике ответ 134689 был получен за 45 секунд. Полный перебор вариантов, не обнаруживший других решений, потребовал 7 минут.
Человек и машина выгодно дополняли друг друга на этом самом коротком пути к ответу. Каждый выполнял ту работу, с которой он справляется наилучшим образом. Зрительный анализ информации, недоступный калькулятору, человеком производился мгновенно. А на долю калькулятора достались рутинные вычисления.
Диалоговый режим оказался эффективнее, чем независимое решение задачи человеком или микрокалькулятором.
С.ШАПИРО (г.Курск)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
К этому моменту "школа" окончательно превратилась в демонстрацию на калькуляторе "элементов нормального программирования". А кому нужно "нормальное программирование" на "ненормальной машине"?
3/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ СЕДЬМОЕ, на котором продолжается разговор о ветвях, циклах, подпрограммах и, в частности, об их комбинировании.
Ведет занятие кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт)
Если посмотреть на три последние программы из числа тех, что мы составляли на прошлом занятии (1/85), то можно заметить, что в каждой из них имеется переменная (скажем, x в самой последней программе, T - в остальных), которая на каждом шаге цикла изменяется регулярным образом, то есть на одно и то же значение. Это столь частая в программировании ситуация, что для подобных циклов имеется специальное название - циклы с параметром (под параметром понимается регулярно меняющаяся переменная). Сюда относится и программа, по которой на втором нашем занятии мы вычисляли среднюю площадь кругов. Напомним последний вариант этой программы (7/85). Здесь мы запишем ее, как условились, с адреса 10:
10. ИП0 11. 1 12. 4 13. П1 14. Сх 15. КИП1 16. Fx2 17. Fgb 18. * 19. 4 20. / 21. + 22. FL0 23. 15 24. x-y 25. /
Пусть число кругов n=12 находится в регистре 0, а диаметры этих двенадцати кругов занесены в следующие регистры: D1 - в РД, D2 - в PC, D3 - в РВ, D4 - в РА, D5 - в Р9, D6 - в Р8, и так далее до Р2. С каждым прохождением цикла (адреса 15-23) вычисляется площадь очередного круга. Иными словами, параметром тут служит индекс в обозначении величины Dk: он изменяется с шагом 1. В регистр 1 перед входом в цикл занесено число 14. Команда КИП1, как мы уже знаем (7/85), при первом же ее выполнении уменьшит содержимое Р1 на единицу (14-1=13) и вызовет в регистр X число, хранящееся в регистре с получившимся в результате вычитания номером. Мы знаем, что номер 13 истолковывается в подобных случаях как обозначение регистра Д. Стало быть, команда КИП1 при первом ее выполнении вызовет в регистр X величину D1, при втором D2 и так далее. И каждый раз будет подсчитываться площадь круга с вызванным в РХ диаметром и результат будет прибавляться к сумме площадей.
Напомним, что автоматическое уменьшение или увеличение адреса, по которому происходит вызов или засылка, называется его модификацией. И еще один термин: совокупность переменных, имеющих одинаковое имя и различающихся номерами, называется массивом. Номер, по которому конкретные переменные отличаются друг от друга, именуется индексом массива. В нашем примере массив образуют диаметры кругов Dk. Здесь D - имя переменной, k - индекс массива, принимающий значение от 1 до 12.
Для программирования циклов, в которых обрабатываются элементы массива, удобны команды косвенного вызова (вида КИПN) и косвенной засылки (вида КПN), при выполнении которых происходит модификация адреса. Если N равно 0, 1, 2 или 3, то перед каждым выполнением такой команды содержимое регистра N уменьшается на единицу. Если же N равно 4, 5 или 6,- то увеличивается на единицу.
Поскольку длина массива, обрабатываемого в таких циклах, всегда строго определена, организуются подобные циклы с помощью операции FLM. Так оно было и в нашей последней программе.
Просмотрите ее вновь, вспомните, как она составлялась. Правила программирования циклов в этих случаях таковы:
1. Занести в регистр с номером М (равным 0, 1, 2 или 3) число повторений цикла.
2. Если для вызова и засылки элементов массива предполагается использовать в теле цикла команды КИПN и КПN, где N = = 0, 1, 2 или 3, то занести в регистр N число, на единицу большее, нежели номер регистра, с которого начнется вызов или засылка. Если N=4, 5 или 6 - занести в регистр N число, на единицу меньшее, нежели номер регистра, с которого начнется вызов или засылка.
3. Запрограммировать тело цикла.
4. Записать операцию FLM и за нею - начальный адрес тела цикла.
(Номера М и N, как правило, не совпадают. Нетрудно сообразить, что при их совпадении косвенный вызов и засылка затрагивали бы регистры, следующие друг за другом не подряд. Впрочем, порою именно это и требуется. Тогда М и N следует полагать совпадающими).
Условимся о форме записи описанных конструкций на алгоритмическом языке. Запись "k:=адрес а" будем понимать "присвоить переменной k значение адреса переменной a"; запись "x:=[k]" будем понимать "присвоить переменной x значение той переменной, адрес которой есть значение переменной k". (Заметим: мы употребили здесь ту же букву, которой обозначили индекс массива, и не случайно). Для того, чтобы отразить модификацию адреса с его уменьшением или увеличением, будем применять запись [-k] и [+k] соответственно. То, что минус и плюс стоят слева от символа k, означает, что значение k изменяется перед его использованием.
С применением этих средств алгоритм вычисления средней площади кругов можно записать так:
алг СРЕДНЕЕ (вещ таб D[1:n] цел n, вещ Сигма;
- арг D, n; рез Сигма;
нач цел k;
- k:=адрес D[n]+1; Сигма:=0
- цикл n раз Сигма:=Сигма+[-k]**2*пи/4 кц
- Сигма:=Сигма/n
кон
(Мы употребили одну и ту же переменную, обозначая сумму площадей и среднюю площадь. Это упростит программирование - позволит использовать один и тот же адресуемый регистр для размещения обеих величин).
Точный перевод этого алгоритма на язык команд калькулятора даст нам иную программу, нежели приведенная выше. Нам понадобятся адресуемые регистры для величин Сигма, n, k, да еще под счетчик повторений цикла, так что под массив останется только 10 адресуемых регистров. Вызов и засылка величины Сигма будут требовать дополнительных команд. Этих неудобств можно избежать, если некоторые величины - скажем, Сигма и n - хранить не в адресуемых регистрах, а в стеке. Величину Сигма лучше хранить в регистре X - тогда ее не надо будет вызывать и засылать; величину n, используемую реже, разместим выше, в регистре Y.
Когда в регистр X будет вызван диаметр очередного круга для вычисления его площади, величины Сигма и n сдвинутся вверх по стековым регистрам. Вычислив площадь очередного круга, надо прибавить ее к сумме площадей Сигма. Площадь получается в регистре X, а сумма к этому моменту находится в регистре Y, как и требуется для сложения. После сложения она вернется в регистр X, а количество кругов окажется также на прежнем месте, в регистре Y. Так оно будет и после последнего сложения, перед вычислением средней площади. Разумеется, перед делением Сигма на n обе величины надо будет поменять местами командой x-y.
Как видим, размещение этих величин в стеке весьма целесообразно. Под счетчик повторений цикла отведем адресуемый регистр 0, под переменную k - регистр 1. Тогда у нас остается 12 регистров под диаметры кругов.
Приступаем к программированию. Займемся сначала присваиваниями k:=адрес D[n] +1, Сигма:=0. Далее вызовем из Р0 в стек величину n. После выполнения этих действий начальное нулевое значение суммы Сигма должно оказаться в регистре X, число n - в регистре Y, а в регистре 1 должно получиться число 14, которое можно "набрать" командами программы (так же, как числа набираются на клавиатуре). Экономнее всего это достигается именно теми командами, с которых начинается знакомый нам вариант программы:
10. ИП0 11. 1 12. 4 13. П1 14. Сх.
Программируем тело цикла. Прежде всего вызовем в регистр X диаметр круга, с которого начнем вычисления,- величину, обозначенную в записи алгоритма символом [-k]. Под переменную к у нас отведен регистр 1, стало быть, нужная нам команда - это 15. КИП1. Дальнейшее программирование формулы Сигма:=Сигма+[-k]**2*пи/4 очевидно:
16. Fx2 17. Fпи 18. * 19. 4 20. / 21. +
Тело цикла запрограммировано. Пишем команду возврата к началу цикла: 22. FL0 23. 15.
Наконец, программируем вычисление средней площади кругов: 24. x-y 25. /. В итоге программа приобретает знакомый нам вид.
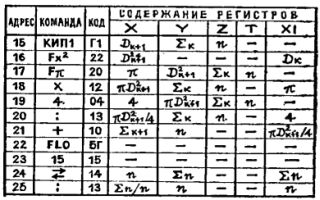
При буквальном переводе алгоритма на язык команд микрокалькулятора программа получилась бы более понятной. Однако при этом она обрабатывала бы меньший массив, была бы длиннее, работала бы дольше. Подобный буквальный перевод естествен для начинающего программиста. Но по мере того, как растет опыт программирования, следует стремиться к составлению как можно более эффективных программ, умело используя все возможности калькулятора.
Отметим в этой связи, что для вызова очередного диаметра мы употребили команду КИП1. Вместо нее можно было написать команду КИП0, КИП2 или КИП3: как и КИП1, они тоже вызывают числа из регистров с убывающими номерами. Но регистр 0, с которым "работает" команда КИП0, уже занят под счетчик повторений цикла. Если же употребить команду КИП2 или КИП3, то тем самым пришлось бы занять регистры 2 или 3 соответственно, и тогда массив, где хранятся диаметры кругов, опять-таки сузился бы. Выбирая для организации цикла регистры 0 (операция FL0) и 1 (команда КИП1), то есть самые первые из адресуемых регистров, мы достигаем предельно возможной длины массива, обрабатываемого в цикле. Такой выбор часто встречается на практике.
Если бы нам требовалось вызывать значения величин, хранящихся в регистрах с нарастающими номерами, то в записи алгоритма мы употребили бы символ [+k], а при программировании - команду вида КИПN, где N=4, 5 или 6. Поскольку регистр N в этом случае находится уже не в начале, а ближе к середине ряда адресуемых регистров, длина обрабатываемого массива будет сильно ограничена. Вот почему в программах для "Электроники Б3-34" в подобных случаях сравнительно редко встречается такая модификация адреса, при которой номера регистров увеличиваются.
Наконец, заметим, что наилучшее программирование не может исправить недостатков алгоритма. У нас же он не безупречен. Если умножать на пи/4 не каждый диаметр, а только итоговую сумму, то программа будет работать раза в два быстрее. Этот прием (вынос повторяющихся вычислений за пределы цикла) называется чисткой циклов.
ПОДПРОГРАММЫ. Обратимся вновь к задаче о вычислении определенного интеграла. Программу для этих целен мы составили, полагая подынтегральную функцию f(x) равной х**2. Ну, а если потребуется вычислить интеграл от другой функции? Нужно заменить команды, по которым вычисляется значение функции, и внести их вместо прежних в программную память калькулятора. Как это делается, мы уже знаем (9/85). Но как быть, если вычисление новой функции требует большего числа команд, чем прежней? Тогда программу придется переписывать и вводить в калькулятор заново.
Чтобы не возникала неприятная необходимость в переписывании всей программы, можно поступить так: вынести за ее пределы фрагмент, где вычисляется подынтегральная функция. Когда потребуется получить ее значение от заданного аргумента, будем передавать управление на начальный адрес такого фрагмента, а после его выполнения возвращаться к основной программе (на тот адрес, который значится за командой передачи управления).
Смена подынтегральной функции теперь повлечет за собой лишь перезапись выносного фрагмента. Будь он короче или длиннее прежнего, перемена никак не отразится на основной программе.
Такие фрагменты, реализующие самостоятельные алгоритмы, и называются подпрограммами. Они оказываются полезными не только в случаях, подобных описанному, но и тогда, когда но ходу выполнения программы приходится в разных ее местах выполнять одну и ту же последовательность команд. Эту последовательность также бывает целесообразно вынести за пределы основной программы в виде подпрограммы и обращаться к ней в нужные моменты так, как описано выше. С подобным примером мы вскоре встретимся.
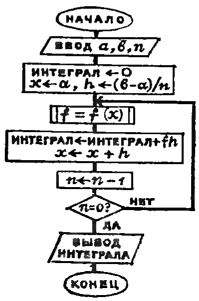
Обращение к подпрограмме следует оговаривать еще на той стадии решения задач, когда на алгоритмическом языке записывается алгоритм ее решения. В его тексте в нужном месте приводится обращение к вспомогательному алгоритму, который будет оформлен в виде подпрограммы. Его записывают отдельно.
Попробуем написать по-новому, со сменным вспомогательным фрагментом, алгоритм для вычисления определенного интеграла. Там, где в прежнем варианте стояла строчка с формулой подынтегральной функции, напишем: ФУНКЦИЯ - озаглавим так нужный нам здесь вспомогательный алгоритм.
алг ИНТЕГРАЛ (вещ a, b, интеграл, цел n);
- арг a, b, n; рез интеграл;
нач вещ h, f, x;
- h:=(b-а)/n; интеграл:=0, x:= a
- цикл n раз
- - ФУНКЦИЯ (х, f);
- - интеграл:=интеграл+f*h; x:=x+h
- кц
кон
Далее запишем вспомогательный алгоритм для вычисления подынтегральной функции. Пусть иа сей раз она будет такой: f(x)=х+х**2.
алг ФУНКЦИЯ (вещ х, f)
- арг х; рез f
нач f:=х+х**2;
кон
Во вспомогательном алгоритме могут использоваться несколько аргументов и получаться несколько результатов. Мы разбираем здесь простейший пример, когда по одному аргументу вычисляется один результат, значение функции.
Для программирования подпрограмм у нашего калькулятора имеется операция ПП ("Переход к Подпрограмме") и команда В/0 (здесь мы ее расшифруем как "Возврат к Основной программе"). Операция ПП выполняет переход на указанный вслед за нею адрес, начальный адрес подпрограммы; при этом калькулятор запоминает место, откуда произошел переход. Команда В/0 ставится в конце подпрограммы и, когда очередь дойдет до нее, совершает возврат на запомненное место, то есть к продолжению основной программы.
Составление подпрограммы требует известной осмотрительности. Например, необходимо следить за тем, чтобы участвующие в ее работе адресуемые регистры не совпадали с теми, где хранятся числа, необходимые для дальнейшей работы основной программы. Аргументы, используемые в подпрограмме, лучше всего к моменту обращения к ней располагать в регистрах стека. Там же рекомендуется размещать результаты работы подпрограммы к моменту возврата к основной программе.
Как всегда в подобных случаях, сформулируем правила программирования подпрограмм:
1. В том месте основной программы, где надо выполнить подпрограмму, записать команды засылки в стек ее аргументов, операцию ПП, а следующий за нею адрес оставить незаполненным; далее записать команды вызова из стека ее результатов.
2. Продолжить запись основной программы.
3. Начиная с адреса, следующего за последним адресом основной программы, записать подпрограмму.
4. В конце подпрограммы поставить команду В/0.
5. В пропущенную на шаге 1 ячейку вписать начальный адрес подпрограммы.
К одной основной программе может быть "приписано" одновременно несколько подпрограмм. Переходы на них в основной программе осуществляются операцией ПП по указываемым вслед за нею соответствующим адресам.
Составим заново программу для вычисления определенного интеграла, полагая подынтегральную функцию f(x)=х+х**2 и вынося ее вычисления в подпрограмму.
Начало программы остается прежним - вплоть до адреса 21, где в регистр X вызывается величина х. Далее пишем обращение к подпрограмме, вычисляющей значение f(x): ставим операцию ПП - а адрес обращения, начальный адрес подпрограммы пока оставляем пустым. Значение подынтегральной функции, очевидно, получится в регистре X (заметим: величины х и f удалось разместить в одном регистре). Так оно было и в прежнем варианте программы. Поэтому новую программу мы можем закончить командами прежней. Они разместятся по адресам 24-35.
А дальше можно писать подпрограмму - начиная прямо с адреса 36. Его и поставим в пустовавшую до сих пор ячейку, вслед за операцией ПП. Вся подпрограмма уложится в три команды: 36. ^ 37. Fx2 38. + (проследите, что в регистре X получается величина х+х**2). Не забудем поставить в конце подпрограммы команду В/0.
10. Сх 11. П5. 12. ИП0 13. П4 14. ИП1 15. НП0 16. - 17. ИП3 18. / 19. П2 20. ИП5 21. ИП4 22. ПП 23. 36 24. ИП2 25. * 26. + 27. П5 28. ИП4 29. ИП2 30. + 31. П4 32. FL3 33. 20 34. ИП5 35. С/П 36. ^ 37. Fx2 38. + 39. В/0.
КОМБИНИРОВАНИЕ ВЕТВЛЕНИЙ И ЦИКЛОВ. Если посмотреть на блок-схемы, где изображены ветвление и цикл (1/86), то можно увидеть, что каждая из этих конструкций имеет один вход и один выход. Во фрагментах программ, реализующих обе конструкции, вход в каждую из них происходит по одному адресу; по выходе из нее мы попадаем опять-таки на один адрес - начальный адрес следующего фрагмента. Это позволяет строить комбинации ветвлений и циклов.
Имеется всего два способа подобного комбинирования: следование и вложение. При следовании выход одной конструкции сцепляется со входом другой. Соответствующие части программы размещаются друг за другом, и при программировании никаких проблем не возникает. Сложнее дело обстоит при вложении, когда в качестве тела цикла, ветви ТО или ветви ИНАЧЕ, в свою очередь, используется цикл или ветвление. Чтобы не ошибаться при программировании столь сложных комбинаций, надо придерживаться простого принципа: каждая конструкция программируется согласно приводившимся выше правилам, независимо от того, является она вложенной или нет.
Запрограммируем ради примера алгоритм нахождения корня функции методом половинного деления. Пусть в концах отрезка [a, b] непрерывная монотонная функция f(х) принимает значения разных знаков. Тогда на отрезке [а, b] у нее есть только один корень. Возьмем середину отрезка х и из двух образованных ею отрезков [а, х] и [х, b] выберем тот, на концах которого функция опять-таки принимает значения разных знаков. С выбранным отрезком повторим тот же процесс. На каждом шаге длина отрезка уменьшается вдвое. Когда она станет меньше некоторого заданного е, то любую точку отрезка (скажем, его середину) можно с абсолютной погрешностью е считать корнем функции f(x).
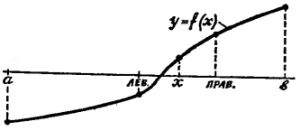
Обозначим левый конец очередного отрезка лев, правый - прав. Их начальные значения: лев = a; прав = b. Выбор нужной половины после деления отрезка пополам будем производить, перемножая значения f(a) и f(x). Допустим, произведение отрицательно. Тогда, в силу монотонности функции, отрицательным будет и произведение ее значений в концах отрезка [лев, x]. Стало быть, функция меняет знак на этом отрезке, его и нужно выбрать - присваиваем переменной прав значение х. Если же произведение f(a)*f(x) положительно, функция не меняет знак на отрезке [лев, х] и меняет его на отрезке [х, прав], который и следует выбрать,- присваиваем значение х переменной лев. Так же поступаем, если произведение f(a)*f(x) равно нулю.
Алгоритм решения задачи можно записать так:
алг КОРЕНЬ (вещ лев, прав, х, е);
- арг лев, прав, е; рез х;
нач вещ fa;
- fa:=f(лев);
- пока прав-лев >= е цикл
- - х:=(лев+прав)/2;
- если f(х)*fa>=0, то лев:=х иначе
- - прав:=х все кц
кон
Вычисление функции оформим в виде подпрограммы, как и при подсчете интеграла.
Приступим к программированию. Начнем с распределения адресуемых регистров. Тот, кто на пятом нашем занятии (11/85) ознакомился с методами ввода исходной информации, легко сообразит, что здесь можно применить СТ-ввод. Величины a, b, e наберем на клавиатуре, перемежая их набор нажатием клавиши ^. Тогда а окажется в регистре Z, b - в регистре Y, е - в регистре X. Величины а и b будут тотчас использованы при выполнении присваиваний а:=лев, b:= прав. Таким образом, на адресуемые регистры претендуют лишь пять величин, и их распределение может быть таким: е - Р0, fa - P1, лев - Р2, прав - Р3, х - Р4.
Поскольку наша задача имеет вполне самостоятельный характер, программу для ее решения будем писать, начиная с адреса 00. Первыми же командами вычислим величину fa, разместим по своим местам величины е и fa, а также начальные значения переменных лев и прав, равные соответственно a и b:
00. П0 01. F() 02. П3 03. F() 04. П2 05. ПП 06. [] 07. П1
После выполнения команд 00-04 величина е оказывается в Р0, b - в Р3, а - в Р2 и в РХ. Далее выполняется подпрограмма, вычисляющая значение функции. Начальный адрес подпрограммы мы пока не знаем и потому оставляем незаполненным. Когда мы будем ее писать, учтем, что аргумент функции берется из регистра X. Напомним попутно, что исходную информацию для выполнения подпрограмм бывает удобно размещать именно так - в стеке. Там же удобно оставлять и результаты их выполнения - в данном случае значение f(a). Командой 07. П1 мы отсылаем эту величину в Р1, чтобы потом ее не надо было многократно вычислять в цикле.
Программируем следующую строку алгоритма - проверку условия цикла:
08. ИП3 09. ИП2 10. - 11. ИП0 12. - 13. Fx>=0 14. []
Оставив незаполненным адрес 14, переходим к программированию тела цикла. Сначала находим величину х - середину отрезка [лев, прав] и отсылаем ее в Р4:
15. ИП2 16. ИП3 17. + 18. 2 19. / 20. П4 21. С/П
После вычисления середины отрезка мы поставили команду С/П. Эта команда поможет нам при отладке программы: определив величину х, калькулятор будет останавливаться, и мы сможем проследить, правильно ли работает программа. Удостоверившись в ее правильной работе, мы заменим эту команду иа "пустую" - КНОП.
Теперь программируем ветвление. Работаем с ним по стандартным правилам, не обращая внимания на то, что оно вложено в цикл. Величину х можно в РХ не вызывать, так как она уже находится там, а сразу обращаться к подпрограмме:
22. ПП 23. [] 24. ИП1 25. * 26. Fx>=0 27. [] 28. ИП4 29. П2 30. БП 31. [] 32. ИП4 33. П3.
В тексте алгоритма мы дошли до служебного слова все, завершающего ветвление. Значит, теперь мы можем заполнить адреса, указывающие порядок переходов в зависимости от выполнения или невыполнения условия
26. Fx>=0. В соответствии с правилами программирования ветвлений (1/86) по адресу 27 записываем 32, адрес начала ветви ИНАЧЕ, а по адресу 31 записываем 34, очередной свободный адрес.
Пройдя в тексте алгоритма служебное слово все, мы оказываемся на служебном слове кц. Оно отмечает конец цикла. Иными словами, оно означает, что тело цикла запрограммировано полностью. Судя по тексту алгоритма, он принадлежит к типу "пока". В соответствии с правилами программирования подобных циклов (1/86) записываем операцию БП и за нею - адрес начала проверки условия цикла, то есть 08:
34. БП 35. 08
Затем, в соответствии с теми же правилами, по адресу 14, который был оставлен незаполненным в конце проверки условия цикла, записываем 36 - очередной свободный адрес.
На этот адрес 36 мы попадаем, когда длина сужающегося с каждым делением отрезка [лев, прав] становится меньше допустимой абсолютной погрешности е. Переменную х, указанную в заголовке алгоритма в качестве результата, выведем на индикатор.
36. ИП4 37. С/П
Так мы запрограммировали последнюю строчку в записи алгоритма: кон.
Итак, составленная нами программа заняла адреса до 37-го включительно. Стало быть, подпрограмму можно размещать с адреса 38. Его и запишем по пустующим до сих пор адресам 06 и 23.
Вот окончательный текст программы:
00. П0 01. F() 02. П3 03. F() 04. П2 05. ПП 06. 38 07. П1 08. ИП3 09. ИП2 10. - 11. ИП0 12. - 13. Fx>=0 14. 36 15. ИП2 16. ИП3 17. + 18. 2 19. / 20. П4 21. С/П 22. ПП 23. 38 24. ИП1 25. * 26. Fx>=0 27. 32 28. ИП4 29. П2 30. БП 31. 34 32. ИП4 33. П3 34. БП 35. 08 36. ИП4 37. С/П.
Возьмем монотонную функцию f(x)=х**2-1 и попробуем отыскать ее корень на отрезке [0, 3] с точностью 0.01 по составленной нами программе.
Дополним текст программы подпрограммой вычисления исследуемой функции. В конце подпрограммы не забудем поставить команду В/0.
38. Fx2 39. 1 40. - 41. В/0
Вводим в калькулятор программу и подпрограмму, возвращаемся в режим вычислений (FАВТ), устанавливаем счетчик адресов на нулевой адрес (В/0), вводим в стек числа, выражающие левый конец отрезка, правый его конец, точность вычислений (0 ^ 3 ^ 0.01), пускаем программу (С/П).
Покуда желаемая точность не достигнута, калькулятор будет останавливаться по команде 21. С/П и на индикаторе будут последовательно загораться числа 1.5, 0.75, 1.125, 0.9375, 1.03125, 0.984375...
Поиск корня идет верно. Заменяем команду 21. С/П командой 21. КНОП (БП 21 FПРГ КНОП), возвращаемся в режим вычислений (FАВТ) и даем команду на продолжение счета (С/П).
Вскоре, достигнув установленной точности, калькулятор останавливается. На индикаторе - приближенное значение корня 1.0019531. От точного значения, единицы, оно отличается менее чем на 0.01.
3/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ СЕДЬМОЕ, на котором продолжается разговор о ветвях, циклах, подпрограммах и, в частности, об их комбинировании.
Ведет занятие кандидат физико-математических наук Л.ШТЕРНБЕРГ (Куйбышевский авиационный институт)
Если посмотреть на три последние программы из числа тех, что мы составляли на прошлом занятии (1/85), то можно заметить, что в каждой из них имеется переменная (скажем, x в самой последней программе, T - в остальных), которая на каждом шаге цикла изменяется регулярным образом, то есть на одно и то же значение. Это столь частая в программировании ситуация, что для подобных циклов имеется специальное название - циклы с параметром (под параметром понимается регулярно меняющаяся переменная). Сюда относится и программа, по которой на втором нашем занятии мы вычисляли среднюю площадь кругов. Напомним последний вариант этой программы (7/85). Здесь мы запишем ее, как условились, с адреса 10:
10. ИП0 11. 1 12. 4 13. П1 14. Сх 15. КИП1 16. Fx2 17. Fgb 18. * 19. 4 20. / 21. + 22. FL0 23. 15 24. x-y 25. /
Пусть число кругов n=12 находится в регистре 0, а диаметры этих двенадцати кругов занесены в следующие регистры: D1 - в РД, D2 - в PC, D3 - в РВ, D4 - в РА, D5 - в Р9, D6 - в Р8, и так далее до Р2. С каждым прохождением цикла (адреса 15-23) вычисляется площадь очередного круга. Иными словами, параметром тут служит индекс в обозначении величины Dk: он изменяется с шагом 1. В регистр 1 перед входом в цикл занесено число 14. Команда КИП1, как мы уже знаем (7/85), при первом же ее выполнении уменьшит содержимое Р1 на единицу (14-1=13) и вызовет в регистр X число, хранящееся в регистре с получившимся в результате вычитания номером. Мы знаем, что номер 13 истолковывается в подобных случаях как обозначение регистра Д. Стало быть, команда КИП1 при первом ее выполнении вызовет в регистр X величину D1, при втором D2 и так далее. И каждый раз будет подсчитываться площадь круга с вызванным в РХ диаметром и результат будет прибавляться к сумме площадей.
Напомним, что автоматическое уменьшение или увеличение адреса, по которому происходит вызов или засылка, называется его модификацией. И еще один термин: совокупность переменных, имеющих одинаковое имя и различающихся номерами, называется массивом. Номер, по которому конкретные переменные отличаются друг от друга, именуется индексом массива. В нашем примере массив образуют диаметры кругов Dk. Здесь D - имя переменной, k - индекс массива, принимающий значение от 1 до 12.
Для программирования циклов, в которых обрабатываются элементы массива, удобны команды косвенного вызова (вида КИПN) и косвенной засылки (вида КПN), при выполнении которых происходит модификация адреса. Если N равно 0, 1, 2 или 3, то перед каждым выполнением такой команды содержимое регистра N уменьшается на единицу. Если же N равно 4, 5 или 6,- то увеличивается на единицу.
Поскольку длина массива, обрабатываемого в таких циклах, всегда строго определена, организуются подобные циклы с помощью операции FLM. Так оно было и в нашей последней программе.
Просмотрите ее вновь, вспомните, как она составлялась. Правила программирования циклов в этих случаях таковы:
1. Занести в регистр с номером М (равным 0, 1, 2 или 3) число повторений цикла.
2. Если для вызова и засылки элементов массива предполагается использовать в теле цикла команды КИПN и КПN, где N = = 0, 1, 2 или 3, то занести в регистр N число, на единицу большее, нежели номер регистра, с которого начнется вызов или засылка. Если N=4, 5 или 6 - занести в регистр N число, на единицу меньшее, нежели номер регистра, с которого начнется вызов или засылка.
3. Запрограммировать тело цикла.
4. Записать операцию FLM и за нею - начальный адрес тела цикла.
(Номера М и N, как правило, не совпадают. Нетрудно сообразить, что при их совпадении косвенный вызов и засылка затрагивали бы регистры, следующие друг за другом не подряд. Впрочем, порою именно это и требуется. Тогда М и N следует полагать совпадающими).
Условимся о форме записи описанных конструкций на алгоритмическом языке. Запись "k:=адрес а" будем понимать "присвоить переменной k значение адреса переменной a"; запись "x:=[k]" будем понимать "присвоить переменной x значение той переменной, адрес которой есть значение переменной k". (Заметим: мы употребили здесь ту же букву, которой обозначили индекс массива, и не случайно). Для того, чтобы отразить модификацию адреса с его уменьшением или увеличением, будем применять запись [-k] и [+k] соответственно. То, что минус и плюс стоят слева от символа k, означает, что значение k изменяется перед его использованием.
С применением этих средств алгоритм вычисления средней площади кругов можно записать так:
алг СРЕДНЕЕ (вещ таб D[1:n] цел n, вещ Сигма;
- арг D, n; рез Сигма;
нач цел k;
- k:=адрес D[n]+1; Сигма:=0
- цикл n раз Сигма:=Сигма+[-k]**2*пи/4 кц
- Сигма:=Сигма/n
кон
(Мы употребили одну и ту же переменную, обозначая сумму площадей и среднюю площадь. Это упростит программирование - позволит использовать один и тот же адресуемый регистр для размещения обеих величин).
Точный перевод этого алгоритма на язык команд калькулятора даст нам иную программу, нежели приведенная выше. Нам понадобятся адресуемые регистры для величин Сигма, n, k, да еще под счетчик повторений цикла, так что под массив останется только 10 адресуемых регистров. Вызов и засылка величины Сигма будут требовать дополнительных команд. Этих неудобств можно избежать, если некоторые величины - скажем, Сигма и n - хранить не в адресуемых регистрах, а в стеке. Величину Сигма лучше хранить в регистре X - тогда ее не надо будет вызывать и засылать; величину n, используемую реже, разместим выше, в регистре Y.
Когда в регистр X будет вызван диаметр очередного круга для вычисления его площади, величины Сигма и n сдвинутся вверх по стековым регистрам. Вычислив площадь очередного круга, надо прибавить ее к сумме площадей Сигма. Площадь получается в регистре X, а сумма к этому моменту находится в регистре Y, как и требуется для сложения. После сложения она вернется в регистр X, а количество кругов окажется также на прежнем месте, в регистре Y. Так оно будет и после последнего сложения, перед вычислением средней площади. Разумеется, перед делением Сигма на n обе величины надо будет поменять местами командой x-y.
Как видим, размещение этих величин в стеке весьма целесообразно. Под счетчик повторений цикла отведем адресуемый регистр 0, под переменную k - регистр 1. Тогда у нас остается 12 регистров под диаметры кругов.
Приступаем к программированию. Займемся сначала присваиваниями k:=адрес D[n] +1, Сигма:=0. Далее вызовем из Р0 в стек величину n. После выполнения этих действий начальное нулевое значение суммы Сигма должно оказаться в регистре X, число n - в регистре Y, а в регистре 1 должно получиться число 14, которое можно "набрать" командами программы (так же, как числа набираются на клавиатуре). Экономнее всего это достигается именно теми командами, с которых начинается знакомый нам вариант программы:
10. ИП0 11. 1 12. 4 13. П1 14. Сх.
Программируем тело цикла. Прежде всего вызовем в регистр X диаметр круга, с которого начнем вычисления,- величину, обозначенную в записи алгоритма символом [-k]. Под переменную к у нас отведен регистр 1, стало быть, нужная нам команда - это 15. КИП1. Дальнейшее программирование формулы Сигма:=Сигма+[-k]**2*пи/4 очевидно:
16. Fx2 17. Fпи 18. * 19. 4 20. / 21. +
Тело цикла запрограммировано. Пишем команду возврата к началу цикла: 22. FL0 23. 15.
Наконец, программируем вычисление средней площади кругов: 24. x-y 25. /. В итоге программа приобретает знакомый нам вид.

При буквальном переводе алгоритма на язык команд микрокалькулятора программа получилась бы более понятной. Однако при этом она обрабатывала бы меньший массив, была бы длиннее, работала бы дольше. Подобный буквальный перевод естествен для начинающего программиста. Но по мере того, как растет опыт программирования, следует стремиться к составлению как можно более эффективных программ, умело используя все возможности калькулятора.
Отметим в этой связи, что для вызова очередного диаметра мы употребили команду КИП1. Вместо нее можно было написать команду КИП0, КИП2 или КИП3: как и КИП1, они тоже вызывают числа из регистров с убывающими номерами. Но регистр 0, с которым "работает" команда КИП0, уже занят под счетчик повторений цикла. Если же употребить команду КИП2 или КИП3, то тем самым пришлось бы занять регистры 2 или 3 соответственно, и тогда массив, где хранятся диаметры кругов, опять-таки сузился бы. Выбирая для организации цикла регистры 0 (операция FL0) и 1 (команда КИП1), то есть самые первые из адресуемых регистров, мы достигаем предельно возможной длины массива, обрабатываемого в цикле. Такой выбор часто встречается на практике.
Если бы нам требовалось вызывать значения величин, хранящихся в регистрах с нарастающими номерами, то в записи алгоритма мы употребили бы символ [+k], а при программировании - команду вида КИПN, где N=4, 5 или 6. Поскольку регистр N в этом случае находится уже не в начале, а ближе к середине ряда адресуемых регистров, длина обрабатываемого массива будет сильно ограничена. Вот почему в программах для "Электроники Б3-34" в подобных случаях сравнительно редко встречается такая модификация адреса, при которой номера регистров увеличиваются.
Наконец, заметим, что наилучшее программирование не может исправить недостатков алгоритма. У нас же он не безупречен. Если умножать на пи/4 не каждый диаметр, а только итоговую сумму, то программа будет работать раза в два быстрее. Этот прием (вынос повторяющихся вычислений за пределы цикла) называется чисткой циклов.
ПОДПРОГРАММЫ. Обратимся вновь к задаче о вычислении определенного интеграла. Программу для этих целен мы составили, полагая подынтегральную функцию f(x) равной х**2. Ну, а если потребуется вычислить интеграл от другой функции? Нужно заменить команды, по которым вычисляется значение функции, и внести их вместо прежних в программную память калькулятора. Как это делается, мы уже знаем (9/85). Но как быть, если вычисление новой функции требует большего числа команд, чем прежней? Тогда программу придется переписывать и вводить в калькулятор заново.
Чтобы не возникала неприятная необходимость в переписывании всей программы, можно поступить так: вынести за ее пределы фрагмент, где вычисляется подынтегральная функция. Когда потребуется получить ее значение от заданного аргумента, будем передавать управление на начальный адрес такого фрагмента, а после его выполнения возвращаться к основной программе (на тот адрес, который значится за командой передачи управления).
Смена подынтегральной функции теперь повлечет за собой лишь перезапись выносного фрагмента. Будь он короче или длиннее прежнего, перемена никак не отразится на основной программе.
Такие фрагменты, реализующие самостоятельные алгоритмы, и называются подпрограммами. Они оказываются полезными не только в случаях, подобных описанному, но и тогда, когда но ходу выполнения программы приходится в разных ее местах выполнять одну и ту же последовательность команд. Эту последовательность также бывает целесообразно вынести за пределы основной программы в виде подпрограммы и обращаться к ней в нужные моменты так, как описано выше. С подобным примером мы вскоре встретимся.

Обращение к подпрограмме следует оговаривать еще на той стадии решения задач, когда на алгоритмическом языке записывается алгоритм ее решения. В его тексте в нужном месте приводится обращение к вспомогательному алгоритму, который будет оформлен в виде подпрограммы. Его записывают отдельно.
Попробуем написать по-новому, со сменным вспомогательным фрагментом, алгоритм для вычисления определенного интеграла. Там, где в прежнем варианте стояла строчка с формулой подынтегральной функции, напишем: ФУНКЦИЯ - озаглавим так нужный нам здесь вспомогательный алгоритм.
алг ИНТЕГРАЛ (вещ a, b, интеграл, цел n);
- арг a, b, n; рез интеграл;
нач вещ h, f, x;
- h:=(b-а)/n; интеграл:=0, x:= a
- цикл n раз
- - ФУНКЦИЯ (х, f);
- - интеграл:=интеграл+f*h; x:=x+h
- кц
кон
Далее запишем вспомогательный алгоритм для вычисления подынтегральной функции. Пусть иа сей раз она будет такой: f(x)=х+х**2.
алг ФУНКЦИЯ (вещ х, f)
- арг х; рез f
нач f:=х+х**2;
кон
Во вспомогательном алгоритме могут использоваться несколько аргументов и получаться несколько результатов. Мы разбираем здесь простейший пример, когда по одному аргументу вычисляется один результат, значение функции.
Для программирования подпрограмм у нашего калькулятора имеется операция ПП ("Переход к Подпрограмме") и команда В/0 (здесь мы ее расшифруем как "Возврат к Основной программе"). Операция ПП выполняет переход на указанный вслед за нею адрес, начальный адрес подпрограммы; при этом калькулятор запоминает место, откуда произошел переход. Команда В/0 ставится в конце подпрограммы и, когда очередь дойдет до нее, совершает возврат на запомненное место, то есть к продолжению основной программы.
Составление подпрограммы требует известной осмотрительности. Например, необходимо следить за тем, чтобы участвующие в ее работе адресуемые регистры не совпадали с теми, где хранятся числа, необходимые для дальнейшей работы основной программы. Аргументы, используемые в подпрограмме, лучше всего к моменту обращения к ней располагать в регистрах стека. Там же рекомендуется размещать результаты работы подпрограммы к моменту возврата к основной программе.
Как всегда в подобных случаях, сформулируем правила программирования подпрограмм:
1. В том месте основной программы, где надо выполнить подпрограмму, записать команды засылки в стек ее аргументов, операцию ПП, а следующий за нею адрес оставить незаполненным; далее записать команды вызова из стека ее результатов.
2. Продолжить запись основной программы.
3. Начиная с адреса, следующего за последним адресом основной программы, записать подпрограмму.
4. В конце подпрограммы поставить команду В/0.
5. В пропущенную на шаге 1 ячейку вписать начальный адрес подпрограммы.
К одной основной программе может быть "приписано" одновременно несколько подпрограмм. Переходы на них в основной программе осуществляются операцией ПП по указываемым вслед за нею соответствующим адресам.
Составим заново программу для вычисления определенного интеграла, полагая подынтегральную функцию f(x)=х+х**2 и вынося ее вычисления в подпрограмму.
Начало программы остается прежним - вплоть до адреса 21, где в регистр X вызывается величина х. Далее пишем обращение к подпрограмме, вычисляющей значение f(x): ставим операцию ПП - а адрес обращения, начальный адрес подпрограммы пока оставляем пустым. Значение подынтегральной функции, очевидно, получится в регистре X (заметим: величины х и f удалось разместить в одном регистре). Так оно было и в прежнем варианте программы. Поэтому новую программу мы можем закончить командами прежней. Они разместятся по адресам 24-35.
А дальше можно писать подпрограмму - начиная прямо с адреса 36. Его и поставим в пустовавшую до сих пор ячейку, вслед за операцией ПП. Вся подпрограмма уложится в три команды: 36. ^ 37. Fx2 38. + (проследите, что в регистре X получается величина х+х**2). Не забудем поставить в конце подпрограммы команду В/0.
10. Сх 11. П5. 12. ИП0 13. П4 14. ИП1 15. НП0 16. - 17. ИП3 18. / 19. П2 20. ИП5 21. ИП4 22. ПП 23. 36 24. ИП2 25. * 26. + 27. П5 28. ИП4 29. ИП2 30. + 31. П4 32. FL3 33. 20 34. ИП5 35. С/П 36. ^ 37. Fx2 38. + 39. В/0.
КОМБИНИРОВАНИЕ ВЕТВЛЕНИЙ И ЦИКЛОВ. Если посмотреть на блок-схемы, где изображены ветвление и цикл (1/86), то можно увидеть, что каждая из этих конструкций имеет один вход и один выход. Во фрагментах программ, реализующих обе конструкции, вход в каждую из них происходит по одному адресу; по выходе из нее мы попадаем опять-таки на один адрес - начальный адрес следующего фрагмента. Это позволяет строить комбинации ветвлений и циклов.
Имеется всего два способа подобного комбинирования: следование и вложение. При следовании выход одной конструкции сцепляется со входом другой. Соответствующие части программы размещаются друг за другом, и при программировании никаких проблем не возникает. Сложнее дело обстоит при вложении, когда в качестве тела цикла, ветви ТО или ветви ИНАЧЕ, в свою очередь, используется цикл или ветвление. Чтобы не ошибаться при программировании столь сложных комбинаций, надо придерживаться простого принципа: каждая конструкция программируется согласно приводившимся выше правилам, независимо от того, является она вложенной или нет.
Запрограммируем ради примера алгоритм нахождения корня функции методом половинного деления. Пусть в концах отрезка [a, b] непрерывная монотонная функция f(х) принимает значения разных знаков. Тогда на отрезке [а, b] у нее есть только один корень. Возьмем середину отрезка х и из двух образованных ею отрезков [а, х] и [х, b] выберем тот, на концах которого функция опять-таки принимает значения разных знаков. С выбранным отрезком повторим тот же процесс. На каждом шаге длина отрезка уменьшается вдвое. Когда она станет меньше некоторого заданного е, то любую точку отрезка (скажем, его середину) можно с абсолютной погрешностью е считать корнем функции f(x).

Обозначим левый конец очередного отрезка лев, правый - прав. Их начальные значения: лев = a; прав = b. Выбор нужной половины после деления отрезка пополам будем производить, перемножая значения f(a) и f(x). Допустим, произведение отрицательно. Тогда, в силу монотонности функции, отрицательным будет и произведение ее значений в концах отрезка [лев, x]. Стало быть, функция меняет знак на этом отрезке, его и нужно выбрать - присваиваем переменной прав значение х. Если же произведение f(a)*f(x) положительно, функция не меняет знак на отрезке [лев, х] и меняет его на отрезке [х, прав], который и следует выбрать,- присваиваем значение х переменной лев. Так же поступаем, если произведение f(a)*f(x) равно нулю.
Алгоритм решения задачи можно записать так:
алг КОРЕНЬ (вещ лев, прав, х, е);
- арг лев, прав, е; рез х;
нач вещ fa;
- fa:=f(лев);
- пока прав-лев >= е цикл
- - х:=(лев+прав)/2;
- если f(х)*fa>=0, то лев:=х иначе
- - прав:=х все кц
кон
Вычисление функции оформим в виде подпрограммы, как и при подсчете интеграла.
Приступим к программированию. Начнем с распределения адресуемых регистров. Тот, кто на пятом нашем занятии (11/85) ознакомился с методами ввода исходной информации, легко сообразит, что здесь можно применить СТ-ввод. Величины a, b, e наберем на клавиатуре, перемежая их набор нажатием клавиши ^. Тогда а окажется в регистре Z, b - в регистре Y, е - в регистре X. Величины а и b будут тотчас использованы при выполнении присваиваний а:=лев, b:= прав. Таким образом, на адресуемые регистры претендуют лишь пять величин, и их распределение может быть таким: е - Р0, fa - P1, лев - Р2, прав - Р3, х - Р4.
Поскольку наша задача имеет вполне самостоятельный характер, программу для ее решения будем писать, начиная с адреса 00. Первыми же командами вычислим величину fa, разместим по своим местам величины е и fa, а также начальные значения переменных лев и прав, равные соответственно a и b:
00. П0 01. F() 02. П3 03. F() 04. П2 05. ПП 06. [] 07. П1
После выполнения команд 00-04 величина е оказывается в Р0, b - в Р3, а - в Р2 и в РХ. Далее выполняется подпрограмма, вычисляющая значение функции. Начальный адрес подпрограммы мы пока не знаем и потому оставляем незаполненным. Когда мы будем ее писать, учтем, что аргумент функции берется из регистра X. Напомним попутно, что исходную информацию для выполнения подпрограмм бывает удобно размещать именно так - в стеке. Там же удобно оставлять и результаты их выполнения - в данном случае значение f(a). Командой 07. П1 мы отсылаем эту величину в Р1, чтобы потом ее не надо было многократно вычислять в цикле.
Программируем следующую строку алгоритма - проверку условия цикла:
08. ИП3 09. ИП2 10. - 11. ИП0 12. - 13. Fx>=0 14. []
Оставив незаполненным адрес 14, переходим к программированию тела цикла. Сначала находим величину х - середину отрезка [лев, прав] и отсылаем ее в Р4:
15. ИП2 16. ИП3 17. + 18. 2 19. / 20. П4 21. С/П
После вычисления середины отрезка мы поставили команду С/П. Эта команда поможет нам при отладке программы: определив величину х, калькулятор будет останавливаться, и мы сможем проследить, правильно ли работает программа. Удостоверившись в ее правильной работе, мы заменим эту команду иа "пустую" - КНОП.
Теперь программируем ветвление. Работаем с ним по стандартным правилам, не обращая внимания на то, что оно вложено в цикл. Величину х можно в РХ не вызывать, так как она уже находится там, а сразу обращаться к подпрограмме:
22. ПП 23. [] 24. ИП1 25. * 26. Fx>=0 27. [] 28. ИП4 29. П2 30. БП 31. [] 32. ИП4 33. П3.
В тексте алгоритма мы дошли до служебного слова все, завершающего ветвление. Значит, теперь мы можем заполнить адреса, указывающие порядок переходов в зависимости от выполнения или невыполнения условия
26. Fx>=0. В соответствии с правилами программирования ветвлений (1/86) по адресу 27 записываем 32, адрес начала ветви ИНАЧЕ, а по адресу 31 записываем 34, очередной свободный адрес.
Пройдя в тексте алгоритма служебное слово все, мы оказываемся на служебном слове кц. Оно отмечает конец цикла. Иными словами, оно означает, что тело цикла запрограммировано полностью. Судя по тексту алгоритма, он принадлежит к типу "пока". В соответствии с правилами программирования подобных циклов (1/86) записываем операцию БП и за нею - адрес начала проверки условия цикла, то есть 08:
34. БП 35. 08
Затем, в соответствии с теми же правилами, по адресу 14, который был оставлен незаполненным в конце проверки условия цикла, записываем 36 - очередной свободный адрес.
На этот адрес 36 мы попадаем, когда длина сужающегося с каждым делением отрезка [лев, прав] становится меньше допустимой абсолютной погрешности е. Переменную х, указанную в заголовке алгоритма в качестве результата, выведем на индикатор.
36. ИП4 37. С/П
Так мы запрограммировали последнюю строчку в записи алгоритма: кон.
Итак, составленная нами программа заняла адреса до 37-го включительно. Стало быть, подпрограмму можно размещать с адреса 38. Его и запишем по пустующим до сих пор адресам 06 и 23.
Вот окончательный текст программы:
00. П0 01. F() 02. П3 03. F() 04. П2 05. ПП 06. 38 07. П1 08. ИП3 09. ИП2 10. - 11. ИП0 12. - 13. Fx>=0 14. 36 15. ИП2 16. ИП3 17. + 18. 2 19. / 20. П4 21. С/П 22. ПП 23. 38 24. ИП1 25. * 26. Fx>=0 27. 32 28. ИП4 29. П2 30. БП 31. 34 32. ИП4 33. П3 34. БП 35. 08 36. ИП4 37. С/П.
Возьмем монотонную функцию f(x)=х**2-1 и попробуем отыскать ее корень на отрезке [0, 3] с точностью 0.01 по составленной нами программе.
Дополним текст программы подпрограммой вычисления исследуемой функции. В конце подпрограммы не забудем поставить команду В/0.
38. Fx2 39. 1 40. - 41. В/0
Вводим в калькулятор программу и подпрограмму, возвращаемся в режим вычислений (FАВТ), устанавливаем счетчик адресов на нулевой адрес (В/0), вводим в стек числа, выражающие левый конец отрезка, правый его конец, точность вычислений (0 ^ 3 ^ 0.01), пускаем программу (С/П).
Покуда желаемая точность не достигнута, калькулятор будет останавливаться по команде 21. С/П и на индикаторе будут последовательно загораться числа 1.5, 0.75, 1.125, 0.9375, 1.03125, 0.984375...
Поиск корня идет верно. Заменяем команду 21. С/П командой 21. КНОП (БП 21 FПРГ КНОП), возвращаемся в режим вычислений (FАВТ) и даем команду на продолжение счета (С/П).
Вскоре, достигнув установленной точности, калькулятор останавливается. На индикаторе - приближенное значение корня 1.0019531. От точного значения, единицы, оно отличается менее чем на 0.01.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
4/86
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Почта принесла еще несколько писем, авторы которых рассказывают о том, как в решении повседневных проблем им помогают компьютеры - "Исrра-226" и "ДВК", "БК-0010" и другие. Проблемы эти просты: составить картотеку распоряжений по лаборатории, построить гистограмму... Но в простоте есть определенное достоинство: разбирая несложные программы, пытаясь составлять их самостоятельно, убеждаясь, что они работают и дают ожидаемый результат, ощущая реальную пользу от них, естественно приобщаться к искусству программирования. А поскольку задачи, о которых рассказывается в нашем разделе, носят повседневный массовый характер, можно надеяться, что их решение облегчит приобщение к программированию многим и многим людям.
Вот почему мы ждем от наших читателей все новых и новых писем подобного рода.
ПЯТИМИНУТКИ С "ИСКРОЙ"
Наш завлаб (назовем его условно Николаем Петровичем, или сокращенно НП) - хороший ученый, отличный человек, но администратор не очень. Как и всякому начальнику, ему приходится отдавать всякого рода распоряжения своим подчиненным. С этой задачей НП справляется неплохо. А вот что касается проверки исполнения - с этим у него не ладится.
Когда НП узнал, как электронно-вычислительная техника облегчает труд руководителя, он вызвал меня, поскольку наша ЭВМ "Искра-226" находится в моем ведении, и поручил составить электронную картотеку приказов по лаборатории. НП высказал свои пожелания к картотеке, перечислил необходимые виды работы с ней:
1. Записать на первую свободную карточку новое распоряжение с указанием дат выдачи и выполнения, имени исполнителя н номера папки, хранящей дополнительную информацию.
2. Снять с контроля выполненное распоряжение.
3. Узнать, что нужно было сделать к текущему дню.
4. Получить информацию о просроченных распоряжениях и о тех, срок исполнения которых приближается.
5. Просмотреть всю картотеку.
6. Просмотреть карточки по отдельным исполнителям.
В тот же день я составил небольшую программу на языке "бэйсик". Как к во всякой программе такого рода (См. например 2/86), здесь используются вещественные и литерные индексные переменные, объединенные в массивы, меню с возвращением к нему после выполнения выбранного вида работы, циклический перебор карточек, логическое сравнение предложенной конструкции с фрагментом текста и т.п.

Картотека записана вместе с программой на гибком магнитном диске. При запуске программы ЭВМ загружает (LOAD; см. строку 2) в свою оперативную память содержание картотеки, которая хранится под именем "КАРТОЧКИ". Там же на диске записана календарная дата последней правки картотеки. Если в процессе работы с картотекой в ней что-то изменили, то старое ее содержание на магнитном диске стирается (SCRATCH). На этом месте будут храниться (SAVE) новые данные (DATA) и новая календарная дата правки картотеки (строка 20).
Впрочем, разберем строки программы по порядку.
Строка 1. В картотеке сто карточек. Индексные литерные переменные: W - названия дней недели, S - формулировка I-го распоряжения (прописная латинская буква I часто используется для индексации), D - двумерный массив: D(1, I) - дата выдачи, a D(2, I) - дата выполнения I-го распоряжения, А - имя исполнителя (длина - 16 знаков по умолчанию). Индексные вещественные переменные: D - номер дня выполнения I-го распоряжения, Т - номер папки с дополнительной информацией по нему. Здесь же считываются (READ) названия дней недели из списка данных (DATA).
Строка 3. Команда GO SUB - это обращение к подпрограмме (строки 22-30), выполнение которой состоит в запросе календарной даты, контроле правильности ее ввода (33.13.86, 29.02.86, 31.06.86 и тому подобные "ляпы" не проходят), определении номера дня на хронологической оси XX века. Зная этот номер, машина легко может определить, что произошло раньше, а что позже и на сколько дней. Кроме того, по номеру дня просто узнать день недели (строка 30; подробнее об алгоритмах работы с календарем можно узнать в книге Я.К.Трохименко и Ф.Д.Любича "Микрокалькулятор, ваш ход". М., Радио и связь, 1985). После выполнения подпрограммы управление возвращается (RETURN, см. строку 30) на старое место.
Строка 4. Меню работы с картотекой и ветвление по участкам программы.
Строки 5-10. Заполнение новой карточки. ЭВМ не допускает очень распространенной в жизни ситуации, когда на вопрос о сроке выполнения отвечают: "Вчера" (строка 8 ).
Строка 11. Снятие с контроля I-го распоряжения.
Строки 12-19. Здесь записаны команды, позволяющие просматривать всю картотеку или ее часть, отвечающую какому-либо заданному признаку. Содержание требуемой карточки выводится на экран дисплея (строка 18 ).
После того как мы завели электронную картотеку распоряжений начальства и своих собственных насущных дел, наши традиционные утренние пятиминутки стали проходить совсем по-иному. Во-первых, они на самом деле стали пятиминутками. Мы включаем машину, загружаем в нее картотеку и работаем по программе. Сначала мы просматриваем, что нужно выполнить сегодня и необходимо сделать в ближайшие дни. Исходя из этого и с учетом новых задач мы составляем или корректируем планы на будущее - записываем что-то за конкретными исполнителями, снимаем с контроля выполненное.
Наш НП преобразился, даже плечи расправил, стал отдавать больше времени своему основному и любимому занятию - науке, а не рутинной работе. Поговаривают, что наша "Искра" стала наиболее вероятным его преемником на должности завлаба.
В.ЩЕГЛОВ (г.Ленинград)
СОСТАВЬТЕ ТАБЛИЦУ КОДОВ
Хотя я еще не могу купить персональный компьютер "БК-1010", у меня была возможность поработать на нем около двух месяцев. Машиной я вполне доволен. К сожалению, инструкция к ней составлена плохо: мало примеров использования тех или иных операторов, нет списка кодов КОИ-7 для работы с функцией ввода и вывода символической информации FCHR(X), а про подачу звукового сигнала вообще ничего не сказано.
Мне удалось найти код подачи звукового сигнала: FCHR(7). Предлагаю программу, с помощью которой, нажимай на клавиши, можно получить их коды на экране телевизора:
10.10 S X=FCHR(-1)
10.15 T!, %3, "КОД=", X
10.20 G 10.10
А.БАТЮК, ученик 10-го класса (г.Москва)
НА ЭКРАНЕ - ГИСТОГРАММА
Вот уже два месяца, как я работаю на микрокомпьютере "Sinclair ZX-81". На нем я выполнил все расчеты, необходимые для дипломного проекта. Одна из моих программ предназначена для построения гистограмм.
Как известно, чтобы построить гистограмму, диапазон изменения исследуемой величины (L, R) необходимо поделить на несколько равных интервалов. Подсчитывается число наблюдений Hi, приходящихся на каждый i-й интервал, и определяется частота, равная отношению числа Нi к общему числу наблюдений. При желании можно получить не только числа-параметры, но и картинку, соответствующую полученным результатам. На рисунке - программа на языке "бэйсик" для решения такой задачи.

Так же, как люди, живущие в разных местностях, говорят на различных диалектах одного языка, так и компьютеры разных марок понимают весьма схожие, но все же отличающиеся друг от друга в деталях версии алгоритмического языка "бэйсик". Чтобы читатели смогли использовать эту программу на доступных им машинах, сделаю некоторые пояснения.
[ В текстах программ на "бэйсике" нуль перечеркивают, чтобы не спутать его с буквой О. Команды нумеруют числами, кратными десяти: это удобно, когда приходится вставлять новую команду между уже пронумерованными ].
Команда 10 присваивает переменной GIST значение числа, первого из введенных с клавиатуры. Команда 20 выделяет область памяти под счетчики числа наблюдений, приходящихся на каждый интервал. Если, к примеру, будет введено число 10, то компьютер отведет область памяти для хранения данных по десяти интервалам. Команды 30 и 40 запрашивают значения левой и правой границ диапазона изменения исследуемой величины (L, R). Команда 50 вычисляет коэффициент X1 по формуле
X1=GIST/(R-L)
Блок команд с 60 по 100 будет выполняться до тех пор, пока мы не введем все значения. Компьютер поймет, что ввод данных закончен, как только мы вместо очередного значения введем число-признак 0.01. Это число следует выбирать так, чтобы оно не входило в интервал (L, R). Получив сигнал о завершении ввода данных, компьютер передаст управление команде 110. Блок команд с 130 по 160 подсчитает суммарное число наблюдений SUM и определит максимальное число наблюдений, приходящихся на один интервал. Теперь осталось лишь вывести на экран содержимое счетчиков. По командам SCROLL и PRINT строки с этой информацией проплывают по экрану снизу вверх.
Чтобы каждый успел переписать с экрана результаты вычислений (печатающими устройствами снабжены не все компьютеры), в программе записан оператор PAUSE. Получив такую команду, компьютер "держит паузу", величина которой определяется числом, стоящим возле ключевого слова: 2E3=2000. Это число колебаний тока в сети за время паузы. Переводя в секунды, получаем 2000/50 = 40 секунд. Паузу можно прервать и раньше - стоит лишь нажать на любую клавишу компьютера.
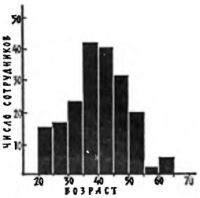
Команда CLS (сокращение от английского clear screen - очистить экран) готовит экран для вывода собственно гистограммы. Команда PLOT рисует квадратик в позиции, определенной значением параметра J, которое, в свою очередь, зависит от номера интервала и количества попавших в
интервал исходных данных.
Б.АЛЕКСЕЕВ (г.Москва)
ИНТЕГРИРОВАНИЕ НА МИКРОКАЛЬКУЛЯТОРЕ
В прошлом году (6/85) читатели нашего раздела приглашались на дискуссию за круглым столом, посвященную вычислению определенных интегралов на микрокалькуляторе "Электроника Б3-34" и ему подобных. В ответ на приглашение редакция получила 143 письма, где предлагаются программы, реализующие различные методы интегрирования. (Самым популярным оказался метод Симпсона - о нем идет речь в каждом втором письме). Есть письма, где говорится о несобственных интегралах, об интегралах с переменным верхним пределом и т.д. Этим темам будут предоставлены страницы одного из предстоящих выпусков. Сейчас под нашей рубрикой выступают С.Г.Волченков (Ярославль), В.Ю.Критинин (Москва), Г.И.Натансон (Ленинград), Н.Б.Никитин (Москва), Л.М.Финк (Ленинград), Ш.Е.Цимринг (Горький), В.А.Яковлев (Москва). Ведет дискуссию Б.Н.ХОДОВ.
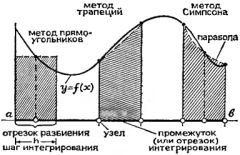
Б.Н.ХОДОВ: Как известно, простейший из приближенных методов интегрирования - метод прямоугольников. Область между графиком интегрируемой функции и осью абсцисс рассекается на вертикальные полоски одинаковой ширины, равной шагу интегрирования h=(b-a)/N (где N - число шагов; а и b-концы промежутка интегрирования, см. на рисунке). Площадь каждой полоски принимается равной площади прямоугольника, одна сторона которого равна h, а другая - значению функции в одной из точек отрезка разбиения. Суммарная площадь прямоугольников S(h) дает приближенное значение интеграла.
В.Ю.КРИТИНИН: Будем брать значения функции в середине каждого отрезка разбиения. Для оценки точности интегрирования станем использовать результаты, полученные при исходном и уменьшенном вдвое шаге интегрирования. Если выполняется условие 3д>|1-S(h)/S(h/2)|, то величина S(h/2) даст значение интеграла с относительной погрешностью, не превышающей д. Предлагаемая программа автоматически дробит шаг, покуда не будет достигнута заданная точность.
00. ПД 01. Cx 02. П3. 03. ИПВ 04. ИПА. 05. - 06. ИПД 07. / 08. П1 09. 2 10. / 11. ИПА 12. + 13. П2 14. ПП 15. 51 16. ИП3 17. + 18. П3 19. ИП2 20. ИП1 21. + 22. П2 23. ИПВ 24. - 25. Fx>=0 26. 14 27. ИП0 28. ИП1 29. ИП3 30. * 31. П3 32. / 33. 1 34. - 35. Fx2 36. Fsqr 37. ИПС 38. - 39. Fx>=0 40. 49 41. ИП3 42. П0 43. Сх 44. П3 45. ИП1 46. 2 47. БП 48. 07 49. ИП3 50. С/П.
Вслед за основной программой ввести, начиная с 51 адреса, подпрограмму вычисления f(x). Ее аргумент берется из Р2, значение должно оказаться в РХ. После ввода перейти в режим вычислений, набрать на клавиатуре а ПА b ПВ 3д ПС 0 П0 1 (или начальное число шагов интегрирования) В/0 С/П. Результат - на индикаторе и в Р3.
Б.Н.ХОДОВ: Согласно другому методу приближенного интегрирования, методу трапеций, каждая полоска, на которые рассекается площадь под графиком интегрируемой функции, заменяется трапецией, чья высота равна h, а основания-значениям функции в концах отрезка разбиения. По сравнению с методом прямоугольников здесь при том же шаге интегрирования обеспечивается примерно вдвое меньшая точность. Оба эти способа превосходит по точности метод Симпсона, когда на каждом отрезке разбиения график функции заменяется параболой, проходящей через точки, соответствующие значениям функции в конце отрезка и в его середине.
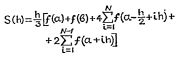
Л.М.ФИНК: Этот метод позволяет быстрее достичь заданной относительной погрешности д, которая на сей раз гарантируется условием со впятеро большей левой частью: 15д>|1-S(h)/S(h/2)|.
00. ИПВ. 01. П6 02. ПП 03. 65 04. ПД 05. ИПА 06. ПП 07. 65 08. ИПД 09. + 10. ПД 11. ИПВ 12. ИПА 13. - 14. П7 15. 1 16. П8 17. ИП7 18. 2 19. / 20. П7 21. ИП8 22. 2 23. * 24. П8 25. П0 26. КИП0 27. 0 28. ПС 29. ИП7 30. ИП0 31. * 32. ИПА 33. + 34. ПП 35. 65 36. ИПС 37. + 38. + 39. FL0 40. 41 41. FL0 42. 28 43. ^ 44. ИПД 45. + 46. ПД 47. + 48. ИП7 49. * 50. ИП6 51. x-y 52. П6 53. - 54. FBx 55. / 56. Fx2 57. ИП9 58. - 59. Fx<0 60. 17 61. ИП6 62. 3 63. / 64. С/П.
Вслед за основной программой ввести, начиная с 65 адреса, подпрограмму вычисления интегрируемой функции (аргумент берется из РХ, результат должен оказаться в РХ и PY; здесь можно прибегнуть к команде ^). После ввода перейти в режим вычислений, набрать на клавиатуре а ПА b ПВ (15д)**2 П9 0 П6 В/0 С/П. Результат - на индикаторе.
Получив величину 3S(h), программа уменьшает шаг h вдвое, число N вдвое увеличивает, в регистр Д заносится (44-46) сумма f(a)+f(b)+2Сигма*f(a+ih/4). Для проверки условия точности к этой сумме добавляется 2Сигма*f(a-h/4+ih/2) (43-47), результат умножается на h (48-49), что дает величину 3S(h/2). Она заносится в Р6 и сравнивается с 3S(h) адреса 50-60. Таким образом, для вычислении с уменьшенным шагом затрачивается минимальное время.
Г.И.НАТАНСОН: Формула Боде В(h)=[16S(h)-S(h/2)]/15, где используются те же величины S(h) и S(h/2), что и при расчетах по формуле Симпсона, дает более точное значение интеграла. Абсолютная погрешность е здесь гарантируется условием 63e>|B(h)-B(h/2)|.
00. ПП 01. 62 02.ПС 03.6 04.3 05.С/П 06. * 07. Fx2 08. ПД 09. ИПА 10. ИПВ 11. - 12. ПВ 13. П5 14. Сх 15. П9 16. ИП5 17. П7 18. 2 19. / 20. П5 21. ИПВ 22. - 23. П8 24. ИПА 25. + 26. ПП 27. 62 28. ИП8 29. ИП7 30. + 31. Fx<0 32. 23 33. ИП6 34. ИП4 35. ИП9 36. ^ 37. + 38. ИПС 39. x-y 40. + 41. ПС 42. FBx 43. + 44. П4 45. 8 46. * 47. - 48. ИП7 49. * 50. 4 51. 5 52. / 53. П6 54. - 55. Fx2 56. ИПД 57. - 58. Fx<0 59. 14 60. ИП6 61. С/П.
Вслед за основной программой ввести, начиная с 62 адреса, подпрограмму расчета подынтегральной функции (аргумент и значение - в РХ), заканчивая ее командами ИП9 + П9 В/0. После ввода перейти в режим вычислений, набрать на клавиатуре Сх П9 а ПА В/0 С/П b ПВ В/0 С/П е С/П. Результат - на индикаторе и в Р6.
Ш.Е.Цимринг: Для гладких функций при заданном числе узлов, в которых вычисляется f(х), наивысшими по точности являются формулы Гаусса. По-видимому, он первый обратил внимание на то, что равномерное расположение узлов не является наилучшим, и указал, что узлы, если всего их n, должны совпадать с нулями многочлена Лежандра n-ной степени. Значения функции в узлах умножаются на коэффициенты, которые приводятся в справочниках по численному интегрированию.
00. ИПВ 01. ^ 02. ИПС 03. - 04. 2 05. / 06. ПС 07. - 08. ПД 09. 0 10. ПВ 11. 1 12. 0 13. П0 14. КИП^ 15. /-/ 16. КП^ 17. ИПС 18. * 19. ИПД 20. + 21. ПП 22. 37 23. КИП0 24. * 25. ИПВ 26. + 27. ПВ 28. FL0 29. 14 30. ИП2 31. Fx>=0 32. 11 33. F() 34. ИПС 35. * 36. С/П.
Программа составлена для случая 10 узлов: больше не позволяют возможности микрокалькулятора. Достигаемой точности, как показывает практика, вполне достаточно.
Ввести программу и далее, с 37 адреса - подпрограмму вычисления интегрируемой функции (аргумент и значение - в РХ). После ввода перейти в режим вычислений, набрать 29552422 ВП 8 /-/ П1 14887434 ВП 8 /-/ П2 26926672 ВП 8 /-/ П3 43339539 ВП 8 /-/ П4 21908636 ВП 8 /-/ П5 67940957 ВП 8 /-/ П6 14945135 ВП 8 /-/ П7 86506337 ВП 8 /-/ П8 66671344 ВП 9 /-/ П9 97390653 ВП 8 /-/ ПА а ПС b ПВ В/0 С/П. Результат - на индикаторе.
С.Г.ВОЛЧЕНКОВ: Обилие констант, используемых в методе Гаусса, не только усложняет пользование программой, но и ограничивает сложность подынтегральной функции, так как сокращает или вовсе сводит к нулю число регистров для хранения констант функции. Предлагаю формулу, аппроксимирующую формулу Гаусса для пяти узлов:
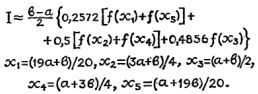
00. ИПА 01. ИПВ 02. + 03. 2 04. / 05. ПД 06. ИПА 07. - 08. ПС 09. 0 10. , 11. 9 12. * 13. ПА 14. ИПД 15. + 16. ПП 17. 52 18. ИПД 19. ИПА 20. - 21. ПП 22. 52 23. + 24. ИП9 25. * 26. ИПД 27. ИПС 28. 2 29. / 30. ПА 31. - 32. ПП 33. 52 34. ИПД 35. ИПА 36. + 37. ПП 38. 52 39. + 40. 2 41. / 42. + 43. ИПД 44. ПП 45. 52 46. ИП8 47. * 48. + 49. ИПС 50. * 51. С/П.
Когда программа введена, ввести с 52 адреса подпрограмму вычисления f(x), аргумент и значение которой помещаются в РХ. Затем перейти в режим вычислений, набрать а ПА b ПВ 0.4856 П8 0.2572 П9 В/0 С/П. Результат - на индикаторе.
Достаточную точность программы подтвердил двухлетний опыт ее использования для контроля студенческих работ по курсу "методы вычислений".
В.А.ЯКОВЛЕВ: Чебышев решил задачу распределения узлов для случая, когда коэффициенты, на которые умножаются значения подынтегральной функции (как в других подобных методах), равны между собой. Такое условие не только сулит большое удобство, но и позволяет уменьшить ошибку, вызванную неточностью задания подынтегральной функции. По точности формулы Чебышева занимают промежуточное положение между методами Гаусса и Симпсона при одинаковом числе использованных значений подынтегральной функции. По предлагаемой программе можно вычислять интегралы по формуле Чебышева для 2, 4 или 6 узлов. По ходу счета исходный отрезок интегрирования последовательно разбивается программой на 2, 4, 8 и более частей для достижения желаемой точности. На каждом из полученных при этом отрезков интеграл вновь вычисляется по формуле с выбранным числом узлов, и результаты складываются.
00. ИПВ 01. ИПА 02. - 03. ПС 04. Сх 05. П2 06. Сх 07. П4 08. ИПА 09. П6 10. ИПД 11. П0 12. КИП0 13. П8 14. ПП 15. 47 16. 1 17. ИП8 18. - 19. ПП 20. 47 21. FL0 22. 12 23. ИП6 24. ИПС 25. + 26. П6 27. ИПВ 28. - 29. Fx>=0 30. 10 31. ИП4 32. ИПС 33. ИПД 34. / 35. * 36. П4 37. ИП2 38. - 39. С/П 40. ИПС 41. 2 42. / 43. ПС 44. ИП4 45. БП 46. 05 47. ИПС 48. * 49. ИП6 50. +.
Ввести программу, и с 51 адреса - подпрограмму вычисления подынтегральной функции (аргумент и значение в РХ), закончить ее командами ИП4 + П4 В/0. После ввода перейти в режим вычислений, набрать а ПА b ПВ N (2, 4 или 6) ПД. В зависимости от выбранного N далее ввести для1 N=2: 21132487 ВП 8 /-/ П1; для N=4: 40620376 ВП 8/-/ П1 10267276 ВП 8/-/ П3; для N=6: 3666823 ВП 7 /-/ П1, 28874067 ВП 8 /-/ П3 66876591 ВП 9 /-/ П5. Запустить программу: В/0 С/П. Результат - на индикаторе. При повторных нажатиях С/П исходный отрезок дробится, а на индикатор выводится разность оценок интеграла при текущем и предыдущем разбиении. Текущее значение интеграла - в Р4, предыдущее - в Р2.
Н.Б.НИКИТИН: Для достижения желаемой точности вычисление интеграла приходится строить как итерационный процесс. А раз так, то можно воспользоваться методами ускорения итерационных процессов, например, методом Эйткина. Если отношение числа шагов на каждой итерации постоянно и равно q. то после выполнения трех итераций можно получить более точный результат.

Применим метод Эйткина к методу прямоугольников.
00. ПА 01. - 02. ПВ 03. x-y 04.ПС 05. 3 06. П0 07. Сх 08. ПД 09. ИПС 10. П1 11. ИП1 12. 2 13. F1/x 14. - 15. ИПВ 16. * 17. ИПС 18. / 19. ИПА 20. + 21. ПП 22. 60 23. ИПД 24. + 25. ПД 26. FL1 27. 11 28. ИПВ 29. * 30. ИПС 31. / 32. КП^ 33. ИПС 34. 2 35. * 36. ПС 37. FL0 38. 07 39. ИП3 40. ИП2 41. - 42. Fx2 43. ИП2 44. 2 45. * 46. ИП3 47. - 48. ИП1 49. - 50. / 51. ИП3 52. + 53. С/П 54. ИП2 55. П3 56. ИП1 57. П2 58. БП 59. 07.
После ввода основной программы ввести с 60 адреса подпрограмму вычисления подынтегральной функции (аргумент и значение- в РХ). перейти в режим вычислений, ввести N (начальное число шагов интегрирования) ^ b ^ a В/0 С/П. Результат - на индикаторе. Последующие нажатия С/П станут давать результаты, полученные по методу Эйткина для уменьшающегося с каждым разом вдвое шага интегрирования. Такое уменьшение позволяет использовать величины S2 и S3 при подсчете S(h/2) и вдвое повысить скорость вычислений.
Б.Н.ХОДОВ. Сравнить предложенные программы позволяет таблица.
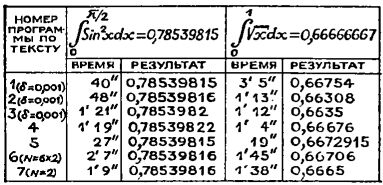
Для обмена опытом с коллегами публикуем адреса читателей, согласившихся на это:
141700, Московская обл., г.Долгопрудный. Лихачевское шоссе 21, кв.128, А.Н.Тулайков;
252027, Киев, ул.Ереванская 32, кв.13, Г.В.Семенов;
410064, Саратов, ул.Тархова 6А, кв.34, Е.С.Левина;
252050, Киев, ул.Кравченко 23, кв.97, А.И.Хоменко;
622023, Нижний Тагил Свердловской обл., ул.Ленина 71А, кв.12, П.И.Чубенко;
198255, Ленинград, просп.Суслова 9, кор.2, кв.97, И.И.Павлов;
150052, Ярославль, Ленинградский проспект 59, кв.63, С.Г.Волченков; 194064, Ленинград, Тихорецкий проспект 7, кор.4, кв.7, Л.М.Финк; 127562, Москва, ул.Санникова 17, кв.217, Н.Б.Никитин;
603025, Горький, ул.Генкиной 19, кв.7, Ш.Е.Цимринг.
ЛИТЕРАТУРА
Калиткин Н.Н. Численные методы. М., Физматгиз, 1978.
Бахвалов Н.С. Численные методы. М., Физматгиз, 1975.
Корн Г., Корн Т. Справочник по математике. М., Физматгиз, 1977.
Инженерные расчеты на ЭВМ. Справочное пособие (под ред. В.А.Троицкого). Л., Машиностроение, 1979.
Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. М., Мир, 1977.
КОГДА ВОСХОДИТ СОЛНЦЕ
Радиолюбителям известно аномально дальнее распространение радиоволн с частотой в несколько мегагерц близ терминатора - границы дня и ночи. Благодаря этому явлению удалось осуществить связь на таких частотах между всеми радиолюбительскими зонами нашей планеты, что считалось невозможным еще лет пятнадцать назад.
Сверхдальняя радиосвязь осуществима лишь тогда, когда оба корреспондента занимают вполне определенное положение относительно терминатора: либо оба находятся на границе дня и ночи, либо один - в зоне терминатора, другой - в зоне ночи. Времени на такую связь отпущено немного, в среднем 5-10 минут: из-за вращения Земли положение корреспондентов относительно терминатора все время меняется. Чтобы планировать связь, нужно наперед знать, когда в местах расположения корреспондентов происходят восходы и заходы солнца. Большую помощь в этом может оказать программируемый микрокалькулятор. Используя его, можно быстро распланировать свое эфирное время при подготовке сеанса, хорош он и во время сеанса. Например, установлена связь с новым корреспондентом: координаты собеседника вводятся в микрокалькулятор и, пока идет обмен сведениями о применяемой аппаратуре, антеннах, свободном эфирном времени, попутно вычисляется и время восходов-заходов в местности корреспондента, что позволяет вполне обоснованно договориться о времени следующего сеанса.

Для расчета используется формула:
Тв/з=[л+/-arccos(tgф*tgд)]/15,
где Тв/з - время восхода или захода: ф - широта места, отсчитываемая к северу от экватора; л - долгота места, отсчитываемая к западу от нулевого меридиана; д - угол склонения солнца для нужной даты. Для определения этого угла удобно использовать соотношение
tgд = cos(15Tв0-л0)/tgф0.
Задавшись какой-либо датой, можно подставить в правую часть равенства тройку чисел ф0, л0, Тв0 для любого города, например, Москвы:
ф0=55o46': л0=-37o37'; Тв0 отыскивается в отрывном календаре на страничке с нужной датой. Это декретное время. Чтобы перевести его в гринвичское, общеупотребительное у радиолюбителей, надо вычесть из него 3 часа. (Из "летнего" времени вычитается 4 часа).
Вычисления производятся по программе:
00. ПД 01. 0 02. , 03. 6 04. П3 05. F1/x 06. П4 07. П6 08. ИПД 09. ПП 10. 64 11. 1 12. 5 13. П0 14. * 15. ИПС 16. ПП 17. 64 18. - 19. Fcos 20. ИПВ 21. ПП 22. 64 23. Ftg 24. / 25. ПА 26. 1 27. С/П 28. П8 29. F() 30. ИП4 31. П6 32. F() 33. ПП 34. 64 35. Ftg 36. ИПА 37. * 38. Farccos 39. П1 40. ИП8 41. ПП 42. 64 43. П8 44. ИП3 45. П6 46. ИП1 47. /-/ 48. ПП 49. 55 50. ИП1 51. ПП 52. 55 53. БП 54. 27 55. ИП8 56. + 57. ИП0 58. / 59. Fx<0 60. 64 61. 2 62. 4 63. + 64. ^ 65. Fx2 66. Fsqr 67. / 68. FBx 69. 1 70. + 71. П9 72. КИП9 73. F() 74. ИП9 75. - 76. ИП6 77. * 78. 1 79. - 80. ИП9 81. + 82. * 83. В/0.
Переключатель Р-Г устанавливается в положение Г. Углы вводятся в виде десятичной дроби, где целая часть - градусы, дробная - минуты (для Москвы ф=55.46; л=-37.37), время - аналогично: целая часть - часы, дробная - минуты. Введя программу, набираем В/0 ф0 ПВ л0 ПС Тв0 С/П. Вскоре на индикаторе появляется единица - значит, микрокалькулятор готов к вычислениям. Набираем координаты интересующего нас места ф ^ л С/П. После счета на табло высвечивается время восхода солнца Тв. Время захода Тз, вызывается нажатием клавиши x-y. Повторить ввод при сбое можно, нажав клавиши БП 29 С/П.
Г.ГУЛЯЕВ (г.Куйбышев)
ЭЛЕКТРОННЫЕ ГОРОДКИ
Электронные городки отличаются от традиционных. Расстояние, с которого производятся броски, выбирается игроком в пределах от 11 до 20 метров. Вместо квадратного "города" используется линия, на которой расставляется от одного до восьми городков. Расстановку показывает индикатор. Незанятые позиции обозначаются единицами, каждый городок - двойкой.
Длина биты выбрана такой, что в случае удачного броска она сшибает пять стоящих рядом городков. Самый удачный бросок - это когда, несмотря на вращение в полете, бита приходит к линии расстановки параллельно ей, а не под углом. Наименее удачны броски, если бита пролетает сквозь строй городков торцом, не задев ни одного из них.
Цель игры - наименьшим числом ударов выбить все городки с линии.
Теперь коротко о правилах диалога (именно в таком режиме проходит игра с микрокалькулятором).
После того как программа введена, требуется ввести в Р9 признак окончания игры - число из восьми единиц. Переключатель Р-Г должен быть установлен в положении Г. Городки располагают в регистрах с восьмого по первый. Набираем, например. 2 П8 - это значит, что в восьмой позиции стоит городок: 1 П7 - седьмая позиция не занята. Так должны быть заполнены все регистры от Р8 до Р1.
Итак, городки расставлены по местам. Можно запускать программу клавишами В/0, С/П. Через 15 секунд иа индикаторе появится изображение, демонстрирующее расстановку городков на линии. Выберем дистанцию для броска, например, 12 метров (12 С/П). Далее выберем угол а (см. рисунок) от -30 до +30o, введем это число и нажмем С/П. Менее чем через минуту на индикаторе демонстрируется положение после броска.
Программа: 00. ^ 01. 8 02. П0 03. Сх 04. КИП^ 05. + 06. 1 07. 0 08. * 09. FL0 10. 04 11. FBx 12. / 13. ^ 14. ИП9 15. - 16. Fln 17. x-y 18. С/П 19. ПВ 20. С/П 21. /-/ 22. ПА 23. 2 24. / 25. Fx2 26. Fsqr 27. ИПВ 28. + 29. 2 30. 0 31. - 32. Fx2 33. Fsqr 34. 5 35. - 36. Fx2 37. Fsqr 38. 1 39. + 40. П0 41. КИП0 42. ИПА 43. Ftg 44. ИПВ 45. * 46. 5 47. + 48. ПС 49. КИПС 50. 1 51. ПП 52. 80 53. ИПС 54. 1 55. + 56. ПС 57. 3 58. ПП 59. 80 60. ИПС 61. 2 62. - 63. ПС 64. ПП 65. 86 66. ИПС 67. 3 68. + 69. ПС 70. 5 71. ПП 72. 80 73. ИПС 74. 4 75. - 76. ПС 77. ПП 78. 86 79. 8 80. ИП0 81. x-y 82. - 83. Fx>=0 84. 01 85. ИПС 86. 1 87. - 88. Fx>=0 89. 97 90. 7 91. x-y 92. - 93. Fx>=0 94. 97 95. 1 96. КПС 97. В/0.
Команда 00. ^ готовит регистр X для приема адреса старшего регистра, начиная с которого предстоит формировать изображение на индикаторе. Адрес старшего регистра записывается в Р0 командами 01-02. Блок команд с 03 по 12 синтезирует изображение, причем каждый регистр соответствует одному разряду. Команда 13 дублирует изображение в регистре Y. Проверку "игра окончена?" ведут команды 14-16.
Если игра не закончена, команды 17-18 выводят на индикатор изображение. После того как команды 20-22 введут в РВ и РА соответственно длину L и угол а, фрагмент 23-41 сформирует длину проекции биты Р по формуле
P=[|||a/2|+L-20|-5|].
Прямые скобки здесь означают абсолютную величину заключенного в них числа, а квадратные - целую часть числа. Формула имитирует влияние вращения биты на длину проекции Р в зависимости от выбранной дистанции L и угла а. Фрагмент с 42 по 49 вычисляет положение центра проекции по формуле
J=[L tg a + 5].
Команды с 50 и 80 и подпрограмма с 80 и 98 проверяют, какие городки задеты битой, и заменяют двойки на единицы.
Потренировавшись, даже самую сложную фигуру можно поразить двумя точными бросками. Однако добиться этого не просто.
А.ЗАЙЦЕВ (г.Щигры, Курской обл.)

Рис. Н.Сущенцова (г.Киров)
[ УЗЕЛКИ НА ПАМЯТЬ
Чтобы выполнить косвенный переход по команде КБПМ или КППМ, в регистр М надо записать двузначный адрес перехода. (Пусть М - один из немодифицируемых регистров от 7 до Д). Но если в регистре М записана константа, то переход произойдет по адресу, выражаемому двумя младшими ее разрядами, считая влево от запятой.
Это обстоятельство позволяет сократить программу, если при ее составлении среди констант оказалась такая, два младших разряда которой совпадают с требуемым адресом перехода.
В.ЛЕСНЯК (г.Днепропетровск) ]
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Почта принесла еще несколько писем, авторы которых рассказывают о том, как в решении повседневных проблем им помогают компьютеры - "Исrра-226" и "ДВК", "БК-0010" и другие. Проблемы эти просты: составить картотеку распоряжений по лаборатории, построить гистограмму... Но в простоте есть определенное достоинство: разбирая несложные программы, пытаясь составлять их самостоятельно, убеждаясь, что они работают и дают ожидаемый результат, ощущая реальную пользу от них, естественно приобщаться к искусству программирования. А поскольку задачи, о которых рассказывается в нашем разделе, носят повседневный массовый характер, можно надеяться, что их решение облегчит приобщение к программированию многим и многим людям.
Вот почему мы ждем от наших читателей все новых и новых писем подобного рода.
ПЯТИМИНУТКИ С "ИСКРОЙ"
Наш завлаб (назовем его условно Николаем Петровичем, или сокращенно НП) - хороший ученый, отличный человек, но администратор не очень. Как и всякому начальнику, ему приходится отдавать всякого рода распоряжения своим подчиненным. С этой задачей НП справляется неплохо. А вот что касается проверки исполнения - с этим у него не ладится.
Когда НП узнал, как электронно-вычислительная техника облегчает труд руководителя, он вызвал меня, поскольку наша ЭВМ "Искра-226" находится в моем ведении, и поручил составить электронную картотеку приказов по лаборатории. НП высказал свои пожелания к картотеке, перечислил необходимые виды работы с ней:
1. Записать на первую свободную карточку новое распоряжение с указанием дат выдачи и выполнения, имени исполнителя н номера папки, хранящей дополнительную информацию.
2. Снять с контроля выполненное распоряжение.
3. Узнать, что нужно было сделать к текущему дню.
4. Получить информацию о просроченных распоряжениях и о тех, срок исполнения которых приближается.
5. Просмотреть всю картотеку.
6. Просмотреть карточки по отдельным исполнителям.
В тот же день я составил небольшую программу на языке "бэйсик". Как к во всякой программе такого рода (См. например 2/86), здесь используются вещественные и литерные индексные переменные, объединенные в массивы, меню с возвращением к нему после выполнения выбранного вида работы, циклический перебор карточек, логическое сравнение предложенной конструкции с фрагментом текста и т.п.

Картотека записана вместе с программой на гибком магнитном диске. При запуске программы ЭВМ загружает (LOAD; см. строку 2) в свою оперативную память содержание картотеки, которая хранится под именем "КАРТОЧКИ". Там же на диске записана календарная дата последней правки картотеки. Если в процессе работы с картотекой в ней что-то изменили, то старое ее содержание на магнитном диске стирается (SCRATCH). На этом месте будут храниться (SAVE) новые данные (DATA) и новая календарная дата правки картотеки (строка 20).
Впрочем, разберем строки программы по порядку.
Строка 1. В картотеке сто карточек. Индексные литерные переменные: W - названия дней недели, S - формулировка I-го распоряжения (прописная латинская буква I часто используется для индексации), D - двумерный массив: D(1, I) - дата выдачи, a D(2, I) - дата выполнения I-го распоряжения, А - имя исполнителя (длина - 16 знаков по умолчанию). Индексные вещественные переменные: D - номер дня выполнения I-го распоряжения, Т - номер папки с дополнительной информацией по нему. Здесь же считываются (READ) названия дней недели из списка данных (DATA).
Строка 3. Команда GO SUB - это обращение к подпрограмме (строки 22-30), выполнение которой состоит в запросе календарной даты, контроле правильности ее ввода (33.13.86, 29.02.86, 31.06.86 и тому подобные "ляпы" не проходят), определении номера дня на хронологической оси XX века. Зная этот номер, машина легко может определить, что произошло раньше, а что позже и на сколько дней. Кроме того, по номеру дня просто узнать день недели (строка 30; подробнее об алгоритмах работы с календарем можно узнать в книге Я.К.Трохименко и Ф.Д.Любича "Микрокалькулятор, ваш ход". М., Радио и связь, 1985). После выполнения подпрограммы управление возвращается (RETURN, см. строку 30) на старое место.
Строка 4. Меню работы с картотекой и ветвление по участкам программы.
Строки 5-10. Заполнение новой карточки. ЭВМ не допускает очень распространенной в жизни ситуации, когда на вопрос о сроке выполнения отвечают: "Вчера" (строка 8 ).
Строка 11. Снятие с контроля I-го распоряжения.
Строки 12-19. Здесь записаны команды, позволяющие просматривать всю картотеку или ее часть, отвечающую какому-либо заданному признаку. Содержание требуемой карточки выводится на экран дисплея (строка 18 ).
После того как мы завели электронную картотеку распоряжений начальства и своих собственных насущных дел, наши традиционные утренние пятиминутки стали проходить совсем по-иному. Во-первых, они на самом деле стали пятиминутками. Мы включаем машину, загружаем в нее картотеку и работаем по программе. Сначала мы просматриваем, что нужно выполнить сегодня и необходимо сделать в ближайшие дни. Исходя из этого и с учетом новых задач мы составляем или корректируем планы на будущее - записываем что-то за конкретными исполнителями, снимаем с контроля выполненное.
Наш НП преобразился, даже плечи расправил, стал отдавать больше времени своему основному и любимому занятию - науке, а не рутинной работе. Поговаривают, что наша "Искра" стала наиболее вероятным его преемником на должности завлаба.
В.ЩЕГЛОВ (г.Ленинград)
СОСТАВЬТЕ ТАБЛИЦУ КОДОВ
Хотя я еще не могу купить персональный компьютер "БК-1010", у меня была возможность поработать на нем около двух месяцев. Машиной я вполне доволен. К сожалению, инструкция к ней составлена плохо: мало примеров использования тех или иных операторов, нет списка кодов КОИ-7 для работы с функцией ввода и вывода символической информации FCHR(X), а про подачу звукового сигнала вообще ничего не сказано.
Мне удалось найти код подачи звукового сигнала: FCHR(7). Предлагаю программу, с помощью которой, нажимай на клавиши, можно получить их коды на экране телевизора:
10.10 S X=FCHR(-1)
10.15 T!, %3, "КОД=", X
10.20 G 10.10
А.БАТЮК, ученик 10-го класса (г.Москва)
НА ЭКРАНЕ - ГИСТОГРАММА
Вот уже два месяца, как я работаю на микрокомпьютере "Sinclair ZX-81". На нем я выполнил все расчеты, необходимые для дипломного проекта. Одна из моих программ предназначена для построения гистограмм.
Как известно, чтобы построить гистограмму, диапазон изменения исследуемой величины (L, R) необходимо поделить на несколько равных интервалов. Подсчитывается число наблюдений Hi, приходящихся на каждый i-й интервал, и определяется частота, равная отношению числа Нi к общему числу наблюдений. При желании можно получить не только числа-параметры, но и картинку, соответствующую полученным результатам. На рисунке - программа на языке "бэйсик" для решения такой задачи.

Так же, как люди, живущие в разных местностях, говорят на различных диалектах одного языка, так и компьютеры разных марок понимают весьма схожие, но все же отличающиеся друг от друга в деталях версии алгоритмического языка "бэйсик". Чтобы читатели смогли использовать эту программу на доступных им машинах, сделаю некоторые пояснения.
[ В текстах программ на "бэйсике" нуль перечеркивают, чтобы не спутать его с буквой О. Команды нумеруют числами, кратными десяти: это удобно, когда приходится вставлять новую команду между уже пронумерованными ].
Команда 10 присваивает переменной GIST значение числа, первого из введенных с клавиатуры. Команда 20 выделяет область памяти под счетчики числа наблюдений, приходящихся на каждый интервал. Если, к примеру, будет введено число 10, то компьютер отведет область памяти для хранения данных по десяти интервалам. Команды 30 и 40 запрашивают значения левой и правой границ диапазона изменения исследуемой величины (L, R). Команда 50 вычисляет коэффициент X1 по формуле
X1=GIST/(R-L)
Блок команд с 60 по 100 будет выполняться до тех пор, пока мы не введем все значения. Компьютер поймет, что ввод данных закончен, как только мы вместо очередного значения введем число-признак 0.01. Это число следует выбирать так, чтобы оно не входило в интервал (L, R). Получив сигнал о завершении ввода данных, компьютер передаст управление команде 110. Блок команд с 130 по 160 подсчитает суммарное число наблюдений SUM и определит максимальное число наблюдений, приходящихся на один интервал. Теперь осталось лишь вывести на экран содержимое счетчиков. По командам SCROLL и PRINT строки с этой информацией проплывают по экрану снизу вверх.
Чтобы каждый успел переписать с экрана результаты вычислений (печатающими устройствами снабжены не все компьютеры), в программе записан оператор PAUSE. Получив такую команду, компьютер "держит паузу", величина которой определяется числом, стоящим возле ключевого слова: 2E3=2000. Это число колебаний тока в сети за время паузы. Переводя в секунды, получаем 2000/50 = 40 секунд. Паузу можно прервать и раньше - стоит лишь нажать на любую клавишу компьютера.

Команда CLS (сокращение от английского clear screen - очистить экран) готовит экран для вывода собственно гистограммы. Команда PLOT рисует квадратик в позиции, определенной значением параметра J, которое, в свою очередь, зависит от номера интервала и количества попавших в
интервал исходных данных.
Б.АЛЕКСЕЕВ (г.Москва)
ИНТЕГРИРОВАНИЕ НА МИКРОКАЛЬКУЛЯТОРЕ
В прошлом году (6/85) читатели нашего раздела приглашались на дискуссию за круглым столом, посвященную вычислению определенных интегралов на микрокалькуляторе "Электроника Б3-34" и ему подобных. В ответ на приглашение редакция получила 143 письма, где предлагаются программы, реализующие различные методы интегрирования. (Самым популярным оказался метод Симпсона - о нем идет речь в каждом втором письме). Есть письма, где говорится о несобственных интегралах, об интегралах с переменным верхним пределом и т.д. Этим темам будут предоставлены страницы одного из предстоящих выпусков. Сейчас под нашей рубрикой выступают С.Г.Волченков (Ярославль), В.Ю.Критинин (Москва), Г.И.Натансон (Ленинград), Н.Б.Никитин (Москва), Л.М.Финк (Ленинград), Ш.Е.Цимринг (Горький), В.А.Яковлев (Москва). Ведет дискуссию Б.Н.ХОДОВ.

Б.Н.ХОДОВ: Как известно, простейший из приближенных методов интегрирования - метод прямоугольников. Область между графиком интегрируемой функции и осью абсцисс рассекается на вертикальные полоски одинаковой ширины, равной шагу интегрирования h=(b-a)/N (где N - число шагов; а и b-концы промежутка интегрирования, см. на рисунке). Площадь каждой полоски принимается равной площади прямоугольника, одна сторона которого равна h, а другая - значению функции в одной из точек отрезка разбиения. Суммарная площадь прямоугольников S(h) дает приближенное значение интеграла.
В.Ю.КРИТИНИН: Будем брать значения функции в середине каждого отрезка разбиения. Для оценки точности интегрирования станем использовать результаты, полученные при исходном и уменьшенном вдвое шаге интегрирования. Если выполняется условие 3д>|1-S(h)/S(h/2)|, то величина S(h/2) даст значение интеграла с относительной погрешностью, не превышающей д. Предлагаемая программа автоматически дробит шаг, покуда не будет достигнута заданная точность.
00. ПД 01. Cx 02. П3. 03. ИПВ 04. ИПА. 05. - 06. ИПД 07. / 08. П1 09. 2 10. / 11. ИПА 12. + 13. П2 14. ПП 15. 51 16. ИП3 17. + 18. П3 19. ИП2 20. ИП1 21. + 22. П2 23. ИПВ 24. - 25. Fx>=0 26. 14 27. ИП0 28. ИП1 29. ИП3 30. * 31. П3 32. / 33. 1 34. - 35. Fx2 36. Fsqr 37. ИПС 38. - 39. Fx>=0 40. 49 41. ИП3 42. П0 43. Сх 44. П3 45. ИП1 46. 2 47. БП 48. 07 49. ИП3 50. С/П.
Вслед за основной программой ввести, начиная с 51 адреса, подпрограмму вычисления f(x). Ее аргумент берется из Р2, значение должно оказаться в РХ. После ввода перейти в режим вычислений, набрать на клавиатуре а ПА b ПВ 3д ПС 0 П0 1 (или начальное число шагов интегрирования) В/0 С/П. Результат - на индикаторе и в Р3.
Б.Н.ХОДОВ: Согласно другому методу приближенного интегрирования, методу трапеций, каждая полоска, на которые рассекается площадь под графиком интегрируемой функции, заменяется трапецией, чья высота равна h, а основания-значениям функции в концах отрезка разбиения. По сравнению с методом прямоугольников здесь при том же шаге интегрирования обеспечивается примерно вдвое меньшая точность. Оба эти способа превосходит по точности метод Симпсона, когда на каждом отрезке разбиения график функции заменяется параболой, проходящей через точки, соответствующие значениям функции в конце отрезка и в его середине.
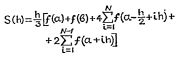
Л.М.ФИНК: Этот метод позволяет быстрее достичь заданной относительной погрешности д, которая на сей раз гарантируется условием со впятеро большей левой частью: 15д>|1-S(h)/S(h/2)|.
00. ИПВ. 01. П6 02. ПП 03. 65 04. ПД 05. ИПА 06. ПП 07. 65 08. ИПД 09. + 10. ПД 11. ИПВ 12. ИПА 13. - 14. П7 15. 1 16. П8 17. ИП7 18. 2 19. / 20. П7 21. ИП8 22. 2 23. * 24. П8 25. П0 26. КИП0 27. 0 28. ПС 29. ИП7 30. ИП0 31. * 32. ИПА 33. + 34. ПП 35. 65 36. ИПС 37. + 38. + 39. FL0 40. 41 41. FL0 42. 28 43. ^ 44. ИПД 45. + 46. ПД 47. + 48. ИП7 49. * 50. ИП6 51. x-y 52. П6 53. - 54. FBx 55. / 56. Fx2 57. ИП9 58. - 59. Fx<0 60. 17 61. ИП6 62. 3 63. / 64. С/П.
Вслед за основной программой ввести, начиная с 65 адреса, подпрограмму вычисления интегрируемой функции (аргумент берется из РХ, результат должен оказаться в РХ и PY; здесь можно прибегнуть к команде ^). После ввода перейти в режим вычислений, набрать на клавиатуре а ПА b ПВ (15д)**2 П9 0 П6 В/0 С/П. Результат - на индикаторе.
Получив величину 3S(h), программа уменьшает шаг h вдвое, число N вдвое увеличивает, в регистр Д заносится (44-46) сумма f(a)+f(b)+2Сигма*f(a+ih/4). Для проверки условия точности к этой сумме добавляется 2Сигма*f(a-h/4+ih/2) (43-47), результат умножается на h (48-49), что дает величину 3S(h/2). Она заносится в Р6 и сравнивается с 3S(h) адреса 50-60. Таким образом, для вычислении с уменьшенным шагом затрачивается минимальное время.
Г.И.НАТАНСОН: Формула Боде В(h)=[16S(h)-S(h/2)]/15, где используются те же величины S(h) и S(h/2), что и при расчетах по формуле Симпсона, дает более точное значение интеграла. Абсолютная погрешность е здесь гарантируется условием 63e>|B(h)-B(h/2)|.
00. ПП 01. 62 02.ПС 03.6 04.3 05.С/П 06. * 07. Fx2 08. ПД 09. ИПА 10. ИПВ 11. - 12. ПВ 13. П5 14. Сх 15. П9 16. ИП5 17. П7 18. 2 19. / 20. П5 21. ИПВ 22. - 23. П8 24. ИПА 25. + 26. ПП 27. 62 28. ИП8 29. ИП7 30. + 31. Fx<0 32. 23 33. ИП6 34. ИП4 35. ИП9 36. ^ 37. + 38. ИПС 39. x-y 40. + 41. ПС 42. FBx 43. + 44. П4 45. 8 46. * 47. - 48. ИП7 49. * 50. 4 51. 5 52. / 53. П6 54. - 55. Fx2 56. ИПД 57. - 58. Fx<0 59. 14 60. ИП6 61. С/П.
Вслед за основной программой ввести, начиная с 62 адреса, подпрограмму расчета подынтегральной функции (аргумент и значение - в РХ), заканчивая ее командами ИП9 + П9 В/0. После ввода перейти в режим вычислений, набрать на клавиатуре Сх П9 а ПА В/0 С/П b ПВ В/0 С/П е С/П. Результат - на индикаторе и в Р6.
Ш.Е.Цимринг: Для гладких функций при заданном числе узлов, в которых вычисляется f(х), наивысшими по точности являются формулы Гаусса. По-видимому, он первый обратил внимание на то, что равномерное расположение узлов не является наилучшим, и указал, что узлы, если всего их n, должны совпадать с нулями многочлена Лежандра n-ной степени. Значения функции в узлах умножаются на коэффициенты, которые приводятся в справочниках по численному интегрированию.
00. ИПВ 01. ^ 02. ИПС 03. - 04. 2 05. / 06. ПС 07. - 08. ПД 09. 0 10. ПВ 11. 1 12. 0 13. П0 14. КИП^ 15. /-/ 16. КП^ 17. ИПС 18. * 19. ИПД 20. + 21. ПП 22. 37 23. КИП0 24. * 25. ИПВ 26. + 27. ПВ 28. FL0 29. 14 30. ИП2 31. Fx>=0 32. 11 33. F() 34. ИПС 35. * 36. С/П.
Программа составлена для случая 10 узлов: больше не позволяют возможности микрокалькулятора. Достигаемой точности, как показывает практика, вполне достаточно.
Ввести программу и далее, с 37 адреса - подпрограмму вычисления интегрируемой функции (аргумент и значение - в РХ). После ввода перейти в режим вычислений, набрать 29552422 ВП 8 /-/ П1 14887434 ВП 8 /-/ П2 26926672 ВП 8 /-/ П3 43339539 ВП 8 /-/ П4 21908636 ВП 8 /-/ П5 67940957 ВП 8 /-/ П6 14945135 ВП 8 /-/ П7 86506337 ВП 8 /-/ П8 66671344 ВП 9 /-/ П9 97390653 ВП 8 /-/ ПА а ПС b ПВ В/0 С/П. Результат - на индикаторе.
С.Г.ВОЛЧЕНКОВ: Обилие констант, используемых в методе Гаусса, не только усложняет пользование программой, но и ограничивает сложность подынтегральной функции, так как сокращает или вовсе сводит к нулю число регистров для хранения констант функции. Предлагаю формулу, аппроксимирующую формулу Гаусса для пяти узлов:
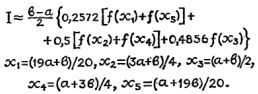
00. ИПА 01. ИПВ 02. + 03. 2 04. / 05. ПД 06. ИПА 07. - 08. ПС 09. 0 10. , 11. 9 12. * 13. ПА 14. ИПД 15. + 16. ПП 17. 52 18. ИПД 19. ИПА 20. - 21. ПП 22. 52 23. + 24. ИП9 25. * 26. ИПД 27. ИПС 28. 2 29. / 30. ПА 31. - 32. ПП 33. 52 34. ИПД 35. ИПА 36. + 37. ПП 38. 52 39. + 40. 2 41. / 42. + 43. ИПД 44. ПП 45. 52 46. ИП8 47. * 48. + 49. ИПС 50. * 51. С/П.
Когда программа введена, ввести с 52 адреса подпрограмму вычисления f(x), аргумент и значение которой помещаются в РХ. Затем перейти в режим вычислений, набрать а ПА b ПВ 0.4856 П8 0.2572 П9 В/0 С/П. Результат - на индикаторе.
Достаточную точность программы подтвердил двухлетний опыт ее использования для контроля студенческих работ по курсу "методы вычислений".
В.А.ЯКОВЛЕВ: Чебышев решил задачу распределения узлов для случая, когда коэффициенты, на которые умножаются значения подынтегральной функции (как в других подобных методах), равны между собой. Такое условие не только сулит большое удобство, но и позволяет уменьшить ошибку, вызванную неточностью задания подынтегральной функции. По точности формулы Чебышева занимают промежуточное положение между методами Гаусса и Симпсона при одинаковом числе использованных значений подынтегральной функции. По предлагаемой программе можно вычислять интегралы по формуле Чебышева для 2, 4 или 6 узлов. По ходу счета исходный отрезок интегрирования последовательно разбивается программой на 2, 4, 8 и более частей для достижения желаемой точности. На каждом из полученных при этом отрезков интеграл вновь вычисляется по формуле с выбранным числом узлов, и результаты складываются.
00. ИПВ 01. ИПА 02. - 03. ПС 04. Сх 05. П2 06. Сх 07. П4 08. ИПА 09. П6 10. ИПД 11. П0 12. КИП0 13. П8 14. ПП 15. 47 16. 1 17. ИП8 18. - 19. ПП 20. 47 21. FL0 22. 12 23. ИП6 24. ИПС 25. + 26. П6 27. ИПВ 28. - 29. Fx>=0 30. 10 31. ИП4 32. ИПС 33. ИПД 34. / 35. * 36. П4 37. ИП2 38. - 39. С/П 40. ИПС 41. 2 42. / 43. ПС 44. ИП4 45. БП 46. 05 47. ИПС 48. * 49. ИП6 50. +.
Ввести программу, и с 51 адреса - подпрограмму вычисления подынтегральной функции (аргумент и значение в РХ), закончить ее командами ИП4 + П4 В/0. После ввода перейти в режим вычислений, набрать а ПА b ПВ N (2, 4 или 6) ПД. В зависимости от выбранного N далее ввести для1 N=2: 21132487 ВП 8 /-/ П1; для N=4: 40620376 ВП 8/-/ П1 10267276 ВП 8/-/ П3; для N=6: 3666823 ВП 7 /-/ П1, 28874067 ВП 8 /-/ П3 66876591 ВП 9 /-/ П5. Запустить программу: В/0 С/П. Результат - на индикаторе. При повторных нажатиях С/П исходный отрезок дробится, а на индикатор выводится разность оценок интеграла при текущем и предыдущем разбиении. Текущее значение интеграла - в Р4, предыдущее - в Р2.
Н.Б.НИКИТИН: Для достижения желаемой точности вычисление интеграла приходится строить как итерационный процесс. А раз так, то можно воспользоваться методами ускорения итерационных процессов, например, методом Эйткина. Если отношение числа шагов на каждой итерации постоянно и равно q. то после выполнения трех итераций можно получить более точный результат.

Применим метод Эйткина к методу прямоугольников.
00. ПА 01. - 02. ПВ 03. x-y 04.ПС 05. 3 06. П0 07. Сх 08. ПД 09. ИПС 10. П1 11. ИП1 12. 2 13. F1/x 14. - 15. ИПВ 16. * 17. ИПС 18. / 19. ИПА 20. + 21. ПП 22. 60 23. ИПД 24. + 25. ПД 26. FL1 27. 11 28. ИПВ 29. * 30. ИПС 31. / 32. КП^ 33. ИПС 34. 2 35. * 36. ПС 37. FL0 38. 07 39. ИП3 40. ИП2 41. - 42. Fx2 43. ИП2 44. 2 45. * 46. ИП3 47. - 48. ИП1 49. - 50. / 51. ИП3 52. + 53. С/П 54. ИП2 55. П3 56. ИП1 57. П2 58. БП 59. 07.
После ввода основной программы ввести с 60 адреса подпрограмму вычисления подынтегральной функции (аргумент и значение- в РХ). перейти в режим вычислений, ввести N (начальное число шагов интегрирования) ^ b ^ a В/0 С/П. Результат - на индикаторе. Последующие нажатия С/П станут давать результаты, полученные по методу Эйткина для уменьшающегося с каждым разом вдвое шага интегрирования. Такое уменьшение позволяет использовать величины S2 и S3 при подсчете S(h/2) и вдвое повысить скорость вычислений.
Б.Н.ХОДОВ. Сравнить предложенные программы позволяет таблица.

Для обмена опытом с коллегами публикуем адреса читателей, согласившихся на это:
141700, Московская обл., г.Долгопрудный. Лихачевское шоссе 21, кв.128, А.Н.Тулайков;
252027, Киев, ул.Ереванская 32, кв.13, Г.В.Семенов;
410064, Саратов, ул.Тархова 6А, кв.34, Е.С.Левина;
252050, Киев, ул.Кравченко 23, кв.97, А.И.Хоменко;
622023, Нижний Тагил Свердловской обл., ул.Ленина 71А, кв.12, П.И.Чубенко;
198255, Ленинград, просп.Суслова 9, кор.2, кв.97, И.И.Павлов;
150052, Ярославль, Ленинградский проспект 59, кв.63, С.Г.Волченков; 194064, Ленинград, Тихорецкий проспект 7, кор.4, кв.7, Л.М.Финк; 127562, Москва, ул.Санникова 17, кв.217, Н.Б.Никитин;
603025, Горький, ул.Генкиной 19, кв.7, Ш.Е.Цимринг.
ЛИТЕРАТУРА
Калиткин Н.Н. Численные методы. М., Физматгиз, 1978.
Бахвалов Н.С. Численные методы. М., Физматгиз, 1975.
Корн Г., Корн Т. Справочник по математике. М., Физматгиз, 1977.
Инженерные расчеты на ЭВМ. Справочное пособие (под ред. В.А.Троицкого). Л., Машиностроение, 1979.
Мак-Кракен Д., Дорн У. Численные методы и программирование на Фортране. М., Мир, 1977.
КОГДА ВОСХОДИТ СОЛНЦЕ
Радиолюбителям известно аномально дальнее распространение радиоволн с частотой в несколько мегагерц близ терминатора - границы дня и ночи. Благодаря этому явлению удалось осуществить связь на таких частотах между всеми радиолюбительскими зонами нашей планеты, что считалось невозможным еще лет пятнадцать назад.
Сверхдальняя радиосвязь осуществима лишь тогда, когда оба корреспондента занимают вполне определенное положение относительно терминатора: либо оба находятся на границе дня и ночи, либо один - в зоне терминатора, другой - в зоне ночи. Времени на такую связь отпущено немного, в среднем 5-10 минут: из-за вращения Земли положение корреспондентов относительно терминатора все время меняется. Чтобы планировать связь, нужно наперед знать, когда в местах расположения корреспондентов происходят восходы и заходы солнца. Большую помощь в этом может оказать программируемый микрокалькулятор. Используя его, можно быстро распланировать свое эфирное время при подготовке сеанса, хорош он и во время сеанса. Например, установлена связь с новым корреспондентом: координаты собеседника вводятся в микрокалькулятор и, пока идет обмен сведениями о применяемой аппаратуре, антеннах, свободном эфирном времени, попутно вычисляется и время восходов-заходов в местности корреспондента, что позволяет вполне обоснованно договориться о времени следующего сеанса.

Для расчета используется формула:
Тв/з=[л+/-arccos(tgф*tgд)]/15,
где Тв/з - время восхода или захода: ф - широта места, отсчитываемая к северу от экватора; л - долгота места, отсчитываемая к западу от нулевого меридиана; д - угол склонения солнца для нужной даты. Для определения этого угла удобно использовать соотношение
tgд = cos(15Tв0-л0)/tgф0.
Задавшись какой-либо датой, можно подставить в правую часть равенства тройку чисел ф0, л0, Тв0 для любого города, например, Москвы:
ф0=55o46': л0=-37o37'; Тв0 отыскивается в отрывном календаре на страничке с нужной датой. Это декретное время. Чтобы перевести его в гринвичское, общеупотребительное у радиолюбителей, надо вычесть из него 3 часа. (Из "летнего" времени вычитается 4 часа).
Вычисления производятся по программе:
00. ПД 01. 0 02. , 03. 6 04. П3 05. F1/x 06. П4 07. П6 08. ИПД 09. ПП 10. 64 11. 1 12. 5 13. П0 14. * 15. ИПС 16. ПП 17. 64 18. - 19. Fcos 20. ИПВ 21. ПП 22. 64 23. Ftg 24. / 25. ПА 26. 1 27. С/П 28. П8 29. F() 30. ИП4 31. П6 32. F() 33. ПП 34. 64 35. Ftg 36. ИПА 37. * 38. Farccos 39. П1 40. ИП8 41. ПП 42. 64 43. П8 44. ИП3 45. П6 46. ИП1 47. /-/ 48. ПП 49. 55 50. ИП1 51. ПП 52. 55 53. БП 54. 27 55. ИП8 56. + 57. ИП0 58. / 59. Fx<0 60. 64 61. 2 62. 4 63. + 64. ^ 65. Fx2 66. Fsqr 67. / 68. FBx 69. 1 70. + 71. П9 72. КИП9 73. F() 74. ИП9 75. - 76. ИП6 77. * 78. 1 79. - 80. ИП9 81. + 82. * 83. В/0.
Переключатель Р-Г устанавливается в положение Г. Углы вводятся в виде десятичной дроби, где целая часть - градусы, дробная - минуты (для Москвы ф=55.46; л=-37.37), время - аналогично: целая часть - часы, дробная - минуты. Введя программу, набираем В/0 ф0 ПВ л0 ПС Тв0 С/П. Вскоре на индикаторе появляется единица - значит, микрокалькулятор готов к вычислениям. Набираем координаты интересующего нас места ф ^ л С/П. После счета на табло высвечивается время восхода солнца Тв. Время захода Тз, вызывается нажатием клавиши x-y. Повторить ввод при сбое можно, нажав клавиши БП 29 С/П.
Г.ГУЛЯЕВ (г.Куйбышев)
ЭЛЕКТРОННЫЕ ГОРОДКИ
Электронные городки отличаются от традиционных. Расстояние, с которого производятся броски, выбирается игроком в пределах от 11 до 20 метров. Вместо квадратного "города" используется линия, на которой расставляется от одного до восьми городков. Расстановку показывает индикатор. Незанятые позиции обозначаются единицами, каждый городок - двойкой.
Длина биты выбрана такой, что в случае удачного броска она сшибает пять стоящих рядом городков. Самый удачный бросок - это когда, несмотря на вращение в полете, бита приходит к линии расстановки параллельно ей, а не под углом. Наименее удачны броски, если бита пролетает сквозь строй городков торцом, не задев ни одного из них.
Цель игры - наименьшим числом ударов выбить все городки с линии.
Теперь коротко о правилах диалога (именно в таком режиме проходит игра с микрокалькулятором).
После того как программа введена, требуется ввести в Р9 признак окончания игры - число из восьми единиц. Переключатель Р-Г должен быть установлен в положении Г. Городки располагают в регистрах с восьмого по первый. Набираем, например. 2 П8 - это значит, что в восьмой позиции стоит городок: 1 П7 - седьмая позиция не занята. Так должны быть заполнены все регистры от Р8 до Р1.
Итак, городки расставлены по местам. Можно запускать программу клавишами В/0, С/П. Через 15 секунд иа индикаторе появится изображение, демонстрирующее расстановку городков на линии. Выберем дистанцию для броска, например, 12 метров (12 С/П). Далее выберем угол а (см. рисунок) от -30 до +30o, введем это число и нажмем С/П. Менее чем через минуту на индикаторе демонстрируется положение после броска.

Программа: 00. ^ 01. 8 02. П0 03. Сх 04. КИП^ 05. + 06. 1 07. 0 08. * 09. FL0 10. 04 11. FBx 12. / 13. ^ 14. ИП9 15. - 16. Fln 17. x-y 18. С/П 19. ПВ 20. С/П 21. /-/ 22. ПА 23. 2 24. / 25. Fx2 26. Fsqr 27. ИПВ 28. + 29. 2 30. 0 31. - 32. Fx2 33. Fsqr 34. 5 35. - 36. Fx2 37. Fsqr 38. 1 39. + 40. П0 41. КИП0 42. ИПА 43. Ftg 44. ИПВ 45. * 46. 5 47. + 48. ПС 49. КИПС 50. 1 51. ПП 52. 80 53. ИПС 54. 1 55. + 56. ПС 57. 3 58. ПП 59. 80 60. ИПС 61. 2 62. - 63. ПС 64. ПП 65. 86 66. ИПС 67. 3 68. + 69. ПС 70. 5 71. ПП 72. 80 73. ИПС 74. 4 75. - 76. ПС 77. ПП 78. 86 79. 8 80. ИП0 81. x-y 82. - 83. Fx>=0 84. 01 85. ИПС 86. 1 87. - 88. Fx>=0 89. 97 90. 7 91. x-y 92. - 93. Fx>=0 94. 97 95. 1 96. КПС 97. В/0.
Команда 00. ^ готовит регистр X для приема адреса старшего регистра, начиная с которого предстоит формировать изображение на индикаторе. Адрес старшего регистра записывается в Р0 командами 01-02. Блок команд с 03 по 12 синтезирует изображение, причем каждый регистр соответствует одному разряду. Команда 13 дублирует изображение в регистре Y. Проверку "игра окончена?" ведут команды 14-16.
Если игра не закончена, команды 17-18 выводят на индикатор изображение. После того как команды 20-22 введут в РВ и РА соответственно длину L и угол а, фрагмент 23-41 сформирует длину проекции биты Р по формуле
P=[|||a/2|+L-20|-5|].
Прямые скобки здесь означают абсолютную величину заключенного в них числа, а квадратные - целую часть числа. Формула имитирует влияние вращения биты на длину проекции Р в зависимости от выбранной дистанции L и угла а. Фрагмент с 42 по 49 вычисляет положение центра проекции по формуле
J=[L tg a + 5].
Команды с 50 и 80 и подпрограмма с 80 и 98 проверяют, какие городки задеты битой, и заменяют двойки на единицы.
Потренировавшись, даже самую сложную фигуру можно поразить двумя точными бросками. Однако добиться этого не просто.
А.ЗАЙЦЕВ (г.Щигры, Курской обл.)

Рис. Н.Сущенцова (г.Киров)
[ УЗЕЛКИ НА ПАМЯТЬ
Чтобы выполнить косвенный переход по команде КБПМ или КППМ, в регистр М надо записать двузначный адрес перехода. (Пусть М - один из немодифицируемых регистров от 7 до Д). Но если в регистре М записана константа, то переход произойдет по адресу, выражаемому двумя младшими ее разрядами, считая влево от запятой.
Это обстоятельство позволяет сократить программу, если при ее составлении среди констант оказалась такая, два младших разряда которой совпадают с требуемым адресом перехода.
В.ЛЕСНЯК (г.Днепропетровск) ]

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Похоже, я потопился обвинить "школу" в избытке классицизма. Авторы честно попытались выжать из ПМК все.
5/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
Занятие восьмое. Заключительные занятия "Школы" проведут авторы известных книг о программируемых микрокалькуляторах - А.И.Цветков, Я.К.Трохименко, М.И.Петров. Публикуемое в этом номере выступление Алексея Николаевича Цветкова посвящено культуре и искусству программирования.
Какая программа лучше - короткая или быстрая, точная или наглядная?
Конечно, неверна сама постановка вопроса. И тем не менее нередко приходится видеть, как автор той или иной конкретной программы отстаивает достоинства своего детища именно с таких позиций.
В то же время ответ станет очевидным, если взять в расчет назначение программы. Программа-справочник для астрономических расчетов требует прежде всего повышенной точности, учебная программа - прозрачности и сосредоточения на том или ином классе операций, программа генерации псевдослучайных чисел - скорости. Главная черта культуры программирования и состоит в умении подчинить все компоненты программы определенному целевому назначению.
Несложную программу для текущего расчета надо постараться написать попроще, не пользуясь изощренными приемами экономии памяти, не добиваясь особого сокращения времени вычислений. Если такая программа считает верно и написана без особых затрат времени и сил, значит, она отвечает целевому назначению, она функциональна. Можно даже считать, что в этой функциональности - ее красота.
Программа может получиться лучше или хуже, короче или длиннее в зависимости от того, насколько ее автору стали привычными известные приемы программирования на микрокалькуляторе данного типа. Это характеризует вторую черту культуры программирования.
Культура н искусство программирования (эти понятия ведут свое начало от известных книг Д.Кнута, вышедших под таким названием) не единственные факторы, которые надо принять во внимание для составления хорошей программы. В частности, надо подобрать алгоритм, соответствующий условиям задачи и свойствам используемого микрокалькулятора. Так что если говорить точнее, речь идет о культуре и искусстве решения вычислительных задач с помощью ЭВМ. Тем не менее, чтобы не нарушать традиций, мы не будем менять терминологию, понимая при этом "культуру" и "искусство" программирования в широком смысле.
Начинается культура программирования с выбора типа ЭВМ. Никому не придет в голову отправиться в командировку из Москвы в Томск на велосипеде, но и в Малаховку из Москвы самолетом не летают. И напрасно иногда считающих на микрокалькуляторах рассматривают как доминошников или, в лучшем случае, извозчиков в эпоху "Жигулей". Прошло время, когда на микрокалькуляторах можно было решать лишь самые простые задачи. Вряд ли просты интегрирование дифференциальных уравнений пятого порядка, проверка статистических гипотез или вычисление значений всех спецфункций из классического справочника Янке и Эмде. А ведь программы для таких расчетов давно составлены, опубликованы и уже никого не удивляют. Но это лишь одна сторона вопроса.
Привлекает внимание любопытный факт: программируемые микрокалькуляторы все шире применяются в организациях, хорошо обеспеченных большими ЭВМ. Одна из главных причин этого - предоставляемая микрокалькуляторами возможность решить поставленную задачу за кратчайшее время. Ситуацию можно проиллюстрировать диаграммой, по вертикальной оси которой отложено, некоторое условное количество результатов, а по горизонтальной оси - календарное время от момента, когда вы решили просчитать задачу по имеющейся программе.
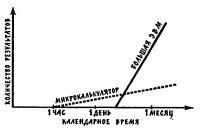
До получения результатов на любой ЭВМ проходит некоторый промежуток времени. В микрокалькулятор надо ввести программу, проверить ее, ввести числовые параметры и выполнить вычисления. Как правило, на это уходит от десяти минут до нескольких часов. По-другому обстоит дело с большой ЭВМ. Здесь вы находитесь в определенной зависимости от намерений и занятости других людей. На ожидание очереди к терминалу или пробивку перфокарт, а также коррекцию исходных параметров по результатам расчета иногда уходит несколько дней. Начав считать, большая ЭВМ, конечно, сразу обгонит микрокалькулятор, но бывает, что задержка, связанная с подготовкой к счету, обесценивает результат. Это случается, например, при анализе вариантов новой конструкции.
Сказанное вовсе не означает, что во всех случаях надо стремиться использовать микрокалькулятор. Сложность задач, решаемых на любой ЭВМ, и, конечно, на микрокалькуляторе, ограничивается вычислительными ресурсами машины. Если, например, не хватает памяти, то резко нарастает время программирования, приходится проявлять чудеса изобретательности, чтобы сэкономить одну-две команды. Можно, конечно, комбинируя методы ручного и машинного счета, решать на "Электронике Б3-34" системы из семи-восьми линейных уравнений, но все же следует признать, что такая задача неадекватна нашей ЭВМ, и надо переходить к машине следующего класса, скажем, "Электронике Д3-28".
Рассмотрим теперь, как составляются программы, отвечающие сформулированным выше требованиям. О программах для текущих расчетов мы уже говорили. Со стандартными программами общематематического профиля можно ознакомиться по опубликованным сборникам прикладных программ. Речь пойдет о программах третьего вида, специализированных, предназначенных для многократного применения.
В практике автора использовалась, например, программа для расчета сверхвысокочастотного радиоизлучения Земли, закрытой облаками. К программе приходилось обращаться достаточно часто, каждый раз, когда варьировались параметры облаков и атмосферы или длина волны. Подобных программ достаточно много у каждого считающего научного работника и инженера.
В подобных случаях результаты вычислений используются исследователем как промежуточные данные при поиске путей решения основной научной задачи. Поэтому программа должна быть построена так, чтобы не тормозить творческого процесса и чтобы в роли оператора мог выступать как сам исследователь или его коллега, так и их помощник менее высокой квалификации.
Поставим задачу так, как ставятся задачи оптимизации в математике: найти минимум по одной переменной, наложив ограничения на остальные.
Считая заданными точность и вычислительные ресурсы микрокалькулятора, будем искать программу, обеспечивающую минимум времени получения результата. Это время - критерий качества составляемой нами программы. Оно определяется не только скоростью работы машины. Сюда входят затраты времени на ввод, вывод, контроль и пересчет в случае ошибки.
Рассмотрим внешние требования к программе, то есть такие, которые существенны для пользователя.
Прежде всего программа должна быть оформлена так, чтобы не заставлять вас искать дополнительные материалы или размышлять над техническими, не важными в данном случае сторонами вопроса. Взяв программу после некоторого перерыва, когда вы успели кое-что подзабыть, вы должны иметь возможность сразу убедиться, что она вычисляет то, что надо, и с достаточной точностью. Для этого в шапке программы должны быть указаны алгоритм, погрешность расчета и область допустимых значений аргументов.
Если для решения задачи надо составлять подпрограмму, должны быть сведения, откуда брать аргументы, куда засылать результаты, какими регистрами можно пользоваться.
Какая запись программы лучше? Для публикации или "карманной" библиотеки важна компактность записи. Команды, бывает, пишут в строчку, без кодов операций, а если в каждой строчке располагается ровно по десятку команд, не пишут и адреса. Однако для ввода такая система не самая лучшая. В поле зрения попадают соседние команды, и ввод идет с определенным напряжением. Для контроля правильности ввода нужна еще таблица кодов операций: не все помнят коды, и здесь нетрудно ошибиться. Запись команд столбиком, с адресами и кодами операций, явно менее компактна, но ввод и контроль менее утомительны. Все это в конечном счете ведет к сохранению высокого темпа вычислений.
Большую роль играет однозначная бессылочная инструкция. К примеру, ссылка вида "далее - как в программе ТТ" заставит вас искать эту программу и разбираться еще и в ней.
Необходим контрольный пример, который не только позволит судить о правильности ввода программы, но и покажет, что вы верно поняли инструкцию. Пример должен быть простым: скажем, если вычисляется коэффициент корреляции, надо ограничиться двумя парами чисел. Конечно, на практике столь малую выборку не анализируют, но для проверки вполне достаточно двух пар.
Надо указать время счета, пусть и ориентировочное. Это поможет правильно спланировать работу.
Теперь рассмотрим внутренние требования к программе, то есть такие, которые существенны с точки зрения программиста.
Засылка констант в адресуемые регистры может выполняться в режимах как ручного, так и автоматического счета. Ручная засылка, когда на клавиатуре набирается число и выполняется команда ПМ, где М - обозначение адресуемого регистра, не удлиняет программы. Однако, если имеются резервы командной памяти, лучше организовать автоматический ввод констант с помощью безликих команд С/П, ПП или циклом. Ввод убыстрится, снизится вероятность ошибки, меньше будет утомляться оператор: ему придется "пропускать через себя" только числа, а номера регистров его не касаются. Это же относится к засылке нулей в сумматоры перед каждым вариантом расчета. Скажем так: "все, что оператор может не делать, пусть он и не делает".
Особое внимание надо уделить программированию ввода больших массивов данных, например, при статистических расчетах. Эти данные после ввода сразу обрабатываются, а в адресуемых регистрах накапливаются соответствующие суммы или произведения. В зависимости от того, как составлена программа первичной обработки, затраты времени на ввод могут измениться в полтора-два раза. Но дело даже не только во времени. Если очередные значения надо вводить через 5-10 секунд, оператор успевает чуть-чуть передохнуть, а если через 15-20 секунд, оператор невольно начинает отвлекаться. Вероятность ошибки растет.
Программа может помочь оператору, если его отвлекли и он спутал, которое число ему предстоит вводить. Для этого перед командой останова в программу ставят команду вызова номера числа, которое надо ввести. Возможны и другие варианты подсказки - это зависит от вашей фантазии. Важно только соблюсти чувство меры, так как для подсказки или, скажем, коррекции неправильного ввода требуются дополнительные команды, и это затягивает обработку.
Вывод результатов расчета в подобных случаях желательно организовать так же, как и ввод исходного материала: не заставлять оператора рыскать по регистрам, а поочередно выводить результаты на индикатор, нажимая клавиши С/П или ПП.
Теперь о компоновке программы. Ошибок и потерь времени будет меньше, если постараться разместить изменяемые части программы, в частности подпрограммы, вне границ основного поля адресов. Такое требование удлинит программу на две-три команды, но коллегам, работающим по вашей программе, не придется путаться при изменении адресов перехода. Темп работы не снизится. Коротко скажем так: "не допускай никого в тело программы".
Не нужно доказывать, что трудно составить хорошую, долго живущую программу, не владея описанными в руководстве по эксплуатации микрокалькулятора способами работы со стеком, способами организации циклов, косвенной адресацией. Обратим внимание на менее очевидные приемы. Это прежде всего тождественные преобразования алгоритма, согласующие его с особенностями микрокалькулятора, затем группирование операций алгоритма и, наконец, выбор наилучшего порядка вычислений.
Пусть, например, требуется вычислить значение двойной суммы:
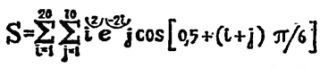
Программа, буквально соответствующая этой формуле, содержит 37 команд. Расчет выполняется примерно за 37 минут.
00. 2 01. 0 02. П0 03. Сх 04. 1 05. 0 06. П1 07. x-y 08. ИП0 09.Fx2 10. ИП0 11. 2 12. * 13. /-/ 14. Fexp 15. * 16. ИП1 17. * 18. ИП0 19. ИП1 20. + 21. Fпи 22. * 23. 6 24. / 25. 0 26. , 27. 5 28. + 29. Fcos 30. * 31. + 32. FL1 33. 08 34. FL0 35. 04 36. С/П.
Тождественное преобразование i**2*exp(-2*i)=(i/exp(i))**2 подсказывает, как обойтись пятью командами ИП0 ^ Fexp / Fx2 вместо восьми команд с адресами 08-15. Для убыстрения счета организуем засылку констант 0.5 и пи/6 в регистры Р3 н Р4 вне цикла, а внутри цикла по мере надобности будем их извлекать. При образовании этих констант для экономии командной памяти используем тождества 0.5=2**-1 и пи/6=arcsin(0.5).
Заметим, что вычислять целиком произведение под знаком двойной суммы 200 раз не обязательно. Можно вынести за скобки j, во внутреннем цикле вычислять сумму по i, а во внешнем - по j. Можно поступить и наоборот: за скобки вынести (i/exp(i))**2, во внутреннем цикле суммировать по j. а во внешнем - по i. Нетрудно показать, что при достаточном числе слагаемых полное время счета меньше там, где быстрее считается каждое слагаемое внутреннего цикла. Короче: "во внутренний цикл ставь то, что считается быстрее". В нашем случае суммирование во внутреннем цикле надо осуществлять по переменной j. Программа потребует также 37 команд, но время счета - около 19 минут, то есть почти вдвое меньше.
00. 2 01. F1/х 02. П3 03. Farcsin 04. П4 05. 2 06. 0 07. П1 08. Сх 09. 1 10. 0 11. П0 12. x-y 13. 0 14. ИП0 15. ИП1 16. + 17. ИП4 18. * 19. ИП3 20. + 21. Fcos 22. ИП0 23. * 24. + 25. FL0 26. 14 27. ИП1 28. ^ 29. Fexp 30. / 31. Fx2 32. * 33. + 34. FL1 35. 09 36. С/П.
Перечислим некоторые тождественные преобразования, позволяющие приспособить исходный алгоритм к совокупности операций микрокалькулятора "Электроника Б3-34" с целью ускорения вычислений в экономии программной памяти.
еxp(2*х)=(еxp**x)**2. Пусть аргумент х находится в регистре М. Левая часть тождества требует четыре команды: ИПМ 2 * Fexp, правая - три: ИПМ Fepx Fx2. Вычисления ускоряются на 0.4-0.5 сек. Далее приводятся только тождества; эффект от их использования предлагается оценить читателю.

Надо знать чисто конструктивные особенности микрокалькулятора "Электроника Б3-34", которые могут оказаться полезными при программировании. Вот некоторые из них.
1. Если стек возврата пуст, то есть выполнены все переходы с возвратом ПП N В/0 (N - адрес перехода), то в режиме автоматического счета команда В/0 эквивалентна составной команде БП 01.
2. В режиме автоматического счета команда ВП, если ей предшествуют команды ИПМ или КИПМ, а также пара команд ^ ВП, если ей предшествуют другие команды, переводит нуль в единицу, но не изменяет других чисел.
3. Если число 0.1<=х<1 находится в регистре М, команды КПМ и КИПМ при М=0, 1, 2, 3 уменьшают его, а при М=4, 5, 6 - увеличивают на 1e-8. Если х<0.1, эти команды изменяют его на другую величину. Читатель может проследить это самостоятельно.
4. Содержимое регистра М при неоднократном выполнении команды FLM уменьшается до единицы, но не далее. В то же время при выполнении команд КПМ или КИПМ (М=0, 1, 2, 3) содержимое регистра М, уменьшаясь, может стать равным нулю.
5. При выполнении команд КПМ или КИПМ (М=0, 1, 2, 3,) числа засылаются (извлекаются) в регистры Д, С, В, А..., 4, 3, 2, 1, 0, 1, 0, Д, С, В, А, затем последовательность с 4-х повторяется. Если же М=4, 5, 6, числа засылаются (извлекаются) в регистры 0, 1, 2..... 9, А, В, С, Д, 0, 1, 0, 1, 2, 3, затем последовательность с А повторяется.
6. Расчет по ряду программ завершают после того, как некоторая переменная х уменьшится по абсолютной величине до заданного предела е. Пусть е находится в регистре М. Если 1e-99<=е<1e-50, для проверки на окончание можно использовать фрагмент программы
A1. Fx<0 А2. А4 A3. /-/ А4. ИПМ А5. - A6. Fx<0 А7. А9 А8. С/П.
Если е>1e-50, используют фрагмент
Fx2 ИПМ - Fx<0 N С/П.
В регистре М при этом хранят величину е**2, N - адрес перехода.
Заметим, что область машинного нуля на "Электронике Б3-34" при выполнении различных операций не одинакова. Например, пара операций arccos(cos(x)) дает в результате нуль уже при значении х<2e-4, тогда как пара операций ln(exp(x)) дает нуль только при х<4e-8. Пользуясь этим обстоятельством, фрагмент проверки на окончание счета при некоторых частных значениях е можно сократить. Не понадобится и специальный регистр для хранения величины е.

В статье невозможно перечислить приемы, используемые на практике. Для совершенствования культуры программирования полезно с карандашом в руках разбирать опубликованные программы.
Мы смело можем считать, что овладели культурой программирования, если каждый этап составления и оформления программы мы умеем согласовать с ее целевым назначением и в работе используем арсенал известных приемов программирования.
Очень хорошо, если для решения задачи хватает командной памяти. А если нет? В этом случае имеются три основных пути. Самый простой, но далеко не лучший - отказ от некоторых "достижений культуры". Очищать счетчики, засылать константы и вводить исходные данные можно вручную прямо в регистры. Выводить результаты можно из регистров командами ИПМ. Останавливать расчет по достижении переменной величиной нуля можно аварийным остановом при помощи команды F1/х. Эти меры позволяют высвободить не так уж много, обычно до десяти команд. Но работать с такой программой более утомительно, а введение дополнительных ручных операций увеличивает вероятность ошибок.
Второй путь - выполнять одну или несколько неразветвленных частей программы в режиме ручного счета. Здесь экономия памяти может быть значительной, но этот способ хорош только при единичных расчетах.
Третий, самый плодотворный, но и трудный путь - замена алгоритма. Характерен призыв автора книги по прикладным программам В.Епанечникова: не ищите экономии в одну команду, экономьте сразу пятьдесят! Первый вариант его программы для решения системы из четырех линейных уравнений требовал 190 команд. Маленькими хитростями тут заведомо не обойтись. А изменив алгоритм, ему удалось сократить программу до 91 команды. Здесь уже можно говорить об искусстве программирования. Под ним мы будем понимать разработку новых способов решения вычислительных задач на микрокалькуляторе неизвестными ранее методами.
Искусство эффективно там, где оно опирается на культуру программирования. Надо знать особенности машины, знать приемы программирования, разработанные другими авторами. Точность вычислений и диапазон допустимых значений параметров должны быть не больше, чем требуется в данной задаче. Тогда появляются резервы, позволяющие создавать простые приближенные формулы, такие, как формула для обратного интеграла вероятности, погрешность которой во всей области доверительных вероятностей 0.8<=Q<=0.999 не превышает 4 процентов.

посвященных программируемым калькуляторам, исходя из заданного объема числовой памяти "Электроники Б3-34", автор утверждает, что интерполировать по формуле Лагранжа на этом микрокалькуляторе можно максимум по пяти узлам. Однако Я.Трохименко и Ф.Любич, применив приближенную формулу и изменив способ ввода, разработали программу интерполяции по 10 узлам и при этом уложились в 42 команды вместо 97 у категоричного автора.
В который раз убеждаешься: там, где начинается искусство, формально верным, но незыблемым методам приходится отступать.
5/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
Занятие восьмое. Заключительные занятия "Школы" проведут авторы известных книг о программируемых микрокалькуляторах - А.И.Цветков, Я.К.Трохименко, М.И.Петров. Публикуемое в этом номере выступление Алексея Николаевича Цветкова посвящено культуре и искусству программирования.
Какая программа лучше - короткая или быстрая, точная или наглядная?
Конечно, неверна сама постановка вопроса. И тем не менее нередко приходится видеть, как автор той или иной конкретной программы отстаивает достоинства своего детища именно с таких позиций.
В то же время ответ станет очевидным, если взять в расчет назначение программы. Программа-справочник для астрономических расчетов требует прежде всего повышенной точности, учебная программа - прозрачности и сосредоточения на том или ином классе операций, программа генерации псевдослучайных чисел - скорости. Главная черта культуры программирования и состоит в умении подчинить все компоненты программы определенному целевому назначению.
Несложную программу для текущего расчета надо постараться написать попроще, не пользуясь изощренными приемами экономии памяти, не добиваясь особого сокращения времени вычислений. Если такая программа считает верно и написана без особых затрат времени и сил, значит, она отвечает целевому назначению, она функциональна. Можно даже считать, что в этой функциональности - ее красота.
Программа может получиться лучше или хуже, короче или длиннее в зависимости от того, насколько ее автору стали привычными известные приемы программирования на микрокалькуляторе данного типа. Это характеризует вторую черту культуры программирования.
Культура н искусство программирования (эти понятия ведут свое начало от известных книг Д.Кнута, вышедших под таким названием) не единственные факторы, которые надо принять во внимание для составления хорошей программы. В частности, надо подобрать алгоритм, соответствующий условиям задачи и свойствам используемого микрокалькулятора. Так что если говорить точнее, речь идет о культуре и искусстве решения вычислительных задач с помощью ЭВМ. Тем не менее, чтобы не нарушать традиций, мы не будем менять терминологию, понимая при этом "культуру" и "искусство" программирования в широком смысле.
Начинается культура программирования с выбора типа ЭВМ. Никому не придет в голову отправиться в командировку из Москвы в Томск на велосипеде, но и в Малаховку из Москвы самолетом не летают. И напрасно иногда считающих на микрокалькуляторах рассматривают как доминошников или, в лучшем случае, извозчиков в эпоху "Жигулей". Прошло время, когда на микрокалькуляторах можно было решать лишь самые простые задачи. Вряд ли просты интегрирование дифференциальных уравнений пятого порядка, проверка статистических гипотез или вычисление значений всех спецфункций из классического справочника Янке и Эмде. А ведь программы для таких расчетов давно составлены, опубликованы и уже никого не удивляют. Но это лишь одна сторона вопроса.
Привлекает внимание любопытный факт: программируемые микрокалькуляторы все шире применяются в организациях, хорошо обеспеченных большими ЭВМ. Одна из главных причин этого - предоставляемая микрокалькуляторами возможность решить поставленную задачу за кратчайшее время. Ситуацию можно проиллюстрировать диаграммой, по вертикальной оси которой отложено, некоторое условное количество результатов, а по горизонтальной оси - календарное время от момента, когда вы решили просчитать задачу по имеющейся программе.

До получения результатов на любой ЭВМ проходит некоторый промежуток времени. В микрокалькулятор надо ввести программу, проверить ее, ввести числовые параметры и выполнить вычисления. Как правило, на это уходит от десяти минут до нескольких часов. По-другому обстоит дело с большой ЭВМ. Здесь вы находитесь в определенной зависимости от намерений и занятости других людей. На ожидание очереди к терминалу или пробивку перфокарт, а также коррекцию исходных параметров по результатам расчета иногда уходит несколько дней. Начав считать, большая ЭВМ, конечно, сразу обгонит микрокалькулятор, но бывает, что задержка, связанная с подготовкой к счету, обесценивает результат. Это случается, например, при анализе вариантов новой конструкции.
Сказанное вовсе не означает, что во всех случаях надо стремиться использовать микрокалькулятор. Сложность задач, решаемых на любой ЭВМ, и, конечно, на микрокалькуляторе, ограничивается вычислительными ресурсами машины. Если, например, не хватает памяти, то резко нарастает время программирования, приходится проявлять чудеса изобретательности, чтобы сэкономить одну-две команды. Можно, конечно, комбинируя методы ручного и машинного счета, решать на "Электронике Б3-34" системы из семи-восьми линейных уравнений, но все же следует признать, что такая задача неадекватна нашей ЭВМ, и надо переходить к машине следующего класса, скажем, "Электронике Д3-28".
Рассмотрим теперь, как составляются программы, отвечающие сформулированным выше требованиям. О программах для текущих расчетов мы уже говорили. Со стандартными программами общематематического профиля можно ознакомиться по опубликованным сборникам прикладных программ. Речь пойдет о программах третьего вида, специализированных, предназначенных для многократного применения.
В практике автора использовалась, например, программа для расчета сверхвысокочастотного радиоизлучения Земли, закрытой облаками. К программе приходилось обращаться достаточно часто, каждый раз, когда варьировались параметры облаков и атмосферы или длина волны. Подобных программ достаточно много у каждого считающего научного работника и инженера.
В подобных случаях результаты вычислений используются исследователем как промежуточные данные при поиске путей решения основной научной задачи. Поэтому программа должна быть построена так, чтобы не тормозить творческого процесса и чтобы в роли оператора мог выступать как сам исследователь или его коллега, так и их помощник менее высокой квалификации.
Поставим задачу так, как ставятся задачи оптимизации в математике: найти минимум по одной переменной, наложив ограничения на остальные.
Считая заданными точность и вычислительные ресурсы микрокалькулятора, будем искать программу, обеспечивающую минимум времени получения результата. Это время - критерий качества составляемой нами программы. Оно определяется не только скоростью работы машины. Сюда входят затраты времени на ввод, вывод, контроль и пересчет в случае ошибки.
Рассмотрим внешние требования к программе, то есть такие, которые существенны для пользователя.
Прежде всего программа должна быть оформлена так, чтобы не заставлять вас искать дополнительные материалы или размышлять над техническими, не важными в данном случае сторонами вопроса. Взяв программу после некоторого перерыва, когда вы успели кое-что подзабыть, вы должны иметь возможность сразу убедиться, что она вычисляет то, что надо, и с достаточной точностью. Для этого в шапке программы должны быть указаны алгоритм, погрешность расчета и область допустимых значений аргументов.
Если для решения задачи надо составлять подпрограмму, должны быть сведения, откуда брать аргументы, куда засылать результаты, какими регистрами можно пользоваться.
Какая запись программы лучше? Для публикации или "карманной" библиотеки важна компактность записи. Команды, бывает, пишут в строчку, без кодов операций, а если в каждой строчке располагается ровно по десятку команд, не пишут и адреса. Однако для ввода такая система не самая лучшая. В поле зрения попадают соседние команды, и ввод идет с определенным напряжением. Для контроля правильности ввода нужна еще таблица кодов операций: не все помнят коды, и здесь нетрудно ошибиться. Запись команд столбиком, с адресами и кодами операций, явно менее компактна, но ввод и контроль менее утомительны. Все это в конечном счете ведет к сохранению высокого темпа вычислений.
Большую роль играет однозначная бессылочная инструкция. К примеру, ссылка вида "далее - как в программе ТТ" заставит вас искать эту программу и разбираться еще и в ней.
Необходим контрольный пример, который не только позволит судить о правильности ввода программы, но и покажет, что вы верно поняли инструкцию. Пример должен быть простым: скажем, если вычисляется коэффициент корреляции, надо ограничиться двумя парами чисел. Конечно, на практике столь малую выборку не анализируют, но для проверки вполне достаточно двух пар.
Надо указать время счета, пусть и ориентировочное. Это поможет правильно спланировать работу.
Теперь рассмотрим внутренние требования к программе, то есть такие, которые существенны с точки зрения программиста.
Засылка констант в адресуемые регистры может выполняться в режимах как ручного, так и автоматического счета. Ручная засылка, когда на клавиатуре набирается число и выполняется команда ПМ, где М - обозначение адресуемого регистра, не удлиняет программы. Однако, если имеются резервы командной памяти, лучше организовать автоматический ввод констант с помощью безликих команд С/П, ПП или циклом. Ввод убыстрится, снизится вероятность ошибки, меньше будет утомляться оператор: ему придется "пропускать через себя" только числа, а номера регистров его не касаются. Это же относится к засылке нулей в сумматоры перед каждым вариантом расчета. Скажем так: "все, что оператор может не делать, пусть он и не делает".
Особое внимание надо уделить программированию ввода больших массивов данных, например, при статистических расчетах. Эти данные после ввода сразу обрабатываются, а в адресуемых регистрах накапливаются соответствующие суммы или произведения. В зависимости от того, как составлена программа первичной обработки, затраты времени на ввод могут измениться в полтора-два раза. Но дело даже не только во времени. Если очередные значения надо вводить через 5-10 секунд, оператор успевает чуть-чуть передохнуть, а если через 15-20 секунд, оператор невольно начинает отвлекаться. Вероятность ошибки растет.
Программа может помочь оператору, если его отвлекли и он спутал, которое число ему предстоит вводить. Для этого перед командой останова в программу ставят команду вызова номера числа, которое надо ввести. Возможны и другие варианты подсказки - это зависит от вашей фантазии. Важно только соблюсти чувство меры, так как для подсказки или, скажем, коррекции неправильного ввода требуются дополнительные команды, и это затягивает обработку.
Вывод результатов расчета в подобных случаях желательно организовать так же, как и ввод исходного материала: не заставлять оператора рыскать по регистрам, а поочередно выводить результаты на индикатор, нажимая клавиши С/П или ПП.
Теперь о компоновке программы. Ошибок и потерь времени будет меньше, если постараться разместить изменяемые части программы, в частности подпрограммы, вне границ основного поля адресов. Такое требование удлинит программу на две-три команды, но коллегам, работающим по вашей программе, не придется путаться при изменении адресов перехода. Темп работы не снизится. Коротко скажем так: "не допускай никого в тело программы".
Не нужно доказывать, что трудно составить хорошую, долго живущую программу, не владея описанными в руководстве по эксплуатации микрокалькулятора способами работы со стеком, способами организации циклов, косвенной адресацией. Обратим внимание на менее очевидные приемы. Это прежде всего тождественные преобразования алгоритма, согласующие его с особенностями микрокалькулятора, затем группирование операций алгоритма и, наконец, выбор наилучшего порядка вычислений.
Пусть, например, требуется вычислить значение двойной суммы:
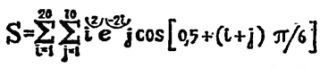
Программа, буквально соответствующая этой формуле, содержит 37 команд. Расчет выполняется примерно за 37 минут.
00. 2 01. 0 02. П0 03. Сх 04. 1 05. 0 06. П1 07. x-y 08. ИП0 09.Fx2 10. ИП0 11. 2 12. * 13. /-/ 14. Fexp 15. * 16. ИП1 17. * 18. ИП0 19. ИП1 20. + 21. Fпи 22. * 23. 6 24. / 25. 0 26. , 27. 5 28. + 29. Fcos 30. * 31. + 32. FL1 33. 08 34. FL0 35. 04 36. С/П.
Тождественное преобразование i**2*exp(-2*i)=(i/exp(i))**2 подсказывает, как обойтись пятью командами ИП0 ^ Fexp / Fx2 вместо восьми команд с адресами 08-15. Для убыстрения счета организуем засылку констант 0.5 и пи/6 в регистры Р3 н Р4 вне цикла, а внутри цикла по мере надобности будем их извлекать. При образовании этих констант для экономии командной памяти используем тождества 0.5=2**-1 и пи/6=arcsin(0.5).
Заметим, что вычислять целиком произведение под знаком двойной суммы 200 раз не обязательно. Можно вынести за скобки j, во внутреннем цикле вычислять сумму по i, а во внешнем - по j. Можно поступить и наоборот: за скобки вынести (i/exp(i))**2, во внутреннем цикле суммировать по j. а во внешнем - по i. Нетрудно показать, что при достаточном числе слагаемых полное время счета меньше там, где быстрее считается каждое слагаемое внутреннего цикла. Короче: "во внутренний цикл ставь то, что считается быстрее". В нашем случае суммирование во внутреннем цикле надо осуществлять по переменной j. Программа потребует также 37 команд, но время счета - около 19 минут, то есть почти вдвое меньше.
00. 2 01. F1/х 02. П3 03. Farcsin 04. П4 05. 2 06. 0 07. П1 08. Сх 09. 1 10. 0 11. П0 12. x-y 13. 0 14. ИП0 15. ИП1 16. + 17. ИП4 18. * 19. ИП3 20. + 21. Fcos 22. ИП0 23. * 24. + 25. FL0 26. 14 27. ИП1 28. ^ 29. Fexp 30. / 31. Fx2 32. * 33. + 34. FL1 35. 09 36. С/П.
Перечислим некоторые тождественные преобразования, позволяющие приспособить исходный алгоритм к совокупности операций микрокалькулятора "Электроника Б3-34" с целью ускорения вычислений в экономии программной памяти.
еxp(2*х)=(еxp**x)**2. Пусть аргумент х находится в регистре М. Левая часть тождества требует четыре команды: ИПМ 2 * Fexp, правая - три: ИПМ Fepx Fx2. Вычисления ускоряются на 0.4-0.5 сек. Далее приводятся только тождества; эффект от их использования предлагается оценить читателю.

Надо знать чисто конструктивные особенности микрокалькулятора "Электроника Б3-34", которые могут оказаться полезными при программировании. Вот некоторые из них.
1. Если стек возврата пуст, то есть выполнены все переходы с возвратом ПП N В/0 (N - адрес перехода), то в режиме автоматического счета команда В/0 эквивалентна составной команде БП 01.
2. В режиме автоматического счета команда ВП, если ей предшествуют команды ИПМ или КИПМ, а также пара команд ^ ВП, если ей предшествуют другие команды, переводит нуль в единицу, но не изменяет других чисел.
3. Если число 0.1<=х<1 находится в регистре М, команды КПМ и КИПМ при М=0, 1, 2, 3 уменьшают его, а при М=4, 5, 6 - увеличивают на 1e-8. Если х<0.1, эти команды изменяют его на другую величину. Читатель может проследить это самостоятельно.
4. Содержимое регистра М при неоднократном выполнении команды FLM уменьшается до единицы, но не далее. В то же время при выполнении команд КПМ или КИПМ (М=0, 1, 2, 3) содержимое регистра М, уменьшаясь, может стать равным нулю.
5. При выполнении команд КПМ или КИПМ (М=0, 1, 2, 3,) числа засылаются (извлекаются) в регистры Д, С, В, А..., 4, 3, 2, 1, 0, 1, 0, Д, С, В, А, затем последовательность с 4-х повторяется. Если же М=4, 5, 6, числа засылаются (извлекаются) в регистры 0, 1, 2..... 9, А, В, С, Д, 0, 1, 0, 1, 2, 3, затем последовательность с А повторяется.
6. Расчет по ряду программ завершают после того, как некоторая переменная х уменьшится по абсолютной величине до заданного предела е. Пусть е находится в регистре М. Если 1e-99<=е<1e-50, для проверки на окончание можно использовать фрагмент программы
A1. Fx<0 А2. А4 A3. /-/ А4. ИПМ А5. - A6. Fx<0 А7. А9 А8. С/П.
Если е>1e-50, используют фрагмент
Fx2 ИПМ - Fx<0 N С/П.
В регистре М при этом хранят величину е**2, N - адрес перехода.
Заметим, что область машинного нуля на "Электронике Б3-34" при выполнении различных операций не одинакова. Например, пара операций arccos(cos(x)) дает в результате нуль уже при значении х<2e-4, тогда как пара операций ln(exp(x)) дает нуль только при х<4e-8. Пользуясь этим обстоятельством, фрагмент проверки на окончание счета при некоторых частных значениях е можно сократить. Не понадобится и специальный регистр для хранения величины е.

В статье невозможно перечислить приемы, используемые на практике. Для совершенствования культуры программирования полезно с карандашом в руках разбирать опубликованные программы.
Мы смело можем считать, что овладели культурой программирования, если каждый этап составления и оформления программы мы умеем согласовать с ее целевым назначением и в работе используем арсенал известных приемов программирования.
Очень хорошо, если для решения задачи хватает командной памяти. А если нет? В этом случае имеются три основных пути. Самый простой, но далеко не лучший - отказ от некоторых "достижений культуры". Очищать счетчики, засылать константы и вводить исходные данные можно вручную прямо в регистры. Выводить результаты можно из регистров командами ИПМ. Останавливать расчет по достижении переменной величиной нуля можно аварийным остановом при помощи команды F1/х. Эти меры позволяют высвободить не так уж много, обычно до десяти команд. Но работать с такой программой более утомительно, а введение дополнительных ручных операций увеличивает вероятность ошибок.
Второй путь - выполнять одну или несколько неразветвленных частей программы в режиме ручного счета. Здесь экономия памяти может быть значительной, но этот способ хорош только при единичных расчетах.
Третий, самый плодотворный, но и трудный путь - замена алгоритма. Характерен призыв автора книги по прикладным программам В.Епанечникова: не ищите экономии в одну команду, экономьте сразу пятьдесят! Первый вариант его программы для решения системы из четырех линейных уравнений требовал 190 команд. Маленькими хитростями тут заведомо не обойтись. А изменив алгоритм, ему удалось сократить программу до 91 команды. Здесь уже можно говорить об искусстве программирования. Под ним мы будем понимать разработку новых способов решения вычислительных задач на микрокалькуляторе неизвестными ранее методами.
Искусство эффективно там, где оно опирается на культуру программирования. Надо знать особенности машины, знать приемы программирования, разработанные другими авторами. Точность вычислений и диапазон допустимых значений параметров должны быть не больше, чем требуется в данной задаче. Тогда появляются резервы, позволяющие создавать простые приближенные формулы, такие, как формула для обратного интеграла вероятности, погрешность которой во всей области доверительных вероятностей 0.8<=Q<=0.999 не превышает 4 процентов.

посвященных программируемым калькуляторам, исходя из заданного объема числовой памяти "Электроники Б3-34", автор утверждает, что интерполировать по формуле Лагранжа на этом микрокалькуляторе можно максимум по пяти узлам. Однако Я.Трохименко и Ф.Любич, применив приближенную формулу и изменив способ ввода, разработали программу интерполяции по 10 узлам и при этом уложились в 42 команды вместо 97 у категоричного автора.
В который раз убеждаешься: там, где начинается искусство, формально верным, но незыблемым методам приходится отступать.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
6/86
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Письма, открывающие очередной выпуск раздела, возвращают к прежним его материалам: здесь собраны отклики читателей на некоторые прошлогодние публикации. А завершают выпуск выступления, обращенные в будущее: они посвящены персональным компьютерам.
ВСЕ ХОРОШО В МЕРУ
В 10/85 год была опубликована статья А.Тулайкова "Стоит ли программировать?". Именно она и побудила меня взяться за перо. А ведь действительно, если внимательно посмотреть все выпуски раздела,- не сквозит ли в них некоторое упоение, умиление возможностями калькулятора? Со страниц журнала на нас смотрят изящные программы, гениальные по простоте алгоритмы... И вот на этом сплошном светлом фоне появилась статья А.Тулайкова. Вопрос он ставит весьма трезвый и своевременный: а всегда ли стоит программировать?
"Ищите удачные алгоритмы!" - призывает А.Бойко в 8/85 год. И вновь вопрос: а всегда ли стоит искать удачные алгоритмы?
Рассмотрим небольшой пример. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных. Искомая вероятность равна отношению числа благоприятствующих событий к числу всех исходов: р=С[4/7]*C[2/3]/C[6/10]=0.5. В общем случае, если всего деталей a, из них стандартных b, вынули c, а ищется вероятность того, что из них будет d стандартных, р=С[d/b]*C[c-d/a-b]/C[c/a]. Для расчета этой величины предлагается следующая программа для "Электроники Б3-34":
00. П5 01. С/П 02. П6 03. С/П 04. П7 05. С/П 06. П8 07. ИП6 08. ПП 09. 40 10. П9 11. ИП7 12. ИП5 13. ПП 14. 40 15. ИП9 16. / 17. П9 18. ИП5 19. ИП6 20. - 21. П1 22. ИП7 23. ИП8 24. - 25. ИП1 26. ПП 27. 40 28. ИП9 29. / 30. С/П... 40. П2 41. x-y 42. П0 43. П1 44. 1 45. П3 46. ИП0 47. ИП3 48. * 49. П3 50. FL0 51. 46 52. ИП3 53. F1/x 54. П3 55. ИП2 56. ИП3 57. * 58. П3 59. ИП2 60. 1 61. - 62. П2 63. FL1 64. 55 65. ИП3 66. В/0
Запуск: В/0 a С/П b С/П c С/П d С/П. После останова на индикаторе - результат p.
Является ли эта программа совершенной, использующей все возможности калькулятора? Естественно, нет. Я думаю, улучшить ее не составит большого труда. А является ли наилучшим алгоритм? Конечно, тоже нет. Но зато у приведенной программы есть два достоинства. Первое: свою задачу она все-таки решает. Второе: на ее составление я потратил всего 30 минут.
В свете вышесказанного возникает вопрос: а так ли уж плоха эта программа? Когда предо мной возникла такая задача, полсотни примеров я прорешал за полтора часа (включая время написания программы, набора и отладки ее). Смею заметить, что, если бы я занялся поиском лучшего алгоритма или оптимальной программы, в полтора часа я бы точно не уложился! Стоит ли овчинка выделки?
Конечно, я отдаю себе отчет в том, что рассмотренная задача достаточно проста. Вполне естественно, что, если при решении начинает сказываться ограниченность ресурсов калькулятора, тогда сразу же встает проблема поиска более эффективного способа решения.
К какому же выводу можно прийти после всех этих размышлений?
Во многих случаях следует искать не наиболее удачный алгоритм, а алгоритм, который нас устраивает в достаточной степени. Точно так же следует и оптимизацию программы производить до такого момента, чтобы она нас удовлетворяла в достаточной степени.
Ваш журнал научно-популярный. Его читает самая различная по своей подготовке массовая аудитория. Нужно показать массовому читателю, что результатов на микрокалькуляторе может добиться не только программист-профессионал, но и любой дилетант, что программирование - дело, доступное каждому, а не только кругу избранных. Поэтому не стоит, по-моему, ставить во главу угла "шлифовку" программ.
Извините за немного резкий тон, но просто мне очень нравится ваше начинание, и хочется, чтобы ваш раздел стал еще лучше.
А.УВАРОВ (г.Обнинск)
ОСТАНАВЛИВАТЬ ЛИ МГНОВЕНИЕ?
Часто в начале фильма на экране появляются титры. Что-то вроде: "Эта история произошла давно, еще в те времена, когда..." Титры ползут, и мы подчас испытываем беспокойство: успеем ли прочесть очередную фразу?
Когда мы звоним в справочные службы и несколько минут слышим гудки или безликие фразы "Ждите ответа", это тоже нервирует.
Подобные проблемы существуют и в области использования вычислительной техники. Как лучше вести общение с ЭВМ? Хоть и есть уже экспериментальные образцы "говорящих" машин, синтезирующих звуки человеческой речи, ориентироваться в ближайшее время следует лишь на визуальный диалог: мы набираем свой вопрос по буквам на клавиатуре, а ЭВМ отвечает фразой на экране. В каком же темпе лучше вести диалог? Через какое время после вопроса машина должна давать ответ? Через минуту после нажатия клавиши, через десяток секунд или мгновенно? И сколько времени этот ответ показывать?
Психологи выяснили, что пользователя нервирует не только долгое ожидание ответа, но и мгновенное его появление. Лучше, если между вопросом и ответом пройдет секунда, две. Это рождает иллюзию "обдумывания" ответа, то есть ситуацию, привычную для общения человека с человеком. Создатели диалоговых систем иногда специально "тормозят" ЭВМ, создавая небольшую паузу перед ее ответом. В данном случае важен не максимальный кпд от использования машинного времени, а максимальный кпд от общения.
А сколько времени должен высвечиваться ответ?
В 10/85 была опубликована заметка А.Бойко и А.Поташова "Остановись, мгновение!". Авторы ее предложили интересное техническое усовершенствование, благодаря которому калькулятор останавливается на несколько секунд, высвечивает результат, а затем продолжает работу.
Так вот, мой опыт работы на больших ЭВМ показывает, что высвечивание информации лишь определенное время, не зависящее от пользователя, порождает такую же нервозность, что и просмотр движущихся кинотитров, и постоянно держит человека в напряжении.
Но если в кино иначе нельзя, то на ЭВМ всегда существует возможность передать управление временем самому пользователю. Лишнее нажатие на клавишу при этом совсем не удлиняет время работы, зато создает ощущение покоя. Пусть у пользователя будет возможность без спешки прочитать показание на индикаторе, осознать его и либо продолжить работу, либо прервать ее. Кстати, если человек увидит, что результат его не устраивает, он нажмет соответствующую кнопку быстрее, чем истекает пауза.
Мне понятна страсть к совершенствованию. Понятно, что пользователи, разобравшись в структуре своей персональной ЭВМ или программируемого калькулятора, хотят усовершенствовать их. Но... человек с паяльником около ЭВМ? Это, на мой взгляд, почти то же, что мастер с кувалдой около наручных часов. Оставим богу богово. Не надо забывать, что одно из основных достоинств персональных ЭВМ и программируемых микрокалькуляторов - в их универсальности. А то скоро нужно будет писать отдельные программы для владельцев калькуляторов со звуковым сигналом или без него, с "паузой" или без оной. Кроме того, попытка модернизировать калькулятор может просто привести к немедленному выводу его из строя или к изменению условий его работы, что также может болезненно отразиться на его "здоровье". Иное дело, что следует доводить предлагаемые модернизации до сведения разрабатывающих и выпускающих организаций. Тогда после прохождения экспертизы и испытаний можно требовать реализации усовершенствований в массовом порядке.
Предвижу возможные возражения рационализаторов: "Не нравится - не используйте". Правильно. Я и не использую.
И.ВЯЗОВСКИЙ (г.Люберцы)
ПОМОГ КАЛЬКУЛЯТОР
Загубленная пленка вызвала у меня сомнения в исправности фотовспышки, в частности, электролитического конденсатора, входящего в ее конструкцию. Подходящего прибора для измерения емкости под рукой не оказалось, и его заменил... калькулятор.
Как известно, при разряде конденсатора через резистор напряжение Ut на его обкладках уменьшается с течением времени t следующим образом:
Ut=U0*exp(-t/RC),
где C - емкость конденсатора; U0 - напряжение на обкладках конденсатора в начальный момент времени; R - сопротивление резистора, соединяющего обкладки конденсатора.
После несложных преобразований получим:
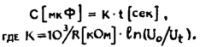
Для измерения времени t я использовал программу "Секундомер" С.Бармина (8/84). Емкость конденсатора оказалась ниже номинальной.
В.АДРИАН (г.Химки)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Введенная в микрокалькулятор программа не будет стираться при отключении блока питания, если концевую часть его пластмассового разъема немного спилить напильником, как показано на рисунке. Таким модифицированным разъемом мы уже несколько месяцев пользуемся на работе.
При аккуратном отключении разъема вначале подключится аккумулятор, а затем отключится блок питания. При аккуратном подключении разъема вначале кратковременно на калькулятор будет подаваться напряжение как от аккумулятора, так и от блока питания (предполагается, что он по-прежнему включен в сеть), после чего концевая часть разъема, отжимая контакты, отключает аккумулятор от электрических цепей калькулятора.
В.ЧУПРИНИН (г.Ростов-ка-Дону) ]
КУСТ И ЦИКАДА
То, что предлагается в публикуемых ниже письмах, можно расценивать н как увлекательные головоломки, и как поучительные, уроки, темы которых закодированы в названиях, предложенных авторами писем: КУСТ - команды управления стеком, ЦИКАДА - циклы и косвенная адресация.
И.ЖУРАВЛЕВА (г.Москва). Когда я осваивала "Электронику Б3-34", то при изучении команд управления стеком мне очень помогли небольшие задачи-головоломки, в которых тесно связаны игровая и обучающая стороны.
Пусть в регистрах стека расположены некоторые однозначные числа. Будем записывать их по порядку размещения в регистрах Т, Z, Y, X, например, 1234 (1 ^ 2 ^ 3 ^ 4). Задача играющего состоит в преобразовании заданной последовательности чисел в стеке к некоторой другой без использования цифровых клавиш микрокалькулятора.
Для этого нужно хорошо знать команды управления стеком и уметь предвидеть результат на несколько ходов вперед, то есть строить в уме алгоритм решения задачи. Как правило, такие головоломки могут быть решены различными способами. Требуется найти оптимальное решение. Играть в эту игру можно и без калькулятора - он нужен лишь для проверки решения. В ходе игры удобно пользоваться табличкой, где записывается содержимое стековых регистров.
Попробуйте выполнить такие преобразования: 1234-4321 (4 хода), 7447-8448 (7 ходов), 6000-7117 (8 ходов), 1234-6060 (12 ходов), 1234-5678 (15 ходов). Содержимое регистра X1 в начале и конце игры игнорируется, однако в ходе решения задачи этот регистр активно используется.
А.НЕКЛЮДОВ (г.Одесса). Предлагаемая мною игра может быть представлена в виде своеобразного пасьянса, где определенным образом переставляется содержимое регистра памяти 1-9, А, В, С. Конкретные числа, хранимые в регистрах, при этом могут быть любыми и лучше абстрагироваться от них с помощью диаграмм перестановок.
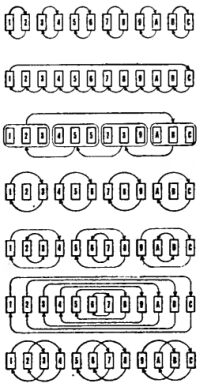
Разберем, к примеру, первую перестановку. Конечно, ничего сложного в ней нет: ИП1 ИП2 П1 x-y П2... ИПВ ИПС ПВ x-y ПС С/П. Всего 31 команда. Можно ли покороче? Можно, если использовать команды косвенной адресации, операторы цикла и регистры 0, Д:
1 2 П0 ИП0 ПД КИП^ КИП0 ККПД x-y КП^ FL0 [] C/П
(условный переход - на команду ИП0).
Решив пару подобных "пасьянсов", вы почувствуете себя значительно увереннее прн применении команд косвенной адресации и циклов, а сборник таких перестановок, оформленный в виде каталога, подобного каталогу вращений кубика Рубика, может оказаться полезным для решения игровых и практических задач.
[ БЮРО СПРАВОК
Рамки раздела не позволяют опубликовать все присылаемые в журнал прикладные программы. Между тем хотелось бы, чтобы они были известны всем, кому моглн бы оказаться полезными. Судя по просьбам читателей, желающих увидеть на наших страницах решения предлагаемых ими задач, такая взаимовыручка была бы целесообразной. Здесь помещены сообщения читателей об имеющихся у них прикладных программах и запросы иа подобные программы. Адреса, приводимые с согласия авторов писем, позволят наладить непосредственную переписку заинтересованных сторон.
У себя в проектном институте мы проводим целенаправленную работу по внедрению программируемого микрокалькулятора "Электроника Б3-34" и его аналогов в производство. Составлено несколько сборникои тематических программ, например, для обработки геодезических светодальномерных измерений на изысканиях новых железных дорог. Программы неплохо зарекомендовали себя на практике.
В.Т.КОНДРАТЕНКО, А.В.СОЛОВЬЕВ.
196105, Ленинград, Московский проспект, 143, "Ленгипротранс".
Предлагаем комплекс прикладных программ для расчета констант устойчивости по данным рН-потеициометрического титрования. Программы составлены для микрокалькулятора "Электроника Б3-34".
И.И.ЖЕЛТВАЙ.
270080, Одесса-80 аб.ящик 33.
В 8/85 была напечатана программа Г.Славина "Микрокалькулятор - советчик врача". По аналогии, на наш взгляд, можно проводить диагностирование машин и оборудования. Желательна диагностическая программа
применительно к таким объектам.
Б.В.КРАСОВ.
433510, Димитровград Ульяновской области, ул.Октябрьская, 74, Димитровградский механико-технологический техникум молочной промышленности.
При изучении теоретических основ электротехники и радиотехники, теории линейных цепей и т.п. часто приходится встречаться с системами из двух уравнений первой степени с комплексными коэффициентами. Многие студенты вузов и техникумов были бы благодарны вам, если бы вы опубликовали оптимальную программу для этой цели.
М.Р.ШЕБЕС.
123423, Москва, ул.Д.Бедного, 19, кор.1, кв.53 ]
ЭЛЕКТРОННЫЙ КОМПОЗИТОР

В 1751 году в Англии музыкант Уильям Гейс написал сатирическое руководство "Искусство сочинять музыку исключительно новым способом, пригодным Для самых захудалых талантов". Там предлагалось, обмакнув в чернила щетку, провести по ней пальцем. К брызгам-кляксам на заблаговременно подложенной нотной бумаге оставалось лишь подрисовать хвостики, чтобы получились "полноценные ноты". В ту пору предлагались и другие неожиданные способы сочинения музыки. Не избежал заразительного увлечения даже Моцарт. В 1793 году он пишет "Руководство, как при помощи двух игральных костей сочинять вальсы, не имея ни малейшего представления о музыке и композиции".
Вероятностный подход к созданию мелодии становится не таким уж бессмысленным, если заложить в ЭВМ некие закономерности, принципы и правила композиции, согласно которым отбираются интервалы натурального звукоряда, выдаваемые программой генерации псевдослучайных чисел Xi, например, с нормальным законом распределения:
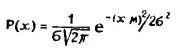
Последовательность интервалов образует мелодию от произвольной начальной ступени. Если менять параметры распределения мю и сигма, будет меняться и характер сочиняемой мелодии. Для мю>0 мелодическая линия будет восходящей, для мю<0 - нисходящей. Для малых значений сигма мелодическая линия оказывается плавной, для больших - скачкообразной. Для знатоков теории вероятностей отметим, что полученная мелодия будет представлять собой марковскую цепь.
Программа: 00. ПП 01. 25 02. ИП2 03. * 04. ИП3 05. + 06. ^ 07. Fx2 08. Fsqr 09. / 10. FBx 11. 1 12. + 13. ПА 14. КИПА 15. + 16. x-y 17. ИПА 18. * 19. ИП1 20. + 21. П1 22. С/П 23. БП 24. 00 25. ИПД 26. 1 27. 1 28. * 29. Fпи 30. + 31. ПД 32. КИПД 33. x-y 34. ИПД 35. - 36. ПД 37. 02 38. * 39. 1 40. - 41. ^ 42. Fx2 43. Fsqr 44. / 45. 1 46. FBx 47. Fx2 48. - 49. Fsqr 50. Fln 51. /-/ 52. Fпи 53. * 54. Fsqr 55. * 56. B/0.
Контрольный пример: в регистр 1 нужно записать номер начальной ступени (например, 8, что соответствует "до" второй октавы, П1), в Р2 - значение сигма (1 П2), в Р3 - значение мю (0 П3), в РД - любое число от 0 до 1 (0.75 ПД), В/0, С/П. На индикаторе читаем номер очередной ступени "7", С/П, "6", С/П... Если продолжить пример, то последовательность будет соответствовать приведенному нотному примеру.
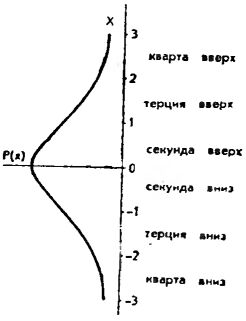
Если придать этой цепочке звуков соответствующий ритм, то первый такт полученной мелодии воспроизведет мотив известной песни "Голубые города" - не правда ли?
Благодарим читателей В.Бирюкова из г.Тюмени - автора программы "Композитор" и нотного примера, А.Андреева из г.Ленинграда и других читателей, чьи письма были использованы при подготовке статьи.

Что общего межцу вычислительной техникой и археологией? По-своему судят об этом Я.Разливинсиий из Тулы и Н.Дорош из поселка Лельчицы Гомельской области.

ЛАБИРИНТ
Лабиринты, публикуемые в развлекательных разделах популярных журналов, отличаются тем, что читатель, ищущий путь к выходу, видит перед собой план лабиринта. В реальном лабиринте приходится двигаться, не имея никакого представления о его плане. Предлагаемая игра в этом смысле весьма приближена к реальности.
Лабиринт представляет собой разграфленное поле размером 7*9 клеток, некоторые из которых заняты. Выход - через одну из клеток девятого ряда, достижение которого означает успешное окончание игры. Начальное положение показывается на индикаторе в виде 204 (второй ряд, четвертый столбец). Так в виде трехзначного числа на индикатор в дальнейшем выводится положение блуждающего по лабиринту после каждого его шага. Направление шага задается нажатием одной из цифровых клавиш: 8 - вперед, 2 - назад, 4 - влево, 6 - вправо.

Например, на индикаторе было число 305. Мы хотим продвинуться вперед и нажимаем клавиши 8 С/П. Если в ответ на индикаторе появится 405, значит, мы действительно продвинулись вперед. Если же опять появилось 305, мы остались на прежнем месте, расположенная впереди клетка занята, и это следует показать штриховкой на плане лабиринта. Нужно искать обходной путь.
У нашего лабиринта есть еще и подвал - другой лабиринт размером 6*9 клеток. Попав в безвыходный
тупик, мы можем опуститься в подвал (если клетка внизу не занята), постараться пройти часть пути там и, выйдя наверх (если верхняя клетка свободна), продолжать путь к выходу.

Координаты подвальных клеток выражаются трехзначными числами со знаком минус. Перемещения по вертикали, с этажа на этаж, требуют нажатия клавиши 0. Пусть мы в подвале, в клетке с координатами -702 и захотели подняться наверх. Нажимаем 0 С/П. Появление 702 говорит об успехе, -702 о неуспехе этого шага: клетка наверху занята, это следует показать штриховкой на плане подвала.
План лабиринта определяется некоторым случайным числом от 10 до 100, которое вводится в калькулятор в начале игры. Начальная клетка 204 может оказаться занятой сразу по выходе из нее. Может также оказаться, что все пути из начальной точки - тупиковые.
00. Fsqr 01. Flg 02. 9 03. П0 04. x-y 05. F10X 06. ^ 07. ВП
08. 7 09. КП^ 10. x-y ll. ^ 12. ПА 13. ВП 14. FL0 15. 05 16. 1 17. П0 18. 2 19. ПА 20. 4 21. ПВ 22. ИПА 23. ВП 24. 2 25. ИПВ 26. + 27. ИП0 28. * 29. С/П 30. Fx!=0 31. 60 32. 3
33. 8 34. + 35. ПД 36. 0 37. ^ 38. 1 39. КБПД 40. /-/ 41. 0 42. /-/ 43. КНОП 44. x-y 45. КНОП 46. ИПА 47. + 48. x-y 49. ИПВ 50. + 51. ПП 52. 74 53. Fx>=0 54. 22 55. F() 56. ПА 57. ИПС 58. БП 59. 21 60. ИП0 61. /-/ 62. П0 63. ИПА 64. ИПВ 65. ПП 66. 74 67. Fx<0 68. 22 69. ИП0 70. /-/ 71. П0 72. БП 73. 22 74. ПС 75. x-y 76. ПД 77. ^ 78. КИПД 79. ИПС 80. F10X 81. / 82. ИП0 83. 2 84. + 85. / 86. ПД 87. КИПД 88. F() 89. ИПД 90. - 91. 2 92. F1/x 93. - 94. В/0.
Адреса 00-15: получение "плана" лабиринта; его задают числа a1..... a9, образуемые из начального случайного числа и рассылаемые по регистрам Р1-Р9. 16-21: формирование координат начальной клетки. 22-29: показ координат клетки в виде m0n, где m координата по направлению "вперед-назад", n - по направлению "вправо-влево". 30-31: проверка "переход на этаж?" и переход на адрес 60 в случае "да". 32-50: формирование координат клетки назначения по заданному направлению перемещения. 51-59: проверка "занята ли клетка назначения?", выполняемая обращением к подпрограмме (см. ниже); если клетка занята, отсылка на адрес 22 для демонстрации неизменившихся координат; если не занята - формирование новых координат. 60-73: проверка "занята ли клетка подвала?", выполняемая обращением к той же подпрограмме, с последующим аналогичным преобразованием координат. 74-94: подпрограмма, позволяющая проверить, занята ли клетка,- деление числа am (см. выше) на 10**n с различными коэффициентами для разных этажей; клетка с координатами m0n считается занятой или незанятой в зависимости от того, какова по сравнению с 0.5 дробная часть частного.
Инструкция. Ввести программу, набрать случайное число, нажать В/0 С/П. На индикаторе - число 204. Нажать цифровую клавишу, задающую перемещение, затем С/П. На индикаторе - координаты местонахождения.
Контрольный пример (см. рисунок) определяется начальным случайным числом 97.123456.
С.ГЕТА (г.Таллин)
ЭКСПЕРИМЕНТ НА ЭВМ
Четыре месяца назад мы приобрели в магазине "Электроника" в Москве бытовой компьютер "БК-0010", и с тех пор сын и жена заболели "компьютерной болезнью". (Я ею болен уже 15 лет, как говорят, по долгу службы и велению сердца).
Для тех, кто еще не знает, что это за ЭВМ, приведу ее очень краткое описание. Внешне это пластмассовая прямоугольная коробка с размерами 36*25*4см, на верхней стороне которой помещена клавиатура, подобная той, что на пишущих машинках (только в компьютере каждая клавиша может нести до шести различных знаков). В качестве дисплея используется телевизор, в качестве внешнего запоминающего устройства для хранения программ и данных - кассетный магнитофон "Электроника-302". Программировать задачи можно как на языке "Фокал" (именно на нем составлены приводимые мною программы), так и в машинных кодах. Информация выводится на дисплей в виде алфавитно-цифровых и графических символов либо по 64, либо по 32 символа в строке.
Для чего нам дома ЭВМ и что мы с ней делаем? Этот вопрос нам задают многие знакомые, и я постараюсь частично на него ответить, хотя сделать это нелегко. Чем больше ты узнаешь о машине и делаешь программ, тем больше хочется узнать и сделать.
Причины, по которым человека охватывает "компьютерная болезнь", можно разбить на две группы: эмоциональные и рациональные. Первая группа связана с удовлетворением его творческих и интеллектуальных потребностей. Программирование - увлекательнейшая игра, дающая возможность думать, изобретать, созидать. Несказанное чувство удовлетворения испытываешь, когда заставишь машину сделать то, что задумал. При этом не всегда важно, имеет ли программа какое-либо практическое применение. Важно, что ты узнал что-то новое, чему-то научился. Примерами таких программ являются созданные моим пятнадцатилетним сыном модель машины Поста, модель игры "Жизнь" ("Эволюция"), просто различные картинки.
Вторая группа связана с практическим применением машины в быту, учебе, работе, отдыхе. Что касается непосредственно быта - скажем, управления варкой супа или стиральной машиной, то реализация подобных программ весьма проблематична, хотя машина имеет соответствующие возможности. А вот помочь составить меню и предложить конкретные рецепты в зависимости от имеющихся у вас продуктов она вполне может. Компьютер также может быть полезен при планировании и анализе семейного бюджета.
Очень большим подспорьем служит ЭВМ в учебе школьников и студентов. Не считая того, что знание программирования само по себе весьма полезно и даже необходимо для современного человека, учебные программы позволяют зрительно представить явления, происходящие в природе и технике, провести в короткое время множество вычислительных экспериментов, исследуя какой-либо процесс.

Приведу две простые программы на эту тему и результаты их работы, выведенные на экран телевизора. Первая программа отображает картину интерференции волн двух когерентных источников колебаний. Это примерно то, что можно увидеть, бросив в воду одновременно два одинаковых камешка на небольшом расстоянии друг от друга. Программа строит картину по точкам. Если разность расстояний от точки до источников волн кратна условной длине волны, точка выделяется светлым крестом. Построение законченной картины требует немало времени, около 30 минут. Зато вторая программа работает практически мгновенно. Она предназначена для исследования траектории тела в вязкой среде, движущегося с заданной начальной скоростью под действием силы тяжести. Решается система дифференциальных уравнений
d2x/dt2=-adx/dt;
d2y/dt2=-ady/dt-b,
и результаты решения отображаются на дисплее. Условия варьируются, и за несколько минут возникает широкий спектр траекторий - от классической параболы (а=0) до круто загибающейся книзу кривой, соответствующей высокому сопротивлению среды.

Домашняя ЭВМ может быть полезна и физикам, и лирикам. Жаль только, что пока еще так редко она появляется в продаже.
И.ЛЬВОВ (г.Москва)
[ У КНИЖНОЙ ПОЛКИ
"Справочник по расчетам на микрокалькуляторах" - новая книга В.П.Дьяконова (М., Наука, 1985г.). Его сравнительно высокий тираж (220000экз.) позволяет надеяться, что 260 программ, собранных в книге, пополнят библиотеку многих энтузиастов программирования на микрокалькуляторах типа "Электроника Б3-34" - научных работников, инженеров, студентов вузов и техникумов.
Существенную помощь окажет справочник владельцам программируемых микрокалькуляторов "TI-58C" и "TI-59". Вторая глава книги и приложения содержат инструкции по применению встроенной библиотеки цифрового магнитофона и печатающего устройства, которыми могут комплектоваться эти машинки. Заинтересованный читатель также найдет в книге несколько эффективных программ из справочника А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для "Электроники Б3-34", "МК-56", "МК 54"".
Пользование справочником несколько затрудняют опечатки и неточности. Так, на стр.20 предлагаются несуществующие команды KL0M, KL1M, KL2M, KL3M; программа 3.2 дает неверный результат для некоторых значений аргумента; глава шестая, посвященная вычислению специальных функций, практически не содержит указаний о точности результатов и допустимых диапазонах изменения аргументов и т.п. Отдельные программы неоптимальны. ]
ГОДИТСЯ ЛЮБОЙ МАГНИТОФОН
Вот уже несколько лет я использую программируемый калькулятор "Электроника Б3-34" для разных расчетов, в том числе и для обработки экспериментальных данных. Большие трудности создает при этом ограниченность памяти калькулятора.
Но вот в продаже появился бытовой компьютер "БК-0010". Покупка его сулила массу преимуществ: скорость более 100 операций в секунду, возможность запомнить более полутора тысяч чисел и, наконец, долгожданная возможность записать программу и данные на магнитофон и не вводить их заново при каждом включении ЭВМ. Запись на магнитную ленту позволяет накапливать библиотеку программ и обмениваться ими с другими владельцами "БК".
Магнитофон (правда, не имеющий линейного выхода, зато имеющий счетчик метража) у меня уже был, однако возникло непредвиденное затруднение. Согласно инструкции, "БК-0010" работает с магнитофоном одной единственной марки - "Электроника-302". Покупать второй магнитофон было нелогично, и я решил попробовать использовать свой. Приложив определенные усилия, я убедился, что "БК-0010" может работать практически с любым магнитофоном - достаточно лишь сделать соответствующий соединительный кабель. Я использую кабель, схема которого приведена на рисунке. Основное условие надежного считывания программы с магнитной ленты - достаточно большая (около 0.5 вольта) амплитуда сигнала. Она устанавливается регулятором громкости.
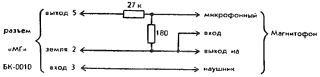
М.МАКСИМОВ (г.Москва)
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ
Письма, открывающие очередной выпуск раздела, возвращают к прежним его материалам: здесь собраны отклики читателей на некоторые прошлогодние публикации. А завершают выпуск выступления, обращенные в будущее: они посвящены персональным компьютерам.
ВСЕ ХОРОШО В МЕРУ
В 10/85 год была опубликована статья А.Тулайкова "Стоит ли программировать?". Именно она и побудила меня взяться за перо. А ведь действительно, если внимательно посмотреть все выпуски раздела,- не сквозит ли в них некоторое упоение, умиление возможностями калькулятора? Со страниц журнала на нас смотрят изящные программы, гениальные по простоте алгоритмы... И вот на этом сплошном светлом фоне появилась статья А.Тулайкова. Вопрос он ставит весьма трезвый и своевременный: а всегда ли стоит программировать?
"Ищите удачные алгоритмы!" - призывает А.Бойко в 8/85 год. И вновь вопрос: а всегда ли стоит искать удачные алгоритмы?
Рассмотрим небольшой пример. В партии из 10 деталей 7 стандартных. Найти вероятность того, что среди 6 взятых наудачу деталей 4 стандартных. Искомая вероятность равна отношению числа благоприятствующих событий к числу всех исходов: р=С[4/7]*C[2/3]/C[6/10]=0.5. В общем случае, если всего деталей a, из них стандартных b, вынули c, а ищется вероятность того, что из них будет d стандартных, р=С[d/b]*C[c-d/a-b]/C[c/a]. Для расчета этой величины предлагается следующая программа для "Электроники Б3-34":
00. П5 01. С/П 02. П6 03. С/П 04. П7 05. С/П 06. П8 07. ИП6 08. ПП 09. 40 10. П9 11. ИП7 12. ИП5 13. ПП 14. 40 15. ИП9 16. / 17. П9 18. ИП5 19. ИП6 20. - 21. П1 22. ИП7 23. ИП8 24. - 25. ИП1 26. ПП 27. 40 28. ИП9 29. / 30. С/П... 40. П2 41. x-y 42. П0 43. П1 44. 1 45. П3 46. ИП0 47. ИП3 48. * 49. П3 50. FL0 51. 46 52. ИП3 53. F1/x 54. П3 55. ИП2 56. ИП3 57. * 58. П3 59. ИП2 60. 1 61. - 62. П2 63. FL1 64. 55 65. ИП3 66. В/0
Запуск: В/0 a С/П b С/П c С/П d С/П. После останова на индикаторе - результат p.
Является ли эта программа совершенной, использующей все возможности калькулятора? Естественно, нет. Я думаю, улучшить ее не составит большого труда. А является ли наилучшим алгоритм? Конечно, тоже нет. Но зато у приведенной программы есть два достоинства. Первое: свою задачу она все-таки решает. Второе: на ее составление я потратил всего 30 минут.
В свете вышесказанного возникает вопрос: а так ли уж плоха эта программа? Когда предо мной возникла такая задача, полсотни примеров я прорешал за полтора часа (включая время написания программы, набора и отладки ее). Смею заметить, что, если бы я занялся поиском лучшего алгоритма или оптимальной программы, в полтора часа я бы точно не уложился! Стоит ли овчинка выделки?
Конечно, я отдаю себе отчет в том, что рассмотренная задача достаточно проста. Вполне естественно, что, если при решении начинает сказываться ограниченность ресурсов калькулятора, тогда сразу же встает проблема поиска более эффективного способа решения.
К какому же выводу можно прийти после всех этих размышлений?
Во многих случаях следует искать не наиболее удачный алгоритм, а алгоритм, который нас устраивает в достаточной степени. Точно так же следует и оптимизацию программы производить до такого момента, чтобы она нас удовлетворяла в достаточной степени.
Ваш журнал научно-популярный. Его читает самая различная по своей подготовке массовая аудитория. Нужно показать массовому читателю, что результатов на микрокалькуляторе может добиться не только программист-профессионал, но и любой дилетант, что программирование - дело, доступное каждому, а не только кругу избранных. Поэтому не стоит, по-моему, ставить во главу угла "шлифовку" программ.
Извините за немного резкий тон, но просто мне очень нравится ваше начинание, и хочется, чтобы ваш раздел стал еще лучше.
А.УВАРОВ (г.Обнинск)
ОСТАНАВЛИВАТЬ ЛИ МГНОВЕНИЕ?
Часто в начале фильма на экране появляются титры. Что-то вроде: "Эта история произошла давно, еще в те времена, когда..." Титры ползут, и мы подчас испытываем беспокойство: успеем ли прочесть очередную фразу?
Когда мы звоним в справочные службы и несколько минут слышим гудки или безликие фразы "Ждите ответа", это тоже нервирует.
Подобные проблемы существуют и в области использования вычислительной техники. Как лучше вести общение с ЭВМ? Хоть и есть уже экспериментальные образцы "говорящих" машин, синтезирующих звуки человеческой речи, ориентироваться в ближайшее время следует лишь на визуальный диалог: мы набираем свой вопрос по буквам на клавиатуре, а ЭВМ отвечает фразой на экране. В каком же темпе лучше вести диалог? Через какое время после вопроса машина должна давать ответ? Через минуту после нажатия клавиши, через десяток секунд или мгновенно? И сколько времени этот ответ показывать?
Психологи выяснили, что пользователя нервирует не только долгое ожидание ответа, но и мгновенное его появление. Лучше, если между вопросом и ответом пройдет секунда, две. Это рождает иллюзию "обдумывания" ответа, то есть ситуацию, привычную для общения человека с человеком. Создатели диалоговых систем иногда специально "тормозят" ЭВМ, создавая небольшую паузу перед ее ответом. В данном случае важен не максимальный кпд от использования машинного времени, а максимальный кпд от общения.
А сколько времени должен высвечиваться ответ?
В 10/85 была опубликована заметка А.Бойко и А.Поташова "Остановись, мгновение!". Авторы ее предложили интересное техническое усовершенствование, благодаря которому калькулятор останавливается на несколько секунд, высвечивает результат, а затем продолжает работу.
Так вот, мой опыт работы на больших ЭВМ показывает, что высвечивание информации лишь определенное время, не зависящее от пользователя, порождает такую же нервозность, что и просмотр движущихся кинотитров, и постоянно держит человека в напряжении.
Но если в кино иначе нельзя, то на ЭВМ всегда существует возможность передать управление временем самому пользователю. Лишнее нажатие на клавишу при этом совсем не удлиняет время работы, зато создает ощущение покоя. Пусть у пользователя будет возможность без спешки прочитать показание на индикаторе, осознать его и либо продолжить работу, либо прервать ее. Кстати, если человек увидит, что результат его не устраивает, он нажмет соответствующую кнопку быстрее, чем истекает пауза.
Мне понятна страсть к совершенствованию. Понятно, что пользователи, разобравшись в структуре своей персональной ЭВМ или программируемого калькулятора, хотят усовершенствовать их. Но... человек с паяльником около ЭВМ? Это, на мой взгляд, почти то же, что мастер с кувалдой около наручных часов. Оставим богу богово. Не надо забывать, что одно из основных достоинств персональных ЭВМ и программируемых микрокалькуляторов - в их универсальности. А то скоро нужно будет писать отдельные программы для владельцев калькуляторов со звуковым сигналом или без него, с "паузой" или без оной. Кроме того, попытка модернизировать калькулятор может просто привести к немедленному выводу его из строя или к изменению условий его работы, что также может болезненно отразиться на его "здоровье". Иное дело, что следует доводить предлагаемые модернизации до сведения разрабатывающих и выпускающих организаций. Тогда после прохождения экспертизы и испытаний можно требовать реализации усовершенствований в массовом порядке.
Предвижу возможные возражения рационализаторов: "Не нравится - не используйте". Правильно. Я и не использую.
И.ВЯЗОВСКИЙ (г.Люберцы)
ПОМОГ КАЛЬКУЛЯТОР
Загубленная пленка вызвала у меня сомнения в исправности фотовспышки, в частности, электролитического конденсатора, входящего в ее конструкцию. Подходящего прибора для измерения емкости под рукой не оказалось, и его заменил... калькулятор.
Как известно, при разряде конденсатора через резистор напряжение Ut на его обкладках уменьшается с течением времени t следующим образом:
Ut=U0*exp(-t/RC),
где C - емкость конденсатора; U0 - напряжение на обкладках конденсатора в начальный момент времени; R - сопротивление резистора, соединяющего обкладки конденсатора.
После несложных преобразований получим:
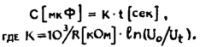
Для измерения времени t я использовал программу "Секундомер" С.Бармина (8/84). Емкость конденсатора оказалась ниже номинальной.
В.АДРИАН (г.Химки)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Введенная в микрокалькулятор программа не будет стираться при отключении блока питания, если концевую часть его пластмассового разъема немного спилить напильником, как показано на рисунке. Таким модифицированным разъемом мы уже несколько месяцев пользуемся на работе.

При аккуратном отключении разъема вначале подключится аккумулятор, а затем отключится блок питания. При аккуратном подключении разъема вначале кратковременно на калькулятор будет подаваться напряжение как от аккумулятора, так и от блока питания (предполагается, что он по-прежнему включен в сеть), после чего концевая часть разъема, отжимая контакты, отключает аккумулятор от электрических цепей калькулятора.
В.ЧУПРИНИН (г.Ростов-ка-Дону) ]
КУСТ И ЦИКАДА
То, что предлагается в публикуемых ниже письмах, можно расценивать н как увлекательные головоломки, и как поучительные, уроки, темы которых закодированы в названиях, предложенных авторами писем: КУСТ - команды управления стеком, ЦИКАДА - циклы и косвенная адресация.
И.ЖУРАВЛЕВА (г.Москва). Когда я осваивала "Электронику Б3-34", то при изучении команд управления стеком мне очень помогли небольшие задачи-головоломки, в которых тесно связаны игровая и обучающая стороны.
Пусть в регистрах стека расположены некоторые однозначные числа. Будем записывать их по порядку размещения в регистрах Т, Z, Y, X, например, 1234 (1 ^ 2 ^ 3 ^ 4). Задача играющего состоит в преобразовании заданной последовательности чисел в стеке к некоторой другой без использования цифровых клавиш микрокалькулятора.
Для этого нужно хорошо знать команды управления стеком и уметь предвидеть результат на несколько ходов вперед, то есть строить в уме алгоритм решения задачи. Как правило, такие головоломки могут быть решены различными способами. Требуется найти оптимальное решение. Играть в эту игру можно и без калькулятора - он нужен лишь для проверки решения. В ходе игры удобно пользоваться табличкой, где записывается содержимое стековых регистров.
Попробуйте выполнить такие преобразования: 1234-4321 (4 хода), 7447-8448 (7 ходов), 6000-7117 (8 ходов), 1234-6060 (12 ходов), 1234-5678 (15 ходов). Содержимое регистра X1 в начале и конце игры игнорируется, однако в ходе решения задачи этот регистр активно используется.
А.НЕКЛЮДОВ (г.Одесса). Предлагаемая мною игра может быть представлена в виде своеобразного пасьянса, где определенным образом переставляется содержимое регистра памяти 1-9, А, В, С. Конкретные числа, хранимые в регистрах, при этом могут быть любыми и лучше абстрагироваться от них с помощью диаграмм перестановок.

Разберем, к примеру, первую перестановку. Конечно, ничего сложного в ней нет: ИП1 ИП2 П1 x-y П2... ИПВ ИПС ПВ x-y ПС С/П. Всего 31 команда. Можно ли покороче? Можно, если использовать команды косвенной адресации, операторы цикла и регистры 0, Д:
1 2 П0 ИП0 ПД КИП^ КИП0 ККПД x-y КП^ FL0 [] C/П
(условный переход - на команду ИП0).
Решив пару подобных "пасьянсов", вы почувствуете себя значительно увереннее прн применении команд косвенной адресации и циклов, а сборник таких перестановок, оформленный в виде каталога, подобного каталогу вращений кубика Рубика, может оказаться полезным для решения игровых и практических задач.
[ БЮРО СПРАВОК
Рамки раздела не позволяют опубликовать все присылаемые в журнал прикладные программы. Между тем хотелось бы, чтобы они были известны всем, кому моглн бы оказаться полезными. Судя по просьбам читателей, желающих увидеть на наших страницах решения предлагаемых ими задач, такая взаимовыручка была бы целесообразной. Здесь помещены сообщения читателей об имеющихся у них прикладных программах и запросы иа подобные программы. Адреса, приводимые с согласия авторов писем, позволят наладить непосредственную переписку заинтересованных сторон.
У себя в проектном институте мы проводим целенаправленную работу по внедрению программируемого микрокалькулятора "Электроника Б3-34" и его аналогов в производство. Составлено несколько сборникои тематических программ, например, для обработки геодезических светодальномерных измерений на изысканиях новых железных дорог. Программы неплохо зарекомендовали себя на практике.
В.Т.КОНДРАТЕНКО, А.В.СОЛОВЬЕВ.
196105, Ленинград, Московский проспект, 143, "Ленгипротранс".
Предлагаем комплекс прикладных программ для расчета констант устойчивости по данным рН-потеициометрического титрования. Программы составлены для микрокалькулятора "Электроника Б3-34".
И.И.ЖЕЛТВАЙ.
270080, Одесса-80 аб.ящик 33.
В 8/85 была напечатана программа Г.Славина "Микрокалькулятор - советчик врача". По аналогии, на наш взгляд, можно проводить диагностирование машин и оборудования. Желательна диагностическая программа
применительно к таким объектам.
Б.В.КРАСОВ.
433510, Димитровград Ульяновской области, ул.Октябрьская, 74, Димитровградский механико-технологический техникум молочной промышленности.
При изучении теоретических основ электротехники и радиотехники, теории линейных цепей и т.п. часто приходится встречаться с системами из двух уравнений первой степени с комплексными коэффициентами. Многие студенты вузов и техникумов были бы благодарны вам, если бы вы опубликовали оптимальную программу для этой цели.
М.Р.ШЕБЕС.
123423, Москва, ул.Д.Бедного, 19, кор.1, кв.53 ]
ЭЛЕКТРОННЫЙ КОМПОЗИТОР

В 1751 году в Англии музыкант Уильям Гейс написал сатирическое руководство "Искусство сочинять музыку исключительно новым способом, пригодным Для самых захудалых талантов". Там предлагалось, обмакнув в чернила щетку, провести по ней пальцем. К брызгам-кляксам на заблаговременно подложенной нотной бумаге оставалось лишь подрисовать хвостики, чтобы получились "полноценные ноты". В ту пору предлагались и другие неожиданные способы сочинения музыки. Не избежал заразительного увлечения даже Моцарт. В 1793 году он пишет "Руководство, как при помощи двух игральных костей сочинять вальсы, не имея ни малейшего представления о музыке и композиции".
Вероятностный подход к созданию мелодии становится не таким уж бессмысленным, если заложить в ЭВМ некие закономерности, принципы и правила композиции, согласно которым отбираются интервалы натурального звукоряда, выдаваемые программой генерации псевдослучайных чисел Xi, например, с нормальным законом распределения:
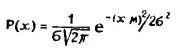
Последовательность интервалов образует мелодию от произвольной начальной ступени. Если менять параметры распределения мю и сигма, будет меняться и характер сочиняемой мелодии. Для мю>0 мелодическая линия будет восходящей, для мю<0 - нисходящей. Для малых значений сигма мелодическая линия оказывается плавной, для больших - скачкообразной. Для знатоков теории вероятностей отметим, что полученная мелодия будет представлять собой марковскую цепь.
Программа: 00. ПП 01. 25 02. ИП2 03. * 04. ИП3 05. + 06. ^ 07. Fx2 08. Fsqr 09. / 10. FBx 11. 1 12. + 13. ПА 14. КИПА 15. + 16. x-y 17. ИПА 18. * 19. ИП1 20. + 21. П1 22. С/П 23. БП 24. 00 25. ИПД 26. 1 27. 1 28. * 29. Fпи 30. + 31. ПД 32. КИПД 33. x-y 34. ИПД 35. - 36. ПД 37. 02 38. * 39. 1 40. - 41. ^ 42. Fx2 43. Fsqr 44. / 45. 1 46. FBx 47. Fx2 48. - 49. Fsqr 50. Fln 51. /-/ 52. Fпи 53. * 54. Fsqr 55. * 56. B/0.
Контрольный пример: в регистр 1 нужно записать номер начальной ступени (например, 8, что соответствует "до" второй октавы, П1), в Р2 - значение сигма (1 П2), в Р3 - значение мю (0 П3), в РД - любое число от 0 до 1 (0.75 ПД), В/0, С/П. На индикаторе читаем номер очередной ступени "7", С/П, "6", С/П... Если продолжить пример, то последовательность будет соответствовать приведенному нотному примеру.

Если придать этой цепочке звуков соответствующий ритм, то первый такт полученной мелодии воспроизведет мотив известной песни "Голубые города" - не правда ли?
Благодарим читателей В.Бирюкова из г.Тюмени - автора программы "Композитор" и нотного примера, А.Андреева из г.Ленинграда и других читателей, чьи письма были использованы при подготовке статьи.

Что общего межцу вычислительной техникой и археологией? По-своему судят об этом Я.Разливинсиий из Тулы и Н.Дорош из поселка Лельчицы Гомельской области.

ЛАБИРИНТ
Лабиринты, публикуемые в развлекательных разделах популярных журналов, отличаются тем, что читатель, ищущий путь к выходу, видит перед собой план лабиринта. В реальном лабиринте приходится двигаться, не имея никакого представления о его плане. Предлагаемая игра в этом смысле весьма приближена к реальности.
Лабиринт представляет собой разграфленное поле размером 7*9 клеток, некоторые из которых заняты. Выход - через одну из клеток девятого ряда, достижение которого означает успешное окончание игры. Начальное положение показывается на индикаторе в виде 204 (второй ряд, четвертый столбец). Так в виде трехзначного числа на индикатор в дальнейшем выводится положение блуждающего по лабиринту после каждого его шага. Направление шага задается нажатием одной из цифровых клавиш: 8 - вперед, 2 - назад, 4 - влево, 6 - вправо.

Например, на индикаторе было число 305. Мы хотим продвинуться вперед и нажимаем клавиши 8 С/П. Если в ответ на индикаторе появится 405, значит, мы действительно продвинулись вперед. Если же опять появилось 305, мы остались на прежнем месте, расположенная впереди клетка занята, и это следует показать штриховкой на плане лабиринта. Нужно искать обходной путь.
У нашего лабиринта есть еще и подвал - другой лабиринт размером 6*9 клеток. Попав в безвыходный
тупик, мы можем опуститься в подвал (если клетка внизу не занята), постараться пройти часть пути там и, выйдя наверх (если верхняя клетка свободна), продолжать путь к выходу.

Координаты подвальных клеток выражаются трехзначными числами со знаком минус. Перемещения по вертикали, с этажа на этаж, требуют нажатия клавиши 0. Пусть мы в подвале, в клетке с координатами -702 и захотели подняться наверх. Нажимаем 0 С/П. Появление 702 говорит об успехе, -702 о неуспехе этого шага: клетка наверху занята, это следует показать штриховкой на плане подвала.
План лабиринта определяется некоторым случайным числом от 10 до 100, которое вводится в калькулятор в начале игры. Начальная клетка 204 может оказаться занятой сразу по выходе из нее. Может также оказаться, что все пути из начальной точки - тупиковые.
00. Fsqr 01. Flg 02. 9 03. П0 04. x-y 05. F10X 06. ^ 07. ВП
08. 7 09. КП^ 10. x-y ll. ^ 12. ПА 13. ВП 14. FL0 15. 05 16. 1 17. П0 18. 2 19. ПА 20. 4 21. ПВ 22. ИПА 23. ВП 24. 2 25. ИПВ 26. + 27. ИП0 28. * 29. С/П 30. Fx!=0 31. 60 32. 3
33. 8 34. + 35. ПД 36. 0 37. ^ 38. 1 39. КБПД 40. /-/ 41. 0 42. /-/ 43. КНОП 44. x-y 45. КНОП 46. ИПА 47. + 48. x-y 49. ИПВ 50. + 51. ПП 52. 74 53. Fx>=0 54. 22 55. F() 56. ПА 57. ИПС 58. БП 59. 21 60. ИП0 61. /-/ 62. П0 63. ИПА 64. ИПВ 65. ПП 66. 74 67. Fx<0 68. 22 69. ИП0 70. /-/ 71. П0 72. БП 73. 22 74. ПС 75. x-y 76. ПД 77. ^ 78. КИПД 79. ИПС 80. F10X 81. / 82. ИП0 83. 2 84. + 85. / 86. ПД 87. КИПД 88. F() 89. ИПД 90. - 91. 2 92. F1/x 93. - 94. В/0.
Адреса 00-15: получение "плана" лабиринта; его задают числа a1..... a9, образуемые из начального случайного числа и рассылаемые по регистрам Р1-Р9. 16-21: формирование координат начальной клетки. 22-29: показ координат клетки в виде m0n, где m координата по направлению "вперед-назад", n - по направлению "вправо-влево". 30-31: проверка "переход на этаж?" и переход на адрес 60 в случае "да". 32-50: формирование координат клетки назначения по заданному направлению перемещения. 51-59: проверка "занята ли клетка назначения?", выполняемая обращением к подпрограмме (см. ниже); если клетка занята, отсылка на адрес 22 для демонстрации неизменившихся координат; если не занята - формирование новых координат. 60-73: проверка "занята ли клетка подвала?", выполняемая обращением к той же подпрограмме, с последующим аналогичным преобразованием координат. 74-94: подпрограмма, позволяющая проверить, занята ли клетка,- деление числа am (см. выше) на 10**n с различными коэффициентами для разных этажей; клетка с координатами m0n считается занятой или незанятой в зависимости от того, какова по сравнению с 0.5 дробная часть частного.
Инструкция. Ввести программу, набрать случайное число, нажать В/0 С/П. На индикаторе - число 204. Нажать цифровую клавишу, задающую перемещение, затем С/П. На индикаторе - координаты местонахождения.
Контрольный пример (см. рисунок) определяется начальным случайным числом 97.123456.
С.ГЕТА (г.Таллин)
ЭКСПЕРИМЕНТ НА ЭВМ
Четыре месяца назад мы приобрели в магазине "Электроника" в Москве бытовой компьютер "БК-0010", и с тех пор сын и жена заболели "компьютерной болезнью". (Я ею болен уже 15 лет, как говорят, по долгу службы и велению сердца).
Для тех, кто еще не знает, что это за ЭВМ, приведу ее очень краткое описание. Внешне это пластмассовая прямоугольная коробка с размерами 36*25*4см, на верхней стороне которой помещена клавиатура, подобная той, что на пишущих машинках (только в компьютере каждая клавиша может нести до шести различных знаков). В качестве дисплея используется телевизор, в качестве внешнего запоминающего устройства для хранения программ и данных - кассетный магнитофон "Электроника-302". Программировать задачи можно как на языке "Фокал" (именно на нем составлены приводимые мною программы), так и в машинных кодах. Информация выводится на дисплей в виде алфавитно-цифровых и графических символов либо по 64, либо по 32 символа в строке.
Для чего нам дома ЭВМ и что мы с ней делаем? Этот вопрос нам задают многие знакомые, и я постараюсь частично на него ответить, хотя сделать это нелегко. Чем больше ты узнаешь о машине и делаешь программ, тем больше хочется узнать и сделать.
Причины, по которым человека охватывает "компьютерная болезнь", можно разбить на две группы: эмоциональные и рациональные. Первая группа связана с удовлетворением его творческих и интеллектуальных потребностей. Программирование - увлекательнейшая игра, дающая возможность думать, изобретать, созидать. Несказанное чувство удовлетворения испытываешь, когда заставишь машину сделать то, что задумал. При этом не всегда важно, имеет ли программа какое-либо практическое применение. Важно, что ты узнал что-то новое, чему-то научился. Примерами таких программ являются созданные моим пятнадцатилетним сыном модель машины Поста, модель игры "Жизнь" ("Эволюция"), просто различные картинки.
Вторая группа связана с практическим применением машины в быту, учебе, работе, отдыхе. Что касается непосредственно быта - скажем, управления варкой супа или стиральной машиной, то реализация подобных программ весьма проблематична, хотя машина имеет соответствующие возможности. А вот помочь составить меню и предложить конкретные рецепты в зависимости от имеющихся у вас продуктов она вполне может. Компьютер также может быть полезен при планировании и анализе семейного бюджета.
Очень большим подспорьем служит ЭВМ в учебе школьников и студентов. Не считая того, что знание программирования само по себе весьма полезно и даже необходимо для современного человека, учебные программы позволяют зрительно представить явления, происходящие в природе и технике, провести в короткое время множество вычислительных экспериментов, исследуя какой-либо процесс.

Приведу две простые программы на эту тему и результаты их работы, выведенные на экран телевизора. Первая программа отображает картину интерференции волн двух когерентных источников колебаний. Это примерно то, что можно увидеть, бросив в воду одновременно два одинаковых камешка на небольшом расстоянии друг от друга. Программа строит картину по точкам. Если разность расстояний от точки до источников волн кратна условной длине волны, точка выделяется светлым крестом. Построение законченной картины требует немало времени, около 30 минут. Зато вторая программа работает практически мгновенно. Она предназначена для исследования траектории тела в вязкой среде, движущегося с заданной начальной скоростью под действием силы тяжести. Решается система дифференциальных уравнений
d2x/dt2=-adx/dt;
d2y/dt2=-ady/dt-b,
и результаты решения отображаются на дисплее. Условия варьируются, и за несколько минут возникает широкий спектр траекторий - от классической параболы (а=0) до круто загибающейся книзу кривой, соответствующей высокому сопротивлению среды.

Домашняя ЭВМ может быть полезна и физикам, и лирикам. Жаль только, что пока еще так редко она появляется в продаже.
И.ЛЬВОВ (г.Москва)
[ У КНИЖНОЙ ПОЛКИ
"Справочник по расчетам на микрокалькуляторах" - новая книга В.П.Дьяконова (М., Наука, 1985г.). Его сравнительно высокий тираж (220000экз.) позволяет надеяться, что 260 программ, собранных в книге, пополнят библиотеку многих энтузиастов программирования на микрокалькуляторах типа "Электроника Б3-34" - научных работников, инженеров, студентов вузов и техникумов.
Существенную помощь окажет справочник владельцам программируемых микрокалькуляторов "TI-58C" и "TI-59". Вторая глава книги и приложения содержат инструкции по применению встроенной библиотеки цифрового магнитофона и печатающего устройства, которыми могут комплектоваться эти машинки. Заинтересованный читатель также найдет в книге несколько эффективных программ из справочника А.Н.Цветкова и В.А.Епанечникова "Прикладные программы для "Электроники Б3-34", "МК-56", "МК 54"".
Пользование справочником несколько затрудняют опечатки и неточности. Так, на стр.20 предлагаются несуществующие команды KL0M, KL1M, KL2M, KL3M; программа 3.2 дает неверный результат для некоторых значений аргумента; глава шестая, посвященная вычислению специальных функций, практически не содержит указаний о точности результатов и допустимых диапазонах изменения аргументов и т.п. Отдельные программы неоптимальны. ]
ГОДИТСЯ ЛЮБОЙ МАГНИТОФОН
Вот уже несколько лет я использую программируемый калькулятор "Электроника Б3-34" для разных расчетов, в том числе и для обработки экспериментальных данных. Большие трудности создает при этом ограниченность памяти калькулятора.
Но вот в продаже появился бытовой компьютер "БК-0010". Покупка его сулила массу преимуществ: скорость более 100 операций в секунду, возможность запомнить более полутора тысяч чисел и, наконец, долгожданная возможность записать программу и данные на магнитофон и не вводить их заново при каждом включении ЭВМ. Запись на магнитную ленту позволяет накапливать библиотеку программ и обмениваться ими с другими владельцами "БК".
Магнитофон (правда, не имеющий линейного выхода, зато имеющий счетчик метража) у меня уже был, однако возникло непредвиденное затруднение. Согласно инструкции, "БК-0010" работает с магнитофоном одной единственной марки - "Электроника-302". Покупать второй магнитофон было нелогично, и я решил попробовать использовать свой. Приложив определенные усилия, я убедился, что "БК-0010" может работать практически с любым магнитофоном - достаточно лишь сделать соответствующий соединительный кабель. Я использую кабель, схема которого приведена на рисунке. Основное условие надежного считывания программы с магнитной ленты - достаточно большая (около 0.5 вольта) амплитуда сигнала. Она устанавливается регулятором громкости.

М.МАКСИМОВ (г.Москва)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Обратите внимание на одну тонкость. Конечно, "машинное время" за прошедшие 40 лет подешевело почти до нуля, но стоимость "нестандартных программ" выросла почти до бесконечности.
7/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ДЕВЯТОЕ, завершающее цикл, предметом которого было обучение работе на программируемых микрокалькуляторах. О границах сферы их применения рассказывает доктор технических наук Я.К.ТРОХИМЕНКО, которым (в соавторстве с кандидатом технических наук Ф.Д.Любичем) написано несколько справочников и популярных книг о программируемых микрокалькуляторах.
Каждому из нас приходится считать. Простейшие вычисления мы выполняем мысленно, но уже при арифметических действиях над многозначными числами обращаемся к авторучке. Если такие операции, особенно умножение и деление, приходится выполнять часто, то целесообразно купить простейший микрокалькулятор.
Приобретение программируемого микрокалькулятора обеспечит возможность успешно решать практически все домашние вычислительные задачи. Но самое главное, ради чего и ведется речь,- программируемый микрокалькулятор способен стать умелым и надежным помощником для работников самых различных специальностей.
Правда, у специалиста, которому доступны различные вычислительные средства, неизбежно возникает вопрос: какие задачи стоит решать на программируемом калькуляторе? Ответ связан со словом "стоит", прямо указывающим на стоимость применения калькулятора. Именно экономические критерии, хотя об этом мы часто забываем, определяют целесообразность создания и применения любых технических средств.
Все вычислительные задачи сводятся к последовательности арифметических операций и могут быть решены (по крайней мере в принципе) с помощью карандаша и бумаги. Однако по мере усложнения задач быстро возрастает количество необходимых операций. Соответственно увеличивается стоимость рабочего времени, затрачиваемого специалистом на получение результата. В этом случае использование даже простейших вычислительных средств, сокращающих затраты времени, дает значительный экономический эффект.
В то же время обращение к ЭВМ окупится лишь тогда, когда с ее помощью данную задачу можно решить дешевле, чем другими способами, например, на вычислительной машине другого типа. По этой причине в каждом поколении ЭВМ имеются типы с различной производительностью, и еще в первом (ламповом) поколении были созданы простейшие машины, названные калькуляторами и явившиеся дальними "предками" современных программируемых микрокалькуляторов.
Стоимость использования ЭВМ оценивают по времени ее работы, необходимому для решения задачи. Стоимость часа машинного времени несложно определить, поделив на расчетный срок службы машины все затраты на ее приобретение и эксплуатацию. Час машинного времени наиболее распространенных стационарных ЭВМ третьего (на интегральных компонентах) поколения стоит от нескольких десятков до нескольких сотен и даже тысяч рублей в зависимости от вычислительных возможностей машины. Стоимость часа машинного времени массовых программируемых микрокалькуляторов без внешней памяти, определяемая стоимостью покупки, ремонта и питания, например, за семилетний срок амортизации составляет около 10 копеек.
Стационарные ЭВМ, машинное время которых недешево, окупаются лишь при практически непрерывном решении последовательности достаточно сложных задач. Для этого необходимо иметь запас (пакет) соответствующих программ, выполняемых по очереди. При таком пакетном режиме результат решения конкретной задачи, вычисляемый машиной за несколько минут или даже секунд, заказчик получит через несколько часов или даже дней. Следует также упомянуть, сколь труден прямой доступ заказчика к таким машинам, сколь значительны затраты времени обслуживающего персонала иа составление нестандартных программ, отсутствующих в машинной библиотеке, и затраты машинного времени на их отладку.
Время, в течение которого приходится ожидать результата решения, существенно уменьшается при использовании ЭВМ в режиме разделения времени между оконечными устройствами ввода и вывода информации (терминалами), к которым имеют прямой доступ пользователи машины. Стоимость таких машин большая, и они окупаются лишь при решении с терминалов достаточно сложных задач по оптимальным программам.
Таким образом, стационарные ЭВМ при любом режиме работы являются коллективными вычислительными средствами, предназначенными для решения достаточно сложных задач. Между тем каждый член коллектива специалистов встречается с множеством повседневных неотложных задач, решение которых (в связи с их относительной простотой) на стационарных и даже современных персональных ЭВМ экономически невыгодно. Именно для решения таких вычислительных задач и предназначены программируемые микрокалькуляторы.
Их применение практически всегда выгодно, если для получения результата с их помощью требуется не более нескольких десятков минут. Наиболее экономичны здесь вычисления по заданным формулам с помощью одной или даже нескольких программ. Относительно быстро на калькуляторах типа "Электроника Б3-34" и аналогичных ему вычисляются многочлены от вещественного и комплексного аргумента с максимальной степенью соответственно 13 и 10. Достаточно удобно применение программируемого микрокалькулятора для решения большинства типовых математических задач, к последовательности которых сводятся практические расчеты: имеется в виду численное интегрирование, решение дифференциальных уравнений первого порядка (например, методом Рунге-Кутта, используемым и "большими" машинами) и т.п. Удобно и экономически выгодно применение программируемых микрокалькуляторов для аппроксимации с требуемой точностью различных специальных функций без обращений к таблицам и номограммам.
Решение нелинейных уравнений часто связано со значительными затратами машинного времени, но обычно и в этом случае рентабельно использовать программируемый микрокалькулятор. В качестве примера рассмотрим решение трансцендентного уравнения
exp(0.274*x)-2.831*x=0
с начальным приближением х=0.4 и абсолютной погрешностью Д не более 1e-3.
На машине "Мир-2" корень этого уравнения x=0.511577 с тремя верными цифрами вычисляется по стандартной программе методом Ньютона с параметром за 60 секунд. На программируемом микрокалькуляторе типа "Электроника Б3-34" это же уравнение решается с той же точностью (х=0.511) методом простых итераций за 40 секунд. Мы видим, следовательно, что даже без учета затрат времени на ввод программы стоимость решения рассмотренной задачи на калькуляторе оказывается в несколько сотен раз (примерно в 450) меньше, чем на машине "Мир-2" с ее относительно низкой стоимостью машинного времени.
В практических приложениях часто приходится решать системы уравнений. С помощью одной программы в автоматическом режиме на калькуляторе типа "Электроника Б3-34" можно решить систему, содержащую от двух до пяти линейных уравнений. При большем числе уравнений целесообразно использовать программу для преобразования системы по методу Жордана-Гаусса, не содержащую обратного хода. В этом случае для системы из n уравнений требуется вычислить и записать n**2(n+1)/2 чисел, из которых п последних являются искомыми корнями. При этом на получение очередного числа затрачивается менее 20 секунд. Для решения, например, системы из шести линейных уравнений в этом случае при отсутствии ошибок в считывании и записи потребуется около 50 минут.
Для получения тех же результатов на машине "Мир-2" по стандартной программе требуется только около 21 минуты, но с учетом стоимости машинного времени использование программируемого микрокалькулятора и тут оказывается экономически значительно более выгодным даже при учете рабочего времени пользователя.
В подобных сравнениях могли бы выступать и большие ЭВМ других типов, но и без дальнейших пояснений очевидно: на программируемом микрокалькуляторе стоит решать все задачи, которые нельзя решить дешевле другими способами. Опыт ряда инженерных коллективов свидетельствует о том, что в среднем свыше 90 процентов задач инженерного расчета целесообразно решать на программируемых микрокалькуляторах без обращения к более дорогим ЭВМ. Опыт свидетельствует также и о том, что близорукое "престижное" увлечение высокопроизводительными ЭВМ, аналогичное "стрельбе из пушек по воробьям" без использования такого "личного оружия" специалиста, каким являются калькуляторы, приводит к значительным явным или, еще чаще, скрытым экономическим потерям.
Естественно, эффективное использование программируемых микрокалькуляторов возможно лишь в том случае, когда их пользователи освоили программирование, методы вычислительной математики и располагают достаточно полной библиотекой оптимальных программ для решения типовых задач. Многие пользователи добиваются этого самостоятельно, но гораздо больший эффект дает обучение. Затраты на него, как показывает опыт ряда технических вузов, полностью окупаются. Студенты-первокурсники, прошедшие такое обучение в объеме 30-40 лекционных часов и 20-30 часов практических занятий под руководством опытных преподавателей, в дальнейшем успешно используют программируемые микрокалькуляторы для решения достаточно сложных задач не только в стенах вуза, но и после его окончания. При этом существенно упрощается последующее изучение алгоритмических языков ЭВМ, а привычка эффективно использовать ограниченные ресурсы памяти калькулятора оказывается весьма полезной при решении сложных задач на больших ЭВМ.
Следует подчеркнуть, что по экономическим показателям и портативности программируемые микрокалькуляторы (несмотря на расширяющееся внедрение персональных ЭВМ) еще долго будут вне конкуренции со стороны ЭВМ других классов при решении относительно простых задач, не требующих вывода информации в графической форме. Это обстоятельство особенно важно учитывать при постановке изучения основ информатики в средней школе, требующей в масштабе всей страны колоссальных затрат на вычислительную технику и ее эксплуатацию.
Точности вычислений ни микрокалькуляторах посвящает свое выступление кандидат технических наук М.И.ПЕТРОВ.
Мы получили результат вычислений на микрокалькуляторе. Исходя из него мы делаем какие-то выводы, предположения, применяем его в нашей практической работе. Для того чтобы правильно использовать или истолковать результат, необходимо знать достоверность проведенных расчетов, выявить ошибки, которые могли повлиять на точность наших вычислений, оценить погрешность полученного результата.
Источниками погрешностей и ошибок при вычислении могут быть недостаточно точное отображение реальных явлений их математической моделью (погрешности модели), приближенное знание величин, входящих в условие задачи (погрешности исходных данных), применение приближенных расчетных формул вместо точных (методические погрешности), особенности работы операционного устройства микрокалькулятора (операционные погрешности).
Все это приводит к тому, что результат вычислений а всегда является приближенным, отличается от точного значения а* искомой величины. Абсолютная величина их разности называется истинной абсолютной погрешностью.
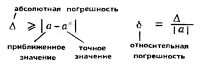
Разумеется, не зная искомую величину точно (иначе зачем ее вычислять?), мы не можем назвать истинную погрешность наших вычислений. Остается лишь оценивать ее заведомо превосходящим числом. Это число обычно обозначают прописной греческой буквой Дельта и называют абсолютной погрешностью приближенной величины а: ее отношение к абсолютной величине |a| именуют относительной погрешностью и обозначают строчной греческой буквой дельта.
Оценка истинной погрешности становится достовернее, если принять число Д достаточно большим. Но практическая ценность оценки при этом, конечно, снижается. Так возникает задача: анализируя процесс получения приближенного результата, оценить его отклонение от истинного по возможности меньшим числом Д, называемым в таком случае предельной абсолютной погрешностью.
Если такая оценка согласуется с допустимой точностью расчета, то приближенный результат можно использовать на практике как точный. Если не согласуется - встает новая задача: повысить точность вычислений.
Эти задачи и будут здесь рассмотрены. Но прежде, чем приступить к их рассмотрению, сделаем несколько замечаний.
На практике точность вычислений чаще оценивают относительной погрешностью, но нередко удобной бывает и абсолютная. Выбор определяется существом проблемы, для решения которой ведется расчет. Отметим, что абсолютная погрешность - величина размерная и размерность у нее та же, что у определяемой величины. Относительная же погрешность - величина безразмерная.
Числа, с которыми оперирует любая вычислительная машина, и микрокалькулятор также, вводятся в нее и выводятся в десятичном представлении. Если погрешность Д не превышает половины единицы некоторого n-ного разряда (Д<=0.5e-n), то все числа в целой части числа и n первых слева цифр в дробной части числа называют верными.
Поскольку величина Д служит лишь оценкой погрешности, не имеет смысла приводить ее с большой точностью. Обычно ее округляют до одной-двух значащих цифр: x=6.72+/-0.01, y=420.52+/-0.15 и т.д. Две значащие цифры в погрешности целесообразно оставлять лишь тогда, когда первая значащая цифра равна 1 или 2 (например, если Дх=0.15, то, округлив погрешность до Дх=0.2, мы весьма сильно изменим ее). Последняя значащая цифра результата вычислений должна быть величиной того же порядка, что и погрешность. Скажем, если абсолютная погрешность составляет 0.05, а на индикаторе микрокалькулятора мы получили число 84.359265, то результат следует записать x=84.36+/-0.05.
ПОГРЕШНОСТЬ МОДЕЛИ. Совокупность факторов реального физического явления невозможно отразить в его математической модели. Чем больше факторов мы учитываем, тем сложнее анализ явления и расчет по его математической модели. Поэтому принимают различные условия и допущения, упрощающие решение задачи.
В небольшой статье трудно дать какие-то общие правила для составления математических моделей ввиду большого разнообразия явлений природы. Поэтому здесь мы ограничимся лишь словами академика А.Н.Крылова, полезными для начинающего программиста: "Сколько бы ни было точно математическое решение, оно не может быть точнее тех приближенных предпосылок, на коих оно основано. Об этом часто забывают, делают вначале какое-нибудь грубое приближенное предположение или допущение, часто даже не оговорив таковое, а затем придают полученной формуле гораздо большее доверие, нежели она заслуживает".
ПОГРЕШНОСТИ ИСХОДНЫХ ДАННЫХ. Вычислителю, как правило, приходится работать с приближенными числами, полученными при проведении экспериментов, при обработке статистических данных, при округлении результатов предыдущих расчетов и т.п. При выполнении любой математической операции над приближенными числами присущие им погрешности обусловливают погрешности результата, причем для каждой операции по-своему (см. таблицу).

Внимательное рассмотрение таблицы подсказывает, что один из самых коварных источников погрешностей - вычитание близких величин. Для примера вычтем из числа x1=110.5+/-0.1 число x2=110.4+/-0.1. Результат: 0.1+/-0.2. Как видим, относительная погрешность равна 0.2/0.1 и составляет 200 процентов, что неприемлемо ни при каком разумном приближении.
Нужно также заметить, что при вычислении элементарных функций на микрокалькуляторе аргумент может попадать в "опасные зоны", где его незначительная относительная погрешность вызывает гораздо более высокую относительную ошибку в определении функции. Так происходит, например, при вычислении arcsin(x) при x, близком к единице.
В подобных случаях говорят о высокой чувствительности результатов операции к погрешностям ее участников (операндов). Кстати, само слово "чувствительность" - строгий математический термин. Так называют коэффициенты в представлении относительной погрешности результата операции через относительные погрешности операндов.
При вычислениях на микрокалькуляторе погрешность конечного результата можно определить шаг за шагом, учитывая погрешности каждой выполненной операции. Так, можно выяснить, насколько точными должны быть исходные данные, чтобы обеспечить приемлемую точность результата. Излишняя точность почти всегда оказывается ненужной. Каждая лишняя цифра в исходных данных увеличивает время их ввода в калькулятор, а следовательно, и общее время счета, не делая результат более точным. Длинный ряд недостоверных цифр в полученном числе может только вводить в заблуждение. "Помните, что каждая неверная цифра - это ошибка, всякая лишняя цифра - это пол-ошибки",- уместно снова процитировать слова академика Л.Н.Крылова.
Обычно округление чисел при их сложении и вычитании производят таким образом, чтобы в них оставалось на один десятичный разряд больше, чем имеется верных знаков в наименее точно заданном числе (если более уточнить его нельзя) или предписано необходимой точностью результата вычислений.
Если при вычислениях не требуется строгий расчет погрешности, то можно рекомендовать такие правила:
- прb сложении и вычитании чисел в результате следует сохранять столько десятичных знаков, сколько их имеет число с наименьшим количеством верных знаков;
- при умножении и делении чисел в результате следует сохранять столько значащих цифр, сколько их имеет число с наименьшим количеством верных значащих цифр;
- при возведении числа в квадрат или куб в результате необходимо сохранить столько значащих цифр, сколько верных значащих цифр в основании степени;
- при извлечении квадратного корня в результате необходимо сохранить столько же значащих цифр, сколько верных значащих цифр в подкоренном числе;
- при вычислении промежуточных результатов в них следует оставлять на одну цифру больше, чем рекомендуют предшествующие правила, а в окончательном результате эту цифру отбросить.
Использование этих правил при расчетах на микрокалькуляторе, конечно, не означает, что надо округлять каждый промежуточный результат. Однако их целесообразно учитывать при ручных расчетах, при вводе исходных данных для решения задачи по программе и при оценке точности окончательного результата.
ОПЕРАЦИОННЫЕ ПОГРЕШНОСТИ обычно возникают из-за ограниченного количества разрядов мантиссы вводимых чисел при их сложении и вычитании, из-за недостаточного числа разрядов в операционных регистрах при умножении и делении чисел, из-за недостаточной точности, с которой вычисляются элементарные функции, и т.п.
Округление результата той или иной математической операции, когда его приходится укладывать в восьмиразрядную сетку калькулятора, производится "Электроникой Б3-34" по-разному - в частности простым отбрасыванием неукладывающихся разрядов. Другие способы округления, которым также "обучен" наш калькулятор, более точны. Они применяются при сложении и вычитании чисел. Однако если приходится оценивать погрешность округления, то для достоверности оценки лучше полагать ее соответствующей отбрасыванию, то есть равной единице самого младшего из разрядов, отображаемых на индикаторе.
Погрешности элементарных функций, вычисляемых на микрокалькуляторе, приведены в руководстве по его эксплуатации. Особенно большие относительные погрешности, как правило, возникают при вычислении sqr(x) и x**y, поэтому многократное применение таких команд в программе может привести к существенной ошибке.
МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ. Применение приближенных формул вместо точных позволяет проводить на микрокалькуляторе расчет достаточно сложных математических выражений. Этот прием основан на замене функций их разложением в ряды, замене производной - разностью, интеграла - суммой и т.д.
Разумеется, используя приближенные формулы, надо всегда четко знать диапазон аргумента, для которого они применимы, и точность вычисления по ним. Обычно такие сведения даются в справочниках. В общем случае при вычислениях на микрокалькуляторе погрешность метода целесообразно выбирать такой, чтобы она была в несколько раз меньше погрешности исходных данных.
Порою расчет по сложной точной формуле удается заменить расчетом по более простой, но применяемой многократно, в процессе последовательных приближений.
Когда вычисления на микрокалькуляторе ведутся с помощью метода последовательных приближений, случается, что при достижении определенного количества верных знаков дальнейшие приближения в силу операционных погрешностей начинают последовательно принимать несколько повторяющихся неодинаковых значений. Эти повторяющиеся результаты различаются между собой на довольно значительную величину. Точность, меньшая этой разности, уже недостижима для избранного метода.
Подобная неприятность нередко затрудняет вычисление рядов и интегралов. Теоретически точность результата должна неограниченно расти, когда увеличивается число слагаемых ряда или число отрезков, на которые разбит промежуток интегрирования. Но при этом увеличивается и число выполняемых операций, а вместе с ними растет и общая операционная погрешность, так что и тут сколь угодно высокая точность результата оказывается недостижимой в рамках избранного метода и алгоритма.
Часто при вычислениях функцию заменяют ее разложением в ряд и оценивают точность вычислений по последнему учтенному члену разложения. Следует заметить, что этот прием не всегда дает приемлемый результат. Вычислять суммы рядов необходимо с особой осторожностью. Например, мы хотим найти сумму ряда
S=1+1/2+1/3+1/4+...,
забыв, что она равняется бесконечности. Тогда, желая получить точность, равную 0.01, при описанном подходе к ее оценке берут последний член в сумме ряда равным 1/100 и получают при расчете на микрокалькуляторе S=5.1873776. Однако ни о какой точности результата при таком подходе здесь вообще говорить нельзя, так как получается, что сумму 5.19 отделяет от бесконечности всего лишь число, близкое к 0.01. Это происходит потому, что значение суммы нарастает очень и очень медленно.
СОВОКУПНАЯ ОЦЕНКА результата вычислений, как видим, требует учитывать не только погрешности всех видов (методические и операционные, погрешности модели и исходных данных), но и их взаимосвязи. Даже в простых на первый взгляд случаях это может оказаться делом нелегким, а достоверная оценка - неочевидной.
Для примера найдем относительную погрешность величины K, вычисленной по формуле K=x1**2*x4/(x2*x3**2). Пусть x1=1.8+/-0.2; x2=2.8+/-0.3; х3=1.1+/-0.1; x4=0.45+/-0.04. Тогда дK = 2*0.2/1.8 + 0.3/2.8 + 2*0.1/1.1 + 0.04/0.45 = 0.6. Относительная погрешность результата составила почти 60 процентов, хотя относительная ошибка каждого из чисел, участвующих в вычислении, находится в пределах между 9 и 11 процентами.
В то же время бывает и так, что погрешности чисел, участвующих в том или ином вычислении, взаимно компенсируются. Учет этого явления вполне возможен, но он требует довольно сложных математических средств. Для ознакомления с ними и с различными другими вопросами приближенных вычислений можно порекомендовать книги Дж.Тейлора "Введение в теорию ошибок" (М, Мир, 1985), Н.Н.Калиткина "Численные методы" (М., Наука, 1978).
ПОВЫШЕНИЕ ТОЧНОСТИ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ. Здесь имеет смысл перечислить лишь несколько простых рецептов, не вдаваясь в их математическое обоснование.
Погрешность суммы нескольких чисел при расчете на микрокалькуляторе уменьшается, если начинать суммирование с меньших по величине слагаемых. Определим ради примера сумму трех чисел, складывая их в том порядке, как онн записаны: S = 200013.11 + 200.05399 + 106.51401 = 200319.67. Проводя суммирование в обратном порядке, от третьего слагаемого до первого, получим более точное значение S=200319.68.
Если складывается достаточно много чисел, то их лучше разбить на группы из чисел, близких по порядку величины, провести суммирование в группах по только что данной рекомендации, после чего полученные суммы сложить, начиная с меньшей.
Как видим, переместительный закон сложения не выполняется при вычислениях на микрокалькуляторе: сумма меняется от перемены мест слагаемых. Дальнейшие примеры покажут нам, что при калькуляторных расчетах не выполняются и другие законы арифметики: сочетательные законы сложения и умножения, переместительный закон умножения, распределительный закон умножения относительно сложения и вычитания. Причины подобных парадоксов - в округлении промежуточных результатов, когда многозначные числа не умещаются в разрядную сетку индикатора. Из-за этой причины и оказывается небезразличным порядок, в котором следует выполнять арифметические операции, чтобы результат был возможно точнее.
Вычисляя разность двух чисел (особенно близких по величине), целесообразно вынести за скобки их общий множитель. Для примера вычислим на нашем микрокалькуляторе величину Р = 6.250001*16 - 25.000003*4 = 1e-5. Вынесем число 4 за скобки и получим более точный результат: Р = 4*(6.250001*4 - 25.000003) = 4e-6.
Уменьшить погрешность разности позволяют преобразования:

Здесь е - малое по сравнению с а число.
Возьмем не совсем обычное квадратное уравнение x**2+1000*x+1=0. Попытаемся найти наименьший по величине корень этого уравнения. Воспользовавшись известной формулой и считая на микрокалькуляторе, получаем:
х1 = -500+sqr(250000-1) = -500+499,99899 = -1.01e-3.
Подставляя значение корня в уравнение, убеждаемся, что решение выполнено с большой погрешностью. Это произошло из-за того, что в примененной нами формуле для x1 присутствует разность двух близких чисел 500 и sqr(250000-1). Значительно более точное значение корня можно получить, если по только что данной рекомендации решение представить в виде:
х1 = -1/(sqr(250000-1)+500) = -1.000001e-3.
При перемножении нескольких чисел сначала надо умножить наибольший множитель на наименьший; из оставшихся сомножителей следует взять либо наибольший, либо наименьший, судя по тому, меньше или больше единицы абсолютная величина промежуточного результата. Если делятся друг на друга два произведения, то рекомендуется чередовать операции умножения и деления, выбирая ту или иную в зависимости от абсолютной величины очередного промежуточного результата, который может оказаться либо больше, либо меньше единицы.
Пренебрежение порядком счета в подобных случаях может привести к тому, что какой-нибудь промежуточный результат не сможет быть представленным на индикаторе с его двумя разрядами для чисел порядка. Если порядок превышает 99, то говорят о переполнении или машинной бесконечности; при этом калькулятор может остановиться, а может и продолжать счет - все зависит от многих конкретных обстоятельств. Если же порядок меньше минус 99, то говорят о машинном нуле. В этом случае калькулятор и впрямь в качестве результата операции записывает в регистр x нуль.
Например, найдем произведение четырех чисел
П = 2e-96 * 0.0001 * 3e95 * 1.4e10, перемножая их на микрокалькуляторе "Электроника Б3-34" в различном порядке:
2e-96 * 0.0001 * 3e95 * 1.4e10 = (0)
3e95 * 1.4e10 (ЕГГОГ) 2e-96 * 0.0001 = (840000)
3e95 * 2e-96 * 1.4e10 * 0.0001 = (840000).
В первом случае перемножение чисел 2e-96 * 0.0001 переводит микрокалькулятор в область машинного нуля, и окончательный результат оказывается равным нулю. Во втором случае перемножение чисел 3e95 * 1.4e10 приводит к машинной бесконечности, и при ручном счете на индикаторе появляется сигнал ошибки ЕГГОГ, однако при продолжении счета результат оказывается правильным. При вычислении по программе в этом случае остановки счета не происходит, и сигнал ошибки на индикаторе не высвечивается. В третьем случае сомножители расположены таким образом, что не возникает ни машинного нуля, ни машинной бесконечности.
Следует помнить, что особенно большие относительные погрешности возникают при вычислении sqr(x) и x**y. Этих операций надо по возможности избегать, изменяя алгоритм вычислений. Надо также следить за тем, чтобы аргумент функции не попадал в "опасные зоны", где ее чувствительность наиболее высока. Замена алгоритма при этом может увеличить число выполняемых операции, но, несмотря на это, погрешность конечного результата может снизиться.
Разумеется, расчетные формулы надо постараться преобразовать так, чтобы общее число операций было наименьшим. Общеизвестный пример такого рода связан с вычислением полинома, где наименьшее число операций обеспечивает схема Горнера.
Иногда для увеличения точности целесообразно комбинировать алгоритмы вычислений. Например, для достаточно быстрого вычисления n! можно использовать формулу Стирлинга:
n! = sqr(2*пи*n)*exp(-n)*n**n * (1 + 1/(12*n) + 1/(288*n**2) - ...).
Однако для значений n<=10 формула дает большую ошибку. Исправить положение можно, введя в программу счета округление результата до единиц, например, с помощью фрагмента 1 ВП 7 + FBx -.
Теперь программа при использовании трех членов в формуле Стирлинга дает точное значение n! для чисел от 1 до 9, а для больших значений n относительная ошибка не превосходит 5e-7. Время счета - всего около 20 секунд.
Так, подбирая удачный алгоритм, грамотно составляя программу вычислений, тщательно готовя исходные данные, контролируя накопление погрешностей, можно достичь желаемой точности результата.
7/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ДЕВЯТОЕ, завершающее цикл, предметом которого было обучение работе на программируемых микрокалькуляторах. О границах сферы их применения рассказывает доктор технических наук Я.К.ТРОХИМЕНКО, которым (в соавторстве с кандидатом технических наук Ф.Д.Любичем) написано несколько справочников и популярных книг о программируемых микрокалькуляторах.
Каждому из нас приходится считать. Простейшие вычисления мы выполняем мысленно, но уже при арифметических действиях над многозначными числами обращаемся к авторучке. Если такие операции, особенно умножение и деление, приходится выполнять часто, то целесообразно купить простейший микрокалькулятор.
Приобретение программируемого микрокалькулятора обеспечит возможность успешно решать практически все домашние вычислительные задачи. Но самое главное, ради чего и ведется речь,- программируемый микрокалькулятор способен стать умелым и надежным помощником для работников самых различных специальностей.
Правда, у специалиста, которому доступны различные вычислительные средства, неизбежно возникает вопрос: какие задачи стоит решать на программируемом калькуляторе? Ответ связан со словом "стоит", прямо указывающим на стоимость применения калькулятора. Именно экономические критерии, хотя об этом мы часто забываем, определяют целесообразность создания и применения любых технических средств.
Все вычислительные задачи сводятся к последовательности арифметических операций и могут быть решены (по крайней мере в принципе) с помощью карандаша и бумаги. Однако по мере усложнения задач быстро возрастает количество необходимых операций. Соответственно увеличивается стоимость рабочего времени, затрачиваемого специалистом на получение результата. В этом случае использование даже простейших вычислительных средств, сокращающих затраты времени, дает значительный экономический эффект.
В то же время обращение к ЭВМ окупится лишь тогда, когда с ее помощью данную задачу можно решить дешевле, чем другими способами, например, на вычислительной машине другого типа. По этой причине в каждом поколении ЭВМ имеются типы с различной производительностью, и еще в первом (ламповом) поколении были созданы простейшие машины, названные калькуляторами и явившиеся дальними "предками" современных программируемых микрокалькуляторов.
Стоимость использования ЭВМ оценивают по времени ее работы, необходимому для решения задачи. Стоимость часа машинного времени несложно определить, поделив на расчетный срок службы машины все затраты на ее приобретение и эксплуатацию. Час машинного времени наиболее распространенных стационарных ЭВМ третьего (на интегральных компонентах) поколения стоит от нескольких десятков до нескольких сотен и даже тысяч рублей в зависимости от вычислительных возможностей машины. Стоимость часа машинного времени массовых программируемых микрокалькуляторов без внешней памяти, определяемая стоимостью покупки, ремонта и питания, например, за семилетний срок амортизации составляет около 10 копеек.
Стационарные ЭВМ, машинное время которых недешево, окупаются лишь при практически непрерывном решении последовательности достаточно сложных задач. Для этого необходимо иметь запас (пакет) соответствующих программ, выполняемых по очереди. При таком пакетном режиме результат решения конкретной задачи, вычисляемый машиной за несколько минут или даже секунд, заказчик получит через несколько часов или даже дней. Следует также упомянуть, сколь труден прямой доступ заказчика к таким машинам, сколь значительны затраты времени обслуживающего персонала иа составление нестандартных программ, отсутствующих в машинной библиотеке, и затраты машинного времени на их отладку.
Время, в течение которого приходится ожидать результата решения, существенно уменьшается при использовании ЭВМ в режиме разделения времени между оконечными устройствами ввода и вывода информации (терминалами), к которым имеют прямой доступ пользователи машины. Стоимость таких машин большая, и они окупаются лишь при решении с терминалов достаточно сложных задач по оптимальным программам.
Таким образом, стационарные ЭВМ при любом режиме работы являются коллективными вычислительными средствами, предназначенными для решения достаточно сложных задач. Между тем каждый член коллектива специалистов встречается с множеством повседневных неотложных задач, решение которых (в связи с их относительной простотой) на стационарных и даже современных персональных ЭВМ экономически невыгодно. Именно для решения таких вычислительных задач и предназначены программируемые микрокалькуляторы.
Их применение практически всегда выгодно, если для получения результата с их помощью требуется не более нескольких десятков минут. Наиболее экономичны здесь вычисления по заданным формулам с помощью одной или даже нескольких программ. Относительно быстро на калькуляторах типа "Электроника Б3-34" и аналогичных ему вычисляются многочлены от вещественного и комплексного аргумента с максимальной степенью соответственно 13 и 10. Достаточно удобно применение программируемого микрокалькулятора для решения большинства типовых математических задач, к последовательности которых сводятся практические расчеты: имеется в виду численное интегрирование, решение дифференциальных уравнений первого порядка (например, методом Рунге-Кутта, используемым и "большими" машинами) и т.п. Удобно и экономически выгодно применение программируемых микрокалькуляторов для аппроксимации с требуемой точностью различных специальных функций без обращений к таблицам и номограммам.
Решение нелинейных уравнений часто связано со значительными затратами машинного времени, но обычно и в этом случае рентабельно использовать программируемый микрокалькулятор. В качестве примера рассмотрим решение трансцендентного уравнения
exp(0.274*x)-2.831*x=0
с начальным приближением х=0.4 и абсолютной погрешностью Д не более 1e-3.
На машине "Мир-2" корень этого уравнения x=0.511577 с тремя верными цифрами вычисляется по стандартной программе методом Ньютона с параметром за 60 секунд. На программируемом микрокалькуляторе типа "Электроника Б3-34" это же уравнение решается с той же точностью (х=0.511) методом простых итераций за 40 секунд. Мы видим, следовательно, что даже без учета затрат времени на ввод программы стоимость решения рассмотренной задачи на калькуляторе оказывается в несколько сотен раз (примерно в 450) меньше, чем на машине "Мир-2" с ее относительно низкой стоимостью машинного времени.
В практических приложениях часто приходится решать системы уравнений. С помощью одной программы в автоматическом режиме на калькуляторе типа "Электроника Б3-34" можно решить систему, содержащую от двух до пяти линейных уравнений. При большем числе уравнений целесообразно использовать программу для преобразования системы по методу Жордана-Гаусса, не содержащую обратного хода. В этом случае для системы из n уравнений требуется вычислить и записать n**2(n+1)/2 чисел, из которых п последних являются искомыми корнями. При этом на получение очередного числа затрачивается менее 20 секунд. Для решения, например, системы из шести линейных уравнений в этом случае при отсутствии ошибок в считывании и записи потребуется около 50 минут.
Для получения тех же результатов на машине "Мир-2" по стандартной программе требуется только около 21 минуты, но с учетом стоимости машинного времени использование программируемого микрокалькулятора и тут оказывается экономически значительно более выгодным даже при учете рабочего времени пользователя.
В подобных сравнениях могли бы выступать и большие ЭВМ других типов, но и без дальнейших пояснений очевидно: на программируемом микрокалькуляторе стоит решать все задачи, которые нельзя решить дешевле другими способами. Опыт ряда инженерных коллективов свидетельствует о том, что в среднем свыше 90 процентов задач инженерного расчета целесообразно решать на программируемых микрокалькуляторах без обращения к более дорогим ЭВМ. Опыт свидетельствует также и о том, что близорукое "престижное" увлечение высокопроизводительными ЭВМ, аналогичное "стрельбе из пушек по воробьям" без использования такого "личного оружия" специалиста, каким являются калькуляторы, приводит к значительным явным или, еще чаще, скрытым экономическим потерям.
Естественно, эффективное использование программируемых микрокалькуляторов возможно лишь в том случае, когда их пользователи освоили программирование, методы вычислительной математики и располагают достаточно полной библиотекой оптимальных программ для решения типовых задач. Многие пользователи добиваются этого самостоятельно, но гораздо больший эффект дает обучение. Затраты на него, как показывает опыт ряда технических вузов, полностью окупаются. Студенты-первокурсники, прошедшие такое обучение в объеме 30-40 лекционных часов и 20-30 часов практических занятий под руководством опытных преподавателей, в дальнейшем успешно используют программируемые микрокалькуляторы для решения достаточно сложных задач не только в стенах вуза, но и после его окончания. При этом существенно упрощается последующее изучение алгоритмических языков ЭВМ, а привычка эффективно использовать ограниченные ресурсы памяти калькулятора оказывается весьма полезной при решении сложных задач на больших ЭВМ.
Следует подчеркнуть, что по экономическим показателям и портативности программируемые микрокалькуляторы (несмотря на расширяющееся внедрение персональных ЭВМ) еще долго будут вне конкуренции со стороны ЭВМ других классов при решении относительно простых задач, не требующих вывода информации в графической форме. Это обстоятельство особенно важно учитывать при постановке изучения основ информатики в средней школе, требующей в масштабе всей страны колоссальных затрат на вычислительную технику и ее эксплуатацию.
Точности вычислений ни микрокалькуляторах посвящает свое выступление кандидат технических наук М.И.ПЕТРОВ.
Мы получили результат вычислений на микрокалькуляторе. Исходя из него мы делаем какие-то выводы, предположения, применяем его в нашей практической работе. Для того чтобы правильно использовать или истолковать результат, необходимо знать достоверность проведенных расчетов, выявить ошибки, которые могли повлиять на точность наших вычислений, оценить погрешность полученного результата.
Источниками погрешностей и ошибок при вычислении могут быть недостаточно точное отображение реальных явлений их математической моделью (погрешности модели), приближенное знание величин, входящих в условие задачи (погрешности исходных данных), применение приближенных расчетных формул вместо точных (методические погрешности), особенности работы операционного устройства микрокалькулятора (операционные погрешности).
Все это приводит к тому, что результат вычислений а всегда является приближенным, отличается от точного значения а* искомой величины. Абсолютная величина их разности называется истинной абсолютной погрешностью.

Разумеется, не зная искомую величину точно (иначе зачем ее вычислять?), мы не можем назвать истинную погрешность наших вычислений. Остается лишь оценивать ее заведомо превосходящим числом. Это число обычно обозначают прописной греческой буквой Дельта и называют абсолютной погрешностью приближенной величины а: ее отношение к абсолютной величине |a| именуют относительной погрешностью и обозначают строчной греческой буквой дельта.
Оценка истинной погрешности становится достовернее, если принять число Д достаточно большим. Но практическая ценность оценки при этом, конечно, снижается. Так возникает задача: анализируя процесс получения приближенного результата, оценить его отклонение от истинного по возможности меньшим числом Д, называемым в таком случае предельной абсолютной погрешностью.
Если такая оценка согласуется с допустимой точностью расчета, то приближенный результат можно использовать на практике как точный. Если не согласуется - встает новая задача: повысить точность вычислений.
Эти задачи и будут здесь рассмотрены. Но прежде, чем приступить к их рассмотрению, сделаем несколько замечаний.
На практике точность вычислений чаще оценивают относительной погрешностью, но нередко удобной бывает и абсолютная. Выбор определяется существом проблемы, для решения которой ведется расчет. Отметим, что абсолютная погрешность - величина размерная и размерность у нее та же, что у определяемой величины. Относительная же погрешность - величина безразмерная.
Числа, с которыми оперирует любая вычислительная машина, и микрокалькулятор также, вводятся в нее и выводятся в десятичном представлении. Если погрешность Д не превышает половины единицы некоторого n-ного разряда (Д<=0.5e-n), то все числа в целой части числа и n первых слева цифр в дробной части числа называют верными.
Поскольку величина Д служит лишь оценкой погрешности, не имеет смысла приводить ее с большой точностью. Обычно ее округляют до одной-двух значащих цифр: x=6.72+/-0.01, y=420.52+/-0.15 и т.д. Две значащие цифры в погрешности целесообразно оставлять лишь тогда, когда первая значащая цифра равна 1 или 2 (например, если Дх=0.15, то, округлив погрешность до Дх=0.2, мы весьма сильно изменим ее). Последняя значащая цифра результата вычислений должна быть величиной того же порядка, что и погрешность. Скажем, если абсолютная погрешность составляет 0.05, а на индикаторе микрокалькулятора мы получили число 84.359265, то результат следует записать x=84.36+/-0.05.
ПОГРЕШНОСТЬ МОДЕЛИ. Совокупность факторов реального физического явления невозможно отразить в его математической модели. Чем больше факторов мы учитываем, тем сложнее анализ явления и расчет по его математической модели. Поэтому принимают различные условия и допущения, упрощающие решение задачи.
В небольшой статье трудно дать какие-то общие правила для составления математических моделей ввиду большого разнообразия явлений природы. Поэтому здесь мы ограничимся лишь словами академика А.Н.Крылова, полезными для начинающего программиста: "Сколько бы ни было точно математическое решение, оно не может быть точнее тех приближенных предпосылок, на коих оно основано. Об этом часто забывают, делают вначале какое-нибудь грубое приближенное предположение или допущение, часто даже не оговорив таковое, а затем придают полученной формуле гораздо большее доверие, нежели она заслуживает".
ПОГРЕШНОСТИ ИСХОДНЫХ ДАННЫХ. Вычислителю, как правило, приходится работать с приближенными числами, полученными при проведении экспериментов, при обработке статистических данных, при округлении результатов предыдущих расчетов и т.п. При выполнении любой математической операции над приближенными числами присущие им погрешности обусловливают погрешности результата, причем для каждой операции по-своему (см. таблицу).

Внимательное рассмотрение таблицы подсказывает, что один из самых коварных источников погрешностей - вычитание близких величин. Для примера вычтем из числа x1=110.5+/-0.1 число x2=110.4+/-0.1. Результат: 0.1+/-0.2. Как видим, относительная погрешность равна 0.2/0.1 и составляет 200 процентов, что неприемлемо ни при каком разумном приближении.
Нужно также заметить, что при вычислении элементарных функций на микрокалькуляторе аргумент может попадать в "опасные зоны", где его незначительная относительная погрешность вызывает гораздо более высокую относительную ошибку в определении функции. Так происходит, например, при вычислении arcsin(x) при x, близком к единице.
В подобных случаях говорят о высокой чувствительности результатов операции к погрешностям ее участников (операндов). Кстати, само слово "чувствительность" - строгий математический термин. Так называют коэффициенты в представлении относительной погрешности результата операции через относительные погрешности операндов.
При вычислениях на микрокалькуляторе погрешность конечного результата можно определить шаг за шагом, учитывая погрешности каждой выполненной операции. Так, можно выяснить, насколько точными должны быть исходные данные, чтобы обеспечить приемлемую точность результата. Излишняя точность почти всегда оказывается ненужной. Каждая лишняя цифра в исходных данных увеличивает время их ввода в калькулятор, а следовательно, и общее время счета, не делая результат более точным. Длинный ряд недостоверных цифр в полученном числе может только вводить в заблуждение. "Помните, что каждая неверная цифра - это ошибка, всякая лишняя цифра - это пол-ошибки",- уместно снова процитировать слова академика Л.Н.Крылова.
Обычно округление чисел при их сложении и вычитании производят таким образом, чтобы в них оставалось на один десятичный разряд больше, чем имеется верных знаков в наименее точно заданном числе (если более уточнить его нельзя) или предписано необходимой точностью результата вычислений.
Если при вычислениях не требуется строгий расчет погрешности, то можно рекомендовать такие правила:
- прb сложении и вычитании чисел в результате следует сохранять столько десятичных знаков, сколько их имеет число с наименьшим количеством верных знаков;
- при умножении и делении чисел в результате следует сохранять столько значащих цифр, сколько их имеет число с наименьшим количеством верных значащих цифр;
- при возведении числа в квадрат или куб в результате необходимо сохранить столько значащих цифр, сколько верных значащих цифр в основании степени;
- при извлечении квадратного корня в результате необходимо сохранить столько же значащих цифр, сколько верных значащих цифр в подкоренном числе;
- при вычислении промежуточных результатов в них следует оставлять на одну цифру больше, чем рекомендуют предшествующие правила, а в окончательном результате эту цифру отбросить.
Использование этих правил при расчетах на микрокалькуляторе, конечно, не означает, что надо округлять каждый промежуточный результат. Однако их целесообразно учитывать при ручных расчетах, при вводе исходных данных для решения задачи по программе и при оценке точности окончательного результата.
ОПЕРАЦИОННЫЕ ПОГРЕШНОСТИ обычно возникают из-за ограниченного количества разрядов мантиссы вводимых чисел при их сложении и вычитании, из-за недостаточного числа разрядов в операционных регистрах при умножении и делении чисел, из-за недостаточной точности, с которой вычисляются элементарные функции, и т.п.
Округление результата той или иной математической операции, когда его приходится укладывать в восьмиразрядную сетку калькулятора, производится "Электроникой Б3-34" по-разному - в частности простым отбрасыванием неукладывающихся разрядов. Другие способы округления, которым также "обучен" наш калькулятор, более точны. Они применяются при сложении и вычитании чисел. Однако если приходится оценивать погрешность округления, то для достоверности оценки лучше полагать ее соответствующей отбрасыванию, то есть равной единице самого младшего из разрядов, отображаемых на индикаторе.
Погрешности элементарных функций, вычисляемых на микрокалькуляторе, приведены в руководстве по его эксплуатации. Особенно большие относительные погрешности, как правило, возникают при вычислении sqr(x) и x**y, поэтому многократное применение таких команд в программе может привести к существенной ошибке.
МЕТОДИЧЕСКИЕ ПОГРЕШНОСТИ. Применение приближенных формул вместо точных позволяет проводить на микрокалькуляторе расчет достаточно сложных математических выражений. Этот прием основан на замене функций их разложением в ряды, замене производной - разностью, интеграла - суммой и т.д.
Разумеется, используя приближенные формулы, надо всегда четко знать диапазон аргумента, для которого они применимы, и точность вычисления по ним. Обычно такие сведения даются в справочниках. В общем случае при вычислениях на микрокалькуляторе погрешность метода целесообразно выбирать такой, чтобы она была в несколько раз меньше погрешности исходных данных.
Порою расчет по сложной точной формуле удается заменить расчетом по более простой, но применяемой многократно, в процессе последовательных приближений.
Когда вычисления на микрокалькуляторе ведутся с помощью метода последовательных приближений, случается, что при достижении определенного количества верных знаков дальнейшие приближения в силу операционных погрешностей начинают последовательно принимать несколько повторяющихся неодинаковых значений. Эти повторяющиеся результаты различаются между собой на довольно значительную величину. Точность, меньшая этой разности, уже недостижима для избранного метода.
Подобная неприятность нередко затрудняет вычисление рядов и интегралов. Теоретически точность результата должна неограниченно расти, когда увеличивается число слагаемых ряда или число отрезков, на которые разбит промежуток интегрирования. Но при этом увеличивается и число выполняемых операций, а вместе с ними растет и общая операционная погрешность, так что и тут сколь угодно высокая точность результата оказывается недостижимой в рамках избранного метода и алгоритма.
Часто при вычислениях функцию заменяют ее разложением в ряд и оценивают точность вычислений по последнему учтенному члену разложения. Следует заметить, что этот прием не всегда дает приемлемый результат. Вычислять суммы рядов необходимо с особой осторожностью. Например, мы хотим найти сумму ряда
S=1+1/2+1/3+1/4+...,
забыв, что она равняется бесконечности. Тогда, желая получить точность, равную 0.01, при описанном подходе к ее оценке берут последний член в сумме ряда равным 1/100 и получают при расчете на микрокалькуляторе S=5.1873776. Однако ни о какой точности результата при таком подходе здесь вообще говорить нельзя, так как получается, что сумму 5.19 отделяет от бесконечности всего лишь число, близкое к 0.01. Это происходит потому, что значение суммы нарастает очень и очень медленно.
СОВОКУПНАЯ ОЦЕНКА результата вычислений, как видим, требует учитывать не только погрешности всех видов (методические и операционные, погрешности модели и исходных данных), но и их взаимосвязи. Даже в простых на первый взгляд случаях это может оказаться делом нелегким, а достоверная оценка - неочевидной.
Для примера найдем относительную погрешность величины K, вычисленной по формуле K=x1**2*x4/(x2*x3**2). Пусть x1=1.8+/-0.2; x2=2.8+/-0.3; х3=1.1+/-0.1; x4=0.45+/-0.04. Тогда дK = 2*0.2/1.8 + 0.3/2.8 + 2*0.1/1.1 + 0.04/0.45 = 0.6. Относительная погрешность результата составила почти 60 процентов, хотя относительная ошибка каждого из чисел, участвующих в вычислении, находится в пределах между 9 и 11 процентами.
В то же время бывает и так, что погрешности чисел, участвующих в том или ином вычислении, взаимно компенсируются. Учет этого явления вполне возможен, но он требует довольно сложных математических средств. Для ознакомления с ними и с различными другими вопросами приближенных вычислений можно порекомендовать книги Дж.Тейлора "Введение в теорию ошибок" (М, Мир, 1985), Н.Н.Калиткина "Численные методы" (М., Наука, 1978).
ПОВЫШЕНИЕ ТОЧНОСТИ РЕЗУЛЬТАТОВ ВЫЧИСЛЕНИЙ. Здесь имеет смысл перечислить лишь несколько простых рецептов, не вдаваясь в их математическое обоснование.
Погрешность суммы нескольких чисел при расчете на микрокалькуляторе уменьшается, если начинать суммирование с меньших по величине слагаемых. Определим ради примера сумму трех чисел, складывая их в том порядке, как онн записаны: S = 200013.11 + 200.05399 + 106.51401 = 200319.67. Проводя суммирование в обратном порядке, от третьего слагаемого до первого, получим более точное значение S=200319.68.
Если складывается достаточно много чисел, то их лучше разбить на группы из чисел, близких по порядку величины, провести суммирование в группах по только что данной рекомендации, после чего полученные суммы сложить, начиная с меньшей.
Как видим, переместительный закон сложения не выполняется при вычислениях на микрокалькуляторе: сумма меняется от перемены мест слагаемых. Дальнейшие примеры покажут нам, что при калькуляторных расчетах не выполняются и другие законы арифметики: сочетательные законы сложения и умножения, переместительный закон умножения, распределительный закон умножения относительно сложения и вычитания. Причины подобных парадоксов - в округлении промежуточных результатов, когда многозначные числа не умещаются в разрядную сетку индикатора. Из-за этой причины и оказывается небезразличным порядок, в котором следует выполнять арифметические операции, чтобы результат был возможно точнее.
Вычисляя разность двух чисел (особенно близких по величине), целесообразно вынести за скобки их общий множитель. Для примера вычислим на нашем микрокалькуляторе величину Р = 6.250001*16 - 25.000003*4 = 1e-5. Вынесем число 4 за скобки и получим более точный результат: Р = 4*(6.250001*4 - 25.000003) = 4e-6.
Уменьшить погрешность разности позволяют преобразования:

Здесь е - малое по сравнению с а число.
Возьмем не совсем обычное квадратное уравнение x**2+1000*x+1=0. Попытаемся найти наименьший по величине корень этого уравнения. Воспользовавшись известной формулой и считая на микрокалькуляторе, получаем:
х1 = -500+sqr(250000-1) = -500+499,99899 = -1.01e-3.
Подставляя значение корня в уравнение, убеждаемся, что решение выполнено с большой погрешностью. Это произошло из-за того, что в примененной нами формуле для x1 присутствует разность двух близких чисел 500 и sqr(250000-1). Значительно более точное значение корня можно получить, если по только что данной рекомендации решение представить в виде:
х1 = -1/(sqr(250000-1)+500) = -1.000001e-3.
При перемножении нескольких чисел сначала надо умножить наибольший множитель на наименьший; из оставшихся сомножителей следует взять либо наибольший, либо наименьший, судя по тому, меньше или больше единицы абсолютная величина промежуточного результата. Если делятся друг на друга два произведения, то рекомендуется чередовать операции умножения и деления, выбирая ту или иную в зависимости от абсолютной величины очередного промежуточного результата, который может оказаться либо больше, либо меньше единицы.
Пренебрежение порядком счета в подобных случаях может привести к тому, что какой-нибудь промежуточный результат не сможет быть представленным на индикаторе с его двумя разрядами для чисел порядка. Если порядок превышает 99, то говорят о переполнении или машинной бесконечности; при этом калькулятор может остановиться, а может и продолжать счет - все зависит от многих конкретных обстоятельств. Если же порядок меньше минус 99, то говорят о машинном нуле. В этом случае калькулятор и впрямь в качестве результата операции записывает в регистр x нуль.
Например, найдем произведение четырех чисел
П = 2e-96 * 0.0001 * 3e95 * 1.4e10, перемножая их на микрокалькуляторе "Электроника Б3-34" в различном порядке:
2e-96 * 0.0001 * 3e95 * 1.4e10 = (0)
3e95 * 1.4e10 (ЕГГОГ) 2e-96 * 0.0001 = (840000)
3e95 * 2e-96 * 1.4e10 * 0.0001 = (840000).
В первом случае перемножение чисел 2e-96 * 0.0001 переводит микрокалькулятор в область машинного нуля, и окончательный результат оказывается равным нулю. Во втором случае перемножение чисел 3e95 * 1.4e10 приводит к машинной бесконечности, и при ручном счете на индикаторе появляется сигнал ошибки ЕГГОГ, однако при продолжении счета результат оказывается правильным. При вычислении по программе в этом случае остановки счета не происходит, и сигнал ошибки на индикаторе не высвечивается. В третьем случае сомножители расположены таким образом, что не возникает ни машинного нуля, ни машинной бесконечности.
Следует помнить, что особенно большие относительные погрешности возникают при вычислении sqr(x) и x**y. Этих операций надо по возможности избегать, изменяя алгоритм вычислений. Надо также следить за тем, чтобы аргумент функции не попадал в "опасные зоны", где ее чувствительность наиболее высока. Замена алгоритма при этом может увеличить число выполняемых операции, но, несмотря на это, погрешность конечного результата может снизиться.
Разумеется, расчетные формулы надо постараться преобразовать так, чтобы общее число операций было наименьшим. Общеизвестный пример такого рода связан с вычислением полинома, где наименьшее число операций обеспечивает схема Горнера.
Иногда для увеличения точности целесообразно комбинировать алгоритмы вычислений. Например, для достаточно быстрого вычисления n! можно использовать формулу Стирлинга:
n! = sqr(2*пи*n)*exp(-n)*n**n * (1 + 1/(12*n) + 1/(288*n**2) - ...).
Однако для значений n<=10 формула дает большую ошибку. Исправить положение можно, введя в программу счета округление результата до единиц, например, с помощью фрагмента 1 ВП 7 + FBx -.
Теперь программа при использовании трех членов в формуле Стирлинга дает точное значение n! для чисел от 1 до 9, а для больших значений n относительная ошибка не превосходит 5e-7. Время счета - всего около 20 секунд.
Так, подбирая удачный алгоритм, грамотно составляя программу вычислений, тщательно готовя исходные данные, контролируя накопление погрешностей, можно достичь желаемой точности результата.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
8/86
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
С недавних пор в разделе сосуществуют программируемые микрокалькуляторы и персональные компьютеры, так что первые его страницы посвящаются то одним, то другим машинам. На сей раз те и другие вместе открывают очередной выпуск раздела, выступают в своеобразном сравнении. Это позволяет отметить смежные области их возможностей, где могли бы сойтись в плодотворном сотрудничестве и микрокалькуляторы, и "большие" ЭВМ.
СКОЛЬКО ВЕСИТ ЗАГОТОВКА?
Я работаю на небольшом механосборочном предприятии. Нашим технологам для расчета норм расхода материалов часто приходится определять вес заготовок различных форм. Делается это с помощью специальных таблиц по предварительно выясненным параметрам заготовки. В принципе это несложно, но малопроизводительно. Поэтому я решил разработать универсальную программу для микрокалькулятора "Электроника Б3-34", позволяющую вычислять вес заготовок наиболее часто встречающихся форм (с круглым, прямоугольным, шестигранным и трубчатым поперечным сечением) без использования таблиц.
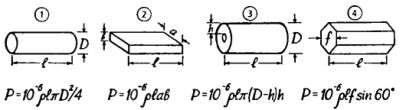
Расчетные формулы для таких заготовок приведены на рисунке. Буквой р обозначен удельный вес материала в г/см3. Линейные размеры задаются в миллиметрах. Множитель 1e-6 введен для получения результата в килограммах. Общие для всех типов заготовок расчетные операции вынесены в основную программу. Расчеты для конкретных типов заготовок оформлены в виде подпрограмм. Чтобы не запоминать адреса переходов, формы кодируются числами от 1 до 4. По этому коду команда КППС вызовет нужную подпрограмму. При этом одна из подпрограмм (вычисление веса прямоугольных в сечении заготовок) получилась пустой: в ней всего одна команда В/0. Сделано это, чтобы не нарушать общей структуры программы.
Для хранения исходных данных использован стек, что позволило унифицировать ввод: в одном и том же месте программы (после останова по адресу 11) можно вводить как три параметра (для прямоугольной и трубчатой заготовок), так и два (для круглого и шестигранного прутков). При создании программы я намеренно пошел на некоторое увеличение ее длины, включив в ее текст все константы, а также адреса подпрограмм (см. адреса 38-49). Общее число нажимаемых клавиш от этого практически не изменилось, работать же с такой программой удобнее, так как любая операция по вводу данных в адресуемые регистры, с точки зрения пользователя, увеличивает объем ручного труда, а это нежелательно.
Программа. 00. ВП 01. 6 02. /-/ 03. ПА 04. С/П 05. ПД 06. КИПД 07. ПС 08. ИПД 09. ИПА 10. + 11. С/П 12. КППС 13. * 14. * 15. ИПА 16. * 17. БП 18. 04 19. x-y 20. Fx2 21. 4 22. / 23. Fпи 24. B/0 25. Fпи 26. F() 27. F() 28. - 29. FBx 30. * 31. В/0 32. x-y 33. Fx2 34. 6 35. 0 36. Fsin 37. В/0 38. 1 39. 9 40. П1 41. 2 42. 4 43. П2 44. 2 45. 5 46. П3 47. 3 48. 2 49. П4 50. С/П.
Инструкция. 1. Ввести программу. 2. Переключатель Р-Г установить в положение Г. 3. Перейти в режим вычислений: FАВТ БП 38 С/П. 4. Ввести удельный вес материала заготовки: р В/0 С/П. 5. Ввести код заготовки (круг: 1 С/П, прямоугольник: 2 С/П, труба: 3 С/П, шестиугольник: 4 С/П). 6. Ввести параметры заготовки (круглой: D ^ l С/П, прямоугольной a ^ b ^ l С/П, трубчатой D ^ h ^ l С/П, шестигранной f ^ l С/П). 7. Прочесть на индикаторе вес заготовки в килограммах. 8. Для продолжения работы: если материал изменился, то перейти к п.4, нет - к п.5.
Для удобства работы с программой после того, как введен код заготовки, на индикатор выводится для контроля число, у которого слева от запятой стоит код заготовки, а справа - первые две-три цифры удельного веса ее материала.
Введя в предложенную программу суммирование результатов, можно вычислять вес деталей, ведь любая деталь состоит из простых элементов (цилиндр, параллелепипед и т.д.). При этом для пустот один из размеров нужно вводить со знаком минус.
В.ДЯДИН (г.Киев)
ОТ РЕДАКЦИИ. В программе В.Дякина реализована структура, называемая в программировании "ВЫБОР" (см. рисунок). Она является своеобразным обобщением структуры "ВЕТВЛЕНИЕ". Но если в последней из блока сравнения имеются только два выхода - по ветви "ДА" и по ветви "НЕТ", то структура "ВЫБОР" допускает произвольное число выходов.
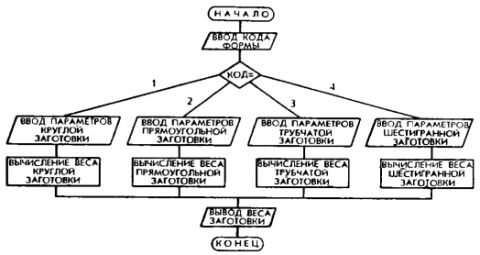
В языке калькулятора "Электроника Б3-34" нет команды, реализующей подобную возможность. Мы можем довольно легко описать однократное ветвление с помощью команд типа Fx=0. Однако структуру "ВЫБОР" приходится программировать "вручную", как это, к примеру, остроумно сделал В.Дякин.
При программировании на языках высокого уровня в подобных ухищрениях нет необходимости. Там существуют специальные операторы для этих целей. К примеру, в алголе-60 это обращение к переключателю goto P(i), в фортране - вычисляемый оператор перехода GO TO (m1, ... mn), I, в ПЛ/1 - оператор перехода, использующий переменную типа метки GO TO L(I), в бейсике - оператор ON ... GOTO или ON ... THEN.
Кстати, при программировании на любом из этих языков, скажем, на бейсике, не было бы необходимости и выносить общие части вычислений в одно место. Это практически бы не сказалось ни на быстродействии, ни на длине программы. Самое же важное, не надо было бы писать инструкции для пользователя. Всю информацию о вводе и смысле выводимых результатов дала бы сама программа.
Возможный вариант такой программы дан ниже.

Конечно, допустим вопрос: а нужна ли такая программа? Если персональный компьютер занимает отдельный стол в вашей рабочей комнате, его не захватишь с собой, идя на склад, где сложены заготовки. А "Электроника Б3-34", "МК-54", "МК-61" умещаются в кармане. Но если цифра, полученная на калькуляторе,- лишь одна из тех, что потребуются для большего расчета, то лучше потом вернуться к персональному компьютеру и провести последующие вычисления на нем.
Мы ждем откликов на выступление В.Дякина. ВНИМАНИЕ! Мы ждем писем, где будет рассказано ЛИБО о том, как на программируемом микрокалькуляторе удалось реализовать алгоритм, для выполнения которого, казалось бы, требуется более мощная вычислительная машина, ЛИБО о том, как микрокалькулятор применяется совместно с большой ЭВМ при решении какой-либо крупной задачи, ЛИБО о том, как опыт работы с программируемыми микрокалькуляторами помог при составлении программ для больших машин.
ТАБЛИЦУ ПЕЧАТАЕТ МАШИНА
В отраслевом экономическом институте, где я работаю, почти ежедневно приходится заниматься расчетами в табличных формах. До недавнего времени основным орудием такой работы в нашей лаборатории служил настольный калькулятор, а приметами этой работы были отрешенный взгляд, еле различимое бормотание и лихорадочное долбление клавиш. Изредка, в особо кризисных ситуациях, раздавались болезненно-надрывные возгласы "О-о-о!", зачастую сопровождаемые энергичным потиранием лба, щек, висков и завершавшиеся сумбурно - лихорадочным поиском ошибок.
Составлению каждой таблицы предшествовали длительные поиски исходной информации. Она обычно находится в разных шкафах, на разных полках, в многочисленных отчетах и справках и уж, конечно, на разных страницах.
Но вот информация подготовлена, таблицы просчитаны, записка составлена. Скорее напечатать!.. Увы! Оказывается, сейчас печатается материал вашего коллеги, а вам придется подождать.
Согласитесь, в таких условиях весьма трудно добиться плодотворного решения серьезных задач. И все же с этим приходилось мириться, пока в нашем институте не установили "Искру-226".
Восхищение мини-ЭВМ, навеянное публикациями, после первого с ней контакта во многом развеялось. Оказалось, что компьютер "не обучен" работе с таблицами. На повестку дня встал вопрос об "изобретении велосипеда" (во всяком случае, так нам тогда казалось).
Первые же размышления над будущей программой поставили нас перед неразрешимой на первый взгляд проблемой. Чтобы использовать различные алгоритмы при обработке одних и тех же данных, последние нужно хранить независимо от программ. Наименования данных, с одной стороны, связаны с ними самими (значит, должны и храниться с ними), с другой - являются частью табличного представления результата (то есть связаны с алгоритмом обработки). Круг замкнулся. Чтобы его разорвать, пришлось расчленить понятие "таблица" на составляющие: шапку, боковик, примечание, форматы представления чисел...
Для облегчения поиска данные по предприятиям объединяются в группы (или файлы, как говорят программисты), которые нумеруются и характеризуют разные признаки данных, например, объемы производства, расходы энергоресурсов, состав технологического оборудования и т.д. Показатели представляются рядом значений, относящихся к разным моментам времени - по годам, кварталам, месяцам. Группа данных может быть дополнительно помечена: "по проекту", "по плану" и т.д.
Возникла структура данных. Для их ввода в программе понадобились команды поиска, считывания. Вот он, шаг от структуры данных к структуре программы. Так шаг за шагом возникла универсальная программа поиска, ввода, печати - программа управления данными.
Как же она работает? Пусть для расчета во второй столбец таблицы нужно внести объем производства, скажем, газовых баллонов, в третий - затраты, а в первый - наименование предприятия, выпускающего газовые баллоны. В режиме диалога "Искра" уточнит у нас число столбцов таблицы, в какой столбец какие данные поместить, за какой год, среди каких предприятий вести поиск (например, по некоторой подотрасли). После этого ЭВМ начинает работать без участия человека.
Прежде всего она "заглядывает" в словарь, где сведены названия предприятий и их шифры. Завод "Вымпел". Его шифр - 501. Поиск касается объемов производства, то есть признака с кодом 001. Из этих двух чисел программа формирует номер файла 001501. В каждом подобном файле хранится двумерный числовой массив из элементов, обозначаемых в программе Z(I,J), а говоря проще - таблица, строение которой понятно из рисунка.

Код газовых баллонов - 103. Именно такое число будет искать машина, просматривая строки первого столбца таблицы. Номер строки, в которой обнаружится искомое число (пусть это будет строка 3), ЭВМ присвоит переменной I. Теперь начинается аналогичный поиск кода года и месяца. Пусть он нашелся в столбце с номером 2. Этот номер ЭВМ присвоит переменной J. Элемент Z(3,2) машина занесет в соответствующее место составляемой таблицы, а из словаря перепишет в строку боковика название предприятия.
По заданным кодам ЭВМ может найти несколько значений затребованного показателя, например, за ряд лет, но в составляемой нами таблице этого не понадобилось.
Бывает, что ЭВМ не находит нужного ей файла или в первом столбце просматриваемой таблицы не обнаруживает нужного кода. Тогда она просто переходит к просмотру файла следующего предприятия.
За составлением таблицы следует расчет (например, средних затрат). Однажды выполнив заданный ей когда-то расчет, машина может запомнить его по соответствующему указанию пользователей, так что впоследствии для его проведения достаточно лишь ввести его шифр.
После расчета нужно напечатать таблицу. К нашим услугам набор готовых шапок. Программа выберет или заново скомпонует требуемую, определит представления чисел. Перед тем, как печатать таблицу, машина "поинтересуется", как заносить в нее нулевые данные - ставить ли "0", прочерк или оставлять пустое место? Как лучше сегментировать таблицу, если полностью на одном листе она не разместится? Каким цветом печатать? Нужно ли сначала вывести таблицу на дисплей?
В итоге "Искра" не только автоматизировала нашу работу, повысила ее качество, высвободила время для постановки и решения сложных задач, создала условия для современной научной работы, но и изменила характер нашей деятельности. Потребность в услугах машинисток сократилась, так как основная часть отчетов - таблицы делаются на ЭВМ. А насколько привлекательнее общение с нею, нежели работа с калькулятором! У сотрудников появился интерес и к программированию, и к решению задач по-новому, стала повышаться квалификация.
Н.НИКИТИН (г.Москва)
МОЮ СЕКРЕТАРШУ ЗОВУТ "ИСКРА"
На моем рабочем столе с недавних пор разместилась ЭВМ "Искра-226". Сам я по специальности инженер-конструктор, а по должности - зав. отделом одного КБ. Нередко мой рабочий день бывает заполнен различными совещаниями, встречами, телефонными звонками. Секретарь мне нужен позарез, но не положен по штату. Вот часто что-то и забываешь, накладки вечно вылезают...
Задумал я поручить своей "Искре" функции секретаря. Много от нее не требуется. В понедельник и четверг (на эти дни мы в КБ стараемся "свалить" все организационные дела) ЭВМ утром должна спросить меня и моих сотрудников о планах на день и далее держать на экране дисплея точное время и информацию о ближайшем или текущем мероприятии, подавать звуковой сигнал в момент их начала и окончания. Только-то и всего.
Соответствующую программу составить было несложно, благо "Искра-226" имеет встроенные часы. Вся программа занимает 18 строк, из которых две последние - это подпрограммы запроса времени.

Строка 1. Названия мероприятия дня (до 200 знаков, то есть байт), время их начала и окончания (в секундах, прошедших от полуночи) хранятся в массивах. На день можно запланировать до 50 дел (ЭВМ может хранить и больше, но кто это выполнит?!). Встроенные часы "Искры-226" останавливаются при выключении машины. При новом ее запуске их нужно поставить - набрать на клавиатуре значение ближайших часов и минут (через запятую) и в момент нулевых секунд нажать на клавишу ВК.
Строки 2-9. Здесь запрограммирован начальный диалог машины с человеком, который сообщает ей свои планы на день. Информацию по текущим делам дня лучше вводить в память ЭВМ в порядке их важности. Машина при этом следит за тем, чтобы новое дело не "наползало" на какое-либо из ранее введенных. Если же это все-таки случится, не беда. "Искра" вежливо сообщит об этом (см. строку 8 ) и попросит выбрать другое время. Ревностно следит она также за тем, чтоб не планировалось что-то на уже прошедшее время (строка 4). Диалог заканчивается либо по инициативе человека, либо машины (см. строку 2).
Строки 10-11. Мы вводили в память машины информацию о делах дня в порядке их важности. Для ЭВМ же они все равны, и она расставляет их так, чтобы было удобнее с ними работать - проводит ранжировку по времени начала. Здесь использован метод перестановок (см., например, 2/86) сравниваются два соседних события (см. строку 10), и если первое должно произойти раньше второго, то они меняются местами. Распорядок дня таким образом "причесывается" до тех пор, пока все события не встанут на свое место и вспомогательная переменная Р останется равной нулю.
Строки 12-16. Здесь запрограммирован монолог ЭВМ, которая "поглядывает на часы" и сообщает о ближайшем или текущем мероприятии дня. Правда, "Искра" разговаривать не может, а подает только звуковой сигнал (зуммер) в момент начала и окончания дела. Шестнадцатиричный код зуммера - 07, перевода курсора дисплея в левый верхний угол экрана 01, то же с его очисткой - 03.
"Поглядывать на часы" машине позволяют подпрограммы, записанные в строках 17 и 18. Команда INPUT хT присваивает переменной Т значение машинного времени, убывающего по одной двухтысячной доле секунды. Перевести все это в часы, минуты и секунды несложно, имея под рукой оператор выделения целой части числа - INT. Здесь S() - это число секунд, прошедших от полуночи до момента запроса машиной точного времени, S - до момента обращения к подпрограмме. В.ГОГОЛЕВ (г.Москва)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Когда однократное нажатие клавиши воспринимается машиной как многократное, говорят про "дребезг" контактов. Это неприятное явление нередко возникает при длительной эксплуатации микрокалькулятора. Клавиши микрокалькулятора используются с различной интенсивностью, поэтому можно заменить дефектный замыкатель на сохранившийся лучше - от другой клавиши, причем такой, дребезг которой не влияет на правильность выполнения операций. Среди таких операций - сброс, очистка регистра памяти, ввод десятичной запятой. Для ремонта понадобится скальпель и пинцет. Чтобы извлечь замыкатель, необходимо удерживающую его пленку прорезать по периметру на половину длины и затем извлечь замыкатель пинцетом. Осталось поменять местами исправный и дефектный замыкатели. Так мне удалось отремонтировать "Электронику Б3-26".
Ш.АХМЕТХАФИЗОВ (г.Казань) ]
ПО ПОРЯДКУ НОМЕРОВ СТАНОВИСЬ!
Выбрать из двух однотипных предметов лучший по какому-либо признаку - задача несложная. Но почти невыполнимой кажется она, если сравниваемых предметов много (скажем, десять), а различаются они едва заметно. Муки подобного выбора знакомы каждому, кто хоть раз состоял в каком-нибудь жюри.
Оказывается, эту сложную задачу можно свести к простейшей - выбору лучшего из двух. Если известны результаты попарных сравнений, то на их основе можно ранжировать всю совокупность. Соответствующий алгоритм известен и положен в основу предлагаемой программы:
00. ПД 01. П0 02. 1 03. КП^ 04. FL0 05. 03 06. ИПД 07. ПС 08. 1 09. - 10. П0 11. ИП0 12. ВП 13. 4 14. ИПС 15. + 16. С/П 17. Fx=0 18. 26 19. FL0 20. 11 21. ИПС 22. 1 23. - 24. БП 25. 07 26. ИПС 27. - 28. Fx=0 29. 36 30. КИПС 31. 1 32. + 33. КПС 34. БП 35. 19 36. КИП^ 37. 1 38. + 39. КП^ 40. БП 41. 19 42. Сх 43. ПС 44. ИПД 45. П0 46. ИПС 47. КИП^ 48. - 49. Fx<0 50. 53 51. FBx 52. ПС 53. FL0 54. 46 55. ИПД 56. П0 57. КИП^ 58. ИПС 59. / 60. КП^ 61.FL0 62. 57 63. Сх 64. С/П.
Программа поможет за несколько минут упорядочить химические вещества по резкости запаха, орнаменты по оригинальности узора, розы по степени отличия цвета лепестков от некоторого идеального и т.п. Сравнению можно подвергнуть не более 11 предметов.
Каждому из сравниваемых по какому-либо свойству объектов программа приписывает число от нуля до единицы - ранг. Объект, у которого это свойство выражено сильнее, чем у всех других, получает ранг, равный единице. Если в одном из сравнений два объекта признаны одинаковыми в отношении этого свойства, они получают одни и тот же ранг.

Процедуру ранжирования освоим на конкретном примере, нарочито простом и наглядном. Представьте, что изображенные здесь палочки требуется упорядочить по длине, а измерить их непосредственно нельзя. Перенумеруем их. Введем вышеприведенную программу в "Электронику Б3-34", нажмем клавишу В/0, наберем число сравниваемых объектов (в нашем случае 5), нажмем клавишу С/П. На индикаторе - 40005. Это вопрос: какая палочка длиннее - четвертая или пятая? Вводим номер той, которая кажется нам длиннее, вновь нажимаем С/П. На индикаторе появляются все новые вопросы, каждый раз в виде i000j. На каждый вопрос дается ответ - указывается номер предмета, i или j, более предпочтительного по свойству, в отношении которого ведется сравнение, или нуль, если предметы практически неразличимы. После опроса на индикаторе появляется 10001, и нажатием клавиши БП 42 С/П мы переходим к расчету рангов, окончание которого отмечается появлением нуля на индикаторе. После этого нажатием клавиш ИП1, ИП2 и т.д. на индикатор выводятся рассчитанные программой ранги: для нашего примера V1=1; V2=0.5; V3=l; V4=0.75; V5=0.25. Для нового расчета описанные действия следует повторить, начиная с нажатия клавиши В/0.
Присваивание рангов объектам различной природы может оказаться единственной возможностью их количественного анализа. Например, сравнивалось несколько роз одного сорта по насыщенности цвета лепестков, и были получены соответствующие ранги. Количество химиката, подсыпавшегося в горшок к каждому цветку, известно. По этим данным была построена эмпирическая зависимость между насыщенностью цвета, выраженного полученными рангами, и количеством химиката. Эта зависимость оказалась весьма полезной растениеводам.
Г.СЛАВИН (г.Таллин)
ТРИВИАЛЬНОЕ РЕШЕНИЕ
Утром первого апреля Виктор Галкин, которого с чьей-то легкой руки все в заводском ВЦ называли "программистом божьей милостью", был вызван к директору завода. В кабинете присутствовало почти все заводское начальство. Директор был краток.
- Товарищ Галкин,- сказал он,- цилиндры, один из которых вы видите у меня на столе,- это четверть всей нашей продукции. Но под эту четверть занята половина станочного парка завода. Так что, товарищ Галкин, вот вам конкретная задача. Подумайте и смоделируйте возможные варианты, прорешайте их на ЭВМ и к первому июля дайте предложения, как нам организовать производство цилиндров, чтобы уменьшить число задействованных под них станков.
Через полмесяца Галкин знал производство цилиндров не хуже главного технолога завода. Он работал с таким вдохновением, которого не испытывал уже давно. Задача была многомерной, и поэтому программа для ее решения оказалась довольно сложной. Для пущей эффектности в ней была предусмотрена выдача результатов на экран дисплея.
Тридцатого июня программа была уже отлажена, а утром следующего дня, когда Галкин еще только приступал к решению задачи, в машинный зал нежданно нагрянуло все начальство. Галкин волновался, как абитуриент на экзамене, когда запускал программу на счет. Наконец что-то щелкнуло, запищало, и на экране дисплея появилась надпись: для производства цилиндров использовать станков - 0, время работы первого станка - 0, второго станка - 0... И вскоре весь экран заполнился одними нулями.
Наступило гробовое молчание, которому, казалось, не будет конца.
- Это,- с трудом выдавил из себя Галкин,- тривиальное решение... Я сейчас...
Он суетливо нажал на какие-то кнопки, вновь что-то щелкнуло, запищало, исчезли с экрана нули, и появилась новая надпись: второго решения нет.
Молчание зала прервал голос директора.
- ВЦ, кажется, ваше хозяйство,- раздраженно обратился он к главному инженеру.- Разберитесь же, чем здесь занимаются.
... Всю ночь Галкину снились кошмары, а утром он шел иа работу, неся в своем "дипломате" заявление об уходе. Галкии уже подходил к зданию ВЦ, когда вдруг увидел спешащего к нему главного инженера. Улыбка не сходила с его лица.
- Сколько ж можно ждать тебя? На, прочти.- И главный инженер протянул ему какую-то бумагу. Это был приказ по министерству, предписывающий заводу с первого июля прекратить производство цилиндров как нерентабельное.
Р.АРАКЕЛОВ (г.Баку)
ПРОСТЫЕ ЧИСЛА
Конкурс на лучшую программу для построения ряда простых чисел (12/83, 6/84, 8/84) продолжал привлекать внимание наших читателей еще долго после того, как были подведены его итоги. Напомним имена и некоторые результаты победителей конкурса. Программа московского студента В.Илюхина отличалась высокими скоростными качествами, программа киевского инженера Г.Пендюры - возможностью получения результатов группами по дюжине простых чисел в каждой. Но, как говаривал К.Прутков, иет столь великой вещи, которую бы не превзошла величина еще большая. Ленинградский врач В.Козлов (Программа 1) и московский рабочий В.Никитин (Программа 2) подтвердили справедливость этих слов.
Программа В.Козлова хотя и работает по тому же алгоритму, как у В.Илюхина, но короче и выполняется быстрее.
Перед пуском счета заносим константы в регистры памяти: 0 в РВ; 2 в РА и Р1, 4 в Р0 и Р2, 6 в Р3 и РД, 12 в Р6. Ряд из восьми чисел 6, 4, 2, 4, 2, 4, 6, 2 формируется при обращении всего к шести регистрам, которое выполняется с помощью оператора КИП4(КИП5) в следующем порядке: Д, 0, 1, 0, 1, 2, 3, А. Последующее обращение (КИП4 или КИП5) вызывает индикацию нуля, ранее записанного в РВ, и приводит по условию х=0 к перезаписи числа 12 из Р6 в Р4 (Р5); цикл обращений в РД ... РВ повторяется. Такой несколько необычный порядок считывания содержимого регистров осуществляется с помощью команд косвенной адресации в тех случаях, когда в регистре-счетчике записано число N>13. Команда КНОП на шаге 01 - "заплата". Ее единственная функция - обеспечить четность адресов 02 и 04 - адресов переходов Kx!=0A, Kx!=0^, КБП^. Контрольный расчет 6121, В/0, С/П, "6131" выполняется за 75 секунд!
На том же принципе, что у В.Козлова, основана программа инженера А.Привеня из г.Константиновки Донецкой области. Она обладает тем же быстродействием, но длиннее на один шаг.
В.Никитин довел вывод результата группами, по-видимому, до предела, обусловленного возможностями "Электроники Б3-34". Его программа выполняется сравнительно долго, позволяя оператору "переключиться" на другие занятия, но уж когда микрокалькулятор закончит вычисления, оператору придется потрудиться, записывая 15 найденных чисел. Предусмотрен удобный ввод числовых данных. После того как программа введена, необходимо лишь набрать наименьшее исследуемое число без двойки и нажать клавиши В/0, С/П. Предположим, вы набрали число 6129. Через 80 минут на индикаторе 6257, а в регистрах Д-А, 9-0 соответственно 6247, 6229, 6221, 6217, 6211, 6203, 6199, 6197, 6173, 6163, 6151, 6143, 6133, 6131.
Программа 1: 00. П8 01. КНОП 02. ИП6 03. П4 04. КИП4 05. Кх!=0А 06. ИП8 07. + 08. П8 09. Fsqr 10. П7 11. 1 12. ПС 13. ИП6 14. П5 15. ИП7 16. КИП5 17. Fx!=0 18. 13 19. ИПС 20. + 21. ПС 22. - 23. Fx>=0 24. 36 25. ИП8 26. ИПС 27. / 28. П9 29. КИП9 30. x-y 31. ИП9 32. - 33. Kx!=0^ 34. БП 35. 15 36. ИП8 37. С/П 38. КБП^.
Программа 2: 00. ^ 01. 1 02. 4 03. П0 04. F() 05. 2 06. + 07. ^ 08. ^ 09. 3 10. ^ 11. F() 12. / 13. FBx 14. - 15. Fx>=0 16. 57 17. FBx 18. + 19. 1 20. , 21. 8 22. F1/x 23. - 24. 7 25. F10X 26. + 27. FBx 28. - 29. F() 30. F() 31. F() 32. * 33. x-y 34. - 35. Fx!=0 36. 54 37. FBx 38. F() 39. F() 40. F() 41. ^ 42. 2 43. + 44. ^ 45. ^ 46. F() 47. F() 48. F() 49. ^ 50. F() 51. F() 52. БП 53. 11 54. FBx 55. БП 56. 05 57. F() 58. ИП0 59. 1 60. 5 61. - 62. Fx<0 63. 68 64. F() 65. КП0 66. БП 67. 05 68. F() 69. С/П 70. БП 71. 00.
А.БОЙКО (г.Москва)

Рис. А.Тягнирядко (пос.Володарсн Ворошиловградской обл.)
МАГИЧЕСКИЙ КВАДРАТ
В этой игре девять чисел (от единицы до девятки) определенным образом перемещаются по полям разграфленного квадрата 3*3. Игра напоминает сборку кубика Рубика. Правда, если бы для нее потребовалась объемная интерпретация, то на эту роль подошел бы не куб, а тор (проще говоря, баранка), чья поверхность разделена на девять пронумерованных сегментов.
Получить такой тор несложно. Мысленно изогнем наш квадрат и склеим верхнюю сторону с нижней. Получим трубочку, как на рисунке. Изогнем трубочку и склеим ее концы, то есть бывшие левую и правую стороны квадрата. Получается тор.

Образ тора сделает более естественными для понимания перемещения чисел по полям нашего квадрата. Будем считать, что при сдвиге какого-либо его столбца сверху вниз содержимое верхнего поля передвигается в среднее, содержимое среднего - в нижнее, содержимое нижнего - в верхнее. Будем считать, что при сдвиге какой-либо строки квадрата слева направо содержимое левого поля попадает в среднее, содержимое среднего - в правое, содержимое правого - в левое. Впрочем, программа игры позволяет сдвигать лишь нижнюю строку, но это отнюдь нс ограничение, поскольку сдвигом столбцов любую строку можно сместить до самого нижнего положения.
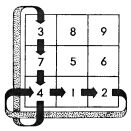
Каждый из желаемых сдвигов выполняется нажатием определенной цифровой клавиши (см. таблицу) и вслед за нею клавиши С/П. После каждого перемещения на индикаторе демонстрируется нижняя строка. Другие строки можно вызвать на индикатор нажатием указанных в той же таблице цифровых клавиш (см. таблицу) и вслед за нею клавиши С/П. (Разобравшись в программе, каждый может добавить дополнительную команду перемещения, если сочтет ее полезной).

Цель игры - превратить допустимыми перемещениями исходное расположение цифр на полях квадрата в такое, в котором они расположены на клавиатуре микрокалькулятора. Каждый просмотр считается за ход, поэтому внимательный игрок имеет больше шансов на победу в коллективной игре.
Введя программу, заполните регистры: 25 - РА 43 - РВ, 52 - PC. Чтобы расположить числа по полям квадрата в нормальном порядке, в регистры с P1 no P9 запишем соответственно 100 20 3, 400, 50, 6, 700, 80, 9. Совершив несколько перемещений, как указано в контрольном примере, приведенном ниже, и убедившись, что программа функционирует без ошибок, сделайте еще пару-другую ходов. Очистите счетчик ходов командами Сх П0. Теперь можно играть. Интереснее, если в игре участвуют несколько человек, задавшись одной и той же исходной ситуацией. Тренируйте память, стараясь обойтись без бумаги и карандаша. После того как контрольный просмотр покажет, что цель достигнута, сравните показания счетчика ходов - регистра Р0 в калькуляторах игроков. Выигрывает тот, кто меньшим числом ходов сумеет решить головоломку.
Для новой игры необходимо лишь очистить регистр Р0 и сделать несколько "запутывающих ходов".
Программа: 00. КБПА 01. КБПВ 02. КБПС 03. БП 04. 61 05. БП 06. 17 07. БП 08. 70 09. БП 10. 77 11. ПД 12. ИП0 13. 1 14. + 15. П0 16. КППД 17. ИП1 18. ИП2 19. + 20. ИП3 21. + 22. С/П 23. БП 24. 11 25. ИП3 26. ИП2 27. ИП1 28. 1 29. 0 30. / 31. П2 32. F() 33. 1 34. 0 35. / 36. П3 37. F() 38. 2 39. F10X 40. * 41. П1 42. В/0 43. ИП1 44. ИП4 45. ИП7 46. П4 47. F() 48. П1 49. F() 50. П7 51. В/0 52. ИП2 53. ИП5 54. ИП8 55. П5 56. F() 57. П2 58. F() 59. П8 60. В/0 61. ИП3 62. ИП6 63. ИП9 64. П6 65. F() 66. П3 67. F() 68. П9 69. В/0 70. ИП4 71. ИП5 72. ИП6 73. + 74. + 75. БП 76. 22 77. ИП9 78. ИП8 79. + 80. ИП7 81. + 82. БП 83. 22.
Контрольный пример: БП 11 5 С/П "123" 7 С/П "456" 9 С/П "789" 0 С/П "312" 1 С/П "412" 2 С/П "452" 3 С/П "456"... Сх П0.
М.ВАХТЕРОВ (г.Москва)
Раздел ведет кандидат физико-математических наук Ю.ПУХНАЧЕВ.
С недавних пор в разделе сосуществуют программируемые микрокалькуляторы и персональные компьютеры, так что первые его страницы посвящаются то одним, то другим машинам. На сей раз те и другие вместе открывают очередной выпуск раздела, выступают в своеобразном сравнении. Это позволяет отметить смежные области их возможностей, где могли бы сойтись в плодотворном сотрудничестве и микрокалькуляторы, и "большие" ЭВМ.
СКОЛЬКО ВЕСИТ ЗАГОТОВКА?
Я работаю на небольшом механосборочном предприятии. Нашим технологам для расчета норм расхода материалов часто приходится определять вес заготовок различных форм. Делается это с помощью специальных таблиц по предварительно выясненным параметрам заготовки. В принципе это несложно, но малопроизводительно. Поэтому я решил разработать универсальную программу для микрокалькулятора "Электроника Б3-34", позволяющую вычислять вес заготовок наиболее часто встречающихся форм (с круглым, прямоугольным, шестигранным и трубчатым поперечным сечением) без использования таблиц.

Расчетные формулы для таких заготовок приведены на рисунке. Буквой р обозначен удельный вес материала в г/см3. Линейные размеры задаются в миллиметрах. Множитель 1e-6 введен для получения результата в килограммах. Общие для всех типов заготовок расчетные операции вынесены в основную программу. Расчеты для конкретных типов заготовок оформлены в виде подпрограмм. Чтобы не запоминать адреса переходов, формы кодируются числами от 1 до 4. По этому коду команда КППС вызовет нужную подпрограмму. При этом одна из подпрограмм (вычисление веса прямоугольных в сечении заготовок) получилась пустой: в ней всего одна команда В/0. Сделано это, чтобы не нарушать общей структуры программы.
Для хранения исходных данных использован стек, что позволило унифицировать ввод: в одном и том же месте программы (после останова по адресу 11) можно вводить как три параметра (для прямоугольной и трубчатой заготовок), так и два (для круглого и шестигранного прутков). При создании программы я намеренно пошел на некоторое увеличение ее длины, включив в ее текст все константы, а также адреса подпрограмм (см. адреса 38-49). Общее число нажимаемых клавиш от этого практически не изменилось, работать же с такой программой удобнее, так как любая операция по вводу данных в адресуемые регистры, с точки зрения пользователя, увеличивает объем ручного труда, а это нежелательно.
Программа. 00. ВП 01. 6 02. /-/ 03. ПА 04. С/П 05. ПД 06. КИПД 07. ПС 08. ИПД 09. ИПА 10. + 11. С/П 12. КППС 13. * 14. * 15. ИПА 16. * 17. БП 18. 04 19. x-y 20. Fx2 21. 4 22. / 23. Fпи 24. B/0 25. Fпи 26. F() 27. F() 28. - 29. FBx 30. * 31. В/0 32. x-y 33. Fx2 34. 6 35. 0 36. Fsin 37. В/0 38. 1 39. 9 40. П1 41. 2 42. 4 43. П2 44. 2 45. 5 46. П3 47. 3 48. 2 49. П4 50. С/П.
Инструкция. 1. Ввести программу. 2. Переключатель Р-Г установить в положение Г. 3. Перейти в режим вычислений: FАВТ БП 38 С/П. 4. Ввести удельный вес материала заготовки: р В/0 С/П. 5. Ввести код заготовки (круг: 1 С/П, прямоугольник: 2 С/П, труба: 3 С/П, шестиугольник: 4 С/П). 6. Ввести параметры заготовки (круглой: D ^ l С/П, прямоугольной a ^ b ^ l С/П, трубчатой D ^ h ^ l С/П, шестигранной f ^ l С/П). 7. Прочесть на индикаторе вес заготовки в килограммах. 8. Для продолжения работы: если материал изменился, то перейти к п.4, нет - к п.5.
Для удобства работы с программой после того, как введен код заготовки, на индикатор выводится для контроля число, у которого слева от запятой стоит код заготовки, а справа - первые две-три цифры удельного веса ее материала.
Введя в предложенную программу суммирование результатов, можно вычислять вес деталей, ведь любая деталь состоит из простых элементов (цилиндр, параллелепипед и т.д.). При этом для пустот один из размеров нужно вводить со знаком минус.
В.ДЯДИН (г.Киев)
ОТ РЕДАКЦИИ. В программе В.Дякина реализована структура, называемая в программировании "ВЫБОР" (см. рисунок). Она является своеобразным обобщением структуры "ВЕТВЛЕНИЕ". Но если в последней из блока сравнения имеются только два выхода - по ветви "ДА" и по ветви "НЕТ", то структура "ВЫБОР" допускает произвольное число выходов.

В языке калькулятора "Электроника Б3-34" нет команды, реализующей подобную возможность. Мы можем довольно легко описать однократное ветвление с помощью команд типа Fx=0. Однако структуру "ВЫБОР" приходится программировать "вручную", как это, к примеру, остроумно сделал В.Дякин.
При программировании на языках высокого уровня в подобных ухищрениях нет необходимости. Там существуют специальные операторы для этих целей. К примеру, в алголе-60 это обращение к переключателю goto P(i), в фортране - вычисляемый оператор перехода GO TO (m1, ... mn), I, в ПЛ/1 - оператор перехода, использующий переменную типа метки GO TO L(I), в бейсике - оператор ON ... GOTO или ON ... THEN.
Кстати, при программировании на любом из этих языков, скажем, на бейсике, не было бы необходимости и выносить общие части вычислений в одно место. Это практически бы не сказалось ни на быстродействии, ни на длине программы. Самое же важное, не надо было бы писать инструкции для пользователя. Всю информацию о вводе и смысле выводимых результатов дала бы сама программа.
Возможный вариант такой программы дан ниже.

Конечно, допустим вопрос: а нужна ли такая программа? Если персональный компьютер занимает отдельный стол в вашей рабочей комнате, его не захватишь с собой, идя на склад, где сложены заготовки. А "Электроника Б3-34", "МК-54", "МК-61" умещаются в кармане. Но если цифра, полученная на калькуляторе,- лишь одна из тех, что потребуются для большего расчета, то лучше потом вернуться к персональному компьютеру и провести последующие вычисления на нем.
Мы ждем откликов на выступление В.Дякина. ВНИМАНИЕ! Мы ждем писем, где будет рассказано ЛИБО о том, как на программируемом микрокалькуляторе удалось реализовать алгоритм, для выполнения которого, казалось бы, требуется более мощная вычислительная машина, ЛИБО о том, как микрокалькулятор применяется совместно с большой ЭВМ при решении какой-либо крупной задачи, ЛИБО о том, как опыт работы с программируемыми микрокалькуляторами помог при составлении программ для больших машин.
ТАБЛИЦУ ПЕЧАТАЕТ МАШИНА
В отраслевом экономическом институте, где я работаю, почти ежедневно приходится заниматься расчетами в табличных формах. До недавнего времени основным орудием такой работы в нашей лаборатории служил настольный калькулятор, а приметами этой работы были отрешенный взгляд, еле различимое бормотание и лихорадочное долбление клавиш. Изредка, в особо кризисных ситуациях, раздавались болезненно-надрывные возгласы "О-о-о!", зачастую сопровождаемые энергичным потиранием лба, щек, висков и завершавшиеся сумбурно - лихорадочным поиском ошибок.
Составлению каждой таблицы предшествовали длительные поиски исходной информации. Она обычно находится в разных шкафах, на разных полках, в многочисленных отчетах и справках и уж, конечно, на разных страницах.
Но вот информация подготовлена, таблицы просчитаны, записка составлена. Скорее напечатать!.. Увы! Оказывается, сейчас печатается материал вашего коллеги, а вам придется подождать.
Согласитесь, в таких условиях весьма трудно добиться плодотворного решения серьезных задач. И все же с этим приходилось мириться, пока в нашем институте не установили "Искру-226".
Восхищение мини-ЭВМ, навеянное публикациями, после первого с ней контакта во многом развеялось. Оказалось, что компьютер "не обучен" работе с таблицами. На повестку дня встал вопрос об "изобретении велосипеда" (во всяком случае, так нам тогда казалось).
Первые же размышления над будущей программой поставили нас перед неразрешимой на первый взгляд проблемой. Чтобы использовать различные алгоритмы при обработке одних и тех же данных, последние нужно хранить независимо от программ. Наименования данных, с одной стороны, связаны с ними самими (значит, должны и храниться с ними), с другой - являются частью табличного представления результата (то есть связаны с алгоритмом обработки). Круг замкнулся. Чтобы его разорвать, пришлось расчленить понятие "таблица" на составляющие: шапку, боковик, примечание, форматы представления чисел...
Для облегчения поиска данные по предприятиям объединяются в группы (или файлы, как говорят программисты), которые нумеруются и характеризуют разные признаки данных, например, объемы производства, расходы энергоресурсов, состав технологического оборудования и т.д. Показатели представляются рядом значений, относящихся к разным моментам времени - по годам, кварталам, месяцам. Группа данных может быть дополнительно помечена: "по проекту", "по плану" и т.д.
Возникла структура данных. Для их ввода в программе понадобились команды поиска, считывания. Вот он, шаг от структуры данных к структуре программы. Так шаг за шагом возникла универсальная программа поиска, ввода, печати - программа управления данными.
Как же она работает? Пусть для расчета во второй столбец таблицы нужно внести объем производства, скажем, газовых баллонов, в третий - затраты, а в первый - наименование предприятия, выпускающего газовые баллоны. В режиме диалога "Искра" уточнит у нас число столбцов таблицы, в какой столбец какие данные поместить, за какой год, среди каких предприятий вести поиск (например, по некоторой подотрасли). После этого ЭВМ начинает работать без участия человека.
Прежде всего она "заглядывает" в словарь, где сведены названия предприятий и их шифры. Завод "Вымпел". Его шифр - 501. Поиск касается объемов производства, то есть признака с кодом 001. Из этих двух чисел программа формирует номер файла 001501. В каждом подобном файле хранится двумерный числовой массив из элементов, обозначаемых в программе Z(I,J), а говоря проще - таблица, строение которой понятно из рисунка.

Код газовых баллонов - 103. Именно такое число будет искать машина, просматривая строки первого столбца таблицы. Номер строки, в которой обнаружится искомое число (пусть это будет строка 3), ЭВМ присвоит переменной I. Теперь начинается аналогичный поиск кода года и месяца. Пусть он нашелся в столбце с номером 2. Этот номер ЭВМ присвоит переменной J. Элемент Z(3,2) машина занесет в соответствующее место составляемой таблицы, а из словаря перепишет в строку боковика название предприятия.
По заданным кодам ЭВМ может найти несколько значений затребованного показателя, например, за ряд лет, но в составляемой нами таблице этого не понадобилось.
Бывает, что ЭВМ не находит нужного ей файла или в первом столбце просматриваемой таблицы не обнаруживает нужного кода. Тогда она просто переходит к просмотру файла следующего предприятия.
За составлением таблицы следует расчет (например, средних затрат). Однажды выполнив заданный ей когда-то расчет, машина может запомнить его по соответствующему указанию пользователей, так что впоследствии для его проведения достаточно лишь ввести его шифр.
После расчета нужно напечатать таблицу. К нашим услугам набор готовых шапок. Программа выберет или заново скомпонует требуемую, определит представления чисел. Перед тем, как печатать таблицу, машина "поинтересуется", как заносить в нее нулевые данные - ставить ли "0", прочерк или оставлять пустое место? Как лучше сегментировать таблицу, если полностью на одном листе она не разместится? Каким цветом печатать? Нужно ли сначала вывести таблицу на дисплей?
В итоге "Искра" не только автоматизировала нашу работу, повысила ее качество, высвободила время для постановки и решения сложных задач, создала условия для современной научной работы, но и изменила характер нашей деятельности. Потребность в услугах машинисток сократилась, так как основная часть отчетов - таблицы делаются на ЭВМ. А насколько привлекательнее общение с нею, нежели работа с калькулятором! У сотрудников появился интерес и к программированию, и к решению задач по-новому, стала повышаться квалификация.
Н.НИКИТИН (г.Москва)
МОЮ СЕКРЕТАРШУ ЗОВУТ "ИСКРА"
На моем рабочем столе с недавних пор разместилась ЭВМ "Искра-226". Сам я по специальности инженер-конструктор, а по должности - зав. отделом одного КБ. Нередко мой рабочий день бывает заполнен различными совещаниями, встречами, телефонными звонками. Секретарь мне нужен позарез, но не положен по штату. Вот часто что-то и забываешь, накладки вечно вылезают...
Задумал я поручить своей "Искре" функции секретаря. Много от нее не требуется. В понедельник и четверг (на эти дни мы в КБ стараемся "свалить" все организационные дела) ЭВМ утром должна спросить меня и моих сотрудников о планах на день и далее держать на экране дисплея точное время и информацию о ближайшем или текущем мероприятии, подавать звуковой сигнал в момент их начала и окончания. Только-то и всего.
Соответствующую программу составить было несложно, благо "Искра-226" имеет встроенные часы. Вся программа занимает 18 строк, из которых две последние - это подпрограммы запроса времени.

Строка 1. Названия мероприятия дня (до 200 знаков, то есть байт), время их начала и окончания (в секундах, прошедших от полуночи) хранятся в массивах. На день можно запланировать до 50 дел (ЭВМ может хранить и больше, но кто это выполнит?!). Встроенные часы "Искры-226" останавливаются при выключении машины. При новом ее запуске их нужно поставить - набрать на клавиатуре значение ближайших часов и минут (через запятую) и в момент нулевых секунд нажать на клавишу ВК.
Строки 2-9. Здесь запрограммирован начальный диалог машины с человеком, который сообщает ей свои планы на день. Информацию по текущим делам дня лучше вводить в память ЭВМ в порядке их важности. Машина при этом следит за тем, чтобы новое дело не "наползало" на какое-либо из ранее введенных. Если же это все-таки случится, не беда. "Искра" вежливо сообщит об этом (см. строку 8 ) и попросит выбрать другое время. Ревностно следит она также за тем, чтоб не планировалось что-то на уже прошедшее время (строка 4). Диалог заканчивается либо по инициативе человека, либо машины (см. строку 2).
Строки 10-11. Мы вводили в память машины информацию о делах дня в порядке их важности. Для ЭВМ же они все равны, и она расставляет их так, чтобы было удобнее с ними работать - проводит ранжировку по времени начала. Здесь использован метод перестановок (см., например, 2/86) сравниваются два соседних события (см. строку 10), и если первое должно произойти раньше второго, то они меняются местами. Распорядок дня таким образом "причесывается" до тех пор, пока все события не встанут на свое место и вспомогательная переменная Р останется равной нулю.
Строки 12-16. Здесь запрограммирован монолог ЭВМ, которая "поглядывает на часы" и сообщает о ближайшем или текущем мероприятии дня. Правда, "Искра" разговаривать не может, а подает только звуковой сигнал (зуммер) в момент начала и окончания дела. Шестнадцатиричный код зуммера - 07, перевода курсора дисплея в левый верхний угол экрана 01, то же с его очисткой - 03.
"Поглядывать на часы" машине позволяют подпрограммы, записанные в строках 17 и 18. Команда INPUT хT присваивает переменной Т значение машинного времени, убывающего по одной двухтысячной доле секунды. Перевести все это в часы, минуты и секунды несложно, имея под рукой оператор выделения целой части числа - INT. Здесь S() - это число секунд, прошедших от полуночи до момента запроса машиной точного времени, S - до момента обращения к подпрограмме. В.ГОГОЛЕВ (г.Москва)
[ МАЛЕНЬКИЕ ХИТРОСТИ
Когда однократное нажатие клавиши воспринимается машиной как многократное, говорят про "дребезг" контактов. Это неприятное явление нередко возникает при длительной эксплуатации микрокалькулятора. Клавиши микрокалькулятора используются с различной интенсивностью, поэтому можно заменить дефектный замыкатель на сохранившийся лучше - от другой клавиши, причем такой, дребезг которой не влияет на правильность выполнения операций. Среди таких операций - сброс, очистка регистра памяти, ввод десятичной запятой. Для ремонта понадобится скальпель и пинцет. Чтобы извлечь замыкатель, необходимо удерживающую его пленку прорезать по периметру на половину длины и затем извлечь замыкатель пинцетом. Осталось поменять местами исправный и дефектный замыкатели. Так мне удалось отремонтировать "Электронику Б3-26".
Ш.АХМЕТХАФИЗОВ (г.Казань) ]
ПО ПОРЯДКУ НОМЕРОВ СТАНОВИСЬ!
Выбрать из двух однотипных предметов лучший по какому-либо признаку - задача несложная. Но почти невыполнимой кажется она, если сравниваемых предметов много (скажем, десять), а различаются они едва заметно. Муки подобного выбора знакомы каждому, кто хоть раз состоял в каком-нибудь жюри.
Оказывается, эту сложную задачу можно свести к простейшей - выбору лучшего из двух. Если известны результаты попарных сравнений, то на их основе можно ранжировать всю совокупность. Соответствующий алгоритм известен и положен в основу предлагаемой программы:
00. ПД 01. П0 02. 1 03. КП^ 04. FL0 05. 03 06. ИПД 07. ПС 08. 1 09. - 10. П0 11. ИП0 12. ВП 13. 4 14. ИПС 15. + 16. С/П 17. Fx=0 18. 26 19. FL0 20. 11 21. ИПС 22. 1 23. - 24. БП 25. 07 26. ИПС 27. - 28. Fx=0 29. 36 30. КИПС 31. 1 32. + 33. КПС 34. БП 35. 19 36. КИП^ 37. 1 38. + 39. КП^ 40. БП 41. 19 42. Сх 43. ПС 44. ИПД 45. П0 46. ИПС 47. КИП^ 48. - 49. Fx<0 50. 53 51. FBx 52. ПС 53. FL0 54. 46 55. ИПД 56. П0 57. КИП^ 58. ИПС 59. / 60. КП^ 61.FL0 62. 57 63. Сх 64. С/П.
Программа поможет за несколько минут упорядочить химические вещества по резкости запаха, орнаменты по оригинальности узора, розы по степени отличия цвета лепестков от некоторого идеального и т.п. Сравнению можно подвергнуть не более 11 предметов.
Каждому из сравниваемых по какому-либо свойству объектов программа приписывает число от нуля до единицы - ранг. Объект, у которого это свойство выражено сильнее, чем у всех других, получает ранг, равный единице. Если в одном из сравнений два объекта признаны одинаковыми в отношении этого свойства, они получают одни и тот же ранг.

Процедуру ранжирования освоим на конкретном примере, нарочито простом и наглядном. Представьте, что изображенные здесь палочки требуется упорядочить по длине, а измерить их непосредственно нельзя. Перенумеруем их. Введем вышеприведенную программу в "Электронику Б3-34", нажмем клавишу В/0, наберем число сравниваемых объектов (в нашем случае 5), нажмем клавишу С/П. На индикаторе - 40005. Это вопрос: какая палочка длиннее - четвертая или пятая? Вводим номер той, которая кажется нам длиннее, вновь нажимаем С/П. На индикаторе появляются все новые вопросы, каждый раз в виде i000j. На каждый вопрос дается ответ - указывается номер предмета, i или j, более предпочтительного по свойству, в отношении которого ведется сравнение, или нуль, если предметы практически неразличимы. После опроса на индикаторе появляется 10001, и нажатием клавиши БП 42 С/П мы переходим к расчету рангов, окончание которого отмечается появлением нуля на индикаторе. После этого нажатием клавиш ИП1, ИП2 и т.д. на индикатор выводятся рассчитанные программой ранги: для нашего примера V1=1; V2=0.5; V3=l; V4=0.75; V5=0.25. Для нового расчета описанные действия следует повторить, начиная с нажатия клавиши В/0.
Присваивание рангов объектам различной природы может оказаться единственной возможностью их количественного анализа. Например, сравнивалось несколько роз одного сорта по насыщенности цвета лепестков, и были получены соответствующие ранги. Количество химиката, подсыпавшегося в горшок к каждому цветку, известно. По этим данным была построена эмпирическая зависимость между насыщенностью цвета, выраженного полученными рангами, и количеством химиката. Эта зависимость оказалась весьма полезной растениеводам.
Г.СЛАВИН (г.Таллин)
ТРИВИАЛЬНОЕ РЕШЕНИЕ
Утром первого апреля Виктор Галкин, которого с чьей-то легкой руки все в заводском ВЦ называли "программистом божьей милостью", был вызван к директору завода. В кабинете присутствовало почти все заводское начальство. Директор был краток.
- Товарищ Галкин,- сказал он,- цилиндры, один из которых вы видите у меня на столе,- это четверть всей нашей продукции. Но под эту четверть занята половина станочного парка завода. Так что, товарищ Галкин, вот вам конкретная задача. Подумайте и смоделируйте возможные варианты, прорешайте их на ЭВМ и к первому июля дайте предложения, как нам организовать производство цилиндров, чтобы уменьшить число задействованных под них станков.
Через полмесяца Галкин знал производство цилиндров не хуже главного технолога завода. Он работал с таким вдохновением, которого не испытывал уже давно. Задача была многомерной, и поэтому программа для ее решения оказалась довольно сложной. Для пущей эффектности в ней была предусмотрена выдача результатов на экран дисплея.
Тридцатого июня программа была уже отлажена, а утром следующего дня, когда Галкин еще только приступал к решению задачи, в машинный зал нежданно нагрянуло все начальство. Галкин волновался, как абитуриент на экзамене, когда запускал программу на счет. Наконец что-то щелкнуло, запищало, и на экране дисплея появилась надпись: для производства цилиндров использовать станков - 0, время работы первого станка - 0, второго станка - 0... И вскоре весь экран заполнился одними нулями.
Наступило гробовое молчание, которому, казалось, не будет конца.
- Это,- с трудом выдавил из себя Галкин,- тривиальное решение... Я сейчас...
Он суетливо нажал на какие-то кнопки, вновь что-то щелкнуло, запищало, исчезли с экрана нули, и появилась новая надпись: второго решения нет.
Молчание зала прервал голос директора.
- ВЦ, кажется, ваше хозяйство,- раздраженно обратился он к главному инженеру.- Разберитесь же, чем здесь занимаются.
... Всю ночь Галкину снились кошмары, а утром он шел иа работу, неся в своем "дипломате" заявление об уходе. Галкии уже подходил к зданию ВЦ, когда вдруг увидел спешащего к нему главного инженера. Улыбка не сходила с его лица.
- Сколько ж можно ждать тебя? На, прочти.- И главный инженер протянул ему какую-то бумагу. Это был приказ по министерству, предписывающий заводу с первого июля прекратить производство цилиндров как нерентабельное.
Р.АРАКЕЛОВ (г.Баку)
ПРОСТЫЕ ЧИСЛА
Конкурс на лучшую программу для построения ряда простых чисел (12/83, 6/84, 8/84) продолжал привлекать внимание наших читателей еще долго после того, как были подведены его итоги. Напомним имена и некоторые результаты победителей конкурса. Программа московского студента В.Илюхина отличалась высокими скоростными качествами, программа киевского инженера Г.Пендюры - возможностью получения результатов группами по дюжине простых чисел в каждой. Но, как говаривал К.Прутков, иет столь великой вещи, которую бы не превзошла величина еще большая. Ленинградский врач В.Козлов (Программа 1) и московский рабочий В.Никитин (Программа 2) подтвердили справедливость этих слов.
Программа В.Козлова хотя и работает по тому же алгоритму, как у В.Илюхина, но короче и выполняется быстрее.
Перед пуском счета заносим константы в регистры памяти: 0 в РВ; 2 в РА и Р1, 4 в Р0 и Р2, 6 в Р3 и РД, 12 в Р6. Ряд из восьми чисел 6, 4, 2, 4, 2, 4, 6, 2 формируется при обращении всего к шести регистрам, которое выполняется с помощью оператора КИП4(КИП5) в следующем порядке: Д, 0, 1, 0, 1, 2, 3, А. Последующее обращение (КИП4 или КИП5) вызывает индикацию нуля, ранее записанного в РВ, и приводит по условию х=0 к перезаписи числа 12 из Р6 в Р4 (Р5); цикл обращений в РД ... РВ повторяется. Такой несколько необычный порядок считывания содержимого регистров осуществляется с помощью команд косвенной адресации в тех случаях, когда в регистре-счетчике записано число N>13. Команда КНОП на шаге 01 - "заплата". Ее единственная функция - обеспечить четность адресов 02 и 04 - адресов переходов Kx!=0A, Kx!=0^, КБП^. Контрольный расчет 6121, В/0, С/П, "6131" выполняется за 75 секунд!
На том же принципе, что у В.Козлова, основана программа инженера А.Привеня из г.Константиновки Донецкой области. Она обладает тем же быстродействием, но длиннее на один шаг.
В.Никитин довел вывод результата группами, по-видимому, до предела, обусловленного возможностями "Электроники Б3-34". Его программа выполняется сравнительно долго, позволяя оператору "переключиться" на другие занятия, но уж когда микрокалькулятор закончит вычисления, оператору придется потрудиться, записывая 15 найденных чисел. Предусмотрен удобный ввод числовых данных. После того как программа введена, необходимо лишь набрать наименьшее исследуемое число без двойки и нажать клавиши В/0, С/П. Предположим, вы набрали число 6129. Через 80 минут на индикаторе 6257, а в регистрах Д-А, 9-0 соответственно 6247, 6229, 6221, 6217, 6211, 6203, 6199, 6197, 6173, 6163, 6151, 6143, 6133, 6131.
Программа 1: 00. П8 01. КНОП 02. ИП6 03. П4 04. КИП4 05. Кх!=0А 06. ИП8 07. + 08. П8 09. Fsqr 10. П7 11. 1 12. ПС 13. ИП6 14. П5 15. ИП7 16. КИП5 17. Fx!=0 18. 13 19. ИПС 20. + 21. ПС 22. - 23. Fx>=0 24. 36 25. ИП8 26. ИПС 27. / 28. П9 29. КИП9 30. x-y 31. ИП9 32. - 33. Kx!=0^ 34. БП 35. 15 36. ИП8 37. С/П 38. КБП^.
Программа 2: 00. ^ 01. 1 02. 4 03. П0 04. F() 05. 2 06. + 07. ^ 08. ^ 09. 3 10. ^ 11. F() 12. / 13. FBx 14. - 15. Fx>=0 16. 57 17. FBx 18. + 19. 1 20. , 21. 8 22. F1/x 23. - 24. 7 25. F10X 26. + 27. FBx 28. - 29. F() 30. F() 31. F() 32. * 33. x-y 34. - 35. Fx!=0 36. 54 37. FBx 38. F() 39. F() 40. F() 41. ^ 42. 2 43. + 44. ^ 45. ^ 46. F() 47. F() 48. F() 49. ^ 50. F() 51. F() 52. БП 53. 11 54. FBx 55. БП 56. 05 57. F() 58. ИП0 59. 1 60. 5 61. - 62. Fx<0 63. 68 64. F() 65. КП0 66. БП 67. 05 68. F() 69. С/П 70. БП 71. 00.
А.БОЙКО (г.Москва)

Рис. А.Тягнирядко (пос.Володарсн Ворошиловградской обл.)
МАГИЧЕСКИЙ КВАДРАТ
В этой игре девять чисел (от единицы до девятки) определенным образом перемещаются по полям разграфленного квадрата 3*3. Игра напоминает сборку кубика Рубика. Правда, если бы для нее потребовалась объемная интерпретация, то на эту роль подошел бы не куб, а тор (проще говоря, баранка), чья поверхность разделена на девять пронумерованных сегментов.
Получить такой тор несложно. Мысленно изогнем наш квадрат и склеим верхнюю сторону с нижней. Получим трубочку, как на рисунке. Изогнем трубочку и склеим ее концы, то есть бывшие левую и правую стороны квадрата. Получается тор.

Образ тора сделает более естественными для понимания перемещения чисел по полям нашего квадрата. Будем считать, что при сдвиге какого-либо его столбца сверху вниз содержимое верхнего поля передвигается в среднее, содержимое среднего - в нижнее, содержимое нижнего - в верхнее. Будем считать, что при сдвиге какой-либо строки квадрата слева направо содержимое левого поля попадает в среднее, содержимое среднего - в правое, содержимое правого - в левое. Впрочем, программа игры позволяет сдвигать лишь нижнюю строку, но это отнюдь нс ограничение, поскольку сдвигом столбцов любую строку можно сместить до самого нижнего положения.

Каждый из желаемых сдвигов выполняется нажатием определенной цифровой клавиши (см. таблицу) и вслед за нею клавиши С/П. После каждого перемещения на индикаторе демонстрируется нижняя строка. Другие строки можно вызвать на индикатор нажатием указанных в той же таблице цифровых клавиш (см. таблицу) и вслед за нею клавиши С/П. (Разобравшись в программе, каждый может добавить дополнительную команду перемещения, если сочтет ее полезной).

Цель игры - превратить допустимыми перемещениями исходное расположение цифр на полях квадрата в такое, в котором они расположены на клавиатуре микрокалькулятора. Каждый просмотр считается за ход, поэтому внимательный игрок имеет больше шансов на победу в коллективной игре.
Введя программу, заполните регистры: 25 - РА 43 - РВ, 52 - PC. Чтобы расположить числа по полям квадрата в нормальном порядке, в регистры с P1 no P9 запишем соответственно 100 20 3, 400, 50, 6, 700, 80, 9. Совершив несколько перемещений, как указано в контрольном примере, приведенном ниже, и убедившись, что программа функционирует без ошибок, сделайте еще пару-другую ходов. Очистите счетчик ходов командами Сх П0. Теперь можно играть. Интереснее, если в игре участвуют несколько человек, задавшись одной и той же исходной ситуацией. Тренируйте память, стараясь обойтись без бумаги и карандаша. После того как контрольный просмотр покажет, что цель достигнута, сравните показания счетчика ходов - регистра Р0 в калькуляторах игроков. Выигрывает тот, кто меньшим числом ходов сумеет решить головоломку.
Для новой игры необходимо лишь очистить регистр Р0 и сделать несколько "запутывающих ходов".
Программа: 00. КБПА 01. КБПВ 02. КБПС 03. БП 04. 61 05. БП 06. 17 07. БП 08. 70 09. БП 10. 77 11. ПД 12. ИП0 13. 1 14. + 15. П0 16. КППД 17. ИП1 18. ИП2 19. + 20. ИП3 21. + 22. С/П 23. БП 24. 11 25. ИП3 26. ИП2 27. ИП1 28. 1 29. 0 30. / 31. П2 32. F() 33. 1 34. 0 35. / 36. П3 37. F() 38. 2 39. F10X 40. * 41. П1 42. В/0 43. ИП1 44. ИП4 45. ИП7 46. П4 47. F() 48. П1 49. F() 50. П7 51. В/0 52. ИП2 53. ИП5 54. ИП8 55. П5 56. F() 57. П2 58. F() 59. П8 60. В/0 61. ИП3 62. ИП6 63. ИП9 64. П6 65. F() 66. П3 67. F() 68. П9 69. В/0 70. ИП4 71. ИП5 72. ИП6 73. + 74. + 75. БП 76. 22 77. ИП9 78. ИП8 79. + 80. ИП7 81. + 82. БП 83. 22.
Контрольный пример: БП 11 5 С/П "123" 7 С/П "456" 9 С/П "789" 0 С/П "312" 1 С/П "412" 2 С/П "452" 3 С/П "456"... Сх П0.
М.ВАХТЕРОВ (г.Москва)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
Круг компьютерных проблем схлопывается...
9/86
ИГРЫ И ДЕЛА ПЕРСОНАЛЬНОГО КОМПЬЮТЕРА
Кандидат технических наук В.БРЯБРИН, кандидат экономических наук Г.КОЧЕТКОВ
В прошлом году мы побывали в Соединенных Штатах Америки в составе небольшой группы советских специалистов, знакомившихся с основными типами выпускаемых в США персональных компьютеров и их характерными применениями. Мы побывали в Стэнфордском и Калифорнийском университетах, а также в Массачусетском технологическом институте, из стен которых вышли многие известные специалисты в области вычислительной техники и информатики и где компьютеры с давних пор служат одним из главных инструментов для научных исследований и обучения. Нам была предоставлена возможность посетить несколько общеобразовательных школ, в которых уже начали широко применяться персональные компьютеры. Побывали мы также в нескольких специальных компьютерных центрах, организованных на основе обычных политехнических музеев; они дают возможность практически каждому желающему посидеть несколько часов за компьютером и посмотреть, что он умеет делать. Наконец, мы познакомились подробнее с тем, для чего и как применяют американцы персональные компьютеры.
В печати публикуются самые различные сведения о масштабах использования в мире персональных компьютеров и разные прогнозы роста их числа. Вот данные, которые приводит популярный журнал "Байт" (число компьютеров - в тысячах штук):

Как видите, в последние годы количество персональных ЭВМ в США росло очень быстро и сегодня исчисляется уже миллионами. С подобным быстрым ростом выпуска определенного вида электронной аппаратуры, пользующейся большим спросом, мы не раз сталкивались и в нашей стране, например, в период быстрого расширения телевизионной сети (3/86), когда, скажем, за 10 лет (1956-1966гг.) число телевизоров у населения возросло в 20 раз и достигло 16 миллионов; к настоящему времени их выпущено около 100 миллионов штук. К сожалению, на такой вид вычислительной техники, как персональные компьютеры, наша промышленность обратила внимание с некоторым опозданием. Но сейчас дело двинулось вперед достаточно энергично, и недалеко, видимо, время, когда количество персональных ЭВМ, выпускаемых в нашей стране, будет полностью удовлетворять спрос на них.
Еще не так давно компьютеры в США были сосредоточены в вычислительных центрах, к ним имел доступ лишь ограниченный круг специалистов, влияние вычислительной техники на общество было косвенным и не столь значительным, как это предсказывалось в прогнозах, сделанных в начале "компьютерной эры". Появление дешевых микропроцессоров и на их основе недорогих микрокомпьютеров в корне изменило ситуацию - информационно-вычислительная техника стала гораздо более доступной, и сфера ее применения быстро расширяется. Компьютеры можно увидеть в конторах и на предприятиях (текстовые процессоры, автоматизированные рабочие места, станки с программным управлением), в магазинах (кассовые аппараты и системы управления товарными запасами), в банках (автоматы для выдачи денег), в индустрии отдыха (системы резервирования мест в гостиницах, продажи билетов в театры и на спортивные мероприятия), на транспорте (системы продажи билетов) и во многих других областях.
Сегодня в ряде стран, в том числе в США, основанная на "использовании персональных компьютеров автоматизация привела к таким значительным изменениям образа жизни, что даже самые смелые эксперты затрудняются предсказать, к чему все это в конце концов придет. В книге "Грядущий разум" американский футуролог Эдвард Лиас отмечает, что персональные компьютеры привели к образованию новой информационной среды, которая пронизывает все общество.
Какие персональные ЭВМ популярны сейчас в Америке? До 1982 года первенство держали машины фирмы Apple, которая одной из первых в США дала толчок индустрии персональных компьютеров. Машины Apple-II и ряд их разновидностей реализованы на основе 8-разрядного микропроцессора, они, как и 8-разрядные машины фирм Radio Schack и Commodore, представляют первое поколение персональных ЭВМ. Их стоимость неуклонно падала и в настоящее время колеблется от нескольких сотен до полутора тысяч долларов.
В конце 1981 года фирма IBM (ИБМ) объявила о выпуске первого своего 16-разрядного персонального компьютера IBM PC, открывшего дорогу новому поколению машин. Репутация известной фирмы, налаженная реклама и сеть продажи сделали свое дело - начиная с 1982 года эти машины стали фаворитами на рынке персональных компьютеров. Вслед за IBM точно такие же машины стали выпускать и другие фирмы - крупные и мелкие. Например, одна из популярных моделей - машина М24 - выпускается совместно американской фирмой АТТ и известной итальянской фирмой Olivetti. Многие небольшие фирмы стали разрабатывать для персональных компьютеров IBM и совместимых с ними машин различные дополнительные устройства и программное обеспечение. В результате популярность этих машин росла, цены падали, и в настоящее время хорошую машину такого класса с жестким диском большого объема (10 или 20Мбайт) и цветным графическим дисплеем можно купить за 3-5тыс. долларов. Наиболее популярны машины двух разновидностей - IBM PC-XT и IBM PC-AT. Вот их основные технические показатели:

Успех компьютеров типа IBM PC заставил другие фирмы искать пути для привлечения новых покупателей. Первый заметный шаг сделала фирма Apple (полное название Apple Computer Incorporeted). В 1984 году ею была объявлена машина Macintosh, которая обладала совершенно новыми свойствами, обеспечивающими простоту и удобство работы пользователей прн выполнении стандартных действий. В основе работы пользователя лежит манипулирование графическими изображениями, обозначающими разные типичные понятия - текстовый документ, таблицу, линию для рисования и др. Эти машины быстро получили признание в университетах, но не вышли на первое место в сравнении с IBM PC. Одна из причин - их довольно высокая стоимость, около 2500 долларов.
Две другие известные фирмы, специализировавшиеся на персональных компьютерах - Commodore и Atari,- в конце 1985 года выпустили почти одинаковые машины - Amiga и Atari-1040, которые при стоимости 1000-1300 долларов обладают замечательными возможностями по обработке цветных графических изображений и синтезу звука. Они могут иметь также очень большую оперативную память - до 16 Мбайт. Сейчас эти машины приобретают все большее число поклонников и постепенно оттесняют машину Macintosh, в которой использован черно-белый дисплей и оперативная память не может быть увеличена более чем до 512 Кбайт. При стоимости около 1000 долларов машины Amiga и Atari-1040 в диапазоне цен занимают место, которое может привлечь значительное число покупателей.
И все же в сфере профессионального использования и в образовании продолжают преобладать компьютеры типа IBM PC-XT и IBM PC-AT, которых выпускается сейчас ежегодно почти 2 миллиона штук. Из этого числа иа саму фирму IBM приходится около 1 миллиона машин.
Помимо широко распространенных дешевых компьютеров, в научно-исследовательских учреждениях и университетах активно используются так называемые профессиональные рабочие станции, самая, так сказать, высокая разновидность персональных вычислительных средств. Это, например, машины Apollo, SLJN-2 и другие, их стоимость около 20 тысяч долларов.
Можно назвать по крайней мере три сферы, где персональные компьютеры используются наиболее широко и оказывают заметное влияние на характер деятельности людей, на их отношение к "компьютерной грамотности", а также на форму и содержание работы, ранее выполнявшейся без применения ЭВМ. Эти сферы - бизнес, наука и образование. Для деловой жизни особенно характерно, во-первых, применение персональных компьютеров как средств текстовой обработки, во-вторых, как инструментов для финансовых расчетов. Удобство применения персональных компьютеров для этих целей в значительной степени определяет коммерческий успех как самих моделей персональных ЭВМ, так и разрабатываемых для них программных средств. Довольно популярно использование персональных компьютеров для создания небольших баз данных и как средства коммуникаций. В последнем случае компьютер, объединенный с телефоном и подключенный к линии связи, играет одновременно роль автоматизированного телефонного справочника, оператора местной АТС, автоответчика, средства доступа к таким источникам информации, как биржевые сводки, библиотечные каталоги, и др. В последнее время все большее внимание начинает уделяться средствам обработки графической информации: хороший персональный компьютер может с успехом использоваться для создания иллюстраций к научным статьям, рекламной графики, чертежей.
Популярность персональных компьютеров и их применение в деловой сфере влияют на внешний облик этих машин. Так, например, ряд фирм уделяет особое внимание так называемым портативным компьютерам - машинам, которые в сложенном виде легко размешаются в небольшом чемодане и могут использоваться в гостиничном номере или даже в дороге - в самолете или в поезде.
Широко применяются персональные компьютеры в научных исследованиях. На столе ученого персональный компьютер служит то пишущей машинкой, то суперкалькулятором, то информационно-справочной системой, то кульманом, то средством управления экспериментальной установкой. В отличие от пользователей в сфере бизнеса, которые редко занимаются программированием, ученые очень часто сами для себя разрабатывают необходимые программы, а затем применяют их в своей научной работе. Возрос интерес к программам с элементами искусственного интеллекта, особенно так называемых экспертных систем: именно дешевые персональные компьютеры позволяют внедрять методы искусственного интеллекта в практических системах, имеющих широкое применение.
Высшее образование в США очень тесно переплетается с научной работой. Согласно университетским программам, студенты значительную часть учебного времени должны посвящать научным исследованиям, и дешевые персональные компьютеры стали почти обязательным элементом студенческого арсенала во многих американских университетах. Крупные фирмы делают большие скидки - до 40 процентов - для студентов. Это преследует сразу несколько целей: во-первых, растет популярность фирмы и изготавливаемых ею машин; во-вторых, студенты, получившие опыт работы на определенных компьютерах, будут, вероятнее всего, и впредь приверженцами и пропагандистами этих моделей; в-третьих, студенты нередко разрабатывают прикладные программы, которые входят в общий фонд программного обеспечения для данного класса персональных компьютеров и способствуют росту их популярности. Любопытно, что в отличие от наших вузовских программ, в университетах США очень мало внимания уделяется обучению программированию как отдельной науке: считается, что студенты так или иначе самостоятельно научатся программировать, если им это будет необходимо. Персональные компьютеры используются студентами чаще всего как вспомогательные средства обучения и самостоятельной работы. При этом они, как и пользователи в сфере бизнеса, применяют стандартные прикладные программы - текстовые процессоры, системы экономических расчетов на основе "электронных таблиц", базы данных.
Сходную картину можно наблюдать и в школах. Правда, вопреки сложившемуся представлению отнюдь не во всех американских школах имеются персональные компьютеры. Но там, где они есть, их применение весьма разнообразно - от ведения административных дел до обучения истории и географии. Директор одной из таких школ - сам бывший выпускник химического факультета Массачусетского технологического института - рассказал, что в его школе пропагандируется применение персональных компьютеров в первую очередь в преподавании гуманитарных дисциплин. Делается это для того, чтобы преподаватели-гуманитарии не испытывали страха перед компьютерами и не оправдывались тем, что ЭВМ относятся прежде всего к области математики и физики. На уроках языка и литературы ученики пользуются текстовым процессором, а на уроках географии - графическим пакетом. Для изучения истории применяются специальные игровые программы: ученик, чтобы набрать во время такой игры побольше очков, должен хорошо знать определенную историческую эпоху, например, историю Франции времен Людовика XIV.
Для изучения основ программирования в младших классах школ чаше всего используется язык Лого.
В США нет государственной программы компьютеризации школьного образования, подобной советской программе или программам, осуществляемым во Франции, Англии и других странах. Большая часть работ в этом направлении в США носит частнопредпринимательский характер. Но некоторые методы и приемы обучения с использованием персональных компьютеров, безусловно, заслуживают внимательного изучения. Предварительная договоренность между Генеральным секретарем ЦК КПСС М.С.Горбачевым и президентом США Р.Рейганом во время женевской встречи о возможном советско-американском сотрудничестве в области школьной информатики открывает перспективы для плодотворного развития идей, методов и конкретных систем, которые могли бы использоваться и в советских, и в американских школах. Первые шаги на этом пути уже делаются и, хочется верить, начнут приносить практические результаты.
Многие американские специалисты сходятся в том, что в ближайшей перспективе сферами, которые окажут радикальное влияние на наше отношение к компьютерам, будут игры, автоматизация конторских работ, использование компьютеров как универсальных приборов для информационных связей. Это подтверждается, в частности, материалами одного из наиболее массовых журналов в данной области - "Персонал компьютинг".
В 1984 году этот журнал имел 625 тысяч подписчиков, в основном руководителей и специалистов (более 85%). Исследование, специально проведенное для журнала, показало, что основной мотив покупки персонального компьютера - это стремление повысить производительность своего труда, сберечь время, улучшить систему деловых и личных связей. В подавляющем большинстве случаев владельцы персональных компьютеров дали положительный ответ на вопрос о том, достигнуты ли их первоначальные цели. А многие указали на то, что перед ними открылись дополнительные возможности, о которых они без новой техники не могли даже подозревать.
Основными сферами применения персональных ЭВМ среди читателей журнала были: обработка текстов (60%); развлекательные программы (40%); ведение личных баз данных (30%); бухгалтерский учет и отчетность (30%); образовательные программы (25%)- По данным журнала, лишь 9% владельцев при покупке воспользовались дотациями своей фирмы, а 91% оплатили покупку из собственных средств. Они объяснили это тем, что не желают ждать, пока их фирма раскачается. Ну, а если она все же примет решение об установке персональных машин в офисах, сотрудники уже будут готовы к этому.
Для крупных фирм основными областями применения персональных ЭВМ стали системы принятия управленческих решений с пакетами программ, позволяющими отвечать на вопросы типа "Что будет, если?..", а также финансовое моделирование, бухгалтерский учет и контроль, ведение кадрового учета, обработка текстов, управление материальными запасами. Несколько меньшей популярностью пользуются программы управления производством.
Практически никто не оценивает персональные компьютеры по критериям типа стоимость/эффективность, не считает прямой экономический эффект от них. В 63% случаев в качестве обоснования использования этих машин называлось повышение качества информационного обеспечения, 47% отметили возможность быстрых и сложных расчетов, 46% - доступ к базам данных. Руководство фирм относится к персональным компьютерам как к необходимому элементу хозяйственной инфраструктуры, такому же, скажем, как телефон.
Долгое время в печати США шли дискуссии относительно того, нужна ли ЭВМ высшим руководителям компаний, фирм и предприятий. Дискуссии эти разрешились самой жизнью - уже в середине 80-х годов многие высшие руководители, особенно в небольших фирмах, имели на своем рабочем месте персональную ЭВМ, которую широко использовали. В мелком бизнесе, где во главе фирм и предприятий стоят в основном молодые воспитанники вузов "компьютерной эпохи", использование ЭВМ почти стопроцентное. Многие руководители имеют дома копии своих рабочих компьютерных систем, чтобы иметь возможность обращаться к ним в любое время.
Процесс компьютеризации охватил все уровни управления экономикой. По оценкам компании "Ксерокс", в 1983 году в США на 54млн. рабочих мест, относящихся к сфере обработки информации, приходилось 55млн. телефонов и 18.5млн. различных компьютерных систем, из которых 4.5 млн.- системы обработки текстов, 10млн.- специализированные терминалы, 2.5млн.- многоцелевые терминалы и 1.5млн.- персональные ЭВМ. Предполагается, что к 1988 году занятость в информационной сфере возрастет до 62млн., число телефонов - до 75млн., компьютерных систем - до 71млн., в том числе 31млн. систем обработки текстов, 32млн. терминалов и 8млн. персональных компьютеров.
Уже довольно давно многие американцы стали ощущать неподготовленность к "компьютерному веку" и стыдятся своей неосведомленности в части возможностей ЭВМ и работы с ней. Со всей остротой встала, как ее называют, проблема компьютерной грамотности. Людям, которые большую часть своей жизни прожили, не зная, что такое компьютер, и лишь изредка встречали это слово на страницах газет и журналов, вдруг было заявлено, что без покупки домашней ЭВМ их дети не смогут учиться в хороших колледжах, в средней школе они наверняка отстанут от своих сверстников, уже имеющих такие машины. Средства массовой информации обрушили на обывателя грозное предупреждение: если он не будет обучаться компьютерной грамотности, то станет с нарастающей скоростью отставать от жизни, от своих коллег, не получит продвижения по службе.
Такая кампания вызвала различные ответные реакции, вплоть до экстремистских - случается, что компьютеры взрывают, в них стреляют, размагничивают магнитную память. Но, конечно, большинство людей стараются подойти к разрешению создавшихся противоречий конструктивными путями.
Известный американский специалист по проблемам искусственного интеллекта профессор Роджер Шенк отметил, что сейчас перед обществом стоит вопрос: что оно должно знать о компьютерах, чтобы жить и процветать в мире, наполненном ими? Задача распространения компьютерной грамотности в традиционном виде подразумевала, что человек должен приспособиться к новому для него типу машин, обучившись несвойственному ему по природе новому занятию - программированию. Но приспособление к системе "человек-машина" идет в двух направлениях, и, как показывает практика последних десятилетий, изменения в компьютерных системах идут гораздо быстрее, чем в "человеческом компоненте".
Чтобы правильно оценить задачи и последствия компьютеризации, нужно прежде всего обратить внимание на человека, на то, как он может измениться под влиянием вычислительных машин. Многочисленные примеры из истории развития технических систем, таких, как автомобиль, радио, телевидение, и других, говорят о том, что в конце концов техника приспосабливается к человеку, а не наоборот. Правда, компьютеры кажутся более значительным достижением техники и более непонятным, нередко высказывают опасения, что они должны резко изменить сам характер нашей жизни.
Многие специалисты, главным образом связанные с созданием искусственного интеллекта, прямо заявляют - ложная тревога! Уже сейчас, указывают они, люди могут обращаться к ЭВМ на языке, довольно близком к разговорному, машины научились воспринимать текст, слушаются команд, поданных голосом. Но во всех случаях, предупреждают нас, для общения с ЭВМ нужно следовать правилам языка, нужно быть просто грамотным человеком: машина ие понимает безграмотных фраз, слов, произнесенных и написанных с ошибками, нечетких, двусмысленных высказываний. В связи с внедрением систем обработки текста, которыми пользуется широкий круг специалистов, перед американским обществом со всей остротой встала проблема родного языка.
Темпы освоения вычислительной техники во многом зависят от обшего уровня компьютерной культуры, которая формируется в США под влиянием множества факторов. В начале 80-х годов было принято несколько программ, имевших своей целью ускорить этот процесс, наибольшую известность приобрел проект "компьютерный город".
Его основная идея заключалась в том, чтобы дать возможность всем желающим познакомиться с компьютером, поработать с ним или поиграть. Для этого организаторы выбрали определенные районы в крупных или небольших городах и установили в них компьютеры в парках, кафе, кинотеатрах, магазинах, аэропортах и других общественных местах. Всем желающим предлагалось подойти к компьютеру и начать с ним диалог. При этом начальное инструктирование сводилось к минимуму, в основном сама машина вела диалог, обучая человека элементарным правилам работы. Основными участниками этих проектов стали дети, которые проводили многие часы возле компьютеров. Наиболее активным выдавались специальные значки с надписью "Мой компьютер любит меня".
Идеи "Компьютерного города" были, естественно, поддержаны производителями оборудования и математического обеспечения, поскольку это позволяло им вести рекламу своей продукции и расширять рынки сбыта. Со временем мероприятия "Компьютерного города" приняли умеренный характер, но контакты компьютера с широкой публикой сохранились и, более того, стали типичным явлением. Во многих универмагах, например, функции справочного бюро выполняют персональные компьютеры, работающие в режиме диалога. В аэропортах мы видели стенды компании ИБМ, на которых установлены персональные компьютеры. Скучающие в ожидании отправки самолета пассажиры могут ознакомиться с основами устройства и работы компьютера, а заодно получить интересующие их справки об аэропорте, местных достопримечательностях, городском транспорте.
Одно из интересных начинаний по формированию компьютерной культуры - создание при бостонском Музее науки Компьютерного центра. Основная форма его работы - уроки для всех желающих. Наибольшей популярностью пользуются воскресные курсы "Язык Лого для детей и родителей". Каждому посетителю выделяется персональная ЭВМ, и в течение полутора часов по специально построенной программе ведется индивидуальное обучение в форме диалога с компьютером.
Но главное, что привлекает посетителей в Центр, считают его руководители, это возможность поработать с новыми пакетами прикладных программ. Ведущие разработчики программных средств предоставляют Центру образцы своих основных программ, к февралю 1985 года библиотека Центра насчитывала более 400 наиболее известных пакетов и продолжала быстро расти. Посетители имеют возможность прямо с полки взять любой пакет и в течение 30 минут делать с ним все, что хотят. Время ограничено из-за большого наплыва желающих приобщиться к новым программам. Центр организует курсы для учителей, в которых они знакомятся с возможностями ЭВМ в обучении, с основами языков Лого, Бейсик, Паскаль и других.
Важный элемент взаимоотношения с персональным компьютером - его эмоциональное воздействие на человека. Давно замечено, что пользователи как бы одушевляют свои компьютер, приписывают ему человеческие чувства, скажем, любовь или ненависть, считают, что он может рассуждать и т.п. С учетом этого многие прикладные программы дополняют различными игровыми элементами, усиливающими эмоциональность контактов человека с ЭВМ. Например, в обучающей программе по арифметике после неправильного ответа раздается взрыв, разрушающий изображение на экране, а после правильного появляется симпатичный герой популярного мультфильма и раздастся веселая музыка. Игровой компонент считается не менее важным, чем содержательный. Среди специалистов укрепляется точка зрения, чго для формирования компьютерной культуры эмоциональный контакт с ЭВМ, который создастся играми, не менее важен, чем способность рационально решать различные задачи. Считается, что именно благодаря эмоциональным контактам и занимательности было разрушено устойчивое представление об ЭВМ, как о большом арифмометре.
Возникает вопрос: что из американского опыта мы можем использовать, что, например, может оказаться полезным в организации учебного процесса в наших школах? На наш взгляд, можно использовать очень многое. С существенными, однако, поправками, учитывающими специфику современного этапа процесса компьютеризации в нашей стране, и, естественно, с учетом принципиальных идеологических различий нашего и капиталистического общества.
Нам чужды задачи, которые, хотя бы и в учебных целях, преследуют прежде всего получение личной выгоды, извлечение максимальных личных доходов из тех или иных предполагаемых хозяйственных мероприятий. Очевидно, для наших людей естественна и понятна ситуация, когда на первый план выдвигаются задачи удовлетворения общественных потребностей, повышения эффективности общественного производства и т.д. Кстати, пакеты программ для решения таких задач созданы и успешно используются при обучении студентов, например, в Московском институте управления имени С.Орджоникидзе. Кроме того, мы должны видеть четкую границу возможностей компьютеризации. В частности, признавая необходимость ускоренной компьютеризации экономики, различных производственных и деловых сфер нашей жизни, нам надо отчетливо представлять, что персональный компьютер вряд ли когда-нибудь может стать помощником при решении проблем нравственного выбора. Компьютерная культура никогда не заменит общую культуру, важнейшим элементом которой было и остается глубокое знание истории, литературы, искусства. Короче говоря, резко повысив темпы внедрения компьютеров в школу, в студенческие аудитории, науку, хозяйственную практику, быт, нам надо избегать фетишизации компьютеров - явления, увы, характерного для многих западных стран. Истоки этого, кстати, есть результат не только общественных потребностей в компьютерном решении задач, но и в естественном для фирм, выпускающих вычислительную технику, стремлении с максимальной выгодой для себя использовать благоприятную конъюнктуру рынка, продать побольше машин даже в тех случаях, когда это не вызывается такой уж срочной и безусловной необходимостью.
В последние годы ни одно нововведение в области электроники не вызывало в США таких бурных и ожесточенных дискуссий, как компьютерные игры. Как отмечают многие исследователи проблем компьютеризации, играм принадлежит важная роль в распространении компьютерной культуры, именно с ними связано появление первых компьютеров в большинстве домов.
Компьютерные игры вырабатывают навыки общения с новой техникой, после нескольких часов игры с ЭВМ не только ребенок, но и взрослый теряет страх к непонятной для него электронной машине. Это обстоятельство сейчас широко используется корпорациями, которые внедряют у себя автоматизированные системы: прежде чем перейти к использованию ЭВМ в рабочих режимах, сотрудникам дают возможность несколько дней и даже недель поиграть с машиной, например, в шахматы. Конечно же, с помощью одних только игр нельзя научить людей программированию и пониманию технических аспектов работы ЭВМ, но в США в последние годы складывается устойчивое мнение, что рядовому гражданину умение программировать не особенно и нужно, что большинству людей достаточно научиться свободно пользоваться вычислительной техникой и знать границы ее применения.
Благодаря некоторым особенностям компьютерных игр они стали мощным ускорителем в деле распространения идей программирования. Дети, которые первоначально лишь пользовались программами, составленными другими, начали проявлять стремление к самостоятельному программистскому творчеству. Многие из них предпочитают получать игры не в виде готовых кассет или дисков, а в виде исходных текстов, так как в этом случае в программу можно вводить любые изменения и создавать таким образом свой собственный вариант игры. Наиболее интересные решения становятся достоянием друзей, и игра начинает жить своей собственной жизнью, развиваясь и совершенствуясь. Создание игр стало популярным способом проведения досуга для серьезных программистов.
Новые компьютерные игры позволяют полностью раскрыться творческим способностям программиста, и только бедность его воображения может положить пределы тем мирам и приключениям, которые возможны на экране ЭВМ. Манипулируя фантастическим миром внутри компьютера, игроки начинают осознавать собственные силы в том реальном мире, который находится за пределами экрана. Считается, что этот новый тип постижения реальности может в корне изменить систему образования. Новое поколение компьютерных игр раскрепощает мышление, позволяет размышлять о немыслимом, и неудивительно, что сценарии большинства игр написаны либо по сказкам, либо по научно-фантастическим романам и рассказам.
Важная особенность компьютерных игр, усиливающая их притягательность,- это способность запоминать прошлый опыт, самообучаться. В большинстве игр компьютер не повторяет ошибок и постепенно усложняет свое поведение по мере того, как его партнер осваивает стратегию победы. Часто компьютеры хранят в своей памяти имена наиболее сильных игроков - каждый игрок должен прежде всего представиться машине, и если его имя уже есть в памяти, то автомат выбирает более сложную стратегию игры. В США появились местные и национальные знаменитости, чемпионы по отдельным видам компьютерных игр.
Достаточно богатый опыт, накопленный в США, подтверждает, что игры позволяют ввести детей, студентов или сложившихся специалистов в мир компьютеров, наиболее быстро и эффективно знакомят их с новой нарождающейся культурой информационного века, помогают создать основу для широкого использования компьютерной техники на производстве и в быту.
В целом процессы, происходящие в обществе под влиянием массовой компьютеризации, пока трудно оценить однозначно. Многое в них неясно, противоречиво. Так, компьютерные игры быстро вводят человека в новую сферу информационной деятельности, но они могут дать эффект "запойности": многие подростки и даже взрослые проводят долгие часы за игровыми пультами, растрачивая впустую свое время. Эти отрицательные последствия игр хорошо описаны в прессе.
Другой пример - компьютеры позволяют резко повысить производительность труда в сфере обработки информации. Но одновременно они интенсифицируют этот труд, что ведет к росту психической и физической нагрузки на операторов. В их среде растет число душевных расстройств, сокращаются масштабы простых человеческих контактов, бесед, обменов новостями и т.п. Это ведет к появлению нездорового климата на рабочем месте. В капиталистическом обществе с его отношением к человеку как к простому носителю товара, рабочей силе подобные процессы являются закономерным результатом автоматизации: машина, на этот раз электронная, в очередной раз противопоставлена человеку. Очевидно, что, взяв на вооружение персональный компьютер как мощное орудие ускорения научно-технического развития, мы, внимательно вникая в уже имеющийся у нас и за рубежом опыт, должны избежать негативных последствий его широкого использования.
...
9/86
ИГРЫ И ДЕЛА ПЕРСОНАЛЬНОГО КОМПЬЮТЕРА
Кандидат технических наук В.БРЯБРИН, кандидат экономических наук Г.КОЧЕТКОВ
В прошлом году мы побывали в Соединенных Штатах Америки в составе небольшой группы советских специалистов, знакомившихся с основными типами выпускаемых в США персональных компьютеров и их характерными применениями. Мы побывали в Стэнфордском и Калифорнийском университетах, а также в Массачусетском технологическом институте, из стен которых вышли многие известные специалисты в области вычислительной техники и информатики и где компьютеры с давних пор служат одним из главных инструментов для научных исследований и обучения. Нам была предоставлена возможность посетить несколько общеобразовательных школ, в которых уже начали широко применяться персональные компьютеры. Побывали мы также в нескольких специальных компьютерных центрах, организованных на основе обычных политехнических музеев; они дают возможность практически каждому желающему посидеть несколько часов за компьютером и посмотреть, что он умеет делать. Наконец, мы познакомились подробнее с тем, для чего и как применяют американцы персональные компьютеры.
В печати публикуются самые различные сведения о масштабах использования в мире персональных компьютеров и разные прогнозы роста их числа. Вот данные, которые приводит популярный журнал "Байт" (число компьютеров - в тысячах штук):

Как видите, в последние годы количество персональных ЭВМ в США росло очень быстро и сегодня исчисляется уже миллионами. С подобным быстрым ростом выпуска определенного вида электронной аппаратуры, пользующейся большим спросом, мы не раз сталкивались и в нашей стране, например, в период быстрого расширения телевизионной сети (3/86), когда, скажем, за 10 лет (1956-1966гг.) число телевизоров у населения возросло в 20 раз и достигло 16 миллионов; к настоящему времени их выпущено около 100 миллионов штук. К сожалению, на такой вид вычислительной техники, как персональные компьютеры, наша промышленность обратила внимание с некоторым опозданием. Но сейчас дело двинулось вперед достаточно энергично, и недалеко, видимо, время, когда количество персональных ЭВМ, выпускаемых в нашей стране, будет полностью удовлетворять спрос на них.
Еще не так давно компьютеры в США были сосредоточены в вычислительных центрах, к ним имел доступ лишь ограниченный круг специалистов, влияние вычислительной техники на общество было косвенным и не столь значительным, как это предсказывалось в прогнозах, сделанных в начале "компьютерной эры". Появление дешевых микропроцессоров и на их основе недорогих микрокомпьютеров в корне изменило ситуацию - информационно-вычислительная техника стала гораздо более доступной, и сфера ее применения быстро расширяется. Компьютеры можно увидеть в конторах и на предприятиях (текстовые процессоры, автоматизированные рабочие места, станки с программным управлением), в магазинах (кассовые аппараты и системы управления товарными запасами), в банках (автоматы для выдачи денег), в индустрии отдыха (системы резервирования мест в гостиницах, продажи билетов в театры и на спортивные мероприятия), на транспорте (системы продажи билетов) и во многих других областях.
Сегодня в ряде стран, в том числе в США, основанная на "использовании персональных компьютеров автоматизация привела к таким значительным изменениям образа жизни, что даже самые смелые эксперты затрудняются предсказать, к чему все это в конце концов придет. В книге "Грядущий разум" американский футуролог Эдвард Лиас отмечает, что персональные компьютеры привели к образованию новой информационной среды, которая пронизывает все общество.
Какие персональные ЭВМ популярны сейчас в Америке? До 1982 года первенство держали машины фирмы Apple, которая одной из первых в США дала толчок индустрии персональных компьютеров. Машины Apple-II и ряд их разновидностей реализованы на основе 8-разрядного микропроцессора, они, как и 8-разрядные машины фирм Radio Schack и Commodore, представляют первое поколение персональных ЭВМ. Их стоимость неуклонно падала и в настоящее время колеблется от нескольких сотен до полутора тысяч долларов.
В конце 1981 года фирма IBM (ИБМ) объявила о выпуске первого своего 16-разрядного персонального компьютера IBM PC, открывшего дорогу новому поколению машин. Репутация известной фирмы, налаженная реклама и сеть продажи сделали свое дело - начиная с 1982 года эти машины стали фаворитами на рынке персональных компьютеров. Вслед за IBM точно такие же машины стали выпускать и другие фирмы - крупные и мелкие. Например, одна из популярных моделей - машина М24 - выпускается совместно американской фирмой АТТ и известной итальянской фирмой Olivetti. Многие небольшие фирмы стали разрабатывать для персональных компьютеров IBM и совместимых с ними машин различные дополнительные устройства и программное обеспечение. В результате популярность этих машин росла, цены падали, и в настоящее время хорошую машину такого класса с жестким диском большого объема (10 или 20Мбайт) и цветным графическим дисплеем можно купить за 3-5тыс. долларов. Наиболее популярны машины двух разновидностей - IBM PC-XT и IBM PC-AT. Вот их основные технические показатели:

Успех компьютеров типа IBM PC заставил другие фирмы искать пути для привлечения новых покупателей. Первый заметный шаг сделала фирма Apple (полное название Apple Computer Incorporeted). В 1984 году ею была объявлена машина Macintosh, которая обладала совершенно новыми свойствами, обеспечивающими простоту и удобство работы пользователей прн выполнении стандартных действий. В основе работы пользователя лежит манипулирование графическими изображениями, обозначающими разные типичные понятия - текстовый документ, таблицу, линию для рисования и др. Эти машины быстро получили признание в университетах, но не вышли на первое место в сравнении с IBM PC. Одна из причин - их довольно высокая стоимость, около 2500 долларов.
Две другие известные фирмы, специализировавшиеся на персональных компьютерах - Commodore и Atari,- в конце 1985 года выпустили почти одинаковые машины - Amiga и Atari-1040, которые при стоимости 1000-1300 долларов обладают замечательными возможностями по обработке цветных графических изображений и синтезу звука. Они могут иметь также очень большую оперативную память - до 16 Мбайт. Сейчас эти машины приобретают все большее число поклонников и постепенно оттесняют машину Macintosh, в которой использован черно-белый дисплей и оперативная память не может быть увеличена более чем до 512 Кбайт. При стоимости около 1000 долларов машины Amiga и Atari-1040 в диапазоне цен занимают место, которое может привлечь значительное число покупателей.
И все же в сфере профессионального использования и в образовании продолжают преобладать компьютеры типа IBM PC-XT и IBM PC-AT, которых выпускается сейчас ежегодно почти 2 миллиона штук. Из этого числа иа саму фирму IBM приходится около 1 миллиона машин.
Помимо широко распространенных дешевых компьютеров, в научно-исследовательских учреждениях и университетах активно используются так называемые профессиональные рабочие станции, самая, так сказать, высокая разновидность персональных вычислительных средств. Это, например, машины Apollo, SLJN-2 и другие, их стоимость около 20 тысяч долларов.
Можно назвать по крайней мере три сферы, где персональные компьютеры используются наиболее широко и оказывают заметное влияние на характер деятельности людей, на их отношение к "компьютерной грамотности", а также на форму и содержание работы, ранее выполнявшейся без применения ЭВМ. Эти сферы - бизнес, наука и образование. Для деловой жизни особенно характерно, во-первых, применение персональных компьютеров как средств текстовой обработки, во-вторых, как инструментов для финансовых расчетов. Удобство применения персональных компьютеров для этих целей в значительной степени определяет коммерческий успех как самих моделей персональных ЭВМ, так и разрабатываемых для них программных средств. Довольно популярно использование персональных компьютеров для создания небольших баз данных и как средства коммуникаций. В последнем случае компьютер, объединенный с телефоном и подключенный к линии связи, играет одновременно роль автоматизированного телефонного справочника, оператора местной АТС, автоответчика, средства доступа к таким источникам информации, как биржевые сводки, библиотечные каталоги, и др. В последнее время все большее внимание начинает уделяться средствам обработки графической информации: хороший персональный компьютер может с успехом использоваться для создания иллюстраций к научным статьям, рекламной графики, чертежей.
Популярность персональных компьютеров и их применение в деловой сфере влияют на внешний облик этих машин. Так, например, ряд фирм уделяет особое внимание так называемым портативным компьютерам - машинам, которые в сложенном виде легко размешаются в небольшом чемодане и могут использоваться в гостиничном номере или даже в дороге - в самолете или в поезде.
Широко применяются персональные компьютеры в научных исследованиях. На столе ученого персональный компьютер служит то пишущей машинкой, то суперкалькулятором, то информационно-справочной системой, то кульманом, то средством управления экспериментальной установкой. В отличие от пользователей в сфере бизнеса, которые редко занимаются программированием, ученые очень часто сами для себя разрабатывают необходимые программы, а затем применяют их в своей научной работе. Возрос интерес к программам с элементами искусственного интеллекта, особенно так называемых экспертных систем: именно дешевые персональные компьютеры позволяют внедрять методы искусственного интеллекта в практических системах, имеющих широкое применение.
Высшее образование в США очень тесно переплетается с научной работой. Согласно университетским программам, студенты значительную часть учебного времени должны посвящать научным исследованиям, и дешевые персональные компьютеры стали почти обязательным элементом студенческого арсенала во многих американских университетах. Крупные фирмы делают большие скидки - до 40 процентов - для студентов. Это преследует сразу несколько целей: во-первых, растет популярность фирмы и изготавливаемых ею машин; во-вторых, студенты, получившие опыт работы на определенных компьютерах, будут, вероятнее всего, и впредь приверженцами и пропагандистами этих моделей; в-третьих, студенты нередко разрабатывают прикладные программы, которые входят в общий фонд программного обеспечения для данного класса персональных компьютеров и способствуют росту их популярности. Любопытно, что в отличие от наших вузовских программ, в университетах США очень мало внимания уделяется обучению программированию как отдельной науке: считается, что студенты так или иначе самостоятельно научатся программировать, если им это будет необходимо. Персональные компьютеры используются студентами чаще всего как вспомогательные средства обучения и самостоятельной работы. При этом они, как и пользователи в сфере бизнеса, применяют стандартные прикладные программы - текстовые процессоры, системы экономических расчетов на основе "электронных таблиц", базы данных.
Сходную картину можно наблюдать и в школах. Правда, вопреки сложившемуся представлению отнюдь не во всех американских школах имеются персональные компьютеры. Но там, где они есть, их применение весьма разнообразно - от ведения административных дел до обучения истории и географии. Директор одной из таких школ - сам бывший выпускник химического факультета Массачусетского технологического института - рассказал, что в его школе пропагандируется применение персональных компьютеров в первую очередь в преподавании гуманитарных дисциплин. Делается это для того, чтобы преподаватели-гуманитарии не испытывали страха перед компьютерами и не оправдывались тем, что ЭВМ относятся прежде всего к области математики и физики. На уроках языка и литературы ученики пользуются текстовым процессором, а на уроках географии - графическим пакетом. Для изучения истории применяются специальные игровые программы: ученик, чтобы набрать во время такой игры побольше очков, должен хорошо знать определенную историческую эпоху, например, историю Франции времен Людовика XIV.
Для изучения основ программирования в младших классах школ чаше всего используется язык Лого.
В США нет государственной программы компьютеризации школьного образования, подобной советской программе или программам, осуществляемым во Франции, Англии и других странах. Большая часть работ в этом направлении в США носит частнопредпринимательский характер. Но некоторые методы и приемы обучения с использованием персональных компьютеров, безусловно, заслуживают внимательного изучения. Предварительная договоренность между Генеральным секретарем ЦК КПСС М.С.Горбачевым и президентом США Р.Рейганом во время женевской встречи о возможном советско-американском сотрудничестве в области школьной информатики открывает перспективы для плодотворного развития идей, методов и конкретных систем, которые могли бы использоваться и в советских, и в американских школах. Первые шаги на этом пути уже делаются и, хочется верить, начнут приносить практические результаты.
Многие американские специалисты сходятся в том, что в ближайшей перспективе сферами, которые окажут радикальное влияние на наше отношение к компьютерам, будут игры, автоматизация конторских работ, использование компьютеров как универсальных приборов для информационных связей. Это подтверждается, в частности, материалами одного из наиболее массовых журналов в данной области - "Персонал компьютинг".
В 1984 году этот журнал имел 625 тысяч подписчиков, в основном руководителей и специалистов (более 85%). Исследование, специально проведенное для журнала, показало, что основной мотив покупки персонального компьютера - это стремление повысить производительность своего труда, сберечь время, улучшить систему деловых и личных связей. В подавляющем большинстве случаев владельцы персональных компьютеров дали положительный ответ на вопрос о том, достигнуты ли их первоначальные цели. А многие указали на то, что перед ними открылись дополнительные возможности, о которых они без новой техники не могли даже подозревать.
Основными сферами применения персональных ЭВМ среди читателей журнала были: обработка текстов (60%); развлекательные программы (40%); ведение личных баз данных (30%); бухгалтерский учет и отчетность (30%); образовательные программы (25%)- По данным журнала, лишь 9% владельцев при покупке воспользовались дотациями своей фирмы, а 91% оплатили покупку из собственных средств. Они объяснили это тем, что не желают ждать, пока их фирма раскачается. Ну, а если она все же примет решение об установке персональных машин в офисах, сотрудники уже будут готовы к этому.
Для крупных фирм основными областями применения персональных ЭВМ стали системы принятия управленческих решений с пакетами программ, позволяющими отвечать на вопросы типа "Что будет, если?..", а также финансовое моделирование, бухгалтерский учет и контроль, ведение кадрового учета, обработка текстов, управление материальными запасами. Несколько меньшей популярностью пользуются программы управления производством.
Практически никто не оценивает персональные компьютеры по критериям типа стоимость/эффективность, не считает прямой экономический эффект от них. В 63% случаев в качестве обоснования использования этих машин называлось повышение качества информационного обеспечения, 47% отметили возможность быстрых и сложных расчетов, 46% - доступ к базам данных. Руководство фирм относится к персональным компьютерам как к необходимому элементу хозяйственной инфраструктуры, такому же, скажем, как телефон.
Долгое время в печати США шли дискуссии относительно того, нужна ли ЭВМ высшим руководителям компаний, фирм и предприятий. Дискуссии эти разрешились самой жизнью - уже в середине 80-х годов многие высшие руководители, особенно в небольших фирмах, имели на своем рабочем месте персональную ЭВМ, которую широко использовали. В мелком бизнесе, где во главе фирм и предприятий стоят в основном молодые воспитанники вузов "компьютерной эпохи", использование ЭВМ почти стопроцентное. Многие руководители имеют дома копии своих рабочих компьютерных систем, чтобы иметь возможность обращаться к ним в любое время.
Процесс компьютеризации охватил все уровни управления экономикой. По оценкам компании "Ксерокс", в 1983 году в США на 54млн. рабочих мест, относящихся к сфере обработки информации, приходилось 55млн. телефонов и 18.5млн. различных компьютерных систем, из которых 4.5 млн.- системы обработки текстов, 10млн.- специализированные терминалы, 2.5млн.- многоцелевые терминалы и 1.5млн.- персональные ЭВМ. Предполагается, что к 1988 году занятость в информационной сфере возрастет до 62млн., число телефонов - до 75млн., компьютерных систем - до 71млн., в том числе 31млн. систем обработки текстов, 32млн. терминалов и 8млн. персональных компьютеров.
Уже довольно давно многие американцы стали ощущать неподготовленность к "компьютерному веку" и стыдятся своей неосведомленности в части возможностей ЭВМ и работы с ней. Со всей остротой встала, как ее называют, проблема компьютерной грамотности. Людям, которые большую часть своей жизни прожили, не зная, что такое компьютер, и лишь изредка встречали это слово на страницах газет и журналов, вдруг было заявлено, что без покупки домашней ЭВМ их дети не смогут учиться в хороших колледжах, в средней школе они наверняка отстанут от своих сверстников, уже имеющих такие машины. Средства массовой информации обрушили на обывателя грозное предупреждение: если он не будет обучаться компьютерной грамотности, то станет с нарастающей скоростью отставать от жизни, от своих коллег, не получит продвижения по службе.
Такая кампания вызвала различные ответные реакции, вплоть до экстремистских - случается, что компьютеры взрывают, в них стреляют, размагничивают магнитную память. Но, конечно, большинство людей стараются подойти к разрешению создавшихся противоречий конструктивными путями.
Известный американский специалист по проблемам искусственного интеллекта профессор Роджер Шенк отметил, что сейчас перед обществом стоит вопрос: что оно должно знать о компьютерах, чтобы жить и процветать в мире, наполненном ими? Задача распространения компьютерной грамотности в традиционном виде подразумевала, что человек должен приспособиться к новому для него типу машин, обучившись несвойственному ему по природе новому занятию - программированию. Но приспособление к системе "человек-машина" идет в двух направлениях, и, как показывает практика последних десятилетий, изменения в компьютерных системах идут гораздо быстрее, чем в "человеческом компоненте".
Чтобы правильно оценить задачи и последствия компьютеризации, нужно прежде всего обратить внимание на человека, на то, как он может измениться под влиянием вычислительных машин. Многочисленные примеры из истории развития технических систем, таких, как автомобиль, радио, телевидение, и других, говорят о том, что в конце концов техника приспосабливается к человеку, а не наоборот. Правда, компьютеры кажутся более значительным достижением техники и более непонятным, нередко высказывают опасения, что они должны резко изменить сам характер нашей жизни.
Многие специалисты, главным образом связанные с созданием искусственного интеллекта, прямо заявляют - ложная тревога! Уже сейчас, указывают они, люди могут обращаться к ЭВМ на языке, довольно близком к разговорному, машины научились воспринимать текст, слушаются команд, поданных голосом. Но во всех случаях, предупреждают нас, для общения с ЭВМ нужно следовать правилам языка, нужно быть просто грамотным человеком: машина ие понимает безграмотных фраз, слов, произнесенных и написанных с ошибками, нечетких, двусмысленных высказываний. В связи с внедрением систем обработки текста, которыми пользуется широкий круг специалистов, перед американским обществом со всей остротой встала проблема родного языка.
Темпы освоения вычислительной техники во многом зависят от обшего уровня компьютерной культуры, которая формируется в США под влиянием множества факторов. В начале 80-х годов было принято несколько программ, имевших своей целью ускорить этот процесс, наибольшую известность приобрел проект "компьютерный город".
Его основная идея заключалась в том, чтобы дать возможность всем желающим познакомиться с компьютером, поработать с ним или поиграть. Для этого организаторы выбрали определенные районы в крупных или небольших городах и установили в них компьютеры в парках, кафе, кинотеатрах, магазинах, аэропортах и других общественных местах. Всем желающим предлагалось подойти к компьютеру и начать с ним диалог. При этом начальное инструктирование сводилось к минимуму, в основном сама машина вела диалог, обучая человека элементарным правилам работы. Основными участниками этих проектов стали дети, которые проводили многие часы возле компьютеров. Наиболее активным выдавались специальные значки с надписью "Мой компьютер любит меня".
Идеи "Компьютерного города" были, естественно, поддержаны производителями оборудования и математического обеспечения, поскольку это позволяло им вести рекламу своей продукции и расширять рынки сбыта. Со временем мероприятия "Компьютерного города" приняли умеренный характер, но контакты компьютера с широкой публикой сохранились и, более того, стали типичным явлением. Во многих универмагах, например, функции справочного бюро выполняют персональные компьютеры, работающие в режиме диалога. В аэропортах мы видели стенды компании ИБМ, на которых установлены персональные компьютеры. Скучающие в ожидании отправки самолета пассажиры могут ознакомиться с основами устройства и работы компьютера, а заодно получить интересующие их справки об аэропорте, местных достопримечательностях, городском транспорте.
Одно из интересных начинаний по формированию компьютерной культуры - создание при бостонском Музее науки Компьютерного центра. Основная форма его работы - уроки для всех желающих. Наибольшей популярностью пользуются воскресные курсы "Язык Лого для детей и родителей". Каждому посетителю выделяется персональная ЭВМ, и в течение полутора часов по специально построенной программе ведется индивидуальное обучение в форме диалога с компьютером.
Но главное, что привлекает посетителей в Центр, считают его руководители, это возможность поработать с новыми пакетами прикладных программ. Ведущие разработчики программных средств предоставляют Центру образцы своих основных программ, к февралю 1985 года библиотека Центра насчитывала более 400 наиболее известных пакетов и продолжала быстро расти. Посетители имеют возможность прямо с полки взять любой пакет и в течение 30 минут делать с ним все, что хотят. Время ограничено из-за большого наплыва желающих приобщиться к новым программам. Центр организует курсы для учителей, в которых они знакомятся с возможностями ЭВМ в обучении, с основами языков Лого, Бейсик, Паскаль и других.
Важный элемент взаимоотношения с персональным компьютером - его эмоциональное воздействие на человека. Давно замечено, что пользователи как бы одушевляют свои компьютер, приписывают ему человеческие чувства, скажем, любовь или ненависть, считают, что он может рассуждать и т.п. С учетом этого многие прикладные программы дополняют различными игровыми элементами, усиливающими эмоциональность контактов человека с ЭВМ. Например, в обучающей программе по арифметике после неправильного ответа раздается взрыв, разрушающий изображение на экране, а после правильного появляется симпатичный герой популярного мультфильма и раздастся веселая музыка. Игровой компонент считается не менее важным, чем содержательный. Среди специалистов укрепляется точка зрения, чго для формирования компьютерной культуры эмоциональный контакт с ЭВМ, который создастся играми, не менее важен, чем способность рационально решать различные задачи. Считается, что именно благодаря эмоциональным контактам и занимательности было разрушено устойчивое представление об ЭВМ, как о большом арифмометре.
Возникает вопрос: что из американского опыта мы можем использовать, что, например, может оказаться полезным в организации учебного процесса в наших школах? На наш взгляд, можно использовать очень многое. С существенными, однако, поправками, учитывающими специфику современного этапа процесса компьютеризации в нашей стране, и, естественно, с учетом принципиальных идеологических различий нашего и капиталистического общества.
Нам чужды задачи, которые, хотя бы и в учебных целях, преследуют прежде всего получение личной выгоды, извлечение максимальных личных доходов из тех или иных предполагаемых хозяйственных мероприятий. Очевидно, для наших людей естественна и понятна ситуация, когда на первый план выдвигаются задачи удовлетворения общественных потребностей, повышения эффективности общественного производства и т.д. Кстати, пакеты программ для решения таких задач созданы и успешно используются при обучении студентов, например, в Московском институте управления имени С.Орджоникидзе. Кроме того, мы должны видеть четкую границу возможностей компьютеризации. В частности, признавая необходимость ускоренной компьютеризации экономики, различных производственных и деловых сфер нашей жизни, нам надо отчетливо представлять, что персональный компьютер вряд ли когда-нибудь может стать помощником при решении проблем нравственного выбора. Компьютерная культура никогда не заменит общую культуру, важнейшим элементом которой было и остается глубокое знание истории, литературы, искусства. Короче говоря, резко повысив темпы внедрения компьютеров в школу, в студенческие аудитории, науку, хозяйственную практику, быт, нам надо избегать фетишизации компьютеров - явления, увы, характерного для многих западных стран. Истоки этого, кстати, есть результат не только общественных потребностей в компьютерном решении задач, но и в естественном для фирм, выпускающих вычислительную технику, стремлении с максимальной выгодой для себя использовать благоприятную конъюнктуру рынка, продать побольше машин даже в тех случаях, когда это не вызывается такой уж срочной и безусловной необходимостью.
В последние годы ни одно нововведение в области электроники не вызывало в США таких бурных и ожесточенных дискуссий, как компьютерные игры. Как отмечают многие исследователи проблем компьютеризации, играм принадлежит важная роль в распространении компьютерной культуры, именно с ними связано появление первых компьютеров в большинстве домов.
Компьютерные игры вырабатывают навыки общения с новой техникой, после нескольких часов игры с ЭВМ не только ребенок, но и взрослый теряет страх к непонятной для него электронной машине. Это обстоятельство сейчас широко используется корпорациями, которые внедряют у себя автоматизированные системы: прежде чем перейти к использованию ЭВМ в рабочих режимах, сотрудникам дают возможность несколько дней и даже недель поиграть с машиной, например, в шахматы. Конечно же, с помощью одних только игр нельзя научить людей программированию и пониманию технических аспектов работы ЭВМ, но в США в последние годы складывается устойчивое мнение, что рядовому гражданину умение программировать не особенно и нужно, что большинству людей достаточно научиться свободно пользоваться вычислительной техникой и знать границы ее применения.
Благодаря некоторым особенностям компьютерных игр они стали мощным ускорителем в деле распространения идей программирования. Дети, которые первоначально лишь пользовались программами, составленными другими, начали проявлять стремление к самостоятельному программистскому творчеству. Многие из них предпочитают получать игры не в виде готовых кассет или дисков, а в виде исходных текстов, так как в этом случае в программу можно вводить любые изменения и создавать таким образом свой собственный вариант игры. Наиболее интересные решения становятся достоянием друзей, и игра начинает жить своей собственной жизнью, развиваясь и совершенствуясь. Создание игр стало популярным способом проведения досуга для серьезных программистов.
Новые компьютерные игры позволяют полностью раскрыться творческим способностям программиста, и только бедность его воображения может положить пределы тем мирам и приключениям, которые возможны на экране ЭВМ. Манипулируя фантастическим миром внутри компьютера, игроки начинают осознавать собственные силы в том реальном мире, который находится за пределами экрана. Считается, что этот новый тип постижения реальности может в корне изменить систему образования. Новое поколение компьютерных игр раскрепощает мышление, позволяет размышлять о немыслимом, и неудивительно, что сценарии большинства игр написаны либо по сказкам, либо по научно-фантастическим романам и рассказам.
Важная особенность компьютерных игр, усиливающая их притягательность,- это способность запоминать прошлый опыт, самообучаться. В большинстве игр компьютер не повторяет ошибок и постепенно усложняет свое поведение по мере того, как его партнер осваивает стратегию победы. Часто компьютеры хранят в своей памяти имена наиболее сильных игроков - каждый игрок должен прежде всего представиться машине, и если его имя уже есть в памяти, то автомат выбирает более сложную стратегию игры. В США появились местные и национальные знаменитости, чемпионы по отдельным видам компьютерных игр.
Достаточно богатый опыт, накопленный в США, подтверждает, что игры позволяют ввести детей, студентов или сложившихся специалистов в мир компьютеров, наиболее быстро и эффективно знакомят их с новой нарождающейся культурой информационного века, помогают создать основу для широкого использования компьютерной техники на производстве и в быту.
В целом процессы, происходящие в обществе под влиянием массовой компьютеризации, пока трудно оценить однозначно. Многое в них неясно, противоречиво. Так, компьютерные игры быстро вводят человека в новую сферу информационной деятельности, но они могут дать эффект "запойности": многие подростки и даже взрослые проводят долгие часы за игровыми пультами, растрачивая впустую свое время. Эти отрицательные последствия игр хорошо описаны в прессе.
Другой пример - компьютеры позволяют резко повысить производительность труда в сфере обработки информации. Но одновременно они интенсифицируют этот труд, что ведет к росту психической и физической нагрузки на операторов. В их среде растет число душевных расстройств, сокращаются масштабы простых человеческих контактов, бесед, обменов новостями и т.п. Это ведет к появлению нездорового климата на рабочем месте. В капиталистическом обществе с его отношением к человеку как к простому носителю товара, рабочей силе подобные процессы являются закономерным результатом автоматизации: машина, на этот раз электронная, в очередной раз противопоставлена человеку. Очевидно, что, взяв на вооружение персональный компьютер как мощное орудие ускорения научно-технического развития, мы, внимательно вникая в уже имеющийся у нас и за рубежом опыт, должны избежать негативных последствий его широкого использования.
...

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
...

Специализированный класс для практической работы на персональных компьютерах в одной из школ Бостона (США).
Приобщение миллионов учащихся к современной компьютерной технике - одна из важнейших задач, поставленных перед советской школой. Уже с прошлого года в девятых и десятых классах наших школ началось изучение основ информатики, в педагогические институты и школы поступило несколько тысяч японских персональных компьютеров "Ямаха" и советских "ДВК-1", "БК-0010", "Агат"; иа их основе во всех регионах страны организованы сотни специализированных классов, где школьники учатся общению с вычислительной машиной. Разработаны и готовятся к производству две новые малые вычислительные машины, специально предназначенные для школьных кабинетов информатики. В некоторых школах практическое подкрепление курса информатики учащиеся получают в виде практикума на больших машинах в вычислительных центрах или в межшкольных учебно-производственных комбинатах. Получен первый опыт приобщения детей к вычислительной машине в детских садах.

В средней школе #18 подмосковного города Павловского-Посада проходят практические занятия по программированию на бытовом компьютере БК-0010.

В этом же городе в детском саду "Золотой петушок" дети рисуют на дисплее компьютера БК-0010; для этого используется программа, в которой нажатие определенной клавиши приводит к появлению на экране готового фрагмента рисунка - дерева, домина, зеленой лужайки, солнца, тучи; дети формируют желаемую картину, вводя в нее по своему выбору эти изобразительные фрагменты и перемещая их по экрану в нужное место.

Три учителя и один ученик - соотношение в данном случае вполне объяснимое: школьная информатика делает первые свои шаги, и случается, что ученик, работая на машине, находит новые пути решения той или иной задачи, вызывающие большой интерес учителей.

Специализированный класс для практической работы на персональных компьютерах в одной из школ Бостона (США).
Приобщение миллионов учащихся к современной компьютерной технике - одна из важнейших задач, поставленных перед советской школой. Уже с прошлого года в девятых и десятых классах наших школ началось изучение основ информатики, в педагогические институты и школы поступило несколько тысяч японских персональных компьютеров "Ямаха" и советских "ДВК-1", "БК-0010", "Агат"; иа их основе во всех регионах страны организованы сотни специализированных классов, где школьники учатся общению с вычислительной машиной. Разработаны и готовятся к производству две новые малые вычислительные машины, специально предназначенные для школьных кабинетов информатики. В некоторых школах практическое подкрепление курса информатики учащиеся получают в виде практикума на больших машинах в вычислительных центрах или в межшкольных учебно-производственных комбинатах. Получен первый опыт приобщения детей к вычислительной машине в детских садах.

В средней школе #18 подмосковного города Павловского-Посада проходят практические занятия по программированию на бытовом компьютере БК-0010.

В этом же городе в детском саду "Золотой петушок" дети рисуют на дисплее компьютера БК-0010; для этого используется программа, в которой нажатие определенной клавиши приводит к появлению на экране готового фрагмента рисунка - дерева, домина, зеленой лужайки, солнца, тучи; дети формируют желаемую картину, вводя в нее по своему выбору эти изобразительные фрагменты и перемещая их по экрану в нужное место.

Три учителя и один ученик - соотношение в данном случае вполне объяснимое: школьная информатика делает первые свои шаги, и случается, что ученик, работая на машине, находит новые пути решения той или иной задачи, вызывающие большой интерес учителей.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
После исчерпания темы ПМК учителя программирования столкнулись с ситуацией несовместимости языков программирования разных моделей ПК. Поэтому интерес представляют не описанные ими подробности, а сам размер бедствия: что мог и какие трудности испытывал программист конкретного компьютера того времени. Почему, имея ПМК, пользователь радовался, что может продуктивно считать, а получив ПК начал радоваться, что считать больше совсем не надо?
Первый прозвучавший здесь "звоночек" - размежевание пользовательского и системного программирования. Мол, человеку легко запрограммировать "C=A+B", трудно запрограммировать "05 10 100 110 200", а программа переводящая "C=A+B" в "05 10 100 110 200" пишется волшебными демонами.
9/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ДЕСЯТОЕ, начальное в цикле, где речь пойдет о языках высокого уровня и главным образом о Бейсике, которому "обучено" большинство современных персональных компьютеров. Занятие носит вводный характер. Здесь объясняются причины появления языков высокого уровня в мире ЭВМ и кратко описываются некоторые характерные черты, свойственные им всем.
Занятия этого цикла ведет кандидат технических наук И.ДАНИЛОВ
Вычислительные машины существуют уже больше четырех десятилетий. За это время сильно изменился их внешний вид - они стали меньше и элегантнее; увеличилось их быстродействие, стало гораздо удобнее с ними работать... Однако, как у любого автомобиля, будь то старичок "Даймлер" или ультрасовременная гоночная "торпеда", осталась неизменной основная идея - двигатель, вращающий колеса, так сохранились и основные принципы устройства вычислительных машин.
Для понимания их работы достаточно знать, что у любой ЭВМ имеются такие структурные элементы: процессор, оперативное запоминающее устройство (или просто память), внешние запоминающие устройства и устройства ввода и вывода. Последние, как видно из их названия, служат для ввода и вывода информации. Вводится информация в память. Туда же вводится и программа. Состоит программа из набора инструкций, следуя которым процессор делает то, ради чего существуют ЭВМ,- обрабатывает информацию.
Память можно представлять в виде длинной ленты, поделенной на сектора, или ячейки. Каждая ячейка имеет свой номер - программисты называют его адресом. По этому адресу процессор может либо прочесть ее содержимое, либо записать туда новую информацию.
Иногда память сравнивают с набором ящиков, как у старого комода. В каждый из ящиков можно нечто положить (то есть записать) или достать (считать). Однако эта аналогия способна сбить с толку. Когда информация считывается из какой-либо ячейки, она оттуда не исчезает, как вещь из опустошаемого ящика. Если уж прибегать к предметным аналогиям, то лучше представлять память в виде грифельной доски, закрытой подвижным экраном с окошком. Подведя окошко к какому-нибудь месту доски (ячейке памяти), можно прочесть, что там написано. Через окошко можно и писать на доске. Естественно, при этом стирается то, что было видно через окошко до этого.
Наконец, внешняя память. Она отличается от внутренней значительно большими размерами. По непосредственного доступа к ней процессор обычно не имеет и, чтобы использовать ее содержимое, нужно предварительно скопировать его в память внутреннюю.
Для того чтобы работать на ЭВМ, надо научиться писать понятные ей программы и понимать самому ее ответные сообщения.
Иначе говоря, надо научиться говорить на одном языке с ЭВМ.
Когда вычислительные машины появились на свет, основными их пользователями были их же создатели. Естественно, что проблемы общения при этом не возникало. Ведь создатели ЭВМ знали язык, на котором они учили разговаривать свое детище. У каждой машины он был особый, понятный только ей. Состояли такие языки из команд.
[ КОМАНДОЙ называется предписание, определяющее очередной шаг процесса выполнения программы. В каждом таком предписании указаны операция, адреса операндов, а также могут содержаться некоторые служебные примечания. ОПЕРАЦИЯ - это то, ЧТО должна сделать машина согласно данной команде. Например, переслать число из одной ячейки в другую, извлечь корень из числа, сложить или вычесть числа, изменить порядок выполнения команд. ОПЕРАНД - это участник операции, то, над ЧЕМ или с ЧЕМ выполняется операция. Как уже было сказано, в каждой команде операнды представлены их адресами - будь то адрес величины, из которой извлекается корень, или адрес команды, которую следует выполнить после данной. Так или иначе это всегда номер некоторой ячейки, некоторое число. Операция, указываемая в команде, также представляется определенным числом. Оно называется КОДОМ ОПЕРАЦИИ ]
Программировать в командах было крайне неудобно. Потребовалось вам, скажем, выполнить сложение - прибавляя к величине А величину В. получить величину С. Чтобы записать команду для выполнения столь несложного арифметического действия, надо произвести немалые изыскания: вспомнить, какой код присвоен операции сложения (предположим, он равен 10), потом осведомиться, в каких ячейках памяти хранятся величины А, В, С (пусть их адреса равны соответственно 0100, 0110, 0200). Вся команда, если она располагается, скажем, по адресу 05, запишется так:
05 10 0100 0110 0200
И так - команда за командой... Сложен был труд программиста, когда программы писались таким вот образом. Велика была и цена ошибки. Предположим, вы оплошали при распределении памяти, разместили величину D в той же ячейке, что и величину А. Будьте любезны - пройдитесь по всей программе и исправьте адрес соответствующего операнда всюду, где он встречается. Или, записывая программу, вы пропустили какую-то команду. Будьте готовы к тому, что вставка повлечет перераспределение памяти: возможно, придется менять адреса каких-то переходов, адреса некоторых операндов. Отладка программ, написанных на языке цифр,- занятие поистине мучительное [Кстати сказать, подобные проблемы хорошо знакомы тем, кто сегодня работает с программируемыми микрокалькуляторами. Ведь эти карманные ЭВМ по принципам программирования мало отличаются от своих прабабушек, о которых только что велась речь].
Естественно встал вопрос: нельзя ли поручить хотя бы часть этой утомительной работы самой машине? Научить ее собственноручно переводить символы операций в коды и самой составлять таблицы, где отражались бы соответствия между величинами, участвующими в расчетах, и адресами, по которым они размещены в памяти.
Оказалось, можно. Так кончилась первобытная эра программирования и появились первые символические языки программирования. Их называют еще автокодами, или языками ассемблера. Здесь для обозначения операций и операндов допускалось пользоваться понятными человеку символами. Появились и первые трансляторы - программы для перевода с языка символов на понятный машине язык цифр.
[ Такой перевод называется ТРАНСЛЯЦИЕЙ (отсюда н термин - ТРАНСЛЯТОР). Заключается он в том, что символы операций заменяются кодами, а символы операндов - адресами, отведенными для этих величин в памяти. Одновременно каждой команде присваивается ее адрес ]
Процесс программирования несколько упростился. Например, команда сложения, которую несколько выше мы разбирали в качестве примера, теперь записывалась так:
+ А В С
Вычислительная техника тем временем развивалась, круг ее пользователей расширялся, в него вовлекалось все больше людей, для которых программирование не было основной специальностью. Для них-то одной из главных проблем становилась именно трудность программирования.
Чтобы лучше ощутить существо проблемы, давайте запишем ту же команду сложения в совсем уж привычном виде:
С = А + В
Из трех записей одного и того же действия вторая, конечно, понятнее первой, но все же еще довольно далека от третьей, наиболее удобной.
Теперь представьте себе, как каждым из трех способов записывалось бы вычисление по какой-либо мало-мальски сложной формуле. Различия между ними стали бы еще разительнее.
[ C = (А+В)/(А-В)
+ А В С
- А В D
/ С D С
05 10 0100 0110 0200
06 11 0100 0110 0210
07 13 0200 0210 0200
Одно и то же вычисление написано здесь в виде привычной математической формулы (вверху), на автокоде (в середине) и в кодах (внизу). Легко понять, какая из записей легче для составления и понимания ]
А ведь электронные вычислительные машины создавались для решения именно сложных задач. Появились они в те времена, когда на повестку дня вставало овладение атомной энергией, конструирование космических ракет. ЭВМ были призваны способствовать осуществлению грандиозных инженерных и научных замыслов.
Первые алгоритмические языки появились в конце 50-х годов, ознаменованных вводом в действие первых атомных электростанций и запуском первых искусственных спутников Земли.
И вот в конце пятидесятых годов, ознаменованных вводом в строй первых атомных электростанций, запуском первых искусственных спутников Земли, в вычислительном деле был совершен шаг, резко увеличивший число людей, способных пользоваться услугами ЭВМ, шаг, позволивший превратить программирование в одну из самых массовых профессий и говорить об овладении им как о "второй грамотности". Появились алгоритмические языки программирования, достаточно близкие к привычному языку математических формул, понятные человеку и избавившие его от необходимости знать особенности конкретной ЭВМ, на которой он работает.
Первенцами в семье этих языков были Фортран, Алгол, Кобол [Названия алгоритмических языков в современных изданиях приводятся весьма по-разному - то в кавычках, то без кавычек, то прописными, то строчными буквами: ФОРТРАН, Фортран, фортран, "фортран"... Возможно, когда эти названия войдут в нашу повседневную речь (что можно предвидеть по темпам компьютеризации нашей жизни), они будут писаться строчными буквами без кавычек. Однако, чтобы не слишком опережать время, мы пишем их пока с прописной буквы]. В силу их близости к языку математических выкладок их назвали языками высокого уровня. Автокоды же в отличие от них отныне стали именовать языками низкого уровня.
Перевод программ с алгоритмического языка на понятный машине язык цифр взяли на себя программы-трансляторы. Естественно, они усложнились, увеличилось время трансляции, но все это было лишь небольшой платой за значительное облегчение процесса программирования, уменьшение времени отладки, упрощение возможного совершенствования программ.
Это, кстати, дало возможность, обсуждая проблемы программирования, говорить не о конкретном типе ЭВМ - например, БЭСМ, ЕС ЭВМ или СМ ЭВМ, а о фиктивных Фортран-машине, Алгол-машине или Бейсик-машине. Дело в том, что специфику конкретной машины учитывает программа-транслятор. Программа же, написанная на алгоритмическом языке, уже рассматривается не как последовательность инструкций для имеющейся ЭВМ, а как инструкции для гипотетической, скажем, Бейсик-машины.
Например, если мы даем Бейсик-машине инструкцию: A=B+C*D-E, то нас не интересует, сколько команд выполнит ЭВМ для получения результата, где будут храниться значения величин А, В, С, D и Е. Мы говорим, что Бейсик-машина вычислит значение выражения, записанного справа от знака равенства, и присвоит его переменной А. В отличие от команд такие инструкции называются операторами.
[ ОПЕРАТОР - это допустимое в данном языке предписание, задающее определенные действия в программе. В отличие от команды, всегда определяющей лишь одно элементарное действие машины, оператор может предписывать такое действие в программе, которое будет реализовано машиной в виде целого ряда элементарных действий.
Использование операторов вместо команд для записи программ является основным различием, между языками высокого и низкого уровней ]
Языков высокого уровня существует сегодня много. Точную цифру назвать затруднительно, однако если перечислять даже наиболее распространенные, получится более десятка. Это различные версии Фортрана, Алгол-60, ПЛ/1, Бейсик, Алгол-68, Паскаль, Рапира, Кобол, Лисп, Снобол, АПЛ, АДА и т.д.
Понимаем, что у иного читателя может возникнуть вопрос: зачем их так много? Неужели их создатели забыли поучительную легенду о вавилонском столпотворении? Сначала на земле, гласит библейская легенда, был одни язык и одно наречие. И собрались люди и стали строить башню высотою до небес. Разгневался господь, сошел на землю и смешал язык их так, чтобы один не понимал другого. Говоря на разных языках, люди не могли работать вместе. Неужели, приступая к широкому освоению вычислительной техники, человечество вновь впадает в "вавилонскую" ошибку?
Не будем спешить с выводами. Не так уж неразумно современное человечество. Появление многих алгоритмических языков вызвано вполне объективными причинами. Дело в том, что самые "умные" электронные вычислительные машины, как и их простоватые предки, по-прежнему понимают лишь язык элементарных команд, записанных цифрами. Поэтому, чем сложнее операторы алгоритмического языка, тем, естественно, сложнее и переводить их в такие команды.
Неоднократные попытки разрешить эту проблему н привели к созданию различных языков. Некоторые из них (Фортран, например) обладают набором лишь сравнительно простых для перевода операторов. Однако для человека это создает трудности при записи сложных алгоритмов. Другие языки (например, Алгол-60) имеют удобные и наглядные средства для записи алгоритмов, но требуют сложной программы-транслятора для перевода их в машинные команды.
Кстати, трансляция программ ставит еще одну проблему: как переводить? Существуют два типа трансляторов - интерпретаторы и компиляторы. Первые переводят "дословно". Каждый оператор алгоритмического языка переводится в команды ЭВМ по мере чтения программы и тут же выполняется, после чего считывается следующий. Можно сказать, что в этом случае программа хранится в памяти машины в том же виде, в каком она написана на бумаге. Если она написана с ошибками, не беда. Запустили такую программу на счет, нашли ошибку, тут же ее исправили н продолжили работу. Захотели что-нибудь изменить, изменили и снова - на счет. Очень удобно. Для человека. А для машины? Во-первых, кроме вашей программы, надо постоянно держать в памяти программу-транслятор. А это накладно. Слишком дорога оперативная память, чтобы транжирить ее на хранение пассивного балласта-транслятора. Вместо этого можно было бы параллельно решать задачу по другой программе. Да и на вашу программу это накладывает дополнительные ограничения по объему. Во-вторых, это замедляет выполнение программы. Ведь если в ней есть конструкции, называемые циклами, когда многократно выполняется одна и та же группа операторов, то переводить их нужно во время каждого прохождения цикла.
От подобных недостатков свободны компиляторы. Трансляторы этой группы сначала переводят программу целиком, так сказать, не по букве, а по смыслу. Полученный "литературный перевод" является уже другой программой, отличающейся от вашей не меньше, чем стихотворение Лермонтова "На севере диком стоит одиноко..." от оригинала Гейне "Ein Fichtenbaum steht einsam...". Однако машиной выполняется именно перевод. После того, как он получен, присутствие транслятора в памяти уже излишне. Нет и необходимости по многу раз переводить одно и то же. Но вот беда: вмешаться в работу "оттранслированной" программы вы не можете - вам не известно, в какие именно команды переведен тот или иной оператор и где эти команды искать. Поэтому при обнаружении ошибки необходимо вернуться к исходному тексту, исправить его и снова повторить трансляцию.
Как видите, свои достоинства и недостатки есть и у компиляторов и у интерпретаторов. Первые чаще применяются при работе на больших ЭВМ с серьезными, объемными программами. Интерпретаторы же в основном используются на микро-ЭВМ. В частности, подавляющее большинство трансляторов с Бейсика - а именно он держит пальму первенства по использованию на малых компьютерах - интерпретаторы.
Но вернемся к размышлению о том, что специфические проблемы взаимоотношения человека с ЭВМ привели к появлению многих и очень различных языков программирования.
Как же разобраться в этом море начинающему, если он к тому же не готовится стать профессиональным программистом? И нужно ли? Может быть, достаточно освоить любой из этих языков, попавший под руку?
Конечно, чтобы понять основы программирования, необходимо выучить хотя бы один язык. Но так же, как для лучшего понимания родного языка полезно познакомиться с иностранными, так и для лучшего понимания конкретного алгоритмического языка полезно иметь понятие о других. Это расширит кругозор пользователя, позволит овладеть целым рядом специальных конструкций, отсутствующих в его "родном" языке, да и, кроме того, при возможности выбора позволит аргументированно выбрать язык для решения конкретной задачи.
Языки высокого уровня отличаются друг от друга довольно сильно, не меньше, чем вода в разных морях. Но так же, как термин "морская вода" подразумевает воду, содержащую большое количество солей, пусть и в разных пропорциях, так и каждый из языков программирования можно разложить на ряд элементов, набор которых есть практически в каждом языке.
Назовем основные из них:
1. Алфавит языка.
2. Структура и способ записи программ.
3. Данные.
4. Операции над данными.
5. Управление последовательностью действий.
6. Операции по трансляции и запуску программ.
Так как эти пункты общи для всех языков, то имеет смысл кратко их охарактеризовать, прежде чем выделять их в каком-либо языке, с которыми мы будем знакомиться на следующих занятиях.
АЛФАВИТ ЯЗЫКА. Каждый язык программирования имеет строго определенный набор символов. Это цифры, математические знаки, буквы и т.д. Только с их помощью дозволяется писать тексты-программы на этом языке. Алфавит алгоритмического языка можно сравнить с набором литер, имеющихся в типографии и используемых для набора книг, журналов и газет. В отличие от символов, употребляемых при письме, этот набор всегда ограничен и с его помощью нельзя изобразить любой знак, пришедший нам в голову.
Каждый символ представляется в машине кодом, по которому его узнает транслятор.
Кроме отдельных символов, в любом алгоритмическом языке употребляются их устойчивые сочетания, называемые иногда иероглифами. Каждый иероглиф при переводе программы выражается, как и символ, одним кодом. К примеру, в любой программе, написанной на Алголе-60, имеются слова begin (начало) и end (конец). Переводя их, транслятор вовсе не кодирует букву за буквой - сначала b, потом e, потом g... Нет, все слово begin заменяется своим кодом, слово end - своим. К иероглифам можно отнести и числа. Встретив в тексте программы, скажем, число 0.02, транслятор тоже не станет заменять отдельными кодами сначала нуль, потом десятичную точку... Впрочем, об особенностях трансляции чисел у нас будет особый разговор.
СТРУКТУРА И СПОСОБ ЗАПИСИ ПРОГРАММ. Способы записи программ сильно различаются в разных языках. В Фортране, например, для этого используется специальный бланк.

Для записи программы на Фортране используется специальный бланк. Символы, помещенные в разные его зоны, интерпретируются по-разному.
Каждая строка бланка поделена на зоны. Символы, находящиеся в разных зонах, интерпретируются по-разному. Такие языки называются позиционированными.
В других языках допускается свободная запись. Для разделения структурных единиц - например, операторов - применяются специальные символы, чаще всего точка с запятой. Так принято писать программы на Алголе-60, Паскале, ПЛ/1.

В Алголе-60 допускается свободная запись, операторы разделяются точкой
с запятой.
Вообще позиционирование является своего рода анахронизмом, исторически перекочевавшим в языки высокого уровня из автокодов. Считается, что лучше использовать для разделения конструкций языка специальные символы, не задумываясь о привязке операторов к началам и концам строк - подобно тому, как при письме мы не заботимся о том, чтобы каждая фраза целиком умещалась на одной строке.
Структура программ - это, пожалуй, одна из наиболее характерных особенностей языка. Когда программа записывается на Фортране, то выглядит набором не связанных друг с другом модулей, каждый из которых может иметь свои особые переменные, транслироваться совершенно автономно.
Программа, записанная на Фортране, выглядит как набор не связанных друг с другом модулей.
Программа, записанная на Алголе-60, состоит из вложенных друг в друга блоков, где из объемлющего блока можно перейти лишь в непосредственно вложенный в него, притом используя либо те же переменные, либо специально оговоренные).
Программа, записанная на Алголе-60, состоит из вложенных друг в друга блоков.
Программа на Бейсике - это единая неделимая структура, состоящая из отдельных строк и т.д.
ДАННЫЕ. Так называется любая информация, находящаяся в ЭВМ. Программа - тоже "данные". Мы, однако, поговорим только о тех данных, которыми оперируют сами программы, написанные на языках высокого уровня.
Эти данные обычно разделяют на постоянные и переменные. Постоянные - это такие величины, которые не меняются на протяжении работы всей программы. Например, если есть в программе константа 2, то и будет она всегда двойкой. Переменные же в процессе выполнения программы могут принимать различные допустимые значения.
Например, если среди данных есть целочисленная переменная, то она может оставаться равной той же двойке во все время работы программы, а может по ходу ее работы стать равной и 15 и 32000, то есть любому целому числу, не превышающему, правда, некоторого максимума, зависящего от конкретной ЭВМ.
Для обозначения переменных во всех языках используются имена (или идентификаторы). Образуются они, как правило, из букв и цифр и начинаются с буквы. Иногда для образования имен допускается использование и других символов - например, знака минус. Длины идентификаторов могут быть различными. Так, в Бейсике допускаются имена, состоящие не более чем из 2-3 символов - A, BI, F4%. В Алголе-60 длина имени не ограничивается. Там возможен, скажем, такой идентификатор; ЛОШАДКАВЕЗУЩАЯХВОРОСТУВОЗ.

Так в ячейках памяти записывается целое число
На каждую постоянную и переменную величину транслятор выделяет для ее хранения определенную зону памяти. Такая зона может состоять из одной или нескольких ячеек. Адреса ячеек, где хранятся данные, собираются в специальные таблицы, из которых ясно, какому адресу соответствует имя той или иной переменной.
Данные, которые можно использовать в арифметических вычислениях, называются числовыми. В свою очередь, они делятся иа целые и вещественные. Такое деление позволяет программисту управлять точностью вычислений и распределением памяти, так как целые и вещественные числа представляются в памяти по-разному. Целые занимают меньше места, и вычисления с их участием проходят быстрее. В некоторых языках допускаются и комплексные числа. Места для их хранения нужно еще больше, чем для вещественных, но и удобства программисту они дают большие. К примеру, решая на машине квадратное уравнение, можно не рассматривать отдельно случаи, когда оно имеет действительные корни, а когда нет. Описали соответствующие переменные как комплексные и все. Дальше машина сама разберется.
Большинство алгоритмических языков допускает работу не только с числами, но с текстами. Для этой цели существуют специальные типы данных, называемые символьными или строковыми. Например, если некоторая переменная описана как символьная, то она может принимать значения, скажем, tract или or. Сложение этих значений даст новую символьную величину tractor.
Бывают данные логического типа. Они обычно принимают одно из двух значений: true (истина) или false (ложь).
Переменные (и постоянные) разных типов представляются в памяти по-разному. Целые числа просто переводятся в двоичную систему. Например, число 17 записывается как 10001.
[ Мы полагаем, что читатель знаком с двоичной системой счисления. Напомним лишь, как "читать" двоичные числа. Под каждым его знаком слева направо припишем последовательные натуральные степени двойки, начиная с нулевой: 2**0=1, 2**1=2, 2**2=4. 2**3= 8 и т.д. Каждое из этих чисел умножим на стоящую над ним единицу или нуль. Полученные произведения сложим. Так, например, из двоичного числа 10011 мы получим 1*1+2*1+16*1=19 ]
Вещественные числа сначала нормализуются, то есть представляются в виде произведения десятичной дроби, меньшей единицы, на десять в некоторой степени, называемой порядком. Дробь эта, называемая мантиссой, должна иметь вслед за нулем и запятой обязательно ненулевую цифру. Например, число 0.02 после нормализации примет вид 0.2e-1, а число 35.6 запишется как 0.356e2. Только после этого транслятор переводит число в двоичную форму, определенным образом упаковывая его в памяти. Так как знаки числа и порядка бывают только двух видов, плюс или минус, то для их обозначения как раз хватает двух символов, которыми оперирует машина: 0 и 1.

произвольное дробное число
Строковые величины записываются в памяти и виде последовательности кодов, каждый из которых соответствует тому или иному символу, образующему строковую величину. (То, что каждый символ имеет свой код, мы уже говорили).
строковая величина.
Очень важным моментом в представлении данных является их классификация по структурам. Те переменные, о которых мы до сих пор говорили, называются "простыми переменными". Они действительно простые: каждая переменная в любой момент времени имеет одно значение. Имя простой переменной записано в специальной таблице, где ей соответствует определенный адрес. По этому адресу она (точнее, ее значение) и отыскивается.
Следующая по сложности структура данных - массив.
Представьте себе, что вам нужно расставить сотню чисел в возрастающем (или убывающем) порядке. Сама по себе задача несложная, имеется много способов таких сортировок. Но вот проблема: как именовать эти числа? Можно так: А, В, С, ..., X, Y, Z, A1, B1... Но если вы попытаетесь написать на любом языке программу расстановки или хотя бы нарисовать схему этого процесса, то сразу же придете к выводу, что сотня имен - это неудобно. Другое дело, если переменные будут иметь одно имя, скажем, X, и разные номера, то есть Х1, Х2, ..., Х100. Тогда можно использовать обозначение Xi, где индекс i указывает на некоторый i-й элемент последовательности наших ста чисел. Такая совокупность данных, каждое из которых имеет одно и то же имя и разные индексы (порядковые номера), и называется массивом.
В зависимости от числа индексов массивы могут быть одномерными (тогда в их обозначении участвует один индекс), двумерными (два индекса) и т.д.
Использование массивов не только облегчает работу программиста, но и "полезно" машине. Дело в том, что элементы массивов располагаются в памяти подряд, поэтому в таблице переменных не нужно перечислять их все. Достаточно указать адрес первого элемента. Тогда адрес i-го элемента можно легко вычислить как сумму адреса первого и величины, кратной i. Кстати, таблица переменных, как и программа, тоже размещается в памяти. Поэтому использование массивов вместо перечней простых переменных экономит память.
Массивы - не единственный способ организации данных. Бывают и более сложные образования - структуры (в ПЛ/I и Алголе-68), файлы. Но если структуры существуют лишь в ограниченном числе алгоритмических языков, то файлы используются почти повсеместно. Упоминание о файлах вы найдете практически в любой книге о программировании. Поэтому и мы посвятим этому понятию несколько слов.
Что же такое "файл"?
В отделе кадров каждого учреждения хранятся карточки на сотрудников. На карточке указаны табельный номер, фамилия сотрудника, его год рождения, должность, домашний адрес. Могут быть и другие сведения. Для отдельного сотрудника информацию, относящуюся к нему, можно записать, например, так: 211 Петров А.Г. 1940 ст.инженер Строительная ул. 16 кв. 2. Совокупность таких записей о сотрудниках учреждения и составит файл.
Другой пример. Перед вами фрагмент программы на Фортране.
IR=0
DO 20 I = 1,N
20 IF(A(I).EQ.0) IR=IR+1
Это тоже файл. Можно привести еще много примеров, но читатель уже, наверное, понял суть дела.
[ ФАЙЛ - это, попросту говоря, организованный набор данных любого типа. Состоит он из ЗАПИСЕЙ. Запись - это, например, строка, где собраны сведения об инженере Петрове, или строка программы на Фортране. Запись служит наименьшей структурной единицей файла, своеобразным атомом, из которых состоят молекулы - сам файл ]
Используются файлы очень широко. Достаточно сказать, что практически вся информация, хранимая во внешних запоминающих устройствах любой ЭВМ, представлена в виде файлов.
Первый прозвучавший здесь "звоночек" - размежевание пользовательского и системного программирования. Мол, человеку легко запрограммировать "C=A+B", трудно запрограммировать "05 10 100 110 200", а программа переводящая "C=A+B" в "05 10 100 110 200" пишется волшебными демонами.
9/86
ШКОЛА НАЧИНАЮЩЕГО ПРОГРАММИСТА
ЗАНЯТИЕ ДЕСЯТОЕ, начальное в цикле, где речь пойдет о языках высокого уровня и главным образом о Бейсике, которому "обучено" большинство современных персональных компьютеров. Занятие носит вводный характер. Здесь объясняются причины появления языков высокого уровня в мире ЭВМ и кратко описываются некоторые характерные черты, свойственные им всем.
Занятия этого цикла ведет кандидат технических наук И.ДАНИЛОВ
Вычислительные машины существуют уже больше четырех десятилетий. За это время сильно изменился их внешний вид - они стали меньше и элегантнее; увеличилось их быстродействие, стало гораздо удобнее с ними работать... Однако, как у любого автомобиля, будь то старичок "Даймлер" или ультрасовременная гоночная "торпеда", осталась неизменной основная идея - двигатель, вращающий колеса, так сохранились и основные принципы устройства вычислительных машин.
Для понимания их работы достаточно знать, что у любой ЭВМ имеются такие структурные элементы: процессор, оперативное запоминающее устройство (или просто память), внешние запоминающие устройства и устройства ввода и вывода. Последние, как видно из их названия, служат для ввода и вывода информации. Вводится информация в память. Туда же вводится и программа. Состоит программа из набора инструкций, следуя которым процессор делает то, ради чего существуют ЭВМ,- обрабатывает информацию.
Память можно представлять в виде длинной ленты, поделенной на сектора, или ячейки. Каждая ячейка имеет свой номер - программисты называют его адресом. По этому адресу процессор может либо прочесть ее содержимое, либо записать туда новую информацию.
Иногда память сравнивают с набором ящиков, как у старого комода. В каждый из ящиков можно нечто положить (то есть записать) или достать (считать). Однако эта аналогия способна сбить с толку. Когда информация считывается из какой-либо ячейки, она оттуда не исчезает, как вещь из опустошаемого ящика. Если уж прибегать к предметным аналогиям, то лучше представлять память в виде грифельной доски, закрытой подвижным экраном с окошком. Подведя окошко к какому-нибудь месту доски (ячейке памяти), можно прочесть, что там написано. Через окошко можно и писать на доске. Естественно, при этом стирается то, что было видно через окошко до этого.
Наконец, внешняя память. Она отличается от внутренней значительно большими размерами. По непосредственного доступа к ней процессор обычно не имеет и, чтобы использовать ее содержимое, нужно предварительно скопировать его в память внутреннюю.
Для того чтобы работать на ЭВМ, надо научиться писать понятные ей программы и понимать самому ее ответные сообщения.
Иначе говоря, надо научиться говорить на одном языке с ЭВМ.
Когда вычислительные машины появились на свет, основными их пользователями были их же создатели. Естественно, что проблемы общения при этом не возникало. Ведь создатели ЭВМ знали язык, на котором они учили разговаривать свое детище. У каждой машины он был особый, понятный только ей. Состояли такие языки из команд.
[ КОМАНДОЙ называется предписание, определяющее очередной шаг процесса выполнения программы. В каждом таком предписании указаны операция, адреса операндов, а также могут содержаться некоторые служебные примечания. ОПЕРАЦИЯ - это то, ЧТО должна сделать машина согласно данной команде. Например, переслать число из одной ячейки в другую, извлечь корень из числа, сложить или вычесть числа, изменить порядок выполнения команд. ОПЕРАНД - это участник операции, то, над ЧЕМ или с ЧЕМ выполняется операция. Как уже было сказано, в каждой команде операнды представлены их адресами - будь то адрес величины, из которой извлекается корень, или адрес команды, которую следует выполнить после данной. Так или иначе это всегда номер некоторой ячейки, некоторое число. Операция, указываемая в команде, также представляется определенным числом. Оно называется КОДОМ ОПЕРАЦИИ ]
Программировать в командах было крайне неудобно. Потребовалось вам, скажем, выполнить сложение - прибавляя к величине А величину В. получить величину С. Чтобы записать команду для выполнения столь несложного арифметического действия, надо произвести немалые изыскания: вспомнить, какой код присвоен операции сложения (предположим, он равен 10), потом осведомиться, в каких ячейках памяти хранятся величины А, В, С (пусть их адреса равны соответственно 0100, 0110, 0200). Вся команда, если она располагается, скажем, по адресу 05, запишется так:
05 10 0100 0110 0200
И так - команда за командой... Сложен был труд программиста, когда программы писались таким вот образом. Велика была и цена ошибки. Предположим, вы оплошали при распределении памяти, разместили величину D в той же ячейке, что и величину А. Будьте любезны - пройдитесь по всей программе и исправьте адрес соответствующего операнда всюду, где он встречается. Или, записывая программу, вы пропустили какую-то команду. Будьте готовы к тому, что вставка повлечет перераспределение памяти: возможно, придется менять адреса каких-то переходов, адреса некоторых операндов. Отладка программ, написанных на языке цифр,- занятие поистине мучительное [Кстати сказать, подобные проблемы хорошо знакомы тем, кто сегодня работает с программируемыми микрокалькуляторами. Ведь эти карманные ЭВМ по принципам программирования мало отличаются от своих прабабушек, о которых только что велась речь].
Естественно встал вопрос: нельзя ли поручить хотя бы часть этой утомительной работы самой машине? Научить ее собственноручно переводить символы операций в коды и самой составлять таблицы, где отражались бы соответствия между величинами, участвующими в расчетах, и адресами, по которым они размещены в памяти.
Оказалось, можно. Так кончилась первобытная эра программирования и появились первые символические языки программирования. Их называют еще автокодами, или языками ассемблера. Здесь для обозначения операций и операндов допускалось пользоваться понятными человеку символами. Появились и первые трансляторы - программы для перевода с языка символов на понятный машине язык цифр.
[ Такой перевод называется ТРАНСЛЯЦИЕЙ (отсюда н термин - ТРАНСЛЯТОР). Заключается он в том, что символы операций заменяются кодами, а символы операндов - адресами, отведенными для этих величин в памяти. Одновременно каждой команде присваивается ее адрес ]
Процесс программирования несколько упростился. Например, команда сложения, которую несколько выше мы разбирали в качестве примера, теперь записывалась так:
+ А В С
Вычислительная техника тем временем развивалась, круг ее пользователей расширялся, в него вовлекалось все больше людей, для которых программирование не было основной специальностью. Для них-то одной из главных проблем становилась именно трудность программирования.
Чтобы лучше ощутить существо проблемы, давайте запишем ту же команду сложения в совсем уж привычном виде:
С = А + В
Из трех записей одного и того же действия вторая, конечно, понятнее первой, но все же еще довольно далека от третьей, наиболее удобной.
Теперь представьте себе, как каждым из трех способов записывалось бы вычисление по какой-либо мало-мальски сложной формуле. Различия между ними стали бы еще разительнее.
[ C = (А+В)/(А-В)
+ А В С
- А В D
/ С D С
05 10 0100 0110 0200
06 11 0100 0110 0210
07 13 0200 0210 0200
Одно и то же вычисление написано здесь в виде привычной математической формулы (вверху), на автокоде (в середине) и в кодах (внизу). Легко понять, какая из записей легче для составления и понимания ]
А ведь электронные вычислительные машины создавались для решения именно сложных задач. Появились они в те времена, когда на повестку дня вставало овладение атомной энергией, конструирование космических ракет. ЭВМ были призваны способствовать осуществлению грандиозных инженерных и научных замыслов.

Первые алгоритмические языки появились в конце 50-х годов, ознаменованных вводом в действие первых атомных электростанций и запуском первых искусственных спутников Земли.
И вот в конце пятидесятых годов, ознаменованных вводом в строй первых атомных электростанций, запуском первых искусственных спутников Земли, в вычислительном деле был совершен шаг, резко увеличивший число людей, способных пользоваться услугами ЭВМ, шаг, позволивший превратить программирование в одну из самых массовых профессий и говорить об овладении им как о "второй грамотности". Появились алгоритмические языки программирования, достаточно близкие к привычному языку математических формул, понятные человеку и избавившие его от необходимости знать особенности конкретной ЭВМ, на которой он работает.
Первенцами в семье этих языков были Фортран, Алгол, Кобол [Названия алгоритмических языков в современных изданиях приводятся весьма по-разному - то в кавычках, то без кавычек, то прописными, то строчными буквами: ФОРТРАН, Фортран, фортран, "фортран"... Возможно, когда эти названия войдут в нашу повседневную речь (что можно предвидеть по темпам компьютеризации нашей жизни), они будут писаться строчными буквами без кавычек. Однако, чтобы не слишком опережать время, мы пишем их пока с прописной буквы]. В силу их близости к языку математических выкладок их назвали языками высокого уровня. Автокоды же в отличие от них отныне стали именовать языками низкого уровня.
Перевод программ с алгоритмического языка на понятный машине язык цифр взяли на себя программы-трансляторы. Естественно, они усложнились, увеличилось время трансляции, но все это было лишь небольшой платой за значительное облегчение процесса программирования, уменьшение времени отладки, упрощение возможного совершенствования программ.
Это, кстати, дало возможность, обсуждая проблемы программирования, говорить не о конкретном типе ЭВМ - например, БЭСМ, ЕС ЭВМ или СМ ЭВМ, а о фиктивных Фортран-машине, Алгол-машине или Бейсик-машине. Дело в том, что специфику конкретной машины учитывает программа-транслятор. Программа же, написанная на алгоритмическом языке, уже рассматривается не как последовательность инструкций для имеющейся ЭВМ, а как инструкции для гипотетической, скажем, Бейсик-машины.
Например, если мы даем Бейсик-машине инструкцию: A=B+C*D-E, то нас не интересует, сколько команд выполнит ЭВМ для получения результата, где будут храниться значения величин А, В, С, D и Е. Мы говорим, что Бейсик-машина вычислит значение выражения, записанного справа от знака равенства, и присвоит его переменной А. В отличие от команд такие инструкции называются операторами.
[ ОПЕРАТОР - это допустимое в данном языке предписание, задающее определенные действия в программе. В отличие от команды, всегда определяющей лишь одно элементарное действие машины, оператор может предписывать такое действие в программе, которое будет реализовано машиной в виде целого ряда элементарных действий.
Использование операторов вместо команд для записи программ является основным различием, между языками высокого и низкого уровней ]
Языков высокого уровня существует сегодня много. Точную цифру назвать затруднительно, однако если перечислять даже наиболее распространенные, получится более десятка. Это различные версии Фортрана, Алгол-60, ПЛ/1, Бейсик, Алгол-68, Паскаль, Рапира, Кобол, Лисп, Снобол, АПЛ, АДА и т.д.
Понимаем, что у иного читателя может возникнуть вопрос: зачем их так много? Неужели их создатели забыли поучительную легенду о вавилонском столпотворении? Сначала на земле, гласит библейская легенда, был одни язык и одно наречие. И собрались люди и стали строить башню высотою до небес. Разгневался господь, сошел на землю и смешал язык их так, чтобы один не понимал другого. Говоря на разных языках, люди не могли работать вместе. Неужели, приступая к широкому освоению вычислительной техники, человечество вновь впадает в "вавилонскую" ошибку?
Не будем спешить с выводами. Не так уж неразумно современное человечество. Появление многих алгоритмических языков вызвано вполне объективными причинами. Дело в том, что самые "умные" электронные вычислительные машины, как и их простоватые предки, по-прежнему понимают лишь язык элементарных команд, записанных цифрами. Поэтому, чем сложнее операторы алгоритмического языка, тем, естественно, сложнее и переводить их в такие команды.
Неоднократные попытки разрешить эту проблему н привели к созданию различных языков. Некоторые из них (Фортран, например) обладают набором лишь сравнительно простых для перевода операторов. Однако для человека это создает трудности при записи сложных алгоритмов. Другие языки (например, Алгол-60) имеют удобные и наглядные средства для записи алгоритмов, но требуют сложной программы-транслятора для перевода их в машинные команды.
Кстати, трансляция программ ставит еще одну проблему: как переводить? Существуют два типа трансляторов - интерпретаторы и компиляторы. Первые переводят "дословно". Каждый оператор алгоритмического языка переводится в команды ЭВМ по мере чтения программы и тут же выполняется, после чего считывается следующий. Можно сказать, что в этом случае программа хранится в памяти машины в том же виде, в каком она написана на бумаге. Если она написана с ошибками, не беда. Запустили такую программу на счет, нашли ошибку, тут же ее исправили н продолжили работу. Захотели что-нибудь изменить, изменили и снова - на счет. Очень удобно. Для человека. А для машины? Во-первых, кроме вашей программы, надо постоянно держать в памяти программу-транслятор. А это накладно. Слишком дорога оперативная память, чтобы транжирить ее на хранение пассивного балласта-транслятора. Вместо этого можно было бы параллельно решать задачу по другой программе. Да и на вашу программу это накладывает дополнительные ограничения по объему. Во-вторых, это замедляет выполнение программы. Ведь если в ней есть конструкции, называемые циклами, когда многократно выполняется одна и та же группа операторов, то переводить их нужно во время каждого прохождения цикла.
От подобных недостатков свободны компиляторы. Трансляторы этой группы сначала переводят программу целиком, так сказать, не по букве, а по смыслу. Полученный "литературный перевод" является уже другой программой, отличающейся от вашей не меньше, чем стихотворение Лермонтова "На севере диком стоит одиноко..." от оригинала Гейне "Ein Fichtenbaum steht einsam...". Однако машиной выполняется именно перевод. После того, как он получен, присутствие транслятора в памяти уже излишне. Нет и необходимости по многу раз переводить одно и то же. Но вот беда: вмешаться в работу "оттранслированной" программы вы не можете - вам не известно, в какие именно команды переведен тот или иной оператор и где эти команды искать. Поэтому при обнаружении ошибки необходимо вернуться к исходному тексту, исправить его и снова повторить трансляцию.
Как видите, свои достоинства и недостатки есть и у компиляторов и у интерпретаторов. Первые чаще применяются при работе на больших ЭВМ с серьезными, объемными программами. Интерпретаторы же в основном используются на микро-ЭВМ. В частности, подавляющее большинство трансляторов с Бейсика - а именно он держит пальму первенства по использованию на малых компьютерах - интерпретаторы.
Но вернемся к размышлению о том, что специфические проблемы взаимоотношения человека с ЭВМ привели к появлению многих и очень различных языков программирования.
Как же разобраться в этом море начинающему, если он к тому же не готовится стать профессиональным программистом? И нужно ли? Может быть, достаточно освоить любой из этих языков, попавший под руку?
Конечно, чтобы понять основы программирования, необходимо выучить хотя бы один язык. Но так же, как для лучшего понимания родного языка полезно познакомиться с иностранными, так и для лучшего понимания конкретного алгоритмического языка полезно иметь понятие о других. Это расширит кругозор пользователя, позволит овладеть целым рядом специальных конструкций, отсутствующих в его "родном" языке, да и, кроме того, при возможности выбора позволит аргументированно выбрать язык для решения конкретной задачи.
Языки высокого уровня отличаются друг от друга довольно сильно, не меньше, чем вода в разных морях. Но так же, как термин "морская вода" подразумевает воду, содержащую большое количество солей, пусть и в разных пропорциях, так и каждый из языков программирования можно разложить на ряд элементов, набор которых есть практически в каждом языке.
Назовем основные из них:
1. Алфавит языка.
2. Структура и способ записи программ.
3. Данные.
4. Операции над данными.
5. Управление последовательностью действий.
6. Операции по трансляции и запуску программ.
Так как эти пункты общи для всех языков, то имеет смысл кратко их охарактеризовать, прежде чем выделять их в каком-либо языке, с которыми мы будем знакомиться на следующих занятиях.
АЛФАВИТ ЯЗЫКА. Каждый язык программирования имеет строго определенный набор символов. Это цифры, математические знаки, буквы и т.д. Только с их помощью дозволяется писать тексты-программы на этом языке. Алфавит алгоритмического языка можно сравнить с набором литер, имеющихся в типографии и используемых для набора книг, журналов и газет. В отличие от символов, употребляемых при письме, этот набор всегда ограничен и с его помощью нельзя изобразить любой знак, пришедший нам в голову.
Каждый символ представляется в машине кодом, по которому его узнает транслятор.
Кроме отдельных символов, в любом алгоритмическом языке употребляются их устойчивые сочетания, называемые иногда иероглифами. Каждый иероглиф при переводе программы выражается, как и символ, одним кодом. К примеру, в любой программе, написанной на Алголе-60, имеются слова begin (начало) и end (конец). Переводя их, транслятор вовсе не кодирует букву за буквой - сначала b, потом e, потом g... Нет, все слово begin заменяется своим кодом, слово end - своим. К иероглифам можно отнести и числа. Встретив в тексте программы, скажем, число 0.02, транслятор тоже не станет заменять отдельными кодами сначала нуль, потом десятичную точку... Впрочем, об особенностях трансляции чисел у нас будет особый разговор.
СТРУКТУРА И СПОСОБ ЗАПИСИ ПРОГРАММ. Способы записи программ сильно различаются в разных языках. В Фортране, например, для этого используется специальный бланк.

Для записи программы на Фортране используется специальный бланк. Символы, помещенные в разные его зоны, интерпретируются по-разному.
Каждая строка бланка поделена на зоны. Символы, находящиеся в разных зонах, интерпретируются по-разному. Такие языки называются позиционированными.
В других языках допускается свободная запись. Для разделения структурных единиц - например, операторов - применяются специальные символы, чаще всего точка с запятой. Так принято писать программы на Алголе-60, Паскале, ПЛ/1.

В Алголе-60 допускается свободная запись, операторы разделяются точкой
с запятой.
Вообще позиционирование является своего рода анахронизмом, исторически перекочевавшим в языки высокого уровня из автокодов. Считается, что лучше использовать для разделения конструкций языка специальные символы, не задумываясь о привязке операторов к началам и концам строк - подобно тому, как при письме мы не заботимся о том, чтобы каждая фраза целиком умещалась на одной строке.
Структура программ - это, пожалуй, одна из наиболее характерных особенностей языка. Когда программа записывается на Фортране, то выглядит набором не связанных друг с другом модулей, каждый из которых может иметь свои особые переменные, транслироваться совершенно автономно.

Программа, записанная на Фортране, выглядит как набор не связанных друг с другом модулей.
Программа, записанная на Алголе-60, состоит из вложенных друг в друга блоков, где из объемлющего блока можно перейти лишь в непосредственно вложенный в него, притом используя либо те же переменные, либо специально оговоренные).

Программа, записанная на Алголе-60, состоит из вложенных друг в друга блоков.
Программа на Бейсике - это единая неделимая структура, состоящая из отдельных строк и т.д.
ДАННЫЕ. Так называется любая информация, находящаяся в ЭВМ. Программа - тоже "данные". Мы, однако, поговорим только о тех данных, которыми оперируют сами программы, написанные на языках высокого уровня.
Эти данные обычно разделяют на постоянные и переменные. Постоянные - это такие величины, которые не меняются на протяжении работы всей программы. Например, если есть в программе константа 2, то и будет она всегда двойкой. Переменные же в процессе выполнения программы могут принимать различные допустимые значения.
Например, если среди данных есть целочисленная переменная, то она может оставаться равной той же двойке во все время работы программы, а может по ходу ее работы стать равной и 15 и 32000, то есть любому целому числу, не превышающему, правда, некоторого максимума, зависящего от конкретной ЭВМ.
Для обозначения переменных во всех языках используются имена (или идентификаторы). Образуются они, как правило, из букв и цифр и начинаются с буквы. Иногда для образования имен допускается использование и других символов - например, знака минус. Длины идентификаторов могут быть различными. Так, в Бейсике допускаются имена, состоящие не более чем из 2-3 символов - A, BI, F4%. В Алголе-60 длина имени не ограничивается. Там возможен, скажем, такой идентификатор; ЛОШАДКАВЕЗУЩАЯХВОРОСТУВОЗ.

Так в ячейках памяти записывается целое число
На каждую постоянную и переменную величину транслятор выделяет для ее хранения определенную зону памяти. Такая зона может состоять из одной или нескольких ячеек. Адреса ячеек, где хранятся данные, собираются в специальные таблицы, из которых ясно, какому адресу соответствует имя той или иной переменной.
Данные, которые можно использовать в арифметических вычислениях, называются числовыми. В свою очередь, они делятся иа целые и вещественные. Такое деление позволяет программисту управлять точностью вычислений и распределением памяти, так как целые и вещественные числа представляются в памяти по-разному. Целые занимают меньше места, и вычисления с их участием проходят быстрее. В некоторых языках допускаются и комплексные числа. Места для их хранения нужно еще больше, чем для вещественных, но и удобства программисту они дают большие. К примеру, решая на машине квадратное уравнение, можно не рассматривать отдельно случаи, когда оно имеет действительные корни, а когда нет. Описали соответствующие переменные как комплексные и все. Дальше машина сама разберется.
Большинство алгоритмических языков допускает работу не только с числами, но с текстами. Для этой цели существуют специальные типы данных, называемые символьными или строковыми. Например, если некоторая переменная описана как символьная, то она может принимать значения, скажем, tract или or. Сложение этих значений даст новую символьную величину tractor.
Бывают данные логического типа. Они обычно принимают одно из двух значений: true (истина) или false (ложь).
Переменные (и постоянные) разных типов представляются в памяти по-разному. Целые числа просто переводятся в двоичную систему. Например, число 17 записывается как 10001.
[ Мы полагаем, что читатель знаком с двоичной системой счисления. Напомним лишь, как "читать" двоичные числа. Под каждым его знаком слева направо припишем последовательные натуральные степени двойки, начиная с нулевой: 2**0=1, 2**1=2, 2**2=4. 2**3= 8 и т.д. Каждое из этих чисел умножим на стоящую над ним единицу или нуль. Полученные произведения сложим. Так, например, из двоичного числа 10011 мы получим 1*1+2*1+16*1=19 ]
Вещественные числа сначала нормализуются, то есть представляются в виде произведения десятичной дроби, меньшей единицы, на десять в некоторой степени, называемой порядком. Дробь эта, называемая мантиссой, должна иметь вслед за нулем и запятой обязательно ненулевую цифру. Например, число 0.02 после нормализации примет вид 0.2e-1, а число 35.6 запишется как 0.356e2. Только после этого транслятор переводит число в двоичную форму, определенным образом упаковывая его в памяти. Так как знаки числа и порядка бывают только двух видов, плюс или минус, то для их обозначения как раз хватает двух символов, которыми оперирует машина: 0 и 1.

произвольное дробное число
Строковые величины записываются в памяти и виде последовательности кодов, каждый из которых соответствует тому или иному символу, образующему строковую величину. (То, что каждый символ имеет свой код, мы уже говорили).

строковая величина.
Очень важным моментом в представлении данных является их классификация по структурам. Те переменные, о которых мы до сих пор говорили, называются "простыми переменными". Они действительно простые: каждая переменная в любой момент времени имеет одно значение. Имя простой переменной записано в специальной таблице, где ей соответствует определенный адрес. По этому адресу она (точнее, ее значение) и отыскивается.
Следующая по сложности структура данных - массив.
Представьте себе, что вам нужно расставить сотню чисел в возрастающем (или убывающем) порядке. Сама по себе задача несложная, имеется много способов таких сортировок. Но вот проблема: как именовать эти числа? Можно так: А, В, С, ..., X, Y, Z, A1, B1... Но если вы попытаетесь написать на любом языке программу расстановки или хотя бы нарисовать схему этого процесса, то сразу же придете к выводу, что сотня имен - это неудобно. Другое дело, если переменные будут иметь одно имя, скажем, X, и разные номера, то есть Х1, Х2, ..., Х100. Тогда можно использовать обозначение Xi, где индекс i указывает на некоторый i-й элемент последовательности наших ста чисел. Такая совокупность данных, каждое из которых имеет одно и то же имя и разные индексы (порядковые номера), и называется массивом.
В зависимости от числа индексов массивы могут быть одномерными (тогда в их обозначении участвует один индекс), двумерными (два индекса) и т.д.
Использование массивов не только облегчает работу программиста, но и "полезно" машине. Дело в том, что элементы массивов располагаются в памяти подряд, поэтому в таблице переменных не нужно перечислять их все. Достаточно указать адрес первого элемента. Тогда адрес i-го элемента можно легко вычислить как сумму адреса первого и величины, кратной i. Кстати, таблица переменных, как и программа, тоже размещается в памяти. Поэтому использование массивов вместо перечней простых переменных экономит память.
Массивы - не единственный способ организации данных. Бывают и более сложные образования - структуры (в ПЛ/I и Алголе-68), файлы. Но если структуры существуют лишь в ограниченном числе алгоритмических языков, то файлы используются почти повсеместно. Упоминание о файлах вы найдете практически в любой книге о программировании. Поэтому и мы посвятим этому понятию несколько слов.
Что же такое "файл"?
В отделе кадров каждого учреждения хранятся карточки на сотрудников. На карточке указаны табельный номер, фамилия сотрудника, его год рождения, должность, домашний адрес. Могут быть и другие сведения. Для отдельного сотрудника информацию, относящуюся к нему, можно записать, например, так: 211 Петров А.Г. 1940 ст.инженер Строительная ул. 16 кв. 2. Совокупность таких записей о сотрудниках учреждения и составит файл.
Другой пример. Перед вами фрагмент программы на Фортране.
IR=0
DO 20 I = 1,N
20 IF(A(I).EQ.0) IR=IR+1
Это тоже файл. Можно привести еще много примеров, но читатель уже, наверное, понял суть дела.
[ ФАЙЛ - это, попросту говоря, организованный набор данных любого типа. Состоит он из ЗАПИСЕЙ. Запись - это, например, строка, где собраны сведения об инженере Петрове, или строка программы на Фортране. Запись служит наименьшей структурной единицей файла, своеобразным атомом, из которых состоят молекулы - сам файл ]
Используются файлы очень широко. Достаточно сказать, что практически вся информация, хранимая во внешних запоминающих устройствах любой ЭВМ, представлена в виде файлов.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Матчасть диванного танкиста
Re: Матчасть диванного танкиста
10/86
МИКРОКАЛЬКУЛЯТОР В ВУЗЕ
Студент проводит лабораторную работу. Сняты показания приборов, пора приниматься за расчеты. В тех цифрах и соотношениях, графиках и диаграммах, которые будут получены сейчас, найдут свое выражение результаты небольшого исследования, выполненного за лабораторным столом.
Не приходится доказывать, что полнота и точность этих результатов во многом зависят от средств, применяемых для расчетов. В век компьютеризации естественно обратиться за помощью в вычислениях к электронной вычислительной машине. Но к какой именно? Очевидно, очень мощная ЭВМ здесь отнюдь не требуется, поскольку студенческая лабораторная работа не предполагает усложненных вычислений. Возможно, здесь был бы наиболее хорош персональный компьютер, но машины этого класса еще не получили желаемого распространения.
А если привлечь к делу карманные ЭВМ, программируемые микрокалькуляторы! При умелом использовании они способны значительно обогатить вузовский учебный процесс. Более того, для некоторых расчетов, которые приходится выполнять студенту, оптимальным вычислительным средством являются именно программируемые микрокалькуляторы.
К такому выводу приходят участвующие в публикуемой ниже беседе доктор технических наук, заведующий кафедрой математической теории микропроцессорных систем управления Ленинградского государственного университета имени А.А.Жданова Г.Г.МЕНЬШИКОВ, доктор технических наук, заведующий кафедрой электротехники Московского станкоинструментального института О.П.МИХАЙЛОВ, кандидат технических наук, заведующий кафедрой экономики, управления и научной организации труда Свердловского инженерно-педагогического института Э.Ф.НИСТРАТОВ и кандидат технических наук, доцент кафедры метрологии и климатологии Томского государственного университета имени В.В.Куйбышева В.И.СЛУЦКИЙ.
Г.Г.МЕНЬШИКОВ. В мнениях многих специалистов по вычислительной технике сквозит незаслуженное пренебрежение к программируемым микрокалькуляторам. Порой доходит до того, что исследователь, выполнивший ключевой расчет своей работы на калькуляторе, стыдится говорить об этом! Но что же в этом плохого? Ведь программируемый микрокалькулятор - это миниатюрная ЭВМ, предназначенная для решения очень многих и весьма непростых задач. Естественно, конкурировать с серьезной вычислительной техникой он не может, но у него есть уникальное преимущество - возможность индивидуального использования в любое время.
В.И.СЛУЦКИЙ. Противопоставлять друг другу имеющиеся вычислительные средства разных типов неразумно - правильнее рассматривать их как набор инструментов для инженерного труда, где каждый инструмент имеет предпочтительную область применения. На практике встречается немало задач, для решения которых наиболее подходит именно программируемый микрокалькулятор.
Выделить эти задачи, создать необходимое программное обеспечение для их решения, научить специалистов именно так их решать проще всего в вузе. Выгоды очевидны: с одной стороны, это реальная помощь производству уже сегодня, в условиях ограниченного пока распространения вычислительной техники, а с другой стороны, это создание и наращивание фонда производственных алгоритмов, без которого о компьютеризации говорить вообще бессмысленно.
Э.Ф.НИСТРАТОВ. Как показывает практика, ограниченных возможностей программируемых микрокалькуляторов вполне хватает для большей части лабораторных работ, расчетов по курсовым и дипломным проектам. Происходит это потому, что здесь мы располагаем в основном старой методической базой, ориентированной на вычисления, которые до сих пор приходилось выполнять вручную или на логарифмической линейке. Программируемый микрокалькулятор существенно облегчает и ускоряет подобные расчеты.
О.П.МИХАЙЛОВ. Это, конечно, не значит, что он лучше других ЭВМ приспособлен к учебному процессу. С помощью более мощных машин учебная сторона диалога "студент-компьютер" может быть существенно расширена. ЭВМ может выступать в роли наставника, помогающего принять верное решение, в качестве информационной системы, поддерживающей необходимые действия человека, в роли экзаменатора, контролирующего знания обучающихся. Однако если придерживаться лишь вычислительного аспекта, то тут я согласен с коллегами: программируемый микрокалькулятор в основном вполне соответствует нуждам индивидуальной работы студента - как в домашних условиях, так и при проведении групповых занятий, насыщенных часто повторяющимися, относительно несложными вычислениями.
"Цель расчетов - не числа, а понимание",- этот афоризм особенно справедлив для высшей школы. Сама процедура решения и средство, которое при этом применено, как бы отступают на задний план. Ради лучшего понимания вопроса, стоящего за расчетами, вычислительная задача разбивается на этапы в рамках логики изучаемой темы: необходимые логические действия на стыках этапов препоручаются обучающемуся, сами же этапы представляют собой задачи несложные, предполагающие лишь рутинные вычисления. При этом становится очевидным излишеством привлечение больших ЭВМ, возможности которых предусматривают решение задач без участия человека в максимально возможном объеме. Программируемый микрокалькулятор в такой ситуации уместнее.
Существуют по крайней мере еще два обстоятельства, которые следует учитывать, выбирая конкретные вычислительные средства для решения учебных задач: расчеты во время занятий с обучающимися должны производиться одновременно всеми студентами группы, причем каждая группа должна находиться в обособленной аудитории или лабораторном помещении. К большой машине сразу все студенты прийти не могут. Принцип "человек идет к машине" в таких условиях должен замениться другим, противоположным - "машина идет к человеку". Соблюдая его, нужно либо создать вычислительные сети во главе с центральной машиной, либо максимально насыщать аудитории элементарными вычислительными средствами, либо развивать оба подхода вместе.
Создать вычислительную сеть, обслуживающую одновременно несколько тысяч пользователей, сложно, дорого и вряд ли по силам большинству институтов. А программируемые микрокалькуляторы нетрудно ввести в состав вычислительной сети на этих этапах, где их возможностей и быстродействия достаточно. Затраты на приобретение 200 программируемых микрокалькуляторов равны затратам на приобретение и установку одной персональной ЭВМ. Иногда в числе решающих факторов могут оказаться габариты вычислительной техники - например, далеко не всегда возможно установить дисплей на рабочем столе.
Э.Ф.НИСТРАТОВ. Учиться работать с ЭВМ сегодня приходится не только студентам, но и преподавателям. Причем последним куда сложнее, поскольку на их плечи ложится ответственность за создание необходимого методического обеспечения для студенческих работ. Здесь преподаватель зачастую вступает на нелегкий путь проб и ошибок, проверяя на практике эффективность того или иного применения вычислительной техники в читаемой им дисциплине.
Нужно ли говорить, что для такого экспериментирования нужен специальный инструмент? Большие ЭВМ на эту роль не подходят - слишком велики затраты времени на подготовку, требуется решать много организационных моментов. Персональные ЭВМ приспособлены для нее значительно лучше, однако пока это еще достаточно редкий инструмент. Остается программируемый микрокалькулятор. С его помощью преподаватель без особых хлопот проверяет задуманные методические приемы, совершенствует используемый математический аппарат решаемых задач, делая его более пригодным для машинного подхода.
Наконец, возникает уверенность в правильности методической постановки задачи. Вот тут уже можно переходить на большую ЭВМ.
О.П.МИХАЙЛОВ. А можно ограничиться и карманными ЭВМ - все теми же программируемыми микрокалькуляторами. На нашей кафедре они широко используются для решения задач лабораторного практикума, несмотря на то, что кафедра имеет свою собственную вычислительную лабораторию, оснащенную значительно более мощными ЭВМ.
Основные задачи, встречающиеся в нашем практикуме по теоретическим основам электротехники, можно условно подразделить на три типа: статистическая обработка результатов эксперимента; расчеты, необходимые для оперативного сравнения экспериментальных данных с теоретическими или для получения исходных параметров в начале эксперимента; расчеты, необходимые для управления экспериментом, выполняемые по ходу его проведения в реальном масштабе времени. В одних лабораторных работах мы используем "Электронику МК-56", в других - "Электронику МК-64", оснащенную встроенным аналого-цифровым устройством, что позволяет автоматизировать снятие разнообразных показателей приборов в нужном темпе.
Г.Г.МЕНЬШИКОВ. С помощью программируемого микрокалькулятора можно решать и многие задачи вузовского курса высшей математики: составление таблиц функций по их явному заданию, вычисление пределов, нахождение корней уравнений и составление таблиц функций по их неявному заданию алгебраическими или трансцедентными уравнениями, вычисление интегралов, в том числе и несобственных, суммирование рядов, вычисление функций двух переменных и построение линий уровня, разложение функций в ряды Фурье, в том числе по произвольной системе базисных функций, интегрирование дифференциальных уравнений первого и второго порядков методом Рунге-Кутта ипи уравнений более высоких порядков методом Эйлера.
Многие программы для решения перечисленных задач имеются в изданных за последнее время сборниках прикладных программ - А.Н.Цветкова и В.А.Епанечникова, Я.К.Трохименко и Ф.Д.Любича. Для решения других задач нужно эти программы составить. Делает это, конечно, не студент. От него в ходе выполнения работы требуется лишь квалифицированно встроить в имеющуюся программу блок непосредственного вычисления заданной функции и расчетом проверить положения проходимого теоретического материала. Мы планируем выполнение работ такого рода как в виде домашних заданий, так и в виде практических занятий в аудитории.
В.И.СЛУЦКИЙ. На нашей кафедре программируемые микрокалькуляторы применяются для проведения лабораторных работ по аэрологии, климатологии и метеорологии. Калькулятор с набором программ позволил отказаться от многих специальных планшетов, линеек, необходимых при ручных методах расчетов. Значительно возросла интенсивность занятий. Существенно изменилась математическая структура учебных задач. Легче стало вычислять интегралы, оперативно решать небольшие системы уравнений и т.п. Большой резерв здесь представляют итерационные методы, практически не используемые при ручных вычислениях.
Однако облегчение труда и экономия времени могут быть достигнуты только при использовании готовых программ и тщательной методической подготовке лабораторных работ. Приступая к их подготовке, прежде всего следует очертить круг задач, которые целесообразно решать с применением программируемых микрокалькуляторов в рамках дисциплины, и составить перечень алгоритмов. Кому-либо из преподавателей приходится изучить калькулятор и ориентировочно оценить его применимость и рентабельность. В соответствии с его возможностями следует изменить математическое содержание решаемых задач, углубить и расширить его.
Следующий этап работ, достаточно сложный и трудоемкий - составление и отладка программ. Большое внимание приходится уделять не только математической стороне решения задач, но также и группировке исходных показателей в виде ясных таблиц, упрощению команд управления программой при расчетах, понятной индикации. Следует заботиться о четкой инструкции к программе, контрольных примерах для проверки ее правильной работы. Сделать все должным образом с первого раза, как правило, не удается. Считать программу готовой к использованию в учебном процессе можно только после того, как она пройдет экспериментальную "обкатку". По этой причине нецелесообразно планировать издание методической литературы сразу большим тиражом - лучше сделать это после года практической эксплуатации программы и методики. Следует учитывать и то, что внедрение микрокалькуляторов в учебный процесс поначалу носит инициативный характер и осуществляется за счет усилий одного-двух преподавателей. Более широкое распространение методики в рамках кафедры требует обучать работе с калькулятором других преподавателей, на что также требуются время и определенные усилия.
О.П.МИХАЙЛОВ. Удобство применения программируемых микрокалькуляторов мы оценили быстро. Правда, в методическом плане они поставили перед нами много проблем. Во-первых, резко возросла точность расчетов, и сегодня мы уже полностью перешли от электромеханических приборов к цифровым, как более точным. Значительно увеличились интенсивность, насыщенность лабораторных занятий, изменился и математический аппарат обработки данных - без достаточно полного статистического анализа, без хорошо выполненной апроксимации экспериментальных данных лабораторную работу у нас сегодня не сдать. Удалось освободиться от всех второстепенных приемов и методов, связанных с математическими трудностями, с применением ручных, графических приближенных вычислений. Внимание студента концентрируется на существе решаемой задачи. Практика показала, что управление микрокалькулятором во время вычислений не требует от студента какой-либо специальной подготовки и уже на самом первом лабораторном занятии, за 5-10 минут он уверенно осваивает команды записи показателей в память калькулятора и пуска программы на счет.
Э.Ф.НИСТРАТОВ. С любопытной неожиданностью столкнулись мы при проведении экспериментальной курсовой работы по дисциплине "Вычислительная техника в учебном процессе", которая появилась в нашем Свердловском инженерно-педагогическом институте в 1983 году. Суть работы проста - будущий преподаватель должен переработать методические указания к одной из действующих лабораторных работ по техническим дисциплинам, вводя в нее вычисления на микрокалькуляторе. Так вот, часть лабораторных работ после текой переработки потеряла смысл, так как, кроме описания расчетов, эти работы ничего не содержали. Во многих работах были обнаружены ошибки, неточности. Но самое главное - пересмотренные таким образом лабораторные работы стали более стройными и логичными в отношении существа изучаемого предмета.
В.И.СЛУЦКИЙ. Думается, что применение программируемых микрокалькуляторов в вузах - это естественный и необходимый шаг не только ввиду учебных задач. Дело имеет серьезную социальную и экономическую подоплеку. Можно не сомневаться, например, в активной позиции специалистов по отношению к вычислительной технике, если в ходе вузовского обучения они использовали хотя бы микрокалькулятор. Считать по старинке там, где много однотипных вычислений, они уже никогда не будут.
Однако чтобы считать на микрокалькуляторе, нужно в достаточной степени его знать. Оптимально было бы, если бы студенты приходили на кафедры специальных дисциплин, уже владея всеми основными приемами работы с ним. Пока что этого нет. В 1984 году наша кафедра ввела в план второго семестра курс "Применение программируемых микрокалькуляторов для решения метеорологических задач", и первокурсники с энтузиазмом освеивают карманную ЭВМ, так как убеждаются в ее практической необходимости. Многие приобретают собственные микрокалькуляторы. Практика показывает, что для занятий с группой достаточно иметь 15-20 вычислительных машинок, чтобы их можно было установить на каждый стол. В целом кафедре нужно 30-35 калькуляторов, чтобы была подмена машинам, вышедшим из строя и требующим ремонта, а также для индивидуальной работы преподавателей и студентов.
О.П.МИХАЙЛОВ. Я занимаю иную позицию в этом вопросе. На мой взгляд, кафедрам специальных дисциплин нецелесообразно обучать студентов программированию на микрокалькуляторах. К тому же, в ходе занятий расточительно было бы тратить время на ручной набор программ, на исправление ошибок набора, связанных с неверными действиями или с ложным срабатыванием клавиш. Мы решили автоматизировать набор, объединив калькуляторы "Электроника МК-56" в вычислительную сеть с ЭВМ "Электроника Д3-28", на магнитной ленте которой записаны все необходимые программы. С помощью завода-изготовителя микрокалькуляторов все "МК-56" в лаборатории были подключены к преобразователю кодов цифровых и операционных клавиш, и процесс ввода программ протекает надежно, хотя и не очень быстро: полторы-две минуты для записи программы полной длины. С помощью специального переключателя можно вести либо запись одной программы на все микрокалькуляторы в лабораторном помещении, либо запись разных программ на отдельные микрокалькуляторы. Это позволяет проводить одновременно различные лабораторные работы, например, во время дополнительных занятий.
Г.Г.МЕНЬШИКОВ. Выгод от применения программируемых микрокалькуляторов в вузе немало. Я, например, убежден, что они способствуют раннему распознаванию склонностей и таланта студента. Нередко слабый, казалось бы, студент оказывается асом в программировании и, почувствовав себя в чем-то сильным, "вытягивает" и все остальное.
Может быть, на мою убежденность повлияла специфика подготовки наших студентов - мы считаем, что для специалиста по микропроцессорной технике практика программирования на мнемокодах должна предшествовать изучению алгоритмических языков высокого уровня. Однако есть и вполне объективные показатели, свидетельствующие о целесообразности освоения программируемых микрокалькуляторов каждым студентом. Так, например, раньше на кафедре мы успевали просчитать с помощью больших ЭВМ 3-4 индивидуальных задания студента в течение семестра (имеется в виду не производительность ЭВМ, а весь комплекс организационно-методических мероприятий, связанных с использованием больших ЭВМ для решения учебных задач). С применением же программируемых микрокалькуляторов число таких заданий возросло до 15-20. Правда, такой выигрыш достижим лишь тогда, когда каждый студент обеспечен вычислительной машинкой для индивидуальной работы. В известной степени делу помогает оснащение специальных классов. Но думается, что в вузах сегодня необходимы специализированные библиотеки ("компьютеки"), где студент мог бы взять микрокалькулятор в личное пользование сроком на год или два.
Э.Ф.НИСТРАТОВ. В нашем институте имеется 400 программируемых микрокалькуляторов "Электроника МК-56". Большая часть находится на кафедрах и в учебных аудиториях, около 50 штук переданы в читальные залы и общежития института. Выдаются они, как и книги, на студенческие билеты. Их ремонтом в институте занимается отдел АСУ. Единственная сложность заключается в том, что выдача микрокалькуляторов не входит в объем работ, учитываемых при определении штатов и фонда заработной платы работников библиотеки.
Студенты к этой системе привыкли очень быстро и берут микрокалькуляторы не только для занятий с применением готовых программ, но и для выполнения индивидуальных работ с большим объемом вычислений. Появились энтузиасты, разрабатывающие разнообразные программы, которыми пользуется вся группа, а иногда и другие группы. Явно напрашивается следующий шаг - выдавать в библиотеке не только микрокалькуляторы, но и сборники учебных программ для них.
Такие сборники еще предстоит создать. Дело это, безусловно, стоящее. Какими бы ни были те ЭВМ, с которыми придется работать выпускнику вуза на производстве, он всегда с благодарностью вспомнит маленький программируемый микрокалькулятор, с помощью которого он когда-то приобщался к вычислительной технике, придумывал нехитрые алгоритмы и составлял свои первые программы.
Беседу вел С.КОМИССАРОВ
На кафедре электротехники Московского станкостроительного института программируемые микрокалькуляторы широко используются для решения задач лабораторного практикума, несмотря на то что кафедра располагает н более мощными ЭВМ.

Учебная лаборатория кафедры электротехники Московского станкостроительного института, оснащенная программируемыми микрокалькуляторами "Электроника МК-56".
На стройплощадке начинаются планировочные работы. Грунт из выемок должен быть перемещен и уложен в насыпи. Трудоемкость н продолжительность планировочных работ во многом зависит от суммарного объема перемещаемого грунта н от дальности его перемещения, характеризуемой некоторым усредненным показателем Lcp. В большинстве случаев при ручных вычислениях его определяют как расстояние между обобщенными центрами тяжести выемок и насыпей. Ради большей точности расчета план площадки приходится подразделять на части, в которых выемки противостоят насыпям.
Подобного подразделения можно избежать за счет модификации расчетного метода - вести расчеты так, как будто грунт вначале перевозится нз выемок или насыпей в соответствующие обобщенные центры тяжести. Конечно, в действительности грунт так никто возить не будет, но точность расчета благодаря такому представлению значительно повышается. Модификация влечет усложнение расчетных формул, но если вычисления ведутся на программируемом микрокалькуляторе, это усложнение практически не ощущается.
Новый подход к определению средней дальности перемещения грунта был предложен в ходя выполнения студенческой научно-исследовательской работы на кафедре технологии строительного производства Московского инженерно-строительного института имени В.В.Куйбышева. Работа отмечена почетным дипломом Всероссийской конференции студенческих работ, состоявшейся в Томске в 1984 году.
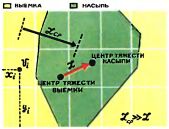
План перемещения грунта из выемок в насыпи, расчет по которому выполняется на программируемом микрокалькуляторе.
В одном из индивидуальных домашних задании, даваемых первокурсникам Ленинградского электротехнического института имени В.И.Ульянова (Ленина), требуется выяснить свойство решений несложного дифференциального уравнения типа x=f(x,y), не решая его в явном виде. Студент должен очертить в координатной плоскости область, в которой существует функция f(x,y), расчетом проверить, что через каждую точку этой области проходит единственная интегральная кривая, отыскать зоны, в которых интегральные кривые возрастают или убывают, выпуклы вверх или вниз, исследовать поведение кривых вблизи границ таких зон и т.д.

Семейство интегральных кривых дифференциального уравнения, построенное с помощью микрокалькулятора.
Расчет ведется на программируемом микрокалькуляторе по методу Рунге-Кутта. программа, реализующая
этот метод, дается студенту в готовом виде. Он должен лишь дополнить ее подпрограммой, где вычисляется правая часть дифференциального уравнения. Программой предусмотрен расчет с некоторым заданным и уменьшенным вдвое шагом по оси х. Это дает представление о точности решения.
При оперативной обработке сигналов радиозонда в аэрологических наблюдениях эффективна автоматизация обработки сигналов с помощью ЭВМ. Программируемый микрокалькулятор может облегчить работу там, где пока еще приходится обрабатывать информацию вручную. Если же калькулятор используется в учебных целях, он демонстрирует работу большой ЭВМ на отдельных этапах, помогает понять на конкретных результатах связь разнообразных параметров. Микрокалькулятор с комплектом нужных программ заменяет применявшиеся ранее для этой цели многочисленные таблицы и номограммы, специальные линейки и планшеты. Требуемые результаты получаются быстрее и проще, возрастает надежность вычислений.
Прикладные программы и методика применения программируемых микрокалькуляторов в аэрологических наблюдениях разработаны на кафедре метеорологии и климатологии Томского Государственного университета имени В.В.Куйбышева. С их помощью определяют параметры ветра на заданных высотах, результирующий ветер для вертикального слоя атмосферы, зависимость скорости ветра от высоты, давление воздуха на заданных высотах, вертикальный градиент температуры и т.д.
Нередко на микрокалькуляторах приходится работать с пакетом программ, поочередно вводя одну за другой. Взять, к примеру, задачу нахождения корней полинома пятой ступени. Программа для ее решения не уместится в памяти "Электроники Б3-34 . Но, используя три микрокалькулятора в "последовательном включении", легко справиться и с этой и многими подобными задачами. В первый калькулятор загружается программа для определения вещественного корня уравнения пятой степени. С ее помощью отыскивается этот корень и коэффициенты полинома четвертой степени, корни которого равны остальным четырем корням исходного полинома. На втором калькуляторе ведется разложение полученного уравнения четвертой степени на два квадратных уравнения. Их действительные или комплексные корни отыскиваются на третьем калькуляторе. При известном навыке таким комплексом сумеет пользоваться даже один человек. Коэффициенты можно выписывать на вычислительный бланк, если программы пакета сильно различаются по быстродействию, или непосредственно переносить с индикатора одного микрокалькулятора в регистры другого, если время выполнения каждой программы примерно одинаково.

Последовательный режим вычислений на нескольких калькуляторах. Решение уравнения пятой степени.
Мыслимо и "параллельное включение" микрокалькуляторов. Допустим, для построения графика или для составления таблицы требуется вычислить значение некоторой быстроменяющейся функции в 200 точках, а каждая точна находится в результате расчета по сложной программе за добрый десяток минут. Объединение трех-четырех калькуляторов ускорит работу во столько же раз. Одновременно на каждом калькуляторе рассчитывается одна из группы точен, расположенных рядом. Затем начинается расчет точек следующей группы и так далее.
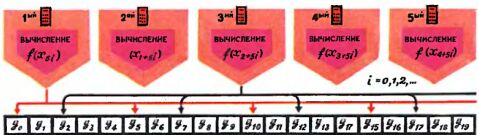
Параллельный режим вычислений на нескольких калькуляторах. Составление таблицы функции.
МИКРОКАЛЬКУЛЯТОР В ВУЗЕ
Студент проводит лабораторную работу. Сняты показания приборов, пора приниматься за расчеты. В тех цифрах и соотношениях, графиках и диаграммах, которые будут получены сейчас, найдут свое выражение результаты небольшого исследования, выполненного за лабораторным столом.
Не приходится доказывать, что полнота и точность этих результатов во многом зависят от средств, применяемых для расчетов. В век компьютеризации естественно обратиться за помощью в вычислениях к электронной вычислительной машине. Но к какой именно? Очевидно, очень мощная ЭВМ здесь отнюдь не требуется, поскольку студенческая лабораторная работа не предполагает усложненных вычислений. Возможно, здесь был бы наиболее хорош персональный компьютер, но машины этого класса еще не получили желаемого распространения.
А если привлечь к делу карманные ЭВМ, программируемые микрокалькуляторы! При умелом использовании они способны значительно обогатить вузовский учебный процесс. Более того, для некоторых расчетов, которые приходится выполнять студенту, оптимальным вычислительным средством являются именно программируемые микрокалькуляторы.
К такому выводу приходят участвующие в публикуемой ниже беседе доктор технических наук, заведующий кафедрой математической теории микропроцессорных систем управления Ленинградского государственного университета имени А.А.Жданова Г.Г.МЕНЬШИКОВ, доктор технических наук, заведующий кафедрой электротехники Московского станкоинструментального института О.П.МИХАЙЛОВ, кандидат технических наук, заведующий кафедрой экономики, управления и научной организации труда Свердловского инженерно-педагогического института Э.Ф.НИСТРАТОВ и кандидат технических наук, доцент кафедры метрологии и климатологии Томского государственного университета имени В.В.Куйбышева В.И.СЛУЦКИЙ.
Г.Г.МЕНЬШИКОВ. В мнениях многих специалистов по вычислительной технике сквозит незаслуженное пренебрежение к программируемым микрокалькуляторам. Порой доходит до того, что исследователь, выполнивший ключевой расчет своей работы на калькуляторе, стыдится говорить об этом! Но что же в этом плохого? Ведь программируемый микрокалькулятор - это миниатюрная ЭВМ, предназначенная для решения очень многих и весьма непростых задач. Естественно, конкурировать с серьезной вычислительной техникой он не может, но у него есть уникальное преимущество - возможность индивидуального использования в любое время.
В.И.СЛУЦКИЙ. Противопоставлять друг другу имеющиеся вычислительные средства разных типов неразумно - правильнее рассматривать их как набор инструментов для инженерного труда, где каждый инструмент имеет предпочтительную область применения. На практике встречается немало задач, для решения которых наиболее подходит именно программируемый микрокалькулятор.
Выделить эти задачи, создать необходимое программное обеспечение для их решения, научить специалистов именно так их решать проще всего в вузе. Выгоды очевидны: с одной стороны, это реальная помощь производству уже сегодня, в условиях ограниченного пока распространения вычислительной техники, а с другой стороны, это создание и наращивание фонда производственных алгоритмов, без которого о компьютеризации говорить вообще бессмысленно.
Э.Ф.НИСТРАТОВ. Как показывает практика, ограниченных возможностей программируемых микрокалькуляторов вполне хватает для большей части лабораторных работ, расчетов по курсовым и дипломным проектам. Происходит это потому, что здесь мы располагаем в основном старой методической базой, ориентированной на вычисления, которые до сих пор приходилось выполнять вручную или на логарифмической линейке. Программируемый микрокалькулятор существенно облегчает и ускоряет подобные расчеты.
О.П.МИХАЙЛОВ. Это, конечно, не значит, что он лучше других ЭВМ приспособлен к учебному процессу. С помощью более мощных машин учебная сторона диалога "студент-компьютер" может быть существенно расширена. ЭВМ может выступать в роли наставника, помогающего принять верное решение, в качестве информационной системы, поддерживающей необходимые действия человека, в роли экзаменатора, контролирующего знания обучающихся. Однако если придерживаться лишь вычислительного аспекта, то тут я согласен с коллегами: программируемый микрокалькулятор в основном вполне соответствует нуждам индивидуальной работы студента - как в домашних условиях, так и при проведении групповых занятий, насыщенных часто повторяющимися, относительно несложными вычислениями.
"Цель расчетов - не числа, а понимание",- этот афоризм особенно справедлив для высшей школы. Сама процедура решения и средство, которое при этом применено, как бы отступают на задний план. Ради лучшего понимания вопроса, стоящего за расчетами, вычислительная задача разбивается на этапы в рамках логики изучаемой темы: необходимые логические действия на стыках этапов препоручаются обучающемуся, сами же этапы представляют собой задачи несложные, предполагающие лишь рутинные вычисления. При этом становится очевидным излишеством привлечение больших ЭВМ, возможности которых предусматривают решение задач без участия человека в максимально возможном объеме. Программируемый микрокалькулятор в такой ситуации уместнее.
Существуют по крайней мере еще два обстоятельства, которые следует учитывать, выбирая конкретные вычислительные средства для решения учебных задач: расчеты во время занятий с обучающимися должны производиться одновременно всеми студентами группы, причем каждая группа должна находиться в обособленной аудитории или лабораторном помещении. К большой машине сразу все студенты прийти не могут. Принцип "человек идет к машине" в таких условиях должен замениться другим, противоположным - "машина идет к человеку". Соблюдая его, нужно либо создать вычислительные сети во главе с центральной машиной, либо максимально насыщать аудитории элементарными вычислительными средствами, либо развивать оба подхода вместе.
Создать вычислительную сеть, обслуживающую одновременно несколько тысяч пользователей, сложно, дорого и вряд ли по силам большинству институтов. А программируемые микрокалькуляторы нетрудно ввести в состав вычислительной сети на этих этапах, где их возможностей и быстродействия достаточно. Затраты на приобретение 200 программируемых микрокалькуляторов равны затратам на приобретение и установку одной персональной ЭВМ. Иногда в числе решающих факторов могут оказаться габариты вычислительной техники - например, далеко не всегда возможно установить дисплей на рабочем столе.
Э.Ф.НИСТРАТОВ. Учиться работать с ЭВМ сегодня приходится не только студентам, но и преподавателям. Причем последним куда сложнее, поскольку на их плечи ложится ответственность за создание необходимого методического обеспечения для студенческих работ. Здесь преподаватель зачастую вступает на нелегкий путь проб и ошибок, проверяя на практике эффективность того или иного применения вычислительной техники в читаемой им дисциплине.
Нужно ли говорить, что для такого экспериментирования нужен специальный инструмент? Большие ЭВМ на эту роль не подходят - слишком велики затраты времени на подготовку, требуется решать много организационных моментов. Персональные ЭВМ приспособлены для нее значительно лучше, однако пока это еще достаточно редкий инструмент. Остается программируемый микрокалькулятор. С его помощью преподаватель без особых хлопот проверяет задуманные методические приемы, совершенствует используемый математический аппарат решаемых задач, делая его более пригодным для машинного подхода.
Наконец, возникает уверенность в правильности методической постановки задачи. Вот тут уже можно переходить на большую ЭВМ.
О.П.МИХАЙЛОВ. А можно ограничиться и карманными ЭВМ - все теми же программируемыми микрокалькуляторами. На нашей кафедре они широко используются для решения задач лабораторного практикума, несмотря на то, что кафедра имеет свою собственную вычислительную лабораторию, оснащенную значительно более мощными ЭВМ.
Основные задачи, встречающиеся в нашем практикуме по теоретическим основам электротехники, можно условно подразделить на три типа: статистическая обработка результатов эксперимента; расчеты, необходимые для оперативного сравнения экспериментальных данных с теоретическими или для получения исходных параметров в начале эксперимента; расчеты, необходимые для управления экспериментом, выполняемые по ходу его проведения в реальном масштабе времени. В одних лабораторных работах мы используем "Электронику МК-56", в других - "Электронику МК-64", оснащенную встроенным аналого-цифровым устройством, что позволяет автоматизировать снятие разнообразных показателей приборов в нужном темпе.
Г.Г.МЕНЬШИКОВ. С помощью программируемого микрокалькулятора можно решать и многие задачи вузовского курса высшей математики: составление таблиц функций по их явному заданию, вычисление пределов, нахождение корней уравнений и составление таблиц функций по их неявному заданию алгебраическими или трансцедентными уравнениями, вычисление интегралов, в том числе и несобственных, суммирование рядов, вычисление функций двух переменных и построение линий уровня, разложение функций в ряды Фурье, в том числе по произвольной системе базисных функций, интегрирование дифференциальных уравнений первого и второго порядков методом Рунге-Кутта ипи уравнений более высоких порядков методом Эйлера.
Многие программы для решения перечисленных задач имеются в изданных за последнее время сборниках прикладных программ - А.Н.Цветкова и В.А.Епанечникова, Я.К.Трохименко и Ф.Д.Любича. Для решения других задач нужно эти программы составить. Делает это, конечно, не студент. От него в ходе выполнения работы требуется лишь квалифицированно встроить в имеющуюся программу блок непосредственного вычисления заданной функции и расчетом проверить положения проходимого теоретического материала. Мы планируем выполнение работ такого рода как в виде домашних заданий, так и в виде практических занятий в аудитории.
В.И.СЛУЦКИЙ. На нашей кафедре программируемые микрокалькуляторы применяются для проведения лабораторных работ по аэрологии, климатологии и метеорологии. Калькулятор с набором программ позволил отказаться от многих специальных планшетов, линеек, необходимых при ручных методах расчетов. Значительно возросла интенсивность занятий. Существенно изменилась математическая структура учебных задач. Легче стало вычислять интегралы, оперативно решать небольшие системы уравнений и т.п. Большой резерв здесь представляют итерационные методы, практически не используемые при ручных вычислениях.
Однако облегчение труда и экономия времени могут быть достигнуты только при использовании готовых программ и тщательной методической подготовке лабораторных работ. Приступая к их подготовке, прежде всего следует очертить круг задач, которые целесообразно решать с применением программируемых микрокалькуляторов в рамках дисциплины, и составить перечень алгоритмов. Кому-либо из преподавателей приходится изучить калькулятор и ориентировочно оценить его применимость и рентабельность. В соответствии с его возможностями следует изменить математическое содержание решаемых задач, углубить и расширить его.
Следующий этап работ, достаточно сложный и трудоемкий - составление и отладка программ. Большое внимание приходится уделять не только математической стороне решения задач, но также и группировке исходных показателей в виде ясных таблиц, упрощению команд управления программой при расчетах, понятной индикации. Следует заботиться о четкой инструкции к программе, контрольных примерах для проверки ее правильной работы. Сделать все должным образом с первого раза, как правило, не удается. Считать программу готовой к использованию в учебном процессе можно только после того, как она пройдет экспериментальную "обкатку". По этой причине нецелесообразно планировать издание методической литературы сразу большим тиражом - лучше сделать это после года практической эксплуатации программы и методики. Следует учитывать и то, что внедрение микрокалькуляторов в учебный процесс поначалу носит инициативный характер и осуществляется за счет усилий одного-двух преподавателей. Более широкое распространение методики в рамках кафедры требует обучать работе с калькулятором других преподавателей, на что также требуются время и определенные усилия.
О.П.МИХАЙЛОВ. Удобство применения программируемых микрокалькуляторов мы оценили быстро. Правда, в методическом плане они поставили перед нами много проблем. Во-первых, резко возросла точность расчетов, и сегодня мы уже полностью перешли от электромеханических приборов к цифровым, как более точным. Значительно увеличились интенсивность, насыщенность лабораторных занятий, изменился и математический аппарат обработки данных - без достаточно полного статистического анализа, без хорошо выполненной апроксимации экспериментальных данных лабораторную работу у нас сегодня не сдать. Удалось освободиться от всех второстепенных приемов и методов, связанных с математическими трудностями, с применением ручных, графических приближенных вычислений. Внимание студента концентрируется на существе решаемой задачи. Практика показала, что управление микрокалькулятором во время вычислений не требует от студента какой-либо специальной подготовки и уже на самом первом лабораторном занятии, за 5-10 минут он уверенно осваивает команды записи показателей в память калькулятора и пуска программы на счет.
Э.Ф.НИСТРАТОВ. С любопытной неожиданностью столкнулись мы при проведении экспериментальной курсовой работы по дисциплине "Вычислительная техника в учебном процессе", которая появилась в нашем Свердловском инженерно-педагогическом институте в 1983 году. Суть работы проста - будущий преподаватель должен переработать методические указания к одной из действующих лабораторных работ по техническим дисциплинам, вводя в нее вычисления на микрокалькуляторе. Так вот, часть лабораторных работ после текой переработки потеряла смысл, так как, кроме описания расчетов, эти работы ничего не содержали. Во многих работах были обнаружены ошибки, неточности. Но самое главное - пересмотренные таким образом лабораторные работы стали более стройными и логичными в отношении существа изучаемого предмета.
В.И.СЛУЦКИЙ. Думается, что применение программируемых микрокалькуляторов в вузах - это естественный и необходимый шаг не только ввиду учебных задач. Дело имеет серьезную социальную и экономическую подоплеку. Можно не сомневаться, например, в активной позиции специалистов по отношению к вычислительной технике, если в ходе вузовского обучения они использовали хотя бы микрокалькулятор. Считать по старинке там, где много однотипных вычислений, они уже никогда не будут.
Однако чтобы считать на микрокалькуляторе, нужно в достаточной степени его знать. Оптимально было бы, если бы студенты приходили на кафедры специальных дисциплин, уже владея всеми основными приемами работы с ним. Пока что этого нет. В 1984 году наша кафедра ввела в план второго семестра курс "Применение программируемых микрокалькуляторов для решения метеорологических задач", и первокурсники с энтузиазмом освеивают карманную ЭВМ, так как убеждаются в ее практической необходимости. Многие приобретают собственные микрокалькуляторы. Практика показывает, что для занятий с группой достаточно иметь 15-20 вычислительных машинок, чтобы их можно было установить на каждый стол. В целом кафедре нужно 30-35 калькуляторов, чтобы была подмена машинам, вышедшим из строя и требующим ремонта, а также для индивидуальной работы преподавателей и студентов.
О.П.МИХАЙЛОВ. Я занимаю иную позицию в этом вопросе. На мой взгляд, кафедрам специальных дисциплин нецелесообразно обучать студентов программированию на микрокалькуляторах. К тому же, в ходе занятий расточительно было бы тратить время на ручной набор программ, на исправление ошибок набора, связанных с неверными действиями или с ложным срабатыванием клавиш. Мы решили автоматизировать набор, объединив калькуляторы "Электроника МК-56" в вычислительную сеть с ЭВМ "Электроника Д3-28", на магнитной ленте которой записаны все необходимые программы. С помощью завода-изготовителя микрокалькуляторов все "МК-56" в лаборатории были подключены к преобразователю кодов цифровых и операционных клавиш, и процесс ввода программ протекает надежно, хотя и не очень быстро: полторы-две минуты для записи программы полной длины. С помощью специального переключателя можно вести либо запись одной программы на все микрокалькуляторы в лабораторном помещении, либо запись разных программ на отдельные микрокалькуляторы. Это позволяет проводить одновременно различные лабораторные работы, например, во время дополнительных занятий.
Г.Г.МЕНЬШИКОВ. Выгод от применения программируемых микрокалькуляторов в вузе немало. Я, например, убежден, что они способствуют раннему распознаванию склонностей и таланта студента. Нередко слабый, казалось бы, студент оказывается асом в программировании и, почувствовав себя в чем-то сильным, "вытягивает" и все остальное.
Может быть, на мою убежденность повлияла специфика подготовки наших студентов - мы считаем, что для специалиста по микропроцессорной технике практика программирования на мнемокодах должна предшествовать изучению алгоритмических языков высокого уровня. Однако есть и вполне объективные показатели, свидетельствующие о целесообразности освоения программируемых микрокалькуляторов каждым студентом. Так, например, раньше на кафедре мы успевали просчитать с помощью больших ЭВМ 3-4 индивидуальных задания студента в течение семестра (имеется в виду не производительность ЭВМ, а весь комплекс организационно-методических мероприятий, связанных с использованием больших ЭВМ для решения учебных задач). С применением же программируемых микрокалькуляторов число таких заданий возросло до 15-20. Правда, такой выигрыш достижим лишь тогда, когда каждый студент обеспечен вычислительной машинкой для индивидуальной работы. В известной степени делу помогает оснащение специальных классов. Но думается, что в вузах сегодня необходимы специализированные библиотеки ("компьютеки"), где студент мог бы взять микрокалькулятор в личное пользование сроком на год или два.
Э.Ф.НИСТРАТОВ. В нашем институте имеется 400 программируемых микрокалькуляторов "Электроника МК-56". Большая часть находится на кафедрах и в учебных аудиториях, около 50 штук переданы в читальные залы и общежития института. Выдаются они, как и книги, на студенческие билеты. Их ремонтом в институте занимается отдел АСУ. Единственная сложность заключается в том, что выдача микрокалькуляторов не входит в объем работ, учитываемых при определении штатов и фонда заработной платы работников библиотеки.
Студенты к этой системе привыкли очень быстро и берут микрокалькуляторы не только для занятий с применением готовых программ, но и для выполнения индивидуальных работ с большим объемом вычислений. Появились энтузиасты, разрабатывающие разнообразные программы, которыми пользуется вся группа, а иногда и другие группы. Явно напрашивается следующий шаг - выдавать в библиотеке не только микрокалькуляторы, но и сборники учебных программ для них.
Такие сборники еще предстоит создать. Дело это, безусловно, стоящее. Какими бы ни были те ЭВМ, с которыми придется работать выпускнику вуза на производстве, он всегда с благодарностью вспомнит маленький программируемый микрокалькулятор, с помощью которого он когда-то приобщался к вычислительной технике, придумывал нехитрые алгоритмы и составлял свои первые программы.
Беседу вел С.КОМИССАРОВ
На кафедре электротехники Московского станкостроительного института программируемые микрокалькуляторы широко используются для решения задач лабораторного практикума, несмотря на то что кафедра располагает н более мощными ЭВМ.

Учебная лаборатория кафедры электротехники Московского станкостроительного института, оснащенная программируемыми микрокалькуляторами "Электроника МК-56".
На стройплощадке начинаются планировочные работы. Грунт из выемок должен быть перемещен и уложен в насыпи. Трудоемкость н продолжительность планировочных работ во многом зависит от суммарного объема перемещаемого грунта н от дальности его перемещения, характеризуемой некоторым усредненным показателем Lcp. В большинстве случаев при ручных вычислениях его определяют как расстояние между обобщенными центрами тяжести выемок и насыпей. Ради большей точности расчета план площадки приходится подразделять на части, в которых выемки противостоят насыпям.
Подобного подразделения можно избежать за счет модификации расчетного метода - вести расчеты так, как будто грунт вначале перевозится нз выемок или насыпей в соответствующие обобщенные центры тяжести. Конечно, в действительности грунт так никто возить не будет, но точность расчета благодаря такому представлению значительно повышается. Модификация влечет усложнение расчетных формул, но если вычисления ведутся на программируемом микрокалькуляторе, это усложнение практически не ощущается.
Новый подход к определению средней дальности перемещения грунта был предложен в ходя выполнения студенческой научно-исследовательской работы на кафедре технологии строительного производства Московского инженерно-строительного института имени В.В.Куйбышева. Работа отмечена почетным дипломом Всероссийской конференции студенческих работ, состоявшейся в Томске в 1984 году.

План перемещения грунта из выемок в насыпи, расчет по которому выполняется на программируемом микрокалькуляторе.
В одном из индивидуальных домашних задании, даваемых первокурсникам Ленинградского электротехнического института имени В.И.Ульянова (Ленина), требуется выяснить свойство решений несложного дифференциального уравнения типа x=f(x,y), не решая его в явном виде. Студент должен очертить в координатной плоскости область, в которой существует функция f(x,y), расчетом проверить, что через каждую точку этой области проходит единственная интегральная кривая, отыскать зоны, в которых интегральные кривые возрастают или убывают, выпуклы вверх или вниз, исследовать поведение кривых вблизи границ таких зон и т.д.

Семейство интегральных кривых дифференциального уравнения, построенное с помощью микрокалькулятора.
Расчет ведется на программируемом микрокалькуляторе по методу Рунге-Кутта. программа, реализующая
этот метод, дается студенту в готовом виде. Он должен лишь дополнить ее подпрограммой, где вычисляется правая часть дифференциального уравнения. Программой предусмотрен расчет с некоторым заданным и уменьшенным вдвое шагом по оси х. Это дает представление о точности решения.
При оперативной обработке сигналов радиозонда в аэрологических наблюдениях эффективна автоматизация обработки сигналов с помощью ЭВМ. Программируемый микрокалькулятор может облегчить работу там, где пока еще приходится обрабатывать информацию вручную. Если же калькулятор используется в учебных целях, он демонстрирует работу большой ЭВМ на отдельных этапах, помогает понять на конкретных результатах связь разнообразных параметров. Микрокалькулятор с комплектом нужных программ заменяет применявшиеся ранее для этой цели многочисленные таблицы и номограммы, специальные линейки и планшеты. Требуемые результаты получаются быстрее и проще, возрастает надежность вычислений.
Прикладные программы и методика применения программируемых микрокалькуляторов в аэрологических наблюдениях разработаны на кафедре метеорологии и климатологии Томского Государственного университета имени В.В.Куйбышева. С их помощью определяют параметры ветра на заданных высотах, результирующий ветер для вертикального слоя атмосферы, зависимость скорости ветра от высоты, давление воздуха на заданных высотах, вертикальный градиент температуры и т.д.
Нередко на микрокалькуляторах приходится работать с пакетом программ, поочередно вводя одну за другой. Взять, к примеру, задачу нахождения корней полинома пятой ступени. Программа для ее решения не уместится в памяти "Электроники Б3-34 . Но, используя три микрокалькулятора в "последовательном включении", легко справиться и с этой и многими подобными задачами. В первый калькулятор загружается программа для определения вещественного корня уравнения пятой степени. С ее помощью отыскивается этот корень и коэффициенты полинома четвертой степени, корни которого равны остальным четырем корням исходного полинома. На втором калькуляторе ведется разложение полученного уравнения четвертой степени на два квадратных уравнения. Их действительные или комплексные корни отыскиваются на третьем калькуляторе. При известном навыке таким комплексом сумеет пользоваться даже один человек. Коэффициенты можно выписывать на вычислительный бланк, если программы пакета сильно различаются по быстродействию, или непосредственно переносить с индикатора одного микрокалькулятора в регистры другого, если время выполнения каждой программы примерно одинаково.

Последовательный режим вычислений на нескольких калькуляторах. Решение уравнения пятой степени.
Мыслимо и "параллельное включение" микрокалькуляторов. Допустим, для построения графика или для составления таблицы требуется вычислить значение некоторой быстроменяющейся функции в 200 точках, а каждая точна находится в результате расчета по сложной программе за добрый десяток минут. Объединение трех-четырех калькуляторов ускорит работу во столько же раз. Одновременно на каждом калькуляторе рассчитывается одна из группы точен, расположенных рядом. Затем начинается расчет точек следующей группы и так далее.

Параллельный режим вычислений на нескольких калькуляторах. Составление таблицы функции.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
Страница 2 из 6 •  1, 2, 3, 4, 5, 6
1, 2, 3, 4, 5, 6 
Страница 2 из 6
Права доступа к этому форуму:
Вы не можете отвечать на сообщения