Синдром го
KRIEGSSPIELE! :: Солдатики :: 3 - Шашки
Страница 1 из 1
 Синдром го
Синдром го
Всем школьникам известен известен "синдром го": существует какой-то предел простоты правил, ниже которого игра представляет интерес только для математиков или историков. И при переходе от "Уголков" к "Шашкам" этот синдром проявляется очень сильно. В "ВЕСЕЛЫХ КАРТИНКАХ" ( ТЕМА #78
ТЕМА #78 ) мы познакомились с играми, которые с этой проблемой справились. Здесь же посмотрим на игры, которым не повезло.
) мы познакомились с играми, которые с этой проблемой справились. Здесь же посмотрим на игры, которым не повезло.
 ТЕМА #78
ТЕМА #78 ) мы познакомились с играми, которые с этой проблемой справились. Здесь же посмотрим на игры, которым не повезло.
) мы познакомились с играми, которые с этой проблемой справились. Здесь же посмотрим на игры, которым не повезло.Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:39 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го

ВЫ ДУМАЛИ ЭТО ИГРА?
Фигушки - это задача по Теории Игр.
Игра "Осада и оборона города".
"Красные" стремятся занять город, синие" обороняют его. У "красных" - два отряда, каждый из которых они могут направить по любой из двух дорог - I и II, ведущих к городу. У "синих" три отряда, которые могут разместиться произвольным образом на любой из двух дорог. Никто из противников не осведомлен об образе действий другого. Условия таковы: если на дороге встречаются равные силы "красных" и "синих", то в 50% случаев "красные" побеждают и занимают город, в 50% - отступают. Если "красные" встречаются с превосходящими силами "синих" (один отряд - с двумя или два - с тремя), они отступают. Определить, как должны распорядиться своими отрядами "красные" и "синие", чтобы обеспечить себе наилучшие возможные результаты игры.
И т.д., и т.п. Если интересно, посмотрите источник - Детскую энциклопедию, том 2-й - про Числа и Фигуры, 1972г. Ну, или - книжку Абчука (
 ТЕМА #26, АБЗАЦ #551
ТЕМА #26, АБЗАЦ #551 )...
)...Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:41 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:41 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Если вы посмотрите в Сети игры "Лисы и Гуси", но увидите огромное количество родственных игр: от "почти шашек", до головоломок на одного. А какова "военная составляющая"?

https://vk.com/@cat_and_raven-istoriya-shashek-ch6-refskak-lisa-i-gusi-asalto-halatafl-ig
ASALTO (ШТУРМ, НАПАДЕНИЕ)
Двое "стражников" защищают "форт". 24 "захватчика" пытаются занять все его девять полей. "Захватчики" не рубят, только ходят вперед, вбок и по любой диагонали по направлению к "форту". В "форте", они ходят лишь ортогонально и не могут двигаться назад.
"Стражники" ходят вперед, назад, вбок и по диагонали вдоль разметки, а кроме того должны рубить "захватчика", если за ним есть свободное поле. Срубленная фишка снимается с поля. "Стражники" должны выбежать из "форта", когда открытие делает это возможным. Если позиция позволяет, "стражник" может срубить больше одного атакующего за ход. Рубка обязательна.
гра заканчивается, когда "захватчики" заняли 9 полей в "форте", или когда "стражники" срубили 15 "захватчиков".
В некоторых вариантах правил простое запирание одного или даже двух "Стражников" не является победой (впрочем, чаще всего после этого нападающим удается занять форт).

В английском варианте игры под названием "Офицеры и сипаи", навеянной индийским восстанием 1857-58 годов, было три фишки-"офицера" и 50 "мятежников".
***
М.Гарднер "Математические досуги"
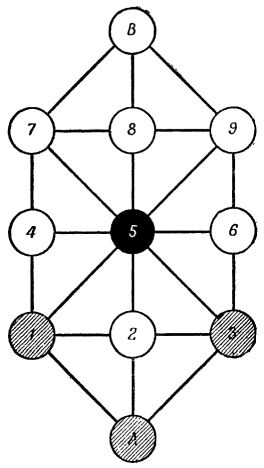
ВОЕННАЯ ИГРА (как ее называют во Франции) представляет собой замечательный пример игры один на один, сочетающей в себе необыкновенную простоту правил с чрезвычайно утонченной стратегией. Эдуард Люка в третьем томе знаменитой книги "Математические развлечения" пишет, что эта игра была популярна во французских военных кругах в течение всей франко-прусской войны 1870—1871 годов и после нее. [А злые языки утверждают, что ее подкинули немецкие шпионы.- G.] К сожалению, с тех пор эту игру совсем забыли: ни в одном солидном руководстве по истории игр на досках она даже не упоминается.
Игровое поле для этой игры изображено на рис.174. Чтобы упростить объяснение правил, кружки пронумерованы. У одного из игроков (условимся называть его ходы ходами "белых") имеются три фишки, которые он в начале игры ставит на три светлых кружка: A, 1 и 3. Второй игрок ("черные") обладает всего одной фишкой, которая перед началом игры занимает кружок 5. (В качестве фишек годятся шахматные пешки или три пятака и одна двадцатикопеечная монета). Игроки делают ходы по очереди; начинают белые. Черная фишка может перейти на любую соседнюю ячейку. Белая фишка ходит так же, но ей запрещено двигаться назад, то есть она может перейти на любую соседнюю ячейку, расположенную слева, справа или спереди от того кружка, на котором она находится. Друг друга фишки не берут. Выигрыш принадлежит белым в том случае, если им удастся запереть черную фишку, то есть загнать ее в кружок, из которого та не сможет сделать ни одного хода. Обычно черная фишка попадает при этом в кружок В, но иногда такая же ситуация возникает, если черные занимают кружок 4 или 6. Во всех остальных случаях выигрывают черные. Для достижения победы им нужно все время держать свою единственную фишку позади фишек противника, не давая ему возможности зайти с тыла. Черные выигрывают и в том случае, когда одни и те же ходы начинают повторяться бесконечное число раз.
Научиться играть в эту игру не сложнее, чем в крестики и нолики, но она гораздо азартнее, а анализ ее более сложен. Люка сумел показать, что белые, играя рационально, могут в каждой партии сдерживать победу, однако простой выигрышной стратегии не существует и игра всегда изобилует ловушками и неожиданностями. Самый лучший на первый взгляд ход нередко оказывается самым худшим. Если черные достаточно опытны, то они с легкостью одерживают победу в игре против менее искушенного противника.
Предположим, что черным предоставлена еще большая свобода: разрешим черным в начале игры ставить свою фишку в любой кружок. Кто в этом случае одерживает победу при рациональной игре обеих сторон?

Из собрания М.С.Костюхиной.
ИГРА НАПОЛЕОН. А. ШОТТЕН, Н. ЛИПНИЦКИЙ. 1890.
В игре используются 4 шашки. Одна из них считается Наполеоном и помещается на точке, называемой Москвой, а остальные три шашки под именем русского корпуса помещаются кругом на ближайших точках к Москве. Игру начинает русский корпус, чтобы дать возможность Наполеону выйти из Москвы. Задача игроков - не дать Наполеону возможность вернуться в Москву. Игра заканчивается, когда русскому корпусу удается загнать Наполеона в точку, названную городом Ковно.

ОСАДА КРЕПОСТИ
На поле располагались бумажные фигурки - три японца помещались в крепость, а 36 китайцев должны были ее захватить.
В "Осаде" китайцы пытались выманить японцев из крепости.
За ход можно было сделать передвижение на одну клетку только по красным линиям. Если за китайцем оказывалось пустое место, японец мог "съесть" его, как в шашках. Китайцы же не имели права "есть" своих противников.
Игра заканчивалась либо когда китайцы занимали места в крепости, либо когда японцы "съедали" всех нападавших.
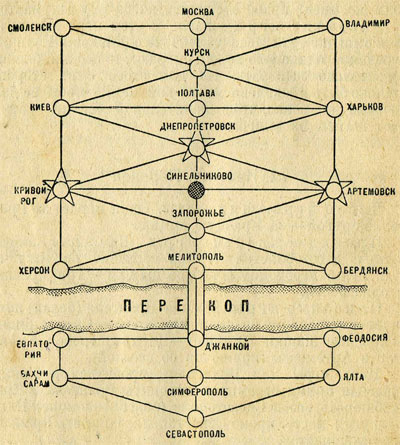
КРАСНЫЙ ПЕРЕКОП
Шашка Врангеля (белая) помещается в заштрихованном кружочке - Синельникове; 3 красные шашки занимают - Днепропетровск, Кривой Рог и Артемовск (кружочки со звездой).
Цель игры для Врангеля - пробиться к Москве; Красная армия стремится оттеснить Врангеля в Крым и запереть его в Севастополе (сбросить в море). Нигде в другом месте, кроме Севастополя, запирать Врангеля на разрешается.
Ходить можно только на ближайший свободный кружок в любом направлении по линиям (вперед, назад, в стороны). Играющие ходят по очереди - один ход делает шашка Врангеля, другой - одна из шашек красных; начинает играть обычно шашка Врангеля.
Бывают такие моменты, когда оба играющие повторяют один и тот же ход по несколько раз под ряд; в этом случае инициативу должны проявить шашки красных, изменяя свои ходы и тем самым изменяя дальнейшее течение игры.
В общем шашки красных имеют некоторое преимущество пред белой и при достаточной внимательности должны выиграть.

https://vk.com/@cat_and_raven-istoriya-shashek-ch6-refskak-lisa-i-gusi-asalto-halatafl-ig
ASALTO (ШТУРМ, НАПАДЕНИЕ)
Двое "стражников" защищают "форт". 24 "захватчика" пытаются занять все его девять полей. "Захватчики" не рубят, только ходят вперед, вбок и по любой диагонали по направлению к "форту". В "форте", они ходят лишь ортогонально и не могут двигаться назад.
"Стражники" ходят вперед, назад, вбок и по диагонали вдоль разметки, а кроме того должны рубить "захватчика", если за ним есть свободное поле. Срубленная фишка снимается с поля. "Стражники" должны выбежать из "форта", когда открытие делает это возможным. Если позиция позволяет, "стражник" может срубить больше одного атакующего за ход. Рубка обязательна.
гра заканчивается, когда "захватчики" заняли 9 полей в "форте", или когда "стражники" срубили 15 "захватчиков".
В некоторых вариантах правил простое запирание одного или даже двух "Стражников" не является победой (впрочем, чаще всего после этого нападающим удается занять форт).

В английском варианте игры под названием "Офицеры и сипаи", навеянной индийским восстанием 1857-58 годов, было три фишки-"офицера" и 50 "мятежников".
***

М.Гарднер "Математические досуги"
ВОЕННАЯ ИГРА (как ее называют во Франции) представляет собой замечательный пример игры один на один, сочетающей в себе необыкновенную простоту правил с чрезвычайно утонченной стратегией. Эдуард Люка в третьем томе знаменитой книги "Математические развлечения" пишет, что эта игра была популярна во французских военных кругах в течение всей франко-прусской войны 1870—1871 годов и после нее. [А злые языки утверждают, что ее подкинули немецкие шпионы.- G.] К сожалению, с тех пор эту игру совсем забыли: ни в одном солидном руководстве по истории игр на досках она даже не упоминается.
Игровое поле для этой игры изображено на рис.174. Чтобы упростить объяснение правил, кружки пронумерованы. У одного из игроков (условимся называть его ходы ходами "белых") имеются три фишки, которые он в начале игры ставит на три светлых кружка: A, 1 и 3. Второй игрок ("черные") обладает всего одной фишкой, которая перед началом игры занимает кружок 5. (В качестве фишек годятся шахматные пешки или три пятака и одна двадцатикопеечная монета). Игроки делают ходы по очереди; начинают белые. Черная фишка может перейти на любую соседнюю ячейку. Белая фишка ходит так же, но ей запрещено двигаться назад, то есть она может перейти на любую соседнюю ячейку, расположенную слева, справа или спереди от того кружка, на котором она находится. Друг друга фишки не берут. Выигрыш принадлежит белым в том случае, если им удастся запереть черную фишку, то есть загнать ее в кружок, из которого та не сможет сделать ни одного хода. Обычно черная фишка попадает при этом в кружок В, но иногда такая же ситуация возникает, если черные занимают кружок 4 или 6. Во всех остальных случаях выигрывают черные. Для достижения победы им нужно все время держать свою единственную фишку позади фишек противника, не давая ему возможности зайти с тыла. Черные выигрывают и в том случае, когда одни и те же ходы начинают повторяться бесконечное число раз.
Научиться играть в эту игру не сложнее, чем в крестики и нолики, но она гораздо азартнее, а анализ ее более сложен. Люка сумел показать, что белые, играя рационально, могут в каждой партии сдерживать победу, однако простой выигрышной стратегии не существует и игра всегда изобилует ловушками и неожиданностями. Самый лучший на первый взгляд ход нередко оказывается самым худшим. Если черные достаточно опытны, то они с легкостью одерживают победу в игре против менее искушенного противника.
Предположим, что черным предоставлена еще большая свобода: разрешим черным в начале игры ставить свою фишку в любой кружок. Кто в этом случае одерживает победу при рациональной игре обеих сторон?

Из собрания М.С.Костюхиной.
ИГРА НАПОЛЕОН. А. ШОТТЕН, Н. ЛИПНИЦКИЙ. 1890.
В игре используются 4 шашки. Одна из них считается Наполеоном и помещается на точке, называемой Москвой, а остальные три шашки под именем русского корпуса помещаются кругом на ближайших точках к Москве. Игру начинает русский корпус, чтобы дать возможность Наполеону выйти из Москвы. Задача игроков - не дать Наполеону возможность вернуться в Москву. Игра заканчивается, когда русскому корпусу удается загнать Наполеона в точку, названную городом Ковно.

ОСАДА КРЕПОСТИ
На поле располагались бумажные фигурки - три японца помещались в крепость, а 36 китайцев должны были ее захватить.
В "Осаде" китайцы пытались выманить японцев из крепости.
За ход можно было сделать передвижение на одну клетку только по красным линиям. Если за китайцем оказывалось пустое место, японец мог "съесть" его, как в шашках. Китайцы же не имели права "есть" своих противников.
Игра заканчивалась либо когда китайцы занимали места в крепости, либо когда японцы "съедали" всех нападавших.

КРАСНЫЙ ПЕРЕКОП
Шашка Врангеля (белая) помещается в заштрихованном кружочке - Синельникове; 3 красные шашки занимают - Днепропетровск, Кривой Рог и Артемовск (кружочки со звездой).
Цель игры для Врангеля - пробиться к Москве; Красная армия стремится оттеснить Врангеля в Крым и запереть его в Севастополе (сбросить в море). Нигде в другом месте, кроме Севастополя, запирать Врангеля на разрешается.
Ходить можно только на ближайший свободный кружок в любом направлении по линиям (вперед, назад, в стороны). Играющие ходят по очереди - один ход делает шашка Врангеля, другой - одна из шашек красных; начинает играть обычно шашка Врангеля.
Бывают такие моменты, когда оба играющие повторяют один и тот же ход по несколько раз под ряд; в этом случае инициативу должны проявить шашки красных, изменяя свои ходы и тем самым изменяя дальнейшее течение игры.
В общем шашки красных имеют некоторое преимущество пред белой и при достаточной внимательности должны выиграть.
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:51 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го

ШТУРМ КРЕПОСТИ / Р.Я.ЮРИК / 1970
"Шашки" примерно по по тем же правилам. Особый интерес - в склеивании солдатиков-конусов (По 15 солдат и одному флагу на игрока).

http://toysland.com.ua/%D0%BD%D0%B0%D1%81%D1%82%D0%BE%D0%BB%D1%8C%D0%BD%D0%B0%D1%8F-%D0%B8%D0%B3%D1%80%D0%B0-%D1%81%D1%80%D0%B0%D0%B6%D0%B5%D0%BD%D0%B8%D0%B5
И, наконец, апофеоз - игра СРАЖЕНИЕ
Полные правила не сохранились. Огрызки (за цифры не поручусь):
- Игровое поле приблизительно 50 на 80см, в клеточку. На фото, вроде, не целиком.
- Кубики - красный и зеленый. Кинешь зеленый, значит хочешь ходить кавалерией (пушкой), красный - стрельнуть из пушки, оба - походить и стрельнуть пехотой.
- Пехотинцы. Уже их изготовление было проблемой, из-за их двусторонности. Помню, я по малолетству постоянно промахивался. У каждого было по 18 штук. Ходили по 6 штук разом (по зеленому кубику). Стреляли по утроенному красному кубику. Атакуя в штыки (только по прямой) - останавливались на первом встреченном вражеском солдатике (снимая его). При стрельбе точное попадание в клетку ближайшего врага, убивало его. Перелет - ранил (раненый начинал со своей стороны поля). Стрелять после штыковой нельзя, перед стрельбой можно повернуть раз за ход и обязательно использовать все очки (или не ходить вовсе). Можно стрелять через голову стоящего вплотную товарища.
- Кавалеристы. Обратите внимание, они тоже влезают на одну клетку. Их вырезать-клеить было кще сложнее. У каждого было по 6 штук. Ходили по трое - по удвоенному зеленому кубику. Атакуя не поворачивает, но рубит всех на пути.
- Пушки. Их надо было клеить из множества частей. У каждого игрока была пушка и мортира, и к каждой - по 3 артиллериста (в т.ч. артиллерийские офицеры). Стреляли по упятеренному красному кубику. Девять клеток у попадания ядра - убиты, бордюр из 16 клеток - ранены. Вроде пушке (но не мортире) мешали местные предметы, и/или сбивала всех солдатиком на траектории полета ядра.
- Мосты. Всего два моста (на поле была нарисована река). Вроде, на поле еще был нарисован брод.
- Заборы. Стрельбе не мешали. Преодолевались пехотой за полный ход, кавалерии не мешали.
- Брустверы. Несколько на игрока (разной длины). Защищал от стрельбы. Можно было стрелять через него, стоя вплотную. Преодолевались как заборы.
- Шатры. По штуке на игрока. Самая объемная из конструкций. Для победы в игре достаточно было подвести трех своих солдатиков вплотную к вражескому.
- Знамена. По штуке на игрока. Совершенно ничего о них не помню. Другой способ победы - захватить вражеское знамя.
Это путь в тупик -
 ТЕМА #80, АБЗАЦ #955
ТЕМА #80, АБЗАЦ #955
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:52 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
А ВОТ ЕЩЕ ОДНА ПОПЫТКА "ПОИГРАТЬ"
Отрывок из книги начала XVI века. Узнали?
В каждом батальоне должно быть 450 человек, из них 400 тяжелой пехоты и 50 легковооруженных; в тяжелой пехоте будет 300 человек со щитами и мечами, которых мы назовем щитоносцами, и 100 человек с пиками, или действующие пикинеры; легкая пехота состоит из 50 человек, вооруженных ружьями, самострелами, алебардами и круглыми щитами; они получают древнее название действующих велитов; во всех 10 батальонах будет 3000 щитоносцев, 1000 действующих пикинеров и 500 действующих велитов, т.е. 4500 человек.
Раньше мы говорили, что в бригаде должно быть 6000 солдат; поэтому нам надо прибавить еще 1500 пехотинцев, именно - 1000 человек с пиками, или запасные пики, и 500 легковооруженных, или запасных велитов. Таким образом, половина моей пехоты состояла бы из щитоносцев, а другая половина получила бы пики или другое оружие. Во главе каждого батальона стоял бы один начальник, 4 центуриона, 40 декурионов; сверх того, еще начальник действующих велитов и при нем 5 декурионов. Во главе 1000 запасных пик я бы поставил 3 начальников при 10 центурионах и 100 декурионах, а запасные велиты получили бы 2 начальников, 5 центурионов и 50 декурионов.
Далее я назначил бы одного командира для всей бригады; каждый батальон получил бы свое знамя и музыку. Итак, бригада в 10 батальонов состояла бы из 3000 щитоносцев с мечами, 1000 действующих и 1000 запасных пик, 500 действующих и 500 запасных велитов, всего 6000 пехоты, в которой бы было 600 декурионов и 15 начальников батальонов с 15 знаменами и трубачами, 55 центурионов, 10 начальников действующих велитов и один командир всей бригады со знаменем и музыкой.
Что касается оружия [конницы], я оставил бы существующее [на 1520 год] вооружение одинаково как для легкой, так и для тяжелой конницы. Мне только казалось бы полезным дать всей легкой коннице арбалеты и присоединить к ним некоторое количество фюзильеров, которые, правда, мало полезны в бою, но великолепны для устрашения противника и лучше всего могут заставить его бросить охраняемый проход; одно ружье стоит двадцати штук любого другого оружия.
... и образовал бы при каждом батальоне отряд не больше чем в 300 лошадей, причем 150 пришлось бы на тяжело вооруженных жандармов, а остальные - на легкую конницу. Во главе каждого эскадрона стоял бы особый начальник и при нем - 15 декурионов, знамя и музыканты. Каждые 10 жандармов получают 5 повозок, а 10 всадников легкой конницы - 2 повозки, нагруженные палатками, котлами для пищи, топорами и кольями, а если будет возможно, то и другим походным снаряжением.
... между бригадами остается пространство в 30 локтей, защищаемое несколькими пушками, а за ними следует командующий [войском из двух бригад и союзных подразделений] с главным знаменем, музыкой и отборным отрядом в 200 человек, главным образом пехоты, из коих, по крайней мере, десять или более могут выполнять любое приказание. Командующий должен быть так вооружен, чтобы он мог, смотря по обстоятельствам, ехать верхом или идти пешком во главе войска.
Для осады крепостей достаточно иметь при войске 10 пушек, стреляющих ядрами весом не больше 50 фунтов, но в поле они служили бы у меня не столько для боя, сколько для защиты лагеря. Всю остальную артиллерию я бы составил из десятифунтовых орудий, которые, по-моему, удобнее пятнадцатифунтовых [по причине их легкости и большего удобства в обращении], и расположил бы ее перед фронтом войска, если только по свойству местности нельзя так поставить ее на флангах, чтобы вполне обеспечить от нападения неприятеля.
Боевое построение, которое я вам только что описал, соединяет выгоды греческой фаланги и римского легиона. Впереди густыми, сомкнутыми рядами стоят пики, так что при наступлении на врага или при обороне вполне возможно, по примеру греческой фаланги, пополнять убыль передних шеренг людьми, стоящими позади.
С другой стороны, если вражеский удар так силен, что фронт пик будет прорван и придется отступить, они вольются в свободное пространство между батальонами второй линии и, соединившись с ними, возобновят сражение единой массой. Если они и тут будут разбиты, то могут тем же порядком снова отойти и опять начать бой уже в третий раз. Таким образом, при этом порядке бой ведется и возобновляется одновременно и по греческому и по римскому образцу.
... Разве вы не слышите уже грома пушек? Наши открыли огонь, но причинили неприятелю лишь малый урон. Запасные велиты выступают теперь вместе с легкой конницей и с отчаянным криком бросаются на неприятеля, рассыпаясь как можно шире. Неприятельская артиллерия дала один залп, но снаряды пронеслись через головы нашей пехоты и не причинили ей никакого вреда. Чтобы помешать ей выстрелить второй раз, наши велиты и конница уже напали на нее, неприятель двинулся им навстречу, и как нашим, так и вражеским пушкам приходится замолчать. Посмотрите, как мужественно бьются наши воины, как крепка их дисциплина, выработанная постоянными военными упражнениями и верой в войско, которое идет за ними вслед. Вот оно мерным своим шагом, в полном боевом порядке выступает вместе с тяжелой конницей навстречу противнику. Наша артиллерия, чтобы пропустить его, отходит на места, только что очищенные велитами. Полководец воодушевляет воинов, обещая им верную победу. Вы видите, что велиты и легкая конница отошли, расположились по сторонам войск и выжидают, нельзя ли налететь на противника с фланга.
Вот войска сошлись! Посмотрите, с каким мужеством и безмолвием наши выдержали удар неприятеля; полководец отдал тяжелой коннице приказ только поддерживать пехоту, не наступая самой и не отдаляясь от пехотных линий. Видели вы, как наша легкая конница ударила на отряд неприятельских стрелков, собиравшихся зайти нам во фланг, как бросились им на помощь эскадроны противника, и как стрелки, стиснутые между двух колонн атак, не в состоянии открыть, огонь и отступают за линию своих батальонов? Смотрите, с какой яростью разят противника наши пики, но тяжелая пехота обеих сторон сблизилась настолько, что пикинеры уже не могут работать и, по правилам нашего боевого построения, они медленно отступают сквозь ряды тяжело вооруженных солдат.
Между тем большой отряд вражеской тяжелой конницы смял наших жандармов на левом крыле. Наши, твердо соблюдая правило, отступили под защиту запасных пик, возобновили с их помощью бой и опрокинули противника, перебив у него множество людей.
Тем временем действующие пики передних батальонов прошли назад сквозь ряды пехоты, и теперь в бой вступают щитоносцы. Смотрите, с какой доблестью, уверенностью и легкостью они уничтожают неприятеля! Разве вы не видите, что ряды так сомкнулись в бою, что солдатам только с большим трудом удается действовать мечами? Смотрите, с какой бессильной злобой умирают враги. Ведь они вооружены только пиками и мечами, а щитов у них нет. Пика бесполезна, потому что слишком длинна, меч бессилен против сильнейшего вооружения наших воинов, и неприятельские солдаты частью падают убитыми или ранеными, частью спасаются бегством. Они бегут и на правом и на левом крыле. Победа за нами!
... Заметьте, что мне даже не пришлось посылать в дело ни вторую, ни третью линию войск; враг побежден силами одной первой...
Отрывок из книги начала XVI века. Узнали?
В каждом батальоне должно быть 450 человек, из них 400 тяжелой пехоты и 50 легковооруженных; в тяжелой пехоте будет 300 человек со щитами и мечами, которых мы назовем щитоносцами, и 100 человек с пиками, или действующие пикинеры; легкая пехота состоит из 50 человек, вооруженных ружьями, самострелами, алебардами и круглыми щитами; они получают древнее название действующих велитов; во всех 10 батальонах будет 3000 щитоносцев, 1000 действующих пикинеров и 500 действующих велитов, т.е. 4500 человек.
Раньше мы говорили, что в бригаде должно быть 6000 солдат; поэтому нам надо прибавить еще 1500 пехотинцев, именно - 1000 человек с пиками, или запасные пики, и 500 легковооруженных, или запасных велитов. Таким образом, половина моей пехоты состояла бы из щитоносцев, а другая половина получила бы пики или другое оружие. Во главе каждого батальона стоял бы один начальник, 4 центуриона, 40 декурионов; сверх того, еще начальник действующих велитов и при нем 5 декурионов. Во главе 1000 запасных пик я бы поставил 3 начальников при 10 центурионах и 100 декурионах, а запасные велиты получили бы 2 начальников, 5 центурионов и 50 декурионов.
Далее я назначил бы одного командира для всей бригады; каждый батальон получил бы свое знамя и музыку. Итак, бригада в 10 батальонов состояла бы из 3000 щитоносцев с мечами, 1000 действующих и 1000 запасных пик, 500 действующих и 500 запасных велитов, всего 6000 пехоты, в которой бы было 600 декурионов и 15 начальников батальонов с 15 знаменами и трубачами, 55 центурионов, 10 начальников действующих велитов и один командир всей бригады со знаменем и музыкой.
Что касается оружия [конницы], я оставил бы существующее [на 1520 год] вооружение одинаково как для легкой, так и для тяжелой конницы. Мне только казалось бы полезным дать всей легкой коннице арбалеты и присоединить к ним некоторое количество фюзильеров, которые, правда, мало полезны в бою, но великолепны для устрашения противника и лучше всего могут заставить его бросить охраняемый проход; одно ружье стоит двадцати штук любого другого оружия.
... и образовал бы при каждом батальоне отряд не больше чем в 300 лошадей, причем 150 пришлось бы на тяжело вооруженных жандармов, а остальные - на легкую конницу. Во главе каждого эскадрона стоял бы особый начальник и при нем - 15 декурионов, знамя и музыканты. Каждые 10 жандармов получают 5 повозок, а 10 всадников легкой конницы - 2 повозки, нагруженные палатками, котлами для пищи, топорами и кольями, а если будет возможно, то и другим походным снаряжением.
... между бригадами остается пространство в 30 локтей, защищаемое несколькими пушками, а за ними следует командующий [войском из двух бригад и союзных подразделений] с главным знаменем, музыкой и отборным отрядом в 200 человек, главным образом пехоты, из коих, по крайней мере, десять или более могут выполнять любое приказание. Командующий должен быть так вооружен, чтобы он мог, смотря по обстоятельствам, ехать верхом или идти пешком во главе войска.
Для осады крепостей достаточно иметь при войске 10 пушек, стреляющих ядрами весом не больше 50 фунтов, но в поле они служили бы у меня не столько для боя, сколько для защиты лагеря. Всю остальную артиллерию я бы составил из десятифунтовых орудий, которые, по-моему, удобнее пятнадцатифунтовых [по причине их легкости и большего удобства в обращении], и расположил бы ее перед фронтом войска, если только по свойству местности нельзя так поставить ее на флангах, чтобы вполне обеспечить от нападения неприятеля.
Боевое построение, которое я вам только что описал, соединяет выгоды греческой фаланги и римского легиона. Впереди густыми, сомкнутыми рядами стоят пики, так что при наступлении на врага или при обороне вполне возможно, по примеру греческой фаланги, пополнять убыль передних шеренг людьми, стоящими позади.
С другой стороны, если вражеский удар так силен, что фронт пик будет прорван и придется отступить, они вольются в свободное пространство между батальонами второй линии и, соединившись с ними, возобновят сражение единой массой. Если они и тут будут разбиты, то могут тем же порядком снова отойти и опять начать бой уже в третий раз. Таким образом, при этом порядке бой ведется и возобновляется одновременно и по греческому и по римскому образцу.
... Разве вы не слышите уже грома пушек? Наши открыли огонь, но причинили неприятелю лишь малый урон. Запасные велиты выступают теперь вместе с легкой конницей и с отчаянным криком бросаются на неприятеля, рассыпаясь как можно шире. Неприятельская артиллерия дала один залп, но снаряды пронеслись через головы нашей пехоты и не причинили ей никакого вреда. Чтобы помешать ей выстрелить второй раз, наши велиты и конница уже напали на нее, неприятель двинулся им навстречу, и как нашим, так и вражеским пушкам приходится замолчать. Посмотрите, как мужественно бьются наши воины, как крепка их дисциплина, выработанная постоянными военными упражнениями и верой в войско, которое идет за ними вслед. Вот оно мерным своим шагом, в полном боевом порядке выступает вместе с тяжелой конницей навстречу противнику. Наша артиллерия, чтобы пропустить его, отходит на места, только что очищенные велитами. Полководец воодушевляет воинов, обещая им верную победу. Вы видите, что велиты и легкая конница отошли, расположились по сторонам войск и выжидают, нельзя ли налететь на противника с фланга.
Вот войска сошлись! Посмотрите, с каким мужеством и безмолвием наши выдержали удар неприятеля; полководец отдал тяжелой коннице приказ только поддерживать пехоту, не наступая самой и не отдаляясь от пехотных линий. Видели вы, как наша легкая конница ударила на отряд неприятельских стрелков, собиравшихся зайти нам во фланг, как бросились им на помощь эскадроны противника, и как стрелки, стиснутые между двух колонн атак, не в состоянии открыть, огонь и отступают за линию своих батальонов? Смотрите, с какой яростью разят противника наши пики, но тяжелая пехота обеих сторон сблизилась настолько, что пикинеры уже не могут работать и, по правилам нашего боевого построения, они медленно отступают сквозь ряды тяжело вооруженных солдат.
Между тем большой отряд вражеской тяжелой конницы смял наших жандармов на левом крыле. Наши, твердо соблюдая правило, отступили под защиту запасных пик, возобновили с их помощью бой и опрокинули противника, перебив у него множество людей.
Тем временем действующие пики передних батальонов прошли назад сквозь ряды пехоты, и теперь в бой вступают щитоносцы. Смотрите, с какой доблестью, уверенностью и легкостью они уничтожают неприятеля! Разве вы не видите, что ряды так сомкнулись в бою, что солдатам только с большим трудом удается действовать мечами? Смотрите, с какой бессильной злобой умирают враги. Ведь они вооружены только пиками и мечами, а щитов у них нет. Пика бесполезна, потому что слишком длинна, меч бессилен против сильнейшего вооружения наших воинов, и неприятельские солдаты частью падают убитыми или ранеными, частью спасаются бегством. Они бегут и на правом и на левом крыле. Победа за нами!
... Заметьте, что мне даже не пришлось посылать в дело ни вторую, ни третью линию войск; враг побежден силами одной первой...

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
ВАЛЕРИЙ ОСИПОВ / ФАКУЛЬТЕТ ЖУРНАЛИСТИКИ
Курдюм давно уже стал бы и настоящим академиком, если бы в его стремительную научную карьеру неожиданно не ворвалась весьма обыденная и банальная страсть. К огромному удивлению и огорчению всего университетского ученого математического мира, Курдюм вдруг оказался совершенно диким, необузданным, первобытным игроком. Причем во что бы он ни играл, его интересовал в первую очередь не конечный результат, а сам процесс игры, так сказать, неисповедимые пути судьбы-индейки, которая одних приводила к счастливому выигрышу, а других - к печальному проигрышу. Получая тайные сигналы из глубин своей гениальной натуры, Курдюм предпринял дерзкую попытку познать законы азартных игрищ с помощью достижений высшей математики.
Он начал с карт. Тарас ввел моложавого гения в круг любителей преферанса и уже через два месяца растерял всех своих бывших партнеров: никто не садился играть против Курдюма, так как это было равносильно игре с электронным запоминающим устройством, в механической "голове" у которого находится загадочное беспроигрышное приспособление.
Курдюм перешел к шахматам и стал потихоньку матовать признанных университетских корифеев. Тарас пытался было направить успехи Курдюма в шахматах по полезной линии, но у того не хватило терпения доиграть до конца ни один квалификационный турнир, и, таким образом, шахматные таланты Курдюма официального признания не получили.
В дальнейшем Курдюм перепробовал все виды игры как таковой, начиная с номеров на автобусных, троллейбусных и всех прочих билетах городского транспорта и кончая ипподромом, где ему дали колоритное прозвище "Кулибин" - очевидно, за то, что он самоучкой постиг все тайные законы бегов. Одним словом, пройдя тернистый путь познания многообразной природы азартных игрищ, Курдюм остановился на древней, бесхитростной народной игре, именуемой в просторечье "подкидным дураком". Курдюм говорил, что его симпатии к этому состязанию вызваны тем, что "подкидной дурак" чрезвычайно точно соответствует той работе в области теории вероятностей, которой он был в последнее время занят, и, таким образом, является для него как бы необходимым практическим подспорьем, чем-то вроде лабораторной работы.
Постоянным соперником Курдюма в этих лабораторных занятиях был, разумеется, Тарас. Тарас и Курдюм играли в "подкидного дурака" исключительно один на один. Они садились друг против друга за шахматный столик и ставили сбоку турнирные часы с двумя циферблатами. Каждый имел перед собой длинную полоску чистой бумаги, на которой, как в шахматах, записывались свои ходы и ответы противника, а также особые комментарии, вызванные спецификой игры, - как, например, "бито", "принято" и т.д. Сдавалось по восемь карт (это правило ввел Курдюм), Тарас объявлял, что младший козырь у него, кощунственным жестом бросал на шахматные клетки какую-нибудь пиковую семерку или бубновую шестерку, включал нажатием кнопки часы противника, и новоизобретенное игрище начиналось по всем строго соблюдаемым правилам русского "подкидного дурака" (в отличие от японского, корейского и т.д.).
Игра велась так называемой большой колодой: то есть с двойками, тройками, четверками, пятерками и джокерами. Впоследствии Курдюм ввел в употребление новую суперколоду и даже ухитрился напечатать несколько экземпляров ее в какой-то малоизвестной типографии. Новая колода-модерн состояла уже не из 52 карт, как обычная, а из 72, так как в каждую масть Курдюм добавил по пять новых карт, а именно: после десятки шли "двадцатки", "тридцатки", "сороковки" и "полсотни", а после обыкновенного туза - еще один туз, старший. Теперь уже старый бубновый туз назывался "туз бубен младший", а новый - "туз бубен старший".
Курдюм пытался также к четырем существующим мастям (бубна, черва, пика и трефа) добавить еще две новые - красную "альфа" и черную "бета", но Тарас, голова у которого и так уже разламывалась от курдюмовских нововведений, решительно восстал против этих добавлений, и Курдюм, чтобы не потерять последнего партнера, вынужден был снять предложение об увеличении мастей.
Каждая серьезная партия в "дурака" продолжалась обычно час, а то и полтора (для тренировки, правда, Тарас и Курдюм гоняли иногда "блицы" по две-три минуты). Противники частенько попадали в жестокий цейтнот, просрочивали время, но потом, имея перед глазами весь записанный ход игры, тщательно анализировали перипетии борьбы и скрупулезно отыскивали те ходы, на которых кто-то из них "дал сок", или "выпал в осадок", или "лег на грунт", или "врезал дуба" и т.д.
Прослышав о карточных оргиях, которым предавался Курдюм, общественность математического факультета призвала доктора наук к ответу. В середине выступления одного из свидетелей обвинения Курдюм неожиданно попросил слова. Оно было ему предоставлено. Курдюм быстро вышел на кафедру и прочитал собравшимся лекцию по одному из разделов теории вероятностей, в которой модернизированная суперколода из 72 карт была представлена на грифельной доске, висевшей за спиной обвиняемого, как некая сложная математическая функция, в которую последовательно включались и исключались следующие величины: "семерка пик", "десятка треф", "валет бубен", "шестерка альфа", "король бета" и т.д.
Аудитория, которая в первую очередь являла собой математику, а потом уже грозную силу общественного воздействия, так заинтриговалась курдюмовской задачей, что первоначальная причина собрания как-то незаметно забылась. Профессора и доценты столпились около грифельной доски, кричали, шумели, спорили, размахивали руками. Курдюма обвиняли и в широте, и в узости, и в простоте, и в сложности, но общее резюме тем не менее было единодушным: для множественных рядов с постоянно взаимодействующими переменными задача Курдюма, построенная на не совсем обычных и даже несколько странных, но весьма убедительных аналогиях, представляла собой несомненный интерес.
Справедливости ради, забегая вперед, следует сказать следующее. К тому времени, когда начались первые запуски искусственных спутников, Курдюм, уже забывший многие "невинные" шалости своей веселой математической юности, занимал довольно видное положение среди теоретиков, подготовивших расчеты орбит, систем управления, телевизионных каналов связи и автоматики. А ту самую сложную математическую функцию, которая впервые родилась на свет божий во время некоего общественного судилища и в системе доказательств которой встречались тогда еще такие странные величины, как "туз треф старший" или "дама альфа", эту сложную функцию, получившую теперь уже вполне пристойный вид, "причесанную" и очищенную от вульгаризмов, можно было найти во всех научных книгах, посвященных космическим полетам, под названием "теоремы Курдюма".
...
***
1. Как следует из этого отрывка, карты вполне могут быть использованы для получения в игре нужных математических функций. Но, не только.
2. Упоминающаяся в отрывке игра - "подкидной дурак", хорошо иллюстрирует баланс, присущий играм 2 категории ("Уголки"). Игрок постоянно решает, что ему важнее - скинуть побольше карт или собрать на руках более сильную комбинацию. Т.е. карты вполне моделируют обе функции - и тактическую, и стратегическую.
3. Наконец, карточный стол является очень удобным интерфейсом/органайзером, позволяющим удобно манипулировать (открыто и втайне) большим количеством сложных информационных объектов.
Конечно, всем этим часто злоупотребляют. И функции переусложняют до полного усреднения результата, и баланс портят введением дополнительных колод на каждый (не)удобный случай, и интерфейс перегружают ненужными операциями, избыточными параметрами карт и дополнительным инструментарием...
Хорошее место для карт в игре - замена, возможно временная, большого логического блока простой, наглядной вероятностной моделью.
Курдюм давно уже стал бы и настоящим академиком, если бы в его стремительную научную карьеру неожиданно не ворвалась весьма обыденная и банальная страсть. К огромному удивлению и огорчению всего университетского ученого математического мира, Курдюм вдруг оказался совершенно диким, необузданным, первобытным игроком. Причем во что бы он ни играл, его интересовал в первую очередь не конечный результат, а сам процесс игры, так сказать, неисповедимые пути судьбы-индейки, которая одних приводила к счастливому выигрышу, а других - к печальному проигрышу. Получая тайные сигналы из глубин своей гениальной натуры, Курдюм предпринял дерзкую попытку познать законы азартных игрищ с помощью достижений высшей математики.
Он начал с карт. Тарас ввел моложавого гения в круг любителей преферанса и уже через два месяца растерял всех своих бывших партнеров: никто не садился играть против Курдюма, так как это было равносильно игре с электронным запоминающим устройством, в механической "голове" у которого находится загадочное беспроигрышное приспособление.
Курдюм перешел к шахматам и стал потихоньку матовать признанных университетских корифеев. Тарас пытался было направить успехи Курдюма в шахматах по полезной линии, но у того не хватило терпения доиграть до конца ни один квалификационный турнир, и, таким образом, шахматные таланты Курдюма официального признания не получили.
В дальнейшем Курдюм перепробовал все виды игры как таковой, начиная с номеров на автобусных, троллейбусных и всех прочих билетах городского транспорта и кончая ипподромом, где ему дали колоритное прозвище "Кулибин" - очевидно, за то, что он самоучкой постиг все тайные законы бегов. Одним словом, пройдя тернистый путь познания многообразной природы азартных игрищ, Курдюм остановился на древней, бесхитростной народной игре, именуемой в просторечье "подкидным дураком". Курдюм говорил, что его симпатии к этому состязанию вызваны тем, что "подкидной дурак" чрезвычайно точно соответствует той работе в области теории вероятностей, которой он был в последнее время занят, и, таким образом, является для него как бы необходимым практическим подспорьем, чем-то вроде лабораторной работы.
Постоянным соперником Курдюма в этих лабораторных занятиях был, разумеется, Тарас. Тарас и Курдюм играли в "подкидного дурака" исключительно один на один. Они садились друг против друга за шахматный столик и ставили сбоку турнирные часы с двумя циферблатами. Каждый имел перед собой длинную полоску чистой бумаги, на которой, как в шахматах, записывались свои ходы и ответы противника, а также особые комментарии, вызванные спецификой игры, - как, например, "бито", "принято" и т.д. Сдавалось по восемь карт (это правило ввел Курдюм), Тарас объявлял, что младший козырь у него, кощунственным жестом бросал на шахматные клетки какую-нибудь пиковую семерку или бубновую шестерку, включал нажатием кнопки часы противника, и новоизобретенное игрище начиналось по всем строго соблюдаемым правилам русского "подкидного дурака" (в отличие от японского, корейского и т.д.).
Игра велась так называемой большой колодой: то есть с двойками, тройками, четверками, пятерками и джокерами. Впоследствии Курдюм ввел в употребление новую суперколоду и даже ухитрился напечатать несколько экземпляров ее в какой-то малоизвестной типографии. Новая колода-модерн состояла уже не из 52 карт, как обычная, а из 72, так как в каждую масть Курдюм добавил по пять новых карт, а именно: после десятки шли "двадцатки", "тридцатки", "сороковки" и "полсотни", а после обыкновенного туза - еще один туз, старший. Теперь уже старый бубновый туз назывался "туз бубен младший", а новый - "туз бубен старший".
Курдюм пытался также к четырем существующим мастям (бубна, черва, пика и трефа) добавить еще две новые - красную "альфа" и черную "бета", но Тарас, голова у которого и так уже разламывалась от курдюмовских нововведений, решительно восстал против этих добавлений, и Курдюм, чтобы не потерять последнего партнера, вынужден был снять предложение об увеличении мастей.
Каждая серьезная партия в "дурака" продолжалась обычно час, а то и полтора (для тренировки, правда, Тарас и Курдюм гоняли иногда "блицы" по две-три минуты). Противники частенько попадали в жестокий цейтнот, просрочивали время, но потом, имея перед глазами весь записанный ход игры, тщательно анализировали перипетии борьбы и скрупулезно отыскивали те ходы, на которых кто-то из них "дал сок", или "выпал в осадок", или "лег на грунт", или "врезал дуба" и т.д.
Прослышав о карточных оргиях, которым предавался Курдюм, общественность математического факультета призвала доктора наук к ответу. В середине выступления одного из свидетелей обвинения Курдюм неожиданно попросил слова. Оно было ему предоставлено. Курдюм быстро вышел на кафедру и прочитал собравшимся лекцию по одному из разделов теории вероятностей, в которой модернизированная суперколода из 72 карт была представлена на грифельной доске, висевшей за спиной обвиняемого, как некая сложная математическая функция, в которую последовательно включались и исключались следующие величины: "семерка пик", "десятка треф", "валет бубен", "шестерка альфа", "король бета" и т.д.
Аудитория, которая в первую очередь являла собой математику, а потом уже грозную силу общественного воздействия, так заинтриговалась курдюмовской задачей, что первоначальная причина собрания как-то незаметно забылась. Профессора и доценты столпились около грифельной доски, кричали, шумели, спорили, размахивали руками. Курдюма обвиняли и в широте, и в узости, и в простоте, и в сложности, но общее резюме тем не менее было единодушным: для множественных рядов с постоянно взаимодействующими переменными задача Курдюма, построенная на не совсем обычных и даже несколько странных, но весьма убедительных аналогиях, представляла собой несомненный интерес.
Справедливости ради, забегая вперед, следует сказать следующее. К тому времени, когда начались первые запуски искусственных спутников, Курдюм, уже забывший многие "невинные" шалости своей веселой математической юности, занимал довольно видное положение среди теоретиков, подготовивших расчеты орбит, систем управления, телевизионных каналов связи и автоматики. А ту самую сложную математическую функцию, которая впервые родилась на свет божий во время некоего общественного судилища и в системе доказательств которой встречались тогда еще такие странные величины, как "туз треф старший" или "дама альфа", эту сложную функцию, получившую теперь уже вполне пристойный вид, "причесанную" и очищенную от вульгаризмов, можно было найти во всех научных книгах, посвященных космическим полетам, под названием "теоремы Курдюма".
...
***
1. Как следует из этого отрывка, карты вполне могут быть использованы для получения в игре нужных математических функций. Но, не только.
2. Упоминающаяся в отрывке игра - "подкидной дурак", хорошо иллюстрирует баланс, присущий играм 2 категории ("Уголки"). Игрок постоянно решает, что ему важнее - скинуть побольше карт или собрать на руках более сильную комбинацию. Т.е. карты вполне моделируют обе функции - и тактическую, и стратегическую.
3. Наконец, карточный стол является очень удобным интерфейсом/органайзером, позволяющим удобно манипулировать (открыто и втайне) большим количеством сложных информационных объектов.
Конечно, всем этим часто злоупотребляют. И функции переусложняют до полного усреднения результата, и баланс портят введением дополнительных колод на каждый (не)удобный случай, и интерфейс перегружают ненужными операциями, избыточными параметрами карт и дополнительным инструментарием...
Хорошее место для карт в игре - замена, возможно временная, большого логического блока простой, наглядной вероятностной моделью.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
ИНДУКТИВНАЯ ИГРА ЭЛУЗИС
Игра придумана Робертом Эбботом и описана Мартином Гарднером: "Математические головоломки и развлечения", М., Мир, 1971.
В элузис можно играть, когда соберется не меньше трех игроков. Для игры берут обычную колоду игральных карт. Играющие сдают карты по очереди. Тот, кто должен сдавать карты, выполнив свою функцию, в дальнейшей игре активного участия не принимает и выступает лишь в роли наблюдателя или арбитра. Последнюю карту кладут посреди стола вверх картинкой. Для того чтобы никто из игроков не оказался обделенным и не получил меньше карт, чем другие, сдающий должен заранее подготовить колоду, изъяв из нее в случае необходимости лишние карты. Изъятые из колоды карты сдающий откладывает в сторону, не показывая их играющим.
После того как все карты сданы и первая карта, образуя начало ряда, положена на свое место, сдающий втайне от остальных игроков задумывает правило, которого нужно придерживаться при выкладке карт в продолжение ряда. (Пример простого правила: "Если верхняя карта в ряду красной масти, пойдите черной, и, наоборот, на черную масть надо класть красную".) Автор правила выступает в роли природы, или, если угодно "всемогущего бога". Задуманное правило сдававший карты записывает на отдельном листке бумаги и, сложив его, откладывает в сторону. Эту нужно для того, чтобы по окончании игры ее участники могли убедится в том, что "арбитр" во время игры не менял своего правила и не нарушал постоянства закона природы. Цель игры для каждого активного участника заключается в том, чтобы избавиться от как можно большего числа карт.
На первом этапе активные игроки по очереди предлагают одну из своих карт для продолжения ряда, а арбитр, либо соглашается ее добавить, если карта удовлетворяет закону, либо заставляет игрока положить эту карту рубашкой вниз перед собой. После того, как все карты перепробованы, производится подсчет очков сдающего. Арбитр получает
Общее-Число-Ошибочных-Карт - Число-Ошибочных-Карт-Лучшего-Игрока * Число-Игроков
очков.
На втором этапе игроки пытаются продолжить цепочку, используя свои ошибочные карты. Игра заканчивается, когда кто-нибудь из них сдаст все свои карты, либо когда тот, кто сдавал карты, увидит, что задуманное правило не позволяет продолжать игру. Каждый активный игрок получает
Общее-Число-Ошибочных-Карт - Число-Ошибочных-Карт-Игрока * Число-Игроков
очков (0, если получилось отрицательное число). Сдавший больше всех карт, получает еще премию в 6 очков. Если таких игроков несколько, премия делится между ними поровну.
Игра придумана Робертом Эбботом и описана Мартином Гарднером: "Математические головоломки и развлечения", М., Мир, 1971.
В элузис можно играть, когда соберется не меньше трех игроков. Для игры берут обычную колоду игральных карт. Играющие сдают карты по очереди. Тот, кто должен сдавать карты, выполнив свою функцию, в дальнейшей игре активного участия не принимает и выступает лишь в роли наблюдателя или арбитра. Последнюю карту кладут посреди стола вверх картинкой. Для того чтобы никто из игроков не оказался обделенным и не получил меньше карт, чем другие, сдающий должен заранее подготовить колоду, изъяв из нее в случае необходимости лишние карты. Изъятые из колоды карты сдающий откладывает в сторону, не показывая их играющим.
После того как все карты сданы и первая карта, образуя начало ряда, положена на свое место, сдающий втайне от остальных игроков задумывает правило, которого нужно придерживаться при выкладке карт в продолжение ряда. (Пример простого правила: "Если верхняя карта в ряду красной масти, пойдите черной, и, наоборот, на черную масть надо класть красную".) Автор правила выступает в роли природы, или, если угодно "всемогущего бога". Задуманное правило сдававший карты записывает на отдельном листке бумаги и, сложив его, откладывает в сторону. Эту нужно для того, чтобы по окончании игры ее участники могли убедится в том, что "арбитр" во время игры не менял своего правила и не нарушал постоянства закона природы. Цель игры для каждого активного участника заключается в том, чтобы избавиться от как можно большего числа карт.
На первом этапе активные игроки по очереди предлагают одну из своих карт для продолжения ряда, а арбитр, либо соглашается ее добавить, если карта удовлетворяет закону, либо заставляет игрока положить эту карту рубашкой вниз перед собой. После того, как все карты перепробованы, производится подсчет очков сдающего. Арбитр получает
Общее-Число-Ошибочных-Карт - Число-Ошибочных-Карт-Лучшего-Игрока * Число-Игроков
очков.
На втором этапе игроки пытаются продолжить цепочку, используя свои ошибочные карты. Игра заканчивается, когда кто-нибудь из них сдаст все свои карты, либо когда тот, кто сдавал карты, увидит, что задуманное правило не позволяет продолжать игру. Каждый активный игрок получает
Общее-Число-Ошибочных-Карт - Число-Ошибочных-Карт-Игрока * Число-Игроков
очков (0, если получилось отрицательное число). Сдавший больше всех карт, получает еще премию в 6 очков. Если таких игроков несколько, премия делится между ними поровну.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
МОЖНО ЛИ ИСПОЛЬЗОВАТЬ В ИГРЕ МАШИНУ ИЗ КОРОБКОВ?
( ТЕМА #63, АБЗАЦ #696
ТЕМА #63, АБЗАЦ #696 )
)
Игра навеяна американским сериалом "Человек - ракета" (50-х годов, но по стилю он ближе к сериалам 30-х годов про всяких Флэш Гордонов). Играем за злобных американских коммунистов против буржуйских суперменов.

Ракетчик, укравший атомную пушку у злобных инопланетян.
Мы можем попытаться провести три вида операций (при желании в сериале можно найти кадры для иллюстрации и их, и ответных действий супергероя): диверсию против суперменского логова, экспроприацию денег на нужды революции или устроить всеамериканский катаклизм на страх буржуям.
На это буржуинство тоже может ответить трояко (повторяю, все по сериалу): устроить гангстерский мордобой (лучше всего помогал от диверсии, хуже - от катастроф), послать ракетчика со своим атомным пистолетом (лучше - от катастроф, хуже - от экспроприаций), слетать по-крупному, на большой ракете (лучше - от экспроприации, хуже - от диверсии).
Прознав, что мы затеваем, главный буржуин, включает свой компьютер и пытается выбрать адекватный способ противодействия. В его компьютере всего три коробка - для трех наших операций. Сначала в каждом по три бусины, для каждого варианта ответа, в дальнейшем при успешном отражении нашей атаки в коробок добавляется бусина успешного ответа, иначе - бусины других цветов.
В ниже приведенной программе (GW-BASIC DOS):
Строки 20-57 - литературная составляющая игры.
60-61 - вероятности успеха буржуйских действий.
70-80 - N - запас денег на бусины у буржуев.
90-91 (закомментированно) - мы выбирает вид операции
92 - операция выбирается случайным образом
100-102 - буржуй тянет бусину из нужного коробка
110-120 - результат противоборства
122-123 (закомментированно) - перепрограммирование коробков для совсем жадного буржуина
124-125 - логичное перепрограммирование коробков
140-150 - количество бусин в коробках на конец игры
10 OPTION BASE 0: DIM R(9),K(9),K$(3),B$(3),U$(18 )
20 K$(0)="ДИВЕРСИЯ":K$(1)="ЭКСПРОПРИАЦИЯ":K$(2)="КАТАСТРОФА"
30 B$(0)="ГАНГСТЕРЫ":B$(1)="РАКЕТЧИК":B$(2)="РАКЕТА"
40 U$(0)="ПОДРЫВНИК ПОГИБ"
41 U$(1)="ЛАБОРАТОРИЯ ВЗОРВАНА"
42 U$(2)="УСТРОЙСТВО НЕЙТРАЛИЗОВАНО":
43 U$(3)="РАКЕТЧИК ОГЛУШЕН"
44 U$(4)="РАКЕТА УЦЕЛЕЛА"
45 U$(5)="РАКЕТА ВЗОРВАЛАСЬ"
46 U$(6)="ДЕНЬГИ ПОТЕРЯНЫ"
47 U$(7)="ДЕНЬГИ ВЫВЕЗЕНЫ"
48 U$(8 )="РАКЕТЧИК ВЫСЛЕДИЛ"
49 U$(9)="РАКЕТЧИК СХВАЧЕН"
50 U$(10)="РАКЕТА РАССТРЕЛЯЛА МАШИНУ"
51 U$(11)="МАШИНА ПРОСКОЧИЛА"
52 U$(12)="ГРУЗ ЗАХВАЧЕН"
53 U$(13)="ГРУЗ ПЕРЕПРАВЛЕН"
54 U$(14)="ПОБЕДА РАКЕТЧИКА"
55 U$(15)="РАКЕТЧИК ПОСТРАДАЛ"
56 U$(16)="РАКЕТА РАЗБОМБИЛА УСТАНОВКУ"
57 U$(17)="РАКЕТА В ЛОВУШКЕ"
60 DATA .8,.5,.2,.5,.2,.8,.2,.8,.5
61 FOR I=0 TO 8:READ R(I):K(I)=1:NEXT I
70 RANDOMIZE TIMER: N=10000
80 IF N<0 GOTO 140
90 REM PRINT "1) ";K$(0);", 2) ";K$(1);", 3) ";K$(2);
91 REM INPUT K:K=K-1:
92 K=INT(RND*3):K3=K*3
100 IF RND<K(K3)/(K(K3)+K(K3+1)+(K3+2))THEN B=0:GOTO 110
101 IF RND<K(K3+1)/(K(K3+1)+K(K3+2))THEN B=1:GOTO 110
102 B=2
110 R=RND<R(K3+B)
120 PRINT N;": ";K$(K);". ";B$(B);". ";U$(K*6+B*2+R+1);"."
121 IF R THEN K(K3+B)=K(K3+B)+1:N=N-1: GOTO 130
122 REM FOR I=0 TO 8:K(I)=K(I)+1:NEXT I
123 REM K(B)=K(B)-1:K(B+3)=K(B+3)-1:K(B+6)=K(B+6)-1:N=N-6
124 FOR I=0 TO 2:K(K3+I)=K(K3+I)+1:NEXT I
125 K(K3+B)=K(K3+B)-1:N=N-2
130 GOTO 80
140 PRINT "FINAL ATTACK:"
150 PRINT K(0);"/";K(1);"/";K(2);"*";K(3);"/";K(4);"/";K(5);"*";K(6);"/";K(7);"/";K(8 )
В таком виде (большое число повторов и логичное программирование коробков) на момент окончание игры количество бусин в коробках примерно соответствует вероятностям успеха буржуйских действий.
Если я поставлю ручное управление революцией (раскомментирую строки 90 и 91, закомментирую 92, и понятно уменьшу N где-то до 100), то смогу попытаться заставить буржуинский компьютер учиться неправильно. Или нет?
Кроме тогу, я могу добавлять буржуину дурости. Например (раскомментировав строки 122-123 вместо 124-125), я заставлю буржуина жалеть потерянных солдатиков, уменьшая их вероятность использования во всех операциях, а не только одного вида. В этом случае выход на правильные вероятности тормозится.
Возможны и другие варианты буржуйского умствования...
Как в это играть? Понятия не имею.
(
 ТЕМА #63, АБЗАЦ #696
ТЕМА #63, АБЗАЦ #696 )
)Игра навеяна американским сериалом "Человек - ракета" (50-х годов, но по стилю он ближе к сериалам 30-х годов про всяких Флэш Гордонов). Играем за злобных американских коммунистов против буржуйских суперменов.

Ракетчик, укравший атомную пушку у злобных инопланетян.
Мы можем попытаться провести три вида операций (при желании в сериале можно найти кадры для иллюстрации и их, и ответных действий супергероя): диверсию против суперменского логова, экспроприацию денег на нужды революции или устроить всеамериканский катаклизм на страх буржуям.
На это буржуинство тоже может ответить трояко (повторяю, все по сериалу): устроить гангстерский мордобой (лучше всего помогал от диверсии, хуже - от катастроф), послать ракетчика со своим атомным пистолетом (лучше - от катастроф, хуже - от экспроприаций), слетать по-крупному, на большой ракете (лучше - от экспроприации, хуже - от диверсии).
Прознав, что мы затеваем, главный буржуин, включает свой компьютер и пытается выбрать адекватный способ противодействия. В его компьютере всего три коробка - для трех наших операций. Сначала в каждом по три бусины, для каждого варианта ответа, в дальнейшем при успешном отражении нашей атаки в коробок добавляется бусина успешного ответа, иначе - бусины других цветов.
В ниже приведенной программе (GW-BASIC DOS):
Строки 20-57 - литературная составляющая игры.
60-61 - вероятности успеха буржуйских действий.
70-80 - N - запас денег на бусины у буржуев.
90-91 (закомментированно) - мы выбирает вид операции
92 - операция выбирается случайным образом
100-102 - буржуй тянет бусину из нужного коробка
110-120 - результат противоборства
122-123 (закомментированно) - перепрограммирование коробков для совсем жадного буржуина
124-125 - логичное перепрограммирование коробков
140-150 - количество бусин в коробках на конец игры
10 OPTION BASE 0: DIM R(9),K(9),K$(3),B$(3),U$(18 )
20 K$(0)="ДИВЕРСИЯ":K$(1)="ЭКСПРОПРИАЦИЯ":K$(2)="КАТАСТРОФА"
30 B$(0)="ГАНГСТЕРЫ":B$(1)="РАКЕТЧИК":B$(2)="РАКЕТА"
40 U$(0)="ПОДРЫВНИК ПОГИБ"
41 U$(1)="ЛАБОРАТОРИЯ ВЗОРВАНА"
42 U$(2)="УСТРОЙСТВО НЕЙТРАЛИЗОВАНО":
43 U$(3)="РАКЕТЧИК ОГЛУШЕН"
44 U$(4)="РАКЕТА УЦЕЛЕЛА"
45 U$(5)="РАКЕТА ВЗОРВАЛАСЬ"
46 U$(6)="ДЕНЬГИ ПОТЕРЯНЫ"
47 U$(7)="ДЕНЬГИ ВЫВЕЗЕНЫ"
48 U$(8 )="РАКЕТЧИК ВЫСЛЕДИЛ"
49 U$(9)="РАКЕТЧИК СХВАЧЕН"
50 U$(10)="РАКЕТА РАССТРЕЛЯЛА МАШИНУ"
51 U$(11)="МАШИНА ПРОСКОЧИЛА"
52 U$(12)="ГРУЗ ЗАХВАЧЕН"
53 U$(13)="ГРУЗ ПЕРЕПРАВЛЕН"
54 U$(14)="ПОБЕДА РАКЕТЧИКА"
55 U$(15)="РАКЕТЧИК ПОСТРАДАЛ"
56 U$(16)="РАКЕТА РАЗБОМБИЛА УСТАНОВКУ"
57 U$(17)="РАКЕТА В ЛОВУШКЕ"
60 DATA .8,.5,.2,.5,.2,.8,.2,.8,.5
61 FOR I=0 TO 8:READ R(I):K(I)=1:NEXT I
70 RANDOMIZE TIMER: N=10000
80 IF N<0 GOTO 140
90 REM PRINT "1) ";K$(0);", 2) ";K$(1);", 3) ";K$(2);
91 REM INPUT K:K=K-1:
92 K=INT(RND*3):K3=K*3
100 IF RND<K(K3)/(K(K3)+K(K3+1)+(K3+2))THEN B=0:GOTO 110
101 IF RND<K(K3+1)/(K(K3+1)+K(K3+2))THEN B=1:GOTO 110
102 B=2
110 R=RND<R(K3+B)
120 PRINT N;": ";K$(K);". ";B$(B);". ";U$(K*6+B*2+R+1);"."
121 IF R THEN K(K3+B)=K(K3+B)+1:N=N-1: GOTO 130
122 REM FOR I=0 TO 8:K(I)=K(I)+1:NEXT I
123 REM K(B)=K(B)-1:K(B+3)=K(B+3)-1:K(B+6)=K(B+6)-1:N=N-6
124 FOR I=0 TO 2:K(K3+I)=K(K3+I)+1:NEXT I
125 K(K3+B)=K(K3+B)-1:N=N-2
130 GOTO 80
140 PRINT "FINAL ATTACK:"
150 PRINT K(0);"/";K(1);"/";K(2);"*";K(3);"/";K(4);"/";K(5);"*";K(6);"/";K(7);"/";K(8 )
В таком виде (большое число повторов и логичное программирование коробков) на момент окончание игры количество бусин в коробках примерно соответствует вероятностям успеха буржуйских действий.
Если я поставлю ручное управление революцией (раскомментирую строки 90 и 91, закомментирую 92, и понятно уменьшу N где-то до 100), то смогу попытаться заставить буржуинский компьютер учиться неправильно. Или нет?
Кроме тогу, я могу добавлять буржуину дурости. Например (раскомментировав строки 122-123 вместо 124-125), я заставлю буржуина жалеть потерянных солдатиков, уменьшая их вероятность использования во всех операциях, а не только одного вида. В этом случае выход на правильные вероятности тормозится.
Возможны и другие варианты буржуйского умствования...
Как в это играть? Понятия не имею.
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 12:54 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Копаясь в старой "Технике - Молодежи".
Попытки 60-х применить ЭВМ в мирных целях.
ТЕХНИКА - МОЛОДЕЖИ 4/1965
КТО ВЫИГРАЕТ?
БОЛЕЛЬЩИК ПРЕДСКАЗЫВАЕТ РЕЗУЛЬТАТ МАТЧА
ТРЕНЕР ФУТБОЛЬНОЙ КОМАНДЫ - МАТЕМАТИК. НЕ ПОТЕРЯЕТ ЛИ ИГРА СВОЙ СПОРТИВНЫЙ ИНТЕРЕС?
А.ВАСИЛЬЕВ И В.ПЕТРОВ, ИНЖЕНЕРЫ
ПРЕДСКАЗАНИЕ МАШИНЫ
Ровно два года назад во время последнего чемпионата мира по футболу в Чили внимание любителей спорта во многих странах привлекла короткая заметка опубликованная в одной из чилийских газет. В статье сообщалось, что два чилийских инженера попытались с помощью вычислительной машины определить заранее исход встречи между лидером подгруппы - сборной командой СССР и аутсайдером - сборной Колумбии. Попытка эта, писала далее газета, окончилась полным провалом, так как машина, несмотря на многократное повторение эксперимента, упорно печатала результат, приводивший в ужас инженеров,- 4:4. Немало насмешливых реплик вызвал этот эксперимент. Однако когда через два дня результат матча между командами СССР и Колумбии стал известен, а, как вы знаете, на табло стадиона после финального свистка стояли две четверки, два чилийских энтузиаста кибернетики, ставшие предметом острот разного сорта, смогли, наконец, вздохнуть свободно. Их бывшие противники были ошеломлены сенсационным совпадением.
Невероятное предсказание в Арике было быстро забыто, хотя техническая сторона эксперимента, бесспорно, заслуживала внимания математиков и инженеров. Забыто... до 1964 года, года Токийской олимпиады. Читателям, конечно, известно, как подробно комментировались предсказанные с помощью вычислительной машины результаты, которые должны были быть показаны в отдельных видах спорта. Но на этот раз результаты не оправдали надежд специалистов. Цифры, которых с нетерпением ожидали эксперты, столпившиеся вокруг машины, мягко говоря, мало чем напоминали показанные впоследствии секунды и набранные очки.
Так "опозорилась" электронно-вычислительная машина. Но значит ли это, что спортивный и, в частности, футбольный прогноз вообще невозможен?
Конечно, нет. Более того, прогнозированием исхода соревнований смогут заняться и притом с большим успехом многие. Не верите? Напрасно.
ЧТО ТАКОЕ ИГРА?
Казалось бы, это вопрос чисто риторический. Каждый читатель наверняка участвовал и в спортивных и в других играх. Но мы говорим об игре с точки зрения математики. А это требует дополнительных замечаний и точных определений. Итак, что такое игра?
Игра - мероприятие, состоящее из ряда действий сторон A и B (чаще всего в игре участвует две стороны). Ход - выбор одного из предусмотренных правилами игры вариантов (не забывайте, товарищи спортсмены, именно предусмотренных правилами!). Чтобы игра была математически определенной, правила игры должны указывать для каждого случайного хода распределение вероятностей возможных последствий.
Значит ли это, что, например, футбол является математически определенной игрой в строгом смысле этого слова?
Конечно, очень трудно предсказать, что гол будет забит именно после прорыва форварда по краю и хорошей навесной передачи. Голы, как известно, забивают и в самых неожиданных ситуациях, но вероятнее всего ожидать взятие ворот, например, после такого прорыва. На трибунах это отлично знают все, даже люди с незаконченным средним образованием. Следовательно, исход борьбы при любых конкретных условиях можно оценить с некоторой, пусть даже небольшой, степенью точности.
Пусть не волнуется читатель, это вовсе не означает, что спортивные игры лишатся прелести неизвестности. Ведь игроки - это не фигурки на шахматной доске, которые может передвигать машина, думая при этом перед каждым ходом. Кроме того, еще раз подчеркнем, что вероятность каждого учитываемого при анализе футбольного матча фактора определяется весьма приблизительно.
Совокупность правил, определяющих личный ход данного игрока в зависимости от ситуации, сложившейся в процессе игры, называется стратегией. Обычно решения принимаются самим игроком в процессе игры в зависимости от сложившейся конкретной ситуации. Однако теоретически дело не изменится, если мы представим себе, что все эти решения принимаются игроком заранее. Для этого игрок должен был бы заблаговременно составить перечень всех возможных ситуаций и предусмотреть свое решение для каждой из них. В принципе (если не практически) это возможно для любой игры. Если такая система решений будет принята, это будет означать, что игрок или тренер выбрали определенную стратегию. Такова, грубо говоря, спортивная игра с точки зрения математики.
В любой спортивной игре можно подобрать стратегию - в большинстве случаев весьма приемлемую. Любой фактор, который мы пожелаем учесть, можно, правда с малой степенью точности, выразить в виде соответствующих коэффициентов в математических уравнениях.
Степень точности конечного результата зависит от того, насколько правильно мы определим вероятность появления того или иного фактора, могущего повлиять на результат соревнования. Например: всем известно, насколько ответственна роль вратаря в любом футбольном матче. По-видимому, при выборе стратегии важно учесть, в хорошей ли форме находится он в последнее время, хорошо ли сыгран с защитниками, считает ли он "трудными" нападающих противника,- да мало ли что влияет на надежную игру стража ворот?
Ведь в подобной игре весьма существенны и моральные факторы. Мы не можем взять на себя смелость и сказать, что мы прекрасно знаем, чем был озабочен, например, заслуженный мастер спорта Г.Качалин перед матчем "Динамо" (Тбилиси) с ЦСКА во втором круге прошлогоднего чемпионата. Ясно было только одно: поражение с крупным счетом не входило в его планы. Скорее всего в этот тяжелый для тбилисцев день их подвела неправильно выбранная стратегия. Но можно предположить, что на исход матча повлияли и случайные обстоятельства - скажем, коллективный просмотр художественного фильма "Страх" или днем в Третьяковской галерее Славе Метревели наступила на ногу девушка в туфельках-шпильках. Все это надо бы иметь в виду тренерам, мы тоже должны это учесть по возможности, если займемся заманчивым делом - предсказанием исхода матча.

МЫ ПРЕДСКАЗЫВАЕМ РЕЗУЛЬТАТ МАТЧА
Любой человек может проделать следующий эксперимент. Возьмите результат матча, состоявшегося, допустим, в прошлом году, отыщите результаты встреч этих команд в прошедшие сезоны и постарайтесь проанализировать все факторы, которые, как вам кажется, влияют (или влияли) на исход интересующего вас последнего матча (в процессе анализа вы, безусловно, можете даже вскрыть какие-то новые факторы, доселе казавшиеся вам несущественными). Потом, опираясь на изученный вами материал, попытайтесь предсказать или, вернее, определить результат последнего матча. Если расхождение будет сильно, попробуйте усилить (или ослабить) влияние того или иного фактора. Пользуясь данными (параметрами) вашей наиболее удачной попытки по использованию известных значений, попробуйте проделать то же самое еще с несколькими известными вам результатами матчей.
Мы можем предложить два способа прогнозирования. Группа московских инженеров уже весьма продолжительное время пользуется несколько более усложненными вариантами этих способов. Они удачно отгадывают результаты футбольных матчей, увлеклись этим занятием и надеются со временем довести свои методы до высокой степени совершенства.
Во-первых, наиболее реально угадать исход матча в очках: победа, ничья или поражение. Более высокой степенью "предсказательства" можно считать определение разницы забитых и пропущенных голов, с которой команда выиграет (проиграет) в предстоящем матче. Но каждому желающему попробовать свои силы в прогнозировании исхода футбольных матчей и получать удовлетворительные результаты мы настоятельно советуем предварительно попытаться определить исход каких-нибудь матчей, проведенных ранее, с тем чтобы сравнить полученный результат с истинным.
Теперь по существу, предлагаемых методов. Чтобы пользоваться первым из них, необходимо составить несложную таблицу.
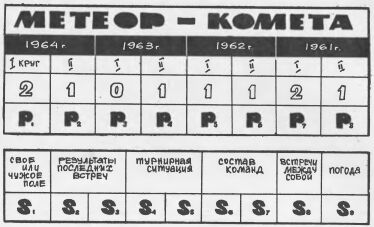
Главная трудность - определить значения символов S.
Здесь должны сказать свое слово ваша интуиция, ваше знание футбола, ваш
опыт болельщика - словом, ваша футбольная эрудиция.
(Мы еще раз посоветуем вам предварительно потренироваться, анализируя уже сыгранные матчи.).
Значение каждого символа S определяется цифрой от 1 до 10. После определения всех S необходимо их просуммировать и посмотреть, в какой интервал попадает полученное вами число:
0-35 - поражение;
36-68 - ничья;
69-90 - победа.
Теперь несколько слов о том, что надо понимать под символами S. Символу S1, относящемуся к вертикальной графе "на своем или чужом поле", должна соответствовать, скажем, цифра 3 (в общем случае меньше 5), если игра происходит на поле противника, или 8 (в общем случае больше 5), если встреча будет на поле противника. Игра на нейтральном поле соответственно будет изображаться числом 5.
Число S2 показывает, насколько успешно для вашей команды были последние 4-5 календарных игр на первенство страны. Если, скажем, ваша команда набрала за эти 5 игр 10 очков, то балл у нее будет высший. Вы ставите в графу число 10. Аналогично в случае очень успешных игр команды противника (10 очков после 5 игр) в третью графу пишем 0... Иначе говоря, S3 показывает, каковы шансы на успех любой команды против команды противника, исходя из результатов последних 4-5 матчей, сыгранных соперником вашей команды.
В четвертую графу вы ставите числа, учитывающие встречи интересующих вас команд на том поле, где предстоит играть командам.
Далее идет графа "состав команд". Тут учитываются появление в командах новых, заведомо сильных игроков, болезнь ведущих футболистов, отсутствие членов сборной СССР, смена тренерского состава и т.д.
Наконец, символы S8 и S9 учитывают встречу команд между собой и погоду с точки зрения выгоды ее для вашей команды.
Рассмотрим теперь второй метод прогнозирования результатов предстоящего футбольного матча. Для этого необходимо сделать следующее: запишите подряд 8 исходов последних матчей интересующих вас команд, например:
"ЗЕНИТ" - "ТОРПЕДО"
1964: I круг - 2*P1, II-1*P2
1963: I-2*P3, II-0*P4
1962: I-0*P5, II-1*P6
1961: I-0*P7, II-1*P8
Числа P1, ... P8 являются десятичными или простыми дробями, сумма которых должна быть равна 1.
При определении чисел P1, ... P8 должно соблюдаться условие:
P1 > P2 > ... > P8
Это условие необходимо выполнять потому, что результат последнего матча несет в себе гораздо больше информации о сравнительной силе команд, нежели результат предпоследнего матча или тем более еще раньше сыгранного.
Первые числа таблицы 2, как вы уже догадались - результаты рассматриваемых вами игр в очках (как при заполнении футбольной таблицы).
После заполнения всех клеток таблицы вам необходимо умножить каждое число-результат на соответствующую дробь и сложить полученные числа. После этого с помощью таблицы интервалов мы определим результат предстоящего матча:
0-0.7 - поражение;
0.7-1.45 - ничья;
1.45-2 - победа.
Можно, разумеется, усложнить задачу, учитывая и счет игры. В этом случае мы будем оценивать результат не только с точки зрения выигрыша или проигрыша. С помощью дополнительной таблицы появится возможность точно угадывать счет. Конечно, "все" будет зависеть от разработанной вами программы, от правильности основных положений таблицы. Значение каждого параметра надо подбирать очень тщательно. Но для этого и существуют предварительные тренировки.
Поработайте как следует. И результат не заставит себя ждать!
Возьмем конкретный пример одного из удачных предсказаний, сделанных авторами. Правда, относится он к сезону 1959 года, но мы даем его просто для иллюстрации наших предложений.
Речь идет о матче ЦСКА МО - СПАРТАК (Москва), состоявшемся 10 октября 1959 года в Москве (второй круг первенства), причем нас интересовал результат армейцев (наша команда - ЦСКА МО).
Начнем предсказание с первой таблицы. S1 и S9 считаем равными 5, так как обе команды московские, а пасмурная погода не благоприятствовала обеим, S4 и S5 - к этому матчу команды пришли, имея на своем счету по 16 очков, но армейцы провели на две игры меньше. Значит, их турнирное положение несколько лучше. Поэтому мы ставим в соответствующих графах по цифре 6. Большинство игроков "Спартака" входило в сборную СССР (Масленкин, Нетто, Ильин и др.). Что касается армейцев, то команда состояла из молодых игроков, значительно менее опытных. Поэтому мы ставим в графе S6 - 4, а в графе S7 - 5.
К этому матчу из 37 встреч армейцы победили в 22, проиграв всего лишь 10 встреч. Следовательно, в графе S7 мы ставим высокий балл - 7.
Наконец, о результатах последних встреч. В предыдущих пяти матчах армейцы, как и спартаковцы, сыграли довольно успешно, поэтому мы ставим S2 - 7, a S3 - 4.
Общий итог составляет:
5+7+4+6+6+4+5+7+5 = 49.
Мы попадаем в интервал результатов, соответствующий ничьей.
Перейдем теперь ко второй таблице.
Вот результаты последних десяти встреч (мы брали тогда 10 результатов, хотя наши читатели могут брать данные, исходя из 9 или даже 8 последних матчей):
1959: 2(3:0)
1958: 1(0:0)
1958: 0(0:2)
1957: 0(1:3)
1957: 2(1:0)
1956: 0(0:3)
1956: 0(3:4)
1955: 1(2:2)
1955: 2(3:1)
1954: 2(1:0)
Соответствующие коэффициенты Р выглядят так:
0.2; 0.18; 0.15; 0.14; 0.12; 0.08; 0.06; 0.04; 0.02; 0.01.
Результат:
0.2*2 + 0.18*1 + 0.12*2 + 0.04*1 + 0.02*2 + 0.01*2 = 0.92
попадает в интервал значений, соответствующий ничейному результату игры. Настал день 10 октября - матч. Команды сыграли 1:1. Ничья! Как мы и предсказали!
ТРЕНЕР ОКАНЧИВАЕТ МЕХМАТ
Итак, мы с вами с помощью элементарных математических выкладок сумели предсказать результат футбольного матча. А как же тренер команды? Стоит ли ему заниматься математикой? Разумеется, но только гораздо более солидной.
Если бы все обстояло так просто, как мы описали, футбольному тренеру вполне хватило бы математических знаний, приобретенных еще в средней школе, а руководимая им команда, овладев секретом нахождения оптимальной стратегии, совершала бы чудеса.
В том-то и дело, что, по старинному выражению, математика - это жернов. И, засыпав в него лебеду, вы никогда не получите пшеничной муки. Иными словами, применять математический аппарат нужно умело, строго отбирая исходные данные для подсчета. А мощные жернова - те самые, что перемигиваются разноцветными лампочками, стрекочут, печатая бесконечные ленты с ответами, и даже говорят человеческим голосом, - быстро дадут ответ (если только данные правильно запрограммированы).
Поэтому не удивляйтесь, если узнаете, что в состава футбольной команды скоро появится квалифицированный математик. Он будет играть не меньшую, а может быть и большую, роль, чем массажист, врач-психолог, тренер по легкой атлетике и администратор. Что же он должен делать?
Прежде всего это накопление максимально возможной информации обо всем, что имеет даже весьма "косвенное" отношение к команде. "Знаем! знаем!- сообразит догадливый читатель.- Футбольная статистика". Да, но несколько отличная от той, что появляется на страницах спортивной прессы и зачастую носит чисто развлекательный характер.
Данные, которые следует собирать и анализировать математику команды, должны гораздо лучше отображать сложную мозаику футбольного соперничества. Сюда, конечно, войдут результаты всех матчей за несколько последних сезонов, но это далеко не все - необходимы и другие сведения, касающиеся составов встречающихся команд, тактического рисунка игр, психологического состояния спортсменов и т.д. Анализируя горы материала, можно будет и без всякой особенной математики и теории игр прийти к определенным выводам, касающимся методов подготовки команды к игре. Будут у тренера задачи и посложнее. Так что мехмат кончать все-таки, наверное, придется.
Выходит, с одной стороны, пользуясь услугами математики, болельщикам легче будет предсказывать результаты матчей, а с другой - математики футбольных команд постараются "спутать карты" и болельщиков и тренеров соперничающих команд. И все это, разумеется, оживит любимую всеми нами игру.
В следующих номерах у нас выступят видные математики, мастера спорта - футболисты и болельщики. Они поделятся своими соображениями о наших методах прогноза.
Любой из вас может принять участие в этой увлекательной игре. Календарный план предстоящих встреч перед вами. Вооружившись карандашом с бумагой, заполняйте таблицы, которые вы видите в тексте статьи и на четвертой странице обложки этого номера.

Тщательно проанализируйте результаты встреч прошлого года, чтобы параметры вашей таблицы оказались наиболее удачными.
КАК СЫГРАЮТ МЕЖДУ СОБОЙ ПОПУЛЯРНЫЕ НАШИ КОМАНДЫ? КТО СТАНЕТ ЧЕМПИОНОМ? ЧЕМ ЗАКОНЧАТСЯ ИГРЫ НА КУБОК?
ПРИСЫЛАЙТЕ НАМ СВОИ ПРОГНОЗЫ, А ТАКЖЕ СООБРАЖЕНИЯ КАК УЛУЧШИТЬ ТАБЛИЦЫ СДЕЛАТЬ ИХ СОВЕРШЕННЕЕ.
ЖДЕМ ВАШИХ ПИСЕМ! САМЫЕ УДАЧНЫЕ ОТВЕТЫ БУДУТ ОПУБЛИКОВАНЫ.
Попытки 60-х применить ЭВМ в мирных целях.
ТЕХНИКА - МОЛОДЕЖИ 4/1965
КТО ВЫИГРАЕТ?
БОЛЕЛЬЩИК ПРЕДСКАЗЫВАЕТ РЕЗУЛЬТАТ МАТЧА
ТРЕНЕР ФУТБОЛЬНОЙ КОМАНДЫ - МАТЕМАТИК. НЕ ПОТЕРЯЕТ ЛИ ИГРА СВОЙ СПОРТИВНЫЙ ИНТЕРЕС?
А.ВАСИЛЬЕВ И В.ПЕТРОВ, ИНЖЕНЕРЫ
ПРЕДСКАЗАНИЕ МАШИНЫ
Ровно два года назад во время последнего чемпионата мира по футболу в Чили внимание любителей спорта во многих странах привлекла короткая заметка опубликованная в одной из чилийских газет. В статье сообщалось, что два чилийских инженера попытались с помощью вычислительной машины определить заранее исход встречи между лидером подгруппы - сборной командой СССР и аутсайдером - сборной Колумбии. Попытка эта, писала далее газета, окончилась полным провалом, так как машина, несмотря на многократное повторение эксперимента, упорно печатала результат, приводивший в ужас инженеров,- 4:4. Немало насмешливых реплик вызвал этот эксперимент. Однако когда через два дня результат матча между командами СССР и Колумбии стал известен, а, как вы знаете, на табло стадиона после финального свистка стояли две четверки, два чилийских энтузиаста кибернетики, ставшие предметом острот разного сорта, смогли, наконец, вздохнуть свободно. Их бывшие противники были ошеломлены сенсационным совпадением.
Невероятное предсказание в Арике было быстро забыто, хотя техническая сторона эксперимента, бесспорно, заслуживала внимания математиков и инженеров. Забыто... до 1964 года, года Токийской олимпиады. Читателям, конечно, известно, как подробно комментировались предсказанные с помощью вычислительной машины результаты, которые должны были быть показаны в отдельных видах спорта. Но на этот раз результаты не оправдали надежд специалистов. Цифры, которых с нетерпением ожидали эксперты, столпившиеся вокруг машины, мягко говоря, мало чем напоминали показанные впоследствии секунды и набранные очки.
Так "опозорилась" электронно-вычислительная машина. Но значит ли это, что спортивный и, в частности, футбольный прогноз вообще невозможен?
Конечно, нет. Более того, прогнозированием исхода соревнований смогут заняться и притом с большим успехом многие. Не верите? Напрасно.
ЧТО ТАКОЕ ИГРА?
Казалось бы, это вопрос чисто риторический. Каждый читатель наверняка участвовал и в спортивных и в других играх. Но мы говорим об игре с точки зрения математики. А это требует дополнительных замечаний и точных определений. Итак, что такое игра?
Игра - мероприятие, состоящее из ряда действий сторон A и B (чаще всего в игре участвует две стороны). Ход - выбор одного из предусмотренных правилами игры вариантов (не забывайте, товарищи спортсмены, именно предусмотренных правилами!). Чтобы игра была математически определенной, правила игры должны указывать для каждого случайного хода распределение вероятностей возможных последствий.
Значит ли это, что, например, футбол является математически определенной игрой в строгом смысле этого слова?
Конечно, очень трудно предсказать, что гол будет забит именно после прорыва форварда по краю и хорошей навесной передачи. Голы, как известно, забивают и в самых неожиданных ситуациях, но вероятнее всего ожидать взятие ворот, например, после такого прорыва. На трибунах это отлично знают все, даже люди с незаконченным средним образованием. Следовательно, исход борьбы при любых конкретных условиях можно оценить с некоторой, пусть даже небольшой, степенью точности.
Пусть не волнуется читатель, это вовсе не означает, что спортивные игры лишатся прелести неизвестности. Ведь игроки - это не фигурки на шахматной доске, которые может передвигать машина, думая при этом перед каждым ходом. Кроме того, еще раз подчеркнем, что вероятность каждого учитываемого при анализе футбольного матча фактора определяется весьма приблизительно.
Совокупность правил, определяющих личный ход данного игрока в зависимости от ситуации, сложившейся в процессе игры, называется стратегией. Обычно решения принимаются самим игроком в процессе игры в зависимости от сложившейся конкретной ситуации. Однако теоретически дело не изменится, если мы представим себе, что все эти решения принимаются игроком заранее. Для этого игрок должен был бы заблаговременно составить перечень всех возможных ситуаций и предусмотреть свое решение для каждой из них. В принципе (если не практически) это возможно для любой игры. Если такая система решений будет принята, это будет означать, что игрок или тренер выбрали определенную стратегию. Такова, грубо говоря, спортивная игра с точки зрения математики.
В любой спортивной игре можно подобрать стратегию - в большинстве случаев весьма приемлемую. Любой фактор, который мы пожелаем учесть, можно, правда с малой степенью точности, выразить в виде соответствующих коэффициентов в математических уравнениях.
Степень точности конечного результата зависит от того, насколько правильно мы определим вероятность появления того или иного фактора, могущего повлиять на результат соревнования. Например: всем известно, насколько ответственна роль вратаря в любом футбольном матче. По-видимому, при выборе стратегии важно учесть, в хорошей ли форме находится он в последнее время, хорошо ли сыгран с защитниками, считает ли он "трудными" нападающих противника,- да мало ли что влияет на надежную игру стража ворот?
Ведь в подобной игре весьма существенны и моральные факторы. Мы не можем взять на себя смелость и сказать, что мы прекрасно знаем, чем был озабочен, например, заслуженный мастер спорта Г.Качалин перед матчем "Динамо" (Тбилиси) с ЦСКА во втором круге прошлогоднего чемпионата. Ясно было только одно: поражение с крупным счетом не входило в его планы. Скорее всего в этот тяжелый для тбилисцев день их подвела неправильно выбранная стратегия. Но можно предположить, что на исход матча повлияли и случайные обстоятельства - скажем, коллективный просмотр художественного фильма "Страх" или днем в Третьяковской галерее Славе Метревели наступила на ногу девушка в туфельках-шпильках. Все это надо бы иметь в виду тренерам, мы тоже должны это учесть по возможности, если займемся заманчивым делом - предсказанием исхода матча.

МЫ ПРЕДСКАЗЫВАЕМ РЕЗУЛЬТАТ МАТЧА
Любой человек может проделать следующий эксперимент. Возьмите результат матча, состоявшегося, допустим, в прошлом году, отыщите результаты встреч этих команд в прошедшие сезоны и постарайтесь проанализировать все факторы, которые, как вам кажется, влияют (или влияли) на исход интересующего вас последнего матча (в процессе анализа вы, безусловно, можете даже вскрыть какие-то новые факторы, доселе казавшиеся вам несущественными). Потом, опираясь на изученный вами материал, попытайтесь предсказать или, вернее, определить результат последнего матча. Если расхождение будет сильно, попробуйте усилить (или ослабить) влияние того или иного фактора. Пользуясь данными (параметрами) вашей наиболее удачной попытки по использованию известных значений, попробуйте проделать то же самое еще с несколькими известными вам результатами матчей.
Мы можем предложить два способа прогнозирования. Группа московских инженеров уже весьма продолжительное время пользуется несколько более усложненными вариантами этих способов. Они удачно отгадывают результаты футбольных матчей, увлеклись этим занятием и надеются со временем довести свои методы до высокой степени совершенства.
Во-первых, наиболее реально угадать исход матча в очках: победа, ничья или поражение. Более высокой степенью "предсказательства" можно считать определение разницы забитых и пропущенных голов, с которой команда выиграет (проиграет) в предстоящем матче. Но каждому желающему попробовать свои силы в прогнозировании исхода футбольных матчей и получать удовлетворительные результаты мы настоятельно советуем предварительно попытаться определить исход каких-нибудь матчей, проведенных ранее, с тем чтобы сравнить полученный результат с истинным.
Теперь по существу, предлагаемых методов. Чтобы пользоваться первым из них, необходимо составить несложную таблицу.

Главная трудность - определить значения символов S.
Здесь должны сказать свое слово ваша интуиция, ваше знание футбола, ваш
опыт болельщика - словом, ваша футбольная эрудиция.
(Мы еще раз посоветуем вам предварительно потренироваться, анализируя уже сыгранные матчи.).
Значение каждого символа S определяется цифрой от 1 до 10. После определения всех S необходимо их просуммировать и посмотреть, в какой интервал попадает полученное вами число:
0-35 - поражение;
36-68 - ничья;
69-90 - победа.
Теперь несколько слов о том, что надо понимать под символами S. Символу S1, относящемуся к вертикальной графе "на своем или чужом поле", должна соответствовать, скажем, цифра 3 (в общем случае меньше 5), если игра происходит на поле противника, или 8 (в общем случае больше 5), если встреча будет на поле противника. Игра на нейтральном поле соответственно будет изображаться числом 5.
Число S2 показывает, насколько успешно для вашей команды были последние 4-5 календарных игр на первенство страны. Если, скажем, ваша команда набрала за эти 5 игр 10 очков, то балл у нее будет высший. Вы ставите в графу число 10. Аналогично в случае очень успешных игр команды противника (10 очков после 5 игр) в третью графу пишем 0... Иначе говоря, S3 показывает, каковы шансы на успех любой команды против команды противника, исходя из результатов последних 4-5 матчей, сыгранных соперником вашей команды.
В четвертую графу вы ставите числа, учитывающие встречи интересующих вас команд на том поле, где предстоит играть командам.
Далее идет графа "состав команд". Тут учитываются появление в командах новых, заведомо сильных игроков, болезнь ведущих футболистов, отсутствие членов сборной СССР, смена тренерского состава и т.д.
Наконец, символы S8 и S9 учитывают встречу команд между собой и погоду с точки зрения выгоды ее для вашей команды.
Рассмотрим теперь второй метод прогнозирования результатов предстоящего футбольного матча. Для этого необходимо сделать следующее: запишите подряд 8 исходов последних матчей интересующих вас команд, например:
"ЗЕНИТ" - "ТОРПЕДО"
1964: I круг - 2*P1, II-1*P2
1963: I-2*P3, II-0*P4
1962: I-0*P5, II-1*P6
1961: I-0*P7, II-1*P8
Числа P1, ... P8 являются десятичными или простыми дробями, сумма которых должна быть равна 1.
При определении чисел P1, ... P8 должно соблюдаться условие:
P1 > P2 > ... > P8
Это условие необходимо выполнять потому, что результат последнего матча несет в себе гораздо больше информации о сравнительной силе команд, нежели результат предпоследнего матча или тем более еще раньше сыгранного.
Первые числа таблицы 2, как вы уже догадались - результаты рассматриваемых вами игр в очках (как при заполнении футбольной таблицы).
После заполнения всех клеток таблицы вам необходимо умножить каждое число-результат на соответствующую дробь и сложить полученные числа. После этого с помощью таблицы интервалов мы определим результат предстоящего матча:
0-0.7 - поражение;
0.7-1.45 - ничья;
1.45-2 - победа.
Можно, разумеется, усложнить задачу, учитывая и счет игры. В этом случае мы будем оценивать результат не только с точки зрения выигрыша или проигрыша. С помощью дополнительной таблицы появится возможность точно угадывать счет. Конечно, "все" будет зависеть от разработанной вами программы, от правильности основных положений таблицы. Значение каждого параметра надо подбирать очень тщательно. Но для этого и существуют предварительные тренировки.
Поработайте как следует. И результат не заставит себя ждать!
Возьмем конкретный пример одного из удачных предсказаний, сделанных авторами. Правда, относится он к сезону 1959 года, но мы даем его просто для иллюстрации наших предложений.
Речь идет о матче ЦСКА МО - СПАРТАК (Москва), состоявшемся 10 октября 1959 года в Москве (второй круг первенства), причем нас интересовал результат армейцев (наша команда - ЦСКА МО).
Начнем предсказание с первой таблицы. S1 и S9 считаем равными 5, так как обе команды московские, а пасмурная погода не благоприятствовала обеим, S4 и S5 - к этому матчу команды пришли, имея на своем счету по 16 очков, но армейцы провели на две игры меньше. Значит, их турнирное положение несколько лучше. Поэтому мы ставим в соответствующих графах по цифре 6. Большинство игроков "Спартака" входило в сборную СССР (Масленкин, Нетто, Ильин и др.). Что касается армейцев, то команда состояла из молодых игроков, значительно менее опытных. Поэтому мы ставим в графе S6 - 4, а в графе S7 - 5.
К этому матчу из 37 встреч армейцы победили в 22, проиграв всего лишь 10 встреч. Следовательно, в графе S7 мы ставим высокий балл - 7.
Наконец, о результатах последних встреч. В предыдущих пяти матчах армейцы, как и спартаковцы, сыграли довольно успешно, поэтому мы ставим S2 - 7, a S3 - 4.
Общий итог составляет:
5+7+4+6+6+4+5+7+5 = 49.
Мы попадаем в интервал результатов, соответствующий ничьей.
Перейдем теперь ко второй таблице.
Вот результаты последних десяти встреч (мы брали тогда 10 результатов, хотя наши читатели могут брать данные, исходя из 9 или даже 8 последних матчей):
1959: 2(3:0)
1958: 1(0:0)
1958: 0(0:2)
1957: 0(1:3)
1957: 2(1:0)
1956: 0(0:3)
1956: 0(3:4)
1955: 1(2:2)
1955: 2(3:1)
1954: 2(1:0)
Соответствующие коэффициенты Р выглядят так:
0.2; 0.18; 0.15; 0.14; 0.12; 0.08; 0.06; 0.04; 0.02; 0.01.
Результат:
0.2*2 + 0.18*1 + 0.12*2 + 0.04*1 + 0.02*2 + 0.01*2 = 0.92
попадает в интервал значений, соответствующий ничейному результату игры. Настал день 10 октября - матч. Команды сыграли 1:1. Ничья! Как мы и предсказали!
ТРЕНЕР ОКАНЧИВАЕТ МЕХМАТ
Итак, мы с вами с помощью элементарных математических выкладок сумели предсказать результат футбольного матча. А как же тренер команды? Стоит ли ему заниматься математикой? Разумеется, но только гораздо более солидной.
Если бы все обстояло так просто, как мы описали, футбольному тренеру вполне хватило бы математических знаний, приобретенных еще в средней школе, а руководимая им команда, овладев секретом нахождения оптимальной стратегии, совершала бы чудеса.
В том-то и дело, что, по старинному выражению, математика - это жернов. И, засыпав в него лебеду, вы никогда не получите пшеничной муки. Иными словами, применять математический аппарат нужно умело, строго отбирая исходные данные для подсчета. А мощные жернова - те самые, что перемигиваются разноцветными лампочками, стрекочут, печатая бесконечные ленты с ответами, и даже говорят человеческим голосом, - быстро дадут ответ (если только данные правильно запрограммированы).
Поэтому не удивляйтесь, если узнаете, что в состава футбольной команды скоро появится квалифицированный математик. Он будет играть не меньшую, а может быть и большую, роль, чем массажист, врач-психолог, тренер по легкой атлетике и администратор. Что же он должен делать?
Прежде всего это накопление максимально возможной информации обо всем, что имеет даже весьма "косвенное" отношение к команде. "Знаем! знаем!- сообразит догадливый читатель.- Футбольная статистика". Да, но несколько отличная от той, что появляется на страницах спортивной прессы и зачастую носит чисто развлекательный характер.
Данные, которые следует собирать и анализировать математику команды, должны гораздо лучше отображать сложную мозаику футбольного соперничества. Сюда, конечно, войдут результаты всех матчей за несколько последних сезонов, но это далеко не все - необходимы и другие сведения, касающиеся составов встречающихся команд, тактического рисунка игр, психологического состояния спортсменов и т.д. Анализируя горы материала, можно будет и без всякой особенной математики и теории игр прийти к определенным выводам, касающимся методов подготовки команды к игре. Будут у тренера задачи и посложнее. Так что мехмат кончать все-таки, наверное, придется.
Выходит, с одной стороны, пользуясь услугами математики, болельщикам легче будет предсказывать результаты матчей, а с другой - математики футбольных команд постараются "спутать карты" и болельщиков и тренеров соперничающих команд. И все это, разумеется, оживит любимую всеми нами игру.
В следующих номерах у нас выступят видные математики, мастера спорта - футболисты и болельщики. Они поделятся своими соображениями о наших методах прогноза.
Любой из вас может принять участие в этой увлекательной игре. Календарный план предстоящих встреч перед вами. Вооружившись карандашом с бумагой, заполняйте таблицы, которые вы видите в тексте статьи и на четвертой странице обложки этого номера.

Тщательно проанализируйте результаты встреч прошлого года, чтобы параметры вашей таблицы оказались наиболее удачными.
КАК СЫГРАЮТ МЕЖДУ СОБОЙ ПОПУЛЯРНЫЕ НАШИ КОМАНДЫ? КТО СТАНЕТ ЧЕМПИОНОМ? ЧЕМ ЗАКОНЧАТСЯ ИГРЫ НА КУБОК?
ПРИСЫЛАЙТЕ НАМ СВОИ ПРОГНОЗЫ, А ТАКЖЕ СООБРАЖЕНИЯ КАК УЛУЧШИТЬ ТАБЛИЦЫ СДЕЛАТЬ ИХ СОВЕРШЕННЕЕ.
ЖДЕМ ВАШИХ ПИСЕМ! САМЫЕ УДАЧНЫЕ ОТВЕТЫ БУДУТ ОПУБЛИКОВАНЫ.
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 1:02 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
В ТОМ ЖЕ НОМЕРЕ ЖУРНАЛА
В. ПЕКЕЛИС
С ФОРМУЛАМИ В ЛАБИРИНТАХ ПРЕСТУПЛЕНИЯ
КИБЕРНЕТИКА В КРИМИНАЛИСТИКЕ
МАТЕМАТИК В РОЛИ СЛЕДОВАТЕЛЯ МАШИНА ПЛАНИРУЕТ РАССЛЕДОВАНИЕ
РИСУНКИ Ю.МАКАРЕНКО И Ю.СЛУЧЕВСКОГО

0.pa1/0.A2.Bpb3/0.Cpc4/3Dpd5/0.E
Сначала - впрочем, давно уже прежде - его занимал один вопрос: почему так легко отыскиваются и выдаются почти все преступления и так явно обозначаются следы почти всех преступников?
/Ф.Достоевский. "Преступление и наказание"/
Помните полную драматического напряжения сцену, нарисованную Достоевским в романе "Преступление и наказание"?
"Лестница к старухе была близко, сейчас из ворот направо. Он уже был на лестнице...
Переведя дух и прижав рукой стукавшее сердце, тут же нащупав и оправив еще раз топор, он стал осторожно и тихо подниматься на лестницу, поминутно прислушиваясь. Но и лестница на ту пору стояла совсем пустая; все двери были заперты; никого-то не встретилось. Во втором этаже одна пустая квартира была, правда, растворена настежь, и в ней работали маляры, но те и не поглядели. Он постоял, подумал и пошел дальше".
Далее следует психологически точное описание того, как Раскольников поднимался по лестнице, звонил к ростовщице, чуть ли не силой открыл к ней дверь, затем, отдав старухе фальшивую табакерку, улучил момент и "...вынул топор совсем, взмахнул его обеими руками, едва себя чувствуя и почти без усилия, почти машинально, опустил на голову обухом". Преступление свершилось. А наказание?
Долог, ой, как долог и многотруден был путь к возмездию! На какие только ухищрения не пускался следователь Порфирий Петрович, чтобы уличить виновного! Какой интуицией, какими аналитическими способностями, какой памятью надо обладать человеку, чтобы безошибочно и в то же время деликатно, не унижая человеческого достоинства подозреваемых, прийти к правильному выводу!
Интуиция... А если вместо нее точный расчет? А если прибегнуть к услугам машины, ее аналитического "ума" и памяти, которые раньше считались чисто человеческими свойствами? Что тогда?
Созданная рукой гениального художника картина убийства, взятая отдельно, лишь в логической последовательности действий, на языке кибернетики была бы записана гораздо лаконичней - формулой, как вы видите в заголовке.
Для чего нужна такая запись? Чтобы ответить, познакомимся с заурядным преступлением, совершенным сто лет спустя, в наши дни.
Когда старый рецидивист вор-"домушник" Чесноков узнал, что одинокий художник, назовем его N, тяжело заболел и отправлен в больницу, он предложил своему зятю Соловьеву "выгодное дельце": проникнуть в квартиру художника и похитить вещи и картины.
Соловьев согласился. Было решено выполнить задуманное вечером, на следующий день. Весь ход ограбления преступники продумали самым тщательным образом, предусмотрев, казалось бы, все до последней мелочи. Обсудили и какими инструментами действовать. Условились захватить с собой отвертку и нож, чтобы выковырять оконную замазку. Не забыли и о свежей замазке, чтобы вставить стекло, а также о мешках и шпагате для упаковки краденого.
План ограбления строился так. После того как в доме погасят огни, проникнуть в квартиру художника через парадный либо через черный ход или через окно в подвале. В крайнем случае через одно из окон со стороны двора.
Предварительная разведка показала: двери парадного и черного ходов нельзя взломать без шума. Окно в подвал, вероятно, удалось бы открыть, но ведь дверь из подвала в квартиру могла быть заперта! Тогда преступники решили пробраться в квартиру через окно со двора.
Как только стемнело и все кругом стихло, Чесноков вытащил из сарая соседнего дома припрятанную заранее лестницу и приставил ее к стене. Соловьев добрался до окна и попытался выдавить стекло. Не удалось. Тогда вор аккуратно удалил замазку ножом и осторожно вынул стекло.
В квартиру забрались вместе, затащив лестницу в окно, которое тут же закрыли. Быстро "обработав" квартиру, перешли в мастерскую. Времени оставалось в обрез, поэтому холсты вырезали бритвами, наспех свертывали в трубки и туго затягивали шпагатом. Вещи и картины, уложенные в мешки, вынесли через окно во двор. Окно закрыли, вставили на место стекло и тщательно замазали щели. Теперь оставалось осторожно перенести мешки в укромное место, а потом "реализовать" награбленное.
АЛГОРИТМ ПРЕСТУПЛЕНИЯ
Вот как выглядит запись этого преступления, если мы условимся, что Чесноков - это X, Соколов - Y, художник - N, а различные ситуации и действия обозначены разными символами.
А: узнать, находится ли N в больнице. pa: находится N в больнице?
В: уговорить Y участвовать в краже. рb: будет Y участвовать?
С: подойти скрытно к месту действия. рс: видел ли кто-нибудь?
D: когда соседи погасят свет, открыть парадную дверь. рd: погашен ли свет? p'd: отворили парадную дверь?
Е: если условие D невыполнимо, то взломать черный ход. ре: заперт ли черныйcход?
F: если условие Е невыполнимо, то проникнуть в квартиру через окно из подвала. pf: доступ в квартиру невозможен?
G: если условие F невыполнимо, то проникнуть в квартиру через окно во дворе. Если нельзя выдавись стекло извне, то удалить замазку. pg: доступ возможен?
H: похитить вещи и картины и вынести во двор. ph: вещи, картины похищены и вынесены?
К: если никто не видит, вмазать стекло на место. рк: никто не видит?
L: удалиться с похищенным добром.
Весь ход событий теперь может быть символически записан так:

0.Apa1/0.Bpb2/0.Cpc3/0.pd4/3.Dp'd5/4.HphСТОП/5.Epe6/5.Fpf7/5.GpgСТОП.Hph8.Kpk9/7.L
Невольно еще раз возникает вопрос: зачем простой и ясный рассказ о преступлении, записанный на понятном всем языке, кодировать условными знаками да еще записывать в виде набора символов со стрелками?
Мы поставили в заголовке "Алгоритм преступления". Алгоритм - это набор очень простых правил, из которых складывается процесс решения даже самой сложной задачи. Для краткости правила записываются в виде формул.
Алгоритм как бы назначает очередность возможных операций и управляет ею. И, что очень ценно, последовательность операций нередко выявляется по ходу дела.
Наряду с описанием операций алгоритм содержит еще и логические требования. Каждому из них можно предпослать такой вопрос, чтобы утвердительный ответ означал бы исполненное требование, а отрицательный - невыполненное.
Такой способ записи очень удобен для детальной оценки преступного действия и для анализа подготовки преступления, его исполнения и сокрытия следов. Теперь мы можем в этом убедиться, если вновь посмотрим на символическую запись всего хода ограбления (если условие исполнено, то следуют по стрелке, направленной вверх, в противном случае - направленной вниз).
ВЫЧИСЛЕНИЕ "ВАРИАБЕЛЬНОСТИ"
Ясно, какое значение для следствия имеет оценка подготовки преступления, его исполнения и сокрытия.
Как правило, вначале суть дела еще не вполне ясна, а преступник неизвестен. Поэтому способ и манеру преступления удается на первых порах обрисовать лишь гипотетически. Как избежать ошибок?
Многочисленные варианты схожих преступлений записываются на специальных карточках и затем сравниваются. Так выявляется, как говорят специалисты, "вариабельность" способов совершения преступления. Но систематизация вариантов сложна, и способ сопоставления карточек весьма громоздок.
Метод алгоритмического изображения позволяет находить более простое и точное решение. Вот пример анализа различных "телефонных" преступлений.
Запишем с помощью символов следующие данные:
P1: действовал подросток (P'1 не подросток);
B1: будка в глухой местности;
B2: подросток приехал на велосипеде;
B3: пользовался инструментом;
B4: был в нетрезвом состоянии;
B5: действовал не один;
B6: днем (В'6 - ночью).
Отдельные операции изобразим так:
p1: бронированный провод оборван;
p2: бронированный провод обрезан;
p3: похищены детали;
p4: диск погнут;
p5: аппарат разбит;
p6: отверстие для монет засорено;
p7: монетный ящик взломан;
p8: осветительные приборы повреждены;
p9: телефонная книга разорвана;
p10: телефонная книга украдена;
p11: дверные ручки сорваны;
p12: двери сняты с петель;
p13: двери погнуты;
p14: будка загрязнена;
p15: стекла разбиты;
p16: детали выброшены.
Давайте запишем с помощью символов следующие данные: A - нарушитель вошел в телефонную будку, Z - вышел из будки, Pn - нарушитель, Bn - обстоятельства преступления, pn - действия преступника. Тогда для общего случая можно написать такую формулу:
(Pn*Bn) ApnZ.
А для конкретного случая: подросток с велосипедом ночью в уединенной местности камнем разбил стекла, изорвал телефонную книгу и взломал кассу - получается формула частного случая:
(P1*B1*B2*B3*B'6) Ap7p9p15Z.

Всего одна строчка, а вместила в себя огромное количество подробнейшей информации! Понятно, насколько легче сравнивать лаконичные и строгие формулы, которые не зависят от стиля изложения, чем многостраничные протокольные записи с возможными разночтениями.

Логический процесс, особенно в машине, удобнее свести к выбору между различными вариантами. Например, в полицейском управлении Нью-Йорка установлена электронно-вычислительная машина. Как только поступает сообщение об очередном преступлении, в устройство закладывается характеристика преступления в виде специального цифрового кода (ведь машина имеет дело не со словами и даже не с формулами, а с цифрами. А формулу очень легко перевести в такой код). Менее чем за три минуты машина информирует следователя обо всех аналогичных преступлениях, совершавшихся раньше в городе. Следователь смотрит: а не поискать ли автора нового преступления среди уже известных лиц, занесенных в картотеку? В конце концов "манера" преступления, повадки, "почерк" нарушителя - очень стойкие характеристики, которые трудно изменить, как ни старайся. Но ведь изучение сходства и различий в характере преступлений - это и есть сравнение вариантов! А краткие формулы, как уже говорилось, сравнить проще, чем пухлые досье.
ИНФОРМАЦИЯ, ИГРА, ВЕРОЯТНОСТЬ
Мы рассказали только об алгоритмизации процесса преступления. Но криминалистика берет на вооружение и другие средства новой науки.
Электронные устройства применяются при экспертизах. Ведь, к примеру, выявление и изучение следов и других данных преступления имеют информационно-техническую природу и поэтому доступны кибернетическому анализу. А доказательство идентичности? Уже сегодня сконструированы автоматы, способные "ощупать" следы ног, отпечатки пальцев царапины от инструмента, воспринять и нужным образом закодировать их информационное содержание, чтобы, сравнив оригинал со следом, установить их полное или неполное соответствие.
Электронные приборы умеют читать и рукописи. Таким образом удается более объективно сравнивать и анализировать почерки. В рукописном тексте распознаются одни и те же, пусть даже по-разному написанные буквы.
Многие признаки, по которым классифицируются почерки, отпечатки пальцев, патронные гильзы и т.д., можно накапливать в машинной картотеке. Использование этих вспомогательных средств сделает все следствие, анализ способов преступления криминалистическую регистрацию, наконец, исследование причин преступности гораздо эффективнее. И прежде всего неизмеримо их ускорит.
Даже то, что раньше в криминалистике было известно как обыкновенное собрание фактов, теперь в терминах кибернетики - "информация" - приобрело новое качество.
В настоящее время в экономике и военном деле применяют автоматы, играющие в стратегические игры. Эти автоматы быстро, объективно и надежно определяют возможное поведение сторон и вычисляют их тактику. В криминалистике тоже приходится решать стратегические задачи. Ведь здесь тоже имеют дело с событиями, которые определяются информацией, поступившей от заявителя или полученной в результате обследования места преступления, допроса свидетелей и т.д. Появляется несколько обоснованных версий, каждая с определенной степенью вероятности.
Иногда бывает, что не только замалчивается информация, полезная для раскрытия преступления, но сознательно или бессознательно вводится так называемый "шум" - посторонняя информация, не имеющая никакого отношения к событию и мешающая раскрытию преступления.
По собранным фактам криминалист составляет стратегический план расследования и отдельных его этапов - шагов. Цель допроса обвиняемого и свидетелей состоит в том, чтобы получить или проверить информацию, касающуюся расследуемого события. Допрос с точки зрения кибернетики - это стратегическая игра, допрашивающий и допрашиваемый противостоят друг другу как противники.
Все это звучит несколько непривычно. Ведь в самом характере допроса есть не только тактические принципы кибернетической игры. Тем не менее в основе поиска правильного решения лежит кибернетическая система. Обе стороны пытаются в соответствии со своей тактикой, поведением, показаниями и вопросами добиться, как говорят кибернетики, "максимально стабильной ситуации".
Информация о преступлении во время допроса анализируется допрашивающим. Результат допроса проверяется. Ведущий допрос убеждается в успехе (или в неудаче) своих действий и на основании этого вырабатывает новую тактику. Противоречия свидетельствуют о неустойчивости системы. Только по устранении всех противоречий система приобретает стабильность и следователь с облегчением может сказать: "Все ясно, преступление раскрыто!"
Конечно, наша криминалистика учитывает и важнейший принцип социалистического законодательства - должное отношение к человеку. Для нас даже возможный преступник - это не просто "противник по кибернетической игре".
ИТАК, ВЫЧИСЛЯЕМ ВИНОВНОГО
В криминалистике применяется не только теория информации, а и такая чисто математическая дисциплина, как теория вероятностей. Без нее не обходятся в почерковедении, дактилоскопии, спектральном анализе вещественных доказательств. Появились работы, использующие логический аппарат теории вероятностей для моделирования процесса доказывания. Математическая статистика участвует как в экспертизе, так и в анализе преступлений.
Применяет криминалистика как дифференциальное, так и интегральное исчисления, когда решаются проблемы причинности. Тригонометрия используется, чтобы математически фиксировать события, запечатленные на фотографии. Не лишены значения для криминалистики номография, алгебра и, конечно, математическая логика.
Вот простой случай применения логики Это, правда, не уголовное дело. Но и тут надо найти виновного.
В классе разбили окно. Сделать это мог только кто-то из четверых: Леня, Дима, Толя или Миша.
При опросе каждый дал по три показания:
Леня: 1) я не виноват, 2) я даже не подходил к окну, 3) Миша знает, кто это сделал.
Дима: 1) стекло разбил не я, 2) с Мишей я не был знаком до поступления в школу, 3) это сделал Толя.
Толя: 1) я не виновен, 2) это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло.
Миша: 1) я не виноват, 2) стекло разбил Леня, 3) Дима может поручиться за меня, так как хорошо знает меня.
При дальнейших расспросах каждый из учеников признал, что из сделанных им трех заявлений два верных и одно ложное. Можно ли логическим путем найти виновника? Попробуем представить задачу в виде формул и уравнений.
Алгебра логики утверждает, что любое сложное высказывание можно представить в виде нескольких простых, употребляя логические связи ИЛИ, И, НЕ. Обычно принято слово ИЛИ обозначать крестиком "плюс", а слово И - знаком умножения - точкой. Теперь остается каждое простое высказывание обозначить для сокращения какой-либо буквой, а его отрицание - той же буквой, но с черточкой наверху.
Известно, что всякое логическое суждение может быть либо истинным, либо ложным. Истинное высказывание обозначается единицей, а ложное - нулем. Например, если какое-либо высказывание В = 1. то В' = 0. И наоборот: если В = 0, то B' = 1.
Разберемся еще с несколькими положениями математической логики.
Ясно, что B+B = B и B*B = B. Столь же очевидны и два положения; В+В' = 1 и В*В' = 0, а также В*0 = 0, В*1 = В, В+0 = В.
Теперь можно приступить к делу - вычислить виновного.
Вспомним, что из трех показаний каждого ученика одно ложно, а два истинных. Значит, сложное высказывание каждого из них будет истинным (равным единице), когда верно первое, второе и третье. Будем обозначать показание каждого из учеников заглавной буквой его имени с номером показания внизу. Тогда заявление Лени логично записать такой формулой:
Л = Л1*Л2*Л3'+Л1*Л2'*Л3+Л1'*Л2*Л3.
Точно так же изобразим показания остальных учеников.
Димы: Д = Д1*Д2*Д3'+Д1*Д2'*Д3+Д1'*Д2*Д3.
Толи: Т = Т1*Т2*Т3'+Т1*Т2'*Т3+Т1'*Т2*Т3.
Миши: М = М1*М2*М3'+М1*М2'*М3+М1'*М2*М3.
Если внимательно проследить показания учеников, то легко заметить, что первое и третье показания Толи равносильны. Действительно, ведь утверждение "Я не виновен", по существу, не отличается от утверждения "Дима говорит неправду, что я разбил стекло". Но тогда Т3 = Т1 а Т3' = Т1' и его заявление можно теперь написать так:
Т = Т1*Т2*Т1'+Т1*Т2'*Т1+Т1'*Т2*Т1
или
Т = (Т1*Т1')*Т2+(Т1*Т1)*Т2'+(Т1*Т1')*Т2.
Но мы знаем уже, что противоречивые высказывания дают ложь. Поэтому
(Т1*Т1')=0.
А если один из сомножителей равен нулю, то все произведение равно нулю, и заявление Толи примет такой вид:
Т = Т1*Т1*Т2' = Т1*Т2'.
Оно будет истинным - равным единице, если каждый из сомножителей равен единице. Следовательно:
Т1 = 1 и Т2' = 1 или Т2 = 0.
Таким образом, мы нашли, что первое показание Толи верно, а второе ложно. А так как он сказал: "1) я не виновен, 2) это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло",- то ясно, что стекло разбил не Толя и не Миша.
Но теперь уже очевидно, что третье показание Димы, в котором он обвиняет Толю, ложно. Значит, Д3 = 0 и Д3' = 1. А раз так, то в заявлении Димы, записанном в виде формулы, последние два слагаемых обратятся в нуль, и формула примет простой вид:
Д = Д1*Д2*Д3'.
И снова заявление будет истинным, если каждый из сомножителей равен единице. Но мы уже нашли, что Д3' = 1 и, следовательно, Д1 = 1 и Д2 = 1. Первое и третье показания Димы верны. Следовательно, Дима не виновен.
Третье показание Миши противоположно второму показанию Димы: М3 = Д2'. Значит, М3 = 0, а М3' = 1, и заявление Миши теперь пишется так: М = М1*М2*М3'. Оно истинно только в том случае, когда M1 = l, М2 = 1, М3' = 1.
Второе показание Миши истинно: стекло разбил Леня! Так формулы математической логики помогли быстро и безошибочно найти виновника.
ПОИСКИ ПОДЖИГАТЕЛЯ
Немного уяснив элементы алгебры логики, мы сможем сейчас смело устремиться вместе со следователем на поиски поджигателя дома в пункте Е, совершившего свое преступление в момент времени t0. Успех следствия здесь во многом зависит от того, сумеем ли мы установить и проверить маршруты следования нескольких человек в течение возможно короткого времени, максимально близкого ко времени поджога Обозначим это время ta < t0 < te.

(Художник сжульничал - по второй оси откладывается время, т.е. все происходит на одной улице.- G.)
При расспросах выяснилось следующее: в указанный промежуток времени, от ta до te, вблизи места пожара побывало 5 человек: Р1, Р2, Р3, Р4 и Рх, причем личность Рх следственным органам еще неизвестна. В связи с этим нужно установить, кто, когда и где находился. Р1, Р3 и Р4 - пешеходы и, как они говорят, шли нормальным шагом (70м в минуту). Р2 пользовался велосипедом (15км/час), а Рх ехал на мотоцикле не быстрее 60км/час. Анализ маршрутов этих людей выявил следующую картину: P1 шел из S1 в S1' во время от t1 до t1'. При этом в точке М13 он встретился с Р3, что последний подтвердил. Далее P1 показал, что видел Рx в точке M1x и Р2 в точке M12.
P2 ехал на велосипеде из S2 ь S2' во время между t2 и t2' и в точке M12 встретился с P1. Никого больше он не видел и не встретил.
Р3 шел из S3 в S3' в промежуток времени от t3 до t3' и в пункте М13 встретил P1. Это подтвердил P1. Далее Р3 сказал, что видел Рх в пункте М3х.
Р4, шедший во время от t4 до t4' из S4 в S4', встретил Р3 в М43, Рх в М4х и Р2 в М42.
Показания Pi1 и Р2 можно принять за истинные, поскольку они не противоречат никаким другим. На основе показаний Р3 и Р4 возникают два предположения: Р3 после встречи с P1 в точке М13 направился в пункт S3', встретившись на этом пути с Рх в точке М3х " или же он направился после этого по пути к пункту Se через Е, встретив Рх на этом пути.
Однако при учете скоростей передвижения Р1, Р3 и Рх оказывается, что Р3 не мог встретить Рх в точке М3х. Отсюда следует, чго Р3 направился по пути к пункту Se, пройдя через Е.
Обозначим высказывание "Р3 направился после встречи с P1 в точке М13 в пункт S3'" через А,
"Р3 встретился с Рх в точке М3х" - В.
"Р3 направился (после точки М13) в пункт Se" - С,
"Р3 прошел через пункт Е" - Е.
Указанные две версии запишутся так: A*B+C*E.
Учитывая, что В не истинно, получим:
(А*В+С*Е)*В' = А*В*В'+С*Е*В' = 0+С*Е*1 = С*Е = 1.
Отсюда Е = 1.
Таким образом получаем указанное выше заключение. Зная время t1 и расстояния от S1 до М13, а также от М13 до Е, нетрудно установить, находился ли Р3 в Е как раз во время t0, то есть в месте, где случился пожар.
Математическое проникновение в запутанные лабиринты преступлений может быть гораздо сложнее. Число и формула в комплексе с другими средствами помогают расследованию причин пожаров, взрывов, аварий, убийств.
Не за горами время, когда при помощи кибернетики можно будет выявить и разрешить самые запутанные противоречия в ходе следствия. А электронные модели позволят "разыгрывать" множество различных вариантов преступлений, основанных на множестве переменных условий. И все это машина сделает с неимоверной быстротой и точностью. Поэтому для следователя не будет даже проблемой "попробовать" на машине вообще все мыслимые варианты расследуемого преступления.
Кибернетика, придя в криминалистику, утверждается в ней основательно, и, вероятно, совсем уж недалека перспектива, когда невозможно будет никакими ухищрениями скрыть преступление или запутать следствие.
***
ДАКТИЛОСКОПИЯ
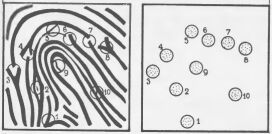
Пальцевый узор (слева) и код его частных признаков (справа). Цифрами слева помечены частные признаки, справа - теми же цифрами - точки координатной сетки, соответствующие признакам.
Как узнать, кто оставил следы пальцев - так называемые папиллярные узоры, которые свойственны каждому человеку и неизменны на протяжении всей жизни? Достаточно проверить, не содержатся ли подобные отпечатки в дактилоскопической картотеке, где зарегистрированы преступники. Это делает электронно-вычислительная машина, просматривая сотни тысяч отпечатков со скоростью тысячи отпечатков в несколько минут.
***
ПОЧЕРКОВЕДЕНИЕ
При сравнении особенностей письма определяется частота, с какой встречается в тексте тот или иной признак. Чем ома меньше, тем ярче выражена индивидуальность почерка.
Для машины составляется программа определения почерка. По ней машина обучается. Затем она исследует текст. Например, машина должна сгруппировать все сведения о буквах "А" (написанных Ивановым) в виде области многомерного пространства и запомнить их.
То же с буквами "А", допустим, Петрова. Машина формирует области всех "А" Иванова и области всех "А" Петрова и проводит между ними границу. Так она обучается, узнает, как пишет букву "А" один и другой. Теперь машина может сравнить свои "энания" с текстом, который ей предъявят, и ответить, кто автор того или иного документа.

Слева - компактная многомерная область всех "А", написанных Ивановым; справа - всех "А", написанных Петровым. Линия между ними условно изображает разграничивающую их поверхность.
***
ПРОГРАММА КВАЛИФИКАЦИИ КРАЖИ, ГРАБЕЖА И РАЗБОЯ
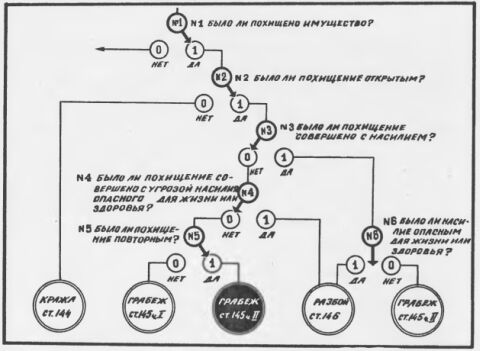
Перед вами электрическая схема, классифицирующая преступления. Поворот переключателя направо - Да, налево - Нет.
Первый вопрос: было ли у потерпевшего похищено имущество? Да. (Если нет, то последующая работа бессмысленна). Поворот направо.
Второй вопрос: тайно или открыто похищено имущество? Материалы следствия говорят: да, открыто. Поворот направо.
Третий вопрос: с насилием или без насилия было изъято имущество. Насилия не было.
Четвертый вопрос: относительно угрозы. Ее тоже не было.
Пятый вопрос: было ли преступление повторным? Да.
Итак, налицо преступление, предусмотренное ч.II, ст.145 УК РСФСР (грабеж, совершенный лицом, уже осужденным ранее за хищение имущества).
Алгоритм квалификации преступления можно выразить и цифрами. Обозначим: Да - 1, а Нет - 0. Тогда описанный случай грабежа обозначится так: 11001. Другие случаи: 1110 и 11000. Разбой можно обозначить двумя наборами цифр: 1101 и 1111. Если теперь эти цифры вместе с программой заложить в машину, то она легко даст квалификацию преступления.
В. ПЕКЕЛИС
С ФОРМУЛАМИ В ЛАБИРИНТАХ ПРЕСТУПЛЕНИЯ
КИБЕРНЕТИКА В КРИМИНАЛИСТИКЕ
МАТЕМАТИК В РОЛИ СЛЕДОВАТЕЛЯ МАШИНА ПЛАНИРУЕТ РАССЛЕДОВАНИЕ
РИСУНКИ Ю.МАКАРЕНКО И Ю.СЛУЧЕВСКОГО

0.pa1/0.A2.Bpb3/0.Cpc4/3Dpd5/0.E
Сначала - впрочем, давно уже прежде - его занимал один вопрос: почему так легко отыскиваются и выдаются почти все преступления и так явно обозначаются следы почти всех преступников?
/Ф.Достоевский. "Преступление и наказание"/
Помните полную драматического напряжения сцену, нарисованную Достоевским в романе "Преступление и наказание"?
"Лестница к старухе была близко, сейчас из ворот направо. Он уже был на лестнице...
Переведя дух и прижав рукой стукавшее сердце, тут же нащупав и оправив еще раз топор, он стал осторожно и тихо подниматься на лестницу, поминутно прислушиваясь. Но и лестница на ту пору стояла совсем пустая; все двери были заперты; никого-то не встретилось. Во втором этаже одна пустая квартира была, правда, растворена настежь, и в ней работали маляры, но те и не поглядели. Он постоял, подумал и пошел дальше".
Далее следует психологически точное описание того, как Раскольников поднимался по лестнице, звонил к ростовщице, чуть ли не силой открыл к ней дверь, затем, отдав старухе фальшивую табакерку, улучил момент и "...вынул топор совсем, взмахнул его обеими руками, едва себя чувствуя и почти без усилия, почти машинально, опустил на голову обухом". Преступление свершилось. А наказание?
Долог, ой, как долог и многотруден был путь к возмездию! На какие только ухищрения не пускался следователь Порфирий Петрович, чтобы уличить виновного! Какой интуицией, какими аналитическими способностями, какой памятью надо обладать человеку, чтобы безошибочно и в то же время деликатно, не унижая человеческого достоинства подозреваемых, прийти к правильному выводу!
Интуиция... А если вместо нее точный расчет? А если прибегнуть к услугам машины, ее аналитического "ума" и памяти, которые раньше считались чисто человеческими свойствами? Что тогда?
Созданная рукой гениального художника картина убийства, взятая отдельно, лишь в логической последовательности действий, на языке кибернетики была бы записана гораздо лаконичней - формулой, как вы видите в заголовке.
Для чего нужна такая запись? Чтобы ответить, познакомимся с заурядным преступлением, совершенным сто лет спустя, в наши дни.
Когда старый рецидивист вор-"домушник" Чесноков узнал, что одинокий художник, назовем его N, тяжело заболел и отправлен в больницу, он предложил своему зятю Соловьеву "выгодное дельце": проникнуть в квартиру художника и похитить вещи и картины.
Соловьев согласился. Было решено выполнить задуманное вечером, на следующий день. Весь ход ограбления преступники продумали самым тщательным образом, предусмотрев, казалось бы, все до последней мелочи. Обсудили и какими инструментами действовать. Условились захватить с собой отвертку и нож, чтобы выковырять оконную замазку. Не забыли и о свежей замазке, чтобы вставить стекло, а также о мешках и шпагате для упаковки краденого.
План ограбления строился так. После того как в доме погасят огни, проникнуть в квартиру художника через парадный либо через черный ход или через окно в подвале. В крайнем случае через одно из окон со стороны двора.
Предварительная разведка показала: двери парадного и черного ходов нельзя взломать без шума. Окно в подвал, вероятно, удалось бы открыть, но ведь дверь из подвала в квартиру могла быть заперта! Тогда преступники решили пробраться в квартиру через окно со двора.
Как только стемнело и все кругом стихло, Чесноков вытащил из сарая соседнего дома припрятанную заранее лестницу и приставил ее к стене. Соловьев добрался до окна и попытался выдавить стекло. Не удалось. Тогда вор аккуратно удалил замазку ножом и осторожно вынул стекло.
В квартиру забрались вместе, затащив лестницу в окно, которое тут же закрыли. Быстро "обработав" квартиру, перешли в мастерскую. Времени оставалось в обрез, поэтому холсты вырезали бритвами, наспех свертывали в трубки и туго затягивали шпагатом. Вещи и картины, уложенные в мешки, вынесли через окно во двор. Окно закрыли, вставили на место стекло и тщательно замазали щели. Теперь оставалось осторожно перенести мешки в укромное место, а потом "реализовать" награбленное.
АЛГОРИТМ ПРЕСТУПЛЕНИЯ
Вот как выглядит запись этого преступления, если мы условимся, что Чесноков - это X, Соколов - Y, художник - N, а различные ситуации и действия обозначены разными символами.
А: узнать, находится ли N в больнице. pa: находится N в больнице?
В: уговорить Y участвовать в краже. рb: будет Y участвовать?
С: подойти скрытно к месту действия. рс: видел ли кто-нибудь?
D: когда соседи погасят свет, открыть парадную дверь. рd: погашен ли свет? p'd: отворили парадную дверь?
Е: если условие D невыполнимо, то взломать черный ход. ре: заперт ли черныйcход?
F: если условие Е невыполнимо, то проникнуть в квартиру через окно из подвала. pf: доступ в квартиру невозможен?
G: если условие F невыполнимо, то проникнуть в квартиру через окно во дворе. Если нельзя выдавись стекло извне, то удалить замазку. pg: доступ возможен?
H: похитить вещи и картины и вынести во двор. ph: вещи, картины похищены и вынесены?
К: если никто не видит, вмазать стекло на место. рк: никто не видит?
L: удалиться с похищенным добром.
Весь ход событий теперь может быть символически записан так:

0.Apa1/0.Bpb2/0.Cpc3/0.pd4/3.Dp'd5/4.HphСТОП/5.Epe6/5.Fpf7/5.GpgСТОП.Hph8.Kpk9/7.L
Невольно еще раз возникает вопрос: зачем простой и ясный рассказ о преступлении, записанный на понятном всем языке, кодировать условными знаками да еще записывать в виде набора символов со стрелками?
Мы поставили в заголовке "Алгоритм преступления". Алгоритм - это набор очень простых правил, из которых складывается процесс решения даже самой сложной задачи. Для краткости правила записываются в виде формул.
Алгоритм как бы назначает очередность возможных операций и управляет ею. И, что очень ценно, последовательность операций нередко выявляется по ходу дела.
Наряду с описанием операций алгоритм содержит еще и логические требования. Каждому из них можно предпослать такой вопрос, чтобы утвердительный ответ означал бы исполненное требование, а отрицательный - невыполненное.
Такой способ записи очень удобен для детальной оценки преступного действия и для анализа подготовки преступления, его исполнения и сокрытия следов. Теперь мы можем в этом убедиться, если вновь посмотрим на символическую запись всего хода ограбления (если условие исполнено, то следуют по стрелке, направленной вверх, в противном случае - направленной вниз).
ВЫЧИСЛЕНИЕ "ВАРИАБЕЛЬНОСТИ"
Ясно, какое значение для следствия имеет оценка подготовки преступления, его исполнения и сокрытия.
Как правило, вначале суть дела еще не вполне ясна, а преступник неизвестен. Поэтому способ и манеру преступления удается на первых порах обрисовать лишь гипотетически. Как избежать ошибок?
Многочисленные варианты схожих преступлений записываются на специальных карточках и затем сравниваются. Так выявляется, как говорят специалисты, "вариабельность" способов совершения преступления. Но систематизация вариантов сложна, и способ сопоставления карточек весьма громоздок.
Метод алгоритмического изображения позволяет находить более простое и точное решение. Вот пример анализа различных "телефонных" преступлений.
Запишем с помощью символов следующие данные:
P1: действовал подросток (P'1 не подросток);
B1: будка в глухой местности;
B2: подросток приехал на велосипеде;
B3: пользовался инструментом;
B4: был в нетрезвом состоянии;
B5: действовал не один;
B6: днем (В'6 - ночью).
Отдельные операции изобразим так:
p1: бронированный провод оборван;
p2: бронированный провод обрезан;
p3: похищены детали;
p4: диск погнут;
p5: аппарат разбит;
p6: отверстие для монет засорено;
p7: монетный ящик взломан;
p8: осветительные приборы повреждены;
p9: телефонная книга разорвана;
p10: телефонная книга украдена;
p11: дверные ручки сорваны;
p12: двери сняты с петель;
p13: двери погнуты;
p14: будка загрязнена;
p15: стекла разбиты;
p16: детали выброшены.
Давайте запишем с помощью символов следующие данные: A - нарушитель вошел в телефонную будку, Z - вышел из будки, Pn - нарушитель, Bn - обстоятельства преступления, pn - действия преступника. Тогда для общего случая можно написать такую формулу:
(Pn*Bn) ApnZ.
А для конкретного случая: подросток с велосипедом ночью в уединенной местности камнем разбил стекла, изорвал телефонную книгу и взломал кассу - получается формула частного случая:
(P1*B1*B2*B3*B'6) Ap7p9p15Z.

Всего одна строчка, а вместила в себя огромное количество подробнейшей информации! Понятно, насколько легче сравнивать лаконичные и строгие формулы, которые не зависят от стиля изложения, чем многостраничные протокольные записи с возможными разночтениями.

Логический процесс, особенно в машине, удобнее свести к выбору между различными вариантами. Например, в полицейском управлении Нью-Йорка установлена электронно-вычислительная машина. Как только поступает сообщение об очередном преступлении, в устройство закладывается характеристика преступления в виде специального цифрового кода (ведь машина имеет дело не со словами и даже не с формулами, а с цифрами. А формулу очень легко перевести в такой код). Менее чем за три минуты машина информирует следователя обо всех аналогичных преступлениях, совершавшихся раньше в городе. Следователь смотрит: а не поискать ли автора нового преступления среди уже известных лиц, занесенных в картотеку? В конце концов "манера" преступления, повадки, "почерк" нарушителя - очень стойкие характеристики, которые трудно изменить, как ни старайся. Но ведь изучение сходства и различий в характере преступлений - это и есть сравнение вариантов! А краткие формулы, как уже говорилось, сравнить проще, чем пухлые досье.
ИНФОРМАЦИЯ, ИГРА, ВЕРОЯТНОСТЬ
Мы рассказали только об алгоритмизации процесса преступления. Но криминалистика берет на вооружение и другие средства новой науки.
Электронные устройства применяются при экспертизах. Ведь, к примеру, выявление и изучение следов и других данных преступления имеют информационно-техническую природу и поэтому доступны кибернетическому анализу. А доказательство идентичности? Уже сегодня сконструированы автоматы, способные "ощупать" следы ног, отпечатки пальцев царапины от инструмента, воспринять и нужным образом закодировать их информационное содержание, чтобы, сравнив оригинал со следом, установить их полное или неполное соответствие.
Электронные приборы умеют читать и рукописи. Таким образом удается более объективно сравнивать и анализировать почерки. В рукописном тексте распознаются одни и те же, пусть даже по-разному написанные буквы.
Многие признаки, по которым классифицируются почерки, отпечатки пальцев, патронные гильзы и т.д., можно накапливать в машинной картотеке. Использование этих вспомогательных средств сделает все следствие, анализ способов преступления криминалистическую регистрацию, наконец, исследование причин преступности гораздо эффективнее. И прежде всего неизмеримо их ускорит.
Даже то, что раньше в криминалистике было известно как обыкновенное собрание фактов, теперь в терминах кибернетики - "информация" - приобрело новое качество.
В настоящее время в экономике и военном деле применяют автоматы, играющие в стратегические игры. Эти автоматы быстро, объективно и надежно определяют возможное поведение сторон и вычисляют их тактику. В криминалистике тоже приходится решать стратегические задачи. Ведь здесь тоже имеют дело с событиями, которые определяются информацией, поступившей от заявителя или полученной в результате обследования места преступления, допроса свидетелей и т.д. Появляется несколько обоснованных версий, каждая с определенной степенью вероятности.
Иногда бывает, что не только замалчивается информация, полезная для раскрытия преступления, но сознательно или бессознательно вводится так называемый "шум" - посторонняя информация, не имеющая никакого отношения к событию и мешающая раскрытию преступления.
По собранным фактам криминалист составляет стратегический план расследования и отдельных его этапов - шагов. Цель допроса обвиняемого и свидетелей состоит в том, чтобы получить или проверить информацию, касающуюся расследуемого события. Допрос с точки зрения кибернетики - это стратегическая игра, допрашивающий и допрашиваемый противостоят друг другу как противники.
Все это звучит несколько непривычно. Ведь в самом характере допроса есть не только тактические принципы кибернетической игры. Тем не менее в основе поиска правильного решения лежит кибернетическая система. Обе стороны пытаются в соответствии со своей тактикой, поведением, показаниями и вопросами добиться, как говорят кибернетики, "максимально стабильной ситуации".
Информация о преступлении во время допроса анализируется допрашивающим. Результат допроса проверяется. Ведущий допрос убеждается в успехе (или в неудаче) своих действий и на основании этого вырабатывает новую тактику. Противоречия свидетельствуют о неустойчивости системы. Только по устранении всех противоречий система приобретает стабильность и следователь с облегчением может сказать: "Все ясно, преступление раскрыто!"
Конечно, наша криминалистика учитывает и важнейший принцип социалистического законодательства - должное отношение к человеку. Для нас даже возможный преступник - это не просто "противник по кибернетической игре".
ИТАК, ВЫЧИСЛЯЕМ ВИНОВНОГО
В криминалистике применяется не только теория информации, а и такая чисто математическая дисциплина, как теория вероятностей. Без нее не обходятся в почерковедении, дактилоскопии, спектральном анализе вещественных доказательств. Появились работы, использующие логический аппарат теории вероятностей для моделирования процесса доказывания. Математическая статистика участвует как в экспертизе, так и в анализе преступлений.
Применяет криминалистика как дифференциальное, так и интегральное исчисления, когда решаются проблемы причинности. Тригонометрия используется, чтобы математически фиксировать события, запечатленные на фотографии. Не лишены значения для криминалистики номография, алгебра и, конечно, математическая логика.
Вот простой случай применения логики Это, правда, не уголовное дело. Но и тут надо найти виновного.
В классе разбили окно. Сделать это мог только кто-то из четверых: Леня, Дима, Толя или Миша.
При опросе каждый дал по три показания:
Леня: 1) я не виноват, 2) я даже не подходил к окну, 3) Миша знает, кто это сделал.
Дима: 1) стекло разбил не я, 2) с Мишей я не был знаком до поступления в школу, 3) это сделал Толя.
Толя: 1) я не виновен, 2) это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло.
Миша: 1) я не виноват, 2) стекло разбил Леня, 3) Дима может поручиться за меня, так как хорошо знает меня.
При дальнейших расспросах каждый из учеников признал, что из сделанных им трех заявлений два верных и одно ложное. Можно ли логическим путем найти виновника? Попробуем представить задачу в виде формул и уравнений.
Алгебра логики утверждает, что любое сложное высказывание можно представить в виде нескольких простых, употребляя логические связи ИЛИ, И, НЕ. Обычно принято слово ИЛИ обозначать крестиком "плюс", а слово И - знаком умножения - точкой. Теперь остается каждое простое высказывание обозначить для сокращения какой-либо буквой, а его отрицание - той же буквой, но с черточкой наверху.
Известно, что всякое логическое суждение может быть либо истинным, либо ложным. Истинное высказывание обозначается единицей, а ложное - нулем. Например, если какое-либо высказывание В = 1. то В' = 0. И наоборот: если В = 0, то B' = 1.
Разберемся еще с несколькими положениями математической логики.
Ясно, что B+B = B и B*B = B. Столь же очевидны и два положения; В+В' = 1 и В*В' = 0, а также В*0 = 0, В*1 = В, В+0 = В.
Теперь можно приступить к делу - вычислить виновного.
Вспомним, что из трех показаний каждого ученика одно ложно, а два истинных. Значит, сложное высказывание каждого из них будет истинным (равным единице), когда верно первое, второе и третье. Будем обозначать показание каждого из учеников заглавной буквой его имени с номером показания внизу. Тогда заявление Лени логично записать такой формулой:
Л = Л1*Л2*Л3'+Л1*Л2'*Л3+Л1'*Л2*Л3.
Точно так же изобразим показания остальных учеников.
Димы: Д = Д1*Д2*Д3'+Д1*Д2'*Д3+Д1'*Д2*Д3.
Толи: Т = Т1*Т2*Т3'+Т1*Т2'*Т3+Т1'*Т2*Т3.
Миши: М = М1*М2*М3'+М1*М2'*М3+М1'*М2*М3.
Если внимательно проследить показания учеников, то легко заметить, что первое и третье показания Толи равносильны. Действительно, ведь утверждение "Я не виновен", по существу, не отличается от утверждения "Дима говорит неправду, что я разбил стекло". Но тогда Т3 = Т1 а Т3' = Т1' и его заявление можно теперь написать так:
Т = Т1*Т2*Т1'+Т1*Т2'*Т1+Т1'*Т2*Т1
или
Т = (Т1*Т1')*Т2+(Т1*Т1)*Т2'+(Т1*Т1')*Т2.
Но мы знаем уже, что противоречивые высказывания дают ложь. Поэтому
(Т1*Т1')=0.
А если один из сомножителей равен нулю, то все произведение равно нулю, и заявление Толи примет такой вид:
Т = Т1*Т1*Т2' = Т1*Т2'.
Оно будет истинным - равным единице, если каждый из сомножителей равен единице. Следовательно:
Т1 = 1 и Т2' = 1 или Т2 = 0.
Таким образом, мы нашли, что первое показание Толи верно, а второе ложно. А так как он сказал: "1) я не виновен, 2) это сделал Миша, 3) Дима говорит неправду, утверждая, что я разбил стекло",- то ясно, что стекло разбил не Толя и не Миша.
Но теперь уже очевидно, что третье показание Димы, в котором он обвиняет Толю, ложно. Значит, Д3 = 0 и Д3' = 1. А раз так, то в заявлении Димы, записанном в виде формулы, последние два слагаемых обратятся в нуль, и формула примет простой вид:
Д = Д1*Д2*Д3'.
И снова заявление будет истинным, если каждый из сомножителей равен единице. Но мы уже нашли, что Д3' = 1 и, следовательно, Д1 = 1 и Д2 = 1. Первое и третье показания Димы верны. Следовательно, Дима не виновен.
Третье показание Миши противоположно второму показанию Димы: М3 = Д2'. Значит, М3 = 0, а М3' = 1, и заявление Миши теперь пишется так: М = М1*М2*М3'. Оно истинно только в том случае, когда M1 = l, М2 = 1, М3' = 1.
Второе показание Миши истинно: стекло разбил Леня! Так формулы математической логики помогли быстро и безошибочно найти виновника.
ПОИСКИ ПОДЖИГАТЕЛЯ
Немного уяснив элементы алгебры логики, мы сможем сейчас смело устремиться вместе со следователем на поиски поджигателя дома в пункте Е, совершившего свое преступление в момент времени t0. Успех следствия здесь во многом зависит от того, сумеем ли мы установить и проверить маршруты следования нескольких человек в течение возможно короткого времени, максимально близкого ко времени поджога Обозначим это время ta < t0 < te.

(Художник сжульничал - по второй оси откладывается время, т.е. все происходит на одной улице.- G.)
При расспросах выяснилось следующее: в указанный промежуток времени, от ta до te, вблизи места пожара побывало 5 человек: Р1, Р2, Р3, Р4 и Рх, причем личность Рх следственным органам еще неизвестна. В связи с этим нужно установить, кто, когда и где находился. Р1, Р3 и Р4 - пешеходы и, как они говорят, шли нормальным шагом (70м в минуту). Р2 пользовался велосипедом (15км/час), а Рх ехал на мотоцикле не быстрее 60км/час. Анализ маршрутов этих людей выявил следующую картину: P1 шел из S1 в S1' во время от t1 до t1'. При этом в точке М13 он встретился с Р3, что последний подтвердил. Далее P1 показал, что видел Рx в точке M1x и Р2 в точке M12.
P2 ехал на велосипеде из S2 ь S2' во время между t2 и t2' и в точке M12 встретился с P1. Никого больше он не видел и не встретил.
Р3 шел из S3 в S3' в промежуток времени от t3 до t3' и в пункте М13 встретил P1. Это подтвердил P1. Далее Р3 сказал, что видел Рх в пункте М3х.
Р4, шедший во время от t4 до t4' из S4 в S4', встретил Р3 в М43, Рх в М4х и Р2 в М42.
Показания Pi1 и Р2 можно принять за истинные, поскольку они не противоречат никаким другим. На основе показаний Р3 и Р4 возникают два предположения: Р3 после встречи с P1 в точке М13 направился в пункт S3', встретившись на этом пути с Рх в точке М3х " или же он направился после этого по пути к пункту Se через Е, встретив Рх на этом пути.
Однако при учете скоростей передвижения Р1, Р3 и Рх оказывается, что Р3 не мог встретить Рх в точке М3х. Отсюда следует, чго Р3 направился по пути к пункту Se, пройдя через Е.
Обозначим высказывание "Р3 направился после встречи с P1 в точке М13 в пункт S3'" через А,
"Р3 встретился с Рх в точке М3х" - В.
"Р3 направился (после точки М13) в пункт Se" - С,
"Р3 прошел через пункт Е" - Е.
Указанные две версии запишутся так: A*B+C*E.
Учитывая, что В не истинно, получим:
(А*В+С*Е)*В' = А*В*В'+С*Е*В' = 0+С*Е*1 = С*Е = 1.
Отсюда Е = 1.
Таким образом получаем указанное выше заключение. Зная время t1 и расстояния от S1 до М13, а также от М13 до Е, нетрудно установить, находился ли Р3 в Е как раз во время t0, то есть в месте, где случился пожар.
Математическое проникновение в запутанные лабиринты преступлений может быть гораздо сложнее. Число и формула в комплексе с другими средствами помогают расследованию причин пожаров, взрывов, аварий, убийств.
Не за горами время, когда при помощи кибернетики можно будет выявить и разрешить самые запутанные противоречия в ходе следствия. А электронные модели позволят "разыгрывать" множество различных вариантов преступлений, основанных на множестве переменных условий. И все это машина сделает с неимоверной быстротой и точностью. Поэтому для следователя не будет даже проблемой "попробовать" на машине вообще все мыслимые варианты расследуемого преступления.
Кибернетика, придя в криминалистику, утверждается в ней основательно, и, вероятно, совсем уж недалека перспектива, когда невозможно будет никакими ухищрениями скрыть преступление или запутать следствие.
***
ДАКТИЛОСКОПИЯ

Пальцевый узор (слева) и код его частных признаков (справа). Цифрами слева помечены частные признаки, справа - теми же цифрами - точки координатной сетки, соответствующие признакам.
Как узнать, кто оставил следы пальцев - так называемые папиллярные узоры, которые свойственны каждому человеку и неизменны на протяжении всей жизни? Достаточно проверить, не содержатся ли подобные отпечатки в дактилоскопической картотеке, где зарегистрированы преступники. Это делает электронно-вычислительная машина, просматривая сотни тысяч отпечатков со скоростью тысячи отпечатков в несколько минут.
***
ПОЧЕРКОВЕДЕНИЕ
При сравнении особенностей письма определяется частота, с какой встречается в тексте тот или иной признак. Чем ома меньше, тем ярче выражена индивидуальность почерка.
Для машины составляется программа определения почерка. По ней машина обучается. Затем она исследует текст. Например, машина должна сгруппировать все сведения о буквах "А" (написанных Ивановым) в виде области многомерного пространства и запомнить их.
То же с буквами "А", допустим, Петрова. Машина формирует области всех "А" Иванова и области всех "А" Петрова и проводит между ними границу. Так она обучается, узнает, как пишет букву "А" один и другой. Теперь машина может сравнить свои "энания" с текстом, который ей предъявят, и ответить, кто автор того или иного документа.

Слева - компактная многомерная область всех "А", написанных Ивановым; справа - всех "А", написанных Петровым. Линия между ними условно изображает разграничивающую их поверхность.
***
ПРОГРАММА КВАЛИФИКАЦИИ КРАЖИ, ГРАБЕЖА И РАЗБОЯ

Перед вами электрическая схема, классифицирующая преступления. Поворот переключателя направо - Да, налево - Нет.
Первый вопрос: было ли у потерпевшего похищено имущество? Да. (Если нет, то последующая работа бессмысленна). Поворот направо.
Второй вопрос: тайно или открыто похищено имущество? Материалы следствия говорят: да, открыто. Поворот направо.
Третий вопрос: с насилием или без насилия было изъято имущество. Насилия не было.
Четвертый вопрос: относительно угрозы. Ее тоже не было.
Пятый вопрос: было ли преступление повторным? Да.
Итак, налицо преступление, предусмотренное ч.II, ст.145 УК РСФСР (грабеж, совершенный лицом, уже осужденным ранее за хищение имущества).
Алгоритм квалификации преступления можно выразить и цифрами. Обозначим: Да - 1, а Нет - 0. Тогда описанный случай грабежа обозначится так: 11001. Другие случаи: 1110 и 11000. Разбой можно обозначить двумя наборами цифр: 1101 и 1111. Если теперь эти цифры вместе с программой заложить в машину, то она легко даст квалификацию преступления.
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 1:05 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Из книги "КОМПЬЮТЕР ОБРЕТАЕТ РАЗУМ" 1990.
УБИЙСТВО В УСАДЬБЕ МАМФРИ
Когда Реджиналд Гартуэйт, граф Мамфри, был обнаружен на полу своей домашней библиотеки, убитый его же собственным ножом для разрезания книг, подозрение почти сразу же пало на хозяина ночного клуба Хью Истуика: решительно всем было известно, что Мамфри недавно обвинил Истуика в попытке обмануть его на крупную сумму. Всего за несколько дней до происшествия многие жители деревни, прогуливаясь по деревенской лужайке, стали свидетелями крупнбго разговора между лордом Мамфри и Истуиком. Разговор этот завершился категорическим отказом лорда заплатить хотя бы пенс и угрозой Истуика отомстить за это.
В день трагического события в числе других гостей в усадьбе Мамфри находился д-р Ричард Хокинс, знаменитый автор детективов, работавший тогда над романом "Байт в ночи". Героем произведения был программист, случайно узнавший о преступлении. Хотя Хокинсу ни разу в жизни не приходилось участвовать в расследовании настоящего убийства, он не сомневался, что ему удастся пролить свет на обстоятельства гибели Мамфри.
Случилось так, что, занимаясь сбором материалов для нового романа, Хокинс присутствовал при совместной работе одного бывалого частного детектива и специалиста по инженерии знаний, которые занимались изготовлением прототипа экспертной системы, предназначенной для расследования преступлений. Хокинс внимательно прислушивался к тому, как программист неутомимо выяснял у детектива его методы раскрытия убийств и допроса подозреваемых. Только после существенных переделок и тщательной проверки детектив согласился, что скопированный с него эрзац-сыщик готов к использованию. Позднее Хокинс приобрел экземпляр программы этой экспертной системы, чтобы иметь возможность украсить свой роман реалистическими деталями.
Почти сразу же после обнаружения тела несчастного лорда Мамфри у писателя возникла мысль, что судьба предоставила ему превосходную возможность проверить, чего стоит его экспертная система. Пока управляющий графа вызывал полицию, а остальные слуги и гости в волнении собрались в бильярдной, Хокинс направился в библиотеку, где несчастный граф встретил свой конец. Для начала Хокинс отметил очевидные обстоятельства случившегося: последний раз лорда Мамфри видели живым за обедом, через полтора часа его тело было обнаружено в домашней библиотеке, на полу рядом с трупом лежал бокал с остатками портвейна...
ПРОНИЦАТЕЛЬНЫЙ НАБЛЮДАТЕЛЬ
Приступив к расследованию, Хокинс мысленно вернулся к моменту, когда было найдено тело. Кто первым упомянул Хью Истуика как наиболее вероятного убийцу? И кто указал на следы на снегу за слегка приоткрытой застекленной дверью? На следах были хорошо видны отпечатки необычного каблука левого ботинка, который Истуику приходилось носить из-за полученного на войне ранения.
Почти все присутствующие пришли к выводу, что лорд Мамфри и на сей раз не отказался от своих привычек, отправившись после обеда в библиотеку отдохнуть с томиком Пруста. Услышав стук в дверь, он встал, чтобы впустить Истуика, жившего примерно в километре от усадьбы, за полем. Между ними вновь разгорелся спор, и в конце концов Истуик вонзил нож для разрезания страниц в сердце лорда.
По-видимому, это объяснение удовлетворило сержанта Блаттерса, который уже прибыл в сопровождении констебля и приступил к опросу всех находившихся в доме. Но Хокинса терзали сомнения. Он быстро спустился к своей машине, достал из отделения для перчаток дискету с экспертной системой и вернулся с ней к домашнему компьютеру лорда Мамфри. Вставив дискету, писатель стал пытаться взвесить все за и против относительно виновности Истуика. Хокинс знал, что прежде всего необходимо сузить круг поисков возможного убийцы. Для этого, исходя из обстоятельств преступления, следует определить, был ли убийца хорошо известен жертве или это был совершенно чужой человек. Все хорошо знали, что лорд Мамфри и Истуик - враги. Но вместе с тем Хокинсу показалось, что разлитый портвейн свидетельствует о том, что в момент убийства Мамфри спокойно держал бокал в руке. Мог ли он быть столь спокоен в присутствии такого человека, как Хью Истуик? Когда Хокинс начал отвечать на возникающие на экране вопросы, его внимание привлекли и другие детали преступления.
На экранах показан диалог между Хокинсом и экспертной системой. Получив от Хокинса вопрос: "Действительно ли убитый знал убийцу и доверял ему?", программа задала относящиеся к делу вопросы, исходя нз своей базы знаний. В данном случае система запрашивает конкретную информацию о месте преступления и состоянии тела жертвы, которая позволит ей построить цепочку рассуждений, приводящих к окончательному ответу.
- Нарушена ли обстановка в комнате?
- Нет
- Есть ли на теле жертвы какие-либо следы насилия, кроме раны, послужившей причиной смерти?
- Нет
- Есть ли следы ног, ведущие к телу снаружи?
- Нет
- Закрыты ли окна и наружные двери, есть ли на них следы взлома?
- Нет
- Где совершено преступление: в кабинете, спальне или гардеробной жертвы?
- Да
ЛОГИЧЕСКАЯ ЦЕПЬ
Сержант Блаттерс проявлял нетерпение, но Хокинс продолжал нажимать клавиши компьютера. Он думал о сотнях правил "если-то" в базе знаний системы. В системах, основанных на правилах, применяются порознь или в комбинации два типа рассуждений - прямая и обратная цепочки. При прямой цепочке рассуждений система начинает с исходных данных и, пользуясь правилами, выводит из них какое-то решение. Фактически пользователь, вводя информацию в систему, задает вопрос: "Какие выводы отсюда следуют?" Если пользователь ввел, например, факт А, система будет искать правило, гласящее "Если А, то В", затем правило "Если В, то С" и т.д. При обратной цепочке рассуждений, которой пользовался Хокинс, решается противоположная задача. Задавшись определенным выводом - в данном случае "убитый знал убийцу и доверял ему" - система пытается доказать этот вывод и проходит логическую цепь в обратном направлении. Если D - это вывод, система ищет все правила вида "Если С, то D", затем правила "Если В, то С" и т.д. Когда процесс достигает точки, в которой часть правила, соответствующая "если", не является выводом из какого-либо другого правила, система требует ввода дополнительной информации. Система Хокинса спрашивала о том, остались ли предметы в комнате на своих местах и были ли царапины на теле убитого. В комнате все оказалось на месте. На руке Мамфри обнаружились царапины, но, по словам управляющего, граф оцарапался о куст розы, когда дрессировал в саду своего бладхаунда. Потом система начала прослеживать другую логическую цепь и спросила, были ли следы вокруг тела. В ответ на этот вопрос Хокинс ответил "Нет", несмотря даже на то, что цепочка следов снаружи указывала, что убийца вошел и вышел через незапертую застекленную дверь. Наблюдательный писатель заметил, что следы ведут к двери и от нее только снаружи, а мокрых (от растаявшего снега) или грязных (от земли в саду) пятен на полу около тела и вообще в комнате нет.
Хокинс знал, что стоит попросить, и система покажет ход своих рассуждений. Он снова запустил программу, но на этот раз, когда система задала тот же вопрос, вместо "Да" или "Нет" ввел ответ "Почему?"; это означало "Почему задан данный вопрос?" Хокинс также мог проверить выводы системы, вводя в ответ "Как?", что означало бы "Каким образом получен этот вывод?" В ответ система перечислила бы все правила "если-то", использованные в ходе рассуждений. Обрабатывая ответы Хокинса на свои вопросы, система выясняла, был ли убийца знаком с жертвой и пользовался ли он ее доверием.
ПРАВИЛА
1) ЕСЛИ жертва не сопротивлялась И нет признаков вторжения И преступление совершено в личных апартаментах жертвы, ТО жертва знала убийцу и доверяла ему.
2) ЕСЛИ обстановка в комнате не нарушена И за исключением смертельной раны следов насилия на теле жертвы нет, ТО жертва не сопротивлялась.
3) ЕСЛИ окна н наружные двери заперты н не имеют следов взлома ИЛИ следы, ведущие к телу жертвы с улицы, отсутствуют, ТО признаков вторжения нет.
4) ЕСЛИ преступление совершено в кабинете жертвы ИЛИ в спальне жертвы ИЛИ в гардеробной жертвы, ТО преступление совершено в личных апартаментах жертвы.
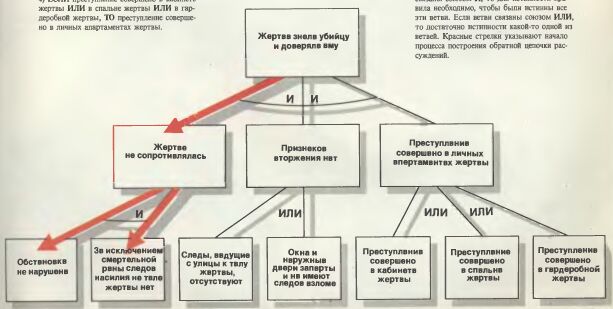
Приведенная диаграмма иллюстрирует взаимосвязи между правилами "если-то", которыми экспертная система пользовалась для выяснения вопроса о знакомстве жертвы с убийцей. Если две или более ветвей правила связаны союзом И, то для истинности правила необходимо, чтобы были истинны все эти ветви. Если ветви связаны союзом ИЛИ, то достаточно истинности какой-то одной из ветвей. Красные стрелки указывают начало процесса построения обратной цепочки рассуждений.
КАК ПОСТУПАЮТ С НЕОПРЕДЕЛЕННОСТЬЮ
Сержант Блаттерс, который уже давно сделал собственный окончательный вывод, ожидал только получения ордера из магистрата, чтобы арестовать Хью Истуика. Опасаясь, что будет арестован невинный, Хокинс на основании выводов экспертной системы подготовил для сержанта свою версию происшедшего. Столь тщательно подготовленная бывалым детективом и специалистом по инженерии знаний экспертная система, как и многие другие подобные ей системы, присваивала численные оценки свидетельским показаниям и выводам из них в зависимости от их надежности, что давало возможность судить, насколько значимы выводы системы.
Как было хорошо известно Хокинсу, реальные детективы часто имеют дело с неполной или неточной информацией - например, со смазанными отпечатками пальцев или сомнительными свидетельскими показаниями. Подобная неопределенность может повлиять и на значимость используемых детективом эмпирических правил. Экспертная система справляется с затруднениями такого рода при помощи коэффициентов уверенности (КУ).
Эти коэффициенты могут быть "встроены" в систему при ее создании с учетом полученного с таким трудом жизненного опыта эксперта. Их может также ввести сам пользователь в ответ на вопросы системы. КУ, равный 1, означает, что эксперт или пользователь абсолютно уверен в данном выводе, а 0 означает "мнения не имею". Если значение КУ лежит в интервале между 0 и 1, то это значит, что эксперт или пользователь не на 100% уверен в выводе или ответе на вопрос. Скажем, лорд Мамфри действительно мог оцарапаться о розовый куст, как утверждал управляющий, но, отвечая на вопрос системы об этом, Хокинс решил, что управляющий мог и солгать, и присвоил своему ответу "Нет" значение КУ, равное 0.8.
Детектив, суждения которого лежали в основе данной экспертной системы, в свою очередь присвоил правилу "Если жертва не сопротивлялась, нет признаков вторжения и преступление совершено в личных апартаментах жертвы, то жертва знала убийцу и доверяла ему" значение коэффициента уверенности 0.9. Иными словами, исходя из своего профессионального опыта, он только на 90% уверен, что если все три условия (все "если") справедливы, то правилен и вывод.
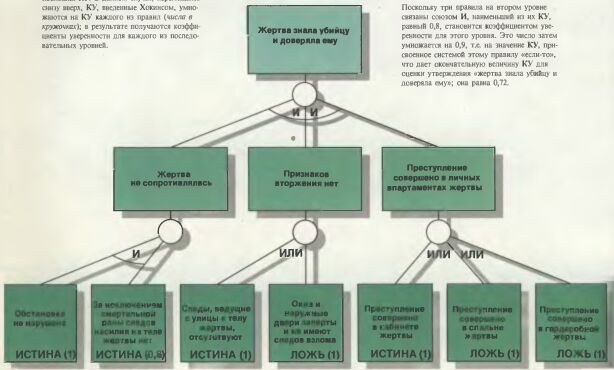
(Тут, в кружках, должны быть числа, но их нет.- G.)
Приведенная здесь диаграмма И-ИЛИ иллюстрирует обычную процедуру оценки достоверности вывода. Если две или более ветвей правила связаны союзом И, то берется наименьший КУ: прочность цепочки определяется прочностью самого слабого звена. Если ветви связаны союзом ИЛИ, то берется наибольший КУ. В данном случае, перемещаясь снизу вверх, КУ, введенные Хокинсом, умножаются на КУ каждого из правил (в кружочках должны быть числа); в результате получаются коэффициенты уверенности для каждого из последовательных уровней.
Значение КУ 0.8 отражает сомнения Хокинса в отношении данного ответа, основанного только на свидетельстве управляющего.
Поскольку три правила на втором уровне связаны союзом И, наименьший из их КУ, равный 0.8, становится коэффициентом уверенности для этого уровня. Это число затем умножается на 0.9, т.е. на значение КУ, присвоенное системой этому правилу "если-то", что дает окончательную величину КУ для оценки утверждения "жертва знала убийцу и доверяла ему"; она равна 0.72.
Разумеется, выводы системы лишь подтвердили первые интуитивные соображения Хокинса о том, что Истуик не мог быть убийцей: лорд Мамфри не мог бы спокойно попивать из бокала портвейн в присутствии человека, который грозил обманом лишить его значительной части состояния. Но если не Истуик, то кто? Хокинс знал, что должен указать Блаттерсу другого подозреваемого. Фальшивые следы в саду привели Хокинса к выводу, что убийцей был кто-то из находившихся в доме, и его размышления обратились к шестерым людям, собравшимся в соседней комнате:
- Джузеппе, повар: его огненный темперамент компенсируется только его кондитерскими талантами.
- Друзилла Тауэрс: при всем своем обаянии эта рыжеволосая обольстительница не сумела занять желаемое место в завещании лорда.
- Дворкинс управляющий: верный слуга лорда Мамфри иа протяжении более 30 лет; играет на скачках.
- Полковник Клилэнд: несмотря на многолетнюю дружбу с Мамфри, приписывает свои недавние денежные неурядицы неудачным советам лорда.
- Хильда, горничная: ее таинственное прошлое дает основания заподозрить связь между ней и кровавым происшествием.
- Фредди Гартуэйт: непутевый племянник лорда; из-за своих сумасбродств и расточительности наделал массу долгов, с которыми невозможно рассчитаться честным путем.
УБИЙЦА НАЙДЕН!
Чтобы не позволить сержанту Блаттерсу арестовать невиновного, Хокинсу пришлось торопиться. Вновь обратившись к экспертной системе, он быстро ввел в нее все, что сумел выяснить, о возможных мотивах к совершению этого преступления у остальных шестерых, находившихся в доме в момент убийства, и удобных случаях, которые могли им для этого предоставиться. За время уик-энда благодаря своей тонкой профессиональной наблюдательности писатель многое узнал о гостях и прислуге. Несколько быстрых вопросов каждому из них, и Хокинс выяснил все, что требовалось, о том, кто где был перед обедом и после него.
Система отделила троих, имевших неоспоримые алиби. У Хокинса возникли серьезные подозрения в отношении одного из оставшихся, но здесь нужны были точные доказательства. Приложив пальцы к губам, он свистнул Рауля, верную собаку покойного графа, заставив ее обнюхать следы за дверью библиотеки. Хокинс был уверен, что следы поддельные, но полагал, что, несмотря на это, они могут помочь найти истинного убийцу. Не прошло и четырех минут, как самые мрачные подозрения Хокинса подтвердились: собака привела его к паре сапог Истуика, спрятанной в комнате юного Фредди Гартуэйта.
Племянник лорда Мамфри, сопротивление которого было сломлено точными вопросами, признал, что несколько дней назад посетил Истуика, назвавшись доверенным графа по их денежному спору, и стащил у хозяина его приметные сапоги. В тот вечер, незадолго до обеда Фредди вышел в поле, отделяющее усадьбу Мамфри от дома Истуика, надел сапоги и прошел около двери библиотеки, чтобы оставить ложные следы. После обеда он, отделившись от других гостей, отсутствовал в точности столько времени, сколько требовалось, чтобы "разобраться" с дядюшкой. Затем, прежде чем присоединиться к полковнику, Друзилле Тауэре и Хокинсу, он приоткрыл стеклянную дверь библиотеки. Бросая на Истуика подозрение в убийстве, Фредди надеялся одним махом отделаться от его претензий на капиталы и приобрести состояние.
После того как сержант Блаттерс приказал констеблю увести арестованного, Хокинс в наступившей тишине подвел итоги своего сотрудничества с "электронным консультантом". Опуская дискету с экспертной системой в карман смокинга, он заявил: "Ничего гениального в этом не было, а была просто цепь логических рассуждений, подобная следам на снегу. За каждым шагом следует новый, и так до тех пор, пока не будет достигнут конечный пункт".
УБИЙСТВО В УСАДЬБЕ МАМФРИ
Когда Реджиналд Гартуэйт, граф Мамфри, был обнаружен на полу своей домашней библиотеки, убитый его же собственным ножом для разрезания книг, подозрение почти сразу же пало на хозяина ночного клуба Хью Истуика: решительно всем было известно, что Мамфри недавно обвинил Истуика в попытке обмануть его на крупную сумму. Всего за несколько дней до происшествия многие жители деревни, прогуливаясь по деревенской лужайке, стали свидетелями крупнбго разговора между лордом Мамфри и Истуиком. Разговор этот завершился категорическим отказом лорда заплатить хотя бы пенс и угрозой Истуика отомстить за это.
В день трагического события в числе других гостей в усадьбе Мамфри находился д-р Ричард Хокинс, знаменитый автор детективов, работавший тогда над романом "Байт в ночи". Героем произведения был программист, случайно узнавший о преступлении. Хотя Хокинсу ни разу в жизни не приходилось участвовать в расследовании настоящего убийства, он не сомневался, что ему удастся пролить свет на обстоятельства гибели Мамфри.
Случилось так, что, занимаясь сбором материалов для нового романа, Хокинс присутствовал при совместной работе одного бывалого частного детектива и специалиста по инженерии знаний, которые занимались изготовлением прототипа экспертной системы, предназначенной для расследования преступлений. Хокинс внимательно прислушивался к тому, как программист неутомимо выяснял у детектива его методы раскрытия убийств и допроса подозреваемых. Только после существенных переделок и тщательной проверки детектив согласился, что скопированный с него эрзац-сыщик готов к использованию. Позднее Хокинс приобрел экземпляр программы этой экспертной системы, чтобы иметь возможность украсить свой роман реалистическими деталями.
Почти сразу же после обнаружения тела несчастного лорда Мамфри у писателя возникла мысль, что судьба предоставила ему превосходную возможность проверить, чего стоит его экспертная система. Пока управляющий графа вызывал полицию, а остальные слуги и гости в волнении собрались в бильярдной, Хокинс направился в библиотеку, где несчастный граф встретил свой конец. Для начала Хокинс отметил очевидные обстоятельства случившегося: последний раз лорда Мамфри видели живым за обедом, через полтора часа его тело было обнаружено в домашней библиотеке, на полу рядом с трупом лежал бокал с остатками портвейна...
ПРОНИЦАТЕЛЬНЫЙ НАБЛЮДАТЕЛЬ
Приступив к расследованию, Хокинс мысленно вернулся к моменту, когда было найдено тело. Кто первым упомянул Хью Истуика как наиболее вероятного убийцу? И кто указал на следы на снегу за слегка приоткрытой застекленной дверью? На следах были хорошо видны отпечатки необычного каблука левого ботинка, который Истуику приходилось носить из-за полученного на войне ранения.
Почти все присутствующие пришли к выводу, что лорд Мамфри и на сей раз не отказался от своих привычек, отправившись после обеда в библиотеку отдохнуть с томиком Пруста. Услышав стук в дверь, он встал, чтобы впустить Истуика, жившего примерно в километре от усадьбы, за полем. Между ними вновь разгорелся спор, и в конце концов Истуик вонзил нож для разрезания страниц в сердце лорда.
По-видимому, это объяснение удовлетворило сержанта Блаттерса, который уже прибыл в сопровождении констебля и приступил к опросу всех находившихся в доме. Но Хокинса терзали сомнения. Он быстро спустился к своей машине, достал из отделения для перчаток дискету с экспертной системой и вернулся с ней к домашнему компьютеру лорда Мамфри. Вставив дискету, писатель стал пытаться взвесить все за и против относительно виновности Истуика. Хокинс знал, что прежде всего необходимо сузить круг поисков возможного убийцы. Для этого, исходя из обстоятельств преступления, следует определить, был ли убийца хорошо известен жертве или это был совершенно чужой человек. Все хорошо знали, что лорд Мамфри и Истуик - враги. Но вместе с тем Хокинсу показалось, что разлитый портвейн свидетельствует о том, что в момент убийства Мамфри спокойно держал бокал в руке. Мог ли он быть столь спокоен в присутствии такого человека, как Хью Истуик? Когда Хокинс начал отвечать на возникающие на экране вопросы, его внимание привлекли и другие детали преступления.
На экранах показан диалог между Хокинсом и экспертной системой. Получив от Хокинса вопрос: "Действительно ли убитый знал убийцу и доверял ему?", программа задала относящиеся к делу вопросы, исходя нз своей базы знаний. В данном случае система запрашивает конкретную информацию о месте преступления и состоянии тела жертвы, которая позволит ей построить цепочку рассуждений, приводящих к окончательному ответу.
- Нарушена ли обстановка в комнате?
- Нет
- Есть ли на теле жертвы какие-либо следы насилия, кроме раны, послужившей причиной смерти?
- Нет
- Есть ли следы ног, ведущие к телу снаружи?
- Нет
- Закрыты ли окна и наружные двери, есть ли на них следы взлома?
- Нет
- Где совершено преступление: в кабинете, спальне или гардеробной жертвы?
- Да
ЛОГИЧЕСКАЯ ЦЕПЬ
Сержант Блаттерс проявлял нетерпение, но Хокинс продолжал нажимать клавиши компьютера. Он думал о сотнях правил "если-то" в базе знаний системы. В системах, основанных на правилах, применяются порознь или в комбинации два типа рассуждений - прямая и обратная цепочки. При прямой цепочке рассуждений система начинает с исходных данных и, пользуясь правилами, выводит из них какое-то решение. Фактически пользователь, вводя информацию в систему, задает вопрос: "Какие выводы отсюда следуют?" Если пользователь ввел, например, факт А, система будет искать правило, гласящее "Если А, то В", затем правило "Если В, то С" и т.д. При обратной цепочке рассуждений, которой пользовался Хокинс, решается противоположная задача. Задавшись определенным выводом - в данном случае "убитый знал убийцу и доверял ему" - система пытается доказать этот вывод и проходит логическую цепь в обратном направлении. Если D - это вывод, система ищет все правила вида "Если С, то D", затем правила "Если В, то С" и т.д. Когда процесс достигает точки, в которой часть правила, соответствующая "если", не является выводом из какого-либо другого правила, система требует ввода дополнительной информации. Система Хокинса спрашивала о том, остались ли предметы в комнате на своих местах и были ли царапины на теле убитого. В комнате все оказалось на месте. На руке Мамфри обнаружились царапины, но, по словам управляющего, граф оцарапался о куст розы, когда дрессировал в саду своего бладхаунда. Потом система начала прослеживать другую логическую цепь и спросила, были ли следы вокруг тела. В ответ на этот вопрос Хокинс ответил "Нет", несмотря даже на то, что цепочка следов снаружи указывала, что убийца вошел и вышел через незапертую застекленную дверь. Наблюдательный писатель заметил, что следы ведут к двери и от нее только снаружи, а мокрых (от растаявшего снега) или грязных (от земли в саду) пятен на полу около тела и вообще в комнате нет.
Хокинс знал, что стоит попросить, и система покажет ход своих рассуждений. Он снова запустил программу, но на этот раз, когда система задала тот же вопрос, вместо "Да" или "Нет" ввел ответ "Почему?"; это означало "Почему задан данный вопрос?" Хокинс также мог проверить выводы системы, вводя в ответ "Как?", что означало бы "Каким образом получен этот вывод?" В ответ система перечислила бы все правила "если-то", использованные в ходе рассуждений. Обрабатывая ответы Хокинса на свои вопросы, система выясняла, был ли убийца знаком с жертвой и пользовался ли он ее доверием.
ПРАВИЛА
1) ЕСЛИ жертва не сопротивлялась И нет признаков вторжения И преступление совершено в личных апартаментах жертвы, ТО жертва знала убийцу и доверяла ему.
2) ЕСЛИ обстановка в комнате не нарушена И за исключением смертельной раны следов насилия на теле жертвы нет, ТО жертва не сопротивлялась.
3) ЕСЛИ окна н наружные двери заперты н не имеют следов взлома ИЛИ следы, ведущие к телу жертвы с улицы, отсутствуют, ТО признаков вторжения нет.
4) ЕСЛИ преступление совершено в кабинете жертвы ИЛИ в спальне жертвы ИЛИ в гардеробной жертвы, ТО преступление совершено в личных апартаментах жертвы.

Приведенная диаграмма иллюстрирует взаимосвязи между правилами "если-то", которыми экспертная система пользовалась для выяснения вопроса о знакомстве жертвы с убийцей. Если две или более ветвей правила связаны союзом И, то для истинности правила необходимо, чтобы были истинны все эти ветви. Если ветви связаны союзом ИЛИ, то достаточно истинности какой-то одной из ветвей. Красные стрелки указывают начало процесса построения обратной цепочки рассуждений.
КАК ПОСТУПАЮТ С НЕОПРЕДЕЛЕННОСТЬЮ
Сержант Блаттерс, который уже давно сделал собственный окончательный вывод, ожидал только получения ордера из магистрата, чтобы арестовать Хью Истуика. Опасаясь, что будет арестован невинный, Хокинс на основании выводов экспертной системы подготовил для сержанта свою версию происшедшего. Столь тщательно подготовленная бывалым детективом и специалистом по инженерии знаний экспертная система, как и многие другие подобные ей системы, присваивала численные оценки свидетельским показаниям и выводам из них в зависимости от их надежности, что давало возможность судить, насколько значимы выводы системы.
Как было хорошо известно Хокинсу, реальные детективы часто имеют дело с неполной или неточной информацией - например, со смазанными отпечатками пальцев или сомнительными свидетельскими показаниями. Подобная неопределенность может повлиять и на значимость используемых детективом эмпирических правил. Экспертная система справляется с затруднениями такого рода при помощи коэффициентов уверенности (КУ).
Эти коэффициенты могут быть "встроены" в систему при ее создании с учетом полученного с таким трудом жизненного опыта эксперта. Их может также ввести сам пользователь в ответ на вопросы системы. КУ, равный 1, означает, что эксперт или пользователь абсолютно уверен в данном выводе, а 0 означает "мнения не имею". Если значение КУ лежит в интервале между 0 и 1, то это значит, что эксперт или пользователь не на 100% уверен в выводе или ответе на вопрос. Скажем, лорд Мамфри действительно мог оцарапаться о розовый куст, как утверждал управляющий, но, отвечая на вопрос системы об этом, Хокинс решил, что управляющий мог и солгать, и присвоил своему ответу "Нет" значение КУ, равное 0.8.
Детектив, суждения которого лежали в основе данной экспертной системы, в свою очередь присвоил правилу "Если жертва не сопротивлялась, нет признаков вторжения и преступление совершено в личных апартаментах жертвы, то жертва знала убийцу и доверяла ему" значение коэффициента уверенности 0.9. Иными словами, исходя из своего профессионального опыта, он только на 90% уверен, что если все три условия (все "если") справедливы, то правилен и вывод.

(Тут, в кружках, должны быть числа, но их нет.- G.)
Приведенная здесь диаграмма И-ИЛИ иллюстрирует обычную процедуру оценки достоверности вывода. Если две или более ветвей правила связаны союзом И, то берется наименьший КУ: прочность цепочки определяется прочностью самого слабого звена. Если ветви связаны союзом ИЛИ, то берется наибольший КУ. В данном случае, перемещаясь снизу вверх, КУ, введенные Хокинсом, умножаются на КУ каждого из правил (в кружочках должны быть числа); в результате получаются коэффициенты уверенности для каждого из последовательных уровней.
Значение КУ 0.8 отражает сомнения Хокинса в отношении данного ответа, основанного только на свидетельстве управляющего.
Поскольку три правила на втором уровне связаны союзом И, наименьший из их КУ, равный 0.8, становится коэффициентом уверенности для этого уровня. Это число затем умножается на 0.9, т.е. на значение КУ, присвоенное системой этому правилу "если-то", что дает окончательную величину КУ для оценки утверждения "жертва знала убийцу и доверяла ему"; она равна 0.72.
Разумеется, выводы системы лишь подтвердили первые интуитивные соображения Хокинса о том, что Истуик не мог быть убийцей: лорд Мамфри не мог бы спокойно попивать из бокала портвейн в присутствии человека, который грозил обманом лишить его значительной части состояния. Но если не Истуик, то кто? Хокинс знал, что должен указать Блаттерсу другого подозреваемого. Фальшивые следы в саду привели Хокинса к выводу, что убийцей был кто-то из находившихся в доме, и его размышления обратились к шестерым людям, собравшимся в соседней комнате:
- Джузеппе, повар: его огненный темперамент компенсируется только его кондитерскими талантами.
- Друзилла Тауэрс: при всем своем обаянии эта рыжеволосая обольстительница не сумела занять желаемое место в завещании лорда.
- Дворкинс управляющий: верный слуга лорда Мамфри иа протяжении более 30 лет; играет на скачках.
- Полковник Клилэнд: несмотря на многолетнюю дружбу с Мамфри, приписывает свои недавние денежные неурядицы неудачным советам лорда.
- Хильда, горничная: ее таинственное прошлое дает основания заподозрить связь между ней и кровавым происшествием.
- Фредди Гартуэйт: непутевый племянник лорда; из-за своих сумасбродств и расточительности наделал массу долгов, с которыми невозможно рассчитаться честным путем.
УБИЙЦА НАЙДЕН!
Чтобы не позволить сержанту Блаттерсу арестовать невиновного, Хокинсу пришлось торопиться. Вновь обратившись к экспертной системе, он быстро ввел в нее все, что сумел выяснить, о возможных мотивах к совершению этого преступления у остальных шестерых, находившихся в доме в момент убийства, и удобных случаях, которые могли им для этого предоставиться. За время уик-энда благодаря своей тонкой профессиональной наблюдательности писатель многое узнал о гостях и прислуге. Несколько быстрых вопросов каждому из них, и Хокинс выяснил все, что требовалось, о том, кто где был перед обедом и после него.
Система отделила троих, имевших неоспоримые алиби. У Хокинса возникли серьезные подозрения в отношении одного из оставшихся, но здесь нужны были точные доказательства. Приложив пальцы к губам, он свистнул Рауля, верную собаку покойного графа, заставив ее обнюхать следы за дверью библиотеки. Хокинс был уверен, что следы поддельные, но полагал, что, несмотря на это, они могут помочь найти истинного убийцу. Не прошло и четырех минут, как самые мрачные подозрения Хокинса подтвердились: собака привела его к паре сапог Истуика, спрятанной в комнате юного Фредди Гартуэйта.
Племянник лорда Мамфри, сопротивление которого было сломлено точными вопросами, признал, что несколько дней назад посетил Истуика, назвавшись доверенным графа по их денежному спору, и стащил у хозяина его приметные сапоги. В тот вечер, незадолго до обеда Фредди вышел в поле, отделяющее усадьбу Мамфри от дома Истуика, надел сапоги и прошел около двери библиотеки, чтобы оставить ложные следы. После обеда он, отделившись от других гостей, отсутствовал в точности столько времени, сколько требовалось, чтобы "разобраться" с дядюшкой. Затем, прежде чем присоединиться к полковнику, Друзилле Тауэре и Хокинсу, он приоткрыл стеклянную дверь библиотеки. Бросая на Истуика подозрение в убийстве, Фредди надеялся одним махом отделаться от его претензий на капиталы и приобрести состояние.
После того как сержант Блаттерс приказал констеблю увести арестованного, Хокинс в наступившей тишине подвел итоги своего сотрудничества с "электронным консультантом". Опуская дискету с экспертной системой в карман смокинга, он заявил: "Ничего гениального в этом не было, а была просто цепь логических рассуждений, подобная следам на снегу. За каждым шагом следует новый, и так до тех пор, пока не будет достигнут конечный пункт".
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 1:06 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
ДИФФЕРЕНЦИАЛЬНЫЕ МОДЕЛИ (ЛАНЧЕСТЕР)
Пусть друг с другом сражаются два отряда по 100 человек, вооруженных винтовками. Так как их боевые характеристики абсолютно идентичны, через некоторое время T отряды полностью друг друга перестреляют. А теперь зададимся вопросом, сколько нужно пулеметчиков, чтобы заменить один из отрядов, если пулемет в 100 раз эффективнее винтовки? Один? Да, он перестреляет 100 человек за время T, однако, по нему ведет огонь отряд, способный перестрелять за это же время 100 человек. Значит, пулеметчик проживет на поле боя только T/100 и сможет пристрелить за это время только 1 солдата противника. А 10 пулеметчиков? Проживут T/10 и перестреляют по 10 солдат каждый - итого 100. Получилось! Значит, есть какая-то формула, связывающая квадрат численности и боевую эффективность. Она и называется уравнением Ланчестера.
***
"В ставке Гитлера все малахольные".
Из книги Philip Sabin, Simulating War: Studying Conflict through Simulation Games, 2012:
В двадцатом веке математическое моделирование боевых действий вошло в моду. Первой ключевой фигурой был Фредерик Ланчестер, который в 1916 году опубликовал анализ новых аспектов воздушной войны [Aircraft in warfare: The dawn of the fourth arm]. В главах 5 и 6 он разработал свой знаменитый закон "N-квадрат", в котором, используя простейшее дифференциальное исчисление, доказывал, что ключевым фактором в современном бою является концентрация превосходящего числа в решающей точке. Его аргументация базировалась на том, что первоначальное численное преимущество во время огневого боя противников с одинаковой огневой мощью стрелков со временем будет неумолимо увеличиваться, поскольку более многочисленные удары, нанесенные и без того более крупными силами, усугубят его пропорциональное преимущество и породят положительную обратную связь. Следовательно, 1000 стрелков теоретически должны уничтожить 500 вражеских, потеряв только 134 своих. Ланчестер утверждал, что разделение вражеских сил на две примерно равные половины и борьба с каждой из них по очереди всеми силами должно, следовательно, позволить победить даже изначально более слабому; он привел план Нельсона перед Трафальгаром как яркий пример стремления победить врага таким образом. Признавая, что огневая мощь в действительности почти всегда не одинакова, Ланчестер предположил, что: "БОЕВАЯ СИЛА подразделения может быть в широком смысле определена как произведение КВАДРАТА ЕЕ ЧИСЛЕННОСТИ на ИНДИВИДУАЛЬНУЮ ОГНЕВУЮ МОЩЬ бойцов".
К сожалению, модель Ланчестера содержит несколько весьма сомнительных предположений. Он не учитывает плотность войск, увеличивающую их уязвимость от огня, в то время как мы знаем, что рассредоточение было ключевым фактором в ограничении потерь, поскольку оружие становилось все более и более эффективным. В его модели все выстрелы нацелены на выжившие вражеские силы, исключая повторное поражение целей и, "дружественный" огонь по своим. Предполагается, что противники стреляют одновременно, и что каждый выстрел имеет лишь небольшой шанс поразить цель. Более реалистичные предположения по перечисленным нюансам могут легко полностью разрушить закон квадратов или даже дать преимущество меньшей силе (особенно если она нанесет упреждающий удар). С другой стороны, модель Ланчестера предполагает, что слабейшие по численности войска продолжают вести огонь с неизменной эффективностью до своего полного уничтожениия, вместо того, чтобы укрываться, спасаться бегством или капитулировать, не нанося врагу потерь, предсказываемых моделью.
В зависимости от того, как складываются условия, реальные бои могут сильно отличаться в любую сторону от упрощенных предсказаний Ланчестера. За последнее столетие ученые провели массу исследований, в которых проверяли уравнения Ланчестера и пытались выяснить, соответствуют ли реальные данные о потерях в битвах, таких как Арденны или Иводзима, описанным им схемам. Однако его модель настолько искусственна, что любое сходство с реальностью обязательно будет в значительной степени случайным, тем более, что нет четкого способа вычислить меняющуюся "огневую мощь" противостоящих сил, кроме как задним числом по самим результатам боя. Для рукопашного боя в древние времена применимость подобных моделей вызывает еще большие сомнения, поскольку реальное соотношение потерь тогда часто составляло десять или даже 100 к одному вместо примерно равных по модели; как это ни парадоксально, но только с появлением порохового оружия, более подходящего для закона квадратов, стали потери немного уравнялись.
Что делает этот вопрос критически важным для настоящего исследования, так это то, что модель Ланчестера гораздо лучше предсказывает поведение простых симуляторов и игр, чем реальных боевых действий, потому что симуляции и игры часто основываются на одних и тех же упрощенных предположениях. Например, в самом первом варгейме, в котором я когда-либо играл, дуэль между противоборствующими отрядами стрелков на расстоянии 300 ярдов в среднем давала безупречные ланчестрийские результаты, поскольку правила устанавливали, что каждый игрок должен поразить выбранного врага на кубике при выбрасывании "шестерки" (раунд соответствовал минуте боя). Даже профессиональные варгеймы и симуляторы, при всей их сложности, часто имеют в основе уравнения Ланчестера и, следовательно, предлагают в лучшем случае примерное приближение к реальности - при увеличении числа специальных условий. По иронии судьбы, именно в области воздушной войны модель Ланчестера наиболее проблемна, как я покажу далее. Также я проиллюстрирую, как более сложное моделирование в военных играх, с одной стороны, эффектов рассредоточения, а, с другой, подавления превосходящей огневой мощью, могут дать гораздо более достоверное представление о современном наземном бое, чем квадратный закон Ланчестера.
Пусть друг с другом сражаются два отряда по 100 человек, вооруженных винтовками. Так как их боевые характеристики абсолютно идентичны, через некоторое время T отряды полностью друг друга перестреляют. А теперь зададимся вопросом, сколько нужно пулеметчиков, чтобы заменить один из отрядов, если пулемет в 100 раз эффективнее винтовки? Один? Да, он перестреляет 100 человек за время T, однако, по нему ведет огонь отряд, способный перестрелять за это же время 100 человек. Значит, пулеметчик проживет на поле боя только T/100 и сможет пристрелить за это время только 1 солдата противника. А 10 пулеметчиков? Проживут T/10 и перестреляют по 10 солдат каждый - итого 100. Получилось! Значит, есть какая-то формула, связывающая квадрат численности и боевую эффективность. Она и называется уравнением Ланчестера.
***
"В ставке Гитлера все малахольные".
Из книги Philip Sabin, Simulating War: Studying Conflict through Simulation Games, 2012:
В двадцатом веке математическое моделирование боевых действий вошло в моду. Первой ключевой фигурой был Фредерик Ланчестер, который в 1916 году опубликовал анализ новых аспектов воздушной войны [Aircraft in warfare: The dawn of the fourth arm]. В главах 5 и 6 он разработал свой знаменитый закон "N-квадрат", в котором, используя простейшее дифференциальное исчисление, доказывал, что ключевым фактором в современном бою является концентрация превосходящего числа в решающей точке. Его аргументация базировалась на том, что первоначальное численное преимущество во время огневого боя противников с одинаковой огневой мощью стрелков со временем будет неумолимо увеличиваться, поскольку более многочисленные удары, нанесенные и без того более крупными силами, усугубят его пропорциональное преимущество и породят положительную обратную связь. Следовательно, 1000 стрелков теоретически должны уничтожить 500 вражеских, потеряв только 134 своих. Ланчестер утверждал, что разделение вражеских сил на две примерно равные половины и борьба с каждой из них по очереди всеми силами должно, следовательно, позволить победить даже изначально более слабому; он привел план Нельсона перед Трафальгаром как яркий пример стремления победить врага таким образом. Признавая, что огневая мощь в действительности почти всегда не одинакова, Ланчестер предположил, что: "БОЕВАЯ СИЛА подразделения может быть в широком смысле определена как произведение КВАДРАТА ЕЕ ЧИСЛЕННОСТИ на ИНДИВИДУАЛЬНУЮ ОГНЕВУЮ МОЩЬ бойцов".
К сожалению, модель Ланчестера содержит несколько весьма сомнительных предположений. Он не учитывает плотность войск, увеличивающую их уязвимость от огня, в то время как мы знаем, что рассредоточение было ключевым фактором в ограничении потерь, поскольку оружие становилось все более и более эффективным. В его модели все выстрелы нацелены на выжившие вражеские силы, исключая повторное поражение целей и, "дружественный" огонь по своим. Предполагается, что противники стреляют одновременно, и что каждый выстрел имеет лишь небольшой шанс поразить цель. Более реалистичные предположения по перечисленным нюансам могут легко полностью разрушить закон квадратов или даже дать преимущество меньшей силе (особенно если она нанесет упреждающий удар). С другой стороны, модель Ланчестера предполагает, что слабейшие по численности войска продолжают вести огонь с неизменной эффективностью до своего полного уничтожениия, вместо того, чтобы укрываться, спасаться бегством или капитулировать, не нанося врагу потерь, предсказываемых моделью.
В зависимости от того, как складываются условия, реальные бои могут сильно отличаться в любую сторону от упрощенных предсказаний Ланчестера. За последнее столетие ученые провели массу исследований, в которых проверяли уравнения Ланчестера и пытались выяснить, соответствуют ли реальные данные о потерях в битвах, таких как Арденны или Иводзима, описанным им схемам. Однако его модель настолько искусственна, что любое сходство с реальностью обязательно будет в значительной степени случайным, тем более, что нет четкого способа вычислить меняющуюся "огневую мощь" противостоящих сил, кроме как задним числом по самим результатам боя. Для рукопашного боя в древние времена применимость подобных моделей вызывает еще большие сомнения, поскольку реальное соотношение потерь тогда часто составляло десять или даже 100 к одному вместо примерно равных по модели; как это ни парадоксально, но только с появлением порохового оружия, более подходящего для закона квадратов, стали потери немного уравнялись.
Что делает этот вопрос критически важным для настоящего исследования, так это то, что модель Ланчестера гораздо лучше предсказывает поведение простых симуляторов и игр, чем реальных боевых действий, потому что симуляции и игры часто основываются на одних и тех же упрощенных предположениях. Например, в самом первом варгейме, в котором я когда-либо играл, дуэль между противоборствующими отрядами стрелков на расстоянии 300 ярдов в среднем давала безупречные ланчестрийские результаты, поскольку правила устанавливали, что каждый игрок должен поразить выбранного врага на кубике при выбрасывании "шестерки" (раунд соответствовал минуте боя). Даже профессиональные варгеймы и симуляторы, при всей их сложности, часто имеют в основе уравнения Ланчестера и, следовательно, предлагают в лучшем случае примерное приближение к реальности - при увеличении числа специальных условий. По иронии судьбы, именно в области воздушной войны модель Ланчестера наиболее проблемна, как я покажу далее. Также я проиллюстрирую, как более сложное моделирование в военных играх, с одной стороны, эффектов рассредоточения, а, с другой, подавления превосходящей огневой мощью, могут дать гораздо более достоверное представление о современном наземном бое, чем квадратный закон Ланчестера.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
И.Ануреев, А.Татарченко Применение математических методов в военном деле.- М.: Воениздат, 1967.
Из главы VI
При планировании операций необходимо иметь возможность производить количественный анализ развития боевых действий между двумя группировками боевых средств с учетом их взаимного огневого воздействия.
Математические методы, изучающие количественные закономерности боя в условиях взаимного воздействия сторон, получают в настоящее время большое развитие. Если рассматривать боевые действия войск с учетом многочисленных факторов, задача становится непомерно сложной. Целесообразно сначала рассматривать лишь упрощенные, схематизированные модели боевых действий.
В таких упрощенных аналитических моделях удается наглядно выявить основные количественные закономерности боя, рассмотреть влияние главных факторов, которые иначе были бы затенены второстепенными, малосущественными факторами.
Математический анализ простейших моделей боевых действий позволяет приближенно оценить влияние таких основных факторов, как огневая мощь и количественный состав применяемых боевых средств, преимущество внезапности, темпы наращивания сил для ответного удара, соотношение сил сторон, темпы восстановления боевых потерь, огневая "производительность" боевых средств и т.д. Математические модели боя, безусловно, явятся ценным вспомогательным средством при планировании операций, не претендуя, разумеется, на то, чтобы подменить собой тактику и оперативное искусство.
Всякий бой между двумя сторонами можно рассматривать как совокупность последовательных ударов каждой стороны по противнику. Процесс развития боя представляется как случайный, так как результат каждого огневого удара в какой-то мере случаен. Ниже будут рассмотрены две простейшие модели боя:
- бой между двумя группировками боевых единиц (модель А);
- бой между двумя плацдармами (модель Б).
Несмотря на значительные допущения, которые делаются для обеих моделей, получаемые с их помощью количественные закономерности дают возможность проанализировать боевые действия с точки зрения учета наиболее существенных факторов.
Дальнейшее развитие моделей такого типа и совершенствование алгоритмов военных задач позволит получать более точные методы теории динамики боя.
УПРОЩЕННЫЕ УРАВНЕНИЯ ДИНАМИКИ БОЯ ДЛЯ МОДЕЛИ А (УРАВНЕНИЯ ЛАНЧЕСТЕРА)
[Ланчестер - английский военный специалист, занимавшийся приложениями математики к исследованию боевых действий. Основная его работа вышла в 1916г.]
Рассмотрим бой между двумя группировками боевых единиц (ракет, самолетов, танков, артиллерийских батарей).
Пусть группировка I состоит из N1 однородных боевых единиц, а группировка II - из N2 боевых единиц. Боевые единицы группировки I не обязательно однородны с боевыми единицами группировки II (например, с одной стороны могут участвовать танки, с другой стороны - артиллерия). Каждая из боевых единиц может вести прицельный огонь по любой из боевых единиц противника. Если боевая единица поражена, то огонь переносится на другую, т.е. пораженная боевая единица в дальнейших боевых действиях не участвует. Будем считать, что каждая боевая единица ведет огонь с некоторой средней скорострельностью л1 и л2 (здесь л обозачает лямбду), а моменты отдельных выстрелов являются случайными. Предположим, что один выстрел боевой единицы группировки I поражает обстрелянную цель с вероятностью Р1, а группировки II - с вероятностью Р2.
Возможности боевых единиц каждой группировки будут характеризоваться их эффективными скорострельностями n1 и n2, при этом
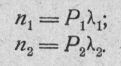
n1 = P1*л1;
n2 = P2*л2.
Рассмотрим обе участвующие в бою группировки как систему, которая в каждый момент времени может находиться в одном из возможных состояний. Под состоянием системы группировок принято понимать число сохранившихся боевых единиц с той и другой стороны.
В дальнейшем будем основываться на допущении, что огневая мощь каждого соединения в каждый момент времени определяется не фактическим числом сохранившихся боевых единиц, а его математическим ожиданием (средним значением).
Такое допущение вполне естественно для соединений и объединений, когда случайности, связанные с поражением или непоражением отдельных единиц, сравнительно мало сказываются на суммарной огневой мощи группировки. Для соединений эти случайности начинают оказывать существенное влияние в конце боя, когда в составе группировок сторон остается совсем небольшое число боевых единиц.
Пусть среднее число (математическое ожидание) сохранившихся на данный момент времени боевых единиц группировок сторон равно соответственно m1 и m2.
Рассмотрим закон уменьшения величины m1 с течением времени.

Каждая из боевых единиц группировки II производит за время Dt [D, здесь - дельта] в среднем P2*л2*Dt = n2Dt успешных выстрелов. Среднее число боевых единиц, воздействующих по группировке I, равно m2. Следовательно, все боевые единицы группировки II за время Dt произведут m2*n2*Dt успешных выстрелов.
Эта величина будет равна числу пораженных единиц группировки I, т.е.
Dm1 = -n2*m2*Dt.
Разделив уравнение на Dt и перейдя к пределу при Dt -> 0, получим дифференциальное уравнение для m1 в виде
dm1/dt = -n2*m2.
Совершенно аналогично можно получить дифференциальные уравнения для m2:
dm2/dt = -n1*m1.
Полученные уравнения называются уравнениями Ланчестера. Они показывают, как убывает число боевых единиц сторон с течением времени боя.
Как уже указывалось, уравнения Ланчестера описывают ход боя однородных боевых средств лишь приближенно и их нельзя применять для последней стадии боя (на этапе "истощения"). Однако эти уравнения дают хорошее приближение к действительности на сравнительно ранних стадиях боя, при большом количестве участвующих в бою однородных боевых средств.
После преобразований уравнения Ланчестера можно привести к виду:
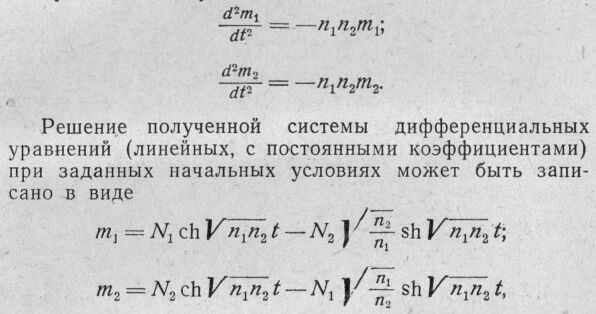
d2m1/dt2 = -n1*n2*m1;
d2m2/dt2 = -n1*n2*m2;
Решение полученной системы дифференциальных уравнений (линейных, с постоянными коэффициентами) при заданных начальных условиях может быть записано в виде
m1 = N1*ch(sqr(n1*n2)*t) - N2*sqr(n2/n1)*sh(sqr(n1*n2)*t);
m2 = N2*ch(sqr(n1*n2)*t) - N1*sqr(n1/n2)*sh(sqr(n1*n2)*t);
где m1 - число боевых единиц первой стороны в некоторый момент боя;
m2 - число боевых единиц второй стороны в тот же момент боя;
N1 - число боевых единиц первой стороны в начале боя;
N2 - число боевых единиц второй стороны в начале боя;
n1 - эффективная скорострельность боевой единицы первой стороны;
n2 - эффективная скорострельность боевой единицы второй стороны;
ch - гиперболический косинус (берется по таблицам);
sh - гиперболический синус (берется по таблицам);
t - момент времени боя.
[Не правда ли, "все очевидно"? Но ведь, никто не заставляет игрока решать дифференциальные уравнения. Приближенные решения, выраженные цветастыми номграммками или табличками, вполне могут обеспечить потребную наукообразность. Просто, не надо считать, что игры для несведующих в математике "чайников" могут делать те же "чайники". "Чувствовать модель" мы просто обязаны. И знать, что гиперболическая тригонометрия это комбинация экспонент, военный моделист обязан знать ровно также, как и любой схемо- или системотехник. Разговоры "здесь добавим 1, там убавим" - исключительно в пользу бедных.- G.]
Для анализа хода боя удобно перейти от абсолютной численности группировок к относительной численности, выражая ее как отношение числа сохранившихся боевых единиц в данный момент, времени к числу боевых единиц в начале, боя.
Введем обозначения:

м1 = m1/N1; м2 = m2/N2; v = N1/N2; a = n1/n2,
где м1, м2 - относительные численности группировок сторон;
v (ню) - соотношение сил сторон в начале боя;
a (альфа) - соотношение эффективных скорострельностей сторон.
Используя введенные обозначения, можно написать уравнения, выражающие зависимость относительной численности боевых средств сторон от времени боя в следующем виде:
м1 = ch(sqr(n1*n2)*t) - 1/v*sqr(1/а)*sh(sqr(n1*n2)*t);
м2 = ch(sqr(n1*n2)*t) - v*sqr(а)*sh(sqr(n1*n2)*t);
Введем еще два обозначения:
т = sqr(n1*n2)*t; X = v*sqr(a).
Величину т можно назвать "приведенным" временем (равносильно изменению масштаба времени).
[Это мы уже наблюдали в простейших полковых моделях, там специально вводилась переменная "напряженность (кровавость) битвы". Во всех же "военных" играх масштаб времени убожески линеен. А ведь, даже фантастически инфантильнфая киношка "STAR WARS", начиная с 6-го эпизода, дает в параллель три финальные битвы - драку на мечах, наземное и космическое сражение. Имеет смысл не делить время на равные промежутки, а идти от события к событию.- G.]
Величину X будем называть коэффициентом преимущества одной стороны над другой.
В этих новых обозначениях уравнения динамики боя для модели А запишутся в виде
м1 = ch(т) - 1/X*sh(т);
м2 = ch(т) - X*sh(т).
Из выражения для коэффициента преимущества следует, что он в большей степени зависит от соотношения сил (в начале боя), чем от соотношения эффективных скорострельностей, так как соотношение сил входит в первой степени, а величина a (соотношение эффективных скорострельностей) - входит под знаком квадратного корня.
Таким образом, при ведении боя между двумя группировками боевых единиц первостепенное значение имеет концентрация сил на направлении главного удара. Вывод получен математически, но он общеизвестен и из практической деятельности. Однако математический вывод дает количественную оценку влияния концентрации сил, а следовательно, дает возможность проанализировать это влияние в ходе боя.
В частном случае, когда обе группировки равносильны (X = 1), уравнение принимает вид
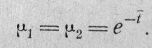
м1 = м2 = exp(-т).
Таким образом, в случае боя равносильных группировок каждая из них уменьшается в ходе боя по простому показательному закону. Если одна из группировок сильнее другой (X > 1), то более сильная сторона с некоторого момента перестает нести существенные потери, тогда как слабая сторона быстро убывает в своей численности, доходя до полного истребления. Следует иметь в виду, что полученные количественные зависимости динамики боя соединений не учитывают тех изменений в тактике действий, которые неизбежно имеются в действительности у обеих сражающихся сторон.
Для иллюстрации приводится таблица, показывающая зависимость соотношения сил сторон m1/m2 (численностей боевых единиц) от приведенного времени для двух значений коэффициента преимущества.
Из приведенной таблицы следует, что в бою по истечении приведенного времени 0.6 первая сторона приобретает преимущество в силах в 1.57 раза больше (при коэффициенте преимущества в начале боя 1.2) и в 8 раз больше второй стороны (при коэффициенте преимущества 1.5). По истечении приведенного времени боя (примерно 1.5) вторая сторона полностью истребляется.
Таким образом, пользуясь полученными уравнения ми, можно дать прогноз боя двух группировок с однородными боевыми средствами в каждой группировке (но не обязательно однородными в обеих группировках).
[Разнородные группировки - чуть позже.- G.]
При этом результаты боя характеризуются количественной зависимостью оставшихся боевых средств сторон (или боевых потерь) к любому моменту времени i зависимости:
- от соотношения сил перед началом боя;
- от скорострельности боевых средств сторон;
- от вероятностей поражения боевых средств сторон при огневом воздействии.
Необходимо заметить, что вероятность пораженя зависит от многих факторов, характеризующих свойства оружия и поражаемого объекта, а именно:
- от тротилового эквивалента ядерного боеприпаса или поражающих характеристик обычных боеприпасов;
- от характеристик рассеивания боеприпаса (характеристик носителя, дальности стрельбы, качества системы управления и др.);
- от размеров цели (противостоящей боевой единицы);
- от прочностных и других защитных свойств цели.
Как видно, уравнения теории динамики боя учитывают довольно много существенных факторов, влияющих на результаты боя, но не учитывают изменений в тактике.
ПРИМЕР. Происходит бой между двумя группировками танков. Группировка I имеет 20, а группировка II - 10 танков. Средняя скорострельность танков группировки I (с учетом переноса огня) - 0.5 выстрела в минуту, вероятность поражения танков противника - 0.06. Танки группировки II обладают средней скорострельностью один выстрел в минуту и имеют среднюю вероятность поражения танков противоположной стороны 0.05.
Победой какой стороны и через какое время завершится бой?
Решение. Определяем численное соотношение сил к началу боя:
v = N1/N2 = 20/10 = 2.

Вычисляем эффективные скорострельности сторон:
n1 = P1*л1 = 0.06*0.5 = 0.03;
n2 = Р2*л2 = 0.05*1 = 0.05.
Определяем соотношение эффективных скорострельностей:
a = n1/n2 = 0.03/0.05 = 0.6.
Коэффициент преимущества будет равен
X = v*sqr(a) = 2*sqr(0.6) = 1.5.
Следовательно, побеждающей стороной будет группировка I. Находим выражение для приведенного времени:
т = sqr(n1*n2)*t = sqr(0.03*0.05)*t = 0.039*t.
Ниже в таблице приводятся результаты расчетов, характеризующих зависимость относительного числа сохранившихся боевых единиц от времени.
Из таблицы следует, что через 10мин. боя потери группировки II составят 52%. тогда как потери группировки I будут равны 19%.
Еще раз заметим, что выведенные зависимости для модели А были основаны на допущении, что каждая боевая единица может вести прицельный огонь по любой из боевых единиц противника, т.е. имеется полная взаимозаменяемость боевых единиц. В действительности такой полной взаимозаменяемости быть не может: для некоторых боевых единиц не все единицы противника будут доступны, не все силы будут введены в бой сразу, будут ограничения по переносу огня с одних целей на другие. Если при этом можно разбить все участвующие в бою единицы на противостоящие группы, взаимодействующие между собой, то бой можно расчленить на отдельные бои между подгруппами. Крайним случаем ограничения взаимозаменяемости будет случай, когда каждая боевая единица может вести огонь только по одной боевой единице противника. В этом случае бой распадается на элементарные бои типа "дуэлей".
Важным условием для применения модели А являются полная разведка объектов противника и наличие информации о результатах обстрела, которая должна быть своевременной. Это условие в действительности также не может быть полностью выполнено.
Вследствие этого темп действительного боя несравненно медленнее, чем дает модель А. Ниже будет рассмотрена другая модель боя, которая дает несколько большее приближение к картине действительного боя.
Остановимся еще на учете пополнения сил и элемента внезапности в модели А.
Допустим, что пополнение сил происходит с темпом k1 боевых единиц группировки I в единицу времени и с темпом k2 боевых единиц для группировки II. В таком случае уравнения динамики боя примут следующий вид:

dm1/dt = -n2*m2+k1;
dm2/dt = -n1*m1+k2;
Темпы пополнения сил могут быть как постоянными, так и переменными. Решение этой системы уравнений дает возможность проанализировать процесс боя в зависимости от темпа пополнения сил и выявить соответствующие требования к темпу пополнения своей группировки для того, чтобы завершить бой разгромом противника в заданное время.
В частном случае, когда темпы пополнения сил постоянные, решение системы уравнений будет иметь вид
m1 = 1/2*(N1-k2/n1)*ch(sqr(n1*n2)*t) + (k1-n2*N2)/(2*sqr(n1*n2))*sh(sqr(n1*n2)*t) + k2/n1;
m2 = 1/2*(N2-k1/n2)*ch(sqr(n1*n2)*t) + (k2-n1*N1)/(2*sqr(n1*n2))*sh(sqr(n1*n2)*t) + k1/n2;
Решение таких уравнений выполняется достаточно просто не только на электронных вычислительных, машинах, но и обычными способами.
ДИНАМИКА БОЯ МЕЖДУ ДВУМЯ ПЛАЦДАРМАМИ (МОДЕЛЬ Б)
Рассмотрим бой между двумя группировками войск при следующих допущениях. Противостоящие друг другу группировки войск ведут огонь не по отдельным разведанным целям, а по некоторой площади (плацдарму), на которой расположены огневые средства противника (стартовые позиции ракет, аэродромы с базирующимися на них бомбардировщиками, артиллерия и т.д.). Кроме того, сведения о причиненных разрушениях и связь между боевыми единицами настолько неполны, что не исключается повторное огневое воздействие по уже пораженным объектам. Такую модель боя называют "боем двух плацдармов" или моделью Б. Ее можно рассматривать как второй крайний случай модели боя, когда отсутствует прицельный огонь и отсутствуют разведывательные данные об объектах противника на площади плацдарма. Действительный бой представляет собой как бы "среднее" между боями, описываемыми моделями А и Б.
Предположим, что плацдармы I и II первоначально находятся в неповрежденном состоянии. Огневое воздействие плацдарма I по плацдарму II за время Dt уничтожает боевые средства на некоторой элементарной площади DS2, которая составляет известную долю от площади плацдарма S2.
Введем в качестве характеристики интенсивности огневого воздействия средний относительный ущерб в единицу времени, который наносит один плацдарм другому в начале боя всеми огневыми средствами.
В таком случае средний ущерб за время Dt, который нанесет плацдарм I по плацдарму II, будет
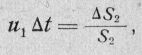
u1*Dt = DS2/S2
где u1 - средний относительный ущерб за единицу времени, наносимый в начале боя плацдармом I по плацдарму II. Аналогичной характеристикой описывается интенсивность огневого воздействия плацдарма II по плацдарму I.
Для определения u1 и u2 нужно найти суммарную среднюю относительную площадь всех разрушений, которые могут нанести противнику все боевые средства за произвольно выбранную единицу времени.
Средний относительный ущерб за единицу времени зависит:
- от количества огневых средств;
- от скорострельности огневых средств;
- от вероятности достижения цели носителями боеприпасов;
- от радиусов поражения объектов поражения;
- от прочности поражаемых объектов.
Для вывода уравнений динамики боя между двумя плацдармами будем рассуждать следующим образом.
Огневой удар за время Dt всеми средствами плацдарма II нанес бы неповрежденному плацдарму I ущерб, равный u2*Dt. Так как к моменту удара плацдарм II располагает только частью сил, сохранившихся на площади, относительную величину которой мы обозначаем через V2, то необходимо умножить относительный ущерб на V2. Кроме того, к моменту удара плацдарм I также уже частично поражен и новый удар огневых средств стороны II может прийтись (полностью или частично) на уже поврежденную площадь. В связи с этим средний ущерб, наносимый плацдармом II плацдарму I за время Dt, нужно умножить на вероятность того, что этот ущерб придется на еще не пораженную часть плацдарма I. Эту вероятность, естественно, нужно принять равной средней доле V1 сохранившейся площади плацдарма I. В результате получим следующее выражение для среднего ущерба:
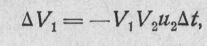
DV1 = -V1*V2*u2*Dt,
где V1 - средняя доля непораженной площади плацдарма I;
V2*u2*Dt - средний ущерб, который был бы нанесен плацдарму I сохранившейся долей V2 плацдарма II, если бы к рассматриваемому моменту времени плацдарм I был бы не поврежден.
Разделив уравнение на Dt и перейдя к пределу при Dt -> 0, получим уравнение

dV1/dt = -u2*V1*V2.
Рассуждая аналогично для стороны II, получим систему двух дифференциальных уравнений для относительных площадей сохранившейся части плацдармов в процессе боя:
dV1/dt = -u2*V1*V2;
dV2/dt = -u1*V1*V2.
Разделив второе уравнение на первое, получим
dV2/dV1 = u1/u2,
откуда
V2 = u1/u2*V1 C.
Постоянную C найдем из условия, что при t = 0, V1 = V2 = 1 (относительная непораженная площадь плацдармов составляет 100%).
В результате имеем
C = (u2-u1)/u2.
Подставляя значение V2 в первое уравнение динамики боя двух плацдармов, будем иметь
dV1/dt = u1*u2*V1*(V1-1).
Аналогично можно получить уравнение для относительной сохранившейся площади V2:
dV2/dt = u1*u2*V2*(V2-1).
Решение приведенных уравнений может быть записано в виде

V1 = (u2-u1)/(u2*exp(u2-u1)*t)-u1);
V2 = (u1-u2)/(u1*exp((u1-u2)*t)-u2).
В частном случае при равной интенсивности огневого воздействия сторон (u1 = u2 = u) относительные сохранившиеся площади будут уменьшаться по такому закону, который получается после раскрытия неопределенности.
V1 = V2 = 1/((1+u)*t)
Отсюда следует, что при равной огневой интенсивности двух плацдармов относительная доля сохранившейся площади каждого плацдарма убывает в процессе боя по гиперболическому закону (а не по показательному, как было в модели А).
Запишем уравнения динамики боя двух плацдармов в следующем виде:
V1 = 2*B/(1+B-(1-B)*exp(-2*B*т));
V2 = 2*B/((1+B)*exp(2*B*т)-(1-B));
где
т = (u1+u2)/2*t - приведенное время;
B = (u1-u2)/(u1+u2) - (В - бета) относительное дифференциальное преимущество плацдарма I перед плацдармом II.
Очевидно, что относительное дифференциальное преимущество зависит:
- от площади плацдармов;
- от плотности огневых средств на плацдармах;
- от разрушительного действия боеприпасов каждого огневого средства;
- от точности стрельбы;
- от противодействия, учитывающего вероятность достижения цели.
Для иллюстрации приводится таблица, показывающая зависимость отношения сохранившихся площадей плацдармов (огневых средств, расположенных на этих площадях) от приведенного времени для двух значений дифференциального относительного преимущества.
Из приведенной таблицы следует, что дифференциальное относительное преимущество очень сильно влияет на результат боя двух плацдармов. Так, например, при B = 0.1 по истечении т = 4 плацдарм I уменьшает огневую мощь плацдарма II в 1.93 раза, тогда как при B = 0.5 к этому же моменту времени плацдарм II оказывается практически полностью уничтоженным.
Приведенные уравнения позволяют выявить влияние на динамику боя двух плацдармов различных факторов, а именно: численности боевых средств, скорострельности каждого средства, радиуса разрушения боеприпасов, точности стрельбы, площади плацдарма и т.д.
ПРИМЕР. Силы сторон I и II размещены на двух плацдармах площадью S1 = 200*200км и S2= 100*100км. Сторона I располагает десятью стартовыми позициями баллистических ракет и двумя фронтовыми аэродромами. Каждая стартовая позиция способна выпускать по плацдарму II в среднем две ракеты в сутки; каждая ракета достигает плацдарма II с вероятностью Wр1д = 0.8; каждая достигшая плацдарма II ракета причиняет разрушения, достаточные для поражения всех боевых средств на площади Sр1 = 20км2 плацдарма II. Каждый аэродром в среднем способен послать по плацдарму II 20 бомбардировщиков в сутки; каждый бомбардировщик достигает плацдарма II с вероятностью Wб1д = 0.6; достигший плацдарма II бомбардировщик причиняет разрушения на площади Sб1 = 10км2. Плацдарм II располагает пятью стартовыми позициями баллистических ракет и одним аэродромом. Средняя скорострельность стартовой позиции - одна ракета в сутки; каждая ракета достигает плацдарма I с вероятностью Wр2д = 0.9 и причиняет ущерб на площади Sр2 = 30км2. Аэродром может послать по плацдарму I десять бомбардировщиков в сутки; посланный бомбардировщик достигает плацдарма I с вероятностью Wб2д = 0.8 и, сбросив бомбы, причиняет разрушения на площади Sб2 = 20км2.
Исследовать количественно динамику боя.
Решение. Определяем характеристику интенсивности воздействия плацдарма I по плацдарму II. Одна ракета наносит средний относительный ущерб

Wp1д*Sp1д/S2 = 0.8*20/10000 = 1.6E-3.
Каждая стартовая позиция наносит в сутки ущерб
2*1.6E-3 = 3.2E-3,
а десять стартовых позиций -
10*3.2E-3 = 3.2E-2.
Каждый бомбардировщик наносит ущерб
Wб1д*Sб1/S2 = 0.6*10/10000 = 0.6E-3.
Каждый аэродром в сутки наносит ущерб
20*0.6E-3 = 1.2E-2,
а два аэродрома -
2*1.2E-2 = 2.4E-2.
Суммарный относительный ущерб в сутки, наносимый плацдармом I плацдарму II:
u1 = 3.2E-2+2.4E-2 = 5.6E-2.
Рассуждая аналогично для плацдарма II, находим
u2 = 0.74E-2.
Переходим к новому масштабу времени:
т = (u1+u2)/28t = (5.6E-2+0.74E-2)/2*t = 3.17E-2*t.
Вычисляем дифференциальное относительное преимущество плацдарма I перед плацдармом II:
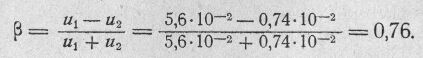
B = (u1-u2)/(u1+u2) = (5.6E-2-0.74E-2)/(5.6E-2+0.74E-2) = 0.76.
Подставляя полученную величину B в формулы для V1 и V2 получим их значения в различные моменты времени. Результаты вычислений приведены в таблице.
Из приведенной таблицы отчетливо видно значительное преимущество плацдарма I. Через приведенное время т = 1.5 плацдарм I потеряет 13% площади (соответственно и огневых средств на этой площади), тогда как плацдарм II будет уничтожен на 81%, т.е. практически выведен из строя. Определим, через какой промежуток времени после начала боя это произойдет:
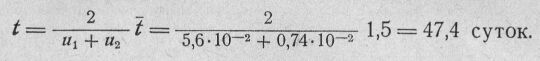
t = 2/(u1+u2)*т = 2*1.5/(5.6E-2+0.74E-2) = 47.4 суток.
Сравнение динамики боя моделей А и Б позволяет сделать следующие выводы:
- модель А соответствует более целеустремленной и интенсивной схеме боя (стрельба по строго определенным целям, перенос огня с пораженной цели на новую);
- процесс боя в модели А развивается более энергично, чем в модели Б; преимущества сильной стороны выражены более ярко;
- бой быстрее заканчивается истощением побежденной стороны в модели А, чем в модели Б;
- бой в модели Б приводит к сравнительно медленному убыванию боевых средств;
- преимущества сильной стороны в модели Б выражены менее ярко; процесс боя с течением времени приобретает затяжной характер.
Аналитические модели могут использоваться для количественной оценки результатов применения боевых средств, для оценки влияния соотношения сил, а также для оценки влияния качества разведки об объектах противника.
Из главы VI
При планировании операций необходимо иметь возможность производить количественный анализ развития боевых действий между двумя группировками боевых средств с учетом их взаимного огневого воздействия.
Математические методы, изучающие количественные закономерности боя в условиях взаимного воздействия сторон, получают в настоящее время большое развитие. Если рассматривать боевые действия войск с учетом многочисленных факторов, задача становится непомерно сложной. Целесообразно сначала рассматривать лишь упрощенные, схематизированные модели боевых действий.
В таких упрощенных аналитических моделях удается наглядно выявить основные количественные закономерности боя, рассмотреть влияние главных факторов, которые иначе были бы затенены второстепенными, малосущественными факторами.
Математический анализ простейших моделей боевых действий позволяет приближенно оценить влияние таких основных факторов, как огневая мощь и количественный состав применяемых боевых средств, преимущество внезапности, темпы наращивания сил для ответного удара, соотношение сил сторон, темпы восстановления боевых потерь, огневая "производительность" боевых средств и т.д. Математические модели боя, безусловно, явятся ценным вспомогательным средством при планировании операций, не претендуя, разумеется, на то, чтобы подменить собой тактику и оперативное искусство.
Всякий бой между двумя сторонами можно рассматривать как совокупность последовательных ударов каждой стороны по противнику. Процесс развития боя представляется как случайный, так как результат каждого огневого удара в какой-то мере случаен. Ниже будут рассмотрены две простейшие модели боя:
- бой между двумя группировками боевых единиц (модель А);
- бой между двумя плацдармами (модель Б).
Несмотря на значительные допущения, которые делаются для обеих моделей, получаемые с их помощью количественные закономерности дают возможность проанализировать боевые действия с точки зрения учета наиболее существенных факторов.
Дальнейшее развитие моделей такого типа и совершенствование алгоритмов военных задач позволит получать более точные методы теории динамики боя.
УПРОЩЕННЫЕ УРАВНЕНИЯ ДИНАМИКИ БОЯ ДЛЯ МОДЕЛИ А (УРАВНЕНИЯ ЛАНЧЕСТЕРА)
[Ланчестер - английский военный специалист, занимавшийся приложениями математики к исследованию боевых действий. Основная его работа вышла в 1916г.]
Рассмотрим бой между двумя группировками боевых единиц (ракет, самолетов, танков, артиллерийских батарей).
Пусть группировка I состоит из N1 однородных боевых единиц, а группировка II - из N2 боевых единиц. Боевые единицы группировки I не обязательно однородны с боевыми единицами группировки II (например, с одной стороны могут участвовать танки, с другой стороны - артиллерия). Каждая из боевых единиц может вести прицельный огонь по любой из боевых единиц противника. Если боевая единица поражена, то огонь переносится на другую, т.е. пораженная боевая единица в дальнейших боевых действиях не участвует. Будем считать, что каждая боевая единица ведет огонь с некоторой средней скорострельностью л1 и л2 (здесь л обозачает лямбду), а моменты отдельных выстрелов являются случайными. Предположим, что один выстрел боевой единицы группировки I поражает обстрелянную цель с вероятностью Р1, а группировки II - с вероятностью Р2.
Возможности боевых единиц каждой группировки будут характеризоваться их эффективными скорострельностями n1 и n2, при этом
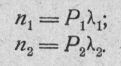
n1 = P1*л1;
n2 = P2*л2.
Рассмотрим обе участвующие в бою группировки как систему, которая в каждый момент времени может находиться в одном из возможных состояний. Под состоянием системы группировок принято понимать число сохранившихся боевых единиц с той и другой стороны.
В дальнейшем будем основываться на допущении, что огневая мощь каждого соединения в каждый момент времени определяется не фактическим числом сохранившихся боевых единиц, а его математическим ожиданием (средним значением).
Такое допущение вполне естественно для соединений и объединений, когда случайности, связанные с поражением или непоражением отдельных единиц, сравнительно мало сказываются на суммарной огневой мощи группировки. Для соединений эти случайности начинают оказывать существенное влияние в конце боя, когда в составе группировок сторон остается совсем небольшое число боевых единиц.
Пусть среднее число (математическое ожидание) сохранившихся на данный момент времени боевых единиц группировок сторон равно соответственно m1 и m2.
Рассмотрим закон уменьшения величины m1 с течением времени.

Каждая из боевых единиц группировки II производит за время Dt [D, здесь - дельта] в среднем P2*л2*Dt = n2Dt успешных выстрелов. Среднее число боевых единиц, воздействующих по группировке I, равно m2. Следовательно, все боевые единицы группировки II за время Dt произведут m2*n2*Dt успешных выстрелов.
Эта величина будет равна числу пораженных единиц группировки I, т.е.
Dm1 = -n2*m2*Dt.
Разделив уравнение на Dt и перейдя к пределу при Dt -> 0, получим дифференциальное уравнение для m1 в виде
dm1/dt = -n2*m2.
Совершенно аналогично можно получить дифференциальные уравнения для m2:
dm2/dt = -n1*m1.
Полученные уравнения называются уравнениями Ланчестера. Они показывают, как убывает число боевых единиц сторон с течением времени боя.
Как уже указывалось, уравнения Ланчестера описывают ход боя однородных боевых средств лишь приближенно и их нельзя применять для последней стадии боя (на этапе "истощения"). Однако эти уравнения дают хорошее приближение к действительности на сравнительно ранних стадиях боя, при большом количестве участвующих в бою однородных боевых средств.
После преобразований уравнения Ланчестера можно привести к виду:
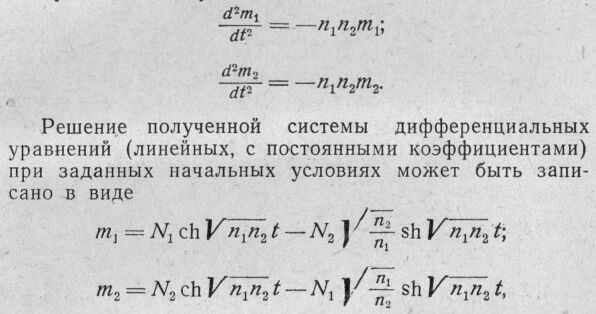
d2m1/dt2 = -n1*n2*m1;
d2m2/dt2 = -n1*n2*m2;
Решение полученной системы дифференциальных уравнений (линейных, с постоянными коэффициентами) при заданных начальных условиях может быть записано в виде
m1 = N1*ch(sqr(n1*n2)*t) - N2*sqr(n2/n1)*sh(sqr(n1*n2)*t);
m2 = N2*ch(sqr(n1*n2)*t) - N1*sqr(n1/n2)*sh(sqr(n1*n2)*t);
где m1 - число боевых единиц первой стороны в некоторый момент боя;
m2 - число боевых единиц второй стороны в тот же момент боя;
N1 - число боевых единиц первой стороны в начале боя;
N2 - число боевых единиц второй стороны в начале боя;
n1 - эффективная скорострельность боевой единицы первой стороны;
n2 - эффективная скорострельность боевой единицы второй стороны;
ch - гиперболический косинус (берется по таблицам);
sh - гиперболический синус (берется по таблицам);
t - момент времени боя.
[Не правда ли, "все очевидно"? Но ведь, никто не заставляет игрока решать дифференциальные уравнения. Приближенные решения, выраженные цветастыми номграммками или табличками, вполне могут обеспечить потребную наукообразность. Просто, не надо считать, что игры для несведующих в математике "чайников" могут делать те же "чайники". "Чувствовать модель" мы просто обязаны. И знать, что гиперболическая тригонометрия это комбинация экспонент, военный моделист обязан знать ровно также, как и любой схемо- или системотехник. Разговоры "здесь добавим 1, там убавим" - исключительно в пользу бедных.- G.]
Для анализа хода боя удобно перейти от абсолютной численности группировок к относительной численности, выражая ее как отношение числа сохранившихся боевых единиц в данный момент, времени к числу боевых единиц в начале, боя.
Введем обозначения:

м1 = m1/N1; м2 = m2/N2; v = N1/N2; a = n1/n2,
где м1, м2 - относительные численности группировок сторон;
v (ню) - соотношение сил сторон в начале боя;
a (альфа) - соотношение эффективных скорострельностей сторон.
Используя введенные обозначения, можно написать уравнения, выражающие зависимость относительной численности боевых средств сторон от времени боя в следующем виде:
м1 = ch(sqr(n1*n2)*t) - 1/v*sqr(1/а)*sh(sqr(n1*n2)*t);
м2 = ch(sqr(n1*n2)*t) - v*sqr(а)*sh(sqr(n1*n2)*t);
Введем еще два обозначения:
т = sqr(n1*n2)*t; X = v*sqr(a).
Величину т можно назвать "приведенным" временем (равносильно изменению масштаба времени).
[Это мы уже наблюдали в простейших полковых моделях, там специально вводилась переменная "напряженность (кровавость) битвы". Во всех же "военных" играх масштаб времени убожески линеен. А ведь, даже фантастически инфантильнфая киношка "STAR WARS", начиная с 6-го эпизода, дает в параллель три финальные битвы - драку на мечах, наземное и космическое сражение. Имеет смысл не делить время на равные промежутки, а идти от события к событию.- G.]
Величину X будем называть коэффициентом преимущества одной стороны над другой.
В этих новых обозначениях уравнения динамики боя для модели А запишутся в виде
м1 = ch(т) - 1/X*sh(т);
м2 = ch(т) - X*sh(т).
Из выражения для коэффициента преимущества следует, что он в большей степени зависит от соотношения сил (в начале боя), чем от соотношения эффективных скорострельностей, так как соотношение сил входит в первой степени, а величина a (соотношение эффективных скорострельностей) - входит под знаком квадратного корня.
Таким образом, при ведении боя между двумя группировками боевых единиц первостепенное значение имеет концентрация сил на направлении главного удара. Вывод получен математически, но он общеизвестен и из практической деятельности. Однако математический вывод дает количественную оценку влияния концентрации сил, а следовательно, дает возможность проанализировать это влияние в ходе боя.
В частном случае, когда обе группировки равносильны (X = 1), уравнение принимает вид
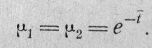
м1 = м2 = exp(-т).
Таким образом, в случае боя равносильных группировок каждая из них уменьшается в ходе боя по простому показательному закону. Если одна из группировок сильнее другой (X > 1), то более сильная сторона с некоторого момента перестает нести существенные потери, тогда как слабая сторона быстро убывает в своей численности, доходя до полного истребления. Следует иметь в виду, что полученные количественные зависимости динамики боя соединений не учитывают тех изменений в тактике действий, которые неизбежно имеются в действительности у обеих сражающихся сторон.
Для иллюстрации приводится таблица, показывающая зависимость соотношения сил сторон m1/m2 (численностей боевых единиц) от приведенного времени для двух значений коэффициента преимущества.
| m1/m2 | т | ||||||
| 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.5 | ||
| X | 1.2 | 1.09 | 1.25 | 1.57 | 2.22 | 4.15 | Истощение |
| 1.5 | 1.38 | 2.10 | 8.0 | Истощение | |||
Из приведенной таблицы следует, что в бою по истечении приведенного времени 0.6 первая сторона приобретает преимущество в силах в 1.57 раза больше (при коэффициенте преимущества в начале боя 1.2) и в 8 раз больше второй стороны (при коэффициенте преимущества 1.5). По истечении приведенного времени боя (примерно 1.5) вторая сторона полностью истребляется.
Таким образом, пользуясь полученными уравнения ми, можно дать прогноз боя двух группировок с однородными боевыми средствами в каждой группировке (но не обязательно однородными в обеих группировках).
[Разнородные группировки - чуть позже.- G.]
При этом результаты боя характеризуются количественной зависимостью оставшихся боевых средств сторон (или боевых потерь) к любому моменту времени i зависимости:
- от соотношения сил перед началом боя;
- от скорострельности боевых средств сторон;
- от вероятностей поражения боевых средств сторон при огневом воздействии.
Необходимо заметить, что вероятность пораженя зависит от многих факторов, характеризующих свойства оружия и поражаемого объекта, а именно:
- от тротилового эквивалента ядерного боеприпаса или поражающих характеристик обычных боеприпасов;
- от характеристик рассеивания боеприпаса (характеристик носителя, дальности стрельбы, качества системы управления и др.);
- от размеров цели (противостоящей боевой единицы);
- от прочностных и других защитных свойств цели.
Как видно, уравнения теории динамики боя учитывают довольно много существенных факторов, влияющих на результаты боя, но не учитывают изменений в тактике.
ПРИМЕР. Происходит бой между двумя группировками танков. Группировка I имеет 20, а группировка II - 10 танков. Средняя скорострельность танков группировки I (с учетом переноса огня) - 0.5 выстрела в минуту, вероятность поражения танков противника - 0.06. Танки группировки II обладают средней скорострельностью один выстрел в минуту и имеют среднюю вероятность поражения танков противоположной стороны 0.05.
Победой какой стороны и через какое время завершится бой?
Решение. Определяем численное соотношение сил к началу боя:
v = N1/N2 = 20/10 = 2.

Вычисляем эффективные скорострельности сторон:
n1 = P1*л1 = 0.06*0.5 = 0.03;
n2 = Р2*л2 = 0.05*1 = 0.05.
Определяем соотношение эффективных скорострельностей:
a = n1/n2 = 0.03/0.05 = 0.6.
Коэффициент преимущества будет равен
X = v*sqr(a) = 2*sqr(0.6) = 1.5.
Следовательно, побеждающей стороной будет группировка I. Находим выражение для приведенного времени:
т = sqr(n1*n2)*t = sqr(0.03*0.05)*t = 0.039*t.
Ниже в таблице приводятся результаты расчетов, характеризующих зависимость относительного числа сохранившихся боевых единиц от времени.
| t, мин | 1 | 2 | 4 | 6 | 10 |
| м1 | 0.98 | 0.95 | 0.91 | 0.88 | 0.82 |
| м2 | 0.94 | 0.88 | 0.78 | 0.66 | 0.44 |
Из таблицы следует, что через 10мин. боя потери группировки II составят 52%. тогда как потери группировки I будут равны 19%.
Еще раз заметим, что выведенные зависимости для модели А были основаны на допущении, что каждая боевая единица может вести прицельный огонь по любой из боевых единиц противника, т.е. имеется полная взаимозаменяемость боевых единиц. В действительности такой полной взаимозаменяемости быть не может: для некоторых боевых единиц не все единицы противника будут доступны, не все силы будут введены в бой сразу, будут ограничения по переносу огня с одних целей на другие. Если при этом можно разбить все участвующие в бою единицы на противостоящие группы, взаимодействующие между собой, то бой можно расчленить на отдельные бои между подгруппами. Крайним случаем ограничения взаимозаменяемости будет случай, когда каждая боевая единица может вести огонь только по одной боевой единице противника. В этом случае бой распадается на элементарные бои типа "дуэлей".
Важным условием для применения модели А являются полная разведка объектов противника и наличие информации о результатах обстрела, которая должна быть своевременной. Это условие в действительности также не может быть полностью выполнено.
Вследствие этого темп действительного боя несравненно медленнее, чем дает модель А. Ниже будет рассмотрена другая модель боя, которая дает несколько большее приближение к картине действительного боя.
Остановимся еще на учете пополнения сил и элемента внезапности в модели А.
Допустим, что пополнение сил происходит с темпом k1 боевых единиц группировки I в единицу времени и с темпом k2 боевых единиц для группировки II. В таком случае уравнения динамики боя примут следующий вид:

dm1/dt = -n2*m2+k1;
dm2/dt = -n1*m1+k2;
Темпы пополнения сил могут быть как постоянными, так и переменными. Решение этой системы уравнений дает возможность проанализировать процесс боя в зависимости от темпа пополнения сил и выявить соответствующие требования к темпу пополнения своей группировки для того, чтобы завершить бой разгромом противника в заданное время.
В частном случае, когда темпы пополнения сил постоянные, решение системы уравнений будет иметь вид
m1 = 1/2*(N1-k2/n1)*ch(sqr(n1*n2)*t) + (k1-n2*N2)/(2*sqr(n1*n2))*sh(sqr(n1*n2)*t) + k2/n1;
m2 = 1/2*(N2-k1/n2)*ch(sqr(n1*n2)*t) + (k2-n1*N1)/(2*sqr(n1*n2))*sh(sqr(n1*n2)*t) + k1/n2;
Решение таких уравнений выполняется достаточно просто не только на электронных вычислительных, машинах, но и обычными способами.
ДИНАМИКА БОЯ МЕЖДУ ДВУМЯ ПЛАЦДАРМАМИ (МОДЕЛЬ Б)
Рассмотрим бой между двумя группировками войск при следующих допущениях. Противостоящие друг другу группировки войск ведут огонь не по отдельным разведанным целям, а по некоторой площади (плацдарму), на которой расположены огневые средства противника (стартовые позиции ракет, аэродромы с базирующимися на них бомбардировщиками, артиллерия и т.д.). Кроме того, сведения о причиненных разрушениях и связь между боевыми единицами настолько неполны, что не исключается повторное огневое воздействие по уже пораженным объектам. Такую модель боя называют "боем двух плацдармов" или моделью Б. Ее можно рассматривать как второй крайний случай модели боя, когда отсутствует прицельный огонь и отсутствуют разведывательные данные об объектах противника на площади плацдарма. Действительный бой представляет собой как бы "среднее" между боями, описываемыми моделями А и Б.
Предположим, что плацдармы I и II первоначально находятся в неповрежденном состоянии. Огневое воздействие плацдарма I по плацдарму II за время Dt уничтожает боевые средства на некоторой элементарной площади DS2, которая составляет известную долю от площади плацдарма S2.
Введем в качестве характеристики интенсивности огневого воздействия средний относительный ущерб в единицу времени, который наносит один плацдарм другому в начале боя всеми огневыми средствами.
В таком случае средний ущерб за время Dt, который нанесет плацдарм I по плацдарму II, будет
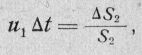
u1*Dt = DS2/S2
где u1 - средний относительный ущерб за единицу времени, наносимый в начале боя плацдармом I по плацдарму II. Аналогичной характеристикой описывается интенсивность огневого воздействия плацдарма II по плацдарму I.
Для определения u1 и u2 нужно найти суммарную среднюю относительную площадь всех разрушений, которые могут нанести противнику все боевые средства за произвольно выбранную единицу времени.
Средний относительный ущерб за единицу времени зависит:
- от количества огневых средств;
- от скорострельности огневых средств;
- от вероятности достижения цели носителями боеприпасов;
- от радиусов поражения объектов поражения;
- от прочности поражаемых объектов.
Для вывода уравнений динамики боя между двумя плацдармами будем рассуждать следующим образом.
Огневой удар за время Dt всеми средствами плацдарма II нанес бы неповрежденному плацдарму I ущерб, равный u2*Dt. Так как к моменту удара плацдарм II располагает только частью сил, сохранившихся на площади, относительную величину которой мы обозначаем через V2, то необходимо умножить относительный ущерб на V2. Кроме того, к моменту удара плацдарм I также уже частично поражен и новый удар огневых средств стороны II может прийтись (полностью или частично) на уже поврежденную площадь. В связи с этим средний ущерб, наносимый плацдармом II плацдарму I за время Dt, нужно умножить на вероятность того, что этот ущерб придется на еще не пораженную часть плацдарма I. Эту вероятность, естественно, нужно принять равной средней доле V1 сохранившейся площади плацдарма I. В результате получим следующее выражение для среднего ущерба:
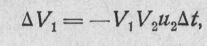
DV1 = -V1*V2*u2*Dt,
где V1 - средняя доля непораженной площади плацдарма I;
V2*u2*Dt - средний ущерб, который был бы нанесен плацдарму I сохранившейся долей V2 плацдарма II, если бы к рассматриваемому моменту времени плацдарм I был бы не поврежден.
Разделив уравнение на Dt и перейдя к пределу при Dt -> 0, получим уравнение

dV1/dt = -u2*V1*V2.
Рассуждая аналогично для стороны II, получим систему двух дифференциальных уравнений для относительных площадей сохранившейся части плацдармов в процессе боя:
dV1/dt = -u2*V1*V2;
dV2/dt = -u1*V1*V2.
Разделив второе уравнение на первое, получим
dV2/dV1 = u1/u2,
откуда
V2 = u1/u2*V1 C.
Постоянную C найдем из условия, что при t = 0, V1 = V2 = 1 (относительная непораженная площадь плацдармов составляет 100%).
В результате имеем
C = (u2-u1)/u2.
Подставляя значение V2 в первое уравнение динамики боя двух плацдармов, будем иметь
dV1/dt = u1*u2*V1*(V1-1).
Аналогично можно получить уравнение для относительной сохранившейся площади V2:
dV2/dt = u1*u2*V2*(V2-1).
Решение приведенных уравнений может быть записано в виде

V1 = (u2-u1)/(u2*exp(u2-u1)*t)-u1);
V2 = (u1-u2)/(u1*exp((u1-u2)*t)-u2).
В частном случае при равной интенсивности огневого воздействия сторон (u1 = u2 = u) относительные сохранившиеся площади будут уменьшаться по такому закону, который получается после раскрытия неопределенности.
V1 = V2 = 1/((1+u)*t)
Отсюда следует, что при равной огневой интенсивности двух плацдармов относительная доля сохранившейся площади каждого плацдарма убывает в процессе боя по гиперболическому закону (а не по показательному, как было в модели А).
Запишем уравнения динамики боя двух плацдармов в следующем виде:
V1 = 2*B/(1+B-(1-B)*exp(-2*B*т));
V2 = 2*B/((1+B)*exp(2*B*т)-(1-B));
где
т = (u1+u2)/2*t - приведенное время;
B = (u1-u2)/(u1+u2) - (В - бета) относительное дифференциальное преимущество плацдарма I перед плацдармом II.
Очевидно, что относительное дифференциальное преимущество зависит:
- от площади плацдармов;
- от плотности огневых средств на плацдармах;
- от разрушительного действия боеприпасов каждого огневого средства;
- от точности стрельбы;
- от противодействия, учитывающего вероятность достижения цели.
Для иллюстрации приводится таблица, показывающая зависимость отношения сохранившихся площадей плацдармов (огневых средств, расположенных на этих площадях) от приведенного времени для двух значений дифференциального относительного преимущества.
| V1/V2 | т | ||||||
| 1 | 2 | 4 | 6 | 8 | 10 | ||
| B | 0.1 | 1.25 | 1.47 | 1.93 | 3.14 | 4.80 | 7.80 |
| 0.5 | 3.2 | 6.4 | 65 | Истощение | |||
Из приведенной таблицы следует, что дифференциальное относительное преимущество очень сильно влияет на результат боя двух плацдармов. Так, например, при B = 0.1 по истечении т = 4 плацдарм I уменьшает огневую мощь плацдарма II в 1.93 раза, тогда как при B = 0.5 к этому же моменту времени плацдарм II оказывается практически полностью уничтоженным.
Приведенные уравнения позволяют выявить влияние на динамику боя двух плацдармов различных факторов, а именно: численности боевых средств, скорострельности каждого средства, радиуса разрушения боеприпасов, точности стрельбы, площади плацдарма и т.д.
ПРИМЕР. Силы сторон I и II размещены на двух плацдармах площадью S1 = 200*200км и S2= 100*100км. Сторона I располагает десятью стартовыми позициями баллистических ракет и двумя фронтовыми аэродромами. Каждая стартовая позиция способна выпускать по плацдарму II в среднем две ракеты в сутки; каждая ракета достигает плацдарма II с вероятностью Wр1д = 0.8; каждая достигшая плацдарма II ракета причиняет разрушения, достаточные для поражения всех боевых средств на площади Sр1 = 20км2 плацдарма II. Каждый аэродром в среднем способен послать по плацдарму II 20 бомбардировщиков в сутки; каждый бомбардировщик достигает плацдарма II с вероятностью Wб1д = 0.6; достигший плацдарма II бомбардировщик причиняет разрушения на площади Sб1 = 10км2. Плацдарм II располагает пятью стартовыми позициями баллистических ракет и одним аэродромом. Средняя скорострельность стартовой позиции - одна ракета в сутки; каждая ракета достигает плацдарма I с вероятностью Wр2д = 0.9 и причиняет ущерб на площади Sр2 = 30км2. Аэродром может послать по плацдарму I десять бомбардировщиков в сутки; посланный бомбардировщик достигает плацдарма I с вероятностью Wб2д = 0.8 и, сбросив бомбы, причиняет разрушения на площади Sб2 = 20км2.
Исследовать количественно динамику боя.
Решение. Определяем характеристику интенсивности воздействия плацдарма I по плацдарму II. Одна ракета наносит средний относительный ущерб

Wp1д*Sp1д/S2 = 0.8*20/10000 = 1.6E-3.
Каждая стартовая позиция наносит в сутки ущерб
2*1.6E-3 = 3.2E-3,
а десять стартовых позиций -
10*3.2E-3 = 3.2E-2.
Каждый бомбардировщик наносит ущерб
Wб1д*Sб1/S2 = 0.6*10/10000 = 0.6E-3.
Каждый аэродром в сутки наносит ущерб
20*0.6E-3 = 1.2E-2,
а два аэродрома -
2*1.2E-2 = 2.4E-2.
Суммарный относительный ущерб в сутки, наносимый плацдармом I плацдарму II:
u1 = 3.2E-2+2.4E-2 = 5.6E-2.
Рассуждая аналогично для плацдарма II, находим
u2 = 0.74E-2.
Переходим к новому масштабу времени:
т = (u1+u2)/28t = (5.6E-2+0.74E-2)/2*t = 3.17E-2*t.
Вычисляем дифференциальное относительное преимущество плацдарма I перед плацдармом II:
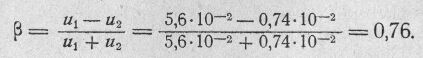
B = (u1-u2)/(u1+u2) = (5.6E-2-0.74E-2)/(5.6E-2+0.74E-2) = 0.76.
Подставляя полученную величину B в формулы для V1 и V2 получим их значения в различные моменты времени. Результаты вычислений приведены в таблице.
| т | 0 | 0.25 | 0.50 | 0.75 | 1.0 | 1.25 | 1.50 |
| V1 | 1.0 | 0.95 | 0.93 | 0.91 | 0.89 | 0.88 | 0.87 |
| V2 | 1.0 | 0.63 | 0.52 | 0.30 | 0.19 | 0.13 | 0.09 |
| V1/V2 | 1.0 | 1.5 | 1.8 | 3.0 | 4.7 | 6.8 | 9.7 |
Из приведенной таблицы отчетливо видно значительное преимущество плацдарма I. Через приведенное время т = 1.5 плацдарм I потеряет 13% площади (соответственно и огневых средств на этой площади), тогда как плацдарм II будет уничтожен на 81%, т.е. практически выведен из строя. Определим, через какой промежуток времени после начала боя это произойдет:
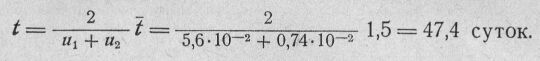
t = 2/(u1+u2)*т = 2*1.5/(5.6E-2+0.74E-2) = 47.4 суток.
Сравнение динамики боя моделей А и Б позволяет сделать следующие выводы:
- модель А соответствует более целеустремленной и интенсивной схеме боя (стрельба по строго определенным целям, перенос огня с пораженной цели на новую);
- процесс боя в модели А развивается более энергично, чем в модели Б; преимущества сильной стороны выражены более ярко;
- бой быстрее заканчивается истощением побежденной стороны в модели А, чем в модели Б;
- бой в модели Б приводит к сравнительно медленному убыванию боевых средств;
- преимущества сильной стороны в модели Б выражены менее ярко; процесс боя с течением времени приобретает затяжной характер.
Аналитические модели могут использоваться для количественной оценки результатов применения боевых средств, для оценки влияния соотношения сил, а также для оценки влияния качества разведки об объектах противника.
Последний раз редактировалось: Gudleifr (Чт Апр 25, 2024 1:19 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
П.Н.Ткаченко и др. МАТЕМАТИЧЕСКИЕ МОДЕЛИ БОЕВЫХ ДЕЙСТВИЙ.- М.: "Советское радио". 1969. Моя любимая книжка. Игры можно делать из каждой главы. Данный источник, по-видимому составлен по материалам каких-то дипломов и/или диссертаций военных ВУЗов , небрежно собранных под одним переплетом. Масса опечаток и нестыковок. Любой материал приходится перепроверять и редактировать.- G.
3.4. УПРОЩЕННАЯ АНАЛИТИЧЕСКАЯ МОДЕЛЬ БОЕВЫХ ДЕЙСТВИЙ ГРУППОВОГО БОЯ ПРИ РАВНОМЕРНОЙ ПЛОТНОСТИ БОЕВЫХ ПОРЯДКОВ
Предположим, что требуется построить модель боевых действий, которая в пределах достаточно грубых допущений позволила бы определить влияние численности боевых средств и их качества на результат боевых действий и найти условия победы для сражающихся сторон. При этом будем считать, что системы разведки и управления обеих сторон работают идеально, что означает наличие полной информации о целях и ее передачу совместно с исполнительной информацией без задержек, т.е. в данном случае в течение времени, которое пренебрежимо мало по сравнению со временем исполнения (tи>>tо). Кроме того, не будем учитывать влияние ввода в бой резервов и относительное перемещение сражающихся сторон на местности. Влияние местности на ход боевых действий также рассматривать не будем. Считая известными размеры целей, примем гипотезу о их равномерном распределении на некоторой площади и представим механизм вооруженной борьбы в виде огневого взаимодействия сторон по схеме рис.3.10. При этом будем учитывать только активные боевые средства, оказывающие непосредственные воздействия на противника. Вспомогательные (пассивные) средства и органы тыла учитывать не будем.
Согласно схеме рис.3.10 любое боевое средство одной стороны может оказывать воздействие на любой объект другой стороны, причем для каждой стороны боевые средства и объекты будем считать однородными. Влияние различных способов распределения боевых средств по объектам противника также учитывать не будем. Введенные ограничения могут быть сняты или уменьшены при переходе к более тонким исследованиям на моделях повышенной точности. По схеме рис. 3.10 в упрощенной постановке может проводиться формализация огневого взаимодействия танков, самолетов, кораблей и наземных средств, включая артиллерийские и ракетно-ядерные удары.

Рис.3.10. Схема огневого взаимодействия сторон; ra - радиус защиты боевой единицы стороны A; rb - то же для стороны B; Ra - радиус поражения боевого средства стороны A; Rb - то же для стороны B.
Каждое боевое средство характеризуется следующими основными параметрами: мощностью удара, скорострельностью, точностью воздействия и степенью защищенности. Для боеприпасов объемного действия мощность определяется радиусом поражения R ~ кубический корень из Q, где Q - тротиловый эквивалент заряда. В частном случае для боеприпасов ударного действия (например, бронебойных) радиус поражения равен радиусу снаряда. Скорострельность c измеряется числом выстрелов в единицу времени. Точность воздействия можно учесть либо при помощи характеристик рассеивания, либо при помощи интегрального коэффициента результативности стрельбы а, устанавливающего относительное число боеприпасов, достигающих цель и попадающих на ее площадь. Степень защищенности объекта можно оценивать различными величинами. В данном случае удобно воспользоваться приведенным радиусом защиты r, определяющим круг, площадь которого равна площади цели. Попадание в эту площадь наносит определенный ущерб цели, а число попаданий k, необходимое для вывода цели из строя, может являться мерой ущерба. Обозначая текущую численность сторон через n, начальную численность - через n0, рассмотрим результат воздействия стороны B по стороне A. Параметры, относящиеся к средствам соответствующей стороны, будем различать индексами a или b.

Рис.3.11. Определение критической площади попадания для поражения объекта одиночным ударом по стороне A.
Сторона B за время Dt сделает по стороне А прицельных выстрелов


где nak и nbk - остаточные численности соответствующих сторон, при которых теряется их способность к дальнейшему ведению боевых действий. Величины коэффициентов фak и фbk зависят от многих факторов, и прежде всего от боевого духа войск, их стойкости, дисциплины, качества командных кадров, наличия средств управления и т.п. Эти факторы в основном имеют качественный характер и не поддаются пока количественному учету. Их суммарное влияние на исход боевых действий можно в первом приближении оценивать при помощи обобщенных коэффициентов потерь боеспособности, определяемых статистическими методами. В среднем для морально стойких войск можно применить фk = 0.4..0.5, для морально нестойких войск фk = 0.7..0.8.
Если обе стороны одновременно достигают критического состояния потери боеспособности, то это означает динамическое равновесие их боевых возможностей, при котором обе стороны должны выйти из боя или объявить перемирие.
Условие динамического равновесия получается из (3.31) в виде

может рассматриваться в качестве условия победы сторон, принимающих участие в сражении. При помощи критерия k можно оценить влияние на результат боевых действий (при принятых допущениях) количества и качества вооружения сторон и их боевой стойкости. Области победы сторон показаны на рис.3.12, на котором Ek - критическая точка, при достижении которой сторона В выходит из боя. Области победы сражающихся сторон существуют и при других, более сложных зависимостях фa = F(фb) по сравнению с соотношением (3.31).

Рис.3.12. Области победы сражающихся сторон: N - линия динамического равновесия; Ek - критическая точка для стороны В (фk = фbk; Фa <> фak)
Граница областей при одной из возможных зависимостей F для постоянных значений фak и фbk показана штрих-пунктирной линией на рис.3.12. Очевидно, что лри любом характере зависимости фa = F(фb) может быть определено условие k, устанавливающее влияние на результат боевых действий параметров na0, nb0, Ba, Bb, фak и фbk.
Однако для анализа хода боевых действий наличие только одного условия (3.32а) часто бывает недостаточным. Важное значение имеет продолжительность боя, определяемая отрезком времени tk от начала боевых действий до момента, когда одна из сторон прекращает сопротивление.
Зависимость относительной численности сторон от времени, полученная из (3.30), имеет вид

При k = 1 выражения (3.35) и (3.36) теряют смысл, так как приводят к значениям tk < 0. В этом случае, например для условий победы стороны А (фbk >фak), из (3.34) получаем величину максимальной продолжительности боевых действий в виде

Графики зависимости т = т(k) согласно (3.38) при нескольких значениях фak = abk изображены на рис. 3.13.

Рис.3.13. График зависимости т = т(k).
Из графиков видно, что при k>3 не достигается сколько-нибудь заметного сокращения длительности боевых действий. Поэтому для победы над противником в сравнительно короткое время не требуется более чем тройного превосходства в значении критерия k. Например, если при фk = 0.5 увеличение значения k от 1 до 2 приводит к уменьшению времени боя на 60%, то дальнейшее повышение величины k до значения k = 3 дает выигрыш во времени только на 15%. Таким образом, установлена верхняя и нижняя границы величины k. Для достижения победы в приемлемое время стороной А необходимо, чтобы соблюдалось условие
2 < k < 3
Условие победы k и входящие в него параметры позволяют в пределах принятых допущений, т.е. довольно приближенно, получить оценку хода боевых действий и предсказать возможное время их завершения. Однако величина k в явном виде не учитывает влияния системы управления на процесс боевых действий, а тот факт, что такое влияние имеется и может быть достаточно существенным, не требует особых доказательств. Система управления влияет на результаты боевых действий, во-первых, за счет затрат времени, необходимых для получения исходных данных, во-вторых, за счет запаздывания в принятии решений по отношению к фактическому состоянию сторон и, в-третьих, за счет точности принимаемых решений и их исполнения. Процесс управления, как правило, состоит из следующих основных этапов: поиск и обнаружение целей, передача информации, обработка данных и принятие решения, передача команд или приказов и их исполнение. Таким образом, можно считать, что продолжительность процесса управления tу определяется временем организации исполнения tо и временем tи, непосредственно затрачиваемым на исполнение принятых решений, т.е.

где c - техническая скорострельность оружия или в более общем случае средняя скорость исполнения команд войсками.
Величина c с индексом a и b соответственно для каждой из сражающихся сторон фигурирует в выражениях (3.29), определяющих параметры Ba и Bb. Не исключена возможность того, что часть процессов по организации управления будет совмещена с процессами исполнения. Так, например, могут совмещаться процессы поиска целей и движения танков, выработки решения и подготовки ракет к пуску и т.д. Поэтому в общем виде

где ac - коэффициент совмещения процессов управления и исполнения в ходе боевых действий.
Если ac = 0, то процессы полностью совмещены и задержек в темпах ведения боевых действий не происходит. При ac = 1 совмещение процессов полностью отсутствует.
При tо >> tи будет иметь место неэффективное использование оружия за счет несовершенства системы управления, что может привести к поражению при прочих равных условиях с противником. Таким образом, критерий победы в виде (3.32) при условии введения коэффициента эффективной скорострельности cэ (3.39) позволяет учесть влияние системы управления на результат боевых действий. Однако при этом не учитывается запаздывание данных о фактическом состоянии сторон, возникающее за счет работы системы управления. В самом деле, удары по каждой из сторон будут наноситься в момент t+tз, где tз=ac*to - время запаздывания в нанесении удара за счет несовмещенности процессов управления и исполнения.
С учетом запаздывания, уравнения (3.28) принимают вид

Для решения системы (3.40) необходимо принять гипотезу о виде функций na и nb с запаздывающими аргументами.
В теории таких систем решение сбычно ищут в виде функции от exp(t+tз), подбирая вид функции так, чтобы удовлетворить исходным уравнениям (3.40). С достаточной степенью приближения функцию n(t+tз) можно представить в виде ряда и ограничиться элементами разложения первого порядка. Тогда

функциями соответственно от фa и фb, причем при фa = фb будет Фa = Фb =1.
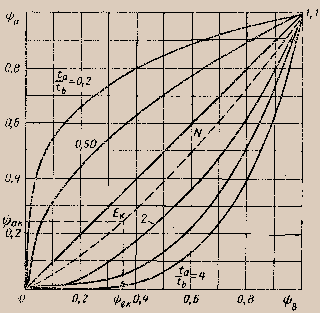
Рис.3.14. График зависимости Фa = F(Фb, ta, tb); Ek - критическая точка; N - линия динамического равновесия.
На рис.3.14 кривая Фa = F(Фb, ta, tb), проходящая через критическую точку Ek(Фa = Фak, Фb = Фbk), будет соответствовать условиям динамического равновесия. В этой точке параметры фa и фb одновременно достигают критического значения. Кривые, проходящие выше точки Ek, соответствуют условиям победы стороны A, так как текущая точка на этих кривых (характеризующая состояние сторон) при перемещении из состояния (1, 1) в состояние

или

Величина k учитывает влияние на результат боевых действий количества и качества вооружения, а величина kу - качество системы управления.
Из (3.46) видно, что за счет системы управления (ta < tb) можно получить некоторое превосходство над противником и при неблагоприятном соотношении по количеству и качеству вооружения. Однако следует иметь в виду, что возможности системы управления довольно ограничены. Если k << 1, а kу ~ 1, то никаким усовершенствованием системы управления в принципе не может быть достигнуто условие победы.
При идеальной системе управления с обеих сторон kу = 1 и неравенство (3.46) превращается в рассмотренное ранее условие k > 1. При исключительно высоких показателях

В этом предельном случае результат боевых действий будет зависеть только от качества системы управления и морального духа войск.
Выражение (3.47), в отличие от общеизвестного качественного выражения о том, что совершенная система вооружения требует и совершенной системы управления, позволяет определить необходимые количественные показатели систем управления. Аналогично тому, как это делалось при оценке верхней и нижней границ условия k, можно показать, что для достижения устойчивой работы в приемлемое время с учетом влияния системы управления должно быть
2 < k*kу < 3
Допустимые пределы изменения произведения параметров определяются на основе интегрирования системы (3.42) при аргументе t и вычислений времени окончания боевых действий.
Полученные зависимости позволяют в первом приближении связать характеристики системы управления с результатами боевых действий и показывают, что средняя продолжительность цикла управления оказывает существенное влияние на динамику вооруженного столкновения и должна приниматься во внимание при оценке качества системы.
Оценка системы вооружения и системы управления в целом может быть произведена на основе различных критериев эффективности, позволяющих установить оптимальные значения основных параметров, характеризующих эти системы.
В качестве основных можно рассматривать совокупность следующих критериев:
а) оперативной эффективности Eо,
б) технической эффективности Eт,
в) экономической эффективности Еэ.
Критерий Ео характеризуется математическим ожиданием (mр) результатов выполнения боевой задачи и определяет, таким образом, боевую эффективность системы в целом с учетом средств вооружения и управления. В числе боевых задач, обеспечение решения которых возлагается на системы управления войсками, можно наметить следующие типовые задачи: выдвижение, наступление, подавление, уничтожение, оборона и отступление. Каждая из этих задач может быть охарактеризована числовой мерой, по величине которой можно судить о качестве выполнения задачи; так, например, выдвижение характеризуется величиной пройденного расстояния или средним темпом перемещения, наступление - величиной захваченной территории или количеством трофеев, подавление или уничтожение - средним числом подавленных или уничтоженных целей, оборона - средним временем удержания обороняемого рубежа (района) или потерями, нанесенными противнику и т.д.
Выполнение боевой задачи может быть достигнуто различными средствами при различных средних потерях (mп) со стороны своих войск. Поэтому можно принять
Ео = mр/mп,
причем математическое ожидание результатов (mр) и потерь (mп) может быть как абсолютным, так и относительным, т.е. отнесенным к единице площади, расстояния, начальной численности и т.п. В некоторых американских работах предлагается боевую эффективность определить отношением стоимости результатов ср к стоимости потерь сп, т.е. считать
Eо = ср[долл.]/сп[долл.].
Однако такой подход вряд ли заслуживает признания, так как в боевых системах не все может быть оценено деньгами и, прежде всего, не поддается финансовому учету стоимость человеческих жизней. Впрочем, не смущаясь этим обстоятельством, американцы оценивают стоимость каждого солдата в 10000долл., т.е. величиной страхового полиса.
С точки зрения оперативной эффективности та система управления будет наилучшей, которая обеспечит получение заданного боевого результата в наименьшее время, причем, само собой разумеется, что это время не должно превышать допустимого значения, установленного из оперативных требований. Поэтому без учета времени выполнения боевой задачи оценка системы не может быть полной. Время выполнения боевой задачи определяется объемом выполняемых физических и информационных работ и зависит от численности технических средств и личного состава, квалификации и обученности обслуживающего персонала, надежности аппаратуры и от ряда других факторов. Наиболее полно влияние всех этих факторов может быть учтено величиной математического ожидания времени выполнения боевой задачи
mt = m(tу).
Иногда можно считать, что mt является суммой математических ожиданий времен выполнения отдельных процессов, из которых состоит процесс функционирования системы в целом. В этом случае критерий Eт может быть охарактеризован величиной mt = m(tп) + m(tо), на основе которой можно провести оценку технической производительности системы.
Что касается экономической эффективности системы, то для ее оценки может быть предложено несколько критериев. Например, она может быть охарактеризована средним временем окупаемости системы за счет более рационального расходования материальных средств, приращением боевых результатов системы на единицу затрачиваемых средств, величинами эксплуатационных расходов в системе и т.д.
Все эти критерии являются частными и могут применяться для анализа отдельных экономических показателей системы. Наиболее общим экономическим показателем системы является математическое ожидание величины капитальных затрат на создание системы m{с), которое складывается из затрат на систему вооружения (св) и на систему управления (су).
Этот показатель входит во все частные критерии и определяется как сумма

Этот критерий наиболее полно характеризует качество системы и из всех возможных вариантов ее построения позволяет выбрать такой оптимальный вариант, который обеспечивает достижение наибольших результатов при минимальных потерях с наименьшими затратами и в наиболее короткое время. Так как все величины, входящие в выражение для E, зависят не только от системы вооружения, но и от системы управления, критерий E позволяет установить правильное соотношение между средствами вооружения и средствами управления, чего нельзя получить при помощи частных критериев. Для того чтобы воспользоваться критерием E, необходимо установить зависимости между величинами mр, mп, mt и mс.
Такие зависимости могут быть получены на основе аналитического или стохастического моделирования процессов функционирования систем с учетом их структурных схем, внешних связей и характера нагрузки.
При применении обобщенного критерия Е следует иметь в виду его пригодность только для сравнительной оценки боевых систем и не пытаться оптимизировать систему путем неограниченного уменьшения величин, стоящих в знаменателе. Все эти величины по физическим соображениям ограничены снизу и не могут быть произвольно приняты сколь угодно малыми.
3.4. УПРОЩЕННАЯ АНАЛИТИЧЕСКАЯ МОДЕЛЬ БОЕВЫХ ДЕЙСТВИЙ ГРУППОВОГО БОЯ ПРИ РАВНОМЕРНОЙ ПЛОТНОСТИ БОЕВЫХ ПОРЯДКОВ
Предположим, что требуется построить модель боевых действий, которая в пределах достаточно грубых допущений позволила бы определить влияние численности боевых средств и их качества на результат боевых действий и найти условия победы для сражающихся сторон. При этом будем считать, что системы разведки и управления обеих сторон работают идеально, что означает наличие полной информации о целях и ее передачу совместно с исполнительной информацией без задержек, т.е. в данном случае в течение времени, которое пренебрежимо мало по сравнению со временем исполнения (tи>>tо). Кроме того, не будем учитывать влияние ввода в бой резервов и относительное перемещение сражающихся сторон на местности. Влияние местности на ход боевых действий также рассматривать не будем. Считая известными размеры целей, примем гипотезу о их равномерном распределении на некоторой площади и представим механизм вооруженной борьбы в виде огневого взаимодействия сторон по схеме рис.3.10. При этом будем учитывать только активные боевые средства, оказывающие непосредственные воздействия на противника. Вспомогательные (пассивные) средства и органы тыла учитывать не будем.
Согласно схеме рис.3.10 любое боевое средство одной стороны может оказывать воздействие на любой объект другой стороны, причем для каждой стороны боевые средства и объекты будем считать однородными. Влияние различных способов распределения боевых средств по объектам противника также учитывать не будем. Введенные ограничения могут быть сняты или уменьшены при переходе к более тонким исследованиям на моделях повышенной точности. По схеме рис. 3.10 в упрощенной постановке может проводиться формализация огневого взаимодействия танков, самолетов, кораблей и наземных средств, включая артиллерийские и ракетно-ядерные удары.

Рис.3.10. Схема огневого взаимодействия сторон; ra - радиус защиты боевой единицы стороны A; rb - то же для стороны B; Ra - радиус поражения боевого средства стороны A; Rb - то же для стороны B.
Каждое боевое средство характеризуется следующими основными параметрами: мощностью удара, скорострельностью, точностью воздействия и степенью защищенности. Для боеприпасов объемного действия мощность определяется радиусом поражения R ~ кубический корень из Q, где Q - тротиловый эквивалент заряда. В частном случае для боеприпасов ударного действия (например, бронебойных) радиус поражения равен радиусу снаряда. Скорострельность c измеряется числом выстрелов в единицу времени. Точность воздействия можно учесть либо при помощи характеристик рассеивания, либо при помощи интегрального коэффициента результативности стрельбы а, устанавливающего относительное число боеприпасов, достигающих цель и попадающих на ее площадь. Степень защищенности объекта можно оценивать различными величинами. В данном случае удобно воспользоваться приведенным радиусом защиты r, определяющим круг, площадь которого равна площади цели. Попадание в эту площадь наносит определенный ущерб цели, а число попаданий k, необходимое для вывода цели из строя, может являться мерой ущерба. Обозначая текущую численность сторон через n, начальную численность - через n0, рассмотрим результат воздействия стороны B по стороне A. Параметры, относящиеся к средствам соответствующей стороны, будем различать индексами a или b.

Рис.3.11. Определение критической площади попадания для поражения объекта одиночным ударом по стороне A.
Сторона B за время Dt сделает по стороне А прицельных выстрелов


где nak и nbk - остаточные численности соответствующих сторон, при которых теряется их способность к дальнейшему ведению боевых действий. Величины коэффициентов фak и фbk зависят от многих факторов, и прежде всего от боевого духа войск, их стойкости, дисциплины, качества командных кадров, наличия средств управления и т.п. Эти факторы в основном имеют качественный характер и не поддаются пока количественному учету. Их суммарное влияние на исход боевых действий можно в первом приближении оценивать при помощи обобщенных коэффициентов потерь боеспособности, определяемых статистическими методами. В среднем для морально стойких войск можно применить фk = 0.4..0.5, для морально нестойких войск фk = 0.7..0.8.
Если обе стороны одновременно достигают критического состояния потери боеспособности, то это означает динамическое равновесие их боевых возможностей, при котором обе стороны должны выйти из боя или объявить перемирие.
Условие динамического равновесия получается из (3.31) в виде

может рассматриваться в качестве условия победы сторон, принимающих участие в сражении. При помощи критерия k можно оценить влияние на результат боевых действий (при принятых допущениях) количества и качества вооружения сторон и их боевой стойкости. Области победы сторон показаны на рис.3.12, на котором Ek - критическая точка, при достижении которой сторона В выходит из боя. Области победы сражающихся сторон существуют и при других, более сложных зависимостях фa = F(фb) по сравнению с соотношением (3.31).

Рис.3.12. Области победы сражающихся сторон: N - линия динамического равновесия; Ek - критическая точка для стороны В (фk = фbk; Фa <> фak)
Граница областей при одной из возможных зависимостей F для постоянных значений фak и фbk показана штрих-пунктирной линией на рис.3.12. Очевидно, что лри любом характере зависимости фa = F(фb) может быть определено условие k, устанавливающее влияние на результат боевых действий параметров na0, nb0, Ba, Bb, фak и фbk.
Однако для анализа хода боевых действий наличие только одного условия (3.32а) часто бывает недостаточным. Важное значение имеет продолжительность боя, определяемая отрезком времени tk от начала боевых действий до момента, когда одна из сторон прекращает сопротивление.
Зависимость относительной численности сторон от времени, полученная из (3.30), имеет вид

При k = 1 выражения (3.35) и (3.36) теряют смысл, так как приводят к значениям tk < 0. В этом случае, например для условий победы стороны А (фbk >фak), из (3.34) получаем величину максимальной продолжительности боевых действий в виде

Графики зависимости т = т(k) согласно (3.38) при нескольких значениях фak = abk изображены на рис. 3.13.

Рис.3.13. График зависимости т = т(k).
Из графиков видно, что при k>3 не достигается сколько-нибудь заметного сокращения длительности боевых действий. Поэтому для победы над противником в сравнительно короткое время не требуется более чем тройного превосходства в значении критерия k. Например, если при фk = 0.5 увеличение значения k от 1 до 2 приводит к уменьшению времени боя на 60%, то дальнейшее повышение величины k до значения k = 3 дает выигрыш во времени только на 15%. Таким образом, установлена верхняя и нижняя границы величины k. Для достижения победы в приемлемое время стороной А необходимо, чтобы соблюдалось условие
2 < k < 3
Условие победы k и входящие в него параметры позволяют в пределах принятых допущений, т.е. довольно приближенно, получить оценку хода боевых действий и предсказать возможное время их завершения. Однако величина k в явном виде не учитывает влияния системы управления на процесс боевых действий, а тот факт, что такое влияние имеется и может быть достаточно существенным, не требует особых доказательств. Система управления влияет на результаты боевых действий, во-первых, за счет затрат времени, необходимых для получения исходных данных, во-вторых, за счет запаздывания в принятии решений по отношению к фактическому состоянию сторон и, в-третьих, за счет точности принимаемых решений и их исполнения. Процесс управления, как правило, состоит из следующих основных этапов: поиск и обнаружение целей, передача информации, обработка данных и принятие решения, передача команд или приказов и их исполнение. Таким образом, можно считать, что продолжительность процесса управления tу определяется временем организации исполнения tо и временем tи, непосредственно затрачиваемым на исполнение принятых решений, т.е.

где c - техническая скорострельность оружия или в более общем случае средняя скорость исполнения команд войсками.
Величина c с индексом a и b соответственно для каждой из сражающихся сторон фигурирует в выражениях (3.29), определяющих параметры Ba и Bb. Не исключена возможность того, что часть процессов по организации управления будет совмещена с процессами исполнения. Так, например, могут совмещаться процессы поиска целей и движения танков, выработки решения и подготовки ракет к пуску и т.д. Поэтому в общем виде

где ac - коэффициент совмещения процессов управления и исполнения в ходе боевых действий.
Если ac = 0, то процессы полностью совмещены и задержек в темпах ведения боевых действий не происходит. При ac = 1 совмещение процессов полностью отсутствует.
При tо >> tи будет иметь место неэффективное использование оружия за счет несовершенства системы управления, что может привести к поражению при прочих равных условиях с противником. Таким образом, критерий победы в виде (3.32) при условии введения коэффициента эффективной скорострельности cэ (3.39) позволяет учесть влияние системы управления на результат боевых действий. Однако при этом не учитывается запаздывание данных о фактическом состоянии сторон, возникающее за счет работы системы управления. В самом деле, удары по каждой из сторон будут наноситься в момент t+tз, где tз=ac*to - время запаздывания в нанесении удара за счет несовмещенности процессов управления и исполнения.
С учетом запаздывания, уравнения (3.28) принимают вид

Для решения системы (3.40) необходимо принять гипотезу о виде функций na и nb с запаздывающими аргументами.
В теории таких систем решение сбычно ищут в виде функции от exp(t+tз), подбирая вид функции так, чтобы удовлетворить исходным уравнениям (3.40). С достаточной степенью приближения функцию n(t+tз) можно представить в виде ряда и ограничиться элементами разложения первого порядка. Тогда

функциями соответственно от фa и фb, причем при фa = фb будет Фa = Фb =1.

Рис.3.14. График зависимости Фa = F(Фb, ta, tb); Ek - критическая точка; N - линия динамического равновесия.
На рис.3.14 кривая Фa = F(Фb, ta, tb), проходящая через критическую точку Ek(Фa = Фak, Фb = Фbk), будет соответствовать условиям динамического равновесия. В этой точке параметры фa и фb одновременно достигают критического значения. Кривые, проходящие выше точки Ek, соответствуют условиям победы стороны A, так как текущая точка на этих кривых (характеризующая состояние сторон) при перемещении из состояния (1, 1) в состояние

или

Величина k учитывает влияние на результат боевых действий количества и качества вооружения, а величина kу - качество системы управления.
Из (3.46) видно, что за счет системы управления (ta < tb) можно получить некоторое превосходство над противником и при неблагоприятном соотношении по количеству и качеству вооружения. Однако следует иметь в виду, что возможности системы управления довольно ограничены. Если k << 1, а kу ~ 1, то никаким усовершенствованием системы управления в принципе не может быть достигнуто условие победы.
При идеальной системе управления с обеих сторон kу = 1 и неравенство (3.46) превращается в рассмотренное ранее условие k > 1. При исключительно высоких показателях

В этом предельном случае результат боевых действий будет зависеть только от качества системы управления и морального духа войск.
Выражение (3.47), в отличие от общеизвестного качественного выражения о том, что совершенная система вооружения требует и совершенной системы управления, позволяет определить необходимые количественные показатели систем управления. Аналогично тому, как это делалось при оценке верхней и нижней границ условия k, можно показать, что для достижения устойчивой работы в приемлемое время с учетом влияния системы управления должно быть
2 < k*kу < 3
Допустимые пределы изменения произведения параметров определяются на основе интегрирования системы (3.42) при аргументе t и вычислений времени окончания боевых действий.
Полученные зависимости позволяют в первом приближении связать характеристики системы управления с результатами боевых действий и показывают, что средняя продолжительность цикла управления оказывает существенное влияние на динамику вооруженного столкновения и должна приниматься во внимание при оценке качества системы.
Оценка системы вооружения и системы управления в целом может быть произведена на основе различных критериев эффективности, позволяющих установить оптимальные значения основных параметров, характеризующих эти системы.
В качестве основных можно рассматривать совокупность следующих критериев:
а) оперативной эффективности Eо,
б) технической эффективности Eт,
в) экономической эффективности Еэ.
Критерий Ео характеризуется математическим ожиданием (mр) результатов выполнения боевой задачи и определяет, таким образом, боевую эффективность системы в целом с учетом средств вооружения и управления. В числе боевых задач, обеспечение решения которых возлагается на системы управления войсками, можно наметить следующие типовые задачи: выдвижение, наступление, подавление, уничтожение, оборона и отступление. Каждая из этих задач может быть охарактеризована числовой мерой, по величине которой можно судить о качестве выполнения задачи; так, например, выдвижение характеризуется величиной пройденного расстояния или средним темпом перемещения, наступление - величиной захваченной территории или количеством трофеев, подавление или уничтожение - средним числом подавленных или уничтоженных целей, оборона - средним временем удержания обороняемого рубежа (района) или потерями, нанесенными противнику и т.д.
Выполнение боевой задачи может быть достигнуто различными средствами при различных средних потерях (mп) со стороны своих войск. Поэтому можно принять
Ео = mр/mп,
причем математическое ожидание результатов (mр) и потерь (mп) может быть как абсолютным, так и относительным, т.е. отнесенным к единице площади, расстояния, начальной численности и т.п. В некоторых американских работах предлагается боевую эффективность определить отношением стоимости результатов ср к стоимости потерь сп, т.е. считать
Eо = ср[долл.]/сп[долл.].
Однако такой подход вряд ли заслуживает признания, так как в боевых системах не все может быть оценено деньгами и, прежде всего, не поддается финансовому учету стоимость человеческих жизней. Впрочем, не смущаясь этим обстоятельством, американцы оценивают стоимость каждого солдата в 10000долл., т.е. величиной страхового полиса.
С точки зрения оперативной эффективности та система управления будет наилучшей, которая обеспечит получение заданного боевого результата в наименьшее время, причем, само собой разумеется, что это время не должно превышать допустимого значения, установленного из оперативных требований. Поэтому без учета времени выполнения боевой задачи оценка системы не может быть полной. Время выполнения боевой задачи определяется объемом выполняемых физических и информационных работ и зависит от численности технических средств и личного состава, квалификации и обученности обслуживающего персонала, надежности аппаратуры и от ряда других факторов. Наиболее полно влияние всех этих факторов может быть учтено величиной математического ожидания времени выполнения боевой задачи
mt = m(tу).
Иногда можно считать, что mt является суммой математических ожиданий времен выполнения отдельных процессов, из которых состоит процесс функционирования системы в целом. В этом случае критерий Eт может быть охарактеризован величиной mt = m(tп) + m(tо), на основе которой можно провести оценку технической производительности системы.
Что касается экономической эффективности системы, то для ее оценки может быть предложено несколько критериев. Например, она может быть охарактеризована средним временем окупаемости системы за счет более рационального расходования материальных средств, приращением боевых результатов системы на единицу затрачиваемых средств, величинами эксплуатационных расходов в системе и т.д.
Все эти критерии являются частными и могут применяться для анализа отдельных экономических показателей системы. Наиболее общим экономическим показателем системы является математическое ожидание величины капитальных затрат на создание системы m{с), которое складывается из затрат на систему вооружения (св) и на систему управления (су).
Этот показатель входит во все частные критерии и определяется как сумма

Этот критерий наиболее полно характеризует качество системы и из всех возможных вариантов ее построения позволяет выбрать такой оптимальный вариант, который обеспечивает достижение наибольших результатов при минимальных потерях с наименьшими затратами и в наиболее короткое время. Так как все величины, входящие в выражение для E, зависят не только от системы вооружения, но и от системы управления, критерий E позволяет установить правильное соотношение между средствами вооружения и средствами управления, чего нельзя получить при помощи частных критериев. Для того чтобы воспользоваться критерием E, необходимо установить зависимости между величинами mр, mп, mt и mс.
Такие зависимости могут быть получены на основе аналитического или стохастического моделирования процессов функционирования систем с учетом их структурных схем, внешних связей и характера нагрузки.
При применении обобщенного критерия Е следует иметь в виду его пригодность только для сравнительной оценки боевых систем и не пытаться оптимизировать систему путем неограниченного уменьшения величин, стоящих в знаменателе. Все эти величины по физическим соображениям ограничены снизу и не могут быть произвольно приняты сколь угодно малыми.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
3.5. ПРИМЕРЫ ПРИМЕНЕНИЯ УПРОЩЕННОЙ МОДЕЛИ
С помощью математической модели, рассмотренной в #3.4, в пределах сделанных допущений и ограничений можно решать реальные типовые задачи, характерные также и для математических моделей более высоких классов. В качестве примера приведем решение некоторых задач, основанных на применении обобщенного критерия эффективности E.
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО СООТНОШЕНИЯ СИЛ И СРЕДСТВ СТОРОН, НЕОБХОДИМЫХ ДЛЯ ВЫПОЛНЕНИЯ ПОСТАВЛЕННОЙ БОЕВОЙ ЗАДАЧИ. В предыдущем параграфе было показано, что соотношение сил и средств сторон, определяемое величиной k, должно быть в пределах 2 < k < 3. Очевидно, чем больше сил, тем меньше времени потребуется для выполнения боевой задачи, но тем больших потерь следует ожидать за счет увеличенной плотности войск при прочих равных условиях. С другой стороны, при уменьшении плотности боевых порядков темп потерь уменьшается, но возрастает время выполнения боевой задачи, что, в свою очередь, приводит к увеличению общих потерь. Интуитивно можно предположить, что существует оптимальное соотношение сил и средств k, при котором выполнение боевой задачи достигается при наименьших потерях в минимально возможное время. Для того чтобы найти это соотношение, воспользуемся критерием эффективности в виде


ОПРЕДЕЛЕНИЕ КАЛИБРА БОЕПРИПАСОВ, ПРИ КОТОРОМ ВЫПОЛНЕНИЕ БОЕВОЙ ЗАДАЧИ ОСУЩЕСТВЛЯЕТСЯ С НАИМЕНЬШИМИ ЭКОНОМИЧЕСКИМИ ЗАТРАТАМИ. Представим с учетом (3.32а) и (3.29) выражение для к в виде

где x - коэффициент, учитывающий параметры, не зависящие от na0, Ra, и k = kопт = const.
Из выражения (3.48) видно, что оптимальное значение kопт можно получить при различных значениях начальной численности (na0) и калибра боеприпасов (Ra).
Очевидно, чем больше калибр, тем меньше боеприпасов требуется для выполнения боевой задачи, но тем выше будет стоимость каждого боеприпаса, что должно отразиться на их общей стоимости. С другой стороны, чем меньше мощность боеприпаса, тем он дешевле, но зато их расход должен возрасти для выполнения той же боевой задачи, что также приведет к общему увеличению экономических затрат. Можно предположить, что существует такой калибр боеприпасов Raопт, при котором выполнение боевой задачи достигается с наименьшими экономическими затратами.

где Q - тротиловый эквивалент; м - коэффициент пропорциональности; n - показатель степени, определяемый статистическим путем.
С другой стороны,

При помощи (3.48) - (3.50) суммарную стоимость выполнения боевой задачи можно представить в виде

Заметим, что при k = kопт = const величина S зависит только от характера целей (rb) и от мощности боеприпасов, определяемой в данном случае радиусом поражения Ra. Если n > 2/3, то S является монотонно возрастающей функцией от Ra, что означает целесообразность применения в экономическом отношении наиболее мелких боеприпасов. С улучшением технологии изготовления боеприпасов и уменьшением их стоимости (n < 2/3), становится выгодным применять боеприпасы более крупных калибров. Оптимальный калибр (радиус поражения) Raопт, обеспечивающий выполнение боевой задачи с наименьшими экономическими затратами, находится из
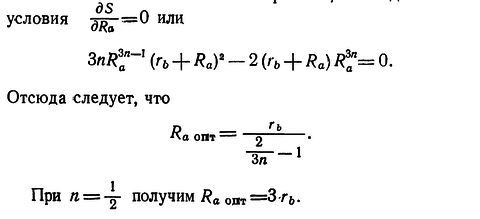
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО СООТНОШЕНИЯ МЕЖДУ ЗАТРАТАМИ НА СИСТЕМУ ВООРУЖЕНИЯ И СИСТЕМУ УПРАВЛЕНИЯ. Для приближенного решения этой задачи воспользуемся формулой (3.44), которая может быть представлена в виде
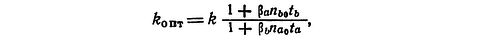
где k определяется выражением (3.32а) и kопт должно быть в пределах 2 < kопт < 3. Увеличение k и уменьшение ta связано с экономическими затратами, поэтому можно предположить, что между этими затратами существует наивыгоднейшее соотношение, обеспечивающее получение необходимой величины kопт.
Обозначим:
Sв - стоимость средств вооружения,
Sу - стоимость средств управления,
w = Sу/Sв - соотношение стоимостей,
и сформулируем задачу следующим образом: при известных значениях tв, Ba и nb0 найти такое значение w, которое приводит к максимуму величину kопт для заданных условий выполнения боевой задачи, например для задачи полного уничтожения противника (фbз = 0).
Очевидно, что для решения этой задачи необходимо установить зависимость между величинами k, ta и w.
Из выражения (3.50) при условии фbз = 0 и F(k) = l получим стоимость боеприпасов S, необходимых для выполнения поставленной боевой задачи:

в выражение для kопт, получим

В случае, когда wо также является оптимальным соотношением, уравнение (3.51) должно удовлетворяться при условии Sо = Sоо, вследствие чего

Рис.3.15. Номограмма для определения wопт.
и m = 0.5, то ао = 2E6. При m = 1 доля затрат на систему управления не зависит от общей суммы затрат So. Для m < 1 с увеличением общих затрат So должна уменьшаться доля затрат w на систему управления. Номограмма для определения wопт = wопт(ао, m) приведена на рис.3.15.
Воспользуемся рис.3.15 для решения контрольного примера. Предположим, что требуется определить wопт при увеличении общих затрат на средства вооружения и управления в три раза (Sо/Sоо = 3) при условиях ko = 2.0, Ba*nb0 = 0.01 1.0/час (темп потерь противника), tа0 = 1 час и m = 0.5.
Для этих условий

Найдя на графике рис.3.15 точку пересечения линий с параметрами m = 0.5 и ао = 5E4, получим wопт = 0.34 = 3.4%. Это означает, что при увеличении общих расходов в три раза, абсолютные расходы на средства управления также должны возрасти, но относительная доля этих расходов несколько уменьшится и составит 3.4% вместо 4%. Этот результат справедлив для случая, когда первоначальные относительные расходы на средства управления (wо = 4%) были определены оптимальным образом. Если первоначальное соотношение расходов не было оптимальным (например, wо < 0.04), то одновременно с увеличением абсолютных расходов на средства управления увеличатся и относительные расходы.
С помощью математической модели, рассмотренной в #3.4, в пределах сделанных допущений и ограничений можно решать реальные типовые задачи, характерные также и для математических моделей более высоких классов. В качестве примера приведем решение некоторых задач, основанных на применении обобщенного критерия эффективности E.
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО СООТНОШЕНИЯ СИЛ И СРЕДСТВ СТОРОН, НЕОБХОДИМЫХ ДЛЯ ВЫПОЛНЕНИЯ ПОСТАВЛЕННОЙ БОЕВОЙ ЗАДАЧИ. В предыдущем параграфе было показано, что соотношение сил и средств сторон, определяемое величиной k, должно быть в пределах 2 < k < 3. Очевидно, чем больше сил, тем меньше времени потребуется для выполнения боевой задачи, но тем больших потерь следует ожидать за счет увеличенной плотности войск при прочих равных условиях. С другой стороны, при уменьшении плотности боевых порядков темп потерь уменьшается, но возрастает время выполнения боевой задачи, что, в свою очередь, приводит к увеличению общих потерь. Интуитивно можно предположить, что существует оптимальное соотношение сил и средств k, при котором выполнение боевой задачи достигается при наименьших потерях в минимально возможное время. Для того чтобы найти это соотношение, воспользуемся критерием эффективности в виде


ОПРЕДЕЛЕНИЕ КАЛИБРА БОЕПРИПАСОВ, ПРИ КОТОРОМ ВЫПОЛНЕНИЕ БОЕВОЙ ЗАДАЧИ ОСУЩЕСТВЛЯЕТСЯ С НАИМЕНЬШИМИ ЭКОНОМИЧЕСКИМИ ЗАТРАТАМИ. Представим с учетом (3.32а) и (3.29) выражение для к в виде

где x - коэффициент, учитывающий параметры, не зависящие от na0, Ra, и k = kопт = const.
Из выражения (3.48) видно, что оптимальное значение kопт можно получить при различных значениях начальной численности (na0) и калибра боеприпасов (Ra).
Очевидно, чем больше калибр, тем меньше боеприпасов требуется для выполнения боевой задачи, но тем выше будет стоимость каждого боеприпаса, что должно отразиться на их общей стоимости. С другой стороны, чем меньше мощность боеприпаса, тем он дешевле, но зато их расход должен возрасти для выполнения той же боевой задачи, что также приведет к общему увеличению экономических затрат. Можно предположить, что существует такой калибр боеприпасов Raопт, при котором выполнение боевой задачи достигается с наименьшими экономическими затратами.

где Q - тротиловый эквивалент; м - коэффициент пропорциональности; n - показатель степени, определяемый статистическим путем.
С другой стороны,

При помощи (3.48) - (3.50) суммарную стоимость выполнения боевой задачи можно представить в виде

Заметим, что при k = kопт = const величина S зависит только от характера целей (rb) и от мощности боеприпасов, определяемой в данном случае радиусом поражения Ra. Если n > 2/3, то S является монотонно возрастающей функцией от Ra, что означает целесообразность применения в экономическом отношении наиболее мелких боеприпасов. С улучшением технологии изготовления боеприпасов и уменьшением их стоимости (n < 2/3), становится выгодным применять боеприпасы более крупных калибров. Оптимальный калибр (радиус поражения) Raопт, обеспечивающий выполнение боевой задачи с наименьшими экономическими затратами, находится из
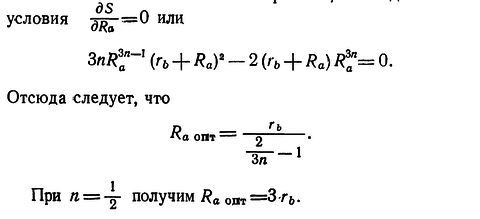
ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНОГО СООТНОШЕНИЯ МЕЖДУ ЗАТРАТАМИ НА СИСТЕМУ ВООРУЖЕНИЯ И СИСТЕМУ УПРАВЛЕНИЯ. Для приближенного решения этой задачи воспользуемся формулой (3.44), которая может быть представлена в виде
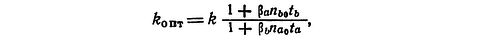
где k определяется выражением (3.32а) и kопт должно быть в пределах 2 < kопт < 3. Увеличение k и уменьшение ta связано с экономическими затратами, поэтому можно предположить, что между этими затратами существует наивыгоднейшее соотношение, обеспечивающее получение необходимой величины kопт.
Обозначим:
Sв - стоимость средств вооружения,
Sу - стоимость средств управления,
w = Sу/Sв - соотношение стоимостей,
и сформулируем задачу следующим образом: при известных значениях tв, Ba и nb0 найти такое значение w, которое приводит к максимуму величину kопт для заданных условий выполнения боевой задачи, например для задачи полного уничтожения противника (фbз = 0).
Очевидно, что для решения этой задачи необходимо установить зависимость между величинами k, ta и w.
Из выражения (3.50) при условии фbз = 0 и F(k) = l получим стоимость боеприпасов S, необходимых для выполнения поставленной боевой задачи:

в выражение для kопт, получим

В случае, когда wо также является оптимальным соотношением, уравнение (3.51) должно удовлетворяться при условии Sо = Sоо, вследствие чего

Рис.3.15. Номограмма для определения wопт.
и m = 0.5, то ао = 2E6. При m = 1 доля затрат на систему управления не зависит от общей суммы затрат So. Для m < 1 с увеличением общих затрат So должна уменьшаться доля затрат w на систему управления. Номограмма для определения wопт = wопт(ао, m) приведена на рис.3.15.
Воспользуемся рис.3.15 для решения контрольного примера. Предположим, что требуется определить wопт при увеличении общих затрат на средства вооружения и управления в три раза (Sо/Sоо = 3) при условиях ko = 2.0, Ba*nb0 = 0.01 1.0/час (темп потерь противника), tа0 = 1 час и m = 0.5.
Для этих условий

Найдя на графике рис.3.15 точку пересечения линий с параметрами m = 0.5 и ао = 5E4, получим wопт = 0.34 = 3.4%. Это означает, что при увеличении общих расходов в три раза, абсолютные расходы на средства управления также должны возрасти, но относительная доля этих расходов несколько уменьшится и составит 3.4% вместо 4%. Этот результат справедлив для случая, когда первоначальные относительные расходы на средства управления (wо = 4%) были определены оптимальным образом. Если первоначальное соотношение расходов не было оптимальным (например, wо < 0.04), то одновременно с увеличением абсолютных расходов на средства управления увеличатся и относительные расходы.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Еще кусочек из П.Н.Ткаченко и др. МАТЕМАТИЧЕСКИЕ МОДЕЛИ БОЕВЫХ ДЕЙСТВИЙ.
Как и ранее, не могу поручиться за правильность всех приведенных здесь формул. Вероятность опечаток очень велика. Так, что, опять, данный материал призван, скорее "очертить район бедствия", чем служить справочником.
ГЛАВА 5. СТОХАСТИЧЕСКИЕ МОДЕЛИ БОЕВЫХ ДЕЙСТВИЙ
Во введении авторы сетуют, что процесс стохастического отыгрывания реальных боев, столь трудоемок, что только чрезвычайные обстоятельства могут заставить человека предпочесть бросание игральных костей приятному процессу решения дифференциальных уравнений.- G.
Суть любой стохастической модели состоит в том, что изучаемое случайное явление формализуется в виде некоторого математического процесса, в общем виде являющего случайным.
При помощи специально разработанных алгоритмов, как правило, на электронной цифровой вычислительной машине воспроизводятся отдельные реализация этого случайного процесса. Методом статистических испытаний учитываются при этом все необходимые вероятностные закономерности влияния случайных факторов. Набор необходимого количества таких реализаций позволяет получить статистические оценки значений параметров процесса.
При изучении исследуемого процесса можно учесть достаточно большое число случайных факторов. Эта возможность появляется за счет того, что каждый раз методом статистических испытаний по известному вероятностному закону определяется конкретных исход случайного события. При этом отсутствует необходимость в выведении общего суммарного вероятностного закона, которому подчиняется конечный исход процесса, что при наличии большого числа случайных факторов является практически неразрешимым. Это обстоятельство как раз и позволило стохастическим моделям занять такое важное место при исследовании боевых действий.
Стохастические модели, позволяя достаточно просто получить отдельные реализации практически любых случайных процессов, в то же время требуют весьма много времени для проведения трудоемкой работы по статистической обработке большого числа реализации изучаемого процесса с целью получения необходимых выводов и рекомендаций. Исходя из того, что для сложных процессов моделей получаются громоздкими и требуют значительных затрат времени и труда для получения достаточно точных результатов, вырисовываются два основных случая применения этих моделей.
В первом случае стохастические модели следует применять тогда, когда метод статистических испытаний позволяет получить окончательные результаты гораздо проще, чем при использовании аналитических моделей. Во втором случае стохастические модели применяются тогда, когда цели исследования аналитическими методами достичь невозможно. [По крайней мере, в тот период времени, когда ведутся исследования].
В дальнейшем будут рассматриваться боевые ситуации и связанные с ними математические задачи, относящиеся, как правило, ко второму случаю применения стохастических моделей.
5.1. ПОСТАНОВКА ЗАДАЧИ И ФОРМАЛИЗАЦИЯ БОЕВОГО ПРОЦЕССА
Обязательная "научно-обоснованная" часть (видимо, это чья-то дипломная работа). Начав с определения всего и всех, авторы, все-таки, проговариваются о том, что они, собственно, собираются отыгрывать.- G.
С формальной точки зрения, любой бой - это реальный процесс, происходящий во времени и в пространстве, характеризующийся наличием двух сторон, состав и численность которых изменяются под взаимным воздействием. Каждая сторона стремится выполнить поставленную перед ней задачу, что достигается чаще всего нанесением противоположной стороне необходимого числа потерь при допустимом уменьшении своей численности. Каждая сторона состоит из некоторого числа элементов, являющихся участниками боя. В зависимости от масштаба боя в качестве элементов могут выбираться: отдельные бойцы, орудия и минометы, танки и самолеты в одном бою, целые подразделения и части в другом.
Каждый такой элемент характеризуется некоторой совокупностью переменных величин, являющих функциями времени и определяющих характер его действия и положение в пространстве. Конкретное значение этих величин в некоторый момент времени называется состоянием элемента. Изменение состояний элементов боя во времени, происходящее в соответствии с конкретными закономерностями течения боя, составляет реальную сущность боя. Бой - процесс конечный и характеризуется своим исходом. С формальной точки зрения исход боя можно определить как совокупность состояний всех элементов в некоторый момент времени, после которого каждое из этих состоянии не меняется.
Исходя из этих интуитивных соображений, можно дать следующее математическое описание боя.
Даны два конечных множества Q и U, где

называется состоянием элемента qi в tз этот момент для l-й реализации и обозначается через Cli(tз). Совокупность {Cli(T0)} для всех i = 1, 2, ..., n называется начальным состоянием стороны Q для l-й реализации. Аналогично описываются элементы Uj (j = 1, 2, ..., m) стороны U и вводятся соответствующие определения и понятия:

получено полное математическое описание боя. Такой бой можно было бы изучать методами теории случайных функций. Однако на практике выделить элементы боя вследствие их многообразия и сложных взаимозависимостей не представляется возможным. Поэтому надо выделить лишь те элементы, которые существенно определяют развитие боя, сводя из число по возможности к минимуму, причем часто полезно объединять элементы в группы, считая каждую группу одним элементом.
Следует иметь в виду, что для всех выделенных параметров характеризующие их одномерные случайные функции будут лишь некоторыми приближениями точных, т.к. задаются они некоторым конечным числом характеристик (на практике чаще всего ограничиваются математическим ожиданием и корреляционной функцией).
В данной главе описывается моделирование танковых боев в тактическом масштабе. Такой масштаб позволяет в качестве элементов боя считать отдельные боевые средства: танк, самоходное орудие, противотанковое средство. Выделяемые параметры элементов характеризуют расположение элементов на местности, их перемещение, характер их деятельности и результат этой деятельности. Изменение этих параметров во времени определяется случайными функциями времени, т.е. некоторыми случайными процессами.
В качестве параметров для выбранных элементов боя применяются следующие случайные функции от действительного аргумента времени t:
h1(t) - функция боеспособности;
h2(t) - функция местоположения;
h3(t) - функция скорости;
h4(t) - функция характера действия;
h5(t) - функция наличия количества боеприпасов.
Создаваемая модель должна давать алгоритмический способ получения приближенных реализаций этих функций, что позволяет в дальнейшем получить приближенные характеристики этих функций для практического их использования. Эти реализации вырабатываются в трех основных моделях:
- перемещения элементов;
- обнаружения элементов (целей);
- стрельбы.
Методика построения этих основных моделей рассматривается в следующем параграфе.
Как и ранее, не могу поручиться за правильность всех приведенных здесь формул. Вероятность опечаток очень велика. Так, что, опять, данный материал призван, скорее "очертить район бедствия", чем служить справочником.
ГЛАВА 5. СТОХАСТИЧЕСКИЕ МОДЕЛИ БОЕВЫХ ДЕЙСТВИЙ
Во введении авторы сетуют, что процесс стохастического отыгрывания реальных боев, столь трудоемок, что только чрезвычайные обстоятельства могут заставить человека предпочесть бросание игральных костей приятному процессу решения дифференциальных уравнений.- G.
Суть любой стохастической модели состоит в том, что изучаемое случайное явление формализуется в виде некоторого математического процесса, в общем виде являющего случайным.
При помощи специально разработанных алгоритмов, как правило, на электронной цифровой вычислительной машине воспроизводятся отдельные реализация этого случайного процесса. Методом статистических испытаний учитываются при этом все необходимые вероятностные закономерности влияния случайных факторов. Набор необходимого количества таких реализаций позволяет получить статистические оценки значений параметров процесса.
При изучении исследуемого процесса можно учесть достаточно большое число случайных факторов. Эта возможность появляется за счет того, что каждый раз методом статистических испытаний по известному вероятностному закону определяется конкретных исход случайного события. При этом отсутствует необходимость в выведении общего суммарного вероятностного закона, которому подчиняется конечный исход процесса, что при наличии большого числа случайных факторов является практически неразрешимым. Это обстоятельство как раз и позволило стохастическим моделям занять такое важное место при исследовании боевых действий.
Стохастические модели, позволяя достаточно просто получить отдельные реализации практически любых случайных процессов, в то же время требуют весьма много времени для проведения трудоемкой работы по статистической обработке большого числа реализации изучаемого процесса с целью получения необходимых выводов и рекомендаций. Исходя из того, что для сложных процессов моделей получаются громоздкими и требуют значительных затрат времени и труда для получения достаточно точных результатов, вырисовываются два основных случая применения этих моделей.
В первом случае стохастические модели следует применять тогда, когда метод статистических испытаний позволяет получить окончательные результаты гораздо проще, чем при использовании аналитических моделей. Во втором случае стохастические модели применяются тогда, когда цели исследования аналитическими методами достичь невозможно. [По крайней мере, в тот период времени, когда ведутся исследования].
В дальнейшем будут рассматриваться боевые ситуации и связанные с ними математические задачи, относящиеся, как правило, ко второму случаю применения стохастических моделей.
5.1. ПОСТАНОВКА ЗАДАЧИ И ФОРМАЛИЗАЦИЯ БОЕВОГО ПРОЦЕССА
Обязательная "научно-обоснованная" часть (видимо, это чья-то дипломная работа). Начав с определения всего и всех, авторы, все-таки, проговариваются о том, что они, собственно, собираются отыгрывать.- G.
С формальной точки зрения, любой бой - это реальный процесс, происходящий во времени и в пространстве, характеризующийся наличием двух сторон, состав и численность которых изменяются под взаимным воздействием. Каждая сторона стремится выполнить поставленную перед ней задачу, что достигается чаще всего нанесением противоположной стороне необходимого числа потерь при допустимом уменьшении своей численности. Каждая сторона состоит из некоторого числа элементов, являющихся участниками боя. В зависимости от масштаба боя в качестве элементов могут выбираться: отдельные бойцы, орудия и минометы, танки и самолеты в одном бою, целые подразделения и части в другом.
Каждый такой элемент характеризуется некоторой совокупностью переменных величин, являющих функциями времени и определяющих характер его действия и положение в пространстве. Конкретное значение этих величин в некоторый момент времени называется состоянием элемента. Изменение состояний элементов боя во времени, происходящее в соответствии с конкретными закономерностями течения боя, составляет реальную сущность боя. Бой - процесс конечный и характеризуется своим исходом. С формальной точки зрения исход боя можно определить как совокупность состояний всех элементов в некоторый момент времени, после которого каждое из этих состоянии не меняется.
Исходя из этих интуитивных соображений, можно дать следующее математическое описание боя.
Даны два конечных множества Q и U, где

называется состоянием элемента qi в tз этот момент для l-й реализации и обозначается через Cli(tз). Совокупность {Cli(T0)} для всех i = 1, 2, ..., n называется начальным состоянием стороны Q для l-й реализации. Аналогично описываются элементы Uj (j = 1, 2, ..., m) стороны U и вводятся соответствующие определения и понятия:

получено полное математическое описание боя. Такой бой можно было бы изучать методами теории случайных функций. Однако на практике выделить элементы боя вследствие их многообразия и сложных взаимозависимостей не представляется возможным. Поэтому надо выделить лишь те элементы, которые существенно определяют развитие боя, сводя из число по возможности к минимуму, причем часто полезно объединять элементы в группы, считая каждую группу одним элементом.
Следует иметь в виду, что для всех выделенных параметров характеризующие их одномерные случайные функции будут лишь некоторыми приближениями точных, т.к. задаются они некоторым конечным числом характеристик (на практике чаще всего ограничиваются математическим ожиданием и корреляционной функцией).
В данной главе описывается моделирование танковых боев в тактическом масштабе. Такой масштаб позволяет в качестве элементов боя считать отдельные боевые средства: танк, самоходное орудие, противотанковое средство. Выделяемые параметры элементов характеризуют расположение элементов на местности, их перемещение, характер их деятельности и результат этой деятельности. Изменение этих параметров во времени определяется случайными функциями времени, т.е. некоторыми случайными процессами.
В качестве параметров для выбранных элементов боя применяются следующие случайные функции от действительного аргумента времени t:
h1(t) - функция боеспособности;
h2(t) - функция местоположения;
h3(t) - функция скорости;
h4(t) - функция характера действия;
h5(t) - функция наличия количества боеприпасов.
Создаваемая модель должна давать алгоритмический способ получения приближенных реализаций этих функций, что позволяет в дальнейшем получить приближенные характеристики этих функций для практического их использования. Эти реализации вырабатываются в трех основных моделях:
- перемещения элементов;
- обнаружения элементов (целей);
- стрельбы.
Методика построения этих основных моделей рассматривается в следующем параграфе.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
5.2. МЕТОДИКА МОДЕЛИРОВАНИЯ ОСНОВНЫХ ПРОЦЕССОВ БОЕВЫХ ДЕЙСТВИЙ
Авторы спохватываются, что в предыдущем параграфе определяли совсем не то, что надо.- G.
МОДЕЛИРОВАНИЕ ПЕРЕМЕЩЕНИЯ. В модели перемещения реализуются h2(t) - функция местоположения; и h3(t) - функция скорости. Отличительной чертой всех сухопутных боев является то, что всякий такой бой происходит на некоторой реальной местности, существенно влияющей на его ход. В любой стохастической модели местность можно учитывать двояко:
1) информация о характеристиках местности не случайна и является частью исходной информации для проигрывания модели на ЭВМ;
2) информация о характеристиках местности является случайной, и конкретные значения этих характеристик в модели учитываются методом статистических испытаний.
Выбор из этих двух возможностей при непосредственном моделировании зависит от цели исследования и имеющихся данных для такого исследования.
Получить постоянную информацию о любой реальной местности нетрудно, в частности она может быть непосредственно взята с карты. Однако выводы, полученные на модели с использованием такого подхода, можно распространить на довольно узкий класс различных типов местности. Второй подход значительно расширяет этот класс, но получение случайных законов изменения характеристик местностей часто бывает затруднительно. Непрерывное отображение местности в стохастической модели невозможно, так как и на картах информация дается не для каждой точки, а усредненно. Это относится к любой информации, кроме координат. Поэтому часто участок местности, на котором происходит реальный бой, разбивается на элеметарные участки, каждая точка которого характерна тем, что она имеет одинаковую информацию с остальными точками элементарного участка.
Принят следующий принцип разбиения местности на элементарные участки. Участок местности, на котором происходит бой, разбивается на одинаковые по величине квадраты со стороной a0. Считается, что все точки одного квадрата имеют информацию, одинаковую с центром квадрата. Принцип разбиения всего участка на элементарные показан на рис.5.1.

Рис.5.1. Порядок нумерации элементарных квадратов.
Если реальный участок имеет неправильную геометрическую форму, то его дополняют до правильного прямоугольника. Совокупность таких элементарных участков упорядочена, т.е. каждому участку соответствует индекс (ij), где i - номер вертикальной полосы, j - горизонтальный (рис.5.1). Между системой таких индексов и географическими координатами установлено взаимно-однозначное соответствие, позволяющее по индексу находить на карте соответствующий участок. Для каждого участка с индексом (ij) задается необходимая для модели информация, характеризующая этот участок как элемент местности: тип рельефа, характер естественных и искусственных сооружений, проходимость и т.д. Количество этих признаков зависит от вида и характера решаемой задачи. Исходя из этого, необходимо задать совокупность функций от аргумента (ij), множества значений которых будут определить количественное значение признаков местности на каждом участке. Таким образом, информация о местности на каждом участке определяется значениями некоторого числа признаков

Местность в модели представлена совокупностью индексов {i, j}, поэтому выработать реализацию h2(t) для некоторого элемента боя - значит для каждого tv, указать индекс (ij) того участка, в котором он находится в момент времени tv. Сечение случайной функции h2(t) для всех tv, будет некоторой случайной величиной, принимающей значения из совокупности {l} (от 1 до Z). Совокупность значений {l} получается при помощи некоторого оператора соответствия, примененного к совокупности {i, j}, например:
i = 1, 2, ..., m,
l = (j - 1)m + i,
j = 1, 2, ..., n.
В данном случае этот оператор пронумеровывает все участки последовательно слева направо и снизу вверх. Причем легко увидеть, что существует и обратное преобразование [l/m]+1 = j, тогда i = l-(j-1)*m, где [A] означает целую часть от любого числа A.
Данный переход не имеет принципиального значения и осуществляется только для снятия некоторых технических трудностей при моделировании.
Очевидно, что перемещение любого элемента за время Dtv = tv - tv-1 характеризуется направлением движения и средней скоростью движения за время Dt [элементы, которые за все время боя не перемещаются, имеют постоянный номер участка (индекс) и нулевую скорость]. В момент времени tv-1 любой элемент находится на некотором участке (iv-1, jv-1) (как правило, считается, что элемент находится в центре участка, это допущение не принципиально, но зато значительно упрощает моделирование, не влияя на конечные результаты). Выбрать дальнейшее направления движения - это значит определить индекс того участка из восьми соседних [если участок с индексом (iv-1, jv-1) граничный, то число соседних может уменьшиться до трех], в который элемент должен переместиться. Выбор индекса такого участка зависит от свойств реальной местности и может производится детерминированно или случайным образом. В первом случае он определяется некоторыми априорными правилами, например уравнением некоторой кривой или совокупностью таких кривых, которые последовательно заменяются во времени.

определенная для всех участков и обладающая следующим свойством: чем предпочтительнее участок (i2, j2) для перемещения в него элемента из участка (i1, j1), тем больше значение весовой функции для участка (i2, j2) должно быть по сравнению с остальными соседними участками.
Пусть элемент находится на некотором участке с индексом (i1, j1). Введем случайную величину X, принимающих одно из восьми значений (1, 2, 3, ..., 8 ), соответствующих индексам соседних участков (i1 - 1, j1), (i1 + 1, j1), (i1 - 1, j1 - 1), (i1 - 1, j1 + 1), (i1 + 1, j1 - 1), (i1 + 1, j1 + 1), (i1, j1 - 1), (i1, j1 + 1) с соответствующими вероятностями p1, p2,...p8. Очевидно, что

так что нормализованные веса участков можно принять за соответствующие вероятности выбора и выбор индекса участка производить методом статистических испытаний.
Конкретный выбор весовой функции w зависит от моделируемой задачи, которая накладывает условия на характер перемещения. Ниже при описании модели боя танкового подразделения будет дан пример выбора такой весовой функции. После выбора направления перемещения необходимо определить скорость перемещения, т.е. получить реализацию случайной функции h3(t). Сечение функции h3(t) при некотором tv-1 =< t =< tv представляется собой случайную величину, принимающую значения на некотором допустимом интервале скоростей, с заданной функцией распределения F(V), причем до левого конца интервала функция распределения равна нулю, после правого - равна 1. Конкретные значения V при одной и тоже реализации функции h3(t), как правило, считаются одинаковыми для всех tv-1 =< t =< tv.
Допустимый интервал скоростей представляет собой отрезок числовой оси, концы которого определяются минимальную и максимальную возможные скорости. Очевидно, что минимально возможной скоростью элемента является нулевая (элемент не двигается). Максимально возможная скорость элемента определяется его техническими характеристиками, условиями проходимости по данной местности и углом наклона движения.
Таким образом, перемещение каждого элемента, для которого V не равна 0, в модели осуществляется следующим образом. Для каждого момента времени tv определяется индекс участка, в котором находится данный элемент. Далее методом статистических испытаний по заданной функции распределения определяется конкретное значение функции h3(t).
Определив путь, пройденный элементом за время tv+1 - tv, узнаем индекс того конечного участка, в который элемент попадает в момент tv+1. Эта процедура проводится для всех перемещающихся элементов и последовательно повторяется для всех моментов времени t1, t2, ..., tv, ..., tN.
Если выбор направления движения происходит по заранее заданным кривым, то индексы участков, в которых последовательно бывает движущийся элемент, определяются уравнениями этих кривых. Скорость на интервалах времени [tv, tv+1] определяется аналогично описанному выше.
МОДЕЛИРОВАНИЕ ОБНАРУЖЕНИЯ ЦЕЛЕЙ. Как правило, при моделировании боев подразделений сухопутных войск предполагают, что каждый элемент в процессе боя ведет наблюдение за элементами противоположного цвета [Для удобства дальнейших рассуждений элементы противоборствующих сторон можно различать по цвету "красные" и "синие", что соответствует традиционному обозначению, приятному в тактике], являющимися в данном случае целями по отношению к элементам, ведущим наблюдение.
Все цели в зависимости от расстояния, разницы высот, рельефа и растительности условно делятся на две группы: невидимы и видимые.
Цели первой группы обнаружить невозможно, а некоторые (иногда все) цели второй группы рано или поздно обнаруживаются. Это значит, что поиск цели - случайное событие и что каждая цель второй группы имеет определенную, отличную от нуля вероятность обнаружения. Естественно, что чем лучше условия наблюдения и чем дольше оно ведется, тем больше вероятность обнаружения.
Конкретный вид функции вероятности обнаружения может быть самым различным - он зависит от типа моделируемого реального боя процесса. Достаточно общепринято предложение, что вероятность обнаружения описывается формулой
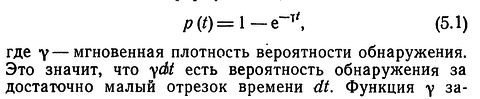
зависит от расстояния до цели, ее размеров, типов средств наблюдения, метеорологических условий наблюдения.
После деления целей на группы для целей второй группы по формуле вероятности обнаружения подсчитываются конкретные значения этих вероятностей и методом статических испытаний по этим значениям выбираются все видимые цели. Информация о всех обнаруженных целях используется в модели для решения задачи об оптимальном целераспределении.
МОДЕЛИРОВАНИЕ ЦЕЛЕРАСПРЕДЕЛЕНИЯ. Обязательной задачей при моделировании боевых действий является задача целераспределения. Однако она имеет и вполне самостоятельное значение для выработки некоторых априорных значений параметров управления боевыми средствами в бою или при подготовке к нему.
Целераспределение как физическая задача заключается в закреплении выявленных целей за боевыми средствами таким образом, чтобы при огневом воздействии по этим целям был получен максимальный эффект в соответствии с выбранным критерием эффективности. Как правило, математически задача целераспределения сводится к целочисленной задаче линейного программирования. Поставка такой задачи может быть сформулирована следующим образом.


По одной и той же цели не могут вести огонь больше средств, чем общее количество элементов, участвующих в распределении. Это требование приводит к следующим условиям:

Введенные таким образом линейные ограничения позволяют отбросить все неосуществимые варианты целераспределения и оставить конечное множество возможных вариантов (определяемых требованием целочисленности искомых переменных), из которых следует выбрать один или несколько наилучших в соответствии с критерием эффективности. Чаще всего применяются критерии, которые линейно завися от искомых переменных и записываются в виде:

где Cij - некоторые действительные числа, характеризующие эффективность закрепления j-ой цели за i-м элементом (например, часто Cij является вероятностью поражения j-й цели i-м элементом).
При выборе линейного критерия задача целераспределения свелась к целочисленной задаче линейного программирования. После решения этой задачи получается некоторая совокупность переменных xij:

Наряду с применением общих методов не следует отказываться от частных методов решения задачи целераспределения. Сущность таких методов стоит в том, что создается некоторый класс алгоритмов, реализующих различные принципы целераспределения (закрепление за средством самой ближайшей цели, самой для него опасной и т.д.). Этот класс алгоритмов используется при создании конкретной стохастической модели для выбора наиболее подходящего принципа целераспределения, причем правомочность выбора должна определиться при анализе результатов моделирования. В этом случае можно получить удовлетворительное приближенное решение задачи целераспределения. В конкретных примерах стохастических моделей, описанных ниже, приводятся результаты такого подхода.
МОДЕЛИРОВАНИЕ СТРЕЛЬБЫ. После целераспределения, которое проводится отдельно для элементов "различного цвета", так что каждый элемент одновременно выступает в двух ролях: боевого средства и цели, некоторые элементы получают номера целей и начинают стрельбу. В модели стрельбы вырабатывается текущая информация о результате стрельбы средств по выделенным целям, при этом определяются вероятности поражения каждой цели.
Вероятность поражения является функцией следующих аргументов: расстояния до цели, ее размеров, скорости движения элемента и цели, количества предыдущих попаданий в цель (параметр, определяющий способность цели выдерживать попадания, чаще всего это среднее количество попаданий, необходимое для поражения цели). Эта функция обозначается Ф(В), где В - суммарный аргумент, определяющий конкретное значение вероятности поражения. Методом статистических испытаний по вычисленному значению вероятности поражения определяется исход случайного события стрельбы.
Результаты стрельбы необходимы для определения реализации функции боеспособности h1(t).
После поражения цели элемент переходит в состояние наблюдателя, благодаря этому строится реализация функции характера действий h4(t).
Т.к. в этой модели всегда можно подсчитать количество боеприпасов, израсходованное на каждую пораженную цель, то при этом получается и реализация функции количества боеприпасов h5(t).
Методика моделирования основных процессов на конкретном примере и получение общей модели боевых действий в тактическом масштабе изложены в следующем параграфе.
Авторы спохватываются, что в предыдущем параграфе определяли совсем не то, что надо.- G.
МОДЕЛИРОВАНИЕ ПЕРЕМЕЩЕНИЯ. В модели перемещения реализуются h2(t) - функция местоположения; и h3(t) - функция скорости. Отличительной чертой всех сухопутных боев является то, что всякий такой бой происходит на некоторой реальной местности, существенно влияющей на его ход. В любой стохастической модели местность можно учитывать двояко:
1) информация о характеристиках местности не случайна и является частью исходной информации для проигрывания модели на ЭВМ;
2) информация о характеристиках местности является случайной, и конкретные значения этих характеристик в модели учитываются методом статистических испытаний.
Выбор из этих двух возможностей при непосредственном моделировании зависит от цели исследования и имеющихся данных для такого исследования.
Получить постоянную информацию о любой реальной местности нетрудно, в частности она может быть непосредственно взята с карты. Однако выводы, полученные на модели с использованием такого подхода, можно распространить на довольно узкий класс различных типов местности. Второй подход значительно расширяет этот класс, но получение случайных законов изменения характеристик местностей часто бывает затруднительно. Непрерывное отображение местности в стохастической модели невозможно, так как и на картах информация дается не для каждой точки, а усредненно. Это относится к любой информации, кроме координат. Поэтому часто участок местности, на котором происходит реальный бой, разбивается на элеметарные участки, каждая точка которого характерна тем, что она имеет одинаковую информацию с остальными точками элементарного участка.
Принят следующий принцип разбиения местности на элементарные участки. Участок местности, на котором происходит бой, разбивается на одинаковые по величине квадраты со стороной a0. Считается, что все точки одного квадрата имеют информацию, одинаковую с центром квадрата. Принцип разбиения всего участка на элементарные показан на рис.5.1.

Рис.5.1. Порядок нумерации элементарных квадратов.
Если реальный участок имеет неправильную геометрическую форму, то его дополняют до правильного прямоугольника. Совокупность таких элементарных участков упорядочена, т.е. каждому участку соответствует индекс (ij), где i - номер вертикальной полосы, j - горизонтальный (рис.5.1). Между системой таких индексов и географическими координатами установлено взаимно-однозначное соответствие, позволяющее по индексу находить на карте соответствующий участок. Для каждого участка с индексом (ij) задается необходимая для модели информация, характеризующая этот участок как элемент местности: тип рельефа, характер естественных и искусственных сооружений, проходимость и т.д. Количество этих признаков зависит от вида и характера решаемой задачи. Исходя из этого, необходимо задать совокупность функций от аргумента (ij), множества значений которых будут определить количественное значение признаков местности на каждом участке. Таким образом, информация о местности на каждом участке определяется значениями некоторого числа признаков

Местность в модели представлена совокупностью индексов {i, j}, поэтому выработать реализацию h2(t) для некоторого элемента боя - значит для каждого tv, указать индекс (ij) того участка, в котором он находится в момент времени tv. Сечение случайной функции h2(t) для всех tv, будет некоторой случайной величиной, принимающей значения из совокупности {l} (от 1 до Z). Совокупность значений {l} получается при помощи некоторого оператора соответствия, примененного к совокупности {i, j}, например:
i = 1, 2, ..., m,
l = (j - 1)m + i,
j = 1, 2, ..., n.
В данном случае этот оператор пронумеровывает все участки последовательно слева направо и снизу вверх. Причем легко увидеть, что существует и обратное преобразование [l/m]+1 = j, тогда i = l-(j-1)*m, где [A] означает целую часть от любого числа A.
Данный переход не имеет принципиального значения и осуществляется только для снятия некоторых технических трудностей при моделировании.
Очевидно, что перемещение любого элемента за время Dtv = tv - tv-1 характеризуется направлением движения и средней скоростью движения за время Dt [элементы, которые за все время боя не перемещаются, имеют постоянный номер участка (индекс) и нулевую скорость]. В момент времени tv-1 любой элемент находится на некотором участке (iv-1, jv-1) (как правило, считается, что элемент находится в центре участка, это допущение не принципиально, но зато значительно упрощает моделирование, не влияя на конечные результаты). Выбрать дальнейшее направления движения - это значит определить индекс того участка из восьми соседних [если участок с индексом (iv-1, jv-1) граничный, то число соседних может уменьшиться до трех], в который элемент должен переместиться. Выбор индекса такого участка зависит от свойств реальной местности и может производится детерминированно или случайным образом. В первом случае он определяется некоторыми априорными правилами, например уравнением некоторой кривой или совокупностью таких кривых, которые последовательно заменяются во времени.

определенная для всех участков и обладающая следующим свойством: чем предпочтительнее участок (i2, j2) для перемещения в него элемента из участка (i1, j1), тем больше значение весовой функции для участка (i2, j2) должно быть по сравнению с остальными соседними участками.
Пусть элемент находится на некотором участке с индексом (i1, j1). Введем случайную величину X, принимающих одно из восьми значений (1, 2, 3, ..., 8 ), соответствующих индексам соседних участков (i1 - 1, j1), (i1 + 1, j1), (i1 - 1, j1 - 1), (i1 - 1, j1 + 1), (i1 + 1, j1 - 1), (i1 + 1, j1 + 1), (i1, j1 - 1), (i1, j1 + 1) с соответствующими вероятностями p1, p2,...p8. Очевидно, что

так что нормализованные веса участков можно принять за соответствующие вероятности выбора и выбор индекса участка производить методом статистических испытаний.
Конкретный выбор весовой функции w зависит от моделируемой задачи, которая накладывает условия на характер перемещения. Ниже при описании модели боя танкового подразделения будет дан пример выбора такой весовой функции. После выбора направления перемещения необходимо определить скорость перемещения, т.е. получить реализацию случайной функции h3(t). Сечение функции h3(t) при некотором tv-1 =< t =< tv представляется собой случайную величину, принимающую значения на некотором допустимом интервале скоростей, с заданной функцией распределения F(V), причем до левого конца интервала функция распределения равна нулю, после правого - равна 1. Конкретные значения V при одной и тоже реализации функции h3(t), как правило, считаются одинаковыми для всех tv-1 =< t =< tv.
Допустимый интервал скоростей представляет собой отрезок числовой оси, концы которого определяются минимальную и максимальную возможные скорости. Очевидно, что минимально возможной скоростью элемента является нулевая (элемент не двигается). Максимально возможная скорость элемента определяется его техническими характеристиками, условиями проходимости по данной местности и углом наклона движения.
Таким образом, перемещение каждого элемента, для которого V не равна 0, в модели осуществляется следующим образом. Для каждого момента времени tv определяется индекс участка, в котором находится данный элемент. Далее методом статистических испытаний по заданной функции распределения определяется конкретное значение функции h3(t).
Определив путь, пройденный элементом за время tv+1 - tv, узнаем индекс того конечного участка, в который элемент попадает в момент tv+1. Эта процедура проводится для всех перемещающихся элементов и последовательно повторяется для всех моментов времени t1, t2, ..., tv, ..., tN.
Если выбор направления движения происходит по заранее заданным кривым, то индексы участков, в которых последовательно бывает движущийся элемент, определяются уравнениями этих кривых. Скорость на интервалах времени [tv, tv+1] определяется аналогично описанному выше.
МОДЕЛИРОВАНИЕ ОБНАРУЖЕНИЯ ЦЕЛЕЙ. Как правило, при моделировании боев подразделений сухопутных войск предполагают, что каждый элемент в процессе боя ведет наблюдение за элементами противоположного цвета [Для удобства дальнейших рассуждений элементы противоборствующих сторон можно различать по цвету "красные" и "синие", что соответствует традиционному обозначению, приятному в тактике], являющимися в данном случае целями по отношению к элементам, ведущим наблюдение.
Все цели в зависимости от расстояния, разницы высот, рельефа и растительности условно делятся на две группы: невидимы и видимые.
Цели первой группы обнаружить невозможно, а некоторые (иногда все) цели второй группы рано или поздно обнаруживаются. Это значит, что поиск цели - случайное событие и что каждая цель второй группы имеет определенную, отличную от нуля вероятность обнаружения. Естественно, что чем лучше условия наблюдения и чем дольше оно ведется, тем больше вероятность обнаружения.
Конкретный вид функции вероятности обнаружения может быть самым различным - он зависит от типа моделируемого реального боя процесса. Достаточно общепринято предложение, что вероятность обнаружения описывается формулой
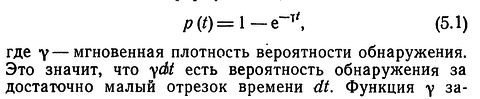
зависит от расстояния до цели, ее размеров, типов средств наблюдения, метеорологических условий наблюдения.
После деления целей на группы для целей второй группы по формуле вероятности обнаружения подсчитываются конкретные значения этих вероятностей и методом статических испытаний по этим значениям выбираются все видимые цели. Информация о всех обнаруженных целях используется в модели для решения задачи об оптимальном целераспределении.
МОДЕЛИРОВАНИЕ ЦЕЛЕРАСПРЕДЕЛЕНИЯ. Обязательной задачей при моделировании боевых действий является задача целераспределения. Однако она имеет и вполне самостоятельное значение для выработки некоторых априорных значений параметров управления боевыми средствами в бою или при подготовке к нему.
Целераспределение как физическая задача заключается в закреплении выявленных целей за боевыми средствами таким образом, чтобы при огневом воздействии по этим целям был получен максимальный эффект в соответствии с выбранным критерием эффективности. Как правило, математически задача целераспределения сводится к целочисленной задаче линейного программирования. Поставка такой задачи может быть сформулирована следующим образом.


По одной и той же цели не могут вести огонь больше средств, чем общее количество элементов, участвующих в распределении. Это требование приводит к следующим условиям:

Введенные таким образом линейные ограничения позволяют отбросить все неосуществимые варианты целераспределения и оставить конечное множество возможных вариантов (определяемых требованием целочисленности искомых переменных), из которых следует выбрать один или несколько наилучших в соответствии с критерием эффективности. Чаще всего применяются критерии, которые линейно завися от искомых переменных и записываются в виде:

где Cij - некоторые действительные числа, характеризующие эффективность закрепления j-ой цели за i-м элементом (например, часто Cij является вероятностью поражения j-й цели i-м элементом).
При выборе линейного критерия задача целераспределения свелась к целочисленной задаче линейного программирования. После решения этой задачи получается некоторая совокупность переменных xij:

Наряду с применением общих методов не следует отказываться от частных методов решения задачи целераспределения. Сущность таких методов стоит в том, что создается некоторый класс алгоритмов, реализующих различные принципы целераспределения (закрепление за средством самой ближайшей цели, самой для него опасной и т.д.). Этот класс алгоритмов используется при создании конкретной стохастической модели для выбора наиболее подходящего принципа целераспределения, причем правомочность выбора должна определиться при анализе результатов моделирования. В этом случае можно получить удовлетворительное приближенное решение задачи целераспределения. В конкретных примерах стохастических моделей, описанных ниже, приводятся результаты такого подхода.
МОДЕЛИРОВАНИЕ СТРЕЛЬБЫ. После целераспределения, которое проводится отдельно для элементов "различного цвета", так что каждый элемент одновременно выступает в двух ролях: боевого средства и цели, некоторые элементы получают номера целей и начинают стрельбу. В модели стрельбы вырабатывается текущая информация о результате стрельбы средств по выделенным целям, при этом определяются вероятности поражения каждой цели.
Вероятность поражения является функцией следующих аргументов: расстояния до цели, ее размеров, скорости движения элемента и цели, количества предыдущих попаданий в цель (параметр, определяющий способность цели выдерживать попадания, чаще всего это среднее количество попаданий, необходимое для поражения цели). Эта функция обозначается Ф(В), где В - суммарный аргумент, определяющий конкретное значение вероятности поражения. Методом статистических испытаний по вычисленному значению вероятности поражения определяется исход случайного события стрельбы.
Результаты стрельбы необходимы для определения реализации функции боеспособности h1(t).
После поражения цели элемент переходит в состояние наблюдателя, благодаря этому строится реализация функции характера действий h4(t).
Т.к. в этой модели всегда можно подсчитать количество боеприпасов, израсходованное на каждую пораженную цель, то при этом получается и реализация функции количества боеприпасов h5(t).
Методика моделирования основных процессов на конкретном примере и получение общей модели боевых действий в тактическом масштабе изложены в следующем параграфе.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
5.3. СТРУКТУРА АЛГОРИТМА, МОДЕЛИРУЮЩЕГО НА ЭВМ НАСТУПАТЕЛЬНЫЙ БОЙ ТАКТИЧЕСКОГО ПОДРАЗДЕЛЕНИЯ
Этакий винегрет из всего того, что пришло моделисту в голову. Однако, формулы, которые мне так трудно было вводить, а вам - рассматривать еще не кончились.- G.
Пусть необходимо исследовать закономерности исхода боя танковой роты (батальона) при наступлении на противотанковый укрепленный район.
Рассматривается следующая тактическая задача. Танковая рота "красных", стоящая из n1 танков, должна прорвать противотанковый укрепленный район "синих". Этот район обороняет n2 танков "синих", которые замаскированы и находятся в специально созданных укрытиях. Рота должна наступать в заданном боевом порядке в полосе шириной a метров и глубиной c метров. Общее направление движения роты определяется взаимным расположением на местности исходной позиции "красных" и "синих". Направление движения для каждого танка "красных" определяется совокупностью ориентиров, которыми являются хорошо различаемые местные предметы.
Бой начинается в некоторое заданное время T0 и продолжается до того момента, когда силы одной из борющихся сторон станут небоеспособными. Концом боя можно также считать тот момент T1 > T0, в который будет выполнена боевая задача или потери одной сторон превысят допустимый относительный уровень.
Одинаковые элементы одного цвета будут отличаться по присвоенным им порядковым номерам, которые не меняются в течение боя. Введенная для характеристики боеспособности случайная функция h1(t) из-за однотипности элементов процесса будет иметь один и тот же вид для всех элементов. Различными для разных элементов будут лишь ее характеристики: математическое ожидание, корреляционная функция и т.д. Это утверждение справедливо и для других параметров элементов. Сечение функции h1(t) (для любого T0 =< t =< T1) представляет собой случайную величину, принимающую значенеие 1, если элемент в данный момент боеспособен, и 0 в противном случае.
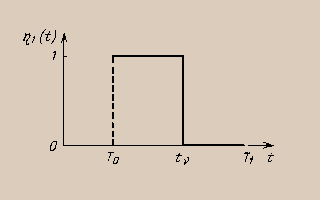
Рис.5.2. Пример случайной реализации функции боеспособности.
Реализация функции h1(t) показана на рис.5.2. Это невозрастающая ступенчатая функция, имеющая скачок в некотором tv (T0 < tv < T1).
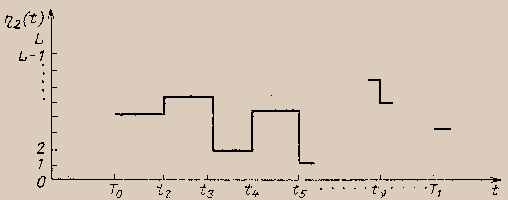
Рис.5.3. Пример случайных реализаций функции h2(t).
Случайная функция h2(t) характеризует местоположение элемента в любой момент времени. Т.к. в любой момент времени элемент находится в одном из L участков, то сечение функции h2(t) представляет собой случайную величину, принимающую одно из значений: 1, 2,..., L. Пример возможных реализаций функции h2(t) показан на рисунке 5.3.
Реализация функции скорости h3(t) вследствие округления получаемых значений будет иметь вид, аналогичный изображенному на рис.5.3., причем возможные значения ординат этой функции будут выбраться из интервала (Vmim, Vmax). Для элементов "синих" параметры h2(t) и h3(t) имеют неслучайный характер и представляют собой заданные константы - номера участков, в которых находятся элементы "синих" и нулевую скорость, т.к. предполагается, что их танки в течение боя не перемещаются.
В модели принято, что если элемент боеспособен, то в каждый момент времени он ведет наблюдение или стрельбу по некоторой цели, порядковый номер которой известен. Поэтому сечение случайной функции h4(t), определяющей характер действия элемента, представляет собой случайную величину, принимающую одно из значений 0, 1, 2, ..., n2 для "красных" и 0, 1, 2,..., n1 - для "синих".
Значение 0 означает, что элемент ведет наблюдение; значение, отличное от нуля, показывает, что элемент стрельбу по цели, порядковый номер которой равен этому значению. Вид реализации случайной функции h4(t) аналогичен виду реализации на рис.5.3.
Реализация случайной функции h5(t) является убывающей ступенчатой функцией, имеющей скачки величиной в единицу в некоторой совокупности значений времени в интервале (T0, T1). Сечение функции h5(t) при любом tн представляет собой случайную величину, принимающую одно из значений 0, 1, 2,..., Qi, где Qi - максимальное значение количества боеприпасов в i элементе.
Значения параметров, рассмотренных выше, достаточно полно определяют состояние значение элемента определяют состояние элемента и позволяют получать данные, характеризующие весь бой в целом. Например, если необходимо получить реализацию случайной функции количества потерь, то сумма реализации функции h1(t) для всех элементов одного цвета и будут искомой реализацией. Задача состоит в том, чтобы составить алгоритмы, позволяющие получать значения параметров состояния элемента в каждый момент tv (v = 1, 2,..., N), используя полученную текущую информацию для моментов времени t1, t2,..., tv-1 и некоторую заданную исходную информацию.
Главной составной частью заданной исходной информации является информация о местности. Анализ тех данных о местности, которые существенно влияют на характер боя, позволяет сделать вывод, что каждый участок должен характеризоваться следующими параметрами, являющимися заданными функциями от порядкового номера участка:
1) параметром проходимости B1(l), где B1 принимает три значения [Такая градация параметра B1, естественно, не обязательна во всех случаях]:
1 - если участок с номером l непроходим для танков "красных";
2 - если труднопроходим;
3 - если хорошо проходим.
Вследствие однотипности танков, участвующих в бою, можно принять, что функция B1(l) зависит только от свойств местности и является постоянной для танков;
2) параметром рельефа B2(l), где функция принимает значение, равное высоте над уровнем моря, для центра участка с номером l;
3) параметром B3(l), где функция B3(l) принимает значение, равное средней высоте искусственных и естественных предметов, занимающих достаточно большую часть площади участка с номером l;
4) параметром B4(l), где функция B4(l) принимает значение, равное коэффициенту сопротивления движения для характерного грунта на участке с номером l.
Моделируемый алгоритм состоит из совокупности основных и вспомогательных блоков. Основные блоки предназначены для моделирования определяющих процессов танкового боя: перемещения, наблюдения, целераспределения и стрельбы. При решении некоторых частных задач методом моделирования эти блоки могут быть использованы как самостоятельные модели.
Вспомогательные блоки предназначены для ввода исходной информации, определения конкретного вида решаемого варианта, управления потоком текущей информации, получаемой в основных блоках и необходимой для них в дальнейшем, для статистической обработки результатов моделирования и выдачи результатов моделирования и выдачи результатов.
Работу всех основных блоков объясняет блок управления, в котором определяется очередность обработки элементов и последовательность получения текущей информации об элементе в основных блоках. Кроме того, в блоке управления происходит регистрация времени, благодаря чему через определенные промежутки происходит выдача текущей информации для статистической обработки и на печать и проверка конца работы программы.
Во все блоки информация поступает и обрабатывается в специально закодированном виде. Всю информацию, как исходную, так и текущую, можно разделить на две группы:
1) информацию о танках, которая задается числовыми параметров состояний элемента;
2) информацию об элементарных участках, которая для каждого участка задается числовыми значениями параметров, характеризующих этот участок.
Каждое числовое значение параметра записывается в виде целого числа в двоичном коде. В задаваемой совокупности исходных констант предусматриваются значения масштаба кодирования, необходимые для декодирования в процессе обработки текущей информации. Такое кодирование позволяет записывать значение параметра в специально отведенных двоичных разрядах ячейки оперативной памяти ЭВМ, причем количество отводимых разрядов определяется верхней границей диапазона изменения параметра. Поэтому количество ячеек, требуемое для записи информации об одном элементе или участке, зависит от числа параметров и диапазонов их изменения.
В таблице 5.1. представлено возможное распределение разрядов ячейки ЭВМ между параметрами состояния элемента.
Таблица 5.1. Возможное распределение разрядов ячейки ЭВМ для записи параметров состояния элемента
Номер разряда. Код и его смысловое значение
1. 0 - танк небоеспособен, 1 - танк боеспособен
2. 0 - "красный" танк, 1 - "синий" танк
3. 0 - танк наблюдает, 1 - танк стреляет
4-12. Номер участка, где стоит танк
13-17. V - скорость танка м/сек
18-21. Номер цели, по которой стреляет танк
22-24. 00 - танк не стреляет, 01 - танк стреляет один раз, 10 - танк стреляет два раза, 11 - танк стреляет три раза
25-30. Количество боеприпасов в танке
31-33. Общее число попадания в танк
34-36. Время непрерывного наблюдения - число шагов dt
38-42. Время, оставшееся у танка при перемещении из одного участка в другой
Таблица 5.2. Возможное распредение разрядов ячейки ЭВМ для записи параметров участка
Номер разряда. Код и его смысловое значение
1-2. 00 - нет танка, 01 - один танк, 10 - два танка
3. 0 - "красный" танк, 1 - "синий" танк
4-5. 01 - непроходимый участок, 10 - труднопроходимый участок, 11 - проходимый участок
6-11. H - Hmin в метрах, где H - высота участка над уровнем моря, Hmin - минимальная высота для всех участков
12-17. hi - высота окружающих предметов, в метрах
18-24. f - коэффициент, определяющий характер грунта 0 < f < 100
25-28. 00 - нет границы, 01 - 1-я граница, 10 - 2-я граница, 11 - 3-я граница, 100 - 4-я граница
Зная номера ячеек, отведенных для записи информации о первом и последних элементах, легко определить номер элемента, информация о котором записана в промежуточной ячейке, при условии, что эти ячейки расположены последовательно.
В таблице 5.2 представлено распределение разрядов ячейки ЭВМ между параметрами участка. Номер участка, информация о котором записана в данной ячейке, определяется номером этой ячейки по способу, аналогичному при определении номера элемента. Исходная информация о каждом элементарном участке берется непосредственно с карты, на которой задается первоначальное распределение танков обеих сторон.
Для работы блока перемещения в алгоритме, построенном по изложенным выше принципам, нужно знать конкретный вид весовой функции w.
Так как танки "красных" однотипны, функция w будет одинакова для всех такнов. Направление перемещения каждого танка определяется совокупностью заданных ориентиров, боевым порядком и условиями проходимости. Так как каждый ориентир обязательно находится на одном из элементарных участков, то, задавая номера участков, в которых находятся ориентиры, получим возможность учитывать их влияние на направление перемещения.
Для определения вида функции w можно считать, что у каждого элемента имеется только один ориентир. Это предположение не нарушит общности модели, т.к. воздействие ориентиров на направление движения происходит последовательно. Переход от одного ориентира к другому происходит в момент, когда данный ориентир перестает определять общее направление движения, т.е. тогда, когда движущийся танк поравняется с ориентиром. Следовательно, направление во всех случаях может определяться по взаимному расположению танка и ближайшего ориентира. Для каждого направления из восьми возможных соседних участков выбираются три.
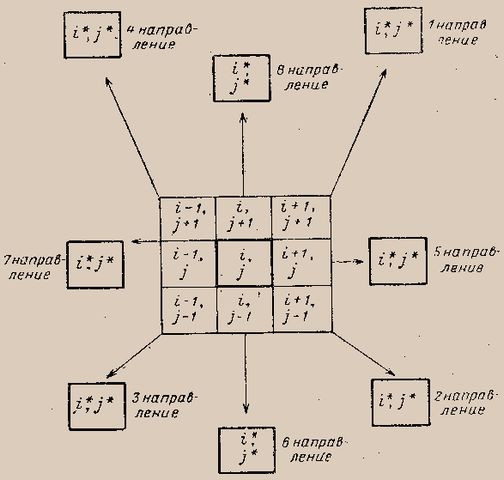
Рис.5.4. Схема выбора возможных направлений движения.
Порядок выбора и характер направлений показаны на рис.5.4., где индекс (i*, j* ) определяют ориентир, а индексы (i, j) - рассматриваемый участок.
В зависимости от назначения разностей (i* - i) и (j* - j) получаются восемь возможных направлений:
1 - при i* > i и j* > j,
2 - при i* > i и j* < j,
3 - при i *< i и j* < j,
4 - при i *< i и j* > j,
5 - при i *> i и j* = j,
6 - при i* = i и j* < j,
7 - при i* < i и j* = j,
8 - при i* = i и j* > j.
Принцип выбора трех участков таков, что, например, для направления 1 выбирается участки с индексами (i, j+1), (i+1, j+1), (i+1, j), а для направления 5 - (i+1, j+1), (i+1, j), (i+1, j-1). Для направлений 2, 3, 4 участки выбираются аналогично направлению 1, а для 6, 7,8 - аналогично направлению 5.
Выделенные участки проверяются на проходимость. Эта проверка включает в себя выделение физически непроходимых участков и выделение участков, перемещение в которые невозможно из-за недопустимого нарушения заданного боевого порядка. Если среди трех выделенных участков есть непроходимые, то каждый такой участок заменяется ближайшим к нему проходным. Выделенным таким образом, трем участкам приписывается положительный вес, остальным участкам - нулевой вес. Распределение вероятностей (весов) среди выделенных трех участков зависит от конкретного вида модели, размеров участка, типов элементов и т.д.
Если размеры элементов и участка примерно одного порядка, то участки должны выбираться равновероятно. Если размеры участков по крайней мере на порядок больше размеров элементов, то центральный участок должен выбираться с гораздо большей вероятностью. В рассматриваемом случае сторона участка была выбрана длиной 100м, размеры элементов составляли 5-7м и веса участка распределились между собой в отношении 1:4:1, что дает следующие вероятности выбора: 1/6; 2/3; 1/6.
Из всех соседних участков хотя бы один должен быть проходным, по крайне мере тот, из которого танк переместится в данный участок. Кроме того, разбиение на элементарные участки должно быть согласовано с размерами допустимых интервалов в принятом боевом порядке для того, чтобы не допустить случая, когда все восемь соседних участков будут непроходимыми из-за нарушения боевого порядка. Для конкретных размеров элементарных участков и допустимых интервалов это осуществить достаточно просто.
При выборе конкретного значения скорости перемещения танка учитывается его тип, характер грунта тех участков, по которым происходит движение, и угол наклона движения. Из общей теории танка известно, что максимальная скорость его движения определяется по формуле:

Значение f для каждого участка задано в исходной информации. При перемещении из участка для определения vmax берется полусумма соответствующих значений коэффициента f.

Рис.5.5. Угол превышения.

Рис.5.6. Возможные варианты расположения соседних элементарных участков.
Значение угла al (альфа) определяется из прямоугольного треугольника (рис.5.5), где h1 - разность высот центров соответствующих участков; d1 - расстояние между центрами этих участков, которое равно или a или а на корень квадратный из 2, где a - сторона участка. Конкретное значение d1 зависит от взаимного расположения участков. Оба случая показаны на рис.5.6.
Конкретное значение скорости выбирается методом, описанным выше, причем Vmin, как правило, принимается равной 0. Характер функции распределения значения скорости на допустимом интервале вследствие почти полного отсутствия необходимых данных неизвестен. Поэтому чаще всего принимается, что значение скорости распределено или равномерно, или по нормальному закону.
Если движущийся элемент не ведет стрельбу, то считается, что он ведет непрерывное наблюдение. Выделение целей в первую группу для каждого танка, ведущего наблюдение, происходит следующим способом. Определяются расстояния танка до каждой цели. Все те цели, расстояния до которых превышают некоторое Rз (слишком удаленные), относятся к первой группе. Для каждой оставшейся цели строится отрезок прямой, соединяющий центры участков, на которых расположены танк и цель, причем построение происходит в трехмерном пространстве, т.е. третьей координатой является высота над уровнем моря участка полюс высота окружающих предметов.
Построенный отрезок проектируется на плоскость XOY. После этого выделяются номера всех тех участков, которые пересекаются проекцией. Для каждого такого участка определяется соответствующая суммарная высота, которая сравнивается со значениями высот, полученными подставкой координат центров участка в уравнение проекции. Если встретятся такие суммарные высоты, которые превосходят значения высот, полученные из уравнения, то это значит, что рельеф не позволяет обнаружить цель.

Рис.5.7. Влияние местности на возможность обнаружения.

Рис.5.8. Схема наблюдения цели.
Рис.5.7 поясняет описанную выше невозможность обнаружения цели, находящейся в точке A, из точки B. Поэтому все такие цели также относятся к первой группе. Оставшиеся цели относятся ко второй группе. Поэтому для каждой из них подсчитывается вероятность ее обнаружения по формуле (5.1). Так как наблюдение ведется из танка за танками, то функция мгновенной плотности может быть определена из следующих соображений. Глаз наблюдателя расположен на некотором расстоянии (рис.5.8 ) от отверстия, образованного фигурой B1-C1-D1-F1, которую можно считать прямоугольником. Цель, наблюдаемая площадь которой равна S, расположена перпендикулярно линии наблюдения и находится на расстоянии r2 от точки A. При этом может наблюдаться фигура B2-C2-D2=F2, подобная B1-C1-D1-F1, площадь которой
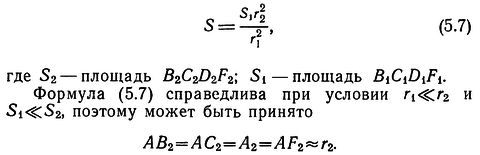
Если предложить, что вероятность обнажения цели, находящейся в плотности B2-C2-D2-F2, пропорциональна отношению соответствующих площадей, т.е.

Таким образом, используя экспериментальные данные p1, можно подобрать значение k, достаточно хорошо учитывающее факторы, действительно влияющие на вероятность обнаружения. Как правило, единого k для всех расстояний от Rз до 0 подобрать не удается, поэтому целесообразно интервал (0, Rз) разбить на отрезки, на каждом из которых справедливо одно значение коэффициента k.
После выяснения всех обнаруженных целей происходит целераспределение. В описываемой модели осуществляется следующий принцип целераспределения.
Из всех обнаруженных данным танком целей сначала выбираются ближайшие стреляющие по нему цели или, если таких нет, просто ближайшие.
Для того чтобы распределение сделать более равномерным, вводятся ограничения: запрещается стрелять по одной и той же цели более чем u огневым средствам, где параметр u можно менять, что дает возможность на модели определять наиболее выгодную степень концентрации огня в тех или иных случаях. После целераспределения на следующем шаге каждый танк с признаком h4 = r начинает стрелять по танку противоположного цвета с порядковым номером r. Стрельба ведется до тех пор, пока не произойдет одно из трех событий: танк поразил цель с номером r, танк поражен каким-нибудь танком противоположного цвета, у танка кончились боеприпасы (h5=0). После каждого выстрела подсчитывается вероятность попадания в цель по формуле

Вследствие невозможности точного аналитического учета поправок при втором и последующих выстрелах, рекомендуемых типовыми правилами стрельбы из танков, в случае непопадания при первом выстреле в модели применяется следующее правило подсчета вероятности при последующих выстрелах. Пусть p2 - вероятность попадания при втором выстреле при условии, что результат первого был отрицателен, тогда

Аналогично

Выбрав соответствующие значения констант на основе статистических данных, можно подсчитать вероятности попадания для последующих выстрелов при достаточно хорошем согласовании с действительными результатами стрельбы. Каждый раз после вычисления вероятности попадания методом статистических испытаний определяется результат стрельбы.
В случае попадания вычисляется вероятность поражения по некоторой заданной при моделирования формуле. Не вызывает возражений, например, формула

произошло попадание, типа цели и типа танка, ведущего стрельбу. Она характеризует среднее число попаданий, необходимое для поражения цели, т.е. огневую мощь стрелявшего танка и броневую защиту.
Этакий винегрет из всего того, что пришло моделисту в голову. Однако, формулы, которые мне так трудно было вводить, а вам - рассматривать еще не кончились.- G.
Пусть необходимо исследовать закономерности исхода боя танковой роты (батальона) при наступлении на противотанковый укрепленный район.
Рассматривается следующая тактическая задача. Танковая рота "красных", стоящая из n1 танков, должна прорвать противотанковый укрепленный район "синих". Этот район обороняет n2 танков "синих", которые замаскированы и находятся в специально созданных укрытиях. Рота должна наступать в заданном боевом порядке в полосе шириной a метров и глубиной c метров. Общее направление движения роты определяется взаимным расположением на местности исходной позиции "красных" и "синих". Направление движения для каждого танка "красных" определяется совокупностью ориентиров, которыми являются хорошо различаемые местные предметы.
Бой начинается в некоторое заданное время T0 и продолжается до того момента, когда силы одной из борющихся сторон станут небоеспособными. Концом боя можно также считать тот момент T1 > T0, в который будет выполнена боевая задача или потери одной сторон превысят допустимый относительный уровень.
Одинаковые элементы одного цвета будут отличаться по присвоенным им порядковым номерам, которые не меняются в течение боя. Введенная для характеристики боеспособности случайная функция h1(t) из-за однотипности элементов процесса будет иметь один и тот же вид для всех элементов. Различными для разных элементов будут лишь ее характеристики: математическое ожидание, корреляционная функция и т.д. Это утверждение справедливо и для других параметров элементов. Сечение функции h1(t) (для любого T0 =< t =< T1) представляет собой случайную величину, принимающую значенеие 1, если элемент в данный момент боеспособен, и 0 в противном случае.
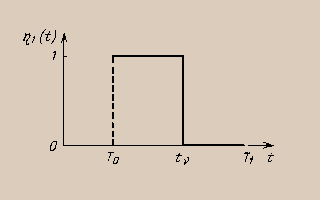
Рис.5.2. Пример случайной реализации функции боеспособности.
Реализация функции h1(t) показана на рис.5.2. Это невозрастающая ступенчатая функция, имеющая скачок в некотором tv (T0 < tv < T1).

Рис.5.3. Пример случайных реализаций функции h2(t).
Случайная функция h2(t) характеризует местоположение элемента в любой момент времени. Т.к. в любой момент времени элемент находится в одном из L участков, то сечение функции h2(t) представляет собой случайную величину, принимающую одно из значений: 1, 2,..., L. Пример возможных реализаций функции h2(t) показан на рисунке 5.3.
Реализация функции скорости h3(t) вследствие округления получаемых значений будет иметь вид, аналогичный изображенному на рис.5.3., причем возможные значения ординат этой функции будут выбраться из интервала (Vmim, Vmax). Для элементов "синих" параметры h2(t) и h3(t) имеют неслучайный характер и представляют собой заданные константы - номера участков, в которых находятся элементы "синих" и нулевую скорость, т.к. предполагается, что их танки в течение боя не перемещаются.
В модели принято, что если элемент боеспособен, то в каждый момент времени он ведет наблюдение или стрельбу по некоторой цели, порядковый номер которой известен. Поэтому сечение случайной функции h4(t), определяющей характер действия элемента, представляет собой случайную величину, принимающую одно из значений 0, 1, 2, ..., n2 для "красных" и 0, 1, 2,..., n1 - для "синих".
Значение 0 означает, что элемент ведет наблюдение; значение, отличное от нуля, показывает, что элемент стрельбу по цели, порядковый номер которой равен этому значению. Вид реализации случайной функции h4(t) аналогичен виду реализации на рис.5.3.
Реализация случайной функции h5(t) является убывающей ступенчатой функцией, имеющей скачки величиной в единицу в некоторой совокупности значений времени в интервале (T0, T1). Сечение функции h5(t) при любом tн представляет собой случайную величину, принимающую одно из значений 0, 1, 2,..., Qi, где Qi - максимальное значение количества боеприпасов в i элементе.
Значения параметров, рассмотренных выше, достаточно полно определяют состояние значение элемента определяют состояние элемента и позволяют получать данные, характеризующие весь бой в целом. Например, если необходимо получить реализацию случайной функции количества потерь, то сумма реализации функции h1(t) для всех элементов одного цвета и будут искомой реализацией. Задача состоит в том, чтобы составить алгоритмы, позволяющие получать значения параметров состояния элемента в каждый момент tv (v = 1, 2,..., N), используя полученную текущую информацию для моментов времени t1, t2,..., tv-1 и некоторую заданную исходную информацию.
Главной составной частью заданной исходной информации является информация о местности. Анализ тех данных о местности, которые существенно влияют на характер боя, позволяет сделать вывод, что каждый участок должен характеризоваться следующими параметрами, являющимися заданными функциями от порядкового номера участка:
1) параметром проходимости B1(l), где B1 принимает три значения [Такая градация параметра B1, естественно, не обязательна во всех случаях]:
1 - если участок с номером l непроходим для танков "красных";
2 - если труднопроходим;
3 - если хорошо проходим.
Вследствие однотипности танков, участвующих в бою, можно принять, что функция B1(l) зависит только от свойств местности и является постоянной для танков;
2) параметром рельефа B2(l), где функция принимает значение, равное высоте над уровнем моря, для центра участка с номером l;
3) параметром B3(l), где функция B3(l) принимает значение, равное средней высоте искусственных и естественных предметов, занимающих достаточно большую часть площади участка с номером l;
4) параметром B4(l), где функция B4(l) принимает значение, равное коэффициенту сопротивления движения для характерного грунта на участке с номером l.
Моделируемый алгоритм состоит из совокупности основных и вспомогательных блоков. Основные блоки предназначены для моделирования определяющих процессов танкового боя: перемещения, наблюдения, целераспределения и стрельбы. При решении некоторых частных задач методом моделирования эти блоки могут быть использованы как самостоятельные модели.
Вспомогательные блоки предназначены для ввода исходной информации, определения конкретного вида решаемого варианта, управления потоком текущей информации, получаемой в основных блоках и необходимой для них в дальнейшем, для статистической обработки результатов моделирования и выдачи результатов моделирования и выдачи результатов.
Работу всех основных блоков объясняет блок управления, в котором определяется очередность обработки элементов и последовательность получения текущей информации об элементе в основных блоках. Кроме того, в блоке управления происходит регистрация времени, благодаря чему через определенные промежутки происходит выдача текущей информации для статистической обработки и на печать и проверка конца работы программы.
Во все блоки информация поступает и обрабатывается в специально закодированном виде. Всю информацию, как исходную, так и текущую, можно разделить на две группы:
1) информацию о танках, которая задается числовыми параметров состояний элемента;
2) информацию об элементарных участках, которая для каждого участка задается числовыми значениями параметров, характеризующих этот участок.
Каждое числовое значение параметра записывается в виде целого числа в двоичном коде. В задаваемой совокупности исходных констант предусматриваются значения масштаба кодирования, необходимые для декодирования в процессе обработки текущей информации. Такое кодирование позволяет записывать значение параметра в специально отведенных двоичных разрядах ячейки оперативной памяти ЭВМ, причем количество отводимых разрядов определяется верхней границей диапазона изменения параметра. Поэтому количество ячеек, требуемое для записи информации об одном элементе или участке, зависит от числа параметров и диапазонов их изменения.
В таблице 5.1. представлено возможное распределение разрядов ячейки ЭВМ между параметрами состояния элемента.
Таблица 5.1. Возможное распределение разрядов ячейки ЭВМ для записи параметров состояния элемента
Номер разряда. Код и его смысловое значение
1. 0 - танк небоеспособен, 1 - танк боеспособен
2. 0 - "красный" танк, 1 - "синий" танк
3. 0 - танк наблюдает, 1 - танк стреляет
4-12. Номер участка, где стоит танк
13-17. V - скорость танка м/сек
18-21. Номер цели, по которой стреляет танк
22-24. 00 - танк не стреляет, 01 - танк стреляет один раз, 10 - танк стреляет два раза, 11 - танк стреляет три раза
25-30. Количество боеприпасов в танке
31-33. Общее число попадания в танк
34-36. Время непрерывного наблюдения - число шагов dt
38-42. Время, оставшееся у танка при перемещении из одного участка в другой
Таблица 5.2. Возможное распредение разрядов ячейки ЭВМ для записи параметров участка
Номер разряда. Код и его смысловое значение
1-2. 00 - нет танка, 01 - один танк, 10 - два танка
3. 0 - "красный" танк, 1 - "синий" танк
4-5. 01 - непроходимый участок, 10 - труднопроходимый участок, 11 - проходимый участок
6-11. H - Hmin в метрах, где H - высота участка над уровнем моря, Hmin - минимальная высота для всех участков
12-17. hi - высота окружающих предметов, в метрах
18-24. f - коэффициент, определяющий характер грунта 0 < f < 100
25-28. 00 - нет границы, 01 - 1-я граница, 10 - 2-я граница, 11 - 3-я граница, 100 - 4-я граница
Зная номера ячеек, отведенных для записи информации о первом и последних элементах, легко определить номер элемента, информация о котором записана в промежуточной ячейке, при условии, что эти ячейки расположены последовательно.
В таблице 5.2 представлено распределение разрядов ячейки ЭВМ между параметрами участка. Номер участка, информация о котором записана в данной ячейке, определяется номером этой ячейки по способу, аналогичному при определении номера элемента. Исходная информация о каждом элементарном участке берется непосредственно с карты, на которой задается первоначальное распределение танков обеих сторон.
Для работы блока перемещения в алгоритме, построенном по изложенным выше принципам, нужно знать конкретный вид весовой функции w.
Так как танки "красных" однотипны, функция w будет одинакова для всех такнов. Направление перемещения каждого танка определяется совокупностью заданных ориентиров, боевым порядком и условиями проходимости. Так как каждый ориентир обязательно находится на одном из элементарных участков, то, задавая номера участков, в которых находятся ориентиры, получим возможность учитывать их влияние на направление перемещения.
Для определения вида функции w можно считать, что у каждого элемента имеется только один ориентир. Это предположение не нарушит общности модели, т.к. воздействие ориентиров на направление движения происходит последовательно. Переход от одного ориентира к другому происходит в момент, когда данный ориентир перестает определять общее направление движения, т.е. тогда, когда движущийся танк поравняется с ориентиром. Следовательно, направление во всех случаях может определяться по взаимному расположению танка и ближайшего ориентира. Для каждого направления из восьми возможных соседних участков выбираются три.

Рис.5.4. Схема выбора возможных направлений движения.
Порядок выбора и характер направлений показаны на рис.5.4., где индекс (i*, j* ) определяют ориентир, а индексы (i, j) - рассматриваемый участок.
В зависимости от назначения разностей (i* - i) и (j* - j) получаются восемь возможных направлений:
1 - при i* > i и j* > j,
2 - при i* > i и j* < j,
3 - при i *< i и j* < j,
4 - при i *< i и j* > j,
5 - при i *> i и j* = j,
6 - при i* = i и j* < j,
7 - при i* < i и j* = j,
8 - при i* = i и j* > j.
Принцип выбора трех участков таков, что, например, для направления 1 выбирается участки с индексами (i, j+1), (i+1, j+1), (i+1, j), а для направления 5 - (i+1, j+1), (i+1, j), (i+1, j-1). Для направлений 2, 3, 4 участки выбираются аналогично направлению 1, а для 6, 7,8 - аналогично направлению 5.
Выделенные участки проверяются на проходимость. Эта проверка включает в себя выделение физически непроходимых участков и выделение участков, перемещение в которые невозможно из-за недопустимого нарушения заданного боевого порядка. Если среди трех выделенных участков есть непроходимые, то каждый такой участок заменяется ближайшим к нему проходным. Выделенным таким образом, трем участкам приписывается положительный вес, остальным участкам - нулевой вес. Распределение вероятностей (весов) среди выделенных трех участков зависит от конкретного вида модели, размеров участка, типов элементов и т.д.
Если размеры элементов и участка примерно одного порядка, то участки должны выбираться равновероятно. Если размеры участков по крайней мере на порядок больше размеров элементов, то центральный участок должен выбираться с гораздо большей вероятностью. В рассматриваемом случае сторона участка была выбрана длиной 100м, размеры элементов составляли 5-7м и веса участка распределились между собой в отношении 1:4:1, что дает следующие вероятности выбора: 1/6; 2/3; 1/6.
Из всех соседних участков хотя бы один должен быть проходным, по крайне мере тот, из которого танк переместится в данный участок. Кроме того, разбиение на элементарные участки должно быть согласовано с размерами допустимых интервалов в принятом боевом порядке для того, чтобы не допустить случая, когда все восемь соседних участков будут непроходимыми из-за нарушения боевого порядка. Для конкретных размеров элементарных участков и допустимых интервалов это осуществить достаточно просто.
При выборе конкретного значения скорости перемещения танка учитывается его тип, характер грунта тех участков, по которым происходит движение, и угол наклона движения. Из общей теории танка известно, что максимальная скорость его движения определяется по формуле:

Значение f для каждого участка задано в исходной информации. При перемещении из участка для определения vmax берется полусумма соответствующих значений коэффициента f.

Рис.5.5. Угол превышения.

Рис.5.6. Возможные варианты расположения соседних элементарных участков.
Значение угла al (альфа) определяется из прямоугольного треугольника (рис.5.5), где h1 - разность высот центров соответствующих участков; d1 - расстояние между центрами этих участков, которое равно или a или а на корень квадратный из 2, где a - сторона участка. Конкретное значение d1 зависит от взаимного расположения участков. Оба случая показаны на рис.5.6.
Конкретное значение скорости выбирается методом, описанным выше, причем Vmin, как правило, принимается равной 0. Характер функции распределения значения скорости на допустимом интервале вследствие почти полного отсутствия необходимых данных неизвестен. Поэтому чаще всего принимается, что значение скорости распределено или равномерно, или по нормальному закону.
Если движущийся элемент не ведет стрельбу, то считается, что он ведет непрерывное наблюдение. Выделение целей в первую группу для каждого танка, ведущего наблюдение, происходит следующим способом. Определяются расстояния танка до каждой цели. Все те цели, расстояния до которых превышают некоторое Rз (слишком удаленные), относятся к первой группе. Для каждой оставшейся цели строится отрезок прямой, соединяющий центры участков, на которых расположены танк и цель, причем построение происходит в трехмерном пространстве, т.е. третьей координатой является высота над уровнем моря участка полюс высота окружающих предметов.
Построенный отрезок проектируется на плоскость XOY. После этого выделяются номера всех тех участков, которые пересекаются проекцией. Для каждого такого участка определяется соответствующая суммарная высота, которая сравнивается со значениями высот, полученными подставкой координат центров участка в уравнение проекции. Если встретятся такие суммарные высоты, которые превосходят значения высот, полученные из уравнения, то это значит, что рельеф не позволяет обнаружить цель.

Рис.5.7. Влияние местности на возможность обнаружения.

Рис.5.8. Схема наблюдения цели.
Рис.5.7 поясняет описанную выше невозможность обнаружения цели, находящейся в точке A, из точки B. Поэтому все такие цели также относятся к первой группе. Оставшиеся цели относятся ко второй группе. Поэтому для каждой из них подсчитывается вероятность ее обнаружения по формуле (5.1). Так как наблюдение ведется из танка за танками, то функция мгновенной плотности может быть определена из следующих соображений. Глаз наблюдателя расположен на некотором расстоянии (рис.5.8 ) от отверстия, образованного фигурой B1-C1-D1-F1, которую можно считать прямоугольником. Цель, наблюдаемая площадь которой равна S, расположена перпендикулярно линии наблюдения и находится на расстоянии r2 от точки A. При этом может наблюдаться фигура B2-C2-D2=F2, подобная B1-C1-D1-F1, площадь которой
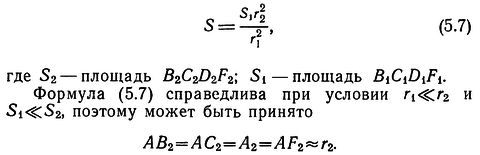
Если предложить, что вероятность обнажения цели, находящейся в плотности B2-C2-D2-F2, пропорциональна отношению соответствующих площадей, т.е.

Таким образом, используя экспериментальные данные p1, можно подобрать значение k, достаточно хорошо учитывающее факторы, действительно влияющие на вероятность обнаружения. Как правило, единого k для всех расстояний от Rз до 0 подобрать не удается, поэтому целесообразно интервал (0, Rз) разбить на отрезки, на каждом из которых справедливо одно значение коэффициента k.
После выяснения всех обнаруженных целей происходит целераспределение. В описываемой модели осуществляется следующий принцип целераспределения.
Из всех обнаруженных данным танком целей сначала выбираются ближайшие стреляющие по нему цели или, если таких нет, просто ближайшие.
Для того чтобы распределение сделать более равномерным, вводятся ограничения: запрещается стрелять по одной и той же цели более чем u огневым средствам, где параметр u можно менять, что дает возможность на модели определять наиболее выгодную степень концентрации огня в тех или иных случаях. После целераспределения на следующем шаге каждый танк с признаком h4 = r начинает стрелять по танку противоположного цвета с порядковым номером r. Стрельба ведется до тех пор, пока не произойдет одно из трех событий: танк поразил цель с номером r, танк поражен каким-нибудь танком противоположного цвета, у танка кончились боеприпасы (h5=0). После каждого выстрела подсчитывается вероятность попадания в цель по формуле

Вследствие невозможности точного аналитического учета поправок при втором и последующих выстрелах, рекомендуемых типовыми правилами стрельбы из танков, в случае непопадания при первом выстреле в модели применяется следующее правило подсчета вероятности при последующих выстрелах. Пусть p2 - вероятность попадания при втором выстреле при условии, что результат первого был отрицателен, тогда

Аналогично

Выбрав соответствующие значения констант на основе статистических данных, можно подсчитать вероятности попадания для последующих выстрелов при достаточно хорошем согласовании с действительными результатами стрельбы. Каждый раз после вычисления вероятности попадания методом статистических испытаний определяется результат стрельбы.
В случае попадания вычисляется вероятность поражения по некоторой заданной при моделирования формуле. Не вызывает возражений, например, формула

произошло попадание, типа цели и типа танка, ведущего стрельбу. Она характеризует среднее число попаданий, необходимое для поражения цели, т.е. огневую мощь стрелявшего танка и броневую защиту.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
5.4. О ТОЧНОСТИ СТОХАСТИЧЕСКОГО МОДЕЛИРОВАНИЯ
А теперь о том, чем "варгеймеры" не занимались никогда. Ведь модель должна дать как можно более точный результат, а игра, наоборот,- большой разброс.- G.
Оценить точность модели - это значит найти расхождения результатов, полученных после реализации этой модели с действительными результатами. Совершенно ясно, что качество выполнения каждого из этапов моделирования влияет на точность модели.
Имеет смысл различать влияние на точность модели двух основных факторов: 1) схематизации "физического" процесса и 2) получения в алгоритме модели лишь приближенных параметров состояний элементов.
После получения результатов моделирования точность модели определяется специалистами, достаточно компетентными в исследуемой вопросе, в соответствии с результатами, полученными методами воспроизведения "физического" процесса в виде натурного эксперимента. Однако необходимо отметить, что весьма часто организация таких экспериментов вообще невозможна, поэтому на повестке дня стоит задача разработки методов определения точности модели теоретическими способами.
При стохастическом моделировании особое значение для математической точности имеет правильное определение числа реализаций, необходимое для получения удовлетворительных оценок характеристик случайных функций. После каждой реализации получается N значений ординат этих функций в точках t1, t2, t3,..., tN.
Пусть проведено n таких реализаций. Требуется найти подходящие значения выборочных характеристик некоторой функции x(t): ее математического ожидания mx(t), дисперсии Dx(t), корреляционной функции kx(t, t') и т.д. Для этого нужно подсчитать соответствующие значения этих характеристик в каждом сечении по известным формулам:

Кроме того, часто бывает необходимо знать частоты появления возможных значений случайной величины в каждом сечении для того, чтобы приближенно оценить функцию распределения этой случайной величины.
После получения простой статистической совокупности

можно определить эмпирическую функцию распределения Fn(x):

Пусть случайная величина x принимает при этом проигрывании одно из возможных значений: c1, c2,..., cm.
Используя полученный вариационный ряд, нетрудно получить совокупность чисел mj.
Тогда частота появления каждого значения mj будет равна

Из теоремы Бореля следует, что частоту, полученную таким образом, можно принять за приближенную вероятность, так как при n, стремящейся к бесконечности, частота стремится в пределе к вероятности. Каково должно быть число n, чтобы, во-первых, полученные частоты достаточно хорошо определяли приближение к вероятности и, во-вторых, эмпирическая функция распределения Fn(x) была хорошим приближением теоретической функции распределения F(x).
Так как характер теоретической функции при моделировании, как правило, бывает неизвестным, то на практике чаще всего поступают следующим образом.
Модель реализуется n1 раз, причем n1 достаточно велико, чтобы обеспечить требование mj >= 5.
По полученным результатами строится эмпирическая функция Fn(x). Из теоремы Гливенко следует, что при стремлении n к бесконечности вероятность стремления к нулю верхней границы модуля разности между эмпирической функцией распределения и теоретической равна единице. Поэтому, если получить две эмпирические функции для некоторых достаточно больших n1 и n2, то с достаточно большой вероятностью можно ожидать, что мера расхождения меду ними достаточно мала. Поэтому, проделав еще некоторое количество реализаций, например l, получим новые статистические данные для n2 = n1 + l. Определив функцию Fn2(x), можно считать ее за теоретическую и проверить гипотезу, что случайная величина h по данным выборки n1 подчинена закону распределения Fn2(x)=F(x).
Эту проверку удобно проводить на основании критерия соответствия xи-квадрат.
Если расхождение выборочных данных с гипотетическим допущением о законе распределения существенно, то наша гипотеза бракуется.
В этом случае проделываем еще l проигрываний и получаем Fn3(x), где n3 = n2 + l, которую принимаем за гипотетическое распределение, а Fn2(x) считаем эмпирической функцией распределения. После этого необходимо вновь проверить по критерию хи-квадрат, существенно ли расхождение Fn2(x) с Fn3(x).
Этот процесс продолжается до тех пор, пока расхождение станет несущественным.
Пусть это произойдет для функции распределения Fnk(x). Тогда можно считать [Это утверждение в общем виде строго не доказано], что получена эмпирическая функциям Fn(x), достаточно хорошо приближающаяся к неизвестной теоретической, где n = nk.
Используя функцию Fn(x), можно получить оценки для неизвестных вероятностных характеристик mx, Dx, (их, как правило, бывает достаточно для дальнейших исследований, другие характеристики можно получить аналогично).
Проделав это для каждого сечения, можно получить последовательность значений:

Часто эти функции аппроксимируются каким-либо удобными аналитическими выражениями. Иногда бывает достаточна проверка: насколько частота p*j хорошо приближает вероятность появления j-го значения случайной величины x.
Задача состоит в том, чтобы по наблюденной частоте указать границы, в которые с достаточно большой вероятностью попадает неизвестная вероятность.
Пусть этот заданный уровень вероятности - доверительная вероятность - равен p, тогда можно найти такое tp > 0, что

Все значения вероятности, лежащие в доверительном интервале, считаются согласующимися с наблюденной на опыте частоте p*j, а лежащие вне его - несогласующимися. Значение tp при каждом выбранном значении a определяется при помощи специально составленных таблиц значений Ф(z). Наиболее часто употребляется при обработке результатов моделирования значения a = 0.95, при котором tp ~ 2.
Задавшись точностью исходных данных, например, исходных значений вероятностей, равной dp, нужно осуществлять реализации процесса до тех пор, пока длина доверительного интервала не станет меньшей или равной значению dp, так как добиваться большей точности не имеет смысла.
Как и при сравнении результатов, полученных с помощью различных математических моделей, следует ожидать, что в качестве критерия оценки степени совпадения результатов натурного и математического моделирования будут выбраны численности противников.
Предположим, что в результате проведенных 15 боев получены значения численности mi наступающей роты в определенный момент боя: 2, 0, 5, 2, 2, 3, 1, 4, 2, 0, 3, 2, 5, 0, 2. Среднее арифметическое численности наступающих танков в этот момент будет равно

можно считать, что результаты натурального и математического моделирования совпадают.

и пределы расхождения сузятся до 2.938..1.462. Аналогичную оценку можно провести для любого фиксированного момента боя, однако она не будет исчерпывающей.
Ниже рассматривается несколько отличный от известных методов статистического анализа способ оценки точности математического моделирования по результатам натурных испытаний.
В рассматриваемом способе дается оценка, когда число реализаций реального процесса небольшое.
Если для боя танков со средствами ПТО построена математическая модель, на которой можно определить число уничтоженных танков и средств ПТО к моменту t от начала боя, то для оценки этой модели по числу уничтоженных средств в N (N = 10..15) взаимно независимых реализациях с соблюдением идентичности всех условий боя, учитываемых в математической модели, в заданные моменты времени t1, t2, t3,..., tk во всех реализациях фиксируется количество уничтоженных боевых единиц для обеих сторон.

Так как доверительный интервал для случайной величины sl записывается в виде


А теперь о том, чем "варгеймеры" не занимались никогда. Ведь модель должна дать как можно более точный результат, а игра, наоборот,- большой разброс.- G.
Оценить точность модели - это значит найти расхождения результатов, полученных после реализации этой модели с действительными результатами. Совершенно ясно, что качество выполнения каждого из этапов моделирования влияет на точность модели.
Имеет смысл различать влияние на точность модели двух основных факторов: 1) схематизации "физического" процесса и 2) получения в алгоритме модели лишь приближенных параметров состояний элементов.
После получения результатов моделирования точность модели определяется специалистами, достаточно компетентными в исследуемой вопросе, в соответствии с результатами, полученными методами воспроизведения "физического" процесса в виде натурного эксперимента. Однако необходимо отметить, что весьма часто организация таких экспериментов вообще невозможна, поэтому на повестке дня стоит задача разработки методов определения точности модели теоретическими способами.
При стохастическом моделировании особое значение для математической точности имеет правильное определение числа реализаций, необходимое для получения удовлетворительных оценок характеристик случайных функций. После каждой реализации получается N значений ординат этих функций в точках t1, t2, t3,..., tN.
Пусть проведено n таких реализаций. Требуется найти подходящие значения выборочных характеристик некоторой функции x(t): ее математического ожидания mx(t), дисперсии Dx(t), корреляционной функции kx(t, t') и т.д. Для этого нужно подсчитать соответствующие значения этих характеристик в каждом сечении по известным формулам:

Кроме того, часто бывает необходимо знать частоты появления возможных значений случайной величины в каждом сечении для того, чтобы приближенно оценить функцию распределения этой случайной величины.
После получения простой статистической совокупности

можно определить эмпирическую функцию распределения Fn(x):

Пусть случайная величина x принимает при этом проигрывании одно из возможных значений: c1, c2,..., cm.
Используя полученный вариационный ряд, нетрудно получить совокупность чисел mj.
Тогда частота появления каждого значения mj будет равна

Из теоремы Бореля следует, что частоту, полученную таким образом, можно принять за приближенную вероятность, так как при n, стремящейся к бесконечности, частота стремится в пределе к вероятности. Каково должно быть число n, чтобы, во-первых, полученные частоты достаточно хорошо определяли приближение к вероятности и, во-вторых, эмпирическая функция распределения Fn(x) была хорошим приближением теоретической функции распределения F(x).
Так как характер теоретической функции при моделировании, как правило, бывает неизвестным, то на практике чаще всего поступают следующим образом.
Модель реализуется n1 раз, причем n1 достаточно велико, чтобы обеспечить требование mj >= 5.
По полученным результатами строится эмпирическая функция Fn(x). Из теоремы Гливенко следует, что при стремлении n к бесконечности вероятность стремления к нулю верхней границы модуля разности между эмпирической функцией распределения и теоретической равна единице. Поэтому, если получить две эмпирические функции для некоторых достаточно больших n1 и n2, то с достаточно большой вероятностью можно ожидать, что мера расхождения меду ними достаточно мала. Поэтому, проделав еще некоторое количество реализаций, например l, получим новые статистические данные для n2 = n1 + l. Определив функцию Fn2(x), можно считать ее за теоретическую и проверить гипотезу, что случайная величина h по данным выборки n1 подчинена закону распределения Fn2(x)=F(x).
Эту проверку удобно проводить на основании критерия соответствия xи-квадрат.
Если расхождение выборочных данных с гипотетическим допущением о законе распределения существенно, то наша гипотеза бракуется.
В этом случае проделываем еще l проигрываний и получаем Fn3(x), где n3 = n2 + l, которую принимаем за гипотетическое распределение, а Fn2(x) считаем эмпирической функцией распределения. После этого необходимо вновь проверить по критерию хи-квадрат, существенно ли расхождение Fn2(x) с Fn3(x).
Этот процесс продолжается до тех пор, пока расхождение станет несущественным.
Пусть это произойдет для функции распределения Fnk(x). Тогда можно считать [Это утверждение в общем виде строго не доказано], что получена эмпирическая функциям Fn(x), достаточно хорошо приближающаяся к неизвестной теоретической, где n = nk.
Используя функцию Fn(x), можно получить оценки для неизвестных вероятностных характеристик mx, Dx, (их, как правило, бывает достаточно для дальнейших исследований, другие характеристики можно получить аналогично).
Проделав это для каждого сечения, можно получить последовательность значений:

Часто эти функции аппроксимируются каким-либо удобными аналитическими выражениями. Иногда бывает достаточна проверка: насколько частота p*j хорошо приближает вероятность появления j-го значения случайной величины x.
Задача состоит в том, чтобы по наблюденной частоте указать границы, в которые с достаточно большой вероятностью попадает неизвестная вероятность.
Пусть этот заданный уровень вероятности - доверительная вероятность - равен p, тогда можно найти такое tp > 0, что

Все значения вероятности, лежащие в доверительном интервале, считаются согласующимися с наблюденной на опыте частоте p*j, а лежащие вне его - несогласующимися. Значение tp при каждом выбранном значении a определяется при помощи специально составленных таблиц значений Ф(z). Наиболее часто употребляется при обработке результатов моделирования значения a = 0.95, при котором tp ~ 2.
Задавшись точностью исходных данных, например, исходных значений вероятностей, равной dp, нужно осуществлять реализации процесса до тех пор, пока длина доверительного интервала не станет меньшей или равной значению dp, так как добиваться большей точности не имеет смысла.
Как и при сравнении результатов, полученных с помощью различных математических моделей, следует ожидать, что в качестве критерия оценки степени совпадения результатов натурного и математического моделирования будут выбраны численности противников.
Предположим, что в результате проведенных 15 боев получены значения численности mi наступающей роты в определенный момент боя: 2, 0, 5, 2, 2, 3, 1, 4, 2, 0, 3, 2, 5, 0, 2. Среднее арифметическое численности наступающих танков в этот момент будет равно

можно считать, что результаты натурального и математического моделирования совпадают.

и пределы расхождения сузятся до 2.938..1.462. Аналогичную оценку можно провести для любого фиксированного момента боя, однако она не будет исчерпывающей.
Ниже рассматривается несколько отличный от известных методов статистического анализа способ оценки точности математического моделирования по результатам натурных испытаний.
В рассматриваемом способе дается оценка, когда число реализаций реального процесса небольшое.
Если для боя танков со средствами ПТО построена математическая модель, на которой можно определить число уничтоженных танков и средств ПТО к моменту t от начала боя, то для оценки этой модели по числу уничтоженных средств в N (N = 10..15) взаимно независимых реализациях с соблюдением идентичности всех условий боя, учитываемых в математической модели, в заданные моменты времени t1, t2, t3,..., tk во всех реализациях фиксируется количество уничтоженных боевых единиц для обеих сторон.

Так как доверительный интервал для случайной величины sl записывается в виде



Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
5.5. ПРИМЕРЫ ПРИМЕНЕНИЯ СТОХАСТИЧЕСКОЙ МОДЕЛИ
Наконец-то. Хоть что-то ощутимое.- G.

Рис.5.10. Блок-схема стохастической модели.
В соответствии с изложенными выше принципами блок-схема стохастической модели построена в виде, приведенном на рис.5.10. В блок-схеме можно выделить следующие основные группы блоков:
- блоки 1, 2, 3, 4, 6, 7, 8, 9, воспроизводящие формализованный процесс боя;
- блоки 0, 5, 10, 11, 12, 13, 15, 16, 17 и др., обеспечивающие функционирование модели (блок времени, блоки получения случайных чисел и т.п.);
- блок 14 обработки результатов.
В блоках, воспроизводящих формализованный процесс, моделируются основные процессы проведения огневых средств в бою: перемещение, поиск, обнаружение цели, целераспределение и стрельба. Функционирование этих блоков координируется блоком времени, который может настраиваться на работу либо с постоянным шагомa, и тогда модель представляет собой dt-модель, либо с переменным шагом dt = var, и переход из состояния в состояние происходит в момент возможного скачкообразного изменения одного из параметров. В этом случае модель становится моделью с квази-узловыми точками.
Такое построение алгоритма модели обеспечивает автономность каждого блока и возможность замены отдельных блоков в зависимости от выбранной схемы формализации процесса.
Приводимые ниже примеры некоторых конкретных случаев применения модели получены при описанных выше способах воспроизведения основных процессов. Результаты, накопленные в ходе отдельных реализаций, подвергались статистической обработке в блоке 14 и в зависимости от объема выборки позволяли с той или иной погрешностью оценить исследуемый параметр. Например, при оценке математического ожидания параметра m в заданный момент боя по N реализациям максимальная погрешность e определяется в виде

Практически, пользуясь формулой (5.15) при оценке параметра, реализующегося в ходе боя один раз, можно ограничиться числом реализаций N = 100..200. Для других параметров это число соответственно меньше или больше.
Как и в предыдущих примерах, исходные данные выбраны произвольно:
- скорость танков V = 15км/час;
- размеры танков: l = 3.0м, m = 2.0м, h = 0.9м для танков в обороне и l = 6.0м, m = 2.5м, h = 2.5м для танка в наступлении;
- характеристики рассеивания при стрельбе из танка на дальностях 500..2500м: Вв = 0.10..0.70, Ввп = 0.20..2.0, Вб = 0.10..0.50, Вбп = 0.25..0.9 при стрельбе с места и при стрельбе с хода: Вв = 0.40..1.2, Ввп = 0.45..1.3, Вб = 0.80..2.5, Вбп = 0.85..2.8;
- среднее число попаданий в танк, необходимое для его поражения, 1.4..2.0;
- размеры ПТУРС, ПТР, РПГ: вертикальная площадь m*h = 1.0*0.5м2, площадь осколочного поражения l*m = 20*10м2;
- вероятность попадания в танк для ПТУРСа на дальностях 500, 1500 и 3000м соответственно 0.4, 0.6, 0.4;
- рассеивание при стрельбе из гранатомета Вбп = Ввп = 0.001 D;
- вероятность попадания из ПТР в танк в первом выстреле 0.5, при пятом выстреле P5 = 0.8;
- вероятность обнаружения из танка на дальностях 500..3000м: танка в окопе 0.9..0.3, ПТУРС, ПТР, РПГ: нестреляющих 0.3..0.0, стреляющих 0.8..0.6;
- дальность открытия огня Dmax: для танков в обороне 2000м, для танков в наступлении 2500м, для ПТУРС 2000м, для ПТР 500м, для РПГ 300м.
В первом примере для легких танков "синих" в окопах:
- среднее число попаданий в танк "синих", необходимое для его поражения, 1.76..1.85 на дальностях соответственно 500..1000м,
- среднее число попаданий в танк "красных", необходимое для его поражения, 1.65..2.25 на дальностях соответственно 500..1000м.
Приведем результаты моделирования в соответствии с предложенной в #5.2 схемой наступательного боя средних танков "красных" с обороняющимися легкими танками в окопах "синих".
В таблице 5.3 приведены значения функции hi, полученные в результате одной реализации боя на модели при атаке "красных" с дальности 1км и начальном соотношении численностей "красных"/"синих"=10/5.
Таблица 5.3. Изменение состояний элементов боя времени
Статистическая обработка результатов моделирования при 100 реализациях для каждого исследуемого варианта позволила определить вероятности победы каждой из сторон и статистические характеристики численности в конце третьей минуты боя и в наиболее вероятный момент его окончания, равный 4.2мин. Эти величины приведенные в таблице 5.4.
Таблица 5.4. Изменение численностей сторон в ходе боя.
При вычислении вероятностей победы победившей считалась сторона, имеющая в своем составе хотя бы один танк к моменту, когда все танки противника уничтожены, т.е. уровни боеспособности принимались нулевыми. При одновременном уничтожении последних из оставшихся неуничтоженными танков на каждой стороне обе стороны считались проигравшими бой. На рис.5.11 представлены зависимости вероятности победы каждой из сторон он начального соотношения численностей противников.

Рис.5.11. Зависимость вероятности победы от начального соотношения численности сторон.
Анализ приведенных результатов позволяет сделать вывод, что для достижения достаточно гарантированной победы необходимо иметь по крайней мере двойное численное превосходство. В остальных случаях победа "красных" менее вероятна, чем победа "синих", а ее достижение происходит с чрезмерными потерями.
Для проверки правильности задания в математических моделях секторов обнаружения огневых средств рассмотрим величины углов обстрела танков в наступательном бою. Результаты решения этой задачи, во-первых, могут быть использованы при выработке обоснованных рекомендаций относительно процесса наблюдения из танков в ходе боя и, во-вторых, при выборе параметров броневой защиты.

Рис.5.12. Схема взаимного распределения цели и поражающего средства в бою:

Углом обстрела a назовем угол между направлением движения танка и направлением на обстреливающее этот танка средство противника (рис.5.12). Статистические данные относительно углов a накапливались при моделировании боя тридцати танков, наступающих в линию на опорные пункты двух пехотных рот, как показано на рис.5.13, и в двух других вариантах, когда эти опорные пункты находились либо на фланге атакующих танков, либо в перовом эшелоне и удар наносился на стыке.

Рис.5.13. Вариант моделируемого боя.
В таблице 5.5 приведены частоты p* появления углов обстрела для различных интервалов D и a, наблюдавшиеся в 12 реализациях каждого варианта боя, и вероятности p, подсчитанные для этих интервалов по формулам нормального закона при M(a) = 0 и sa = 17град.+15град.(2-D).
Таблица 5.5. Частоты углов обстрела танков в ходе боя.
В предпоследнем столбце таблице даны величины критерия xи-квадрат, рассчитанные при уровне 0.05 для каждого значения D, и его контрольные величины. Анализ показывает, что распределение полученных моделированием углов обстрела хорошо аппроксимируется нормальным законом с заданными выше параметрами при изменении D от +2 до -2км.

Основные результаты моделирования максимальных углов обстрела, появляющихся с вероятностью не более 0.05 и 0.10, и соответствующих им величин секторов обнаружения для средств в обороне приведены таблице 5.6. При формализованном описании боя следует задавать секторы обнаружения не менее этих значений.
Таблица 5.6. Максимальные углы обстрела.
Аналогично предыдущему примеру можно проанализировать возможность проявления тех или иных значений углов поворотов башни наступающего танка в момент выбора цели, т.е. решить задачу о величине сектора обнаружения для танка в наступления.
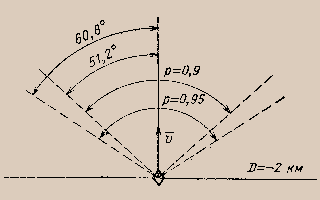
Рис.5.14. Вероятность обстрела цели в секторе данных размеров.
Полученные результаты и методику расчетов кроме использования непосредственно в модели для выбора углов фn можно использовать, например, при задании параметров механизма поворота башни или при выработке рекомендаций относительно наблюдения из танков в ходе боя. Поскольку цели, расположенные пол большими углами к направлению движения, выбираются с малыми вероятностями, возможно ограничить сектор обнаружения из танка до пределов, показанных на рис.5.14. При сокращении сектора обнаружения эффективность поиска целей в нем увеличится.

Рис.5.15. Графики функций Pa и Pф.
На рис. 5.15 показаны в полярных координатах кривые плотностей

В заключение проведем оценку целесообразности применения некоторых схем целераспределения. При решении проблемы выбора цели в стохастических моделях боя неоднородной группировки введением ряда упрощающих допущений можно перейти от решения методами линейного или динамического программирования к простым алгоритмам, не требующим больших затрат машинного времени. В выбранном в модели алгоритме блока целераспределения в качестве основного допущения принято условие, согласно которому вероятность выбора целей одновременно двумя какими-либо средствами равна нулю. В простейшем случае в качестве критерия выбора цели в алгоритме предусматривается выбор наименее удаленной цели (критерий I), так как в боях рассматриваемого класса наименее удаленная из обнаруженных целей, как правило, оказывается и наиболее опасной. В качестве второго критерия можно предложить выбор, максимизирующий потери противника на данном шаге вычислений.
Пусть в момент t боевое средство должно произвести выбор очередной цели для обстрела из числа имеющихся перед ним обнаруженных средств противника. Поскольку в модели каждое средство обоих противников характеризуется в любой момент времени параметрами его состояния, кроме тактико-технических параметров (в том числе номером цели, по которой оно ведет огонь, номерами обнаруженных целей, номерами средств противника, ведущими по нему огонь), то, очевидно, легко провести выбор цели, максимизируюший потери противника или минимизирующий свои потери. При стрельбе с перенацеливанием после каждого выстрела можно найти вероятность поражения j-й цели противника после того, как все ведущие по ней огонь средства произведут по одному выстрелу, в виде

в последнем члене формулы (5.16) максимально. Такой выбор приемлем, когда скорострельности всех участвующих в бою средств приблизительно одинаковы, что вполне справедливо для рассматриваемого класса боев.
При выборе цели может быть наложен ряд дополнительных условий, что зависит от постановки конкретной задачи. Например, согласно третьему из рассматриваемых критериев цель выбирается так, чтобы минимизировать свои потери. Алгоритм при этом не претерпевает существенных изменений, за исключением того, что вероятности pj употребляются с весами, пропорциональными тому ущербу, который j-я цель наносит обстреливаемому ею средству. В общем случае эти веса могут зависеть не только от доли нанесенного ущерба, но и от важности объекта, которому этот ущерб наносится.
Необходимость анализа целесообразности выбора того или иного критерия возникает ввиду значительного увеличения времени одной реализации стохастической модели при применении критерия II, и особенно критерия III. Так, если принять за единицу время одной реализации с использованием критерия I, то при применении критерия II оно возрастает в 4 раза и критерия III в 8 раз. В таблице 5.7 приведены результаты, позволяющие оценить эффективность применения критериев II и III, из которых следует, что к концу боя численность группировки танков может быть увеличена на 15% за счет оптимизации использования своих огневых возможностей, что составит около одной боевой машины в бою, представленном на схеме рис.5.13.
Таблица 5.7. Влияние оптимизации целераспределения на результат боя.
Следует сказать, что в реальных условиях ни танки, ни средства противника в обороне не стремятся оптимизировать использование своих огневых возможностей по таким жестким критериям целераспредления, поэтому при моделировании большинства боев используется критерий I.
Наконец-то. Хоть что-то ощутимое.- G.

Рис.5.10. Блок-схема стохастической модели.
В соответствии с изложенными выше принципами блок-схема стохастической модели построена в виде, приведенном на рис.5.10. В блок-схеме можно выделить следующие основные группы блоков:
- блоки 1, 2, 3, 4, 6, 7, 8, 9, воспроизводящие формализованный процесс боя;
- блоки 0, 5, 10, 11, 12, 13, 15, 16, 17 и др., обеспечивающие функционирование модели (блок времени, блоки получения случайных чисел и т.п.);
- блок 14 обработки результатов.
В блоках, воспроизводящих формализованный процесс, моделируются основные процессы проведения огневых средств в бою: перемещение, поиск, обнаружение цели, целераспределение и стрельба. Функционирование этих блоков координируется блоком времени, который может настраиваться на работу либо с постоянным шагомa, и тогда модель представляет собой dt-модель, либо с переменным шагом dt = var, и переход из состояния в состояние происходит в момент возможного скачкообразного изменения одного из параметров. В этом случае модель становится моделью с квази-узловыми точками.
Такое построение алгоритма модели обеспечивает автономность каждого блока и возможность замены отдельных блоков в зависимости от выбранной схемы формализации процесса.
Приводимые ниже примеры некоторых конкретных случаев применения модели получены при описанных выше способах воспроизведения основных процессов. Результаты, накопленные в ходе отдельных реализаций, подвергались статистической обработке в блоке 14 и в зависимости от объема выборки позволяли с той или иной погрешностью оценить исследуемый параметр. Например, при оценке математического ожидания параметра m в заданный момент боя по N реализациям максимальная погрешность e определяется в виде

Практически, пользуясь формулой (5.15) при оценке параметра, реализующегося в ходе боя один раз, можно ограничиться числом реализаций N = 100..200. Для других параметров это число соответственно меньше или больше.
Как и в предыдущих примерах, исходные данные выбраны произвольно:
- скорость танков V = 15км/час;
- размеры танков: l = 3.0м, m = 2.0м, h = 0.9м для танков в обороне и l = 6.0м, m = 2.5м, h = 2.5м для танка в наступлении;
- характеристики рассеивания при стрельбе из танка на дальностях 500..2500м: Вв = 0.10..0.70, Ввп = 0.20..2.0, Вб = 0.10..0.50, Вбп = 0.25..0.9 при стрельбе с места и при стрельбе с хода: Вв = 0.40..1.2, Ввп = 0.45..1.3, Вб = 0.80..2.5, Вбп = 0.85..2.8;
- среднее число попаданий в танк, необходимое для его поражения, 1.4..2.0;
- размеры ПТУРС, ПТР, РПГ: вертикальная площадь m*h = 1.0*0.5м2, площадь осколочного поражения l*m = 20*10м2;
- вероятность попадания в танк для ПТУРСа на дальностях 500, 1500 и 3000м соответственно 0.4, 0.6, 0.4;
- рассеивание при стрельбе из гранатомета Вбп = Ввп = 0.001 D;
- вероятность попадания из ПТР в танк в первом выстреле 0.5, при пятом выстреле P5 = 0.8;
- вероятность обнаружения из танка на дальностях 500..3000м: танка в окопе 0.9..0.3, ПТУРС, ПТР, РПГ: нестреляющих 0.3..0.0, стреляющих 0.8..0.6;
- дальность открытия огня Dmax: для танков в обороне 2000м, для танков в наступлении 2500м, для ПТУРС 2000м, для ПТР 500м, для РПГ 300м.
В первом примере для легких танков "синих" в окопах:
- среднее число попаданий в танк "синих", необходимое для его поражения, 1.76..1.85 на дальностях соответственно 500..1000м,
- среднее число попаданий в танк "красных", необходимое для его поражения, 1.65..2.25 на дальностях соответственно 500..1000м.
Приведем результаты моделирования в соответствии с предложенной в #5.2 схемой наступательного боя средних танков "красных" с обороняющимися легкими танками в окопах "синих".
В таблице 5.3 приведены значения функции hi, полученные в результате одной реализации боя на модели при атаке "красных" с дальности 1км и начальном соотношении численностей "красных"/"синих"=10/5.
Таблица 5.3. Изменение состояний элементов боя времени
| Номер танка | 1 минута | 2 минута | 3 минута | 4 минута | 5 минута | |||||||||||||||
| h1 | h4 | h2 | h3 | h1 | h4 | h2 | h3 | h1 | h4 | h2 | h3 | h1 | h4 | h2 | h3 | h1 | h4 | h2 | h3 | |
| "Красные" | ||||||||||||||||||||
| 1 | 1 | 1 | 316 | 8 | 1 | 0 | 341 | 4 | ||||||||||||
| 2 | 1 | 1 | 343 | 7 | 1 | |||||||||||||||
| 3 | 1 | 0 | 332 | 4 | 1 | 0 | 370 | 2 | ||||||||||||
| 4 | 1 | 1 | 301 | 2 | 1 | 0 | 324 | 4 | 1 | 1 | 351 | 9 | 1 | 0 | 420 | 8 | 1 | 0 | 444 | 2 |
| 5 | 1 | 1 | 312 | 2 | 0 | 0 | 362 | 10 | 1 | 0 | 405 | 15 | 1 | 0 | 444 | 8 | 1 | 0 | 514 | 3 |
| 6 | 1 | 1 | 310 | 4 | 1 | 1 | 310 | 4 | ||||||||||||
| 7 | 1 | 1 | 311 | 8 | 1 | |||||||||||||||
| 8 | 1 | 1 | 302 | 2 | 1 | 0 | 341 | 2 | 1 | 0 | 364 | 2 | ||||||||
| 9 | 1 | 1 | 301 | 2 | 1 | 0 | 340 | 1 | 1 | 0 | 350 | 8 | 1 | 0 | 407 | 2 | 1 | 0 | 422 | 4 |
| 10 | 1 | 1 | 300 | 3 | 1 | 0 | 325 | 6 | 1 | 0 | 351 | 4 | 1 | 0 | 445 | 2 | ||||
| "Синие" | ||||||||||||||||||||
| 1 | 1 | 1 | ||||||||||||||||||
| 2 | 1 | 1 | 1 | 1 | 0 | 0 | ||||||||||||||
| 3 | 1 | 1 | ||||||||||||||||||
| 4 | 1 | 1 | 1 | 1 | 0 | 0 | ||||||||||||||
| 5 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | ||||||||||
Статистическая обработка результатов моделирования при 100 реализациях для каждого исследуемого варианта позволила определить вероятности победы каждой из сторон и статистические характеристики численности в конце третьей минуты боя и в наиболее вероятный момент его окончания, равный 4.2мин. Эти величины приведенные в таблице 5.4.
Таблица 5.4. Изменение численностей сторон в ходе боя.
| Соотношение начальных численностей сторон | Среднее количество потерь и его среднее квадратическое отклонение через 3 минуты боя | Среднее количество потерь и его среднее квадратическое отклонение в момент окончания боя | Вероятность победы и ее доверительный интервал | |||||||||
| танки "красных" | танки "синих" | танки "красных" | танки "синих" | танки "красных" | танки "синих" | |||||||
| потери | отклонение | потери | отклонение | потери | отклонение | потери | отклонение | вероятность | интервал | вероятность | интервал | |
| 10:5 | 5.46 | 1.45 | 3.53 | 1.08 | 6.7 | 2.26 | 4.66 | 0.81 | 0.8 | 0.664..0.902 | 0.2 | 0.1..0.337 |
| 10:6 | 5.7 | 1.55 | 3.6 | 1.10 | 7.7 | 2.22 | 5.2 | 1.12 | 0.6 | 0.492..0.675 | 0.4 | 0.325..0.508 |
| 10:7 | 6.2 | 1.03 | 3.3 | 1.10 | 9.3 | 1.09 | 5.4 | 1.54 | 0.38 | 0.336..0.446 | 0.62 | 0.554..0.675 |
При вычислении вероятностей победы победившей считалась сторона, имеющая в своем составе хотя бы один танк к моменту, когда все танки противника уничтожены, т.е. уровни боеспособности принимались нулевыми. При одновременном уничтожении последних из оставшихся неуничтоженными танков на каждой стороне обе стороны считались проигравшими бой. На рис.5.11 представлены зависимости вероятности победы каждой из сторон он начального соотношения численностей противников.

Рис.5.11. Зависимость вероятности победы от начального соотношения численности сторон.
Анализ приведенных результатов позволяет сделать вывод, что для достижения достаточно гарантированной победы необходимо иметь по крайней мере двойное численное превосходство. В остальных случаях победа "красных" менее вероятна, чем победа "синих", а ее достижение происходит с чрезмерными потерями.
Для проверки правильности задания в математических моделях секторов обнаружения огневых средств рассмотрим величины углов обстрела танков в наступательном бою. Результаты решения этой задачи, во-первых, могут быть использованы при выработке обоснованных рекомендаций относительно процесса наблюдения из танков в ходе боя и, во-вторых, при выборе параметров броневой защиты.

Рис.5.12. Схема взаимного распределения цели и поражающего средства в бою:

Углом обстрела a назовем угол между направлением движения танка и направлением на обстреливающее этот танка средство противника (рис.5.12). Статистические данные относительно углов a накапливались при моделировании боя тридцати танков, наступающих в линию на опорные пункты двух пехотных рот, как показано на рис.5.13, и в двух других вариантах, когда эти опорные пункты находились либо на фланге атакующих танков, либо в перовом эшелоне и удар наносился на стыке.

Рис.5.13. Вариант моделируемого боя.
В таблице 5.5 приведены частоты p* появления углов обстрела для различных интервалов D и a, наблюдавшиеся в 12 реализациях каждого варианта боя, и вероятности p, подсчитанные для этих интервалов по формулам нормального закона при M(a) = 0 и sa = 17град.+15град.(2-D).
Таблица 5.5. Частоты углов обстрела танков в ходе боя.
| D, км | p, p* | Угол обстрела a | |||||||||||||||||||
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 | 180 | X2 0.05 | n | ||
| 2 | p | 0.325 | 0.269 | 0.194 | 0.116 | 0.060 | 0.024 | 0.008 | 0.002 | 0.001 | |||||||||||
| p* | 0.301 | 0.279 | 0.205 | 0.124 | 0.050 | 0.026 | 0.011 | 0.003 | 0.001 | ||||||||||||
| 1 | p | 0.174 | 0.166 | 0.158 | 0.126 | 0.106 | 0.084 | 0.062 | 0.046 | 0.030 | 0.020 | 0.012 | 0.006 | 0.004 | 0.002 | 0.001 | |||||
| p* | 0.186 | 0.150 | 0.141 | 0.137 | 0.114 | 0.076 | 0.070 | 0.053 | 0.024 | 0.022 | 0.014 | 0.007 | 0.004 | 0.001 | 0.001 | ||||||
| 0 | p | 0.119 | 0.117 | 0.112 | 0.104 | 0.094 | 0.085 | 0.075 | 0.063 | 0.053 | 0.045 | 0.037 | 0.029 | 0.022 | 0.017 | 0.012 | 0.008 | 0.006 | 0.004 | 27.6 | 1350 |
| p* | 0.113 | 0.113 | 0.120 | 0.106 | 0.098 | 0.090 | 0.081 | 0.069 | 0.054 | 0.053 | 0.031 | 0.024 | 0.019 | 0.011 | 0.007 | 0.005 | 0.003 | 0.003 | 18.01 | ||
| -1 | p | 0.092 | 0.089 | 0.086 | 0.084 | 0.081 | 0.076 | 0.072 | 0.066 | 0.060 | 0.052 | 0.044 | 0.038 | 0.033 | 0.029 | 0.025 | 0.020 | 0.016 | 0.012 | 27.6 | 667 |
| p* | 0.099 | 0.086 | 0.095 | 0.083 | 0.080 | 0.068 | 0.073 | 0.069 | 0.061 | 0.057 | 0.051 | 0.042 | 0.035 | 0.032 | 0.028 | 0.018 | 0.014 | 0.009 | 4.41 | ||
| -2 | p | 0.072 | 0.071 | 0.070 | 0.068 | 0.066 | 0.064 | 0.062 | 0.060 | 0.055 | 0.050 | 0.046 | 0.041 | 0.037 | 0.033 | 0.029 | 0.026 | 0.024 | 0.021 | 27.6 | 1012 |
| p* | 0.070 | 0.082 | 0.070 | 0.071 | 0.072 | 0.066 | 0.060 | 0.057 | 0.064 | 0.049 | 0.051 | 0.040 | 0.038 | 0.036 | 0.026 | 0.032 | 0.017 | 0.015 | 10.6 | ||
В предпоследнем столбце таблице даны величины критерия xи-квадрат, рассчитанные при уровне 0.05 для каждого значения D, и его контрольные величины. Анализ показывает, что распределение полученных моделированием углов обстрела хорошо аппроксимируется нормальным законом с заданными выше параметрами при изменении D от +2 до -2км.

Основные результаты моделирования максимальных углов обстрела, появляющихся с вероятностью не более 0.05 и 0.10, и соответствующих им величин секторов обнаружения для средств в обороне приведены таблице 5.6. При формализованном описании боя следует задавать секторы обнаружения не менее этих значений.
Таблица 5.6. Максимальные углы обстрела.
| p | 0.05 | 0.10 | ||||||||
| D, км | 2 | 1 | 0 | -1 | -2 | 2 | 1 | 0 | -1 | -2 |
| amax, град | 47 | 88.5 | 130 | 171 | 213 | 39.6 | 74.6 | 109 | 144 | 179 |
| 2фm >= 2amax, град | 94 | 177 | 260 | 342 | 360 | 79.2 | 149.2 | 218 | 288 | 358 |
Аналогично предыдущему примеру можно проанализировать возможность проявления тех или иных значений углов поворотов башни наступающего танка в момент выбора цели, т.е. решить задачу о величине сектора обнаружения для танка в наступления.

Рис.5.14. Вероятность обстрела цели в секторе данных размеров.
Полученные результаты и методику расчетов кроме использования непосредственно в модели для выбора углов фn можно использовать, например, при задании параметров механизма поворота башни или при выработке рекомендаций относительно наблюдения из танков в ходе боя. Поскольку цели, расположенные пол большими углами к направлению движения, выбираются с малыми вероятностями, возможно ограничить сектор обнаружения из танка до пределов, показанных на рис.5.14. При сокращении сектора обнаружения эффективность поиска целей в нем увеличится.

Рис.5.15. Графики функций Pa и Pф.
На рис. 5.15 показаны в полярных координатах кривые плотностей

В заключение проведем оценку целесообразности применения некоторых схем целераспределения. При решении проблемы выбора цели в стохастических моделях боя неоднородной группировки введением ряда упрощающих допущений можно перейти от решения методами линейного или динамического программирования к простым алгоритмам, не требующим больших затрат машинного времени. В выбранном в модели алгоритме блока целераспределения в качестве основного допущения принято условие, согласно которому вероятность выбора целей одновременно двумя какими-либо средствами равна нулю. В простейшем случае в качестве критерия выбора цели в алгоритме предусматривается выбор наименее удаленной цели (критерий I), так как в боях рассматриваемого класса наименее удаленная из обнаруженных целей, как правило, оказывается и наиболее опасной. В качестве второго критерия можно предложить выбор, максимизирующий потери противника на данном шаге вычислений.
Пусть в момент t боевое средство должно произвести выбор очередной цели для обстрела из числа имеющихся перед ним обнаруженных средств противника. Поскольку в модели каждое средство обоих противников характеризуется в любой момент времени параметрами его состояния, кроме тактико-технических параметров (в том числе номером цели, по которой оно ведет огонь, номерами обнаруженных целей, номерами средств противника, ведущими по нему огонь), то, очевидно, легко провести выбор цели, максимизируюший потери противника или минимизирующий свои потери. При стрельбе с перенацеливанием после каждого выстрела можно найти вероятность поражения j-й цели противника после того, как все ведущие по ней огонь средства произведут по одному выстрелу, в виде

в последнем члене формулы (5.16) максимально. Такой выбор приемлем, когда скорострельности всех участвующих в бою средств приблизительно одинаковы, что вполне справедливо для рассматриваемого класса боев.
При выборе цели может быть наложен ряд дополнительных условий, что зависит от постановки конкретной задачи. Например, согласно третьему из рассматриваемых критериев цель выбирается так, чтобы минимизировать свои потери. Алгоритм при этом не претерпевает существенных изменений, за исключением того, что вероятности pj употребляются с весами, пропорциональными тому ущербу, который j-я цель наносит обстреливаемому ею средству. В общем случае эти веса могут зависеть не только от доли нанесенного ущерба, но и от важности объекта, которому этот ущерб наносится.
Необходимость анализа целесообразности выбора того или иного критерия возникает ввиду значительного увеличения времени одной реализации стохастической модели при применении критерия II, и особенно критерия III. Так, если принять за единицу время одной реализации с использованием критерия I, то при применении критерия II оно возрастает в 4 раза и критерия III в 8 раз. В таблице 5.7 приведены результаты, позволяющие оценить эффективность применения критериев II и III, из которых следует, что к концу боя численность группировки танков может быть увеличена на 15% за счет оптимизации использования своих огневых возможностей, что составит около одной боевой машины в бою, представленном на схеме рис.5.13.
Таблица 5.7. Влияние оптимизации целераспределения на результат боя.
| Критерий | Дальность, км | |||||
| 1.5 | 1 | 0.5 | 0 | -0.5 | -1 | |
| I | 100 | 100 | 100 | 100 | 100 | 100 |
| II | 100.4 | 100.8 | 101.5 | 103.1 | 106.4 | 112.7 |
| III | 100.5 | 100.9 | 101.7 | 103.5 | 107.2 | 114.2 |
Следует сказать, что в реальных условиях ни танки, ни средства противника в обороне не стремятся оптимизировать использование своих огневых возможностей по таким жестким критериям целераспредления, поэтому при моделировании большинства боев используется критерий I.

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
Вернемся к го. В 80-е многие школьники, студенты и младшие научные сотрудники изобретали свои игры - лабиринты  ТЕМА #62
ТЕМА #62 или шашки
или шашки  ТЕМА #78, АБЗАЦ #903
ТЕМА #78, АБЗАЦ #903 - смешивая правила шашек разных видов. Казалось, еще немного и появится какой-то тактический реализм.
- смешивая правила шашек разных видов. Казалось, еще немного и появится какой-то тактический реализм.
Например, такой, вот, мутант:
КАЛЕЙДОСКОП ИГР, 1990
В.А.БРОННИКОВ
НОВАЯ ИНТЕЛЛЕКТУАЛЬНАЯ ИГРА КТОР
Среди огромного разнообразия комбинационных игр есть и такие, которые требуют от играющих не только тщательного логического анализа, но и развитого пространственного (образного) мышления. Новая игра ктор (клеточный тор) относится именно к таким играм. По своим свойствам она может быть поставлена рядом с популярными логическими играми: шахматами, рендзю, реверси.
ПОЛЕ ДЛЯ ИГРЫ
Одна из основных особенностей игры ктор - необычная организация поля. Возьмем лист бумаги и соединим два противоположных края листа - получится цилиндр. Если теперь соединить концы цилиндра между собой, образуется трехмерная фигура тор, или "бублик" (рис.146). Замечательной особенностью этой фигуры является то, что, двигаясь по ее поверхности, мы не сможем обнаружить края, в то время как во всех распространенных сейчас играх поле ограничено краем доски, что, кстати, сильно отражается на стратегиях, используемых в игре (вспомните борьбу за "центр" в шахматном дебюте).

Рис.146. Изготовление игрового тора: а - разметка листа бумаги; б - цилиндр, полученной путем соединения двух сторон листа; в - свернутый цилиндр - тор.
Конечно, играть на таком поле, как тор, не очень удобно. Поэтому для игры используют плоское поле, которое является разверткой тора. Его можно получить, выполнив операцию, обратную проделанной с листом бумаги (то есть развернув "бублик" по линиям, которые показаны на рисунке).
Если оставить поле в таком виде, то игроку все время придется помнить, что это на самом деле поверхность "бублика", и играть будет сложно (особенно начинающим). Поэтому придуманы очень простые и наглядные обозначения крайних клеток плоского поля, которое показано на рис.147. Здесь внутреннее выделенное чертой поле - это собственно игровое поле (или как его называют, "основное поле"), а крайние клетки (за чертой) дополнительное поле - часть основного поля, перенесенная в соответствии с правилами развертки "бублика" на противоположную сторону. Дополнительное поле дублирует все граничные клетки основного поля - так удобнее представлять, что у основного поля нет границ и оно продолжается на противоположной стороне плоского листа.

Поле для игры ктор. Внутри выделено основное поле. Дополнительное поле используется для дублирования фишек, попавших на границу основного поля; для клеток с номерами 1, 2, 3, 4 ставится по три дублирующих фишки, для остальных - по одной.
ПРАВИЛА ИГРЫ
Для игры ктор можно использовать фишки двух цветов или двухсторонние фишки, как в реверси. Число фишек должно быть не меньше числа клеток поля (основного и дополнительного). Поле для игры выбирается размером от 9*9 до 19*19 клеток. Рекомендуем играть на поле размером 15*15 - именно такое поле принято в официальных соревнованиях и выпускается в виде игровых комплектов.
В начале партии поле пустое. Ходы делаются по очереди. Существует правило первого хода: кто ходит первым ставит одну фишку; второй играющий ставит две фишки. Выигрывает тот, у кого после заполнения всех клеток поля больше фишек на основном поле.
Ход может состоять из нескольких отдельных операции.
ПОСТАНОВКА ФИШКИ НА ПОЛЕ. Для этой операции удобно ввести понятие "мощность". Мощность постановки соответствует числу поставленных фишек за один ход одним игроком или тому, сколько раз данная операция применяется за один ход. Так, можно говорить о мощности 2, если правилами предусмотрено, что за один ход противники могут поставить на поле не более, чем по 2 свои фишки.
ЗАМЕНА ФИШКИ ПРОТИВНИКА НА СВОЮ ФИШКУ (или переворот на поле, как в игре реверси). Условием замены является наличие не менее пяти своих фишек вокруг атакуемой фишки противника. Это условие вытекает и из геометрии двухмерной решетки, на которой идет игра, и из соотношения между устойчивостью и неустойчивостью возникающих на поле позиций. Для операции "замена" также вводится понятие "мощность" - количество фишек, которые можно заменить за один ход.
Даже при таких простых правилах игра приобретает новые свойства по сравнению с известными играми. Можно попробовать поиграть и убедиться в этом. Каких же действий еще не хватает с фишками, чтобы игра стала более динамичной? Кстати, если ограничиться изложенными правилами, то игра обладает всеми свойствами реверси (не считая особенностей игрового поля). Через пару партии вы сможете убедиться, что игра в таком варианте не очень интересна. Мы еще не рассказали о других операциях, которые и вносят особый динамизм.
Игра го, которой увлечены сегодня миллионы людей, ставит своей целью захват максимального пространства доски. Создание связных цепочек на доске из своих фишек и организация групп возможна только за счет постановки фишек и взятия в плен групп фишек противника. В то же время в таких играх, как шашки и шахматы, главной является не операция "постановка" (разве что начинающему надо научиться правильно расставлять фигуры на доске), а операция "перемещение" фишек (фигур) по полю. Что, если совместить возможности постановки фишек во время партии и перемещения во время игры своих фишек?
ПЕРЕМЕЩЕНИЕ ФИШКИ. Самый простой вариант перемещения - на одну клетку, например по вертикали или по горизонтали. Мощность этой операции соответствует числу возможных перемещений за один ход.
Итак, за один ход противники могут совершить следующие операции:
- поставить заданное число фишек на свободные клетки поля;
- переместить фишку на заданное число позиций или несколько фишек на это же число позиций;
- заменить заданное число фишек, если выполнено условие замены.
Сколько раз за один ход можно применять каждую операцию? Вариантов было апробировано количество, но наиболее интересными оказались несколько. Один из самых популярных вариантов: за один ход 2 фишки ставятся, 2 фишки могут быть перемещены и 2 фишки могут быть заменены. Другой рекомендуемый вариант: число фишек для постановки - 2, мощность операций "замена" и "перемещение" в сумме равна 4, все операции (или их часть) выполняются в течение одного хода в любом порядке.
При разыгрывании партий по изложенным правилам часто возникает ситуация, когда игрок сосредоточил свои фишки в одной части поля, а события стали развиваться в другой части поля, и у игрока возникает желание перебросить свои силы. Если ставить по две фишки за ход, то потребуется несколько ходов, чтобы укрепить свою позицию. Поэтому в игру вводятся дополнительные операции.
Операция "ДЕСАНТ" позволяет перебросить свои ресурсы из одной части поля в другую (на любое расстояние). Для этого с поля снимаются две любые свои фишки, а вместо них выставляется одна фишка, на любую свободную клетку поля.
Операция "МИГРАЦИЯ" также служит для переброски фишек, причем можно перемешать группу из 2, 3 или 4 фишек (рис.148).

Рис.148. Операции "миграция" фишек. Стрелками показаны возможные направления для перемещения.
И та и другая операции могут выполняться многократно один ход, то есть обладать соответствующей мощностью. Попробуйте теперь сыграть партию, и вы убедитесь, что игра стала намного интереснее.
Осталось рассмотреть необычную операцию, которая еще пока не применяется в официальных соревнованиях. Далее приводится ее описание для тех, кто хочет достигнуть совершенства в игре ктор. Эта необычная операция - "ЧЕРНАЯ ДЫРА". Представим, что у нас в руках спица и мы протыкаем тор (наш "бублик") насквозь так, чтобы спица один раз вошла в него и раз вышла. Точка входа в поверхность называется "истоком" "черной дыры", а точка выхода - "стоком". Игрок с помощью этой операции может контролировать удаленные от его позиций клетки игрового поля и, более того, разрушать устойчивые конфигурации фишек противника.
Перед началом партии противники выбирают (общие для обоих игроков) пары, чтобы затем в ходе игры их можно было использовать для "черных дыр". Создание "черной дыры" происходит следующим образом. Одна из пары клеток окружается 5 своими фишками - это будет означать, что мы организовали исток черной дыры, и сразу же в точке "стока" появляется наша фишка (ставим дополнительную свою фишку в клетку "стока" независимо от того, стояла ли там фишка противника). Эта фишка (стоящая в "стоке") неуязвима для противника, однако она не может перемещаться или мигрировать из места "стока" и не может быть использована в операции "десант". Ее можно использовать только для замены фишки. Причем фишка-"сток" исчезает, когда мы освобождаем "исток".
Число "черных дыр" на поле должно выбираться исходя из того, чтобы на игровом поле не возникло предпочтения одних зон поля перед другими. Это число может варьироваться.
В таблице 2 представлены пять уровней сложности игры ктор, причем мощности отдельных операций указаны в некотором диапазоне. Это означает, что мощность операции в одном ходе может принимать значение от минимального, указанного в таблице (например, 0), до максимального (например. 2, см. уровень 1).

Мощности операций для разных уровней сложности игры ктор. 1 - постановка фишки, 2 - перемещение фишки, 3 - замена фишки, 4 - "десант", 5 - "миграция" группы фишек, 6 - "черная дыра".
Суммарная мощность, указанная в столбце "мощность хода", считается как сумма мощностей всех операций данного уровня сложности без учета операции "черная дыра". Если мощности зафиксированы для каждой операции, то вариант игры называется "жестким". в противном случае - "мягким".
КТОР И КОМПЬЮТЕР
Компьютеры применяются как для разыгрывания партий между двумя партнерами, так и для игры с машинной программой. Особенно удобно использовать компьютер для игр, имеющих высокий уровень сложности. Для пятого уровня сложности можно не только генерировать координаты "черных дыр", но и заставить машину быть третьим партнером в игре, перемещая или генерируя черные дыры по ходу партии. Еще более интересным может оказаться вариант, когда черная дыра "поглощает" часть пространства в истоке и возвращает его в области стока. Механизмом замешивания фишек противника в собственные фишки и появлением вероятностного правила постановки фишек на поле в ходе игры можно также усложнить игру, придав ей необычайный азарт и динамичность. В этом варианте чем больше съедено фишек противника, тем ниже вероятность того, что при постановке своей фишки она действительно окажется своей. Возрастает риск хода. Кроме перечисленных возможностей компьютер, естественно, может использоваться для контроля времени.
Написание играющей ктор-программы может стать увлекательным занятием, которое послужит более эффективному освоению возможностей компьютера.
Игра ктор появилась недавно, в 1986 году. Каково будущее новой игры зависит от вас. Тем, кто не пожалеет времени на освоение самых сложных вариантов правил, откроется мир, в котором для успешной борьбы с противником необходимы не только логическое мышление, внимание и хорошая память, но и умение оперировать геометрическими образами и действовать на основании своей интуиции, подкрепленной практикой игры.
По игре ктор проводятся соревнования и турниры (в том числе международные). Вся деятельность по распространению, пропаганде и изучению игры, а также по компьютерным вариантам ведется под эгидой центрального ктор-клуба (адрес клуба: 191011, Ленинград, Невский, 39, Дворец пионеров, ктор-клуб).
 ТЕМА #62
ТЕМА #62 или шашки
или шашки  ТЕМА #78, АБЗАЦ #903
ТЕМА #78, АБЗАЦ #903 - смешивая правила шашек разных видов. Казалось, еще немного и появится какой-то тактический реализм.
- смешивая правила шашек разных видов. Казалось, еще немного и появится какой-то тактический реализм.Например, такой, вот, мутант:
КАЛЕЙДОСКОП ИГР, 1990
В.А.БРОННИКОВ
НОВАЯ ИНТЕЛЛЕКТУАЛЬНАЯ ИГРА КТОР
Среди огромного разнообразия комбинационных игр есть и такие, которые требуют от играющих не только тщательного логического анализа, но и развитого пространственного (образного) мышления. Новая игра ктор (клеточный тор) относится именно к таким играм. По своим свойствам она может быть поставлена рядом с популярными логическими играми: шахматами, рендзю, реверси.
ПОЛЕ ДЛЯ ИГРЫ
Одна из основных особенностей игры ктор - необычная организация поля. Возьмем лист бумаги и соединим два противоположных края листа - получится цилиндр. Если теперь соединить концы цилиндра между собой, образуется трехмерная фигура тор, или "бублик" (рис.146). Замечательной особенностью этой фигуры является то, что, двигаясь по ее поверхности, мы не сможем обнаружить края, в то время как во всех распространенных сейчас играх поле ограничено краем доски, что, кстати, сильно отражается на стратегиях, используемых в игре (вспомните борьбу за "центр" в шахматном дебюте).

Рис.146. Изготовление игрового тора: а - разметка листа бумаги; б - цилиндр, полученной путем соединения двух сторон листа; в - свернутый цилиндр - тор.
Конечно, играть на таком поле, как тор, не очень удобно. Поэтому для игры используют плоское поле, которое является разверткой тора. Его можно получить, выполнив операцию, обратную проделанной с листом бумаги (то есть развернув "бублик" по линиям, которые показаны на рисунке).
Если оставить поле в таком виде, то игроку все время придется помнить, что это на самом деле поверхность "бублика", и играть будет сложно (особенно начинающим). Поэтому придуманы очень простые и наглядные обозначения крайних клеток плоского поля, которое показано на рис.147. Здесь внутреннее выделенное чертой поле - это собственно игровое поле (или как его называют, "основное поле"), а крайние клетки (за чертой) дополнительное поле - часть основного поля, перенесенная в соответствии с правилами развертки "бублика" на противоположную сторону. Дополнительное поле дублирует все граничные клетки основного поля - так удобнее представлять, что у основного поля нет границ и оно продолжается на противоположной стороне плоского листа.

Поле для игры ктор. Внутри выделено основное поле. Дополнительное поле используется для дублирования фишек, попавших на границу основного поля; для клеток с номерами 1, 2, 3, 4 ставится по три дублирующих фишки, для остальных - по одной.
ПРАВИЛА ИГРЫ
Для игры ктор можно использовать фишки двух цветов или двухсторонние фишки, как в реверси. Число фишек должно быть не меньше числа клеток поля (основного и дополнительного). Поле для игры выбирается размером от 9*9 до 19*19 клеток. Рекомендуем играть на поле размером 15*15 - именно такое поле принято в официальных соревнованиях и выпускается в виде игровых комплектов.
В начале партии поле пустое. Ходы делаются по очереди. Существует правило первого хода: кто ходит первым ставит одну фишку; второй играющий ставит две фишки. Выигрывает тот, у кого после заполнения всех клеток поля больше фишек на основном поле.
Ход может состоять из нескольких отдельных операции.
ПОСТАНОВКА ФИШКИ НА ПОЛЕ. Для этой операции удобно ввести понятие "мощность". Мощность постановки соответствует числу поставленных фишек за один ход одним игроком или тому, сколько раз данная операция применяется за один ход. Так, можно говорить о мощности 2, если правилами предусмотрено, что за один ход противники могут поставить на поле не более, чем по 2 свои фишки.
ЗАМЕНА ФИШКИ ПРОТИВНИКА НА СВОЮ ФИШКУ (или переворот на поле, как в игре реверси). Условием замены является наличие не менее пяти своих фишек вокруг атакуемой фишки противника. Это условие вытекает и из геометрии двухмерной решетки, на которой идет игра, и из соотношения между устойчивостью и неустойчивостью возникающих на поле позиций. Для операции "замена" также вводится понятие "мощность" - количество фишек, которые можно заменить за один ход.
Даже при таких простых правилах игра приобретает новые свойства по сравнению с известными играми. Можно попробовать поиграть и убедиться в этом. Каких же действий еще не хватает с фишками, чтобы игра стала более динамичной? Кстати, если ограничиться изложенными правилами, то игра обладает всеми свойствами реверси (не считая особенностей игрового поля). Через пару партии вы сможете убедиться, что игра в таком варианте не очень интересна. Мы еще не рассказали о других операциях, которые и вносят особый динамизм.
Игра го, которой увлечены сегодня миллионы людей, ставит своей целью захват максимального пространства доски. Создание связных цепочек на доске из своих фишек и организация групп возможна только за счет постановки фишек и взятия в плен групп фишек противника. В то же время в таких играх, как шашки и шахматы, главной является не операция "постановка" (разве что начинающему надо научиться правильно расставлять фигуры на доске), а операция "перемещение" фишек (фигур) по полю. Что, если совместить возможности постановки фишек во время партии и перемещения во время игры своих фишек?
ПЕРЕМЕЩЕНИЕ ФИШКИ. Самый простой вариант перемещения - на одну клетку, например по вертикали или по горизонтали. Мощность этой операции соответствует числу возможных перемещений за один ход.
Итак, за один ход противники могут совершить следующие операции:
- поставить заданное число фишек на свободные клетки поля;
- переместить фишку на заданное число позиций или несколько фишек на это же число позиций;
- заменить заданное число фишек, если выполнено условие замены.
Сколько раз за один ход можно применять каждую операцию? Вариантов было апробировано количество, но наиболее интересными оказались несколько. Один из самых популярных вариантов: за один ход 2 фишки ставятся, 2 фишки могут быть перемещены и 2 фишки могут быть заменены. Другой рекомендуемый вариант: число фишек для постановки - 2, мощность операций "замена" и "перемещение" в сумме равна 4, все операции (или их часть) выполняются в течение одного хода в любом порядке.
При разыгрывании партий по изложенным правилам часто возникает ситуация, когда игрок сосредоточил свои фишки в одной части поля, а события стали развиваться в другой части поля, и у игрока возникает желание перебросить свои силы. Если ставить по две фишки за ход, то потребуется несколько ходов, чтобы укрепить свою позицию. Поэтому в игру вводятся дополнительные операции.
Операция "ДЕСАНТ" позволяет перебросить свои ресурсы из одной части поля в другую (на любое расстояние). Для этого с поля снимаются две любые свои фишки, а вместо них выставляется одна фишка, на любую свободную клетку поля.
Операция "МИГРАЦИЯ" также служит для переброски фишек, причем можно перемешать группу из 2, 3 или 4 фишек (рис.148).

Рис.148. Операции "миграция" фишек. Стрелками показаны возможные направления для перемещения.
И та и другая операции могут выполняться многократно один ход, то есть обладать соответствующей мощностью. Попробуйте теперь сыграть партию, и вы убедитесь, что игра стала намного интереснее.
Осталось рассмотреть необычную операцию, которая еще пока не применяется в официальных соревнованиях. Далее приводится ее описание для тех, кто хочет достигнуть совершенства в игре ктор. Эта необычная операция - "ЧЕРНАЯ ДЫРА". Представим, что у нас в руках спица и мы протыкаем тор (наш "бублик") насквозь так, чтобы спица один раз вошла в него и раз вышла. Точка входа в поверхность называется "истоком" "черной дыры", а точка выхода - "стоком". Игрок с помощью этой операции может контролировать удаленные от его позиций клетки игрового поля и, более того, разрушать устойчивые конфигурации фишек противника.
Перед началом партии противники выбирают (общие для обоих игроков) пары, чтобы затем в ходе игры их можно было использовать для "черных дыр". Создание "черной дыры" происходит следующим образом. Одна из пары клеток окружается 5 своими фишками - это будет означать, что мы организовали исток черной дыры, и сразу же в точке "стока" появляется наша фишка (ставим дополнительную свою фишку в клетку "стока" независимо от того, стояла ли там фишка противника). Эта фишка (стоящая в "стоке") неуязвима для противника, однако она не может перемещаться или мигрировать из места "стока" и не может быть использована в операции "десант". Ее можно использовать только для замены фишки. Причем фишка-"сток" исчезает, когда мы освобождаем "исток".
Число "черных дыр" на поле должно выбираться исходя из того, чтобы на игровом поле не возникло предпочтения одних зон поля перед другими. Это число может варьироваться.
В таблице 2 представлены пять уровней сложности игры ктор, причем мощности отдельных операций указаны в некотором диапазоне. Это означает, что мощность операции в одном ходе может принимать значение от минимального, указанного в таблице (например, 0), до максимального (например. 2, см. уровень 1).

Мощности операций для разных уровней сложности игры ктор. 1 - постановка фишки, 2 - перемещение фишки, 3 - замена фишки, 4 - "десант", 5 - "миграция" группы фишек, 6 - "черная дыра".
Суммарная мощность, указанная в столбце "мощность хода", считается как сумма мощностей всех операций данного уровня сложности без учета операции "черная дыра". Если мощности зафиксированы для каждой операции, то вариант игры называется "жестким". в противном случае - "мягким".
КТОР И КОМПЬЮТЕР
Компьютеры применяются как для разыгрывания партий между двумя партнерами, так и для игры с машинной программой. Особенно удобно использовать компьютер для игр, имеющих высокий уровень сложности. Для пятого уровня сложности можно не только генерировать координаты "черных дыр", но и заставить машину быть третьим партнером в игре, перемещая или генерируя черные дыры по ходу партии. Еще более интересным может оказаться вариант, когда черная дыра "поглощает" часть пространства в истоке и возвращает его в области стока. Механизмом замешивания фишек противника в собственные фишки и появлением вероятностного правила постановки фишек на поле в ходе игры можно также усложнить игру, придав ей необычайный азарт и динамичность. В этом варианте чем больше съедено фишек противника, тем ниже вероятность того, что при постановке своей фишки она действительно окажется своей. Возрастает риск хода. Кроме перечисленных возможностей компьютер, естественно, может использоваться для контроля времени.
Написание играющей ктор-программы может стать увлекательным занятием, которое послужит более эффективному освоению возможностей компьютера.
Игра ктор появилась недавно, в 1986 году. Каково будущее новой игры зависит от вас. Тем, кто не пожалеет времени на освоение самых сложных вариантов правил, откроется мир, в котором для успешной борьбы с противником необходимы не только логическое мышление, внимание и хорошая память, но и умение оперировать геометрическими образами и действовать на основании своей интуиции, подкрепленной практикой игры.
По игре ктор проводятся соревнования и турниры (в том числе международные). Вся деятельность по распространению, пропаганде и изучению игры, а также по компьютерным вариантам ведется под эгидой центрального ктор-клуба (адрес клуба: 191011, Ленинград, Невский, 39, Дворец пионеров, ктор-клуб).

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
 Re: Синдром го
Re: Синдром го
По другую сторону го.
КАЛЕЙДОСКОП ИГР, 1990
В.А.ТРУБИЦЫН
СУГО
В двухтомнике о классическом го, выпущенном в 1974 голу в Токио обществом "Нихон Киин" на русском языке, сказано что "игра достигла такого высочайшего развития, что дальнейшее ее совершенствование будет чрезвычайно затруднительно". Для многих это является очевидной истиной. Совершенствовать самую совершенную игру действительно трудно. Но почему бы не попробовать?
К решению этой непростой задачи автор приступил после многолетнего исследования шахматных и шашечных игр. Итогом явилось создание теории, позволяющей использовать шахматное мышление далеко за пределами известной всем игры. Были созданы различные новые шахматные и шашечные игры, включая игры для трех и более соперников.
Первых результатов по созданию нетрадиционного го удалось добиться в 1977 году. Новая игра получила название суго (от суперго). Предполагается, что читатель уже знаком с правилами классического го хотя бы из настоящего сборника. Поэтому подробное описание этих правил здесь опускается. В суго происходит такая же борьба за территорию между двумя соперниками, с той лишь разницей, что игровая доска специально лишена каких бы то ни было игровых пунктов. Посредством этого великая игра Востока из жесткой координатной сетки вышла на чистую свободную плоскость. Суго требует не только развитого комбинационного мышления, но и гораздо более тонкого, чем прежде, восприятия пространства.
ОПИСАНИЕ ИГРЫ
Суго - настольная комбинационная игра высшего порядка, являющаяся развитием го. В комплект игры входит игровое поле (рис.149) - правильный плоский шестиугольник, сторона которого 33см. По периметру игрового поля имеется бортик высотой 4мм. Цвет игрового поля должен быть нейтральным по отношению к двухцветным камням. Например, светло-коричневый.

Рис.149. Игровое поле суго.
В качестве камней используются 352 шашки (диаметром 30мм и высотой 10мм) из комплектов для игры в шашки (рис.150). Оба игрока имеют по 175 разноцветных камней и по одному красному камню. В игре принимают участие два партнера. Один играет белыми камнями, другой - черными. Цель игры - борьба за территорию посредством поочередной установки камней на свободные пункты игрового поля.

Рис.150. Три типа камней из комплекта для игры в суго (черный, белый, красный).
Игра начинается с пустого игрового поля - за исключением игры с форой, когда более сильный игрок разрешает сопернику установить на игровом поле до начала игры от 1 до 12 своих камней. Ходы делаются поочередно, первый ход - "черных". Камни во время игры не передвигаются.
Соединение в суго - это сплошной ряд камней, установленных с касанием. Валентность камня - его способность присоединить к себе посредством касания одноцветные камни. Максимальная валентность камня в го равняется четырем, в суго - шести. Отдельный камень или группа камней, представляющая из себя соединение, в случае полного окружения немедленно снимаются соперником в качестве пленных, которые после окончания игры, возвращаясь на свою часть поля, занимают полезную территорию и тем самым уменьшают шансы своей стороны на выигрыш. Отдельный камень или соединение из камней считаются полностью окруженными и лишенными "свободных валентностей" в том случае, если к ним посредством касания нельзя присоединить ни одного камня.
Снятие камней в суго происходит при плотной и дальней и дальней блокаде. (рис.151) В первом случае чужие камни должны касаться атакуемого камня, а во втором нет. На практике блокада часто бывает смешанной. Главное ее свойство - невозможность присоединить к атакуемому камню еще один камень и тем самым увеличить его валентность путем образования простейшего соединения.

Рис.151. Плотная и дальняя блокада черного камня.
В середине поля при плотной блокаде для снятия одного камня требуются 4 атакующих камня, у края игрового поля и в тупом углу шестиугольного поля - 2 камня. Если игроки будут ставить камни ближе 12мм от борта поля, то для снятия камня потребуется (как и в го) 3 камня (рис.152 и 153).

Рис.152. Снятие черного камня в середине поля.

Рис.153. Снятие черного камня на стороне (1 и 2) и в углу (3) игрового поля. В позиции 2 черный камень находится не ниже первой линии, поэтому для его снятия требуется не менее грех камней.
Одним из парадоксов суго являются репрессивные ходы, то есть снятие своего камня при дальней блокаде, которая часто смешанной и по типу блокады, и по типу атакующих камней. Последним ходом вы либо включаете в соединение свой гибнущий камень, либо сами снимаете его репрессивным ходом (рис.154). При этом он выбывает из игры, становясь добычей соперника.

Рис.154. Репрессивным ходом 20 "белые" снимают свой камень 18, он выбывает из игры, покинув игровое поле.
В процессе создания суго не сразу было осознано, что при дальней блокаде завершающим ходом возможно снятие своих же камней. Поэтому предполагалось, что такие камни, лишенные валентности, будут оставаться на игровом поле в виде так называемого "нуль-валентного облака", или "болота". Тогда "болото" будучи, например, окружено плотной цепочкой своих камней, являющейся частью "живой" группы, само становится своеобразной "живой" группой, хотя и крайне неэффективной. А если край "болота" не защищен, то от него можно отбирать по одному камню. Одннм ударом все "болото" снять нельзя, так как оно не представляет из себя соединения. В отличие от настоящего соединения такую разобщенную группу камней можно назвать "формальной группой".
После окончания признания репрессивных ходов "болото" уже не может возникнуть, и суго станет более станет более динамичной игрой.
Для определения в спорных случаях наличия свободного места в скоплении камней для очередного хода рекомендуется применять легкую маску из картона с отверстием по размеру камня (30мм). Маска осторожно накладывается сверху на камни без их смещения, затем снимается (см. рис.155). Всякие другие измерения во время игры запрещены.

Рис.155. Контрольная маска.
Запись партий в суго возможна только с применением фотодиаграмм и видеограмм. С этой целью каждый камень получает свой индивидуальный номер: черные камни - нечетные номера от 1 до 349, белые - от 2 до 350. Красные камни не нумеруются, так как по ходу партии красный камень может быть поставлен вместо любого очередного камня. И тогда номер хода перейдет к нему, на диаграмме он будет выделен особо. Первый ход "черные" обязаны сделать камнем 1, второй ход - "белые" камнем 2 и так далее. При такой системе номер хода в партии будет совпадать с номером камня. Для удобства нанесения порядковых номеров на шашки их следует перевернуть гладкой поверхностью вверх.
Применение фотодиаграмм предполагает строгое ориентирование буквенных обозначений углов игрового поля и цифр на выставляемых камнях в одну сторону.
Камень красного цвета - это нейтральный камень, не имеющий никакой способности присоединять камни вообще. Он может занять любой свободный пункт, снять его с поля невозможно. Поэтому он с большим эффектом применяется для борьбы с "живыми" группами, если они имеют менее трех "глаз" (практически замкнутых образований, внутри которых существует хотя бы одна валентность). Как известно, наличие двух "глаз" в го делало группу "живой", то есть неснимаемой.
К запрещенным ходам относятся "самоубийственные" ходы в сплошное окружение из камней, если в результате хода камни не снимаются, и ходы, ведущие к повторению ранее существующей позиции (правило "ко"). Эти ограничения не относятся к нейтральным камням.
Нельзя также делать ход в то место, где территория для камня недостаточна, что выясняется с помощью маски.
Игра прекращается в том случае, если у соперников нет ходов, приносящих хотя бы одно очко. С игрового поля снимаются потенциальные пленные. Такие камни и группы хотя и стоят на поле до конца игры, но они обречены и поэтому называются "мертвыми".
Перед подсчетом итогов игры следует исключить нейтральные пограничные пункты, обозначив их свободными от игры камнями любого цвета. Затем все пленные возвращаются на свою территорию и внутри каждого лагеря производится свободная перестановка камней с целью их плотной упаковки. Свободная от камней территория внутри каждого лагеря считается выигранной территорией. Если визуально выявить победителя трудно, следует сравнить обе территории путем их заполнения камнями при плотной расстановке. При этом ни в коем случае нельзя путать камни, участвовавшие в игре, включая выставленные пленные, и камни, обозначающие ничейные пограничные пункты, с теми камнями, с помощью которых определяют величину полезной территории, выражаемой числом уместившихся на ней камней. Их надо ставить на поле цифрой вниз.
Один камень приравнивается к одному очку. Разница очков у двух соперников составляет цену победы. Чем больше разрыв, тем большую фору следует давать более слабому игроку - примерно один камень за 10 выигранных очков в одной партии.
"Черные", начинающие игру, получают реальное преимущества. Для его компенсации они обязаны отдать "белым" до начала игры 5 своих камней с самыми большими номерами (правило "коми").
Контроль времени в суго производится так же, как и в го (с небольшим увеличением). В обычных любительских встречах игрокам дается по одному часу на всю партию, в официальных встречах и турнирах - по 3 часа (каждому игроку).
НА ПОДСТУПАХ К ТЕОРИИ СУГО
Приступая к созданию новой игры, автор прежде всего проанализировал игровое поле классического го. Игровые пункты этого поля имеют разную валентность: от 2 до 4 (следствие того, что оно имеет форму квадрата). Замкнутое игровое поле можно получить, к примеру, на поверхности тороида. Оно состояло бы из игровых пунктов одинаковой валентности. Такое поле называется однородным.
Следует заметить, что игра в го на однородном поле проходит вяло. Именно борьба на сторонах и в углах квадратного игрового поля, где валентность точек занижена, придает игре особую остроту. Не обогатим ли мы го, если попытаемся расширить диапазон валентности его игрового поля?
Простые исследования показали, что такие структуры создать можно, причем с различным соотношением низкой, средней и высокой валентности игровых пунктов поля. Какое же соотношение является идеальным? В го оно составляет 4:68:289 (при диапазоне валентности от 2 до 4). Такое соотношение предопределено формой и структурой игрового поля.
Если расширить диапазон валентности игрового поля на 4 деления вниз и вверх, получатся игровые поля с валентностью от 0 до 8. (Именно четырехвалентные точки в го являются наиболее типичными).
Располагая свободой выбора, можно, например, создать игровое поле с преобладанием трехвалентных точек не только на периферии, но и во всей структуре поля. После проведения пробных игр станет ясно, что на таких структурах создать "живую" группу значительно труднее. А скажем, на пятивалентных структурах камни становятся слишком "живучими". И поэтому игра проходит вяло.
С помощью многочисленных попыток можно получить можно получить множество неоднородных игровых полей в надежде, что среди них имеется вариант, гарантирующий более высокое качество структуры поля, чем в го. Но новой игры не возникло бы. (Как это ни покажется парадоксальным, именно такие сложные структуры интуитивно искал гениальный русский художник Павел Филонов, чьи полотна появились на свет из запасников Русского музея лишь в 1988 году. Пространство его полотен, переполненное вполне осязаемыми, будто вылепленными из земной праматерии образами, слагается из многоугольных ячеек живописной мозаики). У автора возникла идея заставить самих игроков в каждой партии создавать уникальное поливалентное игровое поле своими ходами. То есть вести игру на чистом листе бумаги
ФОРМА И РАЗМЕР ИГРОВОГО ПОЛЯ СУГО
В го игровые пункты поля в основном являются четырехвалентными. И каждая из этих валентностей направлена на одну из сторон квадратного игрового поля. В суго максимальная валентность одного камня равна 6. Не указывает ли это на то, что игровое поле в суго должно иметь форму шестиугольника?
Имеются и другие доводы. Подобные игры показали, что многовалентным камням суго тесно в прямом углу. Самый же главный довод состоит в том, что суго имеет прямое отношение к плотной упаковке цилиндрических тел и шаров. Если взять одни камень и при плотной упаковке слой за слоем наращивать вокруг него другие камни, то уже первый слой даст шестигранные контуры будущего игрового поля. Остается определить ею размеры.
Игровые поля, полученные таким образом, растут по уровням почти как заряды ядер атомов в таблице Менделеева, но не по физическим, а по геометрическим законам (рис.156). Рост игровых полей определяется по следующим формулам.
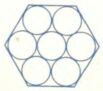
Рис.156 Формирование игрового поля суго второго уровня.
Для го: Х=1+4n(n-1).
Для суго: 1+3n(n-1).
Здесь X-число игровых пунктов или камней при плотной упаковке; n - число слоев (уровней).
Сравнительная таблица 3 для го дает представление о росте игрового поля по указанным параметрам (e - число пунктов или камней в каждом наращиваемом слое, а - число пунктов или камней, умещающихся на одной из сторон поля).

На рис.157 показано формирование игрового поля го третьего уровня. Нетрудно заметить, что все слои (за исключением второго) растут по законам арифметической прогрессии с разностью в 8 пунктов.

Рис.157 Формирование игрового поля го третьего уровня.
Малая доска для игры в го соответствует седьмому, а большая - десятому уровню игрового поля. Число игровых пунктов составляет соответственно 169 и 361.
Сравнительная таблица 4 роста игрового поля суго включает одиннадцать уровней, хотя дальнейший рост поля теория ничем ограничивает.

Для гексагональных структур n=а. Следовательно, по числу пунктов на одной из сторон поля можно определить его уровень.
В данных структурах все слои (за исключением второго) также растут по законам арифметической прогрессии с разностью в 6 пунктов.
Какой же величины должны быть игровые поля в суго? Сравнивая значение X в обеих таблицах, вполне обоснованно можно выбрать во второй таблице восьмой и одиннадцатый уровни (для малой и большой досок). Их числовая величина составит 169 и 331 условных игровых пунктов (то есть пунктов, которые в суго отсутствуют, но при подсчете очков обозначаются плотной упаковкой камней).
При выборе величины игрового поля суго полное совпадение с числовыми параметрами игрового поля го вовсе не является нашей целью, тем более что речь идет о разных структурах. Куда важнее строгая правильность игрового поля и обоснованность его формы.
В частности, выяснилось, что камень в суго, стоящий у бортика, вовсе не находится на первой линии поля (по аналогии с го).
Снятие камней в углу, на боковой стороне и в центре игрового поля в го производится двумя, тремя и четырьмя камнями. В суго камень на стороне снимается, как и в углу, двумя камнями, что делает игру у бортика такой же острой, как и в углу. С этим нельзя согласиться. Камень, который будет сниматься тремя камнями в суго, должен находиться на расстоянии 1.2см от борта. Из этого следует, что первая линия в суго, хотя она и не нанесена, проходит в 2.7см от бортика. А полученные из сравнительных таблиц игровые поля суго надо увеличить по периметру на 1.2см.
Подсчеты площадей показали, что один камень, вписанный в шестиугольную ячейку пространства, вместе с ней составляет 7.78см2. Большое игровое поле суго увеличится на 233.5см2, что будет соответствовать 30 (233.5/7.78 ) дополнительным условным игровым пунктам. Малое поле получит дополнительно 21 игровой пункт.
Оба правильных шестигранных игровых поля будут вписываться в круг. Для малого поля его радиус равен 24см, для большого - 33см. Число условных игровых пунктов составит 190 и 361. Здесь мы снова получили полное совпадение числа игровых пунктов, но уже не на малой, а на большой доске. Но оно является чисто случайным. Однако оказалось, что разместить на указанных игровых полях реальные камни с наиплотнейшей упаковкой невозможно из-за того, что мы увеличили эти поля всего лишь на часть слоя. Поэтому в реальной игре максимальное число камней, необходимых для игры, составит 184 для малой доски и 352 для большой.
Следовательно, в комплекте для игры в суго должно быть 175 черных, 175 белых и 2 красных камня.
Для любителей экстравагантных решений сообщаем, что при игре в суго на поверхности шара с равновеликой площадью он должен иметь диаметр 28.8см.
Плоское шестиугольное игровое поле рекомендуем изготовить из листа прессованной фанеры или картона. Для закрепления бортика радиус описанного круга следует увеличить на 2см. Закрепив по периметру поля бортик, выступающий на 4-5мм, следует обрезать вокруг бортика лишний картон. Бортик можно выполнить за счет приклеивания деревянных реек столярным клеем.
При анализе партии в суго возникает необходимость кратко назвать какой-либо район игрового поля. Предлагается следующий принцип зонирования. Радиус описанного круга, мысленно проведенный через один из углов поля, делится на три части (по 11см). Это позволяет разбить все поле на три зоны: центральную, шатровую и периферийную, включающую площади углов и сторон (рис.158 )

Рис.158. Зонирование игрового поля суго.
Шесть углов поля обозначим латинскими буквами: A, B, C, D, E, F. В игровом комплекте они наносятся на бортике. На самом игровом поле нет никаких обозначений. Тем не менее, изучив схему зонирования, читатель сможет быстро назвать нужный район ноля. Например, бортик AF, Шесть бортов составляют периметр. Угол A - территория между двумя сторонами AB и AF. Сумма территории всех углов и сторон составляет третью периферийную зону.
Шатер af - территория между центром и стороной в секторе AF, Сумма территорий всех шатров составляет вторую шатровую зону. Центральная зона имеет форму шестиугольника. Она составлена из вершин всех шести секторов, имеющих форму правильных треугольников.
Малую доску для игры в суго со стороной игрового поля 24см удобнее всего оформить наклеиванием бортиков на обороте большой доски. Чтобы при этом сохранить устойчивость большой доски, следует снизу выполнить два шестиугольных бортика большой и малый.
В малое суго можно играть и на большой доске, имея дополнительный комплект камней увеличенного диаметра. Для доски со стороной 33см он должен быть равен 42мм. Можно еще значительнее увеличить размер камней. В так называемом детском суго их диаметр равен 8см. В качестве камней можно использовать пластмассовые диски толщиной около 5мм. "Черные" имеют 19 камней, "белые" - 18. Красные камни не применяются.
В заключение этого раздела предлагаем исследовать фрагмент партии в суго, изображенный на рис.159.

Рис.159. Фрагмент партии в суго.
Через игру лежит путь к сложнейшим абстрагированным моделям современной науки. Обе сферы человеческой деятельности обогащают и дополняют друг друга. Регулярно рождающиеся новые игры дают большие возможности для самовыражения каждому человеку. Не является исключением и суго. Что будет после суго? Пока трудно ответить. Может быть, подумаем вместе?
КАЛЕЙДОСКОП ИГР, 1990
В.А.ТРУБИЦЫН
СУГО
В двухтомнике о классическом го, выпущенном в 1974 голу в Токио обществом "Нихон Киин" на русском языке, сказано что "игра достигла такого высочайшего развития, что дальнейшее ее совершенствование будет чрезвычайно затруднительно". Для многих это является очевидной истиной. Совершенствовать самую совершенную игру действительно трудно. Но почему бы не попробовать?
К решению этой непростой задачи автор приступил после многолетнего исследования шахматных и шашечных игр. Итогом явилось создание теории, позволяющей использовать шахматное мышление далеко за пределами известной всем игры. Были созданы различные новые шахматные и шашечные игры, включая игры для трех и более соперников.
Первых результатов по созданию нетрадиционного го удалось добиться в 1977 году. Новая игра получила название суго (от суперго). Предполагается, что читатель уже знаком с правилами классического го хотя бы из настоящего сборника. Поэтому подробное описание этих правил здесь опускается. В суго происходит такая же борьба за территорию между двумя соперниками, с той лишь разницей, что игровая доска специально лишена каких бы то ни было игровых пунктов. Посредством этого великая игра Востока из жесткой координатной сетки вышла на чистую свободную плоскость. Суго требует не только развитого комбинационного мышления, но и гораздо более тонкого, чем прежде, восприятия пространства.
ОПИСАНИЕ ИГРЫ
Суго - настольная комбинационная игра высшего порядка, являющаяся развитием го. В комплект игры входит игровое поле (рис.149) - правильный плоский шестиугольник, сторона которого 33см. По периметру игрового поля имеется бортик высотой 4мм. Цвет игрового поля должен быть нейтральным по отношению к двухцветным камням. Например, светло-коричневый.

Рис.149. Игровое поле суго.
В качестве камней используются 352 шашки (диаметром 30мм и высотой 10мм) из комплектов для игры в шашки (рис.150). Оба игрока имеют по 175 разноцветных камней и по одному красному камню. В игре принимают участие два партнера. Один играет белыми камнями, другой - черными. Цель игры - борьба за территорию посредством поочередной установки камней на свободные пункты игрового поля.

Рис.150. Три типа камней из комплекта для игры в суго (черный, белый, красный).
Игра начинается с пустого игрового поля - за исключением игры с форой, когда более сильный игрок разрешает сопернику установить на игровом поле до начала игры от 1 до 12 своих камней. Ходы делаются поочередно, первый ход - "черных". Камни во время игры не передвигаются.
Соединение в суго - это сплошной ряд камней, установленных с касанием. Валентность камня - его способность присоединить к себе посредством касания одноцветные камни. Максимальная валентность камня в го равняется четырем, в суго - шести. Отдельный камень или группа камней, представляющая из себя соединение, в случае полного окружения немедленно снимаются соперником в качестве пленных, которые после окончания игры, возвращаясь на свою часть поля, занимают полезную территорию и тем самым уменьшают шансы своей стороны на выигрыш. Отдельный камень или соединение из камней считаются полностью окруженными и лишенными "свободных валентностей" в том случае, если к ним посредством касания нельзя присоединить ни одного камня.
Снятие камней в суго происходит при плотной и дальней и дальней блокаде. (рис.151) В первом случае чужие камни должны касаться атакуемого камня, а во втором нет. На практике блокада часто бывает смешанной. Главное ее свойство - невозможность присоединить к атакуемому камню еще один камень и тем самым увеличить его валентность путем образования простейшего соединения.

Рис.151. Плотная и дальняя блокада черного камня.
В середине поля при плотной блокаде для снятия одного камня требуются 4 атакующих камня, у края игрового поля и в тупом углу шестиугольного поля - 2 камня. Если игроки будут ставить камни ближе 12мм от борта поля, то для снятия камня потребуется (как и в го) 3 камня (рис.152 и 153).

Рис.152. Снятие черного камня в середине поля.

Рис.153. Снятие черного камня на стороне (1 и 2) и в углу (3) игрового поля. В позиции 2 черный камень находится не ниже первой линии, поэтому для его снятия требуется не менее грех камней.
Одним из парадоксов суго являются репрессивные ходы, то есть снятие своего камня при дальней блокаде, которая часто смешанной и по типу блокады, и по типу атакующих камней. Последним ходом вы либо включаете в соединение свой гибнущий камень, либо сами снимаете его репрессивным ходом (рис.154). При этом он выбывает из игры, становясь добычей соперника.

Рис.154. Репрессивным ходом 20 "белые" снимают свой камень 18, он выбывает из игры, покинув игровое поле.
В процессе создания суго не сразу было осознано, что при дальней блокаде завершающим ходом возможно снятие своих же камней. Поэтому предполагалось, что такие камни, лишенные валентности, будут оставаться на игровом поле в виде так называемого "нуль-валентного облака", или "болота". Тогда "болото" будучи, например, окружено плотной цепочкой своих камней, являющейся частью "живой" группы, само становится своеобразной "живой" группой, хотя и крайне неэффективной. А если край "болота" не защищен, то от него можно отбирать по одному камню. Одннм ударом все "болото" снять нельзя, так как оно не представляет из себя соединения. В отличие от настоящего соединения такую разобщенную группу камней можно назвать "формальной группой".
После окончания признания репрессивных ходов "болото" уже не может возникнуть, и суго станет более станет более динамичной игрой.
Для определения в спорных случаях наличия свободного места в скоплении камней для очередного хода рекомендуется применять легкую маску из картона с отверстием по размеру камня (30мм). Маска осторожно накладывается сверху на камни без их смещения, затем снимается (см. рис.155). Всякие другие измерения во время игры запрещены.

Рис.155. Контрольная маска.
Запись партий в суго возможна только с применением фотодиаграмм и видеограмм. С этой целью каждый камень получает свой индивидуальный номер: черные камни - нечетные номера от 1 до 349, белые - от 2 до 350. Красные камни не нумеруются, так как по ходу партии красный камень может быть поставлен вместо любого очередного камня. И тогда номер хода перейдет к нему, на диаграмме он будет выделен особо. Первый ход "черные" обязаны сделать камнем 1, второй ход - "белые" камнем 2 и так далее. При такой системе номер хода в партии будет совпадать с номером камня. Для удобства нанесения порядковых номеров на шашки их следует перевернуть гладкой поверхностью вверх.
Применение фотодиаграмм предполагает строгое ориентирование буквенных обозначений углов игрового поля и цифр на выставляемых камнях в одну сторону.
Камень красного цвета - это нейтральный камень, не имеющий никакой способности присоединять камни вообще. Он может занять любой свободный пункт, снять его с поля невозможно. Поэтому он с большим эффектом применяется для борьбы с "живыми" группами, если они имеют менее трех "глаз" (практически замкнутых образований, внутри которых существует хотя бы одна валентность). Как известно, наличие двух "глаз" в го делало группу "живой", то есть неснимаемой.
К запрещенным ходам относятся "самоубийственные" ходы в сплошное окружение из камней, если в результате хода камни не снимаются, и ходы, ведущие к повторению ранее существующей позиции (правило "ко"). Эти ограничения не относятся к нейтральным камням.
Нельзя также делать ход в то место, где территория для камня недостаточна, что выясняется с помощью маски.
Игра прекращается в том случае, если у соперников нет ходов, приносящих хотя бы одно очко. С игрового поля снимаются потенциальные пленные. Такие камни и группы хотя и стоят на поле до конца игры, но они обречены и поэтому называются "мертвыми".
Перед подсчетом итогов игры следует исключить нейтральные пограничные пункты, обозначив их свободными от игры камнями любого цвета. Затем все пленные возвращаются на свою территорию и внутри каждого лагеря производится свободная перестановка камней с целью их плотной упаковки. Свободная от камней территория внутри каждого лагеря считается выигранной территорией. Если визуально выявить победителя трудно, следует сравнить обе территории путем их заполнения камнями при плотной расстановке. При этом ни в коем случае нельзя путать камни, участвовавшие в игре, включая выставленные пленные, и камни, обозначающие ничейные пограничные пункты, с теми камнями, с помощью которых определяют величину полезной территории, выражаемой числом уместившихся на ней камней. Их надо ставить на поле цифрой вниз.
Один камень приравнивается к одному очку. Разница очков у двух соперников составляет цену победы. Чем больше разрыв, тем большую фору следует давать более слабому игроку - примерно один камень за 10 выигранных очков в одной партии.
"Черные", начинающие игру, получают реальное преимущества. Для его компенсации они обязаны отдать "белым" до начала игры 5 своих камней с самыми большими номерами (правило "коми").
Контроль времени в суго производится так же, как и в го (с небольшим увеличением). В обычных любительских встречах игрокам дается по одному часу на всю партию, в официальных встречах и турнирах - по 3 часа (каждому игроку).
НА ПОДСТУПАХ К ТЕОРИИ СУГО
Приступая к созданию новой игры, автор прежде всего проанализировал игровое поле классического го. Игровые пункты этого поля имеют разную валентность: от 2 до 4 (следствие того, что оно имеет форму квадрата). Замкнутое игровое поле можно получить, к примеру, на поверхности тороида. Оно состояло бы из игровых пунктов одинаковой валентности. Такое поле называется однородным.
Следует заметить, что игра в го на однородном поле проходит вяло. Именно борьба на сторонах и в углах квадратного игрового поля, где валентность точек занижена, придает игре особую остроту. Не обогатим ли мы го, если попытаемся расширить диапазон валентности его игрового поля?
Простые исследования показали, что такие структуры создать можно, причем с различным соотношением низкой, средней и высокой валентности игровых пунктов поля. Какое же соотношение является идеальным? В го оно составляет 4:68:289 (при диапазоне валентности от 2 до 4). Такое соотношение предопределено формой и структурой игрового поля.
Если расширить диапазон валентности игрового поля на 4 деления вниз и вверх, получатся игровые поля с валентностью от 0 до 8. (Именно четырехвалентные точки в го являются наиболее типичными).
Располагая свободой выбора, можно, например, создать игровое поле с преобладанием трехвалентных точек не только на периферии, но и во всей структуре поля. После проведения пробных игр станет ясно, что на таких структурах создать "живую" группу значительно труднее. А скажем, на пятивалентных структурах камни становятся слишком "живучими". И поэтому игра проходит вяло.
С помощью многочисленных попыток можно получить можно получить множество неоднородных игровых полей в надежде, что среди них имеется вариант, гарантирующий более высокое качество структуры поля, чем в го. Но новой игры не возникло бы. (Как это ни покажется парадоксальным, именно такие сложные структуры интуитивно искал гениальный русский художник Павел Филонов, чьи полотна появились на свет из запасников Русского музея лишь в 1988 году. Пространство его полотен, переполненное вполне осязаемыми, будто вылепленными из земной праматерии образами, слагается из многоугольных ячеек живописной мозаики). У автора возникла идея заставить самих игроков в каждой партии создавать уникальное поливалентное игровое поле своими ходами. То есть вести игру на чистом листе бумаги
ФОРМА И РАЗМЕР ИГРОВОГО ПОЛЯ СУГО
В го игровые пункты поля в основном являются четырехвалентными. И каждая из этих валентностей направлена на одну из сторон квадратного игрового поля. В суго максимальная валентность одного камня равна 6. Не указывает ли это на то, что игровое поле в суго должно иметь форму шестиугольника?
Имеются и другие доводы. Подобные игры показали, что многовалентным камням суго тесно в прямом углу. Самый же главный довод состоит в том, что суго имеет прямое отношение к плотной упаковке цилиндрических тел и шаров. Если взять одни камень и при плотной упаковке слой за слоем наращивать вокруг него другие камни, то уже первый слой даст шестигранные контуры будущего игрового поля. Остается определить ею размеры.
Игровые поля, полученные таким образом, растут по уровням почти как заряды ядер атомов в таблице Менделеева, но не по физическим, а по геометрическим законам (рис.156). Рост игровых полей определяется по следующим формулам.

Рис.156 Формирование игрового поля суго второго уровня.
Для го: Х=1+4n(n-1).
Для суго: 1+3n(n-1).
Здесь X-число игровых пунктов или камней при плотной упаковке; n - число слоев (уровней).
Сравнительная таблица 3 для го дает представление о росте игрового поля по указанным параметрам (e - число пунктов или камней в каждом наращиваемом слое, а - число пунктов или камней, умещающихся на одной из сторон поля).

На рис.157 показано формирование игрового поля го третьего уровня. Нетрудно заметить, что все слои (за исключением второго) растут по законам арифметической прогрессии с разностью в 8 пунктов.

Рис.157 Формирование игрового поля го третьего уровня.
Малая доска для игры в го соответствует седьмому, а большая - десятому уровню игрового поля. Число игровых пунктов составляет соответственно 169 и 361.
Сравнительная таблица 4 роста игрового поля суго включает одиннадцать уровней, хотя дальнейший рост поля теория ничем ограничивает.

Для гексагональных структур n=а. Следовательно, по числу пунктов на одной из сторон поля можно определить его уровень.
В данных структурах все слои (за исключением второго) также растут по законам арифметической прогрессии с разностью в 6 пунктов.
Какой же величины должны быть игровые поля в суго? Сравнивая значение X в обеих таблицах, вполне обоснованно можно выбрать во второй таблице восьмой и одиннадцатый уровни (для малой и большой досок). Их числовая величина составит 169 и 331 условных игровых пунктов (то есть пунктов, которые в суго отсутствуют, но при подсчете очков обозначаются плотной упаковкой камней).
При выборе величины игрового поля суго полное совпадение с числовыми параметрами игрового поля го вовсе не является нашей целью, тем более что речь идет о разных структурах. Куда важнее строгая правильность игрового поля и обоснованность его формы.
В частности, выяснилось, что камень в суго, стоящий у бортика, вовсе не находится на первой линии поля (по аналогии с го).
Снятие камней в углу, на боковой стороне и в центре игрового поля в го производится двумя, тремя и четырьмя камнями. В суго камень на стороне снимается, как и в углу, двумя камнями, что делает игру у бортика такой же острой, как и в углу. С этим нельзя согласиться. Камень, который будет сниматься тремя камнями в суго, должен находиться на расстоянии 1.2см от борта. Из этого следует, что первая линия в суго, хотя она и не нанесена, проходит в 2.7см от бортика. А полученные из сравнительных таблиц игровые поля суго надо увеличить по периметру на 1.2см.
Подсчеты площадей показали, что один камень, вписанный в шестиугольную ячейку пространства, вместе с ней составляет 7.78см2. Большое игровое поле суго увеличится на 233.5см2, что будет соответствовать 30 (233.5/7.78 ) дополнительным условным игровым пунктам. Малое поле получит дополнительно 21 игровой пункт.
Оба правильных шестигранных игровых поля будут вписываться в круг. Для малого поля его радиус равен 24см, для большого - 33см. Число условных игровых пунктов составит 190 и 361. Здесь мы снова получили полное совпадение числа игровых пунктов, но уже не на малой, а на большой доске. Но оно является чисто случайным. Однако оказалось, что разместить на указанных игровых полях реальные камни с наиплотнейшей упаковкой невозможно из-за того, что мы увеличили эти поля всего лишь на часть слоя. Поэтому в реальной игре максимальное число камней, необходимых для игры, составит 184 для малой доски и 352 для большой.
Следовательно, в комплекте для игры в суго должно быть 175 черных, 175 белых и 2 красных камня.
Для любителей экстравагантных решений сообщаем, что при игре в суго на поверхности шара с равновеликой площадью он должен иметь диаметр 28.8см.
Плоское шестиугольное игровое поле рекомендуем изготовить из листа прессованной фанеры или картона. Для закрепления бортика радиус описанного круга следует увеличить на 2см. Закрепив по периметру поля бортик, выступающий на 4-5мм, следует обрезать вокруг бортика лишний картон. Бортик можно выполнить за счет приклеивания деревянных реек столярным клеем.
При анализе партии в суго возникает необходимость кратко назвать какой-либо район игрового поля. Предлагается следующий принцип зонирования. Радиус описанного круга, мысленно проведенный через один из углов поля, делится на три части (по 11см). Это позволяет разбить все поле на три зоны: центральную, шатровую и периферийную, включающую площади углов и сторон (рис.158 )

Рис.158. Зонирование игрового поля суго.
Шесть углов поля обозначим латинскими буквами: A, B, C, D, E, F. В игровом комплекте они наносятся на бортике. На самом игровом поле нет никаких обозначений. Тем не менее, изучив схему зонирования, читатель сможет быстро назвать нужный район ноля. Например, бортик AF, Шесть бортов составляют периметр. Угол A - территория между двумя сторонами AB и AF. Сумма территории всех углов и сторон составляет третью периферийную зону.
Шатер af - территория между центром и стороной в секторе AF, Сумма территорий всех шатров составляет вторую шатровую зону. Центральная зона имеет форму шестиугольника. Она составлена из вершин всех шести секторов, имеющих форму правильных треугольников.
Малую доску для игры в суго со стороной игрового поля 24см удобнее всего оформить наклеиванием бортиков на обороте большой доски. Чтобы при этом сохранить устойчивость большой доски, следует снизу выполнить два шестиугольных бортика большой и малый.
В малое суго можно играть и на большой доске, имея дополнительный комплект камней увеличенного диаметра. Для доски со стороной 33см он должен быть равен 42мм. Можно еще значительнее увеличить размер камней. В так называемом детском суго их диаметр равен 8см. В качестве камней можно использовать пластмассовые диски толщиной около 5мм. "Черные" имеют 19 камней, "белые" - 18. Красные камни не применяются.
В заключение этого раздела предлагаем исследовать фрагмент партии в суго, изображенный на рис.159.

Рис.159. Фрагмент партии в суго.
Через игру лежит путь к сложнейшим абстрагированным моделям современной науки. Обе сферы человеческой деятельности обогащают и дополняют друг друга. Регулярно рождающиеся новые игры дают большие возможности для самовыражения каждому человеку. Не является исключением и суго. Что будет после суго? Пока трудно ответить. Может быть, подумаем вместе?

Gudleifr- Admin
- Сообщения : 3398
Дата регистрации : 2017-03-29
KRIEGSSPIELE! :: Солдатики :: 3 - Шашки
Страница 1 из 1
Права доступа к этому форуму:
Вы не можете отвечать на сообщения
