О компиляции Машин Тьюринга
Страница 1 из 1
 О компиляции Машин Тьюринга
О компиляции Машин Тьюринга

"К началу 1963г. последними результатами в этом направлении были теорема Ватанабе о существовании универсальной [т.е. способной эмулировать любую другую] машины [Тьюринга] с 5-ю символами и 6-ю состояниями, теорема Минского о существовании машины с 4-мя символами и 7-ю состояниями и теорема Триттера о существовании универсальной машины с 4-мя символами и 6-ю состояниями".
/З.В.Алферова. Теория алгоритмов. 1973/
Для удобства работы на форуме мне понадобилась очень простая машина распаковки баз данных для отображения последних. И я быстренько ее слепил в первой же главе второго тома Заметок, в рамках обсуждения "текстовых игр"
 ТЕМА #70, АБЗАЦ #861
ТЕМА #70, АБЗАЦ #861 . Однако случились две неприятности:
. Однако случились две неприятности:1) практические потребности быстро превратили эту утилитку в нечто совершенно не дидактическое, а местами и просто нечитаемое...
2) все было хорошо в терминах UNIX - текстовые потоки, проходящие через простые программы-фильтры, написанные на простейших языках. Но внутри одного исполняемого файла потоки превратились в винегрет совершенно разнородных структур, каждая из которых жила максимум десяток строк.
Поэтому захотелось решить эту задачу несколько более формально.
Пусть, мы имеем некоторые "Машины Тьюринга"
 ТЕМА #109, АБЗАЦ #1662
ТЕМА #109, АБЗАЦ #1662 , связанные своими лентами в цепочку. На входе первой - байты файла [базы данных]. На выходе последней - эти же данные, но уже размещенные в памяти программы и готовые к выводу на экран. Для удобства примем направление движения информации слева направо. Выходные ленты одной машины служат входными для других. Объем "промежуточных лент" чрезмерно увеличивать не стоит, достаточно, чтобы туда влезли результат одной операции пишущей машины и входные данные машины читающей (что из них объемнее).
, связанные своими лентами в цепочку. На входе первой - байты файла [базы данных]. На выходе последней - эти же данные, но уже размещенные в памяти программы и готовые к выводу на экран. Для удобства примем направление движения информации слева направо. Выходные ленты одной машины служат входными для других. Объем "промежуточных лент" чрезмерно увеличивать не стоит, достаточно, чтобы туда влезли результат одной операции пишущей машины и входные данные машины читающей (что из них объемнее).(В теории, например, в книжке, что я цитировал вначале, обычно используют другой способ - замещение стартовым состоянием одной машины конечного состояния другой, или той же самой, или ее копии... Но это все не так весело).
Наверное, нужна и вторая связующая цепь "лент", благодаря которой машины будут настраивать друг друга. Это имеет смысл, если сигналы настройки будут идти справа налево - цепь синхронизации. Или это будут некоторые состояния и переходы некой объемлющей Машины?
***
Итак, что эти машины будут делать?
В первом приближении задачу извлечения данных из файла будут решать аж 12 машин:
1. FILE. Получатель файлового буфера. На выходе - все байты файла. Сразу по срабатыванию этой машины становятся доступны все байты файла. Можно брать по одному, выбрать нужный (это используется для различения TXT/GIF форматов) или все разом (длина файла тоже известна).
-----> 2/3/10
2. DOS. Символы из DOS 866 в WIN 1251
-----> 10
3. BLK. Разбиратель буфера на блоки. На выходе - отдельно байты заголовков и пакетов. Готовность машины определяется нахождением курсора (здесь и далее - курсора файла) в начале блока. За исключением 1-го блока, тип (и размер блока) определяется его первым байтом. Остальное - как в первой машине, за исключением только того, что доступны становятся байты не до конца файла, а до конца постоянной части блока.
-----> 4/7
4. PCK. Разбиратель пакетов на байты. На выходе - только информационные байты. Готовность - по нахождению курсора в конце постоянной части блока, имеющего пакеты. Далее - работа в цикле: первый байт - длина пакета, остальные байты - содержимое, доступное подобно машинам 1 и 3. Пакет нулевой длины означает возврат (и готовность машины 3). Отличие доступности байтов от машин 1 и 3 состоит в том, что пакеты не представляют собой законченные единицы информации, а разделены просто по размеру.
-----> 5/10
5. CODE. Вырезатель LZW-кодов из байтов. На выходе - коды вместо байтов. Полученные от машины 4 байты накапливаются по одному со сдвигом в накопителе до получения последовательностей битов нужной длины - кодов. Начальная длина определяется в машине 3. Обрабатываются два специальных кода: перезапуск и конец (возврат к машине 4 и, автоматически, к 3).
6. STR. Распаковщик LZW-кодов в строки. На выходе - байты вместо кодов. Коды по одному прогоняются через декодер, выдавая массивы байтов заранее неизвестной длины.
-----> 10
7. BLKS. Выдаватель блоков и пакетов. На выходе - только информационные байты. Заменяет машины 3 и 4, выдавая блоки и пакеты (вместе с их длинами), как единые массивы байтов.
8. B64. Упаковщик в 64base. На выходе - перекодированные байты. Заменяет тройки байтов перекодированными по таблице base64 четверками. Начальные (остаточные) значения накопителя четверок определяются предыдущими запусками этой машины (с учетом типов блоков, определенных машиной 3). Окончание работы машины 7 вызывает завершение и этой машины (и, возможно, дописывание последней четверки).
9. B64S. Генератор полей. На выходе - строки. В зависимости от типов (и их номеров по порядку) блоков, дописывает накопленные четверки в дерево, с добавлением некоего стандартного обрамления.
-----> 12
10. FILD. Искатель в строках границ полей. На выходе - слова. В зависимости от состояния машины 12, копит поступающие байты в слова, которые будут висеть на дереве по отдельности.
11. FLDS. Собиратель полей. На выходе - строки. Отмечая концы строк, формирует наборы слов, как "суперсимволы", управляющие измененением состояния машины 12.
12. TREE. Добавлятор в дерево. На выходе - узлы дерева. Это тот самый автомат разбора базы данных, который я ввел во второй главе второго тома заметок: "GARBAGE - PATH - HEADER - TEXT - PARAM".
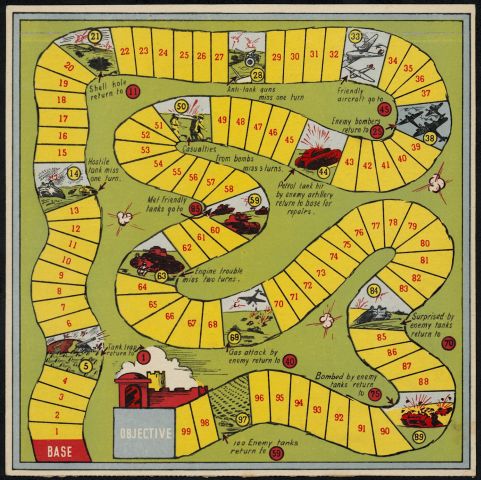
Вся "дорожка" - это файл, который мы читаем побайтно. Каждая клеточка - байт. Т.о. можно пробежать всю дорожку байт за байтом, нигде не задерживаясь. По крайней мере, такая программа будет работать. Но, когда мы доходим до картинки, мы можем ее рассмотреть и прочесть, что надо сделать. Самое хитрое, мы можем "раскрыть" картину, как новое игровое поле, и "сыграть" на нем. Причем, это новое поле может быть построено нами в процессе игры из байтов, считанных ранее. (Во "взрослых" системах такая постепенная сборка реализуется путем построения "Доски объявлений"). Но нам пока важнее не сами эти сложности, а возможность вводить их постепенно, заменяя "просто дорожку" на "живые картинки" по мере понимания задачи.
С точки зрения модели "текстовых машин" из Заметок
 ТЕМА #70, АБЗАЦ #773
ТЕМА #70, АБЗАЦ #773 начальные машины (1-9 ) относятся к "разархиватору", конечные (10-11) - к "разборщику". Очевидно, далее должен следовать "отображатель".
начальные машины (1-9 ) относятся к "разархиватору", конечные (10-11) - к "разборщику". Очевидно, далее должен следовать "отображатель".С точки зрения физического переноса данных машины 2, 3, 4 и 7 практически не нуждаются в хранилищах информации, т.к. могут просто размечать полученный первой машиной файловый буфер.
На первый взгляд кажется, что можно сделать проще всего - пускать байты по одному, с левого конца цепочки, чтобы они проходили весь конвейер. Однако, это перестает быть простым, как только вспомним, что информация может накапливаться на некоторых лентах где-то посредине. Все равно, будет нужно приостанавливать запуск байтов "с самого начала" и разгребать накопившиеся. Значит, нужно будет уметь "переходить к самой правой готовой ленте" (вызов по цепи синхронизации).
Если немного подумать, то станет ясно, что пропуск байтов по одному работает ровно там, где нет надобности в новых хранилищах информации, т.е. в машинах 2, 3, 4 и 7. Это настолько просто, что можно описать таблицей.
Для этих машин - BLK-PCK-BLKS - работающих с одним и тем же входным массивом, выдаваемым машиной FILE, мы имеем следующую инструкцию по обработке байтов, которая может быть оформлена в виде одного цикла, пробегающего по всем байтам файла - от первого до последнего:
| Байты | События | Передача | Далее |
| Заголовок 0-9 | - | B64 начальный | ... |
| Заголовок 10 | Нахождение N | B64 ... | ... |
| Заголовок 11-N | - | B64 ... | Новый блок |
| Блок ";" 0 | Фиксация ";" | - | Конец |
| Блок "," 0 | Фиксация "," | B64 конечный | ... |
| Блок "," 1-8 | - | B64 ... | ... |
| Блок "," 9 | Нахождение N | B64 ... | ... |
| Блок "," 10-N | - | B64 ... | Пакет |
| Блок "," пакет 0 | Нахождение N | B64 ... | Если N=0, новый блок |
| Блок "," пакет 1-N | - | B64 ... | Новый пакет |
| Блок "!-F9" 0-1 | Фиксация "!-F9" | B64 промежуточный | ... |
| Блок "!-F9" 2-8 | - | B64 ... | Новый блок |
| Блок "!-1" 0-1 | Фиксация "!-1" | - | Пакет |
| Блок "!-1" пакет 0 | Нахождение N | - | Если N=0, новый блок |
| Блок "!-1" пакет 1-N | - | FILD ... | Новый пакет |
| Блок "!-2" 0-1 | Фиксация "!-2" | - | Пакет |
| Блок "!-2" пакет 0 | Нахождение N | - | Если N=0, новый блок |
| Блок "!-2" пакет 1-N | - | CODE | Новый пакет |
| Блок "!-3" 0-1 | Фиксация "!-3" | - | Пакет |
| Блок "!-3" пакет 0 | Нахождение N | - | Если N=0, новый блок |
| Блок "!-3" пакет 1-N | - | B64 отдельный | Новый пакет |
| Блок "!-4" 0-1 | Фиксация "!-4" | - | Пакет |
| Блок "!-4" пакет 0 | Нахождение N | - | Если N=0, новый блок |
| Блок "!-4" пакет 1-N | - | Корректировка машин | Новый пакет |
| Блок "!-*" 0-1 | Фиксация "!-что-то непонятное" | - | Пакет |
| Блок "!-*" пакет 0 | Нахождение N | - | Если N=0, новый блок |
| Блок "!-*" пакет 1-N | - | - | Новый пакет |
Но, все равно видно, что связи и по передаче управления (перебору символов), и по управляющим переменным достаточно замысловаты.
Кажется, что на "неструктурном языке" запись этой "программы" будет даже проще - в одну линию, с goto-возвратами к готовым машинам от неготовых. Легко представить, что большинство оптимизаций "проверок и синхронизаций лент" можно будет учесть правильной расстановкой этих самых gotо.
В "структурном" варианте речь, очевидно, должна идти о вложенных циклах:
while(готова лента 1) {
while(готова лента 2) {
while(готова лента 3) {
...
}}}
- чтобы возвращаться каждый раз к самой правой готовой, или переходить к следующей. Однако, вставить в такую "матрешку" еще одну машину, не порушив всю структуру, будет крайне затруднительно. Тем более, что в цепочке есть развилки.
Классики, правда, любят в таком случае говорить о "сопрограммах". Их-то реализовать проще - даже на "структурном языке". Группы операторов "между точками восстановления" нужно заменить функциями. Указатель текущего оператора заменить на переменную, содержащую адрес ф-ии. Goto - на присвоение этой переменной. Чтобы избежать слишком глубокой вложенности вызовов, нужно охватить всю программу циклом "эмуляции", вызывающим ф-ии, адресуемые переменной-указателем. (В крайнем случае, можно использовать оператор switch, выбирающий нужную ф-ию по номеру). Такой "эмулятор" изначально присутствует, например, в любой FORTH-машине.
***
Сами Машины Тьюринга я сразу начал трактовать достаточно широко. Например, я допустил их "усложнение почти произвольным образом". ("Почти" обозначает, что вводить магические операции все-таки нельзя). Например, можно было добавлять составные состояния, сложные символы, возможность обратится к любой части ленты, дополнительные действия в процессе смены состояния...
Например, если в лоб реализовать 8-ю Машину Тьюринга - B64 (преобразование троек 8-битовых символов в четверки 6-битовых "AB..+/"), то понадобится 256 строк таблицы для состояния чтения первого символа, затем 4*256 строк для чтения второго (4 состояния, определяемые недообработанными 2-мя битами первого состояния), 16*256 - для чтения третьего символа, и последние 256 для вывода остатка (всего 5632 строк).
Как-то так
(состояние; символ -> новое состояние; новый символ; сдвиг входной ленты; свиг выходной ленты):
0.0; 00 -> 1.0; "A"; ">"; ">"
...
0.0; 03 -> 1.3; "A"; ">"; ">"
0.0; 04 -> 1.0; "B"; ">"; ">"
...
0.0; FF -> 1.3; "/"; ">"; ">"
1.0; 00 -> 2.0; "A"; ">"; ">"
...
1.0; FF -> 2.F; "O"; ">"; ">"
1.1; 00 -> 2.0; "P"; ">"; ">"
...
1.3; FF -> 2.F; "/"; ">"; ">"
2.0; 00 -> 3.0; "A"; "."; ">"
...
2.F; FF -> 3.0; "/"; "."; ">"
3.0; 00 -> 0.0; "A"; ">"; ">"
...
3.0; 3F -> 0.0; "/"; ">"; ">"
3.0; 40 -> 0.0; "A"; ">"; ">"
...
3.0; FF -> 0.0; "/"; ">"; ">"
Почему "правильная" Машина Тьюринга получилась такой большой? Ислючительно из-за неудачного выбора входного алфавита. 8 бит на символ - слишком много. Обычно теоретики предпочитают работать с однобитными символами... (А, если B64 будет получать пары битов, то ей вообще ничего не надо будет делать! Просто отсчитывать по три символа и все...)
Вообще, возможность преобразований Машин Тьюринга - это классика. Например, можно уменьшить число состояний (в пределе - до двух), вводя сложные символы, и можно уменьшить число символов (опять - до двух), вводя состояния-дешифраторы.
Но удобнее пойти другим путем. Если я дополню процедуры Машины операциями над битами внутри байтов, то понадобится всего 1+4+16+1=22 строки.
0.0; X -> 1.(два младших бита X); F(остальные биты X); ">"; ">"
1.0..3; Y -> 2.(4 младших бита Y); F(мл.биты состояния и остальные биты Y); ">"; ">"
2.0..F; Z -> 3.0; F(мл.биты состояния и 2 старших бита Z); "."; ">"
3.0; Z -> 0.0; F(6 младших битов Z); ">" ; ">"
Это приводит нас к наличию "вычислительных" символов, т.е. таких, которые не будут прописываться в таблицах Машины, но будут служить значениями для вычислений. Если мы будем хранить их на обычной ленте, придется вводить и состояния Машины, нечувствительные к символам на ленте. Что-то вроде:
...
ВВОД-КОДА; "+" -> СЛОЖЕНИЕ; *; *
СЛОЖЕНИЕ; A -> ВВОД-КОДА; {АККУМУЛЯТОР + А}; *
...
Первая строка - часть распознавателя команд, обычная тьюринговская. Во второй же символ "A" означает любое число, над которым производится операция, результат которой записывается на ленту.
Другой вариант добавления процедур к Машине Тьюринга я применял в старой версии машины 12 - TREE. Сама Машина занималась там только переключениями с одного состояния в другое в зависимости от того, какому регулярному выражению соответствует очередная строка, а процедура записи на ленту была заменена ссылкой на функцию, делающую с этой строкой что-то полезное
 ТЕМА #70, АБЗАЦ #762
ТЕМА #70, АБЗАЦ #762 .
.Еще один вариант хранения значений на ленте - прицепить к каждой клетке ленты дополнительное хранилище для чисел. И/или прописывать в клетках таблицы дополнительный параметр - вычислительную операцию. Кстати, можно предвидеть, что в цепочке машин, некоторые символы на правых лентах будут лишь ссылками на символы левых лент, например, машины 2, 3, 4 и 7 могут иметь на своих "рабочих" лентах лишь ссылки на массив выходной ленты FILE.
***
Программа, реализующая один шаг Машины Тьюринга, выглядит как-то так:
ВЫБРАТЬ СТРОКУ, СООТВЕТСТВУЮЩУЮ ТЕКУЩЕМУ СОСТОЯНИЮ И СЧИТАННОМУ СИМВОЛУ;
ЗАПИСАТЬ НА ЛЕНТУ УКАЗАННЫЙ В СТРОКЕ СИМВОЛ;
ПЕРЕЙТИ К НОВЫМ ДАННЫМ НА ЛЕНТЕ;
ИЗМЕНИТЬ СОСТОЯНИЕ НА УКАЗАННОЕ.
Уже здесь можно углядеть помеху нашей попытке ввести сложные символы: получается, что сложный символ нужно читать дважды: первый раз - для нахождения строки таблицы (общим для всех состояний способом) и второй - для вычисления новых значений (уже, возможно, способом, зависящим от состояния.
В "наиболее общей" Машине Тьюринга будет только одна общая операция - нахождения нужной строки таблицы. Остальные операции - записи, протяжки ленты и нахождения состояния должны быть указателями на операции, возможно, уникальные для отдельных состояний. Как, например, битовые вычисления в машине B64.
НАХОЖДЕНИЕ(СОСТОЯНИЕ, СИМВОЛ);
ЗАПИСЬ(СОСТОЯНИЕ, СИМВОЛ, СТРОКА ТАБЛИЦЫ);
ПРОТЯЖКА(СОСТОЯНИЕ, СИМВОЛ, СТРОКА ТАБЛИЦЫ);
СОСТОЯНИЕ = НОВОЕ(СОСТОЯНИЕ, СИМВОЛ, СТРОКА ТАБЛИЦЫ).
И, даже, возможно немного изменить операцию нахождения строки:
ПРОЦЕДУРА НАХОЖДЕНИЯ СЛЕДУЮЩЕЙ = УТОЧНЕНИЕ(СОСТОЯНИЕ, СИМВОЛ, СТРОКА ТАБЛИЦЫ);
Однако, основным свойством наиболее общих программных систем является их полная практическая бесполезность.
Каков же наиболее удобный набор машинных операций, чтобы свести их табличное описание к минимуму? Сколько в таблице будет констант, а сколько функций?
(Для машин с отдельными входными и выходными лентами):
ДЛЯ r(Q) И r(A) ВЫПОЛНИТЬ w(A) w(I) w(O) w(Q),
где Q - состояние, A - символ на ленте, I/O - перемещение по входной/выходной ленте, r() - ф-ия анализа, w() - ф-ия записи/перехода
Т.к. r(A) может отменить успех r(Q) ценой некоторой возможной потери эффективности:
ДЛЯ Q И r(A) ВЫПОЛНИТЬ w(A) w(I) w(O) w(Q)
Т.к. w(A) может (в крайнем случае) просто изменить Q:
ДЛЯ Q И r(A) ВЫПОЛНИТЬ w(A) w(I) w(O) Q
r(A) и w(I) объединять нельзя, т.к. значение на входной ленте используется в w(A). Избавиться от w(I) и w(O) тоже нельзя ввиду сложности устройства клеток лент. Их можно только объединить с w(A):
ДЛЯ Q И r(A) ВЫПОЛНИТЬ w(AIO) Q
Сливать r(A) и w(AIO) не стоит - потеряется наглядность таблицы. Итого - две ф-ии: анализа символа и записи нового.
***
Нет никакого резона писать эмулятор системы Машин Тьюринга потребного размера и переводить всю задачу на ее язык. Просто потому, что обычный язык программирования уже имеет на борту намного более удобные операторы и выражения. Переходя обратно к Машине Тьюринга, мы сами себе будем усложнять жизнь.
Чем программа на "упрощенном алголе" лучше Машины Тьюринга:
1) можно сразу обращаться к нужной переменной, а не проматывать ленту до нужной позиции (или переходить к подмножеству состояний, соответствующему значению переменной);
2) не нужно на каждом шаге проводить полный цикл операций по работе с таблицей Машины;
3) не нужно переводить арифметические операции в элементарные.
Но,
чем лучше Машина Тьюринга (окромя формализмов):
1) можно абстрагироваться от источника информации, лента может изображать и поток ввода-вывода, и блок памяти, и аппаратные управляющие сигналы;
2) можно писать программу не на языке программирования, а в виде заполнения данными таблицы. Можно даже дать пользователю возможность вводить заранее не предусмотренные программой команды - как положено при разработке любых интерпретаторов (например FORTH)
 ТЕМА #43, АБЗАЦ #427
ТЕМА #43, АБЗАЦ #427 .
.Третий минус сильно умаляет второй плюс. Какая выгода от таблиц, если они будут необозримы и трудночитаемы? Поэтому чисто арифметические куски кода все-таки проще оформлять подпрограммами на "алголе".
И, да, тот же "алгол" тоже имеет в себе два практически независимых языка - операторов (смены состояний) и выражений (вычисления значений) - с совершенно разным синтаксисом. Чем Машина Тьюринга хуже?
***
Пусть один шаг машины будет выглядеть так:
ВЫБРАТЬ СТРОКУ;
ЗАПИСАТЬ СИМВОЛ;
ПЕРЕЙТИ К НОВЫМ ДАННЫМ;
ИЗМЕНИТЬ СОСТОЯНИЕ.
Но, т.к. у нас целый коллектив машин, то в начало этой последовательности надо добавить операции:
ВЫПОЛНИТЬ ИНИЦИАЛИЗАЦИЮ;
ПРОВЕРИТЬ ГОТОВНОСТЬ ДАННЫХ;
- а в конец:
ВЫПОЛНИТЬ ФИНАЛИЗАЦИЮ;
ВЫЗВАТЬ ДРУГУЮ МАШИНУ.
Громкими словами - ИНИЦИАЛИЗАЦИЕЙ и ФИНАЛИЗАЦИЕЙ - я обозначил процедуры, ограничивающие жизнь машины - от ее запуска в одном из стартовых состояний, до достижения конечного состояния. Например, машина B64 должна где-то помнить, читает ли она продолжение блока символов или начинает новый, а при окончании блока - добавлять завершающие символы "=" до получения полной четверки символов.
Здесь важно не переусложнить. Например, можно, как в языках программирования высокого уровня сделать ВЫЗОВ ДРУГОЙ МАШИНЫ частью вызова функции вывода значения (т.е. честной подпрограммой).
И, наоборот, реализовать ИНИЦИАЛИЗАЦИИ и ФИНАЛИЗАЦИИ переходом в соответствующие СОСТОЯНИЯ.
***
Согласились мы или нет оформлять отдельные процедуры своей программы (а, может, даже, и целые процессы) в виде Машинок Тьюринга, изначальный вопрос взаимодействия этих машин, так и повис в воздухе.
Уже здесь, даже не вникая в детали синхронизации машин, очевидно, что полный набор операций и учет всех ситуаций избыточен. Многие машины цепочки устроены намного проще. Например, большинство входных лент нашей цепочки будут просматриваться только один раз, без возврата к уже прочитанным символам. Большинство правых машин будут автоматически готовы к работе после срабатывания левых, а большинство левых - после возврата им управления после срабатывания правых...
Есть ли какая-то теория, позволяющая упростить вычисления, пользуясь знанием об ограниченности множеств данных? Есть. См. статью Ершова.
***
С точки зрения структурного программирования, инвариантом рабочего цикла нашей цепочки машин является:
1. Существует некоторая точка T, левее которой все машины уже перешли в конечное состояние. Когда T дойдет до правого конца, работа будет закончена.
2. Существует точка S, между T и правым концом, обозначающая самую правую готовую к работе машину.
Описывая ситуации, на которые машина должна реагировать, можно ввести для каждой тройку условий. si - данные для i-й машины готовы, ti - машина достигла конечного состояния, pi - машина сработала. Под срабатыванием понимаем достижением состояния, требующего проверки возможного изменения S:
- S перемещается вправо, si остается истинным;
- S перемещается вправо, si становится ложным;
- S остается на месте;
- S смещается влево, до ближайшей готовой.
***
Возможность упрощения опять следует искать во взаимной зависимости - теперь si, pi и ti - соседних машин. Например, pi для некоторых машин может автоматически вызывать сдвиг S вправо, или делать si ложным. Тогда нам не придется перебирать всю цепочку в поисках S, проверяя при этом все условия готовности.
***
Что означает соединение машин лентами? Очевидно, что ф-ии r(A) и w(AIO) должны как-то справляться с предикатами si, pi и ti. "Достаточная" запись вызывать запуск следующей машины, неготовность ко вводу - переход влево... Говорить заранее об "общих принципах" тут смысла не имеет.
Языки программирования дают нам множество вариантов:
- вырожденная ситуация, когда одному шагу левой машины соответствует один шаг правой и их можно просто соединить последовательно (друг за другом в тексте программы);
- левая машина может вызывать правую по мере готовности (см. выше вложенные операторы while);
- правая машина может вызывать левую, когда ей нужна новая порция данных;
- на каждом шаге "объемлющая машина" проверяет машины/ленты в поисках самой правой готовой, и передает туда управление.
Все это можно сделать при помощи управляющих операторов, подпрограмм, сопрограмм, системных вызовов и т.п.

Кроме упомянутого соединения машин промежуточными лентами, легко представить себе включение одной машину в другую для сложной обработки одной из ситуаций (например, расчета нового состояния или нового символа); или параллельный запуск нескольких машин для разделения независимых друг от друга вычислений.
Еще можно измыслить (для машин, соединенных промежуточными лентами):
1) объединение двух соседних машин в одну; это возможно только в тех случаях, когда промежуточная лента очень мала или когда обе машины имеют дело практически с одной входной лентой. Компромиссное решение - превратить промежуточную ленту во внутреннюю ленту памяти новой машины;
2) вставку в цепочку новой машины для обеспечения нового функционала; достаточно очевидно "на картинке", но, как я писал выше, именно простая и наглядная реализация вставки подобного кода в программу и явилась проблемой этих рассуждений;
3) разбиение одной машины на две для упрощения структуры ленты; если, конечно, можно разделить состояния машины на два слабо связанные множества;
4) удаление избыточных операций; видимо, в итоге опять сведется к объединению всех машин в одну. С выбрасыванием всех промежуточных лент. По сравнению с поддержкой межмашинного взаимодействия монолитная программа будет по-машинному проще, хотя и совершенно недоступной для понимания человеком...
***
Вспомним машину B64. В этот раз, как имеющую большое разнообразие входных данных. Кроме того, эта машина имеет сложный формат вывода и набор переменных для отображения текущего состояния накопителя машины. См. выше таблицу.
Для описания ее работы проще всего придумать некоторый "язык", на котором можно этой машиной управлять.
Тогда набор команд на кодирование GIF-заголовка должен был бы выглядеть как-то так:
НАКОПИТЕЛЬ СБРОСИТЬ
ВЫВЕСТИ "\GIF\имя_файла.GIF"
ВЫВЕСТИ "ТЕКСТ"
БАЙТЫ адрес размер
ВЫВЕСТИ ПРОБЕЛ
ВЕРНУТЬСЯ
Соответственно, для блока "!-F9":
ВЫВЕСТИ "\GIF\имя_файла.GIF\EXP"
ВЫВЕСТИ "ТЕКСТ"
БАЙТЫ адрес 8
ВЫВЕСТИ ПРОБЕЛ
ВЕРНУТЬСЯ
Для ",":
НАКОПИТЕЛЬ СОХРАНИТЬ
ВЫВЕСТИ "\GIF\имя_файла.GIF\GIF\номер"
ВЫВЕСТИ "ТЕКСТ"
БАЙТЫ адрес размер
ВЕРНУТЬСЯ
...
БАЙТЫ адрес размер
ВЕРНУТЬСЯ
...
БАЙТЫ адрес 1
ЗАВЕРШИТЬ
НАКОПИТЕЛЬ ВОССТАНОВИТЬ
ВЫВЕСТИ ПРОБЕЛ
ВЕРНУТЬСЯ
Чуть проще для "!-3":
НАКОПИТЕЛЬ СОХРАНИТЬ СБРОСИТЬ
ВЫВЕСТИ "\GIF\имя_файла.GIF\IMG\номер"
ВЫВЕСТИ "ТЕКСТ"
ВЕРНУТЬСЯ
...
БАЙТЫ адрес размер
ВЕРНУТЬСЯ
...
ЗАВЕРШИТЬ
НАКОПИТЕЛЬ ВОССТАНОВИТЬ
ВЫВЕСТИ ПРОБЕЛ
ВЕРНУТЬСЯ
Возможно, здесь будет дешевле будет не передавать программу шаг за шагом, а просто строить B64 на лету?
***
Достройка машины на лету может пригодиться и в 6-й машине STR, переводящей LZW-коды в строки байтов. Можно видеть, что ее ядром является постоянно растущий словарь строк. Единственная процедура работы со строкой - вывод ее. Новая строка добавляется приписыванием новой буквы в конец одной из строк словаря (предпоследняя строка кода).
В рамках традиционного программирования словарь создается как древообразная структура пар (буква, ссылка на пару-родителя). А рекурсия без труда справляется с процедурой вывода - выводит (рекурсивно) начало, а потом - букву. К сожалению, Машина Тьюринга работает наоборот: сначала выводит символ, а затем - передает управление.
Т.к. одна и та же строка может иметь много наследников, и все предки любой строки остаются в словаре, другие способы хранения, кроме указанного дерева, неприемлимы. Также необходимым становится и промежуточное хранилище - либо для стека возвратов рекурсии, либо для разворота строки задом наперед.
Словарь растет, и Машина Тьюринга может для реализации этого достраиваться "на лету". Мы, ведь помним, что Машина Тьюринга может быть целиком записана на ленте и скормлена другой машине. (Можно ли "достраивая машину" получить "неожиданное поведение", выходящее за рамки обычной Машины? Конечно, нет. Формально они все эквивалентны).
Но стоит ли этот алгоритм реализовать честной Машиной Тьюринга? Видимо, достаточным будет чтобы он таковой только прикидывался, получая и выдавая ленты.
Последний раз редактировалось: Gudleifr (Ср Окт 25, 2023 12:27 am), всего редактировалось 17 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
Для отдохновения души, почитаем этих самых классиков:

Д.КНУТ. ИСКУССТВО ПРОГРАММИРОВАНИЯ. ТОМ I
1.4.2. СОПРОГРАММЫ
Подпрограммы являются частным случаем более общих программных компонент, называемых "сопрограммами". Если отношения между главной программой и подпрограммой отличаются несимметричностью, то отношения между сопрограммами вполне симметричны, причем КАЖДОЙ из сопрограмм позволено ВЫЗЫВАТЬ ДРУГУЮ.
Чтобы понять концепцию сопрограмм, взглянем еще раз на подпрограммы, но с некоторой другой позиции. Точка зрения, принятая в предыдущем пункте, состояла в том, что подпрограмма является лишь расширением аппаратуры вычислительной машины, которое диктуется желанием сократить количество команд в программе. Может быть, это и так, но допустима и другая точка зрения. Мы можем рассматривать главную программу и подпрограмму как бригаду программ, в которой каждый член бригады обязан выполнять некоторое задание. Главная программа в процессе выполнения своего задания возбуждает подпрограмму; подпрограмма выполняет свою функцию и затем возбуждает главную программу. Мы могли бы напрячь воображение и поверить в то, что с точки зрения подпрограммы выход из нее есть не что иное, как вызов главной программы; главная программа продолжает выполнять свои обязанности, а затем "выходит" в подпрограмму. Теперь работает подпрограмма, и затем она снова вызывает главную программу.
Эти несколько отвлеченные рассуждения становятся вполне реальными, если речь заходит о сопрограммах, когда невозможно отличить, какая из них является подпрограммой другой. Предположим, что у нас есть две сопрограммы A и B; программируя A, мы можем рассматривать B как подпрограмму, но при программировании B мы можем считать, что A является нашей подпрограммой. Таким образом, в сопрограмме A команда "JMP B" используется для того, чтобы возбудить сопрограмму В. В свою очередь, для того чтобы возбудить сопрограмму A, в сопрограмме В используется команда "JMP A". Все это напоминает действия спортсменов в эстафетном беге. Как только сопрограмма активируется, она продолжает выполняться с того самого места, где она была приостановлена в последний раз.
В машине MIX такая связь между сопрограммами реализуется включением в программу следующих четырех команд:
A STJ BX
AX JMP A1
B STJ AX
BX JMP B1 (1)
Для передачи управления в сопрограмму затрачивается четыре машинных такта. Первоначально AX и BX настраиваются на переход в стартовые точки каждой сопрограммы, A1 и B1. Предположим, что первой выполняется команда из ячейки A1 в сопрограмме A. И когда, скажем в ячейке A2, встречается "JMP B", команда в ячейке B сохраняет rJ в AX. Следовательно, в AX окажется "JMP A2+1". Команда, находящаяся в BX, отправит нас в B1, и после этого начнет выполняться сопрограмма B, а в ней в некоторый момент, скажем в ячейке B2, встретится команда "JMP A". Мы сохраним rJ в BX и передадим управление в ячейку A2+1 и тем самым продолжим выполнение сопрограммы A до тех пор, пока вновь не встретится переход в B, в результате которого J сохранится в AX, а управление будет передано в B2+1 и т.д.
Существенное различие между двумя видами связи: программа - подпрограмма и сопрограмма - сопрограмма (и это можно увидеть, изучая приведенный выше пример), состоит в том, что подпрограмма всегда запускается СНАЧАЛА, т.е. с фиксированного места, в то время как главная программа или сопрограмма всегда продолжается С ТОГО МЕСТА, где ее работа была прекращена в последний раз.
На практике сопрограммы являются самым естественным средством при программировании алгоритмов ввода и вывода. Предположим, например, что сопрограмма A должна читать карты и выполнять некоторые преобразования вводимой информации, переводящие ее в последовательность элементов. Другая сопрограмма, которую мы назовем B, выполняет дальнейшую обработку этих элементов и печатает результаты; B будет периодически требовать последовательные входные элементы, получаемые в A. Таким образом, сопрограмма B передает управление A всякий раз, когда ей нужен следующий входной элемент, а сопрограмма A передает управление B всякий раз, когда входной элемент подготовлен. (Читатель может сказать: "Значит, B - основная программа, а A - просто ПОДПРОГРАММА, выполняющая ввод", Однако если процесс, выполняемый A, очень сложный, то это не совсем верно; мы можем даже представить себе A в качестве основной программы, а B - как подпрограмму, выполняющую вывод. При этом приведенное выше описание никоим образом не изменится). Полезность идеи сопрограмм становится очевидной, если мы находимся между этими двумя крайними случаями, т.е. тогда, когда как A, так и B сложны и каждая из них обращается к другой во многих местах. Довольно трудно найти короткие, простые примеры, которые иллюстрируют важность этой идеи; НАИБОЛЕЕ ПОЛЕЗНЫЕ ПРИМЕНЕНИЯ СОПРОГРАММ, КАК ПРАВИЛО, ОЧЕНЬ ДЛИННЫ [выделение мое.- G.].
Чтобы изучить сопрограммы в действии, рассмотрим "надуманный" пример. Предположим, что мы хотим написать программу, которая переводит один код в другой. Входной (транслируемый) код представляет последовательность алфавитно-цифровых литер, оканчивающуюся точкой, например:
A2B5E3426FG0ZYW3210PQ89R. (2)
Такая последовательность перфорируется на картах; пустые колонки (пробелы), встречающиеся на картах, игнорируются. Эту входную информацию следует понимать таким образом (слева направо): если следующая литера - цифра (т.е., 0, 1, ..., 9), скажем n, то это есть указание об n + 1 повторениях следующей литеры независимо от того, является следующая литера цифрой или нет. Нецифровая литера обозначает только себя. Выходом нашей программы должна быть последовательность, полученная указанным образом и разделенная на группы по три литеры в каждой (причем в последней группе может быть меньше чем три литеры). Например, (2) необходимо преобразовать в такую форму:
ABB BEE EEE E44 444 66F GZY W22 220 0PQ 999 999 999 R. (3)
Обратите внимание, что 3426F не означает 3427 повторений буквы F; в результате появляется 4 четверки, 3 шестерки и затем буква F. Наша программа должна отперфорировать результат на картах, по шестнадцать групп на каждой карте.
Для выполнения такого перевода мы напишем две сопрограммы и подпрограмму. Подпрограмма, названная NEXTCHAR, находит следующую литеру, не являющуюся пробелом, во входной последовательчосги и помещает ее в регистр A:
01 * ПОДПРОГРАММА ВВОДА ЛИТЕРЫ
02 READER EQU 16 Номер читающего устройства.
03 INPUT ORIG *+16 Место для входных карт.
04 NEXTCHAR STJ 9F Вход в подпрограмму.
05 - JXNZ 3F Первоначально rX = 0.
06 1H J6N 2F Первоначально rI6 = 0.
07 - IN INPUT(READER) Прочитать следующую карту.
08 - JBUS *(READER) Ждать завершения.
09 - ENN6 16 rI6 указывает на первое слово.
10 2H LDX INPUT+16,6 Взять следующее слово.
11 - INC6 1 Продвинуть стрелку.
12 3H ENTA 0
13 - SLAX 1 Следующая литера ->rA.
14 9H JANZ Пропуск пробелов.
15 - JMP NEXTCHAR+1 []
Эта подпрограмма имеет следующие характеристики:
- Вызов: JMP NEXTCHAR
- Состояние при входе: rI6 указывает на следующее слово, или rI6 = 0, если необходимо прочесть следующую карту; rX = литеры, которые еще будут обрабатываться.
- Состояние при выходе: rA = следующая входная литера (не пробел); rX, rI6 подготовлены для следующего входа в NEXTCHAR.
Наша первая сопрограмма, с названием IN, получает символы из входной последовательности и создает соответствующее количество дубликатов:
16 * ПЕРВАЯ СОПРОГРАММА
17 2H INCA 30 Литера - не цифра.
18 - JMP OUT Передать ее в сопрограмму.
19 IN1 JMP NEXTCHAR Взять литеру.
20 - DECA 30
21 - JAN 2B Буква?
22 - CMPA =10=
23 - JGE 2B Специальная литера?
24 - STA *+1(0:2) Цифра n.
25 - ENT5 * rI5<-n.
26 - JMP NEXTCHAR Взять следующую литеру.
27 - JMP OUT Передать ее в сопрограмму.
28 - DEC5 1 Уменьшить n на 1.
29 - J5NN *-2 Повторить, если это необходимо.
30 - JMP IN1 Начать новый цикл. []
(Напомним, что для MIX цифры 0-9 имеют коды 30-39). Эта сопрограмма имеет следующие характеристики:
- Вызов: JMP IN
- Состояние при выходе (при переходе к OUT): rA = очередная входная литера с учетом размножения; rI4 не изменяет свое значение с момента входа.
- Состояние при входе (после возврата): rA, rX, rI5, rI6 не должны изменять своих значений с момента последнего выхода.
Другая сопрограмма, с названием OUT, размещает код по три литеры и перфорирует карты:
31 * ВТОРАЯ СОПРОГРАММА
32 _ ALF _ Константа для занесения пробелов.
33 OUTPUT ORIG *+16 Буферная область для ответов.
34 PUNCH EQU 17 Номер устройства (перфоратора).
35 OUT1 ENT4 -16 Начать новую карту.
36 - ENT1 OUTPUT
37 - MOVE -1,1(16) Занести пробелы в область вывода.
38 1H JMP IN Взять следующую литеру.
39 - STA OUTPUT+16,4(1:1) Занести в выходную карту.
40 - СМРА PERIOD Это "."?
41 - JE 9F
42 - JMP IN Если нет, то взять следующую литеру.
43 - STA OUTPUT+16,4(2:2) Занести ее.
44 - СМРА PERIOD Это "."?
45 - JE 9F
46 - JMP IN Если нет, то взять следующую литеру.
47 - STA OUTPUT+16,4(3:3) Занести ее.
48 - СМРА PERIOD Это "."?
49 - JE 9F
50 - INC4 1 Перейти к следующему слову.
51 - J4N 1B Конец карты?
52 9H OUT OUTPUT(PUNCH) Если да, то перфорация.
53 - JBUS *(PUNCH) Ждать завершения.
54 - JNE OUT1 Возвратиться и продолжить, если не была принята ".".
55 - HLT
56 PERIOD ALF . []
Эта сопрограмма имеет следующие характеристики:
- Вызов: JMP OUT
- Состояние при выходе (при переходе к IN): rA, rX, rI5, rI6 сохраняют те значения, которые были при входе.
- Состояние при входе (при возврате): rA = (следующая входная литера с учетом размножения); значение r4 сохранилось с момента последнего выхода.
Чтобы завершить программу, мы должны обеспечить связь между сопрограммами [см. (1)] и соответствующие начальные установки. Начальные установки в сопрограммах требуют некоторой изобретательности, хотя и не создают заметных затруднений.
57 * НАЧАЛЬНАЯ УСТАНОВКА И СВЯЗЬ
58 START ENT6 0 Подготовить rI6 для NEXTCHAR.
59 - ENTX 0 Подготовить rX для NEXTCHAR.
60 - JMP OUT1 Начать с OUT.
61 OUT STJ INX Связь сопрограмм.
62 OUTX JMP OUT1
63 IN STJ OUTX
64 INX JMP INI
65 - END START []
Теперь программа написана полностью. Читателю следует тщательно изучить ее, обращая особое внимание на то, как можно написать каждую из сопрограмм независимо, в предположении, что другая сопрограмма является ее подпрограммой.
В программе, приведенной выше, состояния входа и выхода для IN и OUT полностью согласованы. Общий случай может оказаться менее удачным, и тогда для связи сопрограмм потребуется также загрузка и запоминание соответствующих регистров. Например, если сопрограмма OUT изменяет содержимое регистра А, то группа команд для связи сопрограмм примет следующий вид:
OUT STJ INX
- STA HOLD A Запомнить А при выходе из IN.
OUTX JMP OUT1
IN STJ OUTX
- LDA HOLDA Восстановить А при выходе из OUT.
INX JMP IN1
Существует важное родство между сопрограммами и МНОГОПРОХОДНЫМИ АЛГОРИТМАМИ. Например, процесс перевода, который мы только что описали, можно было бы выполнить за два отдельных прохода. Во-первых, мы могли бы сделать в точности то, что делает сопрограмма IN, применяя ее ко всей входной информации и записывая каждую литеру с соответствующим числом дубликатов на магнитную ленту. После того как эта обработка закончится, мы могли бы перемотать ленту в начало и затем сделать в точности то, что делает сопрограмма OUT, принимая литеры с ленты группами по три. Это называют "двухпроходной" обработкой. (Интуитивно под словом "проход" мы подразумеваем полный просмотр входной информации. Это не строгое определение; во многих алгоритмах совсем не ясно количество выполненных проходов. Однако интуитивная концепция "прохода" полезна, несмотря на ее расплывчатость).

Рис.22. Проходы: (а) четырехпроходный алгоритм, (b) однопроходный алгоритм.
На рис.22(а) показана четырехпроходная обработка. Очень часто мы обнаруживаем, что тот же самый процесс может быть выполнен всего в один проход, как показано на рис.22(b), если мы заменим четырьмя сопрограммами A, B, C, D соответствующие проходы A, B, C, D. Сопрограмма A будет переходить к B, тогда как проход записывал бы элемент выходной информации на ленту 1; сопрограмма B будет переходить к A, тогда как проход читал бы элемент входной информации с ленты 1, и B будет переходить к C, тогда как проход B писал бы элемент выходной информации на ленту 2; и т.д.
И наоборот, процесс, реализованный с помощью n сопрограмм, часто можно трансформировать в n-проходный процесс. Поскольку существует такое соответствие, полезно сравнить многопроходные алгоритмы с однопроходными алгоритмами.
a) ПСИХОЛОГИЧЕСКОЕ РАЗЛИЧИЕ. Для решения одной и той же проблемы многопроходный алгоритм, как правило, легче создать и понять, чем однопроходный алгоритм. Процесс, разбитый на ряд небольших этапов, которые выполняются один за другим, легче понять, чем сложный процесс, в котором все происходит одновременно.
Кроме того, если речь идет о большой задаче и если разработкой программы для машины занимается большая группа людей, то многопроходный алгоритм естественным образом обеспечивает разделение работы.
Эти преимущества многопроходного алгоритма присущи также и сопрограммам, поскольку каждую из сопрограмм можно написать независимо от другой, а связь сводит явно многопроходный алгоритм к однопроходному процессу.
b) РАЗЛИЧИЕ ВО ВРЕМЕНИ. Время, необходимое на упаковку, запись, чтение и распаковку промежуточных данных между проходами (например, информации на лентах, см. рис.22), отсутствует в однопроходном алгоритме. Поэтому однопроходные алгоритмы быстрее.
c) РАЗЛИЧИЕ В ОБЪЕМЕ ПАМЯТИ. Однопроходный алгоритм требует места в оперативной памяти одновременно для всех программ, тогда как многопроходный алгоритм требует в каждый момент места только под одну программу. Это может повлиять на скорость даже в большей степени, чем то, о чем говорилось в пункте (b). Например, многие машины имеют ограниченный размер "быстрой памяти" и значительно большую медленную память; если каждый проход может уместиться в быстрой памяти, то результат будет получен значительно быстрее, чем в том случае, если мы используем сопрограммы в одном проходе (поскольку использование сопрограмм, по-видимому, приведет к тому, что большая часть программы окажется в медленной памяти).
Иногда существует необходимость разработать алгоритмы сразу для нескольких конфигураций машины, причем некоторые из них имеют объем памяти больший, чем другие. В этом случае можно было бы написать программу в виде сопрограмм и позволить памяти определять количество проходов: загружать вместе столько сопрограмм, сколько возможно, и компенсировать отсутствующие связи подпрограммами ввода или вывода.
Хотя это родство между сопрограммами и проходами важно, мы должны иметь в виду, что не во всех случаях, когда применяются сопрограммы, возможно расщепление на многопроходные алгоритмы. Например, если сопрограмма B получает входную информацию из A и передает в A информацию, определяющую дальнейшие действия, то преобразование A в проход, за которым следует проход B, становится невозможным.
И конечно, не все многопроходные алгоритмы можно преобразовать в сопрограммы. Некоторым алгоритмам внутренне присуща многопроходность; например, второй проход может требовать кумулятивную информацию от первого прохода (например, суммарное количество появлений некоторого слова во входной информации). Есть старая шутка, которую стоит напомнить в связи с этим.
Старушка, едущая в автобусе: "Мальчик, не скажешь ли, где мне выйти, чтобы попасть на улицу Пасадена?"
Мальчик: "Следите за мной и выходите за две остановки до меня".
(Шутка и состоит в том, что мальчик предлагает двухпроходный алгоритм).
Итак, о многопроходных алгоритмах сказано достаточно. Далее, во многих местах по всей этой книге мы встретимся с примерами сопрограмм, в частности, как с частью схемы буферизации. Сопрограммы играют также важную роль в моделировании дискретных систем...
***
Т.е. оправдать применение сопрограмм может только их сложность. А наша программа изначально проста. Как быть?

Д.КНУТ. ИСКУССТВО ПРОГРАММИРОВАНИЯ. ТОМ I
1.4.2. СОПРОГРАММЫ
Подпрограммы являются частным случаем более общих программных компонент, называемых "сопрограммами". Если отношения между главной программой и подпрограммой отличаются несимметричностью, то отношения между сопрограммами вполне симметричны, причем КАЖДОЙ из сопрограмм позволено ВЫЗЫВАТЬ ДРУГУЮ.
Чтобы понять концепцию сопрограмм, взглянем еще раз на подпрограммы, но с некоторой другой позиции. Точка зрения, принятая в предыдущем пункте, состояла в том, что подпрограмма является лишь расширением аппаратуры вычислительной машины, которое диктуется желанием сократить количество команд в программе. Может быть, это и так, но допустима и другая точка зрения. Мы можем рассматривать главную программу и подпрограмму как бригаду программ, в которой каждый член бригады обязан выполнять некоторое задание. Главная программа в процессе выполнения своего задания возбуждает подпрограмму; подпрограмма выполняет свою функцию и затем возбуждает главную программу. Мы могли бы напрячь воображение и поверить в то, что с точки зрения подпрограммы выход из нее есть не что иное, как вызов главной программы; главная программа продолжает выполнять свои обязанности, а затем "выходит" в подпрограмму. Теперь работает подпрограмма, и затем она снова вызывает главную программу.
Эти несколько отвлеченные рассуждения становятся вполне реальными, если речь заходит о сопрограммах, когда невозможно отличить, какая из них является подпрограммой другой. Предположим, что у нас есть две сопрограммы A и B; программируя A, мы можем рассматривать B как подпрограмму, но при программировании B мы можем считать, что A является нашей подпрограммой. Таким образом, в сопрограмме A команда "JMP B" используется для того, чтобы возбудить сопрограмму В. В свою очередь, для того чтобы возбудить сопрограмму A, в сопрограмме В используется команда "JMP A". Все это напоминает действия спортсменов в эстафетном беге. Как только сопрограмма активируется, она продолжает выполняться с того самого места, где она была приостановлена в последний раз.
В машине MIX такая связь между сопрограммами реализуется включением в программу следующих четырех команд:
A STJ BX
AX JMP A1
B STJ AX
BX JMP B1 (1)
Для передачи управления в сопрограмму затрачивается четыре машинных такта. Первоначально AX и BX настраиваются на переход в стартовые точки каждой сопрограммы, A1 и B1. Предположим, что первой выполняется команда из ячейки A1 в сопрограмме A. И когда, скажем в ячейке A2, встречается "JMP B", команда в ячейке B сохраняет rJ в AX. Следовательно, в AX окажется "JMP A2+1". Команда, находящаяся в BX, отправит нас в B1, и после этого начнет выполняться сопрограмма B, а в ней в некоторый момент, скажем в ячейке B2, встретится команда "JMP A". Мы сохраним rJ в BX и передадим управление в ячейку A2+1 и тем самым продолжим выполнение сопрограммы A до тех пор, пока вновь не встретится переход в B, в результате которого J сохранится в AX, а управление будет передано в B2+1 и т.д.
Существенное различие между двумя видами связи: программа - подпрограмма и сопрограмма - сопрограмма (и это можно увидеть, изучая приведенный выше пример), состоит в том, что подпрограмма всегда запускается СНАЧАЛА, т.е. с фиксированного места, в то время как главная программа или сопрограмма всегда продолжается С ТОГО МЕСТА, где ее работа была прекращена в последний раз.
На практике сопрограммы являются самым естественным средством при программировании алгоритмов ввода и вывода. Предположим, например, что сопрограмма A должна читать карты и выполнять некоторые преобразования вводимой информации, переводящие ее в последовательность элементов. Другая сопрограмма, которую мы назовем B, выполняет дальнейшую обработку этих элементов и печатает результаты; B будет периодически требовать последовательные входные элементы, получаемые в A. Таким образом, сопрограмма B передает управление A всякий раз, когда ей нужен следующий входной элемент, а сопрограмма A передает управление B всякий раз, когда входной элемент подготовлен. (Читатель может сказать: "Значит, B - основная программа, а A - просто ПОДПРОГРАММА, выполняющая ввод", Однако если процесс, выполняемый A, очень сложный, то это не совсем верно; мы можем даже представить себе A в качестве основной программы, а B - как подпрограмму, выполняющую вывод. При этом приведенное выше описание никоим образом не изменится). Полезность идеи сопрограмм становится очевидной, если мы находимся между этими двумя крайними случаями, т.е. тогда, когда как A, так и B сложны и каждая из них обращается к другой во многих местах. Довольно трудно найти короткие, простые примеры, которые иллюстрируют важность этой идеи; НАИБОЛЕЕ ПОЛЕЗНЫЕ ПРИМЕНЕНИЯ СОПРОГРАММ, КАК ПРАВИЛО, ОЧЕНЬ ДЛИННЫ [выделение мое.- G.].
Чтобы изучить сопрограммы в действии, рассмотрим "надуманный" пример. Предположим, что мы хотим написать программу, которая переводит один код в другой. Входной (транслируемый) код представляет последовательность алфавитно-цифровых литер, оканчивающуюся точкой, например:
A2B5E3426FG0ZYW3210PQ89R. (2)
Такая последовательность перфорируется на картах; пустые колонки (пробелы), встречающиеся на картах, игнорируются. Эту входную информацию следует понимать таким образом (слева направо): если следующая литера - цифра (т.е., 0, 1, ..., 9), скажем n, то это есть указание об n + 1 повторениях следующей литеры независимо от того, является следующая литера цифрой или нет. Нецифровая литера обозначает только себя. Выходом нашей программы должна быть последовательность, полученная указанным образом и разделенная на группы по три литеры в каждой (причем в последней группе может быть меньше чем три литеры). Например, (2) необходимо преобразовать в такую форму:
ABB BEE EEE E44 444 66F GZY W22 220 0PQ 999 999 999 R. (3)
Обратите внимание, что 3426F не означает 3427 повторений буквы F; в результате появляется 4 четверки, 3 шестерки и затем буква F. Наша программа должна отперфорировать результат на картах, по шестнадцать групп на каждой карте.
Для выполнения такого перевода мы напишем две сопрограммы и подпрограмму. Подпрограмма, названная NEXTCHAR, находит следующую литеру, не являющуюся пробелом, во входной последовательчосги и помещает ее в регистр A:
01 * ПОДПРОГРАММА ВВОДА ЛИТЕРЫ
02 READER EQU 16 Номер читающего устройства.
03 INPUT ORIG *+16 Место для входных карт.
04 NEXTCHAR STJ 9F Вход в подпрограмму.
05 - JXNZ 3F Первоначально rX = 0.
06 1H J6N 2F Первоначально rI6 = 0.
07 - IN INPUT(READER) Прочитать следующую карту.
08 - JBUS *(READER) Ждать завершения.
09 - ENN6 16 rI6 указывает на первое слово.
10 2H LDX INPUT+16,6 Взять следующее слово.
11 - INC6 1 Продвинуть стрелку.
12 3H ENTA 0
13 - SLAX 1 Следующая литера ->rA.
14 9H JANZ Пропуск пробелов.
15 - JMP NEXTCHAR+1 []
Эта подпрограмма имеет следующие характеристики:
- Вызов: JMP NEXTCHAR
- Состояние при входе: rI6 указывает на следующее слово, или rI6 = 0, если необходимо прочесть следующую карту; rX = литеры, которые еще будут обрабатываться.
- Состояние при выходе: rA = следующая входная литера (не пробел); rX, rI6 подготовлены для следующего входа в NEXTCHAR.
Наша первая сопрограмма, с названием IN, получает символы из входной последовательности и создает соответствующее количество дубликатов:
16 * ПЕРВАЯ СОПРОГРАММА
17 2H INCA 30 Литера - не цифра.
18 - JMP OUT Передать ее в сопрограмму.
19 IN1 JMP NEXTCHAR Взять литеру.
20 - DECA 30
21 - JAN 2B Буква?
22 - CMPA =10=
23 - JGE 2B Специальная литера?
24 - STA *+1(0:2) Цифра n.
25 - ENT5 * rI5<-n.
26 - JMP NEXTCHAR Взять следующую литеру.
27 - JMP OUT Передать ее в сопрограмму.
28 - DEC5 1 Уменьшить n на 1.
29 - J5NN *-2 Повторить, если это необходимо.
30 - JMP IN1 Начать новый цикл. []
(Напомним, что для MIX цифры 0-9 имеют коды 30-39). Эта сопрограмма имеет следующие характеристики:
- Вызов: JMP IN
- Состояние при выходе (при переходе к OUT): rA = очередная входная литера с учетом размножения; rI4 не изменяет свое значение с момента входа.
- Состояние при входе (после возврата): rA, rX, rI5, rI6 не должны изменять своих значений с момента последнего выхода.
Другая сопрограмма, с названием OUT, размещает код по три литеры и перфорирует карты:
31 * ВТОРАЯ СОПРОГРАММА
32 _ ALF _ Константа для занесения пробелов.
33 OUTPUT ORIG *+16 Буферная область для ответов.
34 PUNCH EQU 17 Номер устройства (перфоратора).
35 OUT1 ENT4 -16 Начать новую карту.
36 - ENT1 OUTPUT
37 - MOVE -1,1(16) Занести пробелы в область вывода.
38 1H JMP IN Взять следующую литеру.
39 - STA OUTPUT+16,4(1:1) Занести в выходную карту.
40 - СМРА PERIOD Это "."?
41 - JE 9F
42 - JMP IN Если нет, то взять следующую литеру.
43 - STA OUTPUT+16,4(2:2) Занести ее.
44 - СМРА PERIOD Это "."?
45 - JE 9F
46 - JMP IN Если нет, то взять следующую литеру.
47 - STA OUTPUT+16,4(3:3) Занести ее.
48 - СМРА PERIOD Это "."?
49 - JE 9F
50 - INC4 1 Перейти к следующему слову.
51 - J4N 1B Конец карты?
52 9H OUT OUTPUT(PUNCH) Если да, то перфорация.
53 - JBUS *(PUNCH) Ждать завершения.
54 - JNE OUT1 Возвратиться и продолжить, если не была принята ".".
55 - HLT
56 PERIOD ALF . []
Эта сопрограмма имеет следующие характеристики:
- Вызов: JMP OUT
- Состояние при выходе (при переходе к IN): rA, rX, rI5, rI6 сохраняют те значения, которые были при входе.
- Состояние при входе (при возврате): rA = (следующая входная литера с учетом размножения); значение r4 сохранилось с момента последнего выхода.
Чтобы завершить программу, мы должны обеспечить связь между сопрограммами [см. (1)] и соответствующие начальные установки. Начальные установки в сопрограммах требуют некоторой изобретательности, хотя и не создают заметных затруднений.
57 * НАЧАЛЬНАЯ УСТАНОВКА И СВЯЗЬ
58 START ENT6 0 Подготовить rI6 для NEXTCHAR.
59 - ENTX 0 Подготовить rX для NEXTCHAR.
60 - JMP OUT1 Начать с OUT.
61 OUT STJ INX Связь сопрограмм.
62 OUTX JMP OUT1
63 IN STJ OUTX
64 INX JMP INI
65 - END START []
Теперь программа написана полностью. Читателю следует тщательно изучить ее, обращая особое внимание на то, как можно написать каждую из сопрограмм независимо, в предположении, что другая сопрограмма является ее подпрограммой.
В программе, приведенной выше, состояния входа и выхода для IN и OUT полностью согласованы. Общий случай может оказаться менее удачным, и тогда для связи сопрограмм потребуется также загрузка и запоминание соответствующих регистров. Например, если сопрограмма OUT изменяет содержимое регистра А, то группа команд для связи сопрограмм примет следующий вид:
OUT STJ INX
- STA HOLD A Запомнить А при выходе из IN.
OUTX JMP OUT1
IN STJ OUTX
- LDA HOLDA Восстановить А при выходе из OUT.
INX JMP IN1
Существует важное родство между сопрограммами и МНОГОПРОХОДНЫМИ АЛГОРИТМАМИ. Например, процесс перевода, который мы только что описали, можно было бы выполнить за два отдельных прохода. Во-первых, мы могли бы сделать в точности то, что делает сопрограмма IN, применяя ее ко всей входной информации и записывая каждую литеру с соответствующим числом дубликатов на магнитную ленту. После того как эта обработка закончится, мы могли бы перемотать ленту в начало и затем сделать в точности то, что делает сопрограмма OUT, принимая литеры с ленты группами по три. Это называют "двухпроходной" обработкой. (Интуитивно под словом "проход" мы подразумеваем полный просмотр входной информации. Это не строгое определение; во многих алгоритмах совсем не ясно количество выполненных проходов. Однако интуитивная концепция "прохода" полезна, несмотря на ее расплывчатость).

Рис.22. Проходы: (а) четырехпроходный алгоритм, (b) однопроходный алгоритм.
На рис.22(а) показана четырехпроходная обработка. Очень часто мы обнаруживаем, что тот же самый процесс может быть выполнен всего в один проход, как показано на рис.22(b), если мы заменим четырьмя сопрограммами A, B, C, D соответствующие проходы A, B, C, D. Сопрограмма A будет переходить к B, тогда как проход записывал бы элемент выходной информации на ленту 1; сопрограмма B будет переходить к A, тогда как проход читал бы элемент входной информации с ленты 1, и B будет переходить к C, тогда как проход B писал бы элемент выходной информации на ленту 2; и т.д.
И наоборот, процесс, реализованный с помощью n сопрограмм, часто можно трансформировать в n-проходный процесс. Поскольку существует такое соответствие, полезно сравнить многопроходные алгоритмы с однопроходными алгоритмами.
a) ПСИХОЛОГИЧЕСКОЕ РАЗЛИЧИЕ. Для решения одной и той же проблемы многопроходный алгоритм, как правило, легче создать и понять, чем однопроходный алгоритм. Процесс, разбитый на ряд небольших этапов, которые выполняются один за другим, легче понять, чем сложный процесс, в котором все происходит одновременно.
Кроме того, если речь идет о большой задаче и если разработкой программы для машины занимается большая группа людей, то многопроходный алгоритм естественным образом обеспечивает разделение работы.
Эти преимущества многопроходного алгоритма присущи также и сопрограммам, поскольку каждую из сопрограмм можно написать независимо от другой, а связь сводит явно многопроходный алгоритм к однопроходному процессу.
b) РАЗЛИЧИЕ ВО ВРЕМЕНИ. Время, необходимое на упаковку, запись, чтение и распаковку промежуточных данных между проходами (например, информации на лентах, см. рис.22), отсутствует в однопроходном алгоритме. Поэтому однопроходные алгоритмы быстрее.
c) РАЗЛИЧИЕ В ОБЪЕМЕ ПАМЯТИ. Однопроходный алгоритм требует места в оперативной памяти одновременно для всех программ, тогда как многопроходный алгоритм требует в каждый момент места только под одну программу. Это может повлиять на скорость даже в большей степени, чем то, о чем говорилось в пункте (b). Например, многие машины имеют ограниченный размер "быстрой памяти" и значительно большую медленную память; если каждый проход может уместиться в быстрой памяти, то результат будет получен значительно быстрее, чем в том случае, если мы используем сопрограммы в одном проходе (поскольку использование сопрограмм, по-видимому, приведет к тому, что большая часть программы окажется в медленной памяти).
Иногда существует необходимость разработать алгоритмы сразу для нескольких конфигураций машины, причем некоторые из них имеют объем памяти больший, чем другие. В этом случае можно было бы написать программу в виде сопрограмм и позволить памяти определять количество проходов: загружать вместе столько сопрограмм, сколько возможно, и компенсировать отсутствующие связи подпрограммами ввода или вывода.
Хотя это родство между сопрограммами и проходами важно, мы должны иметь в виду, что не во всех случаях, когда применяются сопрограммы, возможно расщепление на многопроходные алгоритмы. Например, если сопрограмма B получает входную информацию из A и передает в A информацию, определяющую дальнейшие действия, то преобразование A в проход, за которым следует проход B, становится невозможным.
И конечно, не все многопроходные алгоритмы можно преобразовать в сопрограммы. Некоторым алгоритмам внутренне присуща многопроходность; например, второй проход может требовать кумулятивную информацию от первого прохода (например, суммарное количество появлений некоторого слова во входной информации). Есть старая шутка, которую стоит напомнить в связи с этим.
Старушка, едущая в автобусе: "Мальчик, не скажешь ли, где мне выйти, чтобы попасть на улицу Пасадена?"
Мальчик: "Следите за мной и выходите за две остановки до меня".
(Шутка и состоит в том, что мальчик предлагает двухпроходный алгоритм).
Итак, о многопроходных алгоритмах сказано достаточно. Далее, во многих местах по всей этой книге мы встретимся с примерами сопрограмм, в частности, как с частью схемы буферизации. Сопрограммы играют также важную роль в моделировании дискретных систем...
***
Т.е. оправдать применение сопрограмм может только их сложность. А наша программа изначально проста. Как быть?
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:22 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

Стартстопный телеграфный аппарат. Такой стоял вместо терминала на одной из ЭВМ, с которой я работал. Двухленточный агрегат: умел и работать с перфолентой, и выдавать родную телеграфную ленту: "ВРАНГЕЛЬ ОПРАКИНУТ МОРЕ ТЧК ПЛЕНЫХ НЕТ ТЧК".
Из Сборника АВТОМАТЫ (1956).
УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ ВНУТРЕННИМИ СОСТОЯНИЯМИ
КЛОД Э.ШЕННОН
ВВЕДЕНИЕ
В известной статье [Turing A.М., On Computable Numbers, with an Application to the Entscheidungsproblem, Proc. London Math. Soc., (2) 42, 230-265 (1936)] А.М.Тьюринг определил класс вычислительных машин, называемых ныне машинами Тьюринга. Можно представлять себе, что машина Тьюринга состоит из трех частей: управляющего элемента, считывающей и записывающей головки и бесконечной ленты. Лента разделена на последовательность квадратов, каждый из которых может хранить любой символ из конечного алфавита. Считывающая головка в каждый данный момент воспринимает один квадрат ленты. Она может прочесть записанный там символ и под действием управляющего элемента записать новый символ, а также передвинуться на один квадрат вправо или влево. Управляющий элемент представляет собой устройство с конечным числом внутренних "состояний". В каждый данный момент ближайшая операция машины определяется текущим состоянием управляющего элемента и символом, воспринимаемым считывающей головкой. Эта операция состоит из трех частей: 1) записи нового символа в воспринимаемом квадрате (новый символ, конечно, может совпадать с только что прочитанным); 2) перехода управляющего элемента в новое состояние (которое может совпадать с предыдущим состоянием); 3) движения считывающей головки на один квадрат вправо или влево [Иногда предполагают, что считывающая головка может также оставаться на месте.- Прим. ред.].
При подготовке машины к работе на некоторый конечный кусок ленты наносится начальная последовательность символов, а остальная часть ленты оставляется пустой (т.е. заполненной некоторым "пустым" символом). Считывающая головка помещается в некотором начальном квадрате, и машина приступает к вычислениям согласно правилам своей работы. В первоначальной формулировке Тьюринга квадраты через один предназначались для записи окончательного ответа и для промежуточных вычислений. Эта и другие подробности первоначального определения были изменены в позднейших изложениях теории.
Тьюринг показал, что возможно построить универсальную машину, способную работать, как любая частная машина Тьюринга, если ее снабдить описанием этой частной машины. Описание наносится на ленту универсальной машины по определенному коду, подобно начальной последовательности частной машины. Тогда универсальная машина воспроизводит работу частной.
Наша главная цель - показать, что можно построить универсальную машину Тьюринга, использующую одну ленту и имеющую лишь два внутренних состояния. Будет показано также, что с одним внутренним состоянием этого сделать нельзя. В заключение этой статьи дается построение универсальной машины Тьюринга с двумя только символами на ленте.
УНИВЕРСАЛЬНАЯ МАШИНА ТЬЮРИНГА С ДВУМЯ СОСТОЯНИЯМИ
В общих чертах метод построения таков. Для произвольной машины Тьюринга A с алфавитом из m букв (символов, записываемых на ленте, включая пустой квадрат) и с n внутренними состояниями мы построим машину B с двумя внутренними состояниями и алфавитом не более чем из 4mn+m символов. Машина B будет работать, по существу, так же, как и машина A. Во всех квадратах, кроме воспринимаемого считывающей головкой и одного смежного с ним, на ленте машины B записано то же, что и на ленте машины A в соответствующие моменты работы двух машин. Если в качестве A выбрать универсальную машину Тьюринга, то и B будет универсальной машиной Тьюринга.
Машина B моделирует поведение машины A, но хранит информацию о внутреннем состоянии машины A с помощью символов, записанных в квадрате под считывающей головкой и в квадрате, который считывающая головка машины A собирается посетить. Основная задача - своевременно освежать эту информацию и держать ее под считывающей головкой. Если последняя передвигается, то информацию о состоянии надо перенести в новый квадрат, используя всего два внутренних состояния машины B. Пусть, например, следующим состоянием машины A должно быть состояние 17 (согласно какой-нибудь системе счисления). Чтобы перенести его символ, считывающая головка "качается" вперед-назад между старым и новым квадратом 17 раз (точнее 18 раз в новый квадрат и 17 назад в старый). В течение этого процесса символ, стоящий в новом квадрате, пробегает своего рода последовательность счета, которая оканчивается символом, соответствующим состоянию 17 и в то же время сохраняющим информацию о предыдущем символе в этом квадрате. Процесс качания возвращает также старый квадрат к одному из элементарных символов (находящихся во взаимно однозначном соответствии с символами, используемыми машиной A), а именно к тому элементарному символу, который должен быть записан в этом квадрате после окончания этой операции.
Формально машина B строится так. Пусть символы алфавита машины A суть A1, A2, ..., Am, и пусть ее состояния суть S1, S2, ..., Sn. В машине B мы поставим в соответствие алфавиту машины A m элементарных символов B1, B2, ..., Вm. Затем мы определим 4mn новых символов, соответствующих парам из состояния и символа машины A, снабженным двумя новыми двузначными индексами. Эти символы обозначим через B[i,j,x,y] где i = 1, 2, ..., m (соответственно символам), j = 1, 2, ..., n (соответственно состояниям), x = + или - (в зависимости от того, передает или получает информацию квадрат ленты во время качания) и y = R или L (в зависимости от того, вправо или влево от воспринимаемого квадрата должна передвинуться считывающая головка при качании).
Два состояния машины B назовем альфа и бета. Эти состояния используются двояко. Во-первых, при первом шаге качания они переносят в ближайший подлежащий посещению квадрат информацию о том, вправо (альфа) или влево (бета) от нового квадрата лежит старый квадрат. Эта информация нужна в новом квадрате, чтобы управляющий элемент передвинул считывающую головку назад в нужном направлении. После первого шага информация об этом сохраняется в новом квадрате с помощью записанного там символа (последний индекс y). Во-вторых, состояния альфа и бета используются, чтобы сообщить из старого квадрата в новый о конце качания. После первого шага качания состояние бета переносится в новый квадрат вплоть до конца качания, когда переносится альфа. Это означает конец операции, и новый квадрат начинает затем действовать как передатчик и управляет следующим шагом вычисления.
Описывая машину B, указывают, что она выполняет при чтении произвольного символа в произвольном состоянии. Выполняет же она три акта: записывает новый символ, переходит в новое состояние и передвигает считывающую головку вправо или влево. Таблица работы машины B такова:
символ; состояние -> символ; состояние; направление
Bi; альфа -> B[i,1,-,R]; альфа; R (i = 1, 2, ..., m) (1)
Bi; бета -> B[i,1,-,L]; альфа; L (i = 1, 2, ..., m) (2)
B[i,j,-,x]; бета -> B[i,(j+1),-,x]; альфа; x (i = 1, 2, ..., m) (j = 1, 2, ..., n-1) (x = R, L) (3)
B[i,j,+,x]; альфа или бета -> B[i,(j-1),+,x]; бета; x (i = 1, 2, ..., m) (j = 1, 2, ..., n) (x = R, L) (4)
B[i,1,+,x]; альфа или бета -> Bi; алфа; x (i = 1, 2, ..., m) (x = R, L) (5)
Эти операции пока что никак не зависят от таблицы работы машины A (кроме числа используемых символов). Операции же следующего и последнего типа формулируются в терминах таблицы работы моделируемой машины. Предположим, что машина A имеет формулу операций
Ai; Sj -> Ak; Sl; R/L. (6)
Тогда, по определению, машина B имеет формулу
B[i,j,-,x]; альфа -> B[k,l,+,R/L]; бета/альфа; R/L, (7)
причем, если в формуле (6) употреблена верхняя буква (R), то верхние буквы употребляются также и в формуле (7) и обратно.
Чтобы увидеть, как работает эта система, мы проследим цикл, состоящий из одной операции машины A и соответствующей серии операций машины B.
Пусть машина A читает символ A3 и находится в состоянии S7, и пусть ее таблицей работы предусмотрена запись символа A8, переход в состояние S4 и движение вправо. Машина B читает (по индуктивному предположению) символ B[3,7,-,x] (значение х (R или L) зависит от предыдущих операций и безразлично для дальнейшего). Машина B будет находиться в состоянии альфа. Ввиду формулы (7) машина B запишет В[8,4,+,r], перейдет в состояние бета и передвинется вправо. Предположим, что квадрат справа в машине A содержит А13; соответствующий квадрат в машине B содержит В13. Приходя в этот квадрат в состоянии бета, машина B в силу формулы (2) записывает B[13,1,-,L], переходит в состояние альфа и движется назад, влево. Это служит началом переноса информации о состоянии с помощью процесса качания. Приходя в квадрат слева, машина B читает B[8,4,+,R] и в силу формулы (4) записывает B[8,3,+,R], переходит в состояние бета и передвигается опять вправо. Затем в силу формулы (3) она записывает B[13,2,-,L], переходит в состояние альфа и возвращается налево. Весь ход процесса приведен, в табл.1.
Таблица 1.

Указанные операции завершают перенос информации о состоянии в квадрат справа и выполнение команды, отданной квадратом слева. В квадрате слева записан теперь символ B8 (соответствующий символу A8 в машине A), а в квадрате справа - символ B[13,4,-,L]; считывающая головка находится на этом квадрате, имея внутреннее состояние альфа. Это возвращает нас к ситуации, аналогичной той, которая имела место в начале рассмотренного цикла. Рассуждая по индукции, мы видим, что машина B моделирует поведение машины A.
Чтобы заставить машину B работать аналогично машине А, мы заполняем начальную ленту машины B соответственно начальной ленте машины A (с заменой Ai на Bi, за исключением квадрата, занимаемого считывающей головкой в начальный момент. Если Sj - начальное состояние машины A и Ai - начальный символ в этом квадрате, то в соответствующем квадрате ленты машины B записываем B[i,j,-,R (или L)] и приводим B в состояние альфа.
НЕВОЗМОЖНОСТЬ УНИВЕРСАЛЬНОЙ МАШИНЫ ТЬЮРИНГА С ОДНИМ СОСТОЯНИЕМ
Теперь мы покажем, что нельзя построить универсальную машину Тьюринга, использующую одну ленту и одно только внутреннее состояние.
Допустим, что такая машина существует. Если записать подходящее "описательное число" конечной длины на куске ленты (оставив прочую часть ленты пустой) и поместить считывающую головку в подходящий квадрат, то машина будет вычислять любое вычислимое число и, в частности, вычислимые иррациональные числа, например sqr(2) (квадратный корень из двух). Мы покажем, что это невозможно.
Согласно первоначальному замыслу Тьюринга, при вычислении sqr(2) последовательные знаки sqr(2) (скажем, в двоичном представлении) записываются машиной на определенной последовательности квадратов ленты (например, на четных квадратах, тогда как нечетные предназначаются для промежуточных вычислений). Приводимое ниже доказательство исходит из вычисления sqr(2) в таком виде, хотя будет ясно, что, изменив доказательство, можно принять во внимание и другие разумные интерпретации "вычисления sqr(2)".
Ввиду иррациональности sqr(2) его двоичные знаки не станут периодическими ни с какого места. Поэтому если мы покажем, для машины с одним состоянием, что или (1) во всех ее квадратах, кроме конечного числа, будет в конце концов записан один и тот же символ, или (2) во всех квадратах, кроме конечного числа, символы будут без конца сменяться, то тем самым будет получен желаемый результат.
Сначала возьмем ленту, пустую и бесконечную в обе стороны от описательного числа для sqr(2). Если считывающая головка приходит на пустой квадрат, то она должна или остановиться здесь на все время, или же передвинуться вправо либо влево. Так как имеется лишь одно состояние, то ее поведение не зависит от предшествовавшего вычисления. В первом случае считывающая головка никогда не отойдет дальше чем на один квадрат от описательного числа и вся лента, кроме конечного отрезка, будет постоянно пуста. Если же головка передвигается влево с некоторого пустого квадрата, то или левая бесконечная часть пустой ленты не участвует в вычислении и поэтому не требует рассмотрения, или, если она участвует в вычислении, считывающая головка с этого времени беспрерывно движется влево, записывая во всех квадратах, ранее пустых, один и тот же символ. Следовательно, лента становится одинаковой всюду слева от некоторого конечного отрезка и пустой справа от него и не может давать записи числа sqr(2). Аналогичное положение возникает при движении головки вправо от первоначально пустого квадрата. Поэтому двусторонне бесконечная лента ничуть не лучше односторонней, и мы можем из соображений симметрии предположить, что лента односторонне бесконечна вправо от описательного числа.
Теперь рассмотрим следующую операцию. Поместим считывающую головку в первом квадрате бесконечной пустой полосы [Справа от описательного числа.- Прим. ред.]. Машина будет вычислять некоторое время, и, быть может, считывающая головка переместится назад из этой полосы по направлению к описательному числу. Тогда возвратим ее снова в первый квадрат первоначально пустой полосы. Если головка опять переместится к описательному числу, то опять поместим ее в этом первом квадрате и т.д. Число раз, которое головку можно поместить таким образом над этим первым квадратом, будет называться числом отражений машины и обозначаться через R. Оно равно или целому числу 1, 2, 3, ..., или бесконечность.
Теперь поместим считывающую головку в квадрат описательного числа, являющийся начальным для предполагаемого вычисления sqr(2). Спустя некоторое время считывающая головка, возможно, выйдет из части ленты, где записано описательное число. Возвратим ее в последний квадрат описательного числа. Спустя некоторое время она, возможно, опять выйдет. Продолжим этот процесс до тех пор, пока это возможно. Число выходов головки равно или целому числу 0, 1, 2, 3, ..., или бесконечность. Это число S мы назовем числом отражений для данного описания sqr(2).
Если S конечно и R (может быть бесконечность) >= S, то спустя конечное время считывающая головка застрянет в части ленты, где первоначально находилось описательное число. Изменится лишь конечная часть пустой ленты, и машина не вычислит sqr(2).
Если как R, так и S бесконечны, то считывающая головка будет возвращаться неограниченное число раз в часть ленты с описательным числом. Экскурсии в первоначально пустую часть или ограничены по длине, или нет. Если они ограничены, то изменится лишь конечная часть пустой ленты, как и в предыдущем случае. Если же нет, то вся лента, кроме конечной части, будет обрабатываться считывающей головкой неограниченное число раз. Так как имеется только одно состояние и алфавит символов конечен, то символ, записываемый в квадрате, который посещается неограниченное число раз, должен или стать постоянным (одним и тем же для всех таких квадратов), или изменяться циклически бесконечное число раз. В первом случае вся первоначально пустая лента становится одинаковой и не может изображать sqr(2). Во втором случае она непрерывно изменяется и не может изображать никакого результата вычисления.
[Рассуждения автора здесь не вполне ясны, и, кроме того, он использует условие конечности алфавита символов не по существу. Можно дать другое доказательство, без предположения, что число символов конечно.
Пусть вся лента, кроме конечной ее части, обрабатывается головкой неограниченное число раз. A priori возможны два случая: либо во всяком квадрате, кроме конечного их числа, символы сменяются неограниченное число раз (и тогда, очевидно, запись на ленте не может представлять результат вычисления sqr(2)), либо это не так. Во втором случае сколь угодно далеко найдется квадрат q, обладающий тем свойством, что, начиная с некоторого момента, символ в q не изменяется (обозначим этот символ через C); тогда q можно выбрать так, чтобы слева от q имелся некоторый квадрат q*, в который головка возвращается неограниченное число раз.
Пусть головке предписано сдвинуться вправо по прочтении символа C. Тогда головка, попав на квадрат q, после того как в нем постоянно записывается символ C, не сможет, начиная с этого момента, попасть в q*. Аналогично, если по прочтении символа C головка должна сдвинуться влево, то она не сможет, начиная с некоторого момента, посетить квадраты, лежащие правее q.
Это говорит о том, что второй из двух a priori возможных случаев не может иметь места. Итак, возможен лишь первый случай, при котором машина не вычислит sqr(2).
Так как в остальных частях доказательства Шеннон нигде не опирается на условие конечности алфавита символов, то можно считать его теорему справедливой также для "машин", работающих с бесконечным числом символов (и одним состоянием).- Прим. ред.]
Если R < S, то считывающая головка в конце концов уйдет в первоначально пустую часть ленты и там останется. Можно показать, что в этом случае символы в первоначально пустой части становятся, за исключением конечного их числа, одинаковыми. В самом деле, либо головка передвигается вправо из первого пустого квадрата во второй пустой квадрат по меньшей мере R+1 раз, либо нет. В последнем случае спустя конечное время считывающая головка застревает в бывшем первом пустом квадрате, и вся лента, кроме конечной части, остается пустой. Если же головка уходит вправо R+1 раз, то она не вернется в первый квадрат, первоначально пустой, ибо R есть число отражений для пустой ленты. В этом первом квадрате будет записан результат 2R+1 действий над пустым квадратом (при R+1 приходах головки слева и R приходах справа). Во втором первоначально пустом квадрате в конце концов будет записан тот же самый постоянный символ, потому что ко второму квадрату применимо такое же рассуждение, как и к первому. Во всех случаях машина работает на той же самой ленте (бесконечном ряде пустых квадратов) и приходит одно и то же число раз справа (R) и, соответственно, слева (R+1). Тем самым все возможные случаи исчерпаны и доказательство завершено.
МОДЕЛИРОВАНИЕ МАШИНЫ ТЬЮРИНГА С ПОМОЩЬЮ ТОЛЬКО ДВУХ СИМВОЛОВ НА ЛЕНТЕ
Теперь мы покажем, что можно также построить машину C, работающую подобно любой заданной машине Тьюринга A и использующую только два символа 0 и 1 на своей ленте; один из них, например 0, служит символом пустого квадрата. Пусть по прежнему заданная машина A имеет m символов и n внутренних состояний. Пусть l - наименьшее целое число, для которого m<2**l.
Тогда символам машины A можно сопоставить двоичные последовательности длины l таким образом, что различным символам будут соответствовать различные же последовательности. При этом пустому символу машины A мы ставим в соответствие последовательность из l нулей. Машина C будет работать с двоичными последовательностями. Элементарная операция машины A будет соответствовать в машине C переходу считывающей головки на l-1 квадратов вправо (с сохранением считанной информации во внутреннем состоянии головки), затем обратному переходу на l-1 квадратов влево, записи новых символов по пути и, наконец, движению вправо или влево на l квадратов, в соответствии с движением считывающей головки машины A. В течение этого процесса состояние машины A, конечно, сохраняется и в машине C. Замена старого состояния новым происходит в конце операции считывания.
Формально машина C строится так. Состояниям S1, S2, ..., Sn машины A мы ставим в соответствие состояния T1, T2, ..., Tn машины C (последние будут встречаться, когда машина C начинает операцию, считывая первый символ в двоичной последовательности длины l). Для каждого из этих Ti определим два состояния Ti0 и Ti1 Если машина C находится в состоянии Ti и читает символ 0, то она движется вправо и переходит в состояние Ti0. Если она читает 1, то движется вправо и переходит в состояние Ti1 Таким образом, с помощью этих двух состояний машина запоминает, каким был первый символ двоичной последовательности. Для каждого из этих Ti0 и Ti1 определим опять по два состояния: Ti00, Ti01 и Ti10, Ti11. Если, например, машина находится в состоянии Ti0 и читает символ 0, то она переходит в состояние Ti00 и т.д. Таким образом, с помощью этих состояний запоминается начальное состояние и два первых символа, прочитанных в процессе работы машины. Продолжим такое построение состояний вплоть до l-1 шагов, получив в итоге (2**l-1)n состояний. Эти состояния можно обозначить через
T[i,x1,x2,...,xs]; i = 1, 2, ..., n; xj = 0, 1; s = 0, 1, ..., l-1.
Если машина находится в одном из этих состояний (s < l-1) и читает 0 или 1, то она движется вправо и 0 или 1 делается дальнейшим индексом состояния. Когда s = l-1, машина читает последний символ последовательности длины l. Теперь правила операций зависят от конкретных правил машины A. Определим два новых множества состояний, которые несколько похожи на введенное выше множество состояний T, но соответствуют не считыванию, а записи:
R[i,x1,x2,...,xs] и L[i,x1,x2,...,xs].
Последовательность x1, x2, ..., x[l-1], xl соответствует некоторому символу машины A. Предположим, что если машина A читает этот символ и находится в состоянии i, то она записывает символ, соответствующий двоичной последовательности y1, y2, ..., y[l-1], yl, переходит в состояние j и движется, скажем, вправо. Тогда, по определению, машина C, будучи в состоянии T[i,x1,x2,...,x[l-1]] и читая символ хl переходит в состояние R[i,y1,y2,...,y[l-1]], записывает символ y1 и движется влево. В любом из состояний R[i,y1,y2,...,ys] (или L[i,y1,y2,...,ys]) машина C записывает ys, движется влево и переходит в состояние R[i,y1,y2,...,y[s-1]] (или L[i,y1,y2,...,y[s-1]]). Посредством этого процесса двоичная последовательность, соответствующая новому символу, записывается вместо старой двоичной последовательности. При s = 1 эта запись заканчивается на символе y1. Остается только передвинуть считывающую головку на l квадратов вправо или влево, в зависимости от того, находится ли машина в состоянии R или в состоянии L. Это делается с помощью множеств состояний Uis и Vis (i = 1, 2, ..., n; s = 1, 2, ..., l-1). В состоянии R[i,x1] машина записывает x1, движется вправо и переходит в состояние Ui1. В каждом из состояний U машина продолжает движение вправо, не записывая ничего и переходя в состояние U со следующим по величине индексом, пока не будет достигнуто последнее состояние U. Таким образом, Uis вызывает движение вправо и состояние U[i,(s+1)] (s < l-1). Наконец состояние U[i,(l-1)] приводит - после движения вправо - к состоянию Ti, завершая тем самым цикл. Аналогично, L[i,x[1]] приводит к движению влево и состоянию Vi1; Vis дает движение влево и V[i,(s+1)] (s < l-1); наконец V[i,(l-1)] дает движение влево и Тi.
Начальная лента машины C представляет собой, конечно, начальную ленту машины A, где каждый символ замещен соответствующей ему двоичной последовательностью. Ecли работа машины A начинается с какого-то определенного символа, то работа машины С начнется с самого левого двоичного символа соответствующей группы; если машина A начинает работу в состоянии Si, то C начнет работу в состоянии Ti.
Машина C имеет самое большее n(1 + 2 + 4 + ... + 2**(l-1)) = n(2**l - 1) состояний T, самое большее n(2**l - 2) состояний R и n(2**l - 2) состояний L и, наконец, 2n{l-1) состояний U и V. Таким образом, всего требуется не более чем 3n(2**l) + n(2l - 7) состояний. Так как 2**l < 2m, то эта верхняя граница числа состояний меньше, чем 6mn + n(2l - 7), что, в свою очередь, заведомо меньше, чем 8mn.
Полученные нами результаты вместе с интуитивными соображениями подсказывают, что можно заменять символы состояниями и обратно (в некоторых пределах), не изменяя намного произведения mn. При переходе к двум состояниям произведение возрастает приблизительно в восемь раз. При переходе к двум символам произведение возрастает приблизительно в шесть раз, но не более чем в восемь раз. Эти "коэффициенты потерь" - 6 и 8,- вызваны, вероятно, нашим методом микроскопического моделирования, при котором каждая элементарная операция машины A моделируется в машине B. Если конструировать машину B, заботясь лишь о том, чтобы она имела те же вычислительные возможности в широком смысле, что и машина A, то произведение mn изменилось бы значительно меньше. Во всяком случае, число логических элементов (например, реле), необходимых для физической реализации машины, является небольшим постоянным кратным (приблизительно двукратным в случае реле) двоичного логарифма произведения mn, и потому коэффициент 6 или 8 потребует лишь немногих дополнительных реле.
Интересная нерешенная задача - найти минимальное произведение mn для универсальной машины Тьюринга.
***
Таким, образом даже на такой простой модели можно заметить идеи возникновения подпрограмм (как элементарных действий, которые, в силу ограниченности машины, приходится реализовать многочисленным повторением элементарных операций); и организации массивов, как множеств символов/состояний, обладающих одинаковыми свойствами.
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:20 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

В МИРЕ НАУКИ 6/84
А.П.ЕРШОВ
СМЕШАННЫЕ ВЫЧИСЛЕНИЯ
Узкоспециализированные, но эффективные способы решения задач традиционно противопоставляются универсальным, но менее эффективным методам. Смешанные вычисления, осуществляя совместную обработку программы и ее данных, позволяют систематически получать из универсальной программы ее эффективные специализированные версии, не утрачивая знания, заложенного в общий метод
ОДНО ИЗ основных применений ЭВМ заключается в решении задач. Говоря о задаче, мы различаем ее условие, способ ее решения и само решение, результат. Условие задачи обычно обладает определенной степенью общности. В формулировку условия входит один или несколько параметров, называемых исходными данными, так что это условие имеет смысл для некоторого множества значений исходных данных.
Общность условия задачи стимулирует исследователя на поиск общего способа ее решения, т.е. таких правил, которые, будучи некоторым единым образом применены к исходным данным, гарантируют нахождение решения. Поиск общих, или универсальных, методов образует одну из главных парадигм современной науки. Действительно, обладание общим методом, позволяющим точно решить любую задачу из некоторого (обычно бесконечного) их разнообразия, является кульминацией исследования, надежным свидетельством разработки полной теории соответствующей предметной области. В то же время в повседневной практике обнаруживается, что универсальные методы применяются реже, чем можно ожидать.
Обратимся к собственному опыту. Все мы со школы знаем общий метод перемножения двух натуральных чисел столбиком. Но автор готов биться об заклад, что этот алгоритм применяется не более чем в одном из десяти случаев. Каждый из нас обладает целым арсеналом специализированных алгоритмов умножения, которыми старается пользоваться с максимальным предпочтением. Вот наиболее известные:
- таблица умножения однозначных чисел,
- таблица квадратов в пределах тысячи,
- для умножения на десять приписать к числу справа нуль,
- для умножения на число из n девяток, приписать n нулей и вычесть множимое,
- для умножения на пять умножить на десять и разделить на два.
Если нам надо перемножить два числа, обладающих на первый взгляд хоть каким-то своеобразием, скажем 808 и 707, мы можем потратить порядочное время в попытках перемножить его каким-нибудь специальным способом, прежде чем применить универсальный алгоритм.
В чем же здесь дело? Могущество общего метода не только в его универсальности, т.е. применимости к любой задаче из некоторого класса. Он также допускает и максимальную однородность исходных данных и позволяет прийти к решению, используя наименьшее число закономерностей.
Однако, когда от разработки общего метода мы переходим к его массовому практическому применению, многие достоинства метода начинают восприниматься как недостатки. Общий метод трактует исходные данные, не отдавая одному предпочтения перед другими. На практике же одни варианты задачи возникают чаще, чем другие, а их исходные данные обладают определенным своеобразием.
Налицо два взгляда на специальные способы решения задач. Если для теоретика многообразие специальных способов - это признак неразвитости общей теории, то для практика то же разнообразие свидетельствует о дополнительных возможностях решать каждую частную задачу наиболее подходящим методом.
Эти два взгляда на специальные методы формируются в разных контекстах. Если практик вынужден иметь дело с ассортиментом специальных способов при отсутствии общего метода, он постоянно рискует столкнуться с такими частными задачами, для которых у него либо нет метода решения, либо - еще хуже - он не знает, решается эта задача или не решается доступными специальными методами. Картина меняется радикально, когда специальные методы применяются на фоне общего метода, который для практика становится стратегическим тылом по отношению к передовой линии повседневной работы со специальными методами.
ЦЕЛЬ ЭТОЙ статьи - показать, что между общим и специальными методами существует еще более глубокая и дружественная связь. Обычно считается, что специальный метод появляется в результате догадки и не только противостоит общему методу, но и игнорирует его. Автор хочет показать, что специальные методы могут получаться из общего метода систематически, с помощью универсальной процедуры весьма общего характера. Нахождение этой процедуры, названной смешанными вычислениями, стало одним из наиболее интересных достижений современной математической теории вычислений. Оно интересно с познавательной точки зрения, так как проливает свет на глубокие закономерности взаимодействия машинных программ с их данными и на связь программирования с теорией вычислимости. Оно интересно с практической точки зрения, так как позволяет получать большое разнообразие эффективных специальных методов, не порывая со знанием, воплощенным в общей теории. Наконец, оно интересно тем, что раскрывает сущность и подводит теоретический базис под многие методы программирования, возникшие ранее и развивающиеся в виде специальных и не связанных друг с другом приемов.
Если говорить о решении задач на ЭВМ, то способ решения задачи - это программа, которая выполняется на ЭВМ, условие задачи - входные данные для программы, а решение - выходные данные, выдаваемые программой. Поскольку ЭВМ - это детерминированный автомат, то, при фиксированной программе p для любого входного данного x выходное данное z будет некоторой функцией ф, полностью определяемой программой p: z = ф(х). Мы скажем, что функция ф реализуется программой p. Например, если задача состоит в том, чтобы уметь разлагать любое натуральное число на простые сомножители, то входным данным будет само число, допустим 819, способом решения - программа какого-нибудь алгоритма разложения числа на простые сомножители, а выходным данным - список этих сомножителей, в данном случае 3,3,7,13.
Сама программа p вместе с ее данными x выполняется посредством алгоритма Int (от слова "интерпретация"), встроенного в конструкцию ЭВМ. Этот универсальный алгоритм, будучи применен единообразным способом к любой программе и ее входным данным, реализует функцию, реализуемую программой: Int(p;x) = ф(x) = z.
Рассмотрим в этих обозначениях понятие частной задачи. Если частная задача определяется просто одним экземпляром значения x и никакие другие условия нас не интересуют, то специальный метод решения задачи находится тривиально: надо применить программу p к x, получить решение и запомнить его. Всякий раз, когда нужно решить задачу с условием x, например найти простые сомножители числа 819, надо просто взять ответ (3,3,7,13) и использовать его. Такой метод готовых решений широко применялся в виде разного рода математических таблиц во времена "докомпьютерной математики" и сохраняет свое значение и сейчас, когда таблица невелика.
В большинстве случаев, однако, частная задача носит не единичный характер, а сама обладает некоторым разнообразием входных данных. На языке функциональной зависимости это выглядит следующим образом. Предположим, что решение задачи сводится к вычислению функции двух переменных ф(x,y). Множество входных данных образует некоторую область в плоскости координат (х,у). Отдельные точки в этой области соответствуют единичным частным задачам. Универсальный метод решения воспринимает любую точку области исходных данных, не делая никаких различий между ними. Иначе говоря, исходные данные являются независимыми переменными. В общем случае частная задача возникает тогда, когда мы обладаем какой-то дополнительной априорной информацией об исходных данных. Например, может оказаться, что на вход программы разложения числа на множители попадают только простые числа. Тогда и способ решения задачи становится простым: само число и есть свой единственный множитель. Говоря другими словами, частная задача возникает при сужении области исходных данных на некоторое ее подмножество. Максимальной информацией, соответствующей сужению области до одной точки, мы располагаем, когда объект задан конкретно. Например, если натуральное число дано, то мы знаем о нем все: простое оно или нет, оканчивается нулем или нет, равно, скажем, пяти или нет и т.д.
Важным частным случаем, с которым мы будем в основном иметь дело в этой статье, являются сужения-проекции, когда одно независимое переменное задано, или, как говорят, связано некоторым значением, а другое переменное остается полностью неизвестным, свободным. Напомним, что общая задача состоит в вычислении функции ф(x,y). Пусть входной переменной x задано значение a, а переменная y не зафиксирована. Тогда частная задача состоит в вычислении функции ф(a,y), т.е. такой, в которой часть аргументов связана, а другая оставлена свободной.
В этих обозначениях построение специализированного метода решения частной задачи состоит в нахождении такой программы п, которая бы реализовывала функцию ф(a,y). Иначе говоря, если выполнить программу п для некоторого данного y = b на ЭВМ с универсальным алгоритмом выполнения Int, то Int(п;b) = ф(a,b).
| ОБЫЧНЫЕ ВЫЧИСЛЕНИЯ | x = a, y = b | Int(p;a,b) = ф(a,b) |
| СМЕШАННЫЕ ВЫЧИСЛЕНИЯ | x = a, y = b; свободных переменных нет | Mix(p;a,b) = out(c), где c = ф(a,b) |
| x, y - свободные, связанных переменных нет | Mix(p;пусто;x,y) = р | |
| x = a, y - свободная | Mix(p;a;у) = pa, где Int(pa;b) = ф(a,b) |
Mix - процедура смешанных вычислений;
p - конкретная программа;
x,y - входные переменные программы;
ф(x,y) - функция, реализуемая программой.
-----
ОБЫЧНЫЕ И СМЕШАННЫЕ ВЫЧИСЛЕНИЯ связаны друг с другом. Обычные вычисления - это универсальная процедура Int, которая для любой программы p (первый аргумент) и заданных значений всех ее входных переменных (вторая группа аргументов, отделенная точкой с запятой) вычисляет значение функции ф, реализуемой программой. Смешанные вычисления - это универсальная процедура Mix, которая для любой программы (первый аргумент), заданных значений ее связанных входных переменных (вторая группа аргументов, отделенная точками с запятой) и указанных свободных входных переменных (третья группа аргументов) вычисляет другую, так называемую остаточную программу. Если все переменные связаны входными данными, остаточная программа вырождается в команду выдачи предвычисленного результата исходной программы. Если все входные переменные свободны, исходная программа целиком переходит в остаточную программу. Если часть входных переменных связана, а другая оставлена свободной, то остаточная программа pa после задания недостающих данных вычисляет тот же результат, что и исходная программа для тех же данных.
-----
СМЕШАННЫЕ вычисления предлагают универсальную процедуру нахождения программы п как функции исходной общей программы, значений ее связанных входных переменных и указанных свободных переменных. Результат смешанных вычислений называется остаточной программой. Если остаточную программу выполнить, задав значения оставшимся свободным переменным, она выдаст тот же результат, что и исходная программа. Если связать заданными значениями все входные переменные, то остаточная программа выродится в команду выдачи предвычисленного результата. Если, наоборот, все входные переменные оставить свободными, то остаточная программа совпадет с исходной.
Сказанное выше можно рассматривать как функциональное определение смешанных вычислений. Кроме этого, нужно учитывать и некоторые прагматические соображения, которые должны оправдывать применение такой универсальной процедуры. Для начала уместно объяснить, почему среди других способов сужения области исходных данных проекция заслуживает особого рассмотрения. Дело в том, что исходные данные редко входят в условие задачи симметрично, как, например, переменные x и y в формуле длины вектора на плоскости: d = sqr(x**2 + y**2). Чаще бывает так, что одна независимая переменная выступает в качестве параметра, а другая является "истинным" аргументом. Например, в степенной функции y = x**n принято считать вещественное x аргументом функции, а целое n - ее параметром, в том смысле, что степенную функцию, как правило, надо вычислять, когда на одно значение параметра n приходятся разнообразные значения аргумента x. В данном случае, если бы имелся специальный способ вычисления x в заданной степени n, то его применение вместо общего метода позволяло бы решать задачу быстрее. Например, x**16 можно вычислить, сделав только четыре умножения вместо пятнадцати последовательных умножений на x, а именно x**16 = (((X**2)**2)**2)**2. Очевидно, что фиксация параметра и варьирование остальных аргументов есть проекция области исходных данных на значение параметра.
ДЛЯ ТОГО чтобы понять, как можно систематически получать из программы общего метода эффективные программы специальных методов, нужно более подробно узнать, как устроены и выполняются машинные программы.
Все способы записи и выполнения программ опираются на некоторые общие предпосылки. Обрабатываемая информация представляет собой совокупность элементарных данных (чисел или символов). Для элементарных данных существуют их буквальные обозначения, называемые константами. Кроме этого в программе могут фигурировать переменные, значениями которых являются элементарные данные. Эти значения задаются переменным в виде исходных данных или могут быть присвоены этим переменным во время вычислений. Значение переменной остается неизменным до тех пор, пока ей не будет присвоено новое значение. Любая обработка информации сводится к последовательности выполнения небольшого количества базовых операций над элементарными данными, в частности сложения или умножения двух чисел. Не меньшее значение имеют базовые операции проверки некоторых свойств данных, например, равны ли элементарные данные, положительно ли число, четно оно или нет и т.д. Операции, проверяющие свойства данных, называются предикатами - функциями, определенными над данными и принимающими два значения, обычно называемые истина и ложь (true и false), одно из которых соответствует наличию свойства, а другое - его отсутствию.
Программа представляет собой текст, имеющий фразовую структуру и записанный на некотором языке программирования. В этот текст в качестве слов входят константы, переменные, имена базовых операций и предикатов, названия разных частей программы или сгруппированных данных, а также служебные слова и "знаки препинания", которые позволяют делить программный текст на осмысленные части. Описание языка программирования состоит из грамматики (правил записи программ) и операционной семантики, которая интерпретирует программный текст, задавая правила выполнения программы.
Опишем грамматику простого императивного языка программирования МИЛАН (Mini LANguage), обычно используемого в демонстрационных целях. Его фразами являются команды выполнить то или иное действие. Основной командой является присваивание вида X:=E, где x - переменная, а E - выражение, образованное базовыми операциями, константами и переменными. Эта команда предписывает вычислить значение выражения E при текущих значениях входящих в него переменных и полученное значение сделать значением переменной x. Для задания переменным начальных значений - из исходных данных программы - используется команда ввода in(x), где in - служебное слово, а x - переменная, принимающая значение исходного данного. Для того чтобы прочитать результат выполнения программы, используется команда вывода out(E), где E - выражение. Значение выражения при текущих значениях переменных выдается в качестве результата.
Последовательность команд, разделенных точками с запятой, образует серию, в которой команды выполняются в порядке написания.
Программы, однако, не могли бы делать много, если бы состояли только из серий базовых команд. Примером составной команды является альтернатива, имеющая вид if B then S1 else S2 fi, где выражение В - условие, образованное комбинацией базовых предикатов. Альтернатива является сокращенной записью следующего правила: "если свойство данных, выраженное условием B, имеет место, то выполнить серию команд S1, в противном случае выполнить серию команд S2". Служебное слово fi - это перевернутое fi, вместе они символизируют пару скобок, ограничивающих альтернативу.
Наиболее мощной составной командой является итерация, имеющая вид while B do S od. Это сокращенная запись следующего правила: "Проверить соблюдение свойства данных, выраженного условием B. Если оно имеет место, выполнить серию S, после чего снова приступить к проверке B и т.д. При первом же (включая и самую первую проверку) невыполнении условия B завершить выполнение итерации". Таким образом серия S при выполнении итерации либо не выполнится ни разу, либо выполнится конечное число раз, либо будет повторяться бесконечно. Второй случай возможен только тогда, когда B зависит от переменных, значения которых изменяются при выполнении серии S. Именно итерации позволяют с помощью сравнительно коротких программных текстов диктовать машине выполнение огромных по длине последовательностей команд, поспевая тем самым за ее электронной скоростью. Принципиальной трудностью в употреблении итераций является отсутствие общего метода установления того, будет ли данная итерация при данных значениях переменных выполняться конечное число раз. Выяснение этого вопроса требует каждый раз отдельного исследования.

ПРАВИЛА ОБЫЧНЫХ ВЫЧИСЛЕНИЙ в языке МИЛАН представлены в виде его операционной семантики, т.е. универсального алгоритма выполнения любой программы в этом языке. Вычисление выглядит как чтение программного текста и извлечение из него последовательности базовых команд (протокола), при выполнении которых происходит непосредственная обработка информации и проверка ее свойств. Особенностью выполнения программы является то, что она сама направляет порядок своего чтения. Если при этом игнорировать шаги выполнения базовых команд (цветные блоки), а вместо проверки значений условий выбирать true или false произвольно, то операционная семантика сопоставит каждой программе некоторое множество протоколов, называемое детерминантом программы. Если программа содержит хотя бы одну итерацию, ее детерминант будет бесконечным.
-----
ТРАДИЦИОННЫЙ способ описания работы программ заключается в систематическом чтении программного текста и извлечении из него последовательности базовых команд проверки свойств данных (условий), присваиваний, ввода и вывода, которые выполняют фактическую обработку информации. Эту последовательность базовых команд называют протоколом, или историей вычислений. Особенностью выполнения программы является то, что она сама направляет порядок своего чтения. Этот порядок предписывается отчасти текстом программы (текстуальный порядок выполнения команд в серии), отчасти значениями перерабатываемых данных (зависимость выбора команд от значений условий в альтернативе и итерациях). Обычно ЭВМ, снабженная программой, ведет себя как полностью детерминированное устройство. Это значит, что исходные данные и сама программа полностью и единственным образом определяют соответствующий протокол вычислений и благодаря этому обеспечивают единственность результата.
Протокол по своей записи сам является выполнимой программой. Он имеет вид последовательности команд присваивания, ввода и вывода. Правда, если трактовать протокол как программу, остается не вполне ясной роль выражений условий вместе с приписанными им значениями ("+" или "-"). Их наличие, однако, не мешает выполнять протокол как программу. Если протокол вычисления y = x**n, построенный для входных данных, скажем x = 10 и n = 2, выполнить для этих же данных, то в результате мы получим y = 10**2 = 100, а значения всех предикатов, вычисленных в момент их чтения для соответствующих значений переменных, будут совпадать с приписанными им значениями, указанными в протоколе.
-----
ПЕРЕМЕННЫЕ: x, y, n
in(x); in(n); y:=1; while n>0 do while even(n) do n:=n/2; x:=x**2 od; n:=n-1; y:=y*x od; out(y)
-----
ПРОГРАММА ВЫЧИСЛЕНИЯ y = x**n на языке МИЛАН использует то свойство, что для вычисления, например, x**16 достаточно сделать только четыре умножения вместо пятнадцати: x*16 = (((x**2)**2)**2)**2. Программа организует следующий процесс над переменной n. Проверяется четность положительного n. Если оно нечетно, из него вычитается 1, после чего оно становится четным. Если n четно, оно делится пополам, после чего проверка повторяется и все завершается, когда n станет равным нулю. С каждым вычитанием единицы из n связывается умножение y (первоначально равного 1) на текущее значение x. При редукции n к нулю y становится равным x в степени исходного значения n.
-----
Это наблюдение тривиально. Рассмотрим теперь эффект применения этого протокола к каким-либо данным, отличным от тех, для которых он был построен. Если, например, протокол для x = 10 и n = 2 применить к входным данным, скажем x = 20 и n = 2, то мы опять получим правильный результату = 20**2 = 400, а значения, приписанные предикатам-условиям, будут соответствовать значениям, вычисляемым при выполнении протокола. Попробуем теперь протокол для x = 10 и n = 2 применить к x = 10 и n = 3. Сначала все будет в порядке, но при попытке вычислить предикат even(n)+ (означающий, что n должно быть четным) для n = 3 мы обнаружим несовпадение приписанного и вычисленного значений предиката. Это неудивительно, поскольку мы знаем, откуда взялся протокол. Если выполнять программу возведения в степень для x = 10 и n = 3, проверка условия четности even(n) даст значение ложь и тогда мы будем обязаны поместить в протокол условие в виде even(n)- и перейти не к выполнению внутренней итерации, а к вычитанию 1 из n. Таким образом, становится понятной роль предикатных выражений вместе с приписанными им значениями в протоколе. Они являются стражами, отличающими свои данные, т.е. те, к которым для получения результата можно применить построенный единичный протокол, от чужих данных, к которым должны применяться их протоколы. Если программа вычисляет однозначную функцию, то для каждой комбинации входных данных существует в точности один свой протокол. Однако один протокол может обслуживать несколько входных данных или даже их бесконечное множество (как в случае x**n, который отвечает бесконечному разнообразию значений x при фиксированном n).
С логической точки зрения можно рассматривать выполнение программ как двухэтапный процесс декомпозиции, т.е. извлечения базовых команд, образующих протокол, и прямых вычислений, т.е. выполнения команд протокола.
Таким образом, протоколы (истории вычислений) являются конструкциями, вскрывающими механизм работы программы. Именно последовательность команд протокола определяет результат и объем работы, затраченной на его получение. Когда программисты говорят, что две программы работают одинаково, то обычно имеют в виду, что эти две программы, как бы они ни отличались, обладают одним и тем же множеством протоколов. Так постепенно среди теоретиков программирования сложилось представление, что множество протоколов лучше характеризует программу, нежели сам исходный программный текст. Этот взгляд станет еще более справедливым, если удостовериться, что, хотя каждый протокол может быть вычислен только для своих исходных данных, получение всего множества протоколов для данной программы не требует никаких вычислений с данными и может быть достигнуто простым комбинаторным процессом чтения программы.
-----
ПРОГРАММА:
in(x); in(n); y:=1; while n>0 do while even(n) do n:=n/2; x:=x**2 od; n:=n-1; y:=y*x od; out(y)
ПРОТОКОЛЫ:
x = 10, n = 0
in(х); in(n); y:=1; n>0-; out(y)
x = 10, n = 1
in(х); in(n); y:=1; n>0+; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
x = 10, n = 2
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
x = 20, n = 2
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
x = 10, n = 3
in(х); in(n); y:=1; n>0+; even(n)-; n:=n-1; y:=y*x; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
ВЫЧИСЛЕНИЕ ПО ПРОТОКОЛУ, СООТВЕТСТВУЮЩЕМУ x = 10, n = 2.
для x = 10, n = 2
| in(x); | in(n); | y:=1; | n>0+; | even(n)+; | n:=n/2; | x:=x**2; | even(n)-; | n:=n-1; | y:=y*x; | n>0-; | out(y) | |
| x | 10 | 10 | 10 | 10 | 100 | 100 | 100 | |||||
| n | - | 2 | 2 | 2>0+ | even(2)+ | 1 | 1 | even(1)- | 0 | 0 | 0>0- | |
| y | - | - | 1 | 1 | 1 | 1 | 100 | 100 |
для x = 10, n = 3
| in(x); | in(n); | y:=1; | n>0+; | even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y) | |
| x | 10 | 10 | 10 | ||
| n | - | 3 | 3 | 3>0+; | even(3)+ противоречие |
| y | - | - | 1 |
in(х); in(n); y:=1; n>0+; even(n)-; n:=n-1; y:=y*x; n>0+; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
ПРОТОКОЛ имеет вид последовательности команд присваивания, ввода, вывода и предикатных выражений с приписанными им значениями. Каждому набору исходных данных программы соответствует один протокол - тот самый, который возникает при выполнении программы для этих данных. Протокол сам имеет вид выполнимой программы и может применяться к некоторому разнообразию входных данных. При этом вычисляемые значения предикатных выражений сравниваются со значениями ("+" для true, "-" для false), приписанными им при построении протокола. Если эти значения не совпадают, то протокол противоречит взятым исходным данным. Протокол, порожденный какими-то исходными данными, противоречит любым данным, порождающим некоторый другой протокол. В детерминанте программы могут существовать протоколы, которые противоречат любому набору исходных данных. Таким, в частности, является самый нижний протокол, поскольку любое положительное натуральное число при вычитании из него единицы обязательно изменяет свою четность.
-----
...
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:30 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
...
БУДЕМ теперь читать текст программы в порядке, предписываемом алгоритмом, и печатать команды протокола, пропуская шаги выполнения команд. Попадая на шаг проверки условия, вместо проверки значения (которое мы не имеем) будем делать произвольный выбор дальнейшего продвижения по программе. Дойдя до конца программы, мы получим некоторый протокол. Процесс может оказаться бесконечным, что говорит о наличии бесконечных протоколов. Перебирая все возможные варианты произвольного выбора на шагах проверки условий, мы получим и все возможные протоколы. Это множество протоколов называется детерминантом программы. В отличие от отдельных конечных протоколов и текста программы детерминант является абстрактной мысленной конструкцией, как и большинство других бесконечных математических объектов. Однако, чтобы доказать, что детерминант, пусть даже и в теоретическом анализе, заменяет программный текст, следует показать, как можно вычислять по детерминанту. Представим, например, такую схему. Исходные данные подаются на вход всех протоколов детерминанта. Как только при вычислении по какому-то протоколу возникает противоречие, т.е. значение предиката отличается от ему предписанного, так этот протокол выбывает из игры. Здесь возможны четыре исхода: все протоколы оказались противоречивыми - результат не определен, непротиворечивые протоколы оказались бесконечными - результат не определен, несколько конечных протоколов не противоречивы - функция многозначна, нашелся один-единственный непротиворечивый протокол - он и выдает результат вычислений.
Теперь мы в состоянии объяснить природу смешанных вычислений. Примем за основу выполнение программы в два этапа - декомпозицию, формирующую протокол, и прямые вычисления по протоколу. Протокол - это линейная программа и единожды выполненная команда больше не потребуется. Будем сопровождать выполнение протокола его редукцией: выполненная команда или вычисленное условие из протокола убираются, а вычисленные значения переменных подставляются туда, где они используются. Сделаем исключение только для команды выдачи результата, вычислив, однако, стоящее в нем выражение. Тогда при вычислении по протоколу программы возведения в степень для x = 10, n = 2 весь протокол редуцируется к команде out(100). Это и есть готовое решение для единичной задачи: y = 10**2. Попытка применить к входным данным x = 10, n = 2 какой бы то ни было другой протокол в случае нашей программы приведет к противоречию.
Обратимся теперь к опыту школьной алгебры. Нам хорошо понятна задача: вычислить значение (b+sqr(b**2-4*a*c))/(2*a) при a = 3, b = 8 и c = 4. Подставив указанные числа в формулу, мы получим выражение (8+sqr(8**2-4*3*4)/(2*3), которое можно подвергнуть редукциям, состоящим в замене каждого терма, образованного операцией и ее заданными аргументами, константой, обозначающей результат. (Например 8**2 заменяется на 64). Такая полная редукция арифметического выражения соответствует полной редукции протокола при его применении к своим данным.
Так же хорошо нам понятна и другая задача: упростить выражение (b+sqr(b**2-4*a*c))/(2*a) для случая a = 1 и b = 2*d. Подставив указанные числа в формулу, мы получим выражение (2*d+sqr(4*d**2-4*с)/2, которое на этот раз уже не полностью редуцируется, а через цепочку частичных редукций и простых алгебраических преобразований приводится к более простому виду d+sqr(d**2-c). В контексте нашей статьи можно сказать, что мы получили эффективную специализацию общей формулы на сужение входных данных, а именно для любого c, четного b и a = 1.
-----
РЕДУКЦИЯ ФОРМУЛЫ (b+sqr(b**2-4*a*c))/(2*a) для a = 3, b = 8, c = 4:
(8+sqr(8**2-4*3*4))/(2*3)
(8+sqr(64-4*12))/6
(8+sqr(64-48))/6
(8+sqr(16))/6
(8+4)/6
12/6
2
-----
РЕДУКЦИЯ ПРОТОКОЛА ВОЗВЕДЕНИЯ x В СТЕПЕНЬ n для x =10, n = 2
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=10**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
y:=1; 2>0+; even(2)+; n:=2/2; x:=10**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
n:=1; x:=100; even(n)-; n:=n-1; y:=1*x; n>0-; out(y)
x:=100; even(1)-; n:=1-1; y:=1*x; n>0-; out(y)
n:=0; y:=1*100; n>0-; out(y)
y:=100; 0>0-; out(y)
out(100)
-----
ВЫЧИСЛЕНИЕ АРИФМЕТИЧЕСКОГО ВЫРАЖЕНИЯ (вверху) сводится к замене символов переменных их значениями, а затем к выполнению цепочки редукций, которые состоят в замене операции и ее аргументов на результат применения операции к этим аргументам. Вычисление завершается, когда формула редуцируется к одной константе - значению выражения. Поскольку в протоколе каждая команда выполняется однократно, вычислению по нему можно придать аналогичный характер (внизу). Выполняемая команда или вычисляемое условие устраняются из протокола, а вычисленные значения переменных подставляются туда, где они используются. Результат вычисления читается в аргументе команды выдачи out(y).
-----
ПОПРОБУЕМ мысленно обобщить эту ситуацию на случай программ. Вместо одной формулы мы имеем детерминант программы, состоящий из бесконечного множества протоколов. Определим для каждого протокола процесс частичной редукции (частичной из-за того, что значения некоторых переменных не заданы и поэтому вычисления с ними невозможны). Сначала устанавливаем, какие аргументы даны, а какие свободны. Затем читаем протокол и пытаемся выполнять его команды. Те команды, которые можно выполнить, из протокола убираются, а те, что выполнить нельзя, задерживаются в протоколе, чтение которого продолжается, пока не дойдет до конца. При чтении команды in(z) выполняем команду, если входное данное доступно, и делаем значение z равным этому данному. Если входное данное отсутствует, z признается задержанным, т.е. недоступным, и команда пропускается. При чтении присваивания z:=E производится упрощение выражения E за счет возможной доступности его аргументов. Если Е редуцировалось до константы (т.е. вычислилось), его значение присваивается z, переменная объявляется доступной и команда удаляется из протокола. Если же E редуцировалось неполностью, то z объявляется недоступной и команда пропускается. Команда out(E), где E по возможности редуцировано, остается в протоколе всегда.
Предикатные выражения подвергаются такому же упрощению. Если они редуцируются неполностью, то остаются в протоколе с предписанными им значениями ("+" или "-"). Если же условие вычислено, то вычисленный результат сравнивается с предписанным. При совпадении значений предикатное выражение удаляется из протокола. Несовпадение означает противоречие, и в этом случае весь протокол бракуется и удаляется ш детерминанта. Представим себе, что такая процедура проделана с каждым протоколом детерминанта программы. В результате часть протоколов исчезла (из-за противоречий), а другие упростились. При редукции детерминанта были проделаны все вычисления, ставшие возможными благодаря доступным данным, и отброшены все варианты вычислений, противоречащие этим данным. Легко сообразить, что по существу мы максимально использовали дополнительную информацию, возникшую благодаря сужению области входных данных. Если бы мы могли построить программный текст, для которого редуцированный детерминант был бы ее нормальным детерминантом, мы бы сочли такую программу удовлетворительной версией специализированного метода решения частной задачи.
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ ФОРМУЛЫ(b+sqr(b**2-4*a*c))/(2*a) для a = 1, b = 2*d, c и d СВОБОДНЫХ:
(2*d+sqr((2*d)**2-4*1*c))/(2*1)
(2*d+sqr(4*d**2-4*c))/2
(2*d+sqr(4*(d**2-c))/2
(2*d+2*sqr(d**2-c))/2
2*(d+sqr(d**2-c))/2
d+sqr(d**2-c)
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ ПРОТОКОЛА ВОЗВЕДЕНИЯ x В СТЕПЕНЬ n ДЛЯ n = 2 И x СВОБОДНОГО:
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(х); y:=1; 2>0+; even(2)+; n:=2/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(х); n:=1; x:=x**2; even(n)-; n:=n-1; y:=1*x; n>0-; out(y)
in(х); x:=x**2; even(1)-; n:=1-1; y:=1*x; n>0-; out(y)
in(х); x:=x**2; n:=0; y:=1*x; n>0-; out(y)
in(х); x:=x**2; y:=1*x; 0>0-; out(y)
in(х); x:=x**2; y:=1*x; out(y)
СПЕЦИАЛИЗИРОВАННАЯ ПРОГРАММА ВЫЧИСЛЕНИЯ y = x**2:
in(х); x:=x**2; y:=1*x; out(y)
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ арифметического выражения (вверху) происходит в том случае, когда не все значения переменных заданы. При этом замена операции и ее аргументов на результат может дополняться алгебраическими преобразованиями, отражающими свойства операций и величин, входящих в выражение. Результатом частичной редукции является остаточное выражение, получившееся специализацией исходной формулы на суженное разнообразие своих аргументов. Точно так же смешанные вычисления могут трактоваться как совместная частичная редукция всех протоколов, входящих в детерминант общей программы (внизу). При этом часть протоколов сокращается, а часть других отбрасывается как противоречащая доступным данным. Найти остаточную программу - значит найти такой программный текст, чей детерминант был бы как можно ближе к редуцированному детерминанту исходной программы. В случае программы вычисления y = x**n мы, конечно, не можем буквально перебрать все протоколы детерминанта, но зато без особого труда можем доказать, что для n = 2 все протоколы, кроме одного (соответствующего этому значению n), будут противоречивы. В результате частичной редукции этого протокола в качестве своеобразного остатка получаем простую программу, очень близкую к идеальной программе для вычисления y = х**2. Остаточная программа содержит избыточное умножение на 1, но выполнение соответствующего очевидного упрощения требует, понятно, иного знания, нежели то, что используется в редукциях, основанных на доступности значений переменных.
НА ПУТИ к конструктивной реализации только что описанного общего метода лежит, однако, одно принципиальное препятствие. Каждой программе соответствует некоторое множество протоколов (ее детерминант), но не каждое множество протоколов может быть детерминантом какой-либо программы. Характеристическим свойством детерминантов является их принадлежность специальному классу так называемых автоматных множеств. Описанная выше операция редукции в общем случае неконструктивна и выводит получающееся множество протоколов за пределы этого класса. Поэтому, вооружившись общей идеей метода, мы должны организовать процесс частичных редукций так, чтобы в любой момент находиться в пределах некоторого программного текста, который по завершению процесса будет объявлен результатом специализации универсальной программы.
Опишем такой процесс в виде обобщения схемы выполнения программ на языке МИЛАН в двух взаимосвязанных направлениях. Во-первых, определим процесс выполнения программы для неполностью заданных значений переменных - так называемые частичные вычисления. Во-вторых, вместо печати выполнимых команд будем печатать те команды, которые нельзя выполнить из-за отсутствия информации. В отличие от протоколов это будут не только нередуцируемые присваивания, но и нередуцируемые альтернативы и нераскрытые итерации. Эти невыполнимые команды будут печататься в такой логической последовательности, чтобы образовывать в совокупности осмысленную остаточную программу. Сам процесс выполнения частичных вычислений и генерации остаточной программы потому и получил название смешанных вычислений, что при его выполнении шаги обычных вычислений перемежаются шагами формирования остаточной программы. Детерминант остаточной программы - это некоторое непротиворечивое расширение описанной выше редукции детерминанта исходной программы.
Изложенный алгоритм смешанных вычислений в языке МИЛАН соответствует традиционному способу описания операционной семантики языков программирования. Выполнение программы по этому способу напоминает работу ЭВМ, управляемой программой на машинном языке. Обладая сходной организацией, алгоритмы обычных и смешанных вычислений существенно отличаются друг от друга. Получается так, что язык имеет две операционных семантики: одну для обычных вычислений, а другую - для смешанных. Существует, однако, совершенно иной подход к описанию вычислений, который, хотя и восходит к математическим работам 30-х годов, в литературу по программированию вошел совсем недавно. Достоинством этого так называемого трансформационного подхода является то, что в нем обычные и смешанные вычисления выглядят совершенно одинаково.
ИДЕЯ трансформационного подхода состоит в следующем. Мы просматриваем программу и ищем команды, которые могут быть в данный момент выполнены. Выполненную команду редуцируем - убираем из программы. Однако, благодаря итерациям в тексте программы есть команды, которые выполняются многократно и поэтому не могут быть редуцированы после первого выполнения. Выход состоит в том, что в число правил преобразования программного текста кроме редукций включаются так называемые раскрытия, которые "отщепляют" от итерации один ее экземпляр и приносят его в жертву очередной редукции, оставляя саму итерацию в качестве источника последующих экземпляров.
Трансформационная семантика языка МИЛАН состоит из списка правил преобразования текста программы, включая значения переменных. Для каждой конструкции языка есть одно относящееся к ней правило. Правило итерации является раскрытием и составлено так, что раскрывать можно только ту итерацию, которая в программе должна обязательно выполниться и при этом раньше других итераций.
Все остальные правила сводятся к редукциям, их применение приводит к устранению данной конструкции или ее замене более простой конструкцией. Вхождение переменной величины в виде аргумента выражения заменяется на константу только тогда, когда есть уверенность, что должно быть использовано именно то значение переменной, которое она имеет в момент выполнения редукции. Присваивание величине x редуцируется только тогда, когда есть уверенность, что старое значение x, если оно существует, уже не может быть использовано, а само присваивание обязательно должно выполниться. Редукция команды ввода показывает, что ее выполнение эквивалентно присваиванию переменной соответствующего значения исходного данного.
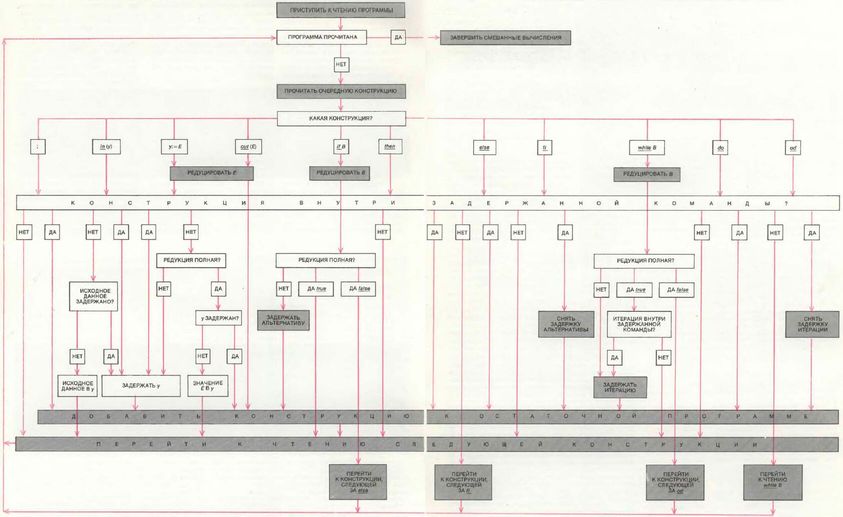
ОРГАНИЗАЦИЯ СМЕШАННЫХ ВЫЧИСЛЕНИЙ в языке МИЛАН напоминает его операционную семантику. Шаги обычных вычислений перемежаются с шагами формирования остаточной программы. Каждая прочитываемая команда либо выполняется, либо задерживается и добавляется к остаточной программе. Причиной задержки команд ввода является незаданность входных переменных, которые при этом объявляются задержанными. Задержанная переменная недоступна для дальнейшего использования. Неполная редукция выражения или условия является причиной задержки присваивания, альтернативы или итерации. Задержка присваивания некоторой переменной, естественно, задерживает эту переменную. Задержка альтернативы и итерации автоматически задерживает все находящиеся внутри них базовые команды и итерации, однако не препятствует редукции выражений, альтернатив и итераций со сложными условиями. Кроме этого, при задержке итерации немедленно задерживаются все переменные, которым возможны присваивания внутри этой итерации.
-----

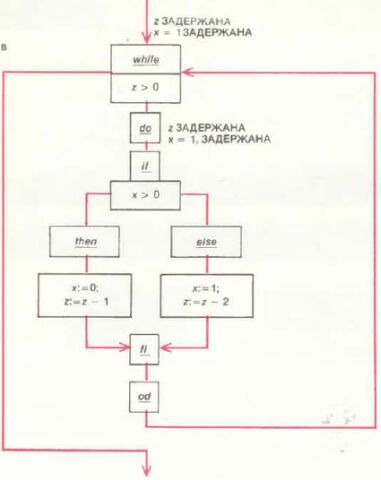
ОСОБЕННОСТИ СМЕШАННЫХ ВЫЧИСЛЕНИЙ при задержке составных команд. На схеме а задержка условия в альтернативе в исходной программе (слева) не позволяет полностью выполнить присваивания переменной y, хотя соответствующие выражения в остаточной программе (справа) редуцируются к константе. Переменная x сохраняет свое значение, но становится задержанной, так как после альтернативы должно использоваться другое, еще не вычисленное значение x. На схеме б истинное условие итерации в исходной программе (слева) провоцирует ее исполнение. Это может сделать, однако, процесс смешанных вычислений бесконечным и в результате остаточная программа не будет получена. В то же время существует такое значение переменной z, при котором будет выбрана левая ветвь альтернативы и потребность в выполнении итерации даже не возникнет. Таким образом, во время смешанных вычислений можно выполнять только такие итерации, которые неизбежны на пути чтения программы. Удаление итераций с ложным условием и редукция альтернативы при известном значении условия возможны, однако, в любом контексте (справа). Схема в демонстрирует необходимость при задержке итерации немедленно задерживать все переменные, которым в этой итерации могут быть сделаны присваивания. Условие x = 1 альтернативы должно проверять не только известное начальное значение x, но и все последующие, которые, однако, будут вычисляться уже только в остаточной программе. Недопустимая редукция альтернативы может быть предотвращена немедленной задержкой переменной x.
-----

ОСТАТОЧНАЯ ПРОГРАММА, построенная согласно трансформационной семантики языка МИЛАН для программы y = x**n, конкретизируемой на случай n = 2. Редуцируемые команды и выражения напечатаны синим, раскрываемые итерации показаны красным. DOD - сокращение итерации по положительности n, dod - сокращение внутренней итерации по четности n. Раскрытие итераций поставляет остальным редукциям "материал для работы". Редукция альтернатив отсекает ветви вычислений, противоречащие доступным данным. "Рабочими редукциями" являются редукции аргументов, операций и присваиваний. В отличие от операционной семантики, предписывающей единственную последовательность вычислений, трансформационная семантика допускает для этой программы несколько сот вариантов смешанных вычислений, которые в силу свойства Черча-Россера приводят к одной и той же остаточной программе, показанной в последней строке схемы.
ОРГАНИЗАЦИЯ вычислений в языке программирования, заданном трансформационной семантикой, имеет ряд существенных отличий от операционной семантики. Главное из них - это изменение модальности предписаний о выполнении команд. Если операционная семантика в каждый момент чтения программы указывает на единственную команду, которая ДОЛЖНА выполниться, то трансформационная семантика в каждый момент работы с программой показывает, какие команды могут "выполниться", т.е. раскрыться или редуцироваться. При этом вполне возможно, что в данный момент в программе существует несколько конструкций, к которым можно применить соответствующие преобразования. Семантика языка не подсказывает, какое из них должно быть выбрано, т.е. допускает в ходе выполнения программы акты произвольного выбора. Среди всех возможных состояний вычислительного процесса естественно выделяется такое, когда ни одно из преобразований не может быть применено ни к одной из оставшихся конструкций. Такое состояние программы и ее данных, т.е. текущих значений переменных, называется неподвижной точкой. Трансформационная семантика определена так, что если все исходные данные в программе заданы и программа для этих данных останавливается и выдает некоторый результат, скажем 78, в качестве значения команды вывода, то неподвижной точкой для этих же исходных данных будет программа, которая редуцируется к одной-единственной команде out(78). Если же часть входных данных окажется не заданной и соответствующие переменные останутся свободными, то неподвижной точкой будет некоторая остаточная программа, та же самая, которая получилась бы в результате смешанных вычислений согласно их операционному определению.
Система преобразований любой текстовой информации, которая приводит к одной и той же неподвижной точке независимо от порядка применения допустимых преобразований, называется системой Черча-Россера по имени известного американского математика А.Черча и его в то время молодого ученика Дж.Россера, которые в 30-е годы впервые исследовали подобного рода системы под названием лямбда-исчислений. Свойство Черча-Россера в применении к трансформационной семантике языка МИЛАН гарантирует однозначность вычислений, не взирая на возможные акты свободного выбора применяемых преобразований. Система преобразований, однако, не гарантирует, что какая-бы то ни было неподвижная точка будет обязательно достигнута. Раскрытие цикла может предлагать свои услуги бесконечно, если возникающее при этом условие альтернативы никогда не получит значение ложь, что привело бы к устранению раскрываемой итерации из программы.
Естественно, что применение "в лоб" трансформационной семантики для обработки программы путем комбинаторного перебора всех возможностей применения преобразований к конструкциям программы очень неэффективно. Достоинства такого способа описания языков программирования лежат в другом. Базовые трансформации программного текста, предписываемые трансформационной семантикой, могут быть основой для достоверного построения разнообразных программных процессоров, существенно более широких, нежели жесткие схемы обычных и смешанных вычислений, задаваемых операционной семантикой. Еще одним достоинством трансформационной семантики является то, что она легко допускает присоединение дополнительных преобразований, содействующих улучшению остаточной программы. Например, присоединение к трансформационной семантике языка МИЛАН преобразования вида E*1 -> E, где E - произвольное арифметическое выражение, позволяет получить идеальную остаточную программу для вычисления x**2 (см. выше).
ТРАНСФОРМАЦИОННАЯ СЕМАНТИКА языка МИЛАН задается набором правил преобразования программного текста и значений переменных. Все правила, кроме правила для итерации, являются редукциями, приводящими к устранению конструкции из программы или замене ее на более простую. В левой колонке таблицы помещено название конструкции, в средней - описывается контекст, в котором преобразование возможно, в правой - указывается, на что заменяется вхождение конструкции, к которому применено правило. Правило для итерации является раскрытием: оно вычленяет один экземпляр условия итерации и ее внутренних команд, к которым могут теперь применяться редукции, сохраняя саму итерацию для возможных повторных раскрытий. Переменная x находится в передовой позиции аргумента выражения, если между ним и началом программы нет присваивания этой переменной и выражение не является условием итерации. Присваивание переменной x находится в передовой позиции, если оно не находится внутри составной команды и между ним и началом программы нет ни одного вхождения x. Итерация находится в передовой позиции, если она не находится внутри составной команды и между ней и началом программы нет других редуцируемых итераций. Выполнение программы в рамках трансформационного подхода состоит в попытках применения к программе любого из правил. При полностью заданных входных переменных программа редуцируется к команде вывода, в аргументе которой читается результат. В общем случае, при наличии свободных входных переменных, исходная программа редуцируется к некоторой остаточной программе.
-----
...
БУДЕМ теперь читать текст программы в порядке, предписываемом алгоритмом, и печатать команды протокола, пропуская шаги выполнения команд. Попадая на шаг проверки условия, вместо проверки значения (которое мы не имеем) будем делать произвольный выбор дальнейшего продвижения по программе. Дойдя до конца программы, мы получим некоторый протокол. Процесс может оказаться бесконечным, что говорит о наличии бесконечных протоколов. Перебирая все возможные варианты произвольного выбора на шагах проверки условий, мы получим и все возможные протоколы. Это множество протоколов называется детерминантом программы. В отличие от отдельных конечных протоколов и текста программы детерминант является абстрактной мысленной конструкцией, как и большинство других бесконечных математических объектов. Однако, чтобы доказать, что детерминант, пусть даже и в теоретическом анализе, заменяет программный текст, следует показать, как можно вычислять по детерминанту. Представим, например, такую схему. Исходные данные подаются на вход всех протоколов детерминанта. Как только при вычислении по какому-то протоколу возникает противоречие, т.е. значение предиката отличается от ему предписанного, так этот протокол выбывает из игры. Здесь возможны четыре исхода: все протоколы оказались противоречивыми - результат не определен, непротиворечивые протоколы оказались бесконечными - результат не определен, несколько конечных протоколов не противоречивы - функция многозначна, нашелся один-единственный непротиворечивый протокол - он и выдает результат вычислений.
Теперь мы в состоянии объяснить природу смешанных вычислений. Примем за основу выполнение программы в два этапа - декомпозицию, формирующую протокол, и прямые вычисления по протоколу. Протокол - это линейная программа и единожды выполненная команда больше не потребуется. Будем сопровождать выполнение протокола его редукцией: выполненная команда или вычисленное условие из протокола убираются, а вычисленные значения переменных подставляются туда, где они используются. Сделаем исключение только для команды выдачи результата, вычислив, однако, стоящее в нем выражение. Тогда при вычислении по протоколу программы возведения в степень для x = 10, n = 2 весь протокол редуцируется к команде out(100). Это и есть готовое решение для единичной задачи: y = 10**2. Попытка применить к входным данным x = 10, n = 2 какой бы то ни было другой протокол в случае нашей программы приведет к противоречию.
Обратимся теперь к опыту школьной алгебры. Нам хорошо понятна задача: вычислить значение (b+sqr(b**2-4*a*c))/(2*a) при a = 3, b = 8 и c = 4. Подставив указанные числа в формулу, мы получим выражение (8+sqr(8**2-4*3*4)/(2*3), которое можно подвергнуть редукциям, состоящим в замене каждого терма, образованного операцией и ее заданными аргументами, константой, обозначающей результат. (Например 8**2 заменяется на 64). Такая полная редукция арифметического выражения соответствует полной редукции протокола при его применении к своим данным.
Так же хорошо нам понятна и другая задача: упростить выражение (b+sqr(b**2-4*a*c))/(2*a) для случая a = 1 и b = 2*d. Подставив указанные числа в формулу, мы получим выражение (2*d+sqr(4*d**2-4*с)/2, которое на этот раз уже не полностью редуцируется, а через цепочку частичных редукций и простых алгебраических преобразований приводится к более простому виду d+sqr(d**2-c). В контексте нашей статьи можно сказать, что мы получили эффективную специализацию общей формулы на сужение входных данных, а именно для любого c, четного b и a = 1.
-----
РЕДУКЦИЯ ФОРМУЛЫ (b+sqr(b**2-4*a*c))/(2*a) для a = 3, b = 8, c = 4:
(8+sqr(8**2-4*3*4))/(2*3)
(8+sqr(64-4*12))/6
(8+sqr(64-48))/6
(8+sqr(16))/6
(8+4)/6
12/6
2
-----
РЕДУКЦИЯ ПРОТОКОЛА ВОЗВЕДЕНИЯ x В СТЕПЕНЬ n для x =10, n = 2
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=10**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
y:=1; 2>0+; even(2)+; n:=2/2; x:=10**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
n:=1; x:=100; even(n)-; n:=n-1; y:=1*x; n>0-; out(y)
x:=100; even(1)-; n:=1-1; y:=1*x; n>0-; out(y)
n:=0; y:=1*100; n>0-; out(y)
y:=100; 0>0-; out(y)
out(100)
-----
ВЫЧИСЛЕНИЕ АРИФМЕТИЧЕСКОГО ВЫРАЖЕНИЯ (вверху) сводится к замене символов переменных их значениями, а затем к выполнению цепочки редукций, которые состоят в замене операции и ее аргументов на результат применения операции к этим аргументам. Вычисление завершается, когда формула редуцируется к одной константе - значению выражения. Поскольку в протоколе каждая команда выполняется однократно, вычислению по нему можно придать аналогичный характер (внизу). Выполняемая команда или вычисляемое условие устраняются из протокола, а вычисленные значения переменных подставляются туда, где они используются. Результат вычисления читается в аргументе команды выдачи out(y).
-----
ПОПРОБУЕМ мысленно обобщить эту ситуацию на случай программ. Вместо одной формулы мы имеем детерминант программы, состоящий из бесконечного множества протоколов. Определим для каждого протокола процесс частичной редукции (частичной из-за того, что значения некоторых переменных не заданы и поэтому вычисления с ними невозможны). Сначала устанавливаем, какие аргументы даны, а какие свободны. Затем читаем протокол и пытаемся выполнять его команды. Те команды, которые можно выполнить, из протокола убираются, а те, что выполнить нельзя, задерживаются в протоколе, чтение которого продолжается, пока не дойдет до конца. При чтении команды in(z) выполняем команду, если входное данное доступно, и делаем значение z равным этому данному. Если входное данное отсутствует, z признается задержанным, т.е. недоступным, и команда пропускается. При чтении присваивания z:=E производится упрощение выражения E за счет возможной доступности его аргументов. Если Е редуцировалось до константы (т.е. вычислилось), его значение присваивается z, переменная объявляется доступной и команда удаляется из протокола. Если же E редуцировалось неполностью, то z объявляется недоступной и команда пропускается. Команда out(E), где E по возможности редуцировано, остается в протоколе всегда.
Предикатные выражения подвергаются такому же упрощению. Если они редуцируются неполностью, то остаются в протоколе с предписанными им значениями ("+" или "-"). Если же условие вычислено, то вычисленный результат сравнивается с предписанным. При совпадении значений предикатное выражение удаляется из протокола. Несовпадение означает противоречие, и в этом случае весь протокол бракуется и удаляется ш детерминанта. Представим себе, что такая процедура проделана с каждым протоколом детерминанта программы. В результате часть протоколов исчезла (из-за противоречий), а другие упростились. При редукции детерминанта были проделаны все вычисления, ставшие возможными благодаря доступным данным, и отброшены все варианты вычислений, противоречащие этим данным. Легко сообразить, что по существу мы максимально использовали дополнительную информацию, возникшую благодаря сужению области входных данных. Если бы мы могли построить программный текст, для которого редуцированный детерминант был бы ее нормальным детерминантом, мы бы сочли такую программу удовлетворительной версией специализированного метода решения частной задачи.
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ ФОРМУЛЫ(b+sqr(b**2-4*a*c))/(2*a) для a = 1, b = 2*d, c и d СВОБОДНЫХ:
(2*d+sqr((2*d)**2-4*1*c))/(2*1)
(2*d+sqr(4*d**2-4*c))/2
(2*d+sqr(4*(d**2-c))/2
(2*d+2*sqr(d**2-c))/2
2*(d+sqr(d**2-c))/2
d+sqr(d**2-c)
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ ПРОТОКОЛА ВОЗВЕДЕНИЯ x В СТЕПЕНЬ n ДЛЯ n = 2 И x СВОБОДНОГО:
in(х); in(n); y:=1; n>0+; even(n)+; n:=n/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(х); y:=1; 2>0+; even(2)+; n:=2/2; x:=x**2; even(n)-; n:=n-1; y:=y*x; n>0-; out(y)
in(х); n:=1; x:=x**2; even(n)-; n:=n-1; y:=1*x; n>0-; out(y)
in(х); x:=x**2; even(1)-; n:=1-1; y:=1*x; n>0-; out(y)
in(х); x:=x**2; n:=0; y:=1*x; n>0-; out(y)
in(х); x:=x**2; y:=1*x; 0>0-; out(y)
in(х); x:=x**2; y:=1*x; out(y)
СПЕЦИАЛИЗИРОВАННАЯ ПРОГРАММА ВЫЧИСЛЕНИЯ y = x**2:
in(х); x:=x**2; y:=1*x; out(y)
-----
ЧАСТИЧНАЯ РЕДУКЦИЯ арифметического выражения (вверху) происходит в том случае, когда не все значения переменных заданы. При этом замена операции и ее аргументов на результат может дополняться алгебраическими преобразованиями, отражающими свойства операций и величин, входящих в выражение. Результатом частичной редукции является остаточное выражение, получившееся специализацией исходной формулы на суженное разнообразие своих аргументов. Точно так же смешанные вычисления могут трактоваться как совместная частичная редукция всех протоколов, входящих в детерминант общей программы (внизу). При этом часть протоколов сокращается, а часть других отбрасывается как противоречащая доступным данным. Найти остаточную программу - значит найти такой программный текст, чей детерминант был бы как можно ближе к редуцированному детерминанту исходной программы. В случае программы вычисления y = x**n мы, конечно, не можем буквально перебрать все протоколы детерминанта, но зато без особого труда можем доказать, что для n = 2 все протоколы, кроме одного (соответствующего этому значению n), будут противоречивы. В результате частичной редукции этого протокола в качестве своеобразного остатка получаем простую программу, очень близкую к идеальной программе для вычисления y = х**2. Остаточная программа содержит избыточное умножение на 1, но выполнение соответствующего очевидного упрощения требует, понятно, иного знания, нежели то, что используется в редукциях, основанных на доступности значений переменных.
НА ПУТИ к конструктивной реализации только что описанного общего метода лежит, однако, одно принципиальное препятствие. Каждой программе соответствует некоторое множество протоколов (ее детерминант), но не каждое множество протоколов может быть детерминантом какой-либо программы. Характеристическим свойством детерминантов является их принадлежность специальному классу так называемых автоматных множеств. Описанная выше операция редукции в общем случае неконструктивна и выводит получающееся множество протоколов за пределы этого класса. Поэтому, вооружившись общей идеей метода, мы должны организовать процесс частичных редукций так, чтобы в любой момент находиться в пределах некоторого программного текста, который по завершению процесса будет объявлен результатом специализации универсальной программы.
Опишем такой процесс в виде обобщения схемы выполнения программ на языке МИЛАН в двух взаимосвязанных направлениях. Во-первых, определим процесс выполнения программы для неполностью заданных значений переменных - так называемые частичные вычисления. Во-вторых, вместо печати выполнимых команд будем печатать те команды, которые нельзя выполнить из-за отсутствия информации. В отличие от протоколов это будут не только нередуцируемые присваивания, но и нередуцируемые альтернативы и нераскрытые итерации. Эти невыполнимые команды будут печататься в такой логической последовательности, чтобы образовывать в совокупности осмысленную остаточную программу. Сам процесс выполнения частичных вычислений и генерации остаточной программы потому и получил название смешанных вычислений, что при его выполнении шаги обычных вычислений перемежаются шагами формирования остаточной программы. Детерминант остаточной программы - это некоторое непротиворечивое расширение описанной выше редукции детерминанта исходной программы.
Изложенный алгоритм смешанных вычислений в языке МИЛАН соответствует традиционному способу описания операционной семантики языков программирования. Выполнение программы по этому способу напоминает работу ЭВМ, управляемой программой на машинном языке. Обладая сходной организацией, алгоритмы обычных и смешанных вычислений существенно отличаются друг от друга. Получается так, что язык имеет две операционных семантики: одну для обычных вычислений, а другую - для смешанных. Существует, однако, совершенно иной подход к описанию вычислений, который, хотя и восходит к математическим работам 30-х годов, в литературу по программированию вошел совсем недавно. Достоинством этого так называемого трансформационного подхода является то, что в нем обычные и смешанные вычисления выглядят совершенно одинаково.
ИДЕЯ трансформационного подхода состоит в следующем. Мы просматриваем программу и ищем команды, которые могут быть в данный момент выполнены. Выполненную команду редуцируем - убираем из программы. Однако, благодаря итерациям в тексте программы есть команды, которые выполняются многократно и поэтому не могут быть редуцированы после первого выполнения. Выход состоит в том, что в число правил преобразования программного текста кроме редукций включаются так называемые раскрытия, которые "отщепляют" от итерации один ее экземпляр и приносят его в жертву очередной редукции, оставляя саму итерацию в качестве источника последующих экземпляров.
Трансформационная семантика языка МИЛАН состоит из списка правил преобразования текста программы, включая значения переменных. Для каждой конструкции языка есть одно относящееся к ней правило. Правило итерации является раскрытием и составлено так, что раскрывать можно только ту итерацию, которая в программе должна обязательно выполниться и при этом раньше других итераций.
Все остальные правила сводятся к редукциям, их применение приводит к устранению данной конструкции или ее замене более простой конструкцией. Вхождение переменной величины в виде аргумента выражения заменяется на константу только тогда, когда есть уверенность, что должно быть использовано именно то значение переменной, которое она имеет в момент выполнения редукции. Присваивание величине x редуцируется только тогда, когда есть уверенность, что старое значение x, если оно существует, уже не может быть использовано, а само присваивание обязательно должно выполниться. Редукция команды ввода показывает, что ее выполнение эквивалентно присваиванию переменной соответствующего значения исходного данного.

ОРГАНИЗАЦИЯ СМЕШАННЫХ ВЫЧИСЛЕНИЙ в языке МИЛАН напоминает его операционную семантику. Шаги обычных вычислений перемежаются с шагами формирования остаточной программы. Каждая прочитываемая команда либо выполняется, либо задерживается и добавляется к остаточной программе. Причиной задержки команд ввода является незаданность входных переменных, которые при этом объявляются задержанными. Задержанная переменная недоступна для дальнейшего использования. Неполная редукция выражения или условия является причиной задержки присваивания, альтернативы или итерации. Задержка присваивания некоторой переменной, естественно, задерживает эту переменную. Задержка альтернативы и итерации автоматически задерживает все находящиеся внутри них базовые команды и итерации, однако не препятствует редукции выражений, альтернатив и итераций со сложными условиями. Кроме этого, при задержке итерации немедленно задерживаются все переменные, которым возможны присваивания внутри этой итерации.
-----


ОСОБЕННОСТИ СМЕШАННЫХ ВЫЧИСЛЕНИЙ при задержке составных команд. На схеме а задержка условия в альтернативе в исходной программе (слева) не позволяет полностью выполнить присваивания переменной y, хотя соответствующие выражения в остаточной программе (справа) редуцируются к константе. Переменная x сохраняет свое значение, но становится задержанной, так как после альтернативы должно использоваться другое, еще не вычисленное значение x. На схеме б истинное условие итерации в исходной программе (слева) провоцирует ее исполнение. Это может сделать, однако, процесс смешанных вычислений бесконечным и в результате остаточная программа не будет получена. В то же время существует такое значение переменной z, при котором будет выбрана левая ветвь альтернативы и потребность в выполнении итерации даже не возникнет. Таким образом, во время смешанных вычислений можно выполнять только такие итерации, которые неизбежны на пути чтения программы. Удаление итераций с ложным условием и редукция альтернативы при известном значении условия возможны, однако, в любом контексте (справа). Схема в демонстрирует необходимость при задержке итерации немедленно задерживать все переменные, которым в этой итерации могут быть сделаны присваивания. Условие x = 1 альтернативы должно проверять не только известное начальное значение x, но и все последующие, которые, однако, будут вычисляться уже только в остаточной программе. Недопустимая редукция альтернативы может быть предотвращена немедленной задержкой переменной x.
-----

ОСТАТОЧНАЯ ПРОГРАММА, построенная согласно трансформационной семантики языка МИЛАН для программы y = x**n, конкретизируемой на случай n = 2. Редуцируемые команды и выражения напечатаны синим, раскрываемые итерации показаны красным. DOD - сокращение итерации по положительности n, dod - сокращение внутренней итерации по четности n. Раскрытие итераций поставляет остальным редукциям "материал для работы". Редукция альтернатив отсекает ветви вычислений, противоречащие доступным данным. "Рабочими редукциями" являются редукции аргументов, операций и присваиваний. В отличие от операционной семантики, предписывающей единственную последовательность вычислений, трансформационная семантика допускает для этой программы несколько сот вариантов смешанных вычислений, которые в силу свойства Черча-Россера приводят к одной и той же остаточной программе, показанной в последней строке схемы.
ОРГАНИЗАЦИЯ вычислений в языке программирования, заданном трансформационной семантикой, имеет ряд существенных отличий от операционной семантики. Главное из них - это изменение модальности предписаний о выполнении команд. Если операционная семантика в каждый момент чтения программы указывает на единственную команду, которая ДОЛЖНА выполниться, то трансформационная семантика в каждый момент работы с программой показывает, какие команды могут "выполниться", т.е. раскрыться или редуцироваться. При этом вполне возможно, что в данный момент в программе существует несколько конструкций, к которым можно применить соответствующие преобразования. Семантика языка не подсказывает, какое из них должно быть выбрано, т.е. допускает в ходе выполнения программы акты произвольного выбора. Среди всех возможных состояний вычислительного процесса естественно выделяется такое, когда ни одно из преобразований не может быть применено ни к одной из оставшихся конструкций. Такое состояние программы и ее данных, т.е. текущих значений переменных, называется неподвижной точкой. Трансформационная семантика определена так, что если все исходные данные в программе заданы и программа для этих данных останавливается и выдает некоторый результат, скажем 78, в качестве значения команды вывода, то неподвижной точкой для этих же исходных данных будет программа, которая редуцируется к одной-единственной команде out(78). Если же часть входных данных окажется не заданной и соответствующие переменные останутся свободными, то неподвижной точкой будет некоторая остаточная программа, та же самая, которая получилась бы в результате смешанных вычислений согласно их операционному определению.
Система преобразований любой текстовой информации, которая приводит к одной и той же неподвижной точке независимо от порядка применения допустимых преобразований, называется системой Черча-Россера по имени известного американского математика А.Черча и его в то время молодого ученика Дж.Россера, которые в 30-е годы впервые исследовали подобного рода системы под названием лямбда-исчислений. Свойство Черча-Россера в применении к трансформационной семантике языка МИЛАН гарантирует однозначность вычислений, не взирая на возможные акты свободного выбора применяемых преобразований. Система преобразований, однако, не гарантирует, что какая-бы то ни было неподвижная точка будет обязательно достигнута. Раскрытие цикла может предлагать свои услуги бесконечно, если возникающее при этом условие альтернативы никогда не получит значение ложь, что привело бы к устранению раскрываемой итерации из программы.
Естественно, что применение "в лоб" трансформационной семантики для обработки программы путем комбинаторного перебора всех возможностей применения преобразований к конструкциям программы очень неэффективно. Достоинства такого способа описания языков программирования лежат в другом. Базовые трансформации программного текста, предписываемые трансформационной семантикой, могут быть основой для достоверного построения разнообразных программных процессоров, существенно более широких, нежели жесткие схемы обычных и смешанных вычислений, задаваемых операционной семантикой. Еще одним достоинством трансформационной семантики является то, что она легко допускает присоединение дополнительных преобразований, содействующих улучшению остаточной программы. Например, присоединение к трансформационной семантике языка МИЛАН преобразования вида E*1 -> E, где E - произвольное арифметическое выражение, позволяет получить идеальную остаточную программу для вычисления x**2 (см. выше).
| РЕДУКЦИЯ АРГУМЕНТА | x в передовой позиции аргумента выражения, x = a | a |
| РЕДУКЦИЯ ПЕРЕМЕННОЙ | x находится в списке переменных, но не входит в текст программы | пусто |
| РЕДУКЦИЯ ОПЕРАЦИИ | f(a1,...,an), где f - операция, а1,...,an - константы, f(a1,...,an) = b | b |
| РЕДУКЦИЯ ВВОДА | in(x), входное значение равно a | x:=a |
| РЕДУКЦИЯ ПРИСВАИВАНИЯ | x:=а; в передовой позиции, a - константа | пусто, x = a |
| РЕДУКЦИЯ АЛЬТЕРНАТИВЫ | if true then S1 else S2 fi или if false then S1 else S2 fi | соответственно S1 или S2 |
| РАСКРЫТИЕ ИТЕРАЦИИ | while В do S od, в передовой позиции | if В then S; while В do S od else fi |
ТРАНСФОРМАЦИОННАЯ СЕМАНТИКА языка МИЛАН задается набором правил преобразования программного текста и значений переменных. Все правила, кроме правила для итерации, являются редукциями, приводящими к устранению конструкции из программы или замене ее на более простую. В левой колонке таблицы помещено название конструкции, в средней - описывается контекст, в котором преобразование возможно, в правой - указывается, на что заменяется вхождение конструкции, к которому применено правило. Правило для итерации является раскрытием: оно вычленяет один экземпляр условия итерации и ее внутренних команд, к которым могут теперь применяться редукции, сохраняя саму итерацию для возможных повторных раскрытий. Переменная x находится в передовой позиции аргумента выражения, если между ним и началом программы нет присваивания этой переменной и выражение не является условием итерации. Присваивание переменной x находится в передовой позиции, если оно не находится внутри составной команды и между ним и началом программы нет ни одного вхождения x. Итерация находится в передовой позиции, если она не находится внутри составной команды и между ней и началом программы нет других редуцируемых итераций. Выполнение программы в рамках трансформационного подхода состоит в попытках применения к программе любого из правил. При полностью заданных входных переменных программа редуцируется к команде вывода, в аргументе которой читается результат. В общем случае, при наличии свободных входных переменных, исходная программа редуцируется к некоторой остаточной программе.
-----
...
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:34 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
...
МЫ ОПИСАЛИ смешанные вычисления как общий метод специализации программ на сужение области их исходных данных. В качестве особого случая сужения мы выделили проекцию области на заданные значения части независимых переменных. Остаточная программа, соответствующая этому сужению, называется проекцией исходной программы на заданные значения переменных.
Пожалуй, наиболее интересным открытием, сделанным на основе понятия смешанных вычислений, было выяснение сущности трансляции - одного из наиболее фундаментальных и часто встречающихся в работе ЭВМ процессов. Способ записи программ, которые могут непосредственно выполняться на ЭВМ,- так называемый машинный язык - "удобен" для машины, но очень не удобен для человека, который придумывает эти программы. Без особого преувеличения можно сказать, что все развитие программирования шло в сторону приспособления языка программирования к удобству человека. При этом основным стимулом было желание составлять программу в тех же обозначениях, в которых человек формулирует задачу. Так появлялись языки программирования все более и более высокого уровня. Проблема внедрения этих языков могла считаться, однако, решенной только в том случае, если перевод их на машинный язык мог быть выполнен с помощью автоматической процедуры, т.е. общей программы, получившей название транслятора или компилятора. Транслятор по тексту программы на входном языке строит программу на машинном языке так, что эти программы реализуют одну и ту же функцию. Построение трансляторов в конце 50-х годов стало весьма специфической и очень трудоемкой областью программного обеспечения. Существует, конечно, и более прямой путь восприятия машинной программы на входном языке высокого уровня. Надо взять операционную семантику входного языка и запрограммировать ее на языке машины. Такие универсальные программы получили название интерпретаторов. Если подать на вход интерпретатора текст программы на входном языке и ее данные, то машина произведет такие действия, как если бы она непосредственно выполняла входную программу. Но, хотя такая техника применяется часто, особенно на персональных компьютерах, в общем случае исполнение входных программ в режиме прямой интерпретации языка высокого уровня очень не экономично, особенно если программа должна выполняться многократно.
Предположим, однако, что на языке машины запрограммированы смешанные вычисления. Соответствующую программу назовем смешанным вычислителем. Он реализует функцию трех переменных: первый аргумент - исходная программа, второй аргумент - ее известные входные данные и третий аргумент - ее свободные переменные. Результат смешанного вычисления - проекция исходной программы на ее известные данные, а сама проекция реализует функцию свободных переменных. Возьмем теперь смешанный вычислитель и применим его к интерпретатору входного языка при некоторой заданной входной программе, но при ее данных, оставленных свободными. В результате мы получим проекцию интерпретатора на входную программу, при этом проекция - это программа на машинном языке. По свойствам остаточной программы, если на вход этой машинной программы подать исходные данные входной программы на языке высокого уровня, она вычислит то же значение, что и входная программа. Другими словами, проекция интерпретатора входного языка на программу в этом языке представляет собой перевод этой программы на машинный язык.
Можно пойти дальше. Рассмотрим смешанный вычислитель как программу, которая сама может быть подвержена смешанным вычислениям - с заданным интерпретатором входного языка, но с его аргументами, оставленными свободными. В результате мы получим проекцию смешанного вычислителя на интерпретатор. Если на вход этой остаточной программы подать текст какой-либо входной программы, то по свойствам смешанных вычислений в качестве результата будет получен ее перевод на машинный язык. Другими словами, проекция смешанного вычислителя на интерпретатор входного языка - это программа транслятора с этого языка на машинный.
Эти замечательные соотношения автор называет проекциями Футамуры по имени молодого японского программиста, который впервые нашел их в 1971г. Они были опубликованы в малоизвестном японском техническом журнале и с тех пор по крайней мере два раза переоткрывались, прежде чем стали общеизвестным фактом.
-----
ОБОЗНАЧЕНИЯ
Int(P;X) - интерпретатор входного языка
Tran(P;X) - транслятор с входного языка
P - входная программа
X - исходные данные входной программы
Mix(P;A;Y) - смешанный вычислитель
P - общая программа
A - заданные значения входных переменных
Y - свободные входные переменные
p - конкретная программа
p(x) - программа p с указанными входными переменными x
p(a) - результат выполнения программы p для исходных данных a
obp(x) - объектная программа, перевод входной программы p на машинный язык
pa(y) - остаточная программа, проекция общей программы p(x,y) на данные значения a части x ее входных переменных
СВОЙСТВА
свойство интерпретатора: Int(p;a) = p(a)
свойство объектной программы: p(a) = obp(a) свойство транслятора: Tran(p;х) = obp(x)
свойство проекции: pa(b) = p(a,b)
свойство смешанного вычислителя: Mix(p;a;y) = pa(y)
ПРОЕКЦИИ ФУТАМУРЫ
Intp(x) = obp(x) (1)
MixInt(P;X) = Tran(Р;Х) (2)
ДОКАЗАТЕЛЬСТВА
1-й проекции: obp(a) = Int(p;a) = p(a)
2-й проекции: Tran(p;x) = Mix(Int;p;x) = Intp(x) = obp(x)
-----
ФОРМУЛИРОВАНИЕ ЗАКОНОМЕРНОСТЕЙ в виде математических выражений зачастую требует большой подготовительной работы в поиске формальных определений и обозначений. Эта работа, однако, вознаграждается общностью, краткостью и точностью формулировки, выразительно раскрывающей природу вещей и явлений. Именно так обстоит дело с проекциями Футамуры, демонстрирующими органическую связь трансляции и смешанных вычислений. Первая проекция гласит, что перевод входной программы на машинный язык может быть получен путем смешанного вычисления интерпретатора входного языка при заданной программе, но ее входных переменных оставленных свободными. В доказательстве справедливости первой проекции первое равенство имеет место в силу свойства проекции, а второе равенство - в силу свойства интерпретатора. Вторая проекция гласит, что сам транслятор может быть получен как проекция смешанного вычислителя на интерпретатор с оставлением аргументов интерпретатора свободными. В доказательстве справедливости второй проекции первое равенство имеет место в силу свойства проекции, второе равенство - в силу свойства смешанного вычислителя и третье равенство - в силу 1-й проекции Футамуры. Важность этих формулировок не в том, что они предлагают еще один подход к получению объектных программ и построению трансляторов, а в том, что они показывают, каким знанием нужно обладать для реализации этих важнейших процедур программирования.
-----
СМЕШАННЫЕ вычисления как конструктивное направление в теории и практике программирования обозначились только в последние несколько лет. В качестве же абстрактной математической концепции они имеют более чем 50-летнюю историю и, мало того, принадлежат к глубинным понятиям оснований математики.
В 20-е годы ученые усиленно размышляли над природой математического языка, одним из главных компонентов которого всегда были функциональные обозначения. Немецкий математик М.Шенфинкель сделал следующее наблюдение, касающееся функций нескольких переменных. Пусть у нас есть функция двух переменных f(x,y). Подстановка вместо одной переменной некоторого значения, скажем x = 10, делает из функции двух переменных f(x,y) новую функцию одной переменной ф(y), связанную с f следующим соотношением: для любого y ф(y) = f(10,y). Можно сказать, что связывание некоторого аргумента конкретным значением создает функциональный оператор, сопоставляющий функции двух переменных функцию одной переменной. Этот оператор, изученный в начале 30-х годов американским математиком X.Карри, получил название карриева оператора и, очевидно, является абстрактным прообразом процедуры смешанных вычислений.
В начале 30-х годов Черч разработал формальное исчисление функций в надежде получить язык конструктивного манипулирования функциональными обозначениями предельной простоты и максимальной общности. Это исчисление, получившее название лямбда-исчисления, сыграло большую роль в нахождении точного определения эффективно вычислимых функций. Именно в рамках лямбда-исчисления в 1936г. Черчем был найден пример задачи, которую можно точно определить математически, но для которой не существует единой процедуры ее эффективного решения. В терминах языка МИЛАН эта задача звучит так: "Для любой программы, содержащей итерации, определить, может ли она войти в бесконечный цикл или нет". В лямбда-исчислении "программы" и "данные" изображались объектами одной природы. Вычислительный процесс задавался правилами, которые можно считать прототипом трансформационной семантики языков программирования. В лямбда-исчислении тоже были правила раскрытия и редукции, удовлетворявшие свойству Черча-Россера, а "смешанные вычисления" использовались в качестве основного метода вычисления функций от нескольких переменных согласно правилу Шенфинкеля-Карри.
В 40-х годах в трудах известного американского математика С.Клини получила большое развитие теория рекурсивных функций как теоретической модели эффективной вычислимости. В книге "Введение в метаматематику", вышедшей в свет в 1952г., Клини привел доказательство так называемой s-m-n-теоремы, которая устанавливала существование процедуры смешанных вычислений для рекурсивных функций. По ходу развития теории рекурсивных функций стало ясно, что s-m-n-теорема играет центральную роль в теории вычислимости.
В конце 50-х годов московский математик В.Успенский в своих "Лекциях о вычислимых функциях" доказал теорему, которая в понятиях этой статьи звучит, примерно, так: "Для того чтобы на данный машинный язык можно было бы перевести любой другой язык программирования, необходимо и достаточно, чтобы в машинном языке были бы определены смешанные вычисления". Это утверждение, по существу, эквивалентно проекциям Футамуры, однако лишь в конце 70-х годов эти два утверждения стали рядом.
Смешанные вычисления в применении к программному обеспечению восходят к итальянскому специалисту по вычислительной науке Л.Ломбарди, который назвал свой подход к обработке программ пошаговыми вычислениями с неполной информацией. В основу его идеи была положена критика основного положения традиционного программирования: использовать ЭВМ для выполнения программы только при полностью определенных данных. Этому требованию полной определенности Ломбарди противопоставил реальные условия, в которых человек постоянно должен принимать решения в условиях неполноты информации. Для того чтобы приблизиться к этим условиям, общая организация вычислений на машинах должна быть изменена. В несколько метафорическом стиле идея Ломбарди выглядит так: двигаясь навстречу постепенно поступающей информации, машина должна редуцировать универсальную программу на основе доступных данных, сохраняя про запас фрагменты обшей программы, подготовленные к восприятию временно отсутствующей информации. Как только появляется порция новой информации, соответствующий фрагмент редуцируется, обеспечивая общий прогресс вычислений.
Ломбарди не развил математической теории вычислений с неполной информацией, хотя и провел эксперимент с разработкой частичного вычислителя для языка программирования Лисп. Его работы дали толчок серии диссертационных работ, выполненных шведскими аспирантами А.Харалдсоном и П.Эмануельсоном, которые построили усовершенствованный смешанный вычислитель для языка Лисп. Коллектив московских специалистов Г.Х.Бабича, Л.Ф.Штернберга и Т.И.Югановой, основываясь на идеях Ломбарди, разработал специальный язык ИНКОЛ для организации вычислений с неполной информацией и применил его для процедуры принятия экономических решений в условиях неопределенности. Наконец, работы Ломбарди привели Футамуру к его проекциям.
СИСТЕМАТИЧЕСКАЯ работа над теорией и применением смешанных вычислений и ее интеграция с другими примыкающими исследованиями началась в 1977г. с работ автора этой статьи и его сотрудников. Это направление быстро развивается и сейчас литература по смешанным вычислениям уже перевалила за полусотню наименований. Теоретические модели смешанных вычислений, реализация смешанных вычислений для главных языков программирования, системы преобразований и редукций программ, аппаратная реализации смешанных вычислений, применения к теории компиляции, рассмотрение аналогичных явлений в процессах логического доказательства, приложения к параллельным вычислениям, построение эффективных специализированных алгоритмов, адаптация и генерация пакетов прикладных программ, рассмотрение сужений, более общих, нежели проекции,- все это заслуживает подробного обзора, но уже в специальной литературе.
Автор хотел бы завершить это изложение двумя методологическими замечаниями. Смешанные вычисления дают яркий пример того, насколько важно в зрелой науке уметь сочетать увлеченность практической работой с широким кругозором и знанием фундаментальных дисциплин, как важно теоретику уметь обнаруживать проблески своих теоретических концепций в пестроте реального мира. Широкая практика программирования, которая сделала актуальными проблемы трансляции и взаимодействия универсальных и специализированных методов, сложилась к концу 50-х годов. К этому времени в теории вычислимости уже существовали теоретические основы смешанных вычислений в виде лямбда-исчислений, s-m-n-теоремы, теоремы о транслируемости. Многие из теоретиков 60-х годов перешли в сферу программирования. Многие из тех, кто сейчас с таким энтузиазмом работают над смешанными вычислениями, в свое время при подготовке к аспирантским экзаменам читали литературу по теории вычислимости. Соответствующие потоки информации проходили рядом или даже пересекались и сосуществовали подолгу в головах исследователей и практиков. Потребовалось, однако, немало лет, чтобы искра догадки осветила все разнообразие практических и теоретических предпосылок этого нового раздела программирования.
Второе замечание - более деловое. Уже начальный опыт использования смешанных вычислений показал, что универсальные алгоритмы нужно создавать с учетом их двухступенчатого применения: получения специализированной версии и ее утилизации в суженной области. Понимание устройства смешанных вычислений позволяет значительно повысить эффективность остаточных программ и упростить их получение. Заметим, что этот подход более удобен для программиста. Как правило, для смешанных вычислений подходит такой универсальный алгоритм, который непосредственно вытекает из обшей теории. Усложненная кодировка исходных данных, излишняя ориентация на особенности ЭВМ, компактификация - все это противопоказано хорошему универсальному алгоритму. Выражаясь метафорически, универсальный алгоритм вместо рабочей лошадки становится элитным производителем остаточных программ, которые, принимая на себя груз рабочих вычислений, объединяют приобретенную эффективность с достоверностью обшей теории, воплощенной в универсальном методе.
МЫ ОПИСАЛИ смешанные вычисления как общий метод специализации программ на сужение области их исходных данных. В качестве особого случая сужения мы выделили проекцию области на заданные значения части независимых переменных. Остаточная программа, соответствующая этому сужению, называется проекцией исходной программы на заданные значения переменных.
Пожалуй, наиболее интересным открытием, сделанным на основе понятия смешанных вычислений, было выяснение сущности трансляции - одного из наиболее фундаментальных и часто встречающихся в работе ЭВМ процессов. Способ записи программ, которые могут непосредственно выполняться на ЭВМ,- так называемый машинный язык - "удобен" для машины, но очень не удобен для человека, который придумывает эти программы. Без особого преувеличения можно сказать, что все развитие программирования шло в сторону приспособления языка программирования к удобству человека. При этом основным стимулом было желание составлять программу в тех же обозначениях, в которых человек формулирует задачу. Так появлялись языки программирования все более и более высокого уровня. Проблема внедрения этих языков могла считаться, однако, решенной только в том случае, если перевод их на машинный язык мог быть выполнен с помощью автоматической процедуры, т.е. общей программы, получившей название транслятора или компилятора. Транслятор по тексту программы на входном языке строит программу на машинном языке так, что эти программы реализуют одну и ту же функцию. Построение трансляторов в конце 50-х годов стало весьма специфической и очень трудоемкой областью программного обеспечения. Существует, конечно, и более прямой путь восприятия машинной программы на входном языке высокого уровня. Надо взять операционную семантику входного языка и запрограммировать ее на языке машины. Такие универсальные программы получили название интерпретаторов. Если подать на вход интерпретатора текст программы на входном языке и ее данные, то машина произведет такие действия, как если бы она непосредственно выполняла входную программу. Но, хотя такая техника применяется часто, особенно на персональных компьютерах, в общем случае исполнение входных программ в режиме прямой интерпретации языка высокого уровня очень не экономично, особенно если программа должна выполняться многократно.
Предположим, однако, что на языке машины запрограммированы смешанные вычисления. Соответствующую программу назовем смешанным вычислителем. Он реализует функцию трех переменных: первый аргумент - исходная программа, второй аргумент - ее известные входные данные и третий аргумент - ее свободные переменные. Результат смешанного вычисления - проекция исходной программы на ее известные данные, а сама проекция реализует функцию свободных переменных. Возьмем теперь смешанный вычислитель и применим его к интерпретатору входного языка при некоторой заданной входной программе, но при ее данных, оставленных свободными. В результате мы получим проекцию интерпретатора на входную программу, при этом проекция - это программа на машинном языке. По свойствам остаточной программы, если на вход этой машинной программы подать исходные данные входной программы на языке высокого уровня, она вычислит то же значение, что и входная программа. Другими словами, проекция интерпретатора входного языка на программу в этом языке представляет собой перевод этой программы на машинный язык.
Можно пойти дальше. Рассмотрим смешанный вычислитель как программу, которая сама может быть подвержена смешанным вычислениям - с заданным интерпретатором входного языка, но с его аргументами, оставленными свободными. В результате мы получим проекцию смешанного вычислителя на интерпретатор. Если на вход этой остаточной программы подать текст какой-либо входной программы, то по свойствам смешанных вычислений в качестве результата будет получен ее перевод на машинный язык. Другими словами, проекция смешанного вычислителя на интерпретатор входного языка - это программа транслятора с этого языка на машинный.
Эти замечательные соотношения автор называет проекциями Футамуры по имени молодого японского программиста, который впервые нашел их в 1971г. Они были опубликованы в малоизвестном японском техническом журнале и с тех пор по крайней мере два раза переоткрывались, прежде чем стали общеизвестным фактом.
-----
ОБОЗНАЧЕНИЯ
Int(P;X) - интерпретатор входного языка
Tran(P;X) - транслятор с входного языка
P - входная программа
X - исходные данные входной программы
Mix(P;A;Y) - смешанный вычислитель
P - общая программа
A - заданные значения входных переменных
Y - свободные входные переменные
p - конкретная программа
p(x) - программа p с указанными входными переменными x
p(a) - результат выполнения программы p для исходных данных a
obp(x) - объектная программа, перевод входной программы p на машинный язык
pa(y) - остаточная программа, проекция общей программы p(x,y) на данные значения a части x ее входных переменных
СВОЙСТВА
свойство интерпретатора: Int(p;a) = p(a)
свойство объектной программы: p(a) = obp(a) свойство транслятора: Tran(p;х) = obp(x)
свойство проекции: pa(b) = p(a,b)
свойство смешанного вычислителя: Mix(p;a;y) = pa(y)
ПРОЕКЦИИ ФУТАМУРЫ
Intp(x) = obp(x) (1)
MixInt(P;X) = Tran(Р;Х) (2)
ДОКАЗАТЕЛЬСТВА
1-й проекции: obp(a) = Int(p;a) = p(a)
2-й проекции: Tran(p;x) = Mix(Int;p;x) = Intp(x) = obp(x)
-----
ФОРМУЛИРОВАНИЕ ЗАКОНОМЕРНОСТЕЙ в виде математических выражений зачастую требует большой подготовительной работы в поиске формальных определений и обозначений. Эта работа, однако, вознаграждается общностью, краткостью и точностью формулировки, выразительно раскрывающей природу вещей и явлений. Именно так обстоит дело с проекциями Футамуры, демонстрирующими органическую связь трансляции и смешанных вычислений. Первая проекция гласит, что перевод входной программы на машинный язык может быть получен путем смешанного вычисления интерпретатора входного языка при заданной программе, но ее входных переменных оставленных свободными. В доказательстве справедливости первой проекции первое равенство имеет место в силу свойства проекции, а второе равенство - в силу свойства интерпретатора. Вторая проекция гласит, что сам транслятор может быть получен как проекция смешанного вычислителя на интерпретатор с оставлением аргументов интерпретатора свободными. В доказательстве справедливости второй проекции первое равенство имеет место в силу свойства проекции, второе равенство - в силу свойства смешанного вычислителя и третье равенство - в силу 1-й проекции Футамуры. Важность этих формулировок не в том, что они предлагают еще один подход к получению объектных программ и построению трансляторов, а в том, что они показывают, каким знанием нужно обладать для реализации этих важнейших процедур программирования.
-----
СМЕШАННЫЕ вычисления как конструктивное направление в теории и практике программирования обозначились только в последние несколько лет. В качестве же абстрактной математической концепции они имеют более чем 50-летнюю историю и, мало того, принадлежат к глубинным понятиям оснований математики.
В 20-е годы ученые усиленно размышляли над природой математического языка, одним из главных компонентов которого всегда были функциональные обозначения. Немецкий математик М.Шенфинкель сделал следующее наблюдение, касающееся функций нескольких переменных. Пусть у нас есть функция двух переменных f(x,y). Подстановка вместо одной переменной некоторого значения, скажем x = 10, делает из функции двух переменных f(x,y) новую функцию одной переменной ф(y), связанную с f следующим соотношением: для любого y ф(y) = f(10,y). Можно сказать, что связывание некоторого аргумента конкретным значением создает функциональный оператор, сопоставляющий функции двух переменных функцию одной переменной. Этот оператор, изученный в начале 30-х годов американским математиком X.Карри, получил название карриева оператора и, очевидно, является абстрактным прообразом процедуры смешанных вычислений.
В начале 30-х годов Черч разработал формальное исчисление функций в надежде получить язык конструктивного манипулирования функциональными обозначениями предельной простоты и максимальной общности. Это исчисление, получившее название лямбда-исчисления, сыграло большую роль в нахождении точного определения эффективно вычислимых функций. Именно в рамках лямбда-исчисления в 1936г. Черчем был найден пример задачи, которую можно точно определить математически, но для которой не существует единой процедуры ее эффективного решения. В терминах языка МИЛАН эта задача звучит так: "Для любой программы, содержащей итерации, определить, может ли она войти в бесконечный цикл или нет". В лямбда-исчислении "программы" и "данные" изображались объектами одной природы. Вычислительный процесс задавался правилами, которые можно считать прототипом трансформационной семантики языков программирования. В лямбда-исчислении тоже были правила раскрытия и редукции, удовлетворявшие свойству Черча-Россера, а "смешанные вычисления" использовались в качестве основного метода вычисления функций от нескольких переменных согласно правилу Шенфинкеля-Карри.
В 40-х годах в трудах известного американского математика С.Клини получила большое развитие теория рекурсивных функций как теоретической модели эффективной вычислимости. В книге "Введение в метаматематику", вышедшей в свет в 1952г., Клини привел доказательство так называемой s-m-n-теоремы, которая устанавливала существование процедуры смешанных вычислений для рекурсивных функций. По ходу развития теории рекурсивных функций стало ясно, что s-m-n-теорема играет центральную роль в теории вычислимости.
В конце 50-х годов московский математик В.Успенский в своих "Лекциях о вычислимых функциях" доказал теорему, которая в понятиях этой статьи звучит, примерно, так: "Для того чтобы на данный машинный язык можно было бы перевести любой другой язык программирования, необходимо и достаточно, чтобы в машинном языке были бы определены смешанные вычисления". Это утверждение, по существу, эквивалентно проекциям Футамуры, однако лишь в конце 70-х годов эти два утверждения стали рядом.
Смешанные вычисления в применении к программному обеспечению восходят к итальянскому специалисту по вычислительной науке Л.Ломбарди, который назвал свой подход к обработке программ пошаговыми вычислениями с неполной информацией. В основу его идеи была положена критика основного положения традиционного программирования: использовать ЭВМ для выполнения программы только при полностью определенных данных. Этому требованию полной определенности Ломбарди противопоставил реальные условия, в которых человек постоянно должен принимать решения в условиях неполноты информации. Для того чтобы приблизиться к этим условиям, общая организация вычислений на машинах должна быть изменена. В несколько метафорическом стиле идея Ломбарди выглядит так: двигаясь навстречу постепенно поступающей информации, машина должна редуцировать универсальную программу на основе доступных данных, сохраняя про запас фрагменты обшей программы, подготовленные к восприятию временно отсутствующей информации. Как только появляется порция новой информации, соответствующий фрагмент редуцируется, обеспечивая общий прогресс вычислений.
Ломбарди не развил математической теории вычислений с неполной информацией, хотя и провел эксперимент с разработкой частичного вычислителя для языка программирования Лисп. Его работы дали толчок серии диссертационных работ, выполненных шведскими аспирантами А.Харалдсоном и П.Эмануельсоном, которые построили усовершенствованный смешанный вычислитель для языка Лисп. Коллектив московских специалистов Г.Х.Бабича, Л.Ф.Штернберга и Т.И.Югановой, основываясь на идеях Ломбарди, разработал специальный язык ИНКОЛ для организации вычислений с неполной информацией и применил его для процедуры принятия экономических решений в условиях неопределенности. Наконец, работы Ломбарди привели Футамуру к его проекциям.
СИСТЕМАТИЧЕСКАЯ работа над теорией и применением смешанных вычислений и ее интеграция с другими примыкающими исследованиями началась в 1977г. с работ автора этой статьи и его сотрудников. Это направление быстро развивается и сейчас литература по смешанным вычислениям уже перевалила за полусотню наименований. Теоретические модели смешанных вычислений, реализация смешанных вычислений для главных языков программирования, системы преобразований и редукций программ, аппаратная реализации смешанных вычислений, применения к теории компиляции, рассмотрение аналогичных явлений в процессах логического доказательства, приложения к параллельным вычислениям, построение эффективных специализированных алгоритмов, адаптация и генерация пакетов прикладных программ, рассмотрение сужений, более общих, нежели проекции,- все это заслуживает подробного обзора, но уже в специальной литературе.
Автор хотел бы завершить это изложение двумя методологическими замечаниями. Смешанные вычисления дают яркий пример того, насколько важно в зрелой науке уметь сочетать увлеченность практической работой с широким кругозором и знанием фундаментальных дисциплин, как важно теоретику уметь обнаруживать проблески своих теоретических концепций в пестроте реального мира. Широкая практика программирования, которая сделала актуальными проблемы трансляции и взаимодействия универсальных и специализированных методов, сложилась к концу 50-х годов. К этому времени в теории вычислимости уже существовали теоретические основы смешанных вычислений в виде лямбда-исчислений, s-m-n-теоремы, теоремы о транслируемости. Многие из теоретиков 60-х годов перешли в сферу программирования. Многие из тех, кто сейчас с таким энтузиазмом работают над смешанными вычислениями, в свое время при подготовке к аспирантским экзаменам читали литературу по теории вычислимости. Соответствующие потоки информации проходили рядом или даже пересекались и сосуществовали подолгу в головах исследователей и практиков. Потребовалось, однако, немало лет, чтобы искра догадки осветила все разнообразие практических и теоретических предпосылок этого нового раздела программирования.
Второе замечание - более деловое. Уже начальный опыт использования смешанных вычислений показал, что универсальные алгоритмы нужно создавать с учетом их двухступенчатого применения: получения специализированной версии и ее утилизации в суженной области. Понимание устройства смешанных вычислений позволяет значительно повысить эффективность остаточных программ и упростить их получение. Заметим, что этот подход более удобен для программиста. Как правило, для смешанных вычислений подходит такой универсальный алгоритм, который непосредственно вытекает из обшей теории. Усложненная кодировка исходных данных, излишняя ориентация на особенности ЭВМ, компактификация - все это противопоказано хорошему универсальному алгоритму. Выражаясь метафорически, универсальный алгоритм вместо рабочей лошадки становится элитным производителем остаточных программ, которые, принимая на себя груз рабочих вычислений, объединяют приобретенную эффективность с достоверностью обшей теории, воплощенной в универсальном методе.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
Это немного напоминает пинбол. Каждая ловушка на игровом поле может взводиться срабатыванием другой, ловит шарик в определенной зоне, отбивает его в другую... Есть совсем простые, есть сложные, но куда бы ни попал шарик, он всегда остается в игре и ничего не ломается.


Из японского 10-томника
Т.2. ПРЕДСТАВЛЕНИЕ И ОБРАБОТКА ЗНАНИЙ
Под редакцией Х.Уэно, М.Исидзука
Перевод И.А.Иванова
М.: "МИР", 1987
...
Расширенным вариантом модели правил является модель доски объявлений (blackboard) [Используется также термин "классная доска".- Прим ред.], которая была предложена в системе распознавания разговорной речи HEARSAY-II как модель представления знаний. Упрощенная структура этой модели приведена на рис.1.3. В центральной ее части, называемой доской объявлений, иерархически определены гипотезы: на самом верхнем уровне находятся заключения, на самом нижнем - факты, на промежуточных - промежуточные гипотезы. Например, при вводе речи в виде сигналов временного ряда, в системе, синтезирующей из них полный текст, определяются уровни гипотез сверху вниз по типу: "предложение - часть предложения - отдельное слово - слог - фонема".
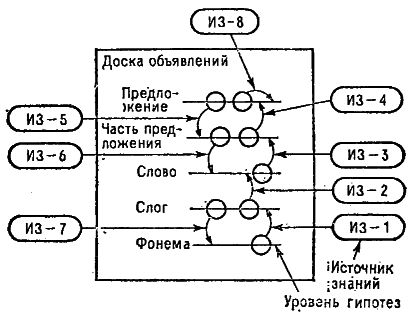
Рис.1.3. Концептуальная схема модели доски объявлений.
Вокруг доски объявлений расположены сгруппированные правила продукций, которые называются источниками знаний (ИЗ), они действуют на соответствующих уровнях гипотез или между уровнями. Например, источник знаний ИЗ-1 служит для формирования гипотез слогов на основании гипотез оценки фонем. Таким образом, последовательно снизу вверх формируются гипотезы верхних уровней, а на самом верхнем уровне образуется полное предложение. Однако образование предложения из последовательности сигналов не всегда проходит успешно: из-за шумов и нечеткости возникает большое число гипотез-кандидатов с высокой вероятностью их достоверности. В таких случаях в направлении сверху вниз используются знания по грамматике и контексту с тем, чтобы ограничить число кандидатов. Например, ИЗ-8 можно подобрать таким, чтобы он оценивал пригодность выдвинутой гипотезы-кандидата в качестве окончательного варианта предложения. Восходящий вывод называется выводом, управляемым данными, а нисходящий - выводом, управляемым моделью, они соответствуют указанным выше прямому и обратному выводам. Таким образом модель доски объявлении выполняет роль канала связи между источниками знаний. Кроме того, поскольку в данной модели четко определены функции каждого ИЗ, ситуации, когда их следует использовать, и эффективность их использования, то она имеет существенное преимущество о точки зрения систематизации знаний и повышения эффективности вывода. Оценка продукции, содержащейся в ИЗ, выполняется только при его активации, поэтому важной проблемой в управлении выводом является выбор порядка запуска ИЗ. Основные методы, используемые при этом,- метод "планировщика" и метод выдвижения кандидатуры "отправителя". В первом случае "планировщик" оценивает ситуацию на доске объявлений и последовательно называет "отправителей" (источники знаний). Во втором случае отправитель сам называет имя следующего отправителя. Однако проблемы имеются в обоих случаях, например, когда выполняется несколько продукций одного ИЗ и указывается более двух ИЗ, причем эти проблемы далеко не простые. В последнее время эту систему используют в комбинации с фреймовой системой.
...
6.3.2. МОДЕЛЬ ДОСКИ ОБЪЯВЛЕНИЙ В СИСТЕМЕ HEARSAY-II
HEARSAY-II - это система понимания речи, разработанная в Университете Карнеги-Меллона, США. Примерно с вероятностью 90% она может понимать связную речь в ограниченном диапазоне среди 1011 слов, относящихся к информатике и поиску литературы. Например, она может понимать вопросы типа
"В каких рефератах есть ссылки на теорию вычислений?",
"Есть ли ссылки на Фейгенбаума и Фельдмана?"
и интерпретировать их до уровня создания команд для поиска в библиографической базе данных.
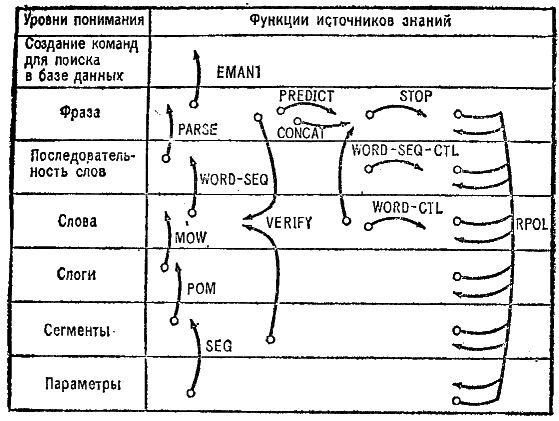
Рис.6.5. Структура знаний в системе понимания речи HEARSAY-II (знания распределены по источникам знаний, кружок указывает место сопоставления данных в условиях, стрелка - место занесения действия). Источники знаний - набор модулей типа "условие-действие".
SEQ - Преобразует речевые сигналы в дискретную форму, измеряет параметры, образует сегменты.
РОМ - На основе сегментов создает гипотезу о слогах.
MOW - На основе слогов создает гипотезы о простых словах.
WORD-CTL - Управляет числом гипотез, созданных модулем MOW.
WORD-SEQ - На основе гипотез о словах и грамматических правил создает гипотезы о последовательности слов.
WORD-SEQ-CTL - Управляет числом гипотез, созданных модулем WORD-SEQ.
PARSE - Делает грамматический разбор последовательности слов, если все верно, создает гипотезы о фразе.
PREDICT - Предсказывает слова, которые предшествуют или следуют за фразой.
VERIFY - Оценивает степень соответствия между гипотезой о сегментах и парой связанных слов.
CONCAT - На основе проверенных пар связанных слов создает гипотезу о фразе.
RPOL - Оценивает степень доверия другим гипотезам на основе информации в гипотезах, созданных другими источниками.
STOP - Оценивает необходимость остановки процесса (закончено ли предложение?) и выбирает гипотезу, которая считается наиболее верной.
5EGMANT - Интерпретирует смысл для системы поиска информации.
Предусмотрено семь уровней понимания от акустических параметров звуковых волн до понимания смысла вопроса (рис.6.5). На этом же рисунке указаны необходимые для этого знания, управление знаниями ведется через отдельные источники знаний. Форма представления знаний - модули (типа правил), состоящие из пар (блок условия - блок действия). Понимание осуществляется на основе данных низшего уровня с переходом к интерпретации на следующий уровень; интерпретация не всегда однозначна и обычно генерируются несколько гипотез. Каждая гипотеза оценивается с использованием информации верхнего уровня, в результате остается одна гипотеза, которая считается правильной. К гипотезам добавляется оценка (число от 0 до 100), указывающая их достоверность, но эта оценка действует ad hoc [На данный случай (лат.).- Прим.перев.]. В конце концов, выбирая наиболее достоверную гипотезу на уровне фразы, извлекается смысл вопроса для поиска литературы.
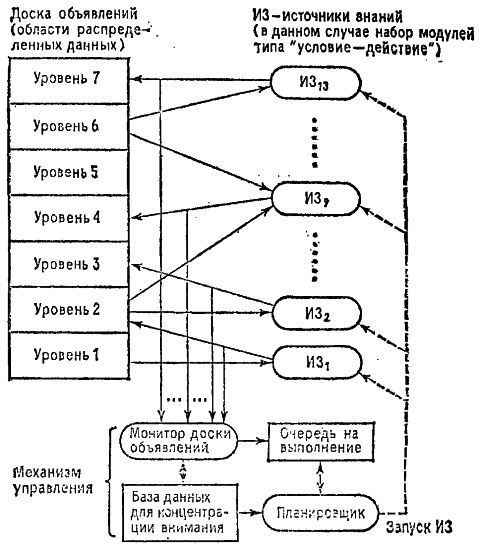
Рис.6.6. Модель доски объявлений в системе HEARSAY-II.
Структура системы HEARSAY-II - это модель доски объявлений (рис. 6.6). Она представляет собой распределенную область данных, каждый источник знаний (ИЗ) обращается к соответствующим областям доски объявлений, вносит гипотезы или дает им оценки в других областях. Эту систему можно рассматривать как распределенную иерархическую высокоуровневую продукционную систему. В принципе можно считать, что все источники знаний, действуя асинхронно и параллельно, переписывают содержимое доски объявлений, что плохо поддается реализации на последовательных компьютерах. Поэтому предусмотрен механизм управления, планирующий работу так, чтобы в первую очередь действовал источник знаний с высшим приоритетом (такой механизм аналогичен механизму списка заявок в программе AM, рассмотренной в разделе 6.2.2). Модель доски объявлений, разработанная в системе HEARSAY-II, в дальнейшем предполагается реализовать как систему представления универсальных знаний. Она дает хороший эффект для согласованного устранения многозначности и нечеткости, возникающих на каждом этапе процесса понимания и интерпретации, с помощью знаний на различных уровнях.


Из японского 10-томника
Т.2. ПРЕДСТАВЛЕНИЕ И ОБРАБОТКА ЗНАНИЙ
Под редакцией Х.Уэно, М.Исидзука
Перевод И.А.Иванова
М.: "МИР", 1987
...
Расширенным вариантом модели правил является модель доски объявлений (blackboard) [Используется также термин "классная доска".- Прим ред.], которая была предложена в системе распознавания разговорной речи HEARSAY-II как модель представления знаний. Упрощенная структура этой модели приведена на рис.1.3. В центральной ее части, называемой доской объявлений, иерархически определены гипотезы: на самом верхнем уровне находятся заключения, на самом нижнем - факты, на промежуточных - промежуточные гипотезы. Например, при вводе речи в виде сигналов временного ряда, в системе, синтезирующей из них полный текст, определяются уровни гипотез сверху вниз по типу: "предложение - часть предложения - отдельное слово - слог - фонема".

Рис.1.3. Концептуальная схема модели доски объявлений.
Вокруг доски объявлений расположены сгруппированные правила продукций, которые называются источниками знаний (ИЗ), они действуют на соответствующих уровнях гипотез или между уровнями. Например, источник знаний ИЗ-1 служит для формирования гипотез слогов на основании гипотез оценки фонем. Таким образом, последовательно снизу вверх формируются гипотезы верхних уровней, а на самом верхнем уровне образуется полное предложение. Однако образование предложения из последовательности сигналов не всегда проходит успешно: из-за шумов и нечеткости возникает большое число гипотез-кандидатов с высокой вероятностью их достоверности. В таких случаях в направлении сверху вниз используются знания по грамматике и контексту с тем, чтобы ограничить число кандидатов. Например, ИЗ-8 можно подобрать таким, чтобы он оценивал пригодность выдвинутой гипотезы-кандидата в качестве окончательного варианта предложения. Восходящий вывод называется выводом, управляемым данными, а нисходящий - выводом, управляемым моделью, они соответствуют указанным выше прямому и обратному выводам. Таким образом модель доски объявлении выполняет роль канала связи между источниками знаний. Кроме того, поскольку в данной модели четко определены функции каждого ИЗ, ситуации, когда их следует использовать, и эффективность их использования, то она имеет существенное преимущество о точки зрения систематизации знаний и повышения эффективности вывода. Оценка продукции, содержащейся в ИЗ, выполняется только при его активации, поэтому важной проблемой в управлении выводом является выбор порядка запуска ИЗ. Основные методы, используемые при этом,- метод "планировщика" и метод выдвижения кандидатуры "отправителя". В первом случае "планировщик" оценивает ситуацию на доске объявлений и последовательно называет "отправителей" (источники знаний). Во втором случае отправитель сам называет имя следующего отправителя. Однако проблемы имеются в обоих случаях, например, когда выполняется несколько продукций одного ИЗ и указывается более двух ИЗ, причем эти проблемы далеко не простые. В последнее время эту систему используют в комбинации с фреймовой системой.
...
6.3.2. МОДЕЛЬ ДОСКИ ОБЪЯВЛЕНИЙ В СИСТЕМЕ HEARSAY-II
HEARSAY-II - это система понимания речи, разработанная в Университете Карнеги-Меллона, США. Примерно с вероятностью 90% она может понимать связную речь в ограниченном диапазоне среди 1011 слов, относящихся к информатике и поиску литературы. Например, она может понимать вопросы типа
"В каких рефератах есть ссылки на теорию вычислений?",
"Есть ли ссылки на Фейгенбаума и Фельдмана?"
и интерпретировать их до уровня создания команд для поиска в библиографической базе данных.

Рис.6.5. Структура знаний в системе понимания речи HEARSAY-II (знания распределены по источникам знаний, кружок указывает место сопоставления данных в условиях, стрелка - место занесения действия). Источники знаний - набор модулей типа "условие-действие".
SEQ - Преобразует речевые сигналы в дискретную форму, измеряет параметры, образует сегменты.
РОМ - На основе сегментов создает гипотезу о слогах.
MOW - На основе слогов создает гипотезы о простых словах.
WORD-CTL - Управляет числом гипотез, созданных модулем MOW.
WORD-SEQ - На основе гипотез о словах и грамматических правил создает гипотезы о последовательности слов.
WORD-SEQ-CTL - Управляет числом гипотез, созданных модулем WORD-SEQ.
PARSE - Делает грамматический разбор последовательности слов, если все верно, создает гипотезы о фразе.
PREDICT - Предсказывает слова, которые предшествуют или следуют за фразой.
VERIFY - Оценивает степень соответствия между гипотезой о сегментах и парой связанных слов.
CONCAT - На основе проверенных пар связанных слов создает гипотезу о фразе.
RPOL - Оценивает степень доверия другим гипотезам на основе информации в гипотезах, созданных другими источниками.
STOP - Оценивает необходимость остановки процесса (закончено ли предложение?) и выбирает гипотезу, которая считается наиболее верной.
5EGMANT - Интерпретирует смысл для системы поиска информации.
Предусмотрено семь уровней понимания от акустических параметров звуковых волн до понимания смысла вопроса (рис.6.5). На этом же рисунке указаны необходимые для этого знания, управление знаниями ведется через отдельные источники знаний. Форма представления знаний - модули (типа правил), состоящие из пар (блок условия - блок действия). Понимание осуществляется на основе данных низшего уровня с переходом к интерпретации на следующий уровень; интерпретация не всегда однозначна и обычно генерируются несколько гипотез. Каждая гипотеза оценивается с использованием информации верхнего уровня, в результате остается одна гипотеза, которая считается правильной. К гипотезам добавляется оценка (число от 0 до 100), указывающая их достоверность, но эта оценка действует ad hoc [На данный случай (лат.).- Прим.перев.]. В конце концов, выбирая наиболее достоверную гипотезу на уровне фразы, извлекается смысл вопроса для поиска литературы.

Рис.6.6. Модель доски объявлений в системе HEARSAY-II.
Структура системы HEARSAY-II - это модель доски объявлений (рис. 6.6). Она представляет собой распределенную область данных, каждый источник знаний (ИЗ) обращается к соответствующим областям доски объявлений, вносит гипотезы или дает им оценки в других областях. Эту систему можно рассматривать как распределенную иерархическую высокоуровневую продукционную систему. В принципе можно считать, что все источники знаний, действуя асинхронно и параллельно, переписывают содержимое доски объявлений, что плохо поддается реализации на последовательных компьютерах. Поэтому предусмотрен механизм управления, планирующий работу так, чтобы в первую очередь действовал источник знаний с высшим приоритетом (такой механизм аналогичен механизму списка заявок в программе AM, рассмотренной в разделе 6.2.2). Модель доски объявлений, разработанная в системе HEARSAY-II, в дальнейшем предполагается реализовать как систему представления универсальных знаний. Она дает хороший эффект для согласованного устранения многозначности и нечеткости, возникающих на каждом этапе процесса понимания и интерпретации, с помощью знаний на различных уровнях.
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:36 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

Эшер. Относительность. Как-то так машины соединяются лентами.
Из книги:
Н.А.КРИНИЦКИЙ, АЛГОРИТМЫ И РОБОТЫ, 1983
ГЛАВА 5. КОЛЛЕКТИВЫ АЛГОРИТМОВ
#5.1. НЕСКОЛЬКО АЛГОРИТМОВ И ОДИН ОПЕРАНД
До сих пор нам встречались случаи, когда алгоритм и операнд "сражались один на один" (одноместные алгоритмы) или один алгоритм имел дело с несколькими операндами (многоместные алгоритмы). При этом "победителем" оказывался алгоритм. Он перерабатывал операнды в искомый результат. Правда, допускались случаи, когда процесс безрезультатно обрывался или затягивался бесконечно. Но и в этих случаях алгоритм оставался верен себе: он никогда не давал различные результаты при повторных "заходах" Когда он противостоял нескольким операндам, они представляли собой коллектив.
Что же получится, если одному операнду противопоставить несколько алгоритмов? По-видимому, их сила должна возрасти? Но оказывается, что в общем случае они потеряют свое главное свойство: однозначность. Они будут друг другу мешать, и это приведет к их "поражению".
Но оставим спортивный стиль и вернемся к математическому. Попробуем разобраться в сущности вопроса. Для этого рассмотрим различные возможные случаи взаимодействия алгоритмов и операндов.
1. Один алгоритм и несколько операндов. Этот случай рассмотрен в #4.5. Как мы помним, несколько операндов (от одного до n) объединены вспомогательной связью в совокупный операнд [В книге наборы данных рассматриваются в виде связных семантических сетей.- G.]. Затем алгоритм и этот совокупный операнд (точнее, их записи) объединены с помощью новой вспомогательной связи в одну конструкцию. И эта конструкция подвергается переработке алгоритмом выполнения [В книге разделяются записи алгоритмов на некотором языке и алгоритмы выполнения этих записей вычислителем (например, алгоритм внутренней работы процессора по исполнению программы).- G.]. Алгоритм выполнения порождает алгоритмический процесс, который представляет собой последовательность шагов. На каждом шаге либо происходит некоторое элементарное преобразование, либо выполняется логическая операция. Что при этом преобразуется или проверяется легко понять, если алгоритм принадлежит классу первичных. Преобразуется, по существу, операнд, а запись первичного алгоритма только просматривается (хотя и это является преобразованием, так как "просматривание" представляет собой связывание отдельных частей записи алгоритма различными выделяющими связями).
В общем случае алгоритмический процесс более сложен, так как отдельные его шаги могут заключаться в выполнении операций, преобразующих совместно элементы записей операнда, алгоритма и даже алгоритма выполнения. Но при этом всегда алгоритмический процесс имеет характер последовательности шагов и является детерминированным (при повторных выполнениях алгоритма в точности воспроизводится).
2. Несколько алгоритмов и несколько операндов при одном алгоритме выполнения. Этот случай ненамного сложнее предыдущего. Рассмотрим его вкратце. Предположим, что, как и в #4.5, заданы два языка: L1 - исходных данных (операндов) и алгоритмический язык L2. С помощью связи m-го жанра и ранга, играющей вспомогательную роль, свяжем m предложений языка L2 (т.е. записей алгоритмов) в совокупную запись. Как и в первом случае, построим совокупный операнд из n предложений языка L1. Далее, с помощью вспомогательной связи 2-го ранга и жанра совокупную запись алгоритмов свяжем с совокупной записью операндов. Именно эту символьную конструкцию должен перерабатывать алгоритм выполнения W. Алгоритм выполнения определит процесс совместного выполнения сразу m алгоритмов над n операндами. Как и в первом случае, этот процесс будет последовательностью актов и будет полностью детерминированным [Примечание для программистов: операционная система мультипрограммного режима, обеспечивающая "одновременное" выполнение с помощью однопроцессорной ЭВМ сразу нескольких программ, является алгоритмом выполнения n алгоритмов, имеющих n операндов].
3. Операнд один, а алгоритмов несколько и каждый со своим алгоритмом выполнения. Процесс выполнения каждого алгоритма является последовательным, а совокупный процесс имеет хаотический характер. Он зависит от соотношения скоростей алгоритмов выполнения, которое в течение выполнения алгоритмов может изменяться и быть различным при повторных применениях алгоритмов к исходному данному. Нет не только детерминированности процесса, но и однозначности результата. Взаимное расположение шагов, совершаемых разными алгоритмами, непредсказуемо, а результат от него зависит. Так будет, если не наделить алгоритмы специальными средствами, обеспечивающими однозначность результата.
В некоторых частных случаях однозначность результата гарантируется и без специальных средств. Например, если операнд содержит столько подконструкций, сколько алгоритмов, и каждый алгоритм перерабатывает отдельную подконструкцию, не затрагивая других. При этом хаотичность совокупного алгоритмического процесса не влияет на окончательный результат: соответствующие операции, выполняемые над операндом, являются локальными и зоны их действия не пересекаются. Но этот случай неинтересен. В нем каждый алгоритм "сражается" со своим операндом (подконструкцией) один на один.
Гораздо интереснее случай, когда возможно преобразование одних и тех же подконструкций операнда несколькими алгоритмами. Во всяком случае ясно, что операции, выполняемые отдельными алгоритмами на отдельных шагах, должны быть локальными (см. #2.7).
Выполнение локальной операции можно расчленить на части: а) обращение к операнду для определения исходных данных операции; б) внесение в преобразуемую символьную конструкцию результата операции. По аналогии с преобразованием символьной конструкции, записанной на бумаге, назовем эти части соответственно ЧТЕНИЕМ и ПИСАНИЕМ. Если два или несколько алгоритмов читают некоторую подконструкцию и ни один из них ее не пишет, то результат чтения будет одним и тем же независимо от того, какой алгоритм будет раньше читать, а какой - позже. Совсем другая картина получится, если один алгоритм будет читать подконструкцию, а другой ее же писать. Может быть сперва написано, а потом прочитано или сперва прочитано (старое состояние подконструкций), а потом написано. Недопустимо также неуправляемое писание двумя алгоритмами одной и той же подконструкций. Писание заключается в замене старого состояния подконструкций новым. При неуправляемом писании новое состояние зависит от того, который из двух алгоритмов будет писать позже.
Теперь мы можем указать еще один случай безконфликтности алгоритмов, имеющих общий операнд. В этом случае операнд состоит из n+1 подконструкций, где n - число алгоритмов. Пронумеруем мысленно алгоритмы числами 1, 2, ..., n и подконструкций - числами 0, 1, ..., n. Предположим, что из подконструкций #0 любой алгоритм может только читать, а в подконструкций #i может как писать, так и читать только алгоритм #i (где i = 1, или 2, ..., или n). Очевидно, при таких условиях хаотичность алгоритмического совокупного процесса не приведет к неоднозначности результата.
В наиболее общем случае можно считать, что операнд состоит из некоторого числа подконструкций, которые можно разбить на две группы. В одну из них входят подконструкции, называемые СОБСТВЕННЫМИ, а в другую - подконструкции, называемые БУФЕРНЫМИ. Каждая собственная подконструкция либо доступна как по письму, так и по чтению только одному алгоритму, либо доступна нескольким алгоритмам, но только по чтению. Каждая буферная подконструкция доступна сразу нескольким алгоритмам и хотя бы одному из них по письму. В описанных выше случаях все подконструкции были собственные. Очевидно, не всегда так просто удается обеспечить бесконфликтность алгоритмов с общим операндом, как в указанных частных случаях.
#5.2. РЕГУЛИРУЮЩИЕ ПРЕДИКАТЫ
Слово ПРЕДИКАТ означает то же, что УСЛОВИЕ. Термин этот принят в математической логике. Введенные нами логические операции (см. #2.7) проверяют выполнение условий или, как говорят в логике, определяют логическое значение предиката.
Описывая ниже алгоритмы, совместно преобразующие один общий операнд, сущность используемых при этом приемов будем пояснять с помощью семантических схем. Для операторных алгоритмов эти схемы будут отражать и их структуру. Для записи семантических схем используем язык схем, введенный в #4.8. Характер этой книги вынуждает меня вместо строгих доказательств ограничиться содержательными рассуждениями и примерами.
Как одно из средств координации алгоритмических процессов нам потребуется один тип операции, который мы сейчас объявим.
Пусть, B - некоторая буферная подконструкция операнда. Обозначим через P(B) логическую локальную операцию, проверяющую, обладает ли B некоторым свойством. Можно построить первичный алгоритм, состоящий из одного условного приказа:
1) Если P(B), то стоп, иначе ->1;
Этот алгоритм осуществляет тождественное преобразование буфера B, если он удовлетворяет условию P(B), и неприменим к нему в противном случае. Отображение, реализуемое этим алгоритмом, объявим операцией и назовем ее "Ожидать P(B)". В составе одиночного первичного алгоритма приказ, например, вида
5) Ожидать P(B), ->6;
не влиял бы на алгоритмический процесс, если условие P(B) выполняется; в противоположном случае он вызывал бы безрезультатную остановку. Другое дело, если этот приказ входит в состав одного из алгоритмов, совместно перерабатывающий общий операнд. Остановка длилась бы до тех пор, пока один из других алгоритмов не преобразовал бы B так, что условие P(B) выполнится. Отмечу, что для выполнения операции "Ожидать P(B)" нужно читать подконструкцию B или ее часть, но не нужно ничего писать.
Рассмотрим теперь случай, когда n алгоритмов A1, A2, ..., An обрабатывают операнд, в котором подконструкция В является буфером, доступным для любого из этих алгоритмов. Предположим, что существуют n предикатов P1(B), P2(B), ..., Pn(B), удовлетворяющих следующим двум условиям: 1) для любого состояния B эти предикаты определены; 2) всегда только одно условие выполняется, а все остальные не выполняются.
Такую совокупность условий будем называть СИСТЕМОЙ РЕГУЛИРУЮЩИХ ПРЕДИКАТОВ N-ГО ПОРЯДКА.
С помощью системы регулирующих предикатов n-го порядка можно обеспечить бесконфликтное обращение алгоритмов к буферу B, если число алгоритмов не более n. Проиллюстрирую это на частном примере, когда n = 3. Пусть семантические схемы алгоритмов имеют вид:
A1:
1) S1 := F11(S1), ->2;
2) Ожидать P1(B), ->3;
3) S1 := F12(S1, B), ->4;
4) B := Ф2(B), ->5;
5) S1 := F13(S1), ->6;
6) Ожидать P1(B), ->7;
7) Если Q(S1, В), то стоп, иначе -> 1;
A2:
1) Ожидать P2(B), ->2;
2) S2 := F21(S2, B), ->3;
3) В = Ф3(B), ->4;
4) S2 := F22(S2), ->1;
A3:
1) Ожидать P3(B), ->2;
2) В = Ф1(B), ->3;
3) S3 := F31(S3), ->1;
В этих схемах алгоритмов P1, P2, P3 - система регулирующих предикатов 3-го порядка. Преобразование B = Фi(B) так перерабатывает B, что становится выполненным условие Pi(B), где i = 1, 2 или 3. Смысл остальных функциональных и предикатных знаков понятен (в нужной степени) из текста схем; S1, S2, S3 - собственные подконструкции алгоритмов.
Защитой от конфликтов являются операции "Ожидать". Только в приказах, которые следуют за приказами, содержащими эту операцию, могут стоять приказы, обращающиеся к буферу, и последним по порядку выполнения является приказ, изменяющий так состояние буфера, что право обращения к нему получает один из остальных алгоритмов. Регулирующие предикаты взаимно-однозначно соответствуют алгоритмам. В принципе, число алгоритмов может быть меньше порядка системы регулирующих предикатов. В этом случае взаимно-однозначное соответствие должно существовать между множеством алгоритмов и некоторым подмножеством регулирующих предикатов.
Если внимательно проследить за процессом выполнения алгоритмов, то можно заметить, что каждый алгоритм может разрешать обращение к буферу другому, запрещая такое обращение себе. При этом нужно иметь в виду, что алгоритмы могут иметь условные приказы, которые приводят к разветвлению процесса выполнения данного алгоритма и могут иметь циклический характер, при котором происходит возврат к уже выполненным один или несколько раз приказам. В процессе выполнения каждого алгоритма до обращения к буферу должна быть обеспечена невозможность одновременного обращения к буферу другого алгоритма. Она обеспечивается тем, что обращению к буферу предшествует (хотя, может быть, не непосредственно) приказ ожидания.
На рис.5.1 схематически показан совокупный процесс выполнения алгоритмов A1, A2, A3 в предположении, что начальное состояние буфера B удовлетворяет условию P3(B) и что при повторном выполнении приказа 7 первого алгоритма реализуется отсылка "стоп". На рисунке в горизонтальных строках записаны номера выполняемых приказов, причем номера приказов ожидания заключены в скобки, а после номеров приказов, изменяющих состояние буфера, в скобках указаны номера алгоритмов, которым эти приказы разрешают обращаться к буферу. Анализируя схему совместного процесса, замечаем, что конец выполнения приказа, разрешающего обращение к буферу, является также концом выполнения приказа об ожидании, стоящего в некотором другом алгоритме. Процесс оканчивается остановкой первого алгоритма, влекущей за собой вход других алгоритмов в бесконечное ожидание. Тем не менее считается, что совокупный процесс заканчивается результативно, так как составитель алгоритмов это заранее предвидел (если, конечно, он не допустил ошибки).

Рис.5.1. Схема совместного выполнения трех алгоритмов, имеющих регулируемый буфер
Если бы одна и та же группа совместно работающих алгоритмов пользовалась не одним, а двумя буферами (каждый со своей системой регулирующих предикатов), то существовала бы возможность того, что все алгоритмы впадут в ожидание и процесс остановится без того, чтобы хотя бы один алгоритм достиг отсылки типа "стоп". Это явление называют схватыванием, или клинчем. При разработке алгоритмов его предусмотреть или исключить трудно, и оно считается нежелательным. Но простейшие примеры схватывания привести легко.
Рассмотрим опять три алгоритма; пусть B1 и B2 - две буферные подконструкции, причем первая связана с регулирующими предикатами P1, P2, P3, а вторая - с регулирующими предикатами Q1, Q2, Q3. Предположим, что первый алгоритм начинается с приказа
1) Ожидать P1(B1), ->2;
второй - с приказа
1) Ожидать Q2(B2), ->2;
а третий - с приказа
1) Ожидать P3(B1), ->2;
Пусть, кроме того, начальное состояние буферов таково, что для них выполняются условия P2(B1) и Q1(B2). Ясно, что все три алгоритма сразу же впадут в бесконечное ожидание, т.е. наступит схватывание.
Заметим, что если бы начальное состояние буферов было таково, что выполняются условия P1(B1), Q2(B2), то схватывания при выполнении первых приказов не произошло бы. А дальнейшие приказы могут благоприятно изменить состояние буферов.
О любых нескольких алгоритмах, имеющих общий буфер, принято говорить, что они СВЯЗАНЫ ЭТИМ БУФЕРОМ. О системе предикатов n-го порядка, регулирующих обращения к буферу B, говорят, что она ЗАДАНА НА ЭТОМ БУФЕРЕ, как и каждый регулирующий предикат. Если в семантической схеме алгоритма A, связанного буфером B, присутствуют приказы "ожидать P(B)", то про алгоритм A и предикат P говорят, что они СООТВЕТСТВУЮТ друг другу.
Мы рассматриваем достаточно общий случай, когда каждому алгоритму, соответствует ТОЛЬКО ОДИН из регулирующих предикатов, заданных на буфере B.
Существуют два очень важных вида связи между алгоритмами и регулирующими предикатами:
1. Каждому из n предикатов, регулирующих обращение к буферу B, соответствует хотя бы один алгоритм. В этом случае буфер B называется ЗАКРЫТЫМ.
2. Лишь некоторым из n регулирующих предикатов, заданных на буфере B, соответствуют алгоритмы из числа перерабатывающих совокупный операнд. В этом случае буфер B называется ОТКРЫТЫМ.
Каждый из этих случаев допускает два варианта: 1) соответствие между регулирующими предикатами и алгоритмами (если оно существует) является взаимно-однозначным; 2) некоторым предикатам соответствует несколько алгоритмов. Соответствие "алгоритм - предикат" однозначное, а "предикат - алгоритм" не однозначное.
Два (или более) алгоритма, соответствующие одному и тому же предикату, называются СОПРЯЖЕННЫМИ ОТНОСИТЕЛЬНО УКАЗАННОГО ПРЕДИКАТА.
Открытые буферы позволяют вводить в операнд, в то время когда ни один алгоритм к этим буферам не обращается, воздействия из внешней среды.
Ясно, что в теории роботов открытые буферы играют существенную роль. Кроме того с их помощью можно обеспечить "одновременный" запуск нескольких алгоритмов. Например, представим себе, что в начале каждого из трех алгоритмов, приведенных выше, стоял бы приказ следующего вида:
0) Ждать x = 1, ->1;
где x - некоторая подконструкция (буфер), которая может принимать одно из двух значений: 0 или 1. Равенство x = 1 является регулирующим предикатом, который вместе с предикатом x = 0 образует систему второго порядка. Буфер x является открытым, и все три алгоритма были бы сопряженными относительно предиката x = 1. Все три алгоритма постоянно находились бы в состоянии ожидания предиката x = 1, и как только человек, который по отношению к совокупности алгоритмов является частью внешней среды, произведет действие x = 1; все алгоритмы одновременно станут выполняться. Отсылка "стоп" может быть заменена отсылкой к приказу вида
100) x := 0, ->0;
и, таким образом, остановка алгоритма будет реализована как ожидание предиката "x = 1". К анализу описанных применений открытых буферов мы еще вернемся.
#5.3. ПОНЯТИЕ КОЛЛЕКТИВА АЛГОРИТМОВ
Совокупность всех алгоритмов, связанных некоторым буфером B (посредством системы регулирующих предикатов), называется ЭЛЕМЕНТАРНЫМ КОЛЛЕКТИВОМ АЛГОРИТМОВ. Однако понятие коллектива алгоритмов шире и не сводится к понятию элементарного коллектива.
КОЛЛЕКТИВОМ АЛГОРИТМОВ называется группа алгоритмов, которые совместно перерабатывают общий для них операнд, приводя к однозначному результату или не давая никакого результата (что зависит только от выбора исходного данного).
Нарушение однозначности результата совокупного выполнения нескольких алгоритмов, преобразующих общий для них операнд, может возникать как следствие беспорядочного обращения к буферным подконструкциям. Поэтому будем буферные подконструкции называть также НЕСОБСТВЕННЫМИ ЭЛЕМЕНТАМИ операнда, а отрезки алгоритмических процессов, при протекании которых происходят обращения к несобственным элементам,- КРИТИЧЕСКИМИ ОТРЕЗКАМИ. В частном случае критический отрезок может сводиться к одному критическому шагу (на котором происходит чтение из буфера, запись в буфер или сразу чтение и следующая за ним запись).
Для исключения неоднозначности результата необходимо, чтобы для каждого несобственного элемента выполнение критических отрезков осуществлялось в некотором порядке, который называется СПЕЦИАЛЬНЫМ. Что же это за порядок? Его можно представить себе как некоторую нумерацию критических отрезков, соответствующих, вообще говоря, различным алгоритмам. В этом порядке каждый критический отрезок, на котором производится запись, имеет некоторый номер, и вся группа критических отрезков, производящих только чтение и подлежащих выполнению после указанного критического отрезка и до другой записи в несобственный элемент,- на единицу больший номер. Следующий номер присваивается записывающему отрезку, если он перед записью читает то состояние критического элемента, которое читалось критическими отрезками группы, уже получившей номер. Если такой критический отрезок отсутствует, то нумерация считается оконченной. При этом возникают так называемые КРИТИЧЕСКИЕ СЕРИИ (отрезков), связанные с данным несобственным элементом.
Самый первый записывающий отрезок серии может быть фиктивным (если обращения к критическому элементу начинаются с группы чтений его начального состояния, содержащегося в исходном данном). В каждой критической серии считаются заданными не только номер записывающих отрезков и групп читающих отрезков, но и количества читающих отрезков в их группах. Например, критическую серию можно себе представить следующим образом:
#1 - пишущий отрезок; #2 - три только читающих отрезка; #3 - читающий и пишущий отрезок; #4 (последний в серии) - два читающих критических отрезка.
Всякое "постороннее" обращение к несобственному элементу после того, как было произведено обращение #1 некоторой серии, и до того, как будут выполнены в присущем серии специальном порядке все ее критические отрезки, должно быть исключено.
С одним и тем же несобственным элементом операнда может быть связано несколько критических серий. При этом возможны два случая: а) критические серии естественно упорядочены в силу того, что в них встречаются критические отрезки одного и того же алгоритмического процесса; такие серии называются ФИКСИРОВАННЫМИ друг относительно друга; б) между двумя критическими сериями нет естественной упорядоченности, так как в них нет критических отрезков, принадлежащих одному и тому же алгоритмическому процессу; такие серии называются ПЛАВАЮЩИМИ друг относительно друга.
Критические серии, связанные с одним несобственным элементом, могут "переплетаться" и даже частично совпадать с критическими сериями, отвечающими другому несобственному элементу. При этом может случиться, что какой-нибудь критический шаг в одной серии предшествует другому критическому шагу, а в другой - следует за ним. В таком случае неминуемо должно произойти схватывание (клинч) и некоторые процессы, а может быть и все, безрезультатно остановятся. Клинч такого типа называется АБСОЛЮТНЫМ, потому что его возникновение или невозникновение целиком зависит от выбора исходного данного (операнда). Наличие в совокупном алгоритмическом процессе пересекающихся с другими критическими сериями плавающих серий может приводить к схватываниям другого вида, которые называются МЕРЦАЮЩИМИ. Эти схватывания при повторных применениях группы алгоритмов к одному и тому же исходному данному могут то возникать, то не возникать. О мерцающих клинчах подробнее будет рассказано в следующем параграфе.
Совокупный процесс выполнения коллектива алгоритмов при любом допустимом исходном данном должен протекать вышеописанным образом и без мерцающих клинчей.
Несобственные элементы (буферы), которым отвечают плавающие друг относительно друга критические серии, иногда называют РЕЗЕРВАМИ, потому что некоторые из алгоритмов коллектива могут их занимать, "работать" в них, использовать для переработки своих собственных подконструкций и затем освобождать.
Как и для отдельного алгоритма, для коллектива алгоритмов возможны два случая: коллектив может делать результативную остановку (и тогда он называется ПРИМЕНИМЫМ к операнду) или быть НЕПРИМЕНИМЫМ к операнду (безрезультатно останавливаться или никогда не останавливаться). Схватывание - это бесконечно длящийся безрезультатный процесс (кроме случаев остановки коллектива на открытом буфере).
Последний раз редактировалось: Gudleifr (Вт Апр 26, 2022 12:37 am), всего редактировалось 1 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
#5.4. ВАЖНЫЕ ВОЗМОЖНОСТИ КОЛЛЕКТИВОВ АЛГОРИТМОВ
Защита буферов с помощью регулирующих предикатов не является единственным способом объединения алгоритмов в коллектив. Рассмотрим случай "захвата" резерва. Если ограничиться коллективом двух алгоритмов, то схема пользования резервом такова: любой алгоритм обращается к резерву, если им не пользуется другой, и на время пользования запрещает другому алгоритму обращаться к резерву. Оказывается, проблема защиты резерва гораздо сложнее, чем проблема защиты буфера другого типа.
Для облегчения анализа этого случая сделаем одно общее замечание. Для защиты как буфера, так и резерва вовсе не обязательно применять предикаты, которые выражали бы глобальные свойства всей защищаемой подконструкций. Можно выбрать в ней очень простую под-подконструкцию и на нее наложить проверяемое условие. Ведь изменить только одну букву - это уже изменить всю подконструкцию. Такие под-подконструкции обычно называют ЯЧЕЙКАМИ. Ячейка, состояние которой используют для проверки состояния всей подконструкции, называется СИГНАЛЬНОЙ. Нужно помнить, что сигнальная ячейка - это часть защищаемой подконструкции. В следующих семантических схемах я буду ячейки обозначать малыми латинскими курсивными буквами с черточкой над ними и, если надо, с постоянным или буквенным (переменным) индексом внизу.
Теория изучает потенциально осуществимые процессы, т.е. отвлекается от ограниченности ресурсов. С помощью такого приема теоретики обеспечивают себе относительно "легкую жизнь". Практики, увы, вынуждены считаться с наличием ресурсов. Если для теоретика резерв - это, в лучшем случае, занятная головоломка, то для практика - это вопрос успеха. Военные специалисты говорят, что резерв - это не запас, а силы для нанесения главного удара.
Итак, вернемся к вопросу защиты резерва, или, если хотите, его захвата и защиты. Пусть даны два алгоритма, претендующих на резерв R. Для обеспечения бесконфликтности нужны три простых буфера, сводящихся к отдельным ячейкам. Обозначим их c1, c2 и x. Предположим, что каждый из двух первых может принимать значения либо 0, либо 1, а третий - либо 1, либо 2. Начальное состояние буферов может быть следующим: с1 = 0; c2 = 0: x = 1; начальное состояние буфера x принципиального значения не имеет. Та часть первого алгоритма, которая производит захват резерва R может иметь следующую семантическую схему (S1 - собственная подконструкция):
...
51) c1 := 1 , ->52;
52) Если c2 = 0, то ->57 , иначе ->53;
53) Если x = 1, то ->54, иначе ->55;
54) Ожидать c2 = 0, ->57;
55) c1 := 0, ->56;
56) Ожидать х = 1, ->51;
57) R := F11(S1), ->58;
58 ) S1 := F12(S1, R), ->59;
59) x := 2, ->60;
60) с1 := 0, ->61;
...
Соответствующую часть схемы второго алгоритма получим, меняя ролями c1 и c2 и предписывая приказом 56 ждать x = 2. Понятно, что номера приказов (метки и отсылки) могут быть сдвинуты. Обе схемы алгоритмов A1 и A2 графически изображены на рис.5.2.
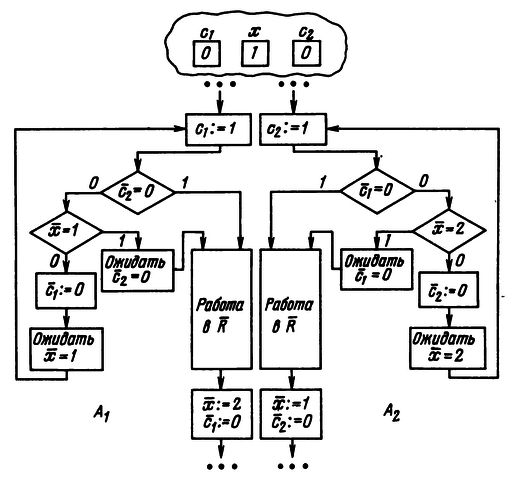
Рис.5.2. Схема двух алгоритмов, "претендующих" на один и тот же резерв R
В приведенной схеме приказы 57 и 58 изображают работу с резервом. В приказе 51 предусмотрена запись в буфер c1 значения 1 (до этого там был 0). Если бы я был педантом, то перед приказом 51 я поставил бы приказ
50) Ожидать c1 = 0, ->51;
но он пропущен потому, что это условие в момент выполнения приказа 51 всегда выполняется. Этим приказом первый алгоритм сообщает второму о том, что захват резерва им начат. Затем приказ 52 предусматривает проверку того, начал ли также захватывать резерв второй алгоритм. Если не начал (т.е. если c2 = 0), то первый алгоритм занимает резерв. Второй алгоритм его уже не сможет занять до конца работы первого. Кончив работу с резервом, первый алгоритм делает x равным 2 и c1 равным 0 (приказы 59 и 60).
Если бы приказ 52 установил, что второй алгоритм тоже начал захват резерва, то было бы проверено значение буфера x, говорящего о том, чья сейчас очередь занимать резерв. Если очередь первого алгоритма, то начинается ожидание условия c2 = 0, которое второй алгоритм должен будет выполнить (своим приказом 55). если же очередь второго, то первый алгоритм начинает ждать свою очередь (приказ 56) и занимает буфер тогда, когда эта очередь придет.
Приказ 52 фактически представляет собой "кусочек" ожидания, оторвавшийся от приказа 54. Прерывать ожидание для выполнения преобразований нельзя, а для выполнения логических операций, не изменяющих состояние буфера,- можно.
В последнем примере буферы c1 и c2 не совсем обычны. Например, буфер c1 может изменяться только первым алгоритмом, тогда как во втором алгоритме предусмотрено только ожидание предикатов c1 = 0. Такое применение буфера называется ЗАДЕРЖКОЙ С ПОМОЩЬЮ ПРЕДИКАТА c1 = 0. В данном случае, записывая (приказ 51) в ячейку c1 значение 1, первый алгоритм ПРОИЗВОДИТ ЗАДЕРЖКУ, а приказом 60 ЕЕ СНИМАЕТ. Аналогично, второй алгоритм производит задержку первого, записывая в ячейку c2 значение 1, а после конца работы с резервом ее снимает.
Задержка предикатом действительно приостанавливает процесс выполнения только в случае, если "задерживаемый" процесс еще не миновал приказа, содержащего операцию ожидания задерживающего предиката. Сработает или нет задержка, зависит от соотношения между скоростями протекания алгоритмических процессов. Это заставляет проявлять большую осторожность, применяя задержки.
Итак, рассмотрев последний пример, мы изучили сразу две новые возможности коллективов: захват резерва и задержку посредством предиката.
Обобщение описанного приема захвата резерва с двух на n алгоритмов оказывается чрезвычайно трудным. Это связано с необходимостью учитывать соотношения между конкурирующими алгоритмическими процессами во всевозможных их сочетаниях. Значительно проще организовать очередь и предоставлять резерв в соответствии с занятой очередью. Для ведения очереди можно отвести один из алгоритмов коллектива. Посмотрим, как это сделать.
Предположим, что для ведения очереди выделены 2n+1 ячеек: x0, x1, ..., xn и c1, c2, ..., cn. Для того чтобы занять очередь, i-й алгоритм должен в ячейку ci записать значение 1 (а до этого там должно быть значение 0). Затем нужно ожидать появления в ячейке x0 числа i (номера алгоритма) и приступить к работе с резервом. Приказы для записи в очередь будут:
1) Ожидать сi = 0, ->2;
2) ci := 1, ->3;
3) Ожидать x0 = i, ->4;
Если в последнем приказе вместо отсылки "4" поставить "стоп", то эти три приказа образуют запись алгоритма. Объявим индуцируемую им функцию операцией и обозначим ее "Занять (x0, i)". Для того чтобы процесс "нахождения в очереди" более заметно выражался в записи семантической схемы алгоритма, объявим еще с помощью алгоритма
1) x0 := 0, стоп;
операцию, которую обозначим "Освободить (x0)".
Теперь участок захвата резерва в записи схемы может иметь вид
...
51) Занять (x0, i), ->52;
52) R := Fi1(Si), ->53;
53) Si := Fi2(R, Si), ->54;
54) Освободить (x0), ->55;
...
Здесь i - номер алгоритма, Si - его собственная подконструкция, R - как и прежде, резервная подконструкция операнда.
Алгоритм ведения очереди может иметь простой вид, если сначала объявить две следующие операции:
1. Операция "j := клиента" объявляется в соответствии с алгоритмом, имеющим запись
1) Если ci = 1, то ->5, иначе ->2;
2) Если i = n, то ->4, иначе ->3;
3) i := i+1, ->1;
4) j := 0, ->9;
5) ci :=0, ->6;
6) j := i, ->7;
7) Если i = n, то ->9, иначе ->8;
8 ) i := i+1, стоп;
9) i := 1, стоп;
До начала работы алгоритма, ведущего очередь, а значит, и до первого выполнения данной операции, i может иметь любое целое значение из интервала [1, n]. На рис.5.3 показано, что до начала работы выполняется операция i := 1 (но это не существенно).
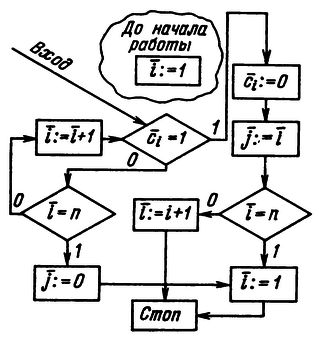
Рис.5.3. Схема алгоритма, индуцирующего операцию "j = клиента"
Алгоритм, индуцирующий операцию "j := клиента", в скрытом виде имеет аргументы c1, с2, . - имена ячеек, в которые алгоритмы-клиенты записывают "заявку" на включение в очередь (Ai - записывает код 1 в ячейку ci). Он эти ячейки просматривает (в кольцевом порядке) и, как только обнаруживает очередную заявку, записывает вместо нее 0, а переменной j присваивает номер алгоритма, сделавшего заявку. Если при просмотре 1-, 2-, ..., n-й ячейки ни одной "заявки" не обнаружено, производится присваивание j : = 0 и алгоритм настраивается на новый просмотр ячеек, начиная с 1-й.
2. Операция "Сделать шаг" объявляется по алгоритму
1) k : = 0, ->2;
2) xk := x[k+1], ->3;
3) Если k = n - 1, то ->4, иначе ->5;
4) xn := 0, стоп;
5) k := k+1, ->2;
Эта операция продвигает очередь на один шаг и освобождает в ней последнее место для очередного "претендента" на резерв.
Теперь без труда сделаем запись алгоритма ведения очереди:
1) i := 1, ->2;
2) j : = клиента, ->3;
3) Ожидать x0 = 0, ->4;
4) Сделать шаг, ->5;
5) xn := j, ->2;
Приведенная семантическая схема алгоритма ведения очереди предполагает простейшую организацию очереди. Ячейки просматриваются в порядке их номеров и все обнаруженные в них заявки последовательно включаются в очередь. Если заявок нет, в очередь заносится нуль. После того, как резерв освобождается, очередь продвигается на один шаг (в том числе и нули, если они стоят в очереди). При необходимости можно реализовать более сложное ведение очереди.
Говоря о захватах резервов, нельзя ничего сказать об особом случае схватывания, который с ними связан.
Захват резерва одним из алгоритмов ЗАПРЕЩАЕТ обращения всех других алгоритмов к этому резерву на время захвата. Представим теперь, что коллектив состоит из двух алгоритмов и что имеется два резерва R и Q. Пусть в первом алгоритме предусмотрен захват резерва Q в то время, когда R уже захвачен, но еще не освобожден, а во втором - захват резерва R, когда уже захвачен, но еще не освобожден резерв Q. Описанную ситуацию поясняет рис.5.4. При выполнении таких алгоритмов возможны два случая: 1) один из алгоритмов успеет захватить оба резерва раньше, чем второй захватит хотя бы один; 2) первый алгоритм успеет захватить R, но не Q, а второй успеет захватить Q, но не R. В первой из указанных ситуаций выполнение обоих алгоритмов произойдет беспрепятственно, а во второй алгоритмы схватятся (будет клинч). Произойдет или не произойдет схватывание - зависит от соотношения скоростей выполнения алгоритмов. Описанное схватывание (клинч) является мерцающим. На рис.5.4. области алгоритмических процессов, одновременное вхождение в которые вызывает наступление мерцающего клинча, обозначены соответственно буквами А и В.
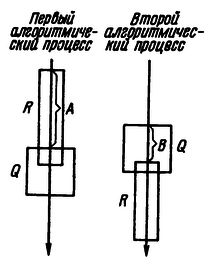
Рис. 5.4. Схема, поясняющая возникновение мерцающего клинча
Мерцающий клинч предотвращается объединением двух ресурсов R и Q в один объединенный ресурс (если невозможно так перестроить алгоритмы, чтобы области А и В отсутствовали). Это должно быть сделано в процессе разработки алгоритмов.
В более общем случае захваты резервов могут осуществляться не одиночными алгоритмами, а их группами.
#5.5. ОТКРЫТЫЕ КОЛЛЕКТИВЫ. ИЕРАРХИЯ
Коллективы алгоритмов, в которых применяется открытый буфер только для "пуска" коллектива, обычно относят к закрытым. Мы будем говорить об открытых коллективах, имеющих и другие открытые буфера, называемые СУЩЕСТВЕННЫМИ.
Наличие открытого буфера может вызывать безрезультатную остановку коллектива алгоритмов. Внося искусственно изменения в состояние открытого буфера, можно добиться продолжения процесса и, поступая так нужное число раз, довести процесс до получения результата. Если, по-разному воздействуя на буфер, можно получать не равные между собой результаты, то открытый буфер называется существенным. Наличие существенного открытого буфера приводит к тому, что коллектив алгоритмов перестает обладать свойством однозначности результата по отношению к исходному данному.
Если для закрытых коллективов справедлива теорема о том, что каждый из них эквивалентен некоторому одиночному алгоритму, то для открытого коллектива это не так (из-за его неоднозначности).
Но посмотрим на открытый коллектив алгоритмов с другой стороны. Будем считать, что операнд X (исходное данное) является некоторым параметром, а последовательность элементов информации b = (b1, b2, ..., bn), которые мы вводим в буфер для того, чтобы совокупный процесс привел к искомому результату (обозначим его Y), примем за значение аргумента. Повторяю, значениями аргумента будем считать не отдельные данные, а их последовательности. Тогда окажется, что каждую последовательность b (при фиксированном X) коллектив алгоритмов отображает на некоторый результат Y. И при этом отображение будет ОДНОЗНАЧНЫМ.
Каждую последовательность b будем называть СЕРИЕЙ [Не смешивать с серией критических отрезков процесса].
Если коллектив алгоритмов имеет несколько открытых существенных буферов, то он индуцирует функцию от многих переменных (зависящую от параметра X). Значениями аргументов этой функции будут серии данных.
Обычно в роботе под параметром X понимают ту информацию, которая хранится в его памяти (запоминающем устройстве), а результат Y расчленяют на части, одну из которых считают новым значением X, другую рассматривают как управляющую информацию и передают эффекторам, а третью вовсе стирают как ненужную (это "отходы производства").
После получения результата и выделения из него нового значения X, выполнение коллектива алгоритмов повторяют и т.д. Таким образом, сигналы рецепторов вместе с информацией, накопленной в памяти, перерабатываются в управляющие сигналы и новое состояние памяти.
Так как при управлении роботом существенное значение имеет своевременность реакции, то в состав коллектива алгоритмов иногда включают алгоритм, играющий роль рецептора, называемый ГЕНЕРАТОРОМ ВРЕМЕНИ. Задаваемое им "время" называют АЛГОРИТМИЧЕСКИМ ВРЕМЕНЕМ.
Генератор времени часто называют АЛГОРИТМИЧЕСКИМИ ЧАСАМИ. Но такой термин неудачен. Часы, по всеобщему мнению, являются измерительным прибором, который позволяет ИЗМЕРЯТЬ время. Я не стану оспаривать эту общепринятую точку зрения, но замечу, что ничего общего с измерением времени генерация алгоритмического времени не имеет.
Пусть T - некоторая подконструкция операнда, которая может принимать состояния T1, T2, ..., TN, где TN - очень большое число, и пусть O - процедура, которая для любого i < N преобразует Ti в T[i+1], а кроме того TN в T1. Генератором времени называется алгоритм
1) T := O(T), ->1;
Другие алгоритмы коллектива могут обращаться в подконструкции T только для чтения, и таким способом они (если это надо) "узнают", каково алгоритмическое время. Если подконструкция T никак не защищена, то в момент обращения к ней нескольких алгоритмов происходит не поддающаяся учету случайная задержка всех процессов, кроме одного. При этом результат, который прочитает тот или иной алгоритм, непредсказуем. Чтобы алгоритмы коллектива между собой не "боролись" за доступ к T, следует организовать очередь из алгоритмов-пользователей. Но это не устранит непредсказуемости результата считывания. Если же подконструкцию T организовать как буфер, защищенный регулирующими предикатами, то непредсказуемость исчезнет, но генератор времени будет останавливаться и ждать, пока алгоритмы-клиенты читают "который час". Разработчик коллектива алгоритмов должен решать, что лучше или, вернее, что хуже.
Обычно в качестве Т берут ЯЧЕЙКУ, которая может принимать последовательные числовые значения, т.е. удовлетворяющую условию Ti = i-1, и тогда генератор времени принимает вид
1) T := (T+1) mod N, ->1;
Здесь выражение (T+1) mod N называется сложением по модулю N и равно остатку от деления суммы T+1 на N. В нашем случае
(T+1) mod N =
= T+1 при T < N-1
= 0 при T = N-1
Можно построить генератор времени так, чтобы "столкновение" алгоритмов при чтении было полностью исключено. Например, для каждого алгоритма Ai отвести свою ячейку связи с часами Ti. Это похоже на ситуацию, в которой каждому прохожему предоставлялся бы отдельный циферблат на уличных часах только для того, чтобы, определяя время, прохожие между собой не передрались... При этом генератор времени может иметь вид:
1) i : = 1, ->2;
2) Ti : = 0, ->3;
3) Если i = n, то ->4, иначе ->5;
4) i := i+1, ->2;
5) Ti := (Ti+1) mod N, ->6;
6) i := (i+1) mod m, ->5;
Легко сообразить, что такие "часы" на разных "циферблатах" одно и то же будут показывать не одновременно. Возможность столкновений между алгоритмами и генератором и здесь не устранена.
ТОЧНОЕ алгоритмическое время алгоритмы коллектива не могут считывать из-за того, что в коллективе возникает "борьба" за обращение к "часам" T. Но если для отсчета времени взята ЯЧЕЙКА, принимающая последовательные целочисленные значения, то границы интервала разброса можно определить и тогда будет известно, с какой ошибкой определяется алгоритмическое время поступления данных или выдачи результата.
В тех случаях, когда коллектив алгоритмов реализован в виде некоторого физического устройства, можно установить экспериментальным способом ЗАВИСИМОСТЬ, существующую МЕЖДУ АЛГОРИТМИЧЕСКИМ И ФИЗИЧЕСКИМ ВРЕМЕНЕМ. Соотношение это должно быть таково, чтобы робот действовал в так называемом РЕАЛЬНОМ ВРЕМЕНИ, т.е. чтобы реакции на внешние воздействия вырабатывались достаточно быстро. Иначе управляющее устройство робота неэффективно. Читателю понятно, что управляющее устройство при нашем подходе - это физическая модель открытого коллектива алгоритмов.
Наряду с регулирующими предикатами, вернее с ожиданием регулирующего предиката, можно допустить и другие бесконфликтные способы обращения к буферу. Я имею в виду такой практически важный прием, как СПАРИВАНИЕ БУФЕРА С СОБСТВЕННОЙ ПОДКОНСТРУКЦИЕЙ алгоритма. Поясню этот прием.
Прежде всего замечу, что каждый алгоритм может иметь много собственных подконструкций. До сих пор я не подчеркивал этого факта. В предыдущих примерах встречалась подконструкция Si. В действительности это может быть ЛЮБАЯ из собственных подконструкций и даже совокупность всех собственных подконструкций. В последнем случае наши примеры приобретают очень частный характер, с которым я мирился ради простоты, учитывая возможность его устранения включением дополнительных приказов. Ниже нам просто нужно, чтобы собственных подконструкций было несколько (хотя бы две).
Пусть теперь B - некоторый буфер, Pi - регулирующий предикат, заданный на этом буфере и соответствующий алгоритму Ai, a Si' - одна из собственных подконструкций алгоритма Ai. Тогда возможна следующая семантическая схема обращения к B:
1) Если Pi(B), то ->2, иначе ->3;
2) Si = Fi1(B, Si), ->4;
3) Si = Fi2(Si', Si), ->4;
4) ...
Эта схема предусматривает проверку истинности регулирующего предиката Pi. Если предикат имеет логическое значение "истина", то выполняется приказ 2, смысл которого в том, что информация из буфера B переносится в подконструкцию Si, после чего, начиная с приказа 4, продолжается выполнение алгоритма Ai. Если же регулирующий предикат имеет логическое значение "ложь", то аналогичная по своей структуре (но другая по смыслу) информация, в силу приказа 3 переносится в собственную подконструкцию Si из Si' и, как в предыдущем случае, продолжается выполнение алгоритма, начиная с приказа 4. Буфер B должен быть открытым. Сущность описанного приема в том, что если внешнее воздействие не закончено к моменту обращения алгоритма к В, то вместо ожидания информации, которая может поступить в буфер, но нарушает требования режима реального времени, алгоритм Ai из подконструкций Si' получает запасенную ранее, может быть, несколько устаревшую, но близкую к нужной информацию.
Мы уже говорили выше, что буферы можно применять для запуска алгоритмов и даже их коллективов. Эту возможность легко использовать для того, чтобы один алгоритм (или коллектив) разрешал или запрещал функционировать другому. Пусть буфер x доступен алгоритму A по записи, а алгоритму B - по чтению и B содержит приказ "Ожидать x = 1", причем вначале x = 0. Достигнув этого приказа, B остановится и будет "ожидать" до тех пор, пока алгоритм А не выполнит приказ
k) x := 1; ->k+1;
Тот же А, своим приказом
l) x := 0, ->l+1;
заставит алгоритм В остановиться при очередном обращении к x.
При такой связи между алгоритмами (коллективами алгоритмов) B и A говорят, что B подчинен A.
Если коллектив алгоритмов K можно разбить на подколлективы так, что каждый из них, кроме одного (ГЛАВНОГО), подчинен одному и только одному подколлективу, то K называют ИЕРАРХИЧЕСКИМ.
Иерархическая структура позволяет четко распределить функции между подколлективами.
Передача подчиненным подколлективом своих результатов старшему допустима, но без задержки процесса выполнения старшего. Один из приемов такой передачи заключается в том, что старший наделяется возможностью "маскировать" буфер, доступный младшему по записи. Допустим, что младший обращается к старшему, заменяя в буфере y код 0 кодом 1. Тогда для старшего предусматривают собственную ячейку z, которая может содержать либо 0, либо 1, и в старшем ставят пару приказов
k) Если z = 1, то ->k+1, иначе k+m;
k+1) Ожидать y = 1, ->k+2;
Защита буферов с помощью регулирующих предикатов не является единственным способом объединения алгоритмов в коллектив. Рассмотрим случай "захвата" резерва. Если ограничиться коллективом двух алгоритмов, то схема пользования резервом такова: любой алгоритм обращается к резерву, если им не пользуется другой, и на время пользования запрещает другому алгоритму обращаться к резерву. Оказывается, проблема защиты резерва гораздо сложнее, чем проблема защиты буфера другого типа.
Для облегчения анализа этого случая сделаем одно общее замечание. Для защиты как буфера, так и резерва вовсе не обязательно применять предикаты, которые выражали бы глобальные свойства всей защищаемой подконструкций. Можно выбрать в ней очень простую под-подконструкцию и на нее наложить проверяемое условие. Ведь изменить только одну букву - это уже изменить всю подконструкцию. Такие под-подконструкции обычно называют ЯЧЕЙКАМИ. Ячейка, состояние которой используют для проверки состояния всей подконструкции, называется СИГНАЛЬНОЙ. Нужно помнить, что сигнальная ячейка - это часть защищаемой подконструкции. В следующих семантических схемах я буду ячейки обозначать малыми латинскими курсивными буквами с черточкой над ними и, если надо, с постоянным или буквенным (переменным) индексом внизу.
Теория изучает потенциально осуществимые процессы, т.е. отвлекается от ограниченности ресурсов. С помощью такого приема теоретики обеспечивают себе относительно "легкую жизнь". Практики, увы, вынуждены считаться с наличием ресурсов. Если для теоретика резерв - это, в лучшем случае, занятная головоломка, то для практика - это вопрос успеха. Военные специалисты говорят, что резерв - это не запас, а силы для нанесения главного удара.
Итак, вернемся к вопросу защиты резерва, или, если хотите, его захвата и защиты. Пусть даны два алгоритма, претендующих на резерв R. Для обеспечения бесконфликтности нужны три простых буфера, сводящихся к отдельным ячейкам. Обозначим их c1, c2 и x. Предположим, что каждый из двух первых может принимать значения либо 0, либо 1, а третий - либо 1, либо 2. Начальное состояние буферов может быть следующим: с1 = 0; c2 = 0: x = 1; начальное состояние буфера x принципиального значения не имеет. Та часть первого алгоритма, которая производит захват резерва R может иметь следующую семантическую схему (S1 - собственная подконструкция):
...
51) c1 := 1 , ->52;
52) Если c2 = 0, то ->57 , иначе ->53;
53) Если x = 1, то ->54, иначе ->55;
54) Ожидать c2 = 0, ->57;
55) c1 := 0, ->56;
56) Ожидать х = 1, ->51;
57) R := F11(S1), ->58;
58 ) S1 := F12(S1, R), ->59;
59) x := 2, ->60;
60) с1 := 0, ->61;
...
Соответствующую часть схемы второго алгоритма получим, меняя ролями c1 и c2 и предписывая приказом 56 ждать x = 2. Понятно, что номера приказов (метки и отсылки) могут быть сдвинуты. Обе схемы алгоритмов A1 и A2 графически изображены на рис.5.2.

Рис.5.2. Схема двух алгоритмов, "претендующих" на один и тот же резерв R
В приведенной схеме приказы 57 и 58 изображают работу с резервом. В приказе 51 предусмотрена запись в буфер c1 значения 1 (до этого там был 0). Если бы я был педантом, то перед приказом 51 я поставил бы приказ
50) Ожидать c1 = 0, ->51;
но он пропущен потому, что это условие в момент выполнения приказа 51 всегда выполняется. Этим приказом первый алгоритм сообщает второму о том, что захват резерва им начат. Затем приказ 52 предусматривает проверку того, начал ли также захватывать резерв второй алгоритм. Если не начал (т.е. если c2 = 0), то первый алгоритм занимает резерв. Второй алгоритм его уже не сможет занять до конца работы первого. Кончив работу с резервом, первый алгоритм делает x равным 2 и c1 равным 0 (приказы 59 и 60).
Если бы приказ 52 установил, что второй алгоритм тоже начал захват резерва, то было бы проверено значение буфера x, говорящего о том, чья сейчас очередь занимать резерв. Если очередь первого алгоритма, то начинается ожидание условия c2 = 0, которое второй алгоритм должен будет выполнить (своим приказом 55). если же очередь второго, то первый алгоритм начинает ждать свою очередь (приказ 56) и занимает буфер тогда, когда эта очередь придет.
Приказ 52 фактически представляет собой "кусочек" ожидания, оторвавшийся от приказа 54. Прерывать ожидание для выполнения преобразований нельзя, а для выполнения логических операций, не изменяющих состояние буфера,- можно.
В последнем примере буферы c1 и c2 не совсем обычны. Например, буфер c1 может изменяться только первым алгоритмом, тогда как во втором алгоритме предусмотрено только ожидание предикатов c1 = 0. Такое применение буфера называется ЗАДЕРЖКОЙ С ПОМОЩЬЮ ПРЕДИКАТА c1 = 0. В данном случае, записывая (приказ 51) в ячейку c1 значение 1, первый алгоритм ПРОИЗВОДИТ ЗАДЕРЖКУ, а приказом 60 ЕЕ СНИМАЕТ. Аналогично, второй алгоритм производит задержку первого, записывая в ячейку c2 значение 1, а после конца работы с резервом ее снимает.
Задержка предикатом действительно приостанавливает процесс выполнения только в случае, если "задерживаемый" процесс еще не миновал приказа, содержащего операцию ожидания задерживающего предиката. Сработает или нет задержка, зависит от соотношения между скоростями протекания алгоритмических процессов. Это заставляет проявлять большую осторожность, применяя задержки.
Итак, рассмотрев последний пример, мы изучили сразу две новые возможности коллективов: захват резерва и задержку посредством предиката.
Обобщение описанного приема захвата резерва с двух на n алгоритмов оказывается чрезвычайно трудным. Это связано с необходимостью учитывать соотношения между конкурирующими алгоритмическими процессами во всевозможных их сочетаниях. Значительно проще организовать очередь и предоставлять резерв в соответствии с занятой очередью. Для ведения очереди можно отвести один из алгоритмов коллектива. Посмотрим, как это сделать.
Предположим, что для ведения очереди выделены 2n+1 ячеек: x0, x1, ..., xn и c1, c2, ..., cn. Для того чтобы занять очередь, i-й алгоритм должен в ячейку ci записать значение 1 (а до этого там должно быть значение 0). Затем нужно ожидать появления в ячейке x0 числа i (номера алгоритма) и приступить к работе с резервом. Приказы для записи в очередь будут:
1) Ожидать сi = 0, ->2;
2) ci := 1, ->3;
3) Ожидать x0 = i, ->4;
Если в последнем приказе вместо отсылки "4" поставить "стоп", то эти три приказа образуют запись алгоритма. Объявим индуцируемую им функцию операцией и обозначим ее "Занять (x0, i)". Для того чтобы процесс "нахождения в очереди" более заметно выражался в записи семантической схемы алгоритма, объявим еще с помощью алгоритма
1) x0 := 0, стоп;
операцию, которую обозначим "Освободить (x0)".
Теперь участок захвата резерва в записи схемы может иметь вид
...
51) Занять (x0, i), ->52;
52) R := Fi1(Si), ->53;
53) Si := Fi2(R, Si), ->54;
54) Освободить (x0), ->55;
...
Здесь i - номер алгоритма, Si - его собственная подконструкция, R - как и прежде, резервная подконструкция операнда.
Алгоритм ведения очереди может иметь простой вид, если сначала объявить две следующие операции:
1. Операция "j := клиента" объявляется в соответствии с алгоритмом, имеющим запись
1) Если ci = 1, то ->5, иначе ->2;
2) Если i = n, то ->4, иначе ->3;
3) i := i+1, ->1;
4) j := 0, ->9;
5) ci :=0, ->6;
6) j := i, ->7;
7) Если i = n, то ->9, иначе ->8;
8 ) i := i+1, стоп;
9) i := 1, стоп;
До начала работы алгоритма, ведущего очередь, а значит, и до первого выполнения данной операции, i может иметь любое целое значение из интервала [1, n]. На рис.5.3 показано, что до начала работы выполняется операция i := 1 (но это не существенно).

Рис.5.3. Схема алгоритма, индуцирующего операцию "j = клиента"
Алгоритм, индуцирующий операцию "j := клиента", в скрытом виде имеет аргументы c1, с2, . - имена ячеек, в которые алгоритмы-клиенты записывают "заявку" на включение в очередь (Ai - записывает код 1 в ячейку ci). Он эти ячейки просматривает (в кольцевом порядке) и, как только обнаруживает очередную заявку, записывает вместо нее 0, а переменной j присваивает номер алгоритма, сделавшего заявку. Если при просмотре 1-, 2-, ..., n-й ячейки ни одной "заявки" не обнаружено, производится присваивание j : = 0 и алгоритм настраивается на новый просмотр ячеек, начиная с 1-й.
2. Операция "Сделать шаг" объявляется по алгоритму
1) k : = 0, ->2;
2) xk := x[k+1], ->3;
3) Если k = n - 1, то ->4, иначе ->5;
4) xn := 0, стоп;
5) k := k+1, ->2;
Эта операция продвигает очередь на один шаг и освобождает в ней последнее место для очередного "претендента" на резерв.
Теперь без труда сделаем запись алгоритма ведения очереди:
1) i := 1, ->2;
2) j : = клиента, ->3;
3) Ожидать x0 = 0, ->4;
4) Сделать шаг, ->5;
5) xn := j, ->2;
Приведенная семантическая схема алгоритма ведения очереди предполагает простейшую организацию очереди. Ячейки просматриваются в порядке их номеров и все обнаруженные в них заявки последовательно включаются в очередь. Если заявок нет, в очередь заносится нуль. После того, как резерв освобождается, очередь продвигается на один шаг (в том числе и нули, если они стоят в очереди). При необходимости можно реализовать более сложное ведение очереди.
Говоря о захватах резервов, нельзя ничего сказать об особом случае схватывания, который с ними связан.
Захват резерва одним из алгоритмов ЗАПРЕЩАЕТ обращения всех других алгоритмов к этому резерву на время захвата. Представим теперь, что коллектив состоит из двух алгоритмов и что имеется два резерва R и Q. Пусть в первом алгоритме предусмотрен захват резерва Q в то время, когда R уже захвачен, но еще не освобожден, а во втором - захват резерва R, когда уже захвачен, но еще не освобожден резерв Q. Описанную ситуацию поясняет рис.5.4. При выполнении таких алгоритмов возможны два случая: 1) один из алгоритмов успеет захватить оба резерва раньше, чем второй захватит хотя бы один; 2) первый алгоритм успеет захватить R, но не Q, а второй успеет захватить Q, но не R. В первой из указанных ситуаций выполнение обоих алгоритмов произойдет беспрепятственно, а во второй алгоритмы схватятся (будет клинч). Произойдет или не произойдет схватывание - зависит от соотношения скоростей выполнения алгоритмов. Описанное схватывание (клинч) является мерцающим. На рис.5.4. области алгоритмических процессов, одновременное вхождение в которые вызывает наступление мерцающего клинча, обозначены соответственно буквами А и В.

Рис. 5.4. Схема, поясняющая возникновение мерцающего клинча
Мерцающий клинч предотвращается объединением двух ресурсов R и Q в один объединенный ресурс (если невозможно так перестроить алгоритмы, чтобы области А и В отсутствовали). Это должно быть сделано в процессе разработки алгоритмов.
В более общем случае захваты резервов могут осуществляться не одиночными алгоритмами, а их группами.
#5.5. ОТКРЫТЫЕ КОЛЛЕКТИВЫ. ИЕРАРХИЯ
Коллективы алгоритмов, в которых применяется открытый буфер только для "пуска" коллектива, обычно относят к закрытым. Мы будем говорить об открытых коллективах, имеющих и другие открытые буфера, называемые СУЩЕСТВЕННЫМИ.
Наличие открытого буфера может вызывать безрезультатную остановку коллектива алгоритмов. Внося искусственно изменения в состояние открытого буфера, можно добиться продолжения процесса и, поступая так нужное число раз, довести процесс до получения результата. Если, по-разному воздействуя на буфер, можно получать не равные между собой результаты, то открытый буфер называется существенным. Наличие существенного открытого буфера приводит к тому, что коллектив алгоритмов перестает обладать свойством однозначности результата по отношению к исходному данному.
Если для закрытых коллективов справедлива теорема о том, что каждый из них эквивалентен некоторому одиночному алгоритму, то для открытого коллектива это не так (из-за его неоднозначности).
Но посмотрим на открытый коллектив алгоритмов с другой стороны. Будем считать, что операнд X (исходное данное) является некоторым параметром, а последовательность элементов информации b = (b1, b2, ..., bn), которые мы вводим в буфер для того, чтобы совокупный процесс привел к искомому результату (обозначим его Y), примем за значение аргумента. Повторяю, значениями аргумента будем считать не отдельные данные, а их последовательности. Тогда окажется, что каждую последовательность b (при фиксированном X) коллектив алгоритмов отображает на некоторый результат Y. И при этом отображение будет ОДНОЗНАЧНЫМ.
Каждую последовательность b будем называть СЕРИЕЙ [Не смешивать с серией критических отрезков процесса].
Если коллектив алгоритмов имеет несколько открытых существенных буферов, то он индуцирует функцию от многих переменных (зависящую от параметра X). Значениями аргументов этой функции будут серии данных.
Обычно в роботе под параметром X понимают ту информацию, которая хранится в его памяти (запоминающем устройстве), а результат Y расчленяют на части, одну из которых считают новым значением X, другую рассматривают как управляющую информацию и передают эффекторам, а третью вовсе стирают как ненужную (это "отходы производства").
После получения результата и выделения из него нового значения X, выполнение коллектива алгоритмов повторяют и т.д. Таким образом, сигналы рецепторов вместе с информацией, накопленной в памяти, перерабатываются в управляющие сигналы и новое состояние памяти.
Так как при управлении роботом существенное значение имеет своевременность реакции, то в состав коллектива алгоритмов иногда включают алгоритм, играющий роль рецептора, называемый ГЕНЕРАТОРОМ ВРЕМЕНИ. Задаваемое им "время" называют АЛГОРИТМИЧЕСКИМ ВРЕМЕНЕМ.
Генератор времени часто называют АЛГОРИТМИЧЕСКИМИ ЧАСАМИ. Но такой термин неудачен. Часы, по всеобщему мнению, являются измерительным прибором, который позволяет ИЗМЕРЯТЬ время. Я не стану оспаривать эту общепринятую точку зрения, но замечу, что ничего общего с измерением времени генерация алгоритмического времени не имеет.
Пусть T - некоторая подконструкция операнда, которая может принимать состояния T1, T2, ..., TN, где TN - очень большое число, и пусть O - процедура, которая для любого i < N преобразует Ti в T[i+1], а кроме того TN в T1. Генератором времени называется алгоритм
1) T := O(T), ->1;
Другие алгоритмы коллектива могут обращаться в подконструкции T только для чтения, и таким способом они (если это надо) "узнают", каково алгоритмическое время. Если подконструкция T никак не защищена, то в момент обращения к ней нескольких алгоритмов происходит не поддающаяся учету случайная задержка всех процессов, кроме одного. При этом результат, который прочитает тот или иной алгоритм, непредсказуем. Чтобы алгоритмы коллектива между собой не "боролись" за доступ к T, следует организовать очередь из алгоритмов-пользователей. Но это не устранит непредсказуемости результата считывания. Если же подконструкцию T организовать как буфер, защищенный регулирующими предикатами, то непредсказуемость исчезнет, но генератор времени будет останавливаться и ждать, пока алгоритмы-клиенты читают "который час". Разработчик коллектива алгоритмов должен решать, что лучше или, вернее, что хуже.
Обычно в качестве Т берут ЯЧЕЙКУ, которая может принимать последовательные числовые значения, т.е. удовлетворяющую условию Ti = i-1, и тогда генератор времени принимает вид
1) T := (T+1) mod N, ->1;
Здесь выражение (T+1) mod N называется сложением по модулю N и равно остатку от деления суммы T+1 на N. В нашем случае
(T+1) mod N =
= T+1 при T < N-1
= 0 при T = N-1
Можно построить генератор времени так, чтобы "столкновение" алгоритмов при чтении было полностью исключено. Например, для каждого алгоритма Ai отвести свою ячейку связи с часами Ti. Это похоже на ситуацию, в которой каждому прохожему предоставлялся бы отдельный циферблат на уличных часах только для того, чтобы, определяя время, прохожие между собой не передрались... При этом генератор времени может иметь вид:
1) i : = 1, ->2;
2) Ti : = 0, ->3;
3) Если i = n, то ->4, иначе ->5;
4) i := i+1, ->2;
5) Ti := (Ti+1) mod N, ->6;
6) i := (i+1) mod m, ->5;
Легко сообразить, что такие "часы" на разных "циферблатах" одно и то же будут показывать не одновременно. Возможность столкновений между алгоритмами и генератором и здесь не устранена.
ТОЧНОЕ алгоритмическое время алгоритмы коллектива не могут считывать из-за того, что в коллективе возникает "борьба" за обращение к "часам" T. Но если для отсчета времени взята ЯЧЕЙКА, принимающая последовательные целочисленные значения, то границы интервала разброса можно определить и тогда будет известно, с какой ошибкой определяется алгоритмическое время поступления данных или выдачи результата.
В тех случаях, когда коллектив алгоритмов реализован в виде некоторого физического устройства, можно установить экспериментальным способом ЗАВИСИМОСТЬ, существующую МЕЖДУ АЛГОРИТМИЧЕСКИМ И ФИЗИЧЕСКИМ ВРЕМЕНЕМ. Соотношение это должно быть таково, чтобы робот действовал в так называемом РЕАЛЬНОМ ВРЕМЕНИ, т.е. чтобы реакции на внешние воздействия вырабатывались достаточно быстро. Иначе управляющее устройство робота неэффективно. Читателю понятно, что управляющее устройство при нашем подходе - это физическая модель открытого коллектива алгоритмов.
Наряду с регулирующими предикатами, вернее с ожиданием регулирующего предиката, можно допустить и другие бесконфликтные способы обращения к буферу. Я имею в виду такой практически важный прием, как СПАРИВАНИЕ БУФЕРА С СОБСТВЕННОЙ ПОДКОНСТРУКЦИЕЙ алгоритма. Поясню этот прием.
Прежде всего замечу, что каждый алгоритм может иметь много собственных подконструкций. До сих пор я не подчеркивал этого факта. В предыдущих примерах встречалась подконструкция Si. В действительности это может быть ЛЮБАЯ из собственных подконструкций и даже совокупность всех собственных подконструкций. В последнем случае наши примеры приобретают очень частный характер, с которым я мирился ради простоты, учитывая возможность его устранения включением дополнительных приказов. Ниже нам просто нужно, чтобы собственных подконструкций было несколько (хотя бы две).
Пусть теперь B - некоторый буфер, Pi - регулирующий предикат, заданный на этом буфере и соответствующий алгоритму Ai, a Si' - одна из собственных подконструкций алгоритма Ai. Тогда возможна следующая семантическая схема обращения к B:
1) Если Pi(B), то ->2, иначе ->3;
2) Si = Fi1(B, Si), ->4;
3) Si = Fi2(Si', Si), ->4;
4) ...
Эта схема предусматривает проверку истинности регулирующего предиката Pi. Если предикат имеет логическое значение "истина", то выполняется приказ 2, смысл которого в том, что информация из буфера B переносится в подконструкцию Si, после чего, начиная с приказа 4, продолжается выполнение алгоритма Ai. Если же регулирующий предикат имеет логическое значение "ложь", то аналогичная по своей структуре (но другая по смыслу) информация, в силу приказа 3 переносится в собственную подконструкцию Si из Si' и, как в предыдущем случае, продолжается выполнение алгоритма, начиная с приказа 4. Буфер B должен быть открытым. Сущность описанного приема в том, что если внешнее воздействие не закончено к моменту обращения алгоритма к В, то вместо ожидания информации, которая может поступить в буфер, но нарушает требования режима реального времени, алгоритм Ai из подконструкций Si' получает запасенную ранее, может быть, несколько устаревшую, но близкую к нужной информацию.
Мы уже говорили выше, что буферы можно применять для запуска алгоритмов и даже их коллективов. Эту возможность легко использовать для того, чтобы один алгоритм (или коллектив) разрешал или запрещал функционировать другому. Пусть буфер x доступен алгоритму A по записи, а алгоритму B - по чтению и B содержит приказ "Ожидать x = 1", причем вначале x = 0. Достигнув этого приказа, B остановится и будет "ожидать" до тех пор, пока алгоритм А не выполнит приказ
k) x := 1; ->k+1;
Тот же А, своим приказом
l) x := 0, ->l+1;
заставит алгоритм В остановиться при очередном обращении к x.
При такой связи между алгоритмами (коллективами алгоритмов) B и A говорят, что B подчинен A.
Если коллектив алгоритмов K можно разбить на подколлективы так, что каждый из них, кроме одного (ГЛАВНОГО), подчинен одному и только одному подколлективу, то K называют ИЕРАРХИЧЕСКИМ.
Иерархическая структура позволяет четко распределить функции между подколлективами.
Передача подчиненным подколлективом своих результатов старшему допустима, но без задержки процесса выполнения старшего. Один из приемов такой передачи заключается в том, что старший наделяется возможностью "маскировать" буфер, доступный младшему по записи. Допустим, что младший обращается к старшему, заменяя в буфере y код 0 кодом 1. Тогда для старшего предусматривают собственную ячейку z, которая может содержать либо 0, либо 1, и в старшем ставят пару приказов
k) Если z = 1, то ->k+1, иначе k+m;
k+1) Ожидать y = 1, ->k+2;

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
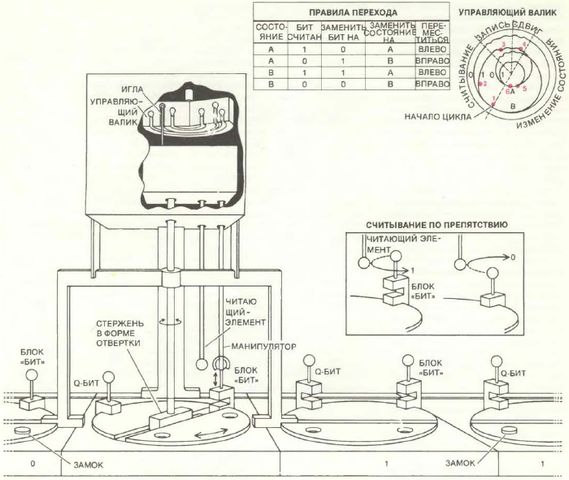
Очередная "механистическая" модель Машины Тьюринга (В МИРЕ НАУКИ 9/85)
Еще из Криницкого...
ГЛАВА 8. КОЛЛЕКТИВЫ РОБОТОВ
#8.1. ЧТО ТАКОЕ КОЛЛЕКТИВ РОБОТОВ?
О коллективах роботов стали говорить, проводя аналогию между системами роботов и коллективами людей. С научной точки зрения такая аналогия не является достаточным основанием для введения нового понятия. Для того чтобы наука стала говорить о коллективах роботов, необходимо точно определить, что это такое.
Основанием точного определения может послужить и интуитивное представление об изучаемом явлении, но такое представление нужно уточнить. Кстати говоря, я уверен, что многие читатели, пользуясь термином "коллектив", и в отношении людей не знают точного смысла этого слова. Посмотрим в энциклопедию. Там сказано: "коллектив - это объединение лиц, связанных совместной работой, общими интересами и целями". Хотя и такое определение не отличается математической точностью, из него все же кое-что можно извлечь. Во-первых, для коллектива характерна связь между его членами. Нет связи - нет и коллектива. Во-вторых, должна быть общая цель, общие интересы. Эта общая цель вовсе не должна быть целью каждого лица. Она должна быть целью всего объединения лиц.
Перейдем теперь к рассмотрению систем роботов. Что нужно понимать под связью между роботами? Чтобы лучше в этом разобраться, рассмотрим ряд примеров.
ПРИМЕР 8.1. В подъезде многоэтажного дома установлен автомат, который отмыкает дверь, если на специальном кнопочном регистре (ряде кнопок, имеющих номера 0, 1, ..., 9) набрать определенный код, например 297. Если после этого в течение минуты никто не входит, автомат опять замыкает дверь. Если кто-то входит, открывая, а затем закрывая дверь, автомат также ее замыкает. Если оставить дверь открытой (а это не просто, так как дверь снабжена пружиной), то через минуту автомат подает сигнал в диспетчерскую, где загорается лампочка. При неверном наборе кода автомат двери не отмыкает. Такой автомат является примитивным роботом. В этом же доме в других подъездах установлены такие же автоматы. Их совокупность не является коллективом, так как между ними нет связи.
ПРИМЕР 8.2. Если бы в подъезде, описанном в предыдущем примере, установили автомат, поддерживающий постоянную освещенность подъезда днем и ночью (а это тоже робот), то такая пара автоматов не стала бы коллективом. Даже находясь в одном помещении, они не связаны. А вот если бы мы второй автомат переделали так, что при полной темноте вместо того, чтобы зажигать дополнительную лампу, он размыкал канал связи, по которому кодовый сигнал с кнопочного регистра поступает в дешифратор первого робота, то совокупность двух роботов была бы коллективом. Между рассматриваемыми роботами возникла бы связь. Кстати, нетрудно выявить и целевое отношение коллектива: днем регулировать освещенность и пропускать в подъезд всех, кто знает соответствующий код, а ночью никого не впускать в подъезд.
Пример 8.2 создает ложное впечатление, что между наличием связи между роботами и наличием общей цели есть зависимость. Очень показателен следующий пример.
ПРИМЕР 8.3. Предположим, что даны два робота, каждый из которых "ощущает" только температуру помещения, в котором он находится, и влияет только на температуру этого помещения. Допустим, что первый из них предназначен для поддержания температуры на уровне +10oС, а второй - на уровне +20oС. Если эти роботы находятся в разных помещениях (изолированных между собой), то между ними практически отсутствует связь. Они не образуют коллектива.
Однако из нашего примера не следует, что такие два робота не могут образовать коллектив. Если их установить в помещениях, которые между собой соединены дверью, то связь между роботами появится. И если нам нужен сложный тепловой режим, который будут теперь в двух комнатах устанавливать два робота, они составляют коллектив. Если же такой сложный режим никому не нужен, т.е. функции его поддержания не существует, то коллектива нет. Это и означает, чго наличие связи между роботами недостаточно для того, чтобы возник коллектив роботов.
Предыдущий пример можно усилить и при этом обнаружить еще одно явление, которое может возникать при объединении роботов.
ПРИМЕР 8.4. Предположим, что роботы, описанные в предыдущем примере, помещены в одну комнату, начальная температура в которой равна +15oС. В таких условиях первый робот будет охлаждать помещение, а второй его нагревать. Кто из них "победит" и "победит" ли один из них, заранее неизвестно. Может быть, ресурсы первого меньше, тогда победит второй. Но в зависимости от таких характеристик, как чувствительность рецепторов, мощность эффекторов и время отклика, возможно и возникновение тепловых колебаний, и даже значительных. Конечно, не исключено и такое соотношение всех факторов, что температура в комнате будет оставаться равной +15oС (хотя этот случай и маловероятен). Еще из известной басни Крылова знаком нам подобный "коллектив": "... Лебедь рвется в облака, Рак пятится назад, а Щука тянет в воду..."
В примере 8.4 мы встретились с так называемым АНТАГОНИЗМОМ роботов. Возникновение антагонизма возможно, если внешние среды роботов связаны. Отмечу, что возможен случай, когда даже один робот сам с собой находится в антагонизме. Это может произойти, если робот влияет на многие параметры внешней среды и эти влияния в скрытом виде противоречивы. Но вернемся к вопросу о возможных видах связей.
Связь между роботами, как следует из вышеприведенных примеров, может возникать благодаря наличию либо связей между их ближними внешними средами, либо канала связи, соединяющего их преобразователи информации. В последнем случае встречаются две разновидности связи: передачей осведомляющей информации и передачей управляющей информации. Первая связь в определенном смысле близка к связи через внешнюю среду, так как под влиянием внешней среды в роботах возникает именно осведомляющая информация. Передача управляющей информации более разнообразна. Она может выражаться в передаче вопроса или ответа на прежде заданный вопрос (это имеет место при управлении одних роботов другими), но может выражаться и во внесении изменений в алгоритм работы робота (как это было в примере 8.2). Другими словами, она может заключаться в передаче операнда или во внесении изменения в алгоритм, управляющий роботом. Последний вид связи может принимать форму передачи записи алгоритма или его части.
Каналом связи может служить специальное приспособление (например, кабель), но возможно, что каналом связи является часть внешней среды (передача звуковых сигналов непосредственно в среде, радиосвязь и т.п.). Независимо от вида канала связи, передачу информации от робота к роботу, осуществляемую АКТИВНО, мы будем всегда отличать от связи, возникающей из-за наличия связи между внешними средами роботов, являющуюся ПАССИВНОЙ.
Нужно еще иметь в виду, что связь между роботами может быть непосредственной или опосредствованной, осуществляемой через другие роботы.
Наконец, нужно не забывать, что в некоторых случаях связь между роботами принимает нежелательную форму антагонизма (я исключаю из рассмотрения случай боевых военных роботов, когда их цель заключается в антагонизме, но ведь "воюющих" между собой роботов не назовешь коллективом).
Теперь мы можем наконец сказать, что следует называть КОЛЛЕКТИВОМ РОБОТОВ. Это - СИСТЕМА РОБОТОВ, В КОТОРОЙ ВСЕ РОБОТЫ МЕЖДУ СОБОЙ СВЯЗАНЫ, НЕ НАХОДЯТСЯ В СОСТОЯНИИ АНТАГОНИЗМА И ИМЕЮТ ГРУППОВОЕ ЦЕЛЕВОЕ ОТНОШЕНИЕ (групповую цель: выполняют групповую функцию).
Не вызывает сомнения, что понятие коллектива роботов целесообразно и заслуживает изучения.
Кончая этот параграф, я хотел бы сделать два замечания общеметодологического характера.
1. Изучая поведение роботов при их взаимодействии, мы описывали их функции и приводили некоторые характеристики внешней среды, а затем анализировали поведение роботов. Такой прием называется МЫСЛЕННЫМ ЭКСПЕРИМЕНТОМ. В последнее время появился ряд работ по философии о значении и месте мысленного эксперимента в познании. Мысленный эксперимент - это моделирование явления или процесса в мыслях. Он существенно отличается от реального эксперимента и может дать не больше чем любая модель. Однако в ряде случаев он существенно помогает анализу явления или процесса. Все же мысленный эксперимент уступает таким моделям, как, например, программная.
2. В некоторых случаях мы считали пример доказательством своего утверждения. Законно ли это? Ведь обычно доказательство проводят путем логических рассуждений. Оказывается законно, и это не противоречит правилам логики. Если нужно опровергнуть какое-либо всеобщее утверждение (т.е. доказать его неверность), то достаточно одного опровергающего примера. Мыс помощью одного примера доказали недостаточность наличия связей для того, чтобы совокупность роботов была коллективом.
#8.2. КЛАССИФИКАЦИЯ КОЛЛЕКТИВОВ РОБОТОВ
В основу всякой классификации обычно кладут какой-либо признак или совокупность признаков, которыми может обладать или не обладать объект из классифицируемого класса объектов. Признак может быть двоичным (отсутствует присутствует) или многозначным. В некоторых случаях классы, полученные по одному какому-то признаку, дальше разбивают на подклассы по другому признаку. При этом, если каждый класс изобразить точкой (или прямоугольником, в котором записано название класса), которую назовем вершиной, и между ними провести отрезки, ведущие от каждого класса к его подклассам, то возникает разветвляющаяся структура, называемая ОДНОАСПЕКТНЫМ КЛАССИФИКАТОРОМ. С математической точки зрения такая структура представляет собой ориентированный граф, имеющий форму дерева (для наглядности добавим обращенного ветвями вниз). Основанием этого дерева является совокупность всех классифицируемых объектов.
Если произведено несколько одноаспектных классификаций и все одно-аспектные классификаторы объединены и при этом одноименные вершины (если такие имеются) совмещены, то получается так называемый МНОГОАСПЕКТНЫЙ КЛАССИФИКАТОР. Входящие в его состав отрезки во избежание неясности следует пометить именем или номером аспекта.
Классифицируя коллективы роботов, мы должны исходить из таких признаков (свойств), которые не являются свойствами роботов, характеризуя именно коллективы их. Таких свойств мы знаем два: 1) характер связей между роботами - членами коллектива и 2) структура коллектива.
Условимся не считать запрос, пересылаемый из одного робота в другой, управляющей информацией, хотя вполне допустимо считать, что запрос - это приказ о выдаче ответа или другого приказа. Кроме того, введем понятие ПОДКОЛЛЕКТИВА. Под коллективом мы будем считать совокупность роботов, входящих в состав некоторого коллектива роботов, и являющуюся коллективом. При этом уточним один вопрос, касающийся коллектива роботов и не освещенный нами до сих пор.
Спрашивается, могут ли элементы коллектива роботов быть связанными с другими роботами, не принадлежащими данному коллективу? В отношении пассивных связей ответ на этот вопрос ясен: могут, потому что всякий робот находится в собственной внешней среде, независимо от того, что влияет на нее. Что же касается активных связей, то проблема сложнее. Если допустить и активные связи, то не получится ли, что любая часть коллектива роботов является подколлективом? С другой стороны, требование отсутствия внешних активных связей явно нецелесообразно, потому что оно привело бы к запрещению связей между коллективами. Но это противоречило бы нашим представлениям о роботах и их коллективах и не позволило бы также отдельный робот считать частным случаем коллектива (одноэлементным коллективом). Ясно, что мы не можем пойти на исключение возможности активных внешних связей. Однако никаких трудностей это не повлечет, так как основной признак коллектива наличие коллективной функции - всегда позволит нам педколлектив отличить от всякой иной части коллектива.
После сделанных выше замечаний мы можем привести классификацию коллективов роботов по видам связей, которые в них существуют (рис.8.1).

Рис.8.1. Классификация коллективов роботов по видам связи между роботами
Недостатком этой классификации является то, что некоторые коллективы роботов могут попасть сразу в несколько классов. Например, если некоторые роботы активно связаны по осведомлению, а другие в том же коллективе активно связаны по управлению. Правда, в таком случае можно считать, что данный коллектив не попадает ни в один класс. Признаюсь, что ради экономии места и терпения читателя я просто опустил в классификаторе ряд "комбинированных" подклассов.
Автономные подколлективы, сами будучи коллективами, должны попасть в один из разделов классификаторов.
Скажем теперь несколько слов о втором возможном аспекте классификации коллективом роботов, связанном с их структурой. Структуру коллектива роботов нам поможет описать теория графов. Придется привести более подробные сведения из этой теории.
СПРАВКА ИЗ ТЕОРИИ ГРАФОВ. Множество точек (назовем их вершинами) и множество ориентированных отрезков линий (назовем их дугами), соединяющих некоторые из этих точек, исходящих из них или входящих в них, называются в своей совокупности ОРИЕНТИРОВАННЫМ ГРАФОМ. Две дуги, имеющие одно и то же начало и один и тот же конец, считаются одной и той же дугой и потому на схеме графа дважды не изображаются. Дуги, не имеющие начала, называются ВХОДАМИ в граф, а не имеющие конца - ВЫХОДАМИ из графа. Если начало дуги и ее конец совпадают, то дуга называется ПЕТЛЕЙ.
Если дуги какого-нибудь ориентированного графа пометить какими-либо значками, а затем провести новые дуги и тоже пометить их, следя за тем, чтобы дуги, имеющие одинаковые начала и одинаковые концы, отличались своими пометками (такую операцию можно проделать многократно), то получится так называемый ОРИЕНТИРОВАННЫЙ РАЗМЕЧЕННЫЙ МУЛЬТИГРАФ.
В дальнейшем слова "ориентированный" и "размеченный" мы будем опускать, так как неориентированные и неразмеченные графы и мультиграфы у нас не будут встречаться.
Графы и мультиграфы называются СВЯЗНЫМИ, если из какой-либо их вершины можно прийти в любую другую вершину, двигаясь по дугам (без учета их направлений и пометок). В противном случае они называются несвязными.
Структуру коллектива роботов мы будем изображать в виде мультиграфа, вершины которого соответствуют роботам, являющимся членами коллектива, а дуги - связям между ними. В данной книге мы ограничимся тремя видами связей, а следовательно и тремя видами пометок на ребрах. Для того чтобы сделать структурные схемы коллективов более наглядными, вместо того, чтобы помечать дуги, будем изображать их пунктиром (пассивные связи), тонкими линиями (связи по осведомляющей информации) и толстыми линиями (активные связи управления). При необходимости можно учитывать большее число видов связей; тогда мультиграф будет сложнее.
Классификацию структур коллективов роботов можно осуществить как классификацию соответствующих им мультиграфов.
Рассмотрим некоторые структуры коллективов роботов. На рис.8.2 приведена структура одноэлементного коллектива, который состоит из одного робота. На этой схеме имеется один вход в мультиграф (воздействие на него внешней среды), один выход (воздействие робота на внешнюю среду) и одна петля (обратная связь). Если имеется робот, управляемый человеком-оператором, то его схема как одноэлементного коллектива будет иметь вид, показанный на рис.8.3.
Рис.8.2. Структура одноэлементного коллектива роботов (одиночного робота)
Рис.8.3. Структура одноэлементного коллектива роботов, управляемого человеком
На рис.8.4 приведена структура двухэлементного коллектива роботов, описанного в примере 8.2.

Рис.8.4. Структура двухэлементного коллектива роботов, описанного в примере 8.2
Рассмотрим некоторые частные случаи коллективов роботов, которые мне кажутся интересными.
#8.3. КОЛЛЕКТИВЫ АВТОНОМНЫХ РОБОТОВ
Коллектив автономных роботов может быть создан намеренно, но может возникнуть и сам собой при совместном использовании нескольких роботов с целью достижения какого-либо эффекта. Необходимым условием для возникновения такого коллектива является связь между внешними средами роботов. При этом кроме внешних обратных связей каждого робота возникаютм внешние прямые связи между роботами. Внешняя обратная связь всего коллектива осуществляется как совокупность внешних обратных связей роботов. Активных связей между роботами в таком коллективе нет. Возможная структура некоторого коллектива автономных роботов приведена на рис.8.5. Воздействие внешней среды на изображенный коллектив описывает совокупность входов в мультиграф (a R1, b R5, c R4, d R3, e R2), а совокупный эффект коллектива автономных роботов коллектива выражает множество выходов из мультиграфа (R1 z, R2 u, R3 y, R4 x, R5 v). Пересечение дуг в точках, не совпадающих с вершинами мультиграфа, не учитывается из-за случайного вида чертежа, который можно и изменить, перемещая вершины.

Рис.8.5. Структура возможного коллектива автономных роботов
При рассмотрении коллективов автономных роботов нужно не забывать о возможности возникновения между ними антагонизмов. Если в некотором резервуаре один робот поддерживает постоянный уровень жидкости, другой - постоянную температуру, третий - постоянное давление, а четвертый постоянный удельный вес (плотность) жидкости, то с высокой степенью уверенности следует ожидать возникновения конфликта между роботами, потому что регулируемые параметры между собой связаны законами физики. Но эта же связь между ними объединяет их в коллектив (если антагонизма нет).
Существенную роль в таких коллективах играет и соотношение между временами отклика роботов-элементов коллектива.
#8.4. ЛИНЕЙНО-ПОСЛЕДОВАТЕЛЬНЫЕ КОЛЛЕКТИВЫ РОБОТОВ
Такие коллективы можно встретить на производстве. Их элементами являются промышленные роботы. Каждый такой робот взаимодействует с обрабатываемым им объектом. Этот объект и является его внешней средой. Получив объект, робот его обрабатывает, контролируя результаты обработки с помощью соответствующих рецепторов. После того, как обработка окончена, он передает сам объект другому роботу, сигнализируя об этом. Следующий в линии робот, после того, как он окончит обработку предыдущего изделия, приступает к обработке нового и т.д.
Если, оканчивая свою работу, каждый робот коллектива перемещает изделие на участок следующего робота, не подавая сигнала, начинает обработку следующего тогда, когда его рецепторы обнаружат появление на его входе следующего изделия, то элементами коллектива являются последовательно работающие автономные роботы. Если же передача изделия имеет место одновременно с подачей сигнала непосредственно в преобразователь информации следующего робота, то коллектив, будучи линейно последовательным, вместе с тем является и иерархическим (о иерархических коллективах см. ниже). Структуры вышеуказанных коллективов роботов приведены на рис.8.6 и 8.7.
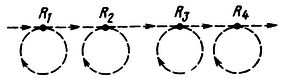
Рис.8.6. Структура линейно-последовательного коллектива автономных роботов
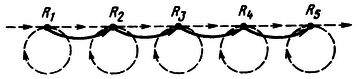
87. Структура линейно-последовательного иерархического коллектива роботов
#8.5. ИЕРАРХИЧЕСКИЕ КОЛЛЕКТИВЫ РОБОТОВ
Рассмотрим коллектив, в котором могут быть как активные, так пассивные связи между роботами. Такой коллектив называется ИЕРАРХИЧЕСКИМ, если для него выполнены следующие три условия:
1. В структурной схеме коллектива можно указать уровни, такие, что каждый робот (i+1)-го непосредственно связан с одним и только одним роботом i-го уровня. Самым старшим считается 0 и уровень и на нем находится только один робот. Уровень с номером i считается старше (i+1)-го.
2. От роботов старшего уровня к роботам младшего уровня осуществляется передача только управляющей информации.
3 От роботов младших уровней к роботам старших уровней может передаваться только осведомляющая информация (активно или пассивно).
На рис.8.8 показана возможная структура иерархического коллектива роботов.
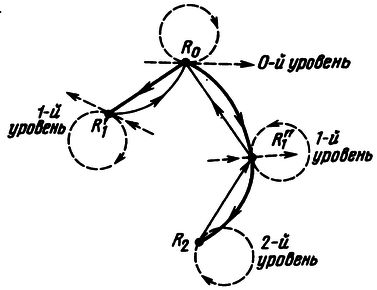
Рис.8.8. Структура иерархического коллектива роботов
Уровень в иерархическом коллективе роботов называется СЛОЕМ, если существуют непосредственные связи между роботами этого уровня. Структурная схема иерархического коллектива роботов, содержащего слой, приведена на рис.8.9.
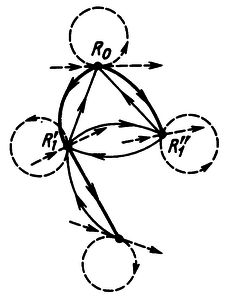
Рис. 8.9. Структура иерархического коллектива роботов, содержащего слой
Возможны иерархические коллективы роботов, в которых робот нулевого уровня не имеет другой внешней среды, кроме роботов коллектива. Такой робот 0-го уровня называется директором коллектива. Структурная схема возможного коллектива с директором показана на рис.8.10.

Рис.8.10. Структура иерархического коллектива роботов с роботом-директором
Рассмотренный нами ранее класс линейно-последовательных роботов во втором его варианте (с передачами управляющих сигналов) является частным случаем иерархических роботов (см. рис.8.7). В роботах этого класса осведомляющая информация передается пассивно.
#8.6. ВОЗМОЖНОСТИ КОЛЛЕКТИВОВ РОБОТОВ
Деятельность человечества иногда сравнивают с борьбой. Человечество сражается с природой и отвоевывает у нее одну позицию за другой. Я ни в коем случае не хочу оправдать действия некоторых западных политических руководителей, которые жизнь человечества представляют себе как войну, да к тому же еще братоубийственную (людей с людьми). Но все же прибегаю к такому сравнению, чтобы нагляднее выявить одно преимущество коллектива сравнительно простых роботов перед большим, сложным роботом, который эквивалентен этому коллективу. Роботов можно уподобить солдатам, сражающимся на стороне человечества.
Спрашивается, что лучше: иметь 100 солдат, каждый из которых оснащен оружием, позволяющим произвести 5 выстрелов в минуту, или одного солдата, огневая мощь которого 500 выстрелов в минуту? По силе огня 100 слабо вооруженных солдат равны одному сильно вооруженному. Но по живучести? Если даже вероятность выхода из строя считать одинаковой (а для более сложного оружия она обычно выше), то живучесть 100 солдат во 100 раз выше живучести одного. [См. формулы Ланчестера.- G.]
Итак, одно преимущество коллектива роботов перед одиночным более сложным роботом мы выяснили: коллектив более НАДЕЖЕН.
Второе преимущество коллектива роботов перед эквивалентным ему одиночным роботом таится в особенностях человеческого мышления, которое вначале является аналитическим, расчленяет сложные проблемы на более простые, а затем уже рассматривает сложную проблему, как систему более простых (т.е. синтезирует ее). Особое развитие получил системный подход во второй половине XXв. Разрабатывая один сложный робот, мы все равно будем создавать его как систему (коллектив). Может быть, только заключим эту систему в общую оболочку. Коллектив роботов проще создать, чем одиночный сложный робот. Да к тому же появляется возможность комплектовать коллективы из некоторого набора стандартных более простых роботов. Это очень важная возможность, которая позволит при производстве роботов существенно экономить материальные средства и научные силы. Уже теперь нужно заняться рассмотрением проблемы стандартизации роботов и списков полного набора возможных роботов-модулей.
Наконец, укажем на еще одно обстоятельство. Если необходимо создать робот, распределенный в большом пространстве, то совершенно неизбежно он примет форму коллектива более простых роботов. Действительно, возникнет вопрос о разработке устройств, связанных между собой каналами связи для дальней передачи информации. Трудности такой передачи информации заставят эффекторы и датчики информации конструктивно группировать вместе с локальными устройствами управления, изолируя такие блоки от вредных воздействий внешней среды. Словом, распределенный робот должен принять форму системы более простых роботов, связанных каналами активной связи.
Следовательно, возможность охвата больших пространств - это одна из особенностей коллективов роботов. Мы знаем, что уже существуют подобные коллективы роботов, в которых один "элемент" находится в космосе, а другой - на земле (имеются в виду межпланетные станции и обслуживающие их ЭВМ; об ЭВМ мы еще поговорим в девятой главе). Легко себе представить, что освоение других планет человечество будет осуществлять, направляя туда роботы, которые вместе с роботами, оставленными на Земле, будут составлять (скорее всего иерархический) коллектив. Менее вероятно, что другие планеты можно будет осваивать с помощью коллектива автономных роботов.
Таким образом, применение коллективов роботов вместо одиночных сложных роботов позволяет повысить надежность системы, облегчает ее разработку, упрощает и удешевляет производство роботов и, наконец, позволяет охватить автоматической системой большие пространства.
Последний раз редактировалось: Gudleifr (Пн Июл 04, 2022 2:42 pm), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
ЛИРИЧЕСКОЕ ОТСТУПЛЕНИЕ

В качестве примера "цепочки Машин Тьюринга" можно привести пример установление межзвездного контакта (с целью "убить всех человеков") из романа Фреда Хойла и Джона Эллиота "А - Андромеда". Начинается все с получения радиосообщения из космоса:
1. На входной ленте, очевидно, двоичная запись сообщения; на выходе:
2. Машина незнамо как, но собрана. Зачем к ней прицеплены два больших высоковольтных электрода, пока неясно. Устройство ввода-вывода - обычный телетайп.
Еще на этапе ввода программы машина начала своевольничать:
3. Машина выдает рецепт живой клетки. И люди пытаются ее вырастить. Чего тут больше, подбора нужной среды или передачи машине данных о наиболее удачных образцах, неясно.
4. Из клетки вырастает многоклеточный монстр:
5. Монстр гипнотизирует лаборантку, заманивая ее между электродами. Девушку убивает током. Машина тоже немного повреждается. Однако получает недостающую информацию об устройстве человека.
6. Машина изготовляет искусственную девушку. Люди ее обучают, превращая в идеального для них оператора машины. Ненужного более монстра машина убивает током. Электроды использует для общения с девушкой и ее наказания в случае ошибки.
7. Тут фантазия авторов исчерпывается. Машина, очевидно, считает, что является столь мощной и полезной, что ее будут использовать в высших эшелонах власти. И она сможет творить, что хочет, во славу пославшего ее высшего разума. Поэтому никаких дальнейших исследований (например, земной культуры) не предпринимает. Передача людям биологических рецептов продолжается для закрепления зависимости последних (в продолжении романа - для терроформирования).
КОНЕЦ ЛИРИЧЕСКОГО ОТСТУПЛЕНИЯ

В качестве примера "цепочки Машин Тьюринга" можно привести пример установление межзвездного контакта (с целью "убить всех человеков") из романа Фреда Хойла и Джона Эллиота "А - Андромеда". Начинается все с получения радиосообщения из космоса:
Далее следует (в разных экранизациях/новеллизациях возможны варианты) примерно следующее:- Морзянка,- сказал Бриджер.
- Знаки не группируются.
Они снова прислушались.
- Длинные и короткие - вот что это такое,- сказал Бриджер.
..
- Кроме того, в этой передаче есть нечто особое, такое, чего я никогда еще не встречал. Между точками и тире шел модулированный сигнал более высокой частоты, и уж там такое количество знаков... В общем нам придется собрать специальную аппаратуру, чтобы принимать все это.
1. На входной ленте, очевидно, двоичная запись сообщения; на выходе:
Разбить сообщение на подобные части вполне возможно - они, очевидно, должны иметь разную энтропию/регулярность, но как понять язык описания машины? Впрочем, работы Минского дают почву некоторому оптимизму (далее я эту статейку выложу).- Видите ли, она распадается на три раздела,- Флеминг переложил свои бумаги, будто это могло что-то объяснить.- Первая часть, так сказать, техническое задание, проект, вернее, набор математических условий, который может быть интерпретирован как техническое задание. Вторая часть - это собственно программа, точнее, система команд, как мы ее называем. И третья, последняя часть - информация, которую нужно ввести в машину, чтобы она над ней работала
2. Машина незнамо как, но собрана. Зачем к ней прицеплены два больших высоковольтных электрода, пока неясно. Устройство ввода-вывода - обычный телетайп.
Еще на этапе ввода программы машина начала своевольничать:
Будучи окончательно запущенной, машина начинает печатать химические константы:- Что-нибудь случилось?
- Сначала ничего. Но там была небольшая группа команд, которыми я сначала пренебрег. Эти команды устраивали все таким образом, что после включения питания первый же импульс тока автоматически запускал все с того места, которое машина выбирала по собственному усмотрению. Я нарочно не стал вводить эти команды, чтобы не давать ей полной воли. И она взбесилась.
Джуди недоверчиво посмотрела на Флеминга.
- Это какая-то ерунда.
- Ну, ладно, скажем, что она просто отметила нарушение. Без всякого предупреждения, прежде чем мы начали вводить данные, она принялась выстукивать на выходе отсутствующую часть кода. Снова, снова и снова, требуя, чтобы я ввел эту часть. Она очень рассердилась.- Флеминг серьезно смотрел в недоверчивые глаза Джуди.- Я выключил ее на минутку и затем начал вводить эти данные. Тогда она успокоилась. Но она сконструирована именно так, чтобы регистрировать нарушения. Одному богу известно, для чего еще она сконструирована!
Цель диалога - уточнить, в какую физическую среду попала машина. Она выводит разные варианты наборов элементов, из которых земляне выбирают важные для земной жизни. Понятно, что при этом машина не столько получает новые данные, сколько отбрасывает те, что в данных условиях ей не пригодятся. Этот этап заканчивается, когда машине объясняют структуру земной ДНК.На бумаге было отпечатано несколько строчек цифр.
...
- Разве это не относительные расстояния между энергетическими уровнями атома водорода?
...
- Ну, водород - самый распространенный элемент во Вселенной. Так? Значит, это очень простая и универсальная единица информации. Если мы ее не опознаем, то машине не имеет смысла продолжать, а если опознаем, то она перейдет к следующему вопросу.
- К какому следующему вопросу?
- Мы еще не знаем. Но бьюсь об заклад, что это только первый шаг в долгой-долгой игре в вопросы и ответы.- Он взял бумагу из рук Дауни и вручил ее Кристин.- Введите-ка это в машину.
3. Машина выдает рецепт живой клетки. И люди пытаются ее вырастить. Чего тут больше, подбора нужной среды или передачи машине данных о наиболее удачных образцах, неясно.
4. Из клетки вырастает многоклеточный монстр:
Люди догадываются, что электроды на машине служат для общения машины и монстра. Видимо, последний является более удобным устройством ввода вывода, чем телетайп. Передает машине информацию о земных условиях и обитающих здесь существах.Оно продолжало расти, пока не достигло размеров овцы; затем рост прекратился. Существо, по-видимому, чувствовало себя хорошо, казалось вполне безвредным, но отнюдь не отличалось красотой.
...
- Полное отсутствие костных образований. Напоминает огромный кусок студня. Но в то же время у него есть глаз и какое-то подобие мозга, напоминающее очень сложные нервные узлы.
- И больше ничего примечательного?- Рейнхарт, прищурившись, рассматривал рентгенограммы.
- Нет, разве что зачатки ног, хотя, вернее всего, это просто раздвоенный кусок ткани. Рейнхарт отложил рентгенограммы и сосредоточенно нахмурился.
- Как оно питается?
- Непосредственно через кожу. Оно живет в питательной среде и усваивает ее прямо клетками тела. Очень просто и очень эффективно.
5. Монстр гипнотизирует лаборантку, заманивая ее между электродами. Девушку убивает током. Машина тоже немного повреждается. Однако получает недостающую информацию об устройстве человека.
6. Машина изготовляет искусственную девушку. Люди ее обучают, превращая в идеального для них оператора машины. Ненужного более монстра машина убивает током. Электроды использует для общения с девушкой и ее наказания в случае ошибки.
7. Тут фантазия авторов исчерпывается. Машина, очевидно, считает, что является столь мощной и полезной, что ее будут использовать в высших эшелонах власти. И она сможет творить, что хочет, во славу пославшего ее высшего разума. Поэтому никаких дальнейших исследований (например, земной культуры) не предпринимает. Передача людям биологических рецептов продолжается для закрепления зависимости последних (в продолжении романа - для терроформирования).
КОНЕЦ ЛИРИЧЕСКОГО ОТСТУПЛЕНИЯ
Последний раз редактировалось: Gudleifr (Пн Апр 25, 2022 1:43 am), всего редактировалось 2 раз(а)

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

ОБЩЕНИЕ С ВНЕЗЕМНЫМ РАЗУМОМ
МАРВИН МИНСКИЙ
Если нам когда-нибудь придется встретиться с инопланетянами, носителями внеземного разума, сможем ли мы разговаривать с ними? Думаю, что да (разумеется, при условии взаимного желания), ибо, несмотря на различие в происхождении, и мы и они должны мыслить одинаково. Приведу два аргумента в пользу своего суждения. Они основаны на том, что решение всех интеллектуальных задач зависит от одних и тех же ограничивающих факторов: времени, пространства и используемых материалов. Чтобы у живых существ могли развиться эффективные средства для работы в рамках названных ограничений, они должны выработать способность формировать представления о ситуации, в которой оказываются, и научиться оперировать этими представлениями. Теперь остановимся на двух важнейших особенностях, характеризующих интеллект как таковой.
1. ЭКОНОМНОСТЬ МЫШЛЕНИЯ. Любой интеллект должен выработать специальные символьные системы для представления объектов, причин, целей, а также для формирования и последующего запоминания процедур, которые он разработал для достижения поставленных целей.
2. УНИКАЛЬНОСТЬ ПРОСТЫХ ИДЕЙ. Любой интеллект в своем развитии неизбежно приходит к ряду специфических представлений, а именно: к арифметике, логике причинно-следственных связей и к математической экономике, т.е. представлениям, которые оказываются наиболее простыми среди всех других, имеющих аналогичное практическое применение.
Требование экономности мышления, как мне кажется, обязательно потому, что сила разума зависит от того, как он использует имеющиеся в его распоряжении ресурсы. Понятие объекта неизбежно возникает, когда рассматривается такой ресурс, как пространство с заполняющими его субстанциями. Понятие цели совершенно необходимо при умозаключениях о том, как мы используем свое время, причем в равной степени это относится и к реальным поступкам, и к воображаемым действиям. Инопланетяне также должны использовать оба этих понятия - объект и цель,- ибо, во-первых, к ним легко прийти и, во-вторых, их вряд ли можно заменить чем-либо другим.
Более строго все эти вопросы рассмотрены в теории уникальности простых идей, где показано, что практически любой эволюционный поиск неизбежно приведет к определенным схемам, которым трудно найти столь же простую замену, т.е. другие идеи, служащие тем же целям. Эти (уникальные) идеи и процессы выделяются тем, что если и существует нечто подобное им, то оно оказывается несравненно более сложным. Мы ограничимся здесь лишь одним примером - законами арифметики; однако я думаю, что понятия "объект", "причина" и "цель" также представляют собой такие изолированные "острова".
КРИТИК. А что если эти инопланетяне настолько опередили нас в своем развитии, что нам не понять ход их мыслей, а их наука и техника в корне отличаются от наших?
- В этом случае общение может и не состояться. Моя аргументация применима только к тому этапу эволюции разума, на котором живые существа еще продолжают бороться за существование, заинтересованы в общении и стремятся расширить свой контроль над окружающим миром. В противном случае у них должны быть различные представления о ценности тех или иных вещей. Но и тогда можно надеяться, что общению будет способствовать сходство механизмов мышления, которыми пользуются все разумные существа для описания времени и пространства. Эти механизмы и могут играть роль своего рода универсальной "разменной монеты".
КРИТИК. А почему вы уверены, что растения, камни, течения и штормы не обладают разумом?
- Если вы не можете сказать, чем их интеллект похож на наш, то нет и смысла использовать для его определения то же название. Ведь им действительно не приходится решать задачи, подобные тем, что решаем мы.
КРИТИК. А что особенного в решении задач? Пожалуйста, определите точнее, что такое интеллект, ибо только тогда будет ясно, о чем идет речь.
- Никто не возьмет на себя смелость объяснить другим людям значение слова, которое они и без того хорошо понимают. Так что будем использовать его в том смысле, в каком оно обычно употребляется: интеллект-это способность решать трудные задачи, скажем, такого типа, как построить ракету или систему дальней связи.
КРИТИК. Тогда, будьте добры, определите, что такое трудная задача. Мы, например, знаем, что человеческий интеллект решал задачу строительства пирамид, однако организмы, населяющие коралловые рифы, "строят" и более грандиозные сооружения. Можно ли сказать, что это дает нам основание для общения с ними?
- Нет. Человек действительно решал подобные задачи, но это заблуждение, что кораллловые полипы делают то же самое. Здесь важным фактором является скорость. Птицы научились летать не за одно поколение - для этого потребовались миллиарды лет эволюции, а человек стал летать за какие-нибудь несколько десятков лет. Чтобы выучиться строить конструкции вроде гнезда иволги или норы бобра, человеку понадобится несколько лет, но бобер способен научиться этому, только используя древний генетический механизм, заложенный в его мозг. Важной особенностью того, что мы называем интеллектом, является способность решать в широком масштабе новые, нетрадиционнные задачи. Вот почему имеет смысл пытаться наладить общение лишь с теми животными, которые способны быстро обучаться решать новые и сложные задачи.
Что позволяет человеку столь быстро решать трудные задачи? На мой взгляд, следует выделить несколько компонентов, участвующих в этом процессе, и эти компоненты столь важны, что инопланетные разумные существа, по-видимому, тоже должны опираться именно на них. Назовем их:
- ПОДЦЕЛИ - разбиение трудной задачи на совокупность более простых подзадач.
- "ПОДОБЪЕКТЫ" - описание объектов через их части и связи между ними.
- ПРИЧИННАЯ СИМВОЛИКА - объяснение и понимание того, как изменяются объекты.
- ПАМЯТЬ - накопление опыта решения сходных задач.
- ЭКОНОМНОСТЬ МЫШЛЕНИЯ - эффективное распределение имеющихся (ограниченных) ресурсов.
- ПЛАНИРОВАНИЕ - мысленная организация работы в общих чертах еще до начала ее выполнения.
- САМОСОЗНАНИЕ - обеспечение благоприятных условий для того, кто решает задачу.
Возникает, однако, вопрос: а разве не существуют мириады других возможностей для решения задач? Почему бы инопланетянам не найти какой-то совершенно иной, "инопланетный" способ? Тем не менее я убежден, что описанные элементы решения задач не столь уж произвольны, как может показаться на первый взгляд.
ПРИНЦИП УНИКАЛЬНОСТИ
Почему всем нам кажется столь очевидным, что дважды два-четыре? Подобные вопросы издавна занимают философов: почему некоторые понятия люди воспринимают так, будто они не нуждаются в предварительной опытной проверке или доказательстве? Я думаю, что это объясняется, по крайней мере отчасти, неким ВЫЧИСЛИТЕЛЬНЫМ ФЕНОМЕНОМ, который я называю ПРИНЦИПОМ УНИКАЛЬНОСТИ ПРОСТЫХ ИДЕЙ: если два относительно простых процесса дают сходные результаты, то с большой вероятностью эти результаты ПОЛНОСТЬЮ идентичны.
В силу этого принципа мы почти всегда априори ожидаем появления вполне определенных структур от определенных вычислительных систем, возникших в ходе эволюции в результате отбора из множества возможных процессов. Примером тому могут служить понятия числа и арифметических действий; возможно, этим и объясняется, почему люди легко находят "общий язык", говоря об этих понятиях, хотя в остальном их мысли и представления могут кардинально различаться. Подобное суждение вполне применимо и к внеземному разуму. Позволю себе пояснить принцип уникальности на примере двух почти анекдотичных случаев. Один из них касается математического эксперимента, а второй - реальный случай из моей жизни.
МАТЕМАТИЧЕСКИЙ ЭКСПЕРИМЕНТ. Как-то я решил проанализировать поведение всех возможных процессов, точнее, всех возможных программ на всех видах компьютеров. Самый простой способ приступить к такому исследованию - просто выписать одно за другим ВСЕ возможные конечные множества правил. Это легко сделать, используя метод, предложенный Аланом Тьюрингом в 1936г. (то, что сейчас называют "машиной Тьюринга"). Естественно, я не слишком преуспел в этом, поскольку количество процессов росло по экспоненте в зависимости от числа правил в каждом множестве. Тем не менее с помощью Дэниела Боброу, бывшего тогда моим студентом, мне удалось проанализировать несколько тысяч таких "машин", и тогда обнаружилось, что поведение всех этих процессов сводится всего лишь к нескольким типам. Одни из них просто прекращались, не приведя ни к каким результатам. Другие стирали входные данные и более не делали ничего. Многие же быстро "зацикливались", снова и снова бессмыслено повторяя одни и те же шаги. И лишь несколько процессов приводили хоть к чему-то интересному - и все они были по сути одинаковыми: в каждом постоянно выполнялась вычислительная операция, которая увеличивала длину некой цепочки символов на единицу; далее снова происходило то же самое. Назовем такие процессы А-МАШИНАМИ, так как они способны делать нечто напоминающее арифметический счет. На мой взгляд, этот эксперимент выявил часть некоторого бесконечного множества возможных вычислительных структур. Тогда этот скромный по масштабам эксперимент говорит о том, что такое множество, вероятно, имеет вид, показанный на рис.1.
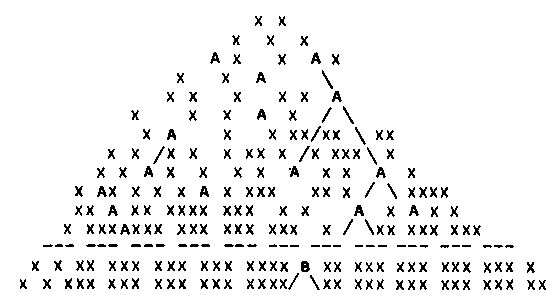
Рис.1. Множество возможных вычислительных процессов.
Символы "X" обозначают бесполезные процессы, т.е. такие, которые почти ничего не дают. Символы "А" представляют те крохотные считающие А-машины, которые в действительности делают одно и то же. Возможно, наш мозг способен выполнять подобные элементарные процессы, в результате которых формируются более сложные представления из области арифметики. Появление А-машин на определенной стадии эволюции любого мозга я считаю неизбежным.
Впрочем, быть может, имеются и другие способы счета. Поэтому на более позднем этапе эволюции мозга могут появиться, скажем, В-МАШИНЫ, которые ведут себя похоже, но не идентично А-машинам. Но наш эксперимент, кажется, наводит на мысль, что даже простейшая В-машина должна быть намного сложнее А-машины, и поэтому маловероятно, чтобы мозг смог ее обнаружить раньше, чем у него появится множество А-машин. Этот коротенький мысленный эксперимент напоминает мне первые эксперименты Стэнли Миллера и Гарольда Юри,в ходе которых ученые исследовали простейшие реальные химические соединения. Начав с нескольких элементов: водорода, кислорода, углерода и фосфора,- они обнаружили, что вначале эти химические вещества, взаимодействуя друг с другом, образуют простые молекулы, и только затем возникают пептиды, сахара, нуклеотиды и т.д. Безусловно, когда образовались эти соединения, до появления тигров, дятлов или пришельцев с Андромеды было еще далеко.
СЛУЧАЙ ИЗ ЖИЗНИ. Когда-то, еще в школе, меня поразило, что минус, умноженный на минус, дает плюс. Как странно, что два отрицания уничтожают друг друга, как будто два ложных утверждения могут дать одно верное или высказывание "это утверждение ложно" может стать правдой. Я задумался, а не существует ли что-то подобное арифметике, но ГДЕ ИСПОЛЬЗУЕТСЯ ЕЩЕ ОДИН ЗНАК? Почему бы не сделать так, чтобы числа были не двух, а трех видов, подумал я. Я стал упорно придумывать новые таблицы умножения. Увы, каждая система приводила либо к невозможной арифметике (например, к такой, где единица равна двум), либо к арифметике вообще без знака или с лишним знаком при числах. Наконец, я сдался. Если бы у меня хватило настойчивости продолжать, то я, быть может, открыл бы арифметику комплексных чисел, как Гаусс, или арифметику спиновых матриц, как Паули. Но никому до сих пор не удалось открыть арифметики с тремя знаками - вероятно, потому, что ее вообще не существует.
Попробуем, к примеру, создать новую систему чисел, в которой все, как в обычной, за исключением того, что там нет одного числа, скажем 4. Эта арифметика не будет работать. Все в ней окажется неверным. Придется выбирать, сколько будет "дважды два". Если мы решим, что это 5, то тогда 5 должно быть четным числом, значит, четными будут 7 и 9. А сколько же тогда будет "5 плюс 5"? Может, 8 или 9, или 10? Следовательно, чтобы создать совершенно новую арифметическую систему, нам придется изменить свойства всех остальных чисел. Когда мы это сделаем, то обнаружим, что изменились только НАЗВАНИЯ чисел, а их свойства остались такими же, как у чисел в обычной арифметике.
Проблемы возникают и в том случае, если мы будем считать равными друг другу два разных числа, например 139 и 145. Но тогда, чтобы было возможным вычитание, придется приравнивать 6 и 0, а 4+5 должно быть равно 3. При этом сумма двух положительных чисел оказывается меньше каждого из них, что уже совсем плохо согласуется с общим представлением об арифметике. (По существу, этот путь ведет к созданию МОДУЛЬНОЙ АРИФМЕТИКИ, находящей применение в некоторых разделах математики, но в повседневной жизни такая арифметика более чем бесполезна).
И так будет всегда: оказывается, невозможно ни отбросить число, ни ввести новое. Нельзя изменить свойства ни одного произведения, ни одной суммы и ни одного простого числа.
Что придает арифметике такую необычайную жесткость? Нельзя ни проделать в ней "дырку", ни растянуть ее, ни согнуть хоть чуточку. Приходится принимать ее такой, как она есть,- целиком, все или ничего, без малейших изменений, потому что арифметика похожа на изолированный остров в "универсуме процессов". А-машина-всегда одна и та же, совершенная и законченная - существует, входя составной частью во все другие процессы, которые могут породить бесконечную цепь разнообразных вещей.
Иногда я думаю, не опасно ли заставлять детей так много заниматься арифметикой: ведь если посмотреть на нее с такой точки зрения, она уводит в совершенно особенный абстрактный мир. Конечно, кое-кого она увлекает, но большинство детей считают ее скучной, для них она источник бесконечной зубрежки и бессмысленной работы - что-то вроде куска холодного и бесформенного пластилина, которому невозможно придать определенную форму.
Из всего сказанного я делаю вывод, что при любом поиске среди простейших процессов в конце концов находится нечто, что не просто напоминает арифметику, но действительно является таковой. При этом изобретательность и воображение роли не играют - важна только "география" этого мира вычислений, который подчинен гораздо более жестким ограничениям, чем реальная жизнь.
УТВЕРЖДЕНИЕ. Все процессы или формализмы, похожие на арифметику, либо тождественны ей, либо безмерно сложнее. Поэтому мы легко находим общий язык, говоря о числах.
Но какое отношение все это имеет к внеземному разуму? Только то, что в своем развитии он, по всей видимости, тоже должен был исследовать множество возможных процессов, начиная с самых простых, и в результате обнаружить те же самые "острова" простых и эффективных идей.
Наконец, возникает вопрос, почему происходят именно такие процессы и не существуют ли наряду с ними какие-то другие процессы, хотя и похожие? Точно ответить на этот вопрос весьма трудно, ибо значение понятия ПОХОЖИЙ зависит от того, в каком смысле мы его употребляем. Один из возможных ответов мог бы сводиться к следующему. Очевидно, что из небольшого количества правил можно вывести чрезвычайно сложную систему следствий и зависимостей. Но обратное утверждение было бы неверным: с помощью небольшого числа правил обычно невозможно описать нечто достаточно большое и сложное. Это простой закон арифметики - не так уж много можно предложить небольших наборов правил! Поэтому нельзя надеяться, что взяв конкретный набор из небольшого числа простейших правил, получив из него сложную систему следствий и слегка изменив эту систему, мы сможем затем описать полученный результат снова небольшим числом правил. Такой измененной системе будут присущи не твердые закономерности, а какие-то волшебные свойства. Короче говоря, небольших совокупностей правил недостаточно, чтобы охватить непрерывное разнообразие возможных систем.
ПРИЧИНЫ И ПРЕДЛОЖЕНИЯ
Если наш способ мыслить - случайный результат эволюционного процесса, то разум инопланетян, возможно, абсолютно не похож на наш. В таком случае общение нереально. Но хотя каждая эволюция - это цепь случайностей, на каждой ее стадии сначала "проигрываются" самые простые варианты. Поскольку на Земле в ходе эволюции человека развились достаточно сложные языки и эти языки, вероятнее всего, строятся на сравнительно простых принципах, не исключено, что другой разум может использовать подобные же принципы. Более того, я утверждаю, что многие аспекты языка (в частности, грамматика) были практически неизбежны. Правда, столь смелое утверждение может многим показаться абсурдным.
Почему в фразе "Скоро пойдет дождь" грамматика заставляет нас употреблять слово "дождь" обязательно в мужском роде и единственном числе? Почему вообще мы не можем сказать этих слов, не указав посредством окончаний род и число существительного, словно дождь - это не явление природы, а актер на сцене? Грамматике безразлично, идет ли речь о реальном действующем лице или нет: мы либо находим его, либо воображаем, что оно есть. Я берусь утверждать, что мы ищем или воображаем причину для каждого различия, изменения или движения. Порой именно грамматика языка навязывает нам подобный подход [В оригинале эти рассуждения иллюстрируются типичным английским выражением: It soon will start to rain (Скоро пойдет дождь), где безличное местоимение it отражает присутствие такого воображаемого действующего лица-причины.- Прим. ред.]; однако, на мой взгляд, причина этого не только в языковых формах, но и в самом способе мышления. Я думаю, что задолго до того, как наши предки научились говорить, у них уже возникли специальные механизмы мозга для представления объектов, различий и причин; эти механизмы позднее легли в основу нашего языка (и грамматики в том числе). В частности, я полагаю, что во многих мыслительных процессах человека используются следующие символьные представления.
- СИМВОЛЫ ОБЪЕКТОВ. Они обозначают вещи, идеи и процессы. В разных языках они чаще всего соответствуют существительным. Наше мышление представляет каждую ситуацию - реальную или воображаемую - через отдельные объекты и связи между ними.
- СИМВОЛЫ РАЗЛИЧИЙ. Обозначая различия между объектами или изменения в объекте, они имеют в языке в основном глагольную форму. Сравнивая два объекта или отмечая изменения, произошедшие в одном объекте, мысль человека отмечает различия.
- СИМВОЛЫ ПРИЧИНЫ. Отметив различие, человек находит его причину, т.е. нечто, ответственное за изменение. При этом мы используем весьма тонкий прием, представляя причины примерно в той же грамматической форме, как и объекты.
- СТРУКТУРА СЛОЖНЫХ ПРЕДЛОЖЕНИЙ. Для описаниях сложных ситуаций наше мышление выработало еще один прием, который позволяет оперировать сложным выражением или описанием так, будто оно - отдельный компонент другого описания. В языке этому соответствует встраивание в фразу, например, сложноподчиненных и вводных предложений, а также причастных и деепричастных оборотов. Такой прием встраивания, когда прежние мысли включаются в текущий мыслительный процесс как отдельные объекты, и придает нашему мышлению особую силу. Именно это позволяет нам повторно использовать те же механизмы мозга, заменяя подчас всю концептуальную картину мира компактным символом. Это позволяет нам легко создавать гигантские построения из наших идей подобно тому, как дети строят домики и башни из кубиков. Благодаря этому мы можем основывать новые идеи на старых. По существу, именно такой механизм обеспечивает нашу способность мыслить. То же относится и к созданным нами вычислительным машинам.
Все языки имеют структуры, допускающие повторное использование, благодаря тому что в самом характере мышления заложен механизм повтора. Этим и обусловлено бесконечное многообразие мысли. Если бы внеземные разумные существа не обладали подобной способностью, они не могли бы обращаться к более ранним результатам мышления. Без этой способности обращать символы к символам вообще невозможно возникновение интеллекта, сколь бы разнообразен и утончен ни был репертуар всех прочих навыков.
КРИТИК. Рассуждая таким путем, вы, пожалуй, придете к выводу, что инопланетяне тоже говорят по-английски, если уж они должны использовать существительные, глаголы и сложноподчиненные предложения. А если они вообще мыслят иначе - не прибегая к понятиям объектов и действий?
- Я думаю, что мы мыслим, пользуясь понятиями объектов и причин неслучайно. В любом случае подобная форма представления порождает вопрос о том, кто или что является причиной? А такое восприятие вещей в их эволюции неизбежно приводит к поискам зависимостей, которые помогают предвидеть, а значит, и КОНТРОЛИРОВАТЬ как внешний мир, так и свой внутренний. Возможно, именно поэтому мы вырастаем с верой в себя; быть может "я" в фразе "Я это здорово придумал" идет именно от такого механизма мышления. Ведь если вам приходится искать причину того, что вы сами делаете, то этой причине надо дать имя. Вы назовете это "я", я назову-"вы".
КРИТИК. А так ли уж важны зависимости? Почему бы каким-нибудь инопланетянам не воспринимать картину мира как единое целое, не разбивая на части? Может, лучше видеть мир каким он есть - ЦЕЛОСТНО, как непрерывный поток изменений во времени и пространстве, а не строить произвольно мысленные фрагментарные копии, лишь приближенно напоминающие реальность?
- В стремлении к более верному, целостному видению мира, безусловно, есть здравый смысл. Но поклонение еще не открытым сверхчувственным способам познания может скрыть от нас возможности обычных способов раздельного восприятия вещей. Каждое живое существо расплачивается энергией (и, следовательно, питанием) за любой механизм, которым обладает его мозг. Подобно тому как фразовая структура языка позволяет нам последовательно концентрировать внимание на каждом фрагменте описания, так и наша способность различать отдельные вещи дает нам возможность разбивать любые ситуации на части и затем последовательно сосредотачивать всю мощь мозга на решении каждой части задачи. Энтузиасты "целостного восприятия мира" не понимают, какой ценой пришлось бы расплачиваться за то, чтобы "увидеть все сразу",- мы просто были бы не в состоянии хоть что-нибудь увидеть достаточно отчетливо.
Высказывается немало суждений относительно того, что в мозге мог бы использоваться голографический принцип организации памяти. Но во-первых, этому пока нет экспериментальных подтверждений, а во-вторых, мы мало бы что при этом выиграли. Голограммы не позволяют хранить больше информации, чем при других способах организации памяти: специалистам по ЭВМ известны другие, причем более эффективные способы дублирования информации в памяти, которые обеспечивают ее более надежную защиту от "помех". Правда, голограммы позволяют упростить некоторые виды распознавания, например в случае, когда надо понять, содержит ли некое изображение копии других вполне определенных изображений. Но в то же время голографическая форма записи сильно затрудняет поиск решения; например, когда нужно установить, содержит ли картина два более мелких фрагмента, которые каким-то образом связаны между собой. По моему мнению, в действительности голограмма - наихудший способ представления отношения между объектами, изображенными на ней, поскольку в сущности память и обучение полезны лишь тогда, когда они дают информацию о связях вещей, которые хотя бы частично можно предсказывать. Вряд ли нам бы понравилось, если бы наша память с одинаковой силой помнила все - в том числе и случайные признаки ситуации. Если какая-то сцена на фотографии содержит 50 признаков, то вряд ли есть смысл с равным вниманием воспринимать весь квадриллион возможных сочетаний этих характеристик. Поэтому необходимы способы выделять и группировать только самые полезные из предсказуемых сочетаний характеристик. Короче говоря, если бы число взаимосвязанных характеристик, по которым люди различают объекты, не было ограниченным, мы просто не могли бы узнавать уже известное, а значит, не могли бы учиться на собственном опыте, не могли бы хранить и накапливать знания.
ПРИЧИНЫ И ЦЕЛИ
Каким образом нам помогает опыт, если не встречается двух абсолютно совпадающих задач? Любой опыт был бы бесполезен, если бы мы не умели различать, что в мире изменилось, а что осталось прежним. Знания нельзя было бы использовать, если бы они не были выражены в виде связей между ПРОГНОЗИРУЕМЫМИ характеристиками и теми действиями, которые мы можем предпринять для установления этих связей. Только при наличии таких связей можно предвидеть, какие действия помогут избавиться от нежелательных свойств.
Сказав "x - причина y", мы, по сути, говорим, что x может подсказать нам, какие действия приводят к y. Животное сможет приспособиться к условиям окружающей среды, если сумеет установить ПРИЧИННУЮ СВЯЗЬ событий, т.е. если найдет фрагменты прогноза, которые помогут ему сделать выбор оптимального варианта. Но прогноз будет неприменим, если зависимостей окажется слишком много. Что же такое причина? Само понятие причины включает определенный элемент стилизации: объяснение причины должно быть кратким, ибо некомпактное объяснение не позволяет строить прогноз. Мы считаем, что x является причиной y, если видим, что y зависит от x больше, чем от чего-либо другого. Но мы не будем считать x причиной y, если х будет состоять из бесконечного потока объяснений, касающихся всего на свете и не приводящих ни к какому итогу. Причем это относится не только к процессам, но и к объектам.
В мире, где все происходящее в большей или меньшей степени зависит от всего остального, нельзя выделить ни объектов, ни вещей, ни причин.
В таком мире понятие ОБЪЕКТ теряет смысл, так как это понятие присваивается предмету по набору свойств, которые либо остаются неизменными, либо меняются предсказуемым образом, несмотря на то что все вокруг меняется. Когда мы двигаем объект, меняется его расположение, но цвет, вес, материал, размер и форма остаются неизменными [Удивительным свойствам КОНСТАНТНОСТИ восприятия нами цвета и формы при перемещении или изменении характера освещения посвящено много исследований, тогда как неизменность веса, материала и т.д. обеспечивается физическими законами сохранения, которые являются следствием однородности пространства.- Прим. ред.]. Не правда ли, это так удобно, что наш мир позволяет нам менять положение вещей, не изменяя их прочих характеристик?! В противном случае число изменений, которые нам пришлось бы учитывать, росло бы по экспоненте в зависимости от числа свойств объекта. В такой ситуации поиск причины происходящего оказался бы бессмысленным.
Чтобы оперировать сложными объектами, мозг должен уметь описывать их с помощью подструктур, в пределах которых можно проследить результат некоторых действий. Знать причину явления - это значит хотя бы в принципе представлять, что меняет его или влияет на него, не меняя при этом всего остального. Это свойство позволяет нам менять один объект, не нарушая других.
Чтобы разумное существо могло обнаруживать причины, вызывающие изменения в окружающем его мире, оно должно иметь органы чувств, регистрирующие изменения, которые предсказуемым образом связаны с действиями, каковые это существо может предпринять. К счастью, в ходе эволюции развился механизм согласованных сочетаний сенсор - эффектор, поскольку практически в любых условиях выживаемость существа значительно возрастает, если его действия основываются на хорошем прогнозе. Поэтому естественно ожидать, что в ходе эволюции должны были возникнуть механизмы, которые отражают причинно-следственные связи, действующие в окружающей нас среде. Самыми мощными оказались механизмы, которые позволяют нам прогнозировать результаты цепочки событий и действий, т.е. заранее планировать свою деятельность.
Когда задачу нельзя решить сразу, она кажется трудной. В самом общем виде решение задачи можно представить как систему действий, которые постепенно "приводят к поставленной цели". В конце 50-х годов А.Ньюэлл и Г.Саймон разработали теорию, которую они назвали "универсальный решатель задач", где развит метод ПОСТЕПЕННОГО ДВИЖЕНИЯ К ЦЕЛИ - путем нахождения действий, которые каждую высокотрудную задачу заменяют совокупностью более простых.
Разумеется, никем не доказано, что любой интеллект (в том числе и инопланетный) должен использовать тот же принцип. Однако другой общей теории решения задач пока нет, и вряд ли она может возникнуть; во всяком случае трудно представить, чтобы разум, каким бы он ни был, не воспользовался идеей цели.
НАДЕЖНОСТЬ КОММУНИКАЦИИ
Прежде чем рассуждать о том, как общаются инопланетяне, следует подумать, как это делаем мы, люди. Есть ли хоть слово, которое значит одно и то же по меньшей мере для двух людей? Каждый из нас, вероятно, задавался вопросом: могут ли два человека, придавая разные значения словам, никогда не почувствовать этого в общении? Что это значит, когда все, что кажется мне зеленым или синим, вам же представляется зеленым и синим? Теория уникальности убеждает нас не бояться такого положения вещей, по крайней мере для технических понятий, поскольку одно из двух словесно неразличимых понятий должно быть гораздо сложнее другого и потому с первого раза их отличие не воспринимается. Уникальность простых идей означает, что мы вполне можем понять друг друга.
Пока трудно судить, к чему может привести теория уникальности, ибо еще не ясно, как именно этот принцип выделяет каждое отдельное понятие. Но в целом данная теория подтверждает основанное на математике и физике интуитивное предположение Ханса Фрюденталя, высказанное в его книге об общении с внеземными цивилизациями [2]. Достаточно вспомнить те несложные модели, которые он предлагает использовать при обсуждении с инопланетянами вопросов социального и административного устройства общества. Впрочем, возникает проблема, связанная с тем, что интроспекция - плохой помощник при решении вопроса о том, какие из наших простых понятий действительно просты,- ведь для понимания многих вещей, кажущихся нам простыми, используются механизмы мозга, сложность которых мы не в состоянии оценить. Например, мы без усилий можем стоять на двух ногах, однако инопланетянам это может показаться поразительным! Какие еще идеи могут выделяться как "острова" в океане всех возможных идей, являясь в этом смысле всеобщими? По-видимому, это математические понятия рациональности, линейной аппроксимации, вероятности и простейшие процессы, напоминающие работу программ ЭВМ. Без них невозможен обмен информацией о производстве и торговле, об основах биологии и даже о многих принципах мышления - объектах, целях, памяти. Впрочем, принцип уникальности, вероятно, работает лишь до определенного предела, так как более сложные идеи допускают варианты, и здесь общение скорее всего будет затруднено.
ЗАКЛЮЧЕНИЕ
Сегодня мало что можно добавить к сказанному с достаточной научной обоснованностью. Однако ожидаемое увеличение вычислительной мощности компьютеров, вероятно, откроет возможности для более глубокого исследования таинственного мира элементарных вычислительных процессов. Тогда мы, быть может, найдем новые уникальные идеи, которые разделят с нами братья по разуму. Подобное исследование позволит получить новые данные о происхождении жизни, выявив элементарные схемы, по которым могло бы идти эволюционное развитие простейших форм.
1. Ernst G.. Newell A. GPS: a Case Study in Generality and Problem Solving.- New York: Academic Press, 1969.
2. Freudenthal H. LINCOS: Design of a Language for Cosmic Intercourse.- Amsterdam: North-Holland, 1960.
3. Lenat D. The Nature of Heuristics. Artificial Intelligence, vol.19, 1982.
4. Turing A. On Computable Numbers. With an Application to the Entscheidungs-problem. Proceedings of the London Mathematical Society, vol.2, 1937; перепечатано в: Davis M. (ed.). The Undecidable.- New York: Raven Press, 1965.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

Даниэль Мруз. Иллюстрация к "Кибериаде" Лема
Один из самых интересных наборов кирпичиков для построения Машины Тьюринга - "Систему из 29 состояний с общим правилом переходов" (т.е. клеточный автомат) - предложил Дж.фон Нейман. "Система" понадобилась для строгого математического доказательства существования универсального конструктора - машины, которая может построить любую другую (даже свою копию), будучи снабженной описанием последней. На книгу фон Неймана очень часто ссылаются
 ТЕМА #98, АБЗАЦ #1242
ТЕМА #98, АБЗАЦ #1242 , особенно любители клеточных автоматов, но очень редко описывают саму "Систему", т.к. описание фон Неймана слишком формально, а его система гораздо сильнее напоминает конструктор, чем саморазвивающийся генератор красивых узоров.
, особенно любители клеточных автоматов, но очень редко описывают саму "Систему", т.к. описание фон Неймана слишком формально, а его система гораздо сильнее напоминает конструктор, чем саморазвивающийся генератор красивых узоров.Попробуем почитать:
ДЖ.ФОН НЕЙМАН
ТЕОРИЯ САМОВОСПРОИЗВОДЯЩИХСЯ АВТОМАТОВ
ГЛАВА 2. СИСТЕМА ИЗ 29 СОСТОЯНИЙ С ОБЩИМ ПРАВИЛОМ ПЕРЕХОДОВ. 2.1. ВВЕДЕНИЕ
[Начало главы посвящено философии понятия "клеточного самовоспроизведения" и формализации понятия "клеточное пространство".- G.].
2.2. ЛОГИЧЕСКИЕ ФУНКЦИИ - ОБЫЧНЫЕ ПЕРЕДАЮЩИЕ СОСТОЯНИЯ
2.2.1. ЛОГИКО-НЕЙРОННЫЕ ФУНКЦИИ
Прежде всего необходимо иметь состояния, выражающие чисто логические, или нейронные, функции [Здесь и далее удаляю ссылки на избыточные формализмы.- G.]. Это требует введения чего-то эквивалентного нейронам, и соединительным линиям.
2.2.2.1. ПЕРЕДАЮЩИЕ СОСТОЯНИЯ - СОЕДИНИТЕЛЬНЫЕ ЛИНИИ
Рассмотрим сначала соединительные линии. Они должны представлять собой ряды клеток, т.е. точек решетки. Так как линия должна обладать способностью передавать (нейронный) импульс, то каждая из составляющих ее клеток уже даже только для этой цели должна иметь состояния ПОКОЯ и ВОЗБУЖДЕНИЯ. Здесь мы интересуемся лишь передачей (нейронного) импульса и потому будем называть эти состояния покоя и возбуждения ПЕРЕДАЮЩИМИ состояниями клетки. Их будем обозначать символом Te, причем e = 0 означает покой, а e = 1 возбуждение.
Эта передача должна быть направленным процессом, ибо линии (заменяемые клетками в передающем состоянии) были проведены так, чтобы соединить определенные точки. Следовательно, надо ввести дополнительные ограничения. Можно условиться, что клетка в передающем состоянии воспринимает только тот импульс, который поступает с одного определенного направления. Мы будем называть это направление ВХОДНЫМ НАПРАВЛЕНИЕМ клетки. Иными словами, возбужденная передающая клетка приводит свою непосредственную соседку (находящуюся в покоящемся передающем состоянии) в возбужденное передающее состояние (а если последняя была в этом состоянии, то сохраняет его) только в том случае, если первая из них посылает импульс во входном направлении последней. Можно также условиться, что клетка в передающем состоянии посылает импульс только в одном определенном направлении. Это направление мы будем называть выходным направлением клетки. Иными словами, возбужденная передающая клетка приводит свою непосредственную соседку (находящуюся в покоящемся передающем состоянии) в возбужденное передающее состояние (а если последняя была в этом состоянии, то сохраняет его) только в том случае, если последняя принимает импульс, посланный в выходном направлении первой. Наконец, можно допустить оба эти условия.
Если рассмотреть все модели, которые здесь возможны, то будет ясно, что удобнее всего выбрать определенное выходное направление. Чтобы избежать некоторых неконтролируемых, а потому нежелательных явлений, связанных с возвратной стимуляцией, целесообразно считать, что выходное направление нечувствительно ко входам, а конкретизировать входное направление даже не обязательно.
Поэтому к символу Те мы добавим еще индекс a (a = 0, 1, 2, 3). Итак, Tae означает, что данная клетка находится в состоянии e и имеет выходное направление a.
2.2.2.2. ЗАДЕРЖКИ, УГЛЫ И ПОВОРОТЫ В СОЕДИНИТЕЛЬНЫХ ЛИНИЯХ
Наша модель для соединительных линий отличается тем, что в ней учитываются конечные задержки распространения импульса. Мы будем предполагать, что между непосредственными соседями имеется единичная задержка.
Заметим также, что наша модель одинаково годится как для синтеза прямых соединительных линий, так и для синтеза линий, образующих углы и повороты.
2.3. НЕЙРОНЫ - КОНФЛЮЕНТНЫЕ СОСТОЯНИЯ
2.3.1. НЕЙРОН "+"
Для нейрона "+" требуется просто возбудимая клетка, которая имеет выход и два возможных входа. Конечно, не будет никакого вреда, если ее снабдить более чем двумя такими входами. В разд.2.2.2.1 мы определили передающую клетку так, что она имеет три возможных входа. Любая из ее 4 сторон, исключая выходную сторону, является входом. Таким образом, наши передающие клетки выполняют не только функции (элементов) соединительных линий между нейронами (для этого они и предназначались), но также играют роль нейронов "+".
2.3.2. КОНФЛЮЕНТНЫЕ СОСТОЯНИЯ: НЕЙРОН "*"
Для нейрона "*" требуется возбудимая клетка, имеющая выход и два входа, которые для получения возбуждения следует раздражать одновременно. Практически удобно было бы ввести класс таких состояний. Но свободный выбор выходного направления и двух входных направлений (из 4 возможных направлений) привел бы к 12 типам, а так как для каждого типа должно быть и покоящееся, и возбужденное состояния, то всего потребовалось бы 24 состояния. Можно получить столь же удовлетворительные результаты более экономно, а именно только с одним типом и поэтому двумя состояниями. Этого можно достичь, если вообще не предписывать определенных входных или выходных направлений, т.е. если договориться, что каждое направление может быть выходным точно так же, как и входным. Кроме того, в качестве необходимого условия возбуждения нужно будет считать наличие не менее двух раздражений, т.е. не менее двух возбужденных передающих клеток, которые являются непосредственными соседями, и при этом наша клетка принимает импульсы, посланные в их выходных направлениях. Еще удобнее придать этому условию более гибкую форму, т.е. считать, что рассматриваемая клетка возбуждается, если возбуждена каждая непосредственно соседствующая передающая клетка, выходное направление которой ориентировано на данную клетку. (Это условие выполняется всегда, если исключить случай, допустимый с точки зрения логики, но, очевидно, противоречащий нашим намерениям,- когда ни одна непосредственная соседка не обладает нужными свойствами, т.е. не является передающей клеткой, выходное направление которой ориентировано на данную клетку).
Такая формулировка правила приводит к тому, что рассматриваемая клетка может работать как нейрон либо с порогом 1 (т.е. с точки зрения входов, как обычная передающая клетка), либо 2 (т.е. как нужный нейрон "*"), либо 3 (т.е. вроде комбинации из двух нейронов "*") в зависимости от того, 1, 2 или 3 непосредственно соседствующие клетки будут передающими клетками, выходные направления которых ориентированы на данную клетку. Так как эта клетка не должна обладать возможностью оказывать стимулирующее действие ни на одну из передающих клеток, выходное направление которых ориентировано на нее, то бессмысленно допускать, чтобы в таком же состоянии были все ее 4 непосредственные соседки, так как тогда возбуждение нашей клетки вообще не привело бы ни к каким последствиям.
Мы будем называть эти состояния клетки КОНФЛЮЕНТНЫМИ СОСТОЯНИЯМИ и обозначать их символом Ce, где e = 0 означает покой, а e = 1 означает возбуждение.
2.3.3. НЕЙРОН "-"
Для нейрона "-" требуется возбудимая клетка, в которой покой и возбуждение поменялись местами (по сравнению с передающими состояниями). Она должна быть нормально возбужденной (т.е. способной возбудить непосредственно соседствующую с ней передающую клетку, на которую указывает ее выходное направление) и в состояние покоя должна приводиться входной стимуляцией (возвращаясь к возбуждению, когда эта стимуляция прекратится). Можно было бы ввести класс таких состояний - например, с данным выходным направлением при условии, что все остальные направления входные (точно так же, как в передающих состояниях). Поскольку возможны 4 направления, это привело бы к 4 типам, а если учесть покой и возбуждение, то потребовалось бы всего 8 состояний. Но тогда мы должны были бы ввести класс состояний, которые при нормальных, невозмущенных условиях не являются состояниями покоя. Эту трудность можно обойти различными путями, с большей или меньшей экономией [Фон Нейман ссылается здесь на прием двойной линии, использованный в другой его работе. С помощью лишь нейронов "+" и нейронов "*" он получил полное множество основных составляющих формальной логики, употребляя пару линий с кодами 01 для "нуля" и 10 для "единицы". Другими словами, каждая линия пары находится в состоянии, противоположном состоянию другой линии этой пары, так что отрицание можно реализовать переменой мест (пересечением) двух линий пары]. Мы обнаружим, что некоторый класс состояний, которые мы введем позже для других целей, можно использовать для формирования функции нейрона "-". Следовательно, на этой стадии можно об этом не беспокоиться.
2.3.4. РАСЩЕПЛЕНИЕ
Мы уже обсудили все типы нейронов, а также их соединительные линии. Остался еще один объект подобного типа, который следует рассмотреть. Логические (т.е. нейронные) сети в большинстве случаев содержат соединительные линии, ведущие от одного выхода к нескольким входам, т.е. линии, которые должны расщепляться. Иными словами, необходимы состояния с несколькими выходами, подобные передающим состояниям.
Однако достаточно отметить, что наше определение конфлюентных состояний предусматривает такую возможность. (См. разд. 2.3.2, в частности обсуждение геометрии, отвечающей "порогу 1" для этого класса состояний. В такой ситуации клетка имеет один вход и, следовательно, до трех возможных выходов).
2.4. ФУНКЦИИ РОСТА: НЕВОЗБУДИМОЕ СОСТОЯНИЕ И СПЕЦИАЛЬНЫЕ ПЕРЕДАЮЩИЕ СОСТОЯНИЯ
2.4.1. МЫШЕЧНЫЕ ФУНКЦИИ, ИЛИ ФУНКЦИИ РОСТА - ОБЫЧНЫЕ ИМПУЛЬСЫ В СРАВНЕНИИ СО СПЕЦИАЛЬНЫМИ
Закончив обсуждение логических (т.е. нейронных) функций, перейдем теперь к другим. Ранее мы временно назвали их мышечными, но другие соображения показали, что правильнее будет подходить к ним как к функциям роста. В любом случае нам необходимы состояния для выражения этих функций. Мы знаем, что изучение функций роста приведет к проблеме обычных и специальных импульсов, т.е. обычных и специальных возбужденных состояний. Обычный класс - это класс импульсов, используемых для логических целей, т.е. класс, который мы до сих пор рассматривали. Специальный класс - это класс, который мы должны ввести сейчас, для того чтобы учесть упомянутые выше функции.
2.4.2. НЕВОЗБУДИМОЕ СОСТОЯНИЕ
Цель возбужденных состояний специального класса - индуцировать рост, т.е. переводить клетки из невозбудимых состояний в возбудимые, а в пределах последней категории и определять тип состояния. Что касается последнего, то мы уже условились, что существует несколько типов: передающие, или состояния T, которые дают 4 типа Тa, а = 0, 1, 2, 3; и конфлюентный тип С (см. разд.2.2.2.1 и 2.3.2). Для каждого из этих 5 типов возможны два состояния: e = 0 (покой) и e = 1 (возбуждение). Но нам нужны здесь лишь состояния Ta0, С0, поскольку достаточно уметь создавать каждый возбудимый тип в покоящемся состоянии. Если требуется возбужденное состояние, то его можно вызвать обычными импульсами.
Итак, необходимо ввести невозбудимое состояние (невозбудимое обычными импульсами). Обозначим его U. Прежде чем дать строгий перечень его свойств, обсудим некоторые родственные вопросы.
2.4.3. ПРЯМОЙ И ОБРАТНЫЙ ПРОЦЕССЫ - СПЕЦИАЛЬНЫЕ ПЕРЕДАЮЩИЕ СОСТОЯНИЯ
Желательно не только иметь возможность осуществить переход от невозбудимого состояния U к возбудимым состояниям (например, T и С, см. разд.2.4.2), но также обеспечить обратимость этого процесса, т.е. иметь возможность осуществить переход от возбудимых состояний к U. В дальнейшем мы приведем примеры использования такой двухсторонней организации. Импульсы, вызывающие эти превращения, должны быть переданы с помощью таких состояний клеток, на которые они (импульсы) не оказывают подобного воздействия. Целесообразно, следовательно, ввести новый класс передающих состояний, скажем T' (аналогичных T по тому, как они соотносятся друг с другом). По аналогии с Tae мы получим e таких состояний: T'ae (a = 0, ..., 3; e = 0, 1).
2.5. ОБРАТНЫЙ ПРОЦЕСС
2.5.1.1. ОБРАТНЫЙ ПРОЦЕСС ДЛЯ ОБЫЧНЫХ СОСТОЯНИЙ
Теперь можно дать определение обратному процессу, т.е. переводу некоторого возбудимого состояния (T, C) в невозбудимое состояние (U) специальными импульсами (от T').
Заметим, что "убийство" клетки, осуществляемое специальным импульсом (от T'), оказывается эффективным даже в выходном направлении (T).
2.5.1.2. ОБРАТНЫЙ ПРОЦЕСС ДЛЯ СПЕЦИАЛЬНЫХ СОСТОЯНИЙ
Причина, вызвавшая введение обратного процесса (от возбудимости к невозбудимости; см. разд.2.4.3 и далее) для обычных возбудимых состояний T, C сохраняется и в случае специальных состояний (T'). Но правило нельзя распространить на состояния T'; влияние такого типа, оказываемое T' на T', недопустимо по той же причине, по какой недопустимо соответствующее влияние T на T (см. разд.2.4.3): оно привело бы к разрушению свойства состояний T' как передающих состояний для специальных импульсов, точно так же как аналогичное воздействие оказалось бы разрушительным для состояний T как передающих состояний для обычных импульсов. Последнее обстоятельство заставило нас ввести T' (чтобы переводить T и C в U); теперь мы можем подобным образом использовать T (чтобы переводить T' в U). Целесообразно, однако, не наделять этим свойством C. Действительно, так как каждое направление является выходным направлением для C, то, если мы припишем C такие возможности, нам будет несравненно труднее направлять и контролировать, чем хотелось бы.
2.5.2. ВОЗНИКНОВЕНИЕ СПЕЦИАЛЬНЫХ ИМПУЛЬСОВ
До сих пор специальные импульсы (т.е. возбуждение клеток, находящихся в состоянии T') возникали у нас лишь друг от друга.
Необходимости во введении полной (логической) нейронной системы, как это было в случае обычных импульсов в разд.2.2.2.1-2.3.4, для специальных импульсов нет. Можно построить всю логику на обычных импульсах, как и предполагалось, когда мы их вводили, и использовать их для того, чтобы обеспечить возникновение цепочек специальных импульсов, когда это потребуется. (Физиологический аналог: логика обеспечивается одной только нейронной активностью и ею же всегда вызывается и контролируется мышечная деятельность). Поэтому нам нужен определенный класс состояний, которые в ответ на обычный импульс испускают специальный импульс, т.е. таких, которые могут быть возбуждены от T, а сами могут возбудить T'.
Прежде чем вводить этот новый класс, проверим, нельзя ли сделать это с помощью уже существующих классов. Состояние T не возбуждает T' (оно "убивает" его); отсюда нельзя использовать для нашей цели ни Т, ни Т'. Остается лишь состояние C. Оно возбуждается от T; поэтому нам надо только наделить его способностью возбуждать T'. Это легко сделать (то, что T' не возбуждает C, а "убивает" его (см. разд.2.5.1.1), сюда отношения не имеет).
2.6. ПРЯМОЙ ПРОЦЕСС - ЧУВСТВИТЕЛЬНЫЕ СОСТОЯНИЯ
2.6.1. ПРЯМОЙ ПРОЦЕСС
Итак, обратный процесс, о котором говорилось в разд.2.4.3 (переход от возбудимости к невозбудимости), уже разобран. Перейдем теперь к рассмотрению (требуемого в первую очередь) прямого процесса разд.2.4.2 (перехода от невозбудимости к возбудимости).
Список состояний, которые должен давать прямой процесс, теперь стал больше. В разд. 2.4.2 были состояния Ta и C; к ним, согласно разд.2.4.3, следует добавить T'a. Другими словами, у нас должна быть возможность создавать следующие состояния (относительно роли e = 0 см. обсуждение в разд. 2.4.2): Ta0, T'a0, C0. Всего здесь 9 состояний.
Таким образом, нам нужен механизм для перевода состояния U в одно из 9 состояний. Сделаем сначала два замечания, касающиеся этого механизма.
2.6.2.1. ПЕРВОЕ ЗАМЕЧАНИЕ: ДУАЛИЗМ ОБЫЧНЫХ И СПЕЦИАЛЬНЫХ СОСТОЯНИЙ
В нашем распоряжении два типа импульсов: обычные и специальные, отвечающие возбуждению состояний T (возможно, вместе с C) и T' соответственно. Мы собирались использовать только специальные импульсы (т.е. состояния T') для трансформации U в одно из 9 состояний (см. разд.2.4.1 и 2.4.5). Но потом, рассматривая обратный процесс (см. разд.2.4.3-2.5.2), мы допустили, что состояния T (на самом деле без C) и T' выполняют симметричные относительно друг друга функции и дополняют друг друга. Поэтому представляется соблазнительным приписать им симметричные роли и в связи с прямым процессом.
Это снова можно было бы сделать двойственным образом, т.е. используя T' для перехода от U к T (и к C), а T для перехода от U к T'. Однако мы увидим, что это ограничение вовсе не необходимо, т.е. можно получить удовлетворительную систему, приняв, что T и T' оказывают на U идентичное и взаимозаменяемое воздействие в смысле переходов во все состояния T, C и T' (т.е. во все 9 состояний).
Отсюда возникает вопрос: зачем вообще понадобилось вводить T', если T может вызывать и контролировать все переходы из U? Ответ заключается в том, что состояния T' требуются в обратном процессе, так как между передачей и стимулированием перехода в состояние U существует различие. Более того, обратный процесс (переход из T, T' или C в U) необходим для осуществления требуемого управления прямым процессом (переходом из U в T, T' или C, или даже только в T или C). Это обстоятельство заслуживает более тщательного рассмотрения.
2.6.2.2. НЕОБХОДИМОСТЬ ОБРАТНОГО ПРОЦЕССА
Пусть клетки 1, ..., 9 занимают площадь размера 3*3. Их предстоит организовать, т.е. перевести из состояния U в различные (наперед заданные) состояния, например в состояния T.
Рассмотрим этот переход для центральной клетки (т.е. для клетки 5). Независимо от того, какие импульсы (обычные или специальные, т.е. возбуждения T или T') вызывают этот переход, от области возникновения и логического контроля этих возбуждений должна быть проложена непрерывающаяся цепочка из передающих клеток (T или Т') к той клетке, на которую должно быть оказано воздействие (в данном случае к клетке 5). Эта цепочка обязательно должна пересечь кольцо клеток, окружающих клетку 5, т.е. кольцо, образованное клетками 1, ..., 4, 6, ..., 9.
Далее, может получиться, что при требуемой организации области 1, ..., 9 состояние клетки пересечения будет другим (покоящимся) состоянием, отличным от состояния цепочки. (Последняя может быть в состоянии Ta или Т'a, где a имеет направление цепи). Поэтому организация клетки пересечения не может произойти до организации клетки 5. Если она происходит после организации клетки 5, то интересующая нас (T или T') клетка цепочки переводится в нужное состояние. Так как прямой процесс обеспечивает перевод из U в любое требуемое состояние, то проще всего обеспечить возможность перевода имеющегося (T или T') состояния в U. Поэтому обратный процесс действительно необходим.
2.6.3.1. ВТОРОЕ ЗАМЕЧАНИЕ: НЕОБХОДИМОСТЬ ФИКСИРОВАННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ ИМПУЛЬСОВ ДЛЯ УПРАВЛЕНИЯ ПРЯМЫМ ПРОЦЕССОМ
В разд.2.6.2.1 мы отмечали, что прямой процесс (перевод из U в состояния Ta0, T'a0 и C0) должен осуществляться импульсами, вызванными возбуждениями T и T', и можно допустить, чтобы оба эти возбуждения давали в этом отношении один и тот же результат. В дальнейшем мы увидим, что такой порядок в некотором важном для нас смысле более экономен, чем его очевидная альтернатива.
Разумно исключить C и из этого процесса. Причины для использования здесь прямого процесса совпадают с причинами использования обратного процесса в разд.2.5.1.2. Заметим, кроме того, что так как каждое направление является выходным для С, то часто бывает необходимо защитить некоторые стороны клетки C; для этой цели естественно использовать U (см. далее). Поэтому было бы крайне неудобно, если бы состояние С оказывало на U какое-нибудь воздействие.
Прямой процесс должен обеспечить перевод из U в любое из 9 состояний. Девять возможностей - это слишком много для того, чтобы получить их одиночным импульсом, даже если бы T и T' оказывали различные воздействия. К тому же мы условились, что в этом процессе T и T' оказывают одинаковое воздействие. Следовательно, нужные нам 9 альтернатив должны выражаться некоторой двоичной последовательностью импульсов. В этом двоичном коде 1 будет соответствовать наличию импульса (T или T'), а 0 - отсутствию импульса. Последовательности из 3 цифр могут выразить 8 альтернатив: 000, 001, . . ., 111. Но так как нам нужно 9 альтернатив, то одну из них (например, первую - 000) мы приспособим для выражения еще 2 возможностей: 0000 и 0001. Итак, мы получаем 9 кодовых последовательностей: 0000, 0001, 001, 010, 011, 100, 101, 110, 111.
Их надо теперь привести в соответствие с 9 состояниями Ta0, T'a0 и C0.
Девять кодовых последовательностей должны строиться из цифр 0 и 1 последовательно. Иными словами, в (прямом) процессе перехода состояние U должно будет проходить через промежуточные состояния, соответствующие подпоследовательностям, встречающимся в процессе построения последовательностей. Такими подпоследовательностями будут 0, 1, 00, 01, 10, 11, 000; всего 7. Наконец, должно быть некоторое состояние, соответствующее началу процесса, когда формирование кодовой последовательности из подпоследовательности еще не началось. Эту кодовую подпоследовательность лучше всего интерпретировать как пустое множество (соответствующее начальному состоянию) и обозначать буквой Q.
2.6.3.2. НЕОБХОДИМЫЕ ДОПОЛНИТЕЛЬНЫЕ СОСТОЯНИЯ
17 кодовых последовательностей Q, ..., 111 соответствуют 17 состояниям. Мы будем обозначать их символом Ss, где s принимает значения Q, 0, ..., 11, 000, 0000, ..., 111. Состояния Ss, отвечающие последовательностям 0000, ..., 111 должны совпадать с 9 состояниями Ta0, T'a0 и C0, т.е. это не новые состояния. Кроме того, мы должны решить, естественно ли и нужно ли требовать, чтобы состояние SQ совпадало с U.
Прямой процесс идет от SQ через Ss списка 0, ..., 000, к Ss списка 0000, ... 111 (т.е. к состояниям Ta0, T'a0, C0), причем к s добавляется 1, когда появляется импульс (T или T'), и 0, когда импульса нет. (Разумеется, когда величина s достигает своего максимального значения, ее рост прекращается. Тогда мы получаем состояния Ta0, T'a0, C0). Это означает, что эволюция от SQ к окончательному состоянию Ss (с s максимальным, т.е. соответствующим последовательностям 0000, ..., 111) должна протекать в строго определенные моменты времени. Отсутствие импульса дает определенный эффект (точно так же, как и его наличие); поэтому нужные импульсы должны подаваться в определенные моменты времени без каких-либо задержек, если только последние специально не потребовались. С другой стороны, мы всегда представляли себе U как состояние покоя; оно не меняется, пока не получит импульса. Учитывая эти два обстоятельства, мы не должны отождествлять U и SQ. Итак, к состояниям Ta0, T'a0 и C0 у нас добавилось еще 8 новых: а именно Ss с s = Q, 0, 1, 00, 01, 10, 11, 000.
2.6.4. ЧУВСТВИТЕЛЬНЫЕ СОСТОЯНИЯ
Назовем новые состояния, к которым привели нас разд.2.6.3.1 и 2.6.3.2, ЧУВСТВИТЕЛЬНЫМИ СОСТОЯНИЯМИ. Как уже говорилось, это состояния Ss, где s принимает значения Q, 0, 1, 00, 01, 10, 11 и 000, но не 0000, 0001, 001, 010, 011, 100, 101, 110, 111 (последние отвечают состояниям, совпадающим со старыми состояниями Ta0, T'a0 и C0).
2.7. ЧЕТНЫЕ И НЕЧЕТНЫЕ ЗАДЕРЖКИ
2.7.1. ЧЕТНЫЕ ЗАДЕРЖКИ, ОБУСЛОВЛЕННЫЕ РАЗЛИЧИЕМ В ДЛИНАХ ПУТЕЙ
Итак, мы закончили описание прямого процесса разд.2.4.2 (см. разд.2.6), т.е. процесса, обеспечивающего переход от U к состояниям Ta0, T'a0 и C0. В разд.2.6.3.2 отмечалось, что прямой процесс строго привязан к определенным моментам времени, т.е. для каждого состояния Ta0, T'a0 и C0 определенные импульсы должны подаваться через определенные промежутки времени. Точнее, чтобы перейти от состояния SQ к состояниям Ta0, T'a0 и C0, т.е. к Ss с s из 0000, ..., 111, требуются непрерывающиеся последовательности импульсов и пауз списка. Эти последовательности имеют длины 3 и 4. Так как на самом деле мы хотим начинать с U, то нужен еще один импульс, идущий непосредственно перед такой последовательностью. Все это приводит к необходимости иметь определенные непрерывающиеся последовательности импульсов и пауз длин 4 и 5.
В правильно организованной управляющей системе такая последовательность может порождаться подходящим (одиночным) управляющим импульсом. Для того чтобы из (одиночного) управляющего импульса получить наперед заданный ряд импульсов в течение 4 или 5 последовательных моментов времени (t целочисленно), необходима некоторая система кратной задержки. Если (одиночный) управляющий импульс появляется в точке А решетки, а заданная последовательность импульсов и пауз должна быть в точке В решетки, то необходимо, чтобы возбуждение прошло из точки А в точку В по нескольким путям - тогда будет создана нужная относительная задержка. Действительно, пусть P - путьт по которому возбуждение из точки А в точку В приходит первым. Тогда другие пути из A в B, скажем P1, P2, ..., должны дать задержки по отношению к P равные расстояниям от первого импульса до заданных импульсов в нужной последовательности импульсов и пауз.
2.7.2.1. НЕЧЕТНЫЕ И ЕДИНИЧНЫЕ ЗАДЕРЖКИ
Ясно, что такимспособом можно получить только четные задержки: разность длин любых двух путей, соединяющих две заданные точки А и В, всегда четна. В то же время последовательности, которым предшествует 1, могут содержать 1 (т.е. импульс) на нечетных расстояниях. Это противоречие должно быть разрешено. Можно поступать по-разному.
Во-первых, принцип четных различий в длинах путей, соединяющих две заданные точки, справедлив лишь для данной кристаллической решетки. Он верен для квадратной решетки (которая лежит в основе всех наших построений), но для некоторых других решеток он не выполняется. Поэтому можно было бы попытаться изменить кристаллическую решетку.
Во-вторых, можно было бы удлинить последовательности, вставляя 0 (паузу) так, чтобы все расстояния между 1 (импульсами), включая вводный разряд 1, стали четными. Это привело бы к увеличению числа подпоследовательностей, встречающихся при построении последовательностей. Таким образом, у нас было бы больше чувствительных состояний.
В-третьих, можно непосредственно ввести нечетные задержки. Ясно, что достаточно ввести единичную задержку. Это значит, что нам нужно возбужденное состояние, появляющееся в момент t, но не после возбуждения, пришедшего в момент t-1 (как во всех до сих пор рассмотренных случаях, т.е. T, T', C), а после возбуждения, пришедшего в момент t-2.
2.7.2.2. ЕДИНИЧНЫЕ ЗАДЕРЖКИ, ДОСТИГНУТЫЕ С ПОМОЩЬЮ КОНФЛЮЕНТНЫХ СОСТОЯНИЙ
Внимательный анализ предыдущих рассмотрений показывает, что из трех возможностей, описанных в разд. 2.7.2.1, последняя наиболее удобна и, в частности, наиболее экономна в смысле числа новых состояний. В этой связи стоит сделать два дополнительных замечания.
Во-первых, достаточно обеспечить введение единичной задержки для обычных (T) импульсов. В самом деле, специальные (T') импульсы можно получить из обычных, применив процесс преобразования с фиксированной задержкой. Иными словами, если требуется строго хронометрированная (в смысле разд.2.7.1) последовательность специальных (T) импульсов, удобно (с помощью системы задержек разд. 2.7.2.1) построить ее на обычных (T) импульсах, а затем преобразовать их в специальные.
Во-вторых, чтобы ввести единичную задержку для обычных импульсов, не обязательно вводить новый тип состояния; достаточно использовать и расширить свойства существующих типов. Удобно наделить таким свойством состояние C, ибо при этом другие нужные нам функции этого состояния не пострадают.
Справедливость этого станет ясна в процессе нашей работы с C. Сейчас же мы ограничимся тем, что формализуем изменения в правилах, управляющих поведением состояния C, необходимые для получения требуемой (единичной) задержки.
Если возбуждение надо задержать на одну единицу времени, то клетка C должна в течение этого промежутка времени помнить, каким должно быть ее следующее состояние возбуждения. Поэтому нужны 2 индекса, например e, e'. Тогда состояниями будут Cee', где индекс e = 0, 1 указывает настоящее состояние возбуждения, а индекс e' = 0, 1 указывает следующее состояние возбуждения.
2.8. РЕЗЮМЕ
2.8.2. НЕФОРМАЛЬНОЕ РЕЗЮМЕ
Существуют 16 ПЕРЕДАЮЩИХ СОСТОЯНИЙ Tuae. Индекс u указывает КЛАСС состояний: u = 0 для ОБЫЧНЫХ и u = 1 для СПЕЦИАЛЬНЫХ. Индекс a показывает ориентацию этого состояния: a = 0 для направления ВПРАВО, a = 1 для направления ВВЕРХ, a = 2 для направления ВЛЕВО, a = 3 для направления ВНИЗ. Индекс e показывает имеющееся состояние ВОЗБУЖДЕНИЯ: e = 0 для ПОКОЯ, e = 1 для ВОЗБУЖДЕНИЯ. Передающее состояние имеет одно ВЫХОДНОЕ направление и три ВХОДНЫХ: первое определяется его ориентацией, последние - это все оставшиеся направления. Передающее состояние может быть возбуждено с ЗАДЕРЖКОЙ 1 от любого непосредственно соседствующего возбужденного передающего состояния того же класса при условии, что первое лежит в выходном направлении второго, а второе лежит в одном из входных направлений первого [Будем говорить, что ОДНО СОСТОЯНИЕ ЛЕЖИТ В ВЫХОДНОМ НАПРАВЛЕНИИ ДРУГОГО, если эти состояния (клетки) являются непосредственными соседями и выходное направление второго состояния ориентировано на первое состояние. Аналогично употребляется выражение СОСТОЯНИЕ ЛЕЖИТ ВО ВХОДНОМ НАПРАВЛЕНИИ ДРУГОГО].
Существуют 4 КОНФЛЮЕНТНЫХ СОСТОЯНИЯ Cee'. Индекс e показывает имеющееся в данный момент состояние возбуждения, индекс e' показывает состояние возбуждения в следующий момент времени: e, e' = 0 для ПОКОЯ и e, e' = 1 для ВОЗБУЖДЕНИЯ. Конфлюентные состояния по определению принадлежат классу 0. Для конфлюентного состояния все направления могут быть как входными, так и выходными. [Но в каждый данный момент времени одно направление не может использоваться одновременно и как входное, и как выходное]. Конфлюентное состояние может быть возбуждено с ЗАДЕРЖКОЙ 2 от тех непосредственно соседствующих передающих состояний его собственного класса (т.е. класса 0), в выходных направлениях которых оно лежит. Возбуждение произойдет, если имеется по крайней мере один такой непосредственный сосед и если все такие непосредственные соседи (сколько бы их ни было) возбуждены.
Передающее состояние (любого класса) может быть также возбуждено с ЗАДЕРЖКОЙ 1 от любого непосредственно соседствующего конфлюентного состояния при условии, что последнее лежит в одном из входных направлений первого.
Существует невозбудимое состояние U. Оно считается покоящимся. Каждое передающее или конфлюентное состояние УБИВАЕТСЯ (т.е. переводится в невозбудимое состояние) любым непосредственно соседствующим возбужденным передающим состоянием противоположного класса при условии, что первое лежит в выходном направлении второго.
Все приведенные состояния (передающие и конфлюентные) принимают покоящуюся форму, если указанные правила не обеспечивают убивание или возбуждение.
Существуют 8 ЧУВСТВИТЕЛЬНЫХ СОСТОЯНИЙ Ss с s из Q, 0, 1, 00, 01, 10, 11, 000. Мы будем рассматривать также состояния Ss с s из 0000, 0001, 001, 010, 011, 100, 101, 110, 111, но эти состояния не относятся к чувствительным. Они совпадают с покоящимися передающими и покоящимися конфлюентными состояниями [S0000 = T000, S0001 = T010, S001 = T020, S010 = T030, S011 = T100, S100 = T110, S101 = T120, S110 = T130, S111 = C00]. Чувствительные состояния в любом случае подвергаются изменению (немедленно, т.е. с ЗАДЕРЖКОЙ 1), а именно переводятся в состояния Ss0 или Ss1. Переход в состояние Ss1 происходит под влиянием каждого непосредственно соседствующего передающего возбужденного состояния (любого класса) при условии, что это чувствительное состояние лежит в выходном направлении последнего. В противном случае происходит переход в Ss0.
Подчеркнем снова, что это последнее правило применимо только к чувствительным состояниям, т.е. лишь при s из Q, ..., 000, но не из 0000, ..., 111 (или, другими словами, если индекс s еще не достиг своего максимального размера).

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга

Михаил Храбрых. Еще "Кибериада".
ГЛАВА 3. СИНТЕЗ НЕКОТОРЫХ ОСНОВНЫХ ОРГАНОВ
3.1. ВВЕДЕНИЕ
3.1.1. СВОБОДНОЕ И ЖЕСТКОЕ ВРЕМЯ, ПЕРИОДИЧЕСКОЕ ПОВТОРЕНИЕ...
Органы, которые мы сконструируем в этой главе, будут характеризоваться двумя важными для нас свойствами
(вместе или по отдельности): СВОБОДНЫМ ВРЕМЕНЕМ и ЖЕСТКИМ ВРЕМЕНЕМ [В оригинале free timing и rigid timing]. СВОБОДНОЕ ВРЕМЯ означает испускание определенных импульсов (в заданной точке и в определенном порядке) без конкретного указания временных интервалов или задержек между двумя актами испускания. Если же эти интервалы заданы, то говорят о ЖЕСТКОМ ВРЕМЕНИ. Иначе это можно выразить, сказав, что периоды задержки заполнены паузами, т.е. на данном месте отсутствуют импульсы. (Ясно, что если заданная задержка между следующими друг за другом импульсами равна d, то пауз на этом интервале будет d-1). Следовательно, последовательность импульсов с жестким временем можно рассматривать как последовательность из непрерывающихся событий, а именно как последовательность типа импульс-пауза.
[В прямом процессе разд.2.6.3.2 используется жесткое время. Фон Нейман говорит там, что при жестком времени "отсутствие импульса дает определенный эффект (точно так же, как и его наличие); поэтому нужные импульсы должны подаваться в определенные моменты времени без каких-либо задержек, если только последние специально не потребовались".
[... нет никаких ограничений на число клеток, которые могут быть в возбужденном состоянии в данный момент времени, хотя, безусловно, это число всегда конечно. Таким образом, клеточная структура, используемая фон Нейманом, допускает неограниченную степень параллелизма. Однако при конструировании своего самовоспроизводящегося автомата фон Нейман не особенно использует этот потенциальный параллелизм клеточной структуры. Его самовоспроизводящийся автомат работает скорее как последовательная цифровая вычислительная машина, в которой большинство органов, как правило, находятся в состоянии покоя. В этом отношении он подобен машине EDVAC.
[Когда на какой-нибудь орган самовоспроизводящегося автомата подается последовательность, содержащая один или более импульсов, то этот орган после некоторой задержки дает выходной сигнал (отклик). Обычно эта задержка между входом и выходом значения не имеет, потому что одновременно не ведется никакого другого конструирования или вычисления. Точно так же задержка от одного входного сигнала, поданного на некоторый орган, до следующего входного сигнала на этот же орган не имеет, как правило, значения при условии, что эта задержка настолько велика, что орган успевает закончить одно действие, прежде чем начать следующее. Основное исключение из этих правил составляет узел ленты, описанной в гл.4. Метод, которым пользуется фон Нейман для удлинения и укорочения ленты, требует одновременной (параллельной) работы в двух соединительных петлях].
Под ПЕРИОДИЧЕСКИМ ПОВТОРЕНИЕМ последовательности подразумевается периодическое повторение с жестким временем, т.е. повторение последовательности в непрерывающиеся последовательные интервалы времени, если только специально не оговаривается противное.
[Далее я немного ускорю изложение, тем более, что в середине своих рассуждений фон Нейман допускает ошибку - на это указал редактор рукописи - и все придется пересчитывать читателю), а на самом интересном месте рукопись просто обрывается...- G.]
3.2. ИМПУЛЬСАТОР,
т.е. орган, превращающие отдельный импульс в последовательность жесткого временем. Правда, время между поступлением входного символа и выдачей результата, очевидно, свободное.
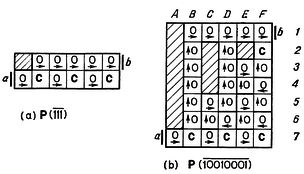
(Символом 0 со стрелкой обозначается T0a; заштрихованные клетки - U).
Первый импульс выходной последовательности - тот, что шел по самому короткому пути. Остальные задерживаются конфлюэнтными состояниями и змейками.
3.2.2. ПЕРИОДИЧЕСКИЙ ИМПУЛЬСАТОР,
после запуска начинающий выдавать последовательность в жестком цикле. Состоит из пульсатора, повторяющей петли (соответствующей длины) и второго пульсатора - прерывателя.
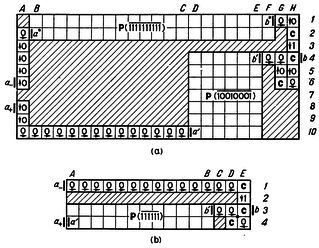
(Символом 1 со стрелкой обозначается T1a).
Прерыватель должен сгенерировать последовательность 11111. Первый ее импульс убивает конфлюэнтное состояние, замыкающее петлю. Остальные 4 создают на его месте новое. Другие последовательности не годятся, т.к. остаточные импульсы петли могли бы их испортить. Здесь и далее фон Нейман свободно использует случайные совпадения. Например, что четыре единицы - код C00. Количество пятерок прерывателя должно быть достаточно длинным, чтобы не дать конфлюэнтному состоянию воскреснуть раньше времени (длиннее повторяющей петли).
Простота "повторителя единиц" вызвана тем, что оставшиеся в повторяющей петле единицы сами воскресят C00.
3.3. ДЕКОДИРУЮЩИЙ ОРГАН
выдает одиночный импульс, если последовательность на входе имеет 1 в определенных позициях. Наличие единиц в других позициях его не интересует.
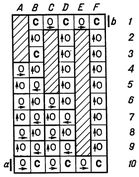
Т.е. "импульсатор наоборот" - имеет на выходе цепочку конфлюэнтных состояний, "собирающих" импульсы с разным запаздыванием.
3.4. ТРОЙНОЙ ВОЗВРАТНЫЙ СЧЕТЧИК -
специальный орган, умеющий считать до трех. Выглядит страшно:
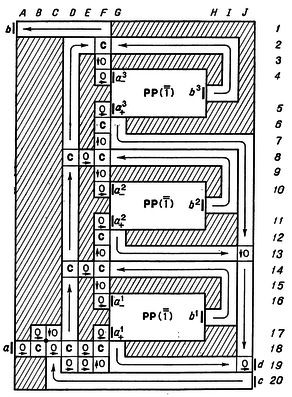
Запускается импульсом, поступающим на вход a. Прежде, чем дойти до конца (посылки импульса на выход b), орган трижды выдает импульс на выход d (в свободном времени) и трижды ждет ответа на входе c. Хитрый "замочек" на пересечении линий a и c (B17..F18) - развязка, позволяющая этим импульсам не перепутаться. Столбец F - "замки" позволяющие пройти импульсу c только, если активирован соответствующий импульсатор. Каждый проход c останавливает работающий импульсатор и запускает следующий (последний - активирует b). Заодно, по столбцу J идет сигнал о запуске на выход d. Столбец D передает сигнал c ко всем "замкам". Первый импульсатор, очевидно запускается импульсом a.
3.5. ДИСКРИМИНАТОР ДЛЯ РАЗЛИЧЕНИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ 1 И 10101
(точнее 1 и 1x1x1) устроен очевидно:

Здесь ДЕКОДЕР 10101 подавляет передачу одиночного импульса на выход b.
3.6. КОДИРОВАННЫЙ КАНАЛ -
развитие идеи "замочка" из тройного счетчика для "пересечения проводов" в двумерном прстранстве.
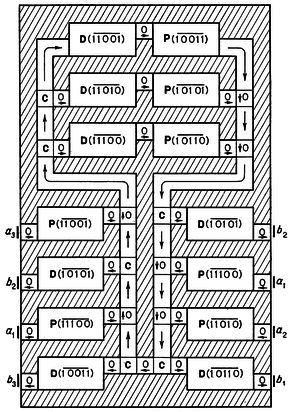
Внутри органа ходят не одиночные импульсы, а соответствующие входным и выходным каналам уникальные последовательности. Что позволяет располагать входы и выходы в произвольном порядке. Обратите внимание, канал замкнут в кольцо, чтобы любой выход был достижим для любого входа, но дополнительное преобразование из входных последовательностей в выходные предотвращает зацикливание. Понятно, что для правильной работы импульсы должны подаваться через большиме промежутки.
ГЛАВА 4. КОНСТРУКЦИЯ ЛЕНТЫ И СИСТЕМЫ УПРАВЛЕНИЯ ЕЮ
В настоящей главе фон Нейман показывает, каким образом в его бесконечную клеточную структуру могут быть встроены неограниченно удлиняемая лента и система управления ею.
Эта лента вместе с системой управления ею состоит из следующих узлов.
1. Линейный массив L, предназначенный для хранения информации: 0 представляется в ячейке xn состоянием U, а 1 - состоянием T03 (стрелка вниз).
2. Соединительная петля C1 для считывания содержимого произвольной ячейки N.
3. ВременнАя петля C2 для изменения длины соединительной петли C1.
4. Узел управления памятью (УУП) для управления работой узлов L, C1 и C2.
5. Конструирующий узел (КУ) для управления узлом УУП.
Это не совсем каноническая Машина Тьюринга:
- Если КУ находится в состоянии A и УУП передает ему значение X (считанное из ячейки N массива L), то КУ переходит в состояние A' = A(A,X).
- Если КУ находится в состоянии A', то он формирует (и передает в УУП для записи в ячейку N массива L) значение X' = X(A).
- Если КУ находится в состоянии A', то он формирует (и передает в УУП для получения N' = N + E') значение E' = E(A').
Фон Нейман разрабатывал свою конструкцию в несколько этапов, продумывая их по мере продвижения вперед. Окончательная схема работает следующим образом.
Конструирующий узел (КУ) посылает импульс в узел управления памятью (УУП), указывая, что должна быть прочитана ячейка N. Этот импульс приводит к тому, что в соединительную петлю С1 поступает последовательность 10101. Затем эта последовательность входит в ячейку N, и, если та находится в состоянии U, то последовательность 1010 переводит ее в состояние T03, а 1 возвращается в УУП. Если же ячейка находится в состоянии T03, то в УУП возвращается вся последовательность 10101. Описанный выше дискриминатор определяет, какая последовательность, 1 или 10101, появилась на выходе, и сообщает в КУ, что хранилось в ячейке N - 0 или 1. В любом случае ячейка остается в состоянии T03.
Затем КУ сообщает УУП, следует ли удлинить петлю С1, чтобы пройти через Ns+1, или сократить C1 чтобы пройти через Ns-1, и следует ли оставить ячейку в состоянии U или T03. Петля C1 используется для хронометрирования удлинения (или укорочения) петли С2. После этого петля С2 используется для хронометрирования удлинения (укорочения) петли С1 (т.е. петли играют друг для друга роль указателя позиции на ленте), а в ячейку тем временем записывается новый бит информации. В конце всего процесса УУП посылает в КУ сигнал окончания.
Мы перечислили функции КУ, касающиеся УУП. Основная же задача КУ заключается в осуществлении конструирования вторичного автомата, описание которого хранится в линейном массиве L. Таким образом, универсальный конструирующий автомат состоит из двух частей: конструирующего узла (КУ) и произвольно большой памяти с устройством для управления ею (УУП, L, С1 и С2).
Но, как будет выглядеть КУ, фон Нейман так и не написал. УУП же - это забавная штука с "микропрограммным управлением".
Можно видеть, что верхние рукава петель C1 и C2 имеют по два входа - для T0 и T1. Это нужно для удлинения, укорочения и записи. Вот, например, как происходит удлинение C1.
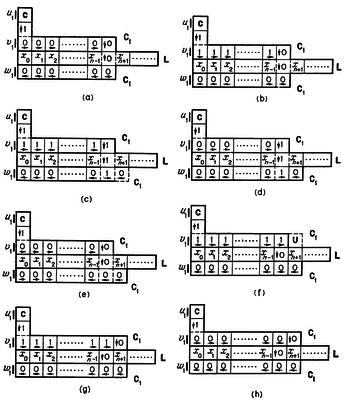
Т.о. УУП - это просто набор "программ" для выполнения операций над L - т.е. последовательностей, подающихся на входы петель C1 и C2.
Можно видеть, что эти "программы" должны иметь что-то вроде "операторов цикла" для перевода в состояние T0/T1 всего "рукава" петли до ячейки N. Фон Нейман опять сыграл на совпадении чисел. Он заметил, что длина последоваельности импульсов для перекодирования одной ячейки - максимум 6 импульсов в жестком времени. Значит, для приведение в нужный вид рукава длиной N достаточно запустить периодический импульсатор нужной последовательности и остановить ее ровно после выдачи 6*N импульсов. Как определить этот момент? Для этого и нужна вторая петля. Импульс проходит ее за 2*N+D шагов. (D - константа, которую можно рассчитать заранее). Прицепив эту петлю к описанному выше тройному счетчику, мы можем отсчитать 6*N импульсов с поправкой на константу. Вычисление константных задержек - это то, в чем и состоит суть "программирования" УУП.

Наиболее важные части УУП: блок считывания-записи-стирания (СЗС) и блок его контроля (КСЗС). Их охватывает кодированный канал "от круглой точки до квадратной" (КСЗС передает команды через блок импульсаторов CC3, СЗС общается с каналом через декодеры-импульсаторы CC1, КСЗС получает ответы через декодеры CC2). Y - блок интерфейса с КУ. X и Z - декодеры и импульсаторы для блоков Y и W.
Блок СЗС - это справочник "микрокоманд" - импульсаторы выдающие последовательности, обеспечивающие пыполнение всех необходимых для работы с L одиночных операций (например, P(10101) - для опроса ячейки L), дискриминатор "Пси" для оценки содержимого ячейки, две пары периодических пульсаторов (PP(110110) и PP(110000)) для переписывания верхних "рукавов" петель C1 и C2, и отключающих их тройных счетчиков Ф1 и Ф2. Входы СЗС - коды команд и сигналы запуска, выходы - содержимое ячейки (от "Пси") и сигналы о перекодировании "рукавов" (от Ф1 и Ф2).
Блок КСЗС, в основном, состоит из периодических импульсаторов PP(1) (для хранения информации о состоянии процесса) и сделанных на их основе Органов Управления:

Входы: a - запуск, d - сигнал о завершении операции (с тройного счетчика). Выходы: c - подтверждение a, b - сигнал о начале операции (запуске счетчика), e - сигнал о подтвержденном завершении операции (от счетчика), e - передача управления следующему Органу Управления.
ГЛАВА 5. САМОВОСПРОИЗВЕДЕНИЕ АВТОМАТОВ
Как один клеточный автомат может построить другой? Очень просто. К КУ первого прицепляется еще один специальный орган: конструирующий рукав. А на L записываются команды, заставляющие его конструировать. От петель УУП рукав отличется тем, что может извиваться в двух измерениях, и тем, что его не надо перестраивать каждый раз сначала, т.к. обе его линии - T0 и T1 проложены параллельно (позднее это решение предлагалось и для петель УУП). Конструирование начинается с дальнего верхнего угла вторичного автомата, а заканчивается снабжением вторичного автомата лентой L и передачей ему управляющего сигнала...

Универсальный конструктор:
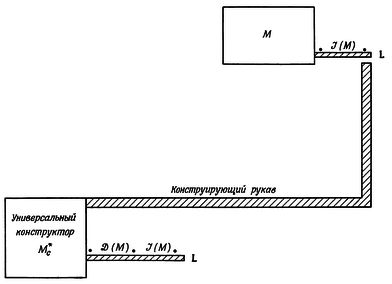
Самовоспроизведение:
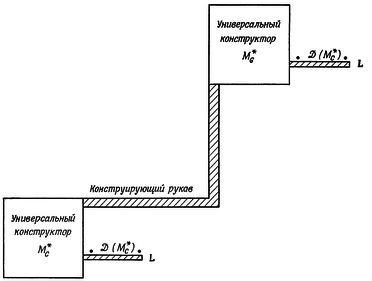
Самовоспроизведение вычислителя:
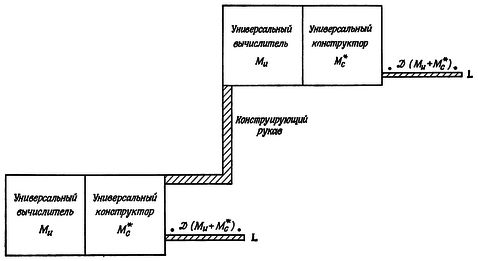


Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
"Послесловие" к фон Нейману.
ВЫЧИСЛЕНИЕ, ПОВЕДЕНИЕ И СТРУКТУРА НЕИЗМЕННЫХ И РАСТУЩИХ АВТОМАТОВ
А.У.БЕРКС (Мичиганский университет, США)
Сб. САМООРГАНИЗУЮЩИЕСЯ СИСТЕМЫ, 1964
#1. ВВЕДЕНИЕ
В этой статье рассматриваются исключительно детерминированные автоматы. Поскольку большинство докладов конференции было посвящено преимущественно вероятностным автоматам, следует сделать некоторые пояснения.
По всей вероятности, справедливо, что детерминистские теории не в состоянии полностью объяснить рост, обучение, мутацию, эволюцию и действительную работу дискретных вычислительных машин, и, следовательно, для полного объяснения всех этих явлений требуется вероятностная теория. Тем не менее обсуждение детерминированных автоматов не является неуместным на конференции по самоорганизующимся системам. Мы не сможем полностью понять вероятностные автоматы до тех пор, пока не будем знать пределы возможностей детерминированных автоматов, т.е. не будем знать, что они не в состоянии выполнять. Более того, вероятностный автомат может рассматриваться как детерминированный, который дополнен вероятностной мерой, определяющей переходы между состояниями. Поскольку как вероятностные, так и детерминистские теории до сих пор играли важную роль в физических науках, мы можем ожидать, что оба вида теорий окажутся плодотворными И при изучении автоматов.
Полная теория самоорганизующихся систем должна точно указать, какую роль в этих системах играет детерминизм. Я согласен с высказыванием Джона фон Неймана о том, что теория автоматов должна включать в себя как вероятностную, так и детерминированную логику [1], но я, так же как и он, уверен и в том, что большой интерес представляет детерминированный анализ такого явления, как самовоспроизведение (см. ниже, разд.4).
Уже изучены различные виды детерминированных автоматов. Усиленно изучались как непосредственно, так и с помощью рекурсивных функций [2] машины Тьюринга. В последнее время уделялось большое внимание неизменным (конечным) автоматам, а фон Нейман работал над самовоспроизводящимися автоматами. Однако очень мало сделано для того, чтобы привести в связь все эти отдельные исследования. В настоящей статье я выскажу некоторые положения, на основании которых можно построить единую теорию детерминированных автоматов.
#2. СТРУКТУРА, ПОВЕДЕНИЕ И ВЫЧИСЛЕНИЕ В НЕИЗМЕННЫХ АВТОМАТАХ И ОБОБЩЕННЫЕ МАШИНЫ ТЬЮРИНГА
Я начну с неизменных автоматов и машин Тьюринга, а затем подвергну общему обсуждению самовоспроизводящиеся машины и растущие автоматы. Неизменный автомат состоит из ограниченного числа переключателей и элементов задержки, которые объединены между собой в некоторую форму или структуру, являющуюся одной и той же в любой данный момент времени [3, 4]. На фиг.1 представлен очень простой неизменный автомат, который исключает через один каждый импульс (1) из серии импульсов, поступающих на вход. Цифровая машина с лентой конечной длины является, конечно, неизменным автоматом.
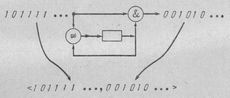
Фиг.1. Поведение неизменного автомата.
Нужно отличать структуру неизменного автомата от его поведения. СТРУКТУРА проявляется в неизменной форме связей между элементами. Структуры двух автоматов являются одинаковыми, если между узлами (т.е. соединениями входов и выходов элементов) этих автоматов может быть установлено взаимно-однозначное соответствие так, чтобы соответствующие узлы являлись узлами идентичных элементов. Например, если соединения, показанные на фиг.1, где-либо разорвать, то мы получим уже другую структуру.
Поведение автомата представляет собой, грубо говоря, связь между входными возбуждениями и выходными реакциями. Более точное определение поведения может быть дано в терминах временных последовательностей состояний, причем соответствующие моменты времени являются неотрицательными целыми числами: 0, 1, 2, 3, ... Условимся называть некоторую неограниченную временную последовательность состояний на входе автомата ИСТОРИЕЙ ВХОДА, а неограниченную временную последовательность состояний на его выходе - ИСТОРИЕЙ ВЫХОДА. ПАРА ПОВЕДЕНИЯ автомата состоит из истории входа и истории выхода, которая вырабатывается, когда данная история входа воздействует на входы автомата. Пара поведения для автомата на фиг.1 показана в нижней части рисунка. ПОВЕДЕНИЕ неизменного автомата - это множество всех пар поведения этого автомата.
Обратимся теперь к машинам Тьюринга. В первоначальном представлении Тьюринга каждая из машин являлась существенно неизменным автоматом, соединенным с одной бесконечной лентой. Неизменный автомат в течение одного такта просматривает один квадратик ленты и может за то же время сдвинуть ленту (или сдвинуться относительно ленты) на один квадратик. Мы несколько обобщим представления Тьюринга в различных направлениях, чтобы получить так называемую ОБОБЩЕННУЮ МАШИНУ ТЬЮРИНГА. Для того чтобы установить связь между машинами Тьюринга и рассмотренными выше неизменными автоматами, предположим, что неизменная часть машины имеет входы и выходы, как это показано на фиг.2. Следствием этого является то, что ранее введенное понятие - ПОВЕДЕНИЕ - оказывается непосредственно применимо к машинам Тьюринга. Затем мы допустим, что существует некоторое ограниченное количество лент. И, наконец, мы будем рассматривать ленту в любой заданный момент времени как конечный автомат и толковать изменение длины ленты как изменение в этом автомате. Таким образом, в каждый данный момент времени лента для нас конечна. "Квадратик" ленты, запоминающий одну двоичную цифру ("0" или "1"), может быть синтезирован из переключателей и элементов задержки различными способами. Квадратики могут добавляться или отниматься для того, чтобы представить удлинение или сокращение ленты [См. ниже, разд.4, а также разд.6 статьи "Логика растущих и неизменных автоматов", которая доложена автором на Гарвардской конференции по теории переключательных схем в 1957г. и должна быть опубликована в Докладах конференции]. Следовательно, хотя обобщенная машина Тьюринга и имеет заданную структуру в любой момент времени, эта структура через такт изменяется очень простым способом, а изменение управляется вычислением, производимым машиной. Цифровая вычислительная машина с печатным выходом и магнитными лентами, длина которых может быть неограниченно увеличена, является обобщенной машиной Тьюринга.

Фиг.2. Вычисление в обобщенной машине Тьюринга.
Для вычисления требуется задача и ответ, причем ответ должен быть где-то представлен. Для этой цели Тьюринг использовал чередующиеся квадратики ленты. Мы условимся, что ответ обобщенной машины Тьюринга должен появляться на выходах. Однако- мы не будем в качестве ответа брать историю выхода, потому что в противном случае мы отождествили бы поведение и вычисление и, следовательно, незаконно ограничили бы область вычисляемого. Вместо этого мы выделим УПРАВЛЯЮЩИЙ ВЫХОД из остальных выходов, которые назовем ВЫХОДАМИ ОТВЕТА. "1" на управляющем выходе означает, что состояние выходов ответа в этот момент является частью ответа, а "0" на управляющем выходе означает, что состояния выходов ответа в этот момент времени не должны приниматься во внимание. Последовательность отобранных таким образом состояний выходов ответа является ВЫЧИСЛЕННОЙ ВЫХОДНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ (computed output sequence). Последовательность 3561 на фиг.2 является начальной частью вычисленной последовательности. Пара, состоящая из истории входа и получающейся в виде результата вычисленной выходной последовательности, является ПАРОЙ ВЫЧИСЛЕНИЯ. ВЫЧИСЛЕНИЕ (computation) автомата - это множество всех пар вычисления этого автомата.
Существует аналогия между поведением и вычислением, с одной стороны, и имитацией "в реальном масштабе времени" и имитацией "в нереальном масштабе времени", с другой стороны. При имитации в реальном масштабе времени ответ вырабатывается со скоростью, определяемой действительным временем, необходимым для процесса, который имитируется машиной, в то время как при имитации в нереальном масштабе времени ответ вырабатывается со скоростью, не зависящей от действительного времени. Подобно этому, поведение автомата включает в себя значения выходов в каждый момент времени, в то время как вычисление содержит только те значения выходов, которые выбираются машиной, и обычно скорость появления этих состояний ответа не постоянна.
Вычисленная выходная последовательность может быть нулевой, ограниченной или неограниченной. Говорят, что вычисление НЕ ОГРАНИЧЕНО, если каждая вычисленная последовательность (т.е. второй элемент каждой пары вычисления) является неограниченной, и ограничено, если каждая вычисленная выходная последовательность является ограниченной или нулевой (т.е. не существует). В противном случае вычисление автомата является смешанным.
Мы можем применить понятие вычисления и другие связанные с ним понятия, которые только что определены, к неизменным автоматам, выделяя управляющий выход неизменного автомата среди других выходов (или выходов ответа). Следовательно, все три понятия - структура, поведение и вычисление - применимы как к неизменным автоматам, так и к обобщенным машинам Тьюринга. Эти три понятия, кроме того, будут применены и к растущим автоматам (см. разд.4).
#3. АНАЛИЗ И СИНТЕЗ АВТОМАТОВ
Наше рассмотрение растущих автоматов, которому будут посвящены разд.4 и 5, предполагает некоторое знакомство с неизменными автоматами и обобщенными машинами Тьюринга, поэтому мы кратко напомним некоторые результаты исследования этих особых случаев растущих автоматов и укажем на некоторые нерешенные проблемы. Поскольку понятия поведения, структуры и вычисления применимы и к растущим автоматам, то все результаты и проблемы, рассматриваемые в настоящем разделе, с надлежащими видоизменениями относятся также и к этим автоматам.
О поведении неизменных автоматов известно довольно много. Например, каждый неизменный автомат имеет ограниченное число выходных состояний с задержкой. Этот факт имеет большое значение для поведения этих устройств. Если неизменный автомат не имеет входов, то это означает, что поведение его периодично [См. [3], теорему 1. Заметим, что в этом случае поведение является единственной историей выхода]. В случае если автомат имеет входы, ограниченность числа состояний означает, что это устройство может обнаруживать только "регулярные события" [5] (а если известно число состояний с задержкой, поведение автомата может быть вычислено по результатам ограниченного по длительности испытания поведения) и что существует метод определения эквивалентности поведения [4, 6]. Поскольку понятие вычисления является новым для неизменных автоматов, оно мало изучено. Из тех же самых доводов, из которых вытекает, что поведение неизменного автомата без входов является периодичным, следует также, что и вычисление такого автомата периодично. Существует алгоритм, который дает возможность установить, является ли вычисление неизменного автомата (со входами) неограниченным, ограниченным или смешанным [Неопубликованные результаты автора и Дж.Райт], но остается нерешенной проблема о существовании алгоритма, с помощью которого можно было бы установить, не имеют ли два неизменных автомата одно и то же вычисление.
Хорошо известны понятие вычислимости по Тьюрингу и такие очень родственные понятия, как алгоритм, общая рекурсивность и частичная рекурсивность. Мы не имеем возможности пояснять здесь эти понятия, однако стоит заметить, что результаты исследования их могут быть изложены с точки зрения нашего понятия обобщенной машины Тьюринга, и они содержат ответы на большинство вопросов о вычислении таких машин. Применение же к обобщенным машинам Тьюринга результатов исследования рекурсивности, алгоритмов и вычисления требует пояснения, потому что существует много различных способов установления связи между обобщенной машиной Тьюринга и этими понятиями. Так, существуют альтернативные методы использования обобщенной машины Тьюринга для вычисления рекурсивной функции. Например, для данной невзаимной рекурсивной функции можно сконструировать машину без входов, вычислением которой является перечень значений этой функции. И, наоборот, можно построить обобщенную машину Тьюринга со входами таким образом, что всякий раз, когда на ее вход поступают аргументы (задачи), вычисленные значения функции (ответы) будут появляться как часть вычисления. Можно провести различие между ограниченным или смешанным вычислением, с одной стороны, и неограниченным вычислением - с другой (см. разд.2), что соответствует различию между частичной рекурсивностью и общей рекурсивноетью.
Установим связь между некоторыми известными нам фактами о вычислимости и рекурсивности и нашим представлением об обобщенной машине Тьюринга. Каждое вычисляемое число (в смысле Тьюринга) может быть выработано как вычисленная выходная последовательность обобщенной машины Тьюринга, имеющей одну ленту и не имеющей входов. Значения функции, которая является общерекурсивной относительно заданной функции, могут быть выработаны как вычисление обобщенной машины Тьюринга, на вход которой поступают значения заданной функции. Не существует алгоритма, с помощью которого можно установить, будет ли вычисление произвольной обобщенной машины Тьюринга ограниченным, смешанным или неограниченным, но имеется алгоритм, который дает возможность установить, сможет ли когда-нибудь измениться структура машины.
Не существует также алгоритма и для того, чтобы установить, не осуществляют ли две обобщенные машины Тьюринга одно и то же вычисление [Неопубликованные результаты Дж.Райт].
Поскольку понятие поведения в применении к машине Тьюринга является новым, то в этой области существует много нерешенных вопросов. Например, является ли класс поведений обобщенных машин Тьюринга с n+1 лентой более широким, чем класс поведений машин с n лентами? Имеется ли алгоритм, с помощью которого можно было бы установить, одинаково ли поведение двух обобщенных машин Тьюринга?
Дальше мы будем рассматривать универсальную КОНСТРУИРУЮЩУЮ МАШИНУ фон Неймана, поэтому универсальная вычислительная машина Тьюринга (фиг.3) представляет здесь особый интерес. Назовем обобщенную машину Тьюринга, которая имеет одну ленту, один выход для ответа и не имеет входов,- специализированной машиной. Переведенный на язык наших понятий результат Тьюринга гласит: существует обобщенная машина Тьюринга с одной лентой и входами, называемая универсальной машиной Тьюринга, обладающая тем свойством, что для каждой специализированной машины M существует ограниченной длины программа или входная последовательность S такая, что если S подать на входы универсальной машины Тьюринга, то вычисленные выходные последовательности машины М и универсальной машины Тьюринга являются тождественными. Это иллюстрируется на фиг.3. Следует заметить, что в общем случае универсальная машина Тьюринга и специализированная машина не вырабатывают одинаковые истории выхода, поэтому тождественность между ними относится к вычислениям, а не к поведению. Следует также заметить, что ограниченная по длительности входная последовательность S может быть подана на универсальную машину Тьюринга присоединением к каждому из входов универсальной машины, не имеющей входов, цепочки задержек без замкнутых петель. На их вход подается противоречие (выход всегда является ложным), а программа запоминается начальными состояниями задержек. После истечения времени, равного длине этой последовательности задержек, вход универсальной машины всегда будет равен нулю.
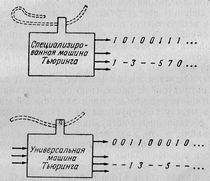
Фиг.3. Универсальная машина Тьюринга.
Очень вероятно, что подобный результат справедлив и в том случае, если специализированную машину снабдить входами и более чем одной лентой, т.е. для каждого множества обобщенных машин Тьюринга с n входами и m выходами существует универсальная машина Тьюринга. Остается ли в силе этот результат для неизменных автоматов? Инженеры по счетной технике часто говорят о коммерческом времени для деталей машины и о выборе между конструированием ("монтажом") операции и составлением инструкции (программированием) этой операции, а это, казалось бы, подразумевает существование универсального неизменного автомата. Но фактически универсальных неизменных автоматов не существует.
Для доказательства этого покажем сначала, что любой неизменный автомат A при подаче на его вход ограниченной последовательности S вырабатывает периодический выход с периодом, не большим чем n, где n - число состояний автомата A с задержкой. Поскольку S ограничено, настанет время, когда входные состояния автомата A не будут изменяться. В этом случае автомат A будет вести себя как устройство без входа, имеющее n состояний с задержкой, и, таким образом, вычисленная выходная последовательность автомата A является периодической с периодом n или меньше. Следовательно, автомат А не может вырабатывать вычисленную выходную последовательность, например с периодом 2n, и поэтому он не является универсальной вычислительной машиной. Таким образом, не существует неизменного автомата, который являлся бы универсальным для класса неизменных автоматов без входа с m выходами, и, следовательно, не существует неизменного автомата для класса неизменных автоматов с n входами и m выходами.
Упомянем далее о проблеме приведения. Увеличивается ли класс вычислений, производимых обобщенной машиной Тьюринга, при увеличении числа лент? Обобщенная машина Тьюринга может иметь только одну многоканальную читающую и записывающую головку на каждую ленту. Наоборот, растущие автоматы, рассматриваемые в следующем разделе, могут иметь ленты с более чем одной многоканальной читающей и записывающей головкой. Какое влияние, если таковое существует, оказывает это на класс поведений или на класс вычислений? В некоторых случаях можно использовать несколько лент с одной головкой для выполнения работы одной ленты с несколькими головками. Это может быть сделано в том случае, если автомат записывает информацию на двух лентах и сравнивает эти ленты, а это, вероятно, всегда может быть сделано. Стоит заметить, что здесь мы сталкиваемся с абстрактной проблемой буфера и планирования.
Обсуждение автоматов на конференции по самоорганизующимся системам было бы неполным, если бы не были рассмотрены машины, синтезирующие другие машины. Этот процесс синтеза можно представить себе различным образом. Один из методов, который был изучен в последнее время [7-10], показан на фиг.4. Предположим, что имеется формальный язык L, на котором человек может удобно и точно сформулировать некоторые условия поведения C, которым, как ему хотелось бы, должен удовлетворять некоторый автомат. Нам интересно знать, существует ли синтезирующая машина S, для которой можно математически доказать следующее положение: если машине S задано некоторое условие поведения C, то она всегда вырабатывает либо конструкцию некоторого автомата A, удовлетворяющего этому условию, либо же скажет нам, что такого автомата нет [Другие задачи в этой области сформулированы Бючи, Элготом и Райт [7]. То, что мы назвали проблемой синтеза, они именовали комбинированной проблемой разрешимости и синтеза]. Условие, записанное сверху фиг.4, заключается в том, что для всех моментов времени, отличных от нуля, на выходе искомого автомата должен быть сигнал (состояние 1), если был сигнал на входе в какой-либо предшествующий момент времени. Существуют неизменные автоматы, удовлетворяющие этому условию, и, следовательно, если существует синтезирующая машина для языка, содержащего это условие, то эта машина произведет в качестве выхода изображение одного из этих автоматов.
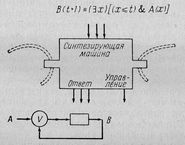
Фиг.4. Синтезирующая машина.
Область исследований здесь очень велика, потому что имеется много проблем только что описанного вида. Процесс синтеза, иллюстрированный на фиг.4, начинает с особого языка L и имеет результатом синтез неизменного автомата, удовлетворяющего условию, наложенному на его поведение. Существует много различных языков L, которые следовало бы изучить. Представляет интерес синтезирование как обобщенных машин Тьюринга, так и неизменных автоматов. В обоих случаях условие может налагаться как на вычисление искомого автомата, так и на его поведение.
Для каждой детализации языка L, условия C и искомого автомата A возникает вопрос: существует ли синтезирующая машина, и если она существует, то какова ее структура? В некоторых случаях машина существует, а в некоторых не существует. Очень важно уяснить себе, что если не существует синтезирующей машины подобного вида, то не существует также и метода использования вычислительных машин для построения вычислительных машин, которые гарантировали бы выработку ответа во всех случаях. Следовательно, основная проблема заключается в том, чтобы определить теоретические границы возможности механизировать процесс синтеза с помощью детерминированных машин этого типа.
ВЫЧИСЛЕНИЕ, ПОВЕДЕНИЕ И СТРУКТУРА НЕИЗМЕННЫХ И РАСТУЩИХ АВТОМАТОВ
А.У.БЕРКС (Мичиганский университет, США)
Сб. САМООРГАНИЗУЮЩИЕСЯ СИСТЕМЫ, 1964
#1. ВВЕДЕНИЕ
В этой статье рассматриваются исключительно детерминированные автоматы. Поскольку большинство докладов конференции было посвящено преимущественно вероятностным автоматам, следует сделать некоторые пояснения.
По всей вероятности, справедливо, что детерминистские теории не в состоянии полностью объяснить рост, обучение, мутацию, эволюцию и действительную работу дискретных вычислительных машин, и, следовательно, для полного объяснения всех этих явлений требуется вероятностная теория. Тем не менее обсуждение детерминированных автоматов не является неуместным на конференции по самоорганизующимся системам. Мы не сможем полностью понять вероятностные автоматы до тех пор, пока не будем знать пределы возможностей детерминированных автоматов, т.е. не будем знать, что они не в состоянии выполнять. Более того, вероятностный автомат может рассматриваться как детерминированный, который дополнен вероятностной мерой, определяющей переходы между состояниями. Поскольку как вероятностные, так и детерминистские теории до сих пор играли важную роль в физических науках, мы можем ожидать, что оба вида теорий окажутся плодотворными И при изучении автоматов.
Полная теория самоорганизующихся систем должна точно указать, какую роль в этих системах играет детерминизм. Я согласен с высказыванием Джона фон Неймана о том, что теория автоматов должна включать в себя как вероятностную, так и детерминированную логику [1], но я, так же как и он, уверен и в том, что большой интерес представляет детерминированный анализ такого явления, как самовоспроизведение (см. ниже, разд.4).
Уже изучены различные виды детерминированных автоматов. Усиленно изучались как непосредственно, так и с помощью рекурсивных функций [2] машины Тьюринга. В последнее время уделялось большое внимание неизменным (конечным) автоматам, а фон Нейман работал над самовоспроизводящимися автоматами. Однако очень мало сделано для того, чтобы привести в связь все эти отдельные исследования. В настоящей статье я выскажу некоторые положения, на основании которых можно построить единую теорию детерминированных автоматов.
#2. СТРУКТУРА, ПОВЕДЕНИЕ И ВЫЧИСЛЕНИЕ В НЕИЗМЕННЫХ АВТОМАТАХ И ОБОБЩЕННЫЕ МАШИНЫ ТЬЮРИНГА
Я начну с неизменных автоматов и машин Тьюринга, а затем подвергну общему обсуждению самовоспроизводящиеся машины и растущие автоматы. Неизменный автомат состоит из ограниченного числа переключателей и элементов задержки, которые объединены между собой в некоторую форму или структуру, являющуюся одной и той же в любой данный момент времени [3, 4]. На фиг.1 представлен очень простой неизменный автомат, который исключает через один каждый импульс (1) из серии импульсов, поступающих на вход. Цифровая машина с лентой конечной длины является, конечно, неизменным автоматом.

Фиг.1. Поведение неизменного автомата.
Нужно отличать структуру неизменного автомата от его поведения. СТРУКТУРА проявляется в неизменной форме связей между элементами. Структуры двух автоматов являются одинаковыми, если между узлами (т.е. соединениями входов и выходов элементов) этих автоматов может быть установлено взаимно-однозначное соответствие так, чтобы соответствующие узлы являлись узлами идентичных элементов. Например, если соединения, показанные на фиг.1, где-либо разорвать, то мы получим уже другую структуру.
Поведение автомата представляет собой, грубо говоря, связь между входными возбуждениями и выходными реакциями. Более точное определение поведения может быть дано в терминах временных последовательностей состояний, причем соответствующие моменты времени являются неотрицательными целыми числами: 0, 1, 2, 3, ... Условимся называть некоторую неограниченную временную последовательность состояний на входе автомата ИСТОРИЕЙ ВХОДА, а неограниченную временную последовательность состояний на его выходе - ИСТОРИЕЙ ВЫХОДА. ПАРА ПОВЕДЕНИЯ автомата состоит из истории входа и истории выхода, которая вырабатывается, когда данная история входа воздействует на входы автомата. Пара поведения для автомата на фиг.1 показана в нижней части рисунка. ПОВЕДЕНИЕ неизменного автомата - это множество всех пар поведения этого автомата.
Обратимся теперь к машинам Тьюринга. В первоначальном представлении Тьюринга каждая из машин являлась существенно неизменным автоматом, соединенным с одной бесконечной лентой. Неизменный автомат в течение одного такта просматривает один квадратик ленты и может за то же время сдвинуть ленту (или сдвинуться относительно ленты) на один квадратик. Мы несколько обобщим представления Тьюринга в различных направлениях, чтобы получить так называемую ОБОБЩЕННУЮ МАШИНУ ТЬЮРИНГА. Для того чтобы установить связь между машинами Тьюринга и рассмотренными выше неизменными автоматами, предположим, что неизменная часть машины имеет входы и выходы, как это показано на фиг.2. Следствием этого является то, что ранее введенное понятие - ПОВЕДЕНИЕ - оказывается непосредственно применимо к машинам Тьюринга. Затем мы допустим, что существует некоторое ограниченное количество лент. И, наконец, мы будем рассматривать ленту в любой заданный момент времени как конечный автомат и толковать изменение длины ленты как изменение в этом автомате. Таким образом, в каждый данный момент времени лента для нас конечна. "Квадратик" ленты, запоминающий одну двоичную цифру ("0" или "1"), может быть синтезирован из переключателей и элементов задержки различными способами. Квадратики могут добавляться или отниматься для того, чтобы представить удлинение или сокращение ленты [См. ниже, разд.4, а также разд.6 статьи "Логика растущих и неизменных автоматов", которая доложена автором на Гарвардской конференции по теории переключательных схем в 1957г. и должна быть опубликована в Докладах конференции]. Следовательно, хотя обобщенная машина Тьюринга и имеет заданную структуру в любой момент времени, эта структура через такт изменяется очень простым способом, а изменение управляется вычислением, производимым машиной. Цифровая вычислительная машина с печатным выходом и магнитными лентами, длина которых может быть неограниченно увеличена, является обобщенной машиной Тьюринга.

Фиг.2. Вычисление в обобщенной машине Тьюринга.
Для вычисления требуется задача и ответ, причем ответ должен быть где-то представлен. Для этой цели Тьюринг использовал чередующиеся квадратики ленты. Мы условимся, что ответ обобщенной машины Тьюринга должен появляться на выходах. Однако- мы не будем в качестве ответа брать историю выхода, потому что в противном случае мы отождествили бы поведение и вычисление и, следовательно, незаконно ограничили бы область вычисляемого. Вместо этого мы выделим УПРАВЛЯЮЩИЙ ВЫХОД из остальных выходов, которые назовем ВЫХОДАМИ ОТВЕТА. "1" на управляющем выходе означает, что состояние выходов ответа в этот момент является частью ответа, а "0" на управляющем выходе означает, что состояния выходов ответа в этот момент времени не должны приниматься во внимание. Последовательность отобранных таким образом состояний выходов ответа является ВЫЧИСЛЕННОЙ ВЫХОДНОЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ (computed output sequence). Последовательность 3561 на фиг.2 является начальной частью вычисленной последовательности. Пара, состоящая из истории входа и получающейся в виде результата вычисленной выходной последовательности, является ПАРОЙ ВЫЧИСЛЕНИЯ. ВЫЧИСЛЕНИЕ (computation) автомата - это множество всех пар вычисления этого автомата.
Существует аналогия между поведением и вычислением, с одной стороны, и имитацией "в реальном масштабе времени" и имитацией "в нереальном масштабе времени", с другой стороны. При имитации в реальном масштабе времени ответ вырабатывается со скоростью, определяемой действительным временем, необходимым для процесса, который имитируется машиной, в то время как при имитации в нереальном масштабе времени ответ вырабатывается со скоростью, не зависящей от действительного времени. Подобно этому, поведение автомата включает в себя значения выходов в каждый момент времени, в то время как вычисление содержит только те значения выходов, которые выбираются машиной, и обычно скорость появления этих состояний ответа не постоянна.
Вычисленная выходная последовательность может быть нулевой, ограниченной или неограниченной. Говорят, что вычисление НЕ ОГРАНИЧЕНО, если каждая вычисленная последовательность (т.е. второй элемент каждой пары вычисления) является неограниченной, и ограничено, если каждая вычисленная выходная последовательность является ограниченной или нулевой (т.е. не существует). В противном случае вычисление автомата является смешанным.
Мы можем применить понятие вычисления и другие связанные с ним понятия, которые только что определены, к неизменным автоматам, выделяя управляющий выход неизменного автомата среди других выходов (или выходов ответа). Следовательно, все три понятия - структура, поведение и вычисление - применимы как к неизменным автоматам, так и к обобщенным машинам Тьюринга. Эти три понятия, кроме того, будут применены и к растущим автоматам (см. разд.4).
#3. АНАЛИЗ И СИНТЕЗ АВТОМАТОВ
Наше рассмотрение растущих автоматов, которому будут посвящены разд.4 и 5, предполагает некоторое знакомство с неизменными автоматами и обобщенными машинами Тьюринга, поэтому мы кратко напомним некоторые результаты исследования этих особых случаев растущих автоматов и укажем на некоторые нерешенные проблемы. Поскольку понятия поведения, структуры и вычисления применимы и к растущим автоматам, то все результаты и проблемы, рассматриваемые в настоящем разделе, с надлежащими видоизменениями относятся также и к этим автоматам.
О поведении неизменных автоматов известно довольно много. Например, каждый неизменный автомат имеет ограниченное число выходных состояний с задержкой. Этот факт имеет большое значение для поведения этих устройств. Если неизменный автомат не имеет входов, то это означает, что поведение его периодично [См. [3], теорему 1. Заметим, что в этом случае поведение является единственной историей выхода]. В случае если автомат имеет входы, ограниченность числа состояний означает, что это устройство может обнаруживать только "регулярные события" [5] (а если известно число состояний с задержкой, поведение автомата может быть вычислено по результатам ограниченного по длительности испытания поведения) и что существует метод определения эквивалентности поведения [4, 6]. Поскольку понятие вычисления является новым для неизменных автоматов, оно мало изучено. Из тех же самых доводов, из которых вытекает, что поведение неизменного автомата без входов является периодичным, следует также, что и вычисление такого автомата периодично. Существует алгоритм, который дает возможность установить, является ли вычисление неизменного автомата (со входами) неограниченным, ограниченным или смешанным [Неопубликованные результаты автора и Дж.Райт], но остается нерешенной проблема о существовании алгоритма, с помощью которого можно было бы установить, не имеют ли два неизменных автомата одно и то же вычисление.
Хорошо известны понятие вычислимости по Тьюрингу и такие очень родственные понятия, как алгоритм, общая рекурсивность и частичная рекурсивность. Мы не имеем возможности пояснять здесь эти понятия, однако стоит заметить, что результаты исследования их могут быть изложены с точки зрения нашего понятия обобщенной машины Тьюринга, и они содержат ответы на большинство вопросов о вычислении таких машин. Применение же к обобщенным машинам Тьюринга результатов исследования рекурсивности, алгоритмов и вычисления требует пояснения, потому что существует много различных способов установления связи между обобщенной машиной Тьюринга и этими понятиями. Так, существуют альтернативные методы использования обобщенной машины Тьюринга для вычисления рекурсивной функции. Например, для данной невзаимной рекурсивной функции можно сконструировать машину без входов, вычислением которой является перечень значений этой функции. И, наоборот, можно построить обобщенную машину Тьюринга со входами таким образом, что всякий раз, когда на ее вход поступают аргументы (задачи), вычисленные значения функции (ответы) будут появляться как часть вычисления. Можно провести различие между ограниченным или смешанным вычислением, с одной стороны, и неограниченным вычислением - с другой (см. разд.2), что соответствует различию между частичной рекурсивностью и общей рекурсивноетью.
Установим связь между некоторыми известными нам фактами о вычислимости и рекурсивности и нашим представлением об обобщенной машине Тьюринга. Каждое вычисляемое число (в смысле Тьюринга) может быть выработано как вычисленная выходная последовательность обобщенной машины Тьюринга, имеющей одну ленту и не имеющей входов. Значения функции, которая является общерекурсивной относительно заданной функции, могут быть выработаны как вычисление обобщенной машины Тьюринга, на вход которой поступают значения заданной функции. Не существует алгоритма, с помощью которого можно установить, будет ли вычисление произвольной обобщенной машины Тьюринга ограниченным, смешанным или неограниченным, но имеется алгоритм, который дает возможность установить, сможет ли когда-нибудь измениться структура машины.
Не существует также алгоритма и для того, чтобы установить, не осуществляют ли две обобщенные машины Тьюринга одно и то же вычисление [Неопубликованные результаты Дж.Райт].
Поскольку понятие поведения в применении к машине Тьюринга является новым, то в этой области существует много нерешенных вопросов. Например, является ли класс поведений обобщенных машин Тьюринга с n+1 лентой более широким, чем класс поведений машин с n лентами? Имеется ли алгоритм, с помощью которого можно было бы установить, одинаково ли поведение двух обобщенных машин Тьюринга?
Дальше мы будем рассматривать универсальную КОНСТРУИРУЮЩУЮ МАШИНУ фон Неймана, поэтому универсальная вычислительная машина Тьюринга (фиг.3) представляет здесь особый интерес. Назовем обобщенную машину Тьюринга, которая имеет одну ленту, один выход для ответа и не имеет входов,- специализированной машиной. Переведенный на язык наших понятий результат Тьюринга гласит: существует обобщенная машина Тьюринга с одной лентой и входами, называемая универсальной машиной Тьюринга, обладающая тем свойством, что для каждой специализированной машины M существует ограниченной длины программа или входная последовательность S такая, что если S подать на входы универсальной машины Тьюринга, то вычисленные выходные последовательности машины М и универсальной машины Тьюринга являются тождественными. Это иллюстрируется на фиг.3. Следует заметить, что в общем случае универсальная машина Тьюринга и специализированная машина не вырабатывают одинаковые истории выхода, поэтому тождественность между ними относится к вычислениям, а не к поведению. Следует также заметить, что ограниченная по длительности входная последовательность S может быть подана на универсальную машину Тьюринга присоединением к каждому из входов универсальной машины, не имеющей входов, цепочки задержек без замкнутых петель. На их вход подается противоречие (выход всегда является ложным), а программа запоминается начальными состояниями задержек. После истечения времени, равного длине этой последовательности задержек, вход универсальной машины всегда будет равен нулю.

Фиг.3. Универсальная машина Тьюринга.
Очень вероятно, что подобный результат справедлив и в том случае, если специализированную машину снабдить входами и более чем одной лентой, т.е. для каждого множества обобщенных машин Тьюринга с n входами и m выходами существует универсальная машина Тьюринга. Остается ли в силе этот результат для неизменных автоматов? Инженеры по счетной технике часто говорят о коммерческом времени для деталей машины и о выборе между конструированием ("монтажом") операции и составлением инструкции (программированием) этой операции, а это, казалось бы, подразумевает существование универсального неизменного автомата. Но фактически универсальных неизменных автоматов не существует.
Для доказательства этого покажем сначала, что любой неизменный автомат A при подаче на его вход ограниченной последовательности S вырабатывает периодический выход с периодом, не большим чем n, где n - число состояний автомата A с задержкой. Поскольку S ограничено, настанет время, когда входные состояния автомата A не будут изменяться. В этом случае автомат A будет вести себя как устройство без входа, имеющее n состояний с задержкой, и, таким образом, вычисленная выходная последовательность автомата A является периодической с периодом n или меньше. Следовательно, автомат А не может вырабатывать вычисленную выходную последовательность, например с периодом 2n, и поэтому он не является универсальной вычислительной машиной. Таким образом, не существует неизменного автомата, который являлся бы универсальным для класса неизменных автоматов без входа с m выходами, и, следовательно, не существует неизменного автомата для класса неизменных автоматов с n входами и m выходами.
Упомянем далее о проблеме приведения. Увеличивается ли класс вычислений, производимых обобщенной машиной Тьюринга, при увеличении числа лент? Обобщенная машина Тьюринга может иметь только одну многоканальную читающую и записывающую головку на каждую ленту. Наоборот, растущие автоматы, рассматриваемые в следующем разделе, могут иметь ленты с более чем одной многоканальной читающей и записывающей головкой. Какое влияние, если таковое существует, оказывает это на класс поведений или на класс вычислений? В некоторых случаях можно использовать несколько лент с одной головкой для выполнения работы одной ленты с несколькими головками. Это может быть сделано в том случае, если автомат записывает информацию на двух лентах и сравнивает эти ленты, а это, вероятно, всегда может быть сделано. Стоит заметить, что здесь мы сталкиваемся с абстрактной проблемой буфера и планирования.
Обсуждение автоматов на конференции по самоорганизующимся системам было бы неполным, если бы не были рассмотрены машины, синтезирующие другие машины. Этот процесс синтеза можно представить себе различным образом. Один из методов, который был изучен в последнее время [7-10], показан на фиг.4. Предположим, что имеется формальный язык L, на котором человек может удобно и точно сформулировать некоторые условия поведения C, которым, как ему хотелось бы, должен удовлетворять некоторый автомат. Нам интересно знать, существует ли синтезирующая машина S, для которой можно математически доказать следующее положение: если машине S задано некоторое условие поведения C, то она всегда вырабатывает либо конструкцию некоторого автомата A, удовлетворяющего этому условию, либо же скажет нам, что такого автомата нет [Другие задачи в этой области сформулированы Бючи, Элготом и Райт [7]. То, что мы назвали проблемой синтеза, они именовали комбинированной проблемой разрешимости и синтеза]. Условие, записанное сверху фиг.4, заключается в том, что для всех моментов времени, отличных от нуля, на выходе искомого автомата должен быть сигнал (состояние 1), если был сигнал на входе в какой-либо предшествующий момент времени. Существуют неизменные автоматы, удовлетворяющие этому условию, и, следовательно, если существует синтезирующая машина для языка, содержащего это условие, то эта машина произведет в качестве выхода изображение одного из этих автоматов.

Фиг.4. Синтезирующая машина.
Область исследований здесь очень велика, потому что имеется много проблем только что описанного вида. Процесс синтеза, иллюстрированный на фиг.4, начинает с особого языка L и имеет результатом синтез неизменного автомата, удовлетворяющего условию, наложенному на его поведение. Существует много различных языков L, которые следовало бы изучить. Представляет интерес синтезирование как обобщенных машин Тьюринга, так и неизменных автоматов. В обоих случаях условие может налагаться как на вычисление искомого автомата, так и на его поведение.
Для каждой детализации языка L, условия C и искомого автомата A возникает вопрос: существует ли синтезирующая машина, и если она существует, то какова ее структура? В некоторых случаях машина существует, а в некоторых не существует. Очень важно уяснить себе, что если не существует синтезирующей машины подобного вида, то не существует также и метода использования вычислительных машин для построения вычислительных машин, которые гарантировали бы выработку ответа во всех случаях. Следовательно, основная проблема заключается в том, чтобы определить теоретические границы возможности механизировать процесс синтеза с помощью детерминированных машин этого типа.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
#4. РАСТУЩИЕ АВТОМАТЫ
Джон фон Нейман показал, как строить универсальные конструирующие машины и самовоспроизводящиеся автоматы, в рамках общего определения автоматов [11-13]. Подробное определение автоматов Неймана содержится в его неопубликованной работе, поэтому я разработал другое определение. Модель Неймана намного ближе к биологическим явлениям, чем представленное здесь определение. Например, каждая ячейка у Неймана обладает единичной задержкой [См. Шеннон [13], стр.127], в то время как многие наши ячейки не имеют задержек. Кроме того, конструкции Неймана базируются на очень слабых основных элементах (его ячейки могут находиться только в 29 различных состояниях), в то время как мы предполагаем использование очень сильных основных элементов (каждая ячейка может иметь любую из приблизительно 28000 структур, и каждая структура может иметь несколько состояний). Хотя предлагаемое здесь определение значительно дальше от естественных систем и менее экономично, чем у Неймана, оно позволяет легко сконструировать и представить различные виды растущих автоматов.
Основой каждого нашего растущего автомата является неограниченная двумерная решетка дискретных ячеек. В момент времени t=0 только ограниченное число этих ячеек содержит элементы, а остальные ячейки пусты (не имеют структуры). Структура в момент времени t+1 определяется в соответствии с правилами, которые будут объяснены ниже, структурой и полным состоянием системы в момент времени t. Эти правила не допускают, чтобы в каждый момент времени создавалась структура одновременно в нескольких ячейках, если их количество больше некоторого ограниченного числа.
Существуют четыре типа элементов, которые могут быть созданы в любой ячейке. Каждый элемент является двоичным в том смысле, что каждый его проводник или узел может находиться в двух состояниях.
1. ВЫЧИСЛИТЕЛЬНЫЙ ЭЛЕМЕНТ может представлять собой переключатель, задержку, комбинацию задержки и переключателя или просто обыкновенный провод. Каждую границу ячейки пересекает не более чем один вычислительный провод (показаны на фигурах жирными линиями), выходящий из ячейки. Конкретно основные вычислительные элементы следующие (фиг.5):
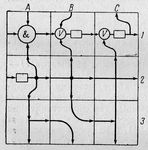
Фиг.5. Вычислительные элементы.
а) Любой переключатель с тремя входами и одним выходом, например ячейка A1 на фиг.5. Их число равно 2**10, если принять во внимание различные ориентации выходов (север, юг, восток и запад), и они дают возможность получить 256 истинностных функций от трех переменных. Заметим, что некоторые из этих истинностных функций не будут зависеть от некоторых входов, потому что эта категория включает в себя как частные случаи переключатели с количеством входов два, один и ноль. Эта категория включает в себя также и некоторые провода, такие, например, как провода ячеек A1, B1 и C1 на фиг.9.
б) Имеются элементы единичной задержки с одним выходом и с одним, двумя или тремя входами. Эти входы подаются через разрыв одной, двух или трех границ ячейки (ячейка B1 на фиг.5).
в) Имеются единичные задержки с двумя выходами и одним или двумя входами (например, ячейка C1 на фиг.5). Их всего 24.
г) Имеются единичные задержки с одним входом и тремя выходами (ячейка A2 на фиг.5). Их всего 4, поскольку вход может приходить со стороны одной из четырех границ ячейки.
д) Имеются провода, проходящие от одной границы к другой, через всю ячейку, у которой более двух границ. Поступающие в ячейку провода могут не соединяться и одну сторону может пересекать не более одного провода. Всего возможно 40 различных вариантов (ячейки B2, C2, A3, B3 и CЗ на фиг.5).
В сумме имеем 1120 различных вычислительных элементов.
2. Существуют НЕСУЩИЕ (scaffolding) ЭЛЕМЕНТЫ, которые имеют один входной провод и один или два выходных. Несущие провода показаны пунктирными линиями (ячейки B1, C1, B2 и C2 на фиг.6). Если рассматривать основные элементы с различными ориентациями как различные основные элементы, то в ячейке может быть любая из 24 различных несущих структур. Несущие элементы будут проводить сигналы построения. Разветвленный несущий элемент (например, ячейка B2 на фиг.6) имеет неявно выраженный переключатель. По условию этот переключатель имеет начальную установку. Установка его может изменяться с помощью переключающих последовательностей, о которых будет сказано ниже.
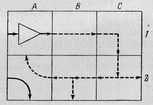
Фиг.6. Несущие и конструирующие элементы.
3. Любой несущий элемент может находиться в одной и той же ячейке с любым вычислительным элементом (см., например, ячейку A5 на фиг.8 ). Существует 24*1120 таких основных элементов.
4. Последний элемент - это ключ к процессу конструирования. Он называется КОНСТРУИРУЮЩИМ ЭЛЕМЕНТОМ и показан в ячейке A1 фиг.6. Конструирующий элемент получает сигналы построения из вычисляющей структуры и направляет их в несущую структуру. Сигналы построения проходят через несущую структуру и в конечном счете вызывают в ячейке построение структуры. Способ построения будет рассмотрен ниже. Конструирующий элемент может получать входные сигналы со стороны любой границы ячейки и передавать свои выходные сигналы к любой другой границе этой ячейки, следовательно, имеется 12 различных конструирующих элементов.
Ячейка может содержать любой элемент из этих четырех типов или же вообще не иметь никакой структуры. Всего имеет место 28049 (что меньше, чем 2**13) возможных случаев, каждый из которых будет изображаться двоичной последовательностью, называемой КОНСТРУИРУЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ. Эти последовательности будут строиться или храниться в структуре вычислительной машины и подаваться на конструирующий элемент. Длина проводов вычислителя или несущих проводов не ограничена, и мы примем идеализированное предположение, что сигналы проходят по проводам мгновенно.
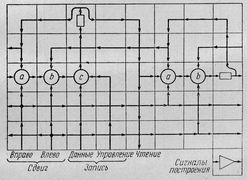
Фиг.7. Два "квадратика" ленты.
Способ функционирования системы и формулирование дальнейших правил лучше всего показать на примере. Мы покажем, как машина может управлять изменением величины ленты, устанавливая тем самым связь между растущими автоматами и обобщенными машинами Тьюринга. На фиг.7 показаны два "квадратика" ленты, каждый из которых запоминает одну двоичную цифру. Переключательные функции (a), (b) и (c) следующие. Пусть N, S, W и E обозначают соответственно северную, южную, западную и восточную границы ячейки. Выход переключателя (a) - E и задается уравнением
E(t) = [{S(t) & N(t)} | {S(t) & W(t)}].
Выход переключателя (b) - E и задается уравнением
E(t) = [{S(t) & W(t)} | {S(t) & N(t)}].
Выход переключателя (c) - N и задается уравнением
N(t) = [{E(t) & W(t)} | {E(t) & S(t)}].
Представим себе, что неизменное вычислительное устройство, связанное с лентой, подсоединяется ко входам и выходам фиг.7. Это вычислительное устройство может производить запись в левом квадратике и считывать хранимую в нем информацию. Оно может информацию на ленте сдвинуть вправо подачей сигнала "сдвиг вправо" и подобным же образом может сдвинуть информацию влево. Посылая сигналы в конструирующий элемент, оно может вызвать справа построение, уничтожение или изменение новых квадратиков ленты тем способом, который должен быть указан. Подобное же устройство существует и для видоизменения ленты слева. Рассмотрим далее построение квадратика ленты. Ячейке A6 на фиг. 8 требуется несущий элемент с разветвлением. Конструирующая последовательность, представляющая этот элемент, вырабатывается неизменным вычислительным устройством и подается в конструирующий элемент, который создает нужный элемент в той ячейке, с которой соприкасается его выход. Следующая конструирующая последовательность пройдет через конструирующий элемент в несущий элемент к его вертикальному выходу и создаст новый элемент в ячейке A5, которая соприкасается с выходом несущего элемента.

Фиг.8. Процесс построения.
В данном случае создаваемой структурой являются горизонтальный вычислительный провод и вертикальный несущий провод. Этот процесс повторяется для построения структур в следующих двух ячейках (A4 и A3). Несущие устройства этих ячеек не показаны, чтобы не усложнять изображение.
После завершения построения в оставшейся части колонки A нужно перенести деятельность в колонку B (фиг.9). Этот переход производится с помощью двоичной ПЕРЕКЛЮЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ, которая проходит через конструирующий элемент в несущий и изменяет установку переключателя несущего устройства ячейки A6 таким образом, что последующие конструирующие последовательности направляются в ячейку B6. После этого мы можем построить колонку B с помощью шести конструирующих последовательностей. Другая переключающая последовательность вновь переставляет переключатели в ячейках A6, A5 и дает возможность построить колонку C. Эта переключающая последовательность действует следующим образом. Она содержит два переключающих сигнала в кодированной форме. Первый сигнал должен быть принят ячейкой A6 и в данном случае должен оставить переключатель в прежнем положении. Второй переключающий сигнал должен пройти в ячейку B6 и изменить в этой ячейке установку переключателя таким образом, чтобы следующая конструирующая последовательность воздействовала бы на ячейку C6 (а не проходила через колонку B). В общем случае переключающая последовательность будет содержать столько переключающих сигналов, сколько имеется переключателей, через которые она должна пройти, чтобы попасть к последнему переключателю, положение которого должно быть изменено.
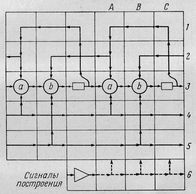
Фиг.9. Завершение построения нового "квадратика" ленты.
Центральное вычислительное устройство должно иметь возможность как сокращать, так и удлинять ленту, т.е. оно должно иметь возможность стирать структуру ячейки. Последнее обеспечивается с помощью двоичных РАЗРУШАЮЩИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. Разрушающая последовательность проходит через конструирующий элемент и через несущее устройство таким же образом, как и конструирующая последовательность. Однако разрушающая последовательность воздействует на ячейку, которая является конечным пунктом данного несущего канала, а не на следующую ячейку. Она разрушает элемент этой ячейки. Существует последовательность из 18 разрушающих последовательностей и 2 переключающих последовательностей, которая может разрушить только что созданный квадратик ленты.
Можно использовать также переключающую последовательность, за которой следуют 3 разрушающие последовательности для стирания элементов нижнего ряда (6), а затем использовать 3 конструирующие последовательности для создания несущего устройства, показанного на фиг.10. Таким образом, с помощью главной последовательности, состоящей из 21 конструирующей, 3 переключающих и 3 разрушающих последовательностей, мы покончили с новым квадратиком ленты и с несущим устройством, которое выбрано так, чтобы каждое повторение этой главной последовательности строило новый квадратик справа. Машина Тьюринга, повторяя эту главную последовательность, может построить ленту любой длины.
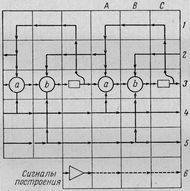
Фиг.10. Подготовка к следующему построению.
Описанный только что процесс построения занимает много тактов времени для создания одного квадратика ленты, и, следовательно, скорость его меньше, чем скорость, оговоренная в качестве условия для обобщенной машины Тьюринга, которая в течение одного такта обрабатывает один квадратик.
Это противоречие можно устранить двумя путями. Во-первых, можно было бы использовать растущие автоматы для имитации обобщенной машины Тьюринга. Для этого мы сопоставляем один большой цикл (т.е. время, требуемое для построения одного квадратика ленты) только что описанного растущего автомата с одним малым циклом (т.е. с одной единицей времени) обобщенной машины Тьюринга. Во-вторых, мы можем расширить базу нашего построения, добавляя элементы и провода, которые могут находиться более чем в двух состояниях. Вводить вычислительные элементы с числом состояний больше двух не обязательно. Достаточно, например, допустить, чтобы несущие элементы имели много состояний, а конструирующие элементы преобразовывали бы двоичные сигналы в надлежащим образом закодированные сигналы для несущих элементов. Заметим, что этот метод не связан с увеличением числа вычислительных или несущих основных элементов и не очень сильно увеличивает число конструирующих основных элементов.
Относительно определения растущих автоматов сказано вполне достаточно, чтобы выявить основные черты этого определения. Но чтобы определение было полным, нужно уточнить некоторые детали. Мы будем считать, что основной элемент становится активным сразу же, как только он создан. Это означает, что часть вычислительного устройства, которая уже построена, может начинать действовать до того, как будет завершено все вычислительное устройство. Это обстоятельство должно быть принято во внимание при построении нашего вычислительного устройства, как это часто делается при построении действительных вычислительных устройств, поскольку эти вычислительные устройства могут потребовать установки в стандартное первоначальное состояние перед тем, как они будут готовы к действию. Две конструирующие последовательности, поступающие от двух различных конструирующих элементов, могут приходить в ячейку в одно и то же время. Необходимо иметь правило старшинства для определения того, какая из них будет управлять построением. Существуют еще и другие детали, которые нужно уточнить, но здесь мы не будем на них останавливаться [Стоит, однако, отметить, что это определение не предотвращает возможности построения неудачно сформированных автоматов (например, имеющих переключательные циклы) и не существует эффективного критерия для того, чтобы определить, "разовьет" ли данный растущий автомат переключательные циклы. Можно было бы добавить некоторые ограничения, чтобы гарантировать, что каждый автомат будет хорошо сформированным. Самым простым ограничением было бы включение задержки в каждый переключатель, но это сильно усложняет автоматы и ограничивает их поведение. Менее строгим ограничением язляется требование, чтобы каждый переключатель или провод с выходом на южную границу содержал бы задержку. Однако мы не будем здесь заниматься исследованием различных возможностей].
Рассмотрим теперь, какие автоматы могут быть отнесены к растущим автоматам в смысле настоящего определения. Каждый неизменный автомат может быть представлен в нормальной форме (см. [4], разд.2.3), и эта нормальная форма может быть построена из вычислительных элементов в ячейках. Следовательно, каждый неизменный автомат является неизменяющимся растущим автоматом. Мы уже показали достаточно подробно, как можно построить изменяющуюся по длине ленту. Следовательно, если исключить вопрос о скорости, то каждая обобщенная машина Тьюринга является растущим автоматом.
Одним из растущих автоматов, которые могут быть построены, является универсальный конструктор фон Неймана. Его блок-схема показана на фиг.11. Универсальный конструктор C является ограниченной структурой и к нему может быть присоединена лента, содержащая спецификацию деталей любого числа автоматов, которые должны быть синтезированы. В общем случае каждая такая спецификация состоит из двух частей.
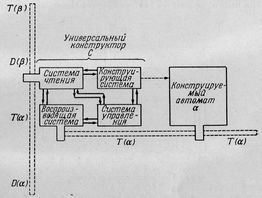
Фиг.11. Универсальный конструктор.
Первая часть спецификации - это главная последовательность конструирующих, переключающих и разрушающих последовательностей, которые обусловливают построение неизменной части искомых автоматов. Этой главной последовательностью является описание D(a). Вторая часть спецификации представляет собой содержимое T(a) ленты, которая должна быть построена и присоединена к автомату а.
Универсальный конструктор действует по указанию своего устройства управления следующим образом. Во-первых, считывающее устройство прочитывает D(a) и передает его конструктору. Одновременно конструктор строит а. Затем считывающее устройство прочитывает T(a). Одновременно с этим воспроизводящее устройство строит ленту, присоединяет ее к a и записывает на ней Т(a). Этот процесс затем повторяется таким образом, что в конце процесса построения T(a) записывается на ленте дважды. (Причина этого дублирования информации на ленте станет понятной из дальнейшего). В общем случае для каждого описания D(a) автомата и каждого содержимого ленты T(a) универсальный конструктор построит a и запишет T(a). T(a) записывается на ленте, присоединенной к автомату a.
Как показал фон Нейман, универсальный конструктор С совместно с соответствующей лентой будет сам себя воспроизводить (фиг.12). Пусть D(C) - последовательность конструирующих, переключающих и разрушающих последовательностей, которая полностью описывает C (включая его несущее устройство). Положим, что универсальный конструктор C, когда он начинает действовать, имеет ленту, на которой дважды записано D(C). Универсальный конструктор сначала прочтет D(C) и построит C. Затем он вторично прочтет D(C) и построит ленту, на которой дважды запишется D(C). (Это и есть причина указанного выше требования, чтобы T(a) записывалась дважды). Таким образом, универсальный конструктор C, снабженный лентой, которая содержит D(C), D(C), воспроизводит универсальный конструктор плюс ленту, содержащую D(C), D(C). Следовательно, С с лентой, содержащей D(C), D(C), воспроизводит сам себя. Новая комбинация C и ленты D(C), D(C) может тогда снова воспроизвести сама себя, и этот процесс будет повторяться до бесконечности.
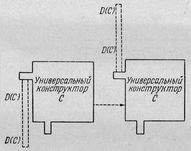
Фиг.12. Самовоспроизведение.
Если объединить универсальный конструктор с универсальным вычислительным устройством (т.е. с универсальной обобщенной машиной Тьюринга) и снабдить эту составную машину лентой, содержащей дважды ее описание, то этот объединенный автомат также будет воспроизводить себя (фиг.13). Следовательно, универсальный конструктор-вычислитель способен к самовоспроизведению.
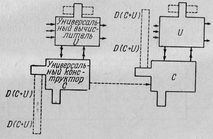
Фиг.13. Универсальный конструктор-вычислитель.
Джон фон Нейман показал, как строить универсальные конструирующие машины и самовоспроизводящиеся автоматы, в рамках общего определения автоматов [11-13]. Подробное определение автоматов Неймана содержится в его неопубликованной работе, поэтому я разработал другое определение. Модель Неймана намного ближе к биологическим явлениям, чем представленное здесь определение. Например, каждая ячейка у Неймана обладает единичной задержкой [См. Шеннон [13], стр.127], в то время как многие наши ячейки не имеют задержек. Кроме того, конструкции Неймана базируются на очень слабых основных элементах (его ячейки могут находиться только в 29 различных состояниях), в то время как мы предполагаем использование очень сильных основных элементов (каждая ячейка может иметь любую из приблизительно 28000 структур, и каждая структура может иметь несколько состояний). Хотя предлагаемое здесь определение значительно дальше от естественных систем и менее экономично, чем у Неймана, оно позволяет легко сконструировать и представить различные виды растущих автоматов.
Основой каждого нашего растущего автомата является неограниченная двумерная решетка дискретных ячеек. В момент времени t=0 только ограниченное число этих ячеек содержит элементы, а остальные ячейки пусты (не имеют структуры). Структура в момент времени t+1 определяется в соответствии с правилами, которые будут объяснены ниже, структурой и полным состоянием системы в момент времени t. Эти правила не допускают, чтобы в каждый момент времени создавалась структура одновременно в нескольких ячейках, если их количество больше некоторого ограниченного числа.
Существуют четыре типа элементов, которые могут быть созданы в любой ячейке. Каждый элемент является двоичным в том смысле, что каждый его проводник или узел может находиться в двух состояниях.
1. ВЫЧИСЛИТЕЛЬНЫЙ ЭЛЕМЕНТ может представлять собой переключатель, задержку, комбинацию задержки и переключателя или просто обыкновенный провод. Каждую границу ячейки пересекает не более чем один вычислительный провод (показаны на фигурах жирными линиями), выходящий из ячейки. Конкретно основные вычислительные элементы следующие (фиг.5):

Фиг.5. Вычислительные элементы.
а) Любой переключатель с тремя входами и одним выходом, например ячейка A1 на фиг.5. Их число равно 2**10, если принять во внимание различные ориентации выходов (север, юг, восток и запад), и они дают возможность получить 256 истинностных функций от трех переменных. Заметим, что некоторые из этих истинностных функций не будут зависеть от некоторых входов, потому что эта категория включает в себя как частные случаи переключатели с количеством входов два, один и ноль. Эта категория включает в себя также и некоторые провода, такие, например, как провода ячеек A1, B1 и C1 на фиг.9.
б) Имеются элементы единичной задержки с одним выходом и с одним, двумя или тремя входами. Эти входы подаются через разрыв одной, двух или трех границ ячейки (ячейка B1 на фиг.5).
в) Имеются единичные задержки с двумя выходами и одним или двумя входами (например, ячейка C1 на фиг.5). Их всего 24.
г) Имеются единичные задержки с одним входом и тремя выходами (ячейка A2 на фиг.5). Их всего 4, поскольку вход может приходить со стороны одной из четырех границ ячейки.
д) Имеются провода, проходящие от одной границы к другой, через всю ячейку, у которой более двух границ. Поступающие в ячейку провода могут не соединяться и одну сторону может пересекать не более одного провода. Всего возможно 40 различных вариантов (ячейки B2, C2, A3, B3 и CЗ на фиг.5).
В сумме имеем 1120 различных вычислительных элементов.
2. Существуют НЕСУЩИЕ (scaffolding) ЭЛЕМЕНТЫ, которые имеют один входной провод и один или два выходных. Несущие провода показаны пунктирными линиями (ячейки B1, C1, B2 и C2 на фиг.6). Если рассматривать основные элементы с различными ориентациями как различные основные элементы, то в ячейке может быть любая из 24 различных несущих структур. Несущие элементы будут проводить сигналы построения. Разветвленный несущий элемент (например, ячейка B2 на фиг.6) имеет неявно выраженный переключатель. По условию этот переключатель имеет начальную установку. Установка его может изменяться с помощью переключающих последовательностей, о которых будет сказано ниже.

Фиг.6. Несущие и конструирующие элементы.
3. Любой несущий элемент может находиться в одной и той же ячейке с любым вычислительным элементом (см., например, ячейку A5 на фиг.8 ). Существует 24*1120 таких основных элементов.
4. Последний элемент - это ключ к процессу конструирования. Он называется КОНСТРУИРУЮЩИМ ЭЛЕМЕНТОМ и показан в ячейке A1 фиг.6. Конструирующий элемент получает сигналы построения из вычисляющей структуры и направляет их в несущую структуру. Сигналы построения проходят через несущую структуру и в конечном счете вызывают в ячейке построение структуры. Способ построения будет рассмотрен ниже. Конструирующий элемент может получать входные сигналы со стороны любой границы ячейки и передавать свои выходные сигналы к любой другой границе этой ячейки, следовательно, имеется 12 различных конструирующих элементов.
Ячейка может содержать любой элемент из этих четырех типов или же вообще не иметь никакой структуры. Всего имеет место 28049 (что меньше, чем 2**13) возможных случаев, каждый из которых будет изображаться двоичной последовательностью, называемой КОНСТРУИРУЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТЬЮ. Эти последовательности будут строиться или храниться в структуре вычислительной машины и подаваться на конструирующий элемент. Длина проводов вычислителя или несущих проводов не ограничена, и мы примем идеализированное предположение, что сигналы проходят по проводам мгновенно.

Фиг.7. Два "квадратика" ленты.
Способ функционирования системы и формулирование дальнейших правил лучше всего показать на примере. Мы покажем, как машина может управлять изменением величины ленты, устанавливая тем самым связь между растущими автоматами и обобщенными машинами Тьюринга. На фиг.7 показаны два "квадратика" ленты, каждый из которых запоминает одну двоичную цифру. Переключательные функции (a), (b) и (c) следующие. Пусть N, S, W и E обозначают соответственно северную, южную, западную и восточную границы ячейки. Выход переключателя (a) - E и задается уравнением
E(t) = [{S(t) & N(t)} | {S(t) & W(t)}].
Выход переключателя (b) - E и задается уравнением
E(t) = [{S(t) & W(t)} | {S(t) & N(t)}].
Выход переключателя (c) - N и задается уравнением
N(t) = [{E(t) & W(t)} | {E(t) & S(t)}].
Представим себе, что неизменное вычислительное устройство, связанное с лентой, подсоединяется ко входам и выходам фиг.7. Это вычислительное устройство может производить запись в левом квадратике и считывать хранимую в нем информацию. Оно может информацию на ленте сдвинуть вправо подачей сигнала "сдвиг вправо" и подобным же образом может сдвинуть информацию влево. Посылая сигналы в конструирующий элемент, оно может вызвать справа построение, уничтожение или изменение новых квадратиков ленты тем способом, который должен быть указан. Подобное же устройство существует и для видоизменения ленты слева. Рассмотрим далее построение квадратика ленты. Ячейке A6 на фиг. 8 требуется несущий элемент с разветвлением. Конструирующая последовательность, представляющая этот элемент, вырабатывается неизменным вычислительным устройством и подается в конструирующий элемент, который создает нужный элемент в той ячейке, с которой соприкасается его выход. Следующая конструирующая последовательность пройдет через конструирующий элемент в несущий элемент к его вертикальному выходу и создаст новый элемент в ячейке A5, которая соприкасается с выходом несущего элемента.

Фиг.8. Процесс построения.
В данном случае создаваемой структурой являются горизонтальный вычислительный провод и вертикальный несущий провод. Этот процесс повторяется для построения структур в следующих двух ячейках (A4 и A3). Несущие устройства этих ячеек не показаны, чтобы не усложнять изображение.
После завершения построения в оставшейся части колонки A нужно перенести деятельность в колонку B (фиг.9). Этот переход производится с помощью двоичной ПЕРЕКЛЮЧАЮЩЕЙ ПОСЛЕДОВАТЕЛЬНОСТИ, которая проходит через конструирующий элемент в несущий и изменяет установку переключателя несущего устройства ячейки A6 таким образом, что последующие конструирующие последовательности направляются в ячейку B6. После этого мы можем построить колонку B с помощью шести конструирующих последовательностей. Другая переключающая последовательность вновь переставляет переключатели в ячейках A6, A5 и дает возможность построить колонку C. Эта переключающая последовательность действует следующим образом. Она содержит два переключающих сигнала в кодированной форме. Первый сигнал должен быть принят ячейкой A6 и в данном случае должен оставить переключатель в прежнем положении. Второй переключающий сигнал должен пройти в ячейку B6 и изменить в этой ячейке установку переключателя таким образом, чтобы следующая конструирующая последовательность воздействовала бы на ячейку C6 (а не проходила через колонку B). В общем случае переключающая последовательность будет содержать столько переключающих сигналов, сколько имеется переключателей, через которые она должна пройти, чтобы попасть к последнему переключателю, положение которого должно быть изменено.

Фиг.9. Завершение построения нового "квадратика" ленты.
Центральное вычислительное устройство должно иметь возможность как сокращать, так и удлинять ленту, т.е. оно должно иметь возможность стирать структуру ячейки. Последнее обеспечивается с помощью двоичных РАЗРУШАЮЩИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ. Разрушающая последовательность проходит через конструирующий элемент и через несущее устройство таким же образом, как и конструирующая последовательность. Однако разрушающая последовательность воздействует на ячейку, которая является конечным пунктом данного несущего канала, а не на следующую ячейку. Она разрушает элемент этой ячейки. Существует последовательность из 18 разрушающих последовательностей и 2 переключающих последовательностей, которая может разрушить только что созданный квадратик ленты.
Можно использовать также переключающую последовательность, за которой следуют 3 разрушающие последовательности для стирания элементов нижнего ряда (6), а затем использовать 3 конструирующие последовательности для создания несущего устройства, показанного на фиг.10. Таким образом, с помощью главной последовательности, состоящей из 21 конструирующей, 3 переключающих и 3 разрушающих последовательностей, мы покончили с новым квадратиком ленты и с несущим устройством, которое выбрано так, чтобы каждое повторение этой главной последовательности строило новый квадратик справа. Машина Тьюринга, повторяя эту главную последовательность, может построить ленту любой длины.

Фиг.10. Подготовка к следующему построению.
Описанный только что процесс построения занимает много тактов времени для создания одного квадратика ленты, и, следовательно, скорость его меньше, чем скорость, оговоренная в качестве условия для обобщенной машины Тьюринга, которая в течение одного такта обрабатывает один квадратик.
Это противоречие можно устранить двумя путями. Во-первых, можно было бы использовать растущие автоматы для имитации обобщенной машины Тьюринга. Для этого мы сопоставляем один большой цикл (т.е. время, требуемое для построения одного квадратика ленты) только что описанного растущего автомата с одним малым циклом (т.е. с одной единицей времени) обобщенной машины Тьюринга. Во-вторых, мы можем расширить базу нашего построения, добавляя элементы и провода, которые могут находиться более чем в двух состояниях. Вводить вычислительные элементы с числом состояний больше двух не обязательно. Достаточно, например, допустить, чтобы несущие элементы имели много состояний, а конструирующие элементы преобразовывали бы двоичные сигналы в надлежащим образом закодированные сигналы для несущих элементов. Заметим, что этот метод не связан с увеличением числа вычислительных или несущих основных элементов и не очень сильно увеличивает число конструирующих основных элементов.
Относительно определения растущих автоматов сказано вполне достаточно, чтобы выявить основные черты этого определения. Но чтобы определение было полным, нужно уточнить некоторые детали. Мы будем считать, что основной элемент становится активным сразу же, как только он создан. Это означает, что часть вычислительного устройства, которая уже построена, может начинать действовать до того, как будет завершено все вычислительное устройство. Это обстоятельство должно быть принято во внимание при построении нашего вычислительного устройства, как это часто делается при построении действительных вычислительных устройств, поскольку эти вычислительные устройства могут потребовать установки в стандартное первоначальное состояние перед тем, как они будут готовы к действию. Две конструирующие последовательности, поступающие от двух различных конструирующих элементов, могут приходить в ячейку в одно и то же время. Необходимо иметь правило старшинства для определения того, какая из них будет управлять построением. Существуют еще и другие детали, которые нужно уточнить, но здесь мы не будем на них останавливаться [Стоит, однако, отметить, что это определение не предотвращает возможности построения неудачно сформированных автоматов (например, имеющих переключательные циклы) и не существует эффективного критерия для того, чтобы определить, "разовьет" ли данный растущий автомат переключательные циклы. Можно было бы добавить некоторые ограничения, чтобы гарантировать, что каждый автомат будет хорошо сформированным. Самым простым ограничением было бы включение задержки в каждый переключатель, но это сильно усложняет автоматы и ограничивает их поведение. Менее строгим ограничением язляется требование, чтобы каждый переключатель или провод с выходом на южную границу содержал бы задержку. Однако мы не будем здесь заниматься исследованием различных возможностей].
Рассмотрим теперь, какие автоматы могут быть отнесены к растущим автоматам в смысле настоящего определения. Каждый неизменный автомат может быть представлен в нормальной форме (см. [4], разд.2.3), и эта нормальная форма может быть построена из вычислительных элементов в ячейках. Следовательно, каждый неизменный автомат является неизменяющимся растущим автоматом. Мы уже показали достаточно подробно, как можно построить изменяющуюся по длине ленту. Следовательно, если исключить вопрос о скорости, то каждая обобщенная машина Тьюринга является растущим автоматом.
Одним из растущих автоматов, которые могут быть построены, является универсальный конструктор фон Неймана. Его блок-схема показана на фиг.11. Универсальный конструктор C является ограниченной структурой и к нему может быть присоединена лента, содержащая спецификацию деталей любого числа автоматов, которые должны быть синтезированы. В общем случае каждая такая спецификация состоит из двух частей.

Фиг.11. Универсальный конструктор.
Первая часть спецификации - это главная последовательность конструирующих, переключающих и разрушающих последовательностей, которые обусловливают построение неизменной части искомых автоматов. Этой главной последовательностью является описание D(a). Вторая часть спецификации представляет собой содержимое T(a) ленты, которая должна быть построена и присоединена к автомату а.
Универсальный конструктор действует по указанию своего устройства управления следующим образом. Во-первых, считывающее устройство прочитывает D(a) и передает его конструктору. Одновременно конструктор строит а. Затем считывающее устройство прочитывает T(a). Одновременно с этим воспроизводящее устройство строит ленту, присоединяет ее к a и записывает на ней Т(a). Этот процесс затем повторяется таким образом, что в конце процесса построения T(a) записывается на ленте дважды. (Причина этого дублирования информации на ленте станет понятной из дальнейшего). В общем случае для каждого описания D(a) автомата и каждого содержимого ленты T(a) универсальный конструктор построит a и запишет T(a). T(a) записывается на ленте, присоединенной к автомату a.
Как показал фон Нейман, универсальный конструктор С совместно с соответствующей лентой будет сам себя воспроизводить (фиг.12). Пусть D(C) - последовательность конструирующих, переключающих и разрушающих последовательностей, которая полностью описывает C (включая его несущее устройство). Положим, что универсальный конструктор C, когда он начинает действовать, имеет ленту, на которой дважды записано D(C). Универсальный конструктор сначала прочтет D(C) и построит C. Затем он вторично прочтет D(C) и построит ленту, на которой дважды запишется D(C). (Это и есть причина указанного выше требования, чтобы T(a) записывалась дважды). Таким образом, универсальный конструктор C, снабженный лентой, которая содержит D(C), D(C), воспроизводит универсальный конструктор плюс ленту, содержащую D(C), D(C). Следовательно, С с лентой, содержащей D(C), D(C), воспроизводит сам себя. Новая комбинация C и ленты D(C), D(C) может тогда снова воспроизвести сама себя, и этот процесс будет повторяться до бесконечности.

Фиг.12. Самовоспроизведение.
Если объединить универсальный конструктор с универсальным вычислительным устройством (т.е. с универсальной обобщенной машиной Тьюринга) и снабдить эту составную машину лентой, содержащей дважды ее описание, то этот объединенный автомат также будет воспроизводить себя (фиг.13). Следовательно, универсальный конструктор-вычислитель способен к самовоспроизведению.

Фиг.13. Универсальный конструктор-вычислитель.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
#5. НЕКОТОРЫЕ ПРОБЛЕМЫ РАСТУЩИХ АВТОМАТОВ
Поскольку растущие автоматы включают в себя неизменные автоматы и обобщенные машины Тьюринга как частные случаи, то проблемы, изложенные в разд.3, относятся также и к растущим автоматам. Существует проблема иного типа, совершенно отличная от всех рассмотренных ранее проблем и приложимая к автоматам любого вида. Это проблема связи между циклической сложностью структуры автомата и его поведением. Поскольку наше прежнее рассмотрение обобщенной машины Тьюринга не выявило, какие циклы подразумеваются на ленте, эту проблему необходимо было отложить до настоящего раздела.
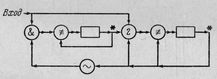
Фиг.14. Автомат второй степени. Троичный счетчик.
Вначале рассмотрим эту проблему для случая неизменного автомата. Структуру неизменного автомата можно разделить на МАКСИМАЛЬНЫЕ ЦИКЛЫ. Степенью максимального цикла является число элементов единичных задержек в этом цикле, а степенью неизменного автомата является максимальная степень его максимальных циклов [Эти понятия подробно поясняются в разд.4.1 работы Беркса и Хао Вана [4]]. На фиг.14 изображен один максимальный цикл степени 2. Выходные узлы помечены звездочками. На фиг.15 показано шесть максимальных циклов, из которых каждый имеет степень 1. Таким образом, на фиг.15 изображен автомат 1-й степени. Выходные узлы также помечены звездочками.
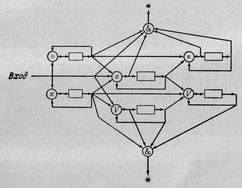
Фиг.15. Автомат первой степени.
Как, однако, степень автомата связана с его поведением? Существует ли некоторая критическая степень n такая, что все поведения неизменных автоматов могут быть реализованы с помощью структур этой степени или степени более низкой? Было высказано предположение, что такой степени не существует. Главная проблема остается открытой, но Дж.Голланд показал, что никакой автомат степени 1 не сможет реализовать поведение автомата, изображенного на фиг.14, который представляет собой троичный счетчик [14].
Эта же проблема может быть поставлена по отношению к вычислению неизменного автомата: существует ли некоторая критическая степень m такая, что все вычисления неизменных автоматов могут быть реализованы с помощью структур этой степени или степени более низкой? Обе проблемы могут быть распространены на обобщенные машины Тьюринга и на растущие автоматы. Конечно, структура любого растущего автомата меняется со временем, а следовательно, меняется также и степень его структуры. Но мы можем определить степень растущего автомата как максимальную степень любой из его структур в любой момент времени для любой истории входа, если этот максимум существует. В противном случае степень автомата является неопределенной.
Теперь мы можем сформулировать следующие вопросы, касающиеся растущих автоматов: 1) Существует ли некоторая конечная степень n такая, что все поведения могут быть реализованы с помощью растущих автоматов этой или меньшей степени? 2) Существует ли некоторая конечная степень m такая, что все вычисления могут быть реализованы с помощью растущих автоматов этой или меньшей степени? Возможно, покажется, что ответом на оба эти вопроса является "нет", поскольку очевидно, что в обоих случаях нет верхнего предела для длины требуемых лент, и лента, построение которой описано в предыдущем разделе, имеет неопределенную степень. Однако можно построить ленту конечной степени, используя изолированные квадратики и движение вдоль ленты головки считывания - записи вместо сдвига информации вдоль ленты. Для того чтобы записать в квадратик "1", автомат строит цикл с задержкой, в котором циркулирует импульс. Для запоминания "0" он строит цикл с задержкой, последовательными состояниями которого является 0. Неизменная часть машины может высылать длинный провод для осуществления таких записей и с помощью другого провода может прочитывать содержимое цикла с задержкой. Содержимое квадратика может быть изменено разрушением существующего в нем цикла с задержкой и построения нового. Когда неизменная часть автомата не производит ни считывания из квадратика, ни записи в него, то она не имеет с ним никакой связи. Таким путем может быть построена обобщенная машина Тьюринга, которая имеет неизменную степень.
Существуют и другие меры сложности обратной связи, которые представляют интерес. Рассмотрим неизменный автомат с n единичными задержками x1, x2, x3, ..., xn. Пусть f(xi) - число задержек, которые прямо и непосредственно воздействуют на элемент задержки xi, т.е. выходы которых управляют входом xi через переключательные элементы. На фиг.14 f(x1) = f(x2) = 2, поскольку каждая задержка управляет сама собой и другой задержкой через переключатель. Среднюю меру сложности обратной связи F для автомата определим как
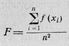
F = SUM[i=1,n]f(xi) / n**2
Существуют "полностью связанные" автоматы, для которых F = 1 [См. [4], стр.291. Конечно, каждый автомат может быть представлен в нормальной форме, которая обладает этим свойством, но нас интересуют здесь сети в "приведенной форме", в которой все неподходящие (неэффективные) входы переключателей устранены]. На фиг.14 в качестве примера показан такой автомат. Но в действительных системах величина сложности обратной связи F обычно много меньше максимума. Для системы, показанной на фиг.15, F = 7/18. Для типичной современной цифровой вычислительной машины F мало. (Заметим, что такая вычислительная машина составляет приблизительно один максимальный цикл, не считая лент). Это обстоятельство имеет прямое отношение к возможности понять большую цифровую машину. Так как отношение числа фактических линий обратной связи (от задержек) к числу возможных линий обратной связи мало, то различные части вычислительной машины имеют значительную местную автономию и поэтому могут быть поняты изолированно от остальных частей машины. (Единообразия внутри этих частей также облегчают нам их понимание). Стоит отметить, что если нейроны представлены в виде переключателей и задержек, то для нервной системы человека F также мало.
Обратимся теперь к некоторым проблемам, которые специфичны только для растущих автоматов. Первой из них является проблема, которая рассматривалась фон Нейманом: насколько сложным должен быть самовоспроизводящийся автомат? В своей модели Нейман использовал ячейки, которые могли иметь около 30 состояний, и по его оценке для самовоспроизведения было бы достаточно около 200000 таких ячеек. Ячейки наших моделей намного сложнее, поскольку ячейка может содержать любой из приблизительно 2**15 различных элементов, и каждый элемент может находиться в нескольких состояниях. Но подсчета числа состояний недостаточно, потому что существует много способов, которыми эти состояния могут быть использованы. Например, основной элемент, который может передавать свою структуру к соседней ячейке по получении одного импульса, намного мощнее, чем любой из принятых нами основных элементов.
Различные модели растущих автоматов можно сравнивать, сведя их к одной общей системе. Например, можно имитировать как модель фон Неймана, так и наши модели с помощью неограниченных однородных неизменных сетей из переключающих элементов и задержек. Мы покажем, как это может быть осуществлено для модели, соответствующей нашему определению. Каждая ячейка имитируется неизменной сетью внутри квадратика. Эти квадратики повторяются неограниченно таким же образом, как ячейки нашей модели. Каждый неизменный автомат в квадратике содержит регистр, главный переключатель, переключатели и задержки, которые выполняют несущие функции и функции вычисления первоначальной ячейки. Каждая неизменная сеть квадратика связана входами и выходами с четырьмя соседними квадратиками. Эти входы и выходы используются в качестве несущих и вычислительных проводов. Конструирующая последовательность, которая должна воздействовать на данный квадратик, пересылается в регистр этого квадратика. Регистр в этом случае с помощью главного переключателя определяет связи переключателей и задержек. Таким образом, неизменный автомат квадратика имитирует первоначальную ячейку.
Для запоминания установок переключателей разветвленных несущих элементов можно использовать триггеры. Переключающая последовательность, проходящая через квадратик, устанавливает триггер надлежащим образом и затем проходит дальше для установки триггеров, относящихся к другим несущим ветвям. Разрушающая последовательность поступает в регистр и восстанавливает первоначальное состояние квадратика.
Заметим, что для нашего определения растущих автоматов необходима только одна неограниченная однородная структура (а именно неограниченное повторение неизменного автомата в квадратиках). Различные автоматы представляются (имитируются) различными состояниями этой структуры, следовательно, мы здесь используем поведение автоматов для имитации структуры автоматов.
Модель фон Неймана может имитироваться подобным же образом. В этом случае сложность самовоспроизводящегося автомата фон Неймана можно сравнить со сложностью описанного нами самовоспроизводящегося автомата, подсчитав число переключателей и задержек, использованных в первоначальной структуре каждого из них. Точно определяя таким методом общий эталон, мы можем свести проблему минимальной сложности воспроизведения ячейки к строго логической проблеме. Имеющийся опыт с задачами минимизации говорит о том, что было бы невероятно трудно, если не вовсе невозможно, найти минимальное решение и доказать, что оно минимально. Можно, однако, получить оценку минимальной сложности, если использовать вычислительную машину для того, чтобы облегчить выработку различных возможных построений.
Существует много других концепций растущих автоматов, которые заслуживают исследования, и они, несомненно, вызовут к жизни новые проблемы. В первой модели фон Неймана опорные элементы, чувствительные органы, соединительные узлы и вычислительные элементы свободно плавали в озере. Как указывает Шеннон ([13], стр.126-127), из-за сложности возможных в этом случае движений было бы чрезвычайно трудно дать точный план универсального конструктора с такой моделью. Можно, однако, так расширить данное нами определение растущих автоматов, чтобы без особого труда получить некоторые эффекты первой модели фон Неймана. Например, можно добавить ЧУВСТВИТЕЛЬНЫЙ ЭЛЕМЕНТ, который прочитывал бы структуру и содержание (состояние) ячейки. Чувствительный элемент проводил бы ЧУВСТВИТЕЛЬНЫЕ КАНАЛЫ через ячейки подобно тому, как конструирующим элементом создается несущее устройство. Эти чувствительные каналы не нарушали бы структуру, уже имеющуюся в ячейках, а передавали бы информацию об исследуемой ячейке к чувствительному элементу. С помощью процесса, подобного процессу построения, описанному в предыдущем разделе, автомат мог бы оппределить, какой элемент содержится в ячейке и каково состояние этого элемента в данный момент времени. Эта информация может быть использована различным образом, например она может быть использована для обнаружения ошибки, которая затем может быть исправлена конструирующим элементом.
Далее возникает вопрос: как много "самопознания" может приобрести и сохранить автомат? Этот вопрос представляет интерес для теории самоорганизующихся систем, поскольку один из возможных методов самоорганизации системы заключается в том, что система имеет картину своей структуры и поведения и использует эту картину для своего собственного управления. Совершенно ясно, что количество знаний о себе самом, которое может приобрести и содержать автомат, имеет предел. Например, возможно, что растущий автомат будет изменяться быстрее, чем его чувствительные элементы смогут чувствовать эти изменения. Существуют также и логические ограничения. Так, если используются все состояния автомата, то соответствующая часть системы не может иметь полностью детализованную картину целого, потому что целое, будучи больше части, будет иметь больше состояний, чем эта часть.
Здесь имеют место логические парадоксы, связанные с ссылками на себя. Хорошо известно, что некоторые ссылочные утверждения ведут к противоречиям. Так, предложение "это предложение ложно" является ложным, если оно истинно (потому что оно говорит о себе, что оно ложно) и является истинным, если оно ложно (потому что если ложно то, что оно ложно, то оно истинно), и, следовательно, оно является как истинным, так и ложным. Для разрешения таких парадоксов Рассел предложил [15] формальный язык, в котором не могут быть сформулированы никакие утверждения со ссылкой на себя. Предложение недопустимости утверждений со ссылкой на себя в формальной системе является, однако, слишком сильным, так как очевидно, что нет ничего ошибочного в следующих утверждениях со ссылкой на себя: 1) "это предложение написано на русском языке" [В оригинале - на английском языке.- Прим. перев.], "это предложение написано по меньшей мере один раз". Оба эти предложения, конечно, истинны. Они иллюстрируют тот факт, что предложение может ссылаться на свои физические свойства, и все же при этом не возникает противоречия. Имеют место также случаи, когда предложение может ссылаться на свои структурные или синтаксические свойства без возникновения противоречий. Предложение: "это предложение грамматически верно" относится к таким предложениям. Другим примером формулы, ссылающейся на свою собственную структуру, является неразрешимая формула, составленная Геделем [Как Гедель отметил в своих лекциях в Институте перспективных исследований (Принстон) в 1933-1934гг., его неразрешимая формула показывает, что решение парадоксов Расселом является слишком экстремальным, потому что неразрешимая формула (истинно) говорит о себе, что она не доказуема. Он соглашался с Расселом, что должны быть некоторые ограничения того, что может сказать о себе предложение, и предположил, что никакое предложение не может правильно говорить о своей истинности и ложности] в его доказательстве неполноты арифметики. Такова формула F, которая в некотором смысле утверждает: "F не доказуемо" [16]. Доказуемость является чисто синтаксическим понятием, поэтому формула ссылается на свой собственный синтаксис, и при этой ссылке не возникает противоречия.
Таким образом, предложение может содержать описание некоторых своих собственных синтаксических или структурных свойств. Отметим сходство этого с тем, что мы имели в предыдущем разделе, а именно что самовоспроизводящийся автомат C содержит в себе описание D(C) своей собственной структуры. Он, однако, не содержит описания состояния своего содержимого (кроме своего начального однородного состояния). Это наводит на мысль, что автомат с чувствительным элементом, вероятно, сможет чувствовать свою собственную структуру, а также может построить и сохранить описание своей структуры. Но создание такого автомата, конечно, представляет еще проблему.
На первый взгляд может показаться, что автомат не может хранить описание своей собственной структуры, потому что сколько бы ячеек он ни имел, для хранения описания потребовалось бы большее число ячеек, подобно парадоксу Тристана Шенди [Тристану Шенди потребовалось два года для описания первых двух дней своей жизни (см. Sterne L., The Life and Opinions of Tristam Shandy, Gentleman, vol.4, ch.13)]. Это возражение неосновательно, потому что в описании можно использовать индексы, символы суммирования и количественные характеристики. Как было показано выше, для описания одного квадратика ленты используется определенная главная последовательность. При составлении описания D(a) структуры автомата a эта главная последовательность не повторяется для каждого квадратика ленты, который должен быть построен, а повторно используется одна и та же последовательность способом, который хорошо известен всем программистам. Это может быть сделано потому, что лента имеет в высшей степени единообразную структуру.
Из этих соображений следует, что для выработки описания собственной структуры, которое было бы настолько мало, чтобы его можно было хранить в этой же структуре, автомат должен обнаруживать некоторые единообразия своей структуры. Он может, например, систематически просматривать структуру каждой из своих ячеек и затем анализировать результаты для того, чтобы найти для них более компактную формулировку, Следовательно, количество информации о своей собственной структуре, которое может приобрести и хранить растущий автомат, зависит от того, какие имеются машинные приемы для обнаружения единообразия структуры.
ЛИТЕРАТУРА
1. Neumann J., "Probabilistic logics and the synthesis of reliable organisms from unreliable components", Automata Studies, (ed. C.E.Shannon and J.McCarthy), Princeton, 1956, pp.43-98; русский перевод см. сб."Автоматы", ИЛ, 1956.
2. К1ееne S.С., Introduction to Metamathematics, New York, 1952; русский перевод см. Клини С., Введение в метаматематику, ИЛ, 1957; Davis M., Computability and Unsolvability, New York., 1958.
3. Burks A.W., Wright J., "Theory of logical nets", Proc. IRE, 41, 1357-1365 (1953).
4. Burks A.W., Hао Wang, "The logic of automata", J. Assoc. Computing Mach., 4, 193-218, 279-297 (1947).
5. Copi I.M., Elgot С.С., Wright J.В., "Realization of events by logical nets", J. Assoc. Computing Mach., 5, 181-196 (1958).
6. Moore E.F., "Gedanken-experiments on sequential machines", Automata Studies, pp.129-153; см. [1].
7. Buchi J.R.,. Elgot С.С., Wright J.В., "The nonexistence of certain algorithms of finite automata theory", Abstract, Not. Amer. Math. Soc., 5, #1, 98 (1958).
8. Church A., "Application of Recursive Arithmetic in the Theory of Computers and Automata", Notes from Summer Session Course in Advanced Theory of the Logical Design of Digital Computers, Univ. Michigan, 1958.
9. Elgоt С.С., Buchi J.R., "Decision problems of weak second order arithmetics and finite automata, Part 1", Abstract, Not. Amer. Math. Soc., 5, #7, 834 (1958).
10. Elgot С.С., "Decision problems of weak second order arithmetics and finite automata, Part II", Abstract, Not. Amer. Math. Soc., 6, #1, 48 (1959).
11. Neumann J., "The general and logical theory of automata", Cerebral Mechanisms in Behavior - The Hixon Symposium (ed. L.A.Jeffress), New York, 1951, pp.1-31; см. также The World of Mathematics (ed. J.R.Newman), vol.4, pp.2070-2098.
12. Кemenу J.G., "Man viewed as a machine", Sci. Amer., 192, 58-67 (1955).
13. Schannon С.Е., "Neumann's contributions to automata theory", Bull. Amer. Math. Soc, 64, 123-129 (1958).
14. Hоlland J.H., "Cycles in logical nets", диссертация, Univ. Michigan, 1959.
15. Russell В., Whitehead A.N., Principia Mathematica, Introduction ("The Theory of Logical Types"), Chap.II.
16. Godel K., "Ueber formal unentscheidbare Saetze der Principia Mathematica und verwandter Systeme", Monat. Math. u. Phys., 38, 173-198 (1931).
ОБСУЖДЕНИЕ
Минский: Хотелось бы узнать, имеются ли какие-либо доказательства для Вашего последнего утверждения? Мне кажется, что автомат довольно простого вида вполне может выяснить все о своей структуре, выяснить, какой она была в определенный момент времени, просто создавая что-то вроде оттиснутой на резине копии своей структуры, и определить, таким образом, свое полное состояние в тот же момент времени.
Это не тривально, это способ обеспечить, чтобы каждая ячейка имела по существу двойные ряды состояний, и этот способ вытекает из того, о чем Вы слышали как о рядовой задаче при посылке волн, которые распространяются через автомат с одномерной или двумерной структурой и одновременно передают полную структуру этого автомата другому слою. На этой стадии машина может не "торопясь исследовать каждую деталь того, что являлось ее структурой в определенный момент, после того как она выработала команду сделать копию, а это равнозначно по смыслу идее о машине, которая не только имеет структуру описанного Вами типа, но имеет еще и руку с глазом на конце и, вероятно, даже располагает зеркалом, так что она может выяснить даже структуру самого глаза. Но, кроме того, она может сделать то же самое и с замороженной копией самой себя, поэтому она может видеть все состояния. Таким образом, у меня возник довольно серьезный вопрос (интересно, возник ли он и у других): можете ли Вы сделать какие-либо обобщения, связанные с самовоспроизведением, которые говорили бы, что, для того чтобы понять самое себя или знать свое состояние, Вы в самом деле должны делать обобщения. Я не вижу, как фон Нейману удалось показать это, и не думаю, чтобы это было достаточно обосновано.
Беркс: Я говорил о ситуации построения универсальной вычислительной машины с не очень единообразной структурой (хотя, очевидно, некоторые единообразия и могли существовать), которая имела, например, один чувствительный элемент. Задача заключается в составлении такой программы, чтобы этот чувствительный элемент делал надлежащий обзор автомата и чтобы автомат закончил описанием самого себя, хранящимся в нем самом. Я не имел в виду, что это не может быть сделано, а хотел лишь сказать, что в этом общем случае необходимо, чтобы автомат имел некоторую возможность резюмировать свое описание.
Соломонов (Фирма "Цейтор", Кембридж, шт.Массачусетс): Мой вопрос касается мотивов для изучения самовоспроизводящихся машин и растущих автоматов. Мне кажется, что в той степени, в какой речь идет о практической задаче создания самовоспроизводящихся машин или заводов, мы можем с теоретической точки зрения вполне хорошо справиться с этой задачей и без такого типа рассмотрения. С практической точки зрения представляется, что мы могли бы построить самовоспооизводящиеся машины или заводы и без того рассмотрения, которое Вы сделали, и что эти проблемы являются в сущности техническими проблемами.
С другой же точки зрения, тот факт, что человек является самовоспроизводящимся, говорит нам, я думаю, очень мало о его структуре. Следовательно, с данной точки зрения это не особенно хороший путь для того, чтобы понять, как в общем и целом работают живые объекты, поэтому мне хотелось бы знать, какие мотивы, кроме математических, есть у Вас для изучения этого вопроса.
Беркс: Я думаю, что последнее из сказанного Вами существенно: математические мотивы. Для целей данного ответа я могу согласиться, что такой математический подход, пожалуй, не очень хороший способ изучения естественных методов самовоспроизведения. Конечно, конкретная модель, предлагаемая мною, является в высшей степени идеализированной в этом отношении, и даже модели, рассмотренные фон Нейманом, являются несколько идеализированными. Но я полагаю, что здесь представляют интерес общие процессы. В частности, я попытался связать функционирование, структуру, вычисления и поведение саморазмножающихся автоматов с аналогичными свойствами других широко изученных автоматов - машин Тьюринга, которые растут очень простым способом (однородно растущая лента), и неизменных автоматов. Конечной целью этой попытки должна явиться всесторонняя теория автоматов, которая включала бы все это как частные случаи.
Кирш (Бюро стандартов): Вы привели пример схемы для количественной оценки, которая, как Вы показали, может быть реализована с помощью некоторой логической сети, и, как Вы намекнули или прямо указали, очевидно, существуют такие схемы для количественной оценки, которые не имеют реализации. Я думаю, что если взять Ваш частный пример и обратить неравенство, то получится утверждение, что существует такая форма, для которой X больше T. Это "предсказатель", для которого Вы, очевидно, не могли бы синтезировать организм.
Мой вопрос заключается в следующем: можете ли Вы сказать что-нибудь о том, до какой степени можно покрыть широкий класс, т.е. до какой степени можно говорить о достаточно широком классе схем для количественной оценки,- могут ли они в действительности изображаться с помощью конечного автомата? Мне хотелось бы найти утверждение такого вида для многих и многих, почти для всех случаев. Или мы можем сделать это для всех важных случаев, или же ни для одного случая?
Беркс: Как Вы заметили, очень легко написать формулы, которые не могут быть реализованы, потому что они требуют от автомата предсказать будущее, а это не в его силах. Было также доказано, что не все автоматы могут быть описаны с помощью формул с "кванторами" (quantifier) такого вида. (Я говорю "такого вида", потому что за имевшееся в моем распоряжении время я не имел возможности дать формальное определение языка, который позволил бы выразить эту и другие разумные формулы).
Вы можете рассмотреть некоторый язык, достаточно сильный для того, чтобы включить в себя формулы с ограниченными кванторами, но не намного сильнее. Для любого такого языка неизвестно, имеется ли синтезирующая машина, которая может сказать, существует ли автомат, удовлетворяющий данному условию, и, если такой автомат существует, описать его.
Я не думаю, чтобы это было очень серьезным возражением против того, что имеется множество формул, которым не соответствует никакой автомат. Если конструктор записывает что-то, соответствующее условиям, которые не могут быть реализованы ни одним автоматом, то машина выполнит свою работу, если скажет, что такой автомат не существует.
Имеется еще одно осложнение, которое заключается в том, что Вы можете расширить сферу проблемы, включив в нее задачу построения автомата, вычисляющего "такие-то" и "такие-то" вещи, и на основании многих формул, которые предсказывают будущее, Вы можете построить автоматы, которые в некотором подходящем смысле будут вычислять вещи такого рода.
Поскольку растущие автоматы включают в себя неизменные автоматы и обобщенные машины Тьюринга как частные случаи, то проблемы, изложенные в разд.3, относятся также и к растущим автоматам. Существует проблема иного типа, совершенно отличная от всех рассмотренных ранее проблем и приложимая к автоматам любого вида. Это проблема связи между циклической сложностью структуры автомата и его поведением. Поскольку наше прежнее рассмотрение обобщенной машины Тьюринга не выявило, какие циклы подразумеваются на ленте, эту проблему необходимо было отложить до настоящего раздела.

Фиг.14. Автомат второй степени. Троичный счетчик.
Вначале рассмотрим эту проблему для случая неизменного автомата. Структуру неизменного автомата можно разделить на МАКСИМАЛЬНЫЕ ЦИКЛЫ. Степенью максимального цикла является число элементов единичных задержек в этом цикле, а степенью неизменного автомата является максимальная степень его максимальных циклов [Эти понятия подробно поясняются в разд.4.1 работы Беркса и Хао Вана [4]]. На фиг.14 изображен один максимальный цикл степени 2. Выходные узлы помечены звездочками. На фиг.15 показано шесть максимальных циклов, из которых каждый имеет степень 1. Таким образом, на фиг.15 изображен автомат 1-й степени. Выходные узлы также помечены звездочками.

Фиг.15. Автомат первой степени.
Как, однако, степень автомата связана с его поведением? Существует ли некоторая критическая степень n такая, что все поведения неизменных автоматов могут быть реализованы с помощью структур этой степени или степени более низкой? Было высказано предположение, что такой степени не существует. Главная проблема остается открытой, но Дж.Голланд показал, что никакой автомат степени 1 не сможет реализовать поведение автомата, изображенного на фиг.14, который представляет собой троичный счетчик [14].
Эта же проблема может быть поставлена по отношению к вычислению неизменного автомата: существует ли некоторая критическая степень m такая, что все вычисления неизменных автоматов могут быть реализованы с помощью структур этой степени или степени более низкой? Обе проблемы могут быть распространены на обобщенные машины Тьюринга и на растущие автоматы. Конечно, структура любого растущего автомата меняется со временем, а следовательно, меняется также и степень его структуры. Но мы можем определить степень растущего автомата как максимальную степень любой из его структур в любой момент времени для любой истории входа, если этот максимум существует. В противном случае степень автомата является неопределенной.
Теперь мы можем сформулировать следующие вопросы, касающиеся растущих автоматов: 1) Существует ли некоторая конечная степень n такая, что все поведения могут быть реализованы с помощью растущих автоматов этой или меньшей степени? 2) Существует ли некоторая конечная степень m такая, что все вычисления могут быть реализованы с помощью растущих автоматов этой или меньшей степени? Возможно, покажется, что ответом на оба эти вопроса является "нет", поскольку очевидно, что в обоих случаях нет верхнего предела для длины требуемых лент, и лента, построение которой описано в предыдущем разделе, имеет неопределенную степень. Однако можно построить ленту конечной степени, используя изолированные квадратики и движение вдоль ленты головки считывания - записи вместо сдвига информации вдоль ленты. Для того чтобы записать в квадратик "1", автомат строит цикл с задержкой, в котором циркулирует импульс. Для запоминания "0" он строит цикл с задержкой, последовательными состояниями которого является 0. Неизменная часть машины может высылать длинный провод для осуществления таких записей и с помощью другого провода может прочитывать содержимое цикла с задержкой. Содержимое квадратика может быть изменено разрушением существующего в нем цикла с задержкой и построения нового. Когда неизменная часть автомата не производит ни считывания из квадратика, ни записи в него, то она не имеет с ним никакой связи. Таким путем может быть построена обобщенная машина Тьюринга, которая имеет неизменную степень.
Существуют и другие меры сложности обратной связи, которые представляют интерес. Рассмотрим неизменный автомат с n единичными задержками x1, x2, x3, ..., xn. Пусть f(xi) - число задержек, которые прямо и непосредственно воздействуют на элемент задержки xi, т.е. выходы которых управляют входом xi через переключательные элементы. На фиг.14 f(x1) = f(x2) = 2, поскольку каждая задержка управляет сама собой и другой задержкой через переключатель. Среднюю меру сложности обратной связи F для автомата определим как
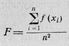
F = SUM[i=1,n]f(xi) / n**2
Существуют "полностью связанные" автоматы, для которых F = 1 [См. [4], стр.291. Конечно, каждый автомат может быть представлен в нормальной форме, которая обладает этим свойством, но нас интересуют здесь сети в "приведенной форме", в которой все неподходящие (неэффективные) входы переключателей устранены]. На фиг.14 в качестве примера показан такой автомат. Но в действительных системах величина сложности обратной связи F обычно много меньше максимума. Для системы, показанной на фиг.15, F = 7/18. Для типичной современной цифровой вычислительной машины F мало. (Заметим, что такая вычислительная машина составляет приблизительно один максимальный цикл, не считая лент). Это обстоятельство имеет прямое отношение к возможности понять большую цифровую машину. Так как отношение числа фактических линий обратной связи (от задержек) к числу возможных линий обратной связи мало, то различные части вычислительной машины имеют значительную местную автономию и поэтому могут быть поняты изолированно от остальных частей машины. (Единообразия внутри этих частей также облегчают нам их понимание). Стоит отметить, что если нейроны представлены в виде переключателей и задержек, то для нервной системы человека F также мало.
Обратимся теперь к некоторым проблемам, которые специфичны только для растущих автоматов. Первой из них является проблема, которая рассматривалась фон Нейманом: насколько сложным должен быть самовоспроизводящийся автомат? В своей модели Нейман использовал ячейки, которые могли иметь около 30 состояний, и по его оценке для самовоспроизведения было бы достаточно около 200000 таких ячеек. Ячейки наших моделей намного сложнее, поскольку ячейка может содержать любой из приблизительно 2**15 различных элементов, и каждый элемент может находиться в нескольких состояниях. Но подсчета числа состояний недостаточно, потому что существует много способов, которыми эти состояния могут быть использованы. Например, основной элемент, который может передавать свою структуру к соседней ячейке по получении одного импульса, намного мощнее, чем любой из принятых нами основных элементов.
Различные модели растущих автоматов можно сравнивать, сведя их к одной общей системе. Например, можно имитировать как модель фон Неймана, так и наши модели с помощью неограниченных однородных неизменных сетей из переключающих элементов и задержек. Мы покажем, как это может быть осуществлено для модели, соответствующей нашему определению. Каждая ячейка имитируется неизменной сетью внутри квадратика. Эти квадратики повторяются неограниченно таким же образом, как ячейки нашей модели. Каждый неизменный автомат в квадратике содержит регистр, главный переключатель, переключатели и задержки, которые выполняют несущие функции и функции вычисления первоначальной ячейки. Каждая неизменная сеть квадратика связана входами и выходами с четырьмя соседними квадратиками. Эти входы и выходы используются в качестве несущих и вычислительных проводов. Конструирующая последовательность, которая должна воздействовать на данный квадратик, пересылается в регистр этого квадратика. Регистр в этом случае с помощью главного переключателя определяет связи переключателей и задержек. Таким образом, неизменный автомат квадратика имитирует первоначальную ячейку.
Для запоминания установок переключателей разветвленных несущих элементов можно использовать триггеры. Переключающая последовательность, проходящая через квадратик, устанавливает триггер надлежащим образом и затем проходит дальше для установки триггеров, относящихся к другим несущим ветвям. Разрушающая последовательность поступает в регистр и восстанавливает первоначальное состояние квадратика.
Заметим, что для нашего определения растущих автоматов необходима только одна неограниченная однородная структура (а именно неограниченное повторение неизменного автомата в квадратиках). Различные автоматы представляются (имитируются) различными состояниями этой структуры, следовательно, мы здесь используем поведение автоматов для имитации структуры автоматов.
Модель фон Неймана может имитироваться подобным же образом. В этом случае сложность самовоспроизводящегося автомата фон Неймана можно сравнить со сложностью описанного нами самовоспроизводящегося автомата, подсчитав число переключателей и задержек, использованных в первоначальной структуре каждого из них. Точно определяя таким методом общий эталон, мы можем свести проблему минимальной сложности воспроизведения ячейки к строго логической проблеме. Имеющийся опыт с задачами минимизации говорит о том, что было бы невероятно трудно, если не вовсе невозможно, найти минимальное решение и доказать, что оно минимально. Можно, однако, получить оценку минимальной сложности, если использовать вычислительную машину для того, чтобы облегчить выработку различных возможных построений.
Существует много других концепций растущих автоматов, которые заслуживают исследования, и они, несомненно, вызовут к жизни новые проблемы. В первой модели фон Неймана опорные элементы, чувствительные органы, соединительные узлы и вычислительные элементы свободно плавали в озере. Как указывает Шеннон ([13], стр.126-127), из-за сложности возможных в этом случае движений было бы чрезвычайно трудно дать точный план универсального конструктора с такой моделью. Можно, однако, так расширить данное нами определение растущих автоматов, чтобы без особого труда получить некоторые эффекты первой модели фон Неймана. Например, можно добавить ЧУВСТВИТЕЛЬНЫЙ ЭЛЕМЕНТ, который прочитывал бы структуру и содержание (состояние) ячейки. Чувствительный элемент проводил бы ЧУВСТВИТЕЛЬНЫЕ КАНАЛЫ через ячейки подобно тому, как конструирующим элементом создается несущее устройство. Эти чувствительные каналы не нарушали бы структуру, уже имеющуюся в ячейках, а передавали бы информацию об исследуемой ячейке к чувствительному элементу. С помощью процесса, подобного процессу построения, описанному в предыдущем разделе, автомат мог бы оппределить, какой элемент содержится в ячейке и каково состояние этого элемента в данный момент времени. Эта информация может быть использована различным образом, например она может быть использована для обнаружения ошибки, которая затем может быть исправлена конструирующим элементом.
Далее возникает вопрос: как много "самопознания" может приобрести и сохранить автомат? Этот вопрос представляет интерес для теории самоорганизующихся систем, поскольку один из возможных методов самоорганизации системы заключается в том, что система имеет картину своей структуры и поведения и использует эту картину для своего собственного управления. Совершенно ясно, что количество знаний о себе самом, которое может приобрести и содержать автомат, имеет предел. Например, возможно, что растущий автомат будет изменяться быстрее, чем его чувствительные элементы смогут чувствовать эти изменения. Существуют также и логические ограничения. Так, если используются все состояния автомата, то соответствующая часть системы не может иметь полностью детализованную картину целого, потому что целое, будучи больше части, будет иметь больше состояний, чем эта часть.
Здесь имеют место логические парадоксы, связанные с ссылками на себя. Хорошо известно, что некоторые ссылочные утверждения ведут к противоречиям. Так, предложение "это предложение ложно" является ложным, если оно истинно (потому что оно говорит о себе, что оно ложно) и является истинным, если оно ложно (потому что если ложно то, что оно ложно, то оно истинно), и, следовательно, оно является как истинным, так и ложным. Для разрешения таких парадоксов Рассел предложил [15] формальный язык, в котором не могут быть сформулированы никакие утверждения со ссылкой на себя. Предложение недопустимости утверждений со ссылкой на себя в формальной системе является, однако, слишком сильным, так как очевидно, что нет ничего ошибочного в следующих утверждениях со ссылкой на себя: 1) "это предложение написано на русском языке" [В оригинале - на английском языке.- Прим. перев.], "это предложение написано по меньшей мере один раз". Оба эти предложения, конечно, истинны. Они иллюстрируют тот факт, что предложение может ссылаться на свои физические свойства, и все же при этом не возникает противоречия. Имеют место также случаи, когда предложение может ссылаться на свои структурные или синтаксические свойства без возникновения противоречий. Предложение: "это предложение грамматически верно" относится к таким предложениям. Другим примером формулы, ссылающейся на свою собственную структуру, является неразрешимая формула, составленная Геделем [Как Гедель отметил в своих лекциях в Институте перспективных исследований (Принстон) в 1933-1934гг., его неразрешимая формула показывает, что решение парадоксов Расселом является слишком экстремальным, потому что неразрешимая формула (истинно) говорит о себе, что она не доказуема. Он соглашался с Расселом, что должны быть некоторые ограничения того, что может сказать о себе предложение, и предположил, что никакое предложение не может правильно говорить о своей истинности и ложности] в его доказательстве неполноты арифметики. Такова формула F, которая в некотором смысле утверждает: "F не доказуемо" [16]. Доказуемость является чисто синтаксическим понятием, поэтому формула ссылается на свой собственный синтаксис, и при этой ссылке не возникает противоречия.
Таким образом, предложение может содержать описание некоторых своих собственных синтаксических или структурных свойств. Отметим сходство этого с тем, что мы имели в предыдущем разделе, а именно что самовоспроизводящийся автомат C содержит в себе описание D(C) своей собственной структуры. Он, однако, не содержит описания состояния своего содержимого (кроме своего начального однородного состояния). Это наводит на мысль, что автомат с чувствительным элементом, вероятно, сможет чувствовать свою собственную структуру, а также может построить и сохранить описание своей структуры. Но создание такого автомата, конечно, представляет еще проблему.
На первый взгляд может показаться, что автомат не может хранить описание своей собственной структуры, потому что сколько бы ячеек он ни имел, для хранения описания потребовалось бы большее число ячеек, подобно парадоксу Тристана Шенди [Тристану Шенди потребовалось два года для описания первых двух дней своей жизни (см. Sterne L., The Life and Opinions of Tristam Shandy, Gentleman, vol.4, ch.13)]. Это возражение неосновательно, потому что в описании можно использовать индексы, символы суммирования и количественные характеристики. Как было показано выше, для описания одного квадратика ленты используется определенная главная последовательность. При составлении описания D(a) структуры автомата a эта главная последовательность не повторяется для каждого квадратика ленты, который должен быть построен, а повторно используется одна и та же последовательность способом, который хорошо известен всем программистам. Это может быть сделано потому, что лента имеет в высшей степени единообразную структуру.
Из этих соображений следует, что для выработки описания собственной структуры, которое было бы настолько мало, чтобы его можно было хранить в этой же структуре, автомат должен обнаруживать некоторые единообразия своей структуры. Он может, например, систематически просматривать структуру каждой из своих ячеек и затем анализировать результаты для того, чтобы найти для них более компактную формулировку, Следовательно, количество информации о своей собственной структуре, которое может приобрести и хранить растущий автомат, зависит от того, какие имеются машинные приемы для обнаружения единообразия структуры.
ЛИТЕРАТУРА
1. Neumann J., "Probabilistic logics and the synthesis of reliable organisms from unreliable components", Automata Studies, (ed. C.E.Shannon and J.McCarthy), Princeton, 1956, pp.43-98; русский перевод см. сб."Автоматы", ИЛ, 1956.
2. К1ееne S.С., Introduction to Metamathematics, New York, 1952; русский перевод см. Клини С., Введение в метаматематику, ИЛ, 1957; Davis M., Computability and Unsolvability, New York., 1958.
3. Burks A.W., Wright J., "Theory of logical nets", Proc. IRE, 41, 1357-1365 (1953).
4. Burks A.W., Hао Wang, "The logic of automata", J. Assoc. Computing Mach., 4, 193-218, 279-297 (1947).
5. Copi I.M., Elgot С.С., Wright J.В., "Realization of events by logical nets", J. Assoc. Computing Mach., 5, 181-196 (1958).
6. Moore E.F., "Gedanken-experiments on sequential machines", Automata Studies, pp.129-153; см. [1].
7. Buchi J.R.,. Elgot С.С., Wright J.В., "The nonexistence of certain algorithms of finite automata theory", Abstract, Not. Amer. Math. Soc., 5, #1, 98 (1958).
8. Church A., "Application of Recursive Arithmetic in the Theory of Computers and Automata", Notes from Summer Session Course in Advanced Theory of the Logical Design of Digital Computers, Univ. Michigan, 1958.
9. Elgоt С.С., Buchi J.R., "Decision problems of weak second order arithmetics and finite automata, Part 1", Abstract, Not. Amer. Math. Soc., 5, #7, 834 (1958).
10. Elgot С.С., "Decision problems of weak second order arithmetics and finite automata, Part II", Abstract, Not. Amer. Math. Soc., 6, #1, 48 (1959).
11. Neumann J., "The general and logical theory of automata", Cerebral Mechanisms in Behavior - The Hixon Symposium (ed. L.A.Jeffress), New York, 1951, pp.1-31; см. также The World of Mathematics (ed. J.R.Newman), vol.4, pp.2070-2098.
12. Кemenу J.G., "Man viewed as a machine", Sci. Amer., 192, 58-67 (1955).
13. Schannon С.Е., "Neumann's contributions to automata theory", Bull. Amer. Math. Soc, 64, 123-129 (1958).
14. Hоlland J.H., "Cycles in logical nets", диссертация, Univ. Michigan, 1959.
15. Russell В., Whitehead A.N., Principia Mathematica, Introduction ("The Theory of Logical Types"), Chap.II.
16. Godel K., "Ueber formal unentscheidbare Saetze der Principia Mathematica und verwandter Systeme", Monat. Math. u. Phys., 38, 173-198 (1931).
ОБСУЖДЕНИЕ
Минский: Хотелось бы узнать, имеются ли какие-либо доказательства для Вашего последнего утверждения? Мне кажется, что автомат довольно простого вида вполне может выяснить все о своей структуре, выяснить, какой она была в определенный момент времени, просто создавая что-то вроде оттиснутой на резине копии своей структуры, и определить, таким образом, свое полное состояние в тот же момент времени.
Это не тривально, это способ обеспечить, чтобы каждая ячейка имела по существу двойные ряды состояний, и этот способ вытекает из того, о чем Вы слышали как о рядовой задаче при посылке волн, которые распространяются через автомат с одномерной или двумерной структурой и одновременно передают полную структуру этого автомата другому слою. На этой стадии машина может не "торопясь исследовать каждую деталь того, что являлось ее структурой в определенный момент, после того как она выработала команду сделать копию, а это равнозначно по смыслу идее о машине, которая не только имеет структуру описанного Вами типа, но имеет еще и руку с глазом на конце и, вероятно, даже располагает зеркалом, так что она может выяснить даже структуру самого глаза. Но, кроме того, она может сделать то же самое и с замороженной копией самой себя, поэтому она может видеть все состояния. Таким образом, у меня возник довольно серьезный вопрос (интересно, возник ли он и у других): можете ли Вы сделать какие-либо обобщения, связанные с самовоспроизведением, которые говорили бы, что, для того чтобы понять самое себя или знать свое состояние, Вы в самом деле должны делать обобщения. Я не вижу, как фон Нейману удалось показать это, и не думаю, чтобы это было достаточно обосновано.
Беркс: Я говорил о ситуации построения универсальной вычислительной машины с не очень единообразной структурой (хотя, очевидно, некоторые единообразия и могли существовать), которая имела, например, один чувствительный элемент. Задача заключается в составлении такой программы, чтобы этот чувствительный элемент делал надлежащий обзор автомата и чтобы автомат закончил описанием самого себя, хранящимся в нем самом. Я не имел в виду, что это не может быть сделано, а хотел лишь сказать, что в этом общем случае необходимо, чтобы автомат имел некоторую возможность резюмировать свое описание.
Соломонов (Фирма "Цейтор", Кембридж, шт.Массачусетс): Мой вопрос касается мотивов для изучения самовоспроизводящихся машин и растущих автоматов. Мне кажется, что в той степени, в какой речь идет о практической задаче создания самовоспроизводящихся машин или заводов, мы можем с теоретической точки зрения вполне хорошо справиться с этой задачей и без такого типа рассмотрения. С практической точки зрения представляется, что мы могли бы построить самовоспооизводящиеся машины или заводы и без того рассмотрения, которое Вы сделали, и что эти проблемы являются в сущности техническими проблемами.
С другой же точки зрения, тот факт, что человек является самовоспроизводящимся, говорит нам, я думаю, очень мало о его структуре. Следовательно, с данной точки зрения это не особенно хороший путь для того, чтобы понять, как в общем и целом работают живые объекты, поэтому мне хотелось бы знать, какие мотивы, кроме математических, есть у Вас для изучения этого вопроса.
Беркс: Я думаю, что последнее из сказанного Вами существенно: математические мотивы. Для целей данного ответа я могу согласиться, что такой математический подход, пожалуй, не очень хороший способ изучения естественных методов самовоспроизведения. Конечно, конкретная модель, предлагаемая мною, является в высшей степени идеализированной в этом отношении, и даже модели, рассмотренные фон Нейманом, являются несколько идеализированными. Но я полагаю, что здесь представляют интерес общие процессы. В частности, я попытался связать функционирование, структуру, вычисления и поведение саморазмножающихся автоматов с аналогичными свойствами других широко изученных автоматов - машин Тьюринга, которые растут очень простым способом (однородно растущая лента), и неизменных автоматов. Конечной целью этой попытки должна явиться всесторонняя теория автоматов, которая включала бы все это как частные случаи.
Кирш (Бюро стандартов): Вы привели пример схемы для количественной оценки, которая, как Вы показали, может быть реализована с помощью некоторой логической сети, и, как Вы намекнули или прямо указали, очевидно, существуют такие схемы для количественной оценки, которые не имеют реализации. Я думаю, что если взять Ваш частный пример и обратить неравенство, то получится утверждение, что существует такая форма, для которой X больше T. Это "предсказатель", для которого Вы, очевидно, не могли бы синтезировать организм.
Мой вопрос заключается в следующем: можете ли Вы сказать что-нибудь о том, до какой степени можно покрыть широкий класс, т.е. до какой степени можно говорить о достаточно широком классе схем для количественной оценки,- могут ли они в действительности изображаться с помощью конечного автомата? Мне хотелось бы найти утверждение такого вида для многих и многих, почти для всех случаев. Или мы можем сделать это для всех важных случаев, или же ни для одного случая?
Беркс: Как Вы заметили, очень легко написать формулы, которые не могут быть реализованы, потому что они требуют от автомата предсказать будущее, а это не в его силах. Было также доказано, что не все автоматы могут быть описаны с помощью формул с "кванторами" (quantifier) такого вида. (Я говорю "такого вида", потому что за имевшееся в моем распоряжении время я не имел возможности дать формальное определение языка, который позволил бы выразить эту и другие разумные формулы).
Вы можете рассмотреть некоторый язык, достаточно сильный для того, чтобы включить в себя формулы с ограниченными кванторами, но не намного сильнее. Для любого такого языка неизвестно, имеется ли синтезирующая машина, которая может сказать, существует ли автомат, удовлетворяющий данному условию, и, если такой автомат существует, описать его.
Я не думаю, чтобы это было очень серьезным возражением против того, что имеется множество формул, которым не соответствует никакой автомат. Если конструктор записывает что-то, соответствующее условиям, которые не могут быть реализованы ни одним автоматом, то машина выполнит свою работу, если скажет, что такой автомат не существует.
Имеется еще одно осложнение, которое заключается в том, что Вы можете расширить сферу проблемы, включив в нее задачу построения автомата, вычисляющего "такие-то" и "такие-то" вещи, и на основании многих формул, которые предсказывают будущее, Вы можете построить автоматы, которые в некотором подходящем смысле будут вычислять вещи такого рода.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
Насколько мы, нейронные автоматы, умнее Машин Тьюринга?

Инопланетяне, пославшие сигнал в "Андромеде"
ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
К. де ЛЕУ, Э.Ф.МУР, К.Э.ШЕННОН и Н.ШАПИРО
Сб. АВТОМАТЫ. 1956
ВВЕДЕНИЕ
В этой статье рассматривается следующий вопрос: имеется ли что-нибудь, что может сделать машина со случайным элементом, но не может сделать детерминистская машина?
Конечно, в таком виде вопрос выглядит слишком неопределенным, чтобы быть доступным для математического анализа. В дальнейшем мы ограничим его в двояком отношении. Будет дано точное определение класса рассматриваемых машин и столь же точное определение задач, выполняемых ими. Ясно, что характер наших результатов сильно зависит от выбора этих двух определений, и поэтому наш ответ нельзя считать полным решением первоначального неформального вопроса. Читатель должен иметь в виду, что полученные нами результаты неприменимы вне области, обусловленной выбранными определениями. В частности, наши результаты указывают на возможность перечисления бесконечных множеств и вычисления бесконечных последовательностей, но не дают информации о типе вероятностных машин, предназначенных для конечных задач, например об их относительной сложности и относительной скорости.
Подобные затруднения присутствуют неявно при всяком применении математики к некоторому поставленному неформально вопросу. Формулировка такого вопроса в точной математической форме неизбежно сосредоточивает внимание на некоторых его сторонах, в то время как другие, одинаково важные и даже более важные в иной ситуации, стороны могут оказаться в полном пренебрежении.
Основной текст настоящей статьи состоит из определений, примеров и формулировок результатов. Доказательства перенесены в приложение, так как большей частью они представляют собой более или менее сложные построения, которые не являются абсолютно необходимыми для понимания результатов.
Читатели, знакомые с теорией рекурсивных функций, без труда увидят, что наши результаты принадлежат этой теории и легко могут быть переведены на ее язык. Ввиду этого наши доказательства получают двоякое значение. Если считать определенным интуитивное понятие ЭФФЕКТИВНОГО ПРОЦЕССА [Об эффективном процессе см. в [9] или [2]. Советуем читателю, не знакомому с понятием эффективного процесса, прочесть одну из этих работ, прежде чем идти дальше. Эффективные процессы рассматриваются также в [1], [7] и [8]], то их можно рассматривать как полные доказательства. С другой стороны, их можно рассматривать как УКАЗАНИЯ, исходя из которых можно теоремы, сформулированные на языке теории рекурсивных функций, доказать формально средствами этой теории. Мы не проводили такой формализации, чтобы не отвлекать читателя от идейного содержания доказательств. Однако возможность такой формализации ясна всякому, кто знаком с теорией рекурсивных функций.
ВЕРОЯТНОСТНЫЕ МАШИНЫ В СРАВНЕНИИ С ДЕТЕРМИНИСТСКИМИ
В этом разделе мы сначала дадим точное определение некоторого класса вычислительных машин. Эти машины имеют вход и выход. Входом является бесконечная последовательность двоичных знаков, которая может подаваться двумя различными способами: 1) как фиксированная последовательность (физически можно представлять заранее подготовленную бесконечную ленту); 2) как выход двоичного случайного устройства (с вероятностью p появления 1). В последнем случае мы имеем вероятностную машину. Затем мы очертим точный класс задач, решения которых этими машинами мы желаем, а именно перечисление с положительной вероятностью множеств выходных символов. После этого ключевой результат настоящей статьи - теорема 1 - используется для ответа на наш вопрос. Ответ дается в теореме 2. Он гласит, что если случайное устройство имеет вероятность p, где p - ВЫЧИСЛИМОЕ ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО (т.е. действительное число, для которого существует эффективный процесс нахождения любого знака в его двоичном разложении), то любое множество, перечислимое посредством вероятностной машины рассматриваемого типа, перечислимо посредством детерминистской машины. Это не имеет места, если p - невычислимое действительное число. Аналогичные результаты получаются для случая, когда учитывается порядок следования выходных символов. Положение подытоживается теоремой 3.
Мы будем мыслить наши машины в виде объектов, которые воспринимают в качестве входа ленту с записанными на ней нулями и единицами и выпускают в качестве выхода ленту, на которой они могут записывать конечную или счетную выборку выходных символов s1, s2, s3, ... (этими символами могут быть конфигурации, образованные из некоторого конечного алфавита). Предполагается, что машина имеет некоторое начальное состояние, в которое она приводится перед началом любой операции (подобно тому, как счетно-клавишная машина гасится перед вычислением). Другое разумное требование к машине таково: должна существовать эффективная процедура, позволяющая определить, какова будет последовательность выходных символов (sj1, ..., sjr) на выходной ленте, если в начальном состоянии машина снабжена входной последовательностью нулей и единиц (a1, ..., an). Эту выходную последовательность мы обозначим через f(a1, ..., an). Так как нас интересует только зависимость между входом и выходом машин, то можно отвлечься от их внутреннего устройства и принять это требование за определение. Хотя мы и дадим сейчас абстрактное определение, мы будем дальше говорить о машинах, пользуясь обычным языком.
ОПРЕДЕЛЕНИЕ. МАШИНА есть функция, которая для каждого n ставит в соответствие каждой конечной последовательности из n нулей и единиц (a1, ..., an) некоторую конечную последовательность f(a1, ..., an) = (sj1, ..., sjr),
состоящую из элементов заданного множества S, причем выполняются следующие два условия:
1) f(a1, ..., an) есть начальный отрезок в f(a1, ..., an, ... a[n+m]) если (a1, ..., an) есть начальный отрезок в (a1, ..., an, ... a[n+m]),
2) f - вычислимая функция, т.е. существует эффективный процесс [См. предыдущее примечание], позволяющий определить f(a1, ..., an) по заданной {a1, ..., an).
Это определение распространяется на бесконечные последовательности следующим образом: если A = (a1, a2, a3, ...), то f(A) есть последовательность с начальными отрезками f(a1, ..., an).
Неформально работу машины можно представить себе следующим образом. Получив вход (a1, ..., an), она воспринимает a1 и записывает последовательность символов f(a1) на выходе; затем она воспринимает a2 и записывает символы на ленте после f(a1), производя f(a1, a2); ...; затем она воспринимает an и записывает символы на ленте после f(a1, ..., a[n-1]), производя f(a1, ..., a[n-1], an); и, наконец, останавливается.
Теперь дадим несколько конкретных примеров машин. Этим мы преследуем двоякую цель: проиллюстрировать наше понятие машины и подготовить материал для иллюстрации новых понятий, вводимых далее. Пока можно читать не все примеры.
МАШИНА #1. Выходными символами этой машины являются упорядоченные пары целых чисел (a, r). Для каждого входного символа a машина записывает выходной символ (a, r), если a был r-м входным символом на входной ленте. Иными словами, f{a1, ..., an) = ((a1, 1), (a2, 2), ..., {an, n)).
МАШИНА #2. Пусть g - целочисленная функция положительных целых чисел, и пусть она вычислима, т.е. существует эффективный процесс для нахождения g(n) по заданному n. Пусть машина записывает выходной символ (r, g(r)) после восприятия r-го входного символа. В этом случае f(a1, ..., an) = ((1, g(1)), (2, g(2)), ..., (n, g(n))) и выход не зависит от входа. Эта машина и машина #1 представляют крайние случаи. #2 забывает о входе, а #1, по существу, копирует вход на выходной ленте. Заметим, что объект #2 не был бы машиной в смысле нашего определения, если бы функция g не была вычислима, ибо в этом случае не существовало бы эффективного процесса, позволяющего определить выход по заданному входу.
МАШИНА #3. Пусть машина записывает символ 0, как только она встретит первый нуль во входной последовательности. В остальное время она не записывает ничего. Тогда f(a1, ..., an) = (0), если один из символов aj является нулем. В противном случае машина не записывает ничего, и мы говорим о "пустой последовательности" (.); f(1, ..., 1) = (.).
МАШИНА #4. Пусть f(a1, ..., an) = (a1). Машина просто копирует на выходной ленте первый входной символ, не записывая больше ничего.
МАШИНА #5. Пусть машина записывает выходной символ r, если максимальная длина групп единиц, воспринятых машиной, равна r. Например, f(1) = (1), f(1, 0) = (1, 1), f(1, 0, 1) = (1, 1, 1), f(1, 0, 1, 1) = (1, 1, 1, 2).
МАШИНА #6. Пусть h(r, s) - вычислимая целочисленная функция, определенная на целых положительных числах. Машина не записывает ничего, пока не встретит первой единицы на входе; если эта единица - первый входной символ, то машина не печатает ничего никогда; если же эта единица встретилась после r нулей, то записывается символ (1, h (r, 1)). После следующего входного символа машина записывает символ (2, h(r, 2)), после следующего - символ (3, h(r, 3)) и т.д. Пусть функция hr{s) с фиксированным r определяется соотношением hr(s) = h(r, s). Тогда работа машины фактически состоит в вычислении функции hr при поступлении в машину начальной группы r нулей и следующей за ними единицы.
МАШИНА #7. Эта машина задается соотношением f{a1, ..., an) = ((1, r1), (2, r2), ..., (q, rq)), где целое число rs получается следующим образом. Возьмем первые 100**s знаков в (a1, ..., an). Пусть ps - доля знаков, равных 1. Тогда rs есть s-й знак в двоичном разложении числа ps. Число q есть наибольшее s, такое, что 100**s <= n. Аналогичная конструкция используется при доказательстве части теоремы 1.
Хотя работа машины определена только для конечных входных последовательностей, тем не менее ясно, что сделала бы такая машина, получая бесконечную входную последовательность A = (a1, a2, a3, ...) и обладая бесконечной выходной лентой для записи. Работа машины определена тем фактом, что мы знаем ее выход для всех конечных входных последовательностей. Таким образом, машина ставит в соответствие каждой бесконечной входной последовательности выходную последовательность, которая может быть или не быть бесконечной. Например, если вводить в машину #1 бесконечную ленту, на которой записаны только единицы, то выходная последовательность будет ((1, 1), (1, 2), (1, 3), ...). Для этой же ленты машина #3 не даст никакого выхода (пустая последовательность (.)), а машина #4 даст выходную последовательность (1).
Рассмотрим множество символов, появляющихся на выходной ленте машины, когда машина получает некоторую бесконечную входную последовательность A. (Например, если выходная последовательность есть (1, 1, 1, ...), то это множество состоит лишь из одного символа 1, а если выходная последовательность есть (1, 3, 5, 7, ...), то это множество символов состоит из всех нечетных чисел). Таким образом, машина ставит в соответствие каждой входной последовательности A некоторое множество выходных символов, которое она перечисляет. (Мы не будем здесь обращать внимание на порядок, в котором это множество перечисляется, а также на то, перечисляется ли оно с повторениями или без повторений. Это будет сделано позже, при рассмотрении вычисления последовательностей).
Например, машина #1 ставит в соответствие любой бесконечной входной последовательности A = (a1, a2, ...) множество выходных символов, состоящее из всех (an, n), где n пробегает целые положительные числа. Машина #2 ставит в соответствие любой входной последовательности множество всех (n, g(n)), где n пробегает целые положительные числа. Машина #3 ставит в соответствие входной последовательности, состоящей только из единиц, пустое множество. Такому же входу машина #5 ставит в соответствие множество всех целых положительных чисел.
ОПРЕДЕЛЕНИЕ. Машина, получающая бесконечную входную последовательность A = (a1, a2, a3, ...), будет называться A-МАШИНОЙ. Будем говорить, что она A-ПЕРЕЧИСЛЯЕТ множество выходных символов, записываемых ею. Множество каких-либо символов называется A-ПЕРЕЧИСЛИМЫМ, если существует A-машина, которая A-перечисляет это множество.
A-перечислимые множества, где A есть последовательность, состоящая только из единиц, обычно называются РЕКУРСИВНО-ПЕРЕЧИСЛИМЫМИ множествами. Мы назовем их 1-ПЕРЕЧИСЛИМЫМИ множествами. A-машина будет называться 1-МАШИНОЙ, если A состоит целиком из единиц.
Каждой бесконечной последовательности A = (a1, a2, ...) можно поставить в соответствие множество всех пар (n, an), где an есть n-й элемент в последовательности A, а n пробегает все целые положительные числа. Это множество обозначим через А'. Последовательность A называется ВЫЧИСЛИМОЙ, если существует эффективный процесс, с помощью которого можно определить n-й член в A для каждого n. Три следующие леммы доказываются в приложении, хотя их доказательства получаются почти немедленно.
ЛЕММА 1. Последовательность A вычислима тогда и только тогда, когда соответствующее множество А' является 1-перечислимым.
ЛЕММА 2. Если А - вычислимая последовательность, то любое А-перечислимое множество 1-перечислимо (и обратно).
ЛЕММА 3. Если А - невычислимая последовательность, то существуют множества А-перечислимые, но не 1-перечислимые.
Лемма 3 и существование невычислимых последовательностей будут важны для нас позже.
Теперь мы хотим присоединить к машине случайное устройство, чтобы построить вероятностную машину. Если у нас есть устройство, записывающее нули и единицы на ленте, и если единицы появляются с вероятностью p, нули - с вероятностью 1-p (0<p<1), причем каждая запись независима от предыдущих, то выход такого устройства можно использовать как входную ленту машины. Такая комбинация случайного устройства и машины будет называться p-МАШИНОЙ.
Поставленный во введении вопрос о существовании вероятностных машин, более общих, чем детерминистские машины, можно теперь сузить до более частного вопроса: можно ли на 1-машине сделать все, что делается на p-машине? (В следующем разделе будет показано, что рассмотрение довольно узкого класса p-машин вместо более широкого класса всех мыслимых вероятностных машин не вызывает большой потери общности. Мы увидим, что широкий класс вероятностных машин эквивалентен (в определяемом далее смысле) 1/2-машинам и что многие свойства машин широкого класса выводятся из свойств 1/2-машин).
Необходимо еще более ограничить наш вопрос, ибо ясно, что нельзя дать никакого точного ответа, пока нет точного определения выполняемой машинами задачи.
Задача, выполняемая машинами в настоящей статье, состоит в перечислении множеств. Эта задача не так уж узка, как это может показаться с первого взгляда. Например, машина может вычислять функцию, перечисляя символы "f(n) = m", или устанавливать истинность или ложность некоторого высказывания о целых положительных числах перечислением символов "P(n) истинно" и "P(n) ложно"; или же может вычислять двоичное разложение действительного числа перечислением символов "n-й знак числа r равен a".
Мы уже определили, что понимается под 1-перечислимым множеством символов. А именно, некоторое множество 1-перечислимо, если существует машина, которая, получая на входе ленту с одними только единицами, производит в итоге это множество на выходе. Необходимо дать определение перечислимости для p-машин, чтобы сравнить их с 1-машинами.
Будет предложено два определения: определение p-перечислимых множеств и определение сильно p-перечислимых множеств. Наш первоначальный неформальный вопрос будет сведен к двум точным вопросам: каждое ли p-перечислимое множество 1-перечислимо? Каждое ли сильно p-перечислимое множество 1-перечислимо?
Остается дать эти два определения. Каждому множеству возможных выходных символов данной p-машины можно приписать вероятность его появления в качестве полного выхода этой машины. Это есть вероятность того, что данное множество будет в точности множеством символов, которые появятся на выходной ленте машины, если машину привести в начальное положение, присоединить случайное устройство и пустить в работу. Указанная вероятность, конечно, равна нулю для большинства множеств. Мы дадим несколько примеров, ссылаясь на описанные выше машины. Предположим, что они присоединены к случайному устройству с p = 1/2 и стали поэтому 1/2-машинами. Машина #1 перечисляет любое множество с нулевой вероятностью. Следует отметить, что конечные множества появиться не могут, и по этой причине они имеют нулевую вероятность. Хотя некоторые бесконечные множества и могут быть выходом, однако это случается лишь с нулевой вероятностью. Не следует забывать о различии между появлением с нулевой вероятностью и невозможностью появления. Машина #2 перечисляет множество всех (n, g(n)) с вероятностью 1 (и притом с достоверностью). Выход машины #3 есть множество, состоящее из единственного символа 0, с вероятностью 1, но без достоверности. Выход машины #5 есть множество всех целых положительных чисел - с вероятностью 1, но без достоверности, ибо бесконечная последовательность нулей и единиц содержит произвольно длинные группы единиц с вероятностью 1, но без достоверности. Машина #6 перечисляет с вероятностью 2**-r множество всех (n, h(r, n)), где r фиксировано, а n пробегает все целые положительные числа. Иными словами, машина вычисляет функцию hr (определяемую соотношением hr(n) = h(r, n)) с вероятностью 2**-r.
...

Инопланетяне, пославшие сигнал в "Андромеде"
ВЫЧИСЛИМОСТЬ НА ВЕРОЯТНОСТНЫХ МАШИНАХ
К. де ЛЕУ, Э.Ф.МУР, К.Э.ШЕННОН и Н.ШАПИРО
Сб. АВТОМАТЫ. 1956
ВВЕДЕНИЕ
В этой статье рассматривается следующий вопрос: имеется ли что-нибудь, что может сделать машина со случайным элементом, но не может сделать детерминистская машина?
Конечно, в таком виде вопрос выглядит слишком неопределенным, чтобы быть доступным для математического анализа. В дальнейшем мы ограничим его в двояком отношении. Будет дано точное определение класса рассматриваемых машин и столь же точное определение задач, выполняемых ими. Ясно, что характер наших результатов сильно зависит от выбора этих двух определений, и поэтому наш ответ нельзя считать полным решением первоначального неформального вопроса. Читатель должен иметь в виду, что полученные нами результаты неприменимы вне области, обусловленной выбранными определениями. В частности, наши результаты указывают на возможность перечисления бесконечных множеств и вычисления бесконечных последовательностей, но не дают информации о типе вероятностных машин, предназначенных для конечных задач, например об их относительной сложности и относительной скорости.
Подобные затруднения присутствуют неявно при всяком применении математики к некоторому поставленному неформально вопросу. Формулировка такого вопроса в точной математической форме неизбежно сосредоточивает внимание на некоторых его сторонах, в то время как другие, одинаково важные и даже более важные в иной ситуации, стороны могут оказаться в полном пренебрежении.
Основной текст настоящей статьи состоит из определений, примеров и формулировок результатов. Доказательства перенесены в приложение, так как большей частью они представляют собой более или менее сложные построения, которые не являются абсолютно необходимыми для понимания результатов.
Читатели, знакомые с теорией рекурсивных функций, без труда увидят, что наши результаты принадлежат этой теории и легко могут быть переведены на ее язык. Ввиду этого наши доказательства получают двоякое значение. Если считать определенным интуитивное понятие ЭФФЕКТИВНОГО ПРОЦЕССА [Об эффективном процессе см. в [9] или [2]. Советуем читателю, не знакомому с понятием эффективного процесса, прочесть одну из этих работ, прежде чем идти дальше. Эффективные процессы рассматриваются также в [1], [7] и [8]], то их можно рассматривать как полные доказательства. С другой стороны, их можно рассматривать как УКАЗАНИЯ, исходя из которых можно теоремы, сформулированные на языке теории рекурсивных функций, доказать формально средствами этой теории. Мы не проводили такой формализации, чтобы не отвлекать читателя от идейного содержания доказательств. Однако возможность такой формализации ясна всякому, кто знаком с теорией рекурсивных функций.
ВЕРОЯТНОСТНЫЕ МАШИНЫ В СРАВНЕНИИ С ДЕТЕРМИНИСТСКИМИ
В этом разделе мы сначала дадим точное определение некоторого класса вычислительных машин. Эти машины имеют вход и выход. Входом является бесконечная последовательность двоичных знаков, которая может подаваться двумя различными способами: 1) как фиксированная последовательность (физически можно представлять заранее подготовленную бесконечную ленту); 2) как выход двоичного случайного устройства (с вероятностью p появления 1). В последнем случае мы имеем вероятностную машину. Затем мы очертим точный класс задач, решения которых этими машинами мы желаем, а именно перечисление с положительной вероятностью множеств выходных символов. После этого ключевой результат настоящей статьи - теорема 1 - используется для ответа на наш вопрос. Ответ дается в теореме 2. Он гласит, что если случайное устройство имеет вероятность p, где p - ВЫЧИСЛИМОЕ ДЕЙСТВИТЕЛЬНОЕ ЧИСЛО (т.е. действительное число, для которого существует эффективный процесс нахождения любого знака в его двоичном разложении), то любое множество, перечислимое посредством вероятностной машины рассматриваемого типа, перечислимо посредством детерминистской машины. Это не имеет места, если p - невычислимое действительное число. Аналогичные результаты получаются для случая, когда учитывается порядок следования выходных символов. Положение подытоживается теоремой 3.
Мы будем мыслить наши машины в виде объектов, которые воспринимают в качестве входа ленту с записанными на ней нулями и единицами и выпускают в качестве выхода ленту, на которой они могут записывать конечную или счетную выборку выходных символов s1, s2, s3, ... (этими символами могут быть конфигурации, образованные из некоторого конечного алфавита). Предполагается, что машина имеет некоторое начальное состояние, в которое она приводится перед началом любой операции (подобно тому, как счетно-клавишная машина гасится перед вычислением). Другое разумное требование к машине таково: должна существовать эффективная процедура, позволяющая определить, какова будет последовательность выходных символов (sj1, ..., sjr) на выходной ленте, если в начальном состоянии машина снабжена входной последовательностью нулей и единиц (a1, ..., an). Эту выходную последовательность мы обозначим через f(a1, ..., an). Так как нас интересует только зависимость между входом и выходом машин, то можно отвлечься от их внутреннего устройства и принять это требование за определение. Хотя мы и дадим сейчас абстрактное определение, мы будем дальше говорить о машинах, пользуясь обычным языком.
ОПРЕДЕЛЕНИЕ. МАШИНА есть функция, которая для каждого n ставит в соответствие каждой конечной последовательности из n нулей и единиц (a1, ..., an) некоторую конечную последовательность f(a1, ..., an) = (sj1, ..., sjr),
состоящую из элементов заданного множества S, причем выполняются следующие два условия:
1) f(a1, ..., an) есть начальный отрезок в f(a1, ..., an, ... a[n+m]) если (a1, ..., an) есть начальный отрезок в (a1, ..., an, ... a[n+m]),
2) f - вычислимая функция, т.е. существует эффективный процесс [См. предыдущее примечание], позволяющий определить f(a1, ..., an) по заданной {a1, ..., an).
Это определение распространяется на бесконечные последовательности следующим образом: если A = (a1, a2, a3, ...), то f(A) есть последовательность с начальными отрезками f(a1, ..., an).
Неформально работу машины можно представить себе следующим образом. Получив вход (a1, ..., an), она воспринимает a1 и записывает последовательность символов f(a1) на выходе; затем она воспринимает a2 и записывает символы на ленте после f(a1), производя f(a1, a2); ...; затем она воспринимает an и записывает символы на ленте после f(a1, ..., a[n-1]), производя f(a1, ..., a[n-1], an); и, наконец, останавливается.
Теперь дадим несколько конкретных примеров машин. Этим мы преследуем двоякую цель: проиллюстрировать наше понятие машины и подготовить материал для иллюстрации новых понятий, вводимых далее. Пока можно читать не все примеры.
МАШИНА #1. Выходными символами этой машины являются упорядоченные пары целых чисел (a, r). Для каждого входного символа a машина записывает выходной символ (a, r), если a был r-м входным символом на входной ленте. Иными словами, f{a1, ..., an) = ((a1, 1), (a2, 2), ..., {an, n)).
МАШИНА #2. Пусть g - целочисленная функция положительных целых чисел, и пусть она вычислима, т.е. существует эффективный процесс для нахождения g(n) по заданному n. Пусть машина записывает выходной символ (r, g(r)) после восприятия r-го входного символа. В этом случае f(a1, ..., an) = ((1, g(1)), (2, g(2)), ..., (n, g(n))) и выход не зависит от входа. Эта машина и машина #1 представляют крайние случаи. #2 забывает о входе, а #1, по существу, копирует вход на выходной ленте. Заметим, что объект #2 не был бы машиной в смысле нашего определения, если бы функция g не была вычислима, ибо в этом случае не существовало бы эффективного процесса, позволяющего определить выход по заданному входу.
МАШИНА #3. Пусть машина записывает символ 0, как только она встретит первый нуль во входной последовательности. В остальное время она не записывает ничего. Тогда f(a1, ..., an) = (0), если один из символов aj является нулем. В противном случае машина не записывает ничего, и мы говорим о "пустой последовательности" (.); f(1, ..., 1) = (.).
МАШИНА #4. Пусть f(a1, ..., an) = (a1). Машина просто копирует на выходной ленте первый входной символ, не записывая больше ничего.
МАШИНА #5. Пусть машина записывает выходной символ r, если максимальная длина групп единиц, воспринятых машиной, равна r. Например, f(1) = (1), f(1, 0) = (1, 1), f(1, 0, 1) = (1, 1, 1), f(1, 0, 1, 1) = (1, 1, 1, 2).
МАШИНА #6. Пусть h(r, s) - вычислимая целочисленная функция, определенная на целых положительных числах. Машина не записывает ничего, пока не встретит первой единицы на входе; если эта единица - первый входной символ, то машина не печатает ничего никогда; если же эта единица встретилась после r нулей, то записывается символ (1, h (r, 1)). После следующего входного символа машина записывает символ (2, h(r, 2)), после следующего - символ (3, h(r, 3)) и т.д. Пусть функция hr{s) с фиксированным r определяется соотношением hr(s) = h(r, s). Тогда работа машины фактически состоит в вычислении функции hr при поступлении в машину начальной группы r нулей и следующей за ними единицы.
МАШИНА #7. Эта машина задается соотношением f{a1, ..., an) = ((1, r1), (2, r2), ..., (q, rq)), где целое число rs получается следующим образом. Возьмем первые 100**s знаков в (a1, ..., an). Пусть ps - доля знаков, равных 1. Тогда rs есть s-й знак в двоичном разложении числа ps. Число q есть наибольшее s, такое, что 100**s <= n. Аналогичная конструкция используется при доказательстве части теоремы 1.
Хотя работа машины определена только для конечных входных последовательностей, тем не менее ясно, что сделала бы такая машина, получая бесконечную входную последовательность A = (a1, a2, a3, ...) и обладая бесконечной выходной лентой для записи. Работа машины определена тем фактом, что мы знаем ее выход для всех конечных входных последовательностей. Таким образом, машина ставит в соответствие каждой бесконечной входной последовательности выходную последовательность, которая может быть или не быть бесконечной. Например, если вводить в машину #1 бесконечную ленту, на которой записаны только единицы, то выходная последовательность будет ((1, 1), (1, 2), (1, 3), ...). Для этой же ленты машина #3 не даст никакого выхода (пустая последовательность (.)), а машина #4 даст выходную последовательность (1).
Рассмотрим множество символов, появляющихся на выходной ленте машины, когда машина получает некоторую бесконечную входную последовательность A. (Например, если выходная последовательность есть (1, 1, 1, ...), то это множество состоит лишь из одного символа 1, а если выходная последовательность есть (1, 3, 5, 7, ...), то это множество символов состоит из всех нечетных чисел). Таким образом, машина ставит в соответствие каждой входной последовательности A некоторое множество выходных символов, которое она перечисляет. (Мы не будем здесь обращать внимание на порядок, в котором это множество перечисляется, а также на то, перечисляется ли оно с повторениями или без повторений. Это будет сделано позже, при рассмотрении вычисления последовательностей).
Например, машина #1 ставит в соответствие любой бесконечной входной последовательности A = (a1, a2, ...) множество выходных символов, состоящее из всех (an, n), где n пробегает целые положительные числа. Машина #2 ставит в соответствие любой входной последовательности множество всех (n, g(n)), где n пробегает целые положительные числа. Машина #3 ставит в соответствие входной последовательности, состоящей только из единиц, пустое множество. Такому же входу машина #5 ставит в соответствие множество всех целых положительных чисел.
ОПРЕДЕЛЕНИЕ. Машина, получающая бесконечную входную последовательность A = (a1, a2, a3, ...), будет называться A-МАШИНОЙ. Будем говорить, что она A-ПЕРЕЧИСЛЯЕТ множество выходных символов, записываемых ею. Множество каких-либо символов называется A-ПЕРЕЧИСЛИМЫМ, если существует A-машина, которая A-перечисляет это множество.
A-перечислимые множества, где A есть последовательность, состоящая только из единиц, обычно называются РЕКУРСИВНО-ПЕРЕЧИСЛИМЫМИ множествами. Мы назовем их 1-ПЕРЕЧИСЛИМЫМИ множествами. A-машина будет называться 1-МАШИНОЙ, если A состоит целиком из единиц.
Каждой бесконечной последовательности A = (a1, a2, ...) можно поставить в соответствие множество всех пар (n, an), где an есть n-й элемент в последовательности A, а n пробегает все целые положительные числа. Это множество обозначим через А'. Последовательность A называется ВЫЧИСЛИМОЙ, если существует эффективный процесс, с помощью которого можно определить n-й член в A для каждого n. Три следующие леммы доказываются в приложении, хотя их доказательства получаются почти немедленно.
ЛЕММА 1. Последовательность A вычислима тогда и только тогда, когда соответствующее множество А' является 1-перечислимым.
ЛЕММА 2. Если А - вычислимая последовательность, то любое А-перечислимое множество 1-перечислимо (и обратно).
ЛЕММА 3. Если А - невычислимая последовательность, то существуют множества А-перечислимые, но не 1-перечислимые.
Лемма 3 и существование невычислимых последовательностей будут важны для нас позже.
Теперь мы хотим присоединить к машине случайное устройство, чтобы построить вероятностную машину. Если у нас есть устройство, записывающее нули и единицы на ленте, и если единицы появляются с вероятностью p, нули - с вероятностью 1-p (0<p<1), причем каждая запись независима от предыдущих, то выход такого устройства можно использовать как входную ленту машины. Такая комбинация случайного устройства и машины будет называться p-МАШИНОЙ.
Поставленный во введении вопрос о существовании вероятностных машин, более общих, чем детерминистские машины, можно теперь сузить до более частного вопроса: можно ли на 1-машине сделать все, что делается на p-машине? (В следующем разделе будет показано, что рассмотрение довольно узкого класса p-машин вместо более широкого класса всех мыслимых вероятностных машин не вызывает большой потери общности. Мы увидим, что широкий класс вероятностных машин эквивалентен (в определяемом далее смысле) 1/2-машинам и что многие свойства машин широкого класса выводятся из свойств 1/2-машин).
Необходимо еще более ограничить наш вопрос, ибо ясно, что нельзя дать никакого точного ответа, пока нет точного определения выполняемой машинами задачи.
Задача, выполняемая машинами в настоящей статье, состоит в перечислении множеств. Эта задача не так уж узка, как это может показаться с первого взгляда. Например, машина может вычислять функцию, перечисляя символы "f(n) = m", или устанавливать истинность или ложность некоторого высказывания о целых положительных числах перечислением символов "P(n) истинно" и "P(n) ложно"; или же может вычислять двоичное разложение действительного числа перечислением символов "n-й знак числа r равен a".
Мы уже определили, что понимается под 1-перечислимым множеством символов. А именно, некоторое множество 1-перечислимо, если существует машина, которая, получая на входе ленту с одними только единицами, производит в итоге это множество на выходе. Необходимо дать определение перечислимости для p-машин, чтобы сравнить их с 1-машинами.
Будет предложено два определения: определение p-перечислимых множеств и определение сильно p-перечислимых множеств. Наш первоначальный неформальный вопрос будет сведен к двум точным вопросам: каждое ли p-перечислимое множество 1-перечислимо? Каждое ли сильно p-перечислимое множество 1-перечислимо?
Остается дать эти два определения. Каждому множеству возможных выходных символов данной p-машины можно приписать вероятность его появления в качестве полного выхода этой машины. Это есть вероятность того, что данное множество будет в точности множеством символов, которые появятся на выходной ленте машины, если машину привести в начальное положение, присоединить случайное устройство и пустить в работу. Указанная вероятность, конечно, равна нулю для большинства множеств. Мы дадим несколько примеров, ссылаясь на описанные выше машины. Предположим, что они присоединены к случайному устройству с p = 1/2 и стали поэтому 1/2-машинами. Машина #1 перечисляет любое множество с нулевой вероятностью. Следует отметить, что конечные множества появиться не могут, и по этой причине они имеют нулевую вероятность. Хотя некоторые бесконечные множества и могут быть выходом, однако это случается лишь с нулевой вероятностью. Не следует забывать о различии между появлением с нулевой вероятностью и невозможностью появления. Машина #2 перечисляет множество всех (n, g(n)) с вероятностью 1 (и притом с достоверностью). Выход машины #3 есть множество, состоящее из единственного символа 0, с вероятностью 1, но без достоверности. Выход машины #5 есть множество всех целых положительных чисел - с вероятностью 1, но без достоверности, ибо бесконечная последовательность нулей и единиц содержит произвольно длинные группы единиц с вероятностью 1, но без достоверности. Машина #6 перечисляет с вероятностью 2**-r множество всех (n, h(r, n)), где r фиксировано, а n пробегает все целые положительные числа. Иными словами, машина вычисляет функцию hr (определяемую соотношением hr(n) = h(r, n)) с вероятностью 2**-r.
...

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
ОПРЕДЕЛЕНИЕ. Для заданного p множество символов будет называться СИЛЬНО P-ПЕРЕЧИСЛИМЫМ, если существует p-машина, производящая (в любом порядке) это множество выходных символов с положительной вероятностью.
Предыдущие примеры показывают, что следующие множества сильно 1/2-перечислимы: множество всех (n, g(n)); множество, состоящее только из 0; множество всех целых положительных чисел; множество всех (n, h{r,n)) с фиксированным r.
Ясно, как употребить p-машину для того, чтобы дать информацию о каком-нибудь сильно p-перечислимом множестве S, производимом ею с положительной вероятностью. Заставим p-машину работать. В том, что перечисляемое ею множество будет S, мы уверены, соответственно вероятности появления S в качестве выхода. Поскольку S обладает положительной вероятностью, p-машину можно использовать с некоторой степенью уверенности. Если же вероятность появления S в качестве выхода равняется нулю, то мы не можем быть уверенными в способности машины перечислить в точности S. Однако даже машина, обладающая высокой вероятностью правильно записать любой отдельный выходной символ, может перечислять S с нулевой вероятностью.
Поэтому мы нуждаемся в более слабом определении.
Существует определенная вероятность того, что данная p-машина M в КОНЦЕ-КОНЦОВ запишет данный выходной символ. Пусть Sm множество всех выходных символов, которые M в конце-концов запишет с вероятностью >1/2. Например, присоединим рассмотренные выше машины к случайному устройству с p = 3/4, так что они станут 3/4-машинами. Sm для машины #2 есть множество всех (n, g(n)); для машины #3 - множество, состоящее только из 0; для машины #4 - множество, состоящее только из 1; для машины #5 - множество целых положительных чисел и для машины #6 - пустое множество.
Если p-машина M начала работать, то с вероятностью >1/2 она в конце концов запишет любой данный элемент из Sm и с вероятностью <=1/2 запишет любой данный элемент, не принадлежащий Sm. Отсюда ясно, как употребить M, чтобы получить информацию о Sm. Существует определенная степень уверенности в том, что любой элемент множества Sm в конце концов появится в качестве выходного символа и что любой элемент, не входящий в Sm не появится в качестве выходного символа. Однако само множество Sm может при этом иметь нулевую вероятность появления, и в таком случае мы не будем уверены в том, что машина перечислит в точности Sm. (Ясно, что все это остается справедливым, если в определении Sm взять вместо 1/2 большее число. Остаются справедливыми и все последующие результаты).
ОПРЕДЕЛЕНИЕ. Множество символов S называется Р-ПЕРЕЧИСЛИМЫМ, если существует такая машина M, что S есть в точности Sm.
Условие p-перечислимости множества совсем слабое, и мы полагаем, что нет более слабого определения, которое все же предусматривало бы существование p-машины, дающей некоторую информацию о каждом элементе множества. Следует заметить, что p-машина p-перечисляет только одно множество, тогда как сильно p-перечислять она может несколько множеств или ни одного.
На первый взгляд понятие сильной p-перечислимости кажется намного сильнее понятия p-перечислимости, и, действительно, мы покажем, что сильно p-перечислимое множество p-перечислимо. Несколько более глубоким и, быть может, неожиданным является обратный результат, означающий фактическую эквивалентность этих двух понятий.
Чтобы сформулировать ключевой результат настоящей статьи и дать с его помощью ответ на два поставленных нами общих вопроса, мы нуждаемся еще в одном определении. Пусть p - действительное число, 0<p<1. Тогда под Ap мы понимаем бесконечную последовательность нулей и единиц (a1, a2, a3, ...), где аn есть n-й знак двоичного разложения действительного числа p, т.е. p == 0.a1a2a3... Так как Ap - бесконечная последовательность нулей и единиц, то она может служить входом машин, и мы будем говорить об Ap-машинах, Ap-перечислимости и т.д.
Теперь для любого числа p между 0 и 1 у нас есть три понятия: Ap-перечислимости, p-перечислимости и сильной p-перечислимости. Из них лишь первое понятие является строго детерминистским, тогда как остальные - вероятностными.
Основной результат гласит:
ТЕОРЕМА 1. Пусть S - множество символов, p - действительное число, 0<p<1. Три следующих предложения эквивалентны:
1) S является Ap-перечислимым;
2) S является p-перечислимым;
3) S является сильно p-перечислимым.
Доказательство этой теоремы дано в приложении, но набросок доказательства мы приведем здесь, показав сначала, что эта теорема дает непосредственный ответ на наши два вопроса.
Пусть p - невычислимое действительное число между 0 и 1. Известно, что такие числа существуют и что в действительности почти все (в смысле меры Лебега) числа невычислимы. Невычислимость p эквивалентна невычислимости Ap. Тогда в силу леммы 3 существует множество S, которое Ap-перечислимо, но не 1-перечислимо. В силу теоремы 1 это множество как p-перечислимо, так и сильно p-перечислимо, но не 1-перечислимо. Следовательно, если имеются случайные устройства, записывающие символ 1 с вероятностью, которая не является вычислимым действительным числом, то можно построить p-машины, которые будут "перечислять" множества, не являющиеся 1-перечислимыми.
Положение совершенно меняется в случае, когда p есть вычислимое действительное число (в частности, когда оно равно 1/2). Это равносильно вычислимости последовательности Ар. Теорема 1 показывает, что любое p-перечислимое или сильно p-перечислимое множество должно быть Ap-перечислимым. Так как Ар вычислимо, то по лемме 2 рассматриваемое множество должно быть 1-перечислимым. Следовательно, p-перечислимое или сильно p-перечислимое множество должно быть 1-перечислимым. Отсюда вывод, что если в качестве p брать только вычислимые действительные числа (в частности 1/2), то машина со случайным устройством не сможет "перечислить" ничего сверх того, что перечисляет детерминистская машина.
Оба случая охватывает
ТЕОРЕМА 2. Если p - вычислимое действительное число, то любое p-перечислимое или сильно p-перечислимое множество 1-перечислимо. Если p - невычислимое действительное число, то существуют p-перечислимые и сильно p-перечислимые множества, не являющиеся 1-перечислимыми.
Теперь мы дадим набросок доказательства теоремы 1. Доказательство состоит из вывода предложения 2 из предложения 3, вывода предложения 1 из предложения 2 и вывода предложения 3 из предложения 1. Эта цепочка заключений дает требуемую эквивалентность.
То, что 3 влечет 2, доказывается тем, что с помощью p-машины, у которой выход S появляется с положительной вероятностью, строится новая машина, у которой S появляется с вероятностью >1/2. Тогда каждый элемент из S появляется с вероятностью >1/2, а любой элемент, не входящий в S, появляется с вероятностью <1/2, так что S p-перечислимо. Следовательно, всякое сильно p-перечислимое множество p-перечислимо.
То, что 2 влечет 1, доказывается следующим образом. Пусть дана p-машина M. Построим Ap-машину, Ap-перечисляющую множество Sm. Предположим, что мы располагаем бесконечной лентой, на которой записано Ap. Используя все более длинные начальные отрезки бесконечной последовательности Ap, можно вычислить сколь угодно хорошие нижние границы для вероятности справедливости высказываний вида "за время, в течение которого из случайного устройства появилось n входных символов, M запишет символ s". Но M запишет s с вероятностью >1/2 тогда и только тогда, когда, существует такое n, что это высказывание справедливо с вероятностью >1/2. В свою очередь, это может случиться лишь тогда, когда одна из сколь угодно хороших нижних границ (которые мы можем вычислить, используя начальные отрезки последовательности Ар) для вероятности справедливости указанного высказывания >1/2. Можно вычислить ПОСЛЕДОВАТЕЛЬНО (используя все более длинные начальные отрезки последовательности Ap) все нижние границы этих вероятностей для каждого n и каждого s. Сразу после получения нижней границы >1/2 записывается соответствующий символ s. Мы видим, что перечисленное таким образом множество символов есть Sm и что перечисление произведено посредством процесса, действительно составляющего Ap-машину. Следовательно, всякое p-перечислимое множество Ap-перечислимо.
То, что 1 влечет 3, доказывается следующим образом. Строится p-машина, вычисляющая с вероятностью >1/2 двоичное разложение действительного числа p. Иными словами, выход машины есть - с вероятностью >1/2 - множество всех (n, an), где an есть n-й знак в двоичном разложении числа p. Машина, делающая это, является видоизменением машины #7. Если выход этой p-машины использовать как вход другой машины M, то выход последней будет с вероятностью >1/2 в точности таким, каким был бы выход машины M, снабженной в качестве входа последовательностью Ар, Если S есть любое Ap-перечислимое множество и M - машина, Ap-перечисляющая его, то построенная выше сложная машина есть p-машина, сильно p-перечисляющая S. Следовательно, любое Aр-перечислимое множество сильно p-перечислимо. Это доказывает, что 1 влечет 3, и набросок доказательства теоремы 1 тем самым закончен.
Исследуем теперь, останутся ли результаты теми же, если учитывать не только совокупность выходных символов, но и порядок их следования. Будет показано, что такое положение можно свести к частному случаю уже полученных результатов.
ОПРЕДЕЛЕНИЕ. Бесконечная последовательность символов S = s1, s2, s3... называется A-ВЫЧИСЛИМОЙ, если она появляется в данном порядке следования на выходе некоторой A-машины. Она называется 1-ВЫЧИСЛИМОЙ, если А состоит целиком из единиц. S СИЛЬНО P-ВЫЧИСЛИМА, если существует p-машина, производящая S в данном порядке с положительной вероятностью. S называется P-ВЫЧИСЛИМОЙ, если существует p-машина, у которой n-й выходной символ есть n-й символ в S с вероятностью >1/2.
Будет показано, что для этих новых понятий справедлив точный аналог теоремы 2.
Пусть S - ПОСЛЕДОВАТЕЛЬНОСТЬ символов (sl, s2, s3, ...). Через S' обозначим МНОЖЕСТВО всех пар (n, sn), где n пробегает все целые положительные числа. Следующие леммы, доказываемые в приложении, суть непосредственные следствия определений.
ЛЕММА 4. Последовательность S {-вычислима тогда и только тогда, когда множество S' 1-перечислимо.
ЛЕММА 5. Если S сильно p-вычислима, то S' сильно p-перечислимо. Если S p-вычислима, то S' p-перечислимо.
Из двух предыдущих лемм и теоремы 2 вытекает.
ЛЕММА 6. Пусть p - вычислимое действительное число (в частности, 1/2). Тогда любая p-вычислимая или сильно p-вычислимая последовательность 1-вычислима.
ДОКАЗАТЕЛЬСТВО. Пусть последовательность S p-вычислима или сильно p-вычислима. Тогда S' p-перечислимо или сильно p-перечислимо по лемме 5. По теореме 2 множество S' 1-перечислимо. По лемме 4 последовательность S должна быть 1-вычислимой.
Это охватывает случай, когда p - вычислимое действительное число. Если p невычислимо, то доказательство теоремы 1, данное в приложении, показывает, что существует p-вычислимая и сильно p-вычислимая, но не 1-вычислимая последовательность (эта последовательность представляет собой двоичное разложение числа p). Объединяя оба случая, получим следующий аналог теоремы 2 для понятий вычислимости.
ТЕОРЕМА 3. Если p - вычислимое действительное число, то любая p-вычислимая или сильно p-вычислимая последовательность 1-вычислима. Если p невычислимо, то существует p-вычислимая и сильно p-вычислимая последовательность, которая не 1-вычислима.
Как частный случай этого мы находим, что 1/2-машина не может записать с положительной вероятностью никакой невычислимой последовательности.
БОЛЕЕ ОБЩИЙ КЛАСС МАШИН
В этом разделе обобщается результат, даваемый теоремой 2 для вычислимого числа p. Мы определим широкий класс вероятностных машин - вычислимо стохастических машин (или в.с.-машин), не покрываемых нашими предыдущими определениями, и предложим понятие эквивалентности для вероятностных машин. Будет показано, что любая машина нового класса эквивалентна 1/2-машине, и, как следствие теоремы 2, мы получим, что любое множество, перечислимое машиной этого класса, должно быть 1-перечислимым. Далее, существует эффективный процесс, позволяющий по описанию машины этого класса найти описание эквивалентной ей 1/2-машины и описание 1-машины, 1-перечисляющей то же самое множество.
Для простоты изложения мы рассматриваем в этом разделе только одно определение перечислимости, соответствующее p-перечислимости, и не даем более сильного определения, соответствующего сильной p-перечислимости. Можно показать, что те же результаты справедливы и для сильного определения.
Сначала определим класс стохастических машин. СТОХАСТИЧЕСКАЯ МАШИНА есть объект со счетным числом состояний X1, X2, X3, ..., выделенным начальным состоянием X0 и счетным набором выходных символов s1, s2, s3, ... При этом указано правило, дающее вероятность прихода машины в состояние Xp и записи ею выходного символа sq, если перед тем она прошла последовательно через состояния X0, Xj1, ..., Xjn. Эту вероятность мы обозначим через P(Xj1, ..., Xjn; Xp; sq). (Мы не требуем, чтобы это правило давало эффективную процедуру для вычисления вероятностей Р).
Любой p-машине M можно поставить в соответствие стохастическую машину в указанном выше смысле. Состояния соответствующей стохастической машины суть конечные последовательности нулей и единиц (a1, ..., an), а начальное состояние - "пустая" последовательность (.). (Фактически мы называем "состоянием" p-машины входную последователь ность, воспринятую ею. Эти "состояния" могут не соответствовать возможным внутренним состояниям конкретной машины, но определяют их полностью). Вероятность перехода из состояния (a1, ..., an) в (a1, ..., an, 1) есть p, а из состояния (a1, ..., an) в (a1, ..., an, 0) есть 1-p. Соответствующая стохастическая машина записывает по приходе в состояние (a1, ..., an, a[n+1]) то же, что и p-машина, принявшая (n+1)-й входной символ a[n+1] после восприятия (a1, . .., an). Тем самым стохастическая машина полностью задана. Она будет в дальнейшем называться стохастической машиной, СООТВЕТСТВУЮЩЕЙ P-МАШИНЕ M. Таким образом, p-машины можно отождествить с частными случаями стохастических машин. Легко видеть, что если p - вычислимое число, то соответствующая стохастическая машина обладает следующим специальным свойством: функция Р ВЫЧИСЛИМА, т.е. существует ЭФФЕКТИВНЫЙ ПРОЦЕСС, позволяющий по заданному целому положительному числу m состояниям Xj1, ..., Xjn и Xp и выходному символу sq вычислить первые m знаков двоичного разложения P(Xj1, ..., Xjn; Xp; sq). Мы назовем стохастические машины с таким свойством вычислимо стохастическими машинами, или в.с.-машинами. Непосредственным следствием этих определений является
ЛЕММА 7. Стохастическая машина, соответствующая p-машине, является в.с.-машиной тогда и только тогда, когда p - вычислимое действительное число.
Остальную часть этого раздела мы посвятим тому, чтобы показать, что результат, сформулированный в теореме 2 для p-машин с вычислимым p, справедлив и для гораздо более широкого класса в.с.-машин. Таким образом, любое множество, перечислимое в.с.-машиной, 1-перечислимо.
Как для стохастических, так и для p-машин можно говорить о вероятности того, что машина в конце концов запишет выходные символы sj1, ..., sjn (подобно тому, как раньше мы говорили о вероятности того, что p-машина в конце концов запишет одиночный символ s). Поскольку наши машины служат для перечисления множеств, то любые две машины, которые в конце концов сделают одно и то же с одной и той же вероятностью, можно считать тождественными с точки зрения окончательного выхода. Поэтому будет дано следующее определение:
ОПРЕДЕЛЕНИЕ. Два объекта - стохастические машины или p-машины - будут называться ЭКВИВАЛЕНТНЫМИ, если для любого конечного множества символов sj1, ..., sjn они имеют одинаковую вероятность включения (в конце концов) этого множества в их выход. Если эти машины суть M1 и M2, то их эквивалентность мы будем обозначать так: M1~M2.
Например, p-машина и соответствующая ей стохастическая машина эквивалентны.
Вспомним, что мы назвали p-машину p-перечисляющей некоторое множество символов, если каждый элемент этого множества появляется на выходе этой машины с вероятностью >1/2, а любой выходной символ, не принадлежащий данному множеству, появляется с вероятностью <1/2. Это определение можно непосредственно применить к стохастическим машинам и в.с.-машинам. Если M - стохастическая машина, то Sm будет множеством всех выходных символов, появляющихся с вероятностью >1/2, в согласии с введенным выше обозначением для p-машин.
Sm есть множество символов, которое машина M перечисляет. Как непосредственное следствие из нашего определения эквивалентности получаем, что M1~M2 влечет Sm1=Sm2, т.е. две эквивалентные машины перечисляют одно и то же множество.
ОПРЕДЕЛЕНИЕ. Множество S в.с.-перечислимо, если существует такая в.с.-машина M, что S=Sm.
Теперь мы ответим на вопрос: каждое ли в.с.-перечислимое множество 1-перечислимо? Ответ вытекает из следующего утверждения, доказанного в приложении.
ТЕОРЕМА 4. Каждая в.с.-машина эквивалентна 1/2-машине.
Следовательно, если M - в.с.-машина, то множество которое M перечисляет, перечислимо также некоторой 1/2-машиной. По теореме 2 множество Sm должно быть 1-перечислимым. Отсюда вытекает
ТЕОРЕМА 5. Любое в.с.-перечислимое множество l-перечислимо.
Этот результат и был упомянут выше.
В действительности доказательство теоремы 4 дает больше, чем было высказано. Могло случиться, что доказательство только устанавливает существование 1/2-машины, эквивалентной произвольной в.с.-машине, но не дает эффективных средств для ее разыскания. Однако это не так, и доказательство дает эффективный процесс.
ТЕОРЕМА 4 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины получить описание эквивалентной ей 1/2-машины.
Следовательно, для заданного описания в.с.-машины М1 существует эффективный процесс, позволяющий найти такую 1/2-машину M2, что Sm1=Sm2. Но это еще не дает эффективного расширения теоремы 5, для которого необходимо следующее эффективное расширение части теоремы 1.
ТЕОРЕМА 1 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию p-машины M (где p - вычислимое число) получить описание 1-машины, 1-перечисляющей то же самое Sm, которое M p-перечисляет.
Из объединения дополнений теорем 1 и 4 вытекает
ТЕОРЕМА 5 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины, в.с.-перечисляющей множество S, получить описание 1-машины, которая 1-перечисляет S.
Результаты относительно вычислимости последовательностей, приведенные в конце предыдущего раздела, остаются справедливыми для в.с.-машин. Очевидным образом можно определить в.с.-вычислимые последовательности. Доказательства лемм 4, 5 и 6 справедливы в этом случае, откуда следует, что любая в.с.-вычислимая последовательность 1-вычислима.
[ПРИЛОЖЕНИЕ я перепечатывать не стал. Там слишком много непечатных символов. Выложил сразу весь сборник АВТОМАТЫ, 1956 DJVU, 4.49Мб
DJVU, 4.49Мб . Слишком уж часто я на него ссылаюсь, особенно, когда пытаюсь кому-то объяснить, что нейронные сети совсем не такие всемогущие, как сейчас принято думать.- G.]
. Слишком уж часто я на него ссылаюсь, особенно, когда пытаюсь кому-то объяснить, что нейронные сети совсем не такие всемогущие, как сейчас принято думать.- G.]
ЛИТЕРАТУРА
1. Church A., An unsolvable problem of elementary number theory, Am. Jourft. Math., 58, 345-363 (1936).
2. Davis M., Готовится книга по рекурсивным функциям и вычислимости, выйдет в изд-ве Мак Гро-Хилл.
3. Dооb J.L., Stochastic processes, John Wiley and Sons (1953) (Русский перевод: Дуб, Вероятностные процессы, Издат. иностр. лит., M., 1956).
4. Феллеp В., Введение в теорию вероятностей и ее приложения, M., 1952.
5. Xалмош П., Теория меры, M., 1953.
6. Hobson E.W., The theory of functions of a real variable and the theory of Fourier's series (1926).
7. К1eene S.C., Introduction to metamathematics, Van Nostrand (1952) (готовится русский перевод).
8. Post E.L., Finite combinatory processes - Formulation I, Journ. Symbolic Logic, 1, 103-105 (1936).
9. Turing A.M., On computable numbers, with an application to the Entscheidungsproblem, Proc. London Math. Soc., ser.2, 42, 230-265 (1936); 43, 544-546 (1937).
Предыдущие примеры показывают, что следующие множества сильно 1/2-перечислимы: множество всех (n, g(n)); множество, состоящее только из 0; множество всех целых положительных чисел; множество всех (n, h{r,n)) с фиксированным r.
Ясно, как употребить p-машину для того, чтобы дать информацию о каком-нибудь сильно p-перечислимом множестве S, производимом ею с положительной вероятностью. Заставим p-машину работать. В том, что перечисляемое ею множество будет S, мы уверены, соответственно вероятности появления S в качестве выхода. Поскольку S обладает положительной вероятностью, p-машину можно использовать с некоторой степенью уверенности. Если же вероятность появления S в качестве выхода равняется нулю, то мы не можем быть уверенными в способности машины перечислить в точности S. Однако даже машина, обладающая высокой вероятностью правильно записать любой отдельный выходной символ, может перечислять S с нулевой вероятностью.
Поэтому мы нуждаемся в более слабом определении.
Существует определенная вероятность того, что данная p-машина M в КОНЦЕ-КОНЦОВ запишет данный выходной символ. Пусть Sm множество всех выходных символов, которые M в конце-концов запишет с вероятностью >1/2. Например, присоединим рассмотренные выше машины к случайному устройству с p = 3/4, так что они станут 3/4-машинами. Sm для машины #2 есть множество всех (n, g(n)); для машины #3 - множество, состоящее только из 0; для машины #4 - множество, состоящее только из 1; для машины #5 - множество целых положительных чисел и для машины #6 - пустое множество.
Если p-машина M начала работать, то с вероятностью >1/2 она в конце концов запишет любой данный элемент из Sm и с вероятностью <=1/2 запишет любой данный элемент, не принадлежащий Sm. Отсюда ясно, как употребить M, чтобы получить информацию о Sm. Существует определенная степень уверенности в том, что любой элемент множества Sm в конце концов появится в качестве выходного символа и что любой элемент, не входящий в Sm не появится в качестве выходного символа. Однако само множество Sm может при этом иметь нулевую вероятность появления, и в таком случае мы не будем уверены в том, что машина перечислит в точности Sm. (Ясно, что все это остается справедливым, если в определении Sm взять вместо 1/2 большее число. Остаются справедливыми и все последующие результаты).
ОПРЕДЕЛЕНИЕ. Множество символов S называется Р-ПЕРЕЧИСЛИМЫМ, если существует такая машина M, что S есть в точности Sm.
Условие p-перечислимости множества совсем слабое, и мы полагаем, что нет более слабого определения, которое все же предусматривало бы существование p-машины, дающей некоторую информацию о каждом элементе множества. Следует заметить, что p-машина p-перечисляет только одно множество, тогда как сильно p-перечислять она может несколько множеств или ни одного.
На первый взгляд понятие сильной p-перечислимости кажется намного сильнее понятия p-перечислимости, и, действительно, мы покажем, что сильно p-перечислимое множество p-перечислимо. Несколько более глубоким и, быть может, неожиданным является обратный результат, означающий фактическую эквивалентность этих двух понятий.
Чтобы сформулировать ключевой результат настоящей статьи и дать с его помощью ответ на два поставленных нами общих вопроса, мы нуждаемся еще в одном определении. Пусть p - действительное число, 0<p<1. Тогда под Ap мы понимаем бесконечную последовательность нулей и единиц (a1, a2, a3, ...), где аn есть n-й знак двоичного разложения действительного числа p, т.е. p == 0.a1a2a3... Так как Ap - бесконечная последовательность нулей и единиц, то она может служить входом машин, и мы будем говорить об Ap-машинах, Ap-перечислимости и т.д.
Теперь для любого числа p между 0 и 1 у нас есть три понятия: Ap-перечислимости, p-перечислимости и сильной p-перечислимости. Из них лишь первое понятие является строго детерминистским, тогда как остальные - вероятностными.
Основной результат гласит:
ТЕОРЕМА 1. Пусть S - множество символов, p - действительное число, 0<p<1. Три следующих предложения эквивалентны:
1) S является Ap-перечислимым;
2) S является p-перечислимым;
3) S является сильно p-перечислимым.
Доказательство этой теоремы дано в приложении, но набросок доказательства мы приведем здесь, показав сначала, что эта теорема дает непосредственный ответ на наши два вопроса.
Пусть p - невычислимое действительное число между 0 и 1. Известно, что такие числа существуют и что в действительности почти все (в смысле меры Лебега) числа невычислимы. Невычислимость p эквивалентна невычислимости Ap. Тогда в силу леммы 3 существует множество S, которое Ap-перечислимо, но не 1-перечислимо. В силу теоремы 1 это множество как p-перечислимо, так и сильно p-перечислимо, но не 1-перечислимо. Следовательно, если имеются случайные устройства, записывающие символ 1 с вероятностью, которая не является вычислимым действительным числом, то можно построить p-машины, которые будут "перечислять" множества, не являющиеся 1-перечислимыми.
Положение совершенно меняется в случае, когда p есть вычислимое действительное число (в частности, когда оно равно 1/2). Это равносильно вычислимости последовательности Ар. Теорема 1 показывает, что любое p-перечислимое или сильно p-перечислимое множество должно быть Ap-перечислимым. Так как Ар вычислимо, то по лемме 2 рассматриваемое множество должно быть 1-перечислимым. Следовательно, p-перечислимое или сильно p-перечислимое множество должно быть 1-перечислимым. Отсюда вывод, что если в качестве p брать только вычислимые действительные числа (в частности 1/2), то машина со случайным устройством не сможет "перечислить" ничего сверх того, что перечисляет детерминистская машина.
Оба случая охватывает
ТЕОРЕМА 2. Если p - вычислимое действительное число, то любое p-перечислимое или сильно p-перечислимое множество 1-перечислимо. Если p - невычислимое действительное число, то существуют p-перечислимые и сильно p-перечислимые множества, не являющиеся 1-перечислимыми.
Теперь мы дадим набросок доказательства теоремы 1. Доказательство состоит из вывода предложения 2 из предложения 3, вывода предложения 1 из предложения 2 и вывода предложения 3 из предложения 1. Эта цепочка заключений дает требуемую эквивалентность.
То, что 3 влечет 2, доказывается тем, что с помощью p-машины, у которой выход S появляется с положительной вероятностью, строится новая машина, у которой S появляется с вероятностью >1/2. Тогда каждый элемент из S появляется с вероятностью >1/2, а любой элемент, не входящий в S, появляется с вероятностью <1/2, так что S p-перечислимо. Следовательно, всякое сильно p-перечислимое множество p-перечислимо.
То, что 2 влечет 1, доказывается следующим образом. Пусть дана p-машина M. Построим Ap-машину, Ap-перечисляющую множество Sm. Предположим, что мы располагаем бесконечной лентой, на которой записано Ap. Используя все более длинные начальные отрезки бесконечной последовательности Ap, можно вычислить сколь угодно хорошие нижние границы для вероятности справедливости высказываний вида "за время, в течение которого из случайного устройства появилось n входных символов, M запишет символ s". Но M запишет s с вероятностью >1/2 тогда и только тогда, когда, существует такое n, что это высказывание справедливо с вероятностью >1/2. В свою очередь, это может случиться лишь тогда, когда одна из сколь угодно хороших нижних границ (которые мы можем вычислить, используя начальные отрезки последовательности Ар) для вероятности справедливости указанного высказывания >1/2. Можно вычислить ПОСЛЕДОВАТЕЛЬНО (используя все более длинные начальные отрезки последовательности Ap) все нижние границы этих вероятностей для каждого n и каждого s. Сразу после получения нижней границы >1/2 записывается соответствующий символ s. Мы видим, что перечисленное таким образом множество символов есть Sm и что перечисление произведено посредством процесса, действительно составляющего Ap-машину. Следовательно, всякое p-перечислимое множество Ap-перечислимо.
То, что 1 влечет 3, доказывается следующим образом. Строится p-машина, вычисляющая с вероятностью >1/2 двоичное разложение действительного числа p. Иными словами, выход машины есть - с вероятностью >1/2 - множество всех (n, an), где an есть n-й знак в двоичном разложении числа p. Машина, делающая это, является видоизменением машины #7. Если выход этой p-машины использовать как вход другой машины M, то выход последней будет с вероятностью >1/2 в точности таким, каким был бы выход машины M, снабженной в качестве входа последовательностью Ар, Если S есть любое Ap-перечислимое множество и M - машина, Ap-перечисляющая его, то построенная выше сложная машина есть p-машина, сильно p-перечисляющая S. Следовательно, любое Aр-перечислимое множество сильно p-перечислимо. Это доказывает, что 1 влечет 3, и набросок доказательства теоремы 1 тем самым закончен.
Исследуем теперь, останутся ли результаты теми же, если учитывать не только совокупность выходных символов, но и порядок их следования. Будет показано, что такое положение можно свести к частному случаю уже полученных результатов.
ОПРЕДЕЛЕНИЕ. Бесконечная последовательность символов S = s1, s2, s3... называется A-ВЫЧИСЛИМОЙ, если она появляется в данном порядке следования на выходе некоторой A-машины. Она называется 1-ВЫЧИСЛИМОЙ, если А состоит целиком из единиц. S СИЛЬНО P-ВЫЧИСЛИМА, если существует p-машина, производящая S в данном порядке с положительной вероятностью. S называется P-ВЫЧИСЛИМОЙ, если существует p-машина, у которой n-й выходной символ есть n-й символ в S с вероятностью >1/2.
Будет показано, что для этих новых понятий справедлив точный аналог теоремы 2.
Пусть S - ПОСЛЕДОВАТЕЛЬНОСТЬ символов (sl, s2, s3, ...). Через S' обозначим МНОЖЕСТВО всех пар (n, sn), где n пробегает все целые положительные числа. Следующие леммы, доказываемые в приложении, суть непосредственные следствия определений.
ЛЕММА 4. Последовательность S {-вычислима тогда и только тогда, когда множество S' 1-перечислимо.
ЛЕММА 5. Если S сильно p-вычислима, то S' сильно p-перечислимо. Если S p-вычислима, то S' p-перечислимо.
Из двух предыдущих лемм и теоремы 2 вытекает.
ЛЕММА 6. Пусть p - вычислимое действительное число (в частности, 1/2). Тогда любая p-вычислимая или сильно p-вычислимая последовательность 1-вычислима.
ДОКАЗАТЕЛЬСТВО. Пусть последовательность S p-вычислима или сильно p-вычислима. Тогда S' p-перечислимо или сильно p-перечислимо по лемме 5. По теореме 2 множество S' 1-перечислимо. По лемме 4 последовательность S должна быть 1-вычислимой.
Это охватывает случай, когда p - вычислимое действительное число. Если p невычислимо, то доказательство теоремы 1, данное в приложении, показывает, что существует p-вычислимая и сильно p-вычислимая, но не 1-вычислимая последовательность (эта последовательность представляет собой двоичное разложение числа p). Объединяя оба случая, получим следующий аналог теоремы 2 для понятий вычислимости.
ТЕОРЕМА 3. Если p - вычислимое действительное число, то любая p-вычислимая или сильно p-вычислимая последовательность 1-вычислима. Если p невычислимо, то существует p-вычислимая и сильно p-вычислимая последовательность, которая не 1-вычислима.
Как частный случай этого мы находим, что 1/2-машина не может записать с положительной вероятностью никакой невычислимой последовательности.
БОЛЕЕ ОБЩИЙ КЛАСС МАШИН
В этом разделе обобщается результат, даваемый теоремой 2 для вычислимого числа p. Мы определим широкий класс вероятностных машин - вычислимо стохастических машин (или в.с.-машин), не покрываемых нашими предыдущими определениями, и предложим понятие эквивалентности для вероятностных машин. Будет показано, что любая машина нового класса эквивалентна 1/2-машине, и, как следствие теоремы 2, мы получим, что любое множество, перечислимое машиной этого класса, должно быть 1-перечислимым. Далее, существует эффективный процесс, позволяющий по описанию машины этого класса найти описание эквивалентной ей 1/2-машины и описание 1-машины, 1-перечисляющей то же самое множество.
Для простоты изложения мы рассматриваем в этом разделе только одно определение перечислимости, соответствующее p-перечислимости, и не даем более сильного определения, соответствующего сильной p-перечислимости. Можно показать, что те же результаты справедливы и для сильного определения.
Сначала определим класс стохастических машин. СТОХАСТИЧЕСКАЯ МАШИНА есть объект со счетным числом состояний X1, X2, X3, ..., выделенным начальным состоянием X0 и счетным набором выходных символов s1, s2, s3, ... При этом указано правило, дающее вероятность прихода машины в состояние Xp и записи ею выходного символа sq, если перед тем она прошла последовательно через состояния X0, Xj1, ..., Xjn. Эту вероятность мы обозначим через P(Xj1, ..., Xjn; Xp; sq). (Мы не требуем, чтобы это правило давало эффективную процедуру для вычисления вероятностей Р).
Любой p-машине M можно поставить в соответствие стохастическую машину в указанном выше смысле. Состояния соответствующей стохастической машины суть конечные последовательности нулей и единиц (a1, ..., an), а начальное состояние - "пустая" последовательность (.). (Фактически мы называем "состоянием" p-машины входную последователь ность, воспринятую ею. Эти "состояния" могут не соответствовать возможным внутренним состояниям конкретной машины, но определяют их полностью). Вероятность перехода из состояния (a1, ..., an) в (a1, ..., an, 1) есть p, а из состояния (a1, ..., an) в (a1, ..., an, 0) есть 1-p. Соответствующая стохастическая машина записывает по приходе в состояние (a1, ..., an, a[n+1]) то же, что и p-машина, принявшая (n+1)-й входной символ a[n+1] после восприятия (a1, . .., an). Тем самым стохастическая машина полностью задана. Она будет в дальнейшем называться стохастической машиной, СООТВЕТСТВУЮЩЕЙ P-МАШИНЕ M. Таким образом, p-машины можно отождествить с частными случаями стохастических машин. Легко видеть, что если p - вычислимое число, то соответствующая стохастическая машина обладает следующим специальным свойством: функция Р ВЫЧИСЛИМА, т.е. существует ЭФФЕКТИВНЫЙ ПРОЦЕСС, позволяющий по заданному целому положительному числу m состояниям Xj1, ..., Xjn и Xp и выходному символу sq вычислить первые m знаков двоичного разложения P(Xj1, ..., Xjn; Xp; sq). Мы назовем стохастические машины с таким свойством вычислимо стохастическими машинами, или в.с.-машинами. Непосредственным следствием этих определений является
ЛЕММА 7. Стохастическая машина, соответствующая p-машине, является в.с.-машиной тогда и только тогда, когда p - вычислимое действительное число.
Остальную часть этого раздела мы посвятим тому, чтобы показать, что результат, сформулированный в теореме 2 для p-машин с вычислимым p, справедлив и для гораздо более широкого класса в.с.-машин. Таким образом, любое множество, перечислимое в.с.-машиной, 1-перечислимо.
Как для стохастических, так и для p-машин можно говорить о вероятности того, что машина в конце концов запишет выходные символы sj1, ..., sjn (подобно тому, как раньше мы говорили о вероятности того, что p-машина в конце концов запишет одиночный символ s). Поскольку наши машины служат для перечисления множеств, то любые две машины, которые в конце концов сделают одно и то же с одной и той же вероятностью, можно считать тождественными с точки зрения окончательного выхода. Поэтому будет дано следующее определение:
ОПРЕДЕЛЕНИЕ. Два объекта - стохастические машины или p-машины - будут называться ЭКВИВАЛЕНТНЫМИ, если для любого конечного множества символов sj1, ..., sjn они имеют одинаковую вероятность включения (в конце концов) этого множества в их выход. Если эти машины суть M1 и M2, то их эквивалентность мы будем обозначать так: M1~M2.
Например, p-машина и соответствующая ей стохастическая машина эквивалентны.
Вспомним, что мы назвали p-машину p-перечисляющей некоторое множество символов, если каждый элемент этого множества появляется на выходе этой машины с вероятностью >1/2, а любой выходной символ, не принадлежащий данному множеству, появляется с вероятностью <1/2. Это определение можно непосредственно применить к стохастическим машинам и в.с.-машинам. Если M - стохастическая машина, то Sm будет множеством всех выходных символов, появляющихся с вероятностью >1/2, в согласии с введенным выше обозначением для p-машин.
Sm есть множество символов, которое машина M перечисляет. Как непосредственное следствие из нашего определения эквивалентности получаем, что M1~M2 влечет Sm1=Sm2, т.е. две эквивалентные машины перечисляют одно и то же множество.
ОПРЕДЕЛЕНИЕ. Множество S в.с.-перечислимо, если существует такая в.с.-машина M, что S=Sm.
Теперь мы ответим на вопрос: каждое ли в.с.-перечислимое множество 1-перечислимо? Ответ вытекает из следующего утверждения, доказанного в приложении.
ТЕОРЕМА 4. Каждая в.с.-машина эквивалентна 1/2-машине.
Следовательно, если M - в.с.-машина, то множество которое M перечисляет, перечислимо также некоторой 1/2-машиной. По теореме 2 множество Sm должно быть 1-перечислимым. Отсюда вытекает
ТЕОРЕМА 5. Любое в.с.-перечислимое множество l-перечислимо.
Этот результат и был упомянут выше.
В действительности доказательство теоремы 4 дает больше, чем было высказано. Могло случиться, что доказательство только устанавливает существование 1/2-машины, эквивалентной произвольной в.с.-машине, но не дает эффективных средств для ее разыскания. Однако это не так, и доказательство дает эффективный процесс.
ТЕОРЕМА 4 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины получить описание эквивалентной ей 1/2-машины.
Следовательно, для заданного описания в.с.-машины М1 существует эффективный процесс, позволяющий найти такую 1/2-машину M2, что Sm1=Sm2. Но это еще не дает эффективного расширения теоремы 5, для которого необходимо следующее эффективное расширение части теоремы 1.
ТЕОРЕМА 1 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию p-машины M (где p - вычислимое число) получить описание 1-машины, 1-перечисляющей то же самое Sm, которое M p-перечисляет.
Из объединения дополнений теорем 1 и 4 вытекает
ТЕОРЕМА 5 (дополнение). Существует эффективный процесс, позволяющий по заданному описанию в.с.-машины, в.с.-перечисляющей множество S, получить описание 1-машины, которая 1-перечисляет S.
Результаты относительно вычислимости последовательностей, приведенные в конце предыдущего раздела, остаются справедливыми для в.с.-машин. Очевидным образом можно определить в.с.-вычислимые последовательности. Доказательства лемм 4, 5 и 6 справедливы в этом случае, откуда следует, что любая в.с.-вычислимая последовательность 1-вычислима.
[ПРИЛОЖЕНИЕ я перепечатывать не стал. Там слишком много непечатных символов. Выложил сразу весь сборник АВТОМАТЫ, 1956
 DJVU, 4.49Мб
DJVU, 4.49Мб . Слишком уж часто я на него ссылаюсь, особенно, когда пытаюсь кому-то объяснить, что нейронные сети совсем не такие всемогущие, как сейчас принято думать.- G.]
. Слишком уж часто я на него ссылаюсь, особенно, когда пытаюсь кому-то объяснить, что нейронные сети совсем не такие всемогущие, как сейчас принято думать.- G.]ЛИТЕРАТУРА
1. Church A., An unsolvable problem of elementary number theory, Am. Jourft. Math., 58, 345-363 (1936).
2. Davis M., Готовится книга по рекурсивным функциям и вычислимости, выйдет в изд-ве Мак Гро-Хилл.
3. Dооb J.L., Stochastic processes, John Wiley and Sons (1953) (Русский перевод: Дуб, Вероятностные процессы, Издат. иностр. лит., M., 1956).
4. Феллеp В., Введение в теорию вероятностей и ее приложения, M., 1952.
5. Xалмош П., Теория меры, M., 1953.
6. Hobson E.W., The theory of functions of a real variable and the theory of Fourier's series (1926).
7. К1eene S.C., Introduction to metamathematics, Van Nostrand (1952) (готовится русский перевод).
8. Post E.L., Finite combinatory processes - Formulation I, Journ. Symbolic Logic, 1, 103-105 (1936).
9. Turing A.M., On computable numbers, with an application to the Entscheidungsproblem, Proc. London Math. Soc., ser.2, 42, 230-265 (1936); 43, 544-546 (1937).

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
До последнего времени никак не мог найти перевод основополагающей статьи Тьюринга 1936 года. Наконец,
повезло - в букинистическом урвал "Читаем Тьюринга" Чарльза Пентцольда. И там статья приведена целиком. Более того, там указаны исправления Тьюринговских описок, найденных другими авторами. В остальном же, книга посвящена единственной теме: как из 40-страничной статьи сделать 400-страничный бестселлер.
Не буду погружаться в проблемы вычислимости, этого достаточно выше. Просто посмотрю, как Тьюринг описывал эту самую первую машину.
Итак, уже можно отметить три особенности первой МТ:
1. Символ указывается в достаточно свободной форме: конкретный символ, (не)пустой и/или любой. Например, "непустой, но не этот".
2. Операции машины - составные. Т.е. несколько операций перемещения головки, стирания, записи за раз.
3. Лента пишется "через клетку" - клетки цифр (результата) и меток чередуются. Впрочем, это свойство не самой машины, а только предложенного Тьюрингом способа ее программирования.
...
повезло - в букинистическом урвал "Читаем Тьюринга" Чарльза Пентцольда. И там статья приведена целиком. Более того, там указаны исправления Тьюринговских описок, найденных другими авторами. В остальном же, книга посвящена единственной теме: как из 40-страничной статьи сделать 400-страничный бестселлер.
Не буду погружаться в проблемы вычислимости, этого достаточно выше. Просто посмотрю, как Тьюринг описывал эту самую первую машину.
О ВЫЧИСЛИМЫХ ЧИСЛАХ ПРИМЕНИТЕЛЬНО К ENTSCHEIDUNGSPROBLEM
А.М.ТЬЮРИНГ
Получено 28 мая, 1936г.- прочитано 12 ноября, 1936г.
Перевод Е.В.Борисова и Л.Н.Чернышова.
ON COMPUTABLE NUMBERS, WITH AN APPLICATION TO THE ENTSCHEIDUNGSPROBLEM
By A.M.Turing.
Received 28 May, 1936.- Read 12 November, 1936.
"Вычислимые" числа кратко можно описать как вещественные, чье десятичное представление можно вычислить конечным способом. Хотя предмет этой статьи - как будто бы вычислимые ЧИСЛА, почти так же легко определить и исследовать вычислимые функции целой, вещественной или вычислимой переменных, вычислимые предикаты и т.д. Однако в любом случае основные проблемы - одни и те же, и для подробного рассмотрения я предпочел вычислимые числа как требующие менее громоздкой техники. Вскоре я надеюсь представить отчет об отношении между вычислимыми числами, функциями, и т.д. Он будет включать развитие теории функций вещественной переменной с точки зрения вычислимых чисел. Согласно моему определению, число вычислимо, если машина может записать его десятичное представление.
В ##9, 10 я привожу некоторые доводы с целью показать, что вычислимые числа включают все числа, которые могли бы считаться естественно вычислимыми. В частности я показываю, что определенные большие классы чисел вычислимы. Они включают, например, вещественные части всех алгебраических чисел, вещественные части нулей функций Бесселя, числа пи, e, и т.д. Однако вычислимые числа не включают все определяемые числа, и приводится пример определяемого числа, которое невычислимо.
Хотя класс вычислимых чисел довольно большой, и в многом похож на класс вещественных чисел, он тем не менее перечислим. В #8 я исследую некоторые аргументы, которые, казалось бы, должны доказывать обратное. При надлежащем применении одного из этих аргументов получаются выводы, которые на первый взгляд похожи на выводы Геделя [Goedel, "Ueber formal unentscheidbare Saetze der Principia Mathematica und verwandter Systeme, I", Monatshefte Math. Phys., 38 (1931), 173-198.]. Эти результаты имеют полезные применения. В частности, они показывает (#11), что гильбертова Entscheidungsproblem не может иметь решения.
В недавней статье Алонзо Черча [Alonzo Church, "An unsolvable problem of elementary number theory", American J. of Math., 58 (1936), 345-363] представлена идея "эффективной вычислимости", которая эквивалентна моей "вычислимости", но определена совсем по-другому. Черч также пришел к похожим выводам об Entscheidungsproblem [Alonzo Church, "A note on the Entscheidungsproblem", J. of Symbolic Logic, 1 (1936), 40-41]. Доказательство эквивалентности между "вычислимостью" и "эффективной вычислимости" приводится в общих чертах в приложении к данной статье.
#1. ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
Мы уже сказали, что вычислимые числа - это десятичные [Здесь десятичные, в смысле записанные обычными арабскими цифрами, через десятичную запятую. На самом деле Тьюринг использует запись в двоичной форме - только цифрами "0" и "1", подразумевая запятую слева от первой цифры.- G.] числа, вычисляемые конечными способом. Это требует несколько более точного определения. Но вплоть до #9 не будет ни одной попытки обосновать данное определение. Пока же я только скажу, что обоснование опирается на тот факт, что человеческая память ограничена.
Мы можем уподобить человека, вычисляющего вещественное число, машине, которая может находиться только в конечном числе состояний q.1, q.2, ..., q.R; которые назовем "m-конфигурациями". Машина снабжена "лентой" (подобием бумаги) по которой она движется, и которая разделена на части (называемые "клетками"), каждая из которых может содержать "символ". В любой момент имеется только одна клетка, скажем r-я, содержащая символ S(r), находится "в машине". Мы можем назвать эту клетку "текущей клеткой". Символ в текущей клетке можно назвать "текущим символом". "Текущий символ" - единственный, который машина, так сказать, "непосредственно осознает". Несмотря на это, за счет изменения своей m-конфигурации машина фактически может помнить некоторые из символов, которые она "видела" раньше. Возможное поведение машины в каждый момент определяется m-конфигурацией q.n и текущим символом S(r) [Здесь у Тьюринга готическая буква, потом появятся и греческие, но я не буду использовать греческие и готические буквы там, где это не вызывает разночтений.- G.]. Эту пару - q.n, S(r) - будет называться "конфигурацией": таким образом конфигурация определяет возможное поведение машины. В некоторых конфигурациях, в которых текущая клетка пуста (то есть не содержит символа), машина записывает в текущую клетку новый символ; в других конфигурациях стирает текущий символ. Машина может также сменить текущую клетку - r, но только, сместившись вправо или влево от нее. Кроме того, каждое из этих действий может изменить m-конфигурацию. Одни из записанных на ленте символов будут образовывать последовательность цифр - цифровое представление вычисляемого вещественного числа. Другие - лишь вспомогательными символами, чтобы "помочь запомнить". Ими будут лишь такие вспомогательные пометки, которые потом подлежат стиранию. [Хитрость состоит в том, что число состояний машины конечно, а длина ленты - нет. И, по мере удлинения последовательности, количество пометок и номера их клеток могут расти вместе с ней. Но, об этом позже.- G.]
Я утверждаю, что эти действия составляют все, что необходимо для вычисления числа. Отстаивать это утверждение будет проще, когда читатель познакомится с теорией машин. Поэтому в следующем разделе я продолжу развитие теории, и, полагаю, станет понятно, что значит "машина", "лента", "текущий", и т.д.
#2. ОПРЕДЕЛЕНИЯ
АВТОМАТИЧЕСКИЕ МАШИНЫ
Если на каждом шаге поведение машины (в смысле #1) ПОЛНОСТЬЮ определяется конфигурацией, мы назовем машину "автоматической машиной" (или a-машиной).
Для некоторых целей мы можем использовать машины (машины выбора или c-машины), чье поведение определяется конфигурацией лишь отчасти (отсюда использование слова "возможное" в #1). Когда такая машина достигает одной из таких неоднозначных конфигураций, она не может двигаться дальше, пока внешний оператор не сделает некоторый произвольный выбор. Так было бы, если бы мы пользовались машинами, имеющими дело с аксиоматическими системами. В этой статье я имею дело только с автоматическими машинами, и поэтому часто буду опускать префикс "a-".
ВЫЧИСЛИТЕЛЬНЫЕ МАШИНЫ
Если a-машина печатает два вида символов, первые из которых (называемые цифрами) состоят только из 0 и 1 (остальные называются символами второго вида), то машина будет называться вычислительной машиной. Если машина снабжена пустой лентой и приведена в движение, начиная с правильной начальной m-конфигурации, то подпоследовательность печатаемых ею символов первого будем называть ПОСЛЕДОВАТЕЛЬНОСТЬЮ, ВЫЧИСЛЯЕМОЙ МАШИНОЙ. Вещественное число, чье представление в виде цифровой двоичной дроби получается путем предварения этой последовательности цифровой точкой, называется ЧИСЛОМ, ВЫЧИСЛЯЕМЫМ МАШИНОЙ.
Будем считать, что на каждом шаге работы машины номер текущей клетки, полная последовательность всех символов на лепте и m-конфигурация описывают ПОЛНУЮ КОНФИГУРАЦИЮ на этом шаге. Изменения машины и ленты между последовательными полными конфигурациями назовем ХОДАМИ машины.
ЦИКЛИЧЕСКИЕ И АЦИКЛИЧЕСКИЕ МАШИНЫ
Если вычислительная машина никогда не записывает более чем конечное число символов первого вида, назовем её ЦИКЛИЧЕСКОЙ. В противном случае говорят, что она АЦИКЛИЧЕСКАЯ.
Машина будет циклической, если она достигнет конфигурации, из которой нет хода, или если она продолжает движение и, возможно, печатает символы второго вида, но больше не может печатать символы первого вида. Значение слова "циклический" будет объяснено в #8.
ВЫЧИСЛИМЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ И ЧИСЛА
Говорят, что последовательность вычислима, если она может быть вычислена ациклической машиной. Число вычислимо, если оно отличается на целое число от числа, вычисляемого ациклической машиной.
Мы избежим путаницы, говоря чаще о вычислимых последовательностях, чем о вычислимых числах.
#3. ПРИМЕРЫ ВЫЧИСЛИТЕЛЬНЫХ МАШИН
I. Можно создать машину для вычисления последовательности 010101... . Машина должна иметь четыре m-конфигурации: "b", "c", "k", "e" [готические. - G.] и уметь печатать "0" и "1". Поведение машины описывается в следующей таблице, в которой "R" означает "машина перемещается так, чтобы просмотреть клетку непосредственно справа от текущей". Аналогично - для "L". "E" означает "текущий символ стирается", а "P" - "печать". Эту таблицу (и все последующие таблицы того же вида) следует понимать так: в конфигурации, описанной и первых двух столбцах, последовательно выполняются операции из третьего столбца, а затем машина переходит в m-конфигурацию, описанную в последнем столбце. [Я использую # для разделения первых двух столбцов.- G.]. Если второй столбец оставлен пустым, это значит, что поведение, заданное третьим и четвертым столбцами, относится к любому символу и к отсутствию символа. ["Шаблоны символов" Тьюринг задает в очень свободной форме, иногда противореча сам себе. Я буду исправлять по мере сил. Пустые клетки буду обозначать подчеркиванием.- G.] Машина начинает с m-конфигурации b при пустой ленте.
Конфигурация -> Поведение
т.е.
m-конфиг.#символ -> операции; заключ.m-конфиг.
b#_ -> P0, R; с
c#_ -> R; e
e#_ -> P0, R; k
k#_ -> R; b
[Уже здесь мы видим, что Тьюринг матричному представлению машины, предпочитает описательное - используя несколько операций в одной строке.- G.]
Если (вопреки описанию в #1) мы позволим символам L, R появляться в столбце операций несколько раз, мы можем значительно упростить таблицу.
b#_ -> P0; b
b#0 -> R, R, P1; b
b#1 -> R, R, P0; b
II. В качестве несколько более сложного примера мы можем создать машину для вычисления последовательности 001011011101111011111... . Машина может иметь пять m-конфигураций, т.е. "о#", "q#", "p#", "s#", "b#", и печатать "э", "x", "0" и "1". Первыми тремя символами налейте будут "ээ0" [два "з" - здесь перестраховка.- перев.]; остальные цифры будут следовать через клетку. В промежуточных клетках мы никогда не печатаем ничего, кроме "х". Эти символы служат нам для "сохранения места" и стираются, когда мы заканчиваем работу с ними. Мы также условимся, что в цифровых клетках пробелов не будет.
b#_ -> Pэ,R,Pэ,R,R0,R,R,P0,L,L; o
o#1 -> R,Pх,L,L,L; o
o#0 -> ; q
q#1 или 0 -> R,R; q
q#_ -> P1,L; p
p#x -> E,R; q
p#э -> R; f
p#_ -> L,L; p
f#1 или 0 -> R,R; f
f#_ -> P0,L,L; o
Для иллюстрации работы этом машины ниже приводится таблица нескольких первых полных конфигураций. Эти полные конфигурации изображаются путем выписывания последовательности символов, которые располагаются на ленте, вместе с m-конфигурацией. Последовательные полные конфигурации отделяются двоеточиями.
(b#)_ : ээ(o#0)_0 : ээ(q#0)_0 : ээ0_(q#0) : ээ0_0_(q#_) : ээ0_0(p#_)1 :
ээ0(p#_)0_1 : э(p#э)0_0_1 : ээ(f#0)_0_1 : ээ0_(f#0)_1 :
ээ0_0_(f#1) : ээ0_0_1_(f#_) : ээ0_0_(o#0) :
ээ0_(o#0)_1x0 : ...
Такую запись обозначим (С). Эту форму не просто соблюдать, но позже мы будем использовать ее в теоретических целях.
Соглашение о записи цифр только через одну клетку очень полезно: я всегда буду делать это. Я буду называть одну последовательность чередующихся клеток F-клетками, а другую последовательность Е-клетками. Символы в E-клетках подлежат стиранию после использования. Символы в F-клетках образуют непрерывную последовательность. Без пропусков, до самого конца. Нет нужды иметь более одной Е-клетки между каждой парой F-клеток: кажущаяся потребность в большем количестве E-клеток может быть удовлетворена наличием достаточно богатого разнообразия символов, которые могли бы печататься в Е-клетках. Если символ b находится в F-клетке S и символ a находится в E-клетке справа от S, то будем говорить, что S и b ПОМЕЧЕНЫ символом a. Процесс печати этого a будет называться пометкой p (или S) символом a.
Итак, уже можно отметить три особенности первой МТ:
1. Символ указывается в достаточно свободной форме: конкретный символ, (не)пустой и/или любой. Например, "непустой, но не этот".
2. Операции машины - составные. Т.е. несколько операций перемещения головки, стирания, записи за раз.
3. Лента пишется "через клетку" - клетки цифр (результата) и меток чередуются. Впрочем, это свойство не самой машины, а только предложенного Тьюрингом способа ее программирования.
...

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
4. Далее, оказывается, что для своей машины Тьюринг придумал препроцессор-макрогенератор.
(И, да, я попробую и здесь обойтись без готики и греции).
5. Можно заметить, что все приведенные m-функции не привязаны к определенной стартовой клетке (и, тем более, к символу в этой клетке). Все они сначала ищут начало или конец ленты и уже оттуда копают. По сути, это строковые операции, рассматривающие всю заполненную часть ленты, как одну строку, литеры которой дополнительно помечены. Вот зачем нужно было писать ответ через клетку!.
...
(И, да, я попробую и здесь обойтись без готики и греции).
***#4. СОКРАЩЕННЫЕ ТАБЛИЦЫ
Существуют определенные типы операций, используемые почти всеми машинами, и в некоторых машинах они применяются во множестве сочетании. Эти операции включают копирование последовательностей символов, сравнение последовательностей, стирание всех символов заданного вида и т.д. Там, где появляются такие операции, за счет применения "скелетных таблиц" мы можем значительно сократить таблицы m-конфигураций. В скелетных таблицах используются прописные немецкие буквы и строчные греческие буквы. Они имеют природу "переменных". Заменив везде каждую прописную немецкую букву на m-конфигурацию и каждую строчную греческую букву - символом, мы получим таблицу для m-конфигурации.
Скелетные таблицы должны считаться лишь сокращениями: они не являются необходимыми. Пока читатель понимает, как получить полные таблицы из скелетных таблиц, нет необходимости давать в связи с ними какие-либо точные определения.
Давайте рассмотрим пример:
f(C,B,a)#э -> L; f.1(C,B,a)
f(C,B,a)#прочее -> L; f(C,B,a)
f.1(C,B,a)#a -> ; C
f.1(C,B,a)#не a -> R; f.1(C,B,a)
f.1(C,B,a)#_ -> R; f.2(C,B,a)
f.2(C,B,a)#a -> ; C
f.2(C,B,a)#не a -> R; f.1(C,B,a)
f.2(C,B,a)#_ -> R; B
Из m-конфигурации f(C,B,a)# машина ищет символ вида а, который является самым первым слева ("первый a"), после чего m-конфигурацией становится С. Если a нет, то m-конфигуpaцией становится B. [Просто запомнить. Параметры состояний - куда переходим по успеху и неуспеху, т.е. просто следующие. Сначала f отматывает ленту в начало, до двойного э. Затем f.1 - ищет, пока не пусто, а f.2 - проверяет, это пусто или совсем пусто. f.1 и f.2 чередуются, пока не найдут a или конец.- G.]
Если мы всюду заменим С на q (например), B на r и a на конкретный x, мы получим полную таблицу для m-конфигурации f(q,r,x). f называют "функцией m-конфигурации", или "m-функцией".
Единственное, что допустимо для подстановки в m-функцию,- это m-конфигурации и символы машины. Они должны быть перечислены более или менее явно: они могут включать такие выражения, как р(e,х); на самом деле - должны, если есть хоть какие-то m-функции. Если бы мы не настаивали на этом явном перечислении, а просто заявили, что машина имеет определенные m-конфигурации (перечисленные) и все m-конфигурации, получаемые подстановкой m-конфигураций в определенные m-функции, мы получили бы бесконечное число m-конфигураций; например, мы могли бы сказать, что машина должна иметь m-конфигурацшо q и все m-конфигурации, получаемые подстановкой m-конфигурации C в p(C). Тогда она должна иметь в качестве конфигураций q, p(q), p(p(q)), p(p(p(q)))...
Тогда наше правило интерпретации таково. Мы придаем m-конфигурациям машины имена, выраженные, главным образом, через m-функции. Мы ввели также скелетные таблицы. Все, что нам нужно,- это полная таблица m-конфигураций машины. Она получается многократной подстановкой в скелетные таблицы.
ДОПОЛНИТЕЛЬНЫЕ ПРИМЕРЫ
(В пояснениях символ "->" употребляется в значении "машина переходит в m-конфигурацию...").
e(C,B,a)# -> ; f(e.1(C,B,a),B,a)
e.1(C,B,a)# -> E; C
Из e(C,B,a)# стирается первый a и ->C. Если a нет ->B. [e - ищем первое вхождение, e.1 - стираем.- G.]
e(B,a)# -> ; e(e(B,a),B,a)
Из e(B,а)# стираются все символы a и ->B. [Заметим, каждый символ заново ищется с самого начала.- G.]
Последний пример кажется чуть труднее для понимания, чем многие другие. Давайте предположим, что в списке m-конфигураций некоторой машины есть e(b,x)# (= q#, например). Ее таблица
e(b,x)# -> e(e(b,x),b,x)
или
q# -> e(q,B,x).
Или подробнее:
q# -> e(q,b,x)
e(q,b,x)# -> ; f(e.1(q,b,x),b,x)
e.1(q,b,x)# -> E; q.
Здесь мы могли бы заменить e.1(q,b,x) на q' и затем задать таблицу для f (с правильными подстановками) и в конечном счете прийти к таблице, в которой m-функции не появляются.
pe(C,b)# -> f(pe.1(C,b),C,э)
pe.1(C,b)#не пусто -> R,R; pe.1(C,b)
pe.1(C,b)#_ -> Pb; C
Из pe(C,b)# машина печатает b в конце последовательности символов и ->C. [pe - тупо отматывает ленту в начало, pe.1 отсчитывает по 2 символа, пока цифры не кончаться. Останавливается на первом же пробеле, т.к. пробелов внутри цифровой последовательности не допускается.- G.]
l(C)# -> L; C
r(С)# -> R; C
f'(C,B,a)# -> ; f(l(C),B,a)
f''(C,B,a)# -> ; f(r(C),B,a)
Из f'(C,B,a)# делается то же самое, что из f(C,B,а)#, шаг влево и ->C. [Т.е. на цифру перед нужной меткой. А f'' - на метку после нужной цифры.- G.]
c(C,B,a)# -> ; f'(c.1(C),B,a)
c.1(C)#(b) -> ; pe(C,b)
c(C,B,a)#. Машина пишет в конце первый символ, отмеченный a и ->C. Последняя строка означает все множество строк, получаемых из нее заменой любым символом, который может встретиться на ленте данной машины. [Оба поиска - и метки, и конца последовательности проводятся с начала ленты.- G.]
ce(C,B,a)# -> ; c(e(C,B,a),B,a)
ce(B,a)# -> ; ce(ce(B,a),B,a)
ce(B,a)#. Машина копирует в конец все символы, помеченные a, и стирает символы a; ->B. [се с двумя параметрами вызывает ce с тремя параметрами с приказом вернуться к себе же. ce с тремя параметрами копирует первый помеченный символ и переходт к e для стирания метки.- G.]
re(C,B,a,b)# -> ; f(re.1(C,B,a,b),B,a)
re.1(C,B,a,b)# -> E, Pb; C
re(C,B,a,b)#. Машина заменяет первую а на b и ->C, если а нет ->B. [re - ищет, re.1 - заменяет.- G.]
re(B,a,b)# -> ; re(re(B,a,b),B,a,b)
re(B,a,b)#. Машина заменяет все а на b, ->B.
cr(C,B,a)# -> ; c(re(C,B,a,a'),B,a)
cr(B,a)# -> ; cr(cr(B,a),re(B,a',a),a)
cr(B,a)# отличается от ce(B,a)# только тем, что символы a не стираются. m-конфитурация cr(B,a)# требует, чтобы на ленте не было символов a'. [cr с тремя параметрами копирует в конец один символ, меняя его метку, cr с двумя параметрами копирует все символы, а потом восстанавливает метки. Одиночные копирования-замены идут путем перехода cr к самой себе, восстановление a - за один раз, переходом к re, когда замены более невозможны.- G.]
cp(C,A,E,a,b)# -> ; f'(cp.1(C,A,b),f(A,E,b),a)
cp.1(C,A,b)#(y) -> ; f'(cp.2(C,A,y),A,b)
cp.2(C,A,b)#(y) -> ; C
cp.2(C,A,b)#прочее -> ; A
Сравниваются первый символ, помеченный a, и первый, помеченный b. Если нет ни a, ни b ->E. Если есть оба и символы подобны ->C. Иначе -> A.
cpe(C,A,E,a,b)# -> ; cp(e(e(C,C,b),C,a),A,E,a,b)
cpe(C,A,E,a,b)# отличается от cp(C,A,E,a,b)# тем, что в случае подобия символов метки a и b стираются.
cpe(A,E,a,b)# -> ; cpe(cpe(A,E,a,b),A,E,a,b),A,E,a,b)
cpe(A,E,a,b)# Последовательность символов, помеченных a, сравнивается с последовательностью, помеченной b. ->E, если они подобны. Иначе -> A. Некоторые метки стираются.
g(C)#не пусто -> R; g(C)
g(C)#_ -> R; g.1(C)
g.1(C)#не пусто -> R; g(C)
g.1(C)#_ -> ; C
g(C,a)# -> ; g(g.1(C,a))
g.1(C,a)#a -> C
g.1(C,a)#прочее -> L; g.1(C,a)
g(C,a)#. Машина ищет последний символ a; ->C. [Сначала g находит конец (две пустых клетки), затем g.1 идет к началу в поисках a.- G.]
pe.2(C,a,b)# -> ; pe(pe(C,b),b)
pe.2(C,a,b). Машина печатает ab в конце.
ce.2(B,a,b)# -> ce(ce(B,b),a)
ce.3(B,a,b)# -> ce(ce(B,b),a)
ce.2(B,a,b,c)# -> ce(ce.2(B,b,c),a)
ce.2(B,a,b,c)#. Сначала машина копирует в конец символы, помеченные a, затем - b и, наконец,- с. Все эти метки стираются.
e(C)#э -> R; e.1(C)
e(C)#не э -> L; e(C)
e.1(C)#не пусто -> R,E,R; e.1(C)
e.1(C)#_ -> ; C
Из e(C)# стираются метки всех помеченных символов; ->C.
5. Можно заметить, что все приведенные m-функции не привязаны к определенной стартовой клетке (и, тем более, к символу в этой клетке). Все они сначала ищут начало или конец ленты и уже оттуда копают. По сути, это строковые операции, рассматривающие всю заполненную часть ленты, как одну строку, литеры которой дополнительно помечены. Вот зачем нужно было писать ответ через клетку!.
...

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
Далее Тьюринг соединил, все описанное в целях создать универсальную машину (мы это уже видели в статье фон Неймана). Для этого он вернулся к упрощенной форме таблицы: одна строка - один символ, одно действие, один сдвиг.
#5. ПЕРЕЧИСЛЕНИЕ ВЫЧИСЛИМЫX ПОСЛЕДОВАТЕЛЬНОСТЕЙ
Вычислимая последовательность y определяется описанием машины, которая вычисляет y. Таким образом, последовательность 001011011101111... определяется таблицей #3, и фактически любая вычислимая последовательность может быть описана подобной таблицей.
Первым делом предположим, что таблица задается в том же виде, что и первая таблица в статье. Т.е., что элемент в столбце операций всегда имеет одну из форм Е; Е,R; Е,L; Pa;, Pa,R: Pa,L; R; L или вообще пусто. Таблица всегда может быть приведена к такому виду путем введения дополнительных m-конфигураций.
Давайте теперь дадим номера m-конфигурациям, назвав их q.1, ..., q.R, как в #1. Начальной ш-конфигурацией всегда должна, быть q.1. Мы также дадим номера символам S.1, ..., S.m и, в частности, пусто = S.0, 0 = S.1, 1 = S.2. Строки таблицы теперь имеют вид
q.i#S.j -> PS.k,L; q.m (N.1)
q.i#S.j -> PS.k,R; q.m (N.2)
q.i#S.j -> PS.k; q.m. (N.3)
Строки вида
q.i#S.j -> E,R; q.m
должжны записываться как
q.i#S.j -> PS.0,R; q.m,
а строки вида
q.i#S.j -> R; q.m
должжны записываться как
q.i#S.j -> PS.j,R; q.m.
Таким образом, мы привели каждую строку таблицы к строке одного из видов (N.1), (N.2), (N.3).
Давайте из каждой строки вида (N.1) образуем выражение вида q.i S.j S.k L q.m; из строки каждой вида (N.2) образуем выражение вида q.i S.j S.k R q.m; из каждой строки вида (N.3) образуем выражение вида q.i S.j S.k N q.m.
Выпишем из таблицы машины все образованные таким образом выражения и разделим их токами с запятой. Таким образом, мы получаем полное описание машины. В этом описании мы заменим q.i буквой "D", за которой следует буква "A", повторенная i раз, а S.j - на "D", за которой следует "C", повторенная j раз. Это новое описание машины можно назвать СТАНДАРТНЫМ ОПИСАНИЕМ (S.D). Оно составлено только из букв "A", "C", "D", "L", "R", "N" и ";".
Наконец, если мы меняем "A" на "1", "C" на "2", "D" на "3", "L" на "4", "R" на "5", "N" на "6" и ";" на "7", у нас будет описание машины в виде арабских цифр. Целое число, представленное этими цифрами, можно назвать ОПИСАТЕЛЬНЫМ НОМЕРОМ (D.N) машины. D.N однозначно определяет S.D и структуру машины. Машину, чей D.N равен n, можно обозначить как М(n).
Каждой вычислимой последовательноетп соответствует хотя бы один описательный номер, тогда как ни одному описательному номеру не соответствует более одной вычислимой последовательности. Следовательно, вычислимые последовательности и числа перечислимы.
Давайте найдем описатель машины I из #3.
Если мы переименуем m-конфигурации, получим таблицу:
q.1#S.0 -> PS.1,R; q.2
q.2#S.0 -> PS.0,R; q.3
q.3#S.0 -> PS.2,R; q.4
q.4#S.0 -> PS.0,R; q.1
Прочие таблицы можно было бы получить, добавляя бесполезные строки, такие как
q.1#S.1 -> PS.1,R; q.2
Наша первая стандартная форма была бы
q.1 S.0 S.1 R q.2; q.2 S.0 S.0 R q.3; q.3 S.0 S.2 R q.4; q.4 S.0 S.0 R q.1;.
Стандартное описание будет таким
DADDCRDAA; DAADDRDAAA; DAAADDCCRDAAAA; DAAAADDRDA;.
Описатель - это
31332531173113353111731113322531111731111335317
а также
3133253117311335311173111332253111173111133531731323253117.
[Ко второму добавлена бесполезная строка.- П.].
Число, которое является описателем ациклической машины, будем назвать ПРИЕМЛЕМЫМ числом. В #8 показывается, что не может быть общего процесса для определения того, что данный номер приемлем или нет.
#6. УНИВЕРСАЛЬНАЯ ВЫЧИСЛИТЕЛЬНАЯ МАШИНА
Можно создать одну-единственную машину, которую можно использовать для вычисления любой вычислимой последователыности. Если этой машине U предоставить ленту, в начале которой записано S.D некоторой вычислительной машины М, то U вычислит ту же последовательность, что и M. В этом разделе я объясняю в общих чертах поведение машины. Следующий раздел посвящается построению полной таблицы для U.
Давайте сначала предположим, что у нас есть машина M', кхоторая запишет в F-клетки последовательные полные конфигурации M. И можно представить, используя описание (С), где все символы идут одной строкой. Или лучше б было преобразовать это описание (как в #5) заменой каждой m-конфигурации на "D" с последующими "A", повторенными нужное число раз, и заменой каждого символа на "D" с последующими "C", повторенными нужное число раз. Число букв "A" и "C" должно соответствовать числам, выбранным в #5, так чтобы, в частности, "0" был заменен на "DC", "1" - на "DCC", а пробелы - на "D". Такие подстановки нужно делать после того, как полные конфигурации собраны вместе, как в (С). Если мы делаем подстановку сразу, возникают трудности. В каждой полной конфигурации все пустые клетки должны быть заменены на "D" так, чтобы полная конфигурация представляла собой конечную последовательность символов.
Если в описании машины II из #3 мы заменяем "o" на "DAA", "э" на "DCCC", "q" на "DAAA", то последовательность (С) становится следующей:
DA:DCCCDCCCDAADCDDC:DCCCDCCCDAAADCDDC:... . (C.1)
(Это - последовательность символов в F-клетках).
Нетрудно видеть, что если можно построить M, то можно построить и М'. Поведение М' могло бы зависеть от правил поведения (т.е. S.D) M, записанных где-то в ней самой (т.е. внутри M'); каждый шаг мог бы выполняться путем обращения к этим правилам. Мы только должны считать, что правила можно вынуть из машины и заменить другими, и мы имеем нечто очень похожее на универсальную машину.
Недостает одного: сейчас машина M' не печатает никаких цифр. Мы можем исправить это, печатая между каждой последовательной парой полных конфигураций цифры, которые появляются в новой конфигурации, но не в старой. Тогда (C.1) становится такой:
DA:0:0:DCCCDCCCDAADCDDC:DCCC... . (С.2)
Не вполне очевидно, что E-клетки предоставляют достаточно места для необходимой "черновой работы", но это действительно так.
Последовательности символов между двоеточиями в таких выражениях, как (C.1), могут использоваться как стандартные описания полных конфигураций. Если буквы заменить цифрами, как в #5, мы получим числовое описание полной конфигурации, которую можно назвать ее описательным номером.
...7. ПОДРОБНОЕ ОПИСАНИЕ УНИВЕРСАЛЬНОЙ МАШИНЫ
Ниже приведена таблица поведения этой универсальной машины. Все возможные m-конфигурации машины появляются в первом и последнем столбцах таблицы вместе со всеми теми, которые появляются при полном выписывании несокращенных таблиц тех, что появляются в таблице в виде m-функций. Например, e(anf) появляется в таблице и является m-функцией. Ее несокращенная таблица (см. конец #4):
e(anf)#э -> R; e.1(anf)
e(anf)#не э -> L; e(anf)
e.1(anf)#не пусто -> R,E,R; e.1(anf)
e.1.(anf)#_ -> anf
Следовательно, e.1(anf) является m-конфигурацией U.
Когда U готова начать работу, на ленту, по которой она движется, нанесены символ э в F-клетке и еще один э в следующей Е-клетке; следом, только в F-клетках, идет S.D машины, за которым следует двойное двоеточие "::" (отдельный символ в F-клетке). S.D состоит из множества команд, разделенных точкой с запятой [далее выясняется, что команда должна начинаться с точи с запятой.- П.].
Каждая команда состоит из пяти следующих друг за другом частей:
(i) "D" с последующей последовательностью букв "A". Описывает соответстиующую m-конфигурацию.
(ii) "D" с последующей последовательностью букв "C". Описывает текущий символ.
(iii) "D" с последующей другой последовательностью букв "C". Описывает символ, на который должен быть заменен текущий символ.
(iv) "L", "R" или "N", описывающие, должна ли машина двигаться влево, вправо или никуда.
(v) "D" с последующей последовательностью букв "A". Описывает заключительную m-конфигурацию.
Машина U должна быть способна печатать "A", "C", "D", "0", "1", "u", "v", "w", "x", "y", "z" [и ":".- П.]. S.D формируется из ";", "A", "C", "D", "L", "R", "N".
Вспомогательная скелетная таблица.
con(C,a)#Not A -> R,R; con(C,a)
con(C,a)#A -> L,Pa; con.1(C,a)
con.1(C,a)#A -> R,Pa; con.1(C,a)
con.1(C,a)#D -> R,Pa,R; con.2(C,a)
con.1(C,a)#_ -> PD,R,Pa,R,R,R; C [Эту строчку добавил Пост.- П.]
con.2(C,a)#C -> R,Pa,R; con.2(C,a)
con.2(C,a)#Not C -> R,R; C
con(C,a). Начиная с F-клетки, скажем S, последовательность С символов, описывающих конфигурацию, ближайшую справа к S, помечается буквам и а. В заключительной конфигурации машина con(C,_) просматривает клетку четырьмя клетками правее клетки с С. С остается непомеченной.
Таблица для U.
b# -> f(b.1,b.1,:: )
b.1# -> R,R,P:,R,R,PD,R,R,PA; anf
b. Машина печатает :DA в F-клетках после :: и ->anf
anf# -> ; g(anf.1,: )
anf.1# -> con(fom,y)
anf. Машина помечает меткой y конфигурацию в последней полной конфигурации. ->fom
fom#: -> R,Pz,L; con(fmp,x)
fom#z -> L,L; fom
fom#не z -> L; fom
fom. Машина находит последнюю точку с запятой, не помеченную z. Она помечает эту точку с занятой z, а последующую конфигурацию - x.
fmp# -> ; cpe(e(fom,x,y),sim,x,y)
[ fmp# -> ; cpe(e(e(anf,x),y)sim,x,y) - исправление Д.Дэвиса.- П.]
fmp. Машина сравнивает последовательности, помеченные x и y. Она стирает все символы x и y. ->sim, если они подобны. Иначе ->fom.
anf. Получив длинное представление, ищется последняя команда, относящаяся к последней конфигурации. Она может быть опознана впоследствии как команда после последней точки с запятой, отмеченная z. ->sim.
sim# -> ; f'(sim.1,sim.1,z)
sim.1# -> ; con(sim.2,)
sim.2#A -> ; sim.3
sim.2#не A -> R,Pu,R,R,R; sim.2 [Неверно. Пост считал, что перед печатью должен быть сдвиг влево.- П.]
sim.3#не A -> L,Py; e(mk,z)
sim.3#A -> L,Py,R,R,R; sim.3
sim. Машина размечает команды. Часть команды, которая относится к выполняемым действиям, будет помечена u, а заключительная m-конфигурация - символом y. Символы z стираются.
mk# -> ; g(mk.1,: )
mk.1#не A -> ; R,R; mk.1
mk.1#A -> ; L,L,L,L; mk.2
mk.2#C -> R,Px,L,L,L; mk.2
mk.2#: -> ; mk.4
mk.2#D -> R,Px,L,L,L; mk.3
mk.3#не : -> R,Pv,L,L,L; mk.3
mk.3#: -> ; mk.4
mk.4# -> ; con(l(l(mk.5)), )
mk.5#символ -> R,Pw,R; mk.3
mk.5#_ -> P:; sh
mk. Последняя полная конфигурация помечается в четырех местах. Конфигурация остается непомеченной. Предшествующий ей символ помечается символом x. Остаток полной конфигурации делится на две части, первая из которых помечается v, вторая - w. После всего печатается двоеточие. ->sh.
sh# -> ; f(sh.1,inst,u)
sh.1# -> L,L,L; sh.2
sh.2#D -> R,R,R,R; sh.3
sh.2#не D -> ; inst
sh.3#C -> R,R; sh.4
sh.3#не C -> ; inst
sh.4#C -> R,R; sh.5
sh.4#не C -> ; pe.2(inst,0,: )
sh.5#C -> R,R; sh.5
sh.5#не C -> ; pe.2(inst,1,: )
sh. Проверяются (помеченные u) команды. Если оказывается, что они включают "Print 0" или "Print 1", то в конце печатается 0: или 1: .
inst# -> ; g(l(inst.1),u)
inst.1#(a) -> R,E; inst.1(a)
inst.1(L)# -> ce.5(ov,v,y,x,u,w)
inst.1(R)# -> ce.5(ov,v,y,x,u,w)
inst.1(N)# -> ce.5(ov,v,y,x,u,w)
ov# -> e(anf)
[Пропущено:
ce.4(B,a,b,c,d)# -> ce(ce.3(B,b,c,d),a)
ce.5(B,a,b,c,d,e)# -> ce(ce.4(B,b,c,d,e),a).- П.]
inst. Выписывается очередная полная конфигурация, выполняются помеченные команды. Символы u, v, w, х, y стираются. ->anf.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
 Re: О компиляции Машин Тьюринга
Re: О компиляции Машин Тьюринга
Далее Тьюринг начинает выяснять пределы вычислимости построенной машины.
Это в общем уже не так весело, так что здесь я остановлюсь, тем более, что с каждой главой моя система обозначения используемых Тьюрингом закорючек становится все менее адекватной. А программирования машины больше не будет.
#8. ПРИМЕНЕНИЕ ДИАГОНАЛЬНОГО ПРОЦЕССА
Можно предположить, что аргументы, которые убеждают в том, что вещественные числа неперечислимы, должны убеждать и в том, что вычислимые числа и последовательности не могут быть перечислимыми [См. Hohson, Theory of functions of a real variable (2-е изд., 1921), 87, 88]. Можно, например, предположить, что предел последовательности вычислимых чисел должен быть вычислимым. Ясно, что это истинно только тогда, когда последовательность вычислимых чисел определяется по некоторому правилу.
Или мы можем применить диагональный процесс. "Если вычислимые последовательности - перечислимые, то пусть a.n - n-я вычислимая последовательность и пусть ф.n(m) - m-я цифра a.n. Пусть b - последовательность с 1-ф.n(n) в качестве ее n-й цифры. Так как b вычислима, то существует номер K - такой, что 1-ф.n(n)=Ф.K(n) Для всех n. Полагая n=K, мы имеем 1=2ф.K(K), т.е. 1 - четное. Это невозможно. Следовательно, вычислимые последовательности неперечислимы".
Ошибка этого вывода кроется в предположении, что b вычислимо. Оно было бы верным, если бы мы могли перечислить вычислимые последовательности конечным образом, но задача перечисления вычислимых последовательностей равносильна задаче выяснения, является ли данное число D.N описателем ациклической машины, а у нас нет общего процесса, чтобы сделать это за конечное число шагов. Фактически, правильно применяя замысел диагонального процесса, мы можем показать, что такого общего процесса не может быть.
Простейшее и самое прямое доказательство этого - показать, что если существует общий процесс, то существует машина, которая вычисляет b. Это доказательство, хоть и кажется безупречным, имеет недостаток, который может оставить читателя с чувством, что "здесь что-то не так". Доказательство, которое я приведу, не имеет этого недостатка и дает некоторое понимание значения идеи "ацикличности". Оно связано не с построением b, а с построением b', чья n-я цифра есть ф.n(n).
Предположим, что такой процесс существует; то есть мы утверждаем, что можем создать машину D, которая, будучи применена к S.D любой вычислительной машины М, проверит это S.D и, если M ~ циклическая, пометит S.D символом "u", а если она без циклов - символом "s". Объединим машины D и U, мы могли бы создать машину H для вычисления последовательности b'. Машине D может потребоваться лента. Мы можем предположить, что она использует помимо всех символов в F-клетках Е-клетки, и когда она вынесет свое решение, вся выполненная D черновая работа стирается.
Движение машины H поделено на участки. В первых N-1 участках, помимо прочего, машиной D выписываются и проверяются целые числа 1, 2, ..., N-1. Некоторое их количество, скажем R(N-1), уже обнаружено, и они должны быть D.N ациклических машин. На N-ом участке машина D проверяет число N. Если N - приемлемое, т.е. если оно - D.N ациклической машины, то R(N)=1+R(N-1) и вычисляются первые R{N) цифр последовательности, D.N которой есть N. R(N)-я цифра этой последовательности записывается как одна из цифр последовательности b', вычисляемой H. Если N не приемлемо, то R(N)=R(N-1) и машина переходит к (N+1)-му участку своего движения.
Из построения H мы можем видеть, что H - ациклическая. Каждый участок движения H заканчивается через конечное число шагов. Поскольку, согласно нашему предположению о D, решение о том, что N приемлемо, достигается за конечное число шагов. Если N не приемлемо, то N-й участок завершается. Если N приемлемо, это означает, что машина M(N), чей D.N есть N,- ациклическая, и поэтому ее R(N)-я цифра может быть вычислена за конечное число шагов. Когда эта цифра вычислена и записана как R(N)-я цифра b', N-й участок завершается. Следовательно, H - ациклическая.
Теперь пусть К будет D.N машины H. Что делает H на К-м участке своего движения? Она должна проверить, приемлемо ли К, приняв решение "s" или "u". Так как K - это D.N машины H так как H - ациклическая, решением не может быть "u". С другой стороны, решением не может быть "s". Ибо, если бы это было, то K-м участке своего движения H была бы обязана вычислить первые R(K-1)+1=R(K) цифр последовательности, вычисляемой машиной с К в качестве ее D.N, и записать R(K)-ю цифру как цифру последовательности, вычисляемой H. Вычисление первых R(K)-1 цифр было бы выполнено хорошо, по команды для вычисления R(K)-й были бы равносильны тому, чтобы "вычислить первые R(K) цифр, вычисленные H, и записать R(K)-ю". Эта R(K)-я цифра никогда не была бы найдена. Т.е. H - циклическая, в противовес тому, что мы выяснили в последнем абзаце, и решению "s". Таким образом, оба решения невозможны, и мы заключаем, что машины D ие может быть.
Далее можно показать, что не может быть машины E которая, получив S.D произвольной машины M, определит, напечатает ли M когда-нибудь заданный символ (скажем, 0).
Сначала покажем, что если существует машина Е, то существует и общий процесс для определения, печатает ли данная машина M 0 бесконечное число раз. Пусть M.1 - машина, которая печатает ту же самую последовательность, что M, за исключением того, что в позиции, где M печатает первый 0, M.1 печатает 0'. M.2 должна заменять два первых символа 0 на 0', и т.д. Так, если M должна напечатать
ABA01AAB0010AB...,
то M.1 напечатала бы
ABA0'1AAB0010AB...,
а M.2 напечатала бы
ABA0'1AAB0'010AB...
Теперь пусть F - это машина, которая, получив S.D M, будет записывать последовательно S.D M.1, M.2, ... (такая машина существует). Объединяем F и E получаем новую машину G. В G сначала применяется F, чтобы записать S.D M, а затем Е проверяет его, записывается :0: , если оказывается, что M никогда не печатает 0; затем F записывает S.D машины M.1, и проверяется она, печатая :0: тогда и только тогда, когда M.1 никогда не печатает 0, и т.д. Теперь давайте проверим G с E. Если оказывается, что G ни когда не печатает 0, то M печатает 0 бесконечное число раз; если M печатает 0 иногда, то M не печатает 0 бесконечное число раз.
Аналогично существует общий процесс для определения того, печатает ли M бесконечное число раз 1. Объединив эти процессы, мы получим процесс для определения, будет ли M печатать цифры бесконечно, т.е. получим процесс для определения, без циклов ли машина M. Поэтому машины Е не может быть.
Всюду в этом разделе выражение "существует общий процесс определения..." употреблялось как эквивалент "существует машина, которая определит..." Такое употребление может быть оправдано тогда и только тогда, когда мы можем подтвердить наше определение "вычислимости". Для каждого из этих "общих процессов" проблему можно свести к проблеме об общем процессе определения, обладает ли данное целое число n свойством G(n) (например, G(n) могло бы означать "n приемлемо" или "n есть Геделево представление доказуемой формулы"), и это равнозначно вычислению числа, чья n-ая цифра есть 1, если G(n) истинно, и 0, если ложно.
Это в общем уже не так весело, так что здесь я остановлюсь, тем более, что с каждой главой моя система обозначения используемых Тьюрингом закорючек становится все менее адекватной. А программирования машины больше не будет.

Gudleifr- Admin
- Сообщения : 3246
Дата регистрации : 2017-03-29
Страница 1 из 1
Права доступа к этому форуму:
Вы не можете отвечать на сообщения|
|
|
